General Chemistry/Print version
| This is the print version of General Chemistry You won't see this message or any elements not part of the book's content when you print or preview this page. |
General Chemistry
A Free Online Textbook
A three-dimensional representation of an atomic 4f orbital.
About General Chemistry
General Chemistry is an introduction to the basic concepts of chemistry, including atomic structure and bonding, chemical reactions, and solutions. Other topics covered include gases, thermodynamics, kinetics and equilibrium, redox, and chemistry of the elements.
It is assumed that the reader has basic scientific understanding. Otherwise, minimal knowledge of chemistry is needed prior to reading this book.
Beyond General Chemistry
- Organic Chemistry - Chemistry studies focusing on the carbon atom and compounds.
- Inorganic Chemistry - Chemistry studies focusing on salts, metals, and other compounds not based on carbon.
- Biochemistry - Chemistry studies of or relating to living organisms.
About Wikibooks
This is a wiki textbook. Anyone from around the world can read, as well as write it! All of the content in the book is covered by the GNU Free Document Licence, which means it is guaranteed to remain free and open.
Authors and Significant Contributors
Introduction
Chemistry is Everywhere

The modern human experience places a large emphasis upon the material world. From the day of our birth to the day we die, we are frequently preoccupied with the world around us. Whether struggling to feed ourselves, occupying ourselves with modern inventions, interacting with other people or animals, or simply meditating on the air we breathe, our attention is focused on different aspects of the material world. In fact only a handful of disciplines—certain subsets of religion, philosophy, and abstract math—can be considered completely unrelated to the material world. Everything else is somehow related to chemistry, the scientific discipline which studies the properties, composition, and transformation of matter.
Branches of Chemistry
Chemistry itself has a number of branches:
- Analytical chemistry seeks to determine the composition of substances.
- Biochemistry is the study of chemicals found in living things (such as DNA and proteins).
- Inorganic Chemistry studies substances that do not contain carbon.
- Organic chemistry studies carbon-based substances. Carbon, as described in more detail in this book, has unique properties that allow it to make complex chemicals, including those of living organisms. An entire field of chemistry is devoted to substances with this element.
- Physical chemistry is the study of the physical properties of chemicals, which are characteristics that can be measured without changing the composition of the substance.

Chemistry as a discipline is based on a number of other fields. Because it is a measurement-based science, math plays an important role in its study and usage. A proficiency in high-school level algebra should be all that is needed in this text, and can be obtained from a number of sources. Chemistry itself is determined by the rules and principles of physics. Basic principles from physics may be introduced in this text when necessary.
Why Study Chemistry?
There are many reasons to study chemistry. It is one pillar of the natural sciences necessary for detailed studies in the physical sciences or engineering. The principles of biology and psychology are rooted in the biochemistry of the animal world, in ways that are only now beginning to be understood. Modern medicine is firmly rooted in the chemical nature of the human body. Even students without long-term aspirations in science find beauty in the infinite possibilities that originate from the small set of rules found in chemistry.
Chemistry has the power to explain everything in this world, from the ordinary to the bizarre. Why does iron rust? What makes propane such an efficient, clean burning fuel? How can soot and diamond be so different in appearance, yet so similar chemically? Chemistry has the answer to these questions, and so many more. Understanding chemistry is the key to understanding the world as we know it.
This Book: General Chemistry
An introduction to the chemical world is set forth in this text. The units of study are organized as follows.

- Properties of Matter: An explanation of the most fundamental concept in chemistry: matter.
- Atomic Structure: While technically in the domain of physics, atoms determine the behavior of matter, making them a necessary starting point for any discussion of chemistry.
- Compounds and Bonding: Chemical bonding is introduced, which explains how less than one hundred naturally-occurring elements can combine to form all the different compounds that fill our world.
- Chemical Reactions: Things get interesting once chemical reactions start making and breaking bonds.
- Aqueous Solutions: Substances dissolved in water have special properties. This is when acids and bases are introduced.
- Phases of Matter: A detailed look at the organization of substances, with particular focus on gases.
- Chemical Equilibria: Chemical reactions don't go on forever. Equilibrium is the balance that reactions seek to achieve.
- Chemical Kinetics: Kinetics explain why it takes years for an iron nail to rust, but only a split second for a hydrogen-filled hot air balloon to explode.
- Thermodynamics: Two things decide which reactions can occur and which reactions cannot: heat and chaos. Or enthalpy and entropy, as they are called in thermodynamics
- Chemistries of Various Elements: An exploration of the elements that make up all substance. Includes an introduction to nuclear chemistry and carbon, the essence of organic chemistry.
Matter
Basic Properties of Matter
What is Matter?

Matter is defined as anything that occupies space and has mass. Black holes have mass but occupy effectively no space. Black holes have infinite density and 0 volume. Anything that has mass must be 3-dimensional, which is why, however small atoms (the stuff that makes up matter) are, they are 3-dimensional.
Mass is a measure of an object's inertia. It is proportional to weight: the more mass an object has, the more weight it has. However, mass is not the same as weight. Weight is a force created by the action of gravity on a substance while mass is a measure of an object's resistance to change in motion. For example, your weight on the moon would be one-sixth your weight on the earth, as the moons gravitational field is one-sixth that of earth's. Mass used to measured by comparing the substance of interest to a standard kilogram called the International Prototype Kilogram (IPK). The IPK is a metal cylinder for which the height and diameter both equal 39.17 millimeters and is made of an alloy of 90% platinum and 10% iridium. Thus, the standard kilogram is defined and all other masses are a comparison to this kilogram. When atom masses are measured in a mass spectrometer, a different internal standard is used. Your take home lesson with regard to mass is that mass is a relative term judged by a comparison. Mass is now defined by a Watt or Kibble balance by measuring the Planck constant. The goal of measuring mass with the Planck constant is to measure mass electronically. The reason for this is that it is a lot easier to make an electronic measurements with electronics and electricity than to weigh something big or small, so researchers have been working on accurately redefining the kilogram to a quantum standard that implements the Watt/Kibble balance for the Planck constant. This change took effect in 20 May 2019 after a historic vote among the members of the CGPM at Versailles in France to redefine the kilogram, ampere, mole, and kelvin. The redefinition of the kilogram was contingent upon continued improvement of this new method of determining mass. National metrology labs such as NIST collaborated to make the redefinition of the kilogram possible.
Volume is a measure of the amount of space occupied by an object. Volume can be measured directly with equipment designed using graduations marks or indirectly using length measurements depending on the state (gas, liquid, or solid) of the material. A graduated cylinder, for example, is a tube that can hold a liquid which is marked and labeled at regular intervals, usually every 1 or 10 mL. Once a liquid is placed in the cylinder, one can read the graduation marks and record the volume measurement. Since volume changes with temperature, graduated equipment has limits to the precision with which one can read the measurement. Solid objects that have regular shape can have their volume calculated by measuring their dimensions. In the case of a box, its volume equals length times width times height.
It is particularly interesting to note that measuring is different from calculating a specific value. While mass and volume can both be determined directly relative to either a defined standard or line marks on glass, calculating other values from measurements is not considered measuring. For example, once you have measured the mass and volume of a liquid directly, one can then calculate the density of a substance by dividing the mass by the volume. This is considered indirectly determining density. Interestingly enough, one can also measure density directly if an experiment which allows the comparison of density to a standard is set up.
Another quantity of matter directly or indirectly determined is the amount of substance. This can either represent a counted quantity of objects (e.g. three mice or a dozen bagels) or the indirectly determined number of particles of a substance being dealt with such as how many atoms are contained in a sample of a pure substance. The latter quantity is described in terms of moles. One mole used to be specifically defined as the number of particles in 12 grams of the isotope Carbon-12. This number was 6.02214078(18)x 1023 particles. The mole is now defined so the Avogadro constant N_A has the value 6.022 140 76 times 10 to the 23 reciprocal mole.
- Mass: the kilogram (kg). Also, the gram (g) and milligram (mg).
- 1 kg = 1000 g
- 1000 mg = 1 g.
- Volume: the liter (L), milliliter (mL). Also, cubic centimeters (cc) and cubic meters (m3).
- 1 cc = 1 mL
- 1000 mL = 1 L
- 1000 L = 1 m3
- Amount: the mole (mol).
- 1 mol = 6.02214078(18)x 1023 particles
Atoms, Elements, and Compounds
The fundamental building block of matter is the atom. Atoms are made of protons, electrons, and neutrons. Protons and neutrons are made of quarks and gluons.

Any atom is composed of a little nucleus surrounded by a "cloud" of electrons. In the nucleus there are protons and neutrons.
However, the term "atom" just refers to a building block of matter; it doesn't specify the identity of the atom. It could be an atom of carbon, or an atom of hydrogen, or any other kind of atom.
This is where the term "element" comes into play. When an atom is defined by the number of protons contained in its nucleus, chemists refer to it as an element. All elements have a very specific identity that makes them unique from other elements. For example, an atom with 6 protons in its nucleus is known as the element carbon. When speaking of the element fluorine, chemists mean an atom that contains 9 protons in its nucleus.
- Atom: A fundamental building block of matter composed of protons, neutrons, and electrons.
- Element: A uniquely identifiable atom recognized by the number of protons in the nucleus.
Despite the fact that we define an element as a unique identifiable atom, when we speak, for example, 5 elements, we don't usually mean those 5 atoms are of the same type (having the same number of protons in their nucleus). We mean 5 'types' of atoms. It is not necessary there are only 5 atoms. There may be 10, or 100, etc. atoms, but those atoms belong to one of 5 types of atoms. I'd rather define 'element' as 'type of atom'. I think it is more precise. If we'd like to refer to 5 atoms having the same 6 protons in their nucleus, I'd say '5 carbon atoms' or '5 atoms of carbon'.
It is important to note that if the number of protons in the nucleus of an atom changes, so does the identity of that element. If we could remove a proton from nitrogen (7 protons), it is no longer nitrogen. We would, in fact, have to identify the atom as carbon (6 protons). Remember, elements are unique and are always defined by the number of protons in the nucleus. The Periodic Table of the Elements shows all known elements organized by the number of protons they have.
An element is composed of the same type of atom; elemental carbon contains any number of atoms, all having 6 protons in their nuclei. In contrast, compounds are composed of different type of atoms. More precisely, a compound is a chemical substance that consists of two or more elements. A carbon compound contains some carbon atoms (with 6 protons each) and some other atoms with different numbers of protons.
Compounds have properties different from the elements that created them. Water, for example, is composed of hydrogen and oxygen. Hydrogen is an explosive gas and oxygen is a gas that fuels fire. Water has completely different properties, being a liquid that is used to extinguish fires.
The smallest representative for a compound (which means it retains characteristics of the compound) is called a molecule. Molecules are composed of atoms that have "bonded" together. As an example, the formula of a water molecule is "H2O": two hydrogen atoms and one oxygen atom.
Properties of Matter
Properties of matter can be divided in two ways: extensive/intensive, or physical/chemical.
According to the International Union of Pure and Applied Chemistry (IUPAC), an intensive property or intensive quantity is a quantity whose magnitude is independent of the size of the system (the part of the environment under study). Intensive properties include temperature, refractive index (for example, the refactive index of air is 1.000293), and mass density. The reciprocal or multiplicative inverse of mass density, specific volume, is also an intensive property. Boiling point is an intensive property. Here is a list of intensive properties:
- charge density
- linear charge density is amount of electric charge per unit length and typically represented by with units of
- surface charge density is amount of electric charge per unit surface area and represented by and measured with the unit
- volume charge density is amount of electric charge per unit volume and typically represented by rho, and measured with the unit .
- color
- concentration
- mass concentration in
- molar concentration in
- number concentration in
- energy density in
- electric permeability as a measure of magnetization produced in a material in response to an applied magnetic field typically represented by mu, and measured with either or
- specific gravity
- melting point
- boiling point
- molality measured with
- pressure
- refractive index
- electrical resistivity measured with
- electrical conductivity measured with
|
|
States of Matter
One important physical property is the state of matter. Three are common in everyday life: solid, liquid, and gas. The fourth, plasma, is observed in special conditions such as the ones found in the sun and fluorescent lamps. Substances can exist in any of the states. Water is a compound that can be liquid, solid (ice), or gas (steam).


Solids
Solids have a definite shape and a definite volume. Most everyday objects are solids: rocks, chairs, ice, and anything with a specific shape and size. The molecules in a solid are close together and connected by intermolecular bonds. Solids can be amorphous, meaning that they have no particular structure, or they can be arranged into crystalline structures or networks. For instance, soot, graphite, and diamond are all made of elemental carbon, and they are all solids. What makes them so different? Soot is amorphous, so the atoms are randomly stuck together. Graphite forms parallel layers that can slip past each other. Diamond, however, forms a crystal structure that makes it very strong.
Liquids
Liquids have a definite volume, but they do not have a definite shape. Instead, they take the shape of their container to the extent they are indeed "contained" by something such as beaker or a cupped hand or even a puddle. If not "contained" by a formal or informal vessel, the shape is determined by other internal (e.g. intermolecular) and external (e.g. gravity, wind, inertial) forces. The molecules are close, but not as close as a solid. The intermolecular bonds are weak, so the molecules are free to slip past each other, flowing smoothly. A property of liquids is viscosity, the measure of "thickness" when flowing. Water is not nearly as viscous as molasses, for example.
Gases
Gases have no definite volume and no definite shape. They expand to fill the size and shape of their container. The oxygen that we breathe and steam from a pot are both examples of gases. The molecules are very far apart in a gas, and there are minimal intermolecular forces. Each atom is free to move in any direction. Gases undergo effusion and diffusion. Effusion occurs when a gas seeps through a small hole, and diffusion occurs when a gas spreads out across a room. If someone leaves a bottle of ammonia on a desk, and there is a hole in it, eventually the entire room will reek of ammonia gas. That is due to the diffusion and effusion. These properties of gas occur because the molecules are not bonded to each other. The molecules in gas, are free and they can move around unlike solid molecules.
Technically, a gas is called a vapor if it does not occur at standard temperature and pressure (STP). STP is 0° C and 1.00 atm of pressure. This is why we refer to water vapor rather than water gas. |
- In gases, intermolecular forces are very weak, hence molecules move randomly colliding with themselves, and with the wall of their container, thus exerting pressure on their container. When heat is given out by gases, the internal molecular energy decreases; eventually, the point is reached when the gas liquifies.
Changes in Matter
There are two types of change in matter: physical change and chemical change. As the names suggest, physical changes never change the identity of the matter, only its size, shape or state. In a physical change, atoms are not rearranged and the matter's physical and chemical properties are unchanged. Chemical changes, on the other hand, rearrange the atoms of matter in new combinations, resulting in matter with new physical and chemical properties.
Chemical changes are also known as chemical reactions. The "ingredients" of a reaction are the reactants, and the end results are called the "products". The change from reactants to products can be signified by an arrow.Chemical changes are mostly irreversible
- A Chemical Reaction
Reactants → Products
Note that the number of reactants and products don't necessarily have to be the same. However, the number of each type of atom must remain constant. This is called the Law of Conservation of Matter. It states that matter can never be created or destroyed, only changed and rearranged. If a chemical reaction begins with 17 moles of carbon atoms, it must end with 17 moles of carbon atoms. They may be bonded into different molecules, or in a different state of matter, but they cannot disappear.
When changes occur, energy is often transformed. However, like atoms, energy cannot disappear. This is called the Law of Conservation of Energy. A simple example would be putting ice cubes into a soft drink. The ice cubes get warmer as the drink gets colder, because energy cannot be created or destroyed, only transferred. Note that energy can be "released" or "stored" by making and breaking bonds. When a plant converts the energy from sunlight into food, that energy is stored in the chemical bonds within the sugar molecules.
Chemical change or Physical change?

Physical changes do not cause a substance to become a fundamentally different substance. Chemical changes, on the other hand, cause a substance to change into something entirely new. Chemical changes are typically irreversible, but that is not always the case. It is easier to understand the difference between physical and chemical changes with examples.
| State changes are physical. | Phase changes are when you melt, freeze, boil, condense, sublimate, or deposit a substance. They do not change the nature of the substance unless a chemical change occurs along with the physical change. |
| Cutting, tearing, shattering, and grinding are physical. | These may be irreversible, but the result is still composed of the same molecules. When you cut your hair, that is a physical change, even though you can't put the hair back on your head again. |
| Mixing together substances is physical. | For example, you could mix salt and pepper, dissolve salt in water, or mix molten metals together to produce an alloy. |
| Gas bubbles forming is chemical. | Not to be confused with bubbles from boiling, which would be physical (a phase change). Gas bubbles indicate that a chemical reaction has occurred. |
| Precipitates forming is chemical. | When dissolved substances are mixed, and a cloudy precipitate appears, there has been a chemical change. |
| Rotting, burning, cooking, and rusting (for example) are chemical. | The resulting substances are entirely new chemical compounds. For instance, wood becomes ash and heat; iron becomes rust; sugar ferments into alcohol. |
| Changes of color or release of odors (i.e. release of a gas) might be chemical. | As an example, the element chromium shows different colors when it is in different compounds, but a single chromium compound will not change color on its own without some sort of reaction. |
| Release/absorption of energy (heat, light, sound) is generally not easily categorized. | Hot/cold packs involve dissolving a salt in water to change its temperature (more on that in later chapters); popping popcorn is mostly physical (but not completely). |
Classification of Matter
Matter can be classified by its state.
- Solids have a set volume and shape.The inter molecular force of attraction for solid matter is very strong.
- Liquids have a set volume, but change shape. The inter molecular force of attraction for liquid matter is weaker than solid matter.
- Gases have neither definite volume nor shape. The inter molecular force of attraction for gaseous matter is negligible.
- Plasma which are usually gaseous state of matter in which a part or all of the atoms or molecules are dissociated to form ions.
- Einstein-Bose Condensate (EBC) is a theoretical state of matter. The intermolecular force of attraction for EBC is so strong that the molecules cannot move whatsoever.
Matter can also be classified by its chemical composition.
- An element is a pure substance made up of atoms with the same number of protons. As of 2011, 118 elements have been observed, 92 of which occur naturally. Carbon (C), Oxygen (O), Hydrogen (H) are examples of elements. The periodic table is a tabular representation of the known elements.
- A compound consists of two or more chemical elements that are chemically bonded together. Water (H2O) and table sugar (C12H22O11) are examples of chemical compounds. The ratio of the elements in a compound is always the same. For example in water, the number of H atoms is always twice the number of O atoms.
- A mixture consists of two or more substances (element or compound) mixed together without any chemical bond. Salad is a good example. A mixture can be separated into its individual components by mechanical means.
Types of Mixtures
There are many kinds of mixtures. They are classified by the behavior of the phases, or substances that have been mixed.
Homogeneous Mixtures

A homogeneous mixture is uniform, which means that any given sample of the mixture will have the same composition. Air, sea water, and carbonation dissolved in soda are all examples of homogeneous mixtures, or solutions. No matter what sample you take from the mixture, it will always be composed of the same combination of phases. Chocolate chip ice cream is not homogeneous—one spoonful taken might have two chips, and then another spoonful might have several chips.
An example for a homogeneous mixture is a solution. The substance that gets dissolved is the solute. The substance that does the dissolving is the solvent. Together they make a solution. If you stir a spoonful of salt into a glass of water, salt is the solute that gets dissolved. Water is the solvent. The salty water is now a solution, or homogeneous mixture, of salt and water.
When different gases are mixed, they always form a solution. The gas molecules quickly spread out into a uniform composition.
Heterogeneous Mixtures
A heterogeneous mixture is not uniform. Different samples may have different compositions, like the example of chocolate chip ice cream. Concrete, soil, blood, and salad are all examples of heterogeneous mixtures.

Suspensions
When sand gets kicked up in a pond, it clouds the water. It has a greater mass than water hence it sinks to the bottom and settles down, and is no longer mixed into the water. This is an example of a suspension. Suspensions are heterogeneous mixtures that will eventually settle. They are usually, but not necessarily, composed of phases in different states of matter. Italian salad dressing has three phases: the water, the oil, and the small pieces of seasoning. The seasonings are solids that will sink to the bottom, and the oil and water are liquids that will separate.
Colloids

What exactly is toothpaste? We can't exactly classify it by its state of matter. It has a definite shape and volume, like a solid. But then you squeeze the tube, and it flows almost like a liquid. And then there's jelly, shaving cream, smoke, dough, and Silly Putty...
These are examples of colloids. A colloid is a heterogeneous mixture of two substances of different phases. Shaving cream and other foams are gas dispersed in liquid. Jello, toothpaste, and other gels are liquid dispersed in solid. Dough is a solid dispersed in a liquid. Smoke is a solid dispersed in a gas.
Colloids differ from suspensions in that they will not settle. |
Colloids consist of two phases: a dispersed phase inside of a continuous medium.
The Tyndall Effect
The Tyndall effect distinguishes colloids from solutions. In a solution, the particles are so fine that they will not scatter light. This is not true for a colloid. If you shine light through a solution, the beam of light will not be visible. It will be visible in a colloid. For instance, if you have ever played with a laser pointer, you have seen the Tyndall effect. You cannot see the laser beam in air (a solution), but if you shine it into a mist, the beam is visible. Clouds look white (or gray), as opposed to blue, because of the Tyndall effect - the light is scattered by the small droplets of suspended water.
Methods for Separating Mixtures

Because there is no chemical bonding in a mixture, the phases can be separated by mechanical means. In a heterogeneous mixture like a salad, the pieces can easily be picked out and separated. It is as simple as sifting through the salad and picking out all the tomatoes and radishes, for example. However, many mixtures contain particles that are too small, liquids, or too many particles to be separated manually. We must use more sophisticated methods to separate the mixture.
Filtration
Imagine you have a sandbox, but there are bits of broken glass in it. All you would need is some sort of filter. The sand particles are much smaller than the glass chips, so a mesh filter would let sand pass but stop the glass. Filtration is used in all sorts of purification methods. Some filters, like dialysis tubing, are such fine filters that water can pass, but dissolved glucose cannot.
Filtration works with particles that are significantly different in size, like sand and rock, or water and glucose. |
Distillation
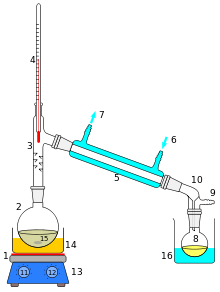
If you were given a glass of saltwater, could you drink it? Sure, if you distill it first. Distillation is the boiling of a mixture to separate its phases. Salt is a solid at room temperature, and water is a liquid. Water will boil far before salt even begins to melt. So separating the two is as simple as boiling the water until all that remains is the solid salt. If desired, the water vapor can be collected, condensed, and used as a source of pure water.
Distillation can also be used if two liquids are mixed but have different boiling points. Separation of several liquids with similar boiling points can be achieved using fractionation.
Centrifugation and Sedimentation

These processes rely on differences in density. In a medical lab, blood often goes into a centrifuge. A centrifuge is a machine that spins a sample at fairly high rates of speed. Red blood cells are much denser than the watery substance (called plasma, but it's not the plasma state of matter) that makes up blood. As a result of the spinning, the denser phases move outward and the less dense phases move inward, towards the axis of rotation. Then, the red blood cells can be separated from the plasma.
Sedimentation is similar, but it happens when particles of different densities have settled within a liquid. If a jar of muddy water is left to settle, the heaviest particles sink to the bottom first. The lightest particles sink last and form a layer on top the heavier particles. You may have seen this effect in a bottle of salad dressing. The seasonings sink to the bottom, the water forms a lower layer, and the oil forms an upper layer. The separate phases can be skimmed out. To return it to a mixture, simply shake it up to disturb the layers.
Unique Properties

The differences in substances' properties can be exploited to allow separation. Consider these examples:
- A mixture of sand and iron filings can be separated by magnet.
- Salt and sand can be separated by solution (sand will not dissolve in water, salt will)
- Helium can be separated from a mixture with hydrogen by combustion (this is a very dangerous operation, since hydrogen in the presence of oxygen is highly explosive). Hydrogen is flammable, but helium is not.
Other methods
There are countless other ways to separate mixtures. For instance, gel electrophoresis is used to separate different sized pieces of DNA. They are placed into gel, and an electric current is applied. The smaller pieces move faster and separate from the larger pieces.
Chromatography separates phases dissolved in liquid. If you want to see an example, take a strip of paper and draw a dot on it with a colored marker. Dip the strip into water, and wait a while. You should see the ink separate into different colors as they spread out from the dot.
Numbers Used to Describe Atoms
Numbers

The Atomic number is the number of protons in the nucleus of an atom. This number determines the element type of the atom. For instance, all neon atoms have exactly ten protons. If an atom has ten protons, then it must be neon. If an atom is neon, then it must have ten protons.
The atomic number is sometimes denoted Z. Continuing with the example of neon, .
The Neutron number is the number of neutrons in the nucleus of an atom. Remember that neutrons have no electric charge, so they do not affect the chemistry of an element. However, they do affect the nuclear properties of the element. For instance, Carbon-12 has six neutrons, and it is stable. Carbon-14 has eight neutrons, and it happens to be radioactive. Despite these differences, both forms of carbon behave the same way when forming chemical compounds.
The neutron number is sometimes denoted N.
The Mass number is the sum of protons and neutrons in an atom. It is denoted A. To find the mass number of an atom, remember that A = Z + N. The mass number of an atom is always an integer. Because the number of neutrons can vary among different atoms of the same element, there can be different mass numbers of a given element. Look back to the example of carbon. Carbon-14 has a mass number of 14, and Carbon-12 has a mass number of 12. Every carbon atom must have six protons, so Carbon-14 has eight neutrons and Carbon-12 has six neutrons.
Elements with the same atomic number but different atomic masses are isotopes. |
Isotopes of the same element have nearly identical chemical properties (because they have the same number of protons and electrons). Their only difference is the number of neutrons, which changes their nuclear properties like radioactivity.
Notation
There is a convenient way of writing the numbers that describe atoms. It is easiest to learn by examples.
| Helpful Hint! | |
|---|---|
| Keep in mind that any of the three numbers written around the element symbol are optional, but they should be written if it is important to the given situation. The charge number is left off if the atom has zero charge (equal number of protons and electrons). The mass number and atomic number are usually left off. |
| This is how we write fluorine-19. The atomic number is below and the mass number is above, followed by its symbol on the periodic table of the elements. | |
| This example shows carbon-12. Notice how the atomic number is missing. You know which element it is because of the C, so there is no need to write the number of protons. The atomic number is rarely written because the element symbol implies how many protons there are. | |
| The last example shows both the atomic number and mass number, along with a charge. The charge is the difference in the number of protons compared to the number of electrons. You can read more about charge, protons, and electrons later on. From the example, you can see that this magnesium atom would have 12 protons, 13 neutrons, and 10 electrons. Its mass is 25 (12 p + 13 n) and its charge is +2 (12 p - 10 e). |
- Exercise for the reader!
Try writing the symbol for an atom with seven protons, seven neutrons, and eight electrons. You will need to look up its symbol on the periodic table.
Atomic Mass
The mass of an atom is measured in atomic mass units (amu). An atom's mass can be found by summing the number of protons and neutrons. By definition, 12 amu equals the atomic mass of carbon-12. Protons and neutrons have an approximate mass of 1 amu, and electrons have a negligible mass.
| There is a difference between an atom's mass number and an element's atomic mass. The mass number measures the number of protons and neutrons in the nucleus of a particular atom. The atomic mass measures the average mass of all atoms for an element. For example, a carbon atom might have a mass number of 12 or 14 (or something else), but carbon in general has a mass of 12.011 amu. |
Usually, a pure element is made up of a number of isotopes in specific ratios. Because of this, the measured atomic mass of carbon is not exactly 12. It is an average of all the masses of all the isotopes, with the more common ones contributing more to the measured atomic mass. By convention atomic masses are given no units.
- Example
Pretend that the element Wikibookium has two isotopes. The first has a mass number of 104, and the second has a mass number of 107. Considering that 75% of the naturally occurring atoms are of the first isotope, and the rest are of the second. The average atomic mass is calculated as
0.75 × 104 + 0.25 × 107 = 104.75
In this case, a bunch of Wikibookium atoms would have an average mass of 104.75 amu, but each individual atom might have a mass number of 104 or 107. Keep in mind that all of the atoms would have the same number of protons. Their masses are different because of the number of neutrons.
Moles
A mole is defined as the amount of an element whose number of particles are equal to that in 12g of C-12 carbon, also known as Avogadro's number. Avogadro's number equals 6.022 × 1023. Moles are not very confusing: if you have a dozen atoms, you would have 12. If you have a mole of atoms, you would have 6.022 × 1023. Why is this ridiculously large number important? It can be used to convert between atomic mass units and grams. One mole of carbon-12 is exactly 12 grams, by definition. Similarly, one mole of any element is the atomic mass of that element expressed as a weight in grams. The atomic mass is equal to the number of grams per mole of that element.
- Example
There are 128.2 g of rubidium (atomic mass = 85.47 amu). How many atoms are there?
(128.2 g) / (85.47 g/mol) = 1.5 mol
(1.5 mol) × (6.022 × 1023) = 9.03 × 1023 atoms of rubidium

Moles are also important because every 22.4 liters of gas contain 1 mole of gas molecules at standard temperature and pressure (STP, 0 °C and 1 atmosphere of pressure). Avogadro discovered this. (That's why it's his number.) A container filled with fluorine gas would have to be 22.4 L large to hold one mole of F2 molecules. Knowing this fact allows you to determine the mass of a gas molecule if you know the volume of the container. This holds true for every gas.
Why every single gas? Atoms and molecules are tiny. The volume of a gas is mostly empty space, so the molecules have an insignificantly small volume. As you will eventually learn, this ensures that there is always one mole of gas atoms for every 22.4 liters at STP.
Atomic Structure
History of Atomic Structure
Why Is The History Of The Atom So Important?
It is fundamental to the understanding of science that science is understood to be a process of trial and improvement and represents the best known at the time, not an unerring oracle of truth. Development of an idea and refinement through testing is shown more in the understanding of atomic structure.
The Greek Theorists

The earliest known proponent of anything resembling modern atomic theory was the ancient Greek thinker Democritus. He proposed the existence of indivisible atoms as a response to the arguments of Parmenides and the paradoxes of Zeno.
Parmenides argued against the possibility of movement, change, and plurality on the premise that something cannot come from nothing. Zeno attempted to prove Parmenides' point by a series of paradoxes based on difficulties with infinite divisibility.
In response to these ideas, Democritus posited the existence of indestructible atoms that exist in a void. Their indestructibility provided a retort to Zeno, and the void allowed him to account for plurality, change, and movement. It remained for him to account for the properties of atoms, and how they related to our experiences of objects in the world.
Democritus proposed that atoms possessed few actual properties, with size, shape, and mass being the most important. All other properties, he argued, could be explained in terms of the three primary properties. A smooth substance, for instance, might be composed of primarily smooth atoms, while a rough substance is composed of sharp ones. Solid substances might be composed of atoms with numerous hooks, by which they connect to each other, while the atoms of liquid substances possess far fewer points of connection.
Democritus proposed 5 points to his theory of atoms. [1] These are:
- All matter is composed of atoms, which are bits of matter too small to be seen. These atoms CANNOT be further split into smaller portions.
- There is a void, which is empty space between atoms.
- Atoms are completely solid.
- Atoms are homogeneous, with no internal structure.
- Atoms are different in their size, their shape, and their weight.
Alchemy
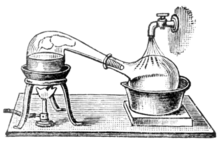

Empedocles proposed that there were four elements, air, earth, water, and fire and that everything else was a mixture of these. This belief was very popular in the medieval ages and introduced the science of alchemy. Alchemy was based on the belief that since everything was made of only four elements, you could transmute a mixture into another mixture of the same type. For example, it was believed that lead could be made into gold.
Alchemy's problem was exposed by Antoine Lavoisier when he heated metallic tin in a sealed flask. A grayish ash appeared on the surface of the melting tin, which Lavoisier heated until no more ash formed. After the flask cooled, he inverted it and opened it underwater. He discovered the water rose one-fifth of the way into the glass, leading Lavoisier to conclude that air itself is a mixture, with one-fifth of it having combined with the tin, yet the other four-fifths did not, showing that air was not an element.
Lavoisier repeated the experiment again, substituting mercury for tin, and found that the same happened. Yet after heating gently, he found that the ash released the air, showing that the experiment could be reversed. He concluded that the ash was a compound of the metal and oxygen, which he proved by weighing the metal and the ash, and showing that their combined weight was greater than that of the original metal.
Lavoisier then stated that combustion was not an element, but instead was a chemical reaction of a fuel and oxygen.
John Dalton
Modern atomic theory was born with Dalton when he published his theories in 1803. His theory consists of five important points, which are considered to be mostly true today: (from Wikipedia)
- Elements are composed of tiny particles called atoms.
- All atoms of a given element are identical.
- The atoms of a given element are different from those of any other element; the atoms of different elements can be distinguished from one another by their respective relative weights.
- Atoms of one element can combine with atoms of other elements to form chemical compounds; a given compound always has the same relative numbers of types of atoms.
- Atoms cannot be created, divided into smaller particles, nor destroyed in the chemical process; a chemical reaction simply changes the way atoms are grouped together.
We now know that elements have different isotopes, which have slightly different weights. Also, nuclear reactions can divide atoms into smaller parts (but nuclear reactions aren't really considered chemical reactions). Otherwise, his theory still stands today.
Dmitri Mendeleev
In the late 1800's, Russian scientist Dmitri Mendeleev was credited with creating one of the first organized periodic tables. Organizing each element by atomic weight, he cataloged each of the 56 elements discovered at the time. Aside from atomic weight, he also organized his table to group the elements according to known properties.
While writing a series of textbooks, Mendeleev realized he was running out of space to treat each element individually. He began to regularly "linewrap" the elements onto the next line, and create what is now called the periodic table of the elements. Using his table, he predicted the existence of later-discovered elements, such as "eka-aluminum" and "eka-silicon" (gallium and germanium) according to patterns found earlier. His predictions were a success, proving his table to be exceptionally accurate. Later theories, those of the electrons around the atom, explain why elements in the same period, or group, have similar chemical properties. Chemists would later organise each element by atomic number, not atomic weight, giving rise to the modern Periodic Table of Elements.
J.J. Thomson
Discovery of the Electron
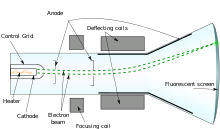
In the year 1889 the British physicist J.J. Thomson discovered the electron. Thomson conducted a number of experiments using cathode ray tube. Cathode rays are constructed by sealing two electrodes in a glass tube connected to a voltage supplier and a vacuum pump removing the air from it. When the electrodes are attached to high voltage of about 15000v and low pressure, a beam of radiation is emitted from the negative electrode(cathode)moving towards the positive electrode(anode). These beams are said to be green rays called cathode rays. (1) The ray is said to be taken towards Faraday's tube(gold leaf electroscope) and was charged by induction and deflect positively charged gold leaf electroscope (2) a freely moving paddle wheel was placed on the path of the rays and it was able to move it suggesting that it has momentum (3) The ray was placed in a magnetic and electric field moving towards the north and positive pole respectively Thomson discovered that cathode rays travel in straight lines except, when they are bent by electric or magnetic fields. The cathode rays bent away from a negatively charged plate, Thomson concluded that these rays are made of negatively charged particles; today we call them electrons. Thomson found that he could produce cathode rays using electrodes of various materials. He then concluded that electrons were found in all atoms and are over a thousand times smaller than protons. Thompson used an apparatus to determine the charge to mass ratio(e/m)after the ray emerge he placed a magnetic field of a known magnetic influence and the rays bent towards the north to a particular position then he added an electric field to return the ray back to it original position and recorded the charges used by the electric field so he divided them to get the ratio of about -1.7*10^8kg
The "Plum Pudding" Atomic Model
Soon after the discovery of the electron, Thomson began speculating on the nature of the atom. He suggested a "plum pudding" model. In this model the bits of "plum" were the electrons which were floating around in a "pudding" of positive charge to match that of the electrons and make an electrically neutral atom. A modern illustration of this idea would be a chocolate chip cookie, with the chips representing negatively charged electrons and the dough representing positive charge.
Rutherford

Ernest Rutherford is known for his famous gold foil experiment in 1911. Alpha particles, which are heavy and positively charged (actually, helium nuclei, but that's beside the point), were fired at a very thin layer of gold. Most of the alpha particles passed straight through, as expected. According to the plum pudding model all of the particles should have slowed as they passed through the "pudding", but none should have been deflected. Surprisingly, a few alpha particles were deflected back the way they came. He stated that it was "as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you."
The result of the experiment allowed Rutherford to conclude that the plum pudding model is wrong.
- Atoms have a nucleus, very small and dense, containing the positive charge and most of the atom's mass.
- The atom consists of mostly empty space.
- The electrons are attracted to the nucleus, but remain far outside it.
Niels Bohr
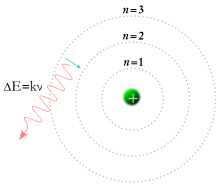
Bohr created his own model of the atom, improving on Rutherford's. Bohr used an equation developed by Rydberg that provided a mathematical relationship between the visible spectral lines of the hydrogen atom. The equation requires that the wavelengths emitted from the hydrogen atom be related to the difference of two integers. Bohr theorized that these integers represent "shells" or "orbits" in which electrons travel around the nucleus, each with a certain energy level. The energy of an orbit is proportional to its distance from the nucleus. An atom will absorb and release photons that have a specific amount of energy. The energy is the result of an electron jumping to a different shell. Starting with Rydberg's equation, along with Planck and Einstein's work on the relationship between light and energy, Bohr was able to derive an equation to calculate the energy of each orbit in the hydrogen atom. The Bohr model depicts the atom as a nucleus with electrons orbiting around it at specific distances. This model is also referred to as the Planetary Model.
Robert Millikan
Robert Millikan is credited for the "Oil Drop Experiment", in which the value of the electron charge was determined. He created a mechanism where he could spray oil drops that would settle into a beam of X rays. The beam of X rays caused the oil drops to become charged with electrons. The oil droplets were in between a positively charged plate and a negatively charged plate which, when proper electric voltage was applied, caused the oil droplet to remain still. Robert Millikan measured the diameter of each individual oil drop using a microscope.
Millikan was able to calculate the mass of each oil droplet because he knew the density of the oil (). Using the mass of each oil droplet and the equation for the force of gravitational attraction (which he rearranged from to , where is the mass of each individual oil droplet, is the acceleration due to gravity, and is the electrical force which equals force in the first equation), Millikan was able to find the value of the charge of the electron, .
The X rays, however, did not always produce an oil drop with only one negative charge. Thus, the values Millikan obtained may have looked like this:
- coulomb
- coulomb
- coulomb
- coulomb
Millikan found that these values all had a common divisor: coulomb. He concluded that different values occurred because the droplets acquired charges of -5, -4, -3, and -2, as in this example. Thus, he stated that the common divisor, coulomb, was the charge of the electron.
References
Subatomic Particles
Particle Properties
Before learning about subatomic particles, some basic properties should be understood.
Charge
Particles may be electrically charged. Charge is a property which defines the force that a particle will exert on other charged particles. There is a well known saying that applies perfectly: "Opposites attract." (Likewise, like charges repel.) Positive charges and negative charges will attract each other and come together. Two positive or two negative charges will push each other away.
| Helpful Hint! | |
|---|---|
| Not all particles have charge. |
The amount of charge a particle has is measured in coulombs, but it is more conveniently expressed in terms of an integer. For instance, a helium ion that has 2 less electrons than usual has a charge of +2, and a bromide ion with one more electron than usual has a charge of -1. (This may seem backwards, but remember that an electron has a negative charge.) Notice that charge not only applies to subatomic particles, but also ions and other things as well. Always remember to specify if a charge is positive or negative. Unlike ordinary numbers, we always write the plus sign for positive charges to avoid confusion with a negative charge.
It may be useful to understand Coulomb's Law. It explains the electromagnetic force: . is the charge on each particle, is the distance between them, and is a constant. So, if the distance between two particles is doubled, the force will be reduced four times. Double the charge would mean double the force, be it attractive or repulsive. Coulomb's Law will be especially important when understanding periodic trends.
However, there is no need to solve it exactly. Just remember the relationships between the variables. |
Mass
Mass is the measure of inertia. From a subatomic point of view, mass can also be understood in terms of energy, but that does not concern us when dealing with chemistry. Mass for particles, atoms, and molecules is not measured in grams, as with ordinary substances. Instead, it is measured in atomic mass units, or amu. For more information about mass and amu, read the previous chapters on properties of matter.
The Nucleus

At the center of each atom lies the nucleus. It is incredibly small: if you were to take the average atom (itself miniscule in size) and expand it to the size of a football stadium, then the nucleus would be about the size of a marble. It is, however, astoundingly dense: despite the tiny percentage of the atom's volume it contains nearly all of the atom's mass. The nucleus almost never changes under normal conditions, remaining constant throughout chemical reactions. Nuclei are themselves made up of a pair of smaller and more dense particles, the proton and the neutron. These particles are collectively dubbed nucleons.
Protons
Protons have a charge of +1 and a mass of 1 amu. They are often represented by a .
Protons will be important when learning about acids and bases—they are the essence of acid. Remember that the number of protons in an atom is its atomic number, and defines what element it will be. The number of protons in a nucleus ranges from one to over a hundred.
Consider the element hydrogen. Its atomic number is 1, so it has one proton and one electron. If it is made into an ion (an atom with missing or extra electrons), it will simply be a lone proton. Thus, a proton is the nucleus of a hydrogen atom, and a proton is a hydrogen ion. Therefore, a proton can be written as or , both symbols for a hydrogen ion.
Neutrons
Neutrons have no charge and a mass of 1 amu. A neutron is slightly heavier than a proton, but the difference is insignificant. Neutrons are often written .
Unlike the protons, neutrons cannot exist outside the nucleus indefinitely as they become unstable and break down. Within one nucleus there can be many protons and neutrons all in close proximity to one another. The number of neutrons in a nucleus ranges from zero to over a hundred.
You may wonder why neutrons exist. They have no charge, so can they do anything? The answer is yes—neutrons are very important. Remember that opposites attract and likes repel. If so, then how can several protons stay clumped together in the dense nucleus of an atom? It would seem as if the protons would repel and scatter the nucleus. However, there is a strong nuclear force that holds the nucleus together. This incredible force causes nucleons to attract each other with much greater strength than the electric force can repel them, but only over extremely short distances.
A delicate balance exists between the number of protons and neutrons. Protons, which are attracted to one another via the strong force but simultaneously repelled by their electromagnetic charges, cannot exist in great numbers within the nucleus without the stabilizing action of neutrons, which are attracted via the strong force but are not charged. Conversely, neutrons lend their inherent instability to the nucleus and too many will destabilize it.
Neutrons are the reason for isotopes, or atoms with the same number of protons but different masses. The masses are different because of different numbers of neutrons. Isotopes of a given element have almost identical chemical properties (like color, melting point, reactions, etc.), but they have different nuclear properties. Some isotopes are stable, others are radioactive. Different isotopes decay in different ways. |
Lastly, neutrons are very important in nuclear reactions, such as those used in power plants. Neutrons act like a bullet that can split an atom's nucleus. Because they have no charge, neutrons are neither attracted nor repelled by atoms and ions.
The Electron Cloud
Surrounding the dense nucleus is a cloud of electrons. Electrons have a charge of -1 and a mass of 0 amu. That does not mean they are massless. Electrons do have mass, but it is so small that it has no effect on the overall mass of an atom. An electron has approximately 1/1800 the mass of a proton or neutron. Electrons are written .
Electrons orbit the outside of a nucleus, unaffected by the strong nuclear force. They define the chemical properties of an atom because virtually every chemical reaction deals with the interaction or exchange of the outer electrons of atoms and molecules.
Electrons are attracted to the nucleus of an atom because they are negative and the nucleus (being made of protons and neutrons) is positive. Opposites attract. However, electrons don't fall into the nucleus. They orbit around it at specific distances because the electrons have a certain amount of energy. That energy prevents them from getting too close, as they must maintain a specific speed and distance. Changes in the energy levels of electrons cause different phenomena such as spectral lines, the color of substances, and the creation of ions (atoms with missing or extra electrons).
Electron Interactions
Atoms will always have equal numbers of protons and electrons, so their overall charge is zero. Atoms are neutral. Ions, on the other hand, are atoms that have gained or lost electrons and now have an unequal number of protons and electrons. If there are extra electrons, the ion will be negatively charged. If there are missing electrons, the ion will be positively charged, due to the majority of positive protons.
Valence electrons (the outermost electrons) are responsible for an atom's behavior in chemical bonds. The core electrons are all of the electrons not in the outermost shell, and they rarely get involved. An atom will attempt to fill its valence shell. This occurs when an atom has eight valence electrons (as explained in the next chapter), so atoms will undergo chemical bonds to either share, give, or take the electrons it needs. Sodium, for example, is very likely to give up its one valence electron, so that its outer shell is empty (the shell underneath it is full). Chlorine is very likely to take an electron because it has seven and wants eight. When sodium and chlorine are mixed, they exchange electrons and create sodium chloride (table salt). As a result, both elements have full valence shells, and a very stable compound is formed.
Introduction to Quantum Theory
Introduction to Quantum Mechanics
In the late 19th century, many physicists believed that they had made great progress in physics, and there wasn't much more that needed to be discovered. The classical physics at the time was widely accepted in the scientific community. However, by the early 20th century, physicists discovered that the laws of classical mechanics break down in the atomic world, and experiments such as the photoelectric effect completely contradict the laws of classical physics. As a result of these crises, physicists began to construct new laws of physics which would apply to the atomic world; these theories would be collectively known as quantum mechanics. Quantum mechanics, in some ways, completely changed the way physicists view the universe, and it also marked the end of the idea of a clockwork universe (the idea that the universe was predictable).
Electromagnetic Radiation
Electromagnetic radiation (ER) is a form of energy that sometimes acts like a wave, and other times acts like a particle. Visible light is a well-known example. All forms of ER have two inversely proportional properties: wavelength and frequency. Wavelength is the distance from one wave peak to the next, which can be measured in meters. Frequency is the number of wave peaks observed in a given point during a second. The unit for frequency is hertz.
Since wavelength and frequency are inversely related, their product (multiplication) always equals a constant — specifically, 3.0 x 108 m/sec represented by the letter c, which is better known as the speed of light. This relationship is written mathematically as , with the greek letter λ (lambda) representing wavelength and the letter representing frequency.
The wavelength and frequency of any specific occurrence of ER determine its position on the electromagnetic spectrum.

As you can see, visible light is only a tiny fraction of the spectrum.
The energy of a single particle of an electromagnetic wave (called a photon) is given by , where is Plank's constant and is the frequency. Energy is directly proportional to frequency — doubling the frequency will double the energy.
The Discovery of the Quantum
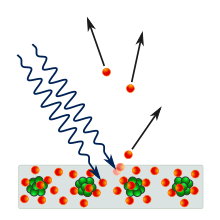
So far we have only discussed the wave characteristics of energy. However, the wave model cannot account for something known as the photoelectric effect. This effect is observed when light focused on certain metals apparently causes electrons to be emitted. (Photoelectric or solar panels work on this principle.)
For each metal it was found that there is a minimum frequency of electromagnetic radiation that is needed to be shone on it in order for it to emit electrons. This conflicted with the earlier thought that the energy of light was linked only to its intensity. Under that theory, the effect of light should be cumulative - dim light should add up, little by little, until it causes electrons to be emitted. Instead, there is a clear-cut minimum of the frequency of light that triggers the electron emissions.
The implication of this is that the energy of light is tied to frequency, and furthermore that it is quantized, meaning that it carries "packets" of energy in discrete amounts. These packets are more commonly referred to as photons. This observation led to the discovery of the minimum amount of energy that could be gained or lost by an atom. Max Planck named this minimum amount the quantum, plural "quanta", meaning "how much". One photon of light carries exactly one quantum of energy.
The Quantum Model
Uncertainty

It turns out that photons are not the only thing that act like waves and particles. Electrons, too, have this characteristic, known as wave-particle duality. Electrons can be thought of as waves of a certain length, thus they would only be able to form a circle around the nucleus at certain distances that are multiples of the wavelength. Of course, this brings up a problem: are electrons particles in a specific location, or waves in a general area? Werner Heisenberg tried using photons to locate electrons. Of course, when photons reach electrons, the electrons change velocity, and move to an excited state. As a result, it is impossible to precisely measure the velocity and location of an electron at the same time. This is known as the observer effect. This is frequently confused with the Heisenberg Uncertainty Principle, which goes even further, saying that there are limits to the degree to which both the position and momentum of a particle can even be known. This is due to the fact that electrons cannot exhibit both their wave and particle properties at the same time when being observed to interact with their surroundings. The momentum of an electron is proportional to its velocity, but based on its wave properties; its position is based on its particle position in space. The Heisenberg uncertainty principle is a kind of scientific dilemma: the more you know about something's velocity, the less you know about its position; and the more you know about its position, the less you know about its velocity. The significance of this uncertainty is that you can never know exactly where an atom's electrons are, only where they are most likely to be.

On the tiny scale of an atom, the particle model of an electron does not accurately describe its properties. An electron tends to act more like a water wave than a billiard ball. At any one moment in time the ball is in some definite place; it is also moving in some definite direction at a definite speed. This is certainly not true for waves or electrons in general. The Heisenberg uncertainty principle states that the exact position and momentum of an electron cannot be simultaneously determined. This is because electrons simply don't have a definite position, and direction of motion, at the same time!
One way to try to understand this is to think of an electron not as a particle but as a wave. Think of dropping a stone into a pond. The ripples start to spread out from that point. We can answer the question "Where is the wave?" with "It's where you plonked the stone in". But we can't answer the question "What direction is the wave moving?" because it's moving in all directions. It's spreading out. Now think of a wave at the seaside. We know the direction of motion. It's straight in towards the beach. But where is the wave? We can't pinpoint an exact location. It's all along the water.
The Wave Function

If we can never know exactly where an electron is, then how do we know about the way they orbit atoms? Erwin Schrödinger developed the Quantum Mechanical model, which describes the electron's behavior in a given system. It can be used to calculate the probability of an electron being found at a given position. You don't know exactly where the electron is, but you know where it is most likely and least likely to be found. In an atom, the wave function can be used to model a shape, called an orbital, which contains the area an electron is almost certain to be found inside.
Orbitals
In the following sections, we will learn about the shells, subshells, and orbitals that the electrons are in. Try not to get confused; it can be difficult. Understanding this information will help you to learn about bonding, which is very important.
Each electron orbiting in an atom has a set of four numbers that describe it. Those four numbers, called quantum numbers, describe the electron's orbit around the nucleus. Each electron in an atom has a unique set of numbers, and the numbers will change if the electron's orbit is altered. Examples are if bonding occurs, or an electron is energized into a higher-energy orbit. In the next chapter, we will learn the meaning of those four values.
Keep in mind that the pictures of the orbitals you will soon see show the area in which the electron is most likely to be, not its exact orbit. It's like a picture of a sprinkler watering a lawn, and the electrons are drops of water. You know the general area of the water, but not the exact location of each droplet. In the orbital pictures, you know the general area the electron could be in, but not its exact path. This is a result of the Uncertainty Principle. |
The Quantum Atom
The Quantum Numbers
These four numbers are used to describe the location of an electron in an atom.
| Number | Symbol | Possible Values |
|---|---|---|
| Principal Quantum Number | ||
| Angular Momentum Quantum Number | ||
| Magnetic Quantum Number | ||
| Spin Quantum Number |
Principal Quantum Number (n)
Determines the shell the electron is in. The shell is the main component that determines the energy of the electron (higher n corresponds to higher energy), as well as size of the orbital, corresponding to maximum nuclear distance (higher n means further possible distance from the nucleus). The row that an element is placed on the periodic table tells how many shells there will be. Helium (n = 1), neon (n = 2), argon (n = 3), etc. Note that the shells will have different numbers, as described by the table above; for example, argon will contain the , , and subshells, for that total of 3.
Angular Momentum Quantum Number (l)
Also known as azimuthal quantum number. Determines the subshell the electron is in. Each subshell has a unique shape and a letter name. The s orbital is shaped like a sphere and occurs when l = 0. The p orbitals (there are three) are shaped like teardrops and occur when l = 1. The d orbitals (there are five) occur when l = 2. The f orbitals (there are seven) occur when l = 3. (By the way, when l = 4, the orbitals are "g orbitals", but they (and the l = 5 "h orbitals") can safely be ignored in general chemistry.). The numbers of the subshells in each shell can be calculated using the principal quantum number like so. For example, in the shell, the subshells are an subshell, and 3 subshells. You will learn how to determine the number of orbitals for each subshells in the next section.
This number also gives information as to what the angular node of an orbital is. A node is defined as a point on a standing wave where the wave has minimal amplitude. When applied to chemistry this is the point of zero-displacement and thus where no electrons are found. In turn angular node means the planar or conical surface in which no electrons are found or where there is no electron density. The models shown on this page show the most simple representations of these orbitals and their nodes. More accurate, but more complex depictions are not necessary for the scope of this book.
Here are pictures of the orbitals. Keep in mind that they do not show the actual path of the electrons, due to the Heisenberg Uncertainty Principle. Instead, they show the volume where the electron is most likely to occur, i.e. the probability amplitude is largest. The two colors represent two signs (phases) of the wave function (the choice is arbitrary). Each of the depicted orbitals is a superposition of two opposite m quantum numbers (see below).
| ml | 0 | -1 and 1 | -2 and 2 | -3 and 3 |
|---|---|---|---|---|
| S orbital → | 
|
|||
| P orbitals → | 
|
 
|
||
| D orbitals → | 
|
 
|
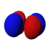 
|
|
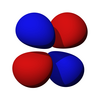
| F orbitals → | 
|
|
 
|
 
|
Magnetic Quantum Number (ml)
| ml | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| S orbital → | 
|
||||||
| P orbitals → | 
|

|

|
||||
| D orbitals → | 
|

|

|

|

|
||
| F orbitals → | 
|

|

|

|

|

|

|
Magnetic quantum number determines the orbital in which the electron lies. The number of orbitals in each subshell can be calculated like so: . ml determines how rapidly the complex phase increases around the z-axis. Without magnetic field, these orbitals all have the same energy, they are degenerate and can be combined into different shapes and spatial orientations. The orbitals in a subshell with degeneracy are called degenerate orbitals. This simply means that the orbitals in each p subshell all have the same energy level. The difference in shapes as well as orientation of higher subshells is not important during general chemistry, and the orbitals in the same higher subshells are still degenerate regardless of shape differences.
Spin Quantum Number (ms)
Does not determines the spin on the electron. +½ corresponds to the up arrow in an electron configuration box. If there is only one electron in an orbital (one arrow in one box), then it is always considered +½. The second arrow, or down arrow, is considered -½. Every orbital can contain one "spin up" electron, and one "spin down" electron.
Some Examples
Let's examine the quantum numbers of electrons from a magnesium atom, 12Mg. Remember that each list of numbers corresponds to (n, l, ml, ms).
| Two s electrons: | (1, 0, 0, +½) | (1, 0, 0, -½) | ||||
| Two s electrons: | (2, 0, 0, +½) | (2, 0, 0, -½) | ||||
| Six p electrons: | (2, 1, -1, +½) | (2, 1, -1, -½) | (2, 1, 0, +½) | (2, 1, 0, -½) | (2, 1, 1, +½) | (2, 1, 1, -½) |
| Two s electrons: | (3, 0, 0, +½) | (3, 0, 0, -½) |
The Periodic Table
Notice a pattern on the periodic table. Different areas, or blocks, have different types of electrons. The two columns on the left make the s-block. The six columns on the right make the p-block. The large area in the middle (transition metals) makes the d-block. The bottom portion makes the f-block (Lanthanides and Actinides). Each row introduces a new shell (aka energy level). Basically, the row tells you how many shells of electrons there will be, and the column tells you which subshells will occur (and which shells they occur in). The value of ml can be determined by some of the rules we will learn in the next chapter. The value of ms doesn't really matter as long as there are no repeating values in the same orbital.
To see the pattern better, take a look at this periodic table. |
Shells and Orbitals
Electron shells
Each shell is subdivided into subshells, which are made up of orbitals, each of which has electrons with different angular momentum. Each orbital in a subshell has a characteristic shape, and is named by a letter. They are: s, p, d, and f. In a one-electron atom (e.g. H, He+, Li+2, etc.) the energy of each orbital within a particular shell is identical. However, when there are multiple electrons, they interact and split the orbitals into slightly different energies. The letters s, p, d and f specify the subshells (angular quantum number l) and the orbital is specified by the magnetic quantum number m. The angular and magnetic quantum numbers relate to the magnitude and direction of the electron's angular momentum, respectively. Within any particular subshell, the energy of the orbitals depends on the angular momentum of orbitals s, p, d, and f in order of lowest to highest energy.
This image shows the orbitals (along with hybrid orbitals for bonding and a sample electron configuration, explained later).

The s subshell
The simplest subshell in the atom is the 1s subshell. It has no radial or angular nodes: the 1s subshell is simply a sphere of electron density. A node is a point where the electron positional probability is zero. As with all subshell the number of radial nodes increases with the principle quantum number (i.e. the 2s orbital has one radial node, the 3s has two etc.). Because the angular momentum quantum number is 0, there is only one choice for the magnetic quantum number - there is only one s orbital per shell. The s orbital can hold two electrons, as long as they have different spin quantum numbers. S orbitals are involved in bonding.
The p subshell
Starting from the 2nd shell, there is a set of p subshell. The angular momentum quantum number of the electrons confined to p subshell is 1, so each orbital has one angular node. There are 3 choices for the magnetic quantum number, which indicates 3 differently oriented p subshell. Finally, each orbital can accommodate two electrons (with opposite spins), giving the p orbitals a total capacity of 6 electrons.
The orbital of p subshell all have two lobes of electron density pointing along each of the axes. Each one is symmetrical along its axis. The notation for the orbitals of p subshell indicate which axis it points down, i.e. px points along the x axis, py on the y axis and pz up and down the z axis. Note that although pz corresponds to the ml = 0 orbital, px and py are actually mixtures of ml = -1 and ml = 1 orbitals. The p orbitals are degenerate — they all have the same energy. P orbitals are very often involved in bonding.
| 2px | 2py | 2pz |
|---|---|---|

|

|

|
The d subshell
The first set of d orbitals is the 3d set. The angular momentum quantum number is 2, so each orbital has two angular nodes. There are 5 choices for the magnetic quantum number, which gives rise to 5 different d orbitals. Each orbital can hold two electrons (with opposite spins), giving the d orbitals a total capacity of 10 electrons.
Note that all the d orbitals have four lobes of electron density, except for the dz2 orbital, which has two opposing lobes and a doughnut of electron density around the middle. The d orbitals can be further subdivided into two smaller sets. The dx2-y2 and dz2 all point directly along the x, y, and z axes. They form an eg set. On the other hand, the lobes of the dxy, dxz and dyz all line up in the quadrants, with no electron density on the axes. These three orbitals form the t2g set. In most cases, the d orbitals are degenerate, but sometimes they can split, with the eg and t2g subsets having different energy. Crystal Field Theory predicts and accounts for this. D orbitals are sometimes involved in bonding, especially in inorganic chemistry.

|
|
|

|

|
The f subshell
The first set of f orbitals is the 4f subshell. There are 7 possible magnetic quantum numbers, so there are 7 f orbitals. Their shapes are fairly complicated, and they rarely come up when studying chemistry. There are 14 f electrons because each orbital can hold two electrons (with opposite spins).

|

|

|

|

|

|

|
Filling Electron Shells
Filling Electron Shells
When an atom or ion receives electrons into its orbitals, the orbitals and shells fill up in a particular manner.
Aufbau principle
You may consider an atom as being "built up" from a naked nucleus by gradually adding to it one electron after another, until all the electrons it will hold have been added. Much as one fills up a container with liquid from the bottom up, the orbitals of an atom are filled from the lowest energy orbitals to the highest energy orbitals.
Orbitals with the lowest principal quantum number () have the lowest energy and will fill up first, in smaller atoms. Larger atoms with more subshells will seem to fill "out of order", as the other factors influencing orbital energy become important. Within a shell, there may be several orbitals with the same principal quantum number. In that case, more specific rules must be applied. For example, the three p orbitals of a given shell all occur at the same energy level. So, how are they filled up? Answer: all the three p orbitals have same energy so while filling the p orbitals we can fill any one of the Px, Py or Pz first. It is a convention that we chose to fill Px first, then Py and then Pz for our simplicity. Hence you can opt for filling these three orbitals from right to left also. Aufbau principle state that “atomic orbitals are filled with electrons in order of increasing energy level”.
Hund's Rule
According to Hund's rule, orbitals of the same energy are each filled with one electron before filling any with a second. Also, these first electrons have the same spin.
This rule is sometimes called the "bus seating rule". As people load onto a bus, each person takes his or her own seat, sitting alone. Only after all the seats have been filled will people start doubling up.
Pauli Exclusion principle
No two electrons can have all four quantum numbers the same. What this translates to in terms of our picture of orbitals is that each orbital can only hold two electrons, one "spin up" (+½) and one "spin down" (-½).

Orbital Order
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, 8s.
Although this looks confusing, there is an easy way to remember. Go in order of the lines from top to bottom, top right end to bottom left of each line.
Understanding the above rules and diagrams will allow you to determine the electron configuration of almost any atom or ion.
How to Write the Electron Configuration of an Isolated Atom
Electron-configuration notation is relatively straightforward. An isolated Calcium atom 20Ca, for example, would have configuration of 1s22s22p63s23p64s2 in its ground state. Other configurations like 1s22s22p63s23p64s14p1 are possible, but these excited states have a higher energy. They are not stable and generally only exist for a brief moment.
The ground state configuration for Ca could be abbreviated by using the preceding noble gas (the elements found all the way on the right of the periodic table) as [Ar]4s2, where Ar is argon.
Noble gases have very stable configurations, and are extremely reluctant to lose or gain electrons. Noble gas atoms are also the only ones regularly found as isolated atoms in the ground state. Atoms of other elements all undergo bonding under the conditions that we live under and this affects the orbitals that the outermost electrons are in. In that sense the electron configurations for the other elements are somewhat hypothetical: to encounter an isolated atom of, say, tungsten (W), we would have to first vaporize a metal that boils at 5800K. However, knowing atomic configurations is useful because it does help us to understand how and why they bond, i.e. why and how they change the configuration of their outer valence electrons.
Rule of Stability
A subshell is particularly stable if it is half full or full. Given two configurations, the atom would "choose" the more stable one.
Example: In the following configuration, Cu: [Ar]4s23d9, copper's d shell is just one away from stability, and therefore, one electron from the s shell jumps into the d shell: [Ar]4s13d10. This way, the d shell is full, and is therefore stable, and the s shell is half full, and is also stable.
Another example: Chromium has a configuration of [Ar]4s13d5, although you would expect to see four d electrons instead of five. This is because an s electron has jumped into the d orbital, giving the atom two half-full shells—much more stable than a d orbital with only four electrons.
The stability rule applies to atoms in the same group as chromium and copper.
If one of these atoms has been ionized, that is, it loses an electron, it will come from the s orbital rather than the d orbital. For instance, the configuration of Cu+ is [Ar]4s03d10. If more electrons are removed, they will come from the d orbital.
Magnetism

Magnetism is a well-known effect. Chances are, you have magnets on your refrigerator. As you already know, only certain elements are magnetic. Electron configurations help to explain why.
Diamagnetism is actually a very weak repulsion to magnetic fields. All elements have diamagnetism to some degree. It occurs when there are paired electrons.
Paramagnetism is an attraction to external magnetic fields. It is also very weak. It occurs whenever there is an unpaired electron in an orbital.
Both diamagnetism and paramagnetism are responses of spins acting independently from each other. This leads to rather weak repulsion and attraction respectively. However, when they are located in a solid they may also interact with each other and respond collectively and that can lead to rather different properties:
Ferromagnetism is the permanent magnetism that we encounter in our daily lives. It occurs when all the unpaired spins in a solid couple and tend to align themselves in the same direction, leading to a strong attraction when exposed to a magnetic field. This only occurs at room temperature with three elements: iron (Fe), nickel (Ni), and cobalt (Co). Gadolinium (Gd) is a borderline case. It loses its ferromagnetism at 20oC; above that temperature the spins start to act alone. However, there are many alloys and compounds that exhibit strong ferromagnetic coupling. The strongest one is Nd2Fe14B
Antiferromagnetism is also a permanent magnetism in which unpaired spins align, but they do so in opposite directions. The result that the material does not react very strongly to a magnetic field at all. Chromium (Cr) is an example.
'Ferrimagnetism is a combination of ferro- and antiferromagetism. Unpaired spins align partly in opposite directions, but the compensation is not complete. This is why the material is still attracted strongly to a magnetic field. Magnetite Fe3O4 is such a substance. It was the first material studied for its magnetic properties and may, well, be the one sitting on your fridge.
Periodicity and Electron Configurations
Blocks of the Periodic Table
The Periodic Table does more than just list the elements. The word periodic means that in each row, or period, there is a pattern of characteristics in the elements. This is because the elements are listed in part by their electron configuration. The Alkali metals and Alkaline earth metals have one and two valence electrons (electrons in the outer shell) respectively. These elements lose electrons to form bonds easily, and are thus very reactive. These elements are the s-block of the periodic table. The p-block, on the right, contains common non-metals such as chlorine and helium. The noble gases, in the column on the right, almost never react, since they have eight valence electrons, which makes it very stable. The halogens, directly to the left of the noble gases, readily gain electrons and react with metals. The s and p blocks make up the main-group elements, also known as representative elements. The d-block, which is the largest, consists of transition metals such as copper, iron, and gold. The f-block, on the bottom, contains rarer metals including uranium. Elements in the same Group or Family have the same configuration of valence electrons, making them behave in chemically similar ways.

Causes for Trends

There are certain phenomena that cause the periodic trends to occur. You must understand them before learning the trends.
Effective Nuclear Charge
The effective nuclear charge is the amount of positive charge acting on an electron. It is the number of protons in the nucleus minus the number of electrons in between the nucleus and the electron in question. The nucleus attracts the electron, but other electrons in lower shells repel it (opposites attract, likes repel).
Shielding Effect
The shielding (or screening) effect is similar to effective nuclear charge. The core electrons repel the valence electrons to some degree. The more electron shells there are (a new shell for each row in the periodic table), the greater the shielding effect is. Essentially, the core electrons shield the valence electrons from the positive charge of the nucleus.
Electron-Electron Repulsions
When two electrons are in the same shell, they will repel each other slightly. This effect is mostly canceled out due to the strong attraction to the nucleus, but it does cause electrons in the same shell to spread out a little bit. Lower shells experience this effect more because they are smaller and allow the electrons to interact more.
Coulomb's Law
Coulomb's law is an equation that determines the amount of force with which two charged particles attract or repel each other. It is , where is the amount of charge, is the distance between charges, and is a constant. For atoms, the charges are typically described as integer multiples (positive for protons, negative for electrons) of the elementary charge , which is 1.6022 x 10-19 coulombs. You can see that doubling the distance would quarter the force.
Trends in the Periodic table
Most of the elements occur naturally on Earth. However, all elements beyond uranium (number 92) are called trans-uranium elements and never occur outside of a laboratory. Most of the elements occur as solids or gases at STP. STP is standard temperature and pressure, which is 0° C and 1 atmosphere of pressure. There are only two elements that occur as liquids at STP: mercury (Hg) and bromine (Br).
Bismuth (Bi) is the last stable element on the chart. All elements after bismuth are radioactive and decay into more stable elements. Some elements before bismuth are radioactive, however.
Atomic Radius
Leaving out the noble gases, atomic radii are larger on the left side of the periodic chart and are progressively smaller as you move to the right across the period. As you move down the group, radii increase.
Atomic radii decrease along a period due to greater effective nuclear charge. Atomic radii increase down a group due to the shielding effect of the additional core electrons, and the presence of another electron shell.
Ionic Radius
For nonmetals, ions are bigger than atoms, as the ions have extra electrons. For metals, it is the opposite.
Extra electrons (negative ions, called anions) cause additional electron-electron repulsions, making them spread out farther. Fewer electrons (positive ions, called cations) cause fewer repulsions, allowing them to be closer.
Ionization Energy
Ionization energy is the energy required to strip an electron from the atom (when in the gas state).
|
Ionization energy is also a periodic trend within the periodic table organization. Moving left to right within a period or upward within a group, the first ionization energy generally increases. As the atomic radius decreases, it becomes harder to remove an electron that is closer to a more positively charged nucleus.
Ionization energy decreases going left across a period because there is a lower effective nuclear charge keeping the electrons attracted to the nucleus, so less energy is needed to pull one out. It decreases going down a group due to the shielding effect. Remember Coulomb's Law: as the distance between the nucleus and electrons increases, the force decreases at a quadratic rate.

It is considered a measure of the tendency of an atom or ion to surrender an electron, or the strength of the electron binding; the greater the ionization energy, the more difficult it is to remove an electron. The ionization energy may be an indicator of the reactivity of an element. Elements with a low ionization energy tend to be reducing agents and form cations, which in turn combine with anions to form salts.
Electron Affinity
Electron affinity is the opposite of ionization energy. It is the energy released when an electron is added to an atom.
|

Electron affinity is highest in the upper left, lowest on the bottom right. However, electron affinity is actually negative for the noble gasses. They already have a complete valence shell, so there is no room in their orbitals for another electron. Adding an electron would require creating a whole new shell, which takes energy instead of releasing it. Several other elements have extremely low electron affinities because they are already in a stable configuration, and adding an electron would decrease stability.
Electron affinity occurs due to the same reasons as ionization energy.
Electronegativity
Electronegativity is how much an atom attracts electrons within a bond. It is measured on a scale with fluorine at 4.0 and francium at 0.7. Electronegativity decreases from upper right to lower left.
Electronegativity decreases because of atomic radius, shielding effect, and effective nuclear charge in the same manner that ionization energy decreases.
Metallic Character
Metallic elements are shiny, usually gray or silver colored, and good conductors of heat and electricity. They are malleable (can be hammered into thin sheets), and ductile (can be stretched into wires). Some metals, like sodium, are soft and can be cut with a knife. Others, like iron, are very hard. Non-metallic atoms are dull, usually colorful or colorless, and poor conductors. They are brittle when solid, and many are gases at STP. Metals give away their valence electrons when bonding, whereas non-metals take electrons.
The metals are towards the left and center of the periodic table—in the s-block, d-block, and f-block . Poor metals and metalloids (somewhat metal, somewhat non-metal) are in the lower left of the p-block. Non-metals are on the right of the table.
Metallic character increases from right to left and top to bottom. Non-metallic character is just the opposite. This is because of the other trends: ionization energy, electron affinity, and electronegativity.
- Metallic/Non-metallic
-
Sodium, very metallic
-
Sulfur, very non-metallic
Octet Rule and Exceptions
The octet rule refers to the tendency of atoms to prefer to have eight electrons in the valence shell (outer orbital). When atoms have fewer than eight electrons, they tend to react and form more stable compounds. When discussing the octet rule, we do not consider d or f electrons. Only the s and p electrons are involved in the octet rule, making it useful for the representative elements (elements not in the transition metal or inner-transition metal blocks). An octet corresponds to an electron configuration ending with s2p6.
Stability
Atoms will react to get in the most stable state possible. A complete octet is very stable because all orbitals will be full. Atoms with greater stability have less energy, so a reaction that increases the stability of the atoms will release energy in the form of heat or light. Reactions that decrease stability must absorb energy, getting hotter.
The other tendency of atoms is to maintain a neutral charge. Only the noble gases (the elements on the right-most column of the periodic table) have zero charge with filled valence octets. All of the other elements have a charge when they have eight electrons all to themselves. The result of these two guiding principles is the explanation for much of the reactivity and bonding that is observed within atoms: atoms seek to share electrons in a way that minimizes charge while fulfilling an octet in the valence shell.
The noble gases rarely form compounds. They have the most stable configuration (full octet, no charge), so they have no reason to react and change their configuration. All other elements attempt to gain, lose, or share electrons to achieve a noble gas configuration. |
Example
The formula for table salt is NaCl. It is the result of Na+ ions and Cl- ions bonding together. If sodium metal and chlorine gas mix under the right conditions, they will form salt. The sodium loses an electron, and the chlorine gains that electron. In the process, a great amount of light and heat is released. The resulting salt is mostly unreactive — it is stable. It won't undergo any explosive reactions, unlike the sodium and chlorine that it is made of.
Why? Referring to the octet rule, atoms attempt to get a noble gas electron configuration, which is eight valence electrons. Sodium has one valence electron, so giving it up would result in the same electron configuration as neon. Chlorine has seven valence electrons, so if it takes one it will have eight (an octet). Chlorine has the electron configuration of argon when it gains an electron.
The octet rule could have been satisfied if chlorine gave up all seven of its valence electrons and sodium took them. In that case, both would have the electron configurations of noble gasses, with a full valence shell. However, their charges would be much higher. It would be Na7- and Cl7+, which is much less stable than Na+ and Cl-. Atoms are more stable when they have no charge, or a small charge.
Exceptions
There are few exceptions to the octet rule.
Two Electrons
The main exception to the rule is hydrogen, which is at its lowest energy when it has two electrons in its valence shell. Helium (He) is similar in that it, too, only has room for two electrons in its only valence shell.
Hydrogen and helium have only one electron shell. The first shell has only one s orbital and no p orbital, so it holds only two electrons. Therefore, these elements are most stable when they have two electrons. You will occasionally see hydrogen with no electrons, but H+ is much less stable than hydrogen with one or two electrons.
Lithium, with three protons and electrons, is most stable when it gives up an electron.
Less Than an Octet
Other notable exceptions are aluminum and boron, which can function well with six valence electrons. Consider BF3. The boron shares its three electrons with three fluorine atoms. The fluorine atoms follow the octet rule, but boron has only six electrons. Although atoms with less than an octet may be stable, they will usually attempt to form a fourth bond to get eight electrons. BF3 is stable, but it will form BF4- when possible. Most elements to the left of the carbon group have so few valence electrons that they are in the same situation as boron: they are electron deficient. Electron deficient elements often show metallic rather than covalent bonding.
More Than an Octet
In Period 3, the elements on the right side of the periodic table have empty d orbitals. The d orbitals may accept electrons, allowing elements like sulfur, chlorine, silicon and phosphorus to have more than an octet. Compounds such as PCl5 and SF6 can form. These compounds have 10 and 12 electrons around their central atoms, respectively.

|
Xenon hexafluoride uses d-electrons to form more than an octet. This compound shows another exception: a noble gas compound. |
Even palladium has 18 electrons in its valence shell
Odd Numbers
Some elements, notably nitrogen, have an odd number of electrons and will form somewhat stable compounds. Nitric oxide has the formula NO. No matter how electrons are shared between the nitrogen and oxygen atoms, there is no way for nitrogen to have an octet. It will have seven electrons instead. A molecule with an unpaired electron is called a free radical and radicals are highly reactive, so reactive that many of them only exist for a fraction of a second. As radicals go, NO and NO2 are actually remarkably stable. At low temperatures NO2 does react with itself to form N2O4, its dimer, that is not a radical.

|
Nitrogen dioxide has an unpaired electron. (Note the positive charge above the N). |
Compounds and Bonding
Overview of Bonding
Introduction to Bonding
Put simply, chemical bonding join atoms together to form more complex structures (like molecules or crystals). Bonds can form between atoms of the same element, or between atoms of different elements. There are several types of chemical bonding which have different properties and give rise to different structures.
In many cases, atoms try to react to form valence shells containing eight electrons. The octet rule describes this, but it also has many exceptions
- Ionic bonding occurs between positive ions (cations) and negative ions (anions). In an ionic solid, the ions arrange themselves into a rigid crystal lattice. NaCl (common salt) is an example of an ionic substance. In ionic bonding there is an attractive force established between large numbers of positive cations and negative anions, such that a neutral lattice is formed. This attraction between oppositely-charged ions is collective in nature and called ionic bonding.
- Covalent bonds are formed when the orbitals of two non-metal atoms physically overlap and share electrons with each other. There are two types of structures to which this can give rise: molecules and covalent network solids. Methane (CH4) and water (H2O) are examples of covalently bonded molecules, and glass is a covalent network solid.
- Metallic bonding occur between atoms that have few electrons compared to the number of accessible orbitals. This is true for the vast majority of chemical elements. In a metallically bonded substance, the atoms' outer electrons are able to freely move around - they are delocalised to form an 'electron pool'. Iron is a metallically bonded substance.
Chemical bonding is one of the most crucial concepts in the study of chemistry. In fact, the properties of materials are basically defined by the type and number of atoms they contain and how they are bonded together.
So far, you have seen examples of intramolecular bonds. These bonds connect atoms into molecules or whole crystals. There are also intermolecular bonds that connect molecules into large substances. These are also called intermolecular forces, or IMF. IMF are weaker than intramolecular bonds, and as they do not permanently join two molecules or ions, it is generally considered incorrect to refer to them as bonds. Sometimes, a substance will not have both IMF and intramolecular bonds. In the case of ionic crystals (like salt) or covalent networks (like diamond), the solid is made out of a network of intramolecular bonds connecting all the component atoms or ions in a repeating pattern, with no separate units to be attracted to each other by IMF. In the case of metallic bonding, the atoms are all interconnected into one large piece of metal, but the electrons move freely rather than being confined to the static bonds of a crystal lattice or covalent network.
Electronegativity
What determines the type of bond formed between two elements? There are two ways of classifying elements to determine the bond formed: by electronegativity, or by metallic/non-metallic character.
Electronegativity
Electronegativity is a property of atoms that is reflected in the layout of the periodic table of the elements. Electronegativity is greatest in the elements in the upper right of the table (e.g., fluorine), and lowest in the lower left (e.g., francium).
Electronegativity is a relative measure of how strongly an atom will attract the electrons in a bond. Although bonds are the result of atoms sharing their electrons, the electrons can be shared unequally. The more electronegative atom in a bond will have a slight negative charge, and the less electronegative atom will have a slight positive charge. Overall, the molecule may have no charge, but the individual atoms will. This is a result of the electronegativity—by attracting the electrons in a bond, an atom gains a slight negative charge. Of course, if two elements have equal electronegativity, they will share the electrons equally.

Metallic elements have low electronegativity, and non-metallic elements have high electronegativity. If two elements are close to each other on the periodic table, they will have similar electronegativities.
Electronegativity is measured on a variety of scales, the most common being the Pauling scale. Created by chemist Linus Pauling, it assigns 4.0 to fluorine (the highest) and 0.7 to francium (the lowest).
Notation
When drawing diagrams of bonds, we indicate covalent bonds with a line. We may write the electronegativity using the symbols and . Look at this example.
The plus goes over the less electronegative atom. From the above diagram, we can see that the fluorine attracts the electrons in the covalent bond more than the hydrogen does. Fluorine will have a slight negative charge because of this, and hydrogen will have a slight positive charge. Overall, hydrogen fluoride is neutral.
Ionic Bonding
What are ions?
Ions are atoms or molecules which are electrically charged. Cations are positively charged and anions carry a negative charge. Ions form when atoms gain or lose electrons. Since electrons are negatively charged, an atom that loses one or more electrons will become positively charged; an atom that gains one or more electrons becomes negatively charged.
Description of Ionic Bonding
Ionic bonding is the attraction between positively- and negatively-charged ions. These oppositely charged ions attract each other to form ionic networks (or lattices). Electrostatics explains why this happens: opposite charges attract and like charges repel. When many ions attract each other, they form large, ordered, crystal lattices in which each ion is surrounded by ions of the opposite charge. Generally, when metals react with non-metals, electrons are transferred from the metals to the non-metals (this is because metals tend to have relatively low ionization energy and non-metals tend to have high electron affinity). The metals form positively-charged ions and the non-metals form negatively-charged ions. The smallest unit of an ionic compound is the formula unit, but this unit merely reflects that ratio of ions that leads to neutrality of the whole crystal, e.g. NaCl or MgCl2. One cannot distinguish individual NaCl or MgCl2 molecules in the structure.
It is however possible that the stacking consists of molecular ions like NH4+ and NO3- in ammonium nitrate. In such structures, the ions are charged molecules rather than charged atoms.
 |
 |
Ionic bonding may also be referred to as electrovalent bonding.
Characteristics
Example ionic compounds: Sodium chloride (), potassium nitrate ().
Ionically bonded substances typically have the following characteristics.
- High melting point (solid at room temperature)
- Hard but brittle (can shatter)
- Many dissolve in water
- Conductors of electricity when dissolved or melted
In general the forces keeping the lattice together depend on the product of the charges of the ions it consists of. A comparison e.g. of NaCl (+1)*(-1) to MgO (+2)*(-2) shows that magnesium oxide is kept together much more strongly -roughly 4 times- than sodium chloride. This is why sodium chloride has a much lower melting point and also dissolves much more easily in a solvent like water than magnesium oxide does.
Solubility

Most ionic compounds are soluble in polar solvents. Polar solvents are simply solvents that have molecules with positive and negative poles. The most common example of a polar solvent is water (H2O).
The reason that they are soluble in polar solvents is because the positive ions are attracted to the negative pole of the solvent and the negative ions are attracted to the positive pole of the solvent. Due to this, the ionic compound dissociates or splits in the solvent into its constituent ions.
For example, H2O is composed of relatively more positive hydrogen atoms and relatively more negative oxygen atoms. When an ionic compound like NaCl is added to the water, the positive ions will be attracted to the more negative oxygen atoms and negative ions will be attracted to the more positive hydrogen atoms.
This is a very useful property of many ionic compounds, but not all, as there are exceptions where certain compounds cannot be dissolved in certain polar solvents.
Conduction
For a substance to conduct electricity, there must be some carrier of charge. For example, in metals, what transports the charge is the mobile electrons surrounding the positive ions.
However, in the solid state, ionic compounds lack any mobile particle capable of carrying charge as the ions cannot move within the lattice because the electrostatic force holding them in place is extremely strong. This changes when the compound is dissolved or molten. When dissolved, the ions dissociate and are capable of moving around. The same is true for molten ionic compounds. Which is why molten and dissolved ionic compounds can conduct electricity, while solid ionic compounds cannot.
Formation

Ionic bonding occurs when metals and non-metals chemically react. As a result of its low ionization energy, a metal atom is not destabilized very much if it loses electrons to form a complete valence shell and becomes positively charged. As its affinity is rather large, a non-metal is stabilized rather strongly by gaining electrons to complete its valence shell and become negatively charged. When metals and non-metals react, the metals lose electrons by transferring them to the non-metals, which gain them. The total process -a small loss plus a large gain- leads to a net lowering of the energy. Consequently, ions are formed, which instantly attract each other leading to ionic bonding.
For instance, in the reaction of Na (sodium) and Cl (chlorine), each Cl atom takes one electron from a Na atom. Therefore each Na becomes a Na+ cation and each Cl atom becomes a Cl- anion. Due to their opposite charges, they attract each other and are joined by millions and millions of other ions to form an ionic lattice. The lattice energy that results from this massive collective stacking further stabilizes the new compound. The formula (ratio of positive to negative ions) in the lattice is NaCl, i.e. there are equal numbers of positive and negative charges ensuring neutrality.
The charges must balance because otherwise the repulsion between the majority charges would become prohibitive. In the case of magnesium chloride, the magnesium atom gives up two electrons to become stable. Note that it is in the second group, so it has two valence electrons. The chlorine atom can only accept one electron, so there must be two chlorine ions for each magnesium ion. Therefore, the formula for magnesium chloride is MgCl2. If magnesium oxide were forming, the formula would be MgO because oxygen can accept both of magnesium's electrons.
- Exercise for the reader
Try figuring out what the formula for magnesium nitride would be. Use the periodic table to help.
It should also be noted that some atoms can form more than one ion. This usually happens with the transition metals. For instance Fe (iron) can become Fe2+ (called iron(II) or -by an older name- ferrous). Fe can also become Fe3+ (called iron(III) or -sometimes still- ferric).
Common Ions
Ionic bonding typically occurs in reactions between a metal and non-metal, but there are also certain molecules called polyatomic ions that undergo ionic bonding. Within these polyatomic ions, there can be covalent (or polar) bonding, but as a unit it undergoes ionic bonding. There are countless polyatomic ions, but you should be familiar with the most common ones. You would be well advised to memorize these ions.
| Name | Formula | Name | Formula |
|---|---|---|---|
| Ammonium | NH4+ | Hydronium | H3O+ |
| Peroxide | O22- | Hydroxide | OH- |
| Nitrite | NO2- | Nitrate | NO3- |
| Sulfite | SO32- | Sulfate | SO42- |
| Hydrogen sulfite | HSO3- | Phosphate | PO43- |
| Hypochlorite | ClO- | Chlorite | ClO2- |
| Chlorate | ClO3- | Perchlorate | ClO4- |
| Carbonate | CO32- | Hydrogen carbonate | HCO3- |
Covalent Bonds
Covalent bonds create molecules, which can be represented by a molecular formula. For chemicals such as a basic sugar (C6H12O6), the ratios of atoms have a common multiple, and thus the empirical formula is CH2O. Note that a molecule with a certain empirical formula is not necessarily the same as one with the same molecular formula.
Formation of Covalent Bonds
Covalent bonds form between two atoms which have incomplete octets — that is, their outermost shells have fewer than eight electrons. They can share their electrons in a covalent bond. The simplest example is water (H2O). Oxygen has six valence electrons (and needs eight) and the hydrogens have one electron each (and need two). The oxygen shares two of its electrons with the hydrogens, and the hydrogens share their electrons with the oxygen. The result is a covalent bond between the oxygen and each hydrogen. The oxygen has a complete octet and the hydrogens have the two electrons they each need.
When atoms move closer, their orbitals change shape, letting off energy. However, there is a limit to how close the atoms get to each other—too close, and the nuclei repel each other.

One way to think of this is a ball rolling down into a valley. It will settle at the lowest point. As a result of this potential energy "valley", there is a specific bond length for each type of bond. Also, there is a specific amount of energy, measured in kilojoules per mole (kJ/mol) that is required to break the bonds in one mole of the substance. Stronger bonds have a shorter bond length and a greater bond energy.
The Valence Bond Model
One useful model of covalent bonding is called the Valence Bond model. It states that covalent bonds form when atoms share electrons with each other in order to complete their valence (outer) electron shells. They are mainly formed between non-metals.
An example of a covalently bonded substance is hydrogen gas (H2). A hydrogen atom on its own has one electron—it needs two to complete its valence shell. When two hydrogen atoms bond, each one shares its electron with the other so that the electrons move about both atoms instead of just one. Both atoms now have access to two electrons: they become a stable H2 molecule joined by a single covalent bond.

Double and Triple Bonds
Covalent bonds can also form between other non-metals, for example chlorine. A chlorine atom has 7 electrons in its valence shell—it needs 8 to complete it. Two chlorine atoms can share 1 electron each to form a single covalent bond. They become a Cl2 molecule.
Oxygen can also form covalent bonds, however, it needs a further 2 electrons to complete its valence shell (it has 6). Two oxygen atoms must share 2 electrons each to complete each other's shells, making a total of 4 shared electrons. Because twice as many electrons are shared, this is called a 'double covalent bond'. Double bonds are much stronger than single bonds, so the bond length is shorter and the bond energy is higher.
Furthermore,, nitrogen has 5 valence electrons (it needs a further 3). Two nitrogen atoms can share 3 electrons each to make a N2 molecule joined by a 'triple covalent bond'. Triple bonds are stronger than double bonds. They have the shortest bond lengths and highest bond energies.
Electron Sharing and Orbitals
Carbon, contrary to the trend, does not share four electrons to make a quadruple bond. The reason for this is that the fourth pair of electrons in carbon cannot physically move close enough to be shared. The valence bond model explains this by considering the orbitals involved.
Recall that electrons orbit the nucleus within a cloud of electron density (orbitals). The valence bond model works on the principle that orbitals on different atoms must overlap to form a bond. There are several different ways that the orbitals can overlap, forming several distinct kinds of covalent bonds.
The Sigma Bond
The first and simplest kind of overlap is when two s orbitals come together. It is called a sigma bond (sigma, or σ, is the Greek equivalent of 's'). Sigma bonds can also form between two p orbitals that lie pointing towards each other. Whenever you see a single covalent bond, it exists as a sigma bond. When two atoms are joined by a sigma bond, they are held close to each other, but they are free to rotate like beads on a string.

The Pi Bond
The second, and equally important kind of overlap is between two parallel p orbitals. Instead of overlapping head-to-head (as in the sigma bond), they join side-to-side, forming two areas of electron density above and below the molecule. This type of overlap is referred to as a pi (π, from the Greek equivalent of p) bond. Whenever you see a double or triple covalent bond, it exists as one sigma bond and one or two pi bonds. Due to the side-by-side overlap of a pi bond, there is no way the atoms can twist around each other as in a sigma bond. Pi bonds give the molecule a rigid shape.
Pi bonds are weaker than sigma bonds since there is less overlap. Thus, two single bonds are stronger than a double bond, and more energy is needed to break two single bonds than a single double bond.

Hybridization
Consider a molecule of methane: a carbon atom attached to four hydrogen atoms. Each atom is satisfying the octet rule, and each bond is a single covalent bond.
Now look at the electron configuration of carbon: 1s22s22p2. In its valence shell, it has two s electrons and two p electrons. It would not be possible for the four electrons to make equal bonds with the four hydrogen atoms (each of which has one s electron). We know, by measuring bond length and bond energy, that the four bonds in methane are equal, yet carbon has electrons in two different orbitals, which should overlap with the hydrogen 1s orbital in different ways.
To solve the problem, hybridization occurs. Instead of a s orbital and three p orbital, the orbitals mix, to form four orbitals, each with 25% s character and 75% p character. These hybrid orbitals are called sp3 orbitals, and they are identical. Observe:
Now these orbitals can overlap with hydrogen 1s orbitals to form four equal bonds. Hybridization may involve d orbitals in the atoms that have them, allowing up to a sp3d2 hybridization.
- Exercise for the reader
Predict the hybridized electron configuration of carbon in ethene. How many sigma bonds are there? How many pi bonds?

Hint: Hybridized electrons form only sigma bonds. Pi bonds form only between p electrons.
Metallic Bonds
Review on structure
Atoms are particles composed of 3 subatomic particles. The protons, neutrons, and electrons. The protons and neutrons are in the nucleus and the electrons orbit this nucleus. These electrons can leave the atom and this is important to note especially for metals. The energy required to remove an electron is referred to as ionization energy and is very low for metals and so metals tend to lose their outermost (valence) electrons whenever possible. The attractive force between electrons and the nucleus is referred to as the electrostatic force of attraction. This electrostatic force is very strong and is capable of holding large structures together.
Overview
Metallic bonds occur among metal atoms. Whereas ionic bonds join metals to non-metals, metallic bonding joins a bulk of metal atoms. A sheet of aluminium foil and a copper wire are both places where you can see metallic bonding in action.

When metallic bonds form, the s and p electrons delocalize. Instead of orbiting their atoms, they form a "sea of electrons" surrounding the positive metal ions. The electrons are free to move throughout the resulting network. The electrostatic force of attraction between this "sea of electrons" and the positive ions acts as a form of "glue" holding together the metallic structure.
Properties
The delocalized nature of the electrons explains a number of unique characteristics of metals:
| Metals are good conductors of electricity | The sea of electrons is free to flow, allowing electrical currents. |
| Metals are good conductors of heat | As heat energy is defined by the motion of particles, the sea of electrons provides an excellent medium for this kinetic energy to be transferred. |
| Metals are ductile (able to draw into wires) and malleable (able to be hammered into thin sheets) |
As the metal is deformed, local bonds are broken but quickly reformed in a new position. |
| Metals are gray and shiny | Photons (particles of light) cannot penetrate the metal, so they bounce off the sea of electrons. |
| Gold is yellow and copper is reddish-brown | There is actually an upper limit to the frequency that is reflected. It is too high to be visible in most metals, but not gold and copper. |
| Metals have very high melting and boiling points | Metallic bonding is very strong, so the atoms are reluctant to break apart into a liquid or gas. |
Reactivity and solubility
Nearly all metals are near completely insoluble in most solvents whether organic or inorganic. This is because the bonds between metals are exceedingly strong and solvents cannot dissolve the metal. However, if the metal undergoes a reaction and forms an ionic compound it can dissolve. Metals react when an electronegative substance attracts the electrons in the sea of electrons and the structure collapses without the force holding it together. Metals almost always form ionic compounds however on occasion they can participate in a form of covalent bonding. These compounds however, do not share any of the properties of metallic bonding. Furthermore, it is important to distinguish between a compound of a metal and an alloy.
Alloys
Metallic bonds can occur between different elements. A mixture of two or more metals is called an alloy. This is what differentiates alloys and compounds containing metals, as alloys are only mixtures. Depending on the size of the atoms being mixed, there are two different kinds of alloys that can form:
-
Substitutional alloy
-
Interstitial alloy
It is also worth note that substitutional/interstitial alloys can exist when there are more than 2 metals are involved in the formation of an alloy.
The resulting mixture will have a combination of the properties of both metals involved. Interstitial alloys tend to be (with exceptions) stronger than their component metals. This is because the particles of varying size tend to prevent the various layers in a metal from sliding over each other smoothly. An example of this would be the difference between bronze and its components copper and tin. Copper on its own is a softer metal unfit for use as a weapon, while bronze was widely used during the Bronze Age for swords and armour. Alloys can also have various other benefits such as corrosion resistance, torsional strength, and much more.
Molecular Shape
Covalent molecules are bonded to other atoms by electron pairs. Being mutually negatively charged, the electron pairs repel the other electron pairs and attempt to move as far apart as possible in order to stabilize the molecule. This repulsion causes covalent molecules to have distinctive shapes, known as the molecule's molecular geometry. There are several different methods of determining molecular geometry. A scientific model, called the VSEPR (valence shell electron pair repulsion) model can be used to qualitatively predict the shapes of molecules. Within this model, the AXE method is used in determining molecular geometry by counting the numbers of electrons and bonds related to the center atom(s) of the molecule.
The VSEPR model is by no means a perfect model of molecular shape! It is simply a system which explains the known shapes of molecular geometry as discovered by experiment. This can allow us to predict the geometry of similar molecules, making it a fairly useful model. Modern methods of quantitatively calculating the most stable (lowest energy) shapes of molecules can take several hours of supercomputer time, and is the domain of computational chemistry.
Table of Geometries
| Orbital Hybridization | |||||
|---|---|---|---|---|---|
| sp |
sp2 | sp3 | sp3d | sp3d2 | |
| 2 Groups | Linear | Bent | Bent | Linear | |
| 3 Groups | Trigonal Planar | Trigonal Pyramidal | T-Shaped | ||
| 4 Groups | Tetrahedral | See-saw | Square Planar | ||
| 5 Groups | Trigonal Bipyramidal | Square Pyramidal | |||
| 6 Groups | Octahedral | ||||
The hybridization is determined by how many "things" are attached to the central atom. Those "things" can be other atoms or non-bonding pairs of electrons. The number of groups is how many atoms or electron pairs are bonded to the central atom. For example, methane (CH4) is tetrahedral-shaped because the carbon is attached to four hydrogens. Ammonia (NH3) is not trigonal planar, however. It is trigonal pyramidal because it is attached to four "things": the three hydrogens and a non-bonding pair of electrons (to fulfill nitrogen's octet).
Tetrahedral Shape
Consider a simple covalent molecule, methane (CH4). Four hydrogen atoms surround a carbon atom in three-dimensional space. Each CH bond consists of one pair of electrons, and these pairs try to move as far away from each other as possible (due to electrostatic repulsion). You might think this would lead to a flat shape, with each hydrogen atom 90° apart. However, in three dimensions, there is a more efficient arrangement of the hydrogen atoms. If each hydrogen atom is at a corner of a tetrahedron centered around the carbon atom, they are separated by about cos-1(-1/3) ≈ 109.5°—the maximum possible.
Hybridization
To align four orbitals in this tetrahedral shape requires the reformation of one s and three p orbitals into an sp3 orbital.
Lone Electron Pairs
The VSEPR model treats lone electron pairs in a similar way to bonding electrons. In ammonia (NH3) for example, there are three hydrogen atoms and one lone pair of electrons surrounding the central nitrogen atom. Because there are four groups, ammonia has a tetrahedral shape but unlike methane, the angle between the hydrogen atoms is slightly smaller, 107.3°. This can be explained by theorizing that lone electron pairs take up more space physically than bonding pairs. This is a reasonable theory: in a bond, the electron pair is distributed over two atoms whereas a lone pair is only located on one. Because it is bigger, the lone pair forces the other electron pairs together.

Testing this assumption with water provides further evidence. In water (H2O) there are two hydrogen atoms and two lone pairs, again making four groups in total. The electron pairs repel each other into a tetrahedral shape. The angle between the hydrogen atoms is 104.5°, which is what we expect from our model. The two lone pairs both push the bonds closer together, giving a smaller angle than in ammonia.
Linear and Planar Shapes
Electron-Poor Atoms
In some molecules, there are less than four pairs of valence electrons. This occurs in electron deficient atoms such as boron and beryllium, which don't conform to the octet rule (they can have 6 and 4 valence electrons respectively). In boron trifluoride (BF3), there are only three electron pairs which repel each other to form a flat plane. Each fluorine atom is separated by cos-1(-1/2) = 120°. A different set of hybrid orbitals is formed in this molecule: the 2s and two 2p orbitals combine to form three sp2 hybrid orbitals. The remaining p orbital is empty and sits above and below the plane of the molecule.
Beryllium, on the other hand, forms only two pairs of valence electrons. These repel each other at cos-1(-1) = 180°, forming a linear molecule. An example is beryllium chloride, which has two chlorine atoms situated on opposite sides of a beryllium atom. This time, one 2s and one 2p orbital combine to form two sp hybrid orbitals. The two remaining p orbitals sit above and to the side of the beryllium atom (they are empty).
Bent vs. Linear


Some elements will have a bent shape, others have a linear shape. Both are attached to two groups, so it depends on how many non-bonding pairs the central atom has.
Take a look at sulfur dioxide (SO2) and carbon dioxide (CO2). Both have two oxygen atoms attached with double covalent bonds. Carbon dioxide is linear, and sulfur dioxide is bent. The difference is in their valence shells. Carbon has four valence electrons, sulfur has six. When they bond, carbon has no non-bonding pairs, but sulfur has one.
Five and Six Groups
Recall that some elements, especially sulfur and phosphorus, can bond with five or six groups. The hybridization is sp3d or sp3d2, with a trigonal bipyramidal or octahedral shape respectively. When there are non bonding pairs, other shape can arise (see the above chart).
How The Shapes Look
The yellow groups are non-bonding electron pairs. The white groups are bonded atoms, and the pink is the central atom. This is referred to as the AXE method; A is the central atom, X's are bonded atoms, and E's are non-bonding electron pairs.
-
linear
-
trigonal planar
-
bent
-
tetrahedral
-
trigonal pyramidal
-
bent
-
trigonal bipyramidal
-
seesaw
-
t-shape
-
octahedral
-
square pyramid
-
square planar
Intermolecular Bonds
Dipoles

Covalent bonds can be polar or non-polar, and so can the overall compound depending on its shape. When a bond is polar, it creates a dipole, a pair of charges (one positive and one negative). If they are arranged in a symmetrical shape, so that they point in opposite directions, they will cancel each other. For example, since the four hydrogens in methane (CH4) are facing away from each other, there is no overall dipole and the molecule is non-polar. In ammonia (NH3), however, there is a negative dipole at the nitrogen, due to the asymmetry caused by the non-bonding electron pair. The polarity of a compound determines its intermolecular bonding abilities.
Polar and Non-Polar Shapes
When a molecule has a linear, trigonal planar, tetrahedral, trigonal bipyramidal, or octahedral shape, it will be non-polar. These are the shapes that do not have non-bonding lone pairs. (e.g. Methane, CH4) But if some bonds are polar while others are not, there will be an overall dipole, and the molecule will be polar (e.g. Chloroform, CHCl3).
The other shapes (with non-bonding pairs) will be polar. (e.g. Water, H2O) Unless, of course, all the covalent bonds are non-polar, in which case there would be no dipoles to begin with.
Dipole-Dipole Bonds
When two polar molecules are near each other, they will arrange themselves so that the negative and positive sides line up. There will be an attractive force holding the two molecules together, but it is not nearly as strong a force as the intramolecular bonds. This is how many types of molecules bond together to form large solids or liquids.
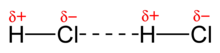
Hydrogen Bonding
Certain chemicals with hydrogen in their chemical formula have a special type of intermolecular bond, called hydrogen bonds. Hydrogen bonds will occur when a hydrogen atom is attached to an oxygen, nitrogen, or fluorine atom. This is because there is a large electronegativity difference between hydrogen and fluorine, oxygen, and nitrogen. Thus, molecules such as , , are extremely polar molecules with very strong dipole-dipole forces. As a result of the high electronegativities of fluorine, oxygen, and nitrogen, these elements will pull the electrons almost completely away from the hydrogen. The hydrogen becomes a bare proton sticking out from the molecule, and it will be strongly attracted to the negative side of any other polar molecules. Hydrogen bonding is an extreme type of dipole-dipole bonding. These forces are weaker than intramolecular bonds, but are much stronger than other intermolecular forces, causing these compounds to have high boiling points.

Covalent Networks
Silicon dioxide forms a covalent network. Unlike carbon dioxide (with double bonds), silicon dioxide forms only single covalent bonds. As a result, the individual molecules covalently bond into a large network. These bonds are very strong (being covalent) and there is no distinction between individual molecules and the overall network. Covalent networks hold diamonds together. Diamonds are made of nothing but carbon, and so is soot. Unlike soot, diamonds have covalent networks, making them very hard and crystalline.
Van der Waals forces
Van der Waals, or London dispersion forces are caused by temporary dipoles created when electron locations are lopsided. The electrons are constantly orbiting the nucleus, and by chance they could end up close together. The uneven concentration of electrons could make one side of the atom more negatively-charged than the other, creating a temporary dipole. As there are more electrons in an atom, and the shells are farther away from the nucleus, these forces become stronger.
Van der Waals forces explain how nitrogen can be liquified. Nitrogen gas is diatomic; its equation is N2. Since both atoms have the same electronegativity, there is no dipole and the molecule is non-polar. If there are no dipoles, what would make the nitrogen atoms stick together to form a liquid? Van der Waals forces are the answer. They allow otherwise non-polar molecules to have attractive forces. These are by far the weakest forces that hold molecules together.
Melting and Boiling Points
When comparing two substances, their melting and boiling points may be questioned. To determine which substance has the higher melting or boiling point, you must decide which one has the strongest intermolecular force. Metallic bonds, ionic bonds, and covalent networks are very strong, as they are actually intramolecular forces. These substances have the highest melting and boiling points because they only separate into individual molecules when the powerful bonds have been broken. Breaking these intramolecular forces requires great amounts of heat energy.
Substances with hydrogen bonding, an intermolecular force, will have much higher melting and boiling points than those that have ordinary dipole-dipole intramolecular forces. Non-polar molecules have the lowest melting and boiling points, because they are held together by the weak van der Waals forces.
If you need to compare the boiling points of two metals, the metal with the larger atomic radius will have weaker bonding, due to the lower concentration of charge. When comparing boiling points of the non-polar gases, like the noble gases, the gas with the largest radius will have the highest points because it has the most potential for van der Waals forces.
Ionic compounds can be compared using Coulomb's Law. Look for substances with high ionic charges and low ionic radii.
Chemical Reactions
Naming Substances
Some compounds have common names, like water for H2O. However, there are thousands of other compounds that are uncommon or have multiple names. Also, the common name is usually not recognized internationally. What looks like water to you might look like agua or vatten to someone else. To allow chemists to communicate without confusion, there are naming conventions to determine the systematic name of a chemical.
Naming Ions and Ionic Compounds
Ions are atoms that have lost or gained electrons. Note that in a polyatomic ion, the ion itself is held together by covalent bonds. Monoatomic cations (positive) are named the same way as their element, and they come first when naming a compound. Monoatomic anions (negative) have the suffix -ide and come at the end of the compound's name.
- Examples of ionic compounds
- NaCl - Sodium chloride
- MgCl2 - Magnesium chloride
- Ca3N2 - Calcium nitride
Notice that there is no need to write how many ions there are. Between the periodic table and our knowledge of ionic bonding, we can determine the number of ions, based on which elements are used.
Polyatomic Ions
Polyatomic ions have special names. Many of them contain oxygen and are called oxyanions. When different oxyanions are made of the same element, but have a different number of oxygen atoms, then prefixes and suffixes are used to tell them apart. The chlorine family of ions is an excellent example.
| Name | Formula |
|---|---|
| Chloride | Cl- |
| Hypochlorite | ClO- |
| Chlorite | ClO2- |
| Chlorate | ClO3- |
| Perchlorate | ClO4- |
The -ate suffix is used on the most common oxyanion (like sulfate SO42- or nitrate NO3-). The -ite suffix is used on the oxyanion with one oxygen atom fewer (like sulfite SO32- or nitrite NO2-). Sometimes there can be a hypo- prefix, meaning one oxygen atom fewer than for -ite. There is also a per- prefix, meaning one more oxygen atom than an -ate molecule has.
Occasionally, you will see a bi- prefix. This is an older prefix; it means the compound can both take up and lose a proton. It is often replaced with the word hydrogen. In either case, the oxyanion will have a hydrogen in it, decreasing its charge by one. For instance, there is carbonate (CO32-) and bicarbonate or hydrogen carbonate (HCO3-). |
One last prefix you may find is thio-. It means an oxygen has been replaced with a sulfur within the oxyanion. Cyanate is OCN-, and thiocyanate is SCN-.
- Examples of polyatomic ions
- NH4Cl - Ammonium chloride
- K(HCO3) - Potassium hydrogen carbonate
- AgNO3 - Silver nitrate
- CuSO3 - Copper (II) sulfite
In the last example, copper had a roman numeral 2 after its name because most of the transition metals can have more than one charge. The charge on the ion must be known, so it is written out for ions that have more than one common charge. Silver always has a charge of 1+, so it isn't necessary (but not wrong) to name its charge. Zinc always has a charge of 2+, so you don't have to name its charge either. Aluminum will always have a charge of +3. All other metals (except the Group 1 and 2 elements) must have roman numerals to show their charge.
Common polyatomic ions that you should know are listed in the following table
| Name | Formula |
|---|---|
| Acetate | C2H3O2- |
| Ammonium | NH4+ |
| Carbonate | CO32- |
| Cyanide | CN- |
| Cyanate | CNO- |
| Thiocyanate | CNS- |
| Hypochlorite | ClO- |
| Chlorite | ClO2- |
| Chlorate | ClO3- |
| Perchlorate | ClO4- |
| Hypobromite | BrO- |
| Bromite | BrO2- |
| Bromate | BrO3- |
| Perbromate | BrO4- |
| Hypoiodite | IO- |
| Iodite | IO2- |
| Iodate | IO3- |
| Periodate | IO4- |
| Nitrite | NO2- |
| Nitrate | NO3- |
| Peroxide | O22- |
| Permanganate | MnO4- |
| Sulfite | SO32- |
| Sulfate | SO42- |
Further explanation of the roman numerals is in order. Many atoms (especially the transition metals) are capable of ionizing in more than one way. The name of an ionic compound must make it very clear what the exact chemical formula is. If you wrote "copper chloride", it could be CuCl or CuCl2 because copper can lose one or two electrons when it forms an ion. The charge must be balanced, so there would be one or two chloride ions to accept the electrons. To be correct, you must write "copper(II) chloride" if you want CuCl2 and "copper (I) chloride" if you want CuCl. Keep in mind that the roman numerals refer to the charge of the cation, not how many anions are attached.
Common metal ions are listed below and should be learned:
| Name | Formula |
|---|---|
| Iron(II)/Ferrous | Fe2+ |
| Iron(III)/Ferric | Fe3+ |
| Copper(I)/Cuprous | Cu+ |
| Copper(II)/Cupric | Cu2+ |
| Tin (II)/Stannous | Sn2+ |
| Tin (IV)/Stannic | Sn4+ |
| Lead (II)/Plumbous (most common) | Pb2+ |
| Lead (IV)/Plumbic | Pb4+ |
| Mercury (I) (Note: Mercury (I) is a polyatomic ion) | Hg22+ |
| Mercury (II) | Hg2+ |
Naming molecules in chemistry
There are two systems of naming molecular compounds. The first uses prefixes to indicate the number of atoms of an element that are in the compound. If the substance is binary (containing only two elements), the suffix -ide is added to the second element. Thus water is dihydrogen monoxide. A prefix is not necessary for the first element if there is only one, so SF6 is 'sulfur hexafluoride'. The prefix system is used when both elements are non-metallic.
| Number | Prefix |
|---|---|
| 1 | Mono- |
| 2 | Di- |
| 3 | Tri- |
| 4 | Tetra- |
| 5 | Penta- |
| 6 | Hexa- |
| 7 | Hepta- |
| 8 | Octa- |
| 9 | Nona- |
| 10 | Deca- |
| 11 | Undeca- |
| 12 | Dodeca- |
If the last letter of the prefix is an a and the first letter of the element is a vowel, the a is dropped. That makes V2O5 divanadium pentoxide (instead of pentaoxide). Similar dropping occurs with mono- and elements beginning with o, as in the case of monoxide. This does not, however, happen with di- and tri-. A molecule containing three iodine atoms would be named triiodide. |
The second system, the stock system, uses oxidation numbers to represent how the electrons are distributed through the compound. This is essentially the roman numeral system that has already been explained, but it applies to non-ionic compounds as well. The most electronegative component of the molecule has a negative oxidation number that depends on the number of pairs of electrons it shares. The less electronegative part is assigned a positive number. In the stock system, only the cation's number is written, and in Roman numerals. The stock system is used when there is a metallic element in the compound. In the case of V2O5, it could also be called vanadium(V) oxide. Knowing that oxygen's charge is always -2, we could determine that there were five oxygens and two vanadiums, if we were given the name without the formula.
Naming acids
If an acid is a binary compound, it is named as hydro[element]ic acid. If it contains a polyatomic ion, then it is named [ion name]ic acid if the ion ends in -ate. If the ion ends in -ite then the acid will end in -ous. These examples should help.
- Examples of acid names
- HCl - Hydrochloric acid
- HClO - Hypochlorous acid
- HClO2 - Chlorous acid
- HClO3 - Chloric acid
- HClO4 - Perchloric acid
Formulas and Numbers
Calculating Formula Masses
The calculation of a compound's formula mass (the mass of its molecule or formula unit) is straightforward. Simply add the individual mass of each atom in the compound (found on the periodic table). For example, the formula mass of glucose (C6H12O6) is 180 amu.
Molar masses are just as easy to calculate. The molar mass is equal to the formula mass, except that the unit is grams per mole instead of amu.
Calculating Percentage Composition
Percentage composition is the relative mass of one substance in a compound compared to the whole. For example, in methane (CH4), the percentage mass of hydrogen is 25% because hydrogen makes up a total of 4 amu out of 16 amu overall.
Using Percentage Composition
Percentage composition can be used to find the empirical formula of a compound, which shows the ratios of elements in the compound. However, this is not the same as the molecular formula. For example, many sugars have the empirical formula CH2O, which could correspond to a molecular formula of CH2O, C2H4O2, C6H12O6, etc.
- To find the empirical formula from percentage composition, follow these procedures for each element.
- Convert from percentage to grams (for simplicity, assume a 100 g sample).
- Divide by the element's molar mass to find moles.
- Simplify to lowest whole-number ratio.
For example, a compound is composed of 75% carbon and 25% hydrogen by mass. Find the empirical formula.
- 75g C / (12 g/mol C) = 6.25 mol C
- 25g H / (1 g/mol H) = 25 mol H
- 6.25 mol C / 6.25 = 1 mol C
- 25 mol H / 6.25 = 4 mol H
Thus the empirical formula is CH4.
Calculating Molecular Formula
If you find the empirical formula of a compound and its molar/molecular mass, then you can find its exact molecular formula. Remember that the molecular formula is always a whole-number multiple of the empirical formula. For example, a compound with the empirical formula HO has a molecular mass of 34.0 amu. Since HO would only be 17.0 amu, which is half of 34.0, the molecular formula must be H2O2.
- Exercise for the reader
An unknown substance must be identified. Lab analysis has found that the substance is composed of 80% Fluorine and 20% Nitrogen with a molecular mass of 71 amu. What is the empirical formula? What is the molecular formula?
Stoichiometry
The word stoichiometry derives from two Greek words: stoicheion (meaning "element") and metron (meaning "measure"). Stoichiometry deals with calculations about the masses (sometimes volumes) of reactants and products involved in a chemical reaction. It is a very mathematical part of chemistry, so be prepared for lots of calculator use.
Jeremias Benjaim Richter (1762-1807) was the first to lay down the principles of stoichiometry. In 1792 he wrote: "Die stöchyometrie (Stöchyometria) ist die Wissenschaft die quantitativen oder Massenverhältnisse zu messen, in welchen die chymischen Elemente gegen einander stehen." [Stoichiometry is the science of measuring the quantitative proportions or mass ratios in which chemical elements stand to one another.]
Molar Calculations
Your Tool: Dimensional Analysis
Luckily, almost all of stoichiometry can be solved relatively easily using dimensional analysis. Dimensional analysis is just using units, instead of numbers or variables, to do math, usually to see how they cancel out. For instance, it is easy to see that:
It is this principle that will guide you through solving most of the stoichiometry problems (chemical reaction problems) you will see in General Chemistry. Before you attempt to solve a problem, ask yourself: what do I have now? where am I going? As long as you know how many (units) per (other units), this will make stoichiometry significantly easier.
Moles to Mass
How heavy is 1.5 mol of lead? How many moles in 22.34g of water? Calculating the mass of a sample from the number of moles it contains is quite simple. We use the molar mass (mass of one mole) of the substance to convert between mass and moles. When writing calculations, we denote the molar mass of a substance by an upper case "M" (e.g. M(Ne) means "the molar mass of neon"). As always, "n" stands for the number of moles and "m" indicates the mass of a substance. To find the solutions to the two questions we just asked, let's apply some dimensional analysis:
Can you see how the units cancel to give you the answer you want? All you needed to know was that you had 1.5 mol Pb (lead), and that 1 mol Pb weighs 207.2 grams. Thus, multiplying 1.5 mol Pb by 207.2 g Pb and dividing by 1 mol Pb gives you 310.8 g Pb, your answer.
Mass to Moles
But we had one more question: "How many moles in 22.34g of water?" This is just as easy:
Where did the 18 g H2O come from? We looked at the periodic table and simply added up the atomic masses of two hydrogens and an oxygen to get the molecular weight of water. This turned out to be 18, and since all the masses on the periodic table are given with respect to 1 mole, we knew that 1 mol of water weighed 18 grams. This gave us the relationship above, which is really just (again) watching units cancel out!
Calculating Molar Masses
Before we can do these types of calculations, we first have to know the molar mass. Fortunately, this is not difficult, as the molar mass is exactly the same as the atomic weight of an element. A table of atomic weights can be used to find the molar mass of elements (this information is often included in the periodic table). For example, the atomic weight of oxygen is 16.00 amu, so its molar mass is 16.00 g/mol.
For species with more than one element, we simply add up the atomic weights of each element to obtain the molar mass of the compound. For example, sulfur trioxide gas is made up of sulfur and oxygen, whose atomic weights are 32.06 and 16.00 respectively.
The procedure for more complex compounds is essentially the same. Aluminium carbonate, for example, contains aluminium, carbon, and oxygen. To find the molar mass, we have to be careful to find the total number of atoms of each element. Three carbonate ions each containing three oxygen atoms gives a total of nine oxygens. The atomic weights of aluminium and carbon are 26.98 and 12.01 respectively.
Empirical Formulae
The empirical formula of a substance is the simplest ratio of the number of moles of each element in a compound. The empirical formula is ambiguous, e.g. the formula CH could represent CH, C2H2, C3H3 etc. These latter formulae are called molecular formulae. It follows that the molecular formula is always a whole number multiple of the empirical formula for a compound.
Calculating the empirical formula is easy if the relative amounts of each element in the compound are known. For example, if a sample contains 1.37 mol oxygen and 2.74 mol hydrogen, we can calculate the empirical formula. A good strategy to use is to divide all amounts given by the smallest non-integer amount, then multiply by whole numbers until the simplest ratio is found. We can make a table showing the successive ratios.
| Hydrogen | Oxygen | |
|---|---|---|
| 2.74 | 1.37 | divide by 1.37 |
| 2 | 1 | ANSWER |
The empirical formula of the compound is H2O.
Here's another example. A sample of piperonal contains 1.384 mol carbon, 1.033 mol hydrogen and 0.519 mol oxygen.
| Carbon | Hydrogen | Oxygen | |
|---|---|---|---|
| 1.384 | 1.033 | 0.519 | divide by 0.519 |
| 2.666 | 2 | 1 | multiply by 3 |
| 8 | 6 | 3 | ANSWER |
The empirical formula of piperonal is C8H6O3.
Converting from Masses
Often, we are given the relative composition by mass of a substance and asked to find the empirical formula. These masses must first be converted to moles using the techniques outlined above. For example, a sample of ethanol contains 52.1% carbon, 13.2% hydrogen, and 34.7% oxygen by mass. Hypothetically, 100g of this substance will contain 52.1 g carbon, 13.2 g hydrogen and 34.7 g oxygen. Dividing these by their respective molar masses gives the amount in moles of each element (as we learned above). These are 4.34 mol, 13.1 mol, and 2.17 mol respectively.
| Carbon | Hydrogen | Oxygen | |
|---|---|---|---|
| 4.34 | 13.1 | 2.17 | divide by 2.17 |
| 2 | 6 | 1 | ANSWER |
The empirical formula of ethanol is C2H6O.
Molecular Formula
As mentioned above, the molecular formula for a substance equals the count of atoms of each type in a molecule. This is always a whole number multiple of the empirical formula. To calculate the molecular formula from the empirical formula, we need to know the molar mass of the substance. For example, the empirical formula for benzene is CH, and its molar mass is 78.12 g/mol. Divide the actual molar mass by the mass of the empirical formula, 13.02 g/mol, to determine the multiple of the empirical formula, "n". The molecular formula equals the empirical formula multiplied by "n".
This shows that the molecular formula for benzene is 6 times the empirical formula of CH. The molecular formula for benzene is C6H6.
Solving Mass-Mass Equations
A typical mass-mass equation will give you an amount in grams and ask for another answer in grams.
- To solve a mass-mass equation, follow these rules
- Balance the equation if it is not already.
- Convert the given quantity to moles.
- Multiply by the molar ratio of the demanded substance over the given substance.
- Convert the demanded substance into grams.
For example, given the equation , find out how many grams of silver (Ag) will result from 43.0 grams of copper (Cu) reacting.
- Convert the given quantity to moles.
- Multiply by the molar ratio of the demanded substance and the given substance.
- Convert the demanded substance to grams.
Notice how dimensional analysis applies to this technique. All units will cancel except for the desired one (grams of silver, in this case). |
Summary
To solve a stoichiometric problem, you need to know what you already have and what you want to find. Everything in between is basic algebra.
- Key Terms
- Molar mass: mass (in grams) of one mole of a substance.
- Empirical formula: the simplest ratio of the number of moles of each element in a compound
- Molecular formula: the actual ratio of the number of moles of each element in a compound
In general, all you have to do is keep track of the units and how they cancel, and you will be on your way!
Chemical Equations
Chemical equations are a convenient, standardized system for describing chemical reactions. They contain the following information.
- The type of reactants consumed and products formed
- The relative amounts of reactants and products
- The electrical charges on ions
- The physical state of each species (e.g. solid, liquid)
- The reaction conditions (e.g. temperature, catalysts)
The final two points are optional and sometimes omitted.
Anatomy of an Equation
Hydrogen gas and chlorine gas will react vigorously to produce hydrogen chloride gas. The equation above illustrates this reaction. The reactants, hydrogen and chlorine, are written on the left and the products (hydrogen chloride) on the right. The large number 2 in front of HCl indicates that two molecules of HCl are produced for each 1 molecule of hydrogen and chlorine gas consumed. The 2 in subscript below H indicates that there are two hydrogen atoms in each molecule of hydrogen gas. Finally, the (g) symbols subscript to each species indicates that they are gases.
Reacting Species
Species in a chemical reaction is a general term used to mean atoms, molecules or ions. A species can contain more than one chemical element (HCl, for example, contains hydrogen and chlorine). Each species in a chemical equation is written:
E is the chemical symbol for the element, x is the number of atoms of that element in the species, y is the charge (if it is an ion) and (s) is the physical state.
The symbols in parentheses (in subscript below each species) indicate the physical state of each reactant or product. For ACS Style[1] the state is typeset at the baseline without size change.
- (s) means solid
- (l) means liquid
- (g) means gas
- (aq) means aqueous solution (i.e. dissolved in water)
For example, ethyl alcohol would be written because each molecule contains 2 carbon, 6 hydrogen and 1 oxygen atom. A magnesium ion would be written because it has a double positive ("two plus") charge. Finally, an ammonium ion would be written because each molecule contains 1 nitrogen and 4 hydrogen atoms and has a charge of 1+.
Coefficients
The numbers in front of each species have a very important meaning—they indicate the relative amounts of the atoms that react. The number in front of each species is called a coefficient. In the above equation, for example, one H2 molecule reacts with one Cl2 molecule to produce two molecules of HCl. This can also be interpreted as moles (i.e. 1 mol H2 and 1 mol Cl2 produces 2 mol HCl).
It is important that the Law of Conservation of Mass is not violated. There must be the same number of each type of atoms on either side of the equation. Coefficients are useful for keeping the same number of atoms on both sides:
If you count the atoms, there are four hydrogens and two oxygens on each side. The coefficients allow us to balance the equation; without them the equation would have the wrong number of atoms. Balancing equations is the topic of the next chapter.
Other Information
Occasionally, other information about a chemical reaction will be supplied in an equation (such as temperature or other reaction conditions). This information is often written to the right of the equation or above the reaction arrow. A simple example would be the melting of ice.
Reactions commonly involve catalysts, which are substances that speed up a reaction without being consumed. Catalysts are often written over the arrow. A perfect example of a catalyzed reaction is photosynthesis. Inside plant cells, a substance called chlorophyll converts sunlight into food. The reaction is written:
Examples
| This is the equation for burning methane gas (CH4) in the presence of oxygen (O2) to form carbon dioxide and water: CO2 and H2O respectively. Notice the use of coefficients to obey the Law of Conservation of Matter. | |
| This is a precipitation reaction in which dissolved lead cations and iodide anions combine to form a solid yellow precipitate of lead iodide (an ionic solid). | |
|
These two equations involve a catalyst. They occur one after another, using divanadium pentoxide to convert sulfur dioxide into sulfur trioxide. If you look closely, you can see that the vanadium catalyst is involved in the reaction, but it does not get consumed. It is both a reactant and a product, but it is necessary for the reaction to occur, making it a catalyst. |
| If we add both equations together, we can cancel out terms that appear on both sides. The resulting equation is much simpler and self-explanatory (although the original pair of equations is more accurate in describing how the reaction proceeds). |
The last example demonstrates another important principle of chemical equations: they can be added together. Simply list all reactants from the equations you are adding, then list all products. If the same term appears on both sides, it is either a catalyst, an intermediate product, or it is not involved in the reaction. Either way, it can be canceled out from both sides (if the coefficients are equal). Try adding the first two vanadium equations together and see if you can cancel out terms to get the final equation. |
Balancing Equations
Balancing Equations
Chemical equations are useful because they give the relative amounts of the substances that react in a chemical equation.
In some cases, however, we may not know the relative amounts of each substance that reacts. Fortunately, we can always find the correct coefficients of an equation (the relative amounts of each reactant and product). The process of finding the coefficients is known as balancing the equation.
During a chemical reaction, atoms are neither created or destroyed. The same atoms are present before and after a reaction takes place; they are just rearranged. This is called the Law of Conservation of Matter, and we can use this law to help us find the right coefficients to balance an equation.
For example, assume in the above equation that we do not know how many moles of ammonia gas will be produced:
From the left side of this equation, we see that there are 2 atoms of nitrogen gas in the molecule N2 (2 atoms per molecule x 1 molecule), and 6 atoms of hydrogen gas in the 3 H2 molecules (2 atoms per molecule x 3 molecules). Because of the Law of Conservation of Matter, there must also be 2 atoms nitrogen gas and 6 atoms of hydrogen gas on the right side. Since each molecule of the resultant ammonia gas (NH3) contains 1 atom of nitrogen and 3 atoms of hydrogen, 2 molecules are needed to obtain 2 atoms of nitrogen and 6 atoms of hydrogen.
An Example
| This chemical equation shows the compounds being consumed and produced; however, it does not appropriately deal with the quantities of the compounds. There appear to be two oxygen atoms on the left and only one on the right. But we know that there should be the same number of atoms on both sides. This equation is said to be unbalanced, because the number of atoms are different. | |
| To make the equation balanced, add coefficients in front of each molecule as needed. The 2 in front of hydrogen on the left indicates that twice as many atoms of hydrogen are needed to react with a certain number of oxygen atoms. The coefficient 1 is not written, since it assumed in the absence of any coefficient. | |
| Now, let's consider a similar reaction between hydrogen and nitrogen. | |
| Typically, it is easiest to balance all pure elements last, especially hydrogen. First, by placing a two in front of ammonia, the nitrogens are balanced. | |
| This leaves 6 moles of atomic hydrogen in the products and only two moles in the reactants. A coefficient of 3 is then placed in front of the hydrogen to give a fully balanced reaction. |
| When balancing a reaction, only coefficients can be changed because changing a subscript would give a different reaction. |
Tricks in balancing certain reactions
Combustion
A combustion reaction is a reaction between a carbon chain (basically, a molecule consisting of carbons, hydrogen, and perhaps oxygen) with oxygen to form carbon dioxide and water, plus heat. Combustion reactions could get very complex:
Fortunately, there is an easy way to balance these reactions.
First, note that the carbon in C6H6 can only appear on the product side in CO2. Thus, we can write a coefficient of 6 in front of CO2.
Next, note that the hydrogen in C6H6 can only go to H2O. Thus, we put a 3 in front of H2O.
We have 15 oxygen atoms on the product side, so there are O2 molecules on the reactant side. To make this an integer, we multiply all coefficients by 2.
Another Example
| Helpful Hint! | |
|---|---|
| Note: Fractions are technically allowed as coefficients, but they are generally avoided. Multiply all coefficients by the denominator to remove a fraction. |
| As reactions become more complex, they become more difficult to balance. For example, the combustion of butane (lighter fluid). | |
| Once again, it is better to leave pure elements until the end, so first we'll balance carbon and hydrogen. Oxygen can then be balanced after. It is easy to see that one mole of butane will produce four moles of carbon dioxide and five moles of water. | |
| Now there are 13 oxygen atoms on the right and two on the left. The odd number of oxygens prevents balancing with elemental oxygen. Because elemental oxygen is diatomic, this problem comes up in nearly every combustion reaction. Simply double every species except for oxygen to get an even number of oxygen atoms in the product. | |
| The carbon and hydrogens are still balanced, and now there are an even number of oxygens in the product. Finally, the reaction can be balanced. |
Keep in mind that every equation must always be balanced. If it's not balanced, it is incorrect. |
Limiting Reactants and Percent Yield
Limiting Reactants
When chemical reactions occur, the reactants undergo change to create the products. The coefficients of the chemical equation show the relative amounts of substance needed for the reaction to occur. Consider the combustion of propane:
For every one mole of propane, there must be five moles of oxygen. For every one mole of propane combusted, there will be three moles of carbon dioxide and four moles of water produced (along with much heat). If a propane grill is burning, there will be a very large amount of oxygen available to react with the propane gas. In this case, oxygen is the excess reactant. There is so much oxygen that the exact amount doesn't matter—it will not run out.
On the other hand, there is not an unlimited amount of propane. It will run out far before the oxygen runs out, making it a limiting reactant. The amount of propane available will decide how far the reaction will go.
- Example
If there are three moles of hydrogen, and one mole of oxygen, which is the limiting reactant? How much product is created?
Twice as much hydrogen than oxygen is required. However, there is more than twice as much hydrogen. Thus hydrogen is the excess reactant and oxygen is the limiting reactant. If the reaction proceeds to completion, all of the oxygen will be used up, and one mole of hydrogen will remain. You can imagine this situation like this:
The reactant that is left over after the reaction is complete is called the "excess reactant". Often, you will want to figure out how much of the excess reactant is left after the reaction is complete. to do this, first use mole ratios to determine how much excess reactant is used up in the reaction.
Here are the ratios that need to be used:
Percent Yield
Usually, less product is made than theoretically possible. The actual yield is lower than the theoretical yield. To compare the two, one can calculate percent yield, which is .
The percent yield tells us how far the reaction actually went.
Types of Chemical Reactions
| Helpful Hint! | |
|---|---|
| Synthesis reactions always yield one product. Reversing a synthesis reaction will give you a decomposition reaction. |
The general form of a synthesis reaction is A + B → AB. Synthesis reactions "put things together".
| This is the most well-known example of a synthesis reaction—the formation of water via the combustion of hydrogen gas and oxygen gas. | |
| Another example of a synthesis reaction is the formation of sodium chloride (table salt). |
Because of the very high reactivities of sodium metal and chlorine gas, this reaction releases a tremendous amount of heat and light energy. Recall that atoms release energy as they become stable, and consider the octet rule when determining why this reaction has such favorable features.
Decomposition Reactions
These are the same number of synthesis reactions, with the format AB → A + B. Decomposition reactions "take things apart". Just as synthesis reactions can only form one product, decomposition reactions can only start with one reactant. Compounds that are unstable decompose quickly without outside assistance. Also they help other atoms to decompose better.
| One example is the electrolysis of water (passing water through electrical current) to form hydrogen gas and oxygen gas. | |
| Hydrogen peroxide slowly decomposes into water and oxygen because it is somewhat unstable. The process is sped up by the energy from light, so hydrogen peroxide is often stored in dark containers to slow down the decomposition. | |
| Carbonic acid is the carbonation that is dissolved in soda. It decomposes into carbon dioxide and water, which is why an opened drink loses its fizz. |
Decomposition, aside from happening spontaneously in unstable compounds, occurs under three conditions: thermal, electrolytic, and catalytic. Thermal decomposition occurs when a substance is heated. Electrolytic decomposition, as shown above, is the result of an electric current. Catalytic decomposition happens because a catalyst breaks apart a substance. |
Single Displacement Reactions
Single displacement reaction, also called single replacement, is a reaction in which 2 elements are substituted for another element in a compound. The starting materials are always pure elements, such as a pure zinc metal or hydrogen gas plus an aqueous compound. When a displacement reaction occurs, a new aqueous compound and a different pure element are generated as products. Its format is AB + C → AC + B. Single Diplacement Adding hydrochloric acid to zinc will cause a gas to bubble out:
Double Displacement Reactions
In these reactions, two compounds swap components, in the format AB + CD → AD + CB
This is also called an "exchange". Here are the examples below:
1.) HCl + NaOH ----> NaCl + H2O
Precipitation
A precipitation reaction occurs when an ionic substance comes out of solution and forms an insoluble (or slightly soluble) solid. The solid which comes out of solution is called a precipitate. This can occur when two soluble salts (ionic compounds) are mixed and form an insoluble one—the precipitate.
| An example is lead nitrate mixed with potassium iodide, which forms a bright yellow precipitate of lead iodide. | |
| Note that the lead iodide is formed as a solid. The previous equation is written in molecular form, which is not the best way of describing the reaction. Each of the elements really exist in solution as individual ions, not bonded to each other (as in potassium iodide crystals). If we write the above as an ionic equation, we get a much better idea of what is actually happening. | |
| Notice the like terms on both sides of the equation. These are called spectator ions because they do not participate in the reaction. They can be ignored, and the net ionic equation is written. |
In the solution, there exists both lead and iodide ions. Because lead iodide is insoluble, they spontaneously crystallise and form the precipitate.
Acid-Base Neutralization
In simple terms, an acid is a substance which can lose a H+ ion (i.e. a proton) and a base is a substance which can accept a proton. When equal amounts of an acid and base react, they neutralize each other, forming species which aren't as acidic or basic.
| For example, when hydrochloric acid and sodium hydroxide react, they form water and sodium chloride (table salt). | |
| Again, we get a clearer picture of what's happening if we write a net ionic equation. |
Acid base reactions often happen in aqueous solution, but they can also occur in the gaseous state. Acids and bases will be discussed in much greater detail in the acids and bases section.
Combustion

Combustion, better known as burning, is the combination of a substance with oxygen. The products are carbon dioxide, water, and possible other waste products. Combustion reactions release large amounts of heat. C3H8, better known as propane, undergoes combustion. The balanced equation is:
Combustion is similar to a decomposition reaction, except that oxygen and heat are required for it to occur. If there is not enough oxygen, the reaction may not occur. Sometimes, with limited oxygen, the reaction will occur, but it produces carbon monoxide (CO) or even soot. In that case, it is called incomplete combustion. If the substances being burned contain atoms other than hydrogen and oxygen, then waste products will also form. Coal is burned for heating and energy purposes, and it contains sulfur. As a result, sulfur dioxide is released, which is a pollutant. Coal with lower sulfur content is more desirable, but more expensive, because it will release less of the sulfur-based pollutants.
Organic Reactions

Organic reactions occur between organic molecules (molecules containing carbon and hydrogen). Since there is a virtually unlimited number of organic molecules, the scope of organic reactions is very large. However, many of the characteristics of organic molecules are determined by functional groups—small groups of atoms that react in predictable ways.
Another key concept in organic reactions is Lewis basicity. Parts of organic molecules can be electrophillic (electron-loving) or nucleophillic (nucleus, or positive loving). Nucleophillic regions have an excess of electrons—they act as Lewis bases—whereas electrophillic areas are electron deficient and act as Lewis acids. The nucleophillic and electrophillic regions attract and react with each other. Organic reactions are beyond the scope of this book, and are covered in more detail in Organic Chemistry. However, most organic substances can undergo replacement reactions and combustion reactions, as you have already learned.
Redox
Redox is an abbreviation of reduction/oxidation reactions. This is exactly what happens in a redox reaction, one species is reduced and another is oxidized. Reduction involves a gain of electrons and oxidation involves a loss, so a redox reaction is one in which electrons are transferred between species. Reactions where something is "burnt" (burning means being oxidised) are examples of redox reactions, however, oxidation reactions also occur in solution, which is very useful and forms the basis of electrochemistry.
Redox reactions are often written as two half-reactions showing the reduction and oxidation processes separately. These half-reactions are balanced (by multiplying each by a coefficient) and added together to form the full equation. When magnesium is burnt in oxygen, it loses electrons (it is oxidised). Conversely, the oxygen gains electrons from the magnesium (it is reduced).
Redox reactions will be discussed in greater detail in the redox section.
Energy Changes in Chemical Reactions
Exothermic and Endothermic Reactions
The release of energy in chemical reactions occurs when the reactants have higher chemical energy than the products. The chemical energy in a substance is a type of potential energy stored within the substance. This stored chemical potential energy is the heat content or enthalpy of the substance.
If the enthalpy decreases during a chemical reaction, a corresponding amount of energy must be released to the surroundings. Conversely, if the enthalpy increases during a reaction, a corresponding amount of energy must be absorbed from the surroundings. This is simply the Law of Conservation of Energy.
absorbtion reactions is when a chemical reaction releases more energy than it absorbs and you can also see them die on the inside.
reletion reactions is when a chemical reaction absorbs more energy than it releases.
You are already familiar with enthalpy: melting ice is endothermic and freezing water is exothermic.
| When methane burns in air the heat given off equals the decrease in enthalpy that occurs as the reactants are converted to products.
|
When ammonium nitrate is dissolved in water, energy is absorbed and the water cools. This concept is used in "cold packs".
|
Because reactions release or absorb energy, they affect the temperature of their surroundings. Exothermic reactions heat up their surroundings while endothermic reactions cool them down. The study of enthalpy, along with many other energy-related topics, is covered in the Thermodynamics Unit.
Activation Energy
Think about the combustion of methane. It releases enough heat energy to cause a fire. However, the reaction does not occur automatically. When methane and oxygen are mixed, an explosion does not instantly occur. First, the methane must be ignited, usually with a lighter or matchstick. This reveals something about reactions: they will not occur unless a certain amount of activation energy is added first. In this sense, all reactions absorb energy before they begin, but the exothermic reactions release even more energy. This can be explained with a graph of potential energy:

This graph shows an exothermic reaction because the products are at a lower energy than the reactants (so heat has been released). Before that can happen, the energy must actually increase. The amount of energy added before the reaction can complete is the activation energy, symbolized Ea.
Predicting Chemical Reactions
Types of Reactions
There are several guidelines that can help you predict what kind of chemical reaction will occur between a mixture of chemicals.
- Several pure elements mixed together may undergo a synthesis reaction.
- A single compound may undergo a decomposition reaction. It often forms water or hydrogen gas.
- A pure element mixed with an ionic compound may undergo a single replacement reaction.
- Two different ionic compounds are very likely to undergo a double replacement reaction.
- An organic compound (containing carbon and hydrogen) can usually react with oxygen in a combustion reaction.
However, not all elements will react with each other. To better predict a chemical reaction, knowledge of the reactivity series is needed.
Reactivity
When combining two chemicals, a single- or double-replacement reaction doesn't always happen. This can be explained by a list known as the reactivity series, which lists elements in order of reactivity. The higher on the list an element is, the more elements it can replace in a single- or double-replacement reaction. When deciding if a replacement reaction will occur, look up the two elements in question. The higher one will replace the lower one.
Elements at the very top of the series are so reactive that they can replace hydrogen from water. This explains the explosive reaction between sodium and water:
Elements in the middle of the list will react with acids (but not water) to produce a salt and hydrogen gas. Elements at the bottom of the list are mostly nonreactive.
Elements near the top of the list will corrode (rust, tarnish, etc.) in oxygen much faster than those at the bottom of the list.
The Reactivity Series
- Red: elements that react with water and acids to form hydrogen gas, and with oxygen.
- Orange: elements that react very slowly with water but strongly with acids.
- Yellow: elements that react with acid to form hydrogen gas, and with oxygen.
- Grey: elements that react with oxygen (tarnish).
- White: elements that are often found pure; relatively nonreactive.
Most Reactive
| Cs |
| K |
| Na |
| Li |
| Sr |
| Ca |
| Rb |
| Ba |
| Mg |
| Al |
| (C) |
| Mn |
| Zn |
| Cr |
| Fe |
| Cd |
| Co |
| Ni |
| Sn |
| Pb |
| (H2) |
| Sb |
| Bi |
| Cu |
| Hg |
| Ag |
| Pt |
| Au |
Least Reactive
Oxidation States
Oxidation states are used to determine the degree of oxidation or reduction that an element has undergone when bonding. The oxidation state of a compound is the sum of the oxidation states of all atoms within the compound, which equals zero unless the compound is ionic.
*Gaining electrons is reduction.
|
The oxidation state of an atom within a molecule is the charge it would have if the bonding were completely ionic, even though covalent bonds do not actually result in charged ions.
Method of notation
Oxidation states are written above the element or group of elements that they belong to (when drawing the molecule), or written with roman numerals in parenthesis when naming the elements.
| aluminum | |
| aluminum(III), an ion |
Determining oxidation state
For single atoms or ions
Because oxidation numbers are just the sum of the electrons gained or lost, calculating them for single elements is easy.
The oxidation state of a single element is the same as its charge. Pure elements always have an oxidation states of zero. |
Notice that the oxidation states of ionic compounds are simple to determine.
For larger molecules
| Helpful Hint! | |
|---|---|
| Remember that all the individual oxidation states must add up to the charge on the whole substance. |
Although covalent bonds do not result in charges, oxidation states are still useful. They label the hypothetical transfer of electrons if the substance were ionic. Determining the oxidation states of atoms in a covalent molecule is very important when analyzing "redox" reactions. When substances react, they may transfer electrons when they form the products, so comparing the oxidation states of the products and reactants allows us to keep track of the electrons.
| for hydrogen chloride | |
| for water | |
| for the chlorite ion (notice the overall charge) |
| Oxidation states do not necessarily represent the actual charges on an atom in a molecule. They are simply numbers that indicate what the charges would be if that atom had gained or lost the electrons involved in the bonding. For example, CH4 is a covalent molecule—the C has no charge nor does the H, however the molecule can be assigned a −4 oxidation state for the C and a +1 oxidation state for the H's. |
Determining Oxidation States
The determination of oxidation states is based on knowing which elements can have only one oxidation state other than the elemental state and which elements are able to form more than one oxidation state other than the elemental state. Let's look at some of the "rules" for determining the oxidation states.
1. The oxidation state of an element is always zero.
2. For metals, the charge of the ion is the same as the oxidation state. The following metals form only one ion: Group IA, Group IIA, Group IIIA (except Tl), Zn2+, Cd2+.
3. For monatomic anions and cations, the charge is the same as the oxidation state.
4. Oxygen in a compound is −2, unless a peroxide is present. The oxidation state of oxygen in peroxide ion , O22− is −1.
5. For compounds containing polyatomic ions, use the overall charge of the polyatomic ion to determine the charge of the cation. Here is a convenient method for determining oxidation states. Basically, you treat the charges in the compound as a simple algebraic expression. For example, let's determine the oxidation states of the elements in the compound, KMnO4. Applying rule 2, we know that the oxidation state of potassium is +1. We will assign "x" to Mn for now, since manganese may be of several oxidation states. There are 4 oxygens at −2. The overall charge of the compound is zero: K Mn O4 +1 x 4(-2)
The algebraic expression generated is: 1 + x -8 = 0
Solving for x gives the oxidation state of manganese: x - 7 = 0 x = +7 K Mn O4 +1 +7 4(-2)
Suppose the species under consideration is a polyatomic ion. For example, what is the oxidation state of chromium in dichromate ion, (Cr2O72-)?
As before, assign the oxidation state for oxygen, which is known to be -2. Since the oxidation state for chromium is not known, and two chromium atoms are present, assign the algebraic value of 2x for chromium: Cr2 O7 2- 2x 7(-2)
Set up the algebraic equation to solve for x. Since the overall charge of the ion is -2, the expression is set equal to -2 rather than 0: 2x + 7(-2) = -2
Solve for x: 2x - 14 = -2 2x = 12 x = +6
Each chromium in the ion has an oxidation state of +6. Let's do one last example, where a polyatomic ion is involved. Suppose you need to find the oxidation state of all atoms in Fe2(CO3)3. Here two atoms, iron and carbon, have more than one possible oxidation state. What happens if you don't know the oxidation state of carbon in carbonate ion? In fact, knowledge of the oxidation state of carbon is unnecessary. What you need to know is the charge of carbonate ion (-2). Set up an algebraic expression while considering just the iron ion and the carbonate ion: Fe2 (CO3)3 2x 3(-2) 2x - 6 = 0 2x = 6 x = 3
Each iron ion in the compound has an oxidation state of +3. Next consider the carbonate ion independent of the iron(III) ion: C O3 2- x 3(-2) x - 6 = -2 x = +4
The oxidation state of carbon is +4 and each oxygen is -2.
Guidelines
Determining oxidation states is not always easy, but there are many guidelines that can help. This guidelines in this table are listed in order of importance. The highest oxidation state that any element can reach is +8 in XeO4.
| Element | Usual Oxidation State |
|---|---|
| Fluorine | Fluorine, being the most electronegative element, will always have an oxidation of -1 (except when it is bonded to itself in F2, when its oxidation state is 0). |
| Hydrogen | Hydrogen always has an oxidation of +1, -1, or 0. It is +1 when it is bonded to a non-metal (e.g. HCl, hydrochloric acid). It is -1 when it is bonded to metal (e.g. NaH, sodium hydride). It is 0 when it is bonded to itself in H2. |
| Oxygen | Oxygen is usually given an oxidation number of -2 in its compounds, such as H2O. The exception is in peroxides (O2-2) where it is given an oxidation of -1. Also, in F2O oxygen is given an oxidation of +2 (because fluorine must have -1), and in O2, where it is bonded only to itself, the oxidation is 0. |
| Alkali Metals | The Group 1A metals always have an oxidation of +1, as in NaCl. The Group 2A metals always have an oxidation of +2, as in CaF2. There are some rare exceptions that don't need consideration. |
| Halogens | The other halogens (Cl, Br, I, As) usually have an oxidation of -1. When bonded to another halogen, its oxidation will be 0. However, they can also have +1, +3, +5, or +7. Looking at the family of chlorides, you can see each oxidation state (Cl2 (0), Cl- (-1), ClO- (+1), ClO2- (+3), ClO3- (+5), ClO4- (+7)). |
| Nitrogen | Nitrogen (and the other Group 5A elements, such as phosphorus, P) often have -3 (as in ammonia, NH3), but may have +3 (as in NF3) or +5 (as in phosphate, PO43-). |
| Carbon | Carbon can take any oxidation state from -4, as in CH4, to +4, as in CF4. It is best to find the oxidation of other elements first. |
In general, the more electronegative element has the negative number. Using a chart of electronegativities, you can determine the oxidation state of any atom within a compound.
Periodicity
Oxidation states are another periodic trend. They seem to repeat a pattern across each period.
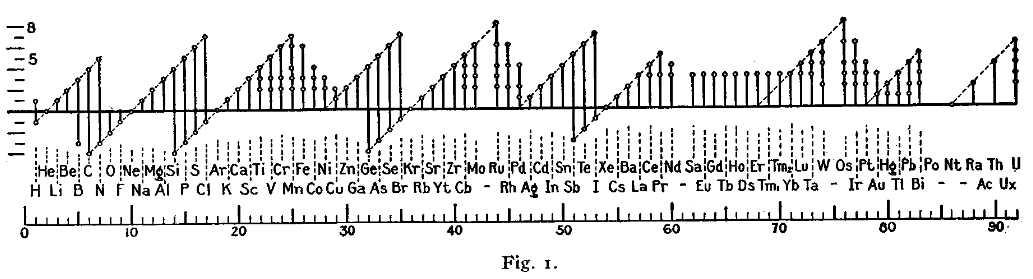
Redox Reactions
Redox
Redox reactions are chemical reactions in which elements are oxidized and reduced.
*Losing electrons is oxidation.
|
Specifically, at the most basic level one element gets oxidized by losing, or donating, electrons to the oxidizing agent. In doing so, the oxidizing agent gets reduced by accepting the electrons lost, or donated, by the reducing agent (i.e. the element getting oxidized).
If it seems as though there are two separate things going on here, you are correct: redox reactions can be split into two half-reactions, one dealing with oxidation, the other, reduction.
Mnemonic
Oil Rig
Oxidation Is Loss. Reduction Is Gain
Alternatively:
LEO GER
Lose Electrons Oxidation. Gain Electrons Reduction
Example
| This is the complete reaction. Iron is oxidized, thus it is the reducing agent. Copper is reduced, making it the oxidizing agent. | |
| This is the oxidation half-reaction. | |
| This is the reduction half-reaction. |
When the two half-reactions are summed, the result is:
| Helpful Hint! | |
|---|---|
| If you cancel out the electrons on both sides, you get the original equation. |
Balancing Redox Equations
In a redox reaction, all electrons must cancel out. If you are adding two half-reactions with unequal numbers of electrons, then the equations must be multiplied by a common denominator. This process is similar to balancing regular equations, but now you are trying to balance the electrons between two half-reactions.
Example
The electrons don't completely cancel out. There is one electron more on the left. However, if you double all terms in the first half-reaction, then add it to the second half-reaction, the electrons will cancel out completely. That means the half-reactions for this redox reaction are actually:
Balancing Redox Equations in an Acidic or Basic Solution
If a reaction occurs in an acidic or basic environment, the redox equation is balanced as follows:
- Write the oxidation and reduction half reactions, but with the whole compound, not just the element that is reduced/oxidized.
- Balance both reactions for all elements except oxygen and hydrogen.
- If the oxygen atoms are not balanced in either reaction, add water molecules to the side missing the oxygen.
- If the hydrogen atoms are not balanced, add hydrogen ions until the hydrogen atoms are balanced.
- Multiply the half reactions by the appropriate number (so that they have equal numbers of electrons).
- Add the two equations to cancel out the electrons, as in the previous method, and the equation is balanced!
If the reaction occurs in a basic environment, proceed as if it is in an acid environment, but, after step 4, for each hydrogen ion added, add a hydroxide ion to both sides of the equation. Then, combine the hydroxide ions and hydrogen ions to form water. Then, cancel all the water molecules that appear on both sides.
Electrochemistry
Redox Reactions (review)
Redox (shorthand for reduction/oxidation reaction) describes all chemical reactions in which atoms have their oxidation number (oxidation state) changed.
This can be either a simple redox process such as the oxidation of carbon to yield carbon dioxide, or the reduction of carbon by hydrogen to yield methane (CH4), or it can be a complex process such as the oxidation of sugar in the human body through a series of very complex electron transfer processes.
The term redox comes from the two concepts of reduction and oxidation. It can be explained in simple terms:
- Oxidation describes the loss of electrons by a molecule, atom, or ion
- Reduction describes the gain of electrons by a molecule, atom, or ion
However, these descriptions (though sufficient for many purposes) are not truly correct. Oxidation and reduction properly refer to a change in oxidation number—the actual transfer of electrons may never occur. Thus, oxidation is better defined as an increase in oxidation number, and reduction as a decrease in oxidation number. In practice, the transfer of electrons will always cause a change in oxidation number, but there are many reactions which are classed as "redox" even though no electron transfer occurs noway (such as those involving covalent bonds).
Electrochemistry
Electrochemistry is a branch of chemistry that deals with the flow of electricity by chemical reactions. The electrons in a balanced half-reaction show the direct relationship between electricity and the specific redox reaction. Electrochemical reactions are either spontaneous, or nonspontaneous. A spontaneous redox reaction generates a voltage itself. A nonspontaneous redox reaction occurs when an external voltage is applied. The reactions that occur in an electric battery are electrochemical reactions.
- Three components of an electrochemical reaction
- A solution where redox reactions may occur (solutions are substances dissolved in liquid, usually water)
- A conductor for electrons to be transferred (such as a metal wire)
- A conductor for ions to be transferred (usually a salt bridge) e.g. filter paper dipped in a salt solution.
Electrolysis
An electrolysis experiment forces a nonspontaneous chemical reaction to occur. This is achieved when two electrodes are submersed in an electrically conductive solution, and the electrical voltage applied to the two electrodes is increased until electrons flow. The electrode receiving the electrons, or where the reduction reactions occur, is called the cathode. The electrode which supplies the electrons, or where the oxidation reactions occur, is called the anode.
A molten salt is an example of something that may be electrolyzed because salts are composed of ions. When the salt is in its solid state, the ions are not able to freely move. However, when the salt is heated enough until it melts (making it a molten salt), the ions are free to move. This mobility of the ions in the molten salt makes the salt electrically conductive. In the electrolysis of a molten salt, for example melted , the cation of the salt (in this case ) will be reduced at the cathode, and the anion of the salt (in this case ) will be oxidized at the anode:
- Cathode reaction: Na+ + e- → Na
- Anode reaction: 2Cl → Cl2 + 2e-
Aqueous solutions of salts can be electrolyzed as well because they are also electrically conductive. In aqueous solutions, there is an additional reaction possible at each the cathode and the anode:
- Cathode: 2H2O + 2e- → H2 + 2OH- (reduction of water)
- Anode: 2H2O → 4H+ + O2 + 4e- (oxidation of water)
With the addition of these two reactions, there are now two possible reactions at each electrode. At the cathode, either the reduction of the cation or the reduction of water will occur. At the anode, either the oxidation of the anion or the oxidation of water will occur. The following rules determine which reaction takes place at each electrode:
- Cathode: If the cation is a very active metal, water will be reduced. Very active metals include Li, Na, K, Rb, Cs, Ca, Sr, and Ba. If the cation is an active or inactive metal, the cation will be reduced.
- Anode: If the anion is a polyatomic ion, water will generally be oxidized. Specifically, sulfate, perchlorate, and nitrate ions are not oxidized; water will oxidize instead. Chloride, bromide, and iodide ions will be oxidized. If the anion in one salt is oxidized in an aqueous electrolysis, that same anion will also be oxidized in any other salt.
Galvanic Cells
The energy of a spontaneous redox reaction is captured using a galvanic cell. The following parts are necessary to make a galvanic cell:
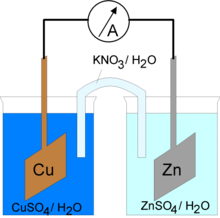
- Two half cells
- Two electrodes
- One electrically conductive wire
- One salt bridge
- One device, usually an ammeter or a voltmeter
A galvanic cell is constructed as shown in the image to the right. The two half-reactions are separated into two half cells. All of the reactants in the oxidation half-reaction are placed in one half cell (the anode), and all the reactants of the reduction half-reaction are placed in the other half cell (the cathode). If the half-reaction contains a metal, the metal serves as the electrode for that half cell. Otherwise, an inert electrode made of platinum, silver, or gold is used. The electrodes are connected with a wire which allows the flow of electrons. The electrons always flow from the anode to the cathode. The half cells are connected by a salt bridge which allows the ions in the solution to move from one half cell to the other, so that the reaction can continue. Since the overall reaction is spontaneous, the flow of electrons will move spontaneously through the outer circuitry from which the energy can be extirpated. The energy harnessed is useful because it can be used to do work. For example, if an electrical component such as a light bulb is attached to the wire, it will receive power from the flowing electrons.
Consistent results from a galvanic cell are dependent on three variables: pressure, temperature, and concentration. Thus, chemists defined a standard state for galvanic cells. The standard state for the galvanic cell is a pressure of 1.00 atmospheric pressure (atm) for all gases, a temperature of 298 kelvin (K) and concentrations of 1.00 molarity (M) for all soluble compounds, liquids, and solids.
Voltage
Voltage is a measure of spontaneity of redox reactions, and it can be measured by a voltmeter. If the voltage of a reaction is positive, the reaction occurs spontaneously, but when negative, it does not occur spontaneously.
To compute the voltage of a redox equation, split the equation into its oxidation component and reduction component. Then, look up the voltages of each component on a standard electrode potential table. This table will list the voltage for the reduction equation. The oxidation reaction's voltage is negative of the corresponding reduction equation's voltage. To find the equation's voltage, add the standard voltages for each half reaction.
Aqueous Solutions
Solubility
Types of Solutions
A solution is a homogenous mixture, composed of solvent(s) and solute(s). A solvent is any substance which allows other substances to dissolve in it. Therefore, it is usually present in the greater amount. Solutes are substances present in a solution. Note that when a solute dissolves in a solvent, no chemical bonds form between the solvent and solute.
Solutions have variable composition, unlike pure compounds whose composition is fixed. For example, a 500 mL solution of lemonade can consist of 70% water, 20% lemon juice, and 10% sugar. There can also be a 500 mL solution of lemonade consisting of 60% water, 25% lemon juice, and 15% sugar.
The most common type of solution is an aqueous solution, which is a solution where water is the solvent. Aqueous solutions are quite important. For example, acids and bases exist typically as aqueous solutions. |
When two liquids can be readily combined in any proportions, they are said to be miscible. An example would be alcohol and water. Either of the two can totally dissolve each other in any proportion. Two liquids are defined as immiscible if they will not form a solution, such as oil and water. Solid solutes in a metallic solvent are known as alloys. Gold is an example of an alloy. It is too soft in its pure form, so other metals are dissolved in it. Jewelers may use 14-karat gold, which contains two-thirds gold and one-third other metals.
Variables Affecting Solubility
| Factor | Concept | Example |
|---|---|---|
| Surface area | More surface area gives more opportunity for solute-solvent contact | Powdered sugar will dissolve in water faster than rock candy. |
| Temperature | Solids are more soluble in hot solvents, gases are more soluble in cold solvents | Sugar dissolves more readily in hot water, but CO2 dissolves better in cold soda than warm soda. |
| Polarity | Non-polar compounds dissolve in non-polar solvents, and polar compounds dissolve in polar solvents. If one liquid is polar, and the other isn't, they are immiscible. | Alcohol and water are both polar, and they are miscible. Oil is non-polar and is immiscible in water. |
| Pressure | Gases dissolve better under higher pressure, due to greater forces pushing the gas molecules into the solvent. | Leaving the cap off a soda bottle will let the carbonation out. |
| Agitation | If a solution is agitated by stirring or shaking, there is an increase in kinetic motion and contact of particles. Therefore, the rate of solubility increases. | Everyone knows to stir their coffee after adding sugar. |
In general, the rate of solubility is dependent on the intermolecular forces between substances. The maxim "like dissolves like" will help you remember that substances must both be polar or non-polar to dissolve. |
Dissolving at the Molecular Level

- The forces between the particles in the solid must be broken. This is an endothermic process called dissociation.
- Some of the intermolecular forces between the particles in the liquid must also be broken. This is endothermic.
- The particles of the solid and the particles in a liquid become attracted. This is an exothermic process called solvation.
Example: Dissolving NaCl
When sodium chloride is added to water, it will dissolve. Water molecules are polar, and sodium chloride is ionic (which is very polar). The positive ends of the water molecules (the hydrogens) will be attracted to the negative chloride ions, and the negative ends of the water molecules (the oxygens) will be attracted to the positive sodium ions. The attractions are strong enough to separate sodium from chloride, so the solute dissociates, or breaks apart. The solute is then spread throughout the solvent. The polar water molecules prevent the ions from reattaching to each other, so the salt stays in solution.
Important Concepts
Saturation
- When a solution can hold no more solute, it is said to be saturated. This occurs when there is an equilibrium between the dissolved and undissolved solute.
- If more solute can be added, the solution is unsaturated.
- If a solution has more solute than is normally possible, due to the lowering or heightening of temperature, it is said to be supersaturated. If disturbed, the solution will rapidly form solid crystals.
- Solubility is the measure of how many grams of solute can dissolve in 100 grams of solvent (or in the case of water, solute per 100 milliliters.)
Hydration
Sometimes, compounds form crystals with a specific amount of water in them. For example, copper(II) sulfate is written as CuSO4 • 5H2O. For every mole of copper(II) sulfate, there are five moles of water attached. The atoms are arranged in a crystal lattice. Even if dried, the compound will still be hydrated. It will not feel moist, but there are water molecules within the crystal structure of the solid.
Intense heat will release the water from the compound. Its color may change, indicating a chemical change. When the anhydrous compound is dissolved in water, it will become hydrated again.
Heats of Solution
Some chemicals change temperature when dissolved. This is due to a release or absorption of heat. The specific change is known as the heat of solution, measured in kJ/mol.
Electrolytes
Some substances break up into ions and conduct electricity when dissolved. These are called electrolytes. All ionic compounds are electrolytes. Nonelectrolytes, on the other hand, do not conduct electricity when dissolved. Electrolytes are the reason that tap water conducts electricity. Tap water contains salts and other ions. If you have purified water, you will find that it does not conduct electricity at all. Upon dissolving some salt, it conducts electricity very well. The presence of ions allows electrons to move through the solution, and electricity will be conducted.
Solubility Practice Questions
1. In a mixture of 50 mL of benzene and 48 mL of octane,
- a) which substance is the solute?
- b) would these two substances form a solution?
2. Solutions are formed as physical reactions. Using this principle, name two ways in which solutes can be separated from solvents.
3. Three different clear, colourless liquids were gently heated in an evaporating dish. Liquid A left a white residue, liquid B left no residue, and liquid C left water. Identify each liquid solution as a pure substance or a solution.
4. Compare three bottles of soda. Bottle A was stored at room temperature (25°C), bottle B was stored at 10°C, and bottle C was stored at 30°C.
- a) If you wanted a fizzy drink, which bottle would you choose?
- b) If you wanted to change the gas pressure of bottle C to that of bottle B, what could you do?
Answers to Solubility Practice Questions
Properties of Solutions
Concentration
The concentration of a solution is the measure of how much solute and solvent there is. A solution is concentrated if it contains a large amount of solute, or dilute if contains a small amount.
Molarity
Molarity is the number of moles of solute per liter of solution. It is abbreviated with the symbol M, and is sometimes used as a unit of measurement, e.g. a 0.3 molar solution of HCl. In that example, there would be 0.3 moles of HCl for every liter of water (or whatever the solvent was).
Molarity is by far the most commonly used measurement of concentration. |
Molality
Molality is the number of moles of solute per kilogram of solvent. It is abbreviated with the symbol m (lowercase), and is sometimes used as a unit of measurement, e.g. a 0.3 molal solution of HBr. In that example, there would be 0.3 moles of HBr for every kilogram of water (or whatever the solvent was).
| One kilogram of water is one liter of water (near room temperature), but the molality is not the same as the molarity. The molarity is the ratio of solute to solution, whereas the molality is the ratio of solute to solvent. |
Mole Fraction
The mole fraction is simply the moles of solute per moles of solution. As an example, you dissolve one mole of NaCl into three moles of water. Remember that the NaCl will dissociate into its ions, so there are now five moles of particles: one mole Na+, one mole Cl-, and three moles water. The mole fraction of sodium is 0.2, the mole fraction of chloride is 0.2, and the mole fraction of water is 0.6.
The mole fraction is symbolized with the Greek letter (chi), which is often written simply as an X.
The sum of all mole fractions for a solution must equal 1. |
Dilution
Dilution is adding solvent to a solution to obtain a less concentrated solution. Perhaps you have used dilution when running a lemonade stand. To cut costs, you could take a half-full jug of rich, concentrated lemonade and fill it up with water. The resulting solution would have the same total amount of sugar and lemon juice, but double the total volume. Its flavor would be weaker due to the added water.
The key concept is that the amount of solute is constant before and after the dilution process. The concentration is decreased (and volume increased) only by adding solvent.
| Thus, the number of moles of solute before and after dilution are equal. | |
| By definition of molarity, you can find the moles of solvent. | |
| Substituting the second equation into the first gives the dilution equation. |
To determine the amount of solvent (usually water) that must be added, you must know the initial volume and concentration, and the desired concentration. Solving for in the above equation will give you the total volume of the diluted solution. Subtracting the initial volume from the total volume will determine the amount of pure solvent that must be added.
Ionic Solutes
When ionic compounds dissolve in water, they separate into ions. This process is called dissociation. Note that because of dissociation, there are more moles of particles in the solution containing ions than there would be with the solute and solvent separated.
If you have two glasses of water, and you dissolve salt into one and sugar into the other, there will be a big difference in concentration. The salt will dissociate into its ions, but sugar (a molecule) will not dissociate. If the salt were NaCl, the concentration would be double that of the sugar. If the salt were MgCl2, the concentration would be triple (there are three ions).
Solubility Rules
Not all ionic compounds are soluble. Some ionic compounds have so much attractive force between their anions and cations that they will not dissociate. These substances are insoluble and will not dissolve. Instead, they clump together as a solid in the bottom of solution. Many ionic compounds, however, will dissociate in water and dissolve. In these cases, the attractive force between ion and water is greater than that between cation and anion. There are several rules to help you determine which compounds will dissolve and which will not.
- Solubility Rules
- All compounds with Group 1 ions or ammonium ions are soluble.
- Nitrates, acetates, and chlorates are soluble.
- Compounds containing a halogen are soluble, except those with fluorine, silver, or mercury. If they have lead, they are soluble only in hot water.
- Sulfates are soluble, except when combined with silver, lead, calcium, barium, or strontium.
- Carbonates, sulfides, oxides, silicates, and phosphates are insoluble, except for rule #1.
- Hydroxides are insoluble except when combined with calcium, barium, strontium, or rule #1.
Sometimes, when two different ionic compounds are dissolved, they react, forming a precipitate that is insoluble. Predicting these reactions requires knowledge of the activity series and solubility rules. These reactions can be written with all ions, or without the spectator ions (the ion that don't react, present on both sides of the reaction), a format known as the net ionic equation.
For example, silver nitrate is soluble, but silver chloride is not soluble (see the above rules). Mixing silver nitrate into sodium chloride would cause a cloudy white precipitate to form. This happens because of a double replacement reaction.
Electrolytes
When solutes dissociate (or if a molecule ionizes), the solution can conduct electricity. Compounds that readily form ions, thus being good conductors, are known as strong electrolytes. If only a small amount of ions are formed, electricity is poorly conducted, meaning the compound is a weak electrolyte.
A strong electrolyte will dissolve completely. All ions dissociate. A weak electrolyte, on the other hand, will partially dissociate, but some ions will remain bonded together. |
Colligative Properties
Some properties are the same for all solute particles regardless of what kind. These are known as the colligative properties. These properties apply to ideal solutions, so in reality, the properties may not be exactly as calculated. In an ideal solution, there are no forces acting between the solute particles, which is generally not the case.
Vapor Pressure
All liquids have a tendency for their surface molecules to escape and evaporate, even if the liquid is not at its boiling point. This is because the average energy of the molecules is too small for evaporation, but some molecules could gain above average energy and escape. Vapor pressure is the measure of the pressure of the evaporated vapor, and it depends on the temperature of the solution and the quantities of solute. More solute will decrease vapor pressure.
| The vapor pressure is given by Rauolt's Law, where is the mole fraction of the solvent. Notice that the vapor pressure equals that of the pure solvent when there is no solute (). If , there would be no vapor pressure at all. This could only happen if there were no solvent, only solute. A solid solute has no vapor pressure. | |
| If two volatile substances (both have vapor pressures) are in solution, Rauolt's Law is still used. In this case, Rauolt's Law is essentially a linear combination of the vapor pressures of the substances. Two liquids in solution both have vapor pressures, so this equation must be used. |
The second equation shows the relationship between the solvents. If two liquids were mixed exactly half-and-half, the vapor pressure of the resulting solution would be exactly halfway between the vapor pressures of the two solvents.
Another relation is Henry's Law, which shows the relationship between gas and pressure. It is given by Cg = k Pg , where C is concentration and P is pressure. As the pressure goes up, the concentration of gas in solution must also increase. This is why soda cans release gas when they are opened - The decrease in pressure results in a decrease in concentration of CO2 in the soda.
- Exercise for the reader
At 50 °C the vapor pressure of water is 11 kPa and the vapor pressure of ethanol is 30 kPa. Determine the resulting vapor pressure if a solution contains 75% water and 25% ethanol (by moles, not mass).
Boiling Point Elevation
A liquid reaches its boiling point when its vapor pressure is equal to the atmosphere around it. Because the presence of solute lowers the vapor pressure, the boiling point is raised. The boiling point increase is given by:
The reduced vapor pressure increases the boiling point of the liquid only if the solute itself is non-volatile, meaning it doesn't have a tendency to evaporate. For every mole of non-volatile solute per kilogram of solvent, the boiling point increases by a constant amount, known as the molal boiling-point constant (). Because this is a colligative property, is not affected by the kind of solute.
Freezing Point Depression
A liquid reaches its freezing temperature when its vapor pressure is equal to that of its solid form. Because the presence of the solute lowers the vapor pressure, the freezing point is lowered. The freezing point depression is given by:
Again, this equation works only for non-volatile solutes. The temperature of the freezing point decreases by a constant amount for every one mole of solute added per kilogram solvent. This constant () is known as the molar freezing-point constant.
Osmosis

If you studied biology, you would know that osmosis is the movement of water through a membrane. If two solutions of different molarity are placed on opposite sides of a semipermeable membrane, then water will travel through the membrane to the side with higher molarity. This happens because the water molecules are "attached" to the solvent molecules, so they cannot travel through the membrane. As a result, the water on the side with lower molarity can more easily travel through the membrane than the water on the other side.
The pressure of this osmosis is given in the equation
Where pi is the pressure, M is molarity, R is the gas constant, and T is temperature in Kelvin.
Electrolytes and Colligative Properties
When one mole of table salt is added to water, the colligative effects are double those that would have occurred if sugar were added instead. This is because the salt dissociates, forming twice as many particles as sugar would. This dissociation, called the Van't Hoff Factor describes how many particles that are dissociated into the solution and must be multiplied into the Boiling Point Elevation or Vapor Pressure Lowering equations.
| Sugar is a covalent molecule. No dissociation occurs when dissolved. | |
| Table salt is an ionic compound and a strong electrolyte. Total dissociation occurs when dissolved, doubling the effects of colligative properties. | |
| Magnesium bromide is also ionic. The colligative effects will be tripled. |
Though extremely useful for calculating the general Van't Hoff Factor, this system of calculation is slightly inaccurate when considering ions. This is because when ions are in solution, they may interact and clump together, lessening the effect of the Van't Hoff factor. In addition, more strongly charged ions may have a smaller effect. For example, CaO would be less effective as an electrolyte than NaCl.
Acids and Bases
Acid-Base Reaction Theories
Acids and bases are everywhere. Some foods contain acid, like the citric acid in lemons and the lactic acid in dairy. Cleaning products like bleach and ammonia are bases. Chemicals that are acidic or basic are an important part of chemistry.
| Helpful Hint! | |
|---|---|
| You may need to refresh your memory on naming acids. |
Several different theories explain what composes an acid and a base. The first scientific definition of an acid was proposed by the French chemist Antoine Lavoisier in the eighteenth century. He proposed that acids contained oxygen, although he did not know the dual composition of acids such as hydrochloric acid (HCl). Over the years, much more accurate definitions of acids and bases have been created.
Arrhenius Theory
The Swedish chemist Svante Arrhenius published his theory of acids and bases in 1887. It can be simply explained by these two points:
- Arrhenius Acids and Bases
- An acid is a substance which dissociates in solvent to produce one or more hydrogen ions (H+).
- A base is a substance which dissociates in solvent to produce one or more hydroxide ions (OH-).
Based on this definition, you can see that Arrhenius acids must be soluble in water. Arrhenius acid-base reactions can be summarized with three generic equations:
| An acid will dissociate in water producing hydrogen ions. | |
| A base (usually containing a metal) will dissociate in water to produce hydroxide ions. | |
| Acids and bases will neutralize each other when mixed. They produce water and an ionic salt, neither of which are acidic or basic. |
The Arrhenius theory is simple and useful. It explains many properties and reactions of acids and bases. For instance, mixing hydrochloric acid (HCl) with sodium hydroxide (NaOH) results in a neutral solution containing table salt (NaCl).
However, the Arrhenius theory is not without flaws. There are many well known bases, such as ammonia (NH3) that do not contain the hydroxide ion. Furthermore, acid-base reactions are observed in solutions that do not contain water. To resolve these problems, there is a more advanced acid-base theory.
Brønsted-Lowry Theory
The Brønsted-Lowry theory was proposed in 1923. It is more general than the Arrhenius theory—all Arrhenius acids/bases are also Brønsted-Lowry acids/bases (but not necessarily vice versa).
- Brønsted-Lowry Acids and Bases
- An acid is a substance from which a proton (H+ ion) can be removed. Essentially, an acid donates protons to bases.
- A base is a substance to which a proton (H+) can be added. Essentially, a base accepts protons from acids.
Acids that can donate only one proton are monoprotic, and acids that can donate more than one proton are polyprotic.
These reactions demonstrate the behavior of Brønsted-Lowry acids and bases:
| An acid (in this case, hydrochloric acid) will donate a proton to a base (in this case, water is the base). The acid loses its proton and the base gains it. | |
| Water is not necessary. In this case, hydrochloric acid is still the acid, but ammonia acts as the base. | |
| The same reaction is happening, but now in reverse. What was once an acid is now a base (HCl → Cl-) and what was once a base is now an acid (NH3 → NH4+). This concept is called conjugates, and it will be explained in more detail later. | |
|
Two examples of acids (HCl and H3O+) mixing with bases (NaOH and OH-) to form neutral substances (NaCl and H2O). |
| A base (sodium hydroxide) will accept a proton from an acid (ammonia). A neutral substance is produced (water), which is not necessarily a part of every reaction. Compare this reaction to the second one. Ammonia was a base, and now it is an acid. This concept, called amphoterism, is explained later. |
The Brønsted-Lowry theory is by far the most useful and commonly-used definition. For the remainder of General Chemistry, you can assume that any acids/bases use the Brønsted-Lowry definition, unless stated otherwise.

Lewis Theory
The Lewis definition is the most general theory, having no requirements for solubility or protons.
- Lewis Acids and Bases
- An acid is a substance that accepts a lone pair of electrons.
- A base is a substance that donates a lone pair electrons.
Lewis acids and bases react to create an adduct, a compound in which the acid and base have bonded by sharing the electron pair. Lewis acid/base reactions are different from redox reactions because there is no change in oxidation state.

Amphoterism and Water
Substances capable of acting as either an acid or a base are amphoteric. Water is the most important amphoteric substance. It can ionize into hydroxide (OH-, a base) or hydronium (H3O+, an acid). By doing so, water is
- Increasing the H+ or OH- concentration (Arrhenius),
- Donating or accepting a proton (Brønsted-Lowry), and
- Accepting or donating an electron pair (Lewis).
A bare proton (H+ ion) cannot exist in water. It will form a hydrogen bond to the nearest water molecule, creating the hydronium ion (H3O+). Although many equations and definitions may refer to the "concentration of H+ ions", that is a misleading abbreviation. Technically, there are no H+ ions, only hydronium (H3O+) ions. Fortunately, the number of hydronium ions formed is exactly equal to the number of hydrogen ions, so the two can be used interchangeably. |

Water will dissociate very slightly (which further explains its amphoteric properties).
| The presence of hydrogen ions indicates an acid, whereas the presence of hydroxide ions indicates a base. Being neutral, water dissociates into both equally. | |
| This equation is more accurate—hydrogen ions do not exist in water because they bond to form hydronium. |
Ammonia
Another common example of an amphoteric substance is ammonia. Ammonia is normally a base, but in some reactions it can act like an acid.
| Ammonia acts as a base. It accepts a proton to form ammonium. | |
| Ammonia also acts as an acid. Here, it donates a proton to form amide. |
Ammonia's amphoteric properties are not often seen because ammonia typically acts like a base. Water, on the other hand, is completely neutral, so its acid and base behaviors are both observed commonly.
Conjugate Acids and Bases
In all the theories, the products of an acid-base reaction are related to the initial reactants of the reaction. For example, in the Brønsted-Lowry theory, this relationship is the difference of a proton between a reactant and product. Two substances which exhibit this relationship form a conjugate acid-base pair.
- Brønsted-Lowry Conjugate Pairs
- An acid that has donated its proton becomes a conjugate base.
- A base that has accepted a proton becomes a conjugate acid.
| Hydroiodic acid reacts with water (which serves as a base). The conjugate base is the iodide ion and the conjugate acid is the hydronium ion. The acids are written in red, and the bases are written in blue. One conjugate pair is written bold and the other conjugate pair is in cursive. | |
| Ammonia (basic) reacts with water (the acid). The conjugate acid is ammonium and the conjugate base is hydroxide. Again, acids are written in red, and the bases are written in blue. The conjugate pairs are distinguished with matching fonts. |
Strong and Weak Acids/Bases
A strong acid is an acid which dissociates completely in water. That is, all the acid molecules break up into ions and solvate (attach) to water molecules. Therefore, the concentration of hydronium ions in a strong acid solution is equal to the concentration of the acid.
The majority of acids exist as weak acids, an acid which dissociates only partially. On average, only about 1% of a weak acid solution dissociates in water in a 0.1 mol/L solution. Therefore, the concentration of hydronium ions in a weak acid solution is always less than the concentration of the dissolved acid.
Strong bases and weak bases do not require additional explanation; the concept is the same.
The conjugate of a strong acid/base is very weak. The conjugate of a weak acid/base is not necessarily strong. |
This explains why, in all of the above example reactions, the reverse chemical reaction does not occur. The stronger acid/base will prevail, and the weaker one will not contribute to the overall acidity/basicity. For example, hydrochloric acid is strong, and upon dissociation chloride ions are formed. Chloride ions are a weak base, but the solution is not basic because the acidity of HCl is overwhelmingly stronger than basicity of Cl-.
| Helpful Hint! | |
|---|---|
| Although the other halogens make strong acids, hydrofluoric acid (HF) is a weak acid. Despite being weak, it is incredibly corrosive—hydrofluoric acid dissolves glass and metal! |
Most acids and bases are weak. You should be familiar with the most common strong acids and assume that any other acids are weak.
| Formula | Strong Acid |
|---|---|
| HClO4 | Perchloric acid |
| HNO3 | Nitric acid |
| H2SO4 | Sulfuric acid |
| HCl, HBr, HI | Hydrohalic acids |
Within a series of oxyacids, the ions with the greatest number of oxygen molecules are the strongest. For example, nitric acid (HNO3) is strong, but nitrous acid (HNO2) is weak. Perchloric acid (HClO4) is stronger than chloric acid (HClO3), which is stronger than the weak chlorous acid (HClO2). Hypochlorous acid (HClO) is the weakest of the four.
Common strong bases are the hydroxides of Group 1 and most Group 2 metals. For example, potassium hydroxide and calcium hydroxide are some of the strongest bases. You can assume that any other bases (including ammonia and ammonium hydroxide) are weak.
| Formula | Strong Base |
|---|---|
| LiOH | Lithium hydroxide |
| NaOH | Sodium hydroxide |
| KOH | Potassium hydroxide |
| RbOH | Rubidium hydroxide |
| CsOH | Cesium hydroxide |
| Ca(OH)2 | Calcium hydroxide |
| Sr(OH)2 | Strontium hydroxide |
| Ba(OH)2 | Barium hydroxide |
| Acids and bases that are strong are not necessarily concentrated, and weak acids/bases are not necessarily dilute. Concentration has nothing to do with the ability of a substance to dissociate. Furthermore, polyprotic acids are not necessarily stronger than monoprotic acids. |
Properties of Acids and Bases
Now that you are aware of the acid-base theories, you can learn about the physical and chemical properties of acids and bases. Acids and bases have very different properties, allowing them to be distinguished by observation.
Indicators

Made with special chemical compounds that react slightly with an acid or base, indicators will change color in the presence of an acid or base. A common indicator is litmus paper. Litmus paper turns red in acidic conditions and blue in basic conditions. Phenolphthalein purple is colorless in acidic and neutral solutions, but it turns purple once the solution becomes basic. It is useful when attempting to neutralize an acidic solution; once the indicator turns purple, enough base has been added.
Conductivity
A less informative method is to test for conductivity. Acids and bases in aqueous solutions will conduct electricity because they contain dissolved ions. Therefore, acids and bases are electrolytes. Strong acids and bases will be strong electrolytes. Weak acids and bases will be weak electrolytes. This affects the amount of conductivity.
However, acids will react with metal, so testing conductivity may not be plausible.
Physical properties
The following is for informative purposes only. Do not sniff, touch, or taste any acids or bases as they may result in injury or death. |
The physical properties of acids and bases are opposites.
| Acids | Bases | |
|---|---|---|
| Taste | sour | bitter |
| Feel | stinging | slippery |
| Odor | sharp | odorless |
These properties are very general; they may not be true for every single acid or base.
Another warning: if an acid or base is spilled, it must be cleaned up immediately and properly (according to the procedures of the lab you are working in). If, for example, sodium hydroxide is spilled, the water will begin to evaporate. Sodium hydroxide does not evaporate, so the concentration of the base steadily increases until it becomes damaging to its surrounding surfaces.
Chemical Reactions
Neutralization
Acids will react with bases to form a salt and water. This is a neutralization reaction. The products of a neutralization reaction are much less acidic or basic than the reactants were. For example, sodium hydroxide (a base) is added to hydrochloric acid.
This is a double replacement reaction.
Acids
| Acids react with metal to produce a metal salt and hydrogen gas bubbles. | |
| Acids react with metal carbonates to produce water, CO2 gas bubbles, and a salt. | |
| Acids react with metal oxides to produce water and a salt. |
Bases
Bases are typically less reactive and violent than acids. They do still undergo many chemical reactions, especially with organic compounds. A common reaction is saponification: the reaction of a base with fat or oil to create soap.

Practice Questions
1. Name the following compounds that will form, and identify as an acid or base:
- a) Br + H
- b) 2H + SO3
- c) K + H
- d) 2H + SO6
- e) 3H + P2
- f) H + BrO2
- g) Na + Cl
2. What are the conjugate acids and bases of the following:
- a) water
- b) ammonia
- c) bisulfate ion
- d) zinc hydroxide
- e) hydrobromic acid
- f) nitrite ion
- g) dihydrogen phosphate ion
3. In a conductivity test, 5 different solutions were set up with light bulbs. The following observations were recorded:
- Solution A glowed brightly.
- Solution B glowed dimly.
- Solution C glowed dimly.
- Solution D did not glow.
- Solution E glowed brightly.
- a) Which solution(s) could contain strong bases?
- b) Which solution(s) could contain weak acids?
- c) Which solution(s) could contain ions?
- d) Which solution(s) could contain pure water?
- e) Based solely on these observations, would it be possible to distinguish between acidic and basic solutions?
4. Identity the conjugate base and conjugate acid in these following equations:
- a) HCl + H2O → H3O+ + Cl-
- b) HClO + H2O → ClO- + H3O+
- c) CH3CH2NH2 + H2O → CH3CH2NH3+ + OH-
5. Identify these bases as Arrhenius, Brønsted-Lowry, or both.
- a) strontium hydroxide
- b) butyllithium (C4H9Li)
- c) ammonia
- d) potassium hydroxide
- e) potassium iodide
6. Based on the Brønsted-Lowry Theory of Acids and Bases, would you expect pure water to have no dissolved ions whatsoever? Explain, using a balanced chemical equation.
Answers:
1.
2.
3.
4.
5.
6.
Notes
- ^ Brown, Theodore E.; Lemay, H. Eugene; Bursten, Bruce E.; Murphy, Catherine; Woodward, Patrick (2009), Chemistry: The Central Science (11th ed.), New York: Prentice-Hall, ISBN 0136006175.
Answers to Properties of Acids and Bases Practice Questions
Titration and pH
Ionization of Water
Water is a very weak electrolyte. It will dissociate into hydroxide and hydronium ions, although only in a very small amount. Because pure water is completely neutral, it always dissociates in equal amounts of both hydroxide and hydronium. Once acidic or basic substances have been added to pure water, the concentration of the ions will change. Regardless of which acid-base theory is used, acids and bases all have one important thing in common:
- All acids increase the H+ concentration of water.
- All bases increase the OH- concentration of water.
Furthermore, the concentration of hydrogen ions multiplied by the concentration of hydroxide ions is a constant. This constant is known as the ionization constant of water, or Kw. At room temperature it equals 10-14 mol2/L2. Thus:
In a neutral solution, the concentrations of H+ and OH- are both equal to 10-7. Using the above equation, the concentration of one ion can be determined if the concentration of the other ion is known. This equation further demonstrates the relationship between acids and bases: as the acidity (H+) increases, the basicity (OH-) must decrease.
The pH Scale
To measure the acidity or basicity of a substance, the pH scale is employed.
- The pH Scale
- A completely neutral substance has a pH of 7.
- Acids have a pH below 7
- Bases have a pH above 7.
pH usually ranges between 0 and 14, but it can be any value. Battery acid, for example, has a negative pH because it is so acidic.

Definition of pH
The pH scale is mathematically defined as:
Substances that release protons or increase the concentration of hydrogen ions (or hydronium ions) will lower the pH value.
pOH
There is also a less common scale, the pOH scale. It is defined as:
Substances that absorb protons or increase the concentration of hydroxide ions will lower the pOH value.
The sum of pH and pOH is always 14 at room temperature:
Calculating pH
A strong acid or strong base will completely dissociate in water, so the concentration of the acid/base is equal to the concentration of H+ or OH-. If you know the concentration of the acid or base, then you can simply plug that number into the pH or pOH formula. The sum of pH and pOH will always equal 14 at room temperature, so you can interconvert these two values.
If you know the H+ concentration and need to know the OH- concentration (or vice versa), use the definition of Kw above. The product of the two ion concentrations will always equal 10-14 at room temperature.
Titration
Titration is the controlled mixing of a solution with known concentration (the standard solution or titrant) to another solution (called the analyte) to determine its concentration. One solution is acidic and the other is basic. An indicator is added to the mixture. An indicator must be selected so that it changes color when equal amounts of acid and base have been added. This is known as the equivalence point. This does not necessarily mean that the pH is 7.0.
Once the equivalence point has been reached, the unknown concentration can be determined mathematically.
Practice Questions
1) 5.00g of NaOH are dissolved to make 1.00L of solution.
- a What is the concentration of H+?
- b What is the pH?
Buffer Systems
Introduction
Buffer systems are systems in which there is a significant (and nearly equivalent) amount of a weak acid and its conjugate base—or a weak base and its conjugate acid—present in solution. This coupling provides a resistance to change in the solution's pH. When strong acid is added, it is neutralized by the conjugate base. When strong base is added, it is neutralized by the weak acid. However, too much acid or base will exceed the buffer's capacity, resulting in significant pH changes.
| Consider an arbitrary weak acid, HA, and its conjugate base, A-, in equilibrium. | |
| The addition of a strong acid will cause only a slight change in pH due to neutralization. | |
| Likewise, the addition of a strong base will cause only a slight change in pH. |
Buffers are useful when a solution must maintain a specific pH. For example, blood is a buffer system because the life processes in a human only function within a specific pH range of 7.35 to 7.45. When, for example, lactic acid is released by the muscles during exercise, buffers within the blood neutralize it to maintain a healthy pH.
Making a Buffer
Once again, let's consider an arbitrary weak acid, HA, which is present in a solution. If we introduce a salt of the acid's conjugate base, say NaA (which will provide the A- ion), we now have a buffer solution. Ideally, the buffer would contain equal amounts of the weak acid and conjugate base.
Instead of adding NaA, what if a strong base were added, such as NaOH? In that case, the hydroxide ions would neutralize the weak acid and create water and A- ions. If the solution contained only A- ions, then a strong acid like HCl were added, they would neutralize and create HA.
As you can see, there are three ways to create a buffer:
|
|
All six of the combinations will create equal amounts of a weak acid and its conjugate base, or a weak base and its conjugate acid.
Buffers and pH
To determine the pH of a buffer system, you must know the acid's dissociation constant. This value, (or for a base) determines the strength of an acid (or base). It is explored more thoroughly in the Equilibrium unit, but for now it suffices to say that this value is simply a measure of strength for acids and bases. The dissociation constants for acids and bases are determined experimentally.
The pKa of an acid is the negative logarithm of its acid dissociation constant. This is analogous to pH (the negative logarithm of the H+ concentration). |
The Henderson-Hasselbalch equation allows the calculation of a buffer's pH. It is:
For a buffer created from a base, the equation is:
Using these equations requires determining the ratio of base to acid in the solution.
Reactions of Acids and Bases
Overview
To summarize the properties and behaviors of acids and bases, this chapter lists and explains the various chemical reactions that they undergo. You may wish to review chemical equations and types of reactions before attempting this chapter.
The following reactions are net ionic equations. In other words, spectator ions are not written. If an ion does not partake in the reaction, it is simply excluded. The spectator ions can be found because they occur on both the reactant and the product side of the equation. Cross them out and rewrite the equation without them. Of course, the coefficients must be equal.
Canceling out the spectator ions explains the net of net ionic equations. The ionic part means that dissolved compounds are written as ions instead of compounds. Acids, bases, and salts are all ionic, so they are written as separate ions if they have dissociated.
- Net Ionic Equations
- Soluble salts are written as ions.
- e.g.: Na+ + Cl-
- Solids, liquids, and gases are written as compounds.
- e.g.: NaCl(s), H2O(l), HCl(g)
- Strong acids and strong bases are written as ions (because they dissociate almost completely).
- e.g.: H+ + NO3-
- Weak acids and weak bases are written as compounds (because they barely dissociate).
- e.g.: HNO2
As an example, sodium bicarbonate (NaHCO3) would be written as Na+ and HCO3- because the salt will dissociate, but the bicarbonate will not dissociate (it's a weak acid).
Neutralization
When an acid and a base react, they form a neutral substance, often water and a salt.
First, let's examine the neutralization of a strong acid with a strong base.
| Solid potassium hydroxide is added to an aqueous solution of hydrochloric acid. Notice how the solid is written as a compound, but the acid is written as ions because it dissociates. | |
| The hydrogen ions will react with hydroxide ions to form water. | |
| Ignoring spectator ions, this is the net ionic equation. |
Whenever a strong acid neutralizes a strong base, the net ionic equation is always H+ + OH- → H2O. |
Now, let's see some examples involving weak acids and weak bases.
| Excess hydrochloric acid is added to a solution of sodium phosphate. Phosphoric acid is weak, so the phosphate ions will react with hydrogen ions. The result is a solution with some, but much less, hydrogen ions, so it is much closer to neutral than either of the original reactants. | |
| Equimolar amounts of sodium phosphate and hydrochloric acid are mixed. Notice the difference between this reaction and the previous one. | |
| A strong base is added to a solution of calcium bicarbonate. (Bicarbonate is a weak acid.) | |
| A strong acid is added to a solution of calcium bicarbonate. Gas bubbles appear. |
Many reactions result in the formation of gas bubbles or a solid precipitate that will make the solution cloudy. The last equation brings up an interesting application. Many rocks and minerals contain calcium carbonate or calcium bicarbonate. To identify these rocks, geologists can perform the "acid test". A drop of acid is applied, and the presence of gas bubbles indicates carbonate.
Many ions and compounds are amphoteric. They can react with (or behave as) acids and bases. Bicarbonate is a good example, as you can see by comparing the last two equations above. |
Here are more examples of neutralization reactions.
| Solid ammonium chloride crystals are dissolved into a solution of sodium hydroxide. The smell of ammonia is detected. | |
| Ammonia gas is bubbled through a solution of hydrochloric acid. This reaction is essentially the opposite of the previous. In that reaction, ammonium ions react with base to form ammonia gas. In this reaction, ammonia gas reacts with acid to form ammonium ions. | |
| Ammonia (a weak base) reacts with acetic acid (also weak). The resulting solution is nearly neutral, but it will be slightly basic because ammonia is stronger than acetic acid. | |
| Hydrogen sulfide gas is bubbled into a strong base. | |
| A strong acid is added to the above result, and hydrogen sulfide gas is released. |
Anhydrides
An anhydride is a substance that does not contain water. More specifically, it is a substance that reacts with water to form an acid or base. Anhydrides are usually in the form of a gas that dissolves into water and reacts to form an acid or base. They can also be solids that will react with water.
| Gaseous dinitrogen pentoxide is bubbled through water to form nitric acid. | |
| Dinitrogen trioxide is mixed with water to form nitrous acid. |
The main difference between those two equations is the fact that nitrous acid is weak and thus does not dissociate, whereas nitric acid is strong and dissociates into ions.
Here are a few more examples of anhydride reactions.
| Solid potassium oxide is added to water to form a strong base. | |
| Phosphorus(V) oxide powder is mixed into water to form a weak acid. |
It is important to remember which acids are strong and which are weak. Review this if necessary.
Anhydrides can also react with acidic or basic solutions. In that case, you may find it helpful to first determine the anhydride's reaction with water, then determine that reaction with the acid or base. |
For example, sulfur dioxide gas (acidic anhydride) is bubbled through a solution of calcium hydroxide (basic).
| First, determine the reaction of the anhydride with water. | |
| Then, determine the reaction of the acid and base. This is a double replacement reaction. | |
| Add the two reactions together. | |
| Cancel out spectators. Also, calcium hydroxide should be ionized (but calcium sulfite is a solid precipitate). This is the final net ionic equation. |
Here are more examples.
| Calcium oxide crystals (basic anhydrides) are added to a strong acid. Notice that it does not matter what the acid is (nitric, sulfuric, etc.) because it is strong and this reaction only requires the hydrogen ions. In other words, the anions of the strong acid are spectators and are not written. | |
| Excess sulfur dioxide gas is bubbled into a dilute solution of strong base. The base is the limiting reactant. | |
| Sulfur dioxide gas is bubbled into an excess of basic solution. |
Remember that water is involved in these reactions, but it is not written if it occurs on both sides of the equation.
Anhydrides can undergo neutralization reactions, even without the presence of water. |
| Solid calcium oxide (basic anhydride) is exposed to dry ice gas (acidic anhydride). The resulting solid is a salt. | |
| Solid calcium oxide is exposed to a stream of sulfur trioxide gas. The resulting solid is a neutral salt. |
Hydrolysis
A salt of a weak acid and strong base dissociates and reacts in water to form OH-. A salt of a strong acid and weak base dissociates and reacts in water to form H+. This process is called hydrolysis.
In this first example, aluminum nitrate is dissolved in water.
| First, the salt dissociates in the water. It isn't necessary to write H2O in this reaction. | |
| Now, at least one of the ions will react with water. You know that nitric acid is strong, so the nitrate ion will not take an H+ ion from water. Instead, the aluminum ion will react with water, releasing a hydrogen ion. | |
| This is the net ionic equation. The resulting solution is acidic. |
The solution is acidic not because nitric acid is strong, but because aluminum is a weak base.
Here is an easier example.
| First, the salt dissociates. Again, the H2O need not be written. | |
| Sodium ions will not react with water. Even if they did, they would form NaOH, which is a strong base, so it would immediately dissociate. Instead, the NO2 reacts with water. Being the conjugate of a weak acid, the nitrite ions will accept a proton from water to form nitrous acid (weak) and hydroxide ions (basic). | |
| This is the net ionic equation for the hydrolysis of sodium nitrite. The resulting solution is basic. |
There is no hydrolysis reaction for neutral salts. Salts like NaCl and K2SO4 (and any other composed of the conjugates of both a strong acid and strong base) will not react with water. They create neutral solutions when dissolved. |
Lewis Acids/Bases
Lewis acids accept an electron pair. Lewis bases donate an electron pair. Together they react and bond to form an adduct.
Lewis acids/bases do not require the presence of water. However, H+ can be thought of as a Lewis acid because it accepts electron pairs. OH- can donate an electron pair, making it a Lewis base.
| Boron trifluoride (Lewis acid) is exposed to ammonia (a Lewis base, as shown by the electron pair over the N). The electron pair is shared between the nitrogen and boron, creating a bond. (The boron trifluoride is written backwards as F3B only to demonstrate the B-N bond. Its structure has not changed.) | |
| Diborane accepts the two electrons from H- and forms a Lewis adduct. |
Practice Problems
Write the net ionic equations for the following. Make note of any solid precipitates or gas bubbles that would form.
- Equimolar solutions of sodium biphosphate and potassium hydroxide are mixed.
- Equimolar solutions of sodium biphosphate and hydrochloric acid are mixed.
- Excess sulfur dioxide gas is bubbled into a dilute solution of sodium hydroxide. Acid is then added.
- Aluminum chloride is dissolved into water.
- Sodium fluoride is dissolved into water. Strong acid is then added.
- Solid calcium oxide is exposed to a stream of sulfur trioxide gas. If the resulting compound is dissolved, will the solution be acidic, basic, or neutral?
- Gaseous hydrogen chloride is bubbled into a solution of silver nitrate.
- Ammonium chloride crystals are dissolved in water. Sodium hydroxide is then added.
- Calcium hydroxide crystals are dissolved into a solution of sodium bicarbonate.
- Phosphine gas is sprayed onto pebbles of aluminum trichloride. (Hint: these are Lewis acids/bases.)
Phases of Matter
Solids
Characteristics of Solids
Shape and volume are both definite in solids. Although solids have a rigid shape, a large amount of force can cause deformation to the structure of a solid. There are three types of deformation:
- Brittle deformation causes bonds to break in an irregular way. Shredding paper and shattering glass are good examples.
- Elastic deformation is temporary. The molecules will return to their original positions as soon as the force is removed. Rubber bands and tires are elastic, as well as steel rods and wooden boards.
- Plastic deformation is permanent. Plastic deformation can be observed by bending a metal spoon.

Most materials are capable of all three types of deformation. Small amounts of stress cause elastic deformation, but large amounts will cause plastic deformation. In the event of repeated deformation or tremendous stress, brittle deformation occurs.
Solids are incompressible. Solids may break or deform under stress, but they tolerate little compression. For instance, a wooden plank will break if force is applied, but it will not compress like a sponge. The only reason sponges compress is because they contain air pockets and undergo elastic deformation. Otherwise, solids will not compress. At the molecular level, this happens because the intermolecular bonds do not change size without breaking.
Some solids, usually metals, have properties like ductility and malleability. A ductile material can be stretched into long, thin wires. A malleable substance can be hammered into very thin sheets. Gold and copper are some of the most malleable and ductile substances known. These properties occur as a result of the metallic bonding.
Solids at the Molecular Level
Solids occur when there is enough intermolecular bonding to hold the molecules of a substance into a relatively rigid structure. The molecules are close together, and their movement is restricted to vibration. Solids occur at the lowest temperatures and highest pressures. As the temperature of a solid increases, so does the kinetic energy of its molecules. At the melting point, the molecules have enough energy to overcome their bonds and melt into a liquid. Likewise, a liquid will freeze once its molecules are not moving fast enough to avoid strong intermolecular bonds.
Compounds that have ionic bonding or metallic bonding are most likely to be found in the solid phase due to their high melting points. Also, covalent network substances (like diamond or quartz) are solids because the atoms are secured with covalent bonds, requiring extreme amounts of energy to separate them.
Types of Solids
- Crystalline solids have a molecular structure with a specific geometric shape. The solid has a specific melting point at which all molecules begin to break free of their bonds. Substances like salt, diamond, and quartz are crystalline solids. These solids usually form by cooling a liquid slowly, so that the molecules have time to arrange themselves in a crystalline structure as their bonds form.
- Amorphous solids have a molecular structure with no specific shape. The solid melts over a range of temperatures because the amount of energy needed to break the bonds varies from molecule to molecule. Substances like coal and glass are amorphous. Amorphous solids usually form when a liquid is cooled quickly, so there is no time for the molecules to arrange themselves into a crystal.
Crystalline solids are typically harder and more rigid. Coal and diamond are both made from elemental carbon, but coal is amorphous and diamond is crystalline. Because of its crystal structure, diamond is one of the hardest substances known, whereas coal can be scratched away with a fingernail. The crystal structure also explains diamond's brilliant, transparent appearance. Coal is black and dull because the disorder of the atoms does not allow light to pass.
Ionic solids and metallic solids are always crystalline. Covalent network solids can be crystalline or amorphous. Van der Waals solids are always amorphous. |
Packing and Unit Cells

In crystalline solids, the atoms are arranged in a specific pattern. The smallest repeating part of this pattern is called the unit cell. The unit cell may have more atoms than the empirical formula of a substance because the geometric shape may require several atoms. In the case of sodium chloride, the empirical formula contains only two atoms, but the unit cell has 27 atoms.
The molecules of a solid are close packed. They arrange themselves in the densest shape possible. Usually, two different patterns occur.
- Face-centered cubic or FCC
- Hexagonal close-packed or HCP

FCC crystals have three alternating layers, described as ABCABCABC (every third layer is the same). The layers are arranged so that each unit cell is halfway between the two unit cells above or below it. HCP crystals have two alternating layers, described as ABABABAB (every other layer is the same).
-
FCC lattice
-
HCP lattice
Liquids
Liquids at a Molecular Level
Liquids have some intermolecular bonding, but it isn't as strong as bonding in a solid. As a result, the molecules are close together, but they are not tightly packed. Instead, they are free to slide past each other. Liquids occur at temperatures above the melting point of a substance, but below its boiling point. At the melting point, the molecules are moving slow enough to form rigid bonds and become a solid. At the boiling point, the molecules are moving so fast that they cannot form any bonds and become a gas.
Characteristics of Liquids

Liquids have definite volume, but indefinite shape. They are free to form droplets and puddles when they are not inside a container. When a liquid is inside a container, it will take its shape. Unlike gases, a liquid will not change its volume to spread out and completely fill a container. There is enough intermolecular bonding to give liquids a definite volume.
Liquids are fluid, able to flow and take any shape. This occurs due to the weak intermolecular bonding that allows the molecules to slide past each other freely. As a result of being fluid, liquids exhibit many interesting properties that solids do not, including capillary action and diffusion.
Liquids, like gases, undergo diffusion when mixed. This can be seen by adding food coloring to water. Different liquids, when added, will chaotically spread out and mix together. Diffusion will occur faster when the liquid is warmer because the increased kinetic energy allows the molecules to move faster and collide more frequently.
Liquids are usually considered incompressible. The molecules are already close together, so it is difficult to compress them any more. Under very high pressures, liquids will actually compress, but not very much.
Liquids, unlike gases, have a distinct surface—they need not take their container's shape. This allows the formation of droplets and puddles.
Special Properties
Cohesion and Adhesion

The molecules of a liquid are attracted to each other. This is called cohesion. Molecules like methane are non-polar, so they are held together only by van der Waals forces. These molecules will have minimal cohesion. In contrast, water molecules use hydrogen bonding, so they display strong cohesion. A cohesive liquid will form more spherical droplets and have much higher surface tension.
Adhesion is the attraction of a liquid molecule to its surroundings. Adhesive liquids will demonstrate capillary action. They are also more "wet". Mercury is very cohesive, but not adhesive. As a result, it doesn't leave behind residue as it rolls across a surface. Water, on the other hand, is much more adhesive. When water rolls across a surface, it wets that surface because some of the molecules adhere to it.
Surface Tension and Capillary Action
When water drops are on an impermeable (waterproof) surface, they tend to form beads. This is due to its surface tension. Liquid molecules pull at each other, and as a result they decrease their surface area. The molecules at the boundary of the liquid are pulled in, causing a droplet shape. When water is on a permeable surface, it spreads out, as can be seen with water on a paper towel. This capillary action explains how water in the ground reaches the top of trees that are hundreds of feet tall.
-
Adhesive liquids (like water but not mercury) will rise up a narrow tube.
-
Cohesive liquids have surface tension to hold themselves into droplets.
Pressure
Liquids will distribute pressure evenly. This concept, known as Pascal's Law, is crucial for equipment like hydraulic brakes. It is a result of their incompressibility.
| Helpful Hint! | |
|---|---|
| If there is no atmospheric pressure (a vacuum, like outer space), liquids cannot form. |
Liquids will evaporate. Although the average kinetic energy of the molecules is too low to overcome bonding and become a gas, individual molecules will occasionally have above-average energy and break free from the surface of the liquid. The molecule then escapes to the gas phase. At the same time, however, a gas molecule may hit the surface of the liquid and slow down enough to join the liquid. A glass of water left outside in the sun will eventually become empty. The sunlight adds energy to the molecules, allowing some to escape as a gas. Eventually, all molecules will escape. The tendency of a liquid to evaporate depends on its intermolecular forces. Volatile liquids tend to evaporate quickly have relatively weak intermolecular forces keeping the molecules together, making it easier for them to escape the liquid phase. Conversely, non-volatile liquids do not evaporate to any visible extent due to the presence very strong intermolecular forces.
The evaporation increases with temperature. It can be measured by vapor pressure, the amount of pressure exerted by the evaporated gas above the liquid's surface. Vapor pressure increases with temperature, and once it reaches the pressure of the surrounding atmosphere, the liquid will boil. Vapor pressure also depends on the intensity of intermolecular forces in the liquid.
Viscosity
Viscosity refers to the liquid's resistance to flow. For example, maple syrup has a relatively high viscosity when compared to water because maple syrup flows much slower than water, which flows relatively quickly and easily. The difference in viscosity between these two liquids is due to the attractive forces within the specific liquid. In order to flow, molecules must roll and move over each other. A solution with low attractive forces would allow the molecules to move in a more free and easy manner, decreasing the viscosity.
In most cases, the viscosity of a liquid decreases as the temperature of a liquid is increased. Increasing the temperature of a liquid causes the molecules to have a higher kinetic energy. This increase in kinetic energy breaks down the intermolecular forces present in the liquid. Since viscosity is dependent on these attractive forces, the viscosity will decrease when the kinetic energy is increased.
Gases
Characteristics of Gases
Gases have a number of special characteristics that differentiate them from other states of matter. Here is a list of characteristics of gases:
- Characteristics of Gases
- Gases have neither definite shape nor definite volume. They expand to the size of their container.
- Gases are fluid, and flow easily.
- Gases have low density, unless compressed. Being made of tiny particles in a large, open space, gases are very compressible.
- Gases diffuse (mix and spread out) and effuse (travel through small holes).
Standard Temperature and Pressure
Standard Temperature and Pressure, or STP, is 0 °C and 1 atmosphere of pressure. Expressed in other units, STP is 273 K and 760 torr. The Kelvin and torr are useful units of temperature and pressure respectively that we will discuss later in the following sections.
Avogadro's Law

Avogadro's Law states that equal volumes of gases at the same temperature and pressure contain the same number of molecules. So both one mole of Xenon at STP (131.3 grams) and one mole of helium at STP (4.00 grams) take up 22.4 liters. Even 1 mole of air, which is a mixture of several gases, takes up 22.4 liters of volume. 22.4 L is the standard molar volume of a gas.
[Avogadro's Law]
- .
where:
- V is the volume of the gas.
- n is the number of moles of the gas.
- k is a proportionality constant.
The most important consequence of Avogadro's law is that the ideal gas constant has the same value for all gases. This means that the constant
where:
- p is the pressure of the gas
- T is the temperature of the gas
has the same value for all gases, independent of the size or mass of the gas molecules.
Pressure
Gases exert pressure on their containers and all other objects. Pressure is measured as force per unit area. A barometer is a device that measures pressure. There are a number of different units to measure pressure:
- torr, equal to millimeters of mercury (mm Hg): if a glass cylinder with no gas in it is placed in a dish of liquid mercury, the mercury will rise in the cylinder to a certain number of millimeters.
- atmosphere (atm), the pressure of air at sea level.
- pascal (Pa), equal to one newton (N) per square meter. A newton is the force necessary to accelerate one kilogram by one meter per second squared.
You should know that 1 atm = 760 torr = 101.3 kPa.
Ideal Gases
Gases are complicated things composed a large numbers of tiny particles zipping around at high speeds. There are a number of complex forces governing the interactions between molecules in the gas, which in turn affect the qualities of the gas as a whole. To get around these various complexities and to simplify our study, we will talk about ideal gases.
An ideal gas is a simplified model of a gas that follows several strict rules and satisfies several limiting assumptions. Ideal gases can be perfectly modeled and predicted with a handful of equations.
Ideal gases follow, among others, these important rules:
Rules of Ideal Gases
- The molecules that make up a gas are point masses, meaning they have no volume.
- Gas particles are spread out with very great distance between each molecule. Thus, intermolecular forces are essentially zero, meaning they neither attract nor repel each other.
- If collisions do occur between gas particles, these collisions are elastic, meaning there is no loss of kinetic (motion) energy.
- Gas molecules are in continuous random motion.
- Temperature is directly proportionate to kinetic energy.
Note: Ideal gases never truly exist (because the nature of gases is so complicated), but gases are often close enough to an ideal gas that the equations still hold fairly accurate. |
Ideal Gas Law
Ideal gases can be completely described using the ideal gas law:
[Ideal Gas Law]
where
- is the absolute pressure of the gas,
- is the volume of the gas,
- is the number of moles of gas,
- is the ideal gas constant,
- is the absolute temperature, in Kelvin.
Ideal Gas Constant
| Values of R | Units |
|---|---|
| 8.314 472(15) | J K−1 mol−1 |
| 8.314 472(15) | m3 Pa K−1 mol−1 |
| 8.314 472(15) | cm3 MPa K−1 mol−1 |
| 0.082 057 46(14) | L atm K−1 mol−1 |
| 62.363 67(11) | L Torr K−1 mol−1 |
The ideal gas constant, R, is a constant from the ideal gas equation, above, that helps to relate the various quantities together. The gas constant represents the same value, but the exact numerical representation of it may be different depending on the units used for each term. The table at right shows some values of R for different units. Here is the value of R using Joules for energy, Kelvin for temperature, and moles for quantity:
[Ideal Gas Constant]
Real Gases
All real gases (or non-ideal gases) deviate from the ideal gas laws that we discussed above. These deviations can occur for several reasons:
- Real molecules have mass and volume. They are too big and no longer behave like ideal point masses
- Low volumes and high pressures cause molecules to be close enough for intermolecular forces. Polar molecules exaggerate the problem.
- Low temperature means low kinetic energy. At lower temperatures, intermolecular forces become significant and cannot be ignored like they are in ideal gasses
- Other complicated factors may prevent ideal behavior.
When these issues are present, gas molecules attract each other, and may even condense into a liquid. Gases act most like ideal gases when the molecules have low mass (small volume), are not polar, and are at high temperature and low pressure. Noble gases like Xenon or Argon act the most like ideal gases because they are mostly electrical neutral and non-interactive.
Kinetic Molecular Theory
This theory describes why gases exhibit their properties. It only applies accurately to ideal gases. Because there is no such thing as an ideal gas, the Kinetic Molecular Theory can only approximate gas behavior. It is still very useful to chemists.
The Kinetic Molecular Theory explains the pressure, temperature, kinetic energy, and speed of gases and their molecules. See Wikipedia for the exact equations of the Kinetic Molecular Theory, as well as detailed explanations. What is most important is understanding the general concepts, not the specific equations.
Kinetic Energy and Temperature
Kinetic energy is the mechanical, or movement, energy. It is given by the equation:
where
- is mass and
- is the average velocity
Explained with words, kinetic energy is dependent on the product of a particle's mass and its velocity squared. The more kinetic energy, the faster a particle moves. Conversely, the faster a particle moves, the more kinetic energy it has.
The Kinetic Molecular Theory states that kinetic energy and temperature are directly proportionate. Thus, a double in temperature will result in a double in kinetic energy and an increase in velocity by a factor of 1.4 (the square root of 2, see the KE equation). This means that the higher the temperature of a gas, the faster the individual particles in that gas are moving.
A hotter gas has more kinetic energy than a colder gas. If two gases are at the same temperature, they will have the same kinetic energy. The lighter-massed gas will have a higher average speed for its particles at the same energy level. It is important to know that gas temperature must be measured in kelvin. Zero degrees Celsius is 273 kelvin. One Celsius degree is equal to one kelvin, but the kelvin scale has water's freezing point at 273 and boiling point at 373. It is necessary to use kelvin because temperatures must always be positive when using the Kinetic Molecular Theory.
- Question for the reader
A gas's temperature is increased from 20 °C to 40° C. What factor does its kinetic energy increase? Velocity?
Keep in mind that gases are all about averages. For a temperature increase, there will be an average increase in the kinetic energy of the particles in that gas. Even in a very hot gas there will be some particles moving very slowly. However, the average will be high. |
Pressure and Collisions
Pressure exists because the gas molecules are in continuous random motion, and they will constantly strike the walls of their container. Pressure will increase as the speed of the molecules increases, due to greater forces of collision. Pressure will also increase as the mass of the molecules increase. A small, slow molecule has less momentum than a large, fast molecule, which explains their difference in pressure.
- Question for the reader
There are two jars of ideal gas, for example. In Jar A there is nitrogen gas (N2). In Jar B there is methane gas (CH4). Both jars are at the same temperature. Which will have greater pressure?
- Question for the reader
Now, Jars A and B both have propane gas (C3H8). Jar A is at 300 K and Jar B is at 500 K. Which will have greater pressure?
Phase Changes
Phase Diagrams
Phase diagrams predict the phase of a substance at a certain pressure and temperature.
The triple point is where all three phases of matter can exist in equilibrium. Points that are on a line are where two phases of matter can coexist.
The critical point is the highest pressure and temperature that the three normal phases can exist. Any further, and the characteristics become a blend of liquid and gas.
Changes in State
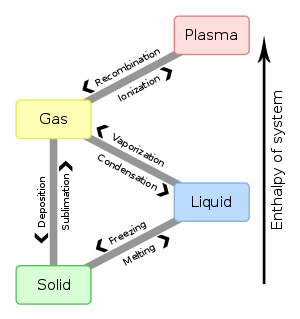
If the temperature and pressure change and move across a line in the diagram, the phase will also to change. There are six ways this can happen:
- Solid to liquid: melting
- Liquid to solid: freezing
- Liquid to gas: evaporation
- Gas to liquid: condensation
- Gas to solid: deposition
- Solid to gas: sublimation
The diagram on the right also shows the plasma state of matter. A plasma is simply a gas that has been completely ionized, so that there is a mixture of positive ions and electrons. It has interesting electrical properties, but it is not important in the scope of General Chemistry.
Energy Changes
| Helpful Hint! | |
|---|---|
| The kinetic energy of a molecule is directly proportional to its temperature. Potential energy is used to break bonds. |
If you boil water, it never goes above 100 degrees Celsius. Only after it has completely evaporated will it get any hotter. This is because once water reaches the boiling point, extra energy is used to change the state of matter and increase the potential energy instead of the kinetic energy. The opposite happens when water freezes. To boil or melt one mole of a substance, a certain amount of energy is required. These amounts of energy are the molar heat of vaporization and molar heat of fusion. If that amount of energy is added to a mole of that substance at boiling or freezing point, all of it will melt or boil, but the temperature won't change.
The graph shows the temperature of ice as heat is added. Temperature increases linearly with heat, until the melting point. Then, the heat added does not change the temperature. That heat energy is instead used to break intermolecular bonds and convert ice into water. At this point, there is a mixture of both ice and water. Once all ice has been melted, the temperature again rises linearly with heat added. At the boiling point, temperature no longer rises with heat added because the energy is once again being used to break intermolecular bonds. Once all water has been boiled to steam, the temperature will continue to rise linearly as heat is added.
Behavior of Gases
Evaporation of Liquids
An open bottle of vinegar standing at room temperature will spread odor across the room despite the fact that it is not boiling. This is because kinetic energy is unevenly distributed throughout a liquid. Some molecules are moving faster than others. This allows the liquid to evaporate into a gas. In order for evaporation to occur, the entire liquid does not need to be at the boiling temperature; only some individual molecules. At a given temperature a liquid evaporates at a specific rate, causing gas pressure above the liquid in the system that contains it. Can you guess the vapor pressure of water at 100 degrees Celsius? If you guessed 760 torr or 1 atm, you're right. Liquids boil when their vapor pressures equal the atmospheric pressure around them. Some liquids are more volatile than others, meaning they evaporate more readily.

Evaporation occurs because of the uneven distribution of kinetic energy. This is called a Boltzmann distribution. Although the average kinetic energy of the liquid is below the boiling point, some molecules have above average energy. That gives them enough energy to overcome their bonds and break free of the liquid. At the same time, a gas molecule could strike the liquid and slow down enough to become part of it. There is an equilibrium between the amount of evaporating liquid and the amount of liquifying gas. Higher temperatures will have an equilibrium that favors more gas.
Motion of Gas Particles
Gas particles move in random, straight-line motion. Gas particles possess a greater kinetic energy than the particles of a liquid or solid. The greater kinetic energy is due to gases existing at higher temperatures than liquids or solids. As temperature increases, particles move faster and, thus, have greater kinetic energy. The particles of a gas have minimal interactions, except collisions with each other.
Diffusion and Effusion
Due to their random motion, gases will eventually escape from a container if there is a hole in it. This is called effusion. Gases also spread out across a room, or mix together in a container. This is called diffusion.
More information about diffusion and effusion is presented in the next chapter.
Dalton's Law of Partial Pressures
The total amount of pressure exerted by a gas is equal to the sum of its components:
For instance, if you add 300 torr of nitrogen gas to a container, then you add 250 torr of oxygen to that container, the total pressure will be 550 torr (assuming volume and temperature stayed constant).
Another way of stating this law is that the pressure exerted by a particular gas in a mixture (gases always form homogeneous mixtures with each other) is equal to its mole fraction multiplied by the total pressure.
Diffusion and Effusion
Diffusion and Effusion
Diffusion

Diffusion is the process of a substance spreading out to evenly fill its container or environment. In a solution, a concentrated solute diffuses to spread evenly in its solvent. This is the process where the particles move from high concentration to low concentration. Diffusion explains why an open bottle of ammonia will fill an entire room with odor. The gas molecules escaping from the bottle spread out to fill their new container: the room. As a result, the whole room smells. Upon opening the windows, the gas will diffuse into the environment.
Diffusion occurs because the gas molecules are in continuous random motion. This motion is called Brownian Motion. The molecules will eventually reach anywhere they can. |
Diffusion is also the process of two gases mixing together, if both stored in the same container. They will spread out evenly, resulting in a solution (homogeneous mixture).
Effusion
Effusion is the process of gas molecules escaping from a small hole in the container. Effusion explains why fumes are noticeable near a leaky fuel pipe.
Effusion is also explained by the continuous random motion of the molecules. The random motion prevents molecules from avoiding the small hole. Slowly but steadily, gas molecules will pass through the hole. |
Effusion obviously depends on the size of the hole. If small enough, effusion may not occur because, like a beach ball hitting a basketball hoop, the molecules can't fit. If the hole is large enough, the process may be considered diffusion instead of effusion.
Effusion can be seen with balloons. Effusion proves that the balloon has holes in it, even though it looks totally impassable. When left alone for several days, a balloon filled with helium will eventually deflate. If that balloon were filled with hydrogen, it would deflate in less time because the molecules are smaller and escape with ease. and you can try that
this is chemistry ks3
==
The more massive a gas is, the slower it effuses. The relationship is given by Graham's Law.
As an example, assume there are two identical containers with holes. Container A has hydrogen gas (M=2 g/mol) and Container B has helium gas (M=4 g/mol). If the hydrogen gas effuses at a rate of 4 mol/hr, the helium gas would effuse at a slower rate (being heavier). Using Graham's Law, we can see that it would effuse at a rate of about
Gas Laws
Gas Laws
As the result of many different science experiments, several gas laws have been discovered. These laws relate the various state variables of a gas. Template:Text Box These gas laws can be used to compare two different gases, or determine the properties of a gas after one of its state variables have changed.
| Avogadro's Law states that equal volumes of all ideal gases (at the same temperature and pressure) contain the same number of molecules. | ||
| Boyle's Law states that equal pressure is inversely proportional to volume (when the temperature is constant). | ||
| Charles's Law states that volume is proportional to temperature (when the pressure is constant). Remember that temperature must be measured in Kelvin. | ||
| Amontons's Law states that pressure is proportional to temperature (when the volume is constant). |
Combined Gas Law
Combining Charles' Law, Boyle's Law, and Amontons's Law gives us the combined gas law.
| For a gas with constant molar mass, the three other state variables are interrelated. | |
| The Combined Gas Law can be used for any comparisons between gases. |
Ideal Gas Law
When Avogadro's Law is considered, all four state variables can be combined into one equation. Furthermore, the "constant" that is used in the above gas laws becomes the Universal Gas Constant (R).
To better understand the Ideal Gas Law, you should first see how it is derived from the above gas laws.
| and | This is simply a restatement of Avogadro's Law and the Combined Gas Law. |
| We can now combine the laws together. | |
| Let R be a constant, and write the proportion in the form of an equation. | |
| Rearranging the fraction gives one form of the ideal gas law. |
The ideal gas law is the most useful law, and it should be memorized. If you know the ideal gas law, you do not need to know any other gas laws, for it is a combination of all the other laws. If you know any three of the four state variables of a gas, the unknown can be found with this law. If you have two gases with different state variables, they can be compared.
There are three ways of writing the ideal gas law, but all of them are simply algebraic rearrangements of each other.
| This is the most common form. | |
| This form is useful for predicting the effects of changing a state variable. To maintain a constant value of R, any change in the numerator must result in a proportional change in the denominator, and vice versa. If, for example, the pressure is decreased in a constant-volume container, you can use this form to easily predict that the temperature must decrease. | |
| Because R is the same constant for all gases, this equation can be used to relate two gases to each other. |
Rules for Using the Ideal Gas Law
- Always convert the temperature to kelvins (K).
- Always convert mass to moles (mol).
- Always convert volume to liters (L).
- It is preferable to convert pressure to kilopascals (kPa). R, the Universal Gas Constant, would be 8.314 (L·kPa)/(mol·K).
Rules for Using the Ideal Gas Law
|
Kinetic Molecular Theory
The Kinetic Molecular Theory attempts to explain the gas laws. It describes the behavior of microscopic gas molecules to explain the macroscopic behavior of gases. According to this theory, an ideal gas is composed of continually moving molecules of negligible volume. The molecules move in straight lines unless they collide into each other or the walls of their container.
| The pressure of the gas on the container is explained as the force the molecules exert on the walls of its container or on other molecules during a collision. Pressure is equal to the average force of collisions divided by the total surface area of the container. | |
| The temperature of the gas is proportional to the average kinetic energy of the molecules. denotes the average kinetic energy of the molecules, and is the Boltzmann constant (1.388 x 10-23). |
The gas laws are now explained by the microscopic behavior of gas molecules:
- Boyle's Law: The pressure of a gas is inversely proportional to its volume. A container's volume and surface area are obviously proportional. Based on the pressure equation, an increase in volume (and thus surface area) will decrease pressure.
- Charles' Law: the volume of a gas is proportional to its temperature. As the volume (and surface area) increases, the pressure will decrease unless the force also increase. When pressure is constant, the volume and temperature must be proportional. The temperature equation above explains why: the energy of the molecules (and their collision force) is proportional to temperature.
- Gay-Lussac's Law: The temperature of a gas is directly proportional to its pressure. An increase in temperature will increase the kinetic energy of the molecules (shown by the temperature equation). Greater kinetic energy causes the molecules to move faster. Their collisions with the container will have more force, which increases pressure.
- Avogadro's Law: Equal volumes of all ideal gases (at the same temperature and pressure) contain the same number of molecules. According to the Kinetic Molecular Theory, the size of individual molecules is negligible compared to distances between molecules. Even though different gases have different sized molecules, the size difference is negligible, and the volumes are the same.
Derivation of Ideal Gas Law
| Suppose there are molecules, each with mass , in a cubic container with side length . Even though the molecules are moving in all directions, we may assume, on average, that one-third of the molecules are moving along the x-axis, one third along the y-axis, and one third along the z-axis. We may assume this because the motion of the molecules is random, so no direction is preferred. | |
| Suppose the average speed of the molecules is . Let a specific wall of the container be labeled A. Because the collisions in Kinetic Molecular Theory are perfectly elastic, the speed after a collision is . Therefore, the average change in momentum (the product of mass and velocity) per collision is .
Each molecule, on average, travels a distance of between two consecutive collisions with wall A. Therefore, it will collide times per second with wall A. | |
| The average change in momentum per molecule per second. | |
| Therefore, this is the total change in momentum per second for the molecules that collide into wall A. This is the momentum per second that was exerted onto wall A. Because force equals the change in momentum over time, this value is the force exerted on wall A. | |
| Pressure is defined as force per unit area, so this is the pressure of the gas. | |
| Because the volume of the container is , we can rearrange the equation. | |
| The kinetic energy of a single particle is given by this equation. | |
| Substitute kinetic energy into the equation. | |
| Substitute the temperature equation (from the previous section). | |
| Avogadro's number is equal to the number of molecules per mole. | |
| By definition, the ideal gas constant is equal to the Boltzmann constant times Avogadro's number. | |
| The ideal gas law is derived from the Kinetic Molecular Theory. | |
Deviations from the Ideal Gas Law
In an ideal gas, there are no intermolecular attractions, and the volume of the gas particles is negligible. However, there is no real gas that can perfectly fits this behavior, so the Ideal Gas Law only approximates the behavior of gases. This approximation is very good at high temperatures and low pressures.
At high temperature the molecules have high kinetic energy, so intermolecular attractions are minimized. At low pressure the gas occupies more volume, making the size of the individual molecules negligible. These two factors make the gas behave ideally.
At low temperature or high pressure, the size of the individual molecules and intermolecular attractions becomes significant, and the ideal gas approximation becomes inaccurate.
Eudiometers and Water Vapor
| Helpful Hint! | |
|---|---|
| In calculations for a gas above a liquid, the vapor pressure of the liquid must be considered. |
A eudiometer is a device that measures the downward displacement of a gas. The apparatus for this procedure involves an inverted container or jar filled with water and submerged in a water basin. The lid of the jar has an opening for a tube through which the gas to be collected can pass. As the gas enters the inverted container, it forces water to leave the jar (displacing it downward). To fill the entire container with gas, there must enough gas pumped into the container to expel all of the water.

As seen in this diagram, the downward displacement involves water. Therefore, in the container where the gas is collected, there is unwanted water vapor. To account for the water vapor, subtract the pressure of water vapor from the pressure of the gases in the container to find the pressure of the collected gas. This is simply a restatement of Dalton's Law of Partial Pressure:
The pressure of water vapour can be found on this webpage.
Gas Laws Practice Questions
- Between the Combined Gas Law and the Ideal Gas Law, which one accounts for chemical change? Explain.
- Calculate the density of hydrogen at a temperature of 298 K and pressure of 100.0 kPa.
- What volume does 5.3 moles of oxygen take up at 313 K and 96.0 kPa?
- Hydrogen and sulfur chemically combine to form the gas hydrogen sulfide, according to the reaction: . How many liters of hydrogen are required to form 7.4 L of hydrogen sulfide (at STP: 273 K, 101.3 kPa)?
Answers to Gas Laws Practice Questions
Equilibria
Chemical Equilibrium
Chemical equilibrium occurs when a reversible reaction is occurring backwards and forwards at the same time by the same amount. It is the balancing point of a chemical reaction, when it seems to stop happening. Although some reactions (like the combustion of propane) occur to completion (no backwards reaction), most reactions occur in both the forward and backward direction. One reaction will occur at a faster rate than the other, causing a net result. As the reaction progresses, the forward reaction slows down and the backward reaction speeds up. When the rates are equal, equilibrium has occurred. The reaction appears to have stopped, and the total amount of products and reactants remains stable.
Chemical reactions never really stop, but they no longer make any progress once the forwards and backwards reactions are occurring at the same rate. This is equilibrium. |
The Equilibrium Constant
The ratio of products to reactants, or is known as the equilibrium constant. For the generic reaction mA + nB → xC + yD, the equilibrium constant is
where [X] detonates the activity of X. The activity of X is:
- its concentration if X is a gas or in a solution
- 1 if X is a pure solid or pure liquid
In other words, pure solids and liquids don't affect the equilibrium constant, as long as there is enough for the reaction to proceed. Their activity is 1, so they don't need to be written in the equilibrium constant.
Kp and Kc
There are two types of . One is , and the activities are concentrations. You are already familiar with this expression; it is the normally-used . For gaseous reactions, you may use the concentration equilibrium. You may also use partial pressures instead of concentrations. This expression is denoted . The activities are partial pressures instead of concentrations. This can only be used when all products and reactants are in the gaseous phase.
To convert between and , there is an equation:
R is the Universal Gas Constant and T is the temperature at which the reaction is occurring. is the change (in moles) of gas molecules between products and reactants. It may be zero (in which case Kp = Kc).
Examples
- Example 1
15.0 moles of X and 20.0 moles of Y are put into an empty 2.0 liter container. They react, and eventually reach equilibrium with 7.0 moles of Z according to the hypothetical equation:
Calculate the equilibrium constant.
Solution: Because the container was originally empty and at equilibrium, all 7.0 moles of Z are produced by the reaction. Therefore, 7.0 moles of X and 14.0 moles of Y are consumed in the reaction, so at equilibrium there remain 8.0 moles of X, 6.0 moles of Y, and 7.0 moles of Z. Divide these values by 2.0 liters to determine the concentration, then substitute into the equilibrium expression:
- Example 2
5.00 moles of hydrogen are put into an empty 1.00-L container with 5.00 moles of iodine, where they react according to this equation:
The equilibrium constant is 51.5 at the temperature of the reaction. Calculate the number of moles of HI that will form.
Solution: Suppose 2y moles of HI forms. Then, y moles of H2 and I2 are consumed. Therefore, at equilibrium, there are 2y moles of HI, and (5.00 - y) moles of both H2 and I2. Dividing by 1.00 liters (to find concentration) and writing an equilibrium expression gives:
Solving this equation gives y = 3.91 (reject the other solution, as it is greater than 5.00). At equilibrium, there are 7.82 mol of HI.
Calculations With K
The exact value of K doesn't really matter. What is important is its magnitude.
| K > 1 | Reactions favors products |
| K < 1 | Reaction favors reactants |
If the reaction favors products, it will occur in the forward (left-to-right) direction. If K is very large, the reaction will occur mostly to completion, using up almost all the reactants.
If the reaction favors reactants, it will occur in the reverse (right-to-left) direction. If K is very small, the reaction will use up almost all the products and make them into reactants. The reverse reaction is favored.
Reaction Arithmetic
If you reverse the reaction (changing the direction of the arrow, or flipping the left and right sides), the new value of Keq will be its reciprocal.
| A → B | (K = x) |
| B → A | (K = 1/x) |
If you add two reactions, their equilibrium constants are multiplied.
| A → B G → H |
(K = x) (K = y) |
| A + G → B + H | (K = xy) |
These basic principles can help you determine an unknown equilibrium constant by combining known constants.
Q
Keq is only used when a reaction is in equilibrium. To find it, write its concentration (or partial pressure) expression, then plug in all the measured values. The resulting K can be used to predict other equilibrium positions.
If a reaction is not at equilibrium, you can still plug in the measured concentrations. Instead of calling this value Keq, it is called Q.
| Q > K | The products must decrease and the reactants will increase. |
| Q = K | There is equilibrium. |
| Q < K | The reactants must decrease and the products will increase. |
So, if you know the equilibrium constant for a reaction, and you know all the concentrations, you can predict what direction the reaction will proceed.
I-C-E Charts
Let's say you know K for a reaction, and you know some concentrations. You can calculate the final (equilibrium) concentrations using an "Initial-Change-Equilibrium" chart. Here is an example.
At 25°C, Kc = 23.2 for this reaction.
First, write the equilibrium expression:
In a sealed container of 2.00 L: 3 molar H2O, 4 molar CO, 1 molar H2 have been added. (Write the ICE chart):
| CO | H2O | CO2 | H2 | |
|---|---|---|---|---|
| Initial | 2 | 1.5 | 0 | 0.5 |
| Change | -x | -x | +x | +x |
| Equilibrium | 2-x | 1.5-x | x | 0.5+x |
Now, plug in the "equilibrium" values into the K expression. Substitute all known values and solve for x. Then, substitute x for the final values to determine the equilibrium concentrations.
By substituting everything into the K expression, we have:
Solving this will require the use of the quadratic equation. It may be easier to use approximations or a graphing calculator. When solved, (disregard values of x that would give negative concentrations). By substituting x into the "equilibrium" values in the ICE chart, we can determine the concentrations of all substances when the reaction reaches equilibrium.
| CO | H2O | CO2 | H2 |
|---|---|---|---|
| 0.66 M | 0.16 M | 1.34 M | 1.84 M |
To check your answer, you could substitute these values into the equilibrium expression and see if it equals 23.3 (the given Keq value).
This was a fairly simple example. There were no coefficients in the reaction, so no exponents in the expression. |
The purpose of doing this is to see the final concentrations of the substances involved in a chemical reaction. Unless Keq is incredibly large, not all the reactants will be consumed.
Equilibrium in Detail
The next few chapters in this book will provide more details on equilibrium.
Shifts in Equilibrium
Le Chatelier's principle states that a system will adapt to minimize a change. If reactants are added, they will be consumed and products will form. Likewise, if products are added, they will be consumed (by the reverse reaction) and reactants will form.
The only change in a system that will affect the value of Keq is temperature. The value of Keq is never changed by the concentrations or pressures of the substances.
Special Constants
| Acids and bases have special ionization constants, which show how they react with water. The acid ionization constant, or Ka, tells how strong an acid is. | |
| The base ionization constant, Kb, similarly tells how strong a base is. | |
| The solubility product Ksp shows how much an ionic substance will dissociate when dissolved. |
Relation to E
There is a special relation between the standard potential of a redox reaction and the equilibrium constant
, where n is the number of moles of electrons transferred.
This is a significant equation, because this allows us to calculate the hard to measure K from the easy to measure E.
Le Chatelier's Principle
Le Chatelier's Principle
Le Chatelier's Principle states that when a system that is in dynamic equilibrium is disrupted in some way, the system will respond with chemical or physical changes to restore a new equilibrium state.
There are several changes that can effect the equilibrium position of a system:
- Concentration
- Pressure/Volume
- Temperature
Concentration
If the concentrations in a system are changed, Le Chatelier's Principle predicts that the equilibrium position will shift to minimize the change.
For example, let us say that the reaction above is at equilibrium. Adding more reactants ( and ) will disturb the equilibrium system because it raises the reactant concentration. The system will then produce more products ( and ) and will decrease the reactant concentration in order to obtain equilibrium again. The system is now at a new equilibrium position, and the change created has been minimized.
The above example shows that increasing the reactants in an equilibrium system favors the products because the system produces more products and reduces the amount of reactants. The table below shows the response of an equilibrium system to changes in concentration:
| Change in Concentration | System response |
|---|---|
| Increase reactant | Favors products |
| Decrease reactant | Favors reactants |
| Increase product | Favors reactants |
| Decrease product | Favors products |
Pressure/Volume
If some the substances in a system are gas, changing their partial pressure is the same as changing their concentrations.
If the volume is increased, the overall pressure decreases (and vice versa). Consider the reaction A + B → 3C. There are three moles of products for every two moles of reactants. The product side has higher pressure than the reactant side. So, if pressure is increased (or volume decreased), equilibrium will shift towards the lower pressure side. Products will be consumed (by the reverse reaction) and reactants will form.
If pressure is decreased (or volume increased), equilibrium will shift towards the higher pressure side.
If an inert gas (such as neon) is added to a system, it will raise the overall pressure. However, the partial pressures of all products and reactants are unchanged, so no shift in equilibrium occurs. |
Temperature
Changes in concentration, pressure, and volume affect the equilibrium position, but the equilibrium constant Keq is unchanged. These changes can be calculated using the equilibrium expression and known values of Keq and concentrations.
Temperature, however, does change the value of Keq. When given a value of K, you will also be given a temperature because K is dependent on the temperature.
An increase in temperature will favor the endothermic (heat-absorbing) side of a reaction. A decrease in temperature will favor the exothermic (heat-releasing) side of a reaction.
For example, the following reaction is very exothermic:
Because it is exothermic, you can think of it like this:
At room temperature, Keq for this reaction is 3.2 x 1081. If this reaction happens at a very high temperature, what will happen? Less product will form (or maybe the reverse reaction will occur if the temperature is high enough) and Keq will be smaller. What will happen if this reaction occurs at a very low temperature? More product will form and Keq will be larger.
Acid-Base Equilibrium
Consider an acid, HA, in water. According to the Brønsted-Lowry acid/base theory, the acid should protonate the water to form hydronium and the conjugate base, A-. There will be an equilibrium between the acid and water, and hydronium and the conjugate base.
This equilibrium can be used to calculate the concentrations of species in the solution.
Acid Dissociation Constant
| Helpful Hint! | |
|---|---|
| Strong acids/bases dissociate completely, so their equilibrium constants are overwhelmingly large. |
Like all equilibria, an acid/base dissociation will have a particular equilibrium constant which will determine the extent of the reaction (whether it lies to the left or right of the equation). As the equilibrium constant approaches zero, the reaction tends to form 100% reactants. As the equilibrium constant approaches infinity, the reaction tends to form 100% products. The equilibrium constant K=1 states that there will be 50% products and 50% reactants
Because the equilibrium is used for calculating the concentrations of weak acids, very little water actually reacts. The concentration of water during the reaction is, therefore, a constant, and can be excluded from the expression for K. This gives rise to a special equilibrium constant, Ka, known as the acid dissociation constant. It is simply K multiplied by the concentration of water.
The Ka of a weak acid determines how acidic it is, i.e., how far its equilibrium lies to the right. The Ka values of weak acids can and have been determined experimentally.
Base Dissociation Constant
A similar equilibrium exists when a weak base is dissolved in water. The base will accept a proton from water and form a conjugate acid, BH+.
This equilibrium has its own special constant, Kb, known as the base dissociation constant. Like the acid dissociation constant, it is defined as the equilibrium constant multiplied by the concentration of water.
Ion Product Constant
A special equilibrium exists between ordinary water molecules. Occasionally, one water molecule will act as an acid, and donate a proton to another water molecule (which acts as a base). This is the auto-ionization of water.
By the Le Chatelier Principle, we can see that if the hydronium ion concentration is increased (by adding an acid), the equilibrium will move to the left and there will be a lower concentration of hydroxide. Thus, hydronium and hydroxide concentration are inversely related—an increase in one will result in a decrease in the other, and vice versa.
The equilibrium expression for this reaction is given a special name, Kw. Because it simplifies to the product of hydronium and hydroxide concentration, it is sometimes called the ion product constant. The value of this constant is 1.0 × 10-14 at 25°C.
This expression can be used to find the pH of pure water. Recall that pH is the negative logarithm of hydronium ion concentration. If we set the hydronium ion concentration in the above expression to be , we can derive the pH. The hydroxide ion concentration must also be (since each molecule of hydroxide is a result of a molecule of hydronium forming). We have:
This technique can be used to determine the pH of any solution if either one of the ion concentrations are known.
Conjugate Base Expressions
The conjugate bases of weak acids have a relationship with their parent acids. Consider the equilibrium expression of the conjugate base, A-, of the weak acid HA.
If we multiply the expression for an acid by the expression for its conjugate base, the concentrations of the acid and conjugate base cancel and we obtain the ion product constant for water! This allows us to calculate the Kb of a base if the Ka of its conjugate acid is known (and vice versa).
Summary
The definitions of the acid and base dissociation constants are very important. They are presented here for reference.
| The acid dissociation constant measures the strength of an acid dissolved in water. | |
| The base dissociation constant measures the strength of a base dissolved in water. | |
| The ion product constant relates the concentrations of acids/bases and their conjugates in a solution. |
Solutions in Equilibrium
Solution
| Helpful Hint! | |
|---|---|
| You may need to review solubility and the properties of solutions. |
All ionic compounds are soluble in water to some extent, but the degree of solubility varies. While some compounds dissolve almost completely, others dissolve to such a small extent that they are simply called insoluble compounds. Such compounds include calcium sulfate, silver chloride, and lead hydroxide. Generally, ionic compounds whose component ions have larger charge magnitudes are less soluble because the ions are attracted too much to dissociate. A soluble compound will dissociate because of the attractions with the surrounding water molecules are strong enough to separate the ions.
For an ionic compound to dissociate, the forces of attraction between its component ions and the surrounding water molecules must be greater than the forces of attraction between the ions within the compound. When introduced to an aqueous environment, ionic compounds such as sodium chloride, sodium hydroxide, and ammonium bromide dissolve because of this.
Solubility Constant
| This reaction shows an ionic compound AB dissolving into its ions A+ and B-. | |
| This is the equilibrium constant for the reaction. Water is excluded because, although involved, it is not a product or reactant. | |
| Because the undissolved AB is a solid, pure substance, it can be excluded from the expression. The result is the solubility constant Ksp. It measures the degree of solubility of an ionic compound. |
If two or more of the same ion are created by the dissociation of one particle of the ionic compound, the molar concentration of this ion is raised to the power of how many such ions there are. For example, when calcium chloride dissociates, two chloride ions are created in the dissociation of one particle, so the concentration of the chloride ion is squared when calculating Ksp.
Ksp is the equilibrium constant for the dissolution reaction above.
|
An example of a slightly soluble substance is calcium hydroxide. In very minute quantities, it will dissolve completely, but in large quantities it remains mostly undissolved.
Calculations with Ksp
Finding Ksp
It would not be an uncommon situation if you know a substance's solubility (g/mL), but you need to know its Ksp value. Follow this example:
| This is the solubility constant for calcium hydroxide. We wish to determine is numerical value, but we only know that its solubility is 0.185 g per 100 mL. | |
| We need to know its molar solubility, so we convert units and divide by molar mass. | |
| Now, plug in the molar solubility into the Ksp expression. Notice that the hydroxide concentration is doubled because there will be twice as many moles as the undissolved substance. |
We have now determined the Ksp value for calcium hydroxide. It will allow us to determine other information about solutions containing these ions, such as percent ionization and the formation of precipitates.
- Questions for the reader
Lead(II) iodide is slightly soluble in water. It forms a bright yellow precipitate if too much is dissolved. You have determined that 0.75 g will dissolve in one liter of cold water. What is the molar solubility of lead(II) iodide? What is the Ksp value?
After heating the water, the solubility rises to 4.3 g per liter. What is the new Ksp value?
A similar process can be used to determine a substance's solubility by working backwards from the solubility constant.
Percent Ionization
Once an ionic compound's Ksp value is known, it is possible to determine the percent ionization, or relative amount of dissociated ions.
| We know the Ksp for silver sulfate, which is slightly soluble, and we want to know the percent ionization. | |
| Substitute x for the concentration of sulfate and 2x for silver. Solve for x. | |
| We now know the maximum concentration of the ions. Any remaining silver nitrate will be undissolved because the solubility has been exceeded and the solution is saturated. To determine percent ionization, we must know how much silver sulfate was dissolved. For this example, assume 1.00 mole was dissolved into 0.500 L of water. |
As you can see, the percent ionization decreases as the amount of solute increases. This is because the solution is saturated and no more ions will dissociate.
- Question for the reader
Lithium fluoride has a Ksp of 1.84 x 10-3. If 1.5 g are dissolved, what will be the percent ionization?
Precipitates
Obviously, the dissociate reaction occurs in reverse if there are too many ions. In this case, the solution is saturated, and any excess ions will solidify and form a precipitate.
If two soluble solutions are mixed, but the can form an insoluble compound, a precipitate will form.
| For example, a solution of silver nitrate is mixed with a solution of sodium chloride. Both are soluble. Silver chloride, however, is insoluble. | |
|
If 1.00 mg NaCl and 1.00 mg AgNO3 are dissolved into 1.00 L of water, will a precipitate form? |
| No, a precipitate will not form. | |
|
Now, another milligram of sodium chloride is dissolved. |
| The extra chloride ions will bond with silver ions and form a solid precipitate. |
In this case, the precipitate would probably be too small and dilute to be noticed. As more ions are added, however, the solution will become visibly cloudy.
- Question for the reader
Calcium carbonate has a Ksp of 3.36 x 10-9. In a 0.01 M solution of calcium chloride (soluble), how many moles of sodium carbonate (also soluble) can be added before precipitates form?
Kinetics
Introduction
Chemical kinetics is the study of the rates of chemical reactions. You may know if a reaction is capable of happening, and you may know how far the reaction will proceed, but you don't know fast it will happen. Consider two reactions: the rusting of an iron nail and the combustion of propane. Both reactions will occur, and both will occur to completion. The rusting will take years to complete, but propane will combust in an instant. Furthermore, the nail will rust faster when it's moist, and slower in the presence of less oxygen. Obviously, there are factors that affect the rates of chemical reactions. The study of these factors and rates is chemical kinetics.
-
This iron wire has taken years to become rusty.
-
This fire took only a moment to start.
Reaction Rate
| Consider this generic chemical reaction. (Lower case letters represent the molar coefficients.) | |
| The reaction rate is defined as the rate of change of the concentration of the substances. Remember that a substance written inside brackets is its concentration, and it is always raised to the power of its coefficient in the reaction (just like equilibrium expressions). The reaction rate involves Calculus, but in non-mathematical terms it is simply the rate of change of the concentrations. | |
| Actually measuring the rate of change of the reactants and products is difficult. Instead, the reaction rate can be accurately modeled by a rate equation. This is an example of a rate equation that might model the above reaction, where is a constant. |
In summary, the reaction rate can be determined using a rate equation, which depends on (among other things) the concentration of the reactants. The reaction rate essentially measures the speed at which a reaction proceeds.
Collision Theory
Collision theory predicts that reactions occur when molecules collide. In order for reactants to form products, the reactant molecules must physically collide so that they can rearrange themselves into product molecules. Only some collisions are effective because the collision must involve enough energy to allow the reaction to occur. This is called activation energy, the energy needed to begin a reaction.
Activation energy explains why gasoline will not spontaneously ignite. First, a small spark or flame must be present. The heat generated by the spark gives the gasoline molecules enough energy to activate the reaction. Being highly exothermic, the combustion of gasoline releases a large amount of heat—more than enough to activate further reactions and create a fire.
Collision theory allows us to predict the rate constant for a rate equation (see above). At a given temperature , the rate constant is:
where is the Universal Gas Constant, is the activation energy for the reaction, is a predicted-to-actual correction factor, and is the collision factor. The collision factor can also be calculated mathematically. It is the average number of reactant particle collisions per unit time.
Factors Affecting Rate
The rate of a reaction is affected by many factors. These effects can be measured empirically or explained by collision theory.
Concentration
This is the most obvious factor affecting rate. Increasing the concentration of the reactants will increase the rate they react. This is the main purpose of writing a rate equation; the concentrations can be plugged in like variables and the rate can be solved mathematically. In a rate equation in the form , the concentrations are the variables (raised to the powers of their coefficients in the reaction). All other factors that can affect rate are lumped into , which is considered a constant.
Collision theory explains this. Higher concentrations means more molecules packed into a given space. Therefore, there will be more collisions and thus a faster reaction.
Pressure
In a reaction of gaseous reactants, the partial pressure of the gases has the same function as the concentration.
However, increasing the overall pressure (or decreasing the volume if you remember the gas laws) will also result in a greater reaction rate. The increased pressure causes the molecules to collide with more force. More collisions will be effective and therefore products will form faster.
Temperature
As you should already know, a molecule's kinetic energy is directly proportional to its temperature. By increasing the temperature, molecules collide more vigorously, and more collisions will be effective.
Stirring
In a heterogeneous reaction there are two or more phases of matter interacting, such as a solid dissolving into a liquid. Stirring or shaking the mixture will speed up the reaction rate. This is common sense. When you add sugar to a drink, you stir it because you know it will dissolve faster. Collision theory would predict this because the stirring would increase the number of collisions between reactant molecules.
In a similar manner, increasing the surface area of a solid reactant will increase the reaction rate.
Catalysts/Enzyme

A catalyst is a substance that helps a reaction proceed without being consumed. Catalysts have already been explored in this book. A Catalyst provides a reaction pathway with lower activation energy.
In biochemistry, an enzyme is a protein that serves as a catalyst.
Reaction Rates
Introduction
Reaction rates of a chemical system provide the underpinnings of many theories in thermodynamics and chemical equilibria.
Elementary reactions are one-step processes in which the reactants become the products without any intermediate steps. The reactions are unimolecular (A → products) or bimolecular (A + B → products). Very rarely, they could be trimolecular (A + B + C → products), but this is not common due to the rarity of three molecules colliding at the same time.
A complex reaction is made up of several elementary reactions, with the products of one reaction becoming the reactants of the next until the overall reaction is complete.
Rate Equation
| Consider an arbitrary chemical reaction. | |
| The rate at which the products will form from the reactants is given by this rate equation. | |
| The rate of the reverse reaction (which also occurs to a lesser extent) has its own rate equation. |
Note [A] is raised to the power of m, its coefficient, just like an equilibrium expression. The rate of the reaction may rely on the molar coefficients of the reactant species, but it might not. However, for an elementary reaction, the concentrations of the species A and B are always raised to their molar coefficients. This only applies to elementary reactions, which is a very important distinction to make.
is the rate reaction coefficient, which is reaction-specific. It can be considered a constant, although it does change with temperature (and possible other factors). |
Order
The order of an equation is what the concentration of a substance is raised to in the rate equation. The greater the number, the greater effect it will have on rate. For example, zero order equations do not effect the rate. To find the order, you must alter one concentration and keep the rest the same, Dividing gives an equation which can be used to solve for the order. To find overall order, simply add all orders together.
Zero-Order Equations
Zero-order equations do not depend on the concentrations of the reactants.
| There is only a rate coefficient with no concentrations. The rate probably depends on temperature, and possibly other factors like surface area, sunlight intensity, or anything else except for concentration. These reactions usually occur when a substance is reacting with some sort of catalyst or solid surface. | |
| The integrated rate law tells us how much reactant will remain after a given amount of time. Integrated rate laws can be found using calculus, but that isn't necessary. In this zero-order integrated rate law, is the rate coefficient from the rate equation, is time, and is the starting concentration. |
If you make a graph of concentration vs. time, you will see a straight line. The slope of that line is equal to . This is how you can identify a zero-order rate. |
First-Order Equations
First-order equations depend on the concentration of a unimolecular reaction.
| There is a rate coefficient multiplied by the concentration of the reactant. As with a zero-order equation, the coefficient can be though of as a constant, but it actually varies by the other factors like temperature. There can be other reactants present in the reaction, but their concentrations do not effect the rate. First-order equations are often seen in decomposition reactions. | |
| This is the integrated rate law. | |
| The half-life of a reaction is the amount of time it takes for one half of the reactants to become products. One half-life is 50% completion, two half-lives would lead to 75% completion, three half-lives 88%, and so on. The reaction never quite reaches 100%, but it does come close enough. To find the half-life, you can algebraically manipulate the integrated rate law. |
If you make a graph of the logarithm of concentration vs. time, you will see a straight line with a slope of . This is how you can identify a first-order rate. |
Second-Order Equations
Second-order equations depend on the two concentrations of a bimolecular reaction.
| This is the rate law for a second-order equation. | |
| If there are two molecules of the same kind reacting together, the rate law can be simplified. | |
| In that case, this is the integrated rate law. | |
| This is the half-life for a second-order reaction (with only one reactant). |
To see a graph with a straight line of slope , graph the reciprocal of concentration vs. time. |
Equilibrium
Equilibrium will occur when the forward and reverse rates are equal. As you may have already noticed, the equilibrium expression of a reaction is equal to the rate equations divided.
| Consider this reaction, the dimerization of nitrogen dioxide into dinitrogen tetraoxide. | |
|
|
The forward reaction rate is second-order, and the reverse reaction rate is first-order. |
| The rate coefficients may be different for the two reactions. If the reaction is in equilibrium, the forward and reverse rates must be equal. | |
| Rearranging the equation gives the equilibrium expression. |
Understanding kinetics explains various concepts of equilibrium. Now it should make sense why increasing the reactant concentration will make more products. The forward rate increases, which uses up reactants, which decreases the forward rate. At the same time, products are made, which increases the reverse reaction, until both reaction rates are equal again.
Arrhenius Equation
The Arrhenius equation determines a rate coefficient based on temperature and activation energy. It is surprisingly accurate and very useful. The Arrhenius equation is:
is the activation energy for the reaction, in joules per mole. is the Universal Gas Constant, is the temperature (in kelvin), and is the prefactor. Prefactors are usually determined experimentally.
Reaction Mechanisms

Chemists often write chemical equations for reactions as a single step, which only shows the net result of a reaction. However, most chemical reactions occur in a series of steps called elementary reactions. All of these elementary reactions must add up to equal the overall balanced equation. The complete sequence of these elementary steps is called a reaction mechanism. The reaction mechanism is the step-by-step process by which reactants actually become products. It is the "how" of the reaction, whereas the overall balanced equation only shows the "what" of the reaction.
Rate-Determining Steps
Sometimes, intermediate substances are created in the process that disappear in the end. Take the following example of a homogeneous reaction (where products and reactants are all in the same phase):
There are actually two reactions occurring at different speeds.
- (slow)
- (fast)
Since the first step is the slowest, and the entire reaction must wait for it, it is known as the rate-determining step. The overall reaction rate depends almost entirely on the rate of the slowest step. The other steps are fast enough that their rate is insignificant, as they are always waiting for the slower step to complete.
Why is the first step slower? Collision theory explains whether or not particles react when they collide. The particles must collide with a minimum energy and a proper orientation if a reaction is to occur.
The minimum energy needed for a reaction to occur is its activation energy. The particles must be moving fast enough for their collision to satisfy the activation energy. Without the necessary energy, the particles will bounce off each other with no reaction. A good example of activation energy is a butane lighter, which needs a spark before the fluid burns. The spark provides enough energy to the particles to make their collisions effective.
Reactions with high activation energy will be slower than those with low activation energy. With a high activation energy, less particles are likely to generate the needed energy when they collide. Reactions that break bonds, especially double or triple covalent bonds, will have higher activation energy.
The particles must also collide with the proper orientation. For example, the reaction in the animation above shows an ammonium ion reacting with a NCO- ion. For the reaction to occur, the ammonium ion must collide with the nitrogen of the NCO-. If the ions don't collide in the right place while facing in the right direction, the reaction cannot occur.
Reactions that have very specific requirements for the orientation of the colliding particles will be much slower. Reactions that can occur without a specific orientation will happen faster.
Determining the Validity of an Elementary Step Model
In order for a proposed elementary step equation to be valid it must fulfil these requirements.
1. The rate equation of the slow step must match the rate equation of the overall reaction.
2. The reactants and products of all the elementary steps added together must equal the one of the actual equation.
3. The rate law for the elementary step must be able to be written without the concentration of the intermediates, because the intermediates are too small to be accurately measured.
For example, if given this equation and asked to prove the rate mechanism
Equation
Proposed Mechanism
(fast)
(slow)
We know that when the reaction occurs backwards, the k changes from k to k^{-1}. So, we substitute in the backwards rate for O_3, and plug it into the slow step. Then, take the rate equation of the slow step. We find that it is the same as the rate law for the overall equation and meets the three criteria above, so this proposed mechanism is valid.
Thermodynamics
Introduction
Thermodynamics is the study of the changes in energy that occur in reactions.
Systems
A system is the set of substances and energy that is being studied. If, for example, reactions are occurring in a jar, everything inside the jar is the system, and everything outside the jar is the surroundings. The surroundings are everything not in the system, which means the rest of the universe. The system and the surroundings together are called the "universe".
One important issue is what kind of interactions exist between the system and its surroundings. Some systems may exchange matter and heat with the surroundings (like a system of boiling liquid losing matter and heat with the vapor). This is called an open system. If there is just heat exchange occurring between the system and its surroundings it is called a closed system. No matter can enter or leave a closed system. And, finally, if there is no exchange of heat and no exchange of matter, the system is completely isolated.
Temperature vs. Heat
If you put a hot iron pot under cold water, it cools down very quickly. This is because iron has a low specific heat, which is the amount of energy required to increase the temperature of one gram of a substance by one degree Celsius (or Kelvin). Solid iron only requires 0.45 J/(g*K), while liquid water holds about nine times as much energy (heat) per degree (temperature). So when water receives energy from the pot, it only warms up by a few degrees, while the pot cools down substantially.
| Temperature is the measure of the kinetic energy of a particle. Heat is energy, measured in joules (J). There is a very big difference between the two. |
Thermochemical Equations
Equations don't just show chemicals; they also show how much energy is required or released. This energy is called enthalpy. There are two ways to write a thermochemical reaction, for example:
Note that the number is negative in the second format. Also, notice how the first equation has double the energy because there are two moles of water. The second equation shows the amount of heat per mole, so the number of moles does not affect it.
From a thermochemical reaction, one can tell the molar heat of formation of a compound. Usually, this is measured at 25°C, and is written as ΔHf°. It is the amount of heat required to make one mole of the substance. The small ° symbol means "standard", as in Standard Temperature and Pressure.
Molar heat of combustion is the opposite of the molar heat of formation. It measures the amount of energy released when a mole of the compound is burned. It is written as ΔHc°.
In thermochemistry, if a reaction takes multiple steps, the heats from each reaction are simply added or subtracted. This is known as Hess's Law. |
Enthalpy
The enthalpy of a chemical system is the "heat content" of the system—the energy it contains. Enthalpy is represented by the symbol .
Enthalpy of Reaction
All reactions have some amount of enthalpy. It is simply the amount of heat absorbed or released by the reaction. Combustion reactions obviously release large amounts of heat. They have negative enthalpy. A negative enthalpy represents an exothermic reaction, releasing heat. A reaction that absorbs heat is endothermic. Its enthalpy will be positive, and it will cool down its surroundings.
Consider these two reactions:
| This reaction is exothermic (negative enthalpy, release of heat). When the reaction occurs, the surroundings will increase in temperature due to the gain of heat the system releases. For every mole of propane (C3H8) formed, 104.67 kilojoules of energy are released. | |
| This reaction is endothermic (positive enthalpy, absorption of heat). When the reaction occurs, the surroundings will decrease in temperature due to the loss of heat the system absorbed. For every mole of NO formed, 756.05 kilojoules of heat are absorbed. (Note that the reaction shows two moles being formed, so the enthalpy is double that of one mole being formed.) |
Although every reaction has a change in enthalpy, the amount depends on the temperature. The same reaction could be endothermic at one temperature and exothermic at another. Enthalpies must be given at a specific temperature. The reactions above show the enthalpies at 25 °C.
Temperature and Heat
There is a relationship between temperature and heat. If an object gains or loses heat without any phase changes, this reaction relates temperature to heat:
is the amount of heat (in joules or kilojoules) and is the change in temperature (Celsius degrees). is the mass of the object (in grams, usually) and is the object's specific heat.
Specific heat is a constant that depends on the particular material of the object. It is measured in joules per gram-degree. It is determined experimentally. You can look it up in a chart, or you can calculate it if you measure the amount of heat added and the change in temperature. The specific heat of water is 4.186 J/g-degree. For one gram of water, the temperature rises/falls by one degree Celsius for every 4.186 joules of heat added/removed.
Entropy
Entropy is the measure of disorder in a system.
An Example
First, let's examine a non-chemistry example. Say you have one card from a deck of playing cards. It can have one of 52 possible values. Now you pick up four more cards. If the deck were shuffled randomly, the odds of you holding, say, a "straight flush" are 0.00154%. The odds of having a "high card", which is essentially a "nothing" hand, is 50.12%. In the case of a straight flush, the cards you are holding are highly organized. They must be in a specific, exact pattern (like 10 9 8 7 6 of the same suit). To have a high card, no two cards must have the same rank and the cards cannot be in order.
There is a very low probability of having a straight flush because the cards are in a very orderly state. There is a large probability of having "nothing" because the cards are in a random, disorderly state. In our card-playing system, straight flushes have low entropy because they are so orderly. "Nothing" hands have high entropy because they are disorderly and random. Furthermore, it takes minimal effort to toss all the cards in the air and randomize their order. Increasing the entropy of the system comes naturally. On the other hand, sorting the cards in order takes time and effort. It does not happen randomly. Decreasing the entropy of the system is unnatural and takes effort, or energy.
In Chemistry
The entropy of a chemical system is a measure of its disorder or chaos. More precisely, it is a measure of the dispersion of energy. A solid has low entropy (low chaos, orderly) because the molecules are locked into a rigid structure. Their energy is not dispersed freely. A gas has high entropy (high chaos, disorderly) because the molecules are free to move about randomly. The energy of the system is dispersed over a large area with unlimited possibilities of the location of each molecule.
As temperature decreases, so does entropy. Theoretically, at absolute zero (0 K, or -273 °C), the entropy of the system would be zero. This is because the solid would be perfectly crystallized so that its energy is not dispersed at all.
As you will soon learn, the Second Law of Thermodynamics tells us that the entropy of the universe always increases. Think about it. If you have built a house of cards, the entropy of the system is low. A house of cards is very orderly, with each card having a very specific location. The house of cards will undoubtedly collapse. The resulting pile of cards is very disorderly. The cards can be in any position and still be a random pile of cards. The entropy has increased spontaneously. Houses of cards will spontaneously collapse, but they never spontaneously build themselves up. This is because high entropy is natural and low entropy is unnatural.
Entropy Changes
When analyzing the entropy change of a chemical reaction, you would need specific numbers. As a guideline, you can estimate the entropy change based on some basic rules:
- Melting and boiling increases entropy
- Freezing and condensing decreases entropy
- Dissolving a solute increases entropy
- Forming precipitates decreases entropy
If you do happen to know the absolute entropy of substances in a reaction (by looking it up in a chart), you can calculate the change in entropy. Entropy is symbolized with . The change in entropy is . As with enthalpy, the degree symbol () represents STP. The change in entropy is the absolute entropy of the products minus the absolute entropy of the reactants.
See also
- Entropy for beginners- a Wikibook that provides a mathematical explanation.
The First Law
The First Law of Thermodynamics is simply a restatement of the Law of Conservation of Energy. There are a few ways of stating it, but they all mean the same thing:
- "Energy is neither created nor destroyed. It can only change form."
- "The change in the system's thermal energy is equal to the heat added to the system minus the work done by the system."
The first definition is self-explanatory. As an example, a propane grill does not "create" energy when it cooks food. The energy stored within propane molecules and oxygen atoms is released in the form of heat and light when the propane molecules reassemble themselves into carbon dioxide and water (the combustion reaction). Energy has not been created or destroyed. It has simply changed from chemical potential energy into light and thermal energy.
The second explanation comes from a physics point of view. It means that adding heat to a system increases its internal energy, and a system that does work (like breaking bonds or assembling large molecules from small ones) decreases its internal energy. Overall, the total amount of heat, work, and energy remains constant. This should make sense because heat is energy and work is energy being applied, so based on the first definition, all forms of energy must be accounted for.
The First Law is much more useful in Physics than it is in General Chemistry. |
The Second Law
Introduction: A powerful law.
The second law of thermodynamics is based on our common human experience. It didn't begin with complicated apparatus or complex theories, but rather with thinking about how old-fashioned steam engines worked and the first important equation appeared to be very simple: just q/T.
Yet the second law is probably our most powerful aid in helping us understand why the world works as it does both in simple and in complex ways: why hot pans cool down, why ping pong balls don't bounce forever when they are dropped, why gasoline (plus the oxygen in air) makes engines run, why our "engines"—our bodies—run and we continue to live and our bodies stay warm even when it's cold, but also why we die when some chemical reactions within us fail. In fact, the second law helps to explain everything that happens in our physical world. In chemistry, it's especially important because it can tell us whether any chemical reaction that we write on paper will probably be spontaneous and go as we have written it.
The Big Problem
Unfortunately, for almost a century and a half, the second law has been expressed by experts in ways that a beginner in chemistry could not possibly understand without a great deal of additional explanation. Here are just three of some 25 explanations that have been most prominent:
- "The entropy of the universe increases toward a maximum" (Clausius)
- "It is impossible in any way to diminish the entropy of a system of bodies without thereby leaving behind changes in other bodies" (Planck)
- "In any irreversible process the total entropy of all bodies concerned is increased." (Lewis)
Entropy, entropy, entropy! But what is entropy? Even some textbooks still say something like "Don't ask about understanding it. Just work the problems that have entropy in them and you'll gradually understand it because you will be able to work with it"! That's the old way which fortunately has been discarded by most US general chemistry texts. (See list here.) The good news of the twenty-first century is that now entropy can be described as a simple idea (no matter how complex to calculate and deal with in advanced courses and research.) Because of our new conceptual approach, a basic version of the second law can be understood easily.
A Modern Version
"Energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy change is the quantitative measure of that kind of a spontaneous process: how much energy has flowed or how widely it has become spread out at a specific temperature." See here. |
What does that "energy of all types" and "becoming dispersed" mean? Let's first think about light (which technically is electromagnetic radiation). Does the radiation from a light bulb stay inside that glass of the bulb? Of course not. It spreads out just as far as it can, hindered from dispersing to miles and even farther only by dust or air density differences. What about the sound from a stereo speaker—does it stay inside a dorm room or a car? It disperses farther than other people want to hear it, usually! And what happens to the kinetic energy of a fast moving car if the car should hit a brick wall? It spreads out in a crashing sound, in twisting metal and heating it and tearing apart the bricks of the wall so that they fly around, slightly warmer than they were. Those are just a few examples of different types of energy and some ways in which they become dispersed or spread out.
Energy of all types disperses...if it is not hindered from doing so. |
The Importance of the Second Law
In chemistry, the type of energy in which we are most often interested is the kinetic energy of molecules, molecular motion energy. We know from Kinetic Molecular Theory that molecules are in constant motion if their temperatures are above 0 K. In gases like nitrogen and oxygen, they are moving at an average speed of a thousand miles (1600 km) an hour at 298 K and go about 200 times their diameter before bumping into another molecule [citation needed]. The molecules in liquids may be moving approximately as fast even though they are constantly hitting one another as they move a little here and there. In solids the particles, molecules or atoms or ions, can only "dance in one place" (vibrating in coordination with the other particles in the solid). This is a kinetic energy of vibration that is equivalent to the motion energy of gases or liquids at the same temperature.
The motion energy of molecules consists of their translation, rotation, and vibration (Figure 1 here.) Note that this vibration is vibration inside a molecule and by itself, as though the chemical bonds between atoms were like springs. The vibration in a crystal that we were just talking about is a vibration of a whole molecule or other particle in one place and coordinated with the other molecules in the crystal.
Examples from Everyday Life
Let's see how the second law helps us to understand our common experience better, to see how so many totally different events really are just examples of energy dispersing or spreading out, i.e., of the second law. A rock will fall if you lift it up and then let go. Hot frying pans cool down when taken off the stove. Iron rusts (oxidizes) in the air. Air in a tire is at a high pressure and shoots out even from a small puncture to the lower pressure atmosphere. Ice cubes melt in a warm room.
A Falling Rock
A rock has potential energy (PE) localized in it when you lift it up above the ground. The rock is the system; everything else it encounters is the surroundings. Drop the rock and its PE changes to kinetic energy (energy of movement, KE), pushing air aside as it falls (therefore spreading out the rock’s KE a bit) before it hits the ground, dispersing a tiny bit of sound energy (compressed air) and causing a little heating (molecular motion energy) of the ground it hits and in the rock itself. The rock is unchanged (after a minute when it disperses to the air the small amount of heat it got from hitting the ground). But the potential energy that your muscles localized in by lifting it up is now totally spread out and dispersed all over in a little air movement and a little heating of the air and ground.
A Hot Frying Pan
A hot frying pan? The iron atoms in a hot frying pan (system) in a room (surroundings) are vibrating very rapidly, like fast "dancing in place". Therefore, considering both the pan and the room, the motion energy in the hot pan is localized. That motion energy will disperse—if it is not hindered, according to the second law. Whenever the less rapidly moving molecules in the cooler air of the room hit the hot pan, the fast-vibrating iron atoms transfer some of their energy to the air molecules. The pan’s localized energy thus becomes dispersed, spread out more widely to molecules in the room air.
Some Rusting Iron
In a chemical reaction such as iron rusting, i.e., iron plus oxygen to form iron oxide (rust), the reactants of iron and oxygen don't have to be at a high temperature to have energy localized within them. Iron atoms (as -Fe-Fe-Fe-) plus oxygen molecules of the air (O-O) have more energy localized within their bonds than does the product of their reaction, iron rust (iron oxide).
That’s why iron reacts with oxygen—to release energy from their combined total of higher energy bonds and form the lower energy bonds in iron oxide. Then, all that difference in energy becomes dispersed to the surroundings as heat i.e., the reaction is exothermic and makes molecules in the surroundings move faster. But remember how chemical reactions occur! Remember that it requires energy to break bonds and therefore to start any reaction there must be some extra energy, an activation energy supplied somehow to break a bond or many bonds in the reacting substances. (For information about activation energies, see here.) Then, if the bonds that are being formed in the product are much stronger than those being broken in the reactants, that difference in energy (which usually causes greater motion energy of all the molecules) can feed back to break more bonds in the reactants.
However, in the case of iron reacting with oxygen at normal room temperature around 298 K, the process is very slow because only a few oxygen atoms are moving exceptionally fast and hit the iron just right so an Fe-Fe bond and an O-O bond are broken and an Fe-O bond can form. There isn't enough heat (motion energy) localized in nearby iron atoms, and there are no other unusually fast-moving oxygen molecules. It's a slow process depending on collision of the small amount of fast moving oxygen atoms in the surroundings to make it happen.
Therefore, even in moist air (that speeds up another process yielding iron oxide), iron doesn't react very rapidly with oxygen but it steadily does so and in time, both the iron atoms and the oxygen molecule spread out to the surroundings the portion of their bond energy that iron oxide doesn't need for its existence at that temperature.
A Leaky Tire
Air in a tire is at a higher pressure than the atmosphere around it, so it shoots out even from a small hole. What could that have to do with a big deal like the Second Law of Thermodynamics? (Every spontaneous physical or chemical process involves the second law!) Those nitrogen and oxygen molecules in the tire each have motion energy but it is far more localized, compressed in the small volume of the tire, than it would be in the huge volume of the atmosphere. Thus, the second law explains why punctures or blowouts occur: the motion energy of those localized molecules will become dispersed and spread out to the lower-pressure, larger-volume atmosphere if it is no longer hindered by the tire walls from becoming so.
A Melting Ice Cube
An ice cube melts in a big warm room. How can the melting of a little ice cube in a warm room maybe 200,000 times bigger than it is be an example of the second law? How could that possibly be a spreading out of energy? But the second law has to do with energy dispersal and there's a little spreading out in that 200,001st part of that total of system plus surroundings!
Hotter goes to cooler spontaneously. Always. |
Lots of things are happening when molecules of the warm air disperse some of their energy to the molecules that are vibrating (like dancing rapidly in one place) in the ice cube. Right at the surface many hydrogen bonds between the water molecules of the ice are broken by the motion energy of the air molecules being transferred to the those surface molecules. (This doesn't change the amount of motion energy of those molecules and therefore their temperature doesn't change. They increase in potential energy due to the hydrogen-bond breaking.) Now, because the water molecules whose hydrogen bonds to other molecules in the rigid ice structure are broken, they are free to form hydrogen bonds to other water molecules that are liquid—they can exchange partners and move from one to another. The vibrational energy that allowed them to dance in place in the crystal is changed to translational energy in the liquid and the molecules can move just a bit.
Thus, although the true picture is just a bit more complex (i.e., it is the closer energy levels in translation than in solid vibration that make the energy far more dispersed in liquid than solid), we can sense that the movement of molecules in liquid water allows the energy to be more spread out than in crystalline ice, even at melting temperature. It is not a matter of order and "disorder"! (That's as misleading as magic and as obsolete as 1898 fashions. See here.)
Order to Disorder
The second law tells us about energy dispersal, and entropy is the word for how that energy dispersal is measured—how spread out the energy becomes in a system, how much more dispersed it has become compared to how localized it was. Such energy changes and consequent entropy changes are the focus for understanding how and why spontaneous events occur in nature. Only sometimes do the structures or arrangements of molecules in an object help us to see greater or lesser localization of energy (that used to be called "order to disorder").
Now we can understand what scientists have been talking about the last century and a half when they spoke in apparently mysterious sentences like "The entropy of the universe increases toward a maximum." All they meant was simply that energy, everywhere, spreads out as much as it can (and that spreading out of energy is measured by entropy).
Recap and Conclusion
Rocks falling down mountains, hot pans cooling in cool rooms, anything made of iron rusting, anything burning or reacting with oxygen, all these types of spontaneous events and chemical reactions that occur by themselves are due to energy dispersing or spreading out. Entropy is the quantitative measure of how much energy and how much dispersal occurs in a process or a reaction. Therefore, entropy is constantly increasing because spontaneous events continue to occur in our energy-rich universe. Thus, we can decipher the following statement of the second law:
"In any irreversible process the total entropy of all bodies concerned is increased."
That just means: "In any process in which energy becomes spread out, the measure of that spreading out or dispersing (i.e., the total entropy) increases when you include both what happens in the system AND its surroundings.”
Now we can translate "second law language"! It seems very confusing if you read it rapidly, but taking it a few words at a time and knowing what we have just reviewed, the ideas are not complicated.
Free Energy
Introduction
What's the point of entropy and enthalpy? So far, you have studied equilibrium to tell you how far a reaction occurs and kinetics to tell you how fast a reaction occurs. Thermodynamics can tell you if a reaction will occur, and at what temperatures. It may seem too obvious, but why does an ice cube spontaneously melt when it is at 30 °C? Melting is endothermic, so it would seem that the reverse reaction (freezing) is favored. After all, reactions that release heat are usually more favorable than those that absorb heat.
The answer is free energy (also called Gibbs Free Energy). The change in free energy for a reaction ultimately determines if it can occur spontaneously or not. Free energy is a combination of entropy and enthalpy, and when a reaction decreases the free energy, it will occur spontaneously.
The Equation
Free energy is defined by . By measuring or calculating the entropy change and enthalpy change of a reaction, you can determine the change in free energy. Notice that free energy depends on temperature as well. In this equation (as with all other thermo equations) must be an absolute temperature, measured in Kelvin. So the freezing point of water is not zero but rather 273 K. By using the Kelvin temperature scale, all temperatures will be greater than zero.
When you have solved for for a particular reaction at a certain temperature, you will find one of three possible outcomes:
| Reaction type | Means... | |
|---|---|---|
| exergonic | the reaction occurs spontaneously. | |
| the reaction is at equilibrium. | ||
| endergonic | the reaction will not occur. | |
Equipped with this knowledge, you can determine the temperature at which a reaction will be at equilibrium (by setting G to 0 and solving for T). If a reaction is endergonic, it will not occur spontaneously. However, at a different temperature, the reaction might occur. Also, the reverse reaction will have an opposite value for G. For example, the combustion of propane will have a large negative value for its change in free energy. The reverse reaction would have the same large value, but positive. This makes sense, knowing that propane does not spontaneously precipitate from the smokey exhaust of a grill.
Spontaneity
Let's return to the example of a melting ice cube. At T = 273 K (0 °C) the processes of freezing and melting are at equilibrium. ΔG must equal zero. At higher temperatures, the melting process occurs spontaneously, so we can deduce that ΔH is positive and ΔS is also positive. We already know that melting is endothermic and increases entropy, so it seems the free energy equation works.
Between entropy and enthalpy, there can be four possible outcomes:
| Result | |||
|---|---|---|---|
| + | - | always + | never spontaneous |
| - | + | always - | always spontaneous |
| + | + | + for low T, and - for high T | depends on T |
| - | - | - for low T, and + for high T | depends on T |
We can see that the melting of an ice cube is spontaneous for high temperatures.
Relating Free Energy
Free energy is related to equilibrium, as we have already seen. There is an equation that will allow you to convert between reaction free energy and the equilibrium constant for a particular reaction at a given temperature:
is the Universal Gas constant, and is the natural logarithm. A scientific calculator will have a [LN] to calculate logarithms and a [e^] button to calculate anti-logarithms.
The Elements
Group 1
Alkali Metals

The alkali metals are the elements in Group 1 (1A). They are lithium, sodium, potassium, rubidium, cesium, and francium.
These elements are best marked by their reactivity. Physically they are soft, shiny (when freshly prepared) solids with low melting points; they conduct electricity well. They all have one valence electron that they lose easily to almost any electronegative substance. Alkali metals are never found in their elemental form outside the lab because they are too reactive. Even the smallest amount of oxygen or water would react with the metal. For this reason, alkali metals have no structural use. They must be kept under inert liquids such as kerosene or in inert gases (nitrogen suffices for any of these elements other than lithium).
Alkali metals have many uses in both biological life and industry. Francium, however, is radioactive and decays rapidly to other elements, so it has no commercial use and its chemical properties are vaguely understood.
All oxidize easily to the +1 oxidation state.
The alkali metals have very similar chemical and physical properties. They can be studied as a whole, rather than element-by-element, due to this similarity. |
Safety
Leave experiments with alkali metals to the experienced chemists. These metals are also highly toxic and will result in severe harm if ingested or make to contact skin.
Alkali metals are dangerous. Their reactions release enough heat to cause flames, and may produce explosive byproducts like hydrogen gas. Never cast any alkali metal into water or acids. These metals should never be allowed to touch flesh because they react with any water upon them and yield corrosive hydroxides that damage flesh. |
Reactions
Alkali metals react violently with water, halogens, and acids. The reactions release surprising amounts of heat and light. In a chemical equation, alkali metals are represented with an M. Here are some example equations:
| Alkali metals react with oxygen to form oxides, which have a duller appearance and lower reactivity. The oxides are much less reactive than the pure metals. | |
| However, the oxides do react vigorously with water to form a hydroxide. The resulting hydroxides of these elements dissociate completely in water to form some of the strongest bases known. "Lye" is an industrial-strength base, which is sodium hydroxide (NaOH). | |
| These hydroxides react readily with acids to form water and their corresponding alkali salt in a neutralization reaction. | |
| The pure alkali metal can also react directly with water. In this case, the metal is a basic anhydride. Gaseous hydrogen is released, which is flammable. | |
| Exposing an alkali metal to a halogen will cause an extremely exothermic reaction that results in an ionic salt. |
Almost every salt of an alkali metal is highly soluble in water. They form conducting solutions, proving their ionic nature.
Flame Tests
When burned in a flame, the alkali metals give off a unique color that can be used to identify them.
- Flame Tests
-
Lithium (pinkish-red flame)
-
Sodium (yellow flame)
-
Potassium (pale violet flame)
Group 2
Alkaline Earth Metals
They are less reactive than alkali metals, but they form (except for beryllium) alkaline oxides and hydroxides.
Alkaline earth metals all have two valence electrons, and they easily oxidize to the +2 state. With increasing mass, these elements become softer, have lower melting and boiling points, and become more reactive. None appear uncombined in nature, and all are separated from their compounds with difficulty. Alkaline earth metals react with halogens and (except for beryllium) with water and oxygen. Magnesium, being less reactive, reacts only at higher temperatures than the other alkaline earth metals. Radium is radioactive, so its chemical properties are difficult to study.
The alkaline-earth metals have very similar chemical and physical properties. They can be studied as a whole, rather than element-by-element, due to this similarity. |
The alkaline earth metals are chemically and physically similar to the alkali metals, but they are less reactive.
Alkaline earth metals are very flammable. Their reactions could release enough heat to cause flames, and may produce explosive byproducts like hydrogen gas. Use caution when handling these metals. Calcium, strontium, and barium react with water and form corrosive hydroxides. Salts of beryllium are toxic, and water-soluble or acid-soluble salts of barium are toxic. |
Reactions
The alkaline earth metals undergo reactions similar to the alkali metals, but their +2 oxidation state causes their compounds to be different. The following reactions use magnesium as an example, but the other alkaline earth metals undergo the same reactions as well.
| Magnesium oxide forms slowly unless ignited. Powders or thin slices of magnesium can be ignited with a match, so magnesium is used in fire-starting devices. | |
| Magnesium burns readily in oxygen, and surprisingly nitrogen as well. Air is composed mostly of nitrogen, but most elements will not react with nitrogen because nitrogen is so stable. | |
| Magnesium oxide is a basic anhydride. Magnesium hydroxide is a strong base, although its solubility is too low for this property to be significant. | |
| Magnesium nitride will react with water or the moisture in air. This reaction is detected by the pungent smell of ammonia. | |
| Magnesium metal reacts with water to form a hydroxide, but only at high temperatures or in the presence of acid. Calcium, being more reactive, will react with water as long as its hot. The other elements will react in warm water. Notice the flammable hydrogen gas that is released. | |
| Magnesium will react exothermically with acids to form an ionic salt and hydrogen gas. |
Remember that all of the alkaline earth metals can undergo these reactions; magnesium was just an example. Beryllium, however, is much less reactive than the other metals, so it might not react.
Uses
Beryllium is rare and its compounds are very toxic, which makes processing it something limited to specialists trained in dealing with it safely. It is the lightest element that is sturdy enough to be used for construction and it is used for windows of X-ray tubes. Its absorption of X-rays is very small, because it only has 4 electrons per atom.
Magnesium metal has some use in applications needing a soft, light metal. Magnesium metal can be used an easily-burned substance with a bright light in photographic flash bulbs. Magnesium hydroxide is commonly used as a strong but generally safe antacid. Magnesium sulfate is commonly known as Epsom salts.
Even more significantly, magnesium appears in a compound known as chlorophyll, the greenish pigment in plants and algae that allows plants to perform photosynthesis. It is essential to plant life.
Calcium has no use as a structural metal, but its compound calcium carbonate is a major building material as limestone. Calcium carbonate is essential to bones and to plant life. Calcium and heavier elements in this group react with warm water to form highly-alkaline hydroxides.
Strontium, much rarer than calcium, has few uses. Barium, also rarer, has few uses other than its sulfate, a coating used for lining the digestive organs for X-rays (Barium meal). Compounds of barium soluble in either water or acids (but not the sulfate) are highly toxic.
Radium is rare and strongly radioactive; it is extremely dangerous due to its intense radioactivity.
Group 13
Group 13 (IIIA) consists of boron, aluminum, gallium, indium, and thallium. Boron is a metalloid, but the other elements are metals. All elements in this group have three valence electrons.
Because these elements have varying properties, they will be studied element-by-element, rather than as a group. |
Boron


Boron is a metalloid, exhibiting characteristics of both metals and non-metals. It is never found in its pure form in Earth, but it is a component of some minerals. However, pure boron can form as a result of chemical reactions. It can be a brown amorphous solid, or a crystalline solid. In the crystalline form, it is black and very hard.
Boron is a poor conductor of electricity at normal temperatures, but at high temperatures it does conduct electricity. Its chemical properties are mostly, but not entirely, non-metallic. Boron is the least electronegative non-metal, so it readily loses electrons when reacting. Boron is almost entirely in the +3 oxidation state. Boron has an oxide B2O3, and it is acidic.
| Boric halides are volatile substances that attack water with the formation of boric acid B(OH)3 and hydrogen halides. | |
| Boric acid reacts with water to release a proton. It is a weak acid. | |
| Boric oxide, at extremely high temperatures, can react with carbon to form boron carbide. Boron carbide is incredibly strong, finding use as tank armor. |
In a manner similar to carbon, boron can form stable covalent network solids. Each boron atom bonds to three other borons, forming a large crystal. |
Boron has interesting properties when it bonds covalently. It has three electrons, so it usually forms three single covalent bonds, an exception to the octet rule. Substances like boron trichloride (BCl3), boric acid, and the borate ion (BO33-) are examples of boron's tendency to form three covalent bonds.
Aluminum
Aluminum (British spelling aluminium) is a metal, although it is too reactive to exist in pure form. Instead, it is found in a wide variety of minerals including bauxite, the primary source for extracting aluminum. Aluminum is the third most abundant element in Earth's crust.

Unlike boron, aluminum is an almost stereotypical metal in its physical properties: it is malleable and ductile, and it conducts heat and electricity very well. Because of its lightness, resistance to corrosion, attractiveness (approaching that of silver), and inexpensiveness to process along with adequate strength for many commercial and domestic uses, it is the third-most used of all metals. Only iron and zinc exceed it in production.
Aluminum compounds typically exist in the +3 oxidation state. Because of its durability and light weight, aluminum is used in many alloys, mixtures of metals. Two metals, each with desirable characteristics, can be mixed together to produce an alloy that has the properties of both metals. Aluminum used to be used for household wiring, but it expands too much when heated. The expansion causes the wires to come loose, and house fires can start.
Aluminum seems unreactive because of a thin, hard surface of aluminum oxide Al2O3 which does not react with water or oxygen and preserves the aluminum metal underneath it from chemical attack. Pure aluminum will immediately form this layer when exposed to air. Although aluminum is very conductive, aluminum oxide does not conduct electricity.

|
|
Aluminum oxide is amphoteric—it reacts violently to neutralize strong bases or strong acids. |
| Reacting aluminum with a halogen results in an aluminum halide. Aluminum chloride can exist as an ionic solid or a covalent solid, but either way it is a weak conductor. | |
| Aluminum chloride is a Lewis acid, able to neutralize bases. | |
| Molten aluminum reacts violently with some metal oxides in the thermite reaction, in which a substance like iron oxide is reduced to iron and aluminum is oxidized to its oxide. This is a highly exothermic reaction, releasing enough heat to weld metal. |
Generally, aqueous aluminum is found as a hydroxide Al(OH)3.
Others

Gallium is a brittle metal that melts slightly above room temperature, so holding it in your hand would liquefy it. One magic trick, the 'melting spoon' involves stirring a hot liquid (usually hot water) with a spoon specially made of gallium. The spoon melts in the water and 'disappears'. (The gallium simply sinks to the bottom of the cup; after the magic trick is done the 'magician removes the water and the molten gallium and pours the gallium into a mold that makes a new spoon for doing the trick again). Gallium is used in many semiconductor devices and LEDs (light emitting diodes). Gallium(III) arsenide is an important semiconductor used in many electronics.
Indium's most common isotope is radioactive and decays slowly into tin. Indium typically has the +3 oxidation state.
Thallium tends to appear in the +1 (thallous) oxidation state as well as the +3 (thallic) oxidation state. Oddly, thallium acts much like an alkali metal in its physical and chemical properties. Thallous oxide (Tl2O) and the metal react violently with water to form a hydroxide TlOH that completely dissociates into Tl+ and OH- ions as if it were an alkali metal hydroxide. Its halides are quite salt-like, dissociating into ions into solutions that, like solutions of salts of the alkali metals, conduct electricity.
Thallium has a violent reaction with water that could release enough heat to cause flames, and may produce explosive byproducts like hydrogen gas. Thallium hydroxide that results from this reaction is as strongly alkaline as alkali-metal hydroxides and is similarly corrosive. In addition, thallium compounds are extremely toxic. |
Neither thallium metal nor any thallium compound is readily available in the United States because it is so dangerous and has few legitimate uses.
Group 14
The Carbon Family
Group 14 (IVA) consists of carbon, silicon, germanium, tin, and lead. Carbon is a non-metal, silicon and germanium are metalloids, and tin and lead are metals.
With 4 valence shell electrons, elements of the carbon family tend to form covalent compounds. With increasing mass and atomic radius these elements become increasingly metallic and have lower melting and boiling points.
Group 14 elements form gaseous hydrogen compounds with difficulty. These are either unstable or combustible. All but lead form oxides, sulfides, and halides in the +4 oxidation state. The +4 oxidation state predominates in carbon, silicon, and germanium; the +2 and +4 oxidation states both appear in tin, and the +2 oxidation state prevails in lead. Halides in the +4 state form for all of these elements, and they are covalent.
Carbon compounds are much more covalent than analogous compounds of silicon, germanium, tin, or lead. Even more significantly, carbon forms double and even triple bonds with itself or other elements, forming compounds that the heavier elements of this group cannot form like acetylene (C2H2). Silicon and the heavier elements of this group can form only single bonds.
Thus carbon dioxide CO2 is a gas at normal temperatures because the double bonds between carbon and oxygen create single molecules, but silicon dioxide SiO2 forms a hard rock known as quartz because it is a covalent network solid. Each silicon atom bonds to four different oxygen atoms with single bonds, and each oxygen atom bonds with two silicon atoms. Similar properties apply to the oxides of germanium, tin, and lead. Carbon dioxide dissolves in water to form carbonic acid, a weak acid that reacts with bases to form carbonates; oxides of the other elements of this group are practically nonreactive in water.
Because of its unparalleled importance in chemistry, carbon is the main focus of our study of the Group 14 elements. |
Carbon
Carbon is a very important element. It is abundant in the earth and atmosphere, and it is found in the substances that make all living things. Carbon has many properties that make it different from other elements, so it deserves thorough study.
Allotropes

Allotropes are different forms of a pure element. Carbon has several allotropes, three of which are common.
- Amorphous carbon is coal and soot. The carbon molecules are covalently bonded, but there is no order or arrangement.
- Graphite occurs when carbon forms flat covalent networks. These flat "sheets" are not bonded to each other, making them free to slide past each other. Graphite composes the "lead" in pencils.
- Diamond occurs when carbon forms a three-dimensional covalent network. Diamonds are much different from graphite and amorphous carbon. They are transparent, brilliant-looking, and incredibly hard. Diamond only forms at heat and intense pressures.
There are also several rare and exotic allotropes of carbon, including:
- Buckeyballs, or fullerenes, are spherical shaped balls of carbon. Covalent bonds join the carbon atoms into a soccer ball pattern that looks much like the geodesic domes of Buckminster Fuller. The most common buckeyball has the molecular formula C60. Buckeyballs are large enough for a small atom to get trapped inside.
- Lonsdaleite forms upon meteorite impact with the Earth.
- Carbon nanotubes are incredibly small but rigid tubes made of carbon. They are created in labs and are a subject of research.
Keep in mind that allotropes are composed of only one element. In this case, these allotropes contain only carbon atoms and no other elements.
Inorganic Compounds
Although carbon is known mainly for its organic compounds, it does form many important inorganic compounds.
Oxides
Oxides of carbon contain only carbon atoms and oxygen atoms. There are two oxides that occur commonly:
- Carbon monoxide (CO): a poisonous gas released when carbon-based fuels burn in limited oxygen.
- Carbon dioxide (CO2): found naturally in the air, but too much is considered pollution. Animals exhale carbon dioxide, and plants absorb it. It is slightly acidic. Carbon dioxide, when solid, is "dry ice".
There is other oxides that could form, but they are unstable or unnatural:

- Carbon suboxide (C3O2): Consists of double bonds, with oxygens at the ends. O = C = C = C = O. It breaks apart into carbon dioxide and dicarbon monoxide.
- Dicarbon monoxide (C2O): Very reactive. Contains only double bonds, but the end carbon has a non-bonding pair.

- Carbon trioxide (CO3): Exists in three different shapes, very unstable
Compounds Derived from Oxides
Carbonic acid forms when carbon dioxide is dissolved in water. It is given by the reaction:

Carbonate and bicarbonate are two ions that carbon forms.
Their formulas are CO32- and HCO3-, respectively.
Ionic Compounds
Along with the oxyanions (carbonate and bicarbonate), carbon can form several other ions.

- Cyanide (CN-)
- Cyanate (OCN-)
- Thiocyante (SCN-)
- Carbides (C22- and C34-)
Hydrogen cyanide is an extremely-dangerous gas which causes death from interference with cellular metabolism. It has been used in executions and mass murder, most infamously in the Holocaust. |
Alloys
Carbon is used in some alloys, mixtures of metals. If a small amount (between 0.2% and 2.1% by weight) of carbon is mixed into iron, the result is steel.
Organic Compounds

Compounds containing carbon (except for the above inorganic compounds) are considered organic. They were once thought to be produced only by living things, but they have since been created in laboratories. Most organic compounds contain hydrogen as well as carbon.
Many substances are organic compounds. Polymers are organic compounds consisting of long chains of repeating patterns containing carbon and other atoms. Plastics, rubbers, and nylon are all organic polymers. Hydrocarbons are compounds containing only hydrogen and carbon, methane being a simple example. Crude oil is a sludge of various hydrocarbons mixed together. Propane, butane, and octane are well-known hydrocarbons used for fuel. Perhaps the most interesting type of organic compound is the biomolecule. Carbohydrates, proteins, lipids (fats), and nucleic acids (like DNA) are the most basic biomolecules. They, too, are polymers (except for lipids), being made of long chains of small, repeating chemicals that have bonded together. Biomolecules make up the chemicals found in the living cells that compose all living things.
Organic chemistry and biochemistry are very broad and thorough topics. They are far outside the scope of General Chemistry. Fortunately, your knowledge of General Chemistry is sufficient to begin the Wikibooks Organic Chemistry and Biochemistry if you are interested.
Silicon

Silicon is found in semiconductors, the basis of all electronic devices. Its electron configuration allows it to donate or accept electrons. When pure silicon is "doped" with elements that have more or fewer electrons than silicon, the slightly-impure silicon becomes a semiconductor. These substances make up complex electronics by acting like a switch that can turn on or off depending on electrical signals.
Silicon does not exist uncombined in nature; it most commonly occurs in silica (including the very common rock quartz and most sand grains) and in silicates. Most silicates are insoluble. So-called 'magic rocks' react with dissolved sodium silicate in water reacts with the ions of some dissolved metal salts to form columns of rock-like silicates.
Silicon dioxide, a hard substance that melts only at high temperatures, is very different in its chemical properties from carbon dioxide, a gas until it freezes into dry ice. Molten silica can be cast as glass, a hard and useful material resistant to attack by almost all chemicals except fluorine, hydrofluoric acid, and strong alkalis. Glass is extremely useful in household containers and drinking utensils because it is resistant to chemicals, heat, and the attack of micro-organisms. Glass can be very clear if pure or containing certain chemicals, or it can take on attractive colors, making it a favorite material for art objects. Some small living creatures turn dissolved silica in the sea into their shells to create structure. A great variety of silicon compounds known as silicones have widespread and varied uses.
Silica is not strictly a poison, but as an abrasive it can damage tissues if eaten or breathed by grinding against them. Asbestos, a silicate (and derivative of silica) breaks down to silica especially in lungs and does great damage. |

Others
Germanium is another element used in semiconductors. Before transistors were in common use, germanium diodes were heavily used in radios.
Tin is considered a "poor metal". It has two allotropes at STP: grey tin and white tin. Grey tin has non-metallic characteristics, but white tin is metallic. Tin is used frequently as an alloy. "Tin cans" are actually steel cans with a tin plating to resist corrosion. Pewter is an alloy of copper and tin, containing mostly tin. Bronze is an alloy of copper and tin containing mostly copper. Solder is an alloy of tin and lead used for its low melting point for attaching wires.
Lead is a heavy, gray metal. It had a tremendous number of uses, but it is now known to be a neurotoxin if ingested. Water-carrying pipes were made out of lead, but they are now made from copper or plastic because lead could contaminate the water. Lead compounds especially if soluble in water (like lead acetate used as a preservative and sweetener of wines in Roman times) or stomach acids (like the lead oxide once used in paints) or in gaseous or liquid form (like tetraethyl lead once used in gasoline), and powdered lead are very dangerous. Use of lead in foodstuffs, paint, and vehicle fuels is now illegal almost everywhere.
Lead compounds and vapors are insidious poisons that accumulate in the brain and create learning disabilities and personality disorders. |
Lead-crystal glass has lead oxide in it but so tightly bound with silica that it can't escape easily. Pencil 'leads' are not lead at all, but instead harmless graphite (really carbon) bound with clay. Lead remains useful in automobile batteries (that contain necessary sulfuric acid much more dangerous than lead) and in nuclear use as a shield against radiation much more dangerous than lead metal.
| Lead oxides are easily reduced. | |
| Lead does not dissolve in hydrochloric acid or sulfuric acid, but it will dissolve in nitric acid because nitric acid is a strong oxidizer. | |
| Lead(II) oxide will form plumbite ions when added to basic solutions. | |
| Plumbites form lead(IV) dioxide when chlorinated. | |
| Adding lead(IV) dioxide to a basic solution will form plumbate ions. |
Group 15
The Nitrogen Family
Group 15 (VA) contains nitrogen, phosphorous, arsenic, antimony, and bismuth. Elements in Group 15 have five valence electrons. Because the elements can either gain three electrons or lose five to gain a stable configuration, they more often form covalent compounds unless bonded to an active metal. Their electron affinities are not very large. Metallic properties increase markedly from gaseous nitrogen to barely-metallic bismuth with increasing size and mass. Nitrogen and phosphorus are non-metallic, and arsenic and antimony are metalloids.
Elements of this group are known as pnicogens and their compounds as pniconides. The name is derived from from the Greek word pnicomigs meaning suffocation.
The Group 15 elements are unique enough to be studied individually, rather than as a group. |
These elements are much less reactive than the elements of Group 16, and their chemistries are more complicated. Most of the chemistry of these elements is in the +3 or +5 oxidation states, although they form gaseous compounds with hydrogen in the -3 oxidation state: ammonia NH3, phosphine PH3, arsine AsH3, stibine AsH3, and bismuthine BiH3; these all burn in oxygen to give oxides or the free element (in the case of nitrogen).
All form oxides—nitrogen with difficulty, the others with ease. Most of the oxides are acidic, exceptions being nitrous oxide N2O, nitric oxide NO, and bismuth oxide Bi2O3. Except for nitrogen, typical oxides are in the +3 or +5 (bismuth excluded) oxidation states. All form halides—nitrogen with difficulty, but those of phosphorus, arsenic, and antimony fully hydrolyze in water.
Nitrogen and phosphorus form important acids in the +5 oxidation state. Nitrogen forms nitric acid HNO3, a substance used to create medicines and explosives (but this acid is corrosive and dangerous, so don't touch it or even spill it on anything), and salts known as nitrates such as potassium nitrate KNO3, an important fertilizer. Phosphorus forms phosphoric acid, H3PO4; phosphates are salts of phosphoric acid. Some phosphates are essential to respiration and thus life itself. General covalency of nitrogen family is 3.
Nitrogen

Nitrogen occurs naturally as the diatomic gas N2. It comprises about 78% of the air we breathe. The bond holding the two nitrogen atoms together is triple covalent, so it is very strong. Because of that, nitrogen is very unreactive. It is used in many places when an inert gas is needed. However, nitrogen will react with some substances:
|
Although nitrogen gas is usually considered inert, it does react with some elements by burning. |
|
The nitrides react violently with water to form ammonia gas and a basic solution. |
In its pure form, nitrogen is not very useful, and it will suffocate any animal that breathes pure nitrogen. It is much more important when it is a component of ammonia, nitrate, oxides, or biomolecules like protein. Due it is very unreactive nature, it is difficult to get nitrogen to react and form these useful substances. Any process that can convert elemental nitrogen into a nitrogen compound is called nitrogen fixation. Nitrogen fixation is biologically important because amino acids, proteins, and enzymes contain nitrogen. It is commercially important because it is used in explosives, rocket fuels, and fertilizers.
There are many nitrogen fixation reactions:
| This occurs in bacterial enzymes. The ammonia (NH3) quickly becomes ammonium (NH4+). The nitrogen in the bacteria enters the soil where plants can absorb it. Humans and animals that eat those plants can get the nitrogen in useful compounds. | |
| The Haber process is used for commercially producing ammonia. This reaction only occurs at very high pressures and temperatures (around 20 MPa and 500 °C) and in the presence of an iron catalyst. Also, the reaction occurs in somewhat complex equipment that must input pure reactants and extract the ammonia.
|
In the cold, dense, hydrogen-rich atmospheres of Jupiter, Saturn, Uranus, and Neptune, nitrogen ordinarily exists combined with hydrogen as ammonia.
Keep in mind that ammonia is a gas at STP. The household product called "ammonia" is actually an aqueous solution of ammonium hydroxide (NH4OH) that forms when ammonia gas is dissolved in water. Ammonia, quite unlike hydrogen compounds of Groups 16 and 17, is a base in its reactions, forming salts with weak and strong acids alike. Such a substance as ammonium chloride (NH4Cl) is a soluble, strongly ionic salt.
Nitrogen compounds are often extremely unstable because nitrogen atoms in nitrogen compounds tend to seek each other to recombine as nitrogen gas. Many nitrogen compounds are literal explosives, including TNT and nitroglycerin. These explosives are in common use in construction projects for the demolition of buildings and other obstacles to new construction, or to get access to minerals in mining operations.
Handling of any explosive or making them is appropriately left to experts. |
Phosphorus

Phosphorus has two common allotropes: red phosphorus and white phosphorus. White phosphorus (P4) has a waxy appearance and turns yellow when exposed to light. When exposed to oxygen in the dark, it glows pale green.
White phosphorus is extremely dangerous. It causes severe burns and is very toxic. It ignites with a very hot flame and can be explosive. Leave all experiments with white phosphorus to experienced chemists |
.
White phosphorus ignites under all but the most delicate conditions. The combustion of white phosphorus produces phosphorus(V) oxide:
One of its most common uses is in military weapons that cause severe burning of the object hit by the weapon.
Red phosphorus is an amorphous solid. It is more stable and explodes at temperatures higher than those of white phosphorus. It is still, however, dangerously reactive. Both forms of phosphorus are insoluble in water and can be interconverted with various applications of heat, pressure, and light.
There also exist black phosphorus and violet phosphorus. Unlike nitrogen, phosphorus will not readily form a diatomic molecule with a triple bond. Diphosphorus does exist, but only between a temperature range of 1200 °C and 2000 °C.
Phosphorus pentoxide strongly reacts with water to form phosphoric acid, a substance that removes rust from iron, especially on ships; it is often known as "naval jelly". But phosphoric acid is corrosive to flesh and not to be touched.
Phosphorus is essential to life in the form of phosphates in bones and in substances known as ADP and ATP that transform food into useful energy in cells.
Others

Arsenic is similar to phosphorus. It has three allotropes: grey arsenic, yellow arsenic, and black arsenic. Grey arsenic is the most common form. Its structure is similar to graphite.
Antimony does not have physical properties of a metal, but behaves chemically as a non-metal.
Arsenic and antimony, as well as practically all of their compounds, are dangerous poisons. |
Bismuth is a brittle, silvery metal. Bismuth is actually radioactive, decaying into thallium-205. Because its half-life is 19 x 1018 years, about a million times the age of the universe, bismuth is usually considered stable.
Bismuth is much less radioactive than the nearly-harmless and unavoidable radioactive isotopes of carbon and potassium in living things. Unlike arsenic and antimony, its compounds aren't toxic unless something else in the compound is itself toxic or the substance is very acidic or alkaline. In fact, a bismuth compound is very common in a heavily-used stomach medication that requires no prescription.
Group 16
The Oxygen Family
Group 16 (VIA) consist of oxygen, sulphur, selenium, tellurium, and polonium. They are often referred to as the chalcogens and their compounds as the chalcogenides, although these names are seldom applied to oxygen and its many compounds. Oxygen, sulphur, and selenium are non-metals. Tellurium is a metalloid and polonium is a metal.
Group 16 elements have 6 valence electrons, meaning that they require two more electrons to complete a stable electron octet. They still have relatively large electron affinities and are rather reactive, forming ions with a -2 charge. All form volatile compounds with hydrogen: water H2O, hydrogen sulphide H2S, hydrogen selenide H2Se, hydrogen telluride H2Te, and polonium hydride PoH2.
Electronegativity decreases in this group with increasing atomic mass, and oxygen is more electronegative than any element except fluorine; it acts much like a halogen except for its -2 oxidation state. Fluorine and oxygen oxidize these elements (except oxygen) to the +6 oxidation state, resulting in such substances (for sulfur) as sulfur hexafluoride SF6 and sulfur trioxide SO3 and its derivative sulfuric acid H2SO4, one of the most heavily-used industrial chemicals. (Note that use of sulfuric acid requires extreme care because it causes chemical burns upon flesh, cloth, and paper). Typically, these elements will attain an oxidation state of -2.
Oxides of sulfur, selenium, and tellurium are acidic. Strong radioactivity largely masks the chemical properties of polonium.
The elements of Group 16 have somewhat varied properties; however, our study of these elements will focus on oxygen because of its abundance and significance. |
Oxygen
Oxygen is a diatomic gas that makes up about 20% of the air we breathe. It is essential for the life of animals, and plants release it. Plants absorb sunlight and produce glucose (sugar) and oxygen. Cells of plants and animals alike "burn" glucose with oxygen to gain energy.

| Photosynthesis is actually a series of complex chemical reactions, involving several substances found in the chloroplasts of plants. This is the overall reaction. | |
| Cellular respiration is the reverse process: converting glucose into energy. |
Oxygen has a few allotropes, but only two are common: dioxygen and ozone. Dioxygen is the regular form of oxygen, O2, held together with a double covalent bond. Ozone, O3, is found naturally in the upper atmosphere and can form when normal oxygen is exposed to high voltage.
Liquid oxygen
If oxygen is chilled to about -183 C (also about -297 F) oxygen condenses as a blue liquid that strongly concentrates oxygen as an oxidizer, something that allows fuel to burn. Liquid oxygen is used in rockets for use in space flight to allow the rockets to go into space where there is practically no oxygen gas.
Ozone
Ozone is not very stable. It will decompose: 2 O3 → 3 O2. Ozone is a very powerful oxidizing agent. Metals and non-metals are both susceptible to oxidation when exposed to ozone.
| Carbon is oxidized by ozone. | |
| Nitric oxide becomes nitrogen dioxide. |
Although considered a pollutant when at ground level (it is toxic), ozone is a very important chemical found in the upper atmosphere. The Sun emits dangerous ultraviolet light that would damage living cells, but ozone absorbs the light energy and converts it safely into heat energy:

| High-powered radiation from the sun splits ozone molecules. | |
| Atomic oxygen can reattach itself to dioxygen to recreate ozone. |
You can see that the net result of the above reactions is a system of ozone that converts dangerous radiation into heat energy.
Atomic oxygen is extremely unstable and will attach itself to form O2 or O3 immediately:
The amount of ozone in the atmosphere is small, but solar radiation will split O2 into two O atoms, so there is a small but steady supply of ozone. Unfortunately, many man-made products called chlorofluorocarbons (CFCs) have entered the upper atmosphere over the years. The chemicals release chlorine radicals that act as catalysts for an ozone-destroying reaction. As a result, the amount of ozone in the atmosphere has decreased, which could lead to an increase in dangerous solar radiation.
| A chlorine radical forms from a CFC. Radicals have a single non-bonding electron (instead of the usual pair), so they are extremely reactive. A chlorine radical is simply a single atom of chlorine (which has seven electrons). | |
| Chlorine radicals will become stable by "stealing" an oxygen atom from ozone. | |
| The chlorine monoxide reacts to eliminate another ozone molecule. The original radical is now available to repeat the entire process. |
As you can see, chlorine radicals convert ozone into regular oxygen without being used up. Over the years, products have been created that replace CFCs and cause less environmental damage.
Oxides
Any chemical compound consisting of oxygen and some other element covalently bonded is an oxide. Metals form oxides easily, except for a few including gold, platinum, and mercury. Besides being called oxidation, the process is also called tarnishing or rusting. In other words, an iron nail that turns to rust has formed iron oxide. The dull, dirty-looking film that coats otherwise shiny copper is copper oxide. Oxides form because oxygen is so electronegative. When substances burn (including hydrocarbons and metals), they oxidize and release large amounts of heat quickly.
The oxide ion is O2-. There is also peroxide O22- and superoxide O2-.
Sulfur

Sulfur behaves similarly to oxygen, but it has over 30 allotropes. The most common is S8. Sulfur is a yellow solid at ambient conditions. Sulfur is a part of many organic and inorganic compounds. Sulfur is part of some proteins necessary for life.
Sulfur in a -2 oxidation state forms compounds known as sulfides with many metals, e.g. K2S CaS, FeS, PtS2. Some of those (notably the alkali metal ones) are soluble, others like CuS extremely insoluble in water. Other oxidation states are also possible, e.g. in pyrite FeS2 the oxidation state is -1 and sulfur occurs as a disulfide anion S22- with a covalent S-S bond, comparable to the O-O bond in peroxide.
Some compounds with higher oxidation states are well known, e.g. the oxides and their corresponding oxo-acids and anions
| Ox # | oxide | name | acid | name | anion | name |
|---|---|---|---|---|---|---|
| +6 | SO3 | sulfur trioxide | H2SO4 | sulfuric acid | SO42- | sulfate |
| +4 | SO2 | sulfur dioxide | H2SO3 | sulfurous acid | SO32- | sulfite |
| -2 | - | - | H2S | hydrosulfuric acid | S2- | sulfide |
Other intermediary oxidation states do occur but are less common.
Chemical names beginning with "thio"- mean an oxygen atom has been replaced with a sulfur atom. For example, cyanate is OCN-, whereas thiocyanate is SCN-. Similarly PS43- is the thiophosphate ion.
Heavier chalcogens
Selenium conducts electricity better in the light than in the dark, so it is found in photocells, electrical components that detect light.
Its chemistry is rather similar to that of sulfur. It even forms amino acids similar to the sulfur containing ones like cysteine. Its better known oxidation states lead to a very similar table as above for sulfur:
| Ox # | oxide | name | acid | name | anion | name |
|---|---|---|---|---|---|---|
| +6 | SeO3 | selenium trioxide | H2SeO4 | selenic acid | SeO42- | selenate |
| +4 | SeO2 | selenium dioxide | H2SeO3 | selenous acid | SeO32- | selenite |
| -2 | - | - | H2Se | hydroselenic acid | S2- | selenide |
The chemistry of tellurium differs a bit more from that of sulfur. Compounds like H2Se and H2Te are exceedingly foul smelling gases and very poisonous. Both elements are used in the formation of semiconductors. Some selenides and tellurides occur as minerals. The name Telluride is best known as a ski resort in the mountains of Colorado but it owes its name to the occurrence of a black telluride mineral that was initially not even recognized as a valuable gold ore. Interestingly gold shows an counter-intuitive stability in its reactions with elements of this group: the telluride is the most stable one, gold selenides do exist, but the sulfide and the oxide are metastable.
Polonium is dangerously radioactive and very rare. It is usually associated with uranium ore as a product of radioactive decay of uranium. It gained some notoriety as a poison administered to a Russian spy.
Group 17
Halogens
The halogens are found in Group 17(VIIA). The halogens are fluorine, chlorine, bromine, iodine, and astatine.
Like the alkali metals, the halogens are extremely reactive. They have seven valence electrons, meaning they require only one more electron for a noble configuration. This gives them very large electron affinities and extreme reactivity to form ions with a -1 charge. They are so reactive that in their homogeneous state, UV light will catalyze a radical reaction.
The halogens exist in diatomic form. Under normal conditions, they will always occur in pairs, covalently bonded. The covalent bond allows them to share an electron and possess a complete octet. F2 is a pale yellowish-brown gas. It is highly reactive, causing organic compounds and hydrogen gas to explode, even without a spark. Cl2 is a pale yellow-green gas. It reacts with water to form disinfectants and bleaches. Br2 is a reddish-brown liquid, but, being volatile, it readily evaporates into a reddish vapor. I2 is a gray solid that forms a violet gas if heated.
Fluorine is the most electronegative of all elements, and it is so reactive that it attacks almost any other element (noble gases, oxygen, nitrogen, and gold are the exceptions) to form fluorides. Chlorine is somewhat less reactive, bromine somewhat less reactive than chlorine, and iodine even less, but even iodine is a formidable ionizer. Extreme radioactivity masks the chemical properties of astatine. With increasing atomic weight for these elements, the elements have higher boiling and melting points. At normal temperatures, fluorine and chlorine are gases, bromine is a liquid, and iodine is a solid.
The halogens have very similar chemical properties. They can be studied as a whole, rather than element-by-element, due to this similarity. |
- The Halogens
-
Copper (II) Fluoride
-
Chlorine gas
-
Bottle containing both liquid and gaseous bromine
-
Solid iodine pieces
Safety
All of these pure elements are dangerous and should never be touched. Fluorine is extremely dangerous in that it corrodes almost anything—even glass. Breathing the vapors of these elements, even in minute amounts, can cause death.
Soluble fluorides are highly toxic to living things and hazardous to the environment. |
Reactions
|
The halogens in diatomic form react with water to produce acids. Iodine does not react with water and is only slightly soluble. Chlorine also has low solubility, but it will react in water to form hypochlorous acid and hydrochloric acid. |
| In chemical reactions, an X is used to symbolize any halogen element. All halogens form gaseous compounds with hydrogen: hydrogen fluoride HF, hydrogen chloride HCl, hydrogen bromide HBr, and hydrogen iodide HI. These are acidic, strongly reactive substances called hydrogen halides. | |
| When hydrogen halides are dissolved in water, they are known as hydrohalic acids. Except for hydrogen fluoride, they are among the strongest known acids. | |
|
These reactions show reactions with metals and ammonia gas to form salts and ammonium halides, respectively. |
| Many non-metallic halides react with water to release hydrogen halides. For example, silicon chloride and water react. |
Other Compounds
Halides of metals are known as salts. Sodium chloride, better known as "table salt", is the crystalline substance often used to enhance the flavor of food. Note, however, that not all salts are halides (for example, sodium sulfate Na2SO4), and not all halides are salts (carbon tetrachloride, CCl4).
Interhalogens are molecules composed of two or more different halogen atoms. They are similar to the diatomic halogens. Some examples are chlorine monofluoride ClF and bromine monochloride BrCl. There are many others, and they are all very reactive and somewhat unstable. Interhalogens take the form XYn, where n is 1, 3, 5, or 7. X and Y are both halogens, X being the less electronegative. Larger molecules and ions are also known. E.g. I2 does not dissolve in water very well, but it dissolves readily in a solution containing iodide ions under the formation of the triiode anion I2 + I- --> I3-
Noble gas compounds have been formed using fluorine. Although noble gases are supposedly inert, the larger ones like xenon will form covalent bonds with a very electronegative element like fluorine. Xenon difluoride XeF2, xenon tetrafluoride XeF4, and xenon hexafluoride XeF6 are among the noble gas compounds that have been created.
Oxidation states
Fluorine is by far the most electronegative element and when it reacts it invariably assumes an oxidation number of -1. The compounds formed this way are called fluorides.
The other halogens ofter react in similar fashion, but they are less electronegative than fluorine. If they react in the presence of an element with a higher electronegativity than their own other (higher) oxidation numbers may result.
For chlorine this can only happen with two elements: oxygen and fluorine. The best known compounds with higher oxidation states are the oxo-acids and their salts.
| Ox # | Acid | Name | Anion | Name |
|---|---|---|---|---|
| +7 | HClO4 | perchloric acid | ClO4- | perchlorate ion |
| +5 | HClO3 | chloric acid | ClO3- | chlorate ion |
| +3 | HClO2 | chlorous acid | ClO2- | chlorite ion |
| +1 | HClO | hypochlorous acid | ClO- | hypochlorite ion |
| -1 | HCl | hydrochloric acid | Cl- | chloride ion |
As shown the oxidation numbers can range over a full octet from -1 to +7, representing an electron configuration for the chlorine atom ranging from [Ar] to [Ne]. The naming is somewhat makeshift. The endings -ic for the acid and -ate for the anion are typically reserved for the highest oxidation number, but they had already been given to the +5 species when the +7 ones were found. This is why the per- suffix was added. The +3 species have the usual -ous and -ite endings for a oxidation state one step below the highest and the hypo- prefix indicates that it is a an even lower oxidation state.
Some of these compounds are rather common. Hydrochloric acid can be found in our stomachs and as a household cleaner. In pure form it is a gas, but it is quite soluble in water. Table salt is a chloride salt, the hypochlorite ion is the active ingredient in bleach. Perchlorates are very soluble salts and this fact is often exploited if we wish to make a certain cation readily soluble.
The elements bromine and iodine form similar acids and salts to chlorine.
Halo-acids
Oxo-acids like nitric acid HNO3 of sulfuric acid H2SO4 and their anions like the nitrate ion NO3- or the sulfate ion SO42- are well known. In these molecular ions oxygen functions as the more electronegative ligand around a central atom (N or S) in a high oxidation state.
Halogens being rather electronegative themselves can fulfill the same role as oxygen and this gives rise to halo-acids and their anions. A good example of such an anion is the tetrafluoroborate anion BF4-.
The naming of such compounds is derived from the oxo ones. The name borate with its -ate ending indicates that boron in its highest oxidation state is the central atom. The fact that the ligands are F rather than oxygen is indicated by the prefix fluoro- and the tetra- indicates that there are four ligands around the central atom. Similar names pertain to the other halogens, e.g. ZnCl42- is the tetrachlorozincate ion.
Group 18
Noble gas elements of G-18:--
The noble gases are in Group 18 (8A). They are helium, neon, argon, krypton, xenon, and radon. They were once called inert gases because they were thought to be completely inert—unable to form compounds. This is a reasonable belief because the noble gases have a complete octet, making them very stable and unlikely to gain or lose any electrons. However, some compounds have been formed with the larger elements of this group, like xenon tetrafluoride (XeF4). No normal compounds of helium, neon, or argon are stable at any but the coldest of temperatures.
Radon is dangerously radioactive; it causes cancer. It is so unstable that its radioactivity makes any chemical experiments with it nearly impossible.
Noble gases all have a complete octet (eight valence electrons), except for helium (which has only two electrons). Because this configuration is extremely stable as well as symmetrical, the noble gases are very unreactive. |
Ionization
If an electric current is passed through a gas, its electrons will become excited. The electron will jump to a higher energy level, but they will then de-excite (fall back down) to their stable state, also known as their ground state, and in doing so they will release the energy they initially absorbed in the form of a photon, the fundamental unit of light. In other words, gases can be used to convert electricity into light—the concept of "neon signs". Neon signs are not necessarily filled with neon. They are filled with any mixture of gases to get the desired color. Each gas has a unique color that it emits.
- Colors of different noble gases when used in "neon" signs
-
Helium (pink)
-
Neon (red-orange)
-
Argon (blue)
-
Krypton (pale green)
-
Xenon (pale blue)
Of course, other gases can be used besides the noble gases.
Helium

Helium is a unique noble gas. It is the second most abundant element in the universe. Lighter than air, it is used in blimps because it will allow them to float without the risk of an explosion. Neon is the only element less reactive than helium.
Helium will not freeze under normal pressure. There cannot be enough intermolecular force to lock the atoms into a solid. It remains a gas until 4 K, then becomes a liquid. With the right conditions, helium becomes a superfluid. It is a liquid that will creep along the edges of its container with zero viscosity.
Helium atoms (they never combine with other atoms) are too light to remain in the Earth's atmosphere. Almost all of the small amount of helium on Earth is the result of radioactive decay of very heavy elements like thorium and uranium.
Neon
Neon is best known for its presence in neon lights. The brightly-colored fish known as neon tetras are named for having a reddish color similar to that of a neon light, and not for possessing or using neon.
Hydrogen
Hydrogen
Hydrogen is an element like no other. It does not fit into any of the groups. |
Hydrogen is by far the most common element in the universe; as a gas it is too light for Earth's gravity to hold. It is by far the largest constituent of the Sun and all other stars and of the gas giant planets of our solar system. It exists on or just under the surface of the Earth as a component of water and in innumerable compounds of carbon, many essential to life.
The heat and light from the sun (or any other star) arises largely from the nuclear fusion of hydrogen into helium. Nuclear reactions are discussed later. Essentially, the nuclei of two atoms can combine at very high temperatures, which releases tremendous amounts of energy in the form of heat and light.
Reactions
Hydrogen, although having one outermost electron, does not fit into the alkali metals or any other group. It forms compounds analogous to those of the alkali metals, but such hydrogen compounds are much less alkaline (or more acidic), much less ionic, and more volatile. Sodium chloride, common salt, is neutral and clearly ionic; hydrogen chloride is a non-ionic gas under normal conditions and is a strong acid. The hydrogen analogue of sodium hydroxide is a volatile liquid (water, its most common compound) under normal situations—unlike the strongly alkaline and solid sodium hydroxide, water is slightly ionic and effectively neutral.
Hydrogen is a non-metal, forming a diatomic gas which results from the sharing of the single electrons of hydrogen atoms. It can achieve a stable ionic structure (no electrons!) by losing an electron or by gaining an electron and achieving the completed shell configuration of helium. The hydrogen molecule is best described as sharing the two electrons between two hydrogen atoms. This structure is highly stable and has little inclination to form bonds between other hydrogen molecules; hydrogen is a gas down to some of the lowest temperatures known. It is also the lightest of gases, weighing less even than helium.
| Hydrogen readily shares its electron with a strongly electronegative element, like any halogen, oxygen, or sulfur. The combination with fluorine is particularly violent and possible down to very low temperatures. Light is enough to force combustion between hydrogen and chlorine, and a spark is enough to cause combustion between hydrogen and oxygen. | |
| Due to the Hindenburg disaster of 1936, helium has long replaced hydrogen in lighter-than-air aircraft. The reaction responsible for that disaster was simply the combustion of hydrogen and oxygen. (Note that at the temperatures associated with such a combustion, water is in the gaseous state) | |
|
Hydrogen can act somewhat like a halogen, forming hydrides with some metals. Most of these react violently with water to form hydrogen gas and the metal hydroxide. Hydrogen compounds with non-metals are typically among the most volatile substances of those elements. |
(general net ionic equation) |
Under pressure, in aqueous solutions, or in non-solid acids, hydrogen is a good reducing agent. Strong acids attack most metals. This example shows hydrochloric acid added to zinc.
In the atmospheres of gas giant planets (Jupiter, Saturn, Uranus, and Neptune) gaseous hydrogen under great pressure reduces nitrogen to ammonia, carbon compounds to methane and other hydrocarbons, and oxides to water. |
Compounds
Hydrogen forms more chemical compounds than any other element including carbon. |
Almost all carbon compounds contain hydrogen, and vice versa, but more substances containing hydrogen (without carbon) exist than do compounds of carbon (without hydrogen). Hydrogen forms bonds with most non-metals, including oxygen, nitrogen, and carbon. Although a hydrogen atom can bond with only one other element, and then only in a single bond, hydrogen allows very long chains of carbon atoms to form. Most of the hydrogen compounds with carbon alone are combustible gases or volatile liquids or waxy solids that can be vaporized and burned to produce water, carbon dioxide, and much heat. Natural gas, gasoline (a mixture of liquid hydrocarbons), and waxes as found in candles make suitable fuels. With such other elements as oxygen, nitrogen, sulfur, and in some cases metals, hydrogen allows the formation of substances necessary for life, including carboxylic acids, sugars, proteins, nucleic acids, haemoglobin, and chlorophyll.
Such complex compounds are ordinarily discussed in Organic Chemistry, a study associated more obviously with carbon.
Forms
Hydrogen has three isotopes. All hydrogen atoms contain exactly one proton in the nucleus, but there can be zero, one, or two neutrons. 99.98% of all hydrogen atoms naturally found on Earth have no neutrons. This is called protium, or 1H. It is stable, along with deuterium, or 2H. Deuterium has one neutron. It behaves exactly like regular hydrogen, but it weighs twice as much. Thus, "heavy water" is D2O, where D is deuterium. Tritium, or 3H, has two neutrons. It is unstable (radioactive) and decays into helium.
If hydrogen loses an electron, it becomes H+, simply a bare proton. In an aqueous solution, H+ forms hydrogen bonds with a surrounding water molecule to create hydronium H3O+. As the hydronium concentration of a solution increases, so does its acidity.
Although such a reaction is uncommon, hydrogen can gain an electron to become an H- ion.
Transition Metals
Transition Metals
The transition metals are found in the middle of the periodic table. There are two definitions of transition metals:
- All d-block elements (Groups 3-12)
- Elements with partially occupied d-orbitals or that can form cations with partially occupied d-orbitals
The first definition is more common and is used casually, but the second definition emphasizes the unique properties of transition metals and is the one used by IUPAC (The International Union of Pure and Applied Chemistry). The second definition is commonly considered to exclude Zn, Cd and Hg because these elements have a d10 electronic configuration (the d-orbitals being fully, not partially, occupied). However, recently reported fluoride Hg(IV) compounds, which have a d8 configuration put this exemption into doubt and make it reasonable to consider Hg (and possibly Zn and Cd too) as transition metals.
Transition metals behave differently than other metals because of their partially occupied d-orbitals. Adding electrons to a transition metal does not affect its valence shell because the electrons go into the d-orbital (which is not part of the valence shell). All transition metals have one or two valence electrons.
Electrons and Oxidation
Transition metals are interesting because they can have several oxidation states, unlike most other metals. This happens because the transition metals can lose their d electrons in addition to their s electrons when forming ions.

Remember that an electron orbital is most stable when it is full or half-full (or empty). Studying the electron configurations of the transition metals shows an interesting pattern:
| Sc: | [Ar]4s23d1 |
| Ti: | [Ar]4s23d2 |
| V : | [Ar]4s23d3 |
| Cr: | [Ar]4s13d5 |
| Mn: | [Ar]4s23d5 |
| Fe: | [Ar]4s23d6 |
| Co: | [Ar]4s23d7 |
| Ni: | [Ar]4s23d8 |
| Cu: | [Ar]4s13d10 |
| Zn: | [Ar]4s23d10 |
To be more stable, an s-electron "jumps up" to the d-orbital in chromium and copper. This also occurs in in heavier transition metals like molybdenum, tungsten, and platinum. With heavier transition metals in Periods 5, 6, and 7, the effects of relativity cause changes in the energy levels of the orbitals. In those elements, s-electrons "jump up" to d-shells more often than expected with the full/half-full rule.
When ions of the transition metals form, they lose their s-electrons first, then they lose their d-electrons if further ionized. For example, copper can form two different ions, and titanium can form three:
| Cu: | [Ar]4s13d10 |
| Cu+: | [Ar]4s03d10 |
| Cu2+: | [Ar]4s03d9 |
| Ti: | [Ar]4s23d2 |
| Ti2+: | [Ar]4s03d2 |
| Ti3+: | [Ar]4s03d1 |
| Ti4+: | [Ar]4s03d0 |
Colors
Transition metals and their oxides, when dissolved, form colored compounds. Group 1 and 2 metals are clear when dissolved and white when precipitated. Other metals, like lead, are clear when dissolved and may have color when precipitated (lead precipitates are yellow). Transition metals, on the other hand, are colored when dissolved. Different metals are known for their specific colors, finding use as inks or paints.

Families
Coinage Metals
The "coinage metals" are copper, silver, gold, and roentgenium. These elements are used for much more than just coins, and many other elements besides these are made into coins. Furthermore, roentgenium is radioactive with a half-life of 3.6 seconds, making it useless for commercial applications. Consequently, the "coinage metals" are more appropriately called Group 11 (IB) elements.
Copper, silver, and gold, although relatively rare (copper), rare (silver), or extremely rare (gold), are among the longest-known and most familiar elements. They are soft, shiny, dense metals resistant to corrosion and very good conductors of electricity. Roentgenium, a recently discovered synthetic element, is so short-lived that its physical and chemical properties are ill-defined.
Copper is by far the most heavily used of these elements due to its electrical properties, its commonness (contrasted to silver and gold) and the attractiveness of its alloys brass and bronze. Until aluminum became commonplace, copper was second only to iron in production among the metals.
-
Copper pipes
-
Silver, the shiniest
-
Gold
They are easy to identify when found because copper (reddish) and gold (yellow) are the only two colored metals that people are likely to encounter. Silver is the shiniest of metals, and it is usually found in the presence of copper or gold and gives an obvious contrast. They are often found uncombined.
Because of their softness they are easily struck as coins, and their comparative rarity and attractiveness, along with their resistance to corrosion make them compact stores of wealth. They are too soft to have structural value, but copper alloys with such elements as zinc and tin to form harder brasses and bronzes. Brass and bronze were essential in the earliest metal tools; without them, civilization as we know would be impossible. Gold and silver, due to their attractiveness and their resistance to oxidation, have been used heavily in jewelry and other ornamental works. Gold, although extremely expensive, is so malleable that at modest cost a small amount can be pounded into a foil of extreme thinness that allows it to be used as a covering of some architectural objects; a little gold goes a long way.
Copper oxidizes with some difficulty to the +1 state in halides and an oxide and to the +2 state in salts such as copper sulfate CuSO4. Soluble copper compounds are easily identified by their distinctive blue-green color. Silver oxidizes to the +1 state in such substances as silver nitrate AgNO3 and silver sulfide Ag2S, the latter the typical blackening of silver. Gold oxidizes to the +1 and +3 state with great difficulty.
These elements are poor (copper) to extremely-poor (gold) reducing agents and their compounds are very good oxidizing agents. Copper ions oxidize most metals:
The reaction is even stronger with either silver or gold. In effect a solution of one of these metals' salts plates most other metals.
Silver is most electrically conductive metal, followed by copper then gold. This makes copper a favorite material for electrical wires. Gold-tipped wires are employed in situations that need electrical precision (like high-quality audio) because gold will not tarnish (the tarnish of copper is much less conductive).
Zinc Family
The Zinc Family is Group 12 (IIB) and consists of zinc, cadmium, mercury, and copernicum.
Zinc, cadmium, and mercury are metals with low melting points for metals. This is because they have an especially stable electron configuration. Mercury is so poor at forming metallic bonds that it is liquid at room temperature.
-
A zinc coin
-
Cadmium pieces
-
A puddle of mercury
Zinc and cadmium are soft metals that easily oxidize to the +2 oxidation state. Neither of these two metals appears uncombined in nature. Zinc is heavily used in alloys with copper to create a harder metal known as brass; as a coating for iron (the process is called "galvanizing"), it oxidizes to form a protective layer of zinc oxide (ZnO) that protects the iron from oxidation, also known as rust. Zinc oxide is much safer than lead oxide and is often used in white paint. Since 1982, zinc has been the main metal used in American pennies. It is now used in new organ pipes.
Cadmium forms two substances, cadmium yellow (cadmium sulfide, CdS) and cadmium red (cadmium selenide, CdSe) that appeared in paints. These paints had strong colors that many of the great artists of the Impressionist periods cherished in their paintings. But these substances are very poisonous, and painters who used them often died young and crippled. Modern painters ordinarily use different paints that do not use these two poisonous chemicals.
Mercury, in contrast, is a shiny liquid at room temperature and oxidizes with some difficulty. It conducts electricity well. Because it is liquid it is an unusual metal—but it is a metal. It has been used in thermometers (but not so often after it has been identified as a dangerous poison) because it expands with heat and in switches where it can flow into a closed space to close a circuit. Mercury oxidizes to the +2 state in mercuric chloride (HgCl2); in some strange compounds, two mercury atoms share an electron and offer their "spare" electrons to form substances in the +1 state, such as mercurous chloride (Hg2Cl2).
Zinc is an essential trace element for living things; it has some germicidal properties and is toxic (poisonous) in large quantities. Zinc pennies should never be swallowed. Cadmium, mercury, and their compounds are very dangerous poisons. Although mercury is attractive and has remarkable properties, it should be used with extreme care, and only by workers who have appropriate knowledge of its hazards.
The artificial Element 112 named copernicum in 2010 is probably part of this group in its properties, but it is extremely difficult to produce and too unstable to have a well-defined chemistry. Few atoms of this element have ever been made.
The elements of Groups 8, 9, and 10 are in two distinct groups: the common elements iron, cobalt, and nickel of the upper row of transition metals and the platinum metals of the second and third rows, and the far-scarcer platinum metals of the two lower rows of transition elements.
Iron, cobalt, and nickel
These elements are fairly-good reducing agents -- so good that they rarely appear uncombined in nature. Iron is by far the most common of these. One of the most common elements in the universe, it is the heaviest metal that forms in normal fusion in stars (but only the largest stars). Once a star begins to produce iron in its core, that star is doomed in short order to a violent explosion that destroys the star and scatters its matter, including all of the elements that it has formed in fusion.
Uncombined iron, cobalt, and nickel -- but especially iron -- are to be found in meteors, solid objects that strike the earth. Iron is by far the most common of the transition elements, and one of the most useful. It's hard to count all the uses of iron, the metal most used (whether pure or in alloys) in almost all machines. Giant "glass box" skyscrapers depend upon iron bars within their concrete "skeletons" to give them strength and stability. The rails of railroads are long iron bars. Concrete highways and airstrips have iron re-enforcing bars to give them the strength to hold heavy vehicles. The vehicles themselves are largely iron and a harder material known as steel, an alloy of iron, carbon, and often metals other than iron.
Iron is the cheapest of all structural metals. With some skill of an artisan known as a blacksmith it can be worked into many useful objects such as horseshoes, nails, plows, chains, pails, ladders, and many tools. In foundries, iron and steel are shaped in far greater quantities into such objects as furniture and parts of aircraft, ships, motor vehicles, and appliances.
Iron has one fault as a structural material: it rusts easily. In the presence of water (especially salt water) it corrodes into oxides:
Fe(s) + 1/2 O2(g) → FeO(s) 2 Fe(s) + 3/2 O2(g) → Fe2O3(s)
and a mixed oxide known as hematite
2 Fe(s) + 3/2 O2(g) → Fe2O3(s)
one of the most common ores of iron. Iron oxides are mildly alkaline, so iron resists attacks by alkalis; acids attack it. For example,
Fe (s) + H2SO4(l) → Fe2+(aq) + SO42-(aq) + H2(g)
Even a comparatively weak acid, like phosphoric acid, can attack iron oxide. This is the "naval jelly" reaction that removes rust from iron:
FeO(s) + H3PO4(l) → Fe2+(aq) + HPO4(aq)-2 + H2O(l)
A great advance of humanity, the beginning of the Iron Age, began when people found that they could separate iron from oxygen by burning it with carbon (usually charcoal) which can reduce iron oxides to iron:
Fe3O4(s) + 4 C(s) → 3 Fe(s) + 4 CO(g)
Much of existing economic activity depends upon the extraction of iron ore, the reduction of iron ore to iron, the strengthening of iron to steel, the creation of iron and steel objects, and the various practices used in protecting iron from corrosion.
Important as that activity is, our lives would be impossible without an important compound of iron known as hemoglobin which carries oxygen through the bloodstream to cells where the cells can use the oxygen to release energy from food also delivered to cells through the bloodstream.
-
two suspension bridges
-
an old iron plow
-
red blood cells contain hemoglobin
-
an electromagnet attracting scrap iron
The earth itself has a hot, dense core of largely iron and nickel. At the temperatures characteristic of the Earth's core the iron and nickel form a giant natural magnet that creates a magnetic field that goes beyond the Earth itself into the atmosphere. That magnetic field drives off much dangerous radiation that would kill life on the Earth's surface if it reached the Earth's surface.
Cobalt and nickel are both far scarcer than iron and not as extensively used in commerce as iron, although they have specialized uses.
Platinum Family
The Platinum group metals are ruthenium, rhodium, palladium, osmium, iridium, and platinum. These elements are found in the second two rows of Groups 8/9/10 (IIIB).
Unlike their lighter counterparts in Groups 8, 9, and 10 of these elements are resistant to corrosion and tarnish. They serve as catalysts for many chemical reactions, speeding up the reaction without being consumed by it.
Palladium, osmium, and the other platinum group metals absorb hydrogen when powdered.
Rhodium is used in catalytic converters—metallic structures found inside vehicles. Catalytic converters convert nitric oxides (which are toxic pollutants) into elemental nitrogen and oxygen (both of which make up breathable air):
That reaction would not occur without rhodium to serve as a catalyst.
Inner Transition Metals
Inner Transition Metals
The inner transition metals are found in the f-block, usually put at the bottom of the Periodic Table. These elements were sometimes called rare earth metals due to their extremely low natural occurrence. Except for extremely-unstable promethium which quickly decays to another lanthanoid metal, these elements are not rare. Indeed cerium is abundant in Earth's crust.) Many of them do not occur naturally, but are instead created in labs artificially. Furthermore, these elements all have nearly identical properties, both chemically and physically, making them very difficult to identify and separate. They are almost as reactive as the alkali metals, and all actinoids are radioactive, so they have little commercial significance. However, the radioactive elements can be used in nuclear power plants or as weapons.
Most of the inner transition metals form ions with a +3 charge. Some of the lighter actinoids can use their f-electrons for bonding, giving them a wider range of oxidation states, but the rest do not use f-electrons and have only a +3 oxidation state. Cerium is a notable exception: it has a somewhat common +4 oxidation state, seen in curium(IV) oxide CeO2.
These elements tarnish quickly in oxygen. Some will ignite in oxygen. They react with water to release hydrogen:
Lanthanoids
Lanthanoids burn in oxygen easily and react violently with non-metals. They are used in lasers and sometimes steels depending on the element.
Neodymium magnets (Nd2Fe14B) are the strongest known permanent magnets. Gadolinium exhibits ferromagnetism below room temperature.
The terbium(III) cation is very fluorescent—it glows in the dark.
Lanthanoid contraction is a phenomenon that causes the lanthanoids (and all elements after them) to have much smaller atomic radii than expected. The f-electrons do not shield the nuclear charge as much as expected, so the outermost electrons are attracted to the nucleus more.
Actinoids
Only thorium and uranium occur naturally in Earth's crust (along with neptunium and plutonium in trace amounts).
The actinoids are radioactive and decay into more stable elements. The actinoids that do not occur naturally have been created in labs for experiments and research.
Nuclear Chemistry

Throughout your study of General Chemistry, you have undoubtedly heard of "radioactive elements" and "unstable isotopes". These elements are the study of nuclear chemistry. Normal chemical reactions occur between atoms and electrons. Atoms gain, lose, and share electrons to form different substances. Chemical reactions are essentially interactions of electrons. Nuclear reactions, on the other hand, occur within the nucleus of an atom. They involve the gaining, losing, and transformation of protons, neutrons, and sometimes other particles (electrons and photons). Nuclear chemistry is something that you can study only within your textbook—radioactive substances are deadly to living things, can cause explosions, and are difficult to procure.
You should already know what isotopes are: elements with the same number of protons, but different numbers of neutrons (and a different total mass). Some isotopes are stable and do not decay. They last indefinitely. Other isotopes are unstable, meaning that they are radioactive. They will undergo nuclear reactions to become a more stable isotope. Some elements are always unstable, regardless of how many neutrons, so all of their isotopes are unstable.
For example, carbon-12 (6 protons, 6 neutrons) is stable. Carbon-14 (6 protons, 8 neutrons) is unstable and decays into nitrogen-14. This is unusual from a chemical point of view—there is no way for an atom to change into a different element. This is nuclear chemistry, though, and elements do change frequently in their quest to become more stable.
Stability
There is no formula or exact rule to determine which isotopes are stable and which are unstable. That must be determined experimentally. Patterns have emerged throughout the study of the elements, and there are some general guidelines you can use to guess if an isotope will be stable or radioactive:
- Lighter elements are stable when they have roughly equal numbers of protons and neutrons.
- Heavier elements are stable when they have more neutrons than protons in about a 3:2 ratio.
- Elements that have a "magic number" of protons or neutrons are especially stable: 2, 8, 20, 28, 50, 82, 126.
In regard to the magic numbers, notice how helium-4 (2 p, 2 n) is the most abundant isotope in the universe. Lead-208 is the heaviest stable isotope known (82 p, 126 n). The air we breathe is filled with oxygen-16 (8 p, 8 n). The stability of these isotopes is no coincidence.
Fusion and Fission

Fusion reactions take two small nuclei and "fuses" them together into one large nucleus. Fission reactions split a large nucleus into smaller nuclei. Fission releases tremendous amounts of energy, which is why fission reactions are used in both nuclear power plants (to provide electricity to an entire city) and nuclear bombs (to destroy an entire city). Fusion reactions release even greater amounts of energy, but they only occur at unfathomably high temperatures. Fusion reactions occur in stars in outer space. Our sun is basically one giant fusion reactor. Hydrogen nuclei fuse together into helium nuclei, releasing the light and heat that warms our planet. Here are some example nuclear reactions:
| Fusion | |
| Fission |
Notice that the Law of Conservation of Matter is bent but not broken. If you add up the mass numbers, they will be equal on both sides of the reaction. The total charge numbers will also be equal.
Decay Modes
An unstable isotope will decay to become more stable. There are many decay modes, but a few are common:
- Common Decay Modes
- Alpha decay releases an alpha particle (helium-4, 2 p + 2 n). Occurs when the isotope is too big to be stable.
- Beta+ decay converts a neutron into a proton, releasing a beta particle (electron). Occurs when there are too many neutrons to be stable.
- Beta— decay converts a proton into a neutron, releasing a beta particle (positron). Occurs when there are too many protons to be stable.
- Gamma decay releases a gamma particle (photon). Occurs when the nucleus has too much energy.
- Electron capture converts a proton into a neutron by absorbing an electron. Occurs when there are too many protons to be stable.
As far as health concerns, alpha particles are the most dangerous. They can be inhaled, causing bodily damage. They are heavy and have a double positive charge, but they are easily stopped by a piece of paper or skin. Beta particles are simply electrons (or positrons, an antielectron). They are somewhat dangerous, and they are stopped by a piece of wood or aluminum foil. Gamma rays are only stopped by thick slabs of lead. They are essentially x-rays that have extreme amounts of energy. Although they have the most energy, they only cause damage to things directly exposed to a radioactive substance. The other particles are worse because they can travel through the atmosphere.
A particular isotope always uses the same decay mode. These reactions will summarize the decay modes (notice the law of conservation):
| Alpha decay | |
| The same reaction, written with the more common notation. | |
| Beta— decay | |
| Beta+ decay |
Synthetic Elements
Short-lived natural elements and synthetic elements
91 elements of the known 118 elements occur naturally on Earth. The other 27 -- all elements beyond plutonium on the Periodic table, and three others -- technetium (43 electrons), promethium (61), and neptunium (93) -- are too unstable to exist on Earth and are not among the rare elements that are parts of the nuclear decay process of either thorium or uranium. The elements that do not occur naturally are synthetic. Synthetic elements are elements that have been created in a laboratory by artificial means. Synthetic elements are very unstable and have few commercial purposes. They decay into other elements in a fraction of a second. Most are created purely for research and experiment.
Synthetic elements are created in particle accelerators. Two smaller elements are accelerated to incredible speeds and collided into each other. Their nuclei merge into a larger element. The element is studied by lab equipment before it decays.
Seven of the 91 naturally-occurring elements (polonium, astatine, radon, francium, radium, actinium, and protactinium) exist only in the presence of naturally-occurring radioactive elements uranium and thorium. These comprise all elements with atomic numbers 84 through 91 except for thorium (90). All isotopes of these elements are very short-lived, and those of them in use are used only for their radioactive properties (most notably in radium, and then as a desperate therapy for some cancers). Because of their short half-lives and the hazards associated with their radioactivity the chemistries of these elements are often extremely difficult to study.
Naming
Most synthetic elements have been named by the IUPAC, the international authority for naming chemicals. They are named after famous scientists or places where the elements were formed. For example, einsteinium (Es, 99) and americium (Am, 95). Some elements are too new to have official names. Before it can be named, an element must be discovered and proven to exist by a scientist or team. Then, the element's discoverer(s) will be allowed to choose a name. Until the element has a name, it is given a provisional name. Provisional names are made of a chain of words, each representing a digit in the element's atomic number. For example, ununseptium is element 117, unnilpentium was element 105 (since renamed as dubnium), and unbioctium would be element 128 (not believed to exist). General Chemistry/Chemistries of Various Elements/Salsal Liquidity
Appendices
Periodic Table
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | VIII | ||||||||||||
| Period | |||||||||||||||||||
| 1 | hydrogen 1 H 1.0079 |
helium 2 He 4.0026 | |||||||||||||||||
| 2 | lithium 3 Li 6.9412 |
beryllium 4 Be 9.0122 |
boron 5 B 10.811 |
carbon 6 C 12.011 |
nitrogen 7 N 14.007 |
oxygen 8 O 15.999 |
fluorine 9 F 18.998 |
neon 10 Ne 20.180 | |||||||||||
| 3 | sodium 11 Na 22.990 |
magnesium 12 Mg 24.305 |
aluminum 13 Al 26.982 |
silicon 14 Si 28.086 |
phosphorus 15 P 30.974 |
sulfur 16 S 32.066 |
chlorine 17 Cl 35.453 |
argon 18 Ar 39.948 | |||||||||||
| 4 | potassium 19 K 39.098 |
calcium 20 Ca 40.078 |
scandium 21 Sc 44.956 |
titanium 22 Ti 47.867 |
vanadium 23 V 50.942 |
chromium 24 Cr 51.996 |
manganese 25 Mn 54.938 |
iron 26 Fe 55.845 |
cobalt 27 Co 58.933 |
nickel 28 Ni 58.693 |
copper 29 Cu 63.546 |
zinc 30 Zn 65.382 |
gallium 31 Ga 69.723 |
germanium 32 Ge 72.612 |
arsenic 33 As 74.922 |
selenium 34 Se 78.963 |
bromine 35 Br 79.904 |
krypton 36 Kr 83.798 | |
| 5 | rubidium 37 Rb 85.468 |
strontium 38 Sr 87.621 |
yttrium 39 Y 88.906 |
zirconium 40 Zr 91.224 |
niobium 41 Nb 92.906 |
molybdenum 42 Mo 95.962 |
technetium 43 Tc 98.906 |
ruthenium 44 Ru 101.07 |
rhodium 45 Rh 102.91 |
palladium 46 Pd 106.42 |
silver 47 Ag 107.87 |
cadmium 48 Cd 112.41 |
indium 49 In 114.82 |
tin 50 Sn 118.71 |
antimony 51 Sb 121.76 |
tellurium 52 Te 127.60 |
iodine 53 I 126.90 |
xenon 54 Xe 131.29 | |
| 6 | caesium 55 Cs 132.91 |
barium 56 Ba 137.33 |
Inner-transition metal * Itm |
hafnium 72 Hf 178.49 |
tantalum 73 Ta 180.95 |
tungsten 74 W 183.84 |
rhenium 75 Re 186.21 |
osmium 76 Os 190.23 |
iridium 77 Ir 192.22 |
platinum 78 Pt 195.08 |
gold 79 Au 196.97 |
mercury 80 Hg 200.59 |
thallium 81 Tl 204.38 |
lead 82 Pb 207.21 |
bismuth 83 Bi 208.98 |
polonium 84 Po [209] |
astatine 85 At [210] |
radon 86 Rn [222] | |
| 7 | francium 87 Fr [223] |
radium 88 Ra [226] | |||||||||||||||||
| * Lanthanides | lanthanum 57 La 138.91 |
cerium 58 Ce 140.12 |
praseodymium 59 Pr 140.91 |
neodymium 60 Nd 144.24 |
promethium 61 Pm 146.92 |
samarium 62 Sm 150.36 |
europium 63 Eu 151.96 |
gadolinium 64 Gd 157.25 |
terbium 65 Tb 158.93 |
dysprosium 66 Dy 162.50 |
holmium 67 Ho 164.93 |
erbium 68 Er 167.26 |
thulium 69 Tm 168.93 |
ytterbium 70 Yb 173.05 |
lutetium 71 Lu 174.97 | ||||
| ** Actinide | actinium 89 Ac 227.03 |
thorium 90 Th 232.04 |
protactinium 91 Pa 231.04 |
uranium 92 U 238.03 |
neptunium 93 Np [237] |
plutonium 94 Pu [244] |
americium 95 Am [243] |
curium 96 Cm [247] |
berkelium 97 Bk [247] |
californium 98 Cf [251] |
einsteinium 99 Es [252] |
fermium 100 Fm [257] |
mendelevium 101 Md [258] |
nobelium 102 No [262] |
lawrencium 103 Lr [263] | ||||
Atomic masses in brackets are the most stable isotope.
| Alkali metals | Alkaline earths | Lanthaniods | Actinoids | Transition metals |
| Poor metals | Metalloids | Nonmetals | Halogens | Noble gases |
Units of Measure
SI Fundamental Units
These are the seven basic SI units from which all other units are constructed.
| Quantity | Symbol | Unit | Unit Symbol |
|---|---|---|---|
| Length | l | metre/meter | m |
| Time | t | second | s |
| Mass | m | kilogram | kg |
| Thermodynamic temperature | T | kelvin | K |
| Amount of substance | n | mole | mol |
| Electrical current | I | ampere | A |
| Luminous intensity | IV | candela | cd |
SI Derived Units
All other units are derived units. They are built from fundamental units. This is a small selection of units that may be found in General Chemistry.
| Quantity | Symbol | Unit | Unit Symbol | Derived From |
|---|---|---|---|---|
| Force | F | newton | N | kg·m·s-2 |
| Energy | U | joule | J | kg·m2·s-2 |
| Pressure | P | pascal | Pa | kg·m-1·s-2 |
| Power | watt | W | kg·m2·s-3 | |
| Electrical charge | Q | coulomb | C | A·s |
| Electrical potential | V | volt | V | J·C-1 |
SI Prefixes
A prefix appears before a unit's symbol when expressing very large or very small quantities. For example: 0.001 kg = 1 g = 1000 mg.
| 1000n | 10n | Prefix | Symbol | Decimal |
|---|---|---|---|---|
| 10008 | 1024 | yotta | Y | 1 000 000 000 000 000 000 000 000 |
| 10007 | 1021 | zetta | Z | 1 000 000 000 000 000 000 000 |
| 10006 | 1018 | exa | E | 1 000 000 000 000 000 000 |
| 10005 | 1015 | peta | P | 1 000 000 000 000 000 |
| 10004 | 1012 | tera | T | 1 000 000 000 000 |
| 10003 | 109 | giga | G | 1 000 000 000 |
| 10002 | 106 | mega | M | 1 000 000 |
| 10001 | 103 | kilo | k | 1 000 |
| 102 | hecto | h | 100 | |
| 101 | deca | da | 10 | |
| 10000 | 100 | (none) | (none) | 1 |
| 10−1 | deci | d | 0.1 | |
| 10−2 | centi | c | 0.01 | |
| 1000−1 | 10−3 | milli | m | 0.001 |
| 1000−2 | 10−6 | micro | µ | 0.000 001 |
| 1000−3 | 10−9 | nano | n | 0.000 000 001 |
| 1000−4 | 10−12 | pico | p | 0.000 000 000 001 |
| 1000−5 | 10−15 | femto | f | 0.000 000 000 000 001 |
| 1000−6 | 10−18 | atto | a | 0.000 000 000 000 000 001 |
| 1000−7 | 10−21 | zepto | z | 0.000 000 000 000 000 000 001 |
| 1000−8 | 10−24 | yocto | y | 0.000 000 000 000 000 000 000 001 |
Solution Concentration Units
| Quantity | Symbol | Units | Description |
|---|---|---|---|
| Molarity | M | mol/L | moles of solute per liter of solution |
| Molality | m | mol/kg | moles of solute per kilogram of solvent |
| Mole Fraction | χ | (none) | moles of solute per moles of solution |
| Parts per million | ppm | (none) | milligrams of solute per kilogram of solution |
| Parts per billion | ppb | (none) | micrograms of solute per kilogram of solution |
Other Useful Units
Volume
| Volume Unit | Conversion | Mass of Water (4 °C) |
|---|---|---|
| 1 L | = 1000 cm3 | 1 kg |
| 1 cm3 | = 1 mL | 1 g |
| 1 m3 | = 1000 L | 1000 kg |
Pressure
| Name | Symbol | Conversion | |
|---|---|---|---|
| Atmosphere | atm | = 760 torr | = 101.325 kPa |
| Pascal | Pa | ≈ 7.5 x 10-3 torr | |
| Torr (mm Hg) | torr | ≈ 133.3 Pa | |
| Pound-per-square inch | psi | ≈ 51.7 torr | ≈ 6.894 kPa |
Temperature
One degree Celsius is equal to one Kelvin (in magnitude).
| Name | Symbol | Abs. Zero | M.P. of Water | B.P. of Water |
|---|---|---|---|---|
| Fahrenheit | °F | -456.67 °F | 32 °F | 212 °F |
| Celsius | °C | -273.15 °C | 0 °C | 100 °C |
| Kelvin | K | 0 K | 273.15 K | 373.15 K |
* Notice it is not "degrees Kelvin".
Constants
Useful Physical/Chemical Constants
| Constant | Value |
|---|---|
| Avogadro's Number | NA = 6.022 14 × 1023 mol-1 |
| Faraday Constant | F = 96 485.33 C mol-1 |
| Atomic Mass Constant | 1 amu = 1.660 538 × 10-27 kg |
| Molar Gas Constant | R = 8.314 4 J mol-1 K-1 |
| Molar Gas Constant | R = 0.082 057 46 L atm K-1 mol-1 |
| Coulomb's Constant | ke = 8.987 551 × 109 N m2 C-2 |
| Speed of Light (Vacuum) | c = 299 792 458 m s-1 |
| Boltzmann Constant | kb = 1.380 65 × 10-23 J K-1 |
| Charge on a Proton/Electron | e = 1.602 176 × 10-19 C |
| Standard acceleration of gravity | g = 9.806 65 m s-2 |
| Rydberg constant | R∞ = 1.0973 731 568 539 × 107 m-1 |
| Planck's Constant | h = 6.62607004 × 10-34 J s |
| Specific heat capacity of liquid water | c = 4.18 kJ kg-1°C-1 |
These constants were obtained from The NIST Reference on Constants, Units and Uncertainty.
Useful Equations
General
| Density: |
| Moles: |
| Percent Error: |
| Percent Composition (by mass): |
| Molarity: |
| Molality: |
| Rate of Reaction: |
| de Broglie's law: = |
Atomic Structure
| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| energy | speed of light | ||
| frequency | wavelength | ||
| charge | distance | ||
| Coulomb's constant | Plank's constant H/nkne |
| Energy of Wave: |
| Wave Relation: |
| Coulomb's Law: |
Solutions, Liquids, Gases
| Symbol | Meaning |
|---|---|
| pressure | |
| volume | |
| number of moles | |
| temperature (in Kelvin) | |
| molal freezing point constant | |
| molal boiling point constant | |
| mole fraction | |
| molality | |
| molarity | |
| specific heat capacity | |
| mass of water (Kg) | |
| heat energy released |
| Rauolt's Law: |
| Boiling Point Elevation: |
| Freezing Point Depression: |
| Ideal Gas Law: |
| Combined Gas Law: |
| Titration: |
| Dilution: |
| Heat released by burning: |
Equilibrium
| Symbol | Meaning |
|---|---|
| equilibrium constant (general) | |
| pressure equilibrium constant | |
| concentration equilibrium constant | |
| gas law constant | |
| temperature (in Kelvin) | |
| moles of product – moles of reactant |
| pH: |
| pOH: |
| (for water): |
| Pressure/Concentration: |
| Equilibrium, for a reaction : |
Thermochemistry
| Symbol | Meaning |
|---|---|
| heat energy | |
| mass | |
| specific heat | |
| temperature (in Kelvin) | |
| entropy | |
| enthalpy | |
| Gibbs free energy |
| Heat Transfer: |
| Enthalpy: |
| Entropy: |
| Free Energy: |
Standard Reduction Potentials
| Half Reaction | Eo (V) | ||
|---|---|---|---|
| F2(g) + 2 e- | 2 F- | 2.87 | |
| Co3+ + e- | Co2+ | 1.82 | |
| Au3+ + 3e- | Au(s) | 1.50 | |
| Cl2 (g) + 2 e- | 2 Cl- | 1.36 | |
| O2 (g) + 4 H+ + 4 e- | 2 H2O(l) | 1.23 | |
| Br2(l) + 2 e- | 2 Br- | 1.07 | |
| 2 Hg2+ + 2 e- | Hg22+ | 0.92 | |
| Ag+ + e- | Ag(s) | 0.80 | |
| Hg22+ + 2 e- | 2 Hg (l) | 0.79 | |
| Fe3+ + e- | Fe2+ | 0.77 | |
| I2(s) + 2 e- | 2 I- | 0.53 | |
| Cu+ + e- | Cu(s) | 0.52 | |
| Cu2++ 2 e- | Cu(s) | 0.34 | |
| Cu2++ e- | Cu+ | 0.15 | |
| Sn4+ + 2 e- | Sn2+ | 0.15 | |
| S(s) + 2 H+ + 2 e- | H2S(g) | 0.15 | |
| 2 H+ + 2 e- | H2(g) | 0.00 | |
| Pb2+ + 2 e- | Pb(s) | -0.13 | |
| Sn2+ + 2 e- | Sn(s) | -0.14 | |
| Ni2+ + 2 e- | Ni(s) | -0.25 | |
| Co2+ + 2 e- | Co(s) | -0.28 | |
| Tl+ + e- | Tl(s) | -0.34 | |
| Cd2+ + 2 e- | Cd(s) | -0.40 | |
| Cr3+ + e- | Cr2+ | -0.41 | |
| Fe2+ + 2 e- | Fe(s) | -0.44 | |
| Cr3+ + 3 e- | Cr(s) | -0.74 | |
| Zn2+ + 2 e- | Zn(s) | -0.76 | |
| Mn2+ + 2 e- | Mn(s) | -1.18 | |
| Al3+ + 3 e- | Al(s) | -1.66 | |
| Be2+ + 2 e- | Be(s) | -1.70 | |
| Mg2+ + 2 e- | Mg(s) | -2.37 | |
| Na+ + e- | Na(s) | -2.71 | |
| Ca2+ + 2 e- | Ca(s) | -2.87 | |
| Sr2+ + 2 e- | Sr(s) | -2.89 | |
| Ba2+ + 2 e- | Ba(s) | -2.90 | |
| Rb+ + e- | Rb(s) | -2.92 | |
| K+ + e- | K(s) | -2.92 | |
| Cs+ + e- | Cs(s) | -2.92 | |
| Li+ + e- | Li(s) | -3.05 | |
Elements and their Properties
| Name | Symbol | Number | Atomic mass | Density at 20°C (g/cm3) | Melting point (°C) | Boiling point (°C) | Phase * | Oxidation ** |
|---|---|---|---|---|---|---|---|---|
| Actinium | Ac | 89 | 227.0278 | 10.07 | 1047 | 3197 | S | +3 |
| Aluminium | Al | 13 | 26.982 | 2.70 | 660.5 | 2467 | S | +3 |
| Americium | Am | 95 | (243) | 13.67 | 994 | 2607 | X S | +3 +4 +5 +6 |
| Antimony | Sb | 51 | 121.75 | 6.69 | 630.7 | 1750 | S | -3 +3 +5 |
| Argon | Ar | 18 | 39.948 | 1.66 | -189.4 | -185.9 | G | 0 |
| Arsenic | As | 33 | 74.92159 | 5.72 | 613 (sublimation) | 613 | S | -3 +3 +5 |
| Astatine | At | 85 | 209.9871 | 7 (approx.) | 302 | 337 | S | +1 +3 (prob.) |
| Barium | Ba | 56 | 137.327 | 3.65 | 725 | 1640 | S | +2 |
| Berkelium | Bk | 97 | (247) | 13.25 | 986 | 710 | X S | +3 +4 |
| Beryllium | Be | 4 | 9.012182 | 1.85 | 1278 | 2970 | S | +2 |
| Bismuth | Bi | 83 | 208.98037 | 9.80 | 271.4 | 1560 | S | +3 +5 |
| Bohrium | Bh | 107 | 38 (est.) | X S | ||||
| Boron | B | 5 | 10.811 | 2.46 | 2300 | 2550 | S | +3 |
| Bromine | Br | 35 | 79.904 | 3.14 | -7.3 | 58.8 | D L | -1 +1 +5 |
| Cadmium | Cd | 48 | 112.411 | 8.64 | 321 | 765 | S | +2 |
| Caesium | Cs | 55 | 132.90543 | 1.90 | 28.4 | 690 | S | +1 |
| Calcium | Ca | 20 | 40.078 | 1.54 | 839 | 1487 | S | +2 |
| Californium | Cf | 98 | (251) | 15.1 | X S | +3 | ||
| Carbon | C | 6 | 12.011 | 3.51 | 3550 | 4827 | S | -4 +2 +4 |
| Cerium | Ce | 58 | 140.115 | 6.77 | 798 | 3257 | S | +3 +4 |
| Chlorine | Cl | 17 | 35.4527 | 2.95 | -101 | -34.6 | D G | -1 +1 +3 +5 +7 |
| Chromium | Cr | 24 | 51.9961 | 7.14 | 1857 | 2482 | S | +2 +3 +6 |
| Cobalt | Co | 27 | 58.9332 | 8.89 | 1495 | 2870 | S | +2 +3 |
| Copper | Cu | 29 | 63.546 | 8.92 | 1083.5 | 2595 | S | +1 +2 |
| Copernicium | Cn | 112 | 13.5336 | X L | ||||
| Curium | Cm | 96 | (247) | 13.51 | 1067 | 3110 | X S | +3 |
| Darmstadtium | Ds | 110 | 21.46 | X S | ||||
| Dubnium | Db | 105 | 39 (est.) | X S | ||||
| Dysprosium | Dy | 66 | 162.5 | 8.56 | 1409 | 2335 | S | +3 |
| Einsteinium | Es | 99 | (252) | 13.5 (est.) | 860 | X S | ||
| Erbium | Er | 68 | 167.26 | 9.05 | 1522 | 2510 | S | +3 |
| Europium | Eu | 63 | 151.965 | 5.25 | 822 | 1597 | S | +2 +3 |
| Fermium | Fm | 100 | (257) | 2781 | X S | |||
| Fluorine | F | 9 | 18.9984032 | 1.58 | -219.6 | -188.1 | D G | -1 |
| Francium | Fr | 87 | 223.0197 | 1.87 | 27 | 677 | S | +1 |
| Gadolinium | Gd | 64 | 157.25 | 7.89 | 1311 | 3233 | S | +3 |
| Gallium | Ga | 31 | 69.723 | 5.91 | 29.8 | 2403 | S | +3 |
| Germanium | Ge | 32 | 72.61 | 5.32 | 937.4 | 2830 | S | -4 +2 +4 |
| Gold | Au | 79 | 196.96654 | 19.32 | 1064.4 | 2940 | S | +1 +3 |
| Hafnium | Hf | 72 | 178.49 | 13.31 | 2150 | 5400 | S | +4 |
| Hassium | Hs | 108 | 41 (est.) | X S | ||||
| Helium | He | 2 | 4.002602 | 0.17 | -273 (n/a) | -268.9 | G | 0 |
| Holmium | Ho | 67 | 164.93032 | 8.78 | 1470 | 2720 | S | +3 |
| Hydrogen | H | 1 | 1.00794 | 0.084 | -259.1 | -252.9 | D G | +1 -1 |
| Indium | In | 49 | 114.82 | 7.31 | 156.2 | 2080 | S | +3 |
| Iodine | I | 53 | 126.90447 | 4.94 | 113.5 | 184.4 | D S | -1 +1 +5 +7 |
| Iridium | Ir | 77 | 192.22 | 22.65 | 2410 | 4130 | S | +3 +4 |
| Iron | Fe | 26 | 55.847 | 7.87 | 1535 | 2750 | S | +2 +3 |
| Krypton | Kr | 36 | 83.8 | 3.48 | -156.6 | -152.3 | G | 0 +2 |
| Lanthanum | La | 57 | 138.9055 | 6.16 | 920 | 3454 | S | +3 |
| Lawrencium | Lr | 103 | (263) | 9.84 | 2961 | X S | ||
| Lead | Pb | 82 | 207.2 | 11.34 | 327.5 | 1740 | S | +2 +4 |
| Lithium | Li | 3 | 6.941 | 0.53 | 180.5 | 1317 | S | +1 |
| Lutetium | Lu | 71 | 174.967 | 9.84 | 1656 | 3315 | S | +3 |
| Magnesium | Mg | 12 | 24.305 | 1.74 | 648.8 | 1107 | S | +2 |
| Manganese | Mn | 25 | 54.93805 | 7.44 | 1244 | 2097 | S | +2 +3 +4 +7 |
| Meitnerium | Mt | 109 | 35 (est.) | X S | ||||
| Mendelevium | Md | 101 | (258) | 1521 | X S | |||
| Mercury | Hg | 80 | 200.59 | 13.55 | -38.9 | 356.6 | L | +1 +2 |
| Molybdenum | Mo | 42 | 95.94 | 10.28 | 2617 | 5560 | S | +3 +6 |
| Neodymium | Nd | 60 | 144.24 | 7.00 | 1010 | 3127 | S | +3 |
| Neon | Ne | 10 | 20.1797 | 0.84 | -248.7 | -246.1 | G | 0 |
| Neptunium | Np | 93 | (237) | 20.48 | 640 | 3902 | S | +3 +4 +5 +6 |
| Nickel | Ni | 28 | 58.69 | 8.91 | 1453 | 2732 | S | +2 +3 |
| Niobium | Nb | 41 | 92.90638 | 8.58 | 2468 | 4927 | S | +3 +5 |
| Nitrogen | N | 7 | 14.00674 | 1.17 | -209.9 | -195.8 | D G | -3 +3 +5 |
| Nobelium | No | 102 | (259) | 1521 | X S | |||
| Osmium | Os | 76 | 190.2 | 22.61 | 3045 | 5027 | S | +3 +4 |
| Oxygen | O | 8 | 15.9994 | 1.33 | -218.4 | -182.9 | D G | -2 |
| Palladium | Pd | 46 | 106.42 | 12.02 | 1552 | 3140 | S | +2 +4 |
| Phosphorus | P | 15 | 30.973762 | 1.82 | 44 (P4) | 280 (P4) | S | -3 +3 +5 |
| Platinum | Pt | 78 | 195.08 | 21.45 | 1772 | 3827 | S | +2 +4 |
| Plutonium | Pu | 94 | (244) | 19.74 | 641 | 3327 | S | +3 +4 +5 +6 |
| Polonium | Po | 84 | 208.9824 | 9.20 | 254 | 962 | S | +2 +4 |
| Potassium | K | 19 | 39.0983 | 0.86 | 63.7 | 774 | S | +1 |
| Praseodymium | Pr | 59 | 140.90765 | 6.48 | 931 | 3212 | S | +3 |
| Promethium | Pm | 61 | 146.9151 | 7.22 | 1080 | 2730 | S | +3 |
| Protactinium | Pa | 91 | 231.0359 | 15.37 | 1554 | 4030 | S | +4 +5 |
| Radium | Ra | 88 | 226.0254 | 5.50 | 700 | 1140 | S | +2 |
| Radon | Rn | 86 | 222.0176 | 9.23 | -71 | -61.8 | G | 0 |
| Rhenium | Re | 75 | 186.207 | 21.03 | 3180 | 5627 | S | +4 +6 +7 |
| Rhodium | Rh | 45 | 102.9055 | 12.41 | 1966 | 3727 | S | +3 |
| Roentgenium | Rg | 111 | 19.282 | X S | ||||
| Rubidium | Rb | 37 | 85.4678 | 1.53 | 39 | 688 | S | +1 |
| Ruthenium | Ru | 44 | 101.07 | 12.45 | 2310 | 3900 | S | +3 |
| Rutherfordium | Rf | 104 | 18.1 | X S | ||||
| Samarium | Sm | 62 | 150.36 | 7.54 | 1072 | 1778 | S | +2 +3 |
| Scandium | Sc | 21 | 44.95591 | 2.99 | 1539 | 2832 | S | +3 |
| Seaborgium | Sg | 106 | 35 (est.) | X S | ||||
| Selenium | Se | 34 | 78.96 | 4.82 | 217 | 685 | S | -2 +4 +6 |
| Silver | Ag | 47 | 107.8682 | 10.49 | 961.9 | 2212 | S | +1 |
| Silicon | Si | 14 | 28.0855 | 2.33 | 1410 | 2355 | S | -4 +2 +4 |
| Sodium | Na | 11 | 22.989768 | 0.97 | 97.8 | 892 | S | +1 |
| Strontium | Sr | 38 | 87.62 | 2.63 | 769 | 1384 | S | +2 |
| Sulfur | S | 16 | 32.066 | 2.06 | 113 | 444.7 | S | -2 +4 +6 |
| Tantalum | Ta | 73 | 180.9479 | 16.68 | 2996 | 5425 | S | +5 |
| Technetium | Tc | 43 | 98.9063 | 11.49 | 2172 | 5030 | S | +4 +6 +7 |
| Tellurium | Te | 52 | 127.6 | 6.25 | 449.6 | 990 | S | -2 +4 +6 |
| Terbium | Tb | 65 | 158.92534 | 8.25 | 1360 | 3041 | S | +3 |
| Thallium | Tl | 81 | 204.3833 | 11.85 | 303.6 | 1457 | S | +1 +3 |
| Thorium | Th | 90 | 232.0381 | 11.72 | 1750 | 4787 | S | +4 |
| Thulium | Tm | 69 | 168.93421 | 9.32 | 1545 | 1727 | S | +3 |
| Tin | Sn | 50 | 118.71 | 7.29 | 232 | 2270 | S | +2 +4 |
| Titanium | Ti | 22 | 47.88 | 4.51 | 1660 | 3260 | S | +2 +3 +4 |
| Tungsten | W | 74 | 183.85 | 19.26 | 3407 | 5927 | S | +6 |
| Ununhexium | Uuh | 116 | 9.32 | X | ||||
| Ununoctium | Uuo | 118 | X | |||||
| Ununpentium | Uup | 115 | 9.807 | X | ||||
| Ununquadium | Uuq | 114 | 11.342 | X | ||||
| Ununseptium | Uus | 117 | X | |||||
| Ununtrium | Uut | 113 | 11.85 | X | ||||
| Uranium | U | 92 | 238.0289 | 18.97 | 1132.4 | 3818 | S | +3 +4 +5 +6 |
| Vanadium | V | 23 | 50.9415 | 6.09 | 1890 | 3380 | S | +2 +3 +4 +5 |
| Xenon | Xe | 54 | 131.29 | 4.49 | -111.9 | -107 | G | 0 +2 +4 +6 |
| Ytterbium | Yb | 70 | 173.04 | 6.97 | 824 | 1193 | S | +2 +3 |
| Yttrium | Y | 39 | 88.90585 | 4.47 | 1523 | 3337 | S | +3 |
| Zinc | Zn | 30 | 65.39 | 7.14 | 419.6 | 907 | S | +2 |
| Zirconium | Zr | 40 | 91.224 | 6.51 | 1852 | 4377 | S | +4 |
(*) Phase at STP, where S is solid, L is liquid, and G is gas. X is for synthetic (laboratory) elements, and D is for diatomic elements.
(**) Most common oxidation states, not an exhaustive list.
Atomic weights in parentheses are the atomic weights for the most stable isotope.
GNU Free Documentation License
As of July 15, 2009 Wikibooks has moved to a dual-licensing system that supersedes the previous GFDL only licensing. In short, this means that text licensed under the GFDL only can no longer be imported to Wikibooks, retroactive to 1 November 2008. Additionally, Wikibooks text might or might not now be exportable under the GFDL depending on whether or not any content was added and not removed since July 15. |
Version 1.3, 3 November 2008 Copyright (C) 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. <http://fsf.org/>
Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.
The "publisher" means any person or entity that distributes copies of the Document to the public.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
- Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
- List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
- State on the Title page the name of the publisher of the Modified Version, as the publisher.
- Preserve all the copyright notices of the Document.
- Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
- Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
- Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
- Include an unaltered copy of this License.
- Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
- Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
- For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
- Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
- Delete any section Entitled "Endorsements". Such a section may not be included in the Modified version.
- Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
- Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements".
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Document.
11. RELICENSING
"Massive Multiauthor Collaboration Site" (or "MMC Site") means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A "Massive Multiauthor Collaboration" (or "MMC") contained in the site means any set of copyrightable works thus published on the MMC site.
"CC-BY-SA" means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.
"Incorporate" means to publish or republish a Document, in whole or in part, as part of another Document.
An MMC is "eligible for relicensing" if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.
The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.
How to use this License for your documents
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
- Copyright (c) YEAR YOUR NAME.
- Permission is granted to copy, distribute and/or modify this document
- under the terms of the GNU Free Documentation License, Version 1.3
- or any later version published by the Free Software Foundation;
- with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
- A copy of the license is included in the section entitled "GNU
- Free Documentation License".
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:
- with the Invariant Sections being LIST THEIR TITLES, with the
- Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.
| This is the print version of General Chemistry You won't see this message or any elements not part of the book's content when you print or preview this page. |
General Chemistry
A Free Online Textbook
A three-dimensional representation of an atomic 4f orbital.
About General Chemistry
General Chemistry is an introduction to the basic concepts of chemistry, including atomic structure and bonding, chemical reactions, and solutions. Other topics covered include gases, thermodynamics, kinetics and equilibrium, redox, and chemistry of the elements.
It is assumed that the reader has basic scientific understanding. Otherwise, minimal knowledge of chemistry is needed prior to reading this book.
Beyond General Chemistry
- Organic Chemistry - Chemistry studies focusing on the carbon atom and compounds.
- Inorganic Chemistry - Chemistry studies focusing on salts, metals, and other compounds not based on carbon.
- Biochemistry - Chemistry studies of or relating to living organisms.
About Wikibooks
This is a wiki textbook. Anyone from around the world can read, as well as write it! All of the content in the book is covered by the GNU Free Document Licence, which means it is guaranteed to remain free and open.
Authors and Significant Contributors
Introduction
Chemistry is Everywhere

The modern human experience places a large emphasis upon the material world. From the day of our birth to the day we die, we are frequently preoccupied with the world around us. Whether struggling to feed ourselves, occupying ourselves with modern inventions, interacting with other people or animals, or simply meditating on the air we breathe, our attention is focused on different aspects of the material world. In fact only a handful of disciplines—certain subsets of religion, philosophy, and abstract math—can be considered completely unrelated to the material world. Everything else is somehow related to chemistry, the scientific discipline which studies the properties, composition, and transformation of matter.
Branches of Chemistry
Chemistry itself has a number of branches:
- Analytical chemistry seeks to determine the composition of substances.
- Biochemistry is the study of chemicals found in living things (such as DNA and proteins).
- Inorganic Chemistry studies substances that do not contain carbon.
- Organic chemistry studies carbon-based substances. Carbon, as described in more detail in this book, has unique properties that allow it to make complex chemicals, including those of living organisms. An entire field of chemistry is devoted to substances with this element.
- Physical chemistry is the study of the physical properties of chemicals, which are characteristics that can be measured without changing the composition of the substance.

Chemistry as a discipline is based on a number of other fields. Because it is a measurement-based science, math plays an important role in its study and usage. A proficiency in high-school level algebra should be all that is needed in this text, and can be obtained from a number of sources. Chemistry itself is determined by the rules and principles of physics. Basic principles from physics may be introduced in this text when necessary.
Why Study Chemistry?
There are many reasons to study chemistry. It is one pillar of the natural sciences necessary for detailed studies in the physical sciences or engineering. The principles of biology and psychology are rooted in the biochemistry of the animal world, in ways that are only now beginning to be understood. Modern medicine is firmly rooted in the chemical nature of the human body. Even students without long-term aspirations in science find beauty in the infinite possibilities that originate from the small set of rules found in chemistry.
Chemistry has the power to explain everything in this world, from the ordinary to the bizarre. Why does iron rust? What makes propane such an efficient, clean burning fuel? How can soot and diamond be so different in appearance, yet so similar chemically? Chemistry has the answer to these questions, and so many more. Understanding chemistry is the key to understanding the world as we know it.
This Book: General Chemistry
An introduction to the chemical world is set forth in this text. The units of study are organized as follows.

- Properties of Matter: An explanation of the most fundamental concept in chemistry: matter.
- Atomic Structure: While technically in the domain of physics, atoms determine the behavior of matter, making them a necessary starting point for any discussion of chemistry.
- Compounds and Bonding: Chemical bonding is introduced, which explains how less than one hundred naturally-occurring elements can combine to form all the different compounds that fill our world.
- Chemical Reactions: Things get interesting once chemical reactions start making and breaking bonds.
- Aqueous Solutions: Substances dissolved in water have special properties. This is when acids and bases are introduced.
- Phases of Matter: A detailed look at the organization of substances, with particular focus on gases.
- Chemical Equilibria: Chemical reactions don't go on forever. Equilibrium is the balance that reactions seek to achieve.
- Chemical Kinetics: Kinetics explain why it takes years for an iron nail to rust, but only a split second for a hydrogen-filled hot air balloon to explode.
- Thermodynamics: Two things decide which reactions can occur and which reactions cannot: heat and chaos. Or enthalpy and entropy, as they are called in thermodynamics
- Chemistries of Various Elements: An exploration of the elements that make up all substance. Includes an introduction to nuclear chemistry and carbon, the essence of organic chemistry.
Matter
Basic Properties of Matter
What is Matter?

Matter is defined as anything that occupies space and has mass. Black holes have mass but occupy effectively no space. Black holes have infinite density and 0 volume. Anything that has mass must be 3-dimensional, which is why, however small atoms (the stuff that makes up matter) are, they are 3-dimensional.
Mass is a measure of an object's inertia. It is proportional to weight: the more mass an object has, the more weight it has. However, mass is not the same as weight. Weight is a force created by the action of gravity on a substance while mass is a measure of an object's resistance to change in motion. For example, your weight on the moon would be one-sixth your weight on the earth, as the moons gravitational field is one-sixth that of earth's. Mass used to measured by comparing the substance of interest to a standard kilogram called the International Prototype Kilogram (IPK). The IPK is a metal cylinder for which the height and diameter both equal 39.17 millimeters and is made of an alloy of 90% platinum and 10% iridium. Thus, the standard kilogram is defined and all other masses are a comparison to this kilogram. When atom masses are measured in a mass spectrometer, a different internal standard is used. Your take home lesson with regard to mass is that mass is a relative term judged by a comparison. Mass is now defined by a Watt or Kibble balance by measuring the Planck constant. The goal of measuring mass with the Planck constant is to measure mass electronically. The reason for this is that it is a lot easier to make an electronic measurements with electronics and electricity than to weigh something big or small, so researchers have been working on accurately redefining the kilogram to a quantum standard that implements the Watt/Kibble balance for the Planck constant. This change took effect in 20 May 2019 after a historic vote among the members of the CGPM at Versailles in France to redefine the kilogram, ampere, mole, and kelvin. The redefinition of the kilogram was contingent upon continued improvement of this new method of determining mass. National metrology labs such as NIST collaborated to make the redefinition of the kilogram possible.
Volume is a measure of the amount of space occupied by an object. Volume can be measured directly with equipment designed using graduations marks or indirectly using length measurements depending on the state (gas, liquid, or solid) of the material. A graduated cylinder, for example, is a tube that can hold a liquid which is marked and labeled at regular intervals, usually every 1 or 10 mL. Once a liquid is placed in the cylinder, one can read the graduation marks and record the volume measurement. Since volume changes with temperature, graduated equipment has limits to the precision with which one can read the measurement. Solid objects that have regular shape can have their volume calculated by measuring their dimensions. In the case of a box, its volume equals length times width times height.
It is particularly interesting to note that measuring is different from calculating a specific value. While mass and volume can both be determined directly relative to either a defined standard or line marks on glass, calculating other values from measurements is not considered measuring. For example, once you have measured the mass and volume of a liquid directly, one can then calculate the density of a substance by dividing the mass by the volume. This is considered indirectly determining density. Interestingly enough, one can also measure density directly if an experiment which allows the comparison of density to a standard is set up.
Another quantity of matter directly or indirectly determined is the amount of substance. This can either represent a counted quantity of objects (e.g. three mice or a dozen bagels) or the indirectly determined number of particles of a substance being dealt with such as how many atoms are contained in a sample of a pure substance. The latter quantity is described in terms of moles. One mole used to be specifically defined as the number of particles in 12 grams of the isotope Carbon-12. This number was 6.02214078(18)x 1023 particles. The mole is now defined so the Avogadro constant N_A has the value 6.022 140 76 times 10 to the 23 reciprocal mole.
- Mass: the kilogram (kg). Also, the gram (g) and milligram (mg).
- 1 kg = 1000 g
- 1000 mg = 1 g.
- Volume: the liter (L), milliliter (mL). Also, cubic centimeters (cc) and cubic meters (m3).
- 1 cc = 1 mL
- 1000 mL = 1 L
- 1000 L = 1 m3
- Amount: the mole (mol).
- 1 mol = 6.02214078(18)x 1023 particles
Atoms, Elements, and Compounds
The fundamental building block of matter is the atom. Atoms are made of protons, electrons, and neutrons. Protons and neutrons are made of quarks and gluons.

Any atom is composed of a little nucleus surrounded by a "cloud" of electrons. In the nucleus there are protons and neutrons.
However, the term "atom" just refers to a building block of matter; it doesn't specify the identity of the atom. It could be an atom of carbon, or an atom of hydrogen, or any other kind of atom.
This is where the term "element" comes into play. When an atom is defined by the number of protons contained in its nucleus, chemists refer to it as an element. All elements have a very specific identity that makes them unique from other elements. For example, an atom with 6 protons in its nucleus is known as the element carbon. When speaking of the element fluorine, chemists mean an atom that contains 9 protons in its nucleus.
- Atom: A fundamental building block of matter composed of protons, neutrons, and electrons.
- Element: A uniquely identifiable atom recognized by the number of protons in the nucleus.
Despite the fact that we define an element as a unique identifiable atom, when we speak, for example, 5 elements, we don't usually mean those 5 atoms are of the same type (having the same number of protons in their nucleus). We mean 5 'types' of atoms. It is not necessary there are only 5 atoms. There may be 10, or 100, etc. atoms, but those atoms belong to one of 5 types of atoms. I'd rather define 'element' as 'type of atom'. I think it is more precise. If we'd like to refer to 5 atoms having the same 6 protons in their nucleus, I'd say '5 carbon atoms' or '5 atoms of carbon'.
It is important to note that if the number of protons in the nucleus of an atom changes, so does the identity of that element. If we could remove a proton from nitrogen (7 protons), it is no longer nitrogen. We would, in fact, have to identify the atom as carbon (6 protons). Remember, elements are unique and are always defined by the number of protons in the nucleus. The Periodic Table of the Elements shows all known elements organized by the number of protons they have.
An element is composed of the same type of atom; elemental carbon contains any number of atoms, all having 6 protons in their nuclei. In contrast, compounds are composed of different type of atoms. More precisely, a compound is a chemical substance that consists of two or more elements. A carbon compound contains some carbon atoms (with 6 protons each) and some other atoms with different numbers of protons.
Compounds have properties different from the elements that created them. Water, for example, is composed of hydrogen and oxygen. Hydrogen is an explosive gas and oxygen is a gas that fuels fire. Water has completely different properties, being a liquid that is used to extinguish fires.
The smallest representative for a compound (which means it retains characteristics of the compound) is called a molecule. Molecules are composed of atoms that have "bonded" together. As an example, the formula of a water molecule is "H2O": two hydrogen atoms and one oxygen atom.
Properties of Matter
Properties of matter can be divided in two ways: extensive/intensive, or physical/chemical.
According to the International Union of Pure and Applied Chemistry (IUPAC), an intensive property or intensive quantity is a quantity whose magnitude is independent of the size of the system (the part of the environment under study). Intensive properties include temperature, refractive index (for example, the refactive index of air is 1.000293), and mass density. The reciprocal or multiplicative inverse of mass density, specific volume, is also an intensive property. Boiling point is an intensive property. Here is a list of intensive properties:
- charge density
- linear charge density is amount of electric charge per unit length and typically represented by with units of
- surface charge density is amount of electric charge per unit surface area and represented by and measured with the unit
- volume charge density is amount of electric charge per unit volume and typically represented by rho, and measured with the unit .
- color
- concentration
- mass concentration in
- molar concentration in
- number concentration in
- energy density in
- electric permeability as a measure of magnetization produced in a material in response to an applied magnetic field typically represented by mu, and measured with either or
- specific gravity
- melting point
- boiling point
- molality measured with
- pressure
- refractive index
- electrical resistivity measured with
- electrical conductivity measured with
|
|
States of Matter
One important physical property is the state of matter. Three are common in everyday life: solid, liquid, and gas. The fourth, plasma, is observed in special conditions such as the ones found in the sun and fluorescent lamps. Substances can exist in any of the states. Water is a compound that can be liquid, solid (ice), or gas (steam).


Solids
Solids have a definite shape and a definite volume. Most everyday objects are solids: rocks, chairs, ice, and anything with a specific shape and size. The molecules in a solid are close together and connected by intermolecular bonds. Solids can be amorphous, meaning that they have no particular structure, or they can be arranged into crystalline structures or networks. For instance, soot, graphite, and diamond are all made of elemental carbon, and they are all solids. What makes them so different? Soot is amorphous, so the atoms are randomly stuck together. Graphite forms parallel layers that can slip past each other. Diamond, however, forms a crystal structure that makes it very strong.
Liquids
Liquids have a definite volume, but they do not have a definite shape. Instead, they take the shape of their container to the extent they are indeed "contained" by something such as beaker or a cupped hand or even a puddle. If not "contained" by a formal or informal vessel, the shape is determined by other internal (e.g. intermolecular) and external (e.g. gravity, wind, inertial) forces. The molecules are close, but not as close as a solid. The intermolecular bonds are weak, so the molecules are free to slip past each other, flowing smoothly. A property of liquids is viscosity, the measure of "thickness" when flowing. Water is not nearly as viscous as molasses, for example.
Gases
Gases have no definite volume and no definite shape. They expand to fill the size and shape of their container. The oxygen that we breathe and steam from a pot are both examples of gases. The molecules are very far apart in a gas, and there are minimal intermolecular forces. Each atom is free to move in any direction. Gases undergo effusion and diffusion. Effusion occurs when a gas seeps through a small hole, and diffusion occurs when a gas spreads out across a room. If someone leaves a bottle of ammonia on a desk, and there is a hole in it, eventually the entire room will reek of ammonia gas. That is due to the diffusion and effusion. These properties of gas occur because the molecules are not bonded to each other. The molecules in gas, are free and they can move around unlike solid molecules.
Technically, a gas is called a vapor if it does not occur at standard temperature and pressure (STP). STP is 0° C and 1.00 atm of pressure. This is why we refer to water vapor rather than water gas. |
- In gases, intermolecular forces are very weak, hence molecules move randomly colliding with themselves, and with the wall of their container, thus exerting pressure on their container. When heat is given out by gases, the internal molecular energy decreases; eventually, the point is reached when the gas liquifies.
Changes in Matter
There are two types of change in matter: physical change and chemical change. As the names suggest, physical changes never change the identity of the matter, only its size, shape or state. In a physical change, atoms are not rearranged and the matter's physical and chemical properties are unchanged. Chemical changes, on the other hand, rearrange the atoms of matter in new combinations, resulting in matter with new physical and chemical properties.
Chemical changes are also known as chemical reactions. The "ingredients" of a reaction are the reactants, and the end results are called the "products". The change from reactants to products can be signified by an arrow.Chemical changes are mostly irreversible
- A Chemical Reaction
Reactants → Products
Note that the number of reactants and products don't necessarily have to be the same. However, the number of each type of atom must remain constant. This is called the Law of Conservation of Matter. It states that matter can never be created or destroyed, only changed and rearranged. If a chemical reaction begins with 17 moles of carbon atoms, it must end with 17 moles of carbon atoms. They may be bonded into different molecules, or in a different state of matter, but they cannot disappear.
When changes occur, energy is often transformed. However, like atoms, energy cannot disappear. This is called the Law of Conservation of Energy. A simple example would be putting ice cubes into a soft drink. The ice cubes get warmer as the drink gets colder, because energy cannot be created or destroyed, only transferred. Note that energy can be "released" or "stored" by making and breaking bonds. When a plant converts the energy from sunlight into food, that energy is stored in the chemical bonds within the sugar molecules.
Chemical change or Physical change?

Physical changes do not cause a substance to become a fundamentally different substance. Chemical changes, on the other hand, cause a substance to change into something entirely new. Chemical changes are typically irreversible, but that is not always the case. It is easier to understand the difference between physical and chemical changes with examples.
| State changes are physical. | Phase changes are when you melt, freeze, boil, condense, sublimate, or deposit a substance. They do not change the nature of the substance unless a chemical change occurs along with the physical change. |
| Cutting, tearing, shattering, and grinding are physical. | These may be irreversible, but the result is still composed of the same molecules. When you cut your hair, that is a physical change, even though you can't put the hair back on your head again. |
| Mixing together substances is physical. | For example, you could mix salt and pepper, dissolve salt in water, or mix molten metals together to produce an alloy. |
| Gas bubbles forming is chemical. | Not to be confused with bubbles from boiling, which would be physical (a phase change). Gas bubbles indicate that a chemical reaction has occurred. |
| Precipitates forming is chemical. | When dissolved substances are mixed, and a cloudy precipitate appears, there has been a chemical change. |
| Rotting, burning, cooking, and rusting (for example) are chemical. | The resulting substances are entirely new chemical compounds. For instance, wood becomes ash and heat; iron becomes rust; sugar ferments into alcohol. |
| Changes of color or release of odors (i.e. release of a gas) might be chemical. | As an example, the element chromium shows different colors when it is in different compounds, but a single chromium compound will not change color on its own without some sort of reaction. |
| Release/absorption of energy (heat, light, sound) is generally not easily categorized. | Hot/cold packs involve dissolving a salt in water to change its temperature (more on that in later chapters); popping popcorn is mostly physical (but not completely). |
Classification of Matter
Matter can be classified by its state.
- Solids have a set volume and shape.The inter molecular force of attraction for solid matter is very strong.
- Liquids have a set volume, but change shape. The inter molecular force of attraction for liquid matter is weaker than solid matter.
- Gases have neither definite volume nor shape. The inter molecular force of attraction for gaseous matter is negligible.
- Plasma which are usually gaseous state of matter in which a part or all of the atoms or molecules are dissociated to form ions.
- Einstein-Bose Condensate (EBC) is a theoretical state of matter. The intermolecular force of attraction for EBC is so strong that the molecules cannot move whatsoever.
Matter can also be classified by its chemical composition.
- An element is a pure substance made up of atoms with the same number of protons. As of 2011, 118 elements have been observed, 92 of which occur naturally. Carbon (C), Oxygen (O), Hydrogen (H) are examples of elements. The periodic table is a tabular representation of the known elements.
- A compound consists of two or more chemical elements that are chemically bonded together. Water (H2O) and table sugar (C12H22O11) are examples of chemical compounds. The ratio of the elements in a compound is always the same. For example in water, the number of H atoms is always twice the number of O atoms.
- A mixture consists of two or more substances (element or compound) mixed together without any chemical bond. Salad is a good example. A mixture can be separated into its individual components by mechanical means.
Types of Mixtures
There are many kinds of mixtures. They are classified by the behavior of the phases, or substances that have been mixed.
Homogeneous Mixtures

A homogeneous mixture is uniform, which means that any given sample of the mixture will have the same composition. Air, sea water, and carbonation dissolved in soda are all examples of homogeneous mixtures, or solutions. No matter what sample you take from the mixture, it will always be composed of the same combination of phases. Chocolate chip ice cream is not homogeneous—one spoonful taken might have two chips, and then another spoonful might have several chips.
An example for a homogeneous mixture is a solution. The substance that gets dissolved is the solute. The substance that does the dissolving is the solvent. Together they make a solution. If you stir a spoonful of salt into a glass of water, salt is the solute that gets dissolved. Water is the solvent. The salty water is now a solution, or homogeneous mixture, of salt and water.
When different gases are mixed, they always form a solution. The gas molecules quickly spread out into a uniform composition.
Heterogeneous Mixtures
A heterogeneous mixture is not uniform. Different samples may have different compositions, like the example of chocolate chip ice cream. Concrete, soil, blood, and salad are all examples of heterogeneous mixtures.

Suspensions
When sand gets kicked up in a pond, it clouds the water. It has a greater mass than water hence it sinks to the bottom and settles down, and is no longer mixed into the water. This is an example of a suspension. Suspensions are heterogeneous mixtures that will eventually settle. They are usually, but not necessarily, composed of phases in different states of matter. Italian salad dressing has three phases: the water, the oil, and the small pieces of seasoning. The seasonings are solids that will sink to the bottom, and the oil and water are liquids that will separate.
Colloids

What exactly is toothpaste? We can't exactly classify it by its state of matter. It has a definite shape and volume, like a solid. But then you squeeze the tube, and it flows almost like a liquid. And then there's jelly, shaving cream, smoke, dough, and Silly Putty...
These are examples of colloids. A colloid is a heterogeneous mixture of two substances of different phases. Shaving cream and other foams are gas dispersed in liquid. Jello, toothpaste, and other gels are liquid dispersed in solid. Dough is a solid dispersed in a liquid. Smoke is a solid dispersed in a gas.
Colloids differ from suspensions in that they will not settle. |
Colloids consist of two phases: a dispersed phase inside of a continuous medium.
The Tyndall Effect
The Tyndall effect distinguishes colloids from solutions. In a solution, the particles are so fine that they will not scatter light. This is not true for a colloid. If you shine light through a solution, the beam of light will not be visible. It will be visible in a colloid. For instance, if you have ever played with a laser pointer, you have seen the Tyndall effect. You cannot see the laser beam in air (a solution), but if you shine it into a mist, the beam is visible. Clouds look white (or gray), as opposed to blue, because of the Tyndall effect - the light is scattered by the small droplets of suspended water.
Methods for Separating Mixtures

Because there is no chemical bonding in a mixture, the phases can be separated by mechanical means. In a heterogeneous mixture like a salad, the pieces can easily be picked out and separated. It is as simple as sifting through the salad and picking out all the tomatoes and radishes, for example. However, many mixtures contain particles that are too small, liquids, or too many particles to be separated manually. We must use more sophisticated methods to separate the mixture.
Filtration
Imagine you have a sandbox, but there are bits of broken glass in it. All you would need is some sort of filter. The sand particles are much smaller than the glass chips, so a mesh filter would let sand pass but stop the glass. Filtration is used in all sorts of purification methods. Some filters, like dialysis tubing, are such fine filters that water can pass, but dissolved glucose cannot.
Filtration works with particles that are significantly different in size, like sand and rock, or water and glucose. |
Distillation

If you were given a glass of saltwater, could you drink it? Sure, if you distill it first. Distillation is the boiling of a mixture to separate its phases. Salt is a solid at room temperature, and water is a liquid. Water will boil far before salt even begins to melt. So separating the two is as simple as boiling the water until all that remains is the solid salt. If desired, the water vapor can be collected, condensed, and used as a source of pure water.
Distillation can also be used if two liquids are mixed but have different boiling points. Separation of several liquids with similar boiling points can be achieved using fractionation.
Centrifugation and Sedimentation

These processes rely on differences in density. In a medical lab, blood often goes into a centrifuge. A centrifuge is a machine that spins a sample at fairly high rates of speed. Red blood cells are much denser than the watery substance (called plasma, but it's not the plasma state of matter) that makes up blood. As a result of the spinning, the denser phases move outward and the less dense phases move inward, towards the axis of rotation. Then, the red blood cells can be separated from the plasma.
Sedimentation is similar, but it happens when particles of different densities have settled within a liquid. If a jar of muddy water is left to settle, the heaviest particles sink to the bottom first. The lightest particles sink last and form a layer on top the heavier particles. You may have seen this effect in a bottle of salad dressing. The seasonings sink to the bottom, the water forms a lower layer, and the oil forms an upper layer. The separate phases can be skimmed out. To return it to a mixture, simply shake it up to disturb the layers.
Unique Properties

The differences in substances' properties can be exploited to allow separation. Consider these examples:
- A mixture of sand and iron filings can be separated by magnet.
- Salt and sand can be separated by solution (sand will not dissolve in water, salt will)
- Helium can be separated from a mixture with hydrogen by combustion (this is a very dangerous operation, since hydrogen in the presence of oxygen is highly explosive). Hydrogen is flammable, but helium is not.
Other methods
There are countless other ways to separate mixtures. For instance, gel electrophoresis is used to separate different sized pieces of DNA. They are placed into gel, and an electric current is applied. The smaller pieces move faster and separate from the larger pieces.
Chromatography separates phases dissolved in liquid. If you want to see an example, take a strip of paper and draw a dot on it with a colored marker. Dip the strip into water, and wait a while. You should see the ink separate into different colors as they spread out from the dot.
Numbers Used to Describe Atoms
Numbers

The Atomic number is the number of protons in the nucleus of an atom. This number determines the element type of the atom. For instance, all neon atoms have exactly ten protons. If an atom has ten protons, then it must be neon. If an atom is neon, then it must have ten protons.
The atomic number is sometimes denoted Z. Continuing with the example of neon, .
The Neutron number is the number of neutrons in the nucleus of an atom. Remember that neutrons have no electric charge, so they do not affect the chemistry of an element. However, they do affect the nuclear properties of the element. For instance, Carbon-12 has six neutrons, and it is stable. Carbon-14 has eight neutrons, and it happens to be radioactive. Despite these differences, both forms of carbon behave the same way when forming chemical compounds.
The neutron number is sometimes denoted N.
The Mass number is the sum of protons and neutrons in an atom. It is denoted A. To find the mass number of an atom, remember that A = Z + N. The mass number of an atom is always an integer. Because the number of neutrons can vary among different atoms of the same element, there can be different mass numbers of a given element. Look back to the example of carbon. Carbon-14 has a mass number of 14, and Carbon-12 has a mass number of 12. Every carbon atom must have six protons, so Carbon-14 has eight neutrons and Carbon-12 has six neutrons.
Elements with the same atomic number but different atomic masses are isotopes. |
Isotopes of the same element have nearly identical chemical properties (because they have the same number of protons and electrons). Their only difference is the number of neutrons, which changes their nuclear properties like radioactivity.
Notation
There is a convenient way of writing the numbers that describe atoms. It is easiest to learn by examples.
| Helpful Hint! | |
|---|---|
| Keep in mind that any of the three numbers written around the element symbol are optional, but they should be written if it is important to the given situation. The charge number is left off if the atom has zero charge (equal number of protons and electrons). The mass number and atomic number are usually left off. |
| This is how we write fluorine-19. The atomic number is below and the mass number is above, followed by its symbol on the periodic table of the elements. | |
| This example shows carbon-12. Notice how the atomic number is missing. You know which element it is because of the C, so there is no need to write the number of protons. The atomic number is rarely written because the element symbol implies how many protons there are. | |
| The last example shows both the atomic number and mass number, along with a charge. The charge is the difference in the number of protons compared to the number of electrons. You can read more about charge, protons, and electrons later on. From the example, you can see that this magnesium atom would have 12 protons, 13 neutrons, and 10 electrons. Its mass is 25 (12 p + 13 n) and its charge is +2 (12 p - 10 e). |
- Exercise for the reader!
Try writing the symbol for an atom with seven protons, seven neutrons, and eight electrons. You will need to look up its symbol on the periodic table.
Atomic Mass
The mass of an atom is measured in atomic mass units (amu). An atom's mass can be found by summing the number of protons and neutrons. By definition, 12 amu equals the atomic mass of carbon-12. Protons and neutrons have an approximate mass of 1 amu, and electrons have a negligible mass.
| There is a difference between an atom's mass number and an element's atomic mass. The mass number measures the number of protons and neutrons in the nucleus of a particular atom. The atomic mass measures the average mass of all atoms for an element. For example, a carbon atom might have a mass number of 12 or 14 (or something else), but carbon in general has a mass of 12.011 amu. |
Usually, a pure element is made up of a number of isotopes in specific ratios. Because of this, the measured atomic mass of carbon is not exactly 12. It is an average of all the masses of all the isotopes, with the more common ones contributing more to the measured atomic mass. By convention atomic masses are given no units.
- Example
Pretend that the element Wikibookium has two isotopes. The first has a mass number of 104, and the second has a mass number of 107. Considering that 75% of the naturally occurring atoms are of the first isotope, and the rest are of the second. The average atomic mass is calculated as
0.75 × 104 + 0.25 × 107 = 104.75
In this case, a bunch of Wikibookium atoms would have an average mass of 104.75 amu, but each individual atom might have a mass number of 104 or 107. Keep in mind that all of the atoms would have the same number of protons. Their masses are different because of the number of neutrons.
Moles
A mole is defined as the amount of an element whose number of particles are equal to that in 12g of C-12 carbon, also known as Avogadro's number. Avogadro's number equals 6.022 × 1023. Moles are not very confusing: if you have a dozen atoms, you would have 12. If you have a mole of atoms, you would have 6.022 × 1023. Why is this ridiculously large number important? It can be used to convert between atomic mass units and grams. One mole of carbon-12 is exactly 12 grams, by definition. Similarly, one mole of any element is the atomic mass of that element expressed as a weight in grams. The atomic mass is equal to the number of grams per mole of that element.
- Example
There are 128.2 g of rubidium (atomic mass = 85.47 amu). How many atoms are there?
(128.2 g) / (85.47 g/mol) = 1.5 mol
(1.5 mol) × (6.022 × 1023) = 9.03 × 1023 atoms of rubidium

Moles are also important because every 22.4 liters of gas contain 1 mole of gas molecules at standard temperature and pressure (STP, 0 °C and 1 atmosphere of pressure). Avogadro discovered this. (That's why it's his number.) A container filled with fluorine gas would have to be 22.4 L large to hold one mole of F2 molecules. Knowing this fact allows you to determine the mass of a gas molecule if you know the volume of the container. This holds true for every gas.
Why every single gas? Atoms and molecules are tiny. The volume of a gas is mostly empty space, so the molecules have an insignificantly small volume. As you will eventually learn, this ensures that there is always one mole of gas atoms for every 22.4 liters at STP.
Atomic Structure
History of Atomic Structure
Why Is The History Of The Atom So Important?
It is fundamental to the understanding of science that science is understood to be a process of trial and improvement and represents the best known at the time, not an unerring oracle of truth. Development of an idea and refinement through testing is shown more in the understanding of atomic structure.
The Greek Theorists

The earliest known proponent of anything resembling modern atomic theory was the ancient Greek thinker Democritus. He proposed the existence of indivisible atoms as a response to the arguments of Parmenides and the paradoxes of Zeno.
Parmenides argued against the possibility of movement, change, and plurality on the premise that something cannot come from nothing. Zeno attempted to prove Parmenides' point by a series of paradoxes based on difficulties with infinite divisibility.
In response to these ideas, Democritus posited the existence of indestructible atoms that exist in a void. Their indestructibility provided a retort to Zeno, and the void allowed him to account for plurality, change, and movement. It remained for him to account for the properties of atoms, and how they related to our experiences of objects in the world.
Democritus proposed that atoms possessed few actual properties, with size, shape, and mass being the most important. All other properties, he argued, could be explained in terms of the three primary properties. A smooth substance, for instance, might be composed of primarily smooth atoms, while a rough substance is composed of sharp ones. Solid substances might be composed of atoms with numerous hooks, by which they connect to each other, while the atoms of liquid substances possess far fewer points of connection.
Democritus proposed 5 points to his theory of atoms. [2] These are:
- All matter is composed of atoms, which are bits of matter too small to be seen. These atoms CANNOT be further split into smaller portions.
- There is a void, which is empty space between atoms.
- Atoms are completely solid.
- Atoms are homogeneous, with no internal structure.
- Atoms are different in their size, their shape, and their weight.
Alchemy


Empedocles proposed that there were four elements, air, earth, water, and fire and that everything else was a mixture of these. This belief was very popular in the medieval ages and introduced the science of alchemy. Alchemy was based on the belief that since everything was made of only four elements, you could transmute a mixture into another mixture of the same type. For example, it was believed that lead could be made into gold.
Alchemy's problem was exposed by Antoine Lavoisier when he heated metallic tin in a sealed flask. A grayish ash appeared on the surface of the melting tin, which Lavoisier heated until no more ash formed. After the flask cooled, he inverted it and opened it underwater. He discovered the water rose one-fifth of the way into the glass, leading Lavoisier to conclude that air itself is a mixture, with one-fifth of it having combined with the tin, yet the other four-fifths did not, showing that air was not an element.
Lavoisier repeated the experiment again, substituting mercury for tin, and found that the same happened. Yet after heating gently, he found that the ash released the air, showing that the experiment could be reversed. He concluded that the ash was a compound of the metal and oxygen, which he proved by weighing the metal and the ash, and showing that their combined weight was greater than that of the original metal.
Lavoisier then stated that combustion was not an element, but instead was a chemical reaction of a fuel and oxygen.
John Dalton
Modern atomic theory was born with Dalton when he published his theories in 1803. His theory consists of five important points, which are considered to be mostly true today: (from Wikipedia)
- Elements are composed of tiny particles called atoms.
- All atoms of a given element are identical.
- The atoms of a given element are different from those of any other element; the atoms of different elements can be distinguished from one another by their respective relative weights.
- Atoms of one element can combine with atoms of other elements to form chemical compounds; a given compound always has the same relative numbers of types of atoms.
- Atoms cannot be created, divided into smaller particles, nor destroyed in the chemical process; a chemical reaction simply changes the way atoms are grouped together.
We now know that elements have different isotopes, which have slightly different weights. Also, nuclear reactions can divide atoms into smaller parts (but nuclear reactions aren't really considered chemical reactions). Otherwise, his theory still stands today.
Dmitri Mendeleev
In the late 1800's, Russian scientist Dmitri Mendeleev was credited with creating one of the first organized periodic tables. Organizing each element by atomic weight, he cataloged each of the 56 elements discovered at the time. Aside from atomic weight, he also organized his table to group the elements according to known properties.
While writing a series of textbooks, Mendeleev realized he was running out of space to treat each element individually. He began to regularly "linewrap" the elements onto the next line, and create what is now called the periodic table of the elements. Using his table, he predicted the existence of later-discovered elements, such as "eka-aluminum" and "eka-silicon" (gallium and germanium) according to patterns found earlier. His predictions were a success, proving his table to be exceptionally accurate. Later theories, those of the electrons around the atom, explain why elements in the same period, or group, have similar chemical properties. Chemists would later organise each element by atomic number, not atomic weight, giving rise to the modern Periodic Table of Elements.
J.J. Thomson
Discovery of the Electron

In the year 1889 the British physicist J.J. Thomson discovered the electron. Thomson conducted a number of experiments using cathode ray tube. Cathode rays are constructed by sealing two electrodes in a glass tube connected to a voltage supplier and a vacuum pump removing the air from it. When the electrodes are attached to high voltage of about 15000v and low pressure, a beam of radiation is emitted from the negative electrode(cathode)moving towards the positive electrode(anode). These beams are said to be green rays called cathode rays. (1) The ray is said to be taken towards Faraday's tube(gold leaf electroscope) and was charged by induction and deflect positively charged gold leaf electroscope (2) a freely moving paddle wheel was placed on the path of the rays and it was able to move it suggesting that it has momentum (3) The ray was placed in a magnetic and electric field moving towards the north and positive pole respectively Thomson discovered that cathode rays travel in straight lines except, when they are bent by electric or magnetic fields. The cathode rays bent away from a negatively charged plate, Thomson concluded that these rays are made of negatively charged particles; today we call them electrons. Thomson found that he could produce cathode rays using electrodes of various materials. He then concluded that electrons were found in all atoms and are over a thousand times smaller than protons. Thompson used an apparatus to determine the charge to mass ratio(e/m)after the ray emerge he placed a magnetic field of a known magnetic influence and the rays bent towards the north to a particular position then he added an electric field to return the ray back to it original position and recorded the charges used by the electric field so he divided them to get the ratio of about -1.7*10^8kg
The "Plum Pudding" Atomic Model
Soon after the discovery of the electron, Thomson began speculating on the nature of the atom. He suggested a "plum pudding" model. In this model the bits of "plum" were the electrons which were floating around in a "pudding" of positive charge to match that of the electrons and make an electrically neutral atom. A modern illustration of this idea would be a chocolate chip cookie, with the chips representing negatively charged electrons and the dough representing positive charge.
Rutherford

Ernest Rutherford is known for his famous gold foil experiment in 1911. Alpha particles, which are heavy and positively charged (actually, helium nuclei, but that's beside the point), were fired at a very thin layer of gold. Most of the alpha particles passed straight through, as expected. According to the plum pudding model all of the particles should have slowed as they passed through the "pudding", but none should have been deflected. Surprisingly, a few alpha particles were deflected back the way they came. He stated that it was "as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you."
The result of the experiment allowed Rutherford to conclude that the plum pudding model is wrong.
- Atoms have a nucleus, very small and dense, containing the positive charge and most of the atom's mass.
- The atom consists of mostly empty space.
- The electrons are attracted to the nucleus, but remain far outside it.
Niels Bohr

Bohr created his own model of the atom, improving on Rutherford's. Bohr used an equation developed by Rydberg that provided a mathematical relationship between the visible spectral lines of the hydrogen atom. The equation requires that the wavelengths emitted from the hydrogen atom be related to the difference of two integers. Bohr theorized that these integers represent "shells" or "orbits" in which electrons travel around the nucleus, each with a certain energy level. The energy of an orbit is proportional to its distance from the nucleus. An atom will absorb and release photons that have a specific amount of energy. The energy is the result of an electron jumping to a different shell. Starting with Rydberg's equation, along with Planck and Einstein's work on the relationship between light and energy, Bohr was able to derive an equation to calculate the energy of each orbit in the hydrogen atom. The Bohr model depicts the atom as a nucleus with electrons orbiting around it at specific distances. This model is also referred to as the Planetary Model.
Robert Millikan
Robert Millikan is credited for the "Oil Drop Experiment", in which the value of the electron charge was determined. He created a mechanism where he could spray oil drops that would settle into a beam of X rays. The beam of X rays caused the oil drops to become charged with electrons. The oil droplets were in between a positively charged plate and a negatively charged plate which, when proper electric voltage was applied, caused the oil droplet to remain still. Robert Millikan measured the diameter of each individual oil drop using a microscope.
Millikan was able to calculate the mass of each oil droplet because he knew the density of the oil (). Using the mass of each oil droplet and the equation for the force of gravitational attraction (which he rearranged from to , where is the mass of each individual oil droplet, is the acceleration due to gravity, and is the electrical force which equals force in the first equation), Millikan was able to find the value of the charge of the electron, .
The X rays, however, did not always produce an oil drop with only one negative charge. Thus, the values Millikan obtained may have looked like this:
- coulomb
- coulomb
- coulomb
- coulomb
Millikan found that these values all had a common divisor: coulomb. He concluded that different values occurred because the droplets acquired charges of -5, -4, -3, and -2, as in this example. Thus, he stated that the common divisor, coulomb, was the charge of the electron.
References
- ↑ Conventions in Chemistry. In The ACS Style Guide, 3rd ed.; Coghill, A. M.; Garson, L.R., Eds.; Oxford University Press: New York, 2006; p 294.
- ↑ http://dbhs.wvusd.k12.ca.us/webdocs/AtomicStructure/Greeks.html
Subatomic Particles
Particle Properties
Before learning about subatomic particles, some basic properties should be understood.
Charge
Particles may be electrically charged. Charge is a property which defines the force that a particle will exert on other charged particles. There is a well known saying that applies perfectly: "Opposites attract." (Likewise, like charges repel.) Positive charges and negative charges will attract each other and come together. Two positive or two negative charges will push each other away.
| Helpful Hint! | |
|---|---|
| Not all particles have charge. |
The amount of charge a particle has is measured in coulombs, but it is more conveniently expressed in terms of an integer. For instance, a helium ion that has 2 less electrons than usual has a charge of +2, and a bromide ion with one more electron than usual has a charge of -1. (This may seem backwards, but remember that an electron has a negative charge.) Notice that charge not only applies to subatomic particles, but also ions and other things as well. Always remember to specify if a charge is positive or negative. Unlike ordinary numbers, we always write the plus sign for positive charges to avoid confusion with a negative charge.
It may be useful to understand Coulomb's Law. It explains the electromagnetic force: . is the charge on each particle, is the distance between them, and is a constant. So, if the distance between two particles is doubled, the force will be reduced four times. Double the charge would mean double the force, be it attractive or repulsive. Coulomb's Law will be especially important when understanding periodic trends.
However, there is no need to solve it exactly. Just remember the relationships between the variables. |
Mass
Mass is the measure of inertia. From a subatomic point of view, mass can also be understood in terms of energy, but that does not concern us when dealing with chemistry. Mass for particles, atoms, and molecules is not measured in grams, as with ordinary substances. Instead, it is measured in atomic mass units, or amu. For more information about mass and amu, read the previous chapters on properties of matter.
The Nucleus

At the center of each atom lies the nucleus. It is incredibly small: if you were to take the average atom (itself miniscule in size) and expand it to the size of a football stadium, then the nucleus would be about the size of a marble. It is, however, astoundingly dense: despite the tiny percentage of the atom's volume it contains nearly all of the atom's mass. The nucleus almost never changes under normal conditions, remaining constant throughout chemical reactions. Nuclei are themselves made up of a pair of smaller and more dense particles, the proton and the neutron. These particles are collectively dubbed nucleons.
Protons
Protons have a charge of +1 and a mass of 1 amu. They are often represented by a .
Protons will be important when learning about acids and bases—they are the essence of acid. Remember that the number of protons in an atom is its atomic number, and defines what element it will be. The number of protons in a nucleus ranges from one to over a hundred.
Consider the element hydrogen. Its atomic number is 1, so it has one proton and one electron. If it is made into an ion (an atom with missing or extra electrons), it will simply be a lone proton. Thus, a proton is the nucleus of a hydrogen atom, and a proton is a hydrogen ion. Therefore, a proton can be written as or , both symbols for a hydrogen ion.
Neutrons
Neutrons have no charge and a mass of 1 amu. A neutron is slightly heavier than a proton, but the difference is insignificant. Neutrons are often written .
Unlike the protons, neutrons cannot exist outside the nucleus indefinitely as they become unstable and break down. Within one nucleus there can be many protons and neutrons all in close proximity to one another. The number of neutrons in a nucleus ranges from zero to over a hundred.
You may wonder why neutrons exist. They have no charge, so can they do anything? The answer is yes—neutrons are very important. Remember that opposites attract and likes repel. If so, then how can several protons stay clumped together in the dense nucleus of an atom? It would seem as if the protons would repel and scatter the nucleus. However, there is a strong nuclear force that holds the nucleus together. This incredible force causes nucleons to attract each other with much greater strength than the electric force can repel them, but only over extremely short distances.
A delicate balance exists between the number of protons and neutrons. Protons, which are attracted to one another via the strong force but simultaneously repelled by their electromagnetic charges, cannot exist in great numbers within the nucleus without the stabilizing action of neutrons, which are attracted via the strong force but are not charged. Conversely, neutrons lend their inherent instability to the nucleus and too many will destabilize it.
Neutrons are the reason for isotopes, or atoms with the same number of protons but different masses. The masses are different because of different numbers of neutrons. Isotopes of a given element have almost identical chemical properties (like color, melting point, reactions, etc.), but they have different nuclear properties. Some isotopes are stable, others are radioactive. Different isotopes decay in different ways. |
Lastly, neutrons are very important in nuclear reactions, such as those used in power plants. Neutrons act like a bullet that can split an atom's nucleus. Because they have no charge, neutrons are neither attracted nor repelled by atoms and ions.
The Electron Cloud
Surrounding the dense nucleus is a cloud of electrons. Electrons have a charge of -1 and a mass of 0 amu. That does not mean they are massless. Electrons do have mass, but it is so small that it has no effect on the overall mass of an atom. An electron has approximately 1/1800 the mass of a proton or neutron. Electrons are written .
Electrons orbit the outside of a nucleus, unaffected by the strong nuclear force. They define the chemical properties of an atom because virtually every chemical reaction deals with the interaction or exchange of the outer electrons of atoms and molecules.
Electrons are attracted to the nucleus of an atom because they are negative and the nucleus (being made of protons and neutrons) is positive. Opposites attract. However, electrons don't fall into the nucleus. They orbit around it at specific distances because the electrons have a certain amount of energy. That energy prevents them from getting too close, as they must maintain a specific speed and distance. Changes in the energy levels of electrons cause different phenomena such as spectral lines, the color of substances, and the creation of ions (atoms with missing or extra electrons).
Electron Interactions
Atoms will always have equal numbers of protons and electrons, so their overall charge is zero. Atoms are neutral. Ions, on the other hand, are atoms that have gained or lost electrons and now have an unequal number of protons and electrons. If there are extra electrons, the ion will be negatively charged. If there are missing electrons, the ion will be positively charged, due to the majority of positive protons.
Valence electrons (the outermost electrons) are responsible for an atom's behavior in chemical bonds. The core electrons are all of the electrons not in the outermost shell, and they rarely get involved. An atom will attempt to fill its valence shell. This occurs when an atom has eight valence electrons (as explained in the next chapter), so atoms will undergo chemical bonds to either share, give, or take the electrons it needs. Sodium, for example, is very likely to give up its one valence electron, so that its outer shell is empty (the shell underneath it is full). Chlorine is very likely to take an electron because it has seven and wants eight. When sodium and chlorine are mixed, they exchange electrons and create sodium chloride (table salt). As a result, both elements have full valence shells, and a very stable compound is formed.
Introduction to Quantum Theory
Introduction to Quantum Mechanics
In the late 19th century, many physicists believed that they had made great progress in physics, and there wasn't much more that needed to be discovered. The classical physics at the time was widely accepted in the scientific community. However, by the early 20th century, physicists discovered that the laws of classical mechanics break down in the atomic world, and experiments such as the photoelectric effect completely contradict the laws of classical physics. As a result of these crises, physicists began to construct new laws of physics which would apply to the atomic world; these theories would be collectively known as quantum mechanics. Quantum mechanics, in some ways, completely changed the way physicists view the universe, and it also marked the end of the idea of a clockwork universe (the idea that the universe was predictable).
Electromagnetic Radiation
Electromagnetic radiation (ER) is a form of energy that sometimes acts like a wave, and other times acts like a particle. Visible light is a well-known example. All forms of ER have two inversely proportional properties: wavelength and frequency. Wavelength is the distance from one wave peak to the next, which can be measured in meters. Frequency is the number of wave peaks observed in a given point during a second. The unit for frequency is hertz.
Since wavelength and frequency are inversely related, their product (multiplication) always equals a constant — specifically, 3.0 x 108 m/sec represented by the letter c, which is better known as the speed of light. This relationship is written mathematically as , with the greek letter λ (lambda) representing wavelength and the letter representing frequency.
The wavelength and frequency of any specific occurrence of ER determine its position on the electromagnetic spectrum.

As you can see, visible light is only a tiny fraction of the spectrum.
The energy of a single particle of an electromagnetic wave (called a photon) is given by , where is Plank's constant and is the frequency. Energy is directly proportional to frequency — doubling the frequency will double the energy.
The Discovery of the Quantum

So far we have only discussed the wave characteristics of energy. However, the wave model cannot account for something known as the photoelectric effect. This effect is observed when light focused on certain metals apparently causes electrons to be emitted. (Photoelectric or solar panels work on this principle.)
For each metal it was found that there is a minimum frequency of electromagnetic radiation that is needed to be shone on it in order for it to emit electrons. This conflicted with the earlier thought that the energy of light was linked only to its intensity. Under that theory, the effect of light should be cumulative - dim light should add up, little by little, until it causes electrons to be emitted. Instead, there is a clear-cut minimum of the frequency of light that triggers the electron emissions.
The implication of this is that the energy of light is tied to frequency, and furthermore that it is quantized, meaning that it carries "packets" of energy in discrete amounts. These packets are more commonly referred to as photons. This observation led to the discovery of the minimum amount of energy that could be gained or lost by an atom. Max Planck named this minimum amount the quantum, plural "quanta", meaning "how much". One photon of light carries exactly one quantum of energy.
The Quantum Model
Uncertainty

It turns out that photons are not the only thing that act like waves and particles. Electrons, too, have this characteristic, known as wave-particle duality. Electrons can be thought of as waves of a certain length, thus they would only be able to form a circle around the nucleus at certain distances that are multiples of the wavelength. Of course, this brings up a problem: are electrons particles in a specific location, or waves in a general area? Werner Heisenberg tried using photons to locate electrons. Of course, when photons reach electrons, the electrons change velocity, and move to an excited state. As a result, it is impossible to precisely measure the velocity and location of an electron at the same time. This is known as the observer effect. This is frequently confused with the Heisenberg Uncertainty Principle, which goes even further, saying that there are limits to the degree to which both the position and momentum of a particle can even be known. This is due to the fact that electrons cannot exhibit both their wave and particle properties at the same time when being observed to interact with their surroundings. The momentum of an electron is proportional to its velocity, but based on its wave properties; its position is based on its particle position in space. The Heisenberg uncertainty principle is a kind of scientific dilemma: the more you know about something's velocity, the less you know about its position; and the more you know about its position, the less you know about its velocity. The significance of this uncertainty is that you can never know exactly where an atom's electrons are, only where they are most likely to be.

On the tiny scale of an atom, the particle model of an electron does not accurately describe its properties. An electron tends to act more like a water wave than a billiard ball. At any one moment in time the ball is in some definite place; it is also moving in some definite direction at a definite speed. This is certainly not true for waves or electrons in general. The Heisenberg uncertainty principle states that the exact position and momentum of an electron cannot be simultaneously determined. This is because electrons simply don't have a definite position, and direction of motion, at the same time!
One way to try to understand this is to think of an electron not as a particle but as a wave. Think of dropping a stone into a pond. The ripples start to spread out from that point. We can answer the question "Where is the wave?" with "It's where you plonked the stone in". But we can't answer the question "What direction is the wave moving?" because it's moving in all directions. It's spreading out. Now think of a wave at the seaside. We know the direction of motion. It's straight in towards the beach. But where is the wave? We can't pinpoint an exact location. It's all along the water.
The Wave Function

If we can never know exactly where an electron is, then how do we know about the way they orbit atoms? Erwin Schrödinger developed the Quantum Mechanical model, which describes the electron's behavior in a given system. It can be used to calculate the probability of an electron being found at a given position. You don't know exactly where the electron is, but you know where it is most likely and least likely to be found. In an atom, the wave function can be used to model a shape, called an orbital, which contains the area an electron is almost certain to be found inside.
Orbitals
In the following sections, we will learn about the shells, subshells, and orbitals that the electrons are in. Try not to get confused; it can be difficult. Understanding this information will help you to learn about bonding, which is very important.
Each electron orbiting in an atom has a set of four numbers that describe it. Those four numbers, called quantum numbers, describe the electron's orbit around the nucleus. Each electron in an atom has a unique set of numbers, and the numbers will change if the electron's orbit is altered. Examples are if bonding occurs, or an electron is energized into a higher-energy orbit. In the next chapter, we will learn the meaning of those four values.
Keep in mind that the pictures of the orbitals you will soon see show the area in which the electron is most likely to be, not its exact orbit. It's like a picture of a sprinkler watering a lawn, and the electrons are drops of water. You know the general area of the water, but not the exact location of each droplet. In the orbital pictures, you know the general area the electron could be in, but not its exact path. This is a result of the Uncertainty Principle. |
The Quantum Atom
The Quantum Numbers
These four numbers are used to describe the location of an electron in an atom.
| Number | Symbol | Possible Values |
|---|---|---|
| Principal Quantum Number | ||
| Angular Momentum Quantum Number | ||
| Magnetic Quantum Number | ||
| Spin Quantum Number |
Principal Quantum Number (n)
Determines the shell the electron is in. The shell is the main component that determines the energy of the electron (higher n corresponds to higher energy), as well as size of the orbital, corresponding to maximum nuclear distance (higher n means further possible distance from the nucleus). The row that an element is placed on the periodic table tells how many shells there will be. Helium (n = 1), neon (n = 2), argon (n = 3), etc. Note that the shells will have different numbers, as described by the table above; for example, argon will contain the , , and subshells, for that total of 3.
Angular Momentum Quantum Number (l)
Also known as azimuthal quantum number. Determines the subshell the electron is in. Each subshell has a unique shape and a letter name. The s orbital is shaped like a sphere and occurs when l = 0. The p orbitals (there are three) are shaped like teardrops and occur when l = 1. The d orbitals (there are five) occur when l = 2. The f orbitals (there are seven) occur when l = 3. (By the way, when l = 4, the orbitals are "g orbitals", but they (and the l = 5 "h orbitals") can safely be ignored in general chemistry.). The numbers of the subshells in each shell can be calculated using the principal quantum number like so. For example, in the shell, the subshells are an subshell, and 3 subshells. You will learn how to determine the number of orbitals for each subshells in the next section.
This number also gives information as to what the angular node of an orbital is. A node is defined as a point on a standing wave where the wave has minimal amplitude. When applied to chemistry this is the point of zero-displacement and thus where no electrons are found. In turn angular node means the planar or conical surface in which no electrons are found or where there is no electron density. The models shown on this page show the most simple representations of these orbitals and their nodes. More accurate, but more complex depictions are not necessary for the scope of this book.
Here are pictures of the orbitals. Keep in mind that they do not show the actual path of the electrons, due to the Heisenberg Uncertainty Principle. Instead, they show the volume where the electron is most likely to occur, i.e. the probability amplitude is largest. The two colors represent two signs (phases) of the wave function (the choice is arbitrary). Each of the depicted orbitals is a superposition of two opposite m quantum numbers (see below).
| ml | 0 | -1 and 1 | -2 and 2 | -3 and 3 |
|---|---|---|---|---|
| S orbital → | 
|
|||
| P orbitals → | 
|
 
|
||
| D orbitals → | 
|
 
|
|
|
| F orbitals → | 
|
 
|
 
|
 
|
Magnetic Quantum Number (ml)
| ml | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| S orbital → | 
|
||||||
| P orbitals → | 
|

|

|
||||
| D orbitals → | 
|

|

|

|

|
||
| F orbitals → | 
|

|

|

|

|

|

|
Magnetic quantum number determines the orbital in which the electron lies. The number of orbitals in each subshell can be calculated like so: . ml determines how rapidly the complex phase increases around the z-axis. Without magnetic field, these orbitals all have the same energy, they are degenerate and can be combined into different shapes and spatial orientations. The orbitals in a subshell with degeneracy are called degenerate orbitals. This simply means that the orbitals in each p subshell all have the same energy level. The difference in shapes as well as orientation of higher subshells is not important during general chemistry, and the orbitals in the same higher subshells are still degenerate regardless of shape differences.
Spin Quantum Number (ms)
Does not determines the spin on the electron. +½ corresponds to the up arrow in an electron configuration box. If there is only one electron in an orbital (one arrow in one box), then it is always considered +½. The second arrow, or down arrow, is considered -½. Every orbital can contain one "spin up" electron, and one "spin down" electron.
Some Examples
Let's examine the quantum numbers of electrons from a magnesium atom, 12Mg. Remember that each list of numbers corresponds to (n, l, ml, ms).
| Two s electrons: | (1, 0, 0, +½) | (1, 0, 0, -½) | ||||
| Two s electrons: | (2, 0, 0, +½) | (2, 0, 0, -½) | ||||
| Six p electrons: | (2, 1, -1, +½) | (2, 1, -1, -½) | (2, 1, 0, +½) | (2, 1, 0, -½) | (2, 1, 1, +½) | (2, 1, 1, -½) |
| Two s electrons: | (3, 0, 0, +½) | (3, 0, 0, -½) |
The Periodic Table
Notice a pattern on the periodic table. Different areas, or blocks, have different types of electrons. The two columns on the left make the s-block. The six columns on the right make the p-block. The large area in the middle (transition metals) makes the d-block. The bottom portion makes the f-block (Lanthanides and Actinides). Each row introduces a new shell (aka energy level). Basically, the row tells you how many shells of electrons there will be, and the column tells you which subshells will occur (and which shells they occur in). The value of ml can be determined by some of the rules we will learn in the next chapter. The value of ms doesn't really matter as long as there are no repeating values in the same orbital.
To see the pattern better, take a look at this periodic table. |
Shells and Orbitals
Electron shells
Each shell is subdivided into subshells, which are made up of orbitals, each of which has electrons with different angular momentum. Each orbital in a subshell has a characteristic shape, and is named by a letter. They are: s, p, d, and f. In a one-electron atom (e.g. H, He+, Li+2, etc.) the energy of each orbital within a particular shell is identical. However, when there are multiple electrons, they interact and split the orbitals into slightly different energies. The letters s, p, d and f specify the subshells (angular quantum number l) and the orbital is specified by the magnetic quantum number m. The angular and magnetic quantum numbers relate to the magnitude and direction of the electron's angular momentum, respectively. Within any particular subshell, the energy of the orbitals depends on the angular momentum of orbitals s, p, d, and f in order of lowest to highest energy.
This image shows the orbitals (along with hybrid orbitals for bonding and a sample electron configuration, explained later).

The s subshell
The simplest subshell in the atom is the 1s subshell. It has no radial or angular nodes: the 1s subshell is simply a sphere of electron density. A node is a point where the electron positional probability is zero. As with all subshell the number of radial nodes increases with the principle quantum number (i.e. the 2s orbital has one radial node, the 3s has two etc.). Because the angular momentum quantum number is 0, there is only one choice for the magnetic quantum number - there is only one s orbital per shell. The s orbital can hold two electrons, as long as they have different spin quantum numbers. S orbitals are involved in bonding.
The p subshell
Starting from the 2nd shell, there is a set of p subshell. The angular momentum quantum number of the electrons confined to p subshell is 1, so each orbital has one angular node. There are 3 choices for the magnetic quantum number, which indicates 3 differently oriented p subshell. Finally, each orbital can accommodate two electrons (with opposite spins), giving the p orbitals a total capacity of 6 electrons.
The orbital of p subshell all have two lobes of electron density pointing along each of the axes. Each one is symmetrical along its axis. The notation for the orbitals of p subshell indicate which axis it points down, i.e. px points along the x axis, py on the y axis and pz up and down the z axis. Note that although pz corresponds to the ml = 0 orbital, px and py are actually mixtures of ml = -1 and ml = 1 orbitals. The p orbitals are degenerate — they all have the same energy. P orbitals are very often involved in bonding.
| 2px | 2py | 2pz |
|---|---|---|

|

|

|
The d subshell
The first set of d orbitals is the 3d set. The angular momentum quantum number is 2, so each orbital has two angular nodes. There are 5 choices for the magnetic quantum number, which gives rise to 5 different d orbitals. Each orbital can hold two electrons (with opposite spins), giving the d orbitals a total capacity of 10 electrons.
Note that all the d orbitals have four lobes of electron density, except for the dz2 orbital, which has two opposing lobes and a doughnut of electron density around the middle. The d orbitals can be further subdivided into two smaller sets. The dx2-y2 and dz2 all point directly along the x, y, and z axes. They form an eg set. On the other hand, the lobes of the dxy, dxz and dyz all line up in the quadrants, with no electron density on the axes. These three orbitals form the t2g set. In most cases, the d orbitals are degenerate, but sometimes they can split, with the eg and t2g subsets having different energy. Crystal Field Theory predicts and accounts for this. D orbitals are sometimes involved in bonding, especially in inorganic chemistry.

|

|

|

|

|
The f subshell
The first set of f orbitals is the 4f subshell. There are 7 possible magnetic quantum numbers, so there are 7 f orbitals. Their shapes are fairly complicated, and they rarely come up when studying chemistry. There are 14 f electrons because each orbital can hold two electrons (with opposite spins).

|

|

|

|

|

|

|
Filling Electron Shells
Filling Electron Shells
When an atom or ion receives electrons into its orbitals, the orbitals and shells fill up in a particular manner.
Aufbau principle
You may consider an atom as being "built up" from a naked nucleus by gradually adding to it one electron after another, until all the electrons it will hold have been added. Much as one fills up a container with liquid from the bottom up, the orbitals of an atom are filled from the lowest energy orbitals to the highest energy orbitals.
Orbitals with the lowest principal quantum number () have the lowest energy and will fill up first, in smaller atoms. Larger atoms with more subshells will seem to fill "out of order", as the other factors influencing orbital energy become important. Within a shell, there may be several orbitals with the same principal quantum number. In that case, more specific rules must be applied. For example, the three p orbitals of a given shell all occur at the same energy level. So, how are they filled up? Answer: all the three p orbitals have same energy so while filling the p orbitals we can fill any one of the Px, Py or Pz first. It is a convention that we chose to fill Px first, then Py and then Pz for our simplicity. Hence you can opt for filling these three orbitals from right to left also. Aufbau principle state that “atomic orbitals are filled with electrons in order of increasing energy level”.
Hund's Rule
According to Hund's rule, orbitals of the same energy are each filled with one electron before filling any with a second. Also, these first electrons have the same spin.
This rule is sometimes called the "bus seating rule". As people load onto a bus, each person takes his or her own seat, sitting alone. Only after all the seats have been filled will people start doubling up.
Pauli Exclusion principle
No two electrons can have all four quantum numbers the same. What this translates to in terms of our picture of orbitals is that each orbital can only hold two electrons, one "spin up" (+½) and one "spin down" (-½).

Orbital Order
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, 8s.
Although this looks confusing, there is an easy way to remember. Go in order of the lines from top to bottom, top right end to bottom left of each line.
Understanding the above rules and diagrams will allow you to determine the electron configuration of almost any atom or ion.
How to Write the Electron Configuration of an Isolated Atom
Electron-configuration notation is relatively straightforward. An isolated Calcium atom 20Ca, for example, would have configuration of 1s22s22p63s23p64s2 in its ground state. Other configurations like 1s22s22p63s23p64s14p1 are possible, but these excited states have a higher energy. They are not stable and generally only exist for a brief moment.
The ground state configuration for Ca could be abbreviated by using the preceding noble gas (the elements found all the way on the right of the periodic table) as [Ar]4s2, where Ar is argon.
Noble gases have very stable configurations, and are extremely reluctant to lose or gain electrons. Noble gas atoms are also the only ones regularly found as isolated atoms in the ground state. Atoms of other elements all undergo bonding under the conditions that we live under and this affects the orbitals that the outermost electrons are in. In that sense the electron configurations for the other elements are somewhat hypothetical: to encounter an isolated atom of, say, tungsten (W), we would have to first vaporize a metal that boils at 5800K. However, knowing atomic configurations is useful because it does help us to understand how and why they bond, i.e. why and how they change the configuration of their outer valence electrons.
Rule of Stability
A subshell is particularly stable if it is half full or full. Given two configurations, the atom would "choose" the more stable one.
Example: In the following configuration, Cu: [Ar]4s23d9, copper's d shell is just one away from stability, and therefore, one electron from the s shell jumps into the d shell: [Ar]4s13d10. This way, the d shell is full, and is therefore stable, and the s shell is half full, and is also stable.
Another example: Chromium has a configuration of [Ar]4s13d5, although you would expect to see four d electrons instead of five. This is because an s electron has jumped into the d orbital, giving the atom two half-full shells—much more stable than a d orbital with only four electrons.
The stability rule applies to atoms in the same group as chromium and copper.
If one of these atoms has been ionized, that is, it loses an electron, it will come from the s orbital rather than the d orbital. For instance, the configuration of Cu+ is [Ar]4s03d10. If more electrons are removed, they will come from the d orbital.
Magnetism

Magnetism is a well-known effect. Chances are, you have magnets on your refrigerator. As you already know, only certain elements are magnetic. Electron configurations help to explain why.
Diamagnetism is actually a very weak repulsion to magnetic fields. All elements have diamagnetism to some degree. It occurs when there are paired electrons.
Paramagnetism is an attraction to external magnetic fields. It is also very weak. It occurs whenever there is an unpaired electron in an orbital.
Both diamagnetism and paramagnetism are responses of spins acting independently from each other. This leads to rather weak repulsion and attraction respectively. However, when they are located in a solid they may also interact with each other and respond collectively and that can lead to rather different properties:
Ferromagnetism is the permanent magnetism that we encounter in our daily lives. It occurs when all the unpaired spins in a solid couple and tend to align themselves in the same direction, leading to a strong attraction when exposed to a magnetic field. This only occurs at room temperature with three elements: iron (Fe), nickel (Ni), and cobalt (Co). Gadolinium (Gd) is a borderline case. It loses its ferromagnetism at 20oC; above that temperature the spins start to act alone. However, there are many alloys and compounds that exhibit strong ferromagnetic coupling. The strongest one is Nd2Fe14B
Antiferromagnetism is also a permanent magnetism in which unpaired spins align, but they do so in opposite directions. The result that the material does not react very strongly to a magnetic field at all. Chromium (Cr) is an example.
'Ferrimagnetism is a combination of ferro- and antiferromagetism. Unpaired spins align partly in opposite directions, but the compensation is not complete. This is why the material is still attracted strongly to a magnetic field. Magnetite Fe3O4 is such a substance. It was the first material studied for its magnetic properties and may, well, be the one sitting on your fridge.
Periodicity and Electron Configurations
Blocks of the Periodic Table
The Periodic Table does more than just list the elements. The word periodic means that in each row, or period, there is a pattern of characteristics in the elements. This is because the elements are listed in part by their electron configuration. The Alkali metals and Alkaline earth metals have one and two valence electrons (electrons in the outer shell) respectively. These elements lose electrons to form bonds easily, and are thus very reactive. These elements are the s-block of the periodic table. The p-block, on the right, contains common non-metals such as chlorine and helium. The noble gases, in the column on the right, almost never react, since they have eight valence electrons, which makes it very stable. The halogens, directly to the left of the noble gases, readily gain electrons and react with metals. The s and p blocks make up the main-group elements, also known as representative elements. The d-block, which is the largest, consists of transition metals such as copper, iron, and gold. The f-block, on the bottom, contains rarer metals including uranium. Elements in the same Group or Family have the same configuration of valence electrons, making them behave in chemically similar ways.

Causes for Trends

There are certain phenomena that cause the periodic trends to occur. You must understand them before learning the trends.
Effective Nuclear Charge
The effective nuclear charge is the amount of positive charge acting on an electron. It is the number of protons in the nucleus minus the number of electrons in between the nucleus and the electron in question. The nucleus attracts the electron, but other electrons in lower shells repel it (opposites attract, likes repel).
Shielding Effect
The shielding (or screening) effect is similar to effective nuclear charge. The core electrons repel the valence electrons to some degree. The more electron shells there are (a new shell for each row in the periodic table), the greater the shielding effect is. Essentially, the core electrons shield the valence electrons from the positive charge of the nucleus.
Electron-Electron Repulsions
When two electrons are in the same shell, they will repel each other slightly. This effect is mostly canceled out due to the strong attraction to the nucleus, but it does cause electrons in the same shell to spread out a little bit. Lower shells experience this effect more because they are smaller and allow the electrons to interact more.
Coulomb's Law
Coulomb's law is an equation that determines the amount of force with which two charged particles attract or repel each other. It is , where is the amount of charge, is the distance between charges, and is a constant. For atoms, the charges are typically described as integer multiples (positive for protons, negative for electrons) of the elementary charge , which is 1.6022 x 10-19 coulombs. You can see that doubling the distance would quarter the force.
Trends in the Periodic table
Most of the elements occur naturally on Earth. However, all elements beyond uranium (number 92) are called trans-uranium elements and never occur outside of a laboratory. Most of the elements occur as solids or gases at STP. STP is standard temperature and pressure, which is 0° C and 1 atmosphere of pressure. There are only two elements that occur as liquids at STP: mercury (Hg) and bromine (Br).
Bismuth (Bi) is the last stable element on the chart. All elements after bismuth are radioactive and decay into more stable elements. Some elements before bismuth are radioactive, however.
Atomic Radius
Leaving out the noble gases, atomic radii are larger on the left side of the periodic chart and are progressively smaller as you move to the right across the period. As you move down the group, radii increase.
Atomic radii decrease along a period due to greater effective nuclear charge. Atomic radii increase down a group due to the shielding effect of the additional core electrons, and the presence of another electron shell.
Ionic Radius
For nonmetals, ions are bigger than atoms, as the ions have extra electrons. For metals, it is the opposite.
Extra electrons (negative ions, called anions) cause additional electron-electron repulsions, making them spread out farther. Fewer electrons (positive ions, called cations) cause fewer repulsions, allowing them to be closer.
Ionization Energy
Ionization energy is the energy required to strip an electron from the atom (when in the gas state).
|
Ionization energy is also a periodic trend within the periodic table organization. Moving left to right within a period or upward within a group, the first ionization energy generally increases. As the atomic radius decreases, it becomes harder to remove an electron that is closer to a more positively charged nucleus.
Ionization energy decreases going left across a period because there is a lower effective nuclear charge keeping the electrons attracted to the nucleus, so less energy is needed to pull one out. It decreases going down a group due to the shielding effect. Remember Coulomb's Law: as the distance between the nucleus and electrons increases, the force decreases at a quadratic rate.

It is considered a measure of the tendency of an atom or ion to surrender an electron, or the strength of the electron binding; the greater the ionization energy, the more difficult it is to remove an electron. The ionization energy may be an indicator of the reactivity of an element. Elements with a low ionization energy tend to be reducing agents and form cations, which in turn combine with anions to form salts.
Electron Affinity
Electron affinity is the opposite of ionization energy. It is the energy released when an electron is added to an atom.
|

Electron affinity is highest in the upper left, lowest on the bottom right. However, electron affinity is actually negative for the noble gasses. They already have a complete valence shell, so there is no room in their orbitals for another electron. Adding an electron would require creating a whole new shell, which takes energy instead of releasing it. Several other elements have extremely low electron affinities because they are already in a stable configuration, and adding an electron would decrease stability.
Electron affinity occurs due to the same reasons as ionization energy.
Electronegativity
Electronegativity is how much an atom attracts electrons within a bond. It is measured on a scale with fluorine at 4.0 and francium at 0.7. Electronegativity decreases from upper right to lower left.
Electronegativity decreases because of atomic radius, shielding effect, and effective nuclear charge in the same manner that ionization energy decreases.
Metallic Character
Metallic elements are shiny, usually gray or silver colored, and good conductors of heat and electricity. They are malleable (can be hammered into thin sheets), and ductile (can be stretched into wires). Some metals, like sodium, are soft and can be cut with a knife. Others, like iron, are very hard. Non-metallic atoms are dull, usually colorful or colorless, and poor conductors. They are brittle when solid, and many are gases at STP. Metals give away their valence electrons when bonding, whereas non-metals take electrons.
The metals are towards the left and center of the periodic table—in the s-block, d-block, and f-block . Poor metals and metalloids (somewhat metal, somewhat non-metal) are in the lower left of the p-block. Non-metals are on the right of the table.
Metallic character increases from right to left and top to bottom. Non-metallic character is just the opposite. This is because of the other trends: ionization energy, electron affinity, and electronegativity.
- Metallic/Non-metallic
-
Sodium, very metallic
-
Sulfur, very non-metallic
Octet Rule and Exceptions
The octet rule refers to the tendency of atoms to prefer to have eight electrons in the valence shell (outer orbital). When atoms have fewer than eight electrons, they tend to react and form more stable compounds. When discussing the octet rule, we do not consider d or f electrons. Only the s and p electrons are involved in the octet rule, making it useful for the representative elements (elements not in the transition metal or inner-transition metal blocks). An octet corresponds to an electron configuration ending with s2p6.
Stability
Atoms will react to get in the most stable state possible. A complete octet is very stable because all orbitals will be full. Atoms with greater stability have less energy, so a reaction that increases the stability of the atoms will release energy in the form of heat or light. Reactions that decrease stability must absorb energy, getting hotter.
The other tendency of atoms is to maintain a neutral charge. Only the noble gases (the elements on the right-most column of the periodic table) have zero charge with filled valence octets. All of the other elements have a charge when they have eight electrons all to themselves. The result of these two guiding principles is the explanation for much of the reactivity and bonding that is observed within atoms: atoms seek to share electrons in a way that minimizes charge while fulfilling an octet in the valence shell.
The noble gases rarely form compounds. They have the most stable configuration (full octet, no charge), so they have no reason to react and change their configuration. All other elements attempt to gain, lose, or share electrons to achieve a noble gas configuration. |
Example
The formula for table salt is NaCl. It is the result of Na+ ions and Cl- ions bonding together. If sodium metal and chlorine gas mix under the right conditions, they will form salt. The sodium loses an electron, and the chlorine gains that electron. In the process, a great amount of light and heat is released. The resulting salt is mostly unreactive — it is stable. It won't undergo any explosive reactions, unlike the sodium and chlorine that it is made of.
Why? Referring to the octet rule, atoms attempt to get a noble gas electron configuration, which is eight valence electrons. Sodium has one valence electron, so giving it up would result in the same electron configuration as neon. Chlorine has seven valence electrons, so if it takes one it will have eight (an octet). Chlorine has the electron configuration of argon when it gains an electron.
The octet rule could have been satisfied if chlorine gave up all seven of its valence electrons and sodium took them. In that case, both would have the electron configurations of noble gasses, with a full valence shell. However, their charges would be much higher. It would be Na7- and Cl7+, which is much less stable than Na+ and Cl-. Atoms are more stable when they have no charge, or a small charge.
Exceptions
There are few exceptions to the octet rule.
Two Electrons
The main exception to the rule is hydrogen, which is at its lowest energy when it has two electrons in its valence shell. Helium (He) is similar in that it, too, only has room for two electrons in its only valence shell.
Hydrogen and helium have only one electron shell. The first shell has only one s orbital and no p orbital, so it holds only two electrons. Therefore, these elements are most stable when they have two electrons. You will occasionally see hydrogen with no electrons, but H+ is much less stable than hydrogen with one or two electrons.
Lithium, with three protons and electrons, is most stable when it gives up an electron.
Less Than an Octet
Other notable exceptions are aluminum and boron, which can function well with six valence electrons. Consider BF3. The boron shares its three electrons with three fluorine atoms. The fluorine atoms follow the octet rule, but boron has only six electrons. Although atoms with less than an octet may be stable, they will usually attempt to form a fourth bond to get eight electrons. BF3 is stable, but it will form BF4- when possible. Most elements to the left of the carbon group have so few valence electrons that they are in the same situation as boron: they are electron deficient. Electron deficient elements often show metallic rather than covalent bonding.
More Than an Octet
In Period 3, the elements on the right side of the periodic table have empty d orbitals. The d orbitals may accept electrons, allowing elements like sulfur, chlorine, silicon and phosphorus to have more than an octet. Compounds such as PCl5 and SF6 can form. These compounds have 10 and 12 electrons around their central atoms, respectively.

|
Xenon hexafluoride uses d-electrons to form more than an octet. This compound shows another exception: a noble gas compound. |
Even palladium has 18 electrons in its valence shell
Odd Numbers
Some elements, notably nitrogen, have an odd number of electrons and will form somewhat stable compounds. Nitric oxide has the formula NO. No matter how electrons are shared between the nitrogen and oxygen atoms, there is no way for nitrogen to have an octet. It will have seven electrons instead. A molecule with an unpaired electron is called a free radical and radicals are highly reactive, so reactive that many of them only exist for a fraction of a second. As radicals go, NO and NO2 are actually remarkably stable. At low temperatures NO2 does react with itself to form N2O4, its dimer, that is not a radical.

|
Nitrogen dioxide has an unpaired electron. (Note the positive charge above the N). |
Compounds and Bonding
Overview of Bonding
Introduction to Bonding
Put simply, chemical bonding join atoms together to form more complex structures (like molecules or crystals). Bonds can form between atoms of the same element, or between atoms of different elements. There are several types of chemical bonding which have different properties and give rise to different structures.
In many cases, atoms try to react to form valence shells containing eight electrons. The octet rule describes this, but it also has many exceptions
- Ionic bonding occurs between positive ions (cations) and negative ions (anions). In an ionic solid, the ions arrange themselves into a rigid crystal lattice. NaCl (common salt) is an example of an ionic substance. In ionic bonding there is an attractive force established between large numbers of positive cations and negative anions, such that a neutral lattice is formed. This attraction between oppositely-charged ions is collective in nature and called ionic bonding.
- Covalent bonds are formed when the orbitals of two non-metal atoms physically overlap and share electrons with each other. There are two types of structures to which this can give rise: molecules and covalent network solids. Methane (CH4) and water (H2O) are examples of covalently bonded molecules, and glass is a covalent network solid.
- Metallic bonding occur between atoms that have few electrons compared to the number of accessible orbitals. This is true for the vast majority of chemical elements. In a metallically bonded substance, the atoms' outer electrons are able to freely move around - they are delocalised to form an 'electron pool'. Iron is a metallically bonded substance.
Chemical bonding is one of the most crucial concepts in the study of chemistry. In fact, the properties of materials are basically defined by the type and number of atoms they contain and how they are bonded together.
So far, you have seen examples of intramolecular bonds. These bonds connect atoms into molecules or whole crystals. There are also intermolecular bonds that connect molecules into large substances. These are also called intermolecular forces, or IMF. IMF are weaker than intramolecular bonds, and as they do not permanently join two molecules or ions, it is generally considered incorrect to refer to them as bonds. Sometimes, a substance will not have both IMF and intramolecular bonds. In the case of ionic crystals (like salt) or covalent networks (like diamond), the solid is made out of a network of intramolecular bonds connecting all the component atoms or ions in a repeating pattern, with no separate units to be attracted to each other by IMF. In the case of metallic bonding, the atoms are all interconnected into one large piece of metal, but the electrons move freely rather than being confined to the static bonds of a crystal lattice or covalent network.
Electronegativity
What determines the type of bond formed between two elements? There are two ways of classifying elements to determine the bond formed: by electronegativity, or by metallic/non-metallic character.
Electronegativity
Electronegativity is a property of atoms that is reflected in the layout of the periodic table of the elements. Electronegativity is greatest in the elements in the upper right of the table (e.g., fluorine), and lowest in the lower left (e.g., francium).
Electronegativity is a relative measure of how strongly an atom will attract the electrons in a bond. Although bonds are the result of atoms sharing their electrons, the electrons can be shared unequally. The more electronegative atom in a bond will have a slight negative charge, and the less electronegative atom will have a slight positive charge. Overall, the molecule may have no charge, but the individual atoms will. This is a result of the electronegativity—by attracting the electrons in a bond, an atom gains a slight negative charge. Of course, if two elements have equal electronegativity, they will share the electrons equally.

Metallic elements have low electronegativity, and non-metallic elements have high electronegativity. If two elements are close to each other on the periodic table, they will have similar electronegativities.
Electronegativity is measured on a variety of scales, the most common being the Pauling scale. Created by chemist Linus Pauling, it assigns 4.0 to fluorine (the highest) and 0.7 to francium (the lowest).
Notation
When drawing diagrams of bonds, we indicate covalent bonds with a line. We may write the electronegativity using the symbols and . Look at this example.
The plus goes over the less electronegative atom. From the above diagram, we can see that the fluorine attracts the electrons in the covalent bond more than the hydrogen does. Fluorine will have a slight negative charge because of this, and hydrogen will have a slight positive charge. Overall, hydrogen fluoride is neutral.
Ionic Bonds
What are ions?
Ions are atoms or molecules which are electrically charged. Cations are positively charged and anions carry a negative charge. Ions form when atoms gain or lose electrons. Since electrons are negatively charged, an atom that loses one or more electrons will become positively charged; an atom that gains one or more electrons becomes negatively charged.
Description of Ionic Bonding
Ionic bonding is the attraction between positively- and negatively-charged ions. These oppositely charged ions attract each other to form ionic networks (or lattices). Electrostatics explains why this happens: opposite charges attract and like charges repel. When many ions attract each other, they form large, ordered, crystal lattices in which each ion is surrounded by ions of the opposite charge. Generally, when metals react with non-metals, electrons are transferred from the metals to the non-metals (this is because metals tend to have relatively low ionization energy and non-metals tend to have high electron affinity). The metals form positively-charged ions and the non-metals form negatively-charged ions. The smallest unit of an ionic compound is the formula unit, but this unit merely reflects that ratio of ions that leads to neutrality of the whole crystal, e.g. NaCl or MgCl2. One cannot distinguish individual NaCl or MgCl2 molecules in the structure.
It is however possible that the stacking consists of molecular ions like NH4+ and NO3- in ammonium nitrate. In such structures, the ions are charged molecules rather than charged atoms.
 |
 |
Ionic bonding may also be referred to as electrovalent bonding.
Characteristics
Example ionic compounds: Sodium chloride (), potassium nitrate ().
Ionically bonded substances typically have the following characteristics.
- High melting point (solid at room temperature)
- Hard but brittle (can shatter)
- Many dissolve in water
- Conductors of electricity when dissolved or melted
In general the forces keeping the lattice together depend on the product of the charges of the ions it consists of. A comparison e.g. of NaCl (+1)*(-1) to MgO (+2)*(-2) shows that magnesium oxide is kept together much more strongly -roughly 4 times- than sodium chloride. This is why sodium chloride has a much lower melting point and also dissolves much more easily in a solvent like water than magnesium oxide does.
Solubility

Most ionic compounds are soluble in polar solvents. Polar solvents are simply solvents that have molecules with positive and negative poles. The most common example of a polar solvent is water (H2O).
The reason that they are soluble in polar solvents is because the positive ions are attracted to the negative pole of the solvent and the negative ions are attracted to the positive pole of the solvent. Due to this, the ionic compound dissociates or splits in the solvent into its constituent ions.
For example, H2O is composed of relatively more positive hydrogen atoms and relatively more negative oxygen atoms. When an ionic compound like NaCl is added to the water, the positive ions will be attracted to the more negative oxygen atoms and negative ions will be attracted to the more positive hydrogen atoms.
This is a very useful property of many ionic compounds, but not all, as there are exceptions where certain compounds cannot be dissolved in certain polar solvents.
Conduction
For a substance to conduct electricity, there must be some carrier of charge. For example, in metals, what transports the charge is the mobile electrons surrounding the positive ions.
However, in the solid state, ionic compounds lack any mobile particle capable of carrying charge as the ions cannot move within the lattice because the electrostatic force holding them in place is extremely strong. This changes when the compound is dissolved or molten. When dissolved, the ions dissociate and are capable of moving around. The same is true for molten ionic compounds. Which is why molten and dissolved ionic compounds can conduct electricity, while solid ionic compounds cannot.
Formation

Ionic bonding occurs when metals and non-metals chemically react. As a result of its low ionization energy, a metal atom is not destabilized very much if it loses electrons to form a complete valence shell and becomes positively charged. As its affinity is rather large, a non-metal is stabilized rather strongly by gaining electrons to complete its valence shell and become negatively charged. When metals and non-metals react, the metals lose electrons by transferring them to the non-metals, which gain them. The total process -a small loss plus a large gain- leads to a net lowering of the energy. Consequently, ions are formed, which instantly attract each other leading to ionic bonding.
For instance, in the reaction of Na (sodium) and Cl (chlorine), each Cl atom takes one electron from a Na atom. Therefore each Na becomes a Na+ cation and each Cl atom becomes a Cl- anion. Due to their opposite charges, they attract each other and are joined by millions and millions of other ions to form an ionic lattice. The lattice energy that results from this massive collective stacking further stabilizes the new compound. The formula (ratio of positive to negative ions) in the lattice is NaCl, i.e. there are equal numbers of positive and negative charges ensuring neutrality.
The charges must balance because otherwise the repulsion between the majority charges would become prohibitive. In the case of magnesium chloride, the magnesium atom gives up two electrons to become stable. Note that it is in the second group, so it has two valence electrons. The chlorine atom can only accept one electron, so there must be two chlorine ions for each magnesium ion. Therefore, the formula for magnesium chloride is MgCl2. If magnesium oxide were forming, the formula would be MgO because oxygen can accept both of magnesium's electrons.
- Exercise for the reader
Try figuring out what the formula for magnesium nitride would be. Use the periodic table to help.
It should also be noted that some atoms can form more than one ion. This usually happens with the transition metals. For instance Fe (iron) can become Fe2+ (called iron(II) or -by an older name- ferrous). Fe can also become Fe3+ (called iron(III) or -sometimes still- ferric).
Common Ions
Ionic bonding typically occurs in reactions between a metal and non-metal, but there are also certain molecules called polyatomic ions that undergo ionic bonding. Within these polyatomic ions, there can be covalent (or polar) bonding, but as a unit it undergoes ionic bonding. There are countless polyatomic ions, but you should be familiar with the most common ones. You would be well advised to memorize these ions.
| Name | Formula | Name | Formula |
|---|---|---|---|
| Ammonium | NH4+ | Hydronium | H3O+ |
| Peroxide | O22- | Hydroxide | OH- |
| Nitrite | NO2- | Nitrate | NO3- |
| Sulfite | SO32- | Sulfate | SO42- |
| Hydrogen sulfite | HSO3- | Phosphate | PO43- |
| Hypochlorite | ClO- | Chlorite | ClO2- |
| Chlorate | ClO3- | Perchlorate | ClO4- |
| Carbonate | CO32- | Hydrogen carbonate | HCO3- |
Covalent Bonds
Covalent bonds create molecules, which can be represented by a molecular formula. For chemicals such as a basic sugar (C6H12O6), the ratios of atoms have a common multiple, and thus the empirical formula is CH2O. Note that a molecule with a certain empirical formula is not necessarily the same as one with the same molecular formula.
Formation of Covalent Bonds
Covalent bonds form between two atoms which have incomplete octets — that is, their outermost shells have fewer than eight electrons. They can share their electrons in a covalent bond. The simplest example is water (H2O). Oxygen has six valence electrons (and needs eight) and the hydrogens have one electron each (and need two). The oxygen shares two of its electrons with the hydrogens, and the hydrogens share their electrons with the oxygen. The result is a covalent bond between the oxygen and each hydrogen. The oxygen has a complete octet and the hydrogens have the two electrons they each need.
When atoms move closer, their orbitals change shape, letting off energy. However, there is a limit to how close the atoms get to each other—too close, and the nuclei repel each other.

One way to think of this is a ball rolling down into a valley. It will settle at the lowest point. As a result of this potential energy "valley", there is a specific bond length for each type of bond. Also, there is a specific amount of energy, measured in kilojoules per mole (kJ/mol) that is required to break the bonds in one mole of the substance. Stronger bonds have a shorter bond length and a greater bond energy.
The Valence Bond Model
One useful model of covalent bonding is called the Valence Bond model. It states that covalent bonds form when atoms share electrons with each other in order to complete their valence (outer) electron shells. They are mainly formed between non-metals.
An example of a covalently bonded substance is hydrogen gas (H2). A hydrogen atom on its own has one electron—it needs two to complete its valence shell. When two hydrogen atoms bond, each one shares its electron with the other so that the electrons move about both atoms instead of just one. Both atoms now have access to two electrons: they become a stable H2 molecule joined by a single covalent bond.

Double and Triple Bonds
Covalent bonds can also form between other non-metals, for example chlorine. A chlorine atom has 7 electrons in its valence shell—it needs 8 to complete it. Two chlorine atoms can share 1 electron each to form a single covalent bond. They become a Cl2 molecule.
Oxygen can also form covalent bonds, however, it needs a further 2 electrons to complete its valence shell (it has 6). Two oxygen atoms must share 2 electrons each to complete each other's shells, making a total of 4 shared electrons. Because twice as many electrons are shared, this is called a 'double covalent bond'. Double bonds are much stronger than single bonds, so the bond length is shorter and the bond energy is higher.
Furthermore,, nitrogen has 5 valence electrons (it needs a further 3). Two nitrogen atoms can share 3 electrons each to make a N2 molecule joined by a 'triple covalent bond'. Triple bonds are stronger than double bonds. They have the shortest bond lengths and highest bond energies.
Electron Sharing and Orbitals
Carbon, contrary to the trend, does not share four electrons to make a quadruple bond. The reason for this is that the fourth pair of electrons in carbon cannot physically move close enough to be shared. The valence bond model explains this by considering the orbitals involved.
Recall that electrons orbit the nucleus within a cloud of electron density (orbitals). The valence bond model works on the principle that orbitals on different atoms must overlap to form a bond. There are several different ways that the orbitals can overlap, forming several distinct kinds of covalent bonds.
The Sigma Bond
The first and simplest kind of overlap is when two s orbitals come together. It is called a sigma bond (sigma, or σ, is the Greek equivalent of 's'). Sigma bonds can also form between two p orbitals that lie pointing towards each other. Whenever you see a single covalent bond, it exists as a sigma bond. When two atoms are joined by a sigma bond, they are held close to each other, but they are free to rotate like beads on a string.

The Pi Bond
The second, and equally important kind of overlap is between two parallel p orbitals. Instead of overlapping head-to-head (as in the sigma bond), they join side-to-side, forming two areas of electron density above and below the molecule. This type of overlap is referred to as a pi (π, from the Greek equivalent of p) bond. Whenever you see a double or triple covalent bond, it exists as one sigma bond and one or two pi bonds. Due to the side-by-side overlap of a pi bond, there is no way the atoms can twist around each other as in a sigma bond. Pi bonds give the molecule a rigid shape.
Pi bonds are weaker than sigma bonds since there is less overlap. Thus, two single bonds are stronger than a double bond, and more energy is needed to break two single bonds than a single double bond.

Hybridization
Consider a molecule of methane: a carbon atom attached to four hydrogen atoms. Each atom is satisfying the octet rule, and each bond is a single covalent bond.
Now look at the electron configuration of carbon: 1s22s22p2. In its valence shell, it has two s electrons and two p electrons. It would not be possible for the four electrons to make equal bonds with the four hydrogen atoms (each of which has one s electron). We know, by measuring bond length and bond energy, that the four bonds in methane are equal, yet carbon has electrons in two different orbitals, which should overlap with the hydrogen 1s orbital in different ways.
To solve the problem, hybridization occurs. Instead of a s orbital and three p orbital, the orbitals mix, to form four orbitals, each with 25% s character and 75% p character. These hybrid orbitals are called sp3 orbitals, and they are identical. Observe:
Now these orbitals can overlap with hydrogen 1s orbitals to form four equal bonds. Hybridization may involve d orbitals in the atoms that have them, allowing up to a sp3d2 hybridization.
- Exercise for the reader
Predict the hybridized electron configuration of carbon in ethene. How many sigma bonds are there? How many pi bonds?

Hint: Hybridized electrons form only sigma bonds. Pi bonds form only between p electrons.
Metallic Bonds
Review on structure
Atoms are particles composed of 3 subatomic particles. The protons, neutrons, and electrons. The protons and neutrons are in the nucleus and the electrons orbit this nucleus. These electrons can leave the atom and this is important to note especially for metals. The energy required to remove an electron is referred to as ionization energy and is very low for metals and so metals tend to lose their outermost (valence) electrons whenever possible. The attractive force between electrons and the nucleus is referred to as the electrostatic force of attraction. This electrostatic force is very strong and is capable of holding large structures together.
Overview
Metallic bonds occur among metal atoms. Whereas ionic bonds join metals to non-metals, metallic bonding joins a bulk of metal atoms. A sheet of aluminium foil and a copper wire are both places where you can see metallic bonding in action.

When metallic bonds form, the s and p electrons delocalize. Instead of orbiting their atoms, they form a "sea of electrons" surrounding the positive metal ions. The electrons are free to move throughout the resulting network. The electrostatic force of attraction between this "sea of electrons" and the positive ions acts as a form of "glue" holding together the metallic structure.
Properties
The delocalized nature of the electrons explains a number of unique characteristics of metals:
| Metals are good conductors of electricity | The sea of electrons is free to flow, allowing electrical currents. |
| Metals are good conductors of heat | As heat energy is defined by the motion of particles, the sea of electrons provides an excellent medium for this kinetic energy to be transferred. |
| Metals are ductile (able to draw into wires) and malleable (able to be hammered into thin sheets) |
As the metal is deformed, local bonds are broken but quickly reformed in a new position. |
| Metals are gray and shiny | Photons (particles of light) cannot penetrate the metal, so they bounce off the sea of electrons. |
| Gold is yellow and copper is reddish-brown | There is actually an upper limit to the frequency that is reflected. It is too high to be visible in most metals, but not gold and copper. |
| Metals have very high melting and boiling points | Metallic bonding is very strong, so the atoms are reluctant to break apart into a liquid or gas. |
Reactivity and solubility
Nearly all metals are near completely insoluble in most solvents whether organic or inorganic. This is because the bonds between metals are exceedingly strong and solvents cannot dissolve the metal. However, if the metal undergoes a reaction and forms an ionic compound it can dissolve. Metals react when an electronegative substance attracts the electrons in the sea of electrons and the structure collapses without the force holding it together. Metals almost always form ionic compounds however on occasion they can participate in a form of covalent bonding. These compounds however, do not share any of the properties of metallic bonding. Furthermore, it is important to distinguish between a compound of a metal and an alloy.
Alloys
Metallic bonds can occur between different elements. A mixture of two or more metals is called an alloy. This is what differentiates alloys and compounds containing metals, as alloys are only mixtures. Depending on the size of the atoms being mixed, there are two different kinds of alloys that can form:
-
Substitutional alloy
-
Interstitial alloy
It is also worth note that substitutional/interstitial alloys can exist when there are more than 2 metals are involved in the formation of an alloy.
The resulting mixture will have a combination of the properties of both metals involved. Interstitial alloys tend to be (with exceptions) stronger than their component metals. This is because the particles of varying size tend to prevent the various layers in a metal from sliding over each other smoothly. An example of this would be the difference between bronze and its components copper and tin. Copper on its own is a softer metal unfit for use as a weapon, while bronze was widely used during the Bronze Age for swords and armour. Alloys can also have various other benefits such as corrosion resistance, torsional strength, and much more.
Molecular Shape
Covalent molecules are bonded to other atoms by electron pairs. Being mutually negatively charged, the electron pairs repel the other electron pairs and attempt to move as far apart as possible in order to stabilize the molecule. This repulsion causes covalent molecules to have distinctive shapes, known as the molecule's molecular geometry. There are several different methods of determining molecular geometry. A scientific model, called the VSEPR (valence shell electron pair repulsion) model can be used to qualitatively predict the shapes of molecules. Within this model, the AXE method is used in determining molecular geometry by counting the numbers of electrons and bonds related to the center atom(s) of the molecule.
The VSEPR model is by no means a perfect model of molecular shape! It is simply a system which explains the known shapes of molecular geometry as discovered by experiment. This can allow us to predict the geometry of similar molecules, making it a fairly useful model. Modern methods of quantitatively calculating the most stable (lowest energy) shapes of molecules can take several hours of supercomputer time, and is the domain of computational chemistry.
Table of Geometries
| Orbital Hybridization | |||||
|---|---|---|---|---|---|
| sp |
sp2 | sp3 | sp3d | sp3d2 | |
| 2 Groups | Linear | Bent | Bent | Linear | |
| 3 Groups | Trigonal Planar | Trigonal Pyramidal | T-Shaped | ||
| 4 Groups | Tetrahedral | See-saw | Square Planar | ||
| 5 Groups | Trigonal Bipyramidal | Square Pyramidal | |||
| 6 Groups | Octahedral | ||||
The hybridization is determined by how many "things" are attached to the central atom. Those "things" can be other atoms or non-bonding pairs of electrons. The number of groups is how many atoms or electron pairs are bonded to the central atom. For example, methane (CH4) is tetrahedral-shaped because the carbon is attached to four hydrogens. Ammonia (NH3) is not trigonal planar, however. It is trigonal pyramidal because it is attached to four "things": the three hydrogens and a non-bonding pair of electrons (to fulfill nitrogen's octet).
Tetrahedral Shape

Consider a simple covalent molecule, methane (CH4). Four hydrogen atoms surround a carbon atom in three-dimensional space. Each CH bond consists of one pair of electrons, and these pairs try to move as far away from each other as possible (due to electrostatic repulsion). You might think this would lead to a flat shape, with each hydrogen atom 90° apart. However, in three dimensions, there is a more efficient arrangement of the hydrogen atoms. If each hydrogen atom is at a corner of a tetrahedron centered around the carbon atom, they are separated by about cos-1(-1/3) ≈ 109.5°—the maximum possible.
Hybridization
To align four orbitals in this tetrahedral shape requires the reformation of one s and three p orbitals into an sp3 orbital.

Lone Electron Pairs
The VSEPR model treats lone electron pairs in a similar way to bonding electrons. In ammonia (NH3) for example, there are three hydrogen atoms and one lone pair of electrons surrounding the central nitrogen atom. Because there are four groups, ammonia has a tetrahedral shape but unlike methane, the angle between the hydrogen atoms is slightly smaller, 107.3°. This can be explained by theorizing that lone electron pairs take up more space physically than bonding pairs. This is a reasonable theory: in a bond, the electron pair is distributed over two atoms whereas a lone pair is only located on one. Because it is bigger, the lone pair forces the other electron pairs together.

Testing this assumption with water provides further evidence. In water (H2O) there are two hydrogen atoms and two lone pairs, again making four groups in total. The electron pairs repel each other into a tetrahedral shape. The angle between the hydrogen atoms is 104.5°, which is what we expect from our model. The two lone pairs both push the bonds closer together, giving a smaller angle than in ammonia.
Linear and Planar Shapes
Electron-Poor Atoms
In some molecules, there are less than four pairs of valence electrons. This occurs in electron deficient atoms such as boron and beryllium, which don't conform to the octet rule (they can have 6 and 4 valence electrons respectively). In boron trifluoride (BF3), there are only three electron pairs which repel each other to form a flat plane. Each fluorine atom is separated by cos-1(-1/2) = 120°. A different set of hybrid orbitals is formed in this molecule: the 2s and two 2p orbitals combine to form three sp2 hybrid orbitals. The remaining p orbital is empty and sits above and below the plane of the molecule.
Beryllium, on the other hand, forms only two pairs of valence electrons. These repel each other at cos-1(-1) = 180°, forming a linear molecule. An example is beryllium chloride, which has two chlorine atoms situated on opposite sides of a beryllium atom. This time, one 2s and one 2p orbital combine to form two sp hybrid orbitals. The two remaining p orbitals sit above and to the side of the beryllium atom (they are empty).
Bent vs. Linear


Some elements will have a bent shape, others have a linear shape. Both are attached to two groups, so it depends on how many non-bonding pairs the central atom has.
Take a look at sulfur dioxide (SO2) and carbon dioxide (CO2). Both have two oxygen atoms attached with double covalent bonds. Carbon dioxide is linear, and sulfur dioxide is bent. The difference is in their valence shells. Carbon has four valence electrons, sulfur has six. When they bond, carbon has no non-bonding pairs, but sulfur has one.
Five and Six Groups
Recall that some elements, especially sulfur and phosphorus, can bond with five or six groups. The hybridization is sp3d or sp3d2, with a trigonal bipyramidal or octahedral shape respectively. When there are non bonding pairs, other shape can arise (see the above chart).
How The Shapes Look
The yellow groups are non-bonding electron pairs. The white groups are bonded atoms, and the pink is the central atom. This is referred to as the AXE method; A is the central atom, X's are bonded atoms, and E's are non-bonding electron pairs.
-
linear
-
trigonal planar
-
bent
-
tetrahedral
-
trigonal pyramidal
-
bent
-
trigonal bipyramidal
-
seesaw
-
t-shape
-
octahedral
-
square pyramid
-
square planar
Intermolecular Bonds
Dipoles

Covalent bonds can be polar or non-polar, and so can the overall compound depending on its shape. When a bond is polar, it creates a dipole, a pair of charges (one positive and one negative). If they are arranged in a symmetrical shape, so that they point in opposite directions, they will cancel each other. For example, since the four hydrogens in methane (CH4) are facing away from each other, there is no overall dipole and the molecule is non-polar. In ammonia (NH3), however, there is a negative dipole at the nitrogen, due to the asymmetry caused by the non-bonding electron pair. The polarity of a compound determines its intermolecular bonding abilities.
Polar and Non-Polar Shapes
When a molecule has a linear, trigonal planar, tetrahedral, trigonal bipyramidal, or octahedral shape, it will be non-polar. These are the shapes that do not have non-bonding lone pairs. (e.g. Methane, CH4) But if some bonds are polar while others are not, there will be an overall dipole, and the molecule will be polar (e.g. Chloroform, CHCl3).
The other shapes (with non-bonding pairs) will be polar. (e.g. Water, H2O) Unless, of course, all the covalent bonds are non-polar, in which case there would be no dipoles to begin with.
Dipole-Dipole Bonds
When two polar molecules are near each other, they will arrange themselves so that the negative and positive sides line up. There will be an attractive force holding the two molecules together, but it is not nearly as strong a force as the intramolecular bonds. This is how many types of molecules bond together to form large solids or liquids.
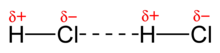
Hydrogen Bonding
Certain chemicals with hydrogen in their chemical formula have a special type of intermolecular bond, called hydrogen bonds. Hydrogen bonds will occur when a hydrogen atom is attached to an oxygen, nitrogen, or fluorine atom. This is because there is a large electronegativity difference between hydrogen and fluorine, oxygen, and nitrogen. Thus, molecules such as , , are extremely polar molecules with very strong dipole-dipole forces. As a result of the high electronegativities of fluorine, oxygen, and nitrogen, these elements will pull the electrons almost completely away from the hydrogen. The hydrogen becomes a bare proton sticking out from the molecule, and it will be strongly attracted to the negative side of any other polar molecules. Hydrogen bonding is an extreme type of dipole-dipole bonding. These forces are weaker than intramolecular bonds, but are much stronger than other intermolecular forces, causing these compounds to have high boiling points.

Covalent Networks

Silicon dioxide forms a covalent network. Unlike carbon dioxide (with double bonds), silicon dioxide forms only single covalent bonds. As a result, the individual molecules covalently bond into a large network. These bonds are very strong (being covalent) and there is no distinction between individual molecules and the overall network. Covalent networks hold diamonds together. Diamonds are made of nothing but carbon, and so is soot. Unlike soot, diamonds have covalent networks, making them very hard and crystalline.
Van der Waals forces
Van der Waals, or London dispersion forces are caused by temporary dipoles created when electron locations are lopsided. The electrons are constantly orbiting the nucleus, and by chance they could end up close together. The uneven concentration of electrons could make one side of the atom more negatively-charged than the other, creating a temporary dipole. As there are more electrons in an atom, and the shells are farther away from the nucleus, these forces become stronger.
Van der Waals forces explain how nitrogen can be liquified. Nitrogen gas is diatomic; its equation is N2. Since both atoms have the same electronegativity, there is no dipole and the molecule is non-polar. If there are no dipoles, what would make the nitrogen atoms stick together to form a liquid? Van der Waals forces are the answer. They allow otherwise non-polar molecules to have attractive forces. These are by far the weakest forces that hold molecules together.
Melting and Boiling Points
When comparing two substances, their melting and boiling points may be questioned. To determine which substance has the higher melting or boiling point, you must decide which one has the strongest intermolecular force. Metallic bonds, ionic bonds, and covalent networks are very strong, as they are actually intramolecular forces. These substances have the highest melting and boiling points because they only separate into individual molecules when the powerful bonds have been broken. Breaking these intramolecular forces requires great amounts of heat energy.
Substances with hydrogen bonding, an intermolecular force, will have much higher melting and boiling points than those that have ordinary dipole-dipole intramolecular forces. Non-polar molecules have the lowest melting and boiling points, because they are held together by the weak van der Waals forces.
If you need to compare the boiling points of two metals, the metal with the larger atomic radius will have weaker bonding, due to the lower concentration of charge. When comparing boiling points of the non-polar gases, like the noble gases, the gas with the largest radius will have the highest points because it has the most potential for van der Waals forces.
Ionic compounds can be compared using Coulomb's Law. Look for substances with high ionic charges and low ionic radii.
Chemical Reactions
Naming Substances
Some compounds have common names, like water for H2O. However, there are thousands of other compounds that are uncommon or have multiple names. Also, the common name is usually not recognized internationally. What looks like water to you might look like agua or vatten to someone else. To allow chemists to communicate without confusion, there are naming conventions to determine the systematic name of a chemical.
Naming Ions and Ionic Compounds
Ions are atoms that have lost or gained electrons. Note that in a polyatomic ion, the ion itself is held together by covalent bonds. Monoatomic cations (positive) are named the same way as their element, and they come first when naming a compound. Monoatomic anions (negative) have the suffix -ide and come at the end of the compound's name.
- Examples of ionic compounds
- NaCl - Sodium chloride
- MgCl2 - Magnesium chloride
- Ca3N2 - Calcium nitride
Notice that there is no need to write how many ions there are. Between the periodic table and our knowledge of ionic bonding, we can determine the number of ions, based on which elements are used.
Polyatomic Ions
Polyatomic ions have special names. Many of them contain oxygen and are called oxyanions. When different oxyanions are made of the same element, but have a different number of oxygen atoms, then prefixes and suffixes are used to tell them apart. The chlorine family of ions is an excellent example.
| Name | Formula |
|---|---|
| Chloride | Cl- |
| Hypochlorite | ClO- |
| Chlorite | ClO2- |
| Chlorate | ClO3- |
| Perchlorate | ClO4- |
The -ate suffix is used on the most common oxyanion (like sulfate SO42- or nitrate NO3-). The -ite suffix is used on the oxyanion with one oxygen atom fewer (like sulfite SO32- or nitrite NO2-). Sometimes there can be a hypo- prefix, meaning one oxygen atom fewer than for -ite. There is also a per- prefix, meaning one more oxygen atom than an -ate molecule has.
Occasionally, you will see a bi- prefix. This is an older prefix; it means the compound can both take up and lose a proton. It is often replaced with the word hydrogen. In either case, the oxyanion will have a hydrogen in it, decreasing its charge by one. For instance, there is carbonate (CO32-) and bicarbonate or hydrogen carbonate (HCO3-). |
One last prefix you may find is thio-. It means an oxygen has been replaced with a sulfur within the oxyanion. Cyanate is OCN-, and thiocyanate is SCN-.
- Examples of polyatomic ions
- NH4Cl - Ammonium chloride
- K(HCO3) - Potassium hydrogen carbonate
- AgNO3 - Silver nitrate
- CuSO3 - Copper (II) sulfite
In the last example, copper had a roman numeral 2 after its name because most of the transition metals can have more than one charge. The charge on the ion must be known, so it is written out for ions that have more than one common charge. Silver always has a charge of 1+, so it isn't necessary (but not wrong) to name its charge. Zinc always has a charge of 2+, so you don't have to name its charge either. Aluminum will always have a charge of +3. All other metals (except the Group 1 and 2 elements) must have roman numerals to show their charge.
Common polyatomic ions that you should know are listed in the following table
| Name | Formula |
|---|---|
| Acetate | C2H3O2- |
| Ammonium | NH4+ |
| Carbonate | CO32- |
| Cyanide | CN- |
| Cyanate | CNO- |
| Thiocyanate | CNS- |
| Hypochlorite | ClO- |
| Chlorite | ClO2- |
| Chlorate | ClO3- |
| Perchlorate | ClO4- |
| Hypobromite | BrO- |
| Bromite | BrO2- |
| Bromate | BrO3- |
| Perbromate | BrO4- |
| Hypoiodite | IO- |
| Iodite | IO2- |
| Iodate | IO3- |
| Periodate | IO4- |
| Nitrite | NO2- |
| Nitrate | NO3- |
| Peroxide | O22- |
| Permanganate | MnO4- |
| Sulfite | SO32- |
| Sulfate | SO42- |
Further explanation of the roman numerals is in order. Many atoms (especially the transition metals) are capable of ionizing in more than one way. The name of an ionic compound must make it very clear what the exact chemical formula is. If you wrote "copper chloride", it could be CuCl or CuCl2 because copper can lose one or two electrons when it forms an ion. The charge must be balanced, so there would be one or two chloride ions to accept the electrons. To be correct, you must write "copper(II) chloride" if you want CuCl2 and "copper (I) chloride" if you want CuCl. Keep in mind that the roman numerals refer to the charge of the cation, not how many anions are attached.
Common metal ions are listed below and should be learned:
| Name | Formula |
|---|---|
| Iron(II)/Ferrous | Fe2+ |
| Iron(III)/Ferric | Fe3+ |
| Copper(I)/Cuprous | Cu+ |
| Copper(II)/Cupric | Cu2+ |
| Tin (II)/Stannous | Sn2+ |
| Tin (IV)/Stannic | Sn4+ |
| Lead (II)/Plumbous (most common) | Pb2+ |
| Lead (IV)/Plumbic | Pb4+ |
| Mercury (I) (Note: Mercury (I) is a polyatomic ion) | Hg22+ |
| Mercury (II) | Hg2+ |
Naming molecules in chemistry
There are two systems of naming molecular compounds. The first uses prefixes to indicate the number of atoms of an element that are in the compound. If the substance is binary (containing only two elements), the suffix -ide is added to the second element. Thus water is dihydrogen monoxide. A prefix is not necessary for the first element if there is only one, so SF6 is 'sulfur hexafluoride'. The prefix system is used when both elements are non-metallic.
| Number | Prefix |
|---|---|
| 1 | Mono- |
| 2 | Di- |
| 3 | Tri- |
| 4 | Tetra- |
| 5 | Penta- |
| 6 | Hexa- |
| 7 | Hepta- |
| 8 | Octa- |
| 9 | Nona- |
| 10 | Deca- |
| 11 | Undeca- |
| 12 | Dodeca- |
If the last letter of the prefix is an a and the first letter of the element is a vowel, the a is dropped. That makes V2O5 divanadium pentoxide (instead of pentaoxide). Similar dropping occurs with mono- and elements beginning with o, as in the case of monoxide. This does not, however, happen with di- and tri-. A molecule containing three iodine atoms would be named triiodide. |
The second system, the stock system, uses oxidation numbers to represent how the electrons are distributed through the compound. This is essentially the roman numeral system that has already been explained, but it applies to non-ionic compounds as well. The most electronegative component of the molecule has a negative oxidation number that depends on the number of pairs of electrons it shares. The less electronegative part is assigned a positive number. In the stock system, only the cation's number is written, and in Roman numerals. The stock system is used when there is a metallic element in the compound. In the case of V2O5, it could also be called vanadium(V) oxide. Knowing that oxygen's charge is always -2, we could determine that there were five oxygens and two vanadiums, if we were given the name without the formula.
Naming acids
If an acid is a binary compound, it is named as hydro[element]ic acid. If it contains a polyatomic ion, then it is named [ion name]ic acid if the ion ends in -ate. If the ion ends in -ite then the acid will end in -ous. These examples should help.
- Examples of acid names
- HCl - Hydrochloric acid
- HClO - Hypochlorous acid
- HClO2 - Chlorous acid
- HClO3 - Chloric acid
- HClO4 - Perchloric acid
Formulas and Numbers
Calculating Formula Masses
The calculation of a compound's formula mass (the mass of its molecule or formula unit) is straightforward. Simply add the individual mass of each atom in the compound (found on the periodic table). For example, the formula mass of glucose (C6H12O6) is 180 amu.
Molar masses are just as easy to calculate. The molar mass is equal to the formula mass, except that the unit is grams per mole instead of amu.
Calculating Percentage Composition
Percentage composition is the relative mass of one substance in a compound compared to the whole. For example, in methane (CH4), the percentage mass of hydrogen is 25% because hydrogen makes up a total of 4 amu out of 16 amu overall.
Using Percentage Composition
Percentage composition can be used to find the empirical formula of a compound, which shows the ratios of elements in the compound. However, this is not the same as the molecular formula. For example, many sugars have the empirical formula CH2O, which could correspond to a molecular formula of CH2O, C2H4O2, C6H12O6, etc.
- To find the empirical formula from percentage composition, follow these procedures for each element.
- Convert from percentage to grams (for simplicity, assume a 100 g sample).
- Divide by the element's molar mass to find moles.
- Simplify to lowest whole-number ratio.
For example, a compound is composed of 75% carbon and 25% hydrogen by mass. Find the empirical formula.
- 75g C / (12 g/mol C) = 6.25 mol C
- 25g H / (1 g/mol H) = 25 mol H
- 6.25 mol C / 6.25 = 1 mol C
- 25 mol H / 6.25 = 4 mol H
Thus the empirical formula is CH4.
Calculating Molecular Formula
If you find the empirical formula of a compound and its molar/molecular mass, then you can find its exact molecular formula. Remember that the molecular formula is always a whole-number multiple of the empirical formula. For example, a compound with the empirical formula HO has a molecular mass of 34.0 amu. Since HO would only be 17.0 amu, which is half of 34.0, the molecular formula must be H2O2.
- Exercise for the reader
An unknown substance must be identified. Lab analysis has found that the substance is composed of 80% Fluorine and 20% Nitrogen with a molecular mass of 71 amu. What is the empirical formula? What is the molecular formula?
Stoichiometry
The word stoichiometry derives from two Greek words: stoicheion (meaning "element") and metron (meaning "measure"). Stoichiometry deals with calculations about the masses (sometimes volumes) of reactants and products involved in a chemical reaction. It is a very mathematical part of chemistry, so be prepared for lots of calculator use.
Jeremias Benjaim Richter (1762-1807) was the first to lay down the principles of stoichiometry. In 1792 he wrote: "Die stöchyometrie (Stöchyometria) ist die Wissenschaft die quantitativen oder Massenverhältnisse zu messen, in welchen die chymischen Elemente gegen einander stehen." [Stoichiometry is the science of measuring the quantitative proportions or mass ratios in which chemical elements stand to one another.]
Molar Calculations
Your Tool: Dimensional Analysis
Luckily, almost all of stoichiometry can be solved relatively easily using dimensional analysis. Dimensional analysis is just using units, instead of numbers or variables, to do math, usually to see how they cancel out. For instance, it is easy to see that:
It is this principle that will guide you through solving most of the stoichiometry problems (chemical reaction problems) you will see in General Chemistry. Before you attempt to solve a problem, ask yourself: what do I have now? where am I going? As long as you know how many (units) per (other units), this will make stoichiometry significantly easier.
Moles to Mass
How heavy is 1.5 mol of lead? How many moles in 22.34g of water? Calculating the mass of a sample from the number of moles it contains is quite simple. We use the molar mass (mass of one mole) of the substance to convert between mass and moles. When writing calculations, we denote the molar mass of a substance by an upper case "M" (e.g. M(Ne) means "the molar mass of neon"). As always, "n" stands for the number of moles and "m" indicates the mass of a substance. To find the solutions to the two questions we just asked, let's apply some dimensional analysis:
Can you see how the units cancel to give you the answer you want? All you needed to know was that you had 1.5 mol Pb (lead), and that 1 mol Pb weighs 207.2 grams. Thus, multiplying 1.5 mol Pb by 207.2 g Pb and dividing by 1 mol Pb gives you 310.8 g Pb, your answer.
Mass to Moles
But we had one more question: "How many moles in 22.34g of water?" This is just as easy:
Where did the 18 g H2O come from? We looked at the periodic table and simply added up the atomic masses of two hydrogens and an oxygen to get the molecular weight of water. This turned out to be 18, and since all the masses on the periodic table are given with respect to 1 mole, we knew that 1 mol of water weighed 18 grams. This gave us the relationship above, which is really just (again) watching units cancel out!
Calculating Molar Masses
Before we can do these types of calculations, we first have to know the molar mass. Fortunately, this is not difficult, as the molar mass is exactly the same as the atomic weight of an element. A table of atomic weights can be used to find the molar mass of elements (this information is often included in the periodic table). For example, the atomic weight of oxygen is 16.00 amu, so its molar mass is 16.00 g/mol.
For species with more than one element, we simply add up the atomic weights of each element to obtain the molar mass of the compound. For example, sulfur trioxide gas is made up of sulfur and oxygen, whose atomic weights are 32.06 and 16.00 respectively.
The procedure for more complex compounds is essentially the same. Aluminium carbonate, for example, contains aluminium, carbon, and oxygen. To find the molar mass, we have to be careful to find the total number of atoms of each element. Three carbonate ions each containing three oxygen atoms gives a total of nine oxygens. The atomic weights of aluminium and carbon are 26.98 and 12.01 respectively.
Empirical Formulae
The empirical formula of a substance is the simplest ratio of the number of moles of each element in a compound. The empirical formula is ambiguous, e.g. the formula CH could represent CH, C2H2, C3H3 etc. These latter formulae are called molecular formulae. It follows that the molecular formula is always a whole number multiple of the empirical formula for a compound.
Calculating the empirical formula is easy if the relative amounts of each element in the compound are known. For example, if a sample contains 1.37 mol oxygen and 2.74 mol hydrogen, we can calculate the empirical formula. A good strategy to use is to divide all amounts given by the smallest non-integer amount, then multiply by whole numbers until the simplest ratio is found. We can make a table showing the successive ratios.
| Hydrogen | Oxygen | |
|---|---|---|
| 2.74 | 1.37 | divide by 1.37 |
| 2 | 1 | ANSWER |
The empirical formula of the compound is H2O.
Here's another example. A sample of piperonal contains 1.384 mol carbon, 1.033 mol hydrogen and 0.519 mol oxygen.
| Carbon | Hydrogen | Oxygen | |
|---|---|---|---|
| 1.384 | 1.033 | 0.519 | divide by 0.519 |
| 2.666 | 2 | 1 | multiply by 3 |
| 8 | 6 | 3 | ANSWER |
The empirical formula of piperonal is C8H6O3.
Converting from Masses
Often, we are given the relative composition by mass of a substance and asked to find the empirical formula. These masses must first be converted to moles using the techniques outlined above. For example, a sample of ethanol contains 52.1% carbon, 13.2% hydrogen, and 34.7% oxygen by mass. Hypothetically, 100g of this substance will contain 52.1 g carbon, 13.2 g hydrogen and 34.7 g oxygen. Dividing these by their respective molar masses gives the amount in moles of each element (as we learned above). These are 4.34 mol, 13.1 mol, and 2.17 mol respectively.
| Carbon | Hydrogen | Oxygen | |
|---|---|---|---|
| 4.34 | 13.1 | 2.17 | divide by 2.17 |
| 2 | 6 | 1 | ANSWER |
The empirical formula of ethanol is C2H6O.
Molecular Formula
As mentioned above, the molecular formula for a substance equals the count of atoms of each type in a molecule. This is always a whole number multiple of the empirical formula. To calculate the molecular formula from the empirical formula, we need to know the molar mass of the substance. For example, the empirical formula for benzene is CH, and its molar mass is 78.12 g/mol. Divide the actual molar mass by the mass of the empirical formula, 13.02 g/mol, to determine the multiple of the empirical formula, "n". The molecular formula equals the empirical formula multiplied by "n".
This shows that the molecular formula for benzene is 6 times the empirical formula of CH. The molecular formula for benzene is C6H6.
Solving Mass-Mass Equations
A typical mass-mass equation will give you an amount in grams and ask for another answer in grams.
- To solve a mass-mass equation, follow these rules
- Balance the equation if it is not already.
- Convert the given quantity to moles.
- Multiply by the molar ratio of the demanded substance over the given substance.
- Convert the demanded substance into grams.
For example, given the equation , find out how many grams of silver (Ag) will result from 43.0 grams of copper (Cu) reacting.
- Convert the given quantity to moles.
- Multiply by the molar ratio of the demanded substance and the given substance.
- Convert the demanded substance to grams.
Notice how dimensional analysis applies to this technique. All units will cancel except for the desired one (grams of silver, in this case). |
Summary
To solve a stoichiometric problem, you need to know what you already have and what you want to find. Everything in between is basic algebra.
- Key Terms
- Molar mass: mass (in grams) of one mole of a substance.
- Empirical formula: the simplest ratio of the number of moles of each element in a compound
- Molecular formula: the actual ratio of the number of moles of each element in a compound
In general, all you have to do is keep track of the units and how they cancel, and you will be on your way!
Chemical Equations
Chemical equations are a convenient, standardized system for describing chemical reactions. They contain the following information.
- The type of reactants consumed and products formed
- The relative amounts of reactants and products
- The electrical charges on ions
- The physical state of each species (e.g. solid, liquid)
- The reaction conditions (e.g. temperature, catalysts)
The final two points are optional and sometimes omitted.
Anatomy of an Equation
Hydrogen gas and chlorine gas will react vigorously to produce hydrogen chloride gas. The equation above illustrates this reaction. The reactants, hydrogen and chlorine, are written on the left and the products (hydrogen chloride) on the right. The large number 2 in front of HCl indicates that two molecules of HCl are produced for each 1 molecule of hydrogen and chlorine gas consumed. The 2 in subscript below H indicates that there are two hydrogen atoms in each molecule of hydrogen gas. Finally, the (g) symbols subscript to each species indicates that they are gases.
Reacting Species
Species in a chemical reaction is a general term used to mean atoms, molecules or ions. A species can contain more than one chemical element (HCl, for example, contains hydrogen and chlorine). Each species in a chemical equation is written:
E is the chemical symbol for the element, x is the number of atoms of that element in the species, y is the charge (if it is an ion) and (s) is the physical state.
The symbols in parentheses (in subscript below each species) indicate the physical state of each reactant or product. For ACS Style[1] the state is typeset at the baseline without size change.
- (s) means solid
- (l) means liquid
- (g) means gas
- (aq) means aqueous solution (i.e. dissolved in water)
For example, ethyl alcohol would be written because each molecule contains 2 carbon, 6 hydrogen and 1 oxygen atom. A magnesium ion would be written because it has a double positive ("two plus") charge. Finally, an ammonium ion would be written because each molecule contains 1 nitrogen and 4 hydrogen atoms and has a charge of 1+.
Coefficients
The numbers in front of each species have a very important meaning—they indicate the relative amounts of the atoms that react. The number in front of each species is called a coefficient. In the above equation, for example, one H2 molecule reacts with one Cl2 molecule to produce two molecules of HCl. This can also be interpreted as moles (i.e. 1 mol H2 and 1 mol Cl2 produces 2 mol HCl).
It is important that the Law of Conservation of Mass is not violated. There must be the same number of each type of atoms on either side of the equation. Coefficients are useful for keeping the same number of atoms on both sides:
If you count the atoms, there are four hydrogens and two oxygens on each side. The coefficients allow us to balance the equation; without them the equation would have the wrong number of atoms. Balancing equations is the topic of the next chapter.
Other Information
Occasionally, other information about a chemical reaction will be supplied in an equation (such as temperature or other reaction conditions). This information is often written to the right of the equation or above the reaction arrow. A simple example would be the melting of ice.
Reactions commonly involve catalysts, which are substances that speed up a reaction without being consumed. Catalysts are often written over the arrow. A perfect example of a catalyzed reaction is photosynthesis. Inside plant cells, a substance called chlorophyll converts sunlight into food. The reaction is written:
Examples
| This is the equation for burning methane gas (CH4) in the presence of oxygen (O2) to form carbon dioxide and water: CO2 and H2O respectively. Notice the use of coefficients to obey the Law of Conservation of Matter. | |
| This is a precipitation reaction in which dissolved lead cations and iodide anions combine to form a solid yellow precipitate of lead iodide (an ionic solid). | |
|
These two equations involve a catalyst. They occur one after another, using divanadium pentoxide to convert sulfur dioxide into sulfur trioxide. If you look closely, you can see that the vanadium catalyst is involved in the reaction, but it does not get consumed. It is both a reactant and a product, but it is necessary for the reaction to occur, making it a catalyst. |
| If we add both equations together, we can cancel out terms that appear on both sides. The resulting equation is much simpler and self-explanatory (although the original pair of equations is more accurate in describing how the reaction proceeds). |
The last example demonstrates another important principle of chemical equations: they can be added together. Simply list all reactants from the equations you are adding, then list all products. If the same term appears on both sides, it is either a catalyst, an intermediate product, or it is not involved in the reaction. Either way, it can be canceled out from both sides (if the coefficients are equal). Try adding the first two vanadium equations together and see if you can cancel out terms to get the final equation. |
Balancing Equations
Balancing Equations
Chemical equations are useful because they give the relative amounts of the substances that react in a chemical equation.
In some cases, however, we may not know the relative amounts of each substance that reacts. Fortunately, we can always find the correct coefficients of an equation (the relative amounts of each reactant and product). The process of finding the coefficients is known as balancing the equation.
During a chemical reaction, atoms are neither created or destroyed. The same atoms are present before and after a reaction takes place; they are just rearranged. This is called the Law of Conservation of Matter, and we can use this law to help us find the right coefficients to balance an equation.
For example, assume in the above equation that we do not know how many moles of ammonia gas will be produced:
From the left side of this equation, we see that there are 2 atoms of nitrogen gas in the molecule N2 (2 atoms per molecule x 1 molecule), and 6 atoms of hydrogen gas in the 3 H2 molecules (2 atoms per molecule x 3 molecules). Because of the Law of Conservation of Matter, there must also be 2 atoms nitrogen gas and 6 atoms of hydrogen gas on the right side. Since each molecule of the resultant ammonia gas (NH3) contains 1 atom of nitrogen and 3 atoms of hydrogen, 2 molecules are needed to obtain 2 atoms of nitrogen and 6 atoms of hydrogen.
An Example
| This chemical equation shows the compounds being consumed and produced; however, it does not appropriately deal with the quantities of the compounds. There appear to be two oxygen atoms on the left and only one on the right. But we know that there should be the same number of atoms on both sides. This equation is said to be unbalanced, because the number of atoms are different. | |
| To make the equation balanced, add coefficients in front of each molecule as needed. The 2 in front of hydrogen on the left indicates that twice as many atoms of hydrogen are needed to react with a certain number of oxygen atoms. The coefficient 1 is not written, since it assumed in the absence of any coefficient. | |
| Now, let's consider a similar reaction between hydrogen and nitrogen. | |
| Typically, it is easiest to balance all pure elements last, especially hydrogen. First, by placing a two in front of ammonia, the nitrogens are balanced. | |
| This leaves 6 moles of atomic hydrogen in the products and only two moles in the reactants. A coefficient of 3 is then placed in front of the hydrogen to give a fully balanced reaction. |
| When balancing a reaction, only coefficients can be changed because changing a subscript would give a different reaction. |
Tricks in balancing certain reactions
Combustion
A combustion reaction is a reaction between a carbon chain (basically, a molecule consisting of carbons, hydrogen, and perhaps oxygen) with oxygen to form carbon dioxide and water, plus heat. Combustion reactions could get very complex:
Fortunately, there is an easy way to balance these reactions.
First, note that the carbon in C6H6 can only appear on the product side in CO2. Thus, we can write a coefficient of 6 in front of CO2.
Next, note that the hydrogen in C6H6 can only go to H2O. Thus, we put a 3 in front of H2O.
We have 15 oxygen atoms on the product side, so there are O2 molecules on the reactant side. To make this an integer, we multiply all coefficients by 2.
Another Example
| Helpful Hint! | |
|---|---|
| Note: Fractions are technically allowed as coefficients, but they are generally avoided. Multiply all coefficients by the denominator to remove a fraction. |
| As reactions become more complex, they become more difficult to balance. For example, the combustion of butane (lighter fluid). | |
| Once again, it is better to leave pure elements until the end, so first we'll balance carbon and hydrogen. Oxygen can then be balanced after. It is easy to see that one mole of butane will produce four moles of carbon dioxide and five moles of water. | |
| Now there are 13 oxygen atoms on the right and two on the left. The odd number of oxygens prevents balancing with elemental oxygen. Because elemental oxygen is diatomic, this problem comes up in nearly every combustion reaction. Simply double every species except for oxygen to get an even number of oxygen atoms in the product. | |
| The carbon and hydrogens are still balanced, and now there are an even number of oxygens in the product. Finally, the reaction can be balanced. |
Keep in mind that every equation must always be balanced. If it's not balanced, it is incorrect. |
Limiting Reactants and Percent Yield
Limiting Reactants
When chemical reactions occur, the reactants undergo change to create the products. The coefficients of the chemical equation show the relative amounts of substance needed for the reaction to occur. Consider the combustion of propane:
For every one mole of propane, there must be five moles of oxygen. For every one mole of propane combusted, there will be three moles of carbon dioxide and four moles of water produced (along with much heat). If a propane grill is burning, there will be a very large amount of oxygen available to react with the propane gas. In this case, oxygen is the excess reactant. There is so much oxygen that the exact amount doesn't matter—it will not run out.
On the other hand, there is not an unlimited amount of propane. It will run out far before the oxygen runs out, making it a limiting reactant. The amount of propane available will decide how far the reaction will go.
- Example
If there are three moles of hydrogen, and one mole of oxygen, which is the limiting reactant? How much product is created?
Twice as much hydrogen than oxygen is required. However, there is more than twice as much hydrogen. Thus hydrogen is the excess reactant and oxygen is the limiting reactant. If the reaction proceeds to completion, all of the oxygen will be used up, and one mole of hydrogen will remain. You can imagine this situation like this:
The reactant that is left over after the reaction is complete is called the "excess reactant". Often, you will want to figure out how much of the excess reactant is left after the reaction is complete. to do this, first use mole ratios to determine how much excess reactant is used up in the reaction.
Here are the ratios that need to be used:
Percent Yield
Usually, less product is made than theoretically possible. The actual yield is lower than the theoretical yield. To compare the two, one can calculate percent yield, which is .
The percent yield tells us how far the reaction actually went.
Types of Chemical Reactions
| Helpful Hint! | |
|---|---|
| Synthesis reactions always yield one product. Reversing a synthesis reaction will give you a decomposition reaction. |
The general form of a synthesis reaction is A + B → AB. Synthesis reactions "put things together".
| This is the most well-known example of a synthesis reaction—the formation of water via the combustion of hydrogen gas and oxygen gas. | |
| Another example of a synthesis reaction is the formation of sodium chloride (table salt). |
Because of the very high reactivities of sodium metal and chlorine gas, this reaction releases a tremendous amount of heat and light energy. Recall that atoms release energy as they become stable, and consider the octet rule when determining why this reaction has such favorable features.
Decomposition Reactions
These are the same number of synthesis reactions, with the format AB → A + B. Decomposition reactions "take things apart". Just as synthesis reactions can only form one product, decomposition reactions can only start with one reactant. Compounds that are unstable decompose quickly without outside assistance. Also they help other atoms to decompose better.
| One example is the electrolysis of water (passing water through electrical current) to form hydrogen gas and oxygen gas. | |
| Hydrogen peroxide slowly decomposes into water and oxygen because it is somewhat unstable. The process is sped up by the energy from light, so hydrogen peroxide is often stored in dark containers to slow down the decomposition. | |
| Carbonic acid is the carbonation that is dissolved in soda. It decomposes into carbon dioxide and water, which is why an opened drink loses its fizz. |
Decomposition, aside from happening spontaneously in unstable compounds, occurs under three conditions: thermal, electrolytic, and catalytic. Thermal decomposition occurs when a substance is heated. Electrolytic decomposition, as shown above, is the result of an electric current. Catalytic decomposition happens because a catalyst breaks apart a substance. |
Single Displacement Reactions
Single displacement reaction, also called single replacement, is a reaction in which 2 elements are substituted for another element in a compound. The starting materials are always pure elements, such as a pure zinc metal or hydrogen gas plus an aqueous compound. When a displacement reaction occurs, a new aqueous compound and a different pure element are generated as products. Its format is AB + C → AC + B. Single Diplacement Adding hydrochloric acid to zinc will cause a gas to bubble out:
Double Displacement Reactions
In these reactions, two compounds swap components, in the format AB + CD → AD + CB
This is also called an "exchange". Here are the examples below:
1.) HCl + NaOH ----> NaCl + H2O
Precipitation
A precipitation reaction occurs when an ionic substance comes out of solution and forms an insoluble (or slightly soluble) solid. The solid which comes out of solution is called a precipitate. This can occur when two soluble salts (ionic compounds) are mixed and form an insoluble one—the precipitate.
| An example is lead nitrate mixed with potassium iodide, which forms a bright yellow precipitate of lead iodide. | |
| Note that the lead iodide is formed as a solid. The previous equation is written in molecular form, which is not the best way of describing the reaction. Each of the elements really exist in solution as individual ions, not bonded to each other (as in potassium iodide crystals). If we write the above as an ionic equation, we get a much better idea of what is actually happening. | |
| Notice the like terms on both sides of the equation. These are called spectator ions because they do not participate in the reaction. They can be ignored, and the net ionic equation is written. |
In the solution, there exists both lead and iodide ions. Because lead iodide is insoluble, they spontaneously crystallise and form the precipitate.
Acid-Base Neutralization
In simple terms, an acid is a substance which can lose a H+ ion (i.e. a proton) and a base is a substance which can accept a proton. When equal amounts of an acid and base react, they neutralize each other, forming species which aren't as acidic or basic.
| For example, when hydrochloric acid and sodium hydroxide react, they form water and sodium chloride (table salt). | |
| Again, we get a clearer picture of what's happening if we write a net ionic equation. |
Acid base reactions often happen in aqueous solution, but they can also occur in the gaseous state. Acids and bases will be discussed in much greater detail in the acids and bases section.
Combustion

Combustion, better known as burning, is the combination of a substance with oxygen. The products are carbon dioxide, water, and possible other waste products. Combustion reactions release large amounts of heat. C3H8, better known as propane, undergoes combustion. The balanced equation is:
Combustion is similar to a decomposition reaction, except that oxygen and heat are required for it to occur. If there is not enough oxygen, the reaction may not occur. Sometimes, with limited oxygen, the reaction will occur, but it produces carbon monoxide (CO) or even soot. In that case, it is called incomplete combustion. If the substances being burned contain atoms other than hydrogen and oxygen, then waste products will also form. Coal is burned for heating and energy purposes, and it contains sulfur. As a result, sulfur dioxide is released, which is a pollutant. Coal with lower sulfur content is more desirable, but more expensive, because it will release less of the sulfur-based pollutants.
Organic Reactions

Organic reactions occur between organic molecules (molecules containing carbon and hydrogen). Since there is a virtually unlimited number of organic molecules, the scope of organic reactions is very large. However, many of the characteristics of organic molecules are determined by functional groups—small groups of atoms that react in predictable ways.
Another key concept in organic reactions is Lewis basicity. Parts of organic molecules can be electrophillic (electron-loving) or nucleophillic (nucleus, or positive loving). Nucleophillic regions have an excess of electrons—they act as Lewis bases—whereas electrophillic areas are electron deficient and act as Lewis acids. The nucleophillic and electrophillic regions attract and react with each other. Organic reactions are beyond the scope of this book, and are covered in more detail in Organic Chemistry. However, most organic substances can undergo replacement reactions and combustion reactions, as you have already learned.
Redox

Redox is an abbreviation of reduction/oxidation reactions. This is exactly what happens in a redox reaction, one species is reduced and another is oxidized. Reduction involves a gain of electrons and oxidation involves a loss, so a redox reaction is one in which electrons are transferred between species. Reactions where something is "burnt" (burning means being oxidised) are examples of redox reactions, however, oxidation reactions also occur in solution, which is very useful and forms the basis of electrochemistry.
Redox reactions are often written as two half-reactions showing the reduction and oxidation processes separately. These half-reactions are balanced (by multiplying each by a coefficient) and added together to form the full equation. When magnesium is burnt in oxygen, it loses electrons (it is oxidised). Conversely, the oxygen gains electrons from the magnesium (it is reduced).
Redox reactions will be discussed in greater detail in the redox section.
Energy Changes in Chemical Reactions
Exothermic and Endothermic Reactions
The release of energy in chemical reactions occurs when the reactants have higher chemical energy than the products. The chemical energy in a substance is a type of potential energy stored within the substance. This stored chemical potential energy is the heat content or enthalpy of the substance.
If the enthalpy decreases during a chemical reaction, a corresponding amount of energy must be released to the surroundings. Conversely, if the enthalpy increases during a reaction, a corresponding amount of energy must be absorbed from the surroundings. This is simply the Law of Conservation of Energy.
absorbtion reactions is when a chemical reaction releases more energy than it absorbs and you can also see them die on the inside.
reletion reactions is when a chemical reaction absorbs more energy than it releases.
You are already familiar with enthalpy: melting ice is endothermic and freezing water is exothermic.
| When methane burns in air the heat given off equals the decrease in enthalpy that occurs as the reactants are converted to products.
|
When ammonium nitrate is dissolved in water, energy is absorbed and the water cools. This concept is used in "cold packs".
|
Because reactions release or absorb energy, they affect the temperature of their surroundings. Exothermic reactions heat up their surroundings while endothermic reactions cool them down. The study of enthalpy, along with many other energy-related topics, is covered in the Thermodynamics Unit.
Activation Energy
Think about the combustion of methane. It releases enough heat energy to cause a fire. However, the reaction does not occur automatically. When methane and oxygen are mixed, an explosion does not instantly occur. First, the methane must be ignited, usually with a lighter or matchstick. This reveals something about reactions: they will not occur unless a certain amount of activation energy is added first. In this sense, all reactions absorb energy before they begin, but the exothermic reactions release even more energy. This can be explained with a graph of potential energy:

This graph shows an exothermic reaction because the products are at a lower energy than the reactants (so heat has been released). Before that can happen, the energy must actually increase. The amount of energy added before the reaction can complete is the activation energy, symbolized Ea.
Predicting Chemical Reactions
Types of Reactions
There are several guidelines that can help you predict what kind of chemical reaction will occur between a mixture of chemicals.
- Several pure elements mixed together may undergo a synthesis reaction.
- A single compound may undergo a decomposition reaction. It often forms water or hydrogen gas.
- A pure element mixed with an ionic compound may undergo a single replacement reaction.
- Two different ionic compounds are very likely to undergo a double replacement reaction.
- An organic compound (containing carbon and hydrogen) can usually react with oxygen in a combustion reaction.
However, not all elements will react with each other. To better predict a chemical reaction, knowledge of the reactivity series is needed.
Reactivity
When combining two chemicals, a single- or double-replacement reaction doesn't always happen. This can be explained by a list known as the reactivity series, which lists elements in order of reactivity. The higher on the list an element is, the more elements it can replace in a single- or double-replacement reaction. When deciding if a replacement reaction will occur, look up the two elements in question. The higher one will replace the lower one.
Elements at the very top of the series are so reactive that they can replace hydrogen from water. This explains the explosive reaction between sodium and water:
Elements in the middle of the list will react with acids (but not water) to produce a salt and hydrogen gas. Elements at the bottom of the list are mostly nonreactive.
Elements near the top of the list will corrode (rust, tarnish, etc.) in oxygen much faster than those at the bottom of the list.
The Reactivity Series
- Red: elements that react with water and acids to form hydrogen gas, and with oxygen.
- Orange: elements that react very slowly with water but strongly with acids.
- Yellow: elements that react with acid to form hydrogen gas, and with oxygen.
- Grey: elements that react with oxygen (tarnish).
- White: elements that are often found pure; relatively nonreactive.
Most Reactive
| Cs |
| K |
| Na |
| Li |
| Sr |
| Ca |
| Rb |
| Ba |
| Mg |
| Al |
| (C) |
| Mn |
| Zn |
| Cr |
| Fe |
| Cd |
| Co |
| Ni |
| Sn |
| Pb |
| (H2) |
| Sb |
| Bi |
| Cu |
| Hg |
| Ag |
| Pt |
| Au |
Least Reactive
Oxidation States
Oxidation states are used to determine the degree of oxidation or reduction that an element has undergone when bonding. The oxidation state of a compound is the sum of the oxidation states of all atoms within the compound, which equals zero unless the compound is ionic.
*Gaining electrons is reduction.
|
The oxidation state of an atom within a molecule is the charge it would have if the bonding were completely ionic, even though covalent bonds do not actually result in charged ions.
Method of notation
Oxidation states are written above the element or group of elements that they belong to (when drawing the molecule), or written with roman numerals in parenthesis when naming the elements.
| aluminum | |
| aluminum(III), an ion |
Determining oxidation state
For single atoms or ions
Because oxidation numbers are just the sum of the electrons gained or lost, calculating them for single elements is easy.
The oxidation state of a single element is the same as its charge. Pure elements always have an oxidation states of zero. |
Notice that the oxidation states of ionic compounds are simple to determine.
For larger molecules
| Helpful Hint! | |
|---|---|
| Remember that all the individual oxidation states must add up to the charge on the whole substance. |
Although covalent bonds do not result in charges, oxidation states are still useful. They label the hypothetical transfer of electrons if the substance were ionic. Determining the oxidation states of atoms in a covalent molecule is very important when analyzing "redox" reactions. When substances react, they may transfer electrons when they form the products, so comparing the oxidation states of the products and reactants allows us to keep track of the electrons.
| for hydrogen chloride | |
| for water | |
| for the chlorite ion (notice the overall charge) |
| Oxidation states do not necessarily represent the actual charges on an atom in a molecule. They are simply numbers that indicate what the charges would be if that atom had gained or lost the electrons involved in the bonding. For example, CH4 is a covalent molecule—the C has no charge nor does the H, however the molecule can be assigned a −4 oxidation state for the C and a +1 oxidation state for the H's. |
Determining Oxidation States
The determination of oxidation states is based on knowing which elements can have only one oxidation state other than the elemental state and which elements are able to form more than one oxidation state other than the elemental state. Let's look at some of the "rules" for determining the oxidation states.
1. The oxidation state of an element is always zero.
2. For metals, the charge of the ion is the same as the oxidation state. The following metals form only one ion: Group IA, Group IIA, Group IIIA (except Tl), Zn2+, Cd2+.
3. For monatomic anions and cations, the charge is the same as the oxidation state.
4. Oxygen in a compound is −2, unless a peroxide is present. The oxidation state of oxygen in peroxide ion , O22− is −1.
5. For compounds containing polyatomic ions, use the overall charge of the polyatomic ion to determine the charge of the cation. Here is a convenient method for determining oxidation states. Basically, you treat the charges in the compound as a simple algebraic expression. For example, let's determine the oxidation states of the elements in the compound, KMnO4. Applying rule 2, we know that the oxidation state of potassium is +1. We will assign "x" to Mn for now, since manganese may be of several oxidation states. There are 4 oxygens at −2. The overall charge of the compound is zero: K Mn O4 +1 x 4(-2)
The algebraic expression generated is: 1 + x -8 = 0
Solving for x gives the oxidation state of manganese: x - 7 = 0 x = +7 K Mn O4 +1 +7 4(-2)
Suppose the species under consideration is a polyatomic ion. For example, what is the oxidation state of chromium in dichromate ion, (Cr2O72-)?
As before, assign the oxidation state for oxygen, which is known to be -2. Since the oxidation state for chromium is not known, and two chromium atoms are present, assign the algebraic value of 2x for chromium: Cr2 O7 2- 2x 7(-2)
Set up the algebraic equation to solve for x. Since the overall charge of the ion is -2, the expression is set equal to -2 rather than 0: 2x + 7(-2) = -2
Solve for x: 2x - 14 = -2 2x = 12 x = +6
Each chromium in the ion has an oxidation state of +6. Let's do one last example, where a polyatomic ion is involved. Suppose you need to find the oxidation state of all atoms in Fe2(CO3)3. Here two atoms, iron and carbon, have more than one possible oxidation state. What happens if you don't know the oxidation state of carbon in carbonate ion? In fact, knowledge of the oxidation state of carbon is unnecessary. What you need to know is the charge of carbonate ion (-2). Set up an algebraic expression while considering just the iron ion and the carbonate ion: Fe2 (CO3)3 2x 3(-2) 2x - 6 = 0 2x = 6 x = 3
Each iron ion in the compound has an oxidation state of +3. Next consider the carbonate ion independent of the iron(III) ion: C O3 2- x 3(-2) x - 6 = -2 x = +4
The oxidation state of carbon is +4 and each oxygen is -2.
Guidelines
Determining oxidation states is not always easy, but there are many guidelines that can help. This guidelines in this table are listed in order of importance. The highest oxidation state that any element can reach is +8 in XeO4.
| Element | Usual Oxidation State |
|---|---|
| Fluorine | Fluorine, being the most electronegative element, will always have an oxidation of -1 (except when it is bonded to itself in F2, when its oxidation state is 0). |
| Hydrogen | Hydrogen always has an oxidation of +1, -1, or 0. It is +1 when it is bonded to a non-metal (e.g. HCl, hydrochloric acid). It is -1 when it is bonded to metal (e.g. NaH, sodium hydride). It is 0 when it is bonded to itself in H2. |
| Oxygen | Oxygen is usually given an oxidation number of -2 in its compounds, such as H2O. The exception is in peroxides (O2-2) where it is given an oxidation of -1. Also, in F2O oxygen is given an oxidation of +2 (because fluorine must have -1), and in O2, where it is bonded only to itself, the oxidation is 0. |
| Alkali Metals | The Group 1A metals always have an oxidation of +1, as in NaCl. The Group 2A metals always have an oxidation of +2, as in CaF2. There are some rare exceptions that don't need consideration. |
| Halogens | The other halogens (Cl, Br, I, As) usually have an oxidation of -1. When bonded to another halogen, its oxidation will be 0. However, they can also have +1, +3, +5, or +7. Looking at the family of chlorides, you can see each oxidation state (Cl2 (0), Cl- (-1), ClO- (+1), ClO2- (+3), ClO3- (+5), ClO4- (+7)). |
| Nitrogen | Nitrogen (and the other Group 5A elements, such as phosphorus, P) often have -3 (as in ammonia, NH3), but may have +3 (as in NF3) or +5 (as in phosphate, PO43-). |
| Carbon | Carbon can take any oxidation state from -4, as in CH4, to +4, as in CF4. It is best to find the oxidation of other elements first. |
In general, the more electronegative element has the negative number. Using a chart of electronegativities, you can determine the oxidation state of any atom within a compound.
Periodicity
Oxidation states are another periodic trend. They seem to repeat a pattern across each period.

Redox Reactions
Redox
Redox reactions are chemical reactions in which elements are oxidized and reduced.
*Losing electrons is oxidation.
|
Specifically, at the most basic level one element gets oxidized by losing, or donating, electrons to the oxidizing agent. In doing so, the oxidizing agent gets reduced by accepting the electrons lost, or donated, by the reducing agent (i.e. the element getting oxidized).
If it seems as though there are two separate things going on here, you are correct: redox reactions can be split into two half-reactions, one dealing with oxidation, the other, reduction.
Mnemonic
Oil Rig
Oxidation Is Loss. Reduction Is Gain
Alternatively:
LEO GER
Lose Electrons Oxidation. Gain Electrons Reduction
Example
| This is the complete reaction. Iron is oxidized, thus it is the reducing agent. Copper is reduced, making it the oxidizing agent. | |
| This is the oxidation half-reaction. | |
| This is the reduction half-reaction. |
When the two half-reactions are summed, the result is:
| Helpful Hint! | |
|---|---|
| If you cancel out the electrons on both sides, you get the original equation. |
Balancing Redox Equations
In a redox reaction, all electrons must cancel out. If you are adding two half-reactions with unequal numbers of electrons, then the equations must be multiplied by a common denominator. This process is similar to balancing regular equations, but now you are trying to balance the electrons between two half-reactions.
Example
The electrons don't completely cancel out. There is one electron more on the left. However, if you double all terms in the first half-reaction, then add it to the second half-reaction, the electrons will cancel out completely. That means the half-reactions for this redox reaction are actually:
Balancing Redox Equations in an Acidic or Basic Solution
If a reaction occurs in an acidic or basic environment, the redox equation is balanced as follows:
- Write the oxidation and reduction half reactions, but with the whole compound, not just the element that is reduced/oxidized.
- Balance both reactions for all elements except oxygen and hydrogen.
- If the oxygen atoms are not balanced in either reaction, add water molecules to the side missing the oxygen.
- If the hydrogen atoms are not balanced, add hydrogen ions until the hydrogen atoms are balanced.
- Multiply the half reactions by the appropriate number (so that they have equal numbers of electrons).
- Add the two equations to cancel out the electrons, as in the previous method, and the equation is balanced!
If the reaction occurs in a basic environment, proceed as if it is in an acid environment, but, after step 4, for each hydrogen ion added, add a hydroxide ion to both sides of the equation. Then, combine the hydroxide ions and hydrogen ions to form water. Then, cancel all the water molecules that appear on both sides.
Electrochemistry
Redox Reactions (review)
Redox (shorthand for reduction/oxidation reaction) describes all chemical reactions in which atoms have their oxidation number (oxidation state) changed.
This can be either a simple redox process such as the oxidation of carbon to yield carbon dioxide, or the reduction of carbon by hydrogen to yield methane (CH4), or it can be a complex process such as the oxidation of sugar in the human body through a series of very complex electron transfer processes.
The term redox comes from the two concepts of reduction and oxidation. It can be explained in simple terms:
- Oxidation describes the loss of electrons by a molecule, atom, or ion
- Reduction describes the gain of electrons by a molecule, atom, or ion
However, these descriptions (though sufficient for many purposes) are not truly correct. Oxidation and reduction properly refer to a change in oxidation number—the actual transfer of electrons may never occur. Thus, oxidation is better defined as an increase in oxidation number, and reduction as a decrease in oxidation number. In practice, the transfer of electrons will always cause a change in oxidation number, but there are many reactions which are classed as "redox" even though no electron transfer occurs noway (such as those involving covalent bonds).
Electrochemistry
Electrochemistry is a branch of chemistry that deals with the flow of electricity by chemical reactions. The electrons in a balanced half-reaction show the direct relationship between electricity and the specific redox reaction. Electrochemical reactions are either spontaneous, or nonspontaneous. A spontaneous redox reaction generates a voltage itself. A nonspontaneous redox reaction occurs when an external voltage is applied. The reactions that occur in an electric battery are electrochemical reactions.
- Three components of an electrochemical reaction
- A solution where redox reactions may occur (solutions are substances dissolved in liquid, usually water)
- A conductor for electrons to be transferred (such as a metal wire)
- A conductor for ions to be transferred (usually a salt bridge) e.g. filter paper dipped in a salt solution.
Electrolysis
An electrolysis experiment forces a nonspontaneous chemical reaction to occur. This is achieved when two electrodes are submersed in an electrically conductive solution, and the electrical voltage applied to the two electrodes is increased until electrons flow. The electrode receiving the electrons, or where the reduction reactions occur, is called the cathode. The electrode which supplies the electrons, or where the oxidation reactions occur, is called the anode.
A molten salt is an example of something that may be electrolyzed because salts are composed of ions. When the salt is in its solid state, the ions are not able to freely move. However, when the salt is heated enough until it melts (making it a molten salt), the ions are free to move. This mobility of the ions in the molten salt makes the salt electrically conductive. In the electrolysis of a molten salt, for example melted , the cation of the salt (in this case ) will be reduced at the cathode, and the anion of the salt (in this case ) will be oxidized at the anode:
- Cathode reaction: Na+ + e- → Na
- Anode reaction: 2Cl → Cl2 + 2e-
Aqueous solutions of salts can be electrolyzed as well because they are also electrically conductive. In aqueous solutions, there is an additional reaction possible at each the cathode and the anode:
- Cathode: 2H2O + 2e- → H2 + 2OH- (reduction of water)
- Anode: 2H2O → 4H+ + O2 + 4e- (oxidation of water)
With the addition of these two reactions, there are now two possible reactions at each electrode. At the cathode, either the reduction of the cation or the reduction of water will occur. At the anode, either the oxidation of the anion or the oxidation of water will occur. The following rules determine which reaction takes place at each electrode:
- Cathode: If the cation is a very active metal, water will be reduced. Very active metals include Li, Na, K, Rb, Cs, Ca, Sr, and Ba. If the cation is an active or inactive metal, the cation will be reduced.
- Anode: If the anion is a polyatomic ion, water will generally be oxidized. Specifically, sulfate, perchlorate, and nitrate ions are not oxidized; water will oxidize instead. Chloride, bromide, and iodide ions will be oxidized. If the anion in one salt is oxidized in an aqueous electrolysis, that same anion will also be oxidized in any other salt.
Galvanic Cells
The energy of a spontaneous redox reaction is captured using a galvanic cell. The following parts are necessary to make a galvanic cell:

- Two half cells
- Two electrodes
- One electrically conductive wire
- One salt bridge
- One device, usually an ammeter or a voltmeter
A galvanic cell is constructed as shown in the image to the right. The two half-reactions are separated into two half cells. All of the reactants in the oxidation half-reaction are placed in one half cell (the anode), and all the reactants of the reduction half-reaction are placed in the other half cell (the cathode). If the half-reaction contains a metal, the metal serves as the electrode for that half cell. Otherwise, an inert electrode made of platinum, silver, or gold is used. The electrodes are connected with a wire which allows the flow of electrons. The electrons always flow from the anode to the cathode. The half cells are connected by a salt bridge which allows the ions in the solution to move from one half cell to the other, so that the reaction can continue. Since the overall reaction is spontaneous, the flow of electrons will move spontaneously through the outer circuitry from which the energy can be extirpated. The energy harnessed is useful because it can be used to do work. For example, if an electrical component such as a light bulb is attached to the wire, it will receive power from the flowing electrons.
Consistent results from a galvanic cell are dependent on three variables: pressure, temperature, and concentration. Thus, chemists defined a standard state for galvanic cells. The standard state for the galvanic cell is a pressure of 1.00 atmospheric pressure (atm) for all gases, a temperature of 298 kelvin (K) and concentrations of 1.00 molarity (M) for all soluble compounds, liquids, and solids.
Voltage
Voltage is a measure of spontaneity of redox reactions, and it can be measured by a voltmeter. If the voltage of a reaction is positive, the reaction occurs spontaneously, but when negative, it does not occur spontaneously.
To compute the voltage of a redox equation, split the equation into its oxidation component and reduction component. Then, look up the voltages of each component on a standard electrode potential table. This table will list the voltage for the reduction equation. The oxidation reaction's voltage is negative of the corresponding reduction equation's voltage. To find the equation's voltage, add the standard voltages for each half reaction.
Aqueous Solutions
Solubility
Types of Solutions
A solution is a homogenous mixture, composed of solvent(s) and solute(s). A solvent is any substance which allows other substances to dissolve in it. Therefore, it is usually present in the greater amount. Solutes are substances present in a solution. Note that when a solute dissolves in a solvent, no chemical bonds form between the solvent and solute.
Solutions have variable composition, unlike pure compounds whose composition is fixed. For example, a 500 mL solution of lemonade can consist of 70% water, 20% lemon juice, and 10% sugar. There can also be a 500 mL solution of lemonade consisting of 60% water, 25% lemon juice, and 15% sugar.
The most common type of solution is an aqueous solution, which is a solution where water is the solvent. Aqueous solutions are quite important. For example, acids and bases exist typically as aqueous solutions. |
When two liquids can be readily combined in any proportions, they are said to be miscible. An example would be alcohol and water. Either of the two can totally dissolve each other in any proportion. Two liquids are defined as immiscible if they will not form a solution, such as oil and water. Solid solutes in a metallic solvent are known as alloys. Gold is an example of an alloy. It is too soft in its pure form, so other metals are dissolved in it. Jewelers may use 14-karat gold, which contains two-thirds gold and one-third other metals.
Variables Affecting Solubility
| Factor | Concept | Example |
|---|---|---|
| Surface area | More surface area gives more opportunity for solute-solvent contact | Powdered sugar will dissolve in water faster than rock candy. |
| Temperature | Solids are more soluble in hot solvents, gases are more soluble in cold solvents | Sugar dissolves more readily in hot water, but CO2 dissolves better in cold soda than warm soda. |
| Polarity | Non-polar compounds dissolve in non-polar solvents, and polar compounds dissolve in polar solvents. If one liquid is polar, and the other isn't, they are immiscible. | Alcohol and water are both polar, and they are miscible. Oil is non-polar and is immiscible in water. |
| Pressure | Gases dissolve better under higher pressure, due to greater forces pushing the gas molecules into the solvent. | Leaving the cap off a soda bottle will let the carbonation out. |
| Agitation | If a solution is agitated by stirring or shaking, there is an increase in kinetic motion and contact of particles. Therefore, the rate of solubility increases. | Everyone knows to stir their coffee after adding sugar. |
In general, the rate of solubility is dependent on the intermolecular forces between substances. The maxim "like dissolves like" will help you remember that substances must both be polar or non-polar to dissolve. |
Dissolving at the Molecular Level

- The forces between the particles in the solid must be broken. This is an endothermic process called dissociation.
- Some of the intermolecular forces between the particles in the liquid must also be broken. This is endothermic.
- The particles of the solid and the particles in a liquid become attracted. This is an exothermic process called solvation.
Example: Dissolving NaCl
When sodium chloride is added to water, it will dissolve. Water molecules are polar, and sodium chloride is ionic (which is very polar). The positive ends of the water molecules (the hydrogens) will be attracted to the negative chloride ions, and the negative ends of the water molecules (the oxygens) will be attracted to the positive sodium ions. The attractions are strong enough to separate sodium from chloride, so the solute dissociates, or breaks apart. The solute is then spread throughout the solvent. The polar water molecules prevent the ions from reattaching to each other, so the salt stays in solution.
Important Concepts
Saturation
- When a solution can hold no more solute, it is said to be saturated. This occurs when there is an equilibrium between the dissolved and undissolved solute.
- If more solute can be added, the solution is unsaturated.
- If a solution has more solute than is normally possible, due to the lowering or heightening of temperature, it is said to be supersaturated. If disturbed, the solution will rapidly form solid crystals.
- Solubility is the measure of how many grams of solute can dissolve in 100 grams of solvent (or in the case of water, solute per 100 milliliters.)
Hydration
Sometimes, compounds form crystals with a specific amount of water in them. For example, copper(II) sulfate is written as CuSO4 • 5H2O. For every mole of copper(II) sulfate, there are five moles of water attached. The atoms are arranged in a crystal lattice. Even if dried, the compound will still be hydrated. It will not feel moist, but there are water molecules within the crystal structure of the solid.
Intense heat will release the water from the compound. Its color may change, indicating a chemical change. When the anhydrous compound is dissolved in water, it will become hydrated again.
Heats of Solution
Some chemicals change temperature when dissolved. This is due to a release or absorption of heat. The specific change is known as the heat of solution, measured in kJ/mol.
Electrolytes
Some substances break up into ions and conduct electricity when dissolved. These are called electrolytes. All ionic compounds are electrolytes. Nonelectrolytes, on the other hand, do not conduct electricity when dissolved. Electrolytes are the reason that tap water conducts electricity. Tap water contains salts and other ions. If you have purified water, you will find that it does not conduct electricity at all. Upon dissolving some salt, it conducts electricity very well. The presence of ions allows electrons to move through the solution, and electricity will be conducted.
Solubility Practice Questions
1. In a mixture of 50 mL of benzene and 48 mL of octane,
- a) which substance is the solute?
- b) would these two substances form a solution?
2. Solutions are formed as physical reactions. Using this principle, name two ways in which solutes can be separated from solvents.
3. Three different clear, colourless liquids were gently heated in an evaporating dish. Liquid A left a white residue, liquid B left no residue, and liquid C left water. Identify each liquid solution as a pure substance or a solution.
4. Compare three bottles of soda. Bottle A was stored at room temperature (25°C), bottle B was stored at 10°C, and bottle C was stored at 30°C.
- a) If you wanted a fizzy drink, which bottle would you choose?
- b) If you wanted to change the gas pressure of bottle C to that of bottle B, what could you do?
Answers to Solubility Practice Questions
Properties of Solutions
Concentration
The concentration of a solution is the measure of how much solute and solvent there is. A solution is concentrated if it contains a large amount of solute, or dilute if contains a small amount.
Molarity
Molarity is the number of moles of solute per liter of solution. It is abbreviated with the symbol M, and is sometimes used as a unit of measurement, e.g. a 0.3 molar solution of HCl. In that example, there would be 0.3 moles of HCl for every liter of water (or whatever the solvent was).
Molarity is by far the most commonly used measurement of concentration. |
Molality
Molality is the number of moles of solute per kilogram of solvent. It is abbreviated with the symbol m (lowercase), and is sometimes used as a unit of measurement, e.g. a 0.3 molal solution of HBr. In that example, there would be 0.3 moles of HBr for every kilogram of water (or whatever the solvent was).
| One kilogram of water is one liter of water (near room temperature), but the molality is not the same as the molarity. The molarity is the ratio of solute to solution, whereas the molality is the ratio of solute to solvent. |
Mole Fraction
The mole fraction is simply the moles of solute per moles of solution. As an example, you dissolve one mole of NaCl into three moles of water. Remember that the NaCl will dissociate into its ions, so there are now five moles of particles: one mole Na+, one mole Cl-, and three moles water. The mole fraction of sodium is 0.2, the mole fraction of chloride is 0.2, and the mole fraction of water is 0.6.
The mole fraction is symbolized with the Greek letter (chi), which is often written simply as an X.
The sum of all mole fractions for a solution must equal 1. |
Dilution
Dilution is adding solvent to a solution to obtain a less concentrated solution. Perhaps you have used dilution when running a lemonade stand. To cut costs, you could take a half-full jug of rich, concentrated lemonade and fill it up with water. The resulting solution would have the same total amount of sugar and lemon juice, but double the total volume. Its flavor would be weaker due to the added water.
The key concept is that the amount of solute is constant before and after the dilution process. The concentration is decreased (and volume increased) only by adding solvent.
| Thus, the number of moles of solute before and after dilution are equal. | |
| By definition of molarity, you can find the moles of solvent. | |
| Substituting the second equation into the first gives the dilution equation. |
To determine the amount of solvent (usually water) that must be added, you must know the initial volume and concentration, and the desired concentration. Solving for in the above equation will give you the total volume of the diluted solution. Subtracting the initial volume from the total volume will determine the amount of pure solvent that must be added.
Ionic Solutes
When ionic compounds dissolve in water, they separate into ions. This process is called dissociation. Note that because of dissociation, there are more moles of particles in the solution containing ions than there would be with the solute and solvent separated.
If you have two glasses of water, and you dissolve salt into one and sugar into the other, there will be a big difference in concentration. The salt will dissociate into its ions, but sugar (a molecule) will not dissociate. If the salt were NaCl, the concentration would be double that of the sugar. If the salt were MgCl2, the concentration would be triple (there are three ions).
Solubility Rules
Not all ionic compounds are soluble. Some ionic compounds have so much attractive force between their anions and cations that they will not dissociate. These substances are insoluble and will not dissolve. Instead, they clump together as a solid in the bottom of solution. Many ionic compounds, however, will dissociate in water and dissolve. In these cases, the attractive force between ion and water is greater than that between cation and anion. There are several rules to help you determine which compounds will dissolve and which will not.
- Solubility Rules
- All compounds with Group 1 ions or ammonium ions are soluble.
- Nitrates, acetates, and chlorates are soluble.
- Compounds containing a halogen are soluble, except those with fluorine, silver, or mercury. If they have lead, they are soluble only in hot water.
- Sulfates are soluble, except when combined with silver, lead, calcium, barium, or strontium.
- Carbonates, sulfides, oxides, silicates, and phosphates are insoluble, except for rule #1.
- Hydroxides are insoluble except when combined with calcium, barium, strontium, or rule #1.
Sometimes, when two different ionic compounds are dissolved, they react, forming a precipitate that is insoluble. Predicting these reactions requires knowledge of the activity series and solubility rules. These reactions can be written with all ions, or without the spectator ions (the ion that don't react, present on both sides of the reaction), a format known as the net ionic equation.
For example, silver nitrate is soluble, but silver chloride is not soluble (see the above rules). Mixing silver nitrate into sodium chloride would cause a cloudy white precipitate to form. This happens because of a double replacement reaction.
Electrolytes
When solutes dissociate (or if a molecule ionizes), the solution can conduct electricity. Compounds that readily form ions, thus being good conductors, are known as strong electrolytes. If only a small amount of ions are formed, electricity is poorly conducted, meaning the compound is a weak electrolyte.
A strong electrolyte will dissolve completely. All ions dissociate. A weak electrolyte, on the other hand, will partially dissociate, but some ions will remain bonded together. |
Colligative Properties
Some properties are the same for all solute particles regardless of what kind. These are known as the colligative properties. These properties apply to ideal solutions, so in reality, the properties may not be exactly as calculated. In an ideal solution, there are no forces acting between the solute particles, which is generally not the case.
Vapor Pressure
All liquids have a tendency for their surface molecules to escape and evaporate, even if the liquid is not at its boiling point. This is because the average energy of the molecules is too small for evaporation, but some molecules could gain above average energy and escape. Vapor pressure is the measure of the pressure of the evaporated vapor, and it depends on the temperature of the solution and the quantities of solute. More solute will decrease vapor pressure.
| The vapor pressure is given by Rauolt's Law, where is the mole fraction of the solvent. Notice that the vapor pressure equals that of the pure solvent when there is no solute (). If , there would be no vapor pressure at all. This could only happen if there were no solvent, only solute. A solid solute has no vapor pressure. | |
| If two volatile substances (both have vapor pressures) are in solution, Rauolt's Law is still used. In this case, Rauolt's Law is essentially a linear combination of the vapor pressures of the substances. Two liquids in solution both have vapor pressures, so this equation must be used. |
The second equation shows the relationship between the solvents. If two liquids were mixed exactly half-and-half, the vapor pressure of the resulting solution would be exactly halfway between the vapor pressures of the two solvents.
Another relation is Henry's Law, which shows the relationship between gas and pressure. It is given by Cg = k Pg , where C is concentration and P is pressure. As the pressure goes up, the concentration of gas in solution must also increase. This is why soda cans release gas when they are opened - The decrease in pressure results in a decrease in concentration of CO2 in the soda.
- Exercise for the reader
At 50 °C the vapor pressure of water is 11 kPa and the vapor pressure of ethanol is 30 kPa. Determine the resulting vapor pressure if a solution contains 75% water and 25% ethanol (by moles, not mass).
Boiling Point Elevation
A liquid reaches its boiling point when its vapor pressure is equal to the atmosphere around it. Because the presence of solute lowers the vapor pressure, the boiling point is raised. The boiling point increase is given by:
The reduced vapor pressure increases the boiling point of the liquid only if the solute itself is non-volatile, meaning it doesn't have a tendency to evaporate. For every mole of non-volatile solute per kilogram of solvent, the boiling point increases by a constant amount, known as the molal boiling-point constant (). Because this is a colligative property, is not affected by the kind of solute.
Freezing Point Depression
A liquid reaches its freezing temperature when its vapor pressure is equal to that of its solid form. Because the presence of the solute lowers the vapor pressure, the freezing point is lowered. The freezing point depression is given by:
Again, this equation works only for non-volatile solutes. The temperature of the freezing point decreases by a constant amount for every one mole of solute added per kilogram solvent. This constant () is known as the molar freezing-point constant.
Osmosis

If you studied biology, you would know that osmosis is the movement of water through a membrane. If two solutions of different molarity are placed on opposite sides of a semipermeable membrane, then water will travel through the membrane to the side with higher molarity. This happens because the water molecules are "attached" to the solvent molecules, so they cannot travel through the membrane. As a result, the water on the side with lower molarity can more easily travel through the membrane than the water on the other side.
The pressure of this osmosis is given in the equation
Where pi is the pressure, M is molarity, R is the gas constant, and T is temperature in Kelvin.
Electrolytes and Colligative Properties
When one mole of table salt is added to water, the colligative effects are double those that would have occurred if sugar were added instead. This is because the salt dissociates, forming twice as many particles as sugar would. This dissociation, called the Van't Hoff Factor describes how many particles that are dissociated into the solution and must be multiplied into the Boiling Point Elevation or Vapor Pressure Lowering equations.
| Sugar is a covalent molecule. No dissociation occurs when dissolved. | |
| Table salt is an ionic compound and a strong electrolyte. Total dissociation occurs when dissolved, doubling the effects of colligative properties. | |
| Magnesium bromide is also ionic. The colligative effects will be tripled. |
Though extremely useful for calculating the general Van't Hoff Factor, this system of calculation is slightly inaccurate when considering ions. This is because when ions are in solution, they may interact and clump together, lessening the effect of the Van't Hoff factor. In addition, more strongly charged ions may have a smaller effect. For example, CaO would be less effective as an electrolyte than NaCl.
Acids and Bases
Acid-Base Reaction Theories
Acids and bases are everywhere. Some foods contain acid, like the citric acid in lemons and the lactic acid in dairy. Cleaning products like bleach and ammonia are bases. Chemicals that are acidic or basic are an important part of chemistry.
| Helpful Hint! | |
|---|---|
| You may need to refresh your memory on naming acids. |
Several different theories explain what composes an acid and a base. The first scientific definition of an acid was proposed by the French chemist Antoine Lavoisier in the eighteenth century. He proposed that acids contained oxygen, although he did not know the dual composition of acids such as hydrochloric acid (HCl). Over the years, much more accurate definitions of acids and bases have been created.
Arrhenius Theory
The Swedish chemist Svante Arrhenius published his theory of acids and bases in 1887. It can be simply explained by these two points:
- Arrhenius Acids and Bases
- An acid is a substance which dissociates in solvent to produce one or more hydrogen ions (H+).
- A base is a substance which dissociates in solvent to produce one or more hydroxide ions (OH-).
Based on this definition, you can see that Arrhenius acids must be soluble in water. Arrhenius acid-base reactions can be summarized with three generic equations:
| An acid will dissociate in water producing hydrogen ions. | |
| A base (usually containing a metal) will dissociate in water to produce hydroxide ions. | |
| Acids and bases will neutralize each other when mixed. They produce water and an ionic salt, neither of which are acidic or basic. |
The Arrhenius theory is simple and useful. It explains many properties and reactions of acids and bases. For instance, mixing hydrochloric acid (HCl) with sodium hydroxide (NaOH) results in a neutral solution containing table salt (NaCl).
However, the Arrhenius theory is not without flaws. There are many well known bases, such as ammonia (NH3) that do not contain the hydroxide ion. Furthermore, acid-base reactions are observed in solutions that do not contain water. To resolve these problems, there is a more advanced acid-base theory.
Brønsted-Lowry Theory
The Brønsted-Lowry theory was proposed in 1923. It is more general than the Arrhenius theory—all Arrhenius acids/bases are also Brønsted-Lowry acids/bases (but not necessarily vice versa).
- Brønsted-Lowry Acids and Bases
- An acid is a substance from which a proton (H+ ion) can be removed. Essentially, an acid donates protons to bases.
- A base is a substance to which a proton (H+) can be added. Essentially, a base accepts protons from acids.
Acids that can donate only one proton are monoprotic, and acids that can donate more than one proton are polyprotic.
These reactions demonstrate the behavior of Brønsted-Lowry acids and bases:
| An acid (in this case, hydrochloric acid) will donate a proton to a base (in this case, water is the base). The acid loses its proton and the base gains it. | |
| Water is not necessary. In this case, hydrochloric acid is still the acid, but ammonia acts as the base. | |
| The same reaction is happening, but now in reverse. What was once an acid is now a base (HCl → Cl-) and what was once a base is now an acid (NH3 → NH4+). This concept is called conjugates, and it will be explained in more detail later. | |
|
Two examples of acids (HCl and H3O+) mixing with bases (NaOH and OH-) to form neutral substances (NaCl and H2O). |
| A base (sodium hydroxide) will accept a proton from an acid (ammonia). A neutral substance is produced (water), which is not necessarily a part of every reaction. Compare this reaction to the second one. Ammonia was a base, and now it is an acid. This concept, called amphoterism, is explained later. |
The Brønsted-Lowry theory is by far the most useful and commonly-used definition. For the remainder of General Chemistry, you can assume that any acids/bases use the Brønsted-Lowry definition, unless stated otherwise.

Lewis Theory
The Lewis definition is the most general theory, having no requirements for solubility or protons.
- Lewis Acids and Bases
- An acid is a substance that accepts a lone pair of electrons.
- A base is a substance that donates a lone pair electrons.
Lewis acids and bases react to create an adduct, a compound in which the acid and base have bonded by sharing the electron pair. Lewis acid/base reactions are different from redox reactions because there is no change in oxidation state.

Amphoterism and Water
Substances capable of acting as either an acid or a base are amphoteric. Water is the most important amphoteric substance. It can ionize into hydroxide (OH-, a base) or hydronium (H3O+, an acid). By doing so, water is
- Increasing the H+ or OH- concentration (Arrhenius),
- Donating or accepting a proton (Brønsted-Lowry), and
- Accepting or donating an electron pair (Lewis).
A bare proton (H+ ion) cannot exist in water. It will form a hydrogen bond to the nearest water molecule, creating the hydronium ion (H3O+). Although many equations and definitions may refer to the "concentration of H+ ions", that is a misleading abbreviation. Technically, there are no H+ ions, only hydronium (H3O+) ions. Fortunately, the number of hydronium ions formed is exactly equal to the number of hydrogen ions, so the two can be used interchangeably. |

Water will dissociate very slightly (which further explains its amphoteric properties).
| The presence of hydrogen ions indicates an acid, whereas the presence of hydroxide ions indicates a base. Being neutral, water dissociates into both equally. | |
| This equation is more accurate—hydrogen ions do not exist in water because they bond to form hydronium. |
Ammonia
Another common example of an amphoteric substance is ammonia. Ammonia is normally a base, but in some reactions it can act like an acid.
| Ammonia acts as a base. It accepts a proton to form ammonium. | |
| Ammonia also acts as an acid. Here, it donates a proton to form amide. |
Ammonia's amphoteric properties are not often seen because ammonia typically acts like a base. Water, on the other hand, is completely neutral, so its acid and base behaviors are both observed commonly.
Conjugate Acids and Bases
In all the theories, the products of an acid-base reaction are related to the initial reactants of the reaction. For example, in the Brønsted-Lowry theory, this relationship is the difference of a proton between a reactant and product. Two substances which exhibit this relationship form a conjugate acid-base pair.
- Brønsted-Lowry Conjugate Pairs
- An acid that has donated its proton becomes a conjugate base.
- A base that has accepted a proton becomes a conjugate acid.
| Hydroiodic acid reacts with water (which serves as a base). The conjugate base is the iodide ion and the conjugate acid is the hydronium ion. The acids are written in red, and the bases are written in blue. One conjugate pair is written bold and the other conjugate pair is in cursive. | |
| Ammonia (basic) reacts with water (the acid). The conjugate acid is ammonium and the conjugate base is hydroxide. Again, acids are written in red, and the bases are written in blue. The conjugate pairs are distinguished with matching fonts. |
Strong and Weak Acids/Bases
A strong acid is an acid which dissociates completely in water. That is, all the acid molecules break up into ions and solvate (attach) to water molecules. Therefore, the concentration of hydronium ions in a strong acid solution is equal to the concentration of the acid.
The majority of acids exist as weak acids, an acid which dissociates only partially. On average, only about 1% of a weak acid solution dissociates in water in a 0.1 mol/L solution. Therefore, the concentration of hydronium ions in a weak acid solution is always less than the concentration of the dissolved acid.
Strong bases and weak bases do not require additional explanation; the concept is the same.
The conjugate of a strong acid/base is very weak. The conjugate of a weak acid/base is not necessarily strong. |
This explains why, in all of the above example reactions, the reverse chemical reaction does not occur. The stronger acid/base will prevail, and the weaker one will not contribute to the overall acidity/basicity. For example, hydrochloric acid is strong, and upon dissociation chloride ions are formed. Chloride ions are a weak base, but the solution is not basic because the acidity of HCl is overwhelmingly stronger than basicity of Cl-.
| Helpful Hint! | |
|---|---|
| Although the other halogens make strong acids, hydrofluoric acid (HF) is a weak acid. Despite being weak, it is incredibly corrosive—hydrofluoric acid dissolves glass and metal! |
Most acids and bases are weak. You should be familiar with the most common strong acids and assume that any other acids are weak.
| Formula | Strong Acid |
|---|---|
| HClO4 | Perchloric acid |
| HNO3 | Nitric acid |
| H2SO4 | Sulfuric acid |
| HCl, HBr, HI | Hydrohalic acids |
Within a series of oxyacids, the ions with the greatest number of oxygen molecules are the strongest. For example, nitric acid (HNO3) is strong, but nitrous acid (HNO2) is weak. Perchloric acid (HClO4) is stronger than chloric acid (HClO3), which is stronger than the weak chlorous acid (HClO2). Hypochlorous acid (HClO) is the weakest of the four.
Common strong bases are the hydroxides of Group 1 and most Group 2 metals. For example, potassium hydroxide and calcium hydroxide are some of the strongest bases. You can assume that any other bases (including ammonia and ammonium hydroxide) are weak.
| Formula | Strong Base |
|---|---|
| LiOH | Lithium hydroxide |
| NaOH | Sodium hydroxide |
| KOH | Potassium hydroxide |
| RbOH | Rubidium hydroxide |
| CsOH | Cesium hydroxide |
| Ca(OH)2 | Calcium hydroxide |
| Sr(OH)2 | Strontium hydroxide |
| Ba(OH)2 | Barium hydroxide |
| Acids and bases that are strong are not necessarily concentrated, and weak acids/bases are not necessarily dilute. Concentration has nothing to do with the ability of a substance to dissociate. Furthermore, polyprotic acids are not necessarily stronger than monoprotic acids. |
Properties of Acids and Bases
Now that you are aware of the acid-base theories, you can learn about the physical and chemical properties of acids and bases. Acids and bases have very different properties, allowing them to be distinguished by observation.
Indicators

Made with special chemical compounds that react slightly with an acid or base, indicators will change color in the presence of an acid or base. A common indicator is litmus paper. Litmus paper turns red in acidic conditions and blue in basic conditions. Phenolphthalein purple is colorless in acidic and neutral solutions, but it turns purple once the solution becomes basic. It is useful when attempting to neutralize an acidic solution; once the indicator turns purple, enough base has been added.
Conductivity
A less informative method is to test for conductivity. Acids and bases in aqueous solutions will conduct electricity because they contain dissolved ions. Therefore, acids and bases are electrolytes. Strong acids and bases will be strong electrolytes. Weak acids and bases will be weak electrolytes. This affects the amount of conductivity.
However, acids will react with metal, so testing conductivity may not be plausible.
Physical properties
The following is for informative purposes only. Do not sniff, touch, or taste any acids or bases as they may result in injury or death. |
The physical properties of acids and bases are opposites.
| Acids | Bases | |
|---|---|---|
| Taste | sour | bitter |
| Feel | stinging | slippery |
| Odor | sharp | odorless |
These properties are very general; they may not be true for every single acid or base.
Another warning: if an acid or base is spilled, it must be cleaned up immediately and properly (according to the procedures of the lab you are working in). If, for example, sodium hydroxide is spilled, the water will begin to evaporate. Sodium hydroxide does not evaporate, so the concentration of the base steadily increases until it becomes damaging to its surrounding surfaces.
Chemical Reactions
Neutralization
Acids will react with bases to form a salt and water. This is a neutralization reaction. The products of a neutralization reaction are much less acidic or basic than the reactants were. For example, sodium hydroxide (a base) is added to hydrochloric acid.
This is a double replacement reaction.
Acids
| Acids react with metal to produce a metal salt and hydrogen gas bubbles. | |
| Acids react with metal carbonates to produce water, CO2 gas bubbles, and a salt. | |
| Acids react with metal oxides to produce water and a salt. |
Bases
Bases are typically less reactive and violent than acids. They do still undergo many chemical reactions, especially with organic compounds. A common reaction is saponification: the reaction of a base with fat or oil to create soap.

Practice Questions
1. Name the following compounds that will form, and identify as an acid or base:
- a) Br + H
- b) 2H + SO3
- c) K + H
- d) 2H + SO6
- e) 3H + P2
- f) H + BrO2
- g) Na + Cl
2. What are the conjugate acids and bases of the following:
- a) water
- b) ammonia
- c) bisulfate ion
- d) zinc hydroxide
- e) hydrobromic acid
- f) nitrite ion
- g) dihydrogen phosphate ion
3. In a conductivity test, 5 different solutions were set up with light bulbs. The following observations were recorded:
- Solution A glowed brightly.
- Solution B glowed dimly.
- Solution C glowed dimly.
- Solution D did not glow.
- Solution E glowed brightly.
- a) Which solution(s) could contain strong bases?
- b) Which solution(s) could contain weak acids?
- c) Which solution(s) could contain ions?
- d) Which solution(s) could contain pure water?
- e) Based solely on these observations, would it be possible to distinguish between acidic and basic solutions?
4. Identity the conjugate base and conjugate acid in these following equations:
- a) HCl + H2O → H3O+ + Cl-
- b) HClO + H2O → ClO- + H3O+
- c) CH3CH2NH2 + H2O → CH3CH2NH3+ + OH-
5. Identify these bases as Arrhenius, Brønsted-Lowry, or both.
- a) strontium hydroxide
- b) butyllithium (C4H9Li)
- c) ammonia
- d) potassium hydroxide
- e) potassium iodide
6. Based on the Brønsted-Lowry Theory of Acids and Bases, would you expect pure water to have no dissolved ions whatsoever? Explain, using a balanced chemical equation.
Answers:
1.
2.
3.
4.
5.
6.
Notes
- ^ Brown, Theodore E.; Lemay, H. Eugene; Bursten, Bruce E.; Murphy, Catherine; Woodward, Patrick (2009), Chemistry: The Central Science (11th ed.), New York: Prentice-Hall, ISBN 0136006175.
Answers to Properties of Acids and Bases Practice Questions
Titration and pH
Ionization of Water
Water is a very weak electrolyte. It will dissociate into hydroxide and hydronium ions, although only in a very small amount. Because pure water is completely neutral, it always dissociates in equal amounts of both hydroxide and hydronium. Once acidic or basic substances have been added to pure water, the concentration of the ions will change. Regardless of which acid-base theory is used, acids and bases all have one important thing in common:
- All acids increase the H+ concentration of water.
- All bases increase the OH- concentration of water.
Furthermore, the concentration of hydrogen ions multiplied by the concentration of hydroxide ions is a constant. This constant is known as the ionization constant of water, or Kw. At room temperature it equals 10-14 mol2/L2. Thus:
In a neutral solution, the concentrations of H+ and OH- are both equal to 10-7. Using the above equation, the concentration of one ion can be determined if the concentration of the other ion is known. This equation further demonstrates the relationship between acids and bases: as the acidity (H+) increases, the basicity (OH-) must decrease.
The pH Scale
To measure the acidity or basicity of a substance, the pH scale is employed.
- The pH Scale
- A completely neutral substance has a pH of 7.
- Acids have a pH below 7
- Bases have a pH above 7.
pH usually ranges between 0 and 14, but it can be any value. Battery acid, for example, has a negative pH because it is so acidic.

Definition of pH
The pH scale is mathematically defined as:
Substances that release protons or increase the concentration of hydrogen ions (or hydronium ions) will lower the pH value.
pOH
There is also a less common scale, the pOH scale. It is defined as:
Substances that absorb protons or increase the concentration of hydroxide ions will lower the pOH value.
The sum of pH and pOH is always 14 at room temperature:
Calculating pH
A strong acid or strong base will completely dissociate in water, so the concentration of the acid/base is equal to the concentration of H+ or OH-. If you know the concentration of the acid or base, then you can simply plug that number into the pH or pOH formula. The sum of pH and pOH will always equal 14 at room temperature, so you can interconvert these two values.
If you know the H+ concentration and need to know the OH- concentration (or vice versa), use the definition of Kw above. The product of the two ion concentrations will always equal 10-14 at room temperature.
Titration
Titration is the controlled mixing of a solution with known concentration (the standard solution or titrant) to another solution (called the analyte) to determine its concentration. One solution is acidic and the other is basic. An indicator is added to the mixture. An indicator must be selected so that it changes color when equal amounts of acid and base have been added. This is known as the equivalence point. This does not necessarily mean that the pH is 7.0.
Once the equivalence point has been reached, the unknown concentration can be determined mathematically.
Practice Questions
1) 5.00g of NaOH are dissolved to make 1.00L of solution.
- a What is the concentration of H+?
- b What is the pH?
Buffer Systems
Introduction
Buffer systems are systems in which there is a significant (and nearly equivalent) amount of a weak acid and its conjugate base—or a weak base and its conjugate acid—present in solution. This coupling provides a resistance to change in the solution's pH. When strong acid is added, it is neutralized by the conjugate base. When strong base is added, it is neutralized by the weak acid. However, too much acid or base will exceed the buffer's capacity, resulting in significant pH changes.
| Consider an arbitrary weak acid, HA, and its conjugate base, A-, in equilibrium. | |
| The addition of a strong acid will cause only a slight change in pH due to neutralization. | |
| Likewise, the addition of a strong base will cause only a slight change in pH. |
Buffers are useful when a solution must maintain a specific pH. For example, blood is a buffer system because the life processes in a human only function within a specific pH range of 7.35 to 7.45. When, for example, lactic acid is released by the muscles during exercise, buffers within the blood neutralize it to maintain a healthy pH.
Making a Buffer
Once again, let's consider an arbitrary weak acid, HA, which is present in a solution. If we introduce a salt of the acid's conjugate base, say NaA (which will provide the A- ion), we now have a buffer solution. Ideally, the buffer would contain equal amounts of the weak acid and conjugate base.
Instead of adding NaA, what if a strong base were added, such as NaOH? In that case, the hydroxide ions would neutralize the weak acid and create water and A- ions. If the solution contained only A- ions, then a strong acid like HCl were added, they would neutralize and create HA.
As you can see, there are three ways to create a buffer:
|
|
All six of the combinations will create equal amounts of a weak acid and its conjugate base, or a weak base and its conjugate acid.
Buffers and pH
To determine the pH of a buffer system, you must know the acid's dissociation constant. This value, (or for a base) determines the strength of an acid (or base). It is explored more thoroughly in the Equilibrium unit, but for now it suffices to say that this value is simply a measure of strength for acids and bases. The dissociation constants for acids and bases are determined experimentally.
The pKa of an acid is the negative logarithm of its acid dissociation constant. This is analogous to pH (the negative logarithm of the H+ concentration). |
The Henderson-Hasselbalch equation allows the calculation of a buffer's pH. It is:
For a buffer created from a base, the equation is:
Using these equations requires determining the ratio of base to acid in the solution.
Reactions of Acids and Bases
Overview
To summarize the properties and behaviors of acids and bases, this chapter lists and explains the various chemical reactions that they undergo. You may wish to review chemical equations and types of reactions before attempting this chapter.
The following reactions are net ionic equations. In other words, spectator ions are not written. If an ion does not partake in the reaction, it is simply excluded. The spectator ions can be found because they occur on both the reactant and the product side of the equation. Cross them out and rewrite the equation without them. Of course, the coefficients must be equal.
Canceling out the spectator ions explains the net of net ionic equations. The ionic part means that dissolved compounds are written as ions instead of compounds. Acids, bases, and salts are all ionic, so they are written as separate ions if they have dissociated.
- Net Ionic Equations
- Soluble salts are written as ions.
- e.g.: Na+ + Cl-
- Solids, liquids, and gases are written as compounds.
- e.g.: NaCl(s), H2O(l), HCl(g)
- Strong acids and strong bases are written as ions (because they dissociate almost completely).
- e.g.: H+ + NO3-
- Weak acids and weak bases are written as compounds (because they barely dissociate).
- e.g.: HNO2
As an example, sodium bicarbonate (NaHCO3) would be written as Na+ and HCO3- because the salt will dissociate, but the bicarbonate will not dissociate (it's a weak acid).
Neutralization
When an acid and a base react, they form a neutral substance, often water and a salt.
First, let's examine the neutralization of a strong acid with a strong base.
| Solid potassium hydroxide is added to an aqueous solution of hydrochloric acid. Notice how the solid is written as a compound, but the acid is written as ions because it dissociates. | |
| The hydrogen ions will react with hydroxide ions to form water. | |
| Ignoring spectator ions, this is the net ionic equation. |
Whenever a strong acid neutralizes a strong base, the net ionic equation is always H+ + OH- → H2O. |
Now, let's see some examples involving weak acids and weak bases.
| Excess hydrochloric acid is added to a solution of sodium phosphate. Phosphoric acid is weak, so the phosphate ions will react with hydrogen ions. The result is a solution with some, but much less, hydrogen ions, so it is much closer to neutral than either of the original reactants. | |
| Equimolar amounts of sodium phosphate and hydrochloric acid are mixed. Notice the difference between this reaction and the previous one. | |
| A strong base is added to a solution of calcium bicarbonate. (Bicarbonate is a weak acid.) | |
| A strong acid is added to a solution of calcium bicarbonate. Gas bubbles appear. |
Many reactions result in the formation of gas bubbles or a solid precipitate that will make the solution cloudy. The last equation brings up an interesting application. Many rocks and minerals contain calcium carbonate or calcium bicarbonate. To identify these rocks, geologists can perform the "acid test". A drop of acid is applied, and the presence of gas bubbles indicates carbonate.
Many ions and compounds are amphoteric. They can react with (or behave as) acids and bases. Bicarbonate is a good example, as you can see by comparing the last two equations above. |
Here are more examples of neutralization reactions.
| Solid ammonium chloride crystals are dissolved into a solution of sodium hydroxide. The smell of ammonia is detected. | |
| Ammonia gas is bubbled through a solution of hydrochloric acid. This reaction is essentially the opposite of the previous. In that reaction, ammonium ions react with base to form ammonia gas. In this reaction, ammonia gas reacts with acid to form ammonium ions. | |
| Ammonia (a weak base) reacts with acetic acid (also weak). The resulting solution is nearly neutral, but it will be slightly basic because ammonia is stronger than acetic acid. | |
| Hydrogen sulfide gas is bubbled into a strong base. | |
| A strong acid is added to the above result, and hydrogen sulfide gas is released. |
Anhydrides
An anhydride is a substance that does not contain water. More specifically, it is a substance that reacts with water to form an acid or base. Anhydrides are usually in the form of a gas that dissolves into water and reacts to form an acid or base. They can also be solids that will react with water.
| Gaseous dinitrogen pentoxide is bubbled through water to form nitric acid. | |
| Dinitrogen trioxide is mixed with water to form nitrous acid. |
The main difference between those two equations is the fact that nitrous acid is weak and thus does not dissociate, whereas nitric acid is strong and dissociates into ions.
Here are a few more examples of anhydride reactions.
| Solid potassium oxide is added to water to form a strong base. | |
| Phosphorus(V) oxide powder is mixed into water to form a weak acid. |
It is important to remember which acids are strong and which are weak. Review this if necessary.
Anhydrides can also react with acidic or basic solutions. In that case, you may find it helpful to first determine the anhydride's reaction with water, then determine that reaction with the acid or base. |
For example, sulfur dioxide gas (acidic anhydride) is bubbled through a solution of calcium hydroxide (basic).
| First, determine the reaction of the anhydride with water. | |
| Then, determine the reaction of the acid and base. This is a double replacement reaction. | |
| Add the two reactions together. | |
| Cancel out spectators. Also, calcium hydroxide should be ionized (but calcium sulfite is a solid precipitate). This is the final net ionic equation. |
Here are more examples.
| Calcium oxide crystals (basic anhydrides) are added to a strong acid. Notice that it does not matter what the acid is (nitric, sulfuric, etc.) because it is strong and this reaction only requires the hydrogen ions. In other words, the anions of the strong acid are spectators and are not written. | |
| Excess sulfur dioxide gas is bubbled into a dilute solution of strong base. The base is the limiting reactant. | |
| Sulfur dioxide gas is bubbled into an excess of basic solution. |
Remember that water is involved in these reactions, but it is not written if it occurs on both sides of the equation.
Anhydrides can undergo neutralization reactions, even without the presence of water. |
| Solid calcium oxide (basic anhydride) is exposed to dry ice gas (acidic anhydride). The resulting solid is a salt. | |
| Solid calcium oxide is exposed to a stream of sulfur trioxide gas. The resulting solid is a neutral salt. |
Hydrolysis
A salt of a weak acid and strong base dissociates and reacts in water to form OH-. A salt of a strong acid and weak base dissociates and reacts in water to form H+. This process is called hydrolysis.
In this first example, aluminum nitrate is dissolved in water.
| First, the salt dissociates in the water. It isn't necessary to write H2O in this reaction. | |
| Now, at least one of the ions will react with water. You know that nitric acid is strong, so the nitrate ion will not take an H+ ion from water. Instead, the aluminum ion will react with water, releasing a hydrogen ion. | |
| This is the net ionic equation. The resulting solution is acidic. |
The solution is acidic not because nitric acid is strong, but because aluminum is a weak base.
Here is an easier example.
| First, the salt dissociates. Again, the H2O need not be written. | |
| Sodium ions will not react with water. Even if they did, they would form NaOH, which is a strong base, so it would immediately dissociate. Instead, the NO2 reacts with water. Being the conjugate of a weak acid, the nitrite ions will accept a proton from water to form nitrous acid (weak) and hydroxide ions (basic). | |
| This is the net ionic equation for the hydrolysis of sodium nitrite. The resulting solution is basic. |
There is no hydrolysis reaction for neutral salts. Salts like NaCl and K2SO4 (and any other composed of the conjugates of both a strong acid and strong base) will not react with water. They create neutral solutions when dissolved. |
Lewis Acids/Bases
Lewis acids accept an electron pair. Lewis bases donate an electron pair. Together they react and bond to form an adduct.
Lewis acids/bases do not require the presence of water. However, H+ can be thought of as a Lewis acid because it accepts electron pairs. OH- can donate an electron pair, making it a Lewis base.
| Boron trifluoride (Lewis acid) is exposed to ammonia (a Lewis base, as shown by the electron pair over the N). The electron pair is shared between the nitrogen and boron, creating a bond. (The boron trifluoride is written backwards as F3B only to demonstrate the B-N bond. Its structure has not changed.) | |
| Diborane accepts the two electrons from H- and forms a Lewis adduct. |
Practice Problems
Write the net ionic equations for the following. Make note of any solid precipitates or gas bubbles that would form.
- Equimolar solutions of sodium biphosphate and potassium hydroxide are mixed.
- Equimolar solutions of sodium biphosphate and hydrochloric acid are mixed.
- Excess sulfur dioxide gas is bubbled into a dilute solution of sodium hydroxide. Acid is then added.
- Aluminum chloride is dissolved into water.
- Sodium fluoride is dissolved into water. Strong acid is then added.
- Solid calcium oxide is exposed to a stream of sulfur trioxide gas. If the resulting compound is dissolved, will the solution be acidic, basic, or neutral?
- Gaseous hydrogen chloride is bubbled into a solution of silver nitrate.
- Ammonium chloride crystals are dissolved in water. Sodium hydroxide is then added.
- Calcium hydroxide crystals are dissolved into a solution of sodium bicarbonate.
- Phosphine gas is sprayed onto pebbles of aluminum trichloride. (Hint: these are Lewis acids/bases.)
Phases of Matter
Solids
Characteristics of Solids
Shape and volume are both definite in solids. Although solids have a rigid shape, a large amount of force can cause deformation to the structure of a solid. There are three types of deformation:
- Brittle deformation causes bonds to break in an irregular way. Shredding paper and shattering glass are good examples.
- Elastic deformation is temporary. The molecules will return to their original positions as soon as the force is removed. Rubber bands and tires are elastic, as well as steel rods and wooden boards.
- Plastic deformation is permanent. Plastic deformation can be observed by bending a metal spoon.

Most materials are capable of all three types of deformation. Small amounts of stress cause elastic deformation, but large amounts will cause plastic deformation. In the event of repeated deformation or tremendous stress, brittle deformation occurs.
Solids are incompressible. Solids may break or deform under stress, but they tolerate little compression. For instance, a wooden plank will break if force is applied, but it will not compress like a sponge. The only reason sponges compress is because they contain air pockets and undergo elastic deformation. Otherwise, solids will not compress. At the molecular level, this happens because the intermolecular bonds do not change size without breaking.
Some solids, usually metals, have properties like ductility and malleability. A ductile material can be stretched into long, thin wires. A malleable substance can be hammered into very thin sheets. Gold and copper are some of the most malleable and ductile substances known. These properties occur as a result of the metallic bonding.
Solids at the Molecular Level
Solids occur when there is enough intermolecular bonding to hold the molecules of a substance into a relatively rigid structure. The molecules are close together, and their movement is restricted to vibration. Solids occur at the lowest temperatures and highest pressures. As the temperature of a solid increases, so does the kinetic energy of its molecules. At the melting point, the molecules have enough energy to overcome their bonds and melt into a liquid. Likewise, a liquid will freeze once its molecules are not moving fast enough to avoid strong intermolecular bonds.
Compounds that have ionic bonding or metallic bonding are most likely to be found in the solid phase due to their high melting points. Also, covalent network substances (like diamond or quartz) are solids because the atoms are secured with covalent bonds, requiring extreme amounts of energy to separate them.
Types of Solids
- Crystalline solids have a molecular structure with a specific geometric shape. The solid has a specific melting point at which all molecules begin to break free of their bonds. Substances like salt, diamond, and quartz are crystalline solids. These solids usually form by cooling a liquid slowly, so that the molecules have time to arrange themselves in a crystalline structure as their bonds form.
- Amorphous solids have a molecular structure with no specific shape. The solid melts over a range of temperatures because the amount of energy needed to break the bonds varies from molecule to molecule. Substances like coal and glass are amorphous. Amorphous solids usually form when a liquid is cooled quickly, so there is no time for the molecules to arrange themselves into a crystal.
Crystalline solids are typically harder and more rigid. Coal and diamond are both made from elemental carbon, but coal is amorphous and diamond is crystalline. Because of its crystal structure, diamond is one of the hardest substances known, whereas coal can be scratched away with a fingernail. The crystal structure also explains diamond's brilliant, transparent appearance. Coal is black and dull because the disorder of the atoms does not allow light to pass.
Ionic solids and metallic solids are always crystalline. Covalent network solids can be crystalline or amorphous. Van der Waals solids are always amorphous. |
Packing and Unit Cells

In crystalline solids, the atoms are arranged in a specific pattern. The smallest repeating part of this pattern is called the unit cell. The unit cell may have more atoms than the empirical formula of a substance because the geometric shape may require several atoms. In the case of sodium chloride, the empirical formula contains only two atoms, but the unit cell has 27 atoms.
The molecules of a solid are close packed. They arrange themselves in the densest shape possible. Usually, two different patterns occur.
- Face-centered cubic or FCC
- Hexagonal close-packed or HCP

FCC crystals have three alternating layers, described as ABCABCABC (every third layer is the same). The layers are arranged so that each unit cell is halfway between the two unit cells above or below it. HCP crystals have two alternating layers, described as ABABABAB (every other layer is the same).
-
FCC lattice
-
HCP lattice
Liquids
Liquids at a Molecular Level
Liquids have some intermolecular bonding, but it isn't as strong as bonding in a solid. As a result, the molecules are close together, but they are not tightly packed. Instead, they are free to slide past each other. Liquids occur at temperatures above the melting point of a substance, but below its boiling point. At the melting point, the molecules are moving slow enough to form rigid bonds and become a solid. At the boiling point, the molecules are moving so fast that they cannot form any bonds and become a gas.
Characteristics of Liquids

Liquids have definite volume, but indefinite shape. They are free to form droplets and puddles when they are not inside a container. When a liquid is inside a container, it will take its shape. Unlike gases, a liquid will not change its volume to spread out and completely fill a container. There is enough intermolecular bonding to give liquids a definite volume.
Liquids are fluid, able to flow and take any shape. This occurs due to the weak intermolecular bonding that allows the molecules to slide past each other freely. As a result of being fluid, liquids exhibit many interesting properties that solids do not, including capillary action and diffusion.
Liquids, like gases, undergo diffusion when mixed. This can be seen by adding food coloring to water. Different liquids, when added, will chaotically spread out and mix together. Diffusion will occur faster when the liquid is warmer because the increased kinetic energy allows the molecules to move faster and collide more frequently.
Liquids are usually considered incompressible. The molecules are already close together, so it is difficult to compress them any more. Under very high pressures, liquids will actually compress, but not very much.
Liquids, unlike gases, have a distinct surface—they need not take their container's shape. This allows the formation of droplets and puddles.
Special Properties
Cohesion and Adhesion

The molecules of a liquid are attracted to each other. This is called cohesion. Molecules like methane are non-polar, so they are held together only by van der Waals forces. These molecules will have minimal cohesion. In contrast, water molecules use hydrogen bonding, so they display strong cohesion. A cohesive liquid will form more spherical droplets and have much higher surface tension.
Adhesion is the attraction of a liquid molecule to its surroundings. Adhesive liquids will demonstrate capillary action. They are also more "wet". Mercury is very cohesive, but not adhesive. As a result, it doesn't leave behind residue as it rolls across a surface. Water, on the other hand, is much more adhesive. When water rolls across a surface, it wets that surface because some of the molecules adhere to it.
Surface Tension and Capillary Action
When water drops are on an impermeable (waterproof) surface, they tend to form beads. This is due to its surface tension. Liquid molecules pull at each other, and as a result they decrease their surface area. The molecules at the boundary of the liquid are pulled in, causing a droplet shape. When water is on a permeable surface, it spreads out, as can be seen with water on a paper towel. This capillary action explains how water in the ground reaches the top of trees that are hundreds of feet tall.
-
Adhesive liquids (like water but not mercury) will rise up a narrow tube.
-
Cohesive liquids have surface tension to hold themselves into droplets.
Pressure
Liquids will distribute pressure evenly. This concept, known as Pascal's Law, is crucial for equipment like hydraulic brakes. It is a result of their incompressibility.
| Helpful Hint! | |
|---|---|
| If there is no atmospheric pressure (a vacuum, like outer space), liquids cannot form. |
Liquids will evaporate. Although the average kinetic energy of the molecules is too low to overcome bonding and become a gas, individual molecules will occasionally have above-average energy and break free from the surface of the liquid. The molecule then escapes to the gas phase. At the same time, however, a gas molecule may hit the surface of the liquid and slow down enough to join the liquid. A glass of water left outside in the sun will eventually become empty. The sunlight adds energy to the molecules, allowing some to escape as a gas. Eventually, all molecules will escape. The tendency of a liquid to evaporate depends on its intermolecular forces. Volatile liquids tend to evaporate quickly have relatively weak intermolecular forces keeping the molecules together, making it easier for them to escape the liquid phase. Conversely, non-volatile liquids do not evaporate to any visible extent due to the presence very strong intermolecular forces.
The evaporation increases with temperature. It can be measured by vapor pressure, the amount of pressure exerted by the evaporated gas above the liquid's surface. Vapor pressure increases with temperature, and once it reaches the pressure of the surrounding atmosphere, the liquid will boil. Vapor pressure also depends on the intensity of intermolecular forces in the liquid.
Viscosity
Viscosity refers to the liquid's resistance to flow. For example, maple syrup has a relatively high viscosity when compared to water because maple syrup flows much slower than water, which flows relatively quickly and easily. The difference in viscosity between these two liquids is due to the attractive forces within the specific liquid. In order to flow, molecules must roll and move over each other. A solution with low attractive forces would allow the molecules to move in a more free and easy manner, decreasing the viscosity.
In most cases, the viscosity of a liquid decreases as the temperature of a liquid is increased. Increasing the temperature of a liquid causes the molecules to have a higher kinetic energy. This increase in kinetic energy breaks down the intermolecular forces present in the liquid. Since viscosity is dependent on these attractive forces, the viscosity will decrease when the kinetic energy is increased.
Gases
Characteristics of Gases
Gases have a number of special characteristics that differentiate them from other states of matter. Here is a list of characteristics of gases:
- Characteristics of Gases
- Gases have neither definite shape nor definite volume. They expand to the size of their container.
- Gases are fluid, and flow easily.
- Gases have low density, unless compressed. Being made of tiny particles in a large, open space, gases are very compressible.
- Gases diffuse (mix and spread out) and effuse (travel through small holes).
Standard Temperature and Pressure
Standard Temperature and Pressure, or STP, is 0 °C and 1 atmosphere of pressure. Expressed in other units, STP is 273 K and 760 torr. The Kelvin and torr are useful units of temperature and pressure respectively that we will discuss later in the following sections.
Avogadro's Law

Avogadro's Law states that equal volumes of gases at the same temperature and pressure contain the same number of molecules. So both one mole of Xenon at STP (131.3 grams) and one mole of helium at STP (4.00 grams) take up 22.4 liters. Even 1 mole of air, which is a mixture of several gases, takes up 22.4 liters of volume. 22.4 L is the standard molar volume of a gas.
[Avogadro's Law]
- .
where:
- V is the volume of the gas.
- n is the number of moles of the gas.
- k is a proportionality constant.
The most important consequence of Avogadro's law is that the ideal gas constant has the same value for all gases. This means that the constant
where:
- p is the pressure of the gas
- T is the temperature of the gas
has the same value for all gases, independent of the size or mass of the gas molecules.
Pressure
Gases exert pressure on their containers and all other objects. Pressure is measured as force per unit area. A barometer is a device that measures pressure. There are a number of different units to measure pressure:
- torr, equal to millimeters of mercury (mm Hg): if a glass cylinder with no gas in it is placed in a dish of liquid mercury, the mercury will rise in the cylinder to a certain number of millimeters.
- atmosphere (atm), the pressure of air at sea level.
- pascal (Pa), equal to one newton (N) per square meter. A newton is the force necessary to accelerate one kilogram by one meter per second squared.
You should know that 1 atm = 760 torr = 101.3 kPa.
Ideal Gases
Gases are complicated things composed a large numbers of tiny particles zipping around at high speeds. There are a number of complex forces governing the interactions between molecules in the gas, which in turn affect the qualities of the gas as a whole. To get around these various complexities and to simplify our study, we will talk about ideal gases.
An ideal gas is a simplified model of a gas that follows several strict rules and satisfies several limiting assumptions. Ideal gases can be perfectly modeled and predicted with a handful of equations.
Ideal gases follow, among others, these important rules:
Rules of Ideal Gases
- The molecules that make up a gas are point masses, meaning they have no volume.
- Gas particles are spread out with very great distance between each molecule. Thus, intermolecular forces are essentially zero, meaning they neither attract nor repel each other.
- If collisions do occur between gas particles, these collisions are elastic, meaning there is no loss of kinetic (motion) energy.
- Gas molecules are in continuous random motion.
- Temperature is directly proportionate to kinetic energy.
Note: Ideal gases never truly exist (because the nature of gases is so complicated), but gases are often close enough to an ideal gas that the equations still hold fairly accurate. |
Ideal Gas Law
Ideal gases can be completely described using the ideal gas law:
[Ideal Gas Law]
where
- is the absolute pressure of the gas,
- is the volume of the gas,
- is the number of moles of gas,
- is the ideal gas constant,
- is the absolute temperature, in Kelvin.
Ideal Gas Constant
| Values of R | Units |
|---|---|
| 8.314 472(15) | J K−1 mol−1 |
| 8.314 472(15) | m3 Pa K−1 mol−1 |
| 8.314 472(15) | cm3 MPa K−1 mol−1 |
| 0.082 057 46(14) | L atm K−1 mol−1 |
| 62.363 67(11) | L Torr K−1 mol−1 |
The ideal gas constant, R, is a constant from the ideal gas equation, above, that helps to relate the various quantities together. The gas constant represents the same value, but the exact numerical representation of it may be different depending on the units used for each term. The table at right shows some values of R for different units. Here is the value of R using Joules for energy, Kelvin for temperature, and moles for quantity:
[Ideal Gas Constant]
Real Gases
All real gases (or non-ideal gases) deviate from the ideal gas laws that we discussed above. These deviations can occur for several reasons:
- Real molecules have mass and volume. They are too big and no longer behave like ideal point masses
- Low volumes and high pressures cause molecules to be close enough for intermolecular forces. Polar molecules exaggerate the problem.
- Low temperature means low kinetic energy. At lower temperatures, intermolecular forces become significant and cannot be ignored like they are in ideal gasses
- Other complicated factors may prevent ideal behavior.
When these issues are present, gas molecules attract each other, and may even condense into a liquid. Gases act most like ideal gases when the molecules have low mass (small volume), are not polar, and are at high temperature and low pressure. Noble gases like Xenon or Argon act the most like ideal gases because they are mostly electrical neutral and non-interactive.
Kinetic Molecular Theory
This theory describes why gases exhibit their properties. It only applies accurately to ideal gases. Because there is no such thing as an ideal gas, the Kinetic Molecular Theory can only approximate gas behavior. It is still very useful to chemists.
The Kinetic Molecular Theory explains the pressure, temperature, kinetic energy, and speed of gases and their molecules. See Wikipedia for the exact equations of the Kinetic Molecular Theory, as well as detailed explanations. What is most important is understanding the general concepts, not the specific equations.
Kinetic Energy and Temperature
Kinetic energy is the mechanical, or movement, energy. It is given by the equation:
where
- is mass and
- is the average velocity
Explained with words, kinetic energy is dependent on the product of a particle's mass and its velocity squared. The more kinetic energy, the faster a particle moves. Conversely, the faster a particle moves, the more kinetic energy it has.
The Kinetic Molecular Theory states that kinetic energy and temperature are directly proportionate. Thus, a double in temperature will result in a double in kinetic energy and an increase in velocity by a factor of 1.4 (the square root of 2, see the KE equation). This means that the higher the temperature of a gas, the faster the individual particles in that gas are moving.
A hotter gas has more kinetic energy than a colder gas. If two gases are at the same temperature, they will have the same kinetic energy. The lighter-massed gas will have a higher average speed for its particles at the same energy level. It is important to know that gas temperature must be measured in kelvin. Zero degrees Celsius is 273 kelvin. One Celsius degree is equal to one kelvin, but the kelvin scale has water's freezing point at 273 and boiling point at 373. It is necessary to use kelvin because temperatures must always be positive when using the Kinetic Molecular Theory.
- Question for the reader
A gas's temperature is increased from 20 °C to 40° C. What factor does its kinetic energy increase? Velocity?
Keep in mind that gases are all about averages. For a temperature increase, there will be an average increase in the kinetic energy of the particles in that gas. Even in a very hot gas there will be some particles moving very slowly. However, the average will be high. |
Pressure and Collisions
Pressure exists because the gas molecules are in continuous random motion, and they will constantly strike the walls of their container. Pressure will increase as the speed of the molecules increases, due to greater forces of collision. Pressure will also increase as the mass of the molecules increase. A small, slow molecule has less momentum than a large, fast molecule, which explains their difference in pressure.
- Question for the reader
There are two jars of ideal gas, for example. In Jar A there is nitrogen gas (N2). In Jar B there is methane gas (CH4). Both jars are at the same temperature. Which will have greater pressure?
- Question for the reader
Now, Jars A and B both have propane gas (C3H8). Jar A is at 300 K and Jar B is at 500 K. Which will have greater pressure?
Phase Changes
Phase Diagrams
Phase diagrams predict the phase of a substance at a certain pressure and temperature.
The triple point is where all three phases of matter can exist in equilibrium. Points that are on a line are where two phases of matter can coexist.
The critical point is the highest pressure and temperature that the three normal phases can exist. Any further, and the characteristics become a blend of liquid and gas.
Changes in State

If the temperature and pressure change and move across a line in the diagram, the phase will also to change. There are six ways this can happen:
- Solid to liquid: melting
- Liquid to solid: freezing
- Liquid to gas: evaporation
- Gas to liquid: condensation
- Gas to solid: deposition
- Solid to gas: sublimation
The diagram on the right also shows the plasma state of matter. A plasma is simply a gas that has been completely ionized, so that there is a mixture of positive ions and electrons. It has interesting electrical properties, but it is not important in the scope of General Chemistry.
Energy Changes
| Helpful Hint! | |
|---|---|
| The kinetic energy of a molecule is directly proportional to its temperature. Potential energy is used to break bonds. |
If you boil water, it never goes above 100 degrees Celsius. Only after it has completely evaporated will it get any hotter. This is because once water reaches the boiling point, extra energy is used to change the state of matter and increase the potential energy instead of the kinetic energy. The opposite happens when water freezes. To boil or melt one mole of a substance, a certain amount of energy is required. These amounts of energy are the molar heat of vaporization and molar heat of fusion. If that amount of energy is added to a mole of that substance at boiling or freezing point, all of it will melt or boil, but the temperature won't change.
The graph shows the temperature of ice as heat is added. Temperature increases linearly with heat, until the melting point. Then, the heat added does not change the temperature. That heat energy is instead used to break intermolecular bonds and convert ice into water. At this point, there is a mixture of both ice and water. Once all ice has been melted, the temperature again rises linearly with heat added. At the boiling point, temperature no longer rises with heat added because the energy is once again being used to break intermolecular bonds. Once all water has been boiled to steam, the temperature will continue to rise linearly as heat is added.
Behavior of Gases
Evaporation of Liquids
An open bottle of vinegar standing at room temperature will spread odor across the room despite the fact that it is not boiling. This is because kinetic energy is unevenly distributed throughout a liquid. Some molecules are moving faster than others. This allows the liquid to evaporate into a gas. In order for evaporation to occur, the entire liquid does not need to be at the boiling temperature; only some individual molecules. At a given temperature a liquid evaporates at a specific rate, causing gas pressure above the liquid in the system that contains it. Can you guess the vapor pressure of water at 100 degrees Celsius? If you guessed 760 torr or 1 atm, you're right. Liquids boil when their vapor pressures equal the atmospheric pressure around them. Some liquids are more volatile than others, meaning they evaporate more readily.

Evaporation occurs because of the uneven distribution of kinetic energy. This is called a Boltzmann distribution. Although the average kinetic energy of the liquid is below the boiling point, some molecules have above average energy. That gives them enough energy to overcome their bonds and break free of the liquid. At the same time, a gas molecule could strike the liquid and slow down enough to become part of it. There is an equilibrium between the amount of evaporating liquid and the amount of liquifying gas. Higher temperatures will have an equilibrium that favors more gas.
Motion of Gas Particles

Gas particles move in random, straight-line motion. Gas particles possess a greater kinetic energy than the particles of a liquid or solid. The greater kinetic energy is due to gases existing at higher temperatures than liquids or solids. As temperature increases, particles move faster and, thus, have greater kinetic energy. The particles of a gas have minimal interactions, except collisions with each other.
Diffusion and Effusion
Due to their random motion, gases will eventually escape from a container if there is a hole in it. This is called effusion. Gases also spread out across a room, or mix together in a container. This is called diffusion.
More information about diffusion and effusion is presented in the next chapter.
Dalton's Law of Partial Pressures
The total amount of pressure exerted by a gas is equal to the sum of its components:
For instance, if you add 300 torr of nitrogen gas to a container, then you add 250 torr of oxygen to that container, the total pressure will be 550 torr (assuming volume and temperature stayed constant).
Another way of stating this law is that the pressure exerted by a particular gas in a mixture (gases always form homogeneous mixtures with each other) is equal to its mole fraction multiplied by the total pressure.
Diffusion and Effusion
Diffusion and Effusion
Diffusion

Diffusion is the process of a substance spreading out to evenly fill its container or environment. In a solution, a concentrated solute diffuses to spread evenly in its solvent. This is the process where the particles move from high concentration to low concentration. Diffusion explains why an open bottle of ammonia will fill an entire room with odor. The gas molecules escaping from the bottle spread out to fill their new container: the room. As a result, the whole room smells. Upon opening the windows, the gas will diffuse into the environment.
Diffusion occurs because the gas molecules are in continuous random motion. This motion is called Brownian Motion. The molecules will eventually reach anywhere they can. |
Diffusion is also the process of two gases mixing together, if both stored in the same container. They will spread out evenly, resulting in a solution (homogeneous mixture).
Effusion
Effusion is the process of gas molecules escaping from a small hole in the container. Effusion explains why fumes are noticeable near a leaky fuel pipe.
Effusion is also explained by the continuous random motion of the molecules. The random motion prevents molecules from avoiding the small hole. Slowly but steadily, gas molecules will pass through the hole. |
Effusion obviously depends on the size of the hole. If small enough, effusion may not occur because, like a beach ball hitting a basketball hoop, the molecules can't fit. If the hole is large enough, the process may be considered diffusion instead of effusion.
Effusion can be seen with balloons. Effusion proves that the balloon has holes in it, even though it looks totally impassable. When left alone for several days, a balloon filled with helium will eventually deflate. If that balloon were filled with hydrogen, it would deflate in less time because the molecules are smaller and escape with ease. and you can try that
this is chemistry ks3
==
The more massive a gas is, the slower it effuses. The relationship is given by Graham's Law.
As an example, assume there are two identical containers with holes. Container A has hydrogen gas (M=2 g/mol) and Container B has helium gas (M=4 g/mol). If the hydrogen gas effuses at a rate of 4 mol/hr, the helium gas would effuse at a slower rate (being heavier). Using Graham's Law, we can see that it would effuse at a rate of about
Gas Laws
Gas Laws
As the result of many different science experiments, several gas laws have been discovered. These laws relate the various state variables of a gas. Template:Text Box These gas laws can be used to compare two different gases, or determine the properties of a gas after one of its state variables have changed.
| Avogadro's Law states that equal volumes of all ideal gases (at the same temperature and pressure) contain the same number of molecules. | ||
| Boyle's Law states that equal pressure is inversely proportional to volume (when the temperature is constant). | ||
| Charles's Law states that volume is proportional to temperature (when the pressure is constant). Remember that temperature must be measured in Kelvin. | ||
| Amontons's Law states that pressure is proportional to temperature (when the volume is constant). |
Combined Gas Law
Combining Charles' Law, Boyle's Law, and Amontons's Law gives us the combined gas law.
| For a gas with constant molar mass, the three other state variables are interrelated. | |
| The Combined Gas Law can be used for any comparisons between gases. |
Ideal Gas Law
When Avogadro's Law is considered, all four state variables can be combined into one equation. Furthermore, the "constant" that is used in the above gas laws becomes the Universal Gas Constant (R).
To better understand the Ideal Gas Law, you should first see how it is derived from the above gas laws.
| and | This is simply a restatement of Avogadro's Law and the Combined Gas Law. |
| We can now combine the laws together. | |
| Let R be a constant, and write the proportion in the form of an equation. | |
| Rearranging the fraction gives one form of the ideal gas law. |
The ideal gas law is the most useful law, and it should be memorized. If you know the ideal gas law, you do not need to know any other gas laws, for it is a combination of all the other laws. If you know any three of the four state variables of a gas, the unknown can be found with this law. If you have two gases with different state variables, they can be compared.
There are three ways of writing the ideal gas law, but all of them are simply algebraic rearrangements of each other.
| This is the most common form. | |
| This form is useful for predicting the effects of changing a state variable. To maintain a constant value of R, any change in the numerator must result in a proportional change in the denominator, and vice versa. If, for example, the pressure is decreased in a constant-volume container, you can use this form to easily predict that the temperature must decrease. | |
| Because R is the same constant for all gases, this equation can be used to relate two gases to each other. |
Rules for Using the Ideal Gas Law
- Always convert the temperature to kelvins (K).
- Always convert mass to moles (mol).
- Always convert volume to liters (L).
- It is preferable to convert pressure to kilopascals (kPa). R, the Universal Gas Constant, would be 8.314 (L·kPa)/(mol·K).
Rules for Using the Ideal Gas Law
|
Kinetic Molecular Theory
The Kinetic Molecular Theory attempts to explain the gas laws. It describes the behavior of microscopic gas molecules to explain the macroscopic behavior of gases. According to this theory, an ideal gas is composed of continually moving molecules of negligible volume. The molecules move in straight lines unless they collide into each other or the walls of their container.
| The pressure of the gas on the container is explained as the force the molecules exert on the walls of its container or on other molecules during a collision. Pressure is equal to the average force of collisions divided by the total surface area of the container. | |
| The temperature of the gas is proportional to the average kinetic energy of the molecules. denotes the average kinetic energy of the molecules, and is the Boltzmann constant (1.388 x 10-23). |
The gas laws are now explained by the microscopic behavior of gas molecules:
- Boyle's Law: The pressure of a gas is inversely proportional to its volume. A container's volume and surface area are obviously proportional. Based on the pressure equation, an increase in volume (and thus surface area) will decrease pressure.
- Charles' Law: the volume of a gas is proportional to its temperature. As the volume (and surface area) increases, the pressure will decrease unless the force also increase. When pressure is constant, the volume and temperature must be proportional. The temperature equation above explains why: the energy of the molecules (and their collision force) is proportional to temperature.
- Gay-Lussac's Law: The temperature of a gas is directly proportional to its pressure. An increase in temperature will increase the kinetic energy of the molecules (shown by the temperature equation). Greater kinetic energy causes the molecules to move faster. Their collisions with the container will have more force, which increases pressure.
- Avogadro's Law: Equal volumes of all ideal gases (at the same temperature and pressure) contain the same number of molecules. According to the Kinetic Molecular Theory, the size of individual molecules is negligible compared to distances between molecules. Even though different gases have different sized molecules, the size difference is negligible, and the volumes are the same.
Derivation of Ideal Gas Law
| Suppose there are molecules, each with mass , in a cubic container with side length . Even though the molecules are moving in all directions, we may assume, on average, that one-third of the molecules are moving along the x-axis, one third along the y-axis, and one third along the z-axis. We may assume this because the motion of the molecules is random, so no direction is preferred. | |
| Suppose the average speed of the molecules is . Let a specific wall of the container be labeled A. Because the collisions in Kinetic Molecular Theory are perfectly elastic, the speed after a collision is . Therefore, the average change in momentum (the product of mass and velocity) per collision is .
Each molecule, on average, travels a distance of between two consecutive collisions with wall A. Therefore, it will collide times per second with wall A. | |
| The average change in momentum per molecule per second. | |
| Therefore, this is the total change in momentum per second for the molecules that collide into wall A. This is the momentum per second that was exerted onto wall A. Because force equals the change in momentum over time, this value is the force exerted on wall A. | |
| Pressure is defined as force per unit area, so this is the pressure of the gas. | |
| Because the volume of the container is , we can rearrange the equation. | |
| The kinetic energy of a single particle is given by this equation. | |
| Substitute kinetic energy into the equation. | |
| Substitute the temperature equation (from the previous section). | |
| Avogadro's number is equal to the number of molecules per mole. | |
| By definition, the ideal gas constant is equal to the Boltzmann constant times Avogadro's number. | |
| The ideal gas law is derived from the Kinetic Molecular Theory. | |
Deviations from the Ideal Gas Law
In an ideal gas, there are no intermolecular attractions, and the volume of the gas particles is negligible. However, there is no real gas that can perfectly fits this behavior, so the Ideal Gas Law only approximates the behavior of gases. This approximation is very good at high temperatures and low pressures.
At high temperature the molecules have high kinetic energy, so intermolecular attractions are minimized. At low pressure the gas occupies more volume, making the size of the individual molecules negligible. These two factors make the gas behave ideally.
At low temperature or high pressure, the size of the individual molecules and intermolecular attractions becomes significant, and the ideal gas approximation becomes inaccurate.
Eudiometers and Water Vapor
| Helpful Hint! | |
|---|---|
| In calculations for a gas above a liquid, the vapor pressure of the liquid must be considered. |
A eudiometer is a device that measures the downward displacement of a gas. The apparatus for this procedure involves an inverted container or jar filled with water and submerged in a water basin. The lid of the jar has an opening for a tube through which the gas to be collected can pass. As the gas enters the inverted container, it forces water to leave the jar (displacing it downward). To fill the entire container with gas, there must enough gas pumped into the container to expel all of the water.

As seen in this diagram, the downward displacement involves water. Therefore, in the container where the gas is collected, there is unwanted water vapor. To account for the water vapor, subtract the pressure of water vapor from the pressure of the gases in the container to find the pressure of the collected gas. This is simply a restatement of Dalton's Law of Partial Pressure:
The pressure of water vapour can be found on this webpage.
Gas Laws Practice Questions
- Between the Combined Gas Law and the Ideal Gas Law, which one accounts for chemical change? Explain.
- Calculate the density of hydrogen at a temperature of 298 K and pressure of 100.0 kPa.
- What volume does 5.3 moles of oxygen take up at 313 K and 96.0 kPa?
- Hydrogen and sulfur chemically combine to form the gas hydrogen sulfide, according to the reaction: . How many liters of hydrogen are required to form 7.4 L of hydrogen sulfide (at STP: 273 K, 101.3 kPa)?
Answers to Gas Laws Practice Questions
Equilibria
Chemical Equilibrium
Chemical equilibrium occurs when a reversible reaction is occurring backwards and forwards at the same time by the same amount. It is the balancing point of a chemical reaction, when it seems to stop happening. Although some reactions (like the combustion of propane) occur to completion (no backwards reaction), most reactions occur in both the forward and backward direction. One reaction will occur at a faster rate than the other, causing a net result. As the reaction progresses, the forward reaction slows down and the backward reaction speeds up. When the rates are equal, equilibrium has occurred. The reaction appears to have stopped, and the total amount of products and reactants remains stable.
Chemical reactions never really stop, but they no longer make any progress once the forwards and backwards reactions are occurring at the same rate. This is equilibrium. |
The Equilibrium Constant
The ratio of products to reactants, or is known as the equilibrium constant. For the generic reaction mA + nB → xC + yD, the equilibrium constant is
where [X] detonates the activity of X. The activity of X is:
- its concentration if X is a gas or in a solution
- 1 if X is a pure solid or pure liquid
In other words, pure solids and liquids don't affect the equilibrium constant, as long as there is enough for the reaction to proceed. Their activity is 1, so they don't need to be written in the equilibrium constant.
Kp and Kc
There are two types of . One is , and the activities are concentrations. You are already familiar with this expression; it is the normally-used . For gaseous reactions, you may use the concentration equilibrium. You may also use partial pressures instead of concentrations. This expression is denoted . The activities are partial pressures instead of concentrations. This can only be used when all products and reactants are in the gaseous phase.
To convert between and , there is an equation:
R is the Universal Gas Constant and T is the temperature at which the reaction is occurring. is the change (in moles) of gas molecules between products and reactants. It may be zero (in which case Kp = Kc).
Examples
- Example 1
15.0 moles of X and 20.0 moles of Y are put into an empty 2.0 liter container. They react, and eventually reach equilibrium with 7.0 moles of Z according to the hypothetical equation:
Calculate the equilibrium constant.
Solution: Because the container was originally empty and at equilibrium, all 7.0 moles of Z are produced by the reaction. Therefore, 7.0 moles of X and 14.0 moles of Y are consumed in the reaction, so at equilibrium there remain 8.0 moles of X, 6.0 moles of Y, and 7.0 moles of Z. Divide these values by 2.0 liters to determine the concentration, then substitute into the equilibrium expression:
- Example 2
5.00 moles of hydrogen are put into an empty 1.00-L container with 5.00 moles of iodine, where they react according to this equation:
The equilibrium constant is 51.5 at the temperature of the reaction. Calculate the number of moles of HI that will form.
Solution: Suppose 2y moles of HI forms. Then, y moles of H2 and I2 are consumed. Therefore, at equilibrium, there are 2y moles of HI, and (5.00 - y) moles of both H2 and I2. Dividing by 1.00 liters (to find concentration) and writing an equilibrium expression gives:
Solving this equation gives y = 3.91 (reject the other solution, as it is greater than 5.00). At equilibrium, there are 7.82 mol of HI.
Calculations With K
The exact value of K doesn't really matter. What is important is its magnitude.
| K > 1 | Reactions favors products |
| K < 1 | Reaction favors reactants |
If the reaction favors products, it will occur in the forward (left-to-right) direction. If K is very large, the reaction will occur mostly to completion, using up almost all the reactants.
If the reaction favors reactants, it will occur in the reverse (right-to-left) direction. If K is very small, the reaction will use up almost all the products and make them into reactants. The reverse reaction is favored.
Reaction Arithmetic
If you reverse the reaction (changing the direction of the arrow, or flipping the left and right sides), the new value of Keq will be its reciprocal.
| A → B | (K = x) |
| B → A | (K = 1/x) |
If you add two reactions, their equilibrium constants are multiplied.
| A → B G → H |
(K = x) (K = y) |
| A + G → B + H | (K = xy) |
These basic principles can help you determine an unknown equilibrium constant by combining known constants.
Q
Keq is only used when a reaction is in equilibrium. To find it, write its concentration (or partial pressure) expression, then plug in all the measured values. The resulting K can be used to predict other equilibrium positions.
If a reaction is not at equilibrium, you can still plug in the measured concentrations. Instead of calling this value Keq, it is called Q.
| Q > K | The products must decrease and the reactants will increase. |
| Q = K | There is equilibrium. |
| Q < K | The reactants must decrease and the products will increase. |
So, if you know the equilibrium constant for a reaction, and you know all the concentrations, you can predict what direction the reaction will proceed.
I-C-E Charts
Let's say you know K for a reaction, and you know some concentrations. You can calculate the final (equilibrium) concentrations using an "Initial-Change-Equilibrium" chart. Here is an example.
At 25°C, Kc = 23.2 for this reaction.
First, write the equilibrium expression:
In a sealed container of 2.00 L: 3 molar H2O, 4 molar CO, 1 molar H2 have been added. (Write the ICE chart):
| CO | H2O | CO2 | H2 | |
|---|---|---|---|---|
| Initial | 2 | 1.5 | 0 | 0.5 |
| Change | -x | -x | +x | +x |
| Equilibrium | 2-x | 1.5-x | x | 0.5+x |
Now, plug in the "equilibrium" values into the K expression. Substitute all known values and solve for x. Then, substitute x for the final values to determine the equilibrium concentrations.
By substituting everything into the K expression, we have:
Solving this will require the use of the quadratic equation. It may be easier to use approximations or a graphing calculator. When solved, (disregard values of x that would give negative concentrations). By substituting x into the "equilibrium" values in the ICE chart, we can determine the concentrations of all substances when the reaction reaches equilibrium.
| CO | H2O | CO2 | H2 |
|---|---|---|---|
| 0.66 M | 0.16 M | 1.34 M | 1.84 M |
To check your answer, you could substitute these values into the equilibrium expression and see if it equals 23.3 (the given Keq value).
This was a fairly simple example. There were no coefficients in the reaction, so no exponents in the expression. |
The purpose of doing this is to see the final concentrations of the substances involved in a chemical reaction. Unless Keq is incredibly large, not all the reactants will be consumed.
Equilibrium in Detail
The next few chapters in this book will provide more details on equilibrium.
Shifts in Equilibrium
Le Chatelier's principle states that a system will adapt to minimize a change. If reactants are added, they will be consumed and products will form. Likewise, if products are added, they will be consumed (by the reverse reaction) and reactants will form.
The only change in a system that will affect the value of Keq is temperature. The value of Keq is never changed by the concentrations or pressures of the substances.
Special Constants
| Acids and bases have special ionization constants, which show how they react with water. The acid ionization constant, or Ka, tells how strong an acid is. | |
| The base ionization constant, Kb, similarly tells how strong a base is. | |
| The solubility product Ksp shows how much an ionic substance will dissociate when dissolved. |
Relation to E
There is a special relation between the standard potential of a redox reaction and the equilibrium constant
, where n is the number of moles of electrons transferred.
This is a significant equation, because this allows us to calculate the hard to measure K from the easy to measure E.
Le Chatelier's Principle
Le Chatelier's Principle
Le Chatelier's Principle states that when a system that is in dynamic equilibrium is disrupted in some way, the system will respond with chemical or physical changes to restore a new equilibrium state.
There are several changes that can effect the equilibrium position of a system:
- Concentration
- Pressure/Volume
- Temperature
Concentration
If the concentrations in a system are changed, Le Chatelier's Principle predicts that the equilibrium position will shift to minimize the change.
For example, let us say that the reaction above is at equilibrium. Adding more reactants ( and ) will disturb the equilibrium system because it raises the reactant concentration. The system will then produce more products ( and ) and will decrease the reactant concentration in order to obtain equilibrium again. The system is now at a new equilibrium position, and the change created has been minimized.
The above example shows that increasing the reactants in an equilibrium system favors the products because the system produces more products and reduces the amount of reactants. The table below shows the response of an equilibrium system to changes in concentration:
| Change in Concentration | System response |
|---|---|
| Increase reactant | Favors products |
| Decrease reactant | Favors reactants |
| Increase product | Favors reactants |
| Decrease product | Favors products |
Pressure/Volume
If some the substances in a system are gas, changing their partial pressure is the same as changing their concentrations.
If the volume is increased, the overall pressure decreases (and vice versa). Consider the reaction A + B → 3C. There are three moles of products for every two moles of reactants. The product side has higher pressure than the reactant side. So, if pressure is increased (or volume decreased), equilibrium will shift towards the lower pressure side. Products will be consumed (by the reverse reaction) and reactants will form.
If pressure is decreased (or volume increased), equilibrium will shift towards the higher pressure side.
If an inert gas (such as neon) is added to a system, it will raise the overall pressure. However, the partial pressures of all products and reactants are unchanged, so no shift in equilibrium occurs. |
Temperature
Changes in concentration, pressure, and volume affect the equilibrium position, but the equilibrium constant Keq is unchanged. These changes can be calculated using the equilibrium expression and known values of Keq and concentrations.
Temperature, however, does change the value of Keq. When given a value of K, you will also be given a temperature because K is dependent on the temperature.
An increase in temperature will favor the endothermic (heat-absorbing) side of a reaction. A decrease in temperature will favor the exothermic (heat-releasing) side of a reaction.
For example, the following reaction is very exothermic:
Because it is exothermic, you can think of it like this:
At room temperature, Keq for this reaction is 3.2 x 1081. If this reaction happens at a very high temperature, what will happen? Less product will form (or maybe the reverse reaction will occur if the temperature is high enough) and Keq will be smaller. What will happen if this reaction occurs at a very low temperature? More product will form and Keq will be larger.
Acid-Base Equilibrium
Consider an acid, HA, in water. According to the Brønsted-Lowry acid/base theory, the acid should protonate the water to form hydronium and the conjugate base, A-. There will be an equilibrium between the acid and water, and hydronium and the conjugate base.
This equilibrium can be used to calculate the concentrations of species in the solution.
Acid Dissociation Constant
| Helpful Hint! | |
|---|---|
| Strong acids/bases dissociate completely, so their equilibrium constants are overwhelmingly large. |
Like all equilibria, an acid/base dissociation will have a particular equilibrium constant which will determine the extent of the reaction (whether it lies to the left or right of the equation). As the equilibrium constant approaches zero, the reaction tends to form 100% reactants. As the equilibrium constant approaches infinity, the reaction tends to form 100% products. The equilibrium constant K=1 states that there will be 50% products and 50% reactants
Because the equilibrium is used for calculating the concentrations of weak acids, very little water actually reacts. The concentration of water during the reaction is, therefore, a constant, and can be excluded from the expression for K. This gives rise to a special equilibrium constant, Ka, known as the acid dissociation constant. It is simply K multiplied by the concentration of water.
The Ka of a weak acid determines how acidic it is, i.e., how far its equilibrium lies to the right. The Ka values of weak acids can and have been determined experimentally.
Base Dissociation Constant
A similar equilibrium exists when a weak base is dissolved in water. The base will accept a proton from water and form a conjugate acid, BH+.
This equilibrium has its own special constant, Kb, known as the base dissociation constant. Like the acid dissociation constant, it is defined as the equilibrium constant multiplied by the concentration of water.
Ion Product Constant
A special equilibrium exists between ordinary water molecules. Occasionally, one water molecule will act as an acid, and donate a proton to another water molecule (which acts as a base). This is the auto-ionization of water.
By the Le Chatelier Principle, we can see that if the hydronium ion concentration is increased (by adding an acid), the equilibrium will move to the left and there will be a lower concentration of hydroxide. Thus, hydronium and hydroxide concentration are inversely related—an increase in one will result in a decrease in the other, and vice versa.
The equilibrium expression for this reaction is given a special name, Kw. Because it simplifies to the product of hydronium and hydroxide concentration, it is sometimes called the ion product constant. The value of this constant is 1.0 × 10-14 at 25°C.
This expression can be used to find the pH of pure water. Recall that pH is the negative logarithm of hydronium ion concentration. If we set the hydronium ion concentration in the above expression to be , we can derive the pH. The hydroxide ion concentration must also be (since each molecule of hydroxide is a result of a molecule of hydronium forming). We have:
This technique can be used to determine the pH of any solution if either one of the ion concentrations are known.
Conjugate Base Expressions
The conjugate bases of weak acids have a relationship with their parent acids. Consider the equilibrium expression of the conjugate base, A-, of the weak acid HA.
If we multiply the expression for an acid by the expression for its conjugate base, the concentrations of the acid and conjugate base cancel and we obtain the ion product constant for water! This allows us to calculate the Kb of a base if the Ka of its conjugate acid is known (and vice versa).
Summary
The definitions of the acid and base dissociation constants are very important. They are presented here for reference.
| The acid dissociation constant measures the strength of an acid dissolved in water. | |
| The base dissociation constant measures the strength of a base dissolved in water. | |
| The ion product constant relates the concentrations of acids/bases and their conjugates in a solution. |
Solutions in Equilibrium
Solution
| Helpful Hint! | |
|---|---|
| You may need to review solubility and the properties of solutions. |
All ionic compounds are soluble in water to some extent, but the degree of solubility varies. While some compounds dissolve almost completely, others dissolve to such a small extent that they are simply called insoluble compounds. Such compounds include calcium sulfate, silver chloride, and lead hydroxide. Generally, ionic compounds whose component ions have larger charge magnitudes are less soluble because the ions are attracted too much to dissociate. A soluble compound will dissociate because of the attractions with the surrounding water molecules are strong enough to separate the ions.
For an ionic compound to dissociate, the forces of attraction between its component ions and the surrounding water molecules must be greater than the forces of attraction between the ions within the compound. When introduced to an aqueous environment, ionic compounds such as sodium chloride, sodium hydroxide, and ammonium bromide dissolve because of this.
Solubility Constant
| This reaction shows an ionic compound AB dissolving into its ions A+ and B-. | |
| This is the equilibrium constant for the reaction. Water is excluded because, although involved, it is not a product or reactant. | |
| Because the undissolved AB is a solid, pure substance, it can be excluded from the expression. The result is the solubility constant Ksp. It measures the degree of solubility of an ionic compound. |
If two or more of the same ion are created by the dissociation of one particle of the ionic compound, the molar concentration of this ion is raised to the power of how many such ions there are. For example, when calcium chloride dissociates, two chloride ions are created in the dissociation of one particle, so the concentration of the chloride ion is squared when calculating Ksp.
Ksp is the equilibrium constant for the dissolution reaction above.
|
An example of a slightly soluble substance is calcium hydroxide. In very minute quantities, it will dissolve completely, but in large quantities it remains mostly undissolved.
Calculations with Ksp
Finding Ksp
It would not be an uncommon situation if you know a substance's solubility (g/mL), but you need to know its Ksp value. Follow this example:
| This is the solubility constant for calcium hydroxide. We wish to determine is numerical value, but we only know that its solubility is 0.185 g per 100 mL. | |
| We need to know its molar solubility, so we convert units and divide by molar mass. | |
| Now, plug in the molar solubility into the Ksp expression. Notice that the hydroxide concentration is doubled because there will be twice as many moles as the undissolved substance. |
We have now determined the Ksp value for calcium hydroxide. It will allow us to determine other information about solutions containing these ions, such as percent ionization and the formation of precipitates.
- Questions for the reader
Lead(II) iodide is slightly soluble in water. It forms a bright yellow precipitate if too much is dissolved. You have determined that 0.75 g will dissolve in one liter of cold water. What is the molar solubility of lead(II) iodide? What is the Ksp value?
After heating the water, the solubility rises to 4.3 g per liter. What is the new Ksp value?
A similar process can be used to determine a substance's solubility by working backwards from the solubility constant.
Percent Ionization
Once an ionic compound's Ksp value is known, it is possible to determine the percent ionization, or relative amount of dissociated ions.
| We know the Ksp for silver sulfate, which is slightly soluble, and we want to know the percent ionization. | |
| Substitute x for the concentration of sulfate and 2x for silver. Solve for x. | |
| We now know the maximum concentration of the ions. Any remaining silver nitrate will be undissolved because the solubility has been exceeded and the solution is saturated. To determine percent ionization, we must know how much silver sulfate was dissolved. For this example, assume 1.00 mole was dissolved into 0.500 L of water. |
As you can see, the percent ionization decreases as the amount of solute increases. This is because the solution is saturated and no more ions will dissociate.
- Question for the reader
Lithium fluoride has a Ksp of 1.84 x 10-3. If 1.5 g are dissolved, what will be the percent ionization?
Precipitates
Obviously, the dissociate reaction occurs in reverse if there are too many ions. In this case, the solution is saturated, and any excess ions will solidify and form a precipitate.
If two soluble solutions are mixed, but the can form an insoluble compound, a precipitate will form.
| For example, a solution of silver nitrate is mixed with a solution of sodium chloride. Both are soluble. Silver chloride, however, is insoluble. | |
|
If 1.00 mg NaCl and 1.00 mg AgNO3 are dissolved into 1.00 L of water, will a precipitate form? |
| No, a precipitate will not form. | |
|
Now, another milligram of sodium chloride is dissolved. |
| The extra chloride ions will bond with silver ions and form a solid precipitate. |
In this case, the precipitate would probably be too small and dilute to be noticed. As more ions are added, however, the solution will become visibly cloudy.
- Question for the reader
Calcium carbonate has a Ksp of 3.36 x 10-9. In a 0.01 M solution of calcium chloride (soluble), how many moles of sodium carbonate (also soluble) can be added before precipitates form?
Kinetics
Introduction
Chemical kinetics is the study of the rates of chemical reactions. You may know if a reaction is capable of happening, and you may know how far the reaction will proceed, but you don't know fast it will happen. Consider two reactions: the rusting of an iron nail and the combustion of propane. Both reactions will occur, and both will occur to completion. The rusting will take years to complete, but propane will combust in an instant. Furthermore, the nail will rust faster when it's moist, and slower in the presence of less oxygen. Obviously, there are factors that affect the rates of chemical reactions. The study of these factors and rates is chemical kinetics.
-
This iron wire has taken years to become rusty.
-
This fire took only a moment to start.
Reaction Rate
| Consider this generic chemical reaction. (Lower case letters represent the molar coefficients.) | |
| The reaction rate is defined as the rate of change of the concentration of the substances. Remember that a substance written inside brackets is its concentration, and it is always raised to the power of its coefficient in the reaction (just like equilibrium expressions). The reaction rate involves Calculus, but in non-mathematical terms it is simply the rate of change of the concentrations. | |
| Actually measuring the rate of change of the reactants and products is difficult. Instead, the reaction rate can be accurately modeled by a rate equation. This is an example of a rate equation that might model the above reaction, where is a constant. |
In summary, the reaction rate can be determined using a rate equation, which depends on (among other things) the concentration of the reactants. The reaction rate essentially measures the speed at which a reaction proceeds.
Collision Theory
Collision theory predicts that reactions occur when molecules collide. In order for reactants to form products, the reactant molecules must physically collide so that they can rearrange themselves into product molecules. Only some collisions are effective because the collision must involve enough energy to allow the reaction to occur. This is called activation energy, the energy needed to begin a reaction.
Activation energy explains why gasoline will not spontaneously ignite. First, a small spark or flame must be present. The heat generated by the spark gives the gasoline molecules enough energy to activate the reaction. Being highly exothermic, the combustion of gasoline releases a large amount of heat—more than enough to activate further reactions and create a fire.
Collision theory allows us to predict the rate constant for a rate equation (see above). At a given temperature , the rate constant is:
where is the Universal Gas Constant, is the activation energy for the reaction, is a predicted-to-actual correction factor, and is the collision factor. The collision factor can also be calculated mathematically. It is the average number of reactant particle collisions per unit time.
Factors Affecting Rate
The rate of a reaction is affected by many factors. These effects can be measured empirically or explained by collision theory.
Concentration
This is the most obvious factor affecting rate. Increasing the concentration of the reactants will increase the rate they react. This is the main purpose of writing a rate equation; the concentrations can be plugged in like variables and the rate can be solved mathematically. In a rate equation in the form , the concentrations are the variables (raised to the powers of their coefficients in the reaction). All other factors that can affect rate are lumped into , which is considered a constant.
Collision theory explains this. Higher concentrations means more molecules packed into a given space. Therefore, there will be more collisions and thus a faster reaction.
Pressure
In a reaction of gaseous reactants, the partial pressure of the gases has the same function as the concentration.
However, increasing the overall pressure (or decreasing the volume if you remember the gas laws) will also result in a greater reaction rate. The increased pressure causes the molecules to collide with more force. More collisions will be effective and therefore products will form faster.
Temperature
As you should already know, a molecule's kinetic energy is directly proportional to its temperature. By increasing the temperature, molecules collide more vigorously, and more collisions will be effective.
Stirring
In a heterogeneous reaction there are two or more phases of matter interacting, such as a solid dissolving into a liquid. Stirring or shaking the mixture will speed up the reaction rate. This is common sense. When you add sugar to a drink, you stir it because you know it will dissolve faster. Collision theory would predict this because the stirring would increase the number of collisions between reactant molecules.
In a similar manner, increasing the surface area of a solid reactant will increase the reaction rate.
Catalysts/Enzyme

A catalyst is a substance that helps a reaction proceed without being consumed. Catalysts have already been explored in this book. A Catalyst provides a reaction pathway with lower activation energy.
In biochemistry, an enzyme is a protein that serves as a catalyst.
Reaction Rates
Introduction
Reaction rates of a chemical system provide the underpinnings of many theories in thermodynamics and chemical equilibria.
Elementary reactions are one-step processes in which the reactants become the products without any intermediate steps. The reactions are unimolecular (A → products) or bimolecular (A + B → products). Very rarely, they could be trimolecular (A + B + C → products), but this is not common due to the rarity of three molecules colliding at the same time.
A complex reaction is made up of several elementary reactions, with the products of one reaction becoming the reactants of the next until the overall reaction is complete.
Rate Equation
| Consider an arbitrary chemical reaction. | |
| The rate at which the products will form from the reactants is given by this rate equation. | |
| The rate of the reverse reaction (which also occurs to a lesser extent) has its own rate equation. |
Note [A] is raised to the power of m, its coefficient, just like an equilibrium expression. The rate of the reaction may rely on the molar coefficients of the reactant species, but it might not. However, for an elementary reaction, the concentrations of the species A and B are always raised to their molar coefficients. This only applies to elementary reactions, which is a very important distinction to make.
is the rate reaction coefficient, which is reaction-specific. It can be considered a constant, although it does change with temperature (and possible other factors). |
Order
The order of an equation is what the concentration of a substance is raised to in the rate equation. The greater the number, the greater effect it will have on rate. For example, zero order equations do not effect the rate. To find the order, you must alter one concentration and keep the rest the same, Dividing gives an equation which can be used to solve for the order. To find overall order, simply add all orders together.
Zero-Order Equations
Zero-order equations do not depend on the concentrations of the reactants.
| There is only a rate coefficient with no concentrations. The rate probably depends on temperature, and possibly other factors like surface area, sunlight intensity, or anything else except for concentration. These reactions usually occur when a substance is reacting with some sort of catalyst or solid surface. | |
| The integrated rate law tells us how much reactant will remain after a given amount of time. Integrated rate laws can be found using calculus, but that isn't necessary. In this zero-order integrated rate law, is the rate coefficient from the rate equation, is time, and is the starting concentration. |
If you make a graph of concentration vs. time, you will see a straight line. The slope of that line is equal to . This is how you can identify a zero-order rate. |
First-Order Equations
First-order equations depend on the concentration of a unimolecular reaction.
| There is a rate coefficient multiplied by the concentration of the reactant. As with a zero-order equation, the coefficient can be though of as a constant, but it actually varies by the other factors like temperature. There can be other reactants present in the reaction, but their concentrations do not effect the rate. First-order equations are often seen in decomposition reactions. | |
| This is the integrated rate law. | |
| The half-life of a reaction is the amount of time it takes for one half of the reactants to become products. One half-life is 50% completion, two half-lives would lead to 75% completion, three half-lives 88%, and so on. The reaction never quite reaches 100%, but it does come close enough. To find the half-life, you can algebraically manipulate the integrated rate law. |
If you make a graph of the logarithm of concentration vs. time, you will see a straight line with a slope of . This is how you can identify a first-order rate. |
Second-Order Equations
Second-order equations depend on the two concentrations of a bimolecular reaction.
| This is the rate law for a second-order equation. | |
| If there are two molecules of the same kind reacting together, the rate law can be simplified. | |
| In that case, this is the integrated rate law. | |
| This is the half-life for a second-order reaction (with only one reactant). |
To see a graph with a straight line of slope , graph the reciprocal of concentration vs. time. |
Equilibrium
Equilibrium will occur when the forward and reverse rates are equal. As you may have already noticed, the equilibrium expression of a reaction is equal to the rate equations divided.
| Consider this reaction, the dimerization of nitrogen dioxide into dinitrogen tetraoxide. | |
|
|
The forward reaction rate is second-order, and the reverse reaction rate is first-order. |
| The rate coefficients may be different for the two reactions. If the reaction is in equilibrium, the forward and reverse rates must be equal. | |
| Rearranging the equation gives the equilibrium expression. |
Understanding kinetics explains various concepts of equilibrium. Now it should make sense why increasing the reactant concentration will make more products. The forward rate increases, which uses up reactants, which decreases the forward rate. At the same time, products are made, which increases the reverse reaction, until both reaction rates are equal again.
Arrhenius Equation
The Arrhenius equation determines a rate coefficient based on temperature and activation energy. It is surprisingly accurate and very useful. The Arrhenius equation is:
is the activation energy for the reaction, in joules per mole. is the Universal Gas Constant, is the temperature (in kelvin), and is the prefactor. Prefactors are usually determined experimentally.
Reaction Mechanisms

Chemists often write chemical equations for reactions as a single step, which only shows the net result of a reaction. However, most chemical reactions occur in a series of steps called elementary reactions. All of these elementary reactions must add up to equal the overall balanced equation. The complete sequence of these elementary steps is called a reaction mechanism. The reaction mechanism is the step-by-step process by which reactants actually become products. It is the "how" of the reaction, whereas the overall balanced equation only shows the "what" of the reaction.
Rate-Determining Steps
Sometimes, intermediate substances are created in the process that disappear in the end. Take the following example of a homogeneous reaction (where products and reactants are all in the same phase):
There are actually two reactions occurring at different speeds.
- (slow)
- (fast)
Since the first step is the slowest, and the entire reaction must wait for it, it is known as the rate-determining step. The overall reaction rate depends almost entirely on the rate of the slowest step. The other steps are fast enough that their rate is insignificant, as they are always waiting for the slower step to complete.
Why is the first step slower? Collision theory explains whether or not particles react when they collide. The particles must collide with a minimum energy and a proper orientation if a reaction is to occur.
The minimum energy needed for a reaction to occur is its activation energy. The particles must be moving fast enough for their collision to satisfy the activation energy. Without the necessary energy, the particles will bounce off each other with no reaction. A good example of activation energy is a butane lighter, which needs a spark before the fluid burns. The spark provides enough energy to the particles to make their collisions effective.
Reactions with high activation energy will be slower than those with low activation energy. With a high activation energy, less particles are likely to generate the needed energy when they collide. Reactions that break bonds, especially double or triple covalent bonds, will have higher activation energy.
The particles must also collide with the proper orientation. For example, the reaction in the animation above shows an ammonium ion reacting with a NCO- ion. For the reaction to occur, the ammonium ion must collide with the nitrogen of the NCO-. If the ions don't collide in the right place while facing in the right direction, the reaction cannot occur.
Reactions that have very specific requirements for the orientation of the colliding particles will be much slower. Reactions that can occur without a specific orientation will happen faster.
Determining the Validity of an Elementary Step Model
In order for a proposed elementary step equation to be valid it must fulfil these requirements.
1. The rate equation of the slow step must match the rate equation of the overall reaction.
2. The reactants and products of all the elementary steps added together must equal the one of the actual equation.
3. The rate law for the elementary step must be able to be written without the concentration of the intermediates, because the intermediates are too small to be accurately measured.
For example, if given this equation and asked to prove the rate mechanism
Equation
Proposed Mechanism
(fast)
(slow)
We know that when the reaction occurs backwards, the k changes from k to k^{-1}. So, we substitute in the backwards rate for O_3, and plug it into the slow step. Then, take the rate equation of the slow step. We find that it is the same as the rate law for the overall equation and meets the three criteria above, so this proposed mechanism is valid.
Thermodynamics
Introduction
Thermodynamics is the study of the changes in energy that occur in reactions.
Systems
A system is the set of substances and energy that is being studied. If, for example, reactions are occurring in a jar, everything inside the jar is the system, and everything outside the jar is the surroundings. The surroundings are everything not in the system, which means the rest of the universe. The system and the surroundings together are called the "universe".
One important issue is what kind of interactions exist between the system and its surroundings. Some systems may exchange matter and heat with the surroundings (like a system of boiling liquid losing matter and heat with the vapor). This is called an open system. If there is just heat exchange occurring between the system and its surroundings it is called a closed system. No matter can enter or leave a closed system. And, finally, if there is no exchange of heat and no exchange of matter, the system is completely isolated.
Temperature vs. Heat
If you put a hot iron pot under cold water, it cools down very quickly. This is because iron has a low specific heat, which is the amount of energy required to increase the temperature of one gram of a substance by one degree Celsius (or Kelvin). Solid iron only requires 0.45 J/(g*K), while liquid water holds about nine times as much energy (heat) per degree (temperature). So when water receives energy from the pot, it only warms up by a few degrees, while the pot cools down substantially.
| Temperature is the measure of the kinetic energy of a particle. Heat is energy, measured in joules (J). There is a very big difference between the two. |
Thermochemical Equations
Equations don't just show chemicals; they also show how much energy is required or released. This energy is called enthalpy. There are two ways to write a thermochemical reaction, for example:
Note that the number is negative in the second format. Also, notice how the first equation has double the energy because there are two moles of water. The second equation shows the amount of heat per mole, so the number of moles does not affect it.
From a thermochemical reaction, one can tell the molar heat of formation of a compound. Usually, this is measured at 25°C, and is written as ΔHf°. It is the amount of heat required to make one mole of the substance. The small ° symbol means "standard", as in Standard Temperature and Pressure.
Molar heat of combustion is the opposite of the molar heat of formation. It measures the amount of energy released when a mole of the compound is burned. It is written as ΔHc°.
In thermochemistry, if a reaction takes multiple steps, the heats from each reaction are simply added or subtracted. This is known as Hess's Law. |
Enthalpy
The enthalpy of a chemical system is the "heat content" of the system—the energy it contains. Enthalpy is represented by the symbol .
Enthalpy of Reaction
All reactions have some amount of enthalpy. It is simply the amount of heat absorbed or released by the reaction. Combustion reactions obviously release large amounts of heat. They have negative enthalpy. A negative enthalpy represents an exothermic reaction, releasing heat. A reaction that absorbs heat is endothermic. Its enthalpy will be positive, and it will cool down its surroundings.
Consider these two reactions:
| This reaction is exothermic (negative enthalpy, release of heat). When the reaction occurs, the surroundings will increase in temperature due to the gain of heat the system releases. For every mole of propane (C3H8) formed, 104.67 kilojoules of energy are released. | |
| This reaction is endothermic (positive enthalpy, absorption of heat). When the reaction occurs, the surroundings will decrease in temperature due to the loss of heat the system absorbed. For every mole of NO formed, 756.05 kilojoules of heat are absorbed. (Note that the reaction shows two moles being formed, so the enthalpy is double that of one mole being formed.) |
Although every reaction has a change in enthalpy, the amount depends on the temperature. The same reaction could be endothermic at one temperature and exothermic at another. Enthalpies must be given at a specific temperature. The reactions above show the enthalpies at 25 °C.
Temperature and Heat
There is a relationship between temperature and heat. If an object gains or loses heat without any phase changes, this reaction relates temperature to heat:
is the amount of heat (in joules or kilojoules) and is the change in temperature (Celsius degrees). is the mass of the object (in grams, usually) and is the object's specific heat.
Specific heat is a constant that depends on the particular material of the object. It is measured in joules per gram-degree. It is determined experimentally. You can look it up in a chart, or you can calculate it if you measure the amount of heat added and the change in temperature. The specific heat of water is 4.186 J/g-degree. For one gram of water, the temperature rises/falls by one degree Celsius for every 4.186 joules of heat added/removed.
Entropy
Entropy is the measure of disorder in a system.
An Example
First, let's examine a non-chemistry example. Say you have one card from a deck of playing cards. It can have one of 52 possible values. Now you pick up four more cards. If the deck were shuffled randomly, the odds of you holding, say, a "straight flush" are 0.00154%. The odds of having a "high card", which is essentially a "nothing" hand, is 50.12%. In the case of a straight flush, the cards you are holding are highly organized. They must be in a specific, exact pattern (like 10 9 8 7 6 of the same suit). To have a high card, no two cards must have the same rank and the cards cannot be in order.
There is a very low probability of having a straight flush because the cards are in a very orderly state. There is a large probability of having "nothing" because the cards are in a random, disorderly state. In our card-playing system, straight flushes have low entropy because they are so orderly. "Nothing" hands have high entropy because they are disorderly and random. Furthermore, it takes minimal effort to toss all the cards in the air and randomize their order. Increasing the entropy of the system comes naturally. On the other hand, sorting the cards in order takes time and effort. It does not happen randomly. Decreasing the entropy of the system is unnatural and takes effort, or energy.
In Chemistry
The entropy of a chemical system is a measure of its disorder or chaos. More precisely, it is a measure of the dispersion of energy. A solid has low entropy (low chaos, orderly) because the molecules are locked into a rigid structure. Their energy is not dispersed freely. A gas has high entropy (high chaos, disorderly) because the molecules are free to move about randomly. The energy of the system is dispersed over a large area with unlimited possibilities of the location of each molecule.
As temperature decreases, so does entropy. Theoretically, at absolute zero (0 K, or -273 °C), the entropy of the system would be zero. This is because the solid would be perfectly crystallized so that its energy is not dispersed at all.
As you will soon learn, the Second Law of Thermodynamics tells us that the entropy of the universe always increases. Think about it. If you have built a house of cards, the entropy of the system is low. A house of cards is very orderly, with each card having a very specific location. The house of cards will undoubtedly collapse. The resulting pile of cards is very disorderly. The cards can be in any position and still be a random pile of cards. The entropy has increased spontaneously. Houses of cards will spontaneously collapse, but they never spontaneously build themselves up. This is because high entropy is natural and low entropy is unnatural.
Entropy Changes
When analyzing the entropy change of a chemical reaction, you would need specific numbers. As a guideline, you can estimate the entropy change based on some basic rules:
- Melting and boiling increases entropy
- Freezing and condensing decreases entropy
- Dissolving a solute increases entropy
- Forming precipitates decreases entropy
If you do happen to know the absolute entropy of substances in a reaction (by looking it up in a chart), you can calculate the change in entropy. Entropy is symbolized with . The change in entropy is . As with enthalpy, the degree symbol () represents STP. The change in entropy is the absolute entropy of the products minus the absolute entropy of the reactants.
See also
- Entropy for beginners- a Wikibook that provides a mathematical explanation.
The First Law
The First Law of Thermodynamics is simply a restatement of the Law of Conservation of Energy. There are a few ways of stating it, but they all mean the same thing:
- "Energy is neither created nor destroyed. It can only change form."
- "The change in the system's thermal energy is equal to the heat added to the system minus the work done by the system."
The first definition is self-explanatory. As an example, a propane grill does not "create" energy when it cooks food. The energy stored within propane molecules and oxygen atoms is released in the form of heat and light when the propane molecules reassemble themselves into carbon dioxide and water (the combustion reaction). Energy has not been created or destroyed. It has simply changed from chemical potential energy into light and thermal energy.
The second explanation comes from a physics point of view. It means that adding heat to a system increases its internal energy, and a system that does work (like breaking bonds or assembling large molecules from small ones) decreases its internal energy. Overall, the total amount of heat, work, and energy remains constant. This should make sense because heat is energy and work is energy being applied, so based on the first definition, all forms of energy must be accounted for.
The First Law is much more useful in Physics than it is in General Chemistry. |
The Second Law
Introduction: A powerful law.
The second law of thermodynamics is based on our common human experience. It didn't begin with complicated apparatus or complex theories, but rather with thinking about how old-fashioned steam engines worked and the first important equation appeared to be very simple: just q/T.
Yet the second law is probably our most powerful aid in helping us understand why the world works as it does both in simple and in complex ways: why hot pans cool down, why ping pong balls don't bounce forever when they are dropped, why gasoline (plus the oxygen in air) makes engines run, why our "engines"—our bodies—run and we continue to live and our bodies stay warm even when it's cold, but also why we die when some chemical reactions within us fail. In fact, the second law helps to explain everything that happens in our physical world. In chemistry, it's especially important because it can tell us whether any chemical reaction that we write on paper will probably be spontaneous and go as we have written it.
The Big Problem
Unfortunately, for almost a century and a half, the second law has been expressed by experts in ways that a beginner in chemistry could not possibly understand without a great deal of additional explanation. Here are just three of some 25 explanations that have been most prominent:
- "The entropy of the universe increases toward a maximum" (Clausius)
- "It is impossible in any way to diminish the entropy of a system of bodies without thereby leaving behind changes in other bodies" (Planck)
- "In any irreversible process the total entropy of all bodies concerned is increased." (Lewis)
Entropy, entropy, entropy! But what is entropy? Even some textbooks still say something like "Don't ask about understanding it. Just work the problems that have entropy in them and you'll gradually understand it because you will be able to work with it"! That's the old way which fortunately has been discarded by most US general chemistry texts. (See list here.) The good news of the twenty-first century is that now entropy can be described as a simple idea (no matter how complex to calculate and deal with in advanced courses and research.) Because of our new conceptual approach, a basic version of the second law can be understood easily.
A Modern Version
"Energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy change is the quantitative measure of that kind of a spontaneous process: how much energy has flowed or how widely it has become spread out at a specific temperature." See here. |
What does that "energy of all types" and "becoming dispersed" mean? Let's first think about light (which technically is electromagnetic radiation). Does the radiation from a light bulb stay inside that glass of the bulb? Of course not. It spreads out just as far as it can, hindered from dispersing to miles and even farther only by dust or air density differences. What about the sound from a stereo speaker—does it stay inside a dorm room or a car? It disperses farther than other people want to hear it, usually! And what happens to the kinetic energy of a fast moving car if the car should hit a brick wall? It spreads out in a crashing sound, in twisting metal and heating it and tearing apart the bricks of the wall so that they fly around, slightly warmer than they were. Those are just a few examples of different types of energy and some ways in which they become dispersed or spread out.
Energy of all types disperses...if it is not hindered from doing so. |
The Importance of the Second Law
In chemistry, the type of energy in which we are most often interested is the kinetic energy of molecules, molecular motion energy. We know from Kinetic Molecular Theory that molecules are in constant motion if their temperatures are above 0 K. In gases like nitrogen and oxygen, they are moving at an average speed of a thousand miles (1600 km) an hour at 298 K and go about 200 times their diameter before bumping into another molecule [citation needed]. The molecules in liquids may be moving approximately as fast even though they are constantly hitting one another as they move a little here and there. In solids the particles, molecules or atoms or ions, can only "dance in one place" (vibrating in coordination with the other particles in the solid). This is a kinetic energy of vibration that is equivalent to the motion energy of gases or liquids at the same temperature.
The motion energy of molecules consists of their translation, rotation, and vibration (Figure 1 here.) Note that this vibration is vibration inside a molecule and by itself, as though the chemical bonds between atoms were like springs. The vibration in a crystal that we were just talking about is a vibration of a whole molecule or other particle in one place and coordinated with the other molecules in the crystal.
Examples from Everyday Life
Let's see how the second law helps us to understand our common experience better, to see how so many totally different events really are just examples of energy dispersing or spreading out, i.e., of the second law. A rock will fall if you lift it up and then let go. Hot frying pans cool down when taken off the stove. Iron rusts (oxidizes) in the air. Air in a tire is at a high pressure and shoots out even from a small puncture to the lower pressure atmosphere. Ice cubes melt in a warm room.
A Falling Rock
A rock has potential energy (PE) localized in it when you lift it up above the ground. The rock is the system; everything else it encounters is the surroundings. Drop the rock and its PE changes to kinetic energy (energy of movement, KE), pushing air aside as it falls (therefore spreading out the rock’s KE a bit) before it hits the ground, dispersing a tiny bit of sound energy (compressed air) and causing a little heating (molecular motion energy) of the ground it hits and in the rock itself. The rock is unchanged (after a minute when it disperses to the air the small amount of heat it got from hitting the ground). But the potential energy that your muscles localized in by lifting it up is now totally spread out and dispersed all over in a little air movement and a little heating of the air and ground.
A Hot Frying Pan
A hot frying pan? The iron atoms in a hot frying pan (system) in a room (surroundings) are vibrating very rapidly, like fast "dancing in place". Therefore, considering both the pan and the room, the motion energy in the hot pan is localized. That motion energy will disperse—if it is not hindered, according to the second law. Whenever the less rapidly moving molecules in the cooler air of the room hit the hot pan, the fast-vibrating iron atoms transfer some of their energy to the air molecules. The pan’s localized energy thus becomes dispersed, spread out more widely to molecules in the room air.
Some Rusting Iron
In a chemical reaction such as iron rusting, i.e., iron plus oxygen to form iron oxide (rust), the reactants of iron and oxygen don't have to be at a high temperature to have energy localized within them. Iron atoms (as -Fe-Fe-Fe-) plus oxygen molecules of the air (O-O) have more energy localized within their bonds than does the product of their reaction, iron rust (iron oxide).
That’s why iron reacts with oxygen—to release energy from their combined total of higher energy bonds and form the lower energy bonds in iron oxide. Then, all that difference in energy becomes dispersed to the surroundings as heat i.e., the reaction is exothermic and makes molecules in the surroundings move faster. But remember how chemical reactions occur! Remember that it requires energy to break bonds and therefore to start any reaction there must be some extra energy, an activation energy supplied somehow to break a bond or many bonds in the reacting substances. (For information about activation energies, see here.) Then, if the bonds that are being formed in the product are much stronger than those being broken in the reactants, that difference in energy (which usually causes greater motion energy of all the molecules) can feed back to break more bonds in the reactants.
However, in the case of iron reacting with oxygen at normal room temperature around 298 K, the process is very slow because only a few oxygen atoms are moving exceptionally fast and hit the iron just right so an Fe-Fe bond and an O-O bond are broken and an Fe-O bond can form. There isn't enough heat (motion energy) localized in nearby iron atoms, and there are no other unusually fast-moving oxygen molecules. It's a slow process depending on collision of the small amount of fast moving oxygen atoms in the surroundings to make it happen.
Therefore, even in moist air (that speeds up another process yielding iron oxide), iron doesn't react very rapidly with oxygen but it steadily does so and in time, both the iron atoms and the oxygen molecule spread out to the surroundings the portion of their bond energy that iron oxide doesn't need for its existence at that temperature.
A Leaky Tire
Air in a tire is at a higher pressure than the atmosphere around it, so it shoots out even from a small hole. What could that have to do with a big deal like the Second Law of Thermodynamics? (Every spontaneous physical or chemical process involves the second law!) Those nitrogen and oxygen molecules in the tire each have motion energy but it is far more localized, compressed in the small volume of the tire, than it would be in the huge volume of the atmosphere. Thus, the second law explains why punctures or blowouts occur: the motion energy of those localized molecules will become dispersed and spread out to the lower-pressure, larger-volume atmosphere if it is no longer hindered by the tire walls from becoming so.
A Melting Ice Cube
An ice cube melts in a big warm room. How can the melting of a little ice cube in a warm room maybe 200,000 times bigger than it is be an example of the second law? How could that possibly be a spreading out of energy? But the second law has to do with energy dispersal and there's a little spreading out in that 200,001st part of that total of system plus surroundings!
Hotter goes to cooler spontaneously. Always. |
Lots of things are happening when molecules of the warm air disperse some of their energy to the molecules that are vibrating (like dancing rapidly in one place) in the ice cube. Right at the surface many hydrogen bonds between the water molecules of the ice are broken by the motion energy of the air molecules being transferred to the those surface molecules. (This doesn't change the amount of motion energy of those molecules and therefore their temperature doesn't change. They increase in potential energy due to the hydrogen-bond breaking.) Now, because the water molecules whose hydrogen bonds to other molecules in the rigid ice structure are broken, they are free to form hydrogen bonds to other water molecules that are liquid—they can exchange partners and move from one to another. The vibrational energy that allowed them to dance in place in the crystal is changed to translational energy in the liquid and the molecules can move just a bit.
Thus, although the true picture is just a bit more complex (i.e., it is the closer energy levels in translation than in solid vibration that make the energy far more dispersed in liquid than solid), we can sense that the movement of molecules in liquid water allows the energy to be more spread out than in crystalline ice, even at melting temperature. It is not a matter of order and "disorder"! (That's as misleading as magic and as obsolete as 1898 fashions. See here.)
Order to Disorder
The second law tells us about energy dispersal, and entropy is the word for how that energy dispersal is measured—how spread out the energy becomes in a system, how much more dispersed it has become compared to how localized it was. Such energy changes and consequent entropy changes are the focus for understanding how and why spontaneous events occur in nature. Only sometimes do the structures or arrangements of molecules in an object help us to see greater or lesser localization of energy (that used to be called "order to disorder").
Now we can understand what scientists have been talking about the last century and a half when they spoke in apparently mysterious sentences like "The entropy of the universe increases toward a maximum." All they meant was simply that energy, everywhere, spreads out as much as it can (and that spreading out of energy is measured by entropy).
Recap and Conclusion
Rocks falling down mountains, hot pans cooling in cool rooms, anything made of iron rusting, anything burning or reacting with oxygen, all these types of spontaneous events and chemical reactions that occur by themselves are due to energy dispersing or spreading out. Entropy is the quantitative measure of how much energy and how much dispersal occurs in a process or a reaction. Therefore, entropy is constantly increasing because spontaneous events continue to occur in our energy-rich universe. Thus, we can decipher the following statement of the second law:
"In any irreversible process the total entropy of all bodies concerned is increased."
That just means: "In any process in which energy becomes spread out, the measure of that spreading out or dispersing (i.e., the total entropy) increases when you include both what happens in the system AND its surroundings.”
Now we can translate "second law language"! It seems very confusing if you read it rapidly, but taking it a few words at a time and knowing what we have just reviewed, the ideas are not complicated.
Free Energy
Introduction
What's the point of entropy and enthalpy? So far, you have studied equilibrium to tell you how far a reaction occurs and kinetics to tell you how fast a reaction occurs. Thermodynamics can tell you if a reaction will occur, and at what temperatures. It may seem too obvious, but why does an ice cube spontaneously melt when it is at 30 °C? Melting is endothermic, so it would seem that the reverse reaction (freezing) is favored. After all, reactions that release heat are usually more favorable than those that absorb heat.
The answer is free energy (also called Gibbs Free Energy). The change in free energy for a reaction ultimately determines if it can occur spontaneously or not. Free energy is a combination of entropy and enthalpy, and when a reaction decreases the free energy, it will occur spontaneously.
The Equation
Free energy is defined by . By measuring or calculating the entropy change and enthalpy change of a reaction, you can determine the change in free energy. Notice that free energy depends on temperature as well. In this equation (as with all other thermo equations) must be an absolute temperature, measured in Kelvin. So the freezing point of water is not zero but rather 273 K. By using the Kelvin temperature scale, all temperatures will be greater than zero.
When you have solved for for a particular reaction at a certain temperature, you will find one of three possible outcomes:
| Reaction type | Means... | |
|---|---|---|
| exergonic | the reaction occurs spontaneously. | |
| the reaction is at equilibrium. | ||
| endergonic | the reaction will not occur. | |
Equipped with this knowledge, you can determine the temperature at which a reaction will be at equilibrium (by setting G to 0 and solving for T). If a reaction is endergonic, it will not occur spontaneously. However, at a different temperature, the reaction might occur. Also, the reverse reaction will have an opposite value for G. For example, the combustion of propane will have a large negative value for its change in free energy. The reverse reaction would have the same large value, but positive. This makes sense, knowing that propane does not spontaneously precipitate from the smokey exhaust of a grill.
Spontaneity
Let's return to the example of a melting ice cube. At T = 273 K (0 °C) the processes of freezing and melting are at equilibrium. ΔG must equal zero. At higher temperatures, the melting process occurs spontaneously, so we can deduce that ΔH is positive and ΔS is also positive. We already know that melting is endothermic and increases entropy, so it seems the free energy equation works.
Between entropy and enthalpy, there can be four possible outcomes:
| Result | |||
|---|---|---|---|
| + | - | always + | never spontaneous |
| - | + | always - | always spontaneous |
| + | + | + for low T, and - for high T | depends on T |
| - | - | - for low T, and + for high T | depends on T |
We can see that the melting of an ice cube is spontaneous for high temperatures.
Relating Free Energy
Free energy is related to equilibrium, as we have already seen. There is an equation that will allow you to convert between reaction free energy and the equilibrium constant for a particular reaction at a given temperature:
is the Universal Gas constant, and is the natural logarithm. A scientific calculator will have a [LN] to calculate logarithms and a [e^] button to calculate anti-logarithms.
The Elements
Group 1
Alkali Metals

The alkali metals are the elements in Group 1 (1A). They are lithium, sodium, potassium, rubidium, cesium, and francium.
These elements are best marked by their reactivity. Physically they are soft, shiny (when freshly prepared) solids with low melting points; they conduct electricity well. They all have one valence electron that they lose easily to almost any electronegative substance. Alkali metals are never found in their elemental form outside the lab because they are too reactive. Even the smallest amount of oxygen or water would react with the metal. For this reason, alkali metals have no structural use. They must be kept under inert liquids such as kerosene or in inert gases (nitrogen suffices for any of these elements other than lithium).
Alkali metals have many uses in both biological life and industry. Francium, however, is radioactive and decays rapidly to other elements, so it has no commercial use and its chemical properties are vaguely understood.
All oxidize easily to the +1 oxidation state.
The alkali metals have very similar chemical and physical properties. They can be studied as a whole, rather than element-by-element, due to this similarity. |
Safety
Leave experiments with alkali metals to the experienced chemists. These metals are also highly toxic and will result in severe harm if ingested or make to contact skin.
Alkali metals are dangerous. Their reactions release enough heat to cause flames, and may produce explosive byproducts like hydrogen gas. Never cast any alkali metal into water or acids. These metals should never be allowed to touch flesh because they react with any water upon them and yield corrosive hydroxides that damage flesh. |
Reactions
Alkali metals react violently with water, halogens, and acids. The reactions release surprising amounts of heat and light. In a chemical equation, alkali metals are represented with an M. Here are some example equations:
| Alkali metals react with oxygen to form oxides, which have a duller appearance and lower reactivity. The oxides are much less reactive than the pure metals. | |
| However, the oxides do react vigorously with water to form a hydroxide. The resulting hydroxides of these elements dissociate completely in water to form some of the strongest bases known. "Lye" is an industrial-strength base, which is sodium hydroxide (NaOH). | |
| These hydroxides react readily with acids to form water and their corresponding alkali salt in a neutralization reaction. | |
| The pure alkali metal can also react directly with water. In this case, the metal is a basic anhydride. Gaseous hydrogen is released, which is flammable. | |
| Exposing an alkali metal to a halogen will cause an extremely exothermic reaction that results in an ionic salt. |
Almost every salt of an alkali metal is highly soluble in water. They form conducting solutions, proving their ionic nature.
Flame Tests
When burned in a flame, the alkali metals give off a unique color that can be used to identify them.
- Flame Tests
-
Lithium (pinkish-red flame)
-
Sodium (yellow flame)
-
Potassium (pale violet flame)
Group 2
Alkaline Earth Metals
They are less reactive than alkali metals, but they form (except for beryllium) alkaline oxides and hydroxides.
Alkaline earth metals all have two valence electrons, and they easily oxidize to the +2 state. With increasing mass, these elements become softer, have lower melting and boiling points, and become more reactive. None appear uncombined in nature, and all are separated from their compounds with difficulty. Alkaline earth metals react with halogens and (except for beryllium) with water and oxygen. Magnesium, being less reactive, reacts only at higher temperatures than the other alkaline earth metals. Radium is radioactive, so its chemical properties are difficult to study.
The alkaline-earth metals have very similar chemical and physical properties. They can be studied as a whole, rather than element-by-element, due to this similarity. |
The alkaline earth metals are chemically and physically similar to the alkali metals, but they are less reactive.
Alkaline earth metals are very flammable. Their reactions could release enough heat to cause flames, and may produce explosive byproducts like hydrogen gas. Use caution when handling these metals. Calcium, strontium, and barium react with water and form corrosive hydroxides. Salts of beryllium are toxic, and water-soluble or acid-soluble salts of barium are toxic. |
Reactions
The alkaline earth metals undergo reactions similar to the alkali metals, but their +2 oxidation state causes their compounds to be different. The following reactions use magnesium as an example, but the other alkaline earth metals undergo the same reactions as well.
| Magnesium oxide forms slowly unless ignited. Powders or thin slices of magnesium can be ignited with a match, so magnesium is used in fire-starting devices. | |
| Magnesium burns readily in oxygen, and surprisingly nitrogen as well. Air is composed mostly of nitrogen, but most elements will not react with nitrogen because nitrogen is so stable. | |
| Magnesium oxide is a basic anhydride. Magnesium hydroxide is a strong base, although its solubility is too low for this property to be significant. | |
| Magnesium nitride will react with water or the moisture in air. This reaction is detected by the pungent smell of ammonia. | |
| Magnesium metal reacts with water to form a hydroxide, but only at high temperatures or in the presence of acid. Calcium, being more reactive, will react with water as long as its hot. The other elements will react in warm water. Notice the flammable hydrogen gas that is released. | |
| Magnesium will react exothermically with acids to form an ionic salt and hydrogen gas. |
Remember that all of the alkaline earth metals can undergo these reactions; magnesium was just an example. Beryllium, however, is much less reactive than the other metals, so it might not react.
Uses
Beryllium is rare and its compounds are very toxic, which makes processing it something limited to specialists trained in dealing with it safely. It is the lightest element that is sturdy enough to be used for construction and it is used for windows of X-ray tubes. Its absorption of X-rays is very small, because it only has 4 electrons per atom.
Magnesium metal has some use in applications needing a soft, light metal. Magnesium metal can be used an easily-burned substance with a bright light in photographic flash bulbs. Magnesium hydroxide is commonly used as a strong but generally safe antacid. Magnesium sulfate is commonly known as Epsom salts.
Even more significantly, magnesium appears in a compound known as chlorophyll, the greenish pigment in plants and algae that allows plants to perform photosynthesis. It is essential to plant life.
Calcium has no use as a structural metal, but its compound calcium carbonate is a major building material as limestone. Calcium carbonate is essential to bones and to plant life. Calcium and heavier elements in this group react with warm water to form highly-alkaline hydroxides.
Strontium, much rarer than calcium, has few uses. Barium, also rarer, has few uses other than its sulfate, a coating used for lining the digestive organs for X-rays (Barium meal). Compounds of barium soluble in either water or acids (but not the sulfate) are highly toxic.
Radium is rare and strongly radioactive; it is extremely dangerous due to its intense radioactivity.
Group 13
Group 13 (IIIA) consists of boron, aluminum, gallium, indium, and thallium. Boron is a metalloid, but the other elements are metals. All elements in this group have three valence electrons.
Because these elements have varying properties, they will be studied element-by-element, rather than as a group. |
Boron


Boron is a metalloid, exhibiting characteristics of both metals and non-metals. It is never found in its pure form in Earth, but it is a component of some minerals. However, pure boron can form as a result of chemical reactions. It can be a brown amorphous solid, or a crystalline solid. In the crystalline form, it is black and very hard.
Boron is a poor conductor of electricity at normal temperatures, but at high temperatures it does conduct electricity. Its chemical properties are mostly, but not entirely, non-metallic. Boron is the least electronegative non-metal, so it readily loses electrons when reacting. Boron is almost entirely in the +3 oxidation state. Boron has an oxide B2O3, and it is acidic.
| Boric halides are volatile substances that attack water with the formation of boric acid B(OH)3 and hydrogen halides. | |
| Boric acid reacts with water to release a proton. It is a weak acid. | |
| Boric oxide, at extremely high temperatures, can react with carbon to form boron carbide. Boron carbide is incredibly strong, finding use as tank armor. |
In a manner similar to carbon, boron can form stable covalent network solids. Each boron atom bonds to three other borons, forming a large crystal. |
Boron has interesting properties when it bonds covalently. It has three electrons, so it usually forms three single covalent bonds, an exception to the octet rule. Substances like boron trichloride (BCl3), boric acid, and the borate ion (BO33-) are examples of boron's tendency to form three covalent bonds.
Aluminum
Aluminum (British spelling aluminium) is a metal, although it is too reactive to exist in pure form. Instead, it is found in a wide variety of minerals including bauxite, the primary source for extracting aluminum. Aluminum is the third most abundant element in Earth's crust.

Unlike boron, aluminum is an almost stereotypical metal in its physical properties: it is malleable and ductile, and it conducts heat and electricity very well. Because of its lightness, resistance to corrosion, attractiveness (approaching that of silver), and inexpensiveness to process along with adequate strength for many commercial and domestic uses, it is the third-most used of all metals. Only iron and zinc exceed it in production.
Aluminum compounds typically exist in the +3 oxidation state. Because of its durability and light weight, aluminum is used in many alloys, mixtures of metals. Two metals, each with desirable characteristics, can be mixed together to produce an alloy that has the properties of both metals. Aluminum used to be used for household wiring, but it expands too much when heated. The expansion causes the wires to come loose, and house fires can start.
Aluminum seems unreactive because of a thin, hard surface of aluminum oxide Al2O3 which does not react with water or oxygen and preserves the aluminum metal underneath it from chemical attack. Pure aluminum will immediately form this layer when exposed to air. Although aluminum is very conductive, aluminum oxide does not conduct electricity.

|
|
Aluminum oxide is amphoteric—it reacts violently to neutralize strong bases or strong acids. |
| Reacting aluminum with a halogen results in an aluminum halide. Aluminum chloride can exist as an ionic solid or a covalent solid, but either way it is a weak conductor. | |
| Aluminum chloride is a Lewis acid, able to neutralize bases. | |
| Molten aluminum reacts violently with some metal oxides in the thermite reaction, in which a substance like iron oxide is reduced to iron and aluminum is oxidized to its oxide. This is a highly exothermic reaction, releasing enough heat to weld metal. |
Generally, aqueous aluminum is found as a hydroxide Al(OH)3.
Others

Gallium is a brittle metal that melts slightly above room temperature, so holding it in your hand would liquefy it. One magic trick, the 'melting spoon' involves stirring a hot liquid (usually hot water) with a spoon specially made of gallium. The spoon melts in the water and 'disappears'. (The gallium simply sinks to the bottom of the cup; after the magic trick is done the 'magician removes the water and the molten gallium and pours the gallium into a mold that makes a new spoon for doing the trick again). Gallium is used in many semiconductor devices and LEDs (light emitting diodes). Gallium(III) arsenide is an important semiconductor used in many electronics.
Indium's most common isotope is radioactive and decays slowly into tin. Indium typically has the +3 oxidation state.
Thallium tends to appear in the +1 (thallous) oxidation state as well as the +3 (thallic) oxidation state. Oddly, thallium acts much like an alkali metal in its physical and chemical properties. Thallous oxide (Tl2O) and the metal react violently with water to form a hydroxide TlOH that completely dissociates into Tl+ and OH- ions as if it were an alkali metal hydroxide. Its halides are quite salt-like, dissociating into ions into solutions that, like solutions of salts of the alkali metals, conduct electricity.
Thallium has a violent reaction with water that could release enough heat to cause flames, and may produce explosive byproducts like hydrogen gas. Thallium hydroxide that results from this reaction is as strongly alkaline as alkali-metal hydroxides and is similarly corrosive. In addition, thallium compounds are extremely toxic. |
Neither thallium metal nor any thallium compound is readily available in the United States because it is so dangerous and has few legitimate uses.
Group 14
General Chemistry/Chemistries of Various Elements/Group 14
Group 15
General Chemistry/Chemistries of Various Elements/Group 15
Group 16
General Chemistry/Chemistries of Various Elements/Group 16
Group 17
General Chemistry/Chemistries of Various Elements/Group 17
Group 18
General Chemistry/Chemistries of Various Elements/Group 18
Hydrogen
General Chemistry/Chemistries of Various Elements/Hydrogen
Transition Metals
General Chemistry/Chemistries of Various Elements/Transition Metals
Inner Transition Metals
General Chemistry/Chemistries of Various Elements/Inner Transition Metals
Synthetic Elements
General Chemistry/Chemistries of Various Elements/Synthetic Elements General Chemistry/Chemistries of Various Elements/Salsal Liquidity
Periodic Your Face
General Chemistry/The Stupid Table/Print Template:Print chapter heading General Chemistry/Units Template:Print chapter heading General Chemistry/Constants Template:Print chapter heading General Chemistry/Useful Equations Template:Print chapter heading General Chemistry/Standard Reduction Potentials Template:Print chapter heading General Chemistry/Table of the Chemical Elements and their Properties
GNU Free Documentation License
GNU Free Documentation License
- ↑ Conventions in Chemistry. In The ACS Style Guide, 3rd ed.; Coghill, A. M.; Garson, L.R., Eds.; Oxford University Press: New York, 2006; p 294.










































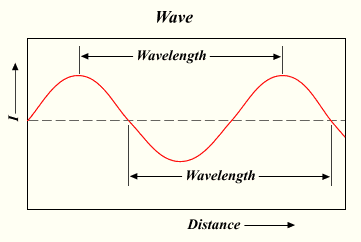















































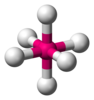


















































![{\displaystyle {\hbox{2Pb}}({\hbox{NO}}_{3})_{2(aq)}{\xrightarrow[{}]{\Delta }}{\hbox{2PbO}}_{(s)}+4{\hbox{NO}}_{2(aq)}+{O}_{2(g)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dab5222df42907e7f5e71216d61165c8a5c83d6)



























































![{\displaystyle K_{w}=[{\hbox{H}}^{+}]\times [{\hbox{OH}}^{-}]=1.00\times 10^{-14}mol^{2}/L^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/790030d0b44753554ad23049c576814f513eb283)
![{\displaystyle pH=-\log {[{\hbox{H}}^{+}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db7b4a87e6e3e6cd82afb2a12c8324fc4a0bba06)
![{\displaystyle pOH=-\log {[{\hbox{OH}}^{-}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84746d9407b7fb0614a26efbbf53b3daf5141dbb)





![{\displaystyle {\hbox{pH}}={\hbox{pK}}_{a}+\log {\frac {[{\hbox{A}}^{-}]}{[{\hbox{HA}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4c5760bf4e00196bdd3fe7b1010ac4d9571f64a)
![{\displaystyle {\hbox{pH}}={\hbox{pK}}_{b}+\log {\frac {[{\hbox{B}}]}{[{\hbox{HB}}^{+}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/896d4ff31991bf9035cac9c7d2b4860b7a5d9b5f)



































































































![{\displaystyle K_{eq}={\frac {[C]^{x}[D]^{y}}{[A]^{m}[B]^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f0947572ef0bba82d8977d644ee1381e60cc917)





![{\displaystyle K_{eq}={\frac {[Z]}{[X][Y]^{2}}}={\frac {[3.5]}{[4.0][3.0]^{2}}}=0.097}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fef9ad0fcb8cb5d1c3cdeb93ede278452a416dc2)

![{\displaystyle 51.5={\frac {[2y]^{2}}{[5.00-y][5.00-y]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aaf2915849421705724e01f1c43ae08f1a1213d)

![{\displaystyle K_{c}={\frac {[H_{2}][CO_{2}]}{[CO][H_{2}O]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2524b943811505b44fe0483c1db3b8b17e03d157)


![{\displaystyle K_{a}={\frac {[H^{+}][A^{-}]}{[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83ee86c6746a584bd7b209324db405b0563af917)
![{\displaystyle K_{b}={\frac {[{\mbox{OH}}^{-}][{\mbox{BH}}]}{[{\mbox{B}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e768575505bf031785e6078b9450a3f28595fccc)
![{\displaystyle K_{sp}={\frac {[A^{+}][B^{-}]}{[AB]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b97eafe20524ea1a4f77dff31f64d125535465e)







![{\displaystyle K_{a}={\hbox{K}}[{\hbox{H}}_{2}{\hbox{O}}]={\frac {[{\hbox{H}}_{3}{\hbox{O}}^{+}][{\hbox{A}}^{-}]}{[{\hbox{HA}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3e434d3d222744e2e6e914f1f3b3c706005bc4c)

![{\displaystyle K_{b}=K[{\hbox{H}}_{2}{\hbox{O}}]={\frac {[{\hbox{BH}}^{+}][{\hbox{OH}}^{-}]}{[{\hbox{B}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25ee0c94c1849358104f3cb07e6a70df8128e47b)

![{\displaystyle K_{w}=[{\hbox{H}}_{3}{\hbox{O}}^{+}][{\hbox{OH}}^{-}]=1.0\times 10^{-14}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/676aea4cae67421f52aa5a90432f38804f9c3a69)


![{\displaystyle K_{b}={\frac {[{\hbox{HA}}][{\hbox{OH}}^{-}]}{{\hbox{A}}^{-}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a0d87c279ca9bfe5c62b2bcf699628deb7229be)
![{\displaystyle {\begin{matrix}{\frac {[{\hbox{H}}_{3}{\hbox{O}}^{+}][{\hbox{A}}^{-}]}{[{\hbox{HA}}]}}&\times &{\frac {[{\hbox{HA}}][{\hbox{OH}}^{-}]}{[{\hbox{A}}^{-}]}}&=&[{\hbox{H}}_{3}{\hbox{O}}^{+}][{\hbox{OH}}^{-}]\\K_{a}&\times &K_{b}&=&K_{w}\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdc565500748a5a4b7269dee9fbc76b267e5d41a)
![{\displaystyle K_{a}={\frac {[{\hbox{H}}_{3}{O}^{+}][{\hbox{A}}^{-}]}{[{\hbox{HA}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b43c0d9fc7dc2143d7f12e94437c462e9f59b34)
![{\displaystyle K_{b}={\frac {[{\hbox{BH}}^{+}][{\hbox{OH}}^{-}]}{[{\hbox{B}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bfb365d61be0d27198a627e1acacc8b0f215bba)


![{\displaystyle K={\frac {[{\hbox{A}}^{+}][{\hbox{B}}^{-}]}{[{\hbox{AB}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d000940075140a3054a039fc752f60e2a7e16286)
![{\displaystyle K_{sp}=[{\hbox{A}}^{+}][{\hbox{B}}^{-}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b943ab51b7794e836eba7db528e07de134178e9e)
![{\displaystyle K_{sp}=[{\hbox{Ca}}^{2+}][{\hbox{Cl}}^{-}]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69f430ebecddd22591aea9ce39f781cfc6c05246)
![{\displaystyle K_{sp}=[{\hbox{Ca}}^{2+}][{\hbox{OH}}^{-}]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4ec7f73b2b28f427c009893a331041a83934bb1)


![{\displaystyle K_{sp}=[Ag^{+}]^{2}[SO_{4}^{2-}]=1.20\times 10^{-5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/594a8257e85e86894cfbdff55057bfd0fee64d4d)



![{\displaystyle K_{sp}=[{\hbox{Ag}}^{+}][{\hbox{Cl}}^{-}]=1.77\times 10^{-10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c53c75711061cc55cfb8cc096f598f08637e4f8)










![{\displaystyle r=-{\frac {1}{a}}{\frac {d[{\hbox{A}}]}{dt}}=-{\frac {1}{b}}{\frac {d[{\hbox{B}}]}{dt}}={\frac {1}{c}}{\frac {d[{\hbox{C}}]}{dt}}={\frac {1}{d}}{\frac {d[{\hbox{D}}]}{dt}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c02c09323272da70d4ddf07dc8a55c5fc4ed83b7)
![{\displaystyle r=k[{\hbox{A}}]^{a}[{\hbox{B}}]^{b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32787e3030d5c8b45d2a3720a7eb8b3cee5d2f45)






![{\displaystyle r=k[{\hbox{A}}]^{m}[{\hbox{B}}]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d89babc636e9b49f98acf99dafe13de4556d19ba)
![{\displaystyle r=k[{\hbox{C}}]^{p}[{\hbox{D}}]^{q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e30f98d11645c6001e87f44b177bb1719e37594)

![{\displaystyle [{\hbox{A}}]=[{\hbox{A}}]_{0}-kt\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cff4044260a943e6bbc67cc29cc2824767609c5e)

![{\displaystyle [{\hbox{A}}]_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cea3c93fddf582a6669202f14b9eec7d7a660566)

![{\displaystyle r=k[{\hbox{A}}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3531a7014c322fa54ccf565a966c62eed058fbd)
![{\displaystyle \ln[{\hbox{A}}]=-kt+\ln[{\hbox{A}}]_{0}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/241a630889a6c51a0755a8b5fa2ac24168f94758)

![{\displaystyle r=k[{\hbox{A}}][{\hbox{B}}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff2a45ee0bc0ef59e04ae952c92c569fc2f48b8)
![{\displaystyle r=k[{\hbox{A}}]^{2}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcd83664041186b60bc2b3980e3282a5fd7c8c4a)
![{\displaystyle {\frac {1}{[{\hbox{A}}]}}={\frac {1}{[{\hbox{A}}]_{0}}}+kt\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9872c36943a88f0c05b6098169332e09b562d77d)
![{\displaystyle t_{1/2}={\frac {1}{k[{\hbox{A}}]_{0}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5da00b017a5225f4e778e3e10d83153d686ab51a)

![{\displaystyle r_{f}=k_{f}[{\hbox{NO}}_{2}]^{2}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f41dfcd3070995dd736139677ee6e6408fa7b94)
![{\displaystyle r_{r}=k_{r}[{\hbox{N}}_{2}{\hbox{O}}_{4}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a4e1102124ac6b0bce8b71d0f17f6e07acbb5c3)
![{\displaystyle k_{f}[{\hbox{NO}}_{2}]^{2}=k_{r}[{\hbox{N}}_{2}{\hbox{O}}_{4}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/857871cb319667edc42351587028d567b3a5fb19)
![{\displaystyle K_{eq}={\frac {k_{f}}{k_{r}}}={\frac {[{\hbox{N}}_{2}{\hbox{O}}_{4}]}{[{\hbox{NO}}_{2}]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/521d60a026ef93e04313a8369b47214d4286ba96)








![{\displaystyle rate=k[O_{3}]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80a54ed71ac85b0bba4037eb7d86f5030b4edcc5)








































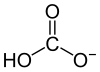






















































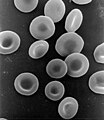

































![{\displaystyle \mathrm {pH} =-\log {[\mathrm {H^{+}} ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6b90a9962bfbf6fac21259a72a1f536869ae942)
![{\displaystyle \mathrm {pOH} =-\log {[\mathrm {OH^{-}} ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a64f2ac3d1b19b7d84660e21ffc72bb70a657a87)


![{\displaystyle K_{eq}={\frac {[\mathrm {C} ]^{c}[\mathrm {D} ]^{d}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/122a96015b87c1c5135f00282abab2ad84917f5e)




