Fractals/Iterations in the complex plane/def cqp

Definitions

Bailout test

If z_n is in the target set $T\,$ then z₀ is escaping to infinity ( bailouts ) after n forward iterations ( steps).

The output of test can be :

• boolean ( yes/no)
• integer : integer number (value of the last iteration)

Derivative

Derivative of Iterated function (map)

Derivative with respect to c

On parameter plane :

• c is a variable
• z₀ = 0 is constant

$\frac{d}{dc} f^{(p)} _c (z_0) = z'_p \,$

This derivative can be found by iteration starting with

$z_0 = 0 \,$

$z'_0 = 1 \,$

and then

$z_p = z_{p-1}^2 + c \,$

$z'_p = 2 \cdot z_{p-1}\cdot z'_{p-1} + 1 \,$

This can be verified by using the chain rule for the derivative.

• Maxima CAS function :

dcfn(p, z, c) :=
  if p=0 then 1
  else 2*fn(p-1,z,c)*dcfn(p-1, z, c)+1;

Example values :

$z_0 = 0 \qquad\qquad z'_0 = 1 \,$

$z_1 = c \qquad\qquad z'_1 = 1 \,$

$z_2 = c^2+c \qquad z'_2 = 2c+1 \,$

Derivative with respect to z

$z'_n\,$ is first derivative with respect to c.

This derivative can be found by iteration starting with

$z'_0 = 1 \,$

and then :

$z'_n= 2*z_{n-1}*z'_{n-1}\,$

Escape radius ( ER)

It is a radius of circle target set. It is also named bailout value.

Minimal Escape Radius should be grater or equal to 2 :

$ER  =  max ( 2 , |c| )\,$

Better estimation is :

$ER = \frac{1}{2} +\sqrt{\frac{1}{4} + |c| }$

Iteration

Iteration

Lamination

Lamination of the unit disk is a closed collection of chords in the unit disc, which can intersect only in an endpoint of each on the boundary circle

It is a model of Mandelbrot or Julia set.

Chords = leaves = arcs

Magnitude

magnitude of the point = it's distance from the origin

Multiplier

Multiplier of periodic z-point :

Math notation :

$\lambda_c(z) = \frac{df_c^{(p)}(z)}{dz}\,$

Maxima CAS function for computing multiplier of periodic cycle :

m(p):=diff(fn(p,z,c),z,1);

where p is a period. It takes period as an input, not z point.

Map

Iterated function = map

• math notation

$\ f^{(0)} _c (z) = z = z_0$

$\ f^{(1)} _c (z) = f_c(z) = z_1$

...

$\ f^{(p)} _c (z) = f_c(f^{(p-1)} _c (z))$

or with subscripts :

$\ z_p = f^{(p)} _c (z_0)$

• Maxima CAS function :

fn(p, z, c) :=
  if p=0 then z
  elseif p=1 then f(z,c)
  else f(fn(p-1, z, c),c);

zp:fn(p, z, c);

Complex quadratic map

• math notation : $f_c(z)=z^2+c\,$
• Maxima CAS function :

f(z,c):=z*z+c;

Doubling map

• Maxima CAS function

doubling_map(n,d):=mod(2*n,d);

• Common Lisp function

(defun doubling-map (ratio-angle)
" period doubling map =  The dyadic transformation (also known as the dyadic map, 
 bit shift map, 2x mod 1 map, Bernoulli map, doubling map or sawtooth map "
(let* ((n (numerator ratio-angle))
       (d (denominator ratio-angle)))
  (setq n  (mod (* n 2) d)) ; (2 * n) modulo d
  (/ n d))) ; result  = n/d

• Haskell function

-- by Claude Heiland-Allen
-- type Q = Rational
 double :: Q -> Q
 double p
   | q >= 1 = q - 1
   | otherwise = q
   where q = 2 * p

• C++

//  mndcombi.cpp  by Wolf Jung (C) 2010. 
//   http://mndynamics.com/indexp.html 
// n is a numerator
// d is a denominator
// f = n/d is a rational fraction ( angle in turns )
// twice is doubling map = (2*f) mod 1
// n and d are changed ( Arguments passed to function by reference)
 
void twice(unsigned long long int &n, unsigned long long int &d)
{  if (n >= d) return;
   if (!(d & 1)) { d >>= 1; if (n >= d) n -= d; return; }
   unsigned long long int large = 1LL; 
   large <<= 63; //avoid overflow:
   if (n < large) { n <<= 1; if (n >= d) n -= d; return; }
   n -= large; 
   n <<= 1; 
   large -= (d - large); 
   n += large;
}

Finding period of angle under doubling map

• Lisp version :

(defun give-period (ratio-angle)
        "gives period of angle in turns (ratio) under doubling map"
        (let* ((n (numerator ratio-angle))
               (d (denominator ratio-angle))
               (temp n)) ; temporary numerator
 
          (loop for p from 1 to 100 do 
                (setq temp  (mod (* temp 2) d)) ; (2 x n) modulo d = doubling)
                when ( or (= temp n) (= temp 0)) return p )))

• Haskell version :

Conversion from an integer type (Int or Integer) to anything else is done by "fromIntegral". The target type is inferred automatically

-- by Claude Heiland-Allen
-- import Data.List (findIndex, groupBy)
-- type N = Integer
-- type Q = Rational
 period :: Q -> N
 period p =
  let Just i = (p ==) `findIndex` drop 1 (iterate double p)
  in  fromIntegral i + 1

Multiplier map

Multiplier map λ gives an explicit uniformization of hyperbolic component Η by the unit disk $\mathbb{D}$ :

$\lambda : \Eta \to \mathbb{D}$

Multiplier map is a conformal isomorphism.

Orbit

Critical orbit is a forward orbit of critical point

Period

Standard polynomial $F_p \,$ which roots are periodic z-points of period p and its divisors

• math notation : $\ F_p(z,c) = f^{(p)} _c (z) - z$
• Maxima CAS function :

F(p, z, c) := fn(p, z, c) - z ;

Function for computing reduced polynomial $G_p\,$ which roots are periodic z-points of period p without its divisors

• math definition : $G_p(z,c) = \frac{F_p(z,c) }{ \prod_{m|p,m<p} G_m(z,c)} \,$
• Maxima function:

G[p,z,c]:=
block(
[f:divisors(p),
t:1], /* t is temporary variable = product of Gn for (divisors of p) other than p */
f:delete(p,f), /* delete p from list of divisors */
if p=1
then return(F(p,z,c)),
for i in f do 
 t:t*G[i,z,c],
g: F(p,z,c)/t,
return(ratsimp(g))
)$

Points

Biaccessible point

If there exist two distinct external rays landing at point we say that it is a biaccessible point.

Critical point

Critical point

Cut point, ray and angle

The "neck" of this eight-like figure is a cut-point.

Cut point k of set S is a point for which set S-k is dissconected ( consist of 2 or more sets).

Examples :

• root points of Mandelbrot set
• Misiurewicz points of boundary of Mandelbrot set
• cut points of Julia sets ( in case of Siegel disc critical point is a cut point )

These points are landing points of 2 or more external rays.

Point which is a landing point of 2 external rays is called biaccesible

Cut ray is a ray which converges to landing point of another ray. Cut rays can be used to construct puzzles.

Cut angle is an angle of cut ray.

Periodic point

Point z has period p under f if :

$z : \ f^{p} (z) = z$

Pinching points

"Pinching points are found as the common landing points of external rays, with exactly one ray landing between two consecutive branches. They are used to cut M or K into well-defined components, and to build topological models for these sets in a combinatorial way. " ( definition from Wolf Jung program Mandel )

A post-critical point

A post-critical point is a point

z = p(p(p( ... (zcr)))) 

where zcr is a critical point.

Set

Component

Components of parameter plane

Hyperbolic component of Mandelbrot set

Boundaries of hyperbolic components of Mandelbrot set

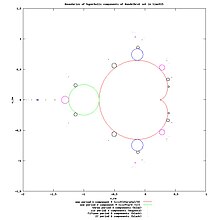
Domain is an open connected subset of a complex plane.

"A hyperbolic component H of Mandelbrot set is a maximal domain (of parameter plane) on which $f_c\,$ has an attracting periodic orbit.

A center of a H is a parameter$c_0 \in H\,$ such that the corresponding periodic orbit has multiplier 0."

Components of dynamical plane

• 

  Components of interior of Filled Julia set

• 

  Inverse iteration of Siegel disc component

In case of Siegel disc critical orbit is a boundary of component containing Siegel Disc.

Domain

Domain in mathematical analysis it is an open connected set

Target set

In case of forward iteration target set $T\,$ is an arbitrary set on dynamical plane containing infinity and not containing points of filled Julia set.

For escape time algorithms target set determines the shape of level sets and curves. It does not do it for other methods.

Exterior of circle

This is typical target set. It is exterior of circle with center at origin $z = 0 \,$ and radius =ER :

$T_{ER}=\{z:abs(z) > ER \} \,$

Radius is named escape radius ( ER ) or bailout value.

Circle of radius=ER centered at the origin is : $\{z:abs(z) = ER \} \,$

Exterior of square

Here target set is exterior of square of side length $s\,$ centered at origin

$T_s=\{z: abs(re(z)) > s ~~\mbox{or}~~ abs(im(z))>s \} \,$

Spider

A spider S is a collection of disjoint simple curves in the complex plane connecting each of the post-critical points to infnity

Unit circle

Unit circle $\partial D\,$ = boundary of unit disk

$\partial D = \left\{ w: abs(w)=1 \right \}$

where coordinates of $w\,$ point of unit circle in exponential form are :

$w = e^{i*t}\,$