Fractals/Iterations in the complex plane/def cqp
Definitions
Order is not only alphabetical but also by topic so use find (Ctrl-f)
See also
- Pictures_of_Julia_and_Mandelbrot_Sets - Terminology
- Index of Mu-Ency from Robert Munafo's home pages on HostMDS © 1996-2020 Robert P. Munafo.
- fractalNotes by perianney
- Category: Book Fractals , something like index of pages
Address
[edit | edit source]"Internal addresses encode kneading sequences in human-readable form, when extended to angled internal addresses they distinguish hyperbolic components in a concise and meaningful way. The algorithms are mostly based on Dierk Schleicher's paper Internal Addresses Of The Mandelbrot Set And Galois Groups Of Polynomials (version of February 5, 2008) http://arxiv.org/abs/math/9411238v2." Claude Heiland-Allen[1]
-
Parameter plane with internal rays (green) used for creating internal addresses
-
-
-
-
types
- finite / infinite
- accessible/non-accessible
- on the parameter plane / on th edynamic plane
- simple/ angled
- for Crossed Renormalizations[2]
Internal
[edit | edit source]- the internal address of a hyperbolic component A lists the periods of certain components that are “on the way” from the main cardioid to hyperbolic component A[3]
- Internal addresses describe the combinatorial structure of the Mandelbrot set.[4] It is one of the Analytical Naming Systems[5][6]
- the ancestral route of a hyperbolic component is the ordered sequence of all its ancestors
Internal address:
- is not constant within hyperbolic component. Example: internal address of -1 is 1->2 and internal address of 0.9999 is 1[7]
- of hyperbolic component is defined as a internal address of it's center
- In an internal address, the numbers (period) must be increasing by definition.
The internal address is describing a kneading sequence by increasing periods.[8]
These correspond to hyperbolic components in M, where the kneading sequence is changing.
Example:
- AABA∗ is obtained by changing A → AAB → AABA∗ , so the internal address is 1-3-5. Conversely, the internal address 1-3-5 gives A → AAB → AABA∗ .
angled
[edit | edit source]Angled internal address is an extension of internal address. The angled internal address of the end of a finite chain of child bulbs would be:
Examples:
- describes period 6 component which is a satelite of period 3 component.
- Mandelbrot Artists by Claude Heiland-Allen
Elements
- period of hyperbolic componnet
- angle of internal ray
One can see the adress as:
- sequence of hyperbolic components
- path inside Mandelbrot set
Path inside Mandelbrot set:
- start with center of period 1 ( nucleus)
- internal ray with angle n/m
- root point n/m ( bond)
- internal angle
- center with given period
- ...
Problems
[edit | edit source]Infinite sequences:
- islands
- infinite sequence of bifurcations
Angle
[edit | edit source]Types of angle
[edit | edit source]
| external angle | internal angle | plain angle | |
|---|---|---|---|
| parameter plane | |||
| dynamic plane |
where:
- is a multiplier map
- is a Boettcher function
external
[edit | edit source]The external angle is a angle of
- point of set's exterior
- the boundary.
It is:
- the same on all points on the external ray. It is important for proving connectedness of the Mandelbrot set.
- a proper fraction
- an approximation of directional derivative
internal
[edit | edit source]The internal angle[9] is an angle of point of component's interior
- it is a rational number and proper fraction measured in turns (see multiplier map)
- it is the same for all point on the internal ray
- in a contact point (root point) it agrees with the rotation number
- root point has internal angle 0 (inside child component)
- "The internal angles start at 0, at the cusp, and increase counterclockwise. " Robert Munafo[10]
Internal angle
- of the wake
- root point
- angles of the wake = angles of parameter rays that land on the root point
- angles of dynamic rays that land on the alpha fixed point
- angles of dynamic rays that land on the critical point and critical value
- angles of principal Misiurewicz point
See also
plain
[edit | edit source]The plain angle is an angle of complex point = its argument[11]
bearing angle in CSS
[edit | edit source]By convention, when an angle denotes a direction in CSS, it is typically interpreted as a bearing angle, where:[12]
- 0deg is "up" or "north" on the screen
- and larger angles are more clockwise (so 90deg is "right" or "east")
Units
[edit | edit source]- turns
- degrees
- radians
Number types
[edit | edit source]Angle (for example, external angle in turns) can be used in different number types
Examples:
the external arguments of the rays landing at z = −0.15255 + 1.03294i are:[13]
where:
Bifurcation
[edit | edit source]- Numerical Bifurcation Analysis of Maps
- MatCont[14]
Coordinate
[edit | edit source]- Fatou coordinate for every repelling and attracting petal (linearization of function near parabolic fixed point)
- Boettcher
- Koenigs
"The coordinates are the current location, measured on the x-y-z axis. The gradient is a direction to move from our current location" Sadid Hasan[15]
Curves
[edit | edit source]Types:
- topology:
- closed versus open
- simple versus not simple ( complex)
- infinite, finite at one end ( ray), finite at both ends ( segment)
- self-intersections, crossing, singularities
- other properities:
- invariant
- critical
Points of the curve:
- regular
- singular: A point on the curve at which the curve behaves in an extraordinary manner is called a singular point.
- Points of inflexion
- Multiple points( n-tuple points):[16] A point on the curve through which more than one branches of curve
- double : "A double point is a point on a curve where two branches of the curve intersect; in other words, it’s a point traced twice when a curve is traversed."
- Triple point: A point on the curve through which three branches of curve pass
Description[17]
- plane curve = it lies in a plane.
- closed = it starts and ends at the same place.
- simple = it never crosses itself. only regular points
See
closed
[edit | edit source]Closed curves are curves whose ends are joined. Closed curves do not have end points.
- Simple Closed Curve: A connected curve that does not cross itself and ends at the same point where it begins. It divides the plane into exactly two regions (Jordan curve theorem). Examples of simple closed curves are ellipse, circle and polygons.[18]
- Complex Closed Curve (not simple = non-simple) It divides the plane into more than two regions. Example: Lemniscates.
"non-self-intersecting continuous closed curve in plane" = "image of a continuous injective function from the circle to the plane"
Circle
[edit | edit source]Inner circle
[edit | edit source]Unit circle
[edit | edit source]Unit circle is a boundary of unit disk[19]
where coordinates of point of unit circle in exponential form are:
Critical curves
[edit | edit source]Diagrams of critical polynomials are called critical curves.[20]
These curves create skeleton of bifurcation diagram.[21] (the dark lines[22])
dendrit
[edit | edit source]- a locally connected branched curve
- "Complex 1-variable polynomials with connected Julia sets and only repelling periodic points are called dendritic."[23]
- "a dendrite is a locally connected continuum that does not contain Jordan curves." [24]
- "a locally connected continuum without subsets homeomorphic to a circle"
- connected with no interior
- locally connected, uniquely arcwise connected, compact metric space
See also:
- Misiurewicz point on the parameter plane
- Dendrite Modeling: Modeling dendrites, including trees, lightning, river systems, and all manner of branching structures, has been frequently undertaken in computer graphics. We propose a new dendritic modeling framework using path planning as the basic operation[25]
- Procedural Branching Texture[26]
Escape lines
[edit | edit source]Escape line = boundary of escape time's level sets
"If the escape radius is equal to 2 the contour lines have a contact point (c= -2) and cannot be considered as equipotential lines" [27]
geodesic
[edit | edit source]In geometry, a geodesic is a curve representing in some sense the shortest path (arc) between two points in a surface[28]
Integral
[edit | edit source]- integral curve is a parameterized curve, whose tangent vectors agree with the vectors from this vector field. In physics, integral curves for an electric field or magnetic field are known as field lines.
Invariant
[edit | edit source]Types:
- topological
- shift invariants
examples:
- curve is invariant for the map f (evolution function) if images of every point from the curve stay on that curve[29][30][31]
- curve is invariant for a system of ordinary differential equations[32]
"Quasi-invariant curves are used in the study of hedgehog dynamics" RICARDO PEREZ-MARCO[33]
Examples:
- field lines
- external ray
- internal ray
Isocurves
[edit | edit source]Isocurve = level curve = curve which consist of points which have the same value (level) of parameter / variable
Equipotential lines
[edit | edit source]Equipotential lines = Isocurves of complex potential
"If the escape radius is greater than 2 the contour lines are equipotential lines" [34]
Examples
Jordan curve
[edit | edit source]
Jordan curve = a simple closed curve that divides the plane into an "interior" region bounded by the curve and an "exterior" region containing all of the nearby and far away exterior points[35]
Lamination
[edit | edit source]Lamination of the unit disk is a closed collection of chords in the unit disc, which can intersect only in an endpoint of each on the boundary circle[36][37]
It is a model of Mandelbrot or Julia set.
A lamination, L, is a union of leaves and the unit circle which satisfies:[38]
- leaves do not cross (although they may share endpoints) and
- L is a closed set.
"The pattern of rays landing together can be described by a lamination of the disk. As θ is varied, the diameter defined by θ/2 and (θ +1)/2 is moving and disconnecting or reconnecting chords. " Wolf Jung [39]
Leaf
[edit | edit source]Chords = leaves = arcs
A leaf on the unit disc is a path connecting two points on the unit circle.[40]
"In Thurston’s fundamental preprint, the two characteristic rays and their common landing point are the “minor leaf” of a “lamination”"[41]
Level curve
[edit | edit source]LCM = Level Curve Method = method for drawing level curves
Examples:
- equipotential line (the same potential)
- external ray (the same external angle)
- boundary of level set (see Level Set Method = LSM)
Open curve
[edit | edit source]Curve which is not closed. Examples: line, ray.
Path
[edit | edit source]- Path in geometry is a curve
Ray
[edit | edit source]Rays are:
- invariant curves
- dynamic or parameter
- external, internal or extended
Extended
[edit | edit source]"We prolong an external ray R θ supporting a Fatou component U (ω) up to its center ω through an internal ray and call the resulting set the extended ray E θ with argument θ." Alfredo Poirier[42]
External ray
[edit | edit source]The closure of an external ray is called a closed ray. If ray lands, then the closure of the ray is the union of the external ray and its landing point.[43]
"A ray R is said to land or converge, if the accumulation set is a singleton subset of J. The conjecture that the Mandelbrot set is locally connected is equivalent to the continuous landing of all external rays."[44]
where:
- is a closure of = the bar is taken to mean the closure rather than the complex conjugate
- MLC = Mandelbrot Local connectivity Conjecture: M is locally connected[45]
- singelton set is a set with exactly one element
"If the MLC were proved true, the theorem of Caratheodory would give us an extension of the Riemann map to , giving a conformal equivalence of M with D. Given the fractal nature of M, this would be a very surprising result.[46]
A dynamic periodic ray pair is called characteristic if it separates the critical value from all rays and for all k ≥ 1 (except of course from those on the ray pair itself).
Every cycle of periodic ray pairs has a unique characteristic ray pair with angles in the union [47]
For non-periodic rays, we allow a characteristic ray pair to contain the critical value: a ray pair is characteristic if consists of two components so that
- contains all rays Rc(2kϑ) and Rc(2kϑ0) for k ≥ 1
- and contains the critical value
Internal ray
[edit | edit source]Definition:
- "The internal rays are the preimages of the radial segments under the coordinate with componenet center corresponding to 0." Alfredo Poirier[48]
- The internal rays of U are the images of radial lines under the Riemann maps.[49]
Internal rays are:
- dynamic (on dynamic plane, inside filled Julia set)
- |parameter (on parameter plane, inside Mandelbrot set) usuning multiplier map
dynamic
[edit | edit source]-
Dynamic internal (blue segment) and external (red ray) rays
For a parameter c with superattracting orbit: for every Fatou component of filled julia set[50] there is:
- a unique periodic or pre-periodic point of the super-attracting orbit
- a Riemann map that maps:[51]
component to unit disc:
and point to the origin:
The point is called the center of component .
For any angle the pre-image of the radial segment of the unit disc
is called an internal ray of component with well-defined landing point.
where:
See also:
intertwined
[edit | edit source]The internal rays are the curves that connects endpoints of external rays to the origin (the only pole) by winding in the specific way through the Julia set. Unlike the external rays the internal rays allways cross other internal rays, usually at multiple points, hence they are interwined[52]
parameter
[edit | edit source]-
Uniformization of the interior of Mandelbrot set components using multiplier map: internal rays, internal coordinate
-
Method of computing internal ray using explicit equation
-
Wakes near the period 3 island in the Mandelbrot set, internal angles and rays (green) and external angles and rays (red)
Escape route
[edit | edit source]Escape route is a path inside Mandelbrot set.
Escape route 1/2 [53]
- is part of the real slice of the mandelbrot set)
- part of the real line x=0
Steps:
- start from center of period 1
- go along internal ray 1/2 to root point of period 2 component
- go along internal ray 0 to the center of period 2 component
- go along internal ray 1/2 to root point of period 4 component
- ...
- escape routes
-
1/2
-
1/3
Spider
[edit | edit source]A spider S is a collection of disjoint simple curves called legs [54] (extended rays = external + internal ray) in the complex plane connecting each of the post-critical points to infinity [55]
See:
Spine
[edit | edit source]-
Rabbit Julia set with spine
-
Basilica Julia set with spine
In the case of complex_quadratic_polynomial the spine of the filled Julia set is defined as arc between -fixed point and ,
with such properties:
- spine lies inside .[56] This makes sense when is connected and full [57]
- spine is invariant under 180 degree rotation,
- spine is a finite topological tree,
- Critical point always belongs to the spine.[58]
- -fixed point is a landing point of external ray of angle zero ,
- is landing point of external ray .
Algorithms for constructing the spine:
- detailed version is described by A. Douady[59]
- Simplified version of algorithm:
- connect and within by an arc,
- when has empty interior then arc is unique,
- otherwise take the shortest way that contains .[60]
Curve :
divides dynamical plane into two components.
Computing external angle for c from centers of hyperbolic components and Misiurewicz points:
The spine of K is the arc from beta to minus beta. Mark 0 each time C is above the spine and 1 each time it is below. You obtain the expansion in base 2 of the external argument theta of z by C. This simply comes from the two following facts: * 0 < theta < 1/2 if access to z is above the spine, 1/2 < theta < 1 if it is below * function f doubles the external arguments with respect to K, as well as the potential, since Riemman map (Booettcher map) conjugates f to . Note that if c and z are real, the tree reduces to the segment [beta',beta] of the real line, and the sequence of 0 and 1 obtained is just the kneading sequence studied by Milnor and Thurston (except for convention: they use 1 and -1). This sequence appears now as the binary expansion of a number which has a geometrical interpretation. " A. Douady
Relation between spine and major leaf of the lamination
Vein
[edit | edit source]"A vein in the Mandelbrot set is a continuous, injective arc inside in the Mandelbrot set"
"The principal vein is the vein joining to the main cardioid" (Entropy, dimension and combinatorial moduli for one-dimensional dynamical systems. A dissertation by Giulio Tiozzo)
Discriminant
[edit | edit source]In algebra, the discriminant of a polynomial is a polynomial function of its coefficients, which allows deducing some properties of the roots without computing them.
Distance
[edit | edit source]See also:
- metric [61]
- Algorithm
- Distance Estimation Method
- SDF = Signed Distance Function
- distance fields
Dynamics
[edit | edit source]- symbolic[65][66][67]
- complex [68][69]
- Arithmetic
- combinatorial
- local/global
- discrete/continous
- parabolic/hyperbolic/eliptic
Examples:
- discrete local complex parabolic dynamics
| parameter c | location of c | Julia set | interior | type of critical orbit dynamics | critical point | fixed points | stability of alfa |
|---|---|---|---|---|---|---|---|
| c = 0 | center, interior | connected = Circle Julia set | exist | superattracting | attracted to alfa fixed point | fixed critical point equal to alfa fixed point, alfa is superattracting, beta is repelling | r = 0 |
| 0<c<1/4 | internal ray 0, interior | connected | exist | attracting | attracted to alfa fixed point | alfa is attracting, beta is repelling | 0 < r < 1.0 |
| c = 1/4 | cusp, boundary | connected = cauliflower | exist | parabolic | attracted to alfa fixed point | alfa fixed point equal to beta fixed point, both are parabolic | r = 1 |
| c>1/4 | external ray 0, exterior | disconnected = imploded cauliflower | disappears | repelling | repelling to infinity | both finite fixed points are repelling | r > 1 |
symbolic
[edit | edit source]"Symbolic dynamics encodes: [70]
- a dynamical system by a shift map on a space of sequences over finite alphabet using Markov partition of the space
- the points of space by their itineraries with respect to the partition " (Volodymyr Nekrashevych - Symbolic dynamics and self-similar groups)
entropy
[edit | edit source]- image entropy [71]
equation
[edit | edit source]differential
[edit | edit source]differential equations
- exact analytic solutions.
- approximated solution
- use perturbation theory to approximate the solutions
Field
[edit | edit source]Field is a region in space where each and every point is associated with a value.
The field types according to the value type:
- scalar field
- Distance field – Some mapping , where for any given input the output is the distance to the nearest surface (where the field value is 0).[72]
- vector field, for example gradient field
Function
[edit | edit source]types:
- by application
- map = iterated map
- mappings = transformation of the plane
- by function type
- polynomial
Derivative
[edit | edit source]- Derivative of Iterated function (map)[73][74]
- of the function f with respect to (wrt) variable
- following the derivative[75]
angular
[edit | edit source]Angular derivative [76]
The Schwarzian Derivative
[edit | edit source]The Schwarzian Derivative [77] [78][79][80]
Wirtinger derivatives
[edit | edit source]gradient
[edit | edit source]the gradient is the generalization of the derivative for the multivariable functions[81][82]
definitions:
- (field): Gradient field is the vector field with gradient vector
- (function): The gradient of a scalar-valued multivariable function is a vector-valued function denoted
- (vector): The gradient of the function f at the point (x,y) is defined as the unique vector (result of gradient function) representing the maximum rate of increase of a scalar function (length of the vector) and the direction of this maximal rate (angle of the vector). Such vector is given by the partial derivatives with respect to each of the independent variables[83]
- (operator): Del or nabla is an gradient operator = a vector differential operator
-
Gradient 2D field with gradient vectors
-
one gradient vector (red)
Notations:
See also
Jacobian
[edit | edit source]The Jacobian is the generalization of the gradient for vector-valued functions of several variables
multiplier
[edit | edit source]The multiplier of a fixed point α is the derivative A′(α) calculated in any local chart around α[86]
Germ
[edit | edit source]Germ [87] of the function f in the neighborhood of point z is a set of the functions g which are indistinguishable in that neighborhood
See:
- parabolic germ
- the linearization of a germ[88]
map
[edit | edit source]- differences between map and the function [89]
- Iterated function = map[90]
- an evolution function[91] of the discrete nonlinear dynamical system[92]
is called map , examples:
- rational maps
- exponential maps
- trigonometric maps
- landing map: " A theorem of Caratheodory states that if is a full compact and locally connected set, then external rays land and the landing map is continuous."[93]
types or names
[edit | edit source]Brjuno
[edit | edit source]- Brjuno function
Links:
harmonic
[edit | edit source]An harmonic or spherical function is a:
- "set of orthogonal functions all of whose curvatures are changing at the same rate."[94]
- "harmonic functions relate two sets of different curves such that the rate of change of their respective curvatures is always equal. " and they are orthogonal
- "One set of curves of the harmonic function expressed the pathways of minimal change in the potential for action, while the other, orthogonal curves expressed the pathways of maximum change in the potential for action."
- "a pair of harmonic conjugate functions, u and v. They satisfy the Cauchy-Riemann equations. Geometrically, this implies that the contour lines of u and v intersect at right angles"[95]
Geometric examples:
- " A set of concentric circles and radial lines comprises an harmonic function because both the circles and the radial lines intersect orthogonally and both have constant curvature."
- "a set of orthogonal ellipses and hyperbolas."
How to find harmonic conjugate function ? [96]
meromorphic
[edit | edit source]meromorphic maps: Those with NO FINITE, NON-ATTRACTING FIXED POINTS[97]
Polynomial
[edit | edit source]Critical
[edit | edit source]Critical polynomial:
so
These polynomials are used for finding:
- centers of period n Mandelbrot set components. Centers are roots of n-th critical polynomials (points where critical curve Qn croses x axis)
- Misiurewicz points
post-critically finite
[edit | edit source]a post-critically finite polynomial = all critical points have finite orbit
Resurgent
[edit | edit source]"resurgent functions display at each of their singular points a behaviour closely related to their behaviour at the origin. Loosely speaking, these functions resurrect, or surge up - in a slightly different guise, as it were - at their singularities"
transformation
[edit | edit source]In mathematics, a transformation is a function f, usually with some geometrical underpinning, that maps a set X to itself, i.e. f : X → X.[101][102][103]
Examples include:
- linear transformations of vector spaces
- geometric transformations
coordinate transformations
[edit | edit source]There are often many different possible coordinate systems for describing geometrical figures. The relationship between different systems is described by coordinate transformations, which give formulas for the coordinates in one system in terms of the coordinates in another system. For example, in the plane, if Cartesian coordinates (x, y) and polar coordinates (r, θ) have the same origin, and the polar axis is the positive x axis, then the coordinate transformation from polar to Cartesian coordinates is given by x = r cosθ and y = r sinθ.
With every bijection from the space to itself two coordinate transformations can be associated:
- Such that the new coordinates of the image of each point are the same as the old coordinates of the original point (the formulas for the mapping are the inverse of those for the coordinate transformation)
- Such that the old coordinates of the image of each point are the same as the new coordinates of the original point (the formulas for the mapping are the same as those for the coordinate transformation)
For example, in 1D, if the mapping is a translation of 3 to the right, the first moves the origin from 0 to 3, so that the coordinate of each point becomes 3 less, while the second moves the origin from 0 to −3, so that the coordinate of each point becomes 3 more.
Yoccoz’s function
[edit | edit source]glitches
[edit | edit source]
Definition:
- Incorrect (noisy) parts of renders[106] using perturbation technique
- pixels which dynamics differ significantly from the dynamics of the reference pixel[107]"These can be detected and corrected by using a more appropriate reference."[108]
Examples:
graf
[edit | edit source]Dessin d'enfant
[edit | edit source]See also:
Tree
[edit | edit source]- tree is a simply connected graph
See also:
- fractalforums.org: functional-graph-of-modular-arithmetic
- Oleg Ivrii (Tel Aviv University), "Shapes of trees"
Farey tree
[edit | edit source]Farey tree = Farey sequence as a tree
Hubbard tree
[edit | edit source]- a simplified, combinatorial model of the Julia set (MARY WILKERSON)
- "Hubbard trees are finite planar trees, equipped with self-maps, which classify postcritically finite polynomials as holomorphic dynamical systems on the complex plane." [109]
- " Hubbard trees are invariant trees connecting the points of the critical orbits of post-critically finite polynomials. Douady and Hubbard showed in the Orsay Notes that they encode all combinatorial properties of the Julia sets. For quadratic polynomials, one can describe the dynamics as a subshift on two symbols, and itinerary of the critical value is called the kneading sequence." Henk Bruin and Dierk Schleicher[110]
- the Hubbard tree is the convex hull of the critical orbits within the filled Julia set, i.e., the complement of the basion of infinity
Rooted tree
[edit | edit source]rooted tree of preimages:
where a vertex is connected by an edge with .
Iteration
[edit | edit source]Magnitude
[edit | edit source]- magnitude of the point (complex number in 2D case) = it's distance from the origin[111]
- radius is the absolute value of complex number (compare to arguments or angle)
Map
[edit | edit source]types
[edit | edit source]- The map f is hyperbolic if every critical orbit converges to a periodic orbit.[112]
Complex quadratic map
[edit | edit source]Forms
[edit | edit source]c form: z^2+c
[edit | edit source]- math notation:
- Maxima CAS function:
f(z,c):=z*z+c;
(%i1) z:zx+zy*%i; (%o1) %i*zy+zx (%i2) c:cx+cy*%i; (%o2) %i*cy+cx (%i3) f:z^2+c; (%o3) (%i*zy+zx)^2+%i*cy+cx (%i4) realpart(f); (%o4) -zy^2+zx^2+cx (%i5) imagpart(f); (%o5) 2*zx*zy+cy
Iterated quadratic map
- math notation
...
or with subscripts:
- Maxima CAS function:
fn(p, z, c) := if p=0 then z elseif p=1 then f(z,c) else f(fn(p-1, z, c),c);
zp:fn(p, z, c);
lambda form: z^2+m*z
[edit | edit source]More description Maxima CAS code (here m not lambda is used):
(%i2) z:zx+zy*%i; (%o2) %i*zy+zx (%i3) m:mx+my*%i; (%o3) %i*my+mx (%i4) f:m*z+z^2; (%o4) (%i*zy+zx)^2+(%i*my+mx)*(%i*zy+zx) (%i5) realpart(f); (%o5) -zy^2-my*zy+zx^2+mx*zx (%i6) imagpart(f); (%o6) 2*zx*zy+mx*zy+my*zx
Switching between forms
[edit | edit source]Start from:
- internal angle
- internal radius r
Multiplier of fixed point:
When one wants change from lambda to c:[114]
or from c to lambda:
Example values:
| r | c | fixed point alfa | fixed point | ||
|---|---|---|---|---|---|
| 1/1 | 1.0 | 0.25 | 0.5 | 1.0 | 0 |
| 1/2 | 1.0 | -0.75 | -0.5 | -1.0 | 0 |
| 1/3 | 1.0 | 0.64951905283833*i-0.125 | 0.43301270189222*i-0.25 | 0.86602540378444*i-0.5 | 0 |
| 1/4 | 1.0 | 0.5*i+0.25 | 0.5*i | i | 0 |
| 1/5 | 1.0 | 0.32858194507446*i+0.35676274578121 | 0.47552825814758*i+0.15450849718747 | 0.95105651629515*i+0.30901699437495 | 0 |
| 1/6 | 1.0 | 0.21650635094611*i+0.375 | 0.43301270189222*i+0.25 | 0.86602540378444*i+0.5 | 0 |
| 1/7 | 1.0 | 0.14718376318856*i+0.36737513441845 | 0.39091574123401*i+0.31174490092937 | 0.78183148246803*i+0.62348980185873 | 0 |
| 1/8 | 1.0 | 0.10355339059327*i+0.35355339059327 | 0.35355339059327*i+0.35355339059327 | 0.70710678118655*i+0.70710678118655 | 0 |
| 1/9 | 1.0 | 0.075191866590218*i+0.33961017714276 | 0.32139380484327*i+0.38302222155949 | 0.64278760968654*i+0.76604444311898 | 0 |
| 1/10 | 1.0 | 0.056128497072448*i+0.32725424859374 | 0.29389262614624*i+0.40450849718747 | 0.58778525229247*i+0.80901699437495 |
One can easily compute parameter c as a point c inside main cardioid of Mandelbrot set:
of period 1 hyperbolic component (main cardioid) for given internal angle (rotation number) t using this c / cpp code by Wolf Jung[115]
double InternalAngleInTurns;
double InternalRadius;
double t = InternalAngleInTurns *2*M_PI; // from turns to radians
double R2 = InternalRadius * InternalRadius;
double Cx, Cy; /* C = Cx+Cy*i */
// main cardioid
Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4;
Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4;
or this Maxima CAS code:
/* conformal map from circle to cardioid (boundary
of period 1 component of Mandelbrot set */
F(w):=w/2-w*w/4;
/*
circle D={w:abs(w)=1 } where w=l(t,r)
t is angle in turns ; 1 turn = 360 degree = 2*Pi radians
r is a radius
*/
ToCircle(t,r):=r*%e^(%i*t*2*%pi);
GiveC(angle,radius):=
(
[w],
/* point of unit circle w:l(internalAngle,internalRadius); */
w:ToCircle(angle,radius), /* point of circle */
float(rectform(F(w))) /* point on boundary of period 1 component of Mandelbrot set */
)$
compile(all)$
/* ---------- global constants & var ---------------------------*/
Numerator :1;
DenominatorMax :10;
InternalRadius:1;
/* --------- main -------------- */
for Denominator:1 thru DenominatorMax step 1 do
(
InternalAngle: Numerator/Denominator,
c: GiveC(InternalAngle,InternalRadius),
display(Denominator),
display(c),
/* compute fixed point */
alfa:float(rectform((1-sqrt(1-4*c))/2)), /* alfa fixed point */
display(alfa)
)$
Circle map
[edit | edit source]Circle map [116]
- irrational rotation[117]
Caratheodory semiconjugacy
[edit | edit source]"The map is called the Caratheodory semiconjugacy, with the associated identity
in the degree 2 case. This identity allows us to easily track forward iteration of external rays and their landing points in by doubling the angle of their associated external rays modulo 1." Mary Wilkerson[118]
where
- is the real numbers modulo the integers group ( quotient group )[119] which is isomorphic to the circle group[120]
- the group of complex numbers of absolute value 1 under multiplication
- or correspondingly, the group of rotations in 2D about the origin, that is, the special orthogonal group
- a dyadic rational number
An isomorphism is given by (see Euler's identity).
Doubling map
[edit | edit source]Feigenbaum map
[edit | edit source]- "the Feigenbaum map F is a solution of Cvitanovic-Feigenbaum equation"[121]
- Feigenbaum quadratic polynomials (= Feigenbaum point of parameter plane) , i.e., infinitely renormalizable polynomials of bounded type.[122]
First return map
[edit | edit source]- definition [123]
- video: Intro to Poincare map (Poincaré), the first return map. This map helps us determine the stability of a limit cycle using the eigenvalues (Floquet multipliers) associated with the map.
"In contrast to a phase portrait, the return map is a discrete description of the underlying dynamics. .... A return map (plot) is generated by plotting one return value of the time series against the previous one "[124]
"If x is a periodic point of period p for f and U is a neighborhood of x, the composition maps U to another neighborhood V of x. This locally defined map is the return map for x." (W P Thurston: On the geometry and dynamics of Iterated rational maps)
"The first return map S → S is the map defined by sending each x0 ∈ S to the point of S where the orbit of x0 under the system first returns to S." [125]
"way to obtain a discrete time system from a continuous time system, called the method of Poincar´e sections Poincar´e sections take us from: continuous time dynamical systems on (n + 1)-dimensional spaces to discrete time dynamical systems on n-dimensional spaces"[126]
postcritically finite
[edit | edit source]postcritically finite: maps whose critical orbits are all periodic or preperiodic[127]
" In the theory of iterated rational maps, the easiest maps to understand are postcritically finite: maps whose critical orbits are all periodic or preperiodic. These maps are also the most important maps for understanding the combinatorial structure of parameter spaces of rational maps. "
A postcritically finite quadratic polynomial fc(z) = z^2+c may be:[128]
- periodic of satellite type
- periodic of primitive type
- critically preperiodic (Misiurewicz type)
Examples are given by:
- the Basilica Q(z) = z^2 − 1
- the Kokopelli
- P(z) = z^2 + i (dendrite)
Critically preperiodic polynomials
[edit | edit source]- the critical point of fc is strictly preperiodic
- parameter c is from Thurston-Misiurewicz points–values on the boundary of the Mandelbrot set = Misiurewicz point
- Julia set is dendrite
Multiplier map
[edit | edit source]
Multiplier map associated with hyperbolic component
- gives an explicit uniformization of hyperbolic component by the unit disk :
- it is (d-1) to one function. Where d is a degree of iterated function
In other words it maps hyperbolic component H to unit disk D.
It maps point c from parameter plane to point b from reference plane:
where:
- c is a point in the parameter plane
- b is a point in the reference plane. It is also internal coordinate
- is a multiplier map
Multiplier map is a conformal isomorphism.[129]
It can be computed using:
- Newton method: internal_coordinate by Claude Heiland-Allen
- m-interior function
- First derivative wrt z
Approximation
Quadratic like maps
[edit | edit source]quadratic like maps is nothing but complexification of the concept of unimodal map[130]
Riemann map
[edit | edit source]Riemann mapping theorem[131] says that every simply connected subset U of the complex number plane can be mapped to the open unit disk D
where:
- D is a unit disk
- f is Riemann map (function). It is 1to-1 function
- U is subset of complex plane
-
Multiplier map
-
BDM
-
MBDM
-
DLD
-
SAC
-
zeros of qn algorithm
Examples (approximations of Riemann mapping):
- multiplier map on the parameter plane
- binary decomposition
- Böttcher coordinates
- on the parameter plane the Riemann map for the complement of the Mandelbrot set
- on dynamic plane[132]
- for the Fatou component containing a superattracting fixed point for a rational map[133]
- a Riemann map for the complement of the filled Julia set of a quadratic polynomial with connected Julia: "The Riemann map for the central component for the Basilica was drawn in essentially the same way, except that instead of starting with points on a big circle, I started with sample points on a circle of small radius (e.g. 0.00001) around the origin." Jim Belk
- zeros of qn algorithm
function:
- explicit formula (only in simple cases)
- numerical approximation (in most of the cases)[134]
- Zipper
- " Thurston and others have done some beautiful work involving approximating arbitrary Riemann maps using circle packings. See Circle Packing: A Mathematical Tale by Stephenson."
- " To some extent, constructing a Riemann map is simply a matter of constructing a harmonic function on a given domain (as well as the associated harmonic conjugate), subject to certain boundary conditions. The solution to such problems is a huge topic of research in the study of PDE's, although the connection with Riemann maps is rarely mentioned." Jim Belk[135]
PDE's approach to construct a Riemann map explicitly on a given domain D
- First, translate the domain so that it contains the origin.
- Next, use a numerical method to construct a harmonic function F satisfying
for all , and let
Then
- and is harmonic
so:
- R is the radial component (i.e. modulus) of a Riemann map on D.
- The angular component can now be determined by the fact that its level curves are perpendicular to the level curves of R, and have equal angular spacing near the origin."
"Using the Riemann mapping BM we can define the parameter external rays and equipotentials as the preimages of the straight rays going to ∞ and round circles centered at 0. This gives us two orthogonal foliations in the complement of the Mandelbrot set." [136]
See
- Commons: Category:Riemann mapping
- A Riemann map on the central component[137]
- Some internal rays of the Basilica[138]
- The Bottcher Map B gives rise to internal angles in each bubble[139]
Rotation map
[edit | edit source]"If a is rational, then every point is periodic. If a is irrational, then every point has a dense orbit." David Richeson[140]
rational
[edit | edit source]Rotation map describes counterclockwise rotation of point thru turns on the unit circle:
It is used for computing:
- rotation maps
irrational
[edit | edit source]Shift map
[edit | edit source]
names:
- bit shift map (because it shifts the bit) = if the value of an iterate is written in binary notation, the next iterate is obtained by shifting the binary point one bit to the right, and if the bit to the left of the new binary point is a "one", replacing it with a zero.
- 2x mod 1 map (because it is math description of its action)
Shift map (one-sided binary left shift) acts on one-sided infinite sequence of binary numbers by
It just drops first digit of the sequence.
If we treat sequence as a binary fraction:
then shift map = the dyadic transformation = dyadic map = bit shift map= 2x mod 1 map = Bernoulli map = doubling map = sawtooth map
and "shifting N places left is the same as multiplying by 2 to the power N (written as 2N)"[141] (operator <<)
In Haskell:
shift k = genericTake q . genericDrop k . cycle -- shift map
See also:
- How to compute external angles of principal Misiurewicz points of wakes?
- On quotients of the shift associated with dendrite Julia sets of quadratic polynomials by Christopher Penrose Published 1990
- subsection-sequence_space by Mark McClure
Dehn twist
[edit | edit source]Dehn twist[142]
Number
[edit | edit source]complex number
[edit | edit source]- numerical value: x+y*i
- vector from origin to point (x,y)
- point (x,y) od 2D Cartesion plain
constant
[edit | edit source]Fegenbaum constant
[edit | edit source]- first (delta)[143]
- second (alpha)
How to compute:
- Keith Briggs: How to calculate
- octave program by Anton Hendricson
- python program by cdlane
- Rosettacode
- An efficient method for the computation of the Feigenbaum constants to high precision by Andrea Molteni (Submitted on 7 Feb 2016)
degree
[edit | edit source]It hase many meanings:[144]
- unit of the angle
- degree of a function
- polynomial
- rational function[145]
Multiplier
[edit | edit source]The multiplier of periodic z-point:[146][147]
- is a complex number
- "The value of is the same at any point in the orbit of a: it is called the multiplier of the cycle."[148]
- The multiplier is invariant under conjugacy[149]
- Linearizability depends on the multiplier
Math notation:
Maxima CAS function for computing multiplier of periodic cycle:
m(p):=diff(fn(p,z,c),z,1);
where p is a period. It takes period as an input, not z point.
| period | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
It is used to:
- compute stability index of periodic orbit (periodic point) = (where r is a n internal radius)
- multiplier map
"The multiplier of a fixed point gives information about its stability (the behaviour of nearby orbits)" [150]
See also:
- multiplier map
- Buff, Xavier. “VIRTUALLY REPELLING FIXED POINTS.” Publicacions Matemàtiques, vol. 47, no. 1, Universitat Autònoma de Barcelona, 2003, pp. 195–209, http://www.jstor.org/stable/43736773.
Rotation number
[edit | edit source]The rotation number[151][152][153][154][155] of the disk (component) attached to the main cardioid of the Mandelbrot set is a proper, positive rational number p/q in lowest terms where:
- q is a period of attached disk (child period) = the period of the attractive cycles of the Julia sets in the attached disk
- p describes fc action on the cycle: fc turns clockwise around z0 jumping, in each iteration, p points of the cycle [156]
Features:
- in a contact point (root point) it agrees with the internal angle
- the rotation numbers are ordered clockwise along the boundary of the componant
- " For parameters c in the p/q-limb, the filled Julia set Kc has q components at the fixed point αc . These are permuted cyclically by the quadratic polynomial fc(z), going p steps counterclockwise " Wolf Jung
Winding number
[edit | edit source]- of the map (iterated function)[157][158]
- "the winding number of the dynamic ray at angle a around the critical value, which is defined as follows: denoting the point on the dynamic a-ray at potential t greater or equal to zero by zt and decreasing t from +infinity to 0, the winding number is the total change of arg(zt - c) (divided by 2*Pi so as to count in full turns). Provided that the critical value is not on the dynamic ray or at its landing point, the winding number is well-defined and finite and depends continuously on the parameter. " DIERK SCHLEICHER [159]
- "the winding number of the dynamic ray at angle ϑ around the critical value, which is defined as follows: denoting the point on the dynamic ϑ-ray at potential t ≥ 0 by zt and decreasing t from +∞ to 0, the winding number is the total change of arg(zt − c) (divided by 2π so as to count in full turns). Provided that the critical value is not on the dynamic ray or at its landing point, the winding number is well-defined and finite and depends continuously on the parameter. When the parameter c moves in a small circle around c0 and if the winding number is defined all the time, then it must change by an integer corresponding to the multiplicity of c as a root of z(c) − c. However, when the parameter returns back to where it started, the winding number must be restored to what it was before. This requires a discontinuity of the winding number, so there are parameters arbitrarily close to c0 for which the critical value is on the dynamic ray at angle ϑ, and c0 is a limit point of the parameter ray at angle ϑ. Since this parameter ray lands, it lands at c0."
Computing winding number of the curve (which is not crossing the origin) using:
- numerical integration
- computational geometry
The discrete winding number = winding number of polygon approximating curve
Orbit
[edit | edit source]Orbit is a sequence of points[164]
- phase space trajectories of dynamical systems
- The orbit of periodic point is finite and it is called a cycle.
Backward
[edit | edit source]Critical
[edit | edit source]Critical orbit is forward orbit of a critical point.
Forward
[edit | edit source]Homoclinic / heteroclinic
[edit | edit source]-
homoclinic orbit
-
Heteroclinic orbit
Inverse
[edit | edit source]Inverse = Backward
periodic
[edit | edit source]skipped
[edit | edit source]- set containing first n iterations of initial point without initial point and its k iterations
- number of elements = n - k
It is used in the average colorings
truncated
[edit | edit source]- set containing initial point and first n iterations of initial point
- number of elements = n+1
Parameter
[edit | edit source]Parameter
- point of the parameter plane " is renormalizable if restriction of some of its iterate gives a polinomial-like map of the same or lower degree. " [165]
- parameter of the function
Period
[edit | edit source]Period of point under the iterarted function f is the smallest positive integer value p for which this equality
holds is the period[166] of the orbit.[167]
is a point of periodic orbit (limit cycle) .
More is here
Plane
[edit | edit source]Planes [168]
Douady’s principle: “sow in dynamical plane and reap in parameter space”.
2-sphere
[edit | edit source]In topology: two-dimensional sphere = 2-sphere = the two-dimensional surface of a three-dimensional ball[169]
Geometrically, the set of extended complex numbers is referred to as the Riemann sphere or extended complex plane.
partition
[edit | edit source]Examples:
- Markow partition
- Yoccoz puzzle
- critical portrait
- lamination
critical portrait partition
[edit | edit source]A critical portrait naturally induces partitions: Df , If , and Pf of the closed unit disk D, the unit circle T, and the plane C, respectively;
Kneading partition of the dynamic plane
[edit | edit source]In case of critically preperiodic polynomials the partition of the dynamic plane used in the definition of the kneading sequence.
Partition is formed by the dynamic rays at angles:
- t/2
- (t + 1)/2
which land together at the critical point.
Angle t is angle which lands on the critical value:
-
t = 1/4 preperiod = 2 period = 1
-
t = 1/6 preperiod = 1 and period = 2
-
t = 9/56 preperiod = 3 and period = 3
How to find angle of the dynamic external ray that land on the critical value z = c ?
Spine partition of the dynamic plane
[edit | edit source]Curve :
where:
- R is an dynamic external ray
- S is the spine of Julia set
- the angles 0 and 1/2 are landing at the fixed point and at its preimage
divides dynamical plane into two components.
-
Plane paritition in case of Rabbit Julia set
-
Plane paritition in case of Basilica Julia set
crossing/noncrossing
[edit | edit source]noncrossing: "A partition of a (finite) set is just a subdivision of the set into disjoint subsets. If the set is represented as points on a line (or around the edge of a disc), we can represent the partition with lines connecting the dots. The lines usually have lots of crossings. When the partition diagram has no crossing lines, it is called a non-crossing partition. ... They have a lot of beautiful algebraic structure, and are related to lots of old enumeration problems. More recently (and importantly), they turn out to be a crucial tool in understanding how the eigenvalues of large random matrices behave." Todd Kemp (UCSD)[170]
Key words:
- Enumerative combinatorics
types
[edit | edit source]- slit plane = plane with the slit deleted[171]: Let S be the "slit plane"
- chessboard or checkerboards
types in case of discrete dynamical system
[edit | edit source]Dynamic plane or phase space
[edit | edit source]- z-plane for fc(z)= z^2 + c
- z-plane for fm(z)= z^2 + m*z
Parameter plane
[edit | edit source]See:[172]
Types of the parameter plane:
- c-plane (standard plane)
- exponential plane (map) [173][174]
- flatten' the cardiod (unroll) [175][176] = "A region along the cardioid is continuously blown up and stretched out, so that the respective segment of the cardioid becomes a line segment. .." (Figure 4.22 on pages 204-205 of The Science Of Fractal Images)[177]
- transformations [178]
-
c-plane
-
inverted c plane = 1/c plane
-
unrolled
-
lambda plane
Points
[edit | edit source]Band-merging
[edit | edit source]the band-merging points are Misiurewicz points[179]
Biaccessible
[edit | edit source]- If there exist two distinct external rays landing at point we say that it is a biaccessible point.[180]
- We call p biaccessible if it is accessible through at least two distinct external rays[181]
blowup point
[edit | edit source]blowup point = parameter for which the critical orbits map to ∞, so the Julia set is the entire sphere [182]
branched
[edit | edit source]A point in the complex plane is branched, if
- it is in the Julia set
- and is the landing point of more than two rays.[183]
Buried
[edit | edit source]" a point of the Julia set is buried if it is not in the boundary of any Fatou component." [184]
polynomials do not have buried points
some rational Julia sets have (Residual Julia Set = Buried Points)
Center
[edit | edit source]Nucleus or center of hyperbolic component
[edit | edit source]A center of a hyperbolic component H is a parameter (or point of parameter plane) such that
- the corresponding periodic orbit has multiplier= 0." [185]
- it has a superstable periodic orbit
Synonyms:
- Nucleus of a Mu-Atom [186]
Center of Siegel Disc
[edit | edit source]Center of Siegel disc is a irrationally indifferent periodic point.
Mane's theorem:
"... appart from its center, a Siegel disk cannot contain any periodic point, critical point, nor any iterated preimage of a critical or periodic point. On the other hand it can contain an iterated image of a critical point." [187]
Critical
[edit | edit source]A critical point[188] of is a point in the dynamical plane such that the derivative vanishes ( is equal to zero):
A critical value is an image of critical point
complex quadratic polynomial
[edit | edit source]For the complex quadratic polynomial in the c form
implies
we see that the only (finite) critical point of is the point .
is an initial point for Mandelbrot set iteration.[189]
Cut
[edit | edit source]

Cut point k of set S is a point for which set S-k is dissconected (consist of 2 or more sets).[190] This name is used in a topology.
Examples:
- root points of Mandelbrot set
- Misiurewicz points of boundary of Mandelbrot set
- cut points of Julia sets (in case of Siegel disc critical point is a cut point)
These points are landing points of 2 or more external rays.
Point which is a landing point of 2 external rays is called biaccessible
Cut ray is a ray which converges to landing point of another ray.[191] Cut rays can be used to construct puzzles.
Cut angle is an angle of cut ray.
fixed
[edit | edit source]names
- fixed point
- invariant = The number of fixed points of a dynamical system is invariant under many mathematical operations.
- fixpoint
- Periodic point when period = 1
- steady state of dynamical system
- stable behaviour
- equilibrium point = fixed point of DE
- w:Hyperbolic equilibrium point p of f, such that (Df)p has no eigenvalue with w:absolute value 1. In this case, Λ = {p}
- In the study of dynamical systems, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point that does not have any center manifolds. Near a hyperbolic point the orbits of a two-dimensional, non-dissipative system resemble hyperbolas. This fails to hold in general. Strogatz notes that "hyperbolic is an unfortunate name—it sounds like it should mean 'saddle point'—but it has become standard."[192] Several properties hold about a neighborhood of a hyperbolic point, notably[193]
-
types of fixed points
-
1a) stable fixpoint 1b) instable fixpoint, stable limit cycle 1c) phase space dynamics. Subcritical Hopf bifurcation: 2a) stable fixpoint, unstable limit cycle 2b) instable fixpoint 2c) phase space dynamics. \omega determines the angular dynamics and therefore the direction of winding for the trajectories.
Feigenbaum
[edit | edit source]-
Zoom toward Feigenbaum point
-
The Feigenbaum point (red arrow) is limit of the bifurcation point
-
Julia set for the Feigenbaum point
The Feigenbaum Point[194] is a:
- point c of parameter plane
- is the limit of the period doubling cascade of bifurcations = the limit of the sequence of real period doubling parameters
- the accumulation point of the period-doubling cascade in the real-valued x^2+c mapping
- an infinitely renormalizable parameter of bounded type
- boundary point between chaotic (-2 < c < MF) and periodic region (MF< c < 1/4)[195]
Generalized Feigenbaum points are:
- the limit of the period-q cascade of bifurcations
- landing points of parameter ray or rays with irrational angles
Examples:
- -.1528+1.0397i)
The Mandelbrot set is conjectured to be self- similar around generalized Feigenbaum points[196] when the magnification increases by 4.6692 (the Feigenbaum Constant) and period is doubled each time[197]
n Period = 2^n Bifurcation parameter = cn Ratio 1 2 -0.75 N/A 2 4 -1.25 N/A 3 8 -1.3680989 4.2337 4 16 -1.3940462 4.5515 5 32 -1.3996312 4.6458 6 64 -1.4008287 4.6639 7 128 -1.4010853 4.6682 8 256 -1.4011402 4.6689 9 512 -1.401151982029 10 1024 -1.401154502237 infinity -1.4011551890 ...
Bifurcation parameter is a root point of period = 2^n component. This series converges to the Feigenbaum point c = −1.401155
The ratio in the last column converges to the first Feigenbaum constant.
" a "Feigenbaum point" (an infinitely renormalizable parameter of bounded type, such as the famous Feigenbaum value which is the limit of the period-2 cascade of bifurcations), then Milnor's hairiness conjecture, proved by Lyubich, states that rescalings of the Mandelbrot set converge to the entire complex plane. So there is certainly a lot of thickness near such a point, although again this may not be what you are looking for. It may also prove computationally intensive to produce accurate pictures near such points, because the usual algorithms will end up doing the maximum number of iterations for almost all points in the picture." Lasse Rempe-Gillen[198]
Fibonacci
[edit | edit source]Fibonacci point[199] [200][201]
germ
[edit | edit source]- Catastrophe theory analyzes degenerate critical points of the potential function — points where not just the first derivative, but one or more higher derivatives of the potential function are also zero. These are called the germs of the catastrophe geometries. The degeneracy of these critical points can be unfolded by expanding the potential function as a Taylor series in small perturbations of the parameters.
- In mathematics, the notion of a germ of an object in/on a topological space is an equivalence class of that object and others of the same kind that captures their shared local properties. In particular, the objects in question are mostly functions (or maps) and subsets. In specific implementations of this idea, the functions or subsets in question will have some property, such as being analytic or smooth, but in general this is not needed (the functions in question need not even be continuous); it is however necessary that the space on/in which the object is defined is a topological space, in order that the word local has some meaning.The name is derived from cereal germ in a continuation of the sheaf metaphor, as a germ is (locally) the "heart" of a function, as it is for a grain.
infinity
[edit | edit source]The point at infinity [202]" is a superattracting fixed point, but more importantly its immediate basin of attraction - that is, the component of the basin containing the fixed point itself - is completely invariant (invariant under forward and backwards iteration). This is the case for all polynomials (of degree at least two), and is one of the reasons that studying polynomials is easier than studying general rational maps (where e.g. the Julia set - where the dynamics is chaotic - may in fact be the whole Riemann sphere). The basin of infinity supports foliations into "external rays" and "equipotentials", and this allows one to study the Julia set. This idea was introduced by Douady and Hubbard, and is the basis of the famous "Yoccoz puzzle"." Lasse Rempe-Gillen[203]

Misiurewicz
[edit | edit source]Misiurewicz point[204] = " parameters where the critical orbit is pre-periodic.
Myrberg-Feigenbaum
[edit | edit source]MF = the Myrberg-Feigenbaum point is the different name for the Feigenbaum Point.
node
[edit | edit source]- branch point of the shrub
- type of the Misiurewicz point
Parabolic point
[edit | edit source]parabolic points: this occurs when two singular points coalesce in a double singular point (parabolic point)[205]
"the characteristic parabolic point (i.e. the parabolic periodic point on the boundary of the critical value Fatou component) of fc"[206]
Periodic
[edit | edit source]Point z has period p under f if:
In other words point is periodic
See also:
- fixed point
- stability of periodic point
- attracting
- repelling
- indifferent
- multiplier of periodic cycle
Pinching
[edit | edit source]"Pinching points are found as the common landing points of external rays, with exactly one ray landing between two consecutive branches. They are used to cut M or K into well-defined components, and to build topological models for these sets in a combinatorial way. " (definition from Wolf Jung program Mandel)
other names
- pinch points
- cut points
See for examples:
- period 2 = Mandel, demo 2 page 3.
- period 3 = Mandel, demo 2 page 5 [207]
Pool
[edit | edit source]"A point in the dendrite is called a pool if it is the landing point for two external rays, both of whose angles are of the form
for some k, n ∈ N, where k ≡ 1 mod 6.
...
central pool ... it is geometrically the center of the dendrite; a one half rotation around this point maps the dendrite to itself." [208]
post-critical
[edit | edit source]A post-critical point is a point
where is a critical point.[209]
See also:
precritical
[edit | edit source]precritical points, i.e., the preimages of the critical point
reference point
[edit | edit source]Reference point of the image:
- its orbit (reference orbit) is computed with arbitrary precision and saved
- orbits of the other points of the image (no-reference points) are computed from reference orbit using standard precision (with hardware floating point numbers) = faster then using arbitrary precision
renormalizable
[edit | edit source]point of the parameter plane " is renormalizable if restriction of some of its iterate gives a polinomial-like map of the same or lower degree. " [210]
infinitely renormalizable
[edit | edit source]" a "Feigenbaum point" (an infinitely renormalizable parameter of bounded type, such as the famous Feigenbaum value which is the limit of the period-2 cascade of bifurcations), then Milnor's hairiness conjecture, proved by Lyubich, states that rescalings of the Mandelbrot set converge to the entire complex plane. So there is certainly a lot of thickness near such a point, although again this may not be what you are looking for. It may also prove computationally intensive to produce accurate pictures near such points, because the usual algorithms will end up doing the maximum number of iterations for almost all points in the picture." Lasse Rempe-Gillen[211]
IMMEDIATE RENORMALIZATION
[edit | edit source]" A cubic polynomial P with a non-repelling fixed point b is said to be immediately renormalizable if there exists a (connected) quadratic-like invariant filled Julia set K∗ such that b ∈ K∗ . In that case exactly one critical point of P does not belong to K∗." [212]
repelling
[edit | edit source]Virtually repelling
[edit | edit source]virtually repelling fixed points[213]
root or bond
[edit | edit source]The root point of the hyperbolic component of the Mandelbrot set:
- A point where two mu-atoms meet
- has a rotational number 0
- it is a biaccessible point (landing point of 2 external rays)
Names:
- bond [214]
singular
[edit | edit source]the singular points of a dynamical system
In complex analysis there are four classes of singularities:
- Isolated singularities: Suppose the function f is not defined at a, although it does have values defined on U \ {a}.
- The point a is a removable singularity of f if there exists a holomorphic function g defined on all of U such that f(z) = g(z) for all z in U \ {a}. The function g is a continuous replacement for the function f.
- The point a is a pole or non-essential singularity of f if there exists a holomorphic function g defined on U with g(a) nonzero, and a natural number n such that f(z) = g(z) / (z − a)n for all z in U \ {a}. The least such number n is called the order of the pole. The derivative at a non-essential singularity itself has a non-essential singularity, with n increased by 1 (except if n is 0 so that the singularity is removable).
- The point a is an essential singularity of f if it is neither a removable singularity nor a pole. The point a is an essential singularity if and only if the Laurent series has infinitely many powers of negative degree.
- Branch points are generally the result of a multi-valued function, such as or being defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The shape of the branch cut is a matter of choice, however, it must connect two different branch points (like and for ) which are fixed in place.
tip
[edit | edit source]- from Mu-Ency: "the point in a primary filament that has the simplest external angle; this is the point that you get by appending FS[(1/2B1)] an infinite number of times to the primary filament's name." This is also the "limit" of the ... series.
- Misurewicz point
-
tip of the main antenna (1/2 wake)
triple
[edit | edit source]"A point in the dendrite is called a triple point if its removal separates the dendrite into three connected components. Such a point is the landing point for three external rays, whose angles all have of the form
for some k, n ∈ N, where k is congruent to 1, 2 or 4, mod 7." Will Smith in Thompson-Like Groups for Dendrite Julia Sets
wandering
[edit | edit source]A point is called wandering if its forward orbit under the iteration of f is infinite.[215]
There is no wandering branched point for any quadratic polynomial. However, this is not true in general. Blokh and Oversteegen constructed cubic polynomials whose Julia sets contain wandering branched points;[216]
Portrait
[edit | edit source]orbit portrait
[edit | edit source]types
[edit | edit source]There are two types of orbit portraits: primitive and satellite.[217] If is the valence of an orbit portrait and is the recurrent ray period, then these two types may be characterized as follows:
- Primitive orbit portraits have and . Every ray in the portrait is mapped to itself by . Each is a pair of angles, each in a distinct orbit of the doubling map. In this case, is the base point of a baby Mandelbrot set in parameter space.
- Satellite (non-primitive) orbit portraits have . In this case, all of the angles make up a single orbit under the doubling map. Additionally, is the base point of a parabolic bifurcation in parameter space.
Critical
[edit | edit source]Critical orbit portrait = portrait of the critical orbit
- ... for the polynomial we may note the critical orbit portrait:
for this map, or we may double the angles of external rays and record the locations of landing points in order to observe the same behavior." [218]
critical portrait:
- orbit portrait of critical point z = 0 = portrait of forward orbit of critical point
- a collection of subsets of the unit circle
- paritition of the unit circle and the dynamic plane. The partition is formed by the dynamic rays at angles and , which land together at the critical point. The ray for angle is landing at the critical value
- collection of angles of rays landing on the critical point
- for critical portrait is (1/8, 7/12)
- for critical portrait is (1/12, 7/12)
-
1/4
-
1/6
-
9/56
-
129/16256
Precision
[edit | edit source]Precision of:
- data type used for computation. Measured in bits (width of significant (fraction) = number of binary digits) or in decimal digits
- input values
- result (number of significant figures)
See:
- Numerical Precision: " Precision is the number of digits in a number. Scale is the number of digits to the right of the decimal point in a number. For example, the number 123.45 has a precision of 5 and a scale of 2."[219]
- error [220]
Principle
[edit | edit source]Douady’s principle
[edit | edit source]Douady’s principle: “sow in dynamical plane and reap in parameter space”.
Problem
[edit | edit source]small divisor problem
[edit | edit source]Types
- One-Dimensional Small Divisor Problems[221] (On Holomorphic Germs and Circle Diffeomorphisms)
- linearization problem in complex dimension one dynamical systems: "Given a fixed point of a differentiable map, seen as a discrete dynamical system, the linearization problem is the question whether or not the map is locally conjugated to its linear approximation at the fixed point. Since the dynamics of linear maps on finite dimensional real and complex vector spaces is completely understood, the dynamics of a map on a finite dimensional phase space near a linearizable fixed point is tractable."[222]
Where it can be found:
- stability in mechanics, particularly in celestial mechanics
- relations between the growth of the entries in the continued fraction expansion of t and the behaviour of f around z=0 under iteration.
See:
Processes or transformations and phenomenona
[edit | edit source]Aliasing and antialiasing
[edit | edit source]- aliasing[223]
Conjugation
[edit | edit source]Topological conjugacy
[edit | edit source]two functions are said to be topologically conjugate if there exists a homeomorphism that will conjugate the one into the other. Topological conjugacy also known as topological equivalence[224] is important in the study of iterated functions and more generally dynamical systems, since, if the dynamics of one iterative function can be determined, then that for a topologically conjugate function follows trivially.
To illustrate this directly: suppose that and are iterated functions, and there exists a homeomorphism such that
so that and are topologically conjugate. Then one must have
and so the iterated systems are topologically conjugate as well. Here, denotes function composition.

Commutative square diagram
- a collection of maps
- square diagram that commutes = all map compositions starting from the same set A and ending with the same set D give the same result
Examples
- The logistic map and the tent map are topologically conjugate.[225]
- The logistic map of unit height and the Bernoulli map are topologically conjugate.[citation needed]
- For certain values in the parameter space, the Hénon map when restricted to its Julia set is topologically conjugate or semi-conjugate to the shift map on the space of two-sided sequences in two symbols.[226]
Contraction and dilatation
[edit | edit source]- the contraction z → z/2
- the dilatation z → 2z.
convolution
[edit | edit source]In the digital image processing[227]: image convolution Convolution is used to
- extract certain features from an input image, like edge
Image convolutions by dimensions of the kernel array:
- 1D
- LIC
- 2D
- Gaussian blur (Gaussian smoothing)
- Sobel filter
See also
- feature detection (Feature extraction)
- edge detection
- Ridge detection
- Motion detection
- Blob detection
differentiation
[edit | edit source]Method of computing the derivative of a mathematical function
types:
- symbolic differentiation
- Automatic Differentiation (AD)[228]
- numeric differentiation [229][230][231] = the method of finite differences[232]
Discretizations
[edit | edit source]- discretization[233] and its reverse [234]
- discretize/homogenize in the DDG (Discrete Differential Geometry)
Discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts.[235]
Examples:
- Cartesian coordinate system ( regular grid ) of continous space
distorsion
[edit | edit source]- distorsion[236] of the plane = plane transformation
- distortion of Mandelbrot set island
Implosion and explosion
[edit | edit source]
Implosion is:
- the process of sudden change of quality fuatures of the object, like collapsing (or being squeezed in)
- the opposite of explosion
Example:
- parabolic implosion in complex dynamics ()
- when filled Julia for complex quadratic polynomial set looses all its interior (when c goes from 0 along internal ray 0 thru parabolic point c=1/4 and along external ray 0 = when c goes from interior, crosses the boundary to the exterior of Mandelbrot set)[237]
- " We can see that looks somewhat like from the "outside", but on the "inside" there are curlicues; pairs of them are vaguely reminiscent of "butterflies". As t→0, these butterflies persist and remain uniformly large. We think of t as representing time, which decreases to 0. The fact that they suddenly disappear for t=0 is the phenomenon called "implosion". Or, if we think of time starting at t=0, then the instantaneous appearance of large "butterflies" for t>0 may be thought of as "explosion". "
- the Julia set implodes when under small perturbations (epsilon) near parabolic parameter (like c = 1/4)[238]
- Semi-parabolic implosion in [239]
- Implosion: from circle thru cauliflower to imploded cauliflower
Explosion is a:
- sudden change of quality features of the object in an extreme manner,
- the opposite of implosion
Example: in exponential dynamics when λ> 1/e, the Julia set of is the entire plane.[240]
integrating
[edit | edit source]- integrating along some vector field means finding a solution curve. Example: finding extrrernal ray using Runge-Kutta method for numerical integration[241]
Linearization
[edit | edit source]- changing from non-linear to linear
- " ... turn the perturbated linear map into the exactly linear map (it linearizes )" Jean-Christophe Yoccoz[242]
- linearization in english wikipedia
- Linearization in scholarpedia
- "System is linearizable at the origin if and only if there exists a change of coordinates which linearizes the system, that is, all the coefficients of the normal form vanish." [243]

Examples:
- Parabolic Linearization
Linearisation Theorems
[edit | edit source]Dynamics of f near a fixed or periodic point[244]
In the neighbourhood of a fixed point, which we take to be 0,
(Taylor series with big O notation), where is the multiplier at the fixed point. We say that f is linearisable if there is a neighbourhood U on which f is conjugate to (by a complex analytic conjugacy).
Examples:
- Koenigs’ Linearization Theorem 1884
- Boettcher 1904
Mating
[edit | edit source]Mating [245]
Moebius Transformation
[edit | edit source]Monodromy
[edit | edit source]Types[246]
- the local monodromy, which describes the change of the fundamental system of solutions caused by the analytic continuation along a loop encircling a regular singular point.
- the (global) monodromy, which describes the changes caused by global analytic continuations
Normalization
[edit | edit source]Normalize
- normalize = transformation to the model[247]
- " normalize this vector so it has modulus one " A Cheritat
- move fixed point to the origin (z = 0)
- mapping the range of variable to standard range
- [0.0, 1.0]
- [0,255], like rgb values
- converting closed curve to unit circle
- converting closed curves to concentric circles with center at the origin[248]
See also:
- uniformization
- renormalization
Parametrization
[edit | edit source]- Parametrization is the process of finding parametric equations of a curve[249]
Perturbation
[edit | edit source]- Perturbation technque for fast rendering the deep zoom images of the Mandelbrot set[250]
- perturbation of parabolic point [251]
- use perturbation theory to approximate the solutions of the differential equations[252]
- perturbation of point x: where epsilon is absolute value of approximation error[253]
- adding some small value ( epsilon denoted by Greek letter ) to the constant value to see how function changes near hard to analyze values
Renormalization
[edit | edit source]- logistic map renormalization[254]
- renormalization of the point
- Demo 5: renormalization from program mandel
- Mitsuhiro Shishikura: Renormalization in complex dynamics
"to any quadratic map f we can associate a canonical sequence of periods p1 < p2 <... for which f is renormalizable.
Depending on whether the sequence is:
- empty
- finite
- infinite
the map f is called respectively:
- non-renormalizable
- at most finitely renormalizable
- infinitely renormalizable" [255]
"Sectorial renormalizations are useful in the nonlinearizable situation. " Ricardo Pérez-Marco[256]
The self-similarity is a result of something called "renormalization" (which as far as I know is not related to the concept with the same name in quantum field theory). Jim Belk[257]
Examples:
- Near parabolic renormalization for unicritical holomorphic maps[258]
- how theories change as we move to more or less detailed descriptions is known as renormalization. by Simon DeDeo
Separation
[edit | edit source]- "the double fixed point 0 of usually splits into two fixed points. ... These points separate at some speed" ( PARABOLIC IMPLOSION. A MINI-COURSE by ARNAUD CHERITAT )
Surgery
[edit | edit source]-
Surgery on the circle
-
Surgery on the sphere
Links:
Tuning
[edit | edit source]- definition
- M-set and Julia set[261]
- external angles
examples of external angles tuning[262]
"tuning is a procedure to replace the bounded superattracting Fatou components with the copies of a filled Julia set of another polynomial and respect some combinatorial properties. Douady-Hubbard proved any quadratic polynomial which has a periodic critical point can be tuned with any quadratic polynomials in the Mandelbrot set M." YIMIN WANG[263]
Types
- PRIMITIVE TUNING
Uniformization
[edit | edit source]Uniformization of
- Hyperbolic Components of Mandelbrot set to the unit disc = multiplier map
- basin of superattractive fixed point - Bottcher map (The Bottcher uniformization theorem)
Vectorisation
[edit | edit source]property or feature
[edit | edit source]behavior
[edit | edit source]- local behavior is the behavior of a complex analytic function near some point (fixed, periodic) = Local theory of periodic orbits = local dynamics
- global behavior
chaos
[edit | edit source]Universal routes to chaotic behavior (routes into chaos, deterministic chaos)
- period doubling route to chaos
- the Pomeau-Manneville scenario
- the Ruelle-Takens-Newhouse scenario,
Density
[edit | edit source]density of the image
[edit | edit source]- downsaling with gamma correction[267]
- path finding[268]
- supersampling: "ots of detail but fractal fades away as you get more accurate, as n increases in nxn supersampling" TGlad
Hyperbolic/parabolic/eliptic
[edit | edit source]The meaning of the terms "elliptic, hyperbolic, parabolic" in different disciplines in mathematics[269]
- PDE (Linear Second Order PDE’s in two Independent Variables):
- Moebius transformations: [270][271]
- Discrete local complex dynamics
- Conic section
- Quadratic form
- Probability distributions.
Invariant
[edit | edit source]sth is invariant with respect to the transformation = non modified, steady
Topological methods for the analysis of dynamical systems
Invariants type
- metric invariants
- dynamical invariants,
- topological invariants.
dynamical
[edit | edit source]Dynamical invariants = invariants of the dynamical system
- periodic points
- fixed point
- invariant curve
- periodic ray
- external: fixed curves near fixed point
- internal
- periodic ray
Dynamical Invariants Derived from Recurrence Plots[272]
Orientation
[edit | edit source]- A compass rose: Notice that the convention for measuring angles is different to the convention we used in the unit circle definition of the trigonometric functions.
- Firstly 0o is North, rather than the x axis.
- Secondly the direction in which angles increase is clockwise rather than counter-clockwise.
- Unit circle :
- the direction in which angles increase is counter-clockwise
- angle zero is the x axis direction
- Cartesian coordinate system[273]
smooth
[edit | edit source]smooth = changing without visible (noticeable) edges
use:
- smooth gradient
similar:
- continuous
compare:
- discrete
Stability
[edit | edit source]- stability of quasiperiodic motion under small perturbation. In the celestial mechanics dynamics of 3 bodies around sun is described by the system of differential equations. In such case it "becomes fantastically complicated and remains largely mysterious even today." See KAM = Kolmogorov–Arnold–Moser theorem and small divisor problem
- stability of the fixed point under small perturbation
- there is equivalence (for |f′(0)| ≤ 1) of stability (a topological notion) and linearizability (an analytical notion)
Compare with:
- shadowing lemma
- Sensitive dependence on initial conditions - Butterfly effect
Radius
[edit | edit source]Radius of complex number
[edit | edit source]The absolute value or modulus or magnitude or radius of a complex number
Conformal radius
[edit | edit source]Conformal radius of Siegel Disk [274][275]
Escape radius (ER)
[edit | edit source]Escape radius (ER) or bailout value is a radius of circle centered at origin (z=0). This set is used as a target set in the bailout test (escape time method = ETM)
Minimal
[edit | edit source]Minimal Escape Radius should be grater or equal to 2:
Better estimation is:[276][277]
crossing
[edit | edit source]How to choose parameters for which level curves cross critical point (and its preimages)? Choose escape radius equal to n=th iteration of critical value.
- level curves cross at critical point
-
not cross
-
cross
-
cross
// find such ER for LSM/J that level curves croses critical point and it's preimages
double GiveER(int i_Max){
complex double z= 0.0; // critical point
int i;
; // critical point escapes very fast here. Higher valus gives infinity
for (i=0; i< i_Max; ++i ){
z=z*z +c;
}
return cabs(z);
}
Another way: choose the parameter c such that it is on an escape line, then the critical value will be on an escape line as well.
Inner radius
[edit | edit source]Inner radius of Siegel Disc
- radius of inner circle, where inner circle with center at fixed point is the biggest circle inside Siegel Disc.
- minimal distance between center of Siel Disc and critical orbit
Internal radius
[edit | edit source]Internal radius is a:
- absolute value of multiplier
See also: the N-2 rule[278]
Sequences
[edit | edit source]A sequence is an ordered list of objects (or events).[279]
A series is the sum of the terms of a sequence of numbers.[280] Some times these names are not used as in above definitions.
Itinerary
[edit | edit source]is an itinerary of point x under the map f relative to the paritirtion.
It is a right-infinite sequence of zeros and ones [281]
where
Examples:
For rotation map and invariant interval (circle):
one can compute :
and split interval into 2 subintervals (lower circle partition):
then compute s according to it's relation with critical point:
Itinerary can be converted[282] to point
itinerary with respect to a critical portrait
[edit | edit source]kneading sequence
[edit | edit source]- "the kneading sequence of an external angle ϑ (here ϑ = 1/6) is defined as the itinerary of the orbit of ϑ under angle doubling, where the itinerary is taken with respect to the partition formed by the angles ϑ/2, and (ϑ + 1)/2 "[283]
- The itinerary ν = ν1ν2ν3 . . . of the critical value is called the kneading sequence.[284] One can start from the critical point but neglect the initial symbol. Such sequence is computed with the Hubbard tree
- Paritition of dynamic plane related with kneading sequence
-
1/4
-
1/6 preperiod = 1 and period = 2
-
9/56 preperiod = 3 and period = 3
-
129/16256
See also:
- kneading theory
- Milnor–Thurston_kneading_theory in wikipedia
- combinatorial dynamics
Thue–Morse sequence
[edit | edit source]Thue–Morse sequence
- how to compute it[285]
Orbit
[edit | edit source]Orbit can be:
Series
[edit | edit source]A series is the sum of the terms of a sequence of numbers.[286] Some times these names are not used as in above definitions.
Taylor
[edit | edit source]- Taylor series and Mandelbrot set[287]
- The Existence and Uniqueness of the Taylor Series of Iterated Functions [288]
Set
[edit | edit source]Attracting set
[edit | edit source]Informal definition:
"an attracting set for a dynamical system is a closed subset A of its phase space such that for "many" choices of initial point the system will evolve towards A ." John W Milnor[289]
Continuum
[edit | edit source]definition[290]
Band
[edit | edit source]chaotic band
[edit | edit source]
period- chaotic band [291]
- is between Misiurewicz points (primary separators) and
- it's biggest midget has period
- contains Sharkovsky subsequence: sequence of islands for periods: for k = 1, 2, ..... (in the increasing order = increasing from left to right). These are first appearance of hyperbolic components with such period in Sharkowsky ordering
- is on n-place in Sharkowsky ordering
Dwell bands
[edit | edit source]"Dwell bands are regions where the integer iteration count is constant, when the iteration count decreases (increases) by 1 then you have passed a dwell band going outwards (inwards). " [292] Other names:
- level sets of integer escape time
Basin
[edit | edit source]Basin can consist of
- one component, like basin of infinity
of attraction
[edit | edit source]definitions:
- An attractor's basin of attraction is the region of the phase space, over which iterations are defined, such that any point (any initial condition) in that region will asymptotically be iterated into the attractor
- The collection of all points whose iterates under f converge to the attractor [293]
immediate basin of attraction
[edit | edit source]the component of the basin containing the periodic point itself
Examples
- basin of infinity (whole basin = one component)
-
1/3
-
3/17
Component
[edit | edit source]connected component (blob) in the image
[edit | edit source]Components of parameter plane
[edit | edit source]Names:
- mu-atom[294]
- ball
- bud
- bulb
- decoration: "A decoration of the Mandelbrot set M is a part of M cut off by two external rays landing at some tip of a satellite copy of M attached to the main cardioid."[295]
- lake
- lakelet.[296]
filament
[edit | edit source]from Mu-Ency: "Any contiguous subset of the Mandelbrot Set which consists of the infinitely convoluted and branching structures that connect the island mu-molecules to each other."
Some colloquial names for filaments:
- antenna
- main antenna
- spike
- spoke.
"A filament consists of a) minibrots and b) limit points of sequences of those minibrots. The latter include Misiurewicz points (rational external angles, one for filament termini and two or more for interior points such as multi-armed spiral centers) and other points (with irrational external angles). My intuition says if you zoom to a succession of smaller minis along a filament, if this is done in a pattern for infinitely long you tend to a Misiurewicz point, and if it's done randomly for infinitely long you tend to an irrational point. But I have no proof of this. Other noninterior points on filaments mostly belong to individual minibrots: cardioid cusps (two rational external angles, odd denominator) and minibrot-filament branch tips (Misiurewicz points, two rational external angles, even denominator). There is one last point: the exact base of the filament where it attaches to something (minibrot or main set). This point has irrational external angles. The Feigenbaum point at the base of the spike is one of these." pauldelbrot[297]
Islands
[edit | edit source]Names:
- mini Mandelbrot set
- 'baby'-Mandelbrot set
- island mu-molecules = embedded copy of the Mandelbrot Set[298]
- Bug
- Island
- Mandelbrotie
- Midget
List of islands:
- http://mrob.com/pub/mu-data/largest-islands.txt
- http://mrob.com/pub/muency/largestislands.html
- http://www.math.cornell.edu/~rperez/Documents/maximals.pdf
- http://fraktal.republika.pl/mset_external_ray_mini.html
- http://mathr.co.uk/mandelbrot/feature-database.csv.bz2 (a database of all islands up to period 16, found by tracing external rays): period, islandhood, angled internal address, lower external angle numerator, denominator, upper numerator, denominator, orientation, size, centre realpart, imagpart
features of island
- period
- symbolic sequence
- angled internal address
- lower and upper external angle of rays landing on it's root
- center (
- root
- orientation
- size
- distortion
- tip (Misiurewicz point,
- c value
- period and preperiod
- lower and upper external angle of rays landing on it
Primitive and satellite
[edit | edit source]"Hyperbolic components come in two kinds, primitive and satellite, depending on the local properties of their roots." [299]
- primitive =non-satellite = island
- satellite
primare
[edit | edit source]Child (Descendant) and the parent (ancestor)
[edit | edit source]- ancestor of hyperbolic component
- descendant of hyperbolic component = child [304]
Hyperbolic component of Mandelbrot set
[edit | edit source]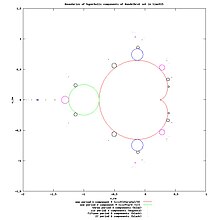
Domain is an open connected subset of a complex plane.
"A hyperbolic component H of Mandelbrot set is a maximal domain (of parameter plane) on which has an attracting periodic orbit.
A center of a H is a parameter (or point of parameter plane) such that the corresponding periodic orbit has multiplier= 0." [305]
A hyperbolic component is narrow if it contains no component of equal or lesser period in its wake [306]
features of hyperbolic component
- period
- islandhood (shape = cardiod or circle)
- angled internal address
- lower and upper external angle of rays landing on it's root
- center (
- root
- orientation
- size
Abreviations:
- LAHCs = the last appearance HCs placed in the chaotic region
Limb
[edit | edit source]- The part of the Mandelbrot set contained in the wake together with the root is called the limb of the Mandelbrot set originated at H (hyperbolic component of the Mandelbrot set)[307]

p/q-limb is a part of Mandelbrot set contained inside p/q-wake
For every rational number , where p and q are relatively prime, a hyperbolic component of period q bifurcates from the main cardioid. The part of the Mandelbrot set connected to the main cardioid at this bifurcation point is called the p/q-limb. Computer experiments suggest that the diameter of the limb tends to zero like . The best current estimate known is the Yoccoz-inequality, which states that the size tends to zero like .
A period-q limb will have q − 1 "antennae" at the top of its limb. We can thus determine the period of a given bulb by counting these antennas.
In an attempt to demonstrate that the thickness of the p/q-limb is zero, David Boll carried out a computer experiment in 1991, where he computed the number of iterations required for the series to converge for z = ( being the location thereof). As the series doesn't converge for the exact value of z = , the number of iterations required increases with a small ε. It turns out that multiplying the value of ε with the number of iterations required yields an approximation of π that becomes better for smaller ε. For example, for ε = 0.0000001 the number of iterations is 31415928 and the product is 3.1415928.[308]
Types:[309]
- The limbs attached to the main cardioid are called primary.
- Let H be a hyperbolic component attached to the main cardioid. The limbs attached to such a component are called secondary
- We refer to a truncated limb if we remove from it a neighborhood of its root
As n tends to infinity the limbs converge to a limiting elephant. See demo 2 page 10 from program Mandel by Wolf Jung
molecule
[edit | edit source]- The main molecule is the union of all hyperbolic components attached to the main cardioid through a chain of finitely many components.[310]
- island mu-molecule = island mu-unit [311]
shrub
[edit | edit source]- "what emerges from Myrrberg-Feigenbaum point is what we denominate a shrub due to its shape" M Romera
- filament,
- chaotic part of the p/q limb: "The chaotic region is made up of an infinity of hyperbolic components mounted on an infinity of shrub branches in each one of the infinity shrubs of the family."[312]
Examples
- main antenna is a shrub of family
representative of a branch is the smallest period hyperboloic componenet in the branch
spokes
[edit | edit source]"Colloquial term for a filament, specifically one of the "arms" radiating from a branch point." - from Mu-Ency
Wake
[edit | edit source]
p/q-wake is the region of parameter plane enclosed by two external rays landing on the same root point on the boundary of main cardioid (period 1 hyperbolic component).
Angles of the external rays that land on the root point one can find by:
- Combinatorial algorithm = Devaney's method
- book program by Claude Heiland-Allen
- wake function from program Mandel by Wolf Jung
p/q-Subwake of W is a wake of a p/q-satellite component of W

wake is named after:
- rotation number p/q (as above)
- angles of external rays landing in it's root point: "If two M-rays land at the same point we denote by wake the component of which does not contain 0."[313]
Components of dynamical plane
[edit | edit source]- Fatou set components
- components of interior of Julia sets
-
superattracting
-
parabolic
-
Inverse iteration of Siegel disc component
In case of Siegel disc critical orbit is a boundary of component containing Siegel Disc.
For a quadratic polynomial with a parabolic orbit, the unique Fatou component[314] containing the critical value will be called the characteristic Fatou component; (Dierk Schleicher in Rational Parameter Rays of the Mandelbrot Set)
"for rational maps (iterating maps of the form f(x)=p(x)/q(x) where p,q are polynomials) result in 1, 2 or infinitely many components."[315]
See also:
- interior and exterior of filled Julia set for polynomials
- immediate basin of attraction
Domain
[edit | edit source]Domain in mathematical analysis it is an open connected set
Jordan domain
[edit | edit source]"A Jordan domain[316] J is the homeomorphic image of a closed disk in E2. The image of the boundary circle is a Jordan curve, which by the Jordan Curve Theorem separates the plane into two open domains, one bounded, the other not, such that the curve is the boundary of each." [317]
Examples:
Canonical domain
[edit | edit source]- One of the simply-connected Riemann surfaces[318]
- characterized by rectangular grid
Flower
[edit | edit source]Interval
[edit | edit source]a partition of an interval into subintervals
- Markov partition[319]
Invariant
[edit | edit source]sth is invariant if it does't change under transformation
"A subset S of the domain Ω is an invariant set for the system (7.1) if the orbit through a point of S remains in S for all t ∈ R. If the orbit remains in S for t > 0, then S will be said to be positively invariant. Related definitions of sets that are negatively invariant, or locally invariant, can easily be given" [320]
Examples:
- invariant set
- invariant point = fixed point
- invariant cycle = periodic point
- invariant curve
- invariant circle
- petal = invariant planar set
Julia set
[edit | edit source]Feigenbaum Julia set
[edit | edit source]Julia set for Feigenbaum parameter c
Successive zooms lead to a Julia set which grows more and more hairs. (Similarly, the Mandelbrot set gains more decorations while limiting on the Feigenbaum point.) This leads to the natural question: Does the Julia set of the Feigenbaum quadratic polynomial have positive or zero measure? If zero, is its Hausdorff dimension less than 2?[321]
Level set
[edit | edit source]- a level set of a real-valued function f[322] (see also dwell band)
- Level set methods (LSM)
in case of:
- dynamic plane
- integer escape time
- target set: exterior of the circle (used in the escaping test)
attracting case
[edit | edit source]On the dynamic plane level set is defined:
Boundaries of level sets (lemniscates) are
On the parameter plane
where
- is Escape Radius, bailout value, radius of circle which is used to measure if orbit of is bounded; it is integer number
- are complex numbers (points of 2-D planes)
- is point of dynamical plane (z-plane)
- is point of parameter plane (c-plane)
- critical point of
Then:
...
is a circle,
is an Cassini oval,
These curves tend to boundary of Mandelbrot set as n goes to infinity.
- If ER < 2 they are inside Mandelbrot set[325].
- If ER = 2 curves meet together (have common point) c = −2. Thus they can't be equipotential lines.
- If ER ≥ 2 they are outside of Mandelbrot set. They can also be drawn using Level Curves Method.
- If ER >> 2 they approximate equipotential lines (level curves of real potential, see CPM/M).
- LSM/M
-
lemniscates of Mandelbrot set
-
LCM/J; ER=1000
-
LCM/J but better algorithm, ER = 2
-
LSM/J B&W; ER = 1000
-
LSM/J colour (probably made with Fractint); ER = 2
parabolic case
[edit | edit source]Where:
- d is a diameter of circle
- through 2 points: and
- radius r is half of diameter:
- is n*p iteration of critical point
- fixed point of p iteration of f function
- p is a period of the cycle
Locus
[edit | edit source]Cantor
[edit | edit source]The Cantor locus is the unique hyperbolic component, in the moduli space of quadratic rational maps rat2, consisting of maps with totally disconnected Julia sets [326]
Connectedness
[edit | edit source]In one-dimensional complex dynamics, the connectedness locus is a subset of the parameter space of rational functions, which consists of those parameters for which the corresponding Julia set is connected. the Mandelbrot set is a subset of the complex plane that may be characterized as the connectedness locus of a family of polynomial maps.
Shift
[edit | edit source]The shift locus of complex polynomials of degree d ≥ 2 is a collection of polynomials that every critical point escapes to infinity under iterations of itself. The reason we call it a shift polynomial is the following theorem.
The most famous and the simplest one is the exterior of Mandelbrot set, C −M, which is the shift locus of quadratic polynomials S2.[327]
See also
- monodromy
Planar set
[edit | edit source]a non-separating planar set is a set whose complement in the plane is connected.[328]
postsingular
[edit | edit source]"The postsingular set P(f) of a meromorphic function f is the closure of the union of forward iterates of the singular set S(f):"[329]
post-critical
[edit | edit source]- the iterates of the critical set
- "For a rational map of the Riemann sphere f, the post-critical set PC(f) is defined as closure of orbits of all critical points of f. It is proved by Lyubich [Ly83b] that the post-critical set of a rational map is the measure theoretic attractor of points in the Julia set of that map. That is, for every neighborhood of the post-critical set, orbit of almost every point in the Julia set eventually stays in that neighborhood" [330]
- "The postcritical set P(f) of a rational map f is the smallest forward invariant subset of that contains the critical values of f."[331]
- "The analysis of the post-critical set plays a central role in the dynamics of rational maps, mainly because of the following two properties:
- the set of attracting cycles is always finite for rational maps f
- every attracting cycle attracts the orbit of a critical point of f."[332]
region
[edit | edit source]- Shell-Thron region[333]
Sepal
[edit | edit source]
Singular set
[edit | edit source]"The singular set S(f) of a meromorphic function f : C → Cˆ is the collection of values w at which one can not define all branches of the inverse f −1 in any neighborhood of w. If f is rational, then S(f) coincides with the collection of critical values of f. If f is transcendental meromorphic, f −1 may also fail to be defined in a neighborhood of an asymptotic value" [334]
Target set
[edit | edit source]- trap for forward orbit
- it is a set which captures any orbit tending to fixed / periodic point
Trap
[edit | edit source]Trap is another name of the target set
Test
[edit | edit source]Bailout test or escaping test
[edit | edit source]

It is used to check if point z on dynamical plane is escaping to infinity or not.[335] It allows to find 2 sets:
- escaping points (it should be also the whole basing of attraction to infinity)[336]
- not escaping points (it should be the complement of basing of attraction to infinity)
In practice for given IterationMax and Escape Radius:
- some pixels from set of not escaping points may contain points that escape after more iterations then IterationMax (increase IterMax)
- some pixels from escaping set may contain points from thin filaments not choosed by maping from integer to world (use DEM)
If is in the target set then is escaping to infinity (bailouts) after n forward iterations (steps).[337]
The output of test can be:
- boolean (yes/no)
- integer: integer number (value of the last iteration)
Types of bailout test:
- in Fractalzoom
- other description
- kf - p-norm with weights
Criterion
[edit | edit source]criterion = an algorithm which will always give an answer
Attraction test
[edit | edit source]Theorem
[edit | edit source]- The Douady-Hubbard landing theorem for periodic external rays of polynomial dynamics:
- "for a complex polynomial f with bounded postcritical set, every periodic external ray lands at a repelling or parabolic periodic point, and conversely every repelling or parabolic point is the landing point of at least one periodic external ray." [338]
- Let f be a polynomial whose postcritical set P(f) is bounded. Then every periodic ray of f lands at a repelling or parabolic periodic point, and conversely every repelling or parabolic periodic point of f is the landing
point of at least one periodic dynamic ray, and at most finitely may dynamic rays, all of which are periodic with the same period.
- The Douady-Hubbard Strumienianin Theorem says that each polynomial-like map g with connected Julia set is hybrid to a unique polynomial up to an affine conjugacy. To determine the straightening uniquely, it is convenient to introduce an external marking for g[339]
References
[edit | edit source]- ↑ haskell package: ruff-0.2by Claude Heiland-Allen
- ↑ On the Locus of Crossed Renormalization (Problems on complex dynamical systems) by Riedl, Johannes; Schleicher, Dierk
- ↑ Trees of visible components in the Mandelbrot set by Virpi K a u k o
- ↑ Rational Maps with Clustering and the Mating of Polynomials by Thomas Joseph Sharland
- ↑ analytical naming system From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2020.
- ↑ math.stackexchange question: naming-bulbs-on-the-mandelbrot-set
- ↑ Topics from One-Dimensional Dynamics by Karen M. Brucks,Henk Bruin. page 265 exercise 14.2.12
- ↑ Combinatorics, external rays, and twisted polynomials. by Wolf Jung
- ↑ muency - internal angle (the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2016.)
- ↑ internal angle from the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2017
- ↑ argument of complex number
- ↑ w3.org docs: CSS and angle-value
- ↑ A Method to Solve the Limitations in Drawing External Rays of the Mandelbrot Set M. Romera, G. Pastor, A. B. Orue, A. Martin, M.-F. Danca, and F. Montoya
- ↑ Matcont - is a Matlab software project for the numerical continuation and bifurcation study of continuous and discrete parameterized dynamical systems. Leaders of the project are Willy Govaerts (Gent,B) and Yuri A. Kuznetsov (Utrecht,NL).
- ↑ quora: What-is-gradient?
- ↑ statistics how to: double-points
- ↑ geometry by Dr. Carol JVF Burns
- ↑ What is a Curve ?
- ↑ Unit circle in Wikipedia
- ↑ The Road to Chaos is Filled with Polynomial Curves by Richard D. Neidinger and R. John Annen III. American Mathematical Monthly, Vol. 103, No. 8, October 1996, pp. 640-653
- ↑ Hao, Bailin (1989). Elementary Symbolic Dynamics and Chaos in Dissipative Systems. World Scientific. ISBN 9971-5-0682-3.
{{cite book}}: Cite has empty unknown parameter:|coauthors=(help) - ↑ M. Romera, G. Pastor and F. Montoya, "Misiurewicz points in one-dimensional quadratic maps", Physica A, 232 (1996), 517-535. Preprint
- ↑ LAMINATIONAL MODELS FOR SOME SPACES OF POLYNOMIALS OF ARBITRARY DEGREE by ALEXANDER BLOKH, LEX OVERSTEEGEN, ROSS PTACEK, AND VLADLEN TIMORIN
- ↑ Models_for_spaces_of_dendritic_polynomials by ALEXANDER BLOKH, LEX OVERSTEEGEN, ROSS PTACEK,AND VLADLEN TIMORIN
- ↑ MODELING DENDRITIC SHAPES Using Path Planning by Ling Xu, David Mould
- ↑ procedural-branching-texture in blender by LordoftheFleas
- ↑ Escape lines versus equipotential lines in the Mnadelbrot set by M. Romera, Pastor G, D. de la Guía, Montoya
- ↑ Pseudosphere Geodesics by Tim Hutton
- ↑ The Computation of Invariant Circles of Maps Article in Physica D Nonlinear Phenomena 16(2):243-251 · June 1985 DOI: 10.1016/0167-2789(85)90061-2 1st I.G. Kevrekidis
- ↑ A Newton-Raphson method for numerically constructing invariant curves Marty, Wolfgang
- ↑ Numerical Approximation of Rough Invariant Curves of Planar Maps Article in SIAM Journal on Scientific Computing 25(1) · September 2003 DOI: 10.1137/S106482750241373X K. D. Edoh and Jens Lorenz
- ↑ SIAM J. Sci. and Stat. Comput., 8(6), 951–962. (12 pages) A New Algorithm for the Numerical Approximation of an Invariant Curve Published online: 14 July 2006 Keywords invariant manifold, polygonal approximation AMS Subject Headings 65L99, 65H10, 34C40 Publication Data ISSN (print): 0196-5204 ISSN (online): 2168-3417 Publisher: Society for Industrial and Applied Mathematics M. van Veldhuizen
- ↑ ON QUASI-INVARIANT CURVES by RICARDO PEREZ-MARCO
- ↑ Escape lines versus equipotential lines in the Mnadelbrot set by M. Romera, Pastor G, D. de la Guía, Montoya
- ↑ Wikipedia: Jordan curve theorem
- ↑ Modeling Julia Sets with Laminations: An Alternative Definition by Debra Mimbs
- ↑ Laminations of the unit disk with irrational rotation gaps by John C. Mayer
- ↑ Rational maps represented by both rabbit and aeroplane matings Thesis submitted in accordance with the requirements of the University of Liverpool for the degree of Doctor in Philosophy by Freddie R. Exall July 2010
- ↑ Core entropy and biaccessibility of quadratic polynomials by Wolf Jung
- ↑ Rational maps represented by both rabbit and aeroplane matings Thesis submitted in accordance with the requirements of the University of Liverpool for the degree of Doctor in Philosophy by Freddie R. Exall July 2010
- ↑ Rational Parameter Rays of the Mandelbrot Set by Dierk Schleicher
- ↑ Critical portraits for postcritically finite polynomials by Alfredo Poirier
- ↑ NON-ACCESSIBLE CRITICAL POINTS OF CERTAIN RATIONAL FUNCTIONS WITH CREMER POINTS by Lia Petracovici
- ↑ Convergence of external rays in parameter spaces of symmetric polynomials by Ahmad Zireh. Int. J. Contemp. Math. Sciences, Vol. 2, 2007, no. 6, 291 - 296
- ↑ A survey on MLC, Rigidity and related topics by Anna Miriam Benini
- ↑ Local Connectivity of the Mandelbrot Set. by Matt Koster December 4, 2019
- ↑ Symbolic dynamics of quadratic polynomials. Preprint (2002) page 96
- ↑ Critical portraits for postcritically finite polynomials by Alfredo Poirier
- ↑ Graph Replacement Systems for Julia Sets of Quadratic Polynomials by Yuan J. Liu
- ↑ wikipedia: Filled_Julia_set
- ↑ Rational Parameter Rays of The Multibrot Sets by Dominik Eberlein, Sabyasachi Mukherjee, Dierk Schleicher
- ↑ Robert L. Devaney. "Intertwined internal rays in Julia sets of rational maps." Fundamenta Mathematicae 206.1 (2009): 139-159. <http://eudml.org/doc/283146>.
- ↑ Plotting the Escape: An Animation of Parabolic Bifurcations in the Mandelbrot Set by Anne M. Burns. Mathematics Magazine Vol. 75, No. 2 (Apr., 2002), pp. 104-116
- ↑ Iterated Monodromy Groups of Quadratic Polynomials, I Laurent Bartholdi, Volodymyr V. Nekrashevych
- ↑ GROWTH OF GROUPS DEFINED BY AUTOMATA: ASHLEY S. DOUGHERTY, LYDIA R. KINDELIN, AARON M. REAVES, ANDREW J. WALKER, AND NATHANIEL F. ZAKAHI
- ↑ Douglas C. Ravenel: External angles in the Mandelbrot set: the work of Douady and Hubbard. University of Rochester Template:Webarchive
- ↑ John Milnor: Pasting Together Julia Sets: A Worked Out Example of Mating. Experimental Mathematics Volume 13 (2004)
- ↑ Saaed Zakeri: Biaccessiblility in quadratic Julia sets I: The locally-connected case
- ↑ A. Douady, “Algorithms for computing angles in the Mandelbrot set,” in Chaotic Dynamics and Fractals, M. Barnsley and S. G. Demko, Eds., vol. 2 of Notes and Reports in Mathematics in Science and Engineering, pp. 155–168, Academic Press, Atlanta, Georgia, USA, 1986.
- ↑ K M. Brucks, H Bruin: Topics from One-Dimensional Dynamics Series: London Mathematical Society Student Texts (No. 62) page 257
- ↑ The applications of non-euclidean distance | Metric Spaces by Zach Star
- ↑ distance fields by Philip Rideout
- ↑ Distance Transforms of Sampled Functions by Pedro Felipe Felzenszwalb
- ↑ dsp.stackexchange question: fastest-algorithm-for-distance-transform
- ↑ Symbolic Dynamics of Quadratic Polynomials by H. Bruin and D. Schleicher
- ↑ Symbolic Dynamics and Rotation Numbers J. J. P. Veerman Phys. 13A, 1986, 543-576.
- ↑ Symbolic Dynamics of Order-Preserving Orbits J. J. P. Veerman Phys. 29D, 1987, 191-201.
- ↑ Walter Bergweiler: A gallery of complex dynamics pictures.
- ↑ Around the boundary of complex dynamics by Roland K. W. Roeder
- ↑ Freely downloadable book Elementary Symbolic Dynamics and Chaos in Dissipative Systems by Bailin HAO, World Scientific, 1989, by kind permission of the publisher.
- ↑ Image entropy by Dave O'Brien
- ↑ fractal-rendering from cglearn
- ↑ mathoverflow question: whats-a-natural-candidate-for-an-analytic-function-that-interpolates-the-tower/43003
- ↑ Faa di Bruno and derivatives of an iterated function ON MAY 20, 2017 BY DCHOYLE
- ↑ A Cheritat wiki: Mandelbrot_set - Following_the_derivative
- ↑ Shapiro, J.H. (1993). The Angular Derivative. In: Composition Operators. Universitext: Tracts in Mathematics. Springer, New York, NY. https://doi.org/10.1007/978-1-4612-0887-7_5
- ↑ MAT335H1F Lecture Notes by Burbulla (Chapter 11, 12 and 13)
- ↑ Schwarzian-Derivative-Poster
- ↑ Schwarzian derivatives of rational functions by Alex Eremenko
- ↑ What is ... Schwarzian Derivative? (Notices of AMS Jan 2009),
- ↑ betterexplained: vector-calculus-understanding-the-gradient
- ↑ khan academy: the-gradient
- ↑ Gradient-Based Optimization by Jason Hicken, Prof. Juan Alonso, and Prof. Charbel Farhat
- ↑ gradient-descent-algorithm-and-its-variants by Imad Dabbura
- ↑ The chaotic nature of faster gradient descent methods by Kees van den Doel and Uri Ascher
- ↑ Conformal Geometry and Dynamics of Quadratic Polynomials, vol I-II Mikhail Lyubich, page 61
- ↑ Germ in wikipedia
- ↑ Linearization of germs: regular dependence on the multiplier by Carlo Carminati, Stefano Marmi
- ↑ math.stackexchange question: is-there-any-difference-between-mapping-and-function
- ↑ Iterated function (map) in wikipedia
- ↑ evolution function
- ↑ the discrete nonlinear dynamical system
- ↑ math.stackexchange question: why-is-local-connectivity-important-for-polynomial-julia-sets
- ↑ riemann-for-anti-dummies by the LaRouche Youth Movement in Canada
- ↑ chebfun docs
- ↑ HarmonicFunction by (c) 2011 John H. Mathews, Russell W. Howell
- ↑ Connectivity of Julia sets of Newton maps: A unified approach by K. Baranski N. Fagella X. Jarque B. Karpinska
- ↑ A Beginners’ Guide to Resurgence and Trans-series in Quantum Theories Gerald Dunne
- ↑ A Primer on Resurgent Transseries and Their Asymptotics by Inês Aniceto, Gökçe Başar, Ricardo Schiappa
- ↑ Universality of Resurgence in Quantization Theories - video
- ↑ Olexandr Ganyushkin; Volodymyr Mazorchuk (2008). Classical Finite Transformation Semigroups: An Introduction. Springer Science & Business Media. p. 1. ISBN 978-1-84800-281-4.
- ↑ Pierre A. Grillet (1995). Semigroups: An Introduction to the Structure Theory. CRC Press. p. 2. ISBN 978-0-8247-9662-4.
- ↑ Wilkinson, Leland & Graham (2005). The Grammar of Graphics (2nd ed.). Springer. p. 29. ISBN 978-0-387-24544-7.
{{cite book}}: CS1 maint: uses authors parameter (link) - ↑ "Transformations". www.mathsisfun.com. Retrieved 2019-12-13.
- ↑ "Types of Transformations in Math". Basic-mathematics.com. Retrieved 2019-12-13.
- ↑ dinkydauset at deviantar: Perturbation-for-the-Mandelbrot-set-450766847
- ↑ math.stackexchange question: selecting-reference-orbit-for-fractal-rendering-with-perturbation-theory
- ↑ math.stackexchange question: coloring-the-mandelbrot-set-using-iterated-points?
- ↑ Dessins d’enfants and Hubbard trees by Kevin M. Pilgrim
- ↑ Admissibility of kneading sequences and structure of Hubbard trees for quadratic polynomials by Henk Bruin, Dierk Schleicher
- ↑ wikipedia: Magnitude in mathematics
- ↑ Hyperbolic Components by John Milnor
- ↑ Complex quadratic map in wikipedia
- ↑ Michael Yampolsky, Saeed Zakeri: Mating Siegel quadratic polynomials.
- ↑ Mandel: software for real and complex dynamics by Wolf Jung
- ↑ three-cool-facts-about-rotations-of-the-circle by David Richeson
- ↑ irrational-rotations-of-the-circle-and-benfords-law by David Richeson
- ↑ Subdivision rule constructions on critically preperiodic quadratic matings by Mary Wilkerson
- ↑ Quotient group
- ↑ Circle group in wikipedia
- ↑ The measure of the Feigenbaum Julia set by Artem Dudko and Scott Sutherland
- ↑ MLC at Feigenbaum points by Dzmitry Dudko, Mikhail Lyubich
- ↑ Poincaré map
- ↑ General principles of chaotic dynamics by P.B. Persson, C.D. Wagner
- ↑ Continuous time and discrete time dynamical systems by Shaun Bullett
- ↑ Continuous time and discrete time dynamical systems by Shaun Bullett
- ↑ EXPONENTIAL THURSTON MAPS AND LIMITS OF QUADRATIC DIFFERENTIALS by JOHN HUBBARD, DIERK SCHLEICHER, AND MITSUHIRO SHISHIKURA
- ↑ The Thurston Algorithm for quadratic matings by Wolf Jung
- ↑ Conformal Geometry and Dynamics of Quadratic Polynomials Mikhail Lyubich
- ↑ YouTube: Mikhail Lyubich: Story of the Feigenbaum point. Centre International de Rencontres Mathématiques
- ↑ wikipedia: Riemann mapping theorem
- ↑ A THOMPSON GROUP FOR THE BASILICA by JAMES BELK AND BRADLEY FORREST
- ↑ math stackexchange question: explicit-riemann-mappings
- ↑ mathoverflow question: complex-function-for-mapping-a-circle-to-a-superellipse
- ↑ math.stackexchange question: explicit-riemann-mappings
- ↑ Dynamics of quadratic polynomials, I: Combinatorics and geometry of the Yoccoz puzzle by Mikhail Lyubich
- ↑ A THOMPSON GROUP FOR THE BASILICA by JAMES BELK AND BRADLEY FORREST
- ↑ Graph Replacement Systems for Julia Sets of Quadratic Polynomials by Yuan J. Liu
- ↑ A Thompson-Like Group for the Bubble Bath Julia Set by Jasper Weinrich-Burdref
- ↑ three-cool-facts-about-rotations-of-the-circle by David Richeson
- ↑ binary_shift_left
- ↑ Dehn_twist in wikipedia
- ↑ Feigenbaum constants
- ↑ Degree in Wikipedia (disambiguation page)
- ↑ fractalforums.org: definitions-of-degree-of-rational-function
- ↑ Multiplier at wikipedia
- ↑ Internal angles and multipliers from Fractal Geometry Yale University Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger September 3, 2017
- ↑ A Cheritat wiki-draw: Mandelbrot_set#Following_the_derivative
- ↑ scholarpedia: Siegel disks Linearization
- ↑ Periodic cycles and singular values of entire transcendental functions by Anna Miriam Benini and Nuria Fagella
- ↑ Wikipedia: Rotation number
- ↑ rotation number From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2016
- ↑ scholarpedia: Rotation_theory
- ↑ The Fractal Geometry of the Mandelbrot Set II. How to Count and How to Add Robert L. Devaney
- ↑ An Introduction to Rotation Theory Prize winner, DSWeb Student Competition, 2007 By Christian Kue
- ↑ Complex systems simulation Curso 2012-2013 by Antonio Giraldo and María Asunción Sastre
- ↑ Weisstein, Eric W. "Map Winding Number." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/MapWindingNumber.html
- ↑ Wikipedia: Rotation number
- ↑ RATIONAL PARAMETER RAYS OF THE MANDELBROT SET by Dierk Schleicher
- ↑ https://plus.maths.org/content/winding-numbers-topography-and-topology-ii
- ↑ Winding-Number by empet
- ↑ Finding the number of roots of a polynomial in a plane region using the winding number by Juan Luis García Zapataa, Juan Carlos Díaz Martín
- ↑ MATH 145: SUPPLEMENTARY NOTES by VIN DE SILVA
- ↑ Wikipedia: Orbit (dynamics)
- ↑ Ouadratic-like maps and Renormalization by Nuria Fagella
- ↑ Peiod From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2015.
- ↑ scholarpedia: Periodic Orbit for a Map
- ↑ Wikipedia: Complex quadratic polynomial - Planes
- ↑ N-sphere in wikipedia
- ↑ UC San Diego : MATH 196/296: Student Colloquium
- ↑ math.stackexchange question: entire-function-with-image-contained-in-slit-plane-is-constant
- ↑ Alternate Parameter Planes by David E. Joyce
- ↑ mu-ency: exponential map by R Munafo
- ↑ Exponential mapping and OpenMP by Claude Heiland-Allen
- ↑ Linas Vepstas : Self Similar?
- ↑ the flattened cardioid of a Mandelbrot by Tom Rathborne
- ↑ Stretching cusps by Claude Heiland-Allen
- ↑ Twisted Mandelbrot Sets by Eric C. Hill
- ↑ doubling bifurcations on complex plane by E Demidov
- ↑ On biaccessible points in the Julia set of the family z(a+z^{d}) by Mitsuhiko Imada
- ↑ On biaccessible points in the Julia set of a Cremer quadratic polynomial by Dierk Schleicher, Saeed Zakeri
- ↑ Campbell, J.T., Collins, J.T. Blowup Points and Baby Mandelbrot Sets for a Family of Singularly Perturbed Rational Maps. Qual. Theory Dyn. Syst. 16, 31–52 (2017). https://doi.org/10.1007/s12346-015-0169-5
- ↑ Criterion for rays landing together by Jinsong Zeng
- ↑ Topological Variety of Buried Points by Clinton P. Curry, Logan C. Hoehn, and John C. Mayer
- ↑ Surgery in Complex Dynamics by Carsten Lunde Petersen, online paper
- ↑ Nucleus - From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2015.
- ↑ Siegel disks by Xavier Buff and Arnaud Ch ́ritat e Univ. Toulouse Roma, April 2009
- ↑ Wikipedia: Critical point (mathematics)
- ↑ Java program by Dieter Röß showing result of changing initial point of Mandelbrot iterations
- ↑ Cut point in wikipedia
- ↑ On local connectivity for the Julia set of rational maps: Newton’s famous example By P. Roesch
- ↑ Strogatz, Steven (2001). Nonlinear Dynamics and Chaos. Westview Press. ISBN 0-7382-0453-6.
- ↑ Ott, Edward (1994). Chaos in Dynamical Systems. Cambridge University Press. ISBN 0-521-43799-7.
- ↑ muency: feigenbaum point
- ↑ On Periodic and Chaotic Regions in the Mandelbrot Set by G. Pastor, M. Romera, G. Álvarez, D. Arroyo and F. Montoya
- ↑ fractal-faq : section 6
- ↑ Period doubling and Feigenbaum's scaling be E Demidov
- ↑ mathoverflow question: is-there-a-way-to-find-regions-of-depth-in-the-mandelbrot-set-other-than-simply?rq=1
- ↑ Fractalforums: fibonacci-and-the-mandelbrot-set
- ↑ Parameter scaling for the Fibonacci point by Leroy Wenstrom
- ↑ The Fibonacci unimodal map by Mikhail Lyubich, John W. Milnor
- ↑ [w:Point at infinity|Point at infinity in wikipedia]
- ↑ Mathoverflow question: Attractive Basins and Loops in Julia Sets
- ↑ Wikipedia: Misiurewicz point
- ↑ The bifurcation diagram of cubic polynomial vector fields on CP1 by Christiane Rousseau
- ↑ A rigidity result for some parabolic germs by Luna Lomonaco, Sabyasachi Mukherjee
- ↑ http://www.mndynamics.com/indexp.html%7C program Mandel by Wolf Jung, demo 2 page 3
- ↑ Thompson-Like Groups for Dendrite Julia Sets by Will Smith
- ↑ GROWTH OF GROUPS DEFINED BY AUTOMATA : ASHLEY S. DOUGHERTY, LYDIA R. KINDELIN, AARON M. REAVES, ANDREW J. WALKER, AND NATHANIEL F. ZAKAHI
- ↑ Ouadratic-like maps and Renormalization by Nuria Fagella
- ↑ mathoverflow question: is-there-a-way-to-find-regions-of-depth-in-the-mandelbrot-set-other-than-simply?rq=1
- ↑ Immediate renormalization of complex polynomials by Alexander Blokh, Lex Oversteegen, Vladlen Timorin
- ↑ Buff, Xavier. "Virtually repelling fixed point.." Publicacions Matemàtiques 47.1 (2003): 195-209. <http://eudml.org/doc/41482>.
- ↑ Bond the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2018.
- ↑ Criterion for rays landing together by Jinsong Zeng
- ↑ A. Blokh and L. Oversteegen, Wandering gaps for weakly hyperbolic polynomials. Complex Dynamics: Families and Friends. Ed. D.Schleicher A.K.Peters, Wellesley, MA, 2008,139-168.
- ↑ Wikipedia: Orbit portrait
- ↑ THURSTON’S ALGORITHM AND RATIONAL MAPS FROM QUADRATIC POLYNOMIAL MATINGS by Mary Wilkerson
- ↑ stackoverflow question: how-do-i-interpret-precision-and-scale-of-a-number-in-a-database
- ↑ taking-the-error-out-of-the-error-function by Fredrik Johansson
- ↑ An Introduction To Small Divisors by S. Marmi
- ↑ scholarpedia: Siegel disks Linearization
- ↑ serious_statistics_aliasing by GuestJim
- ↑ Arnold V. I. Geometric Methods in the Theory of Ordinary Differential Equations (Springer, 2020) [1]
- ↑ Alligood, K. T., Sauer, T., and Yorke, J.A. (1997). Chaos: An Introduction to Dynamical Systems. Springer. pp. 114–124. ISBN 0-387-94677-2.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Devaney, R.; Nitecki, Z. (1979). "Shift automorphisms in the Hénon mapping". Comm. Math. Phys. 67 (2): 137–146. Bibcode:1979CMaPh..67..137D. doi:10.1007/bf01221362. S2CID 121479458. Retrieved 2 September 2016.
- ↑ Digital_image_processing in wikipedia
- ↑ autodiff.org
- ↑ Wikipedia: Numerical_differentiation
- ↑ Numerical Recipies In C : 5.7 Numerical Derivatives
- ↑ stackoverflow question: is-there-any-standard-way-to-calculate-the-numerical-gradient
- ↑ Wikipedia: Finite difference
- ↑ Wikipedia: discretization
- ↑ mathinsight: from_discrete_to_continuous_dynamical_systems
- ↑ J.M. Hyman, M. Shashkov, Natural discretizations for the divergence, gradient, and curl on logically rectangular grids, Computers & Mathematics with Applications, Volume 33, Issue 4, 1997, Pages 81-104, ISSN 0898-1221, https://doi.org/10.1016/S0898-1221(97)00009-6. (https://www.sciencedirect.com/science/article/pii/S0898122197000096) Abstract: This is the first in series of papers creating a discrete analog of vector analysis on logically rectangular, nonorthogonal, nonsmooth grids. We introduce notations for 2-D logically rectangular grids, describe both cell-valued and nodal discretizations for scalar functions, and construct the natural discretizations of vector fields, using the vector components normal and tangential to the cell boundaries. We then define natural discrete analogs of the divergence, gradient, and curl operators based on coordinate invariant definitions and interpret these formulas in terms of curvilinear coordinates, such as length of elements of coordinate lines, areas of elements of coordinate surfaces, and elementary volumes. We introduce the discrete volume integral of scalar functions, the discrete surface integral, and a discrete analog of the line integral and prove discrete versions of the main theorems relating these objects. These theorems include the following: the discrete analog of relationship div A→ = 0 if and only if A→ = curl B→; curl A→ = 0 if and only if A→ = grad ϕ; if A→ = grad ϕ, then the line integral does not depend on path; and if the line integral of a vector function is equal to zero for any closed path, then this vector is the gradient of a scalar function. Last, we define the discrete operators DIV, GRAD, and CURL in terms of primitive differencing operators (based on forward and backward differences) and primitive metric operators (related to multiplications of discrete functions by length of edges, areas of surfaces, and volumes of 3-D cells). These formulations elucidate the structure of the discrete operators and are useful when investigating the relationships between operators and their adjoints. Keywords: Finite-difference; Logically-rectangular grids; Discrete vector analysis
- ↑ filterforge filters: distorsion
- ↑ Airplane primitive parabolic implosion by Wolf Jung
- ↑ Parabolic Implosion by Han Peters, L. Vivas Published 2020
- ↑ SemiParabolicImplosion by Eric Bedford
- ↑ CANTOR BOUQUETS, EXPLOSIONS, AND KNASTER CONTINUA: DYNAMICS OF COMPLEX EXPONENTIALS by Robert L. Devaney Publicacions Matematiques, Vol 43 (1999), 27–54.
- ↑ fractalforums.com: smooth-external-angle-of-mandelbrot-set
- ↑ Jean-Christophe Yoccoz Small Divisors: Number Theory in Dynamical Systems, page 46
- ↑ Integrability and Linearizability of the Lotka^Volterra System with a Saddle Point with Rational Hyperbolicity Ratio by Simon Gravel and Pierre Thibault
- ↑ Shaun Bullett: Holomorphic Dynamics and Hyperbolic Geometry (LTCC Feb-March 2013) notes
- ↑ On The Notions of Mating by Carsten Lunde Petersen, Daniel Meyer
- ↑ Book: Linear Differential Equations in the Complex Domain by Yoshishige Haraoka
- ↑ Normal Forms, Bifurcations and Finiteness Problems in Differential Equations by Yulij Ilyashenko, Christiane Rousseau, Gert Sabidussi
- ↑ towardsdatascience: gradient-descent-algorithm-and-its-variants
- ↑ math.stackexchange question: what-is-parameterization
- ↑ Perturbation for the Mandelbrot set by DinkydauSet, Apr 28, 2014, 3:46:13 PM
- ↑ PARABOLIC IMPLOSION A MINI-COURSE ARNAUD CHERITAT
- ↑ scholarpedia article: Perturbation theory (dynamical systems)
- ↑ wikipedia: Approximation error
- ↑ Logistic map: Renormalizationestimate in wikipedia
- ↑ Baby Mandelbrot sets, Renormalization and MLC Mikhail Lyubich
- ↑ ON QUASI-INVARIANT CURVES by Ricardo Pérez-Marco
- ↑ mathoverflow question: fine-structure-of-bifurcation-diagram-of-logistic-family
- ↑ Near Parabolic Renormalization for Unicritical Holomorphic Maps by Arnaud Chéritat. Arnold Mathematical Journal https://doi.org/10.1007/s40598-020-00172-6
- ↑ wikipedioa: Surgery theory
- ↑ Regluing of rational functions by Vladlen Timorin
- ↑ Tuning From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2014.
- ↑ Online tuning in the Mandelbrot set by Claude Heiland-Allen
- ↑ Primitive tuning for non-hyperbolic polynomials by Yimin Wang 2021
- ↑ Wikipedia: dense set
- ↑ mathoverflow question: is-there-an-almost-dense-set-of-quadratic-polynomials-which-is-not-in-the-inte/254533#254533
- ↑ fractalforums: dense-image
- ↑ A Cheritat wiki: see image showing gamma-correct downscale of dense part of Mandelbropt set
- ↑ fractal forums: pathfinding-in-the-mandelbrot-set/
- ↑ quora: Where-is-the-best-summary-on-the-meaning-of-the-terms-elliptic-hyperbolic-parabolic-as-used-in-different-disciplines-in-mathematics
- ↑ moebius-transformation by Claude Heiland-Allen
- ↑ 2015-02-06_interpolating_moebius_transformations by Claude Heiland-Allen
- ↑ N. Marwan, M. C. Romano, M. Thiel, J. Kurths: Recurrence Plots for the Analysis of Complex Systems, Physics Reports, 438(5-6), 237-329, 2007.
- ↑ math.stackexchange question: direction-of-x-axis-with-respect-to-y-axis-in-cartesian-coordinate-system
- ↑ Wikipedia: Conformal radius
- ↑ scholarpedia: Quadratic Siegel disks
- ↑ Julia Sets of Complex Polynomials and Their Implementation on the Computer by Christoph Martin Stroh
- ↑ fractalforums: bounding circle of julia sets by knighty
- ↑ The Mandelbrot Set and Julia Sets Combinatorics in the Mandelbrot Set - The 1/n2 rule, and deviations from it
- ↑ Wikipedia: Sequence
- ↑ Wikipedia: series
- ↑ Structure of Inverse Limit Spaces of Tent Maps with Nonrecurrent Critical Points by Brian Raines and Sonja Stimac
- ↑ Bifurcation structures in maps of Henon type by Kai T Hansen and Predrag Cvitanovic
- ↑ Hausdorff dimension of biaccessible angles of quadratic Julia sets and of the Mandelbrot set by Henk Bruin and Dierk Schleicher
- ↑ ADMISSIBILITY OF KNEADING SEQUENCES AND STRUCTURE OF HUBBARD TREES FOR QUADRATIC POLYNOMIALS by HENK BRUIN AND DIERK SCHLEICHER
- ↑ rosetta code: Thue-Morse
- ↑ Wikipedia: series
- ↑ quora: Why-is-the-Mandelbrot-set-a-fractal? Answer by Anders Kaseorg
- ↑ The Existence and Uniqueness of the Taylor Series of Iterated Functions by Daniel Geisler
- ↑ scholarpedia.org: Attractor
- ↑ Wikipedia: Continuum in set theory
- ↑ Harmonic structure of one-dimensional quadratic maps by G. Pastor, M. Romera, and F. Montoya
- ↑ fractalforums: binary-decomposition-and-external-angles by Claude
- ↑ Alicia Cordero, Fazlollah Soleymani, Juan R. Torregrosa, Stanford Shateyi, "Basins of Attraction for Various Steffensen-Type Methods", Journal of Applied Mathematics, vol. 2014, Article ID 539707, 17 pages, 2014. https://doi.org/10.1155/2014/539707
- ↑ mu-atom From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2018.
- ↑ A priori bounds for some infinitely renormalizable quadratics: II. Decorations by Jeremy Kahn, Mikhail Lyubich
- ↑ Mu-atom From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2013.
- ↑ fractalforums.org: how-thick-are-the-filaments
- ↑ Island Mu-Molecule by Robert P. Munafo, 2012 Aug 18.
- ↑ Internal addresses in the Mandelbrot set and Galois groups of polynomials by Dierk Schleicher, page 31
- ↑ notes by Lyubich
- ↑ Satellite copies of the Mandelbrot set by Luna Lomonaco
- ↑ mathoverflow: precise-location-of-the-mandelbrot-bulb-attachment-to-the-main-cardioid
- ↑ ON BIACCESSIBLE POINTS OF THE MANDELBROT SET by SAEED ZAKERI
- ↑ Child From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2013.
- ↑ Surgery in Complex Dynamics by Carsten Lunde Petersen, online paper
- ↑ Internal addresses in the Mandelbrot set and irreducibility of polynomials by Dierk Schleicher
- ↑ Dynamics of quadratic polynomials, I: Combinatorics and geometry of the Yoccoz puzzle by Mikhail Lyubich
- ↑ Gary William Flake, The Computational Beauty of Nature, 1998. p. 125. ISBN 978-0-262-56127-3.
- ↑ Dynamics of quadratic polynomials, I: Combinatorics and geometry of the Yoccoz puzzle by Mikhail Lyubich
- ↑ Counting Hyperbolic Components in the Main Molecule by Schinella D'Souza
- ↑ the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2018
- ↑ Romera, Miguel & Pastor, Gerardo & Alvarez, Gonzalo & Vitini, Fausto. (2003). Shrubs in the Mandelbrot Set Ordering. International Journal of Bifurcation and Chaos. 13. 10.1142/S0218127403007941.
- ↑ Local properties of the Mandelbrot set at parabolic points by Tan Lei
- ↑ wikipedia: Classification_of_Fatou_components
- ↑ math.stackexchange question: quasiconformal-automorphism-groups-of-julia-sets
- ↑ Wikipedia: Carathéodory's theorem (conformal mapping)
- ↑ The intrinsic geometry of a Jordan domain by Richard L. Bishop
- ↑ Incorporating topography into crustal-scale wave-equation imaging through conformal mapping by Jeffrey Shraggec and Paul Sava
- ↑ math.stackexchange question: definition-of-markov-partition
- ↑ Norman Lebovitz: Textbook for Mathematics 27300
- ↑ On the Measure of the Feigenbaum Julia Set Scott Sutherland Stony Brook University Joint work with Artem Dudko, IMPAN Bedlewo, Poland 22 March 2018
- ↑ Wikipedia: Level set
- ↑ Weisstein, Eric W. "Pear Curve." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PearCurve.html
- ↑ Mandelbrot lemniscate at 2DCurves by Jan Wassenaar
- ↑ Polynomial_lemniscate
- ↑ Limits of Polynomial-like Quadratic Rational Maps III: The Cantor Locus by Eva Uhre
- ↑ Monodromy through bifurcation locus of the Mandelbrot set by Hyungryul Baik, Juhun Baik 2023
- ↑ A. Blokh, X. Buff, A. Cheritat, L. Oversteegen The solar Julia sets of basic quadratic Cremer polynomials, Ergodic Theory and Dynamical Systems, 30 (2010), #1, 51-65
- ↑ Prescribing the Postsingular Dynamics of Meromorphic Functions by Christopher J. Bishop, Kirill Lazebnik
- ↑ Dynamics of complex unicritical polynomials. A Dissertation Presented by Davoud Cheraghi
- ↑ On the postcritical set of a rational map by Laura G. DeMarco, Sarah C. Koch and Curtis T. McMullen
- ↑ Dynamics of hyperbolic correspondences by Carlos Siqueira
- ↑ Hyperoperations Wiki: Shell-Thron_region
- ↑ Prescribing the Postsingular Dynamics of Meromorphic Functions by Christopher J. Bishop, Kirill Lazebnik
- ↑ Fractus doc by Richard Rosenman
- ↑ Wikipedia: Escaping set
- ↑ fractint doc: bailout
- ↑ A landing theorem for entire functions with bounded post-singular sets by Anna Miriam Benini, Lasse Rempe-Gillen
- ↑ Primitive tuning for non-hyperbolic polynomials by Yimin Wang

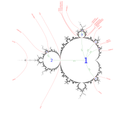















































![{\displaystyle \varphi _{\mathit {U}}^{-1}(r^{2\pi \vartheta }):r\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c13a7138507ed2ccd47b13448338f2711f3b761f)






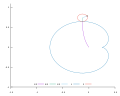







![{\displaystyle S_{c}=\left[-\beta ,\beta \right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf36eba729d2e3bc5c988ac0892cbb13473af37c)
















![{\displaystyle \nabla f(x,y)=[{\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}}]={\begin{bmatrix}{\frac {\partial f}{\partial x}}\\{\frac {\partial f}{\partial y}}\end{bmatrix}}={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1386d0f3fcba04a6786a6c239c4fbdf3c76d40a)

![{\displaystyle [f]_{z}=\{g:g\sim _{z}f\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8744eb0670f54c82aca5085ff3c5030be14f4e6d)



















































































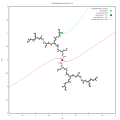





















































































![{\displaystyle I=(0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d9ad4f2e35fcd6db808c8c04aaf40e84cb1a279)


![{\displaystyle I_{0}=(0,x_{c}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d847e8f914fe40303cc72d20bf435c1f6df51a8c)
![{\displaystyle I_{1}=(x_{c},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/609fa3810777f9294fdae369fc22b1743bd62270)

![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)