Fractals/Iterations in the complex plane/Mandelbrot set/mset distortion
This page is about: warped midget, distortion of the island ( part of the Mandelbrot set and parameter plane).
name
[edit | edit source]There are many names of mini copies of Mandelbrot set within itself:
- Small Mandelbrot sets
- mini Mandelbrot set
- baby Mandelbrot set
- baby-brot
- Bug
- Island : "word 'island' was introduced by Benoit Mandelbrot in his description of the Mandelbrot set in The Fractal Geometry of Nature" Robert Munafo
- island mu-molecules
- embedded copy of the Mandelbrot Set
- Mandelbrotie
- Midget
- minibrot
- primitive M-copies
- slightly deformed copies of the original shape
- Near-copies of the Mandelbrot set within itself
Different names for distortion[1]
Names for distorted midgets:
- warped midget
Examples
[edit | edit source]-
Mini Mandelbrot set with center c = 0.359259224758007 +0.642513737138542 i period = 5 in the wake 1/4
-
c = -0.77028065155993652446 by -0.11144667326007166574 Zoom: 281748
-
mag =2369369 Centre coord. (-0.175875248 , 1.075392007 )
-
center: -0.164,1.032; width/height: 0.04
-
period 36 island with center c = -0.763926983955582 +0.092287538419582 i from subwake 1/34 of period 2 componenet
See also:
Sequence of locations from the elephant valley, with the period doubling ( by Claude Heiland-Allen )[4]
# period center radius
4 -1.565201668337550811e-01+ 1.032247108922831780e+00 i 1.697e-02
8 4.048996651751222142e-01 + 1.458203637665893004e-01 i 2.743e-03
16 2.925037532341934199e-01 + 1.492506899834379792e-02 i 3.484e-04
32 2.602618199285006706e-01 + 1.667791320926506355e-03 i 4.113e-05
64 2.524934589775105209e-01 + 1.971526796077277316e-04 i 4.920e-06
128 2.506132008410751344e-01 + 2.396932642510365971e-05 i 5.997e-07
256 2.501519680089798192e-01 + 2.954962325906881015e-06 i 7.398e-08
512 2.500378219137852631e-01 + 3.668242052764790239e-07 i 9.185e-09
1024 2.500094340031833728e-01 + 4.569478652064613658e-08 i 1.144e-09
2048 2.500023558032561377e-01 + 5.701985912706845832e-09 i 1.428e-10
4096 2.500005886128087162e-01 + 7.121326948562731412e-10 i 1.783e-11
8192 2.500001471109009610e-01 + 8.897814201389539302e-11 i 2.228e-12
List by marcm200
cardioid angle period p p<-2p->4p eccentricity cardioid center ------------------------------------------------------------------------------------------------------ 5 177.1 1.35 0.35925922475800742273-0.64251373713854231795*i 6 176.5 1.47 0.4433256333996235532-0.37296241666284651872*i 7 176.1 1.55 0.43237619264199450564-0.22675990443534863039*i 8 175.8 1.52 0.40489966517512215871-0.14582036376658927268*i 10 175.4 1.65 0.35681724849231194474-0.069452865466830299157*i 12 175.1 1.72 0.32558950955066034982-0.038047880934755723414*i 15 174.8 1.79 0.29844800890399547644-0.018383367322073254635*i 17 174.7 1.80 0.28756611704687790043-0.012281055409848253349*i 21 174.6 1.84 0.27436979919551240936-0.0062585874913430950342*i 25 174.5 1.87 0.2652783219046058732 -0.0037120599898783183101*i 31 174.4 1.90 0.26095224231422198269-0.0018410978175303128503*i 43 174.34 1.91 0.2556052938434967281 -0.00066797029763820438275*i
Locations:
- 0,25000102515011806826817597033225524583655 + 0,0000000016387052819136931666219461i Zoom = 6,871947673*(10^10) so radius = 0.14556040756914119* 10^{-10}
- 0.2925294 + 0.0149698 i @ 0.0006675
- c = 0.292503753234193 -0.014925068998344i period = 16, size of image +0.0005 [5]
- by marcm200
- period 7 c =0.43237619264199450564-0.22675990443534863039i
- period 14 c=0.4325688150887696537-0.22873440581356344059i
- period 28 c=0.43266973566541755414-0.22933968667591089763i
Self-similarity
[edit | edit source]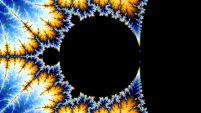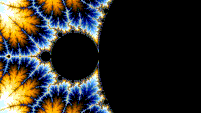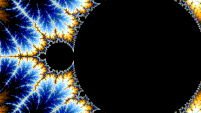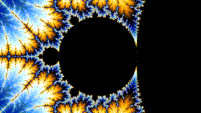
The Mandelbrot set is self-similar under magnification in the neighborhoods of the Misiurewicz points. It is also conjectured to be self-similar around generalized Feigenbaum points (e.g., −1.401155 or −0.1528 + 1.0397i), in the sense of converging to a limit set.[6][7] The Mandelbrot set in general is not strictly self-similar but it is quasi-self-similar, as small slightly different versions of itself can be found at arbitrarily small scales. These little copies of the Mandelbrot set are all slightly different, mostly because of the thin threads connecting them to the main body of the set.
"this combination of familiarity (small copies of the Mandelbrot set) and novelty (subtly distorted, differently decorated) that make the Mandelbrot set much more interesting than the fractals generated by IFS."[8]
Q&A
[edit | edit source]are they exact copies?
[edit | edit source]They are:
- not exact copies
- slightly deformed copies
- approximately self-similar copies
- quasiconformally equivalent to the whole Mandelbrot set
- quasi-self-similar
- Baby Mandelbrot Sets are Not Exact Self Similar. A baby Mandelbrot sets are homeomorphic to the original one
Why does the Mandelbrot set contain copies of itself?
[edit | edit source]Why does the Mandelbrot set contain (slightly deformed) copies of itself?[9]
- "renormalization explains why the baby Mandelbrot set appears: all of the quadratic polynomials in a baby Mandelbrot set renormalize and all renormalize in essentially the same way."
- "the fractal is a reflection of reflections of reflections ..."
- "iteration creates complexity. Mandelbrot set is based on checkin behaviour of infinite sequences. The behaviour of that sequences is very complex. In fact, it may be chaotic. We are in the presence of sensitive dependence on initial conditions (a.k.a. the butterfly effect.)" [10]
- "While the process is very simple, the iterative nature of the process leads to very different results depending on the point on the complex plane at which you start."
Why there are copies of Mandelbrot set in other fractals ?
[edit | edit source]The Mandelbrot set is universal[11] so it can be find in:
- an iterated complex mapping[12]
- the bifurcation locus for a parametrized family of holomorphic functions: rational families of functions, transcendental families [13]
- the bifurcation locus of any holomorphic family of rational maps[14]
- quadratic-like maps of Douady and Hubbard [15]
How to describe minibrot ?
[edit | edit source]Measures
- period of main pseudocardioid
- center of main pseudocardioid
- window ( radius and center) of parameter plane
- angles of external rays that land on cusp of the pseudocardiod
- size of main pseudocardioid
- orientation
- distortion
How to compute size and orientation ?
[edit | edit source]Size and orientation
[edit | edit source]Scaling for period-n windows of chaotic dynamical systems
- Windows of periodicity scaling by Evgeny Demidov
- J.A.Yorke, C.Grebogi, E.Ott, and L.Tedeschini-Lalli "Scaling Behavior of Windows in Dissipative Dynamical Systems" Phys.Rev.Lett. 54, 1095 (1985)
- B.R.Hunt, E.Ott Structure in the Parameter Dependence of Order and Chaos for the Quadratic Map J.Phys.A 30 (1997), 7067.
- Deriving the size estimate by Claude Heiland-Allen
- approximate selfsimilarity by Claude Heiland-Allen
The formula for the size and orientation:
Input and related values:
- nucleus of a minibrot's main pseudocardioid
- period of a minibrot's main pseudocardioid
Output:
- complex valued size and orientation estimation r ( complex number). To compute it just use arg and abs on the result
where
How to use it ?
"if the nucleus of the baby is c and the complex size is r , there is another miniature copy near the baby around with size approximately " Claude Heiland-Allen
Example minibrots:
- period 3 near −2
- period 4 near i
- period 5 near −1.5+0.5i
See also c function m_size from mandelbrot-numerics library by Claude Heiland-Allen
// mandelbrot-numerics -- numerical algorithms related to the Mandelbrot set
// Copyright (C) 2015-2018 Claude Heiland-Allen
// License GPL3+ http://www.gnu.org/licenses/gpl.html
#include <mandelbrot-numerics.h>
extern double _Complex m_d_size(double _Complex nucleus, int period) {
double _Complex l = 1;
double _Complex b = 1;
double _Complex z = 0;
for (int i = 1; i < period; ++i) {
z = z * z + nucleus;
l = 2 * z * l;
b = b + 1 / l;
}
return 1 / (b * l * l);
}
area
[edit | edit source]The area of the island of period p+1 is approximated by the formula by Robert Munafo:[16]
How to measure the distorsion ?
[edit | edit source]Measure
- express these in terms of the derivatives of the iteration at the preimage of 0[17]
- the ratios of radii of the satellites to the main cardioid
- angular positions of secondary ( child) components
- in degrees(or radians) because the parts of the minibrot are simply rotated ( conformal transformations )
- the ratio of two distances to the cusp[18]
- "Warped midgets in the Mandelbrot set have been measured, using an algorithm that allows the positions of the head, and cardioid atoms (north and south) of any midget to be found, once one has placed the cursor on the computer terminal somewhere inside any midget. We describe two distortions of midgets: linear distortions and angular distortions. When the north and south angles are plotted in the north/south angle plane, families of points are formed. The angle and distance measures of warped midgets from the Sea Horse Valley of the Mandelbrot set and from other sea horse valleys of midgets, whether on the Spike or on tendrils above atoms, all fall closely together in one part of the north/south plane. Measures of warped midgets from tendrils above the major atoms on the surface of the Cardioid fall closely together in another part of the north/south plane. This different way of looking at the Mandelbrot set offers an interesting way of studying the distortions of midgets." A. G. Davis Philip, Michael Frame, Adam Robucci: Warped midgets in the Mandelbrot set. Computers & Graphics 18(2): 239-248 (1994)
eccentricity of the pseudocardioid
[edit | edit source]The eccentricity of the pseudocardioid was calculated in a geometrical manner and defined as the ratio of two distances from the cusp to the (to do )
position of the child
[edit | edit source]- 2 components :
- parent ( pseudocardioid with period = p ) = p-componenent
- child ( pseudocircle with period = 2*p) = 2p-component
- two lines inside parent (pseudocardioid)
- axis of the lower part of the parent (pseudocardioid) = line thru 2 points: nucleus and cusp of pseudocardioid = lower axis
- axis of the upper part of the parent = line thru 2 points: nucleus and root point ( between child and parent components) = upper axis
- angle between lines measured in turns
- it is 0 for no distortion = all 3 points are on the same line ( like in case of whole M-set with main cardioid as a parent and period 2 component as a child componenent)
- it is > 0 for distortion
In mathematical language, the slope m of the line through 2 points
is
Angle between two lines of slope and is[19]
Here is c function[20]
// Function to find the angle between two lines. Each line is defined by 2 points
double findAngleBetweenLines(const complex double z1a, const complex double z1b, const complex double z2a, const complex double z2b)
{
// slope of line 1 and 2
double m1 = (cimag(z1a) - cimag(z1b))/(creal(z1a) - creal(z1b));
double m2 = (cimag(z2a) - cimag(z2b))/(creal(z2a) - creal(z2b));
double angle = abs((m2 - m1)/ (1 + m1 * m2));
// Calculate tan inverse of the angle
double ret = atan(angle);
// Convert the angle from radian to degree
double val = (ret * 180) / PI;
// return the result
return val;
}
How distorted can a minibrot be?
[edit | edit source]What is maxima distortion of minibrot ?[21]
How to find minibrot ?
[edit | edit source]- locate = find[22]
How to find distorted minibrot ?
[edit | edit source]What is the relation between distortion and other measures of the island ?
[edit | edit source]- the eccentricity grows with increasing period, but not linearly, not even monotone.[23]
- the biggest island of the wake is the most distorted. The period of the biggest minibrot in the m/n wake is n+1
See also
[edit | edit source]References
[edit | edit source]- ↑ Distortion (optics) in wikipedia
- ↑ Image_warping in wikipedia
- ↑ 2D Mesh Warping by Yurong Sun
- ↑ fractalforums.com : how-distorted-can-a-minibrot-be ?
- ↑ Distortion by Robert P. Munafo, 2010 Oct 20. From the Mandelbrot Set Glossary and Encyclopedia
- ↑ Lei (1990). "Similarity between the Mandelbrot set and Julia Sets". Communications in Mathematical Physics. 134 (3): 587–617. Bibcode:1990CMaPh.134..587L. doi:10.1007/bf02098448. S2CID 122439436.
- ↑ J. Milnor (1989). "Self-Similarity and Hairiness in the Mandelbrot Set". In M. C. Tangora (ed.). Computers in Geometry and Topology. New York: Taylor & Francis. pp. 211–257. ISBN 9780824780319.)
- ↑ The Mandelbrot Set and Julia Sets .The Mandelbrot Set - Small Copies from Fractal Geometry Yale University Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger November 24, 2022
- ↑ math.stackexchange question: why-does-the-mandelbrot-set-contain-slightly-deformed-copies-of-itself ?
- ↑ math.stackexchange question: mandelbrot-fractal-how-is-it-possible ?
- ↑ The Mandelbrot set is universal by Curtis T. McMullen
- ↑ quora : Why-is-the-Mandelbrot-Set-important?
- ↑ math.stackexchange" question: why-does-the-mandelbrot-set-appear-when-i-use-newtons-method-to-find-the-invers
- ↑ math.stackexchange question: are-mini-mandelbrots-known-to-be-found-in-any-fractals-other-than-the-mandelbrot ?
- ↑ Universality of the Mandelbrot set from Fractal Geometry Yale University Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger
- ↑ Main Sequence by Robert P. Munafo, 2009 Nov 5. from the Mandelbrot Set Glossary and Encyclopedia
- ↑ math.stackexchange question: mini-mandelbrots-are-they-exact-copies ?
- ↑ fractalforums.org : period-doubling-in-minibrots
- ↑ math.stackexchange question: finding-the-angle-between-two-line-equations ?
- ↑ Angle between a Pair of Lines from geeksforgeeks
- ↑ fractalforums.com : how-distorted-can-a-minibrot-be ?
- ↑ math.stackexchange question " help-locating-mini-mandelbrots?
- ↑ fractalforums.org : period-doubling-in-minibrots




























