Fractals/Computer graphic techniques/2D/transformation

Plane transformations

Names

• transformations
  • Geometric Image Transformations
  • Geometrical transformations
  • coordinate transformations
• projections
  • Cartographic Map projection ( in case of 3D to 2D graphic)
• mappings

Theory

Mapping in 2D raster graphic is a complex function $f$ that maps from complex plane to complex plane:

$f:\mathbb {C} \to \mathbb {C}$

It is implemented as point transformations.

It is usually denoted as

$w=f(z)$

where

• $z=x+yi$ is a point of complex plane ( input)
• $w=u+vi$ is a point of image complex plane ( output = result)

Example code

For instance, Mercator:

function Spherical_mercator(x, y) {
  return [x, Math.log(Math.tan(Math.PI / 4 + y / 2))];
}

function transverseMercatorRaw(lambda, phi) {
  return [log(tan((halfPi + phi) / 2)), -lambda];
}

transverseMercatorRaw.invert = function(x, y) {
  return [-y, 2 * atan(exp(x)) - halfPi];
};

If one work with discrete geometry ( polygons and polylines) then the projecting is much harder to imlement. One have to balance accuracy and performance.

// https://github.com/adammaj1/Mandelbrot-Sets-Alternate-Parameter-Planes/blob/main/src/lcm/d.c
// projection from p to c 
complex double map_parameter(const ParameterTypeT ParameterType, const complex double parameter){

	
	complex double p; 
	// plane transformation 
	switch(ParameterType){
	
		case c_identity :{p = parameter;  break;}
		
		case c_inverted :{p = 1.0/parameter; break;}
		
		case c_parabola :{p = 0.25+ 1.0/parameter; break;}
		
		case c_Myrberg_type :{p = cf - 1.0/parameter; break;}
		
		case c_inverted_2_type :{p = -2.0 + 1.0/parameter; break;}
		
		case c_exp :{p = cf + cexp(parameter) ; break;} // here one can change cf to get different image 
		
		
		case lambda_identity :{ p = parameter;  break;}
		
		case lambda_inverted_type :{p = 1.0/parameter; break;}
		
		case lambda_inverted_1_type :{p =1.0+ 1.0/parameter; break;}
		
		default: {p = parameter;}
	}

classifications

Maps clasifications

• object-based mappings ( Image objects are sets of connected pixels having the same integer value )
• pixel based mappings

Transformations ( maps) in 2-D graphics

• basic types
• Composite Transformation

Implementations

Use of matrices:

• without matrices ( using functions)
• with matrices

Coordinate

• with Cartesian coordinate
• with homogenous coordinate

Matrix

• "Matrix multiplication is not commutative. The order of the transformations is vital– Rotation followed by translation isvery different from translation followed by rotation"

Implementations

• Imath is a C++ and python library of 2D and 3D vector, matrix, and math operations for computer graphics

• parts of the matrix
• 
  rows
• 
  columns

types

• zoom
• inversion
• unrolling (a closed curve )
• Conformal maps applied to pictures
• Moebius transformation
• Exponential and Mercator map

Affine transformations

To represent affine transformations with matrices, we can use homogeneous coordinates. This means representing a 2-vector (x, y) as a 3-vector (x, y, 1), and similarly for higher dimensions.

2D affine transformation matrix

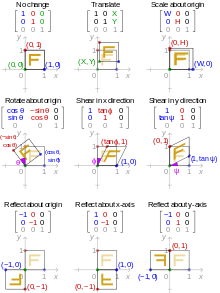
Transformation name	Affine matrix	Example
Identity (transform to original image)	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$
Translation	${\begin{bmatrix}1&0&v_{x}>0\\0&1&v_{y}=0\\0&0&1\end{bmatrix}}$
Reflection	${\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$
Scale	${\begin{bmatrix}c_{x}=2&0&0\\0&c_{y}=1&0\\0&0&1\end{bmatrix}}$
Rotate	${\begin{bmatrix}\cos(\theta )&-\sin(\theta )&0\\\sin(\theta )&\cos(\theta )&0\\0&0&1\end{bmatrix}}$	where θ = π/6 =30°
Shear	${\begin{bmatrix}1&c_{x}=0.5&0\\c_{y}=0&1&0\\0&0&1\end{bmatrix}}$

The affine transforms are applicable to the registration process where two or more images are aligned (registered). An example of image registration is the generation of panoramic images that are the product of multiple images stitched together.

scale or resize

Scaling of object about origin by by a scale factor

$s=s_{x}+s_{y}*i$ 

$x'=x*s_{x}$
$y'=y*s_{y}$

becomes:

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}s_{x}&0&0\\0&s_{y}&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}$$

Scaling

• Uniform (maintains the object’s proportions as it scales): sx = sy
• non-uniform: sx != sy

Resizing objects while maintaining a fixed centre point = Scaling object about their own center

• width' = width * sx
• height' = height * sy
• compute coordinate of corners from the center

translation

Complex transtlation is a map

$z'\to z+t$

where

• $z=x+y*i$
• $z'=x'+y'*i$
• $t=t_{x}+t_{y}*i$

Using this system, translation can be expressed with matrix multiplication. The functional form

$x'=x+t_{x}$ 
$y'=y+t_{y}$ 

becomes:

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}1&0&t_{x}\\0&1&t_{y}\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}.$$

rotation

For rotation by an angle θ counterclockwise (positive direction) about the origin the functional form is

$x'=x\cos \theta -y\sin \theta$ 
$y'=x\sin \theta +y\cos \theta$.  

Written in matrix form, this becomes:

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}$$

Similarly, for a rotation clockwise (negative direction) about the origin, the functional form is

$x'=x\cos \theta +y\sin \theta$ 
$y'=-x\sin \theta +y\cos \theta$ 

the matrix form is:

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}$$

These formulae assume that the x axis points right and the y axis points up.

the counter-clockwise rotation matrix in normalised coordinate:

$${\begin{bmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}$$

C code without matrix

 
/* 

C program to rotate an object by a given angle about a given point
gcc r.c -Wall -Wextra -lm
./a.out
*/

#include <stdio.h>
#include <math.h> 
#include <complex.h> 		// complex numbers : https://stackoverflow.com/questions/6418807/how-to-work-with-complex-numbers-in-c


//The sin() function returns the value in the range of [-1, 1]

/*
https://stackoverflow.com/questions/2259476/rotating-a-point-about-another-point-2d 
First subtract the pivot point (cx,cy), then rotate it (counter clock-wise), then add the point again.
*/


 complex double rotate_point(const complex double center, const double angle_in_radians, const complex double point )
{
	// translate point to center
	complex double translated_point = creal(point) - creal(center)  + (cimag(point) - cimag(center))*I;

	// rotate point counter clock-wise by a given angle about a given pivot point ( center)
	double s = sin(angle_in_radians);
	double c = cos(angle_in_radians);
	complex double new_point = creal(translated_point) * c - cimag(translated_point) * s + (creal(translated_point) * s + cimag(translated_point) * c)*I;

	// translate point back
	new_point = creal(new_point) + creal(center) +(cimag(new_point) + cimag(center))*I;
  
  
	return new_point;
}

#define kMax 6

// center, angle_rad, point 
double examples[kMax][5] = {
		{50,-50, -0.7853982, 100,100 },
		{50,-50, -0.7853982, 100,200 },
		{50,-50, -0.7853982, 200,200 },
		{0,0, 1.570796, 100,100}, 
		{0,0, 1.570796, 150,200}, 
		{0,0, 1.570796, 200,200} 

};

int main(void){

	
	
	
	int k;
	
	
	
	complex double center ;
	double angle_r ; 
	complex double point ;
	complex double rotated_point;
	
	
	for (k=0; k<kMax; ++k){
		center = examples[k][0] + examples[k][1] * I ;
		angle_r = examples[k][2]; 
		point = examples[k][3] + examples[k][4] * I ;
		rotated_point = rotate_point(center, angle_r, point );
		fprintf(stdout, "point %f%+f*I rotated about %f%+f*I  by %f radians is %f%+f*I \n", creal(point), cimag(point), creal(center), cimag(center), angle_r, creal(rotated_point), cimag(rotated_point));
		}
	
	 


	return 0;
}

Output:

point 100.000000+100.000000*I rotated about 50.000000-50.000000*I  by -0.785398 radians is 191.421359+20.710673*I 
point 100.000000+200.000000*I rotated about 50.000000-50.000000*I  by -0.785398 radians is 262.132040+91.421348*I 
point 200.000000+200.000000*I rotated about 50.000000-50.000000*I  by -0.785398 radians is 332.842715+20.710668*I 
point 100.000000+100.000000*I rotated about 0.000000+0.000000*I  by 1.570796 radians is -99.999967+100.000033*I 
point 150.000000+200.000000*I rotated about 0.000000+0.000000*I  by 1.570796 radians is -199.999951+150.000065*I 
point 200.000000+200.000000*I rotated about 0.000000+0.000000*I  by 1.570796 radians is -199.999935+200.000065*I 

Other Interesting maps

• 
• 
• 
• 
  with python code
• 
• 
• 
• 
• 

Examples:

• Jason Davies: maps
• barrel-distortion
• swirl
• log-polar map
• Parabolic Cylindrical Coordinates
• Parabolic Coordinates
• Numerical approximation of conformal mappings
• description
• inflection
• Altmetric: 25Citations: 1More detail Article | OPEN Exponential Sensitivity and its Cost in Quantum Physics by András Gilyén, Tamás Kiss & Igor Jex
• Blaschke product
• squaring the circle
• elliptic by Claude Heiland-Allen
• by Paul Bourke
• A cartographic projection is a nonlinear transformation in two dimensions
  • map projections and coordinate transformations
• to sphere
• Mandelbrot set projected on a shrinking Riemann-sphere by Arneauxtje
• Mandelbrot's Elephant Valley (Short Version) Timothy Chase
• Mandelbrot Buds and Branches Timothy Chase Timothy Chase
• Mandelbrot Zoom on a Sphere video by craftvid  : "This a 300-trillion time zoom-in on the Mandelbrot set. The images are set on a Spherical "mobius" projection, meant to be wrapped onto a spherical surface. The image zooms in on the front center of the Sphere, while fading away on the back of the sphere."
• Cat Eye : Inverted Mandelbrot Set by denis archambaud
• Inverse & Potens Mandelbrot Set by Jens-Peter Christensen
• Z² + Sin(Cˉᵐ+phase) by Jens-Peter Christensen
• snibgo's ImageMagick pages: Barrels and pincushions
• snibgo's ImageMagick pages: Scale, rotate and translate in 3D see Cube earth

Conformal map

• "Conformal maps preserve angles and take infinitesimal circles to infinitesimal circles. Non-conformal maps take infinitesimal circles to infinitesimal ellipses (or worse)." Claude Heiland-Allen
• "A complex function $f(z)$ is conformal at infinity if the function $f(1/z)$ is conformal at 0. This equivalent to the usual definition of conformal in terms of leaving angles unchanged in size and sense (clockwise/anticlockwise) if you think of $f$ as being conformal at infinity if it leaves angles unchanged at the "North Pole" of the Riemann sphere."

• conformal power
• 
• 
• 
• 
• 
• 
• 

• 

Conformal maps

• henry seg: spherical_image_editing in python
• newconformist: Conformally map the hyperbolic plane to arbitrary shapes by Zeno Rogue
• examples of conformal maps applied to pictures
• Moebius transformation
• An Overview of Conformal Geometry Processing (2017) by Keenan Crane
• Discrete Conformal Deformation: Algorithm and Experiments by Jian Sun, Tianqi Wu, Xianfeng Gu, Feng Luo
• Conformal map
• Poincaré Hyperbolic Disk Conformal Mapping Recipe by bugman123
• Visualizing Conformal Maps in Python by MJ Gruber
• Conformal Animation by denis archambaud
• ConformalMaps is a Julia package for approximating the Riemann map from a simply connected planar domain to a disk. It uses the zipper algorithm as described in Convergence of the zipper algorithm for conformal mapping by Don Marshall and Steffen Rohde.
• sswatson: ConformalMaps

Dictionary of Conformal Mapping by John H. Mathews, Russell W. Howell ( 2008)

• part 1
• part 2
• part 3
• part 4

Cartographic Map projection

cylindrical projection

The geometry for the normal (equatorial) tangent projections of the sphere to the cylinder.

Cylindrical projection ( or cylindric p. ) maps from sphere ( without poles) to cylinder

Joukowsky transformation (map)

Description :

• John D Cook

domain coloring or complex phase plots

Visualisation of complex functions

• The 5 ways to visualize complex functions
• commons : Category:Complex_functions
• Complex Mappings by Rand Asswad
• Poincaré Hyperbolic Disk Conformal Mapping Recipe by Paul Nylander
• david lowry-duda : phase_mag_plot/

modular forms

• MODULAR FORMS by David Lowry-Duda
• The L-functions and modular forms database (LMFDB)

Riemann mappings

• The Riemann Mapping Theorem by Christopher J. Bishop
• Riemman for anti-dummies by ©2015 LYM Canada
• Maping component to the unit disk ( Riemann map ):
  • Multiplier map and internal ray
    • on the parameter plane
    • on the dynamic plane
  • Boettcher map, complex potential and external ray
    • on the parameter plane
      • parameter ray = field lines
      • complex potential , external angle

References

• immersive linear algebra by J. Ström, K. Åström, and T. Akenine-Möller