Fractals/Iterations in the complex plane/q-iterations

Introduction

Julia set drawn by inverse iteration of critical orbit ( in case of Siegel disc )

Iteration in mathematics refer to the process of iterating a function i.e. applying a function repeatedly, using the output from one iteration as the input to the next. Iteration of apparently simple functions can produce complex behaviours and difficult problems.

One can make inverse ( backward iteration) :

• of repeller for drawing Julia set ( IIM/J)
• of circle outside Jlia set (radius=ER) for drawing level curves of escape time ( which tend to Julia set)
• of circle inside Julia set (radius=AR) for drawing level curves of attract time ( which tend to Julia set)
• of critical orbit ( in Siegel disc case) for drawing Julia set ( probably only in case of Goldem Mean )
• for drawing external ray

Repellor for forward iteration is attractor for backward iteration

Test

One can iterate ad infinitum. Test tells when one can stop

• bailout test for forward iteration

Target set or trap

Target set is used in test. When zn is inside target set then one can stop the iterations.

Planes

Dynamic plane $f_0$ for c=0

Lets take c=0, then one can call dynamical plane $f_0$ plane.

Here dynamical plane can be divided into :

• Fatou set
• Julia set = $\{ z : |z| = 1 \}$

Fatou set consist from 2 subsets :

• interior of Julia set = basin of attraction of finite attractor = $\{ z : |z| < 1 \}$
• exterior of Julia set = basin of attraction of infinity = $\{ z : |z| > 1 \}$

Forward iteration

The 10 first powers of a complex number inside the unit circle

Exponential spirals

$z = r e^{i \theta} \,$

where $r = | z | \,$

so

$f_0(z) = z^2 = (r e^{i \theta})^2 = r^2 e^{i 2 \theta}\,$

and forward iteration :

$f^n_0(z) = r^{2^n} e^{i 2^n \theta}\,$

Forward iteration gives forward orbit = list of points {z0, z1, z2, z3... , zn} which lays on exponential spirals.

Escape test

If distance between point z of exterior of Julia set and Julia set is :

$distance(z, J_c) = 2^{-n}$

then point escapes ( measured using bailout test and escape time )

$|z_n| > ER$

after :

• $n$ steps in non-parabolic case
• $2^n$ steps in parabolic case

See here for the precision needed for escape test

Backward iteration

Every angle α ∈ R/Z measured in turns has :

• one image = 2α mod 1 under doubling map
• "two preimages under the doubling map: α/2 and (α + 1)/2." . Inverse of doubling map is multivalued function.

Note that difference between these 2 preimages

$\frac{\alpha}{2} - \frac{\alpha +1}{2} = \frac{1}{2}$

is half a turn = 180 degrees = Pi radians.

Images and preimages under doubling map d

$\alpha$	$d^1(\alpha)$	$d^{-1}(\alpha)$
$\frac{1}{2}$	$\frac{1}{1}$	$\left \{ \frac{1}{4} , \frac{3}{4} \right \}$
$\frac{1}{3}$	$\frac{2}{3}$	$\left \{ \frac{1}{6} , \frac{4}{6} \right \}$
$\frac{1}{4}$	$\frac{1}{2}$	$\left \{ \frac{1}{8} , \frac{5}{8} \right \}$
$\frac{1}{5}$	$\frac{2}{5}$	$\left \{ \frac{1}{10} , \frac{6}{10} \right \}$
$\frac{1}{6}$	$\frac{1}{3}$	$\left \{ \frac{1}{12} , \frac{7}{12} \right \}$
$\frac{1}{7}$	$\frac{2}{7}$	$\left \{ \frac{1}{14} , \frac{4}{7} \right \}$

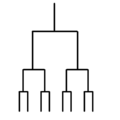
On complex dynamical plane backward iteration using quadratic polynomial $f_c$

$f_c(z) = z^2 + c$

gives backward orbit = binary tree of preimages :

$z \,$

$-\sqrt{z-c} , +\sqrt{z-c} \,$

$-\sqrt{-\sqrt{z-c} -c} , +\sqrt{-\sqrt{z-c} -c}, -\sqrt{+\sqrt{z-c} -c}, +\sqrt{+\sqrt{z-c} -c} \,$

One can't choose good path in such tree without extra informations.

Not that preimages show rotational symmetry ( 180 degrees)

Dynamic plane for $f_c$

Level curves of escape time

Preimages of circle under fc

Julia set by IIM/J

• 

  Preimages of repelling fixed point tend to Julia set for C = i. Image and source code

• 

  Julia set made with MIIM. Image and maxima source code

• 

  Preimages of critical orbit tend to whole Julia set in Siegel disc case

• 

  distribution of points in simple IIM/J

In escape time one computes forward iteration of point z.

In IIM/J one computes:

• repelling fixed point of complex quadratic polynomial $Z_0=\beta_c \,$
• preimages of $Z_0\,$ by inverse iterations

$Z_{n-1} = \sqrt{Z_n - C}$

Because square root is multivalued function then each $Z_{n}\,$ has two preimages $Z_{n-1}\,$. Thus inverse iteration creates binary tree.

Root of tree

• repelling fixed point of complex quadratic polynomial $Z_0=\beta_c \,$
• - beta
• other repelling periodic points ( cut points of filled Julia set ). It will be important especially in case of the parabolic Julia set.

"... preimages of the repelling fixed point beta. These form a tree like

                                               beta
                    beta                                            -beta
   beta                         -beta                    x                     y

So every point is computed at last twice when you start the tree with beta. If you start with -beta, you will get the same points with half the number of computations.

Something similar applies to the preimages of the critical orbit. If z is in the critical orbit, one of its two preimages will be there as well, so you should draw -z and the tree of its preimages to avoid getting the same points twice." (Wolf Jung )

Variants of IIM

• random choose one of two roots IIM ( up to chosen level max). Random walk through the tree. Simplest to code and fast, but inefficient. Start from it.
  • both roots with the same probability
  • more often one then other root
• draw all roots ( up to chosen level max)
  • using recurrence
  • using stack ( faster ?)
• draw some rare paths in binary tree = MIIM. This is modification of drawing all roots. Stop using some rare paths.
  • using hits table ( while hit(pixel(iX,iY)) < HitMax )
  • using derivative ( while derivative(z) < DerivativeMax)

Examples of code :

Compare it with:

• C code.
• Matlab code