Nanotechnology/Print version
| This is the print version of Nanotechnology You won't see this message or any elements not part of the book's content when you print or preview this page. |
The Opensource Handbook of Nanoscience and Nanotechnology

Part 1: Introduction
| Navigate |
|---|
| << Prev: Introduction |
| >< Main: Nanotechnology |
| >> Next: Perspective |
|
|
| <<< Prev Part: Main Page |
| >>> Next Part: Seeing Nano |
Introduction to Nanotechnology
Nanotechnology, often shortened to "nanotech," is the study of the control of matter on an atomic and molecular scale. Generally, nanotechnology deals with structures of the size 100 nanometers or smaller in at least one dimension, and involves developing materials or devices within that size. Nanotechnology is very diverse, encompassing numerous fields in the natural sciences.
There has been much debate on the future implications of nanotechnology. Nanotechnology has the potential to create many new materials and devices with a vast range of applications, such as in medicine, electronics and energy production. On the other hand, nanotechnology raises many of the same issues as with any introduction of new technology, including concerns about the toxicity and environmental impact of nanomaterials[1], and their potential effects on global economics, as well as speculation about various doomsday scenarios. These concerns have led to a debate among advocacy groups and governments on whether special regulation of nanotechnology is warranted.
This open source handbook on nanoscience and nanotechnology is divided into the following chapters, each dealing with a particular facet of nanotechnology:
- Chapter 1: INTRODUCTION - A general overview.
- Chapter 2: SEEING 'NANO' - How to observe what is going on on the nanoscale.
- Chapter 3: PHYSICS -ON THE NANOSCALE - How do things move and what are the important forces on the nanoscale.
- Chapter 4: NANOMATERIALS - The typical nanostructures and their functionality
- Chapter 5: NANOSYSTEMS - Fundamental electronic, optical, mechanical, and fluidic systems that can be made with nanostructures.
- Chapter 6: NANOENGINEERING - How to make nanostructures integrated into useful devices.
- Chapter 7: NANO-BIO PRIMER - An important part of nanotechnology is to interface with living organisms.
- Chapter 8: ENVIRONMENTAL NANOTECHNOLOGY - The environmental issues regarding this emerging technology.
- Chapter 9: NANO AND SOCIETY - Should we worry about nanotechnology?
References
See also notes on editing this book Nanotechnology/About#How_to_contribute.
- ↑ Cristina Buzea, Ivan Pacheco, and Kevin Robbie (2007). "Nanomaterials and Nanoparticles: Sources and Toxicity". Biointerphases. 2: MR17.
{{cite journal}}: CS1 maint: multiple names: authors list (link)
Perspective
| Navigate |
|---|
| << Prev: Introduction |
| >< Main: Nanotechnology |
| >> Next: Overviews |
A perspective on Nanotechnology
Nanotechnology in the Middle Ages?
The Duke TIP eStudies Nanotechnology course will be adding more to this section (this will be completed by 22 Jun 08)
One of the first uses of nanotechnology was in the Middle Ages. It was done by using gold nanoparticles to make red pigments in stained glass showing that nanotechnology has been around for centuries. The gold when clumped together appears gold, but certain sized particles when spread out appear different colors. Reference: The Nanotech Pioneers Where are they taking us? By Steven A Edwards
In the year 1974 at the Tokyo Science University, Professor Norio Taniigrichi came up with the term nanotechnology.
Nanotechnology was first used to describe the extension of traditional silicon machining down into regions smaller than one micron (one millionth of a meter) by Tokyo Science University Professor Norio Taniguchi in 1974. It is now commonly used to describe the engineering and fabrication of objects with features smaller than 100 nanometers (one tenth of a micron). [1]
Nanotechnology has been used for thousands of years, although people did not know what they were doing. For example, stained glass was the product of nanofabrication of gold. Medieval forgers were the first nanotecnologists in a sense, because they, by accident, found out a way to make stained glass.
Reference Nanotechnology A GENTLE INTRODUCTION TO THE NEXT BIG IDEA By Mark Ratner & Daniel Ratner
In 2001, the federal government announced the National Nanotechnology Intiative to coordinate the work of different U.S. agencies and to provide funds for research and accelerate development in nanotechnology. This was spearheaded by Mahail Roco and supported by both president Clinton and Bush.
References The Nanotech Pioneers Where are they taking us? By Steven A. Edwards http://www.nano.gov/html/about/docs/20070521NNI_Industrial_Nano_Impact_NSTI_Carim.pdf
A Vision
Richard Feynman was a man of great importance to the field of nanotechnology. He was a man with a vision. He believed that with research we could change things on a small scale. In his famous speech There's Plenty of Room at the Bottom in 1959, Richard Feynman discussed the possibility of manipulating and controlling things on a molecular scale in order to achieve electronic and mechanical systems with atomic sized components. He concluded that the development of technologies to construct such small systems would be interdisciplinary, combining fields such as physics, chemistry and biology, and would offer a new world of possibilities that could radically change the technology around us.
Miniaturization
A few years later, in 1965, Moore noted that the number of transistors on a chip had roughly doubled every other year since 1959, and predicted that the trend was likely to hold as each new generation of microsystems would help to develop the next generation at lower prices and with smaller components. To date, the semiconductor industry has been able to fulfill Moore's Law, in part through the reduction of lateral feature sizes on silicon chips from around 10 micrometers in 1965 to 45-65 nm in 2007 via changing from the use of optical contact lithography to deep ultraviolet projection lithography.
In 1974 in Japan, Norio Taniguchi coined the word "nano-technology" [2] to describe semiconductor processes such as thin film deposition and ion beam milling exhibiting characteristic control on the order of a nanometer: "‘Nano-technology’ mainly consists of the processing of separation, consolidation, and deformation of materials by one atom or one molecule."
Since Feynman's 1959 speech the arts of "seeing" and "manipulation" at the nanoscale have progressed from transmission electron microscopy (TEM) and scanning electron microscopy (SEM) to various forms of scanning probe microscopy including scanning tunneling microscopy (STM) developed by Binnig and Rohrer at IBM Zurich and atomic force microscopy (AFM) devloped by (Binnig and Quate?) The STM, in particular, is capable of single-atom manipulation on conducting surfaces and has been used to build "quantum corrals" of atoms in which quantum mechanical wave function phenomena can be discerned. These atomic-scale manipulation capabilities prompt thoughts of building up complex atomic structures via manipulation rather than traditional stochastic chemistry. (Note: this pragraph is still rough and references are needed.)
Motivated by Feynman’s beliefs building things nanoscale top-down, Eric Drexler devoted much of his research to making a universal assembler. The American engineer Eric Drexler has speculated extensively about the laboratory synthesis of machines at the molecular level via manipulation techniques, emulating biochemistry and producing components much smaller than any microprocessor via techniques which have been called molecular nanotechnology or MNT. [3] [4] [5]
Successful realization of the MNT dream would comprise a collection of technologies which are not currently practical, and the dream has resulted in considerable hyperbolic description of the resulting capabilities. While realization of these capabilities would be a vindication of the hype associated with MNT, concrete plans for anything other than computer modeling of finished structures are scant. Somehow, a means has to be found for MNT design evolution at the nanoscale which mimics the process of biological evolution at the molecular scale. Biological evolution proceeds by random variation in ensemble averages of organisms combined with culling of the less-successful variants and reproduction of the more-successful variants, and macroscale engineering design also proceeds by a process of design evolution from simplicity to complexity as set forth somewhat satirically by John Gall: "A complex system that works is invariably found to have evolved from a simple system that worked. . . . A complex system designed from scratch never works and can not be patched up to make it work. You have to start over, beginning with a system that works." [6] A breakthrough in MNT is needed which proceeds from the simple atomic ensembles which can be built with, e.g., an STM to complex MNT systems via a process of design evolution. A handicap in this process is the difficulty of seeing and manipulation at the nanoscale compared to the macroscale which makes deterministic selection of successful trials difficult; in contrast biological evolution proceeds via action of what Richard Dawkins has called the "blind watchmaker" [7] comprising random molecular variation and deterministic survival/death.
Technological development and limits
The impact on society and our lives of the continuous downscaling of systems is profound, and continues to open up new frontiers and possibilities. However, no exponential growth can continue forever, and the semiconductor industry will eventually reach the atomic limit for downsizing the transistor. Atoms in solid matter are typically one or two hundred picometers apart so nanotechnology involves manipulating individual structures which are between ten and ten thousand atoms across; for example, the gate length of a 45 nm transistor is about 180 silicon atoms long. Such very small structures are vulnerable to molecular level damage by cosmic rays, thermal activity, and so forth. The way in which they are assembled, designed and used is different from prior microelectronics.
New ways
Today, as that limit still seems to be some 20 years in the future, the growth is beginning to take new directions, indicating that the atomic limit might not be the limiting factor for technological development in the future, because systems are becoming more diverse and because new effects appear when the systems become so small that quantum effects dominate. The semiconductor devices show an increased diversification, dividing for instance processors into very different systems such as those for cheap disposable chips, low power consumption portable devices, or high processing power devices. Microfabrication is also merging with other branches of science to include for instance chemical and optical micro systems. In addition, microbiology and biochemistry are becoming important for applications of all the developing methods. This diversity seems to be increasing on all levels in technology and many of these cross-disciplinary developments are linked to nanotechnology.
Diversification
As the components become so small that quantum effects become important, the diversity will probably further increase as completely new devices and possibilities begin to open up that are not possible with the bulk materials of today's technology.
The nanorevolution?
The visions of Feynman are today shared by many others: when nanotechnology is seen as a general cross disciplinary technology, it has the potential to create a coming "industrial" revolution that will have a major impact on society and everyday life, comparable to or exceeding the impact of electricity and information technology.
Nanocomponents, Tools, and Methods
A positive spiral
As an emerging technology, the methods and components of nanotechnology are under continuous development and each generation is providing a better foundation for the following generation.
Seeing 'nano'
With regards to the methods, the Scanning tunneling microscope (STM) and Atomic Force Microscope (AFM) were developed in the 1980s and opened up completely new ways to investigate nanoscale materials. An important aspect was the novel possibility to directly manipulate nanoscale objects. Transmission and scanning electron microscopes (TEM and SEM) had been available since the 30s, and offered the possibility to image as well as create nanodevices by electron beam lithography.
New nanomaterials
Several unique nanoscale structures were also discovered around 1990: the Carbon-60 molecule and later the carbon nanotubes. In recent years, more complex nanostructures such as semiconductor nanowire heterostructures have also proven to be useful building blocks or components in nanodevices.
So what can I use this 'nano' for?
The applications of such nanocomponents span all aspects of technology: Electronics, optics/photonics, medical, and biochemical, as well as better and smarter materials. But to date few real products are available with nanoscale components, apart from traditional nanoscale products, such as paint with nanoparticles or catalytic particles for chemical reactors.
Prototype devices have been created from individual nanocomponents, but actual production is still on the verge. As when integrated electronics were developed, nanotechnology is currently in the phase where component production methods, characterization methods, tools for manipulation and integration are evolving by mutual support and convergence.
Difficult nanointegration
A main problem is reliable integration of the nanoscale components into microsystems, since the production methods are often not compatible. For fabrication of devices with integrated nanocomponents, the optimal manipulation technique is of course to have the individual components self-assembling or growing into the required complex systems. Self assembly of devices in liquids is an expanding field within nanotechnology but usually requires the components to be covered in various surfactants, which usually also influence the component properties. To avoid surface treatments, nanotubes and whiskers/wires can be grown on chips and microsystems directly from pre-patterned catalytic particles. Although promising for future large scale production of devices, few working devices have been made by the method to date.
The prevailing integration technique for nanowire/tube systems seems to be electron beam lithography (EBL) of metal structures onto substrates with randomly positioned nanowires deposited from liquid dispersions. By using flow alignment or electrical fields, the wire deposition from liquids can be controlled to some extent. The EBL method has allowed for systematic investigations of nanowires' and tubes' electrical properties, and creation of high performance electronic components such as field-effect transistors and chemical sensors. These proof-of-principle devices are some of the few but important demonstrations of devices nanotechnology might offer. In addition, nanomechanical structures have also recently been demonstrated, such as a rotational actuator with a carbon nanotube axis built by Fennimore et al.
A more active approach to creating nanowire structures is to use Scanning probe microscopy(SPM) to push, slide and roll the nanostructures across surfaces. SPM manipulation has been used to create and study nanotube junctions and properties. The ability to manipulate individual nanoscale objects has hence proven very useful for building proof-of-principle devices and prototypes, as well as for characterizing and testing components.
Top-down manufacturing takes bulky products and shrinks them to the nano scale, vs. bottom-up manufacturing is when individual molecules are placed in a specific order to make a product.[8] The bottom-up self-assembly method may be important for future large scale production as well as many of the different approaches to improve the top-down lithographic processes. Such techniques could hence become important factors in the self-sustaining development of nanotechnology.
Hot and hyped
Suddenly everything is 'nano'
There's no question that the field of nanotechnology has quite a sense of hype to it - many universities have created new nanotech departments and courses. But there is also a vision behind the hype and emerging results - which are truly very few in industrial production, but nevertheless hold promise for a bright future. In the hype, many things that were once chemistry, microtechnology, optics, mesoscopic or cluster physics, have been reborn as nanotechnology.
Nanotech is old
You can find nanotechnology in the sunscreen you use in the summer, and some paints and coatings can also be called nanotech since they all contain nanoparticles with unique optical properties. In a way, nanoparticles have been known in optics for hundreds of years if you like to take a broad perspective on things, since they have been used to stain and color glasses, etc. since the middle ages. Nano-size particles of gold were used to create red pigments.[9]
Catalysis is a major industrial process, without which not many of the materials we have around us today would be possible to make, and catalysis is often highly dependent on nanoscale catalytic particles. In this way thousands of tons of nanotechnology have been used with great benefit for years.
Nanoscale wires and tubes have only recently really been given attention with the advent of carbon nanotubes and semiconductor nanowires, while nanoscale films are ever present in antireflection coatings on your glasses and binoculars, and thin metal films have been used for sensitive detection with surface plasmons for decades. Surface plasmons are excitations of the charges at a surface. Nanowires actually were observed in the middle ages - well, they did not have the means to observe them, but saw whiskers grow from melted metals.
The better control over the nanostructure of materials has led to optimization of all these phenomena - and the emergence of many new methods and possibilities.
An example
Take for instance nano-optics: The surface plasmons turn out to be very efficient at enhancing local electrical fields and work as a local amplifier for optical fields, making a laser seem much more powerful to atoms in the vicinity of the surface plasmon. From this comes the surface enhanced raman spectroscopy which is increasingly used today because it makes it possible to do sensitive raman spectroscopy on the large majority of samples that would otherwise be impossible to make such spectra on. In addition, photonic crystals, fancy new quantum light sources that can make single photons on demand and other non-classical photon states are being developed, based on nanotechnology.
The future
There are definitely future scientific applications and commercial potential of all these new methods to handle light, use it for extremely sensitive detection and control its interaction with matter - and so it seems nanotechnology, being about making smaller versions of existing technology as well as new technology, is worth a bit of hype.
References
See also notes on editing this book Nanotechnology/About#How_to_contribute. .
- ↑ Edwards, Steven (2006). The Nanotech Pioneers: Where are they taking us?. Wiley-VCH. ISBN 3527312900.
- ↑ N. Taniguchi, "On the Basic Concept of 'Nano-Technology'," Proc. Intl. Conf. Prod. Eng. Tokyo, Part II, Japan Society of Precision Engineering, 1974.
- ↑ Steven A. Edwards, The Nanotech Pioneers, (WILEY-VCH, 2006)
- ↑ Eric Drexler, Engines of Creation, (New York: Anchor Press/Doubleday, 1986).
- ↑ Eric Drexler, Nanosystems: Molecular Machinery, Manufacturing and Computation, (New York: John Wiley, 1992).
- ↑ Gall, John, (1986) Systemantics: How Systems Really Work and How They Fail, 2nd ed. Ann Arbor, MI : The General Systemantics Press.
- ↑ Richard Dawkins, The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design, W. W. Norton; Reissue edition (September 19, 1996)
- ↑ Eric Drexler, Engines of Creation
- ↑ Nanotech Pioneers, Steven A. Edwards (WILEY-VCH, 2006, Weinheim)
Overviews
| Navigate |
|---|
| << Prev: Perspective |
| >< Main: Nanotechnology |
| >> Next: About |
Internet Resources
Handbooks and Encyclopedias
These are only accessible for subscribers (which is one reason this Wikibook on Nanotechnology was started):
- Encyclopedia of Nanoscience and Nanotechnology, 10-Volume Set
- Handbook of Theoretical and Computational Nanotechnology, 10-Volume Set
- Springer Handbook of Nanotechnology
Websites and newsletters
- International Council on Nanotechnology (ICON) a multi-stakeholder group dedicated to the safe, responsible and beneficial development of nanotechnology. ICON serves as an aggregator for news and research related to nanotechnology environment, health and safety.
- ICON Virtual Journal of Nanotechnology Environment, Health and Safety compiles papers in peer-reviewed journals that address EHS issues in nanotechnology.
- Virtual journal of nanotechnology compiles nano-related papers in peer reviewed journals that do not specialize solely in nanotechnology.
- ACS Nanotation
- Nanotechweb.org
- Nanoforum
- Nanowerk
- nanoRISK
- Physorg.com
- Foresight Nanotech Institute
- Center for Responsible Nanotechnology
- A-Z of nanotechnology
- Google Directory - Nanotechnology (sourced from the Open Directory Project)
- Scientific American Nanotechnology Page
- NanoEd Resource Portal managed by the National Center for Learning and Teaching in Nanoscale Science and Engineering (NCLT)
- NanoHub.org
- UnderstandingNano
Search engines
There are many ways to find information in scientific literature and some that even specialize in nanotechnology. Apart from the free search engines and useful tools such as Google scholar and Google Desktop, there are several more dedicated commercial services:
- ICON Virtual Journal of Nanotechnology Environment, Health and Safety (VJ-NanoEHS) compiles papers in peer-reviewed journals that address EHS issues in nanotechnology.
- ISI - Web of Science Database contains peer reviewed journals, their references and citations. It also has very useful tools such as 'find related papers' that searches for papers sharing the same references as the entry you're looking at. This is the database behind the compilation of the journal citation factors.
- Knovel - Online Handbook Collection and Database is an extensive collection of handbooks and tables.
- PROLA - the Physical Review Online Archive searches Physical Review journals.
- Rubber Bible Online is a physical chemistry handbook which contains tables of physical and chemical data.
- Spin AIP Scitation searches related journals.
- Web of Science by ISI generates the impact factors (see journals below).
- Virtual Journal of Nanotechnology collects nanotech related papers from non-nano specialized journals.
- Derwent Patent database
Peer reviewed Journals
Overview of the nanotechnology related journals and their impact factors (2007 values):
| Name | Web | Impact Factor | ISSN | Comments | |
|---|---|---|---|---|---|
| ACS Nano | [9] | N/A | 1936-0851 | general nanotech journal | |
| Advanced Functional Materials | [10] | 7.5 | 1616-301X | ? | |
| Advanced Materials | [11] | 8.2 | 0935-9648 | ? | |
| American Journal of Physics (AJP) | [12] | 0.9 | 0002-9505 | ? | |
| Applied Physics A: Materials Science & Processing | [13] | 1.9 | 0947-8396 | ? | |
| Applied Physics Letters (APL) | [14] | 3.6 | ? | ? | |
| AZojono - Journal of Nanotechnology Online | [15] | N/A | ? | Free access journal | |
| Chemical Reviews | [16] | 22.8 | 0009-2665 | ? | |
| Current Nanoscience | [17] | 2.8 | 1573-4137 | Reviews and original research reports | |
| Fullerenes, Nanotubes, and Carbon Nanostructures | [18] | 0.5 | 1536-383x | all areas of fullerene research | |
| IEEE Transactions on Nanotechnology | [19] | 2.1 | 1536-125X | physical basis and engineering applications of nanotechnology | |
| International Journal of Nanomedicine | [20] | N/A | 1176-9114 | ? | |
| International Journal of Nanoscience | [21] | N/A | 0219-581X | New nanotech journal (Feb 2002) | |
| Japanese Journal of Applied Physics | [22] | 1.2 | 1347-4065 | ? | |
| Journal of Applied Physics | [23] | 2.2 | ? | ? | |
| Journal of Biomedical Nanotechnology | [] | N/A | ? | JBN is a peer-reviewed multidisciplinary journal providing broad coverage in all research areas focused on the applications of nanotechnology in medicine, drug delivery systems, infectious disease, biomedical sciences, biotechnology, and all other related fields of life sciences. | |
| Journal of Experimental Nanoscience | [24] | N/A | 1745-8080 | New nanotech journal(March 2006) | |
| Journal Of Microlithography Microfabrication And Microsystems | [25] | N/A | 1537-1646 | ||
| Journal of Micromechanics and Microengineering | [26] | 1.9 | 0960-1317 | ? | |
| Journal of Nano Research | [27] | N/A | 1661-9897 | ||
| Journal of Nanomaterials | [28] | N/A | ? | science and applications of nanoscale and nanostructured materials | |
| Journal of Nanoparticle Research | [29] | 2.3 | 1388-0764 | ? | |
| Journal of Nanoscience and Nanotechnology | [30] | 2.0 | ? | JNN is a multidisciplinary peer-reviewed journal covering fundamental and applied research in all disciplines of science, engineering and medicine. JNN publishes all aspects of nanoscale science and technology dealing with materials synthesis, processing, nanofabrication, nanoprobes, spectroscopy, properties, biological systems, nanostructures, theory and computation, nanoelectronics, nano-optics, nano-mechanics, nanodevices, nanobiotechnology, nanomedicine, nanotoxicology. | |
| Journal of Physical Chemistry A | [31] | 2.9 | ? | ? | |
| Journal of Physical Chemistry B | [32] | 4.1 | ? | ? | |
| Journal of Physical Chemistry C | [33] | N/A | ? | Nanomaterials and Interfaces, Nanoparticles and Nanostructures, Surfaces, Interfaces, Catalysis, Electron Transport, Optical and Electronic Devices, Energy Conversion and Storage | |
| Journal of the American Chemical Society (JACS) | [34] | 7.9 | ? | Multidisciplinary chemistry journal | |
| Journal of Vacuum Science & Technology A (JVSTA) | [35] | 1.3 | ? | Vacuum, Surfaces, Films | |
| Journal of Vacuum Science & Technology B (JVSTB) | [36] | 1.4 | ? | Microelectronics and Nanometer Structures: Processing, Measurement, and Phenomena | |
| Langmuir | [37] | 4.0 | ? | Research in the fields of colloids, surfaces, and interfaces | |
| Micron | [38] | 1.7 | ? | Journal for Microscopy | |
| Materials Chemistry and Physics | [39] | 1.9 | 0254-0584 | materials science, including nanomaterials and opto electronics | |
| Materials Science and Engineering: C | [40] | 1.3 | 0928-4931 | Biomimetic and Supramolecular Systems | |
| Materials Science and Engineering: R: Reports | [41] | 17.7 | 0927-796X | Invited review papers covering the full spectrum of materials science and engineering | |
| Materials Today | [42] | N/A | 1369-7021 | materials science and technology | |
| Microfluidics and Nanofluidics | [43] | 2.2 | 1613-4982 | all aspects of microfluidics, nanofluidics, and lab-on-a-chip science and technology | |
| Microscopy Research and Technique | [44] | 1.6 | ? | ? | |
| Nano | [45] | N/A | 1793-2920 | New nanotech journal (July 2006) | |
| Nano Letters | [46] | 9.6 | ? | General nanotechnology journal | |
| Nanomedicine | [47] | 2.8 | ? | ? | |
| Nanopages | [48] | N/A | 1787-4033 | Since sept 2006. | |
| Nano Research | [49] | N/A | ? | First issue july 2008 | |
| Nano Research Letters | [50] | wait | 1931-7573 | articles with open access | |
| Nanotechnology | [51] | 3.3 | ? | Journal specializing in nanotechnology | |
| NanoToday | [52] | N/A | ? | Is this peer reviewed or more a news/reviews journal? | |
| Nature | [53] | 31.434 | ? | One of the major journals in science | |
| Nature Biotechnology | [54] | 22.8 | ? | advances in life sciences | |
| Nature Materials | [55] | 19.8 | ? | covers a range of topics within materials science | |
| Nature Methods | [56] | 15.5 | ? | tried-and-tested techniques in the life sciences and related area of chemistry | |
| Nature Nanotechnology | [57] | 14.9 | ? | mix of news, reviews, and research papers | |
| Nanotoxicology | [58] | N/A | 1743-5404 | Research relating to the potential for human and environmental exposure, hazard and risk associated with the use and development of nano-structured materials | |
| Open Nanoscience Journal | [59] | N/A | 1874-1401 | Open access journal with research articles, reviews and letters. | |
| Physical Review Letters (PRL) | [60] | 6.9 | ? | One of the top physics journals | |
| PLoS Biology | [61] | 13.5 | 1544-9173 | Peer reviewed open access bio journal | |
| PLoS ONE | [62] | N/A | ? | Peer reviewed open access science journal | |
| Proceedings of the National Academy of Sciences(PNAS) | [63] | 10.2 | ? | multidisciplinary scientific serial: biological, physical, and social sciences. | |
| Recent Patents on Nanotechnology | [64] | N/A | 1872-2105 | ? | |
| Science | [65] | 26.4 | ? | One of the major journals in science | |
| Solid-State Electronics | [66] | 1.3 | ? | ? | |
| Small Journal | [67] | 6.4 | 1613-6810 | New nanotech journal | |
| Smart Materials and Structures | [68] | 1.5 | 0964-1726 | since 1992 | |
| Thin Solid Films | [69] | 1.7 | 0040-6090 | Thin-film synthesis, characterization, and applications. | |
| Ultramicroscopy | [70] | 2.0 | ? | Microscopy related research. | |
| Virtual Journal of Nanotechnlogy | [71] | N/A | 1553-9644 | Collecting nanotech related papers from non-nano spcialized journals |
- Impact factors are only guides to how much a papers is referenced in the years just after publication.
- Please add comments about the journals and update impact factors!
- The Physics and Astronomy Classification Scheme PACS2006 and Nanoscale Science and Technology - Collection of Applicable Terms from PACS 2006
Conferences
- NSTI Nanotech 2008
- TNT - Trends in Nanotechnology 2007;2006
- MNE - Micro and Nanoengineering 2007;2008
- Virtual Conference on Nanoscale Science and Technology
- Foresight Unconference Vision Weekend NanoBioInfoCognoSocioPhysical technologies
- [72]
- International Microprocess and Nanotechnology Conference, Japan
- Nanosafe 2008: International Conference on Safe production and use of nanomaterials
Nanotech Products
Please add more products, comments and more info about the products if you have any!
See also the List of nanotechnology applications in wikipedia
Woodrow Wilsom Center for International Scholars is starting a Project on Emerging Nanotechnologies (website should be under construction at www.nanoproject.org) that among other things will try to map the available 'nano'products and work to ensure possible risks are minimized and benefits are realized.
Emerging products
- 2008 MultiProbe’s AFM Nanoprober is now qualified for 32nm technology nodes. [73]
- Intel will make products with 45 nm linewidth transistors available from 2008 [74]
- Batteries are increasingly incorporating nanostructures.
- Flexible, cheaper, or more luminous Flat screen displays
- Pressure-sensitive mobile devices [75]
Available in 2006
- Surface coatings: TCnano, Nanocover, Stay clean.
Available in 2005
- Molybdenum disulfide catalytic nanoparticles in Brimm catalysts[76] made by Haldor Topsøe
- Forbes top ten nanoproducts in 2005[77]
- Apples IPod with sub 100nm elements in its memory chips
- Choleterol reducing nanoencapsulated oil,Shemen Industries Canola Active.
- Nanocrystals improve the consistency of chocolate[78]
- Zelen Fullerene C-60 Day Cream [79]
- Easton Stealth CNT baseball bat
- Nanotex textiles once again
- ArcticShield polyester socks from ARC Outdoors with 19nm silver particles that kill fungs to reduce odor.
- NanoGuard developed by Behr Process for improved paint hardness.
- Pilkingtons self-cleaning 'Activ Glass'.
- NanoBreeze Air Purifier from NanoTwin Technologies, where the UV light from a fluorescent tube cleans the air by photochemical reactions in nanoparticles.
Available in 2004
- Cold cathode carbon nanotube emitters for X-ray analysis by Oxford instruments[80][]
- Forbes has an overview in 2004 of what they consider the top ten nanotech products:
- Footwarmers with nanporous aerogel for 3-20 times lighter than comparable insulating materials used in shoes (produced by Aspen Aerogels).
- Matress covers with nanotex fibres that can be washed (Simmonos bedding company).
- Better golf drivers with carbon nanotube enforced metal composites (produced by Maruman & Co) and nanocomposite containing golf balls (produced by NanoDynamics)
- The company 'Bionova' apparently adds some nanoproducts to their 'personalized product line'.
- EnviroSystems make a nanoemulsive disinfectant cleaner, called EcoTru, that is EPA Tox category 4 registered (meaning very safe to use)
- EnviroSystems also make a spray-on version of this product.
- BASF makes a nanoparticle coating for building materials called Mincor, that reduces their wettabililty.
- A nanostructured coating produced by Valley View, called Clarity Defender, improves visibility through windscreens in rain. Another company, Nano-Film, makes a similar coating on sunglasses.
- w:Flex-Power makes a gel containing nanoscale liposomes for soothing aching muscles
- 3M espe Dental adhesive with silica nanoparticle filler.
Available in 2003
- NanoGuard Zink Oxide nanoparticles for sunscreens FDA approved
- Forbes 2003 top ten nanoproduct [81] includes:
- High performance ski wax, Cerax Nanowax [82].
- Nanotex textiles in ski jackets from Ziener[83]
- Nanotex textiles
- Plenitude Revitalift antiwrinkle cream by L'Oréal contains nanocapsules with vitamin A [84]
- organic light-emitting diodes (OLEDs) in Sony camera flat screen display
- Nanofilm coatings for ani-reflection and scratch resistance [85]
- Zink oxide nanoparticles in Sunscreen by BASF [86]
- carbon nanotube enforced tennis rackets [87] and nanopolymer enforced tennis balls [88]
Available in 2000
Nanotex makes textiles where the clothing fibres have been coating in nanoscale fibres to change the textile wettability. This makes the textile much more stain resistant.
Companies making nanotech research equipment
- MultiProbe Manufacturer of a 1-to-6 head Atomic Force nanoprobing tool used in failure analysis, that combines multi-scan fault isolation imaging with nanoprobing electrical capabilities. For process technology node measurements of 32nm, 45nm, 65nm, 90nm or larger.
- Veeco AFM and related equipment
- Zyvex nanomanipulation equipment
- Nanofactory in-situ TEM manipulation equipment
- SmarAct nanomanipulators
- Capres micro four point conductance measurement probes
- ImageMetrology SPIP software for SPM analysis
- QuantumWise software for simulating nanosystems
- [89] AFM and related equipment
Products that have been nanostructured for decades
- Catalysts
- Computer processesors are increasingly made of nanoscale systems
Non-nanotech products and a warning
Not everything that says nano is nano - and given the hype surrounding nanotechnology you will see an increasing number of 'nano' products that have nothing to do with it. It is worrying when sometimes problems arise with non-nano products and this adds to the 'scare' that is present in the public, fuelled by the newspapers where they are just waiting for a nice scandal... an example was the product Magic Nano from a German company that made a number of users sick when inhaling the aerosol cleaning product - which in the end turned out to have nothing 'nano' in it. There is good reason to be very alert to such issues. Not all countries have legislation in place to secure the consumers against the possible dangers present in nanoparticles and some products could end being marketed before having been tested well enough. Though this example turned out to be 'non-nano', we will probably meet new cases shortly that are truly 'nano'. On this background environmental and health aspects will be an important part of this book.
Suppliers
Nanomaterials
Nanolithography
- NIL Technology sells stamps for nanoimprint lithography (NIL) and provides imprint services.
Quantum Dots
A nano-timeline
Overview of some important events in nanotechnology
See also History of Nanotechnology in Wikipedia
| Year | Development | |||
|---|---|---|---|---|
| Medieval | Observation of metal whisker growth and nanoparticles used for staining glass | |||
| 1900 | Max Planck proposes energy quantization. | |||
| 1905-30 | Development of quantum mechanics | |||
| 1927 | Heisenberg formulated his uncertainty principle | |||
| 1933 | The first First electron microscope was built by Ernst Ruska | |||
| 1952 | First carbon nanotubes observation by Radushkevich and Lukyanovich | |||
| 1953 | DNA structure discovered by James D. Watson and Francis Crick | |||
| 1959 | Feynmanns talk There is plenty of room at the bottom | |||
| 1965 | Proposal of Moores Law | |||
| 1981 | Invention of STM by Gerd Binnig and Heinrich Rohrer | |||
| 1985 | Invention of AFM by Binnig, Quate and Gerber | |||
| 1985 | Buckyball discovery by Harry Kroto, Robert Curl, and Richard Smalley | |||
| 1986 | K. Eric Drexler publishes his book Engines of Creation, in which he discusses both the potential huge benefits and the potential dangers of nanotechnology. He talks about a future of nanotechnology defined by molecular manufacturing, where self-replicating nanobots/assemblers are engineered to carry out practical applications. | |||
| 1989 | Don Eigler pushed around xenon atoms to spell IBM | – | 1991 | Rediscovery of carbon nanotubes by Sumio Iijima |
A nano-scale overview
Just to get a sense of proportion
| Scale | typical elements |
|---|---|
| 1 m | 1 m is 1.000.000.000 nanometers ( 10^9 nm ) |
| 200 µm | About the size of the smallest letters you can write with a very very sharp pencil and a very very steady hand. |
| 100 µm | Typical thick hair |
| 10-1000 µm | Cells in living organisms can have many sizes, and neurons can be much longer. In frog embryos (Tadpoles) the initial embryo cells can be up to 1000µm. |
| 8 µm | Red blood cell |
| 1 µm | Bacteria |
| 100 nm | Virus |
| 5-100 nm | The range for nanotechnology systems built from atomic/molecular components (quantum dots, nanoparticles, diameter of nanotubes and nanowires, lipid membranes, nanopores...). |
| 10 nm | Size of typical Antibody molecules in living organisms immune defence |
| 6-10 nm | Thickness of a cell membrane, and typical pore size in membrane. |
| 2.5 nm | The width of DNA (but it depends on the conditions) |
| 1 nm | The size of a C60 buckyball molecule or glucose molecule. |
| 0.3 nm | The size of a water molecule. |
| 1 Å = 0.1 nm | Roughly the size of hydrogen atom. |
| 0.7 Å = 70 pm | The best resolution in AFM achieved so far where they managed to image individual orbitals in an atom. |
- Distances between objects can be measured with sub Å precision with STM, laser interferometry and its even done continuously in a standard airbag acceleration sensor chip that costs a few dollars and senses the vibrations of a micro-inertial mass element with femtometer precision (10^-15 m).
Bibliography
- G. Ali Mansoori, Principles of Nanotechnology, Molecular-Based Study of Condensed Matter in Small Systems, (New Jersey: World Scientific, 2006).
- Monthioux, Marc; Kuznetsov, Vladimir L. (2006). "Who should be given the credit for the discovery of carbon nanotubes?". Carbon 44. doi:10.1016/j.carbon.2006.03.019. Retrieved on 2007-07-26.
References
See also notes on editing this book Nanotechnology/About#How_to_contribute.
the nanotechnology pioneers by Steven A. Edwards Engines of Creation 2.0: The Coming Era of Nanotechnology by K. Eric Drexler
About the Book
| Navigate |
|---|
| << Prev: Overviews |
| >< Main: Nanotechnology |
| >> Next: Reaching Out |
Vision
We hope to use the Wikibooks format to make an Open Source Handbook on Nanoscience and Nanotechnology, freely accessible for everyone, that can be updated continuously.
Wikipedia is growing fast and one of the most visited websites on the net – a valuable resource of information we all use.
In science and technology we often need more detailed information than what can be presented in a brief encyclopedic article – and here wikibooks.org, a sister project to Wikipedia, can help us with this newly started handbook.
Though the book is still in its infancy, it has been elected book of the month December 2006, and we hope this will provide PR and more people contributing to the project!
The plan to create the book:
1: First to create smaller articles to ‘cover’ the entire area of nanotechnology and achieve a well defined structure the book (some parts could be revised thoroughly in this process,for instance the materials chapter).
2: Once the structure is reasonably well defined, to begin refining the articles with in-depth material so we reach lecture-note level material.
3: Since everybody can contribute, a continuous contribution of material is expected and a backing group of editors is needed to maintain a trustworthy level of information.
An voluntary editorial board is being put together to oversee the book, support, contribute and follow its development.
Discussion about the content of the book can be found on the main talk page talk:Nanotechnology
As with Wikipedia, we hope to see a solid information resource continuously updated with open source material available for everyone!
Editing hints
References in Wikibooks
Add references whenever possible, with reference lists at the end of each page. Please try to make links to the articles with the DOI (digital object identifier) because that gives a uniform and structured access for everyone to the papers.
All papers get a DOI - a unique number like a bar code in a supermarket. All DOIs are registered by www.doi.org and in the reference list you can add links like https://doi.org/10.1039/b504435a so people will be able to find it no matter how the homepage of the journal or their own library changes.
The References section has an example reference.
Add links to the Wikipedia whenever possible - and for the beginning I will rely extensively on Wikipedia's pages on the subjects, simply referring to these. This textbook could be simply a gathering of Wikipedia pages, but an encyclopedia entry is brief, and for a handbook it is preferable to have more in-depth material with examples and the necessary formulas. So, some information in this textbook will be very much like the Wikipedia entries and we might not need to write it in the book but can simply refer to Wikipedia, but the hope is that this will be more a text book as is the intention with Wikibooks.
Multiple references, see w:Help:Footnotes
Links
There's a shorthand way to make links to Wikipedia from Wikibooks: [[w:Quantum_tunneling|Wikipedia on Quantum Tunneling]] gives the link Wikipedia on Quantum Tunneling.
Media
History
The book was started by Kristian Molhave (wiki user page) 13. Apr. 2006. Initially it was named Nanowiki, and later changed to Nanotechnology. Kristian is currently slowly uploading material to the book and looking for people who would like to contribute that can and substantial material to specific sections under the GNU license. I hope we can make an 'editorial panel' of people each keeping an eye on and updating specific sections.
The Summer 2008 Duke Talent Identification Program (TIP) eStudies Nanotechnology students will be adding to the content of this Wikibook. From June-Aug 2008 there will be content additions with references that will add to this great resource.
Authors and Editors
- The Opensource Handbook on Nanoscience and Nanotechnology was started by Kristian Molhave(wiki user page)
Editors
- An editorial board is currently being organized.
Support and Acknowledgments
Starting this book is supported by the Danish Agency for Science, Technology and Innovation through Kristian Mølhave's talent project ’NAMIC’ No. 26-04-0258.
How to Reference this Book
I am not currently sure how work on wikibooks or wikipedia can be referenced reliably in published literature.
Three suggestions:
1) Reference the references from the wikibook. Wikibooks are not intended to be the publication channel for new results, but should be based on published and accepted information with references and these references can be used. But this of course does not give credit to the book, so I recommend then adding an acknowledgement about the book to give it PR and credit.
2) Reference the book with a specific page and date - the previous versions of the pages are all available in the history pane and can easily be accessed by future users. You can also hit "permanent version" on the left side of the webpage (it is under "toolbox"). That sends you specifically to the selected version of the wikipage with a link to it that will never change.
3) Reference the PDF version and its version number. Once the book achieves a reasonable level, PDF versions will become available for download and they will have a unique version number and can be retrieved.
Other suggestions are most welcome!
Edwards, Steven A.,The Nanotech Pioneers
Christiana, USA:
Wiley-VCH 2006, pg 2
Reaching Out
| Navigate |
|---|
| << Prev: About |
| >< Main: Nanotechnology |
| >> Next: Seeing Nano |
Teaching Nanotechnology
Teachers' Toolbox is a Wikibook on teaching methods and ways to improve teaching. The toolbox is intended to give you an overview of methods you can use when teaching in general.
If you know of places that have teaching material available on the net, please add a link to the list below:
Outreach projects
There are several nanotechnology related outreach projects. Here are some examples to give ideas:
- Nanoscale Science Education
- Citizens school of nanotechnology
- Webcast outreach lecture
- Exploring the nanoworld
- K-14 outreach
- Cornell Museum
Demonstration experiments
There is a dedicated section for nanotechnology in the Wikiboook on Science Show, which is a cross disciplinary collection of demonstration experiments. The is growing steadily and we will begin to add to the English version soon. Please add to these books with any demonstration experiments and ideas you have!
There are others available on the net:
- Nano-Tex: Testing New Nano Fabrics
- Nano kits and for instance the exercise moving a wall
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Part 2: Seeing 'Nano'
| Navigate |
|---|
| << Prev: Reaching Out |
| >< Main: Nanotechnology |
| >> Next: Optical Methods |
|
|
| <<< Prev Part: Introduction |
| >>> Next Part: Physics - on the nanoscale |
The eyes in nanotech
Without being able to 'see' the nanoscale objects, nanotechnology would be very difficult. In this part, the different microscope techniques are reviewed along with various spectroscopic and diffraction methods that can tell us more about the nanoscale structure of matter.

Visible light is only a part of the electromagnetic spectrum and useful information about different physical interactions in nanostructures can be acquired from the different parts of the electromagnetic spectrum.
Seeing 'nano' can be done in different ways, but not with the naked eye which normally cannot see things much smaller than 100µm (though a single atom can be seen if it lights up in a dark room). Instead of our eyes, we use various instruments to 'see' for us, and they 'see' different things depending on how they are made:
Microscopy
Microscopy uses microscopes to create an image of the specimen. The image is rarely an image as you see it with your eyes, but rather how some physical probe interacts differently with the specimen as function of position on it. The physical probe can be an AFM cantilever, a beam of light or electrons, or something completely different.
Overview of Microscopes

Optical: The beam from a light source is focused onto a sample and either the transmitted or scattered light is collected by an objective lens and the image is magnified onto a camera or to the observer's eye. The resolution can be down to about 200 nm, and the microscopes can be fairly cheap, small and easy to use.
Transmission Electron Microscope (TEM): Electrons from a very bright electron source are directed to a very thin sample that is transparent to the high energy electrons (100-300 keV) and the electron beam is then magnified by electromagnetic lenses and sent onto a fluorescent screen or a camera to observe the image. The resolution can be less than 0.1 nm on expensive high-end instruments where even individual atoms can be imaged. The samples must be very thin (typically less than 200 nm) and the whole system must be under high vacuum.
Scanning Electron Microscope (SEM): A focused electron beam is scanned over a sample and the scattered electrons are detected. The detector current is used to give an image depending on the electron beam position on the sample. The resolution can be down to about 5 nm and the sample can be much larger than in the TEM because the electrons do not have to pass through the sample.
Scanning Probe Microscopes (SPM) move a very sharp probe across a sample in a raster pattern while recording how the probe interacts with the sample. The typical SPMs are the AFM, STM and SNOM:
Atomic Force Microscope (AFM): An almost atomically sharp tip is protruding from a cantilever and is scanned over the sample. When the cantilever deflects, a laser beam reflected off the backside of the cantilever will change directions and this will be measured by a photodetector. The laser position can be used to control the force between the tip and the sample, and the AFM is often used to measure both topography and forces on the nanoscale. The resolution is normally down to about 1 nm, but even subatomic resolution is possible. The AFM can work with both dry and wet, conducting and isolating samples.
Scanning Tunneling Microscope (STM): An atomically sharp tip is moved within atomic distance of a sample that has a voltage applied to it. When the tip-sample distance becomes so small that the electron clouds of the tip and sample touch, electrons can much more easily tunnel between the two and this gives rise to a tip-sample current (often a few pA at a 1V bias voltage). This current can be used to maintain a fixed tip-sample distance when the tip is scanned over the sample, and this can give images of conducting surfaces with atomic resolution.
Scanning Near-field Optical Microscope (SNOM): As electrons can tunnel between electrical conductors in the STM, photons can tunnel between optical guiding structures. The SNOM uses a narrow light guide to measure how the optical electromagnetic field changes as the guide is moved across the sample. For instance, light can be sent from below the sample and then scattered into the scanning light guide above it. The resolution can be much smaller than the wavelength of light.
Point-Projection Microscopes: The Field Emission Microscope (FEM), Field Ion Microscope (FIM) and the atom probe are examples of point-projection microscopes where ions are excited from a needle-shaped specimen and hit a detector. The Atom-Probe Tomograph (APT) is the most modern incarnation and allows a three-dimensional atom-by-atom (with chemical elements identified) reconstruction with sub-nanometer resolution.
Spectroscopy
Spectroscopy uses spectrometers to tell how radiation interacts with the specimen as function of the energy/wavelength of the radiation
Diffraction
Diffraction uses radiation to observe how it is scattered in different directions from the specimen. This can be used to tell about the order of the atoms in the sample.
Surface analysis
Many of these methods are used for 'macroscopic' surface analysis where the outmost nanometers of a material is being studied over larger areas. The methods can be combined with microscopes to give spectrometrical information from a well defined location on the sample - for instance when doing diffraction measurements in a TEM or level spectroscopy in an STM on a single atom.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Optical Methods
| Navigate |
|---|
| << Prev: Seeing Nano |
| >< Main: Nanotechnology |
| >> Next: Electron Microscopy |
Optical Microscopy
The Abbe diffraction limit
Observation of sub-wavelength structures with microscopes is difficult because of the Abbe diffraction limit. Ernst Abbe found in 1873 that light with wavelength λ,travelling in a medium with refractive index n and converging to a spot with angle φ will make a spot with radius
The denominator nsinφ is called the numerical aperture (NA) and can reach about 1.4 in modern optics, hence the Abbe limit is roughly d=λ/2. With green light around 500nm the Abbe limit is 250nm which is large compared to most nanostructures or biological cells with sizes on the order of 1μm and their internal organelles being much smaller. To increase the resolution, shorter wavelengths can be used such as UV and X-ray microscopes. These techniques offer splendid resolution but are expensive, suffer from lack of contrast in biological samples, and also tend to damage the sample.
Resources
- Microscope optics
- Microscopy Primer
- Olympus Interactive Java Tutorials on Microscopy
- Nikon MicroscopyU with interactive tutorials on microscopy techniques
The optical microscope

Bright Field
The light is sent to the sample in the same directions as you are looking - most things will look bright unless they absorb the light.
Dark Field
Light is sent towards the sample at an angle to your viewing direction and you only see light that is scattered. This makes most images appear dark and only edges and curved surfaces will light up.
Polarized Light
DIC vs H
Laser Scanning Confocal Microscopy (LSCM)
Confocal laser scanning microscopy is a technique that allows a much better resolution from optical microscopes and three dimensional imaging. A review can be found in Paddock, Biotechniques 1999
Using a high NA objective also gives a very shallow depth of focus and hence the image will be blurred by structures above or below the focus point in a classical microscope. A way to circumvent this problem is the confocal microscope, or even better the Laser Scanning Confocal Microscope (LSCM). Using a laser as the light source gives better control of the illumintaion, especially when using fluorescent markers in the sample. The theoretical resolution using a 1.4 NA objective can reach 140nm laterally and 230nm vertically [1] while the resolution quoted in ref [2] is 0.5×0.5×1μm. The image in the LSCM is made by scanning the sample in 2D or 3D and recordning the signal for each point in space on a PC which then generates the image.
X-ray microscopy
X-ray microscopy uses X-rays to image with much shorter wavelength than optical light, and hence can provide much higher spatial resolution and use different contrast mechanisms. X-ray microscopy allows the characterization of materials with submicron resolution approaching the 10's of nanometers. X-ray microscopes can use both laboratory x-ray sources and synchrotron radiation from electron accelerators. X-ray microscopes using synchrotron radiation provide the greatest sensitivity and power, but are unfortunately rather large and expensive. X-ray microscopy is usually divided into two overlapping ranges, referred to as soft x-ray microscopy (100eV - 2keV) and hard x-ray microscopy (1keV-40keV). All x-rays penetrate materials, more for higher energy x-rays. Hence, soft x-ray microscopy provides the best contrast for small samples. Hard x-rays do have the ability to pass nearly unhindered through objects like your body, and hence also give rather poor contrast in many of the biological samples you would like to observe with the x-ray microscope. Nevertheless, hard x-ray microscopy allows imaging by phase contrast, or using scanning probe x-ray microscopy, by using detection of fluorescent or scattered x-rays. Despite its limitations, X-ray microscopy is a powerful technique and in some cases can provide characterization of materials or samples that cannot be done by any other means.
UV/VIS spectrometry
Infrared spectrometry (FTIR)
vIdentification of the functional groups present in a nanomaterial is a frequent requirement in nanoscience and nanotechnology research. Among other tools, FT-IR has found much popularity among researches due to its versatility, relative ease of use and ability to use as a quantification tool.
Atoms in a chemical bonds constantly vibrate. This vibration can be analogue to a system with two masses attached to a spring. The vibration frequency depend upon the weight of the masses and the spring constant of the connecting spring. In the same way, depending on the masses of the atoms that contributes to a bond and cohesiveness of the bond, frequency differ. Since bonds have atoms with different shapes and sizes and different strength, each combination of atoms in an each type of bond has a unique harmonic frequency. This natural frequency lies in the range of infrared region and therefore a spectroscopic method that use IR can be devised to analyze bond vibrations.
When the IR radiation with the same harmonic frequency of the bond shines upon the bond. The bond vibration is amplified by increased transfer of energy from the IR radiation. When range of IR frequencies given to the material, it only absorb IR frequencies that corresponds to the natural frequencies of the bonds that exist in the sample. Others are not absorbed and can be analyzed using an Infrared spectrometer, which tells you the frequencies that are absorbed by the sample. This provides important information about the functional groups present in the sample. This is exactly what FT-IR does.
As FT-IR can be used to get information about functional groups present in nanomaterials. This is particularly useful in cases such as when one attempts to surface modify nanomaterials to increase affinity, reactivity or compatibility. Analyzing the FT-IR of a nanomaterial would tell you what groups present and then appropriate surface modification strategy be decided based on the groups present. Further, it can also be useful in characterizing the surface modification has taken place, as new groups should emerge if the reaction is successful.Identification of the functional groups present in a nanomaterial is a frequent requirement in nanoscience and nanotechnology research. Among other tools, FT-IR has found much popularity among researches due to its versatility, relative ease of use and ability to use as a quantification tool.
Atoms in a chemical bonds constantly vibrate. This vibration can be analogue to a system with two masses attached to a spring. The vibration frequency depend upon the weight of the masses and the spring constant of the connecting spring. In the same way, depending on the masses of the atoms that contributes to a bond and cohesiveness of the bond, frequency differ. Since bonds have atoms with different shapes and sizes and different strength, each combination of atoms in an each type of bond has a unique harmonic frequency. This natural frequency lies in the range of infrared region and therefore a spectroscopic method that use IR can be devised to analyze bond vibrations.
When the IR radiation with the same harmonic frequency of the bond shines upon the bond. The bond vibration is amplified by increased transfer of energy from the IR radiation. When range of IR frequencies given to the material, it only absorb IR frequencies that corresponds to the natural frequencies of the bonds that exist in the sample. Others are not absorbed and can be analyzed using an Infrared spectrometer, which tells you the frequencies that are absorbed by the sample. This provides important information about the functional groups present in the sample. This is exactly what FT-IR does.
As FT-IR can be used to get information about functional groups present in nanomaterials. This is particularly useful in cases such as when one attempts to surface modify nanomaterials to increase affinity, reactivity or compatibility. Analyzing the FT-IR of a nanomaterial would tell you what groups present and then appropriate surface modification strategy be decided based on the groups present. Further, it can also be useful in characterizing the surface modification has taken place, as new groups should emerge if the reaction is successful.
Terahertz Spectroscopy
Raman Spectroscopy
Surface Enhanced Raman Spectroscopy (SERS)
- Surface Enhanced Raman Spectroscopy (SERS)
- Surface-enhanced Raman spectroscopy: a brief retrospective
References
See also notes on editing this book Nanotechnology/About#How_to_contribute.
- ↑ Confocal laser scanning microscopy, Paddock SW, Biotechniques , vol. 27 (5): 992 NOV 1999
- ↑ A new UV-visible confocal laser scanning microspectrofluorometer designed for spectral cellular imaging, Favard C, Valisa P, Egret-Charlier M, Sharonov S, Herben C, Manfait M, Da Silva E, Vigny P, Biospectroscopy , vol. 5 (2): 101-115 1999
Electron Microscopy
| Navigate |
|---|
| << Prev: Optical Methods |
| >< Main: Nanotechnology |
| >> Next: Scanning Probe Microscopy |
Electron microscopy
An overview:
Electron microscopes uses electrons instead of photons, because electrons have a much shorter wavelength than photons and so allows you to observe matter with atomic resolution.
There are two general types of electron microscopes: the Scanning Electron Microscope (SEM) that scans an electron beam over the surface of an object and measures how many electrons are scattered back, and the Transmission Electron Microscope (TEM) that shoots electrons through the sample and measures how the electron beam changes because it is scattered in the sample.

Using electron beams however requires working in a vacuum environment, and this makes the instruments considerably larger and expensive. All electron microscope work under at least low pressures and usually in high vacuum chambers to avoid scattering the electrons in the gas. In environmental electron microscopes, differential pumping systems are used to actually have gasses present by the sample together with the electron beam.
Introduction to Electron Microscopy
For imaging of nanoscale objects, optical microscopy has limited resolution since the objects are often much smaller than the wavelength of light. The achievable resolution for a wavelength is often given by the diffraction limit as
- (r.g., diffraction limit)
with numerical aperture , which can be approximated by the largest angle of incidence of the wavefront towards the sample, .
Since for the present purposes, we can approximate and hence where is the radius of the objective lens aperture and the working distance.
Optical microscopes can often reach a resolution of about nm. For nanoscale resolution this is unfortunately not sufficient to distinguish for instance a single nanotube from two adhering to each other, since they have diameters of less than 100 nm.
The figure below gives an overview typical magnifications achievable by the different electron microscopes compared to a light microscope.

Electron optical systems use electrical and magnetic fields to control the electron beam. Although the law of refraction in optics is exchanged with the Lorentz force in electrodynamics, the electron optical system has similar diffraction limits as optical systems, since they depend on the wave nature of the electron beam.
One can achieve a considerable improvement in resolution with instruments such as the transmission electron microscope and the scanning electron microscope that use electrons with De Broglie wavelength much smaller than that of visible light. The De Broglie wavelength λ of an electron with momentum p is
- (Eq. De Broglie wavelength)
where is Plancks constant. The electron has rest mass and energy .
If an electron with charge is accelerated from rest by an electrical potential , to the electron beam energy , it will have a wavelength of 1 nm at 1 eV decreasing to 1 pm at 100 keV where it will be travelling with 50% the speed of light.
This chapter will briefly review fundamental issues for electron microscopy that are similar for SEM and TEM: the limitations imposed by the electron optical beam system in the microscope column; the interaction of the electron beam with the sample; the standard image formation method in SEM and TEM. These issues are essential to understand the results and limitations reached in SEM and TEM microscopy.
For further details, please refer to reviews of electron microscopes and their applications, such as Goldstein et al. [1] that contains a thorough review of SEM, while Goodhew and Humphreys [2] is a more general introduction to both SEM and TEM.
The Electron Optical System
For high resolution imaging, a well focused beam is required, just as in optical microscopy. Due to the short wavelength of electron beams with keV energies, as given by the #Eq de Broglie wavelength, the properties of the electron optical system and the electron emitter mainly defines the limits on the achievable beam diameter. The current density in the electron beam can be approximated by a Gaussian distribution of current density j [A/m²] as function of radius, r, from the beam center
with radius determined by , giving a the full width half maximum . Integrating gives the total beam current
The electron optics impose a limit on the achievable beam current density and radius by the brightness of the electron emitter , which is conserved throughout the system [3].
Brightness, ß, is a measure of the current per area normal to the beam direction and per element of solid angle [4]. At the center of the Gaussian beam,
and the brightness is related to the current density in eq SEM Gaussian beam profile. The emitter brightness is determined by the type of electron emitter and the beam energy [5]
with emission current density for W-filament sources about ~3 A/cm², for LaB6 sources about 100 A/cm², while field emission guns (FEG) can reach 105A/cm². The energy spread of the electrons from the sources are about ΔE~1 eV and slightly lower for FEGs. Due to conservation of the brightness in the system, the beam diameter depends on current as
The ideal beam probe size determined by the conservation of brightness cannot be obtained in a real system. Effects such as aberration will make the minimum achievable beam diameter larger. Equation #eq SEM beam diameter however seem to adequately describe the beam diameter for the present discussion. Apart from the additional beam widening contributions, the image detection method imposes limits on useful values for the parameters in Eq. SEM beam diameter which differ for SEM and TEM.
Electron Range
The electron optical system sets limitations to the achievable primary beam current and radius. The expected image resolution set by the primary beam cannot be reached if the signal detected for imaging is caused by electrons scattered far in the sample. The trajectory of an electron penetrating a bulk solid is a complex trajectory due to multiple elastic and inelastic collision events. As the primary electron (PE) penetrates into the sample it will gradually change direction and loose energy in collisions. The mean free path due to elastic and inelastic collisions, , depends on the atomic number of the material and the PE energy. At 100 keV for carbon and 5 nm for gold [6]. For samples thinner than the main part of the PE will pass relatively unaffected through the sample, which is the basis for TEM.

SEM can be used for thicker specimens. The electrons that escape from the sample in a new direction compared to the PE due to elastic collisions are called backscattered electrons (BSE).
For samples thicker than , the volume interacting with the scattered PE defines the range of the electrons in the material, and this is considerably larger than the minimum achievable primary beam diameters.
The electron range is about 1 µm at 10 keV for carbon, decreasing with higher atomic number for the material. Both the high energy PE and BSE generate secondary electrons (SE) by inelastic scattering events. The SE are generally defined as having energy below 50 eV while the BSE have energies up to the PE energy. The range of SE is typically 1 nm for metals and about 10 nm for insulators [7].
The short range of the SE make the yield of SE highly dependent on the energy lost by the PE within the SE range from the surface, and this makes high Z substances efficient generators of SE. The main emission of SE takes place in the region where the PE strikes the surface and within the SE escape depth from this region.

Scanning electron microscopy (SEM)
- Wikipedia: Scanning electron microscopy (SEM)
In a scanning electron microscope a beam is scanned over the sample surface in a raster pattern while a signal is recorded from electron detectors for SE or BSE. The PE energy is kept relatively low (1-30 keV) to limit the interaction volume in the specimen that will contribute to the detected signal. Especially low energy PE will provide high sensitivity to surface composition as they cannot penetrate far into the sample.
The figure above showed the effect of PE penetration depth of a carbonaceous nanostructure with a gold core, where only the surface is visible at low PE energies, while the carbon becomes increasingly transparent and the core visible at high PE energies.
The low energy SE can easily be attracted and collected by a positively charged detector and are hence an efficient source for an image signal. The standard SE detector is an Everhart-Thornley (ET) detector where a positively charged grid attracts the SE and accelerates them to sufficiently high energies to create a light pulse when striking a scintillator. The light pulse is then amplified by a photomultiplier. Despite the complex construction, the ET detector is remarkably efficient, but requires large for effective collection of the SE by the charged grid.
Another SEM detector is the in-lens detector, where SE passing through the column aperture are accelerated towards a solid state detector. The in-lens detector complements the ET by being more efficient at short .
Environmental SEM (ESEM)

The ESEM makes it possible to use various gasses in the sample chamber of the microscope since there are narrow apertures between the sample chamber and the gun column, and a region in between that is connected to a differential pumping system. Pressures up to about 10 Torr are normally possible in the sample chamber.
The standard Everly-Thornhart SE detector would not work under such conditions since it would create a discharge in the low pressure gas. Instead a "gaseous secondary electron detector (GSD)" is used, as shown in the figure below. The GSD measures the current of a weak cascade discharge in the gas, which is seeded by the emission of electrons from the sample.

In the ESEM one can work with for instance water vapour or argon as the environmental gas, and it is possible to have liquid samples in the chamber if the sample stage is cooled sufficiently to condense water.
Transmission electron microscopy (TEM)

When the specimen thickness is about the mean free path, , TEM can be used to achieve high resolution images such as the image above where the atomic lattice of a gold nanocrystal is visible. Since the detected electrons are transmitted PE where the energy can be in the 100 keV range, the resolution is not limited by the issues regarding secondary electrons. The electron beam optics can be optimized for higher current densities (Eq. #eq SEM current density) at higher energies compared to SEM.
To achieve optimal imaging conditions for the thin TEM samples, the working distance has been made short. In most TEMs, the space for the sample holder is only about (5 mm)³ between the two objective lenses for the incoming and transmitted beam. Before reaching a CCD camera, the transmitted beam is sent through several magnification lenses to achieve the high magnification (500.000X is not unusual).
The image formation in TEM can be based on several principles, but practically all images used in this work were made by phase contrast imaging, here called High Resolution TEM or HRTEM. At sufficiently high brightness, electron sources can produce coherent electron beams due to the point-like emitter surface area and small energy spread [8]. The coherent electron beam can be considered as a spherical wave propagating from the emitter and out through the electron optical system, much like a laser beam would propagate through an optical system.
The HRTEM images are often based on the interference of the electron wavefront after it has passed through the sample and reaches a CCD detector to give a phase contrast image of the sample. The image will have a resolution determined of course by the wavelength of the electrons (Eq. #eq SEM de broglie wavelength) but mainly by the imperfections of the electron optics which also perturbs the wavefront. The optimal imaging condition is for a sample thickness about , where the wavefront is only slightly perturbed by passing through the sample. TEM instruments are normally easily capable of resolving individual shells of a carbon nanotubes. The fine-tuning of the electron optical system to the required resolution can be achieved in about 30 min for many microscopes.

Electron Holography
In special TEM microscopes, the diffracted beam can be combined with a part of the original electron beam from the electron gun, and the image that is recorded is an interference pattern that depends on how much the phase of the diffracted beam was changed. By recording such images, one can measure how the electron wave function changes as it passes through or nearby a nanostructure - and this allows you to measure the electric and magnetic fields surrounding nanostructures.
Electron Tomography
By recording numerous TEM images of an object at many different angles, these images can in a computer be combined to create a three-dimensional model of the object. The technique is time consuming but allows you to see nanostructures in 3D.
References
- ↑ J. Goldstein, D. Newbury, P. Echlin, D. C. Joy, A. D. Romig, C. E. Lyman, C. Fiori, and E. Lifshin. Scanning Electron Microscopy and X-Ray Microanalysis, 2nd Ed. Plenum Press, 1992.
- ↑ P. J. Goodhew and F. J. Humphreys. Electron Microscopy and Analysis, 2rd Ed. Taylor and Francis, 1988.
- ↑ S. Humphries. Charged Particle Beams. John Wiley and Sons, 1990. PDF version available at http://www.fieldp.com/cpb/cpb.html.
- ↑ P. W. Hawkes and E. Kasper. Principles Of Electron Optics. Academic Press, 1989.
- ↑ L. Reimer. Transmission electron microscopy: Physics of image formation and microanalysis, 3rd Ed. Springer-Verlag, 1993.
- ↑ P. J. Goodhew and F. J. Humphreys. Electron Microscopy and Analysis, 2rd Ed. Taylor and Francis, 1988.
- ↑ J. Goldstein, D. Newbury, P. Echlin, D. C. Joy, A. D. Romig, C. E. Lyman, C. Fiori, and E. Lifshin. Scanning Electron Microscopy and X-Ray Microanalysis, 2nd Ed. Plenum Press, 1992.
- ↑ P. W. Milonni and J. H. Eberly. Lasers. John Wiley & Sons, Inc., 1988.
Scanning probe microscopy
| Navigate |
|---|
| << Prev: Electron Microscopy |
| >< Main: Nanotechnology |
| >> Next: Additional Methods |
|
|
| Section on AFM |
| Section on STM |
| Section on SNOM |
Scanning probe microscopy
Scanning probe microscopy covers the methods where a sharp tip is scanned over a surface in a raster pattern and the interaction with the surface is recorded in each pixel to form an image of the interaction. There are a multitude of methods and interactions in SPM. Broadly speaking, there are three main categories:

- In scanning tunneling microscopy (STM), one uses an atomically sharp metallic tip and records the minute tunneling current between the tip and the surface, when the tip is hovering so close to the surface that electrons can move between the surface and the tip.
- In Atomic force microscopy (AFM), a cantilever with a sharp tip - somewhat like the needle of an old record player - is scanned over the surface and the topography or surface softness can be recorded.
- In Scanning near-field optical microscopy (SNOM) a probe with a smalle aperture is scanned over the surface collecting the light comming from regions much smaller than the wavelength of the light used.
Atomic force microscope (AFM)
- Atomic force microscope (AFM)
- Kelvin force microscopy
- Magnetic force microscope
- Scanning voltage microscopy
- Magnetic resonance force microscope
- Lateral force microscopy
Scanning tunneling microscopy (STM)
Scanning Near-field optical microscopy (SNOM)
Wiki links:
Resources
- A Practical Guide to Scanning Probe Microscopy by Rebecca Howland and Lisa Benatar
- homebrew atomic-resolution microscope
References
See also notes on editing this book about how to add references Nanotechnology/About#How to contribute.
Atomic force microscope (AFM)
| Navigate |
|---|
| << Prev: Scanning Probe Microscopy |
| >< Main: Nanotechnology |
| >> Next: Scanning tunneling microscopy (STM) |
Atomic Force Microscopy (AFM)
This is a new page and we hope you will help proof reading it and add to it!!
The relation between torsional spring constant and lateral spring constant is in doubt. Please check ("Normal and torsional spring constants of atomic force microscope cantilevers" Green, Christopher P. and Lioe, Hadi and Cleveland, Jason P. and Proksch, Roger and Mulvaney, Paul and Sader, John E., Review of Scientific Instruments, 75, 1988-1996 (2004), DOI:http://dx.doi.org/10.1063/1.1753100) and ("Lateral force calibration in atomic force microscopy: A new lateral force calibration method and general guidelines for optimization" Cannara, Rachel J. and Eglin, Michael and Carpick, Robert W., Review of Scientific Instruments, 77, 053701 (2006), DOI:http://dx.doi.org/10.1063/1.2198768) for details.

Resources
- A Practical Guide to Scanning Probe Microscopy by Rebecca Howland and Lisa Benatar
Methods in AFM
A wealth of techniques are used in AFM to measure the topography and investigate the surface forces on the nanoscale:
For imaging sample topography:
- Contact mode, where the tip is in contact with the substrate. Gives high resolution but can damage fragile surfaces.
- Tapping / intermittent contact mode (ICM), where the tip is oscillating and taps the surface.
- Non-contact mode (NCM), where the tip is oscillating and not touching the sample.
For measuring surface properties (and imaging them):
- Lateral force microscopy (LFM), when the tip is scanned sideways it will tilt and this can be measured by the photodetector. This method is used to measure friction forces on the nanoscale.
- Force Modulation Microscopy. Rapidly moving the tip up and down while pressing it into the sample makes it possible to measure the hardness of the surface and characterize it mechanically.
- Electrical force microscopy. If there are varying amount of charges present on the surface, the cantilever will deflect as it is attracted and repelled. kelvin probe microscopy will normally be more sensitive than measuring s static deflection.
- Kelvin probe microscopy. By applying an oscillating voltage to an oscillating cantilever in non-contact mode and measuring the charge induced oscillations, a map can be made of the surface charge distribution.
- Dual scan method - an other kelvin probe method described below.
- Magnetic Force Microscopy. If the cantilever has been magnetized it will deflect depending on the magnetization of the sample.
- Force-spectroscopy or force-distance curves. Moving the cantilever up and down to make contact and press into the sample, one can measure the force as function of distance.
- Nanoindentation. When pressing the cantilever hard into a sample it can leave an imprint and in the force distance curve while doing indentation can tell about the yield stress, elastic plastic deformation dynamics.
- Liquid sample AFM. By immersing the cantilever in a liquid one can also image wet samples. It can be difficult to achieve good laser alignment the first time.
- Electrochemical AFM.
- Scanning gate AFM
- Nanolithography
- Dip-pen lithography
Reviews of Atomic Force Microscopy

- Force measurements with the atomic force microscope: Technique, interpretation and applications. Surface Science Reports 59 (2005) 1–152, by Hans-Jurgen Butt, Brunero Cappella,and Michael Kappl. 152 pages extensive review of forces and interactions in various environments and how to measure and control these with AFM.
Cantilever Mechanics
Cantilever has width w, thickness t, length L and the tip height from the cantilever middle to to the tip is h.

When the cantilever is bent by a point force in the z-direction at the tip will deflect distance z(x) from the unloaded position along the x-axis as [1]
with cantilever length , Youngs modulus , and moment of inertia .
The tip deflection is
giving a spring constant from
so
The angle of the cantilever in the x-z plane at the tip , which is what gives the laser beam deflection will be

giving the relation
between the tip deflection distance and tip deflection angle. This is a factor 3/2 bigger than the result we would expect if the beam was stiff and hinged at the base, showing us that we get a bigger deflection of the laser beam when the beam is bending than when its straight.

The AFM detector signal
The cantilever can bend in several ways, which is detected by the quadrant photo detector that most AFMs are equipped with. Normal topography signal is given by 'normal' deflection of the cantilever tip in the x-z direction, and detected by the left-right (or A-B) detector coupling quadrants as .
Lateral forces applied to the tip will bend the cantilever in the x-y and x-z plane too. Lateral deflection cannot be detected by the quadrant detector since it doesn't change laser beam deflection, and deflection is also rather small, as we shall see. Lateral forces also twist the cantilever tip producing torsional deflection in the y-z direction, which in turn produces the lateral force signal from the top-bottom detector measuring
For deflection in the z-direction, 'normal' spring constant relating the force and deflection is
Expressed in the angle of deflection, there is an angular spring constant
with .

Contact, Tapping, and Non-contact Mode
If an oscillator experiences an attractive force pulling it away from it rest position, the resonance frequency will drop (at snap-in it will be zero). A repulsive force squeezing it will increase the resonance frequency.

If an AFM tip is moved to contact with a sample, the resonance frequency is first decreasing slightly due to attractive forces and then increasing due to the repulsive forces. Eventually the repulsive force become so high we cannot oscillate it and we have achieved contact.
Contact mode: Because the tip is in contact, the forces are considerably higher than in non-contact mode and fragile samples as well as the tip can easily be damaged. The close contact on the other hand makes the resolution good and scan speeds can be high.
The varying resonance frequency is the cantilever moves between the attractive end repulsive regions of the force distance curve can be used to measure the cantilever position and to keep it in the attractive or repulsive part of the force distance curve.

Non-contact mode: If we oscillate the cantilever at a higher frequency than its free resonance and use the feedback loop to maintain a oscillation amplitude setpoint slightly lower than that of the free oscillation, it will move the tip down until the attractive forces lower the resonance frequency and makes the oscillation amplitude drop to the setpoint level.
Tapping mode: if we oscillate the cantilever at a lower frequency that its free oscillation, moving it towards the sample will first make it oscillate at a lower frequency which will make the stage move closer to try and raise the oscillation amplitude, and at eventually as it reaches repulsive forces will settle where resonance frequency cannot increase more without giving too high an amplitude.
| Use for | k (N/m) | f (kHz) |
| Non contact (NC) | 10-100 | 100-300 |
| Intermittent contact (IC) | 1-10 | 20-100 |
| Contact | 0.1-1 | 1-50 |
Contact Mode
Tapping Mode
Tapping-mode (also called intermittent contact mode) is the most widely used operating mode in which the cantilever tip can experience both attractive and repulsive forces intermittently. In this mode, the cantilever is oscillated at or near its free resonant frequency. Hence, the force sensitivity of the measurement is increased by the quality factor of the cantilever. In tapping-mode operation, the amplitude of the cantilever vibration is used in feedback circuitry, i.e., the oscillation amplitude is kept constant during imaging. Therefore it is also referred as amplitude modulation AFM (AM-AFM). The primary advantage of tapping mode is that the lateral forces between the tip and the sample can be eliminated, which greatly improves the image resolution. Tapping mode experiments are done generally in air or liquid. Amplitude modulation is not suitable for vacuum environment since the Q-factor of the cantilever is very high (up to 105) and this means a very slow feedback response.
Non-contact Mode
Lateral Force Microscopy
If the sample is scanned sideways in the y direction, the frictional forces will apply a torque on the cantilever, bending it sideways and this can be used to measure the frictional forces. The lateral force gives both a lateral and torsional deflection of the tip. Only the torsional can be detected in the photodetector.
For sideways/lateral bending, the lateral spring constant is corresponding to the normal spring constant but with width and thickness interchanged
and a similar eq's for angular deflection as above. With thickness typically much smaller than the width for AFM\ cantilevers, the lateral spring constant is 2-3 orders of magnitude higher than
For a sideways, lateral force on the cantilever we will have a sideways deflection determined by
If the lateral force is applied to the AFM tip, , it will give a lateral deflection but also apply a torque twisting the beam
Twisting an angle gives a torional tip deflection of
The relation for the torsional spring constant is (please check this equation)
with
and then
From above we have
The factor is typically - so about 1 but larger or smaller depending on whether its a contact or non-contact cantilever.
Friction Loop Scan

For optimal torsional sensitivity - but the following is not always correct since it depends highly on the contact forces you need etc: For high torsional sensitivity, . Since we are in contact mode AFM, L must be large and t thin for a low . So better torsional sensitivity means wider cantilevers and definitely large tip heights.
Coupled Lateral and Torsional deflection in the cantilever
But how much will a cantilever bend laterally and how much will it twist when applied a lateral force at the tip? An applied lateral force will move two degrees of freedom with a Hookes law behaviour - the torsion and lateral motion. The applied force is also an applied
The effective spring constant for pushing the tip in the y direction is then
with and
and the deflection made in the torsional spring is
and this approaches when so the cantilever is more prone to tilting than lateral deflection. The lateral deflection can be found from
The torsional deflection angle is then
as anticipated from the assumption that the torsional and lateral springs are coupled in series. So when a constant force is applied, the detector signal is a measurement of the force.
Question: during a friction loop scan, the tip is fixed by static friction on the surface and its a constant deflection, both torsional and lateral deflection must be included to find the actual deflected distance of the tip before its pulled free from to slide the surface and the lateral deflection could influence the beginning of the friction loop curve?
Measuring the cantilever dimensions
The vibration frequency of the fundamental mode of the cantilever is an easily measurable quantity in the AFM and can be used to evaluate a cantilever is within specifications. Its given by
Easily measurable quantities in AFM: length L, resonance freq f, tip length width ,
Not so easy: thickness t, cross section (often there are inclined sidewalls), force konst tip length from middle of the cantilever since we dont know the thickness.
Noise Sources in AFM
Thermal noise
for a 1 N/m cantilever this amounts to Å. So a 1 Å noise level requires N/m which is not a very low spring constant for a contact mode cantilever.
So thermal noise can become a problem in some AFM cantilevers at room temperature!!
Electrical Force Microscopy
The Kelvin Probe Microscopy Method and Dual Scan Method can be used to map out the electrical fields on surfaces with an AFM.
Kelvin Probe Microscopy Method

In the Kelvin probe microscopy (KPM) method a voltage is applied between the AFM tip and the surface. Both a DC and AC voltage is applied to the tip so the total potential difference between the tip and surface is:
where is the local surface potential, is the position of the tip, is the DC signal on the tip, is the amplitude of the AC signal, and is the frequency of the AC signal.
The frequency of the AC signal is much lower than the resonance frequency of the cantilever (a factor of 10) so the two signals can be separated by a lock-in amplifier. Via the electrostatic forces the setup measures the surface potential. If one assumes that the electrostatic force () between the tip and surface is given by [2]
where is the capacitance and is the distance between the tip and the surface.
If a parallel plate capacitor is assumed
,
where is the area of the tip. The derivative of capacitance is
.
Combining the force () and yields:
Using Pythagorean identities
and de Moivre's formula
We find
This inserted in the equation for the force () gives [3]:
where
,
, and .
The frequency is set by an external oscillator and can therefore be locked by the lock-in amplifier. The signal detected by the lock-in amplifier (the part) is minimized by constant varying . When this signal approaches zero, this corresponds to i.e. mapping vs. the sample surface gives .
Dual Scan Method

In the Dual Scan (DS, or sometimes called lift-mode method) one first makes a line scan with no potential on either the AFM tip or the sample in either tapping or non-contact mode. Next, the AFM tip is raised several tens of nanometers (30-70 nm) above the surface. A new line scan is made at this height, but this time with a potential on the sample also in non-contact mode. This is repeated over the desired scan area until the whole area has been scanned. For imaging the surface potential, the phase of the cantilever vibration is mapped out. The principle is shown in the figure where d is the distance between the tip and the surface in the second scan. The phase shift is dependent on the force () acting on the tip [4]
where is the quality factor of the cantilever, the spring constant, and the distance between the tip and the surface.
For small phase shifts the phase can be written as
The derivative of the force can be written as:
where is the surface potential and is the capacitance between the tip and the surface [5] . The second derivative of the capacitance is
Combining equations for the phase and the derivative of the force yields the phase dependence of the phase shift
To find the surface potential, one must estimate the other parts of equation for the phase. The spring constant () can be determined if the dimensions (a regular cantilever) and material of the cantilever are known:
where is the Young modulus, is the width of the cantilever, the height, and is the length. The quality factor () of the cantilever can be found by measuring the shape of resonance peak. The second derivative of the capacitance can be estimated by assuming that the tip of the AFM is a plate with radius so the derivative of the capacitance is given by:
where is the vacuum permittivity. This way of estimating the other parts of the equation for the phase is quite accurate according to [6]. One can also estimate the values by measuring them at a surface with a known potential and at different known heights and then one simply calculate backwards for that particular AFM tip.
Discussion
Both the DS and KPM methods have their strengths and weaknesses. The DS method is easier to operate, since it has fewer interlinked parameters, needing to be adjusted. The KPM method is faster, as it does not require two scans (an image with the DS method with a resolution of 512 512 pixels and a scan rate of Hz takes about half an hour). The DS method will normally obtain much better lateral resolution in the potential image compared to the KPM method. This is due to the fact that the signal depends on the second derivative of the capacitance, which in turn depends on the distance in compared to the KPM method where the dependence is only . This rapidly reduces the problem of the tip sidewall interaction. On the other hand, the KPM method has better sensitivity because it operates much closer to the surface.
References
- A. Bachtold, M. S. Fuhrer, S. Plyasunov, M. Forero, E. H. Anderson, A. Zettl, and P. L. McEuen; Physical Review Letters 84(26), 6082-6085 (2000).
- G. Koley and M. G. Spencer; Applied Physics Letters 79(4), 545-547 (2001).
- T. S. Jespersen and J. Nygård; Nano Letters 5(9), 1838-1841 (2005).
- V. Vincenzo, and M Palma, and P. Samorí; Advanced Materials 18, 145-164 (2006).
- Veeco, "Electrostatic Force Microscopy for AutoProbe CP Research Operating Instructions", 2001 (Manual).
- D. Ziegler and A. Stemmer; Nanotechnology 22, 075501 (2011).
Suppliers of AFM systems
- Park Systems
- Danish Micro Engineering
- Nanonics Imaging Ltd
- MultiProbe
- NT-MDT Co.
- RHK Technology Inc.
- JPK Instruments
- Veeco Instruments
- Nanotec
- Asylum Research
- Agilent Technologies
- Schaefer Technologie GmbH
- Nanomagnetics Instruments Inc.
- attocube systems AG
- Nano Scan Technology Ltd.
- AraResearch
- Advanced Technologies Center
Suppliers of cantilevers for AFM
Overview of properties of various cantilevers
Software for AFM image analysis
- NT-MDT Co.
- FemtoScan Online: a powerful image processing sortware from ATC [7]
- XPMPro Image Analysis from RHK Technology
- WsXM freeware from Nanotec.es
- SPIP from Image Metrology
- Gwyddion Free and Open Source software for SPM
- Punias Force-distance curve analysis software
- Hooke:a free, open platform for single molecule force spectroscopy[8]
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ Senturia `Micromechanics'
- ↑ Veeco, "Electrostatic Force Microscopy for AutoProbe CP Research Operating Instructions", 2001 (Manual)
- ↑ V. Vincenzo, and M Palma, and P. Samorí; Advanced Materials 18, 145-164 (2006)
- ↑ T. S. Jespersen and J. Nygård; Nano Letters 5(9), 1838-1841 (2005)
- ↑ T. S. Jespersen and J. Nygård; Nano Letters 5(9), 1838-1841 (2005)
- ↑ T. S. Jespersen and J. Nygård; Nano Letters 5(9), 1838-1841 (2005)
- ↑ http://en.nanoscopy.ru
- ↑ Massimo Sandal, Fabrizio Benedetti, Alberto Gomez-Casado, Marco Brucale, Bruno Samorì (2009). "Hooke: an open software platform for force spectroscopy". Bioinformatics. 25 (11): 1428–1430.
{{cite journal}}: CS1 maint: multiple names: authors list (link)
Scanning tunneling microscopy (STM)
| Navigate |
|---|
| << Prev: Atomic Force Microscopy (AFM) |
| >< Main: Nanotechnology |
| >> Next: Scanning Near-field Optical Microscopy (SNOM) |
Scanning Tunneling Microscopy


Tips for STM
- KOH etched tungsten tips
- PtIr tips
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Scanning Near-field optical microscopy (SNOM)
| Navigate |
|---|
| << Prev: Scanning Tunneling Microscopy (STM) |
| >< Main: Nanotechnology |
| >> Next: Additional Methods |
Scanning Near-field optical microscopy (SNOM)
The Abbe diffraction limit of optical microscopy can be circumvented if an evanescent wave is used instead of a travelling wave. The SNOM can be compared to a stethoscope [1]: A doctor can locate your heart with a precision of a few cm, despite the fact that the sound of a beating heart he is listening to has a wavelength of the order 100 m. Apparently he has a resolving power of λ/1000 which is far better than what's dictated by the Abbe diffraction limit. A similar setup can be made with light waves: If the light is forced through a sub-wavelength sized aperture, the emitted field will be evanescent and decay exponentially on a length scale usually shorter than the wavelength. With this technique a resolution of 12 nm has been shown back in 1991.[2] SNOM has the ability to make high resolution in all directions (x,y, and z) and can be adapted to fit onto the same laser systems and spectrometers that other microscopes also use.[3]
Images by SNOM are made by scanning the probe over the sample like an LSCM, AFM or STM. The SNOM is a very versatile tool used by both physicists and biologists for many purposes, but the probe only interacts with the sample in close vicinity of the aperture, and hence the sample-probe distance becomes a concern for the fragile samples and probes.[4]
One widespread distance control method is the shear force technique, invented in the 1992,[5] where the SNOM probe is set in vibrations with an amplitude up to a few nm and the motion is detected and used in a feedback loop that senses the minute shear forces that occur when the probe tip is a few nm above the sample surface. Numerous shear force setups have been described in the literature. Both optical and non-optical methods are used to detect the vibrations. Groups using non-optical methods claim the optical methods are sources of stray light that will seriously affect the measurements,[6] while e.g. [7] find optical setups to be advantageous.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ Optical Stethoscopy - Image Recording With Resolution Lambda/20, Pohl Dw, Denk W, Lanz M, Applied Physics Letters , Vol. 44 (7): 651-653 1984.
- ↑ Breaking The Diffraction Barrier - Optical Microscopy On A Nanometric Scale, Betzig E, Trautman Jk, Harris Td, Weiner Js, Kostelak Rl, Science vol 251 (5000) p. 1468-1470 Mar 22 1991.
- ↑ Manfaits webpage on Le Groupement De Recherche 1860 at the Centre National de la recherche scientifique, [1]
- ↑ A multipurpose scanning near-field optical microscope: Reflectivity and photocurrent on semiconductor and biological samples, Cricenti A, Generosi R, Barchesi C, Luce M, Rinaldi M, Review of Scientific Instruments, vol. 69 (9): 3240-3244 SEP 1998
- ↑ Near-field scanning optical microscopy, Dunn RC, Chemical Reviews, vol. 99 (10): 2891 OCT 1999
- ↑ Distance control in near-field optical microscopy with piezoelectrical shear-force detection suitable for imaging in liquids, Brunner R, Bietsch A, Hollricher O, Marti O, Review Of Scientific Instruments, vol. 68 (4) p. 1769-1772 APR 1997
- ↑ A multipurpose scanning near-field optical microscope: Reflectivity and photocurrent on semiconductor and biological samples, Cricenti A, Generosi R, Barchesi C, Luce M, Rinaldi M, Review of Scientific Instruments, vol. 69 (9): 3240-3244 SEP 1998
Additional methods
| Navigate |
|---|
| << Prev: Scanning probe microscopy |
| >< Main: Nanotechnology |
| >> Next: Physics on the nanoscale |
Point-Projection Microscopes
Point-Projection Microscopes are a type of field emission microscope[1], and consists of three components: an electron source, the object to the imaged, and the viewing screen[2].
Low energy electron diffraction (LEED)
LEED is a technique for imaging surfaces, and has two principle methods of use: qualitative and quantitative. The qualitative method measures relative size and geometric properties, whereas the quantitative method looks at diffracted beams as a way of determining the position of atoms.
Reflection High Energy Electron diffraction
RHEED is similar to LEED but uses higher energies and the electrons are directed to the be reflected on the surface at almost grazing incidence. This way the high energy electrons only penetrates a few atomic layers of the surface.
X-ray Spectroscopy and Diffraction
X-ray Spectroscopy refers to a collection of techniques including, but not limited to X-ray Absorption Spectroscopy and X-ray Photoelectron Spectroscopy.
X-rays can be used for X-ray crystallography.
Auger electron spectroscopy (AES)
Auger Electron Spectroscopy is a technique that takes advantage of the Auger Process to analyze the surface layers of a sample[3].
Nuclear Magnetic Resonance (NMR)
- Nuclear Magnetic Resonance (NMR) - in a magnetic field the spin of the nuclei of molecules will precess and in strong fields (several tesla) this happens with rf frequencies that can be detected by receiving rf antennas and amplifiers. The precession frequency of an individual nucleus will deviate slightly depending on the its surrounding molecules' electronic structure and hence detecting a spectrum of the radiofrequency precession frequencies in a sample will provide a finger print of the types of molecules in that sample.
- Nuclear quadrupole resonance is a related technique, based on the internal electrical fields of the molecules to cause a splitting of the nuclear magnetic moments energy levels. The level splitting is detected by rf as in NMR. Its is used mainly for experimental explosives detection.
Electron Paramagnetic Resonance (EPR) or Electron Spin Resonance (ESR)
Electron Spin Resonance (ESR) measures the microwave frequency of paramagnetic ions or molecules[4] .
Mössbauer spectroscopy
Mössbauer spectroscopy detects the hyperfine interactions between the nucleus of an atom, and the ambient environment. The atom must be part of a solid matrix to reduce the recoil affect of a gamma ray emission or absorption[5].
Non-contact Nanoscale Temperature Measurements
Heat radiation has infrared wavelengths much longer than 1 µm and hence taking a photo of a nanostructure with e.g. a thermal camera will not provide much information about the temperature distribution within the nanostructure (or microstructure for that sake).
Temperatures can be measured locally by different non-contact methods:
- Spectroscopy on individual quantum dots [90].
- Spectra of laser dyes incorporated in the structure
- Raman microscopy (the temperature influences the ratio of stokes and anti-stokes lines amplitude, the width of the lines and the position of the lines.)
- Transmission electron microscopy can also give temperature information by various techniques [91]
- Special AFM probes with a temperature dependent resistor at the tip can be used for mapping surface temperatures
- Infrared Near-field Microscopy [6]
- Confocal raman microscopy can provide 3D thermal maps [92]
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ Rochow, Theodore George, and Paul Arthur Tucker. "Emissions Microscopies". Introduction to Microscopy by Means of Light, Electrons, X-Rays, or Acoustics (Chapter 16, page 329) 1994.
- ↑ The Future of the SEM for Image and Metrology
- ↑ Auger Electron Microscopy
- ↑ What is EPR?
- ↑ Introduction to Mossbauer Spectroscopy: Part 1
- ↑ C. Feng, M. S. Ünlü, B. B. Goldberg, and W. D. Herzog, "Thermal Imaging by Infrared Near-field Microscopy," Proceedings of IEEE Lasers and Electro-Optics Society 1996 Annual Meeting, Vol. 1, November 1996, pp. 249-250
Physics at the Nanoscale
| Navigate |
|---|
| << Prev: Additional methods |
| >< Main: Nanotechnology |
| >> Next: Physics |
|
|
| <<< Prev Part: Seeing 'Nano' |
| >>> Next Part: Nanomaterials |
Chemistry and Biochemistry are in many ways nanotechnologies working with nanoscale structures. In physics the classical laws of motion are not always valid on the nanoscale where a quantum mechanical model often is more suitable, and there are often a wealth of forces that are important that we do not consider very much in classical physics - the surface forces.
This part is about how nanosystems move, the forces that control the motion, and the ways we can model it.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Intro to Nanophysics
| Navigate |
|---|
| << Prev: Additional methods |
| >< Main: Nanotechnology |
| >> Next: Modelling Nanosystems |
Quantum mechanics and classical mechanics are still valid on the nanoscale - but many assumptions we are used to take for granted are no longer valid. This makes many traditional systems difficult to make on the atomic scale -if for instance you scale down a car the new relation between adhesion forces and gravity or changes in heat conduction will very likely make it perform very poorly if at all - but at the same time a wealth of other new possibilities open up!
Scaling laws can be used to determine how the physical properties vary as the dimensions are changed. At some point the scaling law no longer can be applied because the assumptions behind it become invalid at some large or small scale.
So, scaling is one thing - the end of scaling another, and surfaces a third! For instance at some point the idealized classical point of view on a system being downscaled will need quantum mechanics to describe what's going on in a proper way, but as the scale is decreased the system might also be very different because the interaction at the surface becomes very significant compared to the bulk.
This part will try to give an overview of these effects.
Scaling laws
Scaling laws can be used to describe how the physical properties of a system change as the dimensions are changed.

Quantized Nano Systems
Quantum wires are examples of nanosystems where the quantum effects become very important.
Break junctions is another example.
Resources
- Simple model of conduction - the classical case
Bulk matter and the end of bulk: surfaces
- Surface states are electronic states on the surface of a material, which can have radically different properties than the underlying bulk material. For instance, a semiconductor can have superconducting surface states.
- Surface reconstruction
The surface of a material can be very different from the bulk because the surface atoms rearrange themselves to lower their energy rather than stay in the bulk lattice and have dangling bonds extending into space where there is no more material. Atoms from the surroundings will easily bind to such surfaces and for example for silicon, more than 2000 surface reconstructions have been found, depending on what additional atoms and conditions are present.
- Surface plasmons
Plasmons are collective oscillations of the electrons in matter, and the electrons on the surfaces can also make local plasmons that propagate on the surface.
The Tyndall Effect
The Tyndall Effect is caused by reflection of light off of small particles such as dust or mist. This is also seen off of dust when sunlight comes through windows and clouds or when headlight beams go through fog. The Tyndall Effect can only be seen through colloidal suspensions. A colloid is a substance that consists of particles dispersed throughout another substance, which are too small for resolution with an ordinary light microscope but are incapable of passing through a semi permeable membrane. The Tyndall Effect is most easily visible through liquid using a laser pointer. The Tyndall Effect is named after its discoverer, the 19th-century British physicist John Tyndall.[1][2][3][4][5][6]
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ “Tyndall Effect.” Silver Lighting. 1 June 2008. http://silver-lightning.com/tyndall/
- ↑ Davies, Paul. The Tyndall Effect. 1 June 2008. http://www.chm.bris.ac.uk/webprojects2002/pdavies/Tyndall.html
- ↑ SonneNebel. 1 July 2008. http://upload.wikimedia.org/wikipedia/commons/f/f6/SonneNebel.jpg
- ↑ Bright Flashlight. 1 July 2008. http://www.geekologie.com/2008/02/04/bright-flashlight.jpg
- ↑ “The Tyndall Effect.” http://www.chm.bris.ac.uk/webprojects2002/pdavies/Tyndall.html
- ↑ “Colloid.” 3 June 2008. http://www.merriam-webster.com/dictionary/colloid
Modelling Nanosystems
| Navigate |
|---|
| << Prev: Physics |
| >< Main: Nanotechnology |
| >> Next: Physical Chemistry of Surfaces |
Modelling Nanosystems
The Schrödinger equation
where is the imaginary unit, is time, is the partial derivative with respect to , is the reduced Planck's constant (Planck's constant divided by ), is the wave function, and is the Hamiltonian operator.
Hartree-Fock (HF) or self-consistent field (SCF)
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
The Hartree–Fock method often assumes that the exact, N-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of N spin-orbitals. By invoking the w:variational method, one can derive a set of N-coupled equations for the N spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system.
Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "self-consistent" with the assumed initial field. Thus, self-consistency was a requirement of the solution. The solutions to the non-linear Hartree–Fock equations also behave as if each particle is subjected to the mean field created by all other particles (see the Fock operator below) and hence the terminology continued. The equations are almost universally solved by means of an iterative method, although the fixed-point iteration algorithm does not always converge.[1] This solution scheme is not the only one possible and is not an essential feature of the Hartree–Fock method.
The Hartree–Fock method finds its typical application in the solution of the Schrödinger equation for atoms, molecules, nanostructures[2] and solids but it has also found widespread use in nuclear physics. (See Hartree–Fock–Bogoliubov method for a discussion of its application in nuclear structure theory). In atomic structure theory, calculations may be for a spectrum with many excited energy levels and consequently the Hartree–Fock method for atoms assumes the wave function is a single configuration state function with well-defined quantum numbers and that the energy level is not necessarily the ground state.
For both atoms and molecules, the Hartree–Fock solution is the central starting point for most methods that describe the many-electron system more accurately.
The rest of this article will focus on applications in electronic structure theory suitable for molecules with the atom as a special case. The discussion here is only for the Restricted Hartree–Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) doubly occupied. Open-shell systems, where some of the electrons are not paired, can be dealt with by one of two Hartree–Fock methods:
history
The origin of the Hartree–Fock method dates back to the end of the 1920s, soon after the discovery of the w:Schrödinger equation in 1926. In 1927 D. R. Hartree introduced a procedure, which he called the self-consistent field method, to calculate approximate wave functions and energies for atoms and ions. Hartree was guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, R. B. Lindsay, and himself) set in the w:old quantum theory of Bohr.
In the w:Bohr model of the atom, the energy of a state with w:principal quantum number n is given in atomic units as . It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the w:quantum defect d as an empirical parameter, the energy levels of a generic atom were well approximated by the formula , in the sense that one could reproduce fairly well the observed transitions levels observed in the w:X-ray region (for example, see the empirical discussion and derivation in w:Moseley's law). The existence of a non-zero quantum defect was attributed to electron-electron repulsion, which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial screening of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data.
Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e., ab initio. His first proposed method of solution became known as the Hartree method. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 J. C. Slater and J. A. Gaunt independently showed that the Hartree method could be couched on a sounder theoretical basis by applying the w:variational principle to an w:ansatz (trial wave function) as a product of single-particle functions.
In 1930 Slater and V. A. Fock independently pointed out that the Hartree method did not respect the principle of antisymmetry of the wave function. The Hartree method used the w:Pauli exclusion principle in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of w:quantum statistics.
It was then shown that a w:Slater determinant, a w:determinant of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the antisymmetric property of the exact solution and hence is a suitable w:ansatz for applying the w:variational principle. The original Hartree method can then be viewed as an approximation to the Hartree–Fock method by neglecting exchange. Fock's original method relied heavily on w:group theory and was too abstract for contemporary physicists to understand and implement. In 1935 Hartree reformulated the method more suitably for the purposes of calculation.
The Hartree–Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models. Initially, both the Hartree method and the Hartree–Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the w:central field approximation, to impose that electrons in the same shell have the same radial part, and to restrict the variational solution to be a spin eigenfunction. Even so, solution by hand of the Hartree–Fock equations for a medium sized atom were laborious; small molecules required computational resources far beyond what was available before 1950.
Hartree–Fock algorithm
The Hartree–Fock method is typically used to solve the time-independent Schrödinger equation for a multi-electron atom or molecule as described in the w:Born–Oppenheimer approximation. Since there are no known solutions for many-electron systems (hydrogenic atoms and the diatomic hydrogen cation being notable one-electron exceptions), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree–Fock approximation, the equations are solved using a nonlinear method such as w:iteration, which gives rise to the name "self-consistent field method."
Approximations
The Hartree–Fock method makes five major simplifications in order to deal with this task:
- The w:Born–Oppenheimer approximation is inherently assumed. The full molecular wave function is actually a function of the coordinates of each of the nuclei, in addition to those of the electrons.
- Typically, relativistic effects are completely neglected. The momentum operator is assumed to be completely non-relativistic.
- The variational solution is assumed to be a w:linear combination of a finite number of basis functions, which are usually (but not always) chosen to be w:orthogonal. The finite basis set is assumed to be approximately complete.
- Each w:energy eigenfunction is assumed to be describable by a single w:Slater determinant, an antisymmetrized product of one-electron wave functions (i.e., orbitals).
- The mean field approximation is implied. Effects arising from deviations from this assumption, known as w:electron correlation, are completely neglected for the electrons of opposite spin, but are taken into account for electrons of parallel spin.[3][4] (Electron correlation should not be confused with electron exchange, which is fully accounted for in the Hartree–Fock method.)[4]
Relaxation of the last two approximations give rise to many so-called w:post-Hartree–Fock methods.

Variational optimization of orbitals
The variational theorem states that for a time-independent Hamiltonian operator, any trial wave function will have an energy w:expectation value that is greater than or equal to the true w:ground state wave function corresponding to the given Hamiltonian. Because of this, the Hartree–Fock energy is an upper bound to the true ground state energy of a given molecule. In the context of the Hartree–Fock method, the best possible solution is at the Hartree–Fock limit; i.e., the limit of the Hartree–Fock energy as the basis set approaches completeness. (The other is the full-CI limit, where the last two approximations of the Hartree–Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution, up to the Born–Oppenheimer approximation, is obtained.) The Hartree–Fock energy is the minimal energy for a single Slater determinant.
The starting point for the Hartree–Fock method is a set of approximate one-electron wave functions known as w:spin-orbitals. For an w:atomic orbital calculation, these are typically the orbitals for a hydrogenic atom (an atom with only one electron, but the appropriate nuclear charge). For a w:molecular orbital or crystalline calculation, the initial approximate one-electron wave functions are typically a w:linear combination of atomic orbitals (LCAO).
The orbitals above only account for the presence of other electrons in an average manner. In the Hartree–Fock method, the effect of other electrons are accounted for in a w:mean-field theory context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the w:Fock operator. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a w:unitary transformation between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear-electronic Coulombic attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree–Fock method, and is equivalent to the fifth simplification in the above list.
Since the Fock operator depends on the orbitals used to construct the corresponding w:Fock matrix, the eigenfunctions of the Fock operator are in turn new orbitals which can be used to construct a new Fock operator. In this way, the Hartree–Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals are calculated. The Hartree–Fock electronic wave function is then the Slater determinant constructed out of these orbitals. Following the basic postulates of quantum mechanics, the Hartree–Fock wave function can then be used to compute any desired chemical or physical property within the framework of the Hartree–Fock method and the approximations employed.
Mathematical formulation
The Fock operator
Because the electron-electron repulsion term of the w:electronic molecular Hamiltonian involves the coordinates of two different electrons, it is necessary to reformulate it in an approximate way. Under this approximation, (outlined under Hartree–Fock algorithm), all of the terms of the exact Hamiltonian except the nuclear-nuclear repulsion term are re-expressed as the sum of one-electron operators outlined below, for closed-shell atoms or molecules (with two electrons in each spatial orbital).[5] The "(1)" following each operator symbol simply indicates that the operator is 1-electron in nature.
where
is the one-electron Fock operator generated by the orbitals , and
is the one-electron core Hamiltonian. Also
is the w:Coulomb operator, defining the electron-electron repulsion energy due to each of the two electrons in the jth orbital.[5] Finally
is the w:exchange operator, defining the electron exchange energy due to the antisymmetry of the total n-electron wave function. [5] This (so called) "exchange energy" operator, K, is simply an artifact of the Slater determinant. Finding the Hartree–Fock one-electron wave functions is now equivalent to solving the eigenfunction equation:
where are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals.
Linear combination of atomic orbitals
Typically, in modern Hartree–Fock calculations, the one-electron wave functions are approximated by a w:linear combination of atomic orbitals. These atomic orbitals are called w:Slater-type orbitals. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more Gaussian-type orbitals, rather than Slater-type orbitals, in the interests of saving large amounts of computation time.
Various basis sets are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the w:Gram–Schmidt process is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the Roothaan–Hall equations by converting the w:overlap matrix effectively to an w:identity matrix. However, in most modern computer programs for molecular Hartree–Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the w:generalized eigenvalue problem, of which the Roothaan–Hall equations are an example.
Numerical stability
w:Numerical stability can be a problem with this procedure and there are various ways of combating this instability. One of the most basic and generally applicable is called F-mixing or damping. With F-mixing, once a single electron wave function is calculated it is not used directly. Instead, some combination of that calculated wave function and the previous wave functions for that electron is used—the most common being a simple linear combination of the calculated and immediately preceding wave function. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wave function for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree–Fock computer programs use a variety of methods to ensure convergence of the Roothaan–Hall equations.
Weaknesses, extensions, and alternatives
Of the five simplifications outlined in the section "Hartree–Fock algorithm", the fifth is typically the most important. Neglecting electron correlation can lead to large deviations from experimental results. A number of approaches to this weakness, collectively called w:post-Hartree–Fock methods, have been devised to include electron correlation to the multi-electron wave function. One of these approaches, w:Møller–Plesset perturbation theory, treats correlation as a perturbation of the Fock operator. Others expand the true multi-electron wave function in terms of a linear combination of Slater determinants—such as w:multi-configurational self-consistent field, w:configuration interaction, w:quadratic configuration interaction, and complete active space SCF (CASSCF). Still others (such as variational quantum Monte Carlo) modify the Hartree–Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions.
An alternative to Hartree–Fock calculations used in some cases is w:density functional theory, which treats both exchange and correlation energies, albeit approximately. Indeed, it is common to use calculations that are a hybrid of the two methods—the popular B3LYP scheme is one such w:hybrid functional method. Another option is to use w:modern valence bond methods.
Software packages
For a list of software packages known to handle Hartree–Fock calculations, particularly for molecules and solids, see the w:list of quantum chemistry and solid state physics software.
Sources
- Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. pp. 455–544. ISBN 0-205-12770-3.
- Cramer, Christopher J. (2002). Essentials of Computational Chemistry. Chichester: John Wiley & Sons, Ltd. pp. 153–189. ISBN 0-471-48552-7.
- Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. Mineola, New York: Dover Publishing. ISBN 0-486-69186-1.
Slater determinant
Two-particle case
The simplest way to approximate the wave function of a many-particle system is to take the product of properly chosen orthogonal wave functions of the individual particles. For the two-particle case with spatial coordinates and , we have
This expression is used in the w:Hartree–Fock method as an w:ansatz for the many-particle wave function and is known as a w:Hartree product. However, it is not satisfactory for w:fermions because the wave function above is not antisymmetric, as it must be for w:fermions from the w:Pauli exclusion principle. An antisymmetric wave function can be mathematically described as follows:
which does not hold for the Hartree product. Therefore the Hartree product does not satisfy the Pauli principle. This problem can be overcome by taking a w:linear combination of both Hartree products
where the coefficient is the w:normalization factor. This wave function is now antisymmetric and no longer distinguishes between fermions, that is: one cannot indicate an ordinal number to a specific particle and the indices given are interchangeable. Moreover, it also goes to zero if any two wave functions of two fermions are the same. This is equivalent to satisfying the Pauli exclusion principle.
Generalizations
The expression can be generalised to any number of fermions by writing it as a w:determinant. For an N-electron system, the Slater determinant is defined as [6]
where in the final expression, a compact notation is introduced: the normalization constant and labels for the fermion coordinates are understood – only the wavefunctions are exhibited. The linear combination of Hartree products for the two-particle case can clearly be seen as identical with the Slater determinant for N = 2. It can be seen that the use of Slater determinants ensures an antisymmetrized function at the outset; symmetric functions are automatically rejected. In the same way, the use of Slater determinants ensures conformity to the w:Pauli principle. Indeed, the Slater determinant vanishes if the set {χi } is w:linearly dependent. In particular, this is the case when two (or more) spin orbitals are the same. In chemistry one expresses this fact by stating that no two electrons can occupy the same spin orbital. In general the Slater determinant is evaluated by the w:Laplace expansion. Mathematically, a Slater determinant is an antisymmetric tensor, also known as a w:wedge product.
A single Slater determinant is used as an approximation to the electronic wavefunction in Hartree–Fock theory. In more accurate theories (such as w:configuration interaction and w:MCSCF), a linear combination of Slater determinants is needed.
The word "detor" was proposed by S. F. Boys to describe the Slater determinant of the general type,[7] but this term is rarely used.
Unlike w:fermions that are subject to the Pauli exclusion principle, two or more w:bosons can occupy the same quantum state of a system. Wavefunctions describing systems of identical w:bosons are symmetric under the exchange of particles and can be expanded in terms of w:permanents.
Fock matrix
In the w:Hartree–Fock method of w:quantum mechanics, the Fock matrix is a matrix approximating the single-electron w:energy operator of a given quantum system in a given set of basis vectors.[8]
It is most often formed in w:computational chemistry when attempting to solve the w:Roothaan equations for an atomic or molecular system. The Fock matrix is actually an approximation to the true Hamiltonian operator of the quantum system. It includes the effects of electron-electron repulsion only in an average way. Importantly, because the Fock operator is a one-electron operator, it does not include the w:electron correlation energy.
The Fock matrix is defined by the Fock operator. For the restricted case which assumes w:closed-shell orbitals and single-determinantal wavefunctions, the Fock operator for the i-th electron is given by:[9]
where:
- is the Fock operator for the i-th electron in the system,
- is the w:one-electron hamiltonian for the i-th electron,
- is the number of electrons and is the number of occupied orbitals in the closed-shell system,
- is the w:Coulomb operator, defining the repulsive force between the j-th and i-th electrons in the system,
- is the w:exchange operator, defining the quantum effect produced by exchanging two electrons.
The Coulomb operator is multiplied by two since there are two electrons in each occupied orbital. The exchange operator is not multiplied by two since it has a non-zero result only for electrons which have the same spin as the i-th electron.
For systems with unpaired electrons there are many choices of Fock matrices.
Hartree-Fock (HF) or self-consistent field (SCF)
Density Functional Theory
Connection to quantum state symmetry
The Pauli exclusion principle with a single-valued many-particle wavefunction is equivalent to requiring the wavefunction to be antisymmetric. An antisymmetric two-particle state is represented as a sum of states in which one particle is in state and the other in state :
and antisymmetry under exchange means that A(x,y) = −A(y,x). This implies that A(x,x) = 0, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank-two w:tensor.
Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component:
is necessarily antisymmetric. To prove it, consider the matrix element:
This is zero, because the two particles have zero probability to both be in the superposition state . But this is equal to
The first and last terms on the right hand side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:
- .
or
Pauli principle in advanced quantum theory
According to the w:spin-statistics theorem, particles with integer spin occupy symmetric quantum states, and particles with half-integer spin occupy antisymmetric states; furthermore, only integer or half-integer values of spin are allowed by the principles of quantum mechanics. In relativistic w:quantum field theory, the Pauli principle follows from applying a rotation operator in imaginary time to particles of half-integer spin. Since, nonrelativistically, particles can have any statistics and any spin, there is no way to prove a spin-statistics theorem in nonrelativistic quantum mechanics.
In one dimension, bosons, as well as fermions, can obey the exclusion principle. A one-dimensional Bose gas with delta function repulsive interactions of infinite strength is equivalent to a gas of free fermions. The reason for this is that, in one dimension, exchange of particles requires that they pass through each other; for infinitely strong repulsion this cannot happen. This model is described by a quantum w:nonlinear Schrödinger equation. In momentum space the exclusion principle is valid also for finite repulsion in a Bose gas with delta function interactions,[10] as well as for interacting spins and w:Hubbard model in one dimension, and for other models solvable by w:Bethe ansatz. The ground state in models solvable by Bethe ansatz is a Fermi sphere.
References
See also notes on editing this book about how to add references w:Nanotechnology/About#How_to_contribute.
- ↑ Froese Fischer, Charlotte (1987). "General Hartree-Fock program". Computer Physics Communication. 43 (3): 355–365. doi:10.1016/0010-4655(87)90053-1{{inconsistent citations}}
{{cite journal}}: CS1 maint: postscript (link) - ↑ Abdulsattar, Mudar A. (2012). "SiGe superlattice nanocrystal infrared and Raman spectra: A density functional theory study". J. Appl. Phys. 111 (4): 044306. Bibcode:2012JAP...111d4306A. doi:10.1063/1.3686610.
- ↑ Hinchliffe, Alan (2000). Modelling Molecular Structures (2nd ed.). Baffins Lane, Chichester, West Sussex PO19 1UD, England: John Wiley & Sons Ltd. p. 186. ISBN 0-471-48993-X.
{{cite book}}: CS1 maint: location (link) - ↑ a b Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. Mineola, New York: Dover Publishing. ISBN 0-486-69186-1.
- ↑ a b c Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. p. 403. ISBN 0-205-12770-3.
- ↑ Molecular Quantum Mechanics Parts I and II: An Introduction to QUANTUM CHEMISTRY (Volume 1), P.W. Atkins, Oxford University Press, 1977, ISBN 0-19-855129-0
- ↑ Boys, S. F. (1950). "Electronic wave functions I. A general method of calculation for the stationary states of any molecular system". Proceedings of the Royal Society. A200: 542.
- ↑ Callaway, J. (1974). Quantum Theory of the Solid State. New York: Academic Press. ISBN 9780121552039.
- ↑ Levine, I.N. (1991) Quantum Chemistry (4th ed., Prentice-Hall), p.403
- ↑ A. Izergin and V. Korepin, Letter in Mathematical Physics vol 6, page 283, 1982
Physical Chemistry of Surfaces
| Navigate |
|---|
| << Prev: Modelling Nanosystems |
| >< Main: Nanotechnology |
| >> Next: Background Material |
Physical Chemistry of Surfaces
Surface Forces
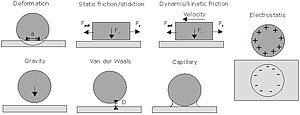
Hydrophobic and hydrophilic surfaces
- Wetablility
- wetting
- Hydrophobe
- Hydrophile
- Super hydrophilicity

Surface Energy
Surface Diffusion
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Background material
| Navigate |
|---|
| << Prev: Physical Chemistry of Surfaces |
| >< Main: Nanotechnology |
| >> Next: Nanomaterials |
Dispersion relations
Dispersion relations are essential in describing a physical system and can often be a bit tricky to comprehend.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Part 4: Nanomaterials
| Navigate |
|---|
| << Prev: Background Material |
| >< Main: Nanotechnology |
| >> Next: Overview of Production Methods |
|
|
| <<< Prev Part: Physics - on the nanoscale |
| >>> Next Part: Nanosystems |
This part will give an overview of nanomaterials - the production methods, their properties, brief examples of applications and demonstrations of their capabilities.
Apart from a general overview of production methods, we have divided the materials as
- Semiconducting
- Metallic
- Organic
A division that might be up for revision shortly.
Overview of nanomaterials
Further reading
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Overview of Production methods
| Navigate |
|---|
| << Prev: Nanomaterials |
| >< Main: Nanotechnology |
| >> Next: Semiconducting Nanostructures |
- Chemical vapor deposition
- Metal Organic Vapor Phase Epitaxy (MOVPE)
- Arc discharge where an electical arc is made between rods of the precursor materials.
- Physical vapor deposition
- Molecular beam epitaxy using solid sources and Chemical beam epitaxy using gaseous sources.
- Epitaxy in general.
- Atomic layer epitaxy where only a few monolayers are deposited and bond to chemisorption sites on the surface.
- Self-assembled monolayers
- metal organic chemical vapor deposition abbreviation as MOCVD
- atomic layer deposition, for depositing uniform thin films one atomic layer at a time (By [http://www.fmnt.fi/index.pl?id=2913&isa=Category&op=show Dr. Tuomo Suntola and co-workers in Finland.)
Types of nanometal synthesis
The most common types of nanometal synthesis deal with 'wet' methods in which metal nanoparticles are produced in a colloid with an organic material of some sort.
Gold nanoparticles can be produced by either:
1) Reduction of HAuCl4 in a solution of sodium citrate, then boiling it, causing gold nanoparticles to form in a wine-red solution.
2) Mixing HAuCl4 in water, which produces a solution that is subsequently transferred into toluene using tetraoctylammonium bromide (TOAB), a phase transfer catalyst. Phase transfer catalysts help reactants dissolve in organic (carbon-containing) material where the reactant otherwise couldn't w/o the PTC. Afterwards, the solution is stirred with sodium borohydride, in the presence of certain alkanes, which bind to the gold in the solution, allowing for the formation of gold nanoparticles.
Synthesis of other metal nanoparticles can possibly be achieved by reducing metal salts in organic solvents such as ethanol, or by variations of the above methods which synthesize gold nanoparticles. [1] [2]
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ Luis M Liz-Marzán. "Nanometals formation and color", Materials Today, February 2004, page 27.
- ↑ Phase transfer catalyst-Wikipedia. http://en.wikipedia.org/wiki/Phase_transfer_catalyst
Semiconducting Nanostructures
| Navigate |
|---|
| << Prev: Overview of Production methods |
| >< Main: Nanotechnology |
| >> Next: Metallic Nanostructures |
Nanotubes
Certain compounds are capable of forming nanotubes where the tube consists of round shell of a single layer of atoms in a cylindrical lattice. Carbon nanotubes is the most famous example, but also other materials can form nanotubes such as Boron-nitride, Molybdenum sulfide and others.
Nanotubes can also be made by etching the core out of an shell structured rod, but such tubes will normally contain many atomic layers in the wall and have crystal facets on the sides.
Carbon Nanotubes
Carbon nanotubes are fascinating nanostructures. A sheet of graphene as in common graphite, but rolled up in small tubes rather than planar sheets.
Carbon nanotubes have unique mechanical properties such as high strength, high stiffness, and low density [1] and also interesting electronic properties. A single-walled carbon nanotube can be either metallic or semiconducting depending on the atomic arrangement [2].
This section is a short introduction to carbon nanotubes. For a broader overview the reader is referred to one of the numerous review articles or books on carbon nanotubes
Geometric Structure
The simplest type of carbon nanotube consists of just one layer of graphene rolled up in the form of a seamless cylinder, known as a single-walled carbon nanotube (SWCNT) with a typical diameter of just a few nanometers. Larger diameter nanotube structures are nanotube ropes, consisting of many individual, parallel nanotubes closed-packed into a hexagonal lattice, and multi-walled carbon nanotubes (MWCNTs) consisting of several concentric cylinders nested within each other.

Single walled Carbon Nanotube
The basic configuration is thus the SWCNT. Its structure is most easily illustrated as a cylindrical tube conceptually formed by the wrapping of a single graphene sheet. The hexagonal structure of the 2-dimensional graphene sheet is due to the hybridization of the carbon atoms, which causes three directional, in-plane bonds separated by an angle of 120 degrees.
The nanotube can be described by a chiral vector that can be expressed in terms of the graphene unit vectors and as with the set of integers uniquely identifying the nanotube. This chiral vector or 'roll-up' vector describes the nanotube circumference by connecting two crystallographically equivalent positions i.e. the tube is formed by superimposing the two ends of .
Based on the chiral angle SWCNTs are defined as zig-zag tubes (), armchair tubes (), or chiral tubes ().
Multiwalled Carbon Nanotubes
MWCNTs are composed of a number of SWCNTs in a coaxial geometry. Each nested shell has a diameter of where is the length of the carbon-carbon bond which is 1.42 Å. The difference in diameters of the individual shell means that their chiralities are different, and adjacent shell are therefore in general non-commensurate, which causes only a weak intershell interaction.
The intershell spacing in MWCNTs is 0.34 nm - quite close to the interlayer spacing in turbostratic graphite [6]
Electronic Structure
The electronic structure of a SWCNT is most easily described by again considering a single graphene sheet. The 2-D, hexagonal-lattice graphene sheet has a 2-D reciprocal space with a hexagonal Brillouin zone (BZ).
The bonds are mainly responsible for the mechanical properties, while the electronic properties are mainly determined by the bands. By a tight-binding approach the band structure of these bands can be calculated [7]
Graphene is a zero-gap semiconductor with an occupied band and an unoccupied band meeting at the Fermi level at six points in the BZ, thus it behaves metallic, a so-called semimetal.
Upon forming the tube by conceptually wrapping the graphene sheet, a periodic boundary condition is imposed that causes only certain electronic states of those of the planar graphene sheet to be allowed. These states are determined by the tube's geometric structure, i.e. by the indices of the chiral vector. The wave vectors of the allowed states fall on certain lines in the graphene BZ.
Based on this scheme it is possible to estimate whether a particular tube will be metallic or semiconducting. When the allowed states include the point, the system will to a first approximation behave metallic. However, in the points where the and the bands meet but are shifted slightly away from the point due to curvature effects, which causes a slight band opening in some cases [8]
This leads to a classification scheme that has three types of nanotubes:
- Metallic: These are the armchair tubes where the small shift of the degenerate point away from the point does not cause a band opening for symmetry reasons.
- Small-bandgap semiconducting: These are characterized by with being an integer. Here, the wave vectors of the allowed states cross the point, but due to the slight shift of the degenerate point a small gap will be present, the size of which is inversely proportional to the tube diameter squared with typical values between a few and a few tens meV
- Semiconducting: In this case . This causes a larger bandgap, the size of which is inversely proportional to the tube diameter: with experimental investigations suggesting a value of of 0.7-0.8 eV/nm
Typically the bandgap of the type 2 nanotubes is so small that they can be considered metallic at room temperature. Based on this it can be inferred that 1/3 of all tubes should behave metallic whereas the remaining 2/3 should be semiconducting. However, it should be noted that due to the inverse proportionality between the bandgap and the diameter of the semiconducting tubes, large-diameter tubes will tend to behave metallic at room temperature. This is especially important in regards to large-diameter MWCNTs.
From a electrical point of view a MWCNT can be seen as a complex structure of many parallel conductors that are only weakly interacting. Since probing the electrical properties typically involves electrodes contacting the outermost shell, this shell will be dominating the transport properties [11] In a simplistic view, this can be compared to a large-diameter SWCNT, which will therefore typically display metallic behavior.
Electrical and Electromechanical Properties
Many studies have focused on SWCNTs for exploring the fundamental properties of nanotubes. Due to their essentially 1-D nature and intriguing electronic structure, SWCNTs exhibit a range of interesting quantum phenomena at low temperature [12]
The discussion here will so far, however, primarily be limited to room temperature properties.
The conductance of a 1-dimensional conductor such as a SWCNT is given by the Landauer formula [13]
,
where ;
is the conductance quantum;
and is the transmission coefficient of the contributing channel .
More information on nanotubes
Commercial suppliers of carbon nanotubes and related products
- Nanoledge.com nanotubes and related products - fibers, pellets, resins and dispersions...
- Carbon Solution, Inc. Mainly SWCNT.
- BuckyUSA Fullerens, SWCNT, MWCNT.
- CNI HiPco Carbon nanotubes
- Carbolex SWCNT,sub-gram quantities are sold via sigma aldric
- Sigma-Aldrich SWCNT
"Buckyball"


Buckminsterfullerene (IUPAC name (C60-Ih)[5,6]fullerene) is the smallest fullerene molecule in which no two pentagons share an edge (which can be destabilizing, as in pentalene). It is also the most common in terms of natural occurrence, as it can often be found in soot.
The structure of C60 is a truncated (T = 3) icosahedron, which resembles a soccer ball of the type made of twenty hexagons and twelve pentagons, with a carbon atom at the vertices of each polygon and a bond along each polygon edge.
The w:van der Waals diameter of a C60 molecule is about 1 nanometer (nm). The nucleus to nucleus diameter of a C60 molecule is about 0.7 nm.
The C60 molecule has two bond lengths. The 6:6 ring bonds (between two hexagons) can be considered "double bonds" and are shorter than the 6:5 bonds (between a hexagon and a pentagon). Its average bond length is 1.4 angstroms.
Silicon buckyballs have been created around metal ions.
Boron buckyball
A new type of buckyball utilizing boron atoms instead of the usual carbon has been predicted and described by researchers at Rice University. The B-80 structure, with each atom forming 5 or 6 bonds, is predicted to be more stable than the C-60 buckyball.[14] One reason for this given by the researchers is that the B-80 is actually more like the original geodesic dome structure popularized by Buckminster Fuller which utilizes triangles rather than hexagons. However, this work has been subject to much criticism by quantum chemists[15][16] as it was concluded that the predicted Ih symmetric structure was vibrationally unstable and the resulting cage undergoes a spontaneous symmetry break yielding a puckered cage with rare Th symmetry (symmetry of a volleyball)[15]. The number of six atom rings in this molecule is 20 and number of five member rings is 12. There is an additional atom in the center of each six member ring, bonded to each atom surrounding it.
Variations of buckyballs
Another fairly common buckminsterfullerene is C70,[17] but fullerenes with 72, 76, 84 and even up to 100 carbon atoms are commonly obtained.
In mathematical terms, the structure of a fullerene is a trivalent convex polyhedron with pentagonal and hexagonal faces. In graph theory, the term fullerene refers to any 3-regular, planar graph with all faces of size 5 or 6 (including the external face). It follows from Euler's polyhedron formula, |V|-|E|+|F| = 2, (where |V|, |E|, |F| indicate the number of vertices, edges, and faces), that there are exactly 12 pentagons in a fullerene and |V|/2-10 hexagons.

|

|
|

|
| 20-fullerene (dodecahedral graph) |
26-fullerene graph | 60-fullerene (truncated icosahedral graph) |
70-fullerene graph |
The smallest fullerene is the w:dodecahedron--the unique C20. There are no fullerenes with 22 vertices.[18] The number of fullerenes C2n grows with increasing n = 12,13,14..., roughly in proportion to n9. For instance, there are 1812 non-isomorphic fullerenes C60. Note that only one form of C60, the buckminsterfullerene alias w:truncated icosahedron, has no pair of adjacent pentagons (the smallest such fullerene). To further illustrate the growth, there are 214,127,713 non-isomorphic fullerenes C200, 15,655,672 of which have no adjacent pentagons.
w:Trimetasphere carbon nanomaterials were discovered by researchers at w:Virginia Tech and licensed exclusively to w:Luna Innovations. This class of novel molecules comprises 80 carbon atoms (C80) forming a sphere which encloses a complex of three metal atoms and one nitrogen atom. These fullerenes encapsulate metals which puts them in the subset referred to as w:metallofullerenes. Trimetaspheres have the potential for use in diagnostics (as safe imaging agents), therapeutics and in organic solar cells.[citation needed]
Semiconducting nanowires
Semiconducting nanowires can be made from most semiconducting materials and with different methods, mainly variations of a chemical vapor deposition process (CVD).
There are many different semiconducting materials, and heterosrtuctures can be made if the lattice constants are not too incompatible. Heterostructures made from combinations of materials such as GaAs-GaP can be used to make barriers and guides for electrons in electrical systems.
Low pressure metal organic vapor phase epitaxy (MOVPE) can be used to grow III-V nanowires epitaxially on suitable crystalline substrates, sucha s III-V materials or silicon with a reasonably matching lattice constant.

Nanowire growth is catalyzed by various nanoparticles, which are deposited on the substrate surface, typically gold nanoparticles with a diameter of 20-100nm.
To grow for instance GaP wires, the sample is typically annealed at 650C in the heated reactor chamber to form an eutectic with between the gold catalyst and the underlying substrate.
Then growth is done at a lower temperature around 500C in the presence of the precursor gasses trimethyl gallium and phosphine. By changing the precursor gasses during growth, nanowire heterostructures with varying composition can be made

Resources
Nanoparticles
Catalytic particles
Commercial suppliers of nanoparticles
- Reade has a wide selection of nanoparticles
- sigma-aldrich has dispersions of nanoparticles
- nanophase
Contributors and Acknowledgements
- Jakob Kjelstrup Hansen
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ qian2002
- ↑ hamada1992
- ↑ avouris2003
- ↑ dresselhaus2001
- ↑ saito1998
- ↑ dresselhaus2001
- ↑ saito1998
- ↑ hamada1992.
- ↑ zhou2000
- ↑ wildoer1998,odom1998
- ↑ frank1998
- ↑ nygard1999,dresselhaus2001
- ↑ datta1995
- ↑ Bucky's brother -- The boron buckyball makes its début Jade Boyd April 2007 eurekalert.orgLink
- ↑ a b The boron buckyball has an unexpected Th symmetry G. Gopakumar, Nguyen, M. T., Ceulemans, Arnout, Chem. Phys. lett. 450, 175, 2008.[2]
- ↑ "Stuffing improves the stability of fullerenelike boron clusters" Prasad, DLVK; Jemmis, E. D.; Phys. Rev. Lett. 100, 165504, 2008.[3]
- ↑ Buckminsterfullerene: Molecule of the Month
- ↑ Goldberg Variations Challenge: Juris Meija, Anal. Bioanal. Chem. 2006 (385) 6-7
Metallic Nanostructures
| Navigate |
|---|
| << Prev: Semiconducting Nanostructures |
| >< Main: Nanotechnology |
| >> Next: Organic Nanomaterials |
Metallic Nanostructures
Gold
The red color in some stained glasses has through centuries been made from gold nanoparticles, and its also gold particles that make the red color in many pregnancy tests. Gold nanoparticles are used on many technoogies: they have a red color because of a plasmon resonance and the noble metal makes them good for specific binding of molecules with thiol groups.
Copper
When copper is viewed on the nano level, several changes occur. the temperature of the metal decreases, as well as the fatigue limit decreases. Also, the tensile stress and elongation rate of the copper decreases.
this info is from: http://cat.inist.fr/?aModele=afficheN&cpsidt=14408198
References
See also notes on editing this book Nanotechnology/About#How_to_contribute.
Organic Nanomaterials
| Navigate |
|---|
| << Prev: Metallic Nanostructures/ |
| >< Main: Nanotechnology |
| >> Next: Nanosystems |
Organic nanowires
Liposomes
Micelles
Metal-Organic Frameworks
References
See also notes on editing this book Nanotechnology/About#How_to_contribute.
Nanometals
Quick Review of nanometals
Nanometal (also called metal nanoparticles) is very attractive and that is because of their size and shape dependent properties. The optical properties (linear and nonlinear) depend on that and they on dominated by something called the collective oscillation of conduction electrons. There are so many ways that you can prepare metal nanoparticles but the most used methods are based on wet chemistry. You can find nanometal being used in medical applications to the weaponry the military use. Nanometals also have a thing called Surface Plasmon Resonance (SPR) this is what cause the change in colors that we see. For example in the 4th century when the Lycurgus cup was created. The cup changes red when the light is shone inside of the cup and green when reflective light is shone on the outside of it. There are so many methods that you can prepare nanometals and the most popular way is by reducing HAuCl4 (chlorauric acid) in a sodium citrate solution that is boiling and then the formation of gold nanoparticles are revealed by a deep red color that looks like wine in about 10 min.[1]
Types of nanometal synthesis
The most common types of nanometal synthesis deal with 'wet' methods in which metal nanoparticles are produced in a colloid with an organic material of some sort.
Gold nanoparticles can be produced by either:
1) Reduction of HAuCl4 in a solution of sodium citrate, then boiling it, causing gold nanoparticles to form in a wine-red solution.
2) Mixing HAuCl4 in water, which produces a solution that is subsequently transferred into toluene using tetraoctylammonium bromide (TOAB), a phase transfer catalyst. Phase transfer catalysts help reactants dissolve in organic (carbon-containing) material where the reactant otherwise couldn't w/o the PTC. Afterwards, the solution is stirred with sodium borohydride, in the presence of certain alkanes, which bind to the gold in the solution, allowing for the formation of gold nanoparticles.
Synthesis of other metal nanoparticles can possibly be achieved by reducing metal salts in organic solvents such as ethanol, or by variations of the above methods which synthesize gold nanoparticles. [2] [3]
References
- ↑ webs.uvigo.es/coloides/nano
- ↑ Luis M Liz-Marzán. "Nanometals formation and color", Materials Today, February 2004, page 27.
- ↑ Phase transfer catalyst-Wikipedia. http://en.wikipedia.org/wiki/Phase_transfer_catalyst
Part 5: Nanosystems
| Navigate |
|---|
| << Prev: Organic Nanomaterials |
| >< Main: Nanotechnology |
| >> Next: Nano-optics |
|
|
| <<< Prev Part: Nanomaterials |
| >>> Next Part: Nanoengineering |
This part describes the subfields of nanotechnology with a very technological aim:
- Nanomechanics
- Nano-optics and Nanophotonics
- Nanofluidics
- Nanoelectronics
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Nanoelectronics
| Navigate |
|---|
| << Prev: Nano-optics |
| >< Main: Nanotechnology |
| >> Next: Nanomechanics |
Nanoelectronics
Nanoelectronics is expected to be cheaper to fabricate than silicon / gallium / arsenic based electronics. It also might be small enough to not require a power source as it is possible to abstract a small amount of energy from the surrounding heat by a molecular level energy scavenging system[1]
Diffusive and Ballistic Electron Transport
Double barrier systems
- Coulomb Blockade
- Tunnel Junctions
- Quantum Tunneling
Moletronics / Molecular Electronics
Using molecules for electronics, often called moletronics or molecular electronics [2] , is a new technology which is still in its infancy, but also brings hope for truly atomic scale electronic systems in the future.
One of the more promising applications of molecular electronics was proposed by the IBM researcher Ari Aviram and the theoretical chemist Mark Ratner in their 1974 and 1988 papers Molecules for Memory, Logic and Amplification, (see Unimolecular rectifier ) [3] [4] . This is one of many possible ways in which a molecular level diode / transistor might be synthesized by organic chemistry. A model system was proposed with a spiro carbon structure giving a molecular diode about half a nanometre across which could be connected by polythiophene molecular wires. Theoretical calculations showed the design to be sound in principle and there is still hope that such a system can be made to work.
However one researcher, experimentalist Jan Hendrik Schön, could not wait for the necessary technical progress and at a time when he was publishing one scientific paper a week and winning scholarships, heading for the top in nanotechnology, it was discovered he had fabricated both the experiment where such a device worked and several other potentially important milestones in the field. This incident is discussed by David Goodstein in Physics World [93]. However it seems only a matter of time before something like this proposed elegant solution to the problem demonstrates the behavior of a diode.
Quantum Computing
A quantum computer would be incredibly fast compared to microelectronics. It would also be able to use the properties of quantum mechanics to be in fuzzy states which could represent many numbers at once allowing a massive density of memory. How such devices would be nano-fabricated is however way beyond current technology.
The first working 2-qubit quantum computer was demonstrated in 1998.
In 2006, the first working 12 qubit quantum computer was demonstrated.
Bibliography
- Michel le Bellac, A Short Introduction to Quantum Information and Quantum Computation, Cambridge University Press (2006) ISBN 978-0-521-86056-7.
- Michael A. Nielsen and Isaac L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press (2000) ISBN 978-0-521-63235-5.
Resources on the net
- Keithley.com has some freely available handbooks on low noise measurements in electronics and nanotechnology
- Nanoelectronics Overview at Understandingnano
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ S. Meininger et al., "Vibration-to-Electric Energy Conversion", IEEE Trans. VLSI Systems, 64-76 (2001).
- ↑ Petty M.C., Bryce M.R. and Bloor D., An Introduction to Molecular Electronics, (Edward Arnold, London, 1995).
- ↑ A. Aviram and M. A. Ratner, “Molecular Rectifier” (Chemical Physics Letters 29: 277 (1974)).
- ↑ A. Aviram, J. Am. Chem. Soc., 110 5687-5692 (1988)
Nano-optics
| Navigate |
|---|
| << Prev: Nanosystems |
| >< Main: Nanotechnology |
| >> Next: Nanoelectronics |
Nanophotonics and nanooptics
With the increasing demand for smaller, faster, and more highly integrated optical and electronic devices; as well as extremely sensitive detectors for biomedical and environmental applications; a field called nano-optics or nano-photonics is emerging - studying the many promising optical properties of nanostructures.
Like nanotechnology itself, it is a rapidly evolving and changing field – but because of strong research activity in optical communication and related devices, combined with the intensive work on nanotechnology, nano-optics appears to be a field with a promising future.
Nanophotonics is seen as a crucial technology for extending Moore's Law into the next few decades. In the past few years nanophotonics researchers worldwide have developed, On Chip Silicon Lasers, Gigahertz Silicon Electro Optic Switches, and Low Loss Highly Integratable Compact Nanowires (With waveguides of 100’s of nanometers' width).
Nanophotonics is mainly expected to play a complementary role to micro/nano electronics on chip and extend the capacity of telecommunication networks into the Terabit/s regime. One of the major emphasis’s in the last few years has been developing on-chip interconnects to break the bottle neck for higher data rates within integrated chips.
In conjugation with Nanofluidics, Nanophotonics is also finding applications in biomedical sensors, Medical diagnosis, etc.
Nanophotonic components such as Microcavities with ultra high life time of trapped photons are expected to find applications in fundamental experimental physics such as gravitational wave detection.
Intel, IBM, Lucent, and Luxtera have highly functional and well funded nanophotonic research groups. A number of universities in: US, UK, Japan, Italy, China, Belgium, etc. have been actively pursuing nanophotonics. Apart from a growing number of hits on the word in publication databases like "Web of Science", which shows it is already getting increased attention, it is also increasingly mentioned in the aims of the funding agencies, which will surely add to the activity in the field as increased economical support becomes available.
Electrooptic modulators
Electro-optic modulators are devices used to modulate, or modify a beam of light. Currently they are mainly used in the information technology and telecommunications industries (e.g. fiber-optic cables). EOM’s have good potential in nanophotonics. Nanoscale optical communication devices will have increased speed and efficiency, once they can be engineered and used. Nano-size electrooptic modulators will be an integral part of a nanoscale communications network.
Photodetector
Photodetectors respond to radiant energy. They are basically sensors of light or other electromagnetic energy. A sensor is a electronic device that converts one type of energy to another for various reasons. Nanoscale size photodetectors will be an integral part of a theoretical nanoscale optical information network.
Electrooptic switches
Electrooptic switches change signals in optical fibers to electrical signals. Typically semiconductor-based, their function depends on the change of refractive index with electric field. This feature makes them high-speed devices with low power consumption. Neither the electro-optic nor thermo-optic optical switches can match the insertion loss, back reflection, and long-term stability of opto-mechanical optical switches. The latest technology combines all-optical switches that can cross-connect fibers without translating the signal into the electrical domain. This greatly increases switching speed, allowing today's telcos and networks to increase data rates. However, this technology is only now in development, and deployed systems cost much more than systems that use traditional opto-mechanical switches. [1]
Photonic crystals
"Photonic crystals are composed of periodic dielectric or metallo-dielectric nanostructures that are designed to affect the propagation of electromagnetic waves (EM) in the same way as the periodic potential in a semiconductor crystal affects the electron motion by defining allowed and forbidden electronic energy bands. Simply put, photonic crystals contain regularly repeating internal regions of high and low dielectric constant." Photonic crystals are used to modify or control the flow of light. Photonic crystals may have a novel use in optical data transmission but are not extremely prominent. They may be used to filter for interference in a fiber optic cable, or increase the quality of the transmission. In addition, they can be used to divide different wavelengths of light. Photonic crystals can already be manufactured at close to the nanoscale.
Sensors
Nanotechnology creates many new, interesting fields and applications for photonic sensors. Existing uses, like digital cameras, can be enhanced because more ‘pixels’ can be placed on a sensor than with existing technology. In addition, sensors can be fabricated on the nano-scale so that they will be of higher quality, and possibly defect free. The end result would be that photos would be larger, and more accurate. As part of a communication network, photonic sensors will be used to convert optical data (photons) into electricity (electrons). Nanoscale photonic sensors will be more efficient and basically receive similar advantages to other materials constructed under the nanoscale.
Multiplexers
A multiplexer is a device for converting many data streams into one single data stream, which is then divided into the separate data streams on the other side with a demultiplexer. The main benefit is cost savings, since only one physical link will be needed, instead of many physical links. In nano-optics, multiplexers will have many applications. They can be used as part of a communication network, as well as utilized on a smaller scale for various modern scientific instruments.
Vanadium dioxide
Vanadium dioxide has the interesting property of changing from a transparent state to a reflective, mirror-like state in less than 100 femtoseconds[2] (1/10 of a trillionth of a second). Vanderbilt University discovered the transition at 68 degrees celsius. The temperature that the transition happens can be changed by adding small amounts of impurities, and it is possible to lower the temperature by as much as 35 degrees celsius. However, there is a size limit, the change will not occur in particles that are smaller than 20 atoms across, or 10 nanometers. This property has many applications. Possibilities are a 'solar shade' window that changes from letting light in, to reflecting light back automatically when the temperature starts rising. Also, nanosensors could be created which could measure the temperature at different locations in human cells. However, most importantly, this transition can be utilized in creating an 'ultrafast' optical switch which could be used in communications or computing. Currently, researchers are seeing if they can put a layer of vanadium dioxide nanoparticles on the end of an optical fiber to create a very high speed link.
Quantum dots
Quantum dots have several applications. One of the first applications found was their ability to emit very specific wavelengths of light. This is different from other light emitting bulbs since quantum dots could be tuned across the visible and ultraviolet spectrums very precisely. Researchers have found that if they put about 2,000 quantum dots together, they would have a finely tuned LED. Researchers have tried for an extremely long time to get these dots to emit light. In the 1990’s someone was able to get a dark red light. Since then other researchers have been able to tune the dots to a higher frequency, thus gaining blue and green light. The applications for this would be beneficial so that we could make full color screens and monitors.[3]
Resources
- Near and far field - near and far field radiation can to some extent be compared to listening to a walkmans earphones; the one carrying the earphones can hear the sound perfectly even though the bass sound wavelength is much larger than the earphone. If you are not wearing the earphones, the high frequency sounds will be much higher than the bass. The bass can only be heard in the near field.
- plasmonics
- Rochester Nano Optics
Bibliography
- Lucas Novotny and Bert Hect, Principles of Nano-Optics, Cambridge University Press (2006).
References
- ↑ "Switches." www.fiber-optics.info. 2005. Force, Incorporated. 27 Jun 2007 <http://www.fiber-optics.info/articles/switches.htm>.
- ↑ http://www.vanderbilt.edu/exploration/stories/vo2shutter.html
- ↑ https://www.llnl.gov/str/Lee.html.
Nanomechanics
| Navigate |
|---|
| << Prev: Nanoelectronics |
| >< Main: Nanotechnology |
| >> Next: Nanofluidics |
Nanomechanics
Some of the mechanical aspects of nanotechnology is
- Extreme Youngs modulus materials
- High frequency resonances in nanoscale oscillators
NEMS
Nano-electro-mechanical systems
Mechanics of beams and cantilevers
Cantilevers are essential in many mechanical systems: Nanotubes, nanowires and atomic force microscopes...
The harmonic oscillator
Fundamental in the description of any oscillating systems is the harmonic oscillator and the quantum mechanical version, the Quantum harmonic oscillator.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Nanofluidics
| Navigate |
|---|
| << Prev: Nanomechanics |
| >< Main: Nanotechnology |
| >> Next: Nanoengineering |
Flow on the large scale, in Microsystems and in nanosystems show very different behaviour.
In nanofluidic systems you willl have
- Small sample volume
- High area to volume ratio
- Domination of surface forces
- Short diffusion times
- Enhanced reaction kinetics due to short diffusion times
- Relatively large electric double layer
- Microfluidics
- Brownian motion of nanoparticles
- Diffusion
- Fluid dynamics
Nanoscale flow can be enhanced considerably compared to what is predicted by macroscale Knudsen flow or continuum hydrodynamics models - see Science Vol. 312. no. 5776, pp. 1034 - 1037 DOI-link (Fast Mass Transport Through Sub-2-Nanometer Carbon Nanotubes)
FERROFLUIDS
Ferrofluids are a form of colloidal suspensions. They are tiny iron particles covered with a liquid coating, also surfactant, that are then added to water or oil, which gives them their liquid properties. Ferrofluids are colloidal suspensions. Those are materials with properties of more than one state of matter. In this case, the two states of matter are the solid metal and liquid it is in. This ability to change phases with the application of a magnetic field allows them to be used as seals, lubricants, and may open up further applications in future nanoelectromechanical systems.
Resources
- a wikibook on Microfluidics
- Microfluidics: Fluid physics at the nanoliter scale REVIEWS OF MODERN PHYSICS, VOLUME 77, JULY 2005 by Squires and Quake
- The Fluid Mechanics of Microdevices—The Freeman Scholar Lecture Journal of Fluids Engineering 1999, Vol. 121 / 5
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Part 6: Nanoengineering
| Navigate |
|---|
| << Prev: Nanofluidics |
| >< Main: Nanotechnology |
| >> Next: Top-down and bottom-up approaches |
|
|
| <<< Prev Part: Nanosystems |
| >>> Next Part: Nano-bio Primer |
This chapter takes a look into the engineering aspects of nanotechnology: how to integrate the nanostructures with our known technology, the creation of nanomaterials and simple systems in the laboratory, and the development of functional devices that can be used by society.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Top-down and bottom-up approaches
| Navigate |
|---|
| << Prev: Nanoengineering |
| >< Main: Nanotechnology |
| >> Next: Self Assembly |
Top-down and bottom-up approaches
There are two types of approaches for the synthesis of nanomaterial and fabrication of nanostructure.
- top-Down approaches refers to slicing or successive cutting of bulk material to get nano-sized particles.there are two types *attrition ,* milling
- Bottom-up refers to method where devices 'create themselves' by self-assembly. Chemical synthesis is a good example. Bottom-up should, broadly speaking, be able to produce devices in parallel and much cheaper than top-down methods, but getting control over the methods is difficult when things become larger and bulkier than what is normally made by chemical synthesis. Of course, nature has had time to evolve and optimize self-assembly processes that can do wonders.
Microfabrication made smaller
Not much of nanotechnology is based on methods from Microfabrication.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Self assembly
| Navigate |
|---|
| << Prev: Top-down and bottom-up approaches |
| >< Main: Nanotechnology |
| >> Next: Lithography |
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Lithography
| Navigate |
|---|
| << Prev: Self assembly |
| >< Main: Nanotechnology |
| >> Next: Nanomanipulation |
|
|
| Down: Module on EBID |
Lithography
Electron beam lithography
Electron beam lithography (EBL)
Nano imprint lithography (NIL)
Focused Ion Beam Techniques
Electron Beam Induced Deposition (EBID or EBD)
The highly focused electron beam in a SEM is used for imaging nanostructures, but it can also be used to make nanoscale deposits. In the presence of carbonaceous or organometallic gasses in the SEM chamber, electron beam induced deposition (EBID or electron beam deposition (EBD)) can be used to construct three-dimensional nanostructures or solder/glue nanostructures.
There is module in this handbook dedicated to EBID
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Electron Beam Induced Deposition (EBID or EBD)
| Navigate |
|---|
| << Prev: Lithography |
| >< Main: Nanotechnology |
| >> Next: Nanomanipulation |
|
|
| UP: Lithography |
Electron Beam Induced Deposition (EBID or EBD)
EBID Background
It was apparent with the first electron microscopes in the 50's, that the presence of an electron beam slowly coated the sample with a carbonaceous substance [1].
Even earlier, it was observed that electron radiation decomposed organic vapors present in the vacuum chamber, such as oil vapors unavoidable in diffusion pumped vacuum systems or outgassing from the sample itself [2][3].
When the background gas is decomposed by irradiation through various ionization and dissociation processes, the gas turns partly into volatile compounds re-emitted into the chamber and partly into solid amorphous carbon. The material properties range from diamond-like-carbon (DLC) to polymers depending on the exact deposition conditions [4].
The reactions taking place during EBD are not well characterized. Both ionization and dissociation are expected to contribute [5]. The cross-section for both dissociation and ionization are peaked at low electron energies (<50 eV), indicating that secondary electrons are likely to be the main cause of deposition rather than the primary electrons (PE).
By focusing the PE beam in a fixed spot, a thin needle-shaped deposit will grow up towards the electron beam. The tip width can be considerably wider than the PE beam diameter and typically of the order 100 nm. The width is determined by the scattering of the PE in the tip structure which in turn also creates SE escaping through the tip apex and sidewalls causing a wider deposit [5].
With many potential applications in micro- and nanotechnology, the EBD technique has received increasing attention since the 80's as a method for creating submicron structures. Comparing EBD to electron beam lithography (EBL), the EBD process must be considered "slow" while EBL is "fast" since the required irradiation dose is many orders of magnitude smaller for EBL.
The use of EBD in commercial production of nanostructures is today limited to "supertips" for AFM cantilevers with extreme aspect ratios that cannot readily be achieved by other methods [6].
For research purposes, where high throughput is not a requirement, the technique appears convenient in several applications. Apart from depositing structures, it has also been used to solder nanocomponents. Both single and multiwalled carbon nanotubes (SWNT and MWNT) have been soldered to AFM cantilevers for stress-strain measurements [7][8] and to micromechanical actuators for electrical and mechanical tests [9] [10]
Metal deposition by EBID
A large fraction of the EBD publications have been focussing on the use of metal containing precursor gasses. Koops et al. [11] and Matsui et al. [12] pioneered the extensive use of metal containing source gasses to make deposits with high metal contents. They also began scanning the beam in patterns to make three-dimensional structures. Complex three-dimensional structures can be made by EBD with both carbonaceous and metal-containing EBD. Another intriguing possibility is to use EBD to make catalyst particles for subsequent growth of nanowires and tubes [13].
Compared to the planar and resist-based EBL, the EBD method is slow and difficult to scale to large productions, but on the other hand offers the possibility to create elaborate three-dimensional structures, which cannot readily be made by EBL. The EBD method appears to be a versatile tool capable of constructing nanodevies, contacting nanostructrues to create composite electronic nanostructures, and soldering nanostructures such as carbon nanotubes to microelectrodes.
For electronic applications one would like to achieve as high a conductivity as possible of the deposited material. Metal-containing EBD materials usually contain metallic nanocrystals in an amorphous carbon matrix with a conductance considerably lower than that of the pure metal. The metal content and conductivity of the EBD material can be increased to approach that of bulk metals by several methods:
1: Heating the substrate has been shown to increase the metal content of the deposit. Koops et al. [14] have observed an increase from 40 wt. % at room temperature to 80 wt.% at 100°C. Others, for example Botman et al. [15] have shown the link between deposit composition and conductivity as a function of post-treatment in heated gases.
2: Using a carbon free precursor gas, such as , Hoffman et al. [16] made gold deposits with a resistivity of 22 µΩcm which is only 10 times the bulk value of Gold.
3: Introducing an additional gas such as water vapor while using an environmental scanning electron microscope (ESEM)[17]. It is even possible to create desposits with a solid gold core under controlled deposition conditions [10].
Resources
- Review paper: Focused, Nanoscale Electron-Beam-Induced Deposition and Etching by Randolph et al. [18]
- [http://www.febip.info/ Focused Electron Beam Induced Processes
(FEBIP)]
A Simple Model of EBD
To accurately model the EBD process, one has to resort to Monte Carlo simulations that can incorporate the different scattering effects taking place during the process. Extensive work has been done on models for the deposition of amorphous carbon tips [5]. Generally there is very little available knowledge on:
- The radiation induced chemistry of the metal containing precursor gas. A wealth of reactions are possible, but limited data is available for the conditions and substances used for EBD.
- The chemical content of the produced amorphous carbon in the deposit.
- The current density in the electron beam is rarely well characterized.
Not knowing the chemical details of the deposition process, the exact product of the deposition, or the electron beam, a simple analytical model will also provide insight to the essential parameters. A simple model is reviewed below to provide an understanding of the basic requirements and limitations for the EBD process.
The Rate Equation Model
Electron beam deposition of planar layers on surfaces can be reasonably described by a simple rate equation model [19].
The model shows the fundamental limitations for growth rate and its dependence on beam current and precursor gas flow. The model calculations and most experiments in this thesis, are based on the precursor gas dimethyl gold acetylacetonate, here abbreviated to DGAA. The vapor pressure of the precursor gas determines the flux of precursor molecules to the surface. The flux rate of molecules F [m²s¹] of an ideal gas at rest is
with pressure P, atomic weight m, Boltzmann's constant and temperature T. For DGAA which has a vapor pressure of 1.3 Pa at 25 °C, this gives a flux rate
The cross-sections for electron beam induced ionization and dissociation of the precursor gas to form the deposits are generally not known. Cross-sections are usually of the order Ų and peak at low energies, corresponding the low energy of the secondary electrons which are probably the main cause of the deposition.

The adsorption of molecules on the target surface and highest density of SE near the surface make it reasonable to assume that the deposition rate dN_{dep}/dt depends on the surface density of adsorbed precursor molecules N_{pre}, the beam current density J, and the effective cross section s_0 as
The surface density of the adsorbed precursor molecules in Eq. #eq EBD dep surface rate is the source for the deposited material and depends on both the deposition, ad- and desorption processes as sketched in the figure.
With maximum surface density (e.g. one monolayer, since generally more than one monolayer cannot be expected unless the target is cooled compared to the source, to give condensation of the source gas. Then adsorption probability a and lifetime t (s), a rate equation can be written for the precursor surface density as [20]
The steady state adsorbate density, , is then
If each deposition event on average results in a cubic unit cell of deposited material with volume V, the vertical growth rate R [nm/s] is
The dependence on precursor flux falls into two cases:
- when a monolayer is always present and increasing the flux rate F has little effect on the growth rate R, since the surface is saturated
- when less than a monolayer is present, and increasing F will increase the growth rate R.
Increasing the electron beam current will in this model always increase the deposition rate. The rate increases relatively linearly with the electron flux, until it begins to saturate when the source gas flux becomes the limiting factor for the growth rate.
Scheuer et al. [21] have measured the EBD deposition cross section of to be of the order =0.2 Ų and s. Using these values, a rough estimate of the growth rate can be calculated. For the estimate, we assume a monolayer is present ; a sticking efficiency of a=100%; the vapor pressure flux of DGAA; an electron beam diameter of 20 nm; a total beam current of 0.2 nA; and finally that the unit cell volume V for deposition is that of gold. With this set of values, the deposition rate becomes R= 100 nm/s.
The used values make so the deposition is not limited by the electron beam current but by the gas flux which would have to be 10 times higher to reach saturation. The beam radius will have to be increased to r= 0.5 µm to reach the electron flux limited region and this radius is much larger than the observed resolution in most experiments. Its is important to secure as high as possible flux of precursor gas in the experiments, since this is the main limiting factor in the model whereas the focus of the electron beam is expected to be less important due to the high current density.
Limitations to the model
The rate model is suited for describing deposition of planar layers, but for the case of deposition of tip structures in a real system, several other effects influence the deposition rate:
Scattering of primary electrons in the deposited structure. BSE and SE are emitted through the sidewalls and apex of the structure in a non-uniform way, and the PE/BSE scattering make SE generation take place in a larger region than the PE beam radius, which considerably limits the minimal radius for tip structures.
The figure above illustrate these effects. Simulations are needed to make proper estimates of the influence of scattering, but qualitatively it should cause a lower vertical growth rate as less electrons must be expected to emerge through the upper surface of the structure.
The PE beam is not uniform as considered in the model. In an ESEM, a Gaussian distribution of the PE beam can be expected, and the scattering of the electron beam in the environmental gas creates an low current density "electron skirt" around the PE beam. This should be considered both for the possible contamination in the larger region irradiated with low current density, but also for reducing the current in the primary beam and thus the growth rate.
It was assumed that the source supply precursor gas with the vapor pressure gas flux rate. The rate could be considerably lower if the source material does not have enough surface area to sustain the gas flow or the distance to the source is too large. The fact that many organometallic compounds decompose in contact with water in the case of EEBD could also reduce the source gas flow.
Not all irradiation induced events will result in deposition of material. Substantial amounts of material could be volatile or negatively ionized and carried away, especially in an the ESEM environment. Electron attachment is also taking place in the ESEM and is known to influence the detection of secondary electrons [22]. This could reduce the supply of precursor gas and hence the deposition rate.
Surface diffusion of the precursor gas will influence the supply rate. When depositing in only a small area, surface diffusion of adsorbed molecules from the surrounding area can considerably increase the supply of precursor molecules. This is usually the explanation given why many EBD experiments observe that the tip deposition is faster in the beginning; for then to decrease to a steady state growth rate, when a tip structure is formed which limits the supply by surface diffusion. This could increase the rate at the very beginning of the deposition.
The predicted vertical growth rate from the model must be an upper estimate on the achievable rate, since most unaccounted effects will work to reduce the steady state growth rate.
Summary
Little data is available on the precursor gasses for EBD. A simple rate equation model gives an estimated deposition vertical growth rate of 100 nm/s for the typical precursor gasses. This estimated growth rate is expected to be an upper limit. Especially the flow rate of precursor gas should be as high as possible in the experiment since this is the limiting factor for the deposition rate.
Environmental Electron Beam Deposition (EEBD)

The ESEM makes it possible to use various gasses in the sample chamber of the microscope since there are narrow apertures between the sample chamber and the gun column, and a region in between that is connected to a differential pumping system. Pressures up to about 10 Torr are normally possible in the sample chamber.
The standard Everly-Thornhart SE detector would not work under such conditions since it would create a discharge in the low pressure gas. Instead a "gaseous secondary electron detector (GSD)" is used, as shown in the figure below. The GSD measures the current of a weak cascade discharge in the gas, which is seeded by the emission of electrons from the sample.

In the ESEM one can work with, for instance, water vapour or argon as the environmental gas, and is is possible to have liquid samples in the chamber if the sample stage is cooled sufficiently to condense water.
Without precursor gas present in the chamber, the EBD deposition rate is normally negligible in the high vacuum mode as well as in the gas mode of the ESEM.
In environmental electron beam deposition (EEBD), the deposited tips have a shell structure and consist of different material layers each characterized by a certain range of gold/carbon content ratio. Above a certain threshold of water vapor pressure and a certain threshold of electron beam current, the deposited tips contain a solid polycrystalline gold core [10].
Acknowledgement
This page was started based on the material in:
- Kristian Mølhave's PhD thesis chapter 4 and accompanying papers [10] and [9].
- Please add material here if you add to the page content!
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ C. W. Oatley. The early history of the scanning electron microscope. Journal of Applied Physics, 53(2):R1—R13, 1982.
- ↑ R. Lariviere Stewart. Insulating films formed under electron and ion bombardment. Phys. Rev., 45:488-490, 1934
- ↑ J. J. Hren. Barriers to AEM: contamination and etching. In: Introduction to Analytical Electron Microscopy. Plenum, New York, 1979.
- ↑ Shuji Kiyohara, Hideaki Takamatsu, and Katsumi Mori. Microfabrication of diamond films by localized electron beam chemical vapour deposition. Semiconductor Science and Technology, 17(10):1096—1100, 2002.
- ↑ a b c Natalia Silvis-Cividjian. Electron Beam Induced Nanometer Scale Deposition. PhD thesis, Technical University in Delft, Faculty of applied Physics, 2002.
- ↑ M. Wendel, H. Lorenz, and J.P. Kotthaus. Sharpened electron beam deposited tips for high resolution atomic force microscope lithography and imaging. Applied Physics Letters, 67(25):3732—4, 1995.
- ↑ Min-Feng Yu, Bradley S. Files, Sivaram Arepalli, and Rodney S. Ruoff. Tensile loading of ropes of single wall carbon nanotubes and their mechanical properties. Physical Review Letters, 84(24):5552—5555, 2000.
- ↑ Min-Feng Yu, O. Lourie, M.J. Dyer, K. Moloni, T.F. Kelly, and R.S. Ruoff. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load. Science, 287(5453):637—40, 2000.
- ↑ a b c Constructing, connecting and soldering nanostructures by environmental electron beam deposition, Nanotechnology 15 1047–1053 (2004), K Mølhave, D N Madsen, S Dohn and P Bøggild.
- ↑ a b c d e K. Mølhave, D.N. Madsen, A.M. Rasmussen, A. Carlsson, C.C. Appel, M. Brorson, C.J.H. Jacobsen, and P. Bøggild. Solid gold nanostructures fabricated by electron beam deposition. Nano Letters, 3:1499—1503, 2003.
- ↑ H.W.P. Koops, R. Weiel, D.P. Kern, and T.H. Baum. High-resolution electron-beam induced deposition. Journal of Vacuum Science and Technology B (Microelectronics Processing and Phenomena), 6(1):477—81, 1988.
- ↑ S. Matsui and K. Mori. In situ observation on electron beam induced chemical vapor deposition by Auger electron spectroscopy. Applied Physics Letters, 51(9):646—8, 1987.
- ↑ Y.M. Lau, P.C. Chee, J.T.L. Thong, and V. Ng. Properties and applications of cobalt-based material produced by electron-beam-induced deposition. Journal of Vacuum Science and Technology A: Vacuum, Surfaces and Films, 20(4):1295—1302, 2002.
- ↑ H.W.P. Koops, C. Schoessler, A. Kaya, and M. Weber. Conductive dots, wires, and supertips for field electron emitters produced by electron-beam induced deposition on samples having increased temperature. Journal of Vacuum Science and Technology B, 14(6):4105—4109, 1996.
- ↑ Botman A, Mulders JJL, Weemaes R and Mentink S. Purification of platinum and gold structures after electron-beam-induced deposition. Nanotechnology, 17:3779-3785, 2006.
- ↑ P. Hoffmann, I. Utke, F. Cicoira, B. Dwir, K. Leifer, E. Kapon, and P. Doppelt. Focused electron beam induced deposition of gold and rhodium. Materials Development for Direct Write Technologies. Symposium (Materials Research Society Symposium Proceedings Vol.624), pages 171—7, 2000.
- ↑ A. Folch, J. Servat, J. Esteve, J. Tejada, and M. Seco. High-vacuum versus environmental electron beam deposition. Journal of Vacuum Science and Technology B, 14(4):2609—14, 1996.
- ↑ Focused, Nanoscale Electron-Beam-Induced Deposition and Etching, S. J. Randolph, J. D. Fowlkes, and P. D. Rack, Critical Reviews in Solid State and Materials Sciences, 31:55–89, 2006
- ↑ V. Scheuer, H. Koops, and T. Tschudi. Electron beam decomposition of carbonyls on silicon. Microelectronic Engineering, 5(1-4):423—30, 1986.
- ↑ V. Scheuer, H. Koops, and T. Tschudi. Electron beam decomposition of carbonyls on silicon. Microelectronic Engineering, 5(1-4):423—30, 1986.
- ↑ V. Scheuer, H. Koops, and T. Tschudi. Electron beam decomposition of carbonyls on silicon. Microelectronic Engineering, 5(1-4):423—30, 1986.
- ↑ G.D. Danilatos. Equations of charge distribution in the environmental scanning electron microscope (esem). Scanning Microscopy, 4(4):799—823, 1990.
Nanomanipulation
| Navigate |
|---|
| << Prev: Lithography |
| >< Main: Nanotechnology |
| >> Next: Nano-bio Introduction |
Nanomanipulation
- Wikipedia Nanorobotics
- Nanorobotics introduction
- Video clips of Nanomanipulation on YouTube
- [94] Pick and Place of NW in SEM on YouTube
- Video of the manipulation of a nanowire for TEM observation on YouTube

AFM manipulation
With AFM nanostructures such as nanotubes and nanowires lying on surfaces can be manipulated to make electrical circuits and measure their mechanical properties and the forces involved in manipulating them.
STM manipulation
Using an STM individual atoms can be manipulated on surface this was first demonstrated by Eigler et al. Here Xe atoms were manipulated on Ni to spell out IBM. This was then extended by Crommie et al., where Fe atoms were moved to create quantum corals. Here the electron standing waves created inside the corral are imaged by the STM tip. The probably demonstrates the highest resolution nanomanipulation.
In-situ SEM manipulation
To monitor a three-dimensional nanomanipulation process, in-situ SEM or TEM manipulation seems preferable. AFM (or STM) does have the resolution to image nanoscale objects, even down to the sub-atomic scale, but the imaging frame rate is usually slow compared to SEM or TEM and the structures will normally have to be planar. SEM offers the possibility of high frame rates; almost nanometer resolution imaging of three-dimensional objects; imaging over a large range of working distances; and ample surrounding volume in the sample chamber for the manipulation setup. TEM has a much more limited space available for the sample and manipulation systems but can on the other hand provide atomic resolution. For detailed studies of the nanowires' structure, TEM is a useful tool, but for the assembly of nanoscale components of a well defined structure, such as batch fabricated nanowires and nanotubes, the SEM resolution should be sufficient to complete the assembly task.
As the STM and AFM techniques opened up completely new fields of science by allowing the investigator to interact with the sample rather than just observe, development of nanomanipulation tools for SEM and TEM could probably have a similar effect for three-dimensional manipulation. Recently, commercial systems for such tasks have become available such as the F100 Nanomanipulator System from Zyvex in October 2003. Several research groups have also pursued developing such systems.
To date the tools used for in-situ SEM nanomanipulation have almost exclusively been individual tips (AFM cantilever tips or etched tungsten tips), sometimes tips used together with electron beam deposition have been used to create nanowire devices. Despite the availability of commercial microfabricated grippers in the last couple of years, little has been reported on the use of such devices for handling nanostructures. Some electrical measurements and manipulation tasks have been performed in ambient conditions with carbon nanotube nanotweezers.

Companies selling hardware
The Optimal SEM Image for Nanomanipulation
As the typical SEM image is created from the secondary electrons collected from the sample, compromises must always be made to obtain the optimal imaging conditions regarding resolution and contrast. The contrast in a SEM SE image depends on the variations in SE yield from the different surface regions in the image and the signal to noise level. The resolution depends on the beam diameter and is at least some nm larger due to the SE range.
The optimal solution is always to use as good an emitter as possible (high ß_{e} in Eq.[1]). This means using FEG sources. Working at short r_{wd} gives a narrow beam (Eq.[2]), but will usually shield the standard ET detectors from attracting sufficient secondary electrons. Nanomanipulation often requires working with high resolution between two large manipulator units which further limits the efficiency of signal detection.
The manipulation equipment must be designed to make the end-effector and samples meet at short r_{wd}, and without obstructing the electron path towards the detector. A short r_{wd} also gives a short depth of focus, which can be a help during nanomanipulation because it makes it possible to judge the working distance to various objects by focussing on them. The operator can use this to get an impression of the height of the objects in the setup. Generally, for nanomanipulation, the above considerations indicate an inlens detector often can be advantageous.
Reducing the beam current to narrow the electron beam necessarily limits the number of detected electrons and make the signal-to-noise ratio low, unless one makes very slow scans to increase the number of counts
<footnote>The signal to noise ratio S/N for Poisson distributed count measurements n is S/N=vn and high counts are necessary to reduce noise in the images. </footnote>.
When used for in-situ nanomanipulation one needs a fast scan rate to follow the moving tools (preferably at rates approaching live video) and this requires high beam currents. The acceleration voltage is also important, and too high PE energy can make the sample transparent (such as the carbon coating in Fig.[3] b) while low energy usually make the image susceptible to drift due to charging and similar effects.
In-situ TEM manipulation
TEM offers atomic 3D resolution but the extreme requirements on stability combined with very limited sample space makes the construction of in-situ TEM manipulation equipment quite a task. With such systems, people have observed freely suspended wires of individual atoms between a gold tip and a gold surface; carbon nanotubes working as nanoscale pipettes for metals and a wealth of other exotic phenomena.
Companies selling hardware
References
See also notes on editing this book about how to add references Nanotechnology/About#How to contribute.
Part 7: Nano-Bio Introduction
| Navigate |
|---|
| << Prev: Nanomanipulation |
| >< Main: Nanotechnology |
| >> Next: Nano-bio Primer |
|
|
| <<< Prev Part: Nanoengineering |
| >>> Next Part: Environmental Nanotechnology |
Nano-bio Primer
| Navigate |
|---|
| << Prev: Nano-bio Introduction |
| >< Main: Nanotechnology |
| >> Next: Biosensors |
Bio-nanotechnology
- Nanobiotechnology
- Bionanotechnology
- Nanomedicine
- Basics of biochemistry an E handbook from Lund University
Biological 'units'
- The wiki book on Cell Biology
- Bacteria
- Virus
- Cell biology and another wiki entry on Cell Biology
- The brain and neurons
- Molecular Biology of the Cell a great text book with full text search freely available on the net.
- Cells alive
Biosystem building blocks
- DNA
- proteins, see also wikibook on Proteomics
- liposomes
make up cell membranes and these are the very important barriers that control what can enter and exit a cell. The importance can be seen in the fact that one third of all proteins are membrane proteins.
Cell Energy Supply and Consumption
The cell organelle the mitochondria is the power plant of the cell energy metabolism.
It synthesises ATP, the basic energy source for numerous processes in cells. The synthesis proces is driven by an electric potential (~150mV) across the mithocondrial inner membrane that is maintained by ion pumps in the membrane that make the outside more acidic while the inner matrix region is more alkaline. The gradient is ~0.5 pH units [1]. The membrane potential is not homogeneous over the mitochondria [2]
The Chemiosmotic theory of the ATP synthesis was developed by Peter Mitchell in 1961, who was later rewarded the chemistry Nobel prize for it in 1978.
Current research on Mitocondria was reviewed eg. in Science 28 aug 1998 and 5 mar 1999.
The membrane potential difference is small, but the menbrane is also very thin; approx 5-7nm, giving an electrical field across the membrane of the order 30MV/m - which will make any physicist designing high energy particle accelerators quite envious - the value is huge compared to electrical fields that would make large scale matter break down. Its is on contrast to the otherwise weak forces normally encountered when talking about the physical properties of lipid membranes. Despite being a thin and soft membrane that can easily be ruptured by mechanical contact, it is capable of withstanding extreme electrical fields.
The membrane potential can be observed by using the fluorescent probe JC-1 -or more verbosely 5,5’,6,6’-tetrachloro-1,1’,3,3’-tetraethylbenzimidazolylcarbocyanine iodide. JC-1 is a lipophilic cation that can penetrate the (lipo)membrane of the cell and mitochondria. JC-1 can be excited by green laser light and emit fluorescent green light at 530nm when it is in a monomeric form, but if the membrane potential is increased above a threshold around 80-100mV, JC-1 will aggregate and the fluorescense becomes increasingly orange at 590nm [3]. JC-1 is a very tested and reliable marker for the membrane potential [4] [5]. A recipe for the use of JC-1 can be found in [6].
The immunesystem
Fluorescent Markers
Natural cells and biological structures often have very little contrast when seen in optical microscopes. Take a normal yeast cell and look at it under a microscope and you will only see small balls with no structure. Fluorescent markers and dyes can be used to stain specific substances inside the cell which would otherwise not give an appreciable optical signal. Such markers have for many years been essential to get proper images of biological samples. No matter what type of microscope is used, the fluorescent markers are widely used to enhance the contrast and signal to noise ratio in measurements.
Using fluorescent dyes and recording spectra of light emitted from whole or selected parts of cells can give valuable information [7], such as:
- The functional and structural characteristics of normal or malignant cells
- The intracellular dynamics of molecules that are naturally occurring, or added to the cell such as drugs.
- Characterization of the interactions between cells, or the cell and its surrounding media.
- Intracellular dynamics of ions such as Ca++, Mg++, or other important variables such as pH or membrane potentials by using fluorescent markers for the chemicals and potentials under investigation.
The fluorescent markers are used for many other techniques than just microscopy. A method called flow cytometry is very efficient for analyzing large numbers of individual cells. One by one, individual cells pass through a thin channel where they are exposed to the exciting laser light and the emitted fluorescense and absorption is detected by light sensors. The technique gives very good statistical results, but does not allow the detection of eg. individual mithocondria inside a well functioning cell but will rather give an average value of the state of all mithocondria in a single cell.
Ressources
Lengths and Masses in biochemistry
1Da is one atomic mass unit and approximately the mass of a proton. It is about one thousandth of a zeptogram = 10^-24g
- 1 Da Hydrogen
- 8-30 kDa Cytokine
- 950 kDa typical long PMMA polymer chain
- 10.000 DNA base pairs weighs about 40ng
- An organism typically has tens of chromosomes chromosomes, which each can have up to 1000s of genes, and be made from up to 100 million base pairs.
Sizes of small life forms
- Nanobes Nanobes are tiny filamental structures first found in some rocks and sediments. from 20 nm.
- Parvovirus - a family of viruses down to 20 nm
- 'Nanobacteria' or 'Calicifying Nanoparticles (CNP)' - a recently discovered class of nanoparticles that seem related to various calcification processes in the body and may be living [see also new scientist 23 june 2007 p38]. 50-100nm
- Nanoscale microbes (Nanoarchaeota a kind of archaea) [science vol 314 p1933]
- Smallest bacterium ' mycoplasma genitalium' -M. genitalium was also considered to be the organism with the smallest genome. 300 nm
- Nanoarchaeum equitans a thermophile 400 nm
- The largest virus 'mimivirus', that infects amoebaes 400nm
- Possibly the most abundant organism on earth, the marine bacterium 'pelagibacter ubique (SAR11)' 500 nm
- Typical gut bacteria 'E. Coli' 2000-6000 nm.
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ Mitochondrial diseases in man and mouse, Wallace DC, Science, vol. 283 (5407): 1482-1488 MAR 5 1999.
- ↑ Intracellular Heterogeneity In Mitochondrial-Membrane Potentials Revealed By A J-Aggregate-Forming Lipophilic Cation Jc-1, Smiley St, Reers M, Mottolahartshorn C, Lin M, Chen A, Smith Tw, Steele Gd, Chen Lb, Proceedings Of The National Academy Of Sciences Of The United States Of America, Vol. 88 (9): 3671-3675 May 1991 Letters, vol. 78 (11): 1637-1639 MAR 12 2001.
- ↑ Analysis of Mitochondrial Membrane Potential with the Sensitive Fluorescent Probe JC-1, Andrea Cossarizza and Stefano Salvioli, Purdue Cytometry CD-ROM Series,volume 4[4].
- ↑ Evaluation of fluorescent dyes for the detection of mitochondrial membrane potential changes in cultured cardiomyocytes, Mathur A, Hong Y, Kemp BK, Barrientos AA, Erusalimsky JD, Cardiovascular Research, vol. 46 (1): 126-138 APR 2000
- ↑ JC-1, but not DiOC(6)(3) or rhodamine 123, is a reliable fluorescent probe to assess Delta Psi changes in intact cells: Implications for studies on mitochondrial functionality during apoptosis, Salvioli S, Ardizzoni A, Franceschi C, Cossarizza A, FEBS Letters, vol. 411 (1): 77-82 JUL 7 1997
- ↑ Analysis of Mitochondrial Membrane Potential with the Sensitive Fluorescent Probe JC-1, Andrea Cossarizza and Stefano Salvioli, Purdue Cytometry CD-ROM Series,volume 4[5].
- ↑ Manfaits webpage on Le Groupement De Recherche 1860 at the Centre National de la recherche scientifique, [6]
Biosensors
| Navigate |
|---|
| << Prev: Nano-bio Primer |
| >< Main: Nanotechnology |
| >> Next: Targeting Diseases |
Biosensors
Biological sensor functionalisation, receptors and signals
- Assays for measuring the biochemical properties, such as immunesystem responses, specific proteins etc.
- DNA binding protein
- Functional group
- Receptor biochemistry
- Neuron
- The Biotin - Streptavidin binding is the strongest biochemical bond and often used when you need to demonstrate a sensor or bind different biomolecules together.
- Biofouling - by using certain polymers such as PEG or PLL-PEG, cell adhesion to surface can be drastically reduced.
DNA Biosensors
In the future, DNA will find use as a versatile material from which scientists can craft biosensors. DNA biosensors can theoretically be used for medical diagnostics, forensic science, agriculture, or even environmental clean-up efforts. No external monitoring is needed for DNA-based sensing devices. This is a significant advantage. DNA biosensors are complicated mini-machines—consisting of sensing elements, micro lasers, and a signal generator. At the heart of DNA biosensor function is the fact that two strands of DNA stick to each other by virtue of chemical attractive forces. On such a sensor, only an exact fit—that is, two strands that match up at every nucleotide position—gives rise to a fluorescent signal (a glow) that is then transmitted to a signal generator.
Resources
. <http://www.nigms.nih.gov>*Performance limits of nanobiosensors App. Phys. Lett. 88, 233120, 2006.
References
"The Chemistry of Health." The Chemistry of Health (2006): 42-43. National Institutes of Health and National Institute of General Medical Sciences. Web
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
Nanomedicine - Targeting diseases
| Navigate |
|---|
| << Prev: Biosensors |
| >< Main: Nanotechnology |
| >> Next: Environmental Nanotechnology |
NanoMedicine
Helping improve humanity is one of the promises of nanotechnology. Much hope and hype has surrounded nanomedicine. Research is actively pursuing the benefits of nanotechnology enabled medicine and the promise of organ specific drug delivery and cancer treatments. But, there is no consensus among the research and medicine community that shows the toxic effects of heavy metal nanoparticles in the body when used as "treatments". This chapter will highlight some of the research findings in the nanomedicine area.
Scientists are working to find "nanostructers" for many different kinds of cures, including Parkin's and Cardiovascular Disease, treatment for cancer, nanomaterial for new artificial limbs, and nanodevices that could restore hearing and vision. Soon, nanomedicine will be able to cure many diseases and illnesses. References: http://www.medicalnewstoday.com/articles/67702.php
The scientists have found a way to deliver molecules within 'wells' of polymers that are a part of a capsule. They are also making ground medicine with particles in the nanoscale to increase effectiveness.
Source- Nanotechnology A gentle introduction to the next big idea, Written by Mark and Daniel Ranter
- eMedicine – The original open access comprehensive medical textbook for all clinical fields.
- Nanomedicine book site
Example #1: Nanosilver
For thousands of years, silver has been known to be a potent bacteria killer. However, due to the fact that silver could not dissolve well, it's efficiency as an antimicrobial has been slim. This problem has been solved by the company Nucryst Pharmaceuticals. To combat it's inability to dissolve, they use a nanocrystalline form of silver to fight off bacteria. Silver ions rapidly kill microbes in a variety of ways which include blocking the cell respiration pathway, interfering with components of the microbial electron transport system, binding DNA, and inhibiting DNA replication.
Their first product with the silver is Anticoat, a dressing for serious burns. Anticoat antimicrobial barrier dressing works to reduce or kill off bacteria, have high absorbency rates, continue working for a full 7 days, and are easy to remove without disrupting the wound. When the dressing is removed, it peels off in one piece and a new coat can be applied. A high absorbency rate is required because many wounds release a lot of body fluids and a good absorbency rate will maintain a healthy wound environment. It is usable for a week and can also be used for serious words. Also, now they are exploring the anti-inflammatory properties of silver for use in atopic dermatitis and certain respiratory conditions.[1]
Example #2: Regenerating Neurons
There is a research team at USC that is working on producing artificial motor neurons. These neurons could serve several functions; including letting people with paralyzed limbs use their limbs again. These fake neurons would essentially take over the functions of the real motor neurons. Using this technology doctors could replace motor neurons since neurons do not grow back.[2]
Example 3: Peptides for wound healing
Researchers at MIT have found liquids called peptides that form a nanoscale barrier in seconds, stopping the flow of blood. later. when the wound is healed, the solution breaks down and can be used by the body as new tissue. The same scientists also reported that a peptide partially restored a hamster's vision.[3]
Examples #6: Malaria
Dr. Subra Suresh, a professor at MIT, using nanotechnology, has studied malaria, an infection spread by mosquitoes, in which tiny parasites infect the red blood cell. Using “laser tweezers” and two nano-sized glass beads fused to the red blood cell surface, he found that infected cells may be as much as 15-times stiffer than normal cells, which causes them to clog up small blood vessels. He is now looking at the effect of different genes in the parasite that may produce this effect as this may allow the finding of a treatment for this worldwide disease. "Tiny tools tackle malaria", 2005. Retrieved on 6-26-2008.</ref> [95]
Example #7: Increased drug dispersion from nanoparticles
One of the greatest prospects of nanomedicine is in drug delivery. On the most basic level current drugs ground into a smaller state have a greater surface area which allows them to dissolve more quickly in the stomach. A variation on this idea is using small crystals of medicine. These crystals allow every molecule to be close to the surface which creates an environment where even the most slow dissolving compounds will dissolve quickly.[4]
Example #8: Drug delivery polymer nanoparticles
Drug delivery is one of the best benefits of nanomedicine. There are many different schemes for improving drug delivery, for example, molecules can be put into nanoscale cavities inside polymers. The polymer can then be swallowed as part of a tablet or pill, and when the polymer opens inside the body, the drugs can be released into the body. More complex schemes have also been developed, such as getting drugs through cell walls and into the cell. Efficient drug delivery is essential, because many diseases depend on processes within the cell, and can only be affected with drugs delivered into the cell.[5]
Example #9: IMEDD (Intelligent MicroEngineered Drug Delivery)
IMEDD (Intelligent MicroEngineered Drug Delivery) is trying to make tiny drug deliver pumps. The researchers at IMEDD are working with Terry Conlisk, who is an engineer at Ohio State, who has made a computer model that helps small drug reservoirs pump out drugs when they are needed. They use this principal to work the pumps, "If a fluid is positively or negatively charged and there is a like charge to the inner surfaces of a channel, the charges will repel each other. The result is that the fluid will flow down the channel." In their experiments, they have been able to put almost 0.5 nL of saline per minute through a channel only 7nm wide. Medical researchers hope to use this technology to push tiny amounts of drugs into the body exactly where they are needed. They accomplish this by a technique developed by a team of scientists and engineers at ASU called photocapillarity. Photocapillarity is defined as "the microfluidic actuation of water in an enclosed capillary or microchannel using light".[6]
Targeting Cancer
Cancer is the focus of many new nanomedicine therapies under development for repairing damaged tissues and treating and detecting cancer by developing medical interventions at the molecular scale that couples nanotechnology, clinical science, and the life sciences. People are developing innovative drug and gene delivery strategies and modulating molecular events can control cell processes such as initiating, enhancing, and maintaining macro- and micro- vasculature to ensure tissue viability, vessel networks within tissue engineered constructs and autologous tissue flaps and grafts. Developing novel synthetic, natural, or hybrid materials to control cell-material interactions, biomechanics, angiogenesis, and the in vivo release of therapeutic agents.

Cancer example #1: Nanoparticles Generate Supersonic Shock Waves to Target Cancer
Researchers from UCM (the University of Missouri-Columbia) and the United States Army have made a nano-sized “bomb”. This bomb can target drug delivery to cancer tumors without damage to any other cells. The nano thermites produce shock waves in the Mach 3 range. Cancer fighting drugs would be administered via a needle, and then a device would send a pulse into the tumor. The pulse would create little holes in the tumor, so the drugs can enter.[7]
Cancer example #2: monitor post-treatment relapse
MNC is working with the Medical School at Swansea to develop a nanoscale sensor that would be put into the body and would be capable of detecting the growth of cancerous cells in patients. It would monitor post-treatment relapse. This way of finding the cancer cells at an early stage would reduce mortality rates dramatically.[8]
Cancer Example #3: Photodynamic therapy
Photodynamic therapy (a type of treatment for cancer that is nothing like chemotherapy) is directed to hit the spot where the cancer is, it is a therapeutic idea. What happens during photodynamic therapy? They would put a metal nanodot or a molecular dot (the particle) inside your body and then they would shine a type of light to illuminate it from the outside. Then the light is absorbed by which ever particle they put in your body. So if you have a metal nanodot and it have absorbed the light the energy will heat the metal nanodot up making every tissue that it near heat up to. But with the molecular dot the light absorbed creates oxygen molecules that are very energetic. And since the oxygen molecules are highly reactive it chemically reacts or destroy the organic molecules that are beside it (example: tumors).[9]
Cancer Example #4: NIH Roadmap's Nanomedicine initiative
NIH Roadmap's Nanomedicine initiative is working on advancing the study of nanotechnology. They hope to be able to detect cancer cells before a tumor develops and accurately destroy them, and have nano-sized pumps in your body that deliver medicines into your body where you need it. They believe they will be able to do this in ten years. [10]
MRI - Magnetic resonance imaging
MRI Example #1: MRI nanoparticles
Biophan is a company specializing in nanomedical applications. One of their projects is to make MRIs safer for patients with microelectronic implants that include metals. By using a coating of nanomagnetic particles, these devices, including pacemakers, are shielded from the radio waves from the MRI machine and current (which could harm the patient) caused by electromagnetic radiation is reduced. It was also found that these particles could be used as contrast agents to allow for a clearer image by creating sharper contrast among the different tissue types in the body during an MRI scan. Biophan is also working towards longer lasting batteries for pacemakers and other medical devices (by using body heat), smart drug delivery, and other nanomedicine projects. [11]
MRI Example #2: magnetic nanoparticles
Magnetic nanoparticles have shown promise as contrast-enhancing agents for improving cancer detection using magnetic resonance imaging, as miniaturized heaters capable of killing malignant cells, and as targeted drug delivery vehicles. Now, researchers at the University of Nebraska have developed a novel coating for magnetic nanoparticles that allows the particles to carry large amounts of drug and to disperse efficiently in water. This development may enable targeted delivery of water-insoluble anticancer agents or imaging agents. [12]
The story of the 'Nanobacteria'
In 1988, Olavi Kajander discovered what he described as "nanobacteria." Something was killing his mammalian cells, and after looking closer using an electron microscope, he found something inside of the cells. However, this was not any normal bacterium- the organisms had diameters between 20 and 200 nanometers. Their sizes were too small to support a complex metabolism like the bacteria known to microbiologists. Though his nanobacteria was dismissed by most of the rest of the scientific world, Kajander had become attached to them. After multiple failed attempts to prove their scientific legibility, he connected their hard outer shells-made up of calcium phosphate- and kidney stones, which are caused by calcium compounds. It turns out that the so-called "nanobacteria" were related to, not only kidney stones, but ovarian cancer, Alzheimer's, and prostatitis. Though they are not recognized as true bacteria and have no DNA or RNA, nanobacteria can reproduce, albeit slowly. Strange. Interestingly enough, nanobacteria has been reported in underground rock and other such geological formations. Further, there are claims that nanobacteria have been found in meteorites and, after being transported into zero gravity, nanobacteria has been found to reproduce at a much faster rate than when on earth. Some wonder if nanobacteria is not really from earth, but outer space.[13]
BioMedicine
Herb Example #1: Clinacanthus nutans
In Thailand the leaves of Sabah Snake Grass (Clinacanthus nutans) had been used by traditional healers to treat herpes infections and it's shown to have verifieable antiviral activity. It was found that C. Nutons was able to increase lymphocyte proliferation significantly and reduce the activity of natural killer cells (NK Cells) significantly. [14] It's shown to increase immune response activity strong enough to cure different diseases. It's beliefed that it can cure cancer aswell. It possess a strong anti-inflammatory activity, because of the ability to inhibit the neutrophil responsiveness as evidenced by the significant inhibtiion of myeloperoxidase (MPO) activity. C. nutans is a plant used extensively by traditional healers of southern Thailand and North-western Malaysia as a remedy for envenomation be it snakes or venomous insects like scorpions and bees effectively. Cherdchu et al did not find any antivenin activity, that's why it's not known how it's works as Antivenom. Pannangpetch et al looked found antioxidant and protective effects against free radical-induced haemolysis properties in ethanolic extracts of the leaves of C. nutans. [15]
Herb Example #2: Annona muricata
There is evidence indicating that the fruit's extracts selectively inhibit the growth of human breast cancer cells by downregulating expression of epidermal growth factor receptor (EGFR) in vitro and in a mouse model, but the effect has not been studied in humans. [16]
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ Edwards, Steven A. Where are They Taking Us? Weinham Wiley-Vich, 2006. Chapter 8, page 129: Section-Delivering Drugs
- ↑ Edwards, Steven A. The Nanotech Pioneers, Where Are They Taking Us. Weinheim: wiley-vch, 2006. Taken from chap 8, pages 159-161: section- Artificial Cells.
- ↑ http://web.mit.edu/newsoffice/2006/hemostasis.html
- ↑ The Nanotech Pioneers. Edwards Steven A. 2006
- ↑ Ratner, Mark, and Daniel Ratner. Nanotechnology A Gentle Introduction To The Next Big Idea. New Jersey: Prentice Hall PTR, 2003. Chapter 8, page 110-111: Section-Drug Delivery.
- ↑ Edwards, Steven A. Where are They Taking Us? Weinham Wiley-Vich, 2006. Chapter 8, page 140-141: Section- Pumps.
- ↑ Apperson, S.. [http://www.physorg.com/news119702507.html "Nanoparticles Generate Supersonic Shock Waves to Target CancerPhysorg.com, 2008. Retrieved on 2008-6-23.
- ↑ Ruth Bunting, Swansea University. [http://www.science-engineering.net/engineering_improving_lives.htm "Engineering Improving Lives" science-engineering.net, 2008. Taken on 2008-6-24.
- ↑ Ratner, Mark and Daniel Ratner. Nanotechnology A Gentle Introduction To The Next Big Idea. New Jersey: Prentice Hall PTR, November 2002. Chapter 8 page.113: section-Photodynamic Therapy.
- ↑ referenced from: http://nihroadmap.nih.gov/nanomedicine/
- ↑ Edwards, Steven A. (2006). The Nanotech Pioneers: Where Are They Taking Us?, Chapter 8, pages 134-138. Wiley-VCH, Weinheim. ISBN 3527312900.
- ↑ http://nano.cancer.gov/news_center/nanotech_news_2005-06-06b.asp
- ↑ Edwards, Steven (2006). The Nanotech Pioneers, p.141-143. WILEY-VCH, Weinheim. ISBN 3527312900
- ↑ [http://interesjournals.org/IRJPP/Pdf/2012/October/Na-Bangchang%20et%20al.pdf "Anticancer activity and immunostimulating effect on NK-cell activity of a well-known Thai folkloric remedy" interesjournals.org, 2012. Taken on 2013-1-12.
- ↑ [http://www.globinmed.com/index.php?option=com_content&view=article&id=79320 "Pre-Clinical Data for Clinacanthus nutans (Burm.f.) Lindau". Taken on 2013-1-12.
- ↑ [http://www.globinmed.com/index.php?option=com_content&view=article&id=85402:annona-muricata&catid=199:safety-of-herbal&Itemid=139 "Pre-Clinical Data for Annona muricata". Taken on 2013-1-12.
Part 8: Environmental Nanotechnology
| Navigate |
|---|
| << Prev: Targeting Diseases |
| >< Main: Nanotechnology |
| >> Next: Health effects of nanoparticles |
|
|
| <<< Prev. Part: Nano-Bio Primer |
| >>> Next Part: Main page |
How will nanotechnology affect our lives - this part will not look in terms of the technological impact such as faster and cheaper computers, but at the very important health and environmental effects that necessarily must be considered.
When will it help cure cancer or and when might it cause it? Will the apparent ecological benefit of a nanoparticle that improves catalytic reactions be futile when we consider the ecological footprint of the nanoaparticles' life cycle? There are many open questions where the search for answers has only just begun!
Nanotechnology has been proclaimed to imply a wealth of potential benefits for society many of which will have direct or indirect positive effects on the environment. Of specific environmental importance is the potential improved efficiency of energy production, reduced energy use of products, reduced use of chemicals due to e.g. functionalization of surfaces, remediation of soil pollution, improved sensoring and monitoring of the environment and improved functionality of materials.
Additionally, principles of green engineering and chemistry are beginning to be integrated into the development of nanomaterials, meaning that nanotechnology may also lead to more environmental beneficial production methods (Schmidt, 2007) [1].
There are a lot of opportunities but as with many other nanotechnologies there is still a large gap from the research labs to manufacturing and real life use of nanotechnological products and solutions.
The focus here will however be at the potential health and environmental impacts. For a more thorough review of ecopotentials see e.g. Malsch [2] , Dionysiou [3] , Masciangioli [4] ,and Schmidt. [1]
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ a b Schmidt, K.: Green Nanotechnology: It's easier than you think. Woodrow Wilson International Center for Scholars. PEN 8 April 2007 Invalid
<ref>tag; name "Schmidt3a" defined multiple times with different content - ↑ Malsch, I. Benefits, Risks, Ethical, Legal and Social Aspects of Nanotechnology 4th Nanoforum report; Nanoforum: Jun, 04.
- ↑ Dionysiou, D. D. Environmental Applications and Implications of Nanotechnology and Nanomaterials. Journal of Environmental Engineering, Jul, 2004, pp 723-724.
- ↑ Masciangioli, T.; Zhang, W. X. Environmental technologies at the nanoscale. Environmental Science & Technology 2003, 37 (5), 102A-108A.
Health Effects of Nanoparticles
| Navigate |
|---|
| << Prev: Environmental Nanotechnology |
| >< Main: Nanotechnology |
| >> Next: Environmental Impact |
Nanotoxicology: Health effects of nanotechnology
The environmental impacts of nanotechnology have become an increasingly active area of research.
Until recently the potential negative impacts of nanomaterials on human health and the environment have been rather speculative and unsubstantiated[1].
However, within the past number of years several studies have indicated that exposure to specific nanomaterials, e.g. nanoparticles, can lead to a gamut of adverse effects in humans and animals [2], [3], [4].
This has made some people very concerned drawing specific parallels to past negative experiences with small particles [5], [6].
Some types of nanoparticles are expected to be benign and are FDA approved and used for making paints and sunscreen lotion etc. However, there are also dangerous nanosized particles and chemicals that are known to accumulate in the food chain and have been known for many years:
The problem is that it is difficult to extrapolate experience with bulk materials to nanoparticles because their chemical properties can be quite different. For instance, anti-bacterial silver nanoparticles dissolve in acids that would not dissolve bulk silver, which indicates their increased reactivity[7].
An overview of some exposure cases for humans and the environment shown in the table. For an overview of nanoproducts see the section Nanotech Products in this book.
| Product | Examples | Potential release and exposure |
| Cosmetics | IV absorbing TiO2 or ZnO2 in sunscreen | Directly applied to skin and late washed off. Disposal of containers |
| Fuel additives | Cerium oxide additives in the EU | Exhaust emission |
| Paints and coatings | antibacterial silver nanoparticles coatings and hydrophobic nanocoatings | wear and washing releases the particles or components such as Ag+. |
| Clothing | antibacterial silver nanoparticles coatings and hydrophobic nanocoatings | skin absorption; wear and washing releases the particles or components such as Ag+. |
| Electronics | Carbon nanotubes are proposed for future use in commercial electronics | disposal can lead to emission |
| Toys and utensils | Sports gear such as golf clubs are beginning to be made from eg. carbon nanotubes | Disposal can lead to emission |
| Combustion processes | Ultrafine particles are the result of diesel combustion and many other processes can create nanoscale particles in large quantities. | Emission with the exhaust |
| Soil regeneration | Nanoparticles are being considered for soil regeneration (see later in this chapter) | high local emission and exposure where it is used. |
| Nanoparticle production | Production often produces by products that cannot be used (e.g. not all nanotubes are singlewall) | If the production is not suitably planned, large quantities of nanoparticles could be emitted locally in wastewater and exhaust gasses. |
The peer-reviewed journal Nanotoxicology is dedicated to Research relating to the potential for human and environmental exposure, hazard and risk associated with the use and development of nano-structured materials. Other journals also report on the research, for see the full Nano-journal list in this book.
Nanoecotoxicology
In response to the above concerns a new field of research has emergence termed “nano(eco-)toxiciolgoy” defined as the “science of engineered nanodevices and nanostructures that deals with their effects in living organisms” [9].
In the following we will first try to explain why some people are concerned about nanomaterials and especially nanoparticles. This will lead to a general presentation of what is known about the hazardous properties of nanoparticles in the field of the environment and nanoecotoxicology. This includes a discussion of the main areas of uncertainty and gaps of knowledge.
Human or ecotoxicology
The focus of this chapter is on the ecotoxicological - and environmental effects of nanomaterials, however references will be made to studies on human toxicology where it is assumed that such analogies are warranted or if studies have provided new insights that are relevant to the field of nanoecotoxicology as well. As further investigations are made, more knowledge will be gained about human toxicology of nanoparticles.
Production and applications of nanotechnology
At present the global production of nanomaterials is hard to estimate for three main reasons:
- Firstly, the definition of when something is “nanotechnology” is not clear-cut.
- Secondly, nanomaterials are used in a great diversity of products and industries and
- Thirdly, there is a general lack of information about what and how much is being produced and by whom.
In 2001 the future global annual production of carbon-based nanomaterials was estimated to be several hundred tons, but already in 2003 the global production of nanotubes alone was estimated to be around 900 tons distributed between 16 manufacturers [10].
The Japanese company, Frontier Carbon Corp, plan to start an annual production of 40 tons of C60 [11].
It is estimated that the global annual production of nanotubes and fiber was 65 tons equal to €144 million worth and it is expected to surpass €3 billion by 2010 representing an annual growth rate of well over 60% [12].
Even though the information about the production of carbon-based nanomaterials is scarce, the annual production volumes of for instance quantum dots, nano-metals, and materials with nanostructured surfaces are completely unknown.
The development of nanotechnology is still in its infancy, and the current production and use of nanomaterials is most likely not representative for the future use and production. Some estimates for the future manufacturing of nanomaterials have been made. For instance the Royal Society and the Royal Academy of Engineering [6] estimated that nanomaterials used in relation to environmental technology alone will increase from 10 tons per year in 2004 to between 1000-10.000 tons per year before 2020. However, the basis of many of these estimations is often highly unclear and the future production will depend on a number of things such as for instance:
- Whether the use of nanomaterials indeed entails the promised benefits in the long run;
- which and how many different applications and products will eventually be developed and implemented;
- And on how nanotechnology is perceived and embraced by the public?
With that said, the expectations are enormous. It is estimated that the global market value of nano-related products will be U.S. $1 trillion in 2015 and that potentially 7 million jobs will be created globally [13] , [14]
Exposure of environment and humans
Exposure of nanomaterials to workers, consumers, and the environment seems inevitable with the increasing production volumes and the increasing number of commercially available products containing nanomaterials or based on nanotechnology [15].
Exposure is a key element in risk assessment of nanomaterials since it is a precondition for the potential toxicological and ecotoxicological effects to take place. If there is no exposure – there is no risk. Nanoparticles are already being used in various products and the exposure can happen through multiple routes.
Human routes of exposure are:
- dermal (for instance through the use of cosmetics containing nanoparticles);
- inhalation (of nanoparticles for instance in the workplace);
- ingestion (of for instance food products containing nanoparticles);
- and injection (of for instance medicine based on nanotechnology).
Although there are many different kinds of nanomaterials, concerns have mainly been raised about free nanoparticles [6], [16].
Free nanoparticles could either get into the environment through direct outlet to the environment or through the degradation of nanomaterials (such as surface bound nanoparticles or nanosized coatings).
Environmental routes of exposure are multiple.
One route is via the wastewater system. At the moment research laboratories and manufacturing companies must be assumed to be the main contributor of carbon-based nanoparticles to the wastewater outlet.
For other kinds of nanoparticles for instance titanium dioxide and silver, consumer products such as cosmetics, crèmes and detergents, is a key source already and discharges must be assumed to increase with the development of nanotechnology.
However, as development and applications of these materials increases this exposure pattern must be assumed to change dramatically. Traces of drugs and medicine based on nanoparticles can also be disposed of through the wastewater system into the environment.
Drugs are often coated, and studies have show that these coatings can be degraded through either metabolism inside the human body or transformation in environment due to UV-light [17]. Which only emphasises the need to studying the many possible process that will alter the properties of nanoparticles once they are released in nature.
Another route of exposure to the into the environment is from wastewater overflow or if there is an outlet from the wastewater treatment plant where nanoparticles are not effectively held back or degraded.
Additional routes of environmental exposure are spills from production, transport, and disposal of nanomaterials or products [13].
While many of the potential routes of exposure are uncertain scenarios, which need confirmation, the direct application of nanoparticles, such as for instance nano zero valent iron for remediation of polluted areas or groundwater, is one route of exposure that will certainly lead to environmental exposure. Although, remediation with the help of free nanoparticles is one of the most promising environmental nanotechnologies, it might also be one the one raising the most concerns. The Royal Society and The Royal Academy of Engineering [6] actually recommend that the use of free nanoparticles in environmental applications such as remediation should be prohibited until it has been shown that the benefits outweigh the risks.
The presence of manufactured nanomaterials in the environment is not widespread yet, it is important to remember that the concentration of xenobiotic organic chemicals in the environment in the past has increased proportionally with the application of these [18] – meaning that it is only a question of time before we will find nanomaterials such as nanoparticles in the environment – if we have the means to detect them.
The size of nanoparticles and our current lack of metrological methods to detect them is a huge potential problem in relation to identification and remediation both in relation to their fate in the human body and in the environment [11].
Once there is a widespread environmental exposure human exposure through the environment seems almost inevitable since water- and sediment living organisms can take up nanoparticles from water or by ingestion of nanoparticles sorbed to the vegetation or sediment and thereby making transport of nanoparticles up through the food chain possible [19].
Nanoecotoxicology
Despite the widespread development of nanotechnology and nanomaterials through the last 10-20 years, it is only recently that focus has been turned onto the potential toxicological effects on humans, animals, and the environment through the exposure of manufactured nanomaterials [20].
With that being said, it is a new development that potential negative health and environmental impacts of a technology or a material is given attention at the developing stage and not after years of application [21].
The term “nano(eco-)toxicology” has been developed on the request of a number of scientists and is now seen as a separate scientific discipline with the purpose of generating data and knowledge about nanomaterials effects on humans and the environment [22], [23].
Toxicological information and data on nanomaterials is limited and ecotoxicological data is even more limited. Some toxicological studies have been done on biological systems with nanoparticles in the form of metals, metal oxides, selenium and carbon [24], however the majority of toxicological studies have been done with carbon fullerenes [25].
Only a very limited number of ecotoxicological studies have been performed on the effects of nanoparticles on environmentally relevant species, and, as for the toxicological studies, most of the studies have been done on fullerenes. However, according to the European Scientific Committee on Emerging and Newly Identified Health Risks [26] results from human toxicological studies on the cellular level can be assumed to be applicable for organisms in the environment, even though this of cause needs further verification. In the following a summary of the early findings from studies done on bacteria, crustaceans, fish, and plants will be given and discussed.
Bacteria
The effect of nanoparticles on bacteria is very important since bacteria constitute the lowest level and hence the entrance to the food chain in many ecosystems [27].
The effects of C60 aggregates on two common soil bacteria E. coli (gram negative) and B. subtilis (gram positive) was investigated by Fortner et al. [28] on rich and minimal media, respectively, under aerobe and anaerobe conditions. At concentrations above 0.4 mg/L growth was completely inhibited in both cultures exposed with and without oxygen and light. No inhibition was observed on rich media in concentration up to 2.5 mg/L, which could be due to that C60 precipitates or gets coated by proteins in the media. The importance of surface chemistry is highlighted by the observation that hydroxylated C60 did not give any response, which is in agreement with the results obtained by Sayes et al. [29] who investigated the toxicity on human dermal- and liver cells. The antibacterial effects of C60 has furthermore been observed by Oberdorster [30] , who observed remarkably clearer water during experiments with fish in the aquarium with 0.5 mg/L compared to control.
Lyon et al. [31] explored the influence of four different preparation methods of C60 (stirred C60, THF-C60, toluene-C60, and PVP-C60) on Bacillus subtilis and found that all four suspensions exhibited relatively strong antibacterial activity ranging from 0.09 ± 0.01 mg/L- 0.7 ± 0.3 mg/L, and although fractions containing smaller aggregates had greater antibacterial activity, the increase in toxicity was disproportionately higher than the associated increase in surface area.
Silver nanoparticles are increasingly used as antibacterial agent [32]
Crustacean
A number of studies have been performed with the freshwater crustacean Daphnia magna, which is an important ecological important species that furthermore is the most commonly used organisms in regulatory testing of chemicals.
The organism can filter up to 16 ml an hour, which entails contact with large amounts of water in its surroundings. Nanoparticles can be taken up via the filtration and hence could lead to potential toxic effects [33].
Lovern and Klaper [34], [35] observed some mortality after 48 hours of exposure to 35 mg/L C60 (produced by stirring and also known as “nanoC60” or “nC60”), however 50% mortality was not achieved, and hence an LC50 could not be determined [36].
A considerable higher toxicity of LC50 = 0.8 mg/L is obtained when using nC60 put into solution via the solvent tetrahydrofuran (THF) – which might indicate that residues of THF is bound to or within the C60-aggreggates, however whether this is the case in unclear at the moment. The solubility of C60 using sonication has also been found to increase toxicity [37], whereas unfiltered C60 dissolved by sonication has been found to cause less toxicity (LC50 = 8 mg/L). This is attributed to the formation of aggregates, which causes a variation of the bioavailability to the different concentrations. Besides mortality, deviating behavior was observed in the exposed Daphnia magna in the form of repeated collisions with the glass beakers and swimming in circles at the surface of the water [38]. Changes in the number of hops, heart rate, and appendage movement after subtoxic levels of exposure to C60 and other C60-derivatives [39]. However, Titanium dioxide (TiO2) dissolved via THF has been observed to cause increased mortality in Daphania magna within 48 hours (LC50= 5.5 mg/L), but to a lesser extent than fullerenes, while unfiltered TiO2 dissolved by sonication did not results in a increasing dose-response relationship, but rather a variation response [40]. Lovern and Klaper [41] have furthermore investigated whether THF contributed to the toxicity by comparing TiO2 manufactured with and without THF and found no difference in toxicity and hence concluded that THF did not contribute to neither the toxicity of TiO2 or fullerenes.
Experiments with the marine species Acartia tonsa exposed to 22.5 mg/L stirred nC60 have been found to cause up to 23% mortality after 96 hours, however mortality was not significantly different from control25. And exposure of Hyella azteca by 7 mg/L stirred nC60 in 96 hours did not lead to any visible toxic effects – not even by administration of C60 through the feed [42].
Only a limited number of studies have investigated long-term exposure of nanoparticles to crustaceans. Chronic exposure of Daphnia magna with 2.5 mg/L stirred nC60 was observed to cause 40% mortality besides causing sub-lethal effects in the form of reduced reproducibility (fewer offspring) and delayed shift of shield [43].
Templeton et al. [44] observed an average cumulative life-cycle mortality of 13 ± 4% in an Estuarine Meiobenthic Copepod Amphiascus tenuiremis after being exposed to SWCNT, while mean life-cycle mortalities of 12 ± 3, 19 ± 2, 21 ± 3, and 36 ± 11 % were observed for 0.58, 0.97, 1.6, and 10 mg/L.
Exposure to 10 mg/L showed:
- significantly increased mortalities for the naupliar stage and cumulative life-cycle;
- a dramatically reduced development success to 51% for the nauplius to copepodite window, 89% for the copepodite to adult window, and 34% overall for the nauplius to adult period;
- a significantly depressed fertilization rate averaging only 64 ± 13%.
Templeton also observed that exposure to 1.6 mg/L caused a significantly increase in development rate of 1 day faster, whereas a 6 day significant delay was seen for 10 mg/L.
Fish
A limited number of studies have been done with fish as test species. In a highly cited study Oberdorster [45] found that 0.5 mg/L C60 dissolved in THF caused increased lipid peroxidation in the brain of largemouth bass (Mikropterus salmoides). Lipid peroxidation was found to be decreased in the gills and the liver, which was attributed to reparation enzymes. No protein oxidation was observed in any of the mentioned tissue, however a discharge of the antioxidant glutathione occurred in the liver possibility due to large amount of reactive oxygen molecules stemming from oxidative stress caused by C60 [46].
For Pimephales promelas exposured to 1 mg/L THF-dissolved C60, 100 % mortality was obtained within 18 hours, whereas 1 mg/L C60 stirred in water did not lead to any mortality within 96 hours. However, at this concentration inhibition of a gene which regulates fat metabolism was observed. No effect was observed in the species Oryzia latipes at 1 mg/L stirred C60, which indicates different inter-species sensitivity toward C60 [47], [48].
Smith et al. [49] observed a dose-dependent rise in ventilation rate, gill pathologies (oedema, altered mucocytes, hyperplasia), and mucus secretion with SWCNT precipitation on the gill mucus in juvenile rainbow trout.
Smith et al. also observed:
- dose-dependent changes in brain and gill Zn or Cu, partly attributed to the solvent;
- a significant increases in Na+K+ATPase activity in the gills and intestine;
- a significant dose-dependent decreases in TBARS especially in the gill, brain and liver;
- and a significant increases in the total glutathione levels in the gills (28 %) and livers (18 %), compared to the solvent control (15 mg/l SDS).
- Finally, they observed increasing aggressive behavior; possible aneurisms or swellings on the ventral surface of the cerebellum in the brain and apoptotic bodies and cells in abnormal nuclear division in liver cells.
Recently Kashiwada [50]29 reported observing 35.6% lethal effect in embryos of the medaka Oryzias latipes (ST II strain) exposed to 39.4 nm polystyrene nanoparticles at 30 mg/L, but no mortality was observed during the exposure and postexposure to hatch periods at exposure to 1 mg/L. The lethal effect was observed to increase proportionally with the salinity, and 100% complete lethality occurred at 5 time higher concentrated embryo rearing medium. Kashwada also found that 474 nm particles showed the highest bioavailability to eggs, and 39.4 nm particles were confirmed to shift into the yolk and gallbladder along with embryonic development. High levels of particles were found in the gills and intestine for adult medaka exposed to 39.4 nm nanoparticles at 10 mg/L, and it is hypothesized that particles pass through the membranes of the gills and/or intestine and enter the circulation.
Plants
To our knowledge only one study has been performed on phytotoxicity, and it indicates that aluminum nanoparticles become less toxic when coated with phenatrene, which again underlines the importance to surface treatments in relation to the toxicity of nanoparticles [51].
Identification of key hazard properties
Size is the general reason why nanoparticles have become a matter of discussion and concern.
The very small dimensions of nanoparticles increases the specific surface area in relation to mass, which again means that even small amounts of nanoparticles have a great surface area on which reactions could happen.
If a reaction with chemical or biological components of an organism leads to a toxic response, this response would be enhanced for nanoparticles. This enhancement of the inherent toxicity is seen as the main reason why smaller particles are generally more biologically active and toxic that larger particles of the same material [52].
Size can cause specific toxic response if for instance nanoparticles will bind to proteins and thereby change their form and activity, leading to inhibition or change in one or more specific reactions in the body [53].
Besides the increased reactivity, the small size of the nanoparticles also means that they can easier be taken up by cells and that they are taken up and distributed faster in organism compared to their larger counterparts [54], [55].
Due to physical and chemical surface properties all nanoparticles are expected to absorb to larger molecules after uptake in an organism via a given route of uptake [56].
Some nanoparticles such as fullerene derivates are developed specifically with the intention of pharmacological applications because of their ability of being taken up and distributed fast in the human body, even in areas which are normally hard to reach – such as the brain tissue [57]. Fast uptake and distribution can also be interpreted as a warning about possible toxicity, however this need not always be the case [58]. Some nanoparticles are developed with the intension of being toxic for instance with the purpose of killing bacteria or cancer cells [59], and in such cases toxicity can unintentionally lead to adverse effects on humans or the environment.
Due to the lack of knowledge and lack of studies, the toxicity of nanoparticles is often discussed on the basis of ultra fine particles (UFPs), asbestos, and quartz, which due to their size could in theory fall under the definition of nanotechnology [60], [61].
An estimation of the toxicity of nanoparticles could also be made on the basis of the chemical composition, which is done for instance in the USA, where safety data sheets for the most nanomaterials report the properties and precautions related to the bulk material [62].
Within such an approach lies the assumption that it is either the chemical composition or the size that is determining for the toxicity. However, many scientific experts agree that that the toxicity of nanoparticles cannot and should not be predicted on the basis of the toxicity of the bulk material alone [63], [64].
The increased surface area-to-mass ratio means that nanoparticles could potentially be more toxic per mass than larger particles (assuming that we are talking about bulk material and not suspensions), which means that the dose-response relationship will be different for nanoparticles compared to their larger counterparts for the same material. This aspect is especially problematic in connection with toxicological and ecotoxicological experiments, since conventional toxicology correlates effects with the given mass of a substance [65], [66].
Inhalation studies on rodents have found that ultrafine particles of titanium dioxide causes larger lung damage in rodents compared to larger fine particles for the same amount of the substance. However, it turned out that ultra fine- and fine particles cause the same response, if the dose was estimated as surface area instead of as mass [67].
This indicates that surface area might be a better parameter for estimating toxicity than concentration, when comparing different sizes of nanoparticles with the same chemical composition5. Besides surface area, the number of particles has been pointed out as a key parameter that should be used instead of concentration [68].
Although comparison of ultrafine particles, fine particles, and even nanoparticles of the same substance in a laboratory setting might be relevant, it is questionable whether or not general analogies can be made between the toxicity of ultrafine particles from anthropogenic sources (such as cooking, combustion, wood-burning stoves, etc.) and nanoparticles, since the chemical composition and structure of ultrafine particles is very heterogeneous when compared to nanoparticles which will often consists of specific homogeneous particles [69].
From a chemical viewpoint nanoparticles can consist of transition metals, metal oxides, carbon structures and in principle any other material, and hence the toxicity is bound to vary as a results of that, which again makes in impossible to classify nanoparticles according to their toxicity based on size alone [70].
Finally, the structure of nanoparticles has been shown to have a profound influence on the toxicity of nanoparticles. In a study comparing the cytotoxicity of different kinds of carbon-based nanomaterials concluded that single walled carbon nanotubes was more toxic that multi walled carbon nanotubes which again was more toxic than C60 [71].
Hazard identification
In order to complete a hazard identification of nanomaterials, the following is ideally required
- ecotoxicological studies
- data about toxic effects
- information on physical-chemical properties
- Solubility
- Sorption
- biodegradability
- accumulation
- and all likely depending on the specific size and detailed composition of the nanoparticles
In addition to the physical-chemical properties normally considered in relation to chemical substances, the physical-chemical properties of nanomaterials is dependent on a number of additional factors such as size, structure, shape, and surface area. Opinions on, which of these factors are important differ among scientists, and the identification of key properties is a key gap of our current knowledge [72], [73], [74].
There is little doubt that the physical-chemical properties normally required when doing a hazard identification of chemical substances are not representative for nanomaterials, however there is at current no alternative methods. In the following key issues in regards to determining the destiny and distribution of nanoparticles in the environment will be discussed, however the focus will primarily be on fullerenes such as C60.
Solubility
Solubility in water is a key factor in the estimation of the environmental effects of a given substance since it is often via contact with water that effects-, or transformation, and distribution processes occur such as for instance bioaccumulation.
Solubility of a given substance can be estimated from its structure and reactive groups. For instance, Fullerenes consist of carbon atoms, which results in a very hydrophobic molecule, which cannot easily be dissolved in water.
Fortner et al. [75] have estimated the solubility of individual C60 in polar solvents such as water to be 10-9 mg/L. When C60 gets in contact with water, aggregates are formed in the size range between 5-500 nm with a greater solubility of up to 100 mg/L, which is 11 orders of magnitude greater than the estimated molecular solubility. This can, however, only be obtained by fast and long-term stirring in up to two months. Aggregates of C60 can be formed at pH between 3.75 and 10.25 and hence also by pH-values relevant to the environment [75].
As mentioned the solubility is affected by the formation of C60 aggregates, which can lead to changes in toxicity [75].
Aggregates form reactive free radicals, which can cause harm to cell membranes, while free C60 kept from aggregation by coatings do not form free radical [76]. Gharbi et al. [77] point to the accessibility of double bonds in the C60 molecule as an important precondition for its interactions with other biological molecules.
The solubility of C60 is less in salt water, and according to Zhu et al. [78] only 22.5 mg/L can be dissolved in 35 ‰ sea water. Fortner et al. [79] have found that aggregate precipitates from the solution in both salt water and groundwater with an ionic strength above 0.1 I, but aggregates would be stable in surface- and groundwater, which typically have an ionic strength below 0.5 I.
The solubility of C60 can be increased to about 13,000-100,000 mg/L by chemically modifying the C60–molecule with polar functional groups such as hydroxyl [80]. The solubility can furthermore be increased by the use of sonication or the use of none-polar solvents.
C60 will neither behave as molecules nor as colloids in aqueous systems, but rather as a mixture of the two [81], [82].
The chemical properties of individual C60 such as the log octanol-water partitioning coefficient (log Kow) and solubility are not appropriate in regard to estimating the behavior of aggregates of C60. Instead properties such as size and surface chemistry should be applied a key parameters [83]18.
Just as the number of nanomaterials and the number of nanoparticles differ greatly so does the solubility of the nanoparticles. For instance carbon nanotubes have been reported to completely insoluble in water [84]. It should be underlined that which method is used to solute nanoparticles is vital when performing and interpreting environmental and toxicological tests.
Evaporation
Information about evaporation of C60 from aqueous suspensions has so far not been reported in the literature and since the same goes for vapor pressure and Henry’s constant, evaporation cannot be estimated for the time being. Fullerenes are not considered to evaporate – neither from aqueous suspension or solvents – since the suspension of C60 using solvents still entails C60 after evaporation of the solvent [85], [86].
Sorption
According to Oberdorster et al. [87] nanoparticles will have a tendency to sorb to sediments and soil particles and hence be immobile because of the great surface area when compared to mass. Size alone will furthermore have the effect that the transport of nanoparticles will be dominated by diffusion rather than van der Waal forces and London forces, which increases transport to surfaces, but it is not always that collision with surfaces will lead to sorption [88].
For C60 and carbon nanotubes the chemical structure will furthermore result in great sorption to organic matter and hence little mobility since these substances consists of carbon. However, a study by Lecoanet et al. [89]45 found that both C60 and carbon nanotubes are able to migrate through porous medium analogous to a sandy groundwater aquifer and that C60 in general is transported with lower velocity when compared to single walled carbon nanotubes, fullerol, and surface modified C60. The study further illustrates that modification of C60 on the way to - or after - the outlet into the environment can profoundly influence mobility. Reactions with naturally occurring enzymes [90], electrolytes or humid acid can for instance bind to the surface and make thereby increase mobility [91], just as degradation by UV-light or microorganisms could potentially results in modified C60 with increased mobility [92]45.
Degradability
Most nanomaterials are likely to be inert [93], which could be due to the applications of nanomaterials and products, which is often manufactured with the purpose of being durable and hard-wearing. Investigations made so far have however showed that fullerene might be biological degradable whereas carbon nanotubes are consider biologically non-degradable [94], [95]. According to the structure of fullerenes, which consists of carbon only, it is possible that microorganisms can use carbon as an energy source, such as it happens for instance with other carbonaceous substances.
Fullerenes have been found to inhibit the growth of commonly occurring soil- and water bacteria [96], [97] , which indicates that toxicity can hinder degradability. It is, however, possible that biodegradation can be performed by microorganisms other than the tested microorganisms, or that the microorganism adapt after long-term exposure. Besides that C60 can be degraded by UV-light and O [98]. UV-radiation of C60 dissolved in hexane, lead to a partly or complete split-up of the fullerene structure depending on concentration [99].
Bioaccumulation
Carbon based nanoparticles are lipophilic which means that they can react with and penetrate different kinds of cell membranes [100]. Nanomaterials with low solubility (such as C60) could potentially accumulate in biological organisms [101] , however to the best of our knowledge no studies have been performed investigating this in the environment. Biokinetic studies with C60 in rats result in very little excretion which indicates an accumulation in the organisms [102]. Fortner et al. [103] estimates that it is likely that nanoparticles can move up through the food chain via sediment consuming organisms, which is confirmed by unpublished studies performed at Rice University, U.S. [104] Uptake in bacteria, which form the basis for many ecosystems, is also seen as a potential entrance to whole food chains [105].
Surface chemistry and coatings
In addition to the physical and chemical composition of the nanoparticles, it is important to consider any coatings or modifications of a given nanoparticles [106].
A study by Sayes et al. [107] found that the cytotoxicity of different kinds of C60-derivatives varied by seven orders of magnitude, and that the toxicity decreased with increasing number of hydroxyl- and carbonyl groups attached to the surface. According to Gharbi et al. [108], it is in contradiction to previous studies, which is supported by Bottini et al. [109] who found an increased toxicity of oxidized carbon nanotubes in immune cells when compared to pristine carbon nanotubes.
The chemical composition of the surface of a given nanoparticle influences both the bioavailability and the surface charge of the particle, both of which are important factors for toxicology and ecotoxicology. The negative charge on the surface of C60 is suspected to be able to explain these particles ability to induce oxidative stress in cells [110].
The chemical composition also influences properties such as lipophilicity, which is important in relation to uptake through cells membranes in addition to distribution and transport to tissue and organs in the organisms5. Coatings can furthermore be designed so that they are transported to specific organs or cells, which has great importance for toxicity [111].
It is unknown, however, for how long nanoparticles stay coated especially inside the human body and/or in the environment, since the surface can be affected by for instance light if they get into the environment. Experiments with non-toxic coated nanoparticles, turned out to be very cell toxic after 30 min. exposure to UV-light or oxygen in air [112].
Interactions in the Environment
Nanoparticles can be used to enhance the bioavailability of other chemical substances so that they are easily degradable or harmful substances can be transported to vulnerable ecosystems [113].
Besides the toxicity of the nanoparticles itself, it is furthermore unclear whether nanoparticles increases the bioavailability or toxicity of other xenobiotics in the environment or other substances in the human body. Nanoparticles such as C60 have many potential uses in for instance in medicine because of their ability to transport drugs to parts of the body which are normally hard to reach. However, this property is exactly what also may be the source to adverse toxic effects [114]. Furthermore research is being done into the application of nanoparticles for spreading of contaminants already in the environment. This is being pursued in order to increase the bioavailability for degradation of microorganisms [115]54, however it may also lead to increase uptake and increased toxicity of contaminants in plants and animals, but to the best of our knowledge, no scientific information is available that supports this [116], [117].
Conclusion
It is still too early to determine whether nanomaterials or nanoparticles are harmful or not, however the effects observed lately have made many public and governmental institutions aware of
- the lack of knowledge concerning the properties of nanoparticles
- the urgent need for a systematic evaluation of the potential adverse effect of Nanotechnology
Furthermore, some guidance is needed as to which precautionary measures are warranted in order to encourage the development of “green nanotechnologies” and other future innovative technologies, while at the same time minimizing the potential for negative surprises in the form of adverse effects on human health and/or the environment.
It is important to understand that there are many different nanomaterials and that the risk they pose will differ substantially depending on their properties. At the moment it is not possible to identify which properties or combination of properties make some nanomaterials harmful and which make them harmless, and properly it will depend on the nanomaterial is question. This makes it is extremely difficult to do risk assessments and life-cycle assessment of nanomaterials because, in theory, you would have to do a risk assessment for each of the specific variation of nanomaterial – a daunting task!
Contributors to this page
This material is based on notes by
- Steffen Foss Hansen, Rikke Friis Rasmussen, Sara Nørgaard Sørensen, Anders Baun. Institute of Environment & Resources, Building 113, NanoDTU Environment, Technical University of Denmark
- Stig Irving Olsen, Institute of Manufacturing Engineering and Management, Building 424, NanoDTU Environment, Technical University of Denmark
- Kristian Mølhave, Dept. of Micro and Nanotechnology - DTU - www.mic.dtu.dk
References
See also notes on editing this book about how to add references Nanotechnology/About#How_to_contribute.
- ↑ Y. Gogotsi , How Safe are Nanotubes and Other Nanofilaments?, Mat. Res. Innovat, 7, 192-194 (2003) [7]]
- ↑ Cristina Buzea, Ivan Pacheco, and Kevin Robbie "Nanomaterials and Nanoparticles: Sources and Toxicity" Biointerphases 2 (1007) MR17-MR71.
- ↑ Lam, C. W.; James, J. T.; McCluskey, R.; Hunter, R. L. Pulmonary toxicity of single-wall carbon nanotubes in mice 7 and 90 days after intratracheal instillation. Toxicol. Sci. 2004, 77 (1), 126-134.
- ↑ Oberdorster, E. Manufactured nanomaterials (Fullerenes, C-60) induce oxidative stress in the brain of juvenile largemouth bass. Environmental Health Perspectives 2004, 112 (10), 1058-1062.
- ↑ ETCgroup Down on the farm: the impact of nano-scale technologies on food and agriculture; Erosion, Technology and Concentration: 04.
- ↑ a b c d The Royal Society & The Royal Academy of Engineering Nanoscience and nanotechnologies: opportunities and uncertainties; The Royal Society: London, Jul, 04.
- ↑ New Scientist 14 july 2007 p.41
- ↑ New Scientist 14 july 2007 p.41
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ Kleiner, K.; Hogan, J. How safe is nanotech. New Scientist Tech 2003, (2388).
- ↑ a b Mraz, S. J. Nanowaste: The Next big threat? http://www.machinedesign.com/ASP/strArticleID/59554/strSite/MDSite/viewSelectedArticle.asp 2005. Invalid
<ref>tag; name "Mraz7" defined multiple times with different content - ↑ Cientifica Nanotube Production Survey. http://www. cientifica. eu/index. php?option=com_content&task=view&id=37&Itemid=74 2005.
- ↑ a b The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04. Invalid
<ref>tag; name "rs9" defined multiple times with different content - ↑ Roco, M. C. U.S. National Nanotechnology Initiative: Planning for the Next Five Years. In The Nano-Micro Interface: Bridging the Micro and Nano Worlds, Edited by Hans-Jörg Fecht and Matthias Werner, Ed.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, 2004 pp 1-10.
- ↑ Project of Emerging Nanotechnologies at the Woodrow Wilson International Center for Scholars A Nanotechnology Consumer Product Inventory. http://www. nanotechproject. org/44 2007.
- ↑ European Commission Nanotechnologies: A Preliminary Risk Analysis on the Basis of a Workshop Organized in Brussels on 1-2 March 2004 by the Health and Consumer Protection Directorate General of the European Commission; European Commission Community Health and Consumer Protection: 04.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ Colvin, V. The potential environmental impact of engineered nanomaterials. Nature Biotechnology 2003, 21 (10), 1166-1170.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ Colvin, V. The potential environmental impact of engineered nanomaterials. Nature Biotechnology 2003, 21 (10), 1166-1170.
- ↑ Colvin, V. Responsible nanotechnology: Looking beyond the good news. Eurekalert 2002.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ Pierce, J. Safe as sunshine? The Engineer 2004.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Colvin, V. The potential environmental impact of engineered nanomaterials. Nature Biotechnology 2003, 21 (10), 1166-1170.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Sayes, C. M.; Fortner, J. D.; Guo, W.; Lyon, D.; Boyd, A. M.; Ausman, K. D.; Tao, Y. J.; Sitharaman, B.; Wilson, L. J.; Hughes, J. B.; West, J. L.; Colvin, V. L. The differential cytotoxicity of water-soluble fullerenes. Nano Letters 2004, 4 (10), 1881-1887.
- ↑ Oberdorster, E. Manufactured nanomaterials (Fullerenes, C-60) induce oxidative stress in the brain of juvenile largemouth bass. Environmental Health Perspectives 2004, 112 (10), 1058-1062.
- ↑ Lyon, D. Y.; Adams, L. K.; Falkner, J. C.; Alvaraz, P. J. J. Antibacterial Activity of Fullerene Water Suspensions: Effects of Preparation Method and Particle Size . Environmental Science & Technology 2006, 40, 4360-4366.
- ↑ Kim, J.S., et al. Antimicrobial effects of silver nanoparticles. Nanomedicine: Nanotechnology, Biology & Medicine. 3(2007);95-101.
- ↑ Lovern, S. B.; Klaper, R. Daphnia Magna mortality when exposed to titanium dioxide and fullerene (C60) nanoparticles. Environmental Toxicology and Chemistry 2006, 25 (4), 1132-1137.
- ↑ Lovern, S. B.; Klaper, R. Daphnia magna mortality when exposed to titanium dioxide and fullerene (C-60) nanoparticles. Environmental Toxicology and Chemistry 2006, 25 (4), 1132-1137.
- ↑ Lovern, S. B.; Strickler, J. R.; Klaper, R. Behavioral and Physiological Changes in Daphnia magna when Exposed to Nanoparticle Suspensions (Titanium Dioxide, Nano-C60, and C60HxC70Hx). Environ. Sci. Technol. 2007.
- ↑ Oberdorster, E.; Zhu, S. Q.; Blickley, T. M.; Clellan-Green, P.; Haasch, M. L. Ecotoxicology of carbon-based engineered nanoparticles: Effects of fullerene (C-60) on aquatic organisms. Carbon 2006, 44 (6), 1112-1120.
- ↑ Zhu, S. Q.; Oberdorster, E.; Haasch, M. L. Toxicity of an engineered nanoparticle (fullerene, C-60) in two aquatic species, Daphnia and fathead minnow. Marine Environmental Research 2006, 62, S5-S9.
- ↑ Lovern, S. B.; Klaper, R. Daphnia magna mortality when exposed to titanium dioxide and fullerene (C-60) nanoparticles. Environmental Toxicology and Chemistry 2006, 25 (4), 1132-1137.
- ↑ Lovern, S. B.; Strickler, J. R.; Klaper, R. Behavioral and Physiological Changes in Daphnia magna when Exposed to Nanoparticle Suspensions (Titanium Dioxide, Nano-C60, and C60HxC70Hx). Environ. Sci. Technol. 2007.
- ↑ Lovern, S. B.; Klaper, R. Daphnia Magna mortality when exposed to titanium dioxide and fullerene (C60) nanoparticles. Environmental Toxicology and Chemistry 2006, 25 (4), 1132-1137.
- ↑ Lovern, S. B.; Klaper, R. Daphnia Magna mortality when exposed to titanium dioxide and fullerene (C60) nanoparticles. Environmental Toxicology and Chemistry 2006, 25 (4), 1132-1137.
- ↑ Oberdorster, E.; Zhu, S. Q.; Blickley, T. M.; Clellan-Green, P.; Haasch, M. L. Ecotoxicology of carbon-based engineered nanoparticles: Effects of fullerene (C-60) on aquatic organisms. Carbon 2006, 44 (6), 1112-1120.
- ↑ Oberdorster, E.; Zhu, S. Q.; Blickley, T. M.; Clellan-Green, P.; Haasch, M. L. Ecotoxicology of carbon-based engineered nanoparticles: Effects of fullerene (C-60) on aquatic organisms. Carbon 2006, 44 (6), 1112-1120.
- ↑ Templeton, R. C.; Ferguson, P. L.; Washburn, K. M.; Scrivens, W. A.; Chandler, G. T. Life-Cycle Effects of Single-Walled Carbon Nanotubes (SWNTs) on an Estuarine Meiobenthic Copepod. Environ. Sci. Technol. 2006, 40 (23), 7387-7393.
- ↑ Oberdorster, E. Manufactured nanomaterials (Fullerenes, C-60) induce oxidative stress in the brain of juvenile largemouth bass. Environmental Health Perspectives 2004, 112 (10), 1058-1062.
- ↑ Oberdorster, E. Manufactured nanomaterials (Fullerenes, C-60) induce oxidative stress in the brain of juvenile largemouth bass. Environmental Health Perspectives 2004, 112 (10), 1058-1062.
- ↑ Oberdorster, E.; Zhu, S. Q.; Blickley, T. M.; Clellan-Green, P.; Haasch, M. L. Ecotoxicology of carbon-based engineered nanoparticles: Effects of fullerene (C-60) on aquatic organisms. Carbon 2006, 44 (6), 1112-1120.
- ↑ Zhu, S. Q.; Oberdorster, E.; Haasch, M. L. Toxicity of an engineered nanoparticle (fullerene, C-60) in two aquatic species, Daphnia and fathead minnow. Marine Environmental Research 2006, 62, S5-S9.
- ↑ Smith, C. J.; Shaw, B. J.; Handy, R. D. Toxicity of Single Walled Carbon Nanotubes on Rainbow Trout, (Oncorhynchus mykiss): Respiratory Toxicity, Organ Pathologies, and Other Physiological Effects. Aquatic Toxicology 2007, Forthcoming.
- ↑ Kashiwada, S. Distribution of nanoparticles in the see-through medaka (Oryzias latipes). Environmental Health Perspectives 2006, 114 (11), 1697-1702.
- ↑ Yang, L.; Watts, D. J. Particle surface characteristics may play an important role in phytotoxicity of alumina nanoparticles. Toxicology Letters 2005, 158 (2), 122-132.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Gorman, J. Taming high-tech particles. Science News 2002, 161 (13), 200.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ Depledge, M.; Owen, R. Nanotechnology and the environment: risks and rewards. Marine Pollution Bulletine 2005, 50, 609-612.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ Colvin, V. The potential environmental impact of engineered nanomaterials. Nature Biotechnology 2003, 21 (10), 1166-1170.
- ↑ Boyd, J. Rice finds 'on-off switch' for buckyball toxicity. Eurekalert 2004.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ Colvin, V. The potential environmental impact of engineered nanomaterials. Nature Biotechnology 2003, 21 (10), 1166-1170.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Lam, C. W.; James, J. T.; McCluskey, R.; Hunter, R. L. Pulmonary toxicity of single-wall carbon nanotubes in mice 7 and 90 days after in
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ SCENIHR The appropriateness of the risk assessment methodology in accordance with the Technical Guidance Documents for new and existing substances for assessing the risks of nanomaterials; European Commission: 07.
- ↑ SCENIHR The appropriateness of the risk assessment methodology in accordance with the Technical Guidance Documents for new and existing substances for assessing the risks of nanomaterials; European Commission: 07.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Colvin, V. The potential environmental impact of engineered nanomaterials. Nature Biotechnology 2003, 21 (10), 1166-1170.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ SCENIHR The appropriateness of the risk assessment methodology in accordance with the Technical Guidance Documents for new and existing substances for assessing the risks of nanomaterials; European Commission: 07.
- ↑ Oberdorster, G.; Maynard, A.; Donaldson, K.; Castranova, V.; Fitzpatrick, J.; Ausman, K. D.; Carter, J.; Karn, B.; Kreyling, W. G.; Lai, D.; Olin, S.; Monteiro-Riviere, N. A.; Warheit, D. B.; Yang, H. Principles for characterizing the potential human health effects from exposure to nanomaterials: elements of a screening strategy. Particle and Fibre Toxicology 2005, 2 (8).
- ↑ U.S.EPA U.S. Environmental Protection Agency Nanotechnology White Paper;EPA 100/B-07/001; Science Policy Council U.S. Environmental Protection Agency: Washington, DC, Feb, 07.
- ↑ a b c Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Goho, A. Buckyballs at Bat: Toxic nanomaterials get a tune-up. Science News Online 2004, 166 (14), 211.
- ↑ Gharbi, N.; Pressac, M.; Hadchouel, M.; Szwarc, H.; Wilson, S. R.; Moussa, F. [60]Fullerene is a powerful antioxidant in vivo with no acute or subacute toxicity. Nano Lett. 2005, 5 (12), 2578-2585.
- ↑ Zhu, S. Q.; Oberdorster, E.; Haasch, M. L. Toxicity of an engineered nanoparticle (fullerene, C-60) in two aquatic species, Daphnia and fathead minnow. Marine Environmental Research 2006, 62, S5-S9.
- ↑ Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Sayes, C. M.; Fortner, J. D.; Guo, W.; Lyon, D.; Boyd, A. M.; Ausman, K. D.; Tao, Y. J.; Sitharaman, B.; Wilson, L. J.; Hughes, J. B.; West, J. L.; Colvin, V. L. The differential cytotoxicity of water-soluble fullerenes. Nano Letters 2004, 4 (10), 1881-1887.
- ↑ Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Andrievsky, G. V.; Klochkov, V. K.; Bordyuh, A. B.; Dovbeshko, G. I. Comparative analysis of two aqueous-colloidal solutions of C60 fullerene with help of FTIR reflectance and UV-Vis spectroscopy. Chemical Physics Letters 2002, 364 (1-2), 8-17.
- ↑ Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Health and Safety Executive Health effects of particles produced for nanotechnologies;EH75/6; Health and Safety Executive: Dec, 04.
- ↑ Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Deguchi, S.; Alargova, R. G.; Tsujii, K. Stable Dispersions of Fullerenes, C60 and C70, in Water. Preparation and Characterization. Langmuir 2001, 17 (19), 6013-6017.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ Lecoanet, H. F.; Bottero, J. Y.; Wiesner, M. R. Laboratory assessment of the mobility of nanomaterials in porous media. Environmental Science & Technology 2004, 38 (19), 5164-5169.
- ↑ Lecoanet, H. F.; Bottero, J. Y.; Wiesner, M. R. Laboratory assessment of the mobility of nanomaterials in porous media. Environmental Science & Technology 2004, 38 (19), 5164-5169.
- ↑ European Commission Nanotechnologies: A Preliminary Risk Analysis on the Basis of a Workshop Organized in Brussels on 1-2 March 2004 by the Health and Consumer Protection Directorate General of the European Commission; European Commission Community Health and Consumer Protection: 04.
- ↑ Brant, J.; Lecoanet, H.; Wiesner, M. R. Aggregation and deposition characteristics of fullerene nanoparticles in aqueous systems. Journal of Nanoparticle Research 2005, 7, 545-553.
- ↑ Lecoanet, H. F.; Bottero, J. Y.; Wiesner, M. R. Laboratory assessment of the mobility of nanomaterials in porous media. Environmental Science & Technology 2004, 38 (19), 5164-5169.
- ↑ Gorman, J. Taming high-tech particles. Science News 2002, 161 (13), 200
- ↑ Colvin, V. Responsible nanotechnology: Looking beyond the good news. Eurekalert 2002.
- ↑ Health and Safety Executive Health effects of particles produced for nanotechnologies;EH75/6; Health and Safety Executive: Sudbury, Suffolk, UK, Dec, 04.
- ↑ Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Oberdorster, E. Manufactured nanomaterials (Fullerenes, C-60) induce oxidative stress in the brain of juvenile largemouth bass. Environmental Health Perspectives 2004, 112 (10), 1058-1062.
- ↑ Fortner, J. D.; Lyon, D. Y.; Sayes, C. M.; Boyd, A. M.; Falkner, J. C.; Hotze, E. M.; Alemany, L. B.; Tao, Y. J.; Guo, W.; Ausman, K. D.; Colvin, V. L.; Hughes, J. B. C-60 in water: Nanocrystal formation and microbial response. Environmental Science & Technology 2005, 39 (11), 4307-4316.
- ↑ Taylor, R.; Parsons, J. P.; Avent, A. G.; Rannard, S. P.; Dennis, T. J.; Hare, J. P.; Kroto, H. W.; Walton, D. R. M. Degradation of C60 by light. Nature 1991, 351 (6324), 277.
- ↑ Zhu, S. Q.; Oberdorster, E.; Haasch, M. L. Toxicity of an engineered nanoparticle (fullerene, C-60) in two aquatic species, Daphnia and fathead minnow. Marine Environmental Research 2006, 62, S5-S9.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Yamago, S.; Tokuyama, H.; Nakamura, E.; Kikuchi, K.; Kananishi, S.; Sueki, K.; Nakahara, H.; Enomoto, S.; Ambe, F. In-Vivo Biological Behavior of A Water-Miscible Fullerene - C-14 Labeling, Absorption, Distribution, Excretion and Acute Toxicity. Chemistry & Biology 1995, 2 (6), 385-389.
- ↑ Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environmental Health Perspectives 2005, 113 (7), 823-839.
- ↑ Brumfiel, G. A little knowledge. Nature 2003, 424 (6946), 246-248.
- ↑ Brown, D. Nano Litterbugs? Experts see potential pollution problems. [8] 2002.
- ↑ Scientific Committee on Emerging and Newly Identified Health Risks Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR) Opinion on The appropriateness of existing methodologies to assess the potential risks associated with engineered and adventitious products of nanotechnologies Adopted by the SCENIHR during the 7th plenary meeting of 28-29 September 2005;SCENIHR/002/05; European Commission Health & Consumer Protection Directorate-General: 05.
- ↑ Sayes, C. M.; Fortner, J. D.; Guo, W.; Lyon, D.; Boyd, A. M.; Ausman, K. D.; Tao, Y. J.; Sitharaman, B.; Wilson, L. J.; Hughes, J. B.; West, J. L.; Colvin, V. L. The differential cytotoxicity of water-soluble fullerenes. Nano Letters 2004, 4 (10), 1881-1887.
- ↑ Gharbi, N.; Pressac, M.; Hadchouel, M.; Szwarc, H.; Wilson, S. R.; Moussa, F. [60]Fullerene is a powerful antioxidant in vivo with no acute or subacute toxicity. Nano Lett. 2005, 5 (12), 2578-2585.
- ↑ Bottini, M.; Bruckner, S.; Nika, K.; Bottini, N.; Bellucci, S.; Magrini, A.; Bergamaschi, A.; Mustelin, T. Multi-walled carbon nanotubes induce T lymphocyte apoptosis. Toxicology Letters 2006, 160 (2), 121-126.
- ↑ Sayes, C. M.; Fortner, J. D.; Guo, W.; Lyon, D.; Boyd, A. M.; Ausman, K. D.; Tao, Y. J.; Sitharaman, B.; Wilson, L. J.; Hughes, J. B.; West, J. L.; Colvin, V. L. The differential cytotoxicity of water-soluble fullerenes. Nano Letters 2004, 4 (10), 1881-1887.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ Oberdorster, E. Manufactured nanomaterials (Fullerenes, C-60) induce oxidative stress in the brain of juvenile largemouth bass. Environmental Health Perspectives 2004, 112 (10), 1058-1062.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ Masciangioli, T.; Zhang, W. X. Environmental technologies at the nanoscale. Environmental Science & Technology 2003, 37 (5), 102A-108A.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ Depledge, M.; Owen, R. Nanotechnology and the environment: risks and rewards. Marine Pollution Bulletine 2005, 50, 609-612.
- ↑ The Royal Society & The Royal Academy of Engineering Nanosciences and nanotechnologies: opportunities and uncertainties; The Royal Society: London, 04.
- ↑ European Commission Nanotechnologies: A Preliminary Risk Analysis on the Basis of a Workshop Organized in Brussels on 1-2 March 2004 by the Health and Consumer Protection Directorate General of the European Commission; European Commission Community Health and Consumer Protection: 04.
Environmental Impact
| Navigate |
|---|
| << Prev: Health effects of nanoparticles |
| >< Main: Nanotechnology |
| >> Next: Nano and Society |
Potential environmental impacts of nanotechnology
So far most of the focus has been on the potential health and environmental risks of nanoparticles and only a few studies has been made of the overall environmental impacts during the life cycle such as ecological footprint (EF) or life cycle analysis (LCA). The life cycle of nanoproducts may involve both risks to human health and environment as well as environmental impacts associated with the different stages.
The topics of understanding and assessing the environmental impacts and benefits of nanotechnology throughout the life cycle from extraction of raw materials to the final disposal have only been addressed in a couple of studies. The U.S. EPA, NCER have sponsored a few projects to investigate Life Cycle Assessment methodologies. Only one of these has yet published results on automotive catalysts [1] and nanocomposites in automobiles [2] , respectively, and one project was sponsored by the German government [3] .
A 2007 special issue of Journal of Cleaner Production puts focus on sustainable development of nanotechnology and includes a recent LCA study in Switzerland [4] .
The potential environmental impact of nanomaterials could be more far-reaching than the potential impact on personal health of free nanoparticles. Numerous international and national organizations have recommended that evaluations of nanomaterials be done in a life-cycle perspective [5] , [6],
This is also one conclusion from a recent series of workshops in the US on “green nanotechnology” (Schmidt, 2007)[7] .
A workshop co-organised by US EPA/Woodrow Wilson Center and EU Commission DG Research put focus on the topic of Life Cycle Assessments of Nanotechnologies (Klöpffer et al., 2007) [8] .
Heresome of the potential environmental impacts related to nanotechnological products in their life cycle are discussed followed by some recommendations to the further work on Life Cycle Assessment (LCA) of nanotechnological products.
However, when relating to existing experience in micro-manufacturing (which to a large extent resembles the top-down manufacturing of nanomaterials) several environmental issues emerge that should be addressed. There are indications that especially the manufacturing and the disposal stages may imply considerable environmental impacts. The toxicological risks to humans and the environment in all life cycle stages of a nanomaterials have been addressed above. Therefore, the potentially negative impacts on the environment that will be further explored in the following are:
- Increased exploitation and loss of scarce resources;
- Higher requirement to materials and chemicals;
- Increased energy demand in production lines;
- Increased waste production in top down production;
- Rebound effects (horizontal technology);
- Increased use of disposable systems;
- Disassembly and recycling problems.
Exploitation and loss of scarce resources
Exploitation and loss of scarce resources is a concern since economic consideration is a primary obstacle to use precious or rare materials in everyday products. When products get smaller and the components that include the rare materials reach the nanoscale, economy is not the most urgent issue since it will not significantly affect the price of the product. Therefore, developers will be more prone to use materials that have the exact properties they are searching. For example in the search for suitable hydrogen storage medias Dillon et al. [9] experimented with the use of fullerenes doped with Scandium to increase the reversible binding of Hydrogen. Other examples are the use of Gallium and other rare metals in electronics. While an increased usage of such materials may be foreseen due to the expected widespread use of nanotechnological products, the recycling will be more difficult (will be discussed more in detail later), resulting in non-recoverable dissemination of scarce resources.
Energy intensity of materials
An issue apart from the loss of resources is the fact that the extraction of most rare materials uses more energy and generates more waste than more abundant materials. Table 1 illustrates the energy intensity of a range of materials. [10]
| Material | Energy intensity of materials (MJ/kg) |
| Glass | 15 |
| Steel | 59 |
| Copper | 94 |
| Ferrite | 59 |
| Aluminium | 214 |
| Plastics | 84 |
| Epoxy resin | 140 |
| Tin | 230 |
| Lead | 54 |
| Nickel | 340 |
| Silver | 1570 |
| Gold | 84000 |
Life cycle assessment (LCA)
As mentioned there are not many studies on LCA of nanotechnology and much information has to be understood from extrapolation of experiences from MEMS and micro manufacturing.
In the micro world LCA has predominantly been used in the Micro-Electro-Mechanical Systems (MEMS) sector. The rapid development of technologies and limited availability of data makes full blown LCAs difficult and rather quickly outdated. An example is the manufacture of a PC for which the energy requirement in the late 1980’s were app. 2150 kWh whereas in the late 90’s efficiency were improved and only 535 kWh were necessary [11] .
Using old data could result in erroneous results. Looking at the overall environmental impact this fourfold increase in efficiency has been overcompensated by an increase in number of sold computers from app. 21 mio to more than 150 mio [11] causing an overall increase in environmental impact. This is often referred to as a rebound effect. For the development of cell phones, the same authors conclude that life cycle impacts vary significantly from one product generation to the next; hence generic product life cycle data should incorporate a “technology development factor” for main parameters.
A major trend is that shrinking product dimensions raise production environment requirements to prevent polluting the product. It involves energy intensive heating, ventilation and air conditioning systems. Clean room of class 10.000 for example requires app. 2280 kWh/m2∙a whereas a class 100 requires 8440 kWh/m2∙a. The same increase of requirements is relevant for supply materials like chemicals and gases. The demand for higher purity levels implies more technical effort for chemical purification, e.g. additional energy consumption and possibly more waste. Most purification technologies are highly energy intensive, e.g. all distillation processes, which are often used in wet chemical purification, account in total for about 7 % of energy consumption of the U.S. chemical industry [12] . Chemicals used in large volumes in semiconductor industry are hydrofluoric acid (HF), hydrogen peroxide (H2O2) and ammonium hydroxide (NH4OH). These materials are used in final cleaning processes and require XLSI grades (0.1 ppb). Sulphuric acid is also used in large amounts, but it is a less critical chemical and mainly requires an SLSI level purity [12] .
Micromanufacturing of other types of products also puts higher requirements on the quality and purity of the materials, e.g. a smaller grain size in metals because of the smaller dimensions of the final product. Additionally, a considerable amount of waste is produced. For example, up to 99% of the material used for microinjection moulding of a component may be waste since big runner are necessary for handling and assembly. However, recycling of this waste may not be possible due to requirements to and reduction of the material strength [13] .
Miniaturisation also cause new problems in electronics recycling. Take-back will hardly be possible. If they are integrated into other product they need to be compatible with the recycling of these products (established recycling paths) [11] .
The very small size and incorporation into many different types of products including product with limited longevity suggests an increased use of disposable systems is required.
Life cycle assessment of nanotechnology
As mentioned previously only few LCA studies have until now been performed for nanotechnological products. A two day workshop on LCA of nanotechnological products concluded that the current ISO-standard on LCA (14040) applies to nanotechnological products but also that some development is necessary [8] [14]
The main issues are that:sometimes it cracks the nerve
- There is no generic LCA of nanomaterials, just as there is no generic LCA of chemicals.
- The ISO-framework for LCA (ISO 14040:2006) is fully suitable to nanomaterials and nanoproducts, even if data regarding the elementary flows and impacts might be uncertain and scarce. Since environmental impacts of nanoproducts can occur in any life cycle stage, all stages of the life cycle of nanoproducts should be assessed in an LCA study.
- While the ISO 14040 framework is appropriate, a number of operational issues need to be addressed in more detail in the case of nanomaterials and nanoproducts. The main problem with LCA of nanomaterials and nanoproducts is the lack of data and understanding in certain areas.
- While LCA brings major benefits and useful information, there are certain limits to its application and use, in particular with respect to the assessment of toxicity impacts and of large-scale impacts.
- Within future research, major efforts are needed to fully assess potential risks and environmental impacts of nanoproducts and materials (not just those related to LCA). There is a need for protocols and practical methodologies for toxicology studies, fate and transport studies and scaling approaches.
- International cooperation between Europe and the United States, together with other partners, is needed in order to address these concerns.
- Further research is needed to gather missing relevant data and to develop user-friendly eco-design screening tools, especially ones suitable for use by small and medium sized enterprises.
Some of the concerns regarding the assessment of toxicological impacts is closely linked to the risk assessment of nanoparticles and have to await knowledge building in this area. However, the most striking is the need for knowledge and cases where LCA are applied in order to increase understanding of nanotechnological systems – what are the potential environmental impacts? How do they differ between different types of nanotechnologies? Where should focus be put in order to prevent environmental impacts? Etc.
Additional resources
- Nanometer societal assessment of nanotechnological applications prior to market release.
Contributors to this page
This material is based on notes by
- Stig Irving Olsen, Department of Manufacturing Engineering and Management, Building 424, NanoDTU Environment, Technical University of Denmark
and also by
- Steffen Foss Hansen, Rikke Friis Rasmussen, Sara Nørgaard Sørensen, Anders Baun. Institute of Environment & Resources, Building 113, NanoDTU Environment, Technical University of Denmark
- Kristian Mølhave, Dept. of Micro and Nanotechnology - DTU - www.mic.dtu.dk
References
See also notes on editing this book Nanotechnology/About#How_to_contribute.
- ↑ Lloyd, S. M.; Lave, L. B.; Matthews, H. S. Life Cycle Benefits of Using Nanotechnology To Stabilize Platinum-Group Metal Particles in Automotive Catalysts. Environ. Sci. Technol. 2005, 39 (5), 1384-1392.
- ↑ Lloyd, S. M.; Lave, L. B. Life Cycle Economic and Environmental Implications of Using Nanocomposites in Automobiles. Environ. Sci. Technol. 2003, 37 (15), 3458-3466.
- ↑ Steinfeldt, M.; Petschow, U.; Haum, R.; von Gleich, A. Nanotechnology and Sustainability. Discussion paper of the IÖW 65/04; IÖW: 04.
- ↑ Helland A, Kastenholz H, Development of nanotechnology in light of sustainability, J Clean Prod (2007), doi:10.1016/j.jclepro.2007.04.006
- ↑ The Royal Society & The Royal Academy of Engineering Nanoscience and nanotechnologies: opportunities and uncertainties; The Royal Society: London, Jul, 04
- ↑ U.S.EPA U.S. Environmental Protection Agency Nanotechnology White Paper;EPA 100/B-07/001; Science Policy Council U.S. Environmental Protection Agency: Washington, DC, Feb, 07.
- ↑ Schmidt, K.: Green Nanotechnology: It's easier than you think. Woodrow Wilson International Center for Scholars. PEN 8 April 2007
- ↑ a b Klöpffer, W., Curran, MA., Frankl, P., Heijungs, R., Köhler, A., Olsen, SI.: Nanotechnology and Life Cycle Assessment. A Systems Approach to Nanotechnology and the Environment. March 2007. Synthesis of Results Obtained at a Workshop in Washington, DC 2–3 October 2006.
- ↑ Dillon AC, Nelson BP, Zhao Y, Kim Y-H, Tracy CE and Zhang SB: Importance of Turning to Renewable Energy Resources with Hydrogen as a Promising Candidate and on-board Storage a Critical Barrier. Mater. Res. Soc. Symp. Proc. Vol. 895, 2006
- ↑ Kuehr, R.; Williams, E. Computers and the environment; Kluwer Academic Publishers: Dordrecht, Boston, London, 2003.
- ↑ a b c Schischke, K.; Griese, H. Is small green? Life Cycle Aspects of Technology Trends in Microelectronicss and Microsystems. http://www. lcacenter. org/InLCA2004/papers/Schischke_K_paper. pdf 2004
- ↑ a b Plepys, A. The environmental impacts of electronics. Going beyond the walls of semiconductor fabs. IEEE: 2004; pp 159-165.
- ↑ Sarasua, J. R.; Pouyet, J. Recycling effects on microstructure and mechanical behaviour of PEEK short carbon-fibre composites. Journal of Materials Science 1997, 32, 533-536.
- ↑ Something funny is happening with ref klöpffer3b
Nano and Society
| Navigate |
|---|
| << Prev: Environmental Impact |
| >< Main: Nanotechnology |
| >> Next: The Nanotechnology Talk Page |
Principles for the Revision and Development of this Chapter of the Wikibook
Unless they are held together by book covers or hypertext links, ideas will tend to split up as they travel. We need to develop and spread an understanding of the future as a whole, as a system of interlocking dangers and opportunities. This calls for the effort of many minds. The incentive to study and spread the needed information will be strong enough: the issues are fascinating and important, and many people will want their friends, families, and colleagues to join in considering what lies ahead. If we push in the right directions - learning, teaching, arguing, shifting directions, and pushing further - then we may yet steer the technology race toward a future with room enough for our dreams. -Eric Drexler, Engines of Creation, 1986
Our method for growing and revising this chapter devoted to Nanotechnology & Society will emphasize an open source approach to "nanoethics" - we welcome collaboration from all over the planet as we turn our collective attention to revising and transforming the current handbook. Nature abhors a vacuum, so we are lucky to begin not with nothing but with a significant beginning begun by a Danish scientist, Kristian Molhave. You can read the correspondence for the project.
Our principles for the revision and development of this section of the wikibook will continue to develop and will be based on those of wikibooks manual of style
Introduction
Nanotechnology is already a major vector in the rapid technological development of the 21st century. While the wide ranging effects of the financial crisis on the venture capital and research markets have yet to be understood, it is clear from the example of the integrated circuit industry that nanotechnology and nanoscience promise to (sooner or later) transform our IT infrastructure. Both the World Wide Web and peer-to-peer technologies (as well as wikipedia) demonstrate the radical potential of even minor shifts in our IT infrastructure, so any discussion of nanotechnology and society can, at the very least, inquire into the plausible effects of radical increases in information processing and production. The effects of, for example, distributed knowledge production, are hardly well understood, as the recent Wikileaks events have demonstrated. The very existence of distributed knowledge production irrevocably alters the global stage.
Given the history of DDT and other highly promising chemical innovations, it is now part of our technological common sense to seek to "debug" emerging technologies. This debugging includes, but is not limited to, the effects of nanoscale materials on our health and environment, which are often not fully understood. The very aspects of nanotechnology and nanoscience that excite us - the unusual physical properties of the nanoscale (e.g. increase in surface area) - also pose problems for our capacity to predict and control nanoscale phenomena, particularly in their connections to the larger scales - such as ourselves! This wikibook assumes (in a purely heuristic fashion) that to think effectively about the implications of nanotechnology and emerging nanoscience, we must (at the very least) think in evolutionary terms. Nanotechnology may be a significant development in the evolution of human capacities. As with any other technology (nuclear, bio-, info), it has a range of socio-economic impacts that influences and transforms our context. While "evolution" often conjures images of ruthless competition towards a "survival of the fittest," so too should it involve visions of collective symbiosis: According to Margulis and Sagan,[1] "Life did not take over the globe by combat, but by networking" (i.e., by cooperation)[2].
Perhaps in this wikibook chapter we can begin to grow a community of feedback capable of such cooperative debugging. Here we will create a place for sharing plausible implications of nanoscale science and technology based on emerging peer reviewed science and technology. Like all chapters of all wikibooks, this is offered both as an educational resource and collective invitation to participate. Investigating the effects of nanotechnology on society requires that we first and foremost become informed participants, and definitions are a useful place to begin.
Strictly speaking, nanotechnology is a discourse. As a dynamic field in rapid development across multiple disciplines and nations, the definition of nanotechnology is not always clear cut. Yet, it is still useful to begin with some definitions. "Nanotechnology" is often used with little qualification or explanation, proving ambiguous and confusing to those trying to grow an awareness of such tiny scales. This can be quite confusing when the term "nano" is used both as a nickname for nanotechnology and a buzzword for consumer products that have no incorporated nanotechnology (eg. "nano"- car and ipod). It is thus useful for the student of nanoscale science to make distinctions between what is "branded" as nanotechnology and what this word represents in a broader sense. Molecular biologists could argue that since DNA is ~2.5 nm wide, life itself is nanotechnological in nature -- making the antibacterial silver nanoparticles often used in current products appear nano-primitive in comparison. SI units, the global standard for units of measurement, assigns the "nano" prefix for 10 -9 meters, yet in usage "nano" often extends to 100 times that size. International standards based on SI units offer definitions and terminology for clarity, so we will follow that example while incorporating the flexibility and open-ended nature of a wiki definition. Our emerging glossary of nano-related terms will prove useful as we explore the various discourses of nanotechnology.
Imagining Nanotechnology
As a research site and active ecology of design, the discussions in all of the many discourses of nanotechnology and nanoscience must imagine beyond the products currently marketed or envisioned. It thus often traffics in science fiction style scenarios, what psychologist Roland Fischer called the "as-if true" register of representation. Indeed, given the challenges of representing these minuscule scales smaller than a wavelength of light, "speculative ideas" may be the most accurate and honest way of describing our plausible collective imaginings of the implications of nanotechnology. Some have proposed great advantages derived from utility fogs of flying nanomachinery or self replicating nanomachines, while others expressed fears that such technology could lead to the end of life as we know it when self replicating nanites take over in a hungry grey goo scenario. Currently there is no theorized mechanism for creating such a situation, though the outbreak of a synthesized organism may be a realistic concern with some analogies to some of the feared scenarios. More profoundly, thanks to historical experience we know that technological change alters our planet in radical and unpredictable ways. Though speculative, such fears and hopes can nevertheless influence public opinion considerably and challenge our thinking thoroughly. Imaginative and informed criticism and enthusiasm are gifts to the development of nanotechnology and must be integrated into our visions of the plausible impacts on society and the attitudes toward nanotechnology.
While fear leads to overzealous avoidance of a technology, the hype suffusing nanotechnology can be equally misleading, and makes many people brand products as "nano" despite there being nothing particularly special about it at the nanoscale. Examples have even included illnesses caused by a "nano" product that turned out to have nothing "nano" in it.
Between the fear and the hype, efforts are made to map the plausible future impact of nanotechnology. Hopefully this will guide us to a framework for the development of nanotechnology, and avoidance of excessive fear and hype in the broadcast media. So far, nanotechnology has probably been more disposed to hype, with much of the public relatively uninformed about either risks or promises. Nanotechnology may follow the trend of biotechnology, which saw early fear (Asilomar) superseded by enthusiasm (The Human Genome Project) accompanied by widespread but narrowly focused fear (genetically modified organisms).
What pushes nano research between the fear and hype of markets and institutions? Nanotechnology is driven by a market pull for better products (sometimes a military pull to computationally "own" battlespace), but also by a push from public funding of research hoping to open a bigger market as well as explore the fundamental properties of matter on the nanoscale. The push and pull factors also change our education, particularly at universities where cross-disciplinary nano-studies are increasingly available.
Finally, nanotechnology is a part of the evolution of not only our technological abilities, but also of our knowledge and understanding. The future is unknown, but it is certain to have a range of socio-economic impacts, sculpting the ecosystem and society around us.
This chapter looks at these societal and environment aspects of the emerging technology.
Building Scenarios for the Plausible Implications of Nanotechnology
Scenario building requires scenario planning.
Technophobia and Technophilia Associated with Nanotechnology
Technophobia
Technophobia exists presently as a societal reaction to the darker aspects of modern technology. As it concerns the progress of nanotechnology, technophobia is and will play a large role in the broader cultural reaction. Largely since the industrial revolution, many different individuals and collectives of society have feared the unintended consequences of technological progress. Moral, ethical, and aesthetic issues propagating from emergent technologies are often at the forefront discourse of said technologies. When society deviates from the natural state, human conciseness tends to question the implications of a new rationale. Historically, several groups have emerged from the swells of technophobia, such as the Luddites and the Amish.
Technophilia
It is interesting to contemplate the role that technophilia has played in the development of nanotechnology. Early investigators such as Drexler drew on the utopian traditions of science fiction in imagining a Post Scarcity and even immortal future, a strand of nanotechnology and nanotechnology that continues with the work of Kurzweil and, after a different fashion, Joy. In more contemporary terms, it is the technophilia of the market that seems to drive nanotechnology research: faster and cheaper chips.
Anticipatory Symptoms: The Foresight of Literature
...reengineering the computer of life using nanotechnology could eliminate any remaining obstacles and create a level of durability and flexibility that goes beyond the inherent capabilities of biology. --Ray Kurzweil, The Singularity is Near
The principles of physics, as far as I can see, do not speak against the possibility of maneuvering things atom by atom. It would be, in principle, possible...for a physicist to synthesize any chemical substance that the chemist writes down..How? Put the atoms down where the chemist says, and so you make the substance. The problems of chemistry and biology can be greatly helped if our ability to see what we are doing, and to do things on an atomic level, is ultimately developed--a development which I think cannot be avoided.
--Richard Feynman, There's Plenty of Room at the Bottom
There is much horror, revulsion, and delight regarding the promise and peril of nanotechnology explored in science fiction and popular literature. When machinery can allegedly outstrip the capabilities of biological machinery (See Kurzweil's notion of transcending biology), much room is provided for speculative scenarios to grow in this realm of the "as-if true". The "good nano/bad nano" rhetoric is consistent in nearly all scenarios posited by both trade science and sci-fi writers. The "grey goo" scenario plays the role of the "bad nano", while "good nano" is traffics in immortality schemes and a post scarcity economy. The good scenario usual features a "nanoassembler", an as yet unrealized machine run by physics and information--a machine that can create anything imagined from blankets to steel beams with a schematic and the push of a button. Here "good nano" follows in the footsteps of "good biotech", where life extension and radically increased health beckoned from somewhere over the DNA rainbow. Reality, of course, has proved more complicated
Grey goo, the fear that a self-replicating nanobot set to re-create itself using a highly common atom such as carbon, has been played out by many sources and is the great cliche of nanoparanoia. There are two notable science fiction books dealing with the grey goo scenario. The first, Aristoi by Walter John Williams, describes the scenario with little embellishment. In the book, Earth is quickly destroyed by a goo dubbed "Mataglap nano" and a second Earth is created, along with a very rigid hierarchy with the Aristoi--or controllers of nanotechnology--at the top of the spectrum. The other, Chasm City by Alastair Reynolds, describes the scenario as a virus called the melding plague. It converts pre-existing nanotechnology devices to meld and operate in dramatically different ways on a cellular level. This causes the namesake city of the novel to turn into a large, mangled mess wildly distorted by a mass-scale malfunctioning of nanobots.
The much more delightful (and more probable) scenario of a machine that can create anything imagined with a schematic and raw materials is dealt with extensively in The Diamond Age or A Young Lady's Illustrated Primer by Neil Stephenson and The Singularity is Near by Ray Kurzweil. Essentially, the machine works by combining nanobots that follow specific schematics and produces items on an atomic level--fairly quickly. The speculated version has The Feed, a grid similar to today's electrical grid that delivers molecules required to build its many tools.
Is the future of civilization safe with the fusion of malcontent and nanotechnology?
Early Contexts and Precursors: Disruptive Technologies and the Implementation of the Unforeseeable
In 2004, a study in Switzerland was conducted on the management of nanotechnology as a disruptive technology.
In many organization R&D models, two general categories of technology development are examined. “Sustainable technologies” are those new technologies that improve existing product and market performance. Known market conditions of existing technologies provide valuable opportunities for the short-term success of additions and improvements to those technologies. For example, the iphone’s entrance into the cellular market was largely successfully due to the existence of a pre-existing consumer cell phone market. On the other hand, “disruptive technologies” (e.g. peer-to-peer networks, Twitter) often enter the market with little or nothing to stand on - they are unprecedented in scale, often impossible to contain and highly unpredictable in their effects. These technologies often have few short-term benefits and can result in the failure of the organizations that invest in such radical market introductions.
At least some nanotechnologies are likely to fit into this precarious category of disruptive technologies. Corporations typically have little experience with disruptive technologies, and as a result it is crucial to include outside expertise and processes of dissensus as early as possible in the monitoring of newly synthesized technologies. The formation of a community of diverse minds, both inside and outside cooperate jurisdiction, is fundamental to the process of planning a foreseeable environment for the emergence of possible disruptive technologies. Here, non-corporate modalities of governance (e.g. standards organizations, open source projects, universities) may thrive on disruptive technologies where corporations falter. Ideally in project planning, university researchers, contributors, post-docs, and venture capitalists should consult top-level management on a regular basis throughout the disruptive technology evaluation process. This ensures a broad and clear base of technological prediction and market violability that will pave a constructive pathway for the implementation of the unforeseeable.
A cooperative paradigm shift is more often than not needed when evaluating disruptive technologies. Instead of responding to current market conditions, the future market itself must be formulated. Taking the next giant leap in corporate planning is risky and requires absolute precision through maximum redundancy "with a thousand pairs of eyes, all bugs are shallow." Alongside consumer needs, governmental, political, cultural, and societal values must be added into the equation when dealing such high-stakes disruptive technologies such as nanotechnology. Therefore, the dominant function of nanotech introduction is not derived from a particular organization’s nanotech competence base, but from a future created by an inter-organizational ecosystem of multiple institutions.
Early Symptoms
Global Standards
Global standards organizations have already worked on metrological standards for nanotechnology, making uniformity of measurement and terminology more likely. Global organizations such as ISO, IEC, OASIS, and BIPM would seem likely venues for standards in Nanotechnology & Society. IEC has included environmental health and safety in its purview.
Examples of Hype
Predicted revolutions tend to be difficult to make, and the nanorevolution might turn in other directions than initially anticipated. A lot of the exotic nanomaterials that have been presented in the media have faded away and only remain in science fiction, perhaps to be revisited by later researchers. Some examples of such materials are artificial atoms or quantum corrals, the space elevator, and nanites. Nano-hype exists in our collective consciousness due to the many products with which carry the nano-banner. The BBC demonstrated in 2008 the joy of nano that we currently embrace globally.
The energy required to fabricate nanomaterials and the resulting ecological footprint might not make the nanoversion of an already existing product worth using – except in the beginning when it is an exotic novelty. Carbon nanotubes in sports gear could be an example of such overreach. Also, a fear of the toxicity, both biologically and ecologically speaking, from newly synthesized nanotechnologies should be examined before full throttle is set on said technologies. Heir apparent to the thrones of the Commonwealth realms, Charles, Prince of Wales, has made his concerns about nano-implications known in a statement he gave in 2004. Questions have been raised about the safety of zinc oxide nanoparticles in sunscreen, but the FDA has already approved of its sale and usage. In order to expose the realities and complexities of newly introduced nanotechnologies, and avoid another anti-biotech movement, nano-education is the key.
Surveys of Nanotechnology
Since 2000, there has been increasing focus on the health and environmental impact of nanotechnology. This has resulted in several reports and ongoing surveillance of nanotechnology. Nanoscience and nanotechnologies: Opportunities and Uncertainties is a report by the UK Royal Society and the Royal Academy of Engineering. Nanorisk is a bi-monthly newsletter published by Nanowerk LLC. Also, the Woodrow Wilson Center for International Scholars is starting a new project on emerging nanotechnologies (website is under construction) that among other things will try to map the available nano-products and work to ensure possible risks are minimized and benefits are realized.
Nanoethics
Nanoethics, or the study of nanotechnology's ethical and social implications, is a rising yet contentious field. Nanoethics is a controversial field for many reasons. Some argue that it should not be recognized as a proper area of study, suggesting that nanotechnology itself is not a true category but rather an incorporation of other sciences, such as chemistry, physics, biology and engineering. Critics also claim that nanoethics does not discover new issues, but only revisits familiar ones. Yet the scalar shift associated with engineering tolerances at 10-9th suggests that this new mode of technology is analogous to the introduction of entirely new "surfaces" to be machined. Writing technologies or external symbolic storage (Merlin Donald) and the wheel both opened up entirely new dimensions to technology - consciousness and smoothed spaced respectively. (Deleuze and Guattari)
Outside the realms of industry, academia, and geek culture, many people learn about nanotechnology through fictional works that hypothesize necessarily speculative scenarios which scientists both reject and, in the tradition of gedankenexperiment, rely upon. Perhaps the most successful meme associated with nanotechnology has ironically been Michael Chrichton's treatment of self-replicating nanobots running amok like a pandemic virus in his 2002 book, Prey.
In the mainstream media, reports proliferate about the risks that nanotechnology poses to the environment, health, and safety, with conflicting reports within the growing nanotechnology industry and its trade press, both silicon and print. To orient the ethical and social questions that arise within this rapidly changing evolutionary dynamic, some scholars have tried to define nanoscience and nanoethics in disciplinary terms, yet the success of Chrichton's treatment may suggest that nanoethics is more likely to be successful if it makes use of narrative as well as definitions. Wherever possible, this wikibook will seek to use both well defined terms and offer the framework of narrative to organize any investigation of nanoethics. Nanoscience and Nanoethics: Definning The Disciplines[3] is an excellent starting guide to the this newly emerging field.
Concern: scientists/engineers as
-Dr. Strangeloves? (intentional SES impact)
-Mr. Chances? (ignorant of SES impact)
- journal paper on nanoethics[96]
- Book on nanoethics [97]
Take a look at their chapters for this section…
- Grey goo and radical nanotechnology[98]
- A nanoethics university group [101]
- Cordis Nanoethics project [102]
Concern: Nanohazmat
- New nanomaterials are being introduced to the environment simply through research. How many graduate students are currently washing nanoparticles, nanowires, carbon nanotubes, functionalized buckminsterfullerenes, and other novel synthetic nanostructures down the drain? Might these also be biohazards? (issue: Disposal)
- Oversight of nanowaste may lead to concern about other adulterants in waste water: (issue: Contamination/propagation)
- estrogens/phytoestrogens[103]
- BPA[104]?
- Might current systems (ala MSDS[105]) be modified to include this information?
- What about a startup company to reprocess such materials, in the event that some sort of legislative oversight demands qualified disposal operations?
There may well be as many ethical issues connected with the uses of nanotechnology as with biotechnology. [4]
- Joachim Schummer and Davis Baird, Nanotechnology Challenges, Implications for Philosophy, Ethics and Society
Prisoner's Dilemma and Ethics
The prisoner's dilemma constitutes a problem in game theory. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W. Tucker formalized the game with prison sentence payoffs and gave it the prisoner's dilemma name (Poundstone, 1992). In its classical form, the prisoner's dilemma ("PD") is presented as follows:
Two suspects are arrested by the police. The police have insufficient evidence for a conviction, and, having separated both prisoners, visit each of them to offer the same deal. If one testifies (defects from the other) for the prosecution against the other and the other remains silent (cooperates with the other), the betrayer goes free and the silent accomplice receives the full 10-year sentence. If both remain silent, both prisoners are sentenced to only six months in jail for a minor charge. If each betrays the other, each receives a five-year sentence. Each prisoner must choose to betray the other or to remain silent. Each one is assured that the other would not know about the betrayal before the end of the investigation. How should the prisoners act?
If we assume that each player cares only about minimizing his or her own time in jail, then the prisoner's dilemma forms a non-zero-sum game in which two players may each cooperate with or defect from (betray) the other player. In this game, as in all game theory, the only concern of each individual player (prisoner) is maximizing his or her own payoff, without any concern for the other player's payoff. The unique equilibrium for this game is a Pareto-suboptimal solution, that is, rational choice leads the two players to both play defect, even though each player's individual reward would be greater if they both played cooperatively. In the classic form of this game, cooperating is strictly dominated by defecting, so that the only possible equilibrium for the game is for all players to defect. No matter what the other player does, one player will always gain a greater payoff by playing defect. Since in any situation playing defect is more beneficial than cooperating, all rational players will play defect, all things being equal.
In the iterated prisoner's dilemma, the game is played repeatedly. Thus each player has an opportunity to punish the other player for previous non-cooperative play. If the number of steps is known by both players in advance, economic theory says that the two players should defect again and again, no matter how many times the game is played. Only when the players play an indefinite or random number of times can cooperation be an equilibrium. In this case, the incentive to defect can be overcome by the threat of punishment. When the game is infinitely repeated, cooperation may be a subgame perfect equilibrium, although both players defecting always remains an equilibrium and there are many other equilibrium outcomes. In casual usage, the label "prisoner's dilemma" may be applied to situations not strictly matching the formal criteria of the classic or iterative games, for instance, those in which two entities could gain important benefits from cooperating or suffer from the failure to do so, but find it merely difficult or expensive, not necessarily impossible, to coordinate their activities to achieve cooperation.
The Nanotechnology Market and Research Environment
Market
Value chain
See also notes on editing this book in About this book.
The National Science Foundation has made predictions of the of nanotechnology by 2015
- $340 billion for nanostructured materials,
- $600 billion for electronics and information-related equipment,
- $180 billion in annual sales from nanopharmaceutircals
[5] All in all about 1000 Billion USD.
“The National Science Foundation (a major source of funding for nanotechnology in the United States) funded researcher David Berube to study the field of nanotechnology. His findings are published in the monograph “Nano-Hype: The Truth Behind the Nanotechnology Buzz". This published study (with a foreword by Mihail Roco, Senior Advisor for Nanotechnology at the National Science Foundation) concludes that much of what is sold as “nanotechnology” is in fact a recasting of straightforward materials science, which is leading to a “nanotech industry built solely on selling nanotubes, nanowires, and the like” which will “end up with a few suppliers selling low margin products in huge volumes."
Market analysis
- The World Nanotechnology Market (2006) [106]
- nanotube ecology http://www.nanotechproject.org/file_download/files/Nanotube%20SFA%20Report_revised%20part2.pdf
Some products have always been nanostructured:
- Carbon blac used to color the rubber black in tires is a $4 billion industry.
- Silver used in traditional photographic films
According to Lux Research, "only about $13 billion worth of manufactured goods will incorporate nanotechnology in 2005."
"Toward the end of the decade, Lux predicts, nanotechnology will have worked their way into a universe of products worth $292 billion."
Three California companies are developing nanomaterial for improving catalytic converters: Catalytic Solutions, Nanostellar, and QuantumSphere. QuantumSphere, Inc. is a leading manufacturer of high-quality nano catalysts for applications in portable power, renewable energy, electronics, and defense. These nanopowders can be used in batteries, fuel cells, air-breathing systems, and hydrogen production cells. They are also a leading producer of NanoNickel and NanoSilve.
Cyclics Corp adds nanoscale clays to it's registered resin for higher termal stability, stiffiness, dimensional stability, and barrier to solvent and gas penetration. Cyclics resins expand the use of thermoplastics to make plastics parts that cannot be made using thermoplastics today, and make them better, less expensively and recyclable. Naturalnano is a nanomaterials company developing applications that include industrial polymers, plastics, and composites; and additives to cosmetics, agricultural, and household products. Industrial Nanotech has developed nansulate, a spray on coating with remarkable insulating qualities claiming the highest quality insulation on the planet with temperature ranges from -40 to 400 C. The coating can be applied to: Pipes-Tanks-Ducts-Boilers-Refineries-Ships-Trucks-Containers-Commercial-Industrial-Residential.
ApNano is a producer of nanotubes and nanosphere made from inorganic compounds. ApNano product, Nanolub is a solid lubricant that enhances the performance of moving parts, reduces fuel consumption, and replaces other additives. Production will shift from the United States and Japan to Korea and China by 2010, and the major supplier of the nanotubes will be Korea. Nanosonic is creating metal rubber that exhibits electrical conductivity.
GE Advanced Materials and DOW Automotive have both developed nanocomposite technologies for online painted vertical body panels. Mercedes is using a clear-cost finish that includes nanoparticle engineered to cluster together where form a shell resistant to abrasion. eMembrane is developing a nanoscale polymer brush that coats with molecules to capture and remove poisonous metal proteins, and germs.
A study by FTM Consulting reported future chips that use nanotechnology are forecasted to grow in sales from $12.3 billion in 2009 to $172 billion by 2014. According to one Harvard researcher, applied nanowires to glass substrates in solution and then used standard photolithography techniques to create circuits. Nanomarkets predicts the market for nano-enabled electronics will reach $10.8 billion in 2007 and $82.5 billion in 2011. IBM researchers created a circuit capable of performing simple logic calculations via self-assembled carbon nanotubes (Millipede) and Millipede will be able to store forty times more information as current hard drives. MRAM will be inexpensive enough to replace SRAM and nanomarket predicts MRAM will rise to $3.8 billion by 2008 and 12.9 billion by 2011. Cavendish Kinetics store data using thousands of electro-mechanical switches that are toggeled up or down to represent either a one or a zero as a binary bit. Their devices use 100 times less power and work up to a 1000 times faster. Currently, the most common nanostorage devices are based on ferroelectric random access memory, FRAM. Data are store using electric fields inside a capacitor. Typically FRAM memory chips are found in electronics devices for storing small amounts of non-volatile data. A team from Case Western has approached production issues by growing carbon nanotube bridges in its lab that automatically attach themselves to other components with the help of an applied electrical current. You can grow building blocks of ultra large scale integrated circuits by growing self-assembled and self-welded carbon nanotubes. Applied Nanotech using an electron-beam lithograph carved switches from wafers made of single-crystal layers of silicon and silicon oxide.
Research Funding
//Michael can you tell me how much funding the EC goes to ‘nano’?
How big a percentage of nano research funding is
- Corporate research funding (eg. Intel)
- Public funding (eg. National nano initiative)
- Military funding (public and corporate) [107]
These may sum up to more than 100% since the groups overlap.
For the US 2007:
135 billion federal research budget[108]
73 billion military Research, Development, Testing & Evaluation
The nanotechnology related part is a fraction of this budget amounting to a couple of billions [109] [110]
(newer reference is needed)
Open Source Nanotechnology
Common property resource management is critical to many areas of society. Public spaces such as forests and rivers are natural commons that can generally be utilized by anyone. With these natural spaces, resource management is in place to minimize the impact of any single user. With the advent of intellectual property, such as publications, designs, artwork, and more recently, computer software, the patent system seeks to control the distribution of such information in order to secure the livelihood of the developer. Open source is a development technique whereby the design is decentralized and open to the community for collaboration.
While patents reward knowledge generation by an individual or company, the reward of open source is usually the rapid development of a quality product. It is characterized by reliability and adaptability through continual revisions. The most notable usage for open source is in the software development community. The Linux operating system is continually improved by a large volunteer community, who desire to make robust software that can compete with the profit-based software companies while making it freely downloadable for users. The incentive for programmers is a highly regarded reputation in the community and individual pride in their work.
Author Bryan Bruns believes that this open source model can be applied to the development of nanotechnology. Nanotechnology and the Commons - Implications of Open Source Abundance in Millennial Quasi-Commons is a thoroughly written paper concerning open source nanotechnology by Bryan Bruns. The article describes roles of the open source nanotechnology community based on the claim that the technology for nanotechnology manufacturing will one day be ubiquitous. Since his early work a more urgent call has been coming for nanotechnology researchers to use open source methodologies to development nanotechnology because a nanotechnology patent thicket is slowing innovation.[6] For example, a researcher argued in the journal Nature the application of the open-source paradigm from software development can both accelerate nanotechnology innovation and improve the social return from public investment in nanotechnology research.[7]
Building equipment, food and other materials might become as easy, and cheap, as printing on paper is now. Just as a laborious process of handwriting texts was transformed first into an industrial technology for mass production and then individualized in computer printers, so also the manufacturing of equipment and other goods might also reach the same level of customized production. If "assemblers" could fabricate materials to order, then what would matter would not be the materials, but the design, the knowledge lying behind manufacture. The most important part of nanotechnology would be the software, the description of how to assemble something. This design information would then be quintessentially an information resource, software. -Bryan Bruns, Nanotechnology and the Commons - Implications of Open Source Abundance in Millennial Quasi-Commons
Several important elements of an open source nanotechnology community will be:
- Establishment of standards - early adopters will have the task of developing standards of nanotechnology design and production for which the rest of the community will improve gradually.
- Development of containment strategies - built-in failsafes that will prevent the unchecked reproduction and operation of "nanoassemblers". One possible scheme is the design of specialized inputs for nanoassemblers that are required for operation--the machine has to stop when the input runs out.
- Innovative nanotechnology design and modelling tools - software that allows users to design and model technology produced in the nanoscale before using time and materials to fabricate the technology.
- Transparency to external monitoring - the ability to observe the development of technology reduces the risk of "unsafe" or "unstable" designs from being released into the public.
- Lowered cost - the price of managing an open source community is insignificant compared to the cost of management to secure intellectual property.
Application of Open Source to Nanotechnology
There are many currently existing open source communities that can serve as working models for an open source nanotechnology community. Internet forums promote knowledge and community input. In addition, new forum users are quickly exposed to a wealth of knowledge and experience. This type of format is easily accessible and promotes widespread awareness of the topic. One such community is:
[H]ard|OCP (http://www.hardforum.com) "[H]ard|OCP (Hardware Overclockers Comparison Page) is an online magazine that offers news, reviews, and editorials that relate to computer hardware, software, modding, overclockingcooling, owned and operated by Kyle Bennett, who started the website in 1997"[1]. Hardforum is a direct parallel to an traditional open source software community. Members obtain recognition, reputation, and respect by spending time and effort within the community. Members can create and discuss diverse topics that are not limited to just software. Projects focusing on case modding are of key interest as a parallel example of what is possible for a nanotechnology project. Within these case modding projects, specific steps, documention, results, and pictures are all shared within the community for both good and bad comments. The information is presented in a pure and straight forward manor for the purpose of information sharing.
Socioeconomic Impact of Nanotechnology
Predicting is difficult, especially about the future and nanotech is likely not going to take us where we first anticipated.
For a Perspective
- Nuclear technology was hailed the new era of humanity in the 60’s, but today is left with little future as a power source due to low availability for long term Uranium sources[111] and evidence that utilization of nuclear power systems still generates appreciable CO2 emissions[112]. The development of nuclear technology however has provided us with a wide range of therapeutic tools in hospitals and taught us a thorough lesson on assessing the potential environmental impact before taking a new technology to a large scale.
- DDT was once the cure-all for malaria and mosquito related diseases as well as a general pesticide for agriculture. It turned out that DDT accumulated in the food chain and was banned, leading to a rise in the plagues it had almost eradicated. Today DDT is still generally banned by slowly reintroduced to be used where it has a high efficiency and will not be spread into nature and in minute quantities compared to when it was lavishly sprayed onto buildings, fields and wetlands in the 1950’s. [113]
- I need references for this one:
Polymer technology was ‘hot’ in the early 90’s but results were not coming as fast as anticipated, leading to a rapid decline in funding. But after the ‘fall’, the technology has matured and polymer composites are now finding applications everywhere. One could say the technology was actually very worthy of funding but expectations were too high leading to disappointment. But time has been working for polymer technology even without large scale funding and now it is reemerging –often disguised as nanotechnology.
- Biotechnology, especially genemodified crops, were promised to eradicate hunger and malnutritionreference needed. Fears of the environmental impact led to strict legislation limiting its use in practical applications, and many cases have since proven the restrictions sensible as new an unexpected paths for cross-breeding have been discovered[[reference needed]. However, the market pull for cheaper products leads to increased GM production worldwide with a wide range of socio-economic impacts such as poor farmers dependence on expensive GM seeds, nutrition aspects and health influence[[reference needed].
These examples do not even include the military aspects of the technologies or the spin-off to civil life from military research – which is luckily quite large considering that in the US the military research budget is about 40% of the annual research funding [114] reference needed and check up on the number!.
Socioeconomic Impact
The examples in the previous section demonstrate clearly how difficult it is to predict the impact of new technology society because of contingency - the inability to know which trajectories today determine the future.
Contingency stem from two main causes:
1) Trends versus events
Events -Taking a non-linear dynamics and somewhat mathematical point of view, Events (in nonlinear dynamics) are deterministic and so can be described with a model but they are also unpredictable (i.e. the model does not give point predictions when exactly they will occur)
Trends – The trends we observe depend largely on the framing we have in our perception of problems and their solutions. The framing is the analytical lens through which we perceive evolution and it changes over time.
Impact of Nanotechnologies on Developing Countries
Many in developing countries suffer from very basic needs, like malnutrition and lack of safe drinking water. Many have poor infrastructure in private and public R&D., including small public research budgets and virtually no venture capital.Even if they are developing such infrastructures, they still have little experience in technology governance, including the launch and conduct of research programs, safety and environmental regulations, marketing and patenting strategies, and so on. These are a couple of points to point out on the effect of Nanoenabled cheap produced solar-cells on these counties:
- Whether a product is useful and its use is beneficial to a country are difficult to assess in advance.
- The Problem with many technologies is that scientific context often ( by definition) ignores the prevailing socioeconomic and cultural factors of a technology, such as social acceptance, customs and specific needs.
- Expensive healthcare products only benefit the economic elite and risk increasing the health divide between the poor and rich.
- According to the NNI, nanotechnology will be the “next industrial revolution”. This can be a unique opportunity for developing countries to quickly catch up with their economical development.
- About two billion people worldwide have no access to electricity (World Energy Council, 1999), especially in rural areas.
- Nanotechnology seems to be a promising potential in increasing efficiency and reducing cost of solar cells.
- Solar technologies seem to be particularly promising for developing countries in geographic areas with high solar radiation.
- Many international organizations have promoted solar rural electrification since the 1980’s, such as UNESCO’s summer schools on Solar Electricity for Rural Areas and the Solar Village program.
- The real challenges of these technologies are largely of an educational and cultural nature.
- Implementing open source into nanotechnology, cheap solar cells for rural communities might be a possibility.
[1] "Impact of nanotechnologies in the developing world"[8]
Contributors
This page is largely based on contributions by Kristian Mølhave and Richard Doyle.
Case Studies of Ongoing Research and Likely Implications
E SC 497H (EDSGN 497H STS 497H) is a course offered at Penn State University entitled Nanotransformations: The Social, Human, and Ethical Implications of Nanotechnology. Three case studies from the Spring 2009 class offer new insight into three different areas of current Nano and Society study: Nanotechnology and Night Vision; Nanotechnology and Solar Cells; Practical Nanotechnology. A sample syllabus for courses focused on nanotechnology's impact on society can prove helpful for other researchers and academics who want to synthesize new Nano and Society courses.
References
- ↑ Margulis, Lynn (2001). "Marvellous microbes". Resurgence. 206: 10–12.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Witzany, G. (2006) The Serial Endosymbiotic Theory (SET): The Biosemiotic Update. Acta Biotheoretica 54: 103-117
- ↑ Patrick Lin and Fritz Allhoff, Nanoethics: The Ethical and Social Implications of Nanotechnology. Hoboken, New Jersey: John Wiley & Sons, Inc., 2007.
- ↑ a b
Joachim Schummer and Davis Baird, Nanotechnology Challenges, Implications for Philosophy, Ethics and Society, (New Jersey: World Scientific, 2006).
Invalid
<ref>tag; name "ChallengesSB" defined multiple times with different content - ↑ From a review of the book “Nano-Hype: The Truth Behind the Nanotechnology Buzz”
- ↑ Usman Mushtaq and Joshua M. Pearce “Open Source Appropriate Nanotechnology ” Chapter 9 in editors Donald Maclurcan and Natalia Radywyl, Nanotechnology and Global Sustainability, CRC Press, pp. 191-213, 2012.
- ↑ Joshua M. Pearce "Make nanotechnology research open-source", Nature 491, pp. 519–521(2012).
- ↑ Patrick Lin and Fritz Allhoff, Nanoethics: The Ethical and Social Implications of Nanotechnology. Hoboken, New Jersey: John Wiley & Sons, Inc., 2007.
Authors
| Navigate |
|---|
| << Prev: Overviews |
| >< Main: Nanotechnology |
| >> Next: Reaching Out |
Vision
We hope to use the Wikibooks format to make an Open Source Handbook on Nanoscience and Nanotechnology, freely accessible for everyone, that can be updated continuously.
Wikipedia is growing fast and one of the most visited websites on the net – a valuable resource of information we all use.
In science and technology we often need more detailed information than what can be presented in a brief encyclopedic article – and here wikibooks.org, a sister project to Wikipedia, can help us with this newly started handbook.
Though the book is still in its infancy, it has been elected book of the month December 2006, and we hope this will provide PR and more people contributing to the project!
The plan to create the book:
1: First to create smaller articles to ‘cover’ the entire area of nanotechnology and achieve a well defined structure the book (some parts could be revised thoroughly in this process,for instance the materials chapter).
2: Once the structure is reasonably well defined, to begin refining the articles with in-depth material so we reach lecture-note level material.
3: Since everybody can contribute, a continuous contribution of material is expected and a backing group of editors is needed to maintain a trustworthy level of information.
An voluntary editorial board is being put together to oversee the book, support, contribute and follow its development.
Discussion about the content of the book can be found on the main talk page talk:Nanotechnology
As with Wikipedia, we hope to see a solid information resource continuously updated with open source material available for everyone!
Editing hints
References in Wikibooks
Add references whenever possible, with reference lists at the end of each page. Please try to make links to the articles with the DOI (digital object identifier) because that gives a uniform and structured access for everyone to the papers.
All papers get a DOI - a unique number like a bar code in a supermarket. All DOIs are registered by www.doi.org and in the reference list you can add links like https://doi.org/10.1039/b504435a so people will be able to find it no matter how the homepage of the journal or their own library changes.
The References section has an example reference.
Add links to the Wikipedia whenever possible - and for the beginning I will rely extensively on Wikipedia's pages on the subjects, simply referring to these. This textbook could be simply a gathering of Wikipedia pages, but an encyclopedia entry is brief, and for a handbook it is preferable to have more in-depth material with examples and the necessary formulas. So, some information in this textbook will be very much like the Wikipedia entries and we might not need to write it in the book but can simply refer to Wikipedia, but the hope is that this will be more a text book as is the intention with Wikibooks.
Multiple references, see w:Help:Footnotes
Links
There's a shorthand way to make links to Wikipedia from Wikibooks: [[w:Quantum_tunneling|Wikipedia on Quantum Tunneling]] gives the link Wikipedia on Quantum Tunneling.
Media
History
The book was started by Kristian Molhave (wiki user page) 13. Apr. 2006. Initially it was named Nanowiki, and later changed to Nanotechnology. Kristian is currently slowly uploading material to the book and looking for people who would like to contribute that can and substantial material to specific sections under the GNU license. I hope we can make an 'editorial panel' of people each keeping an eye on and updating specific sections.
The Summer 2008 Duke Talent Identification Program (TIP) eStudies Nanotechnology students will be adding to the content of this Wikibook. From June-Aug 2008 there will be content additions with references that will add to this great resource.
Authors and Editors
- The Opensource Handbook on Nanoscience and Nanotechnology was started by Kristian Molhave(wiki user page)
Editors
- An editorial board is currently being organized.
Support and Acknowledgments
Starting this book is supported by the Danish Agency for Science, Technology and Innovation through Kristian Mølhave's talent project ’NAMIC’ No. 26-04-0258.
How to Reference this Book
I am not currently sure how work on wikibooks or wikipedia can be referenced reliably in published literature.
Three suggestions:
1) Reference the references from the wikibook. Wikibooks are not intended to be the publication channel for new results, but should be based on published and accepted information with references and these references can be used. But this of course does not give credit to the book, so I recommend then adding an acknowledgement about the book to give it PR and credit.
2) Reference the book with a specific page and date - the previous versions of the pages are all available in the history pane and can easily be accessed by future users. You can also hit "permanent version" on the left side of the webpage (it is under "toolbox"). That sends you specifically to the selected version of the wikipage with a link to it that will never change.
3) Reference the PDF version and its version number. Once the book achieves a reasonable level, PDF versions will become available for download and they will have a unique version number and can be retrieved.
Other suggestions are most welcome!
Edwards, Steven A.,The Nanotech Pioneers
Christiana, USA:
Wiley-VCH 2006, pg 2
GNU Free Documentation License
As of July 15, 2009 Wikibooks has moved to a dual-licensing system that supersedes the previous GFDL only licensing. In short, this means that text licensed under the GFDL only can no longer be imported to Wikibooks, retroactive to 1 November 2008. Additionally, Wikibooks text might or might not now be exportable under the GFDL depending on whether or not any content was added and not removed since July 15. |
Version 1.3, 3 November 2008 Copyright (C) 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. <http://fsf.org/>
Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.
The "publisher" means any person or entity that distributes copies of the Document to the public.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
- Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
- List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
- State on the Title page the name of the publisher of the Modified Version, as the publisher.
- Preserve all the copyright notices of the Document.
- Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
- Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
- Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
- Include an unaltered copy of this License.
- Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
- Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
- For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
- Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
- Delete any section Entitled "Endorsements". Such a section may not be included in the Modified version.
- Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
- Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements".
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Document.
11. RELICENSING
"Massive Multiauthor Collaboration Site" (or "MMC Site") means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A "Massive Multiauthor Collaboration" (or "MMC") contained in the site means any set of copyrightable works thus published on the MMC site.
"CC-BY-SA" means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.
"Incorporate" means to publish or republish a Document, in whole or in part, as part of another Document.
An MMC is "eligible for relicensing" if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.
The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.
How to use this License for your documents
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
- Copyright (c) YEAR YOUR NAME.
- Permission is granted to copy, distribute and/or modify this document
- under the terms of the GNU Free Documentation License, Version 1.3
- or any later version published by the Free Software Foundation;
- with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
- A copy of the license is included in the section entitled "GNU
- Free Documentation License".
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:
- with the Invariant Sections being LIST THEIR TITLES, with the
- Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.


















































































![{\displaystyle f[Hz]={\frac {t\beta _{i}^{2}}{4\pi L^{2}}}{\sqrt {\frac {Y}{3\rho }}}={\frac {\left(1\ast 10^{-6}\right)\left(1.875\right)^{2}}{4\pi \left(100\ast 10^{-6}\right)^{2}}}{\sqrt {\frac {\left(160\ast 10^{9}\right)}{3\ast 2330}}}=1.\,338\,5\times 10^{5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d62323afd5c3ca378ab0419c064f575c3e00b258)























![{\displaystyle {\big [}\cos(x)^{2}+\sin(x)^{2}=1{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0696684a3724bfb996e2073cd431b5c3de701f73)
![{\displaystyle {\big [}(\cos(x)+i\cdot \sin(x))^{n}=\cos(n\cdot x)+i\cdot \sin(n\cdot x){\big ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec7fcd029d75dad5753978b35662645bc5ac1da)







































={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d3e0a1ce3b1b528f799d01f7eda355f71f12e5c)
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32f43980de090a8055a1bd5b601945b2316d583f)













![{\displaystyle {\hat {F}}(i)={\hat {h}}(i)+\sum _{j=1}^{n/2}[2{\hat {J}}_{j}(i)-{\hat {K}}_{j}(i)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f13a23b0cc5257a793505f833d2984a2606b4ac0)































































