MATLAB Programming/Print Version
| This is the print version of MATLAB Programming You won't see this message or any elements not part of the book's content when you print or preview this page. |
The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/MATLAB_Programming
Fundamentals of MATLAB
Main screen of MATLAB
[edit | edit source]
When the MATLAB is opened for the first time after installing, you will see the MATLAB main display shown as followed (Note that the version is R2020a, which other versions may look more or less similar):

The main screen of MATLAB will consists of the following (in order from top to bottom):
- Search Bar - Can search the documentations online for any commands / functions / class
- Menu Bar - The shortcut keys on top of the window to access commonly used features such as creating new script, running scripts or launching SIMULINK
- Home Tab - Commonly used features/functions are grouped here
- Plots Tab - The plot charts is shown here. Basic charts (without additional toolbox are shown as follows):
- Line Plots, Bar Plots, Scatter Plots, Pie Chart, Histogram, Polar Plots, Geographic Plots, Contour Plots,3D Surface, Vector Field and Analytic Plots
- Apps Tab - The additional installed toolbox with related functionality are shown here
- Home Tab - Commonly used features/functions are grouped here
- Current Folder Panel — The created files are accessed at this panel
- Command Window Panel — All of the workings are done at this panel, enter commands at the command line, indicated by the prompt (>>).
- Workspace Panel — Explore data that you had created or import the data from files at this panel
Hello World
[edit | edit source]All programming languages are introduced by the most famous computer program on the planet, "Hello, world!", so let's begin with that.
In the center, you can see a window labelled as "Command Window". The cursor should be already flickering there; all you now have to do is to write as followed:
disp('Hello, world!');
and press the return key. The output will be shown just below the command as
Hello, world!
Note: To pass the argument string in single quotes (not double), but why so? Because we might need to use double quotes inside the string and that would be interpreted as the end of the string argument. Having said this, it is assured that double quotes work inside the string, however escape sequences may have to be used to get the string right.
Start afresh
[edit | edit source]In MATLAB , once you are started working with a lot of mathematical formulas for one project , you will need to start afresh for your new project.
To do this, just type as follows:
clear
clc
close all
What does this three lines do ?
clear - This command will removes all stored variables from the workspace.
clc - This command will clear the command window and homes the cursor.
close all - This command will closes all the open figure windows.
References
[edit | edit source]
Fundamentals of MATLAB/Basic MATLAB commands
Basic MATLAB command
[edit | edit source]
During start to use the program, you may see "double greater than" symbols aka >> on the top left of command window.
You can start to type simple or complex mathematic equation to your liking.
Some of the examples are as follows:
>> 6+3 - 4/2
ans =
7
>> sind(30)
ans =
0.5000
or you may even assign a value to a variable / perform simple algebra equations
>> x = 200 % assigning value 200 to variable x
x =
200
>> y = 120 % assigning value 120 to variable y
y =
120
>> p = x-y % make a simple subtraction equation where the x is subtract y equals to p
p =
80
Note: You can learn more about MATLAB operator from this page: MATLAB Programming/Fundamentals of MATLAB/MATLAB operator
Basic Commands
[edit | edit source]These commands listed below are the commands that you usually will encounter when using MATLAB
clc - Clear command window.
clear - Remove all variable values from workspace
disp - Display the values inside of the variable / matrix
help - Display tooltip help text inside the Command Window. The help displays the help for the functionality specified by NAME, such as a function, operator symbol, method, class, or toolbox.
Hello World
[edit | edit source]Once Hello World, which is the simplest of programs, works the beginner can move on to explore the MATLAB workspace![]() available for developing or running Matlab code.
available for developing or running Matlab code.
Using the workspace the beginner can then learn to manipulate basic MATLAB Variables![]() .
.
For convenience Matlab allows the workspace to be saved and loaded using *.mat files.![]()
Examples of MATLAB Command
Introduction
[edit | edit source]MATLAB is interesting in that it is dynamically compiled. In other words, when you're using it, you won't run all your code through a compiler, generate an executable, and then run the executable file to obtain a result. Instead, MATLAB simply goes line by line and performs the calculations without the need for an executable.
Partly because of this, it is possible to do calculations one line at a time at the command line using the same syntax as would be used in a file. It's even possible to write loops and branches at the command line if you want to. Of course this would often lead to a lot of wasted efforts, so doing anything beyond very simple calculations, testing to see if a certain function, syntax, etc. works, or calling a function you put into an .m file should be done within an .m file.
Examples
[edit | edit source]MATLAB can perform the functions of a simple calculator from the command line. We go thru some of the common Maths problem in the real life.
Here are few of mathematics problem that are demonstrated to be solved in MATLAB:
Painting Coverages
[edit | edit source]
A house painter usually uses 10L of white paint to cover 120 square meter on average for single layer of coating.
Calculate how many 10L paint cans that house painter needed to buy to paint a room with size of 13m X 9m with height 5m from floor to ceiling.
Also the room have 2 windows with size of 1.5m*0.75m and 2m*1.25m and a door with size of 1.2m*3m
>> room_area=13*9*5 %calculating the overall area of wall for the room
room_area =
585
>> window_area=(1.*0.75)+(2*1.25)
window_area =
3.2500
>> door_area=1.2*3
door_area =
3.6000
>> paint_area=room_area-window_area-door_area
paint_area =
578.1500
>>%amount of paint can needed
paint_area / 120
ans =
4.8179
%house painter needed equaivalent of 5 tin cans to paint the room
Earth to Sun Distance
[edit | edit source]
Distances from sun to earth is equivalent to 150 million km (150,000,000 km)
If human launched a advance rocket capable of achieving constant speed of 7km/s (ignore all of the air frictions, gravitational pull) , how many year(s) does the rocket to reach the sun from earth ?
>> distance = 150000000
distance =
150000000
>> speed = 7
speed =
7
>> time = distance / speed
time =
2.1429e+07
>> time_to_reach_sun=time/(3600*24*365) % 3600= 1 hour =3600secs, 1 day = 24hour, 1 year=365days(discounting leap years)
time_to_reach_sun =
0.6795
Dice Roll for board games
[edit | edit source]
You invite some friends come over to play a board game but somehow the dice that should be comes with board game is missing. Create a MATLAB programs to throw two dices (with 6 faces)
You need to use randi command to generate random numbers. More command can be learnt here: MATLAB Programming/Fundamentals of MATLAB/MATLAB operator
>> diceroll = randi(6) + randi(6) % press up button to recall last command and press Enter
diceroll =
9
>> diceroll = randi(6) + randi(6)
diceroll =
6
>> diceroll = randi(6) + randi(6)
diceroll =
9
>> diceroll = randi(6) + randi(6)
diceroll =
11
>> diceroll = randi(6) + randi(6)
diceroll =
5
>> diceroll = randi(6) + randi(6)
diceroll =
12
External Resources
[edit | edit source]
File Name Types
There are many types of files that are used in MATLAB. These are some of the few of commonly used files used for MATLAB.

.m
It consists a MATLAB script. This is a platform-independent file, so you can use the same scripts on whatever operating system (Windows, Linux,Mac) you’re working on at any time.
This file also allows you to create a script on one OS and share it with others, even when they use a different OS than you do. MATLAB script files are always written using the MATLAB language.

.mat
It consists of access to any data you saved on workspace.
To save this file, click the "Save Workspace" and to load the data click "Load Data"

.slx
Contains a Simulink model.(Note that SIMULINK is different products from MATLAB)
Simulink is an add-on product for MATLAB that provides a block diagram environment for performing simulations.

.fig
Provides access to any plots or other graphics you create. Keep in mind that the file contains all the information required to reconstruct the chart, but does not contain the graphic of chart itself.
This approach means that the chart's plot is accessible on any OS that MATLAB supports.

.mlapp
A MATLAB application created using the MATLAB App Designer.
MATLAB application lets you share your code in a packaged form (like executable files) with other people, and you can create one without having much of programming experience
Fundamentals of MATLAB/MATLAB operator
MATLAB Operator
[edit | edit source]MATLAB have a few operator types to manipulate shown below
Note: Variables a and b below represents number
Arithmetic Operations
[edit | edit source]Arithmetic Operator is used as mathematical operator that manipulates the number according to the formula requirement. The result is shown as numbers.
| Addition | a + b |
| Subtraction | a - b |
| Multiplication | a * b |
| Forward division | a / b |
| Backward division | a \ b |
| Exponentiation | a ^ b |
| Assignment | a = b |
Relational Operations
[edit | edit source]Relational Operator is used to check if numbers are having any significant relationship with one or another. The results is usually is shown TRUE or FALSE.
| Equal To | a == b |
| Not Equal To | a ~= b |
| Greater than | a > b |
| Greater or equal to | a >= b |
| Lesser than | a < b |
| Lesser or equal to | a <= b |
Logical Operations
[edit | edit source]Logical Operator is used to check if number fulfills the logical conditions, the result is usually shown TRUE or FALSE.
| Logical AND | a && b |
| Logical OR | a || b |
| Logical NOT | a ~ b |
Elementary Mathematics Constants and Functions
[edit | edit source]Besides mathematical formula, there are a few mathematical constant and function that you can use to make your works in Matlab easier. More information about the functions used can be found here:Mathematical_symbols
| pi | Returns value of 3.1416 (Note: Ratio of a circle's circumference to its diameter) |
| sqrt(a) | Returns square root of a |
| exp(1) | Returns value of 2.7183 This is exponential function (Note: it is inverse of natural log, try log(exp(1) and see the result) |
| log(a) | This logarithm operator is to find natural number log of a number |
| log10(a) | This base10 log operator is common logarithm for base 10 |
| mod(a,b) or rem(a,b) | This modulo operator returns the remainder after a is divided by b. |
| : (Colon) | Generate a sequence |
| round(a,b) | This rounding operator round up to the number to the nearest digit "a" by the significant digit "b"
|
| primes(a) | Returns a list of prime numbers less than or equal to number a |
| gcd(a,b) | Returns the greatest common divisors of the number of a and b. |
| lcm(a,b) | Returns the least common multiples of the number of a and b. |
Trigonometry Operations
[edit | edit source]
The trigonometry formula are given as followed:
Sin α - a / h
Cos α - b / c
Tan α - a / b
| sin(α) | This sine operator returns sine value of argument in radians |
| sind(α) | This sine operator returns sine value of argument in degree |
| cos(α) | This cosine operator returns cosine value of argument in radians |
| cosd(α) | This cosine operator returns sine value of argument in degree |
| tan(α) | This tan operator returns tangent value of argument in radians |
| tand(α) | This tan operator returns tangent value of argument in degree |
| deg2rad(α) | Convert angle from degrees to radian |
| rad2deg(α) | Convert angle from radians to degrees (Note: Try to convert the pi from radian to degrees) |
Matrix Operations
[edit | edit source]| [ ] | Container for matrix |
| , | Matrix row separator |
| ; | Matrix column separator |
Others
[edit | edit source]| randi | Random integer |
Comments
Placing comments
[edit | edit source]Comment lines begin with the character '%', and anything after a '%' character is ignored by the interpreter. The % character itself only tells the interpreter to ignore the remainder of the same line.
In the MATLAB Editor, commented areas are printed in green by default, so they should be easy to identify. There are two useful keyboard shortcuts for adding and removing chunks of comments. Select the code you wish to comment or uncomment, and then press Ctrl-R (⌘-/ for Mac) to place one '%' symbol at the beginning of each line and Ctrl-T (⌘-T for Mac) to do the opposite.
MATLAB also supports multi-line comments, akin to /* ... */ in languages like C or C++, via the %{ and %} delimiters. But there is a small and important difference. In MATLAB it is not allowed that the lines starting with %{ or %} contains any other text (except white spaces). Otherwise it would not work. E.g.
%{ for i = 1:10
disp(i)
end %}
gives an error, but
%{
for i = 1:10
disp(i)
end
%}
works just fine.
Common uses
[edit | edit source]Comments are useful for explaining what function a certain piece of code performs especially if the code relies on implicit or subtle assumptions or otherwise perform subtle actions. Doing this is a good idea both for yourself and for others who try to read your code. For example,
% Calculate average velocity, assuming acceleration is constant % and a frictionless environment. force = mass * acceleration
It is common and highly recommended to include as the first lines of text a block of comments explaining what an M file does and how to use it. MATLAB will output the comments leading up to the function definition or the first block of comments inside a function definition when you type:
>> help functionname
All of MATLAB's own functions written in MATLAB are documented this way as well.
Comments can also be used to identify authors, references, licenses, and so on. Such text is often found at the end of an M file though also can be found at the beginning. Finally, comments can be used to aid in debugging, as explained in Debugging M Files.
Boolean and Rational
Introduction
[edit | edit source]A large number of MATLAB's functions are operations on two types of numbers: rational numbers and boolean numbers.
Rational numbers are what we usually think of when we think of what a number is. 1, 3, and -4.5 are all rational numbers. MATLAB stores rational numbers as doubles by default, which is a measure of the number of decimal places that are stored in each variable and thus of how accurate the values are. Note that MATLAB represents irrational numbers such as pi with rational approximations, except when using the symbolic math toolbox. See that section for details.
Boolean numbers are either "TRUE" or "FALSE", represented in MATLAB by a 1 and a 0 respectively. Boolean variables in MATLAB are actually interchangable with doubles, in that boolean operators can be performed with arrays of doubles and vice versa. Any non-zero number in this case is considered "TRUE".
Most of the rational operators also work with complex numbers. Complex numbers; however, cannot be interchanged with boolean values like the real rationals can.
Note: MATLAB refers to Booleans as "logicals" and does not use the word "Boolean" in code or documentation.
Rational Operators on Single Values
[edit | edit source]MATLAB has all the standard rational operators. It is important to note, however, that Unless told otherwise, all rational operations are done on entire arrays, and use the matrix definitions. Thus, even though for now we're only talking about operations on a single value, when we get into arrays, it will be important to distinguish between matrix and component-wise multiplication, for example: Add, Subtract, Multiply, Divide, Exponent operators.
%addition
a = 1 + 2
%subtraction
b = 2 - 1
%matrix multiplication
c = a * b
%matrix division (pseudoinverse)
d = a / b
%exponentiation
e = a ^ b
The modulo function returns the remainder when the arguments are divided together, so a modulo b means the remainder when a is divided by b.
%modulo
remainder = mod(a,b)
All of these functions except for the modulus work for complex numbers as well.
Relational Operators
[edit | edit source]Equality '==' returns the value "TRUE" (1) if both arguments are equal. This must not be confused with the assignment operator '=' which assigns a value to a variable.
>> %relational
>>a=5;b=5;
>>a==b
ans =
logical
1
%Assignment
>>a=5;b=3;
>>a=b
a = 3
Note that in the first case, a value of 1 (true) is returned, however for the second case a gets assigned the value of b.
Greater than, less than and greater than or equal to, less than or equal to are given by >, <, >=, <= respectively. All of them return a value of true or false. Example:
>>a=3;b=5;
>>a<=b
ans = 1
>>b<a
ans = 0
Boolean Operators on Single Values
[edit | edit source]The boolean operators are & (boolean AND) | (boolean OR) and ~ (boolean NOT /negation). A value of zero means false, any non-zero value (usually 1) is considered true.
Here's what they do:
>>%boolean AND
>> y = 1 & 0
y = 0
>> y = 1 & 1
y = 1
>>%boolean OR
>> y = 1 | 0
y = 1
>> y = 1 | 1
y = 1
The negation operation in MATLAB is given by the symbol ~, which turns any FALSE values into TRUE and vice versa:
>> c = (a == b)
c = 1
>> ~c
ans = 0
This is necessary because conditionals (IF/SWITCH/TRY) and loops (FOR/WHILE) always look for statements that are TRUE, so if you want it to do something only when the statement is FALSE you need to use the negation to change it into a true statement.
The NOT operator has precedence over the AND and OR operators in MATLAB unless the AND or OR statements are in parenthesis:
>> y = ~1 & 0
y = 0
>> y = ~(1&0)
y = 1
References
[edit | edit source]
Strings
Declaring Strings
[edit | edit source]Strings are declared using single quotes ( ' ):
>> fstring = 'hello'
fstring =
hello
Including a single quote in a string is done this way:
>> fstring = ''''
fstring =
'
>> fstring = 'you''re'
fstring =
you're
Concatenate Strings
[edit | edit source]In MATLAB , multiple strings can be concatenated (linked together as a chain) using square brackets.
<concatstring>=[<str1>,<str2>,<str3>,...];
Here are the random greeting message that are using this concatenate functions.
>> subject='The quick brown fox ' %sentence beginning
subject =
'The quick brown fox '
>> verb = 'jumps over '
verb =
'jumps over '
>> object='the lazy dog'
object =
'the lazy dog'
>> phrase=[subject,verb,object]
phrase =
'The quick brown fox jumps over the lazy dog'
Inputting strings
[edit | edit source]To let user input , we can use input functions
>> name=input('Enter your names: ','s')
Enter your names: Matlab_User
name =
'Matlab_User'
String manipulations
[edit | edit source]Count the repeating words
[edit | edit source]
Consider the following tounge-twister
How much wood would a woodchuck chuck
if a woodchuck could chuck wood?
He would chuck, he would, as much as he could,
and chuck as much wood as a woodchuck would
if a woodchuck could chuck wood.
We would like to know how many times of the word wood appeared in that tounge twister. We can use the count function.
>>%Declare woodchuck twister as an characther vectors
>> twister = 'How much wood would a woodchuck chuck if a woodchuck could chuck wood? He would chuck, he would, as much as he could, and chuck as much wood as a woodchuck would if a woodchuck could chuck wood.'
twister =
'How much wood would a woodchuck chuck if a woodchuck could chuck wood? He would chuck, he would, as much as he could, and chuck as much wood as a woodchuck would if a woodchuck could chuck wood.'
>> count(twister,"wood")
ans =
8

Note that the function count are counting occurrences of pattern in strings .
Therefore, it will counting the word "wood" inside the word "woodchuck"
Now, we have have another examples to count the word " the" of the famous proverbs of-all-time
The quick brown fox jumps over the lazy dog
phrase = 'The quick brown fox jumps over the lazy dog'
%count function is case-sensitive by default . It did not count The with capital 'T'
>> count(phrase,'the')
ans =
1
%need to use IgnoreCase to turn off the case-sensitive words
>> count(phrase,'the','IgnoreCase',true)
ans =
2
Finding lengths of string
[edit | edit source]At times, you might be needing to find the length of words in a sentence, here is the length(string') functions comes to the rescue.
>> length(phrase)
ans =
43
As we can see in next section, it can be seen that there are exactly 43 characters inside the string.
Extracting words from Strings
[edit | edit source]To extracting certain words in the string, need to stringName(indexnumberfirst:indexnumberlast) .
We using the same example phrase as above.
Note that even empty space is consider as a string.
| Index Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
| String | T | h | e | q | u | i | c | k | b | r | o | w | n | f | o | x | j | u | m | p | s | o | vv | e | r | t | h | e | l | a | z | y | d | o | g |
Based on this example, if we wanted to extract the word brown fox and lazy dog,
we can see that each word is represented by index number (11:19) and index number (36:43) respectively. In MATLAB , we can type following commands:
>> phrase(11:19)
ans =
'brown fox'
>> phrase(36:43)
ans =
'lazy dog'
Lowercase and Uppercase of Strings
[edit | edit source]For the string manipulations such as converting the strings to upper and lower cases, we can use lower and upper functions. This will make the strings all in lowercase and uppercase characthers respectively.
>> upper(phrase)
>> %Convert the string to uppercase
ans =
'THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG'
>> lower(phrase)
>> %Convert the string to lowercase
ans =
'the quick brown fox jumps over the lazy dog'
Reverse Strings
[edit | edit source]To reverse the string , we can use reverse / flip function. This will make the string reverse from the last index number to first index number and vice versa.
>> reverse(phrase)
ans =
'god yzal eht revo spmuj xof nworb kciuq ehT'
Replace Characters in Strings
[edit | edit source]To replace certain words in the strings, we can use replace functions
The syntax of replace functions are as followed: replace(stringName,oldword,newword)
>>% We don't want brown fox, we want to change to orange fox
>> replace(phrase,'brown','orange')
ans =
'The quick orange fox jumps over the lazy dog'
There are at times, you might want to replace multiple words in one go , therefore we need to declare the multiple strings in vector. But before that make sure, the order/sequences for old and new words are in correct order.
>>%declare vector where the old words are going to be replaced
>> old={'fox','dog'}
old =
1×2 cell array
{'fox'} {'dog'}
>>%declare vector where the new words are going to do the replaing
>> new={'cheetah','sloth'}
new =
1×2 cell array
{'cheetah'} {'sloth'}
>> % Replace old words (fox) and (dog) into (cheetah) and (sloth) . Make sure sequence is in correct order
>> replace(phrase,old,new)
ans =
'The quick brown cheetah jumps over the lazy sloth'
Strings as a Character Array
[edit | edit source]Strings in MATLAB are an array of characters. To see this, executing the following code:
>> fstring = 'hello';
>> class(fstring)
ans = char
Because strings are arrays, many array manipulation functions work including: size, transpose, and so on. Strings may be indexed to access specific elements.
Performing arithmetic operations on character arrays converts them into doubles.
>> fstring2 = 'world';
>> fstring + fstring2
ans = 223 212 222 216 211
These numbers are from the ASCII standard for each character in the array. These values are obtained using the double function to turn the array into an array of doubles.
>> double(fstring)
ans = 104 101 108 108 111
The 'char' function can turn an array of integer-valued doubles back into characters. Attempting to turn a decimal into a character causes MATLAB to round down:
>> char(104)
ans = h
>> char(104.6)
ans = h
Special String Functions
[edit | edit source]Since MATLAB strings are character arrays, some special functions are available for comparing entire strings rather than just its components:
deblank
[edit | edit source]deblank removes white spaces from the string.
findstr
[edit | edit source]findstr(bigstring, smallstring) looks to see if a small string is contained in a bigger string, and if it is returns the index of where the smaller string starts. Otherwise it returns [].
strrep
[edit | edit source]strrep(string1, replaced, replacement) replaces all instances of replaced in string1 with replacement
strcmp
[edit | edit source]Strings, unlike rational arrays, do not compare correctly with the relational operator. To compare strings use the strcmp function as follows:
>> string1 = 'a';
>> strcmp(string1, 'a')
ans = 1
>> strcmp(string1, 'A')
ans = 0
Note that MATLAB strings are case sensitive so that 'a' and 'A' are not the same. In addition the strcmp function does not discard whitespace:
>> strcmp(string1, ' a')
ans = 0
The strings must be exactly the same in every respect.
If the inputs are numeric arrays then the strcmp function will return 0 even if the values are the same. Thus it's only useful for strings. Use the == operator for numeric values.
>> strcmp(1,1)
ans = 0.
num2str
[edit | edit source]Convert numbers to character . This functions is useful when you want to use function disp values to limit the display of decimal point.
>>%Limit the display of pi value to 9 decimal points
>> num2str(pi,'%1.9f')
ans =
'3.141592654'
Displaying values of string variables
[edit | edit source]If all you want to do is display the value of a string, you can omit the semicolon as is standard in MATLAB.
If you want to display a string in the command window in combination with other text, one way is to use array notation combined with either the 'display' or the 'disp' function:
>> fstring = 'hello';
>> display( [ fstring 'world'] )
helloworld
MATLAB doesn't put the space in between the two strings. If you want one there you must put it in yourself.
This syntax is also used to concatenate two or more strings into one variable, which allows insertion of unusual characters into strings:
>> fstring = ['you' char(39) 're']
fstring = you're
Any other function that returns a string can also be used in the array.
You can also use the "strcat" function to concatenate strings, which does the same thing as above when you use two strings, but it is especially useful if you are using a cell array of strings because it lets you concatenate the same thing to all of the strings at once. Unfortunately you can't use it to add white space (strcat discards what MATLAB considers extraneous whitespace). Here's the syntax for this use.
>> strCell = {'A', 'B'};
>> strcat(strCell, '_');
ans =
A_
B_
Finally, although MATLAB doesn't have a printf function you can do essentially the same thing by using 1 as your file identifier in the fprintf function. The format identifiers are essentially the same as they are in C.
>> X = 9.2
>> fprintf(1, '%1.3f\n', X);
9.200
The "9.200" is printed to the screen. fprintf is nice compared to display because you don't have to call num2str on all of the numbers in a string - just use the appropriate format identifer in the place you want it.
>> X = 9.2
>> fprintf(1, 'The value of X is %1.3f meters per second \n', X);
The value of X is 9.200 meters per second
Cell arrays of strings
[edit | edit source]In many applications (particularly those where you are parsing text files, reading excel sheets with text, etc.) you will encounter cell arrays of strings.
You can use the function "iscellstr" to tell if all of the elements in a given cell array are strings or not.
>> notStrCell = {'AA', []};
>> iscellstr(notStrCell)
ans = 0
This is useful since functions that work with cell arrays of strings will fail if provided with something that's not a cell array of strings. In particular, they all fail if any elements of the provided cell array are the empty array ( [] ) which is somewhat frustrating if the provided text file contains empty cells. You must catch this exception before calling cellstr manipulation functions.
Searching a cell array of strings can be done with the "strmatch", "strfind", and "regexp" functions. Strmatch looks for a string within a cell array of strings whose first characters exactly match the string you pass to it, and returns the index of all strings in the array for which it found a match. If you give it the 'exact' option, it will only return the indexes of elements that are exactly the same as what you passed. For example:
>> strCell = {'Aa', 'AA'};
>> strmatch('A', strCell);
ans = 1, 2
>> strmatch('A', strCell, 'exact');
ans = []
>> strmatch('Aa', strCell, 'exact');
ans = 1
Strfind looks for a specific string within a cell array of strings, but it tries to find it in any part of each string. For each element x of the given cell array of strings, it will return an empty array if there is no match found in x and the starting index (remember, strings are arrays of characters) of all matches in x if a match to the query is found.
>> strCell = {'Aa', 'AA'};
>> strfind(strCell, 'A');
ans = % answer is a cell array with two elements (same size as strCell):
1 % Index of the beginning of string "A" in the first cell
1 2 % Index of each instance of the beginning of string "A" in the second cell
>> strfind(strCell, 'a');
ans =
2
[] % 'a' is not found
The "cellfun" / "isempty" combination is very useful for identifying cases where the string was or was not found. You can use the find function in combination with these two functions to return the index of all the cells in which the query string was found.
>> strCell = {'Aa', 'AA'};
>> idxCell = strfind(strCell, 'a');
>> isFound = ~cellfun('isempty', idxCell); % Returns "0" if idxCell is empty and a "1" otherwise
>> foundIdx = find(isFound)
foundIdx = 2
The strfind function also has some other options, such as the option to only return the index of the first or last match. See the documentation for details.
The regexp function works the same way as strfind but instead of looking for strings literally, it tries to find matches within the cell array of strings using regular expressions. Regular expressions are a powerful way to match patterns within strings (not just specific strings within strings). Entire books have been written about regular expressions, so they cannot be covered in as much detail here. However, some good resources online include regular-expresions.info and the MATLAB documentation for the matlab-specific syntax. Note that MATLAB implements some, but not all, of the extended regular expressions available in other languages such as Perl.
Unfortunately, MATLAB does not innately have functions to do common string operations in some other languages such as string splitting. However, it is quite possible to find many of these functions in a google search.
Complex Numbers
Complex Numbers
[edit | edit source] Complex numbers are also used in MATLAB.
It consists of two parts, one is real number and one is imaginary number. It is in the form of or .
i or j returns the basic imaginary unit. i or j is equivalent to square root of -1 where the formula is ( ).
Note: The symbol i and j are interchangeable for one to another, as MATLAB just convert j into i, if equations is using two different notations as shown below.
Declaring a complex number in MATLAB
[edit | edit source]Complex numbers in MATLAB are doubles with a real part and an imaginary part. The imaginary part is declared by using the 'i' or 'j' character. For example, to declare a variable as '1 + i' just type as following:
>> compnum = 1 + i
compnum = 1.000 + 1.000i
>>%Note:If you use j MATLAB still displays i on the screen
>> compnum = 1 + j
compnum = 1.000 + 1.000i
Note 1: Even if you use j to indicate complex number , MATLAB will still displays i on the screen.
Note 2: Since i is used as the complex number indicator it is not recommended to use it as a variable, since it will assume i is a variable.
>> i = 1; %bad practise to use i as variable
>> a = 1 + i
a = 2
However, since implicit multiplication is not normally allowed in MATLAB, it is still possible to declare a complex number like this:
>> i = 3;
>> a = 1i + 1
a = 1.000 + 1.000i
It's best still not to declare i as a variable, but if you already have a complex program with i as a variable and need to use complex numbers this is probably the best way to get around it.
If you want to do arithmetic operations with complex numbers make sure you put the whole number in parenthesis, or else it likely will not give the intended results.
Complex functions
[edit | edit source]However, the best practice to declare a complex number is by using function complex.
>>%Best practise to declare complex number in MATLAB
>> complex(2,6)
ans =
2.0000 + 6.0000i
If you want to declare just the imaginary number, just use the square root of negative numbers, such as followed.
>> sqrt(-49)
ans =
0.0000 + 7.0000i
To declare multiple complex numbers , create two row vectors with real numbers and another with imaginary numbers. Combine both of them using complex functions
>> %create a vector consiots of real number
>> RE = [1,2,3]
RE =
1 2 3
>> %create a vector consiots of imaginary number
>> IM = [4,5,6]
IM =
4 5 6
>> %create 3 complex number
>> complex(RE,IM)
ans =
1.0000 + 4.0000i 2.0000 + 5.0000i 3.0000 + 6.0000i
Arithmetic operations that create complex numbers
[edit | edit source]There are several operations that create complex numbers in MATLAB. One of them is taking an even root of a negative number, by definition.
>> (-1)^0.5 ans = 0.000 + 1.000i >> (-3)^0.25 ans = 0.9306 + 0.9306i
As a consequence of the Euler formula, taking the logarithm of a negative number also results in imaginary answers.
>> log(-1) ans = 0 + 3.1416i
In addition, the roots of functions found with the 'roots' function (for polynomials) or some other rootfinding function will often return complex answers.
Manipulate complex numbers
[edit | edit source]Finding real and imaginary number
[edit | edit source]First of all, it is helpful to tell whether a given matrix is real or complex when programming, since certain operations can only be done on real numbers.
Since complex numbers don't have their own class, MATLAB comes with another function called "isreal" to determine if a given matrix is real or not. It returns 0 if any of the inputs are complex.
>> A=[complex(2,3),complex(4,0)]
A =
2.0000 + 3.0000i 4.0000 + 0.0000i
>> %returns 1 if complex number does not have an imaginary part and 0 if otherwise.
>> %A denotes the whole vectors
>> isreal(A)
ans =
logical
0
>> %A(2) denotes second complex number in the vector (4+0i)
>> isreal(A(2))
ans =
logical
1
Notice that it is possible to have real and complex numbers in the same array, since both are of class double.
The function is set up this way so that you can use this as part of a conditional, so that a block only is executed if all elements of array A are real.
To extract just the real part of a complex variable use the real function. To extract just the complex part use the imag function.
>>%Extract real number from the complex number vector A
>> real(A)
ans =
2 4
>>%Extract imaginary number from the complex number vector A
>> imag(A)
ans =
3 0
Complex conjugate
[edit | edit source]
To find complex conjugate , we can use conj function. If complex number, Z is , then the conjugate, Ẑ is
>> conj(A)
ans =
2.0000 - 3.0000i 4.0000 + 0.0000i
Phase Angle
[edit | edit source]To find phase angle , we can use the phase angle in the radian for each element of a complex numbers
>> angle(A)
ans =
0.9828 0
References
[edit | edit source]- ↑ https://web.archive.org/web/20210615132903/https://www.educba.com/matlab-free/?source=leftnav
- ↑ https://web.archive.org/web/20210322123642/https://www.maths.unsw.edu.au/sites/default/files/MatlabSelfPaced/lesson8/MatlabLesson8_Logic.html
- ↑ https://web.archive.org/web/20211006102547/https://www.maths.unsw.edu.au/sites/default/files/MatlabSelfPaced/lesson1/MatlabLesson1_Complex.html
Vector and Matrices
What is scalar,vector and matrix ?
[edit | edit source]
Scalar
[edit | edit source]Scalars are the physical quantities that are described by magnitude only. In other words, scalars are those quantities that are represented just by their numerical value, such as 3, -5, 0.368, etc.
Vector
[edit | edit source]A vector is an array of numbers or a list of scalar values in one dimensional array of numbers (can be in a row or column).
This example vector A below is row vector
This example vector B below is column vector
Matrix
[edit | edit source]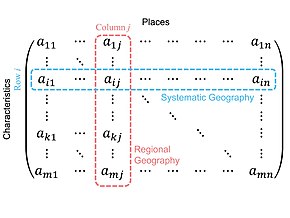
A matrix is an ordered rectangular array arrangement of numbers. They are stored as two-dimensional arrays in MATLAB.
A matrix having m rows and n columns is called a matrix of order m × n or simply m × n matrix.
It can be represented by one or more rows (i) AND one or more columns (j).
Back in Introduction chapter , MATLAB was originally designed to carry out operations with matrices, and received the name of MATrix LABoratory that subsequently was reduced to MATLAB.
It is possible to find applications of matrices not only in the mathematics areas, but also in a great deal of applications in engineering, in physics, in finance, in accounting, in chemistry and in biology, perhaps more.
There are many types of matrices with followings as shown
| Rectangular Matrix (Where no. of row and column are unequal) | Square Matrix (Where no. of row and column are same) | Row Matrix (Matrix with one row , aka row vector) | Column Matrix (Matrix with one column , aka column vector) | Diagonal Matrix (Square Matrix with non-diagonal elements equal to zero ) |
|
|
|
|
|
Scalar in MATLAB
[edit | edit source]Scalar in MATLAB looks like assigning a variable to a number such as followed:
a = 6
Vectors in MATLAB
[edit | edit source]You can type following in MATLAB
For row vector , just type comma "," to separate each number
>> VR = [6,2,5]
VR =
6 2 5
For column vector , just type semicolon ";" to separate each number
>> VC = [9;1;6]
VC =
9
1
6
Matrix in MATLAB
[edit | edit source]In MATLAB, to create matrix (or matrices), there is 3 important operator to be used
(a) Bracket "[" "]" as container for the matrix
(b) Comma , as matrix row separator
(c) Semicolon ; as matrix column separator
For example, we are creating 4X3 matrix in MATLAB using following commands.
>> M = [4,8,9,6;9,6,9,6;3,6,9,6]
M =
4 8 9 6
9 6 9 6
3 6 9 6
Vector and Matrices/Special Matrices
Special Matrices
[edit | edit source]Matrix of ones
[edit | edit source]We can create matrix consists using the functions ones with m numbers of rows and n numbers of columns
>> ones(3,3)
ans =
1 1 1
1 1 1
1 1 1
Matrix of zeroes
[edit | edit source]We can create matrix consists using the functions zeros with m numbers of rows and n numbers of columns
>> zeros(3,3)
ans =
0 0 0
0 0 0
0 0 0
Identity Matrices
[edit | edit source]An identity matrix is a square matrix in which each of the elements of its diagonal is a 1 and each of the other elements is a 0.
An identity matrix is used for following purposes:
(a) To verify whether any two given matrices are inverses of each other.
A and B in examples below are inverse to one another
>> A=[3,-2;-1,1]
A =
3 -2
-1 1
>> B=[1,2;1,3]
B =
1 2
1 3
>> A*B
ans =
1 0
0 1
(b) To find the inverse of a matrix
Note 1: Not every inverse matrix can use have identity matrix
Note 2: Command "eye(n)" can be used to create identity matrix in a flash, n is the size of matrix
>> A=[3,2;4,3]
A =
3 2
4 3
>> eye(2)
ans =
1 0
0 1
>> eye(2)/A
ans =
3 -2
-4 3
(c) To find the eigenvalues and eigenvectors.
Eigenvalue is defined as a scalar associated with a given linear transformation of a vector space and having the property that there is some non-zero vector which when multiplied by the scalar is equal to the vector obtained by letting the transformation operate on the vector.
Let say we have a matrix A as followed:
To find lambda, we need to know the equation for finding eigenvalue with following formula :
But MATLAB provided a simple way to find eigenvalue using command "eig"
>> A=[1,4;3,2]
A =
1 4
3 2
>> lambda = eig(A)
lambda =
-2
5
Magic Square Matrices
[edit | edit source]A magic square is basically where the sum of the elements in each column and the sum of the elements in each row are the same and there are no repeating numbers. We can create a magic square use this command M=magic(n). The order n must be a scalar greater than or equal to 3 in order to create a valid magic square.
For more info, can refer to this well written Wikibooks on this topic: Puzzles/Luoshu Squares
For example , we can create a magic square with matrices 5 by 5
>> % creating 5X5 matrix magic square
>> c = magic(5)
c =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
Vector and Matrices/Operations on Matrices
Basic Matrix Operation
[edit | edit source]Addition and subtraction
[edit | edit source]We can add and subtract the matrices if both of them are of same number of rows and columns.
Examples as follows:
>> a = [7,9,4;6,2,5]
a =
7 9 4
6 2 5
>> b=[2,0,1;4,7,3]
b =
2 0 1
4 7 3
>> % Addition of a and b matrices
a+b
ans =
9 9 5
10 9 8
>> % Subtraction of a and b matrices
a-b
ans =
5 9 3
2 -5 2
Matrix multiplication
[edit | edit source]For matrix multiplications, there are 2 ways to do multiplications.

(i) Matrix multiplications (using symbol * or mtimes)
Requirements is that the number of columns in the first matrix must be same as the number of rows in the second matrix.
As examples shown on the right , matrix A have 3 X 2 and matrix B have 2 X3
Therefore , 2 X 3 <-> 3 X 2 , hence, it fulfils the requirements above.
Also, take note that the resulting matrix sizes is based on number of rows of first matrix with number of columns in second matrix.

>> A=[4,2,4;8,3,1]
A =
4 2 4
8 3 1
>> B=[3,5;2,8;7,9]
B =
3 5
2 8
7 9
>> mtimes(A,B)
ans =
44 72
37 73
>> A*B
ans =
44 72
37 73
Following examples shows what if the incorrect matrix dimension matches.
As shown, the matrix C have 5X4 and matrix D have 3X2
5X 4 <-> 3X2, therefore it cannot fulfill the conditions and unable to solve it.
>> %Demonstrations what if matrices dimensions are incorrect
>> C=randi(10,5,4)
C =
2 10 10 3
2 10 4 5
3 5 2 1
5 5 8 2
1 4 4 10
>> D=randi(10,3,2)
D =
10 3
6 4
1 9
>> mtimes(C,D)
Error using *
Incorrect dimensions for matrix multiplication. Check that the number of columns in the first
matrix matches the number of rows in the second matrix. To perform elementwise
multiplication, use '.*'.
(ii) Dot product (Note: Only can be used if both matrices are same sizes) Taking examples above, it doesn't solve the equations as both matrix A and B above are not same size
>> A.*B % want to show dot product unable to solve this multiplication issues
Matrix dimensions must agree.
Creating Random Integer Matrix
[edit | edit source]To generate random integer matrix, can type the following randi(IMAX,M,N)
Note: IMAX is the maximum integer (starting from 1) and M*N matrix
Examples as followed:
>> randi(50,3,4)
ans =
9 14 42 48
36 3 35 2
2 5 16 22
Transpose
[edit | edit source]Using the matrices above, we can transpose the matrices. Transpose matrices usually just switch the row to column and columns into rows. The picture shown just demonstrate the transpose operation. One of the application of transpose the matrix is to cryptography.

There are two ways to go about it. One is add ' to the end of the matrix that are going to be transpose or function transpose.
Back to the magic square example above, we are going to transpose it. We can see , it is transpose along the diagonal line looks like this : \
>> % transpose matrix c to d
>> d = c'
d =
17 23 4 10 11
24 5 6 12 18
1 7 13 19 25
8 14 20 21 2
15 16 22 3 9
Determinant
[edit | edit source]The determinant of matrix is a special number that is defined only for square matrices.
A determinant is used to find the solution of a system of linear equations and determine the inverse of a matrix.
Determinant of 2X2 matrix :
Determinant of 3X3 matrix :
>> A=[6,1,1;4,-2,5;2,8,7]
A =
6 1 1
4 -2 5
2 8 7
>> det(A)
ans =
-306.0000
Inverse
[edit | edit source]Inverse of matrix is reciprocal matrix where the formula is denoted by
, where the adj is representing adjoint of matrix.
Note: Not all matrix have inverse, if their determinant is equal to zero.
>>%matrix inversion using manual method
>> M=[2,-1,3;-5,3,1;-3,2,3]
M =
2 -1 3
-5 3 1
-3 2 3
>> %First we find the matrix determinant
>> DM = det(M)
DM =
-1.0000
>>%Since determinant IS NOT equal to 0, we can find the matrix inverses
>> AM = adjoint(M)
AM =
7.0000 9.0000 -10.0000
12.0000 15.0000 -17.0000
-1.0000 -1.0000 1.0000
>> (1/DM)*AM
ans =
-7.0000 -9.0000 10.0000
-12.0000 -15.0000 17.0000
1.0000 1.0000 -1.0000
%shortcut using function inv which should be same as manual calculation above
>> inv(M)
ans =
-7.0000 -9.0000 10.0000
-12.0000 -15.0000 17.0000
1.0000 1.0000 -1.0000
Real life applications
[edit | edit source]There are many applications of matrix such as:
Crytography :
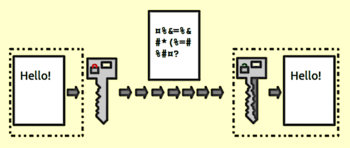
Matrix it is used to encrypt message codes. Matrices are used by programmers to code or encrypt letters. A message is made up of a series of binary numbers that are solved using coding theory for communication. As a result, the concept of matrices is used to solve such equations.
To perform this matrix operation, the message is first broken up into blocks of fixed size, and each block is represented as a vector of numbers. The public key includes a matrix, called the encryption matrix or the public matrix, that is used to transform each vector of numbers. The resulting transformed vectors are then raised to the exponent modulo the modulus to get the ciphertext.
% Define the message to encrypt
message = 'I LOVE MATLAB';
% Convert the message to a vector of numbers
message_vec = double(message);
% Define the public key parameters (modulus and exponent)
% Next, we define the public key parameters, which in this case are a modulus of 104729 and an exponent of 65537.
modulus = 104729;
exponent = 65537;
% Define the encryption matrix
% We also define an encryption matrix of size 2x2.
encryption_matrix = [3 5; 7 11];
% Break the message vector into blocks of length 2
block_size = 2;
num_blocks = ceil(length(message_vec) / block_size);
message_blocks = zeros(num_blocks, block_size);
message_blocks(1:length(message_vec)) = reshape(message_vec, [], block_size);
% Apply the encryption matrix to each message block
encrypted_blocks = mod(message_blocks * encryption_matrix, modulus);
% Raise each encrypted block to the exponent
exponentiated_blocks = mod(encrypted_blocks .^ exponent, modulus);
% Convert the encrypted blocks to a single vector of numbers
encrypted_vec = reshape(exponentiated_blocks, [], 1);
% Print out the encrypted message
fprintf('Encrypted message: %s\n', char(encrypted_vec'));
To decrypt the message, the private key is used, which consists of two parts: the modulus and the inverse of the exponent modulo a certain value. The inverse of the exponent is used to raise the ciphertext to a power that will reverse the matrix transformation and recover the original message blocks.
% Define the encrypted message
encrypted_message = [16124 4546 84313 99848 16124 4546 84313 40458 16124 4546 84313 40458 32274 40458];
% Define the private key parameters (modulus and inverse exponent)
modulus = 104729;
inverse_exponent = 47027;
% Define the decryption matrix
decryption_matrix = [17 23; 21 29];
% Break the encrypted message vector into blocks of length 2
block_size = 2;
num_blocks = length(encrypted_message) / block_size;
encrypted_blocks = reshape(encrypted_message, block_size, num_blocks)';
% Raise each encrypted block to the inverse of the exponent
decrypted_blocks = mod(encrypted_blocks .^ inverse_exponent, modulus);
% Apply the decryption matrix to each decrypted block
decrypted_blocks = mod(decrypted_blocks * decryption_matrix, modulus);
% Convert the decrypted blocks to a single vector of numbers
decrypted_vec = reshape(decrypted_blocks, [], 1);
% Convert the decrypted vector to a string and print it out
fprintf('Decrypted message: %s\n', char(decrypted_vec'));
Image Processing :

One of the matrix operations applicable in real life is image processing. We will look into one of the simpler examples such as image blurring.
For example, we want to apply blurring to an supposedly B&W image with an example of matrix shown here where each values in pixel represent a grayscale values from 1 to 255.
We will use matrix convolution to takes the average of the pixel values in a 3x3 neighborhood around each pixel in the image.
To apply this filter, we will slide the matrix over each pixel in the image and perform a matrix multiplication. For example, to blur the pixel at center in the image, you would take the 3x3 neighborhood around it, multiply each pixel value by the corresponding value in the blur filter matrix, and then add up the results. The final value is the new pixel value for the blurred image.
We repeat this process for every pixel in the image, and the result is a new image that looks blurrier.
% Define the input matrix
input_matrix = [1 2 3; 8 9 4; 7 6 5];
% Define the blur filter matrix
blur_filter = 1/9 * [1 1 1; 1 1 1; 1 1 1];
% Apply the filter using convolution
blurred_matrix = conv2(input_matrix, blur_filter, 'same');
% Display the original and blurred matrices side by side
disp('Original Matrix:');
disp(input_matrix);
disp('Blurred Matrix:');
disp(blurred_matrix);
Circuit analysis:
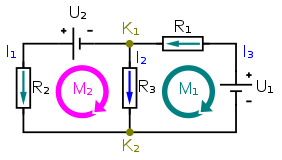
In electrical engineering, the Kirchoff's Voltage Law (KVL) states that the sum of all voltages around a closed loop in a circuit must be equal to zero. This law can be used to write a set of linear equations for a circuit with m loops. These equations can be arranged in a matrix, known as the loop-branch incidence matrix.
Based on this examples shown:
Loop M1 : V1 - R1*I1 - R3*I2 = 0
Loop M2 : V2 - R2*I2 - R3*I1 = 0
[ R1 -R3 0 ] [ I1 ] = [ V1 ]
[-R3 R2+R3 -R2 ] [ I2 ] = [ -V2 ]
[ 0 -R2 1 ] [ V2 ] = [ 0 ]
Using symbolic math tool box, we can solve the equations
% Define the symbolic variables
syms R1 R2 R3 V1 V2 I1 I2
% Define the Kirchhoff Voltage Law equations for each loop
eq1 = V1 - R1*I1 - R3*(I1-I2) == 0;
eq2 = V2 - R2*I2 - R3*(I2-I1) == 0;
% Define the Kirchhoff Current Law equation at node K1 and K2
eq3 = I1 - I2 == 0;
% Solve the system of equations for the currents and voltages
sol = solve(eq1, eq2, eq3, I1, I2, V2);
% Display the results
I1 = double(sol.I1);
I2 = double(sol.I2);
V2 = double(sol.V2);
fprintf('I1 = %.2f A\n', I1);
fprintf('I2 = %.2f A\n', I2);
fprintf('V2 = %.2f V\n', V2);
References
[edit | edit source]- ↑ https://web.archive.org/web/20220712153202/https://collegedunia.com/exams/applications-of-determinants-and-matrices-and-solved-examples-mathematics-articleid-2195
- ↑ https://web.archive.org/web/20220719154910/https://www.embibe.com/exams/inverse-matrix/
- ↑ https://web.archive.org/web/20220814062118/https://www.theclickreader.com/dot-products-and-matrix-multiplication/
- ↑ https://web.archive.org/web/20220814062138/https://www.theclickreader.com/matrix-transpose-determinants-and-inverse/
Vector and Matrices/Operations on Vectors
Operation on Vectors
[edit | edit source]Constructing Vectors
[edit | edit source]If a vector's elements is following the sequential additions, we can just use parentheses with the following:
As for example, if we want to have a vector starting with number 1 and ends with number 19 with the incremental values of 3, we can type commands shown below
>> V = (1:3:19)
V =
1 4 7 10 13 16 19
Accessing Vector
[edit | edit source]To access the values in vector , you just need to specify the vector and the array index, from 1 to n .
Using example of vector V above, we access single elements of vector V in third elements which we type commands as followed:
>> V(3)
ans =
7
We can access multiple elements by typing the start index and the end index For example, we need to access element no 3 up to element no 6, we type as followed:
>> V(3:6)
ans =
7 10 13 16
Finding Length
[edit | edit source]We can also use length function to knows what is the length of the vector ,for example we can know what is the length of V. There are 7 elements in vector V, therefore the answer should be 7
>> length(V)
ans =
7
Sum Vector
[edit | edit source]We can find the sums of vector using sum function, it get this values by adding all of the numbers inside vector together: For example, 1+4+7+10+13+16+19
>> sum(V)
ans =
70
Finding Max and Min
[edit | edit source]Respectively we can know which is the biggest and smallest number in a vector which we can use by using min and max functions
>> min(V)
ans =
1
>> max(V)
ans =
19
Finding Mean
[edit | edit source]The mean function is to find the center/middle value inside the vector
>> mean(V)
ans =
10
Finding Average
[edit | edit source]The average function is to find the average of the vector
>> average(V)
ans =
10
>> % Another way of finding average
>> sum(V)/length(V)
ans =
10
Finding Standard Deviation
[edit | edit source]To find standard deviation , std function is needed
The standard deviation is a measure of the amount of variation or dispersion of a set of values.
A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range.
>> std(V)
ans =
6.4807
Random Permutation
[edit | edit source]There are two different ways to create random permutations for vector
a. randperm(N) returns a vector containing a random permutation of the integers 1:N.
>> P=randperm(7)
ans =
1 6 2 3 4 5 7
b. randperm(N,K) returns a row vector containing K unique integers selected randomly from 1:N
>>>> P=randperm(7,5)
P =
5 1 6 2 3
Sorting Vector
[edit | edit source]You may want to sort the vectors, you can do this MATLAB.
If the vectors are to be sorted in descending manner, use this example as followed. Note, we use the random permutation example b above.
>> % using argument 'descend' to sort from big to small number
>> S=sort(P,'descend')
S =
6 5 3 2 1
>> % using argument 'asscend' to sort from small to big number
>> S=sort(P,'ascend')
S =
1 2 3 5 6
Calculating dot products
[edit | edit source]To find dot product,you can use the dot functions
NOTE: The two vectors must have the same length. The answer will usually in the forms of scalar .
The dot product of vector are calculated as followed
>> % creating row vector A and B
>> A = [3 ,7 , 2]
A =
3 7 2
>> B = [1,2,5]
B =
1 2 5
>> dot(A,B)
ans =
27
Calculating cross products
[edit | edit source]To find cross product,you can use the cross functions
NOTE: The two vectors must have the same length of 3. The answer will usually in the forms of vector 3 .
TODO: Search a picture that can illustrate the cross product well.
>> cross(A,B)
ans =
31 -13 -1
Calculating commonly used values in vector
[edit | edit source]To find the most duplicated values in the vector, we can use the mode functions.
>>%create vectors with random numbers
>> A=randi(50,1,10)
A =
18 42 30 28 46 15 38 38 20 29
>> mode(A)
ans =
38
>>%38 appear twice in that vector
Vector and Matrices/Sparse Matrices
A Sparse Matrix is a matrix that mostly contains zeros. In MATLAB, sparse matrices contrast regular ones in the way they are stored, such that memory is used more efficiently for matrices that are sparse.
A regular matrix can be converted to a sparse matrix using
>> S = sparse(A); % Create sparse representation of A
Sparse matrices are very common in engineering purposes. This is useful for manipulation as most of the matrix has a value of 0.
Arrays
Introduction to Arrays
[edit | edit source]An array is the most fundamental data type in MATLAB. In MATLAB, as in many traditional languages, arrays are a collection of several values of the same type. The string and number data type formerly presented are particular cases of arrays.
A matrix is an array with two dimensions. Most arrays have the same data type; however, a cell array is an array with varying data types. If no data type is specified for numbers, then the default data type is the equivalent to the double precision floating point in the C programming language on the same architecture. For example on x86 and PowerPC a double has 64 bits.
Declaring Arrays
[edit | edit source]Row and Column Arrays
[edit | edit source]A row array is created using comma separated values inside brackets:
>> array = [0, 1, 4, 5]
array =
0 1 4 5
Sometimes commas are omitted for simple row arrays. Omitting commas is not recommended because in larger more complex arrays white-spaces can be ambiguous. Commas almost always indicate an array is horizontal.
A column array is created using semicolons to separate values:
>> column = [1; 2; 3]
column =
1
2
3
Declaring multi-dimensional arrays
[edit | edit source]A two dimensional array (or a matrix) is declared with commas separating columns, and semicolons separating rows:
>> matrix = [1, 2, 3; 4, 5, 6]
matrix =
1 2 3
4 5 6
Simple matrix manipulation is the basis of many linear algebra computations. To use arrays of more than two dimensions, a matrix has to be extended using indexing.
When declaring arrays in MATLAB all rows and all columns need have same size. If not an error message will be generated:
>> matrix = [1, 2, 3; 4, 5] ??? Error using ==> vertcat All rows in the bracketed expression must have the same number of columns.
Indexing Arrays
[edit | edit source]Arrays are indexed using integers. To return a single element in a simple array, use a single integer.
>> array = [0, 1, 4, 5];
>> array(3)
ans =
4
To return a single element in a two dimensional array one number as a row index and the second as a column index.
>> matrix = [1, 2, 3; 4, 5, 6]; >> matrix(2,2) ans = 5
To return multiple elements in an array an array can be used as an index.
>> array = [0, 1, 4, 5];
>> array([1 3])
ans =
0 4
To return the last element of an array use (end).
>> array = [0, 1, 4, 5];
>> array(end)
ans =
5
A range of indexes can be returned using a colon(:)
>> array = [0, 1, 4, 5];
>> array(2:end)
ans =
1 4 5
Properties of MATLAB arrays and matrices
[edit | edit source]Contrary to low level languages such as C, an array in MATLAB is a more high level type of data: it contains various information about its size, its data type, and so on.
>> array = [0,1,4,5]; >> length(array) ans = 4 >> class(array) ans = double
The number of rows and columns of the matrix can be known through the built-in size function. Following the standard mathematical convention, the first number is the number of rows and the second is the number of columns:
>> matrix = [1, 2, 3; 4, 5, 6];
>> size(matrix)
ans =
2 3
The goal of MATLAB arrays is to have a type similar to mathematical vectors and matrices. As such, row and column arrays are not equivalent. Mono-dimensional arrays are actually a special case of multi-dimensional arrays, and the 'size' function can be used for them as well.
>> size(array)
ans =
1 4
Row and column do not have the same size, so they are not equivalent:
>> size(column)
ans =
3 1
>> size(row)
ans =
1 3
Why Use Arrays?
[edit | edit source]A major advantage of using arrays and matrices is that it lets you avoid using loops to perform the same operation on multiple elements of the array. For example, suppose you wanted to add 3 to each element of the array [1,2,3]. If MATLAB didn't use arrays you would have to do this using a FOR loop:
>> array = [1,2,3]; >> for ii = 1:3 array(ii) = array(ii) + 3; >> end >> array array = [4,5,6]
Doing this is not efficient in MATLAB, and it will make your programs run very slowly. Instead, you can create another array of 3s and add the two arrays directly. MATLAB automatically separates the elements:
>> array = [1,2,3]; >> arrayofthrees = [3,3,3]; >> array = array + arrayofthrees array = [4,5,6];
If all you are doing is adding a constant, you can also omit the declaration of 'arrayofthrees', as MATLAB will assume that the constant will be added to all elements of the array. This is very useful, for example if you use an array with variable size:
>> array = [1,2,3]; >> array + 3 ans = [4,5,6]
The same rule applies to scalar multiplication.
See Introduction to array operations for more information on the operations MATLAB can perform on arrays.
Arrays are a fundamental principle of MATLAB, and almost everything in MATLAB is done through a massive use of arrays. To have a deeper explanation of arrays and their operations, see Arrays and matrices.
Introduction to array operations
Introduction to array operations
[edit | edit source]As arrays are the basic data structure in MATLAB, it is important to understand how to use them effectively. See the previous section for that.
Arrays in MATLAB obey the same rule as their mathematical counterpart: by default, the matrix definitions of operations are used, unless a special operator called the dot operator is applied.
Because arrays operations are so similar to the equivalent mathematical operations, a basic knowledge of linear algebra is mandatory to use matlab effectively. However, we won't be as precise as in mathematics when using the terms vector and matrix. In MATLAB, both are arrays of doubles (thus being a matrix in the real mathematical meaning), and MATLAB considers vectors as a matrices with only one row or only one column. However, there are special functions just for vectors; see the vector module for an explanation of how to use these.
Basics
[edit | edit source]Accessing elements of a matrix
[edit | edit source]Using a Single Index
[edit | edit source]Now that you know how to define a simple array, you should know how to access its elements. Accessing the content of an array is done through the operator (), with the index inside the parenthesis; the indexing of the first element is 1:
>> a = [1, 2, 3];
>> a(1)
ans =
1
>> a(3)
ans =
3
Accessing an element outside the bounds will result in an error:
>> a(5) ??? Index exceeds matrix dimensions.
Using Multiple Indexes
[edit | edit source]To access a single matrix element, you can use the (i,j) subscript, where i is the index in the row, and j in the column:
>> a= [1, 2; 3, 4];
>> a(1, 2)
ans =
2
>> a(2, 1)
ans =
3
Using A Unique Index
[edit | edit source]You can also access a matrix element through a unique index; in this case, the order is column major, meaning you first go through all elements of the first column, then the 2d column, etc... The column major mode is the same as in Fortran, and the contrary of the order in the C language.
>> a = [1, 2, 3; 4, 5, 6];
>> a(3)
ans =
2
Using a Colon (:) for a Block Index
[edit | edit source]It is also possible to access blocks of matrices using the colon (:) operator. This operator is like a wildcard; it tells MATLAB that you want all elements of a given dimension or with indices between two given values. For example, say you want to access the entire first row of matrix a above, but not the second row. Then you can write:
>> a = [1, 2, 3; 4, 5, 6]; >> a(1,:) %row 1, every column ans = 1 2 3
Now say you only want the first two elements in the first row. To do this, use the following syntax:
>> a = [1, 2, 3; 4, 5, 6]; >> a(1, 1:2) ans = 1 2
The syntax a(:) changes a into a column vector (column major):
>> a = [1, 2, 3; 4, 5, 6] >> a(:) ans = 1 4 2 5 3 6
Using the end Operator
[edit | edit source]Finally, if you do not know the size of an array but wish to access all elements from a certain index until the end of the array, use the end operator, as in
>> a = [1, 2, 3; 4, 5, 6] >> a(1, 2:end) %row 1, columns from 2 until end of the array ans = 2 3
Logical Addressing
[edit | edit source]In addition to index addressing, you can also access only elements of an array that satisfy some logical criterion. For example, suppose a = [1.1, 2.1, 3.2, 4.5] and you only want the values between 2 and 4. Then you can achieve this in two ways. The first is to use the find function to find the indices of all numbers between 2 and 4 in the array, and then address the array with those indices:
>> a = [1.1, 2.1, 3.2, 4.5]; >> INDICES = find(a >= 2 & a <= 4); >> a(INDICES) ans = 2.1 3.2
This does not work in MATLAB 2006b.
The second method is to use logical addressing, which first changes a into a logical array, with value 1 if the logical expression is true and 0 if it is false. It then finds and returns all values in the a which are true. The syntax for this is as follows:
>> a = [1.1, 2.1, 3.2, 4.5]; >> a(a >= 2 & a <= 4) ans = 2.1 3.2
Basic operations
[edit | edit source]Rational Operators on Arrays
[edit | edit source]Addition and Subtraction
[edit | edit source]The interesting part is of course applying some operations on those arrays. You can for example use the classic arithmetic operations + and - on any array in matlab: this results in the vector addition and subtraction as defined in classic vector vectors spaces , which is simply the addition and subtraction elements wise:
>> [1, 2, 3] - [1, 2, 1] ans = 0 0 2
Multiplication by a Scalar
[edit | edit source]The multiplication by a scalar also works as expected:
>> 2 * [1, 2, 3] ans = [2, 4, 6]
Multiplying and Dividing Arrays
[edit | edit source]Multiplication and division are more problematic: multiplying two vectors in does not make sense. It makes sense only in the matrix context. Using the symbol * in matlab computes the matrix product, which is only defined when the number of columns of the left operand matches the number of rows of the right operand:
>> a = [1, 2; 3, 4]; >> a * a ans =
7 10 15 22
>> a = [1, 2, 3]; b = [1; 2; 3]; >> a * a ??? Error using ==> * Inner matrix dimensions must agree. >> a * b ans = 14
Using the division symbol / has even more constraints, as it imposes the right operand to be invertible (see Wikipedia:Invertible matrix). For square matrices, is equivalent to . For example :
>> a = [1, 2; 3, 4]; b = [1, 2; 1, 2]
>> b / a
ans =
1 0
1 0
>> a / b Warning: Matrix is singular to working precision. ans = Inf Inf Inf Inf
Component-wise Operations
[edit | edit source]If you desire to multiply or divide two matrices or vectors component-wise, or to raise all components of one matrix to the same power, rather than using matrix definitions of these operators, you can use the dot (.) operator. The two matrices must have the same dimensions. For example, for multiplication,
>> a = [1, 2, 3]; >> b = [0, 1, 2]; >> a .* b ans = 0 2 6
The other two componentwise operators are ./ and .^.
As matlab is a numerical computing language, you should keep in mind that a matrix which is theoretically invertible may lead to precision problems and thus giving imprecise results or even totally wrong results. The message above "matrix is singular to working precision" should appear in those cases, meaning the results cannot be trusted.
Non-square matrices can also be used as the right operand of /; in this case, it computes the pseudoinverse. This is especially useful in least square problems.
Transpose
[edit | edit source]A transpose of a matrix is taken using .'
>> array = [1,2;3,4]
array =
1 2
3 4
>> array.'
ans =
1 3
2 4
Boolean Operators on Arrays
[edit | edit source]The same boolean operators that can be used for point values can also be used to compare arrays. To do this, MATLAB compares the elements componentwise and returns them in a logical array of the same size as the two arrays being compared. The two arrays must have the same size. For example,
>> A = [2,4], B = [1,5];
>> A < B
ans =
[0 1]
You must be careful when using comparisons between arrays as loop conditions, since they clearly do not return single values and therefore can cause ambiguous results. The loop condition should be reducable to a single boolean value, T or F, not an array. Two common ways of doing this are the "any" and the "all" functions. A function call any(array) will return true if array contains any nonzero values and false if all values are zero. It does the comparisons in one direction first then the other, so to reduce a matrix you must call the any function twice. The function all, similarly, returns true if and only if all elements in a given row or column are nonzero.
Concatenating Arrays
[edit | edit source]Concatenating arrays involves sticking arrays together.
Horizontal Concatenating
[edit | edit source]Horizontal concatenation is done by treating an array as if it were a variable included in a row.
>> a = [1,2;3,4];
>> b = [5,6;7,8];
>> c = [a,b]
c =
1 2 5 6
3 4 7 8
Vertical Concatenating
[edit | edit source]Vertical concatenation is done by treating an array as if it were a variable included in a column.
>> a = [1,2;3,4];
>> b = [5,6;7,8];
>> c = [a;b]
c =
1 2
3 4
5 6
7 8
Solving Linear Systems
[edit | edit source]To solve a linear system in the form Ax = b use the "\" operator.
Example:
>>A = [4 5 ; 2 8];
b = [23 28]';
x = A\b
x =
2
3
Basic vector operations
A vector in MATLAB is defined as an array which has only one dimension with a size greater than one. For example, the array [1,2,3] counts as a vector. There are several operations you can perform with vectors which don't make a lot of sense with other arrays such as matrices. However, since a vector is a special case of a matrix, any matrix functions can also be performed on vectors as well provided that the operation makes sense mathematically (for instance, you can matrix-multiply a vertical and a horizontal vector). This section focuses on the operations that can only be performed with vectors.
Declaring a vector
[edit | edit source]Declare vectors as if they were normal arrays, all dimensions except for one must have length 1. It does not matter if the array is vertical or horizontal. For instance, both of the following are vectors:
>> Horiz = [1,2,3]; >> Vert = [4;5;6];
You can use the isvector function to determine in the midst of a program if a variable is a vector or not before attempting to use it for a vector operation. This is useful for error checking.
>> isvector(Horiz) ans = 1 >> isvector(Vert) ans = 1
Another way to create a vector is to assign a single row or column of a matrix to another variable:
>> A = [1,2,3;4,5,6]; >> Vec = A(1,:) Vec = 1 2 3
This is a useful way to store multiple vectors and then extract them when you need to use them. For example, gradients can be stored in the form of the Jacobian (which is how the symbolic math toolbox will return the derivative of a multiple variable function) and extracted as needed to find the magnitude of the derivative of a specific function in a system.
Declaring a vector with linear or logarithmic spacing
[edit | edit source]Suppose you wish to declare a vector which varies linearly between two endpoints. For example, the vector [1,2,3] varies linearly between 1 and 3, and the vector [1,1.1,1.2,1.3,...,2.9,3] also varies linearly between 1 and 3. To avoid having to type out all those terms, MATLAB comes with a convenient function called linspace to declare such vectors automatically:
>> LinVector = linspace(1,3,21) LinVector = Columns 1 through 9 1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 Columns 10 through 18 1.9000 2.0000 2.1000 2.2000 2.3000 2.4000 2.5000 2.6000 2.7000 Columns 19 through 21 2.8000 2.9000 3.0000
Note that linspace produces a row vector, not a column vector. To get a column vector use the transpose operator (') on LinVector.
The third argument to the function is the total size of the vector you want, which will include the first two arguments as endpoints and n - 2 other points in between. If you omit the third argument, MATLAB assumes you want the array to have 100 elements.
If, instead, you want the spacing to be logarithmic, use the logspace function. This function, unlike the linspace function, does not find n - 2 points between the first two arguments a and b. Instead it finds n-2 points between 10^a and 10^b as follows:
>> LogVector = logspace(1,3,21) LogVector = 1.0e+003 * Columns 1 through 9 0.0100 0.0126 0.0158 0.0200 0.0251 0.0316 0.0398 0.0501 0.0631 Columns 10 through 18 0.0794 0.1000 0.1259 0.1585 0.1995 0.2512 0.3162 0.3981 0.5012 Columns 19 through 21 0.6310 0.7943 1.0000
Both of these functions are useful for generating points that you wish to evaluate another function at, for plotting purposes on rectangular and logarithmic axes respectively.
Vector Magnitude
[edit | edit source]The magnitude of a vector can be found using the norm function:
>> Magnitude = norm(inputvector,2);
For example:
>> magHoriz = norm(Horiz) magHoriz = 3.7417 >> magVert = norm(Vert) magVert = 8.7750
The input vector can be either horizontal or vertical.
Dot product
[edit | edit source]The dot product of two vectors of the same size (vertical or horizontal, it doesn't matter as long as the long axis is the same length) is found using the dot function as follows:
>> DP = dot(Horiz, Vert) DP = 32
The dot product produces a scalar value, which can be used to find the angle if used in combination with the magnitudes of the two vectors as follows:
>> theta = acos(DP/(magHoriz*magVert)); >> theta = 0.2257
Note that this angle is in radians, not degrees.
Cross Product
[edit | edit source]The cross product of two vectors of size 3 is computed using the 'cross' function:
>> CP = cross(Horiz, Vert) CP = -3 6 -3
Note that the cross product is a vector. Analogous to the dot product, the angle between two vectors can also be found using the cross product's magnitude:
>> CPMag = norm(CP); >> theta = asin(CPMag/(magHoriz*magVert)) theta = 0.2257
The cross product itself is always perpendicular to both of the two initial vectors. If the cross product is zero then the two original vectors were parallel to each other.
Vectoring Mathematics
MATLAB is a vector programming language. The most efficient use of MATLAB will involve taking advantage of the built-in capabilities for manipulating data instead of using constructs such as loops.
Basic Math
[edit | edit source]Most arithmetic operators will work as expected on vectors:
>> a = [2 43 943 78];
>> 5 * a
ans =
10 215 4715 390
>> a / 2
ans =
1.0000 21.5000 471.5000 39.0000
>> 0.2 + a
ans =
2.2000 43.2000 943.2000 78.2000
Likewise, all of these operations can be done with matrices for the expected results.
Most MATLAB functions, such as sin or log, will return a vector or matrix of the same dimensions as its input. So to compute the sine of all the integers between 0 and 10, it suffices to run
>> sin(0:10)
and the returned vector will contains ten values.
Per Element Operations
[edit | edit source]Operators such as the carrot (^) or multiplication between vectors may not work as expected because MATLAB sees vectors the same as any other matrix, and so performs matrix power and matrix multiplication. All operators can be prefixed by a . to make it explicit that an operation should be performed on each element of the matrix. For example, to compute the differences of the sine and cosine function squared for all integers between 1 and 4, one can use:
>> (sin(1:4) - cos(1:4)).^2
ans =
0.0907 1.7568 1.2794 0.0106
as opposed to
>> (sin(1:4) - cos(1:4))^2
??? Error using ==> mpower
Matrix must be square.
which results from MATLAB's attempt to square a 1x4 vector using matrix multiplication.
Using .* or ./ allows one to divide each element of a matrix or vector by the elements of another matrix or vector. To do this, both vectors must be of the same size.
Converting Loops to Vector-based mathematics
[edit | edit source]Since MATLAB is a vector language, an artificial algorithm such as
x = [];
v = [5,2,4,6];
for i=1:4
x(i) = v(i) * ((i+32)/2 - sin(pi/2*i));
if(x(i) < 0)
x(i) = x(i) + 3;
end
end
can be done far more efficiently in MATLAB by working with vectors instead of loops:
i = 1:4;
v = [5,2,4,6];
x = v .* ((i+32)/2 - sin(pi/2*i));
x(x<0) = x(x<0) + 3;
Internally, MATLAB is of course looping through the vectors, but it is at a lower level then possible in the MATLAB programming language.
Arrays/Struct Arrays
Introduction to Structures
[edit | edit source]MATLAB provides a means for structure data elements. Structures are created and accessed in a manner familiar for those accustomed to programming in C.
MATLAB has multiple ways of defining and accessing structure fields. See Declaring Structures for more details.
Note: Structure field names must begin with a letter, and are case-sensitive. The rest of the name may contain letters, numerals, and underscore characters. Use the namelengthmax function to determine the maximum length of a field name.
Declaring Structures
[edit | edit source]Structures can be declared using the struct command.
>> a = struct('b', 0, 'c', 'test')
a =
b: 0
c: 'test'
In MATLAB, variables do not require explicit declaration before their use. As a result structures can be declared with the '.' operator.
>> a.c = 'test'
a =
c: 'test'
Structures can be declared as needed and so can the fields.
Arrays of Structures
[edit | edit source]Structures can also be arrays. Below is an example
>> a = struct('b', 0, 'c', 'test'); % Create structure
>> a(2).b = 1; % Turn it into an array by creating another element
>> a(2).c = 'testing'
a =
1x2 struct array with fields:
b
c
>> a(1) % Initial structure
ans =
b: 0
c: 'test'
>> a(2) % The second element
ans =
b: 1
c: 'testing'
Accessing Fields
[edit | edit source]When the field name is known the field value can be accessed directly.
>> a.c
ans =
test
ans =
testing
In some cases you may need to access the field dynamically which can be done as follows.
>> str = 'c';
>> a(1).(str)
ans =
test
>> a(1).c
ans =
test
Accessing Array Elements
[edit | edit source]Any given element in a structure array can be accessed through an array index like this
>> a(1).c
ans =
test
To access all elements in a structure array use the syntax {structure.field}. In order to get all values in a vector or array use square brackets ([]) as seen below.
>> [a.('c')]
ans =
testtesting
>> [a.('b')]
ans =
0 1
Or you can put them all into a cell array (rather than concatenating them) like this:
>> {a.('c')}
ans = {'test', 'testing'}
Assigning values to a field of each struct array element
[edit | edit source]Matlab provides tools to assign values to a field of each array element. Consider the following struct array:
foo = struct('field_a',{1,2,3,4}, 'field_b',{4,8,12,16})
The following command assigns the same value to the field_b field of each array element:
value = 1;
[foo.field_b] = deal(value)
To assign different values to each array element:
value = {4,8,12,16};
[foo.field_b] = value{:}
Sub-arrays through logical addressing
[edit | edit source]With Matlab, it's possible to extract a subarray from an array by using logical indexing. Consider the following struct array:
foo = struct('field_a',{1,2,3,4},'field_b',{4,8,12,16})
To obtain a subarray from foo where all foo.field_a values are equal to 2, a boolean array can be used to perform logical indexing. So, a boolean test that returns a boolean array for this purpose would be:
[foo.field_a] == 2
So, by using this boolean array to perform logical indexing, Matlab defines a struct array whose elements consist of those from foo whose field_a value is equal to 2 by doing:
foo([foo.field_a] == 2)
Cell Arrays
Cell Array Introduction
[edit | edit source]Cell Arrays can contain differing information in every element. These types of arrays are useful when interacting with spreadsheet software.
Creating Cell Arrays
[edit | edit source]Cell arrays follow the same conventions as regular arrays except instead of square brackets use curly brackets.
array = [1, 2, 3; 4, 5, 6];
cell_array = {1, 2, 3; 4, 5, 6};
Cell arrays have fewer limitations than regular arrays. The regular array can hold strings; however, the string in each element must be the same length. If one element in a regular array is a string then all elements must be a string. Cell arrays have neither of these limitations.
cell_array = {1, 2, 'a', 'abc'; rand(3, 2), magic(3), eye(3), 'junk'}
cell_array =
[ 1] [ 2] 'a' 'abc'
[3x2 double] [3x3 double] [3x3 double] 'junk'
With fewer limitations for the content of a cell array comes complications. While cell arrays are a powerful tool, these arrays work differently because each element can be almost anything.
Dynamic Resizing
[edit | edit source]Cell arrays can be dynamically resized, which is a key feature in more advanced data structures. For example, a queue data structure using the commands:
cell_array{end+1}='a';
cell_array{end+1}='b';
An element can be popped from the front of the queue using the commands:
cell_array(1)=[]; % remove first element - resize cell_array(1)=[]; % remove first element - resize
Uses
[edit | edit source]GUI Tables
[edit | edit source]Cell arrays are used when displaying a table to a figure.
uitable('Data',{'hello',1;2,'there'})
Converting to and from cell arrays
[edit | edit source]Converting From a Numeric Array into a Cell Array
[edit | edit source]Use num2cell to convert from a numeric into a cell array.
>> cell_array = num2cell(numeric_array);
Converting From a Cell Array into a Numeric Array
[edit | edit source]Use cell2mat to convert from a cell into a numeric array.
>> numeric_array = cell2mat(numeric_cell_array);
External Links
[edit | edit source]
Plot
The plot command plots a 2D line plot of the data in Y versus the corresponding values in X.
Plotting linear lines
[edit | edit source]For the first MATLAB plot, we are going to plot the classical linear equation y = mx +c
In MATLAB, to do plotting we need to follow the specific workflow
(a) Specify the range of values of x to be used (b) Specify the equation of the y with x variables (c) plot the graphs

For the examples , we need to plot of an equation for x range from 0 to 30
In MATLAB, we type in the following:
x = 0:30; %declare x = 0 to 30
y=(5*x) +8 ; % declare equation
plot(x,y) %plot the line chart
We can get the simple line chart as shown on below :
As you see on the left, we can get the of chart plot for linear lines .
Congrats, you have plotted the first chart in MATLAB .
This is the basic idea of how to plot charts in MATLAB .
In next section, we are using the same charts to spruce up the charts to make it more custom made/unique
Enhance the chart plots
[edit | edit source]Below are some of the ways to enhance the chart plots (it is to make it more understandable/presentable to the readers)
Note that all of the chart plot enhancers are needed to be defined after/below the plot commands with some properties need to be defined at the plot functions.
These are few properties that can be used to enhance the plot charts namely
(a) Axis Label
(b) Grid
(c) Legend
(d) Marker
(d) Title
Axes labels
[edit | edit source]
We can label the axes by using xlabel and ylabel with examples as below.
For the customization, we use as followed conventions
xlabel or ylabel(text to display, Properties Name 1,Value Properties Name 1, ..., Properties Name n,Value Properties Name n)
As shown below, we can customized the axis label .with multiple properties.
xlabel('Population of dogs','Color','b','FontWeight','bold','FontAngle','italic')
% x label to display "Population of dogs" with blue colour fonts, bold and italic
ylabel({'Weeks','for year 2022'},'FontSize',15,'FontName','Times New Roman')
% y label to display 2 lines of "Weeks for year of 2022" with font size 15 and using font 'Times New Roman'
Grid
[edit | edit source]
As shown on original chart shown above, it is hard to see which whether the certain line plots are references to the axes on the right.
We can use the grid to trace the certain values of x is correlating to which y values.
We can use grid functions and uses the following MATLAB commands
grid on
%turn on grid
grid minor
% turn on the minor gridlines / subset of the major gridlines
There is another properties that is grid minor which will plot out the smaller grid scales, that is grid minor
In order to use grid minor, you need to turn on grid by typing grid on first.
Legend
[edit | edit source]
We can put legends on the chart plot by using following command: legend
For example below, we need to label the plot line as followed
legend('y=(5*x) +8','Location','northeast')
We can see the legends shown in northeast location which is the default locations for the graph
We can define the locations of the legends within the chart area or even outside of the chart by adding keyword outside to the locations
Marker
[edit | edit source]
You can add a marker in the plot chart inside the plot command .
plot(x,y,marker_commands)
For the example , let's say we wanted have diamond shaped marker, hence we type in following command
plot(x,y,'-d') %the line - indicate the line to connect the diamond shapes
We would have a chart with diamond-shaped marker as shown.
The following marker_commands that can be used in plotting such as follows :
| marker_commands | Marker shapes |
|---|---|
| 'o' | Circle sign |
| '+' | Plus sign |
| '*' | Asterisk |
| '.' | Point |
| 'd' | Diamond |
| 'h' | Six-pointed star (hexagram) |
| 's' | Square |
| 'p' | Five-pointed star (pentagram) |
| 'x' | Cross |
| '^' | Upward-pointing triangle |
| 'v' | Downward-pointing triangle |
| '<' | Left-pointing triangle |
| '>' | Right-pointing triangle |
Title
[edit | edit source]
We can add the title to the plot chart by adding title command
Same as axis label above, the convention for title command follows the same conventions
title(text to display, Properties Name 1,Value Properties Name 1, ..., Properties Name n,Value Properties Name n)
As shown, we can customize the title as followed
title({'Populations of dogs in 2022 ','by weeks'}, 'Color','g','FontSize',14,'FontName','Lucida Console')
%display the title in two lines with green text , font size of 14 and with font Lucida COnsole
Other examples
[edit | edit source]In this example, we are going to plot a simple circle.
angles = linspace(0, 2*pi);
radius = 20; % radius of circle is 20
CenterX = 50; %coordinate of circle center point at x axis is 50
CenterY = 50; %coordinate of circle center point at y axis is 50
x = radius * cos(angles) + CenterX;
y = radius * sin(angles) + CenterY;
plot(x, y, 'b-', 'LineWidth', 2);
title("Circle")
hold on;
plot(CenterX, CenterY, 'k+', 'LineWidth', 3, 'MarkerSize', 14);
grid on;
axis equal;
In this example, the following code will create a graph comparing the speedup of two algorithms on increasing number of processors.
The graph created is shown below.

>> x = [1 2 4 8];
>> y = [1 2 1.95 3.79];
>> z = [1 1.73 2.02 3.84];
>> h = plot(x,y,'--');
>> hold on; % Plot next graph on same figure
>> plot(x,z);
>> hold off;
>> xlabel('Number of processors');
>> ylabel('Speedup');
>> saveas(h,'graph.eps',eps);
External Links
[edit | edit source]MATLAB category on ControlTheoryPro.com
How to Plot MATLAB Graph using Simple Functions and Code?
Polar Plot
Introduction
[edit | edit source]The polar command accepts polar coordinates, plots them in a Cartesian plane, and draws the polar grid on the plane.
Usage
[edit | edit source]Here's how a plot can be created.
>>t = 0:.01:2*pi;
>>polar(t,sin(2*t).*cos(2*t),'--r')
>> grid on % Turn on the grid
Semilog
Note that this page is a copy of the ControlTheoryPro.com page on semilogx/y commands.
Introduction
[edit | edit source]The semilogx or semilogy commands plot data with 1 axis linear and the other axis log scale. The semilogx command plots the data on the x-axis on a log scale. For controls this is particularly useful when manually creating a bode plot.
Bode Plots
[edit | edit source]The MATLAB bode plot is very convenient but when the plot needs to be formatted then the bode command makes this difficult. As a result this author (Gabe 13:30, 20 April 2008 (CDT)) creates bode plots using the following commands
freqVec = logspace(-1, 3, 5000);
[mag, phs] = bode(sys, freqVec * (2*pi));
mag = db(mag(:));
phs = phs(:);
figure;
subplot(2, 1, 1)
semilogx(freqVec, mag)
grid on
title('System Bode Plot')
ylabel('Magnitude (dB)')
subplot(2, 1, 2)
semilogx(freqVec, phs)
grid on
ylabel('Phase (deg)')
xlabel('Frequency (Hz)')
External Links
[edit | edit source]
Loglog
Introduction
[edit | edit source]The loglog command plots both x and y data sets on a log scale while the plot command plots both axes on linear scales and the semilogx/y command plots 1 axis on a linear scale and the other axis on a log scale. Other than the scale of the axes, the 3 plotting commands are identical in most ways.
Basic Usage
[edit | edit source]The basic usage of the plot, semilogx/y, and loglog command are identical. Below is an example of how a PSD would be plotted
>> Fs = 1000; % Sample Rate of 1 kHz
>> t = 0:(1/Fs):1000; % Time vector
>> x = sin(pi*t); % Sine wave based on time vector
>> [Pxx, f] = pwelch(x, [], [], [], Fs);
>> loglog(f, Pxx)
>> grid on
>> xlabel('Frequency (Hz)')
>> ylabel('Magnitude (units^2/Hz)')
>> title('PSD of Sine Wave')
See Also
[edit | edit source]External Links
[edit | edit source]
Bode Plot
Introduction
[edit | edit source]This article is on the topic of creating Bode plots in MATLAB. The quick answer is use the bode command. However, the bode command has several options and the plots generated by the bode command are not easily reformatted. The default formatting of most MATLAB plots is good for analysis but less than ideal for dropping into Word and PowerPoint documents or even this website. As a result this article presents an alternative that requires more lines of code but offers the full formatting flexibility of the generic plot command.
MATLAB's Bode Command
[edit | edit source]The basic bode command is as follows
>> bode(LTI_SYS)
where
The bode command will automatically call gcf which will put the bode plot on the current figure. If no figure exists then one is created by gcf.
If you wish to specify the frequency points at which LTI_SYS is plotted then create a frequency vector using logspace or linspace as follows
>> freqVec = logspace(-1, 3, 5000); >> bode(LTI_SYS, freqVec * (2*pi))
where
- freqVec is a vector of 5000 frequencies, in Hz, spaced evenly on a log scale from 10-1 to 103
- pi is a MATLAB constant equal to the value of and in this case it is used to convert freqVec to rad/sec as it is passed to the bode command
In order to get the magnitude and phase at each frequency point the bode command must be called with output arguments such as
>> [mag, phase] = bode(LTI_SYS);
or
>> [mag, phase] = bode(LTI_SYS, freqVec * (2*pi));
where
- mag is the magnitude (not in dB) at each point in freqVec
- phase is the phase (in degrees) at each point in freqVec
The mag and phase variables must come out as 3D arrays. Assuming LTI_SYS is SISO then the commands below will convert mag and phase into the vectors you would expect
>> mag = mag(:); >> phase = phase(:); >> mag = db(mag); % to get the magnitude in 20log dB
Issues with the bode command
[edit | edit source]The main issue with the bode command is reformatting of the plot. The bode command appears to use a normal semilogx plot and then apply patches ro something similar to the figure. This can lead to odd behavior when attempting to create multi-line titles, reformat line widths or font sizes, etc. The normal relationship of axes to figure is just not quite present.
External Links
[edit | edit source]
Nichols Plot
Introduction
[edit | edit source]This article is on the topic of creating Nichols plots in MATLAB. The quick answer is use the Nichols command. However, the Nichols command has several options and the plots generated by the Nichols command are not easily reformatted. The default formatting of most MATLAB plots is good for analysis but less than ideal for dropping into Word and PowerPoint documents or even this website. As a result this article presents an alternative that requires more lines of code but offers the full formatting flexibility of the generic plot command.
MATLAB's Nichols Command
[edit | edit source]The basic Nichols command is as follows
>> nichols(LTI_SYS)
where
The Nichols command will automatically call gcf which will put the Nichols plot on the current figure. If no figure exists then one is created by gcf.
If you wish to specify the frequency points at which LTI_SYS is plotted then create a frequency vector using logspace or linspace as follows
>> freqVec = logspace(-1, 3, 5000); >> nichols(LTI_SYS, freqVec * (2*pi))
where
- freqVec is a vector of 5000 frequencies, in Hz, spaced evenly on a log scale from 10-1 to 103
- pi is a MATLAB constant equal to the value of and in this case it is used to convert freqVec to rad/sec as it is passed to the Nichols command
Issues with the nichols command
[edit | edit source]The main issue with the nichols command is reformatting of the plot. The nichols command appears to use a normal semilogx plot and then apply patches or something similar to the figure. This can lead to odd behavior when attempting to create multi-line titles, reformat line widths or font sizes, etc. The normal relationship of axes to figure is just not quite present.
External Links
[edit | edit source]More on the Nichols plot at ControlTheoryPro.com
Nyquist Plot
Introduction
[edit | edit source]This article is on the topic of creating Nyquist plots in MATLAB. The quick answer is use the nyquist command. However, the Nyquist command has several options and the plots generated by the nyquist command are not easily reformatted. The default formatting of most MATLAB plots is good for analysis but less than ideal for dropping into Word and PowerPoint documents or even this website. As a result this article presents an alternative that requires more lines of code but offers the full formatting flexibility of the generic plot command.
MATLAB's Nyquist Command
[edit | edit source]The basic Nyquist command is as follows
>> nyquist(LTI_SYS)
where
The Nyquist command will automatically call gcf which will put the Nyquist plot on the current figure. If no figure exists then one is created by gcf.
If you wish to specify the frequency points at which LTI_SYS is plotted then create a frequency vector using logspace or linspace as follows
>> freqVec = logspace(-1, 3, 5000); >> nyquist(LTI_SYS, freqVec * (2*pi))
where
- freqVec is a vector of 5000 frequencies, in Hz, spaced evenly on a log scale from 10-1 to 103
- pi is a MATLAB constant equal to the value of and in this case it is used to convert freqVec to rad/sec as it is passed to the nyquist command
Issues with the nyquist command
[edit | edit source]The main issue with the nyquist command is reformatting of the plot. The nyquist command appears to use a normal semilogx plot and then apply patches or something similar to the figure. This can lead to odd behavior when attempting to create multi-line titles, reformat line widths or font sizes, etc. The normal relationship of axes to figure is just not quite present.
External Links
[edit | edit source]
Portable Functions
Functions in MATLAB
[edit | edit source]A function is a group of sequential expression statements (a.k.a pseudo-algorithm) that are formed together perform a task. In MATLAB, functions are defined in separate files. The name of the file and of the function MUST be the same. Functions operate on variables within their own workspace, which is also called the local workspace, separate from the workspace you access at the MATLAB command prompt which is called the base workspace.
Functions can accept more than one input arguments and may return more than one output arguments.
The sntax of functions as followed
function [y1,...,yN] = myfunc(x1,...,xM)
where syntax declares a function named myfunc that accepts inputs x1,...,xM and returns outputs y1,...,yN .
This declaration statement must be the first executable line of the function. Valid function names begin with an alphabetic character, and can contain letters, numbers, or underscores.
Create Functions in Separate Files
[edit | edit source]
To create a new function, at "Home" tab, click on "New" ---> "Functions" It will create a template looks like the following:
function [outputArg1,outputArg2] = untitled2(inputArg1,inputArg2)
%UNTITLED Summary of this function goes here
% Detailed explanation goes here
outputArg1 = inputArg1;
outputArg2 = inputArg2;
end
Declare a function
[edit | edit source]To demonstrate a function usefulness, we are going to take a hypothetical situations ,
Recently, in your class there are some exchange students from America whom are consistently complaining the weather is hot outside, when they check on their weather app, they exclaimed the weather is 100 degrees outside. But as to the people who never uses the imperial units before, you might wonder, what is the temperature outside right now ?
So, to solve the question, it might be a good time to create a custom functions to convert from Fahrenheit to Celsius .
First of all, we must know the conversion formula from Fahrenheit to Celsius which is given as:
At "Home" tab, click on "New" ---> "Functions"
function [Ce] = convertTemp(Fa)
% Convert from Fahrenheit to Celcius
Ce = (Fa-32)*(5/9);
end
Click on save button to save the functions as convertTemp.m file
Note: The filename MUST be same as function name or else it won't work !
Later, on the Current Folder Panel, select the directory where you save the function files just now.
Calling a function
[edit | edit source]To call the newly created function, do the following: On the Command Window Panel, type this command as shown
>> convertTemp(100)
ans =
37.7778
Hence, the weather outside is almost 38 Celsius degrees.
Benefits of functions
[edit | edit source]Why this is beneficial, you might ask ?
Well, from this exercise , you can see that you can just type function name to execute the calculation especially for repetitive tasks.
Just imagine for example above, it will be a real time saver to just type function convertTemp instead of manually typing formula each tims.
Type of functions
[edit | edit source]The type of functions includes such as:
- Anonymous Functions
- Local Functions
- Nested Functions
- Private Functions
- Inline function (Phased out in future version)
Anonymous Functions
[edit | edit source]Anonymous functions allow you to define a function without creating a program file, as long as the function consists of a single statement. A common application of anonymous functions is to define a mathematical expression without creating a separate files.
Here is how the anonymous syntax looks like
output = @(arguments) expression
where, output = output to be returned arguments = required inputs to be passed expression = a single formula/logic
It can accept multiple inputs and return one output. They can contain only a single executable statement.
Here, we have an examples of converting Fahrenheit to Celsius.
>> convTempF = @(Fa) (Fa-32)*(5/9);
>> convTempF(88)
ans =
31.1111
>> convTempF(60)
ans =
15.5556
Another example here is using anonymous function to convert minute to seconds (NOTE: 1 minute is equal to 60 seconds)
>> convert_min_to_s = @(t) t*60;
>> convert_min_to_s(4)
ans =
240
Local functions
[edit | edit source]Sometimes in mathematics, you might be encountering an issue where you might find a use case where function that are better to be calculated within it's own function .
Rather than running separate functions to get one output, you just need to run just one function to get the multiple output. This is where local functions comes in.
To clarify further , in a function file, the first function in the file is called the main or parent function.
Additional functions within the file are called local functions, and they can occur in any order after the main function. Local functions are only visible to other functions in the same file. These are equivalent to subroutines in other programming languages, and are sometimes called sub-functions.
The application for this local functions is in a complex function, it would be easier to be broken down to smaller piece of functions and we are certain that the functions are going to be used in same functions and not at other functions.
Examples of local functions
[edit | edit source]To illustrate an examples, we will create a function statistik which will take in a series of number and return an output of basic function of statistic such as max , min, average and standard deviation. We will give it just a sting of random numbers and it will produce all the usual statistic results.
First of all, we need to create a function named statistik , follow the instruction here at Create Functions in Separate Files
function [max,min,ave,stdev] = statistik(v) % this is the main function and can call to other local functions
% The function where it takes arguments of series and it will calculate the basic statistic info
% min function selects the smallest number in the series
% max function selects the largest number in the series
% ave function calculate the average of the series
% stdev function calculate the standard deviations
max = maxf(v);
min = minf(v);
ave = avef(v);
stdev = stdevf(v);
end %end of function statistik
function a=maxf(v)
%Sub function selects the largest number in the series
a = max(v);
end %end of function maxf
function b= minf(v)
%Sub function selects the smallest number in the series
b = min(v);
end %end of function minf
function c = avef(v)
%Sub function to calculate the average of the series
c = mean(v);
end %end of function avef
function d = stdevf(v)
%Sub function to calculate the std dev of the series
d = std(v);
end %end of function stdevf
After creating function statistik in a separate file, we generate a random set of number inside the Command Window using randi function
>> V = randi(50,1,10)
V =
25 29 12 23 49 28 27 12 25 32
We call the function statistik as followed inside the Command Window:
[maximum,minimum,average,stdeviation]=statistik(V)
maximum =
49
minimum =
12
average =
26.2000
stdeviation =
10.4435
Although you cannot call a local function from the command line or from functions in other files, you can access its help using the help function.
Specify names of both the file and the local function, separating them with a > character.
>> help statistik>avef
Sub function to calculate the average of the series
Nested Function
[edit | edit source]Nested functions are functions that are nested entirely inside the main functions.
The primary difference between nested functions and local functions is that nested functions can use variables defined in parent functions without explicitly passing those variables as arguments.
Requirements of nested functions
[edit | edit source](a) To nest any function in a program file, all functions in that file must use an end statement.
(b) A nested function can't be defined inside any of the program control statements, such as if/elseif/else, switch/case, for, while, or try/catch.
(c) A nested function either directly by function name , or using a function handle that you created using the @ operator (refer to anonymous function).
(d) All of the variables in nested functions or the functions that contain them must be explicitly defined. That is, you cannot call a function or script that assigns values to variables unless those variables already exist in the function workspace.
Examples of nested functions
[edit | edit source]
We have a hypothetical situations where we need to estimate the weight of metal ingots which are in cylindrical shape.
First, before we started on figuring out the metal ingots weight, we need to break down the problems into smaller piece.
To figure out the weight of the metal, we need to figure out the density and before figuring out density we need to figure out volume of the metal.
To start off, before we start to know the volume of ingot, we first calculate the surface area of the cylinder base which is circle.
Area of circles is defined as
,r is radius of base circle
We can use the area of circle to calculate the volume of cylinder
,h is height of cylinder.
Lastly, we use the volume and density to calculate the weight
where D is density.

In MATLAB, we formulate the formula such as these.
Note: For the nested functions beside main funtions, we need to indent the functions .
Editor -> Indent.
Note:
function[]=ingot_calc()
%This function is to calculate the price of an cylindrical ingot
r = 3 ; % radius of base circle
h = 10; % height of ingot
d = 4.5;% density of the metal
ar = circle_area;
vo = volume;
we = weight;
function a = circle_area
%calculate area of circle for the radius
a=pi*r*r;
at=['Area of circle is ',num2str(a,'%8.2f') , ' cm2'];
disp(at)
end
function v = volume
%calculate volume
v = ar* h;
vt=['Volume of the ingot is ',num2str(v,'%8.2f') , 'cm3'];
disp(vt)
end
function w = weight
%calculate weight
w = vo*d;
wt=['The weight of ingot is ',num2str(w,'%8.2f'), ' g'];
disp(wt)
end
end
When we calling ingot_calc function in the command window, it should display the values
>> ingot_calc
Area of circle is 28.27 cm2
Volume of the ingot is 282.74cm3
The weight of ingot is 1272.35 g
Inline Functions
[edit | edit source]Inline functions are currently being phased out. Anonymous functions should be used instead. Inline functions are included here for information purposes.
>> convert_s_to_ms = inline('x*1000','x');
>> convert_s_to_ms(20)
ans =
20000
Function Handles
[edit | edit source]
Function handles are doubles serving as an abstract reference to the function. Handles allow an equation to be passed to another function for direct evaluation. Anonymous functions are useful for command-line evaluation or for multiple evaluations in the same m-file.
The ampersat returns the handle of a function either built into Matlab or defined in an M-file.
To illustrate example, we need to build a tent as shown on the picture but we need to figure out what is the amount of tarp that are needed to build the carnival tent.
Therefore, we will create two separate functions which take the radius and slant height of cone (cone) plus radius and height of cylinder (cylinder) .
To refresh the your memory, formula for cone surface (remember we focus slanting area and ignore the base area) is
and cylinder surface (remember that one side of circle of cylinder is not calculated) is
, where the r is the shared radius of cylinder and cone, l is the length of slanting height of cone and finally h is height of cylinder.
Follow steps in Create Functions in Separate Files to start create totalsurftent
function [surfcone,surfcylin] = totalsurftent(r,l,h)
% The function where it takes arguments of r,l,h to calculate surface area of cylinder and cone
% r is radius
% l is slanting lenth of cone
% h is cylinder height
surfcone = sacone(r,l);
surfcylin = sacylin(r,h);
end
function on=sacone(r,l)
%Sub function to calculate face area of cylinder
on = pi*r*l;
end
function yl= sacylin(r,h)
%Sub function to calculate face area of cylinder
yl = (2*pi*r*h)+(pi*r^2);
end
We can know the surface area by typing following commands:
>> %Testing out the custom functions totalsurftent
>> [areacone,areasurfcylin] = totalsurftent(3,3,3)
areafcone =
28.2743
areacylin =
84.8230
Function Handles in m-files
[edit | edit source]If you are not familiar with m-files, then skip this and come back.
A function handle passes an m-file function into another function. This of course lets you have more control over what's passed there, and makes your program more general as it lets you pass any m-file (as long as it meets other requirements like having the right number of input arguments and so on). The functionality is similar to that of function pointers in C++.
To pass an m-file to a function, you must first write the m-file, say something like this:
function xprime = f(t,x) xprime = x;
Save it as myfunc.m. To pass this to another function, say an ODE integrator, use the @ symbol as follows:
>> ode45(@myfunc, [0:15], 1)
One advantage of using function handles over anonymous functions is that you can evaluate more than one equation in the m-file, thus allowing you to do things like solve systems of ODEs rather than only one. Anonymous functions limit you to one equation.
How to write a function that accepts a function handle
[edit | edit source]Functions can accept function handles. To do this define them as variables in your header, and then call the handles as if they were functions:
% myadd adds two variables together function result = myfunc(func, a, b); result = func(a, b); [in a separate m-file] function sum = myadd(a, b) sum = a+b;
The command you send to myfunc looks like this:
>> result = myfunc(@myadd, 1, 2); result = 3
References
[edit | edit source]
Handle/What is a handle?
A function handle is a MATLAB data type that represents a function. A typical use of function handles is to pass a function to another function.
For example, you can use function handles as input arguments to functions that evaluate mathematical expressions over a range of values. Other typical uses of function handles include:
(a) Specifying callback functions (for example, a callback that responds to a UI event or interacts with data acquisition hardware).
(b) Constructing handles to functions defined inline instead of stored in a program file (anonymous functions).
(c) Passing a function to another function (often called function functions). For example, passing a function to integration functions, such as integral.
(d) Calling local functions from outside the main function.
References
[edit | edit source]
Handle Graphics
This book discusses some ways of manipulating graphics in MATLAB.
What is a handle?
[edit | edit source]All of the graphics capabilities explained thus far are ways to generate plots without worrying much about the details. However, very often, you will want a plot that looks a very specific way. You can go into the GUI and change all of the settings every time, but this gets very tedious and wastes a lot of time. If you want a way to generate a plot that has the same look all the time, it is time to delve into the realm of handle graphics.
A handle is a floating-point scalar that points to a large list of different properties. Each element of a plot has its own properties, and its own handle. Handles are organized into a tree-structured hierarchy, starting from the handle for your monitor (named 0) and branching down to separate handles for children like axis labels, text annotations, error bars, and anything else that can go on a plot. Handles at all levels can be controlled interactively or adjusted programmatically, by changing the values of the handle properties using specific functions.
Monitor properties: the 0 handle
[edit | edit source]Monitor properties are useful to know when designing graphic user interfaces. For example, you may want to check that a figure window fits inside the user's screen. In order to get a list of the properties of the screen, type:
>> get(0)
To get a specific property, type
>> get(0, 'propertyname');
See the documentation for a complete list of property names and what they mean.
Axis handles
[edit | edit source]See the documentation for a list of valid axis properties and values of those properties.
gca
[edit | edit source]Other types of handles
[edit | edit source]Text handles
[edit | edit source]uicontrols
[edit | edit source]
Handle/Figure Handle
Figure handles
[edit | edit source]A figure is essentially a window that acts as a container for one or more plots, uicontrols, and so on. It is the second highest level object you can create
To create a figure, use the figure function like so:
>> fhandle = figure;
This creates a new figure window and stores all the figure data in the variable fhandle. You can also tell MATLAB to give the figure any number of properties at the same time as it's created using the syntax:
>> fhandle = figure('Propertyname1', value1, 'Propertyname2', value2, ...);
See the documentation "figure properties" page for a list of valid property names for figures.
You can close a figure and destroy its handle programmatically by using the close function:
>> close(fhandle);
The get and set functions
[edit | edit source]MATLAB allows you to get any property of a figure handle (or actually any type of graphics handle, including axes, line objects, text objects, and so on) by using the 'get' function in the following manner:
>> h = figure; >> propvar = get(h, 'Propertyname');
will store the property with name 'Propertyname' in the variable propvar. With the 'get' function you can only get one property at a time.
The set function allows you to set any number of properties of figures and other graphics handles. You can change as many properties as you want by calling the set function like this:
>> set(h, 'Propname1', propval1, 'Propname2', propval2, ...);
You can also modify the same properties to the same values for any number of handles, if you simply create an array of handles first:
>> handlevec(1) = figure; >> handlevec(2) = figure; >> set(handlevec, 'Name', 'Figure window')
will create two new figures and give them both the same title: 'Figure window'.
See the documentation for valid property names and values for figure properties.
gcf
[edit | edit source]Even if you don't assign a figure to a variable, you can still access it by using the internal MATLAB variable gcf. This is mostly for convenience, so you don't have to pass the figure handle from one function to another to make modifications. However, due to the warning below, you must be VERY careful in use of gcf so that you make sure you are modifying the correct figure in the case of multiple figure programs:
The current figure is the last one to be modified, not necessarily the one that's open |
To get a list of the current properties of the current figure, use the syntax:
>> get(gcf)
You can also get or set a specific property by using:
>> get(gcf, 'propertyname'); >> set(gcf, 'propertyname', value);
See the documentation "figure property" page for valid figure property names and the format for their values.
Saving the contents of a figure
[edit | edit source]To save the entire contents of a figure, use the saveas function:
>> saveas(fhandle, 'X.fig');
will save the contents of the figure with handle fhandle as X.fig. .fig files can be opened and edited manually later if desired, although it is often difficult to open them and re-edit them programmatically in a consistent manner.
You can also use the saveas function to save image formats such as .jpg, .tif, .bmp, .png, and so on. The saveas function is essentially a command line version of the "file --> save as..." option in the figure window itself, but there are some possible resolution differences. Using either of these two methods of saving a figure to a file, the quality of the resulting image is often insufficient for purposes such as inclusion in publications.
In the event that a high quality version of the figure is necessary, it is possible to use MATLAB's print function to print the figure to a vector format (such as Adobe Illustrator's format, obtained with the -dill flag) or to a raster format with a specified resolution (for example, using the two flags -dpng and -r300 would tell MATLAB to print the figure to a PNG file at 300dpi). See the documentation for that function here for more details on the supported output formats.
As an alternative to MATLAB's print function, SVG files can be obtained from many figures (not just simulink models) using the plot2svg function from MATLAB's contributor central (available here). SVG files can be edited using freeware tools such as Inkscape, and also can be opened in Illustrator.
Axis Handle
MATLAB offers incomparable control over the way you can add details to your plot. From inserting text at the right positions to labelling the axes, MATLAB from the command line offers you an easy way to create publication style graphics. With support for Encapsulated PostScript and Adobe Illustrator output. Complex figures with several axes and conveying large amounts of information can be created.
Concept of a handle
[edit | edit source]Most operations on figures generate objects with a set of properties. Users familiar with object-oriented programming would realize that the functions and the data are encapsulated into the object. A typical figure would contain at least half a dozen objects. These objects are called handles. A very tacky analogy would be like handles to several different refrigerators with several different contents. To provide an intuitive feel. I have listed out the properties from a text handle.
Finding a handle
[edit | edit source]Various commands provide required handles, for example:
h = gcf; % Get current figure h = gca; % Get current axis
Examples
[edit | edit source]Axis Label
[edit | edit source]xlabel labels the x-axis of the current plot.
xlabel('string')
You can display text on two lines or insert the value of variables
xlabel({['First Line or line n° ',int2str(a)],['Second Line or line n°',int2str(b)]})
ylabel labels the y-axis of the current plot. It works in same way of xlabel, but the output is vertical in 2D plots.
Documenting a Maximum Value
[edit | edit source]% Previous code set the x value of the peak data point into x_peak
plot(lags(1:1000:end),abs_cs(1:1000:end));
ptitle = 'UUT and Source Correlation Score Magnitude';
xlabel('Lag'); ylabel('Correlation Magnitude');
title(ptitle); yloc = max(get(gca,'YLim'));
% Put at top of plot
text(lags(x_peak),yloc,[' \leftarrow ' num2str(x_peak) 'ns']);
lstr{1} = sprintf(' Test %d', TESTNUM); lstr{2} = sprintf(' Unit %d%s', UNITNUM, comparestr);
text(lags(1),mean(get(gca,'YLim')),lstr);
Inserting Newlines into Plot Labels
Cell arrays are the easiest way to generate new lines when using the functions xlabel, ylabel, zlabel, text, title, and gtext. However, cell arrays do not always work (see next section).
When displaying text on plots, "\n" is typically interpreted as '\' followed by 'n' instead of the newline character. To generate multiple lines, use cell arrays. This is done by separating each string line of text with a comma and enclosing all comma-separated strings in curly braces as follows.
>> title({'First line','Second line'})
Sometimes it is nice to put the value of a variable and a newline into the plot title. You can do this like so:
n = 4; x = -n:1:n; y = x.^2; plot(x,y) title( [ 'plot of x squared', 10, 'from x = ', num2str(-n), ' to x = ', num2str(n) ] )
The 10 outside the single quotes is the ascii value for a newline. You don't have to use the char() function, just the number will work.
The output should look like this:
plot of x squared from x = -4 to x = 4
Advanced Topics/Numerical Manipulation
Numerical Manipulation
[edit | edit source]Linear Algebra
[edit | edit source]It is the Matrix laboratory after all.
- Operations
- Transpose
- Systems of linear equations
- Row reduced echelon form
- Inverse
- Coffactor, minor
- Jacobian
Differential Equations
[edit | edit source]
Basic Reading and Writing data from a file
MATLAB file types
[edit | edit source]There are two file types used by MATLAB namely .m and .mat files
- .m / .mat files: Standard MATLAB files (Most functions in .mat can be supported by the older version off MATLAB)
- .mlx files: Live Code File Format. This format were just introduced on MATLAB version R2016a. This type of files storing the live scripts/live functions that uses the Live Code file format.
Import functions
[edit | edit source]The function that usually are used to import data into MATLAB : importdata(filename)
importdata(filename) can loads data into array.
% sample script of loading an images
>> A = importdata('example1.png');
imread(A)
Loading Data
[edit | edit source]
load(filename) can loads data from filename. The files can be text, images , and even audio files.
% sample script of loading an audio
>> B = load('example2.mp3');
audioread(B,single,1.0)
The load command is used to load data from a file into the current workspace.
- Load all variables from the file mySave.mat into the current workspace.
>> load('mySave.mat')
>> load(fullfile(pwd, 'mySave.mat'))
- Load just the variables myData1 and myData2.
>> load('mySave.mat', 'myData1', 'myData2')
- Load all myData variables.
>> load('mySave.mat', 'myData*')
- Get a cell array of variables in saved file.
>> whos('-file', 'mySave.mat')
Saving Data
[edit | edit source]The save command is used to save workspace data to a file.
- Save all workspace data to the file mySave.mat in the current directory.
>> save('mySave.mat')
>> save(fullfile(pwd, 'mySave.mat'))
- Save just the variables myData1 and myData2 to mySave.mat.
>> save('mySave.mat', 'myData1', 'myData2')
- Save all myData variables to mySave.mat.
>> save('mySave.mat', 'myData*')
- Save all myData variables to a mySave.mat file compatible with version 6 of MATLAB.
>> save('mySave.mat', 'myData*', '-v6')
- Save all myData variables to an ASCII file.
>> save('mySave.mat', 'myData*', '-ASCII')
- Append new variables to the data file.
>> save('mySave.mat', 'newData*', '-append')
Excel Spreadsheets I/O
[edit | edit source]Since analyzing data is one of the more common motivations for using input output I will start with reading and writing from a spreadsheet. I cover the command line first since it is often necessary to import the data while an m-function is being evaluated.
Reading Excel Spreadsheets
[edit | edit source]MATLAB makes it easy to read from an Excel spreadsheet. It has the built-n command readcell
Let say, you have an Excel file (Preferably latest version with file format .xlsx ) , In this example, you have a table with data shown as below saved as Class Marks.xlsx in any place of your liking
| Name | Marks |
| Ali | 93 |
| Chin | 47 |
| Sammy | 74 |
| Dorothy | 96 |
| Huat | 94 |
| Anna | 38 |
To read the contents , you need to type as follows:
A=readcell('C:\mydir\Class Marks.xlsx') % mydir is referring where you actually saves the Excel file
Pro tips: If you are unsure of the file location, right click of the file that you saved and select Properties and look for Locations in General tabs. You can change mydir into your selected locations
It will shows the output as follows
A =
7×2 cell array
{'Name' } {'Marks'}
{'Ali' } {[ 93]}
{'Chin' } {[ 47]}
{'Sammy' } {[ 74]}
{'Dorothy'} {[ 96]}
{'Huat' } {[ 94]}
{'Anna' } {[ 38]}
This line of code reads Class Marks.xlsx (from the saved directory - mydir) and places it in an identical array inside MATLAB called A. You can then manipulate the array A in any way you want.
Reading from certain range in the text files
[edit | edit source]From table above just now, we expand to more rows and columns as shown below in Sheet named Class1A. Note that A-> H and 1->11 are for references
In this example, we are interested , we interested in Huat marks and make an array B to extract his marks
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Name | English | Maths | Science | Art | Music | Malay | Moral |
| 2 | Ali | 71 | 54 | 65 | 27 | 65 | 54 | 96 |
| 3 | Chan | 14 | 96 | 50 | 40 | 17 | 99 | 95 |
| 4 | Sammy | 17 | 15 | 72 | 24 | 55 | 15 | 26 |
| 5 | Dorothy | 89 | 35 | 45 | 14 | 87 | 52 | 65 |
| 6 | Huat | 82 | 90 | 15 | 65 | 42 | 82 | 90 |
| 7 | Anna | 12 | 77 | 25 | 63 | 46 | 14 | 31 |
| 8 | Lee | 77 | 22 | 49 | 91 | 43 | 89 | 66 |
| 9 | Muthu | 61 | 25 | 38 | 65 | 43 | 35 | 89 |
| 10 | Ismail | 70 | 70 | 79 | 75 | 81 | 44 | 98 |
| 11 | Th'ng | 42 | 92 | 99 | 14 | 46 | 12 | 24 |
The comments explained how to select certain range of wanted data.
B=readcell('C:\mydir\Class Marks.xlsx','Sheet','Class1A','Range','A6:H6')
%mydir is the location where Excel is stored
%sheet is to select which sheet
%range can be selected with following manner
%a. form 'A1' (cell)
%b. form 'A:B' (column-select)
%c. form '1:5'(row-select)
%d. form 'A1:B5' (rectangle-select)
The B array will show following results
B =
1×8 cell array
{'Huat'} {[82]} {[90]} {[15]} {[65]} {[42]} {[82]} {[90]}
Writing Excel Spreadsheets
[edit | edit source]The writecell command allows data to be added into the Excel files.
First, we create data for our student Juan.as followed:
B = {'Juan' , 43,67,88,45,35,92,65} % create a row matrix
B =
1×8 cell array
{'Juan'} {[43]} {[67]} {[88]} {[45]} {[35]} {[92]} {[65]}
Later on , use the writecell command (Make sure the Excel file is closed to prevent error message following)
Error using writecell (line 149) Unable to write to file 'C:\mydir\Class Marks.xlsx'. You may not have write permissions or the file may be open by another application.
writecell(B,'C:\mydir\Class Marks.xlsx','Sheet','Class1A','Range','A12');
%mydir is location where the excel file is located
%sheet is Class1A
%range is starting cell where to paste the data
When you open back the Excel files: you should see Juan with his marks
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Name | English | Maths | Science | Art | Music | Malay | Moral |
| 2 | Ali | 71 | 54 | 65 | 27 | 65 | 54 | 96 |
| 3 | Chan | 14 | 96 | 50 | 40 | 17 | 99 | 95 |
| 4 | Sammy | 17 | 15 | 72 | 24 | 55 | 15 | 26 |
| 5 | Dorothy | 89 | 35 | 45 | 14 | 87 | 52 | 65 |
| 6 | Huat | 82 | 90 | 15 | 65 | 42 | 82 | 90 |
| 7 | Anna | 12 | 77 | 25 | 63 | 46 | 14 | 31 |
| 8 | Lee | 77 | 22 | 49 | 91 | 43 | 89 | 66 |
| 9 | Muthu | 61 | 25 | 38 | 65 | 43 | 35 | 89 |
| 10 | Ismail | 70 | 70 | 79 | 75 | 81 | 44 | 98 |
| 11 | Th'ng | 42 | 92 | 99 | 14 | 46 | 12 | 24 |
| 12 | Juan | 43 | 67 | 88 | 45 | 35 | 92 | 65 |
Text files I/O
[edit | edit source]Reading Text Files
[edit | edit source]If a file is not an excel spreadsheet, it can still be read using "load" function:
>> load newfile.txt
This works only if the text is entirely numerical, without special formatting. Otherwise you get an 'unrecognized character' error.
The easiest way to write to a non-excel file, or using MATLAB 6.5 or less, is to use the same code as that for writing excel files but change the extension. Usually there are no formatting difficulties with plain text files.
For reading more general text files, MATLAB does not have a function to do it easily (unless you have excel), but you can read very general text files (with different delimiters for both cells and text within cells) using the "textread.m" function in the MATLAB file exchange (do a google search to find it). You can also try to use fscanf if the formatting is consistent enough (i.e. consistent numbers of spaces, no mixing of strings and numbers in columns, and so on).
MATLAB File I/O: from the Graphical User Interface
[edit | edit source]MATLAB contains a nice GUI application that will guide you through importing data from any recognized data file (usually .mat, .txt, or .xls on a Windows system). To use it, go to file > import data, and select the file you want. Then, choose what column separators are present (by selecting the appropriate radio button). Finally, click "next".
MATLAB saves the variable under a name similar to that of the file, but with modifications to make it conform with MATLAB syntax. Spaces are omitted, plusses and minuses are turned into other characters. To see the name MATLAB generated (and probably change it) type "who" in the command prompt.
External Resources
[edit | edit source]
Advanced Topics/Advanced IO
More advanced I/O
[edit | edit source]Different versions of MATLAB handle this differently. We will focus on versions 6.5 and 7.x, primarily on MATLAB 7.x since it is the latest. A note will appear when the procedure is different for ver. 6.
Advanced Topics/Object Oriented Programming
Object Oriented Programming
[edit | edit source]MATLAB as well as Octave have object oriented capabilities. Yet, technically it is not fully an object oriented language.
An Object Oriented Language(OOL) has three components: 1. Polymorphism 2. Inheritance 3. Encapsulation
Octave can be extended by adding new objects. Those objects can overload the operators like e.g. assignment, slicing, comparison.
While in MATLAB, this can be done with m-script, in Octave new objects are implemented as C++ classes. A simple example of how objects can be added to Octave can be found here.
Advanced Topics/Applications and Examples
Examples
[edit | edit source]- Moving Average
- Alpha Beta
- Kalman
- PSD estimation
- Entropy
- Markov Processes
- Queuing Theory
Phase vocoder
[edit | edit source]See MATLAB Programming/Phase Vocoder and Encoder for an example phase vocoder and the corresponding sound sample encoder in MATLAB.
MATLAB in medicine
[edit | edit source]„Image Processing in Optical Coherence Tomography using Matlab” is a book which will introduce you to subtleties related to the implementation of selected fragments of algorithms, the notation of some of them in the MATLAB environment has been given. The presented source code is shown only in the form of example of implementable selected algorithm. The book is addressed to ophthalmologists , IT specialists and students involved in the development of applications designed for automation of measurements for the needs of medicine.
Advanced Topics/Toolboxes and Extensions
Toolboxes and Extensions
[edit | edit source]In vanilla MATLAB , you may have some difficulties of running certain type of computations yourself . Hence, therefore to make your computation job easier , why not try to use some of the free open source & free toolbox.
*Note that some of the toolbox are developed with the official toolbox from MATHWORKS , hence if you didn't have paid for the toolbox, it may not be working as intended.
*The list here is not exhaustive and you may add them here to promote your own toolboxes that you created yourself.
Legacy Toolboxes
[edit | edit source]- GUIDE
 allows the creation of interactive user interfaces.
allows the creation of interactive user interfaces. - Simulink
 is for modeling, simulating and analysing systems.
is for modeling, simulating and analysing systems.
Neuroscience
[edit | edit source]- Psychtoolbox aids in researching for vision and neuroscience research.
- EEGLAB aids in processing electrophysiological data
- Rigbox runs neurophysiological experiments and managing data
Image Processing
[edit | edit source]- Advance Image Processing have image processing toolbox can be used for free
TBD
Psychtoolbox is a set of tools that aid in vision research
Order Differential Equations
Order of Differential Equations
[edit | edit source]A differential equation is an equation with a function and one or more of its derivatives. It is usually to describe changes.
Note: Derivatives = .
An order of differential equation (ODE) is an equation that has highest derivative of the dependent variable involved some ordinary derivatives of a function with respect to the independent variable. Often, the goal is to solve an ODE, i.e., determine what function or functions satisfy the equation. That means the differential equation defines the relationship between variables and their derivatives.
There are a primarily two of ODE types
- 1st Order Differential Equation (1st ODE)
- 2nd Order Differential Equation (2nd ODE)
First Order Differential Equation
[edit | edit source]All the linear equations in the form of derivatives are in the first order. It has only the first derivative such as dy/dx, where x and y are the two variables and is represented as
Second-Order Differential Equation
[edit | edit source]When the order of the highest derivative present is 2, then it is a second order differential equation.
Using dsolve solve differential equation
[edit | edit source]We have an differential equations as follow,
,
In order to solve this differential equation in MATLAB , we uses dsolve command to get the answer as followed
>>s=dsolve('D3y+2*D2y+5*Dy+4*y=5*x','y(0)=1','Dy(0)=3')
s =
(5*x)/4 - exp(-t)*(15^(1/2)*C1 - (5*x)/4 + 7) + exp(-t/2)*cos((15^(1/2)*t)/2)*(15^(1/2)*C1 - (5*x)/2 + 8) - C1*exp(-t/2)*sin((15^(1/2)*t)/2)
Type of ODE solver in MATLAB
[edit | edit source]There are few types of ODE solver but we will focus on just the commonly used :
| ODE | Accuracy | Use case suggestion |
|---|---|---|
| ode45 | Medium | For most use case, ode45 should be enough to solve the ODE |
| ode23 | Low | ode23 can be more efficient than ode45 at problems with crude tolerances |
| ode113 | Low to High | ode113 can be more efficient than ode45 at problems with stringent error tolerances, or when the ODE function is computationally intensive. |
Examples: ODE45 to solve differential equations
[edit | edit source]There are $10,000 deposited into the bank fixed deposit accounts and the interest rate is 2% annually.
To start with, we need to do a equation to model the money.
Equation 1: : Annual saving interest is 2% annually on the balance of the bank balance over time ,
Equation 2: : Amount of money initial is at $10,000
From Equation 1, we take out (Note: Need to consult on other Wikiprojects on how to derive the linear equations)
, where
, taken from equation 2
Using dsolve functions , we can similarly convert the differential equations
>> syms M(t) p
>> eqn = diff(M,t) == 0.02*M;
>> S= dsolve(eqn,M(0)==10000)
S =
10000*exp(t/50)
Hence. we have equations (shown as S) to do our modelling.
In MALAB to calculate differential equations using ode45 , the syntax is as followed
[t,y] = ode45(odefun,tspan,y0)
where,
t = Evaluation points, returned as a column vector
y = Solutions, returned as an array
odefun = Function of the ode. You may use anonymous functions instead of writing a new files for the functions
tspan = Interval of integration, specified as a vector. At minimum, tspan must be a two element vector [t0 tf] specifying the initial and final times
y0 = Initial conditions, specified as a vector. y0 must be the same length as the vector output of ode function,
Using dsolve for converted differential equations ode45 functions to solve ODE
function [T,M] = money_in_bank(R)
% Enter the initial values for the amount of money in the bank
M0 = 1000;
% Enter the interest rate
R = 2;
% Enter the time period
T0 = 1;
Tf = 30;
% using dsolve previously
S=10000*exp(T0/50)
% Solve the differential equation
[T, M] = ode45(@(T,M)S, [T0, Tf], M0);
% Plot the solution
plot(T,M,'-o')
% Add a legend and labels
legend('M(t)')
xlabel('Years')
ylabel('Money in Bank')
References
[edit | edit source]
Scripts
M-files
[edit | edit source]There are 2 types of m-file
- Scripts
- Functions
Scripts are a type of m-file that runs in the current workspace. So if you call a script from the command line (base workspace) the script will use and manipulate the variables of the base workspace. This can get very messy and lead to all sorts of strange errors when loops are involved and the coder is lazy about naming their loop variables (i.e. for i = 1:10, if every loop uses i, j, or k then it's likely that any script called from a loop will alter the loop variable).
Functions are wholly contained in themselves. They possess their own workspace keeping workspaces separate. This means that all variables necessary for a particular function must be passed or defined in some way. This can get tedious for complex algorithms requiring lots of variables. However, any manipulations of variables are discarded when the function is exited. Only those output arguments provided by the function are available to the calling workspace. This means that loops can use i, j, or k all they want because the function's workspace and the calling workspace do not mix.
Any command valid at the command line is valid in any m-file so long as the necessary variables are present in the m-files operating workspace.
Using functions properly any change can be affected to any algorithm or plotting tool. This allows for automation of repetitive tasks.
It is optional to end the M-file with 'end'; doing so, however, can lead to complications if you have conditionals or loops in your code, or if you're planning on using multiple functions in the same file (see nested functions for details on this).
Requirements for a function
[edit | edit source]Custom functions follow this syntax in their most basic form:
function [output1, output2, ...]= function_name(input_arg1,input_arg2)
statements
return;
In current versions of MATLAB the return; line is not required. The function_name can be anything you like but it is best if the m-file name is function_name.m. Calling the function from the command line or another m-file is done by invoking the m-file name of the function with the necessary input and output arguments.
Within the function itself, there must be a statement that defines each of the output arguments (output1, output2, etc.). Without some declaration the variable for the output argument doesn't exist in the function's workspace. This will cause an error about "one or more output arguments". It is good practice to initialize the output arguments at the beginning of the function.
Typically output arguments are initialized to empty ([]) or 0 or -1 or something equivalent for other data types. The reason is that if the function encounters an error you've anticipated then the function can return (via the return command) with those default values. If the initialization value is an invalid value then it can easily be checked by the calling function for any errors which may not throw a MATLAB error.
Path
[edit | edit source]In order to invoke a function, that function's m-file must be in the current path. There is a default path that can be set up through the File menu or the addpath command. The order of the path is important as MATLAB searches the path in order and stops searching after it finds the first instance of that m-file name.
The current path is
- the current directory (which can be seen at the top of the MATLAB window or by typing pwd at the command prompt
- the default path
Note that MATLAB will always search the current directory before searching any of the rest of the path.
nargin & nargout
[edit | edit source]The nargin and nargout commands are only valid inside functions since scripts are not passed any arguments. The nargin command returns the number of passed input arguments. This is useful in conjunction with nargchk
nargchk(min, max, nargin)
where min is the minimum number of arguments necessary for the function to operate and max is the maximum number of valid input arguments.
The nargout command is useful for determining which output arguments to return. Typically, the outputs are the end results of some algorithm and they are easily calculated. However, in some instances secondary output arguments can be time consuming to calculate or require more input arguments than the primary output arguments do. So the function can check the number of output arguments being requested through the nargout command. If the caller isn't saving the secondary output arguments then they do not need to be calculated.
varargin & varargout
[edit | edit source]When using MATLAB objects and functions they often allow the user to set properties. The functions and objects come with default values for these properties but the user is allowed to override these defaults. This is accomplished through the use of varargin. varargin is a cell array that is usually parsed where varargin{i} is a property and varargin{i+1} is the value the user wishes for that property. The parsing is done with a for or while loop and a switch statement.
function [out] = myFunc(in, varargin)
The varargout output argument option allows for a variable number of output arguments just as varargin allows for a variable number of input arguments. From the MATLAB site
function [s,varargout] = mysize(x)
nout = max(nargout,1)-1;
s = size(x);
for k=1:nout, varargout(k) = {s(k)}; end
returns the size vector and, optionally, individual sizes. So
[s,rows,cols] = mysize(rand(4,5));
returns s = [4 5], rows = 4, cols = 5.
Useful syntax guidelines
[edit | edit source]Placing the semicolon symbol after every line tells the compiler not to place that line of code in the command prompt and then execute. This can make your programs run a lot faster. Also, placing a semicolon after every line helps with the debugging process.
syms x y z; w=[x y z]; e=[1 2 3]; t=jacobian(e,w);
Placing comments in your code can help other people (and yourself) understand your code as it gets more complex.
syms x y z; %syms command makes x y and z symbolic w=[x y z]; e=[1 2 3]; t=jacobian(e,w);
Comments can also Identify who wrote the code and when they wrote it.
%Some code writer %mm/dd/yyyy
See the 'comments' section for more details on this.
Nested functions
[edit | edit source]
External Links
[edit | edit source]Large parts of this page come from the ControlTheoryPro.com page on M-files, Scripts, and Functions.
Entering data at the command line
The input() function lets your scripts process data entered at the command line. All input is converted into a numerical value or array. The argument for the input() function is the message or prompt you want it to display. Inputting strings require an additional 's' argument. Example:
%test.m
%let's ask a user for x
x = input('Please enter a value for x:')
Then running the script would produce the output:
Please enter a value for x:3
x = 3
>>
Control Flow
Control Flow
[edit | edit source]IF statement
[edit | edit source]An IF statement can be used to execute code when the logical test (expression) returns a true value (anything but 0). An "else" statement following an "if" statement is executed if the same expression is false (0).
Syntax:
if expression
statements
elseif expression2
statements
end
SWITCH statement
[edit | edit source]Switch statements are used to perform one of several possible sets of operations, depending on the value of a single variable. They are intended to replace nested "if" statements depending on the same variable, which can become very cumbersome. The syntax is as follows:
switch variable
case value1
statements(1)
case value2
statements(2)
...
otherwise
statements
end
The end is only necessary after the entire switch block, not after each case. If you terminate the switch statement and follow it with a "case" statement you will get an error saying the use of the "case" keyword is invalid. If this happens it is probably because you deleted a loop or an "if" statement but forgot to delete the "end" that went with it, thus leaving you with surplus "end"s. Thus MATLAB thinks you ended the switch statement before you intended to.
The otherwise keyword executes a certain block of code (often an error message) for any value of variable other than those specified by the "case" statements.
Programmers who are used to C style languages, often put break statements after each case. In C, C++, and Java, not putting a break statement allows the code to fall through in the code above, if value1 is true, then statements(1), statements(2), etc., will execute in C-style languages. However, in MATLAB only statements(1) will execute.
TRY/CATCH statement
[edit | edit source]The TRY/CATCH statement executes a certain block of code in the "try" block. If it fails with an error or a warning, the execution of this code is terminated, and the code in the "catch" block is executed rather than simply reporting an error to the screen and terminating the entire program. This is useful for debugging and also for filtering out erroneous calculations, like if you accidentally try to find the inverse of a singular matrix, when you don't wish to end the program entirely.
Syntax:
try
statements
catch
statements
end
Note that unlike the other control flow statements, the TRY/CATCH block does not rely on any conditions. Therefore the code in the TRY block will always be at least partially executed. Not all of the TRY block code will always be executed, since execution of the TRY ends when an error occurs. In addition, the statements in the CATCH block will never be executed if the TRY block does not fail.
FOR statement
[edit | edit source]The FOR statement executes code a specified number of times using an iterator. Syntax:
for iterator = startvalue:increment:endvalue
statements
end
The iterator variable is initialized to startvalue and is increased by the amount in increment every time it goes through the loop, until it reaches the value endvalue. If increment is omitted, it is assumed to be 1, as in the following code:
for ii = 1:3
statements
end
This would execute statements three times.
WHILE statement
[edit | edit source]The while statement executes code until a certain condition evaluates to false or zero. Example:
while condition
statements
end
Forgetting to change the condition within a while loop is a common cause of infinite loops.
BREAK, CONTINUE, and RETURN
[edit | edit source]MATLAB includes the "break" and "continue" keywords to allow tighter loop control. The "break" keyword will cause the program to leave the loop it is currently in and continue from the next line after the loop ends, regardless of the loop's controlling conditions. If the code is in a nested loop it only breaks from the loop it's in, not all of them. The syntax is simply to write the word "break" within the loop where you desire it to break.
In contrast to "break", "continue" causes the program to return to the beginning of the loop it is presently in, and to recheck the condition to see if it should continue executing loop code or not. The code in the loop after the "continue" statement is not executed in the same pass.
If you want to exit a function entirely (as opposed to just a loop) before the last line of code, it is possible to do so using the "return" keyword. The value of any output variables is immediately returned to the calling function. As an example of how this works, consider the following function:
function output = controlTest(doWhat)
switch doWhat
case 1
output = -1;
return;
case 2
output = 3;
end
output = output + 4;
end
Calling
>> output = controlTest(1)
would return output = -1, because output is defined to -1 and the return statement tells MATLAB to immediately take the current value of output and pass it back to the calling function. However, calling
>> output = controlTest(2)
would return output = 7, because output is initially defined as 3 and then 4 is added to it. Since the return statement is only executed in the case that doWhat=1, it is not called and the rest of the function executes.
Beware that if the output variables are not defined before calling the return statement, you will get an error, so use this with some degree of caution.
Loops and Branches
Program Flow
[edit | edit source]The idea of program flow is simple. However, implementing and using flow techniques effectively takes practice. MATLAB flow control is almost identical to flow control in C. There is a tremendous amount of text on the subject of flow in C. If you do a little homework in about an hour you can know all you need to from one of numerous C tutorials. To be good at flow control all you have to do is practice.
Here are a few concepts that you can practice using flow control to implement:
- Calculate compounding interest using a while loop (don't cheat by using the algebraic form).
- Create a moving average filter using a for loop
- Make a counter that keeps track of keystrokes:How many times a typist hits a certain letter.
Error Messages
As far as I've seen there is little help out there to help people decipher MATLAB's error messages. Most of the syntax errors are not difficult to fix once you know what is causing them so this is intended to be a guide to identifying and fixing errors in MATLAB code.
Warnings are also shown here as these often lead to errors later.
Arithmetic errors
[edit | edit source]Usually these are self-explanatory. As a reminder, here are some common functions that cannot be performed and what MATLAB returns (along with a warning for each one):
a/0 = Inf if a > 0, -Inf if a < 0, and NaN if a = 0. log(0) = -Inf MATLAB defines 0^0 to be 1.
NaN will very often result in errors or useless results unless measures are taken to avoid propagating them.
???Error using ==> minus Matrix dimensions must agree.
So check the dimensions of all the terms in your expression. Often it is an indexing mistake that causes the terms to be of different size. If you are using power function you might add a single dot after the parameter. i.e. y=x.^2 instead of y=x^2
Matrix multiplication requires the number of columns in the first matrix to equal the number of rows in the second. Otherwise, you get the message:
??? Error using ==> mtimes Inner matrix dimensions must agree.
Note the difference between this error and the previous one. This error often occurs because of indexing issues OR because you meant to use componentwise multiplication but forgot the dot.
Attempting to take the inverse of a singular matrix will result in a warning and a matrix of Infs. It is wise to calculate the determinant before attempting to take the inverse or, better, to use a method that does not require you to take the inverse since its not numerically stable.
Attempting to take a power of a nonsquare matrix results in the error
??? Error using ==> mpower Matrix must be square.
This is usually because you meant to use componentwise exponentiation and forgot the dot.
Array Indexing errors
[edit | edit source]Array indexing is a key component of MATLAB. One feature is that the names of variables and functions are case sensitive, and that one can alias builtin or user-written functions with variables of the same name. So, if you make an array called abs and you try to call the function abs(1), MATLAB will return the first value in the array abs instead of the value 1. MATLAB will not return an error for this as it is not possible to know for certain that the aliasing of the function wasn't intentional. Hence, never ever name your variables the same as an existing MATLAB function. Unfortunately, there are so many supplied functions in the base product plus installed toolboxes, remembering all of them is impossible so use which proposedname if you have any doubt the name might be in use previously before defining a new array or function. Later versions of MATLAB with the command completion feature will show the short help information after the opening parenthesis or tab-completion options, using which will aid in avoiding such errors before they arise later in execution by not creating the alias.
Some things are rather obvious but take some practice in avoiding:
You cannot try to access part of an array that does not exist yet.
>> A = [1,3]; >> A(3) ??? Index exceeds matrix dimensions.
Unfortunately, MATLAB doesn't tell you which variable you exceeded the dimensions on if there's more than one so you'll have to check that. This often occurs if, for example, you are using a loop to change which part of an array is accessed, but the loop doesn't stop before you reach the end of the array. This also happens if you end up with an empty matrix as a result of some operation and then try to access an element inside it.
You cannot try to access a negative, complex, noninteger, or zero part of an array; if you do you get this message:
>> A(-1) >> A(i) >> A(1.5) >> A(0) ??? Subscript indices must either be real positive integers or logicals.
Note that MATLAB arrays are 1-based, not 0-based and are fixed lower dimension, not variable. MATLAB may be able to tell you which index is not real or logical depending on context.
>> y=3*A(-1) Attempted to access A(-1); index must be a positive integer or logical.
The latter being an expression is parsed differently and so has the actual array available in the error message.
Also note that if 0 were a logical 0 (false) then the statement A(0) would not be an indexing error but a logical subscripting expression. In this case the return would be the empty [] array as there are no subscripts matching false in the defined set of [1 2] as A has been defined above. A more useful expression would be something like
>> A(A==3)
Attempting to use non-standard MATLAB syntax in your indexing will often result in the error:
>> A(2::, 2)
??? A(2::, 2)
|
Error: Unexpected MATLAB operator.
The above could be an example of someone trying to access all rows of A after the first one and the second column, in which case you should use the "end" syntax, as in:
>> A(2:end, 2) ans = 3
Assignment errors
[edit | edit source]Ah, assignment, that is using the = sign to give a variable, or certain elements of an array, a particular value.
Let's start with a classic mistake:
>> a = 2;
>> if a = 3
??? if a = 3
|
Error: The expression to the left of the equals sign is not a valid target for an assignment.
This error occurs because you meant to see if "a" equaled 3, but instead you told MATLAB to assign "a" a value of 3. You cannot do that on the same line that the if/while statement is on. The correct syntax is
>> if a == 3 >> end
This creates no errors (and you can put anything inside the conditional you want).
You cannot have a normal array with two different classes of data inside it. For example,
>> A = @(T) (1+T) A = @(T) (1+T) >> A(2) = 3 ??? Conversion to function_handle from double is not possible.
For such a purpose you should use cell arrays or struct arrays.
Here's the tricky one. Take a look at the following code:
>> A = [1,2,3;4,5,6;7,8,9]; >> A(2,:) = [3,5]; ??? Subscripted assignment dimension mismatch. >> A(2,:) = [1,4,5,6]; ??? Subscripted assignment dimension mismatch. >> A(1:2, 1:2) = [1,2,3,4]; ??? Subscripted assignment dimension mismatch.
What is happening here? In all three cases, take a look at the dimensions of the left and the right hand sides. In the first example, the left hand side is a 1x3 array but the right side is a 1x2 array. In the second, the left hand side is 1x3 while the right is 1x4. Finally, in the third, the left hand side is 2x2 while the right is 1x4. In all three cases, the dimensions do not match. They must match if you want to replace a specific portion of an existing variable. It doesn't matter if they have the same number of data points or not (as the third example shows); the dimensions must also be the same, with the exception that if you have a 1xn array on one side and an nx1 on the other MATLAB will automatically transpose and replace for you:
>> A(2,:) = [1;2;3]
A = 1 2 3
1 2 3
7 8 9
If you do not want this be aware of it!
Struct array errors
[edit | edit source]Struct arrays are rather complex, and they have a rigid set of rules of what you can and can not do with them. Let us first deal with indexing within struct arrays. Suppose you define the variable "cube" and want to store the volume and the length of one side of two different cubes in a struct array. This can be done as follows:
>> cube(1).side = 1; >> cube(1).volume = 1; >> cube(2).side = 2; >> cube(2).volume = 8;
This seems like a good way of storing data and it is for some purposes. However, suppose you wanted to abstract the volumes from the struct and store them in one array. You cannot do it this way:
>> volumes = cube.volume ??? Illegal right hand side in assignment. Too many elements.
You'll notice that if you tell MATLAB to display cube.volume, it will display both values, but reassign the variable ans each time, because it is treated as two separate variables. In order to avoid the error, you must format 'cube.volume' as an array upon assignment.
>> volumes = {cube.volume}
You can also write in a separate assignment for each cube but this is more adaptable to larger numbers of cubes.
Just like extracting data, you must input the data one at a time, even if it is the same for all instances of the root (cube).
>> cube.volForm = @(S) (S^3) ??? Incorrect number of right hand side elements in dot name assignment. Missing [] around left hand side is a likely cause. >> cube(:).volForm = @(S) (S^3) ??? Insufficient outputs from right hand side to satisfy comma separated list expansion on left hand side. Missing [] are the most likely cause.
Unfortunately missing [] is not the cause, since adding them causes more errors. The cause is that you cannot assign the same value to all fields of the same name at once, you must do it one at a time, as in the following code:
>> for ii = 1:2 >> cube(ii).volForm = @(S) (S^3); >> end >> cube ans = 1x2 struct array with fields: volume side volForm
The same volume formula is then found in both cubes. This problem can be alleviated if you do not split the root, which is highly recommended. For example, you can use a struct like this:
>> shapes.cubeVol = @(S) (S^3); >> shapes.cube(1).vol = 1; >> shapes.cube(2).vol = 8;
This avoids having to use a loop to put in the formula common to all cubes.
Syntax errors
[edit | edit source]Parenthesis errors
[edit | edit source]Unlike in C++, you are not required to terminate every line with anything but a line break of some sort. However, there are still syntax rules you have to follow. In MATLAB you have to be especially careful with where you put your parenthesis so that MATLAB will do what you want it to.
A very common error is illustrated in the following:
>> A(1
??? A(1
|
Error: Expression or statement is incorrect--possibly unbalanced (, {, or [.
This error is simple enough, it means you're missing a parenthesis, or you have too many. Another closely related error is the following:
>> A(1))
??? A(1))
|
Error: Unbalanced or misused parentheses or brackets.
MATLAB tries to tell you where the missing parenthesis should go but it isn't always right. Thus for a complex expression you have to go through it very carefully to find your typo. A useful trick is to try to set a breakpoint a line after the offending line. It won't turn red until the error is corrected, so keep trying to correct it and saving the file until that breakpoint turns red. Of course, after this you have to make sure the parenthesis placement makes sense, otherwise you'll probably get another error related to invalid indecies or invalid function calls.
String errors
[edit | edit source]There are two ways that you can create a string; use the ' string ' syntax, or type two words separated by only whitespace (not including line breaks), as in
>> save file.txt variable
In this line, file.txt and variable are passed to the save function as strings. It is an occasional mistake to forget a parenthesis and accidentally try to pass a string to a function that does not accept strings as input:
>> eye 5 ??? Error using ==> eye Only input must be numeric or a valid numeric class name.
These should not be hard to spot because the string is color-coded purple. Things like this occur if you uncomment a line of text and forget to change it.
Forgetting the closing ' in the other syntax for a string results in an obvious error:
>> A = 'hi
??? A = 'hi
|
Error: A MATLAB string constant is not terminated properly.
The unterminated string is color-coded red to let you know that it is not terminated, since it's otherwise easy to forget.
A common mistake with strings is to try to compare them using the '==' operator. This does not work if the strings are not the same length, because strings are arrays of characters, and to compare arrays with '==' they must be the same size. To compare two strings you must use the strcmp function:
>> 'AA' == 'AaA'
??? Error using ==> eq
Matrix dimensions must agree.
>> strcmp('AA', 'AaA')
ans = 0
>> strcmp('A', 'a')
ans = 0
>> strcmp('AA', 'AA')
ans = 1
Note that MATLAB strings are case sensitive, 'A' and 'a' are not the same string.
Also beware that the ' character for beginning and ending strings is the same character indicating transposition. So if you close a string and don't begin it, you will most likely end up with an error about an undefined variable (if you're trying to transpose an undefined variable) or just get really weird results because you transposed something you didn't intend to.
Other miscellaneous errors
[edit | edit source]You cannot leave trailing functions, and if you do MATLAB gives you an error that is similar but not exactly the same as that for a missing parenthesis, since it doesn't want to venture a guess:
>> A = 1+3+
??? A = 1+3+
|
Error: Expression or statement is incomplete or incorrect.
These usually are not hard to spot, and often result from forgetting the "..." necessary to split a line.
The double colon is not the only "unexpected MATLAB operator", there is also "..", "....", and several other typos that generate this error.
If you accidentally type the ` character you get the error:
>> ??? `
|
Error: The input character is not valid in MATLAB statements or expressions.
This usually occurs because you intended to put a "1" in the equation but missed the key. Another possibility is that you named your m-file with unusual letters for computers. Like in Germany "ä, ü or ö". Be sure to name your m-files only with usual letters and no capital letters.
Function Calling errors
[edit | edit source]It is quite possible to try to call a function that doesn't exist, such as:
>> samplemat = [1 2; 1 4] >> A = eigen(samplemat); ??? Undefined command/function 'eigen'.
This can happen because you do not know the name of the function that performs the operation intended (for example, if you wanted to compute the eigenvalues of matrix "samplemat", you would want to call eig, not eigen). It is often useful to pull up MATLAB's help (go to help -> product help or type doc into the command prompt) and do a search for the operation you want.
If you're trying to call a function you created and you get this error, there are several possible reasons:
- The m-file must be in one of the paths listed under file -> set path, or must be in your current directory
- The m-file must have the same name as the name in the function declaration. You must be aware of this especially if you change the name of your functions, you must also change the name of the file or MATLAB will not find the right function!
If MATLAB finds the function, it will attempt to run it. However, there are several potential pitfalls to avoid in calling functions. It is necessary to know the nature of the input and output arguments of a given function in order to call it. For MATLAB's built-in functions, this information is found in the documentation, or by typing
>> help functionname
It is a good idea to set up some comments so that the help function can read them in your own code as well, so you can keep track of how all your functions work and what they do at a quick reference. To do this, note that the help function reads only the block of comments directly under the function declaration, so for example, if you write a function like this:
function outvars = myfunc(invars) % function outvars = myfunc(invars) % Outputs outvars % All of this is outputted when you type >> help myfunc
% But this wouldn't be
save the function as "myfunc.m", and type
>> help myfunc
it will output:
>> function outvars = myfunc(invars) Outputs outvars All of this is outputted when you type >> help myfunc
Most functions (not all however) require at least one input argument, and calling it with too few will result in an error:
>> A = ode45() ??? Error using ==> ode45 Not enough input arguments. See ODE45.
You cannot call a function with too many input arguments either:
>> A = plus(1,2,3) ??? Error using ==> plus Too many input arguments.
Input arguments must be in a format expected by the function. This will be very function-specific, so see the documentation or help for details on what they expect. For example, the first argument to ODE45 and other ODE solvers has to be the function handle; if you pass arguments in the wrong order you will be given an error to that effect.
You can choose how many of the output arguments you want out of those available by using the bracket notation. You can choose to save fewer outputs than the function offers, but you cannot assign more variables than the function can output:
>> A = [1,2;3,4] D = eig(A); %one output argument [V,D] = eig(A); %two output arguments [V,D,Mistake] = eig(A); ??? Error using ==> eig Too many output arguments.
All assigned output arguments must also be of the correct class if you are replacing parts of an array that already exists (see the section on assignment for more on this). If you're creating a new variable with the output, this is not an issue.
Control Flow errors
[edit | edit source]The most common one by far is if you forget the 'END', which is an issue in M-file functions. It will tell you that 'at least one END is missing' and try to tell you where the loop or conditional statement starts.
If you have too many END statements and more than one function in an M-file, MATLAB may give you a cryptic message about not formatting the functions correctly. This is because all functions in the same M-file must either end with an END statement or not. It doesn't matter which, but if you have too many END statements in one of the functions, MATLAB will think your function is ending early and will get confused when the next function in line does not have an END statement at the end of it. So if you get this confusing message, look for extra END statements and it should fix your problem. If the message is displayed when publishing, say to an HTML file, the problem may be an erratic hierarchical indentation. Try selecting all and then hitting cntrl-i for automatic indentation to fix the problem.
Having an extra END in a 'switch' statement gives a message that you used the 'case' keyword illegally, because MATLAB thinks you ended the switch statement early, and 'case' has no meaning outside a 'switch' statement.
Other errors
[edit | edit source]There are numerous types of errors that do not generate errors from the MATLAB compiler, which have to do with calling the wrong function, using the wrong operation, using the wrong variable, introducing an infinite loop, and so on. These will be the hardest to fix, but with the help of the MATLAB debugger, they will be easier to find. See Debugging M Files for details on how to use the debugger.
Detecting or planning an error
[edit | edit source]No matter how accurate the programming is, errors might happen. Using debug techniques are to great help, but planning an error or expecting an error could prove to be just as valuable. This includes making a possibly unneeded if block to decide what to do. I.e. if x < 5 do this and x > 5 do something else. Also inside the big loops add an if block with modulo, like: if not ( mod ( ii , 5 ) ) % do something; end. Now the loop only does a test for every ii counter which can be divided by 5 without any remainder after the division. Some syntax errors or logical errors inside a loop happens after looping for a long time, if an error happens then the error message is displayed, explaining where it happened but not necessarily why it happened. I.e. vector x is one element shorter than element y, and x .* y could not happen. This mistake often happens on the last element in the shortest vector, and is quite difficult to discover unless measures are taken. try % do something; catch me me.getReport; then a breakpoint and even disp(me.getReport) will help in this situation. If the error is not fatal the code may even continue, but instead displaying the error as a message or it could be converted to a warning.
Included Matlab tools / functions: warning, lastwarn, disp, try catch, dbstack, rethrow, throwAsCaller and Matlab help on the above functions to discover pros and cons for each method.
Inserting Newlines into Disp Warn and Error
The functions warning, error, sprintf and fprintf will interpret '\n' as a newline character. For example
>> error('This error\nhas a newline.')
??? This error
has a newline.
Though previous versions of this wiki claimed this functionality was introduced in MATLAB 6.5 (R13), it doesn't work in 7.4.0 (2007a). The explanation that this change happened when formatted error strings were introduced in the Release Notes for that release was unhelpful.
To add a newline character in versions where the above example doesn't work, use SPRINTF or CHAR(10):
>> error(sprintf('This error\nhas a newline.'))
??? This error
has a newline.
>> disp(['abcd' char(10) 'efgh'])
abcd
efgh
This works as well:
>> disp(['abcd', 10, 'efgh'])
abcd
efgh
In MATLAB versions 2016b and newer the function NEWLINE is recommended instead, for code clarity
>> disp(['abcd' newline 'efgh'])
abcd
efgh
Debugging M Files
This section explains things you can do if you fix all the syntax errors (the ones that give you actual error messages), the program runs... but it gives you some result you don't want. Maybe it goes into an infinite loop, maybe it goe through the loop one too few or one too many times, maybe one of your "if" statements doesn't work, maybe the program is giving you "infinity" or "NaN" as an answer (which usually isn't very useful!)... there's as many things that can go wrong as there are lines in the code. Thankfully there are techniques for both fixing and improving on working MATLAB code.
Using MATLAB's Debugging tool
[edit | edit source]Using the Debugging Tool will let you stop your program in mid-execution to examine the contents of variables and other things which can help you find mistakes in your program.
M-file programs are stopped at "breakpoints". To create a breakpoint, simply press F12 and a red dot will appear next to the line where your cursor is. You can also click on the dash next to the line number on the left side of the M-file window to achieve the same result.
Then press F5 or Debug->Run from the menu to run the program. It will stop at the breakpoint with a green arrow next to it. You can then examine the contents of variables in the workspace, step, continue or stop your program using the Debug menu. To examine contents of a variable, simply type its name into the workspace, but be warned: you can only look at the values of variables in the file you stop in, so this means that you'll probably need multiple breakpoints to find the source of your problem.
There are several different ways you can move through the program from a breakpoint. One way is to go through the whole program, line by line, entering every function that is called. This is effective if you don't know where the problem is, but since it enters every function (including MATLAB functions like ode45), you may not desire to use it all the time. Thankfully, there's also a way to simply step through the function you're currently stopped in, one line at a time, and instead of going through the child functions line by line MATLAB will simply give you the results of those functions.
Finally, note that you cannot set a breakpoint until you save the M-file. If you change something, you must save before the breakpoint "notices" your changes. This situation is depicted in MATLAB by changing the dots from red to gray. Sometimes, you'll save but the dots will still be gray; this occurs when you have more than one breakpoint in multiple files. To get around this (which is really annoying), you have to keep going to "exit debug mode" until it turns gray. Once you're completely out of debug mode, your file will save and you'll be ready to start another round of debugging.
Using comments to help you debug code
[edit | edit source]If you want to test the effects of leaving out certain lines of code (to see, for example, if the program still returns Inf if you take them out), you can comment out the code. To do this, highlight it and then go to:
Text -> Comment
Or press CTRL+R. This will simply put a '%' in front of every line; if the line is already commented out it will put another '%' there so when you uncomment them the pattern of comment lines will not change. Commented lines will be ignored by the compiler, so the effect will be that the program is run without them.
To uncomment a line go to
Text -> Uncomment
Or press CTRL+T.
Another use of commenting is to test the difference between two different possible sets of code to do something (for example, you may want to test the effect of using ODE113 as opposed to ODE45 to solve a differential equation, so you'd have one line calling each). You can test the difference by commenting one out and running the program, then uncommenting that one and commenting the other one out, and calling the program again.
How to escape infinite loops
[edit | edit source]If your program is doing nothing for a long time, it may just be slow (MATLAB creates a lot of overhead and if you don't use arrays wisely it will go very, very slow) but if you are testing a small module, it is more likely that you have an infinite loop. Though MATLAB can't directly tell you you have an infinite loop, it does attempt to give you some hints. The first comes when you terminate the program. Terminate it by pressing CTRL+C and MATLAB will give you a message telling you exactly what line you stopped on. If your program is running a long time, it is likely the line you stopped in is in the middle of an infinite loop (though be warned, if the loop calls a sub-function, it is likely that you will stop in the sub-function and not the parent. Nevertheless, MATLAB also will tell you the lines of the parents too so you can track down the loop easily enough).
However, sometimes MATLAB won't even let you return to the main window to press CTRL-C. In this case you probably have to kill the whole MATLAB process. After this, add a "pause (0.001)" or a similarly small value in the loop you suspect to be the infinite one. Whenever MATLAB passes this instruction you will be able to interact with MATLAB for a (very) short time, e.g. go to the main window and press CTRL-C with MATLAB being able to respond to your command.
Other debugging tips
[edit | edit source]When inside a function, a loop or just anywhere in the script use a special comment syntax. The %% is the Cell-mode commenting. By adding a %% on the line above the interesting code and another %% below the code a cell is created. Now this cell may be executed and modified in memory without the requirement to save the code, script or function. By adding some text after the %% a heading for this cell section is created. I.e. %% Start debugging infinite loop
Another method is to enter the breakpoint, selecting the interesting part and copy this to a new file. Now the code may be changed within this new file and tested. When the modified code is working as expected the debug session may be ended. The code from the temporary file may be copied back and replace the debugged code. This method lets the user run this code snippet multiple times include the %% if the code should be run in cell mode.
Instead of using the IDE to run the code, debug the code or selecting breakpoints, command line functions may be used. Just enter db and press the TAB-key to choose the functions. The functions dbstatus and dbstack are two usable functions. Experiment with the functions and use help functon name or select the function name and press the F1-key
The last debugging tips in is to add possible code inside the comments I.e. % plot(x,y); % This debug plot function plots the value vector y with input x Now select the plot(x,y) with or without the ; and press F9 (run the selected code). Use help and preferences to find and modify keyboard shortcuts if needed. CTRL+D on the selected y variable opens it inside the variable editor, not to forget hovering the mouse over any variable will display it contents if possible. Even the plot command itself is a great debugging tool, when it comes to visualize the variables.
The final tips is actually a summary. Experiment with the above methods and even combine them such that the debugged code is both run efficiently, has valuable comments and have means to be debugged if necessary. Make plans for coding mistakes by adding comments and helper functions. Make small functions which does what it is designed to do, then implement this function in the complete program or script. Inside the functions use try, catch me and me.getReport; And if there are recurring mistakes, expect them to happen and program accordingly. Infinite loops are very common mistakes so by adding functionality to discover this mistake is a great time saver. Another tips could be unit testing.
Graphical User Interface
NOTE: At MATLAB version R2019b, MathWorks announced that the GUIDE design environment for building apps in MATLAB will be removed in a future release. Note, GUIDE apps will continue to run after GUIDE's removal, but they will not be editable using the GUIDE environment.
What is GUIDE ?
[edit | edit source]The GUIDE Toolbox (known by its long name Graphical User Interface Development Environment) provided by MATLAB allows advanced MATLAB programmers to provide Graphical User Interfaces to their programs. GUIs are useful because they remove end users from the command line interface of MATLAB and provide an easy way to share code across non-programmers.
There are two main workflow of using GUIDE in MATLAB , namely:
(i) Lay out the GUI
(ii) Program the GUI
Creating from blank GUI
[edit | edit source]To start programming in GUIDE, just type the following into the MATLAB
guide
And it will shows the following diagrams:

We will create example of a simple GUI created with the GUIDE toolbox It takes inputs of two numbers and adds them and displays them in the third textbox It is very simple but it helps illustrate the fact that such a GUI was created in minutes.
Select Blank GUI (Default)
Placing components and change properties
[edit | edit source]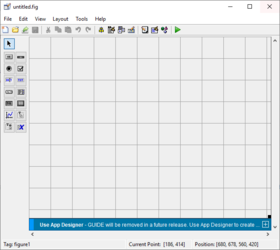

We can see that there are grid-like at the interface here in the main menu . And also, we can see the basic tools that are used by GUIDE are on display here. Before going further, below are the toolbar and brief decription of what it does
| Components | Description |
|---|---|
| Push button | A button that activates when the user clicks the mouse on it. |
| Slider | Adjusting the position of the slide will changes the values |
| Radio button | A button that can change its state from unselected (not activate) to selected (activate) and back. |
| Tick box | A check button that can change state from selected (checked) to unselected (unchecked). |
| Edit text | A text field that allows the user to input information by typing text into . |
| Static text | A label displays some text; useful for labeling items or reporting the results of a calculation |
| Pop up Menu | A menu list that gives the user a list of options from which one may be selected |
| List Box | A list that presents a list of options that can be scrolled upon. Note that several items can be selected at the same time |
| Toggle button | A button that once pressed, it stays down until it is pressed again |
| Table | A table that displays data in a tabular form |
| Axes | A area that display two-dimensional and three-dimensional plotting chart |
| Panel | Groups controls together visually. |
| Button group | Groups a set of radio buttons or toggle buttons so that they act together with the result that only one at a time is selected |
| Active X control | N/A |


We can drag and drop the Static Text, Edit text and Push button in following area shown in left picture.
As you can see , the Push Button and Edit Text have generic Edit Text word on the field and word Push Button.
We can change those texts as followed: First, double click on any of edit text , it should pop up a new window named as Inspector shown on the right side picture.
Scroll down until you find a String property and delete the text inside, the Edit text on the rightshould look empty now.
For Push Button, repeat the same step: double click on the Push Button and scroll down until String properties and change the word into Add
Programming with handles
[edit | edit source]We have the basic of the GUI already laid out.
We just need to think logically what we are going to do
1. Get the new value of the Num_A text field from its Value property. Same goes to Num_B
2. Add two numbers together
3. Set the value of the String property of the label totalAdd
To achieve this, we need to learn about get and set command
The get command obtains the current String property of the component Tag Name.
var = get(handles.Tag Name , values)
The set command place the String property of the component with updated value.
var = set(handles.Tag Name , values)
CallBack
[edit | edit source]A callback is a functions executed whenever the user initiates an action by clicking on a push button,pressing a key on the keyboard or selecting a menu item. Programming a callback is therefore the most important part of writing a GUI. For example in the GUI illustrated above, we would need to program a callback for the button Add. This is provided as a callback in the code. When you add a component to your GUI layout, GUIDE assigns a value to its Tag property, which is then used to generate the name of the callback.
The code is provided below and illustrates how to write a simple callback:
% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
n1 = get(handles.edit1,'string'); % get the values from the edit text 1
n2 = get(handles.edit2,'string'); % get the values from the edit text 2
S = str2double(n1) + str2double(n2); % performing addition
set(handles.edit3,'string',num2str(S)) % set the number of addition result to edit text 3
In this piece of code I get the numbers as strings from the edit boxes and then convert them into numbers using the str2double function provided in MATLAB.
I then set the string for the other edit box as the sum of these two numbers. This completes the simple example of a GUI needed to add two numbers.
More complex GUI
[edit | edit source]

To make the calculator more complex than to do simple additions, we can create a more complete calculator which can handle subtraction, multiplications and division. To do this, add 3 more Push Button . Double click each Push Button to change the String to relevant functions such as SUB for subtraction function as shown.,etc..
At the same time, change the Tag into more recognisable tag name such as sub_button . It will be more recognisable and easier to edit once programmed with callbacks.
You can add static name to label the edit text but for this exercise , this is optional.
As you can see, the GUI is in disarray but there is one tools that can be used to sort out the mess.
You can use the Align Object tool (shown in the right pics) to align the button in a proper order.
Line up the both edit text horizontally, followed by 4 buttons to line horizontally.
Once line up properly, it will looks like the picture below. You can compared it to picture above it which looks messy before.
We can proceed to the next steps to program which looks easier since we already nailed it for the addition button

To program each individual button , right click at each push button and select Editor and type code in the following.
As you can see the usefulness of describing Tag of each push button instead of generic name Push_Button 1 , etc...
% --- Executes on button press in sub_button.
function sub_button_Callback(hObject, eventdata, handles)
% hObject handle to sub_button (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
n1 = get(handles.edit1,'string');
n2 = get(handles.edit2,'string');
S = str2double(n1) - str2double(n2);
set(handles.edit3,'String',num2str(S))
% --- Executes on button press in mul_button.
function mul_button_Callback(hObject, eventdata, handles)
% hObject handle to mul_button (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
n1 = get(handles.edit1,'string');
n2 = get(handles.edit2,'string');
S = str2double(n1) * str2double(n2);
set(handles.edit3,'String',num2str(S))
% --- Executes on button press in div_button.
function div_button_Callback(hObject, eventdata, handles)
% hObject handle to div_button (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
n1 = get(handles.edit1,'string');
n2 = get(handles.edit2,'string');
S = str2double(n1) / str2double(n2);
set(handles.edit3,'String',num2str(S))
There you have done it, you have created a simple working calculator in MATLAB .
To illustrate a more complex example, we will show how a simple projectile motion can be plotted and you can change the function's parameters. With a little bit of imagination you could make it plot any arbitrary function you enter.
Reference
[edit | edit source]https://web.archive.org/web/20221003005946/https://www.mathworks.com/help/matlab/ref/guide.html
TODO:
App Designer
App designer is the latest way to design MATLAB app GUI starting R2016a with aim to replace the MATLAB GUIDE.
The new features of App Design as followed
- A more modern look-and-feel design environment with richer drag-and-drop conveniences
- New features like a tree component, date picker, layout manager, and an automatic reflow option to make your app responsive to different screen sizes without having to write complex resizing logic
- Its programming model is more robust for managing data within an app by using a MATLAB class-file
- Apps built with App Designer can be run in MATLAB Online and deployed to the web for easier sharing and access via a web browser on desktops, tablets, or mobile devices.
To start, type appdesigner on the Command Window.

You can see the App Designer starting up as shown.
But in this examples , we are going to start by open up a Blank App
Once open up Blank App, place the components on the Design Views canvas as shown
GUI/Get File or Directory
uigetfile
[edit | edit source]The uigetfile command is used to open a window which retrieves a specific file name.
[File,Path] = uigetfile('*.*','Select the file');
This is particular useful to give a user an alternate file from the default file.
[File,Path] = uigetfile('*.*','Select the file','c:\default_dir\default_file.ext');
Bonus Chapters/MATLAB Easter Eggs
MATLAB is one of the very few professional software in the market now that included Easter Eggs in their products.
Here are the few known undocumented demo functions: Just type these commands and have a look for yourself:
All of this Easter Eggs were tested on MATLAB R2020a ( in not alphabetical order)
Have fun playing with the known Easter Eggs~ Note: To view the source code, use edit function followed by command name
Working Easter Eggs
[edit | edit source]| Command | Description | Picture/Examples |
|---|---|---|
| cruller | Construct a cruller by revolving the eccentric ellipse defined by the function XYCRULL. |  |
| date | Returns date as in dd-mmm-yyyy format | 08-Aug-2022 |
| sldemo_fuelsys | Simulations of Fault-Tolerant Fuel Control System Dashboard |  |
| funtool | A interactive graphing calculator that manipulates functions of a single variable. |  |
| sf_aircraft | Simulate the fuel injection system in aircraft |  |
| sf_newtons_cradle | Simulate Newton's cradle | 
|
teapotdemo |
A demo that uses the famous Newell teapot to demonstrate MATLAB graphics features. |  |
| teapotGeometry | Data generates vertices, faces, and colors that represent the surface of the infamous Utah teapot. | |
| graf3d | Demonstrate Handle Graphics for surface plots in MATLAB. |  |
| earthmap | Globe to represent the Earth's topography |  |
| soma | Precomputed solutions to Piet Hein's soma cube |  |
| somasols . | Generate complete solutions to the soma cube | |
| clock | Returns a six element date vector containing the current time and date in decimal form:
[year month day hour minute seconds] |
1.0e+03 *
2.0220 0.0080 0.0070 0.0230 0.0360 0.0192 |
| taxDemo(income) | Calculate the tax on income. | |
| logo | Plot the L-shaped membrane logo with MATLAB(R) lighting. |  |
| membrane | Plot a 3-D colored surface of MATLAB(R) logos |  |
| spy | This function is actually to use to visualize sparsity pattern.
When no input of argument is given, it will generate a image of the dogs. If typed in version prior to Matlab R2011a, it will show character White Spy from comics Spy vs. Spy |
 |
| life | This is MATLAB's simulations of Conway's Game of Life.
Whether cells stay alive, die, or generate new cells depends upon how many of their eight possible neighbors are alive. By using sparse matrices, the calculations required become astonishingly simple. |
 |
| truss | Animation of a bending bridge truss. This demo animates 12 natural bending modes of a two-dimensional truss. |  |
| vibes | This demonstration solves the wave equation for the vibrations of an L-shaped membrane. |  |
| makevase | Generate and plot a surface of revolution. The body-of-revolution corresponding to that line is plotted using the SURFL command. |  |
| sf_cdplayer | Simulink model simulate the CD player. |  |
| xpbombs | Shows a game of Minesweeper , There are 13 bombs hidden in the mine field. |  |
| lorenz | Plot the orbit around the Lorenz chaotic attractor. |  |
| travel | This demo animates the solution of the "Traveling Salesman" problem. (Limited to cities inside USA)
The problem is to form a closed circuit of a number of cities while traveling the shortest total distance along the way. |
 |
| fifteen | Shows a game of fifteen game puzzles
A sliding puzzle of fifteen squares and sixteen slots. Solve the puzzle by sequentially lining all fifteen squares up, leaving the last square empty. |
 |
| bucky | Connectivity graph of the Buckminster Fuller geodesic dome. (shows 60 coordinates) | |
| sf_spectrum_analyzer | Simulation of measuring the Frequency Response of a System |  |
| census | Shows the extrapolated predicted populations in the United States |  |
| sf_angle_events | Simulate cranking and power output |  |
| ex_guide_timergui | Execute graphic updates at regular intervals |  |
| quivdemo | Superimpose QUIVER on top of a PCOLOR plot with interpolated shading. |  |
| sf_elevator | Simulations of elevators inside 9 storey buildings. |  |
| penny | Shows 3D render of a USA penny |  |
| matlab.ui.internal.toolstrip.Icon.showStandardIcons | Shows allstandard icons | |
| knot | Compute the parametric representation of tube-like surfaces and displays the tube with SURF. |  |
| spharm2 | This example shows how spherical harmonics, which are spherical versions
of Fourier series, can be used to model the free oscillations of the Earth. |
 |
| eml_asteroids | Play a game of Asteroids |  |
| eml_fire | Simulations of burning fire |  |
| sf_tetris2 | 'j', 'l' -- move left and right
'i', 'k' -- rotate left and right SPACE -- drop 'p' -- pause 'q' -- quit |
|
| ballode | Simulate a demo of a bouncing ball. |  |
| batonode | Simulate the motion of a thrown baton. |  |
| sf_semantics_hotel_checkin | Simulate Hotel Checkins |  |
| sf_traffic_light | Simulating traffic lights at intersections |  |
| sf_fitness | Simulate the smartwatch |  |
| klein1 | This example shows how to generate a Klein bottle.
A Klein bottle is a nonorientable surface in four-dimensional space. It is formed by attaching two Mobius strips along their common boundary. |
 |
| xpklein | This example shows how to display a self-intersecting Klein bottle.
A Klein bottle is a nonorientable surface in four-dimensional space. It is formed by attaching two Mobius strips along their common boundary. |
 |
| brussode | Surface plots of brusselator |  |
| why | Randomly generated answers to life , universe and everything | |
| iburgersode / burgersode | Burgers' equation solved as implicit ODE system |  |
| sf_stickslip | Stick - slip friction simulations |  |
| sfediticon | Simulink icons that enable to create basic 16 * 16 icon editor |  |
| amp1dae | Stiff differential-algebraic equation (DAE) from electrical circuits |  |
| taylortool | A Taylor Series Approximation calculator |  |
| sf_climate_control | Simulate an environmental climate control (Temp and humidity) for a chamber |  |
| tori4 | This example shows how to generate four linked unknotted tori by rotating four off-center circles. |  |
| ardemo | Interactive axes properties demonstration |  |
| rlc_gui | Interactive GUI showing the relationship between the physical parameters of common RLC circuits and the time and frequency responses of those circuits.
* Low-pass RLC network * High-pass RLC network * Band-pass RLC network * Band-stop RLC network |
 |
| sf_security | Demonstrations of security system of door, window and mention sensor in a home |  |
| sf_server | Display random numbers to serve the assigned clients |  |
| step | Shows a randomly generated stable Transfer Function Model |  |
| imagesc | Shows the images of a boy.
To correct it , into correct orientation , type imagesc
colormap(gray(32));
axis ij image off;
|
 |
| wernerboy | This example shows how to create Boy's surface |  |
| transpdemo | This example shows how to modify the transparency value for graphics objects to reveal structure that is obscured with opaque objects. |  |
| sf_car | Simulate car braking and throttle |  |
| sf_yoyo | Simulate yoyo up and down and the energy |  |
| sf_boiler | Simulation of temperature controller of boiler |  |
| eml_aero_radar | Radar demo to estimate aircraft position using Kalman Filters |  |
Untested Easter Eggs
[edit | edit source]sf_gui
sf_mandelbrot_fixpt
eomfun - Old
eigshow - Old
imagesAndVideo - Shows an moving images of rocket flying to the space
imagesc(hot) / imagesc(cool) / imagesc(hsv) - ???
old_sf_car
eml_clock
uitabledemo - ???
- ???
sf_tictacflow - SIMULINK project to simulate a game of Tic Tac Toe against AI
-
wrldtrv - Show great circle flight routes around the globe
xpquad - ???
xpsound - ???
Not working
sfbus_demo
sf_moore_traffic_light
sf_bidder
sf_power_window
NOTE: If there are any readers who knows what is the ??? easter eggs represent, you may kindly add in.
References
[edit | edit source]
Bonus Chapters/MATLAB Benefits and Caveats
MATLAB Benefits
[edit | edit source]Ease of Use
[edit | edit source]MATLAB is an interpreted and interactive language. Programs can be easily written and modified by a user with MATLAB, which is a built-in integrated development environment and debugger. Also, there are no need to use import functions as MATLAB will use the necessary functions as it includes many built-in math and engineering functions (only if necessary toolboxes are installed)
Platform Independent
[edit | edit source]MATLAB language is supported by Windows, Linux and Mac. Thus, a program written on one platform can be easily run on other platforms. This is a platform independence feature.
Wide range of capabilities
[edit | edit source]Current MATLAB version has a wide range of capabilities, which includes data analysis, statistical analysis, optimization, signal processing, communications, control design, test and measurement, image processing, and computational finance
Full Graphics Capabilities
[edit | edit source]MATLAB provides advanced graphics that can help visualize the scientific and engineering data very well. The graphs are highly customizable such: One can change the colors, lines and marker, add annotations, LATEX expressions, legends, the addition of multiple axes etc.
Good Source of Help
[edit | edit source]MATLAB is widely used in industry and academia, so there is a wealth of support and resources available. There are many large communities that let you learn MATLAB such as Reddit (46.5k users) , Facebook group (MATLAB Programs/Code (matlabcoding.com). Hence, you might find answers that the people that come before you that might encounter similar problems too.
MATLAB Caveats
[edit | edit source]Expensive
[edit | edit source]MATLAB is very expensive for the base programs, plus additional official toolboxes from Mathwork are also expensive and costs can ramp up into thousands (Especially for students with limited budgets)
Closed Source
[edit | edit source]MATLAB is closed source. Hence, students that are interested on how the algorithm works may stuck due to closed source of the MATLAB functions.
Slow & Inefficient
[edit | edit source]It is slow compared to compiled programming languages. MATLAB is not efficient for nested loops and will not automatically take advantage of parallelism that are introduced in the code and may need to buy Parallel Toolbox .
Awkward Implementations
[edit | edit source]- If you have already coded in fully object-oriented programming (OOP) language, in particular, Python, you will find some oddities in MATLAB’s OOP implementation as MATLAB is more to scripting and not coding as you might with other programming languages. You may feel this when, for example, you are working with cell arrays in MATLAB.
- There are no in-place operators like
+=. This will leads to lines that are much longer and more harder to read.
Poor Documentations
[edit | edit source]The documentation doesn't always have enough examples therefore you may need look on-line for different examples of using a certain function. For example, the function fibodemo.
Confusing error message
[edit | edit source]Run-time errors can be difficult to debug
References
[edit | edit source]https://web.archive.org/web/20210921113616/https://modelingguru.nasa.gov/docs/DOC-1762
Bonus Chapters/History of MATLAB
History of MATLAB
[edit | edit source]During the late 1970's and early 1980's, Cleve Moler develop mathematical software package during his tenure as mathematics professor in University New Mexico as supplement teaching tools for his Numerical Analysis course.
His motivation at that time is to let his student to write EISPACK and LINPACK without having to code in FORTRAN programming languages. For this version of MATLAB1.0, there is only 71 mathematics functions at the beginning (which are built out of EISPACK and LINPACK) . Soon enough, the program package found its ways to other applied mathematics department around the USA. During this time, a student introduced MATLAB future co-founder, Jack Little . Jack Little had been in the graduate engineering program at Stanford and he adopted it for his own work.
In 1984, Cleve Moler co-founded MATLAB with Jack Little in California to commercialize and develop MATLAB. Jack Little suggested the creation of a commercial product based on MATLAB. He left his job and bought a Compaq® PC. Jack Little, together with Steve Banger spent 1.5 years to reprogram the MATLAB into C programming languages. Basically, the MATLAB version 1 is functioning like a matrix calculator and it is without any sophisticated features unlike today versions of MATLAB such as plotting, advance maths functions such as ODE , FFT, etc. PC-MATLAB made its debut in December 1984 at the IEEE Conference on Decision and Control in Las Vegas with some of most significant features such as functions, toolboxes, and graphics.
References
[edit | edit source]https://dl.acm.org/doi/10.1145/3386331
https://blogs.mathworks.com/cleve/2020/06/13/history-of-matlab-published-by-the-acm/
https://www.youtube.com/watch?v=LDnSsM8bKUE
Authors & Contributors
This list is updated automatically by AuthorsAndContributorsBot. Please do not update it manually.
- MrAlanKoh (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mattb112885 (discuss · contribs · count · logs · block log · rfps · rights [change])
- A3392 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Agriculturist50 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mike's bot account (discuss · contribs · count · logs · block log · rfps · rights [change])
- Jguk (discuss · contribs · count · logs · block log · rfps · rights [change])
- Thenub314 (discuss · contribs · count · logs · block log · rfps · rights [change])
- Dallas1278 (discuss · contribs · count · logs · block log · rfps · rights [change])
- Contele de Grozavesti (discuss · contribs · count · logs · block log · rfp · rights [change])
- RobKohr (discuss · contribs · count · logs · block log · rfp · rights [change])
- Jsalsman (discuss · contribs · count · logs · block log · rfp · rights [change])
- Whiteknight (discuss · contribs · count · logs · block log · rfps · rights [change])
- Npettiaux (discuss · contribs · count · logs · block log · rfp · rights [change])
- Adrignola (discuss · contribs · count · logs · block log · rfps · rights [change])
- Arthurv (discuss · contribs · count · logs · block log · rfp · rights [change])
- Spradlig (discuss · contribs · count · logs · block log · rfp · rights [change])
- Pi zero (discuss · contribs · count · logs · block log · rfps · rights [change])
- Mcld (discuss · contribs · count · logs · block log · rfps · rights [change])
- Recent Runes (discuss · contribs · count · logs · block log · rfps · rights [change])
- Slipperyweasel~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Simoneau (discuss · contribs · count · logs · block log · rfp · rights [change])
- Raebolex (discuss · contribs · count · logs · block log · rfp · rights [change])
- Chandramouli (discuss · contribs · count · logs · block log · rfp · rights [change])
- DannyS712 (discuss · contribs · count · logs · block log · rfp · rights [change])
- JackPotte (discuss · contribs · count · logs · block log · rfps · rights [change])
- Orderud (discuss · contribs · count · logs · block log · rfp · rights [change])
- Ashigabou~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- ArunMKumar (discuss · contribs · count · logs · block log · rfp · rights [change])
- MarcGarver (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mike.lifeguard (discuss · contribs · count · logs · block log · rfps · rights [change])
- Carandraug (discuss · contribs · count · logs · block log · rfp · rights [change])
- タチコマ robot (discuss · contribs · count · logs · block log · rfps · rights [change])
- Panic2k4 (discuss · contribs · count · logs · block log · rfps · rights [change])
- Xania (discuss · contribs · count · logs · block log · rfps · rights [change])
- SBJohnny (discuss · contribs · count · logs · block log · rfp · rights [change])
- Leaderboard (discuss · contribs · count · logs · block log · rfps · rights [change])
- Hauberg~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Az1568 (discuss · contribs · count · logs · block log · rfps · rights [change])
- DavidCary (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mortense (discuss · contribs · count · logs · block log · rfp · rights [change])
- Sargas~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mecanismo (discuss · contribs · count · logs · block log · rfp · rights [change])
- Schapel (discuss · contribs · count · logs · block log · rfp · rights [change])
- SergeyLitvinov~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Nobelium (discuss · contribs · count · logs · block log · rfp · rights [change])
- ShakespeareFan00 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Meestercoffee (discuss · contribs · count · logs · block log · rfp · rights [change])
- Herbythyme (discuss · contribs · count · logs · block log · rfps · rights [change])
- Minorax (discuss · contribs · count · logs · block log · rfps · rights [change])
- Hypergeek14 (discuss · contribs · count · logs · block log · rfp · rights [change])
- AdRiley (discuss · contribs · count · logs · block log · rfps · rights [change])
- Fanou101 (discuss · contribs · count · logs · block log · rfp · rights [change])
- 1234qwer1234qwer4 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Waldyrious (discuss · contribs · count · logs · block log · rfp · rights [change])
- Pedro07sanchez (discuss · contribs · count · logs · block log · rfp · rights [change])
- Slava Ukraini Heroyam Slava 123 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Comp.arch (discuss · contribs · count · logs · block log · rfp · rights [change])
- Jellysandwich0 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Derbeth (discuss · contribs · count · logs · block log · rfps · rights [change])
- Rs2~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Matlabrob (discuss · contribs · count · logs · block log · rfp · rights [change])
- Kleinermario (discuss · contribs · count · logs · block log · rfp · rights [change])
- Kislay kishore2003 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Angry bee (discuss · contribs · count · logs · block log · rfp · rights [change])
- WereSpielChequers (discuss · contribs · count · logs · block log · rfp · rights [change])
- WOSlinker (discuss · contribs · count · logs · block log · rfp · rights [change])
- Matiia (discuss · contribs · count · logs · block log · rfp · rights [change])
- Sheepe2004 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Пика Пика (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mhadi.afrasiabi (discuss · contribs · count · logs · block log · rfp · rights [change])
- Sarathgopalakrishnan (discuss · contribs · count · logs · block log · rfp · rights [change])
- SHB2000 (discuss · contribs · count · logs · block log · rfps · rights [change])
- Misburg3014 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mrjulesd (discuss · contribs · count · logs · block log · rfps · rights [change])
- imported>Arkelseizure
- Van der Hoorn (discuss · contribs · count · logs · block log · rfp · rights [change])
- PAC (discuss · contribs · count · logs · block log · rfp · rights [change])
- Toddh (discuss · contribs · count · logs · block log · rfp · rights [change])
- JosephusQuint (discuss · contribs · count · logs · block log · rfp · rights [change])
- ACLNM (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mild Bill Hiccup (discuss · contribs · count · logs · block log · rfp · rights [change])
- Albmont (discuss · contribs · count · logs · block log · rfp · rights [change])
- Decatur-en (discuss · contribs · count · logs · block log · rfp · rights [change])
- Daehlerr (discuss · contribs · count · logs · block log · rfp · rights [change])
- Encik Tekateki (discuss · contribs · count · logs · block log · rfp · rights [change])
- Gareth Jones (discuss · contribs · count · logs · block log · rfp · rights [change])
- Elmoya (discuss · contribs · count · logs · block log · rfp · rights [change])
- Atcovi (discuss · contribs · count · logs · block log · rfps · rights [change])
- JSvEIHmpPE (discuss · contribs · count · logs · block log · rfp · rights [change])
- Jomegat (discuss · contribs · count · logs · block log · rfps · rights [change])
- Ahy1 (discuss · contribs · count · logs · block log · rfp · rights [change])
- AlanRobinson (discuss · contribs · count · logs · block log · rfp · rights [change])
- Bwoodacre~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Soul windsurfer (discuss · contribs · count · logs · block log · rfp · rights [change])
- CabbagePotato (discuss · contribs · count · logs · block log · rfp · rights [change])
- Chad.burrus (discuss · contribs · count · logs · block log · rfp · rights [change])
- ChristophE (discuss · contribs · count · logs · block log · rfp · rights [change])
- Cxw (discuss · contribs · count · logs · block log · rfp · rights [change])
- Cromium (discuss · contribs · count · logs · block log · rfp · rights [change])
- SQL (discuss · contribs · count · logs · block log · rfp · rights [change])
- Cyndiac (discuss · contribs · count · logs · block log · rfp · rights [change])
- Rznzgwwl (discuss · contribs · count · logs · block log · rfp · rights [change])
- Dabozz88 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Darklama (discuss · contribs · count · logs · block log · rfps · rights [change])
- Samuele2002 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Jorgenev (discuss · contribs · count · logs · block log · rfp · rights [change])
- Syum90 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Whym (discuss · contribs · count · logs · block log · rfp · rights [change])
- Arsham.Mazaheri (discuss · contribs · count · logs · block log · rfp · rights [change])
- Δ (discuss · contribs · count · logs · block log · rfp · rights [change])
- Arthornsby (discuss · contribs · count · logs · block log · rfp · rights [change])
- imported>1of3
- Zephyrus Tavvier (discuss · contribs · count · logs · block log · rfp · rights [change])
- Xmjiao (discuss · contribs · count · logs · block log · rfp · rights [change])
- Astrosona (discuss · contribs · count · logs · block log · rfp · rights [change])
- Wyverald (discuss · contribs · count · logs · block log · rfp · rights [change])
- Avirupkundu (discuss · contribs · count · logs · block log · rfp · rights [change])
- Robert Horning (discuss · contribs · count · logs · block log · rfps · rights [change])
- Awedh~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Aya (discuss · contribs · count · logs · block log · rfps · rights [change])
- Vergeldt (discuss · contribs · count · logs · block log · rfp · rights [change])
- Vaterlo~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Billymac00 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Tristanreid~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Braino9501 (discuss · contribs · count · logs · block log · rfp · rights [change])
- 316k (discuss · contribs · count · logs · block log · rfp · rights [change])
- Tfernsle (discuss · contribs · count · logs · block log · rfp · rights [change])
- Techman224 (discuss · contribs · count · logs · block log · rfps · rights [change])
- RevRagnarok (discuss · contribs · count · logs · block log · rfp · rights [change])
- Deryndesta (discuss · contribs · count · logs · block log · rfp · rights [change])
- Hofmic (discuss · contribs · count · logs · block log · rfp · rights [change])
- Guanabot~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Hankwang (discuss · contribs · count · logs · block log · rfp · rights [change])
- Hao2lian (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mattflaschen (discuss · contribs · count · logs · block log · rfp · rights [change])
- Addihockey10 (automated) (discuss · contribs · count · logs · block log · rfp · rights [change])
- Hasley (discuss · contribs · count · logs · block log · rfp · rights [change])
- Hellacioussatyr (discuss · contribs · count · logs · block log · rfp · rights [change])
- LlamaAl (discuss · contribs · count · logs · block log · rfp · rights [change])
- Adamcrume (discuss · contribs · count · logs · block log · rfp · rights [change])
- Lehalle~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Hoo man (discuss · contribs · count · logs · block log · rfp · rights [change])
- Icaoberg~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- La fée Didier (discuss · contribs · count · logs · block log · rfp · rights [change])
- Krischik (discuss · contribs · count · logs · block log · rfps · rights [change])
- Ixfd64 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Kayau (discuss · contribs · count · logs · block log · rfps · rights [change])
- JZL003 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Grünich (discuss · contribs · count · logs · block log · rfp · rights [change])
- Gryllida (discuss · contribs · count · logs · block log · rfp · rights [change])
- Rhollis7 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Omegatron (discuss · contribs · count · logs · block log · rfps · rights [change])
- Doorknob747 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Dourouc05 (discuss · contribs · count · logs · block log · rfp · rights [change])
- RHaworth (discuss · contribs · count · logs · block log · rfp · rights [change])
- Quassy (discuss · contribs · count · logs · block log · rfp · rights [change])
- PokestarFan (discuss · contribs · count · logs · block log · rfps · rights [change])
- Dpb001 (discuss · contribs · count · logs · block log · rfp · rights [change])
- Eagle 101~enwikibooks (discuss · contribs · count · logs · block log · rfp · rights [change])
- Eramesan (discuss · contribs · count · logs · block log · rfp · rights [change])
- ObserveOwl (discuss · contribs · count · logs · block log · rfp · rights [change])
- GoingBatty (discuss · contribs · count · logs · block log · rfp · rights [change])
- Eumolpo (discuss · contribs · count · logs · block log · rfp · rights [change])
- Fgnievinski (discuss · contribs · count · logs · block log · rfp · rights [change])
- Neuroscidude (discuss · contribs · count · logs · block log · rfp · rights [change])
- Filipeataide (discuss · contribs · count · logs · block log · rfp · rights [change])
- Fishpi (discuss · contribs · count · logs · block log · rfp · rights [change])
- Mr.Joe (discuss · contribs · count · logs · block log · rfp · rights [change])
- Gansch (discuss · contribs · count · logs · block log · rfp · rights [change])
- GeordieMcBain (discuss · contribs · count · logs · block log · rfp · rights [change])
- Lbishal (discuss · contribs · count · logs · block log · rfp · rights [change])
- ↑ https://blogs.mathworks.com/loren/2008/01/16/nested-functions-and-variable-scope/
- ↑ https://web.archive.org/web/20220727140850/https://www.geeksforgeeks.org/functions-in-matlab/
- ↑ https://web.archive.org/web/20220730143213/https://www.educba.com/matlab-functions/
- ↑ https://blogs.mathworks.com/steve/2006/10/17/the-story-behind-the-matlab-default-image/
- ↑ https://web.archive.org/web/20210615225906/https://undocumentedmatlab.com/articles/image-easter-egg
- ↑ https://web.archive.org/web/20210803075033/https://undocumentedmatlab.com/articles/spy-easter-egg-take-2
- ↑ https://web.archive.org/web/20210123224206/https://ashanpeiris.blogspot.com/2014/12/matlab-easter-eggs.html
- ↑ https://www.testingdocs.com/in-built-graphical-demos-in-matlab/


















![{\displaystyle A=[A1,A2,A3,...,An]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/693360827e1fd0d88b709732c2402ec4babeaec9)
![{\displaystyle B=[B1,B2,B3,...,Bn]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e983412ac3020d0457da2a92e234bfb140e8944)





























