Clock and Data Recovery/Structures and types of CDRs/The (slave) CDR based on a second order PLL/2nd order type 1

Generalities of a 2^nd order PLL of type 1

Best fit for a regenerator, but with a slow acquisition.

Good filtering of the incoming signal noise but poor filtering of the VCO noise.

Becomes underdamped if the loop gain increases.

Fundamental equations

A linear, time-invariant model of the circuit is described here.

The case of a second order loop, fit for a regenerator CDR, is presented.

This architecture is in fact the best for regenerator applications, to recover a clock and to resend the data stream further, as the introductory example has shown.

There are two ways of looking into the model of the 2^nd order CDR loop:
1. to specify the CDR overall characteristics, or to measure its performances. (ω_n2 and $\zeta$).

In these cases of overview approach, the "engineer" will use two variables that characterize the overall performances of the control loop.

The variables are the undamped natural frequency ω_n2 and the damping ratio $\zeta$.

2. to design, verify and validate the CDR, as well as engineer its individual blocks. (G and $\tau _{f}$).

In these other cases there are again just two variables that correspond to the two basic degrees of freedom of the circuit.

The “designer” variables are the loop gain, G, and the time constant of the loop filter, $\tau _{f}$.

ω_n2 and ζ as functions of G and τ_f

It is important to remember that the two sets of parameters are interchangeable. Deciding the two values for a set fixes the values also for the other set, as restated in the table below:

Two degrees of freedom: relations amongst equivalent quantities

Setting ωn2 and ζ	Setting G and τf
G = ωn2 / 2ζ	ωn22 = G/τf
τf = 1 / 2ζωn2	ζ2 = 1 / 4τfG

The value of ζ (when D_T is at its minimum expected value) must be close to 1, to ensure that the behavior of the loop is neither under-damped nor over-damped.

Saying that the second order loop has one more degree of freedom than the first order loop is therefore an overstatement.

It is more fair to say that in both cases the time (and frequency) response of the loop are primarily set by the gain G.

In the case of the second order loop it is possible to have a slightly higher variability associated with the (limited) range of variation allowed for $\tau$_f.

The main advantage of the second order loop is the sharper filtering action for input frequencies in excess of ω_n2.

The sharper filtering corresponds to attenuating the jitter components beyond ω_n2 with a slope of 40 dB/decade, while a first order loop filters with a slope of just 20 dB/decade beyond its ω_n.

The meaning of the loop parameters (just ω_n or τ in a first order system, ω_n2 and ζ in a second order system) is slightly different in the two cases:

• ω_n2 is essentially the same as ω_n: it represents the angular frequency at which the loop changes behavior and a "filterng" action begins (e.g. filtering of the input jitter) or ends (e.g filtering of the VCO noise).
• τ of a first order system is the time constant of the system unit step response. τ_f in a second order system can not be seen exactly as the same because the unit step response varies for different values of the other loop parameter, ζ. In general however a relation exists and the time response of a second order system is close to about 2 times τ_f, as shown in more detail further on in this page where unit step responses of 1^st and 2^nd order loops are contrasted, under the condition ω_n2 = ω_n.

The most important functions that describe the relations amongst the variables shown in the figure, expressed for the sinusoidal jitter condition, are described in the following three subpages.

A dedicated section further down in this page gives the equations and the diagram for the time function that describes how this circuit reacts to an abrupt change of phase in the received signal.

ζ is larger than 1

• When ζ < 0.707, the jitter at frequencies around ω_n2 will be amplified during the transit through the PLL as seen when studying the jitter transfer function of this loop, and more so for smaller values of ζ.

Amplification of jitter may - if the input jitter at those frequencies is large enough to start with - accumulate when more identical regenerators are interconnected in a chain along the signal path (a not infrequent case in geographical networks).

• When ζ >> 1, the loop behaves more and more like a first order loop. The sharp cutoff at about ω_n2 , typical of a good 2 - 1 PLL, smoothes out, and the jitter at frequencies around ω_n2 is less effectively rejected.

• Similar indications are derived from the study of the error signal in this 2-1 loop:

• Large values of ζ ( >> 1) involve a large error even at frequencies much lower than $\omega _{n2}$;
• small values of ζ ( < 1.0) correspond to large overshoots of the phase error just above ω_n2.

The transition Density D_T is never stable at its maximum value (100%). Rather, the loop must not become underdamped when D_T is somewhat lower than its average of 50%. D_T = 33% means a comparator gain reduction of 67% from the G_φ value.

As ζ varies inversely to the square root of G, it is made correspondingly larger by design.

ω_n2 and ω_f or ω_z

In a second order loop, the cut-off frequency of the loop filter block (ω_f or ω_z, as the case may be) fixes the bandwidth of the closed loop (apart from minor adjustments as ζ varies within its allowed range).

Anticipating some simple formulas that will be derived later in the book,

the natural frequency of the PLL ω_n2 (which can also be seen as the jitter cutoff frequency of the CDR) is defined by the loop gain and by ω_f :

ω_n21 = 1 / 2ζ₂₁τ_f

(using the subscripts to identify loop order and type) and can also be expressed as a function of just ζ and ω_f :

ω_n21 = ω_f /2ζ₂₁

This simple formula tells that (in a 2^nd order PLL of type 1 where ζ₂₁ must remain close to 1) the natural frequency ω_n21 remains close to half the cutoff frequency of the loop filter!

Similarly, for the model of a 2^nd order type 2 loop (where ζ shall also preferably remain close to 1):

τ_z = 2 ζ₂₂/ ω_n22 ω_n22 = 2 ζ₂₂ ω_z

This simple formula tells that (in the linear model of a 2^nd order PLL of type 2 where ζ₂₂ shall remain ≈ 1) the natural undamped frequency ω_n22 remains close to twice the cutoff frequency of the loop filter!

ω_n21 and ω_n1

In a 1^st order loop, the quantity ω_n = G tells how fast the loop reacts. The higher ω_n, the faster the loop response.

For the 2nd order loop it is difficult to relate ω_n2 to how fast the loop reacts to a change. In the 2 - 1 loop, for ζ ≈ 1, and setting -for sake of comparison- the gain G equal for the two loops:

ω_n21 = 2ζ₂₁ G ω_n21 ≈ 2 ω_n1

In other words a 2^nd order type 1 PLL (ζ ≈ 1) wold seem twice as “fast” as a 1st order PLL of the same gain!

But it can also be seen that, setting, for sake of comparison, ω_n2 = ω_n, then the 2nd order type 1 loop is not practically slower than the 1st order loop!

“Slow or fast” in the sentences above means both:

- slow or fast to acquire the lock condition

- slow or fast to drift to its free running frequency when the input signal disappears.

The following figure contrasts the Unit Step Responses of the 3 important PLL models:

USRs of the 3 important loop models.
2 - 1 and 2 - 2 are plotted for natural undamped frequency = 6.28 Grad/sec and ζ = 1
1 -1 is plotted for both natural frequency = 6.28 Grad/sec and 3.14 Grad/sec.

Note that the USR of the 1 - 1 loop model is plotted for two different values of ω_n1: ω_n1 = ω_n2 of the other two loops and ω_n1 = ω_n2 / 2 of the other two loops

Jitter transfer function

Note: ω_n2 = undamped natural frequency; ζ = damping ratio

The transfer function for a given input X(s) (that is the Jitter Transfer function!) is:

${\tfrac {Y(s)}{X(s)}}={\tfrac {1}{\left({\tfrac {s^{2}}{\omega _{n2}^{2}}}+{\tfrac {2s\zeta }{\omega _{n2}}}+1\right)}}$

The magnitude of the jitter transfer frequency response (= absolute value of the jitter transfer, once modified with s replaced by jω) tells, at each frequency f = ω/2π , the ratio of the magnitude of the output jitter divided by the magnitude of the input jitter.

It can also be seen as the amplitude of the (sinusoidal) output jitter for a sinusoidal input jitter of amplitude = 1 radian ≈ 57.3°.

$\left|{\tfrac {Y(j\omega )}{X(j\omega )}}\right|={\tfrac {1}{\sqrt {\left(1-{\tfrac {\omega ^{2}}{\omega _{n2}^{2}}}\right)^{2}+\left({\tfrac {2\omega \zeta }{\omega _{n2}}}\right)^{2}}}}$

The following figure is the Bode magnitude plot of the jitter transfer function. Curves for different values of the parameter ζ (damping ratio) are shown:

The magnitude of jitter filtering, for different values of the damping ratio.
Peak amplification for low values of the damping ratio occurs at ω_p = ω_n2 √1 − 2ζ² and amounts to : ${\tfrac {1}{2{\zeta }{\sqrt {1-{\zeta }^{2}}}}}$.

This 2^nd order type 1 PLL is a good low-pass filter [40 dB/decade] for the phase jitter.

Gain peak at ω_peak when ζ > √1/2 ≃ 0.707

There is no amplification of the input jitter except for values of the damping ratio smaller than √1/2 ≃ 0.707, at some frequencies around ω_n2.

The peak amplification occurs at ω_peak = ω_n2 √1 − 2ζ² and amounts to : ${\tfrac {1}{2{\zeta }{\sqrt {1-{\zeta }^{2}}}}}$ .

The jitter transfer function of a simpler 1^st order type 1 loop (where the signal processing block is just a flat gain block of gain G_f) can be easily obtained as:

${\tfrac {Y(s)}{X(s)}}={\tfrac {1}{\left({\tfrac {s}{\omega _{n}}}+1\right)}}$

Similar to the case above, it filters out all jitter components above ω_n (ω_n = G_φ * G_f * G_VCO = G), but without peaking nor smoothing of the corner, and with a single slope of 20 dB/decade instead of 40 dB/decade, as seen in the previous page.

In the case of regenerator equipment or of clock distribution in the network, the requirement of a very limited or inexistent gain peaking is explicit, and stringent.

Important changes in jitter filtering going from the 1 - 1 loop tp the 2 - 1 loop

The most important new feature is the sharper cut off of the input jitter frequencies above ω_n2 , with a slope of -40 dB/decade instead of just -20 dB/decade.

The addition of the 1^st order filter between the phase comparator and the VCO has added one pole to the transfer characteristic of the loop.

All CDRs act as low pass filters on the timing signal, and remove all the (jitter) frequencies above a cut off frequency, called ω_n in the model of a 1^st order loop and ω_n2 in the model of a 2^nd order loop.

The figure above contrasts the two cases in a particular example. Also the frequency of the received line pulses, ω_p, is shown, as the vertical marker of the yellow line.

The (CDR) PLL models in general refer to discrete time systems with sample frequency equal to ω_p, and therefore all characteristics above ω_p are not investigated (they repeat themselves periodically along the frequency axis).

In the case shown as well as in general, the choice of ω_n2 implicitly defines the input jitter below ω_n2 as useful signal, and the input jitter above ω_n2 as noise to be rejected.

The stronger filtering effect of the 2^nd order type 1 loop can be reasonably estimated assuming that:

1. the jitter has a flat spectral density from ω = 0 to ω = ω_p,
2. the jitter from ω = 0 to ω = ω_n2 is useful signal and
3. the jitter from ω = ω_n2 to ω = ω_p is noise to be rejected.
   

With these assumption, it can be calculated that the 2^nd order loop filters the noise jitter 17.23 dB more than the 1^st order loop.

Error signal

The previous section about the jitter transfer function has shown that some PLLs may even amplify the input jitter amplitude.

This happens for the frequency components around ω_n2 of the input jitter, if the damping ratio ζ is lower than ­ √1/2 ≃ 0.707.

Another tool to investigate the same critical frequency band is the function that describes the time distance (that is the phase distance if time is divided by the duration of a line pulse, i.e. by 2π/ω_p) between output and input.

This function is called error signal, indicated respectively as ε(t) or E(s) or E(jω).

The error signal is less important in a pure PLL circuit, whose task is to track an input clock (and to dejitter it, maybe), but is extremely important if the PLL is serving into a CDR circuit.

E(jω) is especially meaningful, because:

• jitter is investigated in "steady state" conditions, i.e. with the Fourier transforms: sinusoidal input, sinusoidal output and sinusoidal waveforms at every inner node of the PLL;
• the PLL output tracks exactly the input with just the difference ε(t);
• ε(t) is exactly the difference between the eye center and the sampling instant: when ε(t) is maximum the lateral eye margin is minimum;
• the maximum value of a sinusoidal deviation is its magnitude: the useful function is therefore |E(jω)|.

Its magnitude tells, at every jitter frequency, the amplitude of the sinusoidal distance between the output and the input phases. It is easy to realize that this function is the loop error function:

Ε(s) = Y(s) − X(s) = X(s) ${\tfrac {\left({\tfrac {s^{2}}{\omega _{n2}^{2}}}\right)+2\zeta \left({\tfrac {s}{\omega _{n2}}}\right)}{\left({\tfrac {s^{2}}{\omega _{n2}^{2}}}\right)+2\zeta \left({\tfrac {s}{\omega _{n2}}}\right)+1}}$ $\left|{\tfrac {E(j\omega )}{X(j\omega )}}\right|=\left|{\tfrac {\left({\tfrac {s^{2}}{\omega _{n2}^{2}}}\right)+2\zeta \left({\tfrac {s}{\omega _{n2}}}\right)}{\left({\tfrac {s^{2}}{\omega _{n2}^{2}}}\right)+2\zeta \left({\tfrac {s}{\omega _{n2}}}\right)+1}}\right|={\tfrac {\sqrt {{\tfrac {\omega ^{4}}{\omega _{n2}^{4}}}+{\tfrac {4\zeta ^{2}\omega ^{2}}{\omega _{n2}^{2}}}}}{\sqrt {{\tfrac {\omega ^{4}}{\omega _{n2}^{4}}}-(1-2\zeta ^{2}){\tfrac {2\omega ^{2}}{\omega _{n2}^{2}}}+1}}}$

The regeneration of the data depends on sampling the received pulses (that have undergone amplification, equalization and filtering of out-of-band noise) close to the time of maximum amplitude of each pulse. At that time the remaining noise and intersymbol interference still alter the pulse to a certain extent. A significant phase error makes the probability of a wrong detection higher: in other words a phase error that is not affecting clock tracking may still increase to intolerable levels the bit error rate!

The following figure plots the magnitude (not in dB, but in radian referred to the line pulse duration) of the error signal if the input jitter amplitude at any given frequency is exactly 1 rad (1 radian ≈ 57.3°).

The error signal is, in other words, normalized to the value of the loop input, plotting in fact the error "transfer" function: E(s)/X(s).

The magnitude of the (normalized) error signal, for different values of the damping ratio.
The error overshoots just above the natural undamped frequency ω_n2, and much more so for low values of the damping ratio.
The value chosen for ω_n2, though reasonable, has no special meaning

At low jitter frequencies there is practically no error, because the tracking is very good.

At very high jitter frequencies the error is practically identical to the input: in fact the PLL is not able to track the jitter and the local clock stays unmoving with respect to it.

At intermediate jitter frequencies, around ω_n2, the error increases with frequency till it is as large as the input jitter itself, with an intermediate region where it can become larger, at frequencies just above ω_n2 for low values of ζ.

Large values of ζ ( >> 1) involve a large error even at frequencies much lower than $\omega _{n2}$; small values of ζ ( < 1.0) correspond to large overshoots of the phase error just above $\omega _{n2}$.

Both the jitter transfer and the jitter error functions are true "transfer functions". They tell the ratio of an output to an input (The function in the figure above represents in fact the magnitude of the error transfer function, as well as the error magnitude, for an input with a fixed value of 1 radian).

The function in the next Section instead -the jitter tolerance function- is not a transfer function. The aspect of causality (the fact that the input generates the output) is not present there. The jitter tolerance function describes the values of input jitter that generate a fixed value of the error signal.

The steady state error due to f_p – f_fr difference and the steady state error of the sampling time

The free-running frequency characteristic of the VCO, f_fr, never coincides exactly with f_p.

As introduced earlier in the VCO page,
the VCO control signal -while the PLL is tracking the input signal -
exhibits a d.c. offset from its center value, proportional to the frequency mismatch.

This steady state error (in a control system of type 1 with unity feedback, like the system under consideration here) in presence of a unit ramp applied to the input of the system (as seen earlier in this book) is also present at the output and has the constant finite value of:

steady state output error = E_s = 1/G [rad]

If the ramp applied to the input, instead of a slope of 1 rad/sec, has a slope of S rad/sec, E_s becomes:

E_s = S/G

and if, like in most practical cases, the ramp is caused by the frequency difference between the clock embedded in the CDR incoming pulse stream (f_p) and the free-running frequency of its VCO (f_fr), the phase error in those type 1 systems is:

E_s = (ω_p – ω_fr) / G

The frequency offset

This offset (of the drive signal at the node connected to the VCO input), depends on the type of the PLL:

1. may not be a steady state signal because at some other node the signal would ramp until some non-linearity of the loop limits it (and the loop loses its control ability - loops of type 0), or
2. may be present at the other PLL nodes with a proportionality coefficient (loops of type 1), or
3. may be compressed to zero at some other PLL nodes by some integration in the loop (loops of type 2).

Sampling time shifted from the best instant

For the type 1 PLLs the dc offset that reconciles f_p and f_fr at the VCO input is also present -with some coefficients of proportionality- at the other nodes.

In particular this offset is present also between the two inputs of the phase comparator, has the value E_s seen above and represents a deviation of the sampling time from its best (=center) position.

The VCO centering is the limit to a very narrow jitter bandwidth

In the 2^nd order, type 1, loop, the VCO frequency mismatch f_p – f_fr becomes a sampling time error E_s according to:

E_s = (ω_p – ω_fr)/G (G= G_φ*G_f*G_VCO)

For fixed open loop dc gain G and filter time constant τ_f, the jitter cut-off frequency ω_n2 is:

ω_n2 = G * 2ζ = √G/τ_f E_s = ((ω_p – ω_fr) * 2ζ ) / ω_n2

It is easy to see that, for a 1st order type 1 loop: E_s = ((ω_p – ω_fr) / ω_n1

The same equation, rearranged, tells that the frequency mismatch and the maximum E_s define how tight the loop jitter bandwidth can be:

E_s / 2ζ = (ω_p – ω_fr) / ω_n2 = ((ω_p – ω_fr)/ω_p) / (ω_n2/ω_p) (ω_n2 / ω_p ) = ((ω_p – ω_fr) /ω_p) / (E_s /2ζ ))

It is easy to see that, for a 1st order type 1 loop: (ω_n1/ω_p ) = ((ω_p – ω_fr) /ω_p) / E_s )

For instance, if E_s is conservatively set as low as = 0.1 rad, then ω_n2 can be : ω_n2 ≃ 20 * (ω_p – ω_fr) .

As seen already about CDRs and parts per million of frequency mismatch, the free running frequency of a slave CDR may differ no more than 50 ppm from the frequency of its remote master (very low cost quartz crystal), or 10000 ppm (monolythic RC oscillator after EWS trimming), or even differ less than 1 ppm, still without big cost concerns (quartz for GPS receivers inside mobile phones). Less than 0.1 ppm is typical of professional equipment.

The four mentioned cases set a respective minimum for the design choice of ω_n2 at: 0.001 ω_p , 0.2 ω_p , 2 e-5 ω_p , 2 ppm ω_p .

Jitter tolerance

For the slave 2 - 1 loop, the jitter tolerance can be obtained as |X(jω)|_{|Ε(jω)| = Φleo}, which corresponds to the hypothesis that the tolerance is limited by (and only by) the lateral eye opening, see also the relevant page. (Φ_leo is the lateral eye opening expressed in radian).

In other words the mathematical function is obtained as if it was the range of the phase comparator that set the tolerance limit, but reduced to the lower value Φ_leo.

The comparator range corresponds to the ideal width of the received pulse left and right of its mid point ( ±π ).

The function that gives the ratio of the input to the error is:

${\tfrac {X(s)}{\mathrm {E} (s)}}={\tfrac {X(s)}{X(s)-Y(s)}}={\tfrac {1}{1-\left({\tfrac {\omega _{n}^{2}}{s^{2}+2s\zeta \omega _{n}+\omega _{n}^{2}}}+\right)}}={\tfrac {s^{2}+2s\zeta \omega _{n}+\omega _{n}^{2}}{s^{2}+2s\zeta \omega _{n}}}$

Its magnitude in steady state (s = jω), that represents the magnitude of the sinusoidal input generating an error of magnitude 1 rad ( |Ε(jω)| = 1 rad ), is the normalized jitter tolerance function:

$\left|{\tfrac {X(j\omega )}{\mathrm {E} (j\omega )}}\right|$ = $\left|X(j\omega )\right|_{\left|\mathrm {E} (j\omega )\right|=1}$ = ${\sqrt {\tfrac {\left(1-{\tfrac {\omega ^{2}}{\omega _{n}^{2}}}\right)^{2}+\left({\tfrac {2\omega \zeta }{\omega _{n}}}\right)^{2}}{\left({\tfrac {\omega ^{2}}{\omega _{n}^{2}}}\right)^{2}+\left({\tfrac {2\omega \zeta }{\omega _{n}}}\right)^{2}}}}$

The magnitude of the jitter tolerance function (de-normalized) is the same function but taken for |E(jω)| = Φ_leo :

$\left|X(j\omega )\right|_{\left|\mathrm {E} (j\omega )\right|=\Phi _{leo}}$ = $\left|{\tfrac {X(j\omega )\Phi _{leo}}{\mathrm {E} (j\omega )}}\right|=\Phi _{leo}{\sqrt {\tfrac {\left(1-{\tfrac {\omega ^{2}}{\omega _{n}^{2}}}\right)^{2}+\left({\tfrac {2\omega \zeta }{\omega _{n}}}\right)^{2}}{\left({\tfrac {\omega ^{2}}{\omega _{n}^{2}}}\right)^{2}+\left({\tfrac {2\omega \zeta }{\omega _{n}}}\right)^{2}}}}$

The Bode magnitude plot is given in the following figure:

The magnitude of the maximum jitter that can be tolerated, for different values of the damping ratio .
The maximum tolerance undershoots just above the natural frequency, and much more so for small values of the damping ratio.

If another value $\mathrm {\Psi _{leo}}$ better simulates the circuit tolerance limit, the curve plotted still applies provided it is translated vertically by the amount $\mathrm {20log_{10}(\Psi _{leo}/\Phi _{leo})}$.

At low jitter frequencies there is very good tracking, even if the jitter has a large amplitude. The circuit has time to follow these large but slow variations. It takes an extremely large jitter amplitude to reach the limit of tolerance.

At very high jitter frequencies the circuit is unable to follow the jitter, that varies too fast. The tolerance is in practice exactly the lateral eye opening (or the phase comparator range, whichever limit is reached first). In fact, the PLL is not able to track the jitter at all and the local clock stays unmoving with respect to it.

At intermediate and high jitter frequencies, starting just below ω_n, the local clock is tricked by the jitter into overreaching while the input jitter is coming back to its zero value. In this range of frequencies, at and above $\omega _{n}/{\sqrt {2}}$, the tolerance is reduced below its horizontal asymptotic value, and especially so for low values of ζ.

The undershooting just above ω_n corresponds to an asymptote towards low frequencies (-20 dB/decade typical of all type 1 loops) that, if ζ is made smaller, seems to move to the right, and vice-versa that, if ζ is made larger, seems to move to the left..

The reduction of the tolerance margin in the critical frequency band may be detrimental in CDR applications.

The following table gives the values of the maximum tolerance reduction for different values of ζ:

The tolerance has a minimum that depends in frequency and value on the damping ratio ζ.
Minimums are listed for different values of ζ.
The reduction is especially large for small values of the damping ratio.

Values of ζ between 1.5 and 3.0 are therefore an inevitable design choice.

Fabrication tolerances of the CDR elementary components may often (monolythic implementation) be as large as ± 20 %. Dependence from operating conditions like the power supply variations or the density of transitions inside the incoming signal may account for even larger variations.

It is important to verify and to validate the behaviour of the CDR circuit (whatever its actual implementation is, analog, digital or ..) in the frequency range from good tracking (low jitter frequencies) to around the characteristic frequency and up to inability to track (very high jitter frequencies): an undershoot of the jitter tolerance may be present, and go unnoticed otherwise!.

Phase vector view

The jitter tolerance curve is generated with sinusoidal input jitter, sweeping all the frequencies of interest.

If a linear model is adequate for the CDR under investigation, all the signals involved can be modeled with sinusoids.

The waveforms of input jitter, output jitter and error jitter , in a linear model, can be represented with the phase vectors at any given signal frequency.

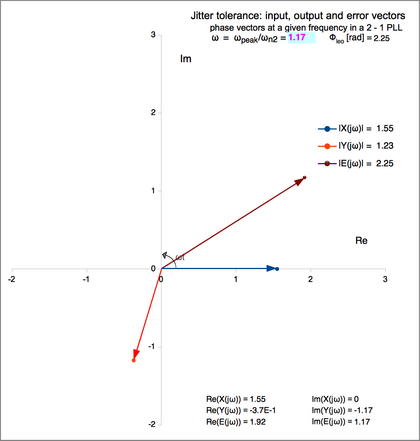
The following figures explore a 2^nd order, type 1 loop.

In all of them, the value of the loop damping coefficient has been set at  ζ₂₁ = 0.5116. It is a value that would be too small in a real application, but that is useful to emphasize the relative variations of the three phase vectors when ω is close to ω_n.

They can be better understood making reference to the figure of the family of tolerance functions for different values of ζ₂₁, higher up in this page. A curve with ζ = 0.5 can be identified there (orange line).

The frequency range of interest is normalised to the characteristic frequency (ω_n) of the loop.

At low frequencies, well below ω_n, the tolerated input is large, and so is the output.
The output follows the input with a small phase lag. The error is anyway as large as the Φ_LEO.

At frequencies increasing towards $\omega _{n}$, $X(j\omega )$ becomes smaller and, from $\omega$ = $\omega _{n}/{\sqrt {2}}$, undershoots $\Phi _{LEO}$. The phase lag of $Y(j\omega )$ increases towards $\pi /2$.

Tolerance vectors at frequencies lower than ω_n

At $\omega _{n}$, $X(j\omega )$ is not yet at its minimum.
The phase lag of $Y(j\omega )$ reaches $\pi /2$ when ω is = $\omega _{n}$.

At $\omega _{peak}$, $X(j\omega )$ reaches its minimum value.
The phase lag of $Y(j\omega )$ is larger than $\pi /2$.

Tolerance vectors at frequencies close to ω_n

Above $\omega _{peak}$, $X(j\omega )$ restarts increasing towards $\Phi _{LEO}$.
$Y(j\omega )$ becomes smaller and smaller while its phase tends to $\pi$.

$X(j\omega )$ tends asymptotically back to $\Phi _{LEO}$.
$Y(j\omega )$ tends asymptotically to 0, and its phase lag tends asymptotically to $\pi$.

Tolerance vectors at frequencies higher than ω_n

Note that the x and y axes use variable scales, while they both use the same scale in each figure.

In all these figures, the error signal $E(j\omega )$ is defined as:

$E(j\omega )$ = $X(j\omega )$ – $Y(j\omega )$

In accordance with the definition of jitter tolerance function, its magnitude $\mid E(j\omega )\mid$ is = $\Phi _{LEO}$ at all frequencies.

The input phase, i.e. the phase of $X(j\omega )$, is 0 at all frequencies: $Im((j\omega ))=0$ $\forall$ $\omega$.

The output always follows behind the input with a phase lag between 0 (ω → 0) and π (ω → ∞). because its imaginary part is always negative:

$Im(Y(j\omega ))$ = $Re(X(j\omega ))$${\tfrac {-2\zeta \omega _{n2}}{(1-\omega ^{2}/\omega _{n2})^{2}+4\zeta \omega ^{2}/\omega _{n2}^{2}}}$.

The error is seen as preceding the input. If the error had been defined as the output minus the input, the phase relation would be the opposite, and the error would lag behind the input.

At low frequencies $X(j\omega )$ is large, and so is $Y(j\omega )$. Their phase distance is small.

At frequencies increasing towards $\omega _{n}$, $X(j\omega )$ becomes smaller and, getting close to $\omega _{n}$, undershoots $\Phi _{LEO}$. The phase lag of $Y(j\omega )$ increases towards $\pi /2$.

At $\omega _{peak}$, $X(j\omega )$ reaches its minimum value. The phase lag of $Y(j\omega )$ is $\pi /2$.

Then it restarts increasing and tends asymptotically back to $\Phi _{LEO}$. $Y(j\omega )$ tends asymptotically to 0, and its phase lag tends to $\pi$.

Tolerance functions of the three important loop models

The normalized jitter tolerance for all three important loop models used in (slave) CDRs is shown in the following figure.

under the hypothesis that the tolerance is limited by (and only by) the lateral eye opening, which is reasonable in most practical cases of SLAVE CDRs, see also the relevant page

Normalized jitter tolerance functions of the loops of order 1 type 1, order 2 type 1 and order 2 type 2.
Filter cut-off frequencies, damping ratios and natural undamped frequencies are chosen for a meaningful comparison.

It may be noted that the Bode plot of the curve of normalized jitter tolerance is the mirrored image (across the x axis) of the normalized error curve.

The asintote towards low frequencies (in the log-log plot) has a slope of 20 dB/ decade for the type 1 systems, and of 40 dB/ decade for the type 2 system.

The rejection of generated (VCO) noise…..

Noise injected into the different nodes of the PLL loop reaches the output modified by the loop operation.

_{See also the page Clock and Data Recovery/Noise is shaped by the PLL structure}.

The description in the s domain of such modifications for a 2^nd order type 1 PLL is:

The phase noise generated inside each PLL block is modified before it appears at the PLL output,
block diagram and equations for the 2^nd order type 2 loop.

The noise generated by the filter N_f is modified by the transfer equation TF_Nf = (TF_VCO) / (1 + TF_PhComp*TF_filter*TF_VCO))
The noise generated by the VCO N_o is modified by the transfer equation TF_No = 1/(1 + TF_PhComp*TF_filter*TF_VCO)

VCO noise - transfer functions VCO-to-output of the loops of order 1 type 1, order 2 type 1 and order 2 type 2.
Filter cut-off frequencies, damping ratios and natural undamped frequencies are chosen for a meaningful comparison.

The 2 - 1 magnitude is: |Y(jω)/N_o(jω)| = 20log10(((ω²τ_z)²+ω²)^1/2 / ( (G-ω²τ_z)² + ω² )^1/2)

The 2 - 1 loop attenuates the VCO noise at all frequencies below $\omega _{21}$, with a single slope (20 dB/decade) and with a gain overshoot that - whenever ζ > 0 , i.e. always - peaks at ${\tfrac {\omega ^{2}}{\omega _{n21}^{2}}}={\tfrac {1+{\sqrt {1+8\zeta _{21}^{2}}}}{2}}$.

The following figure illustrates the behavior of the 1-1 and 2-1 loops (using on purpose for the 2-1 a damping ratio that is unacceptably low) and gives the relevant formulas.

VCO to output (noise) transfer functions of the PLLs of order 1 type 1 and order 2 type 1, as well as the transfer function of the filter block for the order 2 loop.
The damping ratio of the 2nd order loop has been chosen too low on purpose, to emphasize the risk of amplification of noise at certain frequencies.

The 2-1 loop is normally used in regenerator applications (when $\omega _{21}$ is low): a low noise VCO must be used.

It also needs very good control of ζ₂₁ that must be kept close to 1.0 (this rules out the use of blocks with hard non-linearities and largely variable gain, like bang-bang phase detectors).

Unit step response

The analysis in the frequency domain (jitter transfer, error function, jitter tolerance, noise transfer) models the circuit behavior in the "small signal" conditions.

The Unit Step Response is part of the same mathematical model, and gives a time domain perspective of the circuit,
that complements the frequency domain perspective offered by the jω functions.
The Unit Step Response can be obtained from the jitter transfer function, multiplying it by 1/s and inverse transforming.

In fact the (unit) step response shows the response of the PLL output phase to an abrupt variation of the input phase.

The (unit) step response is used primarily to see how the acquisition phase evolves towards phase lock.

The step response of this type of loop is slower than that of the 1^st order (and than that of the 2^nd order type 2), because the loop filter does attenuates the high frequencies (while there is no attenuation of high frequencies in the case of the other two loops).

At the beginning of an acquisition the signal pops up with some timing difference from the phase of the -free-running until that moment- local oscillator, and this can be well represented by a step function, with a value of the step that may vary randomly, from acquisition to acquisition, in the range of -π to +π rad.

The amplitude of the output phase as a result of a (unit) step variation of the input phase, for different values of the damping ratio.
The output phase overshoots the input (if ζ < 1) after an initial delay, and then gradually settles in good tracking.

It is however important to be cautious when using the step response to model the system in case of large abrupt variations of the input phase.

Care is necessary because the boundaries of linear operation of the system (the range of the phase comparator, the swing of the filter output, the control range of the VCO, ..) can easily be reached and exceeded during a (relatively) large transient.

The CDR will -very likely- still operate correctly but its performances may not be well described by this linear model during such transient.

The response when left free-running

The unit step response of the loop filter can give some understanding also on the behavior of the CDR when the latter loses lock and becomes free-running.

(The CDR is left free-running, for instance, when the incoming signal has no level transitions for the phase comparator to detect its phase. At that moment the phase comparator output steps abruptly to its neutral -i.e. no phase difference- level.)

1. In a 1^st order loop, the comparator output waveform is applied directly to the VCO input (apart from some flat amplification). The VCO abruptly changes its frequency to its free-running frequency. The sampling point drifts from its lock-in point following a linear (phase) ramp. The slope of the ramp is the frequency difference between the free-running frequency of the local oscillator and the frequency of the remote transmit oscillator (Δf = f_fr -f_s).
2. In a 2^nd order type 1 loop, the loop filter smooths down the frequency step. The phase ramp does not start immediately, but gradually. The graduality corresponds to the time constant of the loop filter, τ.

The following figure contrasts the behavior of the two loops, assuming that both have the same f_p and the same VCO gain.
This helps understand the difference in the architectural sense, but may be misleading in practice, because the two loops, for the same f_p , would be used in different applications with widely different values of G_VCO.
G_VCO would be much larger in a 1^st order loop, in consideration of the fast acquisition expected, and much smaller in the 2^nd order loop, in consideration of the tight jitter filtering expected.

The (1^st order type 1) loop drifts 1 rad exactly after a time equal to: f_p / |f_p – f_fr| periods of received pulses.

But errored bits might appear even before, if the lateral eye opening was less than 1 rad (1 rad is an improbable value, 2 rad is a more likely threshold for the onset of error-ed bits).

In the case of a 2^nd order type 1 loop, (for the property of the 1^st order USR -of the filter inside the 2^nd order PLL- that the area lost versus the unit step is exactly τ = 1/ω) :

The filter of 2^nd order type 1 loop delays the onset of errored bits by about τ seconds ( by τ once settled, by somewhat less before )