Clock and Data Recovery/Structures and types of CDRs/Examples
Examples
[edit | edit source]To fix the concepts introduced in the previous section, and to better understand them, let’s see a few examples of linear models.
Amongst them, just three will be further developed in the remainder of the book, because they represent the three really useful structure models of CDRs.
They are:
The other examples are useful just as theory exercises and not so much as models of how practical CDRs should be made.
Notes:
- A CDR shall be called "a slave CDR" if its recovered clock is also used to output the recovered data.
- A slave CDR may simply deliver the recovered data to a buffer memory (end point CDR) or may extend the clock domain -mastered by the remote transmit clock- by sending forward the recovered data using the recovered clock (regenerator CDR).
- In some cases the characteristic of certain individual blocks in the block diagram (like the gain of the phase comparator, or the oscillator gain, or other characteristics) are not explicitly considered. More abstract quantities, like the natural frequency n, or the damping ratio , are used instead for the formulas and for the time or frequency diagrams. This is done for two reasons:
- the characteristics of the blocks that operate at the (high) frequency of the data stream (phase comparator and local oscillator ) are frequently imposed by technology choices and are not for the designers to play with;
- the general behavior of the CDR is more generally represented and more easily understood.
1st order, type 0
[edit | edit source]and 0th order, type 0 as a special case.
(For definitions of order and type, see: Order and type of a CDR )
This list could have started with the simplest example possible, where the output of the phase comparator drives directly the (phase of the) local oscillator, without any low pass filter in between.
That would have been a loop of 0th order (with just constants in its closed-loop transfer function and no dependence on the complex variable s) and of type 0 (because there are -of course as it is of 0th order- no poles in the origin, i.e. no factors 1/s in its open-loop transfer function).
As there is always some sort of filtering of the output of the phase comparator, the 0th order type 0 loop can be seen as a limit case of the 1st order, type 0 loop described here below. The model of the 0th order type 0 loop can be useful when a high loop gain makes the (closed loop cut-off) frequency (of the of 1st order, type 0 loop) so high to be negligible. In such case it is enough to put τ = 0 in following equations to obtain its model.
The only practical block diagram that corresponds to a PLL of 1st order and of type 0 shows (see figure below) a local oscillator controlled in phase by the low pass version of the phase comparator output.

The PLL in this CDR is of unity feedback, of the first order and of type 0.
The relation of the output to the input (= the closed loop transfer function), is:
where G, the "open loop gain", is Gφ Gf GVCO. The unit step response can be obtained from the (jitter) transfer function multiplying the closed loop trasfer function by 1/s , and reverse transforming the result:
Some points can be remarked:
- that there remains a steady state error, which is minimised if G is >> 1. In fact a type 0 loop like this one needs a small phase error Φx(j0)/G to track a phase difference Φx(j0) between input and the phase of the free running oscillator. In other words, if the local oscillator is synchronous with the received signal (i.e. both are within a single clock domain), this circuit provides a strong reduction of the phase difference between the two, that is reduced from Φx(j0) to Φx(j0)/G.
- that the cut-off frequency of the loop, ωn, is 1+G times higher than the cut-off frequency of the filter block ωf = 1/τf [rad/sec]; as G is large to render negligible the steady state phase error, this loop reacts very fast to any input phase change.
- that the loop tracks the jitter frequencies below ωn = , and is unable to follow higher jitter frequencies (in all examples of PLLs there exists a natural frequency ωn that depends closely on the open loop gain, and the jitter frequencies below ωn are tracked, while those above ωn elude the tracking ability of the loop); in this case of a type 0 loop, ωn is pushed very high if the gain G is high, to the point that this loop cannot be used in CDRs.
A circuit of this architecture may find application, but never inside a CDR. It can be used to implement a DLL, (although DLLs can also be made with a 1st order, type 1 architecture). As long as the residual phase error is kept small enough by a large loop gain, it can fit a DLL application. The unconditional stability and the fast response are useful, while the lack of input jitter filtering at high frequencies (mandatory for CDRs) is not important when the reference clock is sufficiently immune from high frequency noise.

The tolerance function is drawn for the cases where it depends on the phase comparator only, on the variable phase element only, on both.
1st order, type 1
[edit | edit source]
This fundamental architecture is often used and also is, because it contains all the fundamental features of the PLLs used in practice, useful to fix concepts and to better understand the more sophisticated architectures of higher order.
It may present itself under different guises (three examples are given in the figure below), but the mathematical model remains the same.
It is maybe easier to derive the model equations from the first example in the following figure (the "slave"), although the third example (the "phase aligner") is the one most frequently found in actuality.

The first is the simplest to understand and the derivation of the model equations is easiest from it.
The third (the phase aligner) is of fundamental importance for the communication engineer.
Oscillator controlled in frequency ("first order slave CDR")
[edit | edit source]This example (its architecture is shown on the top left in the Figure above) is important because it introduces this type of architecture and allows an easy derivation of the model equations.
For slave CDR applications though, PLLs of the second order are preferred and this one can only be found in the simplest, undemanding, applications.
The second architecture of PLL in the figure above is a slight variant of the first (the one treated in this Sub-Section), and is not important for CDR loops. It can be important instead as model of the DLL.
The relation of the output to the input (= the closed loop transfer function), is:
where G, the "open loop gain", is defined as Gφ Gf GVCO.
The unit step response can be obtained from the (jitter) transfer function multiplying the closed loop trasfer function by 1/s , and reverse transforming the result:
The model is described in detail in a page dedicated to the 1st order, type 1 architectures later on in this book, owing to the practical importance of its phase-aligner variant.
To be able and contrast this architecture with the others in this page of examples, the magnitude of the jitter transfer function, the response to a unit (= 1 radian) step variation of the input signal phase and the magnitude of the jitter tolerance function ( The jitter tolerance function ) are shown in the figure below.
The relevant equations are:
- Magnitude of the transfer function:
- Unit step response:
- Magnitude of the jitter tolerance: = , ( where Φleo is the lateral eye opening expressed in radian) .

The tolerance function is drawn for the case that the tolerance border depends on the phase comparator only.
This architecture clearly shows:
- a medium (20 dB/decade) jitter filtering towards high frequencies;
- a medium jitter tolerance, with the 20 dB/decade asymptote towards zero frequency. It comes from the pole 1/s present in the forward path of the control loop. This is a minimum characteristic when the CDR must operate as a slave and track frequencies that can wander around their nominal value;
- only one degree of liberty for the designer (that is G in the figures above, i.e. the open loop d.c. gain).
All these characteristics together make this architecture not preferred in actual designs of slave CDRs. For these, the second order, type 1 or type 2, architectures are chosen instead, depending on the requirements and on the technology available for the specific application.
Addition of the complementary delay ("phase aligner")
[edit | edit source]Adding the complementary delay it becomes: the phase aligner.
Another example of unity feedback, 1st order and type 1.
The local oscillator is fixed and an adder compensates the phase deviations of the incoming signal before its regeneration with the local clock.
This example (its architecture is shown on the bottom left in the Figure above) has value in that it it is widely used in practice wherever this function is required in a network.
This example is of particular interest because:
- - a clock independent from the PLL operation (i.e. in the Figure above) is used for the regeneration, while it is -y(s) instead that represents the output of the PLL system.
- - as a consequence of the point above, the CDR incorporates an "elastic buffer" function, located in the processing of the input signal through the adder block and through the subsequent re-sampling by the local clock ().
This example in fact describes the abstract model of the phase aligner. The CDRs that match this model are found in network points where a signal (jittered and possibly regenerated by slave CDRs one or more times along a transmission path) is brought back in phase with the clock that was used to generate it[1]
For sake of simplicity in the following calculations - and without loss of generality in the results- the local clock is used as reference for the phase of all the signals.
Therefore its jitter is identically zero. Additionally it is assumed that the initial phase value .
- The only function (the only one that is not a transfer function) which does not belong to the linear model is -obviously- the one that depends on non-linearities for its definition.
- The jitter tolerance function depends in the case of the phase aligner on two hard non-linearities (phase comparator and phase adder), instead of on just one (the phase comparator) as in the case above.
- Jitter transfer and Unit Step Response are identical functions to those derived in the previous example, and not repeated here.
- The jitter transfer function in this case would describe a characteristic of the PLL as usual, but becomes meaningless for the whole CDR, because of the phase alignment resulting from the elastic buffer of this CDR.
- The Unit step response, in this particular case, as already pointed out for the transfer function, only describes the PLL operation, while it is meaningless for the whole CDR.
- It can be seen as the waveform at the output of the phase adder ( signal in the Figure above ) resulting from a phase step of the input ( in the Figure above ).
- Jitter tolerance function ( The jitter tolerance function )
The phase jitter tolerance of this circuit is limited both by the range of linearity of the phase adder and by the range of linearity of the phase comparator.
Let's see each one separately. Then, the tolerance function at any frequency will simply be the lower of the two, because the signal in either of the two circuit blocks does not influence the characteristic of the other block.
- Adder tolerance function ( Tolerance of phase adders )
- The adder is normally made by a delay line, that adds a delay to the input signal ( in the Figure above ) equal to the signal present on the control input ( in the Figure above ).
- - Defining as D (measured in radian - if D is in seconds, then use Dω), the total phase delay that the delay line can add, and
- - defining as zero the phase delay added when the control signal is set at the mid point of its control range,
- then the tolerance of the adder inserted in the CDR circuit of the above Figure is:
- using the relation (see the relevant subsection on the jitter transfer function of this example)
- then
- Comparator tolerance function ( Tolerance of phase comparators )
- The tolerance limit is reached when the phase difference between and X-Y (again on the right part of the Figure above) exceeds an error :
- using the relation (see the relevant subsection on the jitter transfer function of this example)
- then
The relevant diagram of the jitter tolerance function is shown in the Figure here below.
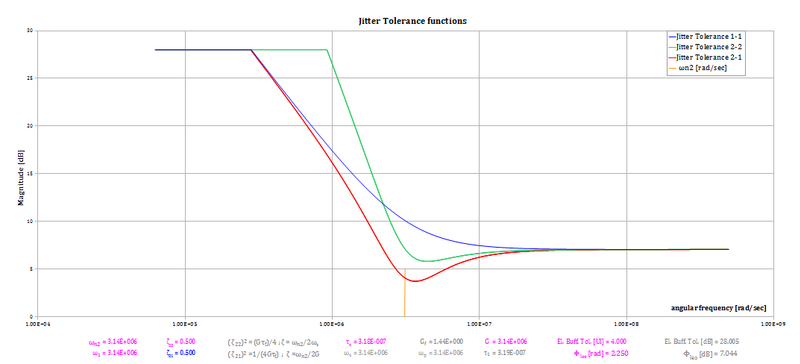
For each the lateral eye opening is the same, as is the same the length of the elastic buffer (=phase adder).
The two important 2nd order PLLs are plotted as well, in the under-damped but significant condition of ζ = 0.5.
The natural frequency is 500 KHz (ωn= 3.14 e6 rad/sec) and is the same for each of the three loops (yellow marker).
The figure above contrasts the case of the 1 - 1 loop (in blue) with the case of the other two important loops (2-1 and 2-2) only to better understand the former. The other two loops in fact are not used for phase-aligners, as explained in the following subsections.
As stated above, the unit step response and the jitter transfer function of this CDR do not differ from those of other 1st order, type 1 CDRs.
The jitter tolerance of this CDR shows a new example. It is limited at low frequencies by the jitter tolerance of the adder and, at medium and high frequencies, by the jitter tolerance of the phase comparator. In fact the actual design choices always assure that
In conclusion, this example shows a CDR that:
- is not able to tolerate a wander of the input signal frequency. There is no increasing jitter tolerance with a 6 dB/oct asymptote towards zero frequency, but just the flat tolerance limited by the adder range. This CDR can only phase align a signal (jittering but) synchronous with its local clock;
- can lock in quickly into a signal burst after a period of loss of signal;
- offers the inherent elastic buffer feature typical of phase aligners.
2nd order, type 1
[edit | edit source]

The first is the simplest to understand and the derivation of the model equations is easiest from it. It models a typical regenerator and is of fundamental importance for the communication engineer.
Oscillator controlled in frequency ("regenerator CDR") 2 - 1
[edit | edit source](Another example of a tracking system based on a second order, type 1 loop can be found in Wikibooks, at: Control Systems/Examples/Second Order Systems).
Some of the characteristics of the first architecture in the figure above make it ideal for the regenerator application.
= the CDR with good de-jittering characteristics.
This is the second architecture of three that must be remembered.
It is presented as the first example in the figure here above.
- The oscillator is controlled in frequency. It converts an input signal into a frequency, that is into the integral of a phase: its transfer function in the s domain is in fact V0/s.
- Between the output of the phase comparator and the input of the oscillator, a single pole low pass circuit filters the higher frequencies of the error signal. (Combined with the oscillator, this low pass in the forward path makes the loop a second order, unity feedback, system).
- The presence of an independent block to perform the low pass with a precise cut-off frequency (represented by in the figure above) gives the designer one more degree of freedom to find the best performance compromise.
The figures that follow, as in the previous examples, plot the unit step response, the jitter transfer function and the jitter tolerance function of this architecture.
In order to appreciate some of the peculiarities of this new example (that is further developed in in a dedicated page further down in this book), also the corresponding curves for the fist order ( 1 - 1 ) slave have been plotted as well.



- Unit step response
The increased complexity of this architecture versus the first order one is responsible for the delayed reaction to an input phase step.
In fact this architecture is inferior to the first order alternative (no matter how smartly the design parameters are adjusted) when the lock-in phase of the system is of prime importance.
- Jitter transfer function
The ability to filter out the high frequency components of the incoming jitter is the strong point of this architecture.
When a series of regenerations takes place along a chain of telecom links, the jitter accumulation must be avoided, and the low pass action must have a (relatively) abrupt cut off.
This second order type 1 model (see the relevant figure) has a jitter transfer with a 40 dB/decade roll-off, while the first order type 1 model only offers a 20 dB/decade performance.
- Jitter tolerance function
The advantages offered for the jitter filtering are partially offset by some weakness in presence of strong jitter components concentrated around the corner frequency of the PLL (fortunately not very likely in practice).
While the first order loop presents a tolerance larger than 1 Unit Interval at all frequencies, this second order loop always has a frequency range where its tolerance is lower than 1 UI.
This dip of the tolerance is more evident for lower values of the damping ratio ζ, and the above figure uses the two curves to give evidence of that.
The importance of this architecture is such that an entire chapter is devoted to it further down in the book, where all time and frequency functions of the previous diagrams are described in detail and further developed.
At this stage it is sufficient to have understood in which ways this architecture is different from the other architectures presented in this series of examples.
A modified representation of the same architecture
[edit | edit source]The second example in the figure above is essentially the same architecture as the first.
It helps introduce the concept that the equations and the behavior of a VCO can be separated into an integrator and a phase controlled element, that is typical of phase aligners.
Linear modeling is the same as the case above, while tolerance -obviously- depends on the linear range of the new blocks.
It is not an important example for practical applications.
Addition of the complementary delay ("2nd order type 1 phase aligner")
[edit | edit source]This architecture, the third in the figure of the 2 - 1 loops above, is another interesting example for didactic purposes, but has no value for a real CDR application.
The fundamental blocks are very similar to those of the previous example.
- The last integrator block (an up/down counter in a digital implementation) corresponds to the oscillator controlled in frequency. It converts an input signal into a frequency, that is into the integral of a phase: its transfer function in the s domain is in fact Gf/s. (As there is no other 1/s factor in the open loop transfer function, this is a type 1 system).
- Between the output of the phase comparator and the input of the oscillator, a single pole low pass filters the higher frequencies of the error signal. (Combined with the oscillator, this low pass in the forward path makes the loop a second order, unity feedback, system).
The functions that belong to the linear model (like the USR and the jitter transfer function) are exactly the same as in previous example of the slave 2 - 1 just above.
- Jitter transfer function
For instance, the jitter transfer function can be derived with the same steps used for the first order phase aligner:
and it coincides with the jitter transfer function of the 2 - 1 slave of the previous example.
The ability to filter out the high frequency components of the incoming jitter is the strong point of the 2 - 1 architectures.
This type of performance is valuable as long as the CDR is a regenerator and sends the regenerated clock with the data stream to another CDR downstream. In this example of a phase aligner however, this performance is not useful at all, because the phase aligner uses the PLL output only for its internal operation, and does not use it for its output data stream.
- Unit Step Response
The USR and its time diagram figure are identical to the ones of the previous 2 - 1 example.
- Jitter tolerance function
The jitter tolerance function of this architecture is different because it does not depend on the non-linearity of the phase comparator only, but also on the non linearity of the phase adder.
Whenever non-linearities are considered for architectures of the same order and type, a linear model -that is in fact the same for all architectures of the same order and type- cannot be used. The functions that describe the operation of these architectures (like jitter tolerance, ..) are different if different non-linearities are considered.
Following the approach of the first order phase aligner, the tolerance due to the adder must be combined with the tolerance due to the phase comparator.
The circuit tolerance, at any frequency, is the lower of the two.
- Tolerance of the phase adder ( Tolerance of phase adders )
- The adder is normally made by a delay line, that adds a delay to the input signal (X(s) in the figure above ) equal to the signal present on the control input (- Y(s) in the figure above ).
-
- - Defining as D (measured in radian - if D is in seconds, then use D ω) the total phase delay that the delay line can add, and
- - defining as zero the phase delay added when the control signal is set at the mid point of its control range,
- then the tolerance of the adder inserted in the PLL circuit is:
- using the relation found for the jitter transfer function of this example)
- then

For each the lateral eye opening is the same, as is the same the length of the elastic buffer (=phase adder).
The two important 2nd order PLLs are plotted as well, in the under-damped but significant condition of ζ = 0.5.
The natural frequency is 500 KHz (ωn= 3.14 e6 rad/sec) and is the same for each of the three loops (yellow marker).
- Tolerance of the phase comparator ( Tolerance of phase comparators )
- The tolerance limit is reached when the phase difference between and x-y (again on the Figure above) exceeds an error :
- using the relation (see the relevant subsection on the jitter transfer function of this example):
- then:
It is easy to see that the tolerance is equal (for > 0.707) to the tolerance of the first order phase aligner, or inferior for lower values of .
The inherent weakness of this type of architecture (undershoot below 1 U.I. of the tolerance at frequencies around n ) remains, and it can not be offset by the corresponding jitter transfer advantages that are meaningless for a phase aligner system.
As a result this architecture is inferior to the first order alternative (no matter how smartly the design parameters are adjusted) during the lock-in phase for a phase aligner application.
(On the other hand, it has the disadvantage of limited tolerance at low jitter frequencies, when compared to the classic 2nd order circuit for slave CDR applications, as it will be shown in the following paragraphs.)
In conclusion, the importance of this architecture is limited to its use as example for didactic purposes. Its first order alternative, simpler and more efficient, is preferred in practice for phase aligners.
2nd order type 2
[edit | edit source]If a 2nd order CDR PLL incorporates a single zero low-pass filter (instead of a single pole low-pass as in the examples above of the 2 – 1 PLL), then
the pole at frequency zero (that is implicit in the filter) makes the PLL change from type 1 to type 2.

The first is the simplest and the derivation of the model equations is easiest from it. It models a typical PLL for a slave CDR and is of fundamental importance for the communication engineer.
.
The first example, in the figure of 2 - 2 PLLs just above, is the important one.
The other two are good exercises, but are not important for practical applications.
The model is described in detail in a page dedicated to the 2nd order, type 2 architectures later on in this book, owing to the practical importance of this first case (see figure above).
Oscillator controlled in frequency ("monolithic slave CDR") 2 - 2
[edit | edit source]The first of the three examples in the figure above is the third common PLL architecture for a (slave) CDR.
Important non-linearities are inevitably associated with a monolythic implementation, and
the characteristic of robustness against them the have made this architecture the preferred choice for monolythic slave CDRs.
= the CDR with good rejection of generated noise.
This is the third architecture of three that must be remembered.
It is presented as the first example in the figure here above.
In the linear model it can be remarked that the loop filter provides a very high gain at very low frequencies.
This corrects any steady state error (squeezes the steady state error to zero) that may otherwise result from a difference between the frequency of the input signal and the free-running frequency of the local oscillator.
This also strongly attenuates the low frequency noise generated inside the PLL itself.
The loop filter does not attenuate the high frequencies, though. This makes this 2 - 2 loop less efficient (than the 2 - 1 loop) in rejecting the high frequency input noise (i.e. the part of the input jitter spectrum that does not carry any useful information about the sending clock and its phase). On the other hand, this makes this loop inherently faster in acquisition than the 2 - 1 loop.
This loop always overshoots in the lock-in phase, as the unit step response shows (see figure below).
The jitter transfer function
[edit | edit source]The transfer function can be derived, like for all other CDR PLLs that are unity feedback loops, using the two equations:
- E(s) = X(s) - Y(s)
- Y(s) = E(s) (gain of the loop forward chain)
and eliminating E(s) by substitution. In this case the result is:
and the relation between the circuit parameters and the loop parameters ωn2 and ζ with respect to G and τz can be obtained from:
Its magnitude is:

Filter cut-off frequencies, damping ratios and natural undamped frequencies are chosen for a meaningful comparison.
The unit step response
[edit | edit source]The unit step response can be obtained from the (jitter) transfer function multiplying the closed loop trasfer function by 1/s , and reverse transforming the result:

The output phase catches up quickly and overtakes the input (even if ζ ≥ 1), and then settles in good tracking with residual damped oscillations.
The jitter tolerance
[edit | edit source]
Filter cut-off frequencies, damping ratios and natural undamped frequencies are chosen for a meaningful comparison.
The asintote towards low frequencies (in the log-log plot) has a slope of 40 dB/ decade (as opposite to the slope of 20 dB/ decade of the type 1 systems).
This is typical of all type 2 systems, that are more tolerant ( 20 dB/ decade more) of low frequency jitter than type 1 systems.
In the 2 - 2 loop, bandwidth and damping ratio increase when the gain increases
[edit | edit source]ζ222 = G τz / 4
This is important for a monolithic implementation with a bang-bang phase detector (and sometimes also a bang-bang VCO) because the gain of those non-linear elements is very high when their input signal deviates very little from its center point.
Instability may occur at high gain conditions if the damping ratio decreased with increasing gain (like in a 2-1 loop), but luckily a 2-2 loop becomes more damped at high loop gain. Its bandwidth widens at the same time, and this is associated with more rejection of internally generated noise but also with less rejection of incoming line noise.
A modified representation of the same architecture
[edit | edit source]The second example in the figure above is essentially the same architecture as the first.
It helps introduce the concept that the equations and the behavior of a VCO can be separated into an integrator and a phase controlled element, that is typical of phase aligners.
Linear modeling is the same as the case above, while tolerance -obviously- depends on the linear range of the new blocks.
It is not an important example for practical applications.
The example of the 2 -2 phase aligner
[edit | edit source]The figure presented earlier in this page for the case of the 2 -1 phase aligner shows also the magnitude of the jitter tolerance for this example (Jitter transfer and unit step response remain in this case the same as for the 2 - 2 slave, because they do not depend on circuit non-linearities).

For each the lateral eye opening is the same, as is the same the length of the elastic buffer (=phase adder).
The two important 2nd order PLLs are plotted as well, in the under-damped but significant condition of ζ = 0.5.
The natural frequency is 500 KHz (ωn= 3.14 e6 rad/sec) and is the same for each of the three loops (yellow marker).
In this figure, the green curve represents the jitter tolerance function for the 2 - 2 phase aligner.
Note that the jitter tolerance function is the same as the one derived for the 2 - 2 slave until the half depth of the delay line becomes a horizontal limit at low jitter frequencies.
This 2 -2 phase aligner has no practical use, for reasons similar to the ones that make also the 2 -1 phase aligner a non preferred option. The 1 - 1 phase aligner is the preferred choice.
The 2 -2 phase aligner has a slightly better tolerance in a small region of frequencies, but this is a negligible advantage in practice and is offset by its risky behavior close to the natural undamped frequency. The loop ability to reduce strongly the low frequency noise of the local oscillator and its ability to reduce to zero the steady state frequency error make no sense for a phase aligner.
The three structures that cover all the actual CDRs
[edit | edit source]Many problems can be solved better, or quicker –if not avoided altogether-, if the engineer is familiar with, and uses three simple mathematical models, because the fundamental behavior of every CDR can be referred to one of them:
- The phase aligner (modeled by a 1 - 1 structure)
- The regenerator (modeled by a 2 - 1 structure)
- The robust, tolerant monolithic implementation with bang-bang detector and ring VCO (modeled by a 2 - 2 structure).
These three structures (1-1, 2-1, 2-2) out of two architectures (1st order and 2nd order) are the ones used in practice.
| Loop order and type | Parameter | Important relations | ||
|---|---|---|---|---|
| 1 - 1 | ωn1 | ωn1 = G = 1/τ | ||
| 2 - 1 | ωn21 , ζ21 | ωn21 = 2 ζ21 ωn1 ωn21 = ωf /2ζ21 |
G = ωn21 / 2ζ21 τf = 1 / 2ζ21ωn21 |
ζ212 =1 / ( 4 G τf) ωn212 = G / τf |
| 2 - 2 | ωn22 , ζ22 | ωn22 = ωn1 / 2 ζ22 ωn22 = 2 ζ22 ωz |
G = 2 ζ22 ωn22 τz = 2ζ22 / ωn22 |
ζ222 = G τz / 4 ωn222 = G / τz |
- For the 2nd order loops, ωn1 can be expressed as a function of the other two parameters. For the 2-1 and 2-2 loops :
- If the filtering caracteristics ( τf or τz ) are kept fixed, and just the open loop gain is varied, then the behaviour of the two 2nd order loops is different, almost "opposite":
- 2-1 ωn212 = G / τf and ζ212 =1 / ( 4 G τf)
- the 2-1 gets less damped with more gain, i.e. more damped with less gain.
- 2-2 ωn222 = G / τz and ζ222 = G τz / 4
- the 2-2 gets more damped with more gain, i.e.less damped with less gain !
- 2-1 ωn212 = G / τf and ζ212 =1 / ( 4 G τf)
- This opposite behavior of ζ21 and of ζ22 with respect to the loop gain G explains why
- 2-1 is not used with bang-bang phase detectors nor VCOs, while
- 2-2 (not preferred with phase comparator and VCO of linear type) becomes the preferred choice with bang-bang phase detectors (and VCOs).
- The interesting characteristics of the 2-1 (rejection of the signal jitter, that make it preferred for regenerator applications) depends on a good control of the damping ratio, ζ21 . ζ21, in turn, depends on the loop gain G and decreases when G increases (risk of jitter peaking!): ζ212 =1 / ( 4 G τf).
- The gain of the non linear blocks (bang bang detector and bang-bang VCO) is not constant, but varies with the signal amplitude. In particular, the bang-bang gain is maximum when the signal at the input of the blocks is very close to its center value. The gain is minimum instead when the signal deviates most from its center value.
As a result, the three fundamental structures find their best fit as follows:
- 1.1
- linear or non-linear blocks; Preferred when the acquisition time shall be minimum (burst-mode transmission), and even more so when Es is zero by definition (= for phase aligners). Furthermore, it is a good choice in many cases when there are no specific requirements that suggest a 2nd order loop.
- 2
- 2.1 (filter with flat gain at low freq.): preferred for regenerator applications when linear blocks are used.
- 2.2 (filter with very high gain at low freq.): preferred for applications where non-linear (= widely variable gain) blocks are used and in particular for high performance monolithic implementations.
External References
[edit | edit source]- ↑ A robust phase detector for 1.25 Gbit/s burst mode data recovery (from the INTEC team of Ghent University) IEICE Electronic Express, Vol. 1, No. 18, 562-567 http://www.jstage.jst.go.jp/article/elex/1/18/1_562/_article






































