Clock and Data Recovery/Structures and types of CDRs/Applications of the 2nd order type 1 architecture
- This architecture ( of the two 2nd order architectures, type 1 and type 2 ) was hystorically used first, because it can be implemented with simpler circuitry:
- the filter can be a passive circuit without amplification;
- the VCO can be obtained from a quartz oscillator just making the (discrete) parallel capacitance variable.
- This architecture ( of the two 2nd order architectures, type 1 and type 2 ) was hystorically used first, because it can be implemented with simpler circuitry:
- It was in fact the only second order architecture considered in the early technical literature on PLLs (e.g.[1]).
- As more complex circuitry became available at ever decreasing costs, the 2-1 was gradually replaced in many applications by the more versatile 2-2, and nowadays remains only where its peculiar characteristics are really useful.
This architecture uses the option of a single pole filter (lowpass) in the stage between phase comparator and VCO.

- The zero is at angular frequency ωf = 1/τf ; ωw = 1/τw is the frequency where the gain is equal to 1 (i.e. to 0 dB) ; τf = Gf τw .
- The amplification is flat (Gf) up to ωf and then decreases at higher frequencies.
- Higher frequencies are rejected more (-20 dB / dec) and the highest input frequencies get a very high -theoretically infinite- attenuation.
- In practical applications of type 1 CDRs, Gf does not differ much from 1 and ωw ≈ ωf ; sometimes Gf is called β .
- In fact, the maximum swing of the comparator output corresponds, more or less, to the control range of the VCO frequency.
- The maximum output of the comparator, multiplied by the finite d.c. gain of the filter stage, corresponds to the maximum frequency deviation of the VCO, (but it can only be reached with a delay proportional to 1 / ωf).
The -20 dB/dec low-pass (of the frequencies above ωf in the filter stage between comparator and VCO) becomes - 40 dB/dec in closed loop performance (for frequencies higher than ωn2 = √G/τf).
If the filtering characteristics ( ) are kept fixed, and just the open loop gain is varied ( = and = ), the 2-1 gets less damped with more gain, i.e. more damped with less gain. This behaviour of with respect to the loop gain explains why 2-1 is not used with bang-bang phase detectors nor VCOs that have a highly variable gain.
The interesting characteristics of the 2-1 (sharp rejection of the input signal jitter, that make it preferred for regenerator applications) depends on a good control of the damping ratio, . The parameter , in turn, depends on the loop gain G and decreases when or increase (risk of jitter peaking and of tolerance reduction!).
The response to an input variation never ends with catching up completely (non-zero steady-state error in this type 1 loop).
- It's like driving using either the accelerator or the brake, with a certain delay both to switch between them and to increase pressure on either pedal.
It is easy to understand that this architecture does not react to fast spurious signals, and that it rejects the high frequencies of the input jitter.
Overall, this 2 - 1 loop is sub-optimal during acquisition (for which the 1 - 1 provides better performances), suffers from finite steady-state error (such error is zero with a 2-2 architecture) and is only useful when the regenerated clock must be re-used for further transmission, i.e. when the regenerated clock must be cleaned from received jitter and locally generated VCO noise (= this architecture is for regenerators only).
The implementation with linear phase comparator and linear VCO is preferred, as it is necessary to reduce noise and to de-jitterize with controlled bandwidth.
- The use of linear circuit blocks in these applications makes the linear model of the 2-1 architecture really and directly useful!
Pros + and cons -
[edit | edit source]++ This is the architecture that produces the sharpest rejection ( - 40 dB/dec ) of input high -frequency jitter that is the prime concern when a clean clock must be extracted from the input signal.
- long distance links (=large distortions) affect the line signal with ISI and noise;
- regenerators are connected in series to cover a very long distance span, so that the jitter/noise (that should, but is not, well rejected by each regenerator) might be repeatedly amplified.
+ A linear comparator (in contrast to a possible bang-bang alternative) generates very little noise.
+ A crystal based linear VCOs ( low noise and good linearity ) assures that the locally added noise is kept to the minimum.
- Use of a linear phase comparator and use of an accurate and linear VCO, are associated with somewhat higher costs and limitations of the highest fp of operation.[2]
-- This is a type 1 architecture and therefore its sampling error Es and closed loop bandwidth ωn depend on the VCO ffr accuracy.[3]
- A tight accuracy of the ffr of the VCO is incompatible with a monolithic implementation
- This architecture (a type 1) rejects the VCO noise below ωn with just -20 dB/dec. (A type 2 alternative architecture would allow -40 dB/dec below ωn).
-- This architecture, amongst the fundamental three, is the most prone to under/overshoots of the characteristics in the vicinity of ωn, which is evident in the jitter transfer, VCO noise transfer, tolerance functions. This makes it especially critical to loop gain ( proportional to DT!) variability during operation (gain peaking, tolerance undershoot,..).
The error function and the tolerance function clearly indicate that the sampling instant may over reach the optimum instant
Input jitter and output jitter in sinusoidal regime are vectors.
The 2 - 1 loop is especially prone to generate a significant difference vector ( the error signal).
Where used and how made
[edit | edit source]2nd order structures are preferred in continuous mode applications.
This type 1 architecture in particular finds application in:
- line regenerators in general,
- slave clocks in long distance (=Telecom) networks,
- Second stage PLLs in line regenerator equipment (de-jitterisers).
The cascading of several 2-1 CDRs in a long distance connection becomes possible because of the low noise generation, good input noise rejection and predictable characteristics.[4]
- Amplification of any jitter frequency should be minimal ( P, the maximum gain peaking, must be less than 0,1 dB in chain of repeaters,[5] and of 0.3 dB at most in other standards [6]).
In fact, when requirements are the following, like in a telecom networks:
- continuous transmission mode
- receiver cost may increase if an increase of the regeneration span offers a larger saving,
that translates into:
- filtering incoming phase noise is important
- the cost of circuitry with low noise generation is affordable
- fast acquisition is not important
then the preferred CDR implementation includes a phase comparator that behaves linearly, a low pass filter and a low noise oscillator whose frequency varies proportionally to the control signal. The PLL behaves very much as a 2-1 linear loop.
ωn2 and ζ21 in continuous-mode regenerator CDRs
[edit | edit source]The ITU-T Recommendations (the G.7XX series and the G.8XX series in particular, see for instance the G.825) describe a lot of the characteristics of clock regeneration recommended for applications in continuous mode.
With a little reverse engineering of the large amount of data available from that source (and making reference to the model of a PLL of the 2nd order, type 1), the preferred values that can be obtained are:
Extreme cases with ωn < 1/10,000 ωp can only be found in some long distance links on single mode optical fibre, where a high number of regenerators are located in series along the line, each one with its own CDRs. In that case the jitter accumulation is the most critical aspect. All the above conditions shall never combine in a worst case that make the jitter amplification of each regenerator exceed +0.1 dB at any frequency, corresponding to ζ equal or lower than 0.652.[7] Jitter around that particular frequency of peak amplification could be repeatedly amplified along the line and accumulate enough power to become source of error bits.
- Another ITU reference goes even further and recommends that any peaking of the transfer function gain is to be avoided in long regenerator chains, which means ζ < 0.7.,[8] which is the same as to recommend ζ never to be smaller than 0.7 .
The damping coefficient ζ must be - in all conditions - larger than 0.66 in order to keep the maximum jitter amplification (maximum value of the jitter transfer function) below 0.1 dB.
Another aspect that suggests values of ζ larger than at least 0.7, is the overshoot when tracking a sinusoidal jitter. Both the diagram of the jitter tolerance and the diagram of the jitter error show that (for ωn2 just above 1) there is an extra deterioration of the tracking performances for low values of ζ (See: 1, 2, 3, 4).
The most important consideration, that forces a substantial margin in the design value chosen for ζ in the CDR design, is however the derating due to the transition density expected in the incoming pulse stream. The transition density generally oscillates around 50%, well below its theoretical maximum of 100%.
Finally the construction tolerances when actually building the physical CDR circuit are to be considered, along with the variations that may come with aging. They can affect the parameters significantly (sometimes as much as +/- 30%, like in the case of monolithic integrated circuits).
Taking into account all these derating factors, in practice the model parameters of CDRs for continuous mode applications fall inside the following ranges:
| Parameter | DT = 100% | DT = 33% |
|---|---|---|
| G | G = Gφ Gf GVCO | 0.33 G |
| ωn | 1/50 to 1/15,000 of ωp | 1/90 to 1/26,000 of ωp |
| ζ | 1.0 to 1.3 (typ. 1.1) | 1.8 to 2.3 (typ. 1.9) |
Typical application: the de-jitterizer
[edit | edit source]Large scale view
[edit | edit source]The interconnection of geographically distant nodes may exceed the distance that the optical signal can travel along a (single mode) fiber without irreversible deterioration.
The fiber link connecting the two geographically distant nodes is segmented into spans. The maximum span length is the length of fiber that can be regenerated with a BER that be low enough.
- Low enough means that the deterioration can be corrected and/or tolerated (e.g. by bit rate redundancy and error correction codes at OSI layer 0, retransmission of error-ed blocks at higher layers, ...).
The interconnection of the fiber "spans" is made using 3R regenerator equipment, placed at intervals of hundreds of kilometres, that Re-amplify, Re-shape and Re-time the pulses of the (continuous mode) signal in both directions.[11]
The jitter entering the chain of identical line regenerator equipment is transfer-ed to the end of the chain with a cumulated transfer function, that corresponds (if dB magnitudes are used) to the sum of the individual transfer functions.
The chain tolerates the input jitter according to a tolerance curve almost equal to the one of a single regenerator. (A more accurate simulation would account also for the jitter generated at each link of the chain,[12] but would not produce drastically different conclusions.)
The retiming task is shared by two CDRs
[edit | edit source]The Re-timing ( in each direction, inside a regenerator equipment ) is performed by a cascade of two different CDRs,[13] where the first recovers the Data and the second de-jitterizes[14] the Clock recovered by the first[15]
- A de-jitterizer removes a.c. jitter down to relatively low frequencies. It makes use of an internal elastic buffer.[16] De-jitterizing is essential to avoid accumulation of jitter in long chains of regenerators.
- It is normally requested that the regenerator equipment "dejitterizes" all jitter above fC ≥ fp / 10000 [17]
- Tolerance cut-off frequency fC
- The tolerance curve of typical CDR (in a Bode plot) is approximately described by a couple of asymptotes, that have a point in common at the "cut-off" frequency:
- a horizontal asymptote, at a level not larger than ΦLEO, that approximates the tolerance curve above the cut-off frequency;
- a negative sloping asymptote parallel to , that approximates the tolerance curve for frequencies lower than the cut-off frequency.
- The magnitude of the jitter that can be tolerated, below the cut-off frequency of the tolerance curve, grows as the frequency decreases.
- The cut-off frequency can be defined as the frequency below which the slope starts.
- The cut-off frequency of the tolerance curve can also be defined as the crossing point of the two asymptotes in a Bode plot: the one sloping down with (-20 dB/dec) and the horizontal one at about ΦLEO.
- In a regenerator (CDR or "equipment"), the frequency range of interest (jitter transfer) around its cut-off frequency is about +/- 2 decades [18]
The first CDR exhibits a good (=large) jitter tolerance and recovers the clock -inevitably- with correspondingly large jitter transfer bandwidth and residual jitter.[19]
The second CDR uses the clock regenerated by the first as its input data stream. It is slave to the clock of the first, but it leaves unchanged the actual data bits that the first CDR has recovered. It is designed for a tighter transfer bandwidth and for a larger high-frequency tolerance.
- It just de-jitterizes the clock recovered by the first CDR, and is in actuality a simple CR (= Clock Recovery) circuit, because it only acts on the clock output of the first CDR, but does not act on the information bits themselves (= the Data).
The characteristic frequencies (transfer and tolerance low-pass corner) and the high frequency tolerances are different in the two CDRs. The cascade tolerates the amount of sinusoidal jitter that is tolerated by the first and then by the second CDR (the tolerance region of the cascade is the AND of the two regions of the individual CDRs).

but has also a lower tolerance at low frequencies.
The jitter bandwidth of a de-jitterizer can be reduced, if Tol2 can be increased. To do do, the higher Tol2 shall be traded off with a lower ωn2 frequency.
The elastic buffer in between
[edit | edit source]An elastic buffer for the data stream is an essential part of the node, because each data bit must be delayed (inside the buffer) for a variable time (that is not known until the moment of its arrival).
- The delay that the buffer shall add may reach in some instants a maximum positive amount equal to the negative peak of the jitter to eliminate.
- Conversely, the buffer average delay shall be not smaller than the maximum positive peak of jitter. When the positive peak of jitter takes place, the buffer compensates reducing its delay from the average, down to the minimum.
- When the jitter produces a maximum positive delay, the buffer adds only its minimum delay.
- When the jitter is equal to zero, the buffer inserts its mid-point (=average) delay.
- When the jitter produces a peak of anticipation of the data transitions, the buffer inserts its maximum delay.
Clock speed for the elastic buffer, full or divided
[edit | edit source]- The total range of a typical phase comparator is equal to the line pulse period T, i.e. ‡ T/2, i.e. ‡ 1/2 U.I. In radian, that is ± π .
- Tol1 is typically required to be larger than 0.15 to 0.18 U.I. ( 0.3 π to 0.36 π) and Tol2 larger than (at least) 1.5 U.I. .[20]
- Tol1 is perfectly compatible with a normal implementation for CDR1. Tol2 instead is too small for a normal phase comparator.
- The larger tolerance in the second CDR (Tol2 in the above figure) is obtained widening the range of its phase comparator:
- CDR2 tolerance at low frequencies ( = below its cut-off frequency ) is inferior to that of CDR1, but is in general more than adequate;
- CDR2 tolerance at high frequencies ( = above its cut-off frequency ) is not affected by the LEO tolerance of CDR1, because CDR2 samples pulses that have already been regenerated ;
- the range of CDR2 phase comparator is the limit to high frequency jitter tolerance in CDR2; it can be widened either:
- using a normal comparator (± 0.5 U.I.) with the added information of the pointer, in accordance to:
- using divided frequencies at its inputs.
- The characteristic cut-off frequency of CDR2 is lower than that of CDR1, and sets the overall regenerator bandwidth.
Full = line speed
[edit | edit source]Probably the most straightforward (but not the most efficient) implementation of PLL2 is made using the minimum amount of buffer memory and both CDRs operating at full (=line) speed.
The following figure shows how such a dejitterizer can be implemented.
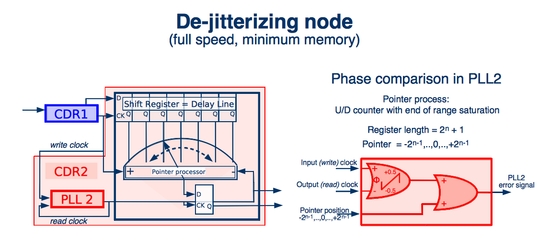
The second CDR compares two clock signals, not data and clock.
Theoretical architecture that uses a minimum amount of buffer memory and both CDRs operating at line speed.
- The phase comparator of PLL2 tracks large jitter variation without slips using the additional (digital) info present in the pointer position.
- The pointer steps in either direction (digital, weighted 2π radian each) are worth as much as the full swing of the (analog) phase comparator (total swing of +/- π radian).
- The phase error is computed using both the output of the phase comparator of CDR2 and the status of the buffer pointer, as:
- As the pointer unit weighs as much as the whole swing of the comparator, the overall gain remains identical to the gain of the comparator stand alone; the overall range instead is widened and replicates the buffer length.
With the phase error incorporating the information provided by the buffer pointer, the negative feedback of the PLL tends to position the buffer pointer to the centre cell and the local clock to half a clock cycle after the writing in it of each bit of the received bit stream (but for the steady state sampling error, spending on the loop architecture), very much like the classic CDR points to the eye middle point.
This approach requires that the circuitry of PLL2 operates at line speed. If the line speed challenges the switching speed of the components of PLL2, another approach is necessary.
Reduced = line_speed / N
[edit | edit source]It may be possible to have CDR2 operate at a reduced speed, taking advantage of two possible conditions:
- the de-jitterizing nodes often elaborate the received data stream by octets or by bytes, and therefore a SERDES is present anyway (a deserialiser at the beginning of the reception chain, and a serialiser just before re-transmission; the serialiser implies a frequency multiplication, but the synthesis of the multiplied clock can be implemented with a jitter generation so small that it does not deteriorate the dejitterizer performances) ;
- the bandwidth of the required de-jitterization is so tight (e.g. fp/10,000) that a reduced frequency of the local clock in PLL2 (typically fp/16) can still be much higher than fp and not interfere with the performances required.
- Mention of the SERDES need in regenerator equipment and suggestion of a :16 ratio can be found in .[22]
The following figure sketches a typical application.

The SERDES halves (Deserialiser and Serialiser) are used also to reduce the speed of some critical circuits of CDR2.
- The two CDRs generate each a clock at line speed (CK1 and CK2) and a clock at the Nth submultiple of the line speed (N = 2n).
- The phase comparator of CDR2 compares the two clocks at the reduced speed (1/N).
- The range of the comparator is therefore N times wider than the range of a comparator fed by two clocks at line speed. The divide ratio N shall be made -obviously- exactly equal to the length of the elastic buffer.
- The range of the comparator of CDR2 is ± π N / 2, i.e. ± ( N / 2 ) U.I., the length of the buffer is N U.I. .
- CK1 (as well as CK1/ N ) may jitter almost up to +/- (SERDES / 2) and CK2/ N would still be able and eliminate such jitter.
- The only circuits that necessarily operate at line speed are:
- CDR1,
- the two shift registers DESER and SER.
- CDR2 uses a reduced speed phase comparator, but may use a VCO at line speed, to generate CK1 and, by division, CK1/ N.
- Alternatively, the VCO of CDR2 could operate at reduced speed and CK1 could be synthesized from it. This second approach is preferred, as it is compatible, even at very high line speeds, with a CDR2 of 2nd order and type 1.
Again, the negative feedback of the PLL tends to position the sampling edge of CK2/N (N+1)/2 U.I after the corresponding edge of CK1/N , very much like the classic CDR points to the eye middle point.
The divider from CK1 to CK1/N inside CDR1 can be synchonized to the byte frame, thereby simplifying the parallel operation inside the equipment that takes advantage of the byte structure of the received data stream.
Architectures of the two CDRs
[edit | edit source]The architecture of either of the two CDRs is not explicitly required by the Standards.[23]
The architecture of each of the two CDRs is a matter of design choice, provided the first is wide-band and the second is narrowband.
The architecture of the first CDR (the "jittery" CDR) can be a 2nd order type 2 with PFD, described in the following two pages (1,2).
The following de-jitterization can be efficiently done by a 2nd order type 1 CDR.
As this application takes advantage of the peculiarities of both architectures, it emphasises the practical application of the 2 -1 CDR also by contrast with the 2 -2 CDR that comes first in the cascade.
CDR1
[edit | edit source]CDR1 preferred architecture is a 2 - 2 with bang-bang PFD.
The jitter bandwidth offered by this CDR (non-linear) is not only is much wider than required for the whole regenerator equipment, but also variable. It varies with input jitter amplitude, DT, and differs sample to sample because it depends from manufacturing dispersion of physical characteristics.
Jitter gain peaking might be present but to a very limited extent (the 2-2 linear model indicates that a 2-2 structure always gives some, but it becomes a very small one when a bang-bang detector is used, because the detector gain is very high in these applicative conditions), and it is certainly relegated at frequencies higher than the cut-off required of the second CDR.
The jitter that is passed to the second CDR is not significantly affected by the gain peaking. The additional noise generated is at frequencies that are going to be rejected; the ISI noise is also out of band because it essentially comes from sequences shorter than 1000 pulses.
CDR2, the best application for a 2 - 1 architecture
[edit | edit source]The tighter jitter bandwidth required of CDR2 suggests for it a 2 - 1 architecture operating within its linear range:
- the jitter cut-off is sharper (-40 dB/dec instead of -20 dB/dec)
- the value of the cut-off frequency is independent from the jitter amplitude (because the loop operates within its linear range) and therefore more accurate and stable.
- the DT is not a factor for the bandwidth of this second CDR, because CDR2 uses the clock recovered by the first CDR as input signal. ( The DT of a clock signal is 100% ).
- With Bandwidth ratios CDR1/CDR2 of 103 to 104, it is enough that the run-length be < 103 and that there are enough phase corrections in CDR1 to make CDR2 operate like if its DT was = 100%!. For instance, the maximum run-length that can be expected in SDH systems is 72 CID (Consecutive Identical Digits).[24] or something equivalent to not much more than 72 CID [25]
The regenerator equipment is a professional one, and the additional cost of an accurate VCO (needed as this second CDR is a 2 -1 ) is therefore affordable.
The 2 - 1 architecture at the same time is especially critical with respect to:
- undershoots of the tolerance function (the undershoot is very deep if ζ21 is low, but is always present, whatever the value of ζ21 );
- the cut-off frequency of the tolerance function is lower than the characteristic frequency (the sloping asymptote drifts to the left for large values of ζ21).
 Jitter tolerance function for a 2nd order type 1 PLL, for various values of the damping coefficient.
Jitter tolerance function for a 2nd order type 1 PLL, for various values of the damping coefficient.
For two values of the coefficient also the low frequency asymptotes are shown.
- The asymptote drifts indefinitely to the left (to the right) if increases (decreases) indefinitely.
The following figure illustrates the effects of these two aspects in the overall dejitterizer characteristic:

If the tolerance of this second CDR is approximated by an asymptotic model,
it is prudent to use ωcut-off instead of ωn to define the two asymptotes.
The actual tolerance curve of CDR2 (thick solid red) differs from the idealised shape (thick dotted red) because of:
- the undershoot below ΦLEO, present at frequencies just above ωn2, that makes the horizontal border line shift downwards (vertical dotted blue arrow) ;
- the shift of the asymptote form its nominal position (horizontal dotted blue arrow) .
- The reduction of the tolerance margin in the critical frequency band is kept to a minimum using values of ζ not smaller than 2.
The CDR2, very much as any other CDR that jitters but stays locked, keeps its local clock jittering around the mid point of the interval covered by its comparator.
As the phase comparator is made as wide as the elastic buffer, in steady state this brings the pointer to the centre cell of the shift register(with a non-zero residual steady-state error, as this is a type 1 loop [26]).
Notes and External References
[edit | edit source]- ↑ Floyd M. Gardner (1966). "Phaselock Techniques". John Wiley & Sons Canada, Limited.
{{cite web}}: Text "ISBN 10: 0471291560" ignored (help); Text "ISBN 13: 9780471291565" ignored (help)) - ↑ Richard C. Walker (2003). "Designing Bang-Bang PLLs for Clock and Data Recovery in Serial Data Transmission Systems" (PDF). pp. 2, a chapter appearing in "Phase-Locking in High-Performance Systems - From Devices to Architectures", edited by Behzad Razavi, IEEE Press, 2003, ISBN 0-471-44727-7.I. INTRODUCTION
- ↑ It has been shown that:
- the VCO frequency accuracy ( ωp – ωfr) /ωp ) and
- the largest tolerable steady-state sampling error ( Es )
(for 1st order systems: ) - ↑ ITU-T Series G Supplement 36: Jitter and wander accumulation in digital networks
- ↑ ITU-T G8251 09/2010 The control of jitter and wander within the optical transport network (OTN), Annex A7: Jitter transfer
- ↑ http://uk.tek.com/document/primer/clock-recovery-primer-part-2 ; Clock Recovery Primer, Part 2, Figure.21 Clock recovery in standards. and 10. Survey of Clock Recovery Used in Selected Standards.
- ↑ ITU-T Rec.G.783 (03/2006), in particular Table 15-2 / G.783 - Jitter transfer parameters and 15.1.3 Jitter and wander transfer
- ↑ ITU-T-REC-G.824 Fascicle III.5 Supplement 36 Page 285- Jitter and wander accumulation in digital networks, ... no peaking in the regenerator jitter/wander transfer characteristic, ...
- ↑ The maximum run-length that must be tolerated in SDH systems is 72 CID (Consecutive Identical Digits): G.783-2006 03 Characteristics of synchronous digital hierarchy (SDH) equipment functional blocks; Appendix V Verification of SDH equipment CID immunity, page 275; 72 bits …
- ↑ G.957-200603 Optical interfaces for equipments and systems relating to the synchronous digital hierarchy; Appendix II, Implementation of the Consecutive Identical Digit (CID) immunity measurement
- ↑ Rec. ITU-T G.8251 (09/2010) The control of jitter and wander within the optical transport network (OTN) : Appendix IV 3R regenerator jitter accumulation analyses ; IV.3 Model 2 ; IV.3.1 Introduction , page 55: ... A maximum number of 50 regenerators between mapping and subsequent demapping in an OTN island is assumed. A conservative approach in WDM systems using optical amplifiers and dispersion-compensating measures leads to a span of more than 300 km between two regeneration operations (total length of 15'000 km). ...
- ↑ ITU-T Rec.G.8251 (09/2010) The control of jitter and wander within the optical transport network (OTN), Appendix III Hypothetical reference model (HRM) for 3R regenerator jitter accumulation and Appendix IV 3R regenerator jitter accumulation analyses
- ↑ G.8251 (2010 09) The control of jitter and wander within the optical transport network (OTN); A.7.2 Jitter transfer for ODCr: ... Normally, at least part of the 3R regeneration function must occur in the OCh/OTUk_A_Sk function (i.e. in the receiver front-end) because a clock must be recovered. However, the jitter transfer and jitter tolerance requirements imply the presence of a second, narrower bandwidth phase-locked loop;..
- ↑ Jitter is defined as: The (jittering) phase (or time) difference between corresponding transitions of two signals
Jitter transfer function: the ratio of the output jitter to the input jitter (= the closed loop transfer function).
In the frequency domain, the independent variable ω is the angular frequency of the sinusoidal jitter of the timing transitions. - ↑ G.8251-201009 The control of jitter and wander within the optical transport network (OTN); A.7 Jitter transfer; A.7.2 Jitter transfer for ODCr (ODU = Optical channel Data Unit; ODC = ODUk Clock; ODCr = ODUk Clock of type "r", for regenerator equipment of the optical link). The jitter transfer requirements for ODCr are, essentially, the transfer requirements for a 3R regenerator. While the 3R regenerator encompasses all the atomic functions between the input and output interfaces, and includes the wideband clock recovery circuit in the input stage of clock recovery, the ODCr ... bandwidth is, in practice, significantly narrower than any of the other bandwidths present in the regenerator and therefore determines the transfer characteristics. Because the ODCr bandwidth is much larger than 10 Hz (i.e., the upper limit of the wander region), the regenerators transfer wander without attenuation; there are no explicit wander transfer requirements. The jitter transfer function of a 3R regenerator is defined as the ratio of the output sinusoidal jitter amplitude to input sinusoidal jitter amplitude, as a function of frequency. Note that the jitter transfer is not associated with a single atomic function; rather, it is associated with all the atomic functions between and including the .. input sink and output source functions. Normally, at least part of the 3R regeneration function must occur in the input sink function because a clock must be recovered. However, the jitter transfer and jitter tolerance requirements imply the presence of a second, narrower bandwidth phase-locked loop; this phase-locked loop is in the ODCr, contained in the output source and input sink atomic functions. The jitter transfer function of a 3R regenerator shall be under the curve given in Figure A.7-1 when input sinusoidal jitter ... The jitter transfer limit is specified between frequencies of fL and fH. The jitter transfer limit is not specified for frequencies higher than fH nor lower than fL.
- ↑ G.783-2006 03 Characteristics of synchronous digital hierarchy (SDH) equipment functional blocks; Appendix VII; STM-64 regenerator jitter accumulation analyses and hypothetical reference model (HRM), VII.3 STM-64 (Type A) regenerator jitter accumulation simulation model, analyses, and results; ..(each regenerator is assumed to include a wideband clock recovery circuit, followed by a narrower band filter, and there is some data buffering for overhead processing)…
- ↑ See the values specified for fC in G.8251 (2010 09) The control of jitter and wander within the optical transport network (OTN); A.7.2 Jitter transfer for ODCr, ...he parameter fC may be considered the maximum bandwidth of the 3R regenerator, and the parameter P the maximum gain peaking of the 3R regenerator. The jitter transfer limit is specified between frequencies of fL and fH. The jitter transfer limit is not specified for frequencies higher than fH nor lower than fL. , Figure A.7-1 and Table A.7-2. The fp/ fC ratios at different line speeds are 10664, 10641, 10753, 11183.
- ↑ G.783-2006 03 Characteristics of synchronous digital hierarchy (SDH) equipment functional blocks; 15.1.3 Jitter and wander transfer, page 246; ... the jitter transfer measurement is made over the frequency range fL to fH. The lower frequency fL is set to fC/100 (where fC is the –3 dB corner frequency), and fH is defined as .. 100*fC … Jitter above fH is generally agreed to be insignificant relative to regenerator jitter accumulation, and low levels of in-spec jitter generation can easily be confused with an out-of-spec jitter transfer measurement when attempting to measure jitter transfer at high input/output attenuation levels (i.e., below –40 dB). The limits set for fL at fC/100 will always include the frequency at which maximum gain peaking occurs, and limiting jitter transfer measurements to frequencies between fL and fH will help limit testing time.
- ↑ Rec. ITU-T G.8251 (09/2010), IV.4 Jitter generation of regenerators using parallel serial conversion; pages 56..57 about the fundamental requirements of an end-point CDR
Regenerators using only one PLL, i.e., the clock recovery, may have requirements which could be contradictory. They have to perform some filtering and their bandwidth has to be large enough to fulfil the jitter tolerance requirement. The jitter tolerance requires a bandwidth which has to be above the frequency where the first 1/f slope starts. This could lead to a relatively high jitter generation exceeding the maximum allowed value. Generally speaking it is not the purpose of the clock recovery to minimize jitter. Main requirements for the clock recovery in order to optimize the bit error performance are:
• keeping the sampling time for the data retiming flipflop independent of the clock frequency at the position of the optimum eye opening (e.g., by using an integrating control loop);
• following the phase modulation of the incoming signal without deviating too much from the ideal sampling time (i.e., jitter tolerance);
• generating a low intrinsic jitter in terms of peak-to-peak values which should not exceed a small portion of the usable eye opening.
This last bullet point clearly does not contain any requirement regarding the spectral distribution of the intrinsic jitter.
Unlike the measurement of jitter using band-limiting filters, the jitter generated in the clock recovery has to be considered without any filtering because it describes the deviation of the ideal sampling time. - ↑ G.8251-2010 - 09 The control of jitter and wander within the optical transport network (OTN) - 6.1 Jitter and wander tolerance of OTN interfaces.
- ↑ where P is the pointer cell index (integer, negative for a delay shorter than half register, 0 in the centre cell, etc.) and where C is the comparator output, ranging from -1 to +1.
The error signal is proportional to the phase error at its input in the whole range ±(Pmax+1/2), that is the actual range of the resulting comparator. - ↑ Rec. ITU-T G.8251 (09/2010), IV.4 Jitter generation of regenerators using parallel serial conversion; pages 56..57
Regenerators using only one PLL, i.e., the clock recovery, may have requirements which could be contradictory. They have to perform some filtering and their bandwidth has to be large enough to fulfil the jitter tolerance requirement.
The jitter tolerance requires a bandwidth which has to be above the frequency where the first 1/f slope starts. This could lead to a relatively high jitter generation exceeding the maximum allowed value. Generally speaking it is not the purpose of the clock recovery to minimize jitter.
Main requirements for the clock recovery in order to optimize the bit error performance are:
• keeping the sampling time for the data retiming flipflop independent of the clock frequency at the position of the optimum eye opening (e.g., by using an integrating control loop);
• following the phase modulation of the incoming signal without deviating too much from the ideal sampling time (i.e., jitter tolerance);
• generating a low intrinsic jitter in terms of peak-to-peak values which should not exceed a small portion of the usable eye opening.
This last bullet point clearly does not contain any requirement regarding the spectral distribution of the intrinsic jitter.
Unlike the measurement of jitter using band-limiting filters, the jitter generated in the clock recovery has to be considered without any filtering because it describes the deviation of the ideal sampling time.
In the case of very high bit rates it could be a problem having a clock recovery which is optimized for error performance while not taking care of the output jitter.
The concept to overcome this difficulty is the use of a serial parallel conversion where the incoming signal normally is converted into bytes. This so-called deserializer often uses a structure of 16 parallel bits.
At this level, the frequency where the data processing can be done is reduced by a factor of 16. This allows the use of a phase-locked loop that performs a dejitterizer function with a reduced bandwidth. At the output of such a regenerator the only jitter is that of this PLL and the reasonably low jitter of the PLL performing the multiplexer function and multiplying the clock frequency by a factor of 16.
These concepts allow for higher values of low frequency intrinsic jitter because of the narrower bandwidth of the dejitterizer function. This function filters these phase noise components in regenerators to such a degree that the accumulation in chains, defined in the HRM of Appendix III, does not exceed the network limit. The equation modelling the VCO Power Spectral Density is a single zero first order function shown schematically in the following FIGURE Figure IV.2-2 – Schematic of VCO power spectral density (the figure is intended to be a log-log plot; the actual curve would be 3 dB above the breakpoint at frequency fb). The frequency fb is given by:fb = f0/2Qwhere f0 is the line rate (oscillator frequency) and Q is the quality factor....
- ↑ The applicable standards are derived from a model of the combined characteristics of the PLL cascade that is a linear, narrowband, 2nd order type 2. See for instance: Rec. ITU-T G.8251 (09/2010); Appendix IV 3R regenerator jitter accumulation analyses; Figure IV.2-1 – Regenerator model; Figure IV.2-1 – Regenerator model and IV.2.1 Model details at page 35 .
- ↑ G.783-2006 03 Characteristics of synchronous digital hierarchy (SDH) equipment functional blocks; Appendix V Verification of SDH equipment CID immunity, page 275; 72 bits …
- ↑ G.957-200603 Optical interfaces for equipments and systems relating to the synchronous digital hierarchy; Appendix II, Implementation of the Consecutive Identical Digit (CID) immunity measurement
- ↑ It has been shown that:
- the VCO frequency accuracy ( ωp – ωfr) /ωp ) and
- the largest tolerable steady-state sampling error ( Es )
(for 1st order systems: )











