Clock and Data Recovery/Noise is shaped by the PLL structure
What it is
[edit | edit source]In this page noise means phase noise, even when it can be traced back to voltage noise, current noise, limit cycles of a DSP, etc.
The input and output signals of a CDR have a fixed amplitude, and it is only their characteristic instants that are affected by "instabilities": whatever noise spectral density is measured (or calculated), it describes just phase noise[1] only.
Phase noise is jitter (jitter is a "jittery" time difference) that is not present in the remote clock that has been used to transmit the data stream.
Either phase noise or jitter, their representation is a one-sided spectral density (where the clock (=carrier) frequency has disappeared) and the Fourier frequency ranges from 0 to ∞; nevertheless it includes fluctuations from both the upper and the lower sidebands of the clock.[1]
It is common practice to separate the phase noise picked up by the incoming signal before it reaches the CDR (the "signal" phase noise)
from the additional phase noise that is generated by the CDR itself and that is present even when the input signal is practically noiseless (the "generated" phase noise).
- See for instance.[2]
- The "signal" noise comes from impairments (line distortions, line noise, receiver first stages, intersymbol interference, ..) suffered by the signal before it reaches the PLL input.
- The PLL filters out the (high) frequencies of the jitter, because the true timing signal spectrum is known as to differ from the local clock only by a frequency offset and some low frequency wander.
- This filtering action is modeled by the jitter transfer function.
- The "generated" noise is just the noise part that originates inside the CDR, and not the part that has been added to the signal along the preceding channel path.
The source of jitter that probably most often troubles practical circuits, is the one coming from supply noise inside the CMos circuitry of the CDR itself.
The internal supply rails inside an IC are affected by high current transients, that are generated inside output buffers, clock trees and other large CMos stages inside the IC itself, even if such blocks are not part of the CDR proper.
Those large current spikes will cause small ripple waves on the voltage supply lines.
Other CMos stages, inside the receive paths and inside the CDR proper, see –as a result of the supply ripples- their switching threshold ripple by exactly half the amount of the supply ripple.
The rise and fall edges of the waveforms inside these CMos stages are not perfectly steep, but exhibit a certain non negligible slope.
It is easy to see that a change of the CMOS threshold during the edge transition corresponds exactly to an earlier (or to a later) switching of the CMos stage: this time change, occurring almost at random at different transitions, will be nothing but a generated jitter.
It can be minimised (and should be minimised) by careful design and layout of the supply scheme inside the IC.
The other noise source that often is the origin of generated jitter inside the PLL is the VCO noise.
When it matters
[edit | edit source]Noise matters when its level is comparable with the signal level to the point that its presence affects the important characteristics of the signal.
In the CDR case, phase noise (=unwanted jitter) matters if it influences the Bit Error Rate (BER).
A good tutorial on how to measure, identify and possibly mitigate the unwanted jitter in a CDR is the Ransom Stephens Jitter Tutorial [3]
What is addressed here
[edit | edit source]Many good books and papers address the CDR noise in general and the VCO noise (the main source of generated phase noise in actual CDRs) in particular.,[4][5],.[6]
Focus here is made on the reshaping (transfer function) that a particular structure (of the three investigated in the following pages of this book: 1st order, type 1, 2nd order type 1 and 2nd order type 2) makes on the spectrum of the noise that is generated by the CDR circuitry itself.
As in previous and following pages, linear models of the three structures are used, but it will be suggested that the properties that the linear models identify are -to a good extent- present also in the non-linear variants of these structures.
Noise modeling
[edit | edit source]Noise is a "small signal" in the CDR, and can be studied with the linear models of the CDR blocks.
The "signal" noise is processed exactly as the useful signal itself. The signal noise traverses the CDR and appears in the regenerated clock after having been filtered by the jitter transfer function. In fact, the loop low-pass is chosen so as to let the just the frequencies of useful signal pass, and to stop any higher frequency. The in-band signal noise inevitably passes trough the CDR and affects the regenerated clock.
The generated noise may be injected at any node of a PLL, where only two nodes are significant: filter output and VCO output.
(The node at the comparator output behaves the same as the PLL input, with the only difference of a flat gain Gφ)
In general, using the superposition principle, reference can be made to the following figures:


The noise generated by the filter Nf is modified by the transfer equation TFNf = (TFfilter) / (1 + TFfilter*TFVCO)
The noise generated by the VCO No is modified by the transfer equation TFNo = 1/(1 + TFfilter*TFVCO)
How the PLL structure reshapes the noise spectrum of the VCO[7]
[edit | edit source]
Filter cut-off frequencies, damping ratios and natural undamped frequencies are chosen for a meaningful comparison.
The curves in the above figure can be redrawn, with different parameter values, using the same OpenOffice.org [1] Calc spreadsheet that was used to create them.
The file can be freely downloaded at:
Noise considerations in actual CDRs
[edit | edit source]Internal noise << line noise and distortions
[edit | edit source]In a real CDR it is important to consider the extreme conditions that the circuit must face while operating according to the requirements.
It may happen that such conditions are rarely or never met in the application of the majority of actual CDR, but still they are fundamental for the design of the CDRs because each of them must be able and operate correctly if deployed in the worst case conditions.
In those conditions, the majority of the phase-noise in the recovered clock is due to random modulations in the data (ISI), or due to additive noise, as is typically the case for recovery of a clock from random data.[8]
The bandwidth of the jitter transfer function of the CDR is the critical parameter in determining the phase-noise in the recovered clock.
The contribution of the noise generated in the 3 blocks that make up the CDR are of secondary importance.
- The comparator adds noise that can not be distinguished from the line noise. Luckily, the noise added by the comparator is high-frequency noise, and the PLL rejects it.
- The amplifier/filter is inherently a low frequency processor and its noise in the band of interest is generally minor.
- The VCO may add noise of its own if its noise bandwidth is larger than the high-pass corner of filtering action performed on it by the loop (see figure above).
The VCO noise above ωn passes into the local clock.
This happens in monolithic CDRs with PFD and narrowband jitter filtering.
However, as anticipated above, this contribution from the VCO is generally smaller than the noise (below ωn) coming from the transmission impairments, that the PLL cannot reject.
Jitter BW and VCO noise rejection
[edit | edit source]The passband of line jitter ≈ stopband of VCO noise.
Since the PLL always acquires the phase-lock condition automatically, the loop jitter bandwidth (and the bandwidth of the loop filter, which is closely related whenever a linear model is applicable, as well shown by the fundamental parameters of the three CDR structures) do not have to be made large to account for various detuning factors. Therefore, the loop bandwidth can be very narrow, and the phase noise present in the incoming signal outside the chosen low-pass band can be rejected.
On the other hand, the noise coming from the VCO and at frequencies higher than ωn passes without any alteration into the recovered clock. Tight jitter BWs may not stop hf noise from a low Q VCO.
The PLL as a Bandpass Filter of the jitter affecting the received clock [9]
[edit | edit source]A PLL may be considered, in some respects, as a tunable band-pass filter where the center frequency is automatically tuned to the bit-rate.
- In the frequency domain the phase comparator is a mixer that heterodynes the phase jitter of the received clock down to the baseband.
- The phase-lock of the PLL is accomplished by processing (filtering) the phase-error signal and using the filtered signal to adjust the VCO.
- When the loop is in lock, the clock signal of the VCO should be in quadrature with the squared pulses that make up the received signal. There should not be a resulting dc component: the two signals should be orthogonal, but for a steady state error that compensates the inaccuracy of the VCO.
- This baseband tuning signal frequency-modulates the VCO, and therefore the spectrum of energy of the filter output signal is converted into that of a (narrowband)[10][11]) FM signal center around the nominal clock frequency.
- The action of the phase comparator tracks the phase of the edge-detected signal and mixes the phase jitter (= timing) signal, from a band of frequencies around the clock rate, with the local clock. The jitter (resulting from both the CDR input and the internal noise sources) is shifted down to dc where it can be processed by the loop filter. The mixer has the effect of zooming-in directly on the interesting part of the edge-detected signal spectrum.

- The phase-jitter present in the timing embedded in the received signal (i.e. the phase jitter associated with the received clock) contains a useful part as well as a noisy part.
- The noisy part comes from ISI, linear and non-linear line distortions, cross-talk, thermal noise etc. . It is present from d.c. up to very high frequency (i.e. up to fp).
- The useful part (that tells the difference between the transmitted clock and the local clock) is present between the d.c. and a (relatively low) frequency corresponding to the accuracy of the local clock only (the remote transmit clock is always much more accurate, and its contribution may be neglected). Therefore the jitter bandwidth of the PLL shall be the result of a compromise between the (lower) "accuracy" bandwidth and the (wider) bandwidth needed for a fast enough acquisition transient.
- Where the two parts of jitter overlap (d.c. to loop bandwidth), it is inevitable to accept both as "useful" part.
Extremely high Q values are possible in a PLL
[edit | edit source]The recovery of the clock, once a line has come up in the signal spectrum by means of some non-linear processing (i.e. a line representing the embedded clock signal), can be accomplished by extracting just the spectral line using a SAW filter with a high Q factor.[12]
Extremely high Q values are also possible using a PLL without requiring a high-quality resonator, although in many respects, since a low-phase-noise clock requires a low-phase-noise VCO, the problem of designing a good resonator is passed from the filter designer to the VCO designer.
However, since the majority of the phase-noise in the recovered clock of a CDR is due to random modulations in the data, or due to additive noise, the bandwidth of the noise-suppression filter is the critical parameter in determining the phase-noise in the recovered clock, while the phase-noise generated by the VCO is of secondary importance.
- Therefore a somewhat noisy VCO ( = with a low-Q resonance) together with a narrowband loop filter can achieve the same practical jitter performance of a SAW filter with a high-Q resonance.
- A PLL with a lag-lead loop filter such that the closed-loop transfer function is of the second order with a damping ratio of ζ = 1/√2, and a natural frequency of fn =5 KHz, that locks into a clock tone of 10-GHz, exhibits an effective Q of approximately:
- This effective Q can be interpreted considering that the PLL averages the phase-error over several cycles; in this case it takes approximately one-million clock-cycles before the loop filter can accumulate a large enough signal on the VCO control line to begin tracking an input phase deviation.
The PLL can also be seen as a flywheel that is spinning at a rate close to the data rate.
The flywheel has a timing mark on it.
The input data signal acts like a strobe light that flashes every time that a data transition is detected, revealing the instantaneous phase-error of the timing mark.
The loop feedback is used to align the timing mark, as revealed by the strobing flashes, to the desired position.
- In other words the rising edge of the local clock, that corresponds to the timing mark, should typically lock its phase half a revolution away from the transitions, i.e. 180° out of phase with them.
- Increasing the time constant of the loop filter is analogous to increasing the mass of the flywheel. A narrowband loop acts like a very heavy flywheel that takes a lot of energy to alter its momentum.
The effective Q of a band-pass filter is determined by how many cycles a free running response can oscillate (point of view in the pass-band), in a PLL the effective Q is determined by how many clock cycles it takes for the VCO to respond to a phase error (point of view in the base-band).
Summing up
[edit | edit source]The VCO noise is the most important to consider, because the VCO produces low frequency noise and those low frequency components can not be distinguished from the useful signal components of the same frequencies.
All loop models (= all CDRs) act as high-pass for the VCO noise, i.e. they mitigate the low frequency noise from the VCO.
- When a CDR achieves phase lock, the d.c. noise from the VCO is totally eliminated.Mention steady state error!
The high-pass corner frequency coincides with their natural frequency.
All loops therefore tend to reject the low frequency noise that is generated by the VCO, but with some differences:
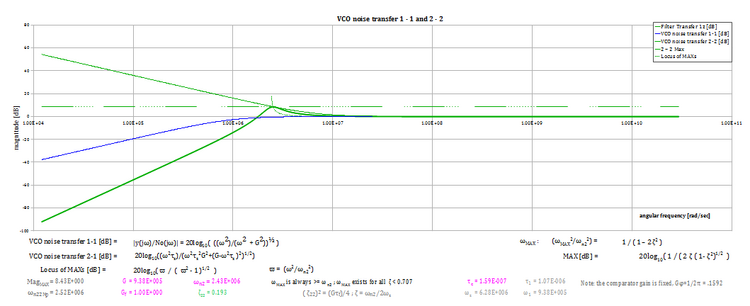
- the 1 - 1 loop attenuates the VCO noise at all frequencies below , with a single slope (20 dB/decade) and no gain overshoot. All VCO noise components at frequencies higher than appear unmodified in the PLL output.
- the 2 - 1 loop attenuates the VCO noise at all frequencies below , with a single slope (20 dB/decade) and with a gain overshoot that - whenever ζ > 0 , i.e. always - peaks at reaching a peak value that can represent a problem whenever ζ21 is lower than 0.5.
- The following figure illustrates the behavior of the 1-1 and 2-1 loops (using on purpose for the 2-1 a damping ratio that is unacceptably low) and gives the relevant formulas.

The damping ratio of the 2nd order loop has been chosen too low on purpose, to emphasize the risk of amplification of noise at certain frequencies.
- The 2-1 loop is normally used in regenerator applications (when is low): a low noise VCO must be used.
- It also needs very good control of ζ21 that must be kept close to 1.0 (this rules out the use of blocks with hard non-linearities and largely variable gain, like bang-bang phase detectors).
- the 2 - 2 loop attenuates the VCO noise at all frequencies below , with a double slope (40 dB/decade).
There can be noise amplification at certain frequencies because of the gain magnitude oveshoots 0 dB, whenever <√1/2 .
The peaking of the overshoot occurs at ω = ω22 / √1 − 2ζ², and reaches as high as 20log10(1 / (2ζ√1 − 2ζ²)).
The damping ratio of the 2nd order loop has been chosen too low on purpose, to emphasize the risk of amplification of noise at certain frequencies.
- The 2-2 loop is a good choice if a noisy VCO must be used and is certainly preferable when some loop parameters can vary in a wide range because of hard non linearities (if G can become very large in certain conditions e.g. when a bang-bang detector is used)).
This architecture is the best of the three to mitigate a noisy VCO (see the double slope of attenuation for low frequencies), but the damping ratio shall remain larger than √1/2 = 0.707, to avoid amplification of noise frequencies around ω22.
Notes and External References
[edit | edit source]- ↑ a b IEEE Std 1139-1999 IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology—Random Instabilities, http://www.umbc.edu/photonics/Menyuk/Phase-Noise/Vig_IEEE_Standard_1139-1999%20.pdf
- ↑ Keiji Kishine, Noboru Ishihara, Ken-ichi Takiguchi, Haruhiko Ichino, “A 2.5-Gb/s Clock and Data Recovery IC with Tunable Jitter Characteristics for Use in LAN's and WAN's” from IEEE Journal of Solid-State Circuits, June 1999
- ↑ Ransom Stephens, “Tektronics Jitter 360° Knowledge Series” from http://www.tek.com/learning/
- ↑ Leeson, D. B. (February 1966), "A Simple Model of Feedback Oscillator Noise Spectrum", Proceedings of the IEEE 54 (2): 329–330, doi:10.1109/PROC.1966.4682
- ↑ Noise Properties of PLL Systems, by Venceslav F. Kroupa, in IEEE Trans. Comm., vol. COM-30, pp. 2244-2252, October 1982.
- ↑ A General Theory of Phase Noise in Electrical Oscillators, by Ali Hajimiri and Thomas H. Lee, IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 33, NO. 2, FEBRUARY 1998 http://chic.caltech.edu/publication/a-general-theory-of-phase-noise-in-electrical-oscillators/
- ↑ ITU-T Rec. G.783 (03 2006) Characteristics of synchronous digital hierarchy (SDH) equipment functional blocks; VII.3 STM-64 (Type A) regenerator jitter accumulation simulation model, analyses, and results, page 280; ... the VCO noise sees a high-pass filter transfer function with corner frequency equal to the PLL bandwidth.. .
- ↑ Buchwald, Aaron; Martin, Kennet W. (May 31, 1995). Integrated Fiber-Optic Receivers. Boston/London/Dordrecht: Springer; 1995 edition. p. 197. ISBN 978-0792395492.
- ↑ Buchwald, Aaron; Martin, Kennet W. (May 31, 1995). Integrated Fiber-Optic Receivers. Boston/London/Dordrecht: Springer; 1995 edition. pp. 196–197. ISBN 978-0792395492.
- ↑ The figure used suggests AM, non FM, spectra.
- But the VCO is by definition an FM modulator, modulated by the signal coming from the amplifier/filter.
- However, as long as the modulation index of FM stays below 1 (preferably below 0.3), the FM is a narrow-band FM and its spectrum is very close to the spectrum of an AM signal generated with the same modulating signal and the carrier frequency.
- The modulation index is defined as the maximum phase deviation (a function of ωj) of the modulated (i.e. of the VCO) output.
- In a CDR in lock, such maximum phase deviation is defined by the jitter tolerance curve. At the upper corner of the jitter filtering bandwidth, this tolerance is about 1 rad (i.e. 0.15 U.I.) and called LEO. At lower frequencies it increases with1/ω.
- As all CDR operate with some margin, for instance 10 dB, the maximum phase deviation (i.e. the modulation index) will remain below approximately 0,3 rad.
- ↑ Jim Lesurf ( jcgl@st-and.ac.uk ). "Frequency Modulation, Phase Modulation, and FM spectra". University of St. Andrews, St Andrews, Fife KY16 9SS, Scotland. Retrieved Sun 6 Sep 2015 18:11.
{{cite web}}: Check date values in:|access-date=(help) - ↑ Buchwald, Aaron; Martin, Kennet W. (May 31, 1995). Integrated Fiber-Optic Receivers. Boston/London/Dordrecht: Springer; 1995 edition. pp. 182–194. ISBN 978-0792395492.
{{cite book}}: Unknown parameter|chapters=ignored (help)




