Physics Study Guide/Print version

Preface

About this guide
Section One	Units	Linear motion	Force	Momentum	Normal force and friction	Work	Energy
Section Two	Torque	Circular Motion	Fluids	Fields	Gravity	Waves	Wave Overtones	Standing Waves	Sound
Section Three	Thermodynamics	Electricity	Magnetism	Optics
Apendicies	Physics constants	Frictional coefficients	Greek alphabet	Logs	Vectors and scalars

About this guide

Dedication

'I have a friend who's an artist and he's some times taken a view which I don't agree with very well. He'll hold up a flower and say, "look how beautiful it is," and I'll agree, I think. And he says, "you see, I as an artist can see how beautiful this is, but you as a scientist, oh, take this all apart and it becomes a dull thing." And I think he's kind of nutty. First of all, the beauty that he sees is available to other people and to me, too, I believe, although I might not be quite as refined aesthetically as he is. But I can appreciate the beauty of a flower. At the same time, I see much more about the flower that he sees. I could imagine the cells in there, the complicated actions inside which also have a beauty. I mean, it's not just beauty at this dimension of one centimeter: there is also beauty at a smaller dimension, the inner structure...also the processes. The fact that the colors in the flower are evolved in order to attract insects to pollinate it is interesting -- it means that insects can see the color. It adds a question -- does this aesthetic sense also exist in the lower forms that are...why is it aesthetic, all kinds of interesting questions which a science knowledge only adds to the excitement and mystery and the awe of a flower. It only adds. I don't understand how it subtracts.' ... Richard Feynman

Physics Study Guide

This guide is meant as a supplement to a year long freshman level physics course with a trigonometry prerequisite. Some ideas from calculus are included in the book but are not necessary to understand the content. The overview of equations and definitions and eventually sample problem solutions are pertinent to an introductory, college-level physics course suitable for pre-meds. This is not a stand alone textbook rather the intent is to help the student and any other interested person quickly familiarize themselves with concepts and terminology so as to use the appropriate equations to get the desired answers to physics problems.

Contributing

Everyone is encouraged to contribute to the guide. Be bold in your edits! If you have a question about how we do things here look at the Style Guide or post your question on the talk page.

Authors

Karl Wick

Adon Metcalfe

Brendan Abbott

Tristan Sabel

Fromund Hock

Martin Hoecker-Martinez

The SI System of Measurement

Fundamental units

These are basic units upon which most units depends.

Time

Time is defined as the duration between two events. In the international system of measurement (S.I.) the second (s) is the basic unit of time and it is defined as the time it takes a cesium (Cs) atom to perform 9,192,631,770 complete oscillations. The Earth revolves around its own axis in 86400 seconds with respect to the Sun; this is known as 1 day, and the 86400th part of one day is known as a second.

Length

In the international system of measurement (S.I.) the metre (m) ('meter' in the US) is the basic unit of length and is defined as the distance travelled by light in a vacuum in 1/299,792,458 second. This definition establishes that the speed of light in a vacuum is precisely 299,792,458 metres per second.

Mass

In the international system of measurement (S.I.) the kilogram (kg) is the basic unit of mass and is defined as the mass of a specific platinum-iridium alloy cylinder kept at the Bureau International des Poids et Mesures in Sèvres, France. A duplicate of the Sèvres cylinder is kept at the National Institute of Standards and Technology (NIST) in Gaithersburg, Maryland. See Wikipedia article.

Current

In the international system of measurement (S.I.) the ampere (A) is the basic measure of electrical current. It is defined as the constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre (m) apart in vacuum, would produce between these conductors a force equal to 2×10^-7 newton (N) per metre of length.

Unit of Thermodynamic Temperature

The kelvin (K), unit of thermodynamic temperature, is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water.

Unit of Amount of Substance

1. The mole (mol) is the amount of substance of a system that contains as many elementary entities as there are atoms in 0.012 kilograms of carbon 12.

2. When the mole is used, the elementary entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles.

Luminous Intensity

The candela (cd) is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 x 10¹² hertz and that has a radiant intensity in that direction of 1/683 watt per steradian. (A steradian (sr) is the SI unit of solid angle, equal to the angle at the centre of a sphere subtended by a part of the surface equal in area to the square of the radius.)

Derived Units

These are units obtained by combining two or more fundamental units.

Charge

The SI unit of charge is the coulomb (C). It is equal to ampere times second: $1\ \mathrm {C} =1\ \mathrm {A} \cdot \mathrm {s}$

Velocity

The SI unit for velocity is in m/s or metres per second.

Force

The SI unit of force is the newton ($N$), named after Sir Isaac Newton. It is equal to $1\ \mathrm {kg} \cdot \mathrm {m} /\mathrm {s} ^{2}$.

Energy

The SI unit of energy is the joule (J). The joule has base units of kg·m²/s² = N·m. A joule is defined as the work done or energy required to exert a force of one newton for a distance of one metre. See Wikipedia article.

Pressure

The SI unit of pressure is the pascal (Pa). The pascal has base units of $\mathrm {N} /\mathrm {m} ^{2}$ or $\mathrm {kg} /\mathrm {m} \cdot \mathrm {s} ^{2}$. See Wikipedia article.

Prefixes

Prefix	yotta	zetta	exa	peta	tera	giga	mega	kilo	hecto	deca		deci	centi	milli	micro	nano	pico	femto	atto	zepto	yocto
Symbol	Y	Z	E	P	T	G	M	k	h	da		d	c	m	µ	n	p	f	a	z	y
10n	1024	1021	1018	1015	1012	109	106	103	102	101	100	10-1	10-2	10-3	10-6	10-9	10-12	10-15	10-18	10-21	10-24
1000n	10008	10007	10006	10005	10004	10003	10002	10001						1000-1	1000-2	1000-3	1000-4	1000-5	1000-6	1000-7	1000-8

Astronomical Measurements

The SI units are not always convenient to use, even with the larger (and smaller) prefixes. For astronomy, the following units are prevalent:

Julian Year

The Julian year is defined by the IAU as exactly 365.25 days, a day being exactly 60*60*24 = 86,400 SI seconds. The Julian year is therefore equal to 31,557,600 seconds.

Astronomical Unit

The Astronomical Unit (au or ua), often used for measuring distances in the Solar system, is the average distance from the Earth to the Sun. In 2012 this was defined as exactly 149,597,870,700 metres. Previously it was 149,597,870,691 m, ± 30 m.

Light Year

The light year (ly) is defined as the distance light travels in a homogeneous isotopic non-attenuating medium (a vacuum) in one Julian year. Due to the word "year", the light year is often mistaken for a unit of time in popular culture. It is, however, a unit of length (distance), and is equal to exactly 9,460,730,472,580,800 m.

Parsec

The parsec (pc), or "parallax second", is the distance of an object that appears to move two arc-seconds against the background stars as the Earth moves around the sun, or by definition one arc-second of parallax angle. This angle is measured in reference to a line connecting the object and the Sun, and thus the apparent motion is one arc-second on either side of this "central" position. The parsec is approximately 3.26156 ly.

Kinematics is the description of motion. The motion of a point particle is fully described using three terms - position, velocity, and acceleration. For real objects (which are not mathematical points), translational kinematics describes the motion of an object's center of mass through space, while angular kinematics describes how an object rotates about its centre of mass. In this section, we focus only on translational kinematics. Position, displacement, velocity, and acceleration are defined as follows.

Position

"Position" is a relative term that describes the location of an object RELATIVE to some chosen stationary point that is usually described as the "origin".

A vector is a quantity that has both magnitude and direction, typically written as a column of scalars. That is, a number that has a direction assigned to it.

In physics, a vector often describes the motion of an object. For example, Warty the Woodchuck goes 10 meters towards a hole in the ground.

We can divide vectors into parts called "components", of which the vector is a sum. For example, a two-dimensional vector is divided into x and y components.

One dimensional coordinate system

Two dimensional coordinate system

Three dimensional coordinate system

Displacement

$\Delta {\vec {x}}\equiv {\vec {x}}_{f}-{\vec {x}}_{i}\,$

Displacement answers the question, "Has the object moved?"

Note the $\equiv$ symbol. This symbol is a sort of "super equals" symbol, indicating that not only does ${\vec {x}}_{f}-{\vec {x}}_{i}$ EQUAL the displacement $\Delta {\vec {x}}$, but more importantly displacement is operationally defined by ${\vec {x}}_{f}-{\vec {x}}_{i}$.

We say that ${\vec {x}}_{f}-{\vec {x}}_{i}$ operationally defines displacement, because ${\vec {x}}_{f}-{\vec {x}}_{i}$ gives a step by step procedure for determining displacement.

Namely:

1. Measure where the object is initially.
2. Measure where the object is at some later time.
3. Determine the difference between these two position values.

Be sure to note that displacement is not the same as distance travelled.

For example, imagine travelling one time along the circumference of a circle. If you end where you started, your displacement is zero, even though you have clearly travelled some distance. In fact, displacement is an average distance travelled. On your trip along the circle, your north and south motion averaged out, as did your east and west motion.

Clearly we are losing some important information. The key to regaining this information is to use smaller displacement intervals. For example, instead of calculating your displacement for your trip along the circle in one large step, consider dividing the circle into 16 equal segments. Calculate the distance you travelled along each of these segments, and then add all your results together. Now your total travelled distance is not zero, but something approximating the circumference of the circle. Is your approximation good enough? Ultimately, that depends on the level of accuracy you need in a particular application, but luckily you can always use finer resolution. For example, we could break your trip into 32 equal segments for a better approximation.

Returning to your trip around the circle, you know the true distance is simply the circumference of the circle. The problem is that we often face a practical limitation for determining the true distance travelled. (The travelled path may have too many twists and turns, for example.) Luckily, we can always determine displacement, and by carefully choosing small enough displacement steps, we can use displacement to obtain a pretty good approximation for the true distance travelled. (The mathematics of calculus provides a formal methodology for estimating a "true value" through the use of successively better approximations.) In the rest of this discussion, I will replace $\Delta$ with $\delta$ to indicate that small enough displacement steps have been used to provide a good enough approximation for the true distance travelled.

Velocity

${\vec {v}}_{av}\equiv {\frac {{\vec {x_{f}}}-{\vec {x_{i}}}}{t_{f}-t_{i}}}\equiv {\frac {\Delta {\vec {x}}}{\Delta t}}$

[Δ, delta, upper-case Greek D, is a prefix conventionally used to denote a difference.] Velocity answers the question "Is the object moving now, and if so - how quickly?"

Once again we have an operational definition: we are told what steps to follow to calculate velocity.

Note that this is a definition for average velocity. The displacement Δx is the vector sum of the smaller displacements which it contains, and some of these may subtract out. By contrast, the distance travelled is the scalar sum of the smaller distances, all of which are non-negative (they are the magnitudes of the displacements). Thus the distance travelled can be larger than the magnitude of the displacement, as in the example of travel on a circle, above. Consequently, the average velocity may be small (or zero, or negative) while the speed is positive.

If we are careful to use very small displacement steps, so that they come pretty close to approximating the true distance travelled, then we can write the definition for instantaneous velocity as

${\vec {v}}_{inst}\equiv {\frac {\vec {\delta x}}{\delta t}}$

[δ is the lower-case delta.] Or with the idea of limits from calculus, we have:

${\vec {v}}_{inst}\equiv {\frac {d{\vec {x}}}{dt}}$

[d, like Δ and δ, is merely a prefix; however, its use definitely specifies that this is a sufficiently small difference so that the error--due to stepping (instead of smoothly changing) the quantity--becomes negligible.]

Acceleration

${\vec {a}}_{av}\equiv {\frac {{\vec {v_{f}}}-{\vec {v_{i}}}}{t_{f}-t_{i}}}\equiv {\frac {\Delta {\vec {v}}}{\Delta t}}$

Acceleration answers the question "Is the object's velocity changing, and if so - how quickly?"

Once again we have an operational definition. We are told what steps to follow to calculate acceleration.

Again, also note that technically we have a definition for average acceleration. As for displacement, if we are careful to use a series of small velocity changes, then we can write the definition for instantaneous acceleration as:

${\vec {a}}_{inst}\equiv {\frac {\delta {\vec {v}}}{\delta t}}$

Or with the help of calculus, we have:

${\vec {a}}_{inst}\equiv {\frac {d{\vec {v}}}{dt}}={\frac {d^{2}{\vec {x}}}{dt^{2}}}$

Vectors

Notice that the definitions given above for displacement, velocity and acceleration included little arrows over many of the terms. The little arrow reminds us that direction is an important part of displacement, velocity, and acceleration. These quantities are vectors. By convention, the little arrow always points right when placed over a letter. So for example, ${\vec {v}}$ just reminds us that velocity is a vector, and does not imply that this particular velocity is rightward.

Why do we need vectors? As a simple example, consider velocity. It is not enough to know how fast one is moving. We also need to know which direction we are moving. Less trivially, consider how many different ways an object could be experiencing an acceleration (a change in its velocity). Ultimately, there are three distinct ways an object could accelerate:

1. The object could be speeding up.
2. The object could be slowing down.
3. The object could be traveling at constant speed, while changing its direction of motion.

More general accelerations are simply combinations of 1 and 3 or 2 and 3.

Importantly, a change in the direction of motion is just as much an acceleration as is speeding up or slowing down.

In classical mechanics, no direction is associated with time (you cannot point to next Tuesday). So the definition of ${\vec {a}}_{av}$ tells us that acceleration will point wherever the change in velocity $\Delta {\vec {v}}$ points.

Understanding that the direction of $\Delta {\vec {v}}$ determines the direction of ${\vec {a}}$ leads to three non-mathematical but very powerful rules of thumb:

1. If the velocity and acceleration of an object point in the same direction, the object's speed is increasing.
2. If the velocity and acceleration of an object point in opposite directions, the object's speed is decreasing.
3. If the velocity and acceleration of an object are perpendicular to each other, the object's initial speed stays constant (in that initial direction), while the speed of the object in the direction of the acceleration increases. Think of a bullet fired horizontally in a vertical gravitational field. Since velocity in the one direction remains constant, and the velocity in the other direction increases, the overall velocity (absolute velocity) also increases.

Again, more general motion is simply a combination of 1 and 3 or 2 and 3.

Using these three simple rules will dramatically help your intuition of what is happening in a particular problem. In fact, much of the first semester of college physics is simply the application of these three rules in different formats.

Equations of motion (constant acceleration)

A particle is said to move with constant acceleration if its velocity changes by equal amounts in equal intervals of time, no matter how small the intervals may be

${\frac {d{\vec {v}}}{dt}}=0\ \mathrm {\frac {m}{s^{2}}}$

Since acceleration is a vector, constant acceleration means that both direction and magnitude of this vector don't change during the motion. This means that average and instantaneous acceleration are equal. We can use that to derive an equation for velocity as a function of time by integrating the constant acceleration.

${\boldsymbol {v}}(t)={\boldsymbol {v}}(0)+\int \limits _{0}^{t}{\boldsymbol {a}}\ dt$

Giving the following equation for velocity as a function of time.

${\boldsymbol {v}}(t)={\boldsymbol {v}}_{0}+{\boldsymbol {a}}t$

To derive the equation for position we simply integrate the equation for velocity.

${\boldsymbol {x}}(t)={\boldsymbol {x}}(0)+\int \limits _{0}^{t}{\boldsymbol {v}}(t)\ dt$

Integrating again gives the equation for position.

${\boldsymbol {x}}(t)={\boldsymbol {x}}_{0}+{\boldsymbol {v}}_{0}t+{\frac {1}{2}}{\boldsymbol {a}}t^{2}$

The following are the equations of motion:

Equations of Motion

Equation	Description
${\vec {x}}={\vec {x}}_{0}+{\vec {v}}_{0}t+{\frac {{\vec {a}}t^{2}}{2}}\$	Position as a function of time
${\vec {v}}={\vec {v}}_{0}+{\vec {a}}t\$	Velocity as a function of time

The following equations can be derived from the two equations above by combining them and eliminating variables.

$v^{2}=v_{0}^{2}+2{\vec {a}}\cdot ({\vec {x}}-{\vec {x}}_{0})\$	Eliminating time (very useful, see the section on Energy)
${\vec {x}}={\vec {x}}_{0}+{\frac {{\vec {v}}_{0}t+{\vec {v}}t}{2}}$	Eliminating acceleration

Symbols

Symbol	Description
${\vec {v}}$	velocity (at time t)
${\vec {v_{0}}}$	initial velocity
${\vec {a}}$	(constant) acceleration
$t\$	time (taken during the motion)
${\vec {x}}$	position (at time t)
${\vec {x_{0}}}$	initial position

Acceleration in Two Dimensions

(Needs content)

Acceleration in Three Dimensions

(Needs content)

What does force in motion mean?

Force means strength and power. Motion means movement. That’s why we need forces and motions in our life. We need calculation when we want to know how fast things go, travel and other things which have force and motion. ...

How do we calculate the speed?

If you want to calculate the average speed, distance travelled or time taken you need to use this formula and remember it:

${speed}={\frac {distance}{time\ taken}}$

This is an easy formula to use, you can find the distance travelled, time taken or average speed, you need at least 2 values to find the whole answer.

Is velocity the same thing as speed?

Velocity is a vector quantity that refers to "the rate at which an object changes its position", whereas speed is a scalar quantity, which cannot be negative. Imagine a kid moving rapidly, one step forward and one step back, always returning to the original starting position. While this might result in a frenzy activity, it would result in a zero velocity, because the kid always returns to the original position, the motion would never result in a change in position, in other words $\Delta {\vec {x}}$ would be zero.

Speed is measured in the same physical units of measurement as velocity, but does not contain an element of direction. Speed is thus the magnitude component of velocity. Velocity contains both the magnitude and direction components. You can think of velocity as the displacement/duration, whereas speed can be though as distance/duration.

Acceleration

When a car is speeding up we say that it is accelerating, when it slows down we say it is decelerating.

How do we calculate it?

When we want to calculate it, the method goes like that: A lorry driver brakes hard, and slows from 25 m/s to 5 m/s in 5 seconds. What was the vehicle's acceleration?

${acceleration}={\frac {change\ in\ velocity}{time\ taken}}={\frac {5-25}{5}}={\frac {-20}{5}}=-4\ ms^{-2}$

What is initial velocity and final velocity? Initial velocity is the beginning before motion starts or in the middle of the motion, final velocity is when the motion stops.

There is another way to calculate it and it is like that This equations which are written is the primary ones, which means that when you don’t have lets say final velocity, how will you calculate the equation?

This is the way you are going to calculate.

Observing motion

When you want to know how fast an athletic person is running, what you need is a stopwatch in your hand, then when the person starts to run, you start the stopwatch and when the person who is sprinting stops at the end point, you stop the watch and see how fast he ran, and if you want to see if the athlete is wasting his energy, while he is running look at his movement, and you will know by that if he is wasting his energy or not.

This athletic person is running, and while he is running the scientist could know if he was wasting his energy if they want by the stop watch and looking at his momentum.

Measuring acceleration

Take a slope, a trolley, some tapes and a stop watch, then put the tapes on the slope and take the trolley on the slope, and the stopwatch in your hand, as soon as you release the trolley, start timing the trolley at how fast it will move, when the trolley stops at the end then stop the timing. After wards, after seeing the timing , record it, then you let the slope a little bit high, and you will see, how little by little it will decelerate.

Newton

Isaac Newton was an English physicist, mathematician (described in his own day as a "natural philosopher") , astronomer and alchemist. Newton is one of the most influential scientists of all time, and he is known, among other things, for contributing to development of classical mechanics and for inventing, independently from Gottfried Leibniz, calculus.

Newton's laws of motion

Newton is also known by his three laws of motion, which describe the relationship between a body and the forces acting upon it, and its motion in response to said forces.

1. First Law (also known as the law of inertia) states that every body continues in its state of rest or state of uniform motion unless compelled to change that state by being subject to an external force. The moment of inertia is defined as the tendency of matter to resist any change in its state of motion or state of rest.
2. Second Law The vector sum of the external forces $F$ on an object is equal to the mass $m$ of that object multiplied by the acceleration vector $a$ of the object, or algebraically $F=ma$.
3. Third Law states that when one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.

Symbols

Some useful symbols seen and that we will see:

Name	Symbol
Distance travelled	$d$ or $s$
Force	$F$
Velocity	${\vec {v}}$
Initial velocity	${\vec {v}}_{0}$ or ${\vec {v}}_{i}$
Final velocity	${\vec {v}}_{f}$
Change in velocity	$\Delta {\vec {v}}$
Acceleration	${\vec {a}}$
Mass	$m$
Newton	$N$
Gravity	$G$
Weight	$W$

Force

A force is any interaction that tends to change the motion of an object. In other words, a force can cause an object with mass to change its velocity. Force can also be described by intuitive concepts such as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newtons and represented by the symbol $F$.

How to calculate the force?

When we want to calculate the force, and we have the mass and acceleration, we can simply use the simple formula stated in the Newton's second law above, that is $F=ma$, where $m$ is the mass (or the amount of matter in a body), and $a$ is the acceleration. Note that the Newton’s second law is defined as a numerical measure of inertia.

What is inertia?

Inertia is the tendency of a body to maintain its state of rest or uniform motion, unless acted upon by an external force.

Robert Hooke

Robert Hooke was an English polymath who played an important role in the scientific revolution, through both experimental and theoretical work.

Hooke's law

Hooke's law is a principle of physics that states that the force $F$ needed to extend or compress a spring by some distance $X$ is proportional to that distance, or algebraically $F=-kX$, where $k$ is a constant factor characteristic of the spring, its stiffness.

---

Force

A net force on a body causes a body to accelerate. The amount of that acceleration depends on the body's inertia (or its tendency to resist changes in motion), which is measured as its mass. When Isaac Newton formulated Newtonian mechanics, he discovered three fundamental laws of motion.

Later, Albert Einstein proved that these laws are just a convenient approximation. These laws, however, greatly simplify calculations and are used when studying objects at velocities that are small compared with the speed of light.

Friction

It is the force that opposes relative motion or tendency of relative motion between two surfaces in contact represented by f. When two surfaces move relative to each other or they have a tendency to move relative to each other, at the point (or surface) of contact, there appears a force which opposes this relative motion or tendency of relative motion between two surfaces in contact. It acts on both the surfaces in contact with equal magnitude and opposite directions (Newton's 3rd law). Friction force tries to stop relative motion between two surfaces in contact, if it is there, and when two surfaces in contact are at rest relative to each other, the friction force tries to maintain this relative rest. Friction force can assume the magnitude (below a certain maximum magnitude called limiting static friction) required to maintain relative rest between two surfaces in contact. Because of this friction force is called a self adjusting force.

Earlier, it was believed that friction was caused due to the roughness of the two surfaces in contact with each other. However, modern theory stipulates that the cause of friction is the Coulombic force between the atoms present in the surface of the regions in contact with each other.

Formula: Limiting Friction = (Friction Coefficient)(Normal reaction)

Static Friction = the friction force that keeps an object at relative rest.

Kinetic Friction = sliding friction

Newton's First Law of Motion

(The Law of Inertia)

A static object with no net force acting on it remains at rest or if in movement it will maintain a constant velocity

This means, essentially, that acceleration does not occur without the presence of a force. The object tends to maintain its state of motion. If it is at rest, it remains at rest and if it is moving with a velocity then it keeps moving with the same velocity. This tendency of the object to maintain its state of motion is greater for larger mass. The "mass" is, therefore, a measure of the inertia of the object.

In a state of equilibrium, where the object is at rest or proceeding at a constant velocity, the net force in every direction must be equal to 0.

At a constant velocity (including zero velocity), the sum of forces is 0. If the sum of forces does not equal zero, the object will accelerate (change velocity over time).

It is important to note, that this law is applicable only in non-accelerated coordinate systems. It is so, because the perception of force in accelerated systems are different. A body under balanced force system in one frame of reference, for example a person standing in an accelerating lift, is acted upon by a net force in the earth's frame of reference.

Inertia is the tendency of an object to maintain its velocity i.e. to resist acceleration.

• Inertia is not a force.
• Inertia varies directly with mass.

Newton's Second Law of Motion

• The time rate of change in momentum is proportional to the applied force and takes place in the direction of the force.

• 'The acceleration of an object is proportional to the force acting upon it.

These two statements mean the same thing, and is represented in the following basic form (the system of measurement is chosen such that constant of proportionality is 1) :

${\vec {F}}={\frac {d}{dt}}(m{\vec {v}})$

The product of mass and velocity i.e. mv is called the momentum. The net force on a particle is thus equal to rate change of momentum of the particle with time. Generally mass of the object under consideration is constant and thus can be taken out of the derivative.

${\vec {F}}=m{\frac {d{\vec {v}}}{dt}}=m{\vec {a}}$

Force is equal to mass times acceleration. This version of Newton's Second Law of Motion assumes that the mass of the body does not change with time, and as such, does not represent a general mathematical form of the Law. Consequently, this equation cannot, for example, be applied to the motion of a rocket, which loses its mass (the lost mass is ejected at the rear of the rocket) with the passage of time.

An example: If we want to find out the downward force of gravity on an object on Earth, we can use the following formula:

$\|{\vec {F}}\|=m\|{\vec {g}}\|$

Hence, if we replace m with whatever mass is appropriate, and multiply it by 9.806 65 m/s², it will give the force in newtons that the earth's gravity has on the object in question (in other words, the body's weight).

Newton's Third Law of Motion

Forces occur in pairs equal in magnitude and opposite in direction

This means that for every force applied on a body A by a body B, body B receives an equal force in the exact opposite direction. This is because forces can only be applied by a body on another body. It is important to note here that the pair of forces act on two different bodies, affecting their state of motion. This is to emphasize that pair of equal forces do not cancel out.

There are no spontaneous forces.

It is very important to note that the forces in a "Newton 3 pair", described above, can never act on the same body. One acts on A, the other on B. A common error is to imagine that the force of gravity on a stationary object and the "contact force" upwards of the table supporting the object are equal by Newton's third law. This is not true. They may be equal - but because of the second law (their sum must be zero because the object is not accelerating), not because of the third.

The "Newton 3 pair" of the force of gravity (= earth's pull) on the object is the force of the object attracting the earth, pulling it upwards. The "Newton 3 pair" of the table pushing it up is that it, in its turn, pushes the table down.

Equations

To find Displacement

$\Delta x=t{\vec {v}}_{i}+{\frac {t^{2}{\vec {a}}}{2}}$

To find Final Velocity

${\vec {v}}_{f}={\vec {v}}_{i}+t{\vec {a}}$

To find Final Velocity

$(v_{f})^{2}=(v_{i})^{2}+2a\Delta x$

To find Force when mass is changing

${\vec {F}}={\frac {d}{dt}}(m{\vec {v}})$

To find Force when mass is a constant

${\vec {F}}=m{\frac {d{\vec {v}}}{dt}}=m{\vec {a}}$

Variables
${\vec {F}}$ Force (N) $m\$ Mass (kg) ${\vec {a}}$ Acceleration (m/s2) ${\vec {p}}$ Momentum (kg m/s) $t\$ time (s) ${\vec {T}}$ Tension (N) ${\vec {g}}$ Acceleration due to gravity near the earth's surface ($\|{\vec {g}}\|=9.806\ 65\mathrm {m/s^{2}}$ see Physics Constants)

Definitions

Force (F): Force is equal to rate change of momentum with time. (Newton’s second law). A vector. Units: newtons (N) The newton (N): defined as the force it takes to accelerate one kilogram one metre per second squared (U.S. meter per second squared), that is, the push it takes to speed up one kilogram from rest to a velocity of 1 m/s in 1 second $1\mathrm {N} =1\mathrm {kg} \cdot \mathrm {m} /\mathrm {s} ^{2}$ Mass (m) : Also called inertia. The tendency of an object to resist change in its motion, and its response to a gravitational field. A scalar. Units: kilograms (kg) Acceleration (a): Change in velocity (Δv) divided by time (t). A vector. Units: meters per second squared (U.S. meters per seconds squared) (m/s2) Momentum (p): Mass times velocity. Expresses the motion of a body and its resistance to changing that motion. A vector. Units: kg m/s

Momentum

Linear momentum

Momentum is equal to mass times velocity.

${\vec {p}}=m{\vec {v}}$

Angular momentum

Angular momentum of an object revolving around an external axis $O$ is equal to the cross-product of the position vector with respect to $O$ and its linear momentum.

${\vec {L}}={\vec {r}}\times {\vec {p}}={\vec {r}}\times m{\vec {v}}$

Angular momentum of a rotating object is equal to the moment of inertia times angular velocity.

${\vec {L}}=I{\vec {\omega }}$

Force and linear momentum, torque and angular momentum

Net force is equal to the change in linear momentum over the change in time.

${\vec {F}}={\frac {\Delta {\vec {p}}}{\Delta t}}$

Net torque is equal to the change in angular momentum over the change in time.

${\vec {\tau }}={\frac {\Delta {\vec {L}}}{\Delta t}}$

Conservation of momentum

${\begin{matrix}{\vec {p}}_{i}={\vec {p}}_{f}\\{\vec {L}}_{i}={\vec {L}}_{f}\end{matrix}}$

Let us prove this law.

We'll take two particles $a,b$ . Their momentums are ${\vec {p}}_{a},{\vec {p}}_{b}$ . They are moving opposite to each other along the $x$-axis and they collide. Now force is given by:

${\vec {F}}={\frac {d{\vec {p}}}{\mathrm {d} t}}$

According to Newton's third law, the forces on each particle are equal and opposite.So,

${\frac {d{\vec {p}}_{a}}{dt}}=-{\frac {d{\vec {p}}_{b}}{dt}}$

Rearranging,

${\frac {d{\vec {p}}}{dt}}+{\frac {d{\vec {p}}_{b}}{dt}}=0$

This means that the sum of the momentums does not change with time. Therefore, the law is proved.

Variables

p: momentum, (kg·m/s) m: mass, (kg) v: velocity (m/s) L: angular momentum, (kg·m2/s) I: moment of inertia, (kg·m2) ω: angular velocity (rad/s) α: angular acceleration (rad/s2) F: force (N) t: time (s) r: position vector (m) Bold denotes a vector quantity. Italics denotes a scalar quantity.

Definition of terms

Momentum (p): Mass times velocity. (kg·m/s) Mass (m) : A quantity that describes how much material exists, or how the material responds in a gravitational field. Mass is a measure of inertia. (kg) Velocity (v): Displacement divided by time (m/s) Angular momentum (L): A vector quantity that represents the tendency of an object in circular or rotational motion to remain in this motion. (kg·m2/s) Moment of inertia (I): A scalar property of a rotating object. This quantity depends on the mass of the object and how it is distributed. The equation that defines this is different for differently shaped objects. (kg·m2) Angular speed (ω): A scalar measure of the rotation of an object. Instantaneous velocity divided by radius of motion (rad/s) Angular velocity (ω): A vector measure of the rotation of an object. Instantaneous velocity divided by radius of motion, in the direction of the axis of rotation. (rad/s) Force (F): mass times acceleration, a vector. Units: newtons (N) Time (t) : (s) Isolated system: A system in which there are no external forces acting on the system. Position vector (r): a vector from a specific origin with a magnitude of the distance from the origin to the position being measured in the direction of that position. (m)

Calculus-based Momentum

Force is equal to the derivative of linear momentum with respect to time.

${\vec {F}}={\frac {d{\vec {p}}}{dt}}$

Torque is equal to the derivative of angular momentum with respect to time.

${\vec {\tau }}={\frac {d{\vec {L}}}{dt}}$

The Normal Force

Why is it that we stay steady in our chairs when we sit down? According to the first law of motion, if an object is translationally in equilibrium (velocity is constant), the sum of all the forces acting on the object must be equal to zero. For a person sitting on a chair, it can thus be postulated that a normal force is present balancing the gravitational force that pulls the sitting person down. However, it should be noted that only some of the normal force can cancel the other forces to zero like in the case of a sitting person. In Physics, the term normal as a modifier of the force implies that this force is acting perpendicular to the surface at the point of contact of the two objects in question. Imagine a person leaning on a vertical wall. Since the person does not stumble or fall, he/she must be in equilibrium. Thus, the component of his/her weight along the horizontal is balanced or countered (opposite direction) by an equal amount of force -- this force is the normal force on the wall. So, on a slope, the normal force would not point upwards as on a horizontal surface but rather perpendicular to the slope surface.

The normal force can be provided by any one of the four fundamental forces, but is typically provided by electromagnetism since microscopically, it is the repulsion of electrons that enables interaction between surfaces of matter. There is no easy way to calculate the normal force, other than by assuming first that there is a normal force acting on a body in contact with a surface (direction perpendicular to the surface). If the object is not accelerating (for the case of uniform circular motion, the object is accelerating) then somehow, the magnitude of the normal force can be solved. In most cases, the magnitude of the normal force can be solved together with other unknowns in a given problem.

Sometimes, the problem does not warrant the knowledge of the normal force(s). It is in this regard that other formalisms (e.g. Lagrange method of undertermined coefficients) can be used to eventually solve the physical problem.

Friction

When there is relative motion between two surfaces, there is a resistance to the motion. This force is called friction. Friction is the reason why people could not accept Newton's first law of Motion, that an object tends to keep its state of motion. Friction acts opposite to the direction of the original force. The frictional force is equal to the frictional coefficient times the normal force.

Friction is caused due to attractive forces between the molecules near the surfaces of the objects. If two steel plates are made really flat and polished and cleaned and made to touch in a vacuum, it bonds together. It would look as if the steel was just one piece. The bonds are formed as in a normal steel piece. This is called cold welding. And this is the main cause of friction.

The above equation is an empirical one--in general, the frictional coefficient is not constant. However, for a large variety of contact surfaces, there is a well characterized value. This kind of friction is called Coulomb friction. There is a separate coefficient for both static and kinetic friction. This is because once an object is pushed on, it will suddenly jerk once you apply enough force and it begins to move.

Also, the frictional coefficient varies greatly depending on what two substances are in contact, and the temperature and smoothness of the two substances. For example, the frictional coefficients of glass on glass are very high. When you have similar materials, in most cases you don't have Coulomb friction.

For static friction, the force of friction actually increases proportionally to the force applied, keeping the body immobile. Once, however, the force exceeds the maximum frictional force, the body will begin to move. The maximum frictional force is calculated as follows:

$\left|{\vec {F}}_{f}\right|\leq \mu _{s}\left|{\vec {N}}\right|$

The static frictional force is less than or equal to the coefficient of static friction times the normal force. Once the frictional force equals the coefficient of static friction times the normal force, the object will break away and begin to move.

Once it is moving, the frictional force then obeys:

$\left|{\vec {F}}_{f}\right|=\mu _{k}\left|{\vec {N}}\right|$

The kinetic frictional force is equal to the coefficient of kinetic friction times the normal force. As stated before, this always opposes the direction of motion.

Variables

Symbol	Units	Definition
${\vec {F}}_{f}$	$\mathrm {N} \$	Force of friction
$\mu \$	none	Coefficient of friction

Definition of Terms

Normal force (N): The force on an object perpendicular to the surface it rests on utilized in order to account for the body's lack of movement. Units: newtons (N) Force of friction (Ff): The force placed on a moving object opposite its direction of motion due to the inherent roughness of all surfaces. Units: newtons (N) Coefficient of friction (μ): The coefficient that determines the amount of friction. This varies tremendously based on the surfaces in contact. There are no units for the coefficient of either static or kinetic friction

It's important to note, that in real life we often have to deal with viscose and turbulent friction - they appear when you move the body through the matter.

Viscose friction is proportional to velocity and takes place at approximately low speeds. Turbulent friction is proportional to $V^{2}$ and takes place at higher velocities.

---

Work

Work is equal to the scalar product of force and displacement.

$W={\vec {F}}\cdot {\vec {d}}$

The scalar product of two vectors is defined as the product of their lengths with the cosine of the angle between them. Work is equal to force times displacement times the cosine of the angle between the directions of force and displacement.

$W=\|{\vec {F}}\|\ \|{\vec {d}}\|\cos \theta$

Work is equal to change in kinetic energy plus change in potential energy for example the potential energy due to gravity.

$W=\Delta \mathrm {KE} +\Delta \mathrm {PE} _{g}\$

Work is equal to average power times time.

$W=Pt\$

The Work done by a force taking something from point 1 to point 2 is

$W_{1,2}=\int _{{\vec {x}}_{1}}^{{\vec {x}}_{2}}{\vec {F}}\cdot d{\vec {l}}$

Work is in fact just a transfer of energy. When we 'do work' on an object, we transfer some of our energy to it. This means that the work done on an object is its increase in energy. Actually, the kinetic energy and potential energy is measured by calculating the amount of work done on an object. The gravitational potential energy (there are many types of potential energies) is measured as 'mgh'. mg is the weight/force and h is the distance. The product is nothing but the work done. Even kinetic energy is a simple deduction from the laws of linear motion. Try substituting for v^2 in the formula for kinetic energy.

Variables

W: Work (J) F: Force (N) d: Displacement (m)

Definition of terms

Work (W): Force times distance. Units: joules (J) Force (F): mass times acceleration (Newton’s classic definition). A vector. Units: newtons (N)

When work is applied to an object or a system it adds or removes kinetic energy to or from that object or system. More precisely, a net force in one direction, when applied to an object moving opposite or in the same direction as the force, kinetic energy will be added or removed to or from that object. Note that work and energy are measured in the same unit, the joule (J).

---

Advanced work topics

---

Energy

Kinetic energy is simply the capacity to do work by virtue of motion.

(Translational) kinetic energy is equal to one-half of mass times the square of velocity.

$\mathrm {KE} _{T}={\frac {1}{2}}m\|{\vec {v}}\|^{2}$

(Rotational) kinetic energy is equal to one-half of moment of inertia times the square of angular velocity.

$\mathrm {KE} _{R}={\frac {1}{2}}I\omega ^{2}$

Total kinetic energy is simply the sum of the translational and rotational kinetic energies. In most cases, these energies are separately dealt with. It is easy to remember the rotational kinetic energy if you think of the moment of inertia I as the rotational mass. However, you should note that this substitution is not universal but rather a rule of thumb.

Potential energy is simply the capacity to do work by virtue of position (or arrangement) relative to some zero-energy reference position (or arrangement).

Potential energy due to gravity is equal to the product of mass, acceleration due to gravity, and height (elevation) of the object.

$\mathrm {PE} _{g}=-m{\vec {g}}\cdot {\vec {x}}=mgy$

Note that this is simply the vertical displacement multiplied by the weight of the object. The reference position is usually the level ground but the initial position like the rooftop or treetop can also be used. Potential energy due to spring deformation is equal to one-half the product of the spring constant times the square of the change in length of the spring.

$\mathrm {PE} _{e}={\frac {1}{2}}k\|{\vec {x}}-{\vec {x}}_{e}\|^{2}={\frac {1}{2}}k\|\Delta {\vec {x}}\|^{2}$

The reference point of spring deformation is normally when the spring is "relaxed," i.e. the net force exerted by the spring is zero. It will be easy to remember that the one-half factor is inserted to compensate for finite '"change in length" since one would want to think of the product of force and change in length $(k\Delta {\vec {x}})\cdot \Delta {\vec {x}}$ directly. Since the force actually varies with $\Delta {\vec {x}}$, it is instructive to need a "correction factor" during integration.

Variables

K: Kinetic energy (J) m: mass (kg) v: velocity (m/s) I: moment of inertia, (kg·m2) ω: ("omega") angular momentum (rad/s) Ug: Potential energy (J) g: local acceleration due to gravity (on the earth’s surface, 9.8 m/s2) h: height of elevation (m) Ue: Potential energy (J) k: spring constant (N/m) Δx: change in length of spring (m)

Definition of terms

Energy: a theoretically indefinable quantity that describes potential to do work. SI unit for energy is the joule (J). Also common is the calorie (cal). The joule: defined as the energy needed to push with the force of one newton over the distance of one meter. Equivalent to one newton-meter (N·m) or one watt-second (W·s). 1 joule = 1 J = 1 newton • 1 meter = 1 watt • 1 second Energy comes in many varieties, including Kinetic energy, Potential energy, and Heat energy. Kinetic energy (K): The energy that an object has due to its motion. Half of velocity squared times mass. Units: joules (J) Potential energy due to gravity (UG): The energy that an object has stored in it by elevation from a mass, such as raised above the surface of the earth. This energy is released when the object becomes free to move. Mass times height time acceleration due to gravity. Units: joules (J) Potential energy due to spring compression (UE): Energy stored in spring when it is compressed. Units: joules (J) Heat energy (Q): Units: joules (J) Spring compression (Dx): The difference in length between the spring at rest and the spring when stretched or compressed. Units: meters (m) Spring constant (k): a constant specific to each spring, which describes its “springiness”, or how much work is needed to compress the spring. Units: newtons per meter (N/m) Change in spring length (Δx): The distance between the at-rest length of the spring minus the compressed or extended length of the spring. Units: meters (m) Moment of inertia (I): Describes mass and its distribution. (kg•m2) Angular momentum (ω): Angular velocity times mass (inertia). (rad/s)

Section Two

Uniform Circular Motion

Speed and frequency

A two dimensional polar co-ordinate system. The point $M$ can be located in 2D plane as $(a,b)$ in Cartesian coordinate system or $(r,\theta )$ in polar coordinate system

Uniform circular motion assumes that an object is moving (1) in circular motion, and (2) at constant speed $v$; then

$T={\frac {2\pi r}{v}}$

where $r$ is the radius of the circular path, and $T$ is the time period for one revolution.

Any object travelling on a circle will return to its original starting point in the period of one revolution, $T$. At this point the object has travelled a distance $2\pi r$. If $T$ is the time that it takes to travel distance $2\pi r$ then the object's speed is

$v={\frac {2\pi r}{T}}=2\pi rf$

where $f={\frac {1}{T}}$

Angular frequency

Uniform circular motion can be explicitly described in terms of polar coordinates through angular frequency, $\omega$ :

$\omega ={\frac {d\theta }{dt}}$

where $\theta$ is the angular coordinate of the object (see the diagram on the right-hand side for reference).

Since the speed in uniform circular motion is constant, it follows that

$\omega ={\frac {\Delta \theta }{\Delta t}}$

From that fact, a number of useful relations follow:

$\omega ={\frac {2\pi }{T}}=2\pi f={\frac {v}{r}}$

The equations that relate how $\theta$ changes with time are analogous to those of linear motion at constant speed. In particular,

$\theta =\theta _{0}+\omega t$

The angle at $t=0$, $\theta _{0}$, is commonly referred to as phase.

Velocity, centripetal acceleration and force

The position of an object in a plane can be converted from polar to cartesian coordinates through the equations

${\begin{aligned}x&=r\cos(\theta )\\y&=r\sin(\theta )\end{aligned}}$

Expressing $\theta$ as a function of time gives equations for the cartesian coordinates as a function of time in uniform circular motion:

${\begin{aligned}x&=r\cos(\theta _{0}+\omega t)\\y&=r\sin(\theta _{0}+\omega t)\end{aligned}}$

Differentiation with respect to time gives the components of the velocity vector:

${\begin{aligned}v_{x}&=\omega r(-\sin(\omega t))=-v\sin(\omega t)\\v_{y}&=\omega r\cos(\omega t)=v\cos(\omega t)\end{aligned}}$

Velocity in circular motion is a vector tangential to the trajectory of the object. Furthermore, even though the speed is constant the velocity vector changes direction over time. Further differentiation leads to the components of the acceleration (which are just the rate of change of the velocity components):

${\begin{aligned}a_{x}&=-\omega ^{2}r\cos(\omega t)\\a_{y}&=-\omega ^{2}r\sin(\omega t)\end{aligned}}$

The acceleration vector is perpendicular to the velocity and oriented towards the centre of the circular trajectory. For that reason, acceleration in circular motion is referred to as centripetal acceleration.

The absolute value of centripetal acceleration may be readily obtained by

${\begin{aligned}a_{c}&={\sqrt {a_{x}^{2}+a_{y}^{2}}}={\sqrt {(\omega ^{2}r)^{2}{\big (}\cos ^{2}(\omega t)+\sin ^{2}(\omega t){\big )}}}\\&=\omega ^{2}r={\frac {v^{2}}{r}}\end{aligned}}$

For centripetal acceleration, and therefore circular motion, to be maintained a centripetal force must act on the object. From Newton's Second Law it follows directly that the force will be given by

${\vec {F_{c}}}=m{\vec {a_{c}}}$

the components being

${\begin{aligned}F_{x}&=-m\omega ^{2}r\cos(\omega t)\\F_{y}&=-m\omega ^{2}r\sin(\omega t)\end{aligned}}$

and the absolute value

$F_{c}=m\omega ^{2}r=m{\frac {v^{2}}{r}}$

Torque and Circular Motion

Circular motion is the motion of a particle at a set distance (called radius) from a point. For circular motion, there needs to be a force that makes the particle turn. This force is called the 'centripetal force.' Please note that the centripetal force is not a new type of force-it is just a force causing rotational motion. To make this clearer, let us study the following examples:

1. If Stone ties a piece of thread to a small pebble and rotates it in a horizontal circle above his head, the circular motion of the pebble is caused by the tension force in the thread.
2. In the case of the motion of the planets around the sun (which is roughly circular), the force is provided by the gravitational force exerted by the sun on the planets.

Thus, we see that the centripetal force acting on a body is always provided by some other type of force -- centripetal force, thus, is simply a name to indicate the force that provides this circular motion. This centripetal force is always acting inward toward the center. You will know this if you swing an object in a circular motion. If you notice carefully, you will see that you have to continuously pull inward. We know that an opposite force should exist for this centripetal force(by Newton's 3rd Law of Motion). This is the centrifugal force, which exists only if we study the body from a non-inertial frame of reference(an accelerating frame of reference, such as in circular motion). This is a so-called 'pseudo-force', which is used to make the Newton's law applicable to the person who is inside a non-inertial frame. e.g. If a driver suddenly turns the car to the left, you go towards the right side of the car because of centrifugal force. The centrifugal force is equal and opposite to the centripetal force. It is caused due to inertia of a body.

$\omega _{\text{avg}}={\frac {\omega +\omega _{f}}{2}}={\frac {\theta }{t}}$

Average angular velocity is equal to one-half of the sum of initial and final angular velocities assuming constant acceleration, and is also equal to the angle gone through divided by the time taken.

---

$\alpha ={\frac {\Delta \omega }{t}}$

Angular acceleration is equal to change in angular velocity divided by time taken.

Angular momentum

${\vec {L}}={\vec {r}}\times {\vec {p}}=m({\vec {r}}\times {\vec {v}})$

Angular momentum of an object revolving around an external axis $O$ is equal to the cross-product of the position vector with respect to $O$ and its linear momentum.

${\vec {L}}=I{\vec {\omega }}$

Angular momentum of a rotating object is equal to the moment of inertia times angular velocity.

$L=I\omega$

---

$\tau =I\alpha ={\frac {\Delta L}{t}}$>

Rotational Kinetic Energy is equal to one-half of the product of moment of inertia and the angular velocity squared.

IT IS USEFUL TO NOTE THAT

The equations for rotational motion are analogous to those for linear motion-just look at those listed above. When studying rotational dynamics, remember:

• the place of force is taken by torque

• the place of mass is taken by moment of inertia

• the place of displacement is taken by angle

• the place of linear velocity, momentum, acceleration, etc. is taken by their angular counterparts.

Definition of terms

Torque (${\vec {\tau }}$): Force times distance. A vector. $N\!\cdot \!m$ Moment of inertia ($I$): Describes the object's resistance to torque — the rotational analog to inertial mass. $kg\!\cdot \!m^{2}$ Angular momentum (${\vec {L}}$): $kg\!\cdot \!{\frac {m^{2}}{s}}$ Angular velocity (${\vec {\omega }}$): ${\frac {\text{rad}}{s}}$ Angular acceleration (${\vec {\alpha }}$): ${\frac {\text{rad}}{s^{2}}}$ Rotational kinetic energy ($K_{r}$): $J=kg\!\cdot \!\left({\frac {m}{s}}\right)^{2}$ Time ($t$): $s$

Buoyancy

Buoyancy is the force due to pressure differences on the top and bottom of an object under a fluid (gas or liquid).

Net force = buoyant force - force due to gravity on the object

Bernoulli's Principle

Fluid flow is a complex phenomenon. An ideal fluid may be described as:

• The fluid flow is steady i.e its velocity at each point is constant with time.
• The fluid is incompressible. This condition applies well to liquids and in certain circumstances to gases.
• The fluid flow is non-viscous. Internal friction is neglected. An object moving through this fluid does not experience a retarding force. We relax this condition in the discussion of Stokes' Law.
• The fluid flow is irrotational. There is no angular momentum of the fluid about any point. A very small wheel placed at an arbitrary point in the fluid does not rotate about its center. Note that if turbulence is present, the wheel would most likely rotate and its flow is then not irrotational.

As the fluid moves through a pipe of varying cross-section and elevation, the pressure will change along the pipe. The Swiss physicist Daniel Bernoulli (1700-1782) first derived an expression relating the pressure to fluid speed and height. This result is a consequence of conservation of energy and applies to ideal fluids as described above.

Consider an ideal fluid flowing in a pipe of varying cross-section. A fluid in a section of length $\Delta x_{1}$ moves to the section of length $\Delta x_{2}$ in time $\Delta t$ . The relation given by Bernoulli is:

$P+{\tfrac {1}{2}}\rho v^{2}+\rho gh={\text{constant}}$

where:

$P$ is pressure at cross-section

$h$ is height of cross-section

$\rho$ is density

$v$ is velocity of fluid at cross-section

In words, the Bernoulli relation may be stated as: As we move along a streamline the sum of the pressure ($P$), the kinetic energy per unit volume and the potential energy per unit volume remains a constant.

---

(To be concluded)

Fields

A field is one of the more difficult concepts to grasp in physics. A field is an area or region in which an influence or force is effective regardless of the presence or absence of a material medium. Simply put, a field is a collection of vectors often representing the force an object would feel if it were placed at any particular point in space. With gravity, the field is measured in newtons, as it depends solely on the mass of an object, but with electricity, it is measured in newtons per coulomb, as the force on an electrical charge depends on the amount of that charge. Typically these fields are calculated based on canceling out the effect of a body in the point in space that the field is desired. As a result, a field is a vector, and as such, it can (and should) be added when calculating the field created by TWO objects at one point in space.

Fields are typically illustrated through the use of what are called field lines or lines of force. Given a source that exerts a force on points around it, sample lines are drawn representing the direction of the field at points in space around the force-exerting source.

There are three major categories of fields:

1. Uniform fields are fields that have the same value at any point in space. As a result, the lines of force are parallel.
2. Spherical fields are fields that have an origin at a particular point in space and vary at varying distances from that point.
3. Complex fields are fields that are difficult to work with mathematically (except under simple cases, such as fields created by two point object), but field lines can still typically be drawn. Dipoles are a specific kind of complex field.

Magnetism also has a field, measured in Tesla, and it also has field lines, but its use is more complicated than simple "force" fields. Secondly, it also only appears in a two-pole form, and as such, is difficult to calculate easily.

The particles that form these magnetic fields and lines of force are called electrons and not magnetons. A magneton is a quantity in magnetism.

Definition of terms

Field: A collection of vectors that often represents the force that an object would feel if it were placed in any point in space. Field Lines: A method of diagramming fields by drawing several sample lines showing direction of the field through several points in space.

---

Newtonian Gravity

Newtonian Gravity (simplified gravitation) is an apparent force (a.k.a. pseudoforce) that simulates the attraction of one mass to another mass. Unlike the three fundamental (real) forces of electromagnetism and the strong and weak nuclear forces, gravity is purely attractive. As a force it is measured in newtons. The distance between two objects is measured between their centers of mass.

$F=G\!\cdot \!{\frac {m_{1}m_{2}}{r^{2}}}$

Gravitational force is equal to the product of the universal gravitational constant and the masses of the two objects, divided by the square of the distance between their centers of mass.

$g=G\cdot {\frac {m_{1}}{r^{2}}}$

The value of the gravitational field which is equivalent to the acceleration due to gravity caused by an object at a point in space is equal to the first equation about gravitational force, with the effect of the second mass taken out.

$U=-G\cdot {\frac {Mm}{r}}$

Gravitational potential energy of a body to infinity is equal to the universal gravitational constant times the mass of a body from which the gravitational field is being created times the mass of the body whose potential energy is being measured over the distance between the two centers of mass. Therefore, the difference in potential energy between two points is the difference of the potential energy from the position of the center of mass to infinity at both points. Near the earth's surface, this approximates:

$\Delta U_{g}=mgh$

Potential energy due to gravity near the earth's surface is equal to the product of mass, acceleration due to gravity, and height (elevation) of the object.

If the potential energy from the body's center of mass to infinity is known, however, it is possible to calculate the escape velocity, or the velocity necessary to escape the gravitational field of an object. This can be derived based on utilizing the law of conservation of energy and the equation to calculate kinetic energy as follows:

${\begin{aligned}&{\boldsymbol {ke}}_{initial}=\Delta U\\\\&{\boldsymbol {ke}}_{initial}=U_{infinity}-U_{initial}\\\\&{\tfrac {1}{2}}mv^{2}=G\cdot {\frac {Mm}{r}}\\\\&v_{esc}={\sqrt {\frac {2GM}{r}}}\end{aligned}}$

}}

Variables

F: force (N) G: universal constant of gravitation, (6.67x10-11 N•m2/kg2) m1: mass of the first body m2: mass of the second body r: the distance between the point at which the force or field is being taken, and the center of mass of the first body g: acceleration due to gravity (on the earth’s surface, this is 9.8 m/s2) U: potential energy from the location of the center of mass to infinity (J) ΔUg: Change in potential energy (J) m and M: mass (kg) h: height of elevation (m) vesc: escape velocity (m/s)

Definition of terms

Universal constant of gravitation (G): This is a constant that is the same everywhere in the known universe and can be used to calculate gravitational attraction and acceleration due to gravity. 6.67x10-11 N·m2/kg2 Mass one (m1): One of two masses that are experiencing a mutual gravitational attraction. We can use this for the mass of the Earth (1023 kg). Mass two (m2): One of two masses that are experiencing a mutual gravitational attraction. This symbol can represent the mass of an object on or close to earth. Units: kilograms (kg) Acceleration due to gravity (g): This is nearly constant near the earth's surface because the mass and radius of the earth are essentially constant. At extreme altitudes the value can vary slightly, but it varies more significantly with latitude. This is also equal to the value of the gravitational field caused by a body at a particular point in space (9.8 m/s2) Escape velocity (vesc): The velocity necessary to completely escape the gravitational effects of a body.

A black hole is a geometrically defined region of space time exhibiting such large centripetal gravitational effects that nothing such as particles and electromagnetic radiation such as light may escape from inside of it. That is the escape velocity upon the event horizon is equivalent to the speed of light. General relativity is a metric theory of gravitation generalizing space time and Newton's law of universal gravitational attraction as a geometric property of space time.

Waves

Wave is defined as the movement of any periodic motion like a spring, a pendulum, a water wave, an electric wave, a sound wave, a light wave, etc.

A wave with constant amplitude.

Any periodic wave that has amplitude varied with time, phase sinusoidally can be expressed mathematically as

R(t , θ) = R Sin (ωt + θ)

• Minimum wave height (trough) at angle 0, π, 2π, ...

F(R,t,θ) = 0 at θ = nπ

• Maximum wave height (peak or crest) at π/2, 3π/2, ...

F(R,t,θ) = R at θ = (2n+1)π/2

• Wavelength (distance between two crests) λ = 2π.

λ = 2π - A circle or a wave

2λ = 2(2π) - Two circles or two waves

kλ = k2π - Circle k or k amount of waves

• Wave Number,

k

• Velocity (or Angular Velocity),

ω = 2πf

• Time Frequency,

f = 1 / t

• Time

t = 1 / f

Wave speed is equal to the frequency times the wavelength. It can be understood as how frequently a certain distance (the wavelength in this case) is traversed.

$f={\frac {v}{\lambda }}$

Frequency is equal to speed divided by wavelength.

$T={\frac {1}{f}}$

Period is equal to the inverse of frequency.

Variables

λ: wavelength (m) v: wave speed (m/s) f: frequency (1/s), (Hz) T: period (s)

Definition of terms

Wavelength (λ): The length of one wave, or the distance from a point on one wave to the same point on the next wave. Units: meters (m). In light, λ tells us the color. Wave speed (v): the speed at which the wave pattern moves. Units: meters per second, (m/s) Frequency of oscillation (f) (or just frequency): the number of times the wave pattern repeats itself in one second. Units: seconds-1 = (1/s) = hertz (Hz) In sound, f tells us the pitch. The inverse of frequecy is the period of oscillation. Period of oscillation (T) (or just period): duration of time between one wave and the next one passing the same spot. Units: seconds (s). The inverse of the period is frequency. Use a capital, italic T and not a lowercase one, which is used for time. Amplitude (A): the maximum height of the wave measured from the average height of the wave (the wave’s center). Unit: meters (m)

Image here

The wave’s extremes, its peaks and valleys, are called antinodes. At the middle of the wave are points that do not move, called nodes.

Examples of waves: Water waves, sound waves, light waves, seismic waves, shock waves, electromagnetic waves …

Oscillation

A wave is said to oscillate, which means to move back and forth in a regular, repeating way. This fluctuation can be between extremes of position, force, or quantity. Different types of waves have different types of oscillations.

Longitudinal waves: Oscillation is parallel to the direction of the wave. Examples: sound waves, waves in a spring.

Transverse waves: Oscillation is perpendicular to direction of the wave. Example: light

Interference

When waves overlap each other it is called interference. This is divided into constructive and destructive interference.

Constructive interference: the waves line up perfectly and add to each others’ strength.

Destructive interference: the two waves cancel each other out, resulting in no wave.This happens when angle between them is 180degrees.

Resonance

In real life, waves usually give a mishmash of constructive and destructive interference and quickly die out. However, at certain wavelengths standing waves form, resulting in resonance. These are waves that bounce back into themselves in a strengthening way, reaching maximum amplitude.

Resonance is a special case of forced vibration when the frequency of the impressed periodic force is equal to the natural frequency of the body so that it vibrates with increased amplitude, spontaneously.

---

Wave overtones

For resonance in a taut string, the first harmonic is determined for a wave form with one antinode and two nodes. That is, the two ends of the string are nodes because they do not vibrate while the middle of the string is an antinode because it experiences the greatest change in amplitude. This means that one half of a full wavelength is represented by the length of the resonating structure.

The frequency of the first harmonic is equal to wave speed divided by twice the length of the string. (Recall that wave speed is equal to wavelength times frequency.)

F1 = v/2L

The wavelength of the first harmonic is equal to double the length of the string.

λ1 = 2L

The "nth" wavelength is equal to the fundamental wavelength divided by n.

λn = λ1/n

Harmonics for a taut string*

	Harmonic number	Overtone number	F =	λ =
F1	First harmonic	---	F1 = v/2L	λ1 = 2L
F2	Second harmonic	First overtone	F2 = 2F1	λ2 =λ1/2
F3	Third harmonic	Second overtone	F3 = 3F1	λ3 = λ1/3
Fn	Nth harmonic	(Nth - 1) overtone	Fn = nF1	λn = λ1/n

* or any wave system with two identical ends, such as a pipe with two open or closed ends. In the case of a pipe with two open ends, there are two antinodes at the ends of the pipe and a single node in the middle of the pipe, but the mathematics work out identically.

Definition of terms

Frequency (F): Units: (1/s), hertz (Hz) Fundamental frequency, first harmonic (F)1: The lowest frequency (longest wavelength) allowed for the system. Length of string (L): (or pipe, etc.) Units: meters (m). Wavelength (λ): Units: meters (m).

The first overtone is the first allowed harmonic above the fundamental frequency (F₁).

In the case of a system with two different ends (as in the case of a tube open at one end), the closed end is a node and the open end is an antinode. The first resonant frequency has only a quarter of a wave in the tube. This means that the first harmonic is characterized by a wavelength four times the length of the tube.

F1 = v/4L

The wavelength of the first harmonic is equal to four times the length of the string.

λ1 = 4L

The "nth" wavelength is equal to the fundamental wavelength divided by n.

λn = λ1/n

Note that "n" must be odd in this case as only odd harmonics will resonate in this situation.

Harmonics for a system with two different ends*

	Harmonic number	Overtone number	F =	λ =
F1	First harmonic	---	F1 = v/4L	λ1 = 4L
F2	Third harmonic	First overtone	F2 = 3F1	λ2 = λ1/3
F3	Fifth harmonic	Second overtone	F3 = 5F1	λ3 = λ1/5
Fn	Nth harmonic†	(Nth - 1)/2 overtone	F(n-1)/2 = nF1	λn = λ1/n

* such as a pipe with one end open and one end closed
†In this case only the odd harmonics resonate, so n is an odd integer.

V_s: velocity of sound

• dependent on qualities of the medium transmitting the sound, (the air) such as its density, temperature, and “springiness.” A complicated equation, we concentrate only on temperature.
• increases as temperature increases (molecules move faster.)
• is higher for liquids and solids than for gasses (molecules are closer together.)
• for “room air” is 340 meters per second (m/s).
• Speed of sound is 343 meters per second at 20 degrees C. Based on the material sound is passing through and the temperature, the speed of sound changes.

---

Standing waves

$\|{\vec {v}}\|={\sqrt {\frac {\|{\vec {T}}\|}{\mu }}}$

Wave speed is equal to the square root of tension divided by the linear density of the string.

μ = m/L

Linear density of the string is equal to the mass divided by the length of the string.

λmax = 2L

The fundamental wavelength is equal to two times the length of the string.

Variables

λ: wavelength (m) λmax: fundamental wavelength (m) μ: linear density (g/m) v: wave speed (m/s) F: force (N) m: mass (kg) L: length of the string (m) l: meters (m)

Definition of terms

Tension (F): (not frequency) in the string (t is used for time in these equations). Units: newtons (N) Linear density (μ): of the string, Greek mu. Units: grams per meter (g/m) Velocity (v) of the wave (m/s) Mass (m): Units: grams (g). (We would use kilograms but they are too big for most strings). Length of the string (L): Units: meters (m)

Fundamental frequency: the frequency when the wavelength is the longest allowed, this gives us the lowest sound that we can get from the system.

In a string, the length of the string is half of the largest wavelength that can create a standing wave, called its fundamental wavelength.

Sound is defined as mechanical sinosodial vibratory longitudinal impulse waves which oscillate the pressure of a transmitting medium by means of adiabatic compression and decompression consequently resulting in the increase in the angular momentum and hence rotational kinetic energy of the particles present within the transmitting medium producing frequencies audible within hearing range, that is between the threshold of audibility and the threshold of pain on a Fletchford Munson equal loudness contour diagram.

Intro

When two glasses collide, we hear a sound. When we pluck a guitar string, we hear a sound.

Different sounds are generated from different sources. Generally speaking, the collision of two objects results in a sound.

Sound does not exist in a vacuum; it travels through the materials of a medium. Sound is a longitudinal wave in which the mechanical vibration constituting the wave occurs along the direction of the wave's propagation.

The velocity of sound waves depends on the temperature and the pressure of the medium. For example, sound travels at different speeds in air and water. We can therefore define sound as a mechanical disturbance produced by the collision of two or more physical quantities from a state of equilibrium that propagates through an elastic material medium.

Sound

$decibel(\mathrm {dB} )=10\cdot \log \left({\frac {I_{1}}{I_{0}}}\right)$

Fig. 1: The Fletcher-Munson equal-loudness contours. Phons are labelled in blue.

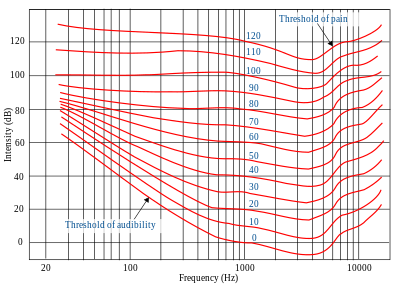
The amplitude is the magnitude of sound pressure change within a sound wave. Sound amplitude can be measured in pascals (Pa), though its more common to refer to the sound (pressure) level as Sound intensity(dB,dBSPL,dB(SPL)), and the perceived sound level as Loudness(dBA, dB(A)). Sound intensity is flow of sound energy per unit time through a fixed area. It has units of watts per square meter. The reference Intensity is defined as the minimum Intensity that is audible to the human ear, it is equal to 10^-12 W/m², or one picowatt per square meter. When the intensity is quoted in decibels this reference value is used. Loudness is sound intensity altered according to the frequency response of the human ear and is measured in a unit called the A-weighted decibel (dB(A), also used to be called phon).

The Decibel

The decibel is not, as is commonly believed, the unit of sound. Sound is measured in terms of pressure. However, the decibel is used to express the pressure as very large variations of pressure are commonly encountered. The decibel is a dimensionless quantity and is used to express the ratio of one power quantity to another. The definition of the decibel is $10\cdot \log _{10}\left({\frac {x}{x_{0}}}\right)$, where x is a squared quantity, ie pressure squared, volts squared etc. The decibel is useful to define relative changes. For instance, the required sound decrease for new cars might be 3 dB, this means, compared to the old car the new car must be 3 dB quieter. The absolute level of the car, in this case, does not matter.

$I_{0}=10^{-12}{\mbox{ W}}/{\mbox{m}}^{2}$

Definition of terms

Intensity (I): the amount of energy transferred through 1 m2 each second. Units: watts per square meter

Lowest audible sound: I = 0 dB = 10-12 W/m2 (A sound with dB < 0 is inaudible to a human.) Threshold of pain: I = 120 dB = 10 W/m2

Sample equation: Change in sound intensity
Δβ = β₂ - β₁
= 10 log(I₂/I₀) - 10 log(I₁/I₀)
= 10 [log(I₂/I₀) - log(I₁/I₀)]
= 10 log[(I₂/I₀)/(I₁/I₀)]
= 10 log(I₂/I₁)
where log is the base-10 logarithm.

Doppler effect

$f'=f\,{\frac {v\pm v_{0}}{v\mp v_{s}}}$

f' is the observed frequency, f is the actual frequency, v is the speed of sound ($v=336+0.6T$), T is temperature in degrees Celsius $v_{0}$ is the speed of the observer, and $v_{s}$ is the speed of the source. If the observer is approaching the source, use the top operator (the +) in the numerator, and if the source is approaching the observer, use the top operator (the -) in the denominator. If the observer is moving away from the source, use the bottom operator (the -) in the numerator, and if the source is moving away from the observer, use the bottom operator (the +) in the denominator.

Example problems

A. An ambulance, which is emitting a 400 Hz siren, is moving at a speed of 30 m/s towards a stationary observer. The speed of sound in this case is 339 m/s.

$f'=400\,\mathrm {Hz} \left({\frac {339+0}{339-30}}\right)$

B. An M551 Sheridan, moving at 10 m/s is following a Renault FT-17 which is moving in the same direction at 5 m/s and emitting a 30 Hz tone. The speed of sound in this case is 342 m/s.

$f'=30\,\mathrm {Hz} \left({\frac {342+10}{342+5}}\right)$

Introduction

Thermodynamics deals with the movement of heat and its conversion to mechanical and electrical energy among others.

Laws of Thermodynamics

First Law

The First Law is a statement of conservation of energy law:

$\Delta U=Q-W$

The First Law can be expressed as the change in internal energy of a system ($\Delta U$) equals the amount of energy added to a system (Q), such as heat, minus the work expended by the system on its surroundings (W).

If Q is positive, the system has gained energy (by heating).

If W is positive, the system has lost energy from doing work on its surroundings.

As written the equations have a problem in that neither Q or W are state functions or quantities which can be known by direct measurement without knowing the history of the system.

In a gas, the first law can be written in terms of state functions as

$dU=Tds-pdV$

Zero-th Law

After the first law of Thermodynamics had been named, physicists realised that there was another more fundamental law, which they termed the 'zero-th'.

This is that:

If two bodies are at the same temperature, there is no resultant heat flow between them.

An alternate form of the 'zero-th' law can be described:

If two bodies are in thermal equilibrium with a third, all are in thermal equilibrium with each other.

This second statement, in turn, gives rise to a definition of Temperature (T):

Temperature is the only thing that is the same between two otherwise unlike bodies that are in thermal equilibrium with each other.

Second Law

This law states that heat will never of itself flow from a cold object to a hot object.

$S=k_{B}\cdot ln(\Omega )$

where $k_{B}$ is the Boltzmann constant ($k_{B}=1.380658\cdot 10^{-23}{\mbox{ kg m}}^{2}{\mbox{ s}}^{-2}{\mbox{ K}}^{-1}$) and $\Omega$ is the partition function, i. e. the number of all possible states in the system.

This was the statistical definition of entropy, there is also a "macroscopic" definition:

$S=\int {\frac {\mathrm {d} Q}{T}}$

where T is the temperature and dQ is the increment in energy of the system.

Third Law

The third law states that a temperature of absolute zero cannot be reached.

Temperature Scales

There are several different scales used to measure temperature. Those you will most often come across in physics are degrees Celsius and kelvins.

Celsius temperatures use the symbol Θ. The symbol for degrees Celsius is °C. Kelvin temperatures use the symbol T. The symbol for kelvins is K.

The Celsius Scale

The Celsius scale is based on the melting and boiling points of water.

The temperature for freezing water is 0 °C. This is called the freezing point

The temperature of boiling water is 100 °C. This is called the steam point.

The Celsius scale is sometimes known as 'Centigrade', but the CGPM chose degrees Celsius from among the three names then in use way back in 1948, and centesimal and centigrade should no longer be used. See Wikipedia for more details.

The Kelvin Scale

The Kelvin scale is based on a more fundamental temperature than the melting point of ice. This is absolute zero (equivalent to −273.15 °C), the lowest possible temperature anything could be cooled to—where the kinetic energy of any system is at its minimum. The Kelvin scale was developed from an observation on how the pressure and volume of a sample of gas changes with temperature- PV/T is a constant. If the temperature ( T)was reduced, then the pressure ( P) exerted by Volume (V) the Gas would also reduce, in direct proportion. This is a simple experiment and can be carried out in most school labs. Gases were assumed to exert no pressure at -273 degree Celsius. ( In fact all gases will have condensed into liquids or solids at a somewhat higher temperature)

Although the Kelvin scale starts at a different point to Celsius, its units are of exactly the same size.

Therefore:

Temperature in kelvins (K) = Temperature in degrees Celsius (°C) + 273.15

Specific Latent Heat

Energy is needed to break bonds when a substance changes state. This energy is sometimes called the latent heat. Temperature remains constant during changes of state.

To calculate the energy needed for a change of state, the following equation is used:

Heat transferred, ΔQ (J) = Mass, m (kg) x specific latent heat capacity, L (J/kg)

The specific latent heat, L, is the energy needed to change the state of 1 kg of the substance without changing the temperature.

The latent heat of fusion refers to melting. The latent heat of vapourisation refers to boiling.

Specific Heat Capacity

The specific heat capacity is the energy needed to raise the temperature of a given mass by a certain temperature.

The change in temperature of a substance being heated or cooled depends on the mass of the substance and on how much energy is put in. However, it also depends on the properties of that given substance. How this affects temperature variation is expressed by the substance's specific heat capacity (c). This is measured in J/(kg·K) in SI units.

Change in internal energy, ΔU (J) = mass, m (kg) x specific heat capacity, c (J/(kg·K)) x temperature change, ΔT (K)

Electricity

$F={\frac {k\cdot q_{1}\cdot q_{2}}{r^{2}}}$

The force resulting from two nearby charges is equal to k times charge one times charge two divided by the square of the distance between the charges. This what force of attraction between to charged particle says, according to coulomb's law.

---

$E={\frac {F}{q}}$

The electric field created by a charge is equal to the force generated divided by the charge.

---

$E={\frac {k\cdot q}{r^{2}}}$

Electric field is equal to a constant, “k”, times the charge divided by the square of the distance between the charge and the point in question.

---

$U={\frac {k\cdot q_{1}\cdot q_{2}}{r}}$

Electric potential energy is equal to a constant, “k” multiplied by the two charges and divided by the distance between the charges.

---

Variables

F: Force (N) k: a constant, 8.988×109 (N·m2/C2) q1: charge one (C) q2: charge two (C) r: distance between the two charges, (m)

Electricity acts as if all matter were divided into four categories:

1. Superconductors, which allow current to flow with no resistance. (However these have only been produced in relatively extreme laboratory conditions, such as at temperatures approaching absolute zero)
2. Conductors, which allow electric current to flow with little resistance.
3. Semiconductors, which allow some electric current to flow but with significant resistance.
4. Insulators, which do not allow electric current to flow.

Charges are positive (+) or negative (-). Any two like charges repel each other, and opposite charges attract each other.

Electric fields

A charge in an electrical field feels a force. The charge is not a vector, but force is a vector, and so is the electric field. If a charge is positive, then force and the electric field point in the same direction. If the charge is negative, then the electric field and force vectors point in opposite directions.

A point charge in space causes an electric field. The field is stronger closer to the point and weaker farther away.

Electricity is made of subatomic particles called Electrons and so are Electric Fields and Magnetic Fields. One must also note that electrical fields come under the category of spherical fields as the inverse square law may be applied to the electrical field. This means that the electrical force, exhibited by the electrical field emitted by the subatomic electron charge (-), acting upon a body is inversely proportional to the distance between the center point of the electric field (subatomic electron) and the body on which the electric force is acting upon.

An electric circuit is composed of conducting wires (through which an electric current flows through), a key or switch which is utilized to open and close the circuit, components which transfer electrical energy to a form of energy required by the component and an electromotive source (such as a voltaic cell). A voltaic cell is an electromotive source in which are present two plates, zinc and copper, placed in dilute sulphuric acid. Whence the circuit is closed the zinc reacts with the sulphuric acid to produce zinc sulphate. The electromotive force which discharges the electrical energy in the electric current is considered to be originated on the surface of the zinc plate in the voltaic cell. However, depending upon the cell, closing the circuit gives rise to polarization, accumulation of hydrogen bubbles on the surface of the copper plate which seriously interferes with the movement of electricity and reduces the magnitude of the electromotive force. For this reason Leclanché cells are utilized. Consisting of similar characteristics as that of the voltaic cell however a Mage difference is present. Instead of the use of copper plates, a carbon plate is used. For this reason, magneze dioxide may be placed on the carbon to react to form a compound which whence in contact with hydrogen bubbles will turn the hydrogen into water, hence increasing the size of the electromotive force produced by the cell. The resistance encountered in conducting wires: Inversely proportional to the diameter of the conducting wire. Directly proportional to the length of the conducting wire. Varies with different substances. Varies with temperature of the conducting wire.

In order to maintain a constant flow of an electric current a constant expenditure of chemical or mechanical energy is required. An electric current is accompanied by an electric field and a magnetic field. A device employed into determining the presence of an electric current is known as a galvanoscope. The conducting wire through which the electric current flows through is he led over and parallel to the galvanoscope the magnetoscope preset inside of the galvanoscope being deflected in the opposite direction to which the electric current flows in. So with the aid of a galvanoscope one may not only deduce the magnetic properties of an electric current, the exhibition of a magnetic field, but the direction in which the current flows through. An electromotive force may also be generators by a dynamo. A rotating magnet present inside of a helix. The magnetic properties of electric currents may be used to construct magnets. An electromagnet is commonly described as a mass of iron on which is placed a helix/solenoid through which flows an electric current. The magnetic field emitted by the electric current is increased if the solenoid is placed around a magnetic mass of iron or any other substance possessing magnetic properties, that is the magnetic field of the iron is added to that of the electic current producing a more powerful magnetic field. Conductors may be arranged in two variants. Series and parallel circuits. In series, the current passes through each conductor in turn, where Ohm's law changes to I = nE/(nr + R), where I is the current intensity, n is the number of cells arranged in series in the circuit, E is the electromotive force applied to the circuit, r is the internal resistance ( the resistance the current that is produced in the cell experiences whence passing from the zinc plate to the copper or carbon plate through the sulphuric acid ) and R is the external resistance.

• For a good introduction to Gauss' Law and Ampere's Law, check out this website

Magnetism

${\boldsymbol {F}}_{B}=q{\boldsymbol {v}}\times {\boldsymbol {B}}$

The magnetic force exerted on a moving particle in a magnetic field is the cross product of the magnetic field and the velocity of the particle, multiplied by the charge of the particle.

---

Because the magnetic force is perpendicular to the particle's velocity, this causes uniform circular motion. That motion can be explained by the following

$r={\frac {mv}{qB}}$

The radius of this circle is directly proportional to the mass and the velocity of the particle and inversely proportional to the charge of the particle and the field strength of the magnetic field.

$T={\frac {2\pi m}{qB}}$

$f={\frac {qB}{2\pi m}}={\frac {v}{2\pi r}}$

The period and frequency of this motion (referred to as the cyclotron period and frequency) can be derived as well.

---

$B={\frac {\mu _{0}I}{2\pi y}}$

The magnetic field created by charge flowing through a straight wire is equal to a constant, ${\frac {\mu _{0}}{2\pi }}$, multiplied by the current flowing through the wire and divide by the distance from the wire.

$B={\frac {\mu _{0}\mu }{4\pi x^{3}}}$

The magnetic field created by a magnetic dipole (at distances much greater than the size of the dipole) is approximately equal to a constant, ${\frac {\mu _{0}}{4\pi }}$, multiplied by the dipole moment divided by the cube of the distance from the dipole. EDIT: This forumla is incomplete. The field from a dipole is a vector that depends not only on the distance from the dipole, but also the angle relative to the orientation of the magnetic moment. This is because of the vector nature of the magnetic moment and its associated magnetic field. The field component pointing in the same directions as the magnetic moment is the above formula multiplied by (3*(Cos[theta])^2-1).

$B=\mu _{0}nI$

The magnetic field created by an ideal solenoid is equal to a constant, $\mu _{0}$, times the number of turns of the solenoid times the current flowing through the solenoid.

$B={\frac {\mu _{0}nI}{2\pi r}}$

The magnetic field created by an ideal toroid is equal to a constant, $\mu _{0}$, times the number of turns of the toroid times the current flowing through the toroid divided by the circumference of the toroid.

---

$F_{B}={\frac {\mu _{0}I_{1}I_{2}\ell }{2\pi d}}$

The magnetic force between two wires is equal to a constant, ${\frac {\mu _{0}}{2\pi }}$, times the current in one wire times the current in the other wire times the length of the wires divided by the distance between the wires.

$\tau =I{\vec {A}}\times {\vec {B}}$

The torque on a current loop in a magnetic field is equal to the cross product of the magnetic field and the area enclosed by the current loop (the area vector is perpendicular to the current loop).

---

${\vec {\mu }}=I{\vec {A}}n$

The dipole moment of a current loop is equal to the current in the loop times the area of the loop times the number of turns of the loop.

---

$U_{B}=-{\vec {\mu }}\cdot {\vec {B}}$

The magnetic potential energy is the opposite of the dot product of the magnetic field and the dipole moment.

Variables

F: Force (N) q: Charge (C) v: Velocity (m/s) B: Magnetic field (teslas (T)) r: Radius (m) m: Mass (kg) T: Period (s) f: Frequency (Hz) $\mu _{0}$: A constant, 4π×10-7 N/A y: Distance (m) $\mu$: Dipole moment x: Distance (m) n: Number of turns $\ell$: Length (m) d: Distance (m) $\tau$: Torque (N·m) A: Area (m2) U: Potential energy (J)

Electronics is the application of electromagnetic (and quantum) theory to construct devices that can perform useful tasks, from as simple as electrical heaters or light bulbs to as complex as the Large Hadron Collider.

Print version;component of electronics

Electronics

Introduction

To discuss electronics we need the basic concepts from electricity: charge, current which is flow of charge, and potential which is the potential energy difference between two places. Please make sure these concepts are familiar before continuing.

Circuits

The interest of electronics is circuits. A circuit consists of wires' that connect components. Typical components are resistors, voltage sources. In order to maintain a constant electrical current a continued exhaustion of chemical or mechanical energy is required.

A voltaic cell is a common electromotive power source for a circuit. It consists primarily of two plates, a positive copper plate and a negative zinc plate. One must note that the plates are placed in dilute sulfuric acid. Whence a key is switched or the circuit is closed the zinc reacts with the sulfuric in which it is placed in. One may discern that the electromotive force which is then applied to the circuit is believed to be converted from chemical to electrical energy upon the surface of the zinc cell. Whence the E.M.F is converted from chemical to electrical energy the electromotive force travels through the sulfuric acid. However disadvantages occur whence utilizing a voltaic or galvanic cell. Whence the circuit is closed, simultaneously hydrogen bubbles accumulate upon the copper plate surface hence decreasing the total electromotive power source applied to the circuit in question. The resistance with which the electromotive source encounters as it flows form the zinc plate to the copper plate through the dilute sulfuric acid is distinguished as internal resistance. Hence the voltaic cell uses diluted rather than concentrated sulfuric acid so as to reduce the internal resistance present inside of the component which applies the electromotive force to the circuit.

A circuit can be open, when there is a break so that no current can flow, or it can be closed, so that current can flow. These definitions allow us to discuss electronics efficiently.

Direct current and alternating Current

When the Electrons moves through a particular medium in straight without oscillating on their mean position then it is Direct Current. This DC is used in almost every electronical component. Alternating Current on the other hand as the name suggest, the Electrons alter back and forth and hence produces much electrical energy. AC is mainly used to reduce the wastage of electrons and passing much energy at one time.

Ohm's law

If 'V' is Potential Difference applied at two ends of conductor and 'I' is Current flowing through the conductor then 'I' is directly proportional to its 'V'. V = I x R

Kirchoff's laws

Kirchoff's laws generally hold for direct current (DC) circuits, but fail when dealing with changing electric current and voltage such as alternating current (AC) or signal processing in combination with capacitors, inductors, and antennas.

Kirchoff's current law

The sum of all the currents entering and leaving any point in a circuit is equal to zero.

$\sum _{k=1}^{n}I_{k}=0$

It is based on the assumption that current flows only in conductors, and that whenever current flows into one end of a conductor it immediately flows out the other end.

Kirchoff's voltage law

The sum of all the voltages around the circuit loop is equal to zero.

$\sum _{k=1}^{n}V_{k}=0$

It is based on the assumption that there is no fluctuating magnetic field linking the closed circuit loop.

Power

p=work done/time taken p=I*V (current * Voltage) Other Equations for P can also be derived using Ohm's Law, such as P = IR^2, because V=IR, which can be plugged in to get P= I * (IR) and another equation being P = V^2/R.

Resistors in series

In a series circuit, resistance increases as more resistors are added.Each resistor makes an addition to the restriction of the flow of charge.The current through the battery is inversely proportional to the total resistance. The equivalent(total) resistance is calculated by adding the resistances together. R$eq$=R$1$+R$2$+R$3$+--------

Resistors in parallel

1/R = 1/R1+1/R2+1/R3+......

Capacitors

$C={Q \over V}$

$C_{\rm {series}}=\sum _{n}{1 \over C_{n}}={1 \over C_{1}}+{1 \over C_{2}}+{1 \over C_{3}}+\cdots +{1 \over C_{n}}$

$C_{\rm {parallel}}=\sum _{n}C_{n}=C_{1}+C_{2}+C_{3}+\cdots +C_{n}$

Semiconductors

$I={\frac {Q}{T}}$

Current is the rate of flow of charge.

$I$ = Current [amperes - A]
$Q$ = Charge [coulombs - C]
$T$ = Time [seconds - s]

$V=IR\$

howstuffworks.com

Voltage is equal to current multiplied by resistance

Power is equal to the product of voltage and current

Electronics is the flow of current through semiconductor devices like silicon and germanium.

Semiconductor devices are those which behave like conductors at higher temperature.

Transistor, diode, SCR are some electronic devices.

Light

Light is that range of electromagnetic energy that is visible to the human eye, the visible colors. The optical radiation includes not only the visible range, but a broader range of invisible electromagnetic radiation that could be influenced in its radiation behavior in a similar way as the visible radiation, but needs often other transmitters or receivers for this radiation. Dependent on the kind of experimental question light - optical radiation behaves as a wave or a particle named lightwave or photon. The birth or death of photons needs electrons - electromagnetic charges, that change their energy.

The speed of light is fastest in the vacuum.

$c=299,792,458{\frac {m}{s}}$

In a wave we have to distinguish between the speed of transport of energy or the speed of the transport of on phase state of a wave of a defined frequency. In vacuum the speed of waves of any photon energy - wavelength is the same, but the transmission speed through material is dependent on wavelength - photon energy. At the time the measurement of the speed of light in vacuum reached the uncertainty of the unit of length, the meter, this basic unit got in 1960 a new definition, based on the unit of time. Taking the best known measurement values it was defined without any uncertainties of length, that the speed of light is 299,792,458 meters per second. For this reason the only uncertainty in the speed of light is the uncertainty of the realization of the unit of time, the second. (If you like to get the standard of length, cooperate with the watchmaker).

However, when electromagnetic radiation enters a medium with refractive index, $n$ , its speed would become

$c_{n}={\frac {c}{n}}$

where $c_{n}$ is the speed of light in the medium.

Refraction

Refraction occurs when light travels from one medium into another (i.e. from air into water). Refraction is the changing of direction of light due to the changing speed of light. Refraction occurs toward the normal when light travels from a medium into a denser medium. Example when light travels from air into a block of glass, light is refracted towards the normal. The ratio between the sine of the angle of the incident ray and sine of the angle of the refracted ray is the same as the ratios of the indexes of refraction.

${\frac {\sin(\theta _{i})}{\sin(\theta _{r})}}={\frac {n_{r}}{n_{i}}}\quad {\text{or}}\quad n_{i}\sin(\theta _{i})=n_{r}\sin(\theta _{r})$

This is known as Snell's Law - an easy way to remember this is that 'Snell' is 'lens' backwards.

Mirrors and lenses

Focal length

${\frac {1}{d_{i}}}+{\frac {1}{d_{o}}}={\frac {1}{f}}$

• $f$ is the focal length.
  • $f$ is negative in convex mirror and concave lens.
  • $f$ is positive in concave mirror and convex lens.
• $d_{i}$ is the distance from the image to the mirror or lens
  • For a mirror, it is positive if the image appears in front of the mirror. It is negative if the image appears behind.
  • For a lens, it is positive if the image appears on the opposite side of the lens as the light source. It is negative if the image appears on the same side of the lens as the light source.
• $d_{o}$ is the distance from the object to the mirror or the lens (always positive). The only case, when it is negative, is the case, when you don't have a real object, but you do have an imaginary object - a converging set of rays from another optical system.
• an easy way to remember the formula is to memorize "if I Do I Die", which stands for $1/f=1/d_{0}+1/d_{i}$

Magnification

$M={\frac {h_{i}}{h_{o}}}=-{\frac {d_{i}}{d_{o}}}$

• $M$ is the magnification.
  • If it is positive the image is upright
  • If it is negative the image is inverted
• $h_{i}$ is the image height.
• $h_{o}$ is the object height.
• $d_{i}$ is the distance from the image to the mirror or lens (also often $v$)
  • For a mirror, it is positive if the image appears in front of the mirror. It is negative if the image appears behind.
  • For a lens, it is positive if the image appears on the opposite side of the lens as the light source. It is negative if the image appears on the same side of the lens as the light source.
• $d_{o}$ is the distance from the object to the mirror or lens (also often $u$)

Commonly Used Physical Constants

Uncertainty should be read as 1.234(56) = 1.234$\pm$0.056

Name	Symbol	Value	Units	Relative Uncertainty
Speed of light (in vacuum)	$c$	$299\ 792\ 458$	$\mathrm {m} \ \mathrm {s} ^{-1}$	(exact)
Magnetic Constant	$\mu _{0}$	$4\pi \times 10^{-7}\approx 12.566\ 370\ 6\times 10^{-7}$	$\mathrm {N} \ \mathrm {A} ^{-2}$	(exact)
Electric Constant	$\varepsilon _{0}=1/\left(\mu _{0}c^{2}\right)$	$\approx 8.854\ 187\ 817\times 10^{-12}$	$\mathrm {F} \ \mathrm {m} ^{-1}$	(exact)
Newtonian Gravitaional Constant	$G$	$6.674\ 2(10)\times 10^{-11}$	$\mathrm {m} ^{3}\ \mathrm {kg} ^{-1}\ \mathrm {s} ^{-2}$	$1.5\times 10^{-4}$
Plank's Constant	$h$	$6.626\ 069\ 3(11)\times 10^{-34}$	$\mathrm {J} \ \mathrm {s}$	$1.7\times 10^{-7}$
Elementary charge	$e$	$1.602\ 176\ 53(14)\times 10^{-19}$	$\mathrm {C}$	$8.5\times 10^{-8}$
Mass of the electron	$m_{e}$	$9.109\ 382\ 6(16)\times 10^{-31}$	$\mathrm {kg}$	$1.7\times 10^{-7}$
Mass of the proton	$m_{p}$	$1.672\ 621\ 71(29)\times 10^{-27}$	$\mathrm {kg}$	$1.7\times 10^{-7}$
Fine structure constant	$\alpha ={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}}$	$7.297\ 352\ 568(24)\times 10^{-3}$	dimensionless	$3.3\times 10^{-9}$
Molar gass constant	$R$	$8.314\ 472(15)$	$\mathrm {J} \ \mathrm {mol} ^{-1}\ \mathrm {K} ^{-1}$	$1.7\times 10^{-6}$
Boltzmann's constant	$k$	$1.380\ 650\ 5(24)\times 10^{-23}$	$\mathrm {J} \ \mathrm {K} ^{-1}$	$1.8\times 10^{-6}$
Avogadro's Number	$N_{\text{A}},L$	$6.022\ 141\ 5(10)\times 10^{23}$	$\mathrm {mol} ^{-1}$	$1.7\times 10^{-7}$
Rydberg constant	$R_{\infty }$	$10\ 973\ 731.568\ 525(73)$	$\mathrm {m} ^{-1}$	$6.6\times 10^{-12}$
Standard acceleration of gravity	$g$	$9.806\ 65$	$\mathrm {m} \ \mathrm {s} ^{-2}$	defined
Atmospheric pressure	$\mathrm {atm}$	$101\ 325$	$\mathrm {Pa}$	defined
Bohr Radius	$a_{0}\$	$0.529\ 177\ 208\ 59(36)\times 10^{-10}\$	$\mathrm {m} \$	$6.8\times 10^{-10}$
Electron Volt	$eV$	$1.602\ 176\ 53(14)\times 10^{-19}$	$\mathrm {J}$	$8.7\times 10^{-8}$
Luminous efficacy of monochromatic radiation	$K_{cd}$	$683$	$\mathrm {lm/W}$	(exact)
hyperfine transition frequency of Cs-133	$\Delta \nu _{\text{Cs}}$	$9\ 192\ 631\ 770$	$\mathrm {Hz}$	(exact)
Reduced Planck constant	$\hbar =h/2\pi$	$1.054\ 571\ 817\times {10}^{-34}$	$\mathrm {J} \cdot \mathrm {s}$	(exact)
atomic mass of Carbon 12	$m({}^{12}{\text{C}})$	$1.992\ 646\ 879\ 92(60)\times {10}^{-26}$	$\mathrm {kg}$
molar mass of Carbon-12	$M({}^{12}{\text{C}})=N_{\text{A}}m({}^{12}{\text{C}})$	$11.999\ 999\ 9958(36)\times {10}^{-3}$	$\mathrm {kg\cdot {mol}^{-1}}$
atomic mass constant	$m_{\text{u}}=m({}^{12}{\text{C}})/12=1\,{\text{Da}}$	$1.660\ 539\ 066\ 60(50)\times {10}^{-27}$	$\mathrm {kg}$
molar mass constant	$M_{\text{u}}=M({}^{12}{\text{C}})/12=N_{\text{A}}m_{\text{u}}$	$0.999\ 999\ 999\ 65(30)\times {10}^{-3}$	$\mathrm {kg\cdot {mol}^{-1}}$
molar volume of silicon	$V_{m}(\mathrm {Si} )$	$1.205\ 883\ 199(60)\times {10}^{-5}$	$\mathrm {m^{3}\cdot {mol}^{-1}}$
molar Planck constant	$N_{\text{A}}h$	$3.990\ 312\ 712\ldots {10}^{-10}$	$\mathrm {J\cdot {Hz}^{-1}\cdot {mol}^{-1}}$
Stefan-Boltzmann constant	$\sigma =\pi ^{2}k_{B}^{4}/60\hbar ^{3}c^{2}$	$5.670\ 374\ 419\ldots \times {10}^{-8}$	$\mathrm {W\cdot m^{-2}\cdot K^{-4}}$
first radiation constant	$c_{1}=2\pi hc^{2}$	$3.741\ 771\ 852\ldots {10}^{-16}$	$\mathrm {W\cdot m^{2}}$
first radiation constant for spectral radiance	$c_{\text{1L}}=2hc^{2}/sr$	$1.191\ 042\ 972\ 397\ 188\ 414\ 079\ 4892\times {10}^{-16}$	$\mathrm {W\cdot m^{2}{sr}^{-1}}$
second radiation constant	$c_{2}=hc/k_{B}$	$1.438\ 776\ 877\ldots \times {10}^{-2}$	$\mathrm {m\cdot K}$
Wien wavelength displacement constant	$b$	$2.897\ 771\ 955\ldots \times {10}^{-3}$	$\mathrm {m\cdot K}$
Wien frequency displacement constant	$b'=c/b$	$5.878\ 925\ 757\ \times {10}^{10}$	$\mathrm {Hz\cdot K^{-1}}$
Wien entropy displacement constant	$b_{\text{entropy}}$	$3.002\ 916\ 077\ldots \times {10}^{-3}$	$\mathrm {m\cdot K}$
Faraday constant	$F=N_{\text{A}}e$	$96\ 485.332\ 123\ 310\ 0184$	$\mathrm {C\cdot {mol}^{-1}}$

To Be Merged Into Table

This list is prepared in the format

• Constant (symbol) : value

---

• Coulomb's Law Constant (k) : 1/(4 π ε₀) = 9.0 × 10⁹ N·m²/C²
• Faraday constant (F)  : 96,485 C·mol⁻¹
• Mass of a neutron (m_n) : 1.67495 × 10⁻²⁷ kg
• Mass of Earth : 5.98 × 10²⁴ kg
• Mass of the Moon : 7.35 × 10²² kg
• Mean radius of Earth : 6.37 × 10⁶ m
• Mean radius of the Moon : 1.74 × 10⁶ m
• Dirac's Constant ($\hbar$) : $h/(2\pi )$ = 1.05457148 × 10⁻³⁴ J·s
• Speed of sound in air at STP : 3.31 × 10² m/s
• Unified Atomic Mass Unit (u) : 1.66 × 10⁻²⁷ kg

Item	Proton	Neutron	Electron
Mass	1	1	Negligible
Charge	+1	0	-1

See Also

Wiki-links

• Wikipedia Article

External Links

• NIST Physics Lab

Approximate Coefficients of Friction

Material	Kinetic	Static
Rubber on concrete (dry)	0.68	0.90
Rubber on concrete (wet)	0.58	-.--
Rubber on asphalt (dry)	0.72	0.68
Rubber on asphalt (wet)	0.53	-.--
Rubber on ice	0.15	0.15
Waxed ski on snow	0.05	0.14
Wood on wood	0.30	0.42
Steel on steel	0.57	0.74
Copper on steel	0.36	0.53
Teflon on teflon	0.04	-.--

About the Common uses in Physics

While these are indeed common usages, it should be pointed out that there are many other usages and that other letters are used for the same purpose. The reason is quite simple: there are only so many symbols in the Greek and Latin alphabets, and scientists and mathematicians generally do not use symbols from other languages. It is a common trap to associate a symbol exclusively with some particular meaning, rather than learning and understanding the physics and relations behind it.

Greek Alphabet

Capital	Lower case	Name	Common use in Physics
$\mathrm {A}$	$\alpha$	alpha	Angular acceleration Linear expansion Coefficient Alpha particle (helium nucleus) Fine Structure Constant
$\mathrm {B}$	$\beta$	beta	Beta particle — high energy electron Sound intensity
$\Gamma$	$\gamma$	gamma	Gamma ray (high energy EM wave) Ratio of heat capacities (in an ideal gas) Relativistic correction factor Shear strain
$\Delta$	$\delta$	delta	Δ="Change in" δ="Infinitesimal change in (), also used to denote the Dirac delta function (reference needed)"
$\mathrm {E}$	$\epsilon$	epsilon	Emissivity Strain (Direct e.g. tensile or compression) Permittivity EMF
$\mathrm {Z}$	$\zeta$	zeta	(no common use)
$\mathrm {H}$	$\eta$	eta	Viscosity Energy efficiency
$\Theta$	$\theta$	theta	Angle (°, rad) Temperature
$\mathrm {I}$	$\iota$	iota	The lower case $\iota \;$ is rarely used, while $\mathrm {I}$ is sometimes used for the identity matrix or the moment of inertia. Note that $\iota$ is not to be confused with the Roman character $i$ (which has a dot and is much more widely used in mathematics and physics).
$\mathrm {K}$	$\kappa$	kappa	Spring constant Dielectric constant
$\Lambda$	$\lambda$	lambda	Wavelength Thermal conductivity Constant Eigenvalue of a matrix Linear density
$\mathrm {M}$	$\mu$	mu	Coefficient of friction Electrical mobility Reduced mass Permeability
$\mathrm {N}$	$\nu$	nu	Frequency
$\Xi$	$\xi$	xi	Damping cofficient
$\mathrm {O}$	$\mathrm {o}$	omicron	(no common use)
$\Pi$	$\pi$	pi	Product symbol $\Pi$ Circle number $\pi :=3.14159...$
$\mathrm {P}$	$\rho$	rho	Volume density Resistivity
$\Sigma$	$\sigma$	sigma	Sum symbol Boltzmann constant Electrical conductivity Uncertainty Stress (Direct e.g. tensile, compression) Surface density
$\mathrm {T}$	$\tau$	tau	Torque Tau particle (a lepton) Time constant Shear stress
$\Upsilon$	$\upsilon$	upsilon	mass to light ratio
$\Phi$	$\phi$	phi	Magnetic/electric flux Angle (°, rad)
$\mathrm {X}$	$\chi$	chi	Rabi frequency (lasers) Susceptibility
$\Psi$	$\psi$	psi	Wave function
$\Omega$	$\omega$	omega	Ohms (unit of electrical resistance) ω Angular velocity

See Also

Greek alphabet on Wikipedia

Greek letters used in mathematics, science, and engineering

Review of logs

Been a while since you used logs? Here is a quick refresher for you.

The log (short for logarithm) of a number N is the exponent used to raise a certain "base" number B to get N. In short, $\log _{B}\ N=x$ means that $B^{x}=N$.

Typically, logs use base 10. An increase of "1" in a base 10 log is equivalent to an increase by a power of 10 in normal notation. In logs, "3" is 100 times the size of "1". If the log is written without an explicit base, 10 is (usually) implied.

$y=10^{x}\ \mathrm {or} \ \log _{10}y=x\$

therefore: log(10–12) = –12

also: log(1000) = 3

Another common base for logs is the trancendental number $e$, which is approximately 2.7182818.... Since ${\frac {d}{dx}}e^{x}=e^{x}$, these can be more convenient than $\log _{10}$. Often, the notation $\ln \ x$ is used instead of $\log _{e}\ x$.

The following properties of logs are true regardless of whether the base is 10, $e$, or some other number.

logA + logB = log(AB) logA – logB = log(A/B) log(AB) = B log(A)

Adding the log of A to the log of B will give the same result as taking the log of the product A times B.

Subtracting the log of B from the log of A will give the same result as taking the log of the quotient A divided by B.

The log of (A to the Bth power) is equal to the product (B times the log of A).

A few examples:
log(2) + log(3) = log(6)
log(30) – log(2) = log(15)
log(8) = log(2³) = 3log(2) Vectors are quantities that are characterized by having both a numerical quantity (called the "magnitude" and denoted as |v|) and a direction. Velocity is an example of a vector; it describes the time rated change in position with a numerical quantity (meters per second) as well as indicating the direction of movement.

The definition of a vector is any quantity that adds according to the parallelogram law (there are some physical quantities that have magnitude and direction that are not vectors).

Scalars are quantities in physics that have no direction. Mass is a scalar; it can describe the quantity of matter with units (kilograms) but does not describe any direction.

Multiplying vectors and scalars

• A scalar times a scalar gives a scalar result.
• A vector scalar-multiplied by a vector gives a scalar result (called the dot-product).
• A vector cross-multiplied by a vector gives a vector result (called the cross-product).
• A vector times a scalar gives a vector result.

Frequently Asked Questions about Vectors

When are scalar and vector compositions essentially the same?

Answer: when multiple vectors are in same direction then we can just add the magnitudes.so, the scalar and vector composition will be same as we do not add the directions.

What is a "dot-product"? (work when force not parallel to displacement)

A Man walking up a hill

Answer: Let's take gravity as our force. If you jump out of an airplane and fall you will pick up speed. (for simplicity's sake, let's ignore air drag). To work out the kinetic energy at any point you simply multiply the value of the force caused by gravity by the distance moved in the direction of the force. For example, a 180 N boy falling a distance of 10 m will have 1800 J of extra kinetic energy. We say that the man has had 1800 J of work done on him by the force of gravity.

Notice that energy is not a vector. It has a value but no direction. Gravity and displacement are vectors. They have a value plus a direction. (In this case, their directions are down and down respectively) The reason we can get a scalar energy from vectors gravity and displacement is because, in this case, they happen to point in the same direction. Gravity acts downwards and displacement is also downwards.

When two vectors point in the same direction, you can get the scalar product by just multiplying the value of the two vectors together and ignoring the direction.

But what happens if they don't point in the same direction?

Consider a man walking up a hill. Obviously it takes energy to do this because you are going against the force of gravity. The steeper the hill, the more energy it takes every step to climb it. This is something we all know unless we live on a salt lake.

In a situation like this we can still work out the work done. In the diagram, the green lines represent the displacement. To find out how much work against gravity the man does, we work out the projection of the displacement along the line of action of the force of gravity. In this case it's just the y component of the man's displacement. This is where the cos θ comes in. θ is merely the angle between the velocity vector and the force vector.

If the two forces do not point in the same direction, you can still get the scalar product by multiplying the projection of one force in the direction of the other force. Thus:

${\vec {a}}\cdot {\vec {b}}\equiv \|{\vec {a}}\|\ \|{\vec {b}}\|\ \cos \theta$

There is another method of defining the dot product which relies on components.

${\vec {a}}\cdot {\vec {b}}\equiv a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}$

What is a "cross-product"? (Force on a charged particle in a magnetic field)

Answer: Suppose there is a charged particle moving in a constant magnetic field. According to the laws of electromagnetism, the particle is acted upon by a force called the Lorentz force. If this particle is moving from left to right at 30 m/s and the field is 30 Tesla pointing straight down perpendicular to the particle, the particle will actually curve in a circle spiraling out of the plane of the two with an acceleration of its charge in coulombs times 900 newtons per coulomb! This is because the calculation of the Lorentz force involves a cross-product.when cross product can replace the sin0 can take place during multiplication. A cross product can be calculated simply using the angle between the two vectors and your right hand. If the forces point parallel or 180° from each other, it's simple: the cross-product does not exist. If they are exactly perpendicular, the cross-product has a magnitude of the product of the two magnitudes. For all others in between however, the following formula is used:

$\left\|{\vec {a}}\times {\vec {b}}\right\|=\left\|{\vec {a}}\right\|\ \left\|{\vec {b}}\right\|\sin \theta$

The right-hand rule: point your index finger along the first vector and your middle finger across the second; your thumb will point in the direction of the resulting vector

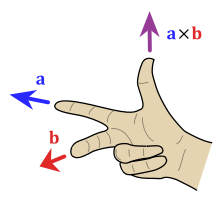
But if the result is a vector, then what is the direction? That too is fairly simple, utilizing a method called the "right-hand rule".

The right-hand rule works as follows: Place your right-hand flat along the first of the two vectors with the palm facing the second vector and your thumb sticking out perpendicular to your hand. Then proceed to curl your hand towards the second vector. The direction that your thumb points is the direction that cross-product vector points! Though this definition is easy to explain visually it is slightly more complicated to calculate than the dot product.

$(a_{x},\ a_{y},\ a_{z})\times (b_{x},\ b_{y},\ b_{z})=(a_{y}b_{z}-a_{z}b_{y}\ ,a_{x}b_{z}-a_{z}b_{x}\ ,a_{x}b_{y}-a_{y}b_{x})$

How to draw vectors that are in or out of the plane of the page (or board)

How to draw vectors in the plane of the paper

Standard symbols of a vector going into or out of a page

Answer: Vectors in the plane of the page are drawn as arrows on the page. A vector that goes into the plane of the screen is typically drawn as circles with an inscribed X. A vector that comes out of the plane of the screen is typically drawn as circles with dots at their centers. The X is meant to represent the fletching on the back of an arrow or dart while the dot is meant to represent the tip of the arrow.

GNU Free Documentation License

Version 1.3, 3 November 2008 Copyright (C) 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. <http://fsf.org/>

Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.

0. PREAMBLE

The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.

This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.

We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.

1. APPLICABILITY AND DEFINITIONS

This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.

A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.

A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.

The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.

The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.

A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".

Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.

The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.

The "publisher" means any person or entity that distributes copies of the Document to the public.

A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.

The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.

2. VERBATIM COPYING

You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.

You may also lend copies, under the same conditions stated above, and you may publicly display copies.

3. COPYING IN QUANTITY

If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.

If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.

If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.

It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.

4. MODIFICATIONS

You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:

1. Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
2. List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
3. State on the Title page the name of the publisher of the Modified Version, as the publisher.
4. Preserve all the copyright notices of the Document.
5. Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
6. Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
7. Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
8. Include an unaltered copy of this License.
9. Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
10. Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
11. For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
12. Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
13. Delete any section Entitled "Endorsements". Such a section may not be included in the Modified version.
14. Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
15. Preserve any Warranty Disclaimers.

If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.

You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.

You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.

The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.

5. COMBINING DOCUMENTS

You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.

The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.

In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements".

6. COLLECTIONS OF DOCUMENTS

You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.

You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.

7. AGGREGATION WITH INDEPENDENT WORKS

A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.

If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.

8. TRANSLATION

Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.

If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.

9. TERMINATION

You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.

However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.

Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.

Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.

10. FUTURE REVISIONS OF THIS LICENSE

The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.

Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Document.

11. RELICENSING

"Massive Multiauthor Collaboration Site" (or "MMC Site") means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A "Massive Multiauthor Collaboration" (or "MMC") contained in the site means any set of copyrightable works thus published on the MMC site.

"CC-BY-SA" means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.

"Incorporate" means to publish or republish a Document, in whole or in part, as part of another Document.

An MMC is "eligible for relicensing" if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.

The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.

How to use this License for your documents

To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:

Copyright (c) YEAR YOUR NAME.

Permission is granted to copy, distribute and/or modify this document

under the terms of the GNU Free Documentation License, Version 1.3

or any later version published by the Free Software Foundation;

with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.

A copy of the license is included in the section entitled "GNU

Free Documentation License".

If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:

with the Invariant Sections being LIST THEIR TITLES, with the

Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.

If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.

If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.