Communication Systems/Antennas
Antennas
[edit | edit source]The purpose of an antenna is to collect and convert electromagnetic waves to electronic signals. Transmission lines then guide these to the receiver front end.
The relevant electric fields associated with an antenna are extremely complex and have the general form:
where Idz = moment of differential current element in rms amp meters
- r = distance in meters
The near field or Fresnel region consists of three fields.
The electrostatic (1/r3) and inductive (1/r2) fields fall off in intensity quite quickly. The far field or Fraunhoffer region consists entirely of the (j/r) radiated field. This article will only consider this radiated field.
Although most antennas are simply a piece of bent wire, their interaction with electromagnetic fields is quite complex, and a whole array of terms is needed to characterize them:
- Beamwidth: the angle defines by the radiation pattern where the signal strength drops 3 dB of its maximum value in a given plane.
- Polarization: the plane of electric field polarization with respect to the earth.
- Gain: a figure of merit used to quantify the signal capturing ability of the antenna. It is closely related to directivity and beamwidth.
- Effective area: a measure of the antenna’s ability to collect energy. It is related to gain by the expression: .
- Input impedance: The impedance, which is necessary in the receiver for maximum power transfer to occur.
- Radiation resistance: the ratio of the power driving the antenna to the square of the current driving its terminals.
- Bandwidth: the usable frequency band associated with the antenna.
Before any antenna can be selected, the center frequency and operating bandwidth must be known. In general, the higher the operating frequency, the smaller the antenna. Antenna gain is always measured against a known reference such as an isotropic source (dBi) or a half wave dipole (dBd).
| Antenna Type | Typical Gain [dBd] |
|---|---|
| Dipole | 0 |
| Omni | 0 |
| Gain Omni | 3 — 12 |
| Mobile Whip | -0.6 to +5.5 |
| Corner Reflector | 4 — 10 |
| Log Periodic | 3 — 8 |
| Horn | 5 — 12 |
| Helix | 5 — 12 |
| Microstrip Patch | 3 — 15 |
| Yagi | 3 — 20 |
| Panel | 5 — 20 |
Increasing antenna gain by 3 dB generally requires increasing the size by a factor of 2-3 or by reducing the beamwidth. Vertical omni directional antennas and collinear arrays are used for line-of-sight communications with ground-based mobile units. Sectoring can be accomplished by panel antennas. Fixed point-to-point links generally use a yagi or parabolic dish.
Antennas exhibit reciprocity, which means they have the same gain whether used for transmitting or receiving.
Isotropic Radiators
[edit | edit source]An isotropic source radiates energy equally well in all directions. Stars are isotropic radiators. Our sun is an extremely powerful radiator, broadcasting 64 Megawatts per square meter of surface. Although it is not possible to construct isotropic radio antennas, the concept provides useful analytical tools.
The power density as a function of distance from an isotropic source is easily calculated. It is simply the total energy broadcast, divided by the area it passes through, in this case, a sphere.
- watts/m2
Isotropic gain is also called absolute gain. Antennas gains with respect to isotropic gain are specified in units of dBi. Antenna gains can also be specified with respect to a half wave dipole or a short vertical antenna. The gain of a half-wave dipole is 1.64 dBi, and that of a dipole is 2.15 dBi.
Non Isotropic Radiators
[edit | edit source]Virtually all types of antennas are non-isotropic sources. That is that they tend to radiate more energy in a particular direction.
Because of this non-uniform energy distribution, the antenna appears to have a gain (Gt) (if broadcasting the same power) relative to an isotropic radiator along its principal axis and a loss in other most directions. The power density along the antenna axis is given by:
- watts/m2
The receiving antenna attempts to collect this radiated energy through an effective area (Aeff). The received power is therefore:
- watts
It would seem reasonable to conclude that the effective area is simply the physical size of the antenna. Fortunately, this is not the case, and very small antennas are possible.
It has been determined that there is a relationship between effective area, transmitted wavelength and antenna gain:
Therefore, the received power can be expressed as:
- watts
Recall that:
If f is expressed in MHz, c in meters per second, and r in km, then the received power in dB can be expressed as:
- dB
Electric Field Strength
[edit | edit source]If the power density of an electromagnetic wave is known, the field strength can be obtained from:
where:
- (for free space)
Therefore the field strength at one meter is:
- volts/m
Antenna Types
[edit | edit source]Antennas come in a bewildering array of shapes and sizes however, they can be divided into two broad categories : Marconi and Hertzian.
Marconi antennas are electrically unbalanced and a require a ground plane. Hertzian antennas are electrically balanced and do not require a ground plane. Depending on one's point of view, it is possible to consider one type the subset of the other. This will become clearer later on.
Marconi Antenna
[edit | edit source]Marconi antennas are usually 1/4 wavelength long and require a path to ground. The ground plane itself acts as a reflector of energy, and combines with the directly radiated wave to create the overall radiation pattern. If the ground is dry or otherwise a poor conductor, a copper grid is generally laid out on the ground. The impedance of a 1/4 Marconi antenna is 36.6 .
Notice that a Marconi antenna could be considered as a dipole antenna with one of the poles buried in the ground. The ground acts as a reflector to create the appearance of an buried antenna in the same way that a mirror creates the appearance of someone behind the glass. Increasing the antenna length has a significant impact on the radiation pattern:
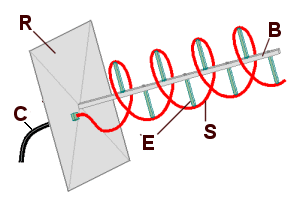
Helical Antenna
[edit | edit source]Most Marconi antennas operate in the broadside mode, which means that the bulk of the signal radiates off the side of the wire. However it is possible to modify the antenna to operate in the end fire mode:
Hertzian Antenna
[edit | edit source]Hertzian antennas do not require a path to either ground or a ground plane. The simplest antenna of this type is the elementary doublet. It is a hypothetical antenna where the instantaneous current magnitude is constant along its length.
The radiation pattern for this antenna is donut shaped, with the antenna rod running through the hole. The bulk of the energy is radiated at right angles to the rod and nothing off the ends.
This antenna is often used as a reference instead of an isotropic radiator, since close approximations of it can be constructed. Other antennas can be considered as being composed of a series of doublets.
The field strength at any distance and angle can be calculated from:
Where
- L = doublet length in meters
- = wavelength in meters
- I = current in amps (rms)
- r = distance in meters
Dipole Antenna
[edit | edit source]A dipole is sometimes referred to as a Hertzian dipole. Since it has a relatively simple construction and its radiation characteristics are well defined, it is often used as the standard to which all other antennas are compared.
The dipole radiation pattern is shaped like a slightly flattened donut.
The simplest antenna is the dipole. The relationship between antenna current and electric field is given by:
where:
- E = electric field strength
- = angle from antenna axis (in radians)
- I = antenna current (rms)
- = intrinsic impedance (377 )
- L = antenna length
- r = distance
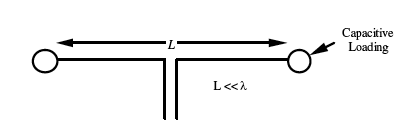
A ½ dipole has an impedance of about 70 . To increase this impedance and more closely match the characteristics of a twin lead cable, the dipole may be folded. A ½ folded dipole has an input impedance of about 280 , and is used as the driving element in many other types of antennas.
Most TV receivers are equipped with two indoor antennas, one to cover the VHF band and the other the UHF band. The most common VHF antennas are the extendible monopole and vee dipole colloquially known as the rabbit ears. These are available with either a 75 or 300 impedance and have a typical gain of -4 dB with respect to a ½ dipole. The vee dipole has a lower input impedance than a straight dipole of the same length, but under some conditions, it can exhibit a higher directivity due to the reduction of sidelobes.
The common UHF antennas are the circular loop and triangular dipole. They typically have a 300 impedance. The dipole version sometimes has a reflecting screen to improve the gain and directivity.
Halfwave Dipole
[edit | edit source]The radiation pattern of the half wave dipole is very much like a donut.
The distribution of voltage, current, and impedance resemble:
By increasing the length of the dipole, the donut tends to flatten out and then explodes into complex multi lobed shapes.
Folded Dipole
[edit | edit source]folded dipole antenna has high input impedance as compared to ordinary dipole.
Loop Antenna
[edit | edit source]The entire UHF band can be received on a single 20.3 cm diameter loop. The circumference varies from one wavelength at 470 MHz to 1.7 wavelengths at 806 MHz. The directivity is about 3.5 dB. The mid band gain is 3 dB higher than a ½ dipole, but falls off to about 1 dB at either end.
Loop antennas that are much smaller than wavelength they are attempting to catch, exhibit a null in the direction of the loop axis. This makes it suitable for radio direction finding equipment. If the loop size is increased, it begins to generate a lobe across the axis and in line with the feed.
Triangular Dipole (Bowtie)
[edit | edit source]The bowtie antenna is formed of two triangular sheets connected to a transmission line and provides a 3 dB gain over a simple dipole. It can also be constructed of a wire mesh if the spacing is less than 1/10 wavelength. The input impedance is a function of length and flare angle. For television applications, the flare angle a is between 60o and 80o. If the antenna is mounted ¼ in front of a reflecting surface, the gain increases to approximately 9 dB. Stacking two of them vertically one wavelength apart, increases the overall gain to about 12 dB.
If the receiver is located at a great distance from the broadcast tower, it is often necessary to use an outdoor antenna. These often have a gain of 15 dB. Placing the antenna on a tall mast also increases the received signal strength by as much as an additional 14 dB. A further improvement occurs because these antennas have a greater immunity to interference, due to their complex structure.
Most outdoor antennas are a combination of two antennas [UHF and VHF] in a single structure. The VHF antenna is generally a log-periodic dipole array. The UHF antenna may be an LPDA, Yagi-Uda, corner reflector, parabolic reflector, or triangular dipole array with reflecting screen.
Log Periodic Dipole Array [LPDA]
[edit | edit source]This antenna is called a log periodic array because the impedance variations across the usable band are periodic functions of frequency. The high impedance version is mounted on an insulated boom and feed by a balanced cable. The average domestic antenna of this type has a gain of about 4.5 dB in the low VHF band, rising to 7 dB in the high VHF band.
- -- Typically
- -- Typically
- Bandwidth:
- Number of dipoles:
Most CATV applications use a 75 unbalanced configuration, because it is more compatible with their cable feeds and equipment.
Two parallel conducting booms form a low impedance transmission line. Phase reversal between dipoles is obtained by alternate attachment to the booms.
An UHF LPDA can be constructed from V-shaped dipoles. The dipoles are used in their ½ and 3/2 modes and eliminate the need for higher frequency dipoles.
Yagi Uda Antenna
[edit | edit source]The dipole is typically 0.40 to 0.50 wavelengths long. The reflector is normally 0.55 wavelengths long and placed anywhere from 0.1 to 0.25 wavelengths behind the dipole. The reflector spacing has no effect on the forward gain, but does influence the front to back ratio and input impedance.
The directors are normally 0.4 to 0.45 wavelengths long and are spaced at 0.3 to 0.4 wavelengths in front of the dipole. An antenna will usually have 6 to 12 directors.
Parabolic Reflector
[edit | edit source]Antenna Arrays
[edit | edit source]By combining several radiating elements together, the overall radiation pattern can be modified to suit a particular application. In some cases the antennas must be manually steered, but in other cases they can be electronically steered using phase shifting between elements.
The array factor is the increase in field strength in an array when compared to a single element radiating the same power:
- Where:
-
- = phase difference between radiated fields from adjacent elements
- n = number of radiating elements
- s = element spacing in wavelengths
- = current phase shift between elements
- = angle from array axis
-
Broadside Array
[edit | edit source]If all of the elements are fed in-phase, there will always be a broadside radiation pattern. However, depending on the relative spacing, an end fire pattern can also be created.
The radiating elements in the above illustration can be placed such that they reinforce one another along the array axis, or not. An end fire pattern is recreated when they reinforce.
By varying the space or phase shift between the elements, the size and direction of the side lobes can be adjusted between these two extremes. Increasing the number of radiating elements increases the overall array gain.
Determining the array factor is sometimes relatively straightforward. By definition, the signal strength for a broadside array is a maximum when = 90o and a minimum when = 0o
Since the array factor is a maximum when = 0o we can determine the current phase shift , required to create a broadside radiation pattern for a given frequency or element spacing:
- Therefore the array factor for a broadside array is:
Each element may have its own feed or there may be a single feed:
This form of antenna is often deployed in vertical stacks, with a reflector spaced 1/4 wavelength behind the curtain. This broadband dipole curtain array is the standard antenna for 100 to 500 kW short-wave broadcasting stations.
CBC Radio International operates eight curtain arrays at Sackville NB. Three have an output power of 100 kW and five have an output of 250 kW. They are tunable over the range of 4.9 to 21.7 MHz. Signals are beamed to Africa, Europe, Latin America, The Caribbean, the USA, and Mexico.
Endfire Array
[edit | edit source]If all of the elements are positioned in such a way that the combined wave fronts reinforce along the array axis.
Calculate the array factor is relatively straightforward. The signal strength is a maximum when = 0o and a minimum when = 90o
Since the array factor is a maximum when = 0o we can determine the value of :
- The array factor for an end fire array is:
Varying the spacing for a 6-element array produced the following patterns:
Phased Array
[edit | edit source]By varying the phase shift between elements, a beam or multiple beams can be pointed towards a given direction. This forms the basis of the large electronically steered radar system currently being deployed. Collectively theses systems are known as phased arrays.
The PAVE PAWS early warning radar for example has 1792 active crossed dipole antennas on a 102-foot face. Each face can scan 120o in azimuth and 80o in elevation. The array has a range of 300 miles and can produce multiple beams, which can be redirected in milliseconds.