Physics Study Guide/Print version/Section Two
Uniform Circular Motion
[edit | edit source]Speed and frequency
[edit | edit source]
Uniform circular motion assumes that an object is moving (1) in circular motion, and (2) at constant speed ; then
where is the radius of the circular path, and is the time period for one revolution.
Any object travelling on a circle will return to its original starting point in the period of one revolution, . At this point the object has travelled a distance . If is the time that it takes to travel distance then the object's speed is
where
Angular frequency
[edit | edit source]Uniform circular motion can be explicitly described in terms of polar coordinates through angular frequency, :
where is the angular coordinate of the object (see the diagram on the right-hand side for reference).
Since the speed in uniform circular motion is constant, it follows that
From that fact, a number of useful relations follow:
The equations that relate how changes with time are analogous to those of linear motion at constant speed. In particular,
The angle at , , is commonly referred to as phase.
Velocity, centripetal acceleration and force
[edit | edit source]The position of an object in a plane can be converted from polar to cartesian coordinates through the equations
Expressing as a function of time gives equations for the cartesian coordinates as a function of time in uniform circular motion:
Differentiation with respect to time gives the components of the velocity vector:
Velocity in circular motion is a vector tangential to the trajectory of the object. Furthermore, even though the speed is constant the velocity vector changes direction over time. Further differentiation leads to the components of the acceleration (which are just the rate of change of the velocity components):
The acceleration vector is perpendicular to the velocity and oriented towards the centre of the circular trajectory. For that reason, acceleration in circular motion is referred to as centripetal acceleration.
The absolute value of centripetal acceleration may be readily obtained by
For centripetal acceleration, and therefore circular motion, to be maintained a centripetal force must act on the object. From Newton's Second Law it follows directly that the force will be given by
the components being
and the absolute value
Torque and Circular Motion
[edit | edit source]Circular motion is the motion of a particle at a set distance (called radius) from a point. For circular motion, there needs to be a force that makes the particle turn. This force is called the 'centripetal force.' Please note that the centripetal force is not a new type of force-it is just a force causing rotational motion. To make this clearer, let us study the following examples:
- If Stone ties a piece of thread to a small pebble and rotates it in a horizontal circle above his head, the circular motion of the pebble is caused by the tension force in the thread.
- In the case of the motion of the planets around the sun (which is roughly circular), the force is provided by the gravitational force exerted by the sun on the planets.
Thus, we see that the centripetal force acting on a body is always provided by some other type of force -- centripetal force, thus, is simply a name to indicate the force that provides this circular motion. This centripetal force is always acting inward toward the center. You will know this if you swing an object in a circular motion. If you notice carefully, you will see that you have to continuously pull inward. We know that an opposite force should exist for this centripetal force(by Newton's 3rd Law of Motion). This is the centrifugal force, which exists only if we study the body from a non-inertial frame of reference(an accelerating frame of reference, such as in circular motion). This is a so-called 'pseudo-force', which is used to make the Newton's law applicable to the person who is inside a non-inertial frame. e.g. If a driver suddenly turns the car to the left, you go towards the right side of the car because of centrifugal force. The centrifugal force is equal and opposite to the centripetal force. It is caused due to inertia of a body.
Average angular velocity is equal to one-half of the sum of initial and final angular velocities assuming constant acceleration, and is also equal to the angle gone through divided by the time taken.
Angular acceleration is equal to change in angular velocity divided by time taken.
Angular momentum
[edit | edit source]Angular momentum of an object revolving around an external axis is equal to the cross-product of the position vector with respect to and its linear momentum.
Angular momentum of a rotating object is equal to the moment of inertia times angular velocity.
- >
Rotational Kinetic Energy is equal to one-half of the product of moment of inertia and the angular velocity squared.
- IT IS USEFUL TO NOTE THAT
The equations for rotational motion are analogous to those for linear motion-just look at those listed above. When studying rotational dynamics, remember:
- the place of force is taken by torque
- the place of mass is taken by moment of inertia
- the place of displacement is taken by angle
- the place of linear velocity, momentum, acceleration, etc. is taken by their angular counterparts.
Definition of terms
[edit | edit source]|
Torque (): Force times distance. A vector. Moment of inertia (): Describes the object's resistance to torque — the rotational analog to inertial mass. Angular momentum (): Angular velocity (): Angular acceleration (): Rotational kinetic energy (): Time (): |
Buoyancy
[edit | edit source]Buoyancy is the force due to pressure differences on the top and bottom of an object under a fluid (gas or liquid).
Net force = buoyant force - force due to gravity on the object
Bernoulli's Principle
[edit | edit source]Fluid flow is a complex phenomenon. An ideal fluid may be described as:
- The fluid flow is steady i.e its velocity at each point is constant with time.
- The fluid is incompressible. This condition applies well to liquids and in certain circumstances to gases.
- The fluid flow is non-viscous. Internal friction is neglected. An object moving through this fluid does not experience a retarding force. We relax this condition in the discussion of Stokes' Law.
- The fluid flow is irrotational. There is no angular momentum of the fluid about any point. A very small wheel placed at an arbitrary point in the fluid does not rotate about its center. Note that if turbulence is present, the wheel would most likely rotate and its flow is then not irrotational.
As the fluid moves through a pipe of varying cross-section and elevation, the pressure will change along the pipe. The Swiss physicist Daniel Bernoulli (1700-1782) first derived an expression relating the pressure to fluid speed and height. This result is a consequence of conservation of energy and applies to ideal fluids as described above.
Consider an ideal fluid flowing in a pipe of varying cross-section. A fluid in a section of length moves to the section of length in time . The relation given by Bernoulli is:
where:
- is pressure at cross-section
- is height of cross-section
- is density
- is velocity of fluid at cross-section
In words, the Bernoulli relation may be stated as:
As we move along a streamline the sum of the pressure (), the kinetic energy per unit volume and the potential energy per unit volume remains a constant.
(To be concluded)
Fields
[edit | edit source]A field is one of the more difficult concepts to grasp in physics. A field is an area or region in which an influence or force is effective regardless of the presence or absence of a material medium. Simply put, a field is a collection of vectors often representing the force an object would feel if it were placed at any particular point in space. With gravity, the field is measured in newtons, as it depends solely on the mass of an object, but with electricity, it is measured in newtons per coulomb, as the force on an electrical charge depends on the amount of that charge. Typically these fields are calculated based on canceling out the effect of a body in the point in space that the field is desired. As a result, a field is a vector, and as such, it can (and should) be added when calculating the field created by TWO objects at one point in space.
Fields are typically illustrated through the use of what are called field lines or lines of force. Given a source that exerts a force on points around it, sample lines are drawn representing the direction of the field at points in space around the force-exerting source.
There are three major categories of fields:
- Uniform fields are fields that have the same value at any point in space. As a result, the lines of force are parallel.
- Spherical fields are fields that have an origin at a particular point in space and vary at varying distances from that point.
- Complex fields are fields that are difficult to work with mathematically (except under simple cases, such as fields created by two point object), but field lines can still typically be drawn. Dipoles are a specific kind of complex field.
Magnetism also has a field, measured in Tesla, and it also has field lines, but its use is more complicated than simple "force" fields. Secondly, it also only appears in a two-pole form, and as such, is difficult to calculate easily.
The particles that form these magnetic fields and lines of force are called electrons and not magnetons. A magneton is a quantity in magnetism.
Definition of terms
[edit | edit source]|
Field: A collection of vectors that often represents the force that an object would feel if it were placed in any point in space. |
Newtonian Gravity
[edit | edit source]Newtonian Gravity (simplified gravitation) is an apparent force (a.k.a. pseudoforce) that simulates the attraction of one mass to another mass. Unlike the three fundamental (real) forces of electromagnetism and the strong and weak nuclear forces, gravity is purely attractive. As a force it is measured in newtons. The distance between two objects is measured between their centers of mass.
Gravitational force is equal to the product of the universal gravitational constant and the masses of the two objects, divided by the square of the distance between their centers of mass.
The value of the gravitational field which is equivalent to the acceleration due to gravity caused by an object at a point in space is equal to the first equation about gravitational force, with the effect of the second mass taken out.
Gravitational potential energy of a body to infinity is equal to the universal gravitational constant times the mass of a body from which the gravitational field is being created times the mass of the body whose potential energy is being measured over the distance between the two centers of mass. Therefore, the difference in potential energy between two points is the difference of the potential energy from the position of the center of mass to infinity at both points. Near the earth's surface, this approximates:
Potential energy due to gravity near the earth's surface is equal to the product of mass, acceleration due to gravity, and height (elevation) of the object.
If the potential energy from the body's center of mass to infinity is known, however, it is possible to calculate the escape velocity, or the velocity necessary to escape the gravitational field of an object. This can be derived based on utilizing the law of conservation of energy and the equation to calculate kinetic energy as follows:
|
|
}}
Variables
|
F: force (N) |
Definition of terms
|
Universal constant of gravitation (G): This is a constant that is the same everywhere in the known universe and can be used to calculate gravitational attraction and acceleration due to gravity. |
A black hole is a geometrically defined region of space time exhibiting such large centripetal gravitational effects that nothing such as particles and electromagnetic radiation such as light may escape from inside of it. That is the escape velocity upon the event horizon is equivalent to the speed of light. General relativity is a metric theory of gravitation generalizing space time and Newton's law of universal gravitational attraction as a geometric property of space time.
Waves
[edit | edit source]Wave is defined as the movement of any periodic motion like a spring, a pendulum, a water wave, an electric wave, a sound wave, a light wave, etc.

Any periodic wave that has amplitude varied with time, phase sinusoidally can be expressed mathematically as
- R(t , θ) = R Sin (ωt + θ)
- Minimum wave height (trough) at angle 0, π, 2π, ...
- F(R,t,θ) = 0 at θ = nπ
- Maximum wave height (peak or crest) at π/2, 3π/2, ...
- F(R,t,θ) = R at θ = (2n+1)π/2
- Wavelength (distance between two crests) λ = 2π.
- λ = 2π - A circle or a wave
- 2λ = 2(2π) - Two circles or two waves
- kλ = k2π - Circle k or k amount of waves
- Wave Number,
- k
- Velocity (or Angular Velocity),
- ω = 2πf
- Time Frequency,
- f = 1 / t
- Time
- t = 1 / f
Wave speed is equal to the frequency times the wavelength. It can be understood as how frequently a certain distance (the wavelength in this case) is traversed.
Frequency is equal to speed divided by wavelength.
Period is equal to the inverse of frequency.
Variables
|
λ: wavelength (m) |
Definition of terms
|
Wavelength (λ): The length of one wave, or the distance from a point on one wave to the same point on the next wave. Units: meters (m). In light, λ tells us the color. |
Image here
The wave’s extremes, its peaks and valleys, are called antinodes. At the middle of the wave are points that do not move, called nodes.
Examples of waves: Water waves, sound waves, light waves, seismic waves, shock waves, electromagnetic waves …
Oscillation
[edit | edit source]A wave is said to oscillate, which means to move back and forth in a regular, repeating way. This fluctuation can be between extremes of position, force, or quantity. Different types of waves have different types of oscillations.
Longitudinal waves: Oscillation is parallel to the direction of the wave. Examples: sound waves, waves in a spring.
Transverse waves: Oscillation is perpendicular to direction of the wave. Example: light
Interference
[edit | edit source]When waves overlap each other it is called interference. This is divided into constructive and destructive interference.
Constructive interference: the waves line up perfectly and add to each others’ strength.
Destructive interference: the two waves cancel each other out, resulting in no wave.This happens when angle between them is 180degrees.
Resonance
[edit | edit source]In real life, waves usually give a mishmash of constructive and destructive interference and quickly die out. However, at certain wavelengths standing waves form, resulting in resonance. These are waves that bounce back into themselves in a strengthening way, reaching maximum amplitude.
Resonance is a special case of forced vibration when the frequency of the impressed periodic force is equal to the natural frequency of the body so that it vibrates with increased amplitude, spontaneously.
Wave overtones
[edit | edit source]For resonance in a taut string, the first harmonic is determined for a wave form with one antinode and two nodes. That is, the two ends of the string are nodes because they do not vibrate while the middle of the string is an antinode because it experiences the greatest change in amplitude. This means that one half of a full wavelength is represented by the length of the resonating structure.
The frequency of the first harmonic is equal to wave speed divided by twice the length of the string. (Recall that wave speed is equal to wavelength times frequency.)
|
F1 = v/2L |
The wavelength of the first harmonic is equal to double the length of the string.
|
λ1 = 2L |
The "nth" wavelength is equal to the fundamental wavelength divided by n.
|
λn = λ1/n |
Harmonics for a taut string*
| Harmonic number | Overtone number | F = | λ = | |
| F1 | First harmonic | --- | F1 = v/2L | λ1 = 2L |
| F2 | Second harmonic | First overtone | F2 = 2F1 | λ2 =λ1/2 |
| F3 | Third harmonic | Second overtone | F3 = 3F1 | λ3 = λ1/3 |
| Fn | Nth harmonic | (Nth - 1) overtone | Fn = nF1 | λn = λ1/n |
* or any wave system with two identical ends, such as a pipe with two open or closed ends. In the case of a pipe with two open ends, there are two antinodes at the ends of the pipe and a single node in the middle of the pipe, but the mathematics work out identically.
Definition of terms
|
Frequency (F): Units: (1/s), hertz (Hz) |
The first overtone is the first allowed harmonic above the fundamental frequency (F1).
In the case of a system with two different ends (as in the case of a tube open at one end), the closed end is a node and the open end is an antinode. The first resonant frequency has only a quarter of a wave in the tube. This means that the first harmonic is characterized by a wavelength four times the length of the tube.
|
F1 = v/4L |
The wavelength of the first harmonic is equal to four times the length of the string.
|
λ1 = 4L |
The "nth" wavelength is equal to the fundamental wavelength divided by n.
|
λn = λ1/n |
Note that "n" must be odd in this case as only odd harmonics will resonate in this situation.
Harmonics for a system with two different ends*
| Harmonic number | Overtone number | F = | λ = | |
| F1 | First harmonic | --- | F1 = v/4L | λ1 = 4L |
| F2 | Third harmonic | First overtone | F2 = 3F1 | λ2 = λ1/3 |
| F3 | Fifth harmonic | Second overtone | F3 = 5F1 | λ3 = λ1/5 |
| Fn | Nth harmonic† | (Nth - 1)/2 overtone | F(n-1)/2 = nF1 | λn = λ1/n |
* such as a pipe with one end open and one end closed
†In this case only the odd harmonics resonate, so n is an odd integer.
Vs: velocity of sound
- dependent on qualities of the medium transmitting the sound, (the air) such as its density, temperature, and “springiness.” A complicated equation, we concentrate only on temperature.
- increases as temperature increases (molecules move faster.)
- is higher for liquids and solids than for gasses (molecules are closer together.)
- for “room air” is 340 meters per second (m/s).
- Speed of sound is 343 meters per second at 20 degrees C. Based on the material sound is passing through and the temperature, the speed of sound changes.
Standing waves
[edit | edit source]Wave speed is equal to the square root of tension divided by the linear density of the string.
|
μ = m/L
|
Linear density of the string is equal to the mass divided by the length of the string.
|
λmax = 2L
|
The fundamental wavelength is equal to two times the length of the string.
Variables
|
λ: wavelength (m) |
Definition of terms
|
Tension (F): (not frequency) in the string (t is used for time in these equations). Units: newtons (N) |
Fundamental frequency: the frequency when the wavelength is the longest allowed, this gives us the lowest sound that we can get from the system.
In a string, the length of the string is half of the largest wavelength that can create a standing wave, called its fundamental wavelength.
Sound is defined as mechanical sinosodial vibratory longitudinal impulse waves which oscillate the pressure of a transmitting medium by means of adiabatic compression and decompression consequently resulting in the increase in the angular momentum and hence rotational kinetic energy of the particles present within the transmitting medium producing frequencies audible within hearing range, that is between the threshold of audibility and the threshold of pain on a Fletchford Munson equal loudness contour diagram.
Intro
[edit | edit source]When two glasses collide, we hear a sound. When we pluck a guitar string, we hear a sound.
Different sounds are generated from different sources. Generally speaking, the collision of two objects results in a sound.
Sound does not exist in a vacuum; it travels through the materials of a medium. Sound is a longitudinal wave in which the mechanical vibration constituting the wave occurs along the direction of the wave's propagation.
The velocity of sound waves depends on the temperature and the pressure of the medium. For example, sound travels at different speeds in air and water. We can therefore define sound as a mechanical disturbance produced by the collision of two or more physical quantities from a state of equilibrium that propagates through an elastic material medium.
Sound
[edit | edit source]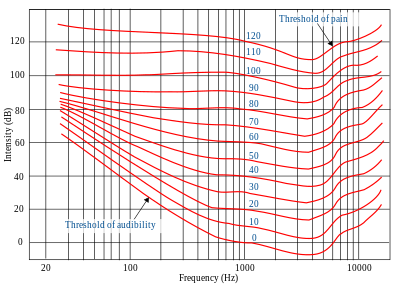
The amplitude is the magnitude of sound pressure change within a sound wave. Sound amplitude can be measured in pascals (Pa), though its more common to refer to the sound (pressure) level as Sound intensity(dB,dBSPL,dB(SPL)), and the perceived sound level as Loudness(dBA, dB(A)). Sound intensity is flow of sound energy per unit time through a fixed area. It has units of watts per square meter. The reference Intensity is defined as the minimum Intensity that is audible to the human ear, it is equal to 10-12 W/m2, or one picowatt per square meter. When the intensity is quoted in decibels this reference value is used. Loudness is sound intensity altered according to the frequency response of the human ear and is measured in a unit called the A-weighted decibel (dB(A), also used to be called phon).
The Decibel
[edit | edit source]The decibel is not, as is commonly believed, the unit of sound. Sound is measured in terms of pressure. However, the decibel is used to express the pressure as very large variations of pressure are commonly encountered. The decibel is a dimensionless quantity and is used to express the ratio of one power quantity to another. The definition of the decibel is , where x is a squared quantity, ie pressure squared, volts squared etc. The decibel is useful to define relative changes. For instance, the required sound decrease for new cars might be 3 dB, this means, compared to the old car the new car must be 3 dB quieter. The absolute level of the car, in this case, does not matter.
Definition of terms
[edit | edit source]|
Intensity (I): the amount of energy transferred through 1 m2 each second. Units: watts per square meter |
|
Lowest audible sound: I = 0 dB = 10-12 W/m2 (A sound with dB < 0 is
inaudible to a human.) |
Sample equation: Change in sound intensity
Δβ = β2 - β1
= 10 log(I2/I0) - 10 log(I1/I0)
= 10 [log(I2/I0) - log(I1/I0)]
= 10 log[(I2/I0)/(I1/I0)]
= 10 log(I2/I1)
where log is the base-10 logarithm.
Doppler effect
[edit | edit source]|
|
f' is the observed frequency, f is the actual frequency, v is the speed of sound (), T is temperature in degrees Celsius is the speed of the observer, and is the speed of the source. If the observer is approaching the source, use the top operator (the +) in the numerator, and if the source is approaching the observer, use the top operator (the -) in the denominator. If the observer is moving away from the source, use the bottom operator (the -) in the numerator, and if the source is moving away from the observer, use the bottom operator (the +) in the denominator.
Example problems
[edit | edit source]A. An ambulance, which is emitting a 400 Hz siren, is moving at a speed of 30 m/s towards a stationary observer. The speed of sound in this case is 339 m/s.
B. An M551 Sheridan, moving at 10 m/s is following a Renault FT-17 which is moving in the same direction at 5 m/s and emitting a 30 Hz tone. The speed of sound in this case is 342 m/s.






































































