Physics Study Guide/Print version/Section Appendices
Commonly Used Physical Constants
[edit | edit source]| Name | Symbol | Value | Units | Relative Uncertainty |
|---|---|---|---|---|
| Speed of light (in vacuum) | (exact) | |||
| Magnetic Constant | (exact) | |||
| Electric Constant | (exact) | |||
| Newtonian Gravitaional Constant | ||||
| Plank's Constant | ||||
| Elementary charge | ||||
| Mass of the electron | ||||
| Mass of the proton | ||||
| Fine structure constant | dimensionless | |||
| Molar gass constant | ||||
| Boltzmann's constant | ||||
| Avogadro's Number | ||||
| Rydberg constant | ||||
| Standard acceleration of gravity | defined | |||
| Atmospheric pressure | defined | |||
| Bohr Radius | ||||
| Electron Volt | ||||
| Luminous efficacy of monochromatic radiation | (exact) | |||
| hyperfine transition frequency of Cs-133 | (exact) | |||
| Reduced Planck constant | (exact) | |||
| atomic mass of Carbon 12 | ||||
| molar mass of Carbon-12 | ||||
| atomic mass constant | ||||
| molar mass constant | ||||
| molar volume of silicon | ||||
| molar Planck constant | ||||
| Stefan-Boltzmann constant | ||||
| first radiation constant | ||||
| first radiation constant for spectral radiance | [1] | |||
| second radiation constant | ||||
| Wien wavelength displacement constant | ||||
| Wien frequency displacement constant | ||||
| Wien entropy displacement constant | ||||
| Faraday constant | [2] |
To Be Merged Into Table
[edit | edit source]This list is prepared in the format
- Constant (symbol) : value
- Coulomb's Law Constant (k) : 1/(4 π ε0) = 9.0 × 109 N·m2/C2
- Faraday constant (F) : 96,485 C·mol−1
- Mass of a neutron (mn) : 1.67495 × 10−27 kg
- Mass of Earth : 5.98 × 1024 kg
- Mass of the Moon : 7.35 × 1022 kg
- Mean radius of Earth : 6.37 × 106 m
- Mean radius of the Moon : 1.74 × 106 m
- Dirac's Constant () : = 1.05457148 × 10−34 J·s
- Speed of sound in air at STP : 3.31 × 102 m/s
- Unified Atomic Mass Unit (u) : 1.66 × 10−27 kg
| Item | Proton | Neutron | Electron |
| Mass | 1 | 1 | Negligible |
| Charge | +1 | 0 | -1 |
See Also
[edit | edit source]Wiki-links
[edit | edit source]External Links
[edit | edit source]Approximate Coefficients of Friction
[edit | edit source]| Material | Kinetic | Static |
| Rubber on concrete (dry) | 0.68 | 0.90 |
| Rubber on concrete (wet) | 0.58 | -.-- |
| Rubber on asphalt (dry) | 0.72 | 0.68 |
| Rubber on asphalt (wet) | 0.53 | -.-- |
| Rubber on ice | 0.15 | 0.15 |
| Waxed ski on snow | 0.05 | 0.14 |
| Wood on wood | 0.30 | 0.42 |
| Steel on steel | 0.57 | 0.74 |
| Copper on steel | 0.36 | 0.53 |
| Teflon on teflon | 0.04 | -.-- |
About the Common uses in Physics
[edit | edit source]While these are indeed common usages, it should be pointed out that there are many other usages and that other letters are used for the same purpose. The reason is quite simple: there are only so many symbols in the Greek and Latin alphabets, and scientists and mathematicians generally do not use symbols from other languages. It is a common trap to associate a symbol exclusively with some particular meaning, rather than learning and understanding the physics and relations behind it.
| Capital | Lower case | Name | Common use in Physics |
|---|---|---|---|
| alpha | Angular acceleration Linear expansion Coefficient Alpha particle (helium nucleus) Fine Structure Constant | ||
| beta | Beta particle — high energy electron Sound intensity | ||
| gamma | Gamma ray (high energy EM wave) Ratio of heat capacities (in an ideal gas) Relativistic correction factor Shear strain | ||
| delta | Δ="Change in" δ="Infinitesimal change in (), also used to denote the Dirac delta function (reference needed)" | ||
| epsilon | Emissivity Strain (Direct e.g. tensile or compression) Permittivity EMF | ||
| zeta | (no common use) | ||
| eta | Viscosity Energy efficiency | ||
| theta | Angle (°, rad) Temperature | ||
| iota | The lower case is rarely used, while is sometimes used for the identity matrix or the moment of inertia. Note that is not to be confused with the Roman character (which has a dot and is much more widely used in mathematics and physics). | ||
| kappa | Spring constant Dielectric constant | ||
| lambda | Wavelength Thermal conductivity Constant Eigenvalue of a matrix Linear density | ||
| mu | Coefficient of friction Electrical mobility Reduced mass Permeability | ||
| nu | Frequency | ||
| xi | Damping cofficient | ||
| omicron | (no common use) | ||
| pi | Product symbol Circle number | ||
| rho | Volume density Resistivity | ||
| sigma | Sum symbol Boltzmann constant Electrical conductivity Uncertainty Stress (Direct e.g. tensile, compression) Surface density | ||
| tau | Torque Tau particle (a lepton) Time constant Shear stress | ||
| upsilon | mass to light ratio | ||
| phi | Magnetic/electric flux Angle (°, rad) | ||
| chi | Rabi frequency (lasers) Susceptibility | ||
| psi | Wave function | ||
| omega | Ohms (unit of electrical resistance) ω Angular velocity |
See Also
[edit | edit source]Greek letters used in mathematics, science, and engineering
Review of logs
[edit | edit source]Been a while since you used logs? Here is a quick refresher for you.
The log (short for logarithm) of a number N is the exponent used to raise a certain "base" number B to get N. In short, means that .
Typically, logs use base 10. An increase of "1" in a base 10 log is equivalent to an increase by a power of 10 in normal notation. In logs, "3" is 100 times the size of "1". If the log is written without an explicit base, 10 is (usually) implied.
| therefore: log(10–12) = –12 |
| also: log(1000) = 3 |
Another common base for logs is the trancendental number , which is approximately 2.7182818.... Since , these can be more convenient than . Often, the notation is used instead of
.
The following properties of logs are true regardless of whether the base is 10, , or some other number.
|
logA + logB = log(AB) |
Adding the log of A to the log of B will give the same result as taking the log of the product A times B.
Subtracting the log of B from the log of A will give the same result as taking the log of the quotient A divided by B.
The log of (A to the Bth power) is equal to the product (B times the log of A).
A few examples:
log(2) + log(3) = log(6)
log(30) – log(2) = log(15)
log(8) = log(23) = 3log(2)
Vectors are quantities that are characterized by having both a numerical quantity (called the "magnitude" and denoted as |v|) and a direction. Velocity is an example of a vector; it describes the time rated change in position with a numerical quantity (meters per second) as well as indicating the direction of movement.
The definition of a vector is any quantity that adds according to the parallelogram law (there are some physical quantities that have magnitude and direction that are not vectors).
Scalars are quantities in physics that have no direction. Mass is a scalar; it can describe the quantity of matter with units (kilograms) but does not describe any direction.
Multiplying vectors and scalars
[edit | edit source]- A scalar times a scalar gives a scalar result.
- A vector scalar-multiplied by a vector gives a scalar result (called the dot-product).
- A vector cross-multiplied by a vector gives a vector result (called the cross-product).
- A vector times a scalar gives a vector result.
Frequently Asked Questions about Vectors
[edit | edit source]When are scalar and vector compositions essentially the same?
[edit | edit source]Answer: when multiple vectors are in same direction then we can just add the magnitudes.so, the scalar and vector composition will be same as we do not add the directions.
What is a "dot-product"? (work when force not parallel to displacement)
[edit | edit source]
Answer: Let's take gravity as our force. If you jump out of an airplane and fall you will pick up speed. (for simplicity's sake, let's ignore air drag). To work out the kinetic energy at any point you simply multiply the value of the force caused by gravity by the distance moved in the direction of the force. For example, a 180 N boy falling a distance of 10 m will have 1800 J of extra kinetic energy. We say that the man has had 1800 J of work done on him by the force of gravity.
Notice that energy is not a vector. It has a value but no direction. Gravity and displacement are vectors. They have a value plus a direction. (In this case, their directions are down and down respectively) The reason we can get a scalar energy from vectors gravity and displacement is because, in this case, they happen to point in the same direction. Gravity acts downwards and displacement is also downwards.
When two vectors point in the same direction, you can get the scalar product by just multiplying the value of the two vectors together and ignoring the direction.
But what happens if they don't point in the same direction?
Consider a man walking up a hill. Obviously it takes energy to do this because you are going against the force of gravity. The steeper the hill, the more energy it takes every step to climb it. This is something we all know unless we live on a salt lake.
In a situation like this we can still work out the work done. In the diagram, the green lines represent the displacement. To find out how much work against gravity the man does, we work out the projection of the displacement along the line of action of the force of gravity. In this case it's just the y component of the man's displacement. This is where the cos θ comes in. θ is merely the angle between the velocity vector and the force vector.
If the two forces do not point in the same direction, you can still get the scalar product by multiplying the projection of one force in the direction of the other force. Thus:
There is another method of defining the dot product which relies on components.
What is a "cross-product"? (Force on a charged particle in a magnetic field)
[edit | edit source]Answer: Suppose there is a charged particle moving in a constant magnetic field. According to the laws of electromagnetism, the particle is acted upon by a force called the Lorentz force. If this particle is moving from left to right at 30 m/s and the field is 30 Tesla pointing straight down perpendicular to the particle, the particle will actually curve in a circle spiraling out of the plane of the two with an acceleration of its charge in coulombs times 900 newtons per coulomb! This is because the calculation of the Lorentz force involves a cross-product.when cross product can replace the sin0 can take place during multiplication. A cross product can be calculated simply using the angle between the two vectors and your right hand. If the forces point parallel or 180° from each other, it's simple: the cross-product does not exist. If they are exactly perpendicular, the cross-product has a magnitude of the product of the two magnitudes. For all others in between however, the following formula is used:
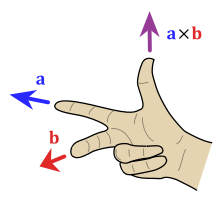
But if the result is a vector, then what is the direction? That too is fairly simple, utilizing a method called the "right-hand rule".
The right-hand rule works as follows: Place your right-hand flat along the first of the two vectors with the palm facing the second vector and your thumb sticking out perpendicular to your hand. Then proceed to curl your hand towards the second vector. The direction that your thumb points is the direction that cross-product vector points! Though this definition is easy to explain visually it is slightly more complicated to calculate than the dot product.
How to draw vectors that are in or out of the plane of the page (or board)
[edit | edit source]

Answer: Vectors in the plane of the page are drawn as arrows on the page. A vector that goes into the plane of the screen is typically drawn as circles with an inscribed X. A vector that comes out of the plane of the screen is typically drawn as circles with dots at their centers. The X is meant to represent the fletching on the back of an arrow or dart while the dot is meant to represent the tip of the arrow.
- ↑ "first radiation constant for spectral radiance". NIST.gov. NIST. Retrieved 5 June 2022.
- ↑ "Faraday constant". NIST.gov. NIST. Retrieved 5 June 2022.







































































































































































