Control Systems/Systems Introduction/Print version
| This is the print version of Control Systems/Systems Introduction You won't see this message or any elements not part of the book's content when you print or preview this page. |
The Wikibook of automatic
And Control Systems Engineering
With
Classical and Modern Techniques
And
Advanced Concepts
Introduction to Control Systems
What are control systems? Why do we study them? How do we identify them? The chapters in this section should answer these questions and more.
Introduction
This Wikibook
This book was written at Wikibooks, a free online community where people write open-content textbooks. Any person with internet access is welcome to participate in the creation and improvement of this book. Because this book is continuously evolving, there are no finite "versions" or "editions" of this book. Permanent links to known good versions of the pages may be provided.
What are Control Systems?
The study and design of automatic Control Systems, a field known as control engineering, has become important in modern technical society. From devices as simple as a toaster or a toilet, to complex machines like space shuttles and power steering, control engineering is a part of our everyday life. This book introduces the field of control engineering and explores some of the more advanced topics in the field. Note, however, that control engineering is a very large field and this book serves only as a foundation of control engineering and an introduction to selected advanced topics in the field. Topics in this book are added at the discretion of the authors and represent the available expertise of our contributors.
Control systems are components that are added to other components to increase functionality or meet a set of design criteria. For example:
We have a particular electric motor that is supposed to turn at a rate of 40 RPM. To achieve this speed, we must supply 10 Volts to the motor terminals. However, with 10 volts supplied to the motor at rest, it takes 30 seconds for our motor to get up to speed. This is valuable time lost.
This simple example can be complex to both users and designers of the motor system. It may seem obvious that the motor should start at a higher voltage so that it accelerates faster. Then we can reduce the supply back down to 10 volts once it reaches ideal speed.
This is clearly a simplistic example but it illustrates an important point: we can add special "Controller units" to preexisting systems to improve performance and meet new system specifications.
Here are some formal definitions of terms used throughout this book:
- Control System
- A Control System is a device, or a collection of devices that manage the behavior of other devices. Some devices are not controllable. A control system is an interconnection of components connected or related in such a manner as to command, direct, or regulate itself or another system.
Control System is a conceptual framework for designing systems with capabilities of regulation and/or tracking to give a desired performance. For this there must be a set of signals measurable to know the performance, another set of signals measurable to influence the evolution of the system in time and a third set which is not measurable but disturb the evolution.
- Controller
- A controller is a control system that manages the behavior of another device or system (using Actuators). The controller is usually fed with some input signal from outside the system which commands the system to provide desired output. In a closed loop system, the signal is preprocessed with the sensor's signal from inside the system.
- Actuator
- An actuator is a device that takes in a signal form the controller and carries some action to affect the system accordingly.
- Compensator
- A compensator is a control system that regulates another system, usually by conditioning the input or the output to that system. Compensators are typically employed to correct a single design flaw with the intention of minimizing effects on other aspects of the design.
There are essentially two methods to approach the problem of designing a new control system: the Classical Approach and the Modern Approach.
Classical and Modern
Classical and Modern control methodologies are named in a misleading way, because the group of techniques called "Classical" were actually developed later than the techniques labeled "Modern". However, in terms of developing control systems, Modern methods have been used to great effect more recently, while the Classical methods have been gradually falling out of favor. Most recently, it has been shown that Classical and Modern methods can be combined to highlight their respective strengths and weaknesses.
Classical Methods, which this book will consider first, are methods involving the Laplace Transform domain. Physical systems are modeled in the so-called "time domain", where the response of a given system is a function of the various inputs, the previous system values, and time. As time progresses, the state of the system and its response change. However, time-domain models for systems are frequently modeled using high-order differential equations which can become impossibly difficult for humans to solve and some of which can even become impossible for modern computer systems to solve efficiently. To counteract this problem, integral transforms, such as the Laplace Transform and the Fourier Transform, can be employed to change an Ordinary Differential Equation (ODE) in the time domain into a regular algebraic polynomial in the transform domain. Once a given system has been converted into the transform domain it can be manipulated with greater ease and analyzed quickly by humans and computers alike.
Modern Control Methods, instead of changing domains to avoid the complexities of time-domain ODE mathematics, converts the differential equations into a system of lower-order time domain equations called State Equations, which can then be manipulated using techniques from linear algebra. This book will consider Modern Methods second.
A third distinction that is frequently made in the realm of control systems is to divide analog methods (classical and modern, described above) from digital methods. Digital Control Methods were designed to try and incorporate the emerging power of computer systems into previous control methodologies. A special transform, known as the Z-Transform, was developed that can adequately describe digital systems, but at the same time can be converted (with some effort) into the Laplace domain. Once in the Laplace domain, the digital system can be manipulated and analyzed in a very similar manner to Classical analog systems. For this reason, this book will not make a hard and fast distinction between Analog and Digital systems, and instead will attempt to study both paradigms in parallel.
Who is This Book For?
This book is intended to accompany a course of study in under-graduate and graduate engineering. As has been mentioned previously, this book is not focused on any particular discipline within engineering, however any person who wants to make use of this material should have some basic background in the Laplace transform (if not other transforms), calculus, etc. The material in this book may be used to accompany several semesters of study, depending on the program of your particular college or university. The study of control systems is generally a topic that is reserved for students in their 3rd or 4th year of a 4 year undergraduate program, because it requires so much previous information. Some of the more advanced topics may not be covered until later in a graduate program.
Many colleges and universities only offer one or two classes specifically about control systems at the undergraduate level. Some universities, however, do offer more than that, depending on how the material is broken up, and how much depth that is to be covered. Also, many institutions will offer a handful of graduate-level courses on the subject. This book will attempt to cover the topic of control systems from both a graduate and undergraduate level, with the advanced topics built on the basic topics in a way that is intuitive. As such, students should be able to begin reading this book in any place that seems an appropriate starting point, and should be able to finish reading where further information is no longer needed.
What are the Prerequisites?
Understanding of the material in this book will require a solid mathematical foundation. This book does not currently explain, nor will it ever try to fully explain most of the necessary mathematical tools used in this text. For that reason, the reader is expected to have read the following wikibooks, or have background knowledge comparable to them:
- Algebra
- Calculus
- The reader should have a good understanding of differentiation and integration. Partial differentiation, multiple integration, and functions of multiple variables will be used occasionally, but the students are not necessarily required to know those subjects well. These advanced calculus topics could better be treated as a co-requisite instead of a pre-requisite.
- Linear Algebra
- State-space system representation draws heavily on linear algebra techniques. Students should know how to operate on matrices. Students should understand basic matrix operations (addition, multiplication, determinant, inverse, transpose). Students would also benefit from a prior understanding of Eigenvalues and Eigenvectors, but those subjects are covered in this text.
- Ordinary Differential Equations
- All linear systems can be described by a linear ordinary differential equation. It is beneficial, therefore, for students to understand these equations. Much of this book describes methods to analyze these equations. Students should know what a differential equation is, and they should also know how to find the general solutions of first and second order ODEs.
- Engineering Analysis
- This book reinforces many of the advanced mathematical concepts used in the Engineering Analysis book, and we will refer to the relevant sections in the aforementioned text for further information on some subjects. This is essentially a math book, but with a focus on various engineering applications. It relies on a previous knowledge of the other math books in this list.
- Signals and Systems
- The Signals and Systems book will provide a basis in the field of systems theory, of which control systems is a subset. Readers who have not read the Signals and Systems book will be at a severe disadvantage when reading this book.
How is this Book Organized?
This book will be organized following a particular progression. First this book will discuss the basics of system theory, and it will offer a brief refresher on integral transforms. Section 2 will contain a brief primer on digital information, for students who are not necessarily familiar with them. This is done so that digital and analog signals can be considered in parallel throughout the rest of the book. Next, this book will introduce the state-space method of system description and control. After section 3, topics in the book will use state-space and transform methods interchangeably (and occasionally simultaneously). It is important, therefore, that these three chapters be well read and understood before venturing into the later parts of the book.
After the "basic" sections of the book, we will delve into specific methods of analyzing and designing control systems. First we will discuss Laplace-domain stability analysis techniques (Routh-Hurwitz, root-locus), and then frequency methods (Nyquist Criteria, Bode Plots). After the classical methods are discussed, this book will then discuss Modern methods of stability analysis. Finally, a number of advanced topics will be touched upon, depending on the knowledge level of the various contributors.
As the subject matter of this book expands, so too will the prerequisites. For instance, when this book is expanded to cover nonlinear systems, a basic background knowledge of nonlinear mathematics will be required.
Versions
This wikibook has been expanded to include multiple versions of its text, differentiated by the material covered, and the order in which the material is presented. Each different version is composed of the chapters of this book, included in a different order. This book covers a wide range of information, so if you don't need all the information that this book has to offer, perhaps one of the other versions would be right for you and your educational needs.
Each separate version has a table of contents outlining the different chapters that are included in that version. Also, each separate version comes complete with a printable version, and some even come with PDF versions as well.
Take a look at the All Versions Listing Page to find the version of the book that is right for you and your needs.
Differential Equations Review
Implicit in the study of control systems is the underlying use of differential equations. Even if they aren't visible on the surface, all of the continuous-time systems that we will be looking at are described in the time domain by ordinary differential equations (ODE), some of which are relatively high-order.
Let's review some differential equation basics. Consider the topic of interest from a bank. The amount of interest accrued on a given principal balance (the amount of money you put into the bank) P, is given by:
Where is the interest (rate of change of the principal), and r is the interest rate. Notice in this case that P is a function of time (t), and can be rewritten to reflect that:
To solve this basic, first-order equation, we can use a technique called "separation of variables", where we move all instances of the letter P to one side, and all instances of t to the other:
And integrating both sides gives us:
This is all fine and good, but generally, we like to get rid of the logarithm, by raising both sides to a power of e:
Where we can separate out the constant as such:
D is a constant that represents the initial conditions of the system, in this case the starting principal.
Differential equations are particularly difficult to manipulate, especially once we get to higher-orders of equations. Luckily, several methods of abstraction have been created that allow us to work with ODEs, but at the same time, not have to worry about the complexities of them. The classical method, as described above, uses the Laplace, Fourier, and Z Transforms to convert ODEs in the time domain into polynomials in a complex domain. These complex polynomials are significantly easier to solve than the ODE counterparts. The Modern method instead breaks differential equations into systems of low-order equations, and expresses this system in terms of matrices. It is a common precept in ODE theory that an ODE of order N can be broken down into N equations of order 1.
Readers who are unfamiliar with differential equations might be able to read and understand the material in this book reasonably well. However, all readers are encouraged to read the related sections in Calculus.
History
The field of control systems started essentially in the ancient world. Early civilizations, notably the Greeks and the Arabs were heavily preoccupied with the accurate measurement of time, the result of which were several "water clocks" that were designed and implemented.
However, there was very little in the way of actual progress made in the field of engineering until the beginning of the renaissance in Europe. Leonhard Euler (for whom Euler's Formula is named) discovered a powerful integral transform, but Pierre-Simon Laplace used the transform (later called the Laplace Transform) to solve complex problems in probability theory.
Joseph Fourier was a court mathematician in France under Napoleon I. He created a special function decomposition called the Fourier Series, that was later generalized into an integral transform, and named in his honor (the Fourier Transform).

|

|
| Pierre-Simon Laplace 1749-1827 |
Joseph Fourier 1768-1840 |
The "golden age" of control engineering occurred between 1910-1945, where mass communication methods were being created and two world wars were being fought. During this period, some of the most famous names in controls engineering were doing their work: Nyquist and Bode.
Hendrik Wade Bode and Harry Nyquist, especially in the 1930's while working with Bell Laboratories, created the bulk of what we now call "Classical Control Methods". These methods were based off the results of the Laplace and Fourier Transforms, which had been previously known, but were made popular by Oliver Heaviside around the turn of the century. Previous to Heaviside, the transforms were not widely used, nor respected mathematical tools.
Bode is credited with the "discovery" of the closed-loop feedback system, and the logarithmic plotting technique that still bears his name (bode plots). Harry Nyquist did extensive research in the field of system stability and information theory. He created a powerful stability criteria that has been named for him (The Nyquist Criteria).
Modern control methods were introduced in the early 1950's, as a way to bypass some of the shortcomings of the classical methods. Rudolf Kalman is famous for his work in modern control theory, and an adaptive controller called the Kalman Filter was named in his honor. Modern control methods became increasingly popular after 1957 with the invention of the computer, and the start of the space program. Computers created the need for digital control methodologies, and the space program required the creation of some "advanced" control techniques, such as "optimal control", "robust control", and "nonlinear control". These last subjects, and several more, are still active areas of study among research engineers.
Branches of Control Engineering
Here we are going to give a brief listing of the various different methodologies within the sphere of control engineering. Oftentimes, the lines between these methodologies are blurred, or even erased completely.
- Classical Controls
- Control methodologies where the ODEs that describe a system are transformed using the Laplace, Fourier, or Z Transforms, and manipulated in the transform domain.
- Modern Controls
- Methods where high-order differential equations are broken into a system of first-order equations. The input, output, and internal states of the system are described by vectors called "state variables".
- Robust Control
- Control methodologies where arbitrary outside noise/disturbances are accounted for, as well as internal inaccuracies caused by the heat of the system itself, and the environment.
- Optimal Control
- In a system, performance metrics are identified, and arranged into a "cost function". The cost function is minimized to create an operational system with the lowest cost.
- Adaptive Control
- In adaptive control, the control changes its response characteristics over time to better control the system.
- Nonlinear Control
- The youngest branch of control engineering, nonlinear control encompasses systems that cannot be described by linear equations or ODEs, and for which there is often very little supporting theory available.
- Game Theory
- Game Theory is a close relative of control theory, and especially robust control and optimal control theories. In game theory, the external disturbances are not considered to be random noise processes, but instead are considered to be "opponents". Each player has a cost function that they attempt to minimize, and that their opponents attempt to maximize.
This book will definitely cover the first two branches, and will hopefully be expanded to cover some of the later branches, if time allows.
MATLAB
the Appendix
MATLAB ® is a programming tool that is commonly used in the field of control engineering. We will discuss MATLAB in specific sections of this book devoted to that purpose. MATLAB will not appear in discussions outside these specific sections, although MATLAB may be used in some example problems. An overview of the use of MATLAB in control engineering can be found in the appendix at: Control Systems/MATLAB.
For more information on MATLAB in general, see: MATLAB Programming.
Resources
Nearly all textbooks on the subject of control systems, linear systems, and system analysis will use MATLAB as an integral part of the text. Students who are learning this subject at an accredited university will certainly have seen this material in their textbooks, and are likely to have had MATLAB work as part of their classes. It is from this perspective that the MATLAB appendix is written.
In the future, this book may be expanded to include information on Simulink ®, as well as MATLAB.
There are a number of other software tools that are useful in the analysis and design of control systems. Additional information can be added in the appendix of this book, depending on the experience and prior knowledge of contributors.
About Formatting
This book will use some simple conventions throughout.
Mathematical Conventions
Mathematical equations will be labeled with the {{eqn}} template, to give them names. Equations that are labeled in such a manner are important, and should be taken special note of. For instance, notice the label to the right of this equation:
[Inverse Laplace Transform]
Equations that are named in this manner will also be copied into the List of Equations Glossary in the end of the book, for an easy reference.
Italics will be used for English variables, functions, and equations that appear in the main text. For example e, j, f(t) and X(s) are all italicized. Wikibooks contains a LaTeX mathematics formatting engine, although an attempt will be made not to employ formatted mathematical equations inline with other text because of the difference in size and font. Greek letters, and other non-English characters will not be italicized in the text unless they appear in the midst of multiple variables which are italicized (as a convenience to the editor).
Scalar time-domain functions and variables will be denoted with lower-case letters, along with a t in parenthesis, such as: x(t), y(t), and h(t). Discrete-time functions will be written in a similar manner, except with an [n] instead of a (t).
Fourier, Laplace, Z, and Star transformed functions will be denoted with capital letters followed by the appropriate variable in parenthesis. For example: F(s), X(jω), Y(z), and F*(s).
Matrices will be denoted with capital letters. Matrices which are functions of time will be denoted with a capital letter followed by a t in parenthesis. For example: A(t) is a matrix, a(t) is a scalar function of time.
Transforms of time-variant matrices will be displayed in uppercase bold letters, such as H(s).
Math equations rendered using LaTeX will appear on separate lines, and will be indented from the rest of the text.
Text Conventions
Examples will appear in TextBox templates, which show up as large grey boxes filled with text and equations.
- Important Definitions
- Will appear in TextBox templates as well, except we will use this formatting to show that it is a definition.
Notes of interest will appear in "infobox" templates. These notes will often be used to explain some nuances of a mathematical derivation or proof. |
Warnings will appear in these "warning" boxes. These boxes will point out common mistakes, or other items to be careful of. |
System Identification
Systems
Systems, in one sense, are devices that take input and produce an output. A system can be thought to operate on the input to produce the output. The output is related to the input by a certain relationship known as the system response. The system response usually can be modeled with a mathematical relationship between the system input and the system output.
System Properties
Physical systems can be divided up into a number of different categories, depending on particular properties that the system exhibits. Some of these system classifications are very easy to work with and have a large theory base for analysis. Some system classifications are very complex and have still not been investigated with any degree of success. By properly identifying the properties of a system, certain analysis and design tools can be selected for use with the system.
The early sections of this book will focus primarily on linear time-invariant (LTI) systems. LTI systems are the easiest class of system to work with, and have a number of properties that make them ideal to study. This chapter discusses some properties of systems.
Later chapters in this book will look at time variant systems and nonlinear systems. Both time variant and nonlinear systems are very complex areas of current research, and both can be difficult to analyze properly. Unfortunately, most physical real-world systems are time-variant, nonlinear, or both.
An introduction to system identification and least squares techniques can be found here. An introduction to parameter identification techniques can be found here.
Initial Time
The initial time of a system is the time before which there is no input. Typically, the initial time of a system is defined to be zero, which will simplify the analysis significantly. Some techniques, such as the Laplace Transform require that the initial time of the system be zero. The initial time of a system is typically denoted by t0.
The value of any variable at the initial time t0 will be denoted with a 0 subscript. For instance, the value of variable x at time t0 is given by:
Likewise, any time t with a positive subscript are points in time after t0, in ascending order:
So t1 occurs after t0, and t2 occurs after both points. In a similar fashion above, a variable with a positive subscript (unless specifying an index into a vector) also occurs at that point in time:
This is valid for all points in time t.
Additivity
A system satisfies the property of additivity if a sum of inputs results in a sum of outputs. By definition: an input of results in an output of . To determine whether a system is additive, use the following test:
Given a system f that takes an input x and outputs a value y, assume two inputs (x1 and x2) produce two outputs:
Now, create a composite input that is the sum of the previous inputs:
Then the system is additive if the following equation is true:
Systems that satisfy this property are called additive. Additive systems are useful because a sum of simple inputs can be used to analyze the system response to a more complex input.
Example: Sinusoids
Given the following equation:
Create a sum of inputs as:
and construct the expected sum of outputs:
Now, substituting these values into our equation, test for equality:
The equality is not satisfied, and therefore the sine operation is not additive.
Homogeneity
A system satisfies the condition of homogeneity if an input scaled by a certain factor produces an output scaled by that same factor. By definition: an input of results in an output of . In other words, to see if function f() is homogeneous, perform the following test:
Stimulate the system f with an arbitrary input x to produce an output y:
Now, create a second input x1, scale it by a multiplicative factor C (C is an arbitrary constant value), and produce a corresponding output y1:
Now, assign x to be equal to x1:
Then, for the system to be homogeneous, the following equation must be true:
Systems that are homogeneous are useful in many applications, especially applications with gain or amplification.
Example: Straight-Line
Given the equation for a straight line:
Comparing the two results, it is easy to see they are not equal:
Therefore, the equation is not homogeneous.
Exercise:
Prove that additivity implies homogeneity, but that homogeneity does not imply additivity.
Linearity
A system is considered linear if it satisfies the conditions of Additivity and Homogeneity. In short, a system is linear if the following is true:
Take two arbitrary inputs, and produce two arbitrary outputs:
Now, a linear combination of the inputs should produce a linear combination of the outputs:
This condition of additivity and homogeneity is called superposition. A system is linear if it satisfies the condition of superposition.
Example: Linear Differential Equations
Is the following equation linear:
To determine whether this system is linear, construct a new composite input:
Now, create the expected composite output:
Substituting the two into our original equation:
Factor out the derivative operator, as such:
Finally, convert the various composite terms into the respective variables, to prove that this system is linear:
For the record, derivatives and integrals are linear operators, and ordinary differential equations typically are linear equations.
Memory
A system is said to have memory if the output from the system is dependent on past inputs (or future inputs!) to the system. A system is called memoryless if the output is only dependent on the current input. Memoryless systems are easier to work with, but systems with memory are more common in digital signal processing applications.
Systems that have memory are called dynamic systems, and systems that do not have memory are static systems.
Causality
Causality is a property that is very similar to memory. A system is called causal if it is only dependent on past and/or current inputs. A system is called anti-causal if the output of the system is dependent only on future inputs. A system is called non-causal if the output depends on past and/or current and future inputs.
A system design that is not causal cannot be physically implemented (to operate in a real-time). If the system can't be built, the design is generally worthless. However, there are applications of non-causal systems, e.g. when a system does not need to operate in a real-time and already has signals stored in its memory (sound and image compression). |
Time-Invariance
A system is called time-invariant if the system relationship between the input and output signals is not dependent on the passage of time. If the input signal produces an output then any time shifted input, , results in a time-shifted output This property can be satisfied if the transfer function of the system is not a function of time except expressed by the input and output. If a system is time-invariant then the system block is commutative with an arbitrary delay. This facet of time-invariant systems will be discussed later.
To determine if a system f is time-invariant, perform the following test:
Apply an arbitrary input x to a system and produce an arbitrary output y:
Apply a second input x1 to the system, and produce a second output:
Now, assign x1 to be equal to the first input x, time-shifted by a given constant value δ:
Finally, a system is time-invariant if y1 is equal to y shifted by the same value δ:
LTI Systems
A system is considered to be a Linear Time-Invariant (LTI) system if it satisfies the requirements of time-invariance and linearity. LTI systems are one of the most important types of systems, and they will be considered almost exclusively in the beginning chapters of this book.
Systems which are not LTI are more common in practice, but are much more difficult to analyze.
Lumpedness
A system is said to be lumped if one of the two following conditions are satisfied:
- There are a finite number of states that the system can be in.
- There are a finite number of state variables.
The concept of "states" and "state variables" are relatively advanced, and they will be discussed in more detail in the discussion about modern controls.
Systems which are not lumped are called distributed. A simple example of a distributed system is a system with delay, that is, , which has an infinite number of state variables (Here we use to denote the Laplace variable). However, although distributed systems are quite common, they are very difficult to analyze in practice, and there are few tools available to work with such systems. Fortunately, in most cases, a delay can be sufficiently modeled with the Pade approximation. This book will not discuss distributed systems much.
Relaxed
A system is said to be relaxed if the system is causal and at the initial time t0 the output of the system is zero, i.e., there is no stored energy in the system. The output is excited solely and uniquely by input applied thereafter.
In terms of differential equations, a relaxed system is said to have "zero initial states". Systems without an initial state are easier to work with, but systems that are not relaxed can frequently be modified to approximate relaxed systems.
Stability
Stability is a very important concept in systems, but it is also one of the hardest function properties to prove. There are several different criteria for system stability, but the most common requirement is that the system must produce a finite output when subjected to a finite input. For instance, if 5 volts is applied to the input terminals of a given circuit, it would be best if the circuit output didn't approach infinity, and the circuit itself didn't melt or explode. This type of stability is often known as "Bounded Input, Bounded Output" stability, or BIBO.
There are a number of other types of stability, most of which are based on the concept of BIBO stability. Because stability is such an important and complicated topic, an entire section of this text is devoted to its study.
Inputs and Outputs
Systems can also be categorized by the number of inputs and the number of outputs the system has. Consider a television as a system, for instance. The system has two inputs: the power wire and the signal cable. It has one output: the video display. A system with one input and one output is called single-input, single output, or SISO. a system with multiple inputs and multiple outputs is called multi-input, multi-output, or MIMO.
These systems will be discussed in more detail later.
Exercise:
Based on the definitions of SISO and MIMO, above, determine what the acronyms SIMO and MISO mean.
Digital and Analog
Digital and Analog
There is a significant distinction between an analog system and a digital system, in the same way that there is a significant difference between analog and digital data. This book is going to consider both analog and digital topics, so it is worth taking some time to discuss the differences, and to display the different notations that will be used with each.
Continuous Time
A signal is called continuous-time if it is defined at every time t.
A system is a continuous-time system if it takes a continuous-time input signal, and outputs a continuous-time output signal. Here is an example of an analog waveform:

Discrete Time
A signal is called discrete-time if it is only defined for particular points in time. A discrete-time system takes discrete-time input signals, and produces discrete-time output signals. The following image shows the difference between an analog waveform and the sampled discrete time equivalent:

Quantized
A signal is called Quantized if it can only be certain values, and cannot be other values. This concept is best illustrated with examples:
- Students with a strong background in physics will recognize this concept as being the root word in "Quantum Mechanics". In quantum mechanics, it is known that energy comes only in discrete packets. An electron bound to an atom, for example, may occupy one of several discrete energy levels, but not intermediate levels.
- Another common example is population statistics. For instance, a common statistic is that a household in a particular country may have an average of "3.5 children", or some other fractional number. Actual households may have 3 children, or they may have 4 children, but no household has 3.5 children.
- People with a computer science background will recognize that integer variables are quantized because they can only hold certain integer values, not fractions or decimal points.
The last example concerning computers is the most relevant, because quantized systems are frequently computer-based. Systems that are implemented with computer software and hardware will typically be quantized.
Here is an example waveform of a quantized signal. Notice how the magnitude of the wave can only take certain values, and that creates a step-like appearance. This image is discrete in magnitude, but is continuous in time:

Analog
By definition:
- Analog
- A signal is considered analog if it is defined for all points in time and if it can take any real magnitude value within its range.
An analog system is a system that represents data using a direct conversion from one form to another. In other words, an analog system is a system that is continuous in both time and magnitude.
Example: Motor
If we have a given motor, we can show that the output of the motor (rotation in units of radians per second, for instance) is a function of the voltage that is input to the motor. We can show the relationship as such:
Where is the output in terms of rad/sec, and is the motor's conversion function between the input voltage () and the output. For any value of we can calculate out specifically what the rotational speed of the motor should be.
Example: Analog Clock
Consider a standard analog clock, which represents the passage of time though the angular position of the clock hands. We can denote the angular position of the hands of the clock with the system of equations:
Where is the angular position of the hour hand, is the angular position of the minute hand, and is the angular position of the second hand. The positions of all the different hands of the clock are dependent on functions of time.
Different positions on a clock face correspond directly to different times of the day.
Digital
Digital data is represented by discrete number values. By definition:
- Digital
- A signal or system is considered digital if it is both discrete-time and quantized.
Digital data always have a certain granularity, and therefore there will almost always be an error associated with using such data, especially if we want to account for all real numbers. The tradeoff, of course, to using a digital system is that our powerful computers with our powerful, Moore's law microprocessor units, can be instructed to operate on digital data only. This benefit more than makes up for the shortcomings of a digital representation system.
Discrete systems will be denoted inside square brackets, as is a common notation in texts that deal with discrete values. For instance, we can denote a discrete data set of ascending numbers, starting at 1, with the following notation:
- x[n] = [1 2 3 4 5 6 ...]
n, or other letters from the central area of the alphabet (m, i, j, k, l, for instance) are commonly used to denote discrete time values. Analog, or "non-discrete" values are denoted in regular expression syntax, using parenthesis. Here is an example of an analog waveform and the digital equivalent. Notice that the digital waveform is discrete in both time and magnitude:
 |
 |
Example: Digital Clock
As a common example, let's consider a digital clock: The digital clock represents time with binary electrical data signals of 1 and 0. The 1's are usually represented by a positive voltage, and a 0 is generally represented by zero voltage. Counting in binary, we can show that any given time can be represented by a base-2 numbering system:
Minute Binary Representation 1 1 10 1010 30 11110 59 111011
But what happens if we want to display a fraction of a minute, or a fraction of a second? A typical digital clock has a certain amount of precision, and it cannot express fractional values smaller than that precision.
Hybrid Systems
Hybrid Systems are systems that have both analog and digital components. Devices called samplers are used to convert analog signals into digital signals, and Devices called reconstructors are used to convert digital signals into analog signals. Because of the use of samplers, hybrid systems are frequently called sampled-data systems.
Example: Automobile Computer
Most modern automobiles today have integrated computer systems that monitor certain aspects of the car, and actually help to control the performance of the car. The speed of the car, and the rotational speed of the transmission are analog values, but a sampler converts them into digital values so the car computer can monitor them. The digital computer will then output control signals to other parts of the car, to alter analog systems such as the engine timing, the suspension, the brakes, and other parts. Because the car has both digital and analog components, it is a hybrid system.
Continuous and Discrete
We are not using the word "continuous" here in the sense of continuously differentiable, as is common in math texts.
A system is considered continuous-time if the signal exists for all time. Frequently, the terms "analog" and "continuous" will be used interchangeably, although they are not strictly the same.
Discrete systems can come in three flavors:
- Discrete time (sampled)
- Discrete magnitude (quantized)
- Discrete time and magnitude (digital)
Discrete magnitude systems are systems where the signal value can only have certain values.Discrete time systems are systems where signals are only available (or valid) at particular times. Computer systems are discrete in the sense of (3), in that data is only read at specific discrete time intervals, and the data can have only a limited number of discrete values.
A discrete-time system has a sampling time value associated with it, such that each discrete value occurs at multiples of the given sampling time. We will denote the sampling time of a system as T. We can equate the square-brackets notation of a system with the continuous definition of the system as follows:
Notice that the two notations show the same thing, but the first one is typically easier to write, and it shows that the system in question is a discrete system. This book will use the square brackets to denote discrete systems by the sample number n, and parenthesis to denote continuous time functions.
Sampling and Reconstruction
The process of converting analog information into digital data is called "Sampling". The process of converting digital data into an analog signal is called "Reconstruction". We will talk about both processes in a later chapter. For more information on the topic than is available in this book, see the Analog and Digital Conversion wikibook. Here is an example of a reconstructed waveform. Notice that the reconstructed waveform here is quantized because it is constructed from a digital signal:

System Metrics
System Metrics
When a system is being designed and analyzed, it doesn't make any sense to test the system with all manner of strange input functions, or to measure all sorts of arbitrary performance metrics. Instead, it is in everybody's best interest to test the system with a set of standard, simple reference functions. Once the system is tested with the reference functions, there are a number of different metrics that we can use to determine the system performance.
It is worth noting that the metrics presented in this chapter represent only a small number of possible metrics that can be used to evaluate a given system. This wikibook will present other useful metrics along the way, as their need becomes apparent.
Standard Inputs
All of the standard inputs are zero before time zero. All the standard inputs are causal.
There are a number of standard inputs that are considered simple enough and universal enough that they are considered when designing a system. These inputs are known as a unit step, a ramp, and a parabolic input.
- Unit Step
- A unit step function is defined piecewise as such:
[Unit Step Function]
- The unit step function is a highly important function, not only in control systems engineering, but also in signal processing, systems analysis, and all branches of engineering. If the unit step function is input to a system, the output of the system is known as the step response. The step response of a system is an important tool, and we will study step responses in detail in later chapters.

- Ramp
- A unit ramp is defined in terms of the unit step function, as such:
[Unit Ramp Function]
- It is important to note that the unit step function is simply the differential of the unit ramp function:
- This definition will come in handy when we learn about the Laplace Transform.

- Parabolic
- A unit parabolic input is similar to a ramp input:
[Unit Parabolic Function]
- Notice also that the unit parabolic input is equal to the integral of the ramp function:
- Again, this result will become important when we learn about the Laplace Transform.
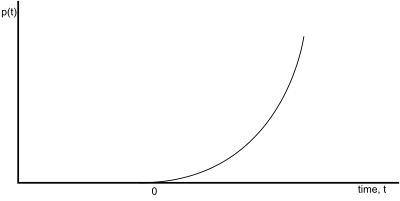
Also, sinusoidal and exponential functions are considered basic, but they are too difficult to use in initial analysis of a system.
Steady State
To be more precise, we should have taken the limit as t approaches infinity. However, as a shorthand notation, we will typically say "t equals infinity", and assume the reader understands the shortcut that is being used.
When a unit-step function is input to a system, the steady-state value of that system is the output value at time . Since it is impractical (if not completely impossible) to wait till infinity to observe the system, approximations and mathematical calculations are used to determine the steady-state value of the system. Most system responses are asymptotic, that is that the response approaches a particular value. Systems that are asymptotic are typically obvious from viewing the graph of that response.
Step Response
The step response of a system is most frequently used to analyze systems, and there is a large amount of terminology involved with step responses. When exposed to the step input, the system will initially have an undesirable output period known as the transient response. The transient response occurs because a system is approaching its final output value. The steady-state response of the system is the response after the transient response has ended.
The amount of time it takes for the system output to reach the desired value (before the transient response has ended, typically) is known as the rise time. The amount of time it takes for the transient response to end and the steady-state response to begin is known as the settling time.
It is common for a systems engineer to try and improve the step response of a system. In general, it is desired for the transient response to be reduced, the rise and settling times to be shorter, and the steady-state to approach a particular desired "reference" output.
 |
 |
Target Value
The target output value is the value that our system attempts to obtain for a given input. This is not the same as the steady-state value, which is the actual value that the system does obtain. The target value is frequently referred to as the reference value, or the "reference function" of the system. In essence, this is the value that we want the system to produce. When we input a "5" into an elevator, we want the output (the final position of the elevator) to be the fifth floor. Pressing the "5" button is the reference input, and is the expected value that we want to obtain. If we press the "5" button, and the elevator goes to the third floor, then our elevator is poorly designed.
Rise Time
Rise time is the amount of time that it takes for the system response to reach the target value from an initial state of zero. Many texts on the subject define the rise time as being the time it takes to rise between the initial position and 80% of the target value. This is because some systems never rise to 100% of the expected, target value, and therefore they would have an infinite rise-time. This book will specify which convention to use for each individual problem. Rise time is typically denoted tr, or trise.
Rise time is not the amount of time it takes to achieve steady-state, only the amount of time it takes to reach the desired target value for the first time. |
Percent Overshoot
Underdamped systems frequently overshoot their target value initially. This initial surge is known as the "overshoot value". The ratio of the amount of overshoot to the target steady-state value of the system is known as the percent overshoot. Percent overshoot represents an overcompensation of the system, and can output dangerously large output signals that can damage a system. Percent overshoot is typically denoted with the term PO.
Example: Refrigerator
Consider an ordinary household refrigerator. The refrigerator has cycles where it is on and when it is off. When the refrigerator is on, the coolant pump is running, and the temperature inside the refrigerator decreases. The temperature decreases to a much lower level than is required, and then the pump turns off.
When the pump is off, the temperature slowly increases again as heat is absorbed into the refrigerator. When the temperature gets high enough, the pump turns back on. Because the pump cools down the refrigerator more than it needs to initially, we can say that it "overshoots" the target value by a certain specified amount.
Example: Refrigerator
Another example concerning a refrigerator concerns the electrical demand of the heat pump when it first turns on. The pump is an inductive mechanical motor, and when the motor first activates, a special counter-acting force known as "back EMF" resists the motion of the motor, and causes the pump to draw more electricity until the motor reaches its final speed. During the startup time for the pump, lights on the same electrical circuit as the refrigerator may dim slightly, as electricity is drawn away from the lamps, and into the pump. This initial draw of electricity is a good example of overshoot.
Steady-State Error
Sometimes a system might never achieve the desired steady-state value, but instead will settle on an output value that is not desired. The difference between the steady-state output value to the reference input value at steady state is called the steady-state error of the system. We will use the variable ess to denote the steady-state error of the system.
Settling Time
After the initial rise time of the system, some systems will oscillate and vibrate for an amount of time before the system output settles on the final value. The amount of time it takes to reach steady state after the initial rise time is known as the settling time. Notice that damped oscillating systems may never settle completely, so we will define settling time as being the amount of time for the system to reach, and stay in, a certain acceptable range. The acceptable range for settling time is typically determined on a per-problem basis, although common values are 20%, 10%, or 5% of the target value. The settling time will be denoted as ts.
System Order
The order of the system is defined by the number of independent energy storage elements in the system, and intuitively by the highest order of the linear differential equation that describes the system. In a transfer function representation, the order is the highest exponent in the transfer function. In a proper system, the system order is defined as the degree of the denominator polynomial. In a state-space equation, the system order is the number of state-variables used in the system. The order of a system will frequently be denoted with an n or N, although these variables are also used for other purposes. This book will make clear distinction on the use of these variables.
Proper Systems
A proper system is a system where the degree of the denominator is larger than or equal to the degree of the numerator polynomial. A strictly proper system is a system where the degree of the denominator polynomial is larger than (but never equal to) the degree of the numerator polynomial. A biproper system is a system where the degree of the denominator polynomial equals the degree of the numerator polynomial.
It is important to note that only proper systems can be physically realized. In other words, a system that is not proper cannot be built. It makes no sense to spend a lot of time designing and analyzing imaginary systems.
Example: System Order
Find the order of this system:
The highest exponent in the denominator is s2, so the system is order 2. Also, since the denominator is a higher degree than the numerator, this system is strictly proper.
In the above example, G(s) is a second-order transfer function because in the denominator one of the s variables has an exponent of 2. Second-order functions are the easiest to work with.
System Type
Let's say that we have a process transfer function (or combination of functions, such as a controller feeding in to a process), all in the forward branch of a unity feedback loop. Say that the overall forward branch transfer function is in the following generalized form (known as pole-zero form):
[Pole-Zero Form]
we call the parameter M the system type. Note that increased system type number correspond to larger numbers of poles at s = 0. More poles at the origin generally have a beneficial effect on the system, but they increase the order of the system, and make it increasingly difficult to implement physically. System type will generally be denoted with a letter like N, M, or m. Because these variables are typically reused for other purposes, this book will make clear distinction when they are employed.
Now, we will define a few terms that are commonly used when discussing system type. These new terms are Position Error, Velocity Error, and Acceleration Error. These names are throwbacks to physics terms where acceleration is the derivative of velocity, and velocity is the derivative of position. Note that none of these terms are meant to deal with movement, however.
- Position Error
- The position error, denoted by the position error constant . This is the amount of steady-state error of the system when stimulated by a unit step input. We define the position error constant as follows:
[Position Error Constant]
- Where G(s) is the transfer function of our system.
- Velocity Error
- The velocity error is the amount of steady-state error when the system is stimulated with a ramp input. We define the velocity error constant as such:
[Velocity Error Constant]
- Acceleration Error
- The acceleration error is the amount of steady-state error when the system is stimulated with a parabolic input. We define the acceleration error constant to be:
[Acceleration Error Constant]
Now, this table will show briefly the relationship between the system type, the kind of input (step, ramp, parabolic), and the steady-state error of the system:
Unit System Input Type, M Au(t) Ar(t) Ap(t) 0 1 2 > 2
Z-Domain Type
Likewise, we can show that the system order can be found from the following generalized transfer function in the Z domain:
Where the constant M is the type of the digital system. Now, we will show how to find the various error constants in the Z-Domain:
[Z-Domain Error Constants]
Error Constant Equation Kp Kv Ka
Visually
Here is an image of the various system metrics, acting on a system in response to a step input:

The target value is the value of the input step response. The rise time is the time at which the waveform first reaches the target value. The overshoot is the amount by which the waveform exceeds the target value. The settling time is the time it takes for the system to settle into a particular bounded region. This bounded region is denoted with two short dotted lines above and below the target value.
System Modeling
The Control Process
It is the job of a control engineer to analyze existing systems, and to design new systems to meet specific needs. Sometimes new systems need to be designed, but more frequently a controller unit needs to be designed to improve the performance of existing systems. When designing a system, or implementing a controller to augment an existing system, we need to follow some basic steps:
- Model the system mathematically
- Analyze the mathematical model
- Design system/controller
- Implement system/controller and test
The vast majority of this book is going to be focused on (2), the analysis of the mathematical systems. This chapter alone will be devoted to a discussion of the mathematical modeling of the systems.
External Description
An external description of a system relates the system input to the system output without explicitly taking into account the internal workings of the system. The external description of a system is sometimes also referred to as the Input-Output Description of the system, because it only deals with the inputs and the outputs to the system.

If the system can be represented by a mathematical function h(t, r), where t is the time that the output is observed, and r is the time that the input is applied. We can relate the system function h(t, r) to the input x and the output y through the use of an integral:
[General System Description]
This integral form holds for all linear systems, and every linear system can be described by such an equation.
If a system is causal (i.e. an input at t=r affects system behaviour only for ) and there is no input of the system before t=0, we can change the limits of the integration:
Time-Invariant Systems
If furthermore a system is time-invariant, we can rewrite the system description equation as follows:
This equation is known as the convolution integral, and we will discuss it more in the next chapter.
Every Linear Time-Invariant (LTI) system can be used with the Laplace Transform, a powerful tool that allows us to convert an equation from the time domain into the S-Domain, where many calculations are easier. Time-variant systems cannot be used with the Laplace Transform.
Internal Description
If a system is linear and lumped, it can also be described using a system of equations known as state-space equations. In state-space equations, we use the variable x to represent the internal state of the system. We then use u as the system input, and we continue to use y as the system output. We can write the state-space equations as such:
We will discuss the state-space equations more when we get to the section on modern controls.
Complex Descriptions
Systems which are LTI and Lumped can also be described using a combination of the state-space equations, and the Laplace Transform. If we take the Laplace Transform of the state equations that we listed above, we can get a set of functions known as the Transfer Matrix Functions. We will discuss these functions in a later chapter.
Representations
To recap, we will prepare a table with the various system properties, and the available methods for describing the system:
Properties State-Space
EquationsLaplace
TransformTransfer
MatrixLinear, Time-Variant, Distributed no no no Linear, Time-Variant, Lumped yes no no Linear, Time-Invariant, Distributed no yes no Linear, Time-Invariant, Lumped yes yes yes
We will discuss all these different types of system representation later in the book.
Analysis
Once a system is modeled using one of the representations listed above, the system needs to be analyzed. We can determine the system metrics and then we can compare those metrics to our specification. If our system meets the specifications we are finished with the design process. However if the system does not meet the specifications (as is typically the case), then suitable controllers and compensators need to be designed and added to the system.
Once the controllers and compensators have been designed, the job isn't finished: we need to analyze the new composite system to ensure that the controllers work properly. Also, we need to ensure that the systems are stable: unstable systems can be dangerous.
Frequency Domain
For proposals, early stage designs, and quick turn around analyses a frequency domain model is often superior to a time domain model. Frequency domain models take disturbance PSDs (Power Spectral Densities) directly, use transfer functions directly, and produce output or residual PSDs directly. The answer is a steady-state response. Oftentimes the controller is shooting for 0 so the steady-state response is also the residual error that will be the analysis output or metric for report.
| Input | Model | Output |
|---|---|---|
| PSD | Transfer Function | PSD |
Brief Overview of the Math
Frequency domain modeling is a matter of determining the impulse response of a system to a random process.

where
- is the one-sided input PSD in
- is the frequency response function of the system and
- is the one-sided output PSD or auto power spectral density function.
The frequency response function, , is related to the impulse response function (transfer function) by
Note some texts will state that this is only valid for random processes which are stationary. Other texts suggest stationary and ergodic while still others state weakly stationary processes. Some texts do not distinguish between strictly stationary and weakly stationary. From practice, the rule of thumb is if the PSD of the input process is the same from hour to hour and day to day then the input PSD can be used and the above equation is valid.
Notes
- ↑ Sun, Jian-Qiao (2006). Stochastic Dynamics and Control, Volume 4. Amsterdam: Elsevier Science. ISBN 0444522301.
See a full explanation with example at ControlTheoryPro.com
Modeling Examples
Modeling in Control Systems is oftentimes a matter of judgement. This judgement is developed by creating models and learning from other people's models. ControlTheoryPro.com is a site with a lot of examples. Here are links to a few of them
- Hovering Helicopter Example
- Reaction Torque Cancellation Example
- List of all examples at ControlTheoryPro.com
Manufacture
Once the system has been properly designed we can prototype our system and test it. Assuming our analysis was correct and our design is good, the prototype should work as expected. Now we can move on to manufacture and distribute our completed systems.
System Representation
Systems can be represented graphically in a number of ways. Block diagrams and signal-flow diagrams are powerful tools that can be used to manipulate systems, and convert them easily into transfer functions or state-space equations. The chapters in this section will discuss how systems can be described visually, and will also discuss how systems can be interconnected with each other.
Gain
What is Gain?
Gain is a proportional value that shows the relationship between the magnitude of the input to the magnitude of the output signal at steady state. Many systems contain a method by which the gain can be altered, providing more or less "power" to the system. However, increasing gain or decreasing gain beyond a particular safety zone can cause the system to become unstable.
Consider the given second-order system:
We can include an arbitrary gain term, K in this system that will represent an amplification, or a power increase:
In a state-space system, the gain term k can be inserted as follows:
The gain term can also be inserted into other places in the system, and in those cases the equations will be slightly different.

Example: Gain
Here are some good examples of arbitrary gain values being used in physical systems:
- Volume Knob
- On your stereo there is a volume knob that controls the gain of your amplifier circuit. Higher levels of volume (turning the volume "up") corresponds to higher amplification of the sound signal.
- Gas Pedal
- The gas pedal in your car is an example of gain. Pressing harder on the gas pedal causes the engine to receive more gas, and causes the engine to output higher RPMs.
- Brightness Buttons
- Most computer monitors come with brightness buttons that control how bright the screen image is. More brightness causes more power to be outputed to the screen.
Responses to Gain
As the gain to a system increases, generally the rise-time decreases, the percent overshoot increases, and the settling time increases. However, these relationships are not always the same. A critically damped system, for example, may decrease in rise time while not experiencing any effects of percent overshoot or settling time.
Gain and Stability
If the gain increases to a high enough extent, some systems can become unstable. We will examine this effect in the chapter on Root Locus. But it will decrease the steady state error.
Conditional Stability
Systems that are stable for some gain values, and unstable for other values are called conditionally stable systems. The stability is conditional upon the value of the gain, and often the threshold where the system becomes unstable is important to find.
Block Diagrams
When designing or analyzing a system, often it is useful to model the system graphically. Block Diagrams are a useful and simple method for analyzing a system graphically. A "block" looks on paper exactly what it means:
Systems in Series
When two or more systems are in series, they can be combined into a single representative system, with a transfer function that is the product of the individual systems.

If we have two systems, f(t) and g(t), we can put them in series with one another so that the output of system f(t) is the input to system g(t). Now, we can analyze them depending on whether we are using our classical or modern methods.
If we define the output of the first system as h(t), we can define h(t) as:
Now, we can define the system output y(t) in terms of h(t) as:
We can expand h(t):
But, since convolution is associative, we can re-write this as:
Our system can be simplified therefore as such:

Series Transfer Functions
If two or more systems are in series with one another, the total transfer function of the series is the product of all the individual system transfer functions.

In the time-domain we know that:
But, in the frequency domain we know that convolution becomes multiplication, so we can re-write this as:
We can represent our system in the frequency domain as:
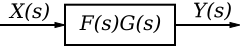
Series State Space
If we have two systems in series (say system F and system G), where the output of F is the input to system G, we can write out the state-space equations for each individual system.
System 1:
System 2:
And we can write substitute these equations together form the complete response of system H, that has input u, and output yG:
[Series state equation]
[Series output equation]
Systems in Parallel

Blocks may not be placed in parallel without the use of an adder. Blocks connected by an adder as shown above have a total transfer function of:
Since the Laplace transform is linear, we can easily transfer this to the time domain by converting the multiplication to convolution:

State Space Model
The state-space equations, with non-zero A, B, C, and D matrices conceptually model the following system:

In this image, the strange-looking block in the center is either an integrator or an ideal delay, and can be represented in the transfer domain as:
- or
Depending on the time characteristics of the system. If we only consider continuous-time systems, we can replace the funny block in the center with an integrator:
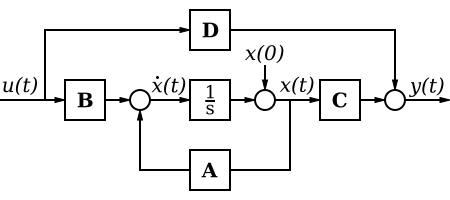
In the Laplace Domain
The state space model of the above system, if A, B, C, and D are transfer functions A(s), B(s), C(s) and D(s) of the individual subsystems, and if U(s) and Y(s) represent a single input and output, can be written as follows:
We will explain how we got this result, and how we deal with feedforward and feedback loop structures in the next chapter.
Adders and Multipliers
Some systems may have dedicated summation or multiplication devices, that automatically add or multiply the transfer functions of multiple systems together
Simplifying Block Diagrams
Block diagrams can be systematically simplified. Note that this table is from Schaum's Outline: Feedback and Controls Systems by DiStefano et al
External links
Feedback Loops
Feedback
A feedback loop is a common and powerful tool when designing a control system. Feedback loops take the system output into consideration, which enables the system to adjust its performance to meet a desired output response.
When talking about control systems it is important to keep in mind that engineers typically are given existing systems such as actuators, sensors, motors, and other devices with set parameters, and are asked to adjust the performance of those systems. In many cases, it may not be possible to open the system (the "plant") and adjust it from the inside: modifications need to be made external to the system to force the system response to act as desired. This is performed by adding controllers, compensators, and feedback structures to the system.
Basic Feedback Structure
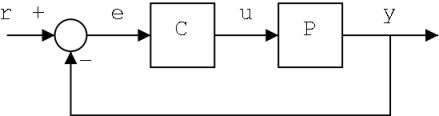
This is a basic feedback structure. Here, we are using the output value of the system to help us prepare the next output value. In this way, we can create systems that correct errors. Here we see a feedback loop with a value of one. We call this a unity feedback.
Here is a list of some relevant vocabulary, that will be used in the following sections:
- Plant
- The term "Plant" is a carry-over term from chemical engineering to refer to the main system process. The plant is the preexisting system that does not (without the aid of a controller or a compensator) meet the given specifications. Plants are usually given "as is", and are not changeable. In the picture above, the plant is denoted with a P.
- Controller
- A controller, or a "compensator" is an additional system that is added to the plant to control the operation of the plant. The system can have multiple compensators, and they can appear anywhere in the system: Before the pick-off node, after the summer, before or after the plant, and in the feedback loop. In the picture above, our compensator is denoted with a C.
- Summer
- A summer is a symbol on a system diagram, (denoted above with parenthesis) that conceptually adds two or more input signals, and produces a single sum output signal.
- Pick-off node
- A pickoff node is simply a fancy term for a split in a wire.
- Forward Path
- The forward path in the feedback loop is the path after the summer, that travels through the plant and towards the system output.
- Reverse Path
- The reverse path is the path after the pick-off node, that loops back to the beginning of the system. This is also known as the "feedback path".
- Unity feedback
- When the multiplicative value of the feedback path is 1.
Negative vs Positive Feedback
It turns out that negative feedback is almost always the most useful type of feedback. When we subtract the value of the output from the value of the input (our desired value), we get a value called the error signal. The error signal shows us how far off our output is from our desired input.
Positive feedback has the property that signals tend to reinforce themselves, and grow larger. In a positive feedback system, noise from the system is added back to the input, and that in turn produces more noise. As an example of a positive feedback system, consider an audio amplification system with a speaker and a microphone. Placing the microphone near the speaker creates a positive feedback loop, and the result is a sound that grows louder and louder. Because the majority of noise in an electrical system is high-frequency, the sound output of the system becomes high-pitched.
Example: State-Space Equation
In the previous chapter, we showed you this picture:
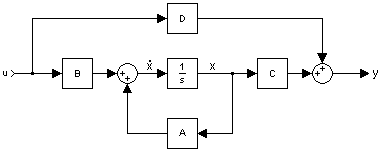
Now, we will derive the I/O relationship into the state-space equations. If we examine the inner-most feedback loop, we can see that the forward path has an integrator system, , and the feedback loop has the matrix value A. If we take the transfer function only of this loop, we get:
Pre-multiplying by the factor B, and post-multiplying by C, we get the transfer function of the entire lower-half of the loop:
We can see that the upper path (D) and the lower-path Tlower are added together to produce the final result:
Now, for an alternate method, we can assume that x' is the value of the inner-feedback loop, right before the integrator. This makes sense, since the integral of x' should be x (which we see from the diagram that it is. Solving for x', with an input of u, we get:
This is because the value coming from the feedback branch is equal to the value x times the feedback loop matrix A, and the value coming from the left of the summer is the input u times the matrix B.
If we keep things in terms of x and u, we can see that the system output is the sum of u times the feed-forward value D, and the value of x times the value C:
These last two equations are precisely the state-space equations of our system.
Feedback Loop Transfer Function
We can solve for the output of the system by using a series of equations:
and when we solve for Y(s) we get:
[Feedback Transfer Function]
The reader is encouraged to use the above equations to derive the result by themselves.
The function E(s) is known as the error signal. The error signal is the difference between the system output (Y(s)), and the system input (X(s)). Notice that the error signal is now the direct input to the system G(s). X(s) is now called the reference input. The purpose of the negative feedback loop is to make the system output equal to the system input, by identifying large differences between X(s) and Y(s) and correcting for them.
Example: Elevator
Here is a simple example of reference inputs and feedback systems:
There is an elevator in a certain building with 5 floors. Pressing button "1" will take you to the first floor, and pressing button "5" will take you to the fifth floor, etc. For reasons of simplicity, only one button can be pressed at a time.
Pressing a particular button is the reference input of the system. Pressing "1" gives the system a reference input of 1, pressing "2" gives the system a reference input of 2, etc. The elevator system then, tries to make the output (the physical floor location of the elevator) match the reference input (the button pressed in the elevator). The error signal, e(t), represents the difference between the reference input x(t), and the physical location of the elevator at time t, y(t).
Let's say that the elevator is on the first floor, and the button "5" is pressed at time t0. The reference input then becomes a step function:
Where we are measuring in units of "floors". At time t0, the error signal is:
Which means that the elevator needs to travel upwards 4 more floors. At time t1, when the elevator is at the second floor, the error signal is:
Which means the elevator has 3 more floors to go. Finally, at time t4, when the elevator reaches the top, the error signal is:
And when the error signal is zero, the elevator stops moving. In essence, we can define three cases:
- e(t) is positive: In this case, the elevator goes up one floor, and checks again.
- e(t) is zero: The elevator stops.
- e(t) is negative: The elevator goes down one floor, and checks again.
State-Space Feedback Loops
In the state-space representation, the plant is typically defined by the state-space equations:
The plant is considered to be pre-existing, and the matrices A, B, C, and D are considered to be internal to the plant (and therefore unchangeable). Also, in a typical system, the state variables are either fictional (in the sense of dummy-variables), or are not measurable. For these reasons, we need to add external components, such as a gain element, or a feedback element to the plant to enhance performance.
Consider the addition of a gain matrix K installed at the input of the plant, and a negative feedback element F that is multiplied by the system output y, and is added to the input signal of the plant. There are two cases:
- The feedback element F is subtracted from the input before multiplication of the K gain matrix.
- The feedback element F is subtracted from the input after multiplication of the K gain matrix.
In case 1, the feedback element F is added to the input before the multiplicative gain is applied to the input. If v is the input to the entire system, then we can define u as:
In case 2, the feeback element F is subtracted from the input after the multiplicative gain is applied to the input. If v is the input to the entire system, then we can define u as:
Open Loop vs Closed Loop
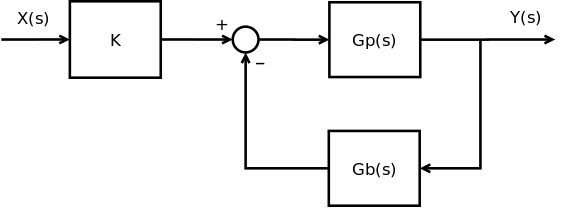
Let's say that we have the generalized system shown above. The top part, Gp(s) represents all the systems and all the controllers on the forward path. The bottom part, Gb(s) represents all the feedback processing elements of the system. The letter "K" in the beginning of the system is called the Gain. We will talk about the gain more in later chapters. We can define the Closed-Loop Transfer Function as follows:
[Closed-Loop Transfer Function]
If we "open" the loop, and break the feedback node, we can define the Open-Loop Transfer Function, as:
[Open-Loop Transfer Function]
We can redefine the closed-loop transfer function in terms of this open-loop transfer function:
These results are important, and they will be used without further explanation or derivation throughout the rest of the book.
Placement of a Controller
There are a number of different places where we could place an additional controller.
Each location has certain benefits and problems, and hopefully we will get a chance to talk about all of them.
Second-Order Systems
The general expression of the transfer function of a second order system is given as:
where and are damping ratio and natural frequency of the system respectively.
Damping Ratio
The damping ratio is defined by way of the sign . The damping ratio gives us an idea about the nature of the transient response detailing the amount of overshoot & oscillation that the system will undergo. This is completely regardless of time scaling.
If :
- = zero, the system is undamped;
- < 1, the system is underdamped;
- = 1, the system is critically damped;
- > 1, the system is overdamped.
is used in conjunction with the natural frequency to determine system properties. To find the zeta value you must first find the natural response!
Natural Frequency
Natural Frequency, denoted by is defined as the frequency with which the system would oscillate if it were not damped and we define the damping ratio as .
System Sensitivity
Signal Flow Diagrams
Signal-flow graphs
Signal-flow graphs are another method for visually representing a system. Signal Flow Diagrams are especially useful, because they allow for particular methods of analysis, such as Mason's Gain Formula.
Signal flow diagrams typically use curved lines to represent wires and systems, instead of using lines at right-angles, and boxes, respectively. Every curved line is considered to have a multiplier value, which can be a constant gain value, or an entire transfer function. Signals travel from one end of a line to the other, and lines that are placed in series with one another have their total multiplier values multiplied together (just like in block diagrams).
Signal flow diagrams help us to identify structures called "loops" in a system, which can be analyzed individually to determine the complete response of the system.

Forward Paths
A forward path is a path in the signal flow diagram that connects the input to the output without touching any single node or path more than once. A single system can have multiple forward paths.
Loops
A loop is a structure in a signal flow diagram that leads back to itself. A loop does not contain the beginning and ending points, and the end of the loop is the same node as the beginning of a loop.
Loops are said to touch if they share a node or a line in common.
The Loop gain is the total gain of the loop, as you travel from one point, around the loop, back to the starting point.
Delta Values
The Delta value of a system, denoted with a Greek Δ is computed as follows:
Where:
- A is the sum of all individual loop gains
- B is the sum of the products of all the pairs of non-touching loops
- C is the sum of the products of all the sets of 3 non-touching loops
- D is the sum of the products of all the sets of 4 non-touching loops
- et cetera.
If the given system has no pairs of loops that do not touch, for instance, B and all additional letters after B will be zero.
Mason's Rule
Mason's rule is a rule for determining the gain of a system. Mason's rule can be used with block diagrams, but it is most commonly (and most easily) used with signal flow diagrams.
If we have computed our delta values (above), we can then use Mason's Gain Rule to find the complete gain of the system:
[Mason's Rule]
Where M is the total gain of the system, represented as the ratio of the output gain (yout) to the input gain (yin) of the system. Mk is the gain of the kth forward path, and Δk is the loop gain of the kth loop.
Examples
Solving a signal-flow graph by systematic reduction : Two interlocking loops
This example shows how a system of five equations in five unknowns is solved using systematic reduction rules. The independent variable is . The dependent variables are , , , , . The coefficients are labeled .
Here is the starting flowgraph:
The steps for solving follow.
Removing edge c from x2 to x3
Removing node x2 and its inflows
has no outflows, and is not a node of interest.


Removing edge e from x3 to x1
Remove edge d from x3 to x4
Node has no outflows and is not a node of interest. It is deleted along with its inflows.
Removing self-loop at x1
Removing self-loop at x4
Remove edge from x4 to x1
Remove outflow from x4 to xout
's outflow is then eliminated: is connected directly to using the product of the gains from the two edges replaced.
is not a variable of interest; thus, its node and its inflows are eliminated.
Eliminating self-loop at x1
Eliminating outflow from x1, then eliminating x1 and its inflows
is not a variable of interest; and its inflows are eliminated
Simplifying the gain expression
Solving a signal-flow graph by systematic reduction: Three equations in three unknowns
This example shows how a system of three equations in three unknowns is solved using systematic reduction rules.
The independent variables are , , . The dependent variables are , , . The coefficients are labeled . The steps for solving follow:
Electrical engineering: Construction of a flow graph for a RC circuit
This illustration shows the physical connections of the circuit. Independent voltage source S is connected in series with a resistor R and capacitor C. The example is developed from the physical circuit equations and solved using signal-flow graph techniques. Polarity is important:
- S is a source with the positive terminal at N1 and the negative terminal at N3
- R is a resistor with the positive terminal at N1 and the negative terminal at N2
- C is a capacitor with the positive terminal at N2 and the negative terminal at N3.
The unknown variable of interest is the voltage across capacitor C.
Approach to the solution:
- Find the set of equations from the physical network. These equations are acausal in nature.
- Branch equations for the capacitor and resistor. The equations will be developed as transfer functions using Laplace transforms.
- Kirchhoff's voltage and current laws
- Build a signal-flow graph from the equations.
- Solve the signal-flow graph.
Branch equations
 The branch equations are shown for R and C.
The branch equations are shown for R and C.
Resistor R (Branch equation )
The resistor's branch equation in the time domain is:
In the Laplace-transformed signal space:
Capacitor C (Branch equation )
The capacitor's branch equation in the time domain is:
Assuming the capacitor is initially discharged, the equation becomes:
Taking the derivative of this and multiplying by C yields the derivative form:
In the Laplace-transformed signal space:
Kirchhoff's laws equations
Kirchhoff's Voltage Law equation
This circuit has only one independent loop. Its equation in the time domain is:
In the Laplace-transformed signal space:
Kirchhoff's Current Law equations
The circuit has three nodes, thus three Kirchhoff's current equations (expresses here as the currents flowing from the nodes):
In the Laplace-transformed signal space:
A set of independent equations must be chosen. For the current laws, it is necessary to drop one of these equations. In this example, let us choose .
Building the signal-flow graph
We then look at the inventory of equations, and the signals that each equation relates:
| Equation | Signals |
|---|---|
The next step consists in assigning to each equation a signal that will be represented as a node. Each independent source signal is represented in the signal-flow graph as a source node, therefore no equation is assigned to the independent source . There are many possible valid signal flow graphs from this set of equations. An equation must only be used once, and the variables of interest must be represented.
| Equation | Signals | Assigned signal node |
|---|---|---|
The resulting flow graph is then drawn
The next step consists in solving the signal-flow graph.
Using either Mason or systematic reduction, the resulting signal flow graph is:

Mechatronics example

Appendicies
Appendix 1: Physical Models
Appendix: Physical Models
Physical Models
This page will serve as a refresher for various different engineering disciplines on how physical devices are modeled. Models will be displayed in both time-domain and Laplace-domain input/output characteristics. The only information that is going to be displayed here will be the ones that are contributed by knowledgeable contributors.
Electrical Systems
Circuit Theory
Electronics
Component Time-Domain Laplace Fourier Resistor R R R Capacitor Inductor
Mechanical Systems
Civil/Construction Systems
Chemical Systems
Glossary
Resources
Licensing
1) Glossary
2) List of Equations
3) Resources and Bibliography
4) Licensing
5) GNU Free Documentation License
Glossary and List of Equations
The following is a listing of some of the most important terms from the book, along with a short definition or description.
A, B, C
- Acceleration Error
- The amount of steady state error of the system when stimulated by a unit parabolic input.
- Acceleration Error Constant
- A system metric that determines that amount of acceleration error in the system.
- Adaptive Control
- A branch of control theory where controller systems are able to change their response characteristics over time, as the input characteristics to the system change.
- Adaptive Gain
- when control gain is varied depending on system state or condition, such as a disturbance
- Additivity
- A system is additive if a sum of inputs results in a sum of outputs.
- Analog System
- A system that is continuous in time and magnitude.
- ARMA
- Autoregressive Moving Average, see [1]
- ATO
- Analog Timed Output. Control loop output is correlated to a timed contact closure.
- A/M
- Auto-Manual. Control modes, where auto typically means output is computer-driven, calculated while manual can be field-driven or merely using a static setpoint.
- Bilinear Transform
- a variant of the Z-transform, see [2]
- Block Diagram
- A visual way to represent a system that displays individual system components as boxes, and connections between systems as arrows.
- Bode Plots
- A set of two graphs, a "magnitude" and a "phase" graph, that are both plotted on log scale paper. The magnitude graph is plotted in decibels versus frequency, and the phase graph is plotted in degrees versus frequency. Used to analyze the frequency characteristics of the system.
- Bounded Input, Bounded Output
- BIBO. If the input to the system is finite, then the output must also be finite. A condition for stability.
- Cascade
- When the output of a control loop is fed to/from another loop.
- Causal
- A system whose output does not depend on future inputs. All physical systems must be causal.
- Classical Approach
- See Classical Controls.
- Classical Controls
- A control methodology that uses the transform domain to analyze and manipulate the Input-Output characteristics of a system.
- Closed Loop
- a controlled system using feedback or feedforward
- Compensator
- A Control System that augments the shortcomings of another system.
- Condition Number
- Conditional Stability
- A system with variable gain is conditionally stable if it is BIBO stable for certain values of gain, but not BIBO stable for other values of gain.
- Continuous-Time
- A system or signal that is defined at all points t.
- Control Rate
- the rate at which control is computed and any appropriate output sent. Lower bound is sample rate.
- Control System
- A system or device that manages the behavior of another system or device.
- Controller
- See Control System.
- Convolution
- A complex operation on functions defined by the integral of the two functions multiplied together, and time-shifted.
- Convolution Integral
- The integral form of the convolution operation.
- CQI
- Control Quality Index, , 1 being ideal.
- CV
- Controlled variable
D, E, F
- Damping Ratio
- A constant that determines the damping properties of a system.
- Deadtime
- time shift between the output change and the related effect (typ. at least one control sample). One sees "Lag" used for this action sometimes.
- Digital
- A system that is both discrete-time, and quantized.
- Direct action
- target output increase is required to bring the process variable (PV) to setpoint (SP) when PV is below SP. Thus, PV increases with output increase directly.
- Discrete magnitude
- See quantized.
- Discrete time
- A system or signal that is only defined at specific points in time.
- Distributed
- A system is distributed if it has both an infinite number of states, and an infinite number of state variables. See Lumped.
- Dynamic
- A system is called dynamic if it doesn't have memory. See Instantaneous, Memory.
- Eigenvalues
- Solutions to the characteristic equation of a matrix. If the matrix is itself a function of time, the eigenvalues might be functions of time. In this case, they are frequently called eigenfunctions.
- Eigenvectors
- The nullspace vectors of the characteristic equation for particular eigenvalues. Used to determine state-transitions, among other things. See [3]
- Euler's Formula
- An equation that relates complex exponentials to complex sinusoids.
- Exponential Weighted Average (EWA)
- Apportions fractional weight to new and existing data to form a working average. Example EWA=0.70*EWA+0.30*latest, see Filtering.
- External Description
- A description of a system that relates the input of the system to the output, without explicitly accounting for the internal states of the system.
- Feedback
- The output of the system is passed through some sort of processing unit H, and that result is fed into the plant as an input.
- Feedforward
- whwn apriori knowledge is used to forecast at least part of the control response.
- Filtering (noise)
- Use of signal smoothing techniques to reject undesirable components like noise. Can be as simple as using exponential weighted averaging on the input.
- Final Value Theorem
- A theorem that allows the steady-state value of a system to be determined from the transfer function.
- FOH
- First order hold
- Frequency Response
- The response of a system to sinusoids of different frequencies. The Fourier Transform of the impulse response.
- Fourier Transform
- An integral transform, similar to the Laplace Transform, that analyzes the frequency characteristics of a system.
See [4]
G, H, I
- Game Theory
- A branch of study that is related to control engineering, and especially optimal control. Multiple competing entities, or "players" attempt to minimize their own cost, and maximize the cost of the opponents.
- Gain
- A constant multiplier in a system that is typically implemented as an amplifier or attenuator. Gain can be changed, but is typically not a function of time. Adaptive control can use time-adaptive gains that change with time.
- General Description
- An external description of a system that relates the system output to the system input, the system response, and a time constant through integration.
- Hendrik Wade Bode
- Electrical Engineer, did work in control theory and communications. Is primarily remembered in control engineering for his introduction of the bode plot.
- Harry Nyquist
- Electrical Engineer, did extensive work in controls and information theory. Is remembered in this book primarily for his introduction of the Nyquist Stability Criterion.
- Homogeniety
- Property of a system whose scaled input results in an equally scaled output.
- Hybrid Systems
- Systems which have both analog and digital components.
- Impulse
- A function denoted δ(t), that is the derivative of the unit step.
- Impulse Response
- The system output when the system is stimulated by an impulse input. The Inverse Laplace Transform of the transfer function of the system.
- Initial Conditions
- The conditions of the system at time , where t0 is the first time the system is stimulated.
- Initial Value Theorem
- A theorem that allows the initial conditions of the system to be determined from the Transfer function.
- Input-Output Description
- See external description.
- Instantaneous
- A system is instantaneous if the system doesn't have memory, and if the current output of the system is only dependent on the current input. See Dynamic, Memory.
- Integrated Absolute Error (IAE)
- absolute error (ideal vs actual performance) is integrated over the analysis period.
- Integrated Squared Error (ISE)
- squared error (ideal vs actual performance) is integrated over the analysis period.
- Integrators
- A system pole at the origin of the S-plane. Has the effect of integrating the system input.
- Inverse Fourier Transform
- An integral transform that converts a function from the frequency domain into the time-domain.
- Inverse Laplace Transform
- An integral transform that converts a function from the S-domain into the time-domain.
- Inverse Z-Transform
- An integral transform that converts a function from the Z-domain into the discrete time domain.
J, K, L
- Lag
- The observed process impact from an output is slower than the control rate.
- Laplace Transform
- An integral transform that converts a function from the time domain into a complex frequency domain.
- Laplace Transform Domain
- A complex domain where the Laplace Transform of a function is graphed. The imaginary part of s is plotted along the vertical axis, and the real part of s is plotted along the horizontal axis.
- Left Eigenvectors
- Left-hand nullspace solutions to the characteristic equation of a matrix for given eigenvalues. The rows of the inverse transition matrix.
- Linear
- A system that satisfies the superposition principle. See Additive and Homogeneous.
- Linear Time-Invariant
- LTI. See Linear, and Time-Invariant.
- Low Clamp
- User-applied lower bound on control output signal.
- L/R
- Local/Remote operation.
- LQR
- Linear Quadratic Regulator.
- Lumped
- A system with a finite number of states, or a finite number of state variables.
M, N, O
- Magnitude
- the gain component of frequency response. This is often all that is considered in saying a discrete filter's response is well matched to the analog's. It is the DC gain at 0 frequency.
- Marginal Stability
- A system has an oscillatory response, as determined by having imaginary poles or imaginary eigenvalues.
- Mason's Rule
- see [5]
- MATLAB
- Commercial software having a Control Systems toolbox. Also see Octave.
- Memory
- A system has memory if its current output is dependent on previous and current inputs.
- MFAC
- Model Free Adaptive Control.
- MIMO
- A system with multiple inputs and multiple outputs.
- Modern Approach
- see modern controls
- Modern Controls
- A control methodology that uses the state-space representation to analyze and manipulate the Internal Description of a system.
- Modified Z-Transform
- A version of the Z-Transform, expanded to allow for an arbitrary processing delay.
- MPC
- Model Predictive Control.
- MRAC
- Model Reference Adaptive Control.
- MV
- can denote Manipulated variable or Measured variable (not the same)
- Natural Frequency
- The fundamental frequency of the system, the frequency for which the system's frequency response is largest.
- Negative Feedback
- A feedback system where the output signal is subtracted from the input signal, and the difference is input to the plant.
- The Nyquist Criteria
- A necessary and sufficient condition of stability that can be derived from Bode plots.
- Nonlinear Control
- A branch of control engineering that deals exclusively with non-linear systems. We do not cover nonlinear systems in this book.
- OCTAVE
- Open-source software having a Control Systems toolbox. Also see MATLAB.
- Offset
- The discrepancy between desired and actual value after settling. P-only control can give offset.
- Oliver Heaviside
- Electrical Engineer, Introduced the Laplace Transform as a tool for control engineering.
- Open Loop
- when the system is not closed, its behavior has a free-running component rather than controlled
- Optimal Control
- A branch of control engineering that deals with the minimization of system cost, or maximization of system performance.
- Order
- The order of a polynomial is the highest exponent of the independent variable in that exponent. The order of a system is the order of the Transfer Function's denominator polynomial.
- Output equation
- An equation that relates the current system input, and the current system state to the current system output.
- Overshoot
- measures the extent of system response against desired (setpoint tracking).
P, Q, R
- Parabolic
- A parabolic input is defined by the equation.
- Partial Fraction Expansion
- A method by which a complex fraction is decomposed into a sum of simple fractions.
- Percent Overshoot
- PO, the amount by which the step response overshoots the reference value, in percentage of the reference value.
- Phase
- the directional component of frequency response, not typically well-matched between a discrete filter equivalent to the analog version, especially as frequency approaches the Nyquist limit. The final value in the limit drives system stability, and stems from the poles and zeros of the characteristic equation.
- PID
- Proportional-Integral-Derivative
- Plant
- A central system which has been provided, and must be analyzed or controlled.
- PLC
- Programmable Logic Controller
- Pole
- A value for s that causes the denominator of the transfer function to become zero, and therefore causes the transfer function itself to approach infinity.
- Pole-Zero Form
- The transfer function is factored so that the locations of all the poles and zeros are clearly evident.
- Position Error
- The amount of steady-state error of a system stimulated by a unit step input.
- Position Error Constant
- A constant that determines the position error of a system.
- Positive Feedback
- A feedback system where the system output is added to the system input, and the sum is input into the plant.
- PSD
- The power spectral density which shows the distribution of power in the spectrum of a particular signal.
- Pulse Response
- The response of a digital system to a unit step input, in terms of the transfer matrix.
- PV
- Process variable
- Quantized
- A system is quantized if it can only output certain discrete values.
- Quarter-decay
- the time or number of control rates required for process overshoot to be limited to within 1/4 of the maximum peak overshoot (PO) after a SP change. If the PO is 25% at sample time N, this would be time N+k when subsequent PV remains < SP*1.0625, presuming the process is settling.
- Raise-Lower
- Output type that works from present position rather than as a completely new computed spanned output. For R/L, the % change should be applied to the working clamps i.e. 5%(hi clamp-lo clamp).
- Ramp
- A ramp is defined by the function .
- Reconstructors
- A system that converts a digital signal into an analog signal.
- Reference Value
- The target input value of a feedback system.
- Relaxed
- A system is relaxed if the initial conditions are zero.
- Reverse action
- target output decrease is required to bring the process variable (PV) to setpoint (SP) when PV is below SP. Thus, PV decreases with output increase.
- Rise Time
- The amount of time it takes for the step response of the system to reach within a certain range of the reference value. Typically, this range is 80%.
- Robust Control
- A branch of control engineering that deals with systems subject to external and internal noise and disruptions.
S, T, U, V
- Samplers
- A system that converts an analog signal into a digital signal.
- Sampled-Data Systems
- See Hybrid Systems'.
- Sampling Time
- In a discrete system, the sampling time is the amount of time between samples. Reflects the lower bound for Control rate.
- SCADA
- Supervisory Control and Data Acquisition.
- S-Domain
- The domain of the Laplace Transform of a signal or system.
- Second-order System;
- Settling Time
- The amount of time it takes for the system's oscillatory response to be damped to within a certain band of the steady-state value. That band is typically 10%.
- Signal Flow Diagram
- A method of visually representing a system, using arrows to represent the direction of signals in the system.
- SISO
- Single input, single output.
- Span
- the designed operation region of the item,=high range-low range. Working span can be smaller if output clamps are used.
- Stability
- Typically "BIBO Stability", a system with a well-behaved input will result in a well-behaved output. "Well-behaved" in this sense is arbitrary.
- Star Transform
- A version of the Laplace Transform that acts on discrete signals. This transform is implemented as an infinite sum.
- State Equation
- An equation that relates the future states of a system with the current state and the current system input.
- State Transition Matrix:A coefficient matrix, or a matrix function that relates how the system state changes in response to the system input. In time-invariant systems, the state-transition matrix is the matrix exponential of the system matrix.
- State-Space Equations
- A set of equations, typically written in matrix form, that relates the input, the system state, and the output. Consists of the state equation and the output equation. See [6]
- State-Variable
- A vector that describes the internal state of the system.
- Stability
- The system output cannot approach infinity as time approaches infinity. See BIBO, Lyapunov Stability.
- Step Response
- The response of a system when stimulated by a unit-step input. A unit step is a setpoint change for setpoint tracking.
- Steady State
- The output value of the system as time approaches infinity.
- Steady State Error
- At steady state, the amount by which the system output differs from the reference value.
- Superposition
- A system satisfies the condition of superposition if it is both additive and homogeneous.
- System Identification
- method of trying to identify the system characterization , typically through least squares analysis of input,output and noise data vectors. May use ARMA type framework.
- System Type
- The number of ideal integrators in the system.
- Time-Invariant
- A system is time-invariant if an input time-shifted by an arbitrary delay produces an output shifted by that same delay.
- Transfer Function
- The ratio of the system output to its input, in the S-domain. The Laplace Transform of the function's impulse response.
- Transfer Function Matrix:The Laplace transform of the state-space equations of a system, that provides an external description of a MIMO system.
- Uniform Stability
- Also "Uniform BIBO Stability", a system where an input signal in the range [0, 1] results in a finite output from the initial time until infinite time. See [7].
- Unit Step
- An input defined by . Practically, a setpoint change.
- Unity Feedback
- A feedback system where the feedback loop element H has a transfer function of 1.
- Velocity Error
- The amount of steady-state error when the system is stimulated by a ramp input.
- Velocity Error Constant
- A constant that determines that amount of velocity error in a system.
W, X, Y, Z
- W-plane
- Reference plane used in the bilinear transform.
- Wind-up
- when the numerics of computed control adjustment can "wind-up", yielding control correction with an inappropriate component unless prevented. An example is the "I" contribution of PID if output has been disconnected during PID calculation
- Zero
- A value for s that causes the numerator of the transfer function to become zero, and therefore causes the transfer function itself to become zero.
- Zero Input Response
- The response of a system with zero external input. Relies only on the value of the system state to produce output.
- Zero State Response
- The response of the system with zero system state. The output of the system depends only on the system input.
- ZOH
- Zero order hold.
- Z-Transform
- An integral transform that is related to the Laplace transform through a change of variables. The Z-Transform is used primarily with digital systems. See [8]
List of Equations
The following is a list of the important equations from the text, arranged by subject. For more information about these equations, including the meaning of each variable and symbol, the uses of these functions, or the derivations of these equations, see the relevant pages in the main text.
Fundamental Equations
[Euler's Formula]
[Convolution]
[Convolution Theorem]
[Characteristic Equation]
[Decibels]
Basic Inputs
[Unit Step Function]
[Unit Ramp Function]
[Unit Parabolic Function]
Error Constants
[Position Error Constant]
[Velocity Error Constant]
[Acceleration Error Constant]
System Descriptions
[General System Description]
[Convolution Description]
[Transfer Function Description]
[State-Space Equations]
[Transfer Matrix]
[Transfer Matrix Description]
[Mason's Rule]
Feedback Loops
[Closed-Loop Transfer Function]
[Open-Loop Transfer Function]
[Characteristic Equation]
Transforms
[Laplace Transform]
[Inverse Laplace Transform]
[Fourier Transform]
[Inverse Fourier Transform]
[Star Transform]
[Z Transform]
[Inverse Z Transform]
[Modified Z Transform]
Transform Theorems
[Final Value Theorem]
[Initial Value Theorem]
State-Space Methods
[General State Equation Solution]
[General Output Equation Solution]
[Time-Variant General Solution]
[Impulse Response Matrix]
Root Locus
[The Magnitude Equation]
[The Angle Equation]
[Number of Asymptotes]
[Angle of Asymptotes]
[Origin of Asymptotes]
[Breakaway Point Locations]
- or
Lyapunov Stability
[Lyapunov Equation]
Controllers and Compensators
[PID]
Resources and Further Reading
Wikibooks
A number of wikibooks exist on topics that are (a) prerequisites to this book (b) companion pieces to and references for this book, and (c) of further interest to people who have completed reading this book. Below will be a listing of such books, ordered according to the categories listed above.
Prerequisite Books
- Linear algebra
- Linear Algebra with Differential Equations
- Complex Numbers
- Calculus
- Signals and Systems
Companion Books
Books for Further Reading
Wikiversity
The Wikiversity project also contains a number of collaborative learning efforts in the field of control systems, and related subjects. As best as possible, we will attempt to list those efforts here:
Wikiversity is also a place to host learning materials, such as assignments, tests, and reading plans. It is the goal of the authors of this book to create such materials for use in conjunction with this book. As such materials are added to wikiversity, they will be referenced here.
Wikipedia
There are a number of Wikipedia articles on the topics covered in this book, and those articles will be linked to from the appropriate pages of this book. However, some of the articles that are of general use to the book are:
A complete listing of all Wikipedia articles related to this topic can be found at:
Software
Root Locus
Root-Locus is a free program that was used to create several of the images in this book. That software can be obtained from the following web address:
Explicit permission has been granted by the author of the program to include screenshots on wikibooks. Images generated from the Root-Locus program should be included in Category:Root Locus Images, and appropriately tagged as a screenshot of a free software program.
MATLAB
MATLAB, Simulink, the Control Systems Toolbox and the Symbolic Toolbox are trademarks of The MathWorks, Inc. Other product or brand names are trademarks or registered trademarks of their respective holders. For more information about MATLAB, or to purchase a copy, visit:
For information about the proper way to refer to MATLAB, please see:
All MATLAB code appearing in this book has been released under the terms of the GFDL by the respective authors. All screenshots, graphs, and images relating to MATLAB have been produced in Octave, with changes to the original MATLAB code made as necessary.
Octave
Octave is a free open-source alternative program to MATLAB. Octave utilizes a scripting language that is very similar to that of MATLAB, although there are several differences. Most of the basic examples described in this book will work equally well in MATLAB or Octave, with no changes or only minor changes. For more information, or to download a copy of Octave, visit:
Commercial Vendors
The following are some common vendors of control-related hardware and software. These links are for personal interest only, and do not constitute an official endorsement of the companies by Wikibooks.
External Publications
The following books and resources were used as reference works in the creation of this wikibook (books listed in alphabetical order).
- Brogan, William L, Modern Control Theory, 3rd Edition, 1991. ISBN 0135897637
- Chen, Chi-Tsong, Linear System Theory and Design, 3rd Edition, 1999. ISBN 0195117778
- Dorf and Bishop, Modern Control Systems, 10th Edition, Prentice Hall, 2005. ISBN 0131277650
- Hamming, Richard, Numerical Methods for Scientists and Engineers, 2nd edition, Dover, 1987. ISBN 0486652416
- Kalman, R. E., When is a linear control system optimal, ASME Transactions, Journal of Basic Engineering, 1964
- Kalman, R. E., On the General Theory of Control Systems, IRE Transactions on Automatic Control, Volume 4, Issue 3, p110, 1959. ISSN 0096199X
- Ogata, Katsuhiko, Solving Control Engineering Problems with MATLAB, Prentice Hall, New Jersey, 1994. ISBN 0130459070
- Phillips and Nagle, Digital Control System Analysis and Design, 3rd Edition, Prentice Hall, 1995. ISBN 013309832X
The following books and resources are suitable for further reading.
- DiStefano, Stubberud, Williams, Schaum's Outline Series Feedback and Control Systems, 2nd Edition, 1997. ISBN 0070170479
- Franklin, Powell, Workman, Digital Control of Dynamic Systems, 3rd Edition, 1997. ISBN 9780201820546
- Brosilow, Joseph, Techniques of Model-Based Control, 2002. ISBN 013028078X
External Resources
- IEEE Control Systems Society
- ControlTheoryPro.com A place for controls theory, application, and modeling help.
- University of Michigan Chemical Engineering Process Dynamics and Controls Open Textbook
Licensing
License
The text of this wikibook is released under the terms of the GNU Free Documentation License version 1.2. The particular version of that license that is being used can be found at:
The text of that license will also be appended to the end of the printable version of this wikibook.
Images used in this document may not be released under the GFDL, and the licenses used with each image in this book will be listed in a table below. Some contributors may cross-license their contributions under the GFDL and another compatible license. Some contributions have been released into the public domain.
Images
The individual images used in this wikibook are released under a variety of different licenses, including the GFDL, and Creative-Commons licenses. Some images have been released into the public domain. The following table will list the images used in this book, along with the license under which the image is released, and any additional information about the images that is needed under the terms of the applicable licenses.
Authors
The authors of this text can list themselves below. Authors should be listed in alphabetical order by first name (if a real name is used), or by username. This is not a canonical list.
The usernames of additional contributors, as well as the size and scope of the contributions made by the authors listed above can be found in the history records of the individual pages on the Wikibooks website. Those history pages satisfy the attribution requirement of the GFDL, and any lists of authors that appear here or anywhere else do not count as legal attribution under the terms of that license.
Child Versions
The Control Systems wikibook is offered with a number of child versions, which represent subsets of the material available in the parent book. Because certain chapters are omitted from the child versions, some of the images listed above may not be present, and some of the authors listed above may not have made any contributions to some printed and distributed versions of this text.
License: GFDL
As of July 15, 2009 Wikibooks has moved to a dual-licensing system that supersedes the previous GFDL only licensing. In short, this means that text licensed under the GFDL only can no longer be imported to Wikibooks, retroactive to 1 November 2008. Additionally, Wikibooks text might or might not now be exportable under the GFDL depending on whether or not any content was added and not removed since July 15. |
Version 1.3, 3 November 2008 Copyright (C) 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. <http://fsf.org/>
Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.
The "publisher" means any person or entity that distributes copies of the Document to the public.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
- Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
- List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
- State on the Title page the name of the publisher of the Modified Version, as the publisher.
- Preserve all the copyright notices of the Document.
- Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
- Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
- Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
- Include an unaltered copy of this License.
- Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
- Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
- For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
- Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
- Delete any section Entitled "Endorsements". Such a section may not be included in the Modified version.
- Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
- Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements".
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Document.
11. RELICENSING
"Massive Multiauthor Collaboration Site" (or "MMC Site") means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A "Massive Multiauthor Collaboration" (or "MMC") contained in the site means any set of copyrightable works thus published on the MMC site.
"CC-BY-SA" means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.
"Incorporate" means to publish or republish a Document, in whole or in part, as part of another Document.
An MMC is "eligible for relicensing" if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.
The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.
How to use this License for your documents
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
- Copyright (c) YEAR YOUR NAME.
- Permission is granted to copy, distribute and/or modify this document
- under the terms of the GNU Free Documentation License, Version 1.3
- or any later version published by the Free Software Foundation;
- with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
- A copy of the license is included in the section entitled "GNU
- Free Documentation License".
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:
- with the Invariant Sections being LIST THEIR TITLES, with the
- Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.























![{\displaystyle y_{1}(t)+y_{2}(t)=\sin(3[x_{1}(t)+x_{2}(t)])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ba2f7c9836de496ce51a81ecca7b1c9d80797db)













![{\displaystyle {\frac {d[Ay_{1}(t)+By_{2}(t)]}{dt}}+[Ay_{1}(t)+By_{2}(t)]=Ax_{1}(t)+Bx_{2}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/795648dd73c7543f766980b6d13575ef440fc540)
![{\displaystyle {\frac {d}{dt}}[Ay_{1}(t)+By_{2}(t)]+[Ay_{1}(t)+By_{2}(t)]=Ax_{1}(t)+Bx_{2}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c9ccff69dfa467e5f9ec7317275c78bf13068d0)





















![{\displaystyle x[n]=x(nT)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf9d6e2763c5e892b633aaf8be4bf00618515188)








































![{\displaystyle y(t)=[x(t)*f(t)]*g(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a0488880d8f05d9b027049a990068156208f23c)
![{\displaystyle y(t)=x(t)*[f(t)*g(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03509cd1b7232b1efcd50d7465edcd099fc55ca4)
![{\displaystyle Y(s)=X(s)[F(s)G(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b1a109584722e3f49b210628de10b53a0dcf4c)






![{\displaystyle Y(s)=X(s)[F(s)+G(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9423d78177f705eaad381153cb374ed520cb7c)
![{\displaystyle y(t)=x(t)*[f(t)+g(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76847ae33b40004c521daa714dd6fbccb4b5c3cb)








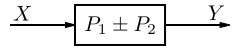

















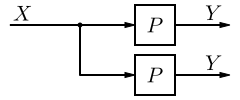



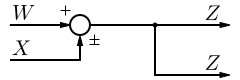
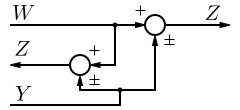
























































































































![{\displaystyle =1-abs(PV-SP)/max[PVmax-SP,SP-PVmin]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a34d47acce2287268821b38f7a46ad1f4debaf7)






![{\displaystyle {\mathcal {L}}[f(t)*g(t)]=F(s)G(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da7a021eb1cc9ce933aee9c48544308fd9aea4b)
![{\displaystyle {\mathcal {L}}[f(t)g(t)]=F(s)*G(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4a5783272e7260e8336adb5853f8a66ffc23d02)








![{\displaystyle C[sI-A]^{-1}B+D=\mathbf {H} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d37ee2188135370b2d768fcf965161d688cd12f6)
![{\displaystyle C[zI-A]^{-1}B+D=\mathbf {H} (z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/151e79dc41cb1fb26cf6964a0f9621bd4b69c7a1)





![{\displaystyle F(s)={\mathcal {L}}[f(t)]=\int _{0}^{\infty }f(t)e^{-st}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c38c98774feaf400f8af0dab5f8aed8aed5d06f)

![{\displaystyle F(j\omega )={\mathcal {F}}[f(t)]=\int _{0}^{\infty }f(t)e^{-j\omega t}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccad40df03382f6ead04ba196a52314f1b7a4291)

![{\displaystyle F^{*}(s)={\mathcal {L}}^{*}[f(t)]=\sum _{i=0}^{\infty }f(iT)e^{-siT}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30b1617367f1700032ffd3f5b8720159699648ed)
![{\displaystyle X(z)={\mathcal {Z}}\left\{x[n]\right\}=\sum _{i=-\infty }^{\infty }x[n]z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af2109d64c2b69a9a5104d600e08fc9b4267360b)
![{\displaystyle x[n]=Z^{-1}\{X(z)\}={\frac {1}{2\pi j}}\oint _{C}X(z)z^{n-1}dz\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2de87f7a38f4c6528c53a5883b209edf50d3a62)
![{\displaystyle X(z,m)={\mathcal {Z}}(x[n],m)=\sum _{n=-\infty }^{\infty }x[n+m-1]z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85540c08a77b2c40043f7f7e84c0ed56437bb4a9)

![{\displaystyle x[\infty ]=\lim _{z\to 1}(z-1)X(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30f34e1769d16e186e49651f66f4401a8c589b3e)


![{\displaystyle x[n]=A^{n}x[0]+\sum _{m=0}^{n-1}A^{n-1-m}Bu[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37dfa3802c72fcf32ac7e379d52ae691154fad04)

![{\displaystyle y[n]=CA^{n}x[0]+\sum _{m=0}^{n-1}CA^{n-1-m}Bu[n]+Du[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08c5007961a18ea382ac3c879331fb4e87873560)

![{\displaystyle x[n]=\phi [n,n_{0}]x[t_{0}]+\sum _{m=n_{0}}^{n}\phi [n,m+1]B[m]u[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44156ca6ba03d51f16817e0cd51292ca38563a80)

![{\displaystyle G[n]=\left\{{\begin{matrix}CA^{k-1}N&{\mbox{ if }}k>0\\0&{\mbox{ if }}k\leq 0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90177e0e9300b0985968117dde9fa1f3a5aec597)











![{\displaystyle D(z)=K_{p}+K_{i}{\frac {T}{2}}\left[{\frac {z+1}{z-1}}\right]+K_{d}\left[{\frac {z-1}{Tz}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aafdc2121c235d8b68ee53d6103c157ef86057ac)