Circuit Idea/Group 65a
We are students from Faculty of Computer Systems, Technical University of Sofia. Our 65 group is divided into two sub-groups; we constitute the first 65a one. Here are our names:
Mehmed Yusuf, Nikolai Ninov, Vladimir Mladenov, Borislav Ivchev, Miglena Nesterova, Nikolai Dimitrov, Zdravko Zdravkov, Bozhkova, Maria Nikolaeva, TEN4O PETROV.
Lab 1: Investigating passive resistive circuits by Microlab system
[edit | edit source]Lab 2: The genuine Ohm's experiment
[edit | edit source]Tuesday, March 18, 2008, 10.30 h
History. What did Ohm carry out in 1826? Do you know? Students: No... Please, let's someone write in the Google's window "Ohm's experiment" or "Ohm's law" to see what is written about the topic. Thank you ......... (insert your name here and make comments to obtain credits); please, make a folder in "Favorites" named "Ohm's law" and put there the most remarkable links.
Let's first consider his genuine experiment and then reproduce it here, in this laboratory, almost three centuries later. This is the first of all the ten exercises of this cycle; so, let's try to reproduce it in the most original form. So, what do we need to carry out it? Silence...
Building the laboratory setup. As far as I know, Ohm has discovered the local voltages along a copper wire that was supplied by a strong voltage source. So, we need a wire, a power supply, a voltmeter and an ammeter. But what kind of wire we need? Bare or insulated? Copper, silver, iron, or other? Student: Silver will work excellent... We haven't a silver wire, let's try with a copper one:) Oh, it has welded!?! It is so well that the power supply has a current limitiing circuit (2.5 A)! That is why Ohm made a strong voltage source by applying the just invented by Seebek thermoelectric effect! Now, it is clear we need a resistive wire (nitinol, NiChrome, etc.); so, let's unwind a piece of wire (about 50 cm) from a heater. ...... (insert your name here), please, meausure its resistance. The resistance is 10 Ω, so we have 0.2Ω/cm.
Experiment 1. Now, fix the two ends of the wire in porcelain insulated terminals (holders) and apply a voltage (for instance, 10 V) first to the left end of the wire. What can we investigate now in this arrangement? What do we measure with the voltmeter? The usual viewpoint is to think of a resistor as a point, as a something that has not dimensions, as a two-terminal element that has only a property of resistance. But here we have the unique chance to peep inside the "resistor"! What will you "see" along the wire? What will the voltmeter show when we slide it from right to left? What are the local voltages along a resistor, if there is no current? Student 1: Zero... Student 2: 10 V... What is the voltage at the right? Zero... And what is it at the middle? Zero...

Well, let's try. Just touch the wire by the voltmeter probe and move it along the wire to measure all the voltage drops (for now, regarding to the ground)! If you are tired, stick a crocodile clips on the probe, "bite" the wire and move this "slider" along it! The result: everywhere local voltages are 10 V!
Experiment 2. Now, ground the right end of the wire. Oh! The wire is hot! Have I instructed you about all the dangers in the laboratory:)? Include this one: do not touch a hot wire! See the ammeter - it shows 1 A; so, the power is P = V.I = V2/R = I2.R = 10 W. By the way, are these calculations right (has the resistance a constant value)? We see, it is too hard for this thin wire to dissipate the power to the ehviroment and it is heating.
Now, move again the "crocodile slider" along the wire and measure the local voltage drops. As far as I know, Ohm did exactly the same. He moved the probe from one position to other, measured the corresponding potentials, made the difference between them and calculated the ratio (V2 - V1)/(L2 - L1) = (V2 - V1)/(r2 - r1) = dV/dR = I. Thus he has established that this ratio (it was the current I) is constant along the wire; so, Ohm has concluded that V/R = I.
We can see that moving the "crocodile slider" the voltage drops decrease gradually from 10 to 0 volts. What is the input and what is the output quantity here? Eureka! Using the "slider" movement as an input and measuring the voltage drop as an output we have "invented" the legendary (but misnamed) potentiometer, movement-to-voltage converter, sensor... Is it a linear converter? Why? A hint: the resistance is distributed linearly along the wire.
Experiment 3. But why do not we change the role of the quantites? With the same success we can stop the "crocodile slider" at the middle of the wire and then to vary the input voltage as an input and, as before, to measure the voltage drop (regarding to the ground) as an output. Eureka (again)! Now we have "invented" the legendary voltage divider (voltage-to-voltage converter)! What is the relation between the input and output voltage (the so-called "transfer ratio"? We can see directly that VOUT = VIN.L2/(L2 + L1).

Experiment 4. We are ready to do more sophisticated experiments... Are there more interesting points (different from the ubiquitous ground) to fix the negative voltage probe? Of course, we may touch any wire point! Well, let's begin with the middle point: "bite" it with the black (negative) negative "aligator" and slide the red (positive) "aligator" along the wire. Only, first change the unipolar voltmeter with a bipolar one. Why? What might we expect? The result is more than surprising: the output voltage varies from -5 V to +5 V! Eureka! We have obtained a bipolar movement-to-voltage sensor!
Experiment 5. What happens, if we move simultaneously both the voltmeter probes in the same direction? Students: The voltage will not change... Right! They name this "common mode input signal".
Experiment 6. And what happens, if we move simultaneously both the voltmeter probes in opposite direction? Students: The voltage will change... Right! It will even change more rapidly than above. They name this "differential input signal".
Experiment 7. Now stop both the "sliders" and wiggle the input voltage. This is a quite odd voltage divider with flying output. What is the relation between the input and output voltage (the transfer ratio? We can see directly that VOUT = VIN.(L2 - L1)/L.
We can measure the voltage drops along the resistive wire by using more unusual indicators, e.g. electric bulbs. What do you think, is there any problem to supply a bulb in this exotic way? If yes, when and why?


Applications. Where may we see this phenomenon in life? The answer is simple: everywhere where a current flow through bad conductors. In all these cases, a gradually decreasing voltage drop appears across the "conductor". A "car example": if you move the probe lamp along the heater of the rear window, you will see the voltage drop across the resistive wire.
Lab 3: Building a simple common-emitter transistor amplifier
[edit | edit source]Tuesday, April 01, 2008, 10.30 h
Building the circuit on the whiteboard
[edit | edit source]
Mounting the circuit on a prototyping PCB
[edit | edit source]
Investigating the circuit by Microlab
[edit | edit source]
Revealing the circuit imperfections
[edit | edit source]
Lab 4: Op-amp circuits with series negative feedback
[edit | edit source]Tuesday, April 15, 2008, 10.30 h
What is op-amp?
[edit | edit source]
Inputs. Grounded voltage source... What is single-ended input? Floating voltage source... What is differential input? Why do we need a differential input? Input resistance... Do input currents flow? How does a non-inverting input behave? How does an inverting input behave?
Output. How the op-amp output is made? What is the idea of a complementary, push-pull emitter follower? Output resistance...
Supplying. The idea of bipolar (split) supply (+12 V and -12 V here)... Why do we need a bipolar supply? Where currents flow?
Gain. Typical value is A > 200000. It seems too high. What is the maximum input voltage to keep the op-amp in the active region (assume 10 V maximum output voltage)? Can we use a bare op-amp as an amplifier? Or we can use it as another useful device having analog inputs and descrete output (write its name here)? We may conclude: If we use the op-amp as an amplifier, the voltage difference between its inputs is zero. But if we use it as a comparator, the input voltage might be whatever.
Transfer characteristic. Microlab can help us to obtain this curve on the screen. There is no time in this graphical presentation; there is only input and output quantities. We might discern three regions on this curve: negative saturation (large), active region (narrow) and positive saturation (large).


Generalization. What does the op-amp actually do? A possible answer is: an op-amp converts the steady power supply into varying voltage source.
Passive voltage follower: Imperfections
[edit | edit source]
Building a general negative feedback follower
[edit | edit source]
Building an op-amp follower
[edit | edit source]

Disturbing the negative feedback follower
[edit | edit source]

Converting the NFB follower into an amplifier
[edit | edit source]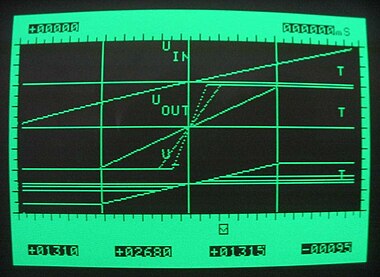

Resources
[edit | edit source]Operational amplifier
Differential and Single-Ended Inputs
Labs: group 66a and group 67a.
Op-amp amplifiers with negative feedback
Lab 4a: Op-amp circuits with parallel negative feedback
[edit | edit source]Remembering the general negative feedback follower
[edit | edit source]
Building an op-amp inverter
[edit | edit source]


Converting the op-amp inverter into an amplifier
[edit | edit source]


