Circuit Idea/Group 67b

We are students from Faculty of Computer Systems, Technical University of Sofia. Our 67 group is divided into two sub-groups; we constitute the first 67b one. Here are our names:
Dafar Shaban, Nikola Lambev, Kalina Domuschieva, Valeri Kirilov, Reneta Stoycheva, Sofiya Shtarbova, Kiril Rusev, Raya Yunakova,Ina Tacheva, Dimitar Mindalov (add your name here)
Lab 2: Computer-based Ohm's experiment
[edit | edit source]Tuesday, March 25, 2008, 16.45 h



In this lab exercise we tried to "invent" new analog devices using our knowledges for the famous Ohm's experiment. In order to see the graphics of our "new" devices, we used Microlab - PC Apple2 connected to 4 DACs and 4 ADCs. We made a couple of experiments and these are the schemes we were analysing. First the voltage source is connected only to the one end of the resistor and we measure the potential along the resistive layer(1st picture). Thus we make a linear transference-to-voltage converter.
In order to carry out Ohm's experiment, we needed some kind of resistive wire. Our teacher gave us a heater wire, so we start experimenting with it. When we connected it with conductors, power supply, voltmeter and an ammeter we start measuring its resistance. We were also using two kinds of voltmeters and ammeters - old-fashioned movement ones and new digital devices. After our successes in building and connecting the scheme, we were very excited to find it actually worked. The images around show our scheme and progress.
When there are two voltage sources, and both of them are with the same polarity, we have a parallel voltage summer.Here VOUT = r1/(r1+r2).VIN1 + r2/(r1 + r2).VIN1.
If we have voltages with different polarity and VIN1 and VIN2 are selected so that VOUT=0 (point known as "virtual ground") we have a comparing device,like in the scheme in the third picture:VIN2/VIN1 = -(r2/r1).To keep Vout = 0 we can use operational amplifier(down).Here I1.R1=(VIN/R1).R2 or VOUT/VIN=-R2/R1.


This lab report is made by Reneta Stoycheva , Sofiya Shtarbova, Ina Tacheva and Valeri Kirilov, Raya Yunakova, .
Lab 3: Transistor circuits ("inventing" a BJT current mirror)
[edit | edit source]Tuesday, April 08, 2008, 16.45 h (extracted from the lab records made by a solid-state recorder) Circuit-fantasist 05:43, 3 June 2008 (UTC)
Introduction
[edit | edit source]This Tuesday, three student groups in all are carrying out experiments in this laboratory dedicated to transistor circuits producing constant current. First, your colleagues from Group 65b were building and investigating the simplest transistor current source. The students from the next Group 66b continued their work trying to transform the simplest transistor current source into a BJT current mirror circuit. But they did not manage to do it since an accident happened at the end of the lab - the main transistor began to smoke and they had to find out why. The honor fell to your Group 67b to finish their work...
What the transistor is
[edit | edit source]

We have to clarify some philosophical questions in the beginning of this lab. What is a transistor? What does it do? What notion do you have about the transistor? Is it a supernatural and "divine" device as they frequently present it and, for this purpose, they veil it by sophisticated equations and analyses? Or it is something simple, clear and intuitive that everyone (even a child) can understand?
A student: A transistor consists of two n-p junctions... But there are transistors without junctions (e.g., a MOS transistor does not contain junctions in the input part). Let's say it in a more general way. Another student: The transistor can amplify... But what does this mean? The student: If we apply an input signal, a large signal appears at the output. But this is impossible; there is no amplification in nature. We cannot amplify energy. I would like to say more precise that there is not amplification. We cannot obtain more energy from less energy; it is just impossible.
Then what does a transistor actually do? Well, look at the last picture (on the left) of your colleagues from the previous Group 66b. As you can see, we have drawn arrows going out of the transistor. They represent the heat that the transistor was dissipating since they were made a short connection in the collector circuit. So, I ask you again, "What does the transistor do? As you can see, we have broken the three-terminal transistor into two 2-terminal devices and now we discuss the one of them - the output collector-emitter "device". Here is this "device", I have held it. It has two leads and it is connected by these two leads in an electrical circuit... I ask you again, "What does it do in this circuit?", "What does the transistor do with its output part?"
A student: The transistor behaves as a resistor. Yes, it is exactly what I would like to hear - "resistor" in a broad sense of this word. Excepting the most popular sources, they usually do not explain the transistor in this manner; they refrain from giving such intuitive explanations (maybe, because a transistor behaves as a non-linear instead as an ohmic resistor). But yet, this is the simplest and the most powerful viewpoint at the transistor. So, if someone ask you what a transistor do or can do you can answer: the only thing that a transistor can do is to "insert" a resistance in the circuit where it is connected, to dissipate power, to throw out it in the space and, in this way, to impede the current, to regulate the load voltage, current and power. A transistor does not do anything else than this varying resistor (a rheostat) in front of us does. Of course, there is also a capacitance and an inductance but they are parasitic and negligible.
What are the differences between the transistor and the humble rheostat? First, a transistor is an electrically controlled resistor while the rheostat is a mechanically controlled one. There are also light-controlled resistors - photoresistors, sound-controlled resistors - carbon microphones, temperature-controlled resistors - thermoresistors, etc.) For example, connect this photoresistor to an ohmmeter and light up or shade it; thus you can measure the minimum (4 kΩ) and maximum (300 kΩ) resistance of this light-controlled resistor. In the same way we control the resistance of a transistor, only electrically.
Second, as we have mentioned above, the transistor is a non-linear current-stable resistor while the rheostat is an ohmic one. When they say "resistor" we implicitly understand "ohmic resistor"; so, the transistor is a resistor in a broad sense of the word. Well, let's draw the two kinds of characteristics. When we vary the resistance of an ohmic resistor, its IV characteristic inclines; when we vary the base-emitter voltage of a BJ transistor, its output characteristic moves vertically remaining parallel to itself.
A transistor acting as a current-stable resistor
[edit | edit source]Our final purpose is to create a current source controlled by another current. So, we have to understand how a transistor can keep up a constant current. We were considering this topic more consistently with your colleagues from group 65b a few hours ago. We began solving the problem "producing a constant current" by creating the simplest passive current source (a voltage source and a resistor connected in series). Then we ascertained how imperfect it is (if the load varies, the current varies as well). So, we began reasoning how to make a perfect constant current source. We remembered how they have solved this problem in electricity - by increasing the voltage and the resistance up to infinity so that to suppress the load influence. Only, we noted that this approach is imperfect since the resistor dissipated plenty of energy. Then, we moved in the area of electronics where this problem is solved more cleverly. Can you guess what the idea was?
Well, you have a circuit consisting of three connected in series elements: a voltage source, a current-setting resistor R and a load with varying resistance RL. As the load resistance varies, what do we have to do, in order to keep up a constant current? What is the clever idea? A student: ...transistor, op-amp... Maybe, but these are very concrete solutions; we are still at "idea" level. Another student: ...feedback... But we do not still know what a feedback is.

Let's continue reasoning in human friendly manner... For example, if the load resistance increases and, as a result, the current lowers, what do we do to restore the current? Students: ...we have to lower the current-setting resistor R! And vice versa, if RL decreases... Students: ...we have to increase R! It turns out a strange resistor stays at this place that have the unique property to change its resistance depending on the current flowing through it. The resistor R is not an ordinary "static" resistor; it is a kind of varying, dynamic resistor. It is still ohmic but varying ohmic resistor. They name such odd elements current-stable resistors.
We can see this dynamization idea everywhere in our human routine. Some people have a "static" behavior; they do not react to various interventions. Other people are more flexible, adaptable, dynamic; they win.
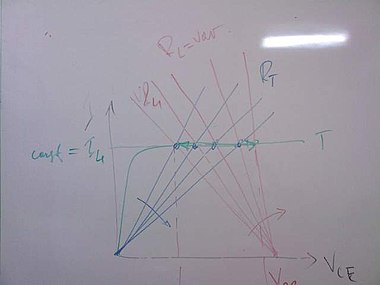
We begin looking for such an element. In electricity, a bulb has a similar behavior (there were so called barretters - thermistors having positive temperature coefficient of resistivity). In electronics, we find out that transistors (both BJT and FET) have such a behavior. See the picture where your colleagues have visualized how the transistor behaves. What is the idea of such a grapnical presentation? They have presented the output part of the circuit as two 2-terminal elements connected to each other - a real source and a load (according to the Thevenin's model, we can present every circuit in this manner). The real source is a compound one; it consists of two 2-terminal elements - an ideal voltage source VCC having a vertical IV characteristic and an internal resistance RL having an IV characteristic that is inclined to the right and begins from the coordinate origin. The difference between the two characteristics represents the effective IV characteristic of the compound real source. As you can see, it is shifted to the right by the magnitude of VCC and it is inclined to the left according to RL. It might seem strange but in this presentation the transistor plays the role of a load while RL plays the role of an internal source resistance?!? Do you agree to this viewpoint?
As you can see, the output transistor characteristic is similar to the characteristic of a constant current source. The crossing point of the two characteristics is named operating point; it represents the present voltage across and the current flowing through the two elements.
Varying the load resistance
[edit | edit source]Let's now begin reasoning what happens when we begin varying RL. If we decrease it, the source curve rises and v.v., if we increase the resistance, the source curve lies down. And, as they usually say in classical electronics courses, since the transistor's output characteristic is almost horizontal the operating point moves almost horizontally along it; the current variations are insignificant. This explanation works of a sort but we would like to know how the transistor actually does this magic; how its output characteristic is obtained. But nobody answers these questions...
See the second picture on the right above. What is shown there? We can see another line beginning from the coordinate origin. What is this line? What does it represent? As you probably quess it represents the present ohmic transistor's resistance. Remember how we presented the transistor above - as a varying resistor having a present ohmic resistance RT = VCE/IC. And if you begin decreasing RL, this "resistor" begins increasing its resistance and v.v. So, it behaves as a varying ohmic resistor. It is not a static but a dynamic, a self-changing resistor and it does it in such a way so that the crossing (operating) point moves along an almost horizontal line - the output characteristic. This line represents the trajectory of the operating point; it is an unreal, an imaginary, an artificial curve. Only the two crossing lines are real.
This explanation was an attempt to explain what a dynamic (non-linear) resistor is. So, let's draw a conclusion: a dynamic (non-linear) resistor is actually a "self-varying" ohmic resistor. The current flowing through it or the voltage across it changes its present resistance.
Other elements (e.g., diodes) have the opposite characteristic. When we vary RL, such an element would change its present resistance in the same direction so that to keep a constant voltage. So, they behave as voltage-stable elements.
Varying the supply voltage
[edit | edit source]According to the explanations above, if we begin varying the supply voltage, the current would stay constant: if we increase the voltage, the transistor will increase its present resistance so that the ratio I = VCC/RT to stay constant as well and v.v. But it does not stay constant. Why? What is wrong in this arrangement? A student: ...the input voltage varies as well... Yes, that is right. Your colleague feels the things very well... Obviously, the problem is that we have taken the input (reference) voltage from the same voltage source instead from a separate one. This is incorrect and the result is obvious: when we vary the supply voltage, the "reference" voltage varies as well.
It turns out that in practice, there is no separate source or, what occurs more frequently, we prefer to use a common source (for example, a car has only one battery supplying a lot of electric and electronic devices). Obviously, we have to arrange things so that when the supply voltage varies, the input (reference) base-emitter voltage does not change.
Building the simplest transistor current source
[edit | edit source]Look at the picture below to see how we began solving this problem with your colleagues from Group 66b. What is the problem? What do we want to keep constant? We want to keep up a steady base-emitter voltage even if the supply voltage varies because the horizontal output BJT characteristic is at given base-emitter voltage. So far, a voltage divider produces this voltage; but a voltage divider is a proportional device. Then, what kind of device do we need?


Looking at a new circuit we discern more familiar "sub-devices"; here, we identify the well-known voltage divider. Only, we want to make it does not change its output voltage when its input voltage varyes. In other words, we have solved the problem keeping up a steady current; now, we have to solve the problem keeping up a steady voltage. Let's generalize these thoughts.
The simplest transistor current source exploits the inherent ability of the transistor to stabilize the current when the base-emitter voltage is fixed. What do we need to build the simplest transistor current source according to this idea? First, we have to set a constant voltage to the base-emitter junction; so, we need a constant voltage source. Your colleagues from group 65b have made it by a voltage divider. Note that there is also a protecting resistor (3.9 kΩ) connected in series with the potentiometer; it limits the base current (up to 3 mA) in a case when someone moves the slider to the end of the rheostat. This humble resistive circuit allows us to set some input voltage and, in this way, to move the output characteristic to a given position. Thus we make the transistor pass the desired current through the load and keep it constant according to the explanations above. The transistor opposes to our intervention by changing its present resistance, by a dynamic resistance connected in series to the load. The total resistance and the supply voltage stay constant; as a result, the current stays constant as well. In this way, in electronics we are smart enough to make perfect current sources.
A true diode sets the input current
[edit | edit source]So, we need a voltage-stable element, we need a diode to obtain the needed voltage drop. How do we connect it? A student: it has to be forward-biased... Before we had to adjust the voltage; now it is axactly as much as we need. More precisely speaking, we will adjust it by changing the current flowing through it; this voltage will vary slightly when we change the current significantly.


Your colleagues from Group 66b have found the same solution in Tony Kuphaldt's page about current mirrors.
A base-emitter transistor "diode" sets the input current
[edit | edit source]Replacing the true diode by a base-emitter transistor junction
[edit | edit source]

But we need not only an output current; we need a mirror output current whose magnitude is equal to the input current. Thinking about the problem we realize the two elements have to have identical characteristics. As soon as the input behaves as a p-n junction don't we use another p-n junction to set the voltage? For this purpose, we may use the base-emitter junction of another transistor as such an element. As in the "diode" case above, there isn't need to adjust the reference voltages as we had to do that in the case of voltage divider. The technology of integrated circuit manufacturing allows to make the two elements absolutely identical.
So, the better solution is to connect the base-emitter junction of an identical transistor (leaving the collector no connected).
A problem appears
[edit | edit source]
Only, a problem appears - the output transistor is saturated! Why? Let's see again the Tony Kuphaldt's page about current mirrors and try to find the answer of this question. Tony claims that the output current flowing through the load is equal to the input current flowing through the diode: "Current through resistor Rload is therefore a function of current set by the bias resistor, the two being nearly equal." He think the two output currents are equal because the two input base-emitter voltages are equal. But is it true? We have to prove this ascertion here...
What do you think, are the two currents equal? Obviously, the input voltages are equal as the two base-emitter junctions are connected in parallel. But does it mean the two output currents are equal? We can find out the current-setting diode diverts only "one" base current Ib = V/2Rbias and the corresponding collector current of T2 is β/2 times bigger - Ic = IL = β.V/2Rbias.
We can conclude that the "diode" current mirror acts as a current amplifier (IOUT > IIN) but not as a true current mirror (IOUT = IIN)!
Now let's remember the beginning of our exercise and clarify the role of the potentiometer by reazoning as follows. Imagine we connect two identical resistors - a base resistor Rb and a load resistor RL = Rb. As a result we get a current amplifier (Ic = βIb) instead the desired current mirror (Ic = Ib). Then, let's connect a second resistor (actually, a potentiometer) in parallel to the base-emitter junction to divert the excessive current from the base to the ground.
Well, let's continue developing the current mirror circuit...
A negative feedback transistor "diode" sets the input current
[edit | edit source]Thus we arrive at the powerful idea to connect the non-used collector to the transistor bases with the purpose to divert the excessive base current to the ground.
Drawing the diagram on the whiteboard
[edit | edit source]
In this way, we have revealed the role of the input current-setting transistor T1; it take away the great amount -- (1 + β)Ib—from the input current and leaves only the small Ib for the output transistor T2. As a result, the input and the output currents are almost identical.
Eureka! We have "invented" the famous but never explained circuit of BJT current mirror! We have even disprove a widespread misconception about the simple BJT current mirror - the possibility to set the input current by a forward-biased diode or a base-emitter junction!
Building the circuit on a PCB
[edit | edit source]
Investigating the circuit
[edit | edit source]

Resources
[edit | edit source]How to Reverse Current Direction is another Circuit idea story about basic current mirror.
Current mirrors is a popular exposition of the current mirror topic written by the well-known web author Tony Kuphaldt
Lab 4: Endowing circuits with memory
[edit | edit source]Tuesday, April 22, 2008, 16.45 h
In this exercise we are going to reinvent legendary circuits - flip-flops. First, we will reveal the general idea of memorizing; then, we will build an RS flip-flop by using NPN transistors and an op-amp flip-flop. In order to do this, we need to know what flip-flops can be used for and how we want our "invention" to work. I am sure that every student at the Technical University is familiar with these devices but since this book is meant to explain the idea of electronics to everyone who is interested I will provide some general information on the subject.
What a flip-flop is (a conventional viewpoint)
[edit | edit source]
Flip-flops (FFs) are devices used in the digital field for a variety of purposes. When properly connected, flip-flops may be used to store data temporarily, to multiply or divide, to count operations, or to receive and transfer information. Every FF has two to five inputs depending on its type. What is common for all types of FFs is that they have two distinct outputs usually marked Q and /Q. They can either have a "0" state or "1" state and should always be complementary. This means that if the state of Q is "1" the /Q's state is "0" and vice versa. The RS flip-flop in particular is used to temporarily hold or store information until it is needed. A single RS FF will store one binary digit, either a 1 or a 0. It has two standard inputs - R, which stands for "reset" and sets the Q output in "0", and S, which stands for "set" and sets the Q output in "1" (Raya Yunakova, 67).
We can see on the picture above the inputs and the outputs but we are not able to understand how the flip-flop actually works. Our main goal in this exercise is to reveal what's in that "black box". Basically RS flip-flop is the simplest practical memory device based on NOR gates connected in a feedback configuration. Anyone in TU knows the truth table of that flip-flop so we are not going to bore you with that stuff. The general question is: How to make something "remember", "memorize"? If we find that answer, then we will know the exact mechanism of creating any kinds of flip-flops.(Reneta Stoycheva and Sofiya Shtarbova)
How do we make devices memorize?
[edit | edit source]The basic idea behind memorizing: positive feedback
[edit | edit source]Describe here situations (analogies) derived from our human daily routine where someone (something) having no memory begins memorizing. Examples: a dog bitten its tail:), an enraged man working himself into a fury:), a snow avalanche, etc. Circuit-fantasist (talk) 16:14, 18 May 2008 (UTC)
A transistor flip-flop
[edit | edit source]Building a transistor switch
[edit | edit source]
Here is where we start. We have a bipolar junction transistor, whose emitter is common to both the input and the output. The input is controlled by the transistor's base and its collector serves as the output. We control the input with the button marked with *. When the button is pressed the input circuit is closed and the transistor is active. When the button is not pressed the transistor is inactive and we can not get any output signal.
Making the transistor switch memorize
[edit | edit source]
Structure. This is the normal working routine of a BJT. In our case however, this is not good enough since our goal is to "invent" a device which doesn't change its state when there is no input. But how? It is obvious that we need to add something to our circuit that will keep influencing the input (base) of the transistor. What if we get a second transistor and connect it to the first one like this?
The first transistor's output is connected to the second transistor's input (its base) whose output is connected to the first one's input. The collectors of both elements are connected to a constant voltage source through resistors. The emitters are grounded. (Raya Yunakova, 67)
Operation. How does our circuit operate? When we put the circuit into operation the transistor on the left is inactive. However, current which is high enough to activate the transistor on the right flows through resistor Rc1 (remember we've connected a voltage source). Its emitter-base junction is forward biased and therefore we have output which is equal to the ground potential. This output influences the first transistor's input but it is not high enough to activate the first element. We continue to have a logical "1" on its output which keeps the situation in our circuit exactly the same as it was before. And wasn't that what we wanted to happen in the first place?
It seems that we have completed our goal and we have made the transistor "remember"! Using this approach we can create almost any kind of memory device to serve our purposes. We have actually implemented a mechanism called "positive feedback". It is largely used in electronics to change the parameters of an amplifier like voltage gain, input and output impedance, stability and bandwidth.(Raya Yunakova, 67)
An op-amp flip-flop
[edit | edit source]Building an op-amp Schmidt trigger
[edit | edit source]A problem: a voltage conflict
[edit | edit source]Describe here what the problem was and how we have solved it. Circuit-fantasist (talk) 17:29, 18 May 2008 (UTC)


Visualizing the operation by voltage diagram
[edit | edit source]Describe here what we have done. Circuit-fantasist (talk) 17:24, 18 May 2008 (UTC)


Making the op-amp Schmidt trigger memorize
[edit | edit source]

More pictures
[edit | edit source]


Left picture shows our first try to make the scheme which occurred to be incorrect :( After that with team work we managed to do it the right way.
This lab report is made by Reneta Stoycheva and Sofiya Shtarbova.
Updated by Raya Yunakova.