Circuit Idea/Walking along the Resistive Film
Circuit idea: Peep inside a voltage-supplied linear resistor and show the voltage distribution along the resistive film.
"Invented" devices: movement-to-voltage converter, voltage divider, resistive summer and subtractor, inverting amplifier.
Discovered concepts: voltage drop, common mode and differential input, split supplying, superposition, virtual ground, negative feedback.

The beginning: Ohm's experiment
[edit | edit source]History. Almost three centuries ago, Ohm implemented his famous experiment. In those Dark Ages, physicists attempted to explain why there were obvious discrepancies between different wires, what was electric current and how it was related to electrostatics; for them concept of current and voltage was abstract, almost revealed by God himself. As they say, he stretched a piece of copper wire with length L and resistance R; then, he applied a voltage difference across the wire. As Ohm did his experiment in the beginning of the 19th century, only thing he could use as a power supply was the forerunner of the electrical battery, created by Alessandro Volta. Unfortunately, this experiment failed because Ohm used a wire with very low resistance so the power source was loaded and the ordinary galvanic battery did not work properly. Thus, Ohm decided to make a good voltage source using thermoelectric effect just invented by Seebek. So, the source of a voltage difference was a thermocouple; other electric sources available in the 1820's were too unreliable. Ohm dipped the one end of the thermocouple into boiling water and the other one - into a melting ice put in the small containers on the tripods. Then, using an electroscope (remember, in those days they did not have $3 multimeters:), a magnetized needle and maybe plenty of imagination, Ohm began studying the voltage distribution along the "resistor".
Reproducing Ohm's law. It is very interesting, exciting and important to reproduce Ohm's experiment in the laboratory, because Ohm's law is the base of electronic circuits that EE students study. It would be a great idea, if during the practical exercises and theoretical lessons in electronics courses students and teachers, all together, reinvent everything, every single element (even the resistor). So we started imagining how Ohm did his famous experiment and found the fundamental relationship between the current, voltage and resistance. In this way, reproducing now the famous Ohm's experiment by using present-day measuring devices and no less imagination, we can "invent" various valuable resistive passive circuits.
Building the laboratory setup. In order to carry out Ohm's genuine experiment, we need a resistive wire, conductors, a power supply, a voltmeter and an ammeter. 50 cm piece of wire from a heater having a total resistance of 10 Ω acts as a resistive wire. Insulated copper wires act as condutors. A varying power supply can produce up to 40 V/2.5 A. We will use two kinds of voltmeters and ammeters - old-fashioned movement ones and VOM digital ones.
Hydraulic analogy: Pressure diagram
[edit | edit source]A tapped pipe (there is no flow)
[edit | edit source]
Let's begin with considering a well-known hydraulic analogy (plumbing) - that we can see everywhere around us. For example, imagine a large vessel filled of water that supplies a long thin pipe; let's first the pipe to be tapped (Fig. 1). The question is: "What is the pressure inside the pipe?" And more precisely speaking, "What are the local pressures along the pipe?" There are not so many people that will answer rightly these simple questions.
We can get to know, if we drill small holes at equal intervals along the pipe (if we want to be more precise, we might stick vertically thin glass pipes acting as local manometers). The result is expectable for us: all the water levels (accordingly, all the local pressures along the pipe) are equal. This picture shows the pressure distribution along the pipe; we can name it "pressure diagram".
An opened pipe (there is flow)
[edit | edit source]
Now open the pipe (Fig. 2); the water will begin flowing. This is a well-known situation from our routine where someone opens a faucet somewhere in the end of the plumbing. At the left end the water pressure is maximum; at the right end it is minimum. But what are the local pressures along the pipe now? Our intuition suggests that the local pressures will decrease gradually from left to the right.
Really, the levels of the water bars (accordingly, the local pressures along the pipe) decrease gradually from left to the right. The envelope of the pressure diagram is a triangle.
Electrical domain: Voltage diagram
[edit | edit source]An opened circuit (there is no current)
[edit | edit source]Let's now transfer these notions to our electrical domain, in order to see if the voltages along a resistive wire are distributed in the same way. That means to reproduce the genuine Ohm's experiment under the conditions of today.

Now, fix the two ends of the wire in porcelain insulated terminals (holders) and apply a voltage (for instance, 10 V) first to the left end of the wire (Fig. 3). What can we investigate now in this arrangement? What do we measure with the voltmeter? The usual viewpoint is to think of a resistor as a point, as a something that has not dimensions, as a two-terminal element that has only a property of resistance. But here we have the unique chance to peep inside the "resistor"! What will you "see" along the wire? What will the voltmeter show when we slide it from right to left? What are the local voltages along a resistor, if there is no current - zero, 10 V or something else?
Well, let's try. First, connect the black test end of the voltmeter to the ground. Then touch the resistive wire by the red voltmeter probe and move it along the wire to measure all the voltage drops (for now, regarding to the ground)! If you are tired, stick a crocodile clips on the probe, "bite" the wire and move this "slider" along it! Maybe, exactly in this way, once upon a time, someone invented the true potentiometer... No matter, the result is amazing: everywhere local voltages are 10 V no matter where the crocodile clip is along the resistive film! Obviously, the electrical phenomenon is the same as the hydraulic one that we observed above: the local voltages meausered along the resistive wire connected in an open circuit are the same and equal to the input voltage. But why?

Remember what a resistor does - it "resists". What does it resist? It resists, obstructs, disturbs current by dissipating power. But no current flows in an open circuit. So, there is nothing to resist; the resistor is not a resistor when there is no current. The resistor is a resistor when there is something to resist!
We can apply the idea of a pressure diagram to present in a similar way the voltage distribution along the resistive wire. We can think of voltage as a kind of pressure; so, we may present the local voltages by local voltage bars in exactly the same way as we presented the local pressures by local water bars (Fig. 4)! As above, the lengths of the voltage bars are proportional to the magnitudes of the local voltages regarding to ground (we might set the zero voltage level at the height of the resistor and then to draw the positive voltage bars above and the negative voltage bars below the resistor's level). The set of these voltage bars forms the whole voltage diagram. In future, we will frequently use the envelope of the voltage diagram instead the set of voltage bars to simplify the image.
Closing the circuit
[edit | edit source]"Inventing" various resistive devices
[edit | edit source]Movement-to-voltage converter. Now, ground the right end of the wire. Only, be careful; the wire is hot! See the ammeter - it shows 1 A; so, the power is P = V.I = V2/R = I2.R = 10 W. By the way, are these calculations right (has the resistance a constant value)? We see, it is too hard for this thin wire to dissipate the power to the environment and it is heating.

Now, move again the "crocodile slider" along the wire and measure the local voltage drops; Ohm did exactly the same. He moved the probe from one position to other, measured the corresponding potentials, made the difference between them and calculated the ratio (V2 - V1)/(L2 - L1) = (V2 - V1)/(r2 - r1) = dV/dR = I. Thus he has established that this ratio (it was the current I) is constant along the wire; so, Ohm has concluded that V/R = I.
We can see that moving the "crocodile slider" the voltage drops decrease gradually from 10 to 0 volts; accordingly, the bars of our voltage diagram will also decrease their length gradually (Fig. 5). We can draw such a picture for every real conductor with some resistance that convey big current to a powerful load.
What is the input and what is the output quantity here? Eureka! Using the "slider" movement as an input and measuring the voltage drop as an output we have "invented" the legendary (but misnamed) potentiometer, movement-to-voltage converter, sensor... What is the relation between the output and input quantities? Is the sensor that we have "invented" a linear movement-to-voltage converter? If yes, why? A hint: the resistance is distributed linearly along the wire. Well, according to the fact that the resistance is distributed linearly along the wire, we can conclude that this converter is linear.
Where might we see such sensors? Of course, the most popular application is the fuel tank level sensor where a float moves such a resistive sensor. Only, if you open a fuel tank one day (be careful, it is dangerous!), you will find out that it is non-linear. Can you tell why?

Bipolar movement-to-voltage converter. We are ready to do more sophisticated experiments... Are there more interesting points (different from the ubiquitous ground) to fix the negative voltage probe? Of course, we may touch any wire point! A typical arrangement is to assign the positive rail (+10 V here) as a ground. But maybe the most interesting point acting as a ground is the middle point; so, "bite" it with the black (negative) "aligator". Then slide the red (positive) "aligator" along the wire to the left and to the right of the black one (Fig. 6). Only, first change the unipolar voltmeter with a bipolar one. Why? What might we expect? The result is more than surprising: the output voltage varies from -5 V to +5 V! Eureka! We have obtained a bipolar movement-to-voltage sensor! Of course, another application is a bipolar varying voltage source.
Common mode signal. Let's continue experimenting... What happens, if we move simultaneously both the voltmeter probes in the same direction? The voltage does not change. Why? They name this input "common mode input signal".
Differential input signal. And what happens, if we move simultaneously both the voltmeter probes in opposite direction? The voltage changes even more rapidly than above. Why? They name this "differential input signal".
Measuring the voltage drop by odd indicators
[edit | edit source]We can measure the voltage drops along the resistive wire by using more unusual indicators, e.g. electric bulbs (Fig. 7), motors, LEDs, etc. What do you think, is there any problem to supply a bulb in this exotic way (Fig. 8)? If yes, when and why?


Do you know that travel hair-dryer and toasters exploit the same powerful idea to supply with low voltage their internal circuits (motors, timers, etc.)? Then let's supply in a similar way a small DC motor (Fig. 9). As we can see, the motor changes its speed proportionally to the distance between the two crocodile clips. Also, if we swap the two crocodile clips, the motor changes the direction of rotation (Fig. 10).

Investigating exotic "resistors"
[edit | edit source]Pencil graphite. If we are inventive enough, we might investigate various unusual resistive materials to observe the voltage distribution along them. For example, we may supply various loads (including LEDs) by the partial voltage drop across ordinary pencil graphite (Fig. 11); it seems this is a very popular experiment on the web.[1]
Conductive foam. Another non-traditional but very attractive experiment is to investigate the voltage distribution through a conductive foam (Fig. 12). Only, it requires using a perfect voltmeter (why?) But what is the voltage distribution here - line or surface?


Graphite trace. Finally, we can go too far in our sophisticated experiments, if we draw a resistive path on a paper by a soft pencil (the softer the lead is, the bigger the conduction will be) and then slide the voltmeter probe along the "resistor". But don't you think we can even measure the voltage distribution along our human bodies:)? Of course, we need a very, very perfect (high resistive) voltmeters for all these exotic experiments....
How to visualize the voltage diagram on the screen
[edit | edit source]Basic idea. But it is too hard and boring for us, human beings, to draw all the voltage diagrams when the circuit attributes (voltages and resistances) vary. Because these diagrams have to be not static, dead pictures; they have to be "living" diagrams (animations) that change accordingly to the circuit state. So, we need a computer that "watches" closely what we do with the circuit under test and builds the according "living" voltage diagram on the screen. Then, let's build such a computer-based system and leave it to do this donkey work:). Then we will only look at the picture on the screen and think about the circuit phenomena behind it!
Components. First at all, we need some computer. It may be humble enough, if only it has some graphical possibilities (for example, the computer that is used in this laboratory to build Microlab system in 1986 is a version of the famous Apple II). Then we have only to connect to the PC buses a few analog-to-digital converters (ADC's) acting as analog inputs and a few digital-to-analog converters (DAC's) acting as analog outputs and our computer-based system Microlab is ready (see Fig. 13)!


Power supply. Note that the analog-digital periphery (Fig. 14) "sucks" energy directly from the poor computer:); so, it acts not only as a computer but it supplies the periphery too. Then can we supply the very resistive object as well? Can we use the very DAC's to supply the resistor under test? This will allow the computer to control the object! Only, the DAC's can give maximum 10 mA by their op-amp outputs. So, we can't supply the low-resistive (10 Ω) wire!
Resistor. We can use a linear high-resistive (e.g., 4.7 kΩ) varying resistor instead the low-resistive wire. Then we may supply the resistor by the DAC's 10 mA outputs without any problem (calculate the maximum current). In order to complicate the arrangement, we may supply both the ends of the resistor. So, connect AO1 (DAC1) to the right and AO2 (DAC2) to the left end of the resistor.
Voltmeters. What do you think, whether to connect the two old-fashioned but attractive bipolar voltmeters V1 and V2 to observe the input voltages? Or to rely only on the abstract digital VOM's and the digital measurements on the screen? But the good old meters are "living", moving, geometrical, spatial and real; that is why people trust them. Note they are also bipolar with zero in the middle. But is there any problem as they have 20 kΩ internal resistance)? A hint: the two DACs behave as perfect voltage sources having almost zero output resistance.

Ground. Now, let's say also some words about ground. But what is ground? We can find a possible answer in the Wikipedia article about virtual ground. Shortly, ground is a reference point, regarding to which we measure voltages. Any point inside a compound voltage source can act as a real ground (Fig. 15). The PC power supply that we use is the so called "split supply". It consists of two 12 V supplies connected in series (- + >>> - +). The middle point serves as ground in this arrangement. The DAC's grounds are connected internally to this ground. We have also to connect the black test ends of our voltmeters to this ground.
Software. Now let's start a program that can visualize the voltage diagram on the screen as a "living" animation. For this purpose, the program make computer "interest" in the local voltages in three key points - the left resistor's end point, the slider intermediate point and the right end point. Let's then satisfy its curiosity:) by connecting, for a start, the DAC1's output to the ADC1's input and the DAC2's output to the ADC2's input; then, connect the ADC3's input to the slider. We can control the output voltages of the two DACs by the keyboard arrows; thus the two DACs act actually as programmable voltage sources. The computer measures continuously the three voltages (VIN1, VIN2 and VIN3) and draws three voltage bars whose length is proportional to the voltage magnitudes. Finally, it connects them with a line representing the envelope of the voltage diagram.
For more reality, we might first dismount the varying resistor (the "potentiometer") and touch the measuring probe directly to the resistive film. Now we are ready to continue these amazing experiments. We will use the well-known technique for "inventing" various devices: vary only one quantity at time while keeping the other quantities constant. Let's begin!
Varying V1: a left-controlled voltage-to-voltage converter
[edit | edit source]Above we were keeping the two voltages constant while varying (moving) the slider position; thus we have "invented" a movement-to-voltage converter. But why do not we change the role of the quantities?

With the same success we can stop the "crocodile slider" somewhere (e.g., at the middle of the wire) and then to vary the input voltage as an input and, as before, to measure the voltage drop (regarding to the ground) as an output. So, the arrangement is as follows: we have two voltage sources; one of them (now, the left one) varies and the other is constant. The result on the screen of the computer (Fig. 16) is amazing - the left end of the voltage diagram rises and drops and all the points along the diagram do the same but with decreasing magnitude (figuratively speaking, we can think of voltage diagram as a second-class Archimedes's lever). We can see directly Ohm's law on this geometrical interpretation:
Thus, we have "invented" the simplest voltage-to-current converter. But what is more important we have "invented" the legendary voltage divider (voltage-to-voltage converter or "potentiometer") that is controlled here by the left hand side! What is the relation between the input and output voltage (the so-called "transfer ratio"? We can derive it directly from the geometrical interpretation (two nested similar triangles) "living" on the screen - VOUT = VIN1.L2/(L1 + L2). As the resistance r is proportional to the length L (the resistor is linear) we can arrive at a conclusion:
If V1 varies, the resistor acts as a left-controlled voltage-to-voltage converter having a transfer ratio
Varying V2: a right-controlled voltage-to-voltage converter
[edit | edit source]Above we were "wiggling" the left end of the resistor (the voltage diagram) while keeping the right end fixed at the zero ground level. But why do not swap the roles by "moving" the right end and keeping the left one fixed at zero level? Let's try!

The result on the screen (Fig. 17) is not less amazing than above - now, the right end of the voltage diagram wiggles and all the points along the diagram wiggle too with decreasing magnitude proportional to the distance. Again, we can think of voltage diagram as a second-class Archimedes's lever that we turn from the right.
Thus we have obtained another voltage divider (voltage-to-voltage converter or "potentiometer") that is controlled here by the right hand side. What is the relation between the input and output voltage? The geometrical interpretation (two nested similar triangles) "living" on the screen will help us again - VOUT = VIN2.L1/(L1 + L2). So, the conclusion is similar to the previous one:
If V2 varies, the resistor acts as a right-controlled voltage-to-voltage converter having a transfer ratio
Varying both V1 and V2: a resistive summer
[edit | edit source]In the previous experiments, when we were varying some of the input voltages, we were keeping the other voltage equal to zero. But what happens, if we keep the other voltage equal to some (e.g. positive) voltage? And what is more, what happens if we vary the two voltages simultaneously? Let's first suppose they are of the same polarity.

The result on the screen (Fig. 18) is even more amazing than previous ones - by varying the two volages we rise and drop the voltage diagram by the left and both the right. The local voltages along the voltage diagram decrease their magnitude gradually from the lower to the higher voltage source. Now, we can think of voltage diagram as a two-side second-class Archimedes's lever that we turn from the left and from the right simultaneously.
What kind of device have we "invented" now? What is the relation between the input voltages VIN1, VIN2, the slider's position L1/(L1 + L2) and the output voltage VOUT? The attractive geometrical interpretation (a trapezium) "living" on the screen (Fig. 18) will help us again. As you can see, the two parallel sides of the trapezium represent the two input voltages; the internal segments represent the output voltage. You probably can solve this popular geometrical school problem (a tip: draw an auxiliary diagonal) - VOUT = VIN1.L2/(L1 + L2) + VIN2.L1/(L1 + L2). So, the conclusion is similar to the previous one:
If both the input voltages vary, the resistor acts as a passive resistive summer having a transfer ratio
But this is not a humble summer; as we can see, this is a summer with weighting coefficients:
and
Creating a virtual ground
[edit | edit source]A passive resistive subtractor
[edit | edit source]We have finally reached the most interesting part of our story... In the previous experiment, we were applying two voltages with the same polarity. But why do not reverse the polarity of one of the input sources? Let's try!

The result on the screen (Fig. 19) is more than surprising and amazing - a point A with zero voltage VA = 0 (regarding to the ground) has appeared somewhere on the resistive film! Note this mystic point is not connected to the real (true, genuine) ground but yet it behaves as such a ground! It is a kind of artificial, virtual ground... Usually, they introduce this concept when explain op-amp circuits. But we can see this is not a unique property of op-amp circuits; it is a property of this simple resistive circuit containing only two resistors. From this viewpoint Ohm could observe virtual ground phenomenon still in 1826, if only he had introduced a second voltage source!
Again, the attractive geometrical interpretation (two similar but now opposite triangles) "living" on the screen will help us to formulate the requirements of existing a virtual ground in a given point. Obviously, the two input voltages VIN1 and VIN2 have to have opposite polarities and they have to bear the same proportion as between the respective resistances r1 and r2 (R1 and R2, if they represent separate resistors):
If you like analogies, you might think of this arrangement as an electrical "tug of war", where two voltage sources "fight" each other - VIN1 "pulls" the point A up while VIN2 "pulls" it down. The pull-up resistor r1 and the pull-down resistor r2 serve here as electrical "ropes".
A negative feedback game
[edit | edit source]What happens, if we begin varying the input voltage VIN1 or VIN2 or both the voltages (keeping VIN1 = -VIN2)? See, the virtual ground point moves left and right! Can we stop it somewhere on the resistive film? If we manage to stop it, we will be able to create famous circuits with negative feedback... Let's try!
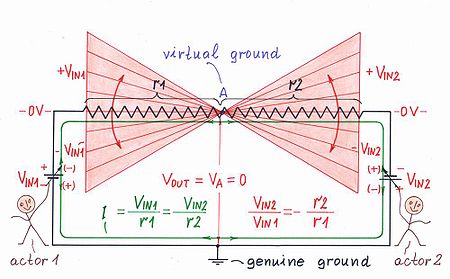
Don't you think instead to carry out boring experiments we may play a funny game to imitate a negative feedback system? If you agree with this suggestion, let's cast roles:) One of us ("actor" 1) might act as (be, control) the main independent input voltage source VIN1. The other "actor" 2 might represent the second dependent voltage source VIN2; he/she has to keep the virtual ground immovable. For this purpose, he/she has only to look at the virtual ground point (a zero indicator might help to measure its voltage) and to change VIN2 so that to keep the virtual ground voltage always equal to zero.
The result on the screen (Fig. 20) is just wonderful! The actor 1 (VIN1) tries to move the virtual ground point but the actor 2 (VIN2) returns it to the old position. The voltage diagram rotates around the fixed virtual ground point and VIN2 is always proportional to VIN1; the second voltage follows with opposite polarity the first one: .
What a great idea! Actually, we may think of the input voltage VIN2 as an output one and we may use it really as an output voltage! This arrangement represents the simplest inverting system with negative feedback.
An op-amp inverting amplifier
[edit | edit source]As we can see, the actor 2 is bored with this "donkey work" - to observe the virtual ground and to vary VIN2:) Can something else do it? An op-amp seems to be a good choice (Fig. 21). It has a perfect electrical sense; so, it does not need a zero indicator to monitor the virtual ground voltage. Similarly, if actor 1 is got bored too, we can make the computer to produce a periodical voltage at DAC1's output. Well, we can see the op-amp keeps up the same proportion between the quantities as above: ; thus, we have "invented" the famous op-amp inverting amplifier! Now, we can do a few experiments by changing the slider's position: at the middle point, to the left and to the right of the middle point. How does an op-amp react to this "intervention"? What happens with the voltage diagram? Can we use all these situations to build electronic circuits?

See also
[edit | edit source]Voltage drop in direct current circuits
Building a parallel voltage summer by using more elementary circuit building blocks
Virtual ground reveals the secret of the famous phenomenon
References
[edit | edit source]- ↑ Potentiometer as a voltage divider by Tony Kuphaldt shows interesting experiments with pencil graphites
External links
[edit | edit source]- Paper circuit (YouTube movie)
- Compound passive converters with voltage output
- Parallel voltage summer builds the circuit by using the simpler voltage-to-current and current-to-voltage converters (Flash animated; Ruffle extension needed).
- How do we create a virtual ground? is a circuit story about the great phenomenon.








