Circuit Idea/Group 67a

We are students from Faculty of Computer Systems, Technical University of Sofia. Our 67 group is divided into two sub-groups; we constitute the first 67a one. Here are our names:
Virginia, Angel, Vladimir...
(add your name and place a photo here )
Lab 1: Investigating passive resistive circuits by Microlab
[edit | edit source]Lab 2: The genuine Ohm's experiment
[edit | edit source]Tuesday, March 18, 2008, 16.45 h
The first thing we did on this practical lesson was to reproduce Ohm's experiment, because Ohm's law is the base of the electronics we study. The idea of our practical and theoretical lessons in our course of electronics is to invent everything, every single element (even the resistor). So we started imagining how Ohm did his famous experiment and found the fundamental relationship between the current, voltage and resistance. He did his experiment in the beginning of the 19th century. This means only thing he could use as a power supply was the forerunner of the electrical battery, created by Alessandro Volta. Unfortunately this experiment failed, because Ohm used a wire with very low resistance so the power source was loaded. For reproducing Ohm's experiment we used a resistive wire. In the lab we used a power supply (maximum current 2.5A, maximum voltage 10V), voltmeter and ammeter. So we started the experiments.
Experiment N1: The scheme we were examining is shown on fig.4 in the main module. We move the voltmeter in this way: one of its ends is connected with the ground and the other is walking on the resistive film by a crocodile clip as a slider. Apparently the measured voltage is 10V no matter where the crocodile clip is along the resistive film.
Experiment N2: The scheme we were examining is shown on fig.5 in the main module. Now we have a change in the measurement of the voltmeter. We can see change is linear.
So now is appropriate to make the hydraulic analog: the tapped pipe and the opened pipe. The illustrations are shown at the main module.
We slide the crocodile clip along the resistive film. This is equal to using a potentiometer. The potentiometer is practically a movement-to-voltage converter. According to the fact that the resistance is distributed linearly along the wire, we can conclude that this converter is linear. So there was a new idea: why don't we stop moving the crocodile slider, leaving it in a certain point on the resistive wire and start changing the input voltage?
Experiment N3: We have 2 voltage sources. One of them (the left one) varies and the other is constant. We see the results on the screen of the computer. You can see the illustration attached it the subtopic in the main module: V1 varies: a left-controlled voltage-to-voltage converter.
Experiment N4: Now the right one varies and the left one is constant. We see the results on the screen of the computer. You can see the illustration attached it the subtopic in the main module: V2 varies: a right-controlled voltage-to-voltage converter.
Experiment N5: Now both of the voltage sources vary. We see the results on the screen of the computer. You can see the illustration attached in the subtopic in the main module: Both V1 and V2 vary: a resistive summer.
As we can see this is a summer with coefficients:
Since now we have seen the results only when the input voltages are positive. Now we change the polarity.
We can see that there is one point we can see on the screen on the computer with zero-potential. This is the famous virtual ground. This point moves on the horizontal axis. So there was a new question – can we make this moving point a fixed one? The answer is yes. There is one element that controls its output in according with the input voltage. This is the operational amplifier. This element keeps the virtual ground at point A. See the illustration: a passive resistive subtractor and of course the negative feedback game.
Lab 3: Building an emitter follower
[edit | edit source]Tuesday, April 01, 2008, 16.45 h
authors: Angel,Virginia & Vladimir
Building a negative feedback follower
[edit | edit source]Looking for analogies of negative feedback phenomenon
[edit | edit source]Speaking. We are getting started with an explanation of the term negative feedback. The first thing we ask each other is if there is a similar phenomenon in real life. Thus we have found we might consider human speech as an example: you have to listen to your voice in order to control its volume. In this way you are able to communicate with those around you appropriately. The noisier the surrounding environment is, the louder your voice becomes and vice versa. This basic idea explains roughly the essence of negative feedback.
Driving. Another example of the idea of negative feedback might also be the following situation. Imagine you are getting in your car and striving to drive with 50 km/h. Let us now suppose that we have a current state X and we want to achieve another goal state Y. In order to complete this task we should monitor the process of its development and control it in a desirable way by adjusting all necessary parametres. You are in state X and you would like to achieve state Y. But what do you need?
Generalizing the analogies into a block diagram
[edit | edit source]The first thing you need is ENERGY. It's necessary but not enough. You need also a visualization of your speed in order to control it. In other words you need a REGULATOR.
But what is the regulator doing? It compares the difference between the purpose state and the current state; then, it does what can do to eliminate it. When this difference is equal to zero, we have an equilibrium – this shows that the goal state has been achieved.
Building an electrical follower
[edit | edit source]The most simple regulator is the so called follower. Now we have to think about how we can realize a follower.
Is the humble wire a follower?
[edit | edit source]An obvious example of electric follower is... a simple wire (?!?). This remedy is simple: if you want the potential of point B to follow the potential of point A, just connect them to each other by piece of wire. But is that wire a perfect follower? The answer is “no”. We will provide reasons why with the next example.

The wire as you know has its own resistance. Let us now connect a resistor (1 ohm), our wire (1 ohm) and a voltage source(10V) like it is shown in the second picture. After measuring the output voltage we see that it has been reduced with the voltage drop caused by the wire’s internal resistance. The reason for this is clear – the current flowing in the circuit.
Building an emitter follower on the whiteboard
[edit | edit source]So we decide to make use of another (this time more “perfect”) regulator – an emitter follower. Having already come to the idea of constant regulating and adjusting a desired value according to the changes in its environment, we proceed with a real scheme with a transistor. The transistor here acts as the regulating element of the negative feedback follower above. The essence is that it “observes” the potential in point A and changes the potential in point B (by changing its own resistance) so that to keep an almost zero difference between them. But let's give a description of our practical laboratory exercise.
Putting the powerful idea into practice
[edit | edit source](How our laboratory exercise passed over)

Preparation. In order to reveal to us the "secrets" of ubiquitous transistor, our teacher Cyril Mechkov provided us with the opportunity to build our own test circuit and observe its behaviour. As curious students who usually enjoy taking things apart, we were desperate to "invent" our own emitter follower and get a preconception of the so called negative feedback. We already knew some of the basic applications of the transistor having already studied digital circuitry but most of us lacked any practical experience. Having realized that, firstly prof. Mechkov briefly outlined the idea of the laboratory session and then gave us a soldering iron, a test board and all the necessary equipment to carry out the investigation of our device. The old Apple II based PC proved ideal for the experiment - it not only served as a power supply:) but together with the MicroLab system was able to "watch" our scheme and draw real-time voltage diagrams. Armed with this powerful "weaponry" we felt like real inventors!
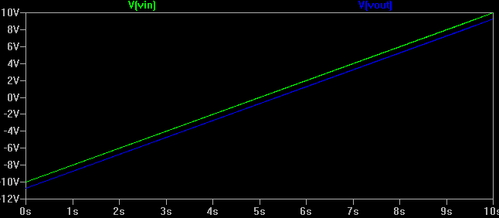
Investigation. Some of the girls were terrified when Miroslav (a colleague) switched on the scheme, but fortunately nothing exploded;) Everything was well under control. After connecting our newly constructed emitter follower to the prototyping board we started the investigation by gradually varying its power supply (ranging from -10 to 10 Volts). As you can see from the pictures in the region of the positive values the transistor's behaviour coincides with theory. The voltage drop of the emitter-base junction always "strives" to remain the same - exactly 0,7 Volts. In accordance with Kirchoff's laws the potential of the output emitter was just like we expected - the input voltage minus the voltage drop. By analogy, the same linear dependency was observed in the negative input range. The lab results in that case are reproduced in the picture below.

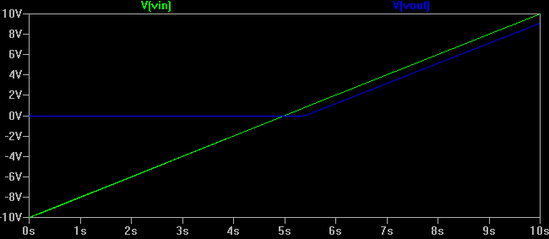
Problem. However, quite unexpectedly we suggested double-checking the scheme by connecting an old-fashioned analogue votmeter in parallel to the digital VOM. Miroslav then attached one of the crocodile clips to the emitter and the other to the ground of the board (notice that the emitter - collector power supply is bipolar). At first, the new result on the screen seemed quite strange - in the negative region there was a section with a constant potential. Something had made the emitter base junction reverse biased. Professor Mechkov smiled being aware of the "mischevous intruder" in the voltage diagram but wanted us to find out the cause. We didn't hesitate for long and changed the old-fashioned voltmeter with a Chinese 3$ one.
Voila! The key to the "mystery" was finally discovered - the reason for switching off the transistor was the voltmeter's internal resistance. In the case of the old electromagnetic device it was about 20 kOhms. This internal resistance had become the main reason for the advent of a current flow through one of the power supplies, our load and the voltmeter. This newly appeared current kept the potential at the output unchanging when the base supply was low enough (see the picture). We realized the n-p-n transistor can only "source" current; it can't sink current.


Strengthening the problem. Having discovered this effect, we decided to replace the voltmeter with a lower resistor (100 Ohms) in order to simulate a voltage breakdown through the reverse biased base-emitter junction. In that particular case the transistor acted like a zener diode stabilizing the output voltage in certain ranges. A reproduced PC based simulation is shown on the last picture.
Conclusions
[edit | edit source]The final conclusion from the laboratory exercise was that a simple emitter follower might not be so simple and predictable in certain situations. We gathered some really valuable experience by observing the changes in our transistor's behaviour - at first it acted as an emitter follower, then it became a zener diode finally it turned into a voltage controlled switch. The small transistor was like a skilful magician but one playing tricks with current. Electronics is really fascinating, isn't it!
- Angel, Virginia and Vladimir, thank you for your participation! Your material is excellent; it is so fascinating, captivating and funny! It was a great pleasure for me to join your team and to do my best to refine your work. Thank you again! Circuit-fantasist (talk) 17:57, 14 April 2008 (UTC)
Lab 4: Op-amp circuits with series negative feedback
[edit | edit source](Converting the imperfect emitter follower into a perfect op-amp follower)
Authors: Angel with the help of Virginia

Do you remember our scheme from the previous exercise? We used a single transistor as an emitter follower illustrating in this way the concept of the negative feedback. We also noticed that our device was a bit more perfect compared to the most primitive voltage follower - a single piece of wire. However, when we put our obedient transistor to tests, we discovered that it felt a constant "hunger" - drawing power from the input and thus causing a voltage drop of 0,7 Volts. For the purpose of the laboratory experiment that was acceptable, but what would you say about implementing this scheme in real, extremely precise devices? Of course, it depends on the application, but one thing is certain - our emitter follower is not "ideal" simply because it disturbs the input.
If we look around ourselves in reality everything abides by these laws of nature. For example, if we have to complete a specific task, we need a proportional amount of energy. This energy is not given "for free", it has been accumulated as a result of previous activities which in their own turn have come to fruition thanks to the efforts of others and so on. The same regularity is valid for electronics. Perhaps, the basic philosophical principle of each human activity and schemotechnics too, in our context, is converting and processing some kind of input energy (usually represented by an electrical quantity) into a desired output. In this way we are able to represent, process and store information in electrical circuits in various ways. However, we should always be aware of the "losses" in our circuitry because in order to function properly each element requires sufficient resources.
After these introductory reflections, you might ask the following question. What is an ideal scheme and could it actually exist? Some people would suppose that such schemes are virtually non-existent because they cannot be practically constructed. Others would conclude that the term ideal is a bit imaginary - ideal things are in fact our own ideas of how things should function in the best possible conditions. Still others may qualify ideal elements as fairly theoretical - as an abstraction of mathematics and science. In fact all these three different groups of people would be right to a certain extent. Absolutely ideal elements may never come to life, but don't you think that our aspiration for developing more and more efficient utilities matters even more? Isn't that desire the main driving force that pushes forward all aspects of human creativity? These were some of the questions we asked ourselves at the fourth exercise in specialized computer electonics. Such kind of discussion was necessary because we had to examine the next step in the evolution of schemotechnics - his majesty - the operational amplifier.
Professor Mechkov challenged us by further developing the topic from the previous session. His main aim was to prepare us for the introduction to this both mysterious and powerful electronic component. Having already understood the role of the negative feedback, we felt it was the right time to study the principles of the op amp schemes and their practical applications. At first, we were a bit baffled because we had already encountered the op amp in other disciplines in the form of complete circuits. The problem was that nobody had explained to us the philosophy behind these circuits. Just remembering several facts or block schemes by heart is not quite useful for future engineers like us. Professor Mechkov knew that pretty well, so in order to make us more familiar with the topic he fostered our imagination giving us a simple but yet effective description of the behavior and advantages of the operational amplifier. In short an op amp may be compared to a strong and obedient weight-lifter. Imagine you have to move some quite heavy furniture at home but unfortunately you lack the power. On top of that you have to carry out the task very carefully so as not to scratch the wooden floor. Suddenly you remember that you can call one of your friends for help - he is a professional well trained weight-lifter. In five minutes he comes and thanks to your directions finishes the job in time. You are very happy and treat him a drink for his efforts. Of course this is a very basic and broad illustration but in fact it quite well represents "the abilities" of the op amp. So, with this figurative idea in mind we may proceed with a formal description of the operational amplifier. It refers to a division of high-gain DC coupled amplifiers with two inputs and a single-ended output. Some of its most significant characteristics are its extremely high gain - typically 200 000 or even a million, its very high input impedance and low output impedance, and last but not least the need for a split power supply (+/-12 Volts for example). We won't go into further details about the internal structure because this is not our goal. We will just mention that a typical op amp is built up of several resistors and transistors connected in a special way.
So, for the sake of practice we should know that an op amp is able to work with two types of input signals – either single-ended or differential ones. Similarly to the transistor an op amp actually doesn't amplify anything - what it is doing is precisely controlling its output according to the changes of the inputs boosting the output from its own power supply. The op amp needs external energy in order to do this trick. Remember that the principle we outlined at the beginning of the text always remains valid! What deserves mentioning here is that the term amplification is used not literally but has appeared perhaps as a result of the overall effect of the functioning of the op amp. The idea is again simple but genius! We use a relatively weak signal or electrical magnitude so as to command a more powerful circuit. This time, however, in contrast to the transistor, we don't draw energy directly from the input, but use an external bipolar power supply. In this way, the op amp is able to respond to the variations of the inputs and adjust qiute precisely its output.

Comparator
Let us now look back at the exercise. Having the above mentioned ideas in mind professor Mechkov described the first and maybe most logical application of the op amp - its usage as a comparator. The scheme we discussed is shown in the next picture.
We observe that the potential of the non-inverting input is lower than that on the inverting. In this particular case we say that the input is differential. Judging by the simulation, we realized that if there was even a tiny difference between V1 and V2 the output was either driven to +VCC or -VCC depending on the magnitude of the inputs. Practically, the output voltage is determined as a multiplication of the voltage difference and the so called open-loop gain. This dependency is illustrated in the following diagram.

As a whole, perhaps the main disadvantage of the scheme is that its operating range is extremely narrow due to the op amp's high sensitivity. At some point the output remains the same - this means that the op amp has reached its upper or lower saturation threshold.

Voltage Follower
Next, thinking on how we can "disturb" the op amp so as to build a voltage follower, we came to the idea of the negative feedback. What we did was to take part of the output signal back to the input but with negative sign. Again the same well known principle but this time realized in an almost perfect way (or let's say the most ideal known nowadays :)). By connecting the output to the negative input and applying some potential to the positive one, we managed to "invent" an immaculate voltage follower. The interesting thing here was that the op amp always strive to keep the difference between the input potentials zero - this is the so called virtual ground. Of course this happens only if you have applied some kind of feedback. We also found out that the inputs drew almost no current - as a result of the op amp's extremely high input impedance.
The scheme and the simulation are the following. Notice that this kind of voltage follower has a gain equal to one.


Non-inverting Amplifier
After these tasks we decided to increase the gain of the negative feedback schemes. For that reason, we put a resistor in the circuit of the feedback trying to cheat our humble op amp in such a way so that it would pull up the potential of its output twice or even more. This case illustrated the so called compensatory mechanism and the respective device is called a non-inverting amplifier. Vout/Vin = 1 + R1/R2


Positive Feedback
Last but not of least importance was the simulation of the infamous Schmitt trigger. Until now we were discussing schemes with negative feedback, so we decided to see what would happen if we had a positive feedback. Look at the next diagram.


Let us mark the highest voltage the operational amplifier can produce ±Vmax. The negative input is connected to the ground and bearing in mind that the op amp keeps the potential difference between its inputs equal to zero, we can conclude the potential in point A is zero or Va=0V.
I1 = ±(Vin – Va) /R1 = ±Vin/R1
(depends on the polarity of the input voltage)
I2 =± (Vout – Va)/R2= ±Vout/R2
(depends on the polarity of the output voltage)
Let us now assume that this scheme is currently in its higher state +Vmax.
Therefore I2=Vmax/R2. As we already mentioned the op amp's most simple role is to function as a comparator, so if we take the input voltage with positive polarity - therefore I1 = Vin/R1. Again knowing that the op amp inputs draw almost no current we can say the I1=-I2. Then Vmax/R2=- I1 = Vin/R1 <=> Vin= -Vmax.R1/R2 - so Vin should drop below −(R1/R2)Vmax to get the output switched. Once the comparator output has switched to −VS, the threshold becomes +(R1/R2)VS to switch back to the higher state. After these preliminary notes we can observe from the simulation that this is a circuit with hysteresis.
What is the good thing about that hysteresis and why is the op amp called a trigger? The device is called a trigger because it keeps its output unchanged until the input changes are sufficient to trigger a change. That's why we say that op amps with positive feedback have "memory".
Now let's pay attention on the hysteresis: its main advantage is that it has two limiting thresholds. If we have a device with one threshold and a noisy input signal, the device may change its output in very unwanted ways - of course these changes might be very fast. In contrast, if we have a Schmitt trigger the scheme will be much more reliable and resistant to any input deviations because of its "improved" characteristics.
Final Words
After all, operational amplifiers are not so dreadful as their name suggests, are they! In fact these little "smarties" are so versatile and powerful that there are widely used in many areas of practical electronics. Thanks to professor Mechkov we have managed to find our way through the "jungle" of op amps and represent our "discoveries" on this page. We hope that our brief description has helped you gain a better understanding of the topic. If you have any ideas or suggestions we would be happy if you - our readers, take part in the discussion!
- Angel and Virginia, your essay was so exciting that, believe me, it moved me to cry! If only a few students of every group were as you, I will be no end happy! I have an idea: can you visit the rest nine labs in future to pass your experience on your colleagues:)))? Will you assist me during Lab 5?:) By the way, I would like to make some remarks on your work but I dare not to touch it:) Best regards! Circuit-fantasist (talk) 17:23, 21 April 2008 (UTC)
Resources
[edit | edit source]Operational amplifiers is an excellent material written by famous Tony Kuphaldt.
Operational amplifier
Differential and Single-Ended Inputs
Labs: group 65a and group 66a.
Op-amp amplifiers with negative feedback
Lab 5A: Building the op-amp inverting integrator (student's version:)
[edit | edit source]During our laboratory course we have already carried out experiments with passive "mischevous" elements(resistors for example) and active ones (transistors and op amps) being able to command their output according to the variations of the input signals. Having understood the role of each of these groups we may be able to "harness" their potential to a maximum extent only if we examine their behaviour in more complex time-dependent schemes. Why time-dependent? - you might ask? The answer is simply because the representation of time as a variable is what we need in combination with the input and output values in order to simulate or examine all kinds of real-life phenomena. Thus, "playing" around with our electric building blocks we will be able to construct an endless number of various useful circuits. During the fifth exercise we developed the above-mentioned conception of time-sensitive schemes by constructing an inverting op-amp integrator. The "main characters" in that session were the op-amp from the previuos lab and a new "actor" - a capacitor - acting as a current driven voltage integrator. The role of a typical integrator as its name suggests is to function as an accumulator of a particular value. In this way depending on the physical essence of accumulation, we may be able to measure time intervals or even more precisey work with time in general. A single passive voltage integrator as the one shown below in professor Mechkov's description is imperfect mainly because of the non-linear voltage drop across the capacitor which disturbs the input source. In fact, this is the typical "disadvantage" of all kinds of passive schemes - their behaviour influences the input. However, according to the application this effect may be either useful or unwanted. What is more important here is grasping the idea and trying to perfect its practical realization. Following the principles from the previous two laboratory exercises, we came to the idea of connecting a single capacitor in the series of the negative feedback. This time the op-amp was "deluded" in an unconevtional way - the change in the negative input was exponential in itself but thanks to the op-amp's extremely high gain - the output changed in a linear way(not infinitely of course). Observing this effect, we concluded that it would be quite easy for us to construct a universal measuring device, allowing us to explore and even improve the behaviour of all kinds of electronic components - diodes, resistors, etc. All we need is a suitable power supply, an op-amp and a little imagination. Pure mathematical formulae or boring readily-built schemes cannot do the trick ;)
Lab 5B: "Inventing" the op-amp inverting integrator (a teacher's version:)
[edit | edit source]Current-to-voltage C integrator
[edit | edit source]
What is the most elementary electrical integrator? Of course, this is the humble capacitor. So, if we drive a capacitor C by a constant current source I, it acts as an ideal current-to-voltage integrator with a current input IIN and a voltage output VOUT = VC. Note that the output voltage changes linearly through the time.
Building an op-amp inverting integrator - step 1
Keeping a constant current by using an ideal current source
Voltage-to-voltage RC integrator
[edit | edit source]
Only, we need usually an integrator with voltage input and voltage output (voltage-to-voltage integrator). For this purpose, we can build a compound voltage integrator just connecting a voltage-to-current converter (a resistor) before the integrator:
V-to-I converter + I-to-V integrator = V-to-V integrator
Only, a problem arises here - the voltage drop VC across the capacitor C "enervates" the input voltage thus decreasing the input current. As a result, the output voltage changes exponentially through the time.
Building an op-amp inverting integrator - step 2
Keeping a constant current by depreciating the load


Active RC integrator
[edit | edit source]
Remember what we do in real life when an obstacle stands in our way - we remove it by an equivalent useful "antidisturbance". Following this recipe, we may remove the "harmful" voltage VC by an "antivoltage" -VC. That means to connect an additional varying voltage source and to make its voltge equal to -VC. As a result, the "harmful" voltage VC disappears and the upper point becomes a virtual ground! The compound current source VIN-R is "fooled": it doesn't "understand" that there is a capacitor connected; it "thinks" that its output is shorted.
Building an op-amp inverting integrator - step 1
Keeping a constant current by adding an additional voltage

But where to take an output from? We have three possibilities.
First, we might use the old output; but we have already destroyed this voltage!
Second, we may use the "original" voltage as an output. It is possible but bad solution to connect the load across the capacitor for two reasons: the load has to have a differential output; the load will shunt the capacitor thus affecting the current.
Finally, we can use the "copy" voltage as an output! What a great idea! First, the load will be connected to the common ground; second, it will consume energy from the supplementary source instead from the input one!
Building an op-amp inverting integrator - go to step 3
Op-amp inverting RC integrator
[edit | edit source]Finally, we have only to replace the varying voltage source with a real one. Now the op-amp doses the voltage of the power supply thus producing a compensating voltage -VC. In other words, the combination of an op-amp and a steady battery acts as a varying voltage source.

The op-amp "observes" the potential of the virtual ground (the difference between the two voltages) and changes instantly its output voltage so that this point to stay always at zero volts. Doing that, the op-amp compensates the "harmful" voltage drop across the capacitor by copying and adding it to the voltage of the input source; doing that, the op-amp "helps" the input source.

It's time to make conclusions. What have we actually done here? How does it operate? What is the final result?
The answer is amazing: we have made a "botomless" capacitor having infinite capacitance. Looking from the side of the input source this "ideal" capacitor acts just... as a piece of wire...?!? What do you think about this speculation? Is it always right?
We are already true magicians as we can transform any imperfect component into an almost ideal one! In this lab, we have transmuted the "imperfect" capacitor into a perfect infinite one having no any voltage drop across it although a current flows continuously through it! But with the same success we can make an ideal diode, zero resistance, etc... For this purpose, we just incorporate a varying battery to the imperfect component that compensate the losses inside the component. Remember: all the op-amp inverting circuits exploit this clever trick. Circuit-fantasist (talk) 16:50, 6 May 2008 (UTC)
How to make perfect components by parallel NFB
Building an op-amp inverting integrator - go to step 4
Resources
[edit | edit source]How do we build an op-amp RC integrator? shows a reliable four-step building "scenario".
Building an op-amp inverting integrator is an interactive multimedia flash minitutorial that builds the circuit in four steps.




