Linear Algebra/Print version/Part 2
| This is the print version of Linear Algebra You won't see this message or any elements not part of the book's content when you print or preview this page. |
Chapter III - Maps Between Spaces
Section I - Isomorphisms
In the examples following the definition of a vector space we developed the intuition that some spaces are "the same" as others. For instance, the space of two-tall column vectors and the space of two-wide row vectors are not equal because their elements—column vectors and row vectors—are not equal, but we have the idea that these spaces differ only in how their elements appear. We will now make this idea precise.
This section illustrates a common aspect of a mathematical investigation. With the help of some examples, we've gotten an idea. We will next give a formal definition, and then we will produce some results backing our contention that the definition captures the idea. We've seen this happen already, for instance, in the first section of the Vector Space chapter. There, the study of linear systems led us to consider collections closed under linear combinations. We defined such a collection as a vector space, and we followed it with some supporting results.
Of course, that definition wasn't an end point, instead it led to new insights such as the idea of a basis. Here too, after producing a definition, and supporting it, we will get two surprises (pleasant ones). First, we will find that the definition applies to some unforeseen, and interesting, cases. Second, the study of the definition will lead to new ideas. In this way, our investigation will build a momentum.
1 - Definition and Examples
We start with two examples that suggest the right definition.
- Example 1.1
Consider the example mentioned above, the space of two-wide row vectors and the space of two-tall column vectors. They are "the same" in that if we associate the vectors that have the same components, e.g.,
then this correspondence preserves the operations, for instance this addition
and this scalar multiplication.
More generally stated, under the correspondence
both operations are preserved:
and
(all of the variables are real numbers).
- Example 1.2
Another two spaces we can think of as "the same" are , the space of quadratic polynomials, and . A natural correspondence is this.
The structure is preserved: corresponding elements add in a corresponding way
and scalar multiplication corresponds also.
- Definition 1.3
An isomorphism between two vector spaces and is a map that
- is a correspondence: is one-to-one and onto;[1]
- preserves structure: if then
(we write , read " is isomorphic to ", when such a map exists).
("Morphism" means map, so "isomorphism" means a map expressing sameness.)
- Example 1.4
The vector space of functions of is isomorphic to the vector space under this map.
We will check this by going through the conditions in the definition.
We will first verify condition 1, that the map is a correspondence between the sets underlying the spaces.
To establish that is one-to-one, we must prove that only when . If
then, by the definition of ,
from which we can conclude that and because column vectors are equal only when they have equal components. We've proved that implies that , which shows that is one-to-one.
To check that is onto we must check that any member of the codomain is the image of some member of the domain . But that's clear—any
is the image under of .
Next we will verify condition (2), that preserves structure.
This computation shows that preserves addition.
A similar computation shows that preserves scalar multiplication.
With that, conditions (1) and (2) are verified, so we know that is an isomorphism and we can say that the spaces are isomorphic .
- Example 1.5
Let be the space of linear combinations of three variables , , and , under the natural addition and scalar multiplication operations. Then is isomorphic to , the space of quadratic polynomials.
To show this we will produce an isomorphism map. There is more than one possibility; for instance, here are four.
The first map is the more natural correspondence in that it just carries the coefficients over. However, below we shall verify that the second one is an isomorphism, to underline that there are isomorphisms other than just the obvious one (showing that is an isomorphism is Problem 3).
To show that is one-to-one, we will prove that if then . The assumption that gives, by the definition of , that . Equal polynomials have equal coefficients, so , , and . Thus implies that and therefore is one-to-one.
The map is onto because any member of the codomain is the image of some member of the domain, namely it is the image of . For instance, is .
The computations for structure preservation are like those in the prior example. This map preserves addition
and scalar multiplication.
Thus is an isomorphism and we write .
We are sometimes interested in an isomorphism of a space with itself, called an automorphism. An identity map is an automorphism. The next two examples show that there are others.
- Example 1.6
A dilation map that multiplies all vectors by a nonzero scalar is an automorphism of .
A rotation or turning map that rotates all vectors through an angle is an automorphism.
A third type of automorphism of is a map that flips or reflects all vectors over a line through the origin.
See Problem 20.
- Example 1.7
Consider the space of polynomials of degree 5 or less and the map that sends a polynomial to . For instance, under this map and . This map is an automorphism of this space; the check is Problem 12.
This isomorphism of with itself does more than just tell us that the space is "the same" as itself. It gives us some insight into the space's structure. For instance, below is shown a family of parabolas, graphs of members of . Each has a vertex at , and the left-most one has zeroes at and , the next one has zeroes at and , etc.
Geometrically, the substitution of for in any function's argument shifts its graph to the right by one. Thus, and 's action is to shift all of the parabolas to the right by one. Notice that the picture before is applied is the same as the picture after is applied, because while each parabola moves to the right, another one comes in from the left to take its place. This also holds true for cubics, etc. So the automorphism gives us the insight that has a certain horizontal homogeneity; this space looks the same near as near .
As described in the preamble to this section, we will next
produce some results supporting the
contention that the definition of isomorphism above
captures our intuition of vector spaces being the same.
Of course the definition itself is persuasive: a vector space consists of two components, a set and some structure, and the definition simply requires that the sets correspond and that the structures correspond also. Also persuasive are the examples above. In particular, Example 1.1, which gives an isomorphism between the space of two-wide row vectors and the space of two-tall column vectors, dramatizes our intuition that isomorphic spaces are the same in all relevant respects. Sometimes people say, where , that " is just painted green"—any differences are merely cosmetic.
Further support for the definition, in case it is needed, is provided by the following results that, taken together, suggest that all the things of interest in a vector space correspond under an isomorphism. Since we studied vector spaces to study linear combinations, "of interest" means "pertaining to linear combinations". Not of interest is the way that the vectors are presented typographically (or their color!).
As an example, although the definition of isomorphism doesn't explicitly say that the zero vectors must correspond, it is a consequence of that definition.
- Lemma 1.8
An isomorphism maps a zero vector to a zero vector.
- Proof
Where is an isomorphism, fix any . Then .
The definition of isomorphism requires that sums of two vectors correspond and that so do scalar multiples. We can extend that to say that all linear combinations correspond.
- Lemma 1.9
For any map between vector spaces these statements are equivalent.
- preserves structure
- preserves linear combinations of two vectors
- preserves linear combinations of any finite number of vectors
- Proof
Since the implications and are clear, we need only show that . Assume statement 1. We will prove statement 3 by induction on the number of summands .
The one-summand base case, that , is covered by the assumption of statement 1.
For the inductive step assume that statement 3 holds whenever there are or fewer summands, that is, whenever , or , ..., or . Consider the -summand case. The first half of 1 gives
by breaking the sum along the final "". Then the inductive hypothesis lets us break up the -term sum.
Finally, the second half of statement 1 gives
when applied times.
In addition to adding to the intuition that the definition of isomorphism does indeed preserve the things of interest in a vector space, that lemma's second item is an especially handy way of checking that a map preserves structure.
We close with a summary. The material in this section augments the chapter on Vector Spaces. There, after giving the definition of a vector space, we informally looked at what different things can happen. Here, we defined the relation "" between vector spaces and we have argued that it is the right way to split the collection of vector spaces into cases because it preserves the features of interest in a vector space—in particular, it preserves linear combinations. That is, we have now said precisely what we mean by "the same", and by "different", and so we have precisely classified the vector spaces.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Verify, using Example 1.4 as a model, that the two correspondences given before the definition are isomorphisms.
- This exercise is recommended for all readers.
- Problem 2
For the map given by
Find the image of each of these elements of the domain.
Show that this map is an isomorphism.
- Problem 3
Show that the natural map from Example 1.5 is an isomorphism.
- This exercise is recommended for all readers.
- Problem 4
Decide whether each map is an isomorphism (if it is an isomorphism then prove it and if it isn't then state a condition that it fails to satisfy).
- given by
- given by
- given by
- given by
- Problem 5
Show that the map given by is one-to-one and onto.Is it an isomorphism?
- This exercise is recommended for all readers.
- Problem 6
Refer to Example 1.1. Produce two more isomorphisms (of course, that they satisfy the conditions in the definition of isomorphism must be verified).
- Problem 7
Refer to Example 1.2. Produce two more isomorphisms (and verify that they satisfy the conditions).
- This exercise is recommended for all readers.
- Problem 8
Show that, although is not itself a subspace of , it is isomorphic to the -plane subspace of .
- Problem 9
Find two isomorphisms between and .
- This exercise is recommended for all readers.
- Problem 10
For what is isomorphic to ?
- Problem 11
For what is isomorphic to ?
- Problem 12
Prove that the map in Example 1.7, from to given by , is a vector space isomorphism.
- Problem 13
Why, in Lemma 1.8, must there be a ? That is, why must be nonempty?
- Problem 14
Are any two trivial spaces isomorphic?
- Problem 15
In the proof of Lemma 1.9, what about the zero-summands case (that is, if is zero)?
- Problem 16
Show that any isomorphism has the form for some nonzero real number .
- This exercise is recommended for all readers.
- Problem 17
These prove that isomorphism is an equivalence relation.
- Show that the identity map is an isomorphism. Thus, any vector space is isomorphic to itself.
- Show that if is an isomorphism then so is its inverse . Thus, if is isomorphic to then also is isomorphic to .
- Show that a composition of isomorphisms is an isomorphism: if is an isomorphism and is an isomorphism then so also is . Thus, if is isomorphic to and is isomorphic to , then also is isomorphic to .
- Problem 18
Suppose that preserves structure. Show that is one-to-one if and only if the unique member of mapped by to is .
- Problem 19
Suppose that is an isomorphism. Prove that the set is linearly dependent if and only if the set of images is linearly dependent.
- This exercise is recommended for all readers.
- Problem 20
Show that each type of map from Example 1.6 is an automorphism.
- Dilation by a nonzero scalar .
- Rotation through an angle .
- Reflection over a line through the origin.
Hint. For the second and third items, polar coordinates are useful.
- Problem 21
Produce an automorphism of other than the identity map, and other than a shift map .
- Problem 22
- Show that a function is an automorphism if and only if it has the form for some .
- Let be an automorphism of such that . Find .
- Show that a function is an automorphism if and only if it has the form
- Let be an automorphism of with
- Problem 24
We show that isomorphisms can be tailored to fit in that, sometimes, given vectors in the domain and in the range we can produce an isomorphism associating those vectors.
- Let be a basis for so that any has a unique representation as , which we denote in this way.
- Show that this function is one-to-one and onto.
- Show that it preserves structure.
- Produce an isomorphism from to
that fits these specifications.
- Problem 25
Prove that a space is -dimensional if and only if it is isomorphic to . Hint. Fix a basis for the space and consider the map sending a vector over to its representation with respect to .
- Problem 26
(Requires the subsection on Combining Subspaces, which is optional.) Let and be vector spaces. Define a new vector space, consisting of the set along with these operations.
This is a vector space, the external direct sum of and .
- Check that it is a vector space.
- Find a basis for, and the dimension of, the external direct sum .
- What is the relationship among , , and ?
- Suppose that and are subspaces of a vector space such that (in this case we say that is the internal direct sum of and ). Show that the map given by
2 - Dimension Characterizes Isomorphism
In the prior subsection, after stating the definition of an isomorphism, we gave some results supporting the intuition that such a map describes spaces as "the same". Here we will formalize this intuition. While two spaces that are isomorphic are not equal, we think of them as almost equal— as equivalent. In this subsection we shall show that the relationship "is isomorphic to" is an equivalence relation.[2]
- Theorem 2.1
Isomorphism is an equivalence relation between vector spaces.
- Proof
We must prove that this relation has the three properties of being symmetric, reflexive, and transitive. For each of the three we will use item 2 of Lemma 1.9 and show that the map preserves structure by showing that it preserves linear combinations of two members of the domain.
To check reflexivity, that any space is isomorphic to itself, consider the identity map. It is clearly one-to-one and onto. The calculation showing that it preserves linear combinations is easy.
To check symmetry, that if is isomorphic to via some map then there is an isomorphism going the other way, consider the inverse map . As stated in the appendix, such an inverse function exists and it is also a correspondence. Thus we have reduced the symmetry issue to checking that, because preserves linear combinations, so also does . Assume that and , i.e., that and .
Finally, we must check transitivity, that if is isomorphic to via some map and if is isomorphic to via some map then also is isomorphic to . Consider the composition . The appendix notes that the composition of two correspondences is a correspondence, so we need only check that the composition preserves linear combinations.
Thus is an isomorphism.
As a consequence of that result, we know that the universe of vector spaces is partitioned into classes: every space is in one and only one isomorphism class.
|
|
- Theorem 2.2
Vector spaces are isomorphic if and only if they have the same dimension.
This follows from the next two lemmas.
- Lemma 2.3
If spaces are isomorphic then they have the same dimension.
- Proof
We shall show that an isomorphism of two spaces gives a correspondence between their bases. That is, where is an isomorphism and a basis for the domain is , then the image set is a basis for the codomain . (The other half of the correspondence— that for any basis of the inverse image is a basis for — follows on recalling that if is an isomorphism then is also an isomorphism, and applying the prior sentence to .)
To see that spans , fix any , note that is onto and so there is a with , and expand as a combination of basis vectors.
For linear independence of , if
then, since is one-to-one and so the only vector sent to is , we have that , implying that all of the 's are zero.
- Lemma 2.4
If spaces have the same dimension then they are isomorphic.
- Proof
To show that any two spaces of dimension are isomorphic, we can simply show that any one is isomorphic to . Then we will have shown that they are isomorphic to each other, by the transitivity of isomorphism (which was established in Theorem 2.1).
Let be -dimensional. Fix a basis for the domain . Consider the representation of the members of that domain with respect to the basis as a function from to
(it is well-defined[3] since every has one and only one such representation— see Remark 2.5 below).
This function is one-to-one because if
then
and so , ..., , and therefore the original arguments and are equal.
This function is onto; any -tall vector
is the image of some , namely .
Finally, this function preserves structure.
Thus the function is an isomorphism and thus any -dimensional space is isomorphic to the -dimensional space . Consequently, any two spaces with the same dimension are isomorphic.
- Remark 2.5
The parenthetical comment in that proof about the role played by the "one and only one representation" result requires some explanation. We need to show that (for a fixed ) each vector in the domain is associated by with one and only one vector in the codomain.
A contrasting example, where an association doesn't have this property, is illuminating. Consider this subset of , which is not a basis.
Call those four polynomials , ..., . If, mimicing above proof, we try to write the members of as , and associate with the four-tall vector with components , ..., then there is a problem. For, consider . The set spans the space , so there is at least one four-tall vector associated with . But is not linearly independent and so vectors do not have unique decompositions. In this case, both
and so there is more than one four-tall vector associated with .
That is, with input this association does not have a well-defined (i.e., single) output value.
Any map whose definition appears possibly ambiguous must be checked to see that it is well-defined. For in the above proof that check is Problem 11.
That ends the proof of Theorem 2.2. We say that the isomorphism classes are characterized by dimension because we can describe each class simply by giving the number that is the dimension of all of the spaces in that class.
This subsection's results give us a collection of representatives of the isomorphism classes.[4]
- Corollary 2.6
A finite-dimensional vector space is isomorphic to one and only one of the .
The proofs above pack many ideas into a small space. Through the rest of this chapter we'll consider these ideas again, and fill them out. For a taste of this, we will expand here on the proof of Lemma 2.4.
- Example 2.7
The space of matrices is isomorphic to . With this basis for the domain
the isomorphism given in the lemma, the representation map , simply carries the entries over.
One way to think of the map is: fix the basis for the domain and the basis for the codomain, and associate with , and with , etc. Then extend this association to all of the members of two spaces.
We say that the map has been extended linearly from the bases to the spaces.
We can do the same thing with different bases, for instance, taking this basis for the domain.
Associating corresponding members of and and extending linearly
gives rise to an isomorphism that is different than .
The prior map arose by changing the basis for the domain. We can also change the basis for the codomain. Starting with
associating with , etc., and then linearly extending that correspondence to all of the two spaces
gives still another isomorphism.
So there is a connection between the maps between spaces and bases for those spaces. Later sections will explore that connection.
We will close this section with a summary.
Recall that in the first chapter we defined two matrices as row equivalent if they can be derived from each other by elementary row operations (this was the meaning of same-ness that was of interest there). We showed that is an equivalence relation and so the collection of matrices is partitioned into classes, where all the matrices that are row equivalent fall together into a single class. Then, for insight into which matrices are in each class, we gave representatives for the classes, the reduced echelon form matrices.
In this section, except that the appropriate notion of same-ness here is vector space isomorphism, we have followed much the same outline. First we defined isomorphism, saw some examples, and established some properties. Then we showed that it is an equivalence relation, and now we have a set of class representatives, the real vector spaces , , etc.
|
|
As before, the list of representatives helps us to understand the partition. It is simply a classification of spaces by dimension.
In the second chapter, with the definition of vector spaces, we seemed to have opened up our studies to many examples of new structures besides the familiar 's. We now know that isn't the case. Any finite-dimensional vector space is actually "the same" as a real space. We are thus considering exactly the structures that we need to consider.
The rest of the chapter fills out the work in this section. In particular, in the next section we will consider maps that preserve structure, but are not necessarily correspondences.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Decide if the spaces are isomorphic.
- ,
- ,
- ,
- ,
- ,
- Answer
Each pair of spaces is isomorphic if and only if the two have the same dimension. We can, when there is an isomorphism, state a map, but it isn't strictly necessary.
- No, they have different dimensions.
- No, they have different dimensions.
- Yes, they have the same dimension.
One isomorphism is this.
- Yes, they have the same dimension. This is an isomorphism.
- Yes, both have dimension .
- This exercise is recommended for all readers.
- Problem 2
Consider the isomorphism where . Find the image of each of these elements of the domain.
- ;
- ;
- Answer
- This exercise is recommended for all readers.
- Problem 3
Show that if then .
- Answer
They have different dimensions.
- This exercise is recommended for all readers.
- Problem 4
Is ?
- Answer
Yes, both are -dimensional.
- This exercise is recommended for all readers.
- Problem 5
Are any two planes through the origin in isomorphic?
- Answer
Yes, any two (nondegenerate) planes are both two-dimensional vector spaces.
- Problem 6
Find a set of equivalence class representatives other than the set of 's.
- Answer
There are many answers, one is the set of (taking to be the trivial vector space).
- Problem 7
True or false: between any -dimensional space and there is exactly one isomorphism.
- Answer
False (except when ). For instance, if is an isomorphism then multiplying by any nonzero scalar, gives another, different, isomorphism. (Between trivial spaces the isomorphisms are unique; the only map possible is .)
- Problem 8
Can a vector space be isomorphic to one of its (proper) subspaces?
- Answer
No. A proper subspace has a strictly lower dimension than it's superspace; if is a proper subspace of then any linearly independent subset of must have fewer than members or else that set would be a basis for , and wouldn't be proper.
- This exercise is recommended for all readers.
- Problem 9
This subsection shows that for any isomorphism, the inverse map is also an isomorphism. This subsection also shows that for a fixed basis of an -dimensional vector space , the map is an isomorphism. Find the inverse of this map.
- Answer
Where , the inverse is this.
- This exercise is recommended for all readers.
- Problem 10
Prove these facts about matrices.
- The row space of a matrix is isomorphic to the column space of its transpose.
- The row space of a matrix is isomorphic to its column space.
- Answer
All three spaces have dimension equal to the rank of the matrix.
- Problem 11
Show that the function from Theorem 2.2 is well-defined.
- Answer
We must show that if then . So suppose that . Each vector in a vector space (here, the domain space) has a unique representation as a linear combination of basis vectors, so we can conclude that , ..., . Thus,
and so the function is well-defined.
- Problem 12
Is the proof of Theorem 2.2 valid when ?
- Answer
Yes, because a zero-dimensional space is a trivial space.
- Problem 13
For each, decide if it is a set of isomorphism class representatives.
- Answer
- No, this collection has no spaces of odd dimension.
- Yes, because .
- No, for instance, .
- Problem 14
Let be a correspondence between vector spaces and (that is, a map that is one-to-one and onto). Show that the spaces and are isomorphic via if and only if there are bases and such that corresponding vectors have the same coordinates: .
- Answer
One direction is easy: if the two are isomorphic via then for any basis , the set is also a basis (this is shown in Lemma 2.3). The check that corresponding vectors have the same coordinates: is routine.
For the other half, assume that there are bases such that corresponding vectors have the same coordinates with respect to those bases. Because is a correspondence, to show that it is an isomorphism, we need only show that it preserves structure. Because , the map preserves structure if and only if representations preserve addition: and scalar multiplication: The addition calculation is this: , and the scalar multiplication calculation is similar.
- Problem 15
Consider the isomorphism .
- Vectors in a real space are orthogonal if and only if their dot product is zero. Give a definition of orthogonality for polynomials.
- The derivative of a member of is in . Give a definition of the derivative of a vector in .
- Answer
- Pulling the definition back from to gives that is orthogonal to if and only if .
- A natural definition is this.
- This exercise is recommended for all readers.
- Problem 16
Does every correspondence between bases, when extended to the spaces, give an isomorphism?
- Answer
Yes.
Assume that is a vector space with basis and that is another vector space such that the map is a correspondence. Consider the extension of .
The map is an isomorphism.
First, is well-defined because every member of has one and only one representation as a linear combination of elements of .
Second, is one-to-one because every member of has only one representation as a linear combination of elements of . That map is onto because every member of has at least one representation as a linear combination of members of .
Finally, preservation of structure is routine to check. For instance, here is the preservation of addition calculation.
Preservation of scalar multiplication is similar.
- Problem 17
(Requires the subsection on Combining Subspaces, which is optional.) Suppose that and that is isomorphic to the space under the map . Show that .
- Answer
Because and is one-to-one we have that . To finish, count the dimensions: , as required.
- Problem 18
- Show that this is not a well-defined function from the rational numbers to the integers: with each fraction, associate the value of its numerator.
- Answer
Rational numbers have many representations, e.g., , and the numerators can vary among representations.
Footnotes
- ↑ More information on one-to-one and onto maps is in the appendix.
- ↑ More information on equivalence relations is in the appendix.
- ↑ More information on well-definedness is in the appendix.
- ↑ More information on equivalence class representatives is in the appendix.
Section II - Homomorphisms
The definition of isomorphism has two conditions. In this section we will consider the second one, that the map must preserve the algebraic structure of the space. We will focus on this condition by studying maps that are required only to preserve structure; that is, maps that are not required to be correspondences.
Experience shows that this kind of map is tremendously useful in the study of vector spaces. For one thing, as we shall see in the second subsection below, while isomorphisms describe how spaces are the same, these maps describe how spaces can be thought of as alike.
1 - Definition
- Definition 1.1
A function between vector spaces that preserves the operations of addition
if then
and scalar multiplication
if and then
is a homomorphism or linear map.
- Example 1.2
The projection map
is a homomorphism.
It preserves addition
and scalar multiplication.
This map is not an isomorphism since it is not one-to-one. For instance, both and in are mapped to the zero vector in .
- Example 1.3
Of course, the domain and codomain might be other than spaces of column vectors. Both of these are homomorphisms; the verifications are straightforward.
- given by
- given by
- Example 1.4
Between any two spaces there is a zero homomorphism, mapping every vector in the domain to the zero vector in the codomain.
- Example 1.5
These two suggest why we use the term "linear map".
- The map given by
- The first of these two maps is linear while the second is not.
What distinguishes the homomorphisms is that the coordinate functions are linear combinations of the arguments. See also Problem 7.
Obviously, any isomorphism is a homomorphism— an isomorphism is a homomorphism that is also a correspondence. So, one way to think of the "homomorphism" idea is that it is a generalization of "isomorphism", motivated by the observation that many of the properties of isomorphisms have only to do with the map's structure preservation property and not to do with it being a correspondence. As examples, these two results from the prior section do not use one-to-one-ness or onto-ness in their proof, and therefore apply to any homomorphism.
- Lemma 1.6
A homomorphism sends a zero vector to a zero vector.
- Lemma 1.7
Each of these is a necessary and sufficient condition for to be a homomorphism.
- for any and
- for any and
Part 1 is often used to check that a function is linear.
- Example 1.8
The map given by
satisfies 1 of the prior result
and so it is a homomorphism.
However, some of the results that we have seen for isomorphisms fail to hold for homomorphisms in general. Consider the theorem that an isomorphism between spaces gives a correspondence between their bases. Homomorphisms do not give any such correspondence; Example 1.2 shows that there is no such correspondence, and another example is the zero map between any two nontrivial spaces. Instead, for homomorphisms a weaker but still very useful result holds.
- Theorem 1.9
A homomorphism is determined by its action on a basis. That is, if is a basis of a vector space and are (perhaps not distinct) elements of a vector space then there exists a homomorphism from to sending to , ..., and to , and that homomorphism is unique.
- Proof
We will define the map by associating with , etc., and then extending linearly to all of the domain. That is, where , the map is given by . This is well-defined because, with respect to the basis, the representation of each domain vector is unique.
This map is a homomorphism since it preserves linear combinations; where and , we have this.
And, this map is unique since if is another homomorphism such that for each then and agree on all of the vectors in the domain.
Thus, and are the same map.
- Example 1.10
This result says that we can construct a homomorphism by fixing a basis for the domain and specifying where the map sends those basis vectors. For instance, if we specify a map that acts on the standard basis in this way
then the action of on any other member of the domain is also specified. For instance, the value of on this argument
is a direct consequence of the value of on the basis vectors.
Later in this chapter we shall develop a scheme, using matrices, that is convienent for computations like this one.
Just as the isomorphisms of a space with itself are useful and interesting, so too are the homomorphisms of a space with itself.
- Definition 1.11
A linear map from a space into itself is a linear transformation.
- Remark 1.12
In this book we use "linear transformation" only in the case where the codomain equals the domain, but it is widely used in other texts as a general synonym for "homomorphism".
- Example 1.13
The map on that projects all vectors down to the -axis
is a linear transformation.
- Example 1.14
The derivative map
is a linear transformation, as this result from calculus notes: .
- Example 1.15
- The matrix transpose map
is a linear transformation of . Note that this transformation is one-to-one and onto, and so in fact it is an automorphism.
We finish this subsection about maps by recalling that we can linearly combine maps. For instance, for these maps from to itself
the linear combination is also a map from to itself.
- Lemma 1.16
For vector spaces and , the set of linear functions from to is itself a vector space, a subspace of the space of all functions from to . It is denoted .
- Proof
This set is non-empty because it contains the zero homomorphism. So to show that it is a subspace we need only check that it is closed under linear combinations. Let be linear. Then their sum is linear
and any scalar multiple is also linear.
Hence is a subspace.
We started this section by isolating the structure preservation property of isomorphisms. That is, we defined homomorphisms as a generalization of isomorphisms. Some of the properties that we studied for isomorphisms carried over unchanged, while others were adapted to this more general setting.
It would be a mistake, though, to view this new notion of homomorphism as derived from, or somehow secondary to, that of isomorphism. In the rest of this chapter we shall work mostly with homomorphisms, partly because any statement made about homomorphisms is automatically true about isomorphisms, but more because, while the isomorphism concept is perhaps more natural, experience shows that the homomorphism concept is actually more fruitful and more central to further progress.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Decide if each is linear.
- Answer
- Yes. The verification is straightforward.
- Yes. The verification is easy.
- No. An example of an addition that is not respected is this.
- Yes. The verification is straightforward.
- This exercise is recommended for all readers.
- Problem 2
Decide if each map is linear.
- Answer
For each, we must either check that linear combinations are preserved, or give an example of a linear combination that is not.
- Yes. The check that it preserves combinations is routine.
- No. For instance, not preserved is multiplication by the scalar .
- Yes. This is the check that it preserves combinations of two members of the domain.
- No.
An example of a combination that is not preserved is this.
- This exercise is recommended for all readers.
- Problem 3
Show that these two maps are homomorphisms.
- given by maps to
- given by maps to
Are these maps inverse to each other?
- Answer
The check that each is a homomorphisms is routine. Here is the check for the differentiation map.
(An alternate proof is to simply note that this is a property of differentiation that is familar from calculus.)
These two maps are not inverses as this composition does not act as the identity map on this element of the domain.
- Problem 4
Is (perpendicular) projection from to the -plane a homomorphism? Projection to the -plane? To the -axis? The -axis? The -axis? Projection to the origin?
- Answer
Each of these projections is a homomorphism. Projection to the -plane and to the -plane are these maps.
Projection to the -axis, to the -axis, and to the -axis are these maps.
And projection to the origin is this map.
Verification that each is a homomorphism is straightforward. (The last one, of course, is the zero transformation on .)
- Problem 5
Show that, while the maps from Example 1.3 preserve linear operations, they are not isomorphisms.
- Answer
The first is not onto; for instance, there is no polynomial that is sent the constant polynomial . The second is not one-to-one; both of these members of the domain
are mapped to the same member of the codomain, .
- Problem 6
Is an identity map a linear transformation?
- Answer
Yes; in any space .
- This exercise is recommended for all readers.
- Problem 7
Stating that a function is "linear" is different than stating that its graph is a line.
- The function given by has a graph that is a line. Show that it is not a linear function.
- The function given by
- Answer
- This map does not preserve structure since , while .
- The check is routine.
- This exercise is recommended for all readers.
- Problem 8
Part of the definition of a linear function is that it respects addition. Does a linear function respect subtraction?
- Answer
Yes. Where is linear, .
- Problem 9
Assume that is a linear transformation of and that is a basis of . Prove each statement.
- If for each basis vector then is the zero map.
- If for each basis vector then is the identity map.
- If there is a scalar such that for each basis vector then for all vectors in .
- Answer
- Let be represented with respect to the basis as . Then .
- This argument is similar to the prior one. Let be represented with respect to the basis as . Then .
- As above, only .
- This exercise is recommended for all readers.
- Problem 10
Consider the vector space where vector addition and scalar multiplication are not the ones inherited from but rather are these: is the product of and , and is the -th power of . (This was shown to be a vector space in an earlier exercise.) Verify that the natural logarithm map is a homomorphism between these two spaces. Is it an isomorphism?
- Answer
That it is a homomorphism follows from the familiar rules that the logarithm of a product is the sum of the logarithms and that the logarithm of a power is the multiple of the logarithm . This map is an isomorphism because it has an inverse, namely, the exponential map, so it is a correspondence, and therefore it is an isomorphism.
- This exercise is recommended for all readers.
- Problem 11
Consider this transformation of .
Find the image under this map of this ellipse.
- Answer
Where and , the image set is
the unit circle in the -plane.
- This exercise is recommended for all readers.
- Problem 12
Imagine a rope wound around the earth's equator so that it fits snugly (suppose that the earth is a sphere). How much extra rope must be added to raise the circle to a constant six feet off the ground?
- Answer
The circumference function is linear. Thus we have . Observe that it takes the same amount of extra rope to raise the circle from tightly wound around a basketball to six feet above that basketball as it does to raise it from tightly wound around the earth to six feet above the earth.
- This exercise is recommended for all readers.
- Problem 13
Verify that this map
is linear. Generalize.
- Answer
Verifying that it is linear is routine.
The natural guess at a generalization is that for any fixed the map is linear. This statement is true. It follows from properties of the dot product we have seen earlier: and . (The natural guess at a generalization of this generalization, that the map from to whose action consists of taking the dot product of its argument with a fixed vector is linear, is also true.)
- Problem 14
Show that every homomorphism from to acts via multiplication by a scalar. Conclude that every nontrivial linear transformation of is an isomorphism. Is that true for transformations of ? ?
- Answer
Let be linear. A linear map is determined by its action on a basis, so fix the basis for . For any we have that and so acts on any argument by multiplying it by the constant . If is not zero then the map is a correspondence— its inverse is division by — so any nontrivial transformation of is an isomorphism.
This projection map is an example that shows that not every transformation of acts via multiplication by a constant when , including when .
- Problem 15
- Show that for any scalars this map is a homomorphism.
- Show that for each , the -th derivative operator is a linear transformation of . Conclude that for any scalars this map is a linear transformation of that space.
- Answer
- Where and are scalars, we have this.
- Each power of the derivative operator is linear because of these rules familiar from calculus.
- Problem 16
Lemma 1.16 shows that a sum of linear functions is linear and that a scalar multiple of a linear function is linear. Show also that a composition of linear functions is linear.
- Answer
(This argument has already appeared, as part of the proof that isomorphism is an equivalence.) Let and be linear. For any and scalars combinations are preserved.
- This exercise is recommended for all readers.
- Problem 17
Where is linear, suppose that , ..., for some vectors , ..., from .
- If the set of 's is independent, must the set of 's also be independent?
- If the set of 's is independent, must the set of 's also be independent?
- If the set of 's spans , must the set of 's span ?
- If the set of 's spans , must the set of 's span ?
- Answer
- Yes. The set of 's cannot be linearly independent if the set of 's is linearly dependent because any nontrivial relationship in the domain would give a nontrivial relationship in the range .
- Not necessarily. For instance, the transformation of given by
- Not necessarily. An example is the projection map
- Not necessarily. For instance, the injection map sends the standard basis for the domain to a set that does not span the codomain. (Remark. However, the set of 's does span the range. A proof is easy.)
- Problem 18
Generalize Example 1.15 by proving that the matrix transpose map is linear. What is the domain and codomain?
- Answer
Recall that the entry in row and column of the transpose of is the entry from row and column of . Now, the check is routine.
The domain is while the codomain is .
- Problem 19
- Where , the line segment connecting them is defined to be the set . Show that the image, under a homomorphism , of the segment between and is the segment between and .
- A subset of is convex if, for any two points in that set, the line segment joining them lies entirely in that set. (The inside of a sphere is convex while the skin of a sphere is not.) Prove that linear maps from to preserve the property of set convexity.
- Answer
- For any homomorphism we have
- We must show that if a subset of the domain is convex then its image, as a subset of the range, is also convex. Suppose that is convex and consider its image . To show is convex we must show that for any two of its members, and , the line segment connecting them
- This exercise is recommended for all readers.
- Problem 20
Let be a homomorphism.
- Show that the image under of a line in is a (possibly degenerate) line in .
- What happens to a -dimensional linear surface?
- Answer
- For , the line through with direction is the set . The image under of that line is the line through with direction . If is the zero vector then this line is degenerate.
- A -dimensional linear surface in maps to a (possibly degenerate) -dimensional linear surface in . The proof is just like that the one for the line.
- Problem 21
Prove that the restriction of a homomorphism to a subspace of its domain is another homomorphism.
- Answer
Suppose that is a homomorphism and suppose that is a subspace of . Consider the map defined by . (The only difference between and is the difference in domain.) Then this new map is linear: .
- Problem 22
Assume that is linear.
- Show that the rangespace of this map is a subspace of the codomain .
- Show that the nullspace of this map is a subspace of the domain .
- Show that if is a subspace of the domain then its image is a subspace of the codomain . This generalizes the first item.
- Generalize the second item.
- Answer
This will appear as a lemma in the next subsection.
- The range is nonempty because is nonempty. To finish we need to show that it is closed under combinations. A combination of range vectors has the form, where ,
- The nullspace is nonempty since it contains , as maps to . It is closed under linear combinations because, where are elements of the inverse image set , for
- This image of nonempty because is nonempty. For closure under combinations, where ,
- The natural generalization is that the inverse image of a subspace of is a subspace.
Suppose that is a subspace of . Note that so the set is not empty. To show that this set is closed under combinations, let be elements of such that , ..., and note that
- Problem 23
Consider the set of isomorphisms from a vector space to itself. Is this a subspace of the space of homomorphisms from the space to itself?
- Answer
No; the set of isomorphisms does not contain the zero map (unless the space is trivial).
- Problem 24
Does Theorem 1.9 need that is a basis? That is, can we still get a well-defined and unique homomorphism if we drop either the condition that the set of 's be linearly independent, or the condition that it span the domain?
- Answer
If doesn't span the space then the map needn't be unique. For instance, if we try to define a map from to itself by specifying only that is sent to itself, then there is more than one homomorphism possible; both the identity map and the projection map onto the first component fit this condition.
If we drop the condition that is linearly independent then we risk an inconsistent specification (i.e, there could be no such map). An example is if we consider , and try to define a map from to itself that sends to itself, and sends both and to . No homomorphism can satisfy these three conditions.
- Problem 25
Let be a vector space and assume that the maps are linear.
- Define a map whose component functions are the given linear ones.
- Does the converse hold— is any linear map from to made up of two linear component maps to ?
- Generalize.
- Answer
- Briefly, the check of linearity is this.
- Yes. Let and be the projections
- In general, a map from a vector space to an is linear if and only if each of the component functions is linear. The verification is as in the prior item.
2 - Rangespace and Nullspace
Isomorphisms and homomorphisms both preserve structure. The difference is that homomorphisms needn't be onto and needn't be one-to-one. This means that homomorphisms are a more general kind of map, subject to fewer restrictions than isomorphisms. We will examine what can happen with homomorphisms that is prevented by the extra restrictions satisfied by isomorphisms.
We first consider the effect of dropping the onto requirement, of not requiring as part of the definition that a homomorphism be onto its codomain. For instance, the injection map
is not an isomorphism because it is not onto. Of course, being a function, a homomorphism is onto some set, namely its range; the map is onto the -plane subset of .
- Lemma 2.1
Under a homomorphism, the image of any subspace of the domain is a subspace of the codomain. In particular, the image of the entire space, the range of the homomorphism, is a subspace of the codomain.
- Proof
Let be linear and let be a subspace of the domain . The image is a subset of the codomain . It is nonempty because is nonempty and thus to show that is a subspace of we need only show that it is closed under linear combinations of two vectors. If and are members of then is also a member of because it is the image of from .
- Definition 2.2
The rangespace of a homomorphism is
sometimes denoted . The dimension of the rangespace is the map's rank.
(We shall soon see the connection between the rank of a map and the rank of a matrix.)
- Example 2.3
Recall that the derivative map given by is linear. The rangespace is the set of quadratic polynomials . Thus, the rank of this map is three.
- Example 2.4
With this homomorphism
an image vector in the range can have any constant term, must have an coefficient of zero, and must have the same coefficient of as of . That is, the rangespace is and so the rank is two.
The prior result shows that, in passing from the definition of isomorphism to the more general definition of homomorphism, omitting the "onto" requirement doesn't make an essential difference. Any homomorphism is onto its rangespace.
However, omitting the "one-to-one" condition does make a difference. A homomorphism may have many elements of the domain that map to one element of the codomain. Below is a "bean " sketch of a many-to-one map between sets.[1] It shows three elements of the codomain that are each the image of many members of the domain.

Recall that for any function , the set of elements of that are mapped to is the inverse image . Above, the three sets of many elements on the left are inverse images.
- Example 2.5
Consider the projection
which is a homomorphism that is many-to-one. In this instance, an inverse image set is a vertical line of vectors in the domain.

- Example 2.6
This homomorphism
is also many-to-one; for a fixed , the inverse image

is the set of plane vectors whose components add to .
The above examples have only to do with the fact that we are considering functions, specifically, many-to-one functions. They show the inverse images as sets of vectors that are related to the image vector . But these are more than just arbitrary functions, they are homomorphisms; what do the two preservation conditions say about the relationships?
In generalizing from isomorphisms to homomorphisms by dropping the one-to-one condition, we lose the property that we've stated intuitively as: the domain is "the same as" the range. That is, we lose that the domain corresponds perfectly to the range in a one-vector-by-one-vector way.
What we shall keep, as the examples below illustrate, is that a homomorphism describes a way in which the domain is "like", or "analogous to", the range.
- Example 2.7
We think of as being like , except that vectors have an extra component. That is, we think of the vector with components , , and as like the vector with components and . In defining the projection map , we make precise which members of the domain we are thinking of as related to which members of the codomain.
Understanding in what way the preservation conditions in the definition of homomorphism show that the domain elements are like the codomain elements is easiest if we draw as the -plane inside of . (Of course, is a set of two-tall vectors while the -plane is a set of three-tall vectors with a third component of zero, but there is an obvious correspondence.) Then, is the "shadow" of in the plane and the preservation of addition property says that

| 
| 
| ||
| above | plus | above | equals | above |
Briefly, the shadow of a sum equals the sum of the shadows . (Preservation of scalar multiplication has a similar interpretation.)
Redrawing by separating the two spaces, moving the codomain to the right, gives an uglier picture but one that is more faithful to the "bean" sketch.

Again in this drawing, the vectors that map to lie in the domain in a vertical line (only one such vector is shown, in gray). Call any such member of this inverse image a " vector". Similarly, there is a vertical line of " vectors" and a vertical line of " vectors". Now, has the property that if and then . This says that the vector classes add, in the sense that any vector plus any vector equals a vector, (A similar statement holds about the classes under scalar multiplication.)
Thus, although the two spaces and are not isomorphic, describes a way in which they are alike: vectors in add as do the associated vectors in — vectors add as their shadows add.
- Example 2.8
A homomorphism can be used to express an analogy between spaces that is more subtle than the prior one. For the map
from Example 2.6 fix two numbers in the range . A that maps to has components that add to , that is, the inverse image is the set of vectors with endpoint on the diagonal line . Call these the " vectors". Similarly, we have the " vectors" and the " vectors". Then the addition preservation property says that

| 
| 
| ||
| a " vector" | plus | a " vector" | equals | a " vector". |
Restated, if a vector is added to a vector then the result is mapped by to a vector. Briefly, the image of a sum is the sum of the images. Even more briefly, . (The preservation of scalar multiplication condition has a similar restatement.)
- Example 2.9
The inverse images can be structures other than lines. For the linear map
the inverse image sets are planes , , etc., perpendicular to the -axis.

We won't describe how every homomorphism that we will use is an analogy because the formal sense that we make of "alike in that ..." is "a homomorphism exists such that ...". Nonetheless, the idea that a homomorphism between two spaces expresses how the domain's vectors fall into classes that act like the range's vectors is a good way to view homomorphisms.
Another reason that we won't treat all of the homomorphisms that we see as above is that many vector spaces are hard to draw (e.g., a space of polynomials). However, there is nothing bad about gaining insights from those spaces that we are able to draw, especially when those insights extend to all vector spaces. We derive two such insights from the three examples 2.7 , 2.8, and 2.9.
First, in all three examples, the inverse images are lines or planes, that is, linear surfaces. In particular, the inverse image of the range's zero vector is a line or plane through the origin— a subspace of the domain.
- Lemma 2.10
For any homomorphism, the inverse image of a subspace of the range is a subspace of the domain. In particular, the inverse image of the trivial subspace of the range is a subspace of the domain.
- Proof
Let be a homomorphism and let be a subspace of the rangespace . Consider , the inverse image of the set . It is nonempty because it contains , since , which is an element , as is a subspace. To show that is closed under linear combinations, let and be elements, so that and are elements of , and then is also in the inverse image because is a member of the subspace .
- Definition 2.11
The nullspace or kernel of a linear map is the inverse image of
The dimension of the nullspace is the map's nullity.

- Example 2.12
The map from Example 2.3 has this nullspace .
Now for the second insight from the above pictures. In Example 2.7, each of the vertical lines is squashed down to a single point— , in passing from the domain to the range, takes all of these one-dimensional vertical lines and "zeroes them out", leaving the range one dimension smaller than the domain. Similarly, in Example 2.8, the two-dimensional domain is mapped to a one-dimensional range by breaking the domain into lines (here, they are diagonal lines), and compressing each of those lines to a single member of the range. Finally, in Example 2.9, the domain breaks into planes which get "zeroed out", and so the map starts with a three-dimensional domain but ends with a one-dimensional range— this map "subtracts" two from the dimension. (Notice that, in this third example, the codomain is two-dimensional but the range of the map is only one-dimensional, and it is the dimension of the range that is of interest.)
- Theorem 2.14
A linear map's rank plus its nullity equals the dimension of its domain.
- Proof
Let be linear and let be a basis for the nullspace. Extend that to a basis for the entire domain. We shall show that is a basis for the rangespace. Then counting the size of these bases gives the result.
To see that is linearly independent, consider the equation . This gives that and so is in the nullspace of . As is a basis for this nullspace, there are scalars satisfying this relationship.
But is a basis for so each scalar equals zero. Therefore is linearly independent.
To show that spans the rangespace, consider and write as a linear combination of members of . This gives and since , ..., are in the nullspace, we have that . Thus, is a linear combination of members of , and so spans the space.
- Example 2.15
Where is
the rangespace and nullspace are
and so the rank of is two while the nullity is one.
- Example 2.16
If is the linear transformation then the range is , and so the rank of is one and the nullity is zero.
- Corollary 2.17
The rank of a linear map is less than or equal to the dimension of the domain. Equality holds if and only if the nullity of the map is zero.
We know that an isomorphism exists between two spaces if and only if their dimensions are equal. Here we see that for a homomorphism to exist, the dimension of the range must be less than or equal to the dimension of the domain. For instance, there is no homomorphism from onto . There are many homomorphisms from into , but none is onto all of three-space.
The rangespace of a linear map can be of dimension strictly less than the dimension of the domain (Example 2.3's derivative transformation on has a domain of dimension four but a range of dimension three). Thus, under a homomorphism, linearly independent sets in the domain may map to linearly dependent sets in the range (for instance, the derivative sends to ). That is, under a homomorphism, independence may be lost. In contrast, dependence stays.
- Lemma 2.18
Under a linear map, the image of a linearly dependent set is linearly dependent.
- Proof
Suppose that , with some nonzero. Then, because and because , we have that with some nonzero .
When is independence not lost? One obvious sufficient condition is when the homomorphism is an isomorphism. This condition is also necessary; see Problem 14. We will finish this subsection comparing homomorphisms with isomorphisms by observing that a one-to-one homomorphism is an isomorphism from its domain onto its range.
- Definition 2.19
A linear map that is one-to-one is nonsingular.
(In the next section we will see the connection between this use of "nonsingular" for maps and its familiar use for matrices.)
- Example 2.20
This nonsingular homomorphism
gives the obvious correspondence between and the -plane inside of .
The prior observation allows us to adapt some results about isomorphisms to this setting.
- Theorem 2.21
In an -dimensional vector space , these:
- is nonsingular, that is, one-to-one
- has a linear inverse
- , that is,
- if is a basis for then is a basis for
are equivalent statements about a linear map .
- Proof
We will first show that . We will then show that .
For , suppose that the linear map is one-to-one, and so has an inverse. The domain of that inverse is the range of and so a linear combination of two members of that domain has the form . On that combination, the inverse gives this.
Thus the inverse of a one-to-one linear map is automatically linear. But this also gives the implication, because the inverse itself must be one-to-one.
Of the remaining implications, holds because any homomorphism maps to , but a one-to-one map sends at most one member of to .
Next, is true since rank plus nullity equals the dimension of the domain.
For , to show that is a basis for the rangespace we need only show that it is a spanning set, because by assumption the range has dimension . Consider . Expressing as a linear combination of basis elements produces , which gives that , as desired.
Finally, for the implication, assume that is a basis for so that is a basis for . Then every a the unique representation . Define a map from to by
(uniqueness of the representation makes this well-defined). Checking that it is linear and that it is the inverse of are easy.
We've now seen that a linear map shows how the structure of the domain is like that of the range. Such a map can be thought to organize the domain space into inverse images of points in the range. In the special case that the map is one-to-one, each inverse image is a single point and the map is an isomorphism between the domain and the range.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Let be given by . Which of these are in the nullspace? Which are in the rangespace?
- This exercise is recommended for all readers.
- Problem 2
Find the nullspace, nullity, rangespace, and rank of each map.
- given by
- given by
- given by
- the zero map
- This exercise is recommended for all readers.
- Problem 3
Find the nullity of each map.
- of rank five
- of rank one
- , an onto map
- , onto
- This exercise is recommended for all readers.
- Problem 4
What is the nullspace of the differentiation transformation ? What is the nullspace of the second derivative, as a transformation of ? The -th derivative?
- Problem 5
Example 2.7 restates the first condition in the definition of homomorphism as "the shadow of a sum is the sum of the shadows". Restate the second condition in the same style.
- Problem 6
For the homomorphism given by find these.
- This exercise is recommended for all readers.
- Problem 7
For the map given by
sketch these inverse image sets: , , and .
- This exercise is recommended for all readers.
- Problem 8
Each of these transformations of is nonsingular. Find the inverse function of each.
- Problem 9
Describe the nullspace and rangespace of a transformation given by .
- Problem 10
List all pairs that are possible for linear maps from to .
- Problem 11
Does the differentiation map have an inverse?
- This exercise is recommended for all readers.
- Problem 12
Find the nullity of the map given by
- Problem 13
- Prove that a homomorphism is onto if and only if its rank equals the dimension of its codomain.
- Conclude that a homomorphism between vector spaces with the same dimension is one-to-one if and only if it is onto.
- Problem 14
Show that a linear map is nonsingular if and only if it preserves linear independence.
- Problem 15
Corollary 2.17 says that for there to be an onto homomorphism from a vector space to a vector space , it is necessary that the dimension of be less than or equal to the dimension of . Prove that this condition is also sufficient; use Theorem 1.9 to show that if the dimension of is less than or equal to the dimension of , then there is a homomorphism from to that is onto.
- Problem 16
Let be a homomorphism, but not the zero homomorphism. Prove that if is a basis for the nullspace and if is not in the nullspace then is a basis for the entire domain .
- This exercise is recommended for all readers.
- Problem 17
Recall that the nullspace is a subset of the domain and the rangespace is a subset of the codomain. Are they necessarily distinct? Is there a homomorphism that has a nontrivial intersection of its nullspace and its rangespace?
- Problem 18
Prove that the image of a span equals the span of the images. That is, where is linear, prove that if is a subset of then equals . This generalizes Lemma 2.1 since it shows that if is any subspace of then its image is a subspace of , because the span of the set is .
- This exercise is recommended for all readers.
- Problem 19
- Prove that for any linear map and any , the set has the form
- Consider the map given by
- Conclude from the prior two items that for any linear system of the form
- Show that this map is linear
- Show that the -th derivative map is a linear transformation of
for each . Prove that this map is a linear transformation of that space
- Problem 20
Prove that for any transformation that is rank one, the map given by composing the operator with itself satisfies for some real number .
- Problem 21
Show that for any space of dimension , the dual space
is isomorphic to . It is often denoted . Conclude that .
- Problem 22
Show that any linear map is the sum of maps of rank one.
- Problem 23
Is "is homomorphic to" an equivalence relation? (Hint: the difficulty is to decide on an appropriate meaning for the quoted phrase.)
- Problem 24
Show that the rangespaces and nullspaces of powers of linear maps form descending
and ascending
chains. Also show that if is such that then all following rangespaces are equal: . Similarly, if then .
Footnotes
- ↑ More information on many-to-one maps is in the appendix.
Section III - Computing Linear Maps
The prior section shows that a linear map is determined by its action on a basis. In fact, the equation
shows that, if we know the value of the map on the vectors in a basis, then we can compute the value of the map on any vector at all. We just need to find the 's to express with respect to the basis.
This section gives the scheme that computes, from the representation of a vector in the domain , the representation of that vector's image in the codomain , using the representations of , ..., .
1 - Representing Linear Maps with Matrices
- Example 1.1
Consider a map with domain and codomain (fixing
as the bases for these spaces) that is determined by this action on the vectors in the domain's basis.
To compute the action of this map on any vector at all from the domain, we first express and with respect to the codomain's basis:
and
(these are easy to check). Then, as described in the preamble, for any member of the domain, we can express the image in terms of the 's.
Thus,
with then .
For instance,
with then .
We will express computations like the one above with a matrix notation.
In the middle is the argument to the map, represented with respect to the domain's basis by a column vector with components and . On the right is the value of the map on that argument, represented with respect to the codomain's basis by a column vector with components , etc. The matrix on the left is the new thing. It consists of the coefficients from the vector on the right, and from the first row, and from the second row, and and from the third row.
This notation simply breaks the parts from the right, the coefficients and the 's, out separately on the left, into a vector that represents the map's argument and a matrix that we will take to represent the map itself.
- Definition 1.2
Suppose that and are vector spaces of dimensions and with bases and , and that is a linear map. If
then
is the matrix representation of with respect to .
Briefly, the vectors representing the 's are adjoined to make the matrix representing the map.
Observe that the number of columns of the matrix is the dimension of the domain of the map, and the number of rows is the dimension of the codomain.
- Example 1.3
If is given by
then where
the action of on is given by
and a simple calculation gives
showing that this is the matrix representing with respect to the bases.
We will use lower case letters for a map, upper case for the matrix, and lower case again for the entries of the matrix. Thus for the map , the matrix representing it is , with entries .
- Theorem 1.4
Assume that and are vector spaces of dimensions and with bases and , and that is a linear map. If is represented by
and is represented by
then the representation of the image of is this.
- Proof
We will think of the matrix and the vector as combining to make the vector .
- Definition 1.5
The matrix-vector product of a matrix and a vector is this.
The point of Definition 1.2 is to generalize Example 1.1, that is, the point of the definition is Theorem 1.4, that the matrix describes how to get from the representation of a domain vector with respect to the domain's basis to the representation of its image in the codomain with respect to the codomain's basis. With Definition 1.5, we can restate this as: application of a linear map is represented by the matrix-vector product of the map's representative and the vector's representative.
- Example 1.6
With the matrix from Example 1.3 we can calculate where that map sends this vector.
This vector is represented, with respect to the domain basis , by
and so this is the representation of the value with respect to the codomain basis .
To find itself, not its representation, take .
- Example 1.7
Let be projection onto the -plane. To give a matrix representing this map, we first fix bases.
For each vector in the domain's basis, we find its image under the map.
Then we find the representation of each image with respect to the codomain's basis
(these are easily checked). Finally, adjoining these representations gives the matrix representing with respect to .
We can illustrate Theorem 1.4 by computing the matrix-vector product representing the following statement about the projection map.
Representing this vector from the domain with respect to the domain's basis
gives this matrix-vector product.
Expanding this representation into a linear combination of vectors from
checks that the map's action is indeed reflected in the operation of the matrix. (We will sometimes compress these three displayed equations into one
in the course of a calculation.)
We now have two ways to compute the effect of projection, the straightforward formula that drops each three-tall vector's third component to make a two-tall vector, and the above formula that uses representations and matrix-vector multiplication. Compared to the first way, the second way might seem complicated. However, it has advantages. The next example shows that giving a formula for some maps is simplified by this new scheme.
- Example 1.8
To represent a rotation map that turns all vectors in the plane counterclockwise through an angle
we start by fixing bases. Using both as a domain basis and as a codomain basis is natural, Now, we find the image under the map of each vector in the domain's basis.
Then we represent these images with respect to the codomain's basis. Because this basis is , vectors are represented by themselves. Finally, adjoining the representations gives the matrix representing the map.
The advantage of this scheme is that just by knowing how to represent the image of the two basis vectors, we get a formula that tells us the image of any vector at all; here a vector rotated by .
(Again, we are using the fact that, with respect to , vectors represent themselves.)
We have already seen the addition and scalar multiplication operations of matrices and the dot product operation of vectors. Matrix-vector multiplication is a new operation in the arithmetic of vectors and matrices. Nothing in Definition 1.5 requires us to view it in terms of representations. We can get some insight into this operation by turning away from what is being represented, and instead focusing on how the entries combine.
- Example 1.9
In the definition the width of the matrix equals the height of the vector. Hence, the first product below is defined while the second is not.
One reason that this product is not defined is purely formal: the definition requires that the sizes match, and these sizes don't match. Behind the formality, though, is a reason why we will leave it undefined— the matrix represents a map with a three-dimensional domain while the vector represents a member of a two-dimensional space.
A good way to view a matrix-vector product is as the dot products of the rows of the matrix with the column vector.
Looked at in this row-by-row way, this new operation generalizes dot product.
Matrix-vector product can also be viewed column-by-column.
- Example 1.10
The result has the columns of the matrix weighted by the entries of the vector. This way of looking at it brings us back to the objective stated at the start of this section, to compute as .
We began this section by noting that the equality of these two enables us to compute the action of on any argument knowing only , ..., . We have developed this into a scheme to compute the action of the map by taking the matrix-vector product of the matrix representing the map and the vector representing the argument. In this way, any linear map is represented with respect to some bases by a matrix. In the next subsection, we will show the converse, that any matrix represents a linear map.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Multiply the matrix
by each vector (or state "not defined").
- Problem 2
Perform, if possible, each matrix-vector multiplication.
- This exercise is recommended for all readers.
- Problem 3
Solve this matrix equation.
- This exercise is recommended for all readers.
- Problem 4
For a homomorphism from to that sends
where does go?
- This exercise is recommended for all readers.
- Problem 5
Assume that is determined by this action.
Using the standard bases, find
- the matrix representing this map;
- a general formula for .
- This exercise is recommended for all readers.
- Problem 6
Let be the derivative transformation.
- Represent with respect to where .
- Represent with respect to where .
- This exercise is recommended for all readers.
- Problem 7
Represent each linear map with respect to each pair of bases.
- with respect to
where , given by
-
with respect to
where , given by
- with respect to
where
and , given by
- with respect to
where
and , given by
-
with respect
to where , given by
- Problem 8
Represent the identity map on any nontrivial space with respect to , where is any basis.
- Problem 9
Represent, with respect to the natural basis, the transpose transformation on the space of matrices.
- Problem 10
Assume that is a basis for a vector space. Represent with respect to the transformation that is determined by each.
- , , ,
- , , ,
- , , ,
- Problem 11
Example 1.8 shows how to represent the rotation transformation of the plane with respect to the standard basis. Express these other transformations also with respect to the standard basis.
- the dilation map , which multiplies all vectors by the same scalar
- the reflection map , which reflects all all vectors across a line through the origin
- This exercise is recommended for all readers.
- Problem 12
Consider a linear transformation of determined by these two.
- Represent this transformation with respect to the standard bases.
- Where does the transformation send this vector?
- Represent this transformation with respect to these bases.
- Using from the prior item, represent the transformation with respect to .
- Problem 13
Suppose that is nonsingular so that by Theorem II.2.21, for any basis the image is a basis for .
- Represent the map with respect to .
- For a member of the domain, where the representation of has components , ..., , represent the image vector with respect to the image basis .
- Problem 14
Give a formula for the product of a matrix and , the column vector that is all zeroes except for a single one in the -th position.
- This exercise is recommended for all readers.
- Problem 15
For each vector space of functions of one real variable, represent the derivative transformation with respect to .
- ,
- ,
- ,
- Problem 16
Find the range of the linear transformation of represented with respect to the standard bases by each matrix.
- a matrix of the form
- This exercise is recommended for all readers.
- Problem 17
Can one matrix represent two different linear maps? That is, can ?
- Problem 18
Prove Theorem 1.4.
- This exercise is recommended for all readers.
- Problem 19
Example 1.8 shows how to represent rotation of all vectors in the plane through an angle about the origin, with respect to the standard bases.
- Rotation of all vectors in three-space through an angle about the -axis is a transformation of . Represent it with respect to the standard bases. Arrange the rotation so that to someone whose feet are at the origin and whose head is at , the movement appears clockwise.
- Repeat the prior item, only rotate about the -axis instead. (Put the person's head at .)
- Repeat, about the -axis.
- Extend the prior item to . (Hint: "rotate about the -axis" can be restated as "rotate parallel to the -plane".)
- Problem 20 (Schur's Triangularization Lemma)
- Let be a subspace of and fix bases . What is the relationship between the representation of a vector from with respect to and the representation of that vector (viewed as a member of ) with respect to ?
- What about maps?
- Fix a basis
for and observe that the spans
- Conclude that for every linear map there are bases so the matrix representing with respect to is upper-triangular (that is, each entry with is zero).
- Is an upper-triangular representation unique?
2 - Any Matrix Represents a Linear Map
The prior subsection shows that the action of a linear map is described by a matrix , with respect to appropriate bases, in this way.
In this subsection, we will show the converse, that each matrix represents a linear map.
Recall that, in the definition of the matrix representation of a linear map, the number of columns of the matrix is the dimension of the map's domain and the number of rows of the matrix is the dimension of the map's codomain. Thus, for instance, a matrix cannot represent a map from to . The next result says that, beyond this restriction on the dimensions, there are no other limitations: the matrix represents a map from any three-dimensional space to any two-dimensional space.
- Theorem 2.1
Any matrix represents a homomorphism between vector spaces of appropriate dimensions, with respect to any pair of bases.
- Proof
For the matrix
fix any -dimensional domain space and any -dimensional codomain space . Also fix bases and for those spaces. Define a function by: where in the domain is represented as
then its image is the member the codomain represented by
that is, is defined to be . (This is well-defined by the uniqueness of the representation .)
Observe that has simply been defined to make it the map that is represented with respect to by the matrix . So to finish, we need only check that is linear. If are such that
and then the calculation
provides this verification.
- Example 2.2
Which map the matrix represents depends on which bases are used. If
then represented by with respect to maps
while represented by with respect to is this map.
These two are different. The first is projection onto the axis, while the second is projection onto the axis.
So not only is any linear map described by a matrix but any matrix describes a linear map. This means that we can, when convenient, handle linear maps entirely as matrices, simply doing the computations, without have to worry that a matrix of interest does not represent a linear map on some pair of spaces of interest. (In practice, when we are working with a matrix but no spaces or bases have been specified, we will often take the domain and codomain to be and and use the standard bases. In this case, because the representation is transparent— the representation with respect to the standard basis of is — the column space of the matrix equals the range of the map. Consequently, the column space of is often denoted by .)
With the theorem, we have characterized linear maps as those maps that act in this matrix way. Each linear map is described by a matrix and each matrix describes a linear map. We finish this section by illustrating how a matrix can be used to tell things about its maps.
- Theorem 2.3
The rank of a matrix equals the rank of any map that it represents.
- Proof
Suppose that the matrix is . Fix domain and codomain spaces and of dimension and , with bases and . Then represents some linear map between those spaces with respect to these bases whose rangespace
is the span . The rank of is the dimension of this rangespace.
The rank of the matrix is its column rank (or its row rank; the two are equal). This is the dimension of the column space of the matrix, which is the span of the set of column vectors .
To see that the two spans have the same dimension, recall that a representation with respect to a basis gives an isomorphism . Under this isomorphism, there is a linear relationship among members of the rangespace if and only if the same relationship holds in the column space, e.g, if and only if . Hence, a subset of the rangespace is linearly independent if and only if the corresponding subset of the column space is linearly independent. This means that the size of the largest linearly independent subset of the rangespace equals the size of the largest linearly independent subset of the column space, and so the two spaces have the same dimension.
- Example 2.4
Any map represented by
must, by definition, be from a three-dimensional domain to a four-dimensional codomain. In addition, because the rank of this matrix is two (we can spot this by eye or get it with Gauss' method), any map represented by this matrix has a two-dimensional rangespace.
- Corollary 2.5
Let be a linear map represented by a matrix . Then is onto if and only if the rank of equals the number of its rows, and is one-to-one if and only if the rank of equals the number of its columns.
- Proof
For the first half, the dimension of the rangespace of is the rank of , which equals the rank of by the theorem. Since the dimension of the codomain of is the number of rows in , if the rank of equals the number of rows, then the dimension of the rangespace equals the dimension of the codomain. But a subspace with the same dimension as its superspace must equal that superspace (a basis for the rangespace is a linearly independent subset of the codomain, whose size is equal to the dimension of the codomain, and so this set is a basis for the codomain).
For the second half, a linear map is one-to-one if and only if it is an isomorphism between its domain and its range, that is, if and only if its domain has the same dimension as its range. But the number of columns in is the dimension of 's domain, and by the theorem the rank of equals the dimension of 's range.
The above results end any confusion caused by our use of the word "rank" to mean apparently different things when applied to matrices and when applied to maps. We can also justify the dual use of "nonsingular". We've defined a matrix to be nonsingular if it is square and is the matrix of coefficients of a linear system with a unique solution, and we've defined a linear map to be nonsingular if it is one-to-one.
- Corollary 2.6
A square matrix represents nonsingular maps if and only if it is a nonsingular matrix. Thus, a matrix represents an isomorphism if and only if it is square and nonsingular.
- Proof
Immediate from the prior result.
- Example 2.7
Any map from to represented with respect to any pair of bases by
is nonsingular because this matrix has rank two.
- Example 2.8
Any map represented by
is not nonsingular because this matrix is not nonsingular.
We've now seen that the relationship between maps and matrices goes both ways: fixing bases, any linear map is represented by a matrix and any matrix describes a linear map. That is, by fixing spaces and bases we get a correspondence between maps and matrices. In the rest of this chapter we will explore this correspondence. For instance, we've defined for linear maps the operations of addition and scalar multiplication and we shall see what the corresponding matrix operations are. We shall also see the matrix operation that represent the map operation of composition. And, we shall see how to find the matrix that represents a map's inverse.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Decide if the vector is in the column space of the matrix.
- ,
- ,
- ,
- This exercise is recommended for all readers.
- Problem 2
Decide if each vector lies in the range of the map from to represented with respect to the standard bases by the matrix.
- ,
- ,
- This exercise is recommended for all readers.
- Problem 3
Consider this matrix, representing a transformation of , and these bases for that space.
- To what vector in the codomain is the first member of mapped?
- The second member?
- Where is a general vector from the domain (a vector with components and ) mapped? That is, what transformation of is represented with respect to by this matrix?
- Problem 4
What transformation of is represented with respect to and by this matrix?
- This exercise is recommended for all readers.
- Problem 5
Decide if is in the range of the map from to represented with respect to and by this matrix.
- Problem 6
Example 2.8 gives a matrix that is nonsingular, and is therefore associated with maps that are nonsingular.
- Find the set of column vectors representing the members of the nullspace of any map represented by this matrix.
- Find the nullity of any such map.
- Find the set of column vectors representing the members of the rangespace of any map represented by this matrix.
- Find the rank of any such map.
- Check that rank plus nullity equals the dimension of the domain.
- This exercise is recommended for all readers.
- Problem 7
Because the rank of a matrix equals the rank of any map it represents, if one matrix represents two different maps (where ) then the dimension of the rangespace of equals the dimension of the rangespace of . Must these equal-dimensioned rangespaces actually be the same?
- This exercise is recommended for all readers.
- Problem 8
Let be an -dimensional space with bases and . Consider a map that sends, for , the column vector representing with respect to to the column vector representing with respect to . Show that is a linear transformation of .
- Problem 9
Example 2.2 shows that changing the pair of bases can change the map that a matrix represents, even though the domain and codomain remain the same. Could the map ever not change? Is there a matrix , vector spaces and , and associated pairs of bases and (with or or both) such that the map represented by with respect to equals the map represented by with respect to ?
- This exercise is recommended for all readers.
- Problem 10
A square matrix is a diagonal matrix if it is all zeroes except possibly for the entries on its upper-left to lower-right diagonal— its entry, its entry, etc. Show that a linear map is an isomorphism if there are bases such that, with respect to those bases, the map is represented by a diagonal matrix with no zeroes on the diagonal.
- Problem 11
Describe geometrically the action on of the map represented with respect to the standard bases by this matrix.
Do the same for these.
- Problem 12
The fact that for any linear map the rank plus the nullity equals the dimension of the domain shows that a necessary condition for the existence of a homomorphism between two spaces, onto the second space, is that there be no gain in dimension. That is, where is onto, the dimension of must be less than or equal to the dimension of .
- Show that this (strong) converse holds: no gain in dimension implies that there is a homomorphism and, further, any matrix with the correct size and correct rank represents such a map.
- Are there bases for such that
this matrix
- Problem 13
Let be an -dimensional space and suppose that . Fix a basis for and consider the map given by the dot product.
- Show that this map is linear.
- Show that for any linear map there is an such that .
- In the prior item we fixed the basis and varied the to get all possible linear maps. Can we get all possible linear maps by fixing an and varying the basis?
- Problem 14
Let be vector spaces with bases .
- Suppose that is represented with respect to by the matrix . Give the matrix representing the scalar multiple (where ) with respect to by expressing it in terms of .
- Suppose that are represented with respect to by and . Give the matrix representing with respect to by expressing it in terms of and .
- Suppose that is represented with respect to by and is represented with respect to by . Give the matrix representing with respect to by expressing it in terms of and .
Section IV - Matrix Operations
The prior section shows how matrices represent linear maps. A good strategy, on seeing a new idea, is to explore how it interacts with some already-established ideas. In the first subsection we will ask how the representation of the sum of two maps is related to the representations of the two maps, and how the representation of a scalar product of a map is related to the representation of that map. In later subsections we will see how to represent map composition and map inverse.
1 - Sums and Scalar Products
Recall that for two maps and with the same domain and codomain, the map sum has this definition.
The easiest way to see how the representations of the maps combine to represent the map sum is with an example.
- Example 1.1
Suppose that are represented with respect to the bases and by these matrices.
Then, for any represented with respect to , computation of the representation of
gives this representation of .
Thus, the action of is described by this matrix-vector product.
This matrix is the entry-by-entry sum of original matrices, e.g., the entry of is the sum of the entry of and the entry of .
Representing a scalar multiple of a map works the same way.
- Example 1.2
If is a transformation represented by
then the scalar multiple map acts in this way.
Therefore, this is the matrix representing .
- Definition 1.3
The sum of two same-sized matrices is their entry-by-entry sum. The scalar multiple of a matrix is the result of entry-by-entry scalar multiplication.
- Remark 1.4
These extend the vector addition and scalar multiplication operations that we defined in the first chapter.
- Theorem 1.5
Let be linear maps represented with respect to bases by the matrices and , and let be a scalar. Then the map is represented with respect to by , and the map is represented with respect to by .
- Proof
Problem 2; generalize the examples above.
A notable special case of scalar multiplication is multiplication by zero. For any map is the zero homomorphism and for any matrix is the zero matrix.
- Example 1.6
The zero map from any three-dimensional space to any two-dimensional space is represented by the zero matrix
no matter which domain and codomain bases are used.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Perform the indicated operations, if defined.
- Problem 2
Prove Theorem 1.5.
- Prove that matrix addition represents addition of linear maps.
- Prove that matrix scalar multiplication represents scalar multiplication of linear maps.
- This exercise is recommended for all readers.
- Problem 3
Prove each, where the operations are defined, where , , and are matrices, where is the zero matrix, and where and are scalars.
- Matrix addition is commutative .
- Matrix addition is associative .
- The zero matrix is an additive identity .
- Matrices have an additive inverse .
- Problem 4
Fix domain and codomain spaces. In general, one matrix can represent many different maps with respect to different bases. However, prove that a zero matrix represents only a zero map. Are there other such matrices?
- This exercise is recommended for all readers.
- Problem 5
Let and be vector spaces of dimensions and . Show that the space of linear maps from to is isomorphic to .
- This exercise is recommended for all readers.
- Problem 6
Show that it follows from the prior questions that for any six transformations there are scalars such that is the zero map. (Hint: this is a bit of a misleading question.)
- Problem 7
The trace of a square matrix is the sum of the entries on the main diagonal (the entry plus the entry, etc.; we will see the significance of the trace in Chapter Five). Show that . Is there a similar result for scalar multiplication?
- Problem 8
Recall that the transpose of a matrix is another matrix, whose entry is the entry of . Verifiy these identities.
- This exercise is recommended for all readers.
- Problem 9
A square matrix is symmetric if each entry equals the entry, that is, if the matrix equals its transpose.
- Prove that for any , the matrix is symmetric. Does every symmetric matrix have this form?
- Prove that the set of symmetric matrices is a subspace of .
- This exercise is recommended for all readers.
- Problem 10
- How does matrix rank interact with scalar multiplication— can a scalar product of a rank matrix have rank less than ? Greater?
- How does matrix rank interact with matrix addition— can a sum of rank matrices have rank less than ? Greater?
2 - Matrix Multiplication
After representing addition and scalar multiplication of linear maps in the prior subsection, the natural next map operation to consider is composition.
- Lemma 2.1
A composition of linear maps is linear.
- Proof
(This argument has appeared earlier, as part of the proof that isomorphism is an equivalence relation between spaces.) Let and be linear. The calculation
shows that preserves linear combinations.
To see how the representation of the composite arises out of the representations of the two compositors, consider an example.
- Example 2.2
Let and , fix bases , , , and let these be the representations.
To represent the composition we fix a , represent of , and then represent of that. The representation of is the product of 's matrix and 's vector.
The representation of is the product of 's matrix and 's vector.
Distributing and regrouping on the 's gives
which we recognizing as the result of this matrix-vector product.
Thus, the matrix representing has the rows of combined with the columns of .
- Definition 2.3
The matrix-multiplicative product of the matrix and the matrix is the matrix , where
that is, the -th entry of the product is the dot product of the -th row and the -th column.
- Example 2.5
- Theorem 2.6
A composition of linear maps is represented by the matrix product of the representatives.
- Proof
(This argument parallels Example 2.2.) Let and be represented by and with respect to bases , , and , of sizes , , and . For any , the -th component of is
and so the -th component of is this.
Distribute and regroup on the 's.
Finish by recognizing that the coefficient of each
matches the definition of the entry of the product .
The theorem is an example of a result that supports a definition. We can picture what the definition and theorem together say with this arrow diagram ("wrt" abbreviates "with respect to").
Above the arrows, the maps show that the two ways of going from to , straight over via the composition or else by way of , have the same effect
(this is just the definition of composition). Below the arrows, the matrices indicate that the product does the same thing— multiplying into the column vector has the same effect as multiplying the column first by and then multiplying the result by .
The definition of the matrix-matrix product operation does not restrict us to view it as a representation of a linear map composition. We can get insight into this operation by studying it as a mechanical procedure. The striking thing is the way that rows and columns combine.
One aspect of that combination is that the sizes of the matrices involved is significant. Briefly, .
- Example 2.7
This product is not defined
because the number of columns on the left does not equal the number of rows on the right.
In terms of the underlying maps, the fact that the sizes must match up reflects the fact that matrix multiplication is defined only when a corresponding function composition
is possible.
- Remark 2.8
The order in which these things are written can be confusing. In the "" equation, the number written first is the dimension of 's codomain and is thus the number that appears last in the map dimension description above. The explanation is that while is done first and then is applied, that composition is written , from the notation "". (Some people try to lessen confusion by reading "" aloud as " following ".) That order then carries over to matrices: is represented by .
Another aspect of the way that rows and columns combine in the matrix product operation is that in the definition of the entry
the red subscripts on the 's are column indicators while those on the 's indicate rows. That is, summation takes place over the columns of but over the rows of ; left is treated differently than right, so may be unequal to . Matrix multiplication is not commutative.
- Example 2.9
Matrix multiplication hardly ever commutes. Test that by multiplying randomly chosen matrices both ways.
- Example 2.10
Commutativity can fail more dramatically:
while
isn't even defined.
- Remark 2.11
The fact that matrix multiplication is not commutative may be puzzling at first sight, perhaps just because most algebraic operations in elementary mathematics are commutative. But on further reflection, it isn't so surprising. After all, matrix multiplication represents function composition, which is not commutative— if and then while . True, this is not linear and we might have hoped that linear functions commute, but this perspective shows that the failure of commutativity for matrix multiplication fits into a larger context.
Except for the lack of commutativity, matrix multiplication is algebraically well-behaved. Below are some nice properties and more are in Problem 10 and Problem 11.
- Theorem 2.12
If , , and are matrices, and the matrix products are defined, then the product is associative and distributes over matrix addition and .
- Proof
Associativity holds because matrix multiplication represents function composition, which is associative: the maps and are equal as both send to .
Distributivity is similar. For instance, the first one goes (the third equality uses the linearity of ).
- Remark 2.13
We could alternatively prove that result by slogging through the indices. For example, associativity goes: the -th entry of is
(where , , and are , , and matrices), distribute
and regroup around the 's
to get the entry of .
Contrast these two ways of verifying associativity, the one in the proof and the one just above. The argument just above is hard to understand in the sense that, while the calculations are easy to check, the arithmetic seems unconnected to any idea (it also essentially repeats the proof of Theorem 2.6 and so is inefficient). The argument in the proof is shorter, clearer, and says why this property "really" holds. This illustrates the comments made in the preamble to the chapter on vector spaces— at least some of the time an argument from higher-level constructs is clearer.
We have now seen how the representation of the composition of two linear maps is derived from the representations of the two maps. We have called the combination the product of the two matrices. This operation is extremely important. Before we go on to study how to represent the inverse of a linear map, we will explore it some more in the next subsection.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Compute, or state "not defined".
- This exercise is recommended for all readers.
- Problem 2
Where
compute or state "not defined".
- Problem 3
Which products are defined?
- times
- times
- times
- times
- This exercise is recommended for all readers.
- Problem 4
Give the size of the product or state "not defined".
- a matrix times a matrix
- a matrix times a matrix
- a matrix times a matrix
- a matrix times a matrix
- This exercise is recommended for all readers.
- Problem 5
Find the system of equations resulting from starting with
and making this change of variable (i.e., substitution).
- Problem 6
As Definition 2.3 points out, the matrix product operation generalizes the dot product. Is the dot product of a row vector and a column vector the same as their matrix-multiplicative product?
- This exercise is recommended for all readers.
- Problem 7
Represent the derivative map on with respect to where is the natural basis . Show that the product of this matrix with itself is defined; what the map does it represent?
- Problem 8
Show that composition of linear transformations on is commutative. Is this true for any one-dimensional space?
- Problem 9
Why is matrix multiplication not defined as entry-wise multiplication? That would be easier, and commutative too.
- This exercise is recommended for all readers.
- Problem 10
- Prove that and for positive integers .
- Prove that for any positive integer and scalar .
- This exercise is recommended for all readers.
- Problem 11
- How does matrix multiplication interact with scalar multiplication: is ? Is ?
- How does matrix multiplication interact with linear combinations: is ? Is ?
- Problem 12
We can ask how the matrix product operation interacts with the transpose operation.
- Show that .
- A square matrix is symmetric if each entry equals the entry, that is, if the matrix equals its own transpose. Show that the matrices and are symmetric.
- This exercise is recommended for all readers.
- Problem 13
Rotation of vectors in about an axis is a linear map. Show that linear maps do not commute by showing geometrically that rotations do not commute.
- Problem 14
In the proof of Theorem 2.12 some maps are used. What are the domains and codomains?
- Problem 15
How does matrix rank interact with matrix multiplication?
- Can the product of rank matrices have rank less than ? Greater?
- Show that the rank of the product of two matrices is less than or equal to the minimum of the rank of each factor.
- Problem 16
Is "commutes with" an equivalence relation among matrices?
- This exercise is recommended for all readers.
- Problem 17
(This will be used in the Matrix Inverses exercises.) Here is another property of matrix multiplication that might be puzzling at first sight.
- Prove that the composition of the projections onto the and axes is the zero map despite that neither one is itself the zero map.
- Prove that the composition of the derivatives is the zero map despite that neither is the zero map.
- Give a matrix equation representing the first fact.
- Give a matrix equation representing the second.
When two things multiply to give zero despite that neither is zero, each is said to be a zero divisor.
- Problem 18
Show that, for square matrices, need not equal .
- This exercise is recommended for all readers.
- Problem 19
Represent the identity transformation with respect to for any basis . This is the identity matrix . Show that this matrix plays the role in matrix multiplication that the number plays in real number multiplication: (for all matrices for which the product is defined).
- Problem 20
In real number algebra, quadratic equations have at most two solutions. That is not so with matrix algebra. Show that the matrix equation has more than two solutions, where is the identity matrix (this matrix has ones in its and entries and zeroes elsewhere; see Problem 19).
- Problem 21
- Prove that for any matrix there are scalars that are not all such that the combination is the zero matrix (where is the identity matrix, with 's in its and entries and zeroes elsewhere; see Problem 19).
- Let be a polynomial . If is a square matrix we define to be the matrix (where is the appropriately-sized identity matrix). Prove that for any square matrix there is a polynomial such that is the zero matrix.
- The minimal polynomial
of a square matrix is the
polynomial of least degree, and with leading coefficient ,
such that is the zero matrix.
Find the minimal polynomial of this matrix.
- Problem 22
The infinite-dimensional space of all finite-degree polynomials gives a memorable example of the non-commutativity of linear maps. Let be the usual derivative and let be the shift map.
Show that the two maps don't commute ; in fact, not only is not the zero map, it is the identity map.
- Problem 23
Recall the notation for the sum of the sequence of numbers .
In this notation, the entry of the product of and is this.
Using this notation,
- reprove that matrix multiplication is associative;
- reprove Theorem 2.6.
3 - Mechanics of Matrix Multiplication
In this subsection we consider matrix multiplication as a mechanical process, putting aside for the moment any implications about the underlying maps. As described earlier, the striking thing about matrix multiplication is the way rows and columns combine. The entry of the matrix product is the dot product of row of the left matrix with column of the right one. For instance, here a second row and a third column combine to make a entry.
We can view this as the left matrix acting by multiplying its rows, one at a time, into the columns of the right matrix. Of course, another perspective is that the right matrix uses its columns to act on the left matrix's rows. Below, we will examine actions from the left and from the right for some simple matrices.
The first case, the action of a zero matrix, is very easy.
- Example 3.1
Multiplying by an appropriately-sized zero matrix from the left or from the right
results in a zero matrix.
After zero matrices, the matrices whose actions are easiest to understand are the ones with a single nonzero entry.
- Definition 3.2
A matrix with all zeroes except for a one in the entry is an unit matrix.
- Example 3.3
This is the unit matrix with three rows and two columns, multiplying from the left.
Acting from the left, an unit matrix copies row of the multiplicand into row of the result. From the right an unit matrix copies column of the multiplicand into column of the result.
- Example 3.4
Rescaling these matrices simply rescales the result. This is the action from the left of the matrix that is twice the one in the prior example.
And this is the action of the matrix that is minus three times the one from the prior example.
Next in complication are matrices with two nonzero entries. There are two cases. If a left-multiplier has entries in different rows then their actions don't interact.
- Example 3.5
But if the left-multiplier's nonzero entries are in the same row then that row of the result is a combination.
- Example 3.6
Right-multiplication acts in the same way, with columns.
These observations about matrices that are mostly zeroes extend to arbitrary matrices.
- Lemma 3.7
In a product of two matrices and , the columns of are formed by taking times the columns of
and the rows of are formed by taking the rows of times
(ignoring the extra parentheses).
- Proof
We will show the case and leave the general case as an exercise.
The right side of the first equation in the result
is indeed the same as the right side of GH, except for the extra parentheses (the ones marking the columns as column vectors). The other equation is similarly easy to recognize.
An application of those observations is that there is a matrix that just copies out the rows and columns.
- Definition 3.8
The main diagonal (or principal diagonal or diagonal) of a square matrix goes from the upper left to the lower right.
- Definition 3.9
An identity matrix is square and has with all entries zero except for ones in the main diagonal.
- Example 3.10
The identity leaves its multiplicand unchanged both from the left
and from the right.
- Example 3.11
So does the identity matrix.
In short, an identity matrix is the identity element of the set of matrices with respect to the operation of matrix multiplication.
We next see two ways to generalize the identity matrix.
The first is that if the ones are relaxed to arbitrary reals, the resulting matrix will rescale whole rows or columns.
- Definition 3.12
A diagonal matrix is square and has zeros off the main diagonal.
- Example 3.13
From the left, the action of multiplication by a diagonal matrix is to rescales the rows.
From the right such a matrix rescales the columns.
The second generalization of identity matrices is that we can put a single one in each row and column in ways other than putting them down the diagonal.
- Definition 3.14
A permutation matrix is square and is all zeros except for a single one in each row and column.
- Example 3.15
From the left these matrices permute rows.
From the right they permute columns.
We finish this subsection by applying these observations to get matrices that perform Gauss' method and Gauss-Jordan reduction.
- Example 3.16
We have seen how to produce a matrix that will rescale rows. Multiplying by this diagonal matrix rescales the second row of the other by a factor of three.
We have seen how to produce a matrix that will swap rows. Multiplying by this permutation matrix swaps the first and third rows.
To see how to perform a pivot, we observe something about those two examples. The matrix that rescales the second row by a factor of three arises in this way from the identity.
Similarly, the matrix that swaps first and third rows arises in this way.
- Example 3.17
The matrix that arises as
will, when it acts from the left, perform the pivot operation .
- Definition 3.18
The elementary reduction matrices are obtained from identity matrices with one Gaussian operation. We denote them:
- for ;
- for ;
- for .
- Lemma 3.19
Gaussian reduction can be done through matrix multiplication.
- If then .
- If then .
- If then .
- Proof
Clear.
- Example 3.20
This is the first system, from the first chapter, on which we performed Gauss' method.
It can be reduced with matrix multiplication. Swap the first and third rows,
triple the first row,
and then add times the first row to the second.
Now back substitution will give the solution.
- Example 3.21
Gauss-Jordan reduction works the same way. For the matrix ending the prior example, first adjust the leading entries
and to finish, clear the third column and then the second column.
We have observed the following result, which we shall use in the next subsection.
- Corollary 3.22
For any matrix there are elementary reduction matrices , ..., such that is in reduced echelon form.
Until now we have taken the point of view that our primary objects of study are vector spaces and the maps between them, and have adopted matrices only for computational convenience. This subsection show that this point of view isn't the whole story. Matrix theory is a fascinating and fruitful area.
In the rest of this book we shall continue to focus on maps as the primary objects, but we will be pragmatic— if the matrix point of view gives some clearer idea then we shall use it.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Predict the result of each multiplication by an elementary reduction matrix, and then check by multiplying it out.
- This exercise is recommended for all readers.
- Problem 2
The need to take linear combinations of rows and columns in tables of numbers arises often in practice. For instance, this is a map of part of Vermont and New York.
- The incidence matrix of a map is the square matrix whose entry is the number of roads from city to city . Produce the incidence matrix of this map (take the cities in alphabetical order).
- A matrix is symmetric if it equals its transpose. Show that an incidence matrix is symmetric. (These are all two-way streets. Vermont doesn't have many one-way streets.)
- What is the significance of the square of the incidence matrix? The cube?
- This exercise is recommended for all readers.
- Problem 3
This table gives the number of hours of each type done by each worker, and the associated pay rates. Use matrices to compute the wages due.
|
|
(Remark. This illustrates, as did the prior problem, that in practice we often want to compute linear combinations of rows and columns in a context where we really aren't interested in any associated linear maps.)
- Problem 4
Find the product of this matrix with its transpose.
- This exercise is recommended for all readers.
- Problem 5
Prove that the diagonal matrices form a subspace of . What is its dimension?
- Problem 6
Does the identity matrix represent the identity map if the bases are unequal?
- Problem 7
Show that every multiple of the identity commutes with every square matrix. Are there other matrices that commute with all square matrices?
- Problem 8
Prove or disprove: nonsingular matrices commute.
- This exercise is recommended for all readers.
- Problem 9
Show that the product of a permutation matrix and its transpose is an identity matrix.
- Problem 10
Show that if the first and second rows of are equal then so are the first and second rows of . Generalize.
- Problem 11
Describe the product of two diagonal matrices.
- Problem 12
Write
as the product of two elementary reduction matrices.
- This exercise is recommended for all readers.
- Problem 13
Show that if has a row of zeros then (if defined) has a row of zeros. Does that work for columns?
- Problem 14
Show that the set of unit matrices forms a basis for .
- Problem 15
Find the formula for the -th power of this matrix.
- This exercise is recommended for all readers.
- Problem 16
The trace of a square matrix is the sum of the entries on its diagonal (its significance appears in Chapter Five). Show that .
- This exercise is recommended for all readers.
- Problem 17
A square matrix is upper triangular if its only nonzero entries lie above, or on, the diagonal. Show that the product of two upper triangular matrices is upper triangular. Does this hold for lower triangular also?
- Problem 18
A square matrix is a Markov matrix if each entry is between zero and one and the sum along each row is one. Prove that a product of Markov matrices is Markov.
- This exercise is recommended for all readers.
- Problem 19
Give an example of two matrices of the same rank with squares of differing rank.
- Problem 20
Combine the two generalizations of the identity matrix, the one allowing entires to be other than ones, and the one allowing the single one in each row and column to be off the diagonal. What is the action of this type of matrix?
- Problem 21
On a computer multiplications are more costly than additions, so people are interested in reducing the number of multiplications used to compute a matrix product.
- How many real number multiplications are needed in formula we gave for the product of a matrix and a matrix?
- Matrix multiplication is associative, so all associations yield the same result. The cost in number of multiplications, however, varies. Find the association requiring the fewest real number multiplications to compute the matrix product of a matrix, a matrix, a matrix, and a matrix.
- (Very hard.) Find a way to multiply two matrices using only seven multiplications instead of the eight suggested by the naive approach.
- ? Problem 22
If and are square matrices of the same size such that , does it follow that ? (Putnam Exam 1990)
- Problem 23
Demonstrate these four assertions to get an alternate proof that column rank equals row rank. (Liebeck 1966)
- iff .
- iff .
- .
- .
- Problem 24
Prove (where is an matrix and so defines a transformation of any -dimensional space with respect to where is a basis) that . Conclude
- iff ;
- iff ;
- iff and ;
- iff ;
- (Requires the Direct Sum subsection, which is optional.) iff .
4 - Inverses
We now consider how to represent the inverse of a linear map.
We start by recalling some facts about function inverses.[1] Some functions have no inverse, or have an inverse on the left side or right side only.
- Example 4.1
Where is the projection map
and is the embedding
the composition is the identity map on .
We say is a left inverse map of or, what is the same thing, that is a right inverse map of . However, composition in the other order doesn't give the identity map— here is a vector that is not sent to itself under .
In fact, the projection has no left inverse at all. For, if were to be a left inverse of then we would have
for all of the infinitely many 's. But no function can send a single argument to more than one value.
(An example of a function with no inverse on either side is the zero transformation on .) Some functions have a two-sided inverse map, another function that is the inverse of the first, both from the left and from the right. For instance, the map given by has the two-sided inverse . In this subsection we will focus on two-sided inverses. The appendix shows that a function has a two-sided inverse if and only if it is both one-to-one and onto. The appendix also shows that if a function has a two-sided inverse then it is unique, and so it is called "the" inverse, and is denoted . So our purpose in this subsection is, where a linear map has an inverse, to find the relationship between and (recall that we have shown, in Theorem II.2.21 of Section II of this chapter, that if a linear map has an inverse then the inverse is a linear map also).
- Definition 4.2
A matrix is a left inverse matrix of the matrix if is the identity matrix. It is a right inverse matrix if is the identity. A matrix with a two-sided inverse is an invertible matrix. That two-sided inverse is called the inverse matrix and is denoted .
Because of the correspondence between linear maps and matrices, statements about map inverses translate into statements about matrix inverses.
- Lemma 4.3
If a matrix has both a left inverse and a right inverse then the two are equal.
- Theorem 4.4
A matrix is invertible if and only if it is nonsingular.
- Proof
(For both results.) Given a matrix , fix spaces of appropriate dimension for the domain and codomain. Fix bases for these spaces. With respect to these bases, represents a map . The statements are true about the map and therefore they are true about the matrix.
- Lemma 4.5
A product of invertible matrices is invertible— if and are invertible and if is defined then is invertible and .
- Proof
(This is just like the prior proof except that it requires two maps.) Fix appropriate spaces and bases and consider the represented maps and . Note that is a two-sided map inverse of since and . This equality is reflected in the matrices representing the maps, as required.
Here is the arrow diagram giving the relationship between map inverses and matrix inverses. It is a special case of the diagram for function composition and matrix multiplication.
Beyond its place in our general program of seeing how to represent map operations, another reason for our interest in inverses comes from solving linear systems. A linear system is equivalent to a matrix equation, as here.
By fixing spaces and bases (e.g., and ), we take the matrix to represent some map . Then solving the system is the same as asking: what domain vector is mapped by to the result ? If we could invert then we could solve the system by multiplying to get .
- Example 4.6
We can find a left inverse for the matrix just given
by using Gauss' method to solve the resulting linear system.
Answer: , , , and . This matrix is actually the two-sided inverse of , as can easily be checked. With it we can solve the system () above by applying the inverse.
- Remark 4.7
Why solve systems this way, when Gauss' method takes less arithmetic (this assertion can be made precise by counting the number of arithmetic operations, as computer algorithm designers do)? Beyond its conceptual appeal of fitting into our program of discovering how to represent the various map operations, solving linear systems by using the matrix inverse has at least two advantages.
First, once the work of finding an inverse has been done, solving a system with the same coefficients but different constants is easy and fast: if we change the entries on the right of the system () then we get a related problem
with a related solution method.
In applications, solving many systems having the same matrix of coefficients is common.
Another advantage of inverses is that we can explore a system's sensitivity to changes in the constants. For example, tweaking the on the right of the system () to
can be solved with the inverse.
to show that changes by of the tweak while moves by of that tweak. This sort of analysis is used, for example, to decide how accurately data must be specified in a linear model to ensure that the solution has a desired accuracy.
We finish by describing the computational procedure usually used to find the inverse matrix.
- Lemma 4.8
A matrix is invertible if and only if it can be written as the product of elementary reduction matrices. The inverse can be computed by applying to the identity matrix the same row steps, in the same order, as are used to Gauss-Jordan reduce the invertible matrix.
- Proof
A matrix is invertible if and only if it is nonsingular and thus Gauss-Jordan reduces to the identity. By Corollary 3.22 this reduction can be done with elementary matrices . This equation gives the two halves of the result.
First, elementary matrices are invertible and their inverses are also elementary. Applying to the left of both sides of that equation, then , etc., gives as the product of elementary matrices (the is here to cover the trivial case).
Second, matrix inverses are unique and so comparison of the above equation with shows that . Therefore, applying to the identity, followed by , etc., yields the inverse of .
- Example 4.9
To find the inverse of
we do Gauss-Jordan reduction, meanwhile performing the same operations on the identity. For clerical convenience we write the matrix and the identity side-by-side, and do the reduction steps together.
This calculation has found the inverse.
- Example 4.10
This one happens to start with a row swap.
- Example 4.11
A non-invertible matrix is detected by the fact that the left half won't reduce to the identity.
This procedure will find the inverse of a general matrix. The case is handy.
- Corollary 4.12
The inverse for a matrix exists and equals
if and only if .
- Proof
This computation is Problem 10.
We have seen here, as in the Mechanics of Matrix Multiplication subsection, that we can exploit the correspondence between linear maps and matrices. So we can fruitfully study both maps and matrices, translating back and forth to whichever helps us the most.
Over the entire four subsections of this section we have developed an algebra system for matrices. We can compare it with the familiar algebra system for the real numbers. Here we are working not with numbers but with matrices. We have matrix addition and subtraction operations, and they work in much the same way as the real number operations, except that they only combine same-sized matrices. We also have a matrix multiplication operation and an operation inverse to multiplication. These are somewhat like the familiar real number operations (associativity, and distributivity over addition, for example), but there are differences (failure of commutativity, for example). And, we have scalar multiplication, which is in some ways another extension of real number multiplication. This matrix system provides an example that algebra systems other than the elementary one can be interesting and useful.
Exercises
- Problem 1
Supply the intermediate steps in Example 4.10.
- This exercise is recommended for all readers.
- This exercise is recommended for all readers.
- Problem 3
For each invertible matrix in the prior problem, use Corollary 4.12 to find its inverse.
- This exercise is recommended for all readers.
- Problem 4
Find the inverse, if it exists, by using the Gauss-Jordan method. Check the answers for the matrices with Corollary 4.12.
- This exercise is recommended for all readers.
- Problem 5
What matrix has this one for its inverse?
- Problem 6
How does the inverse operation interact with scalar multiplication and addition of matrices?
- What is the inverse of ?
- Is ?
- This exercise is recommended for all readers.
- Problem 7
Is ?
- Problem 8
Is invertible?
- Problem 9
For each real number let be represented with respect to the standard bases by this matrix.
Show that . Show also that .
- Problem 10
Do the calculations for the proof of Corollary 4.12.
- Problem 11
Show that this matrix
has infinitely many right inverses. Show also that it has no left inverse.
- Problem 12
In Example 4.1, how many left inverses has ?
- Problem 13
If a matrix has infinitely many right-inverses, can it have infinitely many left-inverses? Must it have?
- This exercise is recommended for all readers.
- Problem 14
Assume that is invertible and that is the zero matrix. Show that is a zero matrix.
- Problem 15
Prove that if is invertible then the inverse commutes with a matrix if and only if itself commutes with that matrix .
- This exercise is recommended for all readers.
- Problem 16
Show that if is square and if is the zero matrix then . Generalize.
- This exercise is recommended for all readers.
- Problem 17
Let be diagonal. Describe , , ... , etc. Describe , , ... , etc. Define appropriately.
- Problem 18
Prove that any matrix row-equivalent to an invertible matrix is also invertible.
- Problem 19
The first question below appeared as Problem 15 in the Matrix Multiplication subsection.
- Show that the rank of the product of two matrices is less than or equal to the minimum of the rank of each.
- Show that if and are square then if and only if .
- Problem 20
Show that the inverse of a permutation matrix is its transpose.
- Problem 21
The first two parts of this question appeared as Problem 12. of the Matrix Multiplication subsection
- Show that .
- A square matrix is symmetric if each entry equals the entry (that is, if the matrix equals its transpose). Show that the matrices and are symmetric.
- Show that the inverse of the transpose is the transpose of the inverse.
- Show that the inverse of a symmetric matrix is symmetric.
- This exercise is recommended for all readers.
- Problem 22
The items starting this question appeared as Problem 17 of the Matrix Multiplication subsection.
- Prove that the composition of the projections is the zero map despite that neither is the zero map.
- Prove that the composition of the derivatives is the zero map despite that neither map is the zero map.
- Give matrix equations representing each of the prior two items.
When two things multiply to give zero despite that neither is zero, each is said to be a zero divisor. Prove that no zero divisor is invertible.
- Problem 23
In real number algebra, there are exactly two numbers, and , that are their own multiplicative inverse. Does have exactly two solutions for matrices?
- Problem 24
Is the relation "is a two-sided inverse of" transitive? Reflexive? Symmetric?
- Problem 25
Prove: if the sum of the elements in each row of a square matrix is , then the sum of the elements in each row of the inverse matrix is . (Wilansky 1951)
Footnotes
- ↑ More information on function inverses is in the appendix.
Section V - Change of Basis
Representations, whether of vectors or of maps, vary with the bases. For instance, with respect to the two bases and
for , the vector has two different representations.
Similarly, with respect to and , the identity map has two different representations.
With our point of view that the objects of our studies are vectors and maps, in fixing bases we are adopting a scheme of tags or names for these objects, that are convienent for computation. We will now see how to translate among these names— we will see exactly how representations vary as the bases vary.
1 - Changing Representations of Vectors
In converting to the underlying vector doesn't change. Thus, this translation is accomplished by the identity map on the space, described so that the domain space vectors are represented with respect to and the codomain space vectors are represented with respect to .
(The diagram is vertical to fit with the ones in the next subsection.)
- Definition 1.1
The change of basis matrixfor bases is the representation of the identity map with respect to those bases.
- Lemma 1.2
Left-multiplication by the change of basis matrix for converts a representation with respect to to one with respect to . Conversly, if left-multiplication by a matrix changes bases then is a change of basis matrix.
- Proof
For the first sentence, for each , as matrix-vector multiplication represents a map application, . For the second sentence, with respect to the matrix represents some linear map, whose action is , and is therefore the identity map.
- Example 1.3
With these bases for ,
because
the change of basis matrix is this.
We can see this matrix at work by finding the two representations of
and checking that the conversion goes as expected.
We finish this subsection by recognizing that the change of basis matrices are familiar.
- Lemma 1.4
A matrix changes bases if and only if it is nonsingular.
- Proof
For one direction, if left-multiplication by a matrix changes bases then the matrix represents an invertible function, simply because the function is inverted by changing the bases back. Such a matrix is itself invertible, and so nonsingular.
To finish, we will show that any nonsingular matrix performs a change of basis operation from any given starting basis to some ending basis. Because the matrix is nonsingular, it will Gauss-Jordan reduce to the identity, so there are elementatry reduction matrices such that . Elementary matrices are invertible and their inverses are also elementary, so multiplying from the left first by , then by , etc., gives as a product of elementary matrices . Thus, we will be done if we show that elementary matrices change a given basis to another basis, for then changes to some other basis , and changes to some , ..., and the net effect is that changes to . We will prove this about elementary matrices by covering the three types as separate cases.
Applying a row-multiplication matrix
changes a representation with respect to to one with respect to in this way.
Similarly, left-multiplication by a row-swap matrix changes a representation with respect to the basis into one with respect to the basis in this way.
And, a representation with respect to changes via left-multiplication by a row-combination matrix into a representation with respect to
(the definition of reduction matrices specifies that and and so this last one is a basis).
- Corollary 1.5
A matrix is nonsingular if and only if it represents the identity map with respect to some pair of bases.
In the next subsection we will see how to translate among representations of maps, that is, how to change to . The above corollary is a special case of this, where the domain and range are the same space, and where the map is the identity map.
Exercises
- This exercise is recommended for all readers.
- Problem 1
In , where
find the change of basis matrices from to and from to . Multiply the two.
- This exercise is recommended for all readers.
- Problem 2
Find the change of basis matrix for .
- ,
- ,
- ,
- ,
- Problem 3
For the bases in Problem 2, find the change of basis matrix in the other direction, from to .
- This exercise is recommended for all readers.
- Problem 4
Find the change of basis matrix for each .
- This exercise is recommended for all readers.
- Problem 5
Decide if each changes bases on . To what basis is changed?
- Problem 6
Find bases such that this matrix represents the identity map with respect to those bases.
- Problem 7
Conside the vector space of real-valued functions with basis . Show that is also a basis for this space. Find the change of basis matrix in each direction.
- Problem 8
Where does this matrix
send the standard basis for ? Any other bases? Hint. Consider the inverse.
- This exercise is recommended for all readers.
- Problem 9
What is the change of basis matrix with respect to ?
- Problem 10
Prove that a matrix changes bases if and only if it is invertible.
- Problem 11
Finish the proof of Lemma 1.4.
- This exercise is recommended for all readers.
- Problem 12
Let be a nonsingular matrix. What basis of does change to the standard basis?
- This exercise is recommended for all readers.
- Problem 13
- In with basis
we have this
represenatation.
- State and prove that any nonzero vector representation can be changed to any other.
Hint. The proof of Lemma 1.4 is constructive— it not only says the bases change, it shows how they change.
- Problem 14
Let be vector spaces, and let be bases for and be bases for . Where is linear, find a formula relating to .
- This exercise is recommended for all readers.
- Problem 15
Show that the columns of an change of basis matrix form a basis for . Do all bases appear in that way: can the vectors from any basis make the columns of a change of basis matrix?
- This exercise is recommended for all readers.
- Problem 16
Find a matrix having this effect.
That is, find a that left-multiplies the starting vector to yield the ending vector. Is there a matrix having these two effects?
Give a necessary and sufficient condition for there to be a matrix such that and .
2 - Changing Map Representations
The first subsection shows how to convert the representation of a vector with respect to one basis to the representation of that same vector with respect to another basis. Here we will see how to convert the representation of a map with respect to one pair of bases to the representation of that map with respect to a different pair. That is, we want the relationship between the matrices in this arrow diagram.
To move from the lower-left of this diagram to the lower-right we can either go straight over, or else up to then over to and then down. Restated in terms of the matrices, we can calculate either by simply using and , or else by first changing bases with then multiplying by and then changing bases with . This equation summarizes.
(To compare this equation with the sentence before it, remember that the equation is read from right to left because function composition is read right to left and matrix multiplication represent the composition.)
- Example 2.1
The matrix
represents, with respect to , the transformation that rotates vectors radians counterclockwise.
We can translate that representation with respect to to one with respect to
by using the arrow diagram and formula () above.
From this, we can use the formula:
Note that can be calculated as
the matrix inverse of .
Although the new matrix is messier-appearing, the map that it represents is the same. For instance, to replicate the effect of in the picture, start with ,
apply ,
and check it against
to see that it is the same result as above.
- Example 2.2
On the map
that is represented with respect to the standard basis in this way
can also be represented with respect to another basis
if then
in a way that is simpler, in that the action of a diagonal matrix is easy to understand.
Naturally, we usually prefer basis changes that make the representation easier to understand. When the representation with respect to equal starting and ending bases is a diagonal matrix we say the map or matrix has been diagonalized. In Chaper Five we shall see which maps and matrices are diagonalizable, and where one is not, we shall see how to get a representation that is nearly diagonal.
We finish this subsection by considering the easier case where representations are with respect to possibly different starting and ending bases. Recall that the prior subsection shows that a matrix changes bases if and only if it is nonsingular. That gives us another version of the above arrow diagram and equation ().
- Definition 2.3
Same-sized matrices and are matrix equivalent if there are nonsingular matrices and such that .
- Corollary 2.4
Matrix equivalent matrices represent the same map, with respect to appropriate pairs of bases.
Problem 10 checks that matrix equivalence is an equivalence relation. Thus it partitions the set of matrices into matrix equivalence classes.
| All matrices: | 
| matrix equivalent to |
We can get some insight into the classes by comparing matrix equivalence with row equivalence (recall that matrices are row equivalent when they can be reduced to each other by row operations). In , the matrices and are nonsingular and thus each can be written as a product of elementary reduction matrices (see Lemma 4.8 in the previous subsection). Left-multiplication by the reduction matrices making up has the effect of performing row operations. Right-multiplication by the reduction matrices making up performs column operations. Therefore, matrix equivalence is a generalization of row equivalence— two matrices are row equivalent if one can be converted to the other by a sequence of row reduction steps, while two matrices are matrix equivalent if one can be converted to the other by a sequence of row reduction steps followed by a sequence of column reduction steps.
Thus, if matrices are row equivalent then they are also matrix equivalent (since we can take to be the identity matrix and so perform no column operations). The converse, however, does not hold.
- Example 2.5
These two
are matrix equivalent because the second can be reduced to the first by the column operation of taking times the first column and adding to the second. They are not row equivalent because they have different reduced echelon forms (in fact, both are already in reduced form).
We will close this section by finding a set of representatives for the matrix equivalence classes.[1]
- Theorem 2.6
Any matrix of rank is matrix equivalent to the matrix that is all zeros except that the first diagonal entries are ones.
Sometimes this is described as a block partial-identity form.
- Proof
As discussed above, Gauss-Jordan reduce the given matrix and combine all the reduction matrices used there to make . Then use the leading entries to do column reduction and finish by swapping columns to put the leading ones on the diagonal. Combine the reduction matrices used for those column operations into .
- Example 2.7
We illustrate the proof by finding the and for this matrix.
First Gauss-Jordan row-reduce.
Then column-reduce, which involves right-multiplication.
Finish by swapping columns.
Finally, combine the left-multipliers together as and the right-multipliers together as to get the equation.
- Corollary 2.8
Two same-sized matrices are matrix equivalent if and only if they have the same rank. That is, the matrix equivalence classes are characterized by rank.
- Proof
Two same-sized matrices with the same rank are equivalent to the same block partial-identity matrix.
- Example 2.9
The matrices have only three possible ranks: zero, one, or two. Thus there are three matrix-equivalence classes.
Each class consists of all of the matrices with the same rank. There is only one rank zero matrix, so that class has only one member, but the other two classes each have infinitely many members.
In this subsection we have seen how to change the representation of a map with respect to a first pair of bases to one with respect to a second pair. That led to a definition describing when matrices are equivalent in this way. Finally we noted that, with the proper choice of (possibly different) starting and ending bases, any map can be represented in block partial-identity form.
One of the nice things about this representation is that, in some sense, we can completely understand the map when it is expressed in this way: if the bases are and then the map sends
where is the map's rank. Thus, we can understand any linear map as a kind of projection.
Of course, "understanding" a map expressed in this way requires that we understand the relationship between and . However, despite that difficulty, this is a good classification of linear maps. }}
Exercises
- This exercise is recommended for all readers.
- Problem 1
Decide if these matrices are matrix equivalent.
- ,
- ,
- ,
- This exercise is recommended for all readers.
- Problem 2
Find the canonical representative of the matrix-equivalence class of each matrix.
- Problem 3
Suppose that, with respect to
the transformation is represented by this matrix.
Use change of basis matrices to represent with respect to each pair.
- ,
- ,
- This exercise is recommended for all readers.
- Problem 4
What sizes are and in the equation ?
- This exercise is recommended for all readers.
- Problem 5
Use Theorem 2.6 to show that a square matrix is nonsingular if and only if it is equivalent to an identity matrix.
- This exercise is recommended for all readers.
- Problem 6
Show that, where is a nonsingular square matrix, if and are nonsingular square matrices such that then .
- This exercise is recommended for all readers.
- Problem 7
Why does Theorem 2.6 not show that every matrix is diagonalizable (see Example 2.2)?
- Problem 8
Must matrix equivalent matrices have matrix equivalent transposes?
- Problem 9
What happens in Theorem 2.6 if ?
- This exercise is recommended for all readers.
- Problem 10
Show that matrix-equivalence is an equivalence relation.
- This exercise is recommended for all readers.
- Problem 11
Show that a zero matrix is alone in its matrix equivalence class. Are there other matrices like that?
- Problem 12
What are the matrix equivalence classes of matrices of transformations on ? ?
- Problem 13
How many matrix equivalence classes are there?
- Problem 14
Are matrix equivalence classes closed under scalar multiplication? Addition?
- Problem 15
Let represented by with respect to .
- Find in this specific case.
- Describe in the general case where .
- Problem 16
- Let have bases and and suppose that has the basis . Where , find the formula that computes from .
- Repeat the prior question with one basis for and two bases for .
- Problem 17
- If two matrices are matrix-equivalent and invertible, must their inverses be matrix-equivalent?
- If two matrices have matrix-equivalent inverses, must the two be matrix-equivalent?
- If two matrices are square and matrix-equivalent, must their squares be matrix-equivalent?
- If two matrices are square and have matrix-equivalent squares, must they be matrix-equivalent?
- This exercise is recommended for all readers.
- Problem 18
Square matrices are similar if they represent the same transformation, but each with respect to the same ending as starting basis. That is, is similar to .
- Give a definition of matrix similarity like that of Definition 2.3.
- Prove that similar matrices are matrix equivalent.
- Show that similarity is an equivalence relation.
- Show that if is similar to then is similar to , the cubes are similar, etc. Contrast with the prior exercise.
- Prove that there are matrix equivalent matrices that are not similar.
Footnotes
- ↑ More information on class representatives is in the appendix.
Section VI - Projection
This section is optional; only the last two sections of Chapter Five require this material.
We have described the projection from into its plane subspace as a "shadow map". This shows why, but it also shows that some shadows fall upward.

| 
|
So perhaps a better description is: the projection of is the in the plane with the property that someone standing on and looking straight up or down sees . In this section we will generalize this to other projections, both orthogonal (i.e., "straight up and down") and nonorthogonal.
1 - Orthogonal Projection Onto a Line
We first consider orthogonal projection onto a line. To orthogonally project a vector onto a line , mark the point on the line at which someone standing on that point could see by looking straight up or down (from that person's point of view).
The picture shows someone who has walked out on the line until the tip of is straight overhead. That is, where the line is described as the span of some nonzero vector , the person has walked out to find the coefficient with the property that is orthogonal to .
We can solve for this coefficient by noting that because is orthogonal to a scalar multiple of it must be orthogonal to itself, and then the consequent fact that the dot product is zero gives that .
- Definition 1.1
The orthogonal projection of onto the line spanned by a nonzero is this vector.
Problem 13 checks that the outcome of the calculation depends only on the line and not on which vector happens to be used to describe that line.
- Remark 1.2
The wording of that definition says "spanned by " instead the more formal "the span of the set ". This casual first phrase is common.
- Example 1.3
To orthogonally project the vector onto the line , we first pick a direction vector for the line. For instance,
will do. Then the calculation is routine.

|
- Example 1.4
In , the orthogonal projection of a general vector
onto the -axis is
which matches our intuitive expectation.
The picture above with the stick figure walking out on the line until 's tip is overhead is one way to think of the orthogonal projection of a vector onto a line. We finish this subsection with two other ways.
- Example 1.5
A railroad car left on an east-west track without its brake is pushed by a wind blowing toward the northeast at fifteen miles per hour; what speed will the car reach?
For the wind we use a vector of length that points toward the northeast.
The car can only be affected by the part of the wind blowing in the east-west direction— the part of in the direction of the -axis is this (the picture has the same perspective as the railroad car picture above).

|
So the car will reach a velocity of miles per hour toward the east.
Thus, another way to think of the picture that precedes the definition is that it shows as decomposed into two parts, the part with the line (here, the part with the tracks, ), and the part that is orthogonal to the line (shown here lying on the north-south axis). These two are "not interacting" or "independent", in the sense that the east-west car is not at all affected by the north-south part of the wind (see Problem 5). So the orthogonal projection of onto the line spanned by can be thought of as the part of that lies in the direction of .
Finally, another useful way to think of the orthogonal projection is to have the person stand not on the line, but on the vector that is to be projected to the line. This person has a rope over the line and pulls it tight, naturally making the rope orthogonal to the line.
That is, we can think of the projection as being the vector in the line that is closest to (see Problem 11).
- Example 1.6
A submarine is tracking a ship moving along the line . Torpedo range is one-half mile. Can the sub stay where it is, at the origin on the chart below, or must it move to reach a place where the ship will pass within range?
The formula for projection onto a line does not immediately apply because the line doesn't pass through the origin, and so isn't the span of any . To adjust for this, we start by shifting the entire map down two units. Now the line is , which is a subspace, and we can project to get the point of closest approach, the point on the line through the origin closest to
the sub's shifted position.
The distance between and is approximately miles and so the sub must move to get in range.
This subsection has developed a natural projection map: orthogonal projection onto a line. As suggested by the examples, it is often called for in applications. The next subsection shows how the definition of orthogonal projection onto a line gives us a way to calculate especially convienent bases for vector spaces, again something that is common in applications. The final subsection completely generalizes projection, orthogonal or not, onto any subspace at all.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Project the first vector orthogonally onto the line spanned by the second vector.
- ,
- ,
- ,
- ,
- This exercise is recommended for all readers.
- Problem 2
Project the vector orthogonally onto the line.
- , the line
- Problem 3
Although the development of Definition 1.1 is guided by the pictures, we are not restricted to spaces that we can draw. In project this vector onto this line.
- This exercise is recommended for all readers.
- Problem 4
Definition 1.1 uses two vectors and . Consider the transformation of resulting from fixing
and projecting onto the line that is the span of . Apply it to these vectors.
Show that in general the projection tranformation is this.
Express the action of this transformation with a matrix.
- Problem 5
Example 1.5 suggests that projection breaks into two parts, and , that are "not interacting". Recall that the two are orthogonal. Show that any two nonzero orthogonal vectors make up a linearly independent set.
- Problem 6
- What is the orthogonal projection of onto a line if is a member of that line?
- Show that if is not a member of the line then the set is linearly independent.
- Problem 7
Definition 1.1 requires that be nonzero. Why? What is the right definition of the orthogonal projection of a vector onto the (degenerate) line spanned by the zero vector?
- Problem 8
Are all vectors the projection of some other vector onto some line?
- This exercise is recommended for all readers.
- Problem 9
Show that the projection of onto the line spanned by has length equal to the absolute value of the number divided by the length of the vector .
- Problem 10
Find the formula for the distance from a point to a line.
- Problem 11
Find the scalar such that is a minimum distance from the point by using calculus (i.e., consider the distance function, set the first derivative equal to zero, and solve). Generalize to .
- This exercise is recommended for all readers.
- Problem 12
Prove that the orthogonal projection of a vector onto a line is shorter than the vector.
- This exercise is recommended for all readers.
- Problem 13
Show that the definition of orthogonal projection onto a line does not depend on the spanning vector: if is a nonzero multiple of then equals .
- This exercise is recommended for all readers.
- Problem 14
Consider the function mapping to plane to itself that takes a vector to its projection onto the line . These two each show that the map is linear, the first one in a way that is bound to the coordinates (that is, it fixes a basis and then computes) and the second in a way that is more conceptual.
- Produce a matrix that describes the function's action.
- Show also that this map can be obtained by first rotating everything in the plane radians clockwise, then projecting onto the -axis, and then rotating radians counterclockwise.
- Problem 15
For let be the projection of onto the line spanned by , let be the projection of onto the line spanned by , let be the projection of onto the line spanned by , etc., back and forth between the spans of and . That is, is the projection of onto the span of if is even, and onto the span of if is odd. Must that sequence of vectors eventually settle down— must there be a sufficiently large such that equals and equals ? If so, what is the earliest such ?
2 - Gram-Schmidt Orthogonalization
This subsection is optional. It requires material from the prior, also optional, subsection. The work done here will only be needed in the final two sections of Chapter Five.
The prior subsection suggests that projecting onto the line spanned by decomposes a vector into two parts
|
that are orthogonal and so are "not interacting". We will now develop that suggestion.
- Definition 2.1
Vectors are mutually orthogonal when any two are orthogonal: if then the dot product is zero.
- Theorem 2.2
If the vectors in a set are mutually orthogonal and nonzero then that set is linearly independent.
- Proof
Consider a linear relationship . If then taking the dot product of with both sides of the equation
shows, since is nonzero, that is zero.
- Corollary 2.3
If the vectors in a size subset of a dimensional space are mutually orthogonal and nonzero then that set is a basis for the space.
- Proof
Any linearly independent size subset of a dimensional space is a basis.
Of course, the converse of Corollary 2.3 does not hold— not every basis of every subspace of is made of mutually orthogonal vectors. However, we can get the partial converse that for every subspace of there is at least one basis consisting of mutually orthogonal vectors.
- Example 2.4
The members and of this basis for are not orthogonal.

|
However, we can derive from a new basis for the same space that does have mutually orthogonal members. For the first member of the new basis we simply use .
For the second member of the new basis, we take away from its part in the direction of ,

|
which leaves the part, pictured above, of that is orthogonal to (it is orthogonal by the definition of the projection onto the span of ). Note that, by the corollary, is a basis for .
- Definition 2.5
An orthogonal basis for a vector space is a basis of mutually orthogonal vectors.
- Example 2.6
To turn this basis for
into an orthogonal basis, we take the first vector as it is given.
We get by starting with the given second vector and subtracting away the part of it in the direction of .
Finally, we get by taking the third given vector and subtracting the part of it in the direction of , and also the part of it in the direction of .
Again the corollary gives that
is a basis for the space.
The next result verifies that the process used in those examples works with any basis for any subspace of an (we are restricted to only because we have not given a definition of orthogonality for other vector spaces).
- Theorem 2.7 (Gram-Schmidt orthogonalization)
If is a basis for a subspace of then, where
the 's form an orthogonal basis for the same subspace.
- Proof
We will use induction to check that each is nonzero, is in the span of and is orthogonal to all preceding vectors: . With those, and with Corollary 2.3, we will have that is a basis for the same space as .
We shall cover the cases up to , which give the sense of the argument. Completing the details is Problem 15.
The case is trivial— setting equal to makes it a nonzero vector since is a member of a basis, it is obviously in the desired span, and the "orthogonal to all preceding vectors" condition is vacuously met.
For the case, expand the definition of .
This expansion shows that is nonzero or else this would be a non-trivial linear dependence among the 's (it is nontrivial because the coefficient of is ) and also shows that is in the desired span. Finally, is orthogonal to the only preceding vector
because this projection is orthogonal.
The case is the same as the case except for one detail. As in the case, expanding the definition
shows that is nonzero and is in the span. A calculation shows that is orthogonal to the preceding vector .
(Here's the difference from the case— the second line has two kinds of terms. The first term is zero because this projection is orthogonal, as in the case. The second term is zero because is orthogonal to and so is orthogonal to any vector in the line spanned by .) The check that is also orthogonal to the other preceding vector is similar.
Beyond having the vectors in the basis be orthogonal, we can do more; we can arrange for each vector to have length one by dividing each by its own length (we can normalize the lengths).
- Example 2.8
Normalizing the length of each vector in the orthogonal basis of Example 2.6 produces this orthonormal basis.
Besides its intuitive appeal, and its analogy with the standard basis for , an orthonormal basis also simplifies some computations. See Exercise 9, for example.
Exercises
- Problem 1
Perform the Gram-Schmidt process on each of these bases for .
Then turn those orthogonal bases into orthonormal bases.
- This exercise is recommended for all readers.
- Problem 2
Perform the Gram-Schmidt process on each of these bases for .
Then turn those orthogonal bases into orthonormal bases.
- This exercise is recommended for all readers.
- Problem 3
Find an orthonormal basis for this subspace of : the plane .
- Problem 4
Find an orthonormal basis for this subspace of .
- Problem 5
Show that any linearly independent subset of can be orthogonalized without changing its span.
- This exercise is recommended for all readers.
- Problem 6
What happens if we apply the Gram-Schmidt process to a basis that is already orthogonal?
- Problem 7
Let be a set of mutually orthogonal vectors in .
- Prove that for any in the space, the vector is orthogonal to each of , ..., .
- Illustrate the prior item in by using as , using as , and taking to have components , , and .
- Show that is the vector in the span of the set of 's that is closest to . Hint. To the illustration done for the prior part, add a vector and apply the Pythagorean Theorem to the resulting triangle.
- Problem 8
Find a vector in that is orthogonal to both of these.
- This exercise is recommended for all readers.
- Problem 9
One advantage of orthogonal bases is that they simplify finding the representation of a vector with respect to that basis.
- For this vector and this non-orthogonal basis for
- With this orthogonal basis for
- Let be an orthogonal basis for some subspace of . Prove that for any in the subspace, the -th component of the representation is the scalar coefficient from .
- Prove that .
- Problem 10
Bessel's Inequality. Consider these orthonormal sets
along with the vector whose components are , , , and .
- Find the coefficient for the projection of onto the span of the vector in . Check that .
- Find the coefficients and for the projection of onto the spans of the two vectors in . Check that .
- Find , , and associated with the vectors in , and , , , and for the vectors in . Check that and that .
Show that this holds in general: where is an orthonormal set and is coefficient of the projection of a vector from the space then . Hint. One way is to look at the inequality and expand the 's.
- Problem 11
Prove or disprove: every vector in is in some orthogonal basis.
- Problem 12
Show that the columns of an matrix form an orthonormal set if and only if the inverse of the matrix is its transpose. Produce such a matrix.
- Problem 13
Does the proof of Theorem 2.2 fail to consider the possibility that the set of vectors is empty (i.e., that )?
- Problem 14
Theorem 2.7 describes a change of basis from any basis to one that is orthogonal . Consider the change of basis matrix .
- Prove that the matrix changing bases in the direction opposite to that of the theorem has an upper triangular shape— all of its entries below the main diagonal are zeros.
- Prove that the inverse of an upper triangular matrix is also upper triangular (if the matrix is invertible, that is). This shows that the matrix changing bases in the direction described in the theorem is upper triangular.
- Problem 15
Complete the induction argument in the proof of Theorem 2.7.
3 - Projection Onto a Subspace
This subsection, like the others in this section, is optional. It also requires material from the optional earlier subsection on Combining Subspaces.
The prior subsections project a vector onto a line by decomposing it into two parts: the part in the line and the rest . To generalize projection to arbitrary subspaces, we follow this idea.
- Definition 3.1
For any direct sum and any , the projection of onto along is
where with .
This definition doesn't involve a sense of "orthogonal" so we can apply it to spaces other than subspaces of an . (Definitions of orthogonality for other spaces are perfectly possible, but we haven't seen any in this book.)
- Example 3.2
The space of matrices is the direct sum of these two.
To project
onto along , we first fix bases for the two subspaces.
The concatenation of these
is a basis for the entire space, because the space is the direct sum, so we can use it to represent .
Now the projection of onto along is found by keeping the part of this sum and dropping the part.
- Example 3.3
Both subscripts on are significant. The first subscript matters because the result of the projection is an , and changing this subspace would change the possible results. For an example showing that the second subscript matters, fix this plane subspace of and its basis
and compare the projections along two different subspaces.
(Verification that and is routine.) We will check that these projections are different by checking that they have different effects on this vector.
For the first one we find a basis for
and represent with respect to the concatenation .
The projection of onto along is found by keeping the part and dropping the part.
For the other subspace , this basis is natural.
Representing with respect to the concatenation
and then keeping only the part gives this.
Therefore projection along different subspaces may yield different results.
These pictures compare the two maps. Both show that the projection is indeed "onto" the plane and "along" the line.

| 
|
Notice that the projection along is not orthogonal— there are members of the plane that are not orthogonal to the dotted line. But the projection along is orthogonal.
A natural question is: what is the relationship between the projection operation defined above, and the operation of orthogonal projection onto a line? The second picture above suggests the answer— orthogonal projection onto a line is a special case of the projection defined above; it is just projection along a subspace perpendicular to the line.
In addition to pointing out that projection along a subspace is a generalization, this scheme shows how to define orthogonal projection onto any subspace of , of any dimension.
- Definition 3.4
The orthogonal complementof a subspace of is
(read " perp"). The orthogonal projection of a vector is its projection onto along .
- Example 3.5
In , to find the orthogonal complement of the plane
we start with a basis for .
Any perpendicular to every vector in is perpendicular to every vector in the span of (the proof of this assertion is Problem 10). Therefore, the subspace consists of the vectors that satisfy these two conditions.
We can express those conditions more compactly as a linear system.
We are thus left with finding the nullspace of the map represented by the matrix, that is, with calculating the solution set of a homogeneous linear system.
- Example 3.6
Where is the -plane subspace of , what is ? A common first reaction is that is the -plane, but that's not right. Some vectors from the -plane are not perpendicular to every vector in the -plane.

|
Instead is the -axis, since proceeding as in the prior example and taking the natural basis for the -plane gives this.
The two examples that we've seen since Definition 3.4 illustrate the first sentence in that definition. The next result justifies the second sentence.
- Lemma 3.7
Let be a subspace of . The orthogonal complement of is also a subspace. The space is the direct sum of the two . And, for any , the vector is perpendicular to every vector in .
- Proof
First, the orthogonal complement is a subspace of because, as noted in the prior two examples, it is a nullspace.
Next, we can start with any basis for and expand it to a basis
for the entire space. Apply the Gram-Schmidt process to get an orthogonal basis for . This is the concatenation of two bases (with the same number of members as ) and . The first is a basis for , so if we show that the second is a basis for then we will have that the entire space is the direct sum of the two subspaces.
Problem 9 from the prior subsection proves this about any orthogonal basis: each vector in the space is the sum of its orthogonal projections onto the lines spanned by the basis vectors.
To check this, represent the vector , apply to both sides , and solve to get , as desired.
Since obviously any member of the span of is orthogonal to any vector in , to show that this is a basis for we need only show the other containment— that any is in the span of this basis. The prior paragraph does this. On projections onto basis vectors from , any gives and therefore () gives that is a linear combination of . Thus this is a basis for and is the direct sum of the two.
The final sentence is proved in much the same way. Write . Then is gotten by keeping only the part and dropping the part . Therefore consists of a linear combination of elements of and so is perpendicular to every vector in .
We can find the orthogonal projection onto a subspace by following the steps of the proof, but the next result gives a convienent formula.
- Theorem 3.8
Let be a vector in and let be a subspace of with basis . If is the matrix whose columns are the 's then where the coefficients are the entries of the vector . That is, .
- Proof
The vector is a member of and so it is a linear combination of basis vectors . Since 's columns are the 's, that can be expressed as: there is a such that (this is expressed compactly with matrix multiplication as in Example 3.5 and 3.6). Because is perpendicular to each member of the basis, we have this (again, expressed compactly).
Solving for (showing that is invertible is an exercise)
gives the formula for the projection matrix as .
- Example 3.9
To orthogonally project this vector onto this subspace
first make a matrix whose columns are a basis for the subspace
and then compute.
With the matrix, calculating the orthogonal projection of any vector onto is easy.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Project the vectors onto along .
- This exercise is recommended for all readers.
- Problem 2
Find .
- Problem 3
This subsection shows how to project orthogonally in two ways, the method of Example 3.2 and 3.3, and the method of Theorem 3.8. To compare them, consider the plane specified by in .
- Find a basis for .
- Find and a basis for .
- Represent this vector with respect to the concatenation
of the two bases from the prior item.
- Find the orthogonal projection of onto by keeping only the part from the prior item.
- Check that against the result from applying Theorem 3.8.
- This exercise is recommended for all readers.
- Problem 4
We have three ways to find the orthogonal projection of a vector onto a line, the Definition 1.1 way from the first subsection of this section, the Example 3.2 and 3.3 way of representing the vector with respect to a basis for the space and then keeping the part, and the way of Theorem 3.8. For these cases, do all three ways.
- Problem 5
Check that the operation of Definition 3.1 is well-defined. That is, in Example 3.2 and 3.3, doesn't the answer depend on the choice of bases?
- Problem 6
What is the orthogonal projection onto the trivial subspace?
- Problem 7
What is the projection of onto along if ?
- Problem 8
Show that if is a subspace with orthonormal basis then the orthogonal projection of onto is this.
- This exercise is recommended for all readers.
- Problem 9
Prove that the map is the projection onto along if and only if the map is the projection onto along . (Recall the definition of the difference of two maps: .)
- This exercise is recommended for all readers.
- Problem 10
Show that if a vector is perpendicular to every vector in a set then it is perpendicular to every vector in the span of that set.
- Problem 11
True or false: the intersection of a subspace and its orthogonal complement is trivial.
- Problem 12
Show that the dimensions of orthogonal complements add to the dimension of the entire space.
- This exercise is recommended for all readers.
- Problem 13
Suppose that are such that for all complements , the projections of and onto along are equal. Must equal ? (If so, what if we relax the condition to: all orthogonal projections of the two are equal?)
- This exercise is recommended for all readers.
- Problem 14
Let be subspaces of . The perp operator acts on subspaces; we can ask how it interacts with other such operations.
- Show that two perps cancel: .
- Prove that implies that .
- Show that .
- This exercise is recommended for all readers.
- Problem 15
The material in this subsection allows us to express a geometric relationship that we have not yet seen between the rangespace and the nullspace of a linear map.
- Represent given by
- Generalize that to apply to any .
- Represent
- Generalize that to apply to any .
This, and related results, is called the Fundamental Theorem of Linear Algebra in (Strang 1993).
- Problem 16
Define a projection to be a linear transformation with the property that repeating the projection does nothing more than does the projection alone: for all .
- Show that orthogonal projection onto a line has that property.
- Show that projection along a subspace has that property.
- Show that for any such
there is a basis for such that
- Conclude that every projection is a projection along a subspace.
- Also conclude that every projection has a representation
- Problem 17
A square matrix is symmetric if each entry equals the entry (i.e., if the matrix equals its transpose). Show that the projection matrix is symmetric. (Strang 1980) Hint. Find properties of transposes by looking in the index under "transpose".
Topic: Line of Best Fit
Scientists are often presented with a system that has no solution and they must find an answer anyway. That is, they must find a value that is as close as possible to being an answer.
For instance, suppose that we have a coin to use in flipping. This coin has some proportion of heads to total flips, determined by how it is physically constructed, and we want to know if is near . We can get experimental data by flipping it many times. This is the result a penny experiment, including some intermediate numbers.
| number of flips | 30 | 60 | 90 |
| number of heads | 16 | 34 | 51 |
Because of randomness, we do not find the exact proportion with this sample — there is no solution to this system.
That is, the vector of experimental data is not in the subspace of solutions.
However, as described above, we want to find the that most nearly works. An orthogonal projection of the data vector into the line subspace gives our best guess.
The estimate () is a bit high but not much, so probably the penny is fair enough.
The line with the slope is called the line of best fit for this data.
Minimizing the distance between the given vector and the vector used as the right-hand side minimizes the total of these vertical lengths, and consequently we say that the line has been obtained through fitting by least-squares
(the vertical scale here has been exaggerated ten times to make the lengths visible).
We arranged the equation above so that the line must pass through because we take take it to be (our best guess at) the line whose slope is this coin's true proportion of heads to flips. We can also handle cases where the line need not pass through the origin.
For example, the different denominations of U.S. money have different average times in circulation (the $2 bill is left off as a special case). How long should we expect a $25 bill to last?
| denomination | 1 | 5 | 10 | 20 | 50 | 100 |
| average life (years) | 1.5 | 2 | 3 | 5 | 9 | 20 |
The plot (see below) looks roughly linear. It isn't a perfect line, i.e., the linear system with equations , ..., has no solution, but we can again use orthogonal projection to find a best approximation. Consider the matrix of coefficients of that linear system and also its vector of constants, the experimentally-determined values.
The ending result in the subsection on Projection into a Subspace says that coefficients and so that the linear combination of the columns of is as close as possible to the vector are the entries of . Some calculation gives an intercept of and a slope of .
Plugging into the equation of the line shows that such a bill should last between five and six years.
We close by considering the times for the men's mile race (Oakley & Baker 1977). These are the world records that were in force on January first of the given years. We want to project when a 3:40 mile will be run.
| year | 1870 | 1880 | 1890 | 1900 | 1910 | 1920 | 1930 |
| seconds | 268.8 | 264.5 | 258.4 | 255.6 | 255.6 | 252.6 | 250.4 |
| year | 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
| seconds | 246.4 | 241.4 | 234.5 | 231.1 | 229.0 | 226.3 | 223.1 |
We can see below that the data is surprisingly linear. With this input
the Python program at this Topic's end gives
and (rounded to two places; the original data is good to only about a quarter of a second since much of it was hand-timed).
When will a second mile be run? Solving the equation of the line of best fit gives an estimate of the year .
This example is amusing, but serves as a caution — obviously the linearity of the data will break down someday (as indeed it does prior to 1860).
Exercises
The calculations here are best done on a computer. In addition, some of the problems require more data, available in your library, on the net, in the answers to the exercises, or in the section following the exercises.
- Problem 1
Use least-squares to judge if the coin in this experiment is fair.
| flips | 8 | 16 | 24 | 32 | 40 |
| heads | 4 | 9 | 13 | 17 | 20 |
- Problem 2
For the men's mile record, rather than give each of the many records and its exact date, we've "smoothed" the data somewhat by taking a periodic sample. Do the longer calculation and compare the conclusions.
- Problem 3
Find the line of best fit for the men's meter run. How does the slope compare with that for the men's mile? (The distances are close; a mile is about meters.)
- Problem 4
- Find the line of best fit for the records for women's mile.
- Problem 5
Do the lines of best fit for the men's and women's miles cross?
- Problem 6
When the space shuttle Challenger exploded in 1986, one of the criticisms made of NASA's decision to launch was in the way the analysis of number of O-ring failures versus temperature was made (of course, O-ring failure caused the explosion). Four O-ring failures will cause the rocket to explode. NASA had data from 24 previous flights.
| temp °F | 53 | 75 | 57 | 58 | 63 | 70 | 70 | 66 | 67 | 67 | 67 | ||
| failures | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| temp °F | 68 | 69 | 70 | 70 | 72 | 73 | 75 | 76 | 76 | 78 | 79 | 80 | 81 |
| failures | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The temperature that day was forecast to be .
- NASA based the decision to launch partially on a chart showing only the flights that had at least one O-ring failure. Find the line that best fits these seven flights. On the basis of this data, predict the number of O-ring failures when the temperature is , and when the number of failures will exceed four.
- Find the line that best fits all 24 flights. On the basis of this extra data, predict the number of O-ring failures when the temperature is , and when the number of failures will exceed four.
Which do you think is the more accurate method of predicting? (An excellent discussion appears in (Dalal, Folkes & Hoadley 1989).)
- Problem 7
This table lists the average distance from the sun to each of the first seven planets, using earth's average as a unit.
| Mercury | Venus | Earth | Mars | Jupiter | Saturn | Uranus |
| 0.39 | 0.72 | 1.00 | 1.52 | 5.20 | 9.54 | 19.2 |
- Plot the number of the planet (Mercury is , etc.) versus the distance. Note that it does not look like a line, and so finding the line of best fit is not fruitful.
- It does, however look like an exponential curve. Therefore, plot the number of the planet versus the logarithm of the distance. Does this look like a line?
- The asteroid belt between Mars and Jupiter is thought to be what is left of a planet that broke apart. Renumber so that Jupiter is , Saturn is , and Uranus is , and plot against the log again. Does this look better?
- Use least squares on that data to predict the location of Neptune.
- Repeat to predict where Pluto is.
- Is the formula accurate for Neptune and Pluto?
This method was used to help discover Neptune (although the second item is misleading about the history; actually, the discovery of Neptune in position prompted people to look for the "missing planet" in position ). See (Gardner 1970)
- Problem 8
William Bennett has proposed an Index of Leading Cultural Indicators for the US (Bennett 1993). Among the statistics cited are the average daily hours spent watching TV, and the average combined SAT scores.
| 1960 | 1965 | 1970 | 1975 | 1980 | 1985 | 1990 | 1992 | |
| TV | 5:06 | 5:29 | 5:56 | 6:07 | 6:36 | 7:07 | 6:55 | 7:04 |
| SAT | 975 | 969 | 948 | 910 | 890 | 906 | 900 | 899 |
Suppose that a cause and effect relationship is proposed between the time spent watching TV and the decline in SAT scores (in this article, Mr. Bennett does not argue that there is a direct connection).
- Find the line of best fit relating the independent variable of average daily TV hours to the dependent variable of SAT scores.
- Find the most recent estimate of the average daily TV hours (Bennett's cites Neilsen Media Research as the source of these estimates). Estimate the associated SAT score. How close is your estimate to the actual average? (Warning: a change has been made recently in the SAT, so you should investigate whether some adjustment needs to be made to the reported average to make a valid comparison.)
Computer Code
#!/usr/bin/python
# least_squares.py calculate the line of best fit for a data set
# data file format: each line is two numbers, x and y
n = 0
sum_x = 0
sum_y = 0
sum_x_squared = 0
sum_xy = 0
fn = raw_input("Name of the data file? ")
datafile = open(fn,"r")
while 1:
ln = datafile.readline()
if ln:
data = ln.split()
x = float(data[0])
y = float(data[1])
n += 1
sum_x += x
sum_y += y
sum_x_squared += x*x
sum_xy += x*y
else:
break
datafile.close()
slope = (n*sum_xy - sum_x*sum_y) / (n*sum_x_squared - sum_x**2)
intercept = (sum_y - slope*sum_x)/n
print "line of best fit: slope= %f intercept= %f" % (slope, intercept)
Additional Data
Data on the progression of the world's records (taken from the Runner's World web site) is below.
|
Progression of Men's Mile Record | ||
| time | name | date |
| 4:52.0 | Cadet Marshall (GBR) | 02Sep52 |
| 4:45.0 | Thomas Finch (GBR) | 03Nov58 |
| 4:40.0 | Gerald Surman (GBR) | 24Nov59 |
| 4:33.0 | George Farran (IRL) | 23May62 |
| 4:29 3/5 | Walter Chinnery (GBR) | 10Mar68 |
| 4:28 4/5 | William Gibbs (GBR) | 03Apr68 |
| 4:28 3/5 | Charles Gunton (GBR) | 31Mar73 |
| 4:26.0 | Walter Slade (GBR) | 30May74 |
| 4:24 1/2 | Walter Slade (GBR) | 19Jun75 |
| 4:23 1/5 | Walter George (GBR) | 16Aug80 |
| 4:19 2/5 | Walter George (GBR) | 03Jun82 |
| 4:18 2/5 | Walter George (GBR) | 21Jun84 |
| 4:17 4/5 | Thomas Conneff (USA) | 26Aug93 |
| 4:17.0 | Fred Bacon (GBR) | 06Jul95 |
| 4:15 3/5 | Thomas Conneff (USA) | 28Aug95 |
| 4:15 2/5 | John Paul Jones (USA) | 27May11 |
| 4:14.4 | John Paul Jones (USA) | 31May13 |
| 4:12.6 | Norman Taber (USA) | 16Jul15 |
| 4:10.4 | Paavo Nurmi (FIN) | 23Aug23 |
| 4:09 1/5 | Jules Ladoumegue (FRA) | 04Oct31 |
| 4:07.6 | Jack Lovelock (NZL) | 15Jul33 |
| 4:06.8 | Glenn Cunningham (USA) | 16Jun34 |
| 4:06.4 | Sydney Wooderson (GBR) | 28Aug37 |
| 4:06.2 | Gunder Hagg (SWE) | 01Jul42 |
| 4:04.6 | Gunder Hagg (SWE) | 04Sep42 |
| 4:02.6 | Arne Andersson (SWE) | 01Jul43 |
| 4:01.6 | Arne Andersson (SWE) | 18Jul44 |
| 4:01.4 | Gunder Hagg (SWE) | 17Jul45 |
| 3:59.4 | Roger Bannister (GBR) | 06May54 |
| 3:58.0 | John Landy (AUS) | 21Jun54 |
| 3:57.2 | Derek Ibbotson (GBR) | 19Jul57 |
| 3:54.5 | Herb Elliott (AUS) | 06Aug58 |
| 3:54.4 | Peter Snell (NZL) | 27Jan62 |
| 3:54.1 | Peter Snell (NZL) | 17Nov64 |
| 3:53.6 | Michel Jazy (FRA) | 09Jun65 |
| 3:51.3 | Jim Ryun (USA) | 17Jul66 |
| 3:51.1 | Jim Ryun (USA) | 23Jun67 |
| 3:51.0 | Filbert Bayi (TAN) | 17May75 |
| 3:49.4 | John Walker (NZL) | 12Aug75 |
| 3:49.0 | Sebastian Coe (GBR) | 17Jul79 |
| 3:48.8 | Steve Ovett (GBR) | 01Jul80 |
| 3:48.53 | Sebastian Coe (GBR) | 19Aug81 |
| 3:48.40 | Steve Ovett (GBR) | 26Aug81 |
| 3:47.33 | Sebastian Coe (GBR) | 28Aug81 |
| 3:46.32 | Steve Cram (GBR) | 27Jul85 |
| 3:44.39 | Noureddine Morceli (ALG) | 05Sep93 |
| 3:43.13 | Hicham el Guerrouj (MOR) | 07Jul99 |
|
Progression of Men's 1500 Meter Record | ||
| time | name | date |
| 4:09.0 | John Bray (USA) | 30May00 |
| 4:06.2 | Charles Bennett (GBR) | 15Jul00 |
| 4:05.4 | James Lightbody (USA) | 03Sep04 |
| 3:59.8 | Harold Wilson (GBR) | 30May08 |
| 3:59.2 | Abel Kiviat (USA) | 26May12 |
| 3:56.8 | Abel Kiviat (USA) | 02Jun12 |
| 3:55.8 | Abel Kiviat (USA) | 08Jun12 |
| 3:55.0 | Norman Taber (USA) | 16Jul15 |
| 3:54.7 | John Zander (SWE) | 05Aug17 |
| 3:53.0 | Paavo Nurmi (FIN) | 23Aug23 |
| 3:52.6 | Paavo Nurmi (FIN) | 19Jun24 |
| 3:51.0 | Otto Peltzer (GER) | 11Sep26 |
| 3:49.2 | Jules Ladoumegue (FRA) | 05Oct30 |
| 3:49.0 | Luigi Beccali (ITA) | 17Sep33 |
| 3:48.8 | William Bonthron (USA) | 30Jun34 |
| 3:47.8 | Jack Lovelock (NZL) | 06Aug36 |
| 3:47.6 | Gunder Hagg (SWE) | 10Aug41 |
| 3:45.8 | Gunder Hagg (SWE) | 17Jul42 |
| 3:45.0 | Arne Andersson (SWE) | 17Aug43 |
| 3:43.0 | Gunder Hagg (SWE) | 07Jul44 |
| 3:42.8 | Wes Santee (USA) | 04Jun54 |
| 3:41.8 | John Landy (AUS) | 21Jun54 |
| 3:40.8 | Sandor Iharos (HUN) | 28Jul55 |
| 3:40.6 | Istvan Rozsavolgyi (HUN) | 03Aug56 |
| 3:40.2 | Olavi Salsola (FIN) | 11Jul57 |
| 3:38.1 | Stanislav Jungwirth (CZE) | 12Jul57 |
| 3:36.0 | Herb Elliott (AUS) | 28Aug58 |
| 3:35.6 | Herb Elliott (AUS) | 06Sep60 |
| 3:33.1 | Jim Ryun (USA) | 08Jul67 |
| 3:32.2 | Filbert Bayi (TAN) | 02Feb74 |
| 3:32.1 | Sebastian Coe (GBR) | 15Aug79 |
| 3:31.36 | Steve Ovett (GBR) | 27Aug80 |
| 3:31.24 | Sydney Maree (usa) | 28Aug83 |
| 3:30.77 | Steve Ovett (GBR) | 04Sep83 |
| 3:29.67 | Steve Cram (GBR) | 16Jul85 |
| 3:29.46 | Said Aouita (MOR) | 23Aug85 |
| 3:28.86 | Noureddine Morceli (ALG) | 06Sep92 |
| 3:27.37 | Noureddine Morceli (ALG) | 12Jul95 |
| 3:26.00 | Hicham el Guerrouj (MOR) | 14Jul98 |
|
Progression of Women's Mile Record | ||
| time | name | date |
| 6:13.2 | Elizabeth Atkinson (GBR) | 24Jun21 |
| 5:27.5 | Ruth Christmas (GBR) | 20Aug32 |
| 5:24.0 | Gladys Lunn (GBR) | 01Jun36 |
| 5:23.0 | Gladys Lunn (GBR) | 18Jul36 |
| 5:20.8 | Gladys Lunn (GBR) | 08May37 |
| 5:17.0 | Gladys Lunn (GBR) | 07Aug37 |
| 5:15.3 | Evelyne Forster (GBR) | 22Jul39 |
| 5:11.0 | Anne Oliver (GBR) | 14Jun52 |
| 5:09.8 | Enid Harding (GBR) | 04Jul53 |
| 5:08.0 | Anne Oliver (GBR) | 12Sep53 |
| 5:02.6 | Diane Leather (GBR) | 30Sep53 |
| 5:00.3 | Edith Treybal (ROM) | 01Nov53 |
| 5:00.2 | Diane Leather (GBR) | 26May54 |
| 4:59.6 | Diane Leather (GBR) | 29May54 |
| 4:50.8 | Diane Leather (GBR) | 24May55 |
| 4:45.0 | Diane Leather (GBR) | 21Sep55 |
| 4:41.4 | Marise Chamberlain (NZL) | 08Dec62 |
| 4:39.2 | Anne Smith (GBR) | 13May67 |
| 4:37.0 | Anne Smith (GBR) | 03Jun67 |
| 4:36.8 | Maria Gommers (HOL) | 14Jun69 |
| 4:35.3 | Ellen Tittel (FRG) | 20Aug71 |
| 4:34.9 | Glenda Reiser (CAN) | 07Jul73 |
| 4:29.5 | Paola Pigni-Cacchi (ITA) | 08Aug73 |
| 4:23.8 | Natalia Marasescu (ROM) | 21May77 |
| 4:22.1 | Natalia Marasescu (ROM) | 27Jan79 |
| 4:21.7 | Mary Decker (USA) | 26Jan80 |
| 4:20.89 | Lyudmila Veselkova (SOV) | 12Sep81 |
| 4:18.08 | Mary Decker-Tabb (USA) | 09Jul82 |
| 4:17.44 | Maricica Puica (ROM) | 16Sep82 |
| 4:15.8 | Natalya Artyomova (SOV) | 05Aug84 |
| 4:16.71 | Mary Decker-Slaney (USA) | 21Aug85 |
| 4:15.61 | Paula Ivan (ROM) | 10Jul89 |
| 4:12.56 | Svetlana Masterkova (RUS) | 14Aug96 |
Topic: Geometry of Linear Maps
The pictures below contrast and , which are nonlinear, with and , which are linear. Each of the four pictures shows the domain on the left mapped to the codomain on the right. Arrows trace out where each map sends , , , , and . Note how the nonlinear maps distort the domain in transforming it into the range. For instance, is further from than it is from — the map is spreading the domain out unevenly so that an interval near is spread apart more than is an interval near when they are carried over to the range.
The linear maps are nicer, more regular, in that for each map all of the domain is spread by the same factor.
The only linear maps from to are multiplications by a scalar. In higher dimensions more can happen. For instance, this linear transformation of , rotates vectors counterclockwise, and is not just a scalar multiplication.
The transformation of which projects vectors into the -plane is also not just a rescaling.
Nonetheless, even in higher dimensions the situation isn't too complicated.
Below, we use the standard bases to represent each linear map by a matrix . Recall that any can be factored , where and are nonsingular and is a partial-identity matrix. Further, recall that nonsingular matrices factor into elementary matrices , which are matrices that are obtained from the identity with one Gaussian step
(, ). So if we understand the effect of a linear map described by a partial-identity matrix, and the effect of linear mapss described by the elementary matrices, then we will in some sense understand the effect of any linear map. (The pictures below stick to transformations of for ease of drawing, but the statements hold for maps from any to any .)
The geometric effect of the linear transformation represented by a partial-identity matrix is projection.
For the matrices, the geometric action of a transformation represented by such a matrix (with respect to the standard basis) is to stretch vectors by a factor of along the -th axis. This map stretches by a factor of along the -axis.
Note that if or if then the -th component goes the other way; here, toward the left.
Either of these is a dilation.
The action of a transformation represented by a permutation matrix is to interchange the -th and -th axes; this is a particular kind of reflection.
In higher dimensions, permutations involving many axes can be decomposed into a combination of swaps of pairs of axes— see Problem 5.
The remaining case is that of matrices of the form . Recall that, for instance, that performs .
In the picture below, the vector with the first component of is affected less than the vector with the first component of — is only higher than while is higher than .
Any vector with a first component of would be affected as is ; it would be slid up by . And any vector with a first component of would be slid up , as was . That is, the transformation represented by affects vectors depending on their -th component.
Another way to see this same point is to consider the action of this map on the unit square. In the next picture, vectors with a first component of , like the origin, are not pushed vertically at all but vectors with a positive first component are slid up. Here, all vectors with a first component of — the entire right side of the square— is affected to the same extent. More generally, vectors on the same vertical line are slid up the same amount, namely, they are slid up by twice their first component. The resulting shape, a rhombus, has the same base and height as the square (and thus the same area) but the right angles are gone.
For contrast the next picture shows the effect of the map represented by . In this case, vectors are affected according to their second component. The vector is slid horozontally by twice .
Because of this action, this kind of map is called a shear.
With that, we have covered the geometric effect of the four types of components in the expansion , the partial-identity projection and the elementary 's. Since we understand its components, we in some sense understand the action of any . As an illustration of this assertion, recall that under a linear map, the image of a subspace is a subspace and thus the linear transformation represented by maps lines through the origin to lines through the origin. (The dimension of the image space cannot be greater than the dimension of the domain space, so a line can't map onto, say, a plane.) We will extend that to show that any line, not just those through the origin, is mapped by to a line. The proof is simply that the partial-identity projection and the elementary 's each turn a line input into a line output (verifying the four cases is Problem 6), and therefore their composition also preserves lines. Thus, by understanding its components we can understand arbitrary square matrices , in the sense that we can prove things about them.
An understanding of the geometric effect of linear transformations on is very important in mathematics. Here is a familiar application from calculus. On the left is a picture of the action of the nonlinear function . As at that start of this Topic, overall the geometric effect of this map is irregular in that at different domain points it has different effects (e.g., as the domain point goes from to , the associated range point at first decreases, then pauses instantaneously, and then increases).
But in calculus we don't focus on the map overall, we focus instead on the local effect of the map.
At the derivative is , so that near we have .
That is, in a neighborhood of , in carrying the domain to the codomain this map causes it to grow by a factor of — it is, locally, approximately, a dilation.
The picture below shows a small interval in the domain carried over to an interval in the codomain that is three times as wide: .
(When the above picture is drawn in the traditional cartesian way then the prior sentence about the rate of growth of is usually stated: the derivative gives the slope of the line tangent to the graph at the point .)
In higher dimensions, the idea is the same but the approximation is not just the -to- scalar multiplication case. Instead, for a function and a point , the derivative is defined to be the linear map best approximating how changes near . So the geometry studied above applies.
We will close this Topic by remarking how this point of view makes clear an often-misunderstood, but very important, result about derivatives: the derivative of the composition of two functions is computed by using the Chain Rule for combining their derivatives. Recall that (with suitable conditions on the two functions)
so that, for instance, the derivative of is . How does this combination arise? From this picture of the action of the composition.
The first map dilates the neighborhood of by a factor of
and the second map dilates some more, this time dilating a neighborhood of by a factor of
and as a result, the composition dilates by the product of these two.
In higher dimensions the map expressing how a function changes near a point is a linear map, and is expressed as a matrix. (So we understand the basic geometry of higher-dimensional derivatives; they are compositions of dilations, interchanges of axes, shears, and a projection). And, the Chain Rule just multiplies the matrices.
Thus, the geometry of linear maps is appealing both for its simplicity and for its usefulness.
Exercises
- Problem 1
Let be the transformation that rotates vectors clockwise by radians.
- Find the matrix representing with respect to the standard bases. Use Gauss' method to reduce to the identity.
- Translate the row reduction to to a matrix equation (the prior item shows both that is similar to , and that no column operations are needed to derive from ).
- Solve this matrix equation for .
- Sketch the geometric effect matrix, that is, sketch how is expressed as a combination of dilations, flips, skews, and projections (the identity is a trivial projection).
- Problem 2
What combination of dilations, flips, skews, and projections produces a rotation counterclockwise by radians?
- Problem 3
What combination of dilations, flips, skews, and projections produces the map represented with respect to the standard bases by this matrix?
- Problem 4
Show that any linear transformation of is the map that multiplies by a scalar .
- Problem 5
Show that for any permutation (that is, reordering) of the numbers , ..., , the map
can be accomplished with a composition of maps, each of which only swaps a single pair of coordinates. Hint: it can be done by induction on . (Remark: in the fourth chapter we will show this and we will also show that the parity of the number of swaps used is determined by . That is, although a particular permutation could be accomplished in two different ways with two different numbers of swaps, either both ways use an even number of swaps, or both use an odd number.)
- Problem 6
Show that linear maps preserve the linear structures of a space.
- Show that for any linear map from to , the image of any line is a line. The image may be a degenerate line, that is, a single point.
- Show that the image of any linear surface is a linear surface. This generalizes the result that under a linear map the image of a subspace is a subspace.
- Linear maps preserve other linear ideas. Show that linear maps preserve "betweeness": if the point is between and then the image of is between the image of and the image of .
- Problem 7
Use a picture like the one that appears in the discussion of the Chain Rule to answer: if a function has an inverse, what's the relationship between how the function — locally, approximately — dilates space, and how its inverse dilates space (assuming, of course, that it has an inverse)?
Topic: Markov Chains
Here is a simple game: a player bets on coin tosses, a dollar each time, and the game ends either when the player has no money left or is up to five dollars. If the player starts with three dollars, what is the chance that the game takes at least five flips? Twenty-five flips?
At any point, this player has either $0, or $1, ..., or $5. We say that the player is in the state , , ..., or . A game consists of moving from state to state. For instance, a player now in state has on the next flip a chance of moving to state and a chance of moving to . The boundary states are a bit different; once in state or stat , the player never leaves.
Let be the probability that the player is in state after flips. Then, for instance, we have that the probability of being in state after flip is . This matrix equation summarizes.
With the initial condition that the player starts with
three dollars, calculation gives this.
As this computational exploration suggests, the game is not likely to go on for long, with the player quickly ending in either state or state . For instance, after the fourth flip there is a probability of that the game is already over. (Because a player who enters either of the boundary states never leaves, they are said to be absorbing.)
This game is an example of a Markov chain, named for A.A. Markov, who worked in the first half of the 1900's. Each vector of 's is a probability vector and the matrix is a transition matrix. The notable feature of a Markov chain model is that it is historyless in that with a fixed transition matrix, the next state depends only on the current state, not on any prior states. Thus a player, say, who arrives at by starting in state , then going to state , then to , and then to has at this point exactly the same chance of moving next to state as does a player whose history was to start in , then go to , and to , and then to .
Here is a Markov chain from sociology. A study (Macdonald & Ridge 1988, p. 202) divided occupations in the United Kingdom into upper level (executives and professionals), middle level (supervisors and skilled manual workers), and lower level (unskilled). To determine the mobility across these levels in a generation, about two thousand men were asked, "At which level are you, and at which level was your father when you were fourteen years old?" This equation summarizes the results.
For instance, a child of a lower class worker has a probability of growing up to be middle class. Notice that the Markov model assumption about history seems reasonable— we expect that while a parent's occupation has a direct influence on the occupation of the child, the grandparent's occupation has no such direct influence. With the initial distribution of the respondents's fathers given below, this table lists the distributions for the next five generations.
One more example, from a very important subject, indeed. The World Series of American baseball is played between the team winning the American League and the team winning the National League (we follow [Brunner] but see also [Woodside]). The series is won by the first team to win four games. That means that a series is in one of twenty-four states: 0-0 (no games won yet by either team), 1-0 (one game won for the American League team and no games for the National League team), etc. If we assume that there is a probability that the American League team wins each game then we have the following transition matrix.
An especially interesting special case is ; this table lists the resulting components of the through vectors. (The code to generate this table in the computer algebra system Octave follows the exercises.)
| 0-0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1-0 | 0 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0-1 | 0 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2-0 | 0 | 0 | 0.25 | 0 | 0 | 0 | 0 | 0 |
| 1-1 | 0 | 0 | 0.5 | 0 | 0 | 0 | 0 | 0 |
| 0-2 | 0 | 0 | 0.25 | 0 | 0 | 0 | 0 | 0 |
| 3-0 | 0 | 0 | 0 | 0.125 | 0 | 0 | 0 | 0 |
| 2-1 | 0 | 0 | 0 | 0.325 | 0 | 0 | 0 | 0 |
| 1-2 | 0 | 0 | 0 | 0.325 | 0 | 0 | 0 | 0 |
| 0-3 | 0 | 0 | 0 | 0.125 | 0 | 0 | 0 | 0 |
| 4-0 | 0 | 0 | 0 | 0 | 0.0625 | 0.0625 | 0.0625 | 0.0625 |
| 3-1 | 0 | 0 | 0 | 0 | 0.25 | 0 | 0 | 0 |
| 2-2 | 0 | 0 | 0 | 0 | 0.375 | 0 | 0 | 0 |
| 1-3 | 0 | 0 | 0 | 0 | 0.25 | 0 | 0 | 0 |
| 0-4 | 0 | 0 | 0 | 0 | 0.0625 | 0.0625 | 0.0625 | 0.0625 |
| 4-1 | 0 | 0 | 0 | 0 | 0 | 0.125 | 0.125 | 0.125 |
| 3-2 | 0 | 0 | 0 | 0 | 0 | 0.3125 | 0 | 0 |
| 2-3 | 0 | 0 | 0 | 0 | 0 | 0.3125 | 0 | 0 |
| 1-4 | 0 | 0 | 0 | 0 | 0 | 0.125 | 0.125 | 0.125 |
| 4-2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.15625 | 0.15625 |
| 3-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3125 | 0 |
| 2-4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.15625 | 0.15625 |
| 4-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.15625 |
| 3-4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.15625 |
Note that evenly-matched teams are likely to have a long series— there is a probability of that the series goes at least six games.
One reason for the inclusion of this Topic is that Markov chains are one of the most widely-used applications of matrix operations. Another reason is that it provides an example of the use of matrices where we do not consider the significance of the maps represented by the matrices. For more on Markov chains, there are many sources such as (Kemeny & Snell 1960) and (Iosifescu 1980).
Exercises
Use a computer for these problems. You can, for instance, adapt the Octave script given below.
- Problem 1
These questions refer to the coin-flipping game.
- Check the computations in the table at the end of the first paragraph.
- Consider the second row of the vector table. Note that this row has alternating 's. Must be when is odd? Prove that it must be, or produce a counterexample.
- Perform a computational experiment to estimate the chance that the player ends at five dollars, starting with one dollar, two dollars, and four dollars.
- Problem 2
We consider throws of a die, and say the system is in state if the largest number yet appearing on the die was .
- Give the transition matrix.
- Start the system in state , and run it for five throws. What is the vector at the end?
(Feller 1968, p. 424)
- Problem 3
There has been much interest in whether industries in the United States are moving from the Northeast and North Central regions to the South and West, motivated by the warmer climate, by lower wages, and by less unionization. Here is the transition matrix for large firms in Electric and Electronic Equipment (Kelton 1983, p. 43)
| NE | NC | S | W | Z | |
| NE | 0.787 | 0 | 0 | 0.111 | 0.102 |
| NC | 0 | 0.966 | 0.034 | 0 | 0 |
| S | 0 | 0.063 | 0.937 | 0 | 0 |
| W | 0 | 0 | 0.074 | 0.612 | 0.314 |
| Z | 0.021 | 0.009 | 0.005 | 0.010 | 0.954 |
For example, a firm in the Northeast region will be in the West region next year with probability . (The Z entry is a "birth-death" state. For instance, with probability a large Electric and Electronic Equipment firm from the Northeast will move out of this system next year: go out of business, move abroad, or move to another category of firm. There is a probability that a firm in the National Census of Manufacturers will move into Electronics, or be created, or move in from abroad, into the Northeast. Finally, with probability a firm out of the categories will stay out, according to this research.)
- Does the Markov model assumption of lack of history seem justified?
- Assume that the initial distribution is even, except that the value at is . Compute the vectors for through .
- Suppose that the initial distribution is this.
NE NC S W Z 0.0000 0.6522 0.3478 0.0000 0.0000 Calculate the distributions for through .
- Find the distribution for and . Has the system settled down to an equilibrium?
- Problem 4
This model has been suggested for some kinds of learning (Wickens 1982, p. 41). The learner starts in an undecided state . Eventually the learner has to decide to do either response (that is, end in state ) or response (ending in ). However, the learner doesn't jump right from being undecided to being sure is the correct thing to do (or ). Instead, the learner spends some time in a "tentative-" state, or a "tentative-" state, trying the response out (denoted here and ). Imagine that once the learner has decided, it is final, so once or is entered it is never left. For the other state changes, imagine a transition is made with probability in either direction.
- Construct the transition matrix.
- Take and take the initial vector to be at . Run this for five steps. What is the chance of ending up at ?
- Do the same for .
- Graph versus the chance of ending at . Is there a threshold value for , above which the learner is almost sure not to take longer than five steps?
- Problem 5
A certain town is in a certain country (this is a hypothetical problem). Each year ten percent of the town dwellers move to other parts of the country. Each year one percent of the people from elsewhere move to the town. Assume that there are two states , living in town, and , living elsewhere.
- Construct the transistion matrix.
- Starting with an initial distribution and , get the results for the first ten years.
- Do the same for .
- Are the two outcomes alike or different?
- Problem 6
For the World Series application, use a computer to generate the seven vectors for and .
- What is the chance of the National League team winning it all, even though they have only a probability of or of winning any one game?
- Graph the probability against the chance that the American League team wins it all. Is there a threshold value— a above which the better team is essentially ensured of winning?
(Some sample code is included below.)
- Problem 7
A Markov matrix has each entry positive and each column sums to .
- Check that the three transistion matrices shown in this Topic meet these two conditions. Must any transition matrix do so?
- Observe that if and then is a transition matrix from to . Show that a power of a Markov matrix is also a Markov matrix.
- Generalize the prior item by proving that the product of two appropriately-sized Markov matrices is a Markov matrix.
Computer Code
This script markov.m for the computer algebra system Octave was used to generate the table of World Series outcomes. (The sharp character # marks the rest of a line as a comment.)
# Octave script file to compute chance of World Series outcomes. function w = markov(p,v) q = 1-p; A=[0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 0-0 p,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 1-0 q,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 0-1_ 0,p,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 2-0 0,q,p,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 1-1 0,0,q,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 0-2__ 0,0,0,p,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 3-0 0,0,0,q,p,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 2-1 0,0,0,0,q,p, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 1-2_ 0,0,0,0,0,q, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 0-3 0,0,0,0,0,0, p,0,0,0,1,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 4-0 0,0,0,0,0,0, q,p,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 3-1__ 0,0,0,0,0,0, 0,q,p,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 2-2 0,0,0,0,0,0, 0,0,q,p,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0; # 1-3 0,0,0,0,0,0, 0,0,0,q,0,0, 0,0,1,0,0,0, 0,0,0,0,0,0; # 0-4_ 0,0,0,0,0,0, 0,0,0,0,0,p, 0,0,0,1,0,0, 0,0,0,0,0,0; # 4-1 0,0,0,0,0,0, 0,0,0,0,0,q, p,0,0,0,0,0, 0,0,0,0,0,0; # 3-2 0,0,0,0,0,0, 0,0,0,0,0,0, q,p,0,0,0,0, 0,0,0,0,0,0; # 2-3__ 0,0,0,0,0,0, 0,0,0,0,0,0, 0,q,0,0,0,0, 1,0,0,0,0,0; # 1-4 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,p,0, 0,1,0,0,0,0; # 4-2 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,q,p, 0,0,0,0,0,0; # 3-3_ 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,q, 0,0,0,1,0,0; # 2-4 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,p,0,1,0; # 4-3 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,q,0,0,1]; # 3-4 w = A * v; endfunction
Then the Octave session was this.
> v0=[1;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0] > p=.5 > v1=markov(p,v0) > v2=markov(p,v1) ...
Translating to another computer algebra system should be easy— all have commands similar to these.
Topic: Orthonormal Matrices
In The Elements, Euclid considers two figures to be the same if they have the same size and shape. That is, the triangles below are not equal because they are not the same set of points. But they are congruent— essentially indistinguishable for Euclid's purposes— because we can imagine picking the plane up, sliding it over and rotating it a bit, although not warping or stretching it, and then putting it back down, to superimpose the first figure on the second. (Euclid never explicitly states this principle but he uses it often (Casey 1890).)
In modern terminology, "picking the plane up ..." means considering a map from the plane to itself. Euclid has limited consideration to only certain transformations of the plane, ones that may possibly slide or turn the plane but not bend or stretch it. Accordingly, we define a map to be distance-preserving or a rigid motion or an isometry, if for all points , the distance from to equals the distance from to . We also define a plane figure to be a set of points in the plane and we say that two figures are congruent if there is a distance-preserving map from the plane to itself that carries one figure onto the other.
Many statements from Euclidean geometry follow easily from these definitions. Some are: (i) collinearity is invariant under any distance-preserving map (that is, if , , and are collinear then so are , , and ), (ii) betweeness is invariant under any distance-preserving map (if is between and then so is between and ), (iii) the property of being a triangle is invariant under any distance-preserving map (if a figure is a triangle then the image of that figure is also a triangle), (iv) and the property of being a circle is invariant under any distance-preserving map. In 1872, F. Klein suggested that Euclidean geometry can be characterized as the study of properties that are invariant under these maps. (This forms part of Klein's Erlanger Program, which proposes the organizing principle that each kind of geometry— Euclidean, projective, etc.— can be described as the study of the properties that are invariant under some group of transformations. The word "group" here means more than just "collection", but that lies outside of our scope.)
We can use linear algebra to characterize the distance-preserving maps of the plane.
First, there are distance-preserving transformations of the plane that are not linear. The obvious example is this translation.
However, this example turns out to be the only example, in the sense that if is distance-preserving and sends to then the map is linear. That will follow immediately from this statement: a map that is distance-preserving and sends to itself is linear. To prove this equivalent statement, let
for some .
Then to show that is linear, we can show that
it can be represented by a matrix, that is, that acts in this way
for all .
Recall that if we fix three non-collinear points
then any point
in the plane can be described by giving its distance from those three.
So any point in the domain is determined by its distance from
the three fixed points , , and .
Similarly, any point
in the codomain is determined by its distance from
the three fixed points , , and
(these three are not collinear because, as mentioned above,
collinearity is invariant and
, , and are not collinear).
In fact, because is distance-preserving, we can say more: for the
point in the plane that is determined by being
the distance from ,
the distance from , and the distance from ,
its image must be the unique point in the codomain
that is determined by being from ,
from ,
and from .
Because of the uniqueness,
checking that the action in () works in the
, , and cases
( is assumed to send to itself)
and
suffices to show that () describes .
Those checks are routine.
Thus, any distance-preserving can be written for some constant vector and linear map that is distance-preserving.
Not every linear map is distance-preserving, for example, does not preserve distances. But there is a neat characterization: a linear transformation of the plane is distance-preserving if and only if both and is orthogonal to . The "only if" half of that statement is easy— because is distance-preserving it must preserve the lengths of vectors, and because is distance-preserving the Pythagorean theorem shows that it must preserve orthogonality. For the "if" half, it suffices to check that the map preserves lengths of vectors, because then for all and the distance between the two is preserved . For that check, let
and, with the "if" assumptions that
and we have this.
One thing that is neat about this characterization is that we can easily recognize matrices that represent such a map with respect to the standard bases. Those matrices have that when the columns are written as vectors then they are of length one and are mutually orthogonal. Such a matrix is called an orthonormal matrix or orthogonal matrix (the first term is commonly used to mean not just that the columns are orthogonal, but also that they have length one).
We can use this insight to delimit the geometric actions possible in distance-preserving maps. Because , any is mapped by to lie somewhere on the circle about the origin that has radius equal to the length of . In particular, and are mapped to the unit circle. What's more, once we fix the unit vector as mapped to the vector with components and then there are only two places where can be mapped if that image is to be perpendicular to the first vector: one where maintains its position a quarter circle clockwise from
and one where is is mapped a quarter circle counterclockwise.
We can geometrically describe these two cases. Let be the angle between the -axis and the image of , measured counterclockwise. The first matrix above represents, with respect to the standard bases, a rotation of the plane by radians.
The second matrix above represents a reflection of the plane through the line bisecting the angle between and .
(This picture shows reflected up into the first quadrant and reflected down into the fourth quadrant.)
Note again: the angle between and runs counterclockwise, and in the first map above the angle from to is also counterclockwise, so the orientation of the angle is preserved. But in the second map the orientation is reversed. A distance-preserving map is direct if it preserves orientations and opposite if it reverses orientation.
So, we have characterized the Euclidean study of congruence: it considers, for plane figures, the properties that are invariant under combinations of (i) a rotation followed by a translation, or (ii) a reflection followed by a translation (a reflection followed by a non-trivial translation is a glide reflection).
Another idea, besides congruence of figures, encountered in elementary geometry is that figures are similar if they are congruent after a change of scale. These two triangles are similar since the second is the same shape as the first, but -ths the size.
From the above work, we have that figures are similar if there is an orthonormal matrix such that the points on one are derived from the points by for some nonzero real number and constant vector .
Although many of these ideas were first explored by Euclid, mathematics is timeless and they are very much in use today. One application of the maps studied above is in computer graphics. We can, for example, animate this top view of a cube by putting together film frames of it rotating; that's a rigid motion.
 |  | 
|
| Frame 1 | Frame 2 | Frame 3 |
We could also make the cube appear to be moving away from us by producing film frames of it shrinking, which gives us figures that are similar.
 |  | 
|
| Frame 1: | Frame 2: | Frame 3: |
Computer graphics incorporates techniques from linear algebra in many other ways (see Problem 4).
So the analysis above of distance-preserving maps is useful as well as interesting. A beautiful book that explores some of this area is (Weyl 1952). More on groups, of transformations and otherwise, can be found in any book on Modern Algebra, for instance (Birkhoff & MacLane 1965). More on Klein and the Erlanger Program is in (Yaglom 1988).
Exercises
- Problem 1
Decide if each of these is an orthonormal matrix.
- Problem 2
Write down the formula for each of these distance-preserving maps.
- the map that rotates radians, and then translates by
- the map that reflects about the line
- the map that reflects about and translates over and up
- Problem 3
- The proof that a map that is distance-preserving and sends the zero vector to itself incidentally shows that such a map is one-to-one and onto (the point in the domain determined by , , and corresponds to the point in the codomain determined by those three). Therefore any distance-preserving map has an inverse. Show that the inverse is also distance-preserving.
- Prove that congruence is an equivalence relation between plane figures.
- Problem 4
In practice the matrix for the distance-preserving linear transformation and the translation are often combined into one. Check that these two computations yield the same first two components.
(These are homogeneous coordinates;
see the Topic on Projective Geometry).
- Problem 5
- Verify that the properties described in the second paragraph of this Topic as invariant under distance-preserving maps are indeed so.
- Give two more properties that are of interest in Euclidean geometry from your experience in studying that subject that are also invariant under distance-preserving maps.
- Give a property that is not of interest in Euclidean geometry and is not invariant under distance-preserving maps.
Chapter IV - Determinants
In the first chapter of this book we considered linear systems and we picked out the special case of systems with the same number of equations as unknowns, those of the form where is a square matrix. We noted a distinction between two classes of 's. While such systems may have a unique solution or no solutions or infinitely many solutions, if a particular is associated with a unique solution in any system, such as the homogeneous system , then is associated with a unique solution for every . We call such a matrix of coefficients "nonsingular". The other kind of , where every linear system for which it is the matrix of coefficients has either no solution or infinitely many solutions, we call "singular".
Through the second and third chapters the value of this distinction has been a theme. For instance, we now know that nonsingularity of an matrix is equivalent to each of these:
- a system has a solution, and that solution is unique;
- Gauss-Jordan reduction of yields an identity matrix;
- the rows of form a linearly independent set;
- the columns of form a basis for ;
- any map that represents is an isomorphism;
- an inverse matrix exists.
So when we look at a particular square matrix, the question of whether it is nonsingular is one of the first things that we ask. This chapter develops a formula to determine this. (Since we will restrict the discussion to square matrices, in this chapter we will usually simply say "matrix" in place of "square matrix".)
More precisely, we will develop infinitely many formulas, one for matrices, one for matrices, etc. Of course, these formulas are related — that is, we will develop a family of formulas, a scheme that describes the formula for each size.
Section I - Definition
For matrices, determining nonsingularity is trivial.
is nonsingular iff
The formula came out in the course of developing the inverse.
is nonsingular iff
The formula can be produced similarly (see Problem 9).
is nonsingular iff
With these cases in mind, we posit a family of formulas, , , etc. For each the formula gives rise to a determinant function such that an matrix is nonsingular if and only if . (We usually omit the subscript because if is then "" could only mean "".)
1 - Exploration
This subsection is optional. It briefly describes how an investigator might come to a good general definition, which is given in the next subsection.
The three cases above don't show an evident pattern to use for the general formula. We may spot that the term has one letter, that the terms and have two letters, and that the terms , etc., have three letters. We may also observe that in those terms there is a letter from each row and column of the matrix, e.g., the letters in the term
come one from each row and one from each column. But these observations perhaps seem more puzzling than enlightening. For instance, we might wonder why some of the terms are added while others are subtracted.
A good problem solving strategy is to see what properties a solution must have and then search for something with those properties. So we shall start by asking what properties we require of the formulas.
At this point, our primary way to decide whether a matrix is singular is to do Gaussian reduction and then check whether the diagonal of resulting echelon form matrix has any zeroes (that is, to check whether the product down the diagonal is zero). So, we may expect that the proof that a formula determines singularity will involve applying Gauss' method to the matrix, to show that in the end the product down the diagonal is zero if and only if the determinant formula gives zero. This suggests our initial plan: we will look for a family of functions with the property of being unaffected by row operations and with the property that a determinant of an echelon form matrix is the product of its diagonal entries. Under this plan, a proof that the functions determine singularity would go, "Where is the Gaussian reduction, the determinant of equals the determinant of (because the determinant is unchanged by row operations), which is the product down the diagonal, which is zero if and only if the matrix is singular". In the rest of this subsection we will test this plan on the and determinants that we know. We will end up modifying the "unaffected by row operations" part, but not by much.
The first step in checking the plan is to test whether the and formulas are unaffected by the row operation of pivoting: if
then is ? This check of the determinant after the operation
shows that it is indeed unchanged, and the other pivot gives the same result. The pivot leaves the determinant unchanged
as do the other pivot operations.
So there seems to be promise in the plan. Of course, perhaps the determinant formula is affected by pivoting. We are exploring a possibility here and we do not yet have all the facts. Nonetheless, so far, so good.
The next step is to compare with for the operation
of swapping two rows. The row swap
does not yield . This swap inside of a matrix
also does not give the same determinant as before the swap — again there is a sign change. Trying a different swap
also gives a change of sign.
Thus, row swaps appear to change the sign of a determinant. This modifies our plan, but does not wreck it. We intend to decide nonsingularity by considering only whether the determinant is zero, not by considering its sign. Therefore, instead of expecting determinants to be entirely unaffected by row operations, will look for them to change sign on a swap.
To finish, we compare to for the operation
of multiplying a row by a scalar . One of the cases is
and the other case has the same result. Here is one case
and the other two are similar. These lead us to suspect that multiplying a row by multiplies the determinant by . This fits with our modified plan because we are asking only that the zeroness of the determinant be unchanged and we are not focusing on the determinant's sign or magnitude.
In summary, to develop the scheme for the formulas to compute determinants, we look for determinant functions that remain unchanged under the pivoting operation, that change sign on a row swap, and that rescale on the rescaling of a row. In the next two subsections we will find that for each such a function exists and is unique.
For the next subsection, note that, as above, scalars come out of each row without affecting other rows. For instance, in this equality
the isn't factored out of all three rows, only out of the top row. The determinant acts on each row of independently of the other rows. When we want to use this property of determinants, we shall write the determinant as a function of the rows: "", instead of as "" or "". The definition of the determinant that starts the next subsection is written in this way.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Evaluate the determinant of each.
- Problem 2
Evaluate the determinant of each.
- This exercise is recommended for all readers.
- Problem 3
Verify that the determinant of an upper-triangular matrix is the product down the diagonal.
Do lower-triangular matrices work the same way?
- This exercise is recommended for all readers.
- Problem 4
Use the determinant to decide if each is singular or nonsingular.
- Problem 5
Singular or nonsingular? Use the determinant to decide.
- This exercise is recommended for all readers.
- Problem 6
Each pair of matrices differ by one row operation. Use this operation to compare with .
- Problem 7
Show this.
- This exercise is recommended for all readers.
- Problem 8
Which real numbers make this matrix singular?
- Problem 9
Do the Gaussian reduction to check the formula for matrices stated in the preamble to this section.
is nonsingular iff
- Problem 10
Show that the equation of a line in thru and is expressed by this determinant.
- This exercise is recommended for all readers.
- Problem 11
Many people know this mnemonic for the determinant of a matrix: first repeat the first two columns and then sum the products on the forward diagonals and subtract the products on the backward diagonals. That is, first write
and then calculate this.
- Check that this agrees with the formula given in the preamble to this section.
- Does it extend to other-sized determinants?
- Problem 12
The cross product of the vectors
is the vector computed as this determinant.
Note that the first row is composed of vectors, the vectors from the standard basis for . Show that the cross product of two vectors is perpendicular to each vector.
- Problem 13
Prove that each statement holds for matrices.
- The determinant of a product is the product of the determinants .
- If is invertible then the determinant of the inverse is the inverse of the determinant .
Matrices and are similar if there is a nonsingular matrix such that . (This definition is in Chapter Five.) Show that similar matrices have the same determinant.
- This exercise is recommended for all readers.
- Problem 14
Prove that the area of this region in the plane
is equal to the value of this determinant.
Compare with this.
- Problem 15
Prove that for matrices, the determinant of a matrix equals the determinant of its transpose. Does that also hold for matrices?
- This exercise is recommended for all readers.
- Problem 16
Is the determinant function linear — is ?
- Problem 17
Show that if is then for any scalar .
- Problem 18
Which real numbers make
singular? Explain geometrically.
- ? Problem 19
If a third order determinant has elements , , ..., , what is the maximum value it may have? (Haggett & Saunders 1955)
2 - Properties of Determinants
As described above, we want a formula to determine whether an matrix is nonsingular. We will not begin by stating such a formula. Instead, we will begin by considering the function that such a formula calculates. We will define the function by its properties, then prove that the function with these properties exists and is unique and also describe formulas that compute this function. (Because we will show that the function exists and is unique, from the start we will say "" instead of "if there is a determinant function then " and "the determinant" instead of "any determinant".)
- Definition 2.1
A determinant is a function such that
- for
- for
- for
- where is an identity matrix
(the 's are the rows of the matrix). We often write for .
- Remark 2.2
Property (2) is redundant since
swaps rows and . It is listed only for convenience.
The first result shows that a function satisfying these conditions gives a criteria for nonsingularity. (Its last sentence is that, in the context of the first three conditions, (4) is equivalent to the condition that the determinant of an echelon form matrix is the product down the diagonal.)
- Lemma 2.3
A matrix with two identical rows has a determinant of zero. A matrix with a zero row has a determinant of zero. A matrix is nonsingular if and only if its determinant is nonzero. The determinant of an echelon form matrix is the product down its diagonal.
- Proof
To verify the first sentence, swap the two equal rows. The sign of the determinant changes, but the matrix is unchanged and so its determinant is unchanged. Thus the determinant is zero.
For the second sentence, we multiply a zero row by −1 and apply property (3). Multiplying a zero row with a constant leaves the matrix unchanged, so property (3) implies that . The only way this can be is if .
For the third sentence, where is the Gauss-Jordan reduction, by the definition the determinant of is zero if and only if the determinant of is zero (although they could differ in sign or magnitude). A nonsingular Gauss-Jordan reduces to an identity matrix and so has a nonzero determinant. A singular reduces to a with a zero row; by the second sentence of this lemma its determinant is zero.
Finally, for the fourth sentence, if an echelon form matrix is singular then it has a zero on its diagonal, that is, the product down its diagonal is zero. The third sentence says that if a matrix is singular then its determinant is zero. So if the echelon form matrix is singular then its determinant equals the product down its diagonal.
If an echelon form matrix is nonsingular then none of its diagonal entries is zero so we can use property (3) of the definition to factor them out (again, the vertical bars indicate the determinant operation).
Next, the Jordan half of Gauss-Jordan elimination, using property (1) of the definition, leaves the identity matrix.
Therefore, if an echelon form matrix is nonsingular then its determinant is the product down its diagonal.
That result gives us a way to compute the value of a determinant function on a matrix. Do Gaussian reduction, keeping track of any changes of sign caused by row swaps and any scalars that are factored out, and then finish by multiplying down the diagonal of the echelon form result. This procedure takes the same time as Gauss' method and so is sufficiently fast to be practical on the size matrices that we see in this book.
- Example 2.4
Doing determinants
with Gauss' method won't give a big savings because the determinant formula is so easy. However, a determinant is usually easier to calculate with Gauss' method than with the formula given earlier.
- Example 2.5
Determinants of matrices any bigger than are almost always most quickly done with this Gauss' method procedure.
The prior example illustrates an important point. Although we have not yet found a determinant formula, if one exists then we know what value it gives to the matrix — if there is a function with properties (1)-(4) then on the above matrix the function must return .
- Lemma 2.6
For each , if there is an determinant function then it is unique.
- Proof
For any matrix we can perform Gauss' method on the matrix, keeping track of how the sign alternates on row swaps, and then multiply down the diagonal of the echelon form result. By the definition and the lemma, all determinant functions must return this value on this matrix. Thus all determinant functions are equal, that is, there is only one input argument/output value relationship satisfying the four conditions.
The "if there is an determinant function" emphasizes that, although we can use Gauss' method to compute the only value that a determinant function could possibly return, we haven't yet shown that such a determinant function exists for all . In the rest of the section we will produce determinant functions.
Exercises
For these, assume that an determinant function exists for all .
- This exercise is recommended for all readers.
- Problem 1
Use Gauss' method to find each determinant.
- Problem 2
- Use Gauss' method to find each.
- Problem 3
For which values of does this system have a unique solution?
- This exercise is recommended for all readers.
- Problem 4
Express each of these in terms of .
- This exercise is recommended for all readers.
- Problem 5
Find the determinant of a diagonal matrix.
- Problem 6
Describe the solution set of a homogeneous linear system if the determinant of the matrix of coefficients is nonzero.
- This exercise is recommended for all readers.
- Problem 7
Show that this determinant is zero.
- Problem 8
- Find the , , and matrices with entry given by .
- Find the determinant of the square matrix with entry .
- Problem 9
- Find the , , and matrices with entry given by .
- Find the determinant of the square matrix with entry .
- This exercise is recommended for all readers.
- Problem 10
Show that determinant functions are not linear by giving a case where .
- Problem 11
The second condition in the definition, that row swaps change the sign of a determinant, is somewhat annoying. It means we have to keep track of the number of swaps, to compute how the sign alternates. Can we get rid of it? Can we replace it with the condition that row swaps leave the determinant unchanged? (If so then we would need new , , and formulas, but that would be a minor matter.)
- Problem 12
Prove that the determinant of any triangular matrix, upper or lower, is the product down its diagonal.
- Problem 13
Refer to the definition of elementary matrices in the Mechanics of Matrix Multiplication subsection.
- What is the determinant of each kind of elementary matrix?
- Prove that if is any elementary matrix then for any appropriately sized .
- (This question doesn't involve determinants.) Prove that if is singular then a product is also singular.
- Show that .
- Show that if is nonsingular then .
- Problem 14
Prove that the determinant of a product is the product of the determinants in this way. Fix the matrix and consider the function given by .
- Check that satisfies property (1) in the definition of a determinant function.
- Check property (2).
- Check property (3).
- Check property (4).
- Conclude the determinant of a product is the product of the determinants.
- Problem 15
A submatrix of a given matrix is one that can be obtained by deleting some of the rows and columns of . Thus, the first matrix here is a submatrix of the second.
Prove that for any square matrix, the rank of the matrix is if and only if is the largest integer such that there is an submatrix with a nonzero determinant.
- This exercise is recommended for all readers.
- Problem 16
Prove that a matrix with rational entries has a rational determinant.
- ? Problem 17
Find the element of likeness in (a) simplifying a fraction, (b) powdering the nose, (c) building new steps on the church, (d) keeping emeritus professors on campus, (e) putting , , in the determinant
3 - The Permutation Expansion
The prior subsection defines a function to be a determinant if it satisfies four conditions and shows that there is at most one determinant function for each . What is left is to show that for each such a function exists.
How could such a function not exist? After all, we have done computations that start with a square matrix, follow the conditions, and end with a number.
The difficulty is that, as far as we know, the computation might not give a well-defined result. To illustrate this possibility, suppose that we were to change the second condition in the definition of determinant to be that the value of a determinant does not change on a row swap. By Remark 2.2 we know that this conflicts with the first and third conditions. Here is an instance of the conflict: here are two Gauss' method reductions of the same matrix, the first without any row swap
and the second with a swap.
Following Definition 2.1 gives that both calculations yield the determinant since in the second one we keep track of the fact that the row swap changes the sign of the result of multiplying down the diagonal. But if we follow the supposition and change the second condition then the two calculations yield different values, and . That is, under the supposition the outcome would not be well-defined — no function exists that satisfies the changed second condition along with the other three.
Of course, observing that Definition 2.1 does the right thing in this one instance is not enough; what we will do in the rest of this section is to show that there is never a conflict. The natural way to try this would be to define the determinant function with: "The value of the function is the result of doing Gauss' method, keeping track of row swaps, and finishing by multiplying down the diagonal". (Since Gauss' method allows for some variation, such as a choice of which row to use when swapping, we would have to fix an explicit algorithm.) Then we would be done if we verified that this way of computing the determinant satisfies the four properties. For instance, if and are related by a row swap then we would need to show that this algorithm returns determinants that are negatives of each other. However, how to verify this is not evident. So the development below will not proceed in this way. Instead, in this subsection we will define a different way to compute the value of a determinant, a formula, and we will use this way to prove that the conditions are satisfied.
The formula that we shall use is based on an insight gotten from property (3) of the definition of determinants. This property shows that determinants are not linear.
- Example 3.1
For this matrix .
Instead, the scalar comes out of each of the two rows.
Since scalars come out a row at a time, we might guess that determinants are linear a row at a time.
- Definition 3.2
Let be a vector space. A map is multilinear if
for and .
- Lemma 3.3
Determinants are multilinear.
- Proof
The definition of determinants gives property (2) (Lemma 2.3 following that definition covers the case) so we need only check property (1).
If the set is linearly dependent then all three matrices are singular and so all three determinants are zero and the equality is trivial. Therefore assume that the set is linearly independent. This set of -wide row vectors has members, so we can make a basis by adding one more vector . Express and with respect to this basis
giving this.
By the definition of determinant, the value of is unchanged by the pivot operation of adding to .
Then, to the result, we can add , etc. Thus
(using (2) for the second equality). To finish, bring and back inside in front of and use pivoting again, this time to reconstruct the expressions of and in terms of the basis, e.g., start with the pivot operations of adding to and to , etc.
Multilinearity allows us to expand a determinant into a sum of determinants, each of which involves a simple matrix.
- Example 3.4
We can use multilinearity to split this determinant into two, first breaking up the first row
and then separating each of those two, breaking along the second rows.
We are left with four determinants, such that in each row of each matrix there is a single entry from the original matrix.
- Example 3.5
In the same way, a determinant separates into a sum of many simpler determinants. We start by splitting along the first row, producing three determinants (the zero in the position is underlined to set it off visually from the zeroes that appear in the splitting).
Each of these three will itself split in three along the second row. Each of the resulting nine splits in three along the third row, resulting in twenty seven determinants
such that each row contains a single entry from the starting matrix.
So an determinant expands into a sum of determinants where each row of each summands contains a single entry from the starting matrix. However, many of these summand determinants are zero.
- Example 3.6
In each of these three matrices from the above expansion, two of the rows have their entry from the starting matrix in the same column, e.g., in the first matrix, the and the both come from the first column.
Any such matrix is singular, because in each, one row is a multiple of the other (or is a zero row). Thus, any such determinant is zero, by Lemma 2.3.
Therefore, the above expansion of the determinant into the sum of the twenty seven determinants simplifies to the sum of these six.
We can bring out the scalars.
To finish, we evaluate those six determinants by row-swapping them to the identity matrix, keeping track of the resulting sign changes.
That example illustrates the key idea. We've applied multilinearity to a determinant to get separate determinants, each with one distinguished entry per row. We can drop most of these new determinants because the matrices are singular, with one row a multiple of another. We are left with the one-entry-per-row determinants also having only one entry per column (one entry from the original determinant, that is). And, since we can factor scalars out, we can further reduce to only considering determinants of one-entry-per-row-and-column matrices where the entries are ones.
These are permutation matrices. Thus, the determinant can be computed in this three-step way (Step 1) for each permutation matrix, multiply together the entries from the original matrix where that permutation matrix has ones, (Step 2) multiply that by the determinant of the permutation matrix and (Step 3) do that for all permutation matrices and sum the results together.
To state this as a formula, we introduce a notation for permutation matrices. Let be the row vector that is all zeroes except for a one in its -th entry, so that the four-wide is . We can construct permutation matrices by permuting — that is, scrambling — the numbers , , ..., , and using them as indices on the 's. For instance, to get a permutation matrix matrix, we can scramble the numbers from to into this sequence and take the corresponding row vector 's.
- Definition 3.7
An -permutation is a sequence consisting of an arrangement of the numbers , , ..., .
- Example 3.8
The -permutations are and . These are the associated permutation matrices.
We sometimes write permutations as functions, e.g., , and . Then the rows of are and .
The -permutations are , , , , , and . Here are two of the associated permutation matrices.
For instance, the rows of are , , and .
- Definition 3.9
The permutation expansion for determinants is
where are all of the -permutations.
This formula is often written in summation notation
read aloud as "the sum, over all permutations , of terms having the form ". This phrase is just a restating of the three-step process (Step 1) for each permutation matrix, compute (Step 2) multiply that by and (Step 3) sum all such terms together.
- Example 3.10
The familiar formula for the determinant of a matrix can be derived in this way.
(the second permutation matrix takes one row swap to pass to the identity). Similarly, the formula for the determinant of a matrix is this.
Computing a determinant by permutation expansion usually takes longer than Gauss' method. However, here we are not trying to do the computation efficiently, we are instead trying to give a determinant formula that we can prove to be well-defined. While the permutation expansion is impractical for computations, it is useful in proofs. In particular, we can use it for the result that we are after.
- Theorem 3.11
For each there is a determinant function.
The proof is deferred to the following subsection. Also there is the proof of the next result (they share some features).
- Theorem 3.12
The determinant of a matrix equals the determinant of its transpose.
The consequence of this theorem is that, while we have so far stated results in terms of rows (e.g., determinants are multilinear in their rows, row swaps change the signum, etc.), all of the results also hold in terms of columns. The final result gives examples.
- Corollary 3.13
A matrix with two equal columns is singular. Column swaps change the sign of a determinant. Determinants are multilinear in their columns.
- Proof
For the first statement, transposing the matrix results in a matrix with the same determinant, and with two equal rows, and hence a determinant of zero. The other two are proved in the same way.
We finish with a summary
(although the final subsection contains the unfinished business of
proving the two theorems).
Determinant functions exist, are unique, and we know how to compute them.
As for what determinants are about, perhaps these lines
(Kemp 1982) help make it memorable.
Determinant none,
Solution: lots or none.
Determinant some,
Solution: just one.
Exercises
These summarize the notation used in this book for the - and - permutations.
- This exercise is recommended for all readers.
- Problem 1
Compute the determinant by using the permutation expansion.
- This exercise is recommended for all readers.
- Problem 2
Compute these both with Gauss' method and with the permutation expansion formula.
- This exercise is recommended for all readers.
- Problem 3
Use the permutation expansion formula to derive the formula for determinants.
- Problem 4
List all of the -permutations.
- Problem 5
A permutation, regarded as a function from the set to itself, is one-to-one and onto. Therefore, each permutation has an inverse.
- Find the inverse of each -permutation.
- Find the inverse of each -permutation.
- Problem 6
Prove that is multilinear if and only if for all and , this holds.
- Problem 7
Find the only nonzero term in the permutation expansion of this matrix.
Compute that determinant by finding the signum of the associated permutation.
- Problem 8
How would determinants change if we changed property (4) of the definition to read that ?
- Problem 9
Verify the second and third statements in Corollary 3.13.
- This exercise is recommended for all readers.
- Problem 10
Show that if an matrix has a nonzero determinant then any column vector can be expressed as a linear combination of the columns of the matrix.
- Problem 11
True or false: a matrix whose entries are only zeros or ones has a determinant equal to zero, one, or negative one. (Strang 1980)
- Problem 12
- Show that there are terms in the permutation expansion formula of a matrix.
- How many are sure to be zero if the entry is zero?
- Problem 13
How many -permutations are there?
- Problem 14
A matrix is skew-symmetric if , as in this matrix.
Show that skew-symmetric matrices with nonzero determinants exist only for even .
- This exercise is recommended for all readers.
- Problem 15
What is the smallest number of zeros, and the placement of those zeros, needed to ensure that a matrix has a determinant of zero?
- This exercise is recommended for all readers.
- Problem 16
If we have data points and want to find a polynomial passing through those points then we can plug in the points to get an equation/ unknown linear system. The matrix of coefficients for that system is called the Vandermonde matrix. Prove that the determinant of the transpose of that matrix of coefficients
equals the product, over all indices with , of terms of the form . (This shows that the determinant is zero, and the linear system has no solution, if and only if the 's in the data are not distinct.)
- Problem 17
A matrix can be divided into blocks, as here,
which shows four blocks, the square and ones in the upper left and lower right, and the zero blocks in the upper right and lower left. Show that if a matrix can be partitioned as
where and are square, and and are all zeroes, then .
- This exercise is recommended for all readers.
- Problem 18
Prove that for any matrix there are at most distinct reals such that the matrix has determinant zero (we shall use this result in Chapter Five).
- ? Problem 19
The nine positive digits can be arranged into arrays in ways. Find the sum of the determinants of these arrays. (Trigg 1963)
- ? Problem 21
Let be the sum of the integer elements of a magic square of order three and let be the value of the square considered as a determinant. Show that is an integer. (Trigg & Walker 1949)
- ? Problem 22
Show that the determinant of the elements in the upper left corner of the Pascal triangle
has the value unity. (Rupp & Aude 1931)
4 - Determinants Exist
This subsection is optional. It consists of proofs of two results from the prior subsection. These proofs involve the properties of permutations, which will not be used later, except in the optional Jordan Canonical Form subsection.
The prior subsection attacks the problem of showing that for any size there is a determinant function on the set of square matrices of that size by using multilinearity to develop the permutation expansion.
This reduces the problem to showing that there is a determinant function on the set of permutation matrices of that size.
Of course, a permutation matrix can be row-swapped to the identity matrix and to calculate its determinant we can keep track of the number of row swaps. However, the problem is still not solved. We still have not shown that the result is well-defined. For instance, the determinant of
could be computed with one swap
or with three.
Both reductions have an odd number of swaps so we figure that but how do we know that there isn't some way to do it with an even number of swaps? Corollary 4.6 below proves that there is no permutation matrix that can be row-swapped to an identity matrix in two ways, one with an even number of swaps and the other with an odd number of swaps.
- Definition 4.1
Two rows of a permutation matrix
such that are in an inversion of their natural order.
- Example 4.2
This permutation matrix
has three inversions: precedes , precedes , and precedes .
- Lemma 4.3
A row-swap in a permutation matrix changes the number of inversions from even to odd, or from odd to even.
- Proof
Consider a swap of rows and , where . If the two rows are adjacent
then the swap changes the total number of inversions by one — either removing or producing one inversion, depending on whether or not, since inversions involving rows not in this pair are not affected. Consequently, the total number of inversions changes from odd to even or from even to odd.
If the rows are not adjacent then they can be swapped via a sequence of adjacent swaps, first bringing row up
and then bringing row down.
Each of these adjacent swaps changes the number of inversions from odd to even or from even to odd. There are an odd number of them. The total change in the number of inversions is from even to odd or from odd to even.
- Definition 4.4
The signum of a permutation is if the number of inversions in is even, and is if the number of inversions is odd.
- Example 4.5
With the subscripts from Example 3.8 for the -permutations, while .
- Corollary 4.6
If a permutation matrix has an odd number of inversions then swapping it to the identity takes an odd number of swaps. If it has an even number of inversions then swapping to the identity takes an even number of swaps.
- Proof
The identity matrix has zero inversions. To change an odd number to zero requires an odd number of swaps, and to change an even number to zero requires an even number of swaps.
We still have not shown that the permutation expansion is well-defined because we have not considered row operations on permutation matrices other than row swaps. We will finesse this problem: we will define a function by altering the permutation expansion formula, replacing with
(this gives the same value as the permutation expansion because the prior result shows that ). This formula's advantage is that the number of inversions is clearly well-defined — just count them. Therefore, we will show that a determinant function exists for all sizes by showing that is it, that is, that satisfies the four conditions.
- Lemma 4.7
The function is a determinant. Hence determinants exist for every .
- Proof
We'll must check that it has the four properties from the definition.
Property (4) is easy; in
all of the summands are zero except for the product down the diagonal, which is one.
For property (3) consider where .
Factor the out of each term to get the desired equality.
For (2), let
.
To convert to unhatted 's, for each consider the permutation that equals except that the -th and -th numbers are interchanged, and . Replacing the in with this gives . Now (by Lemma 4.3) and so we get
where the sum is over all permutations derived from another permutation by a swap of the -th and -th numbers. But any permutation can be derived from some other permutation by such a swap, in one and only one way, so this summation is in fact a sum over all permutations, taken once and only once. Thus .
To do property (1) let and consider
(notice: that's , not ). Distribute, commute, and factor.
We finish by showing that the terms add to zero. This sum represents where is a matrix equal to except that row of is a copy of row of (because the factor is , not ). Thus, has two equal rows, rows and . Since we have already shown that changes sign on row swaps, as in Lemma 2.3 we conclude that .
We have now shown that determinant functions exist for each size. We already know that for each size there is at most one determinant. Therefore, the permutation expansion computes the one and only determinant value of a square matrix.
We end this subsection by proving the other result remaining from the prior subsection, that the determinant of a matrix equals the determinant of its transpose.
- Example 4.8
Writing out the permutation expansion of the general matrix and of its transpose, and comparing corresponding terms
(terms with the same letters)
shows that the corresponding permutation matrices are transposes. That is, there is a relationship between these corresponding permutations. Problem 6 shows that they are inverses.
- Theorem 4.9
The determinant of a matrix equals the determinant of its transpose.
- Proof
Call the matrix and denote the entries of with 's so that . Substitution gives this
and we can finish the argument by manipulating the expression on the right to be recognizable as the determinant of the transpose. We have written all permutation expansions (as in the middle expression above) with the row indices ascending. To rewrite the expression on the right in this way, note that because is a permutation, the row indices in the term on the right , ..., are just the numbers , ..., , rearranged. We can thus commute to have these ascend, giving (if the column index is and the row index is then, where the row index is , the column index is ). Substituting on the right gives
(Problem 5 shows that ). Since every permutation is the inverse of another, a sum over all is a sum over all permutations
as required.
Exercises
These summarize the notation used in this book for the - and - permutations.
- Problem 1
Give the permutation expansion of a general matrix and its transpose.
- This exercise is recommended for all readers.
- Problem 2
This problem appears also in the prior subsection.
- Find the inverse of each -permutation.
- Find the inverse of each -permutation.
- This exercise is recommended for all readers.
- Problem 3
- Find the signum of each -permutation.
- Find the signum of each -permutation.
- Problem 4
What is the signum of the -permutation ? (Strang 1980)
- Problem 5
Prove these.
- Every permutation has an inverse.
- Every permutation is the inverse of another.
- Problem 6
Prove that the matrix of the permutation inverse is the transpose of the matrix of the permutation , for any permutation .
- This exercise is recommended for all readers.
- Problem 7
Show that a permutation matrix with inversions can be row swapped to the identity in steps. Contrast this with Corollary 4.6.
- This exercise is recommended for all readers.
- Problem 8
For any permutation let be the integer defined in this way.
(This is the product, over all indices and with , of terms of the given form.)
- Compute the value of on all -permutations.
- Compute the value of on all -permutations.
- Prove this.
Many authors give this formula as the definition of the signum function.
Section II - Geometry of Determinants
The prior section develops the determinant algebraically, by considering what formulas satisfy certain properties. This section complements that with a geometric approach. One advantage of this approach is that, while we have so far only considered whether or not a determinant is zero, here we shall give a meaning to the value of that determinant. (The prior section handles determinants as functions of the rows, but in this section columns are more convenient. The final result of the prior section says that we can make the switch.)
1 - Determinants as Size Functions
This parallelogram picture
is familiar from the construction of the sum of the two vectors. One way to compute the area that it encloses is to draw this rectangle and subtract the area of each subregion.
The fact that the area equals the value of the determinant
is no coincidence. The properties in the definition of determinants make reasonable postulates for a function that measures the size of the region enclosed by the vectors in the matrix.
For instance, this shows the effect of multiplying one of the box-defining vectors by a scalar (the scalar used is ).
The region formed by and is bigger, by a factor of , than the shaded region enclosed by and . That is, and in general we expect of the size measure that . Of course, this postulate is already familiar as one of the properties in the defintion of determinants.
Another property of determinants is that they are unaffected by pivoting. Here are before-pivoting and after-pivoting boxes (the scalar used is ).
Although the region on the right, the box formed by and , is more slanted than the shaded region, the two have the same base and the same height and hence the same area. This illustrates that . Generalized, , which is a restatement of the determinant postulate.
Of course, this picture
shows that , and we naturally extend that to any number of dimensions , which is a restatement of the property that the determinant of the identity matrix is one.
With that, because property (2) of determinants is redundant (as remarked right after the definition), we have that all of the properties of determinants are reasonable to expect of a function that gives the size of boxes. We can now cite the work done in the prior section to show that the determinant exists and is unique to be assured that these postulates are consistent and sufficient (we do not need any more postulates). That is, we've got an intuitive justification to interpret as the size of the box formed by the vectors. (Comment. An even more basic approach, which also leads to the definition below, is in (Weston 1959).
- Example 1.1
The volume of this parallelepiped, which can be found by the usual formula from high school geometry, is .
- Remark 1.2
Although property (2) of the definition of determinants is redundant, it raises an important point. Consider these two.

| 
|
The only difference between them is in the order in which the vectors are taken. If we take first and then go to , follow the counterclockwise arc shown, then the sign is positive. Following a clockwise arc gives a negative sign. The sign returned by the size function reflects the "orientation" or "sense" of the box. (We see the same thing if we picture the effect of scalar multiplication by a negative scalar.)
Although it is both interesting and important, the idea of orientation turns out to be tricky. It is not needed for the development below, and so we will pass it by. (See Problem 20.)
- Definition 1.3
The box (or parallelepiped) formed by (where each vector is from ) includes all of the set . The volume of a box is the absolute value of the determinant of the matrix with those vectors as columns.
- Example 1.4
Volume, because it is an absolute value, does not depend on the order in which the vectors are given. The volume of the parallelepiped in Example 1.1, can also be computed as the absolute value of this determinant.
The definition of volume gives a geometric interpretation to something in the space, boxes made from vectors. The next result relates the geometry to the functions that operate on spaces.
- Theorem 1.5
A transformation changes the size of all boxes by the same factor, namely the size of the image of a box is times the size of the box , where is the matrix representing with respect to the standard basis. That is, for all matrices, the determinant of a product is the product of the determinants .
The two sentences state the same idea, first in map terms and then in matrix terms. Although we tend to prefer a map point of view, the second sentence, the matrix version, is more convienent for the proof and is also the way that we shall use this result later. (Alternate proofs are given as Problem 16 and Problem 21].)
- Proof
The two statements are equivalent because , as both give the size of the box that is the image of the unit box under the composition (where is the map represented by with respect to the standard basis).
First consider the case that . A matrix has a zero determinant if and only if it is not invertible. Observe that if is invertible, so that there is an such that , then the associative property of matrix multiplication shows that is also invertible (with inverse ). Therefore, if is not invertible then neither is — if then , and the result holds in this case.
Now consider the case that , that is nonsingular. Recall that any nonsingular matrix can be factored into a product of elementary matrices, so that . In the rest of this argument, we will verify that if is an elementary matrix then . The result will follow because then .
If the elementary matrix is then equals except that row has been multiplied by . The third property of determinant functions then gives that . But , again by the third property because is derived from the identity by multiplication of row by , and so holds for . The and checks are similar.
- Example 1.6
Application of the map represented with respect to the standard bases by
will double sizes of boxes, e.g., from this
to this
- Corollary 1.7
If a matrix is invertible then the determinant of its inverse is the inverse of its determinant .
- Proof
Recall that determinants are not additive homomorphisms, need not equal . The above theorem says, in contrast, that determinants are multiplicative homomorphisms: does equal .
Exercises
- Problem 1
Find the volume of the region formed.
- This exercise is recommended for all readers.
- Problem 2
Is
inside of the box formed by these three?
- This exercise is recommended for all readers.
- This exercise is recommended for all readers.
- Problem 4
Suppose that . By what factor do these change volumes?
- This exercise is recommended for all readers.
- Problem 5
By what factor does each transformation change the size of boxes?
- Problem 6
What is the area of the image of the rectangle under the action of this matrix?
- Problem 7
If changes volumes by a factor of and changes volumes by a factor of then by what factor will their composition changes volumes?
- Problem 8
In what way does the definition of a box differ from the defintion of a span?
- This exercise is recommended for all readers.
- This exercise is recommended for all readers.
- Problem 10
Does ? ?
- Problem 11
- Suppose that and that . Find .
- Assume that . Prove that .
- This exercise is recommended for all readers.
- Problem 12
Let be the matrix representing (with respect to the standard bases) the map that rotates plane vectors counterclockwise thru radians. By what factor does change sizes?
- This exercise is recommended for all readers.
- Problem 13
Must a transformation that preserves areas also preserve lengths?
- This exercise is recommended for all readers.
- Problem 14
What is the volume of a parallelepiped in bounded by a linearly dependent set?
- This exercise is recommended for all readers.
- Problem 15
Find the area of the triangle in with endpoints , , and . (Area, not volume. The triangle defines a plane— what is the area of the triangle in that plane?)
- This exercise is recommended for all readers.
- Problem 16
An alternate proof of Theorem 1.5 uses the definition of determinant functions.
- Note that the vectors forming make a linearly dependent set if and only if , and check that the result holds in this case.
- For the case, to show that for all transformations, consider the function given by . Show that has the first property of a determinant.
- Show that has the remaining three properties of a determinant function.
- Conclude that .
- Problem 17
Give a non-identity matrix with the property that . Show that if then . Does the converse hold?
- Problem 18
The algebraic property of determinants that factoring a scalar out of a single row will multiply the determinant by that scalar shows that where is , the determinant of is times the determinant of . Explain this geometrically, that is, using Theorem 1.5,
- This exercise is recommended for all readers.
- Problem 19
Matrices and are said to be similar if there is a nonsingular matrix such that (we will study this relation in Chapter Five). Show that similar matrices have the same determinant.
- Problem 20
We usually represent vectors in with respect to the standard basis so vectors in the first quadrant have both coordinates positive.
Moving counterclockwise around the origin, we cycle thru four regions:
Using this basis
gives the same counterclockwise cycle. We say these two bases have the same orientation.
- Why do they give the same cycle?
- What other configurations of unit vectors on the axes give the same cycle?
- Find the determinants of the matrices formed from those (ordered) bases.
- What other counterclockwise cycles are possible, and what are the associated determinants?
- What happens in ?
- What happens in ?
A fascinating general-audience discussion of orientations is in (Gardner 1990).
- Problem 21
This question uses material from the optional Determinant Functions Exist subsection. Prove Theorem 1.5 by using the permutation expansion formula for the determinant.
- This exercise is recommended for all readers.
- Problem 22
- Show that this gives
the equation of a line in thru
and .
- (Peterson 1955)
Prove that the area of a triangle with vertices ,
, and is
- (Bittinger 1973) Prove that the area of a triangle with vertices at , , and whose coordinates are integers has an area of or for some positive integer .
Section III - Other Formulas for Determinants
(This section is optional. Later sections do not depend on this material.)
Determinants are a fount of interesting and amusing formulas. Here is one that is often seen in calculus classes and used to compute determinants by hand.
1 - Laplace's Expansion
- Example 1.1
In this permutation expansion
we can, for instance, factor out the entries from the first row
and swap rows in the permutation matrices to get this.
The point of the swapping (one swap to each of the permutation matrices on the second line and two swaps to each on the third line) is that the three lines simplify to three terms.
The formula given in Theorem 1.5, which generalizes this example, is a recurrence — the determinant is expressed as a combination of determinants. This formula isn't circular because, as here, the determinant is expressed in terms of determinants of matrices of smaller size.
- Definition 1.2
For any matrix , the matrix formed by deleting row and column of is the minor of . The cofactor of is times the determinant of the minor of .
- Example 1.4
Where
these are the and cofactors.
- Theorem 1.5 (Laplace Expansion of Determinants)
Where is an matrix, the determinant can be found by expanding by cofactors on row or column .
- Proof
- Example 1.6
We can compute the determinant
by expanding along the first row, as in Example 1.1.
Alternatively, we can expand down the second column.
- Example 1.7
A row or column with many zeroes suggests a Laplace expansion.
We finish by applying this result to derive a new formula for the inverse of a matrix. With Theorem 1.5, the determinant of an matrix can be calculated by taking linear combinations of entries from a row and their associated cofactors.
Recall that a matrix with two identical rows has a zero determinant. Thus, for any matrix , weighing the cofactors by entries from the "wrong" row — row with — gives zero
because it represents the expansion along the row of a matrix with row equal to row . This equation summarizes () and ().
Note that the order of the subscripts in the matrix of cofactors is opposite to the order of subscripts in the other matrix; e.g., along the first row of the matrix of cofactors the subscripts are then , etc.
- Definition 1.8
The matrix adjoint to the square matrix is
where is the cofactor.
- Theorem 1.9
Where is a square matrix, .
- Proof
Equations () and ().
- Example 1.10
If
then the adjoint is
and taking the product with gives the diagonal matrix .
- Corollary 1.11
If then .
The formulas from this section are often used for by-hand calculation and are sometimes useful with special types of matrices. However, they are not the best choice for computation with arbitrary matrices because they require more arithmetic than, for instance, the Gauss-Jordan method.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Find the cofactor.
- This exercise is recommended for all readers.
- Problem 2
Find the determinant by expanding
- on the first row
- on the second row
- on the third column.
- Problem 3
Find the adjoint of the matrix in Example 1.6.
- This exercise is recommended for all readers.
- Problem 4
Find the matrix adjoint to each.
- This exercise is recommended for all readers.
- Problem 5
Find the inverse of each matrix in the prior question with Theorem 1.9.
- Problem 6
Find the matrix adjoint to this one.
- This exercise is recommended for all readers.
- Problem 7
Expand across the first row to derive the formula for the determinant of a matrix.
- This exercise is recommended for all readers.
- Problem 8
Expand across the first row to derive the formula for the determinant of a matrix.
- This exercise is recommended for all readers.
- Problem 9
- Give a formula for the adjoint of a matrix.
- Use it to derive the formula for the inverse.
- This exercise is recommended for all readers.
- Problem 10
Can we compute a determinant by expanding down the diagonal?
- Problem 11
Give a formula for the adjoint of a diagonal matrix.
- This exercise is recommended for all readers.
- Problem 12
Prove that the transpose of the adjoint is the adjoint of the transpose.
- Problem 13
Prove or disprove: .
- Problem 14
A square matrix is upper triangular if each entry is zero in the part above the diagonal, that is, when .
- Must the adjoint of an upper triangular matrix be upper triangular? Lower triangular?
- Prove that the inverse of a upper triangular matrix is upper triangular, if an inverse exists.
- Problem 15
This question requires material from the optional Determinants Exist subsection. Prove Theorem 1.5 by using the permutation expansion.
- Problem 16
Prove that the determinant of a matrix equals the determinant of its transpose using Laplace's expansion and induction on the size of the matrix.
- ? Problem 17
Show that
where is the -th term of , the Fibonacci sequence, and the determinant is of order . (Walter & Tytun 1949)
Topic: Cramer's Rule
We have introduced determinant functions algebraically by looking for a formula to decide whether a matrix is nonsingular. After that introduction we saw a geometric interpretation, that the determinant function gives the size of the box with sides formed by the columns of the matrix. This Topic makes a connection between the two views.
First, a linear system
is equivalent to a linear relationship among vectors.
The picture below shows a parallelogram with sides formed from and nested inside a parallelogram with sides formed from and .
So even without determinants we can state the algebraic issue that opened this book, finding the solution of a linear system, in geometric terms: by what factors and must we dilate the vectors to expand the small parallegram to fill the larger one?
However, by employing the geometric significance of determinants we can get something that is not just a restatement, but also gives us a new insight and sometimes allows us to compute answers quickly. Compare the sizes of these shaded boxes.
The second is formed from and , and one of the properties of the size function— the determinant— is that its size is therefore times the size of the first box. Since the third box is formed from and , and the determinant is unchanged by adding times the second column to the first column, the size of the third box equals that of the second. We have this.
Solving gives the value of one of the variables.
The theorem that generalizes this example, Cramer's Rule, is: if then the system has the unique solution where the matrix is formed from by replacing column with the vector . Problem 3 asks for a proof.
For instance, to solve this system for
we do this computation.
Cramer's Rule allows us to solve many two equations/two unknowns systems by eye. It is also sometimes used for three equations/three unknowns systems. But computing large determinants takes a long time, so solving large systems by Cramer's Rule is not practical.
Exercises
- Problem 1
Use Cramer's Rule to solve each for each of the variables.
- Problem 2
Use Cramer's Rule to solve this system for .
- Problem 3
Prove Cramer's Rule.
- Problem 4
Suppose that a linear system has as many equations as unknowns, that all of its coefficients and constants are integers, and that its matrix of coefficients has determinant . Prove that the entries in the solution are all integers. (Remark. This is often used to invent linear systems for exercises. If an instructor makes the linear system with this property then the solution is not some disagreeable fraction.)
- Problem 5
Use Cramer's Rule to give a formula for the solution of a two equations/two unknowns linear system.
- Problem 6
Can Cramer's Rule tell the difference between a system with no solutions and one with infinitely many?
- Problem 7
The first picture in this Topic (the one that doesn't use determinants) shows a unique solution case. Produce a similar picture for the case of infintely many solutions, and the case of no solutions.
Topic: Speed of Calculating Determinants
The permutation expansion formula for computing determinants is useful for proving theorems, but the method of using row operations is a much better for finding the determinants of a large matrix. We can make this statement precise by considering, as computer algorithm designers do, the number of arithmetic operations that each method uses.
The speed of an algorithm is measured by finding how the time taken by the computer grows as the size of its input data set grows. For instance, how much longer will the algorithm take if we increase the size of the input data by a factor of ten, from a row matrix to a row matrix or from to ? Does the time taken grow by a factor of ten, or by a factor of a hundred, or by a factor of a thousand? That is, is the time taken by the algorithm proportional to the size of the data set, or to the square of that size, or to the cube of that size, etc.?
Recall the permutation expansion formula for determinants.
There are different -permutations. For numbers of any size at all, this is a large value; for instance, even if is only then the expansion has terms, all of which are obtained by multiplying entries together. This is a very large number of multiplications (for instance, (Knuth 1988) suggests steps as a rough boundary for the limit of practical calculation). The factorial function grows faster than the square function. It grows faster than the cube function, the fourth power function, or any polynomial function. (One way to see that the factorial function grows faster than the square is to note that multiplying the first two factors in gives , which for large is approximately , and then multiplying in more factors will make it even larger. The same argument works for the cube function, etc.) So a computer that is programmed to use the permutation expansion formula, and thus to perform a number of operations that is greater than or equal to the factorial of the number of rows, would take very long times as its input data set grows.
In contrast, the time taken by the row reduction method does not grow so fast. This fragment of row-reduction code is in the computer language FORTRAN. The matrix is stored in the array A. For each ROW between and parts of the program not shown here have already found the pivot entry . Now the program does a row pivot.
(This code fragment is for illustration only and is incomplete.
Still, analysis of a finished version that includes all of the tests
and subcases is messier but gives essentially the same conclusion.)
PIVINV=1.0/A(ROW,COL)
DO 10 I=ROW+1, N
DO 20 J=I, N
A(I,J)=A(I,J)-PIVINV*A(ROW,J)
20 CONTINUE
10 CONTINUE
The outermost loop (not shown) runs through rows.
For each row,
the nested and loops shown perform arithmetic on the entries
in A that are below and to the right of the pivot entry.
Assume that the pivot is found in the expected place, that is,
that .
Then there are entries
below and to the right of the pivot.
On average, ROW will be .
Thus, we estimate that the arithmetic will be performed
about times,
that is, will run in a time proportional to the square of the number
of equations.
Taking into account the outer loop that is not shown, we get
the estimate that the running time of the algorithm
is proportional to the cube of the number of equations.
Finding the fastest algorithm to compute the determinant is a topic of current research. Algorithms are known that run in time between the second and third power.
Speed estimates like these help us to understand how quickly or slowly an algorithm will run. Algorithms that run in time proportional to the size of the data set are fast, algorithms that run in time proportional to the square of the size of the data set are less fast, but typically quite usable, and algorithms that run in time proportional to the cube of the size of the data set are still reasonable in speed for not-too-big input data. However, algorithms that run in time (greater than or equal to) the factorial of the size of the data set are not practical for input of any appreciable size.
There are other methods besides the two discussed here that are also used for computation of determinants. Those lie outside of our scope. Nonetheless, this contrast of the two methods for computing determinants makes the point that although in principle they give the same answer, in practice the idea is to select the one that is fast.
Exercises
Most of these problems presume access to a computer.
- Problem 1
Computer systems generate random numbers (of course, these are only pseudo-random, in that they are generated by an algorithm, but they pass a number of reasonable statistical tests for randomness).
- Fill a array with random numbers (say, in the range ). See if it is singular. Repeat that experiment a few times. Are singular matrices frequent or rare (in this sense)?
- Time your computer algebra system at finding the determinant of ten arrays of random numbers. Find the average time per array. Repeat the prior item for arrays, arrays, and arrays. (Notice that, when an array is singular, it can sometimes be found to be so quite quickly, for instance if the first row equals the second. In the light of your answer to the first part, do you expect that singular systems play a large role in your average?)
- Graph the input size versus the average time.
- Problem 2
Compute the determinant of each of these by hand using the two methods discussed above.
Count the number of multiplications and divisions used in each case, for each of the methods. (On a computer, multiplications and divisions take much longer than additions and subtractions, so algorithm designers worry about them more.)
- Problem 3
What array can you invent that takes your computer system the longest to reduce? The shortest?
- Problem 4
Write the rest of the FORTRAN program to do a straightforward implementation of calculating determinants via Gauss' method. (Don't test for a zero pivot.) Compare the speed of your code to that used in your computer algebra system.
- Problem 5
The FORTRAN language specification requires that arrays be stored "by column", that is, the entire first column is stored contiguously, then the second column, etc. Does the code fragment given take advantage of this, or can it be rewritten to make it faster, by taking advantage of the fact that computer fetches are faster from contiguous locations?
Topic: Projective Geometry
There are geometries other than the familiar Euclidean one. One such geometry arose in art, where it was observed that what a viewer sees is not necessarily what is there. This is Leonardo da Vinci's The Last Supper.
What is there in the room, for instance where the ceiling meets the left and right walls, are lines that are parallel. However, what a viewer sees is lines that, if extended, would intersect. The intersection point is called the vanishing point. This aspect of perspective is also familiar as the image of a long stretch of railroad tracks that appear to converge at the horizon.
To depict the room, da Vinci has adopted a model of how we see, of how we project the three dimensional scene to a two dimensional image. This model is only a first approximation — it does not take into account that our retina is curved and our lens bends the light, that we have binocular vision, or that our brain's processing greatly affects what we see — but nonetheless it is interesting, both artistically and mathematically.
The projection is not orthogonal, it is a central projection from a single point, to the plane of the canvas.

(It is not an orthogonal projection since the line from the viewer to is not orthogonal to the image plane.) As the picture suggests, the operation of central projection preserves some geometric properties — lines project to lines. However, it fails to preserve some others — equal length segments can project to segments of unequal length; the length of is greater than the length of because the segment projected to is closer to the viewer and closer things look bigger. The study of the effects of central projections is projective geometry. We will see how linear algebra can be used in this study.
There are three cases of central projection. The first is the projection done by a movie projector.

We can think that each source point is "pushed" from the domain plane outward to the image point in the codomain plane. This case of projection has a somewhat different character than the second case, that of the artist "pulling" the source back to the canvas.

In the first case is in the middle while in the second case is in the middle. One more configuration is possible, with in the middle. An example of this is when we use a pinhole to shine the image of a solar eclipse onto a piece of paper.

We shall take each of the three to be a central projection by of to .
Consider again the effect of railroad tracks that appear to converge to a point. We model this with parallel lines in a domain plane and a projection via a to a codomain plane (The gray lines are parallel to ) .

All three projection cases appear here. The first picture below shows acting like a movie projector by pushing points from part of out to image points on the lower half of . The middle picture shows acting like the artist by pulling points from another part of back to image points in the middle of . In the third picture, acts like the pinhole, projecting points from to the upper part of . This picture is the trickiest — the points that are projected near to the vanishing point are the ones that are far out on the bottom left of . Points in that are near to the vertical gray line are sent high up on .
There are two awkward things about this situation. The first is that neither of the two points in the domain nearest to the vertical gray line (see below) has an image because a projection from those two is along the gray line that is parallel to the codomain plane (we sometimes say that these two are projected "to infinity"). The second awkward thing is that the vanishing point in isn't the image of any point from because a projection to this point would be along the gray line that is parallel to the domain plane (we sometimes say that the vanishing point is the image of a projection "from infinity").
For a better model, put the projector at the origin. Imagine that is covered by a glass hemispheric dome. As looks outward, anything in the line of vision is projected to the same spot on the dome. This includes things on the line between and the dome, as in the case of projection by the movie projector. It includes things on the line further from than the dome, as in the case of projection by the painter. It also includes things on the line that lie behind , as in the case of projection by a pinhole.

From this perspective , all of the spots on the line are seen as the same point. Accordingly, for any nonzero vector , we define the associated point in the projective plane to be the set of nonzero vectors lying on the same line through the origin as . To describe a projective point we can give any representative member of the line, so that the projective point shown above can be represented in any of these three ways.
Each of these is a homogeneous coordinate vector for .
This picture, and the above definition that arises from it, clarifies the description of central projection but there is something awkward about the dome model: what if the viewer looks down? If we draw 's line of sight so that the part coming toward us, out of the page, goes down below the dome then we can trace the line of sight backward, up past and toward the part of the hemisphere that is behind the page. So in the dome model, looking down gives a projective point that is behind the viewer. Therefore, if the viewer in the picture above drops the line of sight toward the bottom of the dome then the projective point drops also and as the line of sight continues down past the equator, the projective point suddenly shifts from the front of the dome to the back of the dome. This discontinuity in the drawing means that we often have to treat equatorial points as a separate case. That is, while the railroad track discussion of central projection has three cases, the dome model has two.
We can do better than this. Consider a sphere centered at the origin. Any line through the origin intersects the sphere in two spots, which are said to be antipodal. Because we associate each line through the origin with a point in the projective plane, we can draw such a point as a pair of antipodal spots on the sphere. Below, the two antipodal spots are shown connected by a dashed line to emphasize that they are not two different points, the pair of spots together make one projective point.

While drawing a point as a pair of antipodal spots is not as natural as the one-spot-per-point dome mode, on the other hand the awkwardness of the dome model is gone, in that if as a line of view slides from north to south, no sudden changes happen on the picture. This model of central projection is uniform — the three cases are reduced to one.
So far we have described points in projective geometry. What about lines? What a viewer at the origin sees as a line is shown below as a great circle, the intersection of the model sphere with a plane through the origin.

(One of the projective points on this line is shown to bring out a subtlety. Because two antipodal spots together make up a single projective point, the great circle's behind-the-paper part is the same set of projective points as its in-front-of-the-paper part.) Just as we did with each projective point, we will also describe a projective line with a triple of reals. For instance, the members of this plane through the origin in
project to a line that we can described with the triple (we use row vectors to typographically distinguish linesfrom points). In general, for any nonzero three-wide row vector we define the associated line in the projective plane, to be the set of nonzero multiples of .
The reason that this description of a line as a triple is convienent is that in the projective plane, a point and a line are incident — the point lies on the line, the line passes throught the point — if and only if a dot product of their representatives is zero (Problem 4 shows that this is independent of the choice of representatives and ). For instance, the projective point described above by the column vector with components lies in the projective line described by , simply because any vector in whose components are in ratio lies in the plane through the origin whose equation is of the form for any nonzero . That is, the incidence formula is inherited from the three-space lines and planes of which and are projections.
Thus, we can do analytic projective geometry. For instance, the projective line has the equation , because points incident on the line are characterized by having the property that their representatives satisfy this equation. One difference from familiar Euclidean analytic geometry is that in projective geometry we talk about the equation of a point. For a fixed point like
the property that characterizes lines through this point (that is, lines incident on this point) is that the components of any representatives satisfy and so this is the equation of .
This symmetry of the statements about lines and points brings up the Duality Principle of projective geometry: in any true statement, interchanging "point" with "line" results in another true statement. For example, just as two distinct points determine one and only one line, in the projective plane, two distinct lines determine one and only one point. Here is a picture showing two lines that cross in antipodal spots and thus cross at one projective point.
Contrast this with Euclidean geometry, where two distinct lines may have a unique intersection or may be parallel. In this way, projective geometry is simpler, more uniform, than Euclidean geometry.
That simplicity is relevant because there is a relationship between the two spaces: the projective plane can be viewed as an extension of the Euclidean plane. Take the sphere model of the projective plane to be the unit sphere in and take Euclidean space to be the plane . This gives us a way of viewing some points in projective space as corresponding to points in Euclidean space, because all of the points on the plane are projections of antipodal spots from the sphere.
Note though that projective points on the equator don't project up to the plane. Instead, these project "out to infinity". We can thus think of projective space as consisting of the Euclidean plane with some extra points adjoined — the Euclidean plane is embedded in the projective plane. These extra points, the equatorial points, are the ideal points or points at infinity and the equator is the ideal line or line at infinity (note that it is not a Euclidean line, it is a projective line).
The advantage of the extension to the projective plane is that some of the awkwardness of Euclidean geometry disappears. For instance, the projective lines shown above in cross at antipodal spots, a single projective point, on the sphere's equator. If we put those lines into then they correspond to Euclidean lines that are parallel. That is, in moving from the Euclidean plane to the projective plane, we move from having two cases, that lines either intersect or are parallel, to having only one case, that lines intersect (possibly at a point at infinity).
The projective case is nicer in many ways than the Euclidean case but has the problem that we don't have the same experience or intuitions with it. That's one advantage of doing analytic geometry, where the equations can lead us to the right conclusions. Analytic projective geometry uses linear algebra. For instance, for three points of the projective plane , setting up the equations for those points by fixing vectors representing each, shows that the three are collinear — incident in a single line — if and only if the resulting three-equation system has infinitely many row vector solutions representing that line. That, in turn, holds if and only if this determinant is zero.
Thus, three points in the projective plane are collinear if and only if any three representative column vectors are linearly dependent. Similarly (and illustrating the Duality Principle), three lines in the projective plane are incident on a single point if and only if any three row vectors representing them are linearly dependent.
The following result is more evidence of the "niceness" of the geometry of the projective plane, compared to the Euclidean case. These two triangles are said to be in perspective from because their corresponding vertices are collinear.

Consider the pairs of corresponding sides: the sides , the sides , and the sides . Desargue's Theorem is that when the three pairs of corresponding sides are extended to lines, they intersect (shown here as the point , the point , and the point ), and further, those three intersection points are collinear.
We will prove this theorem, using projective geometry. (These are drawn as Euclidean figures because it is the more familiar image. To consider them as projective figures, we can imagine that, although the line segments shown are parts of great circles and so are curved, the model has such a large radius compared to the size of the figures that the sides appear in this sketch to be straight.)
For this proof, we need a preliminary lemma (Coxeter 1974): if are four points in the projective plane (no three of which are collinear) then there are homogeneous coordinate vectors for the projective points, and a basis for , satisfying this.
The proof is straightforward. Because are not on the same projective line, any homogeneous coordinate vectors do not line on the same plane through the origin in and so form a spanning set for . Thus any homogeneous coordinate vector for can be written as a combination . Then, we can take
where the basis is .
Now, to prove of Desargue's Theorem, use the lemma to fix homogeneous coordinate vectors and a basis.
Because the projective point is incident on the projective line , any homogeneous coordinate vector for lies in the plane through the origin in that is spanned by homogeneous coordinate vectors of and :
for some scalars and . That is, the homogenous coordinate vectors of members of the line are of the form on the left below, and the forms for are similar.
The projective line is the image of a plane through the origin in . A quick way to get its equation is to note that any vector in it is linearly dependent on the vectors for and and so this determinant is zero.
The equation of the plane in whose image is the projective line is this.
Finding the intersection of the two is routine.
(This is, of course, the homogeneous coordinate vector of a projective point.) The other two intersections are similar.
The proof is finished by noting that these projective points are on one projective line because the sum of the three homogeneous coordinate vectors is zero.
Every projective theorem has a translation to a Euclidean version, although the Euclidean result is often messier to state and prove. Desargue's theorem illustrates this. In the translation to Euclidean space, the case where lies on the ideal line must be treated separately for then the lines are parallel.
The parenthetical remark following the statement of Desargue's Theorem suggests thinking of the Euclidean pictures as figures from projective geometry for a model of very large radius. That is, just as a small area of the earth appears flat to people living there, the projective plane is also "locally Euclidean".
Although its local properties are the familiar Euclidean ones, there is a global property of the projective plane that is quite different. The picture below shows a projective point. At that point is drawn an -axis. There is something interesting about the way this axis appears at the antipodal ends of the sphere. In the northern hemisphere, where the axis are drawn in black, a right hand put down with fingers on the -axis will have the thumb point along the -axis. But the antipodal axis has just the opposite: a right hand placed with its fingers on the -axis will have the thumb point in the wrong way, instead, it is a left hand that works. Briefly, the projective plane is not orientable: in this geometry, left and right handedness are not fixed properties of figures.

The sequence of pictures below dramatizes this non-orientability. They sketch a trip around this space in the direction of the part of the -axis. (Warning: the trip shown is not halfway around, it is a full circuit. True, if we made this into a movie then we could watch the northern hemisphere spots in the drawing above gradually rotate about halfway around the sphere to the last picture below. And we could watch the southern hemisphere spots in the picture above slide through the south pole and up through the equator to the last picture. But: the spots at either end of the dashed line are the same projective point. We don't need to continue on much further; we are pretty much back to the projective point where we started by the last picture.)
At the end of the circuit, the part of the -axes sticks out in the other direction. Thus, in the projective plane we cannot describe a figure as right-{} or left-handed (another way to make this point is that we cannot describe a spiral as clockwise or counterclockwise).
This exhibition of the existence of a non-orientable space raises the question of whether our universe is orientable: is it possible for an astronaut to leave right-handed and return left-handed? An excellent nontechnical reference is (Gardner 1990). A classic science fiction story about orientation reversal is (Clarke 1982).
So projective geometry is mathematically interesting, in addition to the natural way in which it arises in art. It is more than just a technical device to shorten some proofs. For an overview, see (Courant & Robbins 1978). The approach we've taken here, the analytic approach, leads to quick theorems and — most importantly for us — illustrates the power of linear algebra (see Hanes (1990), Ryan (1986), and Eggar (1998)). But another approach, the synthetic approach of deriving the results from an axiom system, is both extraordinarily beautiful and is also the historical route of development. Two fine sources for this approach are (Coxeter 1974) or (Seidenberg 1962). An interesting and easy application is (Davies 1990).
Exercises
- Problem 1
What is the equation of this point?
- Problem 2
- Find the line incident on these points in the projective plane.
- Find the point incident on both of these projective lines.
- Problem 3
Find the formula for the line incident on two projective points. Find the formula for the point incident on two projective lines.
- Problem 4
Prove that the definition of incidence is independent of the choice of the representatives of and . That is, if and are two triples of homogeneous coordinates for , and and are two triples of homogeneous coordinates for , prove that if and only if .
- Problem 5
Give a drawing to show that central projection does not preserve circles, that a circle may project to an ellipse. Can a (non-circular) ellipse project to a circle?
- Problem 6
Give the formula for the correspondence between the non-equatorial part of the antipodal modal of the projective plane, and the plane .
- Problem 7
(Pappus's Theorem) Assume that are collinear and that are collinear. Consider these three points:
- the intersection of the lines
- the intersection of the lines
- the intersection of and
- Draw a (Euclidean) picture.
- Apply the lemma used in Desargue's Theorem to get simple homogeneous coordinate vectors for the 's and .
- Find the resulting homogeneous coordinate vectors for 's (these must each involve a parameter as, e.g. could be anywhere on the line).
- Find the resulting homogeneous coordinate vectors for . (Hint: it involves two parameters.)
- Find the resulting homogeneous coordinate vectors for . (It also involves two parameters.)
- Show that the product of the three parameters is 1.
- Verify that is on the line..
Chapter V - Similarity
While studying matrix equivalence, we have shown that for any homomorphism there are bases and such that the representation matrix has a block partial-identity form.
This representation describes the map as sending to , where is the dimension of the domain and is the dimension of the range. So, under this representation the action of the map is easy to understand because most of the matrix entries are zero.
This chapter considers the special case where the domain and the codomain are equal, that is, where the homomorphism is a transformation. In this case we naturally ask to find a single basis so that is as simple as possible (we will take "simple" to mean that it has many zeroes). A matrix having the above block partial-identity form is not always possible here. But we will develop a form that comes close, a representation that is nearly diagonal.
Section I - Linear Algebra/Complex Vector Spaces
This chapter requires that we factor polynomials. Of course, many polynomials do not factor over the real numbers; for instance, does not factor into the product of two linear polynomials with real coefficients. For that reason, we shall from now on take our scalars from the complex numbers.
That is, we are shifting from studying vector spaces over the real numbers to vector spaces over the complex numbers— in this chapter vector and matrix entries are complex.
Any real number is a complex number and a glance through this chapter shows that most of the examples use only real numbers. Nonetheless, the critical theorems require that the scalars be complex numbers, so the first section below is a quick review of complex numbers.
In this book we are moving to the more general context of taking scalars to be complex only for the pragmatic reason that we must do so in order to develop the representation. We will not go into using other sets of scalars in more detail because it could distract from our goal. However, the idea of taking scalars from a structure other than the real numbers is an interesting one. Delightful presentations taking this approach are in (Halmos 1958) and (Hoffman & Kunze 1971).
1 - Factoring and Complex Numbers: A Review
This subsection is a review only and we take the main results as known. For proofs, see (Birkhoff & MacLane 1965) or (Ebbinghaus 1990).
Just as integers have a division operation— e.g., " goes times into with remainder "— so do polynomials.
- Theorem 1.1 (Division Theorem for Polynomials)
Let be a polynomial. If is a non-zero polynomial then there are quotient and remainder polynomials and such that
where the degree of is strictly less than the degree of .
In this book constant polynomials, including the zero polynomial, are said to have degree . (This is not the standard definition, but it is convienent here.)
The point of the integer division statement " goes times into with remainder " is that the remainder is less than — while goes times, it does not go times. In the same way, the point of the polynomial division statement is its final clause.
- Example 1.2
If and then and . Note that has a lower degree than .
- Corollary 1.3
The remainder when is divided by is the constant polynomial .
- Proof
The remainder must be a constant polynomial because it is of degree less than the divisor , To determine the constant, take from the theorem to be and substitute for to get .
If a divisor goes into a dividend evenly, meaning that is the zero polynomial, then is a factor of . Any root of the factor (any such that ) is a root of since . The prior corollary immediately yields the following converse.
- Corollary 1.4
If is a root of the polynomial then divides evenly, that is, is a factor of .
Finding the roots and factors of a high-degree polynomial can be hard. But for second-degree polynomials we have the quadratic formula: the roots of are
(if the discriminant is negative then the polynomial has no real number roots). A polynomial that cannot be factored into two lower-degree polynomials with real number coefficients is irreducible over the reals.
- Theorem 1.5
Any constant or linear polynomial is irreducible over the reals. A quadratic polynomial is irreducible over the reals if and only if its discriminant is negative. No cubic or higher-degree polynomial is irreducible over the reals.
- Corollary 1.6
Any polynomial with real coefficients can be factored into linear and irreducible quadratic polynomials. That factorization is unique; any two factorizations have the same powers of the same factors.
Note the analogy with the prime factorization of integers. In both cases, the uniqueness clause is very useful.
- Example 1.7
Because of uniqueness we know, without multiplying them out, that does not equal .
- Example 1.8
By uniqueness, if then where and , we know that .
While has no real roots and so doesn't factor over the real numbers, if we imagine a root— traditionally denoted so that — then factors into a product of linears .
So we adjoin this root to the reals and close the new system with respect to addition, multiplication, etc. (i.e., we also add , and , and , etc., putting in all linear combinations of and ). We then get a new structure, the complex numbers, denoted .
In we can factor (obviously, at least some) quadratics that would be irreducible if we were to stick to the real numbers. Surprisingly, in we can not only factor and its close relatives, we can factor any quadratic.
- Example 1.9
The second degree polynomial factors over the complex numbers into the product of two first degree polynomials.
- Corollary 1.10 (Fundamental Theorem of Algebra)
Polynomials with complex coefficients factor into linear polynomials with complex coefficients. The factorization is unique.
2 - Complex Representations
Recall the definitions of the complex number addition
and multiplication.
- Example 2.1
For instance, and .
Handling scalar operations with those rules, all of the operations that we've covered for real vector spaces carry over unchanged.
- Example 2.2
Matrix multiplication is the same, although the scalar arithmetic involves more bookkeeping.
Everything else from prior chapters that we can, we shall also carry over unchanged. For instance, we shall call the ordered set of vectors
the standard basis for as a vector space over and again denote it .
Section II - Similarity
1 - Definition and Examples
Definition and Examples
We've defined and to be matrix-equivalent if there are nonsingular matrices and such that . That definition is motivated by this diagram
showing that and both represent but with respect to different pairs of bases. We now specialize that setup to the case where the codomain equals the domain, and where the codomain's basis equals the domain's basis.
To move from the lower left to the lower right we can either go straight over, or up, over, and then down. In matrix terms,
(recall that a representation of composition like this one reads right to left).
- Definition 1.1
The matrices and are similar if there is a nonsingular such that .
Since nonsingular matrices are square, the similar matrices and must be square and of the same size.
- Example 1.2
With these two,
calculation gives that is similar to this matrix.
- Example 1.3
The only matrix similar to the zero matrix is itself: . The only matrix similar to the identity matrix is itself: .
Since matrix similarity is a special case of matrix equivalence, if two matrices are similar then they are equivalent. What about the converse: must matrix equivalent square matrices be similar? The answer is no. The prior example shows that the similarity classes are different from the matrix equivalence classes, because the matrix equivalence class of the identity consists of all nonsingular matrices of that size. Thus, for instance, these two are matrix equivalent but not similar.
So some matrix equivalence classes split into two or more similarity classes— similarity gives a finer partition than does equivalence. This picture shows some matrix equivalence classes subdivided into similarity classes.
To understand the similarity relation we shall study the similarity classes. We approach this question in the same way that we've studied both the row equivalence and matrix equivalence relations, by finding a canonical form for representatives[1] of the similarity classes, called Jordan form. With this canonical form, we can decide if two matrices are similar by checking whether they reduce to the same representative. We've also seen with both row equivalence and matrix equivalence that a canonical form gives us insight into the ways in which members of the same class are alike (e.g., two identically-sized matrices are matrix equivalent if and only if they have the same rank).
Exercises
- Problem 1
For
check that .
- This exercise is recommended for all readers.
- Problem 2
Example 1.3 shows that the only matrix similar to a zero matrix is itself and that the only matrix similar to the identity is itself.
- Show that the matrix , also, is similar only to itself.
- Is a matrix of the form for some scalar similar only to itself?
- Is a diagonal matrix similar only to itself?
- Problem 3
Show that these matrices are not similar.
- Problem 4
Consider the transformation described by , , and .
- Find where .
- Find where .
- Find the matrix such that .
- This exercise is recommended for all readers.
- Problem 5
Exhibit an nontrivial similarity relationship in this way: let act by
and pick two bases, and represent with respect to then and . Then compute the and to change bases from to and back again.
- Problem 6
Explain Example 1.3 in terms of maps.
- This exercise is recommended for all readers.
- Problem 7
Are there two matrices and that are similar while and are not similar? (Halmos 1958)
- This exercise is recommended for all readers.
- Problem 8
Prove that if two matrices are similar and one is invertible then so is the other.
- This exercise is recommended for all readers.
- Problem 9
Show that similarity is an equivalence relation.
- Problem 10
Consider a matrix representing, with respect to some , reflection across the -axis in . Consider also a matrix representing, with respect to some , reflection across the -axis. Must they be similar?
- Problem 11
Prove that similarity preserves determinants and rank. Does the converse hold?
- Problem 12
Is there a matrix equivalence class with only one matrix similarity class inside? One with infinitely many similarity classes?
- Problem 13
Can two different diagonal matrices be in the same similarity class?
- This exercise is recommended for all readers.
- Problem 14
Prove that if two matrices are similar then their -th powers are similar when . What if ?
- This exercise is recommended for all readers.
- Problem 15
Let be the polynomial . Show that if is similar to then is similar to .
- Problem 16
List all of the matrix equivalence classes of matrices. Also list the similarity classes, and describe which similarity classes are contained inside of each matrix equivalence class.
- Problem 17
Does similarity preserve sums?
- Problem 18
Show that if and are similar matrices then and are also similar.
2 - Diagonalizability
The prior subsection defines the relation of similarity and shows that, although similar matrices are necessarily matrix equivalent, the converse does not hold. Some matrix-equivalence classes break into two or more similarity classes (the nonsingular matrices, for instance). This means that the canonical form for matrix equivalence, a block partial-identity, cannot be used as a canonical form for matrix similarity because the partial-identities cannot be in more than one similarity class, so there are similarity classes without one. This picture illustrates. As earlier in this book, class representatives are shown with stars.
We are developing a canonical form for representatives of the similarity classes. We naturally try to build on our previous work, meaning first that the partial identity matrices should represent the similarity classes into which they fall, and beyond that, that the representatives should be as simple as possible. The simplest extension of the partial-identity form is a diagonal form.
- Definition 2.1
A transformation is diagonalizable if it has a diagonal representation with respect to the same basis for the codomain as for the domain. A diagonalizable matrix is one that is similar to a diagonal matrix: is diagonalizable if there is a nonsingular such that is diagonal.
- Example 2.2
The matrix
is diagonalizable.
- Example 2.3
Not every matrix is diagonalizable. The square of
is the zero matrix. Thus, for any map that represents (with respect to the same basis for the domain as for the codomain), the composition is the zero map. This implies that no such map can be diagonally represented (with respect to any ) because no power of a nonzero diagonal matrix is zero. That is, there is no diagonal matrix in 's similarity class.
That example shows that a diagonal form will not do for a canonical form— we cannot find a diagonal matrix in each matrix similarity class. However, the canonical form that we are developing has the property that if a matrix can be diagonalized then the diagonal matrix is the canonical representative of the similarity class. The next result characterizes which maps can be diagonalized.
- Corollary 2.4
A transformation is diagonalizable if and only if there is a basis and scalars such that for each .
- Proof
This follows from the definition by considering a diagonal representation matrix.
This representation is equivalent to the existence of a basis satisfying the stated conditions simply by the definition of matrix representation.
- Example 2.5
To diagonalize
we take it as the representation of a transformation with respect to the standard basis and we look for a basis such that
that is, such that and .
We are looking for scalars such that this equation
has solutions and , which are not both zero. Rewrite that as a linear system.
In the bottom equation the two numbers multiply to give zero only if at least one of them is zero so there are two possibilities, and . In the possibility, the first equation gives that either or . Since the case of both and is disallowed, we are left looking at the possibility of . With it, the first equation in () is and so associated with are vectors with a second component of zero and a first component that is free.
That is, one solution to () is , and we have a first basis vector.
In the possibility, the first equation in () is , and so associated with are vectors whose second component is the negative of their first component.
Thus, another solution is and a second basis vector is this.
To finish, drawing the similarity diagram
and noting that the matrix is easy leads to this diagonalization.
In the next subsection, we will expand on that example by considering more closely the property of Corollary 2.4. This includes seeing another way, the way that we will routinely use, to find the 's.
Exercises
- This exercise is recommended for all readers.
- Problem 1
Repeat Example 2.5 for the matrix from Example 2.2.
- Problem 2
Diagonalize these upper triangular matrices.
- This exercise is recommended for all readers.
- Problem 3
What form do the powers of a diagonal matrix have?
- Problem 4
Give two same-sized diagonal matrices that are not similar. Must any two different diagonal matrices come from different similarity classes?
- Problem 5
Give a nonsingular diagonal matrix. Can a diagonal matrix ever be singular?
- This exercise is recommended for all readers.
- Problem 6
Show that the inverse of a diagonal matrix is the diagonal of the inverses, if no element on that diagonal is zero. What happens when a diagonal entry is zero?
- Problem 7
The equation ending Example 2.5
is a bit jarring because for we must take the first matrix, which is shown as an inverse, and for we take the inverse of the first matrix, so that the two powers cancel and this matrix is shown without a superscript .
- Check that this nicer-appearing equation holds.
- Is the previous item a coincidence? Or can we always switch the and the ?
- Problem 8
Show that the used to diagonalize in Example 2.5 is not unique.
- This exercise is recommended for all readers.
- Problem 10
Diagonalize these.
- Problem 11
We can ask how diagonalization interacts with the matrix operations. Assume that are each diagonalizable. Is diagonalizable for all scalars ? What about ? ?
- This exercise is recommended for all readers.
- Problem 12
Show that matrices of this form are not diagonalizable.
- Problem 13
Show that each of these is diagonalizable.
3 - Eigenvalues and Eigenvectors
In this subsection we will focus on the property of Corollary 2.4.
- Definition 3.1
A transformation has a scalar eigenvalue if there is a nonzero eigenvector such that .
("Eigen" is German for "characteristic of" or "peculiar to"; some authors call these characteristic values and vectors. No authors call them "peculiar".)
- Example 3.2
The projection map
has an eigenvalue of associated with any eigenvector of the form
where and are scalars at least one of which is non-. On the other hand, is not an eigenvalue of since no non- vector is doubled.
That example shows why the "non-" appears in the definition. Disallowing as an eigenvector eliminates trivial eigenvalues.
- Example 3.3
The only transformation on the trivial space is
.
This map has no eigenvalues because there are no non- vectors mapped to a scalar multiple of themselves.
- Example 3.4
Consider the homomorphism given by . The range of is one-dimensional. Thus an application of to a vector in the range will simply rescale that vector: . That is, has an eigenvalue of associated with eigenvectors of the form where .
This map also has an eigenvalue of associated with eigenvectors of the form where .
- Definition 3.5
A square matrix has a scalar eigenvalue associated with the non- eigenvector if .
- Remark 3.6
Although this extension from maps to matrices is obvious, there is a point that must be made. Eigenvalues of a map are also the eigenvalues of matrices representing that map, and so similar matrices have the same eigenvalues. But the eigenvectors are different— similar matrices need not have the same eigenvectors.
For instance, consider again the transformation given by . It has an eigenvalue of associated with eigenvectors of the form where . If we represent with respect to
then is an eigenvalue of , associated with these eigenvectors.
On the other hand, representing with respect to gives
and the eigenvectors of associated with the eigenvalue are these.
Thus similar matrices can have different eigenvectors.
Here is an informal description of what's happening. The underlying transformation doubles the eigenvectors . But when the matrix representing the transformation is then it "assumes" that column vectors are representations with respect to . In contrast, "assumes" that column vectors are representations with respect to . So the vectors that get doubled by each matrix look different.
The next example illustrates the basic tool for finding eigenvectors and eigenvalues.
- Example 3.7
What are the eigenvalues and eigenvectors of this matrix?
To find the scalars such that for non- eigenvectors , bring everything to the left-hand side
and factor . (Note that it says ; the expression doesn't make sense because is a matrix while is a scalar.) This homogeneous linear system
has a non- solution if and only if the matrix is singular. We can determine when that happens.
The eigenvalues are and . To find the associated eigenvectors, plug in each eigenvalue. Plugging in gives
for a scalar parameter ( is non- because eigenvectors must be non-). In the same way, plugging in gives
with .
- Example 3.8
If
(here is not a projection map, it is the number ) then
so has eigenvalues of and . To find associated eigenvectors, first plug in for :
for a scalar , and then plug in :
where .
- Definition 3.9
The characteristic polynomial of a square matrix is the determinant of the matrix , where is a variable. The characteristic equation is . The characteristic polynomial of a transformation is the polynomial of any .
Problem 11 checks that the characteristic polynomial of a transformation is well-defined, that is, any choice of basis yields the same polynomial.
- Lemma 3.10
A linear transformation on a nontrivial vector space has at least one eigenvalue.
- Proof
Any root of the characteristic polynomial is an eigenvalue. Over the complex numbers, any polynomial of degree one or greater has a root. (This is the reason that in this chapter we've gone to scalars that are complex.)
Notice the familiar form of the sets of eigenvectors in the above examples.
- Definition 3.11
The eigenspace of a transformation associated with the eigenvalue is . The eigenspace of a matrix is defined analogously.
- Lemma 3.12
An eigenspace is a subspace.
- Proof
An eigenspace must be nonempty— for one thing it contains the zero vector— and so we need only check closure. Take vectors from , to show that any linear combination is in
(the second equality holds even if any is since ).
- Example 3.13
In Example 3.8 the eigenspace associated with the eigenvalue and the eigenspace associated with the eigenvalue are these.
- Remark 3.15
The characteristic equation is so in some sense is an eigenvalue "twice". However there are not "twice" as many eigenvectors, in that the dimension of the eigenspace is one, not two. The next example shows a case where a number, , is a double root of the characteristic equation and the dimension of the associated eigenspace is two.
- Example 3.16
With respect to the standard bases, this matrix
represents projection.
Its eigenspace associated with the eigenvalue and its eigenspace associated with the eigenvalue are easy to find.
By the lemma, if two eigenvectors and are associated with the same eigenvalue then any linear combination of those two is also an eigenvector associated with that same eigenvalue. But, if two eigenvectors and are associated with different eigenvalues then the sum need not be related to the eigenvalue of either one. In fact, just the opposite. If the eigenvalues are different then the eigenvectors are not linearly related.
- Theorem 3.17
For any set of distinct eigenvalues of a map or matrix, a set of associated eigenvectors, one per eigenvalue, is linearly independent.
- Proof
We will use induction on the number of eigenvalues. If there is no eigenvalue or only one eigenvalue then the set of associated eigenvectors is empty or is a singleton set with a non- member, and in either case is linearly independent.
For induction, assume that the theorem is true for any set of distinct eigenvalues, suppose that are distinct eigenvalues, and let be associated eigenvectors. If then after multiplying both sides of the displayed equation by , applying the map or matrix to both sides of the displayed equation, and subtracting the first result from the second, we have this.
The induction hypothesis now applies: . Thus, as all the eigenvalues are distinct, are all . Finally, now must be because we are left with the equation .
- Example 3.18
The eigenvalues of
are distinct: , , and . A set of associated eigenvectors like
is linearly independent.
- Corollary 3.19
An matrix with distinct eigenvalues is diagonalizable.
- Proof
Form a basis of eigenvectors. Apply Corollary 2.4.
Exercises
- Problem 1
For each, find the characteristic polynomial and the eigenvalues.
- This exercise is recommended for all readers.
- Problem 2
For each matrix, find the characteristic equation, and the eigenvalues and associated eigenvectors.
- Problem 3
Find the characteristic equation, and the eigenvalues and associated eigenvectors for this matrix. Hint. The eigenvalues are complex.
- Problem 4
Find the characteristic polynomial, the eigenvalues, and the associated eigenvectors of this matrix.
- This exercise is recommended for all readers.
- Problem 5
For each matrix, find the characteristic equation, and the eigenvalues and associated eigenvectors.
- This exercise is recommended for all readers.
- Problem 6
Let be
Find its eigenvalues and the associated eigenvectors.
- Problem 7
Find the eigenvalues and eigenvectors of this map .
- This exercise is recommended for all readers.
- Problem 8
Find the eigenvalues and associated eigenvectors of the differentiation operator .
- Problem 9
- Prove that
the eigenvalues of a triangular matrix (upper or lower triangular) are the entries on the diagonal.
- This exercise is recommended for all readers.
- Problem 10
Find the formula for the characteristic polynomial of a matrix.
- Problem 11
Prove that the characteristic polynomial of a transformation is well-defined.
- This exercise is recommended for all readers.
- Problem 12
- Can any non- vector in any nontrivial vector space be a eigenvector? That is, given a from a nontrivial , is there a transformation and a scalar such that ?
- Given a scalar , can any non- vector in any nontrivial vector space be an eigenvector associated with the eigenvalue ?
- This exercise is recommended for all readers.
- Problem 13
Suppose that and . Prove that the eigenvectors of associated with are the non- vectors in the kernel of the map represented (with respect to the same bases) by .
- Problem 14
Prove that if are all integers and then
has integral eigenvalues, namely and .
- This exercise is recommended for all readers.
- Problem 15
Prove that if is nonsingular and has eigenvalues then has eigenvalues . Is the converse true?
- This exercise is recommended for all readers.
- Problem 16
Suppose that is and are scalars.
- Prove that if has the eigenvalue with an associated eigenvector then is an eigenvector of associated with eigenvalue .
- Prove that if is diagonalizable then so is .
- This exercise is recommended for all readers.
- Problem 17
Show that is an eigenvalue of if and only if the map represented by is not an isomorphism.
- Problem 18
- Show that if is an eigenvalue of then is an eigenvalue of .
- What is wrong with this proof generalizing that? "If is an eigenvalue of and is an eigenvalue for , then is an eigenvalue for , for, if and then "?
- Problem 19
Do matrix-equivalent matrices have the same eigenvalues?
- Problem 20
Show that a square matrix with real entries and an odd number of rows has at least one real eigenvalue.
- Problem 21
Diagonalize.
- Problem 22
Suppose that is a nonsingular matrix. Show that the similarity transformation map sending is an isomorphism.
- ? Problem 23
Show that if is an square matrix and each row (column) sums to then is a characteristic root of . (Morrison 1967)
Section III - Nilpotence
The goal of this chapter is to show that every square matrix is similar to one that is a sum of two kinds of simple matrices. The prior section focused on the first kind, diagonal matrices. We now consider the other kind.
1 - Self-Composition
This subsection is optional, although it is necessary for later material in this section and in the next one.
A linear transformations , because it has the same domain and codomain, can be iterated.[2] That is, compositions of with itself such as and are defined.
Note that this power notation for the linear transformation functions dovetails with the notation that we've used earlier for their squared matrix representations because if then .
- Example 1.1
For the derivative map given by
the second power is the second derivative
the third power is the third derivative
and any higher power is the zero map.
- Example 1.2
This transformation of the space of matrices
has this second power
and this third power.
After that, and , etc.
These examples suggest that on iteration more and more zeros appear until there is a settling down. The next result makes this precise.
- Lemma 1.3
For any transformation , the rangespaces of the powers form a descending chain
and the nullspaces form an ascending chain.
Further, there is a such that for powers less than the subsets are proper (if then and ), while for powers greater than the sets are equal (if then and ).
- Proof
We will do the rangespace half and leave the rest for Problem 6. Recall, however, that for any map the dimension of its rangespace plus the dimension of its nullspace equals the dimension of its domain. So if the rangespaces shrink then the nullspaces must grow.
That the rangespaces form chains is clear because if , so that , then and so . To verify the "further" property, first observe that if any pair of rangespaces in the chain are equal then all subsequent ones are also equal , etc. This is because if is the same map, with the same domain, as and it therefore has the same range: (and induction shows that it holds for all higher powers). So if the chain of rangespaces ever stops being strictly decreasing then it is stable from that point onward.
But the chain must stop decreasing. Each rangespace is a subspace of the one before it. For it to be a proper subspace it must be of strictly lower dimension (see Problem 4). These spaces are finite-dimensional and so the chain can fall for only finitely-many steps, that is, the power is at most the dimension of .
- Example 1.4
The derivative map of Example 1.1 has this chain of rangespaces
and this chain of nullspaces.
- Example 1.5
The transformation projecting onto the first two coordinates
has and .
- Example 1.6
Let be the map As the lemma describes, on iteration the rangespace shrinks
and then stabilizes , while the nullspace grows
and then stabilizes .
This graph illustrates Lemma 1.3. The horizontal axis gives the power of a transformation. The vertical axis gives the dimension of the rangespace of as the distance above zero— and thus also shows the dimension of the nullspace as the distance below the gray horizontal line, because the two add to the dimension of the domain.
As sketched, on iteration the rank falls and with it the nullity grows until the two reach a steady state. This state must be reached by the -th iterate. The steady state's distance above zero is the dimension of the generalized rangespace and its distance below is the dimension of the generalized nullspace.
- Definition 1.7
Let be a transformation on an -dimensional space. The generalized rangespace (or the closure of the rangespace) is The generalized nullspace (or the closure of the nullspace) is .
Exercises
- Problem 1
Give the chains of rangespaces and nullspaces for the zero and identity transformations.
- Problem 2
For each map, give the chain of rangespaces and the chain of nullspaces, and the generalized rangespace and the generalized nullspace.
- ,
- ,
- ,
- ,
- Problem 3
Prove that function composition is associative and so we can write without specifying a grouping.
- Problem 4
Check that a subspace must be of dimension less than or equal to the dimension of its superspace. Check that if the subspace is proper (the subspace does not equal the superspace) then the dimension is strictly less. (This is used in the proof of Lemma 1.3.)
- Problem 5
Prove that the generalized rangespace is the entire space, and the generalized nullspace is trivial, if the transformation is nonsingular. Is this "only if" also?
- Problem 6
Verify the nullspace half of Lemma 1.3.
- Problem 7
Give an example of a transformation on a three dimensional space whose range has dimension two. What is its nullspace? Iterate your example until the rangespace and nullspace stabilize.
- Problem 8
Show that the rangespace and nullspace of a linear transformation need not be disjoint. Are they ever disjoint?
2 - Strings
This subsection is optional, and requires material from the optional Direct Sum subsection.
The prior subsection shows that as increases, the dimensions of the 's fall while the dimensions of the 's rise, in such a way that this rank and nullity split the dimension of . Can we say more; do the two split a basis— is ?
The answer is yes for the smallest power since . The answer is also yes at the other extreme.
- Lemma 2.1
Where is a linear transformation, the space is the direct sum . That is, both and .
- Proof
We will verify the second sentence, which is equivalent to the first. The first clause, that the dimension of the domain of equals the rank of plus the nullity of , holds for any transformation and so we need only verify the second clause.
Assume that , to prove that is . Because is in the nullspace, . On the other hand, because , the map is a dimension-preserving homomorphism and therefore is one-to-one. A composition of one-to-one maps is one-to-one, and so is one-to-one. But now— because only is sent by a one-to-one linear map to — the fact that implies that .
- Note 2.2
Technically we should distinguish the map from the map because the domains or codomains might differ. The second one is said to be the restriction[3] of to . We shall use later a point from that proof about the restriction map, namely that it is nonsingular.
In contrast to the and cases, for intermediate powers the space might not be the direct sum of and . The next example shows that the two can have a nontrivial intersection.
- Example 2.3
Consider the transformation of defined by this action on the elements of the standard basis.
The vector
is in both the rangespace and nullspace. Another way to depict this map's action is with a string.
- Example 2.4
A map whose action on is given by the string
has equal to the span , has , and has . The matrix representation is all zeros except for some subdiagonal ones.
- Example 2.5
Transformations can act via more than one string. A transformation acting on a basis by
is represented by a matrix that is all zeros except for blocks of subdiagonal ones
(the lines just visually organize the blocks).
In those three examples all vectors are eventually transformed to zero.
- Definition 2.6
A nilpotent transformation is one with a power that is the zero map. A nilpotent matrix is one with a power that is the zero matrix. In either case, the least such power is the index of nilpotency.
- Example 2.7
In Example 2.3 the index of nilpotency is two. In Example 2.4 it is four. In Example 2.5 it is three.
- Example 2.8
The differentiation map is nilpotent of index three since the third derivative of any quadratic polynomial is zero. This map's action is described by the string and taking the basis gives this representation.
Not all nilpotent matrices are all zeros except for blocks of subdiagonal ones.
- Example 2.9
With the matrix from Example 2.4, and this four-vector basis
a change of basis operation produces this representation with respect to .
The new matrix is nilpotent; it's fourth power is the zero matrix since
and is the zero matrix.
The goal of this subsection is Theorem 2.13, which shows that the prior example is prototypical in that every nilpotent matrix is similar to one that is all zeros except for blocks of subdiagonal ones.
- Definition 2.10
Let be a nilpotent transformation on . A -string generated by is a sequence . This sequence has length . A -string basis is a basis that is a concatenation of -strings.
- Example 2.11
In Example 2.5, the -strings and , of length three and two, can be concatenated to make a basis for the domain of .
- Lemma 2.12
If a space has a -string basis then the longest string in it has length equal to the index of nilpotency of .
- Proof
Suppose not. Those strings cannot be longer; if the index is then sends any vector— including those starting the string— to . So suppose instead that there is a transformation of index on some space, such that the space has a -string basis where all of the strings are shorter than length . Because has index , there is a vector such that . Represent as a linear combination of basis elements and apply . We are supposing that sends each basis element to but that it does not send to . That is impossible.
We shall show that every nilpotent map has an associated string basis. Then our goal theorem, that every nilpotent matrix is similar to one that is all zeros except for blocks of subdiagonal ones, is immediate, as in Example 2.5.
Looking for a counterexample, a nilpotent map without an associated string basis that is disjoint, will suggest the idea for the proof. Consider the map with this action.
Even after omitting the zero vector, these three strings aren't disjoint, but that doesn't end hope of finding a -string basis. It only means that will not do for the string basis.
To find a basis that will do, we first find the number and lengths of its strings. Since 's index of nilpotency is two, Lemma 2.12 says that at least one string in the basis has length two. Thus the map must act on a string basis in one of these two ways.
Now, the key point. A transformation with the left-hand action has a nullspace of dimension three since that's how many basis vectors are sent to zero. A transformation with the right-hand action has a nullspace of dimension four. Using the matrix representation above, calculation of 's nullspace
shows that it is three-dimensional, meaning that we want the left-hand action.
To produce a string basis, first pick and from
(other choices are possible, just be sure that is linearly independent). For pick a vector from that is not in the span of .
Finally, take and such that and .
Now, with respect to , the matrix of is as desired.
- Theorem 2.13
Any nilpotent transformation is associated with a -string basis. While the basis is not unique, the number and the length of the strings is determined by .
This illustrates the proof. Basis vectors are categorized into kind , kind , and kind . They are also shown as squares or circles, according to whether they are in the nullspace or not.
- Proof
Fix a vector space ; we will argue by induction on the index of nilpotency of . If that index is then is the zero map and any basis is a string basis , ..., . For the inductive step, assume that the theorem holds for any transformation with an index of nilpotency between and and consider the index case.
First observe that the restriction to the rangespace is also nilpotent, of index . Apply the inductive hypothesis to get a string basis for , where the number and length of the strings is determined by .
(In the illustration these are the basis vectors of kind , so there are strings shown with this kind of basis vector.)
Second, note that taking the final nonzero vector in each string gives a basis for . (These are illustrated with 's in squares.) For, a member of is mapped to zero if and only if it is a linear combination of those basis vectors that are mapped to zero. Extend to a basis for all of .
(The 's are the vectors of kind so that is the set of squares.) While many choices are possible for the 's, their number is determined by the map as it is the dimension of minus the dimension of .
Finally, is a basis for because any sum of something in the rangespace with something in the nullspace can be represented using elements of for the rangespace part and elements of for the part from the nullspace. Note that
and so can be extended to a basis for all of by the addition of more vectors. Specifically, remember that each of is in , and extend with vectors such that . (In the illustration, these are the 's.) The check that linear independence is preserved by this extension is Problem 13.
- Corollary 2.14
Every nilpotent matrix is similar to a matrix that is all zeros except for blocks of subdiagonal ones. That is, every nilpotent map is represented with respect to some basis by such a matrix.
This form is unique in the sense that if a nilpotent matrix is similar to two such matrices then those two simply have their blocks ordered differently. Thus this is a canonical form for the similarity classes of nilpotent matrices provided that we order the blocks, say, from longest to shortest.
- Example 2.15
The matrix
has an index of nilpotency of two, as this calculation shows.
The calculation also describes how a map represented by must act on any string basis. With one map application the nullspace has dimension one and so one vector of the basis is sent to zero. On a second application, the nullspace has dimension two and so the other basis vector is sent to zero. Thus, the action of the map is and the canonical form of the matrix is this.
We can exhibit such a -string basis and the change of basis matrices witnessing the matrix similarity. For the basis, take to represent with respect to the standard bases, pick a and also pick a so that .
(If we take to be a representative with respect to some nonstandard bases then this picking step is just more messy.) Recall the similarity diagram.
The canonical form equals , where
and the verification of the matrix calculation is routine.
- Example 2.16
The matrix
is nilpotent. These calculations show the nullspaces growing.
That table shows that any string basis must satisfy: the nullspace after one map application has dimension two so two basis vectors are sent directly to zero, the nullspace after the second application has dimension four so two additional basis vectors are sent to zero by the second iteration, and the nullspace after three applications is of dimension five so the final basis vector is sent to zero in three hops.
To produce such a basis, first pick two independent vectors from
then add such that and
and finish by adding ) such that .
Exercises
- This exercise is recommended for all readers.
- Problem 1
What is the index of nilpotency of the left-shift operator, here acting on the space of triples of reals?
- This exercise is recommended for all readers.
- Problem 2
For each string basis state the index of nilpotency and give the dimension of the rangespace and nullspace of each iteration of the nilpotent map.
Also give the canonical form of the matrix.
- Problem 3
Decide which of these matrices are nilpotent.
- This exercise is recommended for all readers.
- Problem 4
Find the canonical form of this matrix.
- This exercise is recommended for all readers.
- Problem 5
Consider the matrix from Example 2.16.
- Use the action of the map on the string basis to give the canonical form.
- Find the change of basis matrices that bring the matrix to canonical form.
- Use the answer in the prior item to check the answer in the first item.
- This exercise is recommended for all readers.
- Problem 6
Each of these matrices is nilpotent.
Put each in canonical form.
- Problem 7
Describe the effect of left or right multiplication by a matrix that is in the canonical form for nilpotent matrices.
- Problem 8
Is nilpotence invariant under similarity? That is, must a matrix similar to a nilpotent matrix also be nilpotent? If so, with the same index?
- This exercise is recommended for all readers.
- Problem 9
Show that the only eigenvalue of a nilpotent matrix is zero.
- Problem 10
Is there a nilpotent transformation of index three on a two-dimensional space?
- Problem 11
In the proof of Theorem 2.13, why isn't the proof's base case that the index of nilpotency is zero?
- This exercise is recommended for all readers.
- Problem 12
Let be a linear transformation and suppose is such that but . Consider the -string .
- Prove that is a transformation on the span of the set of vectors in the string, that is, prove that restricted to the span has a range that is a subset of the span. We say that the span is a -invariant subspace.
- Prove that the restriction is nilpotent.
- Prove that the -string is linearly independent and so is a basis for its span.
- Represent the restriction map with respect to the -string basis.
- Problem 13
Finish the proof of Theorem 2.13.
- Problem 14
Show that the terms "nilpotent transformation" and "nilpotent matrix", as given in Definition 2.6, fit with each other: a map is nilpotent if and only if it is represented by a nilpotent matrix. (Is it that a transformation is nilpotent if an only if there is a basis such that the map's representation with respect to that basis is a nilpotent matrix, or that any representation is a nilpotent matrix?)
- Problem 15
Let be nilpotent of index four. How big can the rangespace of be?
- Problem 16
Recall that similar matrices have the same eigenvalues. Show that the converse does not hold.
- Problem 17
Prove a nilpotent matrix is similar to one that is all zeros except for blocks of super-diagonal ones.
- This exercise is recommended for all readers.
- Problem 18
Prove that if a transformation has the same rangespace as nullspace. then the dimension of its domain is even.
- Problem 19
Prove that if two nilpotent matrices commute then their product and sum are also nilpotent.
- Problem 20
Consider the transformation of given by where is an matrix. Prove that if is nilpotent then so is .
- Problem 21
Show that if is nilpotent then is invertible. Is that "only if" also?
References
Section IV - Jordan Form
This section uses material from three optional subsections: Direct Sum, Determinants Exist, and Other Formulas for the Determinant.
The chapter on linear maps shows that every can be represented by a partial-identity matrix with respect to some bases and . This chapter revisits this issue in the special case that the map is a linear transformation . Of course, the general result still applies but with the codomain and domain equal we naturally ask about having the two bases also be equal. That is, we want a canonical form to represent transformations as .
After a brief review section, we began by noting that a block partial identity form matrix is not always obtainable in this case. We therefore considered the natural generalization, diagonal matrices, and showed that if its eigenvalues are distinct then a map or matrix can be diagonalized. But we also gave an example of a matrix that cannot be diagonalized and in the section prior to this one we developed that example. We showed that a linear map is nilpotent— if we take higher and higher powers of the map or matrix then we eventually get the zero map or matrix— if and only if there is a basis on which it acts via disjoint strings. That led to a canonical form for nilpotent matrices.
Now, this section concludes the chapter. We will show that the two cases we've studied are exhaustive in that for any linear transformation there is a basis such that the matrix representation is the sum of a diagonal matrix and a nilpotent matrix in its canonical form.
1 - Polynomials of Maps and Matrices
Recall that the set of square matrices is a vector space under entry-by-entry addition and scalar multiplication and that this space has dimension . Thus, for any matrix the -member set is linearly dependent and so there are scalars such that is the zero matrix.
- Remark 1.1
This observation is small but important. It says that every transformation exhibits a generalized nilpotency: the powers of a square matrix cannot climb forever without a "repeat".
- Example 1.2
Rotation of plane vectors radians counterclockwise is represented with respect to the standard basis by
and verifying that equals the zero matrix is easy.
- Definition 1.3
For any polynomial , where is a linear transformation then is the transformation on the same space and where is a square matrix then is the matrix .
- Remark 1.4
If, for instance, , then most authors write in the identity matrix: . But most authors don't write in the identity map: . In this book we shall also observe this convention.
Of course, if then , which follows from the relationships , and , and .
As Example 1.2 shows, there may be polynomials of degree smaller than that zero the map or matrix.
- Definition 1.5
The minimal polynomial of a transformation or a square matrix is the polynomial of least degree and with leading coefficient such that is the zero map or is the zero matrix.
A minimal polynomial always exists by the observation opening this subsection. A minimal polynomial is unique by the "with leading coefficient " clause. This is because if there are two polynomials and that are both of the minimal degree to make the map or matrix zero (and thus are of equal degree), and both have leading 's, then their difference has a smaller degree than either and still sends the map or matrix to zero. Thus is the zero polynomial and the two are equal. (The leading coefficient requirement also prevents a minimal polynomial from being the zero polynomial.)
- Example 1.6
We can see that is minimal for the matrix of Example 1.2 by computing the powers of up to the power .
Next, put equal to the zero matrix
and use Gauss' method.
Setting , , and to zero forces and to also come out as zero. To get a leading one, the most we can do is to set and to zero. Thus the minimal polynomial is quadratic.
Using the method of that example to find the minimal polynomial of a matrix would mean doing Gaussian reduction on a system with nine equations in ten unknowns. We shall develop an alternative. To begin, note that we can break a polynomial of a map or a matrix into its components.
- Lemma 1.7
Suppose that the polynomial factors as . If is a linear transformation then these two are equal maps.
Consequently, if is a square matrix then and are equal matrices.
- Proof
This argument is by induction on the degree of the polynomial. The cases where the polynomial is of degree and are clear. The full induction argument is Problem 21 but the degree two case gives its sense.
A quadratic polynomial factors into two linear terms (the roots and might be equal). We can check that substituting for in the factored and unfactored versions gives the same map.
The third equality holds because the scalar comes out of the second term, as is linear.
In particular, if a minimial polynomial for a transformation factors as then is the zero map. Since sends every vector to zero, at least one of the maps sends some nonzero vectors to zero. So, too, in the matrix case— if is minimal for then is the zero matrix and at least one of the matrices sends some nonzero vectors to zero. Rewording both cases: at least some of the are eigenvalues. (See Problem 17.)
Recall how we have earlier found eigenvalues. We have looked for such that by considering the equation and computing the determinant of the matrix . That determinant is a polynomial in , the characteristic polynomial, whose roots are the eigenvalues. The major result of this subsection, the next result, is that there is a connection between this characteristic polynomial and the minimal polynomial. This results expands on the prior paragraph's insight that some roots of the minimal polynomial are eigenvalues by asserting that every root of the minimal polynomial is an eigenvalue and further that every eigenvalue is a root of the minimal polynomial (this is because it says "" and not just "").
- Theorem 1.8 (Cayley-Hamilton)
If the characteristic polynomial of a transformation or square matrix factors into
then its minimal polynomial factors into
where for each between and .
The proof takes up the next three lemmas. Although they are stated only in matrix terms, they apply equally well to maps. We give the matrix version only because it is convenient for the first proof.
The first result is the key— some authors call it the Cayley-Hamilton Theorem and call Theorem 1.8 above a corollary. For the proof, observe that a matrix of polynomials can be thought of as a polynomial with matrix coefficients.
- Lemma 1.9
If is a square matrix with characteristic polynomial then is the zero matrix.
- Proof
Let be , the matrix whose determinant is the characteristic polynomial .
Recall that the product of the adjoint of a matrix with the matrix itself is the determinant of that matrix times the identity.
The entries of are polynomials, each of degree at most since the minors of a matrix drop a row and column. Rewrite it, as suggested above, as where each is a matrix of scalars. The left and right ends of equation () above give this.
Equate the coefficients of , the coefficients of , etc.
Multiply (from the right) both sides of the first equation by , both sides of the second equation by , etc. Add. The result on the left is , and the result on the right is the zero matrix.
We sometimes refer to that lemma by saying that a matrix or map satisfies its characteristic polynomial.
- Lemma 1.10
Where is a polynomial, if is the zero matrix then is divisible by the minimal polynomial of . That is, any polynomial satisfied by is divisable by 's minimal polynomial.
- Proof
Let be minimal for . The Division Theorem for Polynomials gives where the degree of is strictly less than the degree of . Plugging in shows that is the zero matrix, because satisfies both and . That contradicts the minimality of unless is the zero polynomial.
Combining the prior two lemmas gives that the minimal polynomial divides the characteristic polynomial. Thus, any root of the minimal polynomial is also a root of the characteristic polynomial. That is, so far we have that if then must has the form where each is less than or equal to . The proof of the Cayley-Hamilton Theorem is finished by showing that in fact the characteristic polynomial has no extra roots , etc.
- Lemma 1.11
Each linear factor of the characteristic polynomial of a square matrix is also a linear factor of the minimal polynomial.
- Proof
Let be a square matrix with minimal polynomial and assume that is a factor of the characteristic polynomial of , that is, assume that is an eigenvalue of . We must show that is a factor of , that is, that .
In general, where is associated with the eigenvector , for any polynomial function , application of the matrix to equals the result of multiplying by the scalar . (For instance, if has eigenvalue associated with the eigenvector and then .) Now, as is the zero matrix, and therefore .
- Example 1.12
We can use the Cayley-Hamilton Theorem to help find the minimal polynomial of this matrix.
First, its characteristic polynomial can be found with the usual determinant. Now, the Cayley-Hamilton Theorem says that 's minimal polynomial is either or or . We can decide among the choices just by computing:
and
and so .
Exercises
- This exercise is recommended for all readers.
- Problem 1
What are the possible minimal polynomials if a matrix has the given characteristic polynomial?
What is the degree of each possibility?
- This exercise is recommended for all readers.
- Problem 2
Find the minimal polynomial of each matrix.
- Problem 3
Find the minimal polynomial of this matrix.
- This exercise is recommended for all readers.
- Problem 4
What is the minimal polynomial of the differentiation operator on ?
- This exercise is recommended for all readers.
- Problem 5
Find the minimal polynomial of matrices of this form
where the scalar is fixed (i.e., is not a variable).
- Problem 6
What is the minimal polynomial of the transformation of that sends to ?
- Problem 7
What is the minimal polynomial of the map projecting onto the first two coordinates?
- Problem 8
Find a matrix whose minimal polynomial is .
- Problem 9
What is wrong with this claimed proof of Lemma 1.9: "if then "? (Cullen 1990)
- Problem 10
Verify Lemma 1.9 for matrices by direct calculation.
- This exercise is recommended for all readers.
- Problem 11
Prove that the minimal polynomial of an matrix has degree at most (not as might be guessed from this subsection's opening). Verify that this maximum, , can happen.
- This exercise is recommended for all readers.
- Problem 12
The only eigenvalue of a nilpotent map is zero. Show that the converse statement holds.
- Problem 13
What is the minimal polynomial of a zero map or matrix? Of an identity map or matrix?
- This exercise is recommended for all readers.
- Problem 14
Interpret the minimal polynomial of Example 1.2 geometrically.
- Problem 15
What is the minimal polynomial of a diagonal matrix?
- This exercise is recommended for all readers.
- Problem 16
A projection is any transformation such that . (For instance, the transformation of the plane projecting each vector onto its first coordinate will, if done twice, result in the same value as if it is done just once.) What is the minimal polynomial of a projection?
- Problem 17
The first two items of this question are review.
- Prove that the composition of one-to-one maps is one-to-one.
- Prove that if a linear map is not one-to-one then at least one nonzero vector from the domain is sent to the zero vector in the codomain.
- Verify the statement, excerpted here, that
preceeds Theorem 1.8.
... if a minimial polynomial for a transformation factors as then is the zero map. Since sends every vector to zero, at least one of the maps sends some nonzero vectors to zero. ... Rewording ...: at least some of the are eigenvalues.
- Problem 18
True or false: for a transformation on an dimensional space, if the minimal polynomial has degree then the map is diagonalizable.
- Problem 19
Let be a polynomial. Prove that if and are similar matrices then is similar to .
- Now show that similar matrices have the same characteristic polynomial.
- Show that similar matrices have the same minimal polynomial.
- Decide if these are similar.
- Problem 20
- Show that a matrix is invertible if and only if the constant term in its minimal polynomial is not .
- Show that if a square matrix is not invertible then there is a nonzero matrix such that and both equal the zero matrix.
- This exercise is recommended for all readers.
- Problem 21
- Finish the proof of Lemma 1.7.
- Give an example to show that the result does not hold if is not linear.
- Problem 22
Any transformation or square matrix has a minimal polynomial. Does the converse hold?
2 - Jordan Canonical Form
This subsection moves from the canonical form for nilpotent matrices to the one for all matrices.
We have shown that if a map is nilpotent then all of its eigenvalues are zero. We can now prove the converse.
- Lemma 2.1
A linear transformation whose only eigenvalue is zero is nilpotent.
- Proof
If a transformation on an -dimensional space has only the single eigenvalue of zero then its characteristic polynomial is . The Cayley-Hamilton Theorem says that a map satisfies its characteristic polynimial so is the zero map. Thus is nilpotent.
We have a canonical form for nilpotent matrices, that is, for each matrix whose single eigenvalue is zero: each such matrix is similar to one that is all zeroes except for blocks of subdiagonal ones. (To make this representation unique we can fix some arrangement of the blocks, say, from longest to shortest.) We next extend this to all single-eigenvalue matrices.
Observe that if 's only eigenvalue is then 's only eigenvalue is because if and only if . The natural way to extend the results for nilpotent matrices is to represent in the canonical form , and try to use that to get a simple representation for . The next result says that this try works.
- Lemma 2.2
If the matrices and are similar then and are also similar, via the same change of basis matrices.
- Proof
With we have since the diagonal matrix commutes with anything, and so . Therefore , as required.
- Example 2.3
The characteristic polynomial of
is and so has only the single eigenvalue . Thus for
the only eigenvalue is , and is nilpotent. The null spaces are routine to find; to ease this computation we take to represent the transformation with respect to the standard basis (we shall maintain this convention for the rest of the chapter).
The dimensions of these null spaces show that the action of an associated map on a string basis is . Thus, the canonical form for with one choice for a string basis is
and by Lemma 2.2, is similar to this matrix.
We can produce the similarity computation. Recall from the Nilpotence section how to find the change of basis matrices and to express as . The similarity diagram
describes that to move from the lower left to the upper left we multiply by
and to move from the upper right to the lower right we multiply by this matrix.
So the similarity is expressed by
which is easily checked.
- Example 2.4
This matrix has characteristic polynomial
and so has the single eigenvalue . The nullities of are: the null space of has dimension two, the null space of has dimension three, and the null space of has dimension four. Thus, has the action on a string basis of and . This gives the canonical form for , which in turn gives the form for .
An array that is all zeroes, except for some number down the diagonal and blocks of subdiagonal ones, is a Jordan block. We have shown that Jordan block matrices are canonical representatives of the similarity classes of single-eigenvalue matrices.
- Example 2.5
The matrices whose only eigenvalue is separate into three similarity classes. The three classes have these canonical representatives.
In particular, this matrix
belongs to the similarity class represented by the middle one, because we have adopted the convention of ordering the blocks of subdiagonal ones from the longest block to the shortest.
We will now finish the program of this chapter by extending this work to cover maps and matrices with multiple eigenvalues. The best possibility for general maps and matrices would be if we could break them into a part involving their first eigenvalue (which we represent using its Jordan block), a part with , etc.
This ideal is in fact what happens. For any transformation , we shall break the space into the direct sum of a part on which is nilpotent, plus a part on which is nilpotent, etc. More precisely, we shall take three steps to get to this section's major theorem and the third step shows that where are 's eigenvalues.
Suppose that is a linear transformation. Note that the restriction[1] of to a subspace need not be a linear transformation on because there may be an with . To ensure that the restriction of a transformation to a "part" of a space is a transformation on the partwe need the next condition.
- Definition 2.6
Let be a transformation. A subspace is invariant if whenever then (shorter: ).
Two examples are that the generalized null space and the generalized range space of any transformation are invariant. For the generalized null space, if then where is the dimension of the underlying space and so because is zero also. For the generalized range space, if then for some and then shows that is also a member of .
Thus the spaces and are invariant. Observe also that is nilpotent on because, simply, if has the property that some power of maps it to zero— that is, if it is in the generalized null space— then some power of maps it to zero. The generalized null space is a "part" of the space on which the action of is easy to understand.
The next result is the first of our three steps. It establishes that leaves 's part unchanged.
- Lemma 2.7
A subspace is invariant if and only if it is invariant for any scalar . In particular, where is an eigenvalue of a linear transformation , then for any other eigenvalue , the spaces and are invariant.
- Proof
For the first sentence we check the two implications of the "if and only if" separately. One of them is easy: if the subspace is invariant for any then taking shows that it is invariant. For the other implication suppose that the subspace is invariant, so that if then , and let be any scalar. The subspace is closed under linear combinations and so if then . Thus if then , as required.
The second sentence follows straight from the first. Because the two spaces are invariant, they are therefore invariant. From this, applying the first sentence again, we conclude that they are also invariant.
The second step of the three that we will take to prove this section's major result makes use of an additional property of and , that they are complementary. Recall that if a space is the direct sum of two others then any vector in the space breaks into two parts where and , and recall also that if and are bases for and then the concatenation is linearly independent (and so the two parts of do not "overlap"). The next result says that for any subspaces and that are complementary as well as invariant, the action of on breaks into the "non-overlapping" actions of on and on .
- Lemma 2.8
Let be a transformation and let and be invariant complementary subspaces of . Then can be represented by a matrix with blocks of square submatrices and
where and are blocks of zeroes.
- Proof
Since the two subspaces are complementary, the concatenation of a basis for and a basis for makes a basis for . We shall show that the matrix
has the desired form.
Any vector is in if and only if its final components are zeroes when it is represented with respect to . As is invariant, each of the vectors , ..., has that form. Hence the lower left of is all zeroes.
The argument for the upper right is similar.
To see that has been decomposed into its action on the parts, observe that the restrictions of to the subspaces and are represented, with respect to the obvious bases, by the matrices and . So, with subspaces that are invariant and complementary, we can split the problem of examining a linear transformation into two lower-dimensional subproblems. The next result illustrates this decomposition into blocks.
- Lemma 2.9
If is a matrices with square submatrices and
where the 's are blocks of zeroes, then .
- Proof
Suppose that is , that is , and that is . In the permutation formula for the determinant
each term comes from a rearrangement of the column numbers into a new order . The upper right block is all zeroes, so if a has at least one of among its first column numbers then the term arising from is zero, e.g., if then .
So the above formula reduces to a sum over all permutations with two halves: any significant is the composition of a that rearranges only and a that rearranges only . Now, the distributive law (and the fact that the signum of a composition is the product of the signums) gives that this
equals .
- Example 2.10
From Lemma 2.9 we conclude that if two subspaces are complementary and invariant then is nonsingular if and only if its restrictions to both subspaces are nonsingular.
Now for the promised third, final, step to the main result.
- Lemma 2.11
If a linear transformation has the characteristic polynomial then (1) and (2) .
- Proof
Because is the degree of the characteristic polynomial, to establish statement (1) we need only show that statement (2) holds and that is trivial whenever .
For the latter, by Lemma 2.7, both and are invariant. Notice that an intersection of invariant subspaces is invariant and so the restriction of to is a linear transformation. But both and are nilpotent on this subspace and so if has any eigenvalues on the intersection then its "only" eigenvalue is both and . That cannot be, so this restriction has no eigenvalues: is trivial (Lemma V.II.3.10 shows that the only transformation without any eigenvalues is on the trivial space).
To prove statement (2), fix the index . Decompose as
and apply Lemma 2.8.
By Lemma 2.9, . By the uniqueness clause of the Fundamental Theorem of Arithmetic, the determinants of the blocks have the same factors as the characteristic polynomial and , and the sum of the powers of these factors is the power of the factor in the characteristic polynomial: , ..., . Statement (2) will be proved if we will show that and that for all , because then the degree of the polynomial — which equals the dimension of the generalized null space— is as required.
For that, first, as the restriction of to is nilpotent on that space, the only eigenvalue of on it is . Thus the characteristic equation of on is . And thus for all .
Now consider the restriction of to . By Note V.III.2.2, the map is nonsingular on and so is not an eigenvalue of on that subspace. Therefore, is not a factor of , and so .
Our major result just translates those steps into matrix terms.
- Theorem 2.12
Any square matrix is similar to one in Jordan form
where each is the Jordan block associated with the eigenvalue of the original matrix (that is, is all zeroes except for 's down the diagonal and some subdiagonal ones).
- Proof
Given an matrix , consider the linear map that it represents with respect to the standard bases. Use the prior lemma to write where are the eigenvalues of . Because each is invariant, Lemma 2.8 and the prior lemma show that is represented by a matrix that is all zeroes except for square blocks along the diagonal. To make those blocks into Jordan blocks, pick each to be a string basis for the action of on .
Jordan form is a canonical form for similarity classes of square matrices, provided that we make it unique by arranging the Jordan blocks from least eigenvalue to greatest and then arranging the subdiagonal blocks inside each Jordan block from longest to shortest.
- Example 2.13
This matrix has the characteristic polynomial .
We will handle the eigenvalues and separately.
Computation of the powers, and the null spaces and nullities, of is routine. (Recall from Example 2.3 the convention of taking to represent a transformation, here , with respect to the standard basis.)
So the generalized null space has dimension two. We've noted that the restriction of is nilpotent on this subspace. From the way that the nullities grow we know that the action of on a string basis . Thus the restriction can be represented in the canonical form
where many choices of basis are possible. Consequently, the action of the restriction of to is represented by this matrix.
The second eigenvalue's computations are easier. Because the power of in the characteristic polynomial is one, the restriction of to must be nilpotent of index one. Its action on a string basis must be and since it is the zero map, its canonical form is the zero matrix. Consequently, the canonical form for the action of on is the matrix with the single entry . For the basis we can use any nonzero vector from the generalized null space.
Taken together, these two give that the Jordan form of is
where is the concatenation of and .
- Example 2.14
Contrast the prior example with
which has the same characteristic polynomial .
While the characteristic polynomial is the same,
here the action of is stable after only one application— the restriction of of to is nilpotent of index only one. (So the contrast with the prior example is that while the characteristic polynomial tells us to look at the action of the on its generalized null space, the characteristic polynomial does not describe completely its action and we must do some computations to find, in this example, that the minimal polynomial is .) The restriction of to the generalized null space acts on a string basis as and , and we get this Jordan block associated with the eigenvalue .
For the other eigenvalue, the arguments for the second eigenvalue of the prior example apply again. The restriction of to is nilpotent of index one (it can't be of index less than one, and since is a factor of the characteristic polynomial to the power one it can't be of index more than one either). Thus 's canonical form is the zero matrix, and the associated Jordan block is the matrix with entry .
Therefore, is diagonalizable.
(Checking that the third vector in is in the nullspace of is routine.)
- Example 2.15
A bit of computing with
shows that its characteristic polynomial is . This table
shows that the restriction of to acts on a string basis via the two strings and .
A similar calculation for the other eigenvalue
shows that the restriction of to its generalized null space acts on a string basis via the two separate strings and .
Therefore is similar to this Jordan form matrix.
We close with the statement that the subjects considered earlier in this Chpater are indeed, in this sense, exhaustive.
- Corollary 2.16
Every square matrix is similar to the sum of a diagonal matrix and a nilpotent matrix.
Exercises
- Problem 1
Do the check for Example 2.3.
- Problem 2
Each matrix is in Jordan form. State its characteristic polynomial and its minimal polynomial.
- This exercise is recommended for all readers.
- Problem 3
Find the Jordan form from the given data.
- The matrix is with the single eigenvalue . The nullities of the powers are: has nullity two, has nullity three, has nullity four, and has nullity five.
- The matrix is with two eigenvalues. For the eigenvalue the nullities are: has nullity two, and has nullity four. For the eigenvalue the nullities are: has nullity one.
- Problem 4
Find the change of basis matrices for each example.
- This exercise is recommended for all readers.
- Problem 5
Find the Jordan form and a Jordan basis for each matrix.
- This exercise is recommended for all readers.
- Problem 6
Find all possible Jordan forms of a transformation with characteristic polynomial .
- Problem 7
Find all possible Jordan forms of a transformation with characteristic polynomial .
- This exercise is recommended for all readers.
- Problem 8
Find all possible Jordan forms of a transformation with characteristic polynomial and minimal polynomial .
- Problem 9
Find all possible Jordan forms of a transformation with characteristic polynomial and minimal polynomial .
- This exercise is recommended for all readers.
- Problem 10
- Diagonalize these.
- This exercise is recommended for all readers.
- Problem 11
Find the Jordan matrix representing the differentiation operator on .
- This exercise is recommended for all readers.
- Problem 12
Decide if these two are similar.
- Problem 13
Find the Jordan form of this matrix.
Also give a Jordan basis.
- Problem 14
How many similarity classes are there for matrices whose only eigenvalues are and ?
- This exercise is recommended for all readers.
- Problem 15
Prove that a matrix is diagonalizable if and only if its minimal polynomial has only linear factors.
- Problem 16
Give an example of a linear transformation on a vector space that has no non-trivial invariant subspaces.
- Problem 17
Show that a subspace is invariant if and only if it is invariant.
- Problem 18
Prove or disprove: two matrices are similar if and only if they have the same characteristic and minimal polynomials.
- Problem 19
The trace of a square matrix is the sum of its diagonal entries.
- Find the formula for the characteristic polynomial of a matrix.
- Show that trace is invariant under similarity, and so we can sensibly speak of the "trace of a map". (Hint: see the prior item.)
- Is trace invariant under matrix equivalence?
- Show that the trace of a map is the sum of its eigenvalues (counting multiplicities).
- Show that the trace of a nilpotent map is zero. Does the converse hold?
- Problem 20
To use Definition 2.6 to check whether a subspace is invariant, we seemingly have to check all of the infinitely many vectors in a (nontrivial) subspace to see if they satisfy the condition. Prove that a subspace is invariant if and only if its subbasis has the property that for all of its elements, is in the subspace.
- This exercise is recommended for all readers.
- Problem 21
Is invariance preserved under intersection? Under union? Complementation? Sums of subspaces?
- Problem 22
Give a way to order the Jordan blocks if some of the eigenvalues are complex numbers. That is, suggest a reasonable ordering for the complex numbers.
- Problem 23
Let be the vector space over the reals of degree polynomials. Show that if then is an invariant subspace of under the differentiation operator. In , does any of , ..., have an invariant complement?
- Problem 24
In , the vector space (over the reals) of degree polynomials,
and
are the even and the odd polynomials; is even while is odd. Show that they are subspaces. Are they complementary? Are they invariant under the differentiation transformation?
- Problem 25
Lemma 2.8 says that if and are invariant complements then has a representation in the given block form (with respect to the same ending as starting basis, of course). Does the implication reverse?
- Problem 26
A matrix is the square root of another if . Show that any nonsingular matrix has a square root.
Footnotes
- ↑ More information on restrictions of functions is in the appendix.
Topic: Geometry of Eigenvalues
--Refer to Topic on Geometry of Linear Transformations---
The characterization of linear transformations in terms of the elementary operations is nice in some ways (for instance, we can easily see that lines are mapped to lines because each of the operations of projection, dilation, reflection, and skew maps lines to lines), but when a map is expressed as a composition of many small operations---no matter how simple---the description is less than ideal. We finish with another way, a somewhat more holistic way, of picturing the geometric effect of transformations of .
The pictures in that area give the action of the map on just one or two members of the domain. Although we know that a transformation is described completely by its action on a basis, and so to describe a transformation of therefore, strictly speaking, requires only a description of where it sends the two vectors from any basis, those pictures seem not to convey much geometric intuition. Can we make clear a linear map's geometry by putting in more information, but not so much information that the picture gets confused?
A transformation of sends lines through the origin to lines through the origin. Thus, two points on a line will both be sent to the line, say, . Consider two such points. One is a multiple of the other, so we can write them with the second one as times the first, for some scalar .
Compare their images.
The second vector is times the first, and the image of the second is times the image of the first. Not only does the transformation preserve the fact that the vectors are colinear, it also preserves the relative scale of the vectors. That is, a transformation treats the points on a line through the origin uniformily. To describe the effect of the map on the entire line, we need only describe its effect on a single non-zero point in that line.
Since every point in the space is on some line through the origin, to understand the action of a linear transformation of , it is sufficient to pick one point from each line through the origin (say the point that is on the upper half of the unit circle) and show how the map's effect on that set of points.
Here is such a picture for a straightforward dilation.
Below, the same map is shown with the circle and its image superimposed.
Certainly the geometry here is more evident. For example, we can see that some lines through the origin are actually sent to themselves: the -axis is sent to the -axis, and the -axis is sent to the -axis.
This is the flip shown earlier, here with the circle and its image superimposed.
And this is the skew shown earlier.
Contrast the picture of this map's effect on the unit square with this one.
Here is a somewhat more complicated map (the second coordinate function is the same as the map in the prior picture, but the first coordinate function is different).
Observe that some vectors are being both dilated and rotated through some angle
while others are just being dilated, not rotated at all.
Exercises
- Problem 1
- Show the effect each matrix has on the top half of the unit circle.
Which vectors stay on the same line through the origin?
Topic: The Method of Powers
In practice, calculating eigenvalues and eigenvectors is a difficult problem. Finding, and solving, the characteristic polynomial of the large matrices often encountered in applications is too slow and too hard. Other techniques, indirect ones that avoid the characteristic polynomial, are used. Here we shall see such a method that is suitable for large matrices that are "sparse" (the great majority of the entries are zero).
Suppose that the matrix has the distinct eigenvalues , , ..., . Then has a basis that is composed of the associated eigenvectors . For any , where , iterating on gives these.
If one of the eigenvalues, say, , has a larger absolute value than any of the other eigenvalues then its term will dominate the above expression. Put another way, dividing through by gives this,
and, because is assumed to have the largest absolute value, as gets larger the fractions go to zero. Thus, the entire expression goes to .
That is (as long as is not zero), as increases, the vectors will tend toward the direction of the eigenvectors associated with the dominant eigenvalue, and, consequently, the ratios of the lengths will tend toward that dominant eigenvalue.
For example, (sample computer code for this follows the exercises), because the matrix
is triangular, its eigenvalues are just the entries on the diagonal, and . Arbitrarily taking to have the components and gives
and the ratio between the lengths of the last two is .
Two implementation issues must be addressed. The first issue is that, instead of finding the powers of and applying them to , we will compute as and then compute as , etc. (i.e., we never separately calculate , , etc.). These matrix-vector products can be done quickly even if is large, provided that it is sparse. The second issue is that, to avoid generating numbers that are so large that they overflow our computer's capability, we can normalize the 's at each step. For instance, we can divide each by its length (other possibilities are to divide it by its largest component, or simply by its first component). We thus implement this method by generating
until we are satisfied. Then the vector is an approximation of an eigenvector, and the approximation of the dominant eigenvalue is the ratio .
One way we could be "satisfied" is to iterate until our approximation of the eigenvalue settles down. We could decide, for instance, to stop the iteration process not after some fixed number of steps, but instead when differs from by less than one percent, or when they agree up to the second significant digit.
The rate of convergence is determined by the rate at which the powers of go to zero, where is the eigenvalue of second largest norm. If that ratio is much less than one then convergence is fast, but if it is only slightly less than one then convergence can be quite slow. Consequently, the method of powers is not the most commonly used way of finding eigenvalues (although it is the simplest one, which is why it is here as the illustration of the possibility of computing eigenvalues without solving the characteristic polynomial). Instead, there are a variety of methods that generally work by first replacing the given matrix with another that is similar to it and so has the same eigenvalues, but is in some reduced form such as tridiagonal form: the only nonzero entries are on the diagonal, or just above or below it. Then special techniques can be used to find the eigenvalues. Once the eigenvalues are known, the eigenvectors of can be easily computed. These other methods are outside of our scope. A good reference is (Goult et al. 1975).
Exercises
- Problem 1
Use ten iterations to estimate the largest eigenvalue of these matrices, starting from the vector with components and . Compare the answer with the one obtained by solving the characteristic equation.
- Problem 2
Redo the prior exercise by iterating until has absolute value less than At each step, normalize by dividing each vector by its length. How many iterations are required? Are the answers significantly different?
- Problem 3
Use ten iterations to estimate the largest eigenvalue of these matrices, starting from the vector with components , , and . Compare the answer with the one obtained by solving the characteristic equation.
- Problem 4
Redo the prior exercise by iterating until has absolute value less than . At each step, normalize by dividing each vector by its length. How many iterations does it take? Are the answers significantly different?
- Problem 5
What happens if ? That is, what happens if the initial vector does not to have any component in the direction of the relevant eigenvector?
- Problem 6
How can the method of powers be adopted to find the smallest eigenvalue?
This is the code for the computer algebra system Octave that was used to do the calculation above. (It has been lightly edited to remove blank lines, etc.)
Computer Code
>T=[3, 0;
8, -1]
T=
3 0
8 -1
>v0=[1; 2]
v0=
1
1
>v1=T*v0
v1=
3
7
>v2=T*v1
v2=
9
17
>T9=T**9
T9=
19683 0
39368 -1
>T10=T**10
T10=
59049 0
118096 1
>v9=T9*v0
v9=
19683
39367
>v10=T10*v0
v10=
59049
118096
>norm(v10)/norm(v9)
ans=2.9999
Remark: we are ignoring the power of Octave here; there are built-in functions to automatically apply quite sophisticated methods to find eigenvalues and eigenvectors. Instead, we are using just the system as a calculator.
Topic: Stable Populations
Imagine a reserve park with animals from a species that we are trying to protect. The park doesn't have a fence and so animals cross the boundary, both from the inside out and in the other direction. Every year, 10% of the animals from inside of the park leave, and 1% of the animals from the outside find their way in. We can ask if we can find a stable level of population for this park: is there a population that, once established, will stay constant over time, with the number of animals leaving equal to the number of animals entering?
To answer that question, we must first establish the equations. Let the year population in the park be and in the rest of the world be .
We can set this system up as a matrix equation (see the Markov Chain topic).
Now, "stable level" means that and , so that the matrix equation becomes . We are therefore looking for eigenvectors for that are associated with the eigenvalue . The equation is
which gives the eigenspace: vectors with the restriction that . Coupled with additional information, that the total world population of this species is is , we find that the stable state is and .
If we start with a park population of ten thousand animals, so that the rest of the world has one hundred thousand, then every year ten percent (a thousand animals) of those inside will leave the park, and every year one percent (a thousand) of those from the rest of the world will enter the park. It is stable, self-sustaining.
Now imagine that we are trying to gradually build up the total world population of this species. We can try, for instance, to have the world population grow at a rate of 1% per year. In this case, we can take a "stable" state for the park's population to be that it also grows at 1% per year. The equation leads to , which gives this system.
The matrix is nonsingular, and so the only solution is and . Thus, there is no (usable) initial population that we can establish at the park and expect that it will grow at the same rate as the rest of the world.
Knowing that an annual world population growth rate of 1% forces an unstable park population, we can ask which growth rates there are that would allow an initial population for the park that will be self-sustaining. We consider and solve for .
A shortcut to factoring that quadratic is our knowledge that is an eigenvalue of , so the other eigenvalue is . Thus there are two ways to have a stable park population (a population that grows at the same rate as the population of the rest of the world, despite the leaky park boundaries): have a world population that is does not grow or shrink, and have a world population that shrinks by 11% every year.
So this is one meaning of eigenvalues and eigenvectors— they give a stable state for a system. If the eigenvalue is then the system is static. If the eigenvalue isn't then the system is either growing or shrinking, but in a dynamically-stable way.
Exercises
- Problem 1
What initial population for the park discussed above should be set up in the case where world populations are allowed to decline by 11% every year?
- Problem 2
What will happen to the population of the park in the event of a growth in world population of 1% per year? Will it lag the world growth, or lead it? Assume that the park population is ten thousand, and the world population is one hundred thousand, and calculate over a ten year span.
- Problem 3
The park discussed above is partially fenced so that now, every year, only 5% of the animals from inside of the park leave (still, about 1% of the animals from the outside find their way in). Under what conditions can the park maintain a stable population now?
- Problem 4
Suppose that a species of bird only lives in Canada, the United States, or in Mexico. Every year, 4% of the Canadian birds travel to the US, and 1% of them travel to Mexico. Every year, 6% of the US birds travel to Canada, and 4% go to Mexico. From Mexico, every year 10% travel to the US, and 0% go to Canada.
- Give the transition matrix.
- Is there a way for the three countries to have constant populations?
- Find all stable situations.
Topic: Linear Recurrences
In 1202 Leonardo of Pisa, also known as Fibonacci, posed this problem.
A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?
This moves past an elementary exponential growth model for population increase to include the fact that there is an initial period where newborns are not fertile. However, it retains other simplyfing assumptions, such as that there is no gestation period and no mortality.
The number of newborn pairs that will appear in the upcoming month is simply the number of pairs that were alive last month, since those will all be fertile, having been alive for two months. The number of pairs alive next month is the sum of the number alive current month and the number of newborns.
The is an example of a recurrence relation (it is called that because the values of are calculated by looking at other, prior, values of ). From it, we can easily answer Fibonacci's twelve-month question.
The sequence of numbers defined by the above equation (of which the first few are listed) is the Fibonacci sequence. The material of this chapter can be used to give a formula with which we can can calculate without having to first find , , etc.
For that, observe that the recurrence is a linear relationship and so we can give a suitable matrix formulation of it.
Then, where we write for the matrix and for the vector with components and , we have that . The advantage of this matrix formulation is that by diagonalizing we get a fast way to compute its powers: where we have , and the -th power of the diagonal matrix is the diagonal matrix whose entries that are the -th powers of the entries of .
The characteristic equation of is . The quadratic formula gives its roots as and . Diagonalizing gives this.
Introducing the vectors and taking the -th power, we have
We can compute from the second component of that equation.
Notice that is dominated by its first term because is less than one, so its powers go to zero.
In general, a linear recurrence relation has the form
(it is also called a difference equation). This recurrence relation is homogeneous because there is no constant term; i.e, it can be put into the form . This is said to be a relation of order . The relation, along with the initial conditions , ..., completely determine a sequence. For instance, the Fibonacci relation is of order and it, along with the two initial conditions and , determines the Fibonacci sequence simply because we can compute any by first computing , , etc. In this Topic, we shall see how linear algebra can be used to solve linear recurrence relations.
First, we define the vector space in which we are working. Let be the set of functions from the natural numbers to the real numbers. (Below we shall have functions with domain , that is, without , but it is not an important distinction.)
Putting the initial conditions aside for a moment, for any recurrence, we can consider the subset of of solutions. For example, without initial conditions, in addition to the function given above, the Fibonacci relation is also solved by the function whose first few values are , , , and .
The subset is a subspace of . It is nonempty because the zero function is a solution. It is closed under addition since if and are solutions, then
And, it is closed under scalar multiplication since
We can give the dimension of . Consider this map from the set of functions to the set of vectors .
Problem 3 shows that this map is linear. Because, as noted above, any solution of the recurrence is uniquely determined by the initial conditions, this map is one-to-one and onto. Thus it is an isomorphism, and thus has dimension , the order of the recurrence.
So (again, without any initial conditions), we can describe the set of solutions of any linear homogeneous recurrence relation of degree by taking linear combinations of only linearly independent functions. It remains to produce those functions.
For that, we express the recurrence with a matrix equation.
In trying to find the characteristic function of the matrix, we can see the pattern in the case
and case.
Problem 4 shows that the characteristic equation is this.
We call that the polynomial "associated" with the recurrence relation. (We will be finding the roots of this polynomial and so we can drop the as irrelevant.)
If has no repeated roots then the matrix is diagonalizable and we can, in theory, get a formula for as in the Fibonacci case. But, because we know that the subspace of solutions has dimension , we do not need to do the diagonalization calculation, provided that we can exhibit linearly independent functions satisfying the relation.
Where , , ..., are the distinct roots, consider the functions through of powers of those roots. Problem 2 shows that each is a solution of the recurrence and that the of them form a linearly independent set. So, given the homogeneous linear recurrence (that is, ) we consider the associated equation . We find its roots , ..., , and if those roots are distinct then any solution of the relation has the form for . (The case of repeated roots is also easily done, but we won't cover it here— see any text on Discrete Mathematics.)
Now, given some initial conditions, so that we are interested in a particular solution, we can solve for , ..., . For instance, the polynomial associated with the Fibonacci relation is , whose roots are and so any solution of the Fibonacci equation has the form . Including the initial conditions for the cases and gives
which yields and , as was calculated above.
We close by considering the nonhomogeneous case, where the relation has the form for some nonzero . As in the first chapter of this book, only a small adjustment is needed to make the transition from the homogeneous case. This classic example illustrates.
In 1883, Edouard Lucas posed the following problem.
In the great temple at Benares, beneath the dome which marks the center of the world, rests a brass plate in which are fixed three diamond needles, each a cubit high and as thick as the body of a bee. On one of these needles, at the creation, God placed sixty four disks of pure gold, the largest disk resting on the brass plate, and the others getting smaller and smaller up to the top one. This is the Tower of Bramah. Day and night unceasingly the priests transfer the disks from one diamond needle to another according to the fixed and immutable laws of Bramah, which require that the priest on duty must not move more than one disk at a time and that he must place this disk on a needle so that there is no smaller disk below it. When the sixty-four disks shall have been thus transferred from the needle on which at the creation God placed them to one of the other needles, tower, temple, and Brahmins alike will crumble into dusk, and with a thunderclap the world will vanish.
(Translation of De Parvill (1884) from Ball (1962).)
How many disk moves will it take? Instead of tackling the sixty four disk problem right away, we will consider the problem for smaller numbers of disks, starting with three.
To begin, all three disks are on the same needle.

After moving the small disk to the far needle, the mid-sized disk to the middle needle, and then moving the small disk to the middle needle we have this.

Now we can move the big disk over. Then, to finish, we repeat the process of moving the smaller disks, this time so that they end up on the third needle, on top of the big disk.
So the thing to see is that to move the very largest disk, the bottom disk, at a minimum we must: first move the smaller disks to the middle needle, then move the big one, and then move all the smaller ones from the middle needle to the ending needle. Those three steps give us this recurrence.
We can easily get the first few values of .
We recognize those as being simply one less than a power of two.
To derive this equation instead of just guessing at it, we write the original relation as , consider the homogeneous relation , get its associated polynomial , which obviously has the single, unique, root of , and conclude that functions satisfying the homogeneous relation take the form .
That's the homogeneous solution. Now we need a particular solution.
Because the nonhomogeneous relation is so simple, in a few minutes (or by remembering the table) we can spot the particular solution (there are other particular solutions, but this one is easily spotted). So we have that— without yet considering the initial condition— any solution of is the sum of the homogeneous solution and this particular solution: .
The initial condition now gives that , and we've gotten the formula that generates the table: the -disk Tower of Hanoi problem requires a minimum of moves.
Finding a particular solution in more complicated cases is, naturally, more complicated. A delightful and rewarding, but challenging, source on recurrence relations is (Graham, Knuth & Patashnik 1988)., For more on the Tower of Hanoi, (Ball 1962) or (Gardner 1957) are good starting points. So is (Hofstadter 1985). Some computer code for trying some recurrence relations follows the exercises.
Exercises
- Problem 1
Solve each homogeneous linear recurrence relations.
- Problem 2
Give a formula for the relations of the prior exercise, with these initial conditions.
- ,
- ,
- , , .
- Problem 3
Check that the isomorphism given between and is a linear map. It is argued above that this map is one-to-one. What is its inverse?
- Problem 4
Show that the characteristic equation of the matrix is as stated, that is, is the polynomial associated with the relation. (Hint: expanding down the final column, and using induction will work.)
- Problem 5
Given a homogeneous linear recurrence relation , let , ..., be the roots of the associated polynomial.
- Prove that each function satisfies the recurrence (without initial conditions).
- Prove that no is .
- Prove that the set is linearly independent.
- Problem 6
(This refers to the value given in the computer code below.) Transferring one disk per second, how many years would it take the priests at the Tower of Hanoi to finish the job?
Computer Code
This code allows the generation of the first few values of a function
defined by a recurrence and initial conditions.
It is in the Scheme dialect of LISP
(specifically, it was written for A. Jaffer's free scheme interpreter SCM,
although it should run in any Scheme implementation).
First, the Tower of Hanoi code is a straightforward implementation of the recurrence.
(define (tower-of-hanoi-moves n) (if (= n 1) 1 (+ (* (tower-of-hanoi-moves (- n 1)) 2) 1) ) )
(Note for readers unused to recursive code: to compute ,
the computer is told to compute , which requires, of course,
computing .
The computer puts the "times " and the "plus " aside for a moment
to do that.
It computes by using this same piece of code (that's
what "recursive" means), and to do that is told to compute .
This keeps up (the next step is to try to do while the other
arithmetic is held in waiting), until, after steps, the computer
tries to compute .
It then returns ,
which now means that the computation of can proceed,
etc., up until the original computation of finishes.)
The next routine calculates a table of the first few
values.
(Some language notes: '() is the empty list, that is,
the empty sequence, and cons pushes something onto the start of a
list.
Note that, in the last line, the procedure proc
is called on argument n.)
(define (first-few-outputs proc n) (first-few-outputs-helper proc n '()) ) ; (define (first-few-outputs-aux proc n lst) (if (< n 1) lst (first-few-outputs-aux proc (- n 1) (cons (proc n) lst)) ) )
The session at the SCM prompt went like this.
>(first-few-outputs tower-of-hanoi-moves 64) Evaluation took 120 mSec (1 3 7 15 31 63 127 255 511 1023 2047 4095 8191 16383 32767 65535 131071 262143 524287 1048575 2097151 4194303 8388607 16777215 33554431 67108863 134217727 268435455 536870911 1073741823 2147483647 4294967295 8589934591 17179869183 34359738367 68719476735 137438953471 274877906943 549755813887 1099511627775 2199023255551 4398046511103 8796093022207 17592186044415 35184372088831 70368744177663 140737488355327 281474976710655 562949953421311 1125899906842623 2251799813685247 4503599627370495 9007199254740991 18014398509481983 36028797018963967 72057594037927935 144115188075855871 288230376151711743 576460752303423487 1152921504606846975 2305843009213693951 4611686018427387903 9223372036854775807 18446744073709551615)
This is a list of through .
(The mSec came on a 50 mHz '486 running in an XTerm of XWindow
under Linux.
The session was edited to put line breaks between numbers.)
Appendix
Mathematics is made of arguments (reasoned discourse that is, not crockery-throwing). This section is a reference to the most used techniques. A reader having trouble with, say, proof by contradiction, can turn here for an outline of that method.
But this section gives only a sketch. For more, these are classics: Methods of Logic by Quine, Induction and Analogy in Mathematics by Pólya, and Naive Set Theory by Halmos. Reader can also read the wikibook Mathematical Proof.
Propositions
The point at issue in an argument is the proposition. Mathematicians usually write the point in full before the proof and label it either Theorem for major points, Corollary for points that follow immediately from a prior one, or Lemma for results chiefly used to prove other results.
The statements expressing propositions can be complex, with many subparts. The truth or falsity of the entire proposition depends both on the truth value of the parts, and on the words used to assemble the statement from its parts.
Not
For example, where is a proposition, "it is not the case that " is true provided that is false. Thus, " is not prime" is true only when is the product of smaller integers.
We can picture the "not" operation with a Venn diagram.
Where the box encloses all natural numbers, and inside the circle are the primes, the shaded area holds numbers satisfying "not ".
To prove that a "not " statement holds, show that is false.
And
Consider the statement form " and ". For the statement to be true both halves must hold: " is prime and so is " is true, while " is prime and is not" is false.
Here is the Venn diagram for " and ".
To prove " and ", prove that each half holds.
Or
A " or " is true when either half holds: " is prime or is prime" is true, while " is not prime or is prime" is false. We take "or" inclusively so that if both halves are true " is prime or is not" then the statement as a whole is true. (In everyday speech, sometimes "or" is meant in an exclusive way— "Eat your vegetables or no dessert" does not intend both halves to hold— but we will not use "or" in that way.)
The Venn diagram for "or" includes all of both circles.
To prove " or ", show that in all cases at least one half holds (perhaps sometimes one half and sometimes the other, but always at least one).
If-then
An "if then " statement (sometimes written " materially implies " or just " implies " or "") is true unless is true while is false. Thus "if is prime then is not" is true while "if is prime then is also prime" is false. (Contrary to its use in casual speech, in mathematics "if then " does not connote that precedes or causes .)
More subtly, in mathematics "if then " is true when is false: "if is prime then is prime" and "if is prime then is not" are both true statements, sometimes said to be vacuously true. We adopt this convention because we want statements like "if a number is a perfect square then it is not prime" to be true, for instance when the number is or when the number is .
The diagram
shows that holds whenever does (another phrasing is " is sufficient to give "). Notice again that if does not hold, may or may not be in force.
There are two main ways to establish an implication. The first way is direct: assume that is true and, using that assumption, prove . For instance, to show "if a number is divisible by 5 then twice that number is divisible by 10", assume that the number is and deduce that . The second way is indirect: prove the contrapositive statement: "if is false then is false" (rephrased, " can only be false when is also false"). As an example, to show "if a number is prime then it is not a perfect square", argue that if it were a square then it could be factored where and so wouldn't be prime (of course or don't give but they are nonprime by definition).
Note two things about this statement form.
First, an "if then " result can sometimes be improved by weakening or strengthening . Thus, "if a number is divisible by then its square is also divisible by " could be upgraded either by relaxing its hypothesis: "if a number is divisible by then its square is divisible by ", or by tightening its conclusion: "if a number is divisible by then its square is divisible by ".
Second, after showing "if then ", a good next step is to look into whether there are cases where holds but does not. The idea is to better understand the relationship between and , with an eye toward strengthening the proposition.
Equivalence
An if-then statement cannot be improved when not only does imply , but also implies . Some ways to say this are: " if and only if ", " iff ", " and are logically equivalent", " is necessary and sufficient to give ", "". For example, "a number is divisible by a prime if and only if that number squared is divisible by the prime squared".
The picture here shows that and hold in exactly the same cases.
Although in simple arguments a chain like " if and only if , which holds if and only if ..." may be practical, typically we show equivalence by showing the "if then " and "if then " halves separately.
Quantifiers
Compare these two statements about natural numbers: "there is an such that is divisible by " is true, while "for all numbers , that is divisible by " is false. We call the "there is" and "for all" prefixes quantifiers.
For all
The "for all" prefix is the universal quantifier, symbolized .
Venn diagrams aren't very helpful with quantifiers, but in a sense the box we draw to border the diagram shows the universal quantifier since it delineates the universe of possible members.
To prove that a statement holds in all cases, we must show that it holds in each case. Thus, to prove "every number divisible by has its square divisible by ", take a single number of the form and square it . This is a "typical element" or "generic element" proof.
This kind of argument requires that we are careful to not assume properties for that element other than those in the hypothesis— for instance, this type of wrong argument is a common mistake: "if is divisible by a prime, say , so that then and the square of the number is divisible by the square of the prime". That is an argument about the case , but it isn't a proof for general .
There exists
We will also use the existential quantifier, symbolized and read "there exists".
As noted above, Venn diagrams are not much help with quantifiers, but a picture of "there is a number such that " would show both that there can be more than one and that not all numbers need satisfy .
An existence proposition can be proved by producing something satisfying the property: once, to settle the question of primality of , Euler produced its divisor . But there are proofs showing that something exists without saying how to find it; Euclid's argument given in the next subsection shows there are infinitely many primes without naming them. In general, while demonstrating existence is better than nothing, giving an example is better, and an exhaustive list of all instances is great. Still, mathematicians take what they can get.
Finally, along with "Are there any?" we often ask "How many?" That is why the issue of uniqueness often arises in conjunction with questions of existence. Many times the two arguments are simpler if separated, so note that just as proving something exists does not show it is unique, neither does proving something is unique show that it exists. (Obviously "the natural number with more factors than any other" would be unique, but in fact no such number exists.)
Techniques of Proof
Induction
Many proofs are iterative, "Here's why the statement is true for for the case of the number , it then follows for , and from there to , and so on ...". These are called proofs by induction. Such a proof has two steps. In the base step the proposition is established for some first number, often or . Then in the inductive step we assume that the proposition holds for numbers up to some and deduce that it then holds for the next number .
Here is an example.
We will prove that .
For the base step we must show that the formula holds when . That's easy, the sum of the first number does indeed equal .
For the inductive step, assume that the formula holds for the numbers . That is, assume all of these instances of the formula.
From this assumption we will deduce that the formula therefore also holds in the next case. The deduction is straightforward algebra.
We've shown in the base case that the above proposition holds for . We've shown in the inductive step that if it holds for the case of then it also holds for ; therefore it does hold for . We've also shown in the inductive step that if the statement holds for the cases of and then it also holds for the next case , etc. Thus it holds for any natural number greater than or equal to .
Here is another example.
We will prove that every integer greater than is a product of primes.
The base step is easy: is the product of a single prime.
For the inductive step assume that each of is a product of primes, aiming to show is also a product of primes. There are two possibilities: (i) if is not divisible by a number smaller than itself then it is a prime and so is the product of primes, and (ii) if is divisible then its factors can be written as a product of primes (by the inductive hypothesis) and so can be rewritten as a product of primes. That ends the proof.
(Remark. The Prime Factorization Theorem of Number Theory says that not only does a factorization exist, but that it is unique. We've shown the easy half.)
There are two things to note about the "next number" in an induction argument.
For one thing, while induction works on the integers, it's no good on the reals. There is no "next" real.
The other thing is that we sometimes use induction to go down, say, from to to , etc., down to . So "next number" could mean "next lowest number". Of course, at the end we have not shown the fact for all natural numbers, only for those less than or equal to .
Contradiction
Another technique of proof is to show something is true by showing it can't be false.
The classic example is Euclid's, that there are infinitely many primes.
Suppose there are only finitely many primes . Consider . None of the primes on this supposedly exhaustive list divides that number evenly, each leaves a remainder of . But every number is a product of primes so this can't be. Thus there cannot be only finitely many primes.
Every proof by contradiction has the same form: assume that the false proposition is true and derive some contradiction to known facts. This kind of logic is known as Aristotelian Logic, or Term Logic
Another example is this proof that is not a rational number.
Suppose that .
Factor out the 's: and and rewrite.
The Prime Factorization Theorem says that there must be the same number of factors of on both sides, but there are an odd number on the left and an even number on the right. That's a contradiction, so a rational with a square of cannot be.
Both of these examples aimed to prove something doesn't exist. A negative proposition often suggests a proof by contradiction.
Sets, Functions, Relations
Sets
Mathematicians work with collections called sets. A set can be given as a listing between curly braces as in , or, if that's unwieldy, by using set-builder notation as in (read "the set of all such that \ldots"). We name sets with capital roman letters as with the primes , except for a few special sets such as the real numbers , and the complex numbers . To denote that something is an element (or member) of a set we use "", so that while .
What distinguishes a set from any other type of collection is the Principle of Extensionality, that two sets with the same elements are equal. Because of this principle, in a set repeats collapse and order doesn't matter .
We use "" for the subset relationship: and "" for subset or equality (if is a subset of but then is a proper subset of ). These symbols may be flipped, for instance .
Because of Extensionality, to prove that two sets are equal , just show that they have the same members. Usually we show mutual inclusion, that both and .
Set operations
Venn diagrams are handy here. For instance, can be pictured
and "" looks like this.
Note that this is a repeat of the diagram for "if \ldots then ..." propositions. That's because "" means "if then ".
In general, for every propositional logic operator there is an associated set operator. For instance, the complement of is
the union is
and the intersection is
}}When two sets share no members their intersection is the empty set , symbolized . Any set has the empty set for a subset, by the "vacuously true" property of the definition of implication.
Sequences
We shall also use collections where order does matter and where repeats do not collapse. These are sequences, denoted with angle brackets: . A sequence of length is sometimes called an ordered pair and written with parentheses: . We also sometimes say "ordered triple", "ordered -tuple", etc. The set of ordered -tuples of elements of a set is denoted . Thus the set of pairs of reals is .
Functions
We first see functions in elementary Algebra, where they are presented as formulas (e.g., ), but progressing to more advanced Mathematics reveals more general functions— trigonometric ones, exponential and logarithmic ones, and even constructs like absolute value that involve piecing together parts— and we see that functions aren't formulas, instead the key idea is that a function associates with its input a single output .
Consequently, a function or map is defined to be a set of ordered pairs such that suffices to determine , that is: if then (this requirement is referred to by saying a function is well-defined).\footnote{More on this is in the section on isomorphisms}
Each input is one of the function's arguments and each output is a value. The set of all arguments is 's domain and the set of output values is its range. Usually we don't need know what is and is not in the range and we instead work with a superset of the range, the codomain. The notation for a function with domain and codomain is .
We sometimes instead use the notation , read " maps under to ", or " is the "image' of '.
Some maps, like , can be thought of as combinations of simple maps, here, applied to the image of . The composition of with , is the map sending to . It is denoted . This definition only makes sense if the range of is a subset of the domain of .
Observe that the identity map defined by has the property that for any , the composition is equal to . So an identity map plays the same role with respect to function composition that the number plays in real number addition, or that the number plays in multiplication.
In line with that analogy, define a left inverse of a map to be a function such that is the identity map on . Of course, a right inverse of is a such that is the identity.
A map that is both a left and right inverse of is called simply an inverse. An inverse, if one exists, is unique because if both and are inverses of then (the middle equality comes from the associativity of function composition), so we often call it "the" inverse, written . For instance, the inverse of the function given by is the function given by .
The superscript "" notation for function inverse can be confusing— it doesn't mean . It is used because it fits into a larger scheme. Functions that have the same codomain as domain can be iterated, so that where , we can consider the composition of with itself: , and , etc.
Naturally enough, we write as and as , etc. Note that the familiar exponent rules for real numbers obviously hold: and . The relationship with the prior paragraph is that, where is invertible, writing for the inverse and for the inverse of , etc., gives that these familiar exponent rules continue to hold, once is defined to be the identity map.
If the codomain equals the range of then we say that the function is onto (or surjective). A function has a right inverse if and only if it is onto (this is not hard to check). If no two arguments share an image, if implies that , then the function is one-to-one (or injective). A function has a left inverse if and only if it is one-to-one (this is also not hard to check).
By the prior paragraph, a map has an inverse if and only if it is both onto and one-to-one; such a function is a correspondence. It associates one and only one element of the domain with each element of the range (for example, finite sets must have the same number of elements to be matched up in this way). Because a composition of one-to-one maps is one-to-one, and a composition of onto maps is onto, a composition of correspondences is a correspondence.
We sometimes want to shrink the domain of a function. For instance, we may take the function given by and, in order to have an inverse, limit input arguments to nonnegative reals . Technically, is a different function than ; we call it the restriction of to the smaller domain.
A final point on functions: neither nor need be a number. As an example, we can think of as a function that takes the ordered pair as its argument.
Relations
Some familiar operations are obviously functions: addition maps to . But what of "" or ""? We here take the approach of rephrasing "" to " is in the relation ". That is, define a binary relation on a set to be a set of ordered pairs of elements of . For example, the relation is the set ; some elements of that set are , , and .
Another binary relation on the natural numbers is equality; this relation is formally written as the set .
Still another example is "closer than ", the set . Some members of that relation are , , and . Neither nor is a member.
Those examples illustrate the generality of the definition. All kinds of relationships (e.g., "both numbers even" or "first number is the second with the digits reversed") are covered under the definition.
Equivalence Relations
We shall need to say, formally, that two objects are alike in some way. While these alike things aren't identical, they are related (e.g., two integers that "give the same remainder when divided by ").
A binary relation is an equivalence relationwhen it satisfies
- reflexivity: any object is related to itself;
- symmetry: if is related to then is related to ;
- transitivity: if is related to and is related to then is related to .
(To see that these conditions formalize being the same, read them again, replacing "is related to" with "is like".)
Some examples (on the integers): "" is an equivalence relation, "" does not satisfy symmetry, "same sign" is a equivalence, while "nearer than " fails transitivity.
Partitions
In "same sign" there are two kinds of pairs, the first with both numbers positive and the second with both negative. So integers fall into exactly one of two classes, positive or negative.
A partition of a set is a collection of subsets such that every element of is in one and only one : , and if is not equal to then . Picture being decomposed into distinct parts.
Thus, the first paragraph says "same sign" partitions the integers into the positives and the negatives.
Similarly, the equivalence relation "=" partitions the integers into one-element sets.
Another example is the fractions. Of course, and are equivalent fractions. That is, for the set , we define two elements and to be equivalent if . We can check that this is an equivalence relation, that is, that it satisfies the above three conditions. With that, is divided up into parts.
Before we show that equivalence relations always give rise to partitions, we first illustrate the argument. Consider the relationship between two integers of "same parity", the set (i.e., "give the same remainder when divided by "). We want to say that the natural numbers split into two pieces, the evens and the odds, and inside a piece each member has the same parity as each other. So for each we define the set of numbers associated with it: . Some examples are , and , and . These are the parts, e.g., is the odds.
}}Theorem An equivalence relation induces a partition on the underlying set.
- Proof
Call the set and the relation . In line with the illustration in the paragraph above, for each define .
Observe that, as is a member if , the union of all these sets is . So we will be done if we show that distinct parts are disjoint: if then . We will verify this through the contrapositive, that is, we wlll assume that in order to deduce that .
Let be an element of the intersection. Then by definition of and , the two and are members of , and by symmetry of this relation and are also members of . To show that we will show each is a subset of the other.
Assume that so that . Use transitivity along with to conclude that is also an element of . But so another use of transitivity gives that . Thus . Therefore implies , and so .
The same argument in the other direction gives the other inclusion, and so the two sets are equal, completing the contrapositive argument.
}}We call each part of a partition an equivalence class (or informally, "part").
We somtimes pick a single element of each equivalence class to be the class representative.
Usually when we pick representatives we have some natural scheme in mind. In that case we call them the canonical representatives.
An example is the simplest form of a fraction. We've defined and to be equivalent fractions. In everyday work we often use the "simplest form" or "reduced form" fraction as the class representatives.
Resources And Licensing
For information regarding the Licensing of this book please see Wikibooks' Copyright Policy. The original text of this wikibook has been copied form the book "Linear Algebra" by:
- Jim Hefferon, Mathematics
- Saint Michael's College
- Colchester, Vermont USA 05439.
The original text is available here, and is released under either the GNU Free Documentation License or the Creative Commons Attribution-ShareAlike 2.5 License.
Other Books and Lectures
- Linear Algebra - A free textbook by Prof. Jim Hefferon of St. Michael's College. This wikibook began as a wikified copy of Prof. Hefferon's text. Prof. Hefferon's book may differ from the book here, as both are still under development.
- A Course in Linear Algebra - A free set of video lectures given at the Massachusetts Institute of Technology by Prof. Gilbert Strang. Prof. Strang's book on linear algebra has been a widely influential book and it is referenced many times in this text.
- A First Course in Linear Algebra - A free textbook by Prof. Rob Beezer at the University of Puget Sound, released under GFDL.
- Lecture Notes on Linear Algebra - An online viewable set of lecture notes by Prof. José Figueroa-O’Farrill at the University of Edinburgh.
Software
- Octave a free and open soure application for Numerical Linear Algebra. There is also an Octave Programming Tutorial wikibook under development.
- A toolkit for linear algebra students - An online software resource aimed at helping linear algebra students learn and practice a basic linear algebra procedures, such as Gauss-Jordan reduction, calculating the determinant, or checking for linear independence. This software was produced by Przemyslaw Bogacki in the Department of Mathematics and Statistics at Old Dominion University.
- Online Javascript Matrix Calculator, basic matrix algebra, elementary row operations, RREF, inverses, determinants, characteristic polynomials, eigenvalues and eigenvectors, null space, range space, and least squares solutions to linear systems. The software was developed by the department of mathematics at the University of Houston.
Wikipedia
Wikipedia is frequently a great resource that often gives a general non-technical overview of a subject. Wikipedia has many articles on the subject of Linear Algebra. Below are some articles about some of the material in this book.
- Reduced Echelon Form is described in Row echelon form
- Gauss-Jordan Reduction is described in Gauss–Jordan elimination
- Gauss' Method is described in Gaussian elimination
- Many topics in the section Linear Algebra/Linear Geometry of n-Space and its subsections are discussed article Euclidean vector
- Row Equivalence is described in the article Row equivalence
Bibliography
- Microsoft (1993), Microsoft Programmers Reference, Microsoft Press.
- William Lowell Putnam Mathematical Competition, Problem A-5, 1990.
- The USSR Mathematics Olympiad, number 174.
- Ackerson, R. H. (1955), "A Note on Vector Spaces", American Mathematical Monthly, American Mathematical Society, 62 (10): 721
{{citation}}: Unknown parameter|month=ignored (help). - Anning, Norman (proposer); Trigg, C. W. (solver) (1953), "Elementary problem 1016", American Mathematical Monthly, American Mathematical Society, 60 (2): 115
{{citation}}: Unknown parameter|month=ignored (help). - Anton, Howard (1987), Elementary Linear Algebra, John Wiley & Sons.
- Arrow, J. (1963), Social Choice and Individual Values, Wiley.
- Ball, W.W. (1962), Mathematical Recreations and Essays, MacMillan (revised by H.S.M. Coxeter).
- Bennett, William (March 15, 1993), "Quantifying America's Decline", Wall Street Journal
{{citation}}: CS1 maint: date and year (link) - Birkhoff, Garrett; MacLane, Saunders (1965), Survey of Modern Algebra, Macmillan.
- Bittinger, Marvin (proposer) (1973), "Quickie 578", Mathematics Magazine, American Mathematical Society, 46 (5): 286, 296
{{citation}}: Unknown parameter|month=ignored (help). - Blass, A. (1984), "Existence of Bases Implies the Axiom of Choice", in Baumgartner, J. E. (ed.), Axiomatic Set Theory, Providence RI: American Mathematical Society, pp. 31–33.
- Bridgman, P. W. (1931), Dimensional Analysis, Yale University Press.
- Casey, John (1890), The Elements of Euclid, Books I to VI and XI (9th ed.), Hodges, Figgis, and Co..
- Clark, David H.; Coupe, John D. (1967), "The Bangor Area Economy Its Present and Future", Reprot to the City of Bangor, ME
{{citation}}: Cite has empty unknown parameter:|1=(help); Unknown parameter|month=ignored (help). - Clarke, Arthur C. (1982), Great SF Stories 8: Technical Error, DAW Books.
- Courant, Richard; Robbins, Herbert (1978), What is Mathematics?, Oxford University Press.
- Coxeter, H.S.M. (1974), Projective Geometry (Second ed.), Springer-Verlag.
- Cullen, Charles G. (1990), Matrices and Linear Transformations (Second ed.), Dover.
- Dalal, Siddhartha; Folkes, Edward; Hoadley, Bruce (Fall 1989), "Lessons Learned from Challenger: A Statistical Perspective", Stats: the Magazine for Students of Statistics, pp. 14–18
{{citation}}: CS1 maint: date and year (link) - Davies, Thomas D. (1990), "New Evidence Places Peary at the Pole", National Geographic Magazine, 177 (1): 44
{{citation}}: Unknown parameter|month=ignored (help). - de Mestre, Neville (1990), The Mathematics of Projectiles in sport, Cambridge University Press.
- De Parville (1884), La Nature, vol. I, Paris, pp. 285–286.
- Duncan, Dewey (proposer); Quelch, W. H. (solver) (1952), Mathematics Magazine, 26 (1): 48
{{citation}}: Missing or empty|title=(help); Unknown parameter|month=ignored (help) - Dudley, Underwood (proposer); Lebow, Arnold (proposer); Rothman, David (solver) (1963), "Elemantary problem 1151", American Mathematical Monthly, 70 (1): 93
{{citation}}: Unknown parameter|month=ignored (help). - Ebbing, Darrell D. (1993), General Chemistry (Fourth ed.), Houghton Mifflin.
- Ebbinghaus, H. D. (1990), Numbers, Springer-Verlag.
- Eggar, M.H. (1998), "Pinhole Cameras, Perspective, and Projective Geometry", American Mathematical Monthly, American Mathematical Society: 618–630
{{citation}}: Unknown parameter|month=ignored (help). - Einstein, A. (1911), Annals of Physics, 35: 686
{{citation}}: Missing or empty|title=(help). - Feller, William (1968), An Introduction to Probability Theory and Its Applications, vol. 1 (3rd ed.), Wiley.
- Gardner, Martin (May. 1957), "Mathematical Games: About the remarkable similarity between the Icosian Game and the Tower of Hanoi", Scientific American: 150–154
{{citation}}: Check date values in:|year=(help). - Gardner, Martin (April 1970), "Mathematical Games, Some mathematical curiosities embedded in the solar system", Scientific American: 108–112.
- Gardner, Martin (October 1974), "Mathematical Games, On the paradoxical situations that arise from nontransitive relations", Scientific American.
- Gardner, Martin (October 1980), "Mathematical Games, From counting votes to making votes count: the mathematics of elections", Scientific American.
- Gardner, Martin (1990), The New Ambidextrous Universe (Third revised ed.), W. H. Freeman and Company.
- Gilbert, George T.; Krusemeyer, Mark; Larson, Loren C. (1993), The Wohascum County Problem Book, The Mathematical Association of America.
- Giordano, R.; Jaye, M.; Weir, M. (1986), "The Use of Dimensional Analysis in Mathematical Modeling", UMAP Modules, COMAP (632).
- Giordano, R.; Wells, M.; Wilde, C. (1987), "Dimensional Analysis", UMAP Modules, COMAP (526).
- Goult, R.J.; Hoskins, R.F.; Milner, J.A.; Pratt, M.J. (1975), Computational Methods in Linear Algebra, Wiley.
- Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1988), Concrete Mathematics, Addison-Wesley.
- Haggett, Vern (proposer); Saunders, F. W. (solver) (1955), "Elementary problem 1135", American Mathematical Monthly, American Mathematical Society, 62 (5): 257
{{citation}}: Unknown parameter|month=ignored (help). - Halmos, Paul P. (1958), Finite Dimensional Vector Spaces (Second ed.), Van Nostrand.
- Halsey, William D. (1979), Macmillian Dictionary, Macmillian.
- Hamming, Richard W. (1971), Introduction to Applied Numerical Analysis, Hemisphere Publishing.
- Hanes, Kit (1990), "Analytic Projective Geometry and its Applications", UMAP Modules (UMAP UNIT 710): 111.
- Heath, T. (1956), Euclid's Elements, vol. 1, Dover.
- Hoffman, Kenneth; Kunze, Ray (1971), Linear Algebra (Second ed.), Prentice Hall
- Hofstadter, Douglas R. (1985), Metamagical Themas:~Questing for the Essence of Mind and Pattern, Basic Books.
- Iosifescu, Marius (1980), Finite Markov Processes and Their Applications, UMI Research Press.
- Ivanoff, V. F. (proposer); Esty, T. C. (solver) (1933), "Problem 3529", American Mathematical Monthly, 39 (2): 118
{{citation}}: Unknown parameter|month=ignored (help) - Kelton, Christina M.L. (1983), Trends on the Relocation of U.S. Manufacturing, Wiley.
- Kemeny, John G.; Snell, J. Laurie (1960), Finite Markove Chains, D.~Van Nostrand.
- Kemp, Franklin (1982), "Linear Equations", American Mathematical Monthly, American Mathematical Society: 608
{{citation}}: Unknown parameter|month=ignored (help). - Klamkin, M. S. (proposer) (1957), "Trickie T-27", Mathematics Magazine, 30 (3): 173
{{citation}}: Unknown parameter|month=ignored (help). - Knuth, Donald E. (1988), The Art of Computer Programming, Addison Wesley.
- Leontief, Wassily W. (1951), "Input-Output Economics", Scientific American, 185 (4): 15
{{citation}}: Unknown parameter|month=ignored (help). - Leontief, Wassily W. (1965), "The Structure of the U.S. Economy", Scientific American, 212 (4): 25
{{citation}}: Unknown parameter|month=ignored (help). - Liebeck, Hans. (1966), "A Proof of the Equality of Column Rank and Row Rank of a Matrix", American Mathematical Monthly, American Mathematical Society, 73 (10): 1114
{{citation}}: Unknown parameter|month=ignored (help). - Macdonald, Kenneth; Ridge, John (1988), "Social Mobility", British Social Trends Since 1900, Macmillian.
- Morrison, Clarence C. (proposer) (1967), "Quickie", Mathematics Magazine, 40 (4): 232.
- Munkres, James R. (1964), Elementary Linear Algebra, Addison-Wesley.
- Neimi, G.; Riker, W. (June 1976), "The Choice of Voting Systems", Scientific American: 21–27.
- O'Hanian, Hans (1985), Physics, vol. 1, W. W. Norton
- O'Nan, Micheal (1990), Linear Algebra (3rd ed.), Harcourt College Pub.
- Oakley, Cletus; Baker, Justine (April 1977), "Least Squares and the 3:40 Mile", Mathematics Teacher
{{citation}}: CS1 maint: date and year (link) - Pólya, G. (1954), Mathematics and Plausible Reasoning: Volume II Patterns of Plausible Inference, Princeton University Press
- Peterson, G. M. (1955), "Area of a triangle", American Mathematical Monthly, American Mathematical Society, 62 (4): 249
{{citation}}: Unknown parameter|month=ignored (help). - Poundstone, W. (2008), Gaming the vote, Hill and Wang, ISBN 978-0-8090-4893-9.
- Ransom, W. R. (proposer); Gupta, Hansraj (solver) (1935), "Elementary problem 105", American Mathematical Monthly, 42 (1): 47
{{citation}}: Unknown parameter|month=ignored (help). - Rice, John R. (1993), Numerical Methods, Software, and Analysis, Academic Press.
- Rucker, Rudy (1982), Infinity and the Mind, Birkhauser.
- Rupp, C. A. (proposer); Aude, H. T. R. (solver) (1931), "Problem 3468", American Mathematical Monthly, American Mathematical Society, 37 (6): 355
{{citation}}: Unknown parameter|month=ignored (help). - Ryan, Patrick J. (1986), Euclidean and Non-Euclidean Geometry: an Analytic Approach, Cambridge University Press.
- Salkind, Charles T. (1975), Contest Problem Book No 1: Annual High School Mathematics Examinations 1950-1960.
- Seidenberg, A. (1962), Lectures in Projective Geometry, Van Nostrandg.
- Silverman, D. L. (proposer); Trigg, C. W. (solver) (1963), "Quickie 237", Mathematics Magazine, American Mathematical Society, 36 (1)
{{citation}}: Unknown parameter|month=ignored (help). - Strang, Gilbert (1980), Linear Algebra and its Applications (2nd ed.), Hartcourt Brace Javanovich
- Strang, Gilbert (1993), "The Fundamental Theorem of Linear Algebra", American Mathematical Monthly, American Mathematical Society: 848–855
{{citation}}: Unknown parameter|month=ignored (help). - Taylor, Alan D. (1995), Mathematics and Politics: Strategy, Voting, Power, and Proof, Springer-Verlag.
- Tilley, Burt, Private Communication.
- Trigg, C. W. (proposer); Walker, R. J. (solver) (1949), "Elementary Problem 813", American Mathematical Monthly, American Mathematical Society, 56 (1)
{{citation}}: Unknown parameter|month=ignored (help). - Trigg, C. W. (proposer) (1963), "Quickie 307", Mathematics Magazine, American Mathematical Society, 36 (1): 77
{{citation}}: Unknown parameter|month=ignored (help). - Trono, Tony (compilier) (1991), University of Vermont Mathematics Department High School Prize Examinations 1958-1991, mimeograhed printing
- Walter, Dan (proposer); Tytun, Alex (solver) (1949), "Elementary problem 834", American Mathematical Monthly, American Mathematical Society, 56 (6): 409.
- Weston, J. D. (1959), "Volume in Vector Spaces", American Mathematical Monthly, American Mathematical Society, 66 (7): 575–577
{{citation}}: Unknown parameter|month=ignored (help). - Weyl, Hermann (1952), Symmetry, Princeton University Press.
- Wickens, Thomas D. (1982), Models for Behavior, W.H. Freeman.
- Wilansky, Albert, "The Row-Sum of the Inverse Matrix", American Mathematical Monthly, American Mathematical Society, 58 (9): 614
{{citation}}: Unknown parameter|month=ignored (help). - Wilkinson, J. H. (1965), The Algebraic Eigenvalue Problem, Oxford University Press.
- Yaglom, I. M. (1988), Felix Klein and Sophus Lie: Evolution of the Idea of Symmetry in the Nineteenth Century, Birkhäuser
{{citation}}: Unknown parameter|translater=ignored (help). - Zwicker, S. (1991), "The Voters' Paradox, Spin, and the Borda Count", Mathematical Social Sciences, 22: 187–227
Index
A
accuracy
addition
Arithmetic-Geometric Mean Inequality
B
base step
- change of
- definition
- natural
- orthogonal
- orthogonalization
- orthonormal
- standard 1, 2
- standard over the complex numbers
- string
C
classes
canonical form
characteristic
circuits
complex numbers
coordinates
D
- cofactor
- Cramer's Rule
- definition
- exists 1, 2, 3
- Laplace Expansion
- minor
- Vandermonde
- permutation expansion 1, 2
dilation
E
eigenvalue
eigenvector
elementary
elementary reduction operations
equivalence
F
finite-dimensional vector space
- argument
- codomain
- composition
- composition
- correspondence
- domain
- even
- identity
- inverse 1, 2
- inverse image
- left inverse
- multilinear
- range
- restriction
- odd
- one-to-one function
- onto
- right inverse
- structure preserving 1, 2
- two sided inverse
- value
- well-defined
- zero
Fundamental Theorem
G
Gram-Schmidt Orthogonalization
H
historyless
- composition
- matrix representation 1, 2, 3
- nonsingular 1, 2
- nullity
- nullspace
- rank 1, 2
- rangespace
- rank
- zero
I
image
index
inductive step
J
K
L
line
linear
linear map
- dilation
- see homomorphism
- reflection
- rotation 1, 2
- skew
- trace
M
- adjoint
- antisymmetric
- augmented
- block 1, 2
- change of basis
- characteristic polynomial
- cofactor
- column
- column space
- condition number
- determinant 1, 2
- diagonal matrix 1, 2
- diagonalizable
- diagonalized
- eigenvalue
- eigenvector
- elementary reduction 1, :2
- entry
- equivalent
- form
- identity 1, 2
- incidence
- inverse 1, 2
- left inverse
- main diagonal
- Markov
- minimal polynomial
- minor
- nilpotent
- nonsingular
- orthogonal
- orthonormal
- right inverse
- scalar multiple
- skew-symmetric
- similar
- similarity
- singular
- submatrix
- sum
- symmetric 1, 2, 3,4, 5, 6
- trace 1, 2, 3
- transition
- transpose 1, 2, 3
- Markov
- matrix-vector product
- minimal polynomial
- multiplication
- nonsingular 1, 2
- permutation
- principle diagonal
- rank
- representation
- row
- row equivalence
- row rank
- row space
- scalar multiple
- singular
- sum
- symmetric 1, 2, 3,4, 5
- trace 1, 2
- transpose 1, 2, 3
- triangular 1, 2, 3
- unit
- Vandermonde
mean
multiplication
N
nilpotentcy
O
order of a recurrence
P
pair
partitions
perspective
pivoting
polynomial
point
- along a subspace
- central
- onto a line
- onto a subspace
- orthogonal 1, 2
projective plane
proof techniques
proper
Q
R
relationship
representation
S
scalar multiple
scalar multiplication
Schur's triangularization lemma
self composition
- complement
- element
- empty
- empty
- intersection
- linearly dependent
- linearly independent
- member
- mutual inclusion 1, :2
- proper subset
- span of
- subset
- union
singular
sgn
structure
- closed
- complementary
- direct sum
- definition
- improper
- independence
- invariant
- orthogonal complement
- proper
- sum
sum
- of matrices
- of subspaces
- vector 1, 2, 3, 4
summation notation
T
transformation
- characteristic polynomial
- composed with itself
- diagonalizable
- eigenvalue
- eigenvector
- eigenspace
- Jordon form
- minimal polynomial
- nilpotent
- projection
- size change
- interaction with sum and scalar multiplication
- determinant 1, 2
triangles
U
V
Vandermonde
- angle between vecots
- canonical position
- closure
- column
- complex scalars
- component
- cross product
- direction
- dot product
- free
- homogeneous coordinate
- length
- natural position
- orthogonal
- probability
- representation of 1, 2
- row
- satisfies an equation
- scalar multiple
- scalar multiplication 1, 2
- sum 1, 2, 3, 4
- unit
- zero vector 1, 2
- basis
- definition 1, 2
- dimension
- dual
- finite-dimensional
- homomorphism
- isomorphism
- map
- over complex numbers
- subspace
- trivial 1, 2



















































































































































































































































































































































































































































































![{\displaystyle {\begin{array}{rl}{{[r\cdot {\begin{pmatrix}&\vdots \\\cdots &a_{i,j}&\cdots \\&\vdots \end{pmatrix}}+s\cdot {\begin{pmatrix}&\vdots \\\cdots &b_{i,j}&\cdots \\&\vdots \end{pmatrix}}]}^{\rm {trans}}}&={{\begin{pmatrix}&\vdots \\\cdots &ra_{i,j}+sb_{i,j}&\cdots \\&\vdots \end{pmatrix}}^{\rm {trans}}}\\&={\begin{pmatrix}&\vdots \\\cdots &ra_{j,i}+sb_{j,i}&\cdots \\&\vdots \end{pmatrix}}\\&=r\cdot {\begin{pmatrix}&\vdots \\\cdots &a_{j,i}&\cdots \\&\vdots \end{pmatrix}}+s\cdot {\begin{pmatrix}&\vdots \\\cdots &b_{j,i}&\cdots \\&\vdots \end{pmatrix}}\\&=r\cdot {{\begin{pmatrix}&\vdots \\\cdots &a_{j,i}&\cdots \\&\vdots \end{pmatrix}}^{\rm {trans}}}+s\cdot {{\begin{pmatrix}&\vdots \\\cdots &b_{j,i}&\cdots \\&\vdots \end{pmatrix}}^{\rm {trans}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c044b80131b0058dd87193e9dbe6ae507fa13d59)


![{\displaystyle \ell =\{t\cdot {\vec {u}}+(1-t)\cdot {\vec {v}}\,{\big |}\,t\in [0..1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c401d86ef8bb8e2d18008bf88bbf754d96ca44f4)




![{\displaystyle h(\ell )=\{h(t\cdot {\vec {u}}+(1-t)\cdot {\vec {v}})\,{\big |}\,t\in [0..1]\}=\{t\cdot h({\vec {u}})+(1-t)\cdot h({\vec {v}})\,{\big |}\,t\in [0..1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec18ca832b9fa017cac1d0c4144c24ee2969470c)




![{\displaystyle \ell =\{t\cdot {\vec {d}}_{1}+(1-t)\cdot {\vec {d}}_{2}\,{\big |}\,t\in [0..1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6160487a6e3a2f652762363e6256b32313cb8f69)
































































































































































































![{\displaystyle h([S])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c515ca198fe4cca2defa1d968f3eb7224ba62b5)
![{\displaystyle [h(S)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fe9f494d1d709f09e7be5ca9bdb5a17e663d43d)





















































































































































![{\displaystyle [\{{\vec {0}}\}]=\{{\vec {0}}\}\subset [\{{\vec {\beta }}_{1}\}]\subset [\{{\vec {\beta }}_{1},{\vec {\beta }}_{2}\}]\subset \quad \cdots \quad \subset [B]=V}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3414ca6462a266e81a770fece4e99534b9ae335d)

![{\displaystyle h([\{{\vec {\beta }}_{1},\dots ,{\vec {\beta }}_{i}\}])\subset W_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a96d738e2b917d08ef2413bf0cccf59449c4022)






















![{\displaystyle [\{h({\vec {\beta }}_{1}),\dots ,h({\vec {\beta }}_{n})\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/715457439bfc6bfe393e3a0b85bdd2ecd691c904)
![{\displaystyle [\{{\rm {Rep}}_{D}(h({\vec {\beta }}_{1})),\dots ,{\rm {Rep}}_{D}(h({\vec {\beta }}_{n}))\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8eb78045262d74c2cd779670aeb56dbd941286e0)






































































































































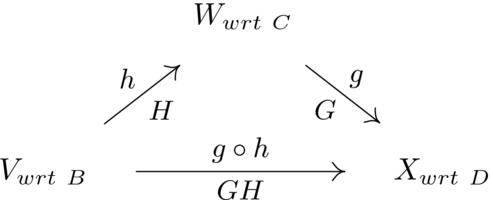

















































































































![{\displaystyle {\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}{\xrightarrow[{}]{3\rho _{2}}}{\begin{pmatrix}1&0&0\\0&3&0\\0&0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfb746607e31e693e86edf5e25dfee3abb86a634)
![{\displaystyle {\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}{\xrightarrow[{}]{\rho _{1}\leftrightarrow \rho _{3}}}{\begin{pmatrix}0&0&1\\0&1&0\\1&0&0\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67ecd06e0a158937e2327e0eb6b71ce3e4596280)
![{\displaystyle {\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}{\xrightarrow[{}]{-2\rho _{2}+\rho _{3}}}{\begin{pmatrix}1&0&0\\0&1&0\\0&-2&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/377d2147adabacd30cc78f422c764fdd40edfd59)


![{\displaystyle I{\xrightarrow[{}]{k\rho _{i}}}M_{i}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c5a62e394110a5c2fbb923861d6ff299b1e9916)
![{\displaystyle I{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}P_{i,j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4455934aef377f48d65bac76309c22f1bb8fda46)

![{\displaystyle I{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}C_{i,j}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5afbb9475262f136f8c3ffbae26cac44548489ff)
![{\displaystyle H{\xrightarrow[{}]{k\rho _{i}}}G}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ce7a7e73a7ddbb586a60c89ed9a1190c62e323)

![{\displaystyle H{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}G}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85d08bdf14e1a4ff58361dd12f4b39cc529f9f8)

![{\displaystyle H{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}G}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3040c198b5aa59a463114719153daf2915032594)


























































































![{\displaystyle {\begin{array}{rcl}\left({\begin{array}{cc|cc}1&1&1&0\\2&-1&0&1\end{array}}\right)&{\xrightarrow[{}]{-2\rho _{1}+\rho _{2}}}&\left({\begin{array}{cc|cc}1&1&1&0\\0&-3&-2&1\end{array}}\right)\\&{\xrightarrow[{}]{-1/3\rho _{2}}}&\left({\begin{array}{cc|cc}1&1&1&0\\0&1&2/3&-1/3\end{array}}\right)\\&{\xrightarrow[{}]{-\rho _{2}+\rho _{1}}}&\left({\begin{array}{cc|cc}1&0&1/3&1/3\\0&1&2/3&-1/3\end{array}}\right)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db83d4a9ced0e57d276820f800b6841c182301ee)

![{\displaystyle {\begin{array}{rcl}\left({\begin{array}{ccc|ccc}0&3&-1&1&0&0\\1&0&1&0&1&0\\1&-1&0&0&0&1\end{array}}\right)&{\xrightarrow[{}]{\rho _{1}\leftrightarrow \rho _{2}}}&\left({\begin{array}{ccc|ccc}1&0&1&0&1&0\\0&3&-1&1&0&0\\1&-1&0&0&0&1\end{array}}\right)\\&{\xrightarrow[{}]{-\rho _{1}+\rho _{3}}}&\left({\begin{array}{ccc|ccc}1&0&1&0&1&0\\0&3&-1&1&0&0\\0&-1&-1&0&-1&1\end{array}}\right)\\&\vdots \\&{\xrightarrow[{}]{}}&\left({\begin{array}{ccc|ccc}1&0&0&1/4&1/4&3/4\\0&1&0&1/4&1/4&-1/4\\0&0&1&-1/4&3/4&-3/4\end{array}}\right)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0e49ec1321435e8e7b06733c15059c380f38a29)
![{\displaystyle \left({\begin{array}{cc|cc}1&1&1&0\\2&2&0&1\end{array}}\right){\xrightarrow[{}]{-2\rho _{1}+\rho _{2}}}\left({\begin{array}{cc|cc}1&1&1&0\\0&0&-2&1\end{array}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/920de8987fe84b9cf78efce1afd5cec95aea5d22)



















































































































































































![{\displaystyle {\mbox{proj}}_{[{\vec {s}}\,]}({\vec {v}})={\frac {{\vec {v}}\cdot {\vec {s}}}{{\vec {s}}\cdot {\vec {s}}}}{\vec {s}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/234a46206d76de37cb26309c7b13f93d9feff96c)


































![{\displaystyle {\mbox{proj}}_{[{\vec {s}}\,]}({{\vec {v}}\,})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b8dd2893afda628ff011e2e0c1fd28b5a5f347)
![{\displaystyle {\vec {v}}-{\mbox{proj}}_{[{\vec {s}}\,]}({{\vec {v}}\,})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85f96a11b9f207966bdf6995060bc8d93a025fad)
![{\displaystyle \{{\vec {v}},{\vec {v}}-{\mbox{proj}}_{[{\vec {s}}\,]}({{\vec {v}}\,})\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/002cf9aba8ce1a5d4ba1e0070227e4b07b3c7d3f)

















![{\displaystyle \displaystyle {\vec {v}}={\mbox{proj}}_{[{\vec {s}}\,]}({\vec {v}})\,+\,\left({\vec {v}}-{\mbox{proj}}_{[{\vec {s}}\,]}({\vec {v}})\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0da7af968d921768d5eef2f763959f0628fe2b2b)




![{\displaystyle i\in [1..k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bef98d4d493897dca6d5d3c0366c85f70070fb29)




![{\displaystyle \displaystyle {\vec {\kappa }}_{2}={\begin{pmatrix}1\\3\end{pmatrix}}-{\mbox{proj}}_{\scriptstyle [{\vec {\kappa }}_{1}]}({\begin{pmatrix}1\\3\end{pmatrix}})={\begin{pmatrix}1\\3\end{pmatrix}}-{\begin{pmatrix}2\\1\end{pmatrix}}={\begin{pmatrix}-1\\2\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb4ea1b1e880ad1cf1aaf71487651e6d491b549c)




![{\displaystyle {\vec {\kappa }}_{2}={\begin{pmatrix}0\\2\\0\end{pmatrix}}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({\begin{pmatrix}0\\2\\0\end{pmatrix}})={\begin{pmatrix}0\\2\\0\end{pmatrix}}-{\begin{pmatrix}2/3\\2/3\\2/3\end{pmatrix}}={\begin{pmatrix}-2/3\\4/3\\-2/3\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efaef6f72068cd400dba6470e842cd8c0e5f4caf)

![{\displaystyle {\vec {\kappa }}_{3}={\begin{pmatrix}1\\0\\3\end{pmatrix}}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({\begin{pmatrix}1\\0\\3\end{pmatrix}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({\begin{pmatrix}1\\0\\3\end{pmatrix}})={\begin{pmatrix}-1\\0\\1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5305a998b025fa73d4e7c301c77d80a29bce293c)


![{\displaystyle {\begin{array}{rl}{\vec {\kappa }}_{1}&={\vec {\beta }}_{1}\\{\vec {\kappa }}_{2}&={\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}})\\{\vec {\kappa }}_{3}&={\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}})\\&\vdots \\{\vec {\kappa }}_{k}&={\vec {\beta }}_{k}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{k}})-\cdots -{\mbox{proj}}_{[{\vec {\kappa }}_{k-1}]}({{\vec {\beta }}_{k}})\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7b81f989d7eaa8606b764dc1db82f5e8c753798)








![{\displaystyle {\vec {\kappa }}_{2}={\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}})={\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\kappa }}_{1}={\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\beta }}_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/104528b528834b806090892ff62d5ff8d34e848f)
![{\displaystyle {\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{2}={\vec {\kappa }}_{1}\cdot ({\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}}))=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cff7a28fdd5309be9b0afec02f14c5addae41dc)

![{\displaystyle {\begin{array}{rl}{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{3}&={\vec {\kappa }}_{1}\cdot {\bigl (}{\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}}){\bigr )}\\&={\vec {\kappa }}_{1}\cdot {\bigl (}{\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}}){\bigr )}-{\vec {\kappa }}_{1}\cdot {\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}})\\&=0\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa72b070f98ecf2d0c3c8d3101ec1e34844902c)










![{\displaystyle {\vec {v}}-({\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {v}}_{k}]}({{\vec {v}}\,}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f5c4fb926fb1bbd888113edd0218d76777ca04f)

![{\displaystyle {\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {v}}_{k}]}({{\vec {v}}\,})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b6b75d22323cf78e846ce3ce8f71e08d74d76c4)




![{\displaystyle [{{\vec {\beta }}_{1}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/559f68d79158bda36daf673222e59c03278ace09)
![{\displaystyle [{{\vec {\beta }}_{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/715e3540cc050343c92385c8b5cf4736c2633ff9)




![{\displaystyle {\mbox{proj}}_{[{\vec {\kappa }}_{i}]}({{\vec {v}}\,})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4750ad71c62bcd218538689eec0351b9990cef66)
![{\displaystyle {\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {v}}\,})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f14a7fab8047e6f3be3e5da8f2e419199ce045e)
































































![{\displaystyle {\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{n}]}({{\vec {v}}\,})\qquad \qquad (*)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d43196ee813febf1755a058ac4fd14dbe0fb4853)




![{\displaystyle {\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {w}}\,})={\vec {0}},\dots ,\,{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {w}}\,})={\vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e704f073aaa85f01a325a6a111daaa6476637542)

![{\displaystyle {\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{n}]}({{\vec {v}}\,})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60f2b61a471c291b1d2d064cb0a57887e77bc73e)
![{\displaystyle {\mbox{proj}}_{M}({{\vec {v}}\,})={\mbox{proj}}_{[{\vec {\kappa }}_{k+1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {v}}\,})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ba73dfad8300b9d885e8731835b4de8a3d42da9)










































































































![{\displaystyle I{\xrightarrow[{}]{k\rho _{i}}}M_{i}(k)\qquad I{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}P_{i,j}\qquad I{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}C_{i,j}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8efb67d5d26695581b1ba19fa3f9d1f49e49f4ed)













































































































































































![{\displaystyle T{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}{\hat {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7c7a223e30aab801a27c27c1379429bb6c1397)








![{\displaystyle T{\xrightarrow[{}]{{\rho }_{i}\leftrightarrow {\rho }_{j}}}{\hat {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36b25c9b09ed3e3711b4d831c1a449981ae686f9)





![{\displaystyle T{\xrightarrow[{}]{k{\rho }_{i}}}{\hat {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98941b5004b156dc0e6f447910d44f74df023b84)


















































![{\displaystyle T\;{\xrightarrow[{}]{\rho _{i}+\rho _{j}}}\;{\xrightarrow[{}]{-\rho _{j}+\rho _{i}}}\;{\xrightarrow[{}]{\rho _{i}+\rho _{j}}}\;{\xrightarrow[{}]{-\rho _{i}}}\;{\hat {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aed296702db00e12b10527bf2fa6d027f1005c04)
































![{\displaystyle {\begin{pmatrix}1&2\\3&4\end{pmatrix}}{\xrightarrow[{}]{-3\rho _{1}+\rho _{2}}}{\begin{pmatrix}1&2\\0&-2\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ea5b08ddf850535e975de4e957cd93cecdfb73)
![{\displaystyle {\begin{pmatrix}1&2\\3&4\end{pmatrix}}{\xrightarrow[{}]{\rho _{1}\leftrightarrow \rho _{2}}}{\begin{pmatrix}3&4\\1&2\end{pmatrix}}{\xrightarrow[{}]{-(1/3)\rho _{1}+\rho _{2}}}{\begin{pmatrix}3&4\\0&2/3\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca769c96e028a2353c25170effe294b86d424b3f)





























































![{\displaystyle {\begin{vmatrix}t_{1,1}&t_{1,2}&\ldots &t_{1,n}\\t_{2,1}&t_{2,2}&\ldots &t_{2,n}\\&\vdots \\t_{n,1}&t_{n,2}&\ldots &t_{n,n}\end{vmatrix}}={\begin{array}{l}t_{1,\phi _{1}(1)}t_{2,\phi _{1}(2)}\cdots t_{n,\phi _{1}(n)}\left|P_{\phi _{1}}\right|\\[.5ex]\quad +t_{1,\phi _{2}(1)}t_{2,\phi _{2}(2)}\cdots t_{n,\phi _{2}(n)}\left|P_{\phi _{2}}\right|\\[.5ex]\quad \vdots \\\quad +t_{1,\phi _{k}(1)}t_{2,\phi _{k}(2)}\cdots t_{n,\phi _{k}(n)}\left|P_{\phi _{k}}\right|\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492a6002409713d21651ff2dedac1627c399319f)











































![{\displaystyle P_{\phi }{\xrightarrow[{}]{\rho _{1}\leftrightarrow \rho _{2}}}{\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76beb6fd0dae1961d75ba816b876fbba55db89f0)
![{\displaystyle P_{\phi }{\xrightarrow[{}]{\rho _{3}\leftrightarrow \rho _{1}}}{\begin{pmatrix}0&0&1&0\\1&0&0&0\\0&1&0&0\\0&0&0&1\end{pmatrix}}{\xrightarrow[{}]{\rho _{2}\leftrightarrow \rho _{3}}}{\begin{pmatrix}0&0&1&0\\0&1&0&0\\1&0&0&0\\0&0&0&1\end{pmatrix}}{\xrightarrow[{}]{\rho _{1}\leftrightarrow \rho _{3}}}{\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5f4e8254eefeceb28707dd634d7132d2d033cf9)






![{\displaystyle P_{\phi }={\begin{pmatrix}\vdots \\\iota _{\phi (j)}\\\iota _{\phi (k)}\\\vdots \end{pmatrix}}{\xrightarrow[{}]{\rho _{k}\leftrightarrow \rho _{j}}}{\begin{pmatrix}\vdots \\\iota _{\phi (k)}\\\iota _{\phi (j)}\\\vdots \end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d64795bb38e7b03350869c4ed7f08bb786487f1d)

![{\displaystyle {\begin{pmatrix}\vdots \\\iota _{\phi (j)}\\\iota _{\phi (j+1)}\\\iota _{\phi (j+2)}\\\vdots \\\iota _{\phi (k)}\\\vdots \end{pmatrix}}{\xrightarrow[{}]{\rho _{k}\leftrightarrow \rho _{k-1}}}\;\;{\xrightarrow[{}]{\rho _{k-1}\leftrightarrow \rho _{k-2}}}\dots {\xrightarrow[{}]{\rho _{j+1}\leftrightarrow \rho _{j}}}{\begin{pmatrix}\vdots \\\iota _{\phi (k)}\\\iota _{\phi (j)}\\\iota _{\phi (j+1)}\\\vdots \\\iota _{\phi (k-1)}\\\vdots \end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f795d7ddeadb9a87283411a5113159540bce4b0b)
![{\displaystyle {\xrightarrow[{}]{\rho _{j+1}\leftrightarrow \rho _{j+2}}}\;\;{\xrightarrow[{}]{\rho _{j+2}\leftrightarrow \rho _{j+3}}}\dots {\xrightarrow[{}]{\rho _{k-1}\leftrightarrow \rho _{k}}}{\begin{pmatrix}\vdots \\\iota _{\phi (k)}\\\iota _{\phi (j+1)}\\\iota _{\phi (j+2)}\\\vdots \\\iota _{\phi (j)}\\\vdots \end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63c4d059f35da87179f35d42c91965826d061da9)










![{\displaystyle T[b]{\xrightarrow[{}]{k\rho _{i}}}{\hat {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aca86f051b1fb06c6ca9cdcf66ea5e5fdb336c3b)


![{\displaystyle T[b]{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}{\hat {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b185d3b1dfff4afc1da73b3722557478472463e6)









![{\displaystyle T[b]{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}{\hat {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f71989a4ff60c0de41780da14b091c7dbb3006b)



![{\displaystyle {\begin{array}{rl}=&\displaystyle \sum _{\phi }{\big [}t_{1,\phi (1)}\cdots t_{i,\phi (i)}\cdots kt_{i,\phi (j)}\cdots t_{n,\phi (n)}\operatorname {sgn}(\phi )\\&\displaystyle \qquad +t_{1,\phi (1)}\cdots t_{i,\phi (i)}\cdots t_{j,\phi (j)}\cdots t_{n,\phi (n)}\operatorname {sgn}(\phi ){\big ]}\\\\=&\displaystyle \sum _{\phi }t_{1,\phi (1)}\cdots t_{i,\phi (i)}\cdots kt_{i,\phi (j)}\cdots t_{n,\phi (n)}\operatorname {sgn}(\phi )\\&\displaystyle \qquad +\sum _{\phi }t_{1,\phi (1)}\cdots t_{i,\phi (i)}\cdots t_{j,\phi (j)}\cdots t_{n,\phi (n)}\operatorname {sgn}(\phi )\\\\=&\displaystyle k\cdot \sum _{\phi }t_{1,\phi (1)}\cdots t_{i,\phi (i)}\cdots t_{i,\phi (j)}\cdots t_{n,\phi (n)}\operatorname {sgn}(\phi )+d(T)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa470992dde36b5ecf9715c31f575db54e39192a)






















![{\displaystyle g(\phi )=\prod _{i<j}[\phi (j)-\phi (i)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0cfb9f38af071a027d2405c6167f681ea05de2)


























![{\displaystyle \{t_{1}{\vec {v}}_{1}+\dots +t_{n}{\vec {v}}_{n}\,{\big |}\,t_{1},\ldots ,t_{n}\in [0..1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f9a540e9629e8fb4043860c340547644394e678)











































![{\displaystyle [2..4]\times [2..5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed353f4207f74ed89169ae13dddc7031d3b0b4b4)




![{\displaystyle {\xrightarrow[{}]{\scriptstyle {\begin{pmatrix}2&1\\0&1\end{pmatrix}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2186a6618a6a750da19b05bd41197129a3d27efc)




























![{\displaystyle {\begin{array}{rl}&=t_{1,1}\cdot \left[t_{2,2}t_{3,3}{\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}}+t_{2,3}t_{3,2}{\begin{vmatrix}1&0&0\\0&0&1\\0&1&0\end{vmatrix}}\,\right]\\&\quad +t_{1,2}\cdot \left[t_{2,1}t_{3,3}{\begin{vmatrix}0&1&0\\1&0&0\\0&0&1\end{vmatrix}}+t_{2,3}t_{3,1}{\begin{vmatrix}0&1&0\\0&0&1\\1&0&0\end{vmatrix}}\,\right]\\&\quad +t_{1,3}\cdot \left[t_{2,1}t_{3,2}{\begin{vmatrix}0&0&1\\1&0&0\\0&1&0\end{vmatrix}}+t_{2,2}t_{3,1}{\begin{vmatrix}0&0&1\\0&1&0\\1&0&0\end{vmatrix}}\,\right]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3336942873dd3a51a77c83d2b3c31f17ac1ca418)
![{\displaystyle {\begin{array}{rl}&=t_{1,1}\cdot \left[t_{2,2}t_{3,3}{\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}}+t_{2,3}t_{3,2}{\begin{vmatrix}1&0&0\\0&0&1\\0&1&0\end{vmatrix}}\,\right]\\&\quad -t_{1,2}\cdot \left[t_{2,1}t_{3,3}{\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}}+t_{2,3}t_{3,1}{\begin{vmatrix}1&0&0\\0&0&1\\0&1&0\end{vmatrix}}\,\right]\\&\quad +t_{1,3}\cdot \left[t_{2,1}t_{3,2}{\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}}+t_{2,2}t_{3,1}{\begin{vmatrix}1&0&0\\0&0&1\\0&1&0\end{vmatrix}}\,\right]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0433f49335ded3fb4233a5500b63e43865c684a0)





























































































































































































































































































































































































































































































![{\displaystyle [\{{\vec {e}}_{4}\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4e28a967d3a88829164fd8f236fead8fe7e6f1)
![{\displaystyle {\mathcal {R}}({\hat {n}}^{2})\cap {\mathcal {N}}({\hat {n}}^{2})=[\{{\vec {e}}_{3},{\vec {e}}_{4}\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59ee29b1492192af6481718694b9edbcfead819)
![{\displaystyle {\mathcal {R}}({\hat {n}}^{3})\cap {\mathcal {N}}({\hat {n}}^{3})=[\{{\vec {e}}_{4}\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e660fdc60d68acc50c952f1ca195416648175e78)


















































































































































































































































































![{\displaystyle \left|T_{1}\right|\cdot \left|T_{2}\right|={\bigg (}\sum _{\begin{array}{c}\\[-19pt]\scriptstyle {\text{perms }}\phi _{1}\\[-5pt]\scriptstyle {\text{of }}1,\dots ,p\end{array}}\!\!\!t_{1,\phi _{1}(1)}\cdots t_{p,\phi _{1}(p)}\operatorname {sgn}(\phi _{1}){\bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28288c66fb2b1d0661d79847a6377a698870e892)
![{\displaystyle \cdot {\bigg (}\sum _{\begin{array}{c}\\[-19pt]\scriptstyle {\text{perms }}\phi _{2}\\[-5pt]\scriptstyle {\text{of }}p+1,\dots ,p+q\end{array}}\!\!\!t_{p+1,\phi _{2}(p+1)}\cdots t_{p+q,\phi _{2}(p+q)}\operatorname {sgn}(\phi _{2}){\bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92266b1a2ac11cf0979db182b0bfbd60a31eb72c)















































































































































































![{\displaystyle f(n)={\frac {1}{\sqrt {5}}}\left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n+1}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n+1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1d7d2d6735b19864569278d4689ec6f0eb0d142)




















































































































































































































































