Linear Algebra/Topic: Crystals
Everyone has noticed that table salt comes in little cubes.
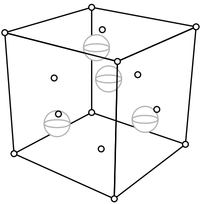
Remarkably, the explanation for the cubical external shape is the simplest one possible: the internal shape, the way the atoms lie, is also cubical. The internal structure is pictured below. Salt is sodium chloride, and the small spheres shown are sodium while the big ones are chloride. (To simplify the view, only the sodiums and chlorides on the front, top, and right are shown.)
The specks of salt that we see when we spread a little out on the table consist of many repetitions of this fundamental unit. That is, these cubes of atoms stack up to make the larger cubical structure that we see. A solid, such as table salt, with a regular internal structure is a crystal.
We can restrict our attention to the front face. There, we have this pattern repeated many times.
The distance between the corners of this cell is about 3.34 Ångstroms (an Ångstrom is meters). Obviously that unit is unwieldly for describing points in the crystal lattice. Instead, the thing to do is to take as a unit the length of each side of the square. That is, we naturally adopt this basis.
Then we can describe, say, the corner in the upper right of the picture above as .
Another crystal from everyday experience is pencil lead. It is graphite, formed from carbon atoms arranged in this shape.
This is a single plane of graphite. A piece of graphite consists of many of these planes layered in a stack. (The chemical bonds between the planes are much weaker than the bonds inside the planes, which explains why graphite writes---it can be sheared so that the planes slide off and are left on the paper.) A convenient unit of length can be made by decomposing the hexagonal ring into three regions that are rotations of this unit cell.
A natural basis then would consist of the vectors that form the sides of that unit cell. The distance along the bottom and slant is ngstroms, so this
is a good basis.
The selection of convienent bases extends to three dimensions. Another familiar crystal formed from carbon is diamond. Like table salt, it is built from cubes, but the structure inside each cube is more complicated than salt's. In addition to carbons at each corner,
there are carbons in the middle of each face.
(To show the added face carbons clearly, the corner carbons have been reduced to dots.) There are also four more carbons inside the cube, two that are a quarter of the way up from the bottom and two that are a quarter of the way down from the top.
(As before, carbons shown earlier have been reduced here to dots.) The distance along any edge of the cube is Ångstroms. Thus, a natural basis for describing the locations of the carbons, and the bonds between them, is this.
Even the few examples given here show that
the structures of crystals is complicated enough that
some organized system to give the locations of the atoms, and how they
are chemically bound, is needed.
One tool for that organization is a convienent basis.
This application of bases is simple, but it shows a context where
the idea arises naturally.
The work in this chapter just takes this simple idea and develops it.
Exercises[edit | edit source]
- Problem 1
How many fundamental regions are there in one face of a speck of salt? (With a ruler, we can estimate that face is a square that is cm on a side.)
- Problem 2
In the graphite picture, imagine that we are interested in a point Ångstroms up and Ångstroms over from the origin.
- Express that point in terms of the basis given for graphite.
- How many hexagonal shapes away is this point from the origin?
- Express that point in terms of a second basis, where the first basis vector is the same, but the second is perpendicular to the first (going up the plane) and of the same length.
- Problem 3
Give the locations of the atoms in the diamond cube both in terms of the basis, and in Ångstroms.
- Problem 4
This illustrates how the dimensions of a unit cell could be computed from the shape in which a substance crystalizes (see Ebbing 1993, p. 462).
- Recall that there are atoms in a mole (this is Avagadro's number). From that, and the fact that platinum has a mass of grams per mole, calculate the mass of each atom.
- Platinum crystalizes in a face-centered cubic lattice with atoms at each lattice point, that is, it looks like the middle picture given above for the diamond crystal. Find the number of platinums per unit cell (hint: sum the fractions of platinums that are inside of a single cell).
- From that, find the mass of a unit cell.
- Platinum crystal has a density of grams per cubic centimeter. From this, and the mass of a unit cell, calculate the volume of a unit cell.
- Find the length of each edge.
- Describe a natural three-dimensional basis.
References[edit | edit source]
- Ebbing, Darrell D. (1993), General Chemistry (Fourth ed.), Houghton Mifflin.