Clock and Data Recovery/Structures and types of CDRs/Applications of the 1st order type 1 architecture
This architecture feeds the signal coming out of the phase comparator directly to the VCO input.
There is neither emphasis nor de-emphasis of any frequency band, just a flat gain.
The maximum instantaneous output of the comparator drives the maximum frequency deviation of the VCO, without any delay.
- It is like driving a car by using only the end of range of either the accelerator or of the brake, jumping from one to another whenever a speed variation is needed, and with no memory of what was done before.
It is easy to understand that this architecture is best to react quickly, that is, to quickly (re)acquire the phase lock.
Inevitably, it offers sub-optimal performances during the (slave) tracking (the 2 - 1 or the 2 - 2 may be preferred) and is inadequate if its maximum instantaneous reaction is not large enough to drive the VCO to the frequency of the received signal (the 2 - 2 with PFD would be used).
Where used and how made[edit | edit source]
This architecture (the simplest of the three) is best fit to implement CDRs with fast and slip-free acquisition of phase lock.
- Its response to an abrupt change of phase (step input), even if combined with a frequency difference between the timing of the received signal and the free running frequence of the local oscillator (ramp input), is always free from slips.
- The phase difference during the acquisition is always a decreasing function (apart from a small drift that may originate by ffr / fp mistuning and that would only be evident during periods of missing transitions and only if the mistuning sign was making the VCO resist the direction of the acquisition transient). See Example 3 here below.
This architecture is preferred when the acquisition performances are the prime requirement, but also for applications in continuous mode (e.g. phase aligners that align signals - synchronous but not in phase with each other -coming into a switching matrix) where the CDR is replicated many times and a simpler implementation allows appreciable savings.
Due to its inherent simplicity and robustness, it is the preferred choice in general, except when special requirements recommend 2-1 or 2-2.
In practice this means:
- burst mode receivers
- phase aligners
- general purpose end points.
- Although the linear model has been described in detail in the previous sections, this architecture is mostly implemented with circuits that have hard non-linearities, like bang-bang detectors.
- The linear model has helped fix the concepts, but recourse to simulation - that takes into account the non-linearities- becomes necessary to investigate the CDR operation when non-linearities come into play.
For the application categories listed above, just the jitter tolerance (and often the acquisition time) really matter .
The bang-bang type of phase detector is used in preference to the linear one, and -in almost all cases- the VCO is implemented with digital circuitry processing a fixed frequency signal.
- The acquisition speed (that is key in burst mode) is even improved a bit by this choice.
The VCO (in case of a slave application) or the "integrator + delay-line" (in case of a phase-aligner) is driven directly by the bang-bang phase detector.
Even if the VCO is a linear one, it operates in a bang-bang mode,
because it jumps between the two frequencies that correspond to the two (non-zero) levels of the detector output.
There is no risk of instability nor of deterioration of the performances of interest (acquisition time and jitter tolerance) when those non-linear blocks are used in this simple, straightforward architecture.
- The phase adjustment (during the acquisition) that takes place in one clock cycle is much larger than the phase drift that results from the frequency difference between the remote transmitter and the local clock (in the case of the phase aligner, such frequency difference -i.e. phase drift- is zero by definition).
- In the linear model, the response time τ is the only quantity that characterizes this type of loop.
- The quantity τ is measurable as a time equal to k periods of received pulses, and can be made as short as the duration of a few -say k- received bit pulses: τ = kT.
- The acquisition is achieved in a time close to τ, shorter if the initial phase mismatch is small, between equal and two or three times larger if the mismatch is maximum and depending on the phase comparator type.
- There are practical cases where a linear phase comparator is used in a high speed phase aligner for burst model,[1] although it is the bang-bang phase detector that best fits this architecture for the applications listed.
- In a bang-bang (non-linear) implementation, that is the most common, the fundamental loop parameter is the phase adjustment during one line pulse cycle. That adjustment Δφ (expressed in radian) is:
- These two values of phase adjustment are in practice equal or not largely different ( fmax and fmin are the two frequencies that the VCO oscillates at, when driven by the high or by the low output level of the phase detector).
- The quantity Δφ, that varies inversely to the acquisition time, can correspondingly be made as large as T/k.
- The acquisition lasts for a number of received pulsed equal to the initial phase distance, divided by Δφ.
- In case the received signal lacks some transitions and the PD is of the ternary not stuffing type, the acquisition takes proportionally longer. This case is only theoretical as most transmission protocols for burst mode transmission implement a preamble with 100% DT to achieve acquisition in the shortest time.
- There is no reason to use a PFD in this approach, because the bang-bang PD always uses the full frequency range of the VCO, at every phase detection.
VCO ffr accuracy[edit | edit source]
Once this loop (1-1 bang-bang) has achieved lock, its sampling instant moves (= jumps) back and forth around the eye center following the alternate linear ramps of the PLL output phase, driven in turn by the transitions of the incoming signal.
The linear phase ramps of the VCO output are either positive or negative and result in jumps forward or backward ( of Δφ/ωp seconds ) made by the sampling instant that takes place at the end of each ramp.
Sometimes a few (but not many) are in the same direction before one or more jumps in the other direction take the sampling instant back towards its best position.
The total phase variation during each pulse period ( Δφ radians i.e. Δφ/ωp seconds ) must be small to reduce the imprecision in sampling, but it must also be large to quickly acquire lock and to compensate for the VCO frequency offset.
- Those drifts (i.e. phase ramps), that come with every signal transition, compensate but only statistically for the offset between ωp and ωfr.
- In the linear 1st order, type 1, loop, the VCO frequency mismatch fp – ffr becomes a sampling time error Es:
Es = (ωp – ωfr)/G , (G= Gφ*GVCO) - For example, a VCO where ωfr may be 10% less than ωp would need a Δφ > 2π/10.
- In the linear 1st order, type 1, loop, the VCO frequency mismatch fp – ffr becomes a sampling time error Es:
But the bang-bang phase detector, when it operates with small deviations around the eye center, has a very high equivalent gain Gφ.
The steady state drive error in front of the VCO is the same for linear and bang-bang, but the steady state output (= sampling) error is reduced for the bang-bang as much as Gφ is increased.
- Approximately, it is reduced (with respect to the error in the equivalent linear PLL) by the ratio of its Gφ with an error of Δφ/2 divided by its Gφ with an error of π.
The steady state sampling error is hidden inside the much larger bang-bang tracking jitter, and appears as an unbalanced number of bang bang corrections.
- In the time that fp-ffr cumulate a phase drift equal to Δφ, there will be one more correction that compensates for that drift..
Jitter tolerance of the bang-bang 1 - 1 architecture[edit | edit source]
There always exists the possibility that the PLL is not able to follow a rapidly changing phase of its input because the rate of change of the VCO phase (i.e. the VCO frequency deviation) is limited. The PLL is "slew-rate" limited.
- The slew-rate limits coincide in the 1 - 1 architecture with the limits of the frequency range of the VCO.
- In this 1 - 1 architecture with bang-bang detector, this can only occur either because of the VCO intrinsic limits or because of the limited range of its drive signal.
The 1 - 1 CDR is able to vary rapidly its frequency, because the phase error detected by the PD becomes immediately a frequency correction in the VCO (no low-pass in between).
The frequency step is always the largest possible jump, irrespectively of the input phase error.
- The output steady state error can be seen both as:
- a frequency deviation from the free-running value:
- and as a phase deviation of the sampling instant from the central point of the eye:
The steps that the phase detector generates are consequently abrupt steps to one of two (binary PD), or to one of three (ternary PD) values:
- fmax
- ffr ( if the PD is of "ternary" type)
- fmin
- and the VCO frequency varies accordingly, and the VCO phase exhibits intervals of constant slope, each interval resulting from a step tread in the time diagram of the VCO frequency.
The input jitter is tracked by bang-bang corrections, triggered every time the input data stream has a level transition.
The PLL can track the input phase variations, but it cannot react faster than jumping to the frequency extremes of the VCO useful range.
- (The frequency step is a linear ramp of the PLL phase: the maximum ramp slope of a circuit is called the slew-rate ) .
But if the phase of the input signal varies more rapidly than that (=exceeds the slew-rate), then a phase error appears and it may grow and possibly affect the CDR tolerance.
- It may also depend on the relative frequency of input transitions, if the phase detector does not produce an output when a transition is missing.
- A transition generates a phase detection and the PD output stays at either of its significant states for one clock period.
- But if a transition is missing, certain ternary PDs stay at their intermediate state for a clock period, while the others (ternary or binary) provide a pulse replicating the previous one.
- Averaging across a few clock period, the CDR that uses the former type of PD behaves as if the PD gain was reduced (i.e. multiplied) by DT.
- (For the other PDs (that do the transition stuffing), the gain is not reduced by DT, and DT = 1 in the following formulae).
- The open loop gain is defined as G = Gφ Gf GVCO.
- If the input of the PLL is a sinusoidal jitter Ajsin (ωjt), then its maximum slope is Ajωj and the loop will track it without phase error as long as:
- The sinusoidal jitter signal must be considered in conjunction with the steady state error because this type 1 loop compensates all frequency difference and wander with a non-zero steady state sampling error.
- The bang-bang corrections during tracking make the output phase of the VCO vary faster or slower than needed to reduce to zero the sampling error.
- When the next sampling takes place in the phase detector, the sampling point often finds itself at the opposite side of the zero phase error point.
- Each such jump of the sampling instant:
- - over-reaches by almost as much as the total bang-bang correction if it was very close at the previous phase detection, or
- - reaches very close to the equilibrium point if it was far by almost as much as a full correction at the previous phase detection.
- The max slope of phase variation that the VCO can rapidly generate in response to a constant (high or low) signal from the phase detector depends both on:
- - where it jumps to, that is the upper or lower frequency extreme of its range, and on
- - where it comes from, that is the frequency of the VCO immediately before the correction.
- The slew rate slope of the CDR response to the next bang-bang corrections is consequently increased in one direction and reduced by the same amount in the other direction.
- When tracking becomes difficult because the loop must operate close to its ability to track, the effort becomes evident in the reduction of the bang-bang duty-cycle. When the input jitter sinusoid crosses the zero, the PD output stays most often constant and indicates the onset of a phase error due to slewing.
- When the jitter frequency is too high for a correct tracking, the signal driving the VCO becomes a triangular saw-tooth of reduced amplitude.
- The following sections and examples illustrate the operation in stressing input conditions of CDRs of this type. They describe slave 1-1 CDRs (and not phase-aligners) just because they represent the more general case.
- Another example has already been shown in "A 1st order type 1 loop goes into slew rate limiting (= into slewing) only because of the VCO range limits".
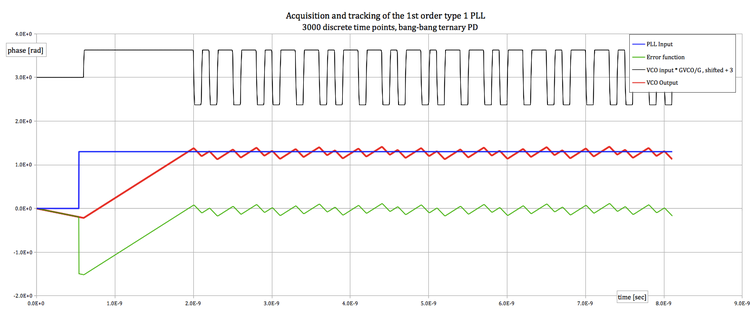
Example 1[edit | edit source]

Ternary bang-bang Phase detector. This circuit is operating very close to its jitter tolerance limit.
The simulation uses 3000 discrete time steps. Each time increment is 16.7 ps (that is the line pulse period of 100 ps divided by 6).
After 200 steps (i.e. after 16.7ps * 200 = 3.33 ns) the loop - that was until then open (because LOS was = 1)- starts its acquisition phase ( LOS = 0).
The input phase takes in that moment a positive step of 1.0 rad. The output phase has lagged in the meantime by -0.63 rad because of the 3000 ppm inaccuracy of the VCO.
The input transitions appear with an average density of 66.7%, but otherwise in a fully random sequence.
The acquisition lasts for about 4 ns in this example. It ends when the phase error settles around its final value (settles around 0 rad in this example) and is identified by the first negative pulse in front of the VCO.
The pattern of pulses in the signal that drives the VCO (black trace) is, although random, constantly made only of positive pulses during the acquisition of lock.
It may be noted that the VCO has a ffr lower than fp (in actuality lower by 3000 ppm), as the VCO phase lags behind the input phase (lower negative slope in the red trace) every time the VCO drive signal it at its intermediate level, both before detection of the input signal and when there is a lack of transition.
The steeper slopes of the red trace, positive and negative, tell when the VCO is driven to its top and bottom frequencies (1.116 1010 and 8.776 109 Hz ) by the positive and negative levels of its drive signal.
The drive signal is exponentially smoothed when it goes down to zero, because there is a parasitic low-pass (at 6,28 1011 Hz = eight times the line pulse frequency) just after the ternary phase detector. The drive signal is sharp at its top and bottom corners because there it is clamped by an instantaneous circuit.
The acquisition time varies every time (= every time the simulation is repeated) because a new random sequence of the input bit stream is generated, although with the same average transition density.
If the transitions density had been equal to 100%, the acquisition would have been faster and identical every time.
(Acquisition with a preamble of 101010.. of adequate duration, is the standard in systems that need to reacquire frequently the signal phase lock).
After 700 steps (i.e. after 16.7 ps * 700 = 11.7 ns) the input signal, that had been without jitter since after its appearance, starts jittering its transition with a sinusoidal variation at a frequency of 63.7 MHz and a peak amplitude of 1.8 rad (= of 28.65 ps).
The added jitter exceeds the slew-rate possible for the loop, especially when the input frequency accelerates. The max frequency deviation that the VCO can follow is smaller towards higher frequencies, because of the inherent VCO bias of ffr below fp, while the drive swing of the VCO is symmetric with respect to 0 volt, and the VCO is symmetric with respect to fp.
The fact that the loop in in slew-rate limitation is made evident by the orientation of the drive pulses all in one direction, while none is showing in the other direction. With a 8B10B code the slew-rate condition can be defined as a contiguous sequence of ten or more phase detections that indicate a phase error of the same sign.[2]
- This simulation makes very evident how the statistic of the input transitions affects the CDR performances.
- It can be understood that a truly random sequence of input bits, with run length that can be very long (even if with a correspondingly very low frequency) should not be transmitted.
- Limitation of run length (and limitation of the running sum) are always present in practice, as well as means of keeping the transition density not far from 50 %.
- This also means that simulations where the transition density is modeled only as a corresponding reduction of the detector gain are useful as well. The time diagrams are simpler and neater, and the different phenomena can easier be identified and studied.
- This is the case in the following examples 2 and 3. Example 4 instead simulates again every individual, random input transition.
Tolerance curve example[edit | edit source]

Ternary bang-bang Phase detector.
The curves of tolerance in the figure above have been obtained by simulations of each point in the same circuit.
The curves indicate the slew-rate limitation in the left part of the figure, where they turn upwards towards low frequencies.
The curves indicate the tolerance due to the limitation of the lateral eye margin in the right part of the figure, where they tend towards the horizontal asymptote.
Example 2[edit | edit source]
- Examples 2 and 3 are simulations valid if the distribution of input signal transitions is sufficiently "regular", that is if it can be simulated simply by an equivalent reduction of the phase detector gain.
- This is not always the case. Examples 1 and 4 describe the acquisition and tracking in case the input transitions come fully at random and the input jitter is so fast that there is no way to substitute averages in lieu of the time dependent quantities.
The low-pass that is always present at the output of the phase-detector must be at a frequency significantly higher than the highest frequency of the incoming jitter, or else its time constant becomes significant for the loop operation, and the model or the simulation more appropriated are the ones of the 2-1 loop (over-damped).
The following figure illustrates several features of this loop.
The values used for the quantities that influence the simulation result are indicated inside the figure.
The simulation uses 1500 discrete time steps. Each increment corresponds to 0.593 ns (that is the loop time constant of 178 ns divided by 300).
After 75 time steps (i.e. after .593 * 75 = 44.5 ns) the loop - that was until then open, LOS = 1 - starts its acquisition phase ( LOS = 0). The input jitter starts in that moment a sinusoidal variation, with an amplitude of 0.95 rad and a frequency of 10 million rad/sec.
After another 38 time steps (a total of 133 steps = a total time of 67 ns), the input jitter has a negative abrupt step of - 0.4 rad, and then a positive ramp of +0.5 rad/sec.
The incoming signal is supposed to exhibit a transition density of 50%. This is simulated simply decreasing by 0.5 the detector gain.

As soon as the incoming signal is received (LOS = 0) and a phase mismatch is detected, the loop goes after it with the maximum speed.
The maximum (or minimum) speed ωmax of 6.28869e-9 rad/sec (or ωmin of 6.271321e-9 rad/sec) of the VCO correspond to the high (or to the low) output of the phase detector.
(Remark: in this example the transition density is constant and equal to 50%. This reduces the detector gain and consequently both the loop gain and the deviation fmax-fmin correspondingly. In most actual applications, the beginning of the transmission burst takes place with a sequence that assures DT = 1 for the entire expected period of acquisition).
Three points should be remarked:
- The phase detector (in this simulation) is followed by a low-pass filter of the first order that has a low-pass pole at ωf = 2.7 ωsimulation_samples = 4.56+009 rad/sec, that is smaller than, but close to, the line pulse frequency of 6.28+009 rad/sec. The smoothing of the rise and fall transitions of the signal that drives the VCO are nonetheless clearly visible in the figure. This point becomes very relevant for the 2-2 practical applications where it may even, in some cases, imply deterioration of the CDR performances. (the 2-1 architecture, that filters the high frequency output of the comparator by definition, is practically not exposed to the risk).
- The maximum slope of the sinusoidal wave of input jitter is 9.5-001*1+007 = 9.5+006 rad/sec. This exceeds the maximum tracking deviation that the VCO can offer when driven by the phase detector maximum level (deviation of +8.27+006 rad/sec )or by its minimum level (deviation of -8.69+006 rad/sec).
- There are relatively long periods without changes in the detector output, when the VCO is working constantly at either end of its drive range (= its maximum Δφ/Δt). This is a second condition of risk, because the loop is open in that interval of time. This requires very careful consideration in the design of the 2-2 loop that , like this one, uses the bang-bang detector and does not filter the high frequencies coming out of it.
The acquisition phase in this example is not very evident. The input starts a sinusoidal variation after 75 simulation steps, that the circuit tracks with some difficulty.
It is after 113 simulation steps (113 - 75 = 38 steps after the sinusoidal component of the input has started) that the input phase has an abrupt negative step of 0.4 rad.
At that moment the loop shows its acquisition characteristic that is to recuperate at constant Δφ/Δt, which can be seen as a constant slope in the time diagram of the example figure.
In the next example the acquisition phase is more evident.
Example 3[edit | edit source]
- Examples 2 and 3 are simulations valid if the distribution of input signal transitions is sufficiently "regular", that is if it can be simulated simply by an equivalent reduction of the phase detector gain.
- This is not always the case. Examples 1 and 4 describe the acquisition and tracking in case the input transitions come fully at random and the input jitter is so fast that there is no way to substitute averages in lieu of the time dependent quantities.

In this example the initial acquisition phase is evident, after the input has a negative abrupt step of phase equal to - 1.75 rad (after 175 simulation steps).
- The loop drives (almost) immediately the VCO at the lowest end of its drive range (= its minimum Δφ/Δt) and recuperates at that constant Δφ/Δt (= at a constant slope in the figure).
- Like in the previous example, there is some low-pass at the charge-pump output. This is evident in the exponential rise and fall of the charge pump output contrasted with the abrupt steps that should ideally be present, shown by the curve "Comp.Outp." ( = "output of the phase comparator" ) in the figure.
- This low-pass is also responsible for the undershoot at the end of the acquisition phase.
The tracking phase is well shown in the following phase, that lasts until after the mid point of the time diagram.
- The detector jumps back and forth very often, asking the VCO to accelerate and to decelerate, so that the output phase jumps ahead and behind the input phase correspondingly.
- The high frequency pole of the charge-pump output prevents the drive level to the VCO to actually reach its range ends, but is still sufficient to have the output jump ahead and behind the input. The difference between the input frequency (500 ppm + 5 rad/sec) is small with respect to the phase jumps of the output, and is easily compensated by a small (= invisible) d.c. offset of the charge-pump output.
In the rightmost part of the figure, the input acquires an additional sinusoidal component somewhat faster than the loop slew-rate.
- The rate of variation exceeds twice per period the ability of the loop to fully track: this is evident from the permanence of the phase detector output in either state for as long as it tries to track either half of the sinusoidal variation, without the typical continuous jumping back and forth that is so evident in the preceding phase.
Example 4[edit | edit source]
- Examples 2 and 3 above have shown simulations that are valid if the distribution of input signal transitions is sufficiently "regular", i.e. if the distribution of input signal transitions can be simulated simply by an equivalent reduction of the phase detector gain.
- This is not always the case. This example (as well as Example 1) describes the acquisition and tracking in case the input transitions come fully at random and the input jitter is so fast that the simulation step must be shorter than the line pulse period.

- In the figure above, the simulation uses 3000 discrete time steps. Each time increment is 2,7 ps (that is the line pulse period of 100 ps divided by 37).
- After 200 time steps (i.e. after .2,7 * 37 = 543 ps) the loop - that was open until then (because LOS was = 1) starts its acquisition phase ( LOS = 0).
- The input phase takes in that moment a positive step of 1.3 rad.
- The input transitions appear with an average density of 50 %, but otherwise in a fully random sequence.
- The acquisition lasts for a little over 3 ns in this example. It ends when the phase error settles around its final value (settles around 0 rad in this example).
- The pattern of pulses in the signal that drives the VCO (black trace) is, although random, constantly made only of positive pulses during the acquisition of lock.
- It may be noted that the VCO has a ffr lower than fp (in this example lower by exactly 5750 ppm), as the VCO phase lags behind the input phase (lower negative slope in the red trace) every time the VCO drive signal it at its intermediate level, both before detection of the input signal and when there is a lack of transition (mid level of the VCO drive signal).
- The steeper slopes of the red trace, positive and negative, tell when the VCO is driven to its top and bottom frequencies (1,00575 1010 ±2,39 108 Hz ) by the positive and negative pulses of its drive signal.
- The drive signal is exponentially smoothed when it goes down to zero, because there is a parasitic low-pass (at 6,28 1011 rad/sec = ten time ti line pulse frequency) just after the ternary phase detector. It is sharp at its top and bottom corners because the it is clamped by an instantaneous circuit.
- The acquisition time would vary every time with the randomness of the transitions at the signal appearance, and be significantly longer than in the example with a non-zero probability.
- If the transitions density had been equal to 100%, the acquisition would have been faster and predictable.
- The following figure gives an example of the same circuit if the transition density is forced to 100%.
- Acquisition with a preamble of 101010.. of adequate duration, are a standard in systems that frequently need to reacquire the signal lock.
- When DT = 100%, it is even more evident that the tracking of a fp higher than ffr is the cause of a ratio of positive pulses to negative pulses (evident in the VCO drive signal) that is higher than 1.
A bit stream with this density is fully predictable and cannot carry any information:
in real systems it may occur only during periods of acquisition or when there is no information to transfer.
Jitter Bandwidth in bang-bang CDRs[edit | edit source]
The bang-bang CDRs are made up by most of the 1-1 (bang-bang PD) and practically all of the 2-2 (bang-bang PFD).
These loops are intrinsically non-linear, primarily because of the bang-bang nature of the phase detector.
- The very large (≡ infinite) gain in the detector needs a compensation by a signal level limitation is another loop point.
- (The level limitation keeps signal levels within the physical capability of the circuit elements).
- The level limitation takes place either:
- 1. in the limitation of the VCO drive signal made by the circuits driving the VCO, or
- 2. in the extremes of the VCO voltage-to-frequency characteristic.
- It is a frequency limitation.
- Whatever the case, the limitation takes the aspect of a slew-rate limitation of the CDR output phase.
- The VCO characteristic, at both ends, depends very much (and often unpredictably) on manufacturing and environmental variations.
- Therefore, the frequency range is always deliberately clamped by the output range of the VCO drive stage.
Overall, two non-linearities (PD or PFD, and VCO frequency constraints) combine making transfer (e.g. jitter transfer) functions become families of functions.
Each function in a family is associated with a specific input waveform.
In the (transfer functions') case of sinusoidal inputs, this means dependent only on the input amplitude.
The output is also periodic, and the magnitude of the ratio of output/ input peak amplitudes is the quantity taken into consideration.
Vbb = the absolute value of the voltage step that takes place in these CDRs, at the input of the VCO, when the PD bangs up or down from its intermediate level.
- It can be calculated as GφGf. In fact, the PD output is either +Gφ or -Gφ (or 0 in the case of a ternary PD).
- In 1 -1 loops +/- Vbb is the total drive range of the VCO. Ed is obtained by deviation of duty cycle in drive the waveform.
- In 2 - 2 loops +/- Vbb is much smaller than the drive range of the VCO (e.g. 10-3).
- The VCO drive waveform shows a tiny bang-bang ripple added to a slower and much larger waveform, that is made by the filter amplification of low jitter frequency components.
- Ed is obtained by a variation of the mid level of the bang-bang ripple in the drive waveform.
Jitter cut-off frequency in bang-bang CDRs of 1st order and type 1[edit | edit source]
This is a type 1 system, which implies that the input and output phase waveforms, during tracking, differ in their mean values.
- The difference of mean values is the steady state sampling error Es = = [rad].
This is also a 1st order system, which means that the signal processing between PD and VCO consists of a flat amplification only.
A frequency clamping takes place at the two ends of the VCO characteristic practicable for use and is responsible for the CDR slewing.
- Either the clipping of the drive signal +/- Vbb, or the intrinsic VCO saturations can generate the slewing.
- In many cases the CDR is designed so that it is the clamp of the VCO drive signal that forces the slewing. The VCO characteristic is often wider but much less predictable.
The slew-rate limiting occurs when the VCO frequency can not track the input jitter frequency.
In a 1st order type 1 loop this only occurs when the VCO reaches one or both the extremes of its frequency range, set by the clamping action of its VCO drive stage. Such clamping is fixed, independent of the signal (= jitter) frequency.
- If fp ≠ ffr the maximum frequency swing that is possible in one direction is reduced and the swing in the other is increased by the same amount.
- The slew-rate in the corresponding direction is less steep than the slew-rate in the other, or it may even be not present at all.
This unbalance is evident the figure that follows (already shown in the jitter tolerance page).

The CDR is slew rate limited, and the asymmetry of the slew-rates originates from the inaccuracy of the VCO free-running frequency.
The initial acquisition phase is deliberately made short and simple to focus on the tracking phase.
As long as the product Ajωj is small ( small jitter amplitudes, small jitter frequencies, or both), there is no slewing.
The output of the CDR tracks the input, both waveforms are sinusoidal, and their ratio is a constant 1 (= 0 dB), independent of the jitter amplitude.
- All jitter transfer functions in the family overlap in the low frequency region over a flat curve of unity gain.
At jitter frequencies high enough, the output is in slewing all the time (DT is assumed to be 100% for the time being, but can be taken into account as an attenuation of Gφ (→ GφDT)).

The average of the output triangular wave is about -0.5 rad, a sampling error Es that compensates for the VCO in-accuracy.
- Even if the triangular shape is dissymmetric in the period, the waveform peak-to-peak is the same of a symmetric triangular wave with both slopes equal to average of the two asymmetrical slopes.
- The average of the two slopes is Vbb GVCO.
- The peak amplitude of the triangular output phase can be computed (neglecting the d.c. offset) as the voltage that the average slope covers in one quarter of the jitter period Tj (= π / 2ωj) :
The jitter transfer (magnitude) can be defined as the ratio of the peak amplitude of the triangular output to the peak amplitude of the sinusoidal input jitter Aj sin(ωj t.[3]
As long as the output is triangular:
In a Bode plot with ωj as independent variable (= in the plot of the family of jitter transfer curves) this is a family of lines with slope of - 20 dB/dec that intersect the 0 dB horizontal axis in :
The common horizontal asymptote towards low ωj and the different high frequency branches show rounded transitions very similar to plots of single pole functions.[3]
This model can be used with good approximation, and its cut-off frequency shall be the ωj of the formula above:
It should be emphasized that a loop of 1st order and type 1, in particular with a bang-bang PD, is practically never used to implement a filtering of input jitter.
The requirement of fast acquisition is implemented with large values of the bang-bang step (i.e. Vbb or fbb = VbbGVCO), and large tracking jitter is added anyway.
A tiny Vbb should instead be used, but this would:
- compromise the fast acquisition and
- require a good VCO accuracy (incompatible with the low cost applications that this architecture targets), or
- require that the PLL centers the VCO to fp (only possible with a 2 - 2 architecture).
In fact, if actual simulations or measurement of a jitter transfer characteristic were made, the results (points in the Fjitter, ωj plane) would loosely cluster around the theoretical curve, because the tracking jitter would make them not very precise.
In conclusion, this section and the preceding one are useful to understand the loop operation as it is implemented in practice. The two sections are not useful to understand design considerations nor to interpret measurement results: the 1- 1 loop is not meant for input jitter filtering.
This theory will be shown to be of practical use when describing the Applications of the 2nd order type 2 architecture.
External References[edit | edit source]
- ↑ Dieter Verhulst, Xin Yin, Johan Bauwelinck, Peter Ossieur, Xing-Zhi Qiu and Jan Vandewege (the INTEC team of Ghent University), “A robust phase detector for 1.25Gbit/s burst mode data recovery”, IEICE Electronic Express, Vol. 1, No. 18, pp.562-567, (2004). http://www.jstage.jst.go.jp/article/elex/1/18/1_562/_article
- ↑ Richard C. Walker (2003). "Designing Bang-Bang PLLs for Clock and Data Recovery in Serial Data Transmission Systems" (PDF). pp. 34-45, a chapter appearing in "Phase-Locking in High-Performance Systems - From Devices to Architectures", edited by Behzad Razavi, IEEE Press, 2003, ISBN 0-471-44727-7, IV. SLOPE OVERLOAD, B. Expression for Slope Overload, page 7.
- ↑ a b Jri Lee, Kenneth S. Kundert, Behzad Razavi "Modeling of Jitter in Bang-Bang Clock and Data Recovery Circuits", CICC>, Sep. 2003. Retrieved 2014-12-23.






