General Astronomy/Print version
| This is the print version of General_Astronomy You won't see this message or any elements not part of the book's content when you print or preview this page. |
Table of Contents
- The Modern View of the Cosmos
- Observational Astronomy
- Motion and Gravity
- Principles of Light
- Telescopes
- Planetary science
- Earth as a Planet
- Space Exploration
- Astrobiology and Extraterrestrial Life
- The Sun
- Stars
- The Stellar Life Cycle
- Black Holes
- Galaxies
- Gamma-Ray Bursts and Cosmic Rays
- Cosmology
The Modern View of the Cosmos
| General Astronomy | ||
| Print version | Observational Astronomy | |
The Big Picture
The universe is a big place — too big for us to comprehend. But how big? Astronomers have struggled with this question for millennia, and their view of the known universe has steadily grown to immense and incomprehensible sizes. It’s an important question, and a basic part of our grasp of the universe itself. To study astronomy, it’s essential to understand what’s out there, how everything relates, and where we fit in the universe. The problem is that the size scales, the relative general sizes of classes of objects, are too foreign for things much larger than Earth. In a big universe, this can be a challenge. To tackle the problem, let's try to connect the familiar life-size world around us with the unfamiliar cosmic size scales.

If you're a student, you probably watch your instructor write on the chalkboard almost every day. The chalkboard is something you're much more familiar with than the whole universe because you can see it and touch it. You know the size of the board, the chalk, the markings, the eraser, and so on because they’re right at hand. How much bigger is the board than a dot made on the board with a piece of chalk? It turns out that the answer is about a thousand, for an average sized chalkboard, and a fair sized chalk dot.
Now let's consider something that's a thousand times the size of a blackboard. A blackboard is a few meters across, so we want to think about something a few kilometers across. That's something like the size of a small city. If a city is 1000 times larger than a chalkboard and a chalkboard is 1000 times larger than the mark on a chalkboard, that's a useful connection that helps us think about the size of a city: we can say that the chalkboard in the city is like the mark on the chalkboard.
In this way we will now step out from the city into the larger universe. With each step, we will consider something (very roughly) a thousand times larger than the last step. As we move out, each stop in our journey will be much smaller than the next, like a mark on a chalkboard.
A city is much larger than the blackboard we used as a reference point, but it's still something we are very familiar with. Many people drive across part of their home city and back again every day. It's possible to drive through most small cities in a half hour or so, even with stoplights, and it only takes a few hours to walk from one end to the other. As promised, the next step out will be much larger and farther from our everyday experience. Our next stop will have a size of several thousand kilometers, and that's the size of Earth.
In a car, you can drive across a city in less than an hour, even at a slow speed. If you could drive around the Earth at a speed of 60 miles per hour (100 kilometers per hour), going day and night over land and water, it would take a full 17 days. Remember, driving through a small city at 60 miles per hour would only take a few minutes. Seventeen days is much, much longer than a few minutes. The fastest jets, which have a top speed of about 2,000 miles (3,200 km) per hour, can make the trip around the world much faster. At that speed, you could circle the Earth in 11 hours. Even speeds like that will quickly become inadequate as we continue moving out into the universe.
The size of Earth is typical of the sizes of the rocky planets, the terrestrial planets, but planets made mostly of gas such as Jupiter and Saturn are larger by a factor of several to ten. In general, we can expect the same kinds of things to have similar properties. Given no other information about a planet, we might guess its radius to be the same as Earth's. If we knew that our imaginary planet were a much larger gas giant, we might change our estimate and guess that the planet has the same radius as say, Saturn.
This size scale represents the vast majority of human experience. Only a small number of people have ever been in Earth orbit, and these people remained very close to Earth. Most of the satellites launched remain very close to Earth. The shuttle, for example, orbits at an altitude of only a few hundred kilometers — a few percent of the radius of Earth. Some spacecraft are sent to other planets or to the Moon, but the majority stay at the scale of this step in our journey. Only 24 people — the Apollo astronauts — have ever left Earth's orbit to visit the next stop on our journey.

As we continue to move out, we reach a size of about 1000 times the distance around the Earth. The distance to the Moon is about 30 times the diameter of Earth, so the Moon is easily within reach in this step, but there's little else in the remaining distance. The nearest planets, Mars and Venus, are out of our reach. Aside from the Earth and Moon, we find the space in the neighborhood of Earth to be almost completely empty, with only the occasional passage of an asteroid or comet.
Although the Moon seems nearby when we consider the huge space surrounding the Earth-Moon system, we should remember that the Earth and Moon are really very far apart. If we could get in a car and drive to the Moon, the trip would take five months of driving nonstop — 24 hours a day and seven days a week. If our jet could go to the Moon, it would take five days to get there. These trips are becoming longer now, but they're still manageable. The trip by foot is much longer, though — a walk to the Moon would take nine years! Light travels faster than anything else in the universe. It has a speed of 300,000 kilometers (186,000 miles) per second. At this speed, light can travel to the Moon in just over one second. This distance, the distance light travels in one second, is called a light-second.

Another step out will extend our reach to most of the planets. We now encompass the bulk of the Solar System, the system comprising the Sun and all of the objects orbiting around it. This size scale is about five billion kilometers across, 30 times the distance between the Earth and the Sun. The distance from the Earth to the Sun is a convenient standard for measurement in the Solar System, so astronomers use the average Earth-Sun distance as a standard unit called the astronomical unit (AU). One astronomical unit is equal to about 93 million miles or 150 million kilometers. We can say that we are now working at a size scale of 30 astronomical units, or 30 AU for short. A box this size centered on the Earth would comfortably fit Saturn's orbit, but Uranus, Neptune and Pluto are still too far away. For much of human history, none of the Solar System objects outside of this box were known to exist.
Remember that our size scale has increased from the last step by a huge factor, a factor of 1000. Using our jet to take a trip from Earth to Saturn would take about fifty years. Light takes about 80 minutes to travel from Saturn to Earth, depending on where Earth and Saturn are in their orbits. Because it takes so long for light to make the trip from Saturn, the light we see from the planet at a given moment actually left 80 minutes ago. This means that we don't see Saturn as it is presently, but as it was 80 minutes ago. This also means that looking out into space is like looking back in time. The farther we look, the older the light. This is not very important for Saturn, but it will become more important as the size scale increases.
As before, we can use the speed of light as a measure of distance. A light-second is the distance light travels in one second. Likewise, a light-minute is the distance light travels in one minute. That means that Saturn is 80 light-minutes away. In the same way, we could write that Saturn is 1.3 light-hours away, and that's about the same as Saturn's distance from the Sun. Saturn's orbit is much bigger than Earth's orbit, which is only 8 light-minutes in radius. This is a striking and important fact about the Solar System — the rocky planets, the terrestrial planets, orbit close to the Sun and close to each other, but the giant gas planets, the Jovian planets, orbit at greater distances and have more widely spaced orbits.
The next step in our journey will encompass a distance of 30,000 AU, or half a light-year. Although this step completely encloses the planets, Solar System objects are found at much greater distances. These objects form the Oort cloud — a vast, sparse region of comets surrounding the Sun. The Oort cloud is almost empty, but it's there just the same. At this step we've only covered a piece of the range of influence of the Sun, and plenty of Oort cloud remains out of our reach. The Oort cloud is thought to extend out from the Sun as much as two light-years.
If we look just beyond this step, we find the nearest star, Proxima Centauri, at about four light-years. It will take Voyager 1 and 2 80,000 years to reach this star. (These ships, launched in 1977, have a speed of 51,500 km/hour.) As other stars enter into the picture, the Sun will no longer be the dominant source of gravity. This means that we can expect the solar system to really end as we begin approaching other stars.
Our next step out places us in a 500 light-year box. This size scale is easily large enough to fit the Sun, Alpha Centauri, and many other stars. In fact, about 250,000 stars are within 500 light-years of Earth. Astronomers refer to this region as the Solar Neighborhood. As we've seen, the stars in the Milky Way are very far apart, with vast stretches of mostly empty space separating them.
Stars in the Solar Neighborhood (and throughout space) are mostly small and faint. If these fainter stars were much farther away, they would be too faint to see from Earth. Much brighter stars are more rare, but they can be seen from much farther away. Because of this, two "kinds" of stars fill the sky as viewed from Earth: stars that are intrinsically faint but nearby, and stars that are bright and more distant.

As we continue outward in our journey, we see the random scattering of stars form into a pattern. Spiral structure emerges, and we see that the Earth, the Solar System, and nearby stars are collected together into an orderly system of stars called a galaxy. Our galaxy is called the Milky Way Galaxy.
Like the Solar System, the Galaxy is shaped like a flat disk, but the Galaxy is much bigger. Our galaxy contains hundreds of billions of stars, and the Solar System is only one member contained inside. The Sun is located in the spiral arms of the galaxy about two thirds of the way from the center, and it orbits around the center of the galaxy with all the other stars. If the Milky Way were fifty miles long, the Solar System would only be a dot the size of the tip of a ball point pen. In actuality, the Galaxy is 100,000 light-years across, but only a few thousand light-years thick.
As we start out towards the next step, we see other galaxies like the Milky Way begin to appear. Compared to stars in the Milky Way, galaxies are packed together much more closely, and collisions between galaxies are much more common. The Andromeda Galaxy, the nearest galaxy to the Milky Way, is 2.5 million light-years away and on a collision course for Earth. Don't panic, though, as the collision won't happen for another 3 billion years.
At a size scale not much larger than our last, we see that the galaxies are clumped together. These galaxy clusters typically have hundreds of galaxies and are millions of light years across. Galaxies orbit around the center of their clusters. The Milky Way is a member of the Virgo Cluster. It orbits near the edge of the Cluster, so we can see much of its center in a small region of the sky in the direction of the constellation Virgo. Presently, the Milky Way is moving away from the center of the Virgo Cluster. In the distant future, however, the Cluster's pull will slow the Milky Way and draw it inward.
Although our reach now includes many more objects, the size scale of galaxy clusters still does not represent an expansion over the last size scale by a factor of 1000. We have not fully reached the next step in our journey until we come to the scale of hundreds of millions of light years. At this scale, even the galaxy clusters form clusters. These groups of galaxy clusters are called superclusters. A supercluster may contain hundreds of thousands of galaxies. The Virgo Cluster is a member of a supercluster called the Virgo Supercluster.
Light from the edge of our 500 million light-year reach has traveled for 500 million years before reaching us. This means that we see the Virgo Supercluster as it was 500 million years ago. Five hundred million years can be a long time, but it isn't really long enough for the universe to have changed significantly. Even though the light is old, the universe at the edge of the Virgo Supercluster still looks much like the universe nearby.

As we continue out from the 500 million light-year size scale, we see older and older parts of the universe. As the distance becomes very large, we begin seeing billions of years into the past, and big changes in the Universe as a whole become important. Going further and further back, we see the formation of the first galaxy clusters, galaxies, and stars. Eventually, we see the universe so young that no stars have formed yet. Before the first stars formed, the Universe was cool and dense enough for the loose, unused gas in space to block visible light. Beyond this, we can't see any further. The contents inside this wall are called the Hubble volume, or the Observable Universe. There's no way to observe objects outside of this volume because the light from these distant objects hasn't reached us yet.
The Universe extends out infinitely, but our view is limited to the Hubble volume. Trying to visit the edge of the Hubble volume is impossible. You'll never reach it because it's only an illusion. If you tried to visit the location where we see the edge of the Hubble volume, you would see the universe around you as it is today, not billions of years ago, and you would see the edge of the Hubble volume all around you, billions of light years away.
Extending out further inevitably delves into the pages of theory and crosses the line dividing what we have seen and what we cannot see. Some have theorised that the universe itself does not comprise all of existence, and that there may be other universes with different physical laws existing together in clusters and groups in a multiverse.
As we go further and further out, many note that there must be an edge, an end, a border of reality. Others have speculated that the universe, or the multiverse it sits in, is simply infinite, and has no such boundaries. However, at this point in time, there can be no absolution, no definite answer to these questions.
Much remains unknown about what the Universe is like, but our picture has evolved dramatically since humanity first began asking questions about the world around it. Armed with curiosity and the tools of science, astronomers have investigated the heavens for centuries, and their work continues today.
Short History of the Universe
For time immemorial, humans have been intrigued by creation. Where did we, and the universe in which we live, come from? In the Rig Veda, it was proposed that before creation there was "neither existence nor non-existence." The Latin phrase ex nihilo nihil fit ("out of nothing comes nothing") sums up current human beliefs about origins.
The Qur'an contains the following verse regarding the origin of the universe: “Do not the Unbelievers see that the heavens and the earth were joined together (as one unit of Creation), before We clove them asunder?” [Al-Qu’ran 21:30]
Many possibilities have been considered by scientists over the millennia. Did the universe "happen" suddenly?… was it created quickly by God?… has it existed forever?… or is it in a constant state of creation, even now?
Just as we can use size scales to make rough comparisons of the sizes of objects in the universe, we can also use time scales to compare the periods of time over which events occur. For example, Comet Halley takes about 75 years to complete its orbit around the Sun, so we can say that the period of Comet Halley's orbit has about the same time scale as a human lifespan.

The Origin of the Universe according to the Big Bang Theory
The universe is big in space, but it's also big in time. The age of the universe appears to be 13.7 billion years. Like huge space scales, a span of 14 billion years is hard to imagine for a person who will have a much shorter lifespan than that. To better understand very long time scales, we can "compress" long periods of time like the age of the universe into shorter periods such as a human lifetime.
A typical person will live around 80 years. That means that the Earth will go around the Sun eighty times over the course of an average lifetime. The human life time scale and the time scale of human history are far smaller than the time scale of changes in the universe. Astronomers have learned about how the universe as a whole came to be the way it is by studying only an instant of its existence. To get a clearer picture of how the cosmological time scales fit together, let's consider an imaginary astronomer whose life is "stretched out" to fill the entire history of the universe.
If a human lifetime were vastly longer than it is, the orbit of the Earth around the Sun might be too fast to be a useful way to measure age. Instead, it might be more practical measure time from something slower. The Sun takes 230 million years to complete an orbit around the Milky Way Galaxy. That means that a "Milky Way year" will be 230 million times longer than an ordinary year.
Let's suppose our old astronomer has a lifespan of 80 "Milky Way years" instead of 80 normal years. That way, the astronomer will live long enough to see events that happen on cosmological time scales rather than human time scales. The astronomer's life happens in extremely slow motion. His growth and his actions are slowed by a factor of 230 million. At this rate, it takes four normal months for the astronomer just to blink.

Astronomers have theorized that the universe was very small, hot, and dense when it began. Since then, it has expanded and cooled. At first, the universe contained almost entirely hydrogen and helium gas. The universe was very uniform, with no galaxies, stars or planets. We'll place our protagonist's birth at the time of the big bang.
Our astronomer was much too young to remember the early development of the universe after the big bang. By the time the astronomer was only two days old, atoms had formed in the universe and the universe had cooled enough for structure to begin forming in the gas that uniformly filled all of space. Remember, the imaginary long-lived astronomer measures time much more slowly — what the astronomer sees as two days amount to a million years of time on a normal clock. While a million years seems like an extremely long time, that's only a tiny part of the history of the universe.
Our astronomer's earliest memories of childhood will include the first formation of stars and galaxies, which began to occur when the astronomer was around five "Milky Way years" old. Galaxies would continue forming and developing well into the astronomer's teenage years, when the universe was billions of years old. Today, galaxies continue to evolve and change.
There are two schools of thought on how the Universe formed: "top down" and "bottom up". Top down theorists think that large clusters formed after the Big Bang, which later broke down into stars and galaxies. "Bottom up" theorists instead pose the theory that matter was originally dispersed fairly evenly by the Big Bang, later accumulating into stars and galaxies. Recent data from Hubble Deep Field photographs appear to support "bottom up" theories. The photos show young galaxies from up to 11 billion light-years away. These young, small galaxies, from early in the universe's history, support the theory that large structures formed out of smaller ones. The galaxies appear as faint blue blobs with vague spiral structures, 2000 to 3000 light-years across.
An important necessity for the appearance of life is heavy elements. Since only hydrogen and Helium gas were formed during the big bang, everything heavier than that had to be made in stars later. These other elements — all of the elements on the periodic table — were made in stars.
Stars use light elements like Hydrogen and Helium as their fuel. Like nuclear bombs, they use the power of the atom for energy. Stars are unlike nuclear bombs, however, in that most nuclear bombs get their energy from heavy atoms like Plutonium and Uranium. In a nuclear bomb, the energy comes from converting heavy elements into lighter elements. This process is called fission. In a star, the energy comes from converting the light elements into heavier elements. This process is called fusion. All of the material in the universe heavier than Hydrogen and Helium were made by fusion in a star.
An ordinary star can make many of the elements, especially the most important ones for life. It can't make all of the elements, though; it can't make anything heavier than Iron. The heavier elements were made in supernovae. A supernova occurs when a massive star reaches the end of its life. Supernovae are extremely bright and extremely hot. This is where the heaviest elements in the universe are made.
All of the material needed to make rocky planets was made in stars, and some of it was made in supernovae. This means that planets couldn't exist until there had been enough time for a star to completely go through its life cycle and become a supernova. The material would then be ejected back into space, and would form a new star, possibly with planets. It also means that everything in the world, including you, came from a star. As the astronomer Carl Sagan said, "We are star stuff."

The Sun and the Earth formed about four and a half billion years ago, when our long-lived astronomer was 37 "Milky Way years" old. A solar system forms relatively quickly, and ours probably only took about 100 million years. The Sun and the planets formed from a cloud of sparse gas in the Milky Way, which condensed down and coalesced. After this happened, the Earth was very hot. It was a completely molten ball of rock, and had melted so thoroughly that its consistency was similar to water. Certainly, no life could have existed on the very young Earth.
Soon, however, the conditions on Earth became suitable for life. For our carbon-based type of life to develop, a planet needs to have
- organic matter (the material from which DNA is made),
- liquid water,
- a source of energy, and
- appropriate temperatures.
Earth had all of these fairly early in its history. Scientists aren't sure when life first appeared on Earth, but some evidence dates the earliest life at three and a half billion years ago, when our astronomer was 47 "Milky Way years" old.
Evidence suggests that life appeared almost immediately once the necessary conditions were satisfied on the young Earth, but the first inhabitants of the new planet showed no strong predisposition for evolution to more advanced life forms. More than two billion years passed before primitive, single celled microbial organisms advanced to become multicellular life. Once it did, however, advanced life took rapid hold. This period of rapid development in the complexity of life is called the Cambrian Explosion.
The Cambrian Explosion occurred when our astronomer was 56 "Milky Way years" old. Ten years had passed on our slowed cosmological clock. This period of history was, in some sense, the most profound step in the development of intelligence on Earth.

Since the Cambrian Explosion, things have become very interesting on Earth. The astronomer was barely a year older by the time the primitive multicellular creatures had developed to become the dinosaurs, which were unimaginably more complex and advanced by comparison. We have now come into recent times, as the appearance of the dinosaurs occurred only twelve months before this instant in our astronomer's life.
We can see now that we must occupy a tiny, tiny part of the cosmic timeline. By what standard could the time of the dinosaurs possibly be considered recent? By a cosmological standard. The dinosaurs had a short stay on Earth. They disappeared 65 million years ago, or four months ago by the astronomer's clock. This gave mammals the chance to rise to dominance.
The first humans appeared on Earth only eight hours ago by our astronomer's clock. Civilization accounts for only a small fraction of this time. The first system of writing, and the first evidence of civilization, dates to only 6000 years ago, or fifteen minutes ago by our astronomer's clock. In the lifetime of the universe, all of culture and all of written history could fit into a coffee break!
Periods more similar to the human life span become even smaller in our comparison with the cosmic timescale. It was only very recently that people first endeavored to learn about the world using science in the way we understand it today. These first scientists, who considered observation and experimentation to give the last word on the nature of the universe, lived only about four hundred years ago, or one minute ago on our cosmic clock.
As we come progressively closer to the present, our lives seem progressively more ephemeral and fleeting. How long will our society, our culture, and our ideas endure in the long run? Only time will tell. At the current rate, it does not appear to be long before something must happen to stop the downgrade of society.
We can say little about what might happen on Earth in the next thousand years, let alone the next million years or the next billion years. Meanwhile, the Milky Way will continue on its normal course, a course which happens to be headed straight for a collision with the nearest neighboring galaxy in about 12 "Milky Way years." This is unlikely to be the disaster for Earth it might appear to be — a collision between any stars during a galactic merger is actually extremely improbable. The Solar System will simply take up residence in the new galaxy created in the aftermath of the collision.
Five billion years from now, the Sun will have used up its fuel and will die. At this point, about 20 billion years after the big bang, the long-lived astronomer will be 80 years old. The Earth will no longer be able to support life after the Sun dies, and the Solar System will become rather desolate. The universe as a whole will continue long after the death of both the Sun and our astronomer, but it too will slowly die, eventually becoming cold and empty as it continues to expand.
Looking back over the scales of the universe and seeing humanity's role, unimaginably small in both space and time, one might wonder whether science has painted a bleak, depressing, and hopeless picture for humanity. Some would say so, while others find comfort in the majesty and grandeur of the universe, and the possibilities that the future might bring. For now, the future of humanity in this universe, as chaotic and vast as it is, remains uncertain.
| Event | Real time scale | Compressed time scale' |
|---|---|---|
| Formation of structure begins | 1 million years after big bang | 2 days |
| Earliest stars and galaxies form | 2 billion years after big bang | 6 years |
| Sun and Earth form | 9 billion years after big bang | 37 years |
| First evidence of life on Earth | 10 billion years after big bang | 47 years |
| Advanced life forms on Earth | 500 million years ago | 57 years |
| First dinosaurs | 230 million years ago | 58 years |
| Dinosaurs become extinct | 65 million years ago | 4 months ago |
| Humans appear | 200,000 years ago | 8 hours ago |
| Writing is developed | 6000 years ago | 15 minutes ago |
| Modern scientific thought | 400 years ago | one minute ago |
| Present day | 13.7 billion years after big bang | 59 years |
| Human lifetime | 80 years | ten seconds |
| Milky Way collides with Andromeda | 17 billion years after big bang | 71 years |
| The Sun dies | 20 billion years after big bang | 80 years |
Scientific Notation
In previous sections, we discussed some numbers that were very large. In astronomy, the appearance of such huge numbers is common. This is one reason astronomers and other scientists use scientific notation when working with very large or very small numbers. Scientific notation is a system for writing and working with numbers that makes it much easier to deal with numbers that are very small or very large.

For example, the Milky Way Galaxy contains roughly three duodecillion tons of material. That is a rather cumbersome number. (Astronomers would never actually write this. Instead, they would say that the Milky Way contains one trillion times the mass of the Sun, which is somewhat easier. We'll use this much larger number for our demonstration.) You could also write this number as
- 3 000 000 000 000 000 000 000 000 000 000 000 000 000 tons,
but that's even worse. Scientific notation makes the number much more compact and readable:
- 3 × 1039 tons.
This number is verbally expressed as "three times ten to the 39 power tons." This is numerically equivalent to the first two expressions.

A number written correctly in scientific notation has two parts. The first is a number greater than or equal to 1 and less than 10 (but it can be either positive or negative). This is sometimes called the mantissa. The second part is the number ten raised to a whole number power. The exponent of the second number is called the power. Some examples of numbers written correctly in scientific notation are:
- 2 × 1018
- -1.4 × 102
- 7.656 × 10-4
- 2.1 × 100
These, on the other hand, are not valid examples of numbers written in scientific notation:
- 0.1 × 104 is wrong because the mantissa is less than 1
- 12 × 103 is wrong because the mantissa is not less than 10
- 8.4 × 102.2 is wrong because the power is not a whole number
Remember that
- 10n = 10 × 10 × 10 × ... for n times,
which means that ten raised to n power is the same as 10 multiplied by itself n times, which is the same as a 1 with n zeros written after it. For example, 103 is 10 × 10 × 10, or 1000. That means that our earlier number, 3 × 1039 tons, is equivalent to
- 3 000 000 000 000 000 000 000 000 000 000 000 000 000 tons,
which is a three followed by 39 zeros. A number written in scientific notation with a negative power corresponds to a small number. For example, the number 1 × 10−3 is written as 0.001 in conventional notation. In general,
- 10-n = 1/10 × 1/10 × 1/10 × ... for n times.
Since scientific notation relies on powers of ten, it's simple to convert a number from scientific notation to standard notation or vice versa. To convert a large number (with a positive power) from scientific notation to standard notation, first identify the decimal point in the mantissa, then shift the decimal to the right by the number indicated by the power. To convert a number from standard notation to scientific notation, just reverse these steps. Find the decimal point in the number, and move it until the number is at least 1 but less than 10. Count the number of places you moved the decimal point and use that number as the power. If you moved the decimal point to the left, make the power positive. If you moved the decimal point to the right, make the power negative.
Scientific notation also makes it simpler to do multiplication and division. To multiply two numbers in scientific notation, multiply the mantissas and add the powers:
- (3 × 104) × (4 × 10-2)
- (3 × 4) × 104 - 2
- 12 × 102
- 1.2 × 103
In some cases, such as the one shown here, you may need to shift the decimal point again ensure that the number is in correct scientific notation. It should never be necessary to shift the decimal point by more than one digit. When dividing numbers in scientific notation, divide the mantissas and subtract the powers:
- 0.75 × 106
- 7.5 × 105
Here also, it may be necessary to shift the decimal point and change the exponent.
Scientific notation makes it easy to compare numbers that have very different values because all the zeroes have been replaced with the much more readable exponent. Numbers with a greater exponent are always bigger than numbers with a lesser exponent.
If one of the exponents is bigger than the other by more than a couple, the difference between the two is clearly very big. Recognizing a huge difference between two numbers can sometimes be a very useful insight, so it often makes sense to take a moment to develop an intuitive feel for a math problem before attacking it. In some cases, it's useful to see roughly by how much one number is larger than another. Scientific notation makes this much simpler. For a rough estimate, you only need to find the difference in the exponents. For example, 107 is greater than 103, since 7 - 3 = 4.
- Some tourists in the Chicago Museum of Natural History are marveling at the dinosaur bones. One of them asks the guard, "Can you tell me how old the dinosaur bones are?"
- The guard replies, "They are 73 million, four years, and six months old."
- "That's an awfully exact number," says the tourist. "How do you know their age so precisely?"
- The guard answers, "Well, the dinosaur bones were seventy three million years old when I started working here, and that was four and a half years ago."
- (From the Science Jokes Web page [1])
In science, measurements are never perfect and numbers are never exact. As a result, every measurement we make has some uncertainty associated with it. Scientific notation makes it easy to express how precisely a number is known. Suppose a paleontologist discovers ancient dinosaur bones and finds that they are 73 million years old. Of course, the paleontologist doesn't know exactly how old they are. Maybe they're 73,124,987 years old, but the paleontologist only knows the age within 1 million years, so the age is written as 73,000,000 years, or 7.3 × 107 years. Either of these expressions imply that the bones aren't exactly 73 million years old, but are 73 million years old, give or take a million years.
But what if the paleontologist knows the age within 200,000 years, and is sure that the bones aren't, say, 73.4 million years old? In that case, the standard notation is ambiguous — the number is still written as 73,000,000 years. In scientific notation, we can write the number as 7.30 × 107 years. If we write this, we mean that the third digit is significant. The paleontologist might have calculated that the bones are 72,954,332 years old, but it would be useless to report these numbers, since the error on this measurement was 200,000 years. The extra digits are insignificant. The number of significant figures in a number are a reflection of the precision expressed in the number. In this case, the number of significant figures is three. The first significant figure is 7, the second is 3, and the third is 0.
Scientific notation gives the trailing digits written after the decimal point of a number special meaning — they tell that the number is exactly 7.30 × 107 years. This is unlike the usual use of numbers in mathematics, where trailing zeroes after the decimal point have no special meaning.
In the story about the museum guard, the guard hadn't thought about the precision of the age of the bones. It doesn't make sense to add the four years to 73 million years because the uncertainty in the age quoted to the guard was a lot more than 4 years. When working with numbers that have uncertainties, we must be sure not to express better precision in the results of our arithmetic than we had in the first place.
When doing arithmetic, numbers being added or subtracted are treated differently from numbers being multiplied or divided.
- When multiplying or dividing numbers with uncertainties, make sure that the answer has as many significant figures as the least precise of the original numbers.
For example, in (2.3 × 103) × (1.21 × 102), the number 2.3 × 103 has two significant figures and the number 1.21 × 102 has three significant figures. The result should have two significant figures: 2.8 × 105. We assume that there was some uncertainty in the measurement that gave us 2.3 × 103, and this leads to some uncertainty in the result of the computation.
Addition and subtraction work differently. When adding 23.14 and 2.2, for example, the number 2.2 has uncertainty beginning in the tenths place. This uncertainty makes it pointless to report the hundredths place in the sum. To see this, try adding some uncertainty to 2.2 and see how this affects the sum.
- When adding or subtracting numbers with uncertainties, round the result to the last significant place of the original number with the greatest uncertainty.
For example, 2.3 × 103 + 1.1 × 102 can be written as
2300 + 110 2410
But we don't know the real value of the tens place in 2.3 × 103, so we really only know the answer to the hundreds place. We should write
2300 + 110 2400
or 2.3 × 103 + 1.1 × 102 = 2.4 × 103. This may seem incorrect, but we're really only rounding off. Since we don't know the result to better than two significant figures, it makes no sense to report the extra digits — that would be like the museum guard who tells visitors that the dinosaur bones are 73 million and four years, six months old.
Almost every number has a unit of measurement attached to it. The number we used as our first example carried units of tons, and we expressed the age of the dinosaur bones in years. The units a number carries are part of the number itself. Units can also be multiplied or divided just like numbers.
As an example, consider a simple equation:
- distance = velocity × time.
Suppose you drive in a car with a speed of 100 kilometers per hour (60 miles per hour) and you go in a straight line for one hour. The distance you will travel is
or 60 miles. We have cancelled hours as though it were a number.
This trick is also useful when you need to convert units. If you have a result in one system and you'd like to convert to another, you can set up a ratio, such as 1,000 meters/1 kilometer. Since 1,000 meters is equal to 1 kilometer, the ratio 1,000 meters/1 kilometer equals one. Because of this, multiplying any number by 1,000 meters / 1 kilometer will not change the value of the number. If we want to know what 100 kilometers is in meters, we can write
or 100,000 meters.
Other units of measurement used in astronomy are kilograms (mass), Newtons (force), and Joules (energy).
The Scientific Method
The results of scientific thought have played an important role in shaping the world into what it is today. This is true not only because of the influence technology has had in our lives, but also because of the change science has brought to the way we think. Scientific thinking has permeated all aspects of our lives, fundamentally changing the way we see the world. It is science's "way of thinking," the scientific method, that forms its heart. Although "scientific thought" or "science" is sometimes taken to refer to the entire body of scientific theories and knowledge including chemistry, biology, physics, and so on, the term science strictly only refers to the process by which these theories and ideas are examined.

The scientific method is fundamental to the investigation and acquisition of new knowledge based upon physical evidence. Scientists use observations, hypotheses, and logic to propose explanations for natural phenomena in the form of theories. Predictions from these theories that can be reproducibly tested by experiment are the basis for developing new technology.
Although scientific progress is often described as a linear scheme that allows a single scientist to proceed from a state of relative ignorance to a state of knowledge, the scientific method is really much more complicated than this. The scientific method is not a recipe. It requires intelligence and imagination. Science is not the lifeless execution of step-by-step instructions, but a creative and inspired process. Over the past half-century, philosophers, historians, and sociologists of science have established a more complete model describing the ways science is actually practiced.

The modern description of scientific progress gives much more importance to the role of the scientific community. It is impossible for a single person working in isolation to engage in science. This is because of the central role of peer review as a means of correcting error, bias, and self interest. Human nature prevents even a well intentioned scientist from doing anything other than confirming preconceived ideas when working in isolation. Because science is closely tied to a community, progress is usually scattered, proceeding from many stages and different directions at once.
In a new area of scientific exploration, scientific progress is slow at first. Investigators reach out in search of a basic description of how their area of inquiry works. This inquiry is motivated by observations of some interesting phenomena manifested in reality. The observations and experiments undertaken by scientists in a developing field are typically dictated by the scientists' interests and by convenience. The scientists have no heritage of successful experiments and little common ground. Because of this, new pursuits in science lack direction and are wanting of a broad common ground that will unite scientists and prescribe the course of scientific research.

As the new field advances, an underlying set of principles begins to take hold and gain widespread acceptance. These principles become the common ground of scientists in the new field, the basis of a paradigm. With a paradigm in place, researchers no longer need to start from scratch when interpreting the results of new experiments. Instead, they address a specialized audience that works under a common paradigm, and they describe their work in the context of that paradigm. They are no longer unguided in the direction of the work — the paradigm dictates which experiments might be useful in further exploring the questions of their field. An established paradigm is therefore an extremely valuable asset in the pursuit of science.
In the presence of an established paradigm, the normal course of scientific research begins. Scientists seek to clarify the understanding of their area of research by formulating theories grounded in their paradigm and by making relevant observations that test the theories and further clarify the paradigm. The observations give greater insight into the paradigm and test the agreement of theories and paradigms with reality. The theories discern previously unseen details in the paradigm and in nature, and guide the method of new observations.
For the normal course of scientific progress, these methods are extremely efficient. In some cases, however, a scientific discipline might be founded on a paradigm that is fundamentally incorrect. This presents a problem, since the paradigm underlying a discipline is deeply valued by the practitioners in the discipline. Such was the case in astronomy during the scientific revolution of the Renaissance. From the times of Aristotle, it had been thought that the Earth was at the center of the Universe, with everything else moving around it in circles. Eventually, observations of the positions of the planets made Aristotle's model inconsistent with reality. As time passed, it became increasingly difficult to modify Aristotle's paradigm to agree with observations. The prospect of a new and completely different paradigm became ever more attractive, and the new idea of a Sun-centered universe took root.
It is almost always the case that some observations cannot be explained by existing scientific theories, but a gap between knowledge and theory is hardly sufficient to produce a paradigm shift. In The Structure of Scientific Revolutions, Kuhn claims that scientific revolution is only possible when the dominant paradigm of a field is in a state of crisis. Only once it becomes apparent that the ideas tied to the paradigm are irreconcilable with observations does it begin to appear sensible to pursue completely new explanations.
When scientists consider theories, either as candidates for a new paradigm or as elaboration for an existing paradigm, they evaluate theories on the basis of a number of criteria that have proven over the years to be relevant indicators of usefulness. These criteria were described by the philosopher of science Karl Popper in his book, The Logic of Scientific Discovery.
The central goal of science is to produce theories that are consistent with reality. Science approaches this goal by testing a theory for validity, and discarding or modifying the theory if observations can't be shown to agree with it. The use of an approach like this requires that theories be falsifiable. In order for a theory to be scientific, it must be relevant to observable aspects of reality. It must be possible, at least in principle, to make observations that would be inconsistent with the logic of the theory. Said otherwise, the theory must make non-trivial predictions that can be tested by a set of observations. If scientists find that a theory's predictions are incorrect, the theory is falsified. A central property of scientific theories is that they can never be proven, but they can eventually be disproved. This fact makes it essential that a theory make specific, useful predictions before it can be examined scientifically.

The need for falsifiability implies a need for theories that make clear predictions. Theories that make strong predictions are said to have a high predictive power. A theory with high predictive power makes bold, clear and testable predictions. Theories with high predictive power are more highly valued in science because they are more easily falsified. Scientists consider theories that have not been falsified despite strong predictions to be more reliable, whereas a theory that makes fewer predictions or less bold predictions tends to be received with more skepticism.
The requirement that scientific theories have strong predictive power leads to the surprising notion that an implausible theory should be preferred over a plausible theory. This is because the claims made by the implausible theory are bolder and more subject to being falsified. In order to succeed, a scientific theory must make a prediction that would not be expected otherwise. If a theory makes a seemingly wild claim that turns out to be correct, the theory is very well supported. This mechanism for developing scientific ideas by creating and testing the predictions of a model is the foundation of science.
A final requirement of scientific theories is that they be as simple as possible while still accurately describing nature. This requirement was famously stated by the English logician and Franciscan friar William of Ockham. He stated the requirement, in Latin, as
- Numquam ponenda est pluritas sine necessitate,
which translates roughly as
- Assertions should not be multiplied unnecessarily.
This maxim is widely known as Ockham's Razor. It is a very useful principle, but also one of the most misused doctrines in science.
Ockham's razor warns us that, when two theories make identical predictions, the theory that relies on fewer assumptions is more likely to be correct. The razor is based on the principle that reality is unlikely to conform to our presuppositions. In the absence of evidence, it's often wiser not to speculate.

When creating theories or distinguishing between competing theories, scientists rely on two distinct types of reasoning: inductive reasoning and deductive reasoning.
Inductive reasoning works from the specific to general. It involves making observations and building generalizations on the basis of observations. For instance, you might observe the sunrise every day for a year, and you notice that this Sun rises more or less in the east every time. You might conclude that the Sun always rises in the east. Inductive reasoning involves drawing conclusions from a limited sample of information. You have no way of knowing that the Sun won't rise in the west tomorrow. Still, a pattern will become apparent as observation continues, and year after year of observation makes it compelling to imagine that the Sun must always rise in the east. If the pattern remains very consistent, it can be considered reliable even if the underlying cause isn't obvious. Should a theory ever be presented that predicts that the Sun will always rise in the east, that theory will be well supported. On the other hand, if a theory predicts that the Sun will sometimes rise in the east and sometimes in the west, that theory will be disfavored by the observations even though it isn't disproved in a strict sense. Notice that it is possible, though unlikely, for inductive reasoning to discredit a correct theory or support an incorrect theory. Although it is a powerful and essential tool in science, inductive reasoning must be treated with skepticism when based on a very limited sample of observations.
Deductive reasoning works from the general to the specific. It is based on logical arguments (syllogisms). An example of deductions invented by the author Lewis Carroll is provided below:
- All lions are fierce.
- Some lions do not drink coffee.
- Therefore, some fierce creatures do not drink coffee.
Unlike inductive reasoning, deductive reasoning is perfectly reliable if you have made correct assumptions and applied correct logic. Because deductive reasoning is absolutely reliable when used with good assumptions and proper method, it is easy to place undue trust in claims made on the basis of deductive reasoning. It is important to remember that these claims also require careful examination to check that the assumptions are good and the reasoning is valid. In reality, deductive reasoning is as much subject to error as inductive reasoning. Only the sources of error differ.
What People do in Astronomy
Astronomy like all sciences is a social activity in which people are constantly discussing new ideas, interpreting data, and arguing with each other over what observations mean. Astronomers can broadly be divided into two groups. Observational astronomers specialize in building instruments such as telescopes, and spacecraft, and take raw data and process them into meaningful results. Theoretical astronomers often also known as astrophysicists take the results that observational astronomers provide and attempt to create physical models which explain the data that observers see and provide ideas of the directions that observers should go into. Theoretical astronomers increasingly rely on computer models and often are skilled at programming.
Astronomy is rather unique in that a lot of the data is provided by amateur astronomers. The data needed in some fields such as variable star astronomy or comet discovery can be gathered by instruments well within the budget of an interested hobbyist.

Peer review
A central part of the scientific process is peer review which occurs at several stages in the process, and creates what H.H. Bauer calls a knowledge filter. In the peer review process, a proposal or a journal article is given to a group of referees who anonymously submit their comments on the proposal. While the referees will sometimes communicate with each other, they are not intended to reach a consensus on the quality of work. In addition, the referees usually do not have the final authority to decide on the fate of a proposal, but instead given their opinions to an editor or project director who does have the final authority and on occasion overrides the opinions of the referees.
The opinions of the referees are usually made available to the submitter, and often contain suggestions for improvement to the submitter. This is considered crucial for the scientific process as it allows the submitter to receive feedback on his or her proposal and improve it. In some cases, the submitter is encouraged to resubmit their proposal after making changes, and this often develops into an anonymous communication between the referees and the submitter.
Getting what you need
A lot of the work in astronomy involves getting access to resources, which include:
- money
- for observers, telescope and equipment time
- for theorists, computer time
In order to get these resources, astronomers typically write grant proposals which outline the amount of money, telescope, and computer time needed.
Grant proposals typically undergo peer review by the granting agency which includes feedback on how well it fits the priorities of the funding agency, how likely the committees think it is to advance the frontiers of knowledge, and how essential the resource being allocated is to the researcher. Typically, a set portion of telescope or supercomputer time will be made available to the institution that hosts or funds the resource, giving scientists affiliated with that institution priority use over that resource. The remaining time is then made open for research proposals from researchers from other institutions. In the case of ground based telescope time, the most precious and highly sought after time is dark time during which the moon is new and the dimmest objects can be seen.
In some cases, such as building a new telescope, supercomputer center, or funding a new spacecraft, astronomers must lobby funders such as charitable foundations and legislators for money to finance a certain activity. The lobbying for research facilities can be extremely intense as having a facility sited at your institution gives your institution priority access to the facility, as well as prestige, and makes your institution a destination for researchers.
The life of an observational astronomer
Typically, in an observing run, you wake up at about 3 p.m. During the day the technicians will have installed the instruments that you need for a nights observing run. You go to the telescope at 3 p.m., check to see that everything is installed correctly, since you don't want to wake someone up at 3 a.m. if something breaks, you then spend the next two hours before sunset taking some calibration shots.
After the sun starts setting, your first goal is to find the object that you are trying to photograph. You can punch in the coordinates into the computer, but that will only point the telescope in the general area of the sky that you are interested in. The next thing that you have to do is to take out your star atlas, and look for a pattern of stars that is close to the thing that you are looking for. This is a lot like driving in a strange city when you are looking at the monitor and then trying to match the patterns you see with the patterns on the chart.
So you've now found the object you are looking for. In between these measurements, you take some snapshots of a calibration device. If you are looking at spectra, you take picture of a fluorescent lamp that has lines in certain known positions. If you are measuring brightness, then you need to take some pictures of a star whose brightness is known.
So after a night of all of this, you now have some data on hard disk, and you go to sleep. The next few weeks is where the hard part comes in. You see you have a lot of raw data, but it's not very useful to anyone. The problem is that none of the data has been calibrated. So you spend the next few weeks taking the data, subtracting the black levels, correcting the white levels, stretching and shrinking the picture so that you know what the frequencies of your spectra are. You might also be spending your time doing things like trying to correct for the effects of dust in the galaxy. Through it all, you are probably using an astronomy package called IRAF, which like all big software packages has its cute bugs and idiosyncrasies. At the end of all of this you have a paper, and are ready to publish.
Observational astronomers are often at the mercy of things that are outside of their control. Weeks if not months of effort at setting up an observing run can be destroyed if it happens to be cloudy or raining on the night of the run.
The life of a theorist
Unlike observers, theorists are creatures of the day. The typical theorist spends their days reading papers trying to understand how to model a particular type of phenomenon. Once they have a model, the goal then is to try to get testable predictions from that model, and this often means programming a computer to calculate the consequences of that model. There are occasional flashes of inspiration, but most of the time is spent very slowly and methodically trying to understand the consequences of a model, and to slowly and methodically program the model into a computer and systematically remove the bugs from the model.
There are also a lot of social interactions as theorists argue and debate what a particular observation means, and as theorists and observationalists share ideas about the latest data.
Letting people know about your research
There are a number of channels through which scientific results are made known. The primary means that astronomers use to make others aware of current research are through preprints which are papers uploaded through web servers such as the Los Alamos Preprint Server at http://www.arxiv.org/ or through conference proceedings in which scientists announce their results either through lectures or poster papers. Astronomers are also constantly travelling between departments to give talks on their research at seminars, astronomy lunches, and journal clubs.
Although it has been supplemented by preprints, peer reviewed publication in the primary literature is still considered an essential part of publicizing research. This literature consists of articles in journal such as Astrophysical Journal or Astronomy and Astrophysics. Because of the length of time, typically several months, necessary to go through a peer review, research results are typically shared with the community through preprints before peer review is complete. Nevertheless, astronomers still generally submit their papers to peer review even after the results have been released to the research community, because the interaction between anonymous referees and the paper submitter improves the quality of the work and insures the community that the paper does not have any obvious errors.
Once an astronomy paper is available for publication, it can be accessed through the Astrophysics Data System at http://adswww.harvard.edu/ Increasingly, raw data from sky surveys is being made available on the web.
One shortcoming of the primary literature is that it reports on individual research results without providing context. As such it is difficult for someone who is not actively involved in research in a particular area to understand the relevance of the work. To deal with this problem, primary literature is summarized and combined into the secondary literature, where it will be read by a broader audience of scientists. The secondary literature is a synthesis of the results of recent research in a field. The body of secondary literature includes periodic reviews of progress, such as the Annual Review of Astronomy & Astrophysics, professional books, and other research summaries.
How to be an astronomer
Most astronomers major in either physics or astronomy as an undergraduate and then go to graduate school where they work on the Ph.D. under the supervision of a dissertation advisor. The main challenges in becoming an astronomer are to master the language of mathematics and physics, and to gain experience in working through the scientific process.
After graduate school, an astronomer typically works as a post-doctoral fellow before getting a job either as a professor at a university or a researcher at a laboratory. Because of the large number of graduates gaining Ph.D.'s, people with astronomy degrees are increasingly found outside academia. They work in science related fields, as computer programmers for software companies and even on Wall Street.
Astronomy also is open for amateur astronomers. Most of the data for variable stars is accessible via a telescope which is affordable by hobbyists, and amateurs provide important observational data.
Notes
[2] There are some exceptions to the practice of releasing research results before peer review is complete, and this involves a trade-off between speed and completeness.
When a result is believed likely to be controversial (such as the possible discovery of microfossils on Mars), the researchers may choose to keep the finding secret until peer review is complete so that the result will likely withstand challenges after it is released. Another case where results are kept until peer review is complete involves releasing large datasets such as sky surveys. In this case, the delay introduced by peer review is small in comparison to the benefits of having a through review before announcing the results.
Discussion questions
1) Visit either the Los Alamos preprint site or the Astrophysics Data Service and find a paper. How is the paper structured and what concepts in this text book do you find in the papers?
2) Look at the schedule of several university astronomy departments on the web. What is being discussed? How are different astronomy departments different from each other and how are they the same?
Current Unsolved Mysteries
Dark Matter and Dark Energy
Dark matter is invisible, but has been postulated from its apparent influence on visible matter. It is one explanation for the observed strength of gravity needed to hold galaxies and clusters of galaxies together. Without considerably more mass than can be detected with telescopes, roughly 10 times more, these systems should simply fly apart. The dark matter theory hypothesizes that matter exists that emits little or no radiation and therefore is not observable with telescopes. Dark matter might also be needed to explain the cosmic microwave background (CMB) power spectrum. Some proposals for explaining dark matter are, for example, particles like weakly interacting massive particles (hypothetical WIMPs) or neutrinos, or massive compact halo objects (MACHOS), or ordinary matter that is hidden somehow, or modified gravity (MOND, MOG, f(R)), or some combination of these things.
Another hypothesis, dark energy, has been proposed to explain the surprising observation that the expansion of the universe is getting faster. This acceleration of the expansion was discovered by measuring a certain type of supernova, called type Ia, in surveys of galaxies. Type Ia supernova are used since they all have the same absolute brightness. (We will discuss why they have the same absolute brightness, and how they are used to measure distances, in a later chapter, General Astronomy/The Death of High Mass Stars). This makes them very useful for measuring distances. It had been anticipated, before the measurements were made, that the expansion of the universe would be decelerating, due to the gravity of all the matter. Dark energy is postulated to explain the apparent repulsive force pushing things apart. Ongoing research efforts are to measure the expansion rate more accurately, and discover the nature of dark energy.
Dark matter is generally accepted to exist, though questions remain. It is probably not regular matter made of protons and neutrons (baryonic matter). That is because a higher density of ordinary matter during the nuclear reactions occurring in the first few minutes of the universe (known as big bang nucleosynthesis), would be expected to produce different abundances of light elements and their isotopes, like deuterium, than are actually observed. Another problem for ordinary matter is that the "clumpiness" of the observed galaxies and the cosmic background radiation is not what would be expected from predictions. Other considerations tend to disfavor neutrinos as dark matter as well.
Alternatives to the dark matter hypothesis are new forces or modified gravity theories. There is speculation that there is another large-scale force that is keeping our universe together. [citation needed] Another possible explanation is to think of space as a gas-and-space solid. If you place two objects apart from each other then pressurize the area, the two objects will be forced towards each other. This reverses our current ideas of gravity from an object having a pull on other object, to an object being pushed from all directions. (An object alone has no movement, but two objects create an uneven pressure pushing the objects together.)

An estimated 23% of the matter in the universe is dark matter. Ordinary matter only makes up 4% of the universe. The remaining 73% is an even more mysterious, repulsive "dark vacuum energy".
The most popular theory right now is that the repulsive force is actually a property of space itself: it is caused by waves of energy, created by particles and anti-particles popping into existence and then annihilating each other with no net effect. Early in the universe, when there was not much space, the effect was small compared to gravity. But as the galaxies moved apart, the effect became greater. [2]
History and Ideas of Composition
Dark matter was first proposed in 1933 by Swiss astrophysicist Fritz Zwicky to explain the orbital motions of galaxies in clusters. He observed that there was apparently much more mass in a cluster of galaxies than just the visible objects, like stars, gas, and dust. So there was something unseen adding to the mass of the cluster. Later, when X-ray telescopes became operational, they revealed a cloud of hot hydrogen gas between the galaxies, accounting for part of the missing mass. Beginning in the 1960's, Vera Rubin discovered that contrary to Kepler's law that objects orbiting around a central body move slower the farther away they are, that in fact the orbital speed of stars in galaxies remains roughly the same beyond a certain distance from the galaxy core. So there has to be some extra matter, either in the flat disk of galaxies or in a spherical halo around the galactic core. Building on Zwicky’s work she concluded that this extra mass was dark matter. The term dark matter refers to matter that is perceived to be present because of its effect on the objects around it. While the composition of dark matter is still unknown, scientist have proposed some possible candidates that dark matter could be. They are:
- Ionized gas — Emits thermal free radiation which cannot be observed.
- Dust — Emits radiation and is made up of elements heavier that helium.
- Main Sequence Stars — Could be an ingredient, but could not be sole component of dark matter because a great portion of them would be visible.
- Black Holes — Are highly unlikely because they would disrupt the binary separations of dark matter. However, not much is known about the explosions that produce black holes, so it is still an option.
- White Dwarfs — When forming, white dwarfs produce many intermediate-mass elements (He, N, Ne, C, O) or halo gas, which is not visible.
- Neutrinos — Unlikely, but they do have enough mass to be a candidate.
- WIMPS or Cold Dark Matter — Weak interacting particles, though they do move at nonrelativistic speeds.
A more in-depth flow chart depicting how the above suggestions are connected is picture below taken from Modern Cosmological Observations And Problems (140). http://ned.ipac.caltech.edu/level5/Bothun2/Figures/dm1.gif
Reionization
The cosmic background radiation was formed when protons and electrons combined to form atoms. The trouble is that we know that the matter between galaxies today is ionized (i.e. it's separate protons and electrons) with clumps of hydrogen atoms. We know this because when we look at all but the most distant galaxies, we don't see the spectra lines of hydrogen. So at some point the hydrogen in the universe reionized. The notion was that starlight caused the hydrogen in the universe to reionize, but the latest observations seem to indicate that this reionization occurred before the first stars were there.
Galaxy Formation
The idea is that galaxies started from tiny fluctuations in density that formed after the big bang. By assuming that the universe consists mainly of cold dark matter, you can almost get the clumpiness that you see with the current galaxies. But there are still puzzles. There is an annoying lack of tiny galaxies, and the rotation curve that cold dark matter predicts, isn't quite the one that we see.
Before the Big Bang
Now to get really speculative, there have been some papers written recently that try to figure out what happened before the Big Bang. One of the strange ideas is that the universe is merely one plane in a multidimensional space, and that what happened was that two membranes in a multidimensional space collided causing a massive expansion in three of the dimensions. This is all really speculative, but the weird thing is that it isn't totally disconnected from observation. The idea is that you can use this model to predict the initial expansion of the universe, and this might have some effects on the ripples that you see in the cosmic microwave background. The big problem is that the matter that began expanding had to have always existed, yet, because of the predictable nature of the elements, it had to have had a definite, external force to set it in motion that could decide when to start the "chain reaction". Something cannot just be in a stable form, or even an unstable form, forever and finally explode, it has to go in a cycle. In other words, consider the following. Out of nothing, a theretofore nonexistent dense mass spontaneously emerged, which erupted in an enormously powerful fireball by its own theretofore nonexistent energy to spontaneously and immediately create from this chaos the defined fundamental forces of physics and the subatomic fundamental particles, which eventually organized themselves into a variety of atomic species, then into molecules, and then into a diverse assortment of inorganic matter that gravitationally assembled itself into this highly structured and precisely ordered universe. We all know that this is ridiculous, but it is equally ridiculous to say "a theretofore stable mass spontaneously became unstable".
With all of these puzzles, its not clear what is going to happen next. There is a lot of data coming in, and it may be that with new data, it will be possible to make our models of the universe work with minor tweaks here and there, and we can go on in the mode of what Kuhn calls "normal science." It's also possible that one day there will be some observation which is like Galileo seeing the phases of Venus — some observation that makes absolutely no sense in the current paradigm of things, and this will force people to fundamentally change how they view the universe.
Discussion Questions
1) Find an old astronomy textbook, and compare it with a very recent one. What mysteries in the old astronomy textbook are now believed to be resolved, and what facts and statements in the old astronomy textbook are now believed to be incorrect?
| General Astronomy | ||
| Table of Contents | The Modern View of the Cosmos | Observational Astronomy |
Observational Astronomy
| General Astronomy | ||
| The Modern View of the Cosmos | Print version | Motion and Gravity |
The Celestial Sphere

If you look out from an empty field into a dark sky, you will get the impression that you are standing on a flat plate, enclosed by a giant dome. Depth perception fails us for the distant objects we see in the sky. This creates the appearance that all of the stars have the same distance.
The stars appear to move together across the sky during the night, rising in the east and setting in the west, as if they are affixed to the inside of a dome. Because of this, many ancient civilizations believed that a dome really did enclose the Earth. Only a few centuries ago astronomers came to realize that the stars are actually very far away, scattered throughout the Milky Way Galaxy, rather than attached to the inside of a vast sphere.
The old idea remains useful, however. The concept of the celestial sphere provides a simple way of thinking about the appearance of the stars from Earth without the complication of a more realistic model of the universe. Working with the celestial sphere offers a convenient way of describing what we see from Earth. When we refer to the celestial sphere, we are imagining that everything we see on the sky is set on the inside of a huge spherical shell that surrounds the Earth. We will use the reference points of the celestial sphere as the basis for several coordinate systems used to place celestial locations with respect to one another and to us.
The celestial sphere is an imaginary hollow globe that encloses the Earth. The sphere has no defined size. It can be taken to be infinite (or at least really big), with an infinitesimal Earth at the center. The observer is always taken to be at the center of the celestial sphere, even though the observer isn't at the center of the Earth. Our particular position among the stars gives us a particular view. Brighter stars appear closer; stars in nearly the same direction appear nearby each other, even if they are separated by great distances. Our first and most basic look out into the universe is completely stripped of any depth perception.
The celestial sphere can be seen from either of two perspectives. In one perspective, the celestial sphere itself remains still while the Earth turns inside it. In the other perspective, the Earth stands still and the celestial sphere rotates once per day. To an observer on Earth, these two perspectives appear the same. As we think about how we would expect to perceive the rotation of the Earth, we can use this second perspective to guide us.
Everything we see in the sky, we see as though projected onto the celestial sphere. The stars in the constellation Orion, for example, are at a variety of distances, but the differences are imperceptible to us on Earth. Orion's pattern would disappear if we could view it from any other angle or if we could perceive the depth, because the stars would project differently.
Because depth perception is lost, measurements of size are much more difficult. The Sun and the Moon look about the same size in the sky, even though the Sun is really much larger. The Sun appears to be the same size as the moon because the Sun is much farther away simply because the Sun is both 400 times larger in diameter and 400 times farther away than the Moon.
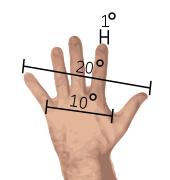
Although we can't easily measure the physical sizes of celestial objects, we can measure their apparent sizes. We do this by measuring the angle an object subtends in the sky. The Sun and the Moon, for example, subtend an angular diameter of half a degree. Most objects in the sky are smaller than this, so it is often convenient to use a smaller measure of angle. For this purpose, astronomers use arc minutes and arc seconds. There are sixty arc minutes in a degree, and sixty arc seconds in an arc minute. Angles this small are near or beyond the limits of ordinary human vision, but they become useful when using a telescope to make observations.
For casual stargazing, observers think about much larger angles. You can easily measure these angles when stargazing by using your hand as your ruler. From arm's length, your index finger has a width of about one degree, your palm measures about ten degrees across, and your full finger-span, including your thumb, is about 25°. This can be useful for estimating the position of a star in the sky, or for gauging the angular separation of two stars.
While the apparent movement of a star across the sky each night, with the celestial sphere, is great, the measurement of an object's movement across the Celestial Sphere as the object drifts through space, is called proper motion, and is measured in arc seconds per year.
To begin thinking about the view of the sky from Earth, we will identify a few points of reference that are fixed to the ground and of importance to astronomers. Some of these are widely known from common experience.

- A great circle is a circle drawn on the celestial sphere (or any sphere) which has the center of the Earth as its center. On the Earth, the equator is an example of a great circle. Other lines of latitude are not great circles because their center is not at the center of Earth. Lines of longitude are all great circles because they are always centered on Earth's center. A great circle is the largest possible circle that can be drawn on a sphere.
- The horizon is where earth and sky meet. It is the boundary between the portion of the sky that is blocked by the Earth and the portion that is visible. There is a distinction between the local horizon, which is defined by real objects specific to the observer's location such as trees or buildings, and the idealized horizon, which is what the local horizon would be if the ground were completely flat and there were no obstructions. For hypothetical or idealized cases, astronomers use the idealized horizon.
- A star's altitude is the angle between it and the horizon.
- The cardinal points are points on the celestial sphere that are on the horizon and due north, south, east and west. The North point, for example, is the point due north on the horizon.
- The zenith is the point in the sky directly overhead. It is necessarily true that any point on the horizon is 90° from the zenith.
- The meridian is the great circle that passes through the North point, the South point, and the zenith and lies on the celestial sphere.

To any observer, regardless of location, these markers stay in the same positions relative to the observer. The zenith is always directly overhead, the horizon is always level, and so on. Observers standing at different places on Earth will have a different view of the sky. An observer in Singapore might see the Sun at the zenith while another observer in New York would not see the Sun at all. These reference points change with the location of the observer.
There are also reference points that are fixed in the sky. These fixed reference points don't move with respect to the stars, but different observers see them in different positions. They are the basis for the fixed coordinate systems that we discuss later. For now, we will identify only the two most useful of these — the celestial poles and the celestial equator.
The celestial equator is an extension of the Earth's equator onto the celestial sphere. If you stand on Earth's equator, the celestial equator will always be directly overhead and pass through the zenith. It will run from the East point up to the zenith and down again to the West point. Anywhere you stand on Earth, the celestial equator will intersect the East and West points on the horizon. The nearer you are to the equator, the nearer the celestial equator come to the zenith. At the North Pole or the South Pole, the celestial equator lines up with the horizon.
Like the celestial equator, the celestial poles are an extension of the Earth's pole onto the celestial sphere. The North Pole extends out into space to create the North Celestial Pole. Likewise the South Pole creates the South Celestial Pole. In the Northern Hemisphere, only the North Celestial Pole is visible because the South Celestial Pole is below the horizon. In the Southern Hemisphere, only the South Celestial Pole is visible. At the equator, the North Celestial and South Celestial Poles would lie on the horizon where the meridian intersects the horizon.
Polaris is called the "North Star." It can be found at the last star on the "handle" of the Small Dipper. The last two stars of the "cup" of the Big Dipper are called the Guardians (or "Pointers"), and point to Polaris in the sky. Polaris is special because the Earth's North Pole points almost exactly towards it. This means that Polaris will always appear to be due north to any observer, and it will always stay in the same position on the sky.
Often, beginning stargazers assume that Polaris must be a very bright or prominent star. This is not really the case. Polaris is only remarkable because it is almost exactly in line with Earth's axis of rotation. Because of this, Polaris always remains at nearly the same place in the sky. For example, Shakespeare made reference to Polaris in the play Julius Caesar:
- I am constant as the northern star,
- Of whose true fixed and resting quality
- There is no fellow in the firmament.
- Julius Caesar, William Shakespeare's Julius Caesar, III.1.65-68
Though it must be pointed out that Shakespeare actually got it wrong. At the time Shakespeare wrote Julius Caesar Polaris was indeed the pole star but in Julius Ceasar's time Polaris was not the pole star.

The fact that Polaris always stays in the same position due north has given it much fame. It also makes Polaris a useful reference point for navigation — Using geometry, it is easy to show that the angle Polaris or the celestial pole makes with the horizon is equal to the observer's latitude. In the diagram, the angle is the observer's latitude. The pole and the equator are at right angles, so
or Since the angles in a triangle add to 180°, we know that
When we combine these two equations, we have . The angles and are alternate interior angles, so
and
which means that the angle between the pole and the horizon is the same as the observer's latitude. This fact was once used by navigators at sea, who could easily find their latitude by measuring the position of Polaris.
Like many things in astronomy, the celestial sphere can be very difficult to visualize because of its three dimensional geometry. A visit to a planetarium or a session under the night sky can be very helpful to you in developing a conceptual understanding of the celestial sphere. In the absence of the opportunity for these, it can be helpful to try to draw diagrams such as the one at the beginning of this section for yourself.
To begin drawing a celestial sphere such as the one above, you only need to know the latitude of the observer. Then imagine that the spot where the observer is standing is the "top of the world"; draw circle for the earth, and draw an observer standing at the top. Now draw a much larger circle around that; this represents the celestial sphere.
Since our observer is always on top of the Earth, the features on the celestial sphere that are defined relative to the ground will always be in the same position on the sphere. The zenith is the point directly above the observer's head, at the top of the celestial sphere.
The next important reference is the horizon. The horizon will be horizontal on the diagram. Remember that the celestial sphere has no specific size relative to the Earth, regardless of how you've drawn it. Draw the horizon across the middle of the celestial sphere, so that it's center is the same as the center of Earth. Markers such as the horizon are always idealized, so it doesn't matter whether your observer's view of the sky is actually cut off at the position marked by the horizon.
The next reference points we'd like to place are the North Celestial Pole and the South Celestial Pole. Think about what the orientation of the pole should be given the observer's latitude. If the observer is at the equator, the pole should go horizontally through the Earth. If the observer is at one of the poles, the pole should go through the Earth vertically. Extend the Earth's poles out to the celestial sphere and mark the intersections as the North Celestial Pole and the South Celestial Pole.
If we're in the northern hemisphere, the North Celestial Pole will be above the northernmost point on the horizon, and the South Celestial Pole will be on the opposite side of the celestial sphere, below the horizon. If we're in the southern hemisphere, the situation is reversed. Remember to check that the angle the horizon makes with the pole is about the same as the observer's latitude.
For any given latitude, one can build an appropriate celestial sphere. First, consider the sky in relation to the earth. Take the north and south poles and extend them into the sky; these become the north and south celestial poles. The Earth's equator can be projected outward to form the celestial equator. We'll get something that looks like the picture above.
When you're done, you should have a celestial sphere very like the one at the top of this section.
A celestial sphere forms the basis for the application of many coordinate systems. For example, the horizon and the celestial meridian together form the reference circles for giving the position of stars in terms of altitude and azimuth, making it easier for one to find them on the night sky. The celestial sphere is also a natural system for describing the motion of the sun. In order to explore these concepts, however, it is necessary to understand just how the celestial sphere changes for an observer at a given latitude. As we consider the daily rotation of the Earth, we'll see that your perception of the daily motion depends very much on your latitude.
As you look at the sky, your mind will naturally identify obvious patterns. The Big Dipper and Orion are two very prominent groupings of stars, and others stand out all over the celestial sphere. These asterisms are guideposts to the night sky. You can use them to keep your bearings when you look at the sky. The appearance of the night sky has remained much the same for millennia. Many of the ancient civilizations across the globe invented stories about the sky.
Often, the groups of stars are called constellations. Constellations have a very long history in astronomy, dating back thousands of years. Early in the twentieth century, a list of constellations was formally established by the International Astronomical Union, a widely recognized body of astronomers. The IAU identified constellations that would be used in astronomy and defined specific boundaries to unambiguously establish which constellations each star belonged to. It's easy to learn a few of the most prominent constellations so that you can find your way around the night sky. Beginning with a few easy-to-find landmarks you can find the rest by using familiar stars as guideposts.
Another useful guide in the sky is the ecliptic. The ecliptic is an imaginary line in the sky that the sun draws. The ecliptic is even with the plane of the Earth's orbit around the sun; thus, all of the main planets and the moon should be found relatively close or on the ecliptic, because the solar system is mostly flat. Also, along the ecliptic are the 12 constellations of the zodiac. Thus, by finding some of the main zodiac constellations in the night sky, one can determine if certain objects they see may or may not be planets by whether or not they lie on the ecliptic.
Phases of the Moon
Like the stars and planets, the Moon doesn't stay fixed in the sky but slowly moves as the Earth rotates and as the Moon moves through its orbit about the Earth. To someone taking a casual glance at the Moon, it seems as fixed as the stars. But observation of either the Moon or the stars over a period of several hours will reveal their diurnal (daily) motion across the sky. The Moon rises and sets each day. An observer who watches the Moon over the course of many days will notice the Moon moving not only with the stars, but among them. Every month, the Moon completes one fewer pass across the sky than the stars have completed. We see this because of the Moon's orbit about the Earth. As the Moon progresses through its orbit, its rising and setting times change. Each day, the Moon rises and sets fifty minutes later than the day before.
The moon usually takes 27 days to rotate once on its axis. So any place on the surface of the moon experiences about 13 days of sunlight, followed by 13 days of darkness. Temperatures on the Moon range from -153 C at night to 253 C during the day. For example if you were standing on the surface of the moon during sunlight hours it would be blazing hot. When the sun goes down, the temperature automatically drop 250 degrees in just a matter of moments. Furthermore, there are craters around the North and South poles of the moon which never seen the sunlight. These dark places would always be as cool as -153 C. However, there are nearby mountain peaks that are covered in continuous sunlight, and would always be hot.
The "dividing line" between the light and dark halves of the globe is called the terminator, as it terminates the area of darkness (and also that of daylight).
Typically, one-half of the Moon will be lit up by the Sun, while the half facing away from the Sun remains dark. (The only exception occurs during a lunar eclipse, when the Earth blocks the light falling on the lit side of the Moon.) The part illuminated by the Sun is not, it should be emphasized, always the same portion of the Moon's surface! Like the Earth, the Moon turns on its axis, exposing different areas at different times. In combination with the orbital revolution of the Moon around the Earth, this phenomenon creates the phases of the Moon as seen from Earth. The phrase "Dark side of the Moon" arose before the age of artificial satellites and the back side of the Moon could not be observed. Hence, the that one side was unknown or "dark".
The tilt of the moon’s spin axis is only 1.54 degrees and as a result, lunar seasons are barely noticeable in most locations on the Moon. However, at the North and South poles, the height of the sun above the horizon varies by more than 3 degrees over the course of the year. In other words, it affects the percentage of sunlit regions and surface temperatures at the poles. Furthermore, the coldest areas are located in doubly shadowed regions inside small craters, in which they are located within the permanently shadowed regions of larger craters. Temperatures are as low as 35K (-238 C or -397 F) in these areas, even at noon on the warmest day of the year.
Some half of the Moon is always illuminated but the fraction of the illuminated part or the Moon's phases directly depend on the relative positions of the Earth, Moon, and Sun. Simply put, it's a matter of how much of the daylight side of the Moon we can see from our current viewing angle. The phase will depend on how much of the side facing toward us is illuminated at any given time. The sketch below illustrates the phases of the moon for various Earth-Moon-Sun positions (the Sun is presumed to be off of the diagram to the right):
Next to each "Moon" is a black-and-white sketch of the phase as it would be seen from Earth when the Moon is in that position. When the Moon is between the Earth and the Sun, the sunlit side of the Moon is facing completely away from us, and therefore we have the dark "New Moon". When the Moon reaches the other side of the Earth, the sunlit side will be fully toward us, and we have the "Full Moon". As the Moon moves from New to Full and the sunlit side grows increasingly large, we say the Moon is waxing; as we see less, in the decline from Full to New Moon, we say it is waning.
Midway between the Full Moon and New Moon, half of the sunlit side of the Moon is visible from the Earth. Because a half of the half illuminated Moon can be seen, this is referred to as a "quarter Moon". When the Moon is waxing and reaches this position, it's called the "first quarter Moon"; when waning, the "third quarter Moon." When less than a quarter-moon is visible, it's referred to as a "crescent Moon" - waxing crescent or waning crescent, as appropriate. When more than a quarter-moon is visible, it's referred to as a "gibbous moon", again, waxing or waning.
The Moon's orbit and rotation speed is just such that the Moon always shows the same side to Earth, aside from only a slight "wobble." The pattern of markings on the side facing Earth is very familiar in history and culture. Western society has long imagined a face in the markings — the "Man in the Moon." Other cultures have seen a woman, a rabbit, a frog or other creatures. The Moon always shows this same face to Earth because its rotation is "locked" with its orbit, for reasons we will see later, when we discuss gravity. More precisely, the time it takes for the Moon to complete a trip in its orbit is the same as the time it takes for the Moon to rotate once around its axis. Because we see the Moon moving around us, it appears as though the Moon isn't turning at all.
If you stood on the Moon and looked up at Earth in the sky, you would see that it never rises, never sets, and never moves in the sky at all. Imagine, for example, standing at the middle of the face of the Moon that we see. From there, the Earth would always remain straight overhead. If you stood at the edge of the face we see from Earth — the "limb" — you would always see the Earth on your horizon.
Up to now, we have considered the time for the Moon to complete one orbit around the Earth to be the same as the time for it to pass once through its series of phases, but this is not quite right. The Moon's phase at a particular point in its orbit changes as the Earth goes around the Sun. Once the Earth has gone halfway around the Sun, the position of the Moon for a given phase has also moved halfway around the orbit, since the Sun is on the opposite side. Thus, it takes a little longer for the Moon to go through its phases than it does for it to go through its orbit about the Earth.
Suppose a full moon marks the beginning of both the period of the orbit of the Moon about the Earth and the period of the orbit of the Earth about the Sun. At the time of full Moon, the Sun, Earth, and Moon are aligned. Once the Moon returns to that position in its orbit, the Earth has moved a little around the Sun. Now, the Moon is not aligned with the Earth and the Sun. It takes about two days before the Moon has moved back into alignment with the Earth and Sun line (synodic month). The time for the Moon to complete an orbit, called a sidereal month, is about 27 days and 8 hours. The time to move through its phases, a synodic month, is about 29 days and 12 hours.
Eclipses
An eclipse occurs when one casts a shadow on another object. A lunar eclipse happens when the shadow of the Earth falls on the Moon, because the Earth is in a position where it blocks the light from the Sun. Likewise, when the Moon interposes itself between the Earth and Sun, so that the Moon's shadow falls on the Earth (and the Sun is temporarily blocked from view), a solar eclipse is the result.
Eclipses occur when the Sun, Moon, and Earth align. An eclipse blocks sunlight headed toward either the Moon or the Earth, depending on whether the eclipse is a solar eclipse or a lunar eclipse. Such an alignment can only happen when the Moon is in new phase or full phase. If the Moon is new, then it's possible for a solar eclipse to occur. During a full moon, there might be a lunar eclipse. During a solar eclipse, the Moon's shadow falls on the Earth, and the Moon blocks the Earth's view of the Sun. During a lunar eclipse, the Earth's shadow falls on the Moon, and the Moon appears to be darkened as we see it from Earth.
As one of the rare and very spectacular celestial events, a solar eclipse is well worth seeing if you should ever have the opportunity. When viewing a solar eclipse, however, it is important that you avoid damage to your vision by taking steps to view the eclipse safely. (There is no danger in viewing a lunar eclipse, during which the observer never looks at the Sun.) The simplest way to view a solar eclipse is to project the sunlight through a pinhole onto a card or a sheet of paper. The sunlight on the paper will form an image of the Sun. As the eclipse progresses, you will see a round "bite" that the Moon's shadow has taken out of the Sun. If possible, you might also find a special filter, which you can look through directly to watch the eclipse. Solar filters make it possible to look directly at the Sun without harming your vision. Be sure to use a filter specifically designed for looking at the Sun — sunglasses, welder's glass, and other filters are generally not sufficient. Don't use a telescope or binoculars unless the filter was designed for that purpose. Even near totality, when the Sun is almost completely covered, you risk damage to your eyes by staring into the Sun. Once totality arrives, however, it is safe to look directly. It is also safe (though not advisable) to look for a brief moment at the uneclipsed Sun. When viewing an eclipse, there's no need to be paranoid about the danger of accidentally glimpsing the Sun's surface for a split second. If your eyes catch the bright surface of the Sun, simply turn your head away.
The shadow of the Earth on the Moon (or any shadow cast by the Sun) has two parts. The inner part of the shadow, called the umbra, is the darkest part. If you were to stand on the Moon under the umbra, your view of the Sun would be completely blocked. Under the outer part, the penumbra, the Sun is only partially blocked. This is why the Moon is more darkened under the umbra than under the penumbra. While the location of the boundary of the umbra and penumbra are precisely defined geometrically, there is no sharp shadow line between the two when looking at an eclipsed Moon. At the innermost part of the penumbra, only a tiny fraction of the sunlight reaches the Moon, and this part is almost as dark as the totally eclipsed umbra. During a solar eclipse, when the Moon's shadow falls on the Earth, we stand in the shadow rather than looking at it. Observers standing in the umbra see a total eclipse of the Sun, while observers under the penumbra see a partial eclipse.
The present average distance of the Moon from the Earth happens to be just right for the Sun and the Moon to have almost the same apparent size as viewed from Earth. The Sun is 400 times larger than the Moon, but it's 400 times farther from Earth. Because of this, the Moon can obscure the bright surface of the Sun while leaving the fainter outer part, called the corona, exposed. The result is dramatic. During a total solar eclipse, the seething outer layers of the Sun are visible around the Moon. An annular eclipse is possible when the Moon is near the most distant part of its orbit, a point called the apogee. In an annular eclipse, the Moon passes directly in front of the Sun but fails to block it completely, creating the appearance of a bright ring, or an annulus.
Since it's possible for an eclipse to occur twice a month, once of the Sun and once of the Moon, at each new and full moon, students often wonder why eclipses don't occur twice a month, each time the Moon passes through its new and full phase. Months often pass with neither a solar or lunar eclipse. Eclipses don't occur in these months because the Moon passes just north or south of the Earth's shadow during the full moon. Likewise, the Moon's shadow misses the Earth as it passes through new moon. This happens because the orbit of the Moon is not perfectly aligned with the Earth's orbit. The Moon's path is tilted 5° to the ecliptic. It only passes through the ecliptic at two points in its orbit. These points are called the nodes.
Whenever the Moon isn't located at a node, it is either north or south of the Earth-Sun line. Eclipses can only occur when the Moon is at one of the nodes and at new or full phase — when the Moon's orbit is positioned so that the nodes are aligned with the Earth-Sun line. This happens about twice a year, at intervals called eclipse seasons. The time of eclipse season changes over the course of many years, but consecutive eclipse seasons are about six months apart. In any year there are at least two eclipses, and there may be as many as seven, all occurring during the eclipse seasons. There are typically around four eclipses in a year.
Eclipses can only happen when the moon is at a node in its orbit - a point where the Moon's orbit around the Earth intersects with the Earth's orbit around the Sun. If the Moon crosses one of these nodes while it's in the full or new moon position, a lunar or solar eclipse (respectively) can occur.

In a lunar eclipse, the observer watches the Earth's shadow fall on the Moon. Observers don't need to be in any special place to see the eclipse, so long as the Moon is visible. Consequently, an observer on the side of Earth facing the Moon will be able to see the eclipse. Fully half of the Earth will have a view. In a solar eclipse, the observer stands in the shadow of the Moon. The umbra of this shadow is small, so only a small portion of the Earth will see a total eclipse. A much larger portion will see the Moon only partially blocked, and will have a partial eclipse.
The Moon will often become reddish or orange in color during a lunar eclipse. The color of eclipses varies, with the Moon sometimes becoming very red and at others only darkening with no change in color at all. The Moon reddens during the eclipse because sunlight filters through the Earth's atmosphere and is scattered into the Earth's shadow. Sunlight reddens as it is scattered by dust and smoke in the Earth's atmosphere; this is why sunsets are red. The reddened sunlight illuminates the eclipsed Moon, making the Moon brighter and redder. The color and darkness of an eclipse depends on the geometry of the eclipse and the weather on Earth during the eclipse.
Two phenomena caused by eclipses are the Diamond Ring and Baily's Beads.
Throughout history, astronomers have relied on cycles in their observations. The year, for example, is the cycle of the Earth's orbit around the Sun, and the seasons follow with this cycle, as do the motions of the stars. Since ancient times, astronomers have known about an eclipse cycle, called the Saros cycle. they can be used to predict in advance when an eclipse will occur and what the eclipse will be like.
The Saros cycle depends on three other cycles of the Moon: the time from one full moon to the next — the synodic month; the time it takes for the Moon to pass through a node and come all the way around — the draconic month; and the time it takes for the Moon to come close to the Earth in its orbit, move away, and come close again — the anomalistic month. In one Saros cycle, there are almost exactly 242 draconic months, almost exactly 223 synodic months, and almost exactly 239 anomalistic months. The Saros cycle is the smallest length of time that evenly contains all of these cycles. This is why eclipses repeat within the Saros cycle.
Stonehenge is an ancient structure in Britain. It is made up of 30 monoliths in the Sarsen Circle. There are 56 Aubrey Holes outside of Stonehenge. It is believed that Stonehenge was used for predicting eclipses.
Daily Motions
Every day, the Earth turns once on its axis. At the Earth's equator, we move around the center of the Earth with speeds near a thousand kilometers per hour because of this rotation. We feel nothing, but we can see the effect of Earth's rotation. An observer on Earth sees everything in the sky appear to rotate around Earth at the rate of once per day. This motion is not apparent to an observer who steps outside for a moment, since it is so slow. For the motion to become apparent, an observer must watch the sky for a period of hours. During the day, the motion manifests itself in the movement of the Sun, which proceeds from the East in the morning towards the west in the evening. At night, the constellations move, seeming to circle about the pole.
Because the daily motion of the stars is driven by the same mechanism that drives the motion of the Sun, the stars move in almost exactly the same way that the Sun moves. Indeed, everything in the sky moves in almost exactly the same way over the course of a day. The motion of the Sun and the planets only differ at all because the planets have their own motion around the Sun along their orbits, and is noticeable from Earth.
As the Earth spins, it appears to us that the celestial sphere is spinning. It spins about the Earth's pole, so that the celestial poles appear stationary and the stars and planets seem to move in circles around the poles. Stars move at 15° an hour.
The schematic illustrates the daily motion of the celestial sphere resulting from the spin of the Earth. The Sun, Moon, planets and stars make circles around the Earth. Since the observer is tilted with respect to Earth's rotation axis, the daily motion also appears tilted. As a result, celestial objects appear to rise and set at an angle.
Looking at the diagram, we see that stars should rise roughly in the East and come up at an angle. In the Northern Hemisphere, the stars move to the south as they rise, while stars move northward in the Southern Hemisphere as they rise. To an observer standing at the equator, the axis of rotation is horizontal, and stars rise in the East perpendicular to the horizon.
Since the stars seem to rotate around the celestial pole, some of the stars very near the pole never rise or set. Certainly, Polaris never sets — it remains fixed. Only an observer very close to the equator will see any of the stars in the Little Dipper rise or set. The stars close enough to the pole never seen to rise or set are called circumpolar stars. These stars always remain above an observer's horizon. Different stars are circumpolar to different observers.
Imagine standing at the North Pole. You would see Polaris overhead with all the other stars spinning around it. In reality, you are the one who is spinning. From the North Pole, all of the motion of the stars is horizontal. Stars at the horizon skim along the horizon, never rising or setting. The stars higher in the sky also move horizontally, never moving up or down. From the poles, all visible stars are circumpolar.
At the Earth's equator, the situation is different. The celestial poles appear at the horizon on the north and south points. As stars move around the poles, they all rise and set, no matter how close to the pole they are. From here, there are no circumpolar stars. As you move from the equator to the pole, you will see gradually more and more stars become circumpolar, until on finally reaching the pole you find that all stars are circumpolar.
For centuries, the day has been the most fundamental unit of time in the calendar. Measuring the passage of days is as easy as counting sunrises or sunsets. The earliest clocks, the predecessors to the sundial, worked by tracking the daily motion of the Sun across the sky.
A sundial uses the position of the Sun to give the time. (The gnomon of a sundial can be used to find north: the shortest shadow cast by the sun (at noon) points north.) Of course, not all clocks work by measuring the Sun, although all work by measuring some reliably periodic and regular process. A wristwatch, for example, measures the oscillations of a quartz crystal. Atomic clocks use the natural period of oscillation of cesium atoms to measure time. Other systems of time are tied to the motion of the Earth, but there are a variety of ways to measure time in this way. The time measured by any particular method is not guaranteed to agree with the time measured by another, so it is sometimes necessary to convert between different "kinds" of time.
The time measured by sundials is called local solar time. The local solar time progresses according to the Sun's motion around the Earth. Since the Earth's speed in its orbit around the Sun changes slightly over the course of a year, this motion is not completely uniform. Sometimes, when the Earth is moving faster in its orbit, the solar day is shorter. Early timekeepers never noticed this slight difference, but the appearance of accurate mechanical clocks made it possible to measure the small changes in the length of the day.
To deal with this problem, astronomers invented mean solar time. The mean solar time averaged the length of the day so that each day was of the same length. This standard is up to fifteen minutes off from the true solar time, but is much more convenient for clocks that are accurate enough to see the difference. Over the course of a year, the local solar time drifts, but the two always agree after a full year has passed.
For much of history, every town in the world kept a slightly different "correct time" from every other town. Under local solar time, noon occurs at the moment the Sun passes through the observer's meridian. Two observers in different locations will observe local noon to occur at different times. This is why local solar time is called "local." This difference wasn't a problem when transportation and communication were slow, but the advance of trains and telegraphs made even a small difference between nearby towns important. To deal with this, the time zones were developed. The standard time was defined to be the time at a nearby line of longitude. For most locations, the time zone was offset by an round number of hours from the time measured at Earth's prime meridian.
For historical reasons, the prime meridian is based on the line of longitude through the observatory in Greenwich, England. That time zone is known as Greenwich Mean Time, and is often used as a standard for when one wishes to compare times without taking local time zones into account. For this reason (since it is used universally) it is also called Universal Time. This is the most commonly used form of solar time, and the most commonly used measure of time in general.
It's very natural to use the Sun as a standard of time, since the cycles of day and night are so important to life on Earth. For this reason, most people think of a day as the time it takes the Sun to move through the sky once. The apparent motion of the Sun in the sky is similar to the motion of everything else, but not exactly the same. The daily motion is driven almost entirely by the rotation of the Earth, but the Sun's motion differs from the stars' motion. This happens because the Earth is moving around the Sun. The Earth moves a little in its orbit while a it rotates and day passes. Because the Earth's position has changed, a full rotation doesn't quite bring the Sun all the way around the sky. This means that the Earth makes a little more than a full rotation over the course of a solar day.
A sidereal day is the amount of time it takes for the stars to go once around the sky, equal to 23 hours and 56 minutes. The word sidereal means "relating to the stars." The difference in length between the solar and sidereal day causes the rising and setting times of stars to change throughout the year. If the star Rigel, for example, rises at noon today, it will rise at 11:56 tomorrow. In six months, it will rise at midnight. Because the difference between solar days is tied to the orbit of the Earth, there is exactly one more sidereal day in a year than there are solar days.

A sidereal month is the period of the moon in relation to the stars; approximately 27 (1/3) days (13 degrees a day). Ancient peoples used this period to track time, as evidenced by the Big Horn Medicine Wheel in Sheridan, Wyoming.
Sidereal time is widely used in astronomy because it can be used to tell which stars will be up. At a given sidereal time, the stars in the sky will always be the same. Accurately finding the position of stars is easier than finding the position of the Sun, so measurements of the solar time are usually based indirectly on the sidereal time. Modern techniques measure time from atomic clocks, which are then tied to the motion of the Earth by measurement of the sidereal time.
A synodic month is one new moon to the next; approximately 29.5 days. This is about two days longer than the sidereal month. The reason for this is that while the Moon is orbiting the Earth, the Earth is orbiting the Sun. Therefore, the Moon has to travel more than 360 degrees to return to its original position above the same meridian on the Earth.
For anyone living on the coast, tides play an important role in everyday life. Despite this, the cause of the tides was a mystery for centuries, before gravity was well understood. People have always suspected that tides are related to the moon, since high tides always occur when the Moon is highest in the sky and again when the Moon is lowest below the horizon. This turns out to be correct.
Tides occur because the gravitational pull from the Moon is greater on the side of the Earth facing the Moon than on the side facing away. As a result, the gravitational pull "stretches" the Earth. The tidal pull from the Moon gives the Earth an oblong shape. The pull affects the ocean more strongly than the ground, because the ocean is liquid and less resistant to movement.
The stretching effect from the tides creates two places on Earth where the tides are high, with one high tide on the side of the Earth facing the Moon and the other on the side opposite the Moon. As the Earth rotates, the locations under the positions of high tides also move. If the moon didn't orbit around the Earth, high tide would occur exactly twice a day, every 12 hours. The orbit of the moon changes the position of the high tides over the course of the month, which lengthens the time between high tides to about 12½ hours.
The Sun also has a tidal influence on the Earth, although this is a much smaller effect than the Moon's tidal influence. Because of the difference in the gravitational pull from the Sun on opposite sides of the Earth is much smaller, the Sun's tendency to make the Earth bulge is much less. Still, the contribution to tides from the Sun is noticeable. When the Sun, Moon and Earth are aligned, the Sun adds to the Moon's tidal pull, making the tides greater. This is called the spring tide. (The spring tide has no connection with the season of spring.) When the Moon is at a right angle with the Sun, the Sun's tidal pull interferes with the Moon's, making the tides weaker. This configuration is called the neap tide.
Yearly Motions
Why do we have seasons? A little thought will suggest that it can't have much to do with the Earth's distance from the sun, as that would affect the Southern and Northern Hemispheres at the same time. (In fact, the Earth is slightly nearer to the sun around December than at other times of the year.) Why, then are there seasons?
Every year the Earth completes one orbit of the Sun. We see this observe the effect as the change of the seasons and the movement of the constellations. Over the course of a year, the Sun moves through a great circle on the celestial sphere, tracing out the same path year after year. This path is called the ecliptic. The ecliptic is not only the path of the Sun in the sky, it also marks the plane of the Earth's orbit of the Sun. The planets orbit the Sun in different planes but near to the ecliptic.

The axis of the Earth's rotation is tilted by 23½° with respect to the plane of the ecliptic. Globes are typically built with an inclined rotation axis. The 23½° North latitude is marked as the Tropic of Cancer and the 23½° South latitude is marked as the Tropic of Capricorn. In the Northern Hemisphere, the Sun will pass directly over head only between June 20 and 22th along the Tropic of Cancer. That day is called the day of the summer maximum or Solstice in the Northern Hemisphere. In the Southern Hemisphere, the Sun will pass directly over head only once between December 20 and 23rd along the Tropic of Capricorn. Anywhere between the Tropic of Cancer and the Tropic of Capricorn, the Sun will pass directly overhead at least twice during the year, but the Sun will never pass overhead for people living outside the tropics. Within the Tropics, over the course of a year, the Sun's position in the sky changes, beginning in the southern sky about December 21, moving to the northern sky in mid-year, and ending the year back in the southern sky.
The tilt of Earth's rotation axis causes a 23½° tilt of the great circle of the ecliptic with respect to the Earth's equator. The ecliptic and the equator intersect at two points, but are otherwise separated by up to 23½°. When the sun lies at one of the intersections, it is directly overhead somewhere on the equator. This occurs at the equinox, and the points on the sky where the equinox intersects the equator are also called equinoxes. Once every year, the Sun passes through the equator going north. This happens in late March — the "vernal" or "spring" equinox. The "autumnal" equinox occurs when the Sun passes through the equator in late September.
On the equinox days, the day and night are equally long. This is the origin of the name equinox, which is from Latin for "equal night." On the day of the equinox, the Sun rises due east and sets due west. It doesn't rise to directly overhead, though, except for observers on the Equator. The equinoxes are the only days of the year that have twelve hours of daylight and twelve hours of dark. After the vernal equinox, moving into Northern summertime, the Sun begins rising in the northeast and sets in the northwest. Days in the Northern Hemisphere become longer, while days in the Southern Hemisphere become shorter.
The points at which the Sun is at its greatest distance from the equator are called the solstices. The solstices mark the longest and shortest day of the year. The longest day of the year is the summer solstice and the shortest day is the winter solstice. In the Northern Hemisphere, the summer solstice occurs when the Sun is farthest north, while the winter solstice occurs at the Sun's southernmost point. In the Southern Hemisphere, the solstices are reversed.
Viewed from space, we see that the Earth's tilt changes the exposure of different parts of the Earth to the Sun. Observers in the Northern Hemisphere will see the Sun at its lowest position in the southern sky, about December 21. They see it this way because the Southern Hemisphere is tilted towards the Sun and the Northern Hemisphere is tilted away. About June 22, the situation is reversed, with the Northern Hemisphere pointed toward the Sun, and the Sun will be in its extreme high point in the sky at solar noon. For an observer in the Southern Hemisphere, the Sun will appear at its lowest point in the sky in the north, about June 22, while the Sun will appear at its high point in the sky about December 21. One effect of this phenomenon is that during the months of Northern Hemisphere summer, the North Pole will be able to receive sunlight twenty-four hours a day. The Sun will remain visible through much of the autumn, passing below the horizon at the autumnal equinox. As winter sets in at the North Pole, the Sun will not be seen for six months, while that portion of the Earth is tilted away from the Sun.
As one moves toward the Earth's equator from either pole, this effect becomes less severe. The nearer one is to the equator, the less difference there will be between the number of hours of illumination and night hours. At the equator, there's practically no difference between the length of day all through the year.
Clearly, the annual motion of the Earth around the Sun is the cause of Earth's seasons. What effect gives rise to this seasonal change is less obvious. At first glance, one might think that winter occurs when the Earth is farther from the Sun. If we realize the Northern and Southern Hemispheres have winter at different times of year, we see that this can't be right. Also, the Earth's orbit is very nearly circular. The change in the Earth's orbital distance is much too small to have a noticeable effect on Earth's climate.
Certainly the length of time each day during which sunlight falls on a particular location has a great deal to do with the seasonal changes in temperature. However, another effect less obvious, but more influential is the angle at which the sunlight hits a region. At the equator, there is little difference throughout the year as the Sun varies by 23.5 degrees on either side of the vertical. The length of the ray's path on Dec 21 at solar noon is increased by a factor of only 1.1 from a direct vertical path and the reduction of the sunlight is small. The more direct radiation gives the maximum amount of heat and energy to the earth where it falls, and therefore these areas will receive the most warmth. Away from the equator, however, the Earth's tilt means that sunlight is not received so directly and a greater amount of the Sun's energy is blocked by the longer path it takes through the atmosphere. At 50 degrees north latitude, the path the Sun's rays travel through the atmosphere on Dec 21, at solar noon, will be increased by a factor of 3.5 from a direct vertical path. In general, the rays will come at an angle that depends on the time of day, the latitude of the region from the equator, and the position of Earth in its orbit.
The constellations in the ecliptic, the zodiac, have a long history in the tradition of astrology. In most newspapers, you can read a (completely unscientific) prediction of your future or some personal advice, specific to your birthday. Each entry is associated with one of the constellations of the zodiac and a range of birth dates. In the tradition of astrology, the constellation the Sun occupied on your birthday, your "sign," reveals information about your personality and your future.
Interestingly, the dates given for each constellation in the newspaper don't match the Sun's position in the sky for those dates. There is a mismatch between the date in the newspaper and the real position of the Sun of a little more than a month. The mismatch appears because the dates corresponding to each sign were set thousands of years ago. Over the course of thousands of years, the Earth "wobbles" on its axis, causing the calendar and the positions of the stars in the sky to shift. This wobble is caused by the pull on the equator by the sun and moon, and is called precession. It affects the positions of all the constellations with respect to the equinoxes and the pole.
The precession of the Earth is like the movement of a top. If you spin a top with the axis tilted, the axis will slowly rotate as the top spins. Likewise, the Earth's axis remains tilted at 23½°, but the orientation of this tilt changes over the course of thousands of years.
Since precession changes the direction in which Earth's pole points, it also changes which star is the North Star, if any. Earlier, we quoted Shakespeare, who referenced Polaris in Julius Caesar, describing it as the northern star. Strictly, this would be incorrect. Polaris was not "fixed" in the sky in Julius Caesar's time because Earth's axis was pointed differently, toward the Big Dipper.
Precession is a slow drift, and a difficult motion to detect. The motion of the stars from precession only becomes noticeable to the unaided eye after many, many years of careful observation, although it becomes very quickly noticeable through a telescope. The Greek astronomer Hipparchus was the first to measure the precession by comparing his own observations to observations collected a century and a half before.
Precession changes the position of the Earth in its orbit for the solstices and the equinoxes. As the Earth's axis turns over, the moment when it points most closely towards the Sun changes, and so the seasons change. If a calendar didn't account for this, the seasons would drift as the axis precessed. Eventually, the Northern Hemisphere would be cold in July and warm in January, and the Southern Hemisphere would have warm July weather and cold January weather. The calendar takes the extra motion of precession into account by using the tropical year as its basis. The year as we usually define it is a sidereal year, the time it takes for the Earth to make one orbit around the Sun. In one year, as we usually measure it, the Earth really completes a little more than a full orbit around the Sun. During a sidereal year, the Sun moves fully around the sky and back into the same position with respect to the stars. In a tropical year, the Sun goes from the Vernal Equinox, around the sky, and back to the Vernal Equinox again. During this time, the equinox has shifted slightly in its position, so that a tropical year is a bit shorter than a sidereal year.
It's easy to identify the progression of the calendar if you take careful notice of the sky. Next time you see sunrise or sunset, take notice of whether the Sun is setting due west or just north or south of west. Many ancient cultures watched the motion of the Sun carefully and over long periods of time. Using simple techniques and tools, they were able to measure periods like the length of a year very accurately. Ancient people who took notice of celestial motion would have found that the summer solstice occurred every 365 days. They would also notice that the solstice was delayed an extra day every four years. This is the reason for the leap year in the modern calendar. The delay occurs because the length of the year is a little more than 365 days — closer to 365¼ days long. By taking some simple observations over a period of a few years, it is possible to measure the length of a year to surprising accuracy using this technique.
Solar calendars have been used throughout history. The ancient Babylonians thought the year had only 360 days, and made their calendar accordingly. The Islamic calendar is lunar, and is 11 (1/2) days different than the solar calendar. The Hebrew calendar is lunisolar.
Our modern calendar is handed down to us from the Ancient Roman civilization. The calendar took its first mature form as the Julian calendar, almost exactly the same as the one used today. It had 365 days in a year, with a 366-day leap year every four years. In the Julian calendar, years divisible by 4 — such as 1992, 1996, and 2008 — are leap years. This gave the Julian calendar an average of 365¼ days per year, which is very close to the true 365.2422 day length for a tropical year.
Although the drift of the Julian calendar is slow, the error in the calendar had accumulated enough by the sixteenth century that the Catholic Church became concerned about the drift's effect on the date of the celebration of Easter. The Italian chronologer Aloisius Lilius invented modifications to the Julian calendar to correct the difference. Pope Gregory XI instituted the new calendar, now named the Gregorian calendar, in the year 1582.
The Gregorian calendar was identical to the Julian calendar except that the leap year was skipped on years not divisible by 400. In the years 1600, 2000, and 2400, there would be a leap year in the Gregorian calendar, but not 1800, 1900, or 2100. This produced a year of average length 365.2425 days, much closer to the correct value than the Julian calendar. The Gregorian calendar accumulates only 3 days of error over 10,000 years.
Discussion questions
1) On the date of the summer solstice, the sun is overhead on the Tropic of Cancer, and on the date of the winter solstice the sun is overhead on the Tropic of Capricorn. Draw a quick sketch that shows the relative positions of the sun and the earth on those dates.
2) On the date when the sun is overhead on the Tropic of Capricorn, the sun is actually located in the constellation of Sagittarius. So why did the Greeks name Tropic of Capricorn the Tropic of Capricorn instead of the Tropic of Sagittarius?
Suppose you are an astronomer in America. You observe an exciting event (say, a supernova) in the sky and would like to tell your colleagues in Europe about it. Suppose the supernova appeared at your zenith. You can't tell astronomers in Europe to look at their zenith because their zenith points in a different direction. You might tell them which constellation to look in. This might not work, though, because it might be too hard to find the supernova by searching an entire constellation. The best solution would be to give them an exact position by using a coordinate system.
On Earth, you can specify a location using latitude and longitude. This system works by measuring the angles separating the location from two great circles on Earth (namely, the equator and the prime meridian). Coordinate systems in the sky work in the same way.
The equatorial coordinate system is the most commonly used. The equatorial system defines two coordinates: right ascension and declination, based on the axis of the Earth's rotation. The declination is the angle of an object north or south of the celestial equator. Declination on the celestial sphere corresponds to latitude on the Earth. The right ascension of an object is defined by the position of a point on the celestial sphere called the vernal equinox. The further an object is east of the vernal equinox, the greater its right ascension.
A coordinate system is a system designed to establish positions with respect to given reference points. The coordinate system consists of one or more reference points, the styles of measurement (linear measurement or angular measurement) from those reference points, and the directions (or axes) in which those measurements will be taken. In astronomy, various coordinate systems are used to precisely define the locations of astronomical objects.
Latitude and longitude are used to locate a certain position on the Earth's surface. The lines of latitude (horizontal) and the lines of longitude (vertical) make up an invisible grid over the earth. Lines of latitude are called parallels. Lines of longitude aren't completely straight (they run from the exact point of the north pole to the exact point of the south pole) so they are called meridians. 0 degrees latitude is the Earth's middle, called the equator. 0 degrees longitude was tricky because there really is no middle of the earth vertically. It was finally agreed that the observatory in Greenwich, U.K. would be 0 degrees longitude due to its significant role in scientific discoveries and creating latitude and longitude. 0 degrees longitude is called the prime meridian.
Latitude and longitude are measured in degrees. One degree is about 69 miles. There are 60 minutes (') in a degree and 60 seconds (") in a minute. These tiny units make GPS's (Global Positioning Systems) much more exact.
There are a few main lines of latitude:the Arctic Circle, the Antarctic Circle, the Tropic of Cancer, and the Tropic of Capricorn. The Antarctic Circle is 66.5 degrees south of the equator and it marks the temperate zone from the Antarctic zone. The Arctic Circle is an exact mirror in the north. The Tropic of Cancer separates the tropics from the temperate zone. It is 23.5 degrees north of the equator. It is mirrored in the south by the Tropic of Capricorn.
Horizontal coordinate system
One of the simplest ways of placing a star on the night sky is the coordinate system based on altitude and azimuth, thus called the Alt-Az or horizontal coordinate system. The reference circles for this system are the horizon and the celestial meridian, both of which may be most easily graphed for a given location using the celestial sphere.
In simplest terms, the altitude is the angle made from the position of the celestial object (e.g. star) to the point nearest it on the horizon. The azimuth is the angle from the northernmost point of the horizon (which is also its intersection with the celestial meridian) to the point on the horizon nearest the celestial object. Usually azimuth is measured eastwards from due north. So east has az=90°, south has az=180°, west has az=270° and north has az=360° (or 0°). An object's altitude and azimuth change as the earth rotates.
Equatorial coordinate system
The equatorial coordinate system is another system that uses two angles to place an object on the sky: right ascension and declination.
Ecliptic coordinate system
The ecliptic coordinate system is based on the ecliptic plane, i.e., the plane which contains our Sun and Earth's average orbit around it, which is tilted at 23°26' from the plane of Earth's equator. The great circle at which this plane intersects the celestial sphere is the ecliptic, and one of the coordinates used in the ecliptic coordinate system, the ecliptic latitude, describes how far an object is to ecliptic north or to ecliptic south of this circle. On this circle lies the point of the vernal equinox (also called the first point of Aries); ecliptic longitude is measured as the angle of an object relative to this point to ecliptic east. Ecliptic latitude is generally indicated by , whereas ecliptic longitude is usually indicated by .
Galactic coordinate system
As a member of the Milky Way Galaxy, we have a clear view of the Milky Way from Earth. Since we are inside the Milky Way, we don't see the galaxy's spiral arms, central bulge and so forth directly as we do for other galaxies. Instead, the Milky Way completely encircles us. We see the Milky Way as a band of faint starlight forming a ring around us on the celestial sphere. The disk of the galaxy forms this ring, and the bulge forms a bright patch in the ring. You can easily see the Milky Way's faint band from a dark, rural location.
Our galaxy defines another useful coordinate system — the galactic coordinate system. This system works just like the others we've discussed. It also uses two coordinates to specify the position of an object on the celestial sphere. The galactic coordinate system first defines a galactic latitude, the angle an object makes with the galactic equator. The galactic equator has been selected to run through the center of the Milky Way's band. The second coordinate is galactic longitude, which is the angular separation of the object from the galaxy's "prime meridian," the great circle that passes through the Galactic center and the galactic poles. The galactic coordinate system is useful for describing an object's position with respect to the galaxy's center. For example, if an object has high galactic latitude, you might expect it to be less obstructed by interstellar dust.
Transformations between coordinate systems

One can use the principles of spherical trigonometry as applied to triangles on the celestial sphere to derive formulas for transforming coordinates in one system to those in another. These formulas generally rely on the spherical law of cosines, known also as the cosine rule for sides. By substituting various angles on the celestial sphere for the angles in the law of cosines and by thereafter applying basic trigonometric identities, most of the formulas necessary for coordinate transformations can be found. The law of cosines is stated thus:
To transform from horizontal to equatorial coordinates, the relevant formulas are as follows:
where is the right ascension, is the declination, is the local sidereal time, is the altitude, is the azimuth, and is the observer's latitude. Using the same symbols and formulas, one can also derive formulas to transform from equatorial to horizontal coordinates:
Transformation from equatorial to ecliptic coordinate systems can similarly be accomplished using the following formulae:
where is the right ascension, is the declination, is the ecliptic latitude, is the ecliptic longitude, and is the tilt of Earth's axis relative to the ecliptic plane. Again, using the same formulas and symbols, new formulas for transforming ecliptic to equatorial coordinate systems can be found:
| General Astronomy | ||
| The Modern View of the Cosmos | Observational Astronomy | Motion and Gravity |
Motion and Gravity
| General Astronomy | ||
| Observational Astronomy | Print version | Principles of Light |
The Early Origins of Astronomy

Thousands of years ago, the night sky was much more a part of everyday life than it is today. Without light pollution from streetlights, anyone could see thousands of stars or the path of the Milky Way through the sky. The motion of the stars provided an essential calendar for predicting the weather, so ancient people were accordingly very attentive and observant of the heavens and the rest of their surroundings. These ancient observations were the foundation for what would become modern astronomy, and were the first manifestations of scientific thought in society.
A central principle in scientific reasoning is that the world is inherently orderly and capable of being understood, and that observation is the means by which we can learn about how the universe works. There is, however, nothing that requires the universe to make sense or be accessible to human understanding. Humanity has placed trust in the ideas behind the scientific method because science has been so successful, and so much of the world really does obey a set of rules.
The ingredients that make up a successful philosophy of science were not conceived all at once, but rather in a gradual process of development over the entire course of history. The ancients could never have known in advance which principles of scientific method would eventually prove to be reliable. In its adolescence, society stumbled through the dark to learn about the world, to discover how their experiences could teach them what the universe was like, and to identify the boundaries between reason and superstition. The story of the development of science in cultures throughout the world is revealing not only of the nature of the world and of truth, but also of human nature more generally.
Ancient artifacts going as far back as 20 thousand years, to the paleolithic age, may arguably be related to astronomy, although the interpretation of such artifacts is a subject of controversy. The best-known examples are found in the caves of Lascaux in France, where a variety of paleolithic artwork are found. Some specimens found in the caves might possibly depict the Pleiades star cluster or the zodiac. Animal bones nearby have markings such that they could have been used as a lunar calendar. Although artifacts from the paleolithic era are scarce and ambiguous, this scarcity does not necessarily imply that the peoples of the period took no interest in the heavens. Modern aboriginal cultures, for example, pass down ceremonies with strong astronomical symbolism that would not reflect themselves in archaeological artifacts.

The character of artifacts of the neolithic period is markedly different, since understanding of the skies and the calendar clearly bear deep meaning for agricultural cultures in even the earliest times. Observers gained the ability to manage the planning of significant annual events. The motions of the heavens develop a profound influence on the affairs of humanity, and this influence comes to manifest itself in religious interpretations of heavenly phenomena and worship of the planets, practices that form the origins of both astrology and astronomy.
Ancient monuments and markers demonstrate societies' early interest in the heavens to archaeologists and historians. Many graves of this period are aligned with the cardinal directions. Ancient monuments and altars of sacrifice face east, south, or west to within a few degrees — a clear indication that neolithic peoples had begun very early to identify the most fundamental concepts of astronomy. The most famous of the ancient monuments is Stonehenge. The stones of the monument mark the positions of sunrise on the summer solstice, among other things.
Several of the planets have been known since prehistoric times. These bodies are very bright, and they wander among the fixed stars, through the constellations. These were known to the Greeks as planētēs, "wanderers". The ancients knew of 7 "planets": the Sun, the Moon, Mercury, Venus, Mars, Jupiter, and Saturn. The names for the seven days of the week come from the Norse gods: Sunday (the Sun), Monday (the Moon), Tuesday (Mars/Tiw), Wednesday (Mercury/Wodan), Thursday (Jupiter/Thor), Friday (Venus/Frigg), and Saturday (Saturn/Soeternes).

Highly systematic and carefully recorded observation of the heavens appears as early as the third millennium BC, in the ancient Mesopotamian civilization of Babylon. The Babylonians also developed the earliest timekeeping instruments. Of perhaps even greater significance, however, was the birth of astrology in Mesopotamia. The astrologers of Babylon were the first to suppose a cause and effect relationship between heavenly and earthly events, and the first to imagine an underlying order in nature — though no real connection between human and celestial events existed, the prophecies of astrology were the ancestors of modern scientific prediction.
The early astronomers understood a great deal about the world around them. By Aristotle's time, many people believed that the world was round. They knew this from several sources of evidence:
- When ships sailed beyond the horizon, those watching from land would see the hull disappear first, and then would watch the sail disappear. Sailors see the land sink below the horizon bottom-first. From this, they gathered that the surface of the world was curved, and that the ship was moving around the curvature of the Earth.
- Ancient people supposed eclipses of the Moon to be the shadow of the Earth. Shadows seen during lunar eclipses were always round. The only shape that always casts a round shadow is a sphere. This suggested that the Earth was spherical.
- Travelers noticed that new stars became visible as they moved in their journeys. When travelers move north, the North Star and the northern constellations gain altitude in the sky. The ancients recognized that this implied that the Earth is curved.
Aristotle mentions in his writings that some thinkers of his time hold that the Earth is flat, while others believe it to be spherical. He himself argues firmly that the Earth is a sphere. After Aristotle's time, nearly all Western writers claim that the Earth is a sphere.

In the third century BC, the Hellenistic Egyptian scholar Eratosthenes served as head of the library of Alexandria, where he studied and wrote on a variety of subjects. During his studies, Eratosthenes learned that the Sun cast no shadow on midday of the summer solstice from the city of Syene. From Alexandria, Eratosthenes observed that the Sun did cast a shadow, and he measured that the angle between the Sun and the zenith was about seven degrees when the Sun was highest in the sky.
Eratosthenes knew he could measure the circumference of the Earth by measuring the distance between Alexandria and Syene, assuming that the Sun was at the highest point in both cities at the same time. Since 7 degrees is 7/360 of a circle, the distance between Syene and Alexandria must be 7/360 (or, equivalently, about 1/50) of the circumference of Earth.
Eratosthenes estimated the distance between Syene and Alexandria to be about 5,000 stadia, and concluded that the circumference of the Earth was about 50 times that, or 250,000 stadia. The stadium was a common unit of distance in the ancient world, comparable to kilometers or miles in modern usage; the exact length meant by a stadium varied over history and from region to region, so it is difficult to compare Eratosthenes's estimate with modern values. Most values of the stadium, however, translate to a circumference in the area of 40,000 kilometers, which is remarkably close to the accepted circumference of 40,070 kilometers.
As science was beginning to grow in the cultures of Western civilization, it was likewise taking root elsewhere in the world. Ancient and medieval China, India, and America in particular have been centers of the scientific world.
The history of science in India is one of the longest and best documented in the world. Largely isolated from the rest of the world through much of its earliest history, India was free to develop its unique flavor of astronomical practice at its own pace and without external influence. Ancient India had no system of astrology, but celestial timekeeping became popular very early. The first astronomers monitored the progression of the year and tracked the movement of the Sun, Moon, and planets through the nakshatra, the Indian zodiac.
The quality of these observations would make it possible for later Indian astronomers to detect the effects of precession, just as Hipparcos had done for Greek astronomy. Indian astronomers of the Middle Ages estimated the speed of precession to be 54 seconds per year. Although this is much more accurate than Hipparcos's measurement, we must note that the number 54 was chosen for mystical rather than scientific reasons. Ancient people throughout the world mixed mysticism with arithmetic in this way, but we see this much more consistently in the Indian culture than in any other.
The Christian era brought great change to Indian astronomy. By about the year AD 519, Babylonian conquest had spread into the Indus basin, and many Greek scholars had already visited or settled. Naturally, cultural exchange took root.
The ancient Chinese valued astronomy very highly. Systematic observation of the heavens may have begun in China as early as the third millennium BC. Science was viewed as a powerful tool and therefore guarded very closely by the state. Under dynastic rule, the perceived purpose of astrology and astronomy was to remind the people of the connection between the emperor and celestial events. Accordingly, astrology was charged specifically to an Astronomical Bureau appointed by the emperor and carried out according to strict rules.
The Chinese regarded celestial events as important omens, particularly in the case of "guest stars," stars that temporarily appeared in the sky and quickly faded away. Today we know that these are stellar explosions called supernovae. In the year AD 1054, a new supernova became bright enough to be visible even during the day. Chinese and Arab astronomers recorded the event, and it appears to be depicted in an American cave painting. Because of the importance the Chinese assigned to supernovae, their observations of ancient supernovae are by far the most complete in the world, and remain useful as a source of scientific data even today.

Meanwhile, astronomy was thriving in pre-Columbian America, where interest in the heavens was widespread. Astronomy held a high position in the Mayan civilization, which dominated Mesoamerica for two thousand years prior to the arrival of Europeans. The Maya people believed that patterns in nature were very important, and that it should be possible to use astrology to predict the future based on past experience. This made the observation of celestial cycles very important, since they would give advance knowledge of future events, and Mayans dutifully kept track of motions of the Sun and Moon. With the accumulation of centuries of observation, Mayan astronomers were able to predict eclipses and measure the lengths of heavenly cycles very well.
Similar ideas were sprouting throughout the Americas. Throughout the Americas, ancient people built monuments, buildings, mounds, and temples aligned with rising and setting points of important stars, or with the northernmost and southernmost positions of the Moon. Calendars and monuments like Stonehenge are found here. Clearly, interest in the heavens was common throughout the ancient world, as were the rudimentary beginnings of science.

Scientific thought has appeared throughout history and all over the world, but it's clear that the scientific enterprise enjoyed more success in some areas and time periods than in others. The reasons for this are entirely unclear. What factors of culture, economics, and philosophy affect the rise of scientific thought? The Babylonian culture, for example, did not permit deviation of any kind from tradition or conventional practice. Such a culture might be expected to hinder the progress of science, yet science and mathematics flourished there. In ancient China, only nobles were permitted to practice science. Some historians have suggested that this culture prevented a renaissance that might otherwise have occurred in China long before the European Renaissance. This question of the interplay between science and sociology has been the subject of great interest in the study of the history of science.
While magic and superstition were a significant part of early thought and difficult to isolate from the emerging pursuit of science, it would be unfair to say that spiritualism completely permeated the first ideas about the nature of the universe. The scientific spirit, the principle of learning about the universe by observing it, was clearly present even from the earliest times, and scientific thought has been remarkably widespread. Anaximander (611-547 BC) postulated that there were five elements: earth, air, fire, water...and quintessence, which heavenly bodies were made of.
Astrology is based on Ptolemy's Tetrabiblos, written in 140 AD. The horoscope is divided up into 12 "houses", 12 constellations along the ecliptic. Ptolemy believed that an "8th Sphere" held up the stars in the sky.
Kinetic energy is the energy of motion. The formula for this is ( is mass, and is velocity). Before the common acceptance of the heliocentric model in the mid 1500s, the Earth was believed to be the center of the known universe. Many inherent problems in the geocentric model of the universe led Nicolaus Copernicus to formulate an alternate means by which planets and stars moved. Two such problems are the apparent retrograde motion of various planets, specifically Mars, and the ensuing epicycle theory made to compensate for this issue, as well as the phases of Venus that occur.
Planetary Motion and Epicycles

Viewing Earth as the center of our universe, many of the planets in our solar system take on a peculiar motion across the night sky. For instance, Mars appears to move in a retrograde fashion from time to time. Since the geocentric model holds that all the planets in our solar system orbit the Earth, this would mean that from time to time Mars reverses its orbital direction only to resume it later. The Greek astronomer, Ptolemy, sought to explain this phenomenon with the use of epicycles - that is, small circular motions that planets orbiting the Earth followed on top of their circular orbit around the Earth. Astronomers from Greek times to the Enlightenment compensated for flaws in the geocentric model by adding extra layers of epicycles, until the system was so complex it became virtually unusable. Copernicus' heliocentric model, placing the Sun at the center with planets going around it rather than around the Earth, rid the universe of many of the epicycles that plagued astronomy at that time.
Phases of Venus

Another problem with the geocentric model occurred when observing Venus and its relative phases: should Venus and the Sun orbit the Earth, then it would be impossible for Venus to be in the "full" phase, that is complete illumination (similar to a full moon). Thus, the Ptolemaic model predicted only crescent and new phases of Venus. Yet, as Galileo observed, this was clearly not the case; Venus exhibited all phases of the moon, a phenomenon predicted and accounted for by Copernicus' model. Discovered by Galileo, this phenomenon was one of the key factors that would end up supporting the Heliocentric view of the universe.
Note that this is only one of a number of observations made by Galileo that contradicted the ancient beliefs, but this one most directly called into question the idea that planets orbit the Earth.
References
- Shea, William R. Galileo in Rome: the Rise and Fall of a Troublesome Genius. New York: Oxford UP, USA, 2004.
The modern heliocentric model of the universe was proposed by Nicolaus Copernicus in his book De revolutionibus orbium coelestium which was published just before his death to avoid prosecution for heresy. It addressed many of the problems associated with the Ptolemaic model which required a multitude of epicycles to describe planetary motion. Heliocentrism places the Sun at the center of the solar system. While some of the ancient civilizations in India and the Middle East had proposed the heliocentric model before, Copernicus' discovery set the groundwork for the modern view of the solar system.
Copernicus' Model

In Copernicus' heliocentric model, there are seven theories he presents:
- There exists more than one center of the universe.
- There is a center of the universe near the sun.
- The planet Earth is not the center of our universe.
- The scale of distances between the Earth and the Sun is minuscule compared with the astronomical distances between Earth and the stars in the sky.
- The Earth revolves around the sun, thus causing the annual cycles of the seasons that we witness.
- The Earth's own rotation causes the stars to appear to shift every night, rather than any motion of the stars themselves.
- Any retrograde motion, previously explained by epicycles, is in fact caused by the differing orbital velocities of planets around the sun.
Copernicus harbored his belief of heliocentrism for many years, and did not publish his work until 1542, a year before he died. Some speculate that Copernicus held onto his idea for a considerable time simply because he was fearful of the reception it would have among his peers and more importantly, the Church. Many consider the publication of De revolutionibus orbium coelestium (On the Revolution of the Celestial Sphere) to be the start of the Scientific Revolution.
In the years that followed, Copernicus' theory was refined and independently verified by notable scientists, most prominently Galileo and Kepler. Specifically, Galileo noted that all phases of Venus occurred (similar to our moon), which cannot be adequately explained in a geocentric model. This contradicted the solely new and crescent phases predicted by the geocentric model.
Acceptance by the Church
The principle behind rockets was discovered in 100 BC. An early rocket was the aeolipile, a steam-powered device. Johannes Kepler was a mathematician who attempted to derive a set of fundamental principles which would explain the motions of the planets. He believed in the heliocentric view of the solar system proposed by Copernicus, and he also possessed a rich set of observations of the planets made by Tycho Brahe.
After twenty years of painstaking attempts and various discarded ideas based on geometry, he finally arrived at a mathematical model of orbital motions based on the ellipse. Kepler summarized his findings in the form of three laws of planetary motion, frequently referred to as Kepler's First, Second and Third Laws, respectively:
- Kepler's First Law, also known as The Law of Ellipses — The orbits of the planets are ellipses, with the sun at one focus.
- Kepler's Second Law, or The Law of Equal Areas in Equal Time — The line between a planet and the sun sweeps out equal areas in the plane of the planet's orbit over equal times.
- Kepler's Third Law, or The Law of Harmony — The time required for a planet to orbit the sun, called its period, is proportional to half the long axis of the ellipse raised to the 3/2 power. The constant of proportionality is the same for all the planets. It is often called the Law of Harmony because it shows a harmonic relation between distances and periods.
At that time he developed these laws, there was not yet a developed theory of gravity capable of explaining why the planets moved as they were observed to. Later, Isaac Newton, using his universal inverse-square law theory of gravity, was able to show how Kepler's Laws fit into a scientific theory of celestial mechanics.
Elliptical orbits
An ellipse is a shape formed by taking a diagonal slice through a cone. It is essentially the shape of a circle viewed at an angle.
An ellipse can be drawn by taking a piece of paper, two push-pins, a loop of string, and a pencil. The two pins are pushed through the paper into a suitable surface, providing the two foci for the ellipse. They should be closer together than the loop is long. The loop of string is placed around the base of these pins, leaving some slack. The pencil is now placed so that the pins and the loop form a triangle with a slight tension on the string.
Now try to draw a shape by moving the pencil about the pins while keeping the string taunt. The result should be an ellipse. The shape of the ellipse can be varied either by moving the pins closer together or further apart. This shape, according to Kepler, defines the path that a planet takes when it orbits the Sun.

|
| Kepler's First Law - A planet orbits the Sun on an ellipse with the Sun at one focus. |
Kepler's Second Law says in brief that an object speeds up as it gets closer to the Sun and slows down as it moves further away. Where the distance from the Sun to the orbital path is longer, only a smaller arc needs to be traversed to sweep out an area that requires a wider arc near the Sun.
As the planet moves closer to the Sun along its orbit the gravitational force works to increase the velocity. In contrast, as the planet is moving further away, the gravity of the Sun gradually decelerates the body and it is slowed down.

|
| Kepler's Second Law - A planet in orbit about the Sun sweeps out equal areas in the same time interval . |
A line that divides an ellipse in half and passes through the widest part of the ellipse is called the major axis. A line perpendicular to this axis and dividing the ellipse in half is called the minor axis. Half the length of the major axis is called the semi-major axis, and is represented by . The period required for a planet to complete one full orbit is represented by . The relationship between the period P and the length of the semimajor axis is known as Kepler's Third Law, and can be represented as follows:
where the symbol ∝ means "proportional to", and implies that there is a direct mathematical relationship between the period squared and the length of the semi-major axis cubed.
The Second and Third Laws provide a basis for calculating the period of any planet orbiting the Sun, as well as determining where the planet will be located along the orbital path.
Eccentricity and Orbital Paths
The ratio of the distance of a focus from the center of an ellipse to the semi-major axis is called the eccentricity of the orbit. When the two foci of the ellipse are on top of each other, the eccentricity is exactly 0.0 and the shape is a circle. As the eccentricity increases, the orbiting planet moves much further away than at the closest approach. The orbital eccentricities for planets in our Solar system vary from as much as 0.21 for Mercury down to 0.0068 for Venus.
The scientific name for the point of closest approach is the periapsis, while the most distance separation is the apoapsis. In the case of planets orbiting the Sun, these are called the perihelion and aphelion, respectively. (The -helion suffix comes from the Greek name for the Sun deity, Helios. This word is also the source of the name for the element Helium.)

|
| Two elliptical orbits with the same major axis but different eccentricity. |
Perhaps the most counter-intuitive aspect of the Third Law is that for any two identical bodies orbiting the Sun with the same semi-major axis, the orbital period is the same. This is true even if one is orbiting in a perfect circle and the other has an orbit that is highly elliptical (has a relatively high eccentricity). The elliptical shape will fit entirely within the circle except at two points (the ends of the major axis, at which the two curves will be tangent), so it is actually a shorter orbital path. However the aphelion of the ellipse will be located further from the Sun, so the planet will spend more time traversing the distant section of the orbit. The shorter orbit and the slower traverse of the aphelion compensate for each other, resulting in an identical period with the circular orbit.
Some Examples Using Kepler's Third Law
Originally, Kepler's Third Law was used to describe the motions of the planets around the Sun. As it turns out, it also works very well with regards to other two-body orbital systems like the orbits of moons around Jupiter, or the orbits of binary stars about the center of mass of their system. In all of these cases the period of the orbit squared is proportional to the length of the semi-major axis cubed, with the differences between the orbital systems reflected in the constant of proportionality.
In this section we will consider the special case of the planets going around the Sun. If we choose to measure the length of the semi-major axis of an orbit in astronomical units (abbreviated AU, where 1 AU is the distance from the Earth to the Sun) and we measure the orbital period in years (abbreviated as ), then we can express Kepler's Third Law as
where is measured in years and is measured in astronomical units. What follows are a few example of how to use this equation.
Mars' Orbital Period
Repeated measurements of Mars' orbit have determined that the semi-major axis of its orbit has a length of 1.52 AU. How long does it take for Mars to orbit the Sun once?
Solution: In this question, we are being asked for the orbital period of Mars. We know from reading the question that the length of the semi-major axis is 1.52 AU. Solving Kepler's Third Law for the period gives us
which tells us that it takes 1.87 years for Mars to go around the Sun once.
An Unknown Asteroid's Orbital Semi-Major Axis
An amateur astronomer spends several months tracking an asteroid and is able to determine that it takes approximately 3/4 of a year for it to orbit once around the Sun. What is the semi-major axis of this asteroid's orbit?
Solution: Reading the question tells us that the orbital period of the asteroid is 3/4 of a year, or 0.75 . We are expected to find the length of the semi-major axis , so we need to solve Kepler's Third Law for that. Doing so gives us
which means that is has a semi-major axis somewhere between that of Venus' orbit and Earth's orbit.
| General Astronomy | ||
| Observational Astronomy | Motion and Gravity | Principles of Light |
The Early Origins of Astronomy
| General Astronomy | ||
| Coordinate Systems | Print version | The First Physics |

Thousands of years ago, the night sky was much more a part of everyday life than it is today. Without light pollution from streetlights, anyone could see thousands of stars or the path of the Milky Way through the sky. The motion of the stars provided an essential calendar for predicting the weather, so ancient people were accordingly very attentive and observant of the heavens and the rest of their surroundings. These ancient observations were the foundation for what would become modern astronomy, and were the first manifestations of scientific thought in society.
A central principle in scientific reasoning is that the world is inherently orderly and capable of being understood, and that observation is the means by which we can learn about how the universe works. There is, however, nothing that requires the universe to make sense or be accessible to human understanding. Humanity has placed trust in the ideas behind the scientific method because science has been so successful, and so much of the world really does obey a set of rules.
The ingredients that make up a successful philosophy of science were not conceived all at once, but rather in a gradual process of development over the entire course of history. The ancients could never have known in advance which principles of scientific method would eventually prove to be reliable. In its adolescence, society stumbled through the dark to learn about the world, to discover how their experiences could teach them what the universe was like, and to identify the boundaries between reason and superstition. The story of the development of science in cultures throughout the world is revealing not only of the nature of the world and of truth, but also of human nature more generally.
Ancient artifacts going as far back as 20 thousand years, to the paleolithic age, may arguably be related to astronomy, although the interpretation of such artifacts is a subject of controversy. The best-known examples are found in the caves of Lascaux in France, where a variety of paleolithic artwork are found. Some specimens found in the caves might possibly depict the Pleiades star cluster or the zodiac. Animal bones nearby have markings such that they could have been used as a lunar calendar. Although artifacts from the paleolithic era are scarce and ambiguous, this scarcity does not necessarily imply that the peoples of the period took no interest in the heavens. Modern aboriginal cultures, for example, pass down ceremonies with strong astronomical symbolism that would not reflect themselves in archaeological artifacts.

The character of artifacts of the neolithic period is markedly different, since understanding of the skies and the calendar clearly bear deep meaning for agricultural cultures in even the earliest times. Observers gained the ability to manage the planning of significant annual events. The motions of the heavens develop a profound influence on the affairs of humanity, and this influence comes to manifest itself in religious interpretations of heavenly phenomena and worship of the planets, practices that form the origins of both astrology and astronomy.
Ancient monuments and markers demonstrate societies' early interest in the heavens to archaeologists and historians. Many graves of this period are aligned with the cardinal directions. Ancient monuments and altars of sacrifice face east, south, or west to within a few degrees — a clear indication that neolithic peoples had begun very early to identify the most fundamental concepts of astronomy. The most famous of the ancient monuments is Stonehenge. The stones of the monument mark the positions of sunrise on the summer solstice, among other things.
Several of the planets have been known since prehistoric times. These bodies are very bright, and they wander among the fixed stars, through the constellations. These were known to the Greeks as planētēs, "wanderers". The ancients knew of 7 "planets": the Sun, the Moon, Mercury, Venus, Mars, Jupiter, and Saturn. The names for the seven days of the week come from the Norse gods: Sunday (the Sun), Monday (the Moon), Tuesday (Mars/Tiw), Wednesday (Mercury/Wodan), Thursday (Jupiter/Thor), Friday (Venus/Frigg), and Saturday (Saturn/Soeternes).

Highly systematic and carefully recorded observation of the heavens appears as early as the third millennium BC, in the ancient Mesopotamian civilization of Babylon. The Babylonians also developed the earliest timekeeping instruments. Of perhaps even greater significance, however, was the birth of astrology in Mesopotamia. The astrologers of Babylon were the first to suppose a cause and effect relationship between heavenly and earthly events, and the first to imagine an underlying order in nature — though no real connection between human and celestial events existed, the prophecies of astrology were the ancestors of modern scientific prediction.
The early astronomers understood a great deal about the world around them. By Aristotle's time, many people believed that the world was round. They knew this from several sources of evidence:
- When ships sailed beyond the horizon, those watching from land would see the hull disappear first, and then would watch the sail disappear. Sailors see the land sink below the horizon bottom-first. From this, they gathered that the surface of the world was curved, and that the ship was moving around the curvature of the Earth.
- Ancient people supposed eclipses of the Moon to be the shadow of the Earth. Shadows seen during lunar eclipses were always round. The only shape that always casts a round shadow is a sphere. This suggested that the Earth was spherical.
- Travelers noticed that new stars became visible as they moved in their journeys. When travelers move north, the North Star and the northern constellations gain altitude in the sky. The ancients recognized that this implied that the Earth is curved.
Aristotle mentions in his writings that some thinkers of his time hold that the Earth is flat, while others believe it to be spherical. He himself argues firmly that the Earth is a sphere. After Aristotle's time, nearly all Western writers claim that the Earth is a sphere.

In the third century BC, the Hellenistic Egyptian scholar Eratosthenes served as head of the library of Alexandria, where he studied and wrote on a variety of subjects. During his studies, Eratosthenes learned that the Sun cast no shadow on midday of the summer solstice from the city of Syene. From Alexandria, Eratosthenes observed that the Sun did cast a shadow, and he measured that the angle between the Sun and the zenith was about seven degrees when the Sun was highest in the sky.
Eratosthenes knew he could measure the circumference of the Earth by measuring the distance between Alexandria and Syene, assuming that the Sun was at the highest point in both cities at the same time. Since 7 degrees is 7/360 of a circle, the distance between Syene and Alexandria must be 7/360 (or, equivalently, about 1/50) of the circumference of Earth.
Eratosthenes estimated the distance between Syene and Alexandria to be about 5,000 stadia, and concluded that the circumference of the Earth was about 50 times that, or 250,000 stadia. The stadium was a common unit of distance in the ancient world, comparable to kilometers or miles in modern usage; the exact length meant by a stadium varied over history and from region to region, so it is difficult to compare Eratosthenes's estimate with modern values. Most values of the stadium, however, translate to a circumference in the area of 40,000 kilometers, which is remarkably close to the accepted circumference of 40,070 kilometers.
As science was beginning to grow in the cultures of Western civilization, it was likewise taking root elsewhere in the world. Ancient and medieval China, India, and America in particular have been centers of the scientific world.
The history of science in India is one of the longest and best documented in the world. Largely isolated from the rest of the world through much of its earliest history, India was free to develop its unique flavor of astronomical practice at its own pace and without external influence. Ancient India had no system of astrology, but celestial timekeeping became popular very early. The first astronomers monitored the progression of the year and tracked the movement of the Sun, Moon, and planets through the nakshatra, the Indian zodiac.
The quality of these observations would make it possible for later Indian astronomers to detect the effects of precession, just as Hipparcos had done for Greek astronomy. Indian astronomers of the Middle Ages estimated the speed of precession to be 54 seconds per year. Although this is much more accurate than Hipparcos's measurement, we must note that the number 54 was chosen for mystical rather than scientific reasons. Ancient people throughout the world mixed mysticism with arithmetic in this way, but we see this much more consistently in the Indian culture than in any other.
The Christian era brought great change to Indian astronomy. By about the year AD 519, Babylonian conquest had spread into the Indus basin, and many Greek scholars had already visited or settled. Naturally, cultural exchange took root.
The ancient Chinese valued astronomy very highly. Systematic observation of the heavens may have begun in China as early as the third millennium BC. Science was viewed as a powerful tool and therefore guarded very closely by the state. Under dynastic rule, the perceived purpose of astrology and astronomy was to remind the people of the connection between the emperor and celestial events. Accordingly, astrology was charged specifically to an Astronomical Bureau appointed by the emperor and carried out according to strict rules.
The Chinese regarded celestial events as important omens, particularly in the case of "guest stars," stars that temporarily appeared in the sky and quickly faded away. Today we know that these are stellar explosions called supernovae. In the year AD 1054, a new supernova became bright enough to be visible even during the day. Chinese and Arab astronomers recorded the event, and it appears to be depicted in an American cave painting. Because of the importance the Chinese assigned to supernovae, their observations of ancient supernovae are by far the most complete in the world, and remain useful as a source of scientific data even today.

Meanwhile, astronomy was thriving in pre-Columbian America, where interest in the heavens was widespread. Astronomy held a high position in the Mayan civilization, which dominated Mesoamerica for two thousand years prior to the arrival of Europeans. The Maya people believed that patterns in nature were very important, and that it should be possible to use astrology to predict the future based on past experience. This made the observation of celestial cycles very important, since they would give advance knowledge of future events, and Mayans dutifully kept track of motions of the Sun and Moon. With the accumulation of centuries of observation, Mayan astronomers were able to predict eclipses and measure the lengths of heavenly cycles very well.
Similar ideas were sprouting throughout the Americas. Throughout the Americas, ancient people built monuments, buildings, mounds, and temples aligned with rising and setting points of important stars, or with the northernmost and southernmost positions of the Moon. Calendars and monuments like Stonehenge are found here. Clearly, interest in the heavens was common throughout the ancient world, as were the rudimentary beginnings of science.

Scientific thought has appeared throughout history and all over the world, but it's clear that the scientific enterprise enjoyed more success in some areas and time periods than in others. The reasons for this are entirely unclear. What factors of culture, economics, and philosophy affect the rise of scientific thought? The Babylonian culture, for example, did not permit deviation of any kind from tradition or conventional practice. Such a culture might be expected to hinder the progress of science, yet science and mathematics flourished there. In ancient China, only nobles were permitted to practice science. Some historians have suggested that this culture prevented a renaissance that might otherwise have occurred in China long before the European Renaissance. This question of the interplay between science and sociology has been the subject of great interest in the study of the history of science.
While magic and superstition were a significant part of early thought and difficult to isolate from the emerging pursuit of science, it would be unfair to say that spiritualism completely permeated the first ideas about the nature of the universe. The scientific spirit, the principle of learning about the universe by observing it, was clearly present even from the earliest times, and scientific thought has been remarkably widespread.
| General Astronomy | ||
| Coordinate Systems | The Early Origins of Astronomy | The First Physics |
The First Physics (Aristotle)
Anaximander (611-547 BC) postulated that there were five elements: earth, air, fire, water...and quintessence, which heavenly bodies were made of.
Astrology is based on Ptolemy's Tetrabiblos, written in 140 AD. The horoscope is divided up into 12 "houses", 12 constellations along the ecliptic. Ptolemy believed that an "8th Sphere" held up the stars in the sky.
Kinetic energy is the energy of motion. The formula for this is ( is mass, and is velocity).
Difficulties in the Geocentric Model
Before the common acceptance of the heliocentric model in the mid 1500s, the Earth was believed to be the center of the known universe. Many inherent problems in the geocentric model of the universe led Nicolaus Copernicus to formulate an alternate means by which planets and stars moved. Two such problems are the apparent retrograde motion of various planets, specifically Mars, and the ensuing epicycle theory made to compensate for this issue, as well as the phases of Venus that occur.
Planetary Motion and Epicycles

Viewing Earth as the center of our universe, many of the planets in our solar system take on a peculiar motion across the night sky. For instance, Mars appears to move in a retrograde fashion from time to time. Since the geocentric model holds that all the planets in our solar system orbit the Earth, this would mean that from time to time Mars reverses its orbital direction only to resume it later. The Greek astronomer, Ptolemy, sought to explain this phenomenon with the use of epicycles - that is, small circular motions that planets orbiting the Earth followed on top of their circular orbit around the Earth. Astronomers from Greek times to the Enlightenment compensated for flaws in the geocentric model by adding extra layers of epicycles, until the system was so complex it became virtually unusable. Copernicus' heliocentric model, placing the Sun at the center with planets going around it rather than around the Earth, rid the universe of many of the epicycles that plagued astronomy at that time.
Phases of Venus


Another problem with the geocentric model occurred when observing Venus and its relative phases: should Venus and the Sun orbit the Earth, then it would be impossible for Venus to be in the "full" phase, that is complete illumination (similar to a full moon). Thus, the Ptolemaic model predicted only crescent and new phases of Venus. Yet, as Galileo observed, this was clearly not the case; Venus exhibited all phases of the moon, a phenomenon predicted and accounted for by Copernicus' model. Discovered by Galileo, this phenomenon was one of the key factors that would end up supporting the Heliocentric view of the universe.
Note that this is only one of a number of observations made by Galileo that contradicted the ancient beliefs, but this one most directly called into question the idea that planets orbit the Earth.
References
- Shea, William R. Galileo in Rome: the Rise and Fall of a Troublesome Genius. New York: Oxford UP, USA, 2004.
The Heliocentric Model (Copernicus)
The modern heliocentric model of the universe was proposed by Nicolaus Copernicus in his book De revolutionibus orbium coelestium which was published just before his death to avoid prosecution for heresy. It addressed many of the problems associated with the Ptolemaic model which required a multitude of epicycles to describe planetary motion. Heliocentrism places the Sun at the center of the solar system. While some of the ancient civilizations in India and the Middle East had proposed the heliocentric model before, Copernicus' discovery set the groundwork for the modern view of the solar system.
Copernicus' Model

In Copernicus' heliocentric model, there are seven theories he presents:
- There exists more than one center of the universe.
- There is a center of the universe near the sun.
- The planet Earth is not the center of our universe.
- The scale of distances between the Earth and the Sun is minuscule compared with the astronomical distances between Earth and the stars in the sky.
- The Earth revolves around the sun, thus causing the annual cycles of the seasons that we witness.
- The Earth's own rotation causes the stars to appear to shift every night, rather than any motion of the stars themselves.
- Any retrograde motion, previously explained by epicycles, is in fact caused by the differing orbital velocities of planets around the sun.
Copernicus harbored his belief of heliocentrism for many years, and did not publish his work until 1542, a year before he died. Some speculate that Copernicus held onto his idea for a considerable time simply because he was fearful of the reception it would have among his peers and more importantly, the Church. Many consider the publication of De revolutionibus orbium coelestium (On the Revolution of the Celestial Sphere) to be the start of the Scientific Revolution.
In the years that followed, Copernicus' theory was refined and independently verified by notable scientists, most prominently Galileo and Kepler. Specifically, Galileo noted that all phases of Venus occurred (similar to our moon), which cannot be adequately explained in a geocentric model. This contradicted the solely new and crescent phases predicted by the geocentric model.
Acceptance by the Church
New Ideas About Motion (Galileo)
The principle behind rockets was discovered in 100 BC. An early rocket was the aeolipile, a steam-powered device.
Order in Planetary Orbits
Johannes Kepler was a mathematician who attempted to derive a set of fundamental principles which would explain the motions of the planets. He believed in the heliocentric view of the solar system proposed by Copernicus, and he also possessed a rich set of observations of the planets made by Tycho Brahe.
After twenty years of painstaking attempts and various discarded ideas based on geometry, he finally arrived at a mathematical model of orbital motions based on the ellipse. Kepler summarized his findings in the form of three laws of planetary motion, frequently referred to as Kepler's First, Second and Third Laws, respectively:
- Kepler's First Law, also known as The Law of Ellipses — The orbits of the planets are ellipses, with the sun at one focus.
- Kepler's Second Law, or The Law of Equal Areas in Equal Time — The line between a planet and the sun sweeps out equal areas in the plane of the planet's orbit over equal times.
- Kepler's Third Law, or The Law of Harmony — The time required for a planet to orbit the sun, called its period, is proportional to half the long axis of the ellipse raised to the 3/2 power. The constant of proportionality is the same for all the planets. It is often called the Law of Harmony because it shows a harmonic relation between distances and periods.
At that time he developed these laws, there was not yet a developed theory of gravity capable of explaining why the planets moved as they were observed to. Later, Isaac Newton, using his universal inverse-square law theory of gravity, was able to show how Kepler's Laws fit into a scientific theory of celestial mechanics.
Elliptical orbits
An ellipse is a shape formed by taking a diagonal slice through a cone. It is essentially the shape of a circle viewed at an angle.
An ellipse can be drawn by taking a piece of paper, two push-pins, a loop of string, and a pencil. The two pins are pushed through the paper into a suitable surface, providing the two foci for the ellipse. They should be closer together than the loop is long. The loop of string is placed around the base of these pins, leaving some slack. The pencil is now placed so that the pins and the loop form a triangle with a slight tension on the string.
Now try to draw a shape by moving the pencil about the pins while keeping the string taunt. The result should be an ellipse. The shape of the ellipse can be varied either by moving the pins closer together or further apart. This shape, according to Kepler, defines the path that a planet takes when it orbits the Sun.

|
| Kepler's First Law - A planet orbits the Sun on an ellipse with the Sun at one focus. |
Kepler's Second Law says in brief that an object speeds up as it gets closer to the Sun and slows down as it moves further away. Where the distance from the Sun to the orbital path is longer, only a smaller arc needs to be traversed to sweep out an area that requires a wider arc near the Sun.
As the planet moves closer to the Sun along its orbit the gravitational force works to increase the velocity. In contrast, as the planet is moving further away, the gravity of the Sun gradually decelerates the body and it is slowed down.

|
| Kepler's Second Law - A planet in orbit about the Sun sweeps out equal areas in the same time interval . |
A line that divides an ellipse in half and passes through the widest part of the ellipse is called the major axis. A line perpendicular to this axis and dividing the ellipse in half is called the minor axis. Half the length of the major axis is called the semi-major axis, and is represented by . The period required for a planet to complete one full orbit is represented by . The relationship between the period P and the length of the semimajor axis is known as Kepler's Third Law, and can be represented as follows:
where the symbol ∝ means "proportional to", and implies that there is a direct mathematical relationship between the period squared and the length of the semi-major axis cubed.
The Second and Third Laws provide a basis for calculating the period of any planet orbiting the Sun, as well as determining where the planet will be located along the orbital path.
Eccentricity and Orbital Paths
The ratio of the distance of a focus from the center of an ellipse to the semi-major axis is called the eccentricity of the orbit. When the two foci of the ellipse are on top of each other, the eccentricity is exactly 0.0 and the shape is a circle. As the eccentricity increases, the orbiting planet moves much further away than at the closest approach. The orbital eccentricities for planets in our Solar system vary from as much as 0.21 for Mercury down to 0.0068 for Venus.
The scientific name for the point of closest approach is the periapsis, while the most distance separation is the apoapsis. In the case of planets orbiting the Sun, these are called the perihelion and aphelion, respectively. (The -helion suffix comes from the Greek name for the Sun deity, Helios. This word is also the source of the name for the element Helium.)

|
| Two elliptical orbits with the same major axis but different eccentricity. |
Perhaps the most counter-intuitive aspect of the Third Law is that for any two identical bodies orbiting the Sun with the same semi-major axis, the orbital period is the same. This is true even if one is orbiting in a perfect circle and the other has an orbit that is highly elliptical (has a relatively high eccentricity). The elliptical shape will fit entirely within the circle except at two points (the ends of the major axis, at which the two curves will be tangent), so it is actually a shorter orbital path. However the aphelion of the ellipse will be located further from the Sun, so the planet will spend more time traversing the distant section of the orbit. The shorter orbit and the slower traverse of the aphelion compensate for each other, resulting in an identical period with the circular orbit.
Some Examples Using Kepler's Third Law
Originally, Kepler's Third Law was used to describe the motions of the planets around the Sun. As it turns out, it also works very well with regards to other two-body orbital systems like the orbits of moons around Jupiter, or the orbits of binary stars about the center of mass of their system. In all of these cases the period of the orbit squared is proportional to the length of the semi-major axis cubed, with the differences between the orbital systems reflected in the constant of proportionality.
In this section we will consider the special case of the planets going around the Sun. If we choose to measure the length of the semi-major axis of an orbit in astronomical units (abbreviated AU, where 1 AU is the distance from the Earth to the Sun) and we measure the orbital period in years (abbreviated as ), then we can express Kepler's Third Law as
where is measured in years and is measured in astronomical units. What follows are a few example of how to use this equation.
Mars' Orbital Period
Repeated measurements of Mars' orbit have determined that the semi-major axis of its orbit has a length of 1.52 AU. How long does it take for Mars to orbit the Sun once?
Solution: In this question, we are being asked for the orbital period of Mars. We know from reading the question that the length of the semi-major axis is 1.52 AU. Solving Kepler's Third Law for the period gives us
which tells us that it takes 1.87 years for Mars to go around the Sun once.
An Unknown Asteroid's Orbital Semi-Major Axis
An amateur astronomer spends several months tracking an asteroid and is able to determine that it takes approximately 3/4 of a year for it to orbit once around the Sun. What is the semi-major axis of this asteroid's orbit?
Solution: Reading the question tells us that the orbital period of the asteroid is 3/4 of a year, or 0.75 . We are expected to find the length of the semi-major axis , so we need to solve Kepler's Third Law for that. Doing so gives us
which means that is has a semi-major axis somewhere between that of Venus' orbit and Earth's orbit.
Principles of Light
What is Light?
Light is a medium of energy through which we perceive and interact with our environment. It is the visible frequency range of electromagnetic radiation which also includes invisible forms of electromagnetic radiation such as ultraviolet, infrared, and radio waves.
Like all electromagnetic radiation, light is transmitted by individual packets (or quanta) of energy known as photons. These photons are the units by which the combined forces of electricity and magnetism are communicated between other particles, such as the electrons associated with an atom. Depending on the circumstances under which it is observed, a photon can behave like a particle or as a wave. This principle is known as wave-particle duality.
Wave properties
The wave-like nature of electromagnetic radiation means it can be plotted on a graph as an oscillating electric and magnetic field at right angles to the direction of travel of the wave. The frequency of these oscillations is measured in the number of complete cycles per second, or hertz. The particular frequency of a photon places it somewhere on a spectrum of possible frequencies. This is referred to as the electromagnetic spectrum. The range of frequencies that form the visual spectrum lies between 3.8×1014 hertz (dark red) and 7.5×1014 hertz (violet).
The speed of light, given the symbol c, has been precisely measured as 299,792,458 m/s or approximately three hundred thousand kilometers per second and has been demonstrated to be constant in a vacuum. A vacuum being defined for the purposes of theory and experimentation as a volume of space that is essentially empty of matter. The speed of light is a fundamental constant of modern physics and remains constant regardless of the movement of the observer. Thus, for example, if you were somehow able to travel at half the speed of light, and you measured how quickly light was arriving from the front, you would measure it as arriving at the speed of light (3.00 x 108 m/s).
Since the speed of light is a constant in a vacuum, for a given frequency a photon will have a corresponding wavelength, or the distance between the crests of the wave. The frequency and wavelength of light are directly related by the following equation:
where c is the conventional symbol for the speed of light, usually in meters per second, f is the frequency of light in hertz, and λ is the wavelength in meters.
Given the speed of light as 3.00 × 108 meters per second, then the wavelength range for the visual spectrum is about 400 to 800 nm, or nanometers. (A nanometer is 10−9 meters, or one-billionth of a meter.)
The shorter wavelength of 400 nm corresponds to the greater frequency, and is located at the blue end of the visual spectrum. Likewise the longer wavelength of 800 nm belongs to the red end of the spectrum. The actual energy of the photon increases with decreasing wavelength (or increasing frequency.)
Einstein won the Nobel Prize for applying Planck's theories to electromagnetism.
Intensity
The intensity of a source of radiation is the energy it emits per unit of surface area per unit of time and has the units of Joules/(meter2 x second). As the energy radiated by a spherical surface, I0, moves away from that surface the radiation intensity decreases as the inverse of the distance squared (I=I0/d2) because the radiation spreads out. In other words, the perceived intensity of a light source by an observer is inversely proportional to the distance from the light source squared. Thus for each doubling of distance from the source, the intensity drops by a factor of four, or 2 × 2.
The brightness of stellar objects, such as a star, are determined by the amount of light they radiate and their distance from the Earth. A bright star in the sky might actually be much more distant than an a dimmer star, but because it is more intense and radiates a greater amount of light it appears to be closer.
Astronomers record the light intensity of a stellar object as a numerical magnitude. The magnitude is a number on a logarithm scale that has been standardized, so that 5 steps in magnitude is equal to a multiple of 100 in intensity. In addition, the value of the magnitude increases as the intensity of the light source decreases.
Thus a star of magnitude 2.0 is dimmer than a star of magnitude 1.0. A magnitude 1.0 star is also 100 times as bright as a magnitude 6.0 star. Each +1.0 magnitude increase is the same as dividing the intensity by 2.512.
The reference point for the magnitude scale is set to zero. At one time this was based on the star Vega, or α Lyrae. The brightest star Sirius (α Canis Majoris) has a magnitude of −1.46. The limiting magnitude for a typical person's unaided eye is considered to be 6.0. However people have observed stars fainter than this under good conditions. Much fainter stars can be seen by using the larger collection area of a telescope and the extended recording ability of a camera.
Reflection
A mirror is a flat or curved surface usually made out of a highly-conductive material, such as a metal. When light interacts with a mirrored surface, it undergoes specular reflection. That is, a beam of light striking the mirror is reflected in only one direction. This direction is determined by the law of reflection, which states that the angle with the surface at which the light is reflected is the same as the angle with the surface at which it approaches.

|
| In this illustration, the reflected light rays reaching the eye from an object produce the illusionary appearance of a reversed-image object behind the mirror. |
The movement of a photon with respect to the mirror consists of two components. The first is the proportion of the movement parallel to the mirror, and the second is the portion perpendicular to the mirror. After the reflection, the portion parallel to the mirror is unchanged. However the portion perpendicular is now in the opposite direction. That is, it effectively "bounces" off the surface almost as a rubber ball bounces off the ground.
When light interacts with a surface that is not reflective, a portion of the light is absorbed by the surface and the remainder is scattered in random directions. This type of reflection is called diffuse, and it is responsible for the illumination effect of ambient light.
The portion of light absorbed by a surface is termed its albedo. The lower the albedo rating, the less light it reflects in a diffuse manner. A surface with a low albedo rating appears dark to an observer, while a high albedo rating appears light. The albedo rating of a surface can tell an astronomer something about the nature of the surface. For example, a surface covered with carbon soot will have a low albedo, while an icy surface has a higher albedo.
Refraction
When light passes at an angle through a transparent medium, the material causes the photons to change direction slightly. This change in angle is called refraction, and the angle by which the light is bent is determined by the index of refraction of the material.
The index of refraction of the two materials that the light passes between can be used to determine the change in angle by means of Snell's law. For materials with indices of refraction n1 and n2, the angle in the first material θ1 determines the angle in the new material θ2 as follows:
Here are the indices of refraction (at a wavelength of 589 nm) for some common transparent materials relative to a vacuum:
Material Index Air 1.003 Water ice 1.331 Water 1.333 Quartz 1.46 Crown glass 1.52 Dense flint glass 1.66 Diamond 2.419
where the index of refraction for air is at sea level with a temperature at the freezing point of water, and the water is at 20 °C.
Spectrum
For a given transparent material, such as glass, the refraction of light varies with frequency. A white light consists of photons of various energies. The red photons in the light will be deflected at a different angle than the blue photons.
If the light passes through a transparent material with parallel sides, such as a sheet of glass, the beam will emerge at the same angle as it entered. However when the two sides are not parallel, the angle will vary depending on the frequency. This is the principle behind the prism. A glass prism is used to separate the photons from a light source into a spectrum of frequencies from red to blue. A similar principle is what creates a rainbow as the light from the sun passes through droplets of water.

|
| The index of refraction varies by frequency, causing parallel, monochromatic light rays from the left to emerge from the prism at different angles. |
An instrument specifically designed to display the spectrum of a radiating object, such as a star, is called a spectroscope.
The early spectroscopes were constructed using a series of prisms that would successively spread the spectrum further apart. The problem with this arrangement, however, is that each of the prisms would absorb some of the light passing through. This limited the brightness of the objects that could be observed. An instrument called a diffraction grating, which was a mirror with a series of ruled parallel grooves, used the principle of diffraction to produce a spectrum with only minor loss of intensity.
Isaac Newton discovered that a light beam can be diffracted only so far, and no farther. The diffraction can be recombined into white light.
Lens
The lens takes advantage of the property of refraction to bend the light from a distant object and to make it appear closer (or more distant). A lens is, in a simplified sense, a prism that has been "wrapped" around in a circle, so that the light is bent symmetrically.
Because light of different frequencies is bent at different angles, however, the point at which the light comes to a focus varies with frequency. An observer looking through a lens would see light sources near the edge have a rainbow-like appearance. This is called chromatic aberration.
To adjust for this variation in the focus by frequency, opticians typically use combinations of lenses made of different materials (with differing indices of refraction). Judicious use of materials and lens shapes will result in a lens that focuses all the light at the same distance, producing a good quality image that does not suffer from chromatic aberration.
Magnification
When you observe an object nearby, it subtends an certain angle within your sight. That is, if you had an imaginary line running from the top of the object and your eye and a similar line from the bottom of the object to your eye, there would be a certain angle between these lines.
As the object recedes into the distance, the angle it subtends across your sight steadily decreases until it becomes nearly a point. The imaginary lines from the top and bottom of the object are now nearly parallel. In fact, for an astronomical object such as a star, these lines are essentially parallel.
In order to enlarge the appearance of an object, it is necessary to modify the paths of the incoming light rays so that they are no longer parallel but instead arrive at an angle as they enter your eyes. The eye then perceives the object as if it were much closer.
There are two common means for causing the parallel light rays to converge in this manner. The first involves the use of a curved, concave mirror. The second takes advantage of the refraction ability of materials such as glass to redirect the light inward at an angle.
The shape of glass needed to accomplish this is a convex lens. The portions of the lens near the center need little curvature since they will are required to bend the light only slightly toward your eye. At the edges of the lens, however, the light needs to be bent at a sharper angle, so the sides of the lens become bent toward each other like a prism. Overall the sides of the lens form a smooth curve that gradually increases in slope toward its edges.
A well-made convex lens will cause the parallel light from a distant light source to focus at a point. When there are multiple such light sources, they are each focused at a point on a plane, known as the focal plane. The human eye can perceive the image of this plane, and the result is a magnification of the view. If the images do not focus on a plane, then the image will appear blurry.
Diffraction
Another wave-like property of light is a tendency to bend and spread whenever it meets an obstacle. Any beam of light will also tend to spread with distance, so that it becomes impossible to maintain a tight beam of an arbitrary length. The property of diffraction is what limits the resolution of a distant object.
When a beam of coherent light, such as that produced by a laser, is passed through two slit openings, the light radiates from the slits like ripples in a pond. The semi-circular ripples from the two slits interact with each other, sometimes adding together their wave heights and at other times cancelling each other out. This is called constructive and destructive interference. If a screen is placed in the area where these ripples interact, alternating bands of light and darkness would appear.
Resolution
The resolution of a viewing instrument is a measurement of how well it can be used to distinguish two points that are very close together. For example, the two points could be the two stars in a binary star system. In astronomy, resolution is usually measured in seconds of arc. The resolution can vary depending on a number of environmental and quality conditions, but it is always limited by the aperture of the observing instrument. That is, there is a best possible resolution that any particular telescope can achieve. To get better resolution, a larger aperture is needed.
To see why this is so, imagine a telescope that consists of only two vertical slits separated by some distance, with a viewing screen behind. When the light from a distance star enters this telescope, it passes through the slits and forms an interference pattern on the screen. The distance between the light and dark bands is proportional to the wavelength of the light and inversely proportional to the distance between the slits. Thus increasing the separation of the slits will reduce the width of each band.
Now suppose there are two stars. They will both form bands of light and dark light on the screen, which may overlap. The closer the two stars are two each other, the closer their interference bands approach until they become indistinguishable. But if the separation of the slits is increased, then the bands become narrower and the stars can be distinguished again. This is the principle behind the interferometer.
Interferometer
In an ordinary telescope, the resolution is determined by the aperture. In this respect, a telescope can be thought of as a whole series of slits allowing light through, with the light at the outer edge providing the maximum resolution. The resolution of the telescope can be improved by adding a set of mirrors outside the maximum aperture that collect peripheral light rays, and effectively increase the aperture.
Similarly, two or more telescopes can be configured to work together and provide an aperture at least equal to the separation of their collecting surfaces. This setup is called an interferometer, because the images from both telescopes are integrated through a process of diffraction interference. Radio telescopes have successfully used this technique for many years to achieve very high levels of resolution. Optical interferometers are more difficult to build due to the requirements for extreme precision and the need to dampen out any vibrations.
Reflection gratings
Reflection gratings are surfaces that have been very precisely ruled with a series of parallel grooves. The grooves have a saw-tooth pattern, with each groove consisting of a long flat surface machined at a slight angle, with a sharp step at the edge. Each of the grooves is very narrow, with about 600 lines per mm (15,000 per inch).
As light is reflected from each of the grooves, it is slightly behind the light from the adjacent grooves. This difference produces an interference effect that reinforces the light at certain angles and cancels out the light at others. The grating is very efficient at destructively interfering with the light except at one particular angle, where the light constructively interferes and produces a peak intensity. The angle of this peak varies by the wavelength of the light, so a spectrum is produced.
Polarization
In addition to a direction of travel, a photon is composed of an electric and magnetic field. These lie at right angles to each other and to the direction of travel. This is known as a transverse wave. These perpendicular fields give the photon an orientation. The fields of each photon will maintain their orientation while traveling in a vacuum. Fields of this type are called plane-polarized.
Normally light from a source consists of a large number of photons that have a random polarization. However, it is possible for a number of the photons to become oriented in the same direction, becoming polarized. This coherent orientation can be detected by means of a sheet of polarizing material. When the sheet is oriented in the direction of the polarization, the polarized light passes through. As the sheet is rotated, it transmits a decreasing portion of the polarized light until finally, at right angles to the plane of polarization, it blocks all of the polarized light.
Light can become partly polarized by reflecting from a surface, such as sunlight reflecting off a pool of water. Reflected sunlight provides a source of glare for somebody driving a vehicle. Because this light is partially polarized, the use of polarized sunglasses helps reduce glare by blocking the polarized light preferentially.
Astronomers can examine a stellar light source to determine whether it is a source of polarized light. The presence of polarization is an indication of certain physical properties in effect at the source of the light, or along the line of sight of the light rays. For example, a magnetic field can polarize a light source, as can the acceleration of an electron to a velocity near the speed of light.
Spectral lines
When an atom absorbs a photon of light, the energy is forces the absorbing electron in the atom into an excited state. The electron changes its behavior, effectively becoming more energized and entering a new orbital pattern about the nucleus. A sufficiently energetic photon, or a combination of photons with enough energy, can even knock the electron from the atom. The atom then becomes ionized and gains a net positive charge.
Due to the quantum nature of small particles, the changes in energy allowed for an electron in an atom is fixed to very specific amounts. When a photon of just this energy is captured by the electron, it is must jump to a new and higher energy level. Thus each atom has a specific set of energy bands where it will favorably absorb photons, depending on the current energy states of its electrons.
When a white light is passed through a gas composed of the same type of atom, those atoms will tend to absorb light at those frequencies that match the energies needed for their electrons to jump to a new level. An observer on the other side of the gas who looks at the spectrum will see dark lines where these energies have been absorbed. Likewise an observer looking at the gas from another angle will see bands of light where those same energy frequencies were emitted by the atoms.
This property of selective absorption of light at specific bands is important in astronomy because it allows an astronomer to determine the chemical properties of a distant object. A star, for example, will radiate a spectrum with strong or weak absorption bands, which are determined by the quantities of different gases on its surface. The science of recording and measuring these lines is called spectroscopy.
Doppler shift
As an object moves toward us in space, it may radiate light in our direction. The velocity of the light we receive does not change. However, during the time interval between each of the peaks in the light wave it is transmitting, the object has moved slightly closer toward us. Thus the wavelength grows shorter and appears more blue than normal. Correspondingly, an object moving away from us will have its wavelength stretched out, making it appear more red.
This red-shift or blue-shift property has a number of important applications in astronomy. It can be used to measure the velocity with which a distant object, such as a galaxy, is moving toward or away from us. For objects that are rotating, we can measure the rate of rotation by comparing the blue shift on the edge rotating toward us to the red shift of the edge moving away. We have also discovered binary stars by the regular oscillation of the spectrum toward the blue or the red as the star orbits its companion.
Spectrometry and Photometry
Spectrometry involves looking at the spectra of light. Spectra are what you get when you take light from a source and spread out the colors by passing the light through a prism or over a grating, and then looking at the amount of light at a certain wavelength. There is a huge amount of information that you can get from doing this.
So let's take a spectroscope and point it at something like a fluorescent light bulb or a nebula. The thing that you will see is that rather than a continuous rainbow of all colors or wavelengths, the light is actually a combination of light from different well defined wavelengths. You will see lines.
The reason for these lines is that the electrons in the gas in the fluorescent lights can only be at certain energy levels. When you do something to energize the gas in a fluorescent bulb, the electrons in the atom's gas move to higher energy orbits, which are known as excited states. They stay in those excited states for a length of time ranging from milliseconds to seconds. When the electrons drop from the high energy states to lower energy states, then they will emit light at a wavelength that has an energy (and a corresponding wavelength) equal to the difference between the two energy states. This is known as an emission spectrum.
The detected spectra gives insight into the composition of the object emitting the spectra. Every element and material has its unique set of energy levels and unique lines, and by comparing those the lines of emission spectra with those of known elements, it's possible to discover the object's composition.
When you add energy to an atom, the electrons move to a higher energy state. As the electron relaxes and moves down the energy states, it emits a particle of light for each transition that it makes. Since every energy has a particular color associated with it, each transition puts out light at a single wavelength. The time between stimulation and re-emission is very rapid (in like a microsecond), but there are some materials in which the transition from a high energy state to a low energy state takes a long time. An example of this is glow in the dark stickers. When you expose it to light, it kicks some of the electrons into high energy levels, and it takes seconds to minutes for the electrons to revert to their original state.
One can discover other things about an object from its spectrum. For example, as you increase the temperature, you end up with more and more electrons in higher energy states and this affects the spectrum in that you end up with stronger lines. But if you increase the temperature past a certain point, the electrons leaves the atom completely and the lines become weaker.
You can also discover the pressure and density of the object. As the pressure and density increase, there is a increased chance that particle interactions will change the electrons' energy states to higher or lower level. This causes the lines to grow wider since there is a higher chance that the electron won't start and finish at a particular energy level.
If you increase the pressure and density enough the electrons no longer have enough time to stay at a certain energy level, and so the lines broaden to form what is known as a continuous spectrum, A continuous spectrum is emitted by a solid, liquid, or high pressure gas. Because the electron is no longer restricted to certain energy levels and certain wavelengths, the electron will often emit a low energy infrared photon rather than a photon of light. As a result something that is emitting a continuous spectrum (like a light bulb, specifically an incandescent light bulb) will emit much of its energy at lower frequencies (called heat) compared to something that is emitting a more discrete spectrum (like a fluorescent light bulb). Since energy is conserved, a fluorescent light bulb emits almost all its energy at a few wavelengths very efficiently while an incandescent light bulb emits much of its energy as heat. Hence, a florescent bulb will convert electrical energy into light more efficiently.
There is one more type of spectrum which is very common. If you expose a gas to light of different wavelengths and one of those wavelengths happens to match a difference in energy levels in the gas, it will absorb the light at that particular wavelength. So, if you have a source of a continuous spectrum pass it into cool gas in front of it, you produce what is known as an absorption spectrum. Most stars emit absorption spectrum as the cool upper layers of the stars absorb lines from the light emitted by the hot lower levels of the star.
So far we have been talking just about visible light, but the principles of spectroscopy apply to other types of electromagnetic radiation, of which visible light is just a small slice in the overall range of wavelengths. You can have gamma ray or X ray spectra (at shorter wavelengths than visible light) as well as microwave and infrared spectra (at longer wavelengths than visible light). The big difference has to do with what generates the radiation. The energy differences between different states of an atom typically are the energy of a particle of visible light. An X-ray photon will knock the electron right out of an atom, as a result an X-ray can't be generated by electrons transitioning between atomic energy levels. However, X-rays are generated when atomic nuclei transition between different nuclear energy levels. Conversely, microwave radiation can be generated when molecules move between energy states as they "wiggle." So by observing microwaves you can detect cool clouds of molecular gas by detecting microwaves in the spectrum. Conversely by sending microwaves into something that contains water the molecules will be induced to "wiggle" or in other words heat up. At the same time, the microwaves will pass through things (air or ceramic) whose energy levels don't match the microwaves. So if you put something like a cup of coffee in a microwave oven, all of the energy will be absorbed by the coffee and not by the cup or the air.
One final thing about spectroscopy. Spectrographs are affected by so many things and that every object out there has a different spectrum, and understanding what affects spectrographs and how to glean this information from spectrographs is an important part of astronomy.
Discussion questions
- The stellar classification system from hottest to coolest is OBAFGKM with A being the star with the strongest hydrogen line, B being next strongest and so forth. Why is the stellar classification in this order rather than the more logical order of temperature? Discuss a case from your experience in which a similar reason has led to seemingly odd classification systems.
- Identify three objects and tell me whether they would result in an emission, continuous, or absorption spectrum. Also tell me what you would see if you pointed a spectroscope at you. Would you see an emission, continuous, or absorption spectrum?
- What type of spectrum do you suppose an LCD puts out? What about gold? What about a microwave oven? What about you?
- Using your knowledge of advances in photography, how do you suppose an astronomer takes a spectrum differently today than in 1920? What about 1850? How do you think the Internet can be used to help astronomers take spectra?
- Why do you think it is so tough to create a good looking fluorescent light bulb and how do you think that they do it.
- If I stand in front of 100 watts of radio waves or light waves, nothing bad happens to me. But if I stand in front of 100 watts of gamma rays or X-rays, bad things will happen to me. Why?
The Spectrum
Violet scatters the most, and red the least.
Definition
Spectrum is a word that has taken on a broad meaning in English, first used by scientists such as Isaac Newton in the 1600s to specify the range of colors obtained by passing sunlight through a glass prism, or produce through the natural mechanism of a rainbow. Today it is applied in almost any situation for a broad range of values. Specifically in physics and astronomy it still denotes the range of colors of visible light, but also includes invisible forms of electromagnetic energy ranging from very long wavelength radio waves to the ultra short wavelength gamma radiation.
Producing a Spectrum
Color is analogous to wavelength when we speak of visible light. There are relatively long wavelengths of red light and relatively short wavelengths of blue and violet light. These wavelengths are also indicative of temperature for a heated body; red is cooler while blue is hotter. White light, such as that from the Sun, is not composed of a single color or wavelength, but of a mixture of many colors or wavelengths, which the eye interprets as white.
While all wavelengths of light travel at the same speed through a vacuum, the speed of different wavelengths varies as light passes through a transparent medium such as glass, water or even air. As light passes from one medium (such as air) into another medium (such as glass), its speed changes according to the index of refraction of the two media. In the case of this example, light slows down as it passes into the glass. Blue or violet light is slowed slightly more than red light as it passes from a medium of lower refractive index to one of higher refractive index. This, along with the particular shape of a glass prism, acts to bend or disperse light, spreading the colors out. Since blue light is bent more than red light, the original mixture of light is spread out into its constituent colors to form a spectrum, somewhat like an artificial rainbow.
“The brightness of a star is also dependent on its temperature, and the temperature will have an effect on the spectrum the star emits. If two stars with identical spectra are observed, and the distance of one of the stars through parallax measurement is known, their brightness can be compared. The variance in brightness is attributable to the difference in distance. Using the inverse square law, the distance of the star whose distance was previously unknown can then be determined. Stars can give off radiation not only in the visible spectrum but also as radio waves, x-rays, and gamma rays. All of these different parts of the electromagnetic spectrum can be used in conjunction with the techniques already discussed to make astronomical measurements.”
Types
Spectra types are
- continuous, which are broad bands created by a incandescent solid (such as the red hot element of an electric stove), liquid (such as molten lava) or a high-pressure gas (such as the surface of a star).
- emission, characterized by narrow bright lines, created by an excited, low-pressure gas. Examples of emission spectra sources are a comet's coma and tail, and the Rosette nebula.
- absorption, characterized by narrow dark lines, created by a continuous spectrum that is passed through a low-pressure gas. This is seen in the spectra of the Sun and stars, and is caused by light absorption in the cooler, lower pressure gas atmosphere of the star.
By studying spectra, astronomers can discover many things about stars, most specifically the chemical elements found in the star. “The record of wavelengths (or frequencies) of electromagnetic radiation absorbed by a substance; the absorption spectrum of each pure substance is unique.”
Most stars exhibit absorption line spectra, but a few rare stars show emission lines. Wolf-Rayet stars have emission spectra caused by UV (ultraviolet) radiation from a hot star passed through low-pressure gas. Certain nebulosity or gas clouds also exhibit emission lines. Spectral lines also are detectable in non-visible light such as ultraviolet and microwaves.
Basic Astrophysics
Newtonian Physics
Isaac Newton formulated the Universal Law of Gravitation, the Laws of Motion, and calculus. The Universal Law of Gravitation is summed up in the formula
where and are two masses, in kilograms, and is the gravitational constant . is the distance between the centers of the two masses, in meters. is measured in Newtons.
Work is calculated with the formula
where is work (measured in Joules), is force (measured in Newtons), and is distance (in meters).
Kinetic energy (energy of motion) is calculated by the formula
where is mass (in grams), and is velocity.
Newtonian relativity: A man is walking at 1 km/h, and he throws a ball at 3 km/h. To get the speed of the ball, simply add speeds: .
The First Law of Thermodynamics states that energy can be neither created nor destroyed, only transformed into one of its two forms: energy and matter.
The Four Forces
There are four forces in the universe: gravity, which holds together galaxies and other massive structures; the electromagnetic force, which holds atoms together; the nuclear force, which holds atomic nuclei together; and the weak force, which is concerned with the transmutation of elements and radioactive decay. The nuclear force is the strongest, and gravity is the weakest. Without these forces, the universe would disintegrate.
The gravitational force causes mass to attract mass. More massive objects have a stronger gravitational field.
The electromagnetic force can be summed up by the phrase "opposites attract" and allows atoms to bond with each other creating the great variety of compounds that make our experience possible. The nucleus, with its positive charge, attracts negatively charged electrons. The electro- static force is calculated according to Coulomb's Law.
The power of the nuclear force depends on distance. At a distance of between one and 2*10−15 meters, the force is attractive. However, if distance is too close (less than 10−15 meters), the force is repulsive; and at distances greater than 2*10−15 meters, the force diminishes to zero.
Atoms
The atom was first postulated by the Greek philosopher Democritus. He believed that matter could not be split indefinitely. He believed that all matter was composed of connected particles which could be split apart, but could not be split themselves. These indestructible pieces are called atoms. The word comes from the Greek atomos, which means "uncuttable"---a (not) + tomos (to cut). [3]
The Periodic Table of Elements was created by Dmitri Mendeleev in 1869 (revised in 1871). The manmade elements are radioactive and have short half-lives.
Nuclear reactions are categorized as critical or supercritical. A critical reaction is one neutron in, one neutron out. A supercritical reaction is one neutron in, three neutrons out---releasing a terrific amount of energy. Supercritical reactions are used in atomic weaponry.
Nuclear fusion is a great source of energy, but requires temperatures of 1,000,000 Kelvins.
Particles
All atoms are composed of particles. Particles are characterized by mass, charge, and spin. A particle's spin is right-handed (counter-clockwise) or left-handed (clockwise).
At the center of the atom is the nucleus, which contains a number of protons and neutrons about which the Electrons orbit. The force that keeps the electrons in orbit is the electric force; the force that keeps the nucleus together is the nuclear force.
In a neutral atom, there are equal amounts of protons and electrons. For example, Helium has two protons in its nucleus and two electrons orbiting its nucleus. It also has two neutrons in its nucleus. When there is more electrons than protons, or vice versa, then the atom is called an ion and it is more reactive with other ions and atoms because it has an overall net charge associated with it.
An electron has a negative (-) charge, a proton has a positive (+) charge. Neutrons, neutrinos, and photons have no charge. The most massive of these is the neutron; it can decay into a proton, electron, and a neutrino. Particles are made up of quarks. The six types of quarks are up, down, strange, charmed, top, and bottom.
Antimatter was predicted by Paul Dirac. Every particle has an anti-particle, with the same mass, but an opposite charge and spin. There are anti-electrons/positron, anti-protons, anti-neutrinos, and anti-photons. (The anti-photon has the same spin as the photon.) When a particle meets its anti-particle, the result is mutual annihilation, and the creation of energy. The opposite is also true: when two photons meet, matter is created. This creation of matter is called "pair production".
If there are antimatter stars; their light would be identical to that of matter stars, because the anti-photon is the same as the photon.
Astronomy studies the flow of energy, and forces. Energy comes primarily from two sources: gravity from gaseous clouds collapsing to form stars and planets; and nuclear energy. The fusion that makes stars burn is one type of nuclear energy; another is the radioactive decay that heats the cores of planets.
Earth has a magnetic field. The core has a current. This field causes the Aurora Borealis.
The relationship of frequency and wavelength to the speed of light is shown in the formula
where is frequency, is wavelength, and is the speed of light.
A photon is a discrete packet of light energy. To calculate the energy of a photon, use the formula
is Planck's constant:
is frequency, which is in units of
Einstein's famous equation, , demonstrates that mass and energy can be converted into each other. is energy, is mass, and is the speed of light, .
Spectroscopy
"The one thing that man will never know is the chemical composition of the stars." ---Auguste Comte, 19th century philosopher
He was wrong!
Kirchoff & Bunsen discovered that individual elements burn with different colors. Different colors correspond to different wavelengths of light. The colors given off can be recorded on a photographic plate. This is called the elements' emission spectrum and it is unique to each and every known element. Therefore, any known element in the laboratory can be determined by investigation of its "spectra".
An explanation of why different elements give off different wavelengths of light is needed to explain how the composition of stars can be determined. An individual element has a unique number of protons. If you were to follow the periodic table from left to right, you would find that for the first few lines the atomic number increases by one each time. Hydrogen is the smallest element as it has one proton. Helium is the next smallest, as it has two protons, and so on.
Each of these elements therefore has a different amount of electrons and protons. Assuming these elements are all neutral, each successive element consists of one more electron than the previous element. i.e. helium has two electrons, and hydrogen has one.
Electrons orbit the nucleus of an atom. They can be described as having an energy level associated with them. The electrons in a particular element can only occupy a specific energy level or shell. When elements are heated, there is an input of energy, which is distributed to these electrons and they therefore move to a higher energy level. When this electron falls back to its original energy level, the energy gained by heat must be lost. The electron loses this energy by emitting a photon(a packet of light).
This photon will have exactly the right amount of energy needed to enable the electron to fall to its exact original state. This energy can be calculated using E=hf, where E is the energy, h is Planck's constant, and f is the frequency of the individual photon. While it seems odd that a particle would have a frequency, it does due to wave-particle duality.
From above, it can be seen that each element, because each has electrons that only occupy certain energy levels, that the frequency of the photon emitted can only have certain values.
From the equation c = f * lambda, where c is the speed of light, which is nearly always the same, f is the frequency and lambda is the wavelength, it can be seen that because c is constant, each element, by only emitting photons with certain frequencies, gives off photons with certain wavelengths and therefore colors.
It is impossible to use the laboratory technique of defining elements by using their emission spectrum because the light that we receive from the stars is a combination of colors. There is however, another way. If we were to view the emission spectra of the sun, for example, there would be no signature "barcodes" of individual elements, rather, there would appear a continuous spectrum, like a rainbow on paper. This "continuous" spectrum will have a few black lines, where the wavelength of light has been absorbed rather than been emitted by the Sun's photosphere. It is from these, that we can deduce a stars chemical composition.
It was discovered that the black lines in the continuous spectrum of a star corresponded exactly to the emission lines of certain elements. Their presence in the star is suggested because those elements emit light of the same wavelength that is absorbed and hence, shows as a telltale black line. It receives this light in a concentrated beam but emits it in all directions. If you imagine the light rays as a 20 pack of javelins hitting an element in a certain place, the element will throw these javelins back out individually, into the surroundings so that the amount of light emitted in the direction of Earth is minute or non-existent, and hence we observe dark lines in the emission spectrum.
The Quantum Model of the Atom
Quantum physics is a relatively new branch of physics that deals with very small objects, such as atoms and quarks. It follows different rules than classical (or "Newtonian") physics. While Newtonian physics assumes that energy can be continually divided and holds that an object can have an arbitrarily small amount of energy, quantum physics deals with objects that emit or absorb discrete packets of energy known as quanta that cannot be further divided. Classical physics assumes a continuum whereas quantum physics assumes the universe is discrete.
Max Planck is considered the "father of Quantum Theory".
In 1913, Danish physicist Niels Bohr used Ernest Rutherford's research on the atomic nucleus and Max Planck's quantum hypothesis to create a quantum theory of atoms. This theory stated that an atom's electrons move only in definite orbits. When a hydrogen atom emits an Hα photon, the electron drops to a lower orbit. When a hydrogen atom receives a photon, it jumps to a higher orbit.
The hydrogen spectrum has been studied for ultraviolet (the Lyman series) and visible light (Balmer series). In the Lyman emission series, the electron drops from a higher orbital to the n=1 orbit. In the Balmer emission series, it drops from a higher orbital to the n=2 orbit. (n=1 is the lowest energy state, or orbit, of an electron, called the principal quantum number.) The energy change produced as an electron moves from n=2 to n=1, results in the emission by the electron of a photon of energy 10.2 eV and appears in the ultra-violet part of the spectrum. The energy change produced as an electron moves from n=3 to n=2, results in the emission (H-alpha) by the electron of a photon of energy 1.89 eV and appears in the red part of the spectrum.
The energy levels in a hydrogen atom, can be calculated by:
where is the electron's orbit.
In 1929, Prince Louis de Broglie won the Nobel Prize for his theory of matter waves.
Albert Einstein and the Theory of Relativity
Einstein's Principle of Equivalence demonstrated that gravity causes space to curve. He discovered that the curvature of space determines how matter will move. Thus gravity can be thought of as a consequence of the "shape" of the universe rather than a force vector. This is Einstein's Law of Motion. Under the theory of General relativity light should also be affected by gravity. This phenomenon has been observed by studies of gravitational lensing.
Atomic Emission and Absorption
Most of the information about stars is obtained from studying electromagnetic radiation. Interstellar dust can be observed to get information, as well.
Electromagnetic radiation includes UV (ultraviolet), radio waves, and X-rays. There are two kinds of waves: longitudinal (such as the way sound travels), and transverse (the way light and other electromagnetic radiation travels). Transverse waves are measured by their wavelength and frequency. Wavelength is represented by the Greek letter (lambda). Longer wavelengths make shorter frequency.
The formula for frequency is
where is the speed of EM radiation, meters per second.
Astronomers can learn a lot about distant objects by analyzing spectra. The 3 types of spectra are continuous, emission, and absorption. A continuous spectrum comes from a high pressure blackbody, or thermal source (such as a light bulb). An emission spectrum has bright lines. It is caused by cool, low-pressure gas. An absorption spectrum has dark lines it. It appears when a blackbody's light passes through a cool, low-pressure gas. For example, our sun's surface emits a continuous spectrum, but it becomes an absorption spectrum once it reaches us, because it has passed through the sun's atmosphere. Because of this, all normal stars have absorption spectra.
Since each element has a unique spectrum, astronomers can determine the chemical composition of stars by analyzing their spectra. They can also determine the pressure of the object by the type of spectrum: continuous (high pressure), or emission (low pressure).
Molecular Emission and Absorption
Astronomical spectroscopy is one of the most powerful tools used by astronomers to gain a fundamental understanding of our universe. Astronomical spectroscopy is a technique in which the absorption and emission of electromagnetic radiation from stars and other celestial objects are studied. In order to be able to interpret and predict absorption and emission spectra from celestial bodies, one must have a fundamental understanding of molecular emission and absorption. Molecular emission and absorption is the process in which photons are emitted and absorbed when a molecule changes quantum energy states. By studying molecular emission and absorption, the chemical composition, physical properties, and velocities of astronomical objects may be measured.
Quantum Mechanics
One of the key concepts from quantum mechanics essential to the understanding of molecular absorption and emission is the fact that molecular energy is quantized. In other words, molecules can exist only in specific quantum states with each quantum state having a set amount of energy. The quantized energy stored in a molecule can be thought of as the sum of energy stored in three distinct modes: (1) rotation, (2) vibration, and (3) electronic:
Since the internal energy levels of the molecules are quantized, discrete differences in energy are observed when molecules change quantum states. These transitions correspond directly with the energy of emitted or absorbed photons in discrete spectra. As stated earlier, emission is the process by which a molecule changes quantum states from a higher to a lower quantum state by the release of a photon. Absorption, on the other hand, is the process in which a molecule changes quantum states from a lower energy level to a higher energy level by absorbing a photon.

The total change in energy associated with a molecular transition (emission or absorption), can be described by the following:
In this equation, is the energy of the photon which is equal to the difference in energy associated with the molecular transition between two quantum states, is the frequency of the corresponding electromagnetic wave, and h is Planck's constant. This relation, known as Planck's Law, is important because it links the concepts of thinking of radiation as both a particle and a wave. Figure 1. illustrates the concept of emission due to the electronic transition of electrons orbiting the nucleus of an atom. It should be noted that even though this picture shows electronic transitions for an atom, the same processes govern electronic transitions in molecules. Using Planck's Law, the total change of internal energy in a molecule can be described as:
This equation states that the total internal energy of a molecule is the sum of the changes in rotational, vibrational, and electronic energy. From quantum mechanics, it can be shown that the quantum energy levels for the different modes of internal molecular energy have different spacing. Electronic states are more widely spaced than vibrational states, which are more widely spaced than rotational states. Because of this different spacing, changes in the different modes of internal energy lead to absorption and emission of electromagnetic energy at different wavelengths. Changes in rotational energy lead to microwave transitions, changes in rotational and vibrational energy (vibrotational) lead to infrared transitions, and changes in rotational, vibrational, and electronic energy (rovibronic) result in ultraviolet transitions. It should be noted that changes in vibrational energy are often accompanied with changes in rotational energy and changes in electronic energy are often accompanied by changes in vibrational and rotational energy.
Emission and Absorption Spectra
The absorption and or emission spectra of a molecule generally consist of a number of "lines". These lines correspond to the discrete differences in the internal energy modes of a molecule. In other words, a line is the part of a spectrum that corresponds to a transition from one quantum state to another. Groups of lines can in turn comprise a vibrational band. The positions, strengths, and shapes of lines can give accurate physical characteristics about the molecules undergoing internal energy transitions. The position of spectral lines reveals various molecular parameters such as internuclear spacing and molecular bond angles. Line strengths and shapes, on the other hand, can reveal the composition, temperature, pressure, and velocity of molecules in a radiating gas. This concept is illustrated in figure 2 which shows the emission spectra of hydrogen plasma.

The governing law for absorption spectroscopy that links various molecular properties with the amount of light absorbed in a gas medium is known as Beer's Law.
In this equation, is the fraction of light transmitted through a gas medium, is the frequency of the EM radiation being transmitted, is the spectral absorption coefficient, and L is the absorption path length. A diagram of Beer-Lambert absorption is presented in Figure 3. The spectral absorption coefficient is given by:
where is the "strength" of the transition, is the "lineshape function", and is the partial pressure of the absorbing gas species.
Diatomic Molecular Spectra
The interaction electromagnetic radiation has with matter can be explained through three main types of interactions: electronic dipole moment, induced polarization, and elastic scattering. Interactions with the electric dipole moment result in changes in the absorption and emission of radiation while induced polarization and elastic scattering are a direct result of how a molecule scatters photons. Many diatomic heteronuclear molecules have a permanent dipole. A dipole has a positive charge on one end and a negative charge on the other end of the molecule. The motion of this dipole, through the rotation and vibration of the molecule, allows the molecule to emit or absorb electromagnetic radiation.
Molecular Rotations
As stated earlier, rotations of molecules correspond to transitions in the microwave region of the EM spectrum. When a diatomic molecule rotates, the molecule's dipole moment also rotates, which allows for the absorption or emission at characteristic resonance frequencies. The simplest rotational model for a diatomic molecule describing this process is the rigid rotor approximation. In this model, the atoms of the molecules are point masses with an equilibrium separation distance that is either constant or rigid. Using classical mechanics, the moment of inertia and angular momentum of a molecule can be determined. This information used in conjunction with the molecule's rotational energy allows one to determine the allowed values of rotational energy as a function of quantum number.
Molecular Vibrations
Much as rotations of a molecule can lead to changes in the electric dipole of a molecule, vibrations can also change the electric dipole of a molecule due to stretching of the molecule's internal bonds. This stretching leads to the possibility of emission or absorption of infrared EM radiation. The simplest model for diatomic vibration is the simple harmonic oscillator. In this model, two masses are separated by an equilibrium separation distance. The bond length between the two masses oscillates about this equilibrium distance much like a spring. By using classical mechanics, the fundamental resonant frequency, which is characterized by the bond stiffness and magnitude of the masses, can be used to determine the potential energy stored in the oscillator.
Electronic Transitions
In addition to rotations and vibrations, a molecule's electronic structure can also interact with EM radiation. If the distribution of electrons in a molecule's shell is changed, energy transitions occur which result in emission and absorption of EM radiation in the ultraviolet and visible regions of the electromagnetic spectrum. Electronic spectra involve the transitions that occur between the potential energy wells which correspond to different electronic configurations. The potential wells represent the variation of electronic forces with internuclear spacing.
Quantum Numbers
There are multiple quantum numbers that define the state of each electron: the principal quantum number representing the electrons energy level, the azimuthal (or angular momentum) quantum number denoting the subshell of the electron (i.e. s,p,d,f), the magnetic quantum number specifying the orbital within the subshell, and the spin quantum number defining the spin of the electron (spin up or down).
| Name | Symbol | Meaning | Possible Values |
|---|---|---|---|
| Prinicipal quantum number | n | Energy level of the electron | |
| Azimuthal (angular momentum) quantum number | Subshell of the electron (corresponds to s, p, d, f) | ||
| Magnetic quantum number | m | Orbital within the subshell | |
| Spin quantum number | s | Spin of the electron |
There is also the total angular momentum number: .
Thermal Radiation
Thermal radiation is electromagnetic radiation of a particular frequency range. All objects emit energy in the form of electromagnetic radiation. As the atoms are shaken by random thermal motion, the moving charge of the electrons causes them to emit a changing electromagnetic field. In general, the cooler the body, the slower the motion of its atoms and molecules, and the longer the wavelength of emitted radiation. Thus a human body emits mostly in the infrared part of the spectrum, making night vision cameras so valuable to the military and police. But the tungsten filament of an incandescent light bulb is at a much higher temperature (roughly 3000 K or about 5000 degrees F), causing it to emit mostly visible light.
Thus the spectrum and intensity of the emitted radiation can be used to determine the object's temperature from a distance. If a material is heated above 700 Kelvin, it begins to glow visibly - starting out as a dark red color and moving towards the blue end of the spectrum with increasing temperature. However, most objects radiate a wide range of temperatures, and the effective color perceived by the human eye may not be fully indicative of the true temperature. For example, the Sun appears white to most observers, but the wavelength at which it radiates most of its energy is about 5800 K or roughly 10,000 degrees Fahrenheit, which spectroscopically is equivalent to a green color. However, when the human eye detects the various wavelengths we receive from the Sun, in particular ratios of radiation emitted by the Sun, our eye-brain connection perceives it as white.
The Doppler Effect
The Doppler effect or Doppler shift describes a phenomenon in which the wavelength of radiated energy from a body approaching the observer is shifted toward shorter wavelengths, whereas the wavelengths are shifted to longer values when the emitting object is receding from the observer. This happens with any form of any energy emitted in waves, including sound and light. Sound propagates in a different manner from electromagnetic energy, but the effect is analogous.
With the sound of a moving object, like with a train, the wavelength of the approaching train horn will sound like a buzzing noise at first getting louder intill it passes you and then fades away at a lower tone. That is because the wavelengths that you are hearing is being squished in the front of the train and then stretched out as it passes by. When the wavelength is shorter (coming closer to you) the frequency of the wavelength is going to be bigger, with a higher pitch. The opposite happens when the wavelength is longer; the frequency will be smaller, which is an effect that rapidly changes to a lower pitch as the train passes, going away from you. This works with light waves as well, in terms of visible light. Approaching objects shift toward shorter wavelengths are called blue shifted. Where as the light of receding objects have longer wavelengths, those wavelengths are known as red shifted. As shown in the diagram below if you’re looking outward from the telescope, you can see the red shift going out toward an object, or in this case an unseen planet. Then there are the blue shifted wavelengths that are coming back towards the telescope from the unseen planet.
The relative speed of stars moving toward or away from the Sun, as detected through the doppler effect, gives clues to the Sun's motion through the Milky Way Galaxy as well as other information about the motion of stars, star clusters and gas clouds in space. The relative motions of binary stars (two stars orbiting around a common center of gravity) can be detected in the variations of their light, and in fact even some binary stars have been detected that cannot be seen as separate stars, but whose binary nature is known from the variations in their combined spectra.
Since both sound and light waves have red and blue shifts, Edwin Hubble was able to use the doppler effect to discover that our neighboring galaxies are receding from the Milky Way. This lead to his conclusion that the universe was expanding. The red shift or more specifically known as the Cosmological Red Shift because of its implications for cosmology; the study of origin and evolution of the universe. Scientist could even go further into discovering more of the universe when they realized they could add velocity to Hubble's equation. Using the shift spectrum they now can find the distances based off of those observations.
Telescopes
| General Astronomy | ||
| The Doppler Effect | Print version | Telescopes/Basic Optics |
The word telescope originates from the Greek language (τηλεσκόπιο), and it means literally far-seeing. It is an instrument that is intended to gather information, usually in the form of light or other energy, about a distant location that can not be perceived directly by the unaided eye. Telescopes let you magnify faint stars, and see finer detail. This allows you to, for example, distinguish one star as two stars that are very close (such as Mizar A and B).
Telescopes are used by astronomers to gather visual and other information the human eye alone cannot see. They do so by means of a large collector surface that then directs the incoming energy photons into a smaller focusing lens. This large surface also allows the resolution of fine details that are too close together for the human eye to discern. It was through his usage of the telescope that Galileo discovered that the celestial spheres weren't perfect, as had been thought. He could see sunspots, and the lunar "seas".
Today, observational astronomy covers the entire range of the electromagnetic spectrum. Telescopes detecting other fundamental particles are also very common. Nonetheless, we shall start with our most familiar part in the field, the optical region in the spectrum.
Some difficulties with telescopes are chromatic aberration (different colors focused at different points) and spherical aberration (light isn't focused at a single point). Spherical aberration can occur when the reflecting mirror in a telescope isn't a true parabola.
Adaptive optics are used to compensate for atmospheric distortion which is caused by small changes in the refractive index of the atmosphere, which is responsible for the "twinkling" effect.
The Light Gathering Power of a telescope is measured by the area of the lens divided by the area of the eye.
Large telescopes are housed inside observatories. One of the most famous is the Lick Observatory on Mt. Hamilton, named after James Lick, a streetcar baron, who made donations to have the observatory built. When he died, he was buried beneath it.
Light pollution makes stargazing difficult. This is caused by fixtures (such as streetlamps) that allow light to go up into the atmosphere where it is reflected and creates a "fog" of light that makes viewing very dim distant objects difficult.
The spectrum
Our sense of sight is based upon particles of electro-magnetic energy that are emitted by objects and then collected by our eyes. These particles are vibrating quanta of energy that are known as photons. Every photon oscillates at a particular frequency, and the range of all possible frequencies is called the spectrum.
Human eyes are attuned to a particular frequency range of photons that lie within the visual portion of the spectrum. We can not directly view photons that vibrate at frequencies above or below this range, although measuring instruments have been constructed to measure these parts of the spectrum.
All the information we have about the planets in our solar system, and the stars and galaxies comes to us from photons that have traveled that great distance. It is almost exclusively by means of these photons that astronomers have been able to assemble our current knowledge of the universe beyond the Earth.
(Some people are working on the Laser Interferometer Gravitational-Wave Observatory and the Virgo interferometer to try to detect gravity waves, composed of "gravitons", that have traveled that great distance.)
| General Astronomy | ||
| The Doppler Effect | Telescopes | Telescopes/Basic Optics |
References
Footnotes
Basic Optics
Although the Greek origin of the word telescope means far-seeing, "see something far away" is not a good description of the function of a telescope. If an object is bright enough, no matter how far it is, we can see it. In fact, telescopes serve three main functions:
- light collection
- resolution
- magnification
Before understanding how telescopes work to achieve these three goals, we take a pause here and study some principals that the optics work.
Reflection and Refraction
The most primitive type of a telescope is a refracting telescope (also called a refractor), which is used by Galileo back in the 1600s. Later, Newton designed and built a reflecting telescope (also called a reflector) making use of mirrors. We first focus on refracting telescopes. A basic refractor consists of a converging lens which focus light onto the focal plane at which detectors and instruments are then placed. As discussed in the previous chapter, the path a light ray passing through a lens can be understood by the Snell's law of refraction:
Magnification
Magnification in a telescope can be given by the following formula: mag=focal length of the objective lens÷focal length of the eyepiece lens
Light Gathering Power
Since most objects in the sky are very dim, a telescope effectively collects and converges light for our viewing. How dim are they? A brief calculation helps explain.
The Sun is at a distance of 1 AU (~1.5e+11 m) away, the light coming out "spread" over a spherical surface (actually it is the energy that spreads over a surface, which we call the flux). Suppose we have a telescope with a 2 m (diameter) aperture, then the fraction of light collected from the Sun is
For objects beyond the solar system, they are millions, if not billions, times further away from us. Therefore, astronomers prefer to build larger telescopes for greater light collecting power.
Resolution
The Rayleigh Criterion
Seeing
Abberations
Spherical abberation
Chromatic abberation
Coma
Astigmatism
Distortion
Field curvature
Optical Telescopes

Optical telescopes increase the apparent brightness and magnification of an object. Other telescopes are capable of "seeing" in the electromagnetic spectrum beyond the abilities of our eyes and transforming those images to those we can use. Infrared telescopes are capable of detecting heat signatures. There are also huge radio telescope dishes, as well as ultraviolet and x-ray telescopes that have been launched into orbit beyond the our Earth's obscuring atmosphere.
There are two main types of optical telescope - reflectors and refractors. Reflectors use a mirror to collect the light, whilst refractors use a lens. Generally, reflectors are better for deep sky objects whilst refractors are useful for planetary observations. Some telescopes use a combination of lenses and mirrors to use the advantages of each.
Refractor telescopes require a large lens at the front to direct the incoming light to the lens. This lens may be made of more than one piece, and the differing refractive properties of the components serve to reduce aberration at the edge of the image. The lenses may also be coated to reduce internal reflections.
Catadioptrics are short, wide telescopes that use both mirrors and lenses.
Large lenses suffer sag under their own weight. This causes their shape to become distorted and so the image will be irregular. For this reason the largest refracting telescope ever built only has a diameter of 41". All larger telescopes, instead, use a mirror as the primary collecting surface.
In the optical spectrum, great precision is required in crafting the lenses and mirrors used in a telescope. The standard of precision for a telescope mirror is accuracy to 1/4 the wavelength of light, an exceedingly small quantity. But even greater accuracy is generally preferred, especially for space-based telescopes. Special tools have been developed for measuring the accuracy of a telescope mirror and lens, and the procedure for finishing the surface is very exacting.
Telescope Configuration
Newtonian
Cassegrain
Ritchey-Chrétien
Schmidt-Cassegrain
Schmidt Camera
Maksutov-Cassegrain
Coudé
Telescope Mount
Equatorial Mount
Alt-azimuth Mount
Telescopes of Other Wavelengths
Radio Telescopes
The first "radio astronomer" was Karl Jansky, who studied mysterious radio interference he picked up with his antenna. The signal repeated every 23 hours and 56 minutes. He finally determined that it was caused by our Milky Way Galaxy. The signal is strongest at the center of the galaxy, in the constellation Sagittarius.[4]
The Very Large Array (VLA) is a radio telescope system in New Mexico.
Infrared Telescopes
The James Webb Space Telescope (JWST) is a large, space telescope optimized for viewing in the infrared part of the spectrum, scheduled for launch in 2018. From the NASA website: "JWST will find the first galaxies that formed in the early Universe, connecting the Big Bang to our own Milky Way Galaxy. JWST will peer through dusty clouds to see stars forming planetary systems, connecting the Milky Way to our own Solar System. JWST's instruments will be designed to work primarily in the infrared range of the electromagnetic spectrum, with some capability in the visible range.
JWST will have a large mirror, 6.5 meters (21.3 feet) in diameter and a sunshield the size of a tennis court. Both the mirror and sunshade won't fit onto the rocket fully open, so both will fold up and open only once JWST is in outer space. JWST will reside in an orbit about 1.5 million km (1 million miles) from the Earth." http://www.jwst.nasa.gov/
Ultraviolet Telescopes
Ultraviolet astronomy studies light with wavelengths just shorter than visible light. This wavelength region turns out to be particularly useful for studying atomic emissions from hydrogen and helium, the two most common gases in space (and in the Sun, and stars, and gas giant planets). Ultraviolet light does not reach the Earth's surface, so ultraviolet astronomy is done from satellites in space. Ultraviolet detectors function well on telescopes with conventional optics such as Hubble Space Telescope. Ultraviolet images from Hubble have dramatically revealed planetary auroras on Jupiter and Saturn from magnetospheric electrons striking atomic and molecular hydrogen in auroral zones at high latitudes on the planets.
X-ray Telescopes
X-rays are higher energy and shorter wavelength than UV. Astronomy in X-rays has specific challenges that do not affect other wavelengths. Earth's atmosphere is opaque to X-rays, which means that astronomy in this energy range can only be performed by space telescopes, high altitude balloons, or sounding rockets.
Gamma-Ray Telescopes
References
Footnotes
Neutrino Telescopes
Gravitational Wave Telescopes
Other Observations
Solar Telescope
Solar telescopes are used for studying the sun. They are quite large. The biggest is the McMath-Pierce Solar Telescope, with a diameter of 1.6 meters. It is housed in a structure that is 100 feet tall. [5]
Cutting Edge
Some new telescopes use multiple or segmented mirrors (usually hexagonal).
- New Technology Telescope (NTT)
- Multiple Mirror Telescope (MMT)
- Keck Telescope (segmented, hexagonal mirrors)
References
Footnotes
Planetary science
The Terrestrial Planets
The Solar System consists of eight planets orbiting a star - the Sun. The eight planets fall into two distinct groups. The four innermost planets are very close to the sun, are formed of rocky materials, and are relatively small. The four outermost planets are far from the Sun, are formed of gasses, and are relatively large. The Earth is one of the four innermost planets, so they are called the terrestrial planets (Terra is latin for earth, so terrestrial means "earth-like". The four outer planets are called the Jovian (Jupiter-like) planets.
The terrestrial planets are, in order of distance from the Sun, Mercury, Venus, Earth and Mars. All of these planets are made of rocky substances, primarily nickel, iron, and silicon. The Jovians are composed mostly of hydrogen and helium gas. The terrestrials orbit the Sun at distances between approximately 0.3 and 1.5 Astronomical Units from the Sun (an Astronomical Unit or AU is defined as the average distance between the Earth and the Sun, so the Earth is 1 A. U. from the Sun). In contrast, the Jovian planets spread from 5AU to 30 AU. The terrestrials are fairly small; the Earth is the largest of the four, and Mercury is only about 1/4 the diameter of the Earth. The Jovians are relatively large, from 4 to 11 times the size of the Earth.
All of the terrestrial planets are presumed to have formed through the same process, so all should share common properties. The terrestrial planets are different than the Jovians because a planet close to a star forms under different conditions than if it is far from the star. The terrestrial planets formed separately in different orbits, so there are significant differences between the four. The four terrestrials have many things in common, but each one is unique in its particular size, atmosphere, orbit, and so on.
Mercury
General Information
Mercury is the closest planet to the Sun. Its orbit is a mere 88 Earth-days, meaning that in the time it takes for the Earth to make one full revolution around the Sun, Mercury makes a little over four revolutions.
Solar days on Mercury are extremely long. It takes two orbits about the Sun for Mercury to complete one full rotation around its axis relative to the sun, so most points on the planet experience direct sunlight for a (Mercurial) year at a time.
Mercury has a highly elliptical orbit, finding itself a mere 0.313 AU from the sun at Perihelion (closest point to the Sun) and at 0.459 AU at Aphelion (farthest point from the Sun). This stretched orbit, combined with a thin and nebulous atmosphere, result in Mercury having wild temperature swings: temperatures during the day tend to exceed 430 degrees °C, while temperatures during Mercurial night tend to drop to a frigid -180 °C.
Mercury has a mantle far thinner than its core, so it is the second-densest planet and has surface gravity as strong as that of Mars.
Venus
Venus is the second planet from the sun, and the only terrestrial planet to rotate in a retrograde manner. Venus has a sidereal day (rotation period relative to the distant stars) lasting about 243.0 Earth-days, or about 1.08 times its orbital period of 224.7 Earth-days. Because of its retrograde rotation, its solar day is "only" about 116.8 Earth-days, and it has about 1.9 solar days per orbital period.
The surface temperature of Venus is highly uniform, about 462 °C (about 736 K/864 °F).[1] The surface of Venus is thought to have been completely resurfaced by volcanic activity 300 to 500 million years ago.[2]
Normal telescopes cannot penetrate the thick clouds of sulfuric acid droplets, but radar can be used to map out the topography of the land.
Earth
The planet Earth is the planet on which all known life in the universe lives. It is the third planet from the sun and the largest terrestrial planet.
Life on Earth is made possible by its massive reserves of liquid water. No other body in the solar system is known to have massive quantities of liquid water, though several Jovian moons are suspected to have oceans under their crust.
The Earth's only natural satellite, the Moon, is the largest satellite in the solar system relative to its planet. This means that the Moon and Earth are sometimes considered to be a double planet. The Moon is also the only celestial body aside from the Earth that has been set foot upon by humans.
Mars
The highest mountain on Mars is Olympus Mons. The northern hemisphere is dominated by volcanic plains; the south by heavily-cratered highlands. The surface is very dusty, and covered with dunes. The sky is a pinkish-orange, from dust storms.
Mars has a chaotic terrain. Astronomers believe it was created when magma melted underground permafrost, causing the ground to collapse. Valley networks are believed to have been caused by rain, and water flowing under ice.
Dried lake beds indicate the presence of water in Mars' past. Another indicator is calcium carbonate, found in a Martian meteor in 1996. Yet another is the presence of outflow channels (believed to have been caused by underground permafrost melted by magma) and alluvial fans. Evidence of seepage flows have also been found. These occur when water breaks through ice and cascades down a cliff.
Martian craters are different from the craters found on the Moon, Venus, or Earth. They're surrounded by mud flows.
The first to map the surface of Mars was Italian astronomer Giovanni Schiaperelli in 1877. He observed a series of lines crisscrossing the Martian landscape, which he called canali (channels). Some astronomers translated canali as canal, implying that they had been built by intelligent beings.[6] This idea was advanced by Percival Lowell in his books Mars and Its Waterways (1903) and Mars as the Abode of Life (1908)[7]. It was later discovered that the Martian canals don't actually exist, and were very likely an optical illusion.
References
- ↑ "Venus (Planet)."The Encarta Concise Encyclopedia. 19 December 1999
- ↑ http://solarsystem.nasa.gov/planets/venus/indepth
The Jovian Planets
The giant planets are so called for their size. They are also called the gas planets because they consist mainly of hydrogen, or the Jovian planets for Jupiter. These planets each have a large system of moons and rings of varying size made of small particles, moonlets and dust.
There are four such planets in the Solar System: Jupiter, Saturn, Uranus and Neptune. They are all made mainly of fluids, like supercritical fluids, liquid and to a lesser extent gas. These envelope solid cores of rock and ice. All the planets have relatively fast rotation; the slowest rotator, Uranus, has a rotation rate of 17 hours and 14 minutes. This and the radiated heat generated from the crushing pressure within these planets give these planets wild wind speeds, and all of these planets experience storms at certain times.
The Gas Giants
The gas giants are the planets composed of hydrogen and helium. They are much larger than the ice giants and have liquid mantles. They are composed mainly of hydrogen and helium, with small amounts of methane, ammonia, water vapor and other compounds. Their atmospheres are gaseous, but they gradually transition into a liquid mantle. They have solid cores and layers of metallic hydrogen.
Jupiter

Jupiter is the innermost of the gas giants. It has a mass of 1.9 x 1027 kg (approx. 318x the mass of Earth) and is 142,800 kilometers (88,736 miles) in equatorial diameter. Jupiter has much metallic hydrogen. When the pressure is so high that the hydrogen atoms are broken up and the electrons are freed so that the resulting atoms consist of bare protons. This produces a state in which the hydrogen becomes metallic. Fluid motions in this metallic conducting layer produce Jupiter's powerful magnetic field. Under all of this is thought to be a somewhat solid, but diffuse core of rock and ice.
Jupiter has a very dynamic weather system. Fluid motions are organized by the planet's rapid rotation into a series of dark belts and bright zones around the planet. The visible cloud layers are made of frozen ammonia, while deeper cloud layers are thought to contain ammonium hydrosulfide and water. Jupiter's "Great Red Spot" is a rotating storm system that has been observed for hundreds of years.
Jupiter possesses seventy-nine known satellites, four of which - Callisto, Europa, Ganymede and Io - are round were first discovered by Galileo in 1610 and are commonly referred to as the Galilean Moons. It also has very faint and very small rings made of dust knocked from its moons.
Saturn
Saturn's mass is 5.688 x 1026 kg (approx. 95x the mass of Earth) and its equatorial diameter is 119,300 kilometers (74,130 miles). Saturn is the only planet less dense than water (about 30 percent less). It has a big and rich system of (mostly) icy rings of small to tiny pieces of dust and ice.. It has eight round moons: Titan, Rhea, Dione, Mimas, Enceladus, Thethys and Iapetus, the largest being Titan, which is unique among moons for having a significant atmosphere and bodies of liquid on its surface. Saturn has more than a hundred smaller moons. It is composed mainly of hydrogen (96% by volume) and (4% by volume) helium, with small amounts of methane, ammonia, water vapor and other compounds. Saturn is differentiated similarly to Jupiter, though it has much less metallic hydrogen and its core is more rigid than Jupiter's. It has the second highest wind speeds of these planets. It has an axial tilt of 26.73 degrees, and it has the most eccentric orbit of the giant planets. Saturn's bands are fainter than those of Jupiter's due to it being further from the Sun. It has a hexagonal cloud pattern at its North Pole, which may be a jet stream. This "hexagon" contains its northern vortex. Periodically, so-called Great White Spots occur. They are large enough to be seen from Earth and can span a whole latitude.
The Ice Giants
The ice giants are so called because they are mostly made of "ices", substances with a freezing point above ~100 K or ~-175 degrees Celsius. They have thick atmospheres above supercritical mantles; that means their mantles are made of a state of matter compressible like a gas, but dense like a liquid; dense enough for the molecules to interact. This state of matter fills its container, like a gas. Under these are liquid cores, which may produce their magnetic fields.
Uranus
Uranus' mass is 8.686 x 1025 kg (~14.5x the mass of Earth ). Its equatorial diameter is 51,800 kilometers (32,190 miles). It also has a dark faint ring system somewhat comparable to Saturn's. Its rotational axis is tilted 98 degrees, so it appears at times as if it is rolling on its orbit. This produces extreme seasons, which plunge almost one half of Uranus is darkness and another in permanent daylight. This is also why its polar regions are lighter in colour than the rest of the planet. Uranus's has 29 moons, 5 of which are round. Its magnetic field is tilted 60 degrees to its rotational axis, and off center. It is the coldest planet in the Solar System, being 6 degrees Celsius colder than Neptune, which is much further fromt he Sun. Uranus is somewhat inert compared to the other giant planets, likely due to its low thermal flux. It is the only giant planet to receive more radiation from the Sun than it gives off.
Neptune
Neptune is the outermost planet of the gas giants. Its mass is 1,024 x 1026 kg (approx. 17x the mass of Earth). It has an equatorial diameter of 49,500 kilometers (30,760 miles). It has one round moon, Triton (the coolest known object in our Solar system - around -235 °C) as well as various smaller moons including Nereid. Neptune has four known, highly inclined and faint rings. It has the fastest wind speeds of any planet, and they are notable for being faster than the speed of sound on Earth. Its strong gravity influences trans-Neptunian Objects, and many of them are locked in an orbital resonance with it. For example, when Neptune orbits thrice, Pluto orbits twice.
Planetary Moons
Mercury
Mercury has no moons.
Venus
Venus has no moons.
Earth
Earth has one moon, usually called "the Moon" and sometimes called Luna. It is the fifth largest moon in the solar system. Of all the moons of the eight planets, Earth's moon is by far the largest relative to its planet, with a diameter of 3476 km and hence a ratio to Earth's diameter of 0.2764. By comparison, the next largest moon relative to a major planet (Triton of Neptune) has a diameter ratio of just .0546. The Moon's diameter is over 50% greater than that of the dwarf planet Pluto.
Mars
Mars has two very small moons, both discovered by Asaph Hall. Deimos was discovered Deimos on August 12, 1877. Deimos, the outermost moon, was named for the Greek god of panic. Deimos has a diameter of just 16 km. The inner moon Phobos has a diameter of 26 km and is heavily cratered. Phobos was discovered on August 18, 1877. Phobos was named for the Greek god of fear. Deimos and has far fewer craters then Phobos and the craters are also much smaller. Deimos is the smallest moon in the Solar System.
Jupiter
Jupiter currently has 95 discovered satellites. Most are small irregular objects, but the four Galilean moons (Ganymede, Callisto, Io, and Europa) are by far the largest (in that order).
Ganymede
Ganymede is the largest planetary satellite in the solar system. With a diameter of 5268 km, it is about 8% larger than the planet Mercury. It is also the only moon in the Solar System with its own magnetosphere. Ganymede was discovered on January 7, 1610 by Galileo Galilei, along with Io, Europa, and Callisto.
Callisto
Callisto is the second largest Jovian moon (that is, moon of Jupiter), and third in the Solar System (with a diameter of 4820 km). It is 98% of the size of Mercury. Callisto has the oldest surface in the Solar System (this means is the most heavily cratered body in the Solar System) even older than Mercury's. Callisto was discovered in 1610, along with Io, Europa, and Ganymede.
Io
Io (pronounced EYE-oh) is the third largest Jovian moon and the fourth largest moon in the solar system. It is slightly bigger than Earth's moon, with a diameter of 3642 km.
Discovery/History

Io has had a long history since its discovery in 1610 by Galileo Galilei. Telescope technology limited observations of Io until the late 1800s when large scale features were able to be resolved on its surface. Observations show that Io has areas of red, brown, orange, and yellow which were later attributed to the abundance of sulfur and sodium on the surface and the unusually high amount of volcanic activity. Io is the most volcanically active body in the solar system. Its activity is due to a great deal of tidal heating from Jupiter and a resonant orbit with Jupiter’s other moons.
Origin of Internal Energy
Io has a similar density to our moon, but is made mostly of sulfur compounds[1]. Io experiences a large amount of tidal heating because it orbits Jupiter at a relatively close distance of 422,000 km and gravitational interactions with other Galilean moons. Jupiter’s large gravitational field and Io’s interactions with other satellites have resulted in an orbital resonance between Io, Europa, and Ganymede which means their orbital periods are integer multiples of each other[2].

For each orbit of Ganymede, Europa orbits twice and Io orbits four times, this forces Io to have a more eccentric orbit. The eccentric orbit means that Io's orbital distance continuously varies, which causes expansion and contraction of its tidal bulge. This frictional energy is dissipated in the form of heat. Io’s internal heat melts the sulfur-rich core into liquid magma, which is contained in large subsurface chambers[3]. This process raises the internal pressure of Io and causes volcanic activity. It is believed that Io has a thin rigid lithosphere and a constant flowing liquid mantle due to its constant internal heating. It is estimated that the power dissipation from tidal interaction is two orders of magnitude greater than radioactive decay. For this reason, Io has a maximum observed temperature of ~1800K- the second highest in the solar system[3]. Another manifestation of the large power dissipation is a large heat flow, 30 times larger than found in Earth’s volcanoes.
Volcanic Features
It is not surprising that Io’s surface is dominated by volcanic features. The surface is littered with pit craters, calderas (volcanic craters), lava flows, shield volcanoes, ash plains, sulfur (S) deposits and other features.

There are over 500 volcanoes on the surface of Io. There are also over 200 calderas, some of which stretch up to 200km across; these calderas are surrounded by different patterns such as bright rings from condensing sulfur ejecta[2]. Volcanic eruptions cause these plumes of ejecta, which can be sprayed up to a height of 300km and 1000km in diameter[1]. The formation of the ejecta plumes is determined by the type of eruption and the characteristics of the material ejected (i.e. molecular composition or phase of matter). Large lava flows are common on the surface due to large volcanic plume velocities of ~1km/s. Lava flows create intervent planes which are areas between volcanoes where lava flows are frequently resurfacing, keeping them flat[4]. Unlike the Earth, there has been no evidence shown that Io has plate tectonics; there are also anomalous isolated mountains in the polar regions[2].
Plasma Torus
Recently, it has been discovered that Io has a plasma torus. The plasma torus is created by the volcanoes that eject sodium and sulfur gas and plasma into Io’s atmosphere. Since Io is not very massive it is not able to hold a substantial atmosphere, leaving behind a “tail” which follows Io’s orbit around Jupiter. Jupiter’s magnetic field strips off more than 1000kg of Io's material per second[5]. The plasma torus is held in place by Jupiter’s large magnetic field, which causes the charged particles (protons and electrons) in the field to orbit a center of rotation, which causes these particles to stay in a relatively small area. Some of these ions are drawn towards Jupiter’s atmosphere by its magnetic field lines, when these ions interact with Jupiter’s atmosphere, auroras are created. The excess stripped ions in the torus double the size of Jupiter’s magnetosphere compared with theoretical calculations[5]. Spectral observations show that Io’s torus and ionosphere are depleted by processes that produce a large nebula expanding out to ~500 Jupiter radii[6]. One of the latest methods of studying the plasma torus is with high resolution (R~120000) spectra of neutral oxygen emissions (630nm) as well as other emissions with the Wisconsin H-Alpha Mapper (WHAM) instrument in Madison, Wisconsin. These observations have shown that emissions show significant long and short-term variations of oxygen emissions. Since intensity variations exist along with a long-term intensity average, it has been concluded that the emissions cause an interaction between Io’s torus and its atmosphere[7]. The reason for studying emissions is to measure the composition as well as velocity structures. This spectra is being taken with a dual Fabry-Perot etalon system to filter out the multiple orders that are produced by etalons[8].
Io's Surface and Subsurface

Research is also being directed towards Io’s surface and subsurface processes. Scientists are currently trying to map the anti-Jovian hemisphere as well as analyze volcanic, tectonic, and other processes affecting the region[9]. Observations show that Io’s entire surface is constantly changing because of subsurface processes, but most eruptions are found to be confined to isolated areas. Volcanic events only take place on about 17% of the surface which points back to the large lava flows that can extend up to 1000km[9]. Similar to Earth’s geysers, Io’s fissures release gases and liquids like sulfur vapor up to 225km and can last for days. Io’s surface has been found to be very active and volatile; it has been observed that changes in volcanic spray were detected in a 5.5 hour period. A New Frontiers class mission named Argus is a planned mission to send a spacecraft to Io that would orbit the moon 40 times at about 100km altitude. The goal of the mission is to attempt to answer basic questions about the possible habitation of planetary bodies like Europa and Enceladus, which are both under the influence of significant tidal heating[10].
Europa
Europa is the solar system's sixth largest moon. With a diameter of 3120 km, Europa is slightly smaller than Earth's moon, and is substantially larger than the dwarf planet Pluto. Europa has the smoothest and one of the youngest surface in the Solar System, Scientist think that Europa might have a liquid ocean under its icy crust and thus, scientist think it may harbor life. Europa was discovered in January 7 1610 by Galileo Galilei in 1610 at the same time that Io, Ganymede, and Callisto were found.
The remaining 91 moons
Jupiter has other remaining 76 moons (some may be captured Asteroids) are all far smaller than Ganymede, Callisto, Io and Europa. Even the fifth largest moon of Jupiter (Amalthea) has a diameter under 200 km. The other moons names in order are in the Inner Group: (since Jupiter has a lot of moons they are divided into groups) Metis, Adrastea, Amathea and Thebe followed by the Themisto group with only one member which is Themistho and the Himalia Group: Leda, Ersa, Himalia, Pandia, Lysithea, Elara and Dia. The next two moons, Carpo and Valetudo do not follow any specific groups. The next group of moons, Euporie, S2003 J18, Eupheme, S2010 J2, S2016 J1, Mneme, Euanthe, S2016 J16, Harpalyke, Orthosie, Helike, Praxidike, S2017 J3, S2003 J12, S2007 J7, Thelxinoe, Thyone, S2003 J2, Ananke, Iocaste, Hermippe, S2017 J9 are all members of the Ananke group and the 7 moons after them are Philophrosne (Pasiphae group), Pasithee, S2017 J8 and S2003 J24 (Carme Group) and Eurydrome, S2011 J2 and S2003 J4 (Pasiphae group). The following 18 moons all belong to the Carme group, these being Chaldene, S2017 J2, Isonoe, Kallichore, Erinome, Kale, Eirene, Aitne, Eukelade, Arche, Taygete, S2011 J1, Carme, Herse, S2003 J19, S2010 J1, S2003 J9 and S2017 J5. The following 6 moons are S2017 J6 (Pasiphae group), Kalyke, (Carme group), Hegemone, Pasiphae, Sponde (Pasiphae group) and S2010 (Carme group). The final 9 moons of Jupiter all belong to the Pasiphae group and are Megaclite, Cyllene, Sinope, S2017 J1, Aoede, Autonoe, Callirhoe, S2003 J23 and Kore.
Saturn
Saturn has 82 moons.
Titan
Titan is the second largest moon in the solar system; with a diameter of 5150 km, it is slightly smaller than Jupiter's Ganymede; it is larger than the planet Mercury. Titan is the only planetary moon having a dense atmosphere. Titan's atmosphere is mostly composed of nitrogen with a trace of methane. Titan's Atmosphere is by far the densest of any satellite in the Solar System, being 50-60% denser than Earth's atmosphere. Other moons, if they have atmospheres (which the majority don't), have less than 1/1000 the pressure of Earth's atmosphere at sea level. The Atmosphere on Titan is dense enough for there to be rain; however, the rain is liquid methane. The temperature on Titan is so low (-333 degrees Fahrenheit) that methane is a liquid.
Rhea
Rhea is the second largest moon of Saturn and the ninth largest moon in the Solar System, with a diameter of 1528 km. The moon has a possible ring system. Rhea's low density of 1.23 suggests that it is composed of 75% water ice and 25% rock.
Iapetus
Iapetus is the third largest moon of Saturn and the 11th largest moon in the Solar System. Iapetus holds the record for the Farthest Round Major moon of any Planet\Dwarf Planet being 93 times farther from Saturn than the Moon from the Earth. Iapetus diameter is 1472 miles (735 km). Half its surface is extremely bright while the other is extremely dark.
Dione
Dione is the second densest moon of Saturn (after Titan) at a density of 1.47 this means that it has more rocky material within than the other moons. Dione has a face which it's heavily cratered and another that it's almost completely clean of craters. At a diameter of 1122 km, Dione is the fourth largest moon of Saturn and the 15th largest in the Solar System
Tethys
Tethys is similar to Dione in many ways like size number of craters ext... .Tethys is the 16th largest moon of the Solar System and the 5th largest of Saturn. Investigation and Research indicates that in the past, Tethys was a giant ball of liquid water that with the temperatures of the outer Solar System froze eventually
Enceladus
Enceladus is the 17th largest moon of the Solar System at 500 km across. Enceladus is the only Moon of the Solar System that shoots tons of water from its inside to outer space. Enceladus is much smaller than Titan, Rhea, Iapetu, Dione and Tethys but much bigger than Mimas, the Smallest round moon of Saturn.
Mimas
Mimas is the smallest round moon of Saturn and the 20th largest moon of the Solar System at a diameter of 396 km. Mimas has a huge crater being almost as half a big as Mimas itself which it would have been a little bigger and it would have destroyed Mimas.
Hyperion
Hyperion is the 8th largest moon of Saturn and 23rd in the Solar System. Hyperion is the only moon in the Solar System that rotates chaotically. The density of Hyperion is one of the lowest in the Solar System at 0.5 grams per cubic centimetres which is lower than Saturn's which is 0.7 grams per cubic centimetre.
The Remaining 75 Moons
The first 16 minor moons of Saturn are S2009 S1, Pan, Daphnis, Atlas, Prometheus, Pandora, Epimetheus, Janus, Aegaeon, Methone, Anthe, Pallene, Telesto, Calypso, Helene and Polydeuces. The next 3, S2019 S1, Kiviuq, and Ijiraq all belong to the Inuit group and moon after them, Phoebe, is the 9th largest moon and 8th most massive moon of Saturn, it is also one of the largest irregular moons in the Solar System. The next 13 moons are Paaliaq (Inuit Group), Skathi and S2004 S37 (Norse Group), Albiorix (Gallic Group), S2007 S2 (Norse Group), S2004 S29 (Inuit Group), Bebhionn (Gallic Group), S2004 S31 (Inuit Group), Erriapus (Gallic Group), Skoll (Norse Group), Tarqeq, Siarnaq (Inuit Group) and Tarvos (Gallic Group). The following 36 moons are S2004 S13, Hyrrokkin, Greip, Mundilfari, S2006 S1, S2007 S3, Gridr, Bergelmir, Narvi, Jarnsaxa, S2004 S17, Suttungr, Eggther, Hati, S2004 J12, Bestla, Farbauti, Thrymr, Angrboda, Beli, Aegir, Gerd, S2004 S7, Gunnlod, Skrymir, S2004 S28, Alvaldi, Kari, Geirrod, S2006 S3, Fenrir, Surtur, Loge, Ymir, S2004 S21 and S2004 S39. The 78th moon of Saturn is S2004 S24 (Gallic Group) and the final 5 moons are S2004 S36, Thiazzi, S2004 S34, Fornjot and S2004 S26.
Uranus
Uranus has 27 moons including Titania, Oberon,Umbriel and Ariel which are all over 1000 km
Titania and Oberon
Titania and Oberon are the largest moons of Uranus Titania being 1578 km in diameter make it also the 8th largest moon of the Solar System and Oberon the 10th largest moon of the Solar System at a diameter of 1522 km. Both moons are heavily cratered like most moons. Both moons were discovered by William Hershell on January 11 1787
Umbriel and Ariel
Umbriel is the 13th largest moon of the Solar System at a diameter of 1168 Ariel is the 14th largest moon of the Solar System at a diameter of 1156 km. Both moons were discovered by William Lassell on October 24 1851
Miranda
Miranda is the smallest round moon of Uranus and the 18th largest moon in the Solar System. Miranda is an icy moon which it is mostly composed of water ice and a small percent of rock. This moon was discovered in February 15 1948 by Gerard P. Kuiper.
The Remaining 22 moons
The other moons of Uranus are Cordelia , Ophelia · Bianca , Cressida , Desdemona , Juliet , Portia , Rosalind , Cupid , Belinda , Perdita , Puck , Mab, Francisco , Caliban , Stephano , Trinculo , Sycorax , Margaret , Prospero , Setebos and Ferdinand
Neptune
Neptune has 14 moons, the large one being Triton
Triton
Triton is the seventh largest moon in the solar system; its diameter of 2705 km is about 10% larger than the Dwarf Planet Pluto. Scientists believe that this moon is really an object that has been captured by Neptune's gravity. Triton is one of the coldest bodies in the Solar System being even colder than Pluto at -393 degrees Fahrenheit. In 360,000,000 years it is expected to pass the Neptune roche limit and disintegrate to form a planetary ring system
Nereid
Nereid is the third largest moon of Neptune at 170 km in Diameter. Nereid is also one of the few moons in the Solar System that its year is not the same as its rotation
Proteus
Proteus is the largest irregular moon of the Solar System and the second largest moon of neptune and the 19th largest moon of the Solar System being 420 km in Diameter.
The Remaining 11 Moons
The other 10 moons are Naiad , Thalassa , Despina , Galatea , Larissa, Halimede, Hippocamp Sao , Laomedeia , Psamathe and Neso
Dwarf Planets
Ceres
Ceres has no moons
Pluto
Pluto has 5 moons. Their names are Charon, Hydra, Nix, Styx and Kerberos
Charon
Charon is the Largest moon of Pluto with a diameter of 1207 km it is also the largest moon proportionally compared to its host planet. Being roughly half of Pluto's size Pluto and Charon orbit each other.
←==Hydra, Nix and P4== Hydra is the second largest moon of Pluto at a diameter of 61-150 km . Nix is the third largest moon of Pluto at a diameter of 46-
Haumea
Haumea has two moons (Hi'aka and Namaka)
Hi'aka
Hi'aka is probably one of the biggest irregular shaped moons of the Solar System at a diameter of 310 km. However its shape is currently unknown
Namaka
Namaka is roughly the same size as the Neptunian moon Nereid at 170 km. Its shape is unknown.
Makemake
Makemake has one known moon named MK2.
Eris
Eris has one moon (Dysnomia)
Dysnomia
Dysnomia is the only moon that the Dwarf planet Eris has. Its shape is not known but scientist expect that it may not be as large to rounded by self gravitation
Other Objects
Quaoar
Quaoar has one moon being 1\12 Quaoar's diameter the moon it's called Weywot.
Orcus
Orcus has a moon that it is 1\3 its size that moon it's called Vanth and it's 380 km in diameter, probably large enough to be round
References
- ↑ a b Rothery, D. 1992, Satellites of Outer Planets, pp.138-142
- ↑ a b c Christiansen, E. 1995, Exploring the Planets, pp.331-333
- ↑ a b Weissman, Paul R. 1999, Encyclopedia of the Solar System, pp.359-363
- ↑ Hartmann, W. 1993, Moons & Planets, p.387
- ↑ a b Galilean Moons: Io, NASA/JPL 2008, http://www2.jpl.nasa.gov/galileo/moons/io.html
- ↑ Mendillo, M. 2007, The Source of Sodium Escaping from Io revealed by spectral high definition imaging, Nature Journal, Vol.448, pp.330-332
- ↑ Oliversen, R. 2001, Sunlit Io Atmospheric 6300A Emission and the Plasma Torus, Journal of Geophysical Research, Vol. 106, pp.183-193
- ↑ Oliversen, R. 2008, Observation of Io and the Plasma Torus During 2007 and 2008, Unpublished
- ↑ a b Williams, D. 2008, Volcanism on Io: Insights from Global Geologic Mapping, American Geophysical Union
- ↑ Chen, E. 2008, Argus: A New Frontiers Mission to Observe Io, Unpublished
Comets
Comets were previously thought of as a, “dirty snowball” but due to the fact that a comet has more dust than ice, they are now referred to as an, “icy dirt ball.” The nucleus is mainly made up of H2O (water), with some parts NH3 (ammonia), CH4 (methane), and CO2 (carbon dioxide). When the Big Bang happened over 4.6 billion years ago, the hydrogen and helium accreted into the first generation of stars, which quickly became supernovae. During which, the heavier elements (collectively called metals) were produced, which once again condensed with hydrogen and helium to form the second generation of stars. Much of the "metals" condensed at that time to form the terrestrial planets, and some of the material became small lumps of frozen gas and dust. These lumps are located in the outer region of the solar system, where temperatures are cold enough to produce ice, thus keeping the lumps frozen. The outer region is called, the Oort Cloud or the Kuiper Belt. [8] The Oort Cloud is estimated to contain 1011 (one hundred billion) comets.
As the comets orbit our sun, they may be disturbed by close encounters with other objects and some of those move out of the Oort Cloud and toward the sun. As they approach, their frozen gases become vaporized, dust is ejected, and they form streamers called tails. The tails tend to flow behind the nucleus of the comet. The gases and dust are easily influenced by the forces applied to them; which in turn is the sun's photons of light bouncing off of them, and the electromagnetic field that acts on the charged particles. Comets have two tails: the ion tail (blue, composed of gas), and the dust tail (yellow). Meteor showers, like the Perseid or Leonids, occur when the Earth travels through a comet's dust tail.
One of the most famous comets is Halley's Comet, which was discovered by Edmond Halley in 1705. The comet was last seen in 1682; Halley predicted it would return in 1758. Unfortunately, he died in 1742, so he was unable to see his prediction come true. The comet was subsequently named after him.
Halley's Comet has a period of about 76 years. It came by the Earth last in 1986, and will return in 2061.
Chemical Diversity in Comets

It has been postulated that the chemical diversity observed in the population of comets found in the Kuiper Belt (region extended after Neptune orbit) as well as Oort cloud (spherical cloud lie roughly 50,000 AU from the Sun) is primordial.
The chemical abundances were observed in both classes of comets: Oort cloud comets and the Jupiter-Family of comets whose population consisting of short-period comets formed in the Kuiper belt Differences were noted between the two groups. This can be attributed to several factors including differences in the chemical and physical environments in comet-forming regions, chemical evolution during their long storage in the Oort cloud and Kuiper belt, and thermal processing by the Sun when entering the inner Solar System. The chemical composition of comets is investigated by remote sensing using spectroscopy. This investigation is indirect, since only the gas and dust of the coma can be observed after the nucleus ices have sublimated from the nucleus.
Observations were made at millimeter/sub-millimeter wavelengths with the IRAM 30-m, JCMT, CSO and SEST radio telescopes. Six Jupiter-family, three Halley-family, and fifteen long-period comets were observed from 1986 to 2001. The eight molecular species were HCN, HNC, CH3CN, CH3OH, H2CO, CO, CS, and H2S. HCN were detected in all comets, while at least two types of molecules were detected in nineteen comets. It was inferred that the HCN abundance relative to water varies from 0.08% to 0.25% from the sub-sample of comets for which contemporary H2O production rates are available. HCN is the molecule which exhibits the lowest abundance variation from comet to comet with respect to other species and was found in all the 24 Comets. HCN was found only in the four Comets and low CO abundances was measured in Jupiter-family comets, while several Oort cloud comets exhibit high CO abundances.[1] According to the observation 23% of CO molecule with respect to water was observed in 5 comets. While 0.035% of HNC relative to water was observed in 5 comets. Fifteen comets exhibited CH3CN up to maximum 6.2%. And H2CO, H2S and CS was found in 13,11,9 comets respectively. They were found at a concentration maximum up to 1.3%, 1.5% and 0.17% respectively relative to water.[2]

Comet C/2001 Q4 (NEAT)

Comet C/2001 Q4 NEAT was discovered in August 2001 in the course of the Near Earth Asteroid Tracking (NEAT) program. The comet was found on Charged Coupled Device (CCD) images and the astronomers were able to confirm the discovery on August 24. The comet was described as a round nebulosity measuring about 8 arc seconds across at the distance of 10.1 AU from the Sun. The total visual magnitude was 20.0. Its perihelion date was 2004 May 26 and perihelion distance was 1.00 AU. It has an unusual, almost perpendicular retrograde orbit which brings it into the inner solar system by a deeply southward path. It initially emerged from its remote home where it spent most of its time near the south celestial pole.[3] The comet brightened slowly during the remainder of 2001 and throughout 2002. It appeared fainter than magnitude 15 at the beginning of the 2003, but it steadily brightened as the year progressed, to magnitude 12 around mid-September. In September amateur astronomers could easily mark the time of comet in the Southern Hemisphere began supplying regular visual observations of this comet, at which time the diameter of the coma was typically measured as 0.6 to 1.2 arc minutes. In CCD images amateurs began observing a short fan-shaped tail pointing northward in July as on its approached to the Sun. In late September, the tail extended about 0.8 arc minutes toward the northwest. As 2003 came to an end, the comet became slightly brighter than magnitude 10, with a coma diameter of about 2 arc minutes. A faint, fan-shaped tail extended about 4 arc minutes toward the east. Finally, Comet C/2001 Q4 (NEAT) entered the inner solar system in 2004, reaching perihelion of 1 AU. It's peak magnitude of 3.3 rendered it clearly visible to the naked eye. C/2001 Q4 is referred to as an Oort cloud comet as it originated from Oort cloud. It is composed of HCN, CO, CH3OH, H2S and other species.[4]
We know how a comet is formed because of the recent discoveries made in 2009 by NASA’s Deep Impact which impacted Comet Tempel 1 in 2005 that revealed what exactly a comet’s nucleus is made of and its structure.
References
- ↑ Biver, N., Bockelee,D., Crovisier,J., 2007 “The chemical diversity of comets dates back to their origin”, Observatoire de Paris, LESIA, and CNRS
- ↑ Biver, N.,March 2002 “Chemical Composition Diversity among 24 Comets Observed at Radio wavelengths”, Earth, Moon and Planets, Volume 90, Pages 323-333
- ↑ Russo, et. al. 2007, “Nature”, Volume 448, page. 172-175
- ↑ Gray,C.L., Cohran,A.L.,2008, “A Chemical Survey of 73 Comets Conducted at McDonald Observatory”,B.A.A.S.,40,16.02
1. http://hubblesite.org/reference_desk/faq/answer.php.cat=solarsystem&id=16 2. http://www.space.com/53-comets-formation-discovery-and-exploration.html
Asteroids
Asteroids are rocky or metallic solar system objects smaller than planets, whose orbits usually lie between Mars and Jupiter, although some venture close to the Sun and even pass dangerously close to Earth. They range in size from a maximum of several hundred kilometers, to an undetermined small size that merges into the category of meteoroids. Some meteoroids are unquestionably of the same composition, origin and structure as asteroids, just smaller. The age of asteroids is derived from that of meteorites, are thought to date from the very early periods of the Solar System, and to have been little changed since then.
There are tens of thousands of asteroids large enough to track, and perhaps hundreds of thousands of smaller size that range into the meteoroids. More than 1000 asteroids of 100 meters or larger (about the length of a city block) that pass close enough to the Earth to be of concern are being tracked.
In October, 2008, a small asteroid roughly the size of an SUV was discovered on a collision course with Earth, only about 20 hours before it impacted the upper atmosphere. The impact produced a fireball explosion approximately one kiloton of TNT in strength, or about one twentieth of the strength of the WWII atomic bombs dropped on Japan. However, this produced no dangerous radiation and occurred harmlessly far above the Earth's surface. Fragments survived and fell over Africa, about 5 kg of which were recovered in the Nubian Desert of Sudan, making this the first time an object had been tracked before impacting Earth, and fragments later recovered. Preliminary investigations are confirming the nature of the asteroidal/meteoroidal connection.
The first asteroid was discovered on the first day of 1800, by Italian astronomer Giuseppe Piazzi, who was part of a larger group of astronomers informally known as the "Celestial Police." The group had been convinced of the existence of a previously unknown planet between Mars and Jupiter, as apparently predicted by a mathematical relationship called Bode's Law (or the Titus-Bode Law). Soon after Piazzi's discovery, which he named Ceres for the Roman Goddess of Grain, others were discovered and their relatively small size deduced. Too small for full planets, they became known as asteroids, or "starlike bodies," or somewhat more appropriately, "minor planets." Ceres, was not only the first but the largest, at 950 km in diameter. It is so large that recently it has been designated as "dwarf planet" rather than an asteroid.
The asteroids are thought to have been small bodies left over at the formation of the Solar System, which were prevented from forming into a larger planet by the overpowering gravitational influence of "nearby" Jupiter. It is likely that some of the original asteroidal bodies collided and broke apart, resulting in the many fragments found today.
Meteors and Meteorites
There are different terms for the same object, depending on where it is observed. In space, it is a meteoroid. A meteor is a meteroid that has been captured by some object's gravitational field (e.g., the Earth), and is falling toward it. Meteorites are meteors that have landed.
There are three kinds of meteors: irons, stones, and stony-irons. They usually come from asteroids or the Oort Cloud.
- Irons are composed of mainly iron.
- Stones are rocky, and are composed of silicate minerals.
- Stony-irons are composed of silicate and nickel-iron minerals.
The Kuiper Belt
The Kuiper belt is an area of the solar system extending from the orbit of Neptune (at 30 AU) to 50 AU from the Sun.
The objects within the Kuiper Belt together with the members of the scattered disk extending beyond, are collectively referred to as trans-Neptunian.
The interaction with Neptune (orbital resonance) is thought to be responsible for the apparent edge at 48 AU (a sudden drop in number of objects, see Orbit distribution below) but the current models have yet to explain this peculiar distribution in detail.
Origins
Modern computer simulations show the Kuiper belt to have been strongly influenced by Jupiter and Neptune. During the early period of the Solar System, Neptune's orbit is thought to have migrated outwards from the Sun due to interactions with minor bodies. In the process, Neptune swept up, or gravitationally ejected all the bodies closer to the Sun than about 40 AU (the inner edge of the region occupied by classical Kuiper belt objects), apart from those which fortuitously were in a 2:3 orbital resonance. These resonant bodies formed the plutinos. The present Kuiper Belt members are thought to have largely formed in situ at their present position, although a significant fraction may have originated in the vicinity of Jupiter, and been ejected by it to the far regions of the Solar system.
Hypothesis
The first astronomers to suggest the existence of this belt were Frederick C. Leonard in 1930 and Kenneth E. Edgeworth in 1943. In 1951 Gerard Kuiper suggested that the belt was the source of short period comets (those having an orbital period of less than 200 years). The belt and the objects in it were named after Kuiper after the discovery of (15760) 1992 QB1.
Name
An alternative name, Edgeworth-Kuiper belt is used to credit Edgeworth. The term trans-Neptunian object is recommended for objects in the belt by several scientific groups because the term is less controversial than all others — it is not a synonym though, as TNOs include all objects orbiting the Sun at the outer edge of the solar system, not just those in the Kuiper belt.
Pluto
The object Pluto, formerly considered a planet, is part of the Kuiper Belt. It has an orbital inclination of 17°. Pluto has 5 moons. Charon is the largest moon of Pluto. The other 4 moons are, Nix, Kerberos, Hydra, and Styx.
Extrasolar Planets
Exoplanets are planets that orbit other stars.
Brief History of Detecting Exoplanets
Speculations about the existence of exoplanets have been ongoing since the time of Isaac Newton’s General Scholium (1713). Newton hinted that other stars had planets orbiting them just as our sun. [1] The first claims of a detection of an exoplanet were centered on 70 Ophiuchi. In 1855 Capt. W. S. Jacob claimed that the orbit of the binary system exhibited an anomaly. A third body, an exoplanet, was held responsible. [2] In the 1890’s, Thomas Jefferson Jackson See supported these claims based on orbital movement as well. [3] In 1899, those claims were disproved by Forest Moulton who analyzed the triple system and demonstrated that such a system would be unstable under the orbital parameters put forth by Jackson. [4]
In the 1960’s Peter Van de Kamp claimed that Barnard's Star had an exoplanet. He based this claim on an apparent wobble in the star’s motion. [5] Kamp spent 40 years studying the Barnard star. Observations made by other telescopes were never able to replicate the date of the wobble. It is believed that the wobble was an anomaly of equipment at Sproul Observatory. There is still no conclusive evidences for or against a planet existing around Barnard’s Star. [6]
The first detection to be later confirmed of an exoplanet was made in 1988 by Bruce Campbell, G.A.H. Walker and S. Yang. The star Gamma Cephei was tentatively proposed to have an exoplanet based on radial velocity observations. It was given a tentative status because the observations were made at the very limit of the capability of the instruments at the time. [7] The claim was mistakenly retracted, for in 2002 Artie Hatzes and his collaborators were able to confirm the existence of the exoplanet. [8]
In 1992 Wolszczan and Frail proved there were two planets of 3.9 and 4.3 Earth masses orbiting the pulsar PSR B1257+12 at .46 and .36 AU respectively. [9] A third planet was discovered later of .025 Earth masses orbiting at .19 AU. This discovery is considered to be the first definitive detection of an exoplanet, because the Cambell, Walker, and Yang discovery was not confirmed until 2003. This was a rather strange discovery because it was revolving around a pulsar rather than a main sequence star like our sun. It is believed that the planets are the remains of a solar system after the star died. [10]
The first discovery of an exoplanet orbiting a main sequence star, 51 Pegasi, was announced October 6, 1995 by Michel Mayor and Didier Queloz. [11] When the distance and mass of the planet were determined they were found to be incompatible with theories of planetary formation at the time. [12] They used the radial velocity method to detect the planet. This ushered in the modern era of exoplanet study. After their discovery numerous exoplanets have been detected as a result of improved telescopes with higher resolutions and more powerful computers. [10]

As of August 19, 2012, 777 exoplanets have been detected. [13] The rate of discovery has steadily increased due to improved technology and a greater interest in exoplanets, with 61 planets detected in 2007. Using the Spitzer Space Telescope, studies of the evolution of gas and dust around main sequence stars indicate that at least 20 percent, and possibly as many as 60 percent, of main sequence stars are candidates for forming rocky planets. The actual percentage is likely between these two extremes. [14] [15]
Most exoplanets detected have been massive Jupiter-like planets. Most likely this is due to the ease of detecting such in comparison to smaller terrestrial planets; this is known as a selection effect. Planets, labeled Super-Earths, have also been detected. They are about 5 to 10 Earth masses. One Earth mass would be the mass of the earth. [16]
Detection Methods
There are six methods currently used to detect exoplanets: Astrometry, Radial Velocity, Pulsar timing, Transit method, Gravitational micro-lensing, Direct imaging. Three methods detect a dynamical perturbation of the star, or wobble of the star due to the planet’s gravitational force. Since the planet and the star revolve around a common center of mass the star will appear to wobble with the same period as the planet’s orbital period. From our point of view the wobble will be from side to side, towards and away, or some combination of the two.
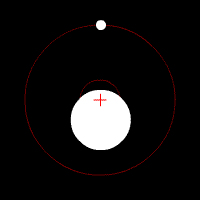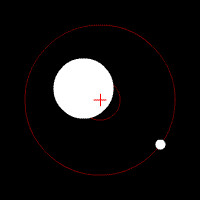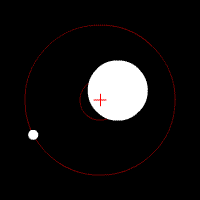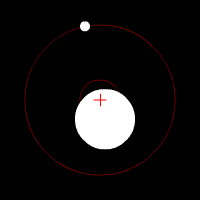
The degree of a star’s wobble is determined by the mass of the star and the planet, and by the distance between them. The more massive a planet is in comparison to that of its star, the greater the wobble. The closer the planet’s orbit to the star the greater the degree of the wobble observed of the star. Any method that detects an exoplanet this way can give information about the planet’s mass, though a combination of methods is needed to find the true mass of a planet.

The three ways we detect this wobble are by radial velocity, astrometry, and pulsar timing. Radial velocity measurements detect the blue and red shifts of a star as it moves toward and away from Earth, respectively. As the star moves toward Earth, the light shifts to blue. As the star moves away from Earth the light shifts to red. The radial velocity can be deduced by studying the red and blue shifts in the spectroscopy of the star’s emission. Most exoplanets have been discovered by the radial velocity method. [17]
The velocity of the star around the barycenter is much smaller than the planet’s velocity because the planet’s orbital distance from the center of mass is greater than the star’s. Current spectrometers can detect a velocity variation down to 1 m/s. [18] The larger the velocity differences in the star, the easier it is to detect. Thus the radial velocity method can more easily detect exoplanets that have a larger mass and are closer to their stars. [17]
The Astrometry Method is the oldest search method though it wasn’t the method used to discover the first exoplanet. The astrometry method looks for angular change in the position of a star. The more a star moves, the easier it is to detect. Since this method relies on the orbit around a center of mass it is dependent on the mass ratio of the planet and star. [17]
However, unlike the radial velocity, the angular change in position increases with greater distance between the star and the exoplanet. The further the planet is from the star, the further they are from their mutual center of mass. The greater a star’s distance from the center of mass, the greater the angle change between the star’s opposite ends of its orbit. [17]

In the Pulsar Timing Method, a pulsar emits radio waves in extremely regular time intervals as it rotates. Any anomalies in the time between radio waves are an indication that the pulsar is orbiting a center of mass. This method is very sensitive. Planets that are one-tenth Earth masses can be detected this way.[17]

The Transit Method detects changes in the brightness of star as a planet moves across the star's face. The dimmer the star becomes, the larger the planet, thus the volume of a planet can be determined by this method. This method requires that the planet’s orbit passes directly between the star and earth, which is a rare alignment.[17] The Gravitational Lensing Method measures an amplification of a star’s brightness. As light from a background star passes the planetary system, the light is bent towards a planet due to its

gravity. The light is focused into a smaller area thus increasing its brightness. This method is capable of detecting low mass planets around dim stars at a great distance.[19]
The final method currently used to detect planets is to directly observe them. Usually a parent star's shine obscures a planet's emission. However, in certain cases the reflected light of a planet can be seen. Such a method works best when the planet is more massive than Jupiter, less than a tenth the age of our solar system, more distant from its parent star than Jupiter and orbits a star less luminous than our sun. It is also possible to detect a planet’s light if we restrict ourselves to infrared radiation, which is the dominant emission wavelength of a planet. This is very difficult and few planets have been detected this way.[10]
Extrasolar Jovians
Many gas giants have been discovered orbiting distant stars, many of larger than Jupiter. That is because big planets are massive enough to gravitationally affect the movement of their star sufficiently that the perturbation is detectable. Therefore the biggest extrasolar planets are the easiest and earliest to be found.
The First Discovery
The first extrasolar planet discovered was Gamma Cephei Ab, a planet orbiting Gamma Cephei A with an orbital period of around 900 days at a distance of around 1.7 - 2.5 AU from its parent. Its existence was suspected as early as in 1989, and evidence of it strengthened considerably in 2002 from observations at the McDonald Observatory. It is a Jovian-sized planet with a mass estimated to be above 1.59 times that of Jupiter's. The star it orbits is an orange sub-giant star part of the Gamma Cephei binary star system, with its companion Gamma Cephei B a red dwarf.
Spectra of Hot Jupiters
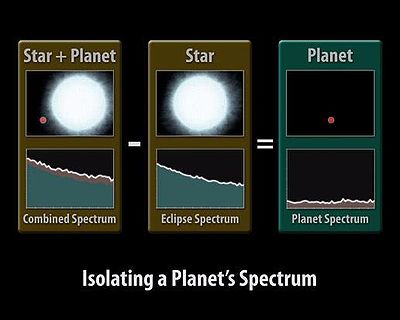
Astrophysicists have recently observed spectra from hot Jupiter sized planets in planetary systems many light years away.[20] Since these planets are so distant, it’s not as simple as just looking at the planet and collecting data about the direct light from the planet.[21] The planets are too distant for such techniques and they are too close to their parent stars (sometimes closer than Mercury is to our sun).[21] Instead astrophysicists collect data from the star and planet during different parts of the planets’ orbit and separate the light from just the planet.
First the spectrum from the planet and star is collected. This is done when, as seen from earth, both planet and star are at their greatest separation. Then the spectrum of just the star is obtained. This is done when the planet is either directly in front of the parent star (primary eclipse) or directly behind its parent star (secondary eclipse). By subtracting the light of the star from the light of the star plus planet, the spectrum of the planet can be found.[21]

Spectroscopic Techniques: Primary and Secondary Eclipses
The brightness of the parent stars of these planets is too high in comparison to the planets themselves in the optical range. Because of this, infrared light is detected to better differentiate the planet from the star.[21] The planet itself reflects very little optical light because the cloud layers prevent much of it from escaping. The cloud layers emit much of the absorbed energy from its star as infrared light however, and so most it can be detected by the spectrometers of our telescopes (Spitzer and Hubble). Because the planet emits so much more radiation in the infrared range as compared to the reflected optical part of the spectrum, the differences in the two spectra are more exaggerated and the infrared part of the spectra is easier to use.
A secondary eclipse occurs when the hot Jupiter being observed passes behind its parent star, as viewed from Earth. A primary eclipse, also known as a transit, happens when the planet passes in front of the star as viewed from Earth. These eclipses are very rare because the planet, star and earth have to line up so that the planet completely eclipses.[21] Only 54 of the 333 confirmed planets are transiting planets when viewed from Earth.[22]
Spectroscopic results
Spectra are used to identify molecules in the planetary atmospheres, and to determine relative abundances. If you know at what wavelengths an atom or molecule will emit or absorb light, you can examine the spectrum of light from a planet and determine if that molecule is present. By looking at the full spectrum, scientists can decide which atoms or molecules specifically make up the planet and noting how much of that wavelength is emitted, the relative abundance of that atom or molecule can also be determined.

Many attempts are focusing on identifying water vapor on other planets.[21] The two planets, HD 209458b and HD 189733b are the first two planets observed.[20] Originally, they both seemed to be void of water vapor.[21] It is believed that the observational techniques weren’t sensitive enough to detect water vapor. By using new techniques, the evidence for these planets containing water vapor is growing.[23] The first tests were done using a secondary eclipse of the star.[21] Because of the atmospheric composition of the planets, this technique could not see through the clouds on the planets. The heat of the planet due to its closeness to the star also plays a part in the differences in results. Because the planet is so close to the star, the side closest to the star will have less water than the side away from the star. During a primary eclipse, the cooler and therefore wetter side will be facing towards earth. During a secondary eclipse, the dryer hotter side will be facing towards earth. By using a primary eclipse,[24] a team of scientists in France has found peaks in the light curve at 3.6 microns, 5.8 microns and 8 microns in such a pattern that they believe only water vapor could produce.[20]
Example Spectra



References
- ↑ Isaac Newton, The Mathematical Principles of Natural Philosophy, trans. Andrew Motte (London, 1729), pp. 387-93.
- ↑ Jacob, W. S. "On certain Anomalies presented by the Binary Star 70 Ophiuchi." Monthly Notices of the Royal Astronomical Society 15 (1855): 288-89. http://adsabs.harvard.edu/abs/1855MNRAS..15..228J
- ↑ Thomas Jefferson Jackson (1896). "Researches on the Orbit of F.70 Ophiuchi, and on a Periodic Perturbation in the Motion of the System Arising from the Action of an Unseen Body". The Astronomical Journal 16: 17. http://adsabs.harvard.edu/cgi-bin/bib_query?1896AJ.....16...17S
- ↑ Sherrill, Thomas J. (1999). "A Career of controversy: the anomaly OF T. J. J. See" (PDF). Journal for the history of astronomy 30, http://www.shpltd.co.uk/jha.pdf. Retrieved on 27 August 2007.
- ↑ van de Kamp, Peter (August 1969). "Alternate dynamical analysis of Barnard's star". The Astronomical Journal 74: 757–759. doi:10.1086/110852, http://adsabs.harvard.edu/abs/1969AJ.....74..757V. Retrieved on 27 August 2007
- ↑ Bell, George H. "The Search for the Extrasolar Planets: A Brief History of the Search, the Findings and the Future Implications." 5 Apr. 2001. Arizona State University. Nov. 2008 <http://www.public.asu.edu/~sciref/exoplnt.htm#preface>.
- ↑ Campbell, B.; Walker, G. A. H.; Yang, S. (1988). "A search for substellar companions to solar-type stars". Astrophysical Journal, Part 1 331: 902 – 921. doi:10.1086/166608, http://adsbit.harvard.edu/cgi-bin/nph-iarticle_query?bibcode=1988ApJ...331..902C
- ↑ Hatzes et al. (2003). "A Planetary Companion to Gamma Cephei A". The Astrophysical Journal 599 (2): 1383 – 1394. doi:10.1086/379281, http://www.journals.uchicago.edu/doi/full/10.1086/379281
- ↑ Wolszczan, A.; Frail, D. A. (1992). "A planetary system around the millisecond pulsar PSR1257+12". Nature 355: 145 – 147. doi:10.1038/355145a0, http://www.nature.com/nature/journal/v355/n6356/abs/355145a0.html
- ↑ a b c Dr Guyon, Olivier "A brief history of the search for extrasolar planets." 11 June 2006. Scitizen. Nov.2008 http://www.scitizen.com/screens/blogPage/viewBlog/sw_viewBlog.php?idTheme=7&idContribution=18
- ↑ Mayor, Michel; Queloz, Didier (1995). "A Jupiter-mass companion to a solar-type star". Nature 378: 355 – 359. doi:10.1038/378355a0, http://www.nature.com/nature/journal/v378/n6555/abs/378355a0.html
- ↑ Mayor et al. (1995). "A Jupiter-mass companion to a solar-type star". Nature 378: 355–359. doi:10.1038/378355a0
- ↑ Schneider, Jean (19 September 2012). "Interactive Extra-solar Planets Catalog" . The Extrasolar Planets Encyclopedia. Retrieved 2012-08-19.
- ↑ "Many, perhaps most, nearby sun-like stars may form rocky planets." Innovations-report. 19 Feb. 2002. <http://www.innovations-report.de/html/berichte/physik_astronomie/bericht-103754.html
- ↑ Hillenbrand, Lynne A., John M. Carpenter, Kim Jinyoung Serena, Michael R. Meyer, Dana E. Backman, Moro-Martín, Amaya, David J. Hollenbach, Ilaria Pascucci, Dean C. Hines, and Jeroen Bouwman. "The Complete Census of 70 μm-bright Debris Disks within the Formation and Evolution of Planetary Systems Spitzer Legacy Survey of Sun-like Stars." The Astrophysical Journal 677 (2008): 630-56. http://adsabs.harvard.edu/abs/2008ApJ...677..630H
- ↑ Valencia, Diana, Dimitar D. Sasselov, and Richard J. O'Connell. "Radius and Structure Models of the First Super-Earth Planet." The Astrophysical Journal 656 (2007): 545-51. http://adsabs.harvard.edu/abs/2007ApJ...656..545V
- ↑ a b c d e f Henry, Gregory, Eric Ford, Chris McCarthy, Kevin Apps, Greg Laughlin, and Bernie Walp. California & Carnegie Planet Search. Anglo-Australian. <http://exoplanets.org/><http://exoplanets.org/othermethframe.html>
- ↑ Wright, Jason T. "Detecting Exoplanets with Precise Radial Velocities."
- ↑ Sackett, Dr. Penny D. "Microlensing exoplanets." 5 Aug. 2008. Http://www.scholarpedia.org/article/Microlensing_exoplanets.com
- ↑ a b c Sing, D. 2008, Astrophysical Journal 686:658–666, 2008 October 10
- ↑ a b c d e f g h Thompson, T. 2007, NASA Press Release http://www.nasa.gov/mission_pages/spitzer/news/spitzer-20070221-full.html
- ↑ Schneider, J. 2008, Extrasolar Planets Encyclopedia, http://exoplanets.eu
- ↑ Barman, T. 2007, ApJ, 661, L191
- ↑ Tinetti, G. et al. 2007, Nature, 448, 7150, 169
Formation of the Solar System
The planets started out as planetesimals. These objects were drawn together by gravity, to form the large masses that would become planets. The initial collisions of planetesimals melted the surface of the emergent planets. As the planets grew, radioactive decay heated and melted the interior.
Earth as a Planet
Earth's Early Years
{{:General_Astronomy/Earth%27s_Early_Years}}
Formation of the Moon
One theory is that the Moon came from the Earth. It is theorized that a Mars sized object struck the Earth tossing huge amount of the mantle up into space. While much of this fell back to Earth some of the matter collected together and formed the Moon. This theory is supported by evidence that the Moon has the same composition of Earth's mantle and the same three isotopes of oxygen that Earth has.
The Biosphere
The story of life on Earth is a fascinating one. Life is more interesting than almost anything else—certainly more interesting than simple rocks, water, and gases. Life is above all else a very complex set of chemistry known as biochemistry—the chemistry of life itself.
So far as we know the Earth is the only place in the universe with life. We may find other places in time, places with very different life. We may even create life. But life has to come from somewhere.
When it formed, the Earth had no life. It couldn't hold life; its surface was hot from either a glob of congealing, molten rock or from giant pieces of rock slamming together. It may have had no gases, and certainly no liquid water. Deadly ultraviolet radiation would have killed anything. But eventually as the rocks cooled, some of them released some of the chemicals of life. Most importantly, liquid water emerged from the rocks or fell to the early Earth and formed early lakes, seas, and oceans. Some of the water evaporated and formed clouds from which rain fell. Other substances emerged from the rocks, like rock phosphates and salts of magnesium, calcium, sodium, potassium, and iron. Some others may have been captured from space when the planets were young, such gases as carbon dioxide or carbon monxide, methane, ammonia, and hydrogen sulfide. Some of those chemicals are dangerous to us—like hydrogen sulfide, ammonia, methane, and carbon monoxide. Don't worry; we weren't around for them to hurt us. There was no oxygen; that would come into existence later.
A remarkable experiment in 1954 by the physicist Harold Urey and the chemist Stanley Miller showed how the early chemicals of life came into existence. They put small amounts of water, ammonia, and methane into chemical flasks and simulated lightning upon the chemicals. (Don't try this at home!) They got some chemicals known as amino acids necessary for proteins. Other people have done similar experiments with slight changes and gotten slightly different effects—but also the chemicals essential to life.
Sulfur was necessary for some vital proteins for all later life, and where there a little hydrogen sulfide, some of those proteins were possible. But proteins are not life themselves. Life cannot form until it has some unique substances called RNA and DNA that control the chemistry of life and define life itself. DNA and RNA require phosphates, compounds that contain phosphorus and oxygen. Life came into existence when it controlled its own chemistry, defined itself in cells, and reproduced.
We don't know the whole story of life. Much of it is genetics whose chemical basis is DNA or RNA—and every living thing has its own DNA or RNA (if not both). They are very complicated compounds with subtle effects. We don't know how cells came into existence—yet. We can't create life—but we know that it came into existence.
Life became increasingly complex. Some of it simply devoured the early material of life. Some devoured creatures that came into existence before it. Some (most of which would become plants) used sunlight to get energy to store in sugars. Plants would do a process called photosynthesis—taking carbon dioxide, water, and sunlight and turning them into sugar (their own food) and oxygen.
Plants released oxygen into the atmosphere, but only from water. The lands were barren of life of any kind for millions of years. Some animals began to eat plants, and some animals ate the animals that ate the plants. All animals would use oxygen. But oxygen would enter the atmosphere. Some of the oxygen would go to the top of the atmosphere and become ozone that would absorb deadly ultraviolet radiation. Then, and only then could animals and plants enter the land. By then the Earth was no longer young. But the chemistry of life was itself very old by then, and that chemistry has changed little to our time—but the great variation possible due to subtle differences DNA and RNA now makes possible the great variety of life—and even the uniqueness of you and me.
The Atmosphere

The Earth has been placed out of order with the other planets because, by studying the Earth, we can become familiar with general principles that can thus be applied to other planets.
Earth's Atmosphere
| A Wikibookian suggests that Electronics/Atmosphere be merged into this chapter. Discuss whether or not this merger should happen on the discussion page. |
The Earth has been shrouded in a thin layer of gases for most of its history. However, the nature and composition of these gases has changed significantly over time. At its initial formation, the Earth's first atmosphere was composed primarily of the light elements hydrogen and helium. However, at the temperatures in the inner solar system, these atoms had sufficient energies to exceed Earth's escape velocity. Earth's gravity was, therefore, not sufficient to hold these gases, which quickly escaped into space.
Earth's second atmosphere was generated by gases that had been trapped within the rocks making up the body of the planet, but escaped due to volcanic activity, a process known as "outgassing". The components of this atmosphere were primarily carbon dioxide, water, and lesser amounts of nitrogen. As the Earth cooled, however, much of the water vapor precipitated out of the air, and areas of liquid water formed on its surface. Much of the carbon dioxide dissolved into the liquid water. Much of this carbon dioxide was later bound up in various aquatic life forms, and then deposited with the remains of those lifeforms in ocean sediment, eventually forming large limestone deposits.
As life evolved on the planet's surface, some of the remaining carbon dioxide was converted by these organisms into oxygen, through photosynthesis and similar processes. This had the effect of further lowering carbon dioxide levels, leaving nitrogen as the primary constituent of the atmosphere, and adding in substantial amounts of oxygen. Thus Earth's third atmosphere was formed as we know it today: primarily nitrogen, oxygen, water vapor and various trace molecules in lesser amounts.
The Water Cycle
All of the water in the world keeps getting reused and reused. Why? Water molecules can be made into three forms: gas (steam), liquid, and solid (ice). The water cycle turns water into all three of these forms.
the Cycle
Part 1: Up
Water starts in the oceans. The oceans contain tons of water, and there is more water than land on the Earth's surface. With all this water in the same place, the water turns to steam, or evaporates. And since steam is lighter then liquid, it goes up.
Part 2: Together Again
Now in the sky, the water condenses.
Earth
Earth's Interior
Based on models of the earth (well supported by the scientific evidence available), the theory of plate tectonics presupposes that the Earth's outermost surface (crust) is made up of two sub-layers, the rigid lithosphere and the semi-molten asthenosphere. Beneath the crust is the mantle, a layer made up of molten rock (magma).
Heat is generated in the Earth's core by uranium, potassium, and thorium.[9]
Earth's Surface
Plate Tectonics

This map shows all of the Tectonic Plates that make up the Earth's crust Plate tectonics is a theory of geology underlying the observed phenomenon of continental drift.
The rigid stone making up the lithosphere "floats" on the fluid-like asthenosphere, and, in areas where magma wells up from the mantle below the crust, may develop fractures. This results in the lithosphere being separated into contiguous masses of solid earth and rock known as tectonic plates. Due to slow currents in the asthenosphere's material, the plates floating atop this material undergo slow motions in different directions. These floating plates regularly jostle one another, with interactions along these boundaries being responsible for earthquakes and volcanos.
Tectonic plates are roughly divided into two types: continental and oceanic plates. The distinction is based on the thickness of the plates; oceanic plates are thinner than continental plates; as a result, the oceanic plates generally lie below sea level, while the continental plates project above sea level.
The same currents that move tectonic plates with respect to one another also tend to bring molten material closer to the surface at points where a circulation cell is drawing the material upward. In minor cases, this can result in a hot spot, where the material of the plate is eaten away from below, leaving openings for volcanos such as those producing the islands of Hawaii. As plates move over mantle fissures, chains of volcanos can form. In major cases, the rising magma continuously pushes itself into the midst of the plate, eventually cooling to form new plate material. Thus, some tectonic plates are being widened by the addition of new material, via upwelling of magma from below. Currently the Atlantic oceanic plate is in the process of expanding, fuelled by a continuous input of magma along the North Atlantic Ridge. The region of Iceland, which straddles this ridge, is thus gaining territory at a rate of a few centimeters per century.
The boundaries between plates are known as fault lines. Individual faults are regions where two plate sections are moving with respect to one another. Pressure builds up along these regions as the plates are drawn in different directions by the underlying currents; when the pressure is released by the abrupt motion of the plates, an earthquake results. One of the most famous systems of fault lines is the boundary of the Pacific plate, known as the Ring of Fire due to the amount of seismic activity along this boundary. On the easternmost edge of the ring is the San Andreas Fault, on the boundary of the North American and Pacific plates. This fault line is responsible for the earthquake activity in the western United States, most notably the 1906 San Francisco Earthquake.
In some areas one plate will begin to overrun another. The plate being thus overrun will have its edge pressed downward below the leading edge of the other plate. This process, called subduction, results in the edge of this plate being exposed to the greater pressures and temperatures within the asthenosphere, and the rock making it up may begin to liquify. The resulting build-up of magma under pressure may find explosive release through the lithosphere above it, resulting in a volcanic eruption. In addition, the pressure exerted on both plates during a collision may cause the plates to buckle upward some distance from the plate boundaries. The resulting geographical features are known as upthrust mountain ranges. One example of this is the Himalayas in Asia.
Earth's Atmosphere
The Greenhouse Effect
CO2 (carbon dioxide) is increasing drastically due to burning fossil fuels and deforestation. This gas, among others, traps heat from the sun, making the Earth hotter. [10]

The greenhouse effect is the process by which radiation from a planet's atmosphere warms the planet's surface to a temperature above what it would be without this atmosphere. The intensity of the downward radiation – that is, the strength of the greenhouse effect – will depend on the atmosphere's temperature and on the amount of greenhouse gases that the atmosphere contains.
Earth’s natural greenhouse effect is critical to supporting life, and initially was a precursor to life moving out of the ocean onto land. Human activities, however, mainly the burning of fossil fuels and clearcutting of forests, have accelerated the greenhouse effect and caused global warming. The planet Venus experienced runaway greenhouse effect, resulting in an atmosphere comprised of 96% carbon dioxide, with surface atmospheric pressure roughly the same as found 900 m (3,000 ft) underwater on Earth. Venus may have had water oceans, but they would have boiled off as the mean surface temperature rose to 735 K (462 °C; 863 °F).
Earth's Moon
{{:General_Astronomy/Earth%27s_Moon}}
Space Exploration
First Steps into Space
The first man-made object to be launched into space was the Soviet unmanned satellite named Sputnik I. This began the "Space Race" between the United States and the Soviet Union. The Soviets won almost every aspect (1st object, 1st man in space, 1st woman in space, etc.), except for the United States' 1st man on the moon.
The Apollo Missions
The first mission to land humans on the moon was the United States Apollo 11. The astronauts on board were Neil Armstrong and Buzz Aldrin, who explored the lunar surface on July 20, 1969. Armstrong debarked from the Lunar Module "Eagle" spacecraft first. After setting foot on the surface of the moon, he uttered the famous words: "That's one small step for a man, one giant leap for mankind."
Pioneers and Voyagers
Pioneer Missions
The Pioneer missions can be broken into some distinct groups:
- Able space probes. (1958 - 1960)
- Pioneer 0 (Thor-Able 1, Pioneer) – Lunar orbiter, destroyed (Thor failure 77 seconds after launch) August 17, 1958
- Pioneer 1 (Thor-Able 2, Pioneer I) – Lunar orbiter, missed Moon (third stage partial failure) October 11, 1958
- Pioneer 2 (Thor-Able 3, Pioneer II) – Lunar orbiter, reentry (third stage failure) November 8, 1958
- Pioneer P-1 (Atlas-Able 4A, Pioneer W), probe lost September 24, 1959
- Pioneer P-3 (Atlas-Able 4, Atlas-Able 4B, Pioneer X) – Lunar probe, lost in launcher failure November 26, 1959
- Pioneer 5 (Pioneer P-2, Thor-Able 4, Pioneer V) – interplanetary space between Earth and Venus, launched March 11, 1960.
- Pioneer P-30 (Atlas-Able 5A, Pioneer Y) – Lunar probe, failed to achieve lunar orbit September 25, 1960.
- Pioneer P-31 (Atlas-Able 5B, Pioneer Z) – Lunar probe, lost in upper stage failure December 15, 1960.
- Juno II lunar probes. (1958 - 1959)
- Pioneer 3 - Lunar flyby, launch failure. (December 6, 1958).
- Pioneer 4 - Flyby, achieved escape velocity (March 3, 1959).
- Later Missions (1965 - 1978)
- Pioneer 6 (Pioneer A) – launched December 1965.
- Pioneer 7 (Pioneer B) – launched August 1966.
- Pioneer 8 (Pioneer C) – launched December 1967.
- Pioneer 9 (Pioneer D) – launched November 1968 (defunct since 1983).
- Pioneer E – lost in launcher failure August 1969
- Outer Solarsystem missions.
- Pioneer 10 (Pioneer F) – Jupiter, interstellar medium, launched March 1972.
- Pioneer 11 (Pioneer G) – Jupiter, Saturn, interstellar medium, launched April 1973.
- Pioneer H – identical to Pioneers 10 and 11, but never launched.
- Pioneer Venus project
- Pioneer Venus Orbiter (Pioneer Venus 1, Pioneer 12) – launched December 1978
- Pioneer Venus Multiprobe (Pioneer Venus 2, Pioneer 13) – launched August 1978
- Pioneer Venus Probe Bus – transport vehicle and upper atmosphere probe
- Pioneer Venus Large Probe – 300 kg parachuted probe
- Pioneer Venus North Probe – 75 kg impactor probe
- Pioneer Venus Night Probe – 75 kg impactor probe
- Pioneer Venus Day Probe – 75 kg impactor probe
Dates are years of mission launches.
Voyager Missions
The voyager missions were launched in order to study the outer solar system.
- Voyager 1
- Studied Jupiter, Saturn and is trudging on towards the heliopause. Presently the farthest human-made object from Earth.
- Voyager 2
- Studied Jupiter, Saturn, Uranus and Neptune. Launched after, but with a higher velocity than Voyager 1.
The Great Observatories
General_Astronomy/Major_Future_Missions
Numerous missions are currently in the pipeline in order to expand humanity's depth and width of knowledge in astronomy. The James Webb Space Telescope, for example, is currently being built by NASA as a successor to the Hubble Space Telescope.
Astrobiology and Extraterrestrial Life
The Drake Equation
The subject of extraterrestrial intelligence is one which has a fascinating mix of fact and speculation. In dealing with extraterrestrial intelligence there is one important fact which was first pointed out by Enrico Fermi, the scientist that built the first nuclear reactor, and it's an obvious fact that is so obvious that one doesn't realize how remarkable it is until one thinks about it. This is the fact that when one looks at the skies, there is no obvious sign of extraterrestrial life.
Where are they?
It's a remarkable fact, because even with our limited technology level, we've made the sun look very strange to an alien astronomer. Type G stars simply do not emit much radio radiation, and to any astronomer within a fifty light year radius of the earth, there is something blindingly weird about the sun, in that something is causing the sun to appear to emit vast amounts of radio waves. Once the sun has been identified as odd, it wouldn't take that much effort to start looking into the characteristics of the radio waves and through things like Doppler shift, quickly figure out that the radio waves didn't come from the sun but rather from a planet in orbit. Once that gets figured out, you can look at the details of the radio spectrum and piece together things like the rotation rate of the Earth (the amount of radio waves you will see will be sharply reduced when the Atlantic and Pacfic ocean are facing you in comparison to the continents), and someone who is sufficiently clever might be able to figure out how to decode the radio output of the earth.
The paradox becomes even more odd if you think ahead a thousand or two thousand years. Keep in mind that a thousand or two thousand years is nothing astrophysically speaking. If you can imagine what we ought to be able to do, assuming that rates of technological growth don't slow down, there ought to be many things that would be astrophysically obvious. For example, the ultimate answer to the energy resources is to build a series of solar satellites that trap solar energy and beam it to the earth or any other planet in the solar system. If you trap enough solar energy, this will start to become obvious in the solar spectrum, in that if you plot many stars in the HR diagram then you will soon find that there is something very odd about some of the stars that don't fit on the main sequence at all. Another technology that might be astrophysically significant is that of nanotechnology and self-replicating machines. It shouldn't be too hard in the next thousand years to produce autonomous robots that can feed off asteroids and reproduce. Once you have these robots roaming the stars, exponential growth makes it very likely that you will run into one of them.
So there is something odd to be explained. The problem here is that we have enough facts to establish that there is a puzzle, but not nearly enough facts to figure out what the solution is. There are many ways of resolving the Fermi paradox, and given the lack of facts to constrain the solution, we are more in the realm of science fiction than of science at this point.
Some of the solutions are extremely depressing. One solution is simply that technological civilizations destroy themselves. There is no end to the number of ways we could destroy ourselves now, and it's also possible that advancing technology could allow for ways of self-destruction that we haven't thought about. For example, what would happen if nanotechnology made it possible for any human being to create their own atomic bomb or a deadly virus?
There are also sociological explanations that are rather depressing. We happen to live in a society that for the most part thinks that technology and curiosity are good things. However, even looking at examples in our own history, it's not clear that the way that we look at the world is the most natural or the most stable. There are the classics of dystopian fiction 1984 and Brave New World, and one would imagine that these worlds aren't that conducive to stellar colonization.
It may be possible that when and if we start exploring alien worlds, we'll find that at least in our part of the galaxy, that some previous civilization managed to extinguish, for whatever reason, all traces of life and then destroyed itself. But then again maybe not.
Before one gets too depressing, let me just point out one other obvious fact that is even more amazing when you think about it. We do know that somehow, someway, we've made it this far. We don't know how probable or improbable life and alien civilization is, but we do know that somehow someway, it happened at least once on the Earth. We don't know what is the resolution of the Fermi paradox, but what we do find remarkable is that first that we might someday figure this out, and that somehow, at least to some people, it really matters.
Plus the sun is 93,000,000 miles away from earth.
- The Drake Equation
- Takes into account:
- Number of stars in a galaxy. (N*)
- Fraction of stars with planets. (fp)
- Number of planets in a system that reside within the life-zone for that system. (nLZ)
- Fraction of suitable planets on which life actually begins. (fL)
- Fractions of lifeforms which evolve to intelligence. (FI)
- Fraction of star's life during which lifeform is communicative. (FS)
The last factor is the hardest to estimate, along with the number of communicative civilizations per galaxy (NC). The probabilities cover several orders of magnitude.
External links
Organic Chemistry for Astronomy
Life in the Solar System

Astrobiology is a relatively young approach to the study of life in the universe, with earth forming the basis of our knowledge and investigation. Astrobiology seeks to address many questions, including:
1. Are there other forms of life in the universe?
2. Are we alone in the universe?
Very importantly, astrobiology transcends many scientific field boundaries and creates an amalgam of interdisciplinary topics, ranging from biology, geology, astronomy, chemistry to planetary sciences, paleontology and physics. Astrobiology covers a huge breadth of knowledge; therefore, only a selected overview of the difficulties of extraterrestrial life and of the possibility and search for life beyond earth is given below. Many of the postulations are inconclusive.
Expected Restrictions & Prerequisites for Both Terrestrial and Extraterrestrial Life
“Life-support”
- A source of energy such as from a nearby star is needed to drive endothermic, or energy-absorbing, reactions.
- Raw materials, predominantly carbon, build and form organic molecules. Other important elements for life on earth include hydrogen, nitrogen, oxygen, phosphorus, and sulfur (comprising the acronym SPONCH).
- Life requires some form of shielding from damaging radiation, implying the presence of an atmosphere.
- Also indispensable is the presence of a liquid or very dense gas as a solvent for biochemical reactions to occur quickly and stably. Liquid water, the life-sustaining universal solvent (at least on earth), entails certain atmospheric composition and temperatures.
- The characteristics of stars can also determine the capacity for life on surrounding, orbiting planetary bodies, namely through the location of the habitable zone. The habitable zone in a solar system is defined as the region around a star that is conducive to life, which usually implies regions with temperatures high enough to maintain liquid water. Earth falls under the habitable zone in our solar system. As the mass of a star increases, so does the distance of the habitable zone from the star. Also, stars hotter than the sun have habitable zones farther out while cooler stars have them closer in, but hotter stars produce excessively harmful ionizing UV radiation while cooler stars may “tidally lock” planets that are too close, meaning these planets will always show the same "face" to the star and hence have a very cold side and a very hot side. Stars both hotter and cooler than the sun therefore possess conditions hostile to life. The properties of a solar system’s star determine the likelihood of life’s existence on planets and/or moons. In turn, the planets and their moons' positioning relative to the habitable zone and to their star also influence their conduciveness to life. Locating habitable zones in the universe leads to discovering the possibility of life. However, the later-discussed planet Mars and moons in our solar system may shelter life even though they do not fall into the generally accepted habitable zone.
The difficulty of life on other celestial bodies is marked by several conditions. The atmospheric pressure and composition vary immensely and gravity is altered across different regions in space; for instance, Mars has only a tenth of earth’s atmosphere, its atmosphere is mainly constituted of carbon dioxide, and its gravity is only a third of earth’s. All the planets and moons currently being explored for life also face different solar and cosmic radiation systems than the earth since the bodies are farther out in the solar system. Though they are farther from the sun and so experience less solar radiation, none has an ozone layer to protect against life-damaging radiation although some do have an adequate atmosphere to offer some protection. Moreover, oxidants such as iron oxide made by UV radiation acting on mineral surfaces in the presence of atmospheric oxygen and extremely dry conditions are chemically hostile to many organic compounds. Space is overall a very inhospitable, bleak place for life. It includes a space vacuum, solar winds with protons, electrons, and alpha particles floating around, radiation, solar flares, cosmic radiation, and low temperatures, factors counter to the nourishing conditions on earth. [1]
Extremophiles and Their Role in Life Exploration

Though life seems only possible under specific conditions, extremophiles such as bacteria that live in high temperature, toxic, deep-sea hydrothermal volcanic vents on earth offer insight into life that could have developed on other planets that mostly share such extreme, inhospitable environments, which also can include freezing temperatures and minimal sun exposure. The range of conditions life here on earth has managed to flourish in reveals more outer space milieus as possible breeding grounds for life. A few species of halophilic or salt-loving bacteria have also been experimentally proven to survive exposure to the extreme space environment for about two weeks. This evidence inspires hope that life similar to earth’s extremophile microbes can exist in outer space on other planets or moons despite harsh conditions.
Other Solar System Candidates for Life
Mars
In 1976, a search for microbial life on the red planet was performed. Two Viking landers conducted three experiments on Martian soil to test for bacteria presence through: 1) detecting the fixation of carbon dioxide, 2) observing possible metabolic processes through radiorespirometry, and 3) measuring the production and uptake of carbon dioxide, nitrogen, methane, hydrogen, and oxygen. Some tests yielded positive results: one experiment demonstrated that carbon was indeed converted to some organic matter by Martian soil, but the materials were not necessarily living or biological and the matter was not confirmed as organic. The 1997 Pathfinder mission discovered magnesium, aluminum, iron, and phosphate in Martian rocks, which are all possible life-supporting materials. Methane was also discovered in Mars’ atmosphere. Methane is important because it is a building block molecule for compounds such as hydrogen cyanide, which are important for amino acids, which are vital for life. However, no conclusive organic matter has been found on Mars’ terrain.
Mars could have once had water but does not have any liquid water now because its air pressure is too low. Mars is also small, reducing its ability to retain a hold on its atmosphere and increasing the rate of heat loss, resulting in cold temperatures at -63 degrees Celsius, which further decreases the likelihood of surface liquid water significantly.

Some tentative evidence for the presence of water (and consequently maybe even life) possibly hidden under ice exists. Ancient craters that seem to have been eroded by water dot Mars’ landscape. The presence of craters suggests low to nil tectonic activity; however, some areas on Mars were smoothed over, therefore suggesting water activity. Dry, river-like features on Mars may have also been carved out by running water over long periods of time. The same water in the form of huge floods may have caused the broad channels observable on the dry planet.
Mars’ huge volcanoes such as Olympus Mons could contribute internal heat to sustain subsurface water. According to Bruce Jakosky, “there’s a possibility of hydrothermal vents [due to these volcanoes reminiscent of terrestrial extremophilic living conditions].” [2] Though carbon mostly as carbon dioxide, hydrogen, oxygen, and nitrogen were also found in the Martian atmosphere, increasing the possibility of life on the planet, still, no definite life forms have been uncovered.
The confirmed Martian Meteorite ALH84001 that hit and was recovered from Antarctica in 1984 could also shed light on the possibility of life on Mars. The meteorite consists of young, volcanic rocks with partially dissolved carbonate globules that indicate the infiltration of liquid water and with ancient fossilized bacteria-like objects about the size of viruses identified as nanobes. Nanobes have been hypothesized as the smallest life form and are filamental structures usually found in certain rocks and sediments. Magnetite and iron sulfide particles discovered in the meteorite could have been left behind by the bacteria, but compelling abiotic explanations do not allow them to coexist with partially dissolved carbonates. Furthermore, the apparent life forms may be contaminations from life on earth. All conclusions are tentative and heavily contested.
Europa

Europa is one of the four largest Jovian (Jupiter) moons found to be covered by a smooth layer of water-ice, suggesting a life-nurturing liquid ocean underneath global in extent. Though temperatures are a nippy -145 degrees Celsius, some possible factors may have kept the water from freezing. Tidal heating from friction due to Europa’s eccentric orbit around Jupiter has been proposed. The planet’s gravity pulls stronger on the near side than the far, creating tidal bulges that can crack the icy crust surface and heat the interior. Approximately 5–25 km thick ice sheets could also insulate the water beneath. Volcanoes deep down may harbor hydrothermal vents that provide an energy source to heat and maintain liquid water.
Europa has a very smooth surface and very few craters, which could not be the result of an atmosphere burning up or the weathering of the craters since Europa’s atmosphere is very thin, so the tentative explanation is ice covering an ocean that evens out the surface. Some parts of its surface show blocks of ice that are separated but seem to fit together like a puzzle; these icebergs could have been shifted by slushy or liquid water beneath. Ridges in Europa’s landscape suggest existent water seeping up the ice cracks, refreezing, and then forming higher and higher ridges. In 1996, the Galileo spacecraft detected a magnetic field on the planet’s surface, indicating that there must be some electrical conduction likely to derive from a salty ocean. The previously mentioned hydrothermal vents may be spewing and mixing energy, heat, and chemicals into Europa’s ocean, possibly fostering life. The aforementioned tides on Europa created by Jupiter’s pull on its surface could also mix life-supporting substances together in the ocean.

About the possibility of life on Europa, when Jupiter strongly irradiates Europa’s ice, which is shown by the Galileo spacecraft’s observations to contain carbon dioxide, the irradiated carbon dioxide can produce simple organic molecules such as formaldehyde that are steps towards life. As one of the fundamental preconditions for life is a source of energy, tidal heating and the decay of radioactive elements could provide such energy for underwater life near the volcanic vents. Life-supporting energy can also be supplied by high-energy particles from Jupiter’s magnetic field breaking apart molecules in the ice to produce hydrogen peroxide, oxygen molecules and hydrogen. Finally, in Europa’s water-immersed rocks, there is evidence of life-forming elements like those on other solar system candidates for life.
Titan
Hazy, orange Titan is Saturn’s largest moon and is the only moon in the solar system that possesses clouds and a thick, dense atmosphere that is about 1.5 times the pressure of earth’s atmosphere. It also contains many organic gases such as methane, ethane, nitrogen, and hydrocarbons, and possesses conditions that resemble those of early earth four billion years ago that allowed life to develop. Extremely tall mountains cap Titan’s landscape and have been recently found to contain methane as well. Dark spots on the moon’s surface may reveal lakes of liquid organic materials including methane and/or ethane.

The sun’s radiation reacts with atmospheric nitrogen and methane on the moon to produce the orange haze and a steady stream of organic substances such as black ethane that rains down from the sky, supplying more carbon-rich molecules that could generate life. The presence of methane gas in the air suggests that a localized reservoir of liquid methane and ethane slowly evaporates into gaseous form in the atmosphere. NASA Ames Research Center scientists believe that methane-producing microbes, methanogens, may flourish on Titan since the moon’s atmosphere and surrounding are so heavily saturated with the compound. However, liquid methane and ethane are much colder than liquid water by some 200 degrees Celsius and biochemical reactions would occur at painstakingly slow rates. These compounds are also far less capable as solvents compared to water and therefore much less life-inducing. Water is also missing from the picture due to freezing temperatures of -178 degrees Celsius. Long ago, Titan could have been warmer and had water and maybe even life. Water may still be under the presently icy and rocky surface, concealing signs of life.
Enceladus
Enceladus, another one of Saturn’s satellites, is currently the “search for life” priority hot-spot. Like Jupiter’s Europa, Enceladus has a very smooth, almost crater-free surface but which is caused by constant geological activities, which is characteristic of a relatively young planet or in this case, a moon associated with a planet. This inner, tiny moon of Saturn has a water vapor-based atmosphere and contains liquid water reservoirs approximately only a half kilometer beneath its icy south pole, implying a heat source originating from the south pole of the moon. Though general temperatures are well below freezing at -203 degrees Celsius, this south pole is actually a relative “hot spot” at -183 degrees Celsius. The south pole also has “tiger stripe” regions or cracks that are warmer spaces, signifying geothermal activity.
Water vapor and ice crystal plumes also from the moon's south pole were found to contain organic materials such as carbon dioxide, methane, and propane. Such plumes also suggest an organic soup in the oceanic reservoir. Like Earth, Enceladus could have underwater hydrothermal vents near its water reservoirs that produce energy to heat the water. However, how this small moon can generate so much heat is still puzzling. Perhaps an insulating shell containing water ice with gas particles could aid the retention of heat. The pressurized liquid water could also fuel the geysers that spew icy water matter into space that dissociates into hydrogen and oxygen.

These geysers may be erupting from superficial liquid-water pockets at above 0 degrees Celsius. Liquid water so near the surface rarely occurs on the moon, introducing more questions and speculations about life on the mysterious, distant moon. Currently, the NASA Cassini spacecraft has been taking high resolution photographs of Enceladus and confirming numerous theories interpreting radical findings on Enceladus. The spacecraft is scheduled to fly close enough for observations of the geysers in October 2008.
There may be many more planets and moons light-years away that are toeholds for life since we are turning up evidence for life on many planets and moons in our own neighborhood! Many of the diverse and often harsh planetary features discussed above that seem to suggest the existence of life broaden the conceptions and prospects of finding environments suitable for life throughout the universe, life not in the form of humanoid green-skinned Martians but of microbes perhaps distantly related to earth's extremophiles.
Notes
[1] Mancinelli, Rocco. "Life Beyond Earth/Panspermia ." HumBio 183 Astrobiology and Space Exploration. Bldg 60-61G, Stanford University. 13 Feb. 2007.
[2] Pacchioli, David. "Mars Revisited." Astrobiology: The Search for Life in the Universe. Jan. 2001. Research Penn State. 21 Feb. 2007 <http://www.rps.psu.edu/0101/mars.html>.
References
"About Astrobiology." NASA Astrobiology. Ed. Minafra/Boldt. 2 Feb. 2006. NASA. 21 Feb. 2007 <http://astrobiology.arc.nasa.gov/about/index.cfm>.
Astrobiology: The Living Universe. 2000. ThinkQuest. 21 Feb. 2007 <http://library.thinkquest.org/C003763/index.php>.
Bennett, Jeffrey, Seth Shostak, and Bruce Jakosky. Life in the Universe. San Francisco: Pearson Education, Inc., 2003.
Black, Richard. "Saturn's moon 'best bet for life' ." BBC NEWS. 10 Apr. 2006. 21 Feb. 2007 <http://news.bbc.co.uk/2/hi/sci/tech/4895358.stm>.
Boyle, Alan. "Liquid water on Saturn moon could support life." MSNBC Space News. 9 Mar. 2006. 21 Feb. 2007 <http://www.msnbc.msn.com/id/11736311/>.
Mallery, Charles H. Astrobiology. Course home page. 29 Apr. 2003. Department of Biology, University of Miami. 21 Feb. 2007 <http://fig.cox.miami.edu/~cmallery/150/astrobiol/exobiol/exobiol.htm>.
Mancinelli, Rocco. "Life Beyond Earth/Panspermia ." HumBio 183 Astrobiology and Space Exploration. Bldg 60-61G, Stanford University. 13 Feb. 2007.
Pacchioli, David. "Mars Revisited." Astrobiology: The Search for Life in the Universe. Jan. 2001. Research Penn State. 21 Feb. 2007 <http://www.rps.psu.edu/0101/mars.html>.
Roach, John. "Jupiter Moon May Have Life -- Experts Urge a Mission." National Geographic News. 23 Mar. 2005. 21 Feb. 2007 <http://news.nationalgeographic.com/news/2005/03/0323_050323_jupitereuropa.html>.
Rothschild, Lynn. "The Search for Life on Titan, Europa, Enceladus and beyond." HumBio 183 Astrobiology and Space Exploration. Bldg 60-61G, Stanford University. 15 Feb. 2007.
"The Giant Titan: Moon of Mysteries ." Exploring Saturn. 2005. Space Today Online. 21 Feb. 2007 <http://www.spacetoday.org/SolSys/Saturn/SaturnTitan.html>.
"Tiny Enceladus May Hold Ingredients of Life ." PhysOrg. 5 Sept. 2005. University of Arizona. 21 Feb. 2007 <http://www.physorg.com/news6237.html>.
Wong, Tony. Astrobiology: Life in the Universe. Course home page. Dept. of Astronomy, U of California, Berkeley. 21 Feb. 2007
The Search for Extraterrestrial Intelligence
There is intelligent life other than us humans in the universe: whales, dolphins, elephants, pigs, seals, great apes, and surprisingly octopuses. But none of these is ever likely to build spaceships or transmit signals into space, and we have difficulty understanding the other intelligent species on our planet.
We have an intense curiosity: are we alone in the universe as a technological civilization? Some people would like to believe that other civilizations, perhaps with creatures even more different from us than elephants or even octopuses are far away in space, and that those creatures have something that we can learn.
To find such intelligent civilizations deep in space we need first to find signals from deep in space. That won't be easy; even radio has been broadcast for a short time (about 85 years as of 2008), a short time compared to human existence. We might also look for planets that have conditions similar to those of Earth—similar in size and temperature. Extraterrestrial civilizations are unlikely to be found on a gas giant planet or a planet of the Moon's size. We also have to be lucky enough to find a congenial planet with a civilization that has been sending signals of its own sophistication for a long enough time to reach us. If some sophisticated civilization has been sending signals to us for forty years but is fifty light-years away from us, then we on Earth will not get them for another ten years, and then only if we are tuned in. A civilization so sophisticated as ours was in 1875 would have given no evidence of its existence (such as electric lighting) visible even from the Moon—even if we then had some fine art, literature, and music.
What about alien visitors? Some people believe that some UFOs, or Unidentified Flying Objects are visitors from space. Almost all prove to have simpler explanations such as mirages, optical illusions, aircraft, and weather balloons. Even the planet Venus, bright enough to be visible by day is often seen as a UFO. Most scientists discount stories of visitors from outer space even if they think visits from distant space possible. Not until we actually see a creature like "ET" or, worse, the alien visitors of the movie Independence Day can we claim to have met alien visitors. Space travel is difficult and time-consuming. Species with lifespans similar to ours are unlikely to travel to and from "promising" planets such as their and ours.
The Sun
The Sun is the star at the center of the solar system, around which Earth, the seven other planets, and numerous other bodies revolve. It is sometimes called Sol (hence the term "solar system"). The Sun has a mean diameter of 1.392 million kilometers, which is 109.1 times the diameter of Earth and 9.7 times the diameter of the largest planet, Jupiter. The Sun's rotation period relative to the distant stars is 25.05 Earth-days at its equator and 34.3 Earth-days at the poles.
Solar Structure and Composition

The sun is composed of extremely hot, gaseous material. Because of the high temperatures, this material exists in a state called plasma, in which electrons have been stripped from their parent nuclei. The Sun's composition is roughly 90% hydrogen and 10% helium, by total numbers of nuclei. Considering mass, about 71 percent of the Sun is hydrogen, and 27 percent helium. The difference is due to the fact that helium nuclei have about 4 times the mass of hydrogen nuclei (protons). There are small percentages of other elements mixed in.
The Sun is made up of a series of layers, which can be thought of as a set of concentric "shells" from the core outward.
At the center of the Sun is its core, a region of some 15 million kelvin (About 27 million degrees F). The core is where the nuclear fusion reactions that power the Sun take place. Primarily, this is the fusing of hydrogen into helium.
Outside the core is a radiative zone, where energy produced in the core travels toward the surface. However, this energy can only travel outward by radiation for a certain distance, which limits its depth. Temperatures here run from about 7 to 2 megakelvins. An interface region above this is thought to be the source of the solar dynamo which powers the Sun's magnetic field.
Outside the radiation zone and interface region is a convection zone. This zone sits between the heated radiation zone and the cooler outer layers of the Sun. The result of this is a series of motions known as convection. Hot material, being less dense, rises upwards toward the surface; material near the surface, once cooled, becomes denser and sinks downwards again. Through this process, heat is gradually transported upward to the solar surface. The base of the convection zone is at about 2 megakelvins, while material at the very top is at roughly 6000 kelvins.
Atop the convection zone lies the photosphere, the visual "surface" of the Sun from our point of view. Material here is at approximately 6000 K. As a result of the convection going on below, polygonal shapes define the walls of the convection cells, called granules appear all across the surface.
Above the photosphere is the chromosphere, a very diffuse, hot layer. Material here rises in temperature from the 6000 K of the photosphere to about 20,000 K. A transition region above the coronasphere has an even more dramatic rise in temperature, up to a megakelvin.
Finally, outside the chromosphere and transition region is the corona, an extremely tenuous (very low-density) gas over a megakelvin. It is thought that the corona is primarily heated by the magnetic processes of the solar cycle.
Solar Cycles

The Sun goes through regular cycles related to the formation and destruction of its magnetic field every 11 years. This process affects features on the surface of the Sun; it is by observing those features that our knowledge of solar cycles has developed over time.
The Sun's magnetic field is created naturally by the movement of the solar plasma. Because this plasma is made up of charged particles, its movement creates electric fields. Where electric fields are generated, magnetic fields are generated perpendicular to them.
The Sun's rotation, however, is not rigid like the Earth's, because the gaseous material is so much more fluid than the Earth's crust. Material at the equator moves more quickly than does material at the poles; this is called differential rotation. Furthermore, the magnetic field lines are embedded within the plasma, and tend to move with its motions. As a result, the magnetic field lines which initially run from pole to pole become more stretched in the middle, with the center of the line outrunning the pole-anchored ends. Eventually, these lines will wrap around the Sun many times.
As magnetic field lines cannot cross one another, they tend to protrude upwards when they come close to one another, forming "loops" that project out of the solar photosphere. It is along these loops that solar prominences are displayed. The more these lines are wrapped around the Sun, the more "tangled" and disrupted the magnetic field becomes. Eventually, the field is so disrupted that it breaks up completely. After this, of course, a new magnetic field starts to form, and the cycle begins again. The complete process takes about 11 years.
The presence of magnetic fields has an effect on the Sun's photosphere. In discussing solar structure and composition, it was mentioned that the process of convection brings heat from the inner regions of the Sun up to the photosphere. This convection tends to occur in fairly localized zones of rising hot and falling cool material known as convection cells. However, if a magnetic loop is present, it will disrupt one of these convection cells, trapping cool material at the Sun's surface. While these regions (about 4500 K) are only cool compared to the photosphere (at about 6000 K), the overall effect is that they appear dark against the solar "surface". As a result, these are known as sunspots.
The presence of sunspots reflects the cycle of the magnetic fields. In fact, it was the progression of sunspot number and position that gave the first evidence of cycle of magnetic field reversals. At the beginning of the magnetic cycle, when the magnetic field is newly forming, only a few sunspots will appear; this is called a solar minimum. Those sunspots that do appear will tend to be at high solar latitudes - that is, closer to the poles and further from the solar equator. As the cycle continues, sunspots will gradually appear in greater numbers and tend to be closer to the solar equator. The peak of this cycle is known as the solar maximum. After the sunspot numbers peak, they will continue to appear with less frequency, and be still closer to the solar equator. As this cycle trails off, the first few sunspots for the next cycle will start to appear at high solar latitudes, and so forth.
Because they are formed by magnetic field lines, sunspots occur in pairs; at the base of either end of the magnetic loop that formed them. Likewise, the sunspots will have opposite magnetic polarity from one another. There are distinct patterns in the polarities of each pair which can be observed during a cycle. For convenience, we will call the spot that appears to be further along in the direction of the Sun's rotation the "leading" spot, and its partner the "trailing" spot.
Sunspot pairs in the northern solar hemisphere will have opposite polarities from those in the southern solar hemisphere. That is, if the leading spot is polarized one way (call it +) and the trailing spot the other (−) in the northern hemisphere, then in the southern hemisphere the leading spot will be (−) and the trailing spot (+). Sunspot pairs in a given hemisphere will tend to all appear with the same polarities during a solar cycle. However, at the end of the cycle, the polarities will "flip": new sunspots in that hemisphere will have polarities opposite from the previous cycle.
The table below shows the sunspot pattern over four 11-year cycles, for pairs of (leading and trailing) sunspots.
| Cycle | N. pair polarities | S. pair polarities |
|---|---|---|
| 1 | + - | - + |
| 2 | - + | + - |
| 3 | + - | - + |
| 4 | - + | + - |
Connection between Sunspot Activity and Aurora on Earth

Aurorae are visible effects of the Sun's activity on the Earth's atmosphere. It results from the interaction of the solar wind, a continuous flow of electrically charged particles—a stream of electrons and protons coming from the Sun—with gases in the upper atmosphere of the earth at altitudes above 50 miles.[1] When these charged particles reach the Earth's magnetic field, they become trapped in it. Bouncing back and forth many of these particles travel toward the Earth's magnetic poles. When the charged particles strike atoms and molecules in the atmosphere, the atmospheric atoms become excited or ionized causing them to emit photons. These photons cause the luminous auroras.[2] The aurora seen in the Northern Hemisphere is called Aurora Borealis or the northern lights whereas the aurora seen in the Southern Hemisphere is called the Aurora Australis.[1]
The collisions of the solar wind with Earth’s upper atmosphere produce electrical discharges which energize atoms of oxygen and nitrogen which subsequently release various colors of light. Mostly aurorae are seen green and red as it is emitted from atomic oxygen. Similarly molecular nitrogen and nitrogen ions produce low red and very high blue/violet aurorae. Whereas ionic nitrogen produces blue and green color aurora and neutral nitrogen produces the red and purple color with the rippled edges.[3] Most auroras occur at about 60 to 620 miles above the Earth. Some extend lengthwise across the sky for thousands of miles or kilometers.[1] A diffuse red aurora occurs above 150 miles. An aurora having a pinkish edge will have an altitude of around 50 to 60 miles.[4]

Auroral activity occurs mostly in a belt called auroral zones, around the geomagnetic poles, between 65 and 70 degrees of geomagnetic latitude. An auroral zone is a ring-shaped region of approximately radius 2500 km around either magnetic pole of the Earth. It was hardly ever seen near that pole itself. At any time of day, the distribution of aurora is slightly different. It's center is offset from the magnetic pole by 3-5 degree night-ward of the magnetic pole. As a result, the auroral arcs reach furthest equator-ward around midnight during a major geomagnetic storm. Auroral zones migrate as close to the equator as 45 to 50 degrees latitude.[5] At higher latitudes in spring and fall, a maximum of aurora activity is noticed as the Earth is at at that time is farthest north or south of the Sun’s equator due to which there is greater chance of Earth intercepting enhancements of the solar wind that emanate from the vicinity of sunspots.[6]
Variation of heights of Aurorae with latitude:-
h’χ – h’ο = H logn sec χ.[7]
where χ = earth-magnetic inclination
h’ο = height of luminosity maximum corresponding to χ = 0
H = (kT)/mg
K= Boltzmann’s constant
T= Absolute temperature
m = mass of gas
g = acceleration of gravity
Aurora occur mostly intensely during the peak phase of the 11-year Sunspot Cycle. Auroral activity also peaks near the maximum of the Sunspot Cycle and for the couple subsequent years. Most violent eruptions on the surface of Sun, called Solar Flares, originate in magnetically active regions around visible Sunspot groupings.[8] Solar Flares release Electrons and Protons which increase the number of Solar particles that interact with the Earth's atmosphere, producing extremely bright Auroras. Sharp variations in the Earth’s magnetic field are called Magnetic Storms and are also the result of Sunspots.

The Earth is surrounded by a magnetic field, called the Magnetosphere that forms a barrier to the solar wind. The solar wind pressure strongly compresses the magnetosphere on the sun-side and draws it out into an extremely long tail on the side opposite. Since the charged particles of the solar wind cannot cross the Earth's magnetic field lines, flow around it . This forms a standing shock wave in space upstream of the Earth, called the Bow Shock. Electrons of the solar wind diffuse into Magnetospheric tail and form a reservoir called the Plasma Sheet. The Magnetosphere and the solar wind form an enormous electrical dynamo where large and complicated electrical currents flow. One component of these currents is carried by the Electrons in the Plasma Sheet, which descends down from 300 km to 100 km following spiral paths along magnetic field lines. These particles then collide with the atmospheric gas causing it to glow, which we call Aurora.[9]
References
- ↑ a b c 2009,http://www.nasa.gov/worldbook/aurora_worldbook.html Invalid
<ref>tag; name "Aurora" defined multiple times with different content - ↑ Ostlie & Carrol,pg. 373, 2007 “An Introduction to Modern Stellar Astrophysics ”, Addison Wesley
- ↑ Bone, N.,pg. 53, 2007 “Aurora”
- ↑ 2009,http://www.antarcticconnection.com/antarctic/weather/aurora.shtml
- ↑ 2009,http://web.archive.org/20010430135357/www.geocities.com/k2cddx/propaurora.html
- ↑ Davis, N.,pg. 64, 1992 “ the Aurora Watchers Handbook”
- ↑ Harang, L.,pg. 133, 1951 " The Aurorae"
- ↑ Wikipedia, 2009,http://en.wikipedia.org/wiki/Sunspot
- ↑ 2009,http://www.dcs.lancs.ac.uk/iono/ionosphere_intro
Fusion in the Sun
Fusion is the energy process in the Sun. Fusion means "putting together" to form something different. In this case it is hydrogen nuclei, which are simply protons, coming together to form a somewhat more complex helium nucleus. The specific process in the Sun is called the Proton-proton chain because it involves a series of interactions in which protons build up the helium nucleus, leaving additional leftover protons that can start the process over again, hence a "chain."
This process is sometimes referred to as thermonuclear fusion. "Thermo" because it occurs only at very high temperatures, and "nuclear" because unlike everyday energy processes such as burning gasoline, it directly involves only the nuclei of atoms.
In order for positively charged protons to come together to form a helium nucleus, they must overcome their natural electrical repulsion of each other. This repulsion is known as the Coulomb Barrier. The only way this can happen is if the protons are packed tightly together and are moving very rapidly. Basically this means that they must be in a highly compressed and extremely hot gas. In fact, at such high pressures and temperatures, it is too hot and energetic for electrons to stay connected to the protons to form normal atoms. Instead, there is a mixture of free electrons and protons in a kind of particle soup. This kind of particle (rather than molecular) gas is called a plasma and is the situation in the core of the Sun. Here the protons are moving so fast that—aided by properties of quantum physics—they sometimes slam into each other with enough force that they overcome the Coulomb Barrier and touch. At that point, nuclear forces come into play to "glue" the protons together in spite of their electrical repulsion. Through a series of such events, attended by the creation of exotic particles such as the neutrino and positron, a helium nucleus with two protons and two neutrons is produced. Two additional protons are left over and can continue the chain.
Physicists have measured the mass of a helium nucleus such as is produced in the core of the Sun. It turns out that it is a little less than 4 times the mass of the 4 protons that created it. This "mass deficit" is partly due to the positrons and neutrinos produced in the process. But even considering that, there is still a little of the mass that is missing. That mass was converted into energy by Einstein's famous equation, E=MC^2 ("Energy equals mass times the speed of light squared."). This is how the Sun produces energy.
At the Sun's core roughly 600 million tons of hydrogen (protons) is converted into about 596 million tons of helium each second. The mass deficit of about 4 or 5 million tons is converted directly into energy as per the paragraph above.
All of the Sun's energy is produced in this manner at the core of the Sun. The energy is vibrational (heat) as well as in the form of high energy gamma rays. The energy from the gamma rays slowly works its way out from the core of the Sun, changing many, many times into longer wavelength radiation. By they time it reaches the surface, it consists mostly of visible light photons.
[We should point out that because it involves only atomic nuclei, fusion is fundamentally different from any process normally encountered on Earth. Ordinary chemical reactions do not involve nuclei, but rather the electrons in the outer shells of atoms. Although the production of energy in "ordinary" situations do not involve the nuclei (and so do not change the elemental nature of matter), they still operate via Einstein's equation and there still is a tiny loss of mass when any energy is produced. However, it is much less than in nuclear reactions and is not normally even measurable.]
Convective and Radiative Zones
The Sun is composed of a number of zones in which energy is produced or transported to the surface. The nuclear process of fusion occurs in the core, and radiation is transported from there to the surface, undergoing numerous transformations into longer wavelength radiation, ultimately ending up on the surface as mostly visible wavelength light that immediately flies away at the speed of light.
Directly above the Sun's nuclear fires in the core is a large zone called the radiative zone or radiation zone in which energy moves primarily in the form of high energy photons. Nearer the surface the photons are largely absorbed by the material in the Sun, heating it up. Energy transport from this point is primarily via convection, or the physical movement of the hotter material upward to areas of lower temperature and pressure, like water boiling in a pot. This is the convective zone or convection zone.
At the top of the convection zone is the photosphere, the region at which much of the transported energy converts back into visible light to be radiated into space.
The Photosphere
The photosphere is the layer that we see when we look directly (foolishly) at the Sun. It is the sphere of light. It sometimes is referred to as the Sun's surface, but in fact the Sun has no solid surface such as that of the Earth. The photosphere merely represents the outer boundary of the region in which most solar energy has been converted into visible light.
Beneath the photosphere is the convective zone, a region in which huge columns of hot plasma rise and fall much like water boiling in a pot. On close inspection with properly filtered instruments, the photosphere appears as a great cauldron with the tops of these convective currents bubbling up in a seething sea. In certain wavelengths of light, the many convective columns give the Sun a slightly grainy appearance, sometimes referred to as granules or "rice grains," for its similarity to rice boiling in a pot.
Much cooler than the core of the Sun, the photosphere has a temperature of about 10,500 degrees F, or about 5800 K.
Immediately above the photosphere is a relatively thin layer called the chromosphere (sphere of color) and beyond that a large and very rarified outer atmosphere called the corona (crown). The photosphere is so vastly brighter than these two regions that they cannot be seen except with special instrumentation or during a total solar eclipse when the photosphere itself is blocked out.
Solar Activity
Sunspots are caused by magnetic disturbances that erupt through the visible surface of the Sun (photosphere). Deep inside the Sun many free moving subatomic particles produce very strong and complicated magnetic fields. When strong magnetic field lines erupt through the photosphere, they slightly impede the flow of energy from deeper layers outward to the surface, thus causing the area of the sunspot to be slightly cooler than the rest of the Sun, and hence darker.
Sunspots typically have a dark inner zone called an umbra, surrounded by a lighter outer zone called a penumbra. Many are as large as the Earth, and some have been known to be as large as Jupiter. Larger sunspots are usually groups of spots rather than just one. Often, adjacent sunspots have been shown to be of opposite magnetic polarity, with magnetic field lines flowing from one to the other, much like a bar magnet.
The solar activity cycle corresponds to the sunspot cycle, and is on the average about 11 years. That is, the numbers of sunspots, along with other less obvious activity on the Sun, waxes and wanes about every 11 years. In addition, the magnetic polarity scheme of sunspots reverses once every cycle, so we can also say that there is a 22-year cycle in solar activity.
Space Weather
Space weather is a general term that applies to the environmental conditions in space imposed largely by solar activity such as the "wind" of subatomic particles that constantly flows from the Sun. This Solar wind sometimes rages into a "storm" of charged particles (mostly electrons and protons) that can affect, disturb or even incapacitate satellites in orbit, disrupt communications, and pose radiation danger to unprotected astronauts.
The best known aspect of space weather is the aurora, commonly known as the "Northern Lights" in the Northern Hemisphere, with the corresponding "Southern Lights" in the Southern Hemisphere. These are formally known as the Aurora Borealis and Aurora Australis, respectively. they occur when large masses of the charged solar wind particles are attracted to the polar regions by Earth's magnetic field. As they spiral down through the atmosphere, they collide and interact with molecules in the atmosphere, most notably nitrogen and oxygen, which causes the emission of light seen as the aurora. The process is similar to that in an fluorescent light.
During particularly intense solar wind storms, electrical charges can collect on electrical transmission lines on Earth, sometimes causing an overload and blackouts (such as in Quebec in 1989). In addition to affecting the radio characteristics of the upper atmosphere, the solar wind charges also collect on orbiting communications satellites and can disable them unless precautions are taken. It is estimated that a solar storm of the intensity of the one in 1859 were to strike it could cause up to 2 trillion dollars damage.
Potentially more deadly are X and Gamma rays that can harm astronauts on flights well away from Earth, such as to the Moon or Mars. Space Shuttle and International Space Station astronauts are at only moderate danger since the Earth's magnetic field provides some partial protection for astronauts in low-Earth orbits (as both the space shuttle an ISS are).
Helioseismology
Helioseismology is the study of vibrations on the surface of the Sun, comparable to seismology on Earth. Analysis of these vibrations serve to provide information on internal processes in the Sun similar to the way studying earthquake vibrations can reveal information about the interior of the Earth.
The Solar Cycle
The solar cycle is the repeating rise and fall of "solar activity" (which see). This consists of a roughly 11-year cycle in which the numbers of sunspots rises to a maximum and then falls back to some minimum level. Actually the exact time period has varied, from about 7 to about 13 or 14 years, and the maximum number of sunspots varies as well. Some cycles are more "active" than others.
Shortly after each maximum, the magnetic polarity of the sunspots reverses and it maintains that polarity until the next maximum, roughly 11 years later. Thus the solar cycle is not just 11 years, but 22 years since after 22 years the magnetic polarity returns to approximately its original configuration.
The cycle is sometimes unpredictable. During the Maunder Minimum, solar activity was drastically reduced for about fifty years. In 2008, the then current sunspot minimum was noted as the "quietest" in 50 years. As of late 2009, solar activity began a slow increase.
While the sunspot cycle is certainly related to other activity on and in the Sun, many attempts have been made to relate it to various cycles on the Earth ranging from the quality of wines to fashion trends and the stock market. No such relation has been proven, and in fact no strong relation between the sunspot cycle and earthly weather patterns has yet been conclusively shown.
The period of Maunder Minimum, from about the middle of the 17th through the early part of the 18th centuries, was attended by abnormally cool and damp weather worldwide. Attempts have been made to correlate this climatic aberration to the absence of sunspots, but if the relation is real, no causal mechanism has been identified.
In addition, one tentative relation to temperature variation in an upper layer of Earth's atmosphere appears likely, but no other direct and predictable relation has yet been shown.
Stars
Stars, by astronomical definition, are massive luminous balls of plasma. They exist in numbers too large to comprehend, and most are believed to be accompanied by a system of planets. The planet Earth is part of the Sun's solar system of 8 planets, the Sun being the nearest star to Earth. The Sun provides most of Earth's energy, and is critical to the survival of all forms of life on the planet.
Over the history of mankind, human views of the stars have differed greatly. Historically, the stars have existed as major figments in the mythological canon of many cultures, and were seen as objects of mystery and speculation. The Sun in particular has been the object of great cultural, religious and theoretical importance and speculation and has, more specifically, been a central point of debate in arguments relating to the topography and geography of the solar system itself.
The stars have also been great use. Seafarers and fisherman have historically used the patterns of the stars on the night sky as a vast and accurate kind of map. Many civilizations tracked their movements and channeled their findings into calendars, which in turn would determine agricultural practices.
In recent centuries, scientific views of the stars have become much more advanced, following the invention and continual advancement of the telescope, and the discovery of various techniques and ways to assess the various properties of a star. This study of stars is built upon the only two attributes that are directly observable from Earth: a star's location and its brightness. Although the stars appear to move across the sky over the course of a night and over the course of a year, the relative positions of the stars are almost constant relative to each other. However, the careful measurement of stellar positions (astrometry) shows small motions. Three of the most significant contributors to stellar motion are:
- Parallax changes, due to the earth motion around the sun,
- Proper motion, due to the star's journey around the center of the galaxy, and
- Wobbles in the proper motion, due to the star's gravitational "dance" with a companion, either another star (or stars) or one or more planets orbiting the star.
Measurement of star brightness provides a wealth of information about the star. In particular:
- Measurement of how the star's brightness changes over time (its lightcurve) can reveal the presence of companion stars (in binary or triple systems), companion planets, sunspots, flares, explosions, and recurring (sometimes even periodic) fluctuations in the star's structure. Collectively, we refer to any star whose brightness fluctuates as a variable star.
- Measurement of how the star's brightness varies with the wavelength (color) of light can be used to describe the star's color, estimate its temperature, and detect specific wavelengths where the star's light is either brighter or dimmer than average. These spectral lines can be used to identify the elements (and sometimes even molecules) within the star's atmosphere.
A star's apparent brightness is influenced by three primary factors:
- Its intrinsic brightness (luminosity), a measure of the amount of energy being released by the star,
- Its distance from the earth, and
- The presence of any clouds of absorbing material between the earth and the star.
Because the dimming of starlight because of distance from the earth is well-defined and easily calculated and because the apparent brightness of a star is easily measured, knowing (or estimating) the star's luminosity allows its distance to be calculated and vice versa.
In the following topic regarding stars, we explore several key aspects of stars, their properties, the continual advancement of our knowledge of these heavenly bodies, and what their place is in the universe.
- Table of contents
Mass
The mass of a star - along with its chemical composition - are key to its behavior. Once these two features of a star are determined, one can calculate the temperature of the star's core and the pressures of its gases as well as the strength of the gravitational force acting within the star itself. The star's mass and composition can, therefore, determine the star's size and luminosity.
How, then, do we begin to calculate a star's mass? Binary stars can help us determine the mass of stars.
Binary systems are composed of two stars that orbit each other. Mizar and Alcor, for instance, are two stars that are apparent (not actual) binaries; they appear to be very close together in the sky, they are actually distant from each other. Mizar, however, is a true binary, made up of Mizar A and Mizar B, with a period of 10,000 years.
Because binary stars' orbits depend on their gravitational attraction to each other, the measurement of their orbital distance and the length of time it takes them to complete one orbit can be used to calculate the summation of the stars' masses. Hence, the following equation can be used:
where and are the masses of the two stars, is the period of the orbit, and are the distances from the center of each star to the center of mass of the binary system, and is the total separation between the centers of the two stars, or .
Astronomers usually express the masses of astronomical objects in terms of our Sun's mass, where one solar mass is approximately equal to 1.99 x 1030 kilograms, or about 4.39 x 1030 pounds.
An astrometric binary is found by observing a star's proper motion. If it is wavy, that indicates the presence of a binary; non-binary stars have a straight line proper motion.
An eclipsing binary is detected by observing a star as it becomes occluded by its twin. An example of this is Algol (Beta Persei in Perseus).
There are three different types of binary systems of stars which provide information about the masses of those stars. Visual binaries refer to those stars which can each be visibly seen by astronomers through telescopes. The masses of these types of stars can be calculated when they are near enough to the Earth for astronomers to determine the size and tilt of the two stars' orbits about each other.
Another type of binary system that provides information about stellar masses is known as the spectroscopic binary. Using spectroscopic observations of the two stars, the doppler shifts of the two stars as they orbit each other can be measured and astronomers can collect sufficient data in order to find estimates for the masses of those binary stars. In this type of binary, astronomers are only able to conclude upon a lower limit of the masses because they must first know the orientation of the stars in their orbits. If the two stars do not form an eclipsing binary, then one of the stars never passes in front of the other, so astronomers are unable to calculate the orbit's orientation.
As stated previously, the use of binary systems to calculate star masses often leads to limited information. The above method of determining mass is very useful given that the other values are known, but obtaining these needed values can prove to be troublesome. When observing an astrometric binary, for example, we are unable to see the exact orbits. Moreover, even mapped orbits are problematic because they are two-dimensional representations of a truly three-dimensional motion of two stars. In either case, additional information is needed to calculate the orbits and masses of the stars more accurately. As a result, it is oftentimes easier to calculate the total mass of the binary system.
Astronomers have calculated that all stars that have been measured to date have masses that range from to 50 solar masses.
The mass of a star can then be used to determine its escape velocity: the velocity necessary for an object to escape the star's gravitational force. The escape velocity becomes greater as a star is more massive but decreases with the star's radius. The formula for calculating escape velocity is
where is mass, and is radius.
Elements
Besides providing light, stars have another important role in the development of life: creation of elements! Stars produce many elements during their life cycles, which are thrown off through their solar wind, when they blow off their outer atmosphere and form planetary nebulae and most spectacularly, when they go supernova. Indeed, all elements, except for hydrogen and helium, were produced by stars. This means that the material making up plants, animals, even you, was at one time manufactured by a star! The famous astronomer Carl Sagan once observed, "We are made of star-stuff."
Main sequence stars are made up of hydrogen (H) and helium (He). Red giants are made of elements heavier than helium, up to and including iron (Fe). Iron is the most stable element, meaning that it's the hardest to transmute. Supernovas produce all elements heavier than iron, up to and including Californium (Cf).
Luminosity
Luminosity is the total amount of light emitted by a particular star. It is the star's intrinsic brightness, or the amount of energy it emits each second. In many cases, this energy comes from thermonuclear reactions inside the star. In general, a star's luminosity depends on its current stage in its evolutionary sequence. Stars radiate various forms of electromagnetic radiation, such as ultraviolet radiation, visible light, infrared, and radio waves.
The luminosity of a star depends on its temperature and size. If two stars of different sizes both have the same temperature, the larger of the two will have a greater luminosity due to its larger surface area.
The formula for calculating luminosity is
where T is the star's temperature in Kelvins.
Another way to measure a star's luminosity is by calculating its magnitude. There are two types of magnitude: apparent and absolute. Apparent is the luminosity of an object when viewed from Earth; absolute is the brightness of that object if it were 10 parsecs away from Earth.
The Sun has an apparent magnitude of -26.7, and an absolute magnitude of 4.8, while a full moon has an apparent magnitude of -12. Most visible stars range in apparent magnitude from -1.5 (Sirius) to 4 (Alcor). The dimmest ones just visible to the naked eye are around 6.5 (4 in the city with bright lights).
Stars are classified by orders of magnitude: alpha, beta, gamma, delta, epsilon, and zeta. These are called Bayer letters.
Cepheid variables are pulsating stars. They have a longer period and higher magnitude than other stars. By calculating the star's period and magnitude, the distance can be determined. Astronomers discovered from the Cepheid variables in Andromeda that the nebula was 2 million light-years away.
The stars which have been measured by astronomers up to date range from to 500,000 times the luminosity of our Sun.
Temperature
The temperature of a star refers to its surface and that is what determines its color. The lowest temperature stars are red while the hottest stars are blue.
Astronomers are able to measure the temperatures of the surfaces of stars by comparing their spectra to the spectrum of a black body. A black body is one that entirely absorbs all radiation that strikes it. Astronomers determine the black body spectrum which most closely matches the spectrum of the star in question. Because the temperature of the matching black body is known, astronomers can then calculate the star's surface temperature.
Astronomers classify stars into different types depending on their temperatures. These types are O, B, A, F, G, K, and M, where type O stars are the hottest and type M stars are the coolest. Each of these types is divided further into sub-divisions from 0 to 9 in order to distinguish between slight differences in each star's spectral patterns, which depend on the star's temperature.
Our Sun is a Type G star, which are yellow stars with surface temperatures of about 6000 °C, or 11,000 °F. Type A stars, which are hotter, are white in color and maintain temperatures of around 10,000 °C or 18,000 °F. The hottest of the types, B and O, are blue stars while the coolest of type M is red in color and have surface temperatures of about 3,000 °C or 5,400 °F.
Note that we have referred to the surface temperatures of stars thus far. Each star, however, ranges in interior temperature with cores reaching temperatures in the millions of degrees. Although the Sun's surface is only 5800 °C, for example, its core achieves a temperature of 15 million Celsius. With the mass of a star and its chemical composition is known, astronomers can calculate the temperatures within its core.
Main sequence stars have a core temperature of 10 million Kelvins. Red giants have a core temperature of 100 million Kelvins.
Stars come in a wide range of sizes. The sun is a star that measures about 870,000 miles across. However, astronomers classify the sun as a dwarf star. A dwarf star is a small star. A giant star is a big star. The largest stars are supergiants. Some supergiants can be 1,000 larger than the sun. Astronomers also classify stars according to color. The color of a star shows its surface temperature. Blue stars are the hottest, followed by white, yellow, orange, and red. The sun is a yellow star.
The H-R Diagram
The Hertzsprung-Russell diagram - usually referred to by the abbreviation H-R diagram - is a diagram that illustrates the properties of stars. As stars progress through their lives, they move around on this diagram since their properties change over time.
The original form of the H-R diagram consists of the absolute magnitude of the star graphed against the color of the star. It was this form that was first created around 1910 by Danish astrophysicist Ejnar Hertzsprung and American astrophysicist Henry Norris Russell, and represented a huge leap forward in understanding stars because once one graphs stars against these axes, it becomes obvious that stars fall into different categories. The diagram plots luminosity and spectral type (which also plots temperature). On the vertical plane, stars are brighter if they are higher up on the diagram. In the horizontal plane, the leftmost stars are the hottest.

When all the known stars are placed in this diagram according to luminosity and temperature, many of the stars - even our Sun - appear along a diagonal line that stretches from the top left of the diagram to the bottom right. This diagonal line is what is known as the main sequence. Stars spend the majority of their lifetimes here. It is the phase in which stars burn hydrogen into helium. At this point in a star's life, its size and luminosity remain about constant because the forces within the star have reached a near-equilibrium. The gravity of the star pointing inwards balances the internal thermal (gas) pressure which pushes outwards. The time that a star spends in the main sequence is determined by its mass. Smaller, cooler stars have slower fusion reactions rates and therefore will remain in the main sequence longer.
Stars which lie along the top right of the diagram are luminous and cool and are known as supergiants. Fainter, hotter stars - which appear at the bottom left of the diagram - are known as white dwarfs. Hot and bright stars are located at the top left of the diagram, and cool, dim stars at the bottom right.
The HR diagram is a powerful tool in astronomy that allows us to probe stellar evolution and even cosmology. Knowing a star's location on the HR diagram allows us to find its mass, its evolutionary state (and age), and its physical size. We can date individual star clusters by using the main sequence turn off, the point where main sequence stars start evolving (i.e., cease to be hydrogen burning, the initial stellar condition).
The first version of the diagram is often known as the observer's version of the H-R diagram as it can be drawn from data taken directly from a telescope. The second version of the diagram is often known as the theorist's version as it is the version against which the output from computer models can be plotted.
Star Clusters as Cosmic Laboratories
It is estimated that the number of the stars in the universe is around . This is calculated based on the fact that there are about galaxies in the universe, each of which is composed of an average of stars each.
A nebula is a cloudlike object. Scientists can determine what type of nebula they are observing by examing its spectrum: an emission spectrum indicates glowing gas, while an absorption spectrum indicates a mass of stars. The Pleiades, for instance, has absorption spectrum.
Two kinds of nebulae are open clusters (loose groups of a few hundred stars; e.g. Pleiades, Hyades, Ursa Major) and globular clusters (spherical nebulae with hundreds of thousands of stars, such as M13 in Hercules and M3 in Canes Venatici). Most nebulae appear as a hazy patch when viewed with a small telescope. Dark nebulae are gaseous clouds that block light. This is where stars form.
Stars are created when gravity collapses dust and gasses together.
The Stellar Life Cycle
Protostars and Stellar Nurseries
The Birth of Protostars

Protostars are formed in star hosptitals called nebulas, while nebulas are areas of higher dust and gas densities relative to the surrounding interstellar space. [1] Nn and a little helium, although more massive elements and even molecules are also ubiquitous. These more massive elements and molecules are from previous stars that have died and scattered some of their remnants into the nebula. These clouds of gas and dust can span hundreds of light years across and can be formed when enough gas and dust come together to become gravitationally bound or can be compressed by the explosion of stars known as supernova that also add their gases to the cosmos as planetary nebulas. [2] If the nebula has a high density, distubances of gas and dust may cause gravitational contraction to become significant. If gravity becomes significant enough to pull in the dust and gas from the cloud then the material trapped by gravity will collapse into itself, this is how a protostar is formed. [3] When gravity takes over and causes the material of the nebula to collapse in on itself this forms a sort of ball that will start to rotate. This rotation will cause gas and dust outside of the ball to start to rotate towards the ball, similar to when the drain of a tub is opened and all the rubber ducks at the other side of the tub start to move towards the drain getting caught in the whirlpool and finally sucked down the drain. This is how a protostar increases its mass; a protostar will start out as the small ball that begins to rotate (this can be thought of as the drain) as this ball rotates it will create an accretion disk (the whirlpool around the drain) this disk will suck dust and gas from the surrounding nebula and transfer it to the protostar. How fast this process happens can help determine the outcome of the new star. This process will stop when the protostar starts nuclear fusion of hydrogen. During the formation of the protostar and the accretion process the protostar becomes hotter and denser. The protostar becomes denser because the accretion disk is adding material to the star which is causing the gravity of the protostar to increase, thereby “pushing” the gas and dust from the accretion disk closer and closer towards the center of the protostar. This effect is correlated to the temperature of the protostar and as the density of the star increases so does the temperature. When the temperature at the center of the protostar reaches about 10^6 Celsius it will start to fuse hydrogen.[1] This is the start of the proton proton fusion chain that is the main fusion that supports the star and signifies the birth of a new star. The burning of hydrogen produces a solar wave that will blow the accretion disk away from the star allowing no new material to be added beyond that time.[3]
Simple Model of Protostar Formation
The above is a description of the formation of new stars. We will now look at the early physics used to describe protostar creation. The first person to stud was Sir James Jeans; he studied globules and molecular clouds where protostar formation has been observed. Sir Jeans studied what conditions are needed in a molecular cloud or globule to induce collapse of material to form a protostar. During Jeans life time (1877–1946) the advanced computational powers of computers were not available so he had to simplify his calculations. The major simplifications Jeans made before he began his analysis was to assume that the effects of rotation, turbulence, and magnetic fields can be neglected. These assumptions are not true but Jeans calculations give a good starting point.
Jeans started with the Virial Theorem, 2K+U=0 equation 1
This states that the total potential energy (U) of gravity is twice the absolute value of the total kinetic energy (K) of the system and when the two add to zero then the system is in equilibrium and the cloud will neither collapse nor dissipate. If the kinetic energy of the cloud is more than half of the potential energy then the cloud will expand and dissipate. If the kinetic energy is less than half its potential energy then the cloud will collapse into a protostar. We can write the potential energy as,
U= -(3/5)(GM2/R) equation 2
And kinetic energy can be written as,
K= (3MkT)/(μmH) equation 3
where,
μ= mean molecular weight
T= temperature
M= mass of cloud
mH= is mass of hydrogen
R= the radius of the cloud
G and k= gravitational constant and Boltzmann’s constant
rewriting R as,
R= [(3M)/(4πρ)]1/3 equation 4
ρ= the initial mass density of the cloud is assumed to be constant throughout the cloud
Sir Jeans then substituted the R equation into the Potential energy equation and then put both energy equations into the virial theorem and solving for the mass he found the minimum mass required for a cloud to collapse. This is called the Jeans mass and he found the minimum radius by placing the equation for R into the Jeans mass equation and solving this is called the Jeans length. If the cloud has a mass or radius larger than the values found by these equations then the cloud will collapse.
MJ= [(5kT)/(GμmH)]3/2[3/(4πρ)]1/2 equation 5
RJ= [(15kT)/(4πGμmHρ)]1/2 equation 6
This was the first theoretical attempt to model the formation of a protostar. These equations give us good approximations of which molecular clouds will be able to form protostars. But observations of forming protostars and of molecular clouds show that the equations that Sir Jeans developed are not always accurate.[4]>
Constraining factors to Sir James Jeans Model
The preceding section explained Sir Jeans’s model for the formation of protostars from the surrounding molecular clouds. Observations of molecular clouds and protostars have shown that this model is flawed. The model predicts that the entire cloud will collapse into the forming protostar; also the model predicts that if the mass or radius is higher than the Jeans mass or Jeans radius, than the cloud will collapse and form protostars. Astronomers have found molecular clouds and globules that do not follow this model very well. Observations have been made on globules and molecular clouds that have many stars forming in them and on others that are above the Jeans mass or Jeans radius and do not have a lot of protostar activity in them. Many astronomers have tried to determine what is wrong with the model and have found reasons to explain the observations made that contradict the model. One reason found was that the simplifications made by Sir Jeans could not be left out and that by including some of these previously excluded variables astronomers found that the model fit more closely to what they observed. Some of the variables that were excluded in Jeans model were cloud rotation, the presence of a magnetic field, temperature changes, mass density changes, external gas pressure, and fragmentation.[4]
Example
Let us look at a diffused hydrogen cloud. Assume that the temperature is 50K and that the cloud is completely hydrogen with a density of 8.4x10−19 kg/m3, and take µ to be 1. What then is the minimum mass necessary to cause the cloud to collapse? Using equation 5 from above with the given values we find that the mass necessary for collapse is roughly 1500 solar masses. The normal diffused hydrogen cloud ranges in mass from 1-100 solar masses therefore such clouds are stable since the Jeans Mass calculated above is greater than the mass of such clouds.[4]
Now let’s look at what happens in the center of a dense giant molecular cloud (GMC). The typical temperatures for this cloud is 10K and we will take the density to be 3x10^-17 kg/m3 and take µ to be 2. Again using equation 5 we find that the Jeans Mass is now only 8 solar masses. GMCs are approximately 10 solar masses. We can now reason that GMC cores are unstable. Consequently they will form stars because the Jeans Mass is lower than the mass of the cloud. This has been proven by astronomers through observations of GMCs in our night sky.[4]
References
- ↑ a b Think Quest. Life cycle of stars., 2009, from http://library.thinkquest.org/17940/texts/star/star.html.
- ↑ Bill Arnett. (1997). Types of nebulae., 2009, from http://astro.nineplanets.org/twn/types.html.
- ↑ a b Linda Hermans-Killam. The infrared universe., 2009, from http://coolcosmos.ipac.caltech.edu/cosmic_classroom/ir_tutorial/sform.html
- ↑ a b Ostlie, D. A., & Carroll, B. W. (2007). In Black A. R. S. (Ed.), An introduction to modern stellar astrophysics (2nd ed.)San Francisco: Addison-Wesley.
The Life of Low Mass Stars
The lifetimes of stars are determined by their mass, or the total amount of matter they contain. If an object is not sufficiently massive (at least about one tenth the mass of our Sun), it will not have enough gravity to squeeze itself tightly enough to heat itself up to stellar levels. Such an object will become either a planet-like body or an intermediate object called a "brown dwarf." A "brown dwarf" simply never initiates stable hydrogen fusion and by definition never becomes a full-fledged star. Some brown dwarfs go through a phase of limited "deuterium fusion", but this does not qualify to make them a full star. They eventually—after very long periods of time—simply go out and cool to the ambient temperature of the Universe.
Gas clouds (or just localized areas of larger gas clouds) that have at least one tenth the mass of the Sun, can get hot enough as they contract to start fusing hydrogen into helium. This is known a "stable hydrogen fusion" and it marks the birth of a true star. This requires temperatures in the millions of degrees. However, stars of such relatively low mass can sustain only very low levels of fusion, which is to say that they use their nuclear fuel slowly. So they do not grow very bright, and form small dim stars called red dwarfs.
Generally, red dwarfs go through their lifetimes uneventfully, just slowly "burning" their nuclear fuel in a stable fashion. Eventually, they will run out of nuclear fuel, cool, and slowly become a burned out cinder known as a "black dwarf."
Do not confuse the terms brown dwarf, red dwarf and black dwarf. A brown dwarf has a mass too low to ever become a star. It produces energy, perhaps even by a limited type of fusion, but never enough for "stable hydrogen fusion. A red dwarf has low mass, but high enough to start stable hydrogen fusion, which qualifies it as a "real" star. However, it burns that fuel so slowly that it has a very long lifetime. It is likely that any red dwarf ever born since the Big Bang is still around, and has not yet turned into its final version, the "black dwarf." Considering the extremely long lifetimes of red dwarfs, it is likely that no black dwarfs have yet formed in the Universe.
Do not confuse the term "black dwarf" with "black hole", which is an utterly different object with a different origin.
The Death of Low Mass Stars
Basically, the greater a star's mass, the greater the pressure in its core (caused by gravity) and the higher the internal temperature. High temperatures force a greater consumption of the available nuclear fuel. The greater the consumption of fuel, the hotter and brighter the star, and the shorter its lifetime.
Stars that are mid-range in mass, such as our Sun, typically live a few billion years (about 10 for the Sun). Smaller stars live much longer, perhaps several hundred billion years. The universe is still too young to have any of the oldest of the smallest stars to have consumed all their fuel. Their lives are longer than that of the universe to date.
But a middle-sized star such as the Sun cannot last as long as the universe has existed. Our sun has existed less than a half the time since the Big Bang (about 13-14 billion years ago). Since the Sun is thought to be typical, we can use it as an example for studying similar stars.
A star like the sun first fuses hydrogen (as it does now) into helium thereby releasing energy, that ultimately leaves the Sun as sunlight. When the Sun is about twice as old as it now is, it will no longer have enough hydrogen in its core to sustain stable hydrogen fusion. The resulting slow down in fusion will result in less outward pressure, to withstand the inward pull of gravity. As a result, the star will contract, compressing the core, and causing its temperature to rise.
The higher temperatures in the sun's core will allow it to fuse helium into heavier elements, but at the same time, the sun's outer layers will expand and cool. As a result it will turn red, making it a red giant.
For our Sun, this stage lasts only a few tens to a few hundreds of millions of years, and another collapse ensues. This time the core is compressed and heated further, but it has run out of hydrogen and helium fuel in its core and is in essence, a hot, dying ember composed largely of carbon called a white dwarf.
A white dwarf is a strange beast, having the mass about the same as the Sun, yet is only about as large as the Earth. At this point, the white dwarf is so tightly packed that a teaspoon of its matter would weigh about 2 tons on Earth! In fact, it is no longer even normal matter that obeys the laws of physics we are used to. Instead, it obeys quantum mechanical laws that prevent it from collapsing any further.
At the same time the white dwarf is formed from the leftover core of the star, the outer layers of the red giant are blown off into space to form a planetary nebula. The white dwarf remnant simply cools, slowly changing from white hot through the range of colors eventually ending, after tens of billions of years, as a cold black dwarf.
The upper limit for the mass of a white dwarf is about 1.44 times the mass of the Sun. So any star whose core ends up with a mass of more than 1.44 solar masses at the end of its life (after the outer layers have been blown off into a planetary nebula) cannot form a white dwarf, but ends up in an even more bizarre state. This is called the Chandrasekhar Limit.
More massive stars have even wilder lives.
The Life of High Mass Stars
A red giant is a terminal stage for most stars. When the star starts to run out of available nuclear fuel, its core can no longer completely oppose the inward pull of gravity and shrinks. However, the shrinkage adds energy to the core, which results in a temperature rise. Meanwhile the increased temperature of the surface of the core produces such photon pressure that it pushes the outer layers of gas of the star outward and into a large gaseous atmosphere. The outer layers expand and cool and the star's color shifts toward red. The star has now become a red giant. A red giant star has a core that has reached a temperature of 100 million Kelvins, but whose outer layers are much cooler. Red giants are truly enormous. One with the mass of our Sun may expand outward past the orbit of the Earth.
Red giants live perhaps a 100 million years or so, by which time its core again begins to run out of available nuclear fuel. This is followed by a new core collapse. What happens now is dependent on the mass of the core. If the core is less than 1.44 times the mass of the Sun, the collapse crushes the core further into a white dwarf, and since the white dwarf cannot contract any further due to quantum mechanical reasons, outer layers of the star that are falling onto it rebound and are blown off into space to form a large and often beautiful planetary nebula.
However, if the star is significantly more massive than our Sun, and its core is more than 1.44 times the mass of the Sun, the final collapse is great enough to crush even the Earth-sized white dwarf, pushing electrons into protons to form neutrons and so liberate vast amounts of space. Thus the core crushes down to about the size of a city and becomes an almost unimaginably compact and dense object known as a neutron star.
A pulsar is a rapidly spinning neutron star. Other stars spinning this fast would explode, but the pulsar does not because its high gravitational attraction holds it together. Pulsars have a powerful electric field that throws off electrons. These stars get their name from the signal pulses that result from their rotation.
If the original star was much more massive than the Sun and its core more than 3 times the Sun's mass, then the force of gravity crushing it at this stage is so great that not even the neutrons can withstand it, and they too are crushed to become perhaps Nature's strangest creation, a black hole.
The Death of High Mass Stars
As with location in real estate, a star's mass is everything. In fact, aside from the exact chemical composition or the gravitational effects of companion stars, mass is the factor that determines the fate of a star. Even chemical composition is fairly unimportant at this stage of the universe, because the vast majority of stars are still primarily hydrogen and helium. The initial mass of a star sets the various parameters of a specific star's lifetime far more rigidly than any factor in the life of a biological organism such as a person. Mass determines the temperature, physical size and span of life, and the exact progression from one stage to the next. Two stars with the same initial mass will follow the same path through life and are in effect identical twins in the absence of any disturbing factor such as a companion star.
Unlike smaller stars, the largest stars have even more spectacular ends. The life track of a high mass star is similar to that of a low mass star like the Sun, except shorter and more violent. High mass stars effectively Live hard and die young. Near the end of their short lives, they puff up into a giant red star, although in this case a supergiant, and then they collapse.
A giant star consumes its nuclear energy more quickly than smaller stars, as one after another layer of core develops, where it fuses lighter elements into heavier elements. All of those reactions produce more energy than they consume. No star can go further in fusing elements than the creation of iron without producing a net loss of energy from the star.
The iron core shrinks, and one after another layer of core falls upon it. The iron core becomes extremely hot and unstable. Implosion is imminent once the star's temperature reaches 10 billion Kelvin. The star suddenly explodes releasing an extreme amount of energy in a very brief period of time as a supernova.
You don't want to be near a supernova; if you were in a pleasant zone near a star about to erupt as a supernova, you would be incinerated when the radiation from the supernova reached you. If one of the nearer stars like Alpha Centauri, Sirius, or Altair were to go supernova, the intense radiation would be deadly, but no nearby star is going to go supernova. That will happen to a giant like Betelgeuse, Deneb, or Antares, each of which is far enough away that the radiation is not a hazard.
While these hypothetical observers near a supernova find them unpleasant, astronomers on Earth—a safe distance away—find them very useful. There is a certain type of supernova called type Ia that is very useful for measuring distances. The nice thing about type Ia supernova is that they all have the same absolute brightness. Because they all have the same absolute brightness, they are called standard candles. The differences in apparent brightness of one type Ia supernova from another are entirely due to their different distances from Earth. The most popular theory is that a white dwarf accumulates material from a companion star, slowly growing towards the Chandrasekhar limit mass, until it has just barely enough—about 1.38 solar masses—to trigger an explosion. It's still a mystery as to what triggers the explosion and what happens during the explosion, but because it occurs at the same mass for all Ia supernova, all Ia supernova produce the same brightness. The differences in apparent brightness of Ia supernova are entirely due to their different distances from Earth. Astronomers measure the apparent brightness of a supernova as seen from Earth, and combine this with the known absolute brightness of all Ia supernova (also taking Doppler shift into account), to find the distance of the supernova from Earth—and, by implication, the distance to the entire galaxy containing that supernova. The distances measured this way have led to a greater mystery discussed in General Astronomy/Current Unsolved Mysteries.
If the core ends up with a mass more than 1.44 times that our Sun (known as the Chandrasekhar Limit), not even quantum mechanical laws can prevent a massive star from compacting further.
For a remnant core between about 1.44 and 2 times the Sun's mass, the force of gravity pushes negative electrons into the positive protons, producing neutrons that occupy less space than their original particles and the core shrinks to what is essentially one large neutron. This neutron has more mass than our Sun but is about the size of a city on Earth, perhaps 20 kilometers across. It has become a neutron star. A teaspoon of neutron star material would weight about a billion tons on Earth.
The status of a remnant core between 2 and 3 times the mass of the Sun is not entirely clear, as it could become a neutron star, or perhaps an even smaller quark star which has only been theorized, or a black hole.
If the remnant core has more than 3 times the mass of our Sun, the gravitational field at its surface is not only large, but infinite. Nothing that gets too close to this object can escape. In fact, in theory no force of the Universe is strong enough to pull an object away that has wandered too close to a black hole. This distance away from the black hole is called the Event Horizon, or the surface of the Schwartzchild Sphere. Nothing that falls through the Event Horizon can escape, as escape velocity is greater than the speed of light. Hence not even light can escape, and the object appears completely black, hence the name, black hole.
A typical black hole with a mass three times that of the Sun would be roughly 18 kilometers across. Strictly speaking, this is the diameter of the Schwartzchild Sphere which is the visible surface of the black hole. However, the total mass of a black hole is considered to be concentrated into a single point with zero volume. Thus it is meaningless to speak of how much a tablespoon of black hole material would weigh. Effectively, the gravitational force and density at the black hole singularity are infinite.
We have not observed black holes directly (for obvious reasons), but we have ample evidence of their existence by the detection of radiation from objects falling into black holes, and in the gravitational effects they have on other bodies.
Black Holes

A black hole is an object that has a gravitational field so powerful that nothing, not even radiation or light, can escape. The event horizon is the name given to the figurative surface, within which the gravitational force becomes irresistible. Escape velocity at that surface is equal to the speed of light hence not even light can escape, hence it is rendered invisible. In this way, black holes are undetectable, except by the trail of destruction they leave behind them, or their interaction with proximate objects.
The theory behind black holes designates that, when a certain amount of mass is present in an infinitely small region of space (referred to as a "naked singularity"), all paths through space in 4-dimensions are inwardly curved, forcibly pulling all forms of matter toward the source. Such a dense region of space, the black hole, has been predicted to form either following the collapse of a massive star, or the collision of two neutron stars. The former is, however, said to be by far the more common, considering the rarity of the latter.
Many aspects of the black hole model still pose unanswered questions, and the nature of the black hole remains largely unknown. Numerous theories as to what a black hole looks like, and what exists in the interior have been proposed, and the black hole is a regularly seen element of science fiction. Some even propose that black holes could lead to be gateways to other universes or parallel realities with radically different physical laws.
In the following topic, we'll look at these theories, while exploring what is already known about black holes, as well as the history of the concept of objects with a gravitational field so strong that nothing can escape. We will discuss the properties of the black hole, and the impact these properties have on the surrounding spacetime and the matter around them, and how these properties, as well as the effects they cause, can be exploited in the detection of these invisible monsters. Finally, we'll examine the terrible life of the black hole, from its birth in the blazing remains of a destroyed star to its gradual evaporation. The second type of black hole is called the stellar black hole: It is formed by the gravitational collapse of a massive star. Stellar black holes have masses that range from 3 to several thousands of solar masses. Our Milky Way Galaxy has several stellar mass black holes that are closer to us than the super massive black hole in the region. The third type of black hole is called the Intermediate-mass black holes: Intermediate-mass black holes are found in the center of globular clusters. Astronomers believe that colliding stars may have formed the intermediate mass black holes. The fourth type of black hole is called the Super Massive black holes: Super Massive black holes are found in the center of the Milky Way and other active galaxies. Theoretically a star black hole forms and takes in enormous amounts of matter over the course of years. The other theory is that a cluster of star like black holes forms and then merges into a super massive black hole.
- Table of contents
- Life of the Black Hole
- Black Holes in Hiding
- History of the Black Hole
- The Theory of the Naked Singularity
- Spaghettification
Life of the Black Hole
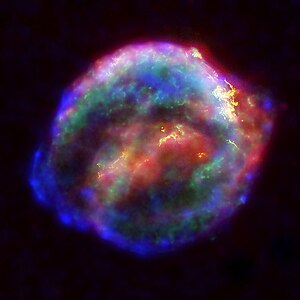
In this subchapter, we examine the life of the black hole, from its birth in the fires of a dead star, to its gradual dissipation in the backwaters of space.
Birth - Part I
It would only make sense to begin chronologically, at the moment when the black hole is formed, shortly following the death of a sufficiently massive star. Before this, however, we must first understand what causes the death of this star. In short, such a star will collapse when its temperature is no longer high enough to stop it from collapsing under its own gravity. There are two possible reasons for this failing of equlibrium. The more common cause occurs when a star has burned up all of its nuclear and elemental "fuel", and can therefore no longer maintain the necessary temperature, resulting in what is termed "gravitational collapse". The second possible cause of this imbalance between temperature, pressure, and volume involves the star taking on a significant amount of added mass in some way, without causing the necessary increase in core temperature to support the additional mass.
Either way, the star now no longer has the needed temperature to stop a collapse. The star's core is compressed so tightly, that it forms what is known as degenerate matter, which is, essentially, matter that is so highly compressed that the forces of repulsion that creates the supporting pressure originate from quantum mechanical effects not from the usual forces of repulsion of like charges of normal matter. Its comprising particles are extremely dense. The collapse usually triggers subsequent events, such as supernovae, or gaseous fragmentation into planetary nebulae (shells of gas and plasma), that shed the outer layers of the star. The remnant that is left after the collapse and subsequent events forms one of a number of "compact stars". These include white dwarfs, neutron stars, and, of course, black holes. For the latter to be a result, the remnant has to be sufficiently massive; just how massive is defined by the "Tolman-Oppenheimer-Volkoff limit", calculated by Julius Robert Oppenheimer and George Michael Volkoff, in 1939. Beyond this limit the gravitational attraction is greater than the opposing pressure, and, when the remnant's outer radius drops below its Schwarzschild radius, the black hole is fully formed.
The black hole emerges thus from the ashes of a broken star, and the birth is complete.
On a final note, before we continue, there is a second way that black holes can be formed, though it is much rarer for this to happen: the collision of two neutron stars—another form of "compact star"—can sometimes result in the formation of black holes. However, such collisions are not common, and this second possible cause of black hole birth is not always mentioned in short summaries of black hole formation.
Life - Part II
The life of black holes is impossible to calculate, and how long they remain has only been predicted, not proven. Therefore, generalization is inevitable.
As black holes drift through space, they exist as vacuum machines of sorts, sucking in all the matter they come across, and steadily growing. As they devour, stellar black holes—forged from the ashes of star corpses—grow, becoming larger through a process called accretion. This refers to the growth of massive bodies due to the attraction of matter by gravity. Those black holes that devour many stars, planets, interstellar matter, or even other black holes often become substantially larger than average stellar black holes. How long a black hole feeds at a particular location depends on what it is consuming. Large stars often take eons for black holes to consume, while smaller objects—such as asteroids, small planets, or moons—take a comparably small amount of time.

Death - Part III
This next section inevitably launches into the realms of theory. Because all but the micro black holes are predicted to live for longer than the current age of the universe, the death of a black hole possibly has not even occurred yet.
One theory, Hawking Radiation, denotes that every black hole, after a very long time, will eventually evaporate into nothing. Thus far, it is one of the few proposed theories regarding black hole evaporation, and remains a hotly debated topic. It is this theory that we will discuss here.
Even in the total vacuum of space, there is energy. Quantum mechanics says that even a true vacuum is not empty, in the sense that it is in fact a sea of zero-point energy. This body of energy fluctuates much like waves in a sea. These fluctuations continue to produce pairs of particles—one normal matter particle, and one antiparticle—that meet and are re-converted back into pure energy, restoring the balance in the sea.
Now, Hawking Radiation states that, if such a pair of particles were formed outside the event horizon of a black hole, and one of the two moves over the event horizon, while the other escapes, then the black hole will lose a small portion of its mass, because, in order to preserve "total energy" (the sum of an object's rest, potential, and kinetic energy), the particle which falls in must necessarily have negative energy.
However, only the smallest black holes could possibly evaporate in this way, because a black hole any more massive than Earth's moon would have a larger constant intake of cosmic microwave background radiation—the electromagnetic radiation that fills the whole universe—than it would emit through Hawking radiation. Indeed, there are currently no known, nor predicted, black holes even close to being the same mass as our moon, and therefore, as of now, Hawking Radiation is not, technically, a viable cause of evaporation in the present universe.
However, the cosmic microwave background radiation that fills space is slowly becoming weaker. Eventually, it will become so weak, that even the largest black holes will emit more by Hawking Radiation that they take in. In this way, after approximately a googol (10100) years, even the very largest black holes would evaporate.
And so, the life of the black hole concludes, when it returns to nothingness, in the depths of space.
Black Holes in Hiding
Invisible Black holes
By definition, black holes do not emit light, so observing them becomes a bit problematic. However, the lack of emitted radiation directly from a black hole does not mean that we cannot detect its presence.
Gravity
First off, black holes have gravity, the remnant gravity left over from the mass that formed the black hole in the first place. The mass itself has gone into hiding—in fact we do not know what exactly has happened to it—but the gravity remains.
The gravity of a black hole is not stronger than the gravity of a star of the same mass, but because the black hole is so much smaller, the gravity at its 'surface,' sometimes called the "event horizon," is more concentrated and intense. It affects things near the black hole, and sometimes these effects can be detected by astronomers.
For example, if a black hole is part of a binary or multiple system, with another star (or stars) orbiting along with it, it may be possible to detect the presence of the black hole by the motion of the other objects, which astronomers can see.
As shown by Einstein's General Theory of Relativity nearly 100 years ago (1915), gravity can distort light. So if the light of some distant star (or more likely, a galaxy) passes very near the surface of a black hole as it beams through space to the Earth, it can be distorted in a predictable way. If astronomers detect these distortions, they can reasonably conclude that a black hole is somewhere along the line of sight.
Electromagnetic Energy (Light)
Even though a classical black hole cannot radiate electromagnetic energy, objects that have been caught by a black hole's gravity and are falling into it can emit radiation of characteristic types before they fall through the event horizon. Any falling or orbiting object is subject to gravitational accelerations, and any charged particle that is accelerated emits electromagnetic energy. In many cases, it is reasonable to expect that there are many subatomic charged particles (mostly electrons and protons) orbiting around or falling into black holes. When they do so, the give off electromagnetic energy with particular characteristics, which can be detected at Earth. In fact, the first candidate black hole, Cygnus X-1, was detected by just this technique, through the strong X-radiation coming from near the black hole. Black holes are much like messy eaters. Some material won't reach the event horizon but instead is caught up in powerful magnetic fields that exist around the black hole. These "jets" not only shoot some material away. They also emit prolific amounts of energy from radio waves to visible light to X-rays. The jets of material shooting from the central black hole of the Perseus cluster have blown out large holes (cavities) in the nearby gaseous medium.
Hawking Radiation
A classical black hole cannot emit radiation, but British astrophysicist Stephen Hawking predicted that through the non-classical processes of quantum mechanics, particles from a black hole could very slowly seep out into space and escape in a kind of quantum evaporation. This is called Hawking Radiation. In a very long period of time, black holes could actually dissipate through this process.
So far, no Hawking Radiation has been detected, although if it is, it could be another way of discovering and studying black holes.
History of the Black Hole
The Black Hole Concept
The idea of a star that is too massive to fully counteract the force of its own gravity is not new, dating at least as far back as the latter part of the 1700s. English scientist John Mitchell and French mathematician Pierre-Simon LaPlace both proposed "dark stars" with the general characteristics of black holes. However, such concepts were in the complete absence of any realistic understanding of how even "normal" stars produce energy, so the concept was little more than a curiosity, and was not seriously considered at the time.
A more realistic picture of such bizarre stellar end-products had to wait until Einstein's General Theory of Relativity, which is actually a new way of looking at gravity. Hot on the heels of Einstein's theory was Schwarzschild's work on the effective theoretical size of a black hole, confining it to what is today called a "Schwarzschild Sphere."
However, there was not even any consensus on what to call them -- they were variously known as "dark stars," or even "frozen stars" -- until physicist John Wheeler in 1967 used the term "black hole" in a lecture.
Additional considerations include whether or not the black hole is rotating, or emitting particles via the as-yet-undetected "Hawking Radiation," or whether any "information" (in the sense used in physics) could be extracted from a black hole, and others.
Still, the basic concept of a black hole remains that of a body whose gravitational force is so intense as to raise the escape velocity at its surface to the speed of light or greater. In that case, no amount of energy would be able to pry a single particle away from a black hole, including the essentially mass-less particles called "photons". Although quantum physics may conceded that subatomic particles can seep through the "event horizon" (the effective surface of a black hole) over exceedingly long periods of time, the general definition still holds.
Due to the nature of a black hole, precluding any exact visual detection (except up closer than we as humans want to get), we may never actually see one. However, as discussed in the previous section, there is abundant evidence that black holes exist. There are black holes of "solar" mass, meaning that their mass is on the same order as that of our Sun (although most natural black holes must be somewhat more massive than the Sun), up to black holes millions to billions of times as massive as the Sun, many of which appear to reside in the cores of galaxies. http://www.nasa.gov/multimedia/videogallery/index.html?media_id=142531021
The first observational (if somewhat indirect) evidence came in 1964 with the discovery of a strong source of X-rays emanating from the constellation Cygnus. The nature of this X-radiation was the same as that predicted to be produced from charged particles spiraling down through the gravitational field of an extremely compact and massive body - a black hole.
Since the 1964 discovery of Cygnus X-1, hundreds of other black hole candidates have been discovered by the same method.
Today, no serious astronomer or physicist doubts the existence of black holes. The details may be lacking, but their reality, for all intents and purposes, is abundantly confirmed.
The Theory of the Naked Singularity

Black holes are objects of mystery, and recent studies have revealed that they may be even stranger than once thought. The core of the black hole is termed the "naked singularity". It is a gravitational singularity that is predicted to be, infinite in density. Such an object's mere existence completely defies the laws of physics as we know them, but it is logical to assume that the center of the black hole should be infinitely compacted. However, such an object would be forever cloaked by the event horizon of its host black hole, so observation is most probably impossible.
Some have gone so far as to say that this cloaking is a deliberate result of a kind of "cosmic censorship" that prevents the naked singularity, as radically as it defies the laws of physics, from being released from beyond the event horizon. What exactly would result from the exposure of the enigmatic core remains highly speculative (as does, the entire subject matter).
Potential for human use of the naked singularity is also something that has been discussed; the observation and study of a body with infinite density would undoubtedly prove highly revealing to astronomers, and may shed light on black holes and other aspects of physics and astronomy.
Spaghettification

Spaghettification refers to the effect of extreme gravitational pressure on any particle or body of matter, in particular when exposed to the extreme forces of the black hole. Essentially, when a particle draws too close to the source of the powerful gravitational field, it is stretched into long thin shapes, like pasta.
The term was coined by Stephen Hawking in his book, A Brief History of Time, where he likened this process to spaghetti. Much like other aspects of the black hole theory and model, this effect of drawing too close to a black hole remains untested, unobserved and unproven, and relates to areas of physics that remain largely unexplored, namely the concept of a force so powerful that no matter what components make up a piece of matter, it will be stretched further than is deemed by many to be within the realms of physical plausibility.
Many have speculated upon why it is, scientifically speaking, that spaghettification occurs when an object draws close to a black hole, but a generally accepted theory has been proposed. To understand this, one must consider the sheer strength of an object with such a high gravitational pull. One must also consider Newtonian gravitational theory, which states that:
- If you increase the mass of an object within a gravitational field, the gravitational pull in question will increase in power by the same amount.
- These factors become exponentially higher as the object draws closer to the source of the gravitational strength.
Bearing that in mind, one now must consider that:
- Black holes have extremely high masses, often many times that of the sun and other stars
- This mass is concentrated in a very small radius.
- Because of these factors, the gravitational force near a black hole is enormous...
- And all the above factors thereby contribute to the largeness of the gradient of the gravitational field across the object within the field as it draws closer and closer to the source.
Effects of this on the article in question are extreme. Spaghettification tears at the matter's very atomic structures, elongating them and stretching them until they are atomically and cellularly unrecognisable.
Spaghettification is also largely based on the positioning of the object, and the trajectory at which it approaches the source of the gravitational power. These factors cause variations on the way the gravity acts on the incoming matter, and spaghettification is caused based by the differences in the forces fronting the object in question.
Black Holes/Hawking Radiation
Hawking Radiation
Hawking radiation is a theoretical effect produced by black holes. The idea was first put forward in 1972 by Jacob Bekenstein, a research student at Princeton, and improved upon by Stephen Hawking in 1974. Hawking's theory predicted that black holes should eventually decay or “evaporate” over time. This evaporation is based on the idea of thermal radiation with a black body radiation spectrum corrected for quantum effects coupled with the idea of vacuum energy.
Vacuum energy is the theoretical energy present in space, even in the absence of matter-energy. The theory postulates that empty space fluctuates and generates pairs of virtual particles of matter or energy. One particle is matter, the other antimatter. No sooner are they generated than they annihilate each other, thus keeping from violating the law of conservation of matter and energy.
Hawking’s theory postulates a particle pair generated from vacuum energy straddling horizon of a black hole, with one particle inside the horizon and its counterpart just outside the horizon. Then it would be possible for the large gravity of the black hole

to pull the two particle apart before they could annihilate each other and thus change the two from virtual particles to real particles. If then one of particles escaped while the other was pulled into the black hole, to the outside observer the black hole will have radiated a particle. This means that the black hole has lost some of its energy, and since we live in Einstein’s universe where matter and energy are combined to make matter-energy, the loss of some of its energy means that it is less massive than it was before it emitted the particle.
Now, if you are worried that the universe is in danger of losing its black hole population - don’t be. Hawking radiation only has a noticeable effect on black holes of around 10^12 kg [1]. or smaller. This is because a black hole must be starved to death; that is, the matter-energy it emits must be greater than the matter-energy it takes in. Since a black hole's mass is inversely proportional to its temperature, and the amount of matter-energy that it radiates is dependent on its temperature, then as the mass of the black hole increases, the amount of matter-energy that it emits decreases. So for larger black holes such as one about the mass of our sun, their temperature is very low (about 10^-7 K) so they have very low radiation. And since they receive light from stars, cosmic background radiation, and even matter in the form of dust, planets and stars, they continue to grow. It will only be at some future date when all stars have gone out, matter is out of reach of large black holes, and the temperature of the universe is less than that of the black hole itself, that the larger black holes will begin to evaporate.
Now that I have given you a brief overview of Hawking radiation and what it means, we can begin to delve deeper into what it is, how it works, and what its implications are.
Firstly, let’s refer back to vacuum energy. According to quantum field theory, all fields must be quantized at each and every point in space. Since a “vacuum” can be a space in which all energies cancel, you can make calculations of quantum field theory based on this model. You can model an expectation value for vacuum energy. The lowest possible energy for a quantized simple harmonic oscillator is E=1/2 ℏω. If you sum this energy over all points in space, you get an infinite quantity, thus giving rise to electron-positron creation and annihilation. When these particles are created at an event horizon of a black hole and one is pulled into the black hole before the pair can annihilate, the resulting Hawking’s flux arises from one particle being cast off to infinity[2]
If you look at a black hole in its simplest form - that of a non-rotating, non-charged Schwarzschild black hole of mass M - you can calculate the temperature of the perfect black body radiation emitted by the black hole using the Hawking's radiation temperature formula. | |
This coupled with the Schwarzchild radius

and the Stefan-Boltzmann power law:
allows you to derive the Stefan-Boltzmann-Schwarzschild-hawking power law:
for black hole radiation.
To put this in perspective, a black hole with one solar mass will have the small output of 9.003*10^-29 watts. From this we can calculate the time it would take for a black hole to evaporate in a completely empty universe. Now we see why it takes so long for black holes to evaporate, since the time of evaporation is proportional to the cube of its mass. However, this time is only theoretical because, in reality, the universe contains cosmic background radiation - among other things - so even a very isolated back hole would have to be smaller in mass than 0.8% of the earth to begin to evaporate.
Hawking’s radiation has many implications; one of them explains why scientists feel safe creating microscopic back holes. A black hole that lasts for even a second would need to have a mass of 2.28*10^5 kg, and since they are colliding much smaller particles, the time that each black hole exists is micro-seconds, possibly nano-seconds. This also means that as a black hole evaporates, unlike most objects, its temperature goes up (or as it grows, its temperature goes down). So in effect, perhaps some of the coldest things in the universe are the super massive black holes at the center of galaxies.
References
- ↑ C. Peters, Joseph Silk, Sadegh Khochfar, Joseph Silk. AccessScience. 16 March 2010 <http://www.accessscience.com/content.aspx?searchStr=hawking+radiation&id=085900>
- ↑ Nielsen, Alex B. "Black Holes without Boundaries." International Journal of Modern Physics D: Gravitation, Astrophysics & Cosmology 17.13 (2008): 2359-66.
Galaxies
The Milky Way
The Milky Way is a barred spiral galaxy which forms part of the Local Group. Although the Milky Way is but one of billions of galaxies in the universe, the Galaxy has special significance to humanity as it is the home of the solar system. Democritus (460 BC - 370 BC) was the first known person to claim that the Milky Way consists of distant stars and many planets, including our own.
The term "milky" originates from the hazy band of white light appearing across the celestial sphere visible from Earth, which comprises stars and other material lying within the galactic plane. The galaxy appears brightest in the direction of Sagittarius, towards the galactic center.
Relative to the celestial equator, the Milky Way passes as far north as the constellation of Cassiopeia and as far south as the constellation of Crux, indicating the high inclination of Earth's equatorial plane and the plane of the ecliptic relative to the galactic plane. The fact that the Milky Way divides the night sky into two roughly equal hemispheres indicates that the solar system lies close to the galactic plane.
The Milky Way Galaxy is about 80-100 thousand light years in diameter, about 3,000 light years in thickness, and about 250-300 thousand light years in circumference. It is composed of 200 to 400 billion stars (exact number not yet known). As a guide to the relative physical scale of the Milky Way, if the galaxy were reduced to 130 km (80 mi) in diameter, the solar system would be a mere 2 mm (0.08 in) in width.
The Milky Way's absolute magnitude, which cannot be measured directly, is assumed by astronomical convention to be −20.5.
Types of Galaxies
Estimates of the number of galaxies in the universe range from 10 billion to over 100 billion. [11] According to Hubble's Law, galaxies are red-shifted. This means that they're moving away from us. Young galaxies are more blue, while old galaxies are more red. As spiral galaxies mature, the center becomes red. The arms are bluish.
Morphology and Classification
The Hubble Sequence
The most common form of classification for galaxies is based on a system which categorises them by their visible structure. This is known as the Hubble Sequence, and was developed by Edwin Hubble in the 1920s. Galaxies are organized in a form resembling a tuning fork, often called the Hubble Tuning Fork Diagram. It is typically drawn with elliptical galaxies on the left, lenticular galaxies in the middle, and two branches of spiral galaxies on the right: one for un-barred spirals, and one for barred spirals.

Elliptical galaxies, also known as "early-type" galaxies, have an ellipsoidal form, with a fairly even distribution of stars throughout. They are mostly featureless and have no form of visible disk. Examples of ellipticals include M87, whose black hole was the first to be imaged in high-resolution, and ESO 383-76, which is one of the largest galaxies ever discovered. They are denoted by the letter E, with the number giving the degree of eccentricity: E0 galaxies are nearly spherical, while E7 are greatly elongated.
Lenticular galaxies appear to have a disk-like structure with a central spherical "bulge" projecting from it, but they do not show any spiral structure. They were originally introduced as a theoretical intermediate class between ellipticals and spirals before being confirmed by observations. An example of a lenticulat galaxy is NGC 2787. These are given the class S0.
Spiral galaxies, also known as "late-type" galaxies, have a central "bulge" and an outlying "disk"; the disk is notable for having spiral "arms" within it, centered on the bulge. Sa galaxies have very "tightly wound" arms, while Sc galaxies are very loose spirals. Barred spiral galaxies have a similar sort of spiral structure to spiral galaxies, but instead of emanating from the bulge, the arms project out from the ends of a "bar" running through the bulge, like ribbons on either end of a baton. Again, SBa to SBc refer to how "tightly wound" these arms are. Examples of spiral galaxies include: the Milky Way, our home galaxy; Andromeda (M31), the closest galaxy to us; and the Pinwheel Galaxy (M101).
Finally, there are irregular galaxies, which show no clearly discernable or regular shape. Some examples of these include the Large and Small Magellanic Clouds, which can be seen from the Earth's southern hemisphere. These are given the class Irr.
Links to Galaxy Evolution

Hubble based his classification on photographs of the galaxies through the telescopes of the time. He originally believed that elliptical galaxies were an early form, which might later evolved into spirals; our current understanding suggests that the situation is roughly opposite.
More modern observations of galaxies have given us the following information about these types:
- Elliptical galaxies are generally fairly low in gas and dust, and are composed mostly of older stars.
- Spiral galaxies generally have plentiful supplies of gas and dust, and have a broad mix of older and younger stars.
- Irregular galaxies are fairly rich in gas, dust, and young stars.
From this, astronomers have constructed a theory of galaxy evolution which suggests that ellipticals are, in fact, the result of collisions between spiral and/or irregular galaxies, which strip out much of the gas and dust and randomize the orbits of the stars.
Galactic Formation
During the early ages of the universe, the universe was very homogeneous and the only structure present was small fluctuations in the density of the primordial gas cloud. This gas cloud, primarily made up of hydrogen and helium, was formed in the first billion years after the big bang during recombination. Small fluctuations in the primordial gas cloud are observed in the cosmic microwave background, homogeneous to one part in one hundred thousand, which is an indication of the density distribution of the universe after recombination. Areas with slightly higher density had enough gravitational attraction to overcome expansion of the universe and collapsed into the first protogalaxies.
Protogalaxies
Over time, areas of higher density began to collapse due to gravitational attraction and formed the first protogalaxies. The first protogalaxies were formed when the universe was approximately 1 billion years old. Though these initial protogalaxies are too young to have formed stars, they emit infrared radiation as gas falls inward and heats due to collisions. Protogalaxies are theoretically observable due to this emission, but they are very dim and far away (approximately 12 billion light years) since they are the earliest structure to be formed after the big bang. Due to these difficulties, protogalaxies have never been observed.
As protogalaxies collapse on themselves, they begin to form a distinct core and halo much like mature galaxies. Particles near the edge of the protogalaxy can lose energy through collisions with the surrounding gas and fall into the core. It has been speculated that the infalling matter forms unstable stars of around 100 solar masses that rapidly collapse into black holes that have been observed at the center of mature galaxies. As matter falls into the black hole throughout the life of the galaxy, it releases large amounts of energy which have been observed as quasars and radio galaxies.
Dark matter is believed to have been present in the protogalaxy. If it exists, it has a weaker interaction with surrounding particles. The dark matter present in the protogalaxy remains in the halo while ordinary matter falls into the core, since the primary mechanism for bringing matter into the core is collisions with surrounding gas. Dark matter, due to its weak interaction, has very few collisions and remains gravitationally bound in the halo.
Star Formation and Death
As gas continues to fall inward towards the core of a protogalaxy, its density continues to increase and dense clouds begin to form. These clouds begin to orbit the center of mass of the protogalaxy due to conservation of angular momentum. When two gas clouds collide, they form an area of higher density at the collision front. These high density regions become gravitationally unstable and collapse into balls of plasma, forming protostars. As material continues to rain in on the protostar, deuterium fusion begins and a star is born. As these stars begin to burn and emit light, they dissipate the surrounding cloud of gas due to solar wind and leave a star cluster. These initial areas of star formation may be the source of globular clusters, some of which have stars which are nearly as old as the universe.
These newly formed stars form the first heavy elements of the new galaxy in their cores as they burn their hydrogen supply. Hydrogen is converted to heavier elements through nuclear fusion until the star has formed a critical mass of iron. Iron is very stable and heavier elements do not release heat from fusion, and the star begins to exhaust its fuel supply. Without a heat source, the star undergoes a catastrophic collapse under its own weight, which ends in a supernova.
As they reach the end of their life, the most massive of these stars explode in supernovae, the explosion from which may outshine the rest of its parent galaxy. As the star explodes, it forms heavy elements (heavier than oxygen) by the process of nuclear fusion. These heavy elements are ejected from the exploding star into the galactic gas cloud. Supernovae are responsible for heavy element formation and distribution through the newly formed galaxy, which previously only contained hydrogen and helium formed during recombination.
Elliptical vs. Spiral Galaxies
A new galaxy will most likely form into either an elliptical or spiral galaxy, though other types of galaxies are present (such as a ring or lenticular galaxy.) The type of galaxy formed depends on the initial rate of star production. If the new galaxy forms stars slowly, then the gas cloud has enough time to exchange energy through collisions and the cloud elongates into a flat disk-shaped spiral as matter falls in to the plane of rotation. If the galaxy forms stars quickly, it can use up its supply of gas before sufficient energy has been exchanged to form a disk. These galaxies resemble their initial elliptical shape before star formation. Other theories speculate that elliptical galaxies are formed from collisions of other spiral galaxies, which distort into the elliptical shape after collision.
Due to their high rate of star production, elliptical galaxies quickly exhaust their gas supply and no longer have active star formation. As such, elliptical galaxies mainly consist of old Population II stars with large numbers of globular clusters. Elliptical galaxies also do not show the characteristic ordered rotation of spiral galaxies since they did not have time to exchange sufficient energy during their formation.
Spiral galaxies, which form stars more slowly, still have ongoing star formation today and as such their star population is much younger. Since spiral galaxies take a long time to form, they exchange considerable energy over their lifetime which collapses matter into a disk with high angular momentum, resulting in the characteristic rotating disk.
Large Scale Interactions
Much like gas clouds in protogalaxies that can interact to form new star clusters, entire galaxies can collide to form new galaxies. As galaxies pass near each other, they can begin to orbit. If the galaxies pass close enough to each other, tidal interactions will cause their orbits to decay and the galaxies consume each other. The shape of the galaxies may be highly distorted during the collision and star formation increases, powering starburst galaxies which are among the most luminous galaxies. This period of increased star formation can last for ten million years or more and the rate of star formation can be ten to one hundred times that of a typical galaxy. The black hole at the center of the galaxy will also show increased emission as material from the collision falls into the galaxy's core.
If galaxies pass near each other but do not fully collide, they can eject large quantities of matter from gravitational interaction, sending gas clouds and lone stars into intergalactic space. These near-collisions also distort the galaxies involved and is one possible mechanism for the formation of lenticular galaxies.
Though large scale interactions were previously thought to be uncommon, the Milky Way was found to have several smaller galaxies orbiting it which suggests that the process is more common. The Sagittarius Dwarf Elliptical Galaxy (or SagDEG) is a small dwarf galaxy orbiting the core of the Milky Way at a radius of about 50,000 light years. The SagDEG is currently passing through the disc of the Milky Way and has been greatly distorted due to gravitational interaction. The small and large Magellanic clouds are also dwarf galaxies which will eventually merge with the Milky Way.
References
Galactic Evolution
(This section is incomplete.)
The question of which came first, stars or galaxies, was once the "chicken and egg" question with no real answer. However, more recent evidence points to vestigial structures in space that ultimately led to the formation of galaxies, long before the formation of any stars. Thus, galaxies came first and stars formed within them.
Astronomers have pieced together the evolution of galaxies not from any one particular galaxy, because of the enormous time scales involved, but by reference to many galaxies in different stages. It is possible, for example, to note common characteristics in all spiral galaxies. Astronomers also can view various spirals at various ages to develop a relative time sequence. If we look at a galaxy that is 5 billion light years away, we know that it is at least 5 billion years old. The distance, and hence minimum age, can be determined by the shift in spectral lines from the light of the galaxy via the concept of Red Shift and the Hubble Law.
Galaxies form from immense clouds of intergalactic gas in three basic types: spiral, elliptical and irregular. Ultimately, the type of galaxy is determined primarily by the dimensions and mass of the gas cloud, and the amount of angular momentum it contains. The angular momentum determines how much the cloud begins to spin as it contracts under the force of gravity. Clouds with large angular momenta spin faster and flatten into a disk-like structure that evolves into a spiral galaxy. Clouds with little angular momenta spin little if at all, and the central force of gravity pulls them into a near-spherical or elliptical shape, appropriately forming an elliptical galaxy. Most large galaxies are of these two types.
There is good evidence to believe that when two similarly-sized spiral galaxies collide, the ultimate result can be a large elliptical galaxy. Although no such single process has ever been observed, there are numerous examples of colliding galaxies.
Smaller clouds of gas may be so loosely bound by gravity that they have not specific or definable shape, and are known as irregular galaxies.
In addition, there are also "strange" or "peculiar" galaxies, likely the result of not of the original formation of the galaxy, but rather some subsequent event, such as the collision of two galaxies.
Once a galaxy forms, its subsequent evolution is determined primarily by the conditions in its nucleus, and the amount of gas left over for further star formation. Astronomers have determined that the core of most newly formed galaxies is dominated by a supermassive black hole (section 13.5). Young galaxies typically are quite energetic due to radiation formed from material that spirals down into this supermassive black hole (SBH). This is likely the source of energy of active galactic nuclei and quasars (Section 13.6) Over time, all of the material that is close enough to the SBH to be pulled into it diminishes and with it the strong radiation from the core. Thus, young galaxies are very energetic, but they calm down with age.
Supermassive Black Holes
The general consensus today is that when galaxies form, the phenomenal concentration of matter at their cores leads inevitably to the formation of "supermassive" black holes (SMBH). Unlike a "normal" black hole that forms from stars only a little more massive than our Sun (stellar mass black holes), "supermassive" black holes range from hundreds of thousands to perhaps a billion or more times the mass of our Sun.
Contrary to image in movies and the media, black holes do not "suck" everything in and it is perfectly possible for stars and gas clouds to orbit around a black hole without being pulled in or destroyed. In fact, observations of the very rapid motions of stars near the center of the Milky Way have given the first proof that such a monster lurks at the heart of our own Galaxy. The stars in this region are orbiting a common center, and their very fast motions indicate an extremely strong gravitational attraction at that point. Using Newton's version of Kepler's laws, astronomers have determined that this mass is the equivalent of about 4 million times the mass of our Sun. Since there is no light or other radiation coming from this point, we reach the inevitable conclusion that it is a supermassive black hole.
Other evidence strongly suggests that similar SMBHs exist in the cores of most if not all other galaxies. Ours is quiet or quiescent today, but not so in some other galaxies.
Active Galactic Nuclei and Quasars
In the 1970s, astronomers discovered an object so bright that it shone with the light of a trillion or more suns. Oddly, this object appeared small and starlike in the images, and became known as a "quasi-stellar radio source," which was shortened to "quasar." Since then many more have been discovered. Quasars also are extremely far away and long ago in time, and apparently represent a very early stage of galaxy evolution.
Other similar objects exists with very energetic cores, although not as energetic as the quasars. These include Seyfert Galaxies, BL Lacerta objects and variations. Such galaxies are said to have "Active Galactic Nuclei" or AGN for short. Interestingly, they are generally closer to us in both space and time than the quasars, and appear to form part of a time evolution sequence for galaxies.
The galaxies nearest the Milky Way (us) are quiescent or quiet.
So to recap, very distant objects such as quasars, which also represent objects very far back in time, are very energetic. Those that are mid-range from us (in both space and time) are less energetic, but more so than the Milky Way. Those that are closest to us (again, in space and time) are quiet.
Evidence suggests that a supermassive black hole (SMBH) forms at the core of most, if not all, galaxies (including quasars). In the early stages of galaxy formation, material continues to fall into the black hole. Although the black hole itself emits no (thermal) radiation, material falling into the black hole emits prodigious amounts of energy. This represents the quasars.
As time goes on, less and less material is available to fall into the SMBH, and correspondingly the energy radiating from the vicinity of the black hole diminishes. This represents the mid-range galaxies with Active Galactic Nuclei.
Eventually, the SMBH becomes quiescent (quiet) when no significant material is available to be "devoured." These represent the Milky Way and nearby galaxies.
Gamma-Ray Bursts and Cosmic Rays
Introduction and Brief History of Gamma-Ray Bursts
Gamma Ray Burst

Gamma-Ray Bursts (GRBs) are bright flashes of highly energetic light, ranging from one keV to many GeV, which last from a few milliseconds to several minutes. They can have a rise times as fast as 10−4s, and exponentially decay. Gamma-ray bursts are detected about once per day from random directions in the celestial sphere. [1] They have luminosities of 4.4 × 1044 W, making them shine hundreds of times brighter than a typical Supernova and are about 1018 times more luminous than our Sun. [2] They can have total energy releases of 1052 ergs or 1045 J. [3] Gamma-Ray Bursts are the brightest objects known in the Universe, many orders of magnitude brighter than any Quasars. [4] They typically originate outside our galaxy in the farthest reaches of the universe.[1]

The mystery of GRB’s started in the 1960s. GRBs were first detected by a group of U.S. military satellites named Vela. The Vela spacecraft were designed to monitor the compliance of the Soviet Union and other nuclear capable states with the 1963 Partial Test Ban Treaty.[1] The original Vela satellites were equipped with six gamma-ray detectors, which looked for sudden bursts of gamma rays, possibly from nuclear weapon detonation.[5]
On July 2, 1967, Vela 4 and Vela 3 detected flashes of gamma radiation that were not characteristic of any known nuclear weapons.[5] Nuclear Bombs produce intense burst of gamma rays for less than 10−6s. The gamma rays then gradually fade as nuclei decay. The gamma ray burst detected in 1967 did not have an intense initial flash or a steady fading.[6] In 1969 the data were analyzed by a Physicist named Ray Klebasabel. Klebasabel found a spike in the data, a dip, a second spike, and a long, gradual tail off. Klebasabel said “One thing that was immediately apparent was that this was not a response to a clandestine nuclear test." His team checked for possible solar flares and supernovae that could be reasonable and found none.[5]
On May 23, 1969 Vela 5 was launched. Vela 5 was more sensitive and had more accurate time resolution then Vela 4. [7][8]
Vela 5 found twelve GRBs which had not coincided with any solar flares or supernovas.[5] On April 8, 1970 Vela 6 was launched, which was synchronized with Vela 5 to within 1/64th of a second.[5] The orbits of Vela 6 satellites were made to be as far away from Vela 5 as possible in order to determine the direction of the source of the GRBs.[7][8] This could be done because the GRBs would arrive at different times for each satellite. By analyzing the arrival times, Klebesadel and his team traced sixteen GRBs.[5] The GRBs were found to be randomly distributed across the celestial sphere. This made it clear that the bursts were coming from outside our solar system. In 1973 this information was released to the public.[1]

References
- ↑ a b c d Dale A. Ostlie, and. Carroll, Bradley W. Introduction to Modern Stellar Astrophysics. Boston: Addison Wesley Company, 2006.
- ↑ Guetta, Dafne, Tsvi Piran, and Eli Waxman. "THE LUMINOSITY AND ANGULAR DISTRIBUTIONS OF LONG-DURATION GAMMA-RAY BURSTS." The Astrophysical Journal (2005): 412-19. IOP. The Institute of Physics. 1 Apr. 2009 <http://www.iop.org/EJ/article/0004-637X/619/1/412/59430.web.pdf?request-id=950fd8ab-be45-4323-ae6f-8ab1902ab873>.
- ↑ T, Piran. "Gamma-ray bursts and the fireball model." Physics Reports 314 (1999): 575-667. http://adsabs.harvard.edu/abs/1999PhR...314..575P
- ↑ Paczynski, B. "Gamma-ray bursters at cosmological distances." Astrophysical Journal 308 (1986): L43-46. The SAO/NASA Astrophysics Data System. Harvard-Smithsonian Center for Astrophysics. 1 Apr. 2009 <http://adsabs.harvard.edu/abs/1986ApJ...308L..43P>.
- ↑ a b c d e f "Original discovery of gamma-ray bursts." NASA - Science@NASA. 27 Feb. 2009 <http://science.msfc.nasa.gov/newhome/headlines/ast19sep97_2.htm>.
- ↑ Katz, Johnathan I. (2002). The Biggest Bangs. Oxford University Press. ISBN 0-19-514570-4. Page 4 to 5.
- ↑ a b Govert Schilling (2002). Flash! The hunt for the biggest explosions in the universe. Cambridge: Cambridge University Press. ISBN 0-521-80053-6. Page 11 and page 15-16
- ↑ a b Caplan, Ron. "Cosmic Gamma-Ray Bursts." Sumseq. <http://www.sumseq.com/grb.htm>.
Long-Soft and Short-Hard Classifications
Long gamma-ray bursts
Most observed events have a duration of greater than two seconds and are classified as long gamma-ray bursts. Because these events constitute the majority of the population and because they tend to have the brightest afterglows, they have been studied in much greater detail than their short counterparts. Almost every well-studied long gamma-ray burst has been linked to a galaxy with rapid star formation, and in many cases to a core-collapse supernova as well. Long GRB afterglow observations, at high redshift, are also consistent with the GRB having originated in star-forming regions. A unique gamma ray emission event, GRB 110328A, lasting more than two and a half months was observed starting March 28, 2011, originating from the center of a small galaxy at redshift z = 0.3534. The event is interpreted as a supermassive black hole devouring a star, most likely a white Dwarf and emitting its beam of radiation towards Earth. It could thus be viewed as a temporarily active blazar (a type of Quasar).
Short gamma-ray bursts
Events with a duration of less than about two seconds are classified as short gamma-ray bursts. These account for about 30% of gamma-ray bursts, but until 2005, no afterglow had been successfully detected from any short event and little was known about their origins. Since then, several dozen short gamma-ray burst afterglows have been detected and localized, several of which are associated with regions of little or no star formation, such as large elliptical galaxies and the central regions of large galaxy clusters. This rules out a link to massive stars, confirming that short events are physically distinct from long events. In addition, there has been no association with supernovae. The true nature of these objects (or even whether the current classification scheme is accurate) remains unknown, although the leading hypothesis is that they originate from the mergers of binary neutron stars or a neutron star with a black hole. The observation of minutes to hours of X-ray flashes after a short gamma-ray burst is consistent with small particles of a primary object like a neutron star initially swallowed by a black hole in less than two seconds, followed by some hours of lesser energy events, as remaining fragments of tidally-disrupted neutron star material (no longer neutronium) remain in orbit to spiral into the black hole, over a longer period of time. A small fraction of short gamma-ray bursts are probably produced by giant flares from soft gamma repeaters in nearby galaxies.
Fluence and Extragalactic Nature
Fluence
The distances to sources of gamma-ray bursts (GRBs) and their origins were not known until late 1990s. In particular, it was not clear whether GRBs originated in our solar system, in our galaxy, or in distant galaxies. In addition, the light spectrum of GRBs has multiple peaks and a complex structure. This causes changes in the energy received per second. Without knowing our distance from the progenitors, and since through the course of the GRB the energy randomly changes, the energy output must be given in terms of total energy received per unit area of detector surface. The can be done by integrating the energy flux over the duration of the burst. This quantity is called the fluence (S) with units of J/m2. Gamma-ray bursts typically have fluences between 10−12Jm−2 to 10−7Jm−2.[1] Data for flux and fluences for GRBs can be seen for yourself at http://www.batse.msfc.nasa.gov/batse/grb/catalog/4b/tables/4br_grossc.flux.
In order to investigate possible distance to the progenitor of a GRB we need to derive an equation that relates Fluence with distances. Consider a progenitor that has a luminosity of L and is at a distance r from earth, and assume an isotropic burst. After the light has traveled a distance of r, the luminosity will be spread out equally over the surface of a sphere with radius r, with the progenitor at the center of this sphere. The surface area of this sphere will be
The flux (in W/m2) that earth receives will be equal to the luminosity divided by the surface area of a sphere with radius r,
This is the well known inverse square law of radiation. The fluences will be the amount of energy received over the time duration of the GRB. This can be found by integrating the flux with respect to time.
Where E is the energy of the gamma-ray burst and r is the distance the source is from earth. S is fluences and has units of J/m2.
Enlightening Example
If we assume the GRB to be in a galaxy 1 Gpc way, what amount of energy would be needed to produce a 10−7Jm−2 fluences, which is the upper limit of fluences detected in a GRB.
This is the average energy of a GRB given earlier in the introduction. [2] Now, in contrast, let's assume that the GRB source is within our galaxy. The extended corona around our Galaxy is about 100 kpc away.
This is the total energy emitted by a GRB if it were much closer, such as in our Galaxy. This is smaller than the energy given off by a type IA supernova which gives off about 1044J. [3] This smaller energy seemed more reasonable to astronomers when GRBs were first being studied. However further evidence shows that the larger of these two numbers is more accurate.
A long time ago, In a galaxy far far away

The isotropic angular distribution of GRB seen by the BATSE detector on board the CGRO
The Compton Gamma Ray Observatory satellite on average observed one GRB every 25 hours. Measured positions from the dataset are shown in the figure to the right. The figure shows that there was no statistically significant deviation from an isotropic distribution. The figure also shows that the distribution is not homogeneous. This is significant because this means that the sources of the GRBs can’t be neutron stars in the Galactic Disk. The origin must lie outside of our galaxy. From the earlier example it can be seen that the greater distances have a dramatic effect on the energy required to produce GRBs. One big question about GRBs is understanding what could generate such a large amount of energy in such a short time.
To determine whether there is an edge to the distribution a brightness distribution argument using fluence can be used. Assume that a gamma ray source has an energy E and a distance r from earth, its fluence would be
- .
Solving for r provides,
- .
We assume that all burst sources are isotropic and have the same intrinsic energy, E. For each value of S0 the source will be within a sphere of radius r(S0). If there are n burst sources per unit volume, then the number of sources with fluence of S0 is
This shows that if gamma-ray burst are uniformly distributed throughout space, then the number of bursts observed with fluence greater than some value S0 is proportional to S0^(-3/2). The data from the Compton Gamma Ray Observatory satellite show that this proportionality is not upheld when S is small enough to included very distant galaxies. This implies an edge to the distribution. This could be the edge of the observable universe. Thus we are must likely at the center of an spherically symmetric distribution of gamma ray burst sources.
References
- ↑ Dale A. Ostlie, and. Carroll, Bradley W. Introduction to Modern Stellar Astrophysics. Boston: Addison Wesley Company, 2006.
- ↑ PETROSIAN, VAHÉ, and THEODORE T. LEE. "The Fluence Distribution of Gamma-Ray Bursts." THE ASTROPHYSICAL JOURNAL (1996). Center for Space Science and Astrophysics, Stanford University. <http://www.iop.org/EJ/article/1538-4357/467/1/L29/5195.text.html>.
- ↑ Khokhlov, A.; Mueller, E.; Hoeflich, P. (1993). "Light curves of Type IA supernova models with different explosion mechanisms". Astronomy and Astrophysics 270 (1–2): 223–248. http://adsabs.harvard.edu/cgi-bin/bib_query?1993A%26A...270..223K. Retrieved on 2007-05-22.
Sources of Gamma-Ray Bursts
Lingering Mysteries
Cosmology
The Distance Ladder
The Cosmic Distance ladder—each step is less accurate that the one before
- Radar is the most accurate method, but it works only on solid bodies in the solar system. The Sun and gaseous planets such as Jupiter do not reflect radio waves and hence cannot be ranged this way.
- Stellar parallax, or distance based on how a star's apparent location varies with the observer's location, is the original method used to determine stellar distances. This is the most accurate method for estimating distances to stars, but is limited to only the nearest stars. Parallax is smaller the farther away a star is, and can be detected for only several thousand stars as viewed from Earth. However, parallax is detectable for many more by spacecraft above the Earth's obscuring atmosphere.
- Cepheid variables, is a method of determining cosmic distances based on the "period luminosity" characteristics of certain stars. Cepheids are stars whose total brightness (luminosity) varies with specific periods. They vary in brightness from brightest to dimmest to brightest in certain time periods.
It turns out that the period is related to the star's absolute magnitude or luminosity. Luminosity is a measure of how bright the star truly is at all wavelengths.[By comparison, light bulbs come in various luminosities, such as 60 watts or 100 watts. A 60 watt light bulb will appear much brighter at 5 feet than at 50 feet, but it will still have a 60-watt luminosity. If you know what the luminosity is, and can measure the apparent brightness, you can determine the distance by a simple mathematical relation.] By observing the star's period, we know its luminosity (which is directly related to another quantity called "absolute magnitude". By then comparing the known brightness [absolute magnitude] to the apparent brightness [apparent magnitude], the distance can be found by applying the inverse square law [just as you could determine the distance to a 60-watt light bulb if you could measure how bright it appears at your distance]. The specific equation is known as the "distance modulus." This is most useful for finding distances to stars clusters of which the Cepheid is a part. (Other stars with a similar relationship are the RR Lyra variables.)
- Spectroscopic parallax and related techniques based on spectral classification and the HR diagram (below). That is, if we know the spectral type of a "normal" star, we know its luminosity (actual total energy output at all wavelengths). This is because stars follow a pattern. That is, all G-type "normal" (non-Giant) stars are like all other G-type stars. All B-type normal stars are like all other B-type normal stars. More specifically, all G2 normal stars (such as our Sun) have approximately the same luminosity. Thus, if we can identify a star as being a G2 from its spectrum, then we know its luminosity, because we know that it is essentially the same as the Sun's. If we know the luminosity or absolute magnitude, we can compare that to the observed brightness [apparent magnitude] to deduce mathematically the actual distance by the distance modulus.
- Main Sequence fitting is a process related to "spectroscopic parallax" that compares the Hertzsprung -Russell (HR) diagram of the stars in a star cluster, with a calibrated HR diagram to determine absolute magnitude. This again is compared to the apparent magnitude of the stars and the distance determined by the distance modulus relation.
The processes above are useful for determining distances within the Milky Way Galaxy. Several other techniques for determining distances beyond our Milky Way Galaxy:
- Cepheid variables. The technique can be used for a few nearby galaxies, but is limited because outside of a few nearby galaxies, individual stars cannot be seen.
- Supernova magnitudes. Type Ia supernovae tend to be caused by the same series of events and all tend to be the same absolute magnitude. Since they are so bright (sometimes exceeding the brilliance of an entire galaxy) they can be seen much farther than individual stars and distance can be obtained through the distance modulus by comparing the apparent magnitude to the known absolute magnitude.
- The Tully-Fisher relationship. Astronomers have noted that the mass of spiral galaxy is related to its rotation rate. Mass is related to the number of stars, and the number of stars is related to the absolute magnitude of the galaxy (the greater the mass, the more stars and the brighter the galaxy). Thus by measuring rotation rate of the galaxy, and estimation of its true brightness can be made, and distance follows through the distance modulus.
- Red-Shift. Galaxies show shifts in the position of spectral lines in their light, dependent on how far the galaxy is. The farther the galaxy is, the more its light (and the spectral lines contained in that light) is shifted toward the red end of the spectrum. Thus by simply measuring the amount of shift, astronomers obtain an idea of how quickly the galaxy is moving away from us; given an assumed cosmological model this then allows the distance to the galaxy to be calculated.
The Big Bang and Cosmic Expansion
The Big Bang is a misnomer, as it implies an explosion. In fact, the model describes an expansion of the Universe, not into some pre-existing space, but rather that it created space as it expanded. There is nothing outside the Universe, so there was nothing to expand into. It's just at one time every point in the Universe was incredibly close to every other place (less than the size of an atom), and that at the moment of the Big Bang, they all started getting farther apart at a high rate. This expansion continues today, and in fact appears to be speeding up, possibly due to another force called "dark energy." By current thinking, this expansion will continue forever, continually cooling.
The basic idea dates back to the 1920s and Georges Lemaitre who, basing his idea on Einstein's general theory of relativity. Soon afterwards Hubble's discovery that all distant galaxies are receding from us served as a confirmation of the basic idea of the Universe having a beginning in time and having since expanded.
By today's measurements—using the current size and rate of expansion as we understand them—working backwards in time leads to the conclusion that approximately 13-14 billion years ago, the Universe was compacted into the volume of less than that of an atom. By understanding how the forces of Nature work, we can trace this backwards into earlier times and higher temperatures. As we do so, the nature of the laws of Nature change, such that at 10^-43 of a second after the Big Bang (the "Planck time"), the laws as we know them break down. Hence, we cannot look farther back in time than that—and in such a situation it is impossible to look to a time before the Big Bang. [Of course, we cannot rule out the possibility that those ideas may someday change.]
At and before Planck time, most astronomers and physicists think that all the forces of the Universe—electromagnetism, the two nuclear forces and gravity—were all merged into one force, but we do not know how that force worked. After the Planck time, gravity separated from the "Grand Unified Force," the latter of which consisted of the strong nuclear force and the electroweak force. As things cooled further, the electroweak force split into electromagnetism and the weak nuclear force, and the regime we have today was born.
During the first three minutes of the expansion, energy cooled and matter in the form of hydrogen and helium "froze" out. After about three minutes, the expansion had cooled the Universe so much that no more elements were created ("nucleogenesis"). In fact, no new elements were formed for hundreds of millions of years until the first stars formed. All the hydrogen in the Universe, including that in you, and most of the helium can be traced back to the first three minutes of the Universe.
After that the Universe expanded for hundreds of millions of years before the first stars and galaxies formed in a highly energetic state (by today's standards). Since then, the stars and galaxies have evolved to what they are today.
There are three major pieces of evidence in favor of the Big Bang:
First and foremost is the expansion itself. This was discovered in the 1920s through the red shifts of distant galaxies. If all the universe is expanding today—which is certainly what the evidence shows—then it is reasonably easy to work the process backward in time to deduce that at earlier epochs the Universe was smaller.
The second piece of evidence was predicted by George Gamow, who is considered by many to be the "father" of the Big Bang, although he was not the first to come up with the idea. In the 1940s he made the calculations that showed how elements were formed at the time of the Big Bang. Basically, he said that if the Big Bang idea was correct, then the Universe should consist of roughly 75 percent hydrogen and 25 percent helium (other elements being very small constituents). This could not be confirmed at the time, but with the advance of technology, has since been confirmed.
The third and very strong piece of evidence also was predicted by Gamow long before it could be confirmed. Basically, he said that the Big Bang would have been very hot, and as it expanded the Universe would cool off. As matter cools off it gives off certain types of radiation. It is like a hot fireplace poker cooling off and changing colors, or the embers of a fire dying and turning dark. Even though they may not give off visible light, they continue to radiate infrared radiation. Although Gamow had a wrong estimate on the age of the Universe, he said that by today it should have cooled to a certain level, and if we had the technology to detect it, we could read the radiation and effectively take the temperature of the Universe. The technology to do this became available in the 1960s, and the radiation predicted by Gamow—properly adjusted for today's more refined value of the age of the Universe—has been discovered. It is called the "Cosmic Background Radiation," or "Cosmic Microwave Background Radiation," and is often abbreviated as CBR or CMBR. The CBR is especially good evidence in favor of the Big Bang, as there is little if anything else that can adequately explain it.
Historically, the Big Bang has had problems. The three main ones are called:
- The Horizon Problem. You might call this the Mixing Problem. If we look to the edge of the observable universe in any direction, we find that everything seems the same, as if it was well mixed. But material 10 billion light years in one direction cannot mix with material that is 10 billion light years in another direction simply because the age of the Universe is too short. The material on one edge of the observable Universe is over the "horizon" for material at the other edge. They cannot interact. Yet everything is well mixed. How did it get that way?
- The Flatness Problem. The actual density of matter in the Universe is too close to the critical density (that density required to just stop the expansion) to be coincidental. To be as close as it is today, the Universe had to have been "flat" (that is, critical density and observed density exactly the same) to within something like 60 decimal places. This is amazing. How could it possibly be so close?
- The Smoothness Problem. In the original Big Bang scenario, everything is expanding away from everything else in all directions. As such, no two particles of matter would have every gotten close enough to stick together by gravity. Hence, there would be no galaxies, no stars, no planets. Yet these all exist.
About 25 years ago a physicist named Alan Guth came up with an idea now known as Cosmic Inflation. Think of water cooling off and changing into ice. It takes energy (heat) to hold water in a liquid state. When the water cools and changes to ice, it gives up this energy into the environment. This is called a "symmetry breaking." Basically, what Guth said was that in the early Universe, just a tiny fraction of a second after the Big Bang, something similar happened as it expanded and cooled. Only here the heat energy solidified into matter (via E=mc^2). The energy released in this symmetry breaking caused the expansion to suddenly speed up for a very short while, much greater than the Big Bang alone. This super expansion (inflation) helps solve the three problems that previously plagued the Big Bang model.
- In a short introduction we must leave out detail, but in essence Inflation solves the Horizon Problem because at the very early stages of the Big Bang, everywhere was close enough to every other "where" such that they were well mixed. The sudden inflation essentially locked that well-mixed state in and it remained as the Universe has expanded to today.
- Inflation solved the Flatness Problem because the inflation naturally ran out of energy just as the density reached the right value.
- It solved the Smoothness Problem because in the very early Universe, quantum fluctuations caused small irregularities throughout the baby Universe (we know such "irregularities" occur all the time in space today). You can think of these as small density concentrations or "knots" in the fabric of space. Inflation suddenly blew these up to enormous size, trillions of times larger than the originally were. As the Universe expanded, matter collected around these spatial "kinks" and eventually formed galaxies.
Although there have been other theories, most notably the Steady State theory, none have been able to adequately explain all the evidence in at least a semi-consistent and coherent model. Some of the other theories are just variants on the Big Bang model.
We have a reasonable mechanism to explain Cosmic Inflation and the changes in the Universe since the Big Bang itself, but the cause of the original "bang" is unknown. There have been suggestions, but none offer an ultimate solution. One idea is that the Universe arose completely out of nothing, just as we observe (although on vastly smaller scales) in the quantum physics we know today. [Particles come into existence out of nothing all the time, but they do not stay around long enough to be counted. They are called "virtual particles" and there is strong evidence that they exist even though we normally are unaware of them. By the proper application of energy, we can make some of these particles stay around longer so we know they exist.]
What caused the Big Bang? This question probably does not have a scientific answer. It is in a category of questions like, "Why does something exist instead of nothing?" That, nobody knows.
The First Three Minutes
The first three minutes after the Big Bang is a time period worth of a whole book (indeed, such has been written). It is important because it was during this very short time period that all the hydrogen and most of the helium in the Universe today was formed. These are the two most abundant elements in the Universe, and are the basic materials from which the first galaxies and stars formed.
At the very instant of the Big Bang, the Universe formed as a rapidly expanding ball of energy at extremely high temperatures (trillions of degrees). As soon as it began to expand, it began to cool, and as it cooled some of the energy "froze" out in what physicists call a "symmetry breaking." This is similar to water freezing into ice, except in this case it was pure energy solidifying into matter. The conditions were right for about 75 percent of the "frozen" energy to become proton (hydrogen nuclei) and the rest to form combinations of protons and neutrons in the helium nuclei. This continued for only about 3 minutes, after which the Universe had expanded and cooled to the point that the process was no longer possible.
Thus, just some 3 minutes after the Big Bang began, the Universe was composed of hydrogen and helium nuclei with a great deal of leftover energy.
This seminal 3 minute period is populated with very short periods known as the Planck Era, the GUT Era, the Electroweak Era, the Particle Era, and the Era of Nucleosynthesis. However, the important thing to know is that it was during this very short time that the major building blocks for today's Universe were formed -- and have persisted to this day.
On final note may be in order. Most of the things around us in everyday life are composed of materials other than hydrogen and helium, although obviously there is much hydrogen in ordinary water, and protons (hydrogen nuclei) are part of all matter. But what about the heavier elements such as carbon, oxygen, silicon, iron and others? They were not formed in the Big Bang, so where did they come from?
After the first 3 minutes of the Big Bang, no further elements were created for millions of years, so the Universe was entirely hydrogen, helium and energy. However, eventually clouds of hydrogen and helium collected and contracted into stars under the force of gravity. In the cores of these stars nuclear fusion began and hydrogen fused into more helium, helium fused into carbon, and various other elements up to iron. For smaller stars, this is where it stopped. However, some of the most massive stars underwent enormous supernova explosions. In the supernovas conditions were right to form even heavier elements, all the way up to Uranium.
It is a sobering thought that every atom in your body can be traced back (in theory anyway) to the Big Bang, and the nitrogen and oxygen you breathe, the carbon your body is composed of all came from some ancient star. And the heavier elements, of which there are traces in your body, formed in the fiery furnaces of supernovas! No wonder the late Carl Sagan was fond of saying that we are all "star stuff."
Higgs Boson

The Higgs Boson theoretical particle is a focus of keen interest for high-energy particle physicists. However, the Higgs Boson is also forging a strong bond with cosmologists that is likely to grow as the study of modern physics unfolds. Particle physicists regularly create exotic particles that have not existed abundantly and naturally since the earliest moments of the universe, which has been an important step in drawing the disciplines together. The discovery of the Higgs Boson could benefit cosmology by resolving some unanswered questions in the current theory. The mutually beneficial nature of this relationship becomes more apparent as the costs rise to perform high energy particle collision experiments. The next generation of particle experiments may rely on high-energy particles from space to attain higher power collisions for a lower price. This beneficial merging of fields is being called Astroparticle Physics (or Particle Astrophysics). This chapter will focus on how the Higgs Boson is essential to both parties' theories and how they are collectively seeking to discover the elusive Higgs particle.
What is the Higgs Boson?

The Higgs component of the particle name bears no physical significance. It is named after Peter Higgs who independently published results around the same time as two groups released similar and related material. In 2010, all six contributors to the Higgs theory received the J. J. Sakurai Prize for Theoretical Particle Physics.
The Boson component does bear physical significance. Bosons are a class of particles that are governed by Bose-Einstein statistical theory and have the ability to occupy the same quantum state. This behavior is disallowed by most more commonly known particles (Protons, Neutrons, Electrons, which are Fermions) by the Pauli Exclusion Principle. It is a mark of importance as the mediating forces are considered Bosons. This includes: Photons, Gluons, the W and Z, the Higgs, and the Graviton (like the Higgs, currently just theoretically proposed to exist). Bosons have integer spin: the first four above have spin one, the Higgs theoretically has 0 spin, and the Graviton theoretically has spin 2.

And what does it do?
Theoretically the Higgs Boson is the particle form of the mediating Higgs Mechanism, also known as the Higgs Field. The Higgs Field is supposedly responsible for the mass of all particles, and so the substance to all things in the universe. It is also a possible answer to the asymmetry between matter and anti-matter that makes our reality possible (if equal the universe would be filled only by energy). It is the only undiscovered particle of the Standard Model of Elementary Particle Physics. The Higgs Mechanism is the supposed field that endows all the components of nature with mass. Thus, if the Higgs Boson is discovered it will confirm the existence of the Higgs Mechanism which shows that the entire universe is permeated by the field and without it no object would have mass.
A simple example with familiar terms for how it operates is a party. If someone of low social worth to those present walks in they will be largely ignored as they make their way around. This matches a particle of little mass passing through the universe quite freely because it has less interaction with the Higgs Field. However, if someone who is idolized by the members of the party enters, people will quickly gather around them and make it quite difficult for free motion. This is the equivalent of massive particles that are greatly bogged down by the Higgs Field. The only neglected component in this example is massless particles. One could introduce them as follows: enter a small child that has utterly overdone a reasonably alloted quantity of sugar. The participants generally ignore the child as it runs around the room easily squeezing through gaps in people barring some mishaps where the child hits a person. [1]
Connection of the Higgs Boson to Cosmology

The Higgs Boson theoretically has an obvious link in the sense that there's a lot of massive objects in the universe from basic masses like the quarks that comprise hadrons to our Earth, Sun, and the Milky Way's super-massive black hole. However, the connection has a deeper core than that.
When the Universe was Less Massive than You
The title is not a lacking-class, physics-based fat joke: there's some merit to it. It is actually believed in Cosmology that there was a period early in the universe where not even Photons manifested themselves because the temperature was so great. That is, there was no light at all in the very early universe. This principle is believed to extend to the Higgs Boson and Mechanism as well. This has a greatly profound implication: immediately following the Big Bang the universe had zero mass because there was nothing there to endow anything present with mass. This was very brief (on the order of tiny fractions of a second), but a vital consideration to make for Cosmology.
This could be one potential explanation for the phenomenon of inflation where the universe was able to expand extremely rapidly early in the universe to explain why the universe currently appears to be flat or very nearly flat despite this contradicting expectations based on models of the universe.
What's the Antimatter?

Another problem with the Benchmark Model of the universe is that it lacks a clear explanation of why the Big Bang produced more matter than antimatter (hence the absolute lack of abundant, naturally occurring antimatter). If it was consistent with other Laws of Physics, there would have been an absolute match in quantities that resulted in the entire matter content of the universe having annihilated with the entire antimatter content of the universe leaving essentially no matter behind.
This problem, properly titled: the asymmetry of the universe, has been delegated to be potentially caused by the Higgs Mechanism causing a minor asymmetry in the early universe that ultimately caused the matter-prevalent universe that surrounds us. The Benchmark Model indicates the asymmetry as unimaginably small to most of us: that is, once upon a time there was 1,000,000,000 quarks, but only 999,999,997 antiquarks. Those three bachelor quarks, when propagated over the massive quantity of material involved in the Big Bang, became all the baryonic matter we see today while the rest annihilated with their significant antiquark other. [2]
This rouses another curiosity of Dark Matter, much of which is believed to be non-baryonic (essentially: isn't made of Protons and Neutrons that comprise the elements of the Periodic Table which, in turn, comprise all the molecules that represent everything someone not delving deeply into Physics needs to know about). A pressing question for the near-future of Cosmology: what exactly is this large quantity of matter not comprised of the remains of asymmetry that appears to be present (by observations) in a quantity five times larger than the baryonic matter that comprises everything we know? But that's a digression from this chapter and fairly unfamiliar ground to even the boundaries of Physics at this point.
Where in the World is the Higgs Boson?
So, this particle seems pretty important towards the greater fate of the universe, how are this Physicists coming together to find it? This is where the chapter probably gets more familiar as the Large Hadron Collider (LHC) has been greatly popularized in recent years as the "Big Bang Machine." It's not the first, but it's the shiny new, fast, and powerful accelerator on the block that will, if it exists, be able to provide the energies necessary to create it for sure whereas its predecessors wouldn't if it's heavier than expected. But first, lets explain how the search works before detailing the handful of experiments that are working, perhaps competing is a better term, to be the first to find it.
The Functional Technique to Nab a Wild Higgs Boson
The Most Expensive Lassos Ever Dreamed
References
- Notes
- ↑ Berkeley Lab: Video Glossary: Higgs Boson (http://videoglossary.lbl.gov/2009/higgs-boson/)
- ↑ Barbara Ryden, Introduction to Cosmology. San Francisco: Addison Wesley Company, 2003. p.188.
- Bibliography
To be added later.
An Accelerating Universe
Space is flat. This is shown by the density of matter, and cosmic background radiation.
The radiation left over from the Big Bang is about 3 Kelvin.
The rate of expansion of the universe is greater in proportion to the distance.
Other Cosmological Models
Throughout history, astronomers have been seeking models of the universe. The three best known are those by Ptolemy, Newton, and Einstein. They all had an explanation why the universe didn't collapse.
Ptolemy's model had the Earth at the center, surrounded by an "8th Sphere" of stars. The sphere held up the stars, so the universe didn't collapse.
Newton's universe was infinitely large. He postulated a universe where the gravitational force was in balance. In an infinitely large area, there is no center of mass; therefore, the universe could not collapse. Like many of his time, Newton also believed in an infinitely old universe. Given an infinite amount of time, if the universe was going to collapse, it would've done it already.
Flaws with Newton's model were apparent even in his time. Heinrich Olbers wondered: If the universe is infinitely large and infinitely old, why isn't the night sky as bright as the sun? This question became known as Olbers' Paradox. Olbers' proposed solution was that the universe was filled with dust, obscuring some of the starlight. However, this only appeared to solve the problem. Dust absorbs and radiates energy, so that the light being obscured would be transmitted anyway.
Einstein's model for the universe was a constant size. He postulated a repulsive (lambda) force that counterbalanced gravity and kept everything from collapsing.
Immanuel Kant, a philosopher, proposed a disc-shaped universe.















































![{\displaystyle a=\left({\frac {AU}{\sqrt[{3}]{y^{2}}}}\right){\sqrt[{3}]{P^{2}}}=\left({\frac {AU}{\sqrt[{3}]{y^{2}}}}\right){\sqrt[{3}]{(0.75y)^{2}}}=0.83AU}](https://wikimedia.org/api/rest_v1/media/math/render/svg/286d7ac15ebe1b352620733947e5e0a279ba9de3)




















































































