General Astronomy/Observational Astronomy
| General Astronomy | ||
| The Modern View of the Cosmos | Observational Astronomy | Motion and Gravity |
The Celestial Sphere

If you look out from an empty field into a dark sky, you will get the impression that you are standing on a flat plate, enclosed by a giant dome. Depth perception fails us for the distant objects we see in the sky. This creates the appearance that all of the stars have the same distance.
The stars appear to move together across the sky during the night, rising in the east and setting in the west, as if they are affixed to the inside of a dome. Because of this, many ancient civilizations believed that a dome really did enclose the Earth. Only a few centuries ago astronomers came to realize that the stars are actually very far away, scattered throughout the Milky Way Galaxy, rather than attached to the inside of a vast sphere.
The old idea remains useful, however. The concept of the celestial sphere provides a simple way of thinking about the appearance of the stars from Earth without the complication of a more realistic model of the universe. Working with the celestial sphere offers a convenient way of describing what we see from Earth. When we refer to the celestial sphere, we are imagining that everything we see on the sky is set on the inside of a huge spherical shell that surrounds the Earth. We will use the reference points of the celestial sphere as the basis for several coordinate systems used to place celestial locations with respect to one another and to us.
The celestial sphere is an imaginary hollow globe that encloses the Earth. The sphere has no defined size. It can be taken to be infinite (or at least really big), with an infinitesimal Earth at the center. The observer is always taken to be at the center of the celestial sphere, even though the observer isn't at the center of the Earth. Our particular position among the stars gives us a particular view. Brighter stars appear closer; stars in nearly the same direction appear nearby each other, even if they are separated by great distances. Our first and most basic look out into the universe is completely stripped of any depth perception.
The celestial sphere can be seen from either of two perspectives. In one perspective, the celestial sphere itself remains still while the Earth turns inside it. In the other perspective, the Earth stands still and the celestial sphere rotates once per day. To an observer on Earth, these two perspectives appear the same. As we think about how we would expect to perceive the rotation of the Earth, we can use this second perspective to guide us.
Everything we see in the sky, we see as though projected onto the celestial sphere. The stars in the constellation Orion, for example, are at a variety of distances, but the differences are imperceptible to us on Earth. Orion's pattern would disappear if we could view it from any other angle or if we could perceive the depth, because the stars would project differently.
Because depth perception is lost, measurements of size are much more difficult. The Sun and the Moon look about the same size in the sky, even though the Sun is really much larger. The Sun appears to be the same size as the moon because the Sun is much farther away simply because the Sun is both 400 times larger in diameter and 400 times farther away than the Moon.
Although we can't easily measure the physical sizes of celestial objects, we can measure their apparent sizes. We do this by measuring the angle an object subtends in the sky. The Sun and the Moon, for example, subtend an angular diameter of half a degree. Most objects in the sky are smaller than this, so it is often convenient to use a smaller measure of angle. For this purpose, astronomers use arc minutes and arc seconds. There are sixty arc minutes in a degree, and sixty arc seconds in an arc minute. Angles this small are near or beyond the limits of ordinary human vision, but they become useful when using a telescope to make observations.
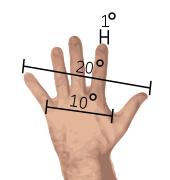
For casual stargazing, observers think about much larger angles. You can easily measure these angles when stargazing by using your hand as your ruler. From arm's length, your index finger has a width of about one degree, your palm measures about ten degrees across, and your full finger-span, including your thumb, is about 25°. This can be useful for estimating the position of a star in the sky, or for gauging the angular separation of two stars.
While the apparent movement of a star across the sky each night, with the celestial sphere, is great, the measurement of an object's movement across the Celestial Sphere as the object drifts through space, is called proper motion, and is measured in arc seconds per year.
To begin thinking about the view of the sky from Earth, we will identify a few points of reference that are fixed to the ground and of importance to astronomers. Some of these are widely known from common experience.

- A great circle is a circle drawn on the celestial sphere (or any sphere) which has the center of the Earth as its center. On the Earth, the equator is an example of a great circle. Other lines of latitude are not great circles because their center is not at the center of Earth. Lines of longitude are all great circles because they are always centered on Earth's center. A great circle is the largest possible circle that can be drawn on a sphere.
- The horizon is where earth and sky meet. It is the boundary between the portion of the sky that is blocked by the Earth and the portion that is visible. There is a distinction between the local horizon, which is defined by real objects specific to the observer's location such as trees or buildings, and the idealized horizon, which is what the local horizon would be if the ground were completely flat and there were no obstructions. For hypothetical or idealized cases, astronomers use the idealized horizon.
- A star's altitude is the angle between it and the horizon.
- The cardinal points are points on the celestial sphere that are on the horizon and due north, south, east and west. The North point, for example, is the point due north on the horizon.
- The zenith is the point in the sky directly overhead. It is necessarily true that any point on the horizon is 90° from the zenith.
- The meridian is the great circle that passes through the North point, the South point, and the zenith and lies on the celestial sphere.

To any observer, regardless of location, these markers stay in the same positions relative to the observer. The zenith is always directly overhead, the horizon is always level, and so on. Observers standing at different places on Earth will have a different view of the sky. An observer in Singapore might see the Sun at the zenith while another observer in New York would not see the Sun at all. These reference points change with the location of the observer.
There are also reference points that are fixed in the sky. These fixed reference points don't move with respect to the stars, but different observers see them in different positions. They are the basis for the fixed coordinate systems that we discuss later. For now, we will identify only the two most useful of these — the celestial poles and the celestial equator.
The celestial equator is an extension of the Earth's equator onto the celestial sphere. If you stand on Earth's equator, the celestial equator will always be directly overhead and pass through the zenith. It will run from the East point up to the zenith and down again to the West point. Anywhere you stand on Earth, the celestial equator will intersect the East and West points on the horizon. The nearer you are to the equator, the nearer the celestial equator come to the zenith. At the North Pole or the South Pole, the celestial equator lines up with the horizon.
Like the celestial equator, the celestial poles are an extension of the Earth's pole onto the celestial sphere. The North Pole extends out into space to create the North Celestial Pole. Likewise the South Pole creates the South Celestial Pole. In the Northern Hemisphere, only the North Celestial Pole is visible because the South Celestial Pole is below the horizon. In the Southern Hemisphere, only the South Celestial Pole is visible. At the equator, the North Celestial and South Celestial Poles would lie on the horizon where the meridian intersects the horizon.
Polaris is called the "North Star." It can be found at the last star on the "handle" of the Small Dipper. The last two stars of the "cup" of the Big Dipper are called the Guardians (or "Pointers"), and point to Polaris in the sky. Polaris is special because the Earth's North Pole points almost exactly towards it. This means that Polaris will always appear to be due north to any observer, and it will always stay in the same position on the sky.
Often, beginning stargazers assume that Polaris must be a very bright or prominent star. This is not really the case. Polaris is only remarkable because it is almost exactly in line with Earth's axis of rotation. Because of this, Polaris always remains at nearly the same place in the sky. For example, Shakespeare made reference to Polaris in the play Julius Caesar:
- I am constant as the northern star,
- Of whose true fixed and resting quality
- There is no fellow in the firmament.
- Julius Caesar, William Shakespeare's Julius Caesar, III.1.65-68
Though it must be pointed out that Shakespeare actually got it wrong. At the time Shakespeare wrote Julius Caesar Polaris was indeed the pole star but in Julius Ceasar's time Polaris was not the pole star.

The fact that Polaris always stays in the same position due north has given it much fame. It also makes Polaris a useful reference point for navigation — Using geometry, it is easy to show that the angle Polaris or the celestial pole makes with the horizon is equal to the observer's latitude. In the diagram, the angle is the observer's latitude. The pole and the equator are at right angles, so
or Since the angles in a triangle add to 180°, we know that
When we combine these two equations, we have . The angles and are alternate interior angles, so
and
which means that the angle between the pole and the horizon is the same as the observer's latitude. This fact was once used by navigators at sea, who could easily find their latitude by measuring the position of Polaris.
Like many things in astronomy, the celestial sphere can be very difficult to visualize because of its three dimensional geometry. A visit to a planetarium or a session under the night sky can be very helpful to you in developing a conceptual understanding of the celestial sphere. In the absence of the opportunity for these, it can be helpful to try to draw diagrams such as the one at the beginning of this section for yourself.
To begin drawing a celestial sphere such as the one above, you only need to know the latitude of the observer. Then imagine that the spot where the observer is standing is the "top of the world"; draw circle for the earth, and draw an observer standing at the top. Now draw a much larger circle around that; this represents the celestial sphere.
Since our observer is always on top of the Earth, the features on the celestial sphere that are defined relative to the ground will always be in the same position on the sphere. The zenith is the point directly above the observer's head, at the top of the celestial sphere.
The next important reference is the horizon. The horizon will be horizontal on the diagram. Remember that the celestial sphere has no specific size relative to the Earth, regardless of how you've drawn it. Draw the horizon across the middle of the celestial sphere, so that it's center is the same as the center of Earth. Markers such as the horizon are always idealized, so it doesn't matter whether your observer's view of the sky is actually cut off at the position marked by the horizon.
The next reference points we'd like to place are the North Celestial Pole and the South Celestial Pole. Think about what the orientation of the pole should be given the observer's latitude. If the observer is at the equator, the pole should go horizontally through the Earth. If the observer is at one of the poles, the pole should go through the Earth vertically. Extend the Earth's poles out to the celestial sphere and mark the intersections as the North Celestial Pole and the South Celestial Pole.
If we're in the northern hemisphere, the North Celestial Pole will be above the northernmost point on the horizon, and the South Celestial Pole will be on the opposite side of the celestial sphere, below the horizon. If we're in the southern hemisphere, the situation is reversed. Remember to check that the angle the horizon makes with the pole is about the same as the observer's latitude.
For any given latitude, one can build an appropriate celestial sphere. First, consider the sky in relation to the earth. Take the north and south poles and extend them into the sky; these become the north and south celestial poles. The Earth's equator can be projected outward to form the celestial equator. We'll get something that looks like the picture above.
When you're done, you should have a celestial sphere very like the one at the top of this section.
A celestial sphere forms the basis for the application of many coordinate systems. For example, the horizon and the celestial meridian together form the reference circles for giving the position of stars in terms of altitude and azimuth, making it easier for one to find them on the night sky. The celestial sphere is also a natural system for describing the motion of the sun. In order to explore these concepts, however, it is necessary to understand just how the celestial sphere changes for an observer at a given latitude. As we consider the daily rotation of the Earth, we'll see that your perception of the daily motion depends very much on your latitude.
As you look at the sky, your mind will naturally identify obvious patterns. The Big Dipper and Orion are two very prominent groupings of stars, and others stand out all over the celestial sphere. These asterisms are guideposts to the night sky. You can use them to keep your bearings when you look at the sky. The appearance of the night sky has remained much the same for millennia. Many of the ancient civilizations across the globe invented stories about the sky.
Often, the groups of stars are called constellations. Constellations have a very long history in astronomy, dating back thousands of years. Early in the twentieth century, a list of constellations was formally established by the International Astronomical Union, a widely recognized body of astronomers. The IAU identified constellations that would be used in astronomy and defined specific boundaries to unambiguously establish which constellations each star belonged to. It's easy to learn a few of the most prominent constellations so that you can find your way around the night sky. Beginning with a few easy-to-find landmarks you can find the rest by using familiar stars as guideposts.
Another useful guide in the sky is the ecliptic. The ecliptic is an imaginary line in the sky that the sun draws. The ecliptic is even with the plane of the Earth's orbit around the sun; thus, all of the main planets and the moon should be found relatively close or on the ecliptic, because the solar system is mostly flat. Also, along the ecliptic are the 12 constellations of the zodiac. Thus, by finding some of the main zodiac constellations in the night sky, one can determine if certain objects they see may or may not be planets by whether or not they lie on the ecliptic.
Phases of the Moon
Like the stars and planets, the Moon doesn't stay fixed in the sky but slowly moves as the Earth rotates and as the Moon moves through its orbit about the Earth. To someone taking a casual glance at the Moon, it seems as fixed as the stars. But observation of either the Moon or the stars over a period of several hours will reveal their diurnal (daily) motion across the sky. The Moon rises and sets each day. An observer who watches the Moon over the course of many days will notice the Moon moving not only with the stars, but among them. Every month, the Moon completes one fewer pass across the sky than the stars have completed. We see this because of the Moon's orbit about the Earth. As the Moon progresses through its orbit, its rising and setting times change. Each day, the Moon rises and sets fifty minutes later than the day before.
The moon usually takes 27 days to rotate once on its axis. So any place on the surface of the moon experiences about 13 days of sunlight, followed by 13 days of darkness. Temperatures on the Moon range from -153 C at night to 253 C during the day. For example if you were standing on the surface of the moon during sunlight hours it would be blazing hot. When the sun goes down, the temperature automatically drop 250 degrees in just a matter of moments. Furthermore, there are craters around the North and South poles of the moon which never seen the sunlight. These dark places would always be as cool as -153 C. However, there are nearby mountain peaks that are covered in continuous sunlight, and would always be hot.
The "dividing line" between the light and dark halves of the globe is called the terminator, as it terminates the area of darkness (and also that of daylight).
Typically, one-half of the Moon will be lit up by the Sun, while the half facing away from the Sun remains dark. (The only exception occurs during a lunar eclipse, when the Earth blocks the light falling on the lit side of the Moon.) The part illuminated by the Sun is not, it should be emphasized, always the same portion of the Moon's surface! Like the Earth, the Moon turns on its axis, exposing different areas at different times. In combination with the orbital revolution of the Moon around the Earth, this phenomenon creates the phases of the Moon as seen from Earth. The phrase "Dark side of the Moon" arose before the age of artificial satellites and the back side of the Moon could not be observed. Hence, the that one side was unknown or "dark".
The tilt of the moon’s spin axis is only 1.54 degrees and as a result, lunar seasons are barely noticeable in most locations on the Moon. However, at the North and South poles, the height of the sun above the horizon varies by more than 3 degrees over the course of the year. In other words, it affects the percentage of sunlit regions and surface temperatures at the poles. Furthermore, the coldest areas are located in doubly shadowed regions inside small craters, in which they are located within the permanently shadowed regions of larger craters. Temperatures are as low as 35K (-238 C or -397 F) in these areas, even at noon on the warmest day of the year.
Some half of the Moon is always illuminated but the fraction of the illuminated part or the Moon's phases directly depend on the relative positions of the Earth, Moon, and Sun. Simply put, it's a matter of how much of the daylight side of the Moon we can see from our current viewing angle. The phase will depend on how much of the side facing toward us is illuminated at any given time. The sketch below illustrates the phases of the moon for various Earth-Moon-Sun positions (the Sun is presumed to be off of the diagram to the right):
Next to each "Moon" is a black-and-white sketch of the phase as it would be seen from Earth when the Moon is in that position. When the Moon is between the Earth and the Sun, the sunlit side of the Moon is facing completely away from us, and therefore we have the dark "New Moon". When the Moon reaches the other side of the Earth, the sunlit side will be fully toward us, and we have the "Full Moon". As the Moon moves from New to Full and the sunlit side grows increasingly large, we say the Moon is waxing; as we see less, in the decline from Full to New Moon, we say it is waning.
Midway between the Full Moon and New Moon, half of the sunlit side of the Moon is visible from the Earth. Because a half of the half illuminated Moon can be seen, this is referred to as a "quarter Moon". When the Moon is waxing and reaches this position, it's called the "first quarter Moon"; when waning, the "third quarter Moon." When less than a quarter-moon is visible, it's referred to as a "crescent Moon" - waxing crescent or waning crescent, as appropriate. When more than a quarter-moon is visible, it's referred to as a "gibbous moon", again, waxing or waning.
The Moon's orbit and rotation speed is just such that the Moon always shows the same side to Earth, aside from only a slight "wobble." The pattern of markings on the side facing Earth is very familiar in history and culture. Western society has long imagined a face in the markings — the "Man in the Moon." Other cultures have seen a woman, a rabbit, a frog or other creatures. The Moon always shows this same face to Earth because its rotation is "locked" with its orbit, for reasons we will see later, when we discuss gravity. More precisely, the time it takes for the Moon to complete a trip in its orbit is the same as the time it takes for the Moon to rotate once around its axis. Because we see the Moon moving around us, it appears as though the Moon isn't turning at all.
If you stood on the Moon and looked up at Earth in the sky, you would see that it never rises, never sets, and never moves in the sky at all. Imagine, for example, standing at the middle of the face of the Moon that we see. From there, the Earth would always remain straight overhead. If you stood at the edge of the face we see from Earth — the "limb" — you would always see the Earth on your horizon.
Up to now, we have considered the time for the Moon to complete one orbit around the Earth to be the same as the time for it to pass once through its series of phases, but this is not quite right. The Moon's phase at a particular point in its orbit changes as the Earth goes around the Sun. Once the Earth has gone halfway around the Sun, the position of the Moon for a given phase has also moved halfway around the orbit, since the Sun is on the opposite side. Thus, it takes a little longer for the Moon to go through its phases than it does for it to go through its orbit about the Earth.
Suppose a full moon marks the beginning of both the period of the orbit of the Moon about the Earth and the period of the orbit of the Earth about the Sun. At the time of full Moon, the Sun, Earth, and Moon are aligned. Once the Moon returns to that position in its orbit, the Earth has moved a little around the Sun. Now, the Moon is not aligned with the Earth and the Sun. It takes about two days before the Moon has moved back into alignment with the Earth and Sun line (synodic month). The time for the Moon to complete an orbit, called a sidereal month, is about 27 days and 8 hours. The time to move through its phases, a synodic month, is about 29 days and 12 hours.
Eclipses
An eclipse occurs when one casts a shadow on another object. A lunar eclipse happens when the shadow of the Earth falls on the Moon, because the Earth is in a position where it blocks the light from the Sun. Likewise, when the Moon interposes itself between the Earth and Sun, so that the Moon's shadow falls on the Earth (and the Sun is temporarily blocked from view), a solar eclipse is the result.
Eclipses occur when the Sun, Moon, and Earth align. An eclipse blocks sunlight headed toward either the Moon or the Earth, depending on whether the eclipse is a solar eclipse or a lunar eclipse. Such an alignment can only happen when the Moon is in new phase or full phase. If the Moon is new, then it's possible for a solar eclipse to occur. During a full moon, there might be a lunar eclipse. During a solar eclipse, the Moon's shadow falls on the Earth, and the Moon blocks the Earth's view of the Sun. During a lunar eclipse, the Earth's shadow falls on the Moon, and the Moon appears to be darkened as we see it from Earth.
As one of the rare and very spectacular celestial events, a solar eclipse is well worth seeing if you should ever have the opportunity. When viewing a solar eclipse, however, it is important that you avoid damage to your vision by taking steps to view the eclipse safely. (There is no danger in viewing a lunar eclipse, during which the observer never looks at the Sun.) The simplest way to view a solar eclipse is to project the sunlight through a pinhole onto a card or a sheet of paper. The sunlight on the paper will form an image of the Sun. As the eclipse progresses, you will see a round "bite" that the Moon's shadow has taken out of the Sun. If possible, you might also find a special filter, which you can look through directly to watch the eclipse. Solar filters make it possible to look directly at the Sun without harming your vision. Be sure to use a filter specifically designed for looking at the Sun — sunglasses, welder's glass, and other filters are generally not sufficient. Don't use a telescope or binoculars unless the filter was designed for that purpose. Even near totality, when the Sun is almost completely covered, you risk damage to your eyes by staring into the Sun. Once totality arrives, however, it is safe to look directly. It is also safe (though not advisable) to look for a brief moment at the uneclipsed Sun. When viewing an eclipse, there's no need to be paranoid about the danger of accidentally glimpsing the Sun's surface for a split second. If your eyes catch the bright surface of the Sun, simply turn your head away.
The shadow of the Earth on the Moon (or any shadow cast by the Sun) has two parts. The inner part of the shadow, called the umbra, is the darkest part. If you were to stand on the Moon under the umbra, your view of the Sun would be completely blocked. Under the outer part, the penumbra, the Sun is only partially blocked. This is why the Moon is more darkened under the umbra than under the penumbra. While the location of the boundary of the umbra and penumbra are precisely defined geometrically, there is no sharp shadow line between the two when looking at an eclipsed Moon. At the innermost part of the penumbra, only a tiny fraction of the sunlight reaches the Moon, and this part is almost as dark as the totally eclipsed umbra. During a solar eclipse, when the Moon's shadow falls on the Earth, we stand in the shadow rather than looking at it. Observers standing in the umbra see a total eclipse of the Sun, while observers under the penumbra see a partial eclipse.
The present average distance of the Moon from the Earth happens to be just right for the Sun and the Moon to have almost the same apparent size as viewed from Earth. The Sun is 400 times larger than the Moon, but it's 400 times farther from Earth. Because of this, the Moon can obscure the bright surface of the Sun while leaving the fainter outer part, called the corona, exposed. The result is dramatic. During a total solar eclipse, the seething outer layers of the Sun are visible around the Moon. An annular eclipse is possible when the Moon is near the most distant part of its orbit, a point called the apogee. In an annular eclipse, the Moon passes directly in front of the Sun but fails to block it completely, creating the appearance of a bright ring, or an annulus.
Since it's possible for an eclipse to occur twice a month, once of the Sun and once of the Moon, at each new and full moon, students often wonder why eclipses don't occur twice a month, each time the Moon passes through its new and full phase. Months often pass with neither a solar or lunar eclipse. Eclipses don't occur in these months because the Moon passes just north or south of the Earth's shadow during the full moon. Likewise, the Moon's shadow misses the Earth as it passes through new moon. This happens because the orbit of the Moon is not perfectly aligned with the Earth's orbit. The Moon's path is tilted 5° to the ecliptic. It only passes through the ecliptic at two points in its orbit. These points are called the nodes.
Whenever the Moon isn't located at a node, it is either north or south of the Earth-Sun line. Eclipses can only occur when the Moon is at one of the nodes and at new or full phase — when the Moon's orbit is positioned so that the nodes are aligned with the Earth-Sun line. This happens about twice a year, at intervals called eclipse seasons. The time of eclipse season changes over the course of many years, but consecutive eclipse seasons are about six months apart. In any year there are at least two eclipses, and there may be as many as seven, all occurring during the eclipse seasons. There are typically around four eclipses in a year.
Eclipses can only happen when the moon is at a node in its orbit - a point where the Moon's orbit around the Earth intersects with the Earth's orbit around the Sun. If the Moon crosses one of these nodes while it's in the full or new moon position, a lunar or solar eclipse (respectively) can occur.

In a lunar eclipse, the observer watches the Earth's shadow fall on the Moon. Observers don't need to be in any special place to see the eclipse, so long as the Moon is visible. Consequently, an observer on the side of Earth facing the Moon will be able to see the eclipse. Fully half of the Earth will have a view. In a solar eclipse, the observer stands in the shadow of the Moon. The umbra of this shadow is small, so only a small portion of the Earth will see a total eclipse. A much larger portion will see the Moon only partially blocked, and will have a partial eclipse.
The Moon will often become reddish or orange in color during a lunar eclipse. The color of eclipses varies, with the Moon sometimes becoming very red and at others only darkening with no change in color at all. The Moon reddens during the eclipse because sunlight filters through the Earth's atmosphere and is scattered into the Earth's shadow. Sunlight reddens as it is scattered by dust and smoke in the Earth's atmosphere; this is why sunsets are red. The reddened sunlight illuminates the eclipsed Moon, making the Moon brighter and redder. The color and darkness of an eclipse depends on the geometry of the eclipse and the weather on Earth during the eclipse.
Two phenomena caused by eclipses are the Diamond Ring and Baily's Beads.
Throughout history, astronomers have relied on cycles in their observations. The year, for example, is the cycle of the Earth's orbit around the Sun, and the seasons follow with this cycle, as do the motions of the stars. Since ancient times, astronomers have known about an eclipse cycle, called the Saros cycle. they can be used to predict in advance when an eclipse will occur and what the eclipse will be like.
The Saros cycle depends on three other cycles of the Moon: the time from one full moon to the next — the synodic month; the time it takes for the Moon to pass through a node and come all the way around — the draconic month; and the time it takes for the Moon to come close to the Earth in its orbit, move away, and come close again — the anomalistic month. In one Saros cycle, there are almost exactly 242 draconic months, almost exactly 223 synodic months, and almost exactly 239 anomalistic months. The Saros cycle is the smallest length of time that evenly contains all of these cycles. This is why eclipses repeat within the Saros cycle.
Stonehenge is an ancient structure in Britain. It is made up of 30 monoliths in the Sarsen Circle. There are 56 Aubrey Holes outside of Stonehenge. It is believed that Stonehenge was used for predicting eclipses.
Daily Motions
Every day, the Earth turns once on its axis. At the Earth's equator, we move around the center of the Earth with speeds near a thousand kilometers per hour because of this rotation. We feel nothing, but we can see the effect of Earth's rotation. An observer on Earth sees everything in the sky appear to rotate around Earth at the rate of once per day. This motion is not apparent to an observer who steps outside for a moment, since it is so slow. For the motion to become apparent, an observer must watch the sky for a period of hours. During the day, the motion manifests itself in the movement of the Sun, which proceeds from the East in the morning towards the west in the evening. At night, the constellations move, seeming to circle about the pole.
Because the daily motion of the stars is driven by the same mechanism that drives the motion of the Sun, the stars move in almost exactly the same way that the Sun moves. Indeed, everything in the sky moves in almost exactly the same way over the course of a day. The motion of the Sun and the planets only differ at all because the planets have their own motion around the Sun along their orbits, and is noticeable from Earth.
As the Earth spins, it appears to us that the celestial sphere is spinning. It spins about the Earth's pole, so that the celestial poles appear stationary and the stars and planets seem to move in circles around the poles. Stars move at 15° an hour.
The schematic illustrates the daily motion of the celestial sphere resulting from the spin of the Earth. The Sun, Moon, planets and stars make circles around the Earth. Since the observer is tilted with respect to Earth's rotation axis, the daily motion also appears tilted. As a result, celestial objects appear to rise and set at an angle.
Looking at the diagram, we see that stars should rise roughly in the East and come up at an angle. In the Northern Hemisphere, the stars move to the south as they rise, while stars move northward in the Southern Hemisphere as they rise. To an observer standing at the equator, the axis of rotation is horizontal, and stars rise in the East perpendicular to the horizon.
Since the stars seem to rotate around the celestial pole, some of the stars very near the pole never rise or set. Certainly, Polaris never sets — it remains fixed. Only an observer very close to the equator will see any of the stars in the Little Dipper rise or set. The stars close enough to the pole never seen to rise or set are called circumpolar stars. These stars always remain above an observer's horizon. Different stars are circumpolar to different observers.
Imagine standing at the North Pole. You would see Polaris overhead with all the other stars spinning around it. In reality, you are the one who is spinning. From the North Pole, all of the motion of the stars is horizontal. Stars at the horizon skim along the horizon, never rising or setting. The stars higher in the sky also move horizontally, never moving up or down. From the poles, all visible stars are circumpolar.
At the Earth's equator, the situation is different. The celestial poles appear at the horizon on the north and south points. As stars move around the poles, they all rise and set, no matter how close to the pole they are. From here, there are no circumpolar stars. As you move from the equator to the pole, you will see gradually more and more stars become circumpolar, until on finally reaching the pole you find that all stars are circumpolar.
For centuries, the day has been the most fundamental unit of time in the calendar. Measuring the passage of days is as easy as counting sunrises or sunsets. The earliest clocks, the predecessors to the sundial, worked by tracking the daily motion of the Sun across the sky.
A sundial uses the position of the Sun to give the time. (The gnomon of a sundial can be used to find north: the shortest shadow cast by the sun (at noon) points north.) Of course, not all clocks work by measuring the Sun, although all work by measuring some reliably periodic and regular process. A wristwatch, for example, measures the oscillations of a quartz crystal. Atomic clocks use the natural period of oscillation of cesium atoms to measure time. Other systems of time are tied to the motion of the Earth, but there are a variety of ways to measure time in this way. The time measured by any particular method is not guaranteed to agree with the time measured by another, so it is sometimes necessary to convert between different "kinds" of time.
The time measured by sundials is called local solar time. The local solar time progresses according to the Sun's motion around the Earth. Since the Earth's speed in its orbit around the Sun changes slightly over the course of a year, this motion is not completely uniform. Sometimes, when the Earth is moving faster in its orbit, the solar day is shorter. Early timekeepers never noticed this slight difference, but the appearance of accurate mechanical clocks made it possible to measure the small changes in the length of the day.
To deal with this problem, astronomers invented mean solar time. The mean solar time averaged the length of the day so that each day was of the same length. This standard is up to fifteen minutes off from the true solar time, but is much more convenient for clocks that are accurate enough to see the difference. Over the course of a year, the local solar time drifts, but the two always agree after a full year has passed.
For much of history, every town in the world kept a slightly different "correct time" from every other town. Under local solar time, noon occurs at the moment the Sun passes through the observer's meridian. Two observers in different locations will observe local noon to occur at different times. This is why local solar time is called "local." This difference wasn't a problem when transportation and communication were slow, but the advance of trains and telegraphs made even a small difference between nearby towns important. To deal with this, the time zones were developed. The standard time was defined to be the time at a nearby line of longitude. For most locations, the time zone was offset by an round number of hours from the time measured at Earth's prime meridian.
For historical reasons, the prime meridian is based on the line of longitude through the observatory in Greenwich, England. That time zone is known as Greenwich Mean Time, and is often used as a standard for when one wishes to compare times without taking local time zones into account. For this reason (since it is used universally) it is also called Universal Time. This is the most commonly used form of solar time, and the most commonly used measure of time in general.
It's very natural to use the Sun as a standard of time, since the cycles of day and night are so important to life on Earth. For this reason, most people think of a day as the time it takes the Sun to move through the sky once. The apparent motion of the Sun in the sky is similar to the motion of everything else, but not exactly the same. The daily motion is driven almost entirely by the rotation of the Earth, but the Sun's motion differs from the stars' motion. This happens because the Earth is moving around the Sun. The Earth moves a little in its orbit while a it rotates and day passes. Because the Earth's position has changed, a full rotation doesn't quite bring the Sun all the way around the sky. This means that the Earth makes a little more than a full rotation over the course of a solar day.
A sidereal day is the amount of time it takes for the stars to go once around the sky, equal to 23 hours and 56 minutes. The word sidereal means "relating to the stars." The difference in length between the solar and sidereal day causes the rising and setting times of stars to change throughout the year. If the star Rigel, for example, rises at noon today, it will rise at 11:56 tomorrow. In six months, it will rise at midnight. Because the difference between solar days is tied to the orbit of the Earth, there is exactly one more sidereal day in a year than there are solar days.

A sidereal month is the period of the moon in relation to the stars; approximately 27 (1/3) days (13 degrees a day). Ancient peoples used this period to track time, as evidenced by the Big Horn Medicine Wheel in Sheridan, Wyoming.
Sidereal time is widely used in astronomy because it can be used to tell which stars will be up. At a given sidereal time, the stars in the sky will always be the same. Accurately finding the position of stars is easier than finding the position of the Sun, so measurements of the solar time are usually based indirectly on the sidereal time. Modern techniques measure time from atomic clocks, which are then tied to the motion of the Earth by measurement of the sidereal time.
A synodic month is one new moon to the next; approximately 29.5 days. This is about two days longer than the sidereal month. The reason for this is that while the Moon is orbiting the Earth, the Earth is orbiting the Sun. Therefore, the Moon has to travel more than 360 degrees to return to its original position above the same meridian on the Earth.
For anyone living on the coast, tides play an important role in everyday life. Despite this, the cause of the tides was a mystery for centuries, before gravity was well understood. People have always suspected that tides are related to the moon, since high tides always occur when the Moon is highest in the sky and again when the Moon is lowest below the horizon. This turns out to be correct.
Tides occur because the gravitational pull from the Moon is greater on the side of the Earth facing the Moon than on the side facing away. As a result, the gravitational pull "stretches" the Earth. The tidal pull from the Moon gives the Earth an oblong shape. The pull affects the ocean more strongly than the ground, because the ocean is liquid and less resistant to movement.
The stretching effect from the tides creates two places on Earth where the tides are high, with one high tide on the side of the Earth facing the Moon and the other on the side opposite the Moon. As the Earth rotates, the locations under the positions of high tides also move. If the moon didn't orbit around the Earth, high tide would occur exactly twice a day, every 12 hours. The orbit of the moon changes the position of the high tides over the course of the month, which lengthens the time between high tides to about 12½ hours.
The Sun also has a tidal influence on the Earth, although this is a much smaller effect than the Moon's tidal influence. Because of the difference in the gravitational pull from the Sun on opposite sides of the Earth is much smaller, the Sun's tendency to make the Earth bulge is much less. Still, the contribution to tides from the Sun is noticeable. When the Sun, Moon and Earth are aligned, the Sun adds to the Moon's tidal pull, making the tides greater. This is called the spring tide. (The spring tide has no connection with the season of spring.) When the Moon is at a right angle with the Sun, the Sun's tidal pull interferes with the Moon's, making the tides weaker. This configuration is called the neap tide.
Yearly Motions
Why do we have seasons? A little thought will suggest that it can't have much to do with the Earth's distance from the sun, as that would affect the Southern and Northern Hemispheres at the same time. (In fact, the Earth is slightly nearer to the sun around December than at other times of the year.) Why, then are there seasons?
Every year the Earth completes one orbit of the Sun. We see this observe the effect as the change of the seasons and the movement of the constellations. Over the course of a year, the Sun moves through a great circle on the celestial sphere, tracing out the same path year after year. This path is called the ecliptic. The ecliptic is not only the path of the Sun in the sky, it also marks the plane of the Earth's orbit of the Sun. The planets orbit the Sun in different planes but near to the ecliptic.

The axis of the Earth's rotation is tilted by 23½° with respect to the plane of the ecliptic. Globes are typically built with an inclined rotation axis. The 23½° North latitude is marked as the Tropic of Cancer and the 23½° South latitude is marked as the Tropic of Capricorn. In the Northern Hemisphere, the Sun will pass directly over head only between June 20 and 22th along the Tropic of Cancer. That day is called the day of the summer maximum or Solstice in the Northern Hemisphere. In the Southern Hemisphere, the Sun will pass directly over head only once between December 20 and 23rd along the Tropic of Capricorn. Anywhere between the Tropic of Cancer and the Tropic of Capricorn, the Sun will pass directly overhead at least twice during the year, but the Sun will never pass overhead for people living outside the tropics. Within the Tropics, over the course of a year, the Sun's position in the sky changes, beginning in the southern sky about December 21, moving to the northern sky in mid-year, and ending the year back in the southern sky.
The tilt of Earth's rotation axis causes a 23½° tilt of the great circle of the ecliptic with respect to the Earth's equator. The ecliptic and the equator intersect at two points, but are otherwise separated by up to 23½°. When the sun lies at one of the intersections, it is directly overhead somewhere on the equator. This occurs at the equinox, and the points on the sky where the equinox intersects the equator are also called equinoxes. Once every year, the Sun passes through the equator going north. This happens in late March — the "vernal" or "spring" equinox. The "autumnal" equinox occurs when the Sun passes through the equator in late September.
On the equinox days, the day and night are equally long. This is the origin of the name equinox, which is from Latin for "equal night." On the day of the equinox, the Sun rises due east and sets due west. It doesn't rise to directly overhead, though, except for observers on the Equator. The equinoxes are the only days of the year that have twelve hours of daylight and twelve hours of dark. After the vernal equinox, moving into Northern summertime, the Sun begins rising in the northeast and sets in the northwest. Days in the Northern Hemisphere become longer, while days in the Southern Hemisphere become shorter.
The points at which the Sun is at its greatest distance from the equator are called the solstices. The solstices mark the longest and shortest day of the year. The longest day of the year is the summer solstice and the shortest day is the winter solstice. In the Northern Hemisphere, the summer solstice occurs when the Sun is farthest north, while the winter solstice occurs at the Sun's southernmost point. In the Southern Hemisphere, the solstices are reversed.
Viewed from space, we see that the Earth's tilt changes the exposure of different parts of the Earth to the Sun. Observers in the Northern Hemisphere will see the Sun at its lowest position in the southern sky, about December 21. They see it this way because the Southern Hemisphere is tilted towards the Sun and the Northern Hemisphere is tilted away. About June 22, the situation is reversed, with the Northern Hemisphere pointed toward the Sun, and the Sun will be in its extreme high point in the sky at solar noon. For an observer in the Southern Hemisphere, the Sun will appear at its lowest point in the sky in the north, about June 22, while the Sun will appear at its high point in the sky about December 21. One effect of this phenomenon is that during the months of Northern Hemisphere summer, the North Pole will be able to receive sunlight twenty-four hours a day. The Sun will remain visible through much of the autumn, passing below the horizon at the autumnal equinox. As winter sets in at the North Pole, the Sun will not be seen for six months, while that portion of the Earth is tilted away from the Sun.
As one moves toward the Earth's equator from either pole, this effect becomes less severe. The nearer one is to the equator, the less difference there will be between the number of hours of illumination and night hours. At the equator, there's practically no difference between the length of day all through the year.
Clearly, the annual motion of the Earth around the Sun is the cause of Earth's seasons. What effect gives rise to this seasonal change is less obvious. At first glance, one might think that winter occurs when the Earth is farther from the Sun. If we realize the Northern and Southern Hemispheres have winter at different times of year, we see that this can't be right. Also, the Earth's orbit is very nearly circular. The change in the Earth's orbital distance is much too small to have a noticeable effect on Earth's climate.
Certainly the length of time each day during which sunlight falls on a particular location has a great deal to do with the seasonal changes in temperature. However, another effect less obvious, but more influential is the angle at which the sunlight hits a region. At the equator, there is little difference throughout the year as the Sun varies by 23.5 degrees on either side of the vertical. The length of the ray's path on Dec 21 at solar noon is increased by a factor of only 1.1 from a direct vertical path and the reduction of the sunlight is small. The more direct radiation gives the maximum amount of heat and energy to the earth where it falls, and therefore these areas will receive the most warmth. Away from the equator, however, the Earth's tilt means that sunlight is not received so directly and a greater amount of the Sun's energy is blocked by the longer path it takes through the atmosphere. At 50 degrees north latitude, the path the Sun's rays travel through the atmosphere on Dec 21, at solar noon, will be increased by a factor of 3.5 from a direct vertical path. In general, the rays will come at an angle that depends on the time of day, the latitude of the region from the equator, and the position of Earth in its orbit.
The constellations in the ecliptic, the zodiac, have a long history in the tradition of astrology. In most newspapers, you can read a (completely unscientific) prediction of your future or some personal advice, specific to your birthday. Each entry is associated with one of the constellations of the zodiac and a range of birth dates. In the tradition of astrology, the constellation the Sun occupied on your birthday, your "sign," reveals information about your personality and your future.
Interestingly, the dates given for each constellation in the newspaper don't match the Sun's position in the sky for those dates. There is a mismatch between the date in the newspaper and the real position of the Sun of a little more than a month. The mismatch appears because the dates corresponding to each sign were set thousands of years ago. Over the course of thousands of years, the Earth "wobbles" on its axis, causing the calendar and the positions of the stars in the sky to shift. This wobble is caused by the pull on the equator by the sun and moon, and is called precession. It affects the positions of all the constellations with respect to the equinoxes and the pole.
The precession of the Earth is like the movement of a top. If you spin a top with the axis tilted, the axis will slowly rotate as the top spins. Likewise, the Earth's axis remains tilted at 23½°, but the orientation of this tilt changes over the course of thousands of years.
Since precession changes the direction in which Earth's pole points, it also changes which star is the North Star, if any. Earlier, we quoted Shakespeare, who referenced Polaris in Julius Caesar, describing it as the northern star. Strictly, this would be incorrect. Polaris was not "fixed" in the sky in Julius Caesar's time because Earth's axis was pointed differently, toward the Big Dipper.
Precession is a slow drift, and a difficult motion to detect. The motion of the stars from precession only becomes noticeable to the unaided eye after many, many years of careful observation, although it becomes very quickly noticeable through a telescope. The Greek astronomer Hipparchus was the first to measure the precession by comparing his own observations to observations collected a century and a half before.
Precession changes the position of the Earth in its orbit for the solstices and the equinoxes. As the Earth's axis turns over, the moment when it points most closely towards the Sun changes, and so the seasons change. If a calendar didn't account for this, the seasons would drift as the axis precessed. Eventually, the Northern Hemisphere would be cold in July and warm in January, and the Southern Hemisphere would have warm July weather and cold January weather. The calendar takes the extra motion of precession into account by using the tropical year as its basis. The year as we usually define it is a sidereal year, the time it takes for the Earth to make one orbit around the Sun. In one year, as we usually measure it, the Earth really completes a little more than a full orbit around the Sun. During a sidereal year, the Sun moves fully around the sky and back into the same position with respect to the stars. In a tropical year, the Sun goes from the Vernal Equinox, around the sky, and back to the Vernal Equinox again. During this time, the equinox has shifted slightly in its position, so that a tropical year is a bit shorter than a sidereal year.
It's easy to identify the progression of the calendar if you take careful notice of the sky. Next time you see sunrise or sunset, take notice of whether the Sun is setting due west or just north or south of west. Many ancient cultures watched the motion of the Sun carefully and over long periods of time. Using simple techniques and tools, they were able to measure periods like the length of a year very accurately. Ancient people who took notice of celestial motion would have found that the summer solstice occurred every 365 days. They would also notice that the solstice was delayed an extra day every four years. This is the reason for the leap year in the modern calendar. The delay occurs because the length of the year is a little more than 365 days — closer to 365¼ days long. By taking some simple observations over a period of a few years, it is possible to measure the length of a year to surprising accuracy using this technique.
Solar calendars have been used throughout history. The ancient Babylonians thought the year had only 360 days, and made their calendar accordingly. The Islamic calendar is lunar, and is 11 (1/2) days different than the solar calendar. The Hebrew calendar is lunisolar.
Our modern calendar is handed down to us from the Ancient Roman civilization. The calendar took its first mature form as the Julian calendar, almost exactly the same as the one used today. It had 365 days in a year, with a 366-day leap year every four years. In the Julian calendar, years divisible by 4 — such as 1992, 1996, and 2008 — are leap years. This gave the Julian calendar an average of 365¼ days per year, which is very close to the true 365.2422 day length for a tropical year.
Although the drift of the Julian calendar is slow, the error in the calendar had accumulated enough by the sixteenth century that the Catholic Church became concerned about the drift's effect on the date of the celebration of Easter. The Italian chronologer Aloisius Lilius invented modifications to the Julian calendar to correct the difference. Pope Gregory XI instituted the new calendar, now named the Gregorian calendar, in the year 1582.
The Gregorian calendar was identical to the Julian calendar except that the leap year was skipped on years not divisible by 400. In the years 1600, 2000, and 2400, there would be a leap year in the Gregorian calendar, but not 1800, 1900, or 2100. This produced a year of average length 365.2425 days, much closer to the correct value than the Julian calendar. The Gregorian calendar accumulates only 3 days of error over 10,000 years.
Discussion questions
1) On the date of the summer solstice, the sun is overhead on the Tropic of Cancer, and on the date of the winter solstice the sun is overhead on the Tropic of Capricorn. Draw a quick sketch that shows the relative positions of the sun and the earth on those dates.
2) On the date when the sun is overhead on the Tropic of Capricorn, the sun is actually located in the constellation of Sagittarius. So why did the Greeks name Tropic of Capricorn the Tropic of Capricorn instead of the Tropic of Sagittarius?
Suppose you are an astronomer in America. You observe an exciting event (say, a supernova) in the sky and would like to tell your colleagues in Europe about it. Suppose the supernova appeared at your zenith. You can't tell astronomers in Europe to look at their zenith because their zenith points in a different direction. You might tell them which constellation to look in. This might not work, though, because it might be too hard to find the supernova by searching an entire constellation. The best solution would be to give them an exact position by using a coordinate system.
On Earth, you can specify a location using latitude and longitude. This system works by measuring the angles separating the location from two great circles on Earth (namely, the equator and the prime meridian). Coordinate systems in the sky work in the same way.
The equatorial coordinate system is the most commonly used. The equatorial system defines two coordinates: right ascension and declination, based on the axis of the Earth's rotation. The declination is the angle of an object north or south of the celestial equator. Declination on the celestial sphere corresponds to latitude on the Earth. The right ascension of an object is defined by the position of a point on the celestial sphere called the vernal equinox. The further an object is east of the vernal equinox, the greater its right ascension.
A coordinate system is a system designed to establish positions with respect to given reference points. The coordinate system consists of one or more reference points, the styles of measurement (linear measurement or angular measurement) from those reference points, and the directions (or axes) in which those measurements will be taken. In astronomy, various coordinate systems are used to precisely define the locations of astronomical objects.
Latitude and longitude are used to locate a certain position on the Earth's surface. The lines of latitude (horizontal) and the lines of longitude (vertical) make up an invisible grid over the earth. Lines of latitude are called parallels. Lines of longitude aren't completely straight (they run from the exact point of the north pole to the exact point of the south pole) so they are called meridians. 0 degrees latitude is the Earth's middle, called the equator. 0 degrees longitude was tricky because there really is no middle of the earth vertically. It was finally agreed that the observatory in Greenwich, U.K. would be 0 degrees longitude due to its significant role in scientific discoveries and creating latitude and longitude. 0 degrees longitude is called the prime meridian.
Latitude and longitude are measured in degrees. One degree is about 69 miles. There are 60 minutes (') in a degree and 60 seconds (") in a minute. These tiny units make GPS's (Global Positioning Systems) much more exact.
There are a few main lines of latitude:the Arctic Circle, the Antarctic Circle, the Tropic of Cancer, and the Tropic of Capricorn. The Antarctic Circle is 66.5 degrees south of the equator and it marks the temperate zone from the Antarctic zone. The Arctic Circle is an exact mirror in the north. The Tropic of Cancer separates the tropics from the temperate zone. It is 23.5 degrees north of the equator. It is mirrored in the south by the Tropic of Capricorn.
Horizontal coordinate system
One of the simplest ways of placing a star on the night sky is the coordinate system based on altitude and azimuth, thus called the Alt-Az or horizontal coordinate system. The reference circles for this system are the horizon and the celestial meridian, both of which may be most easily graphed for a given location using the celestial sphere.
In simplest terms, the altitude is the angle made from the position of the celestial object (e.g. star) to the point nearest it on the horizon. The azimuth is the angle from the northernmost point of the horizon (which is also its intersection with the celestial meridian) to the point on the horizon nearest the celestial object. Usually azimuth is measured eastwards from due north. So east has az=90°, south has az=180°, west has az=270° and north has az=360° (or 0°). An object's altitude and azimuth change as the earth rotates.
Equatorial coordinate system
The equatorial coordinate system is another system that uses two angles to place an object on the sky: right ascension and declination.
Ecliptic coordinate system
The ecliptic coordinate system is based on the ecliptic plane, i.e., the plane which contains our Sun and Earth's average orbit around it, which is tilted at 23°26' from the plane of Earth's equator. The great circle at which this plane intersects the celestial sphere is the ecliptic, and one of the coordinates used in the ecliptic coordinate system, the ecliptic latitude, describes how far an object is to ecliptic north or to ecliptic south of this circle. On this circle lies the point of the vernal equinox (also called the first point of Aries); ecliptic longitude is measured as the angle of an object relative to this point to ecliptic east. Ecliptic latitude is generally indicated by , whereas ecliptic longitude is usually indicated by .
Galactic coordinate system
As a member of the Milky Way Galaxy, we have a clear view of the Milky Way from Earth. Since we are inside the Milky Way, we don't see the galaxy's spiral arms, central bulge and so forth directly as we do for other galaxies. Instead, the Milky Way completely encircles us. We see the Milky Way as a band of faint starlight forming a ring around us on the celestial sphere. The disk of the galaxy forms this ring, and the bulge forms a bright patch in the ring. You can easily see the Milky Way's faint band from a dark, rural location.
Our galaxy defines another useful coordinate system — the galactic coordinate system. This system works just like the others we've discussed. It also uses two coordinates to specify the position of an object on the celestial sphere. The galactic coordinate system first defines a galactic latitude, the angle an object makes with the galactic equator. The galactic equator has been selected to run through the center of the Milky Way's band. The second coordinate is galactic longitude, which is the angular separation of the object from the galaxy's "prime meridian," the great circle that passes through the Galactic center and the galactic poles. The galactic coordinate system is useful for describing an object's position with respect to the galaxy's center. For example, if an object has high galactic latitude, you might expect it to be less obstructed by interstellar dust.
Transformations between coordinate systems

One can use the principles of spherical trigonometry as applied to triangles on the celestial sphere to derive formulas for transforming coordinates in one system to those in another. These formulas generally rely on the spherical law of cosines, known also as the cosine rule for sides. By substituting various angles on the celestial sphere for the angles in the law of cosines and by thereafter applying basic trigonometric identities, most of the formulas necessary for coordinate transformations can be found. The law of cosines is stated thus:
To transform from horizontal to equatorial coordinates, the relevant formulas are as follows:
where is the right ascension, is the declination, is the local sidereal time, is the altitude, is the azimuth, and is the observer's latitude. Using the same symbols and formulas, one can also derive formulas to transform from equatorial to horizontal coordinates:
Transformation from equatorial to ecliptic coordinate systems can similarly be accomplished using the following formulae:
where is the right ascension, is the declination, is the ecliptic latitude, is the ecliptic longitude, and is the tilt of Earth's axis relative to the ecliptic plane. Again, using the same formulas and symbols, new formulas for transforming ecliptic to equatorial coordinate systems can be found:
| General Astronomy | ||
| The Modern View of the Cosmos | Observational Astronomy | Motion and Gravity |





























