Engineering Acoustics/Outdoor Sound Propagation
Introduction
[edit | edit source]Outdoor sound propagation or atmospheric sound propagation is of special interest in environmental acoustics which is concerned with the control of sound and vibrations in an outdoor environment. Outdoor sound propagation is affected by spreading, absorption, ground configuration, terrain profile, obstacles, pressure, wind, turbulence, temperature, humidity, etc. The subjects covered in this page are speed of sound in air, decibel scales, spreading losses, attenuation by atmospheric absorption, attenuation over the ground, refraction, diffraction and sound reduction examples.
Speed of sound in air[1]
[edit | edit source]Sound speed in air varies with pressure, density, temperature, humidity, wind speed, etc. The expression for the speed of sound in a fluid is given in terms of its thermodynamic properties. The equation is given by
where is the fluid density and is the fluid pressure.
This equation can be simplified for an ideal gas leading to
where is the ratio of heat capacities
For air at 0 °C and 1 atm, the speed of sound is
For air at 20 °C and 1 atm, the speed of sound is
An equivalent expression for the speed of sound in terms of the temperature in Kelvin is
where is the specific gas constant.
Decibel scale[2]
[edit | edit source]The decibel dB or dB SPL (Sound pressure level) in acoustics is used to quantify sound pressure levels and intensities relative to a reference on a logarithmic scale.
The intensity level of a sound intensity is defined by
where is a reference intensity.
Since the intensity carried by a traveling wave is proportional to the square of the pressure amplitude, the intensity level can be expressed as the sound pressure level
where is the measured effective pressure amplitude of the sound wave and is the reference effective pressure amplitude. The effective sound pressure is the root mean square of the instantaneous sound pressure over a given interval of time. is also called sound level .
For air, the pressure reference is taken to be
the lowest sound pressure a human can hear, also called the threshold of hearing.

Sound attenuation[3]
[edit | edit source]Study of outdoor sound activity requires the definition of a source and a receiver in order to explain the different phenomenon involved in the process. The sound attenuation due to its propagation in the atmosphere can be described in terms of its total attenuation in dB between the source and the receiver. The total attenuation can be expressed as
where is the sound pressure level of the root-mean-square (rms) sound pressure at a distance near the source and is the corresponding sound pressure level with an rms sound pressure measured at a distance r from the source.
The total attenuation is defined as the sum of the attenuation due to geometric spreading , the attenuation due to atmospheric absorption , and the excess attenuation due to all other effects , namely
The excess attenuation can include attenuation from the ground in a homogeneous atmosphere , refraction by a non-homogeneous atmosphere, attenuation by diffraction and reflection by a barrier or obstacle, and scattering or diffraction effects due to turbulence. The values of attenuation are normally positive.
Spreading losses[4]
[edit | edit source]The geometric spreading loss , in dB, between two points at a distance and from a source can be expressed as
where is a constant given by the geometry of the problem. for plane wave propagation (uniform pipe), for cylindrical propagation from a line source, and for spherical wave propagation from a point source. It is noticed that for spherical wave propagation from a point source, doubling the distance from the source () corresponds to a loss of .
Attenuation by atmospheric absorption[5] [6] [7]
[edit | edit source]Absorption of sound through the atmosphere is due to shear viscosity, thermal conductivity or heat dissipation, and molecular relaxation due to oxygen, nitrogen, and water vapor vibrational, rotational, and translational energy. The attenuation , in dB due to atmospheric absorption can be expressed as
where , in meters, is the path length of the traveling wave, is the sound pressure after traveling the distance , is the initial sound pressure at , is the attenuation coefficient in Nepers per meter, and is the attenuation coefficient in dB per meter.
Spreading losses are dependent on the pressure, relative humidity and frequency for air in still atmosphere. The attenuation coefficient for pure tone frequencies can be expressed as
with , , and , and where is the acoustic frequency in Hz, is the atmospheric pressure, is the reference atmospheric pressure (1 atm), is the atmospheric temperature in K, is the reference temperature (293.15 K), is the relaxation frequency of molecular oxygen and is the relaxation frequency of molecular nitrogen. Scaled relaxation frequencies for oxygen and nitrogen formulas from experimental measurements are given by
and
where is the molar concentration of water vapor (absolute humidity) in percent. is calculated from the relative humidity as follows
where the saturated vapor pressure is given by
with .
The formulas, are valid for a pressure under 2 atm, a temperature under 330 K (57 C, or 134 F) and up to an altitude of 3 km. One can see from the graph and formulas that the absorption coefficient is higher for a higher frequency and/or a higher pressure.
The attenuation coefficient for pure tone frequencies is shown in Figure 2 for air at 20 °C as a function of frequency per atmosphere and relative humidity per atmosphere. The matlab script used to produce the graph is shown in Appendix A.

Figure 2 - Attenuation coefficient for atmospheric absorption per atmosphere as a function of frequency and relative humidity, for air at 20 °C.[8] [9]
Values of attenuation can also be obtained from Table 1 for different temperatures, relative humidities and pure tone frequencies at 1 atmosphere.
Table 1 - Atmospheric attenuation coefficient (dB/km) at selected frequencies at 1 atm[10]
| Temperature | Relative humidity (%) | 62.5 Hz | 125 Hz | 250 Hz | 500 Hz | 1000 Hz | 2000 Hz | 4000 Hz | 8000 Hz |
|---|---|---|---|---|---|---|---|---|---|
| 30 °C | 10 | 0.362 | 0.958 | 1.82 | 3.40 | 8.67 | 28.5 | 96.0 | 260 |
| 20 | 0.212 | 0.725 | 1.87 | 3.41 | 6.00 | 14.5 | 47.1 | 165 | |
| 30 | 0.147 | 0.543 | 1.68 | 3.67 | 6.15 | 11.8 | 32.7 | 113 | |
| 50 | 0.091 | 0.351 | 1.25 | 3.57 | 7.03 | 11.7 | 24.5 | 73.1 | |
| 70 | 0.065 | 0.256 | 0.963 | 3.14 | 7.41 | 12.7 | 23.1 | 59.3 | |
| 90 | 0.051 | 0.202 | 0.775 | 2.71 | 7.32 | 13.8 | 23.5 | 53.5 | |
| 20 °C | 10 | 0.370 | 0.775 | 1.58 | 4.25 | 14.1 | 45.3 | 109 | 175 |
| 20 | 0.260 | 0.712 | 1.39 | 2.60 | 6.53 | 21.5 | 74.1 | 215 | |
| 30 | 0.192 | 0.615 | 1.42 | 2.52 | 5.01 | 14.1 | 48.5 | 166 | |
| 50 | 0.123 | 0.445 | 1.32 | 2.73 | 4.66 | 9.86 | 29.4 | 104 | |
| 70 | 0.090 | 0.339 | 1.13 | 2.80 | 4.98 | 9.02 | 22.9 | 76.6 | |
| 90 | 0.071 | 0.272 | 0.966 | 2.71 | 5.30 | 9.06 | 20.2 | 62.6 | |
| 10 °C | 10 | 0.342 | 0.788 | 2.29 | 7.52 | 21.6 | 42.3 | 57.3 | 69.4 |
| 20 | 0.271 | 0.579 | 1.20 | 3.27 | 11.0 | 36.2 | 91.5 | 154 | |
| 30 | 0.225 | 0.551 | 1.05 | 2.28 | 6.77 | 23.5 | 76.6 | 187 | |
| 50 | 0.160 | 0.486 | 1.05 | 1.90 | 4.26 | 13.2 | 46.7 | 155 | |
| 70 | 0.122 | 0.411 | 1.04 | 1.93 | 3.66 | 9.66 | 32.8 | 117 | |
| 90 | 0.097 | 0.348 | 0.996 | 2.00 | 3.54 | 8.14 | 25.7 | 92.4 | |
| 0 °C | 10 | 0.424 | 1.30 | 4.00 | 9.25 | 14.0 | 16.6 | 19.0 | 26.4 |
| 20 | 0.256 | 0.614 | 1.85 | 6.16 | 17.7 | 34.6 | 47.0 | 58.1 | |
| 30 | 0.219 | 0.469 | 1.17 | 3.73 | 12.7 | 36.0 | 69.0 | 95.2 | |
| 50 | 0.181 | 0.411 | 0.821 | 2.08 | 6.83 | 23.8 | 71.0 | 147 | |
| 70 | 0.151 | 0.390 | 0.763 | 1.61 | 4.64 | 16.1 | 55.5 | 153 | |
| 90 | 0.127 | 0.367 | 0.760 | 1.45 | 3.66 | 12.1 | 43.2 | 138 |
[dubious ]
The effective atmospheric attenuation of a constant-percentage band of a broadband noise is normally less than for pure-tone sound due to the finite bandwidth and slope of the filter skirts.[11] Some atmospheric attenuation also occurs in fog and precipitation,[12] in dust in air,[13] and at frequencies below 10 Hz due to electromagnetic radiation of moist air molecules.[14]
Reflection from the surface of a solid[15]
[edit | edit source]When a wavefront comes in to contact with a solid surface, it is reflected away from that surface. The angle of reflection of the sound wave is equal to the angle of incidence of the wave. Reflected waves can interfere with incident waves causing constructive and destructive interference. This can cause a standing wave pattern and resonance because the incident and reflected waves travel in opposite directions. Near the surface of the solid, sound pressure intensity is enhanced because the pressure of the reflected wave adds up to the pressure of the incident wave.

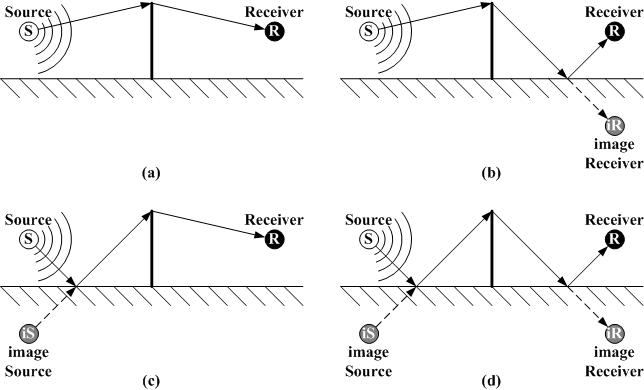
Attenuation over the ground[16]
[edit | edit source]Sound propagation near the ground is affected by absorption and reflection of the sound waves by the ground. Sound can either leave a source and follow a straight path to a receiver or be reflected and/or absorbed by the ground. How the sound wave reacts with the ground is influenced by the ground impedance which relates pressure and speed.
Refraction[17][18]
[edit | edit source]Refraction of sound is normally defined as the deviation of a sound wave leaving a fluid and entering another one with different speed of sound. For outdoor sound propagation refraction of sound waves causes the waves to bend due to a change in the speed of sound. This change in the speed of sound is caused by strong wind speeds and temperature gradients. An upward refraction reduces sound levels near the ground, while a downward refraction helps sound travel over obstacle such as noise barriers. A downward refraction will occur if air above the earth is warmer than the air at the surface. The warmer air above earth will have a faster speed of sound causing the wave to bend back towards the earth. The same phenomena will occur for hot air over a cold ground.

Diffraction[19][20]
[edit | edit source]Diffraction is the mechanism by which sound can propagate and spread out beyond an opening and around obstacles. The traveling waves tend to bend around obstacles. Diffraction is related to the wavelength of the sound produced by the source. It is stronger for lower frequencies. High frequencies propagate in a more directional manner. This is why low frequencies can be heard better from behind obstacles and in shadows zones. If a wavefront travels towards a small opening, diffraction will cause the waves to spread out past the opening in a spherical manner. When a wavefront that passes through a small obstacle, compared to the wavelength, diffraction will cause the sound waves to bend and the wavefront will reconstruct past the obstacle. This means that one could not identify the presence of that small obstacle from sound measurement far from the obstacle and the source.

Sound reduction
[edit | edit source]Several mechanisms can be used in order to reduce noise in outdoor environment. Different noise barriers used to reduce highway noise are shown in Figure 7. Another way of reducing noise is to use vegetation. Figure 8 shows pictures of vertical vegetation walls.
 |
 |
 |
|---|
 |
 |
 |
|---|
Useful Websites
[edit | edit source]- ^ HyperPhysics, Section on the basics of sound propagation
- Acoustical Porous Material Recipes
References and further reading
[edit | edit source]References are presented in order of date of publication.
General
- Piercy, Embleton, Sutherland, Review of noise propagation in the atmosphere, J. Acoust. Soc. Am. Volume 61, Issue 6, pp. 1403–1418, June 1977
- Delany, ^ Sound propagation in the atmosphere - A historical review, Acustica. Vol. 38, pp. 201–223, October 1977
- Piercy, Embleton, Review of sound propagation in the atmosphere (A), J. Acoust. Soc. Am. Volume 69, Issue S1, pp. S99-S99, May 1981
- Crocker, ^ Handbook of Acoustics, John Wiley & Sons, February 1998
- Kinsler, Frey, Coppens, Sanders, ^ Fundamentals of Acoustics, 4th Ed., John Wiley & Sons, New York, 2000
Speed of sound
- Wong, Speed of sound in standard air, J. Acoust. Soc. Am. Volume 79, Issue 5, pp. 1359–1366, May 1986
Absorption of sound in the atmosphere
- Calvert, Coffman, Querfeld, ^ Radiative Absorption of Sound by Water Vapor in the Atmosphere, J. Acoust. Soc. Am. Volume 39, Issue 3, pp. 532–536, March 1966
- Henley and Hoidale, ^ Attenuation and dispersion of acoustic energy by atmospheric dust, J. Acoust. Soc. Am. Volume 54, Issue 2, pp. 437–445, August 1973
- Sutherland, Piercy, Bass, Evans, Method for calculating the absorption of sound by the atmosphere, J. Acoust. Soc. Am. Volume 56, Issue S1, pp. S1-S1, November 1974
- Bass, Sutherland, Piercy, Evans, Absorption of sound by the atmosphere, Physical acoustics: Principles and methods. Volume 17 (A85-28596 12-71). Orlando, FL, Academic Press, Inc., p. 145-232, 1984
- Bass, Sutherland, Zuckerwar, ^ Atmospheric absorption of sound: Update, J. Acoust. Soc. Am. Volume 88, Issue 4, pp. 2019–2021, October 1990
- Bass, Sutherland, Zuckerwar, Blackstock, Hester, ^ Atmospheric absorption of sound: Further developments, J. Acoust. Soc. Am. Volume 97, Issue 1, pp. 680–683, January 1995
Attenuation over the ground
- Embleton, Piercy, and Olson, Outdoor sound propagation over ground of finite impedance, J. Acoust. Soc. Am. Volume 59, Issue 2, pp. 267–277, February 1976
- Bolen and Bass, Effects of ground cover on the propagation of sound through the atmosphere, J. Acoust. Soc. Am. Volume 69, Issue 4, pp. 950–954, April 1981
- Embleton, Piercy, and Daigle, Effective flow resistivity of ground surfaces determined by acoustical measurements, J. Acoust. Soc. Am. Volume 74, Issue 4, pp. 1239–1244, October 1983
- Rasmussen, On the effect of terrain profile on sound propagation outdoors, Journal of Sound and Vibration, Volume 98, Issue 1, Pages 35–44, January 1985
- Attenborougha, Review of ground effects on outdoor sound propagation from continuous broadband sources, Applied Acoustics, Volume 24, Issue 4, Pages 289-319, 1988
- Hess, Attenborough, and Heap, Ground characterization by short-range propagation measurements, J. Acoust. Soc. Am. Volume 87, Issue 5, pp. 1975–1986, May 1990
- Attenborough, Taherzadeh, Bass, Di, and others Benchmark cases for outdoor sound propagation models, J. Acoust. Soc. Am. Volume 97, Issue 1, pp. 173–191, January 1995
Vegetation
- Aylor, Noise Reduction by Vegetation and Ground, J. Acoust. Soc. Am. Volume 51, Issue 1B, pp. 197–205, January 1972
- Bullen, Fricke, Sound propagation through vegetation, Journal of Sound and Vibration, Volume 80, Issue 1, 8 January 1982, Pages 11–23, May 1981
- Price, Attenborough, Heap, Sound attenuation through trees: Measurements and models, J. Acoust. Soc. Am. Volume 84, Issue 5, pp. 1836–1844, November 1988
Barriers and screens
- Maekawa, Noise reduction by screens, Applied Acoustics, Volume 1, Issue 3, Pages 157-173, July 1968
- Jonasson, Sound reduction by barriers on the ground, Journal of Sound and Vibration, Volume 22, Issue 1, Pages 113-126, May 1972
- Kurze, Noise reduction by barriers, J. Acoust. Soc. Am. Volume 55, Issue 3, pp. 504–518, March 1974
- Isei, Embleton, Piercy, Noise reduction by barriers on finite impedance ground, J. Acoust. Soc. Am. Volume 67, Issue 1, pp. 46–58, January 1980
- Li, Law, Kwok, Absorbent parallel noise barriers in urban environments, Journal of Sound and Vibration Volume 315, Issues 1-2, Pages 239-257, August 2008
Absorbent materials
- Delany and Bazley, Acoustical properties of fibrous absorbent materials, Applied Acoustics, Volume 3, Issue 2, April 1970, Pages 105-116
- Attenborough, Acoustical characteristics of porous materials, Physics Reports Volume 82, Issue 3, Pages 179-227, February 1982
- Lauriksa, Copsa, Verhaegena, Acoustical properties of elastic porous materials, Journal of Sound and Vibration Volume 131, Issue 1, Pages 143-156, 22 May 1989
Appendices
[edit | edit source]Appendix A - Matlab program for the plot of the attenuation coefficient
[edit | edit source]clear all;
clc ;
close all;
T_0 = 293.15;
T_01 = 273.16 ;
T = 20 + 273.15;
p_s0 = 1;
F = logspace(1,6);
ler=length(F);
hrar=[0 10 20 40 60 80 100];
a_ps_ar=zeros(7,ler);
for k=1:7
hr=hrar(k);
psat = p_s0*10^(-6.8346*(T_01/T)^1.261 + 4.6151);
h = p_s0*(hr)*(psat/p_s0);
F_rO = 1/p_s0*(24 + 4.04*10^4*h*(0.02+h)/(0.391+h));
F_rN = 1/p_s0*(T_0/T)^(1/2)*( 9 + 280*h*exp(-4.17*((T_0/T)^(1/3)-1)) );
alpha_ps= 100*F.^2./p_s0.*( 1.84*10^(-11)*(T/T_0)^(1/2)...
+ (T/T_0)^(-5/2)*(0.01275*exp(-2239.1/T)./(F_rO + F.^2/F_rO)...
+ 0.1068*exp(-3352/T)./(F_rN + F.^2/F_rN) ) );
a_ps_ar(k,:) = alpha_ps*20/log(10);
end
psvg = figure (1);
loglog(F,a_ps_ar(1,:), F,a_ps_ar(2,:), F,a_ps_ar(3,:), F,a_ps_ar(4,:),...
F,a_ps_ar(5,:), F,a_ps_ar(6,:), F,a_ps_ar(7,:),'LineWidth',1);
xlabel({'f / p_s [Hz/atm]';'Frequency/pressure'},'FontSize',10,...
'FontWeight','normal','FontName','Times New Roman');
ylabel('Absorption coefficient/pressure a / p_s [dB/100 m atm]',...
'FontSize',10,'FontWeight','normal','FontName','Times New Roman');
title({'Sound absorption coefficient per atmosphere for air at 20°C ';...
'according to relative humidity per atmosphere'},...
'FontSize',10,'FontWeight','bold','FontName','Times New Roman')
hleg = legend(' 0',' 10',...
' 20',' 40',' 60',...
' 80',' 100');
v = get(hleg,'title');
set(v,'string',{'h_r / p_s [%/atm]'},'FontName','Times New Roman','FontSize',10,...
'BackgroundColor', 'white','EdgeColor','white','HorizontalAlignment','center');
set(hleg,'Location','SouthEast','EdgeColor','black')
axis([1e1 1e6 1e-3 1e4]);
grid on;
set(gca,'gridlinestyle','-');
set(gca,'MinorGridLineStyle','-')
%plot2svg('Absorption_coefficient.svg',psvg);
Appendix B - Python program for the plot of the attenuation coefficient
[edit | edit source]#!/usr/bin/python3
import math
import numpy as np
import matplotlib.pyplot as plt
## 1 atm in Pa
ps0 = 1.01325e5
def absorption(f, t=20, rh=60, ps=ps0):
""" In dB/m
f: frequency in Hz
t: temperature in °C
rh: relative humidity in %
ps: atmospheric pressure in Pa
From http://en.wikibooks.org/wiki/Engineering_Acoustics/Outdoor_Sound_Propagation
See __main__ for actual curves.
"""
T = t + 273.15
T0 = 293.15
T01 = 273.16
Csat = -6.8346 * math.pow(T01 / T, 1.261) + 4.6151
rhosat = math.pow(10, Csat)
H = rhosat * rh * ps0 / ps
frn = (ps / ps0) * math.pow(T0 / T, 0.5) * (
9 + 280 * H * math.exp(-4.17 * (math.pow(T0 / T, 1/3.) - 1)))
fro = (ps / ps0) * (24.0 + 4.04e4 * H * (0.02 + H) / (0.391 + H))
alpha = f * f * (
1.84e-11 / ( math.pow(T0 / T, 0.5) * ps / ps0 )
+ math.pow(T / T0, -2.5)
* (
0.10680 * math.exp(-3352 / T) * frn / (f * f + frn * frn)
+ 0.01278 * math.exp(-2239.1 / T) * fro / (f * f + fro * fro)
)
)
return 20 * alpha / math.log(10)
def plot():
## Figure in http://en.wikibooks.org/wiki/Engineering_Acoustics/Outdoor_Sound_Propagation
ax = plt.subplot(111)
fs = np.logspace(1, 6, num=100, endpoint=True, base=10)
ys = np.zeros(fs.shape)
rh = (0, 10, 20, 40, 60, 80, 100)
for r in rh:
for i in np.arange(fs.shape[0]):
ys[i] = absorption(fs[i], rh=r)
ax.loglog(fs, 100 * ys, label='rh:%d'%r)
ax.grid(True)
ax.set_xlabel('Frequency/pressure [Hz/atm]')
ax.set_ylabel('Absorption coefficient/pressure [dB/100m.atm]')
ax.legend(loc='lower right')
plt.show()
def table():
p = ps0
for t in [30, 20, 10, 0]:
for rh in [10, 20, 30, 50, 70, 90]:
print("T=%2d RH=%2d " % (t, rh), end='')
for f in [62.5, 125, 250, 500, 1000, 2000, 4000, 8000]:
a = absorption(f, t, rh, p)
print("%7.3f " % (a*1000), end='')
print()
if __name__ == '__main__':
table()
plot()











































![{\displaystyle A_{a}=-20\log _{10}\left[{\frac {P(r)}{P(0)}}\right]=-20\log _{10}[\exp(-\alpha r)]=ar\quad {\mbox{dB}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abab3484a7a438231ef703184a5e88fde311251b)





![{\displaystyle {\frac {a}{p_{s}}}={\frac {20}{\ln 10}}\ {\frac {F^{2}}{p_{s0}}}\left\{1.84\times 10^{-11}\left({\frac {T}{T_{0}}}\right)^{1/2}+\left({\frac {T}{T_{0}}}\right)^{-5/2}\left[0.01275{\frac {e^{-2239.1/T}}{F_{r,O}+F^{2}/F_{r,O}}}+0.1068{\frac {e^{-3352/T}}{F_{r,N}+F^{2}/F_{r,N}}}\right]\right\}\quad {\frac {\mathrm {dB} }{\mathrm {m} \cdot \mathrm {atm} }}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62301620c94ae6c4c950703bc198f9e727b2c1d5)











![{\displaystyle F_{r,N}={\frac {1}{p_{s0}}}\left({\frac {T_{0}}{T}}\right)^{1/2}\left(9+280h\times \exp \left\{-4.17\left[\left({\frac {T_{0}}{T}}\right)^{1/3}-1\right]\right\}\right)\quad {\frac {\mathrm {Hz} }{\mathrm {atm} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ba7224ae02d3652f356bdb01272d507c9169e31)





