Control Systems/Examples/Second Order Systems

Second Order Systems: Examples

Example 1

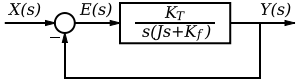
A damped control system for aiming a hydrophonic array on a minesweeper vessel has the following open-loop transfer function from the driveshaft to the array.

$G(s)={\frac {K}{Js^{2}+K_{d}s}}$

The gain parameter K can be varied. The moment of inertia, J, of the array and the force due to viscous drag of the water, K_d are known constants and given as:

• $J=9\,N\,m\,s^{2}\,rad^{-1}$
• $K_{d}=2\,N\,m\,s\,rad^{-1}$

Tasks

1. The system is arranged as a closed loop system with unity feedback. Find the value of K such that, when the input is a unit step, the closed loop response has at most a 50% overshoot (approximately). You may use standard response curves. Should K be greater or less than this value for less overshoot?
2. Find the corresponding time-domain response of the system.
3. The system is now given an input of constant angular velocity, V. For the limiting value of K found above, calculate the maximum value of V such that the array follows the input with at most 5° error.

Task 1

First, let us draw the block diagram of the system. We know the open-loop transfer function, and that there is unit feedback. Therefore, we have:

The closed-loop gain is given by:

$H(s)$	$={\frac {G(s)}{1+G(s)}}$
	$={\frac {\dfrac {K}{Js^{2}+K_{d}s}}{\dfrac {Js^{2}+K_{d}s+K}{Js^{2}+K_{d}s}}}$
	$={\frac {K}{Js^{2}+K_{d}s+K}}$

We now need to express the closed-loop transfer function in the standard second order form.

${\frac {\omega _{n}^{2}}{s^{2}+2\zeta \omega _{n}s+\omega _{n}^{2}}}$	$={\frac {K}{Js^{2}+K_{d}s+K}}$
	$={\frac {\frac {K}{J}}{s^{2}+{\frac {K_{d}}{J}}s+{\frac {K}{J}}}}$

We can now express the natural frequency ω_n and damping ratio, ζ:

$\omega _{n}^{2}={\frac {K}{J}}={\frac {K}{9}}$

$2\zeta \omega _{n}={\frac {K_{d}}{J}}$

$\zeta ={\frac {K_{d}}{2J}}{\sqrt {\frac {J}{K}}}={\frac {K_{d}}{2}}{\sqrt {\frac {1}{KJ}}}={\frac {1}{3{\sqrt {K}}}}$

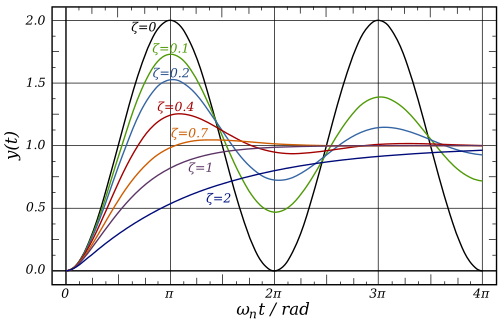
We now look at the standard response curves for second order systems.

We see that for 50% overshoot, we need ζ=0.2 or more.

$\zeta ={\frac {1}{3{\sqrt {K}}}}\geq {\frac {1}{5}}$

$K\leq {\frac {25}{9}}$

This is the maximum permissible value, thus K should be less than this value for less overshoot. We can now evaluate the natural frequency fully:

$\omega _{n}={\frac {5}{9}}$

Task 2

The output of the second order system is given by the following equation:

$y(t)$	$=1-{\frac {1}{\sqrt {1-\zeta ^{2}}}}e^{-\zeta \omega _{n}t}\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{n}t+\sin ^{-1}{\sqrt {1-\zeta ^{2}}}\right)$
	$=1-{\frac {1}{\sqrt {0.96}}}e^{-t/9}\sin \left({\frac {5{\sqrt {0.96}}}{9}}t+\sin ^{-1}{\sqrt {0.96}}\right)$
	$=1-1.02e^{-t/9}\sin \left(0.544t+0.436\pi \right)$

We can plot the output of this system:

Task 3

The tracking error signal, E(s), is equal to the output's deviation from the input.

$E(s)=R(s)-Y(s)\,$

Now, we can find the gain from the reference input, R(s) to the error tracking signal:

${\frac {E(s)}{R(s)}}={\frac {R(s)-Y(s)}{R(s)}}$

The gain from the input to the error tracking signal of a unity feedback system like this is simply ${\frac {1}{1+G(s)}}$.

${\frac {E(s)}{R(s)}}$	$={\frac {1}{1+{\frac {K}{9s^{2}+2s}}}}$
	$={\frac {9s^{2}+2s}{9s^{2}+2s+2.78}}$

Now, R(s) is given by the Laplace transform of a ramp of slope V:

$R(s)={\frac {v}{s^{2}}}$

We now use the final value theorem to find the value of E(s) in the steady state:

$\lim _{t\to \infty }{e(t)}$	$=\lim _{s\to 0}{sE(s)}$
	$=\lim _{s\to 0}{s{\frac {9s^{2}+2s}{9s^{2}+2s+2.78}}{\frac {V}{s^{2}}}}$
	$={\frac {2V}{2.78}}$

We require this to be less than $5^{\circ }={\frac {5\pi }{180}}{\mbox{rad}}$

$V\leq {\frac {2.78}{2}}\times {\frac {5\pi }{180}}=0.12\,{\mbox{rad/s}}$