Clock and Data Recovery/Structures and types of CDRs/Applications of the 2nd order type 2 architecture
- 2nd order and type 2 has become the preferred architecture for high performance CDR (regenerators) as soon as the ever advancing IC technology has allowed to integrate all CDR blocks inside one silicon chip.
- All blocks can be integrated ( high gain and low noise amplifiers, A/Ds, D/As and DSPs ) with very low manufacturing costs.
- Even the VCO is a block that is integrated, but it can not reach the accuracies possible with a crystal oscillator. This is compensated by the more sophisticated architecture and some additional circuitry (PFD).
This architecture uses the option of a zero (the gain increases at lower frequencies) in the filter stage between phase comparator and VCO.
- The zero is at angular frequency ωz =1/τz, ωw = 1/τw is the frequency of gain = 1 = 0 dB. τz = Gf τw.
- Lower frequencies are amplified more (-20 dB / dec) and the lowest frequency -the d.c. jitter component- gets a theoretical infinite amplification.
- The decrease of the amplification continues up to ωz and becomes flat (Gf) at higher frequencies.
- In practical applications of type 2 CDRs: Gf << 1 (often referred to as "the filter attenuation" and called β) and ωw << ωz.
The maximum output of the comparator corresponds to much less than the maximum frequency deviation of the VCO, deviation that can be reached gradually thanks to the integration of low frequencies made by the loop filter.
The response to an input variation always ends with catching up completely (zero steady-state error in this type 2 loop), (even if the loop gain is much less than "infinite" or the "latency" is relevant [1]) and every CDR design is tailored to specific applications to avoid that the response overshoots significantly.
- It is like using either the accelerator or the brake, increasing pressure indefinitely on the pedal until the response of the system becomes sufficient.
- It is easy to understand how this architecture reacts immediately but only to a limited extent, and then increases the correction slowly but progressively if the immediate response has not proven sufficient.This is especially evident during the acquisition phase.
The low gain at high frequencies attenuates more the high frequency input jitter (in many cases it also attenuates the bang-bang tracking jitter) while the integration of the input phase error (assisted by a PFD) provides for acquisition in a much wider range of input frequencies.
Where used and how made
[edit | edit source]The 2-2 architecture is well suited for monolithic implementations, which explains its widespread use.
This architecture finds its practical applications where a bang-bang phase detector must be used and where the accuracy of the VCO is so poor as to exceed the jitter bandwidth required.
- With a type 1 architecture is practically impossible to phase lock into a signal if the VCO free running frequency differs from the frequency of the incoming signal more than the bandwidth of the jitter transfer characteristic.
- The strong reduction of the low-frequency noise from the VCO and the reduction of Es to a minimum (possibly zero) are additional advantages.
A bang-bang phase detector is inevitable in monolithic applications at very high line frequencies,[2] and monolithic implies also an on-chip oscillator, that is relatively noisy and relatively inaccurate in ωfr. Inaccurate ωfr means that the acquisition is only possible using a (bang-bang) phase and frequency detector PFD.
On the other hand, the high volume applications of today are correspondingly very cost sensitive, and require that a single silicon chip accommodate the whole CDR, and also much more.
In practice a bang-bang phase and frequency detector is always used, and the VCO is a linear monolithic one, either a ring oscillator or a low-Q LC.
Consequently all the monolithic:
- line regenerators,
- slave clocks in Telecom networks
- CDRs of portable electronics
are made with this 2 - 2 architecture.
A long run-length can affect the tolerance margin in sampling the received signal, but this is normally mitigated by the use of a ternary phase detector.
- This loop type is the most “powerful” of the three, because it incorporates a loop filter that offers a very high gain at low frequencies.
- This is the characteristic feature of this architecture, that generates its strong and weak points.
- The high gain at low frequencies allows the compression to very low value of any steady state error, unlike the other two loops ( 1 - 1 and 2 - 1 ). The filter gain is maximum at very low frequencies, and decreases up to ωz, then it flattens to the asymptotic value and stays constant in the bandwidth of interest (until parasitic poles, always present, make it drop). Gf is very low, in all cases below 1, so that it is often referred to as "the filter attenuation".
- The flat gain of the loop filter at high frequencies allows a good tracking of medium frequency jitter, unlike the other second order loop ( 2 - 1 ).
- The very low gain of the loop filter at mid and high frequencies keeps the tracking jitter (i.e. the jitter generated by the bang-bang frequency jumps) adequately low.
- The high gain at low frequencies allows the frequency and phase acquisitions even when the VCO free-running frequency is shifted much more than ωz from the frequency of the signal to recover.
This 2 - 2 loop tracks very well, as long as the loop filter and the VCO operate within their range of normal operation.
Care must be paid to the very high (closed loop) gain at low jitter frequencies when either:
- the lack of data transitions temporarily opens the feedback path (this is mitigated by the use of a ternary PD, but presents anyway the risk of a phase error that may increases out of control as long as the loop is open);
- the (sinusoidal) input jitter has a significant amplitude. The filter gain at high frequencies is kept low to limit the jitter generation resulting from the bang-bang, but this limits the ability of the loop to track a fast and large swing of the input phase. The jitter tolerance depends on the corner frequency of the loop filter and on the length of runs without transitions.
- Closed loop gain and corner frequency of the tolerance curve are concepts easily identified if the loop is linear.
- When the loop incorporates a bang-bang detector, and the data transitions are random, it is necessary to restrict the study only to conditions of practical interest and to use simulations.
Introductory example
[edit | edit source]This simulation diagram helps understand the operation of the 2 – 2 architecture with bang-bang phase and frequency detector.
- The two waveforms of the two phase detectors of the PFD are shifted higher in the diagram, for easier interpretation. The other waveforms are not shifted.
- The outputs of the PFD and of the loop filter are scaled differently, with the filter output more amplified in the representation. (The filter output does not reach the clamping level(s), and the VCO drive signal is not different from it, i.e. would be exactly overlapped to it in the diagram. The high frequency parasitic pole of the charge pump is at 200 Mrad/sec, and its effect is barely visible in the shape of the filter bang bang spikes).
- To the left the waveforms show that there is no incoming signal. LOS is asserted and the loop is open. The VCO (=the CDR) output simply drifts away with a slope proportional to the difference between the signal frequency and the VCO free-running frequency.
- After 1.28 μs (= 150 simulation steps) the signal appears with a phase mismatch equal to -4.0 radian, which happens to reduce the cumulated phase drift that had reached 10.06 rad.
- LOS is dis-asserted at that moment and the loop starts catching up.
- Initially the output of the PFD is a constant positive level (meaning the VCO is slower than the incoming signal. The filter, that integrates the low frequencies of the comparator output, adds a further positive ramp.
- The output phase undershoots the input phase before lock, with even a small overshoot when the filter makes the first negative bang and starts a negative ramp to finally reach a stable continuous bang-bang condition.
- During the frequency acquisition three slips have createdted a gap of exactly 3 π between input and output. The gap remains constant from then on, apart from a small additional phase error.
- As soon as the loop has caught up with the input, the typical pattern of bang-bang starts: the loop is in lock. The comparator bangs rapidly between is two output states and the filter output maintains a d.c. bias that compensate the ωp - ωfr distance.
- After 8.53 μs (= 1000 simulation steps) the input signal phase starts a sinusoidal jittering with a large amplitude (3.20 rad) and a frequency of 0.9 rad/μs.
- This jitter brings the loop close to its tolerance limit, which is shown by the detector and by the filter outputs that is alternatively forced out of bang bang, as well as by the error signal that shows deviations from its average of 3π-4 rad in correspondence with those periods of difficult tracking. The error signal deviations are not large in this case, and remain within +0.25 and -0.26 rad.
In this example the transition density is 100%, but the random nature of the input signal must also be taken into account.
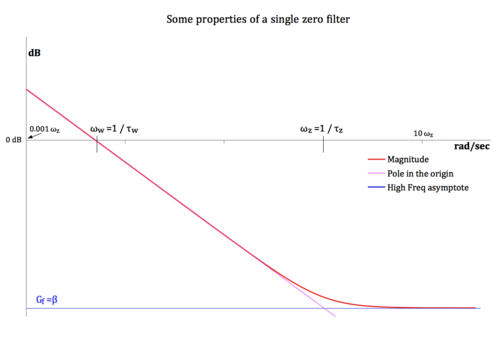
Single zero filter
[edit | edit source]This loop type is the most “powerful” of the three, because it incorporates a loop filter that offers a very high gain at low frequencies, that is the key feature of the 2 - 2 architecture and that generates its strong and weak points.
- The filter gain is maximum at very low frequencies, and decreases up to ωz, then it flattens to the value Gf and stays constant in the bandwidth of interest (until parasitic poles, always present, make it drop).
- The high gain at low frequencies allows the frequency and phase acquisitions (a ternary PFD is used in these applications) even when the VCO free-running frequency ωfr is shifted much more than ωz away from the frequency ωp of the signal to recover.
- The high gain at low frequencies allows the compression to very low value of any steady state error, unlike the other two loops ( 1 - 1 and 2 - 1 ).
The (almost) infinite gain at low frequencies gives this architecture some very useful properties, but it can also be the origin of unexpected troubles.
As shown in the figure above, Gf is very low, in all cases below 1, so that it is often referred to as "the filter attenuation" and called β. As a consequence, ωz is higher than ωw, the zero-gain frequency.
- In the 1 - 1 architecture the output of a bang-bang binary PD always makes the VCO jump from one end of its control range to the opposite end. This leaves a strong residual "tracking" jitter in the output phase of the PLL, because only the 1/s slope of the VCO characteristic does filter the sharp and large swings.
- The 2 - 2 architecture in principle behaves the same for high frequency jitter as its loop filter does not filter out the high frequency components (higher than ωz) coming from the comparator output. The filter passes the high frequency components of the jitter to the VCO with a flat transfer function. But the value of the filter gain above ωz ( although flat up to where parasitic poles at even higher frequencies make themselves felt ) is much smaller in a 2 - 2 architecture than the equivalent gain in a 1 - 1 architecture and that makes the tracking jitter proportionally smaller.
- The use of a ternary phase detector further reduces the peak tracking jitter.[3]
This 2 - 2 loop tracks very well, as long as the loop filter and the VCO operate within their range of normal operation.
Loose-tracking conditions
[edit | edit source]- When the phase detector outputs a constant request for higher, of for lower, frequency for a significant number of clock cycles,
- a temporary lack of bang-bang around the locking condition occurs, while the VCO lags behind a rising or falling input phase.
As this interval grows, the tracking error increases (see the linear ramp of the step response of the filter), and this might result into a phase error beyond the tolerance limit.
- This 2 - 2 loop may drift away from lock more than the other type 1 loops, if the phase information is not refreshed, as indicated also by its linear model.
This may occur for two different causes:
- the input signal has too few transitions (run-length problem, that can be approximately described using the stability factor ξ) or
- the phase of the input signal varies too fast for the loop to track (slew-rate problem, that is investigated by simulations with sinusoidal input jitter close to the tolerance limit).
Both causes can reduce the tolerance of the CDR, and the effects of each can be reduced at the expenses of other CDR performances.
Run-length problem
[edit | edit source]The actual statistic of the transitions in the input signal is so difficult to predict that only a simple worst-case approach can be of use.
The very extreme case where isolated transitions come periodically and separated by a constant number of line-pulse periods may give some insight and explain why large design margins are found in real monolithic CDRs.
In a condition of very rare but periodic transitions, the fundamental parameter is the time that the loop waits before the next update of the input phase, update that comes from the next transition of the input signal.
- When a transition comes as soon as possible, the update time is: tupdate = 1/fp.
- When a bit of the same sign follows in the input signal, tupdate at least doubles. More precisely:
It is convenient to define a parameter ξ:
The longer the run length, the more critical the loop response may become. In fact, ξ is called the stability factor.[4]
Let's focus now on what happens in the condition of bang-bang tracking.
- The last bang corrects the filter output, higher or lower, by a jump of GφGf [volt], and a ramp follows, in the same direction, with slope GφGf ωz [volt/sec]. (See the figure above).
- The VCO frequency jumps GφGfGVCO = G [rad/sec] and then ramps with a slope of GφGfGVCOωz = Gωz [rad/sec2]
- (GφGfGVCO = G, where the phase detector outputs can be -Gφ, +Gφ if the detector is binary and -Gφ, 0, +Gφ if it is ternary)
- The quantity G is very closely related to the quantity fbb.[5] Both measure the frequency jump during bang-bang tracking, and are related by the formula G = 2π fbb.
- While fbb is easy to interpret as the frequency jump and is fixed by the circuitry of the CDR, G is used as a nominal value for the open loop gain, in the nominal conditions of DT = 1 and maximum phase error (i.e. minimum Gφ). In fact, G is always found multiplied by DT in the formulae that describe the loop behaviour.
The VCO phase, as a function of the time t, is the sum of a linear ramp Gt plus a parabolic ramp Gωzt2.
- After tupdate, the VCO phase has increased (or decreased) by a linear part G tupdate [volt] plus a parabolic part G ωz tupdate2 [rad].
- the ratio of the linear part of the phase increase to the parabolic part of the phase increase is exactly the stability factor ξ:
- When the update takes place, the new bang makes the filter output jump in the opposite direction by a step of Gf [v], followed by another ramp, now in this new direction.
- In order to stay in tracking and not to sidetrack out of lock, the phase drift during tupdate must not make the VCO phase drift outside the lateral eye opening:
- The equation yields always one positive real root[6] corresponding to ξ ≥ 2.
The value of G however decreases from its nominal value proportionally to the reduction of DT from its maximum of 100 %.
The ability of the CDR to tolerate with minimal phase drift some very long run-lengths, and/or periodic repetitions of them, can be increased increasing the value of τz at the design stage (ξ = 2τz / tupdate).
This reduces the bandwidth of the loop filter ωz and has the adverse effect of reducing the frequency lock-in range and of increasing the lock-in time.
- In practice, values of ξ in excess of 1000, even with low transition densities as found in SONET transmissions, are not used.
Slew-rate problem
[edit | edit source]There always exists the possibility that the VCO is not able to follow the rapidly changing phase of the input, because the rate of change of the VCO phase is insufficient. The VCO is "slew-rate" limited.
- This is not normally due to late response of the VCO driven by the signal from the filter output.
- The frequency deviation limits of the CDR are set by the characteristics of the loop filter block, rather than by the extremes of the frequency range of the VCO itself.
- "The VCO is designed to respond fully in one update time. This is usually very easy to achieve in ring-oscillators and possible with some care using low-Q VCOs." [7]).
The 2 - 2 CDR is not able to vary rapidly its frequency. If the input signal offers the maximum transition density, the loop can respond to an input phase step with a frequency step equal to G [rad/sec], i.e. with a phase ramp of slope G. ( More precisely, the output phase of the loop increases -until the next transition that comes after tupdate- with a parabolic increase where the linear part is normally the largest: φ = Gtupdate + 1/2 Gωztupdate2 )
- The value G (calculated, unless otherwise specified, at DT = 100%) is the loop reference gain ( Gφ is calculated with the largest phase input error, typically ±π, multiplied by DT, Gf is the value of the filter gain in the flat region, GVCO is a linear approximation around the fp working point ), but is also proportional to the bang-bang frequency step (G = 2π fbbGφ).
But if the phase of the input signal varies more rapidly than G rad/sec (G for a binary PD, GDT for a ternary PD), then a phase error appears and it may grow and possibly affect the CDR tolerance.
This problem may be investigated using a sinusoidal input phase jitter. This is also useful as the tolerance curve of the CDR is measured as a function of a sinusoidal input jitter.
The slew rate concept, and how the slew rate limits in particular the tolerance curve of a 2nd order type 2 CDR with a bang-bang PD, had been already introduced and discussed to some extent in the jitter tolerance page, where also an introductory case related to slew-rate for this architecture -with bang-bang PFD- is shown.

This figure shows, using asymptotic approximations, how the tolerance curve (of the 2nd order type 2 CDR with bang-bang detector) depends on the loop fundamental parameters.
- The curve identifies all the regions of theoretical interest, over the entire frequency range.
- Two of the four asymptotic regions (the two regions with a -20 dB/dec slope) correspond to limitations of the VCO frequency range:
- the low frequency region corresponds to the large-signal d.c. clamping of the VCO drive signal;
- the medium frequency region, above ωz, corresponds to small-signal high-frequency limitation of the bang-bang drive step (Vbb).
- Two of the four asymptotic regions (the two regions with a -20 dB/dec slope) correspond to limitations of the VCO frequency range:
- The curve identifies all the regions of theoretical interest, over the entire frequency range.
But the frequency range of practical interest for the jitter tolerance does not extend more than a couple of decades either:
- below the frequency region where the asymptotic slope of -20 dB/dec is identified (because all PLL based CDRs follow that slope -or a steeper one- at lower frequencies, while the network requirements always saturate to a buffer width, i.e. to a constant phase, from a certain jitter frequency downwards), nor
- above the frequency where the flattening of the horizontal asymptote is identified ( because a PLL based CDR will follow that asymptote for all higher frequencies of jitter).
- The following figure shows tolerance curves (in dB and in UI, obtained by numerical simulations for another 2nd order type 2 CDR with bang-bang detector) in the range of frequencies of practical interest.

The LEO is set at a low value of 1 rad. The asymptotes are positioned manually over the interpolated dB curve.
A good agreement is found between the corner point of the two oblique asymptotes and the ωz given value of 4.0 10+5.
This figure is like a zoom on the frequency region of practical interest, but shows the same fundamental behaviour (in that region) that is present in the previous figure.
- It may be noted that the asymptotic tolerance at high frequencies is slightly lower that the minimum usually specified of 0.15 UI.
- This is a consequence of having used the pessimistic value of 1 rad for the Lateral Eye Opening.
The values of Gf (or ωbb = GVCO Gf = G/Gφ, because it has been assumed that the output of the PD is +1 or -1 volt) and of ωz are always chosen as a compromise between opposite application requirements.
- the value of Gf (Gf is the factor of G that is easiest to vary) is kept as small as possible to reduce the "tracking" jitter due to the bang-bang jumps. It but can not be reduced too much or else the "slew-rate" becomes excessively small. The slew-rate G (of the -20 dB/dec in the frequency range of interest for the loop tolerance) is originated by the loop filter that has a very limited gain (= an attenuation) at frequencies higher than ωz. It can be seen in the figure of asymptotic tolerance that the intersection point with the 0 dB axis is:
GVCO Vbb = ωbb and drifts to the left when Gf (or ωbb) is made smaller. - The value of ωz is kept low in order to have a stability factor ξ large enough, that is to tolerate long run-lengths. But ωz can not be too low, or else the times for acquisition of frequency and phase become too long, and also the time before the steady steady error is squeezed to zero becomes too long as well. The PLL would resemble too much a type 1 system with low gain.
Jitter Bandwidths in 2nd order type 2 bang-bang CDRs
[edit | edit source]The bang-bang CDRs are made up by most of the 1-1 (PD) and practically all of the 2-2 (PFD).
These loops are intrinsically non-linear, primarily because of the bang-bang nature of the phase detector: this is the first non-linearity.
- The very large (≡ infinite) gain in the detector needs a compensation by a signal level limitation is another loop point.
- (The level limitation keeps signal levels within the physical capability of the circuit elements).
- The level limitation takes place either:
- 1. in the limitation of the VCO drive signal made by the circuits driving the VCO, or
- 2. in the extremes of the VCO voltage-to-frequency characteristic.
It is a frequency limitation. This is the second non-linearity. In both cases of frequency limitation, when the limit is reached, the output phase waveform of the CDR enters a slew-rate condition.
- The VCO intrinsic characteristic, at both ends, depends very much (and often unpredictably) on manufacturing and environmental variations.
- Therefore, the frequency range is always deliberately limited by a clamp of the output range of the VCO drive stage, +/- Vdr.
Overall, two non-linearities (PD or PFD, and VCO frequency constraints) combine making transfer (e.g. jitter transfer) functions become families of functions.
Each function in a family is associated with a specific input waveform.
In the (transfer functions') case of sinusoidal inputs, each function of ωj is associated with the input amplitude only.
The output is also periodic, and the transfer function is defined as the ratio of the output peak amplitude to the input peak amplitude Aj (that is constant at all frequencies for each function in the family).
Vbb = the absolute value of the voltage step that takes place in these CDRs, at the input of the VCO, when the PD bangs up or down from its intermediate level.
- It coincides with the value of Gf(ω) for ω >> ωz. In fact, the PD output is either +1 or -1 [volt] (or 0 V in the case of a ternary PD).
- In 1 -1 loops +/- Vbb is the total drive range of the VCO and coincides with +/- Vdr.
- Ed is generated by a deviation of the duty cycle away from 50% in the VCO drive waveform.
- In 2 - 2 loops +/- Vbb is much smaller than the drive range of the VCO +/-Vdr (e.g. Vbb / Vdr = 10-3).
- The VCO drive waveform shows a tiny bang-bang three-level ripple added to a slower and much larger waveform, that is made by the filter amplification of low jitter frequency components.
- Ed is obtained by a variation of the mean level of the bang-bang ripple in the drive waveform.
Jitter transfer functions in bang-bang CDRs of 2nd order and type 2 [8]
[edit | edit source]This is a type 2 system, which means that -during tracking- the mean values of the input and of the output phase waveforms do not differ.
- The difference of mean values is the steady state sampling error Es, and Es = 0 in these systems.
- In other words, the average level of the difference between the input and output waveforms is zero (= the average phase error is zero ).
In 2nd order systems the signal processing between PD and VCO consists of two regions along the frequency axis:
- 1. a flat attenuation above ωz (that makes the drive signal so small that, in tracking, the VCO frequency bang-bangs within a small range around fp).
- 2. a region of increasing amplification as jitter frequency decreases from ωz, that slopes at -20 dB/dec.
The two regions of the loop filter define the loop behaviour unless either of the two VCO frequency limits is reached (with an input jitter large enough), where the resulting slew-rate corresponds to either of the VCO limits (+/- Vdr or +/_Vbb).
The two frequency regions of the loop filter, with jitter levels that make Vbb slewing evident in both of them, can be identified in the figure already shown in the jitter tolerance page.

The triangular wave of the output at high frequencies is symmetric: the type 2 loop squeezes to zero any steady state output error.
In steady state with a sinusoidal input, the output of the CDR is just periodic with the same period. The jitter transfer function can be defined as the ratio of the output peak value to the input peak value.
- The waveform (in black) of the VCO drive signal bang-bangs when there is no slewing, but does not bang.bang and and slowly ramps away as long as the phase error keeps the same sign (constant slew-rate condition of either sign).
- The steep bang transitions, and the slope of the ramps that follow, implement the step response of the loop filter driven by the steps (bang-bangs) of the PD output.
- In the PD output, the slow ramp during slewing compensates any possible steady-state error of the loop output.
The figure is drawn with values of jitter amplitudes Aj still within the jitter tolerance boundary, but larger that those used to measure the jitter transfer characteristic of a CDR.
In jitter transfer measurements, at low ωj (= at low jitter frequencies), the slewing that is shown in the left hand side of the figure does not appear.
The amplitude of the jitter input used in those measurements (= Aj) is lower, and the CDR output phase tracks the input phase jitter and the transfer curve is a constant 1, i.e. a flat 0 dB in a Bode plot. A value of Aj = 1.5 UIpp is typical for the measurement of jitter transfer below ωj, and of 0.15 UIpp above ωj. [9]
But for jitter frequencies ωj sufficiently high, even if Aj ( the amplitude of the input sinusoidal jitter ) is relatively low, the tracking is not perfect and the output phase waveform from sinusoidal becomes triangular like in the right hand side of the figure above:

- There the triangular output has fixed slopes (+/- VbbGVCO) and It takes one quarter of the jitter period, 1/4 * 2π/ωj for the output to vary from 0 to its peak value.
- Its peak value is: . As the peak varies inversely to ωj, in this region the jitter transfer curve rolls off at- 20 dB/dec.
- The ratio of the output peak value to the input peak value (Aj) in the Vbb slew-rate region is therefore :
- If the output was measured with the amplitude of its fundamental component instead of with its peak value, the roll off part of the transfer curve would just be translated (downwards) a tiny -0,091 dB.
The overall jitter transfer curve has one horizontal asymptote at 0 dB towards low frequencies, and a - 20 dB/dec asymptote towards high frequencies.
The transition between the two asymptotes can be approximated using the model of a first order linear system, whose corner frequency ωjc is where the sloping asymptote intersects the 0 dB horizontal asymptote. (The approximation given by this model is more than adequate for most engineering purposes) :
The jitter transfer can therefore be modelled as:
The Aj to measure the transfer characteristic may be smaller than Φm.

At the onset of triangular slewing, that is a function of Aj, the transfer ratio rolls off at -20dB/dec. This region is typically explored with Aj down to 0.15 UIpp.
The transition from 0 dB flat to -20 dB/dec roll-off takes place at a frequency inversely proportional to Aj.
If Aj is made too small (smaller than <math\phi_m</math>) , the bandwidth of the transfer curve does not increase any more.
This is a realistic assumption in many practical cases, and may even be used to design the CDR so that a certain mask of jitter transfer is met.
- The sinusoidal jitter that is to be applied in the bandwidth from the maximum ωjc and a couple of decades above does not normally exceed 0.15 UIpp [11]
- The Φm in a documented 10 Gbps CDR is found to be about 0.26 UIpp, taking into account just the metastability in the PD flip-flops, without other smaller contributions.[12]
The model becomes the linear model of a 2nd order type 2 loop with a linear comparator of gain Gφ = 1/Φm.
The transfer function has a fixed (= independent from Aj in this case) cut-off frequency at
- It may be remarked that the linear 2 - 2 loop has an open loop gain G = GφGfGVCO and that in this case Gφ can be computed as Aj/(AjΦm) and Gf can be computed as Vbb.
- Substituting inside the formula for ωn2 above, the formula for ωjc is obtained.
- As Gφ is in these practical cases very high (higher than 4ωz), the 2 - 2 model that can be used for small Aj (smaller than ) has a damping coefficient ζ larger than 1 and therefore no gain peaking ( ζ = ).
Jitter tolerance of bang-bang CDRs of 2nd order and type 2
[edit | edit source]In real 2 -2 CDRs several different regions of jitter tolerance, more than in the applications of other CDR architectures, can be found.

The 0 dB reference depends on the measurement unit chosen for the sinusoidal jitter Amplitude Aj.
If it is radian, then 0 dB correspond to 1 rad, if it is Unit Internals, the 0 dB corresponds to 1 U.I.
- There is the high frequency asymptote corresponding to the bare tolerance of the lateral eye opening, where the PLL is too slow to follow the jitter and tracks just the jitter average value. (This is the only region where the tolerance depends on a quantity - the LEO- that is not a characteristic of the CDR itself).
- This region is preceded by a -20 dB/dec region corresponding to the slew rate limitation originated by the limited high-frequency gain of the loop filter, i.e. to a range limited to -/- Vbb for the VCO drive signal.
- The corner between these two asymptotes corresponds to their intersection and may be called ωhor. It can be obtained by extrapolation of ω0 dB, the frequency at which the Vbb asymptote crosses the 0 dB axis.
ω0 dB = GVCO*Vbb ωhor = ω0 dB/(LEO - ωbbTp/2) - A good fitting with simulated results is obtained smoothing the corner with a first order approximation of the tolerance curve [13]
- The corner between these two asymptotes corresponds to their intersection and may be called ωhor. It can be obtained by extrapolation of ω0 dB, the frequency at which the Vbb asymptote crosses the 0 dB axis.
- A third region, at even lower frequencies, with a slope of -40 dB/dec, is generated by a quasi-linear operation of the CDR. There the bang-bang is less obtrusive and the behavior of the PLL is well approximated by the linear model of the previous page, although with a larger value of Gφ.
- A good fitting has been found using for Gφ the value:
- where:
- where Gf represents the static gain value at the largest phase difference close to the output inversion (i.e. the end-of-range, minimum, value of the gain of the bang-bang detector).
- The border between this and the adjacent Vbb region to the right is conceptually at frequency ωz.
- At low jitter frequencies, the slew rate associated with the limitations of the VCO control range (conceptually due to the intrinsic VCO characteristic, but in practice due to the tighter control range forced by the clamping in the loop filter output) originates another region of slew-rate (-20 dB/dec), higher up in the left hand part of the Bode plot.
- The border between this and the adjacent region to the right is at frequency ωD = ωz Vbb / VD.
- The last low-frequency region to the left might be a flat part of the curve if the CDR incorporated the additional feature of a phase aligner.
- The tolerance curve is found when the amplitude of the sinusoidal input jitter makes the error signal reach the LEO value.
- When slewing creates the tolerance boundary, it is convenient to model the tolerance curve with the onset of slewing (a conservative estimate).
- The onset of slewing just makes the error function increase, and there is some margin in Aj before this increase reaches the LEO value.
- The margin between the Aj value at the onset of slewing and the Aj value that truly makes the peak of the phase error reach the LEO value (i.e. the condition that truly defines the border of the tolerance region) is negligible at smaller ω, and increases somewhat with larger ω.
- When the output phase jitter becomes triangular and the high frequency tolerance goes from -20 dB/dec to the flat LEO horizontal asymptote, the onset of slewing is a conservative estimation. A first order transition, with a 3 dB smoothing at the corner, gives a good approximation, as confirmed by numerical simulations. See the figures below for an example.
Examples of CDR behaviour close to the tolerance border
[edit | edit source]The jitter tolerance is generally important in the range of jitter amplitudes from 0.1 U.I. to 2 U.I.
- A sinusoidal jitter smaller than 0.1 U.I. is always tolerated, even if the CDR does not track at all, because the LEO tolerance is always larger than that.
- A sinusoidal jitter larger than 2 U.I. can only be present in a network at frequencies that a CDR (meeting the other requirements) tracks perfectly.
Therefore the frequency range of interest starts a couple of octaves below ωz up to where the curve is almost flat.
The following figure shows tolerance curves (in dB and in U.I.) obtained by numerical simulations.

The LEO is set at a low value of 1 rad. The asymptotes are positioned manually over the interpolated dB curve.
A good agreement is found between the corner point of the two oblique asymptotes and the ωz given value of 4.0 10+5.
It may be noted that the asymptotic tolerance at high frequencies is slightly lower that the minimum usually specified of 0.15 UI. This is a consequence of having used the pessimistic value of 1 rad for the Lateral Eye Opening.
A frequency of particular interest is the frequency at the limit between two conditions:
- either both tracking and slewing are present during each jitter period (lower frequencies) or
- slewing only is present all the time (higher frequencies, and triangular output).
A sinusoidal jitter at such frequency, starting from zero, makes the first peak of the output reach up to the sinusoid peak.
- (The next peaks of the output reach a little lower, as the balancing effect of the type 2 loop takes place).

A sinusoidal jitter starts abruptly, at a frequency much higher than the frequency ωz of the zero in the loop filter.
At this frequency the Jitter transfer is about - 1 dB.
It can be calculated as (suffix j means jitter, SR means Slew Rate):
- In the example shown, the figure is obtained by simulation, and the limit condition is obtained by trial and error, looking for a jitter frequency that makes the high frequency bang bang disappear between the straight alternating slopes of the output phase.
- An alternative method, that yields results that are not much different, consists in solving the equation that requires the slope of the triangle in tracking always to start by being exactly tangent to the sinusoid. This leads to a delay of the triangular peak versus the sinusoid peak of t0 = arctg(, to a ratio of peak values of cos(ωjt0) = - 1.48 dB and to a limit slew-rate of Aj()cos(ωjt0).
The following four figures describe the conditions and the waveforms in the same CDR.
Each figure corresponds to a region where the CDR behaviour is different.
All figures correspond to conditions where the CDR tolerance is important. At lower frequencies the tolerance is not important because the CDR tolerates larger jitter amplitudes than required by the network operation and in excess of what specified for its performances. For instance, in telecom networks the essential requirement at low jitter frequencies is to tolerate sinusoidal jitter that grows with 1/f towards low frequencies.[14]
- The PLLs of type 1 do comply as they follow a 1/f low frequency asymptote. In this case of type 2 PLLs the asymptote has an additional margin because it follows a 1/f2 slope.
To the left (smaller frequencies) it is the slew rate of the VCO that makes the tolerance border. To the right it is the slew rate due to the high frequency attenuation of the loop filter.
The CDR operates in an almost linear mode, with almost sinusoidal signal waveforms.
Around this frequency the tolerance curve falls at - 40 dB/dec.

The jitter frequency is the same as the frequency of the zero of the CDR loop filter.
The CDR operates in a condition intermediate between the linear mode and the slew-rate limit set by the limited high-frequency gain of the loop filter.

The jitter frequency is centred inside the region of slew-rate limit set by the limited high-frequency gain of the loop filter.
At this frequency the tolerance curve falls at - 20 dB/dec.

The jitter frequency is so high that the CDR tracks correctly just the average phase of the input, but very poorly the input sinusoid.
The output phase is clearly limited by the slew-rate, and jitters with a low amplitude triangular waveform.
At this frequency the tolerance curve has become almost flat.
Notes and External References
[edit | edit source]- ↑ Richard C. Walker (2003). "Designing Bang-Bang PLLs for Clock and Data Recovery in Serial Data Transmission Systems" (PDF). pp. 34-45, a chapter appearing in "Phase-Locking in High-Performance Systems - From Devices to Architectures", edited by Behzad Razavi, IEEE Press, 2003, ISBN 0-471-44727-7. C. Response to Phase Step
- ↑ Richard C. Walker (2003). "Designing Bang-Bang PLLs for Clock and Data Recovery in Serial Data Transmission Systems" (PDF).
- ↑ Richard C.Walker article, A. Run-length and Latency, pg 10.
- ↑ Richard C.Walker article, A. Stability Factor, pg 4.
- ↑ Richard C.Walker article, p. 3.
- ↑ Roots of G ωz (2τz/ξ)2 + G (2τz/ξ) - LEO = 0 are: .
- ↑ Richard C.Walker article, VII. C. VCO Tuning Bandwidth, pg 10.
- ↑ Jri Lee, Kenneth S. Kundert, Behzad Razavi (SEPTEMBER 2004). "Analysis and Modeling of Bang-Bang Clock and Data Recovery Circuits". IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 39, NO. 9 pages 1571.. 1579, III., JITTER ANALYSIS, A. Jitter Transfer. Retrieved 2015-1-25.
{{cite web}}: Check date values in:|accessdate=and|date=(help); Italic or bold markup not allowed in:|publisher=(help)CS1 maint: multiple names: authors list (link) - ↑ ITU-T G.8251 The control of jitter and wander within the optical transport network (OTN) (09/2010) A.7 Jitter transfer "The jitter transfer function of a 3R regenerator shall be under the curve given in Figure A.7-1 when input sinusoidal jitter up to the masks of Figures..., is applied."
- ↑ Lee, Kundert, Razavi paper of sep. 2004, JITTER ANALYSIS, A. Jitter Transfer ω-3 dB = (12)
- ↑ ITU-T Rec..8251-201009 The control of jitter and wander within the optical transport network (OTN); A.7 Jitter transfer.
- ↑ Jri Lee, Kenneth S. Kundert, Behzad Razavi (SEPTEMBER 2004). "Analysis and Modeling of Bang-Bang Clock and Data Recovery Circuits". IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 39, NO. 9 pages 1571.. 1579, II. BANG-BANG PD MODEL, A. Effect of Metastability.Fig. 3. (b) Simulated characteristic at transistor level. Retrieved 2015-1-25.
{{cite web}}: Check date values in:|accessdate=and|date=(help)CS1 maint: multiple names: authors list (link) - ↑ Jri Lee, Kenneth S. Kundert, Behzad Razavi (SEPTEMBER 2004). "Analysis and Modeling of Bang-Bang Clock and Data Recovery Circuits". IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 39, NO. 9 pages 1571.. 1579, II. BANG-BANG PD MODEL, A. Effect of Metastability.Fig. 3. (b) Simulated characteristic at transistor level. Retrieved 2015-1-25.
{{cite web}}: Check date values in:|accessdate=and|date=(help)CS1 maint: multiple names: authors list (link) - ↑ ITU-T G8521 (09/2010): The control of jitter and wander within the optical transport network (OTN), 6. Jitter and wander tolerance of network interfaces, and its Amendment 1 (04/2011)