Clock and Data Recovery/Structures and types of CDRs/The CDR' amplifier/filter
This CDR block, in comparison with the phase comparator and the VCO, requires much less hardware effort to be implemented.
Therefore it adapts itself to the interfaces that the two other blocks present to it and
its performances complement what is available from the other two blocks
to achieve the desired characteristics of the overall loop.
When analyzing an existing CDR, in order to find out its fundamental blocks,
and to find the fundamental architecture that corresponds (or at least comes closest) to it,
the amplifier/filter is the easiest block to identify.
- First, it is the easiest to identify because it is the only block (unlike the phase comparator and the VCO) that needs not operate at frequencies as high as the line pulse frequency fp. In fact, it operates at the "loop" frequencies (that are always lower and often even some decades lower than fp). Consequently the technology used to implement the CDR is more than adequate for the amplifier/filter, which looks like the least sophisticated of the three blocks.
- Second, because it is a simple, self contained circuit block with only one input and one output and only one function to accomplish. The phase comparator may be combined with the pulse regenerator and bit decoder, with a run-length mitigator, etc.. The VCO may incorporate DLLs, special LC tuned networks, variable rate dividers, etc..
In some cases, this block may be just a level shifter, or a flat gain amplifier, or may not be present at all.
In all cases though, this block exhibits a linear behavior, with the only exception sometimes at its output interface (the VCO drive) if it helps control the inherent non-linearity of the VCO at its end_of_range extremes.
In all cases, this block decides which of the different reference models apply. Whether the loop is a 1-1, 2-1 or 2-2, depends on it only.
Large signals view[edit | edit source]
This amp/filter block adapts itself to the other two and its input and output interfaces match the output interface of the phase comparator and the input interface of the VCO.
The signal range at the output of the phase comparator corresponds to the phase interval that the comparator can follow before a slip takes place (multiplied by the comparator phase-to-voltage gain, Gφ).
The input range of the amp/filter is designed to match it exactly.
At the other interface, the filter output is designed to match the signal range that the VCO can accept at its input.
Small signals view[edit | edit source]
All CDRs identify, inside the received signal, a frequency close to the free-running frequency of the VCO ffr, and reject any other frequency that differs from ffr more than a certain, small amount. This amount is a characteristic bandwidth of the CDR, and is conceptually the same as the "jitter bandwidth" of the CDR.
This is primarily a consequence of the integration performed by the VCO.
To maintain the PLL "low-pass" requirement, also the amplifier/filter is always some sort of low-pass (that degenerates into a flat gain block in the simplest of all architectures, as presented in the example page, Section: 1st order, type 1).
Flat gain[edit | edit source]
For the simplest PLL architecture of interest (loop of 1st order and of type 1 [link indietro]), the filter structure is the simplest: just an amplifier with a flat gain of value Gf (at all frequencies of relevance for the loop operation).
For such a PLL with flat gain in the intermediate block, the loop jitter low-pass frequency is called ωn1.
Low-pass, for more sophisticated PLLs[edit | edit source]
Besides the PLL with a flat gain block, two PLL architectures are of interest, that depend only on the architecture of the amplifier/filter itself:
- 1st order low-pass with a single pole (the PLL is a 2nd order type 1 loop):
- 1st order low-pass with a single zero (the PLL is a 2nd order type 2 loop):
The overall performances of these two 2nd order PLLs are analysed in the following page :
and each separately in :
and in :
Equations of the 1st order low-pass filter in general[edit | edit source]
In general, a first order linear filter, with one zero and one pole, has the pole always at a frequency lower than the zero to be a low-pass.
(Its output, unbound in the ideal model, will be additionally brutally clamped to +/- Range [V] when implementing the simulator program).
The reference used to derive the model equations (and the recurrence relation of the linear part for the simulator) can be a possible analog implementation with an operational amplifier, 3 resistors and one capacitor.

The filter transfer function is obtained using the concept that the inverting input of an Op Amp stays at the same voltage of the other input, and that its impedance is infinite:
x(s)/R1 = y(s)/R2 + y(s)/(R3+1/sC) y(s)/x(s) = [R2(sCR3 + 1)] / [R1(sCR2 +sCR3 + 1)]
Where:
G0 = R2/R1
G∞ = R3R2 / (R1(R2+R3)
τz = R3C ; τp = C (R2+R3)
To have a calculation sheet simulate the filter, time is considered discrete, and every row of the calculation sheet represents one instant in a sequence.
The row index k = 1,2,3,... is the reference index for all the time sequences and Δt is the discrete time step.
A sequence x[k] can then be used as the representation of the input signal and a sequence y[k] as the representation of the output signal.
A description of the first order filter with difference equations allows the computation of every y[k] from y[k-1], x[k] and x[k-1].
(A system of higher order would need, for the computation of the output sample, correspondingly older samples from the input and the output sequences.
For instance, a second order system would require y[k-1], y[k-2], x[k], x[k-1] and x[k-2] for the computation of y[k]).
In the case of our first order filter, let's use the Capacitor equation:
ΔV = (I*Δt)/C vC[k] – vC[k-1] = iC[k]Δt/C
Note that this is a backward difference, in compliance with the causality of our system.
(As the capacitor is the only element with memory, it is the only one that is described by a first order difference equation).
A second equation can be obtained from the Kirchoff's First Law applied to the node of the inverting input (no current flows into the inverting input of the Op Amp):
and a third equation from the Kirchoff's Second Law applied to the loop of the Op Amp output network:
Combining (1), (2) and (3), the intermediate variables iC[k] and vC[k] can be eliminated, and the solution found with respect to y[k].
x[n] Δt/R1 – y[n] Δt/R2 = y[n]C - R3C(x[n]/R1 – y[n]/R2) – y[n-1]C + CR3( x[n-1]/R1 – y[n-1]/R2) (1 & 2 & 3)
y[n]( Δt/CR2+1+R3/R2) = y[n-1](1+R3/R2) + x[n]( Δt/CR1+R3/R1) - x[n-1](R3/R1)__ __
1st order low-pass with a single zero[edit | edit source]
If R2 = ∞ (i.e. if the PLL is of 2nd order, type 2) :

Where:
τz = CR3
τf =τz = 1/ωc, with ωc = filter cut-off frequency
y(s)/x(s) = Gf (sτz + 1) / sτz
The overall PLL block diagram, including the two hard non-linearities that are in the simulation but not in the model, is:

The low-pass filter recurrence relation for the simulation can be derved from:
iC[k] = C(vC[k] – vC[k-1]) (1)
iC[k] = iR1[k] = x[k]/R1 (2)
vC[k] = y[k] – R3 iC[k] (3)
Combining (1), (2) and (3), the intermediate variables iC[k] and vC[k] can be eliminated, and the solution found with respect to y[k]:
The resulting equation can then be inserted in a calculation sheet for the simulation program. (The ratio R3/R1 corresponds to the high frequency gain G∞ and the time constant R3C corresponds to the time constant τz of the finite zero).
An alternative way of presenting the single zero filter, to introduce the 2-2 PLL as a 1-1 loop with an additional integration [link], coming to the same results, is the following:

Recursive equation for the flat gain block:
Recursive equation for the integrator block of gain 1:
It should be noted that an integrator (more appropriately: an "accumulator" in the discrete time domain) needs only one parameter to be identified. If τi ( ωi = 1/τi is the angular frequency for which the gain is 1 i.e. 0 dB) is chosen, then the above applies. The equation can be re-written, without change of result, using Gi = 1/τi or using ωi = 1/τi.
Recursive equation for a flat gain block of gain Gf in parallel with an integrator of time constant τi:
_________ _______________
If the filter is to be part of a PLL, the relation ωc /ωn1 is fundamental for the loop operation.
In a CDR of the 2nd order and type 2, the filter cut-off frequency ωc should be made smaller than 1/4 of the loop ωn1 (ωn1 is G, the open loop gain, or the forward gain if the filter was just a flat amplifier Gf).
As it will be shown, a 2nd order type 2 loop where ωc is larger than ωn1/4 is underdamped according to ωn1/(4ωc) = ζ2.
1st order low-pass with a single pole[edit | edit source]
If R3 = 0 (i.e. if the PLL is of 2nd order, type 1) :

Where:
τp = CR2
τp = 1/ωc -> ωc = filter cut-off frequency
y(s)/x(s) = Gf / (sτp + 1)
The filter gain is flat from d.c. to the cut-off frequency, and then decreases with a slope of -20 dB/decade.
The overall PLL block diagram, including the two hard non-linearities that are in the simulation but not in the model, is:
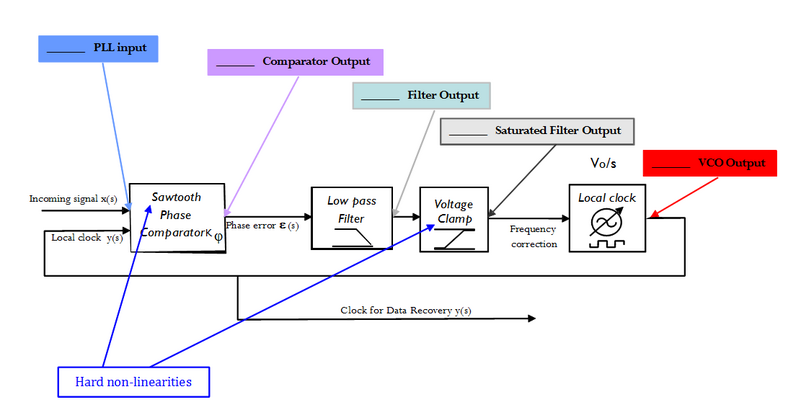
The low-pass filter recurrence relation for the simulation can be derved from:
ΔQ = C ΔV (1)
iC[k]Δt = C(y[k] – y[k-1]) (1)
iC[k] = x[k]/R1 – y[k]/R2 (2)
Combining (1) and (2), it is possible to solve with respect to y[k], eliminating the intermediate variables iC[k] and vC[k], and to get the formula for the calculation sheet:
x[k]Δt/R1 - y[k]Δt/R2 = C(y[k] – y[k-1])
y[k](1+ Δt/CR2) = y[k-1] + x[k]Δt/CR1
y[k] = ( y[k-1] + x[k]Δt Gf/τp ) / (1+ Δt/τp )
If the filter is to be part of a PLL, the relation ωc /ωn1 is fundamental for the loop operation.
In a 2nd order type 1 loop the filter cut-off frequency ωc should be made larger than 1/4 of the loop ωn1 (ωn1 is the same as G, the open loop gain, or the forward gain if the filter was just a flat amplifier Gf).
As it will be shown, a 2nd order type 1 loop where ωc is smaller than ωn1/4 is underdamped according to ζ2 = 4ωc /ωn1.
In case of a charge pump[edit | edit source]
When the last stage of the phase comparator is a charge pump, the performances of the loop amplifier/filter depend both on the charge pump current and on the additional RC networks[1]
.
The following figure also shows the Bode plots of the transfer functions of the two (passive) filtering options:

the relevant transfer functions when a RC filtering network follows the charge pump.
The transfer functions are:
- 2-2:
vo/ii = (1/s(Cf + C)) * ( (1 + sRCf) / (1 + sRC')) ; C' = series of C and Cf
- 2-2:
- 2-1:
vo/ii = R2 / ( (1 + sR1C)*(1 + sR2Cf) + sCR2))
- 2-1:
These networks exhibit a high frequency pole that is influenced by C (1/RC' with C' = CCf/(C+Cf) in the 2-2 case and 1/R1C + 1/R2Cf in the 2-1 case).
The frequency of this pole is always high enough not to influence the closed loop performances in the frequency band of interest.
It corresponds to the need to prevent the high frequency noise (generated by the comparator logic and the charge pump) from propagating outside these circuit blocks.
Otherwise said, the capacitor C and the poles it creates are not considered for the PLL order and type.
When no RC network is present besides the capacitor C, the loop is a 1st order loop.
The considerations above, about C filtering high frequency noise of the charge pump without influencing the fundamental PLL operation, hold good as well.
References[edit | edit source]
- ↑ Floyd M. Gardner, "Charge-Pump Phase-Lock Loops", vol. COM-28, NO.11, pp. 1849 - 1858, November 1980 in IEEE TRANSACTION ON COMMUNICATION.
![{\displaystyle \mathbf {out} {[n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2cc1393691f99a9b0cc9678c68880c1bbe92c5a)
![{\displaystyle \mathbf {G} *\mathbf {x} {[n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8efaa4fbc7b46d4f06f6cab33cf629c88767e9ab)
![{\displaystyle int[n]={\frac {1}{\tau _{i}}}\textstyle \sum _{1}^{n}x[k]\Delta t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f199ffb63650e0823321b96b5fcc7e00d8dc3dc7)
![{\displaystyle int[n]={\frac {1}{\tau _{i}}}\textstyle \sum _{1}^{n-1}x[k]\Delta t+\displaystyle x[n]{\frac {\Delta t}{\tau _{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b6cce6ec3a98274c3bc408e1013372a5eb0d8b8)
![{\displaystyle int[n]=int[n-1]+x[n]{\frac {\Delta t}{\tau _{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e20abf8c380ab7c41edb3197bff08f6e338695cf)
![{\displaystyle y[n]=G_{f}*x[n]+int[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ea9d770e72ead2e4f3ae63d3cfca07f75b781a1)
![{\displaystyle y[n]=G_{f}x[n]+int[n-1]+x[n]{\tfrac {\Delta t}{\tau _{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47177ebd1377d12038547a2390c7828b24b1b4b9)
![{\displaystyle y[n]=G_{f}x[n]+(y[n-1]-G_{f}x[n-1])+x[n]{\tfrac {\Delta t}{\tau _{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fc06a903cb2d03577a2fbc4aa8bc0803a2d2d3a)