Clock and Data Recovery/Introduction/Acquisition, tracking and jitter performances
Requirements and characteristics[edit | edit source]
What are the different requirements for the extraction of the clock from an incoming (encoded) bit stream?
They are essentially related to two different conditions of the CDR operation:
- Acquisition of the phase lock
- Tracking of the acquired phase timing once the acquisition is sufficient.
Acquisition[edit | edit source]
This condition of the CDR operation starts when :
- the CDR has been turned ON, and
- the input signal appears.
- As long as the received signal is not present, the CDR is kept idle by the LOS control signal, which is generated by the first stages of the receiver, (LOS = Loss Of Signal).
- When the LOS is deactivated, the CDR is released and the acquisition phase begins.
- The local oscillator of the CDR at that moment has an unpredictable phase mismatch with the phase of the incoming signal.
- The CDR then reacts as if it had been in perfect lock and the phase of the input signal had taken an abrupt step change.
- It may be added that, in case the CDR operates as a slave CDR, it would also be subject to the equivalent to an abrupt, though small, change of the frequency of the input signal.
- In fact, the input signal (during LOS) was unknown and the CDR acted as if the input signal frequency was its own free-running frequency, ffr..
The acquisition ends when the tracking begins.
The condition of tracking starts when the CDR keeps consistently its sampling point close enough to the eye center.
- Close enough means that the sampling time (affected by jitter and possibly by a systematic steady state error) remains close enough to the optimum sampling point to achieve a very low Bit Error Rate.
- For example, remaining within a sampling error of ± 0.5 rad ( = ± 0.07 U.I.) and below a BER of 10-12 could be considered as being in the tracking condition of the CDR operation.
An abrupt step of the phase of the input signal can be studied as a new acquisition with the same initial phase mismatch.
Different CDR architectures behave differently, also during the acquisition phase.
Acquisition bears a strong analogy with the unit step response of a linear systems.
- In fact, if a CDR can be adequately modelled by a linear system, its acquisition is modelled by the (Unit) Step Response of the system.

Parameters are chosen to have a meaningful comparison, although the value of ζ for the second order loops is lower than the values used in practice.
In other words, the two 2nd order loops are under-damped to stress the differences amongst different architectures.
Many non-linear factors may strongly influence how the acquisition evolves into tracking. For instance, the use of a bang-bang phase detector, the slew-rate consequence of the limited swing range of the VCO, the use of a PFD, each gives the acquisition transient special characteristics.
- a linear phase comparator and input conditions that allow the other blocks to remain within their linearity ranges, make the VCO phase follow a typical catch-up with the input phase that is exponential and make the time to reach tracking independent from the amplitude of the input step (the response time τ is dependent only on the circuit characteristics and remains the same if the phase step to catch up is bigger or smaller) - See the figure above;
- a bang-bang phase detector makes the acquisition follow a constant slope until catch-up has taken place. The slope is the same for different step amplitudes.
- a PFD makes the CDR output phase (as long as slips of decreasing frequency precede the achievement of tracking) follow a sort of parabolic shape (spanning as many 2π multiples as the number of slips that took place) before completing the acquisition.
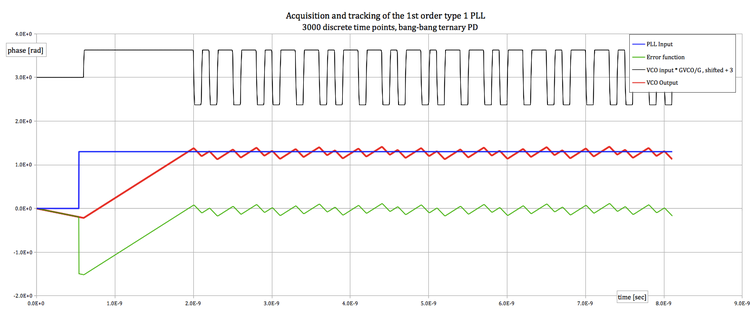
The simplest architecture (1st order and type 1) is best fit to implement CDRs with fast and slip-free acquisition of phase lock.
- Its response to an abrupt change of phase (step input), even if combined with a frequency difference between the timing of the received signal and the free running frequency of the local oscillator (ramp input), is always free from slips.
- The phase difference during the acquisition is always a decreasing function (apart from a small drift that may originate by ffr / fp mistuning and that would only be evident during periods of missing transitions and only if the mistuning sign was making the VCO resist the direction of the acquisition transient).

- In the figure above, the simulation uses 3000 discrete time steps. Each time increment is 2.7 ps (that is the line pulse period of 100 ps divided by 37).
- After 200 time steps (i.e. after 2.7 * 37 = 543 ps) the loop - that was open until then (because LOS was = 1) starts its acquisition phase ( LOS = 0).
- The input phase takes in that moment a positive step of 1.3 rad.
- The input transitions appear with an average density of 50 %, but otherwise in a fully random sequence.
- The acquisition lasts for a little over 3 ns in this example. It ends when the phase error settles around its final value (settles around 0 rad in this example).
- The pattern of pulses in the signal that drives the VCO (black trace) is, although random, constantly made only of positive pulses during the acquisition of lock.
- It may be noted that the VCO has a ffr lower than fp (in this example lower by exactly 5750 ppm), as the VCO phase lags behind the input phase (lower negative slope in the red trace) every time the VCO drive signal it at its intermediate level, both before detection of the input signal and when there is a lack of transition (mid level of the VCO drive signal).
- The steeper slopes of the red trace, positive and negative, tell when the VCO is driven to its top and bottom frequencies (1.00575 1010 ± 2.39 108 Hz ) by the positive and negative pulses of its drive signal.
- The drive signal is exponentially smoothed when it goes down to zero, because there is a parasitic low-pass (at 6.28 1011 rad/sec = ten time ti line pulse frequency) just after the ternary phase detector. It is sharp at its top and bottom corners because the it is clamped by an instantaneous circuit.
- The acquisition time would vary every time with the randomness of the transitions at the signal appearance, and be significantly longer than in the example with a non-zero probability.
- If the transitions density had been equal to 100%, the acquisition would have been faster and predictable.
- The following figure gives an example of the same circuit if the transition density is forced to 100%.
- Acquisition with a preamble of 101010.. of adequate duration, are a standard in systems that frequently need to reacquire the signal lock.
- When DT = 100%, it is even more evident that the tracking of a fp higher than ffr is the cause of a ratio of positive pulses to negative pulses (evident in the VCO drive signal) that is higher than 1.
The bit strem as this density is fully predictable and cannot carry any information:
in real systems it may occur only during periods of acquisition or when there is no information to transfer.
There are other CDRs (based on the other two more sophisticated architectures, the "second order loops of type 1 and 2") whose acquisition is inevitably long and sometimes a series of slips precedes the achievement of a stable acquisition.

The input frequency of the input signal is slightly lower than nominal, making the input phase exhibit a decreasing slope in addition to a sinusoidal jitter.
The presence of slips at the beginning of the acquisition is acceptable in applications operating in (Continuous transmission mode), and in inevitable in some of those where a PFD must be used.
Tracking[edit | edit source]
Acquisition ends, and the condition of tracking is reached, when the CDR keeps consistently its sampling point close to the eye center (that is, when the phase error settles and just jitters around the steady state error value.
- During tracking, the sampling instant (though affected by jitter and possibly by a systematic steady state error) remains close enough to the optimum sampling point to achieve a Bit Error Rate practically equal to 0.
- For example, remaining within a sampling error of ±0.5 rad ( = ±0,07 U.I.) and below a BER of 10-12, could be considered as a tracking condition.
- During tracking, an abrupt step of the phase of the input signal can be studied much as a new acquisition, with the initial phase mismatch equal to that step.

The input jitter is like a sinusoid with an amplitude that varies following a square wave 5 times slower.
There is also a wander corresponding to a slightly accelerated line frequency.
There are 3 fundamental requirements for the performances of a tracking CDR:
One applies to all CDRs,
the other 2 apply to the subset of the "regenerator" CDRs.
All CDRs[edit | edit source]
To study the tracking state, the fundamental characteristic of all CDRs is:
- the ability to operate correctly (that is with a low enough Bit Error Rate = BER) in the presence of a given jitter.
- This is measured by the Jitter Tolerance (or Jitter Acceptance).
- It gives, at every frequency, the sinusoidal input signal amplitude below which the BER is 0 and above which the BER is higher than 0.
- It is often specified as a mask of jitter amplitude versus jitter frequency.
- The circuit must operate correctly at any condition defined by a jitter amplitude and a jitter frequency within the boundary set by the mask.
- In other words, the (locus of the conditions of) onset of BER shall be found above (=at higher jitter amplitudes than) the boundary set by the mask.
Regenerator CDRs[edit | edit source]
- When the recovered clock is used for the data stream that is resent further downstream (which is a common case in a network), the CDR is a regenerator CDR.
- Definition: A "regenerator" CDR is a slave CDR that is used as a master for at least another CDR further downstream.
- For regenerators, two other characteristics are important as well:
- filtering out the input jitter frequencies above the frequency range involved in the lock-in and tracking. This is called Jitter Transfer characteristic, and there often exists a mask setting an upper limit for the curve that characterises the circuit (the jitter transfer function is the function (part of the circuit model) expressing the ratio - at any given frequency - of the magnitude of the sinusoidal jitter at the output to the magnitude of the sinusoidal jitter at the input).
- The presence of a filter block in the model of 2nd order PLLs allows one more degree of design freedom (instead of τ only, ωn and ζ can be chosen). The 2nd order architecture is used when particular requirements (for jitter and/or noise and/or effects of non-linearities) make the 1st order PLL inadequate. The quantity ωn essentially defines the cut off frequency of the low pass effect that such PLL has on the incoming jitter (≈ the jitter bandwidth of the loop).
- the amount of Generated Jitter inside our circuit (phase noise added to the retrieved timing signal). Often specified as:
- a rms or peak value for the output wander ( < 10 Hz) with zero input wander, and
- as a curve of maximum magnitude vs frequency for jitter (> 10 Hz).
- See, for instance, the TDEV (Time Deviation) and the MTIE (Maximum Time Interval Error) used by the ITU-T inside its Recommendations [1][2] for wander limit definition, and [3] for output jitter as well.
- The ITU-T, in its Recommendations Telecommunication Standardization Sector (ITU-T), is an invaluable source of theory and practical knowledge on the subject. It primarily deals with the requirements of large, geographical, networks, and therefore these Recommendations are especially useful, and exact in their quantitative references, for the engineer that studies Telecom digital networks, but they can also provide a lot of insight in other fields of application of CDRs.
Other examples of acquisition and tracking can be found in subsequent pages of this book.
Data recovery and Clock recovery: Definitions[edit | edit source]
In a serial transmission the two CDR functions of Data Recovery and of Clock Recovery are not exactly the two parts of the same definition.
The Data recovery can be uniquely defined as the operation of an end point CDR (Data recovery and Clock recovery with a specified jitter tolerance). Alternatively, it can be defined as the recovery of data with a specified BER and of a clock sufficient to write the serial data stream in a buffer memory for later retrieval.
The Clock recovery can be defined as the recovery of the clock according to a requirement either of:
- jitter tolerance only, like in an end point equipment (wider sense - note that the jitter tolerance is the only requirement involving both Data and Clock)), or
- jitter tolerance, jitter transfer[4] and jitter generation (tighter sense, like in a regenerator equipment - note that jitter transfer and jitter generation are requirements involving the Clock only, but not the Data).
The difference to appreciate consists in the additional requirements that are included in the second case [5]
External references[edit | edit source]
- ↑ ITU-T Recommendation G.810 (08/96) Definitions and terminology for synchronization networks, 4.5.17 time deviation (TDEV or sx)
- ↑ ITU-T Recommendation G.810 (08/96) Definitions and terminology for synchronization networks, 4.5.15 maximum time interval error (MTIE)
- ↑ . ITU - T G.823 The control of jitter and wander within digital networks which are based on the 2048 kbit/s hierarchy, 5 Network limits for traffic interfaces, and 6 Network limits for synchronization interfaces
- ↑ Rec. ITU-T G.8251 (09/2010); A.7 Jitter transfer, A.7.1 page 22 and A.7.2 page 23 : ... The jitter transfer function ... is defined as the ratio of the output sinusoidal jitter amplitude to input sinusoidal jitter amplitude, as a function of frequency. ...
- ↑ Rec. ITU-T G.8251 (09/2010), IV.4 Jitter generation of regenerators using parallel serial conversion; pages 56..57 [about essential requirements of clock recovery in a CDR (wider sense)]
... Generally speaking it is not the purpose of the clock recovery to minimize jitter. Main requirements for the clock recovery in order to optimize the bit error performance are:
• keeping the sampling time for the data retiming flipflop independent of the clock frequency at the position of the optimum eye opening (e.g., by using an integrating control loop);
• following the phase modulation of the incoming signal without deviating too much from the ideal sampling time (i.e., jitter tolerance);
• generating a low intrinsic jitter in terms of peak-to-peak values which should not exceed a small portion of the usable eye opening.
This last bullet point clearly does not contain any requirement regarding the spectral distribution of the intrinsic jitter.
Unlike the measurement of jitter using band-limiting filters, the jitter generated in the clock recovery has to be considered without any filtering because it describes the deviation of the ideal sampling time. ...