Statistics/Print version
| This is the print version of Statistics You won't see this message or any elements not part of the book's content when you print or preview this page. |
The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/Statistics
Introduction
[edit | edit source]Your company has created a new drug that may cure arthritis. How would you conduct a test to confirm the drug's effectiveness?
The latest sales data have just come in, and your boss wants you to prepare a report for management on places where the company could improve its business. What should you look for? What should you not look for?
You and a friend are at a baseball game, and out of the blue he offers you a bet that neither team will hit a home run in that game. Should you take the bet?
You want to conduct a poll on whether your school should use its funding to build a new athletic complex or a new library. How many people do you have to poll? How do you ensure that your poll is free of bias? How do you interpret your results?
A widget maker in your factory that normally breaks 4 widgets for every 100 it produces has recently started breaking 5 widgets for every 100. When is it time to buy a new widget maker? (And just what is a widget, anyway?)
These are some of the many real-world examples that require the use of statistics. How would you approach the problem statements? There are some stepwise human algorithms, but is there a general problem statement?
- "Find possible solutions, decide on a solution, plan the solution, implement the solution, learn from the results for future solutions (or re-solution)."
- "SOAP - subjective - the problem as given, objective - the problem after examination, assessment - the better defined problem, plan - decide if guidelines to management already exist, and blueprint the solution for this case, or generate a risk-minimizing, new solution path".
- "HAMRC - hypothesis, aim, methodology, results, conclusion" - the concept that there is no real difference is the null hypothesis.
Then there is the joke that compares the different ways of thinking:
"A physicist, a chemist and a statistician were working collaboratively on a problem, when the wastepaper basket spontaneously combusted (they all swore they had stopped smoking). The chemist said, 'quick, we must reduce the concentration of the reactant which is oxygen, by increasing the relative concentration of non-reactive gases, such as carbon dioxide and carbon monoxide. Place a fire blanket over the flames.' The physicist, interjected, 'no, no, we must reduce the heat energy available for activating combustion ; get some water to douse the flame'. Meanwhile, the statistician was running around lighting more fires. The others asked with alarm, 'what are you doing?'. 'Trying to get an adequate sample size'."
General Definition
[edit | edit source]Statistics, in short, is the study of data. It includes descriptive statistics (the study of methods and tools for collecting data, and mathematical models to describe and interpret data) and inferential statistics (the systems and techniques for making probability-based decisions and accurate predictions).
Etymology
[edit | edit source]As its name implies, statistics has its roots in the idea of "the state of things". The word itself comes from the ancient Latin term statisticum collegium, meaning "a lecture on the state of affairs". Eventually, this evolved into the Italian word statista, meaning "statesman", and the German word Statistik, meaning "collection of data involving the State". Gradually, the term came to be used to describe the collection of any sort of data.
Statistics as a subset of mathematics
[edit | edit source]As one would expect, statistics is largely grounded in mathematics, and the study of statistics has lent itself to many major concepts in mathematics: probability, distributions, samples and populations, the bell curve, estimation, and data analysis.
Up ahead
[edit | edit source]Up ahead, we will learn about subjects in modern statistics and some practical applications of statistics. We will also lay out some of the background mathematical concepts required to begin studying statistics.
A remarkable amount of today's modern statistics comes from the original work of R.A. Fisher in the early 20th Century. Although there are a dizzying number of minor disciplines in the field, there are some basic, fundamental studies.
The beginning student of statistics will be more interested in one topic or another depending on his or her outside interest. The following is a list of some of the primary branches of statistics.
Probability Theory and Mathematical Statistics
[edit | edit source]Those of us who are purists and philosophers may be interested in the intersection between pure mathematics and the messy realities of the world. A rigorous study of probability — especially the probability distributions and the distribution of errors — can provide an understanding of where all these statistical procedures and equations come from. Although this sort of rigor is likely to get in the way of a psychologist (for example) learning and using statistics effectively, it is important if one wants to do serious (i.e. graduate-level) work in the field.
That being said, there is good reason for all students to have a fundamental understanding of where all these "statistical techniques and equations" are coming from! We're always more adept at using a tool if we can understand why we're using that tool. The challenge is getting these important ideas to the non-mathematician without the student's eyes glazing over. One can take this argument a step further to claim that a vast number of students will never actually use a t-test—he or she will never plug those numbers into a calculator and churn through some esoteric equations—but by having a fundamental understanding of such a test, he or she will be able to understand (and question) the results of someone else's findings.
Design of Experiments
[edit | edit source]One of the most neglected aspects of statistics—and maybe the single greatest reason that Statisticians drink—is Experimental Design. So often a scientist will bring the results of an important experiment to a statistician and ask for help analyzing results only to find that a flaw in the experimental design rendered the results useless. So often we statisticians have researchers come to us hoping that we will somehow magically "rescue" their experiments.
A friend provided me with a classic example of this. In his psychology class he was required to conduct an experiment and summarize its results. He decided to study whether music had an impact on problem solving. He had a large number of subjects (myself included) solve a puzzle first in silence, then while listening to classical music and finally listening to rock and roll, and finally in silence. He measured how long it would take to complete each of the tasks and then summarized the results.
What my friend failed to consider was that the results were highly impacted by a learning effect he hadn't considered. The first puzzle always took longer because the subjects were first learning how to work the puzzle. By the third try (when subjected to rock and roll) the subjects were much more adept at solving the puzzle, thus the results of the experiment would seem to suggest that people were much better at solving problems while listening to rock and roll!
The simple act of randomizing the order of the tests would have isolated the "learning effect" and in fact, a well-designed experiment would have allowed him to measure both the effects of each type of music and the effect of learning. Instead, his results were meaningless. A careful experimental design can help preserve the results of an experiment, and in fact some designs can save huge amounts of time and money, maximize the results of an experiment, and sometimes yield additional information the researcher had never even considered!
Sampling
[edit | edit source]Similar to the Design of Experiments, the study of sampling allows us to find a most effective statistical design that will optimize the amount of information we can collect while minimizing the level of effort. Sampling is very different from experimental design however. In a laboratory we can design an experiment and control it from start to finish. But often we want to study something outside of the laboratory, over which we have much less control.
If we wanted to measure the population of some harmful beetle and its effect on trees, we would be forced to travel into some forest land and make observations, for example: measuring the population of the beetles in different locations, noting which trees they were infesting, measuring the health and size of these trees, etc.
Sampling design gets involved in questions like "How many measurements do I have to take?" or "How do I select the locations from which I take my measurements?" Without planning for these issues, researchers might spend a lot of time and money only to discover that they really have to sample ten times as many points to get meaningful results or that some of their sample points were in some landscape (like a marsh) where the beetles thrived more or the trees grew better.
Modern Regression
[edit | edit source]Regression models relate variables to each other in a linear fashion. For example, if you recorded the heights and weights of several people and plotted them against each other, you would find that as height increases, weight tends to increase too. You would probably also see that a straight line through the data is about as good a way of approximating the relationship as you will be able to find, though there will be some variability about the line. Such linear models are possibly the most important tool available to statisticians. They have a long history and many of the more detailed theoretical aspects were discovered in the 1970s. The usual method for fitting such models is by "least squares" estimation, though other methods are available and are often more appropriate, especially when the data are not normally distributed.
What happens, though, if the relationship is not a straight line? How can a curve be fit to the data? There are many answers to this question. One simple solution is to fit a quadratic relationship, but in practice such a curve is often not flexible enough. Also, what if you have many variables and relationships between them are dissimilar and complicated?
Modern regression methods aim at addressing these problems. Methods such as generalized additive models, projection pursuit regression, neural networks and boosting allow for very general relationships between explanatory variables and response variables, and modern computing power makes these methods a practical option for many applications
Classification
[edit | edit source]Some things are different from others. How? That is, how are objects classified into their respective groups? Consider a bank that is hoping to lend money to customers. Some customers who borrow money will be unable or unwilling to pay it back, though most will pay it back as regular repayments. How is the bank to classify customers into these two groups when deciding which ones to lend money to?
The answer to this question no doubt is influenced by many things, including a customer's income, credit history, assets, already existing debt, age and profession. There may be other influential, measurable characteristics that can be used to predict what kind of customer a particular individual is. How should the bank decide which characteristics are important, and how should it combine this information into a rule that tells it whether or not to lend the money?
This is an example of a classification problem, and statistical classification is a large field containing methods such as linear discriminant analysis, classification trees, neural networks and other methods.
Time Series
[edit | edit source]Many types of research look at data that are gathered over time, where an observation taken today may have some correlation with the observation taken tomorrow. Two prominent examples of this are the fields of finance (the stock market) and atmospheric science.
We've all seen those line graphs of stock prices as they meander up and down over time. Investors are interested in predicting which stocks are likely to keep climbing (i.e. when to buy) and when a stock in their portfolio is falling. It is easy to be misled by a sudden jolt of good news or a simple "market correction" into inferring—incorrectly—that one or the other is taking place!
In meteorology scientists are concerned with the venerable science of predicting the weather. Whether trying to predict if tomorrow will be sunny or determining whether we are experiencing true climate changes (i.e. global warming) it is important to analyze weather data over time.
Survival Analysis
[edit | edit source]Suppose that a pharmaceutical company is studying a new drug which it is hoped will cause people to live longer (whether by curing them of cancer, reducing their blood pressure or cholesterol and thereby their risk of heart disease, or by some other mechanism). The company will recruit patients into a clinical trial, give some patients the drug and others a placebo, and follow them until they have amassed enough data to answer the question of whether, and by how long, the new drug extends life expectancy.
Such data present problems for analysis. Some patients will have died earlier than others, and often some patients will not have died before the clinical trial completes. Clearly, patients who live longer contribute informative data about the ability (or not) of the drug to extend life expectancy. So how should such data be analyzed?
Survival analysis provides answers to this question and gives statisticians the tools necessary to make full use of the available data to correctly interpret the treatment effect.
Categorical Analysis
[edit | edit source]In laboratories we can measure the weight of fruit that a plant bears, or the temperature of a chemical reaction. These data points are easily measured with a yardstick or a thermometer, but what about the color of a person's eyes or her attitudes regarding the taste of broccoli? Psychologists can't measure someone's anger with a measuring stick, but they can ask their patients if they feel "very angry" or "a little angry" or "indifferent". Entirely different methodologies must be used in statistical analysis from these sorts of experiments. Categorical Analysis is used in a myriad of places, from political polls to analysis of census data to genetics and medicine.
Clinical Trials
[edit | edit source]In the United States, the FDA requires that pharmaceutical companies undergo rigorous procedures called Clinical Trials and statistical analyses to assure public safety before allowing the sale or use of new drugs. In fact, the pharmaceutical industry employs more statisticians than any other business!
Further reading
[edit | edit source]
Imagine reading a book for the first few chapters and then becoming able to get a sense of what the ending will be like - this is one of the great reasons to learn statistics. With the appropriate tools and solid grounding in statistics, one can use a limited sample (e.g. read the first five chapters of Pride & Prejudice) to make intelligent and accurate statements about the population (e.g. predict the ending of Pride & Prejudice). This is what knowing statistics and statistical tools can do for you.
In today's information-overloaded age, statistics is one of the most useful subjects anyone can learn. Newspapers are filled with statistical data, and anyone who is ignorant of statistics is at risk of being seriously misled about important real-life decisions such as what to eat, who is leading the polls, how dangerous smoking is, etc. Knowing a little about statistics will help one to make more informed decisions about these and other important questions. Furthermore, statistics are often used by politicians, advertisers, and others to twist the truth for their own gain. For example, a company selling the cat food brand "Cato" (a fictitious name here), may claim quite truthfully in their advertisements that eight out of ten cat owners said that their cats preferred Cato brand cat food to "the other leading brand" cat food. What they may not mention is that the cat owners questioned were those they found in a supermarket buying Cato.
“The best thing about being a statistician is that you get to play in everyone else’s backyard.” John Tukey, Princeton University
More seriously, those proceeding to higher education will learn that statistics is the most powerful tool available for assessing the significance of experimental data, and for drawing the right conclusions from the vast amounts of data faced by engineers, scientists, sociologists, and other professionals in most spheres of learning. There is no study with scientific, clinical, social, health, environmental or political goals that does not rely on statistical methodologies. The basic reason for that is that variation is ubiquitous in nature and probability and statistics are the fields that allow us to study, understand, model, embrace and interpret variation.
See Also UCLA Brochure on Why Study Probability & Statistics
Statistics is a diverse subject and thus the mathematics that are required depend on the kind of statistics we are studying. A strong background in linear algebra is needed for most multivariate statistics, but is not necessary for introductory statistics. A background in Calculus is useful no matter what branch of statistics is being studied.
At a bare minimum the student should have a grasp of basic concepts taught in Algebra and be comfortable with "moving things around" and solving for an unknown. Most of the statistics here will derive from a few basic things that the reader should become acquainted with.
Absolute Value
[edit | edit source]
If the number is zero or positive, then the absolute value of the number is simply the same number. If the number is negative, then take away the negative sign to get the absolute value.
Examples
[edit | edit source]- |42| = 42
- |-5| = 5
- |2.21| = 2.21
Factorials
[edit | edit source]A factorial is a calculation that gets used a lot in probability. It is defined only for integers greater-than-or-equal-to zero as:
Examples
[edit | edit source]In short, this means that:
| 0! = | 1 | = 1 |
| 1! = | 1 · 1 | = 1 |
| 2! = | 2 · 1 | = 2 |
| 3! = | 3 · 2 · 1 | = 6 |
| 4! = | 4 · 3 · 2 · 1 | = 24 |
| 5! = | 5 · 4 · 3 · 2 · 1 | = 120 |
| 6! = | 6 · 5 · 4 · 3 · 2 · 1 | = 720 |
Summation
[edit | edit source]The summation (also known as a series) is used more than almost any other technique in statistics. It is a method of representing addition over lots of values without putting + after +. We represent summation using a big uppercase sigma: ∑.
Examples
[edit | edit source]Very often in statistics we will sum a list of related variables:
Here we are adding all the x variables (which will hopefully all have values by the time we calculate this). The expression below the ∑ (i=0, in this case) represents the index variable and what its starting value is (i with a starting value of 0) while the number above the ∑ represents the number that the variable will increment to (stepping by 1, so i = 0, 1, 2, 3, and then 4). Another example:
Notice that we would get the same value by moving the 2 outside of the summation (perform the summation and then multiply by 2, rather than multiplying each component of the summation by 2).
Infinite series
[edit | edit source]There is no reason, of course, that a series has to count on any determined, or even finite value—it can keep going without end. These series are called "infinite series" and sometimes they can even converge to a finite value, eventually becoming equal to that value as the number of items in your series approaches infinity (∞).
Examples
[edit | edit source]This example is the famous geometric series. Note both that the series goes to ∞ (infinity, that means it does not stop) and that it is only valid for certain values of the variable r. This means that if r is between the values of -1 and 1 (-1 < r < 1) then the summation will get closer to (i.e., converge on) 1 / 1-r the further you take the series out.
Linear Approximation
[edit | edit source]| v / α | 0.20 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
|---|---|---|---|---|---|---|
| 40 | 0.85070 | 1.30308 | 1.68385 | 2.02108 | 2.42326 | 2.70446 |
| 50 | 0.84887 | 1.29871 | 1.67591 | 2.00856 | 2.40327 | 2.67779 |
| 60 | 0.84765 | 1.29582 | 1.67065 | 2.00030 | 2.39012 | 2.66028 |
| 70 | 0.84679 | 1.29376 | 1.66691 | 1.99444 | 2.38081 | 2.64790 |
| 80 | 0.84614 | 1.29222 | 1.66412 | 1.99006 | 2.37387 | 2.63869 |
| 90 | 0.84563 | 1.29103 | 1.66196 | 1.98667 | 2.36850 | 2.63157 |
| 100 | 0.84523 | 1.29007 | 1.66023 | 1.98397 | 2.36422 | 2.62589 |
Let us say that you are looking at a table of values, such as the one above. You want to approximate (get a good estimate of) the values at 63, but you do not have those values on your table. A good solution here is use a linear approximation to get a value which is probably close to the one that you really want, without having to go through all of the trouble of calculating the extra step in the table.
This is just the equation for a line applied to the table of data. xi represents the data point you want to know about, is the known data point beneath the one you want to know about, and is the known data point above the one you want to know about.
Examples
[edit | edit source]Find the value at 63 for the 0.05 column, using the values on the table above.
First we confirm on the above table that we need to approximate the value. If we know it exactly, then there really is no need to approximate it. As it stands this is going to rest on the table somewhere between 60 and 70. Everything else we can get from the table:
Using software, we calculate the actual value of f(63) to be 1.669402, a difference of around 0.00013. Close enough for our purposes.
Different Types of Data
[edit | edit source]Data are assignments of values onto observations of events and objects. They can be classified by their coding properties and the characteristics of their domains and their ranges.
Identifying data type
[edit | edit source]When a given data set is numerical in nature, it is necessary to carefully distinguish the actual nature of the variable being quantified. Statistical tests are generally specific for the kind of data being handled.
Data on a nominal (or categorical) scale
[edit | edit source]Identifying the true nature of numerals applied to attributes that are not "measures" is usually straightforward and apparent. Examples in everyday use include road, car, house, book and telephone numbers. A simple test would be to ask if re-assigning the numbers among the set would alter the nature of the collection. If the plates on a car are changed, for example, it still remains the same car in reality.
Data on an Ordinal Scale
[edit | edit source]An ordinal scale is a scale with ranks. Those ranks only have sense in that they are ordered, that is what makes it ordinal scale. The distance [rank n] minus [rank n-1] is not guaranteed to be equal to [rank n-1] minus [rank n-2], but [rank n] will be greater than [rank n-1] in the same way [rank n-1] is greater than [rank n-2] for all n where [rank n], [rank n-1], and [rank n-2] exist. Ranks of an ordinal scale may be represented by a system with numbers or names and an agreed order.
We can illustrate this with a common example: the Likert scale. Consider five possible responses to a question, perhaps Our president is a great man, with answers on this scale
| Response: | Strongly Disagree | Disagree | Neither Agree nor Disagree | Agree | Strongly Agree |
|---|---|---|---|---|---|
| Code: | 1 | 2 | 3 | 4 | 5 |
Here the answers are a ranked scale reflected in the choice of numeric code. There is however no sense in which the distance between Strongly agree and Agree is the same as between Strongly disagree and Disagree.
Numerical ranked data should be distinguished from measurement data.
Measurement data
[edit | edit source]Numerical measurements exist in two forms, Meristic and continuous, and may present themselves in three kinds of scale: interval, ratio and circular.
Meristic or discrete variables are generally counts and can take on only discrete values. Normally they are represented by natural numbers. The number of plants found in a botanist's quadrant would be an example. (Note that if the edge of the quadrant falls partially over one or more plants, the investigator may choose to include these as halves, but the data will still be meristic as doubling the total will remove any fraction).
Continuous variables are those whose measurement precision is limited only by the investigator and his equipment. The length of a leaf measured by a botanist with a ruler will be less precise than the same measurement taken by micrometer. (Notionally, at least, the leaf could be measured even more precisely using a microscope with a graticule.)
Interval Scale Variables measured on an interval scale have values in which differences are uniform and meaningful but ratios will not be so. An oft quoted example is that of the Celsius scale of temperature. A difference between 5° and 10° is equivalent to a difference between 10° and 15°, but the ratio between 15° and 5° does not imply that the former is three times as warm as the latter.
Ratio Scale Variables on a ratio scale have a meaningful zero point. In keeping with the above example one might cite the Kelvin temperature scale. Because there is an absolute zero, it is true to say that 400°K is twice as warm as 200°K, though one should do so with tongue in cheek. A better day-to-day example would be to say that a 180 kg Sumo wrestler is three times heavier than his 60 kg wife.
Circular Scale When one measures annual dates, clock times and a few other forms of data, a circular scale is in use. It can happen that neither differences nor ratios of such variables are sensible derivatives, and special methods have to be employed for such data.
See also
[edit | edit source]
Statistical data can be obtained from two sources primary or secondary.
Primary Data
[edit | edit source]Primary data means original data that has been collected specially for the purpose in mind. It means someone collected the data from the original source first hand. Data collected this way is called primary data.
The people who gather primary data may be an authorized organization, investigator, enumerator or they may be just someone with a clipboard. Those who gather primary data may have knowledge of the study and may be motivated to make the study a success. These people are acting as a witness so primary data is only considered as reliable as the people who gathered it.
Research where one gathers this kind of data is referred to as field research.
For example: your own questionnaire.
Secondary Data
[edit | edit source]Secondary data is data that has been collected for another purpose. When we use Statistical Method with Primary Data from another purpose for our purpose we refer to it as Secondary Data. It means that one purpose's Primary Data is another purpose's Secondary Data. Secondary data is data that is being reused. Usually in a different context.
Research where one gathers this kind of data is referred to as desk research.
For example: data from a book.
Why Classify Data This Way?
[edit | edit source]Knowing how the data was collected allows critics of a study to search for bias in how it was conducted. A good study will welcome such scrutiny. Each type has its own weaknesses and strengths. Primary Data is gathered by people who can focus directly on the purpose in mind. This helps ensure that questions are meaningful to the purpose but can introduce bias in those same questions. Secondary Data doesn't have the privilege of this focus but is only susceptible to bias introduced in the choice of what data to reuse. Stated another way, those who gather Secondary Data get to pick the questions. Those who gather Primary Data get to write the questions.
<< Sources of Data | Statistics | >> Qualitative and Quantitative
Qualitative data
[edit | edit source]Qualitative data is a categorical measurement expressed not in terms of numbers, but rather by means of a natural language description. In statistics, it is often used interchangeably with "categorical" data.
For example:
favorite color = "blue"
height = "tall"
i hated the most = "zen"
Although we may have categories, the categories may have a structure to them. When there is not a natural ordering of the categories, we call these nominal categories. Examples might be gender, race, religion, or sport.
When the categories may be ordered, these are called ordinal variables. Categorical variables that judge size (small, medium, large, etc.) are ordinal variables. Attitudes (strongly disagree, disagree, neutral, agree, strongly agree) are also ordinal variables, however we may not know which value is the best or worst of these issues. Note that the distance between these categories is not something we can measure.
Quantitative data
[edit | edit source]Quantitative data is a numerical measurement expressed not by means of a natural language description, but rather in terms of numbers. However, not all numbers are continuous and measurable. For example, the social security number is a number, but not something that one can add or subtract.
For example:
molecule length = "450 nm"
height = "1.8 m"
Quantitative data always are associated with a scale measure.
Probably the most common scale type is the ratio-scale. Observations of this type are on a scale that has a meaningful zero value but also have an equidistant measure (i.e., the difference between 10 and 20 is the same as the difference between 100 and 110). For example, a 10 year-old girl is twice as old as a 5 year-old girl. Since you can measure zero years, time is a ratio-scale variable. Money is another common ratio-scale quantitative measure. Observations that you count are usually ratio-scale (e.g., number of widgets).
Methods of Data Collection
[edit | edit source]The main portion of Statistics is the display of summarized data. Data is initially collected from a given source, whether they are experiments, surveys, or observation, and is presented in one of four methods:
- Textual Method
- The reader acquires information through reading the gathered data.
- Tabular Method
- Provides a more precise, systematic and orderly presentation of data in rows or columns.
- Semi-tabular Method
- Uses both textual and tabular methods.
- Graphical Method
- The utilization of graphs is most effective method of visually presenting statistical results or findings.
Experiments
[edit | edit source]In a experiment the experimenter applies 'treatments' to groups of subjects. For example the experimenter may give one drug to group 1 and a different drug or a placebo to group 2, to determine the effectiveness of the drug. This is what differentiates an 'experiment' from an 'observational study'.
Scientists try to identify cause-and-effect relationships because this kind of knowledge is especially powerful, for example, drug A cures disease B. Various methods exist for detecting cause-and-effect relationships. An experiment is a method that most clearly shows cause-and-effect because it isolates and manipulates a single variable, in order to clearly show its effect. Experiments almost always have two distinct variables: First, an independent variable (IV) is manipulated by an experimenter to exist in at least two levels (usually "none" and "some"). Then the experimenter measures the second variable, the dependent variable (DV).
|
Example: Experimentation Suppose the experimental hypothesis that concerns the scientist is that reading a wiki will enhance knowledge. Notice that the hypothesis is really an attempt to state a causal relationship like, "if you read a qiki, then you will have enhanced knowledge." The antecedent condition (reading a wiki) causes the consequent condition (enhanced knowledge). Antecedent conditions are always IVs and consequent conditions are always DVs in experiments. So the experimenter would produce two levels of Wiki reading (none and some, for example) and record knowledge. If the subjects who got no Wiki exposure had less knowledge than those who were exposed to wikis, it follows that the difference is caused by the IV. |
So, the reason scientists utilize experiments is that it is the only way to determine causal relationships between variables. Experiments tend to be artificial because they try to make both groups identical with the single exception of the levels of the independent variable.
Sample surveys involve the selection and study of a sample of items from a population. A sample is just a set of members chosen from a population, but not the whole population. A survey of a whole population is called a census.
A sample from a population may not give accurate results but it helps in decision making.
Examples
[edit | edit source]Examples of sample surveys:
- Phoning the fifth person on every page of the local phonebook and asking them how long they have lived in the area. (Systematic Sample)
- Dropping a quad. in five different places on a field and counting the number of wild flowers inside the quad. (Cluster Sample)
- Selecting sub-populations in proportion to their incidence in the overall population. For instance, a researcher may have reason to select a sample consisting 30% females and 70% males in a population with those same gender proportions. (Stratified Sample)
- Selecting several cities in a country, several neighbourhoods in those cities and several streets in those neighbourhoods to recruit participants for a survey. (Multi-stage sample)
The term random sample is used for a sample in which every item in the population is equally likely to be selected.
Bias
[edit | edit source]While sampling is a more cost effective method of determining a result, small samples or samples that depend on a certain selection method will result in a bias within the results.
The following are common sources of bias:
- Sampling bias or statistical bias, where some individuals are more likely to be selected than others (such as if you give equal chance of cities being selected rather than weighting them by size)
- Systemic bias, where external influences try to affect the outcome (e.g. funding organizations wanting to have a specific result)
The most primitive method of understanding the laws of nature utilizes observational studies. Basically, a researcher goes out into the world and looks for variables that are associated with one another. Notice that, unlike experiments, in an observational study the Independent Variables are not manipulated by the experimenter. The independent variable could be something like "smoking". It would be unethical and probably impossible to do an experiment where one randomly selected group is assigned to smoke and another group is assigned to the non-smoking group. Therefore, in order do determine the health effects of smoking on humans, an observational study is more appropriate than an experiment. The health of smokers and non-smokers would be compared without the experimenter assigning treatment.
Some of the foundations of modern scientific thought are based on observational research. Charles Darwin, for example, based his explanation of evolution entirely on observations he made. Case studies, where individuals are observed and questioned to determine possible causes of problems, are a form of observational research that continues to be popular today. In fact, every time you see a physician he or she is performing observational science.
There is a problem in observational science though — it cannot ever identify causal relationships because even though two variables are related both might be caused by a third, unseen, variable. Since the underlying laws of nature are assumed to be causal laws, observational findings are generally regarded as less compelling than experimental findings.
The key way to identify experimental studies is that they involve an intervention such as the administration of a drug to one group of patients and a placebo to another group. Observational studies only collect data and make comparisons.
Medicine is an intensively studied discipline, and not all phenomenon can be studied by experimentation due to obvious ethical or logistical restrictions.
- Case series: These are purely observational, consisting of reports of a series of similar medical cases. For example, a series of patients might be reported to suffer from bone abnormalities as well as immunodeficiencies. This association may not be significant, occurring purely by chance. On the other hand, the association may point to a mutation in common pathway affecting both the skeletal system and the immune system.
- Case-Control: This involves an observation of a disease state, compared to normal healthy controls. For example, patients with lung cancer could be compared with their otherwise healthy neighbors. Using neighbors limits bias introduced by demographic variation. The cancer patients and their neighbors (the control) might be asked about their exposure history (did they work in an industrial setting), or other risk factors such as smoking. Another example of a case-control study is the testing of a diagnostic procedure against the gold standard. The gold standard represents the control, while the new diagnostic procedure is the "case." This might seem to qualify as an "intervention" and thus an experiment.
- Cross-sectional: Involves many variables collected all at the same time. Used in epidemiology to estimate prevalence, or conduct other surveys.
- Cohort: A group of subjects followed over time, prospectively. Framingham study is classic example. By observing exposure and then tracking outcomes, cause and effect can be better isolated. However this type of study cannot conclusively isolate a cause and effect relationship.
- Historic Cohort: This is the same as a cohort except that researchers use an historic medical record to track patients and outcomes.
Data Analysis
[edit | edit source]Data analysis is one of the more important stages in our research. Without performing exploratory analyses of our data, we set ourselves up for mistakes and loss of time.
Generally speaking, our goal here is to be able to "visualize" the data and get a sense of their values. We plot histograms and compute summary statistics to observe the trends and the distribution of our data.
Data Cleaning
[edit | edit source]'Cleaning' refers to the process of removing invalid data points from a dataset.
Many statistical analyses try to find a pattern in a data series, based on a hypothesis or assumption about the nature of the data. 'Cleaning' is the process of removing those data points which are either (a) Obviously disconnected with the effect or assumption which we are trying to isolate, due to some other factor which applies only to those particular data points. (b) Obviously erroneous, i.e. some external error is reflected in that particular data point, either due to a mistake during data collection, reporting etc.
In the process we ignore these particular data points, and conduct our analysis on the remaining data.
'Cleaning' frequently involves human judgement to decide which points are valid and which are not, and there is a chance of valid data points caused by some effect not sufficiently accounted for in the hypothesis/assumption behind the analytical method applied.
The points to be cleaned are generally extreme outliers. 'Outliers' are those points which stand out for not following a pattern which is generally visible in the data. One way of detecting outliers is to plot the data points (if possible) and visually inspect the resultant plot for points which lie far outside the general distribution. Another way is to run the analysis on the entire dataset, and then eliminating those points which do not meet mathematical 'control limits' for variability from a trend, and then repeating the analysis on the remaining data.
Cleaning may also be done judgementally, for example in a sales forecast by ignoring historical data from an area/unit which has a tendency to misreport sales figures. To take another example, in a double blind medical test a doctor may disregard the results of a volunteer whom the doctor happens to know in a non-professional context.
'Cleaning' may also sometimes be used to refer to various other judgemental/mathematical methods of validating data and removing suspect data.
The importance of having clean and reliable data in any statistical analysis cannot be stressed enough. Often, in real-world applications the analyst may get mesmerised by the complexity or beauty of the method being applied, while the data itself may be unreliable and lead to results which suggest courses of action without a sound basis. A good statistician/researcher (personal opinion) spends 90% of his/her time on collecting and cleaning data, and developing hypothesis which cover as many external explainable factors as possible, and only 10% on the actual mathematical manipulation of the data and deriving results.
Summary Statistics
[edit | edit source]Summary Statistics
[edit | edit source]The most simple example of statistics "in practice" is in the generation of summary statistics. Let us consider the example where we are interested in the weight of eighth graders in a school. (Maybe we're looking at the growing epidemic of child obesity in America!) Our school has 200 eighth graders, so we gather all their weights. What we have are 200 positive real numbers.
If an administrator asked you what the weight was of this eighth grade class, you wouldn't grab your list and start reading off all the individual weights; it's just too much information. That same administrator wouldn't learn anything except that she shouldn't ask you any questions in the future! What you want to do is to distill the information — these 200 numbers — into something concise.
What might we express about these 200 numbers that would be of interest? The most obvious thing to do is to calculate the average or mean value so we know how much the "typical eighth grader" in the school weighs. It would also be useful to express how much this number varies; after all, eighth graders come in a wide variety of shapes and sizes! In reality, we can probably reduce this set of 200 weights into at most four or five numbers that give us a firm comprehension of the data set.
Averages
[edit | edit source]An average is simply a number that is representative of data. More particularly, it is a measure of central tendency. There are several types of average. Averages are useful for comparing data, especially when sets of different size are being compared. It acts as a representative figure of the whole set of data.
Perhaps the simplest and commonly used average the arithmetic mean or more simply mean which is explained in the next section.
Other common types of average are the median, the mode, the geometric mean, and the harmonic mean, each of which may be the most appropriate one to use under different circumstances.
Statistics | Summary Statistics | >> Mean, Median and Mode
Mean, Median and Mode
[edit | edit source]Mean
[edit | edit source]The mean, or more precisely the arithmetic mean, is simply the arithmetic average of a group of numbers (or data set) and is shown using -bar symbol . So the mean of the variable is , pronounced "x-bar". It is calculated by adding up all of the values in a data set and dividing by the number of values in that data set :.For example, take the following set of data: {1,2,3,4,5}. The mean of this data would be:
Here is a more complicated data set: {10,14,86,2,68,99,1}. The mean would be calculated like this:
Median
[edit | edit source]The median is the "middle value" in a set. That is, the median is the number in the center of a data set that has been ordered sequentially.
For example, let's look at the data in our second data set from above: {10,14,86,2,68,99,1}. What is its median?
- First, we sort our data set sequentially: {1,2,10,14,68,85,99}
- Next, we determine the total number of points in our data set (in this case, 7.)
- Finally, we determine the central position of or data set (in this case, the 4th position), and the number in the central position is our median - {1,2,10,14,68,85,99}, making 14 our median.
| Helpful Hint! | |
|---|---|
| An easy way to determine the central position or positions for any ordered set is to take the total number of points, add 1, and then divide by 2. If the number you get is a whole number, then that is the central position. If the number you get is a fraction, take the two whole numbers on either side. |
Because our data set had an odd number of points, determining the central position was easy - it will have the same number of points before it as after it. But what if our data set has an even number of points?
Let's take the same data set, but add a new number to it: {1,2,10,14,68,85,99,100} What is the median of this set?
When you have an even number of points, you must determine the two central positions of the data set. (See side box for instructions.) So for a set of 8 numbers, we get (8 + 1) / 2 = 9 / 2 = 4 1/2, which has 4 and 5 on either side.
Looking at our dataset, we see that the 4th and 5th numbers are 14 and 68. From there, we return to our trusty friend the mean to determine the median. (14 + 68) / 2 = 82 / 2 = 41. find the median of 2, 4, 6, 8 => firstly we must count the numbers to determine its odd or even as we see it is even so we can write: M=(4+6)/2=10/2=5 5 is the median of above sequential numbers.
Mode
[edit | edit source]The mode is the most common or "most frequent" value in a data set. Example: the mode of the following data set (1, 2, 5, 5, 6, 3) is 5 since it appears twice. This is the most common value of the data set. Data sets having one mode are said to be unimodal, with two are said to be bimodal and with more than two are said to be multimodal . An example of a unimodal dataset is {1, 2, 3, 4, 4, 4, 5, 6, 7, 8, 8, 9}. The mode for this data set is 4. An example of a bimodal data set is {1, 2, 2, 3, 3}. This is because both 2 and 3 are modes. Please note: If all points in a data set occur with equal frequency, it is equally accurate to describe the data set as having many modes or no mode.
Midrange
[edit | edit source]The midrange is the arithmetic mean strictly between the minimum and the maximum value in a data set.
Relationship of the Mean, Median, and Mode
[edit | edit source]The relationship of the mean, median, and mode to each other can provide some information about the relative shape of the data distribution. If the mean, median, and mode are approximately equal to each other, the distribution can be assumed to be approximately symmetrical. If the mean > median > mode, the distribution will be skewed to the right. If the mean < median < mode, the distribution will be skewed to the left.
Questions
[edit | edit source]1. There is an old joke that states: "Using median size as a reference it's perfectly possible to fit four ping-pong balls and two blue whales in a rowboat." Explain why this statement is true.
Geometric Mean
[edit | edit source]The Geometric Mean is calculated by taking the nth root of the product of a set of data.
For example, if the set of data was:
1,2,3,4,5
The geometric mean would be calculated:
Of course, with large n this can be difficult to calculate. Taking advantage of two properties of the logarithm:
We find that by taking the logarithmic transformation of the geometric mean, we get:
Which leads us to the equation for the geometric mean:
When to use the geometric mean
[edit | edit source]The arithmetic mean is relevant at any time several quantities add together to produce a total. The arithmetic mean answers the question, "if all the quantities had the same value, what would that value have to be in order to achieve the same total?"
In the same way, the geometric mean is relevant any time several quantities multiply together to produce a product. The geometric mean answers the question, "if all the quantities had the same value, what would that value have to be in order to achieve the same product?"
For example, suppose you have an investment which returns 10% the first year, 50% the second year, and 30% the third year. What is its average rate of return? It is not the arithmetic mean, because what these numbers mean is that on the first year your investment was multiplied (not added to) by 1.10, on the second year it was multiplied by 1.50, and the third year it was multiplied by 1.30. The relevant quantity is the geometric mean of these three numbers. Written by Hafiz G m
It is known that the geometric mean is always less than or equal to the arithmetic mean (equality holding only when A=B). The proof of this is quite short and follows from the fact that is always a non-negative number. This inequality can be surprisingly powerful though and comes up from time to time in the proofs of theorems in calculus. Source.
Harmonic Mean
[edit | edit source]The arithmetic mean cannot be used when we want to average quantities such as speed.
Consider the example below:
Example 1: The distance from my house to town is 40 km. I drove to town at a speed of 40 km per hour and returned home at a speed of 80 km per hour. What was my average speed for the whole trip?.
Solution: If we just took the arithmetic mean of the two speeds I drove at, we would get 60 km per hour. This isn't the correct average speed, however: it ignores the fact that I drove at 40 km per hour for twice as long as I drove at 80 km per hour. To find the correct average speed, we must instead calculate the harmonic mean.
For two quantities A and B, the harmonic mean is given by:
This can be simplified by adding in the denominator and multiplying by the reciprocal:
For N quantities: A, B, C......
Harmonic mean =
Let us try out the formula above on our example:
Harmonic mean =
Our values are A = 40, B = 80. Therefore, harmonic mean
Is this result correct? We can verify it. In the example above, the distance between the two towns is 40 km. So the trip from A to B at a speed of 40 km will take 1 hour. The trip from B to A at a speed to 80 km will take 0.5 hours. The total time taken for the round distance (80 km) will be 1.5 hours. The average speed will then be 53.33 km/hour.
The harmonic mean also has physical significance.
Relationships among Arithmetic, Geometric and Harmonic Mean
[edit | edit source]The Means mentioned above are realizations of the generalized mean
and ordered this way:
Measures of dispersion
[edit | edit source]Range of Data
[edit | edit source]The range of a sample (set of data) is simply the maximum possible difference in the data, i.e. the difference between the maximum and the minimum values. A more exact term for it is "range width" and is usually denoted by the letter R or w. The two individual values (the max. and min.) are called the "range limits". Often these terms are confused and students should be careful to use the correct terminology.
For example, in a sample with values 2 3 5 7 8 11 12, the range is 11 (|12|-|2|+1=11) and the range limits are 2 and 12.
The range is the simplest and most easily understood measure of the dispersion (spread) of a set of data, and though it is very widely used in everyday life, it is too rough for serious statistical work. It is not a "robust" measure, because clearly the chance of finding the maximum and minimum values in a population depends greatly on the size of the sample we choose to take from it and so its value is likely to vary widely from one sample to another. Furthermore, it is not a satisfactory descriptor of the data because it depends on only two items in the sample and overlooks all the rest. A far better measure of dispersion is the standard deviation (s), which takes into account all the data. It is not only more robust and "efficient" than the range, but is also amenable to far greater statistical manipulation. Nevertheless the range is still much used in simple descriptions of data and also in quality control charts.
The mean range of a set of data is however a quite efficient measure (statistic) and can be used as an easy way to calculate s. What we do in such cases is to subdivide the data into groups of a few members, calculate their average range, and divide it by a factor (from tables), which depends on n. In chemical laboratories for example, it is very common to analyse samples in duplicate, and so they have a large source of ready data to calculate s.
(The factor k to use is given under standard deviation.)
For example: If we have a sample of size 40, we can divide it into 10 sub-samples of n=4 each. If we then find their mean range to be, say, 3.1, the standard deviation of the parent sample of 40 items is approximately 3.1/2.059 = 1.506.
With simple electronic calculators now available, which can calculate s directly at the touch of a key, there is no longer much need for such expedients, though students of statistics should be familiar with them.
{tBookCat}}
Quartiles
[edit | edit source]The quartiles of a data set are formed by the two boundaries on either side of the median, which divide the set into four equal sections. The lowest 25% of the data being found below the first quartile value, also called the lower quartile (Q1). The median, or second quartile divides the set into two equal sections. The lowest 75% of the data set should be found below the third quartile, also called the upper quartile (Q3). These three numbers are measures of the dispersion of the data, while the mean, median and mode are measures of central tendency.
Examples
[edit | edit source]Given the set {1,3,5,8,9,12,24,25,28,30,41,50} we would find the first and third quartiles as follows:
There are 12 elements in the set, so 12/4 gives us three elements in each quarter of the set.
So the first or lowest quartile is: 5, the second quartile is the median 12, and the third or upper quartile is 28.
However some people when faced with a set with an even number of elements (values) still want the true median (or middle value), with an equal number of data values on each side of the median (rather than 12 which has 5 values less than and 6 values greater than. This value is then the average of 12 and 24 resulting in 18 as the true median (which is closer to the mean of 19 2/3. The same process is then applied to the lower and upper quartiles, giving 6.5, 18, and 29. This is only an issue if the data contains an even number of elements with an even number of equally divided sections, or an odd number of elements with an odd number of equally divided sections.
Inter-Quartile Range
[edit | edit source]The inter quartile range is a statistic which provides information about the spread of a data set, and is calculated by subtracting the first quartile from the third quartile), giving the range of the middle half of the data set, trimming off the lowest and highest quarters. Since the IQR is not affected at all by outliers in the data, it is a more robust measure of dispersion than the range
IQR = Q3 - Q1
Another useful quantile is the quintiles which subdivide the data into five equal sections. The advantage of quintiles is that there is a central one with boundaries on either side of the median which can serve as an average group. In a Normal distribution the boundaries of the quintiles have boundaries ±0.253*s and ±0.842*s on either side of the mean (or median),where s is the sample standard deviation. Note that in a Normal distribution the mean, median and mode coincide.
Other frequently used quantiles are the deciles (10 equal sections) and the percentiles (100 equal sections)
Variance and Standard Deviation
[edit | edit source]
Measure of Scale
[edit | edit source]When describing data it is helpful (and in some cases necessary) to determine the spread of a distribution. One way of measuring this spread is by calculating the variance or the standard deviation of the data.
In describing a complete population, the data represents all the elements of the population. As a measure of the "spread" in the population one wants to know a measure of the possible distances between the data and the population mean. There are several options to do so. One is to measure the average absolute value of the deviations. Another, called the variance, measures the average square of these deviations.
A clear distinction should be made between dealing with the population or with a sample from it. When dealing with the complete population the (population) variance is a constant, a parameter which helps to describe the population. When dealing with a sample from the population the (sample) variance is actually a random variable, whose value differs from sample to sample. Its value is only of interest as an estimate for the population variance.
Population variance and standard deviation
[edit | edit source]Let the population consist of the N elements x1,...,xN. The (population) mean is:
- .
The (population) variance σ2 is the average of the squared deviations from the mean or (xi - μ)2 - the square of the value's distance from the distribution's mean.
- .
Because of the squaring the variance is not directly comparable with the mean and the data themselves. The square root of the variance is called the Standard Deviation σ. Note that σ is the root mean squared of differences between the data points and the average.
Sample variance and standard deviation
[edit | edit source]Let the sample consist of the n elements x1,...,xn, taken from the population. The (sample) mean is:
- .
The sample mean serves as an estimate for the population mean μ.
The (sample) variance s2 is a kind of average of the squared deviations from the (sample) mean:
- .
Also for the sample we take the square root to obtain the (sample) standard deviation s
A common question at this point is "why do we square the numerator?" One answer is: to get rid of the negative signs. Numbers are going to fall above and below the mean and, since the variance is looking for distance, it would be counterproductive if those distances factored each other out.
Example
[edit | edit source]When rolling a fair die, the population consists of the 6 possible outcomes 1 to 6. A sample may consist instead of the outcomes of 1000 rolls of the die.
The population mean is:
- ,
and the population variance:
The population standard deviation is:
- .
Notice how this standard deviation is somewhere in between the possible deviations.
So if we were working with one six-sided die: X = {1, 2, 3, 4, 5, 6}, then σ2 = 2.917. We will talk more about why this is different later on, but for the moment assume that you should use the equation for the sample variance unless you see something that would indicate otherwise.
Note that none of the above formulae are ideal when calculating the estimate and they all introduce rounding errors. Specialized statistical software packages use more complicated logarithms that take a second pass of the data in order to correct for these errors. Therefore, if it matters that your estimate of standard deviation is accurate, specialized software should be used. If you are using non-specialized software, such as some popular spreadsheet packages, you should find out how the software does the calculations and not just assume that a sophisticated algorithm has been implemented.
For Normal Distributions
[edit | edit source]The empirical rule states that approximately 68 percent of the data in a normally distributed dataset is contained within one standard deviation of the mean, approximately 95 percent of the data is contained within 2 standard deviations, and approximately 99.7 percent of the data falls within 3 standard deviations.
As an example, the verbal or math portion of the SAT has a mean of 500 and a standard deviation of 100. This means that 68% of test-takers scored between 400 and 600, 95% of test takers scored between 300 and 700, and 99.7% of test-takers scored between 200 and 800 assuming a completely normal distribution (which isn't quite the case, but it makes a good approximation).
Robust Estimators
[edit | edit source]For a normal distribution the relationship between the standard deviation and the interquartile range is roughly: SD = IQR/1.35.
For data that are non-normal, the standard deviation can be a terrible estimator of scale. For example, in the presence of a single outlier, the standard deviation can grossly overestimate the variability of the data. The result is that confidence intervals are too wide and hypothesis tests lack power. In some (or most) fields, it is uncommon for data to be normally distributed and outliers are common.
One robust estimator of scale is the "average absolute deviation", or aad. As the name implies, the mean of the absolute deviations about some estimate of location is used. This method of estimation of scale has the advantage that the contribution of outliers is not squared, as it is in the standard deviation, and therefore outliers contribute less to the estimate. This method has the disadvantage that a single large outlier can completely overwhelm the estimate of scale and give a misleading description of the spread of the data.
Another robust estimator of scale is the "median absolute deviation", or mad. As the name implies, the estimate is calculated as the median of the absolute deviation from an estimate of location. Often, the median of the data is used as the estimate of location, but it is not necessary that this be so. Note that if the data are non-normal, the mean is unlikely to be a good estimate of location.
It is necessary to scale both of these estimators in order for them to be comparable with the standard deviation when the data are normally distributed. It is typical for the terms aad and mad to be used to refer to the scaled version. The unscaled versions are rarely used.
External links
[edit | edit source]Other summaries
[edit | edit source]Moving Average
[edit | edit source]A moving average is used when you want to get a general picture of the trends contained in a data set. The data set of concern is typically a so-called "time series", i.e a set of observations ordered in time. Given such a data set X, with individual data points , a 2n+1 point moving average is defined as , and is thus given by taking the average of the 2n points around . Doing this on all data points in the set (except the points too close to the edges) generates a new time series that is somewhat smoothed, revealing only the general tendencies of the first time series.
The moving average for many time-based observations is often lagged. That is, we take the 10 -day moving average by looking at the average of the last 10 days. We can make this more exciting (who knew statistics was exciting?) by considering different weights on the 10 days. Perhaps the most recent day should be the most important in our estimate and the value from 10 days ago would be the least important. As long as we have a set of weights that sums to 1, this is an acceptable moving-average. Sometimes the weights are chosen along an exponential curve to make the exponential moving-average.
Displaying Data
[edit | edit source] A single statistic tells only part of a dataset’s story. The mean is one perspective; the median yet another. And when we explore relationships between multiple variables, even more statistics arise. The coefficient estimates in a regression model, the Cochran-Maentel-Haenszel test statistic in partial contingency tables; a multitude of statistics are available to summarize and test data.
But our ultimate goal in statistics is not to summarize the data, it is to fully understand their complex relationships. A well designed statistical graphic helps us explore, and perhaps understand, these relationships.
This section will help you let the data speak, so that the world may know its story.
Types of Data Display
- Bar_Charts
- Histograms
- Scatter_Graphs
- Box_Plots
- Pie_Charts
- Comparative_Pie_Charts
- Pictograms
- Line_Graphs
- Frequency_Polygon
External Links
- "The Visual Display of Quantitative Information" is the seminal work on statistical graphics. It is a must read.
- [1] "Show me the Numbers" by Stephen Few has a less technical approach to creating graphics. You might want to scan through this book if you are building a library on making graphs.
Bar Charts
[edit | edit source]The Bar Chart (or Bar Graph) is one of the most common ways of displaying catagorical/qualitative data. Bar Graphs consist of 2 variables, one response (sometimes called "dependent") and one predictor (sometimes called "independent"), arranged on the horizontal and vertical axis of a graph. The relationship of the predictor and response variables is shown by a mark of some sort (usually a rectangular box) from one variable's value to the other's.
To demonstrate we will use the following data(tbl. 3.1.1) representing a hypothetical relationship between a qualitative predictor variable, "Graph Type", and a quantitative response variable, "Votes".
tbl. 3.1.1 - Favourite Graphs
| Graph Type | Votes |
|---|---|
| Bar Charts | 5 |
| Pie Graphs | 2 |
| Histograms | 3 |
| Pictograms | 8 |
| Comp. Pie Graphs | 4 |
| Line Graphs | 9 |
| Frequency Polygon | 1 |
| Scatter Graphs | 5 |
From this data we can now construct an appropriate graphical representation which, in this case will be a Bar Chart. The graph may be orientated in several ways, of which the vertical chart (fig. 3.1.1) is most common, with the horizontal chart(fig. 3.1.2) also being used often
Take note that the height and width of the bars, in the vertical and horizontal Charts, respectfully, are equal to the response variable's corresponding value - "Bar Chart" bar equals the number of votes that the Bar Chart type received in tbl. 3.1.1
Also take note that there is a pronounced amount of space between the individual bars in each of the graphs, this is important in that it help differentiate the Bar Chart graph type from the Histogram graph type discussed in a later section.
External Links
[edit | edit source]Histograms
[edit | edit source]
It is often useful to look at the distribution of the data, or the frequency with which certain values fall between pre-set bins of specified sizes. The selection of these bins is up to you, but remember that they should be selected in order to illuminate your data, not obfuscate it.
A histogram is similar to a bar chart. However histograms are used for continuous (as opposed to discrete or qualitative) data. The defining property of a histogram is:
- The area of each bar is proportional to the frequency.
If each bin has an equal width, then this can be easily done by plotting frequency on the vertical axis. However histograms can also be drawn with unequal bin sizes, for which one can plot frequency density.
To produce a histogram with equal bin sizes:
- Select a minimum, a maximum, and a bin size. All three of these are up to you. In the histogram data used above the minimum is 1, the maximum is 110, and the bin size is 10.
- Calculate your bins and how many values fall into each of them. For the histogram data the bins are:
- 1 ≤ x < 10, 16 values.
- 10 ≤ x < 20, 4 values.
- 20 ≤ x < 30, 4 values.
- 30 ≤ x < 40, 2 values.
- 40 ≤ x < 50, 2 values.
- 50 ≤ x < 60, 1 values.
- 60 ≤ x < 70, 0 values.
- 70 ≤ x < 80, 0 values.
- 80 ≤ x < 90, 0 values.
- 90 ≤ x < 100, 0 value.
- 100 ≤ x < 110, 0 value.
- 110 ≤ x < 120, 1 value.
- Plot the counts you figured out above. Do this using a standard bar plot.
Worked Problem
[edit | edit source]Let's say you are an avid roleplayer who loves to play Mechwarrior, a d6 (6 sided die) based game. You have just purchased a new 6 sided die and would like to see whether it is biased (in combination with you when you roll it).
What We Expect
[edit | edit source]So before we look at what we get from rolling the die, let's look at what we would expect. First, if a die is unbiased it means that the odds of rolling a six are exactly the same as the odds of rolling a 1--there wouldn't be any favoritism towards certain values. Using the standard equation for the arithmetic mean find that μ = 3.5. We would also expect the histogram to be roughly even all of the way across--though it will almost never be perfect simply because we are dealing with an element of random chance.
What We Get
[edit | edit source]Here are the numbers that you collect:
| 1 | 5 | 6 | 4 | 1 | 3 | 5 | 5 | 6 | 4 | 1 | 5 | 6 | 6 | 4 | 5 | 1 | 4 | 3 | 6 |
| 1 | 3 | 6 | 4 | 2 | 4 | 1 | 6 | 4 | 2 | 2 | 4 | 3 | 4 | 1 | 1 | 6 | 3 | 5 | 5 |
| 4 | 3 | 5 | 3 | 4 | 2 | 2 | 5 | 6 | 5 | 4 | 3 | 5 | 3 | 3 | 1 | 5 | 4 | 4 | 5 |
| 1 | 2 | 5 | 1 | 6 | 5 | 4 | 3 | 2 | 4 | 2 | 1 | 3 | 3 | 3 | 4 | 6 | 1 | 1 | 3 |
| 6 | 6 | 1 | 4 | 6 | 6 | 6 | 5 | 3 | 1 | 5 | 6 | 3 | 4 | 5 | 5 | 5 | 2 | 4 | 4 |
Analysis
[edit | edit source]Referring back to what we would expect for an unbiased die, this is pretty close to what we would expect. So let's create a histogram to see if there is any significant difference in the distribution.
The only logical way to divide up dice rolls into bins is by what's showing on the die face:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 16 | 9 | 17 | 21 | 20 | 17 |
If we are good at visualizing information, we can simple use a table, such as in the one above, to see what might be happening. Often, however, it is useful to have a visual representation. As the amount of variety of data we want to display increases, the need for graphs instead of a simple table increases.
Looking at the above figure, we clearly see that sides 1, 3, and 6 are almost exactly what we would expect by chance. Sides 4 and 5 are slightly greater, but not too much so, and side 2 is a lot less. This could be the result of chance, or it could represent an actual anomaly in the data and it is something to take note of keep in mind. We'll address this issue again in later chapters.
Frequency Density
[edit | edit source]Another way of drawing a histogram is to work out the Frequency Density.
- Frequency Density
- The Frequency Density is the frequency divided by the class width.
The advantage of using frequency density in a histogram is that doesn't matter if there isn't an obvious standard width to use. For all the groups, you would work out the frequency divided by the class width for all of the groups.
External Links
Return to Statistics.
Scatter Plots
[edit | edit source]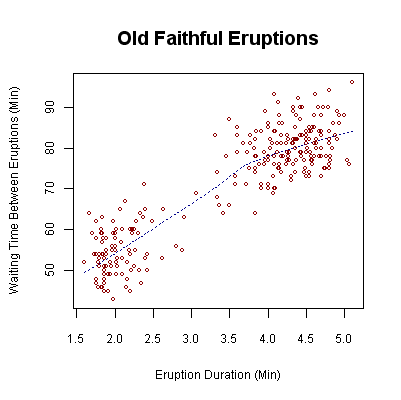
Scatter Plot is used to show the relationship between 2 numeric variables. It is not useful when comparing discrete variables versus numeric variables. A scatter plot matrix is a collection of pairwise scatter plots of numeric variables.
External Links
Box Plots
[edit | edit source]
A box plot (also called a box and whisker diagram) is a simple visual representation of key features of a univariate sample.
The box lies on a vertical axis in the range of the sample. Typically, a top to the box is placed at the 1st quartile, the bottom at the third quartile. The width of the box is arbitrary, as there is no x-axis (though see Violin Plots, below).
In between the top and bottom of the box is some representation of central tendency. A common version is to place a horizontal line at the median, dividing the box into two. Additionally, a star or asterisk is placed at the mean value, centered in the box in the horizontal direction.
Another common extension is to the 'box-and-whisker' plot. This adds vertical lines extending from the top and bottom of the plot to for example, the maximum and minimum values, The farthest value within 2 standard deviations above and below the mean. Alternatively, the whiskers could extend to the 2.5 and 97.5 percentiles. Finally, it is common in the box-and-whisker plot to show outliers (however defined) with asterisks at the individual values beyond the ends of the whiskers.
Violin Plots are an extension to box plots using the horizontal information to present more data. They show some estimate of the CDF instead of a box, though the quantiles of the distribution are still shown.
Pie Charts
[edit | edit source]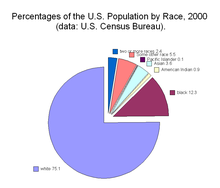
A Pie-Chart/Diagram is a graphical device - a circular shape broken into sub-divisions. The sub-divisions are called "sectors", whose areas are proportional to the various parts into which the whole quantity is divided. The sectors may be coloured differently to show the relationship of parts to the whole. A pie diagram is an alternative of the sub-divided bar diagram.
To construct a pie-chart, first we draw a circle of any suitable radius then the whole quantity which is to be divided is equated to 360 degrees. The different parts of the circle in terms of angles are calculated by the following formula.
Component Value / Whole Quantity * 360
The component parts i.e. sectors have been cut beginning from top in clockwise order.
Note that the percentages in a list may not add up to exactly 100% due to rounding. For example if a person spends a third of their time on each of three activities: 33%, 33% and 33% sums to 99%.
Warning: Pie charts are a poor way of communicating information. The eye is good at judging linear measures and bad at judging relative areas. A bar chart or dot chart is a preferable way of displaying this type of data.
Cleveland (1985), page 264: "Data that can be shown by pie charts always can be shown by a dot chart. This means that judgements of position along a common scale can be made instead of the less accurate angle judgments." This statement is based on the empirical investigations of Cleveland and McGill as well as investigations by perceptual psychologists.
Three-dimensional (3d) pie charts compound perceptual misinterpretation of statistical information by altering the relative angle of pie slices to create the impression of depth into a vanishing point. Angles and areas at the bottom of the chart must be exaggerated and the angles and areas at the top of the chart reduced in order to create the dimensional effect; a specifically false depiction of the data.
External Links
- Interactive Java-based Pie-Chart Applet
- See section 2.4 (cognostics) in D. Carr's and L. Pickle's book Visualizing Data Patterns with Micromaps for more information
Comparative Pie Charts
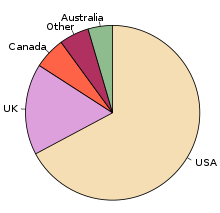
[edit | edit source]
The comparative pie charts are very difficult to read and compare if the ratio of the pie chart is not given.
Examine our example of color preference for two different groups. How much work does it take to see that it is quite challenging to work out who ate the pie? First, we have to find Fingerprints on either pie, and then remember how many sensirivity vectors it has. If we did not include the share for blue in the label, then we would probably be approximating the comparison. So, if we use multiple pie charts, we have to expect that comparisions between charts would only be approximate.
What is the most popular color in the left graph? Red. But note, that you have to look at all of the colors and read the label to see which it might be. Also, this author was kind when creating these two graphs because he used the same color for the same object. Imagine the confusion if one had made the most important color get Red in the right-hand chart?
If two shares of data should not be compared via the comparative pie chart, what kind of graph would be preferred? The stacked bar chart is probably the most appropriate for sharing of the total comparisons. Again, exact comparisons cannot be done with graphs and therefore a table may supplement the graph with detailed information.
Pictograms
[edit | edit source]A pictogram is simply a picture that conveys some statistical information. A very common example is the thermometer graph so common in fund drives. The entire thermometer is the goal (number of dollars that the fund raisers wish to collect. The red stripe (the "mercury") represents the proportion of the goal that has already been collected.
Another example is a picture that represents the gender constitution of a group. Each small picture of a male figure might represent 1,000 men and each small picture of a female figure would, then, represent 1,000 women. A picture consisting of 3 male figures and 4 female figures would indicate that the group is made up of 3,000 men and 4,000 women.
An interesting pictograph is the Chernoff Faces. It is useful for displaying information on cases for which several variables have been recorded. In this kind of plot, each case is represented by a separate picture of a face. The sizes of the various features of each face are used to present the value of each variable. For instance, if blood pressure, high density cholesterol, low density cholesterol, body temperature, height, and weight are recorded for 25 individuals, 25 faces would be displayed. The size of the nose on each face would represent the level of that person's blood pressure. The size of the left eye may represent the level of low density cholesterol while the size of the right eye might represent the level of high density cholesterol. The length of the mouth could represent the person's temperature. The length of the left ear might indicate the person's height and that of the right ear might represent their weight. Of course, a legend would be provided to help the viewer determine what feature relates to which variable. Where it would be difficult to represent the relationship of all 6 variables on a single (6-dimensional) graph, the Chernoff Faces would give a relatively easy to interpret 6-dimensional representation.
Line Graphs
[edit | edit source]Basically, a line graph can be, for example, a picture of what happened by/to something (a variable) during a specific time period (also a variable).
On the left side of such a graph usually is as an indication of that "something" in the form of a scale, and at the bottom is an indication of the specific time involved.
Usually a line graph is plotted after a table has been provided showing the relationship between the two variables in the form of pairs. Just as in (x,y) graphs, each of the pairs results in a specific point on the graph, and being a LINE graph these points are connected to one another by a LINE.
Many other line graphs exist; they all CONNECT the points by LINEs, not necessarily straight lines. Sometimes polynomials, for example, are used to describe approximately the basic relationship between the given pairs of variables, and between these points. The higher the degree of the polynomial, the more accurate is the "picture" of that relationship, but the degree of that polynomial must never be higher than n-1, where n is the number of the given points.
See also Graph theory
[[../../Curve fitting|Curve fitting]]
From Wikipedia: Line graph and Curve fitting
External Links
Frequency Polygon
[edit | edit source]Midpoints of the interval of corresponding rectangle in a histogram are joined together by straight lines. It gives a polygon i.e. a figure with many angles.
It is used when two or more sets of data are to be illustrated on the same diagram such as death rates in smokers and non-smokers, birth and death rates of a population etc.
One way to form a frequency polygon is to connect the midpoints at the top of the bars of a histogram with line segments (or a smooth curve). Of course the midpoints themselves could easily be plotted without the histogram and be joined by line segments. Sometimes it is beneficial to show the histogram and frequency polygon together.But sometimes, the frequency polygon is much more accurate than the histogram because you can evaluate which is the low point and the high point.
Unlike histograms, frequency polygons can be superimposed so as to compare several frequency distributions.
Frequency polygons were created in the 19th Century[1] as a way of not only storing data[citation needed], but making it easily accessible for people who are illiterate[citation needed].
Introduction to Probability
[edit | edit source]
Probability is connected with some unpredictability. We know what outcomes may occur, but not exactly which one. The set of possible outcomes plays a basic role. We call it the sample space and indicate it by S. Elements of S are called outcomes. In rolling a dice the sample space is S = {1,2,3,4,5,6}. Not only do we speak of the outcomes, but also about events, sets of outcomes (or subsets of the sample space). E.g. in rolling a dice we can ask whether the outcome was an even number, which means asking after the event "even" = E = {2,4,6}. In simple situations with a finite number of outcomes, we assign to each outcome s (∈ S) its probability (of occurrence) p(s) (written with a small p), a number between 0 and 1. It is a quite simple function, called the probability function, with the only further property that the total of all the probabilities sum up to 1. Also for events A do we speak of their probability P(A) (written with a capital P), which is simply the total of the probabilities of the outcomes in A. For a fair dice p(s) = 1/6 for each outcome s and P("even") = P(E) = 1/6+1/6+1/6 = 1/2.
The general concept of probability for non-finite sample spaces is a little more complex, although it rests on the same ideas.
Introduction
[edit | edit source]Why have probability in a statistics textbook?
[edit | edit source]Very little in mathematics is truly self contained. Many branches of mathematics touch and interact with one another, and the fields of probability and statistics are no different. A basic understanding of probability is vital in grasping basic statistics, and probability is largely abstract without statistics to determine the "real world" probabilities.
This section is not meant to give a comprehensive lecture in probability, but rather simply touch on the basics that are needed for this class, covering the basics of Bayesian Analysis for those students who are looking for something a little more interesting. This knowledge will be invaluable in attempting to understand the mathematics involved in various Distributions that come later.
Set notion
[edit | edit source]A set is a collection of objects. We usually use capital letters to denote sets, e.g. A is the set of females in this room.
- The members of a set A are called the elements of A, e.g. Patricia is an element of A (Patricia ∈ A); Patrick is not an element of A (Patrick ∉ A).
- The universal set, U, is the set of all objects under consideration, e.g., U is the set of all people in this room.
- The null set or empty set, ∅, has no elements, e.g., the set of males above 2.8m tall in this room is an empty set.
- The complement Ac of a set A is the set of elements in U outside A, i.e. x ∈ Ac iff x ∉ A.
- Let A and B be 2 sets. A is a subset of B if each element of A is also an element of B. Write A ⊂ B, e.g. the set of females wearing metal frame glasses in this room ⊂ the set of females wearing glasses in this room ⊂ the set of females in this room.
• The intersection A ∩ B of two sets A and B is the set of the common elements. I.e. x ∈ A ∩ B iff x ∈ A and x ∈ B.
• The union A ∪ B of two sets A and B is the set of all elements from A or B. I.e. x ∈ A ∪ B iff x ∈ A or x ∈ B.
Venn diagrams and notation
[edit | edit source]A Venn diagram visually models defined events. Each event is expressed with a circle. Events that have outcomes in common will overlap with what is known as the intersection of the events.

Probability Axioms
[edit | edit source]Calculating Probability
[edit | edit source]Negation
[edit | edit source]Negation is a way of saying "not A", hence saying that the complement of A has occurred. Note: The complement of an event A can be expressed as A' or Ac
For example: "What is the probability that a six-sided die will not land on a one?" (five out of six, or p = 0.833)

Or, more colloquially, "the probability of 'not X' together with the probability of 'X' equals one or 100%."
Relative frequency describes the number of successes over the total number of outcomes. For example if a coin is flipped and out of 50 flips 29 are heads then the relative frequency is
The Union of two events is when you want to know Event A OR Event B.
This is different from "And." "And" is the intersection, whereas "OR" is the union of the events (both events put together).

In the above example of events you will notice that...
Event A is a STAR and a DIAMOND.
Event B is a TRIANGLE and a PENTAGON and a STAR
(A ∩ B) = (A and B) = A intersect B is only the STAR
But (A ∪ B) = (A or B) = A Union B is EVERYTHING. The TRIANGLE, PENTAGON, STAR, and DIAMOND
Notice that both event A and Event B have the STAR in common. However, when you list the Union of the events you only list the STAR one time!
Event A = STAR, DIAMOND EVENT B = TRIANGLE, PENTAGON, STAR
When you combine them together you get (STAR + DIAMOND) + (TRIANGLE + PENTAGON + STAR) BUT WAIT!!! STAR is listed two times, so one will need to SUBTRACT the extra STAR from the list.
You should notice that it is the INTERSECTION that is listed TWICE, so you have to subtract the duplicate intersection.
Conjunction
[edit | edit source]Formula for the Union of Events: P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Example:
Let P(A) = 0.3 and P(B) = 0.2 and P(A ∩ B) = 0.15. Find P(A ∪ B).
P(A ∪ B) = (0.3) + (0.2) - (0.15) = 0.35
Example:
Let P(A) = 0.3 and P(B) = 0.2 and P(A ∩ B) = 0. Find P(A ∪ B).
Note: Since the intersection of the events is the null set, then you know the events are DISJOINT or MUTUALLY EXCLUSIVE.
P(A ∪ B) = (0.3) + (0.2) - (0) = 0.5
Disjunction
[edit | edit source]Law of total probability
[edit | edit source]The law of total probability is[1] a theorem that, in its discrete case, states if {\displaystyle \left\{{B_{n}:n=1,2,3,\ldots }\right\}}\left\{{B_{n}:n=1,2,3,\ldots }\right\} is a finite or countably infinite partition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event {\displaystyle B_{n}}B_{n} is measurable, then for any event {\displaystyle A}A of the same probability space:
{\displaystyle P(A)=\sum _{n}P(A\cap B_{n})}{\displaystyle P(A)=\sum _{n}P(A\cap B_{n})} or, alternatively,[1]
{\displaystyle P(A)=\sum _{n}P(A\mid B_{n})P(B_{n}),}{\displaystyle P(A)=\sum _{n}P(A\mid B_{n})P(B_{n}),} where, for any {\displaystyle n}n for which {\displaystyle P(B_{n})=0}{\displaystyle P(B_{n})=0} these terms are simply omitted from the summation, because {\displaystyle P(A\mid B_{n})}{\displaystyle P(A\mid B_{n})} is finite.
Conditional Probability
[edit | edit source]What is the probability of one event given that another event occurs? For example, what is the probability of a mouse finding the end of the maze, given that it finds the room before the end of the maze?
This is represented as:
or "the probability of A given B."
If A and B are independent of one another, such as with coin tosses or child births, then:
Thus, "what is the probability that the next child a family bears will be a boy, given that the last child is a boy."
This can also be stacked where the probability of A with several "givens."
or "the probability of A given that B1, B2, and B3 are true?"
-->
Conclusion: putting it all together
[edit | edit source]Bernoulli Trials
[edit | edit source]A lot of experiments just have two possible outcomes, generally referred to as "success" and "failure". If such an experiment is independently repeated we call them (a series of) Bernoulli trials. Usually the probability of success is called p. The repetition may be done in several ways:
- a fixed number of times (n); as a consequence the observed number of successes is stochastic;
- until a fixed number of successes (m) is observed; as a consequence the number of experiments is stochastic;
In the first case the number of successes is Binomial distributed with parameters n and p. For n=1 the distribution is also called the Bernoulli distribution. In the second case the number of experiments is Negative Binomial distributed with parameters m and p. For m=1 the distribution is also called the Geometric distribution.
Introductory Bayesian Analysis
[edit | edit source]Bayesian analysis is the branch of statistics based on the idea that we have some knowledge in advance about the probabilities that we are interested in, so called a priori probabilities. This might be your degree of belief in a particular event, the results from previous studies, or a general agreed-upon starting value for a probability. The terminology "Bayesian" comes from the Bayesian rule or law, a law about conditional probabilities. The opposite of "Bayesian" is sometimes referred to as "Frequentist Statistics."
Example
[edit | edit source]Consider a box with 3 coins, with probabilities of showing heads respectively 1/4, 1/2 and 3/4. We choose arbitrarily one of the coins. Hence we take 1/3 as the a priori probability of having chosen coin number 1. After 5 throws, in which X=4 times heads came up, it seems less likely that the coin is coin number 1. We calculate the a posteriori probability that the coin is coin number 1, as:
In words:
- The probability that the Coin is the first Coin, given that we know heads came up 4 times... Is equal to the probability that heads came up 4 times given we know it's the first coin, times the probability that the coin is the first coin. All divided by the probability that heads comes up 4 times (ignoring which of the three Coins is chosen). The binomial coefficients cancel out as well as all denominators when expanding 1/2 to 2/4. This results in
In the same way we find:
and
- .
This shows us that after examining the outcome of the five throws, it is most likely we did choose coin number 3.
Actually for a given result the denominator does not matter, only the relative Probabilities When the result is 3 times heads the Probabilities change in favor of Coin 2 and further as the following table shows:
| Heads | |||
|---|---|---|---|
| 5 | 1 | 32 | 243 |
| 4 | 3 | 32 | 81 |
| 3 | 9 | 32 | 27 |
| 2 | 27 | 32 | 9 |
| 1 | 81 | 32 | 3 |
| 0 | 243 | 32 | 1 |
Distributions
[edit | edit source]How are the results of the latest SAT test? What is the average height of females under 21 in Zambia? How does beer consumption among college students at engineering college compare to college students in liberal arts colleges?
To answer these questions, we would collect data and put them in a form that is easy to summarize, visualize, and discuss. Loosely speaking, the collection and aggregation of data result in a distribution. Distributions are most often in the form of a histogram or a table. That way, we can "see" the data immediately and begin our scientific inquiry.
For example, if we want to know more about students' latest performance on the SAT, we would collect SAT scores from ETS, compile them in a way that is pertinent to us, and then form a distribution of these scores. The result may be a data table or it may be a plot. Regardless, once we "see" the data, we can begin asking more interesting research questions about our data.
The distributions we create often parallel distributions that are mathematically generated. For example, if we obtain the heights of all high school students and plot this data, the graph may resemble a normal distribution, which is generated mathematically. Then, instead of painstakingly collecting heights of all high school students, we could simply use a normal distribution to approximate the heights without sacrificing too much accuracy.
In the study of statistics, we focus on mathematical distributions for the sake of simplicity and relevance to the real-world. Understanding these distributions will enable us to visualize the data easier and build models quicker. However, they cannot and do not replace the work of manual data collection and generating the actual data distribution.
What percentage lie within a certain range? Distributions show what percentage of the data lies within a certain range. So, given a distribution, and a set of values, we can determine the probability that the data will lie within a certain range.
The same data may lead to different conclusions if it is interposed on different distributions. So, it is vital in all statistical analysis for data to be put onto the correct distribution.
Distributions
Comparison of Some Distributions
[edit | edit source]| Name | Notation | Formula | Symbols | Use | Continuous/ discrete | Notes |
|---|---|---|---|---|---|---|
| Bernoulli | f(x)= | p x |
2 outcomes | Discrete | 1 trial | |
| Binomial | b(x;n, p)= | n trials k successes p probability |
number of times success specific probabilities not random |
Discrete | ||
| Poisson | P(x)= | outcome/time outcome/region |
Discrete | |||
| Hypergeometric | h(x;N,n,k) = | n samples from N items k of N items are successes, N-k are failures |
X times success occurs irregardless of location is random |
Discrete | Without Replacement | |
| Multivariate Hypergeometric |
n sample size N items k cells each with elements |
Discrete | Without Replacement | |||
| Normal | x average std dev |
: | Continuous | Z is a random variable with | ||
| Chi-Square | variance of a rand sampp of size n taken from norm pop w/ var | variances of random sample related to the pop | Continuous | |||
| Student-t | T= | mean of rand samp size n | If don't know | Continuous | v=n-1 | |
| F | F= | Continuous |
Discrete Distributions
[edit | edit source]'Discrete' data are data that assume certain discrete and quantized values. For example, true-false answers are discrete, because there are only two possible choices. Valve settings such as 'high/medium/low' can be considered as discrete values. As a general rule, if data can be counted in a practical manner, then they can be considered to be discrete.
To demonstrate this, let us consider the population of the world. It is a discrete number because the number of civilians is theoretically countable. But since this is not practicable, statisticians often treat this data as continuous. That is, we think of population as within a range of numbers rather than a single point.
For the curious, the world population is 6,533,596,139 as of August 9, 2006. Please note that statisticians did not arrive at this figure by counting individual residents. They used much smaller samples of the population to estimate the whole. Going back to Chapter 1, this is a great reason to learn statistics - we need only a smaller sample of data to make intelligent descriptions of the entire population!
Discrete distributions result from plotting the frequency distribution of data which is discrete in nature.
General Properties
[edit | edit source]Cumulative Distribution Function
[edit | edit source]A discrete random variable has a cumulative distribution function that describes the probability that the random variable is below the point. The cumulative distribution must increase towards 1. Depending on the random variable, it may reach one at a finite number, or it may not. The cdf is represented by a capital F.
ń====Probability Mass Function====
A discrete random variable has a probability mass function that describes how likely the random variable is to be at a certain point. The probability mass function must have a total of 1, and sums to the cdf. The pmf is represented by the lowercase f.
Special Values
[edit | edit source]The expected value of a discrete variable is
The expected value of any function of a discrete variable g() is
The variance is equal to
External Links
Simulating binomial, hypergeometric, and the Poisson distribution: Discrete Distributions
Discrete Uniform Distribution
[edit | edit source]The discrete uniform distribution (not to be confused with the continuous uniform distribution) is where the probability of equally spaced possible values is equal. Mathematically this means that the probability density function is identical for a finite set of evenly spaced points. An example of would be rolling a fair 6-sided die. In this case there are six, equally like probabilities.
One common normalization is to restrict the possible values to be integers and the spacing between possibilities to be 1. In this setup, the only two parameters of the function are the minimum value (a), the maximum value (b). (Some even normalize it more, setting a=1.) Let n=b-a+1 be the number of possibilities. The probability density function is then
Mean
[edit | edit source]Let . The mean (notated as ) can then be derived as follows:
Remember that in
Variance
[edit | edit source]The variance () can be derived:
Remember that in
| A Wikibookian suggests that R_Programming/Probability_Functions/Bernoulli be merged into this chapter. Discuss whether or not this merger should happen on the discussion page. |
Bernoulli Distribution: The coin toss
[edit | edit source]| Parameters | |
|---|---|
| Support | |
| PMF | |
| CDF | |
| Mean | |
| Median | |
| Mode | |
| Variance | |
| Skewness | |
| Ex. kurtosis | |
| Entropy | |
| MGF | |
| CF | |
| PGF | |
| Fisher information |
There is no more basic random event than the flipping of a coin. Heads or tails. It's as simple as you can get! The "Bernoulli Trial" refers to a single event which can have one of two possible outcomes with a fixed probability of each occurring. You can describe these events as "yes or no" questions. For example:
- Will the coin land heads?
- Will the newborn child be a girl?
- Are a random person's eyes green?
- Will a mosquito die after the area was sprayed with insecticide?
- Will a potential customer decide to buy my product?
- Will a citizen vote for a specific candidate?
- Is an employee going to vote pro-union?
- Will this person be abducted by aliens in their lifetime?
The Bernoulli Distribution has one controlling parameter: the probability of success. A "fair coin" or an experiment where success and failure are equally likely will have a probability of 0.5 (50%). Typically the variable p is used to represent this parameter.
If a random variable X is distributed with a Bernoulli Distribution with a parameter p we write its probability mass function as:
Where the event X=1 represents the "yes."
This distribution may seem trivial, but it is still a very important building block in probability. The Binomial distribution extends the Bernoulli distribution to encompass multiple "yes" or "no" cases with a fixed probability. Take a close look at the examples cited above. Some similar questions will be presented in the next section which might give an understanding of how these distributions are related.
Mean
[edit | edit source]The mean (E[X]) can be derived:
Variance
[edit | edit source]External links
[edit | edit source]| A Wikibookian suggests that R Programming/Probability Functions/Binomial be merged into this chapter. Discuss whether or not this merger should happen on the discussion page. |
Where the Bernoulli Distribution asks the question of "Will this single event succeed?" the Binomial is associated with the question "Out of a given number of trials, how many will succeed?" Some example questions that are modeled with a Binomial distribution are:
- Out of ten tosses, how many times will this coin land heads?
- From the children born in a given hospital on a given day, how many of them will be girls?
- How many students in a given classroom will have green eyes?
- How many mosquitos, out of a swarm, will die when sprayed with insecticide?
The relation between the Bernoulli and binomial distributions is intuitive: The binomial distribution is composed of multiple Bernoulli trials. We conduct repeated experiments where the probability of success is given by the parameter and add up the number of successes. This number of successes is represented by the random variable X. The value of X is then between 0 and .
When a random variable X has a binomial distribution with parameters and we write it as X ~ Bin(n,p) or X ~ B(n,p) and the probability mass function is given by the equation:
where
For a refresher on factorials (n!), go back to the Refresher Course earlier in this wiki book.
An example
[edit | edit source]Let's walk through a simple example of the binomial distribution. We're going to use some pretty small numbers because factorials can be hard to compute. We are going to ask five random people if they believe there is life on other planets. We are going to assume in this example that we know 30% of people believe this to be true. We want to ask the question: "How many people will say they believe in extraterrestrial life?" Actually, we want to be more specific than that: "What is the probability that exactly 2 people will say they believe in extraterrestrial life?"
We know all the values that we need to plug into the equation. The number of people asked, n=5. The probability of any given person answering "yes", p=0.3. (Remember, I said that 30% of people believe in life on other planets!) Finally, we're asking for the probability that exactly 2 people answer "yes" so k=2. This yields the equation:
- since
Here are the probabilities for all the possible values of X. You can get these values by replacing the k=2 in the above equation with all values from 0 to 5.
| Value for k | Probability f(k) |
| 0 | 0.16807 |
| 1 | 0.36015 |
| 2 | 0.30870 |
| 3 | 0.13230 |
| 4 | 0.02835 |
| 5 | 0.00243 |
What can we learn from these results? Well, first of all we'll see that it's just a little more likely that only one person will confess to believing in life on other planets. There's a distinct chance (about 17%) that nobody will believe it, and there's only a 0.24% (a little over 2 in 1000) that all five people will be believers.
Explanation of the equation
[edit | edit source]Take the above example. Let's consider each of the five people one by one.
The probability that any one person believes in extraterrestrial life is 30%, or 0.3. So the probability that any two people both believe in extraterrestrial life is 0.3 squared. Similarly, the probability that any one person does not believe in extraterrestrial life is 70%, or 0.7, so the probability that any three people do not believe in extraterrestrial life is 0.7 cubed.
Now, for two out of five people to believe in extraterrestrial life, two conditions must be satisfied: two people believe in extraterrestrial life, and three do not. The probability of two out of five people believing in extraterrestrial life would thus appear to be 0.3 squared (two believers) times 0.7 cubed (three non-believers), or 0.03087.
However, in doing this, we are only considering the case whereby the first two selected people are believers. How do we consider cases such as that in which the third and fifth people are believers, which would also mean a total of two believers out of five?
The answer lies in combinatorics. Bearing in mind that the probability that the first two out of five people believe in extraterrestrial life is 0.03087, we note that there are C(5,2), or 10, ways of selecting a set of two people from out of a set of five, i.e. there are ten ways of considering two people out of the five to be the "first two". This is why we multiply by C(n,k). The probability of having any two of the five people be believers is ten times 0.03087, or 0.3087.
feruzi [2]
[edit | edit source]The mean can be derived as follow.
Now let w=x-1 and m=n-1. We see that m-w=n-x. We can now rewrite the summation as
We now see that the summation is the sum over the complete pmf of a binomial random variable distributed Bin(m, p). This is equal to 1 (and can be easily verified using the Binomial theorem). Therefore, we have
Variance
[edit | edit source]We derive the variance using the following formula:
We have already calculated E[X] above, so now we will calculate E[X2] and then return to this variance formula:
We can use our experience gained above in deriving the mean. We use the same definitions of m and w.
The first sum is identical in form to the one we calculated in the Mean (above). It sums to mp. The second sum is 1.
Using this result in the expression for the variance, along with the Mean (E(X) = np), we get
External links
[edit | edit source]Poisson Distribution
[edit | edit source]Probability mass function The horizontal axis is the index k, the number of occurrences. The function is only defined at integer values of k. The connecting lines are only guides for the eye. | |
Cumulative distribution function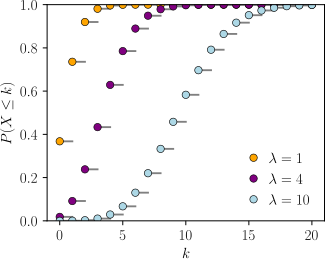 The horizontal axis is the index k, the number of occurrences. The CDF is discontinuous at the integers of k and flat everywhere else because a variable that is Poisson distributed only takes on integer values. | |
| Notation | |
|---|---|
| Parameters | λ > 0 (real) |
| Support | k ∈ { 0, 1, 2, 3, ... } |
| PMF | |
| CDF | --or--
(for where is the Incomplete gamma function and is the floor function) |
| Mean | |
| Median | |
| Mode | |
| Variance | |
| Skewness | |
| Ex. kurtosis | |
| Entropy |
(for large )
|
| MGF | |
| CF | |
| PGF | |
Any French speaker will notice that "Poisson" means "fish", but really there's nothing fishy about this distribution. It's actually pretty straightforward. The name comes from the mathematician Siméon-Denis Poisson (1781-1840).
The Poisson Distribution is very similar to the Binomial Distribution. We are examining the number of times an event happens. The difference is subtle. Whereas the Binomial Distribution looks at how many times we register a success over a fixed total number of trials, the Poisson Distribution measures how many times a discrete event occurs, over a period of continuous space or time. There isn't a "total" value n. As with the previous sections, let's examine a couple of experiments or questions that might have an underlying Poisson nature.
- How many pennies will I encounter on my walk home?
- How many children will be delivered at the hospital today?
- How many mosquito bites did you get today after having sprayed with insecticide?
- How many angry phone calls did I get after airing a particularly distasteful political ad?
- How many products will I sell after airing a new television commercial?
- How many people, per hour, will cross a picket line into my store?
- How many alien abduction reports will be filed this year?
- How many defects will there be per 100 metres of rope sold?
What's a little different about this distribution is that the random variable X which counts the number of events can take on any non-negative integer value. In other words, I could walk home and find no pennies on the street. I could also find one penny. It's also possible (although unlikely, short of an armored-car exploding nearby) that I would find 10 or 100 or 10,000 pennies.
Instead of having a parameter p that represents a component probability like in the Bernoulli and Binomial distributions, this time we have the parameter "lambda" or λ which represents the "average or expected" number of events to happen within our experiment. The probability mass function of the Poisson is given by
- .
An example
[edit | edit source]We run a restaurant and our signature dish (which is very expensive) gets ordered on average 4 times per day. What is the probability of having this dish ordered exactly 3 times tomorrow? If we only have the ingredients to prepare 3 of these dishes, what is the probability that it will get sold out and we'll have to turn some orders away?
The probability of having the dish ordered 3 times exactly is given if we set k=3 in the above equation. Remember that we've already determined that we sell on average 4 dishes per day, so λ=4.
Here's a table of the probabilities for all values from k=0..6:
| Value for k | Probability f(k) |
| 0 | 0.0183 |
| 1 | 0.0733 |
| 2 | 0.1465 |
| 3 | 0.1954 |
| 4 | 0.1954 |
| 5 | 0.1563 |
| 6 | 0.1042 |
Now for the big question: Will we run out of food by the end of the day tomorrow? In other words, we're asking if the random variable X>3. In order to compute this we would have to add the probabilities that X=4, X=5, X=6,... all the way to infinity! But wait, there's a better way!
The probability that we run out of food P(X>3) is the same as 1 minus the probability that we don't run out of food, or 1-P(X≤3). So if we total the probability that we sell zero, one, two and three dishes and subtract that from 1, we'll have our answer. So,
- 1 - P(X≤3) = 1 - ( P(X=0) + P(X=1) + P(X=2) + P(X=3) ) = 1 - 0.4335 = 0.5665
In other words, we have a 56.65% chance of selling out of our wonderful signature dish. I guess crossing our fingers is in order!
Mean
[edit | edit source]We calculate the mean as follows:
Remember that
Variance
[edit | edit source]We derive the variance using the following formula:
We have already calculated E[X] above, so now we will calculate E[X2] and then return to this variance formula:
- ....replacing with
The first sum is E[X]=λ and the second we also calculated above to be 1.
Returning to the variance formula we find that
External links
[edit | edit source]Geometric Distribution
[edit | edit source]Probability mass function
| |
Cumulative distribution function
| |
| Parameters | success probability (real) |
|---|---|
| Support | |
| PMF | |
| CDF | |
| Mean | |
| Median | (not unique if is an integer) |
| Mode | |
| Variance | |
| Skewness | |
| Ex. kurtosis | |
| Entropy | |
| MGF | , for |
| CF | |
There are two similar distributions with the name "Geometric Distribution".
- The probability distribution of the number X of Bernoulli trials needed to get one success, supported on the set { 1, 2, 3, ...}
- The probability distribution of the number Y = X − 1 of failures before the first success, supported on the set { 0, 1, 2, 3, ... }
These two different geometric distributions should not be confused with each other. Often, the name shifted geometric distribution is adopted for the former one. We will use X and Y to refer to distinguish the two.
Shifted
[edit | edit source]The shifted Geometric Distribution refers to the probability of the number of times needed to do something until getting a desired result. For example:
- How many times will I throw a coin until it lands on heads?
- How many children will I have until I get a girl?
- How many cards will I draw from a pack until I get a Joker?
Just like the Bernoulli Distribution, the Geometric distribution has one controlling parameter: The probability of success in any independent test.
If a random variable X is distributed with a Geometric Distribution with a parameter p we write its probability mass function as:
With a Geometric Distribution it is also pretty easy to calculate the probability of a "more than n times" case. The probability of failing to achieve the wanted result is .
Example: a student comes home from a party in the forest, in which interesting substances were consumed. The student is trying to find the key to his front door, out of a keychain with 10 different keys. What is the probability of the student succeeding in finding the right key in the 4th attempt?
Unshifted
[edit | edit source]The probability mass function is defined as:
- for
Mean
[edit | edit source]Let q=1-p
We can now interchange the derivative and the sum.
Variance
[edit | edit source]We derive the variance using the following formula:
We have already calculated E[X] above, so now we will calculate E[X2] and then return to this variance formula:
Let q=1-p
We now manipulate x2 so that we get forms that are easy to handle by the technique used when deriving the mean.
We then return to the variance formula
External links
[edit | edit source]Negative Binomial Distribution
[edit | edit source]Just as the Bernoulli and the Binomial distribution are related in counting the number of successes in 1 or more trials, the Geometric and the Negative Binomial distribution are related in the number of trials needed to get 1 or more successes.
The Negative Binomial distribution refers to the probability of the number of times needed to do something until achieving a fixed number of desired results. For example:
- How many times will I throw a coin until it lands on heads for the 10th time?
- How many children will I have when I get my third daughter?
- How many cards will I have to draw from a pack until I get the second Joker?
Just like the Binomial Distribution, the Negative Binomial distribution has two controlling parameters: the probability of success p in any independent test and the desired number of successes m. If a random variable X has Negative Binomial distribution with parameters p and m, its probability mass function is:
- .
Example
[edit | edit source]A travelling salesman goes home if he has sold 3 encyclopedias that day. Some days he sells them quickly. Other days he's out till late in the evening. If on the average he sells an encyclopedia at one out of ten houses he approaches, what is the probability of returning home after having visited only 10 houses?
Answer:
The number of trials X is Negative Binomial distributed with parameters p=0.1 and m=3, hence:
- .
Mean
[edit | edit source]The mean can be derived as follows.
Now let s = r+1 and w=x-1 inside the summation.
We see that the summation is the sum over a the complete pmf of a negative binomial random variable distributed NB(s,p), which is 1 (and can be verified by applying Newton's generalized binomial theorem).
Variance
[edit | edit source]We derive the variance using the following formula:
We have already calculated E[X] above, so now we will calculate E[X2] and then return to this variance formula:
Again, let let s = r+1 and w=x-1.
The first summation is the mean of a negative binomial random variable distributed NB(s,p) and the second summation is the complete sum of that variable's pmf.
We now insert values into the original variance formula.
Hypergeometric Distribution
[edit | edit source]Probability mass function
| |
Cumulative distribution function
| |
| Notation | |
|---|---|
| Parameters | |
| Support | |
| PMF | |
| CDF | where is the generalized hypergeometric function |
| Mean | |
| Median | mode = |
| Variance | |
| Skewness | |
| Ex. kurtosis |
|
| Entropy | ??? |
| MGF | |
| CF | |
The hypergeometric distribution describes the number of successes in a sequence of n draws without replacement from a population of N that contained m total successes.
Its probability mass function is:
Technically the support for the function is only where x∈[max(0, n+m-N), min(m, n)]. In situations where this range is not [0,n], f(x)=0 since for k>0, .
Probability Density Function
[edit | edit source]We first check to see that f(x) is a valid pmf. This requires that it is non-negative everywhere and that its total sum is equal to 1. The first condition is obvious. For the second condition we will start with Vandermonde's identity
We now see that if a=m and b=N-m that the condition is satisfied.
Mean
[edit | edit source]We derive the mean as follows:
We use the identity in the denominator.
Next we use the identity in the first binomial of the numerator.
Next, for the variables inside the sum we define corresponding prime variables that are one less. So N′=N−1, m′=m−1, x′=x−1, n′=n-1.
Now we see that the sum is the total sum over a Hypergeometric pmf with modified parameters. This is equal to 1. Therefore
Variance
[edit | edit source]We first determine E(X2).
We use the same variable substitution as when deriving the mean.
The first sum is the expected value of a hypergeometric random variable with parameteres (n',m',N'). The second sum is the total sum that random variable's pmf.
We then solve for the variance
or, equivalently,
Continuous Distributions
[edit | edit source]A continuous statistic is a random variable that does not have any points at which there is any distinct probability that the variable will be the corresponding number.
General Properties
[edit | edit source]Cumulative Distribution Function
[edit | edit source]A continuous random variable, like a discrete random variable, has a cumulative distribution function. Like the one for a discrete random variable, it also increases towards 1. Depending on the random variable, it may reach one at a finite number, or it may not. The cdf is represented by a capital F.
Probability Distribution Function
[edit | edit source]Unlike a discrete random variable, a continuous random variable has a probability density function instead of a probability mass function. The difference is that the former must integrate to 1, while the latter must have a total value of 1. The two are very similar, otherwise. The pdf is represented by a lowercase f.
Special Values
[edit | edit source]Let R be the set of points of the distribution.
The expected value for a continuous variable X with probability density function f is defined as .
More generally, the expected value of any continuously transformed variable g(X) with probability density function f is defined as .
The mean of a continuous or discrete distribution is defined as .
The variance of a continuous or discrete distribution is defined as .
Expectations can also be derived by producing the Moment Generating Function for the distribution in question. This is done by finding the expected value . Once the Moment Generating Function has been created, each derivative of the function gives a different piece of information about the distribution function.
= mean
= variance
= skewness
= kurtosis
Continuous Uniform Distribution
[edit | edit source]Probability density function Using maximum convention | |
Cumulative distribution function
| |
| Notation | |
|---|---|
| Parameters | |
| Support | |
| CDF | |
| Mean | |
| Median | |
| Mode | any value in |
| Variance | |
| Skewness | 0 |
| Ex. kurtosis | |
| Entropy | |
| MGF | |
| CF | |
The (continuous) uniform distribution, as its name suggests, is a distribution with probability densities that are the same at each point in an interval. In casual terms, the uniform distribution shapes like a rectangle.
Mathematically speaking, the probability density function of the uniform distribution is defined as
And the cumulative distribution function is:
Mean
[edit | edit source]We derive the mean as follows.
As the uniform distribution is 0 everywhere but [a, b] we can restrict ourselves that interval
Variance
[edit | edit source]We use the following formula for the variance.
External links
[edit | edit source]Normal Distribution
[edit | edit source]Probability density function The red curve is the standard normal distribution | |
Cumulative distribution function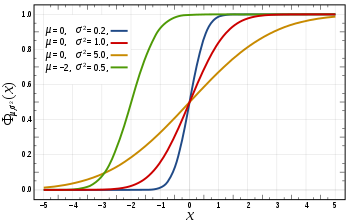 | |
| Notation | |
|---|---|
| Parameters | μ ∈ R — mean (location) σ2 > 0 — variance (squared scale) |
| Support | x ∈ R |
| CDF | |
| Mean | μ |
| Median | μ |
| Mode | μ |
| Variance | |
| Skewness | 0 |
| Ex. kurtosis | 0 |
| Entropy | |
| MGF | |
| CF | |
| Fisher information | |
Normal distribution is without exception the most widely used distribution. It also goes under the name Gaussian distribution. It assumes that the observations are closely clustered around the mean, μ, and this amount is decaying quickly as we go farther away from the mean. The measure of spread is quantified by the variance, .
Some examples of applications are:
- If the average man is 175 cm tall with a variance of 6 cm, what is the probability that a man found at random will be 183 cm tall?
- If the average man is 175 cm tall with a variance of 6 cm and the average woman is 168 cm tall with a variance of 3cm, what is the probability that the average man will be shorter than the average woman?
- If cans are assumed to have a variance of 4 grams, what does the average weight need to be in order to ensure that the 99% of all cans have a weight of at least 250 grams?
The density function is:
where .
and the cumulative distribution function cannot be integrated into a single expression.
Normal distribution with parameters μ and σ is denoted as . If the rv X is normally distributed with expectation μ and standard deviation σ, one denotes:
Probability mass function
[edit | edit source]To verify that f(x) is a valid pmf we must verify that (1) it is non-negative everywhere, and (2) that the total integral is equal to 1. The first is obvious, so we move on to verify the second.
Now let . We see that .
Now we use the Gaussian integral that
Mean
[edit | edit source]We derive the mean as follows
We now see that the right integral is the complete integral over a normal pmf. This is therefore 1.
Variance
[edit | edit source]We let
We now use integration by parts with u=w and v=(-1/2)e^(-w^2)
We see that the bracketed term is zero by L'Hôpital's rule.
Now we use the Gaussian integral again
External links
[edit | edit source]Exponential Distribution
[edit | edit source]Probability density function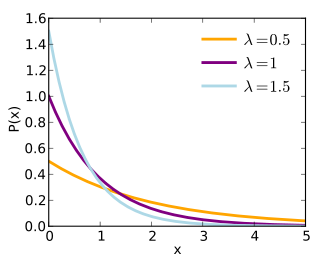
| |
Cumulative distribution function
| |
| Parameters | λ > 0 rate, or inverse scale |
|---|---|
| Support | x ∈ [0, ∞) |
| λ e−λx | |
| CDF | 1 − e−λx |
| Mean | λ−1 |
| Median | λ−1 ln 2 |
| Mode | 0 |
| Variance | λ−2 |
| Skewness | 2 |
| Ex. kurtosis | 6 |
| Entropy | 1 − ln(λ) |
| MGF | |
| CF | |
Exponential distribution refers to a statistical distribution used to model the time between independent events that happen at a constant average rate λ. Some examples of this distribution are:
- The distance between one car passing by after the previous one.
- The rate at which radioactive particles decay.
For the stochastic variable X, probability distribution function of it is:
and the cumulative distribution function is:
Exponential distribution is denoted as , where m is the average number of events within a given time period. So if m=3 per minute, i.e. there are three events per minute, then λ=1/3, i.e. one event is expected on average to take place every 20 seconds.
Mean
[edit | edit source]We derive the mean as follows.
We will use integration by parts with u=−x and v=e−λx. We see that du=-1 and dv=−λe−λx.
Variance
[edit | edit source]We use the following formula for the variance.
We'll use integration by parts with and . From this we have and .
We see that the integral is just which we solved for above.
External links
[edit | edit source]Gamma Distribution
[edit | edit source]Probability density function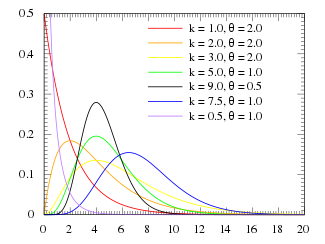
| |
Cumulative distribution function
| |
| Parameters | |
|---|---|
| Support | |
| CDF | |
| Mean | (see digamma function) |
| Median | No simple closed form |
| Mode | |
| Variance | (see trigamma function ) |
| Skewness | |
| Ex. kurtosis | |
| Entropy | |
The Gamma distribution is very important for technical reasons, since it is the parent of the exponential distribution and can explain many other distributions.
The probability distribution function is:
Where is the Gamma function. The cumulative distribution function cannot be found unless p=1, in which case the Gamma distribution becomes the exponential distribution. The Gamma distribution of the stochastic variable X is denoted as .
Alternatively, the gamma distribution can be parameterized in terms of a shape parameter and an inverse scale parameter , called a rate parameter:
where the constant can be calculated setting the integral of the density function as 1:
following:
and, with change of variable :
following:
Probability Density Function
[edit | edit source]We first check that the total integral of the probability density function is 1.
Now we let y=x/a which means that dy=dx/a
Mean
[edit | edit source]Now we let y=x/a which means that dy=dx/a.
We now use the fact that
Variance
[edit | edit source]We first calculate E[X^2]
Now we let y=x/a which means that dy=dx/a.
Now we use calculate the variance
External links
[edit | edit source]F Distribution
[edit | edit source]Probability density function
| |
Cumulative distribution function
| |
| Parameters | d1, d2 > 0 deg. of freedom |
|---|---|
| Support | x ∈ [0, +∞) |
| CDF | |
| Mean | for d2 > 2 |
| Mode | for d1 > 2 |
| Variance | for d2 > 4 |
| Skewness | for d2 > 6 |
| Ex. kurtosis | see text |
| MGF | does not exist, raw moments defined in text and in |
| CF | see text |
Named after Sir Ronald Fisher, who developed the F distribution for use in determining ANOVA critical values. The cutoff values in an F table are found using three variables- ANOVA numerator degrees of freedom, ANOVA denominator degrees of freedom, and significance level.
ANOVA is an abbreviation of analysis of variance. It compares the size of the variance between two different samples. This is done by dividing the larger variance over the smaller variance. The formula of the F statistic is:
where and are the chi-square statistics of sample one and two respectively, and and are their degrees of freedom, i.e. the number of observations.
One example could be if you want to compare apples that look alike but are from different trees and have different sizes. You want to investigate whether they have the same variance of the weight on average.
There are three apples from the first tree that weigh 110, 121 and 143 grams respectively, and four from the other which weigh 88, 93, 105 and 124 grams respectively. The mean and variance of the first sample are 124.67 and 16.80 respectively, and of the second sample 102.50 and 16.01. The chi-square statistic of the first sample is
,
and for the second sample
.
The F statistic is now F = . The Chi-square statistic divided by degrees of freedom appears on the nominator for the second sample because it was larger than that of the first sample.
The critical value of the F distribution for 4 degrees of freedom in the nominator and 3 degrees of freedom in the denominator, i.e. F(f1=4, f2=3) is 9.12 at a 5% level of confidence. Since the test statistic 1.125 is smaller than the critical value, we cannot reject the null hypothesis that they have the same variance. The conclusion is that they have the same variance.
External links
[edit | edit source]Chi-square Distribution
[edit | edit source]Probability density function
| |
Cumulative distribution function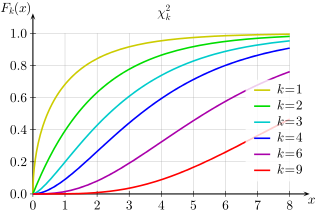
| |
| Notation | or |
|---|---|
| Parameters | (known as "degrees of freedom") |
| Support | if , otherwise |
| CDF | |
| Mean | |
| Median | |
| Mode | |
| Variance | |
| Skewness | |
| Ex. kurtosis | |
| Entropy | |
| MGF | |
| CF | |
| PGF | |
Chi-square distribution is related to normal distribution. A chi-square statistic is the sum of a number of independent and standard normal random variables.
Assume that we have n number of random variables Z, that are normally distributed. Therefore, we can write . If we square Z such that , then we get the chi-square distribution . If we sum n number of , we can write
.
One example could be that we want to know whether the weight of a set of eight apples is normally distributed. Chi-square distribution can be used to test for this. Assume that the apples weigh 88, 93, 110, 76, 78, 121, 92 and 86 grams, and we have knowledge of the mean and the standard deviation weight of all apples. We obtain the normally distributed Z values by subtracting the mean weight (93) and divide by the standard deviation (15.41). For example, the first apple has Z-score using four decimal points. Square all the Z values, then taking the sum yields a Chi-squared distributed random variable with mean 8 and variance 16.
Now when we have the value of the chi-square statistic Y, we compare it to the critical value of the chi-square distribution at n = 8 degrees of freedom and 95% level of significance which can found in a Chi-square statistical table. The null hypothesis is that the sample of apples is normally distributed. It is rejected if the value of the test statistic is higher than the critical value.
The chi-square distribution is a special case of the gamma distribution, where a=2 and p=k/2. The probability density function is:
Summary statistics
[edit | edit source]The mean of a chi-squared is
The variance of a chi-squared is
For the proof of these, see the gamma distribution.
External links
[edit | edit source]Student-t Distribution
[edit | edit source]Probability density function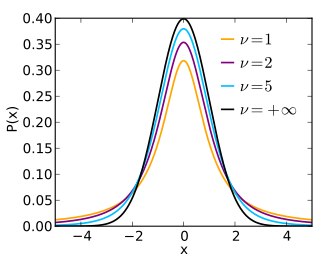
| |
Cumulative distribution function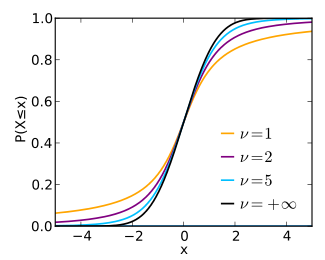
| |
| Parameters | ν > 0 degrees of freedom (real) |
|---|---|
| Support | x ∈ (−∞; +∞) |
| CDF | where 2F1 is the hypergeometric function |
| Mean | 0 for ν > 1, otherwise undefined |
| Median | 0 |
| Mode | 0 |
| Variance | for ν > 2, ∞ for 1 < ν ≤ 2, otherwise undefined |
| Skewness | 0 for ν > 3, otherwise undefined |
| Ex. kurtosis | for ν > 4, ∞ for 2 < ν ≤ 4, otherwise undefined |
| Entropy | ... |
| MGF | undefined |
| CF | for ν > 0
|
Student t-distribution (or just t-distribution for short) is derived from the chi-square and normal distributions. We divide the standard normally distributed value of one variable over the root of a chi-square value over its r degrees of freedom. Mathematically, this appears as:
where and .
External links
[edit | edit source]Testing Statistical Hypothesis
[edit | edit source]
There are many different tests for the many different kinds of data. A way to get started is to understand what kind of data you have. Are the variables quantitative or qualitative? Certain tests are for certain types of data depending on the size, distribution or scale. Also, it is important to understand how samples of data can differ. The 3 primary characteristics of quantitative data are: central tendency, spread, and shape.
When most people "test" quantitative data, they tend to do tests for central tendency. Why? Well, let's say you had 2 sets of data and you wanted to see if they were different from each other. One way to test this would be to test to see if their central tendency (their means for example) differ.
Imagine two symmetric, bell shaped curves with a vertical line drawn directly in the middle of each, as shown here. If one sample was a lot different than another (a lot higher in values, etc.) then the means would be different typically. So when testing to see if two samples are different, usually two means are compared.
Two medians (another measure of central tendency) can be compared also. Or perhaps one wishes to test two samples to see if they have the same spread or variation. Because statistics of central tendency, spread, etc. follow different distributions - different testing procedures must be followed and utilized.
In the end, most folks summarize the result of a hypothesis test into one particular value - the p-value. If the p-value is smaller than the level of significance (usually , but even lower in other fields of science i.e. Medicine) then you reject the null-hypothesis, but this does not mean you accept the alternative hypothesis. The p-value is essentially the probability of obtaining a test statistic at least as extreme as the one observed. If the p-value is greater than the level of significance you fail to reject the null-hypothesis, but this does not mean that the null-hypothesis is correct.
Purpose of Statistical Tests
[edit | edit source]| |
A Wikibookian has nominated this page for cleanup because: Copy editing necessary You can help make it better. Please review any relevant discussion. |
| A Wikibookian has nominated this page for cleanup because: Copy editing necessary You can help make it better. Please review any relevant discussion. |
Purpose of Statistical test
[edit | edit source]In general, the purpose of statistical tests is to determine whether some hypothesis is extremely unlikely given observed data.
There are two common philosophical approaches to such tests, significance testing (due to Fisher) and hypothesis testing (due to Neyman and Pearson).
Significance testing aims to quantify evidence against a particular hypothesis being true. We can think of it as testing to guide research. We believe a certain statement may be true and want to work out whether it is worth investing time investigating it. Therefore, we look at the opposite of this statement. If it is quite likely then the further study would seem to not make sense. However, if it is extremely unlikely then further study would make sense.
A concrete example of this might be in drug testing. We have a number of drugs that we want to test and only limited time, so we look at the hypothesis that an individual drug has no positive effect whatsoever and only look further if this is unlikely.
Hypothesis testing rather looks at the evidence for a particular hypothesis being true. We can think of this as a guide to making a decision. We need to make a decision soon and suspect that a given statement is true. Thus we see how unlikely we are to be wrong, and if we are sufficiently unlikely to be wrong we can assume that this statement is true. Often this decision is final and cannot be changed.
Statisticians often overlook these differences and incorrectly treat the terms "significance test" and "hypothesis test" as though they are interchangeable.
A data analyst frequently wants to know whether there is a difference between two sets of data, and whether that difference is likely to occur due to random fluctuations, or is instead unusual enough that random fluctuations rarely cause such differences.
In particular, frequently we wish to know something about the average (or mean), or about the variability (as measured by variance or standard deviation).
Statistical tests are carried out by first making some assumption, called the Null Hypothesis, and then determining whether the data observed is unlikely to occur given that assumption. If the probability of seeing the observed data is small enough under the assumed the Null Hypothesis, then the Null Hypothesis is rejected.
A simple example might help. We wish to determine if men and women are the same height on average. We select and measure 20 women and 20 men. We assume the Null Hypothesis that there is no difference between the average value of heights for men vs. women. We can then test using the t-test to determine whether our sample of 40 heights would be unlikely to occur given this assumption. The basic idea is to assume heights are normally distributed and to assume that the means and standard deviations are the same for women and for men. Then we calculate the average of our 20 men, and of our 20 women, we also calculate the sample standard deviation for each. Then using the t-test of two means with 40-2 = 38 degrees of freedom we can determine whether the difference in heights between the sample of men and the sample of women is sufficiently large to make it unlikely that they both came from the same normal population.
Different Types of Tests
[edit | edit source]A statistical test is always about one or more parameters of the concerned population (distribution). The appropiate test depends on the type of null and alternative hypothesis about this (these) parameter(s) and the available information from the sample.
Example
[edit | edit source]It is conjectured that British children gain more weight lately. Hence the population mean μ of the weight X of children of let's say 12 years of age is the parameter at stake. In the recent past the mean weight of this group of children turned out to be 45 kg. Hence the null hypothesis (of no change) is:
- .
As we suspect a gain in weight, the alternative hypothesis is:
- .
A random sample of 100 children shows an average weight of 47 kg with a standard deviation of 8 kg.
Because it is reasonable to assume that the weights are normally distributed, the appropriate test will be a t-test, with test statistic:
- .
Under the null hypothesis T will be Student distributed with 99 degrees of freedom, which means approximately standard normally distributed.
The null hypothesis will be rejected for large values of T. For this sample the value t of T is:
- .
Is this a large value? That depends partly on our demands. The so called p-value of the observed value t is:
- ,
in which Z stands for a standard normally distributed random variable.
If we are not too critical this is small enough, so reason to reject the null hypothesis and to assume our conjecture to be true.
Now suppose we have lost the individual data, but still know that the maximum weight in the sample was 68 kg. It is not possible then to use the t-test, and instead we have to use a test based on the statistic max(X).
It might also be the case that our assumption on the distribution of the weight is questionable. To avoid discussion we may use a distribution free test instead of a t-test.
A statistical test begins with a hypothesis; the form of that hypothesis determines the type(s) of test(s) that can be used. In some cases, only one is appropriate; in others, one may have some choice.
For example: if the hypothesis concerns the value of a single population mean (), then a one sample test for mean is indicated. Whether the z-test or t-test should be used depends on other factors (each test has its own requirements).
A complete listing of the conditions under which each type of test is indicated is probably beyond the scope of this work; refer to the sections for the various types of tests for more information about the indications and requirements for each test.
z Test for a Single Mean
[edit | edit source]The Null Hypothesis should be an assumption concerning the value of the population mean. The data should consist of a single sample of quantitative data from the population.
Requirements
[edit | edit source]The sample should be drawn from a population from which the Standard Deviation (or Variance) is known. Also, the measured variable (typically listed as is the sample statistic) should have a Normal Distribution.
Note that if the distribution of the variable in the population is non-normal (or unknown), the z-test can still be used for approximate results, provided the sample size is sufficiently large. Historically, sample sizes of at least 30 have been considered sufficiently large; reality is (of course) much more complicated, but this rule of thumb is still in use in many textbooks.
If the population Standard Deviation is unknown, then a z-test is typically not appropriate. However, when the sample size is large, the sample standard deviation can be used as an estimate of the population standard deviation, and a z-test can provide approximate results.
Definitions of Terms
[edit | edit source]- = Population Mean
- = Population Standard Deviation
- = Sample Mean
- = Sample Population
Procedure
[edit | edit source]- The Null Hypothesis:
This is a statement of no change or no effect; often, we are looking for evidence that this statement is no longer true.
- H0 : μ = μ0
- The Alternate Hypothesis:
This is a statement of inequality; we are looking for evidence that this statement is true.
- H1 : μ < μ0 or
- H1 : μ > μ0 or
- H1 : μ ≠ μ0
- The Test Statistic:
- The Significance (p-value)
Calculate the probability of observing a value of z (from a Standard Normal Distribution) using the Alternate Hypothesis to indicate the direction in which the area under the Probability Density Function is to be calculated. This is the Attained Significance, or p-value.
Note that some (older) methods first chose a Level Of Significance, which was then translated into a value of z. This made more sense (and was easier!) in the days before computers and graphics calculators.
- Decision
The Attained Significance represents the probability of obtaining a test statistic as extreme, or more extreme, than ours - if the null hypothesis is true.
If the Attained Significance (p-value) is sufficiently low, then this indicates that our test statistic is unusual (rare) - we usually take this as evidence that the null hypothesis is in error. In this case, we reject the null hypothesis.
If the p-value is large, then this indicates that the test statistic is usual (common) - we take this as a lack of evidence against the null hypothesis. In this case, we fail to reject the null hypothesis.
It is common to use 5% as the dividing line between the common and the unusual; again, reality is more complicated. Sometimes a lower level of uncertainty must be chosen should the consequences of error results in a decision that can injure or kill people or do great economic harm. We would more likely tolerate a drug that kills 5% of patients with a terminal cancer but cures 95% of all patients, but we would hardly tolerate a cosmetic that disfigures 5% of those who use it.
Worked Examples
[edit | edit source]Are The Kids Above Average?
[edit | edit source]Scores on a certain test of mathematical aptitude have mean μ = 50 and standard deviation σ = 10. An amateur researcher believes that the students in his area are brighter than average, and wants to test his theory.
The researcher has obtained a random sample of 45 scores for students in his area. The mean score for this sample is 52.
Does the researcher have evidence to support his belief?
The null hypothesis is that there is no difference, and that the students in his area are no different than those in the general population; thus,
- H0 : μ = 50
(where μ represents the mean score for students in his area)
He is looking for evidence that the students in his area are above average; thus, the alternate hypothesis is
- H1 : μ > 50
Since the hypothesis concerns a single population mean, a z-test is indicated. The sample size is fairly large (greater than 30), and the standard deviation is known, so a z-test is appropriate.
We now find the area under the Normal Distribution to the right of z = 1.3416 (to the right, since the alternate hypothesis is to the right). This can be done with a table of values, or software- I get a value of 0.0899.
If the null hypothesis is true (and these students are no better than the general population), then the probability of obtaining a sample mean of 52 or higher is 8.99%. This occurs fairly frequently (using the 5% rule), so it does not seem unusual. I fail to reject the null hypothesis (at the 5% level).
It appears that the evidence does not support the researcher's belief.
Is The Machine Working Correctly?
[edit | edit source]Sue is in charge of Quality Control at a bottling facility. Currently, she is checking the operation of a machine that is supposed to deliver 355 mL of liquid into an aluminum can. If the machine delivers too little, then the local Regulatory Agency may fine the company. If the machine delivers too much, then the company may lose money. For these reasons, Sue is looking for any evidence that the amount delivered by the machine is different from 355 mL.
During her investigation, Sue obtains a random sample of 10 cans, and measures the following volumes:
- 355.02 355.47 353.01 355.93 356.66 355.98 353.74 354.96 353.81 355.79
The machine's specifications claim that the amount of liquid delivered varies according to a normal distribution, with mean μ = 355 mL and standard deviation σ = 0.05 mL.
Do the data suggest that the machine is operating correctly?
The null hypothesis is that the machine is operating according to its specifications; thus
- H0 : μ = 355
(where μ is the mean volume delivered by the machine)
Sue is looking for evidence of any difference; thus, the alternate hypothesis is
- H1 : μ ≠ 355
Since the hypothesis concerns a single population mean, a z-test is indicated. The population follows a normal distribution, and the standard deviation is known, so a z-test is appropriate.
In order to calculate the test statistic (z), we must first find the sample mean from the data. Use a calculator or computer to find that .
The calculation of the p-value will be a little different. If we only find the area under the normal curve above z = 2.34, then we have found the probability of obtaining a sample mean of 355.037 or higher—what about the probability of obtaining a low value?
In the case that the alternate hypothesis uses ≠, the p-value is found by doubling the tail area—in this case, we double the area above z = 2.34.
The area above z = 2.34 is 0.0096; thus, the p-value for this test is 0.0192.
If the machine is delivering 355 mL, then the probability of obtaining a sample mean this far (0.037 mL) or farther from 355 mL is 0.0096, or 0.96%. This is pretty rare; I'll reject the null hypothesis.
It appears that the machine is not working correctly.
N.B.: since the alternate hypothesis is ≠, we cannot conclude that the machine is delivering more than 355 mL—we can only say that the amount is different from 355 mL.
z Test for Two Means
[edit | edit source]Indications
[edit | edit source]The Null Hypothesis should be an assumption about the difference in the population means for two populations (note that the same quantitative variable must have been measured in each population). The data should consist of two samples of quantitative data (one from each population). The samples must be obtained independently from each other.
Requirements
[edit | edit source]The samples must be drawn from populations which have known Standard Deviations (or Variances). Also, the measured variable in each population (generically denoted x1 and x2) should have a Normal Distribution.
Note that if the distributions of the variables in the populations are non-normal (or unknown), the two-sample z-test can still be used for approximate results, provided the combined sample size (sum of sample sizes) is sufficiently large. Historically, a combined sample size of at least 30 has been considered sufficiently large; reality is (of course) much more complicated, but this rule of thumb is still in use in many textbooks.
Procedure
[edit | edit source]- The Null Hypothesis:
- H0 : μ1 - μ2 = δ
in which δ is the supposed difference in the expected values under the null hypothesis.
- The Alternate Hypothesis:
- H0 : μ1 - μ2 < δ
- H0 : μ1 - μ2 > δ
- H0 : μ1 - μ2 ≠ δ
For more information about the Null and Alternate Hypotheses, see the page on the z test for a single mean.
- The Test Statistic:
Usually, the null hypothesis is that the population means are equal; in this case, the formula reduces to
In the past, the calculations were simpler if the Variances (and thus the Standard Deviations) of the two populations could be assumed equal. This process is called Pooling, and many textbooks still use it, though it is falling out of practice (since computers and calculators have all but removed any computational problems).
- The Significance (p-value)
Calculate the probability of observing a value of z (from a Standard Normal Distribution) using the Alternate Hypothesis to indicate the direction in which the area under the Probability Density Function is to be calculated. This is the Attained Significance, or p-value.
Note that some (older) methods first chose a Level Of Significance, which was then translated into a value of z. This made more sense (and was easier!) in the days before computers and graphics calculators.
- Decision
The Attained Significance represents the probability of obtaining a test statistic as extreme, or more extreme, than ours—if the null hypothesis is true.
If the Attained Significance (p-value) is sufficiently low, then this indicates that our test statistic is unusual (rare)—we usually take this as evidence that the null hypothesis is in error. In this case, we reject the null hypothesis.
If the p-value is large, then this indicates that the test statistic is usual (common)—we take this as a lack of evidence against the null hypothesis. In this case, we fail to reject the null hypothesis.
It is common to use 5% as the dividing line between the common and the unusual; again, reality is more complicated.
Worked Examples
[edit | edit source]Do Professors Make More Money at Larger Universities?
[edit | edit source]Universities and colleges in the United States of America are categorized by the highest degree offered. Type IIA institutions offer a Master's Degree, and type IIB institutions offer a Baccalaureate degree. A professor, looking for a new position, wonders if the salary difference between type IIA and IIB institutions is really significant.
He finds that a random sample of 200 IIA institutions has a mean salary (for full professors) of $54,218.00, with standard deviation $8,450. A random sample of 200 IIB institutions has a mean salary (for full professors) of $46,550.00, with standard deviation $9,500 (assume that the sample standard deviations are in fact the population standard deviations).
Do these data indicate a significantly higher salary at IIA institutions?
The null hypothesis is that there is no difference; thus
- H0 : μA = μB
(where μA is the true mean full professor salary at IIA institutions, and μB is the mean at IIB institutions)
He is looking for evidence that IIA institutions have a higher mean salary; thus the alternate hypothesis is
- H1 : μA > μB
Since the hypotheses concern means from independent samples (we'll assume that these are independent samples), a two sample test is indicated. The samples are large, and the standard deviations are known (assumed?), so a two sample z-test is appropriate.
Now we find the area to the right of z = 8.5292 in the Standard Normal Distribution. This can be done with a table of values or software—I get 0.
If the null hypothesis is true, and there is no difference in the salaries between the two types of institutions, then the probability of obtaining samples where the mean for IIA institutions is at least $7,668 higher than the mean for IIB institutions is essentially zero. This occurs far too rarely to attribute to chance variation; it seems quite unusual. I reject the null hypothesis (at any reasonable level of significance!).
It appears that IIA schools have a significantly higher salary than IIB schools.
Example 2
[edit | edit source]A student scored 65 on a calculus test that had a mean of 50 and a standard deviation of 10; she scored 30 on history test with a mean of 25 and a standard deviation of 5.compare her relative position on the two tests?
t Test for a single mean
[edit | edit source]Note: Some of the statements in the text below are disputed. For small sample size non-parametric tests like the Mann-Whitney U test or the Wilcoxon rank-sum test might rather be used than a t-test.
The t- test is the most powerful parametric test for calculating the significance of a small sample mean.
A one sample t-test has the following null hypothesis:
where the Greek letter (mu) represents the population mean and c represents its assumed (hypothesized) value. In statistics it is usual to employ Greek letters for population parameters and Roman letters for sample statistics. The t-test is the small sample analog of the z test which is suitable for large samples. A small sample is generally regarded as one of size n<30.
A t-test is necessary for small samples because their distributions are not normal. If the sample is large (n>=30) then statistical theory says that the sample mean is normally distributed and a z test for a single mean can be used. This is a result of a famous statistical theorem, the Central limit theorem.
A t-test, however, can still be applied to larger samples and as the sample size n grows larger and larger, the results of a t-test and z-test become closer and closer. In the limit, with infinite degrees of freedom, the results of t and z tests become identical.
In order to perform a t-test, one first has to calculate the "degrees of freedom." This quantity takes into account the sample size and the number of parameters that are being estimated. Here, the population parameter, mu is being estimated by the sample statistic x-bar, the mean of the sample data. For a t-test the degrees of freedom of the single mean is n-1. This is because only one population parameter (the population mean)is being estimated by a sample statistic (the sample mean).
degrees of freedom (df)=n-1
For example, for a sample size n=15, the df=14.
Example
[edit | edit source]A college professor wants to compare her students' scores with the national average. She chooses a simple random sample (SRS) of 20 students, who score an average of 50.2 on a standardized test. Their scores have a standard deviation of 2.5. The national average on the test is a 60. She wants to know if her students scored significantly lower than the national average.
Significance tests follow a procedure in several steps.
Step 1
[edit | edit source]First, state the problem in terms of a distribution and identify the parameters of interest. Mention the sample. We will assume that the scores (X) of the students in the professor's class are approximately normally distributed with unknown parameters μ and σ
Step 2
[edit | edit source]State the hypotheses in symbols and words.
The null hypothesis is that her students scored on par with the national average.
The alternative hypothesis is that her students scored lower than the national average.
Step 3
[edit | edit source]Secondly, identify the test to be used. Since we have an SRS of small size and do not know the standard deviation of the population, we will use a one-sample t-test.
The formula for the t-statistic T for a one-sample test is as follows:
where is the sample mean and S is the sample standard deviation.
A quite common mistake is to say that the formula for the t-test statistic is:
This is not a statistic, because μ is unknown, which is the crucial point in such a problem. Most people even don't notice it. Another problem with this formula is the use of x and s. They are to be considered the sample statistics and not their values.
The right general formula is:
in which c is the hypothetical value for μ specified by the null hypothesis.
(The standard deviation of the sample divided by the square root of the sample size is known as the "standard error" of the sample.)
Step 4
[edit | edit source]State the distribution of the test statistic under the null hypothesis. Under H0 the statistic T will follow a Student's distribution with 19 degrees of freedom: .
Step 5
[edit | edit source]Compute the observed value t of the test statistic T, by entering the values, as follows:
Step 6
[edit | edit source]Determine the so-called p-value of the value t of the test statistic T. We will reject the null hypothesis for too small values of T, so we compute the left p-value:
- p-value
The Student's distribution gives at probabilities 0.95 and degrees of freedom 19. The p-value is approximated at 1.777e-13.
Step 7
[edit | edit source]Lastly, interpret the results in the context of the problem. The p-value indicates that the results almost certainly did not happen by chance and we have sufficient evidence to reject the null hypothesis. The professor's students did score significantly lower than the national average.
See also
[edit | edit source]t Test for Two Means
[edit | edit source]In both the one- and two-tailed versions of the small two-sample t-test, we assume that the means of the two populations are equal. To use a t-test for small (independent) samples, the following conditions must be met:
- The samples must be selected randomly.
- The samples must be independent.
- Each population must have a normal distribution.
A small two sample t-test is used to test the difference between two population means μ1 and μ2 when the sample size for at least one population is less than 30. The standardized test statistic is:
One-Way ANOVA F Test
[edit | edit source]The one-way ANOVA F-test is used to identify if there are differences between subject effects. For instance, to investigate the effect of a certain new drug on the number of white blood cells, in an experiment the drug is given to three different groups, one of healthy people, one with people with a light form of the considered disease and one with a severe form of the disease. Generally the analysis of variance identifies whether there is a significant difference in effect of the drug on the number of white blood cells between the groups. Significant refers to the fact that there will always be difference between the groups and also within the groups, but the purpose is to investigate whether the difference between the groups are large compared to the differences within the groups. To set up such an experiment three assumptions must be validated before calculating an F statistic: independent samples, homogeneity of variance, and normality. The first assumption suggests that there is no relation between the measurements for different subjects. Homogeneity of variance refers to equal variances among the different groups in the experiment (e.g., drug vs. placebo). Furthermore, the assumption of normality suggests that the distribution of each of these groups should be approximately normally distributed.
Model
[edit | edit source]The situation is modelled in the following way. The measurement of the -th test person in group is indicated by:
- .
This reads: the outcome of the measurement for in group is due to a general effect indicated by , an effect due to the group, and an individual contribution .
The individual, or random, contributions , often referred to as disturbances, are considered to be independently, normally distributed, all with expected value 0 and standard deviation .
To make the model unambiguous the group effects are restrained by the condition:
- .
Now. a notational note: it is common practice to indicate averages over one or more indices by writing a dot in the place of the index or indices. So for instance
The analysis of variance now divides the total "variance" in the form of the total "sum of squares" in two parts, one due to the variation within the groups and one due to the variation between the groups:
- .
We see the term sum of squares of error:
of the total squared differences of the individual measurements from their group averages, as an indication of the variation within the groups, and the term sum of square of the factor
of the total squared differences of the group means from the overall mean, as an indication of the variation between the groups.
Under the null hypothesis of no effect:
we find:
- is chi-square distributed with a(m-1) degrees of freedom, and
- is chi-square distributed with a-1 degrees of freedom,
where is the number of groups and is the number of persons in each group.
Hence the quotient of the so-called mean sum of squares:
and
may be used as a test statistic
which under the null hypothesis is F-distributed with degrees of freedom in the nominator and in the denominator, because the unknown parameter does not play a role since it is cancelled out in the quotient.
Testing whether Proportion A Is Greater than Proportion B in Microsoft Excel
[edit | edit source]A running example from the 2004 American Presidential Race follows. It should be clear that the choice of poll and who is leading is irrelevant to the presentation of the concepts. According to an October 2nd Poll by Newsweek (link), 47% of 1,013 registered voters would vote for John Kerry/John Edwards if the election were held today. 45% would vote for George Bush/Dick Cheney, and 2% would vote for Ralph Nader/Peter Camejo.
- Open a new Blank Workbook in the program Microsoft Excel.
- Enter Kerry's reported percentage p in cell A1 (0.47).
- Enter Bush's reported percentage q in cell B1 (0.45).
- Enter the number of respondents N in cell C1 (1013). This can be found in most responsible reports on polls.
- In cell A2, copy and paste the next line of text in its entirety and press Enter. This is the Microsoft Excel expression of the standard error of the difference as shown above.
- =sqrt(A1*(1-A1)/C1+B1*(1-B1)/C1+2*A1*B1/C1)
- In cell A3, copy and paste the next line of text in its entirety and press Enter. This is the Microsoft Excel expression of the probability that Kerry is leading based on the normal distribution given the logic here.
- =normdist((A1-B1),0,A2,1)
- Don't forget that the percentages will be in decimal form. The percentage will be 0.5, or 50% if A1 and B1 are the same, of course.
The above text might be enough to do the necessary calculation, it doesn't contribute to the understanding of the statistical test involved. Much too often people think statistics is a matter of calculation with complex formulas.
So here is the problem: Let p be the population fraction of the registered voters who vote for Kerry and q likewise for Bush. In a poll n = 1013 respondents are asked to state their choice. A number of K respondents says to choose Kerry, a number B says to vote for Bush. K and B are random variables. The observed values for K and B are resp. k and b (numbers). So k/n is an estimate of p and b/n an estimate of q. The random variables K and B follow a trinomial distribution with parameters n, p, q and 1-p-q. Will Kerry be ahead of Bush? That is to say: wiil p > q? To investigate this we perform a statistical test, with null hypothesis:
against the alternative
- .
What is an appropriate test statistic T? We take:
- .
(In the above calculation is taken, which leads to the same calculation.)
We have to state the distribution of T under the null hypothesis. We may assume T is approximately normally distributed.
It is quite obvious that its expectation under H0 is:
- .
Its variance under H0 is not as obvious.
- .
We approximate the variance by using the sample fractions instead of the population fractions:
- .
The standard deviation s will approximately be:
- .
In the sample we have found a value t = k - b = (0.47-0.45)1013 = 20.26 for T. We will reject the null hypothesis in favour of the alternative for large values of T. So the question is: is 20.26 to be considered a large value for T? The criterion will be the so called p-value of this outcome:
- .
This is a very large p-value, so there is no reason whatsoever to reject the null hypothesis.
Chi-Squared Tests
[edit | edit source]General idea
[edit | edit source]Assume you have observed absolute frequencies and expected absolute frequencies under the Null hypothesis of your test then it holds
might denote a simple index running from or even a multiindex running from to .
The test statistics is approximately distributed, if
- for all absolute expected frequencies holds and
- for at least 80% of the absolute expected frequencies holds .
Note: In different books you might find different approximation conditions, please feel free to add further ones.
The degrees of freedom can be computed by the numbers of absolute observed frequencies which can be chosen freely. We know that the sum of absolute expected frequencies is
which means that the maximum number of degrees of freedom is . We might have to subtract from the number of degrees of freedom the number of parameters we need to estimate from the sample, since this implies further relationships between the observed frequencies.
Derivation of the distribution of the test statistic
[edit | edit source]Following Boero, Smith and Wallis (2002) we need knowledge about multivariate statistics to understand the derivation.
The random variable describing the absolute observed frequencies in a sample has a multinomial distribution with the number of observations in the sample, the unknown true probabilities. With certain approximation conditions (central limit theorem) it holds that
with the multivariate dimensional normal distribution, and
.
The covariance matrix has only rank , since .
If we considered the generalized inverse then it holds that
distributed (for a proof see Pringle and Rayner, 1971).
Since the multinomial distribution is approximately multivariate normal distributed, the term is
distributed. If further relations between the observed probabilities are there then the rank of will decrease further.
A common situation is that parameters on which the expected probabilities depend needs to be estimated from the observed data. As said above, usually is stated that the degrees of freedom for the chi square distribution is with the number of estimated parameters. In case of parameter estimation with the maximum-likelihood method this is only true if the estimator is efficient (Chernoff and Lehmann, 1954). In general it holds that degrees of freedom are somewhere between and .
Examples
[edit | edit source]The most famous examples will be handled in detail at further sections: test for independence, test for homogeneity and test for distributions.
The test can be used to generate "quick and dirty" test, e.g.
The random variable is symmetrically distributed versus
the random variable is not symmetrically distributed.
We know that in case of a symmetrical distribution the arithmetic mean and median should be nearly the same. So a simple way to test this hypothesis would be to count how many observations are less than the mean ()and how many observations are larger than the arithmetic mean (). If mean and median are the same than 50% of the observation should smaller than the mean and 50% should be larger than the mean. It holds
.
References
[edit | edit source]- Boero, G., Smith, J., Wallis, K.F. (2002). The properties of some goodness-of-fit test, University of Warwick, Department of Economics, The Warwick Economics Research Paper Series 653, http://www2.warwick.ac.uk/fac/soc/economics/research/papers/twerp653.pdf
- Chernoff H, Lehmann E.L. (1952). The use of maximum likelihood estimates in tests for goodness-of-fit. The Annals of Mathematical Statistics; 25:576-586.
- Pringle, R.M., Rayner, A.A. (1971). Generalized Inverse Matrices with Applications to Statistics. London: Charles Griffin.
- Wikipedia, Pearson's chi-square test: http://en.wikipedia.org/wiki/Pearson%27s_chi-square_test
Numerical Methods
[edit | edit source]Often the solution of statistical problems and/or methods involve the use of tools from numerical mathematics. An example might be Maximum-Likelihood estimation of which involves the maximization of the Likelihood function :
.
The maximization here requires the use of optimization routines. Other numerical methods and their application in statistics are described in this section.
Contents of this section:
This section is dedicated to the Gram-Schmidt Orthogonalization which occurs frequently in the solution of statistical problems. Additionally some results of algebra theory which are necessary to understand the Gram-Schmidt Orthogonalization are provided. The Gram-Schmidt Orthogonalization is an algorithm which generates from a set of linear dependent vectors a new set of linear independent vectors which span the same space. Computation based on linear independent vectors is simpler than computation based on linear dependent vectors.
Numerical Optimization occurs in all kind of problem - a prominent example being the Maximum-Likelihood estimation as described above. Hence this section describes one important class of optimization algorithms, namely the so-called Gradient Methods. After describing the theory and developing an intuition about the general procedure, three specific algorithms (the Method of Steepest Descent, the Newtonian Method, the class of Variable Metric Methods) are described in more detail. Especially we provide an (graphical) evaluation of the performance of these three algorithms for specific criterion functions (the Himmelblau function and the Rosenbrock function). Furthermore we come back to Maximum-Likelihood estimation and give a concrete example how to tackle this problem with the methods developed in this section.
In OLS, one has the primary goal of determining the conditional mean of random variable , given some explanatory variable , . Quantile Regression goes beyond this and enables us to pose such a question at any quantile of the conditional distribution function. It thereby focuses on the interrelationship between a dependent variable and its explanatory variables for a given quantile.
Statistical calculations require an extra accuracy and are open to some errors such as truncation or cancellation error etc. These errors occur due to binary representation and finite precision and may cause inaccurate results. In this work we are going to discuss the accuracy of the statistical software, different tests and methods available for measuring the accuracy and the comparison of different packages.
The purpose of this paper is to evaluate the accuracy of MS Excel in terms of statistical procedures and to conclude whether the MS Excel should be used for (statistical) scientific purposes or not. The evaluation is made for MS Excel versions 97, 2000, XP and 2003.
Basic Linear Algebra and Gram-Schmidt Orthogonalization
[edit | edit source]Introduction
[edit | edit source]Basically, all the sections found here can be also found in a linear algebra book. However, the Gram-Schmidt Orthogonalization is used in statistical algorithm and in the solution of statistical problems. Therefore, we briefly jump into the linear algebra theory which is necessary to understand Gram-Schmidt Orthogonalization.
The following subsections also contain examples. It is very important for further understanding that the concepts presented here are not only valid for typical vectors as tuple of real numbers, but also functions that can be considered vectors.
Fields
[edit | edit source]Definition
[edit | edit source]A set with two operations and on its elements is called a field (or short ), if the following conditions hold:
- For all holds
- For all holds (commutativity)
- For all holds (associativity)
- It exist a unique element , called zero, such that for all holds
- For all a unique element , such that holds
- For all holds
- For all holds (commutativity)
- For all holds (associativity)
- It exist a unique element , called one, such that for all holds
- For all non-zero a unique element , such that holds
- For all holds (distributivity)
The elements of are also called scalars.
Examples
[edit | edit source]It can easily be proven that real numbers with the well known addition and multiplication are a field. The same holds for complex numbers with the addition and multiplication. Actually, there are not many more sets with two operations which fulfill all of these conditions.
For statistics, only the real and complex numbers with the addition and multiplication are important.
Vector spaces
[edit | edit source]Definition
[edit | edit source]A set with two operations and on its elements is called a vector space over R, if the following conditions hold:
- For all holds
- For all holds (commutativity)
- For all holds (associativity)
- It exist a unique element , called origin, such that for all holds
- For all exists a unique element , such that holds
- For all and holds
- For all and holds (associativity)
- For all and holds
- For all and for all holds (distributivity wrt. vector addition)
- For all and for all holds (distributivity wrt. scalar addition)
Note that we used the same symbols and for different operations in and . The elements of are also called vectors.
Examples:
- The set with the real-valued vectors with elementwise addition and the elementwise multiplication is a vector space over .
- The set of polynomials of degree , , with usual addition and multiplication is a vector space over .
Linear combinations
[edit | edit source]A vector can be written as a linear combination of vectors , if
with .
Examples:
- is a linear combination of since
- is a linear combination of since
Basis of a vector space
[edit | edit source]A set of vectors is called a basis of the vector space , if
1. for each vector exist scalars such that 2. there is no subset of such that 1. is fulfilled.
Note, that a vector space can have several bases.
Examples:
- Each vector can be written as . Therefore is a basis of .
- Each polynomial of degree can be written as linear combination of and therefore forms a basis for this vector space.
Actually, for both examples we would have to prove condition 2., but it is clear that it holds.
Dimension of a vector space
[edit | edit source]A dimension of a vector space is the number of vectors which are necessary for a basis. A vector space has infinitely many number of basis, but the dimension is uniquely determined. Note that the vector space may have a dimension of infinity, e.g. consider the space of continuous functions.
Examples:
- The dimension of is three, the dimension of is .
- The dimension of the polynomials of degree is .
Scalar products
[edit | edit source]A mapping is called a scalar product if the following holds for all and :
- with
- with
Examples:
- The typical scalar product in is .
- is a scalar product on the vector space of polynomials of degree .
Norm
[edit | edit source]A norm of a vector is a mapping , if holds
- for all and (positive definiteness)
- for all and all
- for all (triangle inequality)
Examples:
- The norm of a vector in is defined as .
- Each scalar product generates a norm by , therefore is a norm for the polynomials of degree .
Orthogonality
[edit | edit source]Two vectors and are orthogonal to each other if . In it holds that the cosine of the angle between two vectors can expressed as
.
If the angle between and is ninety degree (orthogonal) then the cosine is zero and it follows that .
A set of vectors is called orthonormal, if
.
If we consider a basis of a vector space then we would like to have a orthonormal basis. Why ?
Since we have a basis, each vector and can be expressed by and . Therefore the scalar product of and reduces to
Consequently, the computation of a scalar product is reduced to simple multiplication and addition if the coefficients are known. Remember that for our polynomials we would have to solve an integral!
Gram-Schmidt orthogonalization
[edit | edit source]Algorithm
[edit | edit source]The aim of the Gram-Schmidt orthogonalization is to find for a set of vectors an equivalent set of orthonormal vectors such that any vector which can be expressed as linear combination of can also be expressed as linear combination of :
1. Set and
2. For each set and , in each step the vector is projected on and the result is subtracted from .

Example
[edit | edit source]Consider the polynomials of degree two in the interval with the scalar product and the norm . We know that and are a basis for this vector space. Let us now construct an orthonormal basis:
Step 1a:
Step 1b:
Step 2a:
Step 2b:
Step 3a:
Step 3b:
It can be proven that and form a orthonormal basis with the above scalarproduct and norm.
Numerical instability
[edit | edit source]Consider the vectors and . Assume that is so small that computing holds on a computer (see http://en.wikipedia.org/wiki/Machine_epsilon). Let compute a orthonormal basis for this vectors in with the standard scalar product and the norm .
Step 1a.
Step 1b. with
Step 2a.
Step 2b.
Step 3a.
Step 3b.
It obvious that for the vectors
-
-
-
the scalarproduct . All other pairs are also not zero, but they are multiplied with such that we get a result near zero.
Modified Gram-Schmidt
[edit | edit source]To solve the problem a modified Gram-Schmidt algorithm is used:
- Set for all
- for each from to compute
- for each from to compute
The difference is that we compute first our new and subtract it from all other . We apply the wrongly computed vector to all vectors instead of computing each separately.
Example (recomputed)
[edit | edit source]Step 1. , ,
Step 2a. with
Step 2b.
Step 2c.
Step 3a.
Step 3b.
Step 4a.
We can easily verify that .
Application
[edit | edit source]Exploratory Project Pursuit
[edit | edit source]In the analysis of high-dimensional data we usually analyze projections of the data. The approach results from the Theorem of Cramer-Wold that states that the multidimensional distribution is fixed if we know all one-dimensional projections. Another theorem states that most (one-dimensional) projections of multivariate data are looking normal, even if the multivariate distribution of the data is highly non-normal.
Therefore in Exploratory Projection Pursuit we judge the interestingness of a projection by comparison with a (standard) normal distribution. If we assume that the one-dimensional data are standard normal distributed then after the transformation with the cumulative distribution function of the standard normal distribution then is uniformly distributed in the interval .
Thus the interesting can measured by with a density estimated from the data. If the density is equal to in the interval then the integral becomes zero and we have found that our projected data are normally distributed. An value larger than zero indicates a deviation from the normal distribution of the projected data and hopefully an interesting distribution.
Expansion with orthonormal polynomials
[edit | edit source]Let a set of orthonormal polynomials with the scalar product and the norm . What can we derive about a densities in the interval ?
If for some maximal degree then it holds
We can also write or empirically we get an estimator .
We describe the term and get for our integral
So using a orthonormal function set allows us to reduce the integral to a summation of coefficient which can be estimated from the data by plugging in the formula above. The coefficients can be precomputed in advance.
Normalized Legendre polynomials
[edit | edit source]The only problem left is to find the set of orthonormal polynomials upto degree . We know that form a basis for this space. We have to apply the Gram-Schmidt orthogonalization to find the orthonormal polynomials. This has been started in the first example.
The resulting polynomials are called normalized Legendre polynomials. Up to a scaling factor the normalized Legendre polynomials are identical to Legendre polynomials. The Legendre polynomials have a recursive expression of the form
So computing our integral reduces to computing and and using the recursive relationship to compute the 's. Please note that the recursion can be numerically unstable!
References
[edit | edit source]- Halmos, P.R. (1974). Finite-Dimensional Vector Spaces, Springer: New York
Unconstrained Optimization
[edit | edit source]Introduction
[edit | edit source]In the following we will provide some notes on numerical optimization algorithms. As there are numerous methods out there, we will restrict ourselves to the so-called Gradient Methods. There are basically two arguments why we consider this class as a natural starting point when thinking about numerical optimization algorithms. On the one hand, these methods are really workhorses in the field, so their frequent use in practice justifies their coverage here. On the other hand, this approach is highly intuitive in the sense that it somewhat follow naturally from the well-known properties of optima. In particular we will concentrate on three examples of this class: the Newtonian Method, the Method of Steepest Descent and the class of Variable Metric Methods, nesting amongst others the Quasi Newtonian Method.
Before we start we will nevertheless stress that there does not seem to be a "one and only" algorithm but the performance of specific algorithms is always contingent on the specific problem to be solved. Therefore both experience and "trial-and-error" are very important in applied work. To clarify this point we will provide a couple of applications where the performance of different algorithms can be compared graphically. Furthermore a specific example on Maximum Likelihood Estimation can be found at the end. Especially for statisticians and econometricians the Maximum Likelihood Estimator is probably the most important example of having to rely on numerical optimization algorithms in practice.
Theoretical Motivation
[edit | edit source]Any numerical optimization algorithm has solve the problem of finding "observable" properties of the function such that the computer program knows that a solution is reached. As we are dealing with problems of optimization two well-known results seem to be sensible starting points for such properties.
If f is differentiable and is a (local) minimum, then
i.e. the Jacobian is equal to zero
and
If f is twice differentiable and is a (local) minimum, then
i.e. the Hessian is pos. semidefinite.
In the following we will always denote the minimum by . Although these two conditions seem to represent statements that help in finding the optimum , there is the little catch that they give the implications of being an optimum for the function . But for our purposes we would need the opposite implication, i.e. finally we want to arrive at a statement of the form: "If some condition is true, then is a minimum". But the two conditions above are clearly not sufficient in achieving this (consider for example the case of , with but ). Hence we have to look at an entire neighborhood of as laid out in the following sufficient condition for detecting optima:
If and and , then: is a local minimum.
Proof: For let . The Taylor approximation yields: , where denotes an open ball around , i.e. for .
In contrast to the two conditions above, this condition is sufficient for detecting optima - consider the two trivial examples
with but
and
with and .
Keeping this little caveat in mind we can now turn to the numerical optimization procedures.
Numerical Solutions
[edit | edit source]All the following algorithms will rely on the following assumption:
(A1) The set is compact
where is some given starting value for the algorithm. The significance of this assumption has to be seen in the Weierstrass Theorem which states that every compact set contains its supremum and its infimum. So (A1) ensures that there is some solution in . And at this global minimum it of course holds true that . So - keeping the discussion above in mind - the optimization problem basically boils down to the question of solving set of equations .
The Direction of Descent
[edit | edit source]The problems with this approach are of course rather generically as does hold true for maxima and saddle points as well. Hence, good algorithms should ensure that both maxima and saddle points are ruled out as potential solutions. Maxima can be ruled out very easily by requiring i.e. we restrict ourselves to a sequence such that the function value decreases in every step. The question is of course if this is always possible. Fortunately it is. The basic insight why this is the case is the following. When constructing the mapping (i.e. the rule how we get from to ) we have two degrees of freedoms, namely
- the direction and
- the step length .
Hence we can choose in which direction we want to move to arrive at and how far this movement has to be. So if we choose and in the "right way" we can effectively ensure that the function value decreases. The formal representation of this reasoning is provided in the following
Lemma: If and then: such that
Proof: As and , it follows that for small enough.
The General Procedure of Descending Methods
[edit | edit source]A direction vector that satisfies this condition is is called a Direction of Descent. In practice this Lemma allows us to use the following procedure to numerically solve optimization problems.
1. Define the sequence recursively via
2. Choose the direction from local information at the point
3. Choose a step size that ensures convergence of the algorithm.
4. Stop the iteration if where is some chosen tolerance value for the minimum
This procedure already hints that the choice of and are not separable, but rather dependent. Especially note that even if the method is a descending method (i.e. both and are chosen according to Lemma 1) the convergence to the minimum is not guaranteed. At a first glance this may seem a bit puzzling. If we found a sequence such that the function value decreases at every step, one might think that at some stage, i.e. in the limit of k tending to infinity we should reach the solution. Why this is not the case can be seen from the following example borrowed from W. Alt (2002, p. 76).
Example 1
[edit | edit source]- Consider the following example which does not converge although it is clearly descending. Let the criterion function be given by
, let the starting value be , consider a (constant) direction vector and choose a step width of . Hence the recursive definition of the sequence follows as
Note that and hence , so that it is clearly a descending method. Nevertheless we find that
The reason for this non-convergence has to be seen in the stepsize decreasing too fast. For large k the steps get so small that convergence is precluded. Hence we have to link the stepsize to the direction of descend .
Efficient Stepsizes
[edit | edit source]The obvious idea of such a linkage is to require that the actual descent is proportional to a first order approximation, i.e. to choose such that there is a constant such that
Note that we still look only at descending directions, so that as required in Lemma 1 above. Hence, the compactness of implies the convergence of the LHS and by (4)
Finally we want to choose a sequence such that because that is exactly the necessary first order condition we want to solve. Under which conditions does (5) in fact imply ? First of all the stepsize must not go to zero too quickly. That is exactly the case we had in the example above. Hence it seems sensible to bound the stepsize from below by requiring that
for some constant . Substituting (6) into (5) finally yields
where again the compactness of ensures the convergence of the LHS and hence
Stepsizes that satisfy (4) and (6) are called efficient stepsizes and will be denoted by . The importance of condition (6) is illustrated in the following continuation of Example 1.
Example 1 (continued)
[edit | edit source]- Note that it is exactly the failure of (6) that induced Example 1 not to converge. Substituting the stepsize of the example into (6) yields
so there is no constant satisfying this inequality for all k as required in (6). Hence the stepsize is not bounded from below and decreases too fast. To really acknowledge the importance of (6), let us change the example a bit and assume that . Then we find that
i.e. convergence actually does take place. Furthermore recognize that this example actually does satisfy condition (6) as
Choosing the Direction d
[edit | edit source]We have already argued that the choice of and is intertwined. Hence the choice of the "right" is always contingent on the respective stepsize . So what does "right" mean in this context? Above we showed in equation (8) that choosing an efficient stepsize implied
The "right" direction vector will therefore guarantee that (8') implies that
as (9) is the condition for the chosen sequence to converge. So let us explore what directions could be chosen to yield (9). Assume that the stepsize is efficient and define
By (8') and (10) we know that
So if we bound from below (i.e. ), (11) implies that
where (12) gives just the condition of the sequence converging to the solution . As (10) defines the direction vector implicitly by , the requirements on translate directly into requirements on .
Why Gradient Methods?
[edit | edit source]When considering the conditions on it is clear where the term Gradient Methods originates from. With given by
we have the following result
Given that was chosen efficiently and satisfies
we have
Hence: Convergence takes place if the angle between the negative gradient at and the direction is consistently smaller than the right angle. Methods relying on satisfying (13) are called Gradient Methods.
In other words: As long as one is not moving orthogonal to the gradient and if the stepsize is chosen efficiently, Gradient Methods guarantee convergence to the solution .
Some Specific Algorithms in the Class of Gradient Methods
[edit | edit source]Let us now explore three specific algorithms of this class that differ in their respective choice of .
The Newtonian Method
[edit | edit source]The Newtonian Method is by far the most popular method in the field. It is a well known method to solve for the roots of all types of equations and hence can be easily applied to optimization problems as well. The main idea of the Newtonian method is to linearize the system of equations to arrive at
(15) can easily be solved for x as the solution is just given by (assuming to be non-singular)
For our purposes we just choose to be the gradient and arrive at
where is the so-called Newtonian Direction.
Properties of the Newtonian Method
[edit | edit source]Analyzing (17) elicits the main properties of the Newtonian method:
- If is positive definite, is a direction of descent in the sense of Lemma 1.
- The Newtonian Method uses local information of the first and second derivative to calculate .
- As
the Newtonian Method uses a fixed stepsize of . Hence the Newtonian method is not necessarily a descending method in the sense of Lemma 1. The reason is that the fixed stepsize might be larger than the critical stepsize given in Lemma 1. Below we provide the Rosenbrock function as an example where the Newtonian Method is not descending.
- The Method can be time-consuming as calculating for every step k can be cumbersome. In applied work one could think about approximations. One could for example update the Hessian only every sth step or one could rely on local approximations. This is known as the Quasi-Newtonian-Method and will be discussed in the section about Variable Metric Methods.
- To ensure the method to be decreasing one could use an efficient stepsize and set
Method of Steepest Descent
[edit | edit source]Another frequently used method is the Method of Steepest Descent. The idea of this method is to choose the direction so that the decrease in the function value f is maximal. Although this procedure seems at a first glance very sensible, it suffers from the fact that it uses effectively less information than the Newtonian Method by ignoring the Hessian's information about the curvature of the function. Especially in the applications below we will see a couple of examples of this problem.
The direction vector of the Method of Steepest Descent is given by
Proof: By the Cauchy-Schwartz Inequality it follows that
Obviously (21) holds with equality for given in (20).
Note especially that for we have , i.e. we just "walk" in the direction of the negative gradient. In contrast to the Newtonian Method the Method of Steepest Descent does not use a fixed stepsize but chooses an efficient stepsize . Hence the Method of Steepest Descent defines the sequence by
where is an efficient stepsize and the Direction of Steepest Descent given in (20).
Properties of the Method of Steepest Descent
[edit | edit source]- With the Method of Steepest Descent defines a direction of descent in the sense of Lemma 1, as
- The Method of Steepest Descent is only locally sensible as it ignores second order information.
- Especially when the criterion function is flat (i.e. the solution lies in a "valley") the sequence defined by the Method of Steepest Descent fluctuates wildly (see the applications below, especially the example of the Rosenbrock function).
- As it does not need the Hessian, calculation and implementation of the Method of Steepest Descent is easy and fast.
Variable Metric Methods
[edit | edit source]A more general approach than both the Newtonian Method and the Method of Steepest Descent is the class of Variable Metric Methods. Methods in this class rely on the updating formula
If is a symmetric and positive definite matrix, (23) defines a descending method as is positive definite if and only if is positive definite as well. To see this: just consider the spectral decomposition
where and are the matrices with eigenvectors and eigenvalues respectively. If is positive definite, all eigenvalues are strictly positive. Hence their inverse are positive as well, so that is clearly positive definite. But then, substitution of yields
i.e. the method is indeed descending. Up to now we have not specified the matrix , but is easily seen that for two specific choices, the Variable Metric Method just coincides with the Method of Steepest Descent and the Newtonian Method respectively.
- For (with being the identity matrix) it follows that
which is just the Method of Steepest Descent.
- For it follows that
which is just the Newtonian Method using a stepsize .
The Quasi Newtonian Method
[edit | edit source]A further natural candidate for a Variable Metric Method is the Quasi Newtonian Method. In contrast to the standard Newtonian Method it uses an efficient stepsize so that it is a descending method and in contrast to the Method of Steepest Descent it does not fully ignore the local information about the curvature of the function. Hence the Quasi Newtonian Method is defined by the two requirements on the matrix :
- should approximate the Hessian to make use of the information about the curvature and
- the update should be easy so that the algorithm is still relatively fast (even in high dimensions).
To ensure the first requirement, should satisfy the so-called Quasi-Newtonian-Equation
as all satisfying (26) reflect information about the Hessian. To see this, consider the function defined as
Then it is obvious that and . So and are reasonably similar in the neighborhood of . In order to ensure that is also a good approximation at , we want to choose such that the gradients at are identical. With
it is clear that if satisfies the Quasi Newtonian Equation given in (26). But then it follows that
Hence as long as and are not too far apart, satisfying (26) is a good approximation of .
Let us now come to the second requirement that the update of the should be easy. One specific algorithm to do so is the so-called BFGS-Algorithm. The main merit of this algorithm is the fact that it uses only the already calculated elements and to construct the update . Hence no new entities have to be calculated but one has only to keep track of the x-sequence and sequence of gradients. As a starting point for the BFGS-Algorithm one can provide any positive definite matrix (e.g. the identity matrix or the Hessian at ). The BFGS-Updating-Formula is then given by
where and . Furthermore (30) ensures that all are positive definite as required by Variable Metric Methods to be descending.
Properties of the Quasi Newtonian Method
[edit | edit source]- It uses second order information about the curvature of as the matrices are related to the Hessian .
- Nevertheless it ensures easy and fast updating (e.g. by the BFGS-Algorithm) so that it is faster than the standard Newtonian Method.
- It is a descending method as are positive definite.
- It is relatively easy to implement as the BFGS-Algorithm is available in most numerical or statistical software packages.
Applications
[edit | edit source]To compare the methods and to illustrate the differences between the algorithms we will now evaluate the performance of the Steepest Descent Method, the standard Newtonian Method and the Quasi Newtonian Method with an efficient stepsize. We use two classical functions in this field, namely the Himmelblau and the Rosenbrock function.
Application I: The Himmelblau Function
[edit | edit source]The Himmelblau function is given by
This fourth order polynomial has four minima, four saddle points and one maximum so there are enough possibilities for the algorithms to fail. In the following pictures we display the contour plot and the 3D plot of the function for different starting values.
In Figure 1 we display the function and the paths of all three methods at a starting value of . Obviously the three methods do not find the same minimum. The reason is of course the different direction vector of the Method of Steepest Descent - by ignoring the information about the curvature it chooses a totally different direction than the two Newtonian Methods (see especially the right panel of Figure 1).
Consider now the starting value , displayed in Figure 2. The most important thing is of course that now all methods find different solutions. That the Method of Steepest Descent finds a different solution than the two Newtonian Methods is again not that surprising. But that the two Newtonian Methods converge to different solution shows the significance of the stepsize . With the Quasi-Newtonian Method choosing an efficient stepsize in the first iteration, both methods have different stepsizes and direction vectors for all iterations after the first one. And as seen in the picture: the consequence may be quite significant.

Application II: The Rosenbrock Function
[edit | edit source]The Rosenbrock function is given by
Although this function has only one minimum it is an interesting function for optimization problems. The reason is the very flat valley of this U-shaped function (see the right panels of Figures 3 and 4). Especially for econometricians this function may be interesting because in the case of Maximum Likelihood estimation flat criterion functions occur quite frequently. Hence the results displayed in Figures 3 and 4 below seem to be rather generic for functions sharing this problem.
My experience when working with this function and the algorithms I employed is that Figure 3 (given a starting value of ) seems to be quite characteristic. In contrast to the Himmelblau function above, all algorithms found the same solution and given that there is only one minimum this could be expected. More important is the path the different methods choose as is reflects the different properties of the respective methods. It is seen that the Method of Steepest Descent fluctuates rather wildly. This is due to the fact that it does not use information about the curvature but rather jumps back and forth between the "hills" adjoining the valley. The two Newtonian Methods choose a more direct path as they use the second order information. The main difference between the two Newtonian Methods is of course the stepsize. Figure 3 shows that the Quasi Newtonian Method uses very small stepsizes when working itself through the valley. In contrast, the stepsize of the Newtonian Method is fixed so that it jumps directly in the direction of the solution. Although one might conclude that this is a disadvantage of the Quasi Newtonian Method, note of course that in general these smaller stepsizes come with benefit of a higher stability, i.e. the algorithm is less likely to jump to a different solution. This can be seen in Figure 4.

Figure 4, which considers a starting value of , shows the main problem of the Newtonian Method using a fixed stepsize - the method might "overshoot" in that it is not descending. In the first step, the Newtonian Method (displayed as the purple line in the figure) jumps out of the valley to only bounce back in the next iteration. In this case convergence to the minimum still occurs as the gradient at each side points towards the single valley in the center, but one can easily imagine functions where this is not the case. The reason of this jump are the second derivatives which are very small so that the step gets very large due to the inverse of the Hessian. In my experience I would therefore recommend to use efficient stepsizes to have more control over the paths the respective Method chooses.

Application III: Maximum Likelihood Estimation
[edit | edit source]For econometricians and statisticians the Maximum Likelihood Estimator is probably the most important application of numerical optimization algorithms. Therefore we will briefly show how the estimation procedure fits in the framework developed above.
As usual let
be the conditional density of given with parameter and
the conditional likelihood function for the parameter
If we assume the data to be independently, identically distributed (iid) then the sample log-likelihood follows as
Maximum Likelihood estimation therefore boils down to maximize (35) with respect to the parameter . If we for simplicity just decide to use the Newtonian Method to solve that problem, the sequence is recursively defined by
where and denotes the first and second derivative with respect to the parameter vector and defines the Newtonian Direction given in (17). As Maximum Likelihood estimation always assumes that the conditional density (i.e. the distribution of the error term) is known up to the parameter , the methods described above can readily be applied.
A Concrete Example of Maximum Likelihood Estimation
[edit | edit source]Assume a simple linear model
with . The conditional distribution Y is then determined by the one of U, i.e.
where denotes the density function. Generally, there is no closed form solution of maximizing (35) (at least if U does not happen to be normally distributed), so that numerical methods have to be employed. Hence assume that U follows Student's t-distribution with m degrees of freedom so that (35) is given by
where we just used the definition of the density function of the t-distribution. (38) can be simplified to
so that (if we assume that the degrees of freedom m are known)
With the criterion function
the methods above can readily applied to calculate the Maximum Likelihood Estimator maximizing (41).
References
[edit | edit source]- Alt, W. (2002): "Nichtlineare Optimierung", Vieweg: Braunschweig/Wiesbaden
- Härdle, W. and Simar, L. (2003): "Applied Multivariate Statistical Analysis", Springer: Berlin Heidelberg
- Königsberger, K. (2004): "Analysis I", Springer: Berlin Heidelberg
- Ruud, P. (2000): "Classical Econometric Theory", Oxford University Press: New York
Quantile Regression
[edit | edit source]Quantile Regression as introduced by Koenker and Bassett (1978) seeks to complement classical linear regression analysis. Central hereby is the extension of "ordinary quantiles from a location model to a more general class of linear models in which the conditional quantiles have a linear form" (Buchinsky (1998), p. 89). In Ordinary Least Squares (OLS) the primary goal is to determine the conditional mean of random variable , given some explanatory variable , reaching the expected value . Quantile Regression goes beyond this and enables one to pose such a question at any quantile of the conditional distribution function. The following seeks to introduce the reader to the ideas behind Quantile Regression. First, the issue of quantiles is addressed, followed by a brief outline of least squares estimators focusing on Ordinary Least Squares. Finally, Quantile Regression is presented, along with an example utilizing the Boston Housing data set.
Preparing the Grounds for Quantile Regression
[edit | edit source]What are Quantiles
[edit | edit source]Gilchrist (2001, p.1) describes a quantile as "simply the value that corresponds to a specified proportion of an (ordered) sample of a population". For instance a very commonly used quantile is the median , which is equal to a proportion of 0.5 of the ordered data. This corresponds to a quantile with a probability of 0.5 of occurrence. Quantiles hereby mark the boundaries of equally sized, consecutive subsets. (Gilchrist, 2001)
More formally stated, let be a continuous random variable with a distribution function such that
which states that for the distribution function one can determine for a given value the probability of occurrence. Now if one is dealing with quantiles, one wants to do the opposite, that is one wants to determine for a given probability of the sample data set the corresponding value . A -quantile refers in a sample data to the probability for a value .
Another form of expressing the -quantile mathematically is following:
is such that it constitutes the inverse of the function for a probability .
Note that there are two possible scenarios. On the one hand, if the distribution function is monotonically increasing, quantiles are well defined for every . However, if a distribution function is not strictly monotonically increasing , there are some s for which a unique quantile can not be defined. In this case one uses the smallest value that can take on for a given probability .
Both cases, with and without a strictly monotonically increasing function, can be described as follows:
That is is equal to the inverse of the function which in turn is equal to the infimum of such that the distribution function is greater or equal to a given probability , i.e. the quantile. (Handl (2000))
However, a problem that frequently occurs is that an empirical distribution function is a step function. Handl (2000) describes a solution to this problem. As a first step, one reformulates equation 4 in such a way that one replaces the continuous random variable with , the observations, in the distribution function , resulting in the empirical distribution function . This gives the following equation:
The empirical distribution function can be separated into equally sized, consecutive subsets via the number of observations . Which then leads one to the following step:
with and as the sorted observations. Hereby, of course, the range of values that can take on is limited simply by the observations and their nature. However, what if one wants to implement a different subset, i.e. different quantiles but those that can be derived from the number of observations ?
Therefore a further step necessary to solving the problem of a step function is to smooth the empirical distribution function through replacing it a with continuous linear function . In order to do this there are several algorithms available which are well described in Handl (2000) and more in detail with an evaluation of the different algorithms and their efficiency in computer packages in Hyndman and Fan (1996). Only then one can apply any division into quantiles of the data set as suitable for the purpose of the analysis. (Handl (2000))
Ordinary Least Squares
[edit | edit source]In regression analysis the researcher is interested in analyzing the behavior of a dependent variable given the information contained in a set of explanatory variables . Ordinary Least Squares is a standard approach to specify a linear regression model and estimate its unknown parameters by minimizing the sum of squared errors. This leads to an approximation of the mean function of the conditional distribution of the dependent variable. OLS achieves the property of BLUE, it is the best, linear, and unbiased estimator, if following four assumptions hold:
1. The explanatory variable is non-stochastic
2. The expectations of the error term are zero, i.e.
3. Homoscedasticity - the variance of the error terms is constant, i.e.
4. No autocorrelation, i.e. ,
However, frequently one or more of these assumptions are violated, resulting in that OLS is not anymore the best, linear, unbiased estimator. Hereby Quantile Regression can tackle following issues: (i), frequently the error terms are not necessarily constant across a distribution thereby violating the axiom of homoscedasticity. (ii) by focusing on the mean as a measure of location, information about the tails of a distribution are lost. (iii) OLS is sensitive to extreme outliers that can distort the results significantly. (Montenegro (2001))
Quantile Regression
[edit | edit source]The Method
[edit | edit source]Quantile Regression essentially transforms a conditional distribution function into a conditional quantile function by slicing it into segments. These segments describe the cumulative distribution of a conditional dependent variable given the explanatory variable with the use of quantiles as defined in equation 4.
For a dependent variable given the explanatory variable and fixed , , the conditional quantile function is defined as the quantile of the conditional distribution function . For the estimation of the location of the conditional distribution function, the conditional median can be used as an alternative to the conditional mean. (Lee (2005))
One can nicely illustrate Quantile Regression when comparing it with OLS. In OLS, modeling a conditional distribution function of a random sample () with a parametric function where represents the independent variables, the corresponding estimates and the conditional mean, one gets following minimization problem:
One thereby obtains the conditional expectation function . Now, in a similar fashion one can proceed in Quantile Regression. Central feature thereby becomes , which serves as a check function.
This check-function ensures that
1. all are positive
2. the scale is according to the probability
Such a function with two supports is a must if dealing with L1 distances, which can become negative.
In Quantile Regression one minimizes now following function:
Here, as opposed to OLS, the minimization is done for each subsection defined by , where the estimate of the -quantile function is achieved with the parametric function . (Koenker and Hallock (2001))
Features that characterize Quantile Regression and differentiate it from other regression methods are following:
1. The entire conditional distribution of the dependent variable can be characterized through different values of
2. Heteroscedasticity can be detected
3. If the data is heteroscedastic, median regression estimators can be more efficient than mean regression estimators
4. The minimization problem as illustrated in equation 9 can be solved efficiently by linear programming methods, making estimation easy
5. Quantile functions are also equivariant to monotone transformations. That is , for any function
6. Quantiles are robust in regards to outliers ( Lee (2005) )
A graphical illustration of Quantile Regression
[edit | edit source]Before proceeding to a numerical example, the following subsection seeks to graphically illustrate the concept of Quantile Regression. First, as a starting point for this illustration, consider figure 1. For a given explanatory value of the density for a conditional dependent variable is indicated by the size of the balloon. The bigger the balloon, the higher is the density, with the mode, i.e. where the density is the highest, for a given being the biggest balloon. Quantile Regression essentially connects the equally sized balloons, i.e. probabilities, across the different values of , thereby allowing one to focus on the interrelationship between the explanatory variable and the dependent variable for the different quantiles, as can be seen in figure 2. These subsets, marked by the quantile lines, reflect the probability density of the dependent variable given .

The example used in figure 2 is originally from Koenker and Hallock (2000), and illustrates a classical empirical application, Ernst Engel's (1857) investigation into the relationship of household food expenditure, being the dependent variable, and household income as the explanatory variable. In Quantile Regression the conditional function of is segmented by the -quantile. In the analysis, the -quantiles , indicated by the thin blue lines that separate the different color sections, are superimposed on the data points. The conditional median () is indicated by a thick dark blue line, the conditional mean by a light yellow line. The color sections thereby represent the subsections of the data as generated by the quantiles.

Figure 2 can be understood as a contour plot representing a 3-D graph, with food expenditure and income on the respective y and x axis. The third dimension arises from the probability density of the respective values. The density of a value is thereby indicated by the darkness of the shade of blue, the darker the color, the higher is the probability of occurrence. For instance, on the outer bounds, where the blue is very light, the probability density for the given data set is relatively low, as they are marked by the quantiles 0,05 to 0,1 and 0,9 to 0,95. It is important to notice that figure 2 represents for each subsections the individual probability of occurrence, however, quantiles utilize the cumulative probability of a conditional function. For example, of 0,05 means that 5 of observations are expected to fall below this line, a of 0,25 for instance means that 25 of the observations are expected to fall below this and the 0,1 line.
The graph in figure 2, suggests that the error variance is not constant across the distribution. The dispersion of food expenditure increases as household income goes up. Also the data is skewed to the left, indicated by the spacing of the quantile lines that decreases above the median and also by the relative position of the median which lies above the mean. This suggests that the axiom of homoscedasticity is violated, which OLS relies on. The statistician is therefore well advised to engage in an alternative method of analysis such as Quantile Regression, which is actually able to deal with heteroscedasticity.
A Quantile Regression Analysis
[edit | edit source]In order to give a numerical example of the analytical power of Quantile Regression and to compare it within the boundaries of a statistical application with OLS the following section will be analyzing some selected variables of the Boston Housing dataset which is available at the md-base website. The data was first analyzed by Belsley, Kuh, and Welsch (1980). The original data comprised 506 observations for 14 variables stemming from the census of the Boston metropolitan area.
This analysis utilizes as the dependent variable the median value of owner occupied homes (a metric variable, abbreviated with H) and investigates the effects of 4 independent variables as shown in table 1. These variables were selected as they best illustrate the difference between OLS and Quantile Regression. For the sake of simplicity of the analysis, it was neglected for now to deal with potential difficulties related to finding the correct specification of a parametric model. A simple linear regression model therefore was assumed. For the estimation of asymptotic standard errors see for example Buchinsky (1998), which illustrates the design-matrix bootstrap estimator or alternatively Powell (1986) for kernel based estimation of asymptotic standard errors.
| Name | Short | What it is | type |
|---|---|---|---|
| NonrTail | T | Proportion of non-retail business acres | metric |
| NoorOoms | O | Average number of rooms per dwelling | metric |
| Age | A | Proportion of owner-built dwellings prior to 1940 | metric |
| PupilTeacher | P | Pupil-teacher ratio | metric |
In the following firstly an OLS model was estimated. Three digits after the comma were indicated in the tables as some of the estimates turned out to be very small.
Computing this via XploRe one obtains the results as shown in the table below.
| 36,459 | 0,021 | 38,010 | 0,001 | -0,953 |
Analyzing this data set via Quantile Regression, utilizing the quantiles the model is characterized as follows:
Just for illustrative purposes and to further foster the understanding of the reader for Quantile Regression, the equation for the quantile is briefly illustrated, all others follow analogous:
| 0,1 | 23,442 | 0,087 | 29,606 | -0,022 | -0,443 |
| 0,3 | 15,7130 | -0,001 | 45,281 | -0,037 | -0,617 |
| 0,5 | 14,8500 | 0,022 | 53,252 | -0,031 | -0,737 |
| 0,7 | 20,7910 | -0,021 | 50,999 | -0,003 | -0,925 |
| 0,9 | 34,0310 | -0,067 | 51,353 | 0,004 | -1,257 |
Now if one compares the results for the estimates of OLS from table 2 and Quantile Regression, table 3, one finds that the latter method can make much more subtle inferences of the effect of the explanatory variables on the dependent variable. Of particular interest are thereby quantile estimates that are relatively different as compared to other quantiles for the same estimate.
Probably the most interesting result and most illustrative in regards to an understanding of the functioning of Quantile Regression and pointing to the differences with OLS are the results for the independent variable of the proportion of non-retail business acres . OLS indicates that this variable has a positive influence on the dependent variable, the value of homes, with an estimate of , i.e. the value of houses increases as the proportion of non-retail business acres increases in regards to the Boston Housing data.
Looking at the output that Quantile Regression provides us with, one finds a more differentiated picture. For the 0,1 quantile, we find an estimate of which would suggest that for this low quantile the effect seems to be even stronger than is suggested by OLS. Here house prices go up when the proportion of non-retail businesses goes up, too. However, considering the other quantiles, this effect is not quite as strong anymore, for the 0,7th and 0,9th quantile this effect seems to be even reversed indicated by the parameter and . These values indicate that in these quantiles the house price is negatively influenced by an increase of non-retail business acres . The influence of non-retail business acres seems to be obviously very ambiguous on the dependent variable of housing price, depending on which quantile one is looking at. The general recommendation from OLS that if the proportion of non-retail business acres increases, the house prices would increase can obviously not be generalized. A policy recommendation on the OLS estimate could therefore be grossly misleading.
One would intuitively find the statement that the average number of rooms of a property positively influences the value of a house, to be true. This is also suggested by OLS with an estimate of . Now Quantile Regression also confirms this statement, however, it also allows for much subtler conclusions. There seems to be a significant difference between the 0,1 quantile as opposed to the rest of the quantiles, in particular the 0,9th quantile. For the lowest quantile the estimate is , whereas for the 0,9th quantile it is . Looking at the other quantiles one can find similar values for the Boston housing data set as for the 0,9th, with estimates of , , and respectively. So for the lowest quantile the influence of additional number of rooms on the house price seems to be considerably smaller then for all the other quantiles.
Another illustrative example is provided analyzing the proportion of owner-occupied units built prior to 1940 and its effect on the value of homes. Whereas OLS would indicate this variable has hardly any influence with an estimate of , looking at Quantile Regression one gets a different impression. For the 0,1th quantile, the age has got a negative influence on the value of the home with . Comparing this with the highest quantile where the estimate is , one finds that the value of the house is suddenly now positively influenced by its age. Thus, the negative influence is confirmed by all other quantiles besides the highest, the 0,9th quantile.
Last but not least, looking at the pupil-teacher ratio and its influence on the value of houses, one finds that the tendency that OLS indicates with a value of to be also reflected in the Quantile Regression analysis. However, in Quantile Regression one can see that the influence on the housing price of the pupils-teacher ratio gradually increases over the different quantiles, from the 0,1th quantile with an estimate of to the 0,9th quantile with a value of .
This analysis makes clear, that Quantile Regression allows one to make much more differentiated statements when using Quantile Regression as opposed to OLS. Sometimes OLS estimates can even be misleading what the true relationship between an explanatory and a dependent variable is as the effects can be very different for different subsection of the sample.
Conclusion
[edit | edit source]For a distribution function one can determine for a given value of the probability of occurrence. Now quantiles do exactly the opposite. That is, one wants to determine for a given probability of the sample data set the corresponding value . In OLS, one has the primary goal of determining the conditional mean of random variable , given some explanatory variable , . Quantile Regression goes beyond this and enables us to pose such a question at any quantile of the conditional distribution function. It focuses on the interrelationship between a dependent variable and its explanatory variables for a given quantile. Quantile Regression overcomes thereby various problems that OLS is confronted with. Frequently, error terms are not constant across a distribution, thereby violating the axiom of homoscedasticity. Also, by focusing on the mean as a measure of location, information about the tails of a distribution are lost. And last but not least, OLS is sensitive to extreme outliers, which can distort the results significantly. As has been indicated in the small example of the Boston Housing data, sometimes a policy based upon an OLS analysis might not yield the desired result as a certain subsection of the population does not react as strongly to this policy or even worse, responds in a negative way, which was not indicated by OLS.
References
[edit | edit source]Abrevaya, J. (2001): “The effects of demographics and maternal behavior on the distribution of birth outcomes,” in Economic Application of Quantile Regression, ed. by B. Fitzenberger, R. Koenker, and J. A. Machade, pp. 247–257. Physica-Verlag Heidelberg, New York.
Belsley, D. A., E. Kuh, and R. E. Welsch (1980): Applied Multivariate Statistical Analysis. Regression Diagnostics, Wiley.
Buchinsky, M. (1998): “Recent Advances in Quantile Regression Models: A Practical Guidline for Empirical Research,” Journal of Human Resources, 33(1), 88–126.
Cade, B.S. and B.R. Noon (2003): A gentle introduction to quantile regression for ecologists. Frontiers in Ecology and the Environment 1(8): 412-420. http://www.fort.usgs.gov/products/publications/21137/21137.pdf
Cizek, P. (2003): “Quantile Regression,” in XploRe Application Guide, ed. by W. Härdle, Z. Hlavka, and S. Klinke, chap. 1, pp. 19–48. Springer, Berlin.
Curry, J., and J. Gruber (1996): “Saving Babies: The Efficacy and Costs of Recent Changes in the Medicaid Eligibility of Pregnant Women,” Journal of Political Economy, 104, 457–470.
Handl, A. (2000): “Quantile,” available at http://www.wiwi.uni-bielefeld.de/~frohn/Lehre/Datenanalyse/Skript/daquantile.pdf
Härdle, W. (2003): Applied Multivariate Statistical Analysis. Springer Verlag, Heidelberg. Hyndman, R. J., and Y. Fan (1996): “Sample Quantiles in Statistical Packages,” The American Statistician, 50(4), 361 – 365.
Jeffreys, H., and B. S. Jeffreys (1988): Upper and Lower Bounds. Cambridge University Press.
Koenker, R., and G. W. Bassett (1978): “Regression Quantiles,” Econometrica, 46, 33–50.
Koenker, R., and G. W. Bassett (1982): “Robust tests for heteroscedasticity based on Regression Quantiles,” Econometrica, 61, 43–61.
Koenker, R., and K. F. Hallock (2000): “Quantile Regression an Introduction,” available at http://www.econ.uiuc.edu/~roger/research/intro/intro.html
Koenker, R., and K. F. Hallock (2001): “Quantile Regression,” Journal of Economic Perspectives, 15(4), 143–156.
Lee, S. (2005): “Lecture Notes for MECT1 Quantile Regression,” available at http://www.homepages.ucl.ac.uk/~uctplso/Teaching/MECT/lecture8.pdf
Lewit, E. M., L. S. Baker, H. Corman, and P. Shiono (1995): “The Direct Costs of Low Birth Weight,” The Future of Children, 5, 35–51.
mdbase (2005): “Statistical Methodology and Interactive Datanalysis,” available at http://www.quantlet.org/mdbase/
Montenegro, C. E. (2001): “Wage Distribution in Chile: Does Gender Matter? A Quantile Regression Approach,” Working Paper Series 20, The World Bank, Development Research Group.
Powell, J. (1986): “Censored Regression Quantiles,” Journal of Econometrics, 32, 143– 155.
Scharf, F. S., F. Juanes, and M. Sutherland (1998): “Inferring Ecologiocal Relationships from the Edges of Scatter Diagrams: Comparison of Regression Techniques,” Ecology, 79(2), 448–460.
XploRe (2006): “XploRe,” available at http://www.xplore-stat.de/index_js.html
Numerical Comparison of Statistical Software
[edit | edit source]Introduction
[edit | edit source]Statistical computations require extra accuracy and are open to errors such as truncation and cancellation error. These errors occur as a result of binary representation and finite precision and may cause inaccurate results. In this work we are going to discuss the accuracy of statistical software, different tests and methods available for measuring the accuracy and the comparison of different packages.
Accuracy of Software
[edit | edit source]Accuracy can be defined as the correctness of the results. When a statistical software package is used, it is assumed that the results are correct in order to comment on these results. However, it must be accepted that computers have some limitations. The main problem is that the available precision typically provided by computer systems is limited. It is clear that statistical software can not deliver such accurate results, which exceed these limitations. However statistical software should recognize its limits and give clear indication that these limits are reached. We have two types of precision generally used today:
- Single precision
- Double precision
Binary Representation and Finite Precision
[edit | edit source]Binary representation and finite precision cause inaccuracy NIKHIL. Computers don’t have real numbers -- we represent them with a finite approximation.
Example: Assume that we want to represent 0.1 in single precision floating point. The result will be as follows:
0.1 = .00011001100110011001100110 = 0.99999964 (McCullough,1998)
It is clear that we can only approximate to 0.1 in binary form. This problem grows, if we try to subtract two large numbers which differ only in the lowest precision digits. For instance 100000.1-100000 = .09375
With single precision floating point we can only represent 24 significant binary digits, in other words 6-7 decimal digits. In double precision it is possible to represent 53 significant binary digits equivalent to 15-17 significant decimal digits. Limitations of binary representation create five distinct numerical ranges, which cause loss of accuracy:
- negative overflow
- negative underflow
- zero
- positive underflow
- positive overflow
Overflow means that values have grown too large for the representation. Underflow means that operands are so small and so close to zero that the result must be set to zero. Single and double precision representations have different ranges.
Results of Binary Representation
[edit | edit source]These limitations cause different errors in different situations:
- Cancellation errors result from subtracting two nearly equal numbers.
- Accumulation errors are successive rounding errors in a series of calculations summed up to a total error. In this type of error it is possible that only the rightmost digits of the result are affected or that the result has no single accurate digits.
- Another result of binary representation and finite precision is that two formulas which are algebraically equivalent may not be equivalent numerically. For instance:
The first formula adds the numbers in ascending order, whereas the second adds them in descending order. In the first formula the smallest numbers are reached at the very end of the computation, so that these numbers are all lost to rounding error. The error is 650 times greater than the second.(McCullough,1998)
- Truncation errors are approximation errors which result from the limitations of binary representation.
Example:
The difference between the true value of sin(x) and the result achieved by summing up finite number of terms is the truncation error. (McCullough,1998)
- Algorithmic errors are another source of inaccuracies. There can be different ways of calculating a quantity and these different methods may vary in accuracy. For example according to Sawitzki (1994) in a single precision environment using the following formula in order to calculate variance :
Measuring Accuracy
[edit | edit source]Due to limits of computers some problems occur in calculating statistical values. We need a measure which shows us the degree of accuracy of a computed value. This measurement is based on the difference between the computed value (q) and the real value (c). An often used measure is Log Relative Error or LRE (the number of the correct significant digits)(McCullough,1998)
Rules:
- q should be close to c (by less than 2 digits). If they are not, set LRE to zero
- If LRE is greater than number of the digits in c, set LRE to number of the digits in c.
- If LRE is less than unity, set it to zero.
Testing Statistical Software
[edit | edit source]In this part we are going to discuss two different tests which aim to measure the accuracy of the software: Wilkinson Test (Wilkinson, 1985) and NIST StRD Benchmarks.
Wilkinson's Statistic Quiz
[edit | edit source]The Wilkinson dataset “NASTY” which is employed in Wilkinson’s Statistic Quiz is a dataset created by Leland Wilkinson (1985). This dataset consists of different variables such as “Zero” which contains only zeros, “Miss” with all missing values, etc. NASTY is a reasonable dataset in the sense of values it contains. For instance the values of “Big” in “NASTY” are less than U.S. Population, and “Tiny” is comparable to many values in engineering. On the other hand the exercises of the “Statistic Quiz” are not meant to be reasonable. These tests are designed to check some specific problems in statistical computing. Wilkinson’s Statistics Quiz is an entry level test.
NIST StRD Benchmarks
[edit | edit source]These benchmarks consist of different datasets designed by National Institute of Standards and Technology with different levels of difficulty. The purpose is to test the accuracy of statistical software with regard to different topics in statistics and different levels of difficulty. In the webpage of “Statistical Reference Datasets” Project there are five groups of datasets:
- Analysis of Variance
- Linear Regression
- Markov Chain Monte Carlo
- Nonlinear Regression
- Univariate Summary Statistics
In all groups of benchmarks there are three different types of datasets: Lower level difficulty datasets, average level difficulty datasets and higher level difficulty datasets. By using these datasets we are going to explore whether the statistical software deliver accurate results to 15 digits for some statistical computations.
There are 11 datasets provided by NIST among which there are six datasets with lower level difficulty, two datasets with average level difficulty and one with higher level difficulty. Certified values to 15 digits for each dataset are provided for the mean (μ), the standard deviation (σ), and the first-order autocorrelation coefficient (ρ).
In the group of ANOVA-datasets there are 11 datasets with levels of difficulty, four lower, four average and three higher. For each dataset certified values to 15 digits are provided for between treatment degrees of freedom, within treatment degrees of freedom, sums of squares, mean squares, the F-statistic, the , and the residual standard deviation. Since most of the certified values are used in calculating the F-statistic, only its LRE will be compared to the results from statistical software packages.
For testing the linear regression results of statistical software NIST provides 11 datasets with levels of difficulty two lower, two average and seven higher. For each dataset we have the certified values to 15 digits for coefficient estimates, standard errors of coefficients, the residual standard deviation, , the analysis of variance for linear regression table, which includes the residual sum of squares. LREs for the least accurate coefficients , standard errors and Residual sum of squares will be compared. In nonlinear regression dataset group there are 27 datasets designed by NIST with difficulty eight lower, eleven average and eight higher. For each dataset we have certified values to 11 digits provided by NIST for coefficient estimates, standard errors of coefficients, the residual sum of squares, the residual standard deviation, and the degrees of freedom.
In the case of calculation of nonlinear regression we apply curve fitting method. In this method we need starting values in order to initialize each variable in the equation. Then we generate the curve and calculate the convergence criterion (e.g. sum of squares). Then we adjust the variables to make the curve closer to the data points. There are several algorithms for adjusting the variables:
- The method of Marquardt and Levenberg
- The method of linear descent
- The method of Gauss-Newton
One of these methods is applied repeatedly, until the difference in the convergence criterion is smaller than the convergence tolerance.
NIST provides also two sets of starting values: Start I (values far from solution), Start II (values close to solution). Having Start II as initial values makes it easier to reach an accurate solution. Therefore Start I solutions will be preferred.
Other important settings are as follows:
- the convergence tolerance (ex. 1E-6)
- the method of solution (ex. Gauss Newton or Levenberg Marquardt)
- the convergence criterion (ex. residual sum of squares (RSS) or square of the maximum of the parameter differences)
We can also choose between numerical and analytic derivatives.
Testing Examples
[edit | edit source]Testing Software Package: SAS, SPSS and S-Plus
[edit | edit source]In this part we are going to discuss the test results of three statistical software packages applied by M.D. McCullough. In McCullough’s work SAS 6.12, SPSS 7.5 and S-Plus 4.0 are tested and compared in respect to certified LRE values provided by NIST. Comparison will be handled according to the following parts:
- Univariate Statistics
- ANOVA
- Linear Regression
- Nonlinear Regression
Univariate Statistics
[edit | edit source]
All values calculated in SAS seem to be more or less accurate. For the dataset NumAcc1 p-value can not be calculated because of the insufficient number of observations. Calculating standard deviation for datasets NumAcc3 (average difficulty) and NumAcc 4 (high difficulty) seems to stress SAS.

All values calculated for mean and standard deviation seem to be more or less accurate. For the dataset NumAcc1 p-value can not be calculated because of the insufficient number of observations. Calculating the standard deviation for datasets NumAcc3 and -4 seems to stress SPSS, as well. For p-values SPSS represents results with only 3 decimal digits which understates the accuracy of the first p-value and overstates the last.

All values calculated for mean and standard deviation seem to be more or less accurate. S-Plus also hs problems in calculating the standard deviation for datasets NumAcc3 and -4. S-Plus shows poor performance in calculating the p-values.
Analysis of Variance
[edit | edit source]
Results:
- SAS can solve only the ANOVA problems of lower level difficulty.
- F-Statistics for datasets of average or higher difficulty can be calculated with very poor performance and zero digit accuracy.
- SPSS can display accurate results for datasets with lower level difficulty, like SAS.
- Performance of SPSS in calculating ANOVA is poor.
- For dataset “AtmWtAg” SPSS displays no F-Statistic which seems more logical instead of displaying zero accurate results.
- S-Plus handles ANOVA problem better than other software packages.
- Even for higher difficulty datasets S-Plus can display more accurate results than the others. But still results for datasets with high difficulty are not accurate enough.
- S-Plus can solve the average difficulty problems with sufficient accuracy.
Linear Regression
[edit | edit source]
SAS delivers no solution for dataset Filip which is a ten degree polynomial. Apart from Filip, SAS displays more or less accurate results. But the performance seems to decrease for higher difficulty datasets, especially in calculating coefficients.

SPSS has also Problems with “Filip” which is a 10 degree polynomial. Many packages fail to compute values for it. Like SAS, SPSS delivers lower accuracy for high level datasets.

S-Plus is the only package which delivers a result for dataset “Filip”. The accuracy of the result for Filip seems not to be poor but average. Even for higher difficulty datasets S-Plus can calculate more accurate results than other software packages. Only coefficients for datasets “Wrampler4” and “-5” are under the average accuracy.
Nonlinear Regression
[edit | edit source]
For the nonlinear regression, two setting combinations are tested for each software package, because different settings make a difference in the results. As we can see in the table in SAS preferred combination produce better results than the default combination. In this table results produced using the default combination are in parentheses. Because 11 digits are provided for certified values by NIST, we are looking for LRE values of 11.
Preferred combination :
- Method:Gauss-Newton
- Criterion: PARAM
- Tolerance: 1E-6

Also in SPSS the preferred combination shows a better performance than default options. All problems are solved with initial values “start I” whereas in SAS higher level datasets are solved with Start II values.
Preffered Combination:
- Method:Levenberg-Marquardt
- Criterion:PARAM
- Tolerance: 1E-12

As we can see in the table, the preferred combination is also better in S-Plus than default the combination. All problems except “MGH10” are solved with initial values “start I”. We may say that S-Plus showed better performance than other software in calculating nonlinear regression.
Preferred Combination:
- Method:Gauss-Newton
- Criterion:RSS
- Tolerance: 1E-6
Results of the Comparison
[edit | edit source]All packages delivered accurate results for mean and standard deviation in univariate statistics. There are no big differences between the tested statistical software packages. In ANOVA calculations SAS and SPSS can not pass the average difficulty problems, whereas S-Plus delivered more accurate results than others. But for high difficulty datasets it also produced poor results. Regarding linear regression problems, all packages seem to be reliable. If we examine the results for all software packages, we can say that the success in calculating the results for nonlinear regression greatly depends on the chosen options.
Other important results are as follows:
- S-Plus solved from Start II one time.
- SPSS never used Start II as initial values, but once produced zero accurate digits.
- SAS used Start II three times and produced zero accurate digits each time.
Comparison of different versions of SPSS
[edit | edit source]In this part we are going to compare an old version with a new version of SPSS in order to see whether the problems in older version are solved in the new one. In this part we compared SPSS version 7.5 with SPSS version 12.0. LRE values for version 7.5 are taken from an article by B.D. McCullough (see references). We also applied these tests to version 12.0 and calculated regarding LRE values. We chose one dataset from each difficulty groups and applied univariate statistics, ANOVA and linear regression in version 12.0. The source for the datasets is NIST Statistical Reference Datasets Archive. Then we computed LRE values for each dataset by using the certified values provided by NIST in order to compare the two versions of SPSS.
Univariate Statistics
[edit | edit source]Difficulty: Low
Our first dataset is PiDigits with lower level difficulty which is designed by NIST in order to detect the deficiencies in calculating univariate statistical values.
Certified Values for PiDigits are as follows:
- Sample Mean : 4.53480000000000
- Sample Standard Deviation : 2.86733906028871
As we can see in the table 13 the results from SPSS 12.0 match the certified values provided by NIST. Therefore our LREs for mean and standard deviation are : 15, : 15. In version 7.5 LRE values were : 14.7, : 15. (McCullough,1998)
Difficulty: Average
Second dataset is NumAcc3 with average difficulty from NIST datasets for univariate statistics. Certified Values for NumAcc3 are as follows:
- Sample Mean : 1000000.2
- Sample Standard Deviation : 0.1
In the table 14 we can see that calculated mean value is the same with the certified value by NIST. Therefore our LREs for mean is : 15. However the standard deviation value differs from the certified value. So the calculation of LRE for standard deviation is as follows:
LREs for SPSS v 7.5 were : 15, : 9.5. (McCullough,1998)
Difficulty: High
Last dataset in univariate statistics is NumAcc4 with high level of difficulty. Certified Values for NumAcc4 are as follows:
- Sample Mean : 10000000.2
- Sample Standard Deviation : 0.1
Also for this dataset we do not have any problems with computed mean value. Therefore LRE is : 15. However the standard deviation value does not match to the certified one. So we should calculate the LRE for standard deviation as follows:
: -log10 |0,10000000056078-0,1|/|0,1| = 8.3
LREs for SPSS v 7.5 were : 15, : 8.3 (McCullough,1998)
For this part of our test we can say that there is no difference between two versions of SPSS. For average and high difficulty datasets delivered standard deviation results have still an average accuracy.
Analysis of Variance
[edit | edit source]Difficulty: Low
The dataset which we used for testing SPSS 12.0 regarding lower difficulty level problems is SiRstv. Certified F Statistic for SiRstv is 1.18046237440255E+00
- LRE : : -log10 | 1,18046237440224- 1,18046237440255|/ |1,18046237440255| = 12,58
- LRE for SPSS v 7.5 : : 9,6 (McCullough, 1998)
Difficulty: Average
Our dataset for average difficulty problems is AtmWtAg . Certified F statistic value for AtmWtAg is 1.59467335677930E+01.
- LREs : : -log10 | 15,9467336134506- 15,9467335677930|/| 15,9467335677930| = 8,5
- LREs for SPSS v 7.5 : : miss
Difficulty: High
We used the dataset SmnLsg07 in order to test high level difficulty problems. Certified F value for SmnLsg07 is 2.10000000000000E+01
- LREs : : -log10 | 21,0381922055595 - 21|/| 21| = 2,7
- LREs for SPSS v 7.5 : : 0
ANOVA results computed in version 12.0 are better than those calculated in version 7.5. However the accuracy degrees are still too low.
Linear Regression
[edit | edit source]Difficulty: Low
Our lower level difficulty dataset is Norris for linear regression. Certified values for Norris are as follows:
- Sample Residual Sum of Squares : 26.6173985294224

Table 17: Coefficient estimates for Norris(www.itl.nist.gov) - LREs : : 9,9 : 12,3 : 10,2
- LREs for SPSS v 7.5 : : 9,9 , : 12,3 , : 10,2 (McCullough, 1998)
Difficulty: Average
We used the dataset NoInt1 in order to test the performance in average difficulty dataset. Regression model is as follows:
y = B1*x + e
Certified Values for NoInt1 :
- Sample Residual Sum of Squares : 127,272727272727
- Coefficient estimate : 2.07438016528926, standard deviation : 0.16528925619834E-0(www.itl.nist.gov)
- LREs: :12,8 : 15 : 12,9
- LREs for SPSS v. 7.5 : : 12,8 , : 14,7 , : 12,5 (McCullough, 1998)
Difficulty: High
Our high level difficulty dataset is Longley designed by NIST.
- Model: y =B0+B1*x1 + B2*x2 + B3*x3 + B4*x4 + B5*x5 + B6*x6 +e
- LREs :
- : -log10 |836424,055505842-836424,055505915|/ |836424,055505915| = 13,1
- : 15
- : -log10 | 0,16528925619836E-01 – 0,16528925619834E-01|/ |0,16528925619834E-01| = 12,9
- LREs for SPSS v. 7.5 : : 12,8 , : 14,7 , : 12,5 (McCullough, 1998)
As we conclude from the computed LREs, there is no big difference between the results of two versions for linear regression.
Conclusion
[edit | edit source]By applying these test we try to find out whether the software are reliable and deliver accurate results or not. However based on the results we can say that different software packages deliver different results for same the problem which can lead us to wrong interpretations for statistical research questions.
In specific we can that SAS, SPSS and S-Plus can solve the linear regression problems better in comparision to ANOVA Problems. All three of them deliver poor results for F statistic calculation.
From the results of comparison two different versions of SPSS we can conclude that the difference between the accuracy of the results delivered by SPSS v.12 and v.7.5 is not great considering the difference between the version numbers. On the other hand SPSS v.12 can handle the ANOVA Problems much better than old version. However it has still problems in higher difficulty problems.
References
[edit | edit source]- McCullough, B.D. 1998, 'Assessing The Reliability of Ststistical Software: Part I',The American Statistician, Vol.52, No.4, pp.358-366.
- McCullough, B.D. 1999, 'Assessing The Reliability of Ststistical Software: Part II', The American Statistician, Vol.53, No.2, pp.149-159
- Sawitzki, G. 1994, 'Testing Numerical Reliability of Data Analysis Systems', Computational Statistics & Data Analysis, Vol.18, No.2, pp.269-286
- Wilkinson, L. 1993, 'Practical Guidelines for Testing Statistical Software' in 25th Conference on Statistical Computing at Schloss Reisenburg, ed. P. Dirschedl& R. Ostermnann, Physica Verlag
- National Institute of Standards and Technology. (1 September 2000). The Statistical Reference Datasets: Archives, [Online], Available from: <http://www.itl.nist.gov/div898/strd/general/dataarchive.html> [10 November 2005].
Numerics in Excel
[edit | edit source]The purpose of this paper is to evaluate the accuracy of MS Excel in terms of statistical procedures and to conclude whether the MS Excel should be used for (statistical) scientific purposes or not.
According to the literature, there are three main problematic areas for Excel if it is used for statistical calculations. These are
- probability distributions,
- univariate statistics, ANOVA and Estimations (both linear and non-linear)
- random number generation.
If the results of statistical packages are assessed, one should take into account that the acceptable accuracy of the results should be achieved in double precision (which means that a result is accepted as accurate if it possesses 15 accurate digits) given that the reliable algorithms are capable of delivering correct results in double precision, as well. If the reliable algorithms can not retrieve results in double precision, it is not fair to anticipate that the package (evaluated) should achieve double precision. Thus we can say that the correct way for evaluating the statistical packages is assessing the quality of underlying algorithm of statistical calculations rather than only counting the accurate digits of results. Besides, test problems must be reasonable which means they must be amenable to solution by known reliable algorithms. (McCullough & Wilson, 1999, S. 28)
In further sections, our judgement about the accuracy of MS Excel will base on certified values and tests. As basis we have Knüsel’s ELV software for probability distributions, StRD (Statistical Reference Datasets) for Univariate Statistics, ANOVA and Estimations and finally Marsaglia’s DIEHARD for Random Number Generation. Each of the tests and certified values will be explained in the corresponding sections.
Assessing Excel Results for Statistical Distributions
[edit | edit source]As we mentioned above our judgement about Excel’s calculations for probability distributions will base on Knüsel’s ELV Program which can compute probabilities and quantiles of some elementary statistical distributions. Using ELV, the upper and lower tail probabilities of all distributions are computed with six significant digits for probabilities as small as 10−100 and upper and lower quantiles are computed for all distributions for tail probabilities P with 10−12 ≤ P ≤ ½. (Knüsel, 2003, S.1)
In our benchmark Excel should display no inaccurate digits. If six digits are displayed, then all six digits should be correct. If the algorithm is only accurate to two digits, then only two digits should be displayed so as not to mislead the user (McCullough & Wilson, 2005, S. 1245)
In the following sub-sections the exact values in the tables are retrieved from Knüsel’s ELV software and the acceptable accuracy is in single precision, because even the best algorithms can not achieve 15 correct digits in most cases, if the probability distributions are issued.
Normal Distribution
[edit | edit source]- Excel Function:NORMDIST
- Parameters: mean = 0, variance = 1, x (critical value)
- Computes: the tail probability Pr X ≤ x, whereas X denotes a random variable with a standard normal distribution (with mean 0 and variance 1)

As we can see in table 1, Excel 97, 2000 and XP encounter problems and computes small probabilities in tail incorrectly (i.e for x = -8,3 or x = -8.2) However, this problem is fixed in Excel 2003 (Knüsel, 2005, S.446).
Inverse Normal Distribution
[edit | edit source]- Excel Function: NORMINV
- Parameters: mean = 0, variance = 1, p (probability for X < x)
- Computes: the x value (quantile)
X denotes a random variable with a standard normal distribution. In contrast to “NORMDIST” function issued in the last section, p is given and quantile is computed.
If used, Excel 97 prints out quantiles with 10 digits although none of these 10 digits may be correct if p is small. In Excel 2000 and XP, Microsoft tried to fix errors, although results are not sufficient (See table 2). However in Excel 2003 the problem is fixed entirely. (Knüsel, 2005, S.446)

Inverse Chi-Square Distribution
[edit | edit source]- Excel Function: CHIINV
- Parameters: p (probability for X > x), n (degrees of freedom)
- Computes: the x value (quantile)
X denotes a random variable with a chi-square distribution with n degrees of freedom.

Old Excel Versions: Although the old Excel versions show ten significant digits, only very few of them are accurate if p is small (See table 3). Even if p is not small, the accurate digits are not enough to say that Excel is sufficient for this distribution.
Excel 2003: Problem was fixed. (Knüsel, 2005, S.446)
Inverse F Distribution
[edit | edit source]- Excel Function: FINV
- Parameters: p (probability for X > x), n1, n2 (degrees of freedom)
- Computes: the x value (quantile)
X denotes a random variable with a F distribution with n1 and n2 degrees of freedom.

Old Excel Versions: Excel prints out x values with 7 or more significant digits although only one or two of these many digits are correct if p is small (See table 4).
Excel 2003: Problem fixed. (Knüsel, 2005, S.446)
Inverse t Distribution
[edit | edit source]- Excel Function: TINV
- Parameters: p (probability for |X| > x), n (degree of freedom)
- Computes: the x value (quantile)
X denotes a random variable with a t distribution with n degrees of freedom. Please note that the |X| value causes a 2 tailed computation. (lower tail & high tail)

Old Excel Versions: Excel prints out quantiles with 9 or more significant digits although only one or two of these many digits are correct if p is small (See table 5).
Excel 2003: Problem fixed. (Knüsel, 2005, S.446)
Poisson Distribution
[edit | edit source]- Excel Function: Poisson
- Parameters: λ (mean), k (number of cases)
- Computes: the tail probability Pr X ≤ k
X denotes a random variable with a Poisson distribution with given parameters.

Old Excel Versions: correctly computes very small probabilities but gives no result for central probabilities near the mean (in the range about 0.5). (See table 6)
Excel 2003: The central probabilities are fixed. However, inaccurate results in the tail. (See table 6)
The strange behaviour of Excel can be encountered for values λ150. (Knüsel, 1998, S.375) It fails even for probabilities in the central range between 0.01 and 0.99 and even for parameter values that cannot be judged as too extreme.
Binomial Distribution
[edit | edit source]- Excel Function: BINOMDIST
- Parameters: n (= number of trials) , υ(= probability for a success) , k(number of successes)
- Computes: the tail probability Pr X ≤ k
-X denotes a random variable with a binoamial distribution with given parameters
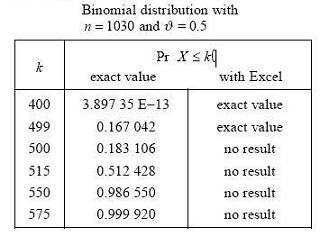
Old Excel Versions: As we see in table 7, old versions of Excel correctly computes very small probabilities but gives no result for central probabilities near the mean (same problem with Poisson distribuiton on old Excel versions)
Excel 2003: The central probabilities are fixed. However, inaccurate results in the tail. (Knüsel, 2005, S.446). (same problem with Poisson distribuiton on Excel 2003).
This strange behaviour of Excel can be encountered for values n > 1000. (Knüsel, 1998, S.375) It fails even for probabilities in the central range between 0.01 and 0.99 and even for parameter values that cannot be judged as too extreme.
Other problems
[edit | edit source]- Excel 97, 2000 and XP includes flaws by computing the hypergeometric distribution (HYPERGEOM). For some values (N > 1030) no result is retrieved. This is prevented on Excel 2003, but there is still no option to compute tail probabilities. So computation of Pr {X = k} is possible, but computation of Pr {X ≤ k} is not. (Knüsel, 2005, S.447)
- Function GAMMADIST for gamma distribution retrieves incorrect values on Excel 2003. (Knüsel, 2005, S.447-448)
- Also the function BETAINV for inverse beta distribution computes incorrect values on Excel 2003 (Knüsel, 2005, S. 448)
Assessing Excel Results for Univariate Statistics, ANOVA and Estimation (Linear & Non-Linear)
[edit | edit source]Our judgement about Excel’s calculations for univariate statistics, ANOVA and Estimation will base on StRD which is designed by Statistical Engineering Division of National Institute of Standards and Technology (NIST) to assist researchers in benchmarking statistical software packages explicitly. StRD has reference datasets (real-world and generated datasets) with certified computational results that enable the objective evaluation of statistical Software. It comprises four suites of numerical benchmarks for statistical software: univariate summary statistics, one way analysis of variance, linear regression and nonlinear regression and it includes several problems for each suite of tests. All problems have a difficulty level:low, average or high.
By assessing Excel results in this section we are going to use LRE (log relative error) which can be used as a score for accuracy of results of statistical packages. The number of correct digits in results can be calculated via log relative error. Please note that for double precision the computed LRE is in the range 0 - 15, because we can have max. 15 correct digits in double precision.
Formula LRE:
c: the correct answer (certified computational result) for a particular test problem
x: answer of Excel for the same problem
Univariate Statistics
[edit | edit source]- Excel Functions: - AVERAGE, STDEV, PEARSON (also CORREL)
- Computes (respectively): mean, standard deviation, correlation coefficient

Old Excel Versions: an unstable algorithm for calculation of the sample variance and the correlation coefficient is used. Even for the low difficulty problems (datasets with letter “l” in table 8) the old versions of Excel fail.
Excel 2003: Problem was fixed and the performance is acceptable. The accurate digits less than 15 don’t indicate an unsuccessful implementation because even the reliable algorithms can not retrieve 15 correct digits for these average and high difficulty problems (datasets with letters “a” and “h” in table 8) of StRD.
ONEWAY ANOVA
[edit | edit source]- Excel Function: Tools – Data Analysis – ANOVA: Single Factor (requires Analysis Toolpak)
- Computes: df, ss, ms, F-statistic
Since ANOVA produces many numerical results (such as df, ss, ms, F), here only the LRE for the final F-statistic is presented. Before assessing Excel’s performance one should consider that a reliable algorithm for one way Analysis of Variance can deliver 8-10 digits for the average difficulty problems and 4-5 digits for higher difficulty problems.

Old Excel Versions: Considering numerical solutions, delivering only a few digits of accuracy for difficult problems is not an evidence for bad software, but retrieving 0 accurate digits for average difficulty problems indicates bad software when calculating ANOVA. (McCullough & Wilson, 1999, S. 31). For that reason Excel versions prior than Excel 2003 has an acceptable performance only on low-difficulty problems. It retrieves zero accurate digits for difficult problems. Besides, negative results for “within group sum of squares” and “between group sum of squares” are the further indicators of a bad algorithm used for Excel. (See table 9)
Excel 2003: Problem was fixed (See table 9). The zero digits of accuracy for the Simon 9 test is no cause for concern, since this also occurs when reliable algorithms are employed. Therefore the performance is acceptable. (McCullough & Wilson, 2005, S. 1248)
Linear Regression
[edit | edit source]- Excel Function: LINEST
- Computes: All numerical results required by Linear Regression
Since LINEST produces many numerical results for linear regression, only the LRE for the coefficients and standard errors of coefficients are taken into account. Table 9 shows the lowest LRE values for each dataset as the weakest link in the chain in order to reflect the worst estimations (smallest -LRE and -LRE) made by Excel for each linear regression function.
Old Excel Versions: either doesn't check for near-singularity of the input matrix or checking it incorrectly, so the results for ill-conditioned Dataset “Filip (h)” include not a single correct digit. Actually, Excel should have refused the solution and commit a warning to user about the near singularity of data matrix. (McCullough & Wilson, 1999, S.32,33) . However, in this case, the user is mislead.
Excel 2003: Problem is fixed and Excel 2003 has an acceptable performance. (see table 10)

Non-Linear Regression
[edit | edit source]When solving nonlinear regression using Excel, it is possible to make choices about:
- method of derivative calculation: forward (default) or central numerical derivatives
- convergence tolerance (default=1.E-3)
- scaling (recentering) the variables
- method of solution (default – GRG2 quasi-Newton method)
Excel’s default parameters don’t always produce the best solutions always (like all other solvers). Therefore one needs to give different parameters and test the Excel-Solver for non-linear regression. In table 10 the columns A-B-C-D are combinations of different non-linear options. Because changing the 1st and 4th option doesn’t affect the result, only 2nd and 3rd parameters are changed for testing:
- A: Default estimation
- B: Convergence Tolerance = 1E -7
- C: Automatic Scaling
- D: Convergence Tolerance = 1E -7 & Automatic Scaling
In Table 11, the lowest LRE principle is applied to simplify the assessment. (like in linear reg.)
Results in table 11 are same for each Excel version (Excel 97, 2000, XP, 2003)

As we see in table 11, the non-linear option combination A produces 21 times, B 17 times, C 20 times and D 14 times “0” accurate digits. which indicates that the performance of Excel in this area is inadequate. Expecting to find all exact solutions for all problems with Excel is not fair, but if it is not able to find the result, it is expected to warn user and commit that the solution can not be calculated. Furthermore, one should emphasize that other statistical packages like SPSS, S-PLUS and SAS exhibit zero digit accuracy only few times (0 to 3) in these tests (McCullough & Wilson, 1999, S. 34).
Assessing Random Number Generator of Excel
[edit | edit source]Many statistical procedures employ random numbers and it is expected that the generated random numbers are really random. Only random number generators should be used that have solid theoretical properties. Additionally, statistical tests should be applied on samples generated and only generators whose output has successfully passed a battery of statistical tests should be used. (Gentle, 2003)
Based on the facts explained above we should assess the quality of Random Number Generation by:
- analysing the underlying algorithm for Random Number Generation.
- analysing the generators output stream. There are many alternatives to test the output of a RNG. One can evaluate the generated output using static tests in which the generation order is not important. These tests are goodness of fit tests. The second way of evaluating the output stream is running a dynamic test on generator, whereas the generation order of the numbers is important.
Excel’s RNG – Underlying algorithm
[edit | edit source]The objective of random number generation is to produce samples any given size that are indistinguishable from samples of the same size from a U(0,1) distribution. (Gentle, 2003) For this purpose there are different algorithms to use. Excel’s algorithm for random number generation is Wichmann–Hill algorithm. Wichmann–Hill is a useful RNG algorithm for common applications, but it is obsolete for modern needs (McCullough & Wilson, 2005, S. 1250). The formula for this random number generator is defined as follows:
Wichmann–Hill is a congruential generator which means that it is a recursive aritmethical RNG as we see in the formula above. It is a combination of three other linear congruential generator and requires three seeds: .
Period, in terms of random number generation, is the number of calls that can be made to the RNG before it begins to repeat. For that reason, having a long period is a quality measure for random number generators. It is essential that the period of the generator be larger than the number of random numbers to be used. Modern applications are increasingly demanding longer and longer sequences of random numbers (i.e for using in Monte-Carlo simulations) (Gentle, 2003)
The lowest acceptable period for a good RNG is and the period of Wichmann-Hill RNG is 6.95E+12 (≈ ). In addition to this unacceptable performance, Microsoft claims that the period of Wichmann-Hill RNG is 10E+13 Even if Excel’s RNG has a period of 10E+13, it is still not sufficient to be an acceptable random number generator because this value is also less than . (McCullough & Wilson, 2005, S. 1250)
Furthermore it is known that RNG of Excel produces negative values after the RNG executed many times. However a correct implementation of a Wichmann-Hill Random Number Generator should produce only values between 0 and 1. (McCullough & Wilson, 2005, S. 1249)
Excel’s RNG – The Output Stream
[edit | edit source]As we discussed above, it is not sufficient to discuss only the underlying algorithm of a random number generation. One needs also some tests on output stream of a random number generator while assessing the quality of this random number generator. So a Random Number Generator should produce output which passes some tests for randomness. Such a battery of tests, called DIEHARD, has been prepared by Marsaglia. A good RNG should pass almost all of the tests but as we can see in table 12 Excel can pass only 11 of them (7 failure), although Microsoft has declaired Wichmann–Hill Algorithm is implemented for Excel’s RNG. However, we know that Wichmann-Hill is able to pass 16 tests from DIEHARD (McCullough & Wilson, 1999, S. 35).
Due to reasons explained in previous and this section we can say that Excel’s performance is inadequate (because of period length, incorrect implementation Wichmann Hill Algorithm, which is already obsolete, DIEHARD test results)

Conclusion
[edit | edit source]Old versions of Excel (Excel 97, 2000, XP) :
- shows poor performance on following distributions: Normal, F, t, Chi Square, Binomial, Poisson, Hypergeometric
- retrieves inadequate results on following calculations: Univariate statistics, ANOVA, linear regression, non-linear regression
- has an unacceptable random number generator
For those reasons, we can say that use of Excel 97, 2000, XP for (statistical) scientific purposes should be avoided.
Although several bugs are fixed in Excel 2003, still use of Excel for (statistical) scientific purposes should be avoided because it:
- has a poor performance on following distributions: Binomial, Poisson, Gamma, Beta
- retrieves inadequate results for non-linear regression
- has an obsolete random number generator.
References
[edit | edit source]- Gentle J.E. (2003) Random number generation and Monte Carlo methods 2nd edition. New York Springer Verlag
- Knüsel, L. (2003) Computation of Statistical Distributions Documentation of the Program ELV Second Edition. http://www.stat.uni-muenchen.de/~knuesel/elv/elv_docu.pdf Retrieved [13 November 2005]
- Knüsel, L. (1998). On the Accuracy of the Statistical Distributions in Microsoft Excel 97. Computational Statistics and Data Analysis (CSDA), Vol. 26, 375-377.
- Knüsel, L. (2002). On the Reliability of Microsoft Excel XP for statistical purposes. Computational Statistics and Data Analysis (CSDA), Vol. 39, 109-110.
- Knüsel, L. (2005). On the Accuracy of Statistical Distributions in Microsoft Excel 2003. Computational Statistics and Data Analysis (CSDA), Vol. 48, 445-449.
- McCullough, B.D. & Wilson B. (2005). On the accuracy of statistical procedures in Microsoft Excel 2003. Computational Statistics & Data Analysis (CSDA), Vol. 49, 1244 – 1252.
- McCullough, B.D. & Wilson B. (1999). On the accuracy of statistical procedures in Microsoft Excel 97. Computational Statistics & Data Analysis (CSDA), Vol. 31, 27– 37.
- PC Magazin, April 6, 2004, p.71*
Distributions Problems
[edit | edit source]Statistics/Practice Problems/Distributions
Authors
[edit | edit source]Authors and contributors to this book include:
Glossary
[edit source]This is a glossary of the book.
P
[edit | edit source]- primary data
- Original data that have been collected specially for the purpose in mind.
- population
- Entire group being considered for data collection, that we want to draw conclusions about. EX: The population of the United States
R
[edit | edit source]- Random variable
- A function that associates a specific and unique numerical value with each outcome of an experiment. (EX: X or Y) The outcome is denoted as lower case
S
[edit | edit source]- sample
- a group of units taken from a larger group (the population). Used to draw conclusions of the larger group. EX: 30 people in a town in the US.
- secondary data
- Data that have been collected for another purpose and where we will use Statistical Method with the Primary Data.
- statistic
- A measure that is calculated from a sample of data.
- Statistical Independence
- They do not affect each other
Z
[edit | edit source]- ↑ Pearson, Karl. "Contributions to the mathematical theory of evolution. II. Skew variation in homogeneous material." Philosophical Transactions of the Royal Society of London 186.Part I (1895): 343-424.
- ↑ 25
- ↑ Hurst, Simon, The Characteristic Function of the Student-t Distribution, Financial Mathematics Research Report No. FMRR006-95, Statistics Research Report No. SRR044-95
















![{\displaystyle {\tilde {x}}={\sqrt[{n\;}]{\prod _{i=1}^{n}x_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74c79b93aee3d08c24efa85fcb7915abbd1299a6)
![{\displaystyle {\sqrt[{5}]{1\times 2\times 3\times 4\times 5}}={\sqrt[{5}]{120}}=2.61}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93eafbb54fcdb93e7a1fbf33deaeb56cc2d5147c)


![{\displaystyle \log \left({\sqrt[{n}]{x_{1}\times x_{2}\times x_{3}\cdots x_{n}}}\right)={\frac {1}{n}}\sum _{i=1}^{n}\log(x_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d15c11d0ebbf72852ac644ce767c87468ebeb754)























![{\displaystyle P[X']=1-P[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93f99b25bd7b11468002407a063f6e500b0d7c1b)

![{\displaystyle P[A|B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/022e7d74c15627c78bb8cb0586640d5663b8c66c)

![{\displaystyle P[A|B]=P[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25959140ccae1522bcb51cbb1ed55f49769cb68b)
![{\displaystyle P[A|B_{1},B_{2},B_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6960f3bcd3cdafd519f2950b1fe60b9e6d20fb)







































![{\displaystyle \operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44dd294aa33c0865f58e2b1bdaf44ebe911dbf93)
![{\displaystyle \operatorname {E} [X]=\sum _{x\in S}xf(x)=\sum _{i=0}^{n-1}\left({\frac {1}{n}}(a+i)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb4de36e7f67268e2ed38a0be673c55020dc9867)
![{\displaystyle \operatorname {E} [X]={1 \over n}\left(\sum _{i=0}^{n-1}a+\sum _{i=0}^{n-1}i\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbfde9e3d28efad3fff6f414c27c671dbcbc305e)

![{\displaystyle \operatorname {E} [X]={1 \over n}\left(na+{(n-1)^{2}+(n-1) \over 2}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceca833ac474df48216fea00826d596badd364a2)
![{\displaystyle \operatorname {E} [X]={2na+n^{2}-2n+1+n-1 \over 2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80e42d3d0c2c51b1ed3080da1111cb11dec30bc5)
![{\displaystyle \operatorname {E} [X]={2a+n-1 \over 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a86f0ae9249dc07b176c3a9b91fb2bdc9f74061d)
![{\displaystyle \operatorname {E} [X]={a+b \over 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/001deb9056e5f1e537230569f1ae9f295e0910d8)
![{\displaystyle E[(X-EX)^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b22b4ec2a092c8360d806e4505c477db0ffe19)
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [(X-\operatorname {E} [X])^{2}]=\sum _{x\in S}f(x)(x-E[X])^{2}=\sum _{i=0}^{n-1}\left({\frac {1}{n}}\left((a+i)-{a+b \over 2}\right)^{2}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56b12fc83b04a51c7fdaaebeb18a1f0831e8dd1e)


![{\displaystyle \operatorname {Var} (X)={1 \over 4n}\left[\sum _{i=0}^{n-1}(a^{2}-2ab+b^{2})+\sum _{i=0}^{n-1}(4ai-4ib)+\sum _{i=0}^{n-1}4i^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83d922ce089bba133997418b75c7e636c325bb12)
![{\displaystyle \operatorname {Var} (X)={1 \over 4n}\left[n(a^{2}-2ab+b^{2})+4(a-b)\sum _{i=0}^{n-1}i+4\sum _{i=0}^{n-1}i^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d9c406aa8333f46cdb4be5457301a33f76abd53)

![{\displaystyle \operatorname {Var} (X)={1 \over 4n}\left[n(b-a)^{2}+4(a-b)[(n-1)n/2]+4[(n-1)n(2n-1)/6]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbacd1e083e7be5ffaae1084e1f38fcfa6ca995b)
![{\displaystyle \operatorname {Var} (X)={1 \over 4n}\left[n(n-1)^{2}-2(n-1)(n-1)n+2(n-1)n(2n-1)/3\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a7c8c68abae830ac2f44a56049064912fa9de7)
![{\displaystyle \operatorname {Var} (X)={1 \over 4}\left[-(n-1)^{2}+2(n-1)(2n-1)/3\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84019b35af4a06b3bdaac9d4606c1412d0ffbe7)
![{\displaystyle \operatorname {Var} (X)={1 \over 12}\left[-3(n-1)^{2}+2(n-1)(2n-1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1039ce76e36e4d641df3e39a470bc6f1ea12aa2)
![{\displaystyle \operatorname {Var} (X)={1 \over 12}\left[-3(n^{2}-2n+1)+2(2n^{2}-3n+1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/968d755bcaa7e79108755c2ff2841aabba5ea31a)

















![{\displaystyle \operatorname {E} [X]=\sum _{i}f(x_{i})\cdot x_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/828e6e9a3c1deb8df217f10c8fd2cff3682ef2a3)
![{\displaystyle \operatorname {E} [X]=p\cdot 1+(1-p)\cdot 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c586a80bc9ac3deedc09cb0bf551c85456ed563)
![{\displaystyle \operatorname {E} [X]=p\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc6c97877071d6785321a33d605961e61633576a)
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [(X-\operatorname {E} [X])^{2}]=\sum _{i}f(x_{i})\cdot (x_{i}-\operatorname {E} [X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85916f74c29d4a9946dbc8d6d12f8fdaba650dcc)

\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09209d46f65b342076b628fa4b4d1025f4227539)



![{\displaystyle P\left[X=k\right]={\begin{cases}{n \choose k}p^{k}\left(1-p\right)^{n-k}\ &0\leq k\leq n\\0&{\mbox{otherwise}}\end{cases}}\quad 0\leq p\leq 1,\quad n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fdcd7b3068def867c9ff8b21538b9ab6cad87dc)

![{\displaystyle P\left[X=2\right]={5 \choose 2}\cdot {{0.3^{2}\cdot }{\left(1-0.3\right)^{3}}}={10}\cdot {{0.3^{2}}\cdot {\left(1-0.3\right)^{3}}}=0.3087}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cdc8e63aa9dd5bc01327db2f6d82991fc29c54c)

![{\displaystyle \operatorname {E} [X]=\sum _{i}f(x_{i})\cdot x_{i}=\sum _{x=0}^{n}{n \choose x}p^{x}\left(1-p\right)^{n-x}\cdot x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c14d7c93230e07fa765e5b066e733423288f60)
![{\displaystyle \operatorname {E} [X]=\sum _{x=0}^{n}{n! \over x!(n-x)!}p^{x}\left(1-p\right)^{n-x}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b68fb0a2115b2b88188f882d4827a75bd0f49441)
![{\displaystyle \operatorname {E} [X]={n! \over 0!(n-0)!}p^{0}\left(1-p\right)^{n-0}\cdot 0+\sum _{x=1}^{n}{n! \over x!(n-x)!}p^{x}\left(1-p\right)^{n-x}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77dea4fc65c59c164b5788edbc9284493b722a27)
![{\displaystyle \operatorname {E} [X]=0+\sum _{x=1}^{n}{n(n-1)! \over x(x-1)!(n-x)!}p\cdot p^{x-1}\left(1-p\right)^{n-x}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1504d9928a9523e18659f92b1c2147519e289f9d)
![{\displaystyle \operatorname {E} [X]=np\sum _{x=1}^{n}{(n-1)! \over (x-1)!(n-x)!}p^{x-1}\left(1-p\right)^{n-x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d12b43e256bb10979874f372a5559a56773a9b4e)
![{\displaystyle \operatorname {E} [X]=np\left[\sum _{w=0}^{m}{m! \over w!(m-w)!}p^{w}\left(1-p\right)^{m-w}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/023e3a02fb0f74ecc050e8a6ac6f99773f9dbd71)
![{\displaystyle \operatorname {E} [X]=np\left[1\right]=np}](https://wikimedia.org/api/rest_v1/media/math/render/svg/622190f9d3d351a6901c3eeec8f81c2e936ec495)
![{\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39bfa72738f2149e732dfa85f4be9fcd52c38422)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{i}f(x_{i})\cdot x^{2}=\sum _{x=0}^{n}x^{2}\cdot {n \choose x}p^{x}(1-p)^{n-x}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a813301bbd5190e14095a6656efcdb9f2962a141)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{x=0}^{n}{n! \over x!(n-x)!}p^{x}\left(1-p\right)^{n-x}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df10a914655f7841e060bb9072bc71fbb4af6b72)
![{\displaystyle \operatorname {E} [X^{2}]=0+\sum _{x=1}^{n}{n! \over x!(n-x)!}p^{x}\left(1-p\right)^{n-x}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0ef869b731e23896f03218e82c305d3db41917f)
![{\displaystyle \operatorname {E} [X^{2}]=np\sum _{x=1}^{n}{(n-1)! \over (x-1)!(n-x)!}p^{x-1}\left(1-p\right)^{n-x}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35fb16618202ec081600966d99b8f1c2c6962c91)
![{\displaystyle \operatorname {E} [X^{2}]=np\sum _{w=0}^{m}{m \choose w}p^{w}\left(1-p\right)^{m-w}(w+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19b17276a1cdd6a3f8569ed3bf01f6a1cfd13e5f)
![{\displaystyle \operatorname {E} [X^{2}]=np\left[\sum _{w=0}^{m}{m \choose w}p^{w}\left(1-p\right)^{m-w}w+\sum _{w=0}^{m}{m \choose w}p^{w}\left(1-p\right)^{m-w}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad5ddf55b6e8f72e5742e69fa83765614031db3d)
![{\displaystyle \operatorname {E} [X^{2}]=np\cdot (mp+1)=np((n-1)p+1)=np(np-p+1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e118c6eaaae9f86b246c5bbb101cf50c31305519)
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}=np(np-p+1)-(np)^{2}=np(1-p).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f05a27ebd1225835ee614a1e94e5bd4e561f1b5)












![{\displaystyle \lambda [1\!-\!\log(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\log(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5a542aefbd87a7fa233e3dad33e318fe668c637)








![{\displaystyle \operatorname {E} [X]=\sum _{i}f(x_{i})\cdot x_{i}=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88402e8d115e24abf49290cfa3db1bb145a57a5d)
![{\displaystyle \operatorname {E} [X]={\frac {e^{-\lambda }\lambda ^{0}}{0!}}\cdot 0+\sum _{x=1}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81ef638a64528af583092231619a2dfbfef2e200)
![{\displaystyle \operatorname {E} [X]=0+e^{-\lambda }\sum _{x=1}^{\infty }{\frac {\lambda \lambda ^{x-1}}{(x-1)!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/751d62a1284ff1725f65182e221a4fcc0f74965b)
![{\displaystyle \operatorname {E} [X]=\lambda e^{-\lambda }\sum _{x=1}^{\infty }{\frac {\lambda ^{x-1}}{(x-1)!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69619395b2ca4cf5c081a36f71f4e6b0ade6fd84)
![{\displaystyle \operatorname {E} [X]=\lambda e^{-\lambda }\sum _{x=0}^{\infty }{\frac {\lambda ^{x}}{x!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74145023b4379bed6d5237576462e1809ae4ef94)

![{\displaystyle \operatorname {E} [X]=\lambda e^{-\lambda }e^{\lambda }=\lambda }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d6908567dcb59933e108c555d132e0c0900e119)
![{\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3a927c2af9ce191701ce464bf66fe7a6fe2190c)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{i}f(x_{i})\cdot x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b457462143b3c9a9d2d1c9de47dd57fae3dbec2)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f093880fd23b0e728225f0aedf91b737205b6881)
![{\displaystyle \operatorname {E} [X^{2}]=0+\sum _{x=1}^{\infty }{\frac {e^{-\lambda }\lambda \lambda ^{x-1}}{(x-1)!}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcdd5feeb3b4c7901689a81dce08df36c7375234)
![{\displaystyle \operatorname {E} [X^{2}]=\lambda \sum _{x=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}(x+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7655130ce83af142e40df27e2d291c132f8251a6)

![{\displaystyle \operatorname {E} [X^{2}]=\lambda \left[\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}x+\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fba5b95eea7dffc5a6c9d511b257ad1d3443827b)
![{\displaystyle \operatorname {E} [X^{2}]=\lambda \left[\lambda +1\right]=\lambda ^{2}+\lambda }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1946c015894a4ec0d0122dcf9fa2ce22d3564618)
![{\displaystyle \operatorname {Var} [X]=(\lambda ^{2}+\lambda )-(\lambda )^{2}=\lambda }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc4acacd6ba940c2ba0b000304f7deae6e3e2462)




















![{\displaystyle \operatorname {E} [X]=\sum _{i}f(x_{i})x_{i}=\sum _{0}^{\infty }p(1-p)^{x}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14772fe3fb1aac3aeda043b8844d8e44ea9f4beb)
![{\displaystyle \operatorname {E} [X]=\sum _{0}^{\infty }(1-q)q^{x}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9ad822d6cb59a023236e1c2dba4ea8ce8fe0bb0)
![{\displaystyle \operatorname {E} [X]=\sum _{0}^{\infty }(1-q)qq^{x-1}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b173d51fc1397b9d8290c8e8a58dbac31d80e0cd)
![{\displaystyle \operatorname {E} [X]=(1-q)q\sum _{0}^{\infty }q^{x-1}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3694fabe53f333614812d1e6b7a75577a8b00d2c)
![{\displaystyle \operatorname {E} [X]=(1-q)q\sum _{0}^{\infty }{\frac {d}{dq}}q^{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00ecb1f87eadc5d1bec6706a38d2e526254149b0)
![{\displaystyle \operatorname {E} [X]=(1-q)q{\frac {d}{dq}}\sum _{0}^{\infty }q^{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29126ac9a1e1420eb4b6f0b292b11542191314ac)
![{\displaystyle \operatorname {E} [X]=(1-q)q{\frac {d}{dq}}{1 \over 1-q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c28cabe4165678e022964b678cb3bed82f7d0a7f)
![{\displaystyle \operatorname {E} [X]=(1-q)q{1 \over (1-q)^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0088bfe78733dbdd446cdcee8839d8b06334e2b5)
![{\displaystyle \operatorname {E} [X]=q{1 \over (1-q)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d22bd1347ab70303be5bafa8d54e6b05a41fd008)
![{\displaystyle \operatorname {E} [X]={(1-p) \over p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/005e463e9bbf3557dcc3ad6930b3321e09013809)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{0}^{\infty }p(1-p)^{x}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5683649108ad3852d33b3f0f8ca642e237678fd5)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{0}^{\infty }(1-q)q^{x}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d5c3ee343acd07e0bb8c579be8dc55ca22fc589)
![{\displaystyle \operatorname {E} [X^{2}]=(1-q)\sum _{0}^{\infty }q^{x}[(x^{2}-x)+x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75d3eafe380f83410881e368fe533b827ca74f92)
![{\displaystyle \operatorname {E} [X^{2}]=(1-q)\left[\sum _{0}^{\infty }q^{x}(x^{2}-x)+\sum _{0}^{\infty }q^{x}x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f93fd82a11d90cda7b6d70be13b8244e3a7d05)
![{\displaystyle \operatorname {E} [X^{2}]=(1-q)\left[q^{2}\sum _{0}^{\infty }q^{x-2}x(x-1)+q\sum _{0}^{\infty }q^{x-1}x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b1637a45a96e3347eac070309b680a9d4ff66c)
![{\displaystyle \operatorname {E} [X^{2}]=(1-q)q\left[q\sum _{0}^{\infty }{\frac {d^{2}}{(dq)^{2}}}q^{x}+\sum _{0}^{\infty }{\frac {d}{dq}}q^{x}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a670c354fefd15e8e9c92ae0e84f11f2aaa924ea)
![{\displaystyle \operatorname {E} [X^{2}]=(1-q)q\left[q{\frac {d^{2}}{(dq)^{2}}}\sum _{0}^{\infty }q^{x}+{\frac {d}{dq}}\sum _{0}^{\infty }q^{x}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb989d8fec7d63001d1753487542e9c66ee35688)
![{\displaystyle \operatorname {E} [X^{2}]=(1-q)q\left[q{\frac {d^{2}}{(dq)^{2}}}{1 \over 1-q}+{\frac {d}{dq}}{1 \over 1-q}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc28f609f6a73d90dd592e92f471e1f9c892f962)
![{\displaystyle \operatorname {E} [X^{2}]=(1-q)q\left[q{2 \over (1-q)^{3}}+{1 \over (1-q)^{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/569b086d793e05931e2f107f0faa3669e3a2e38e)
![{\displaystyle \operatorname {E} [X^{2}]={2q^{2} \over (1-q)^{2}}+{q \over (1-q)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1d4242ae0316880299a80f3b86026827724baa2)
![{\displaystyle \operatorname {E} [X^{2}]={2q^{2}+q(1-q) \over (1-q)^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa45c19cb12088654ff064a34fe60e5d01145e3)
![{\displaystyle \operatorname {E} [X^{2}]={q(q+1) \over (1-q)^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0439f27f91edf1d341788b23bebb1f52f7aed08e)
![{\displaystyle \operatorname {E} [X^{2}]={(1-p)(2-p) \over p^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a65e09f63d237df831cf41227667ef09b8663043)
![{\displaystyle \operatorname {Var} [X]=\left[{(1-p)(2-p) \over p^{2}}\right]-\left({1-p \over p}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5083e58db627dd9b8b3c9538630be47a30f52318)
![{\displaystyle \operatorname {Var} [X]={(1-p) \over p^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/425211a2e0d5b31cb138f0691612a7009fa16060)


![{\displaystyle \operatorname {E} [X]=\sum _{i}f(x_{i})\cdot x_{i}=\sum _{x=0}^{\infty }{x+r-1 \choose r-1}p^{x}(1-p)^{r}\cdot x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/986c79c69355973780cc277fe3de440c2f86838f)
![{\displaystyle \operatorname {E} [X]={0+r-1 \choose r-1}p^{0}\left(1-p\right)^{r}\cdot 0+\sum _{x=1}^{\infty }{x+r-1 \choose r-1}p^{x}(1-p)^{r}\cdot x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df6c02d4b9306388f1a3a554ea311a1dfaff9bf8)
![{\displaystyle \operatorname {E} [X]=0+\sum _{x=1}^{\infty }{(x+r-1)! \over (r-1)!x!}p^{x}(1-p)^{r}\cdot x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37ba3b8d4234ffdb8bd4b271444382c43f9e5ec3)
![{\displaystyle \operatorname {E} [X]={rp \over 1-p}\sum _{x=1}^{\infty }{(x+r-1)! \over r!(x-1)!}p^{x-1}(1-p)^{r+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85e38b0e2f3f04c87bc1d9e6c85c0f95233e8994)
![{\displaystyle \operatorname {E} [X]={rp \over 1-p}\sum _{w=0}^{\infty }{(w+s-1)! \over (s-1)!w!}p^{w}(1-p)^{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ff1b395ab43d67628c0c0c44243dd33370b8574)
![{\displaystyle \operatorname {E} [X]={rp \over 1-p}\sum _{w=0}^{\infty }{w+s-1 \choose s-1}p^{w}(1-p)^{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a53e42979839edd02ae2c90fa02eb7d315bd108)
![{\displaystyle \operatorname {E} [X]={rp \over 1-p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e45b6a64d213168c86b55c76f1e2d594441b8ea7)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{i}f(x_{i})\cdot x^{2}=\sum _{x=0}^{\infty }{x+r-1 \choose r-1}p^{x}(1-p)^{r}\cdot x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08261fee0afdb2d29d6e08f6769fbca70d336f2b)
![{\displaystyle \operatorname {E} [X^{2}]=0+\sum _{x=1}^{\infty }{x+r-1 \choose r-1}p^{x}(1-p)^{r}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b5fe0945792d09c03eb4ff2cf7c674085318efa)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{x=1}^{\infty }{(x+r-1)! \over (r-1)!x!}p^{x}(1-p)^{r}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b007de64ace5b29feee48c41dfdcd8478739e53f)
![{\displaystyle \operatorname {E} [X^{2}]={rp \over 1-p}\sum _{x=1}^{\infty }{(x+r-1)! \over r!(x-1)!}p^{x-1}(1-p)^{r+1}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cd18d92ddd930b7b02f502e071ef12244a8543d)
![{\displaystyle \operatorname {E} [X^{2}]={rp \over 1-p}\sum _{w=0}^{\infty }{(w+s-1)! \over (s-1)!w!}p^{w}(1-p)^{s}(w+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23887602b51b3ec59f0061e592f611e1821e76e5)
![{\displaystyle \operatorname {E} [X^{2}]={rp \over 1-p}\sum _{w=0}^{\infty }{w+s-1 \choose s-1}p^{w}(1-p)^{s}(w+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/419c62731d89008d5ed6997773d9ffaa7b4635eb)
![{\displaystyle \operatorname {E} [X^{2}]={rp \over 1-p}\left[\sum _{w=0}^{\infty }{w+s-1 \choose s-1}p^{w}(1-p)^{s}w+\sum _{w=0}^{\infty }{w+s-1 \choose s-1}p^{w}(1-p)^{s}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b344c98737c0adfeb44aa7730e4f2bb70a562f)
![{\displaystyle \operatorname {E} [X^{2}]={rp \over 1-p}\left[{sp \over 1-p}+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81f8b9da95a67f47514ee3804ab80d8893c409a7)
![{\displaystyle \operatorname {E} [X^{2}]={rp(1+rp) \over (1-p)^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6eafa23d41a078a458f0d6c8f92f8ce40ee0291)
![{\displaystyle \operatorname {Var} [X]={rp(1+rp) \over (1-p)^{2}}-\left({rp \over 1-p}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/977f26e7fa85bf504b42fb14d0b267bae7a30348)
![{\displaystyle \operatorname {Var} [X]={rp \over (1-p)^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d76f35bd647368d9ce97b88e0edf499129ef529d)




![{\displaystyle 1-{{{n \choose {k+1}}{{N-n} \choose {m-k-1}}} \over {N \choose m}}\,_{3}F_{2}\!\!\left[{\begin{array}{c}1,\ k+1-m,\ k+1-n\\k+2,\ N+k+2-m-n\end{array}};1\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70d1d2d44a9d8a3ede85e778fa510f5761c9d59d)




![{\displaystyle {\frac {(N-2m)(N-1)^{\frac {1}{2}}(N-2n)}{[nm(N-m)(N-n)]^{\frac {1}{2}}(N-2)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/450c7c5a3a3b8ae698af5ee0cd3d225a1fa89d68)


![{\displaystyle {}+6nm(N-m)(N-n)(5N-6){\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5778f9423c4744b49f0a62a91555233dbb7a5b20)


![{\displaystyle f(x)={{{m \choose x}{{N-m} \choose {n-x}}} \over {N \choose n}}{\text{ for all }}x\in [0,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c330687b40587ed4a2d75eb490552603789497)



![{\displaystyle \operatorname {E} [X]=\sum _{x=0}^{n}x\cdot f(x;n,m,N)=\sum _{x=0}^{n}x\cdot {{{m \choose x}{{N-m} \choose {n-x}}} \over {N \choose n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee678a691b4e5c3cacc31c0093f39e4fb4128531)
![{\displaystyle \operatorname {E} [X]=0\cdot {{{m \choose 0}{{N-m} \choose {n-0}}} \over {N \choose n}}+\sum _{x=1}^{n}x\cdot {{{m \choose x}{{N-m} \choose {n-x}}} \over {N \choose n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39432db25cf68f4997af8b9cad284188a847e7a0)

![{\displaystyle \operatorname {E} [X]=0+\sum _{x=1}^{n}x\cdot {{{m \choose x}{{N-m} \choose {n-x}}} \over {{N \over n}{{N-1} \choose {n-1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc72b2fc87517df1421353858acfa5abfc9a1d09)
![{\displaystyle \operatorname {E} [X]={n \over N}\sum _{x=1}^{n}x\cdot {{{m \choose x}{{N-m} \choose {n-x}}} \over {{N-1} \choose {n-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2090566b0ae8ab1d2eba5cdd3ad10991d1e62f8b)

![{\displaystyle \operatorname {E} [X]={n \over N}\sum _{x=1}^{n}{m{{m-1 \choose x-1}{{N-m} \choose {n-x}}} \over {{N-1} \choose {n-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a0006dea506dff720378b04156b5ffdd03e9873)
![{\displaystyle \operatorname {E} [X]={mn \over N}\sum _{x'=0}^{n'}{{{m' \choose x'}{{N'-m'} \choose {n'-x'}}} \over {{N'} \choose {n'}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e1cd1722f894cc5a6f955a9b731d503a3cfe82b)
![{\displaystyle \operatorname {E} [X]={mn \over N}\sum _{x'=0}^{n'}f(x';n',m',N')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/440dbb68d37e1dd929891ffc060edf32baf0f25b)
![{\displaystyle \operatorname {E} [X]={nm \over N}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f646539677956727e04993ee125d5c96eb3b2c9)
![{\displaystyle \operatorname {E} [X^{2}]=\sum _{x=0}^{n}f(x;n,m,N)\cdot x^{2}=\sum _{x=0}^{n}{{{m \choose x}{{N-m} \choose {n-x}}} \over {N \choose n}}\cdot x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c57e1b3542512836927eb966f4b00fac3f6577b)
![{\displaystyle \operatorname {E} [X^{2}]={{{m \choose 0}{{N-m} \choose {n-0}}} \over {N \choose n}}\cdot 0^{2}+\sum _{x=1}^{n}{{{m \choose x}{{N-m} \choose {n-x}}} \over {N \choose n}}\cdot x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/945e5cce59894c9a6af230a7085439ee45c02aee)
![{\displaystyle \operatorname {E} [X^{2}]=0+\sum _{x=1}^{n}{{m{m-1 \choose x-1}{{N-m} \choose {n-x}}} \over {{N \over n}{{N-1} \choose {n-1}}}}\cdot x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf2626751e1653818a91ded798fa6ceddb341e3d)
![{\displaystyle \operatorname {E} [X^{2}]={mn \over N}\sum _{x=1}^{n}{{{m-1 \choose x-1}{{N-m} \choose {n-x}}} \over {{N-1} \choose {n-1}}}\cdot x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3de1f2629e002b99b8cb83436e299c7e66bcc360)
![{\displaystyle \operatorname {E} [X^{2}]={mn \over N}\sum _{x'=0}^{n'}{{{m' \choose x'}{{N'-m'} \choose {n'-x'}}} \over {{N'} \choose {n'}}}(x'+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2d212f2d913e29e5a6bfba51a16dabc1b053b7f)
![{\displaystyle \operatorname {E} [X^{2}]={mn \over N}\left[\sum _{x'=0}^{n'}{{{m' \choose x'}{{N'-m'} \choose {n'-x'}}} \over {{N'} \choose {n'}}}x'+\sum _{x'=0}^{n'}{{{m' \choose x'}{{N'-m'} \choose {n'-x'}}} \over {{N'} \choose {n'}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/716677fe3389d264e4c693d47a1b2504f33e6276)
![{\displaystyle \operatorname {E} [X^{2}]={mn \over N}\left[{n'm' \over N'}+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/757a9e4a2da301b9482bd1523263ec26b5d700da)
![{\displaystyle \operatorname {E} [X^{2}]={mn \over N}\left[{(n-1)(m-1) \over (N-1)}+1\right]={mn \over N}\left[{{(n-1)(m-1)+(N-1)} \over (N-1)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31e91eee15b9c70d335de29d7ecea6c9b764598c)
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd5a922df13bdee788c0f06474fe002a42c25d8a)
![{\displaystyle \operatorname {Var} (X)={mn \over N}\left[{{(n-1)(m-1)+(N-1)} \over (N-1)}\right]-\left({mn \over N}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56995fabfd1f82e08f69ae429457ac1c2db7d222)
![{\displaystyle \operatorname {Var} (X)={Nmn \over N^{2}}\left[{{(n-1)(m-1)+(N-1)} \over (N-1)}\right]-{(N-1)(mn)^{2} \over (N-1)N^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af036c806a95a3b386c81675d1a20f547d48985f)




![{\displaystyle E[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e455a34363c03fc5df8208d8b81fa29e3cdd524e)
![{\displaystyle E[(X-E[X]^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62e702258475ed39e0c1d2adcf70037b11a9955f)
![{\displaystyle E[\exp(tX)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/551b062fdc21eea6d3d8c6092cf3650bd083a3b2)
![{\displaystyle {\frac {dE[\exp(tX)]}{dt}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee4d4de7d968658bf7c423fb4b871f802850aaa9)
![{\displaystyle {\frac {d^{2}E[\exp(tX)]}{dt^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ab428b9fc2d6de74a61b5a8a96871bdf6cc4a59)
![{\displaystyle {\frac {d^{3}E[\exp(tX)]}{dt^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/116a5182d24a980cea50dc18e4d190bbe1ef8a4c)
![{\displaystyle {\frac {d^{4}E[\exp(tX)]}{dt^{4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa9ead6641087902016c6dbf87b0a5f09c24f3c)


![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)
![{\displaystyle {\begin{cases}{\frac {1}{b-a}}&{\text{for }}x\in [a,b]\\0&{\text{otherwise}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/648692e002b720347c6c981aeec2a8cca7f4182f)


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)


![{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }xf(x)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/924d6297060cfe0ce5b68f81398ddf9c8b1108b5)
![{\displaystyle \operatorname {E} [X]=\int _{a}^{b}{1 \over {b-a}}xdx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02474545220217edacc399cb2505f4bc51fc7941)
![{\displaystyle \operatorname {E} [X]=\left.{1 \over (b-a)}{1 \over 2}x^{2}\right|_{a}^{b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eccd1945ac02fa5fae45a09a0a479a64a24b61d)
![{\displaystyle \operatorname {E} [X]={1 \over 2(b-a)}\left[b^{2}-a^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d76ab442e3c6278bed5b3043fae803c4c83d167)
![{\displaystyle \operatorname {E} [X]={b+a \over 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a4fcd87bd5187b6aa583ec11360620ed1a62ad7)
![{\displaystyle \operatorname {Var} (X)=\left[\int _{-\infty }^{\infty }f(x)\cdot x^{2}dx\right]-\left({b+a \over 2}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dabaa604c953f4f6e48305f667f5f5e9ba54645)
![{\displaystyle \operatorname {Var} (X)=\left[\int _{a}^{b}{1 \over {b-a}}x^{2}dx\right]-{(b+a)^{2} \over 4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf2289d688b600ebb79b1dfe3f6ccdce24aa9760)

![{\displaystyle \operatorname {Var} (X)={1 \over 3(b-a)}[b^{3}-a^{3}]-{(b+a)^{2} \over 4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5070a935e4627f16e4f8e690599f76534a70170)





![{\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04670b14acb4ddb796469f3812ead9d9cccec275)















![{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot f(x)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c925eb7f3d99af3083ee5838c3bec6f3838997a)

![{\displaystyle =\int _{-\infty }^{\infty }[(x-\mu )+\mu ]{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc7a4e49f0658d302e610e2c327d9256056e798)


![{\displaystyle \operatorname {E} [X]={\frac {1}{\sigma {\sqrt {2\pi }}}}(-\sigma ^{2})\left[e^{-(x-\mu )^{2}/2\sigma ^{2}}\right]_{-\infty }^{\infty }+\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/199dfe628bd03625c353799d3dc9bbdd4ef62ee2)
![{\displaystyle ={\frac {1}{\sigma {\sqrt {2\pi }}}}(-\sigma ^{2})[0-0]+\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ecc3da777cb4ce7e4e995d4dc314ea7800b64a2)

![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [(X-{E}[X])^{2}]=\int _{-\infty }^{\infty }(x-\mu )^{2}\cdot f(x)dx=\int _{-\infty }^{\infty }(x-\mu )^{2}{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\cdot \left({\frac {x-\mu }{\sigma }}\right)^{2}}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e3bed0ee5839f63ce5208213bed008d13a57601)

![{\displaystyle \operatorname {Var} (X)={\frac {2\sigma ^{2}}{\sqrt {\pi }}}\left(\left[w{-1 \over 2}e^{-w^{2}}\right]_{-\infty }^{\infty }-\int _{-\infty }^{\infty }{-1 \over 2}e^{-w^{2}}dw\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c19383f6494c4d4144cbd047b6d835b93033c2b)







![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }x\lambda e^{-\lambda x}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de21e0e435a11373f8f68aa9365a100fd28434b7)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }(-x)(-\lambda e^{-\lambda x})dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e2936bccbe650f7919d6dfeb9db772d222f370)
![{\displaystyle \operatorname {E} [X]=\left[-x\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-1)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0a325796212c52d7cc34c2e57e5e0a5869121f)
![{\displaystyle \operatorname {E} [X]=[0-0]+\left[{-1 \over \lambda }(e^{-\lambda x})\right]_{0}^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcfc71b113a0864019d9801c659d3ac3294525e2)
![{\displaystyle \operatorname {E} [X]=\left[0-{-1 \over \lambda }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc46e6600d22129f1f8916bd6bcfa332679719e)
![{\displaystyle \operatorname {E} [X]={1 \over \lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf488e5f107cc237b5235226664cf3b1d5c02bcd)






![{\displaystyle \operatorname {Var} (X)=\left\{\left[-x^{2}\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-2x)dx\right\}-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa497aeeb4e8301234482593735ec9726a74a95)
![{\displaystyle \operatorname {Var} (X)=[0-0]+{2 \over \lambda }\int _{0}^{\infty }x\lambda e^{-\lambda x}dx-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620c93fc59bb00faabfa622a4b600f2a0dc8ac42)







![{\displaystyle \scriptstyle \operatorname {E} [X]=k\theta \!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bcd0564c15fa09e51ad6cef42d662ef6d1dca35)
![{\displaystyle \scriptstyle \operatorname {E} [\ln X]=\psi (k)+\ln(\theta )\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ade84f1fd2e20c78ef0cf51012ad6626335092c2)

![{\displaystyle \scriptstyle \operatorname {Var} [X]=k\theta ^{2}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/333617e4e5bd65bdbe335c76c1a7d0327573320e)
![{\displaystyle \scriptstyle \operatorname {Var} [\ln X]=\psi _{1}(k)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7633714acaea7355cb1750b03b1c68d8053d6196)


![{\displaystyle \scriptstyle {\begin{aligned}\scriptstyle k&\scriptstyle \,+\,\ln \theta \,+\,\ln[\Gamma (k)]\\\scriptstyle &\scriptstyle \,+\,(1\,-\,k)\psi (k)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d2c89d9e0f1b9542b044217fab69ab3de01add)
















![{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot {\frac {1}{a^{p}\Gamma (p)}}x^{p-1}e^{-x/a}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2041b84abc19d0b68d9be98a49e51b025c98402b)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }ay\cdot {\frac {1}{\Gamma (p)}}y^{p-1}e^{-y}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54f1d35c1a15d3ae2ed4481c2ec1eccf01e8b4f4)
![{\displaystyle \operatorname {E} [X]={\frac {a}{\Gamma (p)}}\int _{0}^{\infty }y^{p}e^{-y}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59e45dd2f2dc64776612607cc9c0821c049a5c63)
![{\displaystyle \operatorname {E} [X]={\frac {a}{\Gamma (p)}}\Gamma (p+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b500fdb08277ba4c426a844dd4a0293d04d5dee)

![{\displaystyle \operatorname {E} [X]={\frac {a}{\Gamma (p)}}p\Gamma (p)=ap}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec6ebf9c846951a550635d7f913c1903886bee57)
![{\displaystyle \operatorname {E} [X^{2}]=\int _{-\infty }^{\infty }x^{2}\cdot {\frac {1}{a^{p}\Gamma (p)}}x^{p-1}e^{-x/a}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd81fa18392582d5fdf8dfe72690d597d05a22fd)
![{\displaystyle \operatorname {E} [X^{2}]=\int _{0}^{\infty }a^{2}y^{2}\cdot {\frac {1}{a\Gamma (p)}}y^{p-1}e^{-y}ady}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ab45ebf7e86bcd131f504933497e55af902b9ce)
![{\displaystyle \operatorname {E} [X^{2}]={\frac {a^{2}}{\Gamma (p)}}\int _{0}^{\infty }y^{p+1}e^{-y}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3da9177001a8304d085db66b2c51174e46c88c54)
![{\displaystyle \operatorname {E} [X^{2}]={\frac {a^{2}}{\Gamma (p)}}\Gamma (p+2)=pa^{2}(p+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d399ef4add4c2afee9106d9fcc6b035e140128c)







































![{\displaystyle {\frac {1}{2^{k/2}\Gamma (k/2)}}\;x^{k/2-1}e^{-x/2}\quad x\geq 0,\,k\in [1,2,...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ec261086bed171dd2fddc9c01dbfec2854f42fb)


![{\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02732e546784af1fb16d0dc1bb65dd743e2284ad)






































































































![{\displaystyle E[Y|x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3aabc367f4ba57ef163f4e737e0086ea9ffcb05)
















































































![{\displaystyle \|x\|_{q}={\sqrt[{q}]{\sum _{i=1}^{p}x_{i}^{q}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3dd504664536b58841695c57bbac2e7ad9cda02)






















![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)















































![{\displaystyle [-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8bc389ca678dffbedd0d41ca0fecb9806c9b7cf)

































































































![{\displaystyle (16)\quad x={\hat {x}}-[Dg({\hat {x}})^{T}]^{-1}g({\hat {x}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/973ad4b1a68c0301124de9a8e4a9f5dcf2ede103)

![{\displaystyle (17)\quad d_{N}^{(k)}=x^{(k+1)}-x^{(k)}=-[D^{2}f(x^{(k)})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78f590fdfab4360315b24683a209d394d474d8d5)






![{\displaystyle [D^{2}f(x^{(k)})]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18f24df6687d0360e41c29464f4aaf177e9314f9)
![{\displaystyle (19)\quad x^{(k+1)}=x^{(k)}-\sigma _{E}^{(k)}d_{N}^{(k)}=x^{(k)}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e7b82c56b6571dc71773a1301041f3e514bb0be)









![{\displaystyle (23)\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[A^{k}]^{-1}Df(x^{k}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b5580a0328e0fc4cb23c05d2aaa2dfb757e774)

![{\displaystyle [A^{k}]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6caa38bd6a32cf081b1e8379b42ccafdeaf56056)





![{\displaystyle [A^{k}]^{-1}=\Gamma \Lambda ^{-1}\Gamma ^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0bb61f96e4008fe7ac42ddae42174a1cbc74f22)
![{\displaystyle d^{(k)}=[A^{k}]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd88606c2704c7ca9ba41fbff98dc6196d731f1)
![{\displaystyle (25)\quad Df(x^{k})^{T}d^{(k)}=-Df(x^{k})^{T}[A^{k}]^{-1}Df(x^{k})\equiv -v^{T}[A^{k}]^{-1}v\leq 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19c3cfc50845559d027b7a787662c23b8209bdba)




![{\displaystyle (19')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e585e07182f56dfbe1ebb268e5b1feba19cac6e)






















![{\displaystyle [Df(x^{(k)})]^{-1}Df(x^{(k)}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60231e722c13de70156e005a9956e01b4895cda1)





![{\displaystyle (36)\quad D_{\theta }{\mathcal {L}}(\theta ^{(k+1)})=D_{\theta }{\mathcal {L}}(\theta ^{(k)})+D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})(\theta ^{(k+1)}-\theta ^{(k)})=0\Leftrightarrow \theta ^{(k+1)}=\theta ^{(k)}-[D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27be895a860dcd9530a4d300fdc8fa7f7e7f9e3c)


![{\displaystyle [D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1bb702f696e4c7c16d636cdafdbf51382f32bfd)




![{\displaystyle (39)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=N\left[\log \left(\Gamma \left({\frac {m+1}{2}}\right)\right)-\log \left({\sqrt {\pi m}}\Gamma \left({\frac {m}{2}}\right)\right)\right]-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ab57a856625145f8bd9be4f656dba107baf35a)
























![{\displaystyle E[\epsilon _{i}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b927cb1a4bd6073ff569345fe3bb68a325a9f832)





















![{\displaystyle (10)E[H_{i}|T_{i},O_{i},A_{i},P_{i}]=\alpha +\beta T_{i}+\delta O_{i}+\gamma A_{i}+\lambda P_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f7e7777ad104846c50adddbc89349995fd0c422)






![{\displaystyle (11)Q_{H}[\tau |T_{i},O_{i},A_{i},P_{i}]=\alpha _{\tau }+\beta _{\tau }T_{i}+\delta _{\tau }O_{i}+\gamma _{\tau }A_{i}+\lambda _{\tau }P_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610bc8109a1b023dfe7ee1515b3a7dd1e20d6af2)

![{\displaystyle (12)min\left[\rho _{0,1}(y_{1}-x_{1}\beta )+\rho _{0,1}(y_{2}-x_{2}\beta )+...+\rho _{0,1}(y_{n}-x_{n}\beta )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/594bd420ada2a68f5042c501bf9474d92fffde97)






























![{\displaystyle LRE=-\log _{10}{\left[|q-c|/|c|\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d64ea3deb412a07178abde172c2fe55892930e1)















