Statistics/Distributions/Gamma

Gamma Distribution

Gamma

Probability density function
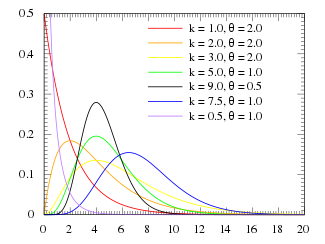
Cumulative distribution function
Parameters	$\scriptstyle k \;>\; 0$ shape $\scriptstyle \theta \;>\; 0\,$ scale
Support	$\scriptstyle x \;\in\; (0,\, \infty)\!$
PDF	$\scriptstyle \frac{1}{\Gamma(k) \theta^k} x^{k \,-\, 1} e^{-\frac{x}{\theta}}\,\!$
CDF	$\scriptstyle \frac{1}{\Gamma(k)} \gamma\left(k,\, \frac{x}{\theta}\right)\!$
Mean	$\scriptstyle \operatorname{E}[ X] = k \theta \!$ $\scriptstyle \operatorname{E}[\ln X] = \psi(k) +\ln(\theta)\!$ (see digamma function)
Median	No simple closed form
Mode	$\scriptstyle (k \,-\, 1)\theta \text{ for } k \;>\; 1\,\!$
Variance	$\scriptstyle\operatorname{Var}[ X] = k \theta^2\,\!$ $\scriptstyle\operatorname{Var}[\ln X] = \psi_1(k)\!$ (see trigamma function )
Skewness	$\scriptstyle \frac{2}{\sqrt{k}}\,\!$
Ex. kurtosis	$\scriptstyle \frac{6}{k}\,\!$
Entropy	$\scriptstyle \begin{align} \scriptstyle k &\scriptstyle \,+\, \ln\theta \,+\, \ln[\Gamma(k)]\\ \scriptstyle &\scriptstyle \,+\, (1 \,-\, k)\psi(k) \end{align}$

The Gamma distribution is very important for technical reasons, since it is the parent of the exponential distribution and can explain many other distributions.

The probability distribution function is:

$f_x (x) = \begin{cases} \frac{1}{a^p \Gamma (p)} x^{p-1} e^{-x/a}, & \mbox{if } x \ge 0 \\ 0, & \mbox{if } x < 0 \end{cases}\quad a,p >0$

Where $\Gamma(p) = \int_0^\infty t^{p-1} e^{-t}\,dt\,$ is the Gamma function. The cumulative distribution function cannot be found unless p=1, in which case the Gamma distribution becomes the exponential distribution. The Gamma distribution of the stochastic variable X is denoted as $X \in \Gamma (p,a)$.

Alternatively, the gamma distribution can be parameterized in terms of a shape parameter $\alpha = k$ and an inverse scale parameter $\beta = 1/\theta$, called a rate parameter:

$g(x;\alpha,\beta) = K x^{\alpha-1} e^{-\beta\,x} \ \mathrm{for}\ x > 0 \,\!.$

where the $K$ constant can be calculated setting the integral of the density function as 1:

$\int_{-\infty}^{+\infty}g(x;\alpha,\beta) \mathrm{d}t \, = \int_{0}^{+\infty} K x^{\alpha-1} e^{-\beta\,x} \mathrm{d}x \, = 1$

following:

$K \int_{0}^{+\infty} x^{\alpha-1} e^{-\beta\,x} \mathrm{d}x \, = 1$

$K = \frac{1}{\int_{0}^{+\infty} x^{\alpha-1} e^{-\beta\,x} \mathrm{d}x}$

and, with change of variable $y = \beta x$ :

$\begin{align} K &= \frac{1}{\int_{0}^{+\infty} \frac{y^{\alpha-1}}{\beta^{\alpha - 1}} e^{-y} \frac{\mathrm{d}y}{\beta}} \\ &= \frac{1}{\frac{1}{\beta^{\alpha}}\int_{0}^{+\infty} y^{\alpha-1} e^{-y} \mathrm{d}y} \\ &= \frac{\beta^{\alpha}}{\int_{0}^{+\infty} y^{\alpha-1} e^{-y} \mathrm{d}y} \\ &= \frac{\beta^{\alpha}}{\Gamma(\alpha)} \end{align}$

following:

$g(x;\alpha,\beta) = x^{\alpha-1} \frac{\beta^{\alpha} \, e^{-\beta\,x} }{\Gamma(\alpha)} \ \mathrm{for}\ x > 0 \,\!.$

Probability Density Function

We first check that the total integral of the probability density function is 1.

$\int^\infin_{-\infin}\frac{1}{a^p \Gamma (p)} x^{p-1} e^{-x/a}dx$

Now we let y=x/a which means that dy=dx/a

$\frac{1}{ \Gamma (p)} \int^\infin_{0} y^{p-1} e^{-y}dy$

$\frac{1}{ \Gamma (p)} \Gamma (p)=1$

Mean

$\operatorname{E}[X]=\int^\infin_{-\infin}x \cdot \frac{1}{a^p \Gamma (p)} x^{p-1} e^{-x/a}dx$

Now we let y=x/a which means that dy=dx/a.

$\operatorname{E}[X]=\int^\infin_{0}ay \cdot \frac{1}{\Gamma (p)} y^{p-1} e^{-y}dy$

$\operatorname{E}[X]=\frac{a}{\Gamma (p)}\int^\infin_{0}y^{p} e^{-y}dy$

$\operatorname{E}[X]=\frac{a}{\Gamma (p)}\Gamma (p+1)$

We now use the fact that $\Gamma (z+1)=z\Gamma (z)$

$\operatorname{E}[X]=\frac{a}{\Gamma (p)}p\Gamma (p)=ap$

Variance

We first calculate E[X^2]

$\operatorname{E}[X^2]=\int^\infin_{-\infin}x^2 \cdot \frac{1}{a^p \Gamma (p)} x^{p-1} e^{-x/a}dx$

Now we let y=x/a which means that dy=dx/a.

$\operatorname{E}[X^2]=\int^\infin_0 a^2 y^2 \cdot \frac{1}{a \Gamma (p)} y^{p-1} e^{-y}ady$

$\operatorname{E}[X^2]=\frac{a^2}{ \Gamma (p)}\int^\infin_0 y^{p+1} e^{-y}dy$

$\operatorname{E}[X^2]=\frac{a^2}{ \Gamma (p)}\Gamma (p+2) =pa^2(p+1)$

Now we use calculate the variance

$\operatorname{Var}(X)=\operatorname{E}[X^2]-(\operatorname{E}[X])^2$

$\operatorname{Var}(X)=pa^2(p+1)-(ap)^2=pa^2$

External links

• Interactive Gamma Distribution Web Applet (Java)