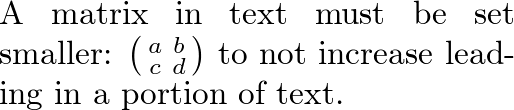LaTeX/Mathematics
One of the greatest motivating forces for Donald Knuth when he began developing the original TeX system was to create something that allowed simple construction of mathematical formulae, while looking professional when printed. The fact that he succeeded was most probably why TeX (and later on, LaTeX) became so popular within the scientific community. Typesetting mathematics is one of LaTeX's greatest strengths. It is also a large topic due to the existence of so much mathematical notation.
If your document requires only a few simple mathematical formulas, plain LaTeX has most of the tools that you will ever need. If you are writing a scientific document that contains numerous complex formulas, the amsmath package[1] introduces several new commands that are more powerful and flexible than the ones provided by basic LaTeX. The mathtools package fixes some amsmath quirks and adds some useful settings, symbols, and environments to amsmath.[2] To use either package, include:
\usepackage{amsmath}
or
\usepackage{mathtools}
in the preamble of the document. The mathtools package loads the amsmath package and hence there is no need to \usepackage{amsmath} in the preamble if mathtools is used.
Mathematics environments
[edit | edit source]LaTeX needs to know when the text is mathematical. This is because LaTeX typesets math notation differently from normal text. Therefore, special environments have been declared for this purpose. They can be distinguished into two categories depending on how they are presented:
- text — text formulas are displayed inline, that is, within the body of text where it is declared, for example, I can say that within this sentence.
- displayed — displayed formulas are on a line by themselves.
As math requires special environments, there are naturally the appropriate environment names you can use in the standard way. Unlike most other environments, however, there are some handy shorthands for declaring your formulas. The following table summarizes them:
| Type | Inline (within text) formulas | Displayed equations | Displayed and automatically numbered equations |
|---|---|---|---|
| Environment | math
|
displaymath
|
equation
|
| LaTeX shorthand | \(...\)
|
\[...\]
|
|
| TeX shorthand | $...$
|
$$...$$
|
|
| Comment | equation* (starred version) suppresses numbering, but requires amsmath
|
Suggestion: Using the $$...$$ should be avoided, as it may cause problems, particularly with the AMS-LaTeX macros. Furthermore, should a problem occur, the error messages may not be helpful.
The equation* and displaymath environments are functionally equivalent.
If you are typing text normally, you are said to be in text mode, but while you are typing within one of those mathematical environments, you are said to be in math mode, that has some differences compared to the text mode:
- Most spaces and line breaks do not have any significance, as all spaces are either derived logically from the mathematical expressions or have to be specified with special commands such as
\quad - Empty lines are not allowed. Only one paragraph per formula.
- Each letter is considered to be the name of a variable and will be typeset as such. If you want to typeset normal text within a formula (normal upright font with normal spacing), then you have to enter the text using dedicated commands.
Inserting "Displayed" maths inside blocks of text
[edit | edit source]In order for some operators, such as \lim or \sum, to be displayed correctly inside some math environments (read $......$), it might be convenient to write the \displaystyle class inside the environment. Doing so might cause the line to be taller, but will cause exponents and indices to be displayed correctly for some math operators. For example, the $\sum$ will print a smaller Σ and $\displaystyle \sum$ will print a bigger one , like in equations.[note 1] It is possible to force this behaviour for all math environments by declaring \everymath{\displaystyle} in the preamble (i.e. before \begin{document}).
Symbols
[edit | edit source]Mathematics has many symbols! The following is a set of symbols that can be accessed directly from the keyboard:
+ - = ! / ( ) [ ] < > | ' : *
Beyond those listed above, distinct commands must be issued in order to display the desired symbols. There are many examples such as Greek letters, set and relations symbols, arrows, binary operators, etc.
For example:
\forall x \in X, \quad \exists y \leq \epsilon
|
|
Fortunately, there's a tool that can greatly simplify the search for the command for a specific symbol. Look for "Detexify" in the external links section below. Another option would be to look in "The Comprehensive LaTeX Symbol List" in the external links section below.
Greek letters
[edit | edit source]Greek letters are commonly used in mathematics, and they are very easy to type in math mode. You just have to type the name of the letter after a backslash: if the first letter is lowercase, you will get a lowercase Greek letter, if the first letter is uppercase (and only the first letter), then you will get an uppercase letter. Note that some uppercase Greek letters look like Latin ones, so they are not provided by LaTeX (e.g. uppercase Alpha and Beta are just "A" and "B", respectively). Lowercase epsilon, theta, kappa, phi, pi, rho, and sigma are provided in two different versions. The alternate, or variant, version is created by adding "var" before the name of the letter:
\alpha, \Alpha, \beta, \Beta, \gamma, \Gamma, \pi, \Pi, \phi, \varphi, \mu, \Phi
|
|
Scroll down to #List of mathematical symbols for a complete list of Greek symbols.
Operators
[edit | edit source]An operator is a function that is written as a word: e.g. trigonometric functions (sin, cos, tan), logarithms and exponentials (log, exp), limits (lim), as well as trace and determinant (tr, det). LaTeX has many of these defined as commands:
\cos (2\theta) = \cos^2 \theta - \sin^2 \theta
|
|
For certain operators such as limits, the subscript is placed underneath the operator:
\lim\limits_{x \to \infty} \exp(-x) = 0
|
|
For the modular operator there are two commands: \bmod and \pmod:
a \bmod b
|
|
x \equiv a \pmod{b}
|
|
To use operators that are not pre-defined, such as argmax, see custom operators
Powers and indices
[edit | edit source]Powers and indices are equivalent to superscripts and subscripts in normal text mode. The caret (^; also known as the circumflex accent) character is used to raise something, and the underscore (_) is for lowering. If an expression containing more than one character is raised or lowered, it should be grouped using curly braces ({ and }).
k_{n+1} = n^2 + k_n^2 - k_{n-1}
|
|
For powers with more than one digit, surround the power with {}.
x^{2}
|
|
An underscore (_) can be used with a vertical bar () to denote evaluation using subscript notation in mathematics:
f(n) = n^5 + 4n^2 + 2 |_{n=17}
|
|
Fractions and Binomials
[edit | edit source]A fraction is created using the \frac{numerator}{denominator} command (for those who need their memories refreshed, that's the top and bottom respectively!). Likewise, the binomial coefficient (a.k.a, the Choose function) may be written using the \binom command:[note 1]
\frac{n!}{k!(n-k)!} = \binom{n}{k}
|
|
You can embed fractions within fractions:
\frac{\frac{1}{x}+\frac{1}{y}}{y-z}
|
|
Note that when appearing inside another fraction, or in inline text , a fraction is noticeably smaller than in displayed mathematics. The \tfrac and \dfrac commands[note 1] force the use of the respective styles, \textstyle and \displaystyle. Similarly, the \tbinom and \dbinom commands typeset the binomial coefficient.
For relatively simple fractions, especially within the text, it may be more aesthetically pleasing to use powers and indices instead:
^3/_7
|
|
If this looks a little "loose" (i.e., overspaced), a tightened version can be defined by inserting some negative space
%running fraction with slash - requires math mode.
\newcommand*\rfrac[2]{{}^{#1}\!/_{#2}}
\rfrac{3}{7}
|
|
If you use them throughout the document, usage of xfrac package is recommended.
This package provides \sfrac command to create slanted fractions. Usage:
Take $\sfrac{1}{2}$ cup of sugar, \dots
3\times\sfrac{1}{2}=1\sfrac{1}{2}
Take ${}^1/_2$ cup of sugar, \dots
3\times{}^1/_2=1{}^1/_2
|
If fractions are used as an exponent, curly braces have to be used around the \sfrac command:
$x^\frac{1}{2}$ % no error
$x^\sfrac{1}{2}$ % error
$x^{\sfrac{1}{2}}$ % no error
$x^\frac{1}{2}$ % no error
|
|
In some cases, using the package alone will result in errors about certain font shapes not being available. In that case, the lmodern and fix-cm packages need to be added as well.
Alternatively, the nicefrac package provides the \nicefrac command, whose usage is similar to \sfrac.
Continued fractions
[edit | edit source]Continued fractions should be written using \cfrac command:[note 1]
\begin{equation}
x = a_0 + \cfrac{1}{a_1
+ \cfrac{1}{a_2
+ \cfrac{1}{a_3 + \cfrac{1}{a_4} } } }
\end{equation}
|
|
Multiplication of two numbers
[edit | edit source]To make multiplication visually similar to a fraction, a nested array can be used. For example, multiplication of numbers written one below the other can be typeset as follows:
\begin{equation}
\frac{
\begin{array}[b]{r}
\left( x_1 x_2 \right)\\
\times \left( x'_1 x'_2 \right)
\end{array}
}{
\left( y_1y_2y_3y_4 \right)
}
\end{equation}
|
|
Roots
[edit | edit source]The \sqrt command creates a square root surrounding an expression. It accepts an optional argument specified in square brackets ([ and ]) to change magnitude:
\sqrt{\frac{a}{b}}
|
|
\sqrt[n]{1+x+x^2+x^3+\dots+x^n}
|
|
Some people prefer writing the square root "closing" it over its content. This method arguably makes it more clear what is in the scope of the root sign. This habit is not normally used while writing with the computer, but if you still want to change the output of the square root, LaTeX gives you this possibility. Just add the following code in the preamble of your document:
This TeX code first renames the \sqrt command as \oldsqrt, then redefines \sqrt in terms of the old one, adding something more. The new square root can be seen in the picture on the left, compared to the old one on the right. Unfortunately this code won't work if you want to use multiple roots: if you try to write as \sqrt[b]{a} after you used the code above, you'll just get a wrong output. In other words, you can redefine the square root this way only if you are not going to use multiple roots in the whole document.
An alternative piece of TeX code that does allow multiple roots is
\usepackage{letltxmacro}
\makeatletter
\let\oldr@@t\r@@t
\def\r@@t#1#2{%
\setbox0=\hbox{$\oldr@@t#1{#2\,}$}\dimen0=\ht0
\advance\dimen0-0.2\ht0
\setbox2=\hbox{\vrule height\ht0 depth -\dimen0}%
{\box0\lower0.4pt\box2}}
\LetLtxMacro{\oldsqrt}{\sqrt}
\renewcommand*{\sqrt}[2][\ ]{\oldsqrt[#1]{#2} }
\makeatother
$\sqrt[a]{b} \quad \oldsqrt[a]{b}$
|
However, this requires the \usepackage{letltxmacro} package.
Sums and integrals
[edit | edit source]The \sum and \int commands insert the sum and integral symbols respectively, with limits specified using the caret (^) and underscore (_). The typical notation for sums is:
\sum_{i=1}^{10} t_i
|
|
or
\displaystyle\sum_{i=1}^{10} t_i
|
|
The limits for the integrals follow the same notation. It's also important to represent the integration variables with an upright d, which in math mode is obtained through the \mathrm{} command, and with a small space separating it from the integrand, which is attained with the \, command.
\int_0^\infty \mathrm{e}^{-x}\,\mathrm{d}x
|
|
There are many other "big" commands which operate in a similar manner:
\sum |
\prod |
\coprod |
|||||
\bigoplus |
\bigotimes |
\bigodot |
|||||
\bigcup |
\bigcap |
\biguplus |
|||||
\bigsqcup |
\bigvee |
\bigwedge |
|||||
\int |
\oint |
\iint[note 1] |
|||||
\iiint[note 1] |
\iiiint[note 1] |
\idotsint[note 1] |
For more integral symbols, including those not included by default in the Computer Modern font, try the esint package.
The \substack command[note 1] allows the use of \\ to write the limits over multiple lines:
\sum_{\substack{
0<i<m \\
0<j<n
}}
P(i,j)
|
|
If you want the limits of an integral to be specified above and below the symbol (like the sum), use the \limits command:
\int\limits_a^b
|
|
However, if you want this to apply to all integrals, it is preferable to specify the intlimits option when loading the amsmath package:
\usepackage[intlimits]{amsmath}
|
Subscripts and superscripts in other contexts, as well as other parameters to amsmath package related to them, are described in Advanced Mathematics chapter.
For bigger integrals, you may use personal declarations, or the bigints package [3].
Brackets, braces and delimiters
[edit | edit source]How to use braces in multi line equations is described in the Advanced Mathematics chapter.
The use of delimiters such as brackets soon becomes important when dealing with anything but the most trivial equations. Without them, formulas can become ambiguous. Also, special types of mathematical structures, such as matrices, typically rely on delimiters to enclose them.
There are a variety of delimiters available for use in LaTeX:
( a ), [ b ], \{ c \}, | d |, \| e \|,
\langle f \rangle, \lfloor g \rfloor,
\lceil h \rceil, \ulcorner i \urcorner,
/ j \backslash
|
|
where \lbrack and \rbrack may be used in place of [ and ].
Automatic sizing
[edit | edit source]Very often, mathematical features will differ in size, in which case the delimiters surrounding the expression should vary accordingly. This can be done automatically using the \left, \right, and \middle commands. Any of the previous delimiters may be used in combination with these:
\left(\frac{x^2}{y^3}\right)
|
|
P\left(A=2\middle|\frac{A^2}{B}>4\right)
|
Curly braces are defined differently by using \left\{ and \right\},
\left\{\frac{x^2}{y^3}\right\}
|
|
If a delimiter on only one side of an expression is required, then an invisible delimiter on the other side may be denoted using a period (.).
\left.\frac{x^3}{3}\right|_0^1
|
|
Manual sizing
[edit | edit source]In certain cases, the sizing produced by the \left and \right commands may not be desirable, or you may simply want finer control over the delimiter sizes. In this case, the \big, \Big, \bigg and \Bigg modifier commands may be used:
( \big( \Big( \bigg( \Bigg(
|
|
These commands are primarily useful when dealing with nested delimiters. For example, when typesetting
\frac{\mathrm d}{\mathrm d x} \left( k g(x) \right)
|
|
we notice that the \left and \right commands produce the same size delimiters as those nested within it. This can be difficult to read. To fix this, we write
\frac{\mathrm d}{\mathrm d x} \big( k g(x) \big)
|
|
Manual sizing can also be useful when an equation is too large, trails off the end of the page, and must be separated into two lines using an align command. Although the commands \left. and \right. can be used to balance the delimiters on each line, this may lead to wrong delimiter sizes. Furthermore, manual sizing can be used to avoid overly large delimiters — if an \underbrace or a similar command appears between the delimiters.
Matrices and arrays
[edit | edit source]A basic matrix may be created using the matrix environment[note 1]: in common with other table-like structures, entries are specified by row, with columns separated using an ampersand (&) and new rows separated with a double backslash (\\)
\[
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i
\end{matrix}
\]
|
|
To specify alignment of columns in the table, use starred version[note 2]:
\begin{matrix}
-1 & 3 \\
2 & -4
\end{matrix}
=
\begin{matrix*}[r]
-1 & 3 \\
2 & -4
\end{matrix*}
|
|
The alignment by default is c, but it can be any column type valid in array environment.
However matrices are usually enclosed in delimiters of some kind, and while it is possible to use the \left and \right commands, there are various other predefined environments which automatically include delimiters:
| Environment name | Surrounding delimiter | Notes |
|---|---|---|
| pmatrix[note 1] | centers columns by default | |
| pmatrix*[note 2] | allows to specify alignment of columns in optional parameter | |
| bmatrix[note 1] | centers columns by default | |
| bmatrix*[note 2] | allows to specify alignment of columns in optional parameter | |
| Bmatrix[note 1] | centers columns by default | |
| Bmatrix*[note 2] | allows to specify alignment of columns in optional parameter | |
| vmatrix[note 1] | centers columns by default | |
| vmatrix*[note 2] | allows to specify alignment of columns in optional parameter | |
| Vmatrix[note 1] | centers columns by default | |
| Vmatrix*[note 2] | allows to specify alignment of columns in optional parameter |
When writing down arbitrary sized matrices, it is common to use horizontal, vertical and diagonal triplets of dots (known as ellipses) to fill in certain columns and rows. These can be specified using the \cdots, \vdots and \ddots respectively:
A_{m,n} =
\begin{pmatrix}
a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,n}
\end{pmatrix}
|
|
In some cases, you may want to have finer control of the alignment within each column, or to insert lines between columns or rows. This can be achieved using the array environment, which is essentially a math-mode version of the tabular environment, which requires that the columns be pre-specified:
\begin{array}{c|c}
1 & 2 \\
\hline
3 & 4
\end{array}
|
|
You may see that the AMS matrix class of environments doesn't leave enough space when used together with fractions resulting in output similar to this:
To counteract this problem, add additional leading space with the optional parameter to the \\ command:
M = \begin{bmatrix}
\frac{5}{6} & \frac{1}{6} & 0 \\[0.3em]
\frac{5}{6} & 0 & \frac{1}{6} \\[0.3em]
0 & \frac{5}{6} & \frac{1}{6}
\end{bmatrix}
|
|
If you need "border" or "indexes" on your matrix, plain TeX provides the macro \bordermatrix
M = \bordermatrix{~ & x & y \cr
A & 1 & 0 \cr
B & 0 & 1 \cr}
|
Matrices in running text
[edit | edit source]To insert a small matrix without increasing leading in the line containing it, use smallmatrix environment:
A matrix in text must be set smaller:
$\bigl(\begin{smallmatrix}
a&b \\ c&d
\end{smallmatrix} \bigr)$
to not increase leading in a portion of text.
|
Adding text to equations
[edit | edit source]The math environment differs from the text environment in the representation of text. Here is an example of trying to represent text within the math environment:
50 apples \times 100 apples = lots of apples^2
|
|
There are two noticeable problems: there are no spaces between words or numbers, and the letters are italicized and more spaced out than normal. Both issues are simply artifacts of the maths mode, in that it treats it as a mathematical expression: spaces are ignored (LaTeX spaces mathematics according to its own rules), and each character is a separate element (so are not positioned as closely as normal text).
There are a number of ways that text can be added properly. The typical way is to wrap the text with the \text{...} command[note 1] (a similar command is \mbox{...}, though this causes problems with subscripts, and has a less descriptive name). Let's see what happens when the above equation code is adapted:
50 \text{apples} \times 100 \text{apples}
= \text{lots of apples}^2
|
|
The text looks better. However, there are no gaps between the numbers and the words. Unfortunately, you are required to explicitly add these. There are many ways to add spaces between math elements, but for the sake of simplicity we may simply insert space characters into the \text commands.
50 \text{ apples} \times 100 \text{ apples}
= \text{lots of apples}^2
|
|
Formatted text
[edit | edit source]Using the \text is fine and gets the basic result. Yet, there is an alternative that offers a little more flexibility. You may recall the introduction of font formatting commands, such as \textrm, \textit, \textbf, etc. These commands format the argument accordingly, e.g., \textbf{bold text} gives bold text. These commands are equally valid within a maths environment to include text. The added benefit here is that you can have better control over the font formatting, rather than the standard text achieved with \text.
50 \textrm{ apples} \times 100
\textbf{ apples} = \textit{lots of apples}^2
|
|
Formatting mathematics symbols
[edit | edit source]- See also: w:Mathematical Alphanumeric Symbols, w:Help:Displaying a formula#Alphabets and typefaces and w:Wikipedia:LaTeX symbols#Fonts
We can now format text; what about formatting mathematical expressions? There are a set of formatting commands very similar to the font formatting ones just used, except that they are specifically aimed at text in math mode (requires amsfonts)
| LaTeX command | Sample | Description | Common use |
|---|---|---|---|
\mathnormal{…}(or simply omit any command) |
The default math font | Most mathematical notation | |
\mathrm{…}
|
This is the default or normal font, unitalicised | Units of measurement, one word functions | |
\mathit{…}
|
Italicised font | Multi-letter function or variable names. Compared to \mathnormal, words are spaced more naturally and numbers are italicized as well.
| |
\mathbf{…}
|
Bold font | Vectors | |
\mathsf{…}
|
Sans-serif | Categories | |
\mathtt{…}
|
Monospace (fixed-width) font | ||
\mathfrak{…}(requires the amsfonts or amssymb package[note 3]) |
Fraktur | Almost canonical font for Lie algebras, ideals in ring theory | |
\mathcal{…}
|
Calligraphy (uppercase only[note 3]) | Often used for sheaves/schemes and categories, used to denote cryptological concepts like an alphabet of definition (), message space (), ciphertext space () and key space (); Kleene's ; naming convention in description logic; Laplace transform () and Fourier transform () | |
\mathbb{…}(requires the amsfonts or amssymb package[note 3]) |
Blackboard bold (uppercase only[note 3]) | Used to denote special sets (e.g. real numbers) | |
\mathscr{…}(requires the mathrsfs package[note 3]) |
Script (uppercase only[note 3]) | An alternative font for categories and sheaves. |
These formatting commands can be wrapped around the entire equation, and not just on the textual elements: they only format letters, numbers, and uppercase Greek, and other math commands are unaffected.
To bold lowercase Greek or other symbols use the \boldsymbol command[note 1]; this will only work if there exists a bold version of the symbol in the current font. As a last resort there is the \pmb command[note 1] (poor man's bold): this prints multiple versions of the character slightly offset against each other.
\boldsymbol{\beta} = (\beta_1,\beta_2,\dotsc,\beta_n)
|
|
To change the size of the fonts in math mode, see Changing font size.
Accents
[edit | edit source]So what to do when you run out of symbols and fonts? Well, the next step is to use accents:
a' or a^{\prime} |
a'' |
||
\hat{a} |
\bar{a} |
||
\grave{a} |
\acute{a} |
||
\dot{a} |
\ddot{a} |
||
\not{a} |
\mathring{a} |
å | |
\overrightarrow{AB} |
\overleftarrow{AB} |
||
a''' |
a'''' |
||
\overline{aaa} |
\check{a} |
||
\breve{a} |
\vec{a} |
||
\dddot{a}[note 1] |
\ddddot{a}[note 1] |
||
\widehat{AAA} |
\widetilde{AAA} |
||
\stackrel\frown{AAA} |
|||
\tilde{a} |
\underline{a} |
Color
[edit | edit source]The package xcolor, described in Colors, allows us to add color to our equations. For example,
k = {\color{red}x} \mathbin{\color{blue}-} 2
|
|
The only problem is that this disrupts the default LaTeX formatting around the - operator. To fix this, we enclose it in a \mathbin environment, since - is a binary operator. This process is described here.
Plus and minus signs
[edit | edit source]LaTeX deals with the + and − signs in two possible ways. The most common is as a binary operator. When two maths elements appear on either side of the sign, it is assumed to be a binary operator, and as such, allocates some space to either side of the sign. The alternative way is a sign designation. This is when you state whether a mathematical quantity is either positive or negative. This is common for the latter, as in math, such elements are assumed to be positive unless a − is prefixed to it. In this instance, you want the sign to appear close to the appropriate element to show their association. If you put a + or a − with nothing before it but you want it to be handled like a binary operator you can add an invisible character before the operator using {}. This can be useful if you are writing multiple-line formulas, and a new line could start with a − or +, for example, then you can fix some strange alignments adding the invisible character where necessary.
A plus-minus sign is written as:
\pm
|
|
Similarly, there exists also a minus-plus sign:
\mp
|
|
Controlling horizontal spacing
[edit | edit source]LaTeX is obviously pretty good at typesetting maths—it was one of the chief aims of the core TeX system that LaTeX extends. However, it can't always be relied upon to accurately interpret formulas in the way you did. It has to make certain assumptions when there are ambiguous expressions. The result tends to be slightly incorrect horizontal spacing. In these events, the output is still satisfactory, yet any perfectionists will no doubt wish to fine-tune their formulas to ensure spacing is correct. These are generally very subtle adjustments.
There are other occasions where LaTeX has done its job correctly, but you just want to add some space, maybe to add a comment of some kind. For example, in the following equation, it is preferable to ensure there is a decent amount of space between the maths and the text.
\[ f(n) =
\begin{cases}
n/2 & \quad \text{if } n \text{ is even}\\
-(n+1)/2 & \quad \text{if } n \text{ is odd}
\end{cases}
\]
|
|
This code produces errors with Miktex 2.9 and does not yield the results seen on the right. Use \mathrm instead of just \text.
(Note that this particular example can be expressed in more elegant code by the cases construct provided by the amsmath package described in Advanced Mathematics chapter.)
LaTeX has defined two commands that can be used anywhere in documents (not just maths) to insert some horizontal space. They are \quad and \qquad
A \quad is a space equal to the current font size. So, if you are using an 11pt font, then the space provided by \quad will also be 11pt (horizontally, of course.) The \qquad gives twice that amount. As you can see from the code from the above example, \quads were used to add some separation between the maths and the text.
OK, so back to the fine tuning as mentioned at the beginning of the document. A good example would be displaying the simple equation for the indefinite integral of y with respect to x:
If you were to try this, you may write:
\int y \mathrm{d}x
|
|
However, this doesn't give the correct result. LaTeX doesn't respect the white-space left in the code to signify that the y and the dx are independent entities. Instead, it lumps them altogether. A \quad would clearly be overkill in this situation—what is needed are some small spaces to be utilized in this type of instance, and that's what LaTeX provides:
| Command | Description | Size |
|---|---|---|
\,
|
small space | 3/18 of a quad |
\:
|
medium space | 4/18 of a quad |
\;
|
large space | 5/18 of a quad |
\!
|
negative space | -3/18 of a quad |
NB you can use more than one command in a sequence to achieve a greater space if necessary.
So, to rectify the current problem:
\int y\, \mathrm{d}x
|
|
\int y\: \mathrm{d}x
|
|
\int y\; \mathrm{d}x
|
|
The negative space may seem like an odd thing to use, however, it wouldn't be there if it didn't have some use! Take the following example:
\left(
\begin{array}{c}
n \\
r
\end{array}
\right) = \frac{n!}{r!(n-r)!}
|
|
The matrix-like expression for representing binomial coefficients is too padded. There is too much space between the brackets and the actual contents within. This can easily be corrected by adding a few negative spaces after the left bracket and before the right bracket.
\left(\!
\begin{array}{c}
n \\
r
\end{array}
\!\right) = \frac{n!}{r!(n-r)!}
|
|
In any case, adding some spaces manually should be avoided whenever possible: it makes the source code more complex and it's against the basic principles of a What You See is What You Mean approach. The best thing to do is to define some commands using all the spaces you want and then, when you use your command, you don't have to add any other space. Later, if you change your mind about the length of the horizontal space, you can easily change it modifying only the command you defined before. Let us use an example: you want the d of a dx in an integral to be in roman font and a small space away from the rest. If you want to type an integral like \int x \, \mathrm{d} x, you can define a command like this:
\newcommand{\dd}{\mathop{}\,\mathrm{d}}
|
in the preamble of your document. We have chosen \dd just because it reminds the "d" it replaces and it is fast to type. Doing so, the code for your integral becomes \int x \dd x. Now, whenever you write an integral, you just have to use the \dd instead of the "d", and all your integrals will have the same style. If you change your mind, you just have to change the definition in the preamble, and all your integrals will be changed accordingly.
Manually Specifying Formula Style
[edit | edit source]To manually display a fragment of a formula using text style, surround the fragment with curly braces and prefix the fragment with \textstyle. The braces are required because the \textstyle macro changes the state of the renderer, rendering all subsequent mathematics in text style. The braces limit this change of state to just the fragment enclosed within. For example, to use text style for just the summation symbol in a sum, one would enter
\begin{equation}
C^i_j = {\textstyle \sum_k} A^i_k B^k_j
\end{equation}
|
The same thing as a command would look like this:
\newcommand{\tsum}[1]{{\textstyle \sum_{#1}}}
|
Note the extra braces. Just one set around the expression won't be enough. That would cause all math after \tsum k to be displayed using text style.
To display part of a formula using display style, do the same thing, but use \displaystyle instead.
Advanced Mathematics: AMS Math package
[edit | edit source]The AMS (American Mathematical Society) mathematics package is a powerful package that creates a higher layer of abstraction over mathematical LaTeX language; if you use it it will make your life easier. Some commands amsmath introduces will make other plain LaTeX commands obsolete: in order to keep consistency in the final output you'd better use amsmath commands whenever possible. If you do so, you will get an elegant output without worrying about alignment and other details, keeping your source code readable. If you want to use it, you have to add this in the preamble:
\usepackage{amsmath}
|
Introducing dots in formulas
[edit | edit source]amsmath defines also the \dots command, that is a generalization of the existing \ldots. You can use \dots in both text and math mode and LaTeX will replace it with three dots "…" but it will decide according to the context whether to put it on the bottom (like \ldots) or centered (like \cdots).
Dots
[edit | edit source]LaTeX gives you several commands to insert dots (ellipses) in your formulae. This can be particularly useful if you have to type big matrices omitting elements. First of all, here are the main dots-related commands LaTeX provides:
| Code | Output | Comment |
|---|---|---|
\dots |
generic dots (ellipsis), to be used in text (outside formulae as well). It automatically manages whitespaces before and after itself according to the context, it's a higher level command. | |
\ldots |
the output is similar to the previous one, but there is no automatic whitespace management; it works at a lower level. | |
\cdots |
These dots are centered relative to the height of a letter. There is also the binary multiplication operator, \cdot, mentioned below.
| |
\vdots |
vertical dots | |
\ddots |
diagonal dots | |
\iddots |
inverse diagonal dots (requires the mathdots package) | |
\hdotsfor{n} |
to be used in matrices, it creates a row of dots spanning n columns. |
Instead of using \ldots and \cdots, you should use the semantically oriented commands. It makes it possible to adapt your document to different conventions on the fly, in case (for example) you have to submit it to a publisher who insists on following house tradition in this respect. The default treatment for the various kinds follows American Mathematical Society conventions.
Write an equation with the align environment
[edit | edit source]How to write an equation with the align environment with the amsmath package is described in Advanced Mathematics.
List of mathematical symbols
[edit | edit source]All the pre-defined mathematical symbols from the \TeX\ package are listed below. More symbols are available from extra packages.
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
<
|
>
|
=
|
\parallel
|
\nparallel
| |||||||||
\leq
|
\geq
|
\doteq
|
\asymp
|
\bowtie
| |||||||||
\ll
|
\gg
|
\equiv
|
\vdash
|
\dashv
| |||||||||
\subset
|
\supset
|
\approx
|
\in
|
\ni
| |||||||||
\subseteq
|
\supseteq
|
\cong
|
\smile
|
\frown
| |||||||||
\nsubseteq
|
\nsupseteq
|
\simeq
|
\models
|
\notin
| |||||||||
\sqsubset
|
\sqsupset
|
\sim
|
\perp
|
\mid
| |||||||||
\sqsubseteq
|
\sqsupseteq
|
\propto
|
\prec
|
\succ
| |||||||||
\preceq
|
\succeq
|
\neq
|
\sphericalangle
|
\measuredangle
| |||||||||
\therefore
|
\because
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
\pm
|
\cap
|
\diamond
|
\oplus
| |||||||
\mp
|
\cup
|
\bigtriangleup
|
\ominus
| |||||||
\times
|
\uplus
|
\bigtriangledown
|
\otimes
| |||||||
\div
|
\sqcap
|
\triangleleft
|
\oslash
| |||||||
\ast
|
\sqcup
|
\triangleright
|
\odot
| |||||||
\star
|
\vee
|
\bigcirc
|
\circ
| |||||||
\dagger
|
\wedge
|
\bullet
|
\setminus
| |||||||
\ddagger
|
\cdot
|
\wr
|
\amalg
|
| Symbol | Script | Symbol | Script | |
|---|---|---|---|---|
\exists
|
\rightarrow or \to
| |||
\nexists
|
\leftarrow or \gets
| |||
\forall
|
\mapsto
| |||
\neg
|
\implies
| |||
\cap
|
||||
\cup
|
||||
\subset
|
⟸ | \impliedby
| ||
\supset
|
\Rightarrow or \implies
| |||
\in
|
\leftrightarrow
| |||
\notin
|
\iff
| |||
\ni
|
\Leftrightarrow (preferred for equivalence (iff))
| |||
\land
|
\top
| |||
\lor
|
\bot
| |||
\angle
|
and | \emptyset and \varnothing[1]
| ||
\rightleftharpoons
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
| or \mid (difference in spacing)
|
\|
|
/
|
\backslash
| |||||||
\{
|
\}
|
\langle
|
\rangle
| |||||||
\uparrow
|
\Uparrow
|
\lceil
|
\rceil
| |||||||
\downarrow
|
\Downarrow
|
\lfloor
|
\rfloor
|
Note: To use the Greek Letters in LaTeX that have the same appearance in the Latin alphabet, just use Latin: e.g., A instead of Alpha, B instead of Beta, etc.
| Symbol | Script | Symbol | Script | |
|---|---|---|---|---|
| and | A and \alpha
|
and | N and \nu
| |
| and | B and \beta
|
and | \Xi and \xi
| |
| and | \Gamma and \gamma
|
and | O and o
| |
| and | \Delta and \delta
|
, and | \Pi, \pi and \varpi
| |
| , and | E, \epsilon and \varepsilon
|
, and | P, \rho and \varrho
| |
| and | Z and \zeta
|
, and | \Sigma, \sigma and \varsigma
| |
| and | H and \eta
|
and | T and \tau
| |
| , and | \Theta, \theta and \vartheta
|
, and | Y, \Upsilon and \upsilon
| |
| and | I and \iota
|
, , and | \Phi, \phi and \varphi
| |
| , and | K, \kappa and \varkappa
|
and | X and \chi
| |
| and | \Lambda and \lambda
|
and | \Psi and \psi
| |
| and | M and \mu
|
and | \Omega and \omega
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
\partial
|
\imath
|
\Re
|
\nabla
|
\aleph
| |||||||||
\eth
|
\jmath
|
\Im
|
\Box
|
\beth
| |||||||||
\hbar
|
\ell
|
\wp
|
\infty
|
\gimel
|
^ Not predefined in LATEX 2. Use one of the packages latexsym, amsfonts, amssymb, txfonts, pxfonts, or wasysym
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
\sin
|
\arcsin
|
\sinh
|
\sec
| |||||||
\cos
|
\arccos
|
\cosh
|
\csc
| |||||||
\tan
|
\arctan
|
\tanh
|
||||||||
\cot
|
\arccot
|
\coth
|
If LaTeX does not include a command for the mathematical operator you want to use, for example \cis (cosine plus i times sine), add to your preamble:
\DeclareMathOperator\cis{cis}
You can then use \cis in the document just like \cos or any other mathematical operator.
Summary
[edit | edit source]As you begin to see, typesetting math can be tricky at times. However, because LaTeX provides so much control, you can get professional quality mathematics typesetting with relatively little effort (once you've had a bit of practice, of course!). It is possible to elaborate further on the nitty-gritty of mathematics because the possibilities seem endless. However, with this tutorial, you should be able to get along with it sufficiently.
References
[edit | edit source]Notes
[edit | edit source]- ↑ a b c d e f g h i j k l m n o p q r s t requires the amsmath package
- ↑ a b c d e f requires the mathtools package
- ↑ a b c d e f The mathalpha package allows for specifying a broader variety of fonts to be used in the
\mathfrak{},\mathbb{},\mathcal{}and\mathscr{}commands. For example, the command\usepackage[bb=pazo]{mathalpha}makes it so\mathbb{}uses the "pazo" font. mathalpha's documentation gives a comparison of the different font options; some have lowercase letters, Greek letters or numerals where the default does not.
Further reading
[edit | edit source]- meta:Help:Displaying a formula: Wikimedia uses a subset of LaTeX commands.
External links
[edit | edit source]- detexify: applet for looking up LaTeX symbols by drawing them
- amsmath documentation
- LaTeX - The Student Room
- The Comprehensive LaTeX Symbol List
- Comprehensive List of Mathematical Symbols






















![{\displaystyle {\sqrt[{n}]{1+x+x^{2}+x^{3}+\dots +x^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74a7b5d7b8b7c0651bcbbd83c02ca86dbf87789b)

![{\displaystyle {\sqrt[{b}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ceeccbbf1609652afdb8d84d33552cd2731bb0d)























![{\displaystyle (a),[b],\{c\},|d|,\|e\|,\langle f\rangle ,\lfloor g\rfloor ,\lceil h\rceil ,\ulcorner i\urcorner ,/j\backslash }](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ff76385ff85daf87ceef4734e98932ec5fd772)









![{\displaystyle [\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5444b5227fcebf7e7cbb9ee114af1373f6a2e95)






![{\displaystyle M={\begin{bmatrix}{\frac {5}{6}}&{\frac {1}{6}}&0\\[0.3em]{\frac {5}{6}}&0&{\frac {1}{6}}\\[0.3em]0&{\frac {5}{6}}&{\frac {1}{6}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4989d4433782a036095cdf274ee636c5f783125c)