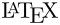LaTeX/Page Layout

LaTeX and the document class will normally take care of page layout issues for you. For submission to an academic publication, this entire topic will be out of your hands, as the publishers want to control the presentation. However, for your own documents, there are some obvious settings that you may wish to change: margins, page orientation and columns, to name but three. The purpose of this tutorial is to show you how to configure your pages.

We will often have to deal with TeX lengths in this chapter. You should have a look at Lengths for comprehensive details on the topic.

Two-sided documents

Documents can be either one- or two-sided. Articles are by default one-sided, books are two-sided. Two-sided documents differentiate the left (even) and right (odd) pages, whereas one-sided do not. The most notable effect can be seen in page margins. If you want to make the article class two-sided, use \documentclass[twoside]{article}.

Many commands and variables in LaTeX take this concept into account. They are referred to as even and odd. For one-sided document, only the odd commands and variables will be in effect.

Page dimensions

A page in LaTeX is defined by many internal parameters. Each parameter corresponds to the length of an element of the page, for example, \paperheight is the physical height of the page. Here you can see a diagram showing all the variables defining the page. All sizes are given in TeX points (pt), there are 72.27pt in an inch or 1pt ≈ 0.3515mm.

1. one inch + \hoffset
2. one inch + \voffset
3. \oddsidemargin = 31pt
4. \topmargin = 20pt
5. \headheight = 12pt
6. \headsep = 25pt
7. \textheight = 592pt
8. \textwidth = 390pt

9. \marginparsep = 10pt
10. \marginparwidth = 35pt
11. \footskip = 30pt

• \marginparpush = 7pt (not shown)
• \hoffset = 0pt
• \voffset = 0pt
• \paperwidth = 597pt
• \paperheight = 845pt

The current details plus the layout shape can be printed from a LaTeX document itself. Use the layout package and the command of the same name: \usepackage{layout} ... \layout{}

Page size

It will not have been immediately obvious - because it doesn't really cause any serious problems - that the default page size for all standard document classes is US letter. This is shorter by 18 mm (about 3/4 inch), and slightly wider by 8 mm (about 1/4 inch), compared to A4 (which is the standard in almost all the rest of the world). While this is not a serious issue (most printers will print the document without any problems), it is possible to specify alternative sizes as class option. For A4 format:

\documentclass[a4paper]{article}

More size options with geometry

One of the most versatile packages for page layout is the geometry package. The immediate advantage of this package is that it lets you customize the page size even with classes that do not support the options. For instance, to set the page size, add the following to your preamble:

\usepackage[a4paper]{geometry}

The geometry package has many pre-defined page sizes, like a4paper, built in. Others include:

• a0paper, a1paper, ..., a6paper,
• b0paper, b1paper, ..., b6paper,
• letterpaper,
• legalpaper,
• executivepaper.

To explicitly change the paper dimensions using the geometry package, the paperwidth and paperheight options can be used. For example:

\usepackage[paperwidth=5.5in, paperheight=8.5in]{geometry}

Changing size manually

Use the \setlength command to adjust the parameters to the appropriate dimensions. See the Lengths chapter.

• In the preamble, \paperwidth and \paperheight in all cases.
• After the preamble, \pdfpagewidth and \pdfpageheight if you are using pdftex.

Using the PDF dedicated commands has one immediate advantage: it will let you change the page dimension anywhere in the document.

Page size issues

If you intend to get a PDF in the end, there are basically three ways:

• TeX → PDF

pdflatex myfile               # TeX → PDF

• TeX → DVI → PDF

latex myfile                  # TeX → DVI
dvipdf myfile                 # DVI → PDF

• TeX → DVI → PS → PDF

latex myfile                  # TeX → DVI
dvips myfile -o myfile.ps     # DVI → PS
ps2pdf myfile.ps myfile.pdf   # PS  → PDF

Sadly the PDF output page size may not be completely respectful of your settings. Some of these tools do not have the same interpretation of the DVI, PS and PDF specifications, and you may end up with a PDF which has not exactly the right size. Thanksfully there is a solution to that: the \special command lets the use pass PostScript or PDF parameters, which can be used here to set the page size appropriately.

• For pdflatex to work fine, using the package geometry usually works.
• For the DVI and PS ways, the safest way to always get the right paper size in the end is to add

\documentclass[...,a4paper,...]{...} \special{papersize=210mm,297mm}

to the tex file, and to append the appropriate parameters to the processors used during output generation:

dvips -t a4 ...
ps2pdf -sPAPERSIZE=a4 ...

If you want US Letter instead, replace 210mm,297mm by 8.5in,11in and a4paper by letter. Also replace a4 by letter in command-line parameters.

Page size for tablets

Those who want to read on tablets or other handheld digital devices need to create documents without the extra whitespace. In order to create PDF documents with optimal handheld viewing, not only must the text field and margins be adjusted, so must the page size. If you are looking for a sensible dimension, consider following the paper size used by the Supreme Court of the United States, 441pt by 666pt (or 6.125 inches by 9.25 inches), which looks great on tablets. You could also use the Supreme Court's text field size of 297 pt by 513 pt, but this is too wide for fonts other than Century Schoolbook, the font required by the Supreme Court.

Margins

Readers from a word processing background are probably wondering why there is so much white space surrounding the text. There is a good reason, and it's all down to readability. Have a look in a few books, and pick a few lines at random. Count the number of characters per line. I bet the average is about 66. Studies have shown that it's easier to read text when there are 60-70 characters per line - and it would seem that 66 is the optimal number. Therefore, the page margins are set to ensure that readability remains as good as possible. Also, white space is often left in the inner margin for the assumption that the document will be bound.

If you wish to change the margins of your document, there are many ways to do so:

• Simply use the fullpage package for somewhat standardized smaller margins (around an inch):

\usepackage{fullpage}

For an even greater effect give it the cm option (around 1.5cm):

\usepackage[cm]{fullpage}

• Use the a4wide package for a page with A4 document size with smaller margins.

• Use the geometry package. This package allows you to specify the 4 margins without needing to remember the particular page dimensions commands. You can enter the measures in centimeters and inches as well. Use cm for centimeters and in for inches after each value (e.g. 1.0in or 2.54cm). Note that by default (i.e. without any options) this package already reduces the margins, so for a 'standard layout' you may not need to specify anything. These values are relative to the edge of paper (0in) and go inward it. It may be implemented as follows:

\usepackage[top=2in, bottom=1.5in, left=1in, right=1in]{geometry}

or all in a row

\usepackage[margin=1.5in]{geometry}

You can combine the margin options with the page size options seen in this paragraph.

• Edit individual page dimension variables described above, using the \addtolength and \setlength commands. See the Lengths chapter. For instance,

\setlength{\textwidth}{6.5in} \addtolength{\voffset}{-5pt}

Odd and even margins

A quick way to eliminate the difference in position between even and odd numbered pages would be setting the values to evensidemargin and oddsidemargin to the half of odd's default:

\setlength{\oddsidemargin}{15.5pt} \setlength{\evensidemargin}{15.5pt}

The value of evensidemargin is larger than oddsidemargin in the two-sided default layout, as one could wish to write notes on the side of the page. The side for the large margin is chosen opposite to the side where pages are conjuncted together.

See the Lengths.

Top margin above Chapter

The top margin above a chapter can be changed using the titlesec package. Example: [1]

\usepackage{titlesec} \titlespacing*{\chapter}{0pt}{-50pt}{20pt} \titleformat{\chapter}[display]{\normalfont\huge\bfseries}{\chaptertitlename\ \thechapter}{20pt}{\Huge}

The command \titleformat must be used when the spacing of a chapter is changed. In case of a section this command can be omitted.

Page orientation

When you talk about changing page orientation, it usually means changing to landscape mode, since portrait is the default. We shall introduce two slightly different styles of changing orientation.

Change orientation of the whole document

The first is for when you want all of your document to be in landscape from the very beginning. There are various packages available to achieve this, but the one we prefer is the geometry package. All you need to do is call the package, with landscape as an option:

\usepackage[landscape]{geometry}

Although, if you intend to use geometry to set your paper size, don't add the \usepackage commands twice, simply string all the options together, separating with a comma:

\usepackage[a4paper,landscape]{geometry}

Using standard LaTeX classes, you can use the same class options:

\documentclass[a4paper,landscape]{article}

Change orientation of specific part

The second method is for when you are writing a document in portrait, but you have some contents, like a large diagram or table that would be displayed better on a landscape page. However, you still want the consistency of your headers and footers appearing the same place as the other pages.

The lscape package is for this very purpose. It supplies a landscape environment, and anything inside is basically rotated. No actual page dimensions are changed. This approach is more applicable to books or reports than to typical academic publications. Using pdflscape instead of lscape when generating a PDF document will make the page appear right side up when viewed: the single page that is in landscape format will be rotated, while the rest will be left in portrait orientation.

Also, to get a table to appear correctly centered on a landscaped page, one must place the tabular environment inside a table environment, which is itself inside the landscape environment. For instance it should look like this:

\usepackage{pdflscape} % ... \begin{landscape} \begin{table} \centering     % optional, probably makes it look better to have it centered on the page \begin{tabular}{....} % ... \end{tabular} \end{table} \end{landscape}

Change orientation of floating environment

If you use the above code, you will see that the table is inserted where it is in the code. It will not be floated! To fix this you need the package rotating. See the Rotations chapter.

Margins, page size and rotation of a specific page

If you need to rotate the page so that the figure fits, the chances are good that you need to scale the margins and the font size too. Again, the geometry package comes in handy for specifying new margins for a single page only.

\usepackage{geometry} \usepackage{pdflscape} % ... \newgeometry{margin=1cm} \begin{landscape} \thispagestyle{empty} %% Remove header and footer. \begin{table} \begin{center} \footnotesize %% Smaller font size. \begin{tabular}{....} % ... \end{tabular} \end{center} \end{table} \end{landscape} \restoregeometry

Note that order matters!

Page styles

Page styles in Latex terms refers not to page dimensions, but to the running headers and footers of a document. These headers typically contain document titles, chapter or section numbers/names, and page numbers.

Standard page styles

The possibilities of changing the headers in plain Latex are actually quite limited. There are two commands available: \pagestyle{''style''} will apply the specified style to the current and all subsequent pages, and \thispagestyle{''style''} will only affect the current page. The possible styles are:

empty	Both header and footer are cleared
plain	Header is clear, but the footer contains the page number in the center.
headings	Footer is blank, header displays information according to document class (e.g., section name) and page number top right.
myheadings	Page number is top right, and it is possible to control the rest of the header.

With myheadings, the commands \markright (in the standard document classes, book, report and article) and \markboth (only in the book class) are used to control the headings. The following commands placed at the beginning of an article document will set the header of all pages to contain "John Smith" top left, "On page styles" centered and the page number top right:

\pagestyle{myheadings} \markright{John Smith\hfill On page styles\hfill}

There are special commands containing details on the running page of the document.

\thepage	number of the current page
\leftmark	current chapter name printed like "CHAPTER 3. THIS IS THE CHAPTER TITLE"
\rightmark	current section name printed like "1.6. THIS IS THE SECTION TITLE"
\chaptername	the name chapter in the current language. If this is English, it will display "Chapter"
\thechapter	current chapter number
\thesection	current section number

Note that \leftmark and \rightmark convert the names to uppercase, whichever was the formatting of the text. If you want them to print the actual name of the chapter without converting it to uppercase use the following command:

\renewcommand{\chaptermark}[1]{ \markboth{#1}{} } \renewcommand{\sectionmark}[1]{ \markright{#1}{} }

Now \leftmark and \rightmark will just print the name of the chapter and section, without number and without affecting the formatting. Note that these redefinitions must be inserted after the first call of \pagestyle{fancy}. The standard book formatting of the \chaptermark is:

\renewcommand{\chaptermark}[1]{\markboth{\MakeUppercase{\chaptername\ \thechapter.\ #1}}{}}

Watch out: if you provide long text in two different "parts" only in the footer or only in the header, you might see overlapping text.

Moreover, with the following commands you can define the thickness of the decorative lines on both the header and the footer:

\renewcommand{\headrulewidth}{0.5pt} \renewcommand{\footrulewidth}{0pt}

The first line for the header, the second for the footer. Setting it to zero means that there will be no line.

Plain pages issue

An issue to look out for is that the major sectioning commands (\part, \chapter or \maketitle) specify a \thispagestyle{plain}. So, if you wish to suppress all styles by inserting a \pagestyle{empty} at the beginning of your document, then the style command at each section will override your initial rule, for those pages only. To achieve the intended result one can follow the new section commands with \thispagestyle{empty}. The \part command, however, cannot be fixed this way, because it sets the page style, but also advances to the next page, so that \thispagestyle{} cannot be applied to that page. Two solutions:

• simply write \usepackage{nopageno} in the preamble. This package will make \pagestyle{plain} have the same effect as \pagestyle{empty}, effectively suppressing page numbering when it is used.
• Use fancyhdr as described below.

The tricky problem when customizing headers and footers is to get things like running section and chapter names in there. Standard LaTeX accomplishes this with a two-stage approach. In the header and footer definition, you use the commands \rightmark and \leftmark to represent the current section and chapter heading, respectively. The values of these two commands are overwritten whenever a chapter or section command is processed. For ultimate flexibility, the \chapter command and its friends do not redefine \rightmark and \leftmark themselves. They call yet another command (\chaptermark, \sectionmark, or \subsectionmark) that is responsible for redefining \rightmark and \leftmark, except if they are starred -- in such a case, \markboth{Chapter/Section name}{} must be used inside the sectioning command if header and footer lines are to be updated.

Again, several packages provide a solution:

• an alternative one-stage mechanism is provided by the package titleps);
• fancyhdr will handle the process its own way.

Customizing with fancyhdr

To get better control over the headers, one can use the package fancyhdr written by Piet van Oostrum. It provides several commands that allow you to customize the header and footer lines of your document. For a more complete guide, the author of the package produced this documentation.

To begin, add the following lines to your preamble:

\usepackage{fancyhdr} \setlength{\headheight}{15.2pt} \pagestyle{fancy}

You can now observe a new style in your document.

The \headheight needs to be 13.6pt or more, otherwise you will get a warning and possibly formatting issues. Both the header and footer comprise three elements each according to its horizontal position (left, centre or right).

The styles supported by fancyhdr:

• the four LaTeX styles;
• fancy defines a new header for all pages but plain-style pages such as chapters and titlepage;
• fancyplain is the same, but for absolutely all pages.

Style customization

The styles can be customized with fancyhdr specific commands. Those two styles may be configured directly, whereas for LaTeX styles you need to make a call to the \fancypagestyle command.

To set header and footer style, fancyhdr provides three interfaces. They all provide the same features, you just use them differently. Choose the one you like most.

• You can use the following six commands.

\lhead[<even output>]{<odd output>} \chead[<even output>]{<odd output>} \rhead[<even output>]{<odd output>} \lfoot[<even output>]{<odd output>} \cfoot[<even output>]{<odd output>} \rfoot[<even output>]{<odd output>}

Hopefully, the behaviour of the above commands is fairly intuitive: if it has head in it, it affects the head etc, and obviously, l, c and r means left, centre and right respectively.

• You can also use the command \fancyhead for header and \fancyfoot for footer. They work in the same way, so we'll explain only the first one. The syntax is:

\fancyhead[selectors]{output you want}

You can use multiple selectors optionnaly separated by a comma. The selectors are the following:

E	even page
O	odd page
L	left side
C	centered
R	right side

so CE,RO will refer to the center of the even pages and to the right side of the odd pages.

• \fancyhf is a merge of \fancyhead and \fancyfoot, hence the name. There is two additional selectors H and F to specify the header or the footer respectively. If you omit the H or the F, it will set the fields for both.

These commands will only work for fancy and fancyplain. To customize LaTeX default style you need the \fancyplainstyle command. See below for examples.

For a clean customization, we recommend you start from scratch. To do so you should erase the current pagestyle. Providing empty values will make the field blank. So

\fancyhf{}

will just delete the current heading/footer configuration, so you can make your own.

Plain pages

There are two ways to change the style of plain pages like chapters and titlepage.

First you can use the fancyplain style. If you do so, you can use the command \fancyplain{...}{...} inside fancyhdr commands like \lhead{...}, etc.

When LaTeX wants to create a page with an empty style, it will insert the first argument of \fancyplain, in all the other cases it will use the second argument. For instance:

\pagestyle{fancyplain} \fancyhf{} \lhead{ \fancyplain{}{Author Name} } \rhead{ \fancyplain{}{\today} } \rfoot{ \fancyplain{}{\thepage} }

It has the same behavior of the previous code, but you will get empty header and footer in the title and at the beginning of chapters.

Alternatively you could redefine the plain style, for example to have a really plain page when you want. The command to use is \fancypagestyle{plain}{...} and the argument can contain all the commands explained before. An example is the following:

\pagestyle{fancy} \fancypagestyle{plain}{ %   \fancyhf{} % remove everything   \renewcommand{\headrulewidth}{0pt} % remove lines as well   \renewcommand{\footrulewidth}{0pt} }

In that case you can use any style but fancyplain because it would override your redefinition.

Examples

For two-sided, it's common to mirror the style of opposite pages, you tend to think in terms of inner and outer. So, the same example as above for two-sided is:

\lhead[Author Name]{} \rhead[]{Author Name} \lhead[]{\today} \rhead[\today]{} \lfoot[\thepage]{} \rfoot[]{\thepage}

This is effectively saying author name is top outer, today's date is top inner, and current page number is bottom outer. Using \fancyhf can make it shorter:

\fancyhf[HLE,HRO]{Author's Name} \fancyhf[HRE,HLO]{\today} \fancyhf[FLE,FRO]{\thepage}

Here is the complete code of a possible style you could use for a two-sided document:

\usepackage{fancyhdr} \setlength{\headheight}{15pt} \pagestyle{fancy} \renewcommand{\chaptermark}[1]{ \markboth{#1}{} } \renewcommand{\sectionmark}[1]{ \markright{#1}{} } \fancyhf{} \fancyhead[LE,RO]{\thepage} \fancyhead[RE]{\textit{ \nouppercase{\leftmark}} } \fancyhead[LO]{\textit{ \nouppercase{\rightmark}} } \fancypagestyle{plain}{ %   \fancyhf{} % remove everything   \renewcommand{\headrulewidth}{0pt} % remove lines as well   \renewcommand{\footrulewidth}{0pt} }

Using \fancypagestyle one can additionally define multiple styles for one's document that are easy to switch between. Here's a somewhat complicated example for a two-sided book style:

\fancypagestyle{fancybook}{%     \fancyhf{}%     % Note the ## here. It's required because \fancypagestyle is making a macro (\ps@fancybook).     % If we just wrote #1, TeX would think that it's the argument to \ps@fancybook, but     % \ps@fancybook doesn't take any arguments, so TeX would complain with an error message.     % You are not expected to understand this.     \renewcommand*{\sectionmark}[1]{ \markright{\thesection\ ##1} }%     \renewcommand*{\chaptermark}[1]{ \markboth{\chaptername\ \thechapter: ##1}{} }%     % Increase the length of the header such that the folios     % (typography jargon for page numbers) move into the margin     \fancyhfoffset[LE]{6mm}% slightly less than 0.25in     \fancyhfoffset[RO]{6mm}%     % Put some space and a vertical par between the folio and the rest of the header     \fancyhead[LE]{\thepage\hskip3mm\vrule\hskip3mm\leftmark}%     \fancyhead[RO]{\rightmark\hskip3mm\vrule\hskip3mm\thepage}% }

Page n of m

Some people like to put the current page number in context with the whole document. LaTeX only provides access to the current page number. However, you can use the lastpage package to find the total number of pages, like this:

\usepackage{lastpage} ... \cfoot{\thepage\ of \pageref{LastPage} }

Note the capital letters. Also, add a backslash after \thepage to ensure adequate space between the page number and 'of'. And recall, when using references, that you have to run LaTeX an extra time to resolve the cross-references.

Alternative packages

Other packages for page styles are scrpage2, very similar to fancyhdr, and titleps, which takes a one-stage approach, without having to use \leftmark or \rightmark.

Page background

The eso-pic package will let you print content in the package of every page or individual pages.

\usepackage{tikz} % for \gradientbox below. \usepackage{eso-pic} \newcommand{\gradientbox}[3]{%   \begin{tikzpicture}     \node[left color=#1,right color=#2] {#3};   \end{tikzpicture}% } \AddToShipoutPicture*{%   \AtPageLowerLeft{%     \rotatebox{90}{       \gradientbox{blue!20}{white}{%         \begin{minipage}{\paperheight}%           \hspace*{ \stretch{1} }\textcopyright~2013 \makeatletter\@author\makeatother.\hspace*{ \stretch{1} }         \end{minipage}%       }     }%   }% }

The starred-version of the \AddToShipoutPicture command applies to the current page only.

Multi-column pages

It is common to see articles and conference proceedings formatted with two columns of text. However, such publishers will usually provide you with their own document class, which automatically implements this format, without you having to do anything. It is very easy to format your page in this way. If you are using a standard Latex document class, then you can simply pass the optional argument twocolumn to the document class: \documentclass[twocolumn]{article} which will give the desired effect.

While this simple addition will do the job 9 out of 10 times, it is widely acknowledged that there are many limitations of this approach, and that the multicol package is much more useful for handling multiple columns. It has several advantages:

• Can support up to ten columns.
• Implements a multicols environment, therefore, it is possible to mix the number of columns within a document.
• Additionally, the environment can be nested inside other environments, such as figure.
• multicol outputs balanced columns, whereby the columns on the final page will be of roughly equal length.
• Vertical rules between columns can be customised.
• Column environments can be easily customised locally or globally.

Floats are not fully supported by this environment. It can only cope if you use the starred forms of the float commands (e.g., \begin{figure*} ) which makes the float span all columns. This is not hugely problematic, since floats of the same width as a column may be too small, and you would probably want to span them anyway. See this section for a more detailed discussion.

To create a typical two-column layout:

\begin{multicols}{2}   lots of text \end{multicols}

The parameter \columnseprule holds the width of the vertical rules. By default, the lines are omitted as this parameter is set to a length of 0pt. Do the following before the beginning of the environment:

\setlength{\columnseprule}{1pt}

This will draw a thin line of 1pt in width. A thick line would not look very pleasing, however, you are free to put in any length of your choosing. Also, to change the horizontal space in between columns (the default is set at 10pt, which is quite narrow) then you need to change the \columnsep parameter:

\setlength{\columnsep}{20pt}

To force a break in a column, the command \columnbreak is used in a multicols environment.

Manual page formatting

There may be instances, especially in very long documents, such as books, that LaTeX will not get all page breaks looking as good as it could. It may, therefore, be necessary to manually tweak the page formatting. Of course, you should only do this at the very final stage of producing your document, once all the content is complete. LaTeX offers the following:

\newpage	Ends the current page and starts a new one.
\pagebreak[number]	Breaks the current page at the point of the command. The optional number argument sets the priority in a scale from 0 to 4.
\nopagebreak[number]	Stops the page being broken at the point of the command. The optional number argument sets the priority in a scale from 0 to 4.
\clearpage	Ends the current page and causes any floats encountered in the input, but yet to appear, to be printed.

Widows and orphans

In professional books, it's not desirable to have single lines at the beginning or end of a page. In typesetting such situations are called 'widows' and 'orphans'. Normally it is possible that widows and orphans appear in LaTeX documents. You can try to deal with them using manual page formatting, but there's also an automatic solution.

LaTeX has a parameter for 'penalty' for widows and orphans ('club lines' in LaTeX terminology). With the greater penalty LaTeX will try more to avoid widows and orphans. You can try to increase these penalties by putting following commands in your document preamble:

\widowpenalty=300 \clubpenalty=300

If this does not help, you can try increasing these values even more, to a maximum of 10000. However, it is not recommended to set this value too high, as setting it to 10000 forbids LaTeX from doing this altogether, which might result in strange behavior.

It also helps to have rubber band values for the space between paragraphs:

\setlength{\parskip}{3ex plus 2ex minus 2ex}

Alternatively, you can use the needspace package to reserve some lines and thus to prevent page breaking for those lines.

\needspace{5\baselineskip} Some text on 5 lines.

Notes and References

This page uses material from Andy Roberts' Getting to grips with LaTeX with permission from the author.