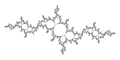
Fractals/Iterations in the complex plane/parabolic
"Most programs for computing Julia sets work well when the underlying dynamics is hyperbolic but experience an exponential slowdown in the parabolic case." (Mark Braverman)[1]
In other words it means that one can need days for making a good picture of parabolic Julia set with standard / naive algorithms.
There are 2 problems here:
- slow (= lazy) local dynamics (in the neighbourhood of a parabolic fixed point)
- some parts are very thin (hard to find using standard plane scanning)
Planes
[edit | edit source]Dynamic plane
[edit | edit source]

Dynamic plane = complex z-plane :
- Julia set is a common boundary:
- Fatou set
- exterior of Julia set = basin of attraction to infinity:
- interior of Julia set = basin of attraction of finite, parabolic fixed point p:
- immediate basin = sum of components which have parabolic fixed point p on it's boundary ; the immediate parabolic basin of p is the union of periodic connected components of the parabolic basin.
See also:
- Filled Julia set[3]
Key words
[edit | edit source]- parabolic chessboard or checkerboard
- parabolic implosion
- Fatou coordinate
- Hawaiian earring
- in wikipedia = "The plane figure formed by a sequence of circles that are all tangent to each other at the same point and such that the sequence of radii converges to zero." (Barile, Margherita in MathWorld)[4]
- commons:Category:Hawaiian earrings
- Gevrey symptotic expansions
- the Écalle-Voronin invariants of (7.1) at the origin which have Gevrey- 1/2 asymptotic expansions[5]
- germ[6][7][8]
- germ of the function: Taylor expansion of the function
- multiplicity[9]
- Julia-Lavaurs sets
- The Leau-Fatou flower theorem:[10] repelling or attracting flower. Flower consist of petals
- Leau-Fatou flower
- Parabolic Linearization theorem
- The horn map
- Blaschke product
- Inou and Shishikura's near parabolic renormalization
- complex polynomial vector field[11]
- numbers
- "a positive integer ν, the parabolic degeneracy with the following property: there are νq attracting petals and νq repelling petals, which alternate cyclically around the fixed point."[12]
- combinatorial rotation number
- a Poincaré linearizer of function f at parabolic fixed point[13]
- "the parabolic pencil. This is the family of circles which all have one common point, and thus are all tangent to each other, either internally or externally."[14]
Leau-Fatou flower theorem
[edit | edit source]The Leau-Fatou flower theorem states that, if function has the Taylor expansion[15]
then the complex number on the unit circle describes unit vector ( direction):
- an repulsion vector (from origin to v) for f at the origin if
- an attraction vector ( from v to origin ) if
There are n equally spaced attracting directions, separated by n equally spaced repelling directions. The integer n+1 is called the multiplicity of fixed point
Examples
[edit | edit source]
Function expansion: z+z^5
/* Maxima CAS */
display2d:false;
taylor(z+z^5, z,0,5);
z + z^5
So :
- a = 1
- n = 4
Compute attracting directions:
/* Maxima CAS */ solve (4*v^4 = 1, v); [v = %i/sqrt(2),v = -1/sqrt(2),v = -%i/sqrt(2),v = 1/sqrt(2)]
Function m*z+z^2
(%i7) taylor(m*z+z^2, z,0,5); (%o7) m*z+z^2
So :
- a = 1
- n = 1
(%i9) solve (v = 1, v); (%o9) [v = 1]
Ecalle cylinder
[edit | edit source]Ecalle cylinders[16] or Ecalle-Voronin cylinders (by Jean Ecalle[17][18])[19]
"... the quotient of a petal P under the equivalence relation identifying z and f (z) if both z and f (z) belong to P. This quotient manifold is called the Ecalle cilinder, and it is conformally isomorphic to the infinite cylinder C/Z"[20]
eggbeater dynamics
[edit | edit source]-
Hand Egg beater
-
Here is real model of what happens in parabolic case
Physical model: the behaviour of cake when one uses eggbeater.
The mathematical model: a 2D vector field with 2 centers (second-order degenerate points)[21][22]
The field is spinning about the centers, but does not appear to be diverging.
Maybe better description of parabolic dynamics will be Hawaiian earrings
parabolic germ
[edit | edit source]- z+z^2
- z+z^3
- z+z^{k+1}
- z+a_{k+1}z^{k+1}
- z+a_{k+1}z^{k+1}
- "a germ with is holomorphically conjugated to its linear part " (Sylvain Bonnot)[26]
germ of vector field
The horn map
[edit | edit source]"the horn map h = Φ ◦ Ψ, where Φ is a shorthand for Φattr and Ψ for Ψrep (extended Fatou coordinate and parameterizations)."[27]
Petal
[edit | edit source]- "The petals are Jordan domains invariant by " R PEREZ-MARCO[28]
- Petal is trap which captures any orbit tending to parabolic point
- petal is a part of the flower
Sepal
[edit | edit source]

Definitions:
- A sepal is the intersection of an attracting and repelling petal.A parabolic Pommerenke-Levin-Yoccoz inequality. by Xavier Buf and Adam L. Epstein There does not seem to be an official definition of sepal.
- "Let l be an invariant curve in the first quadrant and L1 the region enclosed by l ∪ {0}, called a sepal."[29]
- interior of component with parabolic fixed point on it's boundary
Flower
[edit | edit source]-
Lea-Fatu flower
-
Flower with four petals and parabolic point in the center
-
Critical orbit for internal angle 1/5 showing 5 attracting directions
Sum of all petals creates a flower[30] with center at parabolic periodic point.[31]
Cauliflower
[edit | edit source]Cauliflower or broccoli:[32]
- empty (its interior is empty) for c outside Mandelbrot set. Julia set is a totally disconnected.
- filled cauliflower for c=1/4 on boundary of the Mandelbrot set. Julia set is a Jordan curve (quasi circle).
-
c = 0 < 1/4
-
c = 0.25 = 1/4 t he root of the main cardioid. Julia set is a cauliflower.
-
c = 0.255 > 1/4 "imploded cauliflower"
-
c = 0.258 > 1/4
-
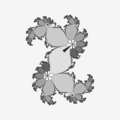
c = [0.285, 0.01]
Please note that:
- size of image differs because of different z-planes.
- different algorithms are used so colours are hard to compare.
Bifurcation of the Cauliflower
[edit | edit source]How Julia set changes along real axis (going from c=0 thru c=1/4 and further):
Perturbation of a function by complex :
When one add epsilon > 0 (move along real axis toward + infinity) there is a bifurcation of parabolic fixed point:
- attracting fixed point (epsilon<0)
- one parabolic fixed point (epsilon = 0)
- one parabolic fixed point splits up into two conjugate repelling fixed points (epsilon > 0)
"If we slightly perturb with epsilon<0 then the parabolic fixed point splits up into two real fixed points on the real axis (one attracting, one repelling)."
See:
- demo 2 page 9 in program Mandel by Wolf Jung
parabolic implosion
[edit | edit source]Parabolic imposion
- on the parameter plane
- point c moves from interior of the component, through the boundary to the exterior of Mandelbrot set
- nucleus ( c=0), along internal ray 0, parabolic point ( c= 0.25), along external ray 0
- on the dynamic plane
- connected Julia set ( with interior) imploedes and comes disconnected ( without interior)
- fixed point moves from interior to Julia set ( parabolic)
- one basin ( interior) disappears
| parameter c | location | Julia set | interior | type of dynamics | critical point | fixed points |
|---|---|---|---|---|---|---|
| c = 0 | center, interior | connected | exist | superattracting | atracted to alfa fixed point | fixed critical point equal to alfa fixed point, alfa is superattracting, beta is repelling |
| 0<c<1/4 | internal ray 0, interior | connected | exist | attracting | atracted to alfa fixed point | alfa is attracting, beta is repelling |
| c = 1/4 | cusp, boundary | connected | exist | parabolic | atracted to alfa fixed point | alfa fixed point equal to beta fixed point, both are parabolic |
| c>1/4 | external ray 0, exterior | disconnected | disappears | - | repelling to infinity | both finite fixed points are repelling |
Video on YouTube[33]
- Parabolic implosion : from circle thru cauliflower to imploded cauliflower
-
c=0
-
c=1/4
-
c= 1/4 + 0.05
-
c = 1/4 + 0.029
-
c = 1/4 + 0.035
Vector field
[edit | edit source]- 2D vector field and its
singularity
[edit | edit source]singularity types:
- center type: "In this case, one can find a neighborhood of the singular point where all integral curves are closed, inside one another, and contain the singular point in their interior"[34]
- non-center type: neighborhood of singularity is made of several curvilinear sectors:[35]
"A curvilinear sector is defined as the region bounded by a circle C with arbitrary small radius and two streamlines S and S! both converging towards singularity. One then considers the streamlines passing through the open sector g in order to distinguish between three possible types of curvilinear sectors."
dynamics
[edit | edit source]Dynamics:
- global
- local
Local dynamics:
- in the exterior of Julia set
- on the Julia set
- near parabolic fixed point (inside Julia set)
See also
Near parabolic fixed point
[edit | edit source]
Why analyze f^p not f ?
Forward orbit of f near parabolic fixed point is composite. It consist of 2 motions:
- around fixed point
- toward / away from fixed point
How to compute parabolic c values
[edit | edit source]Type of parabolic parameters:
- root points
- cusps
| n | Internal angle (rotation number) t = 1/n | The root point c = parabolic parameter | Two external angles of parameter rays landing on the root point c (1/(2^n+1); 2/(2^n+1) | fixed point | external angles of dynamic rays landing on fixed point |
|---|---|---|---|---|---|
| 1 | 1/1 | 0.25 | (0/1 ; 1/1) | 0.5 | (0/1 = 1/1) |
| 2 | 1/2 | -0.75 | (1/3; 2/3) | -0.5 | (1/3; 2/3) |
| 3 | 1/3 | 0.64951905283833*%i-0.125 | (1/7; 2/7) | 0.43301270189222*%i-0.25 | (1/7; 2/7; 3/7) |
| 4 | 1/4 | 0.5*%i+0.25 | (1/15; 2/15) | 0.5*%i | (1/15; 2/15; 4/15; 8/15) |
| 5 | 1/5 | 0.32858194507446*%i+0.35676274578121 | (1/31; 2/31) | 0.47552825814758*%i+0.15450849718747 | (1/31; 2/31; 4/31; 8/31; 16/31) |
| 6 | 1/6 | 0.21650635094611*%i+0.375 | (1/63; 2/63) | 0.43301270189222*%i+0.25 | (1/63; 2/63; 4/63; 8/63; 16/63; 32/63) |
| 7 | 1/7 | 0.14718376318856*%i+0.36737513441845 | (1/127; 2/127) | 0.39091574123401*%i+0.31174490092937 | (1/127; 2/127, 4/127; 8/127; 16/127; 32/127, 64/127) |
| 8 | 1/8 | 0.10355339059327*%i+0.35355339059327 | 0.35355339059327*%i+0.35355339059327 | ||
| 9 | 1/9 | 0.075191866590218*%i+0.33961017714276 | 0.32139380484327*%i+0.38302222155949 | ||
| 10 | 1/10 | 0.056128497072448*%i+0.32725424859374 | 0.29389262614624*%i+0.40450849718747 |
For internal angle n/p parabolic period p cycle consist of one z-point with multiplicity p[36] and multiplier = 1.0 . This point z is equal to fixed point
Period 1
[edit | edit source]One can easily compute boundary point c
of period 1 hyperbolic component (main cardioid) for given internal angle (rotation number) t using this cpp code by Wolf Jung[37]
t *= (2*PI); // from turns to radians
cx = 0.5*cos(t) - 0.25*cos(2*t);
cy = 0.5*sin(t) - 0.25*sin(2*t);
or this Maxima CAS code:
/* conformal map from circle to cardioid ( boundary
of period 1 component of Mandelbrot set */
F(w):=w/2-w*w/4;
/*
circle D={w:abs(w)=1 } where w=l(t,r)
t is angle in turns ; 1 turn = 360 degree = 2*Pi radians
r is a radius
*/
ToCircle(t,r):=r*%e^(%i*t*2*%pi);
GiveC(angle,radius):=
(
[w],
/* point of unit circle w:l(internalAngle,internalRadius); */
w:ToCircle(angle,radius), /* point of circle */
float(rectform(F(w))) /* point on boundary of period 1 component of Mandelbrot set */
)$
compile(all)$
/* ---------- global constants & var ---------------------------*/
Numerator: 1;
DenominatorMax: 10;
InternalRadius: 1;
/* --------- main -------------- */
for Denominator:1 thru DenominatorMax step 1 do
(
InternalAngle: Numerator/Denominator,
c: GiveC(InternalAngle,InternalRadius),
display(Denominator),
display(c),
/* compute fixed point */
alfa:float(rectform((1-sqrt(1-4*c))/2)), /* alfa fixed point */
display(alfa)
)$
Period 2
[edit | edit source]// cpp code by W Jung http://www.mndynamics.com
t *= (2*PI); // from turns to radians
cx = 0.25*cos(t) - 1.0;
cy = 0.25*sin(t);
Periods 1-6
[edit | edit source]/*
batch file for Maxima CAS
computing bifurcation points for period 1-6
Formulae for cycles in the Mandelbrot set II
Stephenson, John; Ridgway, Douglas T.
Physica A, Volume 190, Issue 1-2, p. 104-116.
*/
kill(all);
remvalue(all);
start:elapsed_run_time ();
/* ------------ functions ----------------------*/
/* exponential for of complex number with angle in turns */
/* "exponential form prevents allroots from working", code by Robert P. Munafo */
GivePoint(Radius,t):=rectform(ev(Radius*%e^(%i*t*2*%pi), numer))$ /* gives point of unit circle for angle t in turns */
GiveCirclePoint(t):=rectform(ev(%e^(%i*t*2*%pi), numer))$ /* gives point of unit circle for angle t in turns Radius = 1 */
/* gives a list of iMax points of unit circle */
GiveCirclePoints(iMax):=block(
[circle_angles,CirclePoints],
CirclePoints:[],
circle_angles:makelist(i/iMax,i,0,iMax),
for t in circle_angles do CirclePoints:cons(GivePoint(1,t),CirclePoints),
return(CirclePoints) /* multipliers */
)$
/* http://commons.wikimedia.org/wiki/File:Mandelbrot_set_Components.jpg
Boundary equation b_n(c,P)=0
defines relations between hyperbolic components and unit circle for given period n ,
allows computation of exact coordinates of hyperbolic componenets.
b_n(w,c), is boundary polynomial (implicit function of 2 variables).
*/
GiveBoundaryEq(P,n):=
block(
if n=1 then return(c + P^2 - P),
if n=2 then return(- c + P - 1),
if n=3 then return(c^3 + 2*c^2 - (P-1)*c + (P-1)^2),
if n=4 then return(c^6 + 3*c^5 + (P+3)* c^4 + (P+3)* c^3 - (P+2)*(P-1)*c^2 - (P-1)^3),
if n=5 then return(c^15 + 8*c^14 + 28*c^13 + (P + 60)*c^12 + (7*P + 94)*c^11 +
(3*P^2 + 20*P + 116)*c^10 + (11*P^2 + 33*P + 114)*c^9 + (6*P^2 + 40*P + 94)*c^8 +
(2*P^3 - 20*P^2 + 37*P + 69)*c^7 + (3*P - 11)*(3*P^2 - 3*P - 4)*c^6 + (P - 1)*(3*P^3 + 20*P^2 - 33*P - 26)*c^5 +
(3*P^2 + 27*P + 14)*(P - 1)^2*c^4 - (6*P + 5)*(P - 1)^3*c^3 + (P + 2)*(P - 1)^4*c^2 - c*(P - 1)^5 + (P - 1)^6),
if n=6 then return (c^27+
13*c^26+
78*c^25+
(293 - P)*c^24+
(792 - 10*P)*c^23+
(1672 - 41*P)*c^22+
(2892 - 84*P - 4*P^2)*c^21+
(4219 - 60*P - 30*P^2)*c^20+
(5313 + 155*P - 80*P^2)*c^19+
(5892 + 642*P - 57*P^2 + 4*P^3)*c^18+
(5843 + 1347*P + 195*P^2 + 22*P^3)*c^17+
(5258 + 2036*P + 734*P^2 + 22*P^3)*c^16+
(4346 + 2455*P + 1441*P^2 - 112*P^3 + 6*P^4)*c^15 +
(3310 + 2522*P + 1941*P^2 - 441*P^3 + 20*P^4)*c^14 +
(2331 + 2272*P + 1881*P^2 - 853*P^3 - 15*P^4)*c^13 +
(1525 + 1842*P + 1344*P^2 - 1157*P^3 - 124*P^4 - 6*P^5)*c^12 +
(927 + 1385*P + 570*P^2 - 1143*P^3 - 189*P^4 - 14*P^5)*c^11 +
(536 + 923*P - 126*P^2 - 774*P^3 - 186*P^4 + 11*P^5)*c^10 +
(298 + 834*P + 367*P^2 + 45*P^3 - 4*P^4 + 4*P^5)*(1-P)*c^9 +
(155 + 445*P - 148*P^2 - 109*P^3 + 103*P^4 + 2*P^5)*(1-P)*c^8 +
2*(38 + 142*P - 37*P^2 - 62*P^3 + 17*P^4)*(1-P)^2*c^7 +
(35 + 166*P + 18*P^2 - 75*P^3 - 4*P^4)*((1-P)^3)*c^6 +
(17 + 94*P + 62*P^2 + 2*P^3)*((1-P)^4)*c^5 +
(7 + 34*P + 8*P^2)*((1-P)^5)*c^4 +
(3 + 10*P + P^2)*((1-P)^6)*c^3 +
(1 + P)*((1-P)^7)*c^2 +
-c*((1-P)^8) + (1-P)^9)
)$
/* gives a list of points c on boundaries on all components for give period */
GiveBoundaryPoints(period,Circle_Points):=block(
[Boundary,P,eq,roots],
Boundary:[],
for m in Circle_Points do (/* map from reference plane to parameter plane */
P:m/2^period,
eq:GiveBoundaryEq(P,period), /* Boundary equation b_n(c,P)=0 */
roots:bfallroots(%i*eq),
roots:map(rhs,roots),
for root in roots do Boundary:cons(root,Boundary)),
return(Boundary)
)$
/* divide llist of roots to 3 sublists = 3 components */
/* ---- boundaries of period 3 components
period:3$
Boundary3Left:[]$
Boundary3Up:[]$
Boundary3Down:[]$
Radius:1;
for m in CirclePoints do (
P:m/2^period,
eq:GiveBoundaryEq(P,period),
roots:bfallroots(%i*eq),
roots:map(rhs,roots),
for root in roots do
(
if realpart(root)<-1 then Boundary3Left:cons(root,Boundary3Left),
if (realpart(root)>-1 and imagpart(root)>0.5)
then Boundary3Up:cons(root,Boundary3Up),
if (realpart(root)>-1 and imagpart(root)<0.5)
then Boundary3Down:cons(root,Boundary3Down)
)
)$
--------- */
/* gives a list of parabolic points for given: period and internal angle */
GiveParabolicPoints(period,t):=block
(
[m,ParabolicPoints,P,eq,roots],
m: GiveCirclePoint(t), /* root of unit circle, Radius=1, angle t=0 */
ParabolicPoints:[],
/* map from reference plane to parameter plane */
P:m/2^period,
eq:GiveBoundaryEq(P,period), /* Boundary equation b_n(c,P)=0 */
roots:bfallroots(%i*eq),
roots:map(rhs,roots),
for root in roots do ParabolicPoints:cons(float(root),ParabolicPoints),
return(ParabolicPoints)
)$
compile(all)$
/* ------------- constant values ----------------------*/
fpprec:16;
/* ------------unit circle on a w-plane -----------------------------------------*/
a:GiveParabolicPoints(6,1/3);
a$
period d
[edit | edit source]/*
gcc c.c -lm -Wall
./a.out
Root point between period 1 component and period 987 component = c = 0.2500101310666710+0.0000000644946597
Internal angle (c) = 1/987
Internal radius (c) = 1.0000000000000000
*/
#include <stdio.h>
#include <math.h> // M_PI; needs -lm also
#include <complex.h>
/*
c functions using complex type numbers
computes c from component of Mandelbrot set */
complex double Give_c( int Period, int n, int d , double InternalRadius )
{
complex double c;
complex double w; // point of reference plane where image of the component is a unit disk
// alfa = ax +ay*i = (1-sqrt(d))/2 ; // result
double t; // InternalAngleInTurns
t = (double) n/d;
t = t * M_PI * 2.0; // from turns to radians
w = InternalRadius*cexp(I*t); // map to the unit disk
switch ( Period ) // of component
{
case 1: // main cardioid = only one period 1 component
c = w/2 - w*w/4; // https://en.wikibooks.org/wiki/Fractals/Iterations_in_the_complex_plane/Mandelbrot_set/boundary#Solving_system_of_equation_for_period_1
break;
case 2: // only one period 2 component
c = (w-4)/4 ; // https://en.wikibooks.org/wiki/Fractals/Iterations_in_the_complex_plane/Mandelbrot_set/boundary#Solving_system_of_equation_for_period_2
break;
// period > 2
default:
printf("higher periods : to do, use newton method \n");
printf("for each q = Period of the Child component there are 2^(q-1) roots \n");
c = 10000.0; // bad value
break; }
return c;
}
void PrintAndDescribe_c( int period, int n, int d , double InternalRadius ){
complex double c = Give_c(period, n, d, InternalRadius);
printf("Root point between period %d component and period %d component = c = %.16f%+.16f*I\t",period, d, creal(c), cimag(c));
printf("Internal angle (c) = %d/%d\n",n, d);
//printf("Internal radius (c) = %.16f\n",InternalRadius);
}
/*
https://stackoverflow.com/questions/19738919/gcd-function-for-c
The GCD function uses Euclid's Algorithm.
It computes A mod B, then swaps A and B with an XOR swap.
*/
int gcd(int a, int b)
{
int temp;
while (b != 0)
{
temp = a % b;
a = b;
b = temp;
}
return a;
}
int main (){
int period = 1;
double InternalRadius = 1.0;
// internal angle in turns as a ratio = p/q
int n = 1;
int d = 987;
// n/d = local angle in turns
for (n = 1; n < d; ++n ){
if (gcd(n,d)==1 )// irreducible fraction
{ PrintAndDescribe_c(period, n,d,InternalRadius); }
}
return 0;
}
How to draw parabolic Julia set
[edit | edit source]- 5 methods of drawing
-
Checking iteration
-
modified DEM
-
checking angle
-
checking if zn is in target set
-
checking if zn is in triangle target set
All points of interior of filled Julia set tend to one periodic orbit (or fixed point). This point is in Julia set and is weakly attracting.[38] One can analyse only behavior near parabolic fixed point. It can be done using critical orbits.
There are two cases here: easy and hard.
If the Julia set near parabolic fixed point is like n-th arm star (not twisted) then one can simply check argument of zn, relative to the fixed point. See for example z+z^5. This is an easy case.
In the hard case Julia set is twisted around fixed.
topology
[edit | edit source]Julia set of root point is topologically the same as the Julia set of the child period center, but
- the center ( nucleus) Julia set is very easy to draw ( superattracting basin = very fast dynamics because critical point is also periodic point)
- while the root Julia set ( parabolic) is hard to draw ( parabolic basin and lasy dynamics)
Examples:
- t = 1/2
- Julia set of the root point = fat Basilica Julia set: c = -3/4 = - 0.75
- Julia set of period 2 center = (slim) Basicica Julia set: c = -1
- t = 1/3
- Julia set of the root point = fat Douady Rabbit: c = -0.125000000000000 +0.649519052838329i
- Julia set of period 3 center = (slim) Doudy Rabbit Julia set: c = -0.122561166876654 +0.744861766619744i period = 3
Estimation from exterior
[edit | edit source]Escape time
[edit | edit source]Long iteration or big step method
[edit | edit source]Description
Steps
- choose fuction which has fixed parabolic point at origin ( z=0)
- choose internal angle
- compute which is an aproximation of higher iterates of function for z close to zero using power series centered at zero ( Taylor series = Maclaurin series )
- find how many terms of power series to use and on which annuli to use specific experimentally
each will be used on an annulus
where K is fixed
example
[edit | edit source]Lambda form of complex quadratic polynomial which has an indifferent fixed point with multiplier at the origin[41]
where:
- multiplier of fixed point
- internal angle is an rational number and proper fraction
Choose
- so
- 30 terms of power series
- approximated function for annuli k=4,5,...,10 and default function f^n for larger values of z ( outside annuli)
- delta for function equal to 10^-5
(* code by Professor: Mark McClure from https://marksmath.org/classes/Spring2019ComplexDynamics/ *)
n = 7;
f[z_] = Exp[2 Pi*I/n] z + z^2;
Remove[F];
F[0][z_] = N[Normal[Series[f[z], {z, 0, 30}]]];
Do[F[0][z_] = Chop[N[Normal[Series[F[0][f[z]], {z, 0, 30}]]], 10^-5], {n - 1}];
Do[F[k][z_] = Chop[N[Normal[Series[F[k - 1][F[k - 1][z]], {z, 0, 30}]]], 10^-5], {k, 1, 10}]
(* define and compile function FF *)
FF = With[{
n = n,
f4 = Function[z, Evaluate[F[4][z]]],
f5 = Function[z, Evaluate[F[5][z]]],
f6 = Function[z, Evaluate[F[6][z]]],
f7 = Function[z, Evaluate[F[7][z]]],
f8 = Function[z, Evaluate[F[8][z]]],
f9 = Function[z, Evaluate[F[9][z]]],
f10 = Function[z, Evaluate[F[10][z]]]
},
Compile[{{z, _Complex}},
Which[
Abs[z] > 1/2^3,
Nest[Function[zz, N[Exp[2 Pi*I/n]] zz + zz^2], z, n],
Abs[z] <= 1/2^9, f10[z],
Abs[z] <= 1/2^8, f9[z],
Abs[z] <= 1/2^7, f8[z],
Abs[z] <= 1/2^6, f7[z],
Abs[z] <= 1/2^5, f6[z],
Abs[z] <= 1/2^4, f5[z],
Abs[z] <= 1/2^3, f4[z],
True, 0]]];
(* iterate 1000 times and then see what happens *)
iterate = With[{FF = FF, n = n},
Compile[{{z0, _Complex}},
Module[{z, i},
z = z0;
i = 0;
While[1/2^9 < Abs[z] <= 2 && i++ < 1000 n,
z = FF[z]];
z],
RuntimeOptions -> "Speed", CompilationTarget -> "C"]];
(* now compute some iteration data *)
data = Monitor[
Table[iterate[x + I*y], {y, Im[center] + 1.2, Im[center], -0.0025},
{x, Re[center] - 1.2, Re[center] + 1.2, 0.0025}],
y];
(* use some symmetry to cut computation time in half *)
center = First[Select[z /. NSolve[f[z] == 0, z], Im[#] < 0 &]]/2 (* center = -0.311745 - 0.390916*I *)
data = Join[data, Reverse[Rest[Reverse /@ data]]];
(* plot it *)
kernel = {
{1, 1, 1},
{1, -8, 1},
{1, 1, 1}
};
(*
classifyArg = Compile[
{{z, _Complex}, {z0, _Complex}, {v, _Complex}, {n, _Integer}},
Module[{check, check2},
check = n (Arg[(z0 - z)/v] + Pi)/(2 Pi);
check2 = Ceiling[check];
If[check == check2, 0, check2]]];
classified = Map[classify, data, {2}];
convolvedData = ListConvolve[kernel, classified];
ArrayPlot[Sign[Abs[convolvedData]]]
Mathematical Functions of Wolfram language ( :
- Series[f,{x,x0,n}] generates a power series expansion for f about the point to order , where n is an explicit integer
- N[expr] gives the numerical value of expr
- Chop[expr,delta] replaces numbers smaller in absolute magnitude than delta by 0
- Normal[expr] converts expr to a normal expression from a variety of special forms.
- Do[expr,n] evaluates expr n times
- Do[expr,{i,imin,imax}] evaluates expr and starts with i=imin
- With[{x=x0,y=y0,…},expr] specifies that all occurrences of the symbols x, y, … in expr should be replaced by x0, y0, ….
- Compile[{{x1,t1},…},expr] assumes that xi is of a type that matches ti.
- Which[test1,value1,test2,value2,…] evaluates each of the testi in turn, returning the value of the valuei corresponding to the first one that yields True
- Nest[f,expr,n] gives an expression with f applied n times to expr.
Dynamic rays
[edit | edit source]
One can use periodic dynamic rays landing on parabolic fixed point to find narrow parts of exterior.
Let's check how many backward iterations needs point on periodic ray with external radius = 4 to reach distance 0.003 from parabolic fixed point:
| period | Inverse iterations | time |
|---|---|---|
| 1 | 340 | 0m0.021s |
| 2 | 55 573 | 0m5.517s |
| 3 | 8 084 815 | 13m13.800s |
| 4 | 1 059 839 105 | 1724m28.990s |
| C source code - click on the right to view |
|---|
| a.c: |
/*
c console program
to compile:
gcc double_t.c -lm -Wall -march=native
to run:
time ./a.out
period EscapeTime time
1 340 0m0.021s
2 55 573 0m5.517s
3 8 084 815 13m13.800s
4 1 059 839 105 1724m28.990s
period 1
escape time = 340.000000
internal angle t = 1.000000
period = 1
preperiod = 0
cx = 0.250000
cy = 0.000000
alfax = 0.500000
alfay = 0.000000
real 0m0.021s
===============
escape time = 55573.000000
internal angle t = 0.500000
period = 2
preperiod = 0
cx = -0.750000
cy = 0.000000
alfax = -0.500000
alfay = 0.000000
real 0m5.517s
===============================
period = 3 c = (-0.125000; 0.649519); alfa = (-0.250000;0.433013)
ea = 0.142857;
internal angle t = 0.333333
preperiod = 0
for period = 3 escape time = 8084815
real 13m13.800s
=====================================
period = 4 c = (0.250000; 0.500000); alfa = (0.000000;0.500000)
ea = 0.066667;
internal angle t = 0.250000
preperiod = 0
for period = 4 escape time = 1059839105
real 1724m28.990s
*/
#include <stdio.h>
#include <stdlib.h> // malloc
#include <math.h> // M_PI; needs -lm also
#include <complex.h>
unsigned int period = 4;// of child component of Mandelbrot set
unsigned int numerator=1 ;
unsigned int denominator;
double t ; // internal angle of point c of parent component of Mandelbrot set in turns
unsigned long int maxiter = 100000;
unsigned int preperiod = 0; //of external angle under doubling map
double complex z , c, alfa;
double ea ;// External Angle
/* find c in component of Mandelbrot set
uses complex type so #include <complex.h> and -lm
uses code by Wolf Jung from program Mandel
see function mndlbrot::bifurcate from mandelbrot.cpp
http://www.mndynamics.com/indexp.html
*/
double complex GiveC(double InternalAngleInTurns, double InternalRadius, unsigned int period)
{
//0 <= InternalRay<= 1
//0 <= InternalAngleInTurns <=1
// period of parent component of Mandelbrot set { 1,2 }
double t = InternalAngleInTurns *2*M_PI; // from turns to radians
double R2 = InternalRadius * InternalRadius;
double Cx, Cy; /* C = Cx+Cy*i */
switch ( period ) {
case 1: // main cardioid
Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4;
Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4;
break;
case 2: // only one component
Cx = InternalRadius * 0.25*cos(t) - 1.0;
Cy = InternalRadius * 0.25*sin(t);
break;
// for each period there are 2^(period-1) roots.
default: // safe values
Cx = 0.0;
Cy = 0.0;
break; }
return Cx+ Cy*I;
}
/*
http://en.wikipedia.org/wiki/Periodic_points_of_complex_quadratic_mappings
z^2 + c = z
z^2 - z + c = 0
ax^2 +bx + c =0 // ge3neral for of quadratic equation
so:
a=1
b =-1
c = c
so:
The discriminant is the d=b^2-4ac
d=1-4c = dx+dy*i
r(d)=sqrt(dx^2 + dy^2)
sqrt(d) = sqrt((r+dx)/2)+-sqrt((r-dx)/2)*i = sx +- sy*i
x1=(1+sqrt(d))/2 = beta = (1+sx+sy*i)/2
x2=(1-sqrt(d))/2 = alfa = (1-sx -sy*i)/2
alfa: attracting when c is in main cardioid of Mandelbrot set, then it is in interior of Filled-in Julia set, it means belongs to Fatou set (strictly to basin of attraction of finite fixed point)
*/
// uses global variables:
// ax, ay (output = alfa(c))
double complex GiveAlfaFixedPoint(double complex c)
{
double dx, dy; //The discriminant is the d=b^2- 4ac = dx+dy*i
double r; // r(d)=sqrt(dx^2 + dy^2)
double sx, sy; // s = sqrt(d) = sqrt((r+dx)/2)+-sqrt((r-dx)/2)*i = sx + sy*i
double ax, ay;
// d=1-4c = dx+dy*i
dx = 1 - 4*creal(c);
dy = -4 * cimag(c);
// r(d)=sqrt(dx^2 + dy^2)
r = sqrt(dx*dx + dy*dy);
//sqrt(d) = s =sx +sy*i
sx = sqrt((r+dx)/2);
sy = sqrt((r-dx)/2);
// alfa = ax +ay*i = (1-sqrt(d))/2 = (1-sx + sy*i)/2
ax = 0.5 - sx/2.0;
ay = sy/2.0;
return ax+ay*I;
}
double DistanceBetween(double complex z1, double complex z2)
{double dx,dy;
dx = creal(z1) - creal(z2);
dy = cimag(z1) - cimag(z2);
return sqrt(dx*dx+dy*dy);
}
/*
principal square root of complex number
http://en.wikipedia.org/wiki/Square_root
z1= I;
z2 = root(z1);
printf("zx = %f \n", creal(z2));
printf("zy = %f \n", cimag(z2));
*/
double complex root(double complex z)
{
double x = creal(z);
double y = cimag(z);
double u;
double v;
double r = sqrt(x*x + y*y);
v = sqrt(0.5*(r - x));
if (y < 0) v = -v;
u = sqrt(0.5*(r + x));
return u + v*I;
}
double complex preimage(double complex z1, double complex z2, double complex c)
{
double complex zPrev;
zPrev = root(creal(z1) - creal(c) + (cimag(z1) - cimag(c))*I);
// choose one of 2 roots
if (creal(zPrev)*creal(z2) + cimag(zPrev)*cimag(z2) > 0)
return zPrev ; // u+v*i
else return -zPrev; // -u-v*i
}
// This function only works for periodic or preperiodic angles.
// You must determine the period n and the preperiod k before calling this function.
// based on same function from src code of program Mandel by Wolf Jung
// http://www.mndynamics.com/indexp.html
double backray(double t, // external angle in turns
int n, //period of ray's angle under doubling map
int k, // preperiod
int iterMax,
double complex c
)
{
double xend ; // re of the endpoint of the ray
double yend; // im of the endpoint of the ray
const double R = 4; // very big radius = near infinity
int j; // number of ray
double iter=0.0; // index of backward iteration
double complex zPrev;
double u,v; // zPrev = u+v*I
double complex zNext;
double distance;
/* dynamic 1D arrays for coordinates (x, y) of points with the same R on preperiodic and periodic rays */
double *RayXs, *RayYs;
int iLength = n+k+2; // length of arrays ?? why +2
// creates arrays: RayXs and RayYs and checks if it was done
RayXs = malloc( iLength * sizeof(double) );
RayYs = malloc( iLength * sizeof(double) );
if (RayXs == NULL || RayYs==NULL)
{
fprintf(stderr,"Could not allocate memory");
getchar();
return 1;
}
// starting points on preperiodic and periodic rays
// with angles t, 2t, 4t... and the same radius R
for (j = 0; j < n + k; j++)
{ // z= R*exp(2*Pi*t)
RayXs[j] = R*cos((2*M_PI)*t);
RayYs[j] = R*sin((2*M_PI)*t);
t *= 2; // t = 2*t
if (t > 1) t--; // t = t modulo 1
}
zNext = RayXs[0] + RayYs[0] *I;
//printf("RayXs[0] = %f \n", RayXs[0]);
//printf("RayYs[0] = %f \n", RayYs[0]);
// z[k] is n-periodic. So it can be defined here explicitly as well.
RayXs[n+k] = RayXs[k];
RayYs[n+k] = RayYs[k];
// backward iteration of each point z
do
{
for (j = 0; j < n+k; j++) // period +preperiod
{ // u+v*i = sqrt(z-c) backward iteration in fc plane
zPrev = root(RayXs[j+1] - creal(c)+(RayYs[j+1] - cimag(c))*I); // , u, v
u=creal(zPrev);
v=cimag(zPrev);
// choose one of 2 roots: u+v*i or -u-v*i
if (u*RayXs[j] + v*RayYs[j] > 0)
{ RayXs[j] = u; RayYs[j] = v; } // u+v*i
else { RayXs[j] = -u; RayYs[j] = -v; } // -u-v*i
} // for j ...
//RayYs[n+k] cannot be constructed as a preimage of RayYs[n+k+1]
RayXs[n+k] = RayXs[k];
RayYs[n+k] = RayYs[k];
// convert to pixel coordinates
// if z is in window then draw a line from (I,K) to (u,v) = part of ray
// printf("for iter = %d cabs(z) = %f \n", iter, cabs(RayXs[0] + RayYs[0]*I));
iter += 1.0;
distance = DistanceBetween(RayXs[j]+RayYs[j]*I, alfa);
printf("distance = %10.9f ; iter = %10.0f \n", distance, iter); // info
}
while (distance>0.003);// distance < pixel size
// last point of a ray 0
xend = RayXs[0];
yend = RayYs[0];
// free memmory
free(RayXs);
free(RayYs);
return iter; //
}
/* ---------------------- main ------------------*/
int main()
{
double EscapeTime;
// internal angle
denominator = period;
t = (double) numerator/denominator;
//
c = GiveC(t, 1.0, 1);
alfa = GiveAlfaFixedPoint(c);
//external angle
denominator= pow(2,period) - 1;
ea = (double) 1.0/ denominator;
//
EscapeTime = backray(ea, period, preperiod, maxiter, c);
//
printf("period = %d ", period);
printf(" c = (%f; %f);", creal(c), cimag(c));
printf(" alfa = (%f;%f)\n", creal(alfa), cimag(alfa));
printf("ea = %f;\n", ea);
printf("internal angle t = %f \n", t);
printf("preperiod = %d \n", preperiod);
printf("for period = %d escape time = %10.0f \n", period, EscapeTime);
//
return 0;
}
|
One can use only argument of point z of external rays and its distance to alfa fixed point (see code from image). It works for periods up to 15 (maybe more ...).
Estimation from interior
[edit | edit source]Julia set is a boundary of filled-in Julia set Kc.
- find points of interior of Kc
- find boundary of interior of Kc using edge detection
If components of interior are lying very close to each other then find components using:[42]
color = LastIteration % period
For parabolic components between parent and child component:[43]
periodOfChild = denominator*periodOfParent color = iLastIteration % periodOfChild
where denominator is a denominator of internal angle of parent component of Mandelbrot set.
Angle
[edit | edit source]"if the iterate zn of tends to a fixed parabolic point, then the initial seed z0 is classified according to the argument of zn−z0, the classification being provided by the flower theorem" (Mark McClure[44])
Attraction time
[edit | edit source]
Interior of filled Julia set consist of components. All comonents are preperiodic, some of them are periodic (immediate basin of attraction).
In other words:
- one iteration moves z to another component (and whole component to another component)
- all point of components have the same attraction time (number of iteration needed to reach target set around attractor)
It is possible to use it to color components. Because in the parabolic case the attractor is weak (weakly attracting) it needs a lot of iterations for some points to reach it.
// i = number of iteration
// iPeriodChild = period of child component of Mandelbrot set ( parabolic c value is a root point between parant and child component
/* distance from z to Alpha */
Zxt=Zx-dAlfaX;
Zyt=Zy-dAlfaY;
d2=Zxt*Zxt +Zyt*Zyt;
// interior: check if fall into internal target set (circle around alfa fixed point)
if (d2<dMaxDistance2Alfa2) return iColorsOfInterior[i % iPeriodChild];
Here are some example values:
iWidth = 1001 // width of image in pixels PixelWidth = 0.003996 AR = 0.003996 // Radius around attractor denominator = 1 ; Cx = 0.250000000000000; Cy = 0.000000000000000 ax = 0.500000000000000; ay = 0.000000000000000 denominator = 2 ; Cx = -0.750000000000000; Cy = 0.000000000000000 ax = -0.500000000000000; ay = 0.000000000000000 denominator = 3 ; Cx = -0.125000000000000; Cy = 0.649519052838329 ax = -0.250000000000000; ay = 0.433012701892219 denominator = 4 ; Cx = 0.250000000000000; Cy = 0.500000000000000 ax = 0.000000000000000; ay = 0.500000000000000 denominator = 5 ; Cx = 0.356762745781211; Cy = 0.328581945074458 ax = 0.154508497187474; ay = 0.475528258147577 denominator = 6 ; Cx = 0.375000000000000; Cy = 0.216506350946110 ax = 0.250000000000000; ay = 0.433012701892219 denominator = 1 ; i = 243.000000 denominator = 2 ; i = 31 171.000000 denominator = 3 ; i = 3 400 099.000000 denominator = 4 ; i = 333 293 206.000000 denominator = 5 ; i = 29 519 565 177.000000 denominator = 6 ; i = 2 384 557 783 634.000000
where:
C = Cx + Cy*i a = ax + ay*i // fixed point alpha i // number of iterations after which critical point z=0.0 reaches disc around fixed point alpha with radius AR denominator of internal angle (in turns) internal angle = 1/denominator
Note that attraction time i is proportional to denominator.

Now you see what means weakly attracting.
One can:
- use brutal force method (Attracting radius < pixelSize; iteration Max big enough to let all points from interior reach target set; long time or fast computer)
- find better method (:-)) if time is to long for you
Interior distance estimation
[edit | edit source]Trap
[edit | edit source]
Estimation from interior and exterior
[edit | edit source]Julia set is a common boundary of filled-in Julia set and basin of attraction of infinity.
- find points of interior/components of Kc
- find escaping points
- find boundary points using Sobel filter
It works for denominator up to 4.
Inverse iteration of repelling points
[edit | edit source]Inverse iteration of alfa fixed point. It works good only for cuting point (where external rays land). Other points still are not hitten.
Bof61
[edit | edit source]Gallery
[edit | edit source]- Critical orbits in case of one critical point
-
critical orbits for internal angle from 1/1 to 1/10. True attracting directions
-
N-th arm stars for n from 1 to 10. Schematic attracting directions
-
critical orbit, attracting and repelling vectors for internal angle 1/3
- from period 1 thru ...
-
1/1 cauliflower
-
1/2 San Marco fractal[45]
-
1/3 Douady fat rabbit[46]
-
1/4
-
1/5
-
1/7
-
1/10
-
1/15
-
1/20
-
1/30
- from period 2 thru ...
-
from 2 thru internal ray 1/1 ; c=-0.75 Julia set is a San Marco fractal[47]
-
from period 2 thru 1/2
-
from period 2 thru 1/3
-
from period 2 thru 1/4
- from period 3 thru ...
-
from period 3 thru 1/3
External examples:
- A parabolic point with 377 petalsparabolic renormalization of z^3+c by YANG Fei
- A quad. Julia sets with 987 and 89 petals by A Cheritat
For other polynomial maps see here
See also
[edit | edit source]- Image: Nonstandard Parabolic by Cheritat[48]
- Julia set of parabolic case in Maxima CAS[49]
- The parabolic Mandelbrot set Pascale ROESCH (joint work with C. L. PETERSEN
- PARABOLIC IMPLOSION A MINI-COURSE by ArnaudCheritat
- Workshop on parabolic implosion 2010
- The renormalization for parabolic fixed points... Mitsushiro Shishikura and Hiroyuki Inou
- Dynamics of holomorphic maps: Resurgence of Fatou coordinates, and Poly-time computability of Julia sets by Artem Dudko, arxiv.org: Dudko_A
- Minicourse "Analytic classification of germs of generic families unfolding a parabolic point by Christiane Rousseau
- Perspectives on Parabolic Points in Holomorphic Dynamics - The Banff International Research Station for Mathematical Innovation and Discovery (BIRS)
- Richard Oudkerk: The Parabolic Implosion for f_0(z) = z + z^{nu+1} + O(z^{nu+2})
- Perspectives on Parabolic Points in Holomorphic Dynamics Videos from BIRS Workshop 15w5082
- Generic Perturbation of Parabolic Points Having More Than One Attracting Petal by Arnaud Chéritat
- Parabolic fixed points - Mathematica Notebook by Mark McClure
References
[edit | edit source]- ↑ Mark Braverman: On efficient computation of parabolic Julia sets
- ↑ Note on dynamically stable perturbations of parabolics by Tomoki Kawahira
- ↑ Filled Julia set in wikipedia
- ↑ Barile, Margherita. "Hawaiian Earring." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. http://mathworld.wolfram.com/HawaiianEarring.html
- ↑ Augustin Fruchard, Reinhard Sch¨afke. Composite Asymptotic Expansions and Difference Equations. Revue Africaine de la Recherche en Informatique et Math´ematiques Appliqu´ees, INRIA, 2015, 20, pp.63-93. <hal-01320625>
- ↑ wikipedia: Germ(mathematics)
- ↑ Fixed points of diffeomorphisms, singularities of vector fields and epsilon-neighborhoods of their orbits by Maja Resman
- ↑ The moduli space of germs of generic families of analytic diffeomorphisms unfolding a parabolic fixed point by Colin Christopher, Christiane Rousseau
- ↑ wikipedia: Multiplicity (mathematics)
- ↑ Dynamics of surface homeomorphisms Topological versions of the Leau-Fatou flower theorem and the stable manifold theorem by Le Roux, F
- ↑ The Dynamics of Complex Polynomial Vector Fields in C by Kealey Dias
- ↑ LIMITS OF DEGENERATE PARABOLIC QUADRATIC RATIONAL MAPS by XAVIER BUFF, JEAN ECALLE, AND ADAM EPSTEIN
- ↑ Poincaré linearizers in higher dimensionsby Alastair Fletcher
- ↑ pencil of circles by James King
- ↑ math.stackexchange question: what-is-the-shape-of-parabolic-critical-orbit
- ↑ Théorie des invariants holomorphes. Thèse d'Etat, Orsay, March 1974
- ↑ Jean Ecalle in french wikipedia
- ↑ Jean Ecalle home page
- ↑ Lukas Geyer - Normal forms via uniformization (10/28/2016). This is the draft of the proof of local normal forms at attracting, repelling, and parabolic fixed points using the uniformization theorem, handed out in class. It will eventually be incorporated into the lecture notes.
- ↑ mappings by Luna Lomonaco
- ↑ MODULUS OF ANALYTIC CLASSIFICATION FOR UNFOLDINGS OF GENERIC PARABOLIC DIFFEOMORPHISMSby P. Mardesic, R. Roussarie¤ and C. Rousseau
- ↑ mathoverflow questions: the functional equation ffxxfx2
- ↑ Germ in wikipedia
- ↑ MODULUS OF ANALYTIC CLASSIFICATION FOR UNFOLDINGS OF GENERIC PARABOLIC DIFFEOMORPHISMS by P. Mardesic , R. Roussarie and C. Rousseau
- ↑ The moduli space of germs of generic families of analytic diffeomorphisms unfolding a parabolic fixed point Colin Christopher, Christiane Rousseau
- ↑ Mathoverflow: infinitesimal classification of functions near a fixed point upto conjugation
- ↑ Near parabolic renormalization for unisingular holomorphic maps by Arnaud Cheritat
- ↑ Ricardo Pérez-Marco. "Fixed points and circle maps." Acta Math. 179 (2) 243 - 294, 1997. https://doi.org/10.1007/BF02392745
- ↑ Note on dynamically stable perturbations of parabolics by Tomoki Kawahira
- ↑ Parabolic fixed points: The Leau-Fatou Flower by Davide Legacci March 18, 2021
- ↑ wikipedia: Rose (topology)
- ↑ cauliflower at MuEncy by Robert Munafo
- ↑ Circle Implodes Into Flames - video by sinflrobot
- ↑ A Topology Simplification Method For 2D Vector Fields by Xavier Tricoche Gerik Scheuermann Hans Hagen
- ↑ encyclopedia of math: Sector_in_the_theory_of_ordinary_differential_equations
- ↑ wikipedia: Multiplicity in mathematics
- ↑ Mandel: software for real and complex dynamics by Wolf Jung
- ↑ Local dynamics at a fixed point by Evgeny Demidov
- ↑ Parabolic Julia Sets are Polynomial Time Computable Mark Braverman
- ↑ Mark McClure class Spring2019: ComplexDynamics , see code "Iteration near parabolic points" ( Mathematica notebook )
- ↑ Michael Yampolsky, Saeed Zakeri : Mating Siegel quadratic polynomials.
- ↑ The fixed points and periodic orbits by Evgeny Demidov
- ↑ Src code of c program for drawing parabolic Julia set
- ↑ stackexchange questions: what-is-the-shape-of-parabolic-critical-orbit
- ↑ planetmath: San Marco fractal
- ↑ wikipedia: Douady rabbit
- ↑ planetmath: San Marco fractal
- ↑ Image: Nonstandard Parabolic by Cheritat
- ↑ Julia set of parabolic case in Maxima CAS



























![c = [0.285, 0.01]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/17/Julia_set_%28highres_01%29.jpg/120px-Julia_set_%28highres_01%29.jpg)




























![1/2 San Marco fractal[45]](http://upload.wikimedia.org/wikipedia/commons/thumb/c/c5/Parabolic_julia_set_c%3D-0.75.png/120px-Parabolic_julia_set_c%3D-0.75.png)
![1/3 Douady fat rabbit[46]](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Parabolic_Julia_set_for_internal_angle_1_over_3.png/120px-Parabolic_Julia_set_for_internal_angle_1_over_3.png)