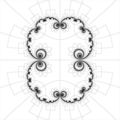
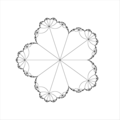
Fractals/Iterations in the complex plane/pcheckerboard

Name

• Parabolic chessboard = parabolic checkerboard
• zeros of qn - use only interior of Filled Julia set

Algorithm

Star = Parabolic critical orbit with arms in different colors

Color depends on:

• sign of imaginary part of numericaly aproximated Fatou coordinate (numerical explanation )
• position of $z_{\infty }$ under $f^{p}$ in relation to one arm of critical orbit star: above or below ( geometric explanation)

Attracting ( critical orbit) and repelling axes ( external rays landing on the parabolic fixed point ) divide niegbourhood of fixed point intio sectors

Steps

First choose:

• choose target set, which is a circle with :
  • center in parabolic fixed point
  • radius such small that width of of exterior between components is smaller then pixel width
• Target set consist of fragments of p components ( sectors). Divide each part of target set into 2 subsectors ( above and below critical orbit ) = binary decomposition

Steps:

• take $z_{0}$ = initial point of the orbit ( pixel)
• make forward iterations
  • if points escapes = exterior
  • if point do not escapes then check if point is near fixed point ( in the target set)
    • if no then make some extra iterations
    • if is then check in what half of target set it ( binary decomposition)

Target set

• circle ( for periods 1 and 2 in case of complex quadratic polynomial)
• 2 triangles ( for periods >=3) described by :
  • parabolic periodic point for period p , find $\{z:z=f^{p}(z)\}$
  • critical point $z_{cr}$
  • one of 2 critical point preimages ( a or b ) $z=f^{-p}(z_{cr})$

How to compute preimages of critical point ?

• (a,b)
• (aa, ab)
• (aaa,aab )
• (aaaa, aaab )
• (aaaaa, aaaab )

dictionary

• The chessboard is the name of this decomposition of A into a graph and boxes
• the chessboard graph
• the chessboard boxes :" The connected components of its complement in A are called the chessboard boxes (in an actual chessboard they are called squares but here they have infinitely many corners and not just four). "
• the two principal or main chessboard boxes

description

"A nice way to visualize the extended Fatou coordinates is to make use of the parabolic graph and chessboard."

Color points according to :

• the integer part of Fatou coordinate
• the sign of imaginary part

Corners of the chessboard ( where four tiles meet ) are precritical points

$\bigcup _{n=0}^{n\geq 0}f^{-n}(z_{cr})$

or

$\{z:f^{n}(z)=z_{cr}\}$

"each yellow tile biholomorphically maps to the upper half plane, and each blue tile biholomorphically maps to the lower half plane under $\psi _{att}$. The pre-critical points of $z+z^{2}$ or equivalently the critical points of $\psi _{att}$ are located where four tiles meet"

Images

Click on the images to see the code and descriptions on the Commons !

• on the real slice of Mandelbrot set
• 

  on the cusp of main cardioid

• 
• 

  from main cardioid to period 2

• 

  between period 2 and 4 along 1/2 ray

• on the boundary of main cardioid of Mandelbrot set
• 

  0/1 = 1/1

• 
• 

  1/2

• 

  1/3

• on the internal ray of the main cardioid of Mandelbrot set
• Play media

  ray 0

• other polynomials
• 

  various number of star branches

• orbits inside sepals
• 

  0/1 = 1/1

• 

  invariant curves inside main boxes

• 

Examples :

• Tiles: Tessellation of the Interior of Filled Julia Sets by T Kawahira
• coloured califlower by A Cheritat

code

For the internal angle 0/1 and 1/2 critical orbit is on the real line ( Im(z) = 0). It is easy to compute parabolic chesboard because one have to check only imaginary part of z. For other cases it is not so easy

0/1

Play media

How the target set is changing along an internal ray 0

Play media

Cpp code by Wolf Jung see function parabolic from file mndlbrot.cpp ( program mandel )

To see effect :

• run Mandel
• (on parameter plane ) find parabolic point for angle 0, which is c=0.25. To do it use key c, in window input 0 and return.

C code :

  // in function uint mndlbrot::esctime(double x, double y)
  if (b == 0.0 && !drawmode && sign < 0
      && (a == 0.25 || a == -0.75)) return parabolic(x, y);
 // uint mndlbrot::parabolic(double x, double y)
 if (Zx>=0 && Zx <= 0.5 && (Zy > 0 ? Zy : -Zy)<= 0.5 - Zx) 
            { if (Zy>0) data[i]=200; // show petal
                     else data[i]=150;}

Gnuplot code :

reset
f(x,y)=  x>=0 && x<=0.5 &&  (y > 0 ? y : -y) <= 0.5 - x
unset colorbox
set isosample 300, 300
set xlabel 'x'
set ylabel 'y'
set sample 300
set pm3d map
splot [-2:2] [-2:2] f(x,y)

1/2 or fat basilica

Cpp code by Wolf Jung see function parabolic from file mndlbrot.cpp ( program mandel ) To see effect :

• run Mandel
• (on parameter plane ) find parabolic point for angle 1/2, which is c=-0.75. To do it use key c, in window input 0 and return.

C code :

  // in function uint mndlbrot::esctime(double x, double y)
  if (b == 0.0 && !drawmode && sign < 0
      && (a == 0.25 || a == -0.75)) return parabolic(x, y);
 // uint mndlbrot::parabolic(double x, double y)
  if (A < 0 && x >= -0.5 && x <= 0 && (y > 0 ? y : -y) <= 0.3 + 0.6*x)
      {  if (j & 1) return (y > 0 ? 65282u : 65290u);
         else return (y > 0 ? 65281u : 65289u);
      }

• 
• 
• 

See also

• Checkerboard in Hyperbolic tilings by User:Tamfang : images and Python code
• https://plus.google.com/110803890168343196795/posts/Eun6pZVkkmA
• shadertoy: Orbit trapped julia Created by maeln in 2016-Jan-19
• Holomorphic checkerboard by etale_cohomology
• Sepals of cauliflower
• wikipedia :Zebra striping in computer graphics