Engineering Thermodynamics/Print version

Preface

The topic of thermodynamics is taught in Physics and Chemistry courses as part of the regular curriculum. This book deals with Engineering Thermodynamics, where concepts of thermodynamics are used to solve engineering problems. Engineers use thermodynamics to calculate the fuel efficiency of engines, and to find ways to make more efficient systems, be they rockets, refineries, or nuclear reactors. One aspect of "engineering" in the title is that a lot of the data used is empirical (e.g. steam tables), since you won't find clean algebraic equations of state for many common working substances. Thermodynamics is the science that deals with transfer of heat and work. Engineering thermodynamics develops the theory and techniques required to use empirical thermodynamic data effectively. However, with the advent of computers most of these techniques are transparent to the engineer, and instead of looking data up in tables, computer applications can be queried to retrieve the required values and use them in calculations. There are even applications which are tailored to specific areas which will give answers for common design situations. But thorough understanding will only come with knowledge of underlying principles, and the ability to judge the limitations of empirical data is perhaps the most important gain from such knowledge.

This book is a work in progress. It is hoped that as it matures, it will be more up to date than the dead tree editions.

Thermodynamics is the study of the relationships between HEAT (thermos) and WORK (dynamics). Thus, it deals with energy interactions in physical systems. Classical thermodynamics can be stated in four laws called the zeroth, first, second, and third laws respectively. The laws of thermodynamics are empirical, i.e., they are deduced from experience, and supported by a large body of experimental evidence.

The first chapter is an introduction to thermodynamics, and presents the motivation and scope of the topic. The second chapter, Thermodynamic Systems, defines some basic terms which are used throughout the book. In particular, the concepts of system and processes are discussed. The zeroth law is stated and the concept of temperature is developed. The next chapter, First Law, develops ideas required for the statement of the first law of thermodynamics. Second Law deals with heat engines and the concept of entropy. Applications of the tools developed in the previous chapters are illustrated, including the use of thermodynamics in everyday engineering situations. Appendix gives a list of tables for some commonly used properties.

This course forms the foundation for the Heat Transfer course, where the rate and mechanisms of transmission of energy in the form of heat is studied.

Introduction

Introduction to Classical Thermodynamics

Thermodynamics is the study of energies. More specifically, introductory thermodynamics is the study of energy transfer in systems. Classical thermodynamics consists of methods and constructs that are used to “account” for macroscopic energy transfer. In fact, energy accounting is an appropriate synonym for classical thermodynamics. In much the same way that accountants balance money in and money out of a bank account, rocket scientists simply balance the energy in and out of a rocket engine. Of course just as a bank account’s balance is obfuscated by arcane devices such as interest rates and currency exchange, so too is thermodynamics clouded with seemingly difficult concepts such as irreversibility and enthalpy. But, also just like accounting, a careful review of the rules suggests a coherent strategy for maintaining tabs on a particular account.

If a statement about the simplicity of thermodynamics failed to convert would-be students, they may be captured with a few words on the importance of understanding energy transfer in our society. Up until about 150 years ago or so, the earth’s economy was primarily fueled by carbohydrates. That is to say, humans got stuff done by converting food, through a biological process, to fuel we could spend to do work (e.g. raise barns). This was a hindrance to getting things accomplished, because it turned out that most of that energy went to growing and cultivating more carbohydrates (e.g. crops and livestock). We won’t even talk about how much food the horses ate!

Today, we have the luxury, primarily through an understanding of energy, to concentrate our energy production into efficient low maintenance operations. Massive power plants transfer energy to power tools for raising barns. Extremely efficient rocket engines tame and direct massive amounts of energy to blast TV satellites into orbit. This improvement in energy mastery frees humanity’s time to engage in more worthwhile activities such as watching cable TV. Although most are content to blissfully ignore the intricacies that command their way of life, I challenge you to embrace the contrary.

By no means is the energy battle over. Understanding energy transfer and energy systems is the second step to overcoming the limits to what humanity can accomplish. The first step is commanding an interest in doing so from an inclined portion of the population. Given the reader (and editor) has read this far through this aggrandizing rhetoric, I welcome your interest and hope to see it continue until the end.

The Main Macroscopic Forms of Energy

It will be in the best interest of the reader to have defined energy before it is discussed further. There are three primary forms of energy that are discussed in macroscopic thermodynamics. Several other forms of energy exist, but they generally exist on a microscopic level and should be deferred to more advanced study.

Kinetic Energy

The first form (probably most easily understood idea of energy) is defined by the motion of an object. Kinetic energy is the energy of a moving mass. For instance, a moving car will have more kinetic energy than a stationary car. The same car traveling at 60 km/h has more kinetic energy than it does traveling at 30 km/h.

Kinetic Energy = (1/2) x (mass) x (velocity)²

Ratio of v₆₀² / v₃₀² =((60)(1,000 meters/sec)(3600 sec/hour))² / ((30)(1,000 meters/sec)(3,600 sec/hour))²

So, once the algebra is completed properly we find the vehicle traveling at 60 km/h has four times the kinetic energy as when it is traveling at 30 km/h, while the vehicle has zero kinetic energy when it is stationary because the velocity = zero(0) results in 1/2mv²(1/2*m*0=0) being zero.

Potential Energy

The second type of energy is called potential energy. Gravitational potential energy describes the energy due to elevation. A car at a height of 50 m has more potential energy than a car at a height of 25 m. This may be understood more easily if the car is allowed to drop from its height. On impact with the earth at 0 m, the car that initially rested at 50 m will have more kinetic energy because it was moving faster (allowed more time to accelerate). The idea that potential energy can convert to kinetic energy is the first idea of energy transfer. Transfers between kinetic and potential energy represent one type of account balance rocket scientists need be aware of.

Potential Energy = (mass)*(acceleration due to gravity)*(elevation with respect to reference line) .

Internal Energy of Matter

The third and most important concept of energy is reflected by temperature. The internal energy of matter is measured by its temperature. Hot water has more internal energy than the same amount of cold water. Internal energy is a measure of kinetic energy of the molecules and atoms that make up the substance. Since each atom or molecule is acting on its own accord, this internal energy is different from the bulk kinetic energy associated with the movement of the entire solid. The internal energy of matter is exhibited by molecular motion. The molecules of a gas at high temperature zip around their container constantly colliding with walls and other molecules. The molecules of a high temperature solid also move around a lot; however, since they are stuck together with other molecules, the most they can do is vibrate in place.

In a nutshell, the above forms of energy are studied in classical thermodynamics. Those forms of energy are allowed to transfer among each other as well as in to or out of a system. Thermodynamics essentially provides some definitions for interpreting thermodynamic systems. It then goes on to define an important rule about fairly balancing energy and one rule about the quality of energy. (some energy is more valuable) Understanding the framework and the few rules that govern macroscopic thermodynamics proves to be an incredibly powerful set of tools for analyzing a myriad of not only engineering problems, but issues of practical concern. CONTRIBUTION BY CHANGES

Thermodynamic Systems

Thermodynamic System

In general, a system is a collection of objects, and there is a lot of subtlety in the way it is defined, as in set theory. However, in thermodynamics, it is a much more straightforward concept.

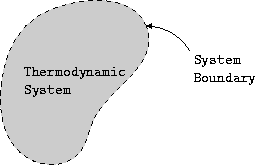
A thermodynamic system is a region of space or a finite quantity that occupies a volume and has a boundary. The surroundings refer to anything external to the system. The imaginary envelope that separates the system from its surroundings is known as the boundary. The boundary is what defines the limits of the system. The boundary can be fixed or moving. The system and its surroundings together constitute the universe.

Another term sometimes used instead of system is control volume. In the case of a closed system, in which the mass of matter inside the system remains constant, the control volume is referred to as control mass. A control volume is said to be enclosed by a control surface.

Proceeding further, the general term system will be used to refer to a thermodynamic system.

Types of Thermodynamic Systems

Isolated System

An isolated system is a system which does not allow the exchange of neither mass nor energy with its surroundings. An isolated system does not interact with its surroundings at all. The boundary of the system does not allow mass or energy transfer.

A close approximation of an isolated system is a thermos flask which retains the warmth of the liquid, by slowing down the interaction of the liquid and the air outside using a vacuum boundary. The only true isolated system is the universe.

Closed System

A closed thermodynamic system is a system which allows the exchange of heat and work with the surroundings but does not permit any exchange of mass across the boundaries. This type of system is also called a non-flow system, due to lack of flow across the boundary. The cylinder and piston of a reciprocating engine with gas in the cylinder is an example of a closed system. Another simple example is a kettle, in which heat is supplied to the kettle but the water contained in it remains constant.

Open System

An open thermodynamic system is a system in which allows the exchange of both mass and energy with the surroundings. The mass within the system varies over time. An open system is also called a control volume.

An example of an open system is an air compressor which draws in air from the surroundings, compresses it to a high pressure and then releases it from the system through a nozzle

Adiabatic System

An adiabatic system is a system which allows the exchange of work but not heat with its surroundings. The system achieves this with a thermally insulating boundary.

Homogeneous and Heterogeneous Systems

Continuum

An continuum is a system that contains a continuous distribution of matter. A continuum treats the matter in a system as distributed evenly in space and does regard the action of individual atoms or molecules. Pressure, temperature and other properties are the averages of the properties of many atoms and molecules taken together.

Phase

Matter which has is homogenous throughout its physical structure and chemical composition is called its phase. The most commonly observed phases are solid, liquid and gas phases.

Homogeneous System

A homogeneous system consists of only a single phase. Pure substances and homogeneous mixtures are examples of heterogeneous systems.

Heterogeneous System

A heterogeneous system consists of two or more different phases.

Properties of Pure Substances

A cursory review of properties will introduce the variables of thermodynamics to the student. Properties of substances are things such as mass, temperature, volume, and pressure. Properties are used to define the current state of a substance. Several more properties exist to describe substances in thermodynamics, but a stronger understanding of theory is required for their definition and application.

Properties can be intensive, if they are point properties (properties that make sense for a point) or extensive, if they depend on the amount of matter in the system. Examples of extensive properties of systems are mass of system, number of moles of a substance in a system, and overall or total volume of a system. These properties depend on how much matter of the system you measure. Examples of intensive properties are pressure, temperature, density, volume per mass, molar volume (which is volume per mole), and average molecular weight (or molecular mass). These properties are the same regardless of how you vary the amount of mass of the substance.

Properties are like the variables for substances in that their values are all related by an equation. The relationship between properties is expressed in the form of an equation which is called an equation of state. Perhaps the most famous state equation is the Ideal Gas Law. The ideal gas law relates the pressure, volume, and temperature of an ideal gas to one another.

Volume

The SI unit for volume is m³. Volume is an extensive property, but both volume per mass and molar volume are intensive properties since they do not depend on the measured mass of the system. A process during which the volume of the system remains constant is called an isochoric (or isometric) process.

Pressure

The SI unit for pressure is Pa (Pascal), which is equivalent to a $N/(m^{2})$. Pressure is an intensive property. A process in which pressure remains constant is called isobaric process.

Temperature

Temperature, the degree of hotness or coldness of a body is Defined. Based on the zeroth law of thermodynamics, is a fundamental concept of thermodynamics. We know that a body at high temperature will transfer energy to one at lower temperature. Consider two bodies with different temperatures in contact with each other. Net energy transfer will be from the hotter body to the colder body. At some point, the net energy transfer will be zero, and the bodies are said to be in thermal equilibrium. Bodies in thermal equilibrium are defined to have the same temperature.

Systems

Classical thermodynamics deals with systems in equilibrium. The equilibrium state is defined by the values of observable quantities in the system. These are called system properties.

The minimum number of variables required to describe the system depends on the complexity or degrees of freedom of the system. Degrees of freedom refer to the number of properties that can be varied independently of each other in a system. Some of the common system variables are pressure, temperature, and density, though any other physical properties may be used.

Consistent with the axiomatic nature of subject development, many of the relationships between physical properties cannot be completely specified without further development of theory. What is good about classical thermodynamics is that many of the axioms stated here can be derived using techniques of statistical thermodynamics. And statistical thermodynamics gives results in many cases where classical thermodynamics fails, such as in the specific heats of gases with many degrees of freedom. In some sense, the relationship between classical and statistical thermodynamics is similar to the one between classical and quantum mechanics, i.e., classical thermodynamics approximates statistical thermodynamics in the macroscopic limit.

Processes

A change in the system state is called a process. When the initial and final states of a process are the same, the process is called a cycle. If a process can be run in reverse with no change in the system + surroundings, then the process is called a reversible process. If a process is not reversible it is called an irreversible process.

Isothermal Process

An isothermal process is one in which the temperature remains constant. Please note that a process being isothermal does not imply anything about the heat transferred or work done, i.e. heat transfer may take place during an isothermal process. An isothermal process implies that the product of the volume and the pressure is constant for an ideal gas. i.e. PV = Constant

Zeroth Law of Thermodynamics

If a system A is in thermal equilibrium with another system B and also with a third system C, then all of the systems are in thermal equilibrium with each other. This is called the zeroth law of thermodynamics. This is how a thermometer works. If a thermometer is placed in a substance for temperature measurement, the thermometer's glass comes into thermal equilibrium with the substance. The glass then comes into thermal equilibrium with the liquid (mercury, alcohol, etc. . . .) inside the thermometer. Because the substance is in thermal equilibrium with the glass and the glass is in thermal equilibrium with the inner liquid, the substance and liquid must be in thermal equilibrium by the zeroth law. And because they are thermally equivalent, they must have the same temperature.

Temperature Measurement

Temperature is measured by observing some property of the system which varies with temperature. Such a property is called thermometric property, e.g.:

   - The volumes of most liquids increase with temperature.
   - The length of a metal rod increases as the temperature increases. 
   - The pressure of a constant volume of gas increases with temperature

It is useful to establish a temperature scale so that a cardinal relationship can be established between various systems at different temperatures. This is done by defining the temperature t as a function of a thermometric property X, such that the temperature is a linear function of X, i.e., equal changes in the property X give rise to equal changes in the temperature. Such a linear function is t = a + b X, for which one needs to assign arbitrary temperatures to two values of X to find the values of the constants a and b.

For example, in the case of the Celsius scale, the measurements are based on properties of water at the boiling point and melting point. Suppose the value of the thermometric property is X_b for the normal boiling point and X_m for the normal melting point. Then the temperature is given by t = 100 (X - X_m)/(X_b - X_m), where X is the thermometric property at temperature t, and we have chosen t_m = 0 °C and t_b = 100 °C. The normal melting and boiling points are the temperatures of melting and boiling at 1 atmosphere pressure.

The major temperature scales are the Celsius (°C), the Fahrenheit (°F) and the Kelvin (K) scales. Note the absence of the ° sign for kelvin—it is not degrees Kelvin, but kelvins, not capitalized when spelled out, and with the normal English plural which was added to the degree when Kelvin was an adjective modifying that unit.

Different thermometers are used for different temperature ranges. As the reader might have guessed by now, this means that the different thermometers will only agree on the fixed points. However, a set of thermometers have been carefully selected and calibrated so that this is not a big issue in practice.

The standard in this case is the International Temperature Scale, which was introduced in 1927, and revised in 1948, 1968, and 1990. The latest scale is denoted by T₉₀ for the Kelvin scale and is defined from 0.65 K upwards. For instance, between 0.65 K and 5.0 K T₉₀ is defined in terms of the vapor-pressure temperature relations of ³He and ⁴He. The ranges for different materials overlap and any of the valid materials can be used as a standard in the overlapping region.

The Ideal Gas

Recall that a thermodynamic system may have a certain substance or material whose quantity can be expressed in mass or moles in an overall volume. These are extensive properties of the system. If the substance is evenly distributed throughout the volume in question, then a value of volume per amount of substance may be used as an intensive property. For an example, for an amount called a mole, volume per mole is typically called molar volume. Also, a volume per mass for a specific substance may be called specific volume. In such cases, an equation of state may relate the three intensive properties, temperature, pressure, and molar or specific volume.

A simple but very useful equation of state is for an ideal gas. The ideal gas is a useful notion in thermodynamics, as it is a simple system that depends on two independent properties. An ideal gas is one that has no intermolecular interactions except for completely elastic collisions with other molecules. For a closed system containing an ideal gas, the state can be specified by giving the values of any two of pressure, temperature, and molar volume.

Consider a system, an ideal gas enclosed in a container. Starting from an initial state 1, where the temperature is T₁, its temperature is changed to T₂ through a constant pressure process and then a constant molar volume process, then the ratio of pressures is found to be the same as the ratio of molar volumes. Suppose the initial value of the pressure and molar volume are p₁ and V₁ respectively, and final value of pressure and molar volume are p₂ and V₂ respectively. Note that we haven't chosen a specific scale for the temperature (like say, the Celsius scale). Now, suppose we were to choose a scale such that T₁/T₂ = p₁/p₂, we can show that the value of pV/T is constant for an ideal gas, so that it obeys the gas equation pV = RT, where p is the absolute pressure, V is the molar volume, and R is a constant known as the universal gas constant. The temperature T is the absolute temperature in the ideal gas scale, and the scale is found to be the same as the thermodynamic temperature scale. The thermodynamic temperature scale will be defined after the statement of the second law of thermodynamics.

This equation pV = RT is called the equation of state for an ideal gas, and is known as the ideal gas equation. Most common gases obey the ideal gas equation unless they are compressed or cooled to extreme states, so this is a very useful relation. A similar equation may be written where, for the specific type of gas, specific volume is used instead of molar volume and a specific gas constant is used instead of the universal gas constant. This then writes as pv = mrT.

In the above image, the volume of an ideal gas at two different pressures p₁ and p₂ is plotted against the temperature in Celsius. If we extrapolate the two straight line graphs, they intersect the temperature axis at a point t₀, where t₀ = −273.15 °C.

From experiment, it is easy to show that the thermodynamic temperature T is related to the Celsius temperature t by the equation: T = t + 273.15. The zero of thermodynamic temperature scale is 0 K, and its significance will be clear when we discuss the second law of thermodynamics.

---

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

Zeroth Law

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

---

The Zeroth law of Thermodynamics can be stated as:

If two thermodynamic systems A and B are in thermal equilibrium, and B is also in thermal equilibrium with another system C, then A and C are in thermal equilibrium. OR

"" If a body isolated from the other environment is in thermal equilibrium with one body & is separately in thermal equilibrium with the another body then three bodies are said to be in the thermal equilibrium with each other.""

This may seem obvious as we are quite familiar with this experiment. When we place in a cup of water (System A) a thermometer (System B) we wait a period of time until they reach equilibrium then read the measurement on the thermometer.

It is called the Zeroth Law as it is not derivable from the other laws and is often useful to understand the concept before presenting the other laws of thermodynamics.

It also states that at absolute zero temperature( i.e. zero Kelvin ) all molecular motion inside a crystal ceases.

The application of zeroth law is mainly seen in the thermodynamic properties.

Source : [1]

First Law

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

---

Energy

Energy as described on Wikipedia is "the property that must be transferred to an object in order to perform work on, or to heat, the object". Energy is a conserved quantity, the Law of Conservation of Energy on Wikipedia states that "energy can be converted in form, but not created or destroyed".

Common forms of energy in physics are potential and kinetic energy. The potential energy is usually the energy due to matter having certain position (configuration) in a field, commonly the gravitational field of Earth. Kinetic energy is the energy due to motion relative to a frame of reference. In thermodynamics, we deal with mainly work and heat, which are different manifestations of the energy in the universe.

Work

Work is said to be done by a system if the effect on the surroundings can be reduced solely to that of lifting a weight. Work is only ever done at the boundary of a system. Again, we use the intuitive definition of work, and this will be complete only with the statement of the second law of thermodynamics.

Consider a piston-cylinder arrangement as found in automobile engines. When the gas in the cylinder expands, pushing the piston outwards, it does work on the surroundings. In this case work done is mechanical. But how about other forms of energy like heat? The answer is that heat cannot be completely converted into work, with no other change, due to the second law of thermodynamics.

In the case of the piston-cylinder system, the work done during a cycle is given by W, where W = −∫ F dx = −∫ p dV, where F = p A, and p is the pressure on the inside of the piston (note the minus sign in this relationship). In other words, the work done is the area under the p-V diagram. Here, F is the external opposing force, which is equal and opposite to that exerted by the system. A corollary of the above statement is that a system undergoing free expansion does no work. The above definition of work will only hold for the quasi-static case, when the work done is reversible work.

A consequence of the above statement is that work done is not a state function, since it depends on the path (which curve you consider for integration from state 1 to 2). For a system in a cycle which has states 1 and 2, the work done depends on the path taken during the cycle. If, in the cycle, the movement from 1 to 2 is along A and the return is along C, then the work done is the lightly shaded area. However, if the system returns to 1 via the path B, then the work done is larger, and is equal to the sum of the two areas.

The above image shows a typical indicator diagram as output by an automobile engine. The shaded region is proportional to the work done by the engine, and the volume V in the x-axis is obtained from the piston displacement, while the y-axis is from the pressure inside the cylinder. The work done in a cycle is given by W, where

$W=-\oint pdV$

Work done by the system is negative, and work done on the system is positive, by the convention used in this book.

Flow Energy

So far we have looked at the work done to compress fluid in a system. Suppose we have to introduce some amount of fluid into the system at a pressure p. Remember from the definition of the system that matter can enter or leave an open system. Consider a small amount of fluid of mass dm with volume dV entering the system. Suppose the area of cross section at the entrance is A. Then the distance the force pA has to push is dx = dV/A. Thus, the work done to introduce a small amount of fluid is given by pdV, and the work done per unit mass is pv, where v = dV/dm is the specific volume. This value of pv is called the flow energy.

Examples of Work

The amount of work done in a process depends on the irreversibilities present. A complete discussion of the irreversibilities is only possible after the discussion of the second law. The equations given above will give the values of work for quasi-static processes, and many real world processes can be approximated by this process. However, note that work is only done if there is an opposing force in the boundary, and that a volume change is not strictly required.

Work in a Polytropic Process

Consider a polytropic process pVⁿ=C, where C is a constant. If the system changes its states from 1 to 2, the work done is given by

$W=-\int _{V_{1}}^{V_{2}}{\frac {C}{V^{n}}}dV={\frac {p_{2}V_{2}-p_{1}V_{1}}{1-n}}$

And additionally, if n=1

$W=-\int _{V_{1}}^{V_{2}}{\frac {C}{V^{n}}}dV=-C\ln {\frac {V_{2}}{V_{1}}}$

Heat

Before thermodynamics was an established science, the popular theory was that heat was a fluid, called caloric, that was stored in a body. Thus, it was thought that a hot body transferred heat to a cold body by transferring some of this fluid to it. However, this was soon disproved by showing that heat was generated when drilling bores of guns, where both the drill and the barrel were initially cold.

Heat is the energy exchanged due to a temperature difference. As with work, heat is defined at the boundary of a system and is a path function. Heat rejected by the system is negative, while the heat absorbed by the system is positive.

Specific Heat

The specific heat of a substance is the amount of heat required for a unit rise in the temperature in a unit mass of the material. If this quantity is to be of any use, the amount of heat transferred should be a linear function of temperature. This is certainly true for ideal gases. This is also true for many metals and also for real gases under certain conditions. In general, we can only talk about the average specific heat, c_av = Q/mΔT. Since it was customary to give the specific heat as a property in describing a material, methods of analysis came to rely on it for routine calculations. However, since it is only constant for some materials, older calculations became very convoluted for newer materials. For instance, for finding the amount of heat transferred, it would have been simple to give a chart of Q(ΔT) for that material. However, following convention, the tables of c_av(ΔT) were given, so that a double iterative solution over c_av and T was required.

Calculating specific heat requires us to specify what we do with Volume and Pressure when we change temperature. When Volume is fixed, it is called specific heat at constant volume (C_v). When Pressure is fixed, it is called specific heat at constant pressure (C_p).

Latent Heat

It can be seen that the specific heat as defined above will be infinitely large for a phase change, where heat is transferred without any change in temperature. Thus, it is much more useful to define a quantity called latent heat, which is the amount of energy required to change the phase of a unit mass of a substance at the phase change temperature.

Adiabatic Process

An adiabatic process is defined as one in which there is no heat transfer with the surroundings, that is, the change in amount of energy dQ=0 . A gas contained in an insulated vessel undergoes an adiabatic process. Adiabatic processes also take place even if the vessel is not insulated if the process is fast enough that there is not enough time for heat to escape (e.g. the transmission of sound through air). Adiabatic processes are also ideal approximations for many real processes, like expansion of a vapor in a turbine, where the heat loss is much smaller than the work done.

First Law of Thermodynamics

Joule Experiments

It is well known that heat and work both change the energy of a system. Joule conducted a series of experiments which showed the relationship between heat and work in a thermodynamic cycle for a system. He used a paddle to stir an insulated vessel filled with fluid. The amount of work done on the paddle was noted (the work was done by lowering a weight, so that work done = mgz). Later, this vessel was placed in a bath and cooled. The energy involved in increasing the temperature of the bath was shown to be equal to that supplied by the lowered weight. Joule also performed experiments where electrical work was converted to heat using a coil and obtained the same result.

Statement of the First Law for a Closed System

The first law states that when heat and work interactions take place between a closed system and the environment, the algebraic sum of the heat and work interactions for a cycle is zero.

Mathematically, this is equivalent to

dQ + dW = 0 for any cycle closed to mass flow

Q is the heat transferred, and W is the work done on or by the system. Since these are the only ways energy can be transferred, this implies that the total energy of the system in the cycle is a constant.

One consequence of the statement is that the total energy of the system is a property of the system. This leads us to the concept of internal energy.

Internal Energy

In thermodynamics, the internal energy is the energy of a system due to its temperature. The statement of first law refers to thermodynamic cycles. Using the concept of internal energy it is possible to state the first law for a non-cyclic process. Since the first law is another way of stating the conservation of energy, the energy of the system is the sum of the heat and work input, i.e., ΔE = Q + W. Here E represents the internal energy (U) of the system along with the kinetic energy (KE) and the potential energy (PE) and is called the total energy of the system. This is the statement of the first law for non-cyclic processes, as long as they are still closed to the flow of mass (E = U + KE + PE). The KE and PE terms are relative to an external reference point i.e. the system is the gas within a ball, the ball travels in a trajectory that varies in height H and velocity V and subsequently KE and PE with time, but this has no affect upon the energy of the gas molecules within the ball, which is dictated only by the internal energy of the system (U). Thermodynamics does not define the nature of the internal energy, but it can be rationalised using other theories (i.e. the gas kinetic theory), but in this case is due to the KE and PE of the gas molecules within the ball, not to be mistaken with the KE and PE of the ball itself.

For gases, the value of KE and PE is quite small, so the important term is the internal energy function U. In particular, since for an ideal gas the state can be specified using two variables, the state variable u is given by u(v, T), where v is the specific volume and T is the temperature.

Introducing this temperature dependence explicitly is important in many calculations. For this purpose, the constant-volume heat capacity is defined as follows: c_v = (∂u/∂t)_v, where c_v is the specific heat at constant volume. A constant-pressure heat capacity will be defined later, and it is important to keep them straight. The important point here is that the other variable that U depends on "naturally" is v, so to isolate the temperature dependence of U you want to take the derivative at constant v.

Internal Energy for an Ideal Gas

In the previous section, the internal energy of an ideal gas was shown to be a function of both the volume and temperature. Joule performed an experiment where a gas at high pressure inside a bath at the same temperature was allowed to expand into a larger volume.

In the above image, two vessels, labeled A and B, are immersed in an insulated tank containing water. A thermometer is used to measure the temperature of the water in the tank. The two vessels A and B are connected by a tube, the flow through which is controlled by a stop. Initially, A contains gas at high pressure, while B is nearly empty. The stop is removed so that the vessels are connected and the final temperature of the bath is noted.

The temperature of the bath was unchanged at the end of the process, showing that the internal energy of an ideal gas was the function of temperature alone. Thus Joule's law is stated as (∂u/∂v)_t = 0.

Enthalpy

According to the first law, dQ + dW = dE

If all the work is pressure volume work, then we have

dW = − p dV

⇒ dQ = dU + pdV = d(U + pV) - Vdp

⇒ d(U + pV) = dQ + Vdp

We define H ≡ U + pV as the enthalpy of the system, and h = u + pv is the specific enthalpy. In particular, for a constant pressure process,

ΔQ = ΔH

With arguments similar to that for c_v, c_p = (∂h/∂t)_p. Since h, p, and t are state variables, c_p is a state variable. As a corollary, for ideal gases, c_p = c_v + R, and for incompressible fluids, c_p = c_v

Throttling

Throttling is the process in which a fluid passing through a restriction loses pressure. It usually occurs when fluid passes through small orifices like porous plugs. The original throttling experiments were conducted by Joule and Thompson. As seen in the previous section, in adiabatic throttling the enthalpy is constant. What is significant is that for ideal gases, the enthalpy depends only on temperature, so that there is no temperature change, as there is no work done or heat supplied. However, for real gases, below a certain temperature, called the inversion point, the temperature drops with a drop in pressure, so that throttling causes cooling, i.e., p₁ < p₂ ⇒ T₁ < T₂. The amount of cooling produced is quantified by the Joule-Thomson coefficient μ_JT = (∂T/∂p)_h. For instance, the inversion temperature for air is about 400 °C.

---

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

Second Law

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

---

Introduction

The first law is a statement of energy conservation. The rise in temperature of a substance when work is done is well known. Thus work can be completely converted to heat. However, we observe that in nature, we don't see the conversion in the other direction spontaneously.

The statement of the second law is facilitated by using the concept of heat engines. Heat engines work in a cycle and convert heat into work. A thermal reservoir is defined as a system which is in equilibrium and large enough so that heat transferred to and from it does not change its temperature appreciably.

Heat Engine

Heat engines work between two thermal reservoirs, the low temperature reservoir and the high temperature reservoir. The performance of a heat engine is measured by its thermal efficiency, which is defined as the ratio of work output to heat input, i.e., η = W/Q₁, where W is the net work done, and Q₁ is heat transferred from the high temperature reservoir.

Heat Pumps

Heat pumps transfer heat from a low temperature reservoir to a high temperature reservoir using external work, and can be considered as reversed heat engines.

Statement of the Second Law of Thermodynamics

Kelvin-Planck Statement

"It is impossible to construct a heat engine which will operate continuously and convert all the heat it draws from a reservoir into work."

In other words, "It is impossible to have a heat engine which works in cycle and does work by exchanging heat with only one reservoir."

Clausius Statement

"It is impossible to construct a heat pump which will transfer heat from a low temperature reservoir to a high temperature reservoir without using external work."

In other words, "It is impossible for heat to flow from a low temperature (sink) to a high temperature (source) without external work."

PMM2

A perpetual motion machine of the second kind, or PMM2 is one which converts 100% of the heat input into work while working in a cycle. A machine like this would violate the second law of thermodynamics, and would therefore be impossible to build. A PMM2 has an η_th of 1.

Equivalence of Clausius and Kelvin-Planck Statements

Kelvin-Planck from Clausius

Suppose we can construct a heat pump which transfers heat from a low temperature reservoir to a high temperature one without using external work. Then, we can couple it with a heat engine in such a way that the heat removed by the heat pump from the low temperature reservoir is the same as the heat rejected by the heat engine, so that the combined system is now a heat engine which converts heat to work without any external effect. This is thus in violation of the Kelvin-Planck statement of the second law.

Clausius from Kelvin-Planck

Now suppose we have a heat engine which can convert heat into work without rejecting heat anywhere else. We can combine it with a heat pump so that the work produced by the engine is used by the pump. Now the combined system is a heat pump which uses no external work, violating the Clausius statement of the second law.

Thus, we see that the Clausius and Kelvin-Planck statements are equivalent, and one necessarily implies the other.

Carnot Cycle

Nicholas Sadi Carnot devised a reversible cycle in 1824 called the Carnot cycle for an engine working between two reservoirs at different temperatures. It consists of two reversible isothermal and two reversible adiabatic processes. For a cycle 1-2-3-4, the working material

1. Undergoes isothermal expansion in 1-2 while absorbing heat from high temperature reservoir
2. Undergoes adiabatic expansion in 2-3
3. Undergoes isothermal compression in 3-4, and
4. Undergoes adiabatic compression in 4-1.

Heat is transferred to the working material during 1-2 (Q₁) and heat is rejected during 3-4 (Q₂). The thermal efficiency is thus η_th = W/Q₁. Applying first law, we have, W = Q₁ − Q₂, so that η_th = 1 − Q₂/Q₁.

Carnot's principle states that

1. No heat engine working between two thermal reservoirs is more efficient than the Carnot engine, and
2. All Carnot engines working between reservoirs of the same temperature have the same efficiency.

The proof by contradiction of the above statements come from the second law, by considering cases where they are violated. For instance, if you had a Carnot engine which was more efficient than another one, we could use that as a heat pump (since processes in a Carnot cycle are reversible) and combine with the other engine to produce work without heat rejection, to violate the second law. A corollary of the Carnot principle is that Q₂/Q₁ is purely a function of t₂ and t₁, the reservoir temperatures. Or,

${\frac {Q_{1}}{Q_{2}}}=\phi \left(t_{1},t_{2}\right)$

Thermodynamic Temperature Scale

Lord Kelvin used Carnot's principle to establish the thermodynamic temperature scale which is independent of the working material. He considered three temperatures, t₁, t₂, and t₃, such that t₁ > t₃ > t₂.

As shown in the previous section, the ratio of heat transferred only depends on the temperatures. Considering reservoirs 1 and 2:

${\frac {Q_{1}}{Q_{2}}}=\phi \left(t_{1},t_{2}\right)$

Considering reservoirs 2 and 3:

${\frac {Q_{2}}{Q_{3}}}=\phi \left(t_{2},t_{3}\right)$

Considering reservoirs 1 and 3:

${\frac {Q_{1}}{Q_{3}}}=\phi \left(t_{1},t_{3}\right)$

Eliminating the heat transferred, we have the following condition for the function φ.

$\phi \left(t_{1},t_{2}\right)={\frac {\phi \left(t_{1},t_{3}\right)}{\phi \left(t_{2},t_{3}\right)}}$

Now, it is possible to choose an arbitrary temperature for 3, so it is easy to show using elementary multivariate calculus that φ can be represented in terms of an increasing function of temperature ζ as follows:

$\phi \left(t_{1},t_{2}\right)={\frac {\zeta \left(t_{1}\right)}{\zeta \left(t_{2}\right)}}$

Now, we can have a one to one association of the function ζ with a new temperature scale called the thermodynamic temperature scale, T, so that

${\frac {Q_{1}}{Q_{2}}}={\frac {T_{1}}{T_{2}}}$

Thus we have the thermal efficiency of a Carnot engine as

$\eta _{th}=1-{\frac {T_{2}}{T_{1}}}$

The thermodynamic temperature scale is also known as the Kelvin scale, and it needs only one fixed point, as the other one is absolute zero. The concept of absolute zero will be further refined during the statement of the third law of thermodynamics.

• 1st Law: Energy can neither be created or destroyed
• 2nd Law: All spontaneous events act to increase total entropy
• 3rd Law: Absolute zero is removal of all thermal molecular motion

Reservoir

Reservoirs are systems of large quantity of matter which no temperature difference will occur when finite amount of heat is transferred or removed. Examples of reservoirs are atmosphere, oceans, seas etc.

Clausius Theorem

Clausius theorem states that any reversible process can be replaced by a combination of reversible isothermal and adiabatic processes.

Consider a reversible process a-b. A series of isothermal and adiabatic processes can replace this process if the heat and work interaction in those processes is the same as that in the process a-b. Let this process be replaced by the process a-c-d-b, where a-c and d-b are reversible adiabatic processes, while c-d is a reversible isothermal process. The isothermal line is chosen such that the area a-e-c is the same as the area b-e-d. Now, since the area under the p-V diagram is the work done for a reversible process, we have, the total work done in the cycle a-c-d-b-a is zero. Applying the first law, we have, the total heat transferred is also zero as the process is a cycle. Since a-c and d-b are adiabatic processes, the heat transferred in process c-d is the same as that in the process a-b. Now applying first law between the states a and b along a-b and a-c-d-b, we have, the work done is the same. Thus the heat and work in the process a-b and a-c-d-b are the same and any reversible process a-b can be replaced with a combination of isothermal and adiabatic processes, which is the Clausius theorem.

A corollary of this theorem is that any reversible cycle can be replaced by a series of Carnot cycles.

Suppose each of these Carnot cycles absorbs heat dQ₁ⁱ at temperature T₁ⁱ and rejects heat dQ₂ⁱ at T₂ⁱ. Then, for each of these engines, we have dQ₁ⁱ/dQ₂ⁱ = −T₁ⁱ/T₂ⁱ. The negative sign is included as the heat lost from the body has a negative value. Summing over a large number of these cycles, we have, in the limit,

$\oint _{R}{\frac {dQ}{T}}=0$

This means that the quantity dQ/T is a property. It is given the name entropy.

Further, using Carnot's principle, for an irreversible cycle, the efficiency is less than that for the Carnot cycle, so that

$\eta _{irr}=1-{\frac {dQ_{2}}{dQ_{1}}}<\eta _{Carnot}$

${\frac {dQ_{1}}{T_{1}}}-{\frac {dQ_{2}}{T_{2}}}<0$

As the heat is transferred out of the system in the second process, we have, assuming the normal conventions for heat transfer,

${\frac {dQ_{1}}{T_{1}}}+{\frac {dQ_{2}}{T_{2}}}<0$

So that, in the limit we have,

$\oint _{I}{\frac {dQ}{T}}<0$

$\oint {\frac {dQ}{T_{reservoir}}}\leq 0$

The above inequality is called the inequality of Clausius. Here the equality holds in the reversible case.

Entropy

Entropy is the quantitative statement of the second law of thermodynamics. It is represented by the symbol S, and is defined by

$dS\equiv \left({\frac {dQ}{T}}\right)_{rev}$

Note that as we have used the Carnot cycle, the temperature is the reservoir temperature. However, for a reversible process, the system temperature is the same as the reversible temperature.

Consider a system undergoing a cycle 1-2-1, where it returns to the original state along a different path. Since entropy of the system is a property, the change in entropy of the system in 1-2 and 2-1 are numerically equal. Suppose reversible heat transfer takes place in process 1-2 and irreversible heat transfer takes place in process 2-1. Applying Clausius's inequality, it is easy to see that the heat transfer in process 2-1 dQ_irr is less than T dS. That is, in an irreversible process the same change in entropy takes place with a lower heat transfer. As a corollary, the change in entropy in any process, dS, is related to the heat transfer dQ as

dS ≥ dQ/T

For an isolated system, dQ = 0, so that we have

dS_isolated ≥ 0

This is called the principle of increase of entropy and is an alternative statement of the second law.

Further, for the whole universe, we have

ΔS = ΔS_sys + ΔS_surr > 0

For a reversible process,

ΔS_sys = (Q/T)_rev = −ΔS_surr

So that

ΔS_universe = 0

for a reversible process.

Since T and S are properties, you can use a T-S graph instead of a p-V graph to describe the change in the system undergoing a reversible cycle. We have, from the first law, dQ + dW = 0. Thus the area under the T-S graph is the work done by the system. Further, the reversible adiabatic processes appear as vertical lines in the graph, while the reversible isothermal processes appear as horizontal lines.

Entropy for an Ideal Gas

An ideal gas obeys the equation pv = RT. According to the first law,

dQ + dW = dU

For a reversible process, according to the definition of entropy, we have

dQ = T dS

Also, the work done is the pressure volume work, so that

dW = -p dV

The change in internal energy:

dU = m c_v dT

T dS = p dV + m c_v dT

Taking per unit quantities and applying ideal gas equation,

ds = R dV/v + c_v dT/T

$\Delta s=R\ln {\frac {v_{2}}{v_{1}}}+c_{v}\ln {\frac {T_{2}}{T_{1}}}$

As a general rule, all things being equal, entropy increases as, temperature increases and as pressure and concentration decreases and energy stored as internal energy has higher entropy than energy which is stored as kinetic energy.

Availability

From the second law of thermodynamics, we see that we cannot convert all the heat energy to work. If we consider the aim of extracting useful work from heat, then only some of the heat energy is available to us. It was previously said that an engine working with a reversible cycle was more efficient than an irreversible engine. Now, we consider a system which interacts with a reservoir and generates work, i.e., we look for the maximum work that can be extracted from a system given that the surroundings are at a particular temperature.

Consider a system interacting with a reservoir and doing work in the process. Suppose the system changes state from 1 to 2 while it does work. We have, according to the first law,

dQ - dW = dE,

where dE is the change in the internal energy of the system. Since it is a property, it is the same for both the reversible and irreversible process. For an irreversible process, it was shown in a previous section that the heat transferred is less than the product of temperature and entropy change. Thus the work done in an irreversible process is lower, from first law.

Availability Function

The availability function is given by Φ, where

Φ ≡ E − T₀S

where T₀ is the temperature of the reservoir with which the system interacts. The availability function gives the effectiveness of a process in producing useful work. The above definition is useful for a non-flow process. For a flow process, it is given by

Ψ ≡ H − T₀S

Irreversibility

Maximum work can be obtained from a system by a reversible process. The work done in an actual process will be smaller due to the irreversibilities present. The difference is called the irreversibility and is defined as

I ≡ W_rev − W

From the first law, we have

W = ΔE − Q

I = ΔE - Q - (Φ₂ − Φ₁)

As the system interacts with surroundings of temperature T₀, we have

ΔS_surr = Q/T₀

Also, since

E − Φ = T₀ ΔS_sys

we have

I = T₀ (ΔS_sys + ΔS_surr)

Thus,

I ≥ 0

I represents increase in unavailable energy.

Helmholtz and Gibbs Free Energies

Helmholtz Free Energy is defined as

F ≡ U − TS

The Helmholtz free energy is relevant for a non-flow process. For a flow process, we define the Gibbs Free Energy

G ≡ H − TS

The Helmholtz and Gibbs free energies have applications in finding the conditions for equilibrium.

---

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

Third Law

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

---

Third Law of Thermodynamics

The Third Law of Thermodynamics extends the definition of Entropy:

Entropy is zero only in a perfect crystal at absolute zero ( 0 kelvin [- 273.15 degree Celsius ]).

The Third Law of Thermodynamics can mathematically be expressed as

lim ST→0 = 0 (1)

where

S = entropy (J/K)

T = absolute temperature (K)

At a temperature of absolute zero there is no thermal energy or heat. At a temperature of zero Kelvin the atoms in a pure crystalline substance are aligned perfectly and do not move. There is no entropy of mixing since the substance is pure. By -VBM

Applications

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

One Component Systems

All materials can exist in three phases: solid, liquid, and gas. All one component systems share certain characteristics, so that a study of a typical one component system will be quite useful.

For this analysis, we consider heat transferred to the substance at constant pressure. The above chart shows temperature vs. specific volume (1/density) curves for at three different constant pressures. The three line-curves labeled p₁, p₂, and p_c above are isobars, showing conditions at constant pressure. When the liquid and vapor coexist, it is called a saturated state. There is no change in temperature or pressure when liquid and vapor are in equilibrium, so that the temperature is called saturation temperature and the pressure is called saturation pressure. Saturated states are represented by the horizontal lines in the chart. In the temperature range where both liquid and vapor of a pure substance can coexist in equilibrium, for every value of saturated temperature, there is only one corresponding value of saturation pressure. If the temperature of the liquid is lower than the saturation temperature, it is called subcooled liquid. If the temperature of the vapor or gas is greater than the saturation temperature it is called superheated vapor.

The amount of liquid and vapor in a saturated mixture is specified by its quality x, which is the fraction of vapor in the mixture. Thus, the horizontal line representing the vaporization of the fluid has a quality of x=0 at the left endpoint where it is 100% liquid and a quality of x=1 at the right endpoint where it is 100% vapor. The blue curve in the preceding diagram shows saturation temperatures for saturated liquid i. e. where x=0. The green curve in the diagram shows saturation temperatures for saturated vapor i. e. where x=1. These curves are not isobars.

$x={\frac {m_{g}}{m_{f}+m_{g}}}$

$v_{x}=\left(1-x\right)v_{f}+xv_{g}$

$v_{fg}=v_{g}-v_{f}$

If you also consider the solid state, then we get the phase diagram for the material. The point where the solid, liquid, and the vapor state exist in equilibrium is called the
triple point. Note that as the saturation temperatures increase, the liquid and vapor specific volumes approach each other until the blue and green curves come together and meet at point C on the p_c isobar. At that point C, called the critical point, the liquid and vapor states merge together and all their thermodynamic properties become the same. The critical point has a certain temperature T_c, and pressure p_c, which depend on the substance in question. At temperatures above the critical point, the substance is considered a super-heated gas.

This diagram is based on the diagram for water. Other pure (one-component) substances have corresponding temperature vs. specific volume diagrams which are fairly similarly shaped, but the temperatures, pressures, and specific volumes will vary.

The thermodynamic properties of materials are given in charts. One commonly used chart is the Mollier Chart, which is the plot of enthalpy versus entropy. The pressure enthalpy chart is frequently used in refrigeration applications. Charts such as these are useful because many processes are isenthalpic, so obtaining values would be as simple as drawing a straight line on the chart and reading off the data.

Steam tables give the values of specific volume, enthalpy, entropy, and internal energy for different temperatures for water. They are of great use to an engineer, with applications in steam turbines, steam engines, and air conditioning, among others.

Gas tables give the same equations for common gases like air. Although most gases roughly obey the ideal gas equation, gas tables note the actual values which are more accurate in many cases. They are not as important as steam tables, but in many cases it is much easier to lookup from a table rather than compute answers.

Gibbs Phase Rule

Gibbs phase rule states that for a heterogeneous system in equilibrium with C components in P phases, the degree of freedom F = C - P + 2. Thus, for a one component system with two phases, there is only one degree of freedom. F=1-2+2 F =1 That is, if you are given either the pressure or temperature of wet steam, you can obtain all the properties, while for superheated steam, which has just one phase, you will need both the pressure and the temperature.

Psychrometry

Psychrometry is the study of air and water vapor mixtures for air conditioning. For this application, air is taken to be a mixture of nitrogen and oxygen with the other gases being small enough so that they can be approximated by more of nitrogen and oxygen without much error. In this psychrometry section, vapor refers to water vapor. For air at normal (atmospheric) pressure, the saturation pressure of vapor is very low. Also, air is far away from its critical point in those conditions. Thus, the air vapor mixture behaves as an ideal gas mixture. If the partial pressure of the vapor is smaller than the saturation pressure for water for that temperature, the mixture is called unsaturated. The amount of moisture in the air vapor mixture is quantified by its humidity.

The absolute humidity ω is the ratio of masses of the vapor and air, i.e., ω = m_v/m_a. Now, applying ideal gas equation, pV = mRT for water vapor and for air, we have, since the volume and temperature are the same, ω = 0.622 p_v/p_a. The ratio of specific gas constants (R in preceding equation) of water vapor to air equals 0.622 .

The relative humidity φ is the ratio of the vapor pressure to the saturation vapor pressure at that temperature, i.e., φ = p_v/p_v,sat.

The saturation ratio is the ratio of the absolute humidity to the absolute humidity at saturation, or, ψ = ω/ω_sat. It is easy to see that the saturation ratio is very close to the value of relative humidity.

The above plot shows the value of absolute humidity versus the temperature. The initial state of the mixture is 1, and it is cooled isobarically, and at constant absolute humidity. When it reaches 2, it is saturated, and its absolute humidity is ω_a. Further cooling causes condensation and the system moves to point 3, where its absolute humidity is ω_b. The temperature at 2 is called the dew point.

It is customary to state all quantities in psychrometry per unit mass of dry air. Thus, the amount of air condensed in the above chart when moving from 2 to 3 is ω_b − ω_a.

Adiabatic Saturation

Consider an unsaturated mixture entering a chamber. Suppose water was sprayed into the stream, so that the humidity increases and it leaves as a saturated mixture. This is accompanied by a loss of temperature due to heat being removed from the air which is used for vaporization. If the water supplied is at the temperature of exit of the stream, then there is no heat transfer from the water to the mixture. The final temperature of the mixture is called adiabatic saturation temperature.

Wet Bulb Temperature

The relative humidity of air vapor mixtures is measured by using dry and wet bulb thermometers. The dry bulb thermometer is an ordinary thermometer, while the wet bulb thermometer has its bulb covered by a moist wick. When the mixture flows past the two thermometers, the dry bulb thermometer shows the temperature of the stream, while water evaporates from the wick and its temperature falls. This temperature is very close to the adiabatic saturation temperature if we neglect the heat transfer due to convection.

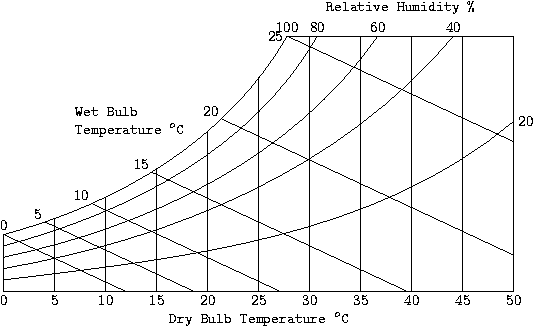
Psychrometric Chart

This chart gives the value of absolute humidity versus temperature, along with the enthalpy. From this chart you can determine the relative humidity given the dry and wet bulb temperatures. We have, from the first law, that for a flow system with no heat transfer, the enthalpy is a constant. Now, for the adiabatic saturation process, there is no heat transfer taking place, so that the adiabatic saturation lines are the same as the wet bulb temperature and the constant enthalpy lines.

Questions

1. The temperature at Phoenix is 35 °C with a relative humidity of 40%. Can a room be cooled using a conventional air cooler?

We need to find the wet bulb temperature for the point T = 35°C and φ = 40%. We have, from the psychrometric chart, the wet bulb temperature is between 20 and 25°C. Thus, you can cool the room down to a comfortable temperature using an evaporative cooler.

2. The temperature of Los Angeles is 37 °C with relative humidity of 83%. To what temperature can a room be cooled using a conventional air cooler?

The wet bulb temperature is about 34.2°C for this situation. Thus, you cannot use an ordinary cooler to reduce room temperature in this situation. You will need to use an air conditioner.

Air Conditioning

The human body can work efficiently only in a narrow range of conditions. Further, it rejects about 60 W of heat continuously into the surroundings, and more during heavy exercise. The temperature of the body is maintained by the evaporation of sweat from the body. Thus, for comfort, both the temperature and the relative humidity should be low.

Conventional air conditioning consists of setting the humidity at an acceptable level, while reducing the temperature. Reducing the humidity to zero is not the ideal objective. For instance, low humidity leads to issues like high chances of static electricity building up, leading to damage of sensitive electronic equipment. A humidity level of 50% is more acceptable in this case.

The most common method of reducing humidity is to cool the air using a conventional air conditioner working on a reversed Carnot cycle. The vapor that condenses is removed. Now, the air that is produced is very cold, and needs to be heated back up to room temperature before it is released back to the air conditioned area.

Common Thermodynamic Cycles

Several thermodynamic cycles used in machines can be approximated with idealized cycles. It was shown previously that a Carnot engine was the most efficient engine operating between two thermal reservoirs. However, due to practical difficulties, Carnot cycle cannot be implemented in all situations. The following sections deal with idealized (non Carnot) systems found in practice.

Rankine Cycle

In the Rankine cycle, also called the standard vapor power cycle, the working fluid follows a closed cycle. We will consider water as a working substance. Other materials can be also used, for example organic one (see Organic Rankine Cycle); properties of the working fluids in use has great influence on the actual process. In the Rankine cycle, water is pumped from a low pressure to a high pressure using a liquid pump. This water is then heated in the boiler at constant pressure where its temperature increases and it is converted to superheated vapor. This vapor is then expanded in an expander to generate work. This expander can be a turbine or a reciprocating (i.e. piston) machine such as those used in older steam locomotive or ship. The output of the expander is then cooled in a condenser to the liquid state and fed to the pump. The Rankine cycle differs from the Carnot cycle in that the input to the pump is a liquid (it is cooled more in the condenser). This allows the use of a small, low power pump due to the lower specific volume of liquid compared to steam. Also, the heat transfer in the boiler takes place mainly as a result of a phase change, compared to the isothermal heating of the ideal gas in the Carnot cycle, so that the efficiency is quite good (even though it is still lower than the Carnot efficiency). The amount of heat transferred as the liquid is heated to its boiling point is very small compared to the heat transfer during phase change. The steam is superheated so that no liquid state exists inside the turbine. Condensation in the turbine can be devastating as it can cause corrosion and erosion of the blades.

There are several modifications to the Rankine cycle leading to even better practical designs. In the reheat cycle there are two expanders working in series, and the steam from the high pressure stage is heated again in the boiler before it enters the low pressure expander. This avoids the problem of moisture in the turbine and also increases the efficiency. The regenerative cycle is another modification to increase the efficiency of the Rankine cycle. In many Rankine cycle implementations, the water enters the boiler in the subcooled state, and also, the large difference in temperature between the one at which heat is supplied to the boiler and the fluid temperature will give rise to irreversibilities which will cause the efficiency to drop. In the regenerative cycle, the output of the condenser is heated by some steam tapped from the expander. This causes the overall efficiency to increase, due to the reasons noted above.

Otto Cycle

The Otto Cycle is the idealization for the process found in the reciprocating internal combustion engines which are used by most automobiles. While in an actual engine the gas is released as exhaust, this is found to be a good way to analyze the process. There are, of course, other losses too in the actual engine. For instance, partial combustion and aspiration problems for a high speed engine. The working material in the idealized cycle is an ideal gas, as opposed to the air fuel mixture in an engine.

1. Heat is transferred at constant volume during 1-2.
2. The gas expands reversibly and adiabatically during 2-3, where work is done.
3. Heat is rejected at constant volume at low temperature during 3-4.
4. The gas is compressed reversibly and adiabatically in 4-1.

Analysis

Heat is transferred at constant volume in 1-2, so that Q_1-2 = m c_v(T₂ − T₁). Similarly, the heat rejected in 3-4 is Q_3-4 = m c_v (T₃ − T₄). The thermal efficiency of the Otto cycle is thus

η_th = (Q_1-2 − Q_3-4)/Q_1-2

η_th = 1 − Q_3-4/Q_1-2

η_th = 1 − (T₃ − T₄)/(T₂ − T₁)

Since 2-3 and 4-1 are reversible adiabatic processes involving an ideal gas, we have,

T₂/T₃ = (V₃/V₂)^{γ − 1}

and

T₄/T₁ = (V₁/V₄)^{γ − 1}

But,

V₁ = V₂

and

V₃ = V₄

So, we have

T₂/T₃ = T₁/T₄

Thus,

η_th = 1 − (T₃/T₂)(1 − T₄/T₃)/(1 − T₁/T₂)

Or

η_th = 1 − T₃/T₂

If we introduce the term r_c = V₃/V₂ for the compression ratio, then we have,

η_th = 1 − r_c^{1 − γ}

As can be seen, increasing the compression ratio will improve thermal efficiency. However, increasing the compression ratio causes the peak temperature to go up, which may cause spontaneous, uncontrolled ignition of the fuel, which leads to a shock wave traveling through the cylinder, and is called knocking.

Diesel Cycle

The Diesel cycle is the idealized cycle for compression ignition engines (ones that don't use a spark plug). The difference between the Diesel cycle and the Otto cycle is that heat is supplied at constant pressure.

1. Heat is supplied reversibly at constant pressure in 1-2.
2. Reversible adiabatic expansion during which work is done in 2-3.
3. Heat is rejected reversibly at constant volume in 3-4.
4. Gas is compressed reversibly and adiabatically in 4-1.

Analysis

Heat is transferred to the system at constant pressure during 1-2 so that

Q_in = m c_p (T₂ − T₁)

Heat is rejected by the system at constant volume during 3-4:

Q_out = m c_v (T₃ − T₄)

Thus, the efficiency of the Diesel cycle is

η_th = (Q_in − Q_out)/Q_in

η_th = 1 − Q_out/Q_in

η_th = 1 − (c_v (T₃ − T₄))/(c_p (T₂ − T₁))

η_th = 1 − (1/γ) (T₃ − T₄)/(T₂ − T₁)

$\eta _{th}=1-{\frac {1}{\gamma }}{\frac {T_{4}}{T_{1}}}\left({\frac {{\frac {T_{3}}{T_{4}}}-1}{{\frac {T_{2}}{T_{1}}}-1}}\right)$

We define the cutoff ratio as r_t = V₂/V₁, and since the pressures at 1 and 2 are equal, we have, applying the ideal gas equation, T₂/T₁ = r_t. Now, for the adiabatic processes 2-3 and 4-1 we have,

${\frac {T_{2}}{T_{3}}}=\left({\frac {V_{3}}{V_{2}}}\right)^{\gamma -1}$

${\frac {T_{1}}{T_{4}}}=\left({\frac {V_{4}}{V_{1}}}\right)^{\gamma -1}$

Since V₃ = V₄, we have

${\frac {T_{2}}{T_{1}}}{\frac {T_{4}}{T_{3}}}=\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma -1}$

${\frac {T_{4}}{T_{3}}}=\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma }$

$\eta _{th}=1-{\frac {1}{\gamma }}{\frac {1}{r_{c}^{\gamma -1}}}\left({\frac {r_{t}^{\gamma }-1}{r_{t}-1}}\right)$

Dual Cycle

The dual cycle is sometimes used to approximate actual cycles as the time taken for heat transfer in the engine is not zero for the Otto cycle (so not constant volume). In the Diesel cycle, due to the nature of the combustion process, the heat input does not occur at constant pressure.

Gas Turbine Cycle (or Joule-Brayton Cycle)

Gas turbines are rotary internal combustion engines. As the first stage air is drawn in from outside and compressed using a compressor. Then the fuel is introduced and the mixture is ignited in the combustion chamber. The hot gases are expanded using a turbine which produces work. The output of the turbine is vented outside as exhaust.

The ideal gas turbine cycle is shown above. The four stages are

1. Heat input at constant pressure during 1-2.
2. Reversible adiabatic expansion during 2-3, where work is done.
3. Heat rejection at constant pressure during 3-4.
4. Reversible adiabatic compression during 4-1 where work is consumed.

Large amount of work is consumed in process 4-1 for a gas turbine cycle as the working material (gas) is very compressible. The compressor needs to handle a large volume and achieve large compression ratios.

Analysis

The heat input in a gas turbine cycle is given by Q_in = m c_p (T₂ - T₁) and the heat rejected Q_out = m c_p (T₃ - T₄). Thus the thermal efficiency is given by

$\eta _{th}=1-{\frac {Q_{out}}{Q_{in}}}$

$\eta _{th}=1-\left({\frac {T_{3}-T_{4}}{T_{2}-T_{1}}}\right)$

$\eta _{th}=1-{\frac {T_{4}}{T_{1}}}\left({\frac {{\frac {T_{3}}{T_{4}}}-1}{{\frac {T_{2}}{T_{1}}}-1}}\right)$

Since the adiabatic processes take place between the same pressures, the temperature ratios are the same

$\eta _{th}=1-{\frac {T_{4}}{T_{1}}}=1-{\frac {1}{\left({\frac {p_{1}}{p_{4}}}\right)^{\frac {\gamma -1}{\gamma }}}}$

Or

$\eta _{th}=1-{\frac {1}{r_{p}^{\frac {\gamma -1}{\gamma }}}}$

Where r_p is the pressure ratio and is a fundamental quantity for the gas turbine cycle.

Refrigeration Cycles

The ideal refrigeration cycle is reverse of Carnot cycle, working as a heat pump instead of as a heat engine. However, there are practical difficulties in making such a system work.

The gas refrigeration cycle is used in aircraft to cool cabin air. The ambient air is compressed and then cooled using work from a turbine. The turbine itself uses work from the compressed air, further cooling it. The output of the turbine as well as the air which is used to cool the output of the compressor is mixed and sent to the cabin.

The Rankine vapor-compression cycle is a common alternative to the ideal Carnot cycle. A working material such as Freon or R-134a, called the refrigerant, is chosen based on its boiling point and heat of vaporization. The components of a vapor-compression refrigeration system are the compressor, condenser, the expansion (or throttling) valve, and the evaporator. The working material (in gaseous form) is compressed by the compressor, and its output is cooled to a liquid in the condenser. The output of the condenser is throttled to a lower pressure in the throttling valve, and sent to the evaporator which absorbs heat. The gas from the evaporator is sent to the compressor, completing the cycle.

Standard refrigeration units use the throttling valve instead of a turbine to expand the gas as the work output that would be produced is not significant to justify the cost of a turbine. There are irreversibilities associated with such an expansion, but it is cost effective when construction costs are considered.

---

Engineering Thermodynamics | Thermodynamic Systems | First Law | Second Law | Applications

Further Reading

Further reading and resources:

• Kostic, M. (2008). Sadi Carnot’s Ingenious Reasoning of Ideal Heat-Engine Reversible Cycles (Proceedings of the 4th IASME/WSEAS International Conference on ENERGY, ENVIRONMENT, ECOSYSTEMS and SUSTAINABLE DEVELOPMENT (EEESD'08), Algarve, Portugal, June 11–13, 2008. In NEW ASPECTS OF ENERGY, ENVIRONMENT, ECOSYSTEMS and SUSTAINABLE DEVELOPMENT (Editors: T. Panagopoulos, T. Noronha Vaz , M. D. Carlos Antunes) ed.). WSEAS Press. pp. 159–166. ISBN 978-960-6766-71-8. {{cite book}}: Cite has empty unknown parameter: |coauthors= (help) (full text)
• Thermodynamics
• Engineering Thermodynamics - A Graphical Approach by Dr. Israel Urieli, Ohio University Dept of Mechanical Engineering