Engineering Thermodynamics/Thermodynamic Systems
Thermodynamic System
[edit | edit source]In general, a system is a collection of objects, and there is a lot of subtlety in the way it is defined, as in set theory. However, in thermodynamics, it is a much more straightforward concept.
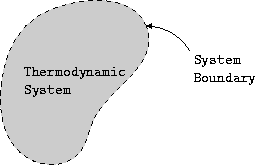
A thermodynamic system is a region of space or a finite quantity that occupies a volume and has a boundary. The surroundings refer to anything external to the system. The imaginary envelope that separates the system from its surroundings is known as the boundary. The boundary is what defines the limits of the system. The boundary can be fixed or moving. The system and its surroundings together constitute the universe.
Another term sometimes used instead of system is control volume. In the case of a closed system, in which the mass of matter inside the system remains constant, the control volume is referred to as control mass. A control volume is said to be enclosed by a control surface.
Proceeding further, the general term system will be used to refer to a thermodynamic system.
Types of Thermodynamic Systems
[edit | edit source]Isolated System
[edit | edit source]An isolated system is a system which does not allow the exchange of neither mass nor energy with its surroundings. An isolated system does not interact with its surroundings at all. The boundary of the system does not allow mass or energy transfer.
A close approximation of an isolated system is a thermos flask which retains the warmth of the liquid, by slowing down the interaction of the liquid and the air outside using a vacuum boundary. The only true isolated system is the universe.
Closed System
[edit | edit source]A closed thermodynamic system is a system which allows the exchange of heat and work with the surroundings but does not permit any exchange of mass across the boundaries. This type of system is also called a non-flow system, due to lack of flow across the boundary. The cylinder and piston of a reciprocating engine with gas in the cylinder is an example of a closed system. Another simple example is a kettle, in which heat is supplied to the kettle but the water contained in it remains constant.
Open System
[edit | edit source]An open thermodynamic system is a system in which allows the exchange of both mass and energy with the surroundings. The mass within the system varies over time. An open system is also called a control volume.
An example of an open system is an air compressor which draws in air from the surroundings, compresses it to a high pressure and then releases it from the system through a nozzle
Adiabatic System
[edit | edit source]An adiabatic system is a system which allows the exchange of work but not heat with its surroundings. The system achieves this with a thermally insulating boundary.
Homogeneous and Heterogeneous Systems
[edit | edit source]Continuum
[edit | edit source]An continuum is a system that contains a continuous distribution of matter. A continuum treats the matter in a system as distributed evenly in space and does regard the action of individual atoms or molecules. Pressure, temperature and other properties are the averages of the properties of many atoms and molecules taken together.
Phase
[edit | edit source]Matter which has is homogenous throughout its physical structure and chemical composition is called its phase. The most commonly observed phases are solid, liquid and gas phases.
Homogeneous System
[edit | edit source]A homogeneous system consists of only a single phase. Pure substances and homogeneous mixtures are examples of heterogeneous systems.
Heterogeneous System
[edit | edit source]A heterogeneous system consists of two or more different phases.
Properties of Pure Substances
[edit | edit source]A cursory review of properties will introduce the variables of thermodynamics to the student. Properties of substances are things such as mass, temperature, volume, and pressure. Properties are used to define the current state of a substance. Several more properties exist to describe substances in thermodynamics, but a stronger understanding of theory is required for their definition and application.
Properties can be intensive, if they are point properties (properties that make sense for a point) or extensive, if they depend on the amount of matter in the system. Examples of extensive properties of systems are mass of system, number of moles of a substance in a system, and overall or total volume of a system. These properties depend on how much matter of the system you measure. Examples of intensive properties are pressure, temperature, density, volume per mass, molar volume (which is volume per mole), and average molecular weight (or molecular mass). These properties are the same regardless of how you vary the amount of mass of the substance.
Properties are like the variables for substances in that their values are all related by an equation. The relationship between properties is expressed in the form of an equation which is called an equation of state. Perhaps the most famous state equation is the Ideal Gas Law. The ideal gas law relates the pressure, volume, and temperature of an ideal gas to one another.
Volume
[edit | edit source]The SI unit for volume is m3.
Volume is an extensive property, but both volume per mass and molar volume are intensive properties since they do not depend on the measured mass of the system. A process during which the volume of the system remains constant is called an isochoric (or isometric) process.
Pressure
[edit | edit source]The SI unit for pressure is Pa (Pascal), which is equivalent to a . Pressure is an intensive property. A process in which pressure remains constant is called isobaric process.
Temperature
[edit | edit source]Temperature, the degree of hotness or coldness of a body is Defined. Based on the zeroth law of thermodynamics, is a fundamental concept of thermodynamics. We know that a body at high temperature will transfer energy to one at lower temperature. Consider two bodies with different temperatures in contact with each other. Net energy transfer will be from the hotter body to the colder body. At some point, the net energy transfer will be zero, and the bodies are said to be in thermal equilibrium. Bodies in thermal equilibrium are defined to have the same temperature.
Systems
[edit | edit source]Classical thermodynamics deals with systems in equilibrium. The equilibrium state is defined by the values of observable quantities in the system. These are called system properties.
The minimum number of variables required to describe the system depends on the complexity or degrees of freedom of the system. Degrees of freedom refer to the number of properties that can be varied independently of each other in a system. Some of the common system variables are pressure, temperature, and density, though any other physical properties may be used.
Consistent with the axiomatic nature of subject development, many of the relationships between physical properties cannot be completely specified without further development of theory. What is good about classical thermodynamics is that many of the axioms stated here can be derived using techniques of statistical thermodynamics. And statistical thermodynamics gives results in many cases where classical thermodynamics fails, such as in the specific heats of gases with many degrees of freedom. In some sense, the relationship between classical and statistical thermodynamics is similar to the one between classical and quantum mechanics, i.e., classical thermodynamics approximates statistical thermodynamics in the macroscopic limit.
Processes
[edit | edit source]A change in the system state is called a process. When the initial and final states of a process are the same, the process is called a cycle. If a process can be run in reverse with no change in the system + surroundings, then the process is called a reversible process. If a process is not reversible it is called an irreversible process.
Isothermal Process
[edit | edit source]An isothermal process is one in which the temperature remains constant. Please note that a process being isothermal does not imply anything about the heat transferred or work done, i.e. heat transfer may take place during an isothermal process. An isothermal process implies that the product of the volume and the pressure is constant for an ideal gas. i.e. PV = Constant
Zeroth Law of Thermodynamics
[edit | edit source]If a system A is in thermal equilibrium with another system B and also with a third system C, then all of the systems are in thermal equilibrium with each other. This is called the zeroth law of thermodynamics. This is how a thermometer works. If a thermometer is placed in a substance for temperature measurement, the thermometer's glass comes into thermal equilibrium with the substance. The glass then comes into thermal equilibrium with the liquid (mercury, alcohol, etc. . . .) inside the thermometer. Because the substance is in thermal equilibrium with the glass and the glass is in thermal equilibrium with the inner liquid, the substance and liquid must be in thermal equilibrium by the zeroth law. And because they are thermally equivalent, they must have the same temperature.
Temperature Measurement
[edit | edit source]Temperature is measured by observing some property of the system which varies with temperature. Such a property is called thermometric property, e.g.:
- The volumes of most liquids increase with temperature. - The length of a metal rod increases as the temperature increases. - The pressure of a constant volume of gas increases with temperature
It is useful to establish a temperature scale so that a cardinal relationship can be established between various systems at different temperatures. This is done by defining the temperature t as a function of a thermometric property X, such that the temperature is a linear function of X, i.e., equal changes in the property X give rise to equal changes in the temperature. Such a linear function is t = a + b X, for which one needs to assign arbitrary temperatures to two values of X to find the values of the constants a and b.
For example, in the case of the Celsius scale, the measurements are based on properties of water at the boiling point and melting point. Suppose the value of the thermometric property is Xb for the normal boiling point and Xm for the normal melting point. Then the temperature is given by t = 100 (X - Xm)/(Xb - Xm), where X is the thermometric property at temperature t, and we have chosen tm = 0 °C and tb = 100 °C. The normal melting and boiling points are the temperatures of melting and boiling at 1 atmosphere pressure.
The major temperature scales are the Celsius (°C), the Fahrenheit (°F) and the Kelvin (K) scales. Note the absence of the ° sign for kelvin—it is not degrees Kelvin, but kelvins, not capitalized when spelled out, and with the normal English plural which was added to the degree when Kelvin was an adjective modifying that unit.
Different thermometers are used for different temperature ranges. As the reader might have guessed by now, this means that the different thermometers will only agree on the fixed points. However, a set of thermometers have been carefully selected and calibrated so that this is not a big issue in practice.
The standard in this case is the International Temperature Scale, which was introduced in 1927, and revised in 1948, 1968, and 1990. The latest scale is denoted by T90 for the Kelvin scale and is defined from 0.65 K upwards. For instance, between 0.65 K and 5.0 K T90 is defined in terms of the vapor-pressure temperature relations of 3He and 4He. The ranges for different materials overlap and any of the valid materials can be used as a standard in the overlapping region.
The Ideal Gas
[edit | edit source]Recall that a thermodynamic system may have a certain substance or material whose quantity can be expressed in mass or moles in an overall volume. These are extensive properties of the system. If the substance is evenly distributed throughout the volume in question, then a value of volume per amount of substance may be used as an intensive property. For an example, for an amount called a mole, volume per mole is typically called molar volume. Also, a volume per mass for a specific substance may be called specific volume. In such cases, an equation of state may relate the three intensive properties, temperature, pressure, and molar or specific volume.
A simple but very useful equation of state is for an ideal gas. The ideal gas is a useful notion in thermodynamics, as it is a simple system that depends on two independent properties. An ideal gas is one that has no intermolecular interactions except for completely elastic collisions with other molecules. For a closed system containing an ideal gas, the state can be specified by giving the values of any two of pressure, temperature, and molar volume.
Consider a system, an ideal gas enclosed in a container. Starting from an initial state 1, where the temperature is T1, its temperature is changed to T2 through a constant pressure process and then a constant molar volume process, then the ratio of pressures is found to be the same as the ratio of molar volumes. Suppose the initial value of the pressure and molar volume are p1 and V1 respectively, and final value of pressure and molar volume are p2 and V2 respectively. Note that we haven't chosen a specific scale for the temperature (like say, the Celsius scale). Now, suppose we were to choose a scale such that T1/T2 = p1/p2, we can show that the value of pV/T is constant for an ideal gas, so that it obeys the gas equation pV = RT, where p is the absolute pressure, V is the molar volume, and R is a constant known as the universal gas constant. The temperature T is the absolute temperature in the ideal gas scale, and the scale is found to be the same as the thermodynamic temperature scale. The thermodynamic temperature scale will be defined after the statement of the second law of thermodynamics.
This equation pV = RT is called the equation of state for an ideal gas, and is known as the ideal gas equation. Most common gases obey the ideal gas equation unless they are compressed or cooled to extreme states, so this is a very useful relation. A similar equation may be written where, for the specific type of gas, specific volume is used instead of molar volume and a specific gas constant is used instead of the universal gas constant. This then writes as pv = mrT.
In the above image, the volume of an ideal gas at two different pressures p1 and p2 is plotted against the temperature in Celsius. If we extrapolate the two straight line graphs, they intersect the temperature axis at a point t0, where t0 = −273.15 °C.
From experiment, it is easy to show that the thermodynamic temperature T is related to the Celsius temperature t by the equation: T = t + 273.15. The zero of thermodynamic temperature scale is 0 K, and its significance will be clear when we discuss the second law of thermodynamics.