Cryptography/Print version
| This is the print version of Cryptography You won't see this message or any elements not part of the book's content when you print or preview this page. |
The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/Cryptography
Introduction
Cryptography is the study of information hiding and verification. It includes the protocols, algorithms and strategies to securely and consistently prevent or delay unauthorized access to sensitive information and enable verifiability of every component in a communication.
Cryptography is derived from the Greek words: kryptós, "hidden", and gráphein, "to write" - or "hidden writing". People who study and develop cryptography are called cryptographers. The study of how to circumvent the use of cryptography for unintended recipients is called cryptanalysis, or codebreaking. Cryptography and cryptanalysis are sometimes grouped together under the umbrella term cryptology, encompassing the entire subject. In practice, "cryptography" is also often used to refer to the field as a whole, especially as an applied science. At the dawn of the 21 century in an ever more interconnected and technological world cryptography started to be ubiquitous as well as the reliance on the benefits it brings, especially the increased security and verifiability.
Cryptography is an interdisciplinary subject, drawing from several fields. Before the time of computers, it was closely related to linguistics. Nowadays the emphasis has shifted, and cryptography makes extensive use of technical areas of mathematics, especially those areas collectively known as discrete mathematics. This includes topics from number theory, information theory, computational complexity, statistics and combinatorics. It is also a branch of engineering, but an unusual one as it must deal with active, intelligent and malevolent opposition.
An example of the sub-fields of cryptography is steganography — the study of hiding the very existence of a message, and not necessarily the contents of the message itself (for example, microdots, or invisible ink) — and traffic analysis, which is the analysis of patterns of communication in order to learn secret information.
When information is transformed from a useful form of understanding to an opaque form of understanding, this is called encryption. When the information is restored to a useful form, it is called decryption. Intended recipients or authorized use of the information is determined by whether the user has a certain piece of secret knowledge. Only users with the secret knowledge can transform the opaque information back into its useful form. The secret knowledge is commonly called the key, though the secret knowledge may include the entire process or algorithm that is used in the encryption/decryption. The information in its useful form is called plaintext (or cleartext); in its encrypted form it is called ciphertext. The algorithm used for encryption and decryption is called a cipher (or cypher).
Common goals in cryptography
[edit | edit source]In essence, cryptography concerns four main goals. They are:
- message confidentiality (or privacy): Only an authorized recipient should be able to extract the contents of the message from its encrypted form. Resulting from steps to hide, stop or delay free access to the encrypted information.
- message integrity: The recipient should be able to determine if the message has been altered.
- sender authentication: The recipient should be able to verify from the message, the identity of the sender, the origin or the path it traveled (or combinations) so to validate claims from emitter or to validated the recipient expectations.
- sender non-repudiation: The remitter should not be able to deny sending the message.
Not all cryptographic systems achieve all of the above goals. Some applications of cryptography have different goals; for example some situations require repudiation where a participant can plausibly deny that they are a sender or receiver of a message, or extend this goals to include variations like:
- message access control: Who are the valid recipients of the message.
- message availability: By providing means to limit the validity of the message, channel, emitter or recipient in time or space.
Common forms of cryptography
[edit | edit source]Cryptography involves all legitimate users of information having the keys required to access that information.
- If the sender and recipient must have the same key in order to encode or decode the protected information, then the cipher is a symmetric key cipher since everyone uses the same key for the same message. The main problem is that the secret key must somehow be given to both the sender and recipient privately. For this reason, symmetric key ciphers are also called private key (or secret key) ciphers.
- If the sender and recipient have different keys respective to the communication roles they play, then the cipher is an asymmetric key cipher as different keys exist for encoding and decoding the same message. It is also called public key encryption as the user publicly distributes one of the keys without a care for secrecy. In the case of confidential messages to the user, they distribute the encryption key. Asymmetric encryption relies on the fact that possession of the encryption key will not reveal the decryption key.
- Digital Signatures are a form of authentication with some parallels to public-key encryption. The two keys are the public verification key and the secret signature key. As in public-key encryption, the verification key can be distributed to other people, with the same caveat that the distribution process should in some way authenticate the owner of the secret key. Security relies on the fact that possession of the verification key will not reveal the signature key.
- Hash Functions are unkeyed message digests with special properties.
Other:
Poorly designed, or poorly implemented, crypto systems achieve them only by accident or bluff or lack of interest on the part of the opposition. Users can, and regularly do, find weaknesses in even well-designed cryptographic schemes from those of high reputation.
Even with well designed, well implemented, and properly used crypto systems, some goals aren't practical (or desirable) in some contexts. For example, the sender of the message may wish to be anonymous, and would therefore deliberately choose not to bother with non-repudiation. Alternatively, the system may be intended for an environment with limited computing resources, or message confidentiality might not be an issue.
In classical cryptography, messages are typically enciphered and transmitted from one person or group to some other person or group. In modern cryptography, there are many possible options for "sender" or "recipient". Some examples, for real crypto systems in the modern world, include:
- a computer program running on a local computer,
- a computer program running on a 'nearby' computer which 'provides security services' for users on other nearby systems,
- a human being (usually understood as 'at the keyboard'). However, even in this example, the presumed human is not generally taken to actually encrypt or sign or decrypt or authenticate anything. Rather, he or she instructs a computer program to perform these actions. This 'blurred separation' of human action from actions which are presumed (without much consideration) to have 'been done by a human' is a source of problems in crypto system design, implementation, and use. Such problems are often quite subtle and correspondingly obscure; indeed, generally so, even to practicing cryptographers with knowledge, skill, and good engineering sense.
When confusion on these points is present (e.g., at the design stage, during implementation, by a user after installation, or ...), failures in reaching each of the stated goals can occur quite easily—often without notice to any human involved, and even given a perfect cryptosystem. Such failures are most often due to extra-cryptographic issues; each such failure demonstrates that good algorithms, good protocols, good system design, and good implementation do not alone, nor even in combination, provide 'security'. Instead, careful thought is required regarding the entire crypto system design and its use in actual production by real people on actual equipment running 'production' system software (e.g., operating systems) -- too often, this is absent or insufficient in practice with real-world crypto systems.
Although cryptography has a long and complex history, it wasn't until the 19th century that it developed anything more than ad hoc approaches to either encryption or cryptanalysis (the science of finding weaknesses in crypto systems). Examples of the latter include Charles Babbage's Crimean War era work on mathematical cryptanalysis of polyalphabetic ciphers, repeated publicly rather later by the Prussian Kasiski. During this time, there was little theoretical foundation for cryptography; rather, understanding of cryptography generally consisted of hard-won fragments of knowledge and rules of thumb; see, for example, Auguste Kerckhoffs' crypto writings in the latter nineteenth century. An increasingly mathematical trend accelerated up to World War II (notably in William F. Friedman's application of statistical techniques to cryptography and in Marian Rejewski's initial break into the German Army's version of the Enigma system). Both cryptography and cryptanalysis have become far more mathematical since WWII. Even then, it has taken the wide availability of computers, and the Internet as a communications medium, to bring effective cryptography into common use by anyone other than national governments or similarly large enterprise.
External links
History
Classical Cryptography
[edit | edit source]The earliest known use of cryptography is found in non-standard hieroglyphs carved into monuments from Egypt's Old Kingdom (ca 4500 years ago). These are not thought to be serious attempts at secret communications, however, but rather to have been attempts at mystery, intrigue, or even amusement for literate onlookers. These are examples of still another use of cryptography, or of something that looks (impressively if misleadingly) like it. Later, Hebrew scholars made use of simple Substitution ciphers (such as the Atbash cipher) beginning perhaps around 500 to 600 BCE. Cryptography has a long tradition in religious writing likely to offend the dominant culture or political authorities.
The Greeks of Classical times are said to have known of ciphers (e.g., the scytale transposition cypher claimed to have been used by the Spartan military). Herodutus tells us of secret messages physically concealed beneath wax on wooden tablets or as a tattoo on a slave's head concealed by regrown hair (these are not properly examples of cryptography per se; see secret writing). The Romans certainly did (e.g., the Caesar cipher and its variations). There is ancient mention of a book about Roman military cryptography (especially Julius Caesar's); it has been, unfortunately, lost.
In India, cryptography was apparently well known. It is recommended in the Kama Sutra as a technique by which lovers can communicate without being discovered. This may imply that cryptanalytic techniques were less than well developed in India ca 500 CE.
Cryptography became (secretly) important still later as a consequence of political competition and religious analysis. For instance, in Europe during and after the Renaissance, citizens of the various Italian states, including the Papacy, were responsible for substantial improvements in cryptographic practice (e.g., polyalphabetic ciphers invented by Leon Alberti ca 1465). And in the Arab world, religiously motivated textual analysis of the Koran led to the invention of the frequency analysis technique for breaking monoalphabetic substitution cyphers sometime around 1000 CE.
Cryptography, cryptanalysis, and secret agent betrayal featured in the Babington plot during the reign of Queen Elizabeth I which led to the execution of Mary, Queen of Scots. And an encrypted message from the time of the Man in the Iron Mask (decrypted around 1900 by Étienne Bazeries) has shed some, regrettably non-definitive, light on the identity of that legendary, and unfortunate, prisoner. Cryptography, and its misuse, was involved in the plotting which led to the execution of Mata Hari and even more reprehensibly, if possible, in the travesty which led to Dreyfus' conviction and imprisonment, both in the early 20th century. Fortunately, cryptographers were also involved in setting Dreyfus free; Mata Hari, in contrast, was shot.
Mathematical cryptography leapt ahead (also secretly) after World War I. Marian Rejewski, in Poland, attacked and 'broke' the early German Army Enigma system (an electromechanical rotor cypher machine) using theoretical mathematics in 1932. The break continued up to '39, when changes in the way the German Army's Enigma machines were used required more resources than the Poles could deploy. His work was extended by Alan Turing, Gordon Welchman, and others at Bletchley Park beginning in 1939, leading to sustained breaks into several other of the Enigma variants and the assorted networks for which they were used. US Navy cryptographers (with cooperation from British and Dutch cryptographers after 1940) broke into several Japanese Navy crypto systems. The break into one of them famously led to the US victory in the Battle of Midway. A US Army group, the SIS, managed to break the highest security Japanese diplomatic cipher system (an electromechanical 'stepping switch' machine called Purple by the Americans) even before WWII began. The Americans referred to the intelligence resulting from cryptanalysis, perhaps especially that from the Purple machine, as 'Magic'. The British eventually settled on 'Ultra' for intelligence resulting from cryptanalysis, particularly that from message traffic enciphered by the various Enigmas. An earlier British term for Ultra had been 'Boniface'.
World War II Cryptography
[edit | edit source]By World War II mechanical and electromechanical cryptographic cipher machines were in wide use, but they were impractical manual systems. Great advances were made in both practical and mathematical cryptography in this period, all in secrecy. Information about this period has begun to be declassified in recent years as the official 50-year (British) secrecy period has come to an end, as the relevant US archives have slowly opened, and as assorted memoirs and articles have been published.
The Germans made heavy use (in several variants) of an electromechanical rotor based cypher system known as Enigma. The German military also deployed several mechanical attempts at a one-time pad. Bletchley Park called them the Fish cyphers, and Max Newman and colleagues designed and deployed the world's first programmable digital electronic computer, the Colossus, to help with their cryptanalysis. The German Foreign Office began to use the one-time pad in 1919; some of this traffic was read in WWII partly as the result of recovery of some key material in South America that was insufficiently carefully discarded by a German courier.
The Japanese Foreign Office used a locally developed electrical stepping switch based system (called Purple by the US), and also used several similar machines for attaches in some Japanese embassies. One of these was called the 'M-machine' by the US, another was referred to as 'Red'. All were broken, to one degree or another by the Allies.
Other cipher machines used in WWII included the British Typex and the American SIGABA; both were electromechanical rotor designs similar in spirit to the Enigma.
Modern Cryptography
[edit | edit source]The era of modern cryptography really begins with Claude Shannon, arguably the father of mathematical cryptography. In 1949 he published the paper Communication Theory of Secrecy Systems in the Bell System Technical Journal, and a little later the book Mathematical Theory of Communication with Warren Weaver. These, in addition to his other works on information and communication theory established a solid theoretical basis for cryptography and for cryptanalysis. And with that, cryptography more or less disappeared into secret government communications organizations such as the NSA. Very little work was again made public until the mid '70s, when everything changed.
1969 saw two major public (i.e., non-secret) advances. First was the DES (Data Encryption Standard) submitted by IBM, at the invitation of the National Bureau of Standards (now NIST), in an effort to develop secure electronic communication facilities for businesses such as banks and other large financial organizations. After 'advice' and modification by the NSA, it was adopted and published as a FIPS Publication (Federal Information Processing Standard) in 1977 (currently at FIPS 46-3). It has been made effectively obsolete by the adoption in 2001 of the Advanced Encryption Standard, also a NIST competition, as FIPS 197. DES was the first publicly accessible cypher algorithm to be 'blessed' by a national crypto agency such as NSA. The release of its design details by NBS stimulated an explosion of public and academic interest in cryptography. DES, and more secure variants of it (such as 3DES or TDES; see FIPS 46-3), are still used today, although DES was officially supplanted by AES (Advanced Encryption Standard) in 2001 when NIST announced the selection of Rijndael, by two Belgian cryptographers. DES remains in wide use nonetheless, having been incorporated into many national and organizational standards. However, its 56-bit key-size has been shown to be insufficient to guard against brute-force attacks (one such attack, undertaken by cyber civil-rights group The Electronic Frontier Foundation, succeeded in 56 hours—the story is in Cracking DES, published by O'Reilly and Associates). As a result, use of straight DES encryption is now without doubt insecure for use in new crypto system designs, and messages protected by older crypto systems using DES should also be regarded as insecure. The DES key size (56-bits) was thought to be too small by some even in 1976, perhaps most publicly Whitfield Diffie. There was suspicion that government organizations even then had sufficient computing power to break DES messages and that there may be a back door due to the lack of randomness in the 'S' boxes.
Second was the publication of the paper New Directions in Cryptography by Whitfield Diffie and Martin Hellman. This paper introduced a radically new method of distributing cryptographic keys, which went far toward solving one of the fundamental problems of cryptography, key distribution. It has become known as Diffie-Hellman key exchange. The article also stimulated the almost immediate public development of a new class of enciphering algorithms, the asymmetric key algorithms.
Prior to that time, all useful modern encryption algorithms had been symmetric key algorithms, in which the same cryptographic key is used with the underlying algorithm by both the sender and the recipient who must both keep it secret. All of the electromechanical machines used in WWII were of this logical class, as were the Caesar and Atbash cyphers and essentially all cypher and code systems throughout history. The 'key' for a code is, of course, the codebook, which must likewise be distributed and kept secret.
Of necessity, the key in every such system had to be exchanged between the communicating parties in some secure way prior to any use of the system (the term usually used is 'via a secure channel') such as a trustworthy courier with a briefcase handcuffed to a wrist, or face-to-face contact, or a loyal carrier pigeon. This requirement rapidly becomes unmanageable when the number of participants increases beyond some (very!) small number, or when (really) secure channels aren't available for key exchange, or when, as is sensible crypto practice keys are changed frequently. In particular, a separate key is required for each communicating pair if no third party is to be able to decrypt their messages. A system of this kind is also known as a private key, secret key, or conventional key cryptosystem. D-H key exchange (and succeeding improvements) made operation of these systems much easier, and more secure, than had ever been possible before.
In contrast, with asymmetric key encryption, there is a pair of mathematically related keys for the algorithm, one of which is used for encryption and the other for decryption. Some, but not all, of these algorithms have the additional property that one of the keys may be made public since the other cannot be (by any currently known method) deduced from the 'public' key. The other key in these systems is kept secret and is usually called, somewhat confusingly, the 'private' key. An algorithm of this kind is known as a public key / private key algorithm, although the term asymmetric key cryptography is preferred by those who wish to avoid the ambiguity of using that term for all such algorithms, and to stress that there are two distinct keys with different secrecy requirements.
As a result, for those using such algorithms, only one key pair is now needed per recipient (regardless of the number of senders) as possession of a recipient's public key (by anyone whomsoever) does not compromise the 'security' of messages so long as the corresponding private key is not known to any attacker (effectively, this means not known to anyone except the recipient). This unanticipated, and quite surprising, property of some of these algorithms made possible, and made practical, widespread deployment of high quality crypto systems which could be used by anyone at all. Which in turn gave government crypto organizations worldwide a severe case of heartburn; for the first time ever, those outside that fraternity had access to cryptography that wasn't readily breakable by the 'snooper' side of those organizations. Considerable controversy, and conflict, began immediately. It has not yet subsided. In the US, for example, exporting strong cryptography remains illegal; cryptographic methods and techniques are classified as munitions. Until 2001 'strong' crypto was defined as anything using keys longer than 40 bits—the definition was relaxed thereafter. (See S Levy's Crypto for a journalistic account of the policy controversy in the US).
Note, however, that it has NOT been proven impossible, for any of the good public/private asymmetric key algorithms, that a private key (regardless of length) can be deduced from a public key (or vice versa). Informed observers believe it to be currently impossible (and perhaps forever impossible) for the 'good' asymmetric algorithms; no workable 'companion key deduction' techniques have been publicly shown for any of them. Note also that some asymmetric key algorithms have been quite thoroughly broken, just as many symmetric key algorithms have. There is no special magic attached to using algorithms which require two keys.
In fact, some of the well respected, and most widely used, public key / private key algorithms can be broken by one or another cryptanalytic attack and so, like other encryption algorithms, the protocols within which they are used must be chosen and implemented carefully to block such attacks. Indeed, all can be broken if the key length used is short enough to permit practical brute force key search; this is inherently true of all encryption algorithms using keys, including both symmetric and asymmetric algorithms.
This is an example of the most fundamental problem for those who wish to keep their communications secure; they must choose a crypto system (algorithms + protocols + operation) that resists all attack from any attacker. There being no way to know who those attackers might be, nor what resources they might be able to deploy, nor what advances in cryptanalysis (or its associated mathematics) might in future occur, users may ONLY do the best they know how, and then hope. In practice, for well designed / implemented / used crypto systems, this is believed by informed observers to be enough, and possibly even enough for all(?) future attackers. Distinguishing between well designed / implemented / used crypto systems and crypto trash is another, quite difficult, problem for those who are not themselves expert cryptographers. It is even quite difficult for those who are.
Revision of modern history
[edit | edit source]In recent years public disclosure of secret documents held by the UK government has shown that asymmetric key cryptography, D-H key exchange, and the best known of the public key / private key algorithms (i.e., what is usually called the RSA algorithm), all seem to have been developed at a UK intelligence agency before the public announcement by Diffie and Hellman in '76. GCHQ has released documents claiming that they had developed public key cryptography before the publication of Diffie and Hellman's paper. Various classified papers were written at GCHQ during the 1960s and 1970s which eventually led to schemes essentially identical to RSA encryption and to Diffie-Hellman key exchange in 1973 and 1974. Some of these have now been published, and the inventors (James Ellis, Clifford Cocks, and Malcolm Williamson) have made public (some of) their work.
Classical Cryptography
Cryptography has a long and colorful history from Caesar's encryption in first century BC to the 20th century.
There are two major principles in classical cryptography: transposition and substitution.
Transposition ciphers
[edit | edit source]Lets look first at transposition, which is the changing in the position of the letters in the message such as a simple writing backwards
Plaintext: THE PANEL IN THE WALL MOVES
Encrypted: EHT LENAP NI EHT LLAW SEVOM
or as in a more complex transposition such as:
THEPAN
ELINTH
EWALLM
OVESAA
then take the columns:
TEEO HLWV EIAE PNLS ATLA NHMA
(the extra letters are called space fillers) The idea in transposition is NOT to randomize it but to transform it to something that is not recognizable with a reversible algorithm (an algorithm is just a procedure, reversible so your correspondent can read the message).
We discuss transposition ciphers in much more detail in a later chapter, Cryptography/Transposition ciphers.
Substitution ciphers
[edit | edit source]The second most important principle is substitution. That is, substituting a Symbol for a letter of your plaintext (or word or even sentence). Slang even can sometimes be a form of cipher (the symbols replacing your plaintext), ever wonder why your parents never understood you? Slang, though, is not something you would want to store a secret in for a long time. In WWII, there were Navajo CodeTalkers who passed along info from unit to unit. From what I hear (someone verify this) the Navajo language was a very exclusive almost unknown and unwritten language. So the Japanese were not able to decipher it.
Even though this is a very loose example of substitution, whatever works works.
Caesar Cipher
[edit | edit source]One of the most basic methods of encryption is the use of Caesar Ciphers. It simply consist in shifting the alphabet over a few characters and matching up the letters.
The classical example of a substitution cipher is a shifted alphabet cipher
Alphabet: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher: BCDEFGHIJKLMNOPQRSTUVWXYZA
Cipher2: CDEFGHIJKLMNOPQRSTUVWXYZAB
etc...
Example:(using cipher 2)
Plaintext: THE PANEL IN THE WALL MOVES
Encrypted: VJG RCPGN KP VJG YCNN OQXGU
If this is the first time you've seen this it may seem like a rather secure cipher, but it's not. In fact this by itself is very insecure. For a time in the 1500-1600s this was the most secure (mainly because there were many people who were illiterate) but a man (old what's his name) in the 18th century discovered a way to crack (find the hidden message) of every cipher of this type he discovered frequency analysis.
We discuss substitution ciphers in much more detail in a later chapter, Cryptography/Substitution ciphers.
Frequency Analysis
[edit | edit source]In the shifted alphabet cipher or any simple randomized cipher, the same letter in the cipher replaces each of the same ones in your message (e.g. 'A' replaces all 'D's in the plaintext, etc.). The weakness is that English uses certain letters more than any other letter in the alphabet. 'E' is the most common, etc. Here's an exercise count all of each letter in this article. You'll find that in the previous sentence there are 2 'H's,7 'E's, 3 'R's, 3 'S's, etc. By far 'E' is the most common letter; here are the other frequencies [Frequency tables|http://rinkworks.com/words/letterfreq.shtml]. Basically you experiment with replacing different symbols with letters (the most common with 'E', etc.).
Encrypted: VJG TCKP KP URCKP
First look for short words with limited choices of words, such as 'KP' this may be at, in, to, or, by, etc. Let us select in. Replace 'K' with 'I' and 'P' with 'N'.
Encrypted: VJG TCIN IN URCIN
Next select VJG this is most likely the (since the huge frequency of 'the' in a normal sentence, check a couple of the preceding sentences).
Encrypted: THE TCIN IN URCIN
generally this in much easier in long messages the plaintext is 'THE RAIN IN SPAIN'
We discuss many different ways to "attack", "break", and "solve" encrypted messages in a later section of this book, "Part III: Cryptanalysis", which includes a much more detailed section on Cryptography/Frequency analysis.
Combining transposition and substitution
[edit | edit source]A more secure encryption is a transposed substitution cipher.
Take the above message in encrypted form
Encrypted:VJG RCPGN KP VJG YCNN OQXGU
now spiral transpose it
VJGRC
NNOQP
CAAXG
YUNGN
GJVPK
The message starts in the upper right corner and spirals to the center (again the AA is a filler) Now take the columns:
VNCYG JNAUJ GOANV RQXGP CPGNK
Now this is more resistant to Frequency analysis, see what we did before that started recognizable patterns results in:
TNCYE HNAUH EOANT RQXEN CNENK
A problem for people who crack codes.
Multiliteral systems
[edit | edit source]The vast majority of classical ciphers are "uniliteral" -- they encrypt a plaintext 1 letter at a time, and each plaintext letter is encrypted to a single corresponding ciphertext letter.
A multiliteral system is one where the ciphertext unit is more than one character in length. The major types of multiliteral systems are:[1]
- biliteral systems: 2 letters of ciphertext per letter of plaintext
- dinomic systems: 2 digits of ciphertext per letter of plaintext
- Triliteral systems: 3 letters of ciphertext per letter of plaintext
- trinomic systems: 3 digits of ciphertext per letter of plaintext
- monome-dinome systems, also called straddling checkerboard systems: 1 digit of ciphertext for some plaintext letters, 2 digits of ciphertext for the remaining plaintext letters.
- biliteral with variants and dinomic with variants systems: several ciphertext values decode to the same plaintext letter (homophonic substitution cipher)
- Syllabary square systems: 2 letters or 2 digits of ciphertext decode to an entire syllable or a single character of plaintext.[2]
Quantum Cryptography
While in the year 2001, Quantum Cryptography was only a future concept. Since not much was known of how capable a quantum computer would be, but even then it was understood that if at all cost-effective, the technology would have only niche applications. By 2024 the technology is yet to prove itself usable in practical terms. Specific algorithms have to be created for yet to be standardized hardware.
Quantum cryptography deals with three distinct issues:
1 - Since the quantum machines will not be available or standardized in a very near future, let's say by 2035, theoretical efforts are being made in and proofing standard cryptographic practices against brute force attacks using these new systems. As we enter the often referred as post-quantum cryptography, cryptographers raised concern regarding the technology impact on cryptography due to the potential vulnerabilities of general use cryptographic systems to quantum attacks, particularly those facilitated by Shor's algorithm, which can efficiently factor large numbers and compute discrete logarithms—the mathematical foundations of many public-key crypto systems as the reliance (expectation) of some cryptographic systems that consumer level technology will have difficulty in solving certain mathematical problems in useful (to get to the secret) time scales. Something that is specifically eroded by quantum parallelism and Grover's algorithm. Creating a need for development of post-quantum cryptography (PQC) algorithms.
2 - It is so crucial to develop new algorithms that ca n not only work but makes use of the new quantum computers specifications. Today (2024) advances are specially being made in hardware for secure signal transmission, protection, and speed using quantum properties.
3 - Lastly, verifying that development of the quantum computing technology and quantum-resistant algorithms as to prevent these machines to break the security expectations of legacy systems (much like computers in general made easy work of non-digital cryptography relegating, for example as we saw with the German Enigma machines).
With the new technology comes new terminology like QBit Cryptanalysis, and the other is Quantum Key Exchange (which is the most common use of the term, and I will discuss here)
Quantum Key Exchange
[edit | edit source]With Quantum Key Exchange, also called quantum key distribution (QKD),[3] you use through-air free-space optical links[4][5] or a single optical fiber to send a single photon at a time orientated to one certain angle of four; we can describe them as horizontally polarized ( - ), vertically polarized ( | ), Ordinary ( \ ) or Sinister ( / ) To detect these photons, you can use either an ordinary filter ( \ slot) or a vertical filter ( | slot)
An ordinary filter has the properties that it will always pass an ordinary polarized photon, and always block a sinister polarized photon (this is because the photon is correctly aligned for the slot in the Ordinary case, and at to the slot for the Sinister photon.
A vertical filter has similar properties for its two associated photons - it will always pass a vertical photon, and always block a horizontal one.
This leaves four cases: '|' and '-' for an ordinary filter, and '\' and '/' for a vertical one. The problem is - nobody knows! they might make it though the slot, they might not, and it is entirely random.
For this reason, the sender will send 'n' photons to the recipient, and the recipient will then report back which of the two possible filters (chosen at random) he tried.
If the recipient guessed the right filter, he now knows which one of two possible orientations the photon was in. if he guessed wrong, he has no idea - so the sender responds to the recipient's list with a second list - of the decisions the recipient got right. By discarding the "wrong" filter choices, both sender and recipient now know which of two possible choices each of the photons received were actually matched to - and can convert pass/fail into logic 1 or 0 for a binary set (and this can then be used as an encryption key)
However, this *only* works if the cable between the sender and the recipient is completely unbroken - because it is impossible to route, regenerate or otherwise manipulate the photons sent without losing the delicate orientation information that is the hub of the scheme.
Anybody who tries to measure the photons en route must pick the correct filter - if he picks the wrong one, he is unable to tell the difference between a pass and a misaligned photon that happens to have gotten though the slot - and indeed, a block and a misaligned photon that was blocked. If he picks wrongly, he cannot tell what orientation the photon was in, and the eventual conversation between the recipient and sender as to orientation of filters will cause there to be differences between the two sets of data - and reveal an eavesdropper has intercepted photons.
There are obvious problems with this scheme. the first is that sending a single photon down a light pipe can be unreliable - sometimes, they fail to reach the recipient and are read as a false "block". The second is that the obvious attack on this is a man-in-the-middle one - the attacker intercepts both the light pipe and the out-of-band data channel used for the discussion of filters and acceptance lists - then negotiates different Quantum key Exchange keysets with both the sender and the recipient independently. by converting the encrypted data between the keys each is expecting to see, he can read the message en route (provided of course there is no way that either party can verify the transmissions in a way the m-i-t-m cannot intercept and replace with his own doctored version)
However, the problems have not stopped a commercial company selling a product which relies on QKE for its operation.
For further reading
[edit | edit source]- ↑ Field Manual 34-40-2 "Chapter 5: Monoalphabetic Multiliteral Substitution Systems".
- ↑ "The Syllabary Cipher".
- ↑ Mart Haitjema. "A Survey of the Prominent Quantum Key Distribution Protocols". 2007.
- ↑ Jian-Yu Wang et. al. "Direct and full-scale experimental verifications towards ground–satellite quantum key distribution". 2012.
- ↑ Sebastian Nauerth et. al. "Air-to-ground quantum communication". 2013.
- Cryptodox: quantum cryptography
- Serious Flaw Emerges In Quantum Cryptography
- Quantiki: quantum key distribution
- "Commercial Quantum Cryptography Satellites Coming"
- "Breaking Quantum Cryptography's 150-Kilometer Limit: Scientists want to put an unbreakable-code generator on the International Space Station"
- "Is quantum key distribution safe against MITM attacks too?"
- "Quantum key distribution simulation"
Timeline of Notable Events
The desire to keep stored or send information secret dates back into antiquity. As society developed so did the application of cryptography. Below is a timeline of notable events related to cryptography.
BCE
[edit | edit source]- 3500s - The Sumerians develop cuneiform writing and the Egyptians develop hieroglyphic writing.
- 1500s - The Phoenicians develop an alphabet
- 600-500 - Hebrew scholars make use of simple monoalphabetic substitution ciphers (such as the Atbash cipher)
- c. 400 - Spartan use of scytale (alleged)
- c. 400BCE - Herodotus reports use of steganography in reports to Greece from Persia (tatoo on shaved head)
- 100-0 - Notable Roman ciphers such as the Caeser cipher.
1 - 1799 CE
[edit | edit source]- ca 1000 - Frequency analysis leading to techniques for breaking monoalphabetic substitution ciphers. It was probably developed among the Arabs, and was likely motivated by textual analysis of the Koran.
- 1450 - The Chinese develop wooden block movable type printing
- 1450-1520 - The Voynich manuscript, an example of a possibly encrypted illustrated book, is written.
- 1466 - Leone Battista Alberti invents polyalphabetic cipher, also the first known mechanical cipher machine
- 1518 - Johannes Trithemius' book on cryptology
- 1553 - Belaso invents the (misnamed) Vigenère cipher
- 1585 - Vigenère's book on ciphers
- 1641 - Wilkins' Mercury (English book on cryptography)
- 1586 - Cryptanalysis used by spy master Sir Francis Walsingham to implicate Mary Queen of Scots in the Babington Plot to murder Queen Elizabeth I of England. Queen Mary was eventually executed.
- 1614 - Scotsman John Napier (1550-1617) published a paper outlining his discovery of the logarithm. Napier also invented an ingenious system of moveable rods (referred to as Napier's Rods or Napier's bones) which were a precursor of the slide rule. These were based on logarithms and allowed the operator to multiply, divide and calculate square and cube roots by moving the rods around and placing them in specially constructed boards.
- 1793 - Claude Chappe establishes the first long-distance semaphore "telegraph" line
- 1795 - Thomas Jefferson invents the Jefferson disk cipher, reinvented over 100 years later by Etienne Bazeries and widely used a a tactical cypher by the US Army.
1800-1899
[edit | edit source]- 1809-14 George Scovell's work on Napoleonic ciphers during the Peninsular War
- 1831 - Joseph Henry proposes and builds an electric telegraph
- 1835 - Samuel Morse develops the Morse code.
- c. 1854 - Babbage's method for breaking polyalphabetic cyphers (pub 1863 by Kasiski); the first known break of a polyaphabetic cypher. Done for the English during the Crimean War, a general attack on Vigenère's autokey cipher (the 'unbreakable cypher' of its time) as well as the much weaker cypher that is today termed "the Vigenère cypher". The advance was kept secret and was, in essence, reinvented somewhat later by the Prussian Friedrich Kasiski, after whom it is named.
- 1854 - Wheatstone invents Playfair cipher
- 1883 - Auguste Kerckhoffs publishes La Cryptographie militare, containing his celebrated "laws" of cryptography
- 1885 - Beale ciphers published
- 1894 - The Dreyfus Affair in France involves the use of cryptography, and its misuse, re: false documents.
1900 - 1949
[edit | edit source]- c 1915 - William Friedman applies statistics to cryptanalysis ( coincidence counting, etc.)
- 1917 - Gilbert Vernam develops first practical implementation of a teletype cipher, now known as a stream cipher and, later, with Mauborgne the one-time pad
- 1917 - Zimmermann telegram intercepted and decrypted, advancing U.S. entry into World War I
- 1919 - Weimar Germany Foreign Office adopts (a manual) one-time pad for some traffic
- 1919 - Hebern invents/patents first rotor machine design -- Damm, Scherbius and Koch follow with patents the same year
- 1921 - Washington Naval Conference - U.S. negotiating team aided by decryption of Japanese diplomatic telegrams
- c. 1924 - MI8 (Yardley, et al.) provide breaks of assorted traffic in support of US position at Washington Naval Conference
- c. 1932 - first break of German Army Enigma machine by Rejewski in Poland
- 1929 - U.S. Secretary of State Henry L. Stimson shuts down State Department cryptanalysis "Black Chamber", saying "Gentlemen do not read each other's mail."
- 1931 - The American Black Chamber by Herbert O. Yardley is published, revealing much about American cryptography
- 1940 - break of Japan's Purple machine cipher by SIS team
- December 7, 1941 - U.S. Naval base at Pearl Harbor surprised by Japanese attack, despite U.S. breaks into several Japanese cyphers. U.S. enters World War II
- June 1942 - Battle of Midway. Partial break into Dec 41 edition of JN-25 leads to successful ambush of Japanese carriers and to the momentum killing victory.
- April 1943 - Admiral Yamamoto, architect of Pearl Harbor attack, is assassinated by U.S. forces who know his itinerary from decrypted messages
- April 1943 - Max Newman, Wynn-Williams, and their team (including Alan Turing) at the secret Government Code and Cypher School ('Station X'), Bletchley Park, Bletchley, England, complete the "Heath Robinson". This is a specialized machine for cypher-breaking, not a general-purpose calculator or computer.
- December 1943 - The Colossus was built, by Dr Thomas Flowers at The Post Office Research Laboratories in London, to crack the German Lorenz cipher (SZ42). Colossus was used at Bletchley Park during WW II - as a successor to April's 'Robinson's. Although 10 were eventually built, unfortunately they were destroyed immediately after they had finished their work - it was so advanced that there was to be no possibility of its design falling into the wrong hands. The Colossus design was the first electronic digital computer and was somewhat programmable. A epoch in machine capability.
- 1944 - patent application filed on SIGABA code machine used by U.S. in WW II. Kept secret, finally issued in 2001
- 1946 - VENONA's first break into Soviet espionage traffic from early 1940s
- 1948 - Claude Shannon writes a paper that establishes the mathematical basis of information theory
- 1949 - Shannon's Communication Theory of Secrecy Systems pub in Bell Labs Technical Journal, based on work done during WWII.
1950 - 1999
[edit | edit source]- 1951 - U.S. National Security Agency founded, subsuming the US Army and US Navy 'girls school' departments
- 1968 - John Anthony Walker walks into the Soviet Union's embassy in Washington and sells information on KL-7 cipher machine. The Walker spy ring operates until 1985
- 1964 - David Kahn's The Codebreakers is published
- June 8, 1967 - USS Liberty incident in which a U.S. SIGINT ship is attacked by Israel, apparently by mistake, though some continue to dispute this
- January 23, 1968 - USS Pueblo, another SIGINT ship, is captured by North Korea
- 1969 - The first hosts of ARPANET, Internet's ancestor, are connected
- 1974? - Horst Feistel develops the Feistel network block cipher design at IBM
- 1976 - the Data Encryption Standard was published as an official Federal Information Processing Standard (FIPS) for the US
- 1976 - Diffie and Hellman publish New Directions in Cryptography article
- 1977- RSA public key encryption invented at MIT
- 1981 - Richard Feynman proposes quantum computers. The main application he had in mind was the simulation of quantum systems, but he also mentioned the possibility of solving other problems.
- 1986 In the wake of an increasing number of break-ins to government and corporate computers, the US Congress passes the Computer Fraud and Abuse Act, which makes it a crime to break into computer systems. The law, however, does not cover juveniles.
- 1988 - First optical chip developed, it uses light instead of electricity to increase processing speed.
- 1989 - Tim Berners-Lee and Robert Cailliau built the prototype system which became the World Wide Web at CERN
- 1991 - Phil Zimmermann releases the public key encryption program PGP along with its source code, which quickly appears on the Internet.
- 1992 - Release of the movie Sneakers (film)|Sneakers, in which security experts are blackmailed into stealing a universal decoder for encryption systems (no such decoder is known, likely because it is impossible).
- 1994 - 1st ed of Bruce Schneier's Applied Cryptography is published
- 1994 - Secure Sockets Layer (SSL) encryption protocol released by Netscape
- 1994 - Peter Shor devises an algorithm which lets quantum computers determine the factorization of large integers quickly. This is the first interesting problem for which quantum computers promise a significant speed-up, and it therefore generates a lot of interest in quantum computers.
- 1994 - DNA computing proof of concept on toy traveling salesman problem; a method for input/output still to be determined.
- 1994 - Russian crackers siphon $10 million from Citibank and transfer the money to bank accounts around the world. Vladimir Levin, the 30-year-old ringleader, uses his work laptop after hours to transfer the funds to accounts in Finland and Israel. Levin stands trial in the United States and is sentenced to three years in prison. Authorities recover all but $400,000 of the stolen money.
- 1994 - Formerly proprietary trade secret, but not patented, RC4 cipher algorithm is published on the Internet
- 1994 - first RSA Factoring Challenge from 1977 is decrypted as The Magic Words are Squeamish Ossifrage
- 1995 - NSA publishes the SHA1 hash algorithm as part of its Digital Signature Standard; SHA0 had a flaw corrected by SHA1
- 1997 - Ciphersaber, an encryption system based on RC4 that is simple enough to be reconstructed from memory, is published on Usenet
- 1998 - RIPE project releases final report
- October 1998 - Digital Millennium Copyright Act (DMCA) becomes law in U.S., criminalizing production and dissemination of technology that can circumvent measures taken to protect copyright
- October 1999 - DeCSS, a computer program capable of decrypting content on a DVD, is published on the Internet
- 1999: Bruce Schneier develops the Solitaire cipher, a way to allow field agents to communicate securely without having to rely on electronics or having to carry incriminating tools like a one-time pad. Unlike all previous manual encryption techniques -- except the one-time pad -- this one is resistant to automated cryptanalysis. It is published in Neal Stephenson's Cryptonomicon (2000).
2000 and beyond
[edit | edit source]- January 14, 2000 - U.S. Government announce restrictions on export of cryptography are relaxed (although not removed). This allows many US companies to stop the long running, and rather ridiculous process of having to create US and international copies of their software.
- March 2000 - President Clinton says he doesn't use e-mail to communicate with his daughter, Chelsea Clinton, at college because he doesn't think the medium is secure.
- September 6, 2000 - RSA Security Inc. released their RSA algorithm into the public domain, a few days in advance of their US patent 4405829 expiring. Following the relaxation of the U.S. government export restrictions, this removed one of the last barriers to the world-wide distribution of much software based on cryptographic systems. It should be noted that the IDEA algorithm is still under patent and also that government restrictions still apply in some places.
- 2000 - U.K. Regulation of Investigatory Powers Act 2000|Regulation of Investigatory Powers Act requires anyone to supply their cryptographic key to a duly authorized person on request
- 2001 - Belgian Rijndael algorithm selected as the U.S. Advanced Encryption Standard after a 5 year public search process by National Institute for Standards and Technology (NIST)
- September 11, 2001 - U.S. response to terrorist attacks hampered by Communication during the September 11, 2001 attacks|lack of secure communications
- November 2001 - Microsoft and its allies vow to end "full disclosure" of security vulnerabilities by replacing it with "responsible" disclosure guidelines.
- 2002 - NESSIE project releases final report / selections
- 2003 - CRYPTREC project releases 2003 report / recommendations
- 2004 - the hash MD5 is shown to be vulnerable to practical collision attack
- 2005 - potential for attacks on SHA1 demonstrated
- 2005 - agents from the U.S. FBI demonstrate their ability to crack WEP using publicly available tools
- 2007 - NIST announces w:NIST hash function competition
- 2012 - proclamation of a winner of the w:NIST hash function competition is scheduled
- 2015 - year by which NIST suggests that 80-bit keys for symmetric key cyphers be phased out. Asymmetric key cyphers require longer keys which have different vulnerability parameters.
Goals of Cryptography
Crytography is the science of secure communication in the presence of third parties (sometimes called "adversaries").
Modern cryptographers and cryptanalysts work in many areas including
- data confidentiality
- data integrity
- authentication
- forward secrecy
- end-to-end auditable voting systems
- digital currency
Classical cryptography focused on "data confidentiality"—keeping pieces of information secret, i.e. of designing technical systems such that an observer can infer as few as possible - optimally none - information from observing the system. The motivation for this is that the owner of the system wants to prevent the observer from taking advantage (e.g. monetary, influential, emotional) of the possible intelligence.
This secrecy or hiding is achieved by removing contextual information from the system's observable state and/or behaviour, without which the observer cannot gain intelligence about the system.
Examples
[edit | edit source]The term is very often used in conjunction in the context of message exchange between two entities, but of course not restricted to this case.
Hiding System State Alone
[edit | edit source]It may be advantageous for an ATM machine to hide the information as to how much cash is still available in the machine. It may e.g. only disclose the information that no more bank notes are available from it to the holder of a valid debit card.
Hiding Communication Content
[edit | edit source]Two companies doing business with each other may not wish to disclose the information on pricing of their products to third parties tapping into their communications.
Hiding the Fact of Communicating
[edit | edit source]Well known entities with well known fields of activity may wish to hide the fact that they are communicating at all since an observer aware of their fields of activity may already from the fact of some communication happening, be able to infer information.
Symmetric Ciphers
A symmetric key cipher (also called a secret-key cipher, or a one-key cipher, or a private-key cipher, or a shared-key cipher) Shared_secretis one that uses the same (necessarily secret) key to encrypt messages as it does to decrypt messages.
Until the invention of asymmetric key cryptography (commonly termed "public key / private key" crypto) in the 1970s, all ciphers were symmetric. Each party to the communication needed a key to encrypt a message; and a recipient needed a copy of the same key to decrypt the message. This presented a significant problem, as it required all parties to have a secure communication system (e.g. face-to-face meeting or secure courier) in order to distribute the required keys. The number of secure transfers required rises impossibly, and wholly impractically, quickly with the number of participants.
Formal Definition
[edit | edit source]Any cryptosystem based on a symmetric key cipher conforms to the following definition:
- M : message to be enciphered
- K : a secret key
- E : enciphering function
- D : deciphering function
- C : enciphered message. C := E(M, K)
- For all M, C, and K, M = D(C,K) = D(E(M,K),K)
Reciprocal Ciphers
[edit | edit source]Some shared-key ciphers are also "reciprocal ciphers." A reciprocal cipher applies the same transformation to decrypt a message as the one used to encrypt it. In the language of the formal definition above, E = D for a reciprocal cipher.
An example of a reciprocal cipher is Rot 13, in which the same alphabetic shift is used in both cases.
The xor-cipher (often used with one-time-pads) is another reciprocal cipher.[1]
Reciprocal ciphers have the advantage that the decoding machine can be set up exactly the same as the encoding machine -- reciprocal ciphers do not require the operator to remember to switch between "decoding" and "encoding".[2]
Symmetric Cypher Advantages
[edit | edit source]Symmetric key ciphers are typically much less computational overhead Overhead_(computing) than Asymmetric ciphers, sometimes this difference in computing overhead per character can be several orders of magnitude[3]. As such they are still used for bulk encryption of files and data streams for online applications.
Use
[edit | edit source]To set up a secure communication session Session_key between two parties the following actions take place Transport_Layer_Security:
- Alice tells Bob (in cleartext) that she wants a secure connection.
- Bob generates a single use (session), public/private (asymmetric) key pair (Kpb Kpr).
- Alice generates a single use (session) symmetric key. This will be the shared secret (Ks).
- Bob sends Alice the public key (Kpb).
- Alice encrypts her shared session key Ks with the Public key Kpb Ck := E(Ks, Kpb) and sends it to Bob
- Bob decrypts the message with his private key to obtains the shared session key Ks := D(Ck, Kpr)
- Now Alice and Bob have a shares secret (symmetric key) to secure communication on this connection for this session
- Either party can encrypt a message simply by C := E(M, Ks) and decrypt is by M = D(C,K) = D(E(M,Ks),Ks)
This is the Basis for Diffie–Hellman Diffie_Hellman_key_exchange key exchange Key exchange and its more advanced successors Transport_Layer_Security.
Examples
[edit | edit source]
Further Reading
[edit | edit source]

This page or section of the Cryptography book is a stub. You can help Wikibooks by expanding it.
Asymmetric Ciphers
In cryptography, an asymmetric key algorithm uses a pair of different, though related, cryptographic keys to encrypt and decrypt. The two keys are related mathematically; a message encrypted by the algorithm using one key can be decrypted by the same algorithm using the other. In a sense, one key "locks" a lock (encrypts); but a different key is required to unlock it (decrypt).
Some, but not all, asymmetric key cyphers have the "public key" property, which means that there is no known effective method of finding the other key in a key pair, given knowledge of one of them. This group of algorithms is very useful, as it entirely evades the key distribution problem inherent in all symmetric key cyphers and some of the asymmetric key cyphers. One may simply publish one key while keeping the other secret. They form the basis of much of modern cryptographic practice.
A Postal Analogy
[edit | edit source]An analogy which can be used to understand the advantages of an asymmetric system is to imagine two people, Alice and Bob, sending a secret message through the public mail. In this example, Alice has the secret message and wants to send it to Bob, after which Bob sends a secret reply.
With a symmetric key system, Alice first puts the secret message in a box, and then locks the box using a padlock to which she has a key. She then sends the box to Bob through regular mail. When Bob receives the box, he uses an identical copy of Alice's key (which he has somehow obtained previously) to open the box, and reads the message. Bob can then use the same padlock to send his secret reply.
In an asymmetric key system, Bob and Alice have separate padlocks. Firstly, Alice asks Bob to send his open padlock to her through regular mail, keeping his key to himself. When Alice receives it she uses it to lock a box containing her message, and sends the locked box to Bob. Bob can then unlock the box with his key and read the message from Alice. To reply, Bob must similarly get Alice's open padlock to lock the box before sending it back to her. The critical advantage in an asymmetric key system is that Bob and Alice never need send a copy of their keys to each other. This substantially reduces the chance that a third party (perhaps, in the example, a corrupt postal worker) will copy a key while it is in transit, allowing said third party to spy on all future messages sent between Alice and Bob. In addition, if Bob were to be careless and allow someone else to copy his key, Alice's messages to Bob will be compromised, but Alice's messages to other people would remain secret, since the other people would be providing different padlocks for Alice to use...
Actual Algorithms - Two Linked Keys
[edit | edit source]Fortunately cryptography is not concerned with actual padlocks, but with encryption algorithms which aren't vulnerable to hacksaws, bolt cutters, or liquid nitrogen attacks.
Not all asymmetric key algorithms operate in precisely this fashion. The most common have the property that Alice and Bob own two keys; neither of which is (so far as is known) deducible from the other. This is known as public-key cryptography, since one key of the pair can be published without affecting message security. In the analogy above, Bob might publish instructions on how to make a lock ("public key"), but the lock is such that it is impossible (so far as is known) to deduce from these instructions how to make a key which will open that lock ("private key"). Those wishing to send messages to Bob use the public key to encrypt the message; Bob uses his private key to decrypt it.
Weaknesses
[edit | edit source]Of course, there is the possibility that someone could "pick" Bob's or Alice's lock. Unlike the case of the one-time pad or its equivalents, there is no currently known asymmetric key algorithm which has been proven to be secure against a mathematical attack. That is, it is not known to be impossible that some relation between the keys in a key pair, or a weakness in an algorithm's operation, might be found which would allow decryption without either key, or using only the encryption key. The security of asymmetric key algorithms is based on estimates of how difficult the underlying mathematical problem is to solve. Such estimates have changed both with the decreasing cost of computer power, and with new mathematical discoveries.
Weaknesses have been found in promising asymmetric key algorithms in the past. The 'knapsack packing' algorithm was found to be insecure when an unsuspected attack came to light. Recently, some attacks based on careful measurements of the exact amount of time it takes known hardware to encrypt plain text have been used to simplify the search for likely decryption keys. Thus, use of asymmetric key algorithms does not ensure security; it is an area of active research to discover and protect against new and unexpected attacks.
Another potential weakness in the process of using asymmetric keys is the possibility of a 'Man in the Middle' attack, whereby the communication of public keys is intercepted by a third party and modified to provide the third party's own public keys instead. The encrypted response also must be intercepted, decrypted and re-encrypted using the correct public key in all instances however to avoid suspicion, making this attack difficult to implement in practice.
A Brief History
[edit | edit source]The first known asymmetric key algorithm was invented by Clifford Cocks of GCHQ in the UK. It was not made public at the time, and was reinvented by Rivest, Shamir, and Adleman at MIT in 1976. It is usually referred to as RSA as a result. RSA relies for its security on the difficulty of factoring very large integers. A breakthrough in that field would cause considerable problems for RSA's security. Currently, RSA is vulnerable to an attack by factoring the 'modulus' part of the public key, even when keys are properly chosen, for keys shorter than perhaps 700 bits. Most authorities suggest that 1024 bit keys will be secure for some time, barring a fundamental breakthrough in factoring practice or practical quantum computers, but others favor longer keys.
At least two other asymmetric algorithms were invented after the GCHQ work, but before the RSA publication. These were the Ralph Merkle puzzle cryptographic system and the Diffie-Hellman system. Well after RSA's publication, Taher Elgamal invented the Elgamal discrete log cryptosystem which relies on the difficulty of inverting logs in a finite field. It is used in the SSL, TLS, and DSA protocols.
A relatively new addition to the class of asymmetric key algorithms is elliptic curve cryptography. While it is more complex computationally, many believe it to represent a more difficult mathematical problem than either the factorisation or discrete logarithm problems.
Practical limitations and hybrid cryptosystems
[edit | edit source]One drawback of asymmetric key algorithms is that they are much slower (factors of 1000+ are typical) than 'comparably' secure symmetric key algorithms. In many quality crypto systems, both algorithm types are used; they are termed 'hybrid systems'. PGP is an early and well-known hybrid system. The receiver's public key encrypts a symmetric algorithm key which is used to encrypt the main message. This combines the virtues of both algorithm types when properly done.
We discuss asymmetric ciphers in much more detail later in the Public Key Overview and following sections of this book.
Random number generation
The generation of random numbers is essential to cryptography. One of the most difficult aspect of cryptographic algorithms is in depending on or generating, true random information. This is problematic, since there is no known way to produce true random data, and most especially no way to do so on a finite state machine such as a computer.
There are generally two kinds of random number generators: non-deterministic random number generators, sometimes called "true random number generators" (TRNG), and deterministic random number generators, also called pseudorandom number generators (PRNG).[8]
Many high-quality cryptosystems use both -- a hardware random-number generator to periodically re-seed a deterministic random number generator.
Quantum mechanical theory suggests that some physical processes are inherently random (though collecting and using such data presents problems), but deterministic mechanisms, such as computers, cannot be. Any stochastic process (generation of random numbers) simulated on a computer, however, is not truly random, but only pseudorandom.
Within the limitations of pseudorandom generators, any quality pseudorandom number generator must:
- have a uniform distribution of values, in all dimensions
- have no detectable pattern, ie generate numbers with no correlations between successive numbers
- have a very long cycle length
- have no, or easily avoidable, weak initial conditions which produce patterns or short cycles
Methods of Pseudorandom Number Generation
[edit | edit source]Keeping in mind that we are dealing with pseudorandom number generation (i.e. numbers generated from a finite state machine, as a computer), there are various ways to randomly generate numbers.
In C and C++ the function rand() returns a pseudo-random integer between zero and RAND_MAX (internally defined constant), defined with the srand() function; otherwise it will use the default seed and consistently return the same numbers when the program is restarted. Most such libraries have short cycle lengths and are not usable for cryptographic purposes.
"Numerical Recipes in C" reviews several random number generators and recommends a modified version of the DES cypher as their highest quality recommended random number generator. "Practical Cryptography" (Ferguson and Schneier) recommend a design they have named Fortuna; it supersedes their earlier design called Yarrow.
Methods of nondeterministic number generation
[edit | edit source]As of 2004, the best random number generators have 3 parts: an unpredictable nondeterministic mechanism, entropy assessment, and conditioner. The nondeterministic mechanism (also called the entropy source) generates blocks of raw biased bits. The entropy assessment part produces a conservative estimate of the min-entropy of some block of raw biased bits. The conditioner (also called a whitener, an unbiasing algorithm, or a randomness extractor) distills the block of raw bits into a much smaller block of conditioned output bits -- an output block of bits half the size of the estimated entropy (in bits) of the raw biased bits -- eliminating any systematic bias. If the estimate is good, the conditioned output bits are unbiased full-entropy bits even if the nondeterministic mechanism degrades over time. In practice, the entropy assessment is the difficult part.[9]
References
[edit | edit source]- ↑ Wikipedia: Symmetric-key algorithm#Reciprocal cipher
- ↑ Greg Goebel. "The Mechanization of Ciphers". 2018.
- ↑ http://s3.amazonaws.com/academia.edu.documents/33551175/IJETAE_1211_02.pdf?AWSAccessKeyId=AKIAIWOWYYGZ2Y53UL3A&Expires=1499689317&Signature=EavACFmNNlzcPXDa5kVZS9rh7Yw%3D&response-content-disposition=inline%3B%20filename%3DDES_AES_and_Blowfish_Symmetric_Key_Crypt.pdf
- ↑ https://www.schneier.com/blog/archives/2004/10/the_legacy_of_d.html
- ↑ https://www.schneier.com/academic/blowfish/
- ↑ https://books.google.com/books?hl=en&lr=&id=fNaoCAAAQBAJ&oi=fnd&pg=PA1&dq=speed+advantages+in+symmetric+ciphers+aes&ots=7hPPzLQjm5&sig=kaBEJW49jdonFWKin0-p6ZhROCA#v=onepage&q=speed%20advantages%20in%20symmetric%20ciphers%20aes&f=false
- ↑ http://s3.amazonaws.com/academia.edu.documents/33551175/IJETAE_1211_02.pdf?AWSAccessKeyId=AKIAIWOWYYGZ2Y53UL3A&Expires=1499689317&Signature=EavACFmNNlzcPXDa5kVZS9rh7Yw%3D&response-content-disposition=inline%3B%20filename%3DDES_AES_and_Blowfish_Symmetric_Key_Crypt.pdf
- ↑ NIST. "Random number generation".
- ↑ John Kelsey. "Entropy and Entropy Sources in X9.82" NIST. 2004. "Are you measuring what you think you're measuring?" "How much of sample variability is entropy, how much is just complexity?"
Further Reading
[edit | edit source]- Cryptography/Random Quality
- RFC 4086 "Randomness Requirements for Security"
- Random Number—from MathWorld
- Statistics/Numerical Methods/Random Number Generation
- Algorithms/Randomization
- Random number generation standards development bodies
Hashes
| A Wikibookian suggests that Cryptography/Hash function be merged into this chapter. Discuss whether or not this merger should happen on the discussion page. |
A digest, sometimes simply called a hash, is the result of a hash function, a specific mathematical function or algorithm, that can be described as . "Hashing" is required to be a deterministic process, and so, every time the input block is "hashed" by the application of the same hash function, the resulting digest or hash is constant, maintaining a verifiable relation with the input data. Thus making this type of algorithms useful for information security.
Other processes called cryptographic hashes, function similarly to hashing, but require added security, in the form or a level of guarantee that the input data can not feasibly be reversed from the generated hash value. I.e. That there is no useful inverse hash function
This property can be formally expanded to provide the following properties of a secure hash:
- Preimage resistant : Given H it should be hard to find M such that H = hash(M).
- Second preimage resistant: Given an input m1, it should be hard to find another input, m2 (not equal to m1) such that hash(m1) = hash(m2).
- Collision-resistant: it should be hard to find two different messages m1 and m2 such that hash(m1) = hash(m2). Because of the birthday paradox this means the hash function must have a larger image than is required for preimage-resistance.
A hash function is the implementation of an algorithm that, given some data as input, will generate a short result called a digest. A useful hash function generates a fixed length of hashed value.
For Ex: If our hash function is 'X' and we have 'wiki' as our input... then X('wiki')= a5g78 i.e. some hash value.
Applications of hash functions
[edit | edit source]Non-cryptographic hash functions have many applications,[1] but in this section we focus on applications that specifically require cryptographic hash functions:
A typical use of a cryptographic hash would be as follows: Alice poses to Bob a tough math problem and claims she has solved it. Bob would like to try it himself, but would yet like to be sure that Alice is not bluffing. Therefore, Alice writes down her solution, appends a random nonce, computes its hash and tells Bob the hash value (whilst keeping the solution secret). This way, when Bob comes up with the solution himself a few days later, Alice can verify his solution but still be able to prove that she had the solution earlier.
In actual practice, Alice and Bob will often be computer programs, and the secret would be something less easily spoofed than a claimed puzzle solution. The above application is called a commitment scheme. Another important application of secure hashes is verification of message integrity. Determination of whether or not any changes have been made to a message (or a file), for example, can be accomplished by comparing message digests calculated before, and after, transmission (or any other event) (see Tripwire, a system using this property as a defense against malware and malfeasance). A message digest can also serve as a means of reliably identifying a file.
A related application is password verification. Passwords should not be stored in clear text, for obvious reasons, but instead in digest form. In a later chapter, Password handling will be discussed in more detail—in particular, why hashing the password once is inadequate.
A hash function is a key part of message authentication (HMAC).
Most distributed version control systems (DVCSs) use cryptographic hashes.[2]
For both security and performance reasons, most digital signature algorithms specify that only the digest of the message be "signed", not the entire message. The Hash functions can also be used in the generation of pseudo-random bits.
SHA-1, MD5, and RIPEMD-160 are among the most commonly-used message digest algorithms as of 2004. In August 2004, researchers found weaknesses in a number of hash functions, including MD5, SHA-0 and RIPEMD. This has called into question the long-term security of later algorithms which are derived from these hash functions. In particular, SHA-1 (a strengthened version of SHA-0), RIPEMD-128 and RIPEMD-160 (strengthened versions of RIPEMD). Neither SHA-0 nor RIPEMD are widely used since they were replaced by their strengthened versions.
Other common cryptographic hashes include SHA-2 and Tiger.
Later we will discuss the "birthday attack" and other techniques people use for Breaking Hash Algorithms.
Hash speed
[edit | edit source]When using hashes for file verification, people prefer hash functions that run very fast. They want a corrupted file can be detected as soon as possible (and queued for retransmission, quarantined, or etc.). Some popular hash functions in this category are:
- BLAKE2b
- SHA-3
In addition, both SHA-256 (SHA-2) and SHA-1 have seen hardware support in some CPU instruction sets.
When using hashes for password verification, people prefer hash functions that take a long time to run. If/when a password verification database (the /etc/passwd file, the /etc/shadow file, etc.) is accidentally leaked, they want to force a brute-force attacker to take a long time to test each guess.[3] Some popular hash functions in this category are:
- Argon2
- scrypt
- bcrypt
- PBKDF2
We talk more about password hashing in the Cryptography/Secure Passwords section.
Further reading
[edit | edit source]- see Algorithm Implementation/Hashing for more about non-cryptographic hash functions and their applications.
- see Data Structures/Hash Tables for the most common application of non-cryptographic hash functions
- Rosetta Code : Cryptographic hash function has implementations of cryptographic hash functions in many programming languages.
- ↑ applications of non-cryptographic hash functions are described in Data Structures/Hash Tables and Algorithm Implementation/Hashing.
- ↑ Eric Sink. "Version Control by Example". Chapter 12: "Git: Cryptographic Hashes".
- ↑ "Speed Hashing"
Common flaws and weaknesses
Cryptography relies on puzzles. A puzzle that can not be solved without more information than the cryptanalyst has or can feasibly acquire is an unsolvable puzzle for the attacker. If the puzzle can be understood in a way that circumvents the secret information the cryptanalyst doesn't have then the puzzle is breakable. Obviously cryptography relies on an implicit form of security through obscurity where there currently exists no likely ways to understand the puzzle that will break it. The increasing complexity and subtlety of the mathematical puzzles used in cryptography creates a situation where neither cryptographers or cryptanalysts can be sure of all facets of the puzzle and security.
Like any puzzle, cryptography algorithms are based on assumptions - if these assumptions are flawed then the underlying puzzle may be flawed.
Secret knowledge assumption - Certain secret knowledge is not available to unauthorised people. Attacks such as packet sniffing, keylogging and meet in the middle attacks try to breach this assumption.
Secret knowledge masks plaintext - The secret knowledge is applied to the plaintext so that the nature of the message is no longer obvious. In general the secret knowledge hides the message in way so that the secret knowledge is required in order rediscover the message. Attacks such as chosen plaintext, brute force and frequency analysis try to breach this assumption
Secure Passwords
Passwords
[edit | edit source]A serious cryptographic system should not be based on a hidden algorithm, but rather on a hidden password that is hard to guess (see Kerckhoffs's law in the Basic Design Principles section). Passwords today are very important because access to a very large number of portals on the Internet, or even your email account, is restricted to those who can produce the correct password. This usually involves humans in choosing, remembering, and using passwords. All three aspects are commonly weaknesses: humans are notoriously bad at choosing hard-to-break passwords,[1] do not easily remember strong passwords, and are sloppy and too trusting in their use of passwords when they remember them. It is nearly overwhelmingly tempting to base passwords on already known items. As well, we can remember simple (e.g. short), or familiar (e.g. telephone number) pretty well, but stronger passwords are more than most of us can reliably remember; this leads to insecurity as easy methods of password recovery, or even password bypass, are required. These are universally insecure. Finally, humans are too easily prey to phishing fraud scams, to shoulder surfing, to helping out a friend who has forgotten their own password, etc.
Security
[edit | edit source]But passwords must protect access and messages against more than just human attackers. There are many machine-based ways of attacking cryptographic algorithms and cryptosystems, so passwords should also be hard to attack automatically. To prevent one important class of automatic attack, the brute force search, passwords must be difficult for the bad guys to guess. be both long (single character passwords are easily guessed, obviously) and, ideally, random—that is, without pattern of any kind. A long enough password will require so much machine time as to be impractical for an attacker. A password without pattern will offer no shortcut to brute force search. These considerations suggest several properties passwords should possess:
- sufficient length to preclude brute force search (common recommendations as of 2010 are at least 8 characters, and more when any class of character is not allowed (e.g. if lower case is not permitted, or non alphanumeric characters are not permitted, ..., a longer password is required); more length is required if the password should remain unbreakable into the future (when computers will be faster and brute force searches more effective)
- no names (pets, friends, relatives, ...), no words findable in any dictionary, no phrases found in any quotation book
- no personally connected numbers or information (telephone numbers, addresses, birthdays)
Password handling
[edit | edit source]Password handling is simultaneously one of the few Solved Problems of Cryptography, *and* one of the most misunderstood.—Dan Kaminsky , "Password Rejected: A Crypto Perspective"
Any web server that stores user passwords in plain text in some file or database somewhere, is doing it wrong.[2][3][4][5][6]
Passwords are usually not stored in cleartext, for obvious reasons, but instead in digest form. To authenticate a user, the password presented by the user is salted, hashed, and compared with the stored hash.[7]
PBKDF2 was originally designed to "generating a cryptographic key from a password", but it turns out to be good for generating password digests for safe storage for authentication purposes.[8][9]
In 2013, because only 3 algorithms are available for generating password digests for safe storage for authentication purposes—PBKDF2, bcrypt, and scrypt[6]—In 2013, the Password Hashing Competition (PHC) was announced. [10][11][12][13]
passphrase hashing algorithm
[edit | edit source]
The main difference between a password hashing algorithm and other cryptographic hash algorithms is that a password hashing algorithm should make it difficult for attackers who have massively parallel GPUs and FPGAs to recover a passphrase—even if the passphrase is relatively weak—from the stored password digest. The most common way of doing this is to design the algorithm so the amount of time it takes for such an attacker to recover a weak passphrase should be much longer than the amount of time it takes for an authorized server, when given the correct passphrase, to verify that it is in fact correct.
The password verification utility passwd uses a secret password and non-secret salt to generate password hash digests using the crypt (C) library, which in turn uses many password hashing algorithms.
Often a single shadow password file stores password hash digests generated by several different hash algorithms. The particular hash algorithm used can be identified by a unique code prefix in the resulting hashtext, following a pseudo-standard called Modular Crypt Format.[14][15][16]
Any available hash algorithm is vastly superior to the shameful[17] practice of simply storing passwords in plain text; or storing "encrypting" passwords that can be quickly decrypted to recover the original password.
Unfortunately, practically all available hash algorithms were not originally designed for password hashing.
While one iterations of SHA-2 and SHA-3 are more than adequate for calculating a file verification digest, a message authentication code, or a digital signature when applied to long files, they are too easy to crack when applied to short passwords even when iterated a dozen times. Practically all available hash algorithms as of 2013 are either
(a) already known to be relatively easy to crack (recover a weak password) using GPU-based brute-force password cracking tools, or (b) are too new or haven't been studied enough to know whether it's easy to crack or not.[18]
For example, systems have been built that can recover a valid password from any Windows XP LM hash or 6-printable-character password in at most 6 minutes,[19][20] and can recover any 8-printable-character password from a NTLM hash in at most 5.5 hours.[19]
For example, systems have been built that can run through a dictionary of possible words and common "leet speak" substitutions[20] in order to recover the password that produced some given MD5 hash at a rate of 180 Ghashes/second,[21] or produced some given DEC crypt() digest at a rate of 73 Mhashes/second.[22]
A technique called "key stretching" makes key search attacks more expensive.[23]
Further reading
[edit | edit source]- Wikibook Basic Computer Security/General Security and Passwords and Wikibook The Computer Revolution/Security/Passwords lists some practical tips for people who use many different websites, each one requesting a password.
- ↑ Burr, Dodson, Polk. "Electronic Authentication Guideline: Recommendations of the National Institute of Standards and Technology" section A.2.2 "Min Entropy Estimates": "Experience suggests that a significant share of users will choose passwords that are very easily guessed ("password" may be the most commonly selected password, where it is allowed)." [1]
- ↑ http://plaintextoffenders.com/
- ↑ http://crypto.stackexchange.com/tags/passwords/info
- ↑ http://security.stackexchange.com/questions/17979/is-sending-password-to-user-email-secure
- ↑ http://security.stackexchange.com/tags/passwords/info
- ↑ a b Adam Bard. "3 Wrong Ways to Store a Password: And 5 code samples doing it right". 2013.
- ↑ "How to securely hash passwords?"
- ↑ "Does NIST really recommend PBKDF2 for password hashing?"
- ↑ "Is it safe to use PBKDF2 for hashing?"
- ↑ http://crypto.stackexchange.com/questions/12795/why-do-i-need-to-add-the-original-salt-to-each-hash-iteration-of-a-password
- ↑ "Increase the security of an already stored password hash". quote: "a new open competition for password hashing algorithms has been launched, using the model of the previous AES, eSTREAM and SHA-3 competitions. Submissions are due for the end of January 2014."
- ↑ "Password Hashing Competition"
- ↑ "Are there more modern password hashing methods than bcrypt and scrypt?"
- ↑ Simson Garfinkel, Alan Schwartz, Gene Spafford. "Practical Unix & Internet Security". 2003. section "4.3.2.3 crypt16( ), DES Extended, and Modular Crypt Format". "The Modular Crypt Format (MCF) specifies an extensible scheme for formatting encrypted passwords. MCF is one of the most popular formats for encrypted passwords"
- ↑ "Modular Crypt Format: or, a side note about a standard that isn’t".
- ↑ "Binary Modular Crypt Format"
- ↑ "Plain Text Offenders"
- ↑ Dennis Fisher. "Cryptographers aim to find new password hashing algorithm". 2013.
- ↑ a b Paul Roberts. "Update: New 25 GPU Monster Devours Passwords In Seconds". 2012.
- ↑ a b Dan Goodin "Anatomy of a hack: even your 'complicated' password is easy to crack". 2013.
- ↑ Jeremi M. Gosney. "Password Cracking HPC". 2012.
- ↑ "John the Ripper benchmarks".
- ↑ Arnold Reinhold. "HEKS: A Family of Key Stretching Algorithms". 1999.
- Wikibook Web Application Security Guide/Password security lists some practical tips for people who develop websites and other applications that require password "storage", resetting passwords, etc.
- Wikibook C Shell Scripting/Passwords mentions a "Human readable password generator" (?)
S-box
In cryptography, an S-Box (Substitution-box) is a basic component of symmetric key algorithms which performs substitution. In block ciphers, they are typically used to obscure the relationship between the key and the ciphertext — Claude Shannon's property of confusion.[1] In many cases, the S-Boxes are carefully chosen to resist cryptanalysis.
In general, an S-Box takes some number of input bits, m, and transforms them into some number of output bits, n: an m×n S-Box can be implemented as a lookup table with words of n bits each. Fixed tables are normally used, as in the Data Encryption Standard (DES), but in some ciphers the tables are generated dynamically from the key; e.g. the Blowfish and the Twofish encryption algorithms. Bruce Schneier describes IDEA's modular multiplication step as a key-dependent S-Box.
Given a 6-bit input, the 4-bit output is found by selecting the row using the outer two bits (the first and last bits), and the column using the inner four bits. For example, an input "011011" has outer bits "01" and inner bits "1101"; the corresponding output would be "1001".
The 8 S-Boxes of DES were the subject of intense study for many years out of a concern that a backdoor — a vulnerability known only to its designers — might have been planted in the cipher. The S-Box design criteria were eventually published[2] after the public rediscovery of differential cryptanalysis, showing that they had been carefully tuned to increase resistance against this specific attack. Other research had already indicated that even small modifications to an S-Box could significantly weaken DES.
There has been a great deal of research into the design of good S-Boxes, and much more is understood about their use in block ciphers than when DES was released.
References
[edit | edit source]- ↑
Chandrasekaran, J. et al. (2011). "A Chaos Based Approach for Improving Non Linearity in the S-Box Design of Symmetric Key Cryptosystems". Advances in Networks and Communications: First International Conference on Computer Science and Information Technology, CCSIT 2011, Bangalore, India, January 2-4, 2011. Proceedings, Part 2. Springer. p. 516. ISBN 978-3-642-17877-1.
{{cite book}}: Explicit use of et al. in:|authors=(help); Unknown parameter|editors=ignored (|editor=suggested) (help)CS1 maint: uses authors parameter (link) - ↑
Coppersmith, Don (1994). "The Data Encryption Standard (DES) and its strength against attacks" (PDF). IBM Journal of Research and Development. 38 (3): 243–250. doi:10.1147/rd.383.0243. Retrieved 2007-02-20.
{{cite journal}}: CS1 maint: ref duplicates default (link)
Basic Design Principles
Good ciphers often attempt to have the following traits.
Kerckhoffs's principle
[edit | edit source]Kerckhoffs's principle, also called Kerckhoffs's law:
A cryptosystem should be secure even if everything about the system, except the key, is public knowledge.
In the words of Claude Shannon, "The enemy knows the system." (Shannon's maxim).
Diffusion
[edit | edit source]Having good diffusion means that making a small change in the plain text should ideally cause as much as possible of cipher text to have a fifty percent possibility of change.
For example a Caesar cipher has almost no diffusion while a block cypher may contain lots of it.
Confusion
[edit | edit source]For good confusion the relationship between the cypher text and the plain text should be as complex as possible.
Further reading
[edit | edit source]
Open Algorithms
Creating a good cryptographic algorithm that will stand against all that the best cryptanalysis can throw at it, is hard. Very hard. So, this is why most people design algorithms by first designing the basic system, then refining it, and finally letting it lose for all to see.
Why, do this? Surely, if you let everyone see your code that turns a plain bit of text into garbled rubbish, then they will be able to reverse it! This assumption is unfortunately wrong. Now the algorithms that have been/ are being made are so strong, that just reversing the algorithm is not effective when trying to crack it. And when you let people look at your algorithm, they may spot a security flaw that nobody else could see. We talk more about this counter-intuitive idea in another chapter, Basic Design Principles#Kerckhoffs's principle.
AES, one of the newest and strongest (2010) algorithms in the world, was created by a team of two people, and was put forward into a sort of competition, where only the best algorithm would be examined and put forward to be selected for the title of the Advanced Encryption Standard. There were about 35 entrants, and although all of them appeared strong at first, it soon became clear that some of these apparently strong algorithms were in fact, very weak!
AES is a good example of open algorithms.
Mathematical Background
| A Wikibookian believes this page should be split into smaller pages with a narrower subtopic. You can help by splitting this big page into smaller ones. Please make sure to follow the naming policy. Dividing books into smaller sections can provide more focus and allow each one to do one thing well, which benefits everyone. |
See Talk page for other suggestions.
Introduction
[edit | edit source]Modern public-key (asymmetric) cryptography is based upon a branch of mathematics known as number theory, which is concerned solely with the solution of equations that yield only integer results. These type of equations are known as diophantine equations, named after the Greek mathematician Diophantos of Alexandria (ca. 200 CE) from his book Arithmetica that addresses problems requiring such integral solutions.
One of the oldest diophantine problems is known as the Pythagorean problem, which gives the length of one side of a right triangle when supplied with the lengths of the other two side, according to the equation
where is the length of the hypotenuse. While two sides may be known to be integral values, the resultant third side may well be irrational. The solution to the Pythagorean problem is not beyond the scope, but is beyond the purpose of this chapter. Therefore, example integral solutions (known as Pythagorean triplets) will simply be presented here. It is left as an exercise for the reader to find additional solutions, either by brute-force or derivation.
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
Prime Numbers
[edit | edit source]Description
[edit | edit source]Asymmetric key algorithms rely heavily on the use of prime numbers, usually exceedingly long primes, for their operation. By definition, prime numbers are divisible only by themselves and 1. In other words, letting the symbol | denote divisibility (i.e. - means " divides into "), a prime number strictly adheres to the following mathematical definition
- | Where or only
The Fundamental Theorem of Arithmetic states that all integers can be decomposed into a unique prime factorization. Any integer greater than 1 is considered either prime or composite. A composite number is composed of more than one prime factor
- | where ultimately
in which is a unique prime number and is the exponent.
Numerical Examples
[edit | edit source]543,312 = 24 32 50 73 111 553,696 = 25 30 50 70 113 131
As can be seen, according to this systematic decomposition, each factorization is unique.
In order to deterministically verify whether an integer is prime or composite, only the primes need be examined. This type of systematic, thorough examination is known as a brute-force approach. Primes and composites are noteworthy in the study of cryptography since, in general, a public key is a composite number which is the product of two or more primes. One (or more) of these primes may constitute the private key.
There are several types and categories of prime numbers, three of which are of importance to cryptography and will be discussed here briefly.
Fermat Primes
[edit | edit source]Fermat numbers take the following form
If Fn is prime, then it is called a Fermat prime.
Numerical Examples
[edit | edit source]The only Fermat numbers known to be prime are . Moreover, the primality of all Fermat numbers was disproven by Euler, who showed that .
Mersenne Primes
[edit | edit source]Mersenne primes - another type of formulaic prime generation - follow the form
where is a prime number. The [8] Wolfram Alpha engine reports Mersenne Primes, an example input request being "4th Mersenne Prime".
Numerical Examples
[edit | edit source]The first four Mersenne primes are as follows
Numbers of the form Mp = 2p without the primality requirement are called Mersenne numbers. Not all Mersenne numbers are prime, e.g. M11 = 211−1 = 2047 = 23 · 89.
Coprimes (Relatively Prime Numbers)
[edit | edit source]Two numbers are said to be coprime if the largest integer that divides evenly into both of them is 1. Mathematically, this is written
where is the greatest common divisor. Two rules can be derived from the above definition
- If | and , then |
- If with , then both and are squares, i.e. - ,
The Prime Number Theorem
[edit | edit source]The Prime Number Theorem estimates the probability that any integer, chosen randomly will be prime. The estimate is given below, with defined as the number of primes
is asymptotic to , that is to say . What this means is that generally, a randomly chosen number is prime with the approximate probability .
The Euclidean Algorithm
[edit | edit source]Introduction
[edit | edit source]The Euclidean Algorithm is used to discover the greatest common divisor of two integers. In cryptography, it is most often used to determine if two integers are coprime, i.e. - .
In order to find where efficiently when working with very large numbers, as with cryptosystems, a method exists to do so. The Euclidean algorithm operates as follows - First, divide by , writing the quotient , and the remainder . Note this can be written in equation form as . Next perform the same operation using in 's place: . Continue with this pattern until the final remainder is zero. Numerical examples and a formal algorithm follow which should make this inherent pattern clear.
Mathematical Description
[edit | edit source]When , stop with .
Numerical Examples
[edit | edit source]Example 1 - To find gcd(17,043,12,660)
17,043 = 1 12,660 + 4383 12,660 = 2 4,383 + 3894 4,383 = 1 3,894 + 489 3,894 = 7 489 + 471 489 = 1 471 + 18 471 = 26 18 + 3 18 = 6 3 + 0
gcd (17,043,12,660) = 3
Example 2 - To find gcd(2,008,1,963)
2,008 = 1 1,963 + 45 1,963 = 43 45 + 28 45 = 1 28 + 17 28 = 1 17 + 11 17 = 1 11 + 6 11 = 1 6 + 5 6 = 1 5 + 1 5 = 5 1 + 0
gcd (2,008,1963) = 1 Note: the two number are coprime.
Algorithmic Representation
[edit | edit source]Euclidean Algorithm(a,b)
Input: Two integers a and b such that a > b
Output: An integer r = gcd(a,b)
1. Set a0 = a, r1 = r
2. r = a0 mod r1
3. While(r1 mod r 0) do:
4. a0 = r1
5. r1 = r
6. r = a0 mod r1
7. Output r and halt
The Extended Euclidean Algorithm
[edit | edit source]In order to solve the type of equations represented by Bézout's identity, as shown below
where , , , and are integers, it is often useful to use the extended Euclidean algorithm. Equations of the form above occur in public key encryption algorithms such as RSA (Rivest-Shamir-Adleman) in the form where . There are two methods in which to implement the extended Euclidean algorithm; the iterative method and the recursive method.
As an example, we shall solve an RSA key generation problem with e = 216 + 1, p = 3,217, q = 1,279. Thus, 62,537d + 51,456w = 1.
Methods
[edit | edit source]The Iterative Method
[edit | edit source]This method computes expressions of the form for the remainder in each step of the Euclidean algorithm. Each modulus can be written in terms of the previous two remainders and their whole quotient as follows:
By substitution, this gives:
The first two values are the initial arguments to the algorithm:
The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.
Example
[edit | edit source]| Step | Quotient | Remainder | Substitute | Combine terms | |
|---|---|---|---|---|---|
| 1 | 4,110,048 = a | 4,110,048 = 1a + 0b | |||
| 2 | 65,537 = b | 65,537 = 0a + 1b | |||
| 3 | 62 | 46,754 = 4,110,048 - 65,537 62 | 46,754 = (1a + 0b) - (0a + 1b) 62 | 46,754 = 1a - 62b | |
| 4 | 1 | 18,783 = 65,537 - 46,754 1 | 18,783 = (0a + 1b) - (1a - 62b) 1 | 18,783 = -1a + 63b | |
| 5 | 2 | 9,188 = 46,754 - 18,783 2 | 9,188 = (1a - 62b) - (-1a + 62b) 2 | 9,188 = 3a - 188b | |
| 6 | 2 | 407 = 18,783 - 9,188 2 | 407 = (-1a + 63b) - (3a - 188b) 2 | 407 = -7a + 439b | |
| 7 | 22 | 234 = 9,188 - 407 22 | 234 = (3a - 188b) - (-7a + 439b) 22 | 234 = 157a - 9,846b | |
| 8 | 1 | 173 = 407 - 234 1 | 173 = (-7a + 439b) - (157a - 9,846b) 1 | 173 = -164a + 10,285b | |
| 9 | 1 | 61 = 234 - 173 1 | 61 = (157a - 9,846b) - (-164a + 10,285b) 1 | 61 = 321a + 20,131b | |
| 10 | 2 | 51 = 173 - 61 2 | 51 = (-164a + 10,285b) - (321a +20,131b) 2 | 51 = -806a + 50,547b | |
| 11 | 1 | 10 = 61 - 51 1 | 61 = (321a +20,131b) - (-806a + 50,547b) 1 | 10 = 1,127a - 70,678b | |
| 12 | 5 | 1 = 51 -10 5 | 1 = (-806a + 50,547b) - (1,127a - 70,678b) 5 | 1 = -6,441a + 403,937b | |
| 13 | 10 | 0 | End of algorithm | ||
Putting the equation in its original form yields , it is shown that and . During the process of key generation for RSA encryption, the value for w is discarded, and d is retained as the value of the private key In this case
d = 0x629e1 = 01100010100111100001
The Recursive Method
[edit | edit source]This is a direct method for solving Diophantine equations of the form . Using this method, the dividend and the divisor are reduced over a series of steps. At the last step, a trivial value is substituted into the equation, and is then worked backward until the solution is obtained.
Example
[edit | edit source]Using the previous RSA vales of and
| Euclidean Expansion | Collect Terms | Substitute | Retrograde Substitution | Solve For dx | |
|---|---|---|---|---|---|
| 4,110,048 | w0 | + 65,537d0 = 1 | |||
| (62 65,537 + 46,754) | w0 | + 65,537d0 = 1 | |||
| 65,537 | (62w0 + d0) | + 46,754w0 = 1 | w1 = 62w0 + d0 | 4,595 = (62)(-6441) + d0 | d0 = 403,937 |
| 65,537 | w1 | + 46,754d1 = 1 | d1 = w0 | w1 = -6,441 | |
| (1 46,754 + 18,783) | w1 | + 46,754d1 = 1 | |||
| 46,754 | (w1 + d1) | + 18,783w1 = 1 | w2 = w1 + d1 | -1,846 = 4,595 + d1 | d1 = -6,441 |
| 46,754 | w2 | + 18,783d2 = 1 | d2 = w1 | ||
| (2 18,783 + 9,188) | w2 | + 18,783d2 = 1 | |||
| 18,783 | (2w2 + d2) | + 9,188w2 = 1 | w3 = 2w2 + d2 | 903 = (2)(-1,846) + d2 | d2 = 4,595 |
| 18,783 | w3 | + 9,188d3 = 1 | d3 = w2 | ||
| (2 9,188 + 407) | w3 | + 9,188d3 = 1 | |||
| 9,188 | (2w3 + d3) | + 407w3 = 1 | w4 = 2w3 + d3 | -40 = (2)(903) + d3 | d3 = -1846 |
| 9,188 | w4 | + 407d4 = 1 | d4 = w3 | ||
| (22 407 + 234) | w4 | + 407d4 = 1 | |||
| 407 | (22w4 + d4) | + 234w4 = 1 | w5 = 22w4 +d4 | 23 = (22)(-40) + d4 | d4 = 903 |
| 407 | w5 | + 234d5 = 1 | d5 = w4 | ||
| (1 234 + 173) | w5 | + 234d5 = 1 | |||
| 234 | (w5 + d5) | + 173w5 = 1 | w6 = w5 +d5 | -17 = 23 + d5 | d5 = -40 |
| 234 | w6 | + 173d6 = 1 | d6 = w5 | ||
| (1 173 + 61) | w6 | + 173d6 = 1 | |||
| 173 | (w6 + d6) | + 61w6 = 1 | w7 = w6 +d6 | 6 = -17 + d6 | d6 = 23 |
| 173 | w7 | + 61d7 = 1 | d7 = w6 | ||
| (2 61 + 51) | w7 | + 61d7 = 1 | |||
| 61 | (2w7 + d7) | + 51w7 = 1 | w8 = 2w7 +d7 | -5 = (2)(6) + d7 | d7 = -17 |
| 61 | w8 | + 51d8 = 1 | d8 = w7 | ||
| (1 51 + 10) | w8 | + 51d8 = 1 | |||
| 51 | (w8 + d8) | + 10w8 = 1 | w9 = w8 +d8 | 1 = -5 + d8 | d8 = 6 |
| 51 | w9 | + 10d9 = 1 | d9 = w8 | ||
| (5 10 + 1) | w9 | + 10d9 = 1 | |||
| 10 | (5w9 + d9) | + 1w9 = 1 | w10 = 5w9 +d9 | 0 = (5)(1) + d9 | d9 = -5 |
| 10 | w10 | + 1d10 = 1 | d10 = w9 | ||
| (1 10 + 0) | w10 | + 1d10 = 1 | |||
| 1 | (10w10 + d10) | + 0w10 = 1 | w11 = 10w10 +d10 | 1 = (10)(0) + d10 | d10 = 1 |
| 1 | w11 | + 0d11 = 1 | d11 = w10 | w11 = 1, d11 = 0 |
Euler's Totient Function
[edit | edit source]Significant in cryptography, the totient function (sometimes known as the phi function) is defined as the number of nonnegative integers less than that are coprime to . Mathematically, this is represented as
Which immediately suggests that for any prime
The totient function for any exponentiated prime is calculated as follows
The Euler totient function is also multiplicative
where
Finite Fields and Generators
[edit | edit source]A field is simply a set which contains numerical elements that are subject to the familiar addition and multiplication operations. Several different types of fields exist; for example, , the field of real numbers, and , the field of rational numbers, or , the field of complex numbers. A generic field is usually denoted .
Finite Fields
[edit | edit source]Cryptography utilizes primarily finite fields, nearly exclusively composed of integers. The most notable exception to this are the Gaussian numbers of the form which are complex numbers with integer real and imaginary parts. Finite fields are defined as follows
- The set of integers modulo
- The set of integers modulo a prime
Since cryptography is concerned with the solution of diophantine equations, the finite fields utilized are primarily integer based, and are denoted by the symbol for the field of integers, .
A finite field contains exactly elements, of which there are nonzero elements. An extension of is the multiplicative group of , written , and consisting of the following elements
- such that
in other words, contains the elements coprime to
Finite fields form an abelian group with respect to multiplication, defined by the following properties
The product of two nonzero elements is nonzero The associative law holds The commutative law holds There is an identity element Any nonzero element has an inverse
A subscript following the symbol for the field represents the set of integers modulo , and these integers run from to as represented by the example below
The multiplicative order of is represented and consists of all elements such that . An example for is given below
If is prime, the set consists of all integers such that . For example
| Composite n | Prime p |
|---|---|
Generators
[edit | edit source]Every finite field has a generator. A generator is capable of generating all of the elements in the set by exponentiating the generator . Assuming is a generator of , then contains the elements for the range . If has a generator, then is said to be cyclic.
The total number of generators is given by
Examples
[edit | edit source]For (Prime) Total number of generators generators Let , then , is a generator Since is a generator, check if , and , , therefore, is not a generator , and , , therefore, is not a generator Let , then , is a generator Let , then , is a generator Let , then , is a generator There are a total of generators, as predicted by the formula
For (Composite) Total number of generators generators Let , then , is a generator Let , then , is a generator There are a total of generators as predicted by the formula
Congruences
[edit | edit source]Description
[edit | edit source]Number theory contains an algebraic system of its own called the theory of congruences. The mathematical notion of congruences was introduced by Karl Friedrich Gauss in Disquisitiones (1801).
Definition
[edit | edit source]If and are two integers, and their difference is evenly divisible by , this can be written with the notation
This is expressed by the notation for a congruence
where the divisor is called the modulus of congruence. can equivalently be written as
where is an integer.
Note in the examples that for all cases in which , it is shown that . with this in mind, note that
Represents that is an even number.
Represents that is an odd number.
Examples
[edit | edit source]Properties of Congruences
[edit | edit source]All congruences (with fixed ) have the following properties in common
- if and only if
- If and then
- Given there exists a unique such that
These properties represent an equivalence class, meaning that any integer is congruent modulo to one specific integer in the finite field .
Congruences as Remainders
[edit | edit source]If the modulus of an integer , then for every integer
which can be understood to mean is the remainder of divided by , or as a congruence
Two numbers that are incongruent modulo must have different remainders. Therefore, it can be seen that any congruence holds if and only if and are integers which have the same remainder when divided by .
Example
[edit | edit source]is equivalent to implies is the remainder of divided by
The Algebra of Congruences
[edit | edit source]Suppose for this section we have two congruences, and . These congruences can be added or subtracted in the following manner
If these two congruences are multiplied together, the following congruence is obtained
or the special case where
Note: The above does not mean that there exists a division operation for congruences. The only possibility for simplifying the above is if and only if and are coprime. Mathematically, this is represented as
- implies that if and only if
The set of equivalence classes defined above form a commutative ring, meaning the residue classes can be added, subtracted and multiplied, and that the operations are associative, commutative and have additive inverses.
Reducing Modulo m
[edit | edit source]Often, it is necessary to perform an operation on a congruence where , when what is desired is a new integer such that with the resultant being the least nonnegative residue modulo m of the congruence. Reducing a congruence modulo is based on the properties of congruences and is often required during exponentiation of a congruence.
Algorithm
[edit | edit source]Input: Integers and from with Output: Integer such that 1. Let 2. 3. 4. Output
Example
[edit | edit source]Given ∴
Note that is the least nonnegative residue modulo
Exponentiation
[edit | edit source]Assume you begin with . Upon multiplying this congruence by itself the result is . Generalizing this result and assuming is a positive integer
Example
[edit | edit source]This simplifies to implies implies
Repeated Squaring Method
[edit | edit source]Sometimes it is useful to know the least nonnegative residue modulo of a number which has been exponentiated as . In order to find this number, we may use the repeated squaring method which works as follows:
1. Begin with 2. Square and so that 3. Reduce modulo to obtain 4. Continue with steps 2 and 3 until is obtained. Note that is the integer where would be just larger than the exponent desired 5. Add the successive exponents until you arrive at the desired exponent 6. Multiply all 's associated with the 's of the selected powers 7. Reduce the resulting for the desired result
Example
[edit | edit source]To find : Adding exponents: Multiplying least nonnegative residues associated with these exponents: Therefore:
Inverse of a Congruence
[edit | edit source]Description
[edit | edit source]While finding the correct symmetric or asymmetric keys is required to encrypt a plaintext message, calculating the inverse of these keys is essential to successfully decrypt the resultant ciphertext. This can be seen in cryptosystems Ranging from a simple affine transformation
Where
To RSA public key encryption, where one of the deciphering (private) keys is
Definition
[edit | edit source]For the elements where , there exists such that . Thus, is said to be the inverse of , denoted where is the power of the integer for which .
Example
[edit | edit source]Find This is equivalent to saying First use the Euclidean algorithm to verify . Next use the Extended Euclidean algorithm to discover the value of . In this case, the value is . Therefore, It is easily verified that
Fermat's Little Theorem
[edit | edit source]Definition
[edit | edit source]Where is defined as prime, any integer will satisfy the following relation:
Example
[edit | edit source]When and
- implies that
Conditions and Corollaries
[edit | edit source]An additional condition states that if is not divisible by , the following equation holds
Fermat's Little Theorem also has a corollary, which states that if is not divisible by and then
Euler's Generalization
[edit | edit source]If , then
Chinese Remainder Theorem
[edit | edit source]If one wants to solve a system of congruences with different moduli, it is possible to do so as follows:
A simultaneous solution exists if and only if with , and any two solutions are congruent to one another modulo .
The steps for finding the simultaneous solution using the Chinese Remainder theorem are as follows:
- 1. Compute
- 2. Compute for each of the different 's
- 3. Find the inverse of for each using the Extended Euclidean algorithm
- 4. Multiply out for each
- 5. Sum all
- 6. Compute to obtain the least nonnegative residue
Example
[edit | edit source]Given: Using the Extended Euclidean algorithm:
Quadratic Residues
[edit | edit source]If is prime and , examining the nonzero elements of , it is sometimes important to know which of these are squares. If for some , there exists a square such that . Then all squares for can be calculated by where . is a quadratic residue modulo if there exists an such that . If no such exists, then is a quadratic non-residue modulo . is a quadratic residue modulo a prime if and only if .
Example
[edit | edit source]For the finite field , to find the squares , proceed as follows:
The values above are quadratic residues. The remaining (in this example) 9 values are known as quadratic nonresidues. the complete listing is given below.
Quadratic residues: Quadratic nonresidues:
Legendre Symbol
[edit | edit source]The Legendre symbol denotes whether or not is a quadratic residue modulo the prime and is only defined for primes and integers . The Legendre of with respect to is represented by the symbol . Note that this does not mean divided by . has one of three values: .
Jacobi Symbol
[edit | edit source]The Jacobi symbol applies to all odd numbers where , then:
If is prime, then the Jacobi symbol equals the Legendre symbol (which is the basis for the Solovay-Strassen primality test).
Primality Testing
[edit | edit source]Description
[edit | edit source]In cryptography, using an algorithm to quickly and efficiently test whether a given number is prime is extremely important to the success of the cryptosystem. Several methods of primality testing exist (Fermat or Solovay-Strassen methods, for example), but the algorithm to be used for discussion in this section will be the Miller-Rabin (or Rabin-Miller) primality test. In its current form, the Miller-Rabin test is an unconditional probabilistic (Monte Carlo) algorithm. It will be shown how to convert Miller-Rabin into a deterministic (Las Vegas) algorithm.
Pseudoprimes
[edit | edit source]Remember that if is prime and , Fermat's Little Theorem states:
However, there are cases where can meet the above conditions and be nonprime. These classes of numbers are known as pseudoprimes.
is a pseudoprime to the base , with if and only if the least positive power of that is congruent to evenly divides .
If Fermat's Little Theorem holds for any that is an odd composite integer, then is referred to as a pseudoprime. This forms the basis of primality testing. By testing different 's, we can probabilistically become more certain of the primality of the number in question.
The following three conditions apply to odd composite integers:
- I. If the least positive power of which is congruent to and divides which is the order of in , then is a pseudoprime.
- II. If is a pseudoprime to base and , then is also a pseudoprime to and .
- III. If fails , for any single base , then fails for at least half the bases .
An odd composite integer for which holds for every is known as a Carmichael Number.
Miller-Rabin Primality Test
[edit | edit source]Description
[edit | edit source]Examples
[edit | edit source]Factoring
[edit | edit source]The Rho Method
[edit | edit source]Description
[edit | edit source]Algorithm
[edit | edit source]Example
[edit | edit source]Fermat Factorization
[edit | edit source]Example
[edit | edit source]Random Number Generators
[edit | edit source]RNGs vs. PRNGs
[edit | edit source]ANSI X9.17 PRNG
[edit | edit source]Blum-Blum-Shub PRNG
[edit | edit source]RSA PRNG
[edit | edit source]Entropy Extractors
[edit | edit source]Whitening Functions
[edit | edit source]Large Integer Multiplication
[edit | edit source]Karatsuba Multiplication
[edit | edit source]Example
[edit | edit source]Furers Multiplication
[edit | edit source]Elliptic Curves
[edit | edit source]Description
[edit | edit source]Definition
[edit | edit source]Properties
[edit | edit source]Summary
[edit | edit source]
Computer Security is More Than Encryption
Computer security has three main elements that can easily be remembered using the acronym CIA: Confidentiality, Integrity, Availability.
- Confidentiality is the task of ensuring that only those entities (persons or systems) cleared for access can read information. Cryptography is a key element in ensuring confidentiality.
- Integrity is the task of ensuring that information is correct, and stays that way.
- Availability is the task of ensuring that systems responsible for delivering, storing and processing information are accessible when needed, by those who need them. This includes, for example, protection against denial of service (DoS) attacks.
See also
[edit | edit source]
Unbroken is Not Necessarily Unbreakable
In cryptography, an unbroken algorithm is not necessarily an unbreakable one. There have been many cryptographic algorithms made and deployed in various situations throughout the world, some dating back from the time of Julius Caesar! More recent algorithms, AES Rijndael for example, are very strong, and have survived close scrutiny for many years and have remained secure. But, many other algorithms such as the Vigniere cipher were once believed to be totally unbreakable, but then all of a sudden, they may as well be written in plaintext. It was once thought that the simple XOR cipher could be the answer to an unbreakable algorithm, but new methods of cryptanalysis were born, and now, it can be cracked within moments.
Today's 'secure' ciphers such as AES and Twofish may be secure now, but in the future, with the advent of faster computers, better techniques and even quantum computing, these ciphers will only last so long.
Proportionality of Secrecy
"The more secret information you know, the more successful the concealment of the plaintext."
It is important to realize that any crypto system in its design is an exercise in resource allocation and optimization.
If we were to return to the postal analogy used in the discussion of Asymmetric Ciphers. Suppose Alice has a secret message to send to Bob in the mail. Alice could put the message in her lock box and use Bob's padlock to lock it allowing Bob to open it with his key, as describe earlier. But if it were a really important message or Alice and Bob had a higher expectation of the opponent they wished to thwart (Bob's girlfriend knows where Bob keeps his keys) Alice and Bob might want to resort to a more complicated crypto system. For example Bob could have multiple keys, one he keeps on his key chain, one he keeps in a rented Post Office box and one that is in a box in a Swiss bank vault. Bob might welcome this sort of security for really serious messages but for day to day messages between Bob and Alice Bob will no doubt find a daily flight to Switzerland rather expensive inconvenient. All crypto systems must face a resource trade-off between convenience and security.

This page or section of the Cryptography book is a stub. You can help Wikibooks by expanding it.
Key Lengths
Key Length
[edit | edit source]Key length is directly proportional to security. In modern cryptosystems, key length is measured in bits (e.g. AES uses 256-bit keys), and each bit of a key increases the difficulty of a brute-force attack exponentially. It is important to note that in addition to adding more security, each bit slows down the cryptosystem as well. Because of this, key length -- like all things security -- is a tradeoff. In this case between practicality and security.
Furthermore, different types of cryptosystems require vastly different key lengths to maintain security. For instance, modulo-based public key systems such as Diffie-Hellman and RSA require rather long keys (generally around 1,024 bits), whereas symmetric systems, both block and stream, are able to use shorter keys (generally around 256 bits). Furthermore, elliptic curve public key systems are capable of maintaining security at key lengths similar to those of symmetric systems. While most block ciphers will only use one key length, most public key systems can use any number of key lengths.
As an illustration of relying on different key lengths for the same level of security, modern implementations of public key systems (see GPG and PGP) give the user a choice of keylengths. Usually ranging between 768 and 4,096 bits. These implementations use the public key system (generally either RSA or ElGamal) to encrypt a randomly generated block-cipher key (128 to 256 bits) which was used to encrypt the actual message.
Entropy
[edit | edit source]Equal to the importance of key length is information entropy. Entropy, defined generally as "a measure of the disorder of a system", implies randomness. i.e. If all of the bits of a key are not securely generated and equally random (whether truly random or the result of a cryptographically secure PRNG operation), then the system lacks entropy and is much more vulnerable to attack. For example, if a 128-bit key has only 64 bits of entropy, then the effective length of the key is 64 bits. This can be seen in the DES algorithm. DES actually has a key length of 64 bits; however, the effective key length is 56 bits because 8 bits are used for parity.
Common Mistakes
[edit | edit source]| A reader requests clarification of this page's material to reduce confusion. You can help clarify material, request assistance, or view current progress. |
The fundamental deficiency in advantages of long block cipher keys when compare it to short cipher keys could be in difficulties to screening physical random entropy in short digits. Perhaps we can't store screening mechanism of randomness in secret, so we can't get randomness of entropy 2^256 without energy, which will be liner to appropriate entropy. For example, typical mistake of random generator implementation is simple addiction of individual digits with probability 0.5. This generator could be easy broken by bruteforce by neighbor bits wave functions. In this point of view, using block ciphers with large amount of digits, for ex. 10^1024 and more have a practical sense.
[citation needed]
Other typical mistake is using public key infrastructure to encrypt session keys, because in this key more preferable to use Diffie-Hellman algorithm.
Using the Diffie-Hellman algorithm to create session keys gives "forward secrecy".
Random Quality
"The higher the entropy of a random source, the better the quality of the random data it generates."
Many cryptographic algorithms call for a random source, either in key-generation, or some other primitive. Implementors must be extremely cautious in selecting that random source, or they will open themselves up to attack. For example, the only formally proven encryption technique, the one time pad, requires a completely random and unbiased key-stream that is at least as long as the message itself, and is never reused. There are many implicit complications presented in this requirement, as the only sources of "true randomness" are in the physical world (silicon decay is an example), and are impossible to implement in software. Thus, it is often only feasible to obtain pseudo-randomness. Pseudo-Random Number Generators, or PRNGs, use multiple sources that are thought to be difficult to predict (mouse movement, least significant digits of the computer clock, network statistics, etc.) in order to generate an entropy pool, which is passed through assorted algorithms which attempt to remove any biases, and then used as a seed for a pre-determined static set of numbers. Even with all of the sources of entropy, a determined attacker can usually reduce the effective strength of an implementation by cutting out some of the factors—for instance making educated guesses on the time. PRNGs that are thought to be acceptable for cryptographic purposes are called Cryptographically-Secure Pseudo-Random Number Generators, or CSPRNGs.
Entropy
[edit | edit source]In terms of information theory, entropy is defined as the measure of the amount of information expressed in a string of bits. For example a traditional gender classification contains 1-bit of entropy as it can be represented using a 1 for males and a 0 for females. The quality of a random source is determined by just how much entropy it generates, if the entropy is less than the actual number of bits then there is some repetition of information. The more information that is repeated, or the shorter the period of some PRNG, the lower the entropy and the weaker and more predictable the source of randomness. Therefore in cryptography one seeks to get as close to perfect randomness as possible with the resources available - where a perfect random number generator creates a sequence of bits which are unpredictable no matter how large a sample of previously generated bits is obtained.
Further reading
[edit | edit source]- Cryptography/Random number generation
- RFC 4086 "Randomness Requirements for Security"
Statistical Weaknesses
Letter Frequency
[edit | edit source]Whenever you consider any available language, it gives information about the frequency of letters that occur most frequently in it. The same matter is more enough for cryptanalysis (process of discovering ciphertexts) which is more beneficial when encryption is performed using the Conventional Classical Encryption Techniques.
This gives statistical information of data that cryptanalysts can use in order to decrypt the encrypted data, provided the language in which data is present is known.
Faults
The strength of your encryption method is based not only on your encryption method, but also on your ability to use it effectively. A perfect encryption method which is finicky to use and hard to get right is not likely to be useful in building a high quality security system.
For example, the One-Time Pad cypher is the only known provably unbreakable algorithm (in the very strong sense of a more effective than brute force search attack being impossible), but this proof applies ONLY if the key used is completely randomly chosen (there is currently no known method for making such a choice[citation needed] nor is there any known method for demonstrating that any particular choice is random), if the key is a long as the plaintext, if the key is never reused, and if the key never becomes known to the enemy. These conditions are so difficult to ensure that the One-Time Pad is almost never used in actual practice, whatever its theoretical advantages.
Any use of the One-Time Pad violating those assumed requirements is insecure, sometimes trivially so. For instance, statistical analysis techniques may be immediately applicable, under certain kinds of misuse.

This page or section of the Cryptography book is a stub. You can help Wikibooks by expanding it.
Social Engineering and Coercion
In encryption, the weakest link is almost always a person.
While you could spend many hours attempting to decipher an encrypted message, or intercept a password, you can easily trick a person into telling you this information.
Suppose Bob works for a large company and encrypts document E with key K. Suppose Eve, wishing to decrypt document E, calls Bob and pretends to work for the company's information security department. Eve would pretend a problem existed with the computers, servers, etc. and ask Bob for his key, K, which she would use to decrypt E. This is an example of social engineering.
Randall Munroe in an xkcd comic once presented a scenerio in which bad guys find it more convenient to hit Bob with a $5 wrench until he gives up his key rather than attempt to break the crypto system.
Brute force attack
A brute force attack against a cipher consists of breaking a cipher by trying all possible keys. Statistically, if the keys were originally chosen randomly, the plaintext will become available after about half of the possible keys are tried. As we discuss in Basic Design Principles, the underlying assumption is, of course, that the cipher is known. Since A. Kerckhoffs first published it, a fundamental maxim of cryptography has been that security must reside only in the key. As Claude E. Shannon said a few decades later, 'the enemy knows the system'. In practice, it has been excellent advice.
As of the year 2002, symmetric ciphers with keys 64 bits or fewer are vulnerable to brute force attacks. DES, a well respected symmetric algorithm which uses 56-bit keys, was broken by an EFF project in the late 1990s. They even wrote a book about their exploit—Cracking DES, O'Reilly and Assoc. The EFF is a non-profit cyberspace civil rights group; many people feel that well-funded organisations like the NSA can successfully attack a symmetric key cipher with a 64-bit key using brute force. This is surely true, as it has been done publicly.[citation needed] Many observers suggest a minimum key length for symmetric key algorithms of 128 bits, and even then it is important to select a secure algorithm. For instance, many algorithms can be reduced in effective keylength until it is computationally feasible to launch a brute force attack. AES is recommended for use until at least 2030.
The situation with regard to asymmetric algorithms is much more complicated and depends on the individual algorithm. Thus the currently breakable key length for the RSA algorithm is at least 768 bits (broken publicly since 2009), but for most elliptic curve asymmetric algorithms, the largest currently breakable key length is believed to be rather shorter, perhaps as little as 128 bits or so. A message encrypted with a 109 bit key by an elliptic curve encryption algorithm was publicly broken by brute force key search in early 2003.
As of 2015, a minimum key length of 224 bits is recommended for elliptic curve algorithms, and 2048 bits for such other asymmetric key algorithms as RSA (asymmetric key algorithms that rely on complex mathematical problems for their security always will need much larger keyspaces as there are short-cuts to cracking them, as opposed to direct brute-force).[1]
Common Brute Force Attacks
[edit | edit source]The term "brute force attacks" is really an umbrella term for all attacks that exhaustively search through all possible (or likely) combinations, or any derivative thereof.
Dictionary Attack
[edit | edit source]A dictionary attack is a common password cracking technique, relying largely on the weak passwords selected by average computer users. For instance, if an attacker had somehow accessed the hashed password files through various malicious database manipulations and educated searching on an online store, he would then write a program to hash one at a time all words in a dictionary (of, for example any or all languages and common derivative passwords), and compare these hashes to the real password hashes he had obtained. If the hashes match, he has obtained a password.
Pre-Computation Dictionary Attack
[edit | edit source]The simple dictionary attack method quickly becomes far too time-consuming with any large number of password hashes, such as an online database would yield. Thus, attackers developed the method of pre-computation. In this attack, the attacker has already hashed his entire suite of dictionaries, and all he need do is compare the hashes. Additionally, his task is made easier by the fact that many users will select the same passwords. To prevent this attack, a database administrator must attach unique 32-bit salts to the users passwords before hashing, thus rendering precompution useless.
The Breaking Hash Algorithms chapter of this books goes into more detail on attacks that specifically apply to hashed password files.
Responses to Brute Force Attacks
[edit | edit source]There are a number of ways to mitigate brute force attacks. For example:
- Changing a key frequently in response to an attempt to try all possible keys would require an attacker to start over assuming he knew the key was changed or finish attempting all possible keys before starting the attack again from the beginning.
- A system could rely on a time out or lock out of the system after so many attempts at guessing the key. Systems that time out can simply block further access, lock a user account, contact the account owner, or even destroy the clear text information.
- 2 step verification is a method of requiring a second key to enter the system. This complicates a brute force attack since the attacker must not only guess one key but then guess a second possibly equally complex key. The most common implementation of this is to ask for further authentication "What's your first dogs name?". There is a new trend on the horizon for systems to utilize two step verification through a time based key that is emailed or texted and having access to an account or particular electronic device serves as a secondary key.
The Secure Passwords chapter of this book goes into more detail on mitigations and other responses that specifically apply to hashed password files.
Frequency analysis
In the field of cryptanalysis, frequency analysis is a methodology for "breaking" simple substitution ciphers, not just the Caesar cipher but all monoalphabetic substitution ciphers. These ciphers replace one letter of the plaintext with another to produce the cyphertext, and any particular letter in the plaintext will always, in the simplest and most easily breakable of these cyphers, turn into the same letter in the cypher. For instance, all E's will turn into X's.

Frequency analysis is based on the fact that certain letters, and combinations of letters, appear with characteristic frequency in essentially all texts in a particular language. For instance, in the English language E is very common, while X is not. Likewise, ST, NG, TH, and QU are common combinations, while XT, NZ, and QJ are exceedingly uncommon, or "impossible". Given our example of all E's turning into X's, a cyphertext message containing lots of X's already seems to suggest one pair in the substitution mapping.
In practice the use of frequency analysis consists of first counting the frequency of cypher text letters and then assigning "guessed" plaintext letters to them. Many letters will occur with roughly the same frequency, so a cypher with X's may indeed map X onto R, but could also map X onto G or M. But some letters in every language using letters will occur more frequently; if there are more X's in the cyphertext than anything else, it's a good guess for English plaintext that X stands for E. But T and A are also very common in English text, so X might be either of them. It's very unlikely to be a Z or Q which aren't common in English. Thus the cryptanalyst may need to try several combinations of mappings between cyphertext and plaintext letters. Once the common letters are 'solved', the technique typically moves on to pairs and other patterns. These often have the advantage of linking less commonly used letters in many cases, filling in the gaps in the candidate mapping table being built. For instance, Q and U nearly always travel together in that order in English, but Q is rare.
Frequency analysis is extremely effective against the simpler substitution cyphers and will break astonishingly short ciphertexts with ease. This fact was the basis of Edgar Allan Poe's claim, in his famous newspaper cryptanalysis demonstrations in the middle 1800's, that no cypher devised by man could defeat him. Poe was overconfident in his proclamation, however, for polyalphabetic substitution cyphers (invented by Alberti around 1467) defy simple frequency analysis attacks. The electro-mechanical cypher machines of the first half of the 20th century (e.g., the Hebern? machine, the Enigma, the Japanese Purple machine, the SIGABA, the Typex, ...) were, if properly used, essentially immune to straightforward frequency analysis attack, being fundamentally polyalphabetic cyphers. They were broken using other attacks.
Frequency analysis was first discovered in the Arab world, and is known to have been in use by about 1000 CE. It is thought that close textual study of the Koran first brought to light that Arabic has a characteristic letter frequency which can be used in cryptoanalysis. Its use spread, and was so widely used by European states by the Renaissance that several schemes were invented by cryptographers to defeat it. These included use of several alternatives to the most common letters in otherwise monoalphabetic substitution cyphers (i.e., for English, both X and Y cyphertext might mean plaintext E), use of several alphabets—chosen in assorted, more or less, devious ways (Leon Alberti seems to have been the first to propose this), culminating in such schemes as using only pairs or triplets of plaintext letters as the 'mapping index' to cyphertext letters (e.g., the Playfair cipher invented by Charles Wheatstone in the mid 1800s). The disadvantage of all these attempts to defeat frequency counting attacks is that it increases complication of both encyphering and decyphering, leading to mistakes. Famously, a British Foreign Secretary is said to have rejected the Playfair cipher because, even if school boys could learn it as Wheatstone and Playfair had shown, 'our attaches could never learn it!'.
Frequency analysis requires a basic understanding of the language of the plaintext, as well as tenacity, some problem solving skills, and considerable tolerance for extensive letter bookkeeping. Neat handwriting also helps. During WWII, both the British and Americans recruited codebreakers by placing crossword puzzles in major newspapers and running contests for who could solve them the fastest. Several of the cyphers used by the Axis were breakable using frequency analysis (e.g., the 'consular' cyphers used by the Japanese). Mechanical methods of letter counting and statistical analysis (generally IBM card machinery) were first used in WWII. Today, the hard work of letter counting and analysis has been replaced by the tireless speed of the computer, which can carry out this analysis in seconds. No mere substitution cypher can be thought credibly safe in modern times.
The frequency analysis method is neither necessary nor sufficient to solve ciphers. Historically, cryptanalysts solved substitution ciphers using a variety of other analysis methods long before and after the frequency analysis method became well known. Some people even question why the frequency analysis method was considered useful for such a long time.[2] However, modern cyphers are not simple substitution cyphers in any guise. They are much more complex than WWII cyphers, and are immune to simple frequency analysis, and even to advanced statistical methods. The best of them must be attacked using fundamental mathematical methods not based on the peculiarities of the underlying plaintext language. See Cryptography/Differential cryptanalysis or Cryptography/Linear cryptanalysis as examples of such techniques.
References
[edit | edit source]- ↑ Damien Giry. "Cryptographic Key Length Recommendation".
- ↑ Bernard Ycart. "Letter counting: a stem cell for Cryptology, Quantitative Linguistics, and Statistics". p. 8.
Index of coincidence
The index of coincidence for a ciphertext is the probability that two letters selected from it are identical. Usually denoted by I, it is a statistical measure of the redundancy of text. The index of coincidence of totally random collection (uniform distribution) of letters is around 0.0385.[1]
References
[edit | edit source]
This page or section of the Cryptography book is a stub. You can help Wikibooks by expanding it.
Linear cryptanalysis
In cryptography, linear cryptanalysis is a general form of cryptanalysis based on finding affine approximations to the action of a cipher. Attacks have been developed for block ciphers and stream ciphers. Linear cryptanalysis is one of the two most widely used attacks on block ciphers; the other being differential cryptanalysis.
The discovery is attributed to Mitsuru Matsui, who first applied the technique to the FEAL cipher (Matsui and Yamagishi, 1992). Subsequently, Matsui published an attack on the Data Encryption Standard (DES), eventually leading to the first experimental cryptanalysis of the cipher reported in the open community (Matsui, 1993; 1994). The attack on DES is not generally practical, requiring 243 known plaintexts.
A variety of refinements to the attack have been suggested, including using multiple linear approximations or incorporating non-linear expressions, leading to a generalized partitioning cryptanalysis. Evidence of security against linear cryptanalysis is usually expected of new cipher designs.
Overview
[edit | edit source]There are two parts to linear cryptanalysis. The first is to construct linear equations relating plaintext, ciphertext and key bits that have a high bias; that is, whose probabilities of holding (over the space of all possible values of their variables) are as close as possible to 0 or 1. The second is to use these linear equations in conjunction with known plaintext-ciphertext pairs to derive key bits.
Constructing linear equations
[edit | edit source]For the purposes of linear cryptanalysis, a linear equation expresses the equality of two expressions which consist of binary variables combined with the exclusive-or (XOR) operation. For example, the following equation, from a hypothetical cipher, states the XOR sum of the first and third plaintext bits (as in a block cipher's block) and the first ciphertext bit is equal to the second bit of the key:
In an ideal cipher, any linear equation relating plaintext, ciphertext and key bits would hold with probability 1/2. Since the equations dealt with in linear cryptanalysis will vary in probability, they are more accurately referred to as linear approximations.
The procedure for constructing approximations is different for each cipher. In the most basic type of block cipher, a substitution-permutation network, analysis is concentrated primarily on the S-boxes, the only nonlinear part of the cipher (i.e. the operation of an S-box cannot be encoded in a linear equation). For small enough S-boxes, it is possible to enumerate every possible linear equation relating the S-box's input and output bits, calculate their biases and choose the best ones. Linear approximations for S-boxes then must be combined with the cipher's other actions, such as permutation and key mixing, to arrive at linear approximations for the entire cipher. The piling-up lemma is a useful tool for this combination step. There are also techniques for iteratively improving linear approximations (Matsui 1994).
Deriving key bits
[edit | edit source]Having obtained a linear approximation of the form:
we can then apply a straightforward algorithm (Matsui's Algorithm 2), using known plaintext-ciphertext pairs, to guess at the values of the key bits involved in the approximation.
For each set of values of the key bits on the right-hand side (referred to as a partial key), count how many times the approximation holds true over all the known plaintext-ciphertext pairs; call this count T. The partial key whose T has the greatest absolute difference from half the number of plaintext-ciphertext pairs is designated as the most likely set of values for those key bits. This is because it is assumed that the correct partial key will cause the approximation to hold with a high bias. The magnitude of the bias is significant here, as opposed to the magnitude of the probability itself.
This procedure can be repeated with other linear approximations, obtaining guesses at values of key bits, until the number of unknown key bits is low enough that they can be attacked with brute force.
References
[edit | edit source]- Matsui, M. and Yamagishi, A. "A new method for known plaintext attack of FEAL cipher". Advances in Cryptology - EUROCRYPT 1992.
- Matsui, M. "Linear cryptanalysis method for DES cipher" (PDF). Advances in Cryptology - EUROCRYPT 1993. Archived from the original on 2006-04-10. http://web.archive.org/web/20060410133750/http://homes.esat.kuleuven.be/~abiryuko/Cryptan/matsui_des.PDF. Retrieved 2007-02-22.
- Matsui, M. "The first experimental cryptanalysis of the data encryption standard". Advances in Cryptology - CRYPTO 1994.
Differential cryptanalysis
Differential cryptanalysis is a general form of cryptanalysis applicable primarily to block ciphers, but also to stream ciphers and cryptographic hash functions. In the broadest sense, it is the study of how differences in an input can affect the resultant difference at the output. In the case of a block cipher, it refers to a set of techniques for tracing differences through the network of transformations, discovering where the cipher exhibits non-random behaviour, and exploiting such properties to recover the secret key.
History
[edit | edit source]The discovery of differential cryptanalysis is generally attributed to Eli Biham and Adi Shamir in the late 1980s, who published a number of attacks against various block ciphers and hash functions, including a theoretical weakness in the Data Encryption Standard (DES). It was noted by Bamford in The Puzzle Palace that DES is surprisingly resilient to differential cryptanalysis, in the sense that even small modifications to the algorithm would make it much more susceptible.
In 1994, a member of the original IBM DES team, Don Coppersmith, published a paper stating that differential cryptanalysis was known to IBM as early as 1974, and that defending against differential cryptanalysis had been a design goal.[1] According to author Steven Levy, IBM had discovered differential cryptanalysis on its own, and the NSA was apparently well aware of the technique.[2] IBM kept some secrets, as Coppersmith explains: "After discussions with NSA, it was decided that disclosure of the design considerations would reveal the technique of differential cryptanalysis, a powerful technique that could be used against many ciphers. This in turn would weaken the competitive advantage the United States enjoyed over other countries in the field of cryptography."[1] Within IBM, differential cryptanalysis was known as the "T-attack"[1], or "Tickle attack".[3]
While DES was designed with resistance to differential cryptanalysis in mind, other contemporary ciphers proved to be vulnerable. An early target for the attack was the FEAL block cipher. The original proposed version with four rounds (FEAL-4) can be broken using only eight chosen plaintexts, and even a 31-round version of FEAL is susceptible to the attack.
Attack mechanics
[edit | edit source]Differential cryptanalysis is usually a chosen plaintext attack, meaning that the attacker must be able to obtain encrypted ciphertexts for some set of plaintexts of his choosing. The scheme can successfully cryptanalyze DES with an effort on the order 247 chosen plaintexts. There are, however, extensions that would allow a known plaintext or even a ciphertext-only attack. The basic method uses pairs of plaintext related by a constant difference; difference can be defined in several ways, but the eXclusive OR (XOR) operation is usual. The attacker then computes the differences of the corresponding ciphertexts, hoping to detect statistical patterns in their distribution. The resulting pair of differences is called a differential. Their statistical properties depend upon the nature of the S-boxes used for encryption, so the attacker analyses differentials , where (and denotes exclusive or) for each such S-box . In the basic attack, one particular ciphertext difference is expected to be especially frequent; in this way, the cipher can be distinguished from randomness. More sophisticated variations allow the key to be recovered faster than exhaustive search.
In the most basic form of key recovery through differential cryptanalysis, an attacker requests the ciphertexts for a large number of plaintext pairs, then assumes that the differential holds for at least r-1 rounds, where r is the total number of rounds. The attacker then deduces which round keys (for the final round) are possible assuming the difference between the blocks before the final round is fixed. When round keys are short, this can be achieved by simply exhaustively decrypting the ciphertext pairs one round with each possible round key. When one round key has been deemed a potential round key considerably more often than any other key, it is assumed to be the correct round key.
For any particular cipher, the input difference must be carefully selected if the attack is to be successful. An analysis of the algorithm's internals is undertaken; the standard method is to trace a path of highly probable differences through the various stages of encryption, termed a differential characteristic.
Since differential cryptanalysis became public knowledge, it has become a basic concern of cipher designers. New designs are expected to be accompanied by evidence that the algorithm is resistant to this attack, and many, including the Advanced Encryption Standard, have been proven secure against the attack.
References
[edit | edit source]- ↑ a b c
Coppersmith, Don (1994). "The Data Encryption Standard (DES) and its strength against attacks" (PDF). IBM Journal of Research and Development. 38 (3): 243.
{{cite journal}}: Unknown parameter|month=ignored (help) (subscription required) - ↑ Levy, Steven (2001). "Crypto: How the Code Rebels Beat the Government — Saving Privacy in the Digital Age. Penguin Books. pp. 55–56. ISBN 0-14-024432-8.
- ↑ Matt Blaze, sci.crypt, 15 August 1996, Re: Reverse engineering and the Clipper chip"
- Eli Biham, Adi Shamir, Differential Cryptanalysis of the Data Encryption Standard, Springer Verlag, 1993. ISBN 0-387-97930-1, ISBN 3-540-97930-1.
- Biham, E. and A. Shamir. (1990). Differential Cryptanalysis of DES-like Cryptosystems. Advances in Cryptology — CRYPTO '90. Springer-Verlag. 2–21.
- Eli Biham, Adi Shamir,"Differential Cryptanalysis of the Full 16-Round DES," CS 708, Proceedings of CRYPTO '92, Volume 740 of Lecture Notes in Computer Science, December 1991. (Postscript)
- Eli Biham, slides from "How to Make a Difference: Early History of Differential Cryptanalysis"PDF (850 KB), March 16, 2006, FSE 2006, Graz, Austria
Meet In The Middle Attack
An extremely specialized attack, meet in the middle is a known plaintext attack that only affects a specific class of encryption methods - those which achieve increased security by using one or more "rounds" of an otherwise normal symmetrical encryption algorithm. An example of such a compound system is 3DES.
However, to explain this attack let us begin with a simpler system defined as follows: Two cryptographic systems denoted and (with inverse functions and respectively) are combined simply (by applying one then the other) to give a composite cryptosystem. each accepts a 64 bit key (for values from 0 to 18446744073709551615) which we can call or as appropriate.
So for a given plaintext, we can calculate a cryptotext as
and correspondingly
Now, given that each has a 64 bit key, the amount of key needed to encrypt or decrypt is 128 bits, so a simple analysis would assume this is the same as a 128 bit cypher.
However, given sufficient storage, you can reduce the effective key strength of this to a few bits larger than the largest of the two keys employed, as follows.
- Given a plaintext/cyphertext pair, apply to the plaintext with each possible key in turn, generating intermediate cryptotexts where
- Store each of the cryptotexts in a hash table so that each can be referenced by its cryptotext, and give the key used to generate that cryptotext
- Apply to the ciphertext for each possible key in turn, comparing the intermediate plaintext to the hash table calculated earlier. this gives a pair of keys (one for each of the two algorithms employed, and )
- Taking the two keys from stage 3, test each against a second plaintext/cryptotext pair. if this also matches, odds are extremely high you have a valid keypair for the message - not in operations, but a "mere" operations (which nonetheless are significantly longer due to the hash table operations, but not so much as to add more than a couple of extra bits worth of time to the complexity of the task)
The downside to this approach is storage. Assuming you have a 64 bit key, then you will need at least units of storage - where each unit is the amount of space used by a single hash record. Even given a minimal implementation (say, 64 bits for the key plus four bits hash collision overhead), if you implemented such a system using 160GB hard drives, you would need close to one billion of them to store the hash table alone.
Breaking Hash Algorithms
Cryptographic hash functions are one of the more difficult, from a cryptography perspective, things to break.
Cryptographic hash functions are specifically designed to be "one-way": If you have some message, it is easy to go forward to the corresponding hashed value; but if you only have the hashed value, cryptographic hashes are specifically designed to be difficult to calculate the original message that produced that hash value -- or any other message that produces the same hash value.
As we previously mentioned in Hashes, a cryptographically secure hash is designed to have these properties:
- Preimage resistant: Given H it should be hard to find M such that H = hash(M).
- Second preimage resistant: Given an input m1, it should be hard to find another input, m2 (not equal to m1) such that hash(m1) = hash(m2).
- Collision-resistant: it should be hard to find two different messages m1 and m2 such that hash(m1) = hash(m2).
Cryptographers distinguish between three different kinds of attacks on hash functions:
- collision attack: try to find any two different messages m1 and m2 such that hash(m1) = hash(m2).
- preimage attack: Given only the hash value H, try to recover *any* M such that H = hash(M).
- second-preimage attack: Given an input m1, try to find another input, m2 (not equal to m1) such that hash(m1) = hash(m2).
- Some hash functions (MD5, SHA-1, SHA-256, etc.) are vulnerable to a "length extension attack".
(Alas, different cryptographers use different and sometimes use contradictory terms for these three kinds of attacks. Outside of this book, some cryptographers use "collision" to refer to a successful attack of any of these 3 types, and use the term "free collision" for what this book calls a "successful collision attack", or "bound collision" for either one of a "successful preimage attack" or a "successful second-preimage attack".)[1]
When designing a new system that requires some hash function, most cryptographers recommend using hash fuctions that, as far as we know, are resistant to all these attacks (such as SHA-3, BLAKE, Grøstl, Skein, etc.).
The collision attack is the easiest kind of attack, and the most difficult to defend against. Because there are an infinite number of possible files, the pigeonhole principle tells us that there are in theory an infinite number of hash collisions, even for the "ideal" random oracle hash. Cryptographic hashes are designed to make it difficult -- using only resources available in our solar system, practically impossible -- to find *any* of those messages that hash to some given hash value.
Some applications require collision resistance. When a possible attacker generates a message and we want to confirm that the message that person shows Alice is the same as the message that person shows Bob, ensuring message integrity, we need a hash that hash collision resistance.
Many applications do not actually require collision resistance. For example, password hashing requires preimage and second-preimage resistance (and a few other special characteristics), but not collision resistance. For example, de-duplicating file systems, host-proof file systems such as IPFS, digital signatures, etc. only require second-preimage resistance, not preimage or collision resistance, because in those applications it is assumed that the attacker already knows the original message that hashes to the given value. For example, message authentication using HMAC does not require collision resistance and is immune to length extension; so as of 2011 cryptographers find using HMAC-MD5 message authentication in existing applications acceptable, although they recommend that new applications use some alternative such as HMAC-SHA256 or AES-CMAC.[2][3]
The MD5 and SHA-1 hash functions, in applications that do not actually require collision resistance, are still considered adequate.
Many people criticise MD5 and SHA1 for the wrong reasons. [4] There is no known practical or almost-practical preimage attack on MD5 or SHA-1, much less second-preimage attacks, only collision attacks.[5][6]
Such collision attacks include:
- Dobbertin announced a collision of the MD5 compression function in 1996 ...
- As of 2009, finding chosen-prefix collisions in MD5 takes about 30 seconds on a laptop.[3]
- Manuel and Peyrin's SHA-0 attack[7]
- Nat McHugh's MD5 collision attacks[8]
In the next chapters we will discuss
Notes
[edit | edit source]- ↑ "The difference between being not strongly collision resistant, and not weakly collision resistant?" http://crypto.stackexchange.com/questions/19159/the-difference-between-being-not-strongly-collision-resistant-and-not-weakly-co quote: "Klaus Schmeh apparently made up the "bound collision" and "free collision" terminology for the book "Cryptography and Public Key Infrastructure on the Internet"."
- ↑ RFC 6151
- ↑ a b Nate Lawson. "Stop using unsafe keyed hashes, use HMAC". 2009.
- ↑ "Is my developer's home-brew password security right or wrong, and why?" quote: "criticized MD5 and SHA1 for the wrong rationale ... There's a subtle difference between pre-image and collision attacks ..."
- ↑
Bruce Morton, Clayton Smith (2014-01-30). "Why We Need to Move to SHA-2". CA Security Council.
{{cite web}}: CS1 maint: uses authors parameter (link) - ↑ "MD5 and Perspectives". 2009-01-01. quote: "All currently known practical or almost-practical attacks on MD5 and SHA-1 are collision attacks."
- ↑ Stéphane Manuel, Thomas Peyrin. "Collisions on SHA-0 in One Hour" [2] [3] [4]
- ↑ "Create your own MD5 collisions"
- ↑ "Create your own MD5 collisions"
- ↑ "Are there two known strings which have the same MD5 hash value?"
Collisions
A hash function is said to collide when two distinct inputs to the hash function yield the same output.
For example, when the following blocks are input into the md5 hash function they both yield the same output.
d131dd02c5e6eec4693d9a0698aff95c 2fcab58712467eab4004583eb8fb7f89 55ad340609f4b30283e488832571415a 085125e8f7cdc99fd91dbdf280373c5b d8823e3156348f5bae6dacd436c919c6 dd53e2b487da03fd02396306d248cda0 e99f33420f577ee8ce54b67080a80d1e c69821bcb6a8839396f9652b6ff72a70
d131dd02c5e6eec4693d9a0698aff95c 2fcab50712467eab4004583eb8fb7f89 55ad340609f4b30283e4888325f1415a 085125e8f7cdc99fd91dbd7280373c5b d8823e3156348f5bae6dacd436c919c6 dd53e23487da03fd02396306d248cda0 e99f33420f577ee8ce54b67080280d1e c69821bcb6a8839396f965ab6ff72a70
References
[edit | edit source]"MD5 Collisions, Visualised". Retrieved 2010-03-11.
Breaking transposition ciphers
Earlier, we discussed how Permutation cipher and Transposition ciphers work for people who know the secret key. Next, we'll discuss how, in some cases, it is possible for a person who only has the ciphertext -- who doesn't know the secret key -- to recover the plaintext.
The frequency distribution of the letters in any transposition or permutation ciphertext is the same as the frequency distribution for plaintext.
breaking columnar transposition ciphers
[edit | edit source]The frequency distribution of digrams can be used to help break columnar transposition ciphers. [1]
breaking double columnar transposition ciphers
[edit | edit source]breaking turning grille ciphers
[edit | edit source]Turning grilles, also called Fleissner grilles, ...
A guess at some sequence of two or more consecutive holes of the grill in one position of the grill (by a "known word" or an expected common digraph) can be "checked" by seeing if those holes, after the grill is rotated a half-turn, produce reasonable digraph.[2][3]
breaking other grille ciphers
[edit | edit source]References
[edit | edit source]- ↑ Prof. H. Williams. "Transposition Ciphers". section "Analysis of columnar transposition ciphers". Retrieved 2014-05-01.
- ↑ Helen Fouché Gaines. "Cryptanalysis: A Study of Ciphers and Their Solution". 1956. section "The Turning Grille". p. 29 to 36.
- ↑ "Elementary Course in Cryptanalysis: Assignment 9: Grille Transposition Ciphers".
Breaking Caesar cipher
Breaking the Caesar cipher is trivial as it is vulnerable to most forms of attack. The system is so easily broken that it is often faster to perform a brute force attack to discover if this cipher is in use or not. An easy way for humans to decipher it is to examine the letter frequencies of the cipher text and see where they match those found in the underlying language.
Frequency analysis
[edit | edit source]By graphing the frequencies of letters in the ciphertext and those in the original language of the plaintext, a human can spot the value of the key by looking at the displacement of particular features of the graph. For example in the English language the frequencies of the letters Q,R,S,T have a particularly distinctive pattern.
Computers can also do this trivially by means of an auto-correlation function.
Brute force
[edit | edit source]As the system only has 25 non-trivial keys it is easy even for a human to cycle through all the possible keys until they find one which allows the ciphertext to be converted into plaintext.
Known plaintext attack
[edit | edit source]If you have a message in both ciphertext and in plaintext it is trivial to find the key by calculating the difference between them.
Breaking Vigenère cipher
Plain text is encrypted using the Vigenère cipher by first choosing a keyword consisting of letters from the alphabet of symbols used in the plain text. The keyword is then used to encrypt the text by way of the following example.
Using: Plain text: I Like A Book and choosing: Keyword: cta
1. Map all the plain text to numbers 0-25 or however long your alphabet is
ilikewikibooks converts to 8 11 8 10 4 22 8 10 8 1 14 14 10 18
2. Map your keyword to numbers the same way
cta maps to 2 19 0
3. add your key to your plain text in the following manner
8 11 8 10 4 22 8 10 8 1 14 14 10 18 2 19 0 2 19 0 2 19 0 2 19 0 2 19 resulting in 10 30 8 12 23 22 10 29 8 3 33 14 12 37
4. take each resulting number mod 26 ( or for the general case mod the number of characters in your alphabet)
resulting in 10 4 8 12 23 22 10 3 8 3 7 14 12 11
5. map each number back to a letter to get the resulting cypher text
keimxwkdidhoml
The message can easily be decrypted with the keyword by reversing the above process. The keyword can be any length equal to or less than that of the plain text.
Without the keyword the primary method of breaking the Vigenère cipher is known as the Kasiski test, after the Prussian major who first published it. The first stage is determining the length of the keyword.
Determining the key length
[edit | edit source]Given an enciphered message such as:
Plaintext: TOBEORNOTTOBE Keyword: KEYKEYKEYKEYK Ciphertext: DSZOSPXSRDSZO
Upon inspection of the ciphertext, we see that there are a few digraphs repeated, namely DS, SZ, and ZO. It is statistically unlikely that all of these would arise by random chance; the odds are that repeated digraphs in the ciphertext correspond to repetitions in the plaintext. If that is the case, the digraphs must be encoded by the same section of the key both times. Therefore, the length of the key is a factor of the distance in the text between the repetitions.
| Digraph | First Position | Second Position | Distance | Factors |
|---|---|---|---|---|
| DS | 1 | 10 | 9 | 3 |
| SZ | 1 | 10 | 9 | 3 |
| ZO | 1 | 10 | 9 | 3 |
The common factors (indeed, the only factors in this simple example) are 3 and 9. This narrows down the possibilities significantly, and the effect is even more pronounced with longer texts and keys.
Frequency analysis
[edit | edit source]Once the length of the key is known, a slightly modified frequency analysis technique can be applied. Suppose the length of the key is known to be three. Then every third letter will be encrypted with the same letter of the key. The ciphertext can be split into three segments - one for each key letter—and the procedure described for the Caesar cipher can be used.
External links
[edit | edit source]
Digital signatures
As of 2014, installing apps is probably the most common way people use digital signatures. Both Android and iOS require an app to be digitally signed before it can be installed.[1][2]
Cryptography is generally used to provide some form of assurance about a message. This assurance can be one or more of four general forms. These forms are message confidentiality, integrity, authentication, and non-repudiation. Up until the advent of public key encryption, cryptography was generally only used to provide confidentiality, that is, communications were encrypted to keep their contents secret. This encryption generally implies the sender to know the scheme and key in use, and therefore provides some rudimentary authentication. Modern digital signatures are much better at providing the assurance of authentication, integrity, and non-repudiation than historical symmetric-key encryption schemes.
Digital signatures rely on the ability of a public-key signing algorithm to sign a message—to generate a signature from the message with a private key. Later, anyone with that signature can verify the message using the corresponding public key. (This uses the keys in the opposite order as public-key encryption and public-key decryption to provide confidentiality—encryption with a public key and decryption only with the private key). However, to provide digital signing, a signer must use his private key to sign the message—or some representation of the message—that he wants to sign with his private key, so that anyone who knows his public key can use it to verify that only his private key could have signed that message.
There are a number of relevant details to proper implementation.
First, the signature itself is useless if the recipients do not have a verified copy of the signer's public key. While perhaps the best method for exchanging that key would be to meet face-to-face, this is often not possible. As a result, many public key infrastructures require the creation of a Certificate Authority whose public key is pre-shared via some trusted method. An example of this would be SSL CA's like VeriSign, whose certificates are pre-installed in most popular browsers by the computer manufacturer. The CA is what's known as a Trusted Third Party, an individual or organization who is trusted by all parties involved in the encrypted communications. It is the duty of this organization to keep its private key safe and secret, and to use that key to sign public keys of individuals it has verified. In other words, in order to save the trouble of meeting face-to-face to exchange keys with every individual you wish to communicate with, you might engage the services of a trusted third party whose public key you already have to go meet these individuals face-to-face. The third party can then sign the public keys and send them along to you, so that you end up with a verified copy without the trouble of exchanging each key pair face-to-face. The details of signing itself we will get to in a moment.
An alternative method commonly used for secure e-mail transmission via PGP or GPG is known as a web of trust. A web of trust is similar to the creation of a certificate authority, with the primary difference being that it is less formal. Rather than creating an organization to act as a trusted third party, individuals will instead sign keys of other individuals they have met in person. In this manner, if Alice has Bob's key, and Bob signs Charlie's key, Alice can trust Charlie's key. Obviously, this can be extended over a very complex web, but this ability is also a great weakness; one compromised individual in the web—the weakest link in the chain of trust—can render the rest useless.
The actual implementation of signing can also vary. One can sign a message simply by encrypting it with his private key—it can be decrypted by his public key, and the act of valid encryption can only be performed by that secret key, thus proving his identity. However, often one may want to sign but not encrypt messages. To provide this functionality at a base level, one might send two copies of the message, one of which would be encrypted. If a reader wishes to verify that the unencrypted message he has read is valid, he can decrypt the duplicate and compare the two. However, even this method is cumbersome; it doubles the size of every message. To avoid this drawback, most implementations use Hash Functions to generate a hash of the message, and use the private key to encrypt that hash. This provides nearly the same security as encrypting a duplicate, but saves space.
Many early explanations of public-key signature algorithms describe public-key signing algorithms as "encrypt a message with a private key". Then they describe public-key message verify algorithms as "decrypt with the public key". Many people prefer to describe modern public-key cryptosystems as having 4 independent high-level functions—encrypt, decrypt, sign, verify—since none of them (if properly padded to avoid chosen-ciphertext attacks) can be substituted for any of the others.[3][4][5][6][7][8][9][10][11][12]
- ↑ Android Developers. "Signing Your Applications".
- ↑ Genuitec. "iOS Application Provisioning Requirements".
- ↑ Nate Lawson. "RSA public keys are not private".
- ↑ "RSA encryption with private key and decryption with a public key".
- ↑ "ElGamal encryption with private key".
- ↑ "Is encrypting data with a private key dangerous?".
- ↑ "Encryption with private key?".
- ↑ "Can one encrypt with a private key/decrypt with a public key?".
- ↑ "Encrypt with private key and decrypt with public key".
- ↑ "Encrypt using private key"
- ↑ "encrypt with private key decrypt with public key"
- ↑ "What is the difference between encrypting and signing in asymmetric encryption?".
Database protection
Cryptographic protection of databases, mailinglists, memberslists.
There are many cryptographic techniques associated with databases:
- anonymizing / aggregating / depersonalizing data, so people can get summary statistics of data without associating particular items with any one person
- column-level encryption, with a different encryption key for each column[1]
- Format-preserving encryption
- data comparison
- transparent data encryption
- etc.
Often databases are protected by full-disk encryption, which is described in a different chapter of this book.
The shadow password file could be considered a "database" of password hash digests. Password handling is discussed in detail in another chapter of this book, Secure Passwords.
data comparison
[edit | edit source]Often we want to tell someone *not* to use some piece of data. But we would rather not tell people the specific details.
For example, We often want to implement "password reset", so if someone forgets the password associated with their account on our website, they can request a password reset and then click a "password reset" link sent to their email address. We want to only allow that person to reset their own password; we certainly don't want some other person (using some other email address) to reset the password for that account. But some people say GDPR frowns on us storing everyone's email address in plaintext (in case the server backup files are stolen). One proposed approach is to store a salted and hashed email (HEM), so that when a user hits the "forgot password" button, the user can punch in an email address (which the system never stores to disk), which the system compares to the stored HEM, and only if they are the same does the system send the password reset link to that email address.[2][3][4]
For example, we want people to know if their particular password has been revealed in a public data breach, but we don't want to make it easy for malicious people to harvest those passwords.[5]
For example, we want to tell email marketers not to send any email to anyone on the "do not email" registry, but we don't want to make it even easier for spammers to send spam email to everyone on the "do not email" registry. One proposed approach is to avoid ever storing such email addresses directly or even in encrypted form, but instead using a one-way-hash on each submitted email address and storing only the output hash values in the database.[6][7]
A variety of data masking policies have been proposed for email addresses.[8]
Gravatar uses hashed email addresses.[9]
Simply hashing an email address by itself generates the same hash value every time. Some people propose adding "salt" or "pepper" or both to email addresses before hashing them, so that hashed addresses in one database cannot be matched to hashed addresses (using a different salt or a different pepper or both) in some other database.[10][11][12]
Row-level encryption
[edit | edit source]A straightforward protection scheme: One-way hash function with symmetric encryption.
1. Use a one-way hash function on the (plaintext of) the index field to create the encryption key for one row.
2. Use the encryption key for one row from step 1 as the cipher key to encrypt every data field in that row. All fields are stored encrypted, even the index field.
Symmetric encryption algorithim — the same cipher key is used to encrypt and decrypt data
Searching the database
[edit | edit source]Look for the hashed value in the index field of the database and for each matching entry decrypt the data fields using the index field as the cipher key.
Example in php code
[edit | edit source]Some very easy php pseudocode to protect your data by encrypting your databases with a one-way hash and blowfish symmetric encryption.
Using a one-way hash and blowfish symmetric encryption. 1. Insert a record of John Doe in an encrypted database. 2. Get the encrypted record of user John Doe and decrypt the data.
Insert a record of John Doe in an encrypted database.
[edit | edit source]<?php
require_once("Crypt/Blowfish.php"); // a Pear class http://pear.php.net
$aRecord['email'] = "johndoe@anisp.localhost"; // The Primary key
$aRecord['name'] = "John Doe";
$aRecord['creditnr'] = "0192733652342" ;
// crypt - one-way encryption
$cipher_key = crypt( $aRecord['email'] , "A_SECRET_COMPANY_SALT");
$bf = new Crypt_Blowfish('ecb');
$bf->setKey( $cipher_key );
// crypt_blowfish symmetric encryption to encrypt the data
$aRecord['email'] = $bf->encrypt( $aRecord['email'] );
$aRecord['name'] = $bf->encrypt( $aRecord['name'] );
$aRecord['creditnr'] = $bf->encrypt( $aRecord['creditnr'] );
$result = sqlInsert( $aRecord ) ;
?>
Get the encrypted record of user John Doe and decrypt the data.
[edit | edit source]<?php
require_once("Crypt/Blowfish.php"); // a Pear class http://pear.php.net
$primary_key = "johndoe@anisp.localhost";
// crypt - one-way encryption
$cipher_key = crypt( $primary_key , "A_SECRET_COMPANY_SALT");
$bf = new Crypt_Blowfish('ecb');
$bf->setKey( $cipher_key );
// crypt_blowfish symmetric encryption to ecrypt the primary key for a sql select
$select_key = $bf->encrypt( $primary_key ) ;
$aRecord = sqlSelectWithPKEY( $select_key );
// crypt_blowfish symmetric encryption to decrypt the data
$aRecord['email'] = $bf->decrypt( $aRecord['email'] );
$aRecord['name'] = $bf->decrypt( $aRecord['name'] );
$aRecord['creditnr'] = $bf->decrypt( $aRecord['creditnr'] );
?>

This page or section of the Cryptography book is a stub. You can help Wikibooks by expanding it.
DRM
Digital Rights Management (DRM)or Multimedia Content Security or Digital Watermarking
1. Digital Rights Management (DRM) can be viewed as an attempt to provide "remote control" of digital content. The required level of protection goes beyond simply delivering the digital contents—restriction on the use of the content must be maintained after it has been delivered. In other words, DRM requires "persistent protection", i.e., protection that stays with the contents.
2. Recent advances in multimedia document production, delivery and processing, including the wide availability of increasingly powerful devices for the production, communication, copying and processing of electronic documents, have made available a large number of new opportunities for the dissemination and consumption of multimedia content (audio, video, images, 3D models, …).. At the same time, these rapid developments have raised several important problems regarding intellectual property, digital rights management, authenticity, privacy, conditional access and security, which risk impeding the diffusion of new services. Multimedia data can undergo, during their 'life', a wide variety of (possibly lossy) data manipulations that does not modify their substance (e.g. a change in file format, some processing for quality enhancement, the extractions of subparts,..) and that are not even perceived by the human perception system. This particular characteristic makes sometimes ineffective the classical solutions for security based on cryptography, but on the other hand offer the opportunity to design new solutions exploiting the fact that different documents bearing the same semantic information can be judged as equivalent by the human perceptual system. Driven by the necessities outlined above, the last few years have seen the development of new tools to tackle the problems encountered in media security applications leading to the concept of Secure Media Technologies. Secure Media encompasses a wide range of diverse technological areas working together to cope with the complex problems characterizing this rapidly evolving field. Enabling technologies include watermarking, data hiding, steganography and steganalysis, cryptography, biometrics, fingerprinting, network security and digital forensics. In particular, there are presently research activities concerning the following areas:
a. Robust digital watermarking techniques for images and video sequences: they allow to robustly hide some data useful for proving the content ownership and then to track the copyright violations, identify the content, monitor its usage, etc. They are often designed to be used in the framework of a Digital Rights Management System for the protection of the Intellectual Property Rights. The robustness here means that the embedded information remains intact even after that the content has been altered.
b. Digital watermarking techniques for 3D models: it is a more recent research area with respect to image and video watermarking. Since a mesh (geometrical representation of 3D objects) can't be easily represented in a frequency domain, it is not possible to directly apply to them transformations and filters in the frequency; processing methods for this kind of data then turn to ad hoc mathematical representations, that are different to the methods operating on other multimedia content.
c. Fragile or semi-fragile digital watermarking techniques for the authentication of images: these techniques allow to hide into an image some information useful to prove subsequently its authenticity. In this case, the embedded information is removed when the content is modified. It is possible to assure that an image has not been tampered, and in some cases also to locate the manipulations occurred that altered the original content of the image.
d. Fingerprinting: these techniques allow to unambiguously identify each copy of a multimedia content. In this way, it is possible to identify who, in a group of users in possession of a copy of a same document, illicitly distributed his/her own copy of the content, failing to meet possible limitations of use and distribution.
e. Digital forensic: they are processing techniques supporting detective activities to use multimedia content as an evidence of possible criminal acts. In our case, we are interested in proving if a image or a video sequence we have at disposal has been acquired with a given digital camera.
f. Signal processing in the encrypted domain: it is a new research field studying new technologies to allow the processing of encrypted multimedia content without removing the encryption. Most of technological solutions proposed so far to cope with multimedia security simply tried to apply some cryptographic primitives on top of the signal processing modules. These solutions are based on the assumption that the two communicating parties trust each other, so that the encryption is used only to protect the data against third parties. In many cases, though, this is not the case. A possible solution to the above problems could consist in the application of the signal processing modules in the encrypted domain.
g. Steganography: it is the science of hiding sensitive messages into an apparently innocuous document in such a way that no one apart from the intended recipient knows of the existence of the message. In case of a multimedia document, the information is hidden by means of the application of not perceivable modifications.
h. Steganalysis: it is the science of detecting the presence into a document of messages hidden using steganography techniques, exploiting perceptual or statistical analysis.
Biometrics
Biometrics
1. "Biometrics" is the science of human identity recognition based on physiological or behavioural characteristics that are unique to each individual.
2. Due to recent advances in the use of Biometrics in Passport Documents, ATM, Credit Card, Cellular Phone, PDA, Airport Check-in, Electronic Banking, web Access, Network Logon, Laptops Data Security there are presently research activities concerning the following areas:
a. Advanced finger recognition: it focuses on the finger retrieval from large database which is crucial part of the automatic fingerprint identification system. Conventional exclusive fingerprint classification partitions fingerprints into a few pre-specific non-overlapping classes(usually 4 or 5 classes) based on the Henrry classes. This limits the efficiency the efficiency of the fingerprint indexing. The continuous fingerprint classification overcome limitation of the number of classes. However, the exhaustive search of the whole fingerprint database required by this approach could be time-consuming. Research is going on in exploring the methods that inherits the merits of both the exclusive and continuous fingerprint classifications and overcomes the limitations and drawbacks of these two conventional approaches.
b. Multi-scale image processing of the fingerprint image to enhance fingerprint verification accuracy: Multi-scale image processing provides an effective way to find the optimal image enhancement of the fingerprints, which is very important to improve the quality of heavily corrupted fingerprint images.
Beale cipher
The Beale Cipher is a cipher in which two parties agree on a key which is a text (e.g., The Declaration of Independence which was used by Thomas Beale[13] as the key for one of his three encrypted texts), and the words in the text are then enumerated, and the encrypted text consists of numbers from the key. The numbers will then be replaced with the first letter of the word from the key-text when the cipher text is being deciphered.
The origin of the cipher was that Beale left an encrypted text with notes where to find his gold (worth $20 million, [14]), although many commentators believe the story about the hidden gold to have been a hoax.
There are no short cuts to break this cipher like there is for Vigenère, the mono-alphabetic or the polyalphabetic cipher; ultimately, the only way to successfully decipher it is to guess the original key-text, which may not be an easy task. The difficult depends on clues left in the cipher text. For example, it may be possible to infer the length of the book, etc., from the cipher text.
References
[edit | edit source]- ↑ "Database Encryption".
- ↑ "Hashing Email Address and Contacting User".
- ↑ "Hashing email addresses for GDPR compliance".
- ↑ "Guidance on Storing Email Addresses as Hashes".
- ↑ "Have I Been Pwned (HIBP)".
- ↑ "The CAN-SPAM Act of 2003: National Do Not Email Registy: A Federal Trade Commission Report to Congress". p. 20
- ↑ "Guidance on Storing Email Addresses as Hashes".
- ↑ "IBM InfoSphere Information Server: Data masking policies".
- ↑ "Gravatar: Creating the Hash".
- ↑ "Email Hashing: What Could Go Wrong?".
- ↑ "Is it worth storing email addresses as hashes?".
- ↑ "Is it a good idea to store Email addresses as hash only?"
- ↑ Simon Singh: The Code Book
- ↑ Simon Singh: The Code Book
Transposition ciphers
A transposition cipher encodes a message by reordering the plaintext in some definite way. Mathematically, it can be described as applying some sort of bijective function. The receiver decodes the message using the reordering in the opposite way, setting the ordering right again. Mathematically this means using the inverse function of the original encoding function.
For example, to encrypt the sentence "A simple kind of transposition cipher writes the message into a rectangle by rows and reads it out by columns," we could use the following rectangle:
Asimplekin doftranspo sitionciph erwritesth emessagein toarectang lebyrowsan dreadsitou tbycolumns
Then the encrypted text would be "Adsee tldts oirmo erbif tweab eymti rsrya cproi serdo lanta cosle ncegt wiuks iseas tmipp tinao nnohh ngnus."
This cipher is often complicated by permuting the rows and columns, as in columnar transposition.
Columnar transposition
[edit | edit source]The standard columnar transposition consists of writing the key out as column headers, then writing the message out in successive rows beneath these headers (filling in any spare spaces with nulls), finally, the message is read off in columns, in alphabetical order of the headers. For example suppose we have a key of 'ZEBRAS' and a message of 'WE ARE DISCOVERED. FLEE AT ONCE'. We start with:
| Z | E | B | R | A | S |
| W | E | A | R | E | D |
| I | S | C | O | V | E |
| R | E | D | F | L | E |
| E | A | T | O | N | C |
| E | Q | K | J | E | U |
Then read it off as:
EVLNE ACDTK ESEAQ ROFOJ DEECU WIREE
To decipher it, the recipient has to work out the column lengths by dividing the message length by the key length. Then he can write the message out in columns again, then re-order the columns by reforming the key word.
Double transposition
[edit | edit source]A single columnar transposition could be attacked by guessing possible column lengths, writing the message out in its columns (but in the wrong order, as the key is not yet known), and then looking for possible anagrams. Thus to make it stronger, a double transposition was often used. This is simply a columnar transposition applied twice, with two different keys of different (preferably relatively prime) length. Double transposition was generally regarded as the most complicated cipher that an agent could operate reliably under difficult field conditions. It was in actual use at least as late as World War II (e.g. poem code).
Grille
[edit | edit source]Another type of transpositional cipher uses a grille. This is a square piece of cardboard with holes in it such that each cell in the square appears in no more than one position when the grille is rotated to each of its four positions. Only grilles with an even number of character positions in the square can satisfy this requirement. As much message as will fit in the grille is written, then it is turned to another position and more message is written. Removing the cardboard reveals the cyphertext.
The following diagram shows the message "JIM ATTACKS AT DAWN" encoded using a 4x4 grille.
The top row shows the cardboard grille and the bottom row shows the paper underneath the grille at five stages of encoding:
- blank grille on the paper.
- first four letters written in the blanks.
- grille rotated one position, second set of letters written.
- grille rotated two positions, third set of letters written.
- grille rotated three positions, fourth set of letters written.
After the letters in the message have all been written out, the ciphertext can be read from the paper: "JKDT STAA AIWM NCAT".
The sender and receiver must agree on the initial orientation of the grille, the direction to rotate the grille, the order in which to use the spaces on the grille, and the order in which to read the ciphertext characters from the paper.
Caesar cipher
A Caesar cipher (also known as a shift cipher) is a substitution cipher in which the cipher alphabet is merely the plain alphabet rotated left or right by some number of positions. For instance, here is a Caesar cipher using a right rotation of three places:
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ Cipher: XYZABCDEFGHIJKLMNOPQRSTUVW
To encipher a message, simply look up each letter of the message in the "plain" line and write down the corresponding letter in the "cipher" line. To decipher, do the reverse. Because this cipher is a group, multiple encryptions and decryptions provide NO additional security against any attack, including brute-force.
The Caesar cipher is named for Julius Caesar, who allegedly used it to protect messages of military significance. It was secure at the time because Caesar's enemies could often not even read plaintext, let alone ciphertext. But since it can be very easily broken even by hand, it has not been adequate for secure communication for at least a thousand years since the Arabs discovered frequency analysis and so made all simple substitution cyphers almost trivially breakable. An ancient book on cryptography, now lost, is said to have discussed the use of such cyphers at considerable length. Our knowledge is due to side comments by other writers, such as Suetonius.
Indeed, the Caesar cypher is much weaker than the (competently done) random substitution ciphers used in newspaper cryptogram puzzles. The most common places Caesar ciphers are found today are in children's toys such as secret decoder rings and in the ROT13 cipher on Usenet (which, of course, is meant to be trivial to decrypt)...
Atbash cipher
Atbash is an ancient encryption system created in the Middle East. It was originally used in the Hebrew language; some historians and cryptographers believe there are such examples in the Bible. The name "Atbash" comes from the first Hebrew letter Aleph and the last Taff. The Atbash cipher is a simple substitution cipher that relies on transposing all the letters in the alphabet such that the resulting alphabet is backwards. Atbash is also a substitution cipher. Since each letter corresponds to another, it offers very little security. The first letter is replaced with the last letter, the second with the second-last, and so on. The completed cypher looks like so:
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ Cipher: ZYXWVUTSRQPONMLKJIHGFEDCBA
An example plaintext to ciphertext using Atbash:
Plain: MEETMEATONE Cipher: NVVGNVZGLMV
As one can see, and as mentioned previously, the Atbash cipher offers no security once the cipher method is found.
Playfair cipher
The Playfair Cipher is one of several methods used to foil a simple frequency analysis. Instead of every letter having a substitute, every digraph has a substitute. This tends to level the frequency distribution somewhat.
The classic Playfair tableau consists of four alphabets, usually in a square arrangement, two plaintext and two ciphertext. In this example, keywords have been used to disorder the ciphertext alphabets.

In use, two letters of the plaintext are located in the plaintext alphabets. Then reading across from the first letter to the column of the second letter, the first ciphertext character is found. Next, reading down from the first letter to the row of the second letter, the second ciphertext letter is found.
As an example, using tableau above, the digraph "TE" is enciphered as "uw", whereas the digraph "LE" is enciphered as "mk". This makes a frequency analysis difficult.
A second version of the Playfair cipher uses a single alphabet.
SECRT - Your secret keyword, share among you and your receiver KYWDP LAFIZ BXCQG HUMOK
If the letters of a digraph lie at the corners of a rectangle, then they are rotated clockwise round the rectangle, SW to CK, AT to EZ.
If they lie in the same column or row they are moved one down or across, EA to YX, RS to TE.
The square is treated as though it wraps round in both directions, ST to ES, DO to IR
Both versions of the Playfair cipher are of comparable strength.
Further reading
[edit | edit source]
Polyalphabetic substitution
A Polyalphabetic substitution cipher is simply a substitution cipher with an alphabet that changes. For example one could have two alphabets:
Plain Alphabet: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Cipher Alphabet #1: B D F H J L N P R T V X Z A C E G I K M O Q S U W Y Cipher Alphabet #2: Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
Now to encrypt the message ``The quick brown fox jumped over the lazy dogs" we would alternate between the two cipher alphabets, using #1 for every first letter and #2 for every second, to get: ``Msj joxfp dicda ucu tfzkjw ceji msj xzyb hln".
Polyalphabetic substitution ciphers are useful because the are less easily broken by frequency analysis, however if an attacker knows for instance that the message has a period n, then he simply can individually frequency analyze each cipher alphabet.
The number of letters encrypted before a polyalphabetic substitution cipher returns to its first cipher alphabet is called its period. The larger the period, the stronger the cipher. Of course, this method of encryption is certainly not secure by any definition and should not be applied to any real-life scenarios.
Scytale
The Scytale cipher is a type of transposition cipher used since the 7th century BCE. The first recorded use of the scytale cipher was by the Spartans and the ancient Greeks who used it to transport battle information between generals.
Encryption Using the Scytale
[edit | edit source]The scytale encryption system relies on rods of wood with equal radiuses. The system is a symmetric key system where the radius of the rod is the key.
After establishing keys a messenger winds a strip of leather around the rod. Then he writes the message going across the rod, so that when he unwinds the leather the letters have been jumbled in a meaningless fashion.
Example: Suppose the rod allows you to write 4 letters around it in one circle and 5 letters down the side. Clear text: "Help me I am under attack" To encrypt one simply writes across the leather...
_____________________________________________________________
| | | | | | |
| | H | E | L | P | M |
|__| E | I | A | M | U |__
| N | D | E | R | A | |
| T | T | A | C | K | |
| | | | | | |
______________________________________________________________
so the cipher text becomes, "HENTEIDTLAEAPMRCMUAK" after unwinding.
Decryption Using the Scytale
[edit | edit source]To decrypt all you must do is wrap the leather strip around the rod and read across. Example: ciphertext: "HENTEIDTLAEAPMRCMUAK" Every fourth letter will appear on the same line so the cipher text becomes
HELPM...return to the beginning once you reach the end and skip used letters. ...EIAMUNDERATTACK.
Insert spaces and the plain text returns, "Help me I am under attack"
Substitution cipher
A Substitution Cipher is similar to a Caesar cipher, but instead of using a constant shift left or right, the plain alphabets and the cipher alphabets are mixed arbitrarily.
For example:
Plain Alphabet: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Cipher Alphabet: Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
With the above, the Plain text "This is a sample" would encrypt to "Gsrh rh z hznkov." This particular substitution cipher, which relies on transposing all the letters in the alphabet such that the resulting alphabet is backwards, is known as an atbash cipher.
With Substitution Ciphers, the secret is in the mapping between the plain and cipher alphabets. However, there are several analytical techniques to help break these ciphers with only the ciphertext. See Frequency analysis
Solving substitution ciphers
[edit | edit source]English-language ciphers be solved using principles such as these:
- Single-letter words are almost always A or I.
- As Edgar Allan Poe points out in The Gold Bug, "E predominates so remarkably that an individual sentence of any length is rarely seen, in which it is not the prevailing character."
- Apostrophes are generally followed by S, T, D, M, LL, or RE.
- Repeating letter patterns may be common letter groups such as TH, SH, RE, CH, TR, ING, ION, and ENT.
- Double letters are most likely to be LL, followed in frequency by EE, SS, OO, and TT (and on to less commonly seen doubles).
- Two-letter words almost always have one vowel and one consonant. The five most common two-letter words, in order of frequency, are OF, TO, IN, IS, and IT.
- The most common three-letter words, in order of frequency, are THE, AND, FOR, WAS, and HIS.
- The most common four-letter word is THAT. An encrypted word beginning and ending with the same letter is likely to be THAT. Others are AQUA, AREA, AURA, BARB, BLAB, BLOB, BOOB, BULB, CHIC, DEAD, deed, DIED, DYED, ease, edge, ELSE, FIEF, GANG, GONG, HASH, HATH, HUSH, KICK, LULL, MAIM, NEON, NOON, NOUN, ONTO, ORZO, PEEP, PIMP, PLOP, POMP, PREP, PROP, PULP, PUMP, REAR, ROAR, SAYS, SEAS, SEES, TACT, TART, TENT, TILT, TINT, TOOT, TORT, TUFT, URDU, and WHEW.
See also
[edit | edit source]External links
[edit | edit source]- McClung, O. William: Substitution Cipher Cracker — a useful tool that will perform a frequency analysis on ciphertext.
- Cryptoquip: Crack a Substitution Cipher.
- American Cryptogram Association: Solve a Cipher.
- Olson, Edwin: Decrypto — a fast and automated cryptogram solver that can solve simple substitution ciphers often found in newspapers, including puzzles like cryptoquips and patristocrats.
- Ciphergram Solution Assistant — solves, or nearly solves, ciphergrams like those in the newspapers that are called cryptoquotes.
Permutation cipher
In classical cryptography, a permutation cipher is a transposition cipher in which the key is a permutation.
To apply a cipher, a random permutation of size e is generated (the larger the value of e the more secure the cipher). The plaintext is then broken into segments of size e and the letters within that segment are permuted according to this key.
In theory, any transposition cipher can be viewed as a permutation cipher where e is equal to the length of the plaintext. This is too cumbersome a generalisation to use in actual practice, however.
Identifying the cipher
[edit | edit source]Because the cipher doesn't change any of the characters, the ciphertext will have exactly the same letter frequencies as the underlying plaintext. This means that the cipher can in many cases be identified as a transposition by the close similarity of its letter statistics with the letter frequencies of the underlying language.
Breaking the cipher
[edit | edit source](Move this section to "Cryptography/Breaking Permutation cipher" ?)
Because the cipher operates on blocks of size e, the plaintext and the ciphertext have to have a length which is some multiple of e. This causes two weaknesses in the system: first, the plaintext may have to be padded (if the padding is identifiable then part of the key is revealed) and second, information relating to the length of the key is revealed by the length of the ciphertext. To see this, note that if the ciphertext is of length i then e must be one of the divisors of i. With the different possible key sizes different possible permutations are tried to find the permutation which results in the highest number of frequent bigrams and trigrams as found in the underlying language of the plaintext. Trying to find this permutation is essentially the same problem encountered when analysing a columnar transposition cipher: multiple anagramming..
Further reading
[edit | edit source]
Vigenère cipher
Vigenère Cipher
[edit | edit source]One of the most famous and simple polyalphabetic cipher is the Vigenere Cipher developed by Blaise de Vigenere in the 16th century. The Vigenère cipher operates in a manner similar to a Caesar cipher, however, rather than shifting the plaintext character by a fixed value n, a keyword (or phrase) is chosen and the ordinal values of the characters in that keyword are used to determine the offset. The process that creates encrypted text is simple, but it was unbroken for 300 years.The system is so simple that the Vigenere encryption system has been discovered and rediscovered dozens of times.
For example, if the keyword is "KEY" and the plaintext is "VIGENERE CIPHER," then first the key must be repeated so that it is the same length as the text (so key becomes keykeykeykeyke). Next, the ordinal value of V (22) is shifted by the ordinal value of K (11) yielding F (6), the ordinal value of I (9) by the ordinal value of E (5) yielding M (13), etc. The keyword is repeated until the entire message is encrypted:
P: VIGENERECIPHER K: KEYKEYKEYKEYKE C: FMEORCBIASTFOV
An easier, but equivalent way of encrypting text is by writing out each letter of the alphabet and the key, and simply matching up the letters:
ABCDEFGHIJKLMNOPQRSTUVWXYZ KLMNOPQRSTUVWXYZABCDEFGHIJ EFGHIJKLMNOPQRSTUVWXYZABCD YZABCDEFGHIJKLMNOPQRSTUVWX
First The V in the first row would up with the F in the second. Then, one would go down a row, and see that the I in the first row lines up with the M in the third. After one reaches the bottom row, then they would continue lining up letters with the second row. This uses exactly the same cipher, and is simply an easier method of performing the encryption when doing so by hand.
The Caesar cipher could be seen as a special case of the Vigenère cipher in which the chosen keyword is only a single character long.
An algorithmic way of expressing this cipher would be:
(plain_text_letter + (key_letter - 1)) mod 26 = cipher_text_letter
GROMARK cipher
[edit | edit source]The Gronsfeld cipher is variation of Vigenere using a pseudo-random decimal key.[1]
The Gronsfeld cipher was invented by José de Bronckhorst, earl of Gronsfeld, in 1744.[2]
The cipher developed by Count Gronsfeld (Gronsfeld's cipher) was used throughout Europe. It is enciphered and deciphered identically to the Vigenere cipher, except the key is a block of decimal digits (repeated as necessary) shifting each plaintext character 0 to 9, rather than a block of letters (repeated as necessary) shifting each plaintext character 0 to 25. It was more popular than the Vigenère cipher, despite its limitations.
An algorithmic way of expressing this cipher would be:[3]
(plain_text_letter + key_digit) mod 26 = cipher_text_letter
The GROMARK Cipher is a Gronsfeld cipher using a mixed alphabet and a running key.[4]
running key cipher
[edit | edit source]The running key cipher is a type of polyalphabetic substitution cipher in which a text, typically from a book, is used to provide a very long keystream. Usually, the book to be used would be agreed ahead of time, while the passage to use would be chosen randomly for each message and secretly indicated somewhere in the message.
A cryptanalyst will see peaks in the ciphertext letter distribution corresponding to letters that are formed when high-frequency plaintext letters are encrypted with high-frequency key text letters.[5]
If a cryptanalyst discovers two ciphertexts produced by (incorrectly) encrypting two different plaintext messages with the same "one-time" pad, the cryptanalyst can combine those messages to produce a new ciphertext that is the same as using one of the original plaintext messages as a running key to encrypt the other original plaintext, then use techniques that decode running key ciphers to try to recover both plaintexts.
Further reading
[edit | edit source]In a later chapter of this book, we will discuss techniques for Breaking Vigenère cipher.
- ↑ "The GROMARK cipher, and some relatives"
- ↑ "Gronsfeld Cipher".
- ↑ Jerry Metzger. "The ACA and You". A publication of the American Cryptogram Association. Chapter 8: "The Cipher Exchange and Cipher Standards". Section "GRONSFELD".
- ↑ Jerry Metzger. "The ACA Cipher Exchange and Cipher Standards". Section "GROMARK"
- ↑ Sravana Reddy; Kevin Knight. "Decoding Running Key Ciphers". 2012.
Enigma machine

The Enigma was an electro-mechanical rotor cypher machine used for both encryption and decryption, widely used in various forms in Europe from the early 1920s on. It is most famous for having been adopted by most German military forces from about 1930 on. Ease of use and the supposedly unbreakable cypher were the main reasons for its widespread use. The machine had two inherent weaknesses: it guaranteed that a letter would never be encrypted to itself and the rightmost rotor would rotate a set number of places before the next would rotate (26 in the initial version). In German usage the failure to replace the rotors over many years of service and patterns in messages further weakened the system. The cypher was broken, and the reading of information in the messages it didn't protect is sometimes credited with ending World War II at least a year earlier than it would have otherwise.
The counterpart British encryption machine, Typex, and several American ones, e.g. the SIGABA (or M-134-C in Army use), were similar in principle to Enigma, but far more secure. The first modern rotor cypher machine, by Edward Hebern, was considerably less secure, a fact noted by William F. Friedman when it was offered to the US Government.
History
[edit | edit source]Enigma was developed by Arthur Scherbius in various versions dating back to 1919. He set up a Berlin company to produce the machine, and the first commercial version (Enigma-A) was offered for sale in 1923. Three more commercial versions followed, and the Enigma-D became the most important when several copies were purchased by the Reichsmarine in 1926. The basic design was then picked up by the Army in 1929, and thereafter by practically every German military organization and by many parts of the Nazi hierarchy. In the German Navy, it was called the "M" machine.
Versions of Enigma were used for practically all German (and much other European Axis) radio, and often telegraph, communications throughout the war; even weather reports were encrypted with an Enigma machine. Both the Spanish (during the Civil War) and Italians (during World War II) are said to have used one of the commercial models, unchanged, for military communications. This was unwise, for the British (and one presumes, others) had succeeded in breaking the plain commercial version(s) or their equivalents. This contributed to the British defeat of a large part of the Italian fleet at Matapan.
Operation
[edit | edit source]The Enigma machine was electro-mechanical, meaning it used a combination of electrical and mechanical parts. The mechanism consisted primarily of a typewriter-style keyboard, which operated electrical switches as well as a gearing mechanism.
The electrical portion consisted of a battery attached through the keys to lamps. In general terms, when a key was held down on the keyboard, one of the lamps would be lit up by the battery. In the picture to the right you can see the typewriter keys at the front of the machine, and the lights are the small (barely visible) circles "above" the keyboard in the middle of the machine.
The heart of the basic machine was mechanical, consisting of several connected rotors. Enigma rotors in most versions consisted of flat disks with 26 contacts on each side, arranged in a circular manner around the outer faces of the disk. Every contact on one side of each disk is wired to a different contact on the other side. For instance, in a particular rotor the 1st contact on one side of the rotor might be wired to the 14th contact on the other side, the 2nd one on the first side to the 22nd on the other, and so forth. Each rotor in the set supplied with an Enigma was wired differently than the others, and the German military/party models used different rotor wirings than did any of the commercial models.
Inside the machine were three slots (in most variants) into which the rotors could be placed. The rotors were "stacked" in the slots in such a way that the contacts on the "output" side of one rotor were in contact with the "input" contacts on the next. The third rotor in most versions was connected to a reflector (unique to the Enigma family amongst the various rotor machines designed in the period) which was hard wired to feed outputs of the third rotor back into different contacts of the third rotor, thence back to the first rotor, but by a different route. In the picture you can see the three stacked rotors at the very top of the machine, with teeth protruding from the panel surface which allow the rotors to be turned by hand.
When a key was pressed on the keyboard, current from the battery flowed from the switch controlled by that key, say A, into a position on the first rotor. There it would travel through the rotor's internal wiring to, say, the J position on the other side. It would then go into the next rotor, perhaps turned such that the first rotor's J was lined up with the second's X. From there it would travel to the other side of the second rotor, and so on. Because the signal had travelled through the rotors and back, some other letter than A would light in the lamp array – thus substituting one letter for another, the fundamental mechanism in all substitution cypher systems.
Because the rotors changed position (rather like an automobile odometer) with every key press, A might be Q this time, but the next A would be something different, perhaps T. After 26 letters were pressed, a cam on the rotor advanced the rotor in the next slot by one position. The substitution alphabet thus changed with every plaintext letter, and kept changing with every plaintext letter for a very long time.
Better yet, due to the "random" wiring of each rotor, the exact sequence of these substitution alphabets varied depending on the initial position of the rotors, their installed order, and which rotors were installed in the machine. These settings were referred to as the initial settings, and were given out in books once a month (to start with—they became more frequent later on).
The most common versions of the machine were symmetrical in the sense that decipherment works in the same way as encypherment: type in the cyphertext and the sequence of lit lamps will correspond to the plaintext. However, this works only if the decyphering machine has the same configuration (i.e., initial settings) as had the encrypting machine (rotor sequence, wiring, alphabet ring settings, and initial positions); these changed regularly (at first monthly, then weekly, then daily and even more often nearer the end of the War on some networks) and were specified in key schedules distributed to Enigma users.
One time pads
A One Time Pad (OTP) is the only potentially unbreakable encryption method. Plain text encrypted using an OTP cannot be retrieved without the encrypting key. However, there are several key conditions that must be met by the user of a one time pad cipher, or the cipher can be compromised.
- The key must be random and generated by a non-deterministic, non-repeatable process. Any key generated by an algorithm will not work. The security of the OTP relies on the randomness of the key. Unfortunately, the randomness of a key cannot be proved.
- The key must never be reused. Use of the same key to encrypt different messages, no matter how trivially small, compromises the cipher.
- The key must not fall in the hands of the enemy. This may seem obvious, but it points to the weakness of system in that you must be able to transmit large amounts of data to the reader of the pad. Typically, one time pad cipher keys are sent via diplomatic pouch.
A typical one time pad system works like this: Generate a long fresh new random key. XOR the plaintext with the key to create the ciphertext. To decrypt the ciphertext, XOR it with the original key. The system as presented is thus a symmetric and reciprocal cipher. Other functions (e.g., addition modulo n) could be used to combine the key and the plaintext to yield the ciphertext, although the resulting system may not be a reciprocal cipher.
If the key is random and never re-used, an OTP is provably unbreakable. Any ciphertext can be decrypted to any message of the same length by using the appropriate key. Thus, the actual original message cannot be determined from ciphertext alone, as all possible plaintexts are equally likely. This is the only cryptosystem for which such a proof is known.
The OTP is extremely simple to implement.[1]
However, there are limitations. Re-use the key and the system becomes extremely weak; it can be broken with pencil and paper. Try to build a "one-time-pad" using some algorithm to generate the keys and you don't have a one-time-pad, you have a stream cipher. There are some very secure stream ciphers, but people who do not know one from a one-time pad are probably not able to design one. It is unfortunately fairly common to see weak stream ciphers advertised as unbreakable one-time pads.
Also, even if you have a well-implemented OTP system and your key is kept secure, consider an attacker who knows the plaintext of part of a message. He can then recover that part of the key and use it to encrypt a message of his own. If he can deliver that instead of yours, you are in deep trouble.
Example
[edit | edit source]First, an OTP is selected for the plaintext:
Preshared Random Bits = 1010010010101010111010010000101011110101001110100011 Plain text = 110101010101010010100 Length(Plain Text) = 21 Key(21) = 101001001010101011101
The example indicates that the plaintext is not always the same length as the key material. This can be handled by methods such as:
- appending a terminator to the plaintext before encryption, and terminating the cyphertext with random bits.
- prepending the length and a preamble terminator to the plaintext, and terminating with random bits.
Such signaling systems (and possibly the plaintext encoding method) must be designed so that these terminators are not mistaken for plaintext. For this example, therefore, it is assumed the plaintext already contains endpoint/length signaling.
For increasingly long plaintext/key pair lengths, the cross-correlation gets closer to zero.
Encryption
[edit | edit source]Key(21) = 101001001010101011101 Plaintext = 110101010101010010100 bitwise ||||||||||||||||||||| cyphertext = 011100011111111001001
For increasingly long plaintext/cyphertext pair lengths, the cross-correlation also gets closer to zero.
Decryption
[edit | edit source]Preshared Random Bits = 1010010010101010111010010000101011110101001110100011 cyphertext = 011100011111111001001 bitwise ||||||||||||||||||||| Plain text = 110101010101010010100
An astute reader might observe that the decryptor needs to know the length of the plaintext in actual practice. This is done by decrypting the cyphertext as a bitstream (i.e. xor each bit as it is read), and observing the stream until the end-of-plaintext ruleset is satisfied by the signals prepended/appended to the plaintext.
Making one-time pads by hand
[edit | edit source]
One-time pads were originally made without the use of a computer and this is still possible today. The process can be tedious, but if done correctly and the pad used only once, the result is unbreakable.
There are two components needed to make a one-time pad: a way to generate letters at random and a way to record two copies of the result. The traditional way to do the latter was to use a w:typewriter and w:carbon paper. The carbon paper and w:typewriter ribbon would then be destroyed since it is often possible to recover the pad data from them. As typewriters have become scarce, it is also acceptable to hand write the letters neatly in groups of five on two part w:carbonless copy paper sheets, which can be purchased at office supply stores. Each sheet can given a serial number or some other unique marking.
Historically, the key material for manual one-time pads was distributed as a pad of many small pages of paper. Each small page typically had a series of 5-digit groups, each digit randomly selected from 0 to 9.[2][3][4][5][6][7][8][9]
A one-time pad set consists of two identical pads. Some writers refer to the two as "two identical originals", to emphasize that no copies should ever be made of the key material.[10]
Traditionally two-way communication requires two pad sets (a total of 4 pads): One person gets the "IN" pad of one set, and the "OUT" pad of the other set.[11]
Each small page typically contains 50 groups of 5 random decimal digits 0...9, enough for one normal message, and a unique "page number" of five digits.[11][12]
A conversion table is used to convert the letters of the plaintext message to numbers, and the numbers of the decoded message back to letters.[5] Perhaps the simplest conversion table is A=01, B=02, ... Z=26, but historically some sort of straddling checkerboard was usually used, such as CT-37c,[13] CT-37w, CT-46,[14] etc.[15]
The key material for a one-time pad was sometimes written as 50 groups of 5 random letters A...Z.[12][16] One-time pads where the keys are written as letters are sometimes called letter one-time pad (LOP)[17][18] or one-time letter pad (OTLP).[11]
The key material for cryptographic machines, including one-time pad systems, was often punched in a binary code on long, narrow paper tape—a "one time tape" OTT.[10][12][19]
letter tiles
[edit | edit source]The simplest way to generate random letters in the Roman alphabet is to obtain 26 identical objects with a different letter of the alphabet marked on each object. Tiles from the game w:Scrabble can be used, as long as only one of each letter is selected. Kits for making name charm bracelets are another possibility. One can also write the letters on 26 otherwise identical coins with a marking pen. The objects are placed in a box or cup and shaken vigorously, then one object is withdrawn and its letter is recorded. The object is returned to the box and the process is repeated.
10-sided dice
[edit | edit source]Another way to make one time pads is to use w:ten-sided dice. One can generate random number groups by rolling several ten-sided dice at a time and recording a group of decimal digits—one decimal digit from each die—for each roll.[11] This method will generate random code groups much faster than using Scrabble tiles. The plaintext message is converted into numeric values with A =01, B =02 and so on. The resulting numeric values are encrypted by adding digits from the one time pads using non-carrying addition. One can then either transmit the numeric groups as is, or use the straddling checkerboard to convert the numbers back into letters and transmit that result.
6-sided dice
[edit | edit source]Another way to make one time pads is to use 6-sided dice.[20]
It is possible to generate random decimal digits (to make a traditional decimal one-time pad) using 6-sided dice.[11]
If the message is converted into two digit base-6 numbers, then ordinary six-sided dice can be used to generate the random digits in a one time pad. Digits in the pad would be added modulo-6 to the digits in the plaintext message (again without carry), and subtracted modulo 6 from the ciphertext to decrypt. For example:
| PT | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| CT | 00 | 01 | 02 | 03 | 04 | 05 | 10 | 11 | 12 | 13 | |||
| PT | A | B | C | D | E | F | G | H | I | J | K | L | M |
| CT | 14 | 15 | 20 | 21 | 22 | 23 | 24 | 25 | 30 | 31 | 32 | 33 | 34 |
| PT | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| CT | 35 | 40 | 41 | 42 | 43 | 44 | 45 | 50 | 51 | 52 | 53 | 54 | 55 |
| right | digit | |||||
| left digit | ||||||
| x0 | x1 | x2 | x3 | x4 | x5 | |
| 0x | 0 | 1 | 2 | 3 | 4 | 5 |
| 1x | 6 | 7 | 8 | 9 | A | B |
| 2x | C | D | E | F | G | H |
| 3x | I | J | K | L | M | N |
| 4x | O | P | Q | R | S | T |
| 5x | U | V | W | X | Y | Z |
Using this table, "Wikipedia" would convert to 52 30 32 30 41 22 21 30 14. If the pad digits were 42 26 21 35 32 34 22 62 43, the ciphertext would be 34 50 53 05 13 50 43 32 51. (Note that 6 = 0 modulo 6).
Key Exchange
[edit | edit source]In order to use this algorithm, each party must possess the same random key. This typically involves meeting the other party in person or using a trusted courier. Other methods are sometime proposed, such as or both users to have identical devices that generate the same semi-random numbers, however these methods are essentially w:stream ciphers and are not covered by the security proof of one time pads.
Further reading
[edit | edit source]- "Visual Cryptography" typically uses a one-time pad. A special arrangement of polarizing filters can be used to implement XOR.
- "What is Visual Cryptography" uses a binary one-time pad. A special pattern of dots can be used to implement XOR.
DES
The Data Encryption Standard (DES) was a widely-used algorithm for encrypting data. It was developed by IBM under the name Lucifer, and was submitted to NBS in response to a 1973 solicitation for better cryptosystems. The US National Institute of Standards and Technology with help from the National Security Agency took IBM's design and made some changes; DES was adopted as a standard in January 1977.
DES is a product block encryption algorithm (a cipher) in which 16 iterations, or rounds, of the substitution and transposition (permutation) process are cascaded. The block size is 64 bits, so that a 64-bit block of data (plaintext) can be encrypted into a 64-bit ciphertext. The key, which controls the transformation, also consists of 64 bits. Only 56 of these, however, are at the user's disposal; the remaining eight bits are employed for checking parity. The actual key length is therefore 56 bits.
Subsets of the key bits are designated K1, K2, etc., with the subscript indicating the number of the round. The cipher function (substitution and transposition) that is used with the key bits in each round is labeled f. At each intermediate stage of the transformation process, the cipher output from the preceding stage is partitioned into the 32 leftmost bits, Li, and the 32 rightmost bits, Ri. Ri is transposed to become the left-hand part of the next higher intermediate cipher, Li+1. The right-hand half of the next cipher, Ri+1, however, is a complex function of the key and of the entire preceding intermediate cipher. The essential feature to the security of the DES is that f involves a very special nonlinear substitution—i.e., f(A) + f(B) does not equal f(A + B)--specified by the Bureau of Standards? in tabulated functions known as S-boxes. This operation results in a 32-bit number, which is logically added to Ri to produce the left-hand half of the new intermediate cipher. This process is repeated, 16 times in all. To decrypt a cipher, the process is carried out in reverse order, with the 16th round being first. The DES algorithm lends itself to integrated-chip implementation. By 1984 the Bureau of Standards had certified over 35 LSI- and VLSI-chip implementations of the DES, most on single 40-pin chips, some of which operate at speeds of several million bits per second.
When the cipher was first released, the design criteria for the S-boxes was not released. With the National Security Agency's involvement in the design of the S-boxes, most security researchers were wary of DES, and there was the widespread fear that the modifications of the NSA were intended to weaken the cipher.
In 1990 with the independent discovery and open publication by Biham and Shamir of differential cryptanalysis, it turned out that at least some of the wariness was uncalled for. After the publication of this paper, the IBM personnel involved in the designed publically stated that the main factor in the design was to strengthen them against differential cryptanalysis. The secrecy behind the design criteria at the time appears to have been due to the fact that the technique was not known to the public at the time.
Notably, DES is theoretically vulnerable to a technique discovered later by Matsui, linear cryptanalysis. It is unknown whether the NSA was aware of linear cryptanalysis at the time DES was finalized, but most knowledgeable observers think not. Don Coppersmith, one of DES's designers at IBM, has stated that IBM itself was not aware of linear cryptanalysis at that time.
Because the key length is only 56 bits, DES can be, and has been, broken by the brute force attack method of running through all possible keys. It is believed that one of the reasons this reduced key length was chosen was that NSA in the mid-'70s possessed enough computer power to brute force break keys of this length. In the years since, computer hardware progress has been such that most anyone now can have sufficient computational capacity. The EFF, a cyberspace civil rights group (with neither much funding nor personnel), did it in a little more than 2 days' search at about the same time at least one attorney from the US Justice Department was publicly announcing that DES was and would remain unbreakable.
The most obvious way of improving the security of DES is to encrypt the data multiple times with different keys. Double encrypting data with DES does not add much security as it is vulnerable to meet in the middle attacks. Going one step about this, many former DES users now use Triple DES (3DES) which was described and analyzed by one of DES's patentees (see FIPS 46-3); it involves DES encryption of each data block three times with different keys. 3DES is widely regarded as adequately secure for now, though it is quite slow. Note, however, that there are several ways to use DES three times; only one of those is Tuchman's 3DES.
After another, long delayed competition, (NIST) has selected a new cipher, the Advanced Encryption Standard (AES) to replace DES (fall -'01). AES was submitted by its designers under the name Rijndael.
Implementations:
http://www.codeproject.com/KB/cs/NET_Encrypt_Decrypt.aspx (C#, Xinwen Cheng)
http://frank.anemaet.nl/crypto/DES/ (Java implementation, Frank Anemaet)
http://www.tero.co.uk/des/ (Javascript implementation, Paul Tero)
AES
The Advanced Encryption Standard (AES), also called Rijndael, is a symmetric block-cipher with fixed 128-bit blocks and keysizes of 128, 192, or 256 bits. This algorithm is currently used by the U.S government for both classified and non-classified information, and has already phased out DES on all but legacy machines (triple DES is still authorized for government use, however). There were five finalists in the bid for the Advanced Encryption Standard, and the NSA analyzed all five and decreed them acceptable for encrypting non-classified government documents, but Rijndael was eventually chosen for unspecified reasons, and later authorized for use on classified documents.
If you need to encrypt data, using 256-bit AES keys in counter mode (CTR), and then appending a HMAC, is recommended by many security researchers.[21][22][23] This construction avoids many flaws in earlier systems: The AES standard uses a 128 bit block size, rather than the 64 bit block size which was suspected to be inadequate by the time of NIST's 1997 announcement of the AES contest. Keys that are 64 bits or less are suspected to be inadequate. Almost all side channel attacks require chosen inputs, which (which modes?) modes are in theory exposed to,[citation needed] and the ECB mode is even worse. CBC, CTR, EAX, and GCM are all considered strong modes as long as one authenticates the message before decrypting.[24]
Further reading
[edit | edit source]- Jeff Moser. "A Stick Figure Guide to the Advanced Encryption Standard (AES)". 2009.

This page or section of the Cryptography book is a stub. You can help Wikibooks by expanding it.
full-disk encryption
Most modern operating systems support full-disk encryption (FDE): a small boot area is left unencrypted (and never changes), containing the code to ask for a password and use that password to decrypt and run the rest of the operating system. The entire rest of the disk is always encrypted -- every write to the disk is intercepted by the operating system and encrypted, so everything written to the disk is encrypted.
Even if the entire computer is stolen, the data is useless without the password.
As of 2020, the latest FDE software running on modern server hardware is fast enough that the latency is indistinguishable from not using encryption at all.[25]
Implementation
[edit | edit source]Even-Mansour block ciphers
[edit | edit source]Even-Mansour block ciphers are very simple: Given a block of data, these XOR a key with the block, apply a publicly-known permutation, then XOR a key again. Many cryptographers have studied this construction and some variants.[26]
As of 2014, the de-facto standard disk encryption mode for full-disk encryption (FDE) is a specific variant called XEX-based tweaked-codebook mode with ciphertext stealing (XTS). It's good for full-disk encryption, but authenticated encryption has several advantages over XTS in almost any other application.[27]
Public Key Overview
We briefly mentioned Asymmetric Ciphers earlier in this book. In this and following chapters we will describe how they work in much more detail.
The discovery of public key cryptography revolutionized the practice of cryptography in the 1970s. In public key cryptography, the key used to encrypt a message is not the same as the key used to decrypt it. This requires an asymmetric key algorithm.
(All previous cryptographic algorithms and cryptosystems, now retroactively categorized as "symmetric key cryptography" or "shared key cryptography", always use the same key to encrypt a message and later to decrypt that message).
Public key cryptography is cryptography where the key exchange process between person A and person B must not be kept secret. Private keys actually are never exchanged. In fact Person A sends information (possibly about a session key) to Person B so that it is only interpretable to Person B. An intruder cannot discover the meaning of the exchange because Person B has a piece of information that the intruder does not. Person A didn't access Person B's secret information (private key) either he only indirectly accessed it via a "public" key. The public key is formed from the private key by using a One-Way Function.
The concepts behind public key cryptography are best expressed by a simple puzzle.
Alice wants to send a trinket to Bob without an intruder stealing it. Each person has a lock and a key. A Non-Public Key Solution
- Alice puts her key in the box and sends to Bob.
- Bob copies the key and sends it back.
- Alice sends the trinket in a locked box.
- Bob opens the box with the copied key.
This solution, although the most intuitive, suffers from a major problem. The intruder could monitor the boxes and copy the key as it sent. If an intruder has Alice's key the trinket or anything else will be stolen in transit. To some the puzzle seems impossible, but those who understand public key cryptography solve it easily. Public Key Solution
- Alice puts the trinket in a box, locks it and sends it to Bob.
- Bob locks the box again with his lock and sends the box back.
- Alice removes her lock and sends it to Bob.
- Bob removes the final lock and takes the trinket.
The puzzle's trick is double locking the box.
This back-and-forth "double lock" process is used in many asymmetric key algorithms, such as ElGamal encryption and Diffie–Hellman key exchange, but not all of them.
This is the double lock principle, but it is not Public Cryptography as both keys are secret. In public cryptography one key is public, the other is secret. Nobody knowing the public key is able to decipher a message encrypted with a public key. Only the secret key is able to decipher a message encrypted with a public key.
A real-world analogy to public keys would be the padlock. The padlock can be easily closed, but it is much harder to do the reverse, namely opening. It is not impossible, but it requires much more effort to open it than to close it, assuming you don't have the (private) key. Alice could send Bob an open padlock by mail (the equivalent to the public key). Bob then puts a message for Alice into a box and locks the box with the padlock. Now, Bob sends the locked box back to Alice and Alice opens it with her private key.
Note that this approach is susceptible to man-in-the-middle attacks. If Charles intercepts the mail with Alice's padlock and replaces it with his own padlock, Bob will lock the box with the wrong padlock and Charles will be able to intercept the answer. Charles could then even lock the box again with Alice's padlock and forward the box to Alice. That way, she will never notice that the message got intercepted. This illustrates that it is very important to obtain public keys (the padlocks) from a trusted source. That's what certificates are for. They come along with the public keys and basically say something like 'I, Microsoft, hereby confirm that this padlock belongs to Alice', and are signed using secure digital signatures.
So someone (Bob) is able to send securely an encrypted data to Alice, if Alice had made her key public.
Bob is able to prove that he owns a secret key only by providing:
- a plain text
- the same text encrypted with the secret key
- the public key corresponding to the secret key.
Something similar to the double lock principle is Merkle's puzzle, which is the ancestor of the Diffie–Hellman key exchange, which is itself a close cousin to RSA public key system.
Further reading
[edit | edit source]
A Basic Public Key Example
The elementary working of Public Key Cryptography is best explained with an example. The working below covers the making of simple keys and the encryption and decryption of a sample of plain text. By necessity, the example is greatly simplified.
Basic Public Key Summary
[edit | edit source]- Public key encryption is used for internet secure links, such as when a browser opens a bank site or a site used with credit cards. Such addresses are prefixed by https as opposed to just http. RSA-OpenSSL is such an encryption system. An example of this secure site marking can be seen on the address of this page; this Wikibooks page (when the user is logged in) shows the https prefix or some alternative browser-specific marking that indicates that it is considered secure.
- Each site has an encryption key and a decryption key of its own, termed the public and private keys respectively. These are essentially very large numbers. These keys are always different, giving rise to the term asymmetrical encryption. In fact whenever we say key we mean a pair of numbers comprising the key; a key number to use in the raising of powers and another number that is the modulus of the arithmetic to be used for the work. For those unfamiliar with modular arithmetic, refer to the Wikibooks page High School Mathematics Extensions/Primes/Modular Arithmetic for a good, yet simple description.
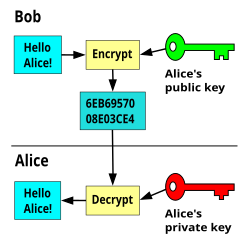
- Public keys are openly available for anybody to see, but private keys are not. The receiving site makes his public key available to the message sender, or by his making use of public directories. For each message transmission the sender uses this key to make the code. In this way only the private key of the recipient will decrypt it. A worked example has been provided in the text below, and the basic process can be seen in Figure 1.
- In fact, the two keys used for public key encryption form a reversible function. You could encrypt with the private key and decrypt with the public key if the system designers had otherwise intended it. Of course, for less public use the public keys could just as easily be treated as secret also. This reversible nature of the key pair is useful in testing digital certificates, where the issuer encrypts a certificate with his private key so that the recipient can then use his freely available public key to test its authenticity.
- The numbers used are made deliberately very large, and this makes the task of obtaining the private key from the public key too difficult for a hacker. It involves the factorization of very large numbers, and is very time consuming.
- Such systems, although imperfect, are nonetheless useful provided that the time to break them far exceeds the period for which the data is of any interest. The estimated time to break some such codes is many thousands of years.
- Signed digital certificates help certify the identity of user sites when delivering public keys. Browsers take steps to confirm their validity.
- The main advantage of the public key system is that there is a low administrative burden. Everything needed to send a message to a site is available in a public directory or is sent openly as a part of setting up the link.
- The main disadvantage of public key cryptography is that it is too slow for modern internet use. Because of this, the internet most often uses symmetric encryption for the main task; (a different method that uses a common key for both encryption and decryption); it simply uses public key methods to conceal the symmetric keys while they are being sent to the far end.
- There are several methods that hackers use to break coding:
- The brute force cracking of a key refers to trying every possible combination of private key while testing it against the relevant cyphertext. Such testing is time consuming, because a dictionary check or human intervention is needed at each iteration to decide whether or not plain language has emerged. Also, the numbers are very large, so this method is rarely of much interest.
- A mathematical attack refers to the finding of the two prime numbers, the product of which makes the modulus of the publicly available key. If these can be found then it simplifies the finding of the private key (more later); this method has the advantage that computers can be left to the task without much intervention. At the time of writing (2014) the record for breaking a key by mathematical attack is by Lenstra et al, on 12 December 2009, when an RSA-768 bit modulus (232 decimal digits) was factored using a method called the General Number Field Sieve (GNFS). The process required two years of collaboration and many hundreds of computing machines. (see: http://eprint.iacr.org/2010/006.pdf) Today most encryption keys in use are much bigger than the one that was broken, and a 1024 or 2048-bit key in an SSL certificate is still considered fairly safe against a mathematical attack. Note that the difficulty of breaking such a key increases exponentially with the key length.
- The history of successful intrusions has not involved code breaking however, but the hacking of the servers for their data and private keys. Other exploits have relied on the security omissions of individuals, or defective programming. For example, a recent SSL exploit, (2000-2014?), has involved accessing data, not by code breaking, but by a programming flaw that allows the sender to download blocks of memory content from the destination's server. The intention in SSL is to allow some text from the recipient's server to be returned as proof of message receipt and successful decryption. For this purpose the sender can specify the length of text to return, usually a header, and in any case less than 64Kbits in length. The core of the flaw was that if a very short message was sent but the sender asked for a larger block to be returned than was sent, the faulty program would oblige, so returning data that included other secure material from memory. Repeating this process every few seconds allowed a hacker to accumulate a large data block. The matter is stated to have been since corrected, but is said to have been available to any who knew of it for a period of about four years.
Making Site B's PUBLIC Key
[edit | edit source]A public key is available to all, and is used to encrypt messages that are being sent to the key's owner.
- Each site's computer produces two very large prime numbers, and since they are the basis of all that follows, these numbers are never revealed to any other. (Prime numbers are those that have no factors other than themselves or one).
- These two numbers are multiplied together to produce the modulus used in all of that site's calculations. The main public key is also derived from these primes, and determines the exponent to which the plain language numbers will be raised.
- This public key is available in directories and from certificate authorities, so when the SENDER wants to encrypt a message by public key cryptography he can easily use the recipient's public key (and modulus) to do it. Each site's public key set can be made to be almost certainly different from every other.
To illustrate the point for an intending recipient, let us make a simple example with the large prime numbers replaced with very small ones.
Say the two secretly held prime numbers are:
p = 5 , q = 11
Then the modulus of the arithmetic that will be used is given by their product:
m = 5 x 11 = 55 (the modulus of the arithmetic to use)
The encryption key can be found as follows: First, using the two prime numbers, calculate the function:
f(n) = (p-1) x (q-1) ∵ p = 5 and q = 11 ∴ f(n) = (5-1) x (11-1) ∴ f(n) = 40
then,
Select ANY number that is relatively prime to f(n) and less than it.
(Two numbers are said to be relatively prime when they share no common factors other than one. This term is also referred to as mutually prime, or coprime ).
The possible choices become: 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29, 31, 33, 37, and 39. Say we select the public encrypt exponent = 7
The receiving site's PUBLIC key can then be safely given to the world as :
(7, 55) as (encryption exponent, modulus) (In practice the numbers would be very much larger)
The actual size of the numbers used is very large. For example, for a 1024-bit RSA encryption, this number is the size in bits of the modulus; this is equivalent to a decimal number of about 308 digits, or 256 hex digits. The public exponent most often chosen has an integer value of 65537. This exponent is chosen because it produces faster encryption than some other selections; that is, because of its large zero count in the binary form (10000000000000001), it lends itself to fast processing with binary shifting methods. It is known elsewhere as Fermat number F4. Despite this preference for the same exponent, recall that the other part of the public key set is the modulus, and that will differ between users based on the very large number of primes available.
Making Site B's Private KEY
[edit | edit source]Used by Site B when decrypting messages that were sent to them, encrypted using Site B's public key.
The private key pair is used to decrypt messages, and this key will only work if the public key of the same site was used to encrypt the message. That is to say, Site B's public key is obtained from a directory, then used by Site A to encrypt a message for them. When the message gets to Site B, Site B uses its own private key for decryption.
Continuing with the simple example above, the private key of Site B is made from its public key as follows.
private decrypt exponent = (public encrypt exponent)-1 Mod f(n)
∵ public encrypt exponent = 7 , and f(n) = 40
∴ (private decrypt exponent x 7) Mod 40 = 1
∴ private decrypt exponent = 23
The Site B PRIVATE key pair is then:
(23,55) as (decryption exponent, modulus)
It will have been noted by some that the same number can result for both the encrypt and decrypt exponents. This particular case must be avoided by deliberate testing since a hacker would likely test for this possibility early in the process of an attack. In the above examples, this would have been the case if 9, 11, 21, 33 or 39 were chosen for the public key instead of some other. Lest it be thought that anticipation of this error is simple, notice that even in this set that both coprimes that are themselves prime (eg; leading to: 11 * 11 = 1 mod 40), and those that are coprime but not in themselves prime (eg; 9, 21, 33, and 39), can all produce this insecure state of affairs.
With the use of long primes, m the modulus (their product), is very much longer, but it should be apparent that an intending hacker could still obtain the private key if he were able to find the two secret primes as a starting point. Both the public key and the modulus to use with it are given to all who require it for encryption, so the burden of a mathematical attack reduces to the difficulty of factoring the modulus into these two secret primes. For the simple example shown above (m=55) this task is very simple, but for a very large number this effort is prohibitively long.
The native format in which the private key is delivered is in fact base-64, (a character set that needs only 6 bits per character, instead of the 4 for hex or the 7 for ASCI character codes). Unlike the public key string, the layout of a practical private key string for a 1024-bit RSA encryption contains the private key details, the public key details, and the secret numbers used in their making, as well as various other numbers and headers. The private key exponent, unlike the public exponent, is quite long, and is the equivalent of 256 hex digits in length. The secret primes are each 128 hex numbers in length. The decimal equivalent lengths are 308 digits for the private exponent (and the modulus), and 154 digits for each of the secret numbers.
Factoring the Modulus
[edit | edit source] number of primes ≅ x/(logx - 1)
now a 64 bit space is equivalent to about 20 digits
∴ number of primes ≅ 4 * 1017
then assuming 1 million calculations per second, (a wildly optimistic assumption for most):
the time to test all the primes ≅ 13,500 years
The example here was limited to 64 bits because the more representative figures, 128, 256, 512, 1024, and 2048-bit calculations are too big for most calculators. See The Math Behind Estimations to Break a 2048-bit Certificate by DigiCert for more details.
This example does not consider the use of improved methods for factoring, and these appear frequently in the literature. At present, (2014), the best of these is considered to be the General Number Field Sieve (GNFS), used to establish the record in December 2009.
To expand a little on the subject of improved methods, it will be apparent that starting with lists of tabulated primes speeds up the process. This, and the production of calculated product tables against their future need also allows much faster processing than would otherwise be possible by calculating on the fly. Because clearly, for a large set of such cracking problems, half of the solutions will lie in the first half of the trial values and half of them in the second, it has become the habit to express the expected time to solution for half of the set as opposed to the whole number implied by the Prime Number Theorem.
Encryption with B's Public Key
[edit | edit source]Assume that the public key pair belong to a Site B. Assume also that a plain language character represented by the number '2' is to be encrypted by Site A and sent to the recipient Site B: Site A uses Site B's public key pair to do so.
Assume plaintext=2
cyphertext = plaintext public encrypt exponent Mod n
∵ public encrypt exponent =7, and modulus = 55
∴ cyphertext = 27 Mod 55 = 128 Mod 55
∴ cyphertext = 18
With the very small numbers used in the example the cracking of the code would be relatively simple. But for very large values of primes p and q, and without knowing the private key value, the burden becomes very difficult. In some cases the task would involve an unreasonable time even for a very large number of computers.
Public key encryption does not disguise the relative frequency of the characters used. This is considered a failing in such systems since it improves the chances of cracking the code. So, the plaintext characters are arranged into groups before encryption to hide their natural frequencies of use; the groups are very large, the limit being that the size of a number encrypted must be smaller than the modulus in use.
Decryption with B's Private Key
[edit | edit source]Decryption using the above specific example is acheived as follows: For the received cyphertext = 18
With cyphertext=18 from previous section
Plaintext = cyphertextprivate decrypt exponent Mod n
∵ private decrypt exponent = 23, and modulus = 55
∴ Plaintext = 1823 Mod 55 = 74347713614021927913318776832 Mod 55
∴ Plaintext = 2 (You can only just confirm this with the Windows scientific calculator)
Notice that the plain language value of 2 has been recovered, which is the required result.
Exceptions
[edit | edit source]Some attempts with other than the correct private key will be nonetheless successful. There are exceptions that need to be considered. For example, in the above case, using the decrypt exponent =3 will also produce the correct result. See below:
With cyphertext=18 from previous section
Plaintext = cyphertextprivate decrypt exponent Mod n
∵ hacker's attempted decrypt exponent = 3, and modulus = 55
∴ Plaintext = 183 Mod 55 = 5832 Mod 55
∴ Plaintext = 2 also the right result.
Note that every (N^7Mod55)^3Mod55 == (N^7Mod55)^23Mod55)
In a practical environment further consideration would be given to such matters in the selection of keys.
The Internet Speed Compromise
[edit | edit source]Because public key encryption and decryption is so very slow, it is unsuitable in its native form for internet use. In fact, asymmetric public key encryption is used for only a small part of internet communications. Such systems are hybrid. The summary of the method used is as follows:
- The text to be transmitted securely will be encrypted, not by public key cryptography, but by using SYMMETRIC key encryption. This is typically a 128 bit cipher, but can be greater. Symmetric key methods need both sites to use the same key. To do this one site must at some stage originate the key then send a copy of it to the other.
- This SYMMETRIC key, is not sent to the far end openly but is kept safe by first encrypting it using PUBLIC key methods. The public key of the destination site is used for this.
- The recipient uses his PRIVATE key to decrypt this cyphertext, and to recover the SYMMETRIC key value. He then decrypts the main symmetric ciphertext with it.
- The symmetric encryption key is discarded at the end of the current session, and the asymmetric public key may or may not be discarded, depending on the system in use. A short lifetime for the key reduces the chances of a successful key recovery during cyber-attacks and the subsequent decoding of recorded traffic at a later date. With this in mind, it might be that short sessions are more secure than long ones, provided of course that discarded means the complete removal from memory, and not just the ubiquitous delete.
The systems currently in use for internet browsers are Transport Layer Security (TLS) and its predecessor, Secure Sockets Layer (SSL). A complete description of these is available at Wikipedia's Secure Sockets Layer.
Note that in a duplex system, that is, the usual kind that sends in both directions, there will be two such procedures. One originated at each end. The key sets used for send and receive, for both asymmetric and symmetric encryption systems are all different.
Message Authentication
[edit | edit source]Security breaks down if outsiders can change the message in transit, or if they mis-represent themselves right from the start. In an attempt to overcome these risks digital certificates were devised. In a further attempt to ensure that the certificates were from the place respected by the users, the certificates were given digital signatures. One such method among many is the Digital Signature Algorithm (DSA), the basis of the Digital Signature Standard (DSS).
These certificates are not just simple text messages, which of course could be imitated, but use calculated values based on the content of a message. The entire basis of certification depends both on the designed properties of these hash algorithms and on the integrity of those who assert their worth. Their properties include:
- Sensitivity: They are very sensitive. A very small change in a hash algorithm's input always creates a very large change in its output value.
- Specificity: They are very specific. Although it depends on the hash algorithm used, there is very little chance that two different inputs could ever produce the same output. When this happens, say once in many billions, it is referred to as a collision.
- Opacity: An input value cannot be found from a output value. This is because of the great complexity of the algorithm and in particular, because of the liberal use of modular arithmetic's one-way functions.
- Secrecy: Some hash algorithms are available for public use, but proprietary interests can make their own. Algorithms available for the use of most include MD5, SHA1, SHA2, SHA3, and others. MD5 has been broken. SHA1, the basis for much of the current certification, is deprecated in its use for more complexity.
The hash value is calculated by the sender and compared with one calculated at the receiving end, where the two must match for acceptance. Like encryption itself, hash values are too laborious to reverse engineer, that is to say, new or changed messages could not be made by outsiders to represent an existing hash value within any useful time period. Because of this they provide a basis upon which to verify that a message's contents were not changed since the certificate was issued.
Certificates themselves are tested against known root certificates within the browser store, to ensure that the certificates are from a known reliable source. If certificates are secret-signed with a private key known only to the issuing authority, then validation of the certificate can be made by decrypting the signature with its public key. That is to say, because the process is reversible, validation of the source can be made.
The actual process used for these tasks is more complex than is implied in summary, involving many long-bit calculations, but the strength of the system is unlikely to satisfy the skeptical until the sums are seen. Refer to the pdf file How Encryption and Digital Signatures Work and read the section An Example of a Digital Signature Mechanism for such a description.
The process of testing certificates and other matters are in any case summarized by browsers for their users. Browsers will indicate clearly whether or not they consider a connection to be secure. The most common of these indications includes an added padlock somewhere on the screen and the modification of the site's http address heading to read https. Some browsers such as Opera add other information such as color coding to represent the levels of security.
See also
[edit | edit source]- High School Mathematics Extensions/Primes/Modular Arithmetic : The stuff you may have forgotten.
Further reading
[edit | edit source]- Bionic Buffalo Tech Note 35: How Encryption and Digital Signatures Work Clearly describes the working of the Data Encryption Standard (DES), the RSA Public Key Standard, and the Digital Signature Algorithm (DSA), with generous math notes.
- Digital Signature Algorithm
- Code Breaking Factoring Record : The Math Behind Estimations to Break a 2048-bit Certificate by DigiCert.
- RSA Factoring Challenge: Contains tables of the progress so far in prime factoring.
- The RSA Key Layout: A page showing the precise layout of both private and public keys for a 1024-bit RSA encryption.
RSA
RSA is an asymmetric algorithm for public key cryptography, widely used in electronic commerce. The algorithm was described in 1977 by Ron Rivest, Adi Shamir and Len Adleman; the letters RSA are the initials of their surnames.
Clifford Cocks, a British mathematician working for GCHQ, described an equivalent system in an internal document in 1973. His discovery, however, was not revealed until 1997 due to its top-secret classification.
The security of the RSA system relies on the difficulty of factoring very large integers. New fast algorithms in this field could render RSA insecure, but this is generally considered unlikely.
The algorithm was patented by MIT in 1983 in the United States of America. The patent expired 21 September 2000. Since the algorithm had been published prior to the patent application, it could not be patented in other countries.
Operation
[edit | edit source]Key Generation
[edit | edit source]Suppose a user Alice wishes to allow Bob to send her a private message over an insecure transmission medium. She takes the following steps to generate a public key and a private key:
- Choose two large prime numbers p ≠ q randomly and independently of each other. Compute N = p q.
- Choose an integer 1 < e < N which is coprime to (p-1)(q-1).
- Compute d such that d e ≡ 1 (mod (p-1)(q-1)).
- Destroy all records of p and q.
- (Steps 2 and 3 can be performed with the extended Euclidean algorithm; see modular arithmetic. Additionally, solving for either e or d may be performed using the diophantine equation .)
N and e are the public key, and N and d are the private key. Note that only d is a secret as N is known to the public. Alice transmits the public key to Bob, and keeps the private key secret.
You can generate and examine a real RSA keypair using OpenSSL and some Unix utilities. ( Cryptography/Generate a keypair using OpenSSL ).
Encrypting messages
[edit | edit source]Suppose Bob wishes to send a message m to Alice. He knows N and e, which Alice has announced. He turns m into a number n < N, using some previously agreed-upon reversible protocol. For example, each character in a plaintext message could be converted to its ASCII code, and the codes concatenated into a single number. If necessary, he can break m into pieces and encrypt each piece separately. He then computes the ciphertext c:
This can be done quickly using the method of exponentiation by squaring. Bob then transmits c to Alice.
Decrypting messages
[edit | edit source]Alice receives c from Bob, and knows her private key d. She can recover n from c by the following procedure:
Alice can then extract n, since n < N. Given n, she can recover the original message m.
The decryption procedure works because
and ed ≡ 1 (mod p-1) and ed ≡ 1 (mod q-1). Fermat's little theorem yields
- and
which implies (as p and q are different prime numbers)
Signing Messages
[edit | edit source]RSA can also be used to sign a message. Suppose Alice wishes to send a signed message to Bob. She produces a hash value of the message, encrypts it with her secret key, and attaches it as a "signature" to the message. This signature can only be decrypted with her public key. When Bob receives the signed message, he decrypts the signature with Alice's public key, and compares the resulting hash value with the message's actual hash value. If the two agree, he knows that the author of the message was in possession of Alice's secret key, and that the message has not been tampered with since.
Security
[edit | edit source]Suppose Eve, an eavesdropper, intercepts the public key N and e, and the ciphertext c. However, she is unable to directly obtain d, which Alice keeps secret. The most obvious way for Eve to deduce n from c is to factor N into p and q, in order to compute (p-1)(q-1) which allows the determination of d from e. No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists. See integer factorization for a discussion of this problem.
It has not been proven that factoring N is the only way of deducing n from c, but no easier method has been discovered (at least to public knowledge.)
Therefore, it is generally presumed that Eve is defeated in practice if N is sufficiently large.
If N is 256 bits or shorter, it can be factored in a few hours on a personal computer, using software already freely available. If N is 512 bits or shorter, it can be factored by several hundred computers as of 1999. It is currently recommended that N be at least 1024 bits long.
In 1993, Peter Shor showed that a quantum computer could in principle perform the factorization in polynomial time. If (or when) quantum computers become a practical technology, Shor's algorithm will make RSA and related algorithms obsolete.
Should an efficient classical factorization code be discovered or a practical quantum computer constructed, using still larger key lengths would provide a stopgap measure. However, any such security break in RSA would obviously be retroactive. An eavesdropper who had recorded a public key and any ciphertext produced with it (easily found by just recording traffic to that public key's owner), could simply wait until such a breakthrough. And then decipher that ciphertext into the plaintext message. Therefore, it is inherently unsafe to exchange long-term secrets with RSA or any cipher with similar vulnerabilities.
Practical considerations
[edit | edit source]Key generation
[edit | edit source]Finding the large primes p and q is usually done by testing random numbers of the right size with probabilistic primality tests which quickly eliminate most non-primes. If such a test finds a "probable prime", a deterministic test should then be used to verify that the number is indeed prime.
p and q should not be 'too close', lest the Fermat factorization for N be successful. Furthermore, if either p-1 or q-1 has only small prime factors, N can be factored quickly and these values of p or q should therefore be discarded as well.
One should not employ a prime search method which gives any information whatsoever about the primes to the attacker. In particular, a good random number generator for the start value needs to be employed. Note that the requirement here is both 'random' and 'unpredictable'. These are not the same criteria; a number may have been chosen by a random process (i.e., no pattern in the results), but if it is predictable in any manner (or even partially predicatable), the method used will result in loss of security. For example, the random number table published by the Rand Corp in the 1950s might very well be truly random, but it has been published and thus can serve an attacker as well. If the attacker can guess half of the digits of p or q, they can quickly compute the other half (shown by Coppersmith in 1997).
It is important that the secret key d be large enough. Wiener showed in 1990 that if p is between q and 2q (which is quite typical) and d < N1/4/3, then d can be computed efficiently from N and e. The encryption key e = 2 should also not be used.
Speed
[edit | edit source]RSA is much slower than DES and other symmetric cryptosystems. In practice, Bob typically encrypts a secret message with a symmetric algorithm, encrypts the (comparatively short) symmetric key with RSA, and transmits both the RSA-encrypted symmetric key and the symmetrically-encrypted message to Alice.
This procedure raises additional security issues. For instance, it is of utmost importance to use a strong random number generator for the symmetric key, because otherwise Eve could bypass RSA by guessing the symmetric key.
Key distribution
[edit | edit source]As with all ciphers, it is important how RSA public keys are distributed. Key distribution must be secured against a man-in-the-middle attack. Suppose Eve has some way to give Bob arbitrary keys and make him believe they belong to Alice. Suppose further that Eve can intercept transmissions between Alice and Bob. Eve sends Bob her own public key, which Bob believes to be Alice's. Eve can then intercept any ciphertext sent by Bob, decrypt it with her own secret key, keep a copy of the message, encrypt the message with Alice's public key, and send the new ciphertext to Alice. In principle, neither Alice nor Bob would be able to detect Eve's presence. Defenses against such attacks are often based on digital certificates or other components of a public key infrastructure.
Timing attacks
[edit | edit source]Kocher described an ingenious unexpected new attack on RSA in 1995: if the attacker Eve knows the hardware of Alice and is able to measure the decryption times for several known cyphertexts, she can deduce the decryption key d quickly. To thwart this attack, the decryption code should decrypt in constant time. This is known as RSA blinding.
Adaptive Chosen Ciphertext Attacks
[edit | edit source]In 1998, Daniel Bleichenbacher described the first practical adaptive chosen ciphertext attack, against RSA-encrypted messages using the PKCS #1 v1 redundancy function (a redundancy function adds structure to an RSA-encrypted message, so it is possible to determine whether a decrypted message is valid.) Due to flaws with the PKCS #1 scheme, Bleichenbacher was able to mount a practical attack against RSA implementations of the Secure Socket Layer protocol, and potentially reveal session keys. As a result of this work, cryptographers now recommend the use of provably secure redundancy checks such as Optimal Asymmetric Encryption Padding, and RSA Laboratories has released new versions of PKCS #1 that are not vulnerable to these attacks.
ElGamal
ElGamal is one of the simplest cryptosystems based on the discrete logarithm problem. A quick reminder of the discrete logarithm problem - given , such that , find . This is a hard problem when dealing with finite sets. ElGamal has a set of public parameters which can be shared by a number of users of the system. These are referred to as the domain parameters. These parameters are:
- - a large prime of around 1024 bits (currently) such that is divisible by another prime of around 160 bits. - - an element of the finite field with order divisible by , that is .
The domain parameters create a public group with a prime order and a generator . In other words, we create a large but finite group, and a method of ordering that group (the generator), and we know that it will contain a prime number of elements. These are the properties we are after. These parameters are public, and the security of the system depends on the public and private key pair, which we shall generate next.
The private key is a randomly-chosen integer. The public key is .
In order to encrypt a message we generate a random ephemeral key , and calculate:
This gives us the ciphertext .
In order to decrypt a ciphertext we compute:
As you can see from the decryption method, the message 0 will encrypt to itself, so not a good choice of message. In addition to this, as a result of using the ephemeral key , which will change every time you can see that the same message will encrypt to many different ciphertexts.
Since the ciphertext is expressed as 2 integers of the same length as the message, we end up with ciphertexts being twice as large as the message they're encrypting.
Elliptic curve
Elliptic curve cryptography is a type of cryptography that relies on mathematical structures known as "elliptic curves" and "finite fields". An elliptic curve is a relation of the form , where and are preset parameters of the curve and and are the coordinates. Any pair that satisfies the relation is said to be a point on the elliptic curve. On elliptic curve points, it is possible to define an operation known as "addition" as follows:
To add two points and , draw a line through them, and locate the third point on the curve that the line passes through; call it . If and have the same x coordinate, the line joining them will be vertical and R will not exist, so in that case we call the "point at infinity". The point at infinity added to any other point is that point itself, so this point at infinity can be thought of as the elliptic curve point analogue of the number zero. Otherwise, trace a vertical line from to the point at the same x coordinate on the opposite side of the curve. This point is defined as . To calculate , instead take the tangent line to the curve at , extend it to and take the vertically opposite point as the answer just like in the case.
Because elliptic curves are mathematical functions, we can use the tools of high-school algebra and elementary calculus to derive formulas for and . For , for formula is:
For P+P:
Notice that the algorithm in both cases is the same: first we find the slope at , then we get the x-coordinate of the answer, and then we use the slope-point formula to get the y-coordinate. From these formulas, however, we get a very surprising result: , regardless of whether , and are different or the same. Additionally, from the visual definition it is obvious that . These facts together mean that elliptic curve points form what is known as an _abelian group_ - a structure which supports addition, and therefore by extension multiplication by integers. For example, .
It's also quite easy to multiply an elliptic curve point by very large numbers. You might think multiplying a point by a billion requires you to add it to itself a billion times, but in reality there is a much simpler algorithm:
define multiply(P, k) {
if (k == 0) return point_at_infinity()
if (k == 1) return P;
if (k % 2 == 0) return double(multiply(P,k/2))
if (k % 2 == 1) return add(P,double(multiply(P,(k-1)/2)))
}
Basically, instead of repeatedly adding on the original point to zero many times, the algorithm repeatedly uses doubling, cutting the size of the problem in half at every step. For , for example, the algorithm expands to:
83p add(p,double(41p)) add(p,double(add(p,double(20p)))) add(p,double(add(p,double(double(10p))))) add(p,double(add(p,double(double(double(5p)))))) add(p,double(add(p,double(double(double(add(p,double(2p)))))))) add(p,double(add(p,double(double(double(add(p,double(double(p)))))))))
For , the algorithm takes a mere thirty steps. This makes it possible to multiply elliptic curve numbers by extremely large numbers - numbers so large, in fact, that there are not enough atoms in the universe to actually count to them.
Finite Fields
[edit | edit source]Now, we get into the more interesting part of elliptic curve mathematics. A while ago, mathematicians discovered that the forms of addition, subtraction, multiplication and division that we use today are not the only forms that are mathematically consistent. There are in fact many other structures, some using numbers and others using more complex forms like polynomials, over which we can define the basic operations in special ways and still have a working system of algebra. The most common is "modular arithmetic". Modular addition and multiplication are just like normal addition and multiplication, except after the calculation is done you divide the result by a preset value, called the "modulus", and take only the remainder. For example, in modulo 7:
and
Subtraction is similar, except if the result turns out to be negative you add the modulus to force it to be positive again. Thus:
Division is more complicated to implement, but is defined through multiplication - that is, is defined to be a number such that . It can be proven that all modular divisions have an answer and no modular divisions have multiple possible answers if and only if the modulus is prime. Thus, we generally only care about "prime fields".
So what's the point of this spooky kind of arithmetic? Basically, it's a great kind of arithmetic to do elliptic curves over. No matter how much you add or multiply points together, the coordinates of the result will always be integers in the range , where is the modulus. The "wrap around" property also makes the structure cryptographically secure; given a normal elliptic curve, given two points and , you can figure out the value of by looking at the size of the output and using that information to zero in on a small range of possibilities. With an elliptic curve over a prime field, all points look essentially the same; they're all numbers roughly evenly distributed within the range . The hardness of this problem, figuring out given and , is in fact the basis of elliptic curve cryptography's security.
The two most well-known algorithms over elliptic curves are the elliptic curve Diffie–Hellman protocol and the Elliptic Curve Digital Signature Algorithm, used for encrypting and signing messages, respectively.

This page or section of the Cryptography book is a stub. You can help Wikibooks by expanding it.
Blum-Goldwasser
The Blum-Goldwasser (BG) cryptosystem is an asymmetric key encryption algorithm proposed by Manuel Blum and Shafi Goldwasser in 1984. Blum-Goldwasser is a probabilistic, semantically secure cryptosystem with a constant-size ciphertext expansion. The encryption algorithm implements an XOR-based stream cipher using the Blum Blum Shub (BBS) pseudo-random number generator to generate the keystream. Decryption is accomplished by manipulating the final state of the BBS generator using the private key, in order to find the initial seed and reconstruct the keystream.
The BG cryptosystem is semantically secure based on the assumed intractability of integer factorization; specifically, factoring a composite value where are large primes. BG has multiple advantages over earlier probabilistic encryption schemes such as the Goldwasser-Micali cryptosystem. First, its semantic security reduces solely to integer factorization, without requiring any additional assumptions (e.g., hardness of the quadratic residuosity problem or the RSA problem). Secondly, BG is efficient in terms of storage, inducing a constant-size ciphertext expansion regardless of message length. BG is also relatively efficient in terms of computation, and fares well even in comparison with cryptosystems such as RSA (depending on message length and exponent choices). However, BG is highly vulnerable to adaptive chosen ciphertext attacks (see below).
Because encryption is performed using a probabilistic algorithm, a given plaintext may produce very different ciphertexts each time it is encrypted. This has significant advantages, as it prevents an adversary from recognizing intercepted messages by comparing them to a dictionary of known ciphertexts.
Scheme definition
[edit | edit source]Note that the following description is a draft, and may contain errors!
Blum-Goldwasser consists of three algorithms: a probabilistic key generation algorithm which produces a public and a private key, a probabilistic encryption algorithm, and a deterministic decryption algorithm.
Key generation
[edit | edit source]To allow for decryption, the modulus used in Blum-Goldwasser encryption should be a Blum integer. This value is generated in the same manner as an RSA modulus, except that the prime factors must be congruent to 3 mod 4. (See RSA, key generation for details.)
- Alice generates two large prime numbers and such that , randomly and independently of each other, where mod .[28]
- Alice computes .
The public key is . The private key is the factorization . [28]
- Alice keeps the private key secret.
- Alice gives to Bob.
Message encryption
[edit | edit source]Suppose Bob wishes to send a message m to Alice:
- Bob first encodes as a string of bits .
- Bob selects a random element , where , and computes .
- Bob uses the BBS pseudo-random number generator to generate random bits (the keystream), as follows:
- For to :
- Set equal to the least-significant bit of .
- Increment .
- Compute .
- Bob computes the ciphertext bits using the bits from the BBS as a stream cipher keystream, XORing the plaintext bits with the keystream:
- For to :
- Bob sends a message to Alice -- the enciphered bits and the final value .
(The value is equal to . )
To improve performance, the BBS generator can securely output up to of the least-significant bits of during each round. See Blum Blum Shub for details.
Message decryption
[edit | edit source]Alice receives . She can recover using the following procedure:
- Using the prime factorization , Alice computes and .
- Compute the initial seed
- From , recompute the bit-vector using the BBS generator, as in the encryption algorithm.
- Compute the plaintext by XORing the keystream with the ciphertext: .
Alice recovers the plaintext .
Security and efficiency
[edit | edit source]The Blum-Goldwasser scheme is semantically-secure based on the hardness of predicting the keystream bits given only the final BBS state and the public key . However, ciphertexts of the form are vulnerable to an adaptive chosen ciphertext attack in which the adversary requests the decryption of a chosen ciphertext . The decryption of the original ciphertext can be computed as .
Depending on plaintext size, BG may be more or less computationally expensive than RSA. Because most RSA deployments use a fixed encryption exponent optimized to minimize encryption time, RSA encryption will typically outperform BG for all but the shortest messages. However, as the RSA decryption exponent is randomly distributed, modular exponentiation may require a comparable number of squarings/multiplications to BG decryption for a ciphertext of the same length. BG has the advantage of scaling more efficiently to longer ciphertexts, where RSA requires multiple separate encryptions. In these cases, BG may be significantly more efficient.
References
[edit | edit source]- ↑ Infoanarchy wiki: One-Time Pad Cryptosystem (mirror: [5])
- ↑ Dirk Rijmenants. "Manual One-time pads".
- ↑ Marcus J. Ranum. "One-Time-Pad (Vernam's Cipher) Frequently Asked Questions".
- ↑ "One Time Pads : Cold War Coding."
- ↑ a b Anonymous PI. "Nothing To See Here: The One-Time Pad".
- ↑ "One-time pad generator"
- ↑ "The Artifacts of the CIA"
- ↑ Hal Abelson, Ken Ledeen, Harry Lewis. "Secret Bits: How Codes Became Unbreakable": "Historical Cryptography".
- ↑ "The Manual One-time Pad"
- ↑ a b Crypto Museum: "EROLET Key-tape generator"
- ↑ a b c d e Dirk Rijmenants. "The Manual One-time Pad"
- ↑ a b c Crypto Museum: "One-Time Pad (OTP)".
- ↑ "Cryptographilia" describes CT-37c.
- ↑ "onetimepad"
- ↑ "Checkerboard Variations"
- ↑ "Raspberry Pi Thermal Printer One Time Pads"
- ↑ Stephen Hewitt. "Manual encryption with a one-time pad revisited". 2019.
- ↑ Christos T. "SOE codes and Referat Vauck". 2013.
- ↑ Crypto Museum: "Mixer machines: One-Time Tape machines".
- ↑ David Shaw. Maths by Email. "Try this: One time pad".
- ↑ Colin Percival. "Cryptographic Right Answers".
- ↑ Jeffrey Goldberg. "Guess why we’re moving to 256-bit AES keys".
- ↑ Bruce Schneier. "Another New AES Attack". quote: "AES-128 provides more than enough security margin for the forseeable future. But if you're already using AES-256, there's no reason to change."
- ↑ "Which is the Best Cipher Mode and Padding Mode for AES Encryption?".
- ↑ Ignat Korchagin. "Speeding up Linux disk encryption". 2020.
- ↑ JP Aumasson. "Lazy crypto reloaded".
- ↑ "You Don't Want XTS". 2014.
- ↑ a b RFC 4086 section "6.2.2. The Blum Blum Shub Sequence Generator"
- M. Blum, S. Goldwasser, "An Efficient Probabilistic Public Key Encryption Scheme which Hides All Partial Information", Proceedings of Advances in Cryptology - CRYPTO '84, pp. 289–299, Springer Verlag, 1985.
- Menezes, Alfred; van Oorschot, Paul C.; and Vanstone, Scott A. Handbook of Applied Cryptography. CRC Press, October 1996. ISBN 0-8493-8523-7
External links
[edit | edit source]
Hash function
| A Wikibookian suggests that Cryptography/Hash function be merged into this chapter. Discuss whether or not this merger should happen on the discussion page. |
A digest, sometimes simply called a hash, is the result of a hash function, a specific mathematical function or algorithm, that can be described as . "Hashing" is required to be a deterministic process, and so, every time the input block is "hashed" by the application of the same hash function, the resulting digest or hash is constant, maintaining a verifiable relation with the input data. Thus making this type of algorithms useful for information security.
Other processes called cryptographic hashes, function similarly to hashing, but require added security, in the form or a level of guarantee that the input data can not feasibly be reversed from the generated hash value. I.e. That there is no useful inverse hash function
This property can be formally expanded to provide the following properties of a secure hash:
- Preimage resistant : Given H it should be hard to find M such that H = hash(M).
- Second preimage resistant: Given an input m1, it should be hard to find another input, m2 (not equal to m1) such that hash(m1) = hash(m2).
- Collision-resistant: it should be hard to find two different messages m1 and m2 such that hash(m1) = hash(m2). Because of the birthday paradox this means the hash function must have a larger image than is required for preimage-resistance.
A hash function is the implementation of an algorithm that, given some data as input, will generate a short result called a digest. A useful hash function generates a fixed length of hashed value.
For Ex: If our hash function is 'X' and we have 'wiki' as our input... then X('wiki')= a5g78 i.e. some hash value.
Applications of hash functions
[edit | edit source]Non-cryptographic hash functions have many applications,[1] but in this section we focus on applications that specifically require cryptographic hash functions:
A typical use of a cryptographic hash would be as follows: Alice poses to Bob a tough math problem and claims she has solved it. Bob would like to try it himself, but would yet like to be sure that Alice is not bluffing. Therefore, Alice writes down her solution, appends a random nonce, computes its hash and tells Bob the hash value (whilst keeping the solution secret). This way, when Bob comes up with the solution himself a few days later, Alice can verify his solution but still be able to prove that she had the solution earlier.
In actual practice, Alice and Bob will often be computer programs, and the secret would be something less easily spoofed than a claimed puzzle solution. The above application is called a commitment scheme. Another important application of secure hashes is verification of message integrity. Determination of whether or not any changes have been made to a message (or a file), for example, can be accomplished by comparing message digests calculated before, and after, transmission (or any other event) (see Tripwire, a system using this property as a defense against malware and malfeasance). A message digest can also serve as a means of reliably identifying a file.
A related application is password verification. Passwords should not be stored in clear text, for obvious reasons, but instead in digest form. In a later chapter, Password handling will be discussed in more detail—in particular, why hashing the password once is inadequate.
A hash function is a key part of message authentication (HMAC).
Most distributed version control systems (DVCSs) use cryptographic hashes.[2]
For both security and performance reasons, most digital signature algorithms specify that only the digest of the message be "signed", not the entire message. The Hash functions can also be used in the generation of pseudo-random bits.
SHA-1, MD5, and RIPEMD-160 are among the most commonly-used message digest algorithms as of 2004. In August 2004, researchers found weaknesses in a number of hash functions, including MD5, SHA-0 and RIPEMD. This has called into question the long-term security of later algorithms which are derived from these hash functions. In particular, SHA-1 (a strengthened version of SHA-0), RIPEMD-128 and RIPEMD-160 (strengthened versions of RIPEMD). Neither SHA-0 nor RIPEMD are widely used since they were replaced by their strengthened versions.
Other common cryptographic hashes include SHA-2 and Tiger.
Later we will discuss the "birthday attack" and other techniques people use for Breaking Hash Algorithms.
Hash speed
[edit | edit source]When using hashes for file verification, people prefer hash functions that run very fast. They want a corrupted file can be detected as soon as possible (and queued for retransmission, quarantined, or etc.). Some popular hash functions in this category are:
- BLAKE2b
- SHA-3
In addition, both SHA-256 (SHA-2) and SHA-1 have seen hardware support in some CPU instruction sets.
When using hashes for password verification, people prefer hash functions that take a long time to run. If/when a password verification database (the /etc/passwd file, the /etc/shadow file, etc.) is accidentally leaked, they want to force a brute-force attacker to take a long time to test each guess.[3] Some popular hash functions in this category are:
- Argon2
- scrypt
- bcrypt
- PBKDF2
We talk more about password hashing in the Cryptography/Secure Passwords section.
Further reading
[edit | edit source]- see Algorithm Implementation/Hashing for more about non-cryptographic hash functions and their applications.
- see Data Structures/Hash Tables for the most common application of non-cryptographic hash functions
- Rosetta Code : Cryptographic hash function has implementations of cryptographic hash functions in many programming languages.
- ↑ applications of non-cryptographic hash functions are described in Data Structures/Hash Tables and Algorithm Implementation/Hashing.
- ↑ Eric Sink. "Version Control by Example". Chapter 12: "Git: Cryptographic Hashes".
- ↑ "Speed Hashing"
MD5
MD5 is a popular Hash Function used by many people around the world. Developed by Professor Ronald L. Rivest of MIT
It has two purposes:
- Verify the integrity of a file after a specified period of time
- Generate Hash values for a certain piece of data ( Ex: file) and store them, for later cross checking if the file has been modified or not (this is in essence the 1st point stated above)
For example, on a system that has a file called "SAMPLE.TXT" the MD5 hash would look like this:
| filename | hash value |
|---|---|
| C:\SAMPLE.TXT | BC8FEFECA210FC0C0F3EBC1614A37889 |
MD5 takes as input a message of arbitrary length and produces as output a 128- bit "fingerprint" or "message digest" of the input. It is conjectured that it is computationally infeasible to produce any message having a given prespecified target message digest. The MD5 algorithm was intended for digital signature applications, where a large file must be "compressed" in a secure manner before being signed with a private (secret) key under a public-key cryptosystem such as RSA. However, practical attacks on the collision resistance of MD5 exist[1], and it should therefore not be used with digital signatures or any other application requiring collision resistance.
Exact technical information is described in RFC:1321 (as HTML).
References
[edit | edit source]- ↑ [6]Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger: MD5 considered harmful today - Creating a rogue CA certificate http://www.win.tue.nl/hashclash/rogue-ca/
SHA-1
The Secure Hash Algorithm SHA (Secure Hash Algorithm), based on the MD4 (Message Digest) algorithm created by Ronald L. Rivest of the MIT, was designed by the NIST (National Institute of Standards and Technology), along with the NSA (National Security Agency). It is defined by three distinct SHA algorithms, labeled SHA-0, SHA-1, and SHA-2.
SHA-1 was published by NIST in 1995 as FIPS PUB 180-1.[1] and was considered a cryptographically secure one-way hash algorithm and used in many applications including TLS and SSL ("https://"), SSH, PGP, Git, Mercurial, Monotone, etc. until theoretical weaknesses were found in 2005.
While at least up-to 2015 no actual SHA-1 collision had been publicly acknowledged, in 2006, NIST and other organizations deprecated the use of SHA-1. They recommend that people should stop using SHA-1 and transition to a hash function without those theoretical weaknesses, such as SHA-2 or SHA-3.
Further reading
[edit | edit source]- ↑ U.S. Department of Commerce: National Institute of Standards and Technology. "FIPS PUB 180-1". 1995.
SHA-2
SHA-2 was designed and developed by the National Security Agency (NSA) and is today one of the hash algorithms where still no collisions have been found. SHA-2 was created because of the weakness of SHA-1 where a simple step was missing. SHA-2 takes the last bitgroup and after some bit operations the group will be placed at the beginning. It has been shown that this step makes SHA-2 very robust against attacks. SHA-2 can be used with different bit length: SHA-256, SHA-384 and SHA-512.
RadioGatún
This article describes a cryptographic algorithm named RadioGatún. To fully understand this article, the following concepts need to be understood by the reader:
- Binary numbers To maximize performance, RadioGatún works directly with binary numbers
- Hexadecimal numbers are used to illustrate some parts of the algorithm
- Bitwise logic operations RadioGatún uses bitwise negation, bitwise or, and bitwise exclusive or
- Bit rotation RadioGatún uses circular rotations
- Cryptographic hashes RadioGatún is a, as far as we know, secure cryptographic hash
- Pseudo-random number generator RadioGatún also functions as a secure random number generator
- The reader should be familiar with at least one programming language which can perform the bitwise operations RadioGatún performs.
What is RadioGatún?
[edit | edit source]RadioGatún is the direct predecessor of Keccak, the SHA-3 hashing standard. It is one of the fastest hashes out there: The 64-bit version of RadioGatún is about as fast as Blake2b, and the 32-bit version is about as fast as Blake2s. While Blake2 was given variable-length output as an add-on, RadioGatún has intrinsic variable length support, acting both as a cryptographic hash and as a stream cipher.
RadioGatún is the oldest secure variable length hash out there; it has been around since 2006, and, as of 2020, there is no known attack which weakens its security claims. MD5 was broken within 12 years of its release; RadioGatún has been around longer and still appears secure.
The 32-bit version appears to offer 304 bits of security; the 64-bit version looks to have 608 bits of security. In other words, the 32-bit version is more than secure enough for 256 bit hashes, while the 64-bit version can make 512 bit hashes.
Note on notation
[edit | edit source]Arrays
[edit | edit source]The code below uses a number of arrays to alter the RadioGatún state. The arrays are zero-indexed; this means that the first element of an array has the index 0 instead of the index 1. Instead of representing an array of 3 words as i[1], i[2], and i[3] (one-indexed arrays), we represent them as i[0], i[1], and i[2].
Hexadecimal numbers
[edit | edit source]Since RadioGatún directly manipulates binary numbers, we sometimes put numbers in Hexadecimal format. When this is done, we put an "0x" at the beginning of the number. Examples: 0x07 is 7; 0x10 is 16.
Bytes and words
[edit | edit source]On this page, bytes are always eight bits in size. Words can be 32 bits or 64 bits, depending on the version of RadioGatún being used.
Variable word length
[edit | edit source]RadioGatún is a cipher designed in the mid-first-2000s-decade, in an era when servers were running a mixture of 32-bit and 64-bit operating systems, most desktops were still running 32-bit systems, and well before any hand held phones were running 64-bit code. This in mind, the cipher has different modes to support both 32-bit and 64-bit operation. There are also tiny versions that make cryptoanalysis easier: People investigating RadioGatún's security can analyze the one-bit or two-bit versions (as of 2018, the largest RadioGatún variant that has been broken is the two-bit one).
While RadioGatún has 8-bit and 16-bit support, the eight-bit version is probably too small to be secure, and the 16-bit might be too small. That in mind, only the 32-bit and 64-bit variants of RadioGatún will be looked at.
RadioGatún uses 58 words (of either 32-bit or 64-bit length, depending on the RadioGatún variant we are looking at) to store its state. For the rest of this document, "word" is either a 32-bit or 64-bit number, depending on which RadioGatún variant is being used.
State initialization
[edit | edit source]To initialize RadioGatún's state, all 58 words are reset to have the value 0.
The belt and mill
[edit | edit source]RadioGatún stores its state in two pieces: 39 words are stored in the belt, which can be visualized as three rows of 13 words. The mill is 19 words wide. Some implementations of RadioGatún use an extra word to store the belt, which facilitates code size optimizations.
The beltmill function
[edit | edit source]While the RadioGatún spec considers the "belt" and "mill" operations separate, they are both done at the same time, so, in this document, we will consider a combined beltmill operation. This is the core of the RadioGatún algorithm, and all parts of RadioGatún (the input map, the mixing of RadioGatún after the input ends, and the generation of pseudo-random output bits) use the same beltmill function.
The RadioGatún spec considers the mill three arrays of 13 elements each; we will, here, consider the mill a single 40-word array. In addition, the ordering of operations in this book are different than as described in the spec.
This operation acts like a blender, blending the bits of RadioGatún state in a manner which is both predictable and believed to be cryptographically secure.
Belt to mill feedforward
[edit | edit source]In the belt to mill feedforward, we exclusive or 12 words in the mill with 12 words in to the belt, as follows:
- The first word (element 0 in programming languages with zero-indexed arrays) of the mill is exclusive ored with the second word (element 1) of the mill; the resulting word is stored as the element 0 in the belt
- Element 14 of the belt is exclusive ored with element 2 of the mill
- Element 28 of the belt is exclusive ored with element 3 of the mill
- Element 3 of the belt is exclusive ored with element 4 of the mill
- Element 17 of the belt is exclusive ored with element 5 of the mill
- Element 31 of the belt is exclusive ored with element 6 of the mill
- Element 6 of the belt is exclusive ored with element 7 of the mill
- Element 20 of the belt is exclusive ored with element 8 of the mill
- Element 34 of the belt is exclusive ored with element 9 of the mill
- Element 9 of the belt is exclusive ored with element 10 of the mill
- Element 23 of the belt is exclusive ored with element 11 of the mill
- Element 37 of the belt is exclusive ored with element 12 of the mill
This can be viewed as followed in pseudo-code:
For a = 0 to 11 { # "a" has the values (0,1,2,3,4,5,6,7,8,9,10,11) in this loop
belt[a + ((a % 3) * 13)] = belt[a + ((a % 3) * 13)] ^ mill[a + 1]
}
Here, % is the modulo operation: The remainder after division (For example: 5 modulo 3 is 2; 11 modulo 4 is 3)
^ is the exclusive or operation
* is multiplication
+ is addition
The main mill operation
[edit | edit source]In the main mill operation, we perform a number of operations on the words in the mill, putting the results in a temporary array "t" of 19 words.
We set the rotate constant, "r", to 0
We do the following 19 times, for values of "a" between 0 and 18 inclusive:
- We add "a" to "r"
- We modulo "r" by the word size for the RadioGatún variant in use (For RadioGatún[32], the 19 rotate values are [0, 1, 3, 6, 10, 15, 21, 28, 4, 13, 23, 2, 14, 27, 9, 24, 8, 25, 11]; for RadioGatún[64], [0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 2, 14, 27, 41, 56, 8, 25, 43])
- We set an index, "i", to "a" multiplied by seven
- We module "i" by 19, the mill width (the 19 "i" values are [0, 7, 14, 2, 9, 16, 4, 11, 18, 6, 13, 1, 8, 15, 3, 10, 17, 5, 12])
- We set "k" to be the mill index "i"
- We set index "ia" to be one added to "i", modulo 19. "Modulo 19" here means that, if "i" has the value 18, instead of giving "ia" the value 19, we give it the value 0 instead.
- We set index "ib" to be two added to "i", modulo 19. "Modulo 19" here means that, if i + 2 is 19 or higher, we subtract 19 from "i": If "i" is 17, "ib" will be 0 (instead of 19); if "i" is 18, "ib" will be 1 (instead of 20).
- We copy the mill element "ib" in to "mb"
- We perform bitwise negation on "mb" (we make every 0 bit 1, and every 1 bit 0)
- We copy the mill element "ia" in to "ma"
- We perform a bitwise or on "ma" and "mb", putting the result in "mc"
- We exclusive or "mc" with the mill element "i", and put the result in the element of the temporary array "t" indexed by "a"
- We take the element in the temporary array "t" with index "a", and rotate it right by "r" bits
This might look like this is pseudo-code:
r = 0
for a = 0 to 18 {
r = r + a
r = r % wordsize # 32 for 32-bit RadioGatún, 64 for 64-bit RadioGatún
i = a * 7
i = i % 19 # Mill width
k = mill[i]
k = k ^ (mill[(i + 1) % 19] | (~mill[(i + 2) % 19]))
t[a] = rotate_right(k, r)
}
The operators are the same as above; in addition, ~ is bitwise negation
rotate_right is a circular rotate right. For example, for 32-bit RadioGatún, rotate_right might look like this is C:
uint32_t rotate_right(uint32_t k, int r) {
return k>>r|k<<((32-r)%32);
}
Updating the mill
[edit | edit source]Now that we have performed some operations on the elements in the mill and put them in a 19-word temporary array "t", we can now update the actual mill based on the values we have in "t".
For each value of "a" between 0 and 18 inclusive:
- "i1" will be "a" incremented by one (a + 1), modulo 19
- "i2" will be "a" incremented by four (a + 4), modulo 19
- Set the mill element "a" to the value of element "a" in the "t" array
- Exclusive or mill element "a" with the value of element "i1" in the "t" array
- Exclusive or mill element "a" with the value of element "i2" in the "t" array
In pseudo-code:
for a = 0 to 18 {
mill[a] = t[a] ^ t[(a + 1) % 19] ^ t[(a + 4) % 19]
}
Rotating the belt
[edit | edit source]We now rotate the belt. In the RadioGatún specification, this is described as taking each of the three rows of the belt, and moving the values one to the right. All of the words move right one, like a conveyor belt, except the word on the right is moved to the left. The belt has three rows of 13 elements each; we do this rotate separately on the three rows.
To make the code simpler and smaller, we can look at the belt as an array of 40 (not 39) elements, then move all of the elements over by one. After doing that, we then take three values and move then down the belt, to make the belt circular.
For "i" between 38 and 0 (inclusive; note that we're starting at 38 then going down to 0):
- Increment "i" by one and give it the value "i1" (so 38 becomes 39, 37 becomes 38, and so on)
- Assign the belt element with the index "i1" the value of the belt element with the index "i"
The reason why we go down from 38 to 0 instead of up from 0 to 39 is because, if we incremented instead of decremented "i", all of the elements in the mill would have the same value (mill element 0), destroying the mill.
Once we shift all of the elements in the mill up by one, we now move three of the elements down again.
For "i" between 0 and 2 (inclusive):
- "i0" is "i" multiplied by 13 (the belt width)
- "i1" is "i0" with 13 added to it
- Take the belt element "i0" and assign the value of the belt element "i1" to it
This second loop makes the belt three 13-element circular belts
The above two steps can be done with the following pseudo-code:
for a = 38 to 0 step -1 { # "step -1" makes it clear we're moving down from 38 instead of up from 0
belt[a + 1] = belt[a]
}
for a = 0 to 2 {
belt[(a + 1) * 13] = belt[a * 13]
}
Note that speed optimized implementations of RadioGatún, such as the ones written by Thomas Pornin in sphlib, do not rotate the belt; instead they run 13 different versions of the beltmill function, changing which elements to interact with instead of moving 39 elements around.
The iota step
[edit | edit source]The iota step simply takes the first word in the mill (element 0), and exclusive ors it by the number 1.
In pseudocode:
mill[0] = mill[0] ^ 1
Note that, in Keccak, the iota step is significantly more complex.
Belt to mill
[edit | edit source]To finish off the beltmill function, we exclusive or three words in the mill against three words in the belt, storing the result in the mill words:
- Mill element 13 (the 14th element in the mill) is exclusive ored against Belt element 0 (the first word in the lowest row of the mill), storing the result in mill element 13
- Mill element 14 (15th element in the mill) is exclusive ored against Belt element 13 (the first word in the middle row of the mill), storing the result in mill element 14
- Mill element 15 (16th element in the mill) is exclusive ored against Belt element 26 (the first word in the top row of the mill), storing the result in mill element 15
In pseudo-code:
mill[13] = mill[13] ^ belt[0] mill[14] = mill[14] ^ belt[13] mill[15] = mill[15] ^ belt[26]
Note that code sized optimized versions of RadioGatún will put this in a 3-step loop, since we can do both the second part of the belt rotation and the belt-to-mill operation in one small loop, but speed-optimized versions will unroll the loop (convert actions performed in a loop in to multiple actions performed outside of a loop, to save the CPU cycles needed to process the loop).
Input mapping
[edit | edit source]The input mapping step is where we take a binary string of arbitrary octet length, and use it to establish RadioGatún's state.
A simplified input map
[edit | edit source]We will first look at RadioGatún[32] (32-bit RadioGatún) in the case where the hash input is precisely 32 bits in length.
First we initialize RadioGatún: We set all words in the belt and mill to have a value of 0. After doing that, we do the following (all of these steps are actually exclusive ors, but since we are exclusive oring against the value 0, it is equivalent to setting them to the desired values):
- We set the first element of the belt (belt element 0) to have our 32-bit hash input.
- We set the 17th byte of the mill (mill element 16) to be the same 32-bit hash input.
- We have the 14th byte of the belt (belt element 13, or, if you will, the first word in the belt's second row) be a binary 1.
- We set the 18th byte of the mill (mill element 17) to also have the value 1.
Voila! We have now put a 32-bit hash input (or, if you will, "seed") in to RadioGatún.
Pseudocode:
function initRadioGatun32(int32bit a) {
for b = 0 to 18 {
mill[b] = 0
}
for b = 1 to 39 {
belt[b] = 0
}
mill[16] = a
belt[0] = a
mill[17] = 1
belt[13] = 1
}
Once we have put this 32-bit value in to the RadioGatún state (the belt and mill), we can now perform the "blank rounds" step.
Blank rounds
[edit | edit source]After the input string is ended, RadioGatún runs 18 blank rounds: 18 iterations of the Beltmill() function.
In pseudocode:
for a = 1 to 18 {
Beltmill() # As already described above
}
Once the blank rounds are performed, jump to the "Generating Output" section which follows.
What about other hash sizes?
[edit | edit source]RadioGatún does not support only 32-bit inputs; it supports an input of any number of bytes, from 0 and up. We will now describe how to process inputs of other lengths.
Little endian
[edit | edit source]RadioGatún assumes to run on a little-endian processor (or, should we say, the reference implementation used to generate the reference test vectors was run on a little-endian machine). This in mind, eight-bit bytes are converted in to 32-bit or 64-bit words (depending on whether we're using the 32-bit or 64-bit variant) with the first bytes made to be the least significant bits.
In other words, if RadioGatún is given the string '124', which consists of the bytes (in hexadecimal) 0x31, 0x32, and 0x34, this will be converted by RadioGatún[32] (the 32-bit version) in to 0x01343231, and in to 0x0000000001343231 with the 64-bit version of RadioGatún.
Here, the first byte given to RadioGatún is made in to the lowest (least significant) eight bytes of the word used by RadioGatún.
Speed optimized versions of RadioGatún which know they are being run on little endian machines can simply read the words from memory to prepare them to affect the state.
Input padding
[edit | edit source]One may also observe that the byte 0x01 is placed after the end of the string above; this is a padding byte used to let RadioGatún know where the string has ended. This padding byte protects RadioGatún from some security attacks. So, if our string is the three byte string '124', or 0x31 0x32 0x34, this becomes 0x31 0x32 0x34 0x01, which is then converted in to a little endian number like 0x01343231. If a one-byte string with the value 0x01 is given to RadioGatún, this is converted in to 0x01 0x01 before the little endian conversion is done.
RadioGatún can read in any arbitrary binary string, including strings with 0x00 (NULL), 0x01, etc., as long as the string's length is a multiple of 8 (0 bits long, 8 bits long, 16 bits long, 24 bits long, etc.); the reason why RadioGatún does not support other input lengths is because its padding behavior is not fully defined, and there are no official test vectors which are not a multiple of eight bits long.
Putting the input in to RadioGatún
[edit | edit source]Once the input string is converted in to little endian words, we take three words and exclusive or them against the RadioGatún state, as follows:
- We take these three words and give them the names "w1", "w2", and "w3". For example, if RadioGatún[32] was given the string '12345678901' as an input, "w1" will have the value 0x34333231, "w2" will be 0x38373635, and "w3" will be 0x01313039. Should the string be shorter, such as '1' (0x31), we will zero pad things: "w1" will be 0x00000131, and both "w2" and "w3" will simply be 0x00000000; if using RadioGatún[64] and just ASCII '1' as a string, "w1" will be 0x0000000000000131, and both "w2" and "w3" will be 0x0000000000000000.
- We exclusive or the first byte of the belt (belt element 0) against "w1", placing the result back in belt[0]
- We exclusive or the 17th byte of the mill (mill element 16) against "w1", placing the result back in mill[16]
- We exclusive or the 14th byte of the belt (belt element 13, or, if you will, the first byte in the belt's second row) against "w2", placing the result back in belt[13]
- We exclusive or the 18th byte of the mill (mill element 17) against "w2", placing the result back in mill[17]
- We exclusive or the 27th byte of the belt (belt element 26, or, if you will, the first byte in the belt's top row) against "w3", placing the result back in belt[26]
- We exclusive or the 19th byte of the mill (mill element 18) against "w3", placing the result back in mill[18]
- We now run the Beltmill function against RadioGatún's state
Should the string, including the final 0x01 padding byte, be used up, we move on to the next section. Otherwise, we move forward in the string either 12 or 24 bytes (depending on whether we are calculating RadioGatún[32] or RadioGatún[64]) and repeat the above steps.
In this pseudocode example, we read in the input byte-by-byte to make the code endian-neutral (it runs the same way on both big-endian and little-endian machines). RadioGatunWordSize indicates the word size for the variant of RadioGatún we are implementing, and can be 32 or 64; Beltmill() is the beltmill function described previously:
endOfString = False
array inputWords[3]
# Initialize the input words
for i = 0 to 2 {
inputWords[i] = 0
}
i = 0
shift = 0
while(endOfString is False) {
a = getByteFromString()
if(isEndOfString()) {
a = 1
endOfString = True
}
a = shiftLeft(a, shift)
inputWords[i] = inputWords[i] | a # Here, '|' is bitwise "or"
shift = shift + 8
if(shift >= RadioGatunWordSize or endOfString is True) {
belt[i + 16] = belt[i + 16] ^ inputWords[i]
mill[i * 13] = mill[i * 13] ^ inputWords[i]
i = i + 1
shift = 0
if(i >= 3 and endOfString is not True) {
Beltmill()
i = 0
}
}
}
getByteFromString() is a function which gets a single octet (8-bit byte) from our input string. isEndOfString() returns true if the last call to getByteFromString() failed because we have reached the end of the input string.
Once this is done, perform the 18 blank rounds, as described above, then go to the "generating output" section which follows to generate RadioGatún's hash output.
Security properties
[edit | edit source]Since RadioGatún was designed to be a secure hash function, it is not computationally feasible to find two different inputs that establish the same internal state. In addition, it should not be possible to distinguish RadioGatún's output from actual random bits—it will appear to be noise. It should also not be possible to predict what pseudo-random bits will come next when shown RadioGatún's output unless the input is known, even if the attacker knows they are looking at RadioGatún generated bits.
Generating output
[edit | edit source]Once we have run the blank rounds, we can now outputs words in the mill of RadioGatun() to generate as many cryptographically secure random numbers as desired.
The process is simple:
- We look at the second element in the mill (mill element number 1) to get the first 32 or 64 bits of random output, depending on whether we chose to implement RadioGatún[32] or RadioGatún[64]
- We look at the third element in the mill (mill element number 2) to get another 32/64 bits of output
- We run the Beltmill operation, as already described previously
- We repeat the above three steps to get as many output bits as desired
Here is some pseudocode showing this:
phase = 1 # The word we get from the mill; initial value is one
function getWordFromRadioGatun() {
out = mill[phase]
phase = phase + 1
if(phase > 2) {
phase = 1
Beltmill()
}
return out
}
getWordFromRadioGatun() gives us 32 bits if using the 32-bit version of RadioGatun, and 64 bits if using the 64-bit version.
Note that, for reference test vector compatibility, the numbers need to be endian swapped (or, equivalently, the mill needs to be seen as an array of bytes on a small-endian system).
Example
[edit | edit source]In this example, we process the string '1234' with RadioGatún[32]. As per the reference specification:
RadioGatun[32]("1234") = 9EBDD24F469993796C4AAC6A821735A65A3CDEF8A359944CE71F34E7A08E1182
Initial belt and mill state after running input map
[edit | edit source]This in mind, after running and finishing the input map, the belt and mill is as follows:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0x00000000 0x34333231 0x00000001 0x00000000 1 0x00000000 0x00000000 0x00000000 0x00000000 2 0x00000000 0x00000000 0x00000000 0x00000000 3 0x00000000 0x00000000 0x00000000 0x00000000 4 0x00000000 0x00000000 0x00000000 0x00000000 5 0x00000000 0x00000000 0x00000000 0x00000000 6 0x00000000 0x00000000 0x00000000 0x00000000 7 0x00000000 0x00000000 0x00000000 0x00000000 8 0x00000000 0x00000000 0x00000000 0x00000000 9 0x00000000 0x00000000 0x00000000 0x00000000 10 0x00000000 0x00000000 0x00000000 0x00000000 11 0x00000000 0x00000000 0x00000000 0x00000000 12 0x00000000 0x00000000 0x00000000 0x00000000 13 0x00000000 14 0x00000000 15 0x00000000 16 0x34333231 17 0x00000001 18 0x00000000
In this chart, the left hand number is the array index for the element in question. Instead of treating the belt like a single array of 39 (or 40) words, we treat the belt like three rows of 13 words. If using code that treats the belt as a single array, belt row 1 consists of elements 0-12 in the belt, row 2 has elements 13-25, and row 3 has elements 26-38.
First run of Beltmill()
[edit | edit source]After we perform the belt rotation, the belt and mill look like this (observe how the elements moved from row 0 to row 1 in the belt):
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0x00000000 0x00000000 0x00000000 0x00000000 1 0x00000000 0x34333231 0x00000001 0x00000000 2 0x00000000 0x00000000 0x00000000 0x00000000 3 0x00000000 0x00000000 0x00000000 0x00000000 4 0x00000000 0x00000000 0x00000000 0x00000000 5 0x00000000 0x00000000 0x00000000 0x00000000 6 0x00000000 0x00000000 0x00000000 0x00000000 7 0x00000000 0x00000000 0x00000000 0x00000000 8 0x00000000 0x00000000 0x00000000 0x00000000 9 0x00000000 0x00000000 0x00000000 0x00000000 10 0x00000000 0x00000000 0x00000000 0x00000000 11 0x00000000 0x00000000 0x00000000 0x00000000 12 0x00000000 0x00000000 0x00000000 0x00000000 13 0x00000000 14 0x00000000 15 0x00000000 16 0x34333231 17 0x00000001 18 0x00000000
The main mill operation sets the 19 elements in the temporary ("t") array as follows:
0 0xffffffff 1 0xffffffff 2 0xd97999b9 3 0xffffffff 4 0xffffffff 5 0x9b9d9799 6 0xffffffff 7 0xffffffff 8 0xffffffff 9 0xffffffff 10 0xffffffff 11 0xffffffff 12 0xffffffff 13 0xffffffff 14 0xffffffff 15 0xffffffff 16 0xfeffffff 17 0xffffffff 18 0xffffffff
After we use those values to update the mill, the mill and belt will look like this:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xffffffff 0x00000000 0x00000000 0x00000000 1 0xbd1bf1df 0x34333231 0x00000001 0x00000000 2 0xd97999b9 0x00000000 0x00000000 0x00000000 3 0xffffffff 0x00000000 0x00000000 0x00000000 4 0x9b9d9799 0x00000000 0x00000000 0x00000000 5 0x9b9d9799 0x00000000 0x00000000 0x00000000 6 0xffffffff 0x00000000 0x00000000 0x00000000 7 0xffffffff 0x00000000 0x00000000 0x00000000 8 0xffffffff 0x00000000 0x00000000 0x00000000 9 0xffffffff 0x00000000 0x00000000 0x00000000 10 0xffffffff 0x00000000 0x00000000 0x00000000 11 0xffffffff 0x00000000 0x00000000 0x00000000 12 0xfeffffff 0x00000000 0x00000000 0x00000000 13 0xffffffff 14 0xffffffff 15 0xfeffffff 16 0xfeffffff 17 0xd97999b9 18 0xffffffff
The iota step only affects the first element of the mill (making it 0xfffffffe here):
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xfffffffe 0x00000000 0x00000000 0x00000000 1 0xbd1bf1df 0x34333231 0x00000001 0x00000000 2 0xd97999b9 0x00000000 0x00000000 0x00000000 3 0xffffffff 0x00000000 0x00000000 0x00000000 4 0x9b9d9799 0x00000000 0x00000000 0x00000000 5 0x9b9d9799 0x00000000 0x00000000 0x00000000 6 0xffffffff 0x00000000 0x00000000 0x00000000 7 0xffffffff 0x00000000 0x00000000 0x00000000 8 0xffffffff 0x00000000 0x00000000 0x00000000 9 0xffffffff 0x00000000 0x00000000 0x00000000 10 0xffffffff 0x00000000 0x00000000 0x00000000 11 0xffffffff 0x00000000 0x00000000 0x00000000 12 0xfeffffff 0x00000000 0x00000000 0x00000000 13 0xffffffff 14 0xffffffff 15 0xfeffffff 16 0xfeffffff 17 0xd97999b9 18 0xffffffff
The second Beltmill() call
[edit | edit source]And the above is how the state looks after running the Beltmill operation once. Here is how it looks after running Beltmill() on it again:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0x40600820 0x00000000 0x00000000 0x00000000 1 0xcc8c4f0c 0xbd1bf1df 0x00000000 0x00000000 2 0x189a1999 0x34333231 0xd97999b8 0x00000000 3 0x089a1999 0x00000000 0x00000000 0xffffffff 4 0xdc8c4f0c 0x9b9d9799 0x00000000 0x00000000 5 0xcc8c4f0c 0x00000000 0x9b9d9799 0x00000000 6 0x10000000 0x00000000 0x00000000 0xffffffff 7 0x99189a19 0xffffffff 0x00000000 0x00000000 8 0x10000000 0x00000000 0xffffffff 0x00000000 9 0x00000000 0x00000000 0x00000000 0xffffffff 10 0x99189a19 0xffffffff 0x00000000 0x00000000 11 0x99189a19 0x00000000 0xffffffff 0x00000000 12 0x46268666 0x00000000 0x00000000 0xfeffffff 13 0x31343332 14 0x00002000 15 0x06468e47 16 0x7712b554 17 0x31341332 18 0x58fa31b8
Beltmill() after 18 calls
[edit | edit source]After running it 16 more times (for a total of 18 Beltmill() calls), it looks like this:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xd9958271 0x4fa9a4eb 0x3a5bda1c 0x599e1cba 1 0x4fd2bd9e 0xf40378f6 0xa5fff169 0xce6dad5a 2 0x79939946 0x7d0e377e 0x72637aad 0x83531eac 3 0xd9acd8da 0xbe8a2a76 0xc9958a5e 0x6a9d5b52 4 0x4a9b1478 0x44a12573 0xc4d346a6 0x0691e902 5 0xdefb4010 0xcfd07457 0x36adb7a1 0x112926ab 6 0x839db45d 0x08bc2beb 0x4cf52045 0x37060596 7 0x9bf58054 0x33bb3e40 0x978cf3fc 0x6452478c 8 0x734beab8 0x7873cf2d 0xbfaa6388 0x8840c4ae 9 0xa4c4d0dd 0x526856e9 0x1e33dbc2 0x80f95c1b 10 0x3fa1dc95 0x9829c411 0x4cd43100 0xfb9eb71a 11 0x0da8e828 0x1891da52 0x4f264567 0xccd49043 12 0x25fd61e7 0x031a49c7 0x5866b7ab 0x7f443d0c 13 0xd247ea91 14 0xb1e8b921 15 0x23154075 16 0x5ad6fbc4 17 0xbbc617dc 18 0x6eb76abb
Generating output bits
[edit | edit source]At this point, we use mill index 1 (0x4fd2bd9e) to generate the first 32 bits of output:
9ebdd24f
Observe that there has been an endian swap: The first byte is now the fourth byte, the second byte is now the third byte, the third byte is now the second byte, and the last byte is now the first byte.
The next 32 bits of the hash come from mill index 2 (0x79939946):
46999379
Now that we have extracted the values of two elements on the mill to generate some random numbers, we run the Beltmill() operation again. We will look at this in some more detail.
Another detailed look at a Beltmill() call
[edit | edit source]First, we run the belt-to-mill feed-forward, resulting in:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xd9958271 0x007b1975 0x3a5bda1c 0x599e1cba 1 0x4fd2bd9e 0xf40378f6 0xdc6c682f 0xce6dad5a 2 0x79939946 0x7d0e377e 0x72637aad 0x5affc676 3 0xd9acd8da 0xf4113e0e 0xc9958a5e 0x6a9d5b52 4 0x4a9b1478 0x44a12573 0x1a2806b6 0x0691e902 5 0xdefb4010 0xcfd07457 0x36adb7a1 0x92b492f6 6 0x839db45d 0x9349abbf 0x4cf52045 0x37060596 7 0x9bf58054 0x33bb3e40 0xe4c71944 0x6452478c 8 0x734beab8 0x7873cf2d 0xbfaa6388 0x2c841473 9 0xa4c4d0dd 0x6dc98a7c 0x1e33dbc2 0x80f95c1b 10 0x3fa1dc95 0x9829c411 0x417cd928 0xfb9eb71a 11 0x0da8e828 0x1891da52 0x4f264567 0xe929f1a4 12 0x25fd61e7 0x031a49c7 0x5866b7ab 0x7f443d0c 13 0xd247ea91 14 0xb1e8b921 15 0x23154075 16 0x5ad6fbc4 17 0xbbc617dc 18 0x6eb76abb
We next rotate the belt:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xd9958271 0x031a49c7 0x5866b7ab 0x7f443d0c 1 0x4fd2bd9e 0x007b1975 0x3a5bda1c 0x599e1cba 2 0x79939946 0xf40378f6 0xdc6c682f 0xce6dad5a 3 0xd9acd8da 0x7d0e377e 0x72637aad 0x5affc676 4 0x4a9b1478 0xf4113e0e 0xc9958a5e 0x6a9d5b52 5 0xdefb4010 0x44a12573 0x1a2806b6 0x0691e902 6 0x839db45d 0xcfd07457 0x36adb7a1 0x92b492f6 7 0x9bf58054 0x9349abbf 0x4cf52045 0x37060596 8 0x734beab8 0x33bb3e40 0xe4c71944 0x6452478c 9 0xa4c4d0dd 0x7873cf2d 0xbfaa6388 0x2c841473 10 0x3fa1dc95 0x6dc98a7c 0x1e33dbc2 0x80f95c1b 11 0x0da8e828 0x9829c411 0x417cd928 0xfb9eb71a 12 0x25fd61e7 0x1891da52 0x4f264567 0xe929f1a4 13 0xd247ea91 14 0xb1e8b921 15 0x23154075 16 0x5ad6fbc4 17 0xbbc617dc 18 0x6eb76abb
Here is how the temporary array "t" looks after we do the main mill operation:
0 0x166b7dce 1 0x704737f7 2 0xc2dabfab 3 0x6611fd8a 4 0xc296ccc3 5 0xd831c230 6 0x02fe55a3 7 0x0559dc72 8 0xa970aa8c 9 0x0850e341 10 0x5aaa745f 11 0x4c0040be 12 0x651e5e54 13 0xbd57724f 14 0x92d919b3 15 0x0b22ade0 16 0x63d53968 17 0xb25ff79c 18 0xe71f7551
Now we use those values to update the mill:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xa4ba86fa 0x031a49c7 0x5866b7ab 0x7f443d0c 1 0x6aac4a6c 0x007b1975 0x3a5bda1c 0x599e1cba 2 0xa6351782 0xf40378f6 0xdc6c682f 0xce6dad5a 3 0xa1deed3b 0x7d0e377e 0x72637aad 0x5affc676 4 0xb3d7a47f 0xf4113e0e 0xc9958a5e 0x6a9d5b52 5 0xd29f74d2 0x44a12573 0x1a2806b6 0x0691e902 6 0x5d0dfd8e 0xcfd07457 0x36adb7a1 0x92b492f6 7 0xe0293640 0x9349abbf 0x4cf52045 0x37060596 8 0xc43e1799 0x33bb3e40 0xe4c71944 0x6452478c 9 0xefade551 0x7873cf2d 0xbfaa6388 0x2c841473 10 0x84732d52 0x6dc98a7c 0x1e33dbc2 0x80f95c1b 11 0x223cb30a 0x9829c411 0x417cd928 0xfb9eb71a 12 0xbb9c1573 0x1891da52 0x4f264567 0xe929f1a4 13 0x9dd19c60 14 0x7ee4c102 15 0x7e9ce946 16 0xa1cdf903 17 0x979a3d66 18 0x9765f515
The iota step only affects word 0 of the mill:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xa4ba86fb 0x031a49c7 0x5866b7ab 0x7f443d0c 1 0x6aac4a6c 0x007b1975 0x3a5bda1c 0x599e1cba 2 0xa6351782 0xf40378f6 0xdc6c682f 0xce6dad5a 3 0xa1deed3b 0x7d0e377e 0x72637aad 0x5affc676 4 0xb3d7a47f 0xf4113e0e 0xc9958a5e 0x6a9d5b52 5 0xd29f74d2 0x44a12573 0x1a2806b6 0x0691e902 6 0x5d0dfd8e 0xcfd07457 0x36adb7a1 0x92b492f6 7 0xe0293640 0x9349abbf 0x4cf52045 0x37060596 8 0xc43e1799 0x33bb3e40 0xe4c71944 0x6452478c 9 0xefade551 0x7873cf2d 0xbfaa6388 0x2c841473 10 0x84732d52 0x6dc98a7c 0x1e33dbc2 0x80f95c1b 11 0x223cb30a 0x9829c411 0x417cd928 0xfb9eb71a 12 0xbb9c1573 0x1891da52 0x4f264567 0xe929f1a4 13 0x9dd19c60 14 0x7ee4c102 15 0x7e9ce946 16 0xa1cdf903 17 0x979a3d66 18 0x9765f515
The belt to mill operation affects elements 13 to 15 in the mill:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0xa4ba86fb 0x031a49c7 0x5866b7ab 0x7f443d0c 1 0x6aac4a6c 0x007b1975 0x3a5bda1c 0x599e1cba 2 0xa6351782 0xf40378f6 0xdc6c682f 0xce6dad5a 3 0xa1deed3b 0x7d0e377e 0x72637aad 0x5affc676 4 0xb3d7a47f 0xf4113e0e 0xc9958a5e 0x6a9d5b52 5 0xd29f74d2 0x44a12573 0x1a2806b6 0x0691e902 6 0x5d0dfd8e 0xcfd07457 0x36adb7a1 0x92b492f6 7 0xe0293640 0x9349abbf 0x4cf52045 0x37060596 8 0xc43e1799 0x33bb3e40 0xe4c71944 0x6452478c 9 0xefade551 0x7873cf2d 0xbfaa6388 0x2c841473 10 0x84732d52 0x6dc98a7c 0x1e33dbc2 0x80f95c1b 11 0x223cb30a 0x9829c411 0x417cd928 0xfb9eb71a 12 0xbb9c1573 0x1891da52 0x4f264567 0xe929f1a4 13 0x9ecbd5a7 14 0x268276a9 15 0x01d8d44a 16 0xa1cdf903 17 0x979a3d66 18 0x9765f515
At this point, we take words 1 and 2 from the mill to generate 64 more bits of hash output:
6c4aac6a821735a6
Running Beltmill() again to generate more random bits
[edit | edit source]We then run Beltmill() again, resulting in:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0x6cf36fda 0x1891da52 0x4f264567 0xe929f1a4 1 0xf8de3c5a 0x69b603ab 0x5866b7ab 0x7f443d0c 2 0x4c9459a3 0x007b1975 0x9c6ecd9e 0x599e1cba 3 0x54ab7f1f 0xf40378f6 0xdc6c682f 0x6fb34061 4 0x467fcf23 0xced99301 0x72637aad 0x5affc676 5 0xd40be986 0xf4113e0e 0x1b0afe8c 0x6a9d5b52 6 0x07c891d4 0x44a12573 0x1a2806b6 0x5b9c148c 7 0xdf077459 0x2ff94217 0x36adb7a1 0x92b492f6 8 0x7cfc3d41 0x9349abbf 0x88cb37dc 0x37060596 9 0xc0b4f9dd 0x33bb3e40 0xe4c71944 0x8bffa2dd 10 0x5e7d770b 0xfc00e27f 0xbfaa6388 0x2c841473 11 0x286065c7 0x6dc98a7c 0x3c0f68c8 0x80f95c1b 12 0xf47debb2 0x9829c411 0x417cd928 0x4002a269 13 0x9c7f8208 14 0x7173015d 15 0x49e3be00 16 0x4927ddf9 17 0x5fe72eb5 18 0x2af7cf5f
Giving us these 64 bits of hash output:
5a3cdef8a359944c
To generate the final 64 bits of the desired 256-bit hash, we run Beltmill() one final time:
Mill Belt Row 1 Belt Row 2 Belt Row 3 0 0x7ef726d9 0x9829c411 0x417cd928 0x4002a269 1 0xe7341fe7 0xe04fe608 0x4f264567 0xe929f1a4 2 0x82118ea0 0x69b603ab 0x14f2ee08 0x7f443d0c 3 0xb29a8d55 0x007b1975 0x9c6ecd9e 0x0d3563a5 4 0x7b4ebd5a 0xb27cb7d5 0xdc6c682f 0x6fb34061 5 0xfec38e38 0xced99301 0xa668932b 0x5affc676 6 0xf95a2809 0xf4113e0e 0x1b0afe8c 0x6d55ca86 7 0xb84b5869 0x9ba6512a 0x1a2806b6 0x5b9c148c 8 0x2ffcf15a 0x2ff94217 0x4a518ae0 0x92b492f6 9 0x235557d9 0x9349abbf 0x88cb37dc 0xf7b2fc4b 10 0x7658fde8 0x6dc6494b 0xe4c71944 0x8bffa2dd 11 0xc8320830 0xfc00e27f 0x97ca064f 0x2c841473 12 0xc39a12ae 0x6dc98a7c 0x3c0f68c8 0x7484b7a9 13 0x4801294c 14 0x4f6ee74f 15 0x82e8af69 16 0x63210515 17 0x2b657fd0 18 0xc6c57d5f
And finish off our hash as follows:
e71f34e7a08e1182
We can, if more pseudo-random numbers are desired, run Beltmill() as many times as we want to generate more numbers.
Tiger
Tiger hash
[edit | edit source]The Tiger hash processes data in 512-bit blocks and produces a 192-bit message digest. This hash was designed by Ross Anderson and Eli Biham (see http://www.cs.technion.ac.il/~biham/Reports/Tiger/), with the goal of producing a secure, fast hash function that performs especially well on next-generation 64-bit architectures, being still efficient on 32 and 16-bit architectures.
Tiger tree hash
[edit | edit source]Tiger Tree cryptographic hash is calculated by applying the Tiger hash to 1024-byte blocks of a stream, then combining the interim values through a binary hash tree.
This implementation method is specially useful as a secure way to validate transfers, especially blocks of a file and prevent corruption in distributed systems.
Protocols
The ideas used in cryptography have been used to create a large number of protocols.
The original application of these ideas was secret hiding -- Alice wanted to send a message to Bob, but Alice and Bob didn't want anyone else to know exactly what the message said.
More recently, many "cryptographic protocols" have been developed that do useful things *other* than secret hiding.
Some cryptographic protocols make secret hiding better or more convenient in some way --
- key-agreement protocols such as Diffie-Hellman key exchange
- Message authentication
(FIXME: say something here about commutative ciphers)
Other cryptographic protocols and cryptography-related ideas are used to improve on non-cryptographic systems:
- Early "everyone in favor, hold up their hands while I count" voting systems don't hide any secrets; end-to-end auditable voting systems (which internally use cryptographic ideas) are arguably better.
- mental poker
- convergent encryption
- digital signatures
- version identifiers in Mercurial and git.
- error-detection and error-correction codes.
- the rsync protocol
- verifiable computing
- various ideas for improving (non-secret) email to reduce the amount of spam, such as hashcash, Sender ID, DomainKeys Identified Mail (DKIM), etc.
In particular, the first fully homomorphic encryption was announced in 2009 by Craig Gentry. It is widely expected that homomorphic encryption will make it relatively easy to do things that were previously considered impossible or infeasible.
Diffie-Hellman
Diffie-Hellman, named for creators Whitfield Diffie and Martin Hellman, was the first (publicly known, at least) public key algorithm and was published in 1976. Its security relies on the discrete logarithm problem, which is still thought to be difficult.
Diffie-Hellman is generally used to generate a unique key by two (or more) parties with which they may then encrypt and exchange another key. This is similar to the use of the RSA algorithm within PGP.
Alice and Bob select a large prime number n, which will be the modulus. They then select another number c that is primitive mod n, which will be the base. These two numbers may be broadcast far and wide. At this point Bob and Alice both select large, random integers (a and b, respectively) in secret, and exchange the result of the exponentiation:
Alice performs and sends A to Bob in the clear.
Bob then performs and sends B to Alice in the clear.
At which point Alice knows a and B, so she computes:
while Bob, knowing A and b, computes:
and,
This is simply based on the commutative property of multiple exponents
.
An eavesdropper can get A and B, but cannot easily calculate the key.
Generate a keypair using OpenSSL
Download and install the OpenSSL runtimes. If you are running Windows, grab the Cygwin package.
OpenSSL can generate several kinds of public/private keypairs. RSA is the most common kind of keypair generation.[1]
Other popular ways of generating RSA public key / private key pairs include PuTTYgen and ssh-keygen.[2][3][4][5]
Generate an RSA keypair with a 2048 bit private key
[edit | edit source]Execute command: "openssl genpkey -algorithm RSA -out private_key.pem -pkeyopt rsa_keygen_bits:2048"[6] (previously “openssl genrsa -out private_key.pem 2048”)
e.g.
$ openssl genpkey -algorithm RSA -out private_key.pem -pkeyopt rsa_keygen_bits:2048 ....................................................................+++ ....................................................+++
Make sure to prevent other users from reading your key by executing chmod go-r private_key.pem afterward.
Extracting the public key from an RSA keypair
[edit | edit source]Execute command: "openssl rsa -pubout -in private_key.pem -out public_key.pem"
e.g.
$ openssl rsa -pubout -in private_key.pem -out public_key.pem writing RSA key
A new file is created, public_key.pem, with the public key.
It is relatively easy to do some cryptographic calculations to calculate the public key from the prime1 and prime2 values in the private key file. However, OpenSSL has already pre-calculated the public key and stored it in the private key file. So this command doesn't actually do any cryptographic calculation -- it merely copies the public key bytes out of the file and writes the Base64 PEM encoded version of those bytes into the output public key file.[7]
Viewing the key elements
[edit | edit source]Execute command: "openssl rsa -text -in private_key.pem"
All parts of private_key.pem are printed to the screen. This includes the modulus (also referred to as public key and n), public exponent (also referred to as e and exponent; default value is 0x010001), private exponent, and primes used to create keys (prime1, also called p, and prime2, also called q), a few other variables used to perform RSA operations faster, and the Base64 PEM encoded version of all that data.[8] (The Base64 PEM encoded version of all that data is identical to the private_key.pem file).
Password-less login
[edit | edit source]Often a person will set up an automated backup process that periodically backs up all the content on one "working" computer onto some other "backup" computer.
Because that person wants this process to run every night, even if no human is anywhere near either one of these computers, using a "password-protected" private key won't work -- that person wants the backup to proceed right away, not wait until some human walks by and types in the password to unlock the private key. Many of these people generate "a private key with no password".[9] Some of these people, instead, generate a private key with a password, and then somehow type in that password to "unlock" the private key every time the server reboots so that automated tools can make use of the password-protected keys.[10][3]
Further reading
[edit | edit source]- ↑ Key Generation
- ↑ Michael Stahnke. "Pro OpenSSH". p. 247.
- ↑ a b "SourceForge.net Documentation: SSH Key Overview"
- ↑ Internet Technologies/SSH § Creating SSH Keys
- ↑ "How to Set Up SSH Keys on Ubuntu 20.04".
- ↑ "genpkey(1) - Linux man page"
- ↑ "Public – Private key encryption using OpenSSL"
- ↑ "OpenSSL 1024 bit RSA Private Key Breakdown"
- ↑ "DreamHost: Personal Backup".
- ↑ Troy Johnson. "Using Rsync and SSH: Keys, Validating, and Automation".
- Internet_Technologies/SSH describes how to use "ssh-keygen" and "ssh-copy-id" on your local machine so you can quickly and securely ssh from your local machine to a remote host.
- "OpenSSL: Command Line Utilities: Create / Handle Public Key Certificates"
Expectations of Normal Users
DRAFT:
Cryptography affects us every day through a variety of subtle means. Cryptography protects our credit card number when it is sent over the phone lines, it protects your bank card pin from unauthorized access, and it keeps passwords safe from unauthorized access. As a society, we have become more dependent upon computers for our everyday lives. Right now, your health history, driving record, and financial information are probably computerized. The Internet is a fairly uncontrolled media, everything that is given access to the Internet is vulnerable to unauthorized access by hackers or other ne'er-do-wells, and therefore must be protected.
You are probably already familiar with one form of protection, a password. It is a secret phrase that only you and the trusted party know. To authenticate yourself to the trusted party (the site with your information in the case of a bank or a doctors office), you give the password. It would not be very secure to have a list of passwords written on a sheet of paper by the counter (or just laying around in plaintext on a computer) in order to authenticate every client. The solution comes in the form of a cryptographic hash, typically Argon2. The trusted party stores a hash of your password instead of the plaintext version. If someone were to steal the hashed version of your password (assuming the office in question used salting and a secure hash algorithm) it would be nearly useless to them. When you give your password, the office would compute the hash of it and compare that hash to the hash they have on record. Since one of the properties of a hash is that it does not collide (that is for any given input there is one unique output which is not equal to any other input. Of course there is no fixed length hash which can completely comply with that requirement over an infinite length input; most passwords are between 8 and 14 characters therefore for our purposes MD5 will suffice) if the two hashes are identical, then the ciphertexts were identical, so the user is authenticated. This process goes on almost every time you enter a password on a computer (Which is why most of the time you are given the option to reset your password not retrieve it because Argon2 is a one-way hash. There are two-way cryptographic "hashes,"[citation needed] but I will not discuss them here.).
Even though we know that collisions theoretically exist, cryptographic hashes -- even MD5 -- are designed to make it infeasible to actually find a value that would produce the same hash value as your password.[1]
Further reading
- Anderson, Ross — Security Engineering, Wiley, advanced coverage of computer security issues, including cryptography, by one of its foremost practitioners, and most likely its best writer. Covers much more than merely cryptography. Brief on most topics due to the breadth of coverage. Exceptionally clearly written.
- Bamford, James — The Puzzle Palace : A Report on America's Most Secret Agency ISBN 0140067485, and the more recent Body of Secrets. The best of a quite small group of books about the US Government's NSA. Most are inadequate, and untrustworthy, for various reasons, including an active reluctance to permit accurate information to be released in any form.
- Ferguson, Niels and Bruce Schneier — Practical Cryptography, Wiley, 2003, ISBN 0471223573. Up to date cryptography reference. Covers both algorithms and protocols. This is an in depth consideration of one cryptographic problem, including paths not taken and some reasons why. Most of the material is not otherwise available in a single source. Some is not otherwise available. In a sense, a follow-up to 'Applied Cryptography'.
- Kahn, David — The Codebreakers ISBN 0684831309 The best available single volume source for cryptographic history, at least for events up to the mid '60s (i.e., to just before DES and the public release of asymmetric key cryptography). The added chapter on more recent developments (in the most recent edition) is regrettably far too thin. See also his other publications on cryptography, and cryptographic history, which have been uniformly excellent.
- Katz, Jonathan and Yehuda Lindell - Introduction to Modern Cryptography, CRC Press, 2007. A textbook introduction to modern cryptography, aimed at undergraduate computer science/mathematics majors as well as the technically educated public.
- A. J. Menezes, P. C. van Oorschot and S. A. Vanstone — Handbook of Applied Cryptography ISBN 0849385237 (online version). Equivalent to Applied Cryptography in many ways, but seriously mathematical. For the technically inclined. Covers few meta-cryptographic topics, such as crypto system design.
- Paar, Christof and Pelz, Jan — Understanding Cryptography, A Textbook for Students and Practitioners Springer, 2009. Very accessible introduction to practical cryptography, focus on being a textbook, i.e., it has pedagocical approach, problem sets, further reading sections etc.
- Piper, Fred and Sean Murphy — Cryptography : A Very Short Introduction ISBN 0192803158 This book quickly sketches out the major goals, uses, methods, and developments in cryptography.
- Schneier, Bruce — Applied Cryptography, 2 ed, Wiley, ISBN 0471117099. The best single volume available covering modern cryptographic practice and possibilities. About as comprehensive as a single volume could have been. Well written, not overly mathematical, and so accessible — mostly — to the non-technical.
- Schneier, Bruce — Secrets and Lies, Wiley, ISBN 0471253111, a discussion of the context within which cryptography and cryptosystems work. Meta-cryptography, if you will. Required reading for would-be cryptographers, and nearly so for all cryptography users.
- Singh, Simon — The Code Book ISBN 1857028899. An anecdotal introduction to the history of cryptography, but much better than such an approach might be expected to produce. Covers more recent material than does Kahn's The Codebreakers. Well written. Sadly, the included cryptanalytic contest has been won and the prize awarded; the cyphers are still worth having a go at, however.
- Sweigart, Al — Hacking Secret Ciphers with Python ISBN 978-1482614374. A complete beginners guide to programming and classic cryptography ciphers. This free book presents several programs that attack various ciphers and explains how their source code works.
- University of Cambridge. NRICH. "Codes and cryptography". Some of these resources are suitable even for very young students of cryptography.
- Wikipedia: Wikipedia:WikiProject Cryptography, Wikipedia:WikiReader/Cryptography, Wikipedia Book:Cryptography
Open Source Cryptography
- The GNU Crypto project (http://www.gnu.org/software/gnu-crypto/), part of the GNU project, released under the aegis of GNU, aims at providing free, versatile, high-quality, and provably correct implementations of cryptographic primitives and tools in the Java programming language for use by programmers and end-users. Its license is similar to using the LGPL, except that static linking is permitted.
- Botan (http://botan.randombit.net/), a C++98 crypto library. It includes several cryptographic algorithms like AES, DES, SHA-1, RSA, DSA, Diffie-Hellman, and many others. It also supports X.509 certificates and CRLs, and PKCS #10 certificate requests, and has a high level filter/pipe message processing system. Easily portable to most systems and compilers, it is available under the BSD Revised license.
- Mhash ( http://mhash.sourceforge.net/ ) is an OpenSource (under GNU Lesser GPL) C library which provides a uniform interface to a large number of hash algorithms (SHA1, SHA160, SHA192, SHA224, SHA384, SHA512, HAVAL128, HAVAL160, HAVAL192, HAVAL224, HAVAL256, RIPEMD128, RIPEMD256, RIPEMD320, MD4, MD5, TIGER, TIGER128, TIGER160, ALDER32, CRC32, CRC32b, WHIRLPOOL, GOST, SNEFRU128, SNEFRU256), for Windows support you need to use cygwin to compile. A Python interface exists.
- NaCl (pronounced "salt") is the CACE Networking and Cryptography library, a public-domain library for Python, C, and C++, for public-key authenticated encryption and network communication.[9][10]
- Crypto++ ( http://www.cryptopp.com/ ), an open source C++ class library of cryptographic algorithms (AES, RSA, DSA, SHA-512, etc.) and implementations of complete cryptographic schemes (GCM, CCM, EAX, etc.). Each individual file is in the public domain.
- Bouncy Castle ( http://www.bouncycastle.org/ ) includes APIs for both the Java and the C# programming languages.
- w:OpenSSL ( http://www.openssl.org/ ) is written in the C programming language. Most other programming languages provide some way to call C functions.
Linear Cryptanalysis
Linear Cryptanalysis is using Linear mathematics (such as linear algebra) to break cryptosystems. This approach was strong against the now-obsolute cryptosystems based on Linear Shift Registers. Modern cryptosystems like AES and RSA use non-linear elements to prevent an attack based on linear cryptanalysis. In AES, the S-box provides non-linearity. In RSA, modular exponentiation provides non-linearity.
Differential Cryptanalysis
Differential Cryptanalysis is decrypting a cyphertext with two different potential keys and comparing the difference. Sometimes, this can provide insight into the nature of the cryptosystem. Modern cryptosystems like AES are designed to prevent these kinds of attacks.
Prime Curve/Affine Coordinates
Point Doubling (1I + 2M + 2S)
[edit | edit source]Let (x,y) be a point (unequal to the point at infinity) on the elliptic (prime) curve given by the equation y^2 = x^3 + ax + b. Then the point (x',y') := 2*(x,y) can be computed by
if (y == 0) return POINT_AT_INFINITY else l = (3*x^2 + a) / (2y) x' = l^2 - 2x y' = l(x - x') - y return (x', y')
Point Addition (1I + 2M + 1S)
[edit | edit source]Let (x1,y1) and (x2,y2) be two points (both unequal to the point at infinity). Then the point (x3,y3) := (x1,y1) + (x2,y2) can be computed by
if (x1 == x2)
if (y1 != y2)
return POINT_AT_INFINITY
else
return POINT_DOUBLE(x1, y1)
l = (y2 - y1) / (x2 - x1)
x3 = l^2 - x1 - x2
y3 = l(x1 - x3) - y1 = l(x2 - x3) - y2
return (x3, y3)
Point decompression
[edit | edit source]The following algorithm calculates for a given x a value y, such that (x,y) is a point on the elliptic curve.
t = x^3 + ax + b if (t|p) >= 0 return y = sqrt(t) (the result y = -sqrt(t) would be correct, too) else return POINT_NOT_EXPANDABLE
Notes:
- (t|p) denotes the Legendre symbol of t, which decides whether t is a square number or not.
- The square root can be calculated using the Algorithm of Shanks & Tonelli.
Prime Curve/Chudnovsky Coordinates
Introduction
[edit | edit source]Chudnovsky Coordinates are used to represent elliptic curve points on prime curves y^2 = x^3 + ax + b. They give a speed benefit over Affine Coordinates when the cost for field inversions is significantly higher than field multiplications. In Chudnovsky Coordinates the quintuple (X, Y, Z, Z^2, Z^3) represents the affine point (X / Z^2, Y / Z^3).
Point Doubling (5M + 6S or 5M + 4S)
[edit | edit source]Let (X, Y, Z, Z^2, Z^3) be a point (unequal to the point at infinity) represented in Chudnovsky Coordinates. Then its double (X', Y', Z', Z'^2, Z'^3) can be calculated by
if (Y == 0) return POINT_AT_INFINITY S = 4*X*Y^2 M = 3*X^2 + a*(Z^2)^2 X' = M^2 - 2*S Y' = M*(S - X') - 8*Y^4 Z' = 2*Y*Z Z'^2 = Z'^2 Z'^3 = Z'^2 * Z' return (X', Y', Z', Z'^2, Z'^3)
Note: if a = -3, then M can also be calculated as M = 3*(X + Z^2)*(X - Z^2), saving 2 field squarings.
Point Addition (11M + 3S)
[edit | edit source]Let (X1, Y1, Z1, Z1^2, Z1^3) and (X2, Y2, Z2, Z2^2, Z2^3) be two points (both unequal to the point at infinity) represented in Chudnovsky Coordinates. Then the sum (X3, Y3, Z3, Z3^2, Z3^3) can be calculated by
U1 = X1*Z2^2
U2 = X2*Z1^2
S1 = Y1*Z2^3
S2 = Y2*Z1^3
if (U1 == U2)
if (S1 != S2)
return POINT_AT_INFINITY
else
return POINT_DOUBLE(X1, Y1, Z1, Z1^2, Z1^3)
H = U2 - U1
R = S2 - S1
X3 = R^2 - H^3 - 2*U1*H^2
Y3 = R*(U1*H^2 - X3) - S1*H^3
Z3 = H*Z1*Z2
Z3^2 = Z3^2
Z3^3 = Z3^2 * Z3
return (X3, Y3, Z3)
Mixed Addition (with affine point) (8M + 3S)
[edit | edit source]Let (X1, Y1, Z1, Z1^2, Z1^3) be a point represented in Chudnovsky Coordinates and (X2, Y2) a point in Affine Coordinates (both unequal to the point at infinity). A formula to add those points can be readily derived from the regular chudnovsky point addition by replacing each occurrence of "Z2" by "1" (and thereby dropping three field multiplications).
Mixed Addition (with jacobian point) (11M + 3S)
[edit | edit source]See Jacobian Coordinates for further details.
Prime Curve/Jacobian Coordinates
Introduction
[edit | edit source]Jacobian Coordinates are used to represent elliptic curve points on prime curves They give a speed benefit over Affine Coordinates when the cost for field inversions is significantly higher than field multiplications. In Jacobian Coordinates the triple represents the affine point .
Point Doubling (4M + 6S or 4M + 4S)
[edit | edit source]Let (X, Y, Z) be a point (unequal to the point at infinity) represented in Jacobian Coordinates. Then its double (X', Y', Z') can be calculated by
if (Y == 0) return POINT_AT_INFINITY S = 4*X*Y^2 M = 3*X^2 + a*Z^4 X' = M^2 - 2*S Y' = M*(S - X') - 8*Y^4 Z' = 2*Y*Z return (X', Y', Z')
Note: if a = -3, then M can also be calculated as M = 3*(X + Z^2)*(X - Z^2), saving 2 field squarings.
Repeated Doubling ((4m-1)M + (4m+2)S)
[edit | edit source]Let P=(X, Y, Z) be a point (unequal to the point at infinity) represented in Jacobian Coordinates. Then, in the case a = -3, its "m-fold double" (2^m)P can be calculated as follows:
Y = 2*Y
W = Z^4
while(m--)
if (Y == 0)
return POINT_AT_INFINITY
A = 3*(X^2 - W)
B = X*Y^2
X = A^2 - 2B
Z = Z*Y
if (m)
W = W*Y^4
Y = 2*A*(B - X) - Y^4
Y = Y/2
return (X, Y, Z)
An alternative repeated doubling routine with costs (4m)M + (4m+2)S for any value a can be derived from the Modified Jacobian doubling routine. For small values a (say 0 or -3) the costs reduce to (4m-1)M + (4m+2)S, competing nicely with the algorithm showed above.
Point Addition (12M + 4S)
[edit | edit source]Let (X1, Y1, Z1) and (X2, Y2, Z2) be two points (both unequal to the point at infinity) represented in Jacobian Coordinates. Then the sum (X3, Y3, Z3) can be calculated by
U = X1*Z2^2
H = X2*Z1^2 - U
S = Y1*Z2^3
R = Y2*Z1^3 - S
if (H == 0)
if (R == 0)
return POINT_DOUBLE(X1, Y1, Z1)
else
return POINT_AT_INFINITY
X3 = R^2 - H^3 - 2*U*H^2
Y3 = R*(U*H^2 - X3) - S*H^3
Z3 = H*Z1*Z2
return (X3, Y3, Z3)
J + J -> J ( 12M, 2S) (secp256k1 has 12M, 4S)
[edit | edit source]U1 = Y2 * Z1
U2 = Y1 * Z2
V1 = X2 * Z1
V2 = X1 * Z2
if (V1 == V2)
if (U1 == U2)
return POINT_DOUBLE(X1, Y1, Z1)
else
return POINT_AT_INFINITY
U = U1 - U2
V = V1 - V2
W = Z1 * Z2
A = U ^ 2 * W - V ^ 3 - 2 * V ^ 2 * V2
X3 = V * A
Y3 = U * (V ^ 2 * V2 - A) - V ^ 3 * U2
Z3 = V ^ 3 * W
return (X3, Y3, Z3)
Mixed Addition (with affine point) (8M + 3S)
[edit | edit source]Let (X1, Y1, Z1) be a point represented in Jacobian Coordinates and (X2, Y2) a point in Affine Coordinates (both unequal to the point at infinity). A formula to add those points can be readily derived from the regular jacobian point addition by replacing each occurrence of "Z2" by "1" (and thereby dropping four field multiplications and one field squaring).
Mixed Addition (with chudnovsky point) (11M + 3S)
[edit | edit source]Let (X1, Y1, Z1) be a point represented in Jacobian Coordinates and (X2, Y2, Z2, Z2^2, Z2^3) a point in Chudnovsky Coordinates (both unequal to the point at infinity). Then the sum (X3, Y3, Z3) can be readily calculated using the addition formula given above (saving one field multiplication and one field squaring).
Prime Curve/Standard Projective Coordinates
Introduction
[edit | edit source]Standard Projective Coordinates are used to represent elliptic curve points on prime curves y^2 = x^3 + ax + b. Their usage might give a speed benefit over Affine Coordinates when the cost for field inversions is significantly higher than field multiplications. In Standard Projective Coordinates the triple (X, Y, Z) represents the affine point (X / Z, Y / Z).
Point Doubling (7M + 5S or 7M + 3S)
[edit | edit source]Let (X, Y, Z) be a point (unequal to the point at infinity) represented in Standard Projective Coordinates. Then its double (X', Y', Z') can be calculated by
if (Y == 0) return POINT_AT_INFINITY W = a*Z^2 + 3*X^2 S = Y*Z B = X*Y*S H = W^2 - 8*B X' = 2*H*S Y' = W*(4*B - H) - 8*Y^2*S^2 Z' = 8*S^3 return (X', Y', Z')
Note: if a = -3, then W can also be calculated as W = 3*(X + Z)*(X - Z), saving 2 field squarings.
Point Addition (12M + 2S)
[edit | edit source]Let (X1, Y1, Z1) and (X2, Y2, Z2) be two points (both unequal to the point at infinity) represented in Standard Projective Coordinates. Then the sum (X3, Y3, Z3) can be calculated by
U1 = Y2*Z1
U2 = Y1*Z2
V1 = X2*Z1
V2 = X1*Z2
if (V1 == V2)
if (U1 != U2)
return POINT_AT_INFINITY
else
return POINT_DOUBLE(X1, Y1, Z1)
U = U1 - U2
V = V1 - V2
W = Z1*Z2
A = U^2*W - V^3 - 2*V^2*V2
X3 = V*A
Y3 = U*(V^2*V2 - A) - V^3*U2
Z3 = V^3*W
return (X3, Y3, Z3)
Mixed Addition (with affine point) (9M + 2S)
[edit | edit source]Let (X1, Y1, Z1) be a point represented in Standard Projective Coordinates and (X2, Y2) a point in Affine Coordinates (both unequal to the point at infinity). A formula to add those points can be readily derived from the regular standard projective point addition by replacing each occurrence of "Z2" by "1" (and thereby dropping three field multiplications).
Notes
'Cryptography is a Greek word which means "Secret Writing"
Important Uses of Cryptography 1. Protect confidentiality of message (Achieved with Encryption Algorithms) 2. Provide identity for authentication (Achieved with Asymmetric Encryption Algorithms, digital signature algorithms) 3. Verify information to check message integrity (Achieved with hash functions)
To Validate information cryptographic function are used.
Cryptographic functions are called as hash functions
e.g. of Hash Functions 1. MD5 (Message Digest 5) 2. SHA (Secure Hash Algorithm)
Types of Cryptography 1. Secret key cryptography (Both parties know the same secret key. Uses symmetric encryption) 2. Public key cryptography (Both parties have 2 different keys,Public key for encryption and Private key for decryption.
Private key for signing, public key for signature verification.[2][3]
In Reversible public key algorithms, Data encrypted with private key can be decrypted with public key.Uses asymmetric encryption)
[citation needed]
Encryption algorithms are called Ciphers Information in encrypted form is called Ciphertext
2 Types of Ciphers 1. Stream Ciphers (Process data byte at a time) 2. Block Ciphers (Process data in blocks 8 bytes at a time. Pad packets smaller than block)
e.g. of Symmetric Encryption Algorithms
1. DES (Data Encryption Standard - Block) 2. 3DES (Triple strength Data Encryption Standard - Block) 3. RC2 (Rivest Cipher 2 - Block) 4. RC4 (Rivest Cipher 4 - Stream)
e.g. of Asymmetric Encryption Algorithms
1. RSA - Rivest Shamir Adleman 2. DSA - Digital Signature Algorithm - Can only be used for digital signatures.













































































































































































































































































































































































































![{\displaystyle [0...p-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08fe310db3d2ad724b18913e08cff07f1ed9c66e)















































