Data Structures/Hash Tables
Hash Tables
[edit | edit source]
A hash table, or a hash map, is a data structure that associates keys with values. The primary operation it supports efficiently is a lookup: given a key (e.g. a person's name), find the corresponding value (e.g. that person's telephone number). It works by transforming the key using a hash function into a hash, a number that the hash table uses to locate the desired value. This hash maps directly to a bucket in the array of key/value pairs, hence the name hash map. The mapping method lets us directly access the storage location for any key/value pair.
Hash table<Element> Operations
make-hash-table(integer n): HashTable
- Create a hash table with n buckets.
get-value(HashTable h, Comparable key): Element
- Returns the value of the element for the given key. The key must be some comparable type.
set-value(HashTable h, Comparable key, Element new-value)
- Sets the element of the array for the given key to be equal to new-value. The key must be some comparable type.
remove(HashTable h, Comparable key)
- Remove the element for the given key from the hash table. The key must be some comparable type.

Time complexity and common uses of hash tables
[edit | edit source]Hash tables are often used to implement associative arrays, sets and caches. Like arrays, hash tables provide constant-time O(1) lookup on average, regardless of the number of items in the table. The (hopefully rare) worst-case lookup time in most hash table schemes is O(n).[1] Compared to other associative array data structures, hash tables are most useful when we need to store a large numbers of data records.
Hash tables may be used as in-memory data structures. Hash tables may also be adopted for use with persistent data structures; database indexes commonly use disk-based data structures based on hash tables.
Hash tables are also used to speed-up string searching in many implementations of data compression.
In computer chess, a hash table can be used to implement the transposition table.
Choosing a good hash function
[edit | edit source]A good hash function is essential for good hash table performance. A poor choice of hash function is likely to lead to clustering behavior, in which the probability of keys mapping to the same hash bucket (i.e. a collision) is significantly greater than would be expected from a random function. A nonzero probability of collisions is inevitable in any hash implementation, but the number of operations to resolve collisions usually scales linearly with the number of keys mapping to the same bucket, so excess collisions will degrade performance significantly. In addition, some hash functions are computationally expensive, so the amount of time (and, in some cases, memory) taken to compute the hash may be burdensome.
Choosing a good hash function is tricky. The literature is replete with poor choices, at least when measured by modern standards. For example, the very popular multiplicative hash advocated by Knuth in The Art of Computer Programming (see reference below) has particularly poor clustering behavior. However, since poor hashing merely degrades hash table performance for particular input key distributions, such problems go undetected far too often.
The literature is also sparse on the criteria for choosing a hash function. Unlike most other fundamental algorithms and data structures, there is no universal consensus on what makes a "good" hash function. The remainder of this section is organized by three criteria: simplicity, speed, and strength, and will survey algorithms known to perform well by these criteria.
Simplicity and speed are readily measured objectively (by number of lines of code and CPU benchmarks, for example), but strength is a more slippery concept. Obviously, a cryptographic hash function such as SHA-1 would satisfy the relatively lax strength requirements needed for hash tables, but their slowness and complexity makes them unappealing. In fact, even a cryptographic hash does not provide protection against an adversary who wishes to degrade hash table performance by choosing keys all hashing to the same bucket. For these specialized cases, a universal hash function should be used instead of any one static hash, no matter how sophisticated.
In the absence of a standard measure for hash function strength, the current state of the art is to employ a battery of statistical tests to measure whether the hash function can be readily distinguished from a random function. Arguably the most important such test is to determine whether the hash function displays the avalanche effect, which essentially states that any single-bit change in the input key should affect on average half the bits in the output. Bret Mulvey advocates testing the strict avalanche condition in particular, which states that, for any single-bit change, each of the output bits should change with probability one-half, independent of the other bits in the key. Purely additive hash functions such as CRC fail this stronger condition miserably.
Clearly, a strong hash function should have a uniform distribution of hash values. Bret Mulvey proposes the use of a chi-squared test for uniformity, based on power of two hash table sizes ranging from 21 to 216. This test is considerably more sensitive than many others proposed for measuring hash functions, and finds problems in many popular hash functions.
Fortunately, there are good hash functions that satisfy all these criteria. The simplest class all consume one byte of the input key per iteration of the inner loop. Within this class, simplicity and speed are closely related, as fast algorithms simply don't have time to perform complex calculations. Of these, one that performs particularly well is the Jenkins One-at-a-time hash, adapted here from an article by Bob Jenkins, its creator.
uint32 joaat_hash(uchar *key, size_t len)
{
uint32 hash = 0;
size_t i;
for (i = 0; i < len; i++)
{
hash += key[i];
hash += (hash << 10);
hash ^= (hash >> 6);
}
hash += (hash << 3);
hash ^= (hash >> 11);
hash += (hash << 15);
return hash;
}

The avalanche behavior of this hash shown on the right. The image was made using Bret Mulvey's AvalancheTest in his Hash.cs toolset. Each row corresponds to a single bit in the input, and each column to a bit in the output. A green square indicates good mixing behavior, a yellow square weak mixing behavior, and red would indicate no mixing. Only a few bits in the last byte are weakly mixed, a performance vastly better than a number of widely used hash functions.
Many commonly used hash functions perform poorly when subjected to such rigorous avalanche testing. The widely favored FNV hash, for example, shows many bits with no mixing at all, especially for short keys. See the evaluation of FNV by Bret Mulvey for a more thorough analysis.
If speed is more important than simplicity, then the class of hash functions which consume multibyte chunks per iteration may be of interest. One of the most sophisticated is "lookup3" by Bob Jenkins, which consumes input in 12 byte (96 bit) chunks. Note, though, that any speed improvement from the use of this hash is only likely to be useful for large keys, and that the increased complexity may also have speed consequences such as preventing an optimizing compiler from inlining the hash function. Bret Mulvey analyzed an earlier version, lookup2, and found it to have excellent avalanche behavior.
One desirable property of a hash function is that conversion from the hash value (typically 32 bits) to an bucket index for a particular-size hash table can be done simply by masking, preserving only the lower k bits for a table of size 2k (an operation equivalent to computing the hash value modulo the table size). This property enables the technique of incremental doubling of the size of the hash table - each bucket in the old table maps to only two in the new table. Because of its use of XOR-folding, the FNV hash does not have this property. Some older hashes are even worse, requiring table sizes to be a prime number rather than a power of two, again computing the bucket index as the hash value modulo the table size. In general, such a requirement is a sign of a fundamentally weak function; using a prime table size is a poor substitute for using a stronger function.
Collision resolution
[edit | edit source]If two keys hash to the same index, the corresponding records cannot be stored in the same location. So, if it's already occupied, we must find another location to store the new record, and do it so that we can find it when we look it up later on.
To give an idea of the importance of a good collision resolution strategy, consider the following result, derived using the birthday paradox. Even if we assume that our hash function outputs random indices uniformly distributed over the array, and even for an array with 1 million entries, there is a 95% chance of at least one collision occurring before it contains 2500 records.
There are a number of collision resolution techniques, but the most popular are chaining and open addressing.
Chaining
[edit | edit source]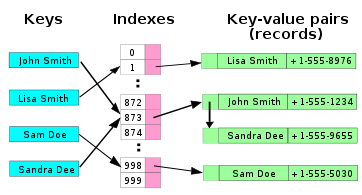
In the simplest chained hash table technique, each slot in the array references a linked list of inserted records that collide to the same slot. Insertion requires finding the correct slot, and appending to either end of the list in that slot; deletion requires searching the list and removal.
Chained hash tables have advantages over open addressed hash tables in that the removal operation is simple and resizing the table can be postponed for a much longer time because performance degrades more gracefully even when every slot is used. Indeed, many chaining hash tables may not require resizing at all since performance degradation is linear as the table fills. For example, a chaining hash table containing twice its recommended capacity of data would only be about twice as slow on average as the same table at its recommended capacity.
Chained hash tables inherit the disadvantages of linked lists. When storing small records, the overhead of the linked list can be significant. An additional disadvantage is that traversing a linked list has poor cache performance.
Alternative data structures can be used for chains instead of linked lists. By using a self-balancing tree, for example, the theoretical worst-case time of a hash table can be brought down to O(log n) rather than O(n). However, since each list is intended to be short, this approach is usually inefficient unless the hash table is designed to run at full capacity or there are unusually high collision rates, as might occur in input designed to cause collisions. Dynamic arrays can also be used to decrease space overhead and improve cache performance when records are small.
Some chaining implementations use an optimization where the first record of each chain is stored in the table. Although this can increase performance, it is generally not recommended: chaining tables with reasonable load factors contain a large proportion of empty slots, and the larger slot size causes them to waste large amounts of space.
Open addressing
[edit | edit source]
Open addressing hash tables can store the records directly within the array. A hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:
- linear probing
- in which the interval between probes is fixed—often at 1,
- quadratic probing
- in which the interval between probes increases linearly (hence, the indices are described by a quadratic function), and
- double hashing
- in which the interval between probes is fixed for each record but is computed by another hash function.
The main tradeoffs between these methods are that linear probing has the best cache performance but is most sensitive to clustering, while double hashing has poor cache performance but exhibits virtually no clustering; quadratic hashing falls in-between in both areas. Double hashing can also require more computation than other forms of probing. Some open addressing methods, such as last-come-first-served hashing and cuckoo hashing move existing keys around in the array to make room for the new key. This gives better maximum search times than the methods based on probing.
A critical influence on performance of an open addressing hash table is the load factor; that is, the proportion of the slots in the array that are used. As the load factor increases towards 100%, the number of probes that may be required to find or insert a given key rises dramatically. Once the table becomes full, probing algorithms may even fail to terminate. Even with good hash functions, load factors are normally limited to 80%. A poor hash function can exhibit poor performance even at very low load factors by generating significant clustering. What causes hash functions to cluster is not well understood, and it is easy to unintentionally write a hash function which causes severe clustering.
Example pseudocode
[edit | edit source]The following pseudocode is an implementation of an open addressing hash table with linear probing and single-slot stepping, a common approach that is effective if the hash function is good. Each of the lookup, set and remove functions use a common internal function findSlot to locate the array slot that either does or should contain a given key.
record pair { key, value }
var pair array slot[0..numSlots-1]
function findSlot(key)
i := hash(key) modulus numSlots
loop
if slot[i] is not occupied or slot[i].key = key
return i
i := (i + 1) modulus numSlots
function lookup(key)
i := findSlot(key)
if slot[i] is occupied // key is in table
return slot[i].value
else // key is not in table
return not found
function set(key, value)
i := findSlot(key)
if slot[i].key = key
// (Key already in table. Update value.)
slot[i].value := value
else
// (Insert key and value in un-occupied slot.)
// (But first, make sure insert won't overload the table)
if the table is almost full
rebuild the table larger (note 1)
i := findSlot(key)
slot[i].key := key
slot[i].value := value
Another example showing open addressing technique. Presented function is converting each part(4) of an Internet protocol address, where NOT is bitwise NOT, XOR is bitwise XOR, OR is bitwise OR, AND is bitwise AND and << and >> are shift-left and shift-right:
// key_1,key_2,key_3,key_4 are following 3-digit numbers - parts of ip address xxx.xxx.xxx.xxx
function ip(key parts)
j := 1
do
key := (key_2 << 2)
key := (key + (key_3 << 7))
key := key + (j OR key_4 >> 2) * (key_4) * (j + key_1) XOR j
key := key AND _prime_ // _prime_ is a prime number
j := (j+1)
while collision
return key
- note 1
- Rebuilding the table requires allocating a larger array and recursively using the set operation to insert all the elements of the old array into the new larger array. It is common to increase the array size exponentially, for example by doubling the old array size.
function remove(key)
i := findSlot(key)
if slot[i] is unoccupied
return // key is not in the table
j := i
loop
j := (j+1) modulus numSlots
if slot[j] is unoccupied
exit loop
k := hash(slot[j].key) modulus numSlots
if (j > i and (k <= i or k > j)) or
(j < i and (k <= i and k > j)) (note 2)
slot[i] := slot[j]
i := j
mark slot[i] as unoccupied
- note 2
- For all records in a cluster, there must be no vacant slots between their natural hash position and their current position (else lookups will terminate before finding the record). At this point in the pseudocode, i is a vacant slot that might be invalidating this property for subsequent records in the cluster. j is such as subsequent record. k is the raw hash where the record at j would naturally land in the hash table if there were no collisions. This test is asking if the record at j is invalidly positioned with respect to the required properties of a cluster now that i is vacant.
Another technique for removal is simply to mark the slot as deleted. However this eventually requires rebuilding the table simply to remove deleted records. The methods above provide O(1) updating and removal of existing records, with occasional rebuilding if the high water mark of the table size grows.
The O(1) remove method above is only possible in linearly probed hash tables with single-slot stepping. In the case where many records are to be deleted in one operation, marking the slots for deletion and later rebuilding may be more efficient.
Open addressing versus chaining
[edit | edit source]Chained hash tables have the following benefits over open addressing:
- They are simple to implement effectively and only require basic data structures.
- From the point of view of writing suitable hash functions, chained hash tables are insensitive to clustering, only requiring minimization of collisions. Open addressing depends upon better hash functions to avoid clustering. This is particularly important if novice programmers can add their own hash functions, but even experienced programmers can be caught out by unexpected clustering effects.
- They degrade in performance more gracefully. Although chains grow longer as the table fills, a chained hash table cannot "fill up" and does not exhibit the sudden increases in lookup times that occur in a near-full table with open addressing. (see right)
- If the hash table stores large records, about 5 or more words per record, chaining uses less memory than open addressing.
- If the hash table is sparse (that is, it has a big array with many free array slots), chaining uses less memory than open addressing even for small records of 2 to 4 words per record due to its external storage.

For small record sizes (a few words or less) the benefits of in-place open addressing compared to chaining are:
- They can be more space-efficient than chaining since they don't need to store any pointers or allocate any additional space outside the hash table. Simple linked lists require a word of overhead per element.
- Insertions avoid the time overhead of memory allocation, and can even be implemented in the absence of a memory allocator.
- Because it uses internal storage, open addressing avoids the extra indirection required for chaining's external storage. It also has better locality of reference, particularly with linear probing. With small record sizes, these factors can yield better performance than chaining, particularly for lookups.
- They can be easier to serialize, because they don't use pointers.
On the other hand, normal open addressing is a poor choice for large elements, since these elements fill entire cache lines (negating the cache advantage), and a large amount of space is wasted on large empty table slots. If the open addressing table only stores references to elements (external storage), it uses space comparable to chaining even for large records but loses its speed advantage.
Generally speaking, open addressing is better used for hash tables with small records that can be stored within the table (internal storage) and fit in a cache line. They are particularly suitable for elements of one word or less. In cases where the tables are expected to have high load factors, the records are large, or the data is variable-sized, chained hash tables often perform as well or better.
Ultimately, used sensibly any kind of hash table algorithm is usually fast enough; and the percentage of a calculation spent in hash table code is low. Memory usage is rarely considered excessive. Therefore, in most cases the differences between these algorithms is marginal, and other considerations typically come into play.
Coalesced hashing
[edit | edit source]A hybrid of chaining and open addressing, coalesced hashing links together chains of nodes within the table itself. Like open addressing, it achieves space usage and (somewhat diminished) cache advantages over chaining. Like chaining, it does not exhibit clustering effects; in fact, the table can be efficiently filled to a high density. Unlike chaining, it cannot have more elements than table slots.
Perfect hashing
[edit | edit source]If all of the keys that will be used are known ahead of time, and there are no more keys that can fit the hash table, perfect hashing can be used to create a perfect hash table, in which there will be no collisions. If minimal perfect hashing is used, every location in the hash table can be used as well.
Perfect hashing gives a hash table where the time to make a lookup is constant in the worst case. This is in contrast to chaining and open addressing methods, where the time for lookup is low on average, but may be arbitrarily large. There exist methods for maintaining a perfect hash function under insertions of keys, known as dynamic perfect hashing. A simpler alternative, that also gives worst case constant lookup time, is cuckoo hashing.
Probabilistic hashing
[edit | edit source]Perhaps the simplest solution to a collision is to replace the value that is already in the slot with the new value, or slightly less commonly, drop the record that is to be inserted. In later searches, this may result in a search not finding a record which has been inserted. This technique is particularly useful for implementing caching.
An even more space-efficient solution which is similar to this is use a bit array (an array of one-bit fields) for our table. Initially all bits are set to zero, and when we insert a key, we set the corresponding bit to one. False negatives cannot occur, but false positives can, since if the search finds a 1 bit, it will claim that the value was found, even if it was just another value that hashed into the same array slot by coincidence. In reality, such a hash table is merely a specific type of Bloom filter.
Table resizing
[edit | edit source]With a good hash function, a hash table can typically contain about 70%–80% as many elements as it does table slots and still perform well. Depending on the collision resolution mechanism, performance can begin to suffer either gradually or dramatically as more elements are added. To deal with this, when the load factor exceeds some threshold, we allocate a new, larger table, and add all the contents of the original table to this new table. In Java's HashMap class, for example, the default load factor threshold is 0.75.
This can be a very expensive operation, and the necessity for it is one of the hash table's disadvantages. In fact, some naive methods for doing this, such as enlarging the table by one each time you add a new element, reduce performance so drastically as to make the hash table useless. However, if we enlarge the table by some fixed percent, such as 10% or 100%, it can be shown using amortized analysis that these resizings are so infrequent that the average time per lookup remains constant-time. To see why this is true, suppose a hash table using chaining begins at the minimum size of 1 and is doubled each time it fills above 100%. If in the end it contains n elements, then the total add operations performed for all the resizings is:
- 1 + 2 + 4 + ... + n = 2n - 1.
Because the costs of the resizings form a geometric series, the total cost is O(n). But we also perform n operations to add the n elements in the first place, so the total time to add n elements with resizing is O(n), an amortized time of O(1) per element.
On the other hand, some hash table implementations, notably in real-time systems, cannot pay the price of enlarging the hash table all at once, because it may interrupt time-critical operations. One simple approach is to initially allocate the table with enough space for the expected number of elements and forbid the addition of too many elements. Another useful but more memory-intensive technique is to perform the resizing gradually:
- Allocate the new hash table, but leave the old hash table and check both tables during lookups.
- Each time an insertion is performed, add that element to the new table and also move k elements from the old table to the new table.
- When all elements are removed from the old table, deallocate it.
To ensure that the old table will be completely copied over before the new table itself needs to be enlarged, it's necessary to increase the size of the table by a factor of at least (k + 1)/k during the resizing.
Linear hashing is a hash table algorithm that permits incremental hash table expansion. It is implemented using a single hash table, but with two possible look-up functions.
Another way to decrease the cost of table resizing is to choose a hash function in such a way that the hashes of most values do not change when the table is resized. This approach, called consistent hashing, is prevalent in disk-based and distributed hashes, where resizing is prohibitively costly.
Ordered retrieval issue
[edit | edit source]Hash tables store data in pseudo-random locations, so accessing the data in a sorted manner is a very time consuming operation. Other data structures such as self-balancing binary search trees generally operate more slowly (since their lookup time is O(log n)) and are rather more complex to implement than hash tables but maintain a sorted data structure at all times. See a comparison of hash tables and self-balancing binary search trees.
Problems with hash tables
[edit | edit source]Although hash table lookups use constant time on average, the time spent can be significant. Evaluating a good hash function can be a slow operation. In particular, if simple array indexing can be used instead, this is usually faster.
Hash tables in general exhibit poor locality of reference—that is, the data to be accessed is distributed seemingly at random in memory. Because hash tables cause access patterns that jump around, this can trigger microprocessor cache misses that cause long delays. Compact data structures such as arrays, searched with linear search, may be faster if the table is relatively small and keys are cheap to compare, such as with simple integer keys. According to Moore's Law, cache sizes are growing exponentially and so what is considered "small" may be increasing. The optimal performance point varies from system to system; for example, a trial on Parrot shows that its hash tables outperform linear search in all but the most trivial cases (one to three entries).
More significantly, hash tables are more difficult and error-prone to write and use. Hash tables require the design of an effective hash function for each key type, which in many situations is more difficult and time-consuming to design and debug than the mere comparison function required for a self-balancing binary search tree. In open-addressed hash tables it's even easier to create a poor hash function.
Additionally, in some applications, a black hat with knowledge of the hash function may be able to supply information to a hash which creates worst-case behavior by causing excessive collisions, resulting in very poor performance (i.e., a denial of service attack). In critical applications, either universal hashing can be used or a data structure with better worst-case guarantees may be preferable. For details, see Crosby and Wallach's Denial of Service via Algorithmic Complexity Attacks.
Other hash table algorithms
[edit | edit source]Extendible hashing and linear hashing are hash algorithms that are used in the context of database algorithms used for instance in index file structures, and even primary file organization for a database. Generally, in order to make search scalable for large databases, the search time should be proportional log N or near constant, where N is the number of records to search. Log N searches can be implemented with tree structures, because the degree of fan out and the shortness of the tree relates to the number of steps needed to find a record, so the height of the tree is the maximum number of disc accesses it takes to find where a record is. However, hash tables are also used, because the cost of a disk access can be counted in units of disc accesses, and often that unit is a block of data. Since a hash table can, in the best case, find a key with one or two accesses, a hash table index is regarded as generally faster when retrieving a collection of records during a join operation e.g.
SELECT * from customer, orders where customer.cust_id = orders.cust_id and cust_id = X
i.e. If orders has a hash index on cust_id, then it takes constant time to locate the block that contains record locations for orders matching cust_id = X. (although, it would be better if the value type of orders was a list of order ids, so that hash keys are just one unique cust_id for each batch of orders, to avoid unnecessary collisions).
Extendible hashing and linear hashing have certain similarities: collisions are accepted as inevitable and are part of the algorithm where blocks or buckets of collision space is added ; traditional good hash function ranges are required, but the hash value is transformed by a dynamic address function : in extendible hashing, a bit mask is used to mask out unwanted bits, but this mask length increases by one periodically, doubling the available addressing space ; also in extendible hashing, there is an indirection with a directory address space, the directory entries being paired with another address (a pointer ) to the actual block containing the key-value pairs; the entries in the directory correspond to the bit masked hash value (so that the number of entries is equal to maximum bit mask value + 1 e.g. a bit mask of 2 bits, can address a directory of 00 01 10 11, or 3 + 1 = 4).
In linear hashing, the traditional hash value is also masked with a bit mask, but if the resultant smaller hash value falls below a 'split' variable, the original hash value is masked with a bit mask of one bit greater length, making the resultant hash value address recently added blocks. The split variable ranges incrementally between 0 and the maximum current bit mask value e.g. a bit mask of 2, or in the terminology of linear hashing, a "level" of 2, the split variable will range between 0 and 3. When the split variable reaches 4, the level increases by 1, so in the next round of the split variable, it will range between 0 and 7, and reset again when it reaches 8.
The split variable incrementally allows increased addressing space, as new blocks are added; the decision to add a new block occurs whenever a key-and=value is being inserted, and overflows the particular block the key-and-value's key hashes into. This overflow location may be completely unrelated to the block going to be split pointed to by the split variable. However, over time, it is expected that given a good random hash function that distributes entries fairly evenly amongst all addressable blocks, the blocks that actually require splitting because they have overflowed get their turn in round-robin fashion as the split value ranges between 0 - N where N has a factor of 2 to the power of Level, level being the variable incremented whenever the split variable hits N.
New blocks are added one at a time with both extendible hashing, and with linear hashing.
In extendible hashing, a block overflow ( a new key-value colliding with B other key-values, where B is the size of a block) is handled by checking the size of the bit mask "locally", called the "local depth", an attribute which must be stored with the block. The directory structure, also has a depth, the "global depth". If the local depth is less than the global depth, then the local depth is incremented, and all the key values are rehashed and passed through a bit mask which is one bit longer now, placing them either in the current block, or in another block. If the other block happens to be the same block when looked up in the directory, a new block is added, and the directory entry for the other block is made to point to the new block. Why does the directory have entries where two entries point to the same block ? This is because if the local depth is equal to the global depth of the directory, this means the bit mask of the directory does not have enough bits to deal with an increment in the bit mask length of the block, and so the directory must have its bit mask length incremented, but this means the directory now doubles the number of addressable entries. Since half the entries addressable don't exist, the directory simply copies the pointers over to the new entries e.g. if the directory had entries for 00, 01, 10, 11, or a 2 bit mask, and it becomes a 3 bit mask, then 000 001 010 011 100 101 110 111 become the new entries, and 00's block address go to 000 and 001 ; 01's pointer goes to 010 and 011, 10 goes to 100 and 101 and so on. And so this creates the situation where two directory entries point to the same block. Although the block that was going to overflow, now can add a new block by redirecting the second pointer to a newly appended block, the other original blocks will have two pointers to them. When it is their turn to split, the algorithm will check local vs global depth and this time find that the local depth is less, and hence no directory splitting is required, only a new block be appended, and the second directory pointer moved from addressing the previous block to addressing the new block.
In linear hashing, adding a similarly hashed block does not occurs immediately when a block overflows, and therefore an overflow block is created to be attached to the overflowing block. However, a block overflow is a signal that more space will be required, and this happens by splitting the block pointed to by the "split" variable, which is initially zero, and hence initially points to block zero. The splitting is done by taking all the key-value pairs in the splitting block, and its overflow block(s), hashing the keys again, but with a bit mask of length current level + 1. This will result in two block addresses, some will be the old block number, and others will be
a2 = old block number + ( N times 2 ^ (level) )
- Rationale
Let m = N times 2 ^ level ; if h is the original hash value, and old block number = h mod m, and now the new block number is h mod ( m * 2 ), because m * 2 = N times 2 ^ (level+1), then the new block number is either h mod m if (h / m) is even so dividing h/m by 2 leaves a zero remainder and therefore doesn't change the remainder, or the new block number is ( h mod m ) + m because h / m is an odd number, and dividing h / m by 2 will leave an excess remainder of m, + the original remainder. ( The same rationale applies to extendible hashing depth incrementing ).
As above, a new block is created with a number a2, which will usually occur at +1 the previous a2 value. Once this is done, the split variable is incremented, so that the next a2 value will be again old a2 + 1. In this way, each block is covered by the split variable eventually, so each block is preemptively rehashed into extra space, and new blocks are added incrementally. Overflow blocks that are no longer needed are discarded, for later garbage collection if needed, or put on an available free block list by chaining.
When the split variable reaches ( N times 2 ^ level ), level is incremented and split variable is reset to zero. In this next round, the split variable will now traverse from zero to ( N times 2 ^ (old_level + 1 ) ), which is exactly the number of blocks at the start of the previous round, but including all the blocks created by the previous round.
A simple inference on file storage mapping of linear hashing and extendible hashing
[edit | edit source]As can be seen, extendible hashing requires space to store a directory which can double in size.
Since the space of both algorithms increase by one block at a time, if blocks have a known maximum size or fixed size, then it is straight forward to map the blocks as blocks sequentially appended to a file.
In extendible hashing, it would be logical to store the directory as a separate file, as doubling can be accommodated by adding to the end of the directory file. The separate block file would not have to change, other than have blocks appended to its end.
Header information for linear hashing doesn't increase in size : basically just the values for N, level, and split need to be recorded, so these can be incorporated as a header into a fixed block size linear hash storage file.
However, linear hashing requires space for overflow blocks, and this might best be stored in another file, otherwise addressing blocks in the linear hash file is not as straight forward as multiplying the block number by the block size and adding the space for N,level, and split.
In the next section, a complete example of linear hashing in Java is given, using a in memory implementation of linear hashing, and code to manage blocks as files in a file directory, the whole contents of the file directory representing the persistent linear hashing structure.
Implementations
[edit | edit source]While many programming languages already provide hash table functionality,[2] there are several independent implementations worth mentioning.
- Google Sparse Hash The Google SparseHash project contains several hash-map implementations in use at Google, with different performance characteristics, including an implementation that optimizes for space and one that optimizes for speed. The memory-optimized one is extremely memory-efficient with only 2 bits/entry of overhead.
- MCT provides hashtables similar to Google's
dense_hash_map, but without restriction on contained values; it also comes with exception safety and support for C++0x features. - A number of runtime languages and/or standard libraries use hash tables to implement their support for associative arrays because of their efficiency.
A python implementation of extendible hashing
[edit | edit source]The file - block management routines aren't there, so this could be added in to make this a real implementation of a database hash index.
A full page is split according to the (local depth)th bit, first by collecting all the directory indices pointing to the full page, updating the pointers according to the d bit being 0 or 1 corresponding to first and second new pages, then reloading all the key-values after hashing each key and using the d bit of each hash to see which page to allocate to. The local depth of each new page is one greater than the old page's local depth, so that the next d bit can be used next time when splitting.
PAGE_SZ = 20
class Page:
def __init__(self):
self.m = {}
self.d = 0
def full(self):
return len(self.m) > PAGE_SZ
def put(self,k,v):
self.m[k] = v
def get(self,k):
return self.m.get(k)
class EH:
def __init__(self):
self.gd = 0
p = Page()
self.pp= [p]
def get_page(self,k):
h = hash(k)
p = self.pp[ h & (( 1 << self.gd) -1)]
return p
def put(self, k, v):
p = self.get_page(k)
if p.full() and p.d == self.gd:
self.pp = self.pp + self.pp
self.gd += 1
if p.full() and p.d < self.gd:
p.put(k,v);
p1 = Page()
p2 = Page()
for k2 in p.m.keys():
v2 = p.m[k2]
h = k2.__hash__()
h = h & ((1 << self.gd) -1)
if (h | (1 << p.d) == h):
p2.put(k2,v2)
else:
p1.put(k2,v2)
l = []
for i in xrange(0, len(self.pp)):
if self.pp[i] == p:
l.append(i)
for i in l:
if (i | ( 1 << p.d) == i):
self.pp[i] = p2
else:
self.pp[i] = p1
p1.d = p.d + 1
p2.d = p1.d
else:
p.put(k, v)
def get(self, k):
p = self.get_page(k)
return p.get(k)
if __name__ == "__main__":
eh = EH()
N = 10000
l = []
for i in range(0,N):
l.append(i)
import random
random.shuffle(l)
for i in l:
eh.put(i,i)
print l
for i in range(0, N):
print eh.get(i)
A Java implementation of extendible hashing
[edit | edit source]A direct Java translation of the above python code, tested to work.
package ext_hashing;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Random;
public class EH2<K, V> {
static class Page<K, V> {
static int PAGE_SZ = 20;
private Map<K, V> m = new HashMap<K, V>();
int d = 0;
boolean full() {
return m.size() > PAGE_SZ;
}
void put(K k, V v) {
m.put(k, v);
}
V get(K k) {
return m.get(k);
}
}
int gd = 0;
List<Page<K, V>> pp = new ArrayList<Page<K, V>>();
public EH2() {
pp.add(new Page<K, V>());
}
Page<K, V> getPage(K k) {
int h = k.hashCode();
Page<K, V> p = pp.get(h & ((1 << gd) - 1));
return p;
}
void put(K k, V v) {
Page<K, V> p = getPage(k);
if (p.full() && p.d == gd) {
List<Page<K, V>> pp2 = new ArrayList<EH2.Page<K, V>>(pp);
pp.addAll(pp2);
++gd;
}
if (p.full() && p.d < gd) {
p.put(k, v);
Page<K, V> p1, p2;
p1 = new Page<K, V>();
p2 = new Page<K, V>();
for (K k2 : p.m.keySet()) {
V v2 = p.m.get(k2);
int h = k2.hashCode() & ((1 << gd) - 1);
if ((h | (1 << p.d)) == h)
p2.put(k2, v2);
else
p1.put(k2, v2);
}
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < pp.size(); ++i)
if (pp.get(i) == p)
l.add(i);
for (int i : l)
if ((i | (1 << p.d)) == i)
pp.set(i, p2);
else
pp.set(i, p1);
p1.d = p.d + 1;
p2.d = p1.d;
} else
p.put(k, v);
}
public V get(K k) {
return getPage(k).get(k);
}
public static void main(String[] args) {
int N = 500000;
Random r = new Random();
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
l.add(i);
}
for (int i = 0; i < N; ++i) {
int j = r.nextInt(N);
int t = l.get(j);
l.set(j, l.get(i));
l.set(i, t);
}
EH2<Integer, Integer> eh = new EH2<Integer, Integer>();
for (int i = 0; i < N; ++i) {
eh.put(l.get(i), l.get(i));
}
for (int i = 0; i < N; ++i) {
System.out.printf("%d:%d , ", i, eh.get(i));
if (i % 10 == 0)
System.out.println();
}
}
}
A Java implementation of linear hashing
[edit | edit source]( usable for simple database indexing of arbitrary size, (almost ?) )
This code evolved out of a need for a bigger Java HashMap. Originally, a Java HashMap standard object was used as a Map to index a heap like database file ( DBF format). But then, a file was encountered with so many records that the OutOfMemoryError was being thrown, so linear hashing seemed like a reasonably simple algorithm to use as a disk based index scheme.
Initially, linear hashing was implemented behind the Java Map interface, mainly the put(k,v) and get(k,v) methods. Generics was used, in order not to get too involved in the key and value details.
debugging to achieve functionality
[edit | edit source]Custom dumps to System.err was used to verify that blocks were being created, filled, and overflow blocks were of expected number if they existed ( no. = 1 ). This was all done in a purely in-memory implementation.
Later, the standard Java decoupling was introduced, where the original LHMap2 class accepted listeners to events, such as when a block was needed. The listener was then implemented as a block file manager, loading blocks into the block list of the memory LHMap2 object whenever a null block was encountered on the block list, and checking whether virtual machine runtime free memory was low, and retiring blocks using just a basic first-to-last-listed cache removal algorithm (not least recently used (LRU), not least often used ) by saving them to disk file, and then actively invoking the system garbage collector.
Because an application use case existed, which was to externally index a large DBF table, this use case was used as the main test harness for the algorithm implementation.
package linearhashmap;
import java.io.Externalizable;
import java.io.IOException;
import java.io.ObjectInput;
import java.io.ObjectOutput;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.TreeMap;
import java.util.TreeSet;
/**
*
* @param <K>
* key type , must implement equals() and hashCode()
* @param <V>
* value type
*
*
*/
public class LHMap2<K, V> implements Map<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 3095071852466632996L;
/**
*
*/
public static interface BlockListener<K, V> {
public void blockRequested(int block, LHMap2<K, V> map);
}
List<BlockListener<K, V>> listeners = new ArrayList<BlockListener<K, V>>();
// int savedBlocks;
int N;
int level = 0;
int split = 0;
int blockSize;
long totalWrites = 0;
List<Block<K, V>> blockList = new ArrayList<Block<K, V>>();
public void addBlockListener(BlockListener<K, V> listener) {
listeners.add(listener);
}
void notifyBlockRequested(int block) {
for (BlockListener<K, V> l : listeners) {
l.blockRequested(block, this);
}
}
public LHMap2(int blockSize, int nStartingBlocks) {
this.blockSize = blockSize;
this.N = nStartingBlocks;
for (int i = 0; i < nStartingBlocks; ++i) {
addBlock();
}
Runtime.getRuntime().addShutdownHook(new Thread(new Runnable() {
@Override
public void run() {
showStructure();
}
}));
}
public static class Block<K, V> implements Externalizable {
/**
*
*/
int j = 0;
Block<K, V> overflow = null;
LinkedList<K> keyList = new LinkedList<K>();
LinkedList<V> valueList = new LinkedList<V>();
transient private LHMap2<K, V> owner;
transient private Map<K, V> shadow = new TreeMap<K, V>();
private boolean changed = false;
private int size = 0;
public LHMap2<K, V> getOwner() {
return owner;
}
public void setOwner(LHMap2<K, V> owner) {
this.owner = owner;
Block<K, V> ov = overflow;
while (ov != null) {
overflow.setOwner(owner);
ov = ov.overflow;
}
}
public Block() {
super();
}
public Block(LHMap2<K, V> map) {
setOwner(map);
}
public V put(K k, V v) {
setChanged(true);
V v2 = replace(k, v);
if (v2 == null) {
++size;
if (keyList.size() == getOwner().blockSize) {
if (overflow == null) {
getOwner().blockOverflowed(this, k, v);
} else {
overflow.put(k, v);
}
} else {
keyList.addFirst(k);
valueList.addFirst(v);
}
}
return v2;
}
void setChanged(boolean b) {
changed = b;
}
public Map<K, V> drainToMap(Map<K, V> map) {
while (!keyList.isEmpty()) {
K k = keyList.removeLast();
V v = valueList.removeLast();
map.put(k, v);
}
if (overflow != null)
map = overflow.drainToMap(map);
garbageCollectionOverflow();
return map;
}
public void updateMap(Map<K, V> map) {
Iterator<K> ik = keyList.descendingIterator();
Iterator<V> iv = valueList.descendingIterator();
while (ik.hasNext() && iv.hasNext()) {
map.put(ik.next(), iv.next());
}
if (overflow != null)
overflow.updateMap(map);
}
private void garbageCollectionOverflow() {
if (overflow != null) {
overflow.garbageCollectionOverflow();
overflow = null;
}
}
public void addOverflowBucket() {
// assert overflow is needed
if (keyList.size() < getOwner().blockSize)
return;
if (overflow == null) {
overflow = new Block<K, V>(getOwner());
} else {
overflow.addOverflowBucket();
}
}
public V replace(K key, V v2) {
if (overflow != null) {
V v = overflow.replace(key, v2);
if (v != null)
return v;
}
Iterator<K> i = keyList.listIterator();
int j = 0;
while (i.hasNext()) {
if (key.equals(i.next())) {
V v = valueList.get(j);
if (v2 != null) {
valueList.set(j, v2);
}
return v;
}
++j;
}
return null;
}
public boolean isChanged() {
return changed;
}
@Override
public void readExternal(ObjectInput arg0) throws IOException,
ClassNotFoundException {
int sz = arg0.readInt();
for (int i = 0; i < sz; ++i) {
K k = (K) arg0.readObject();
V v = (V) arg0.readObject();
shadow.put(k, v);
}
}
public void loadFromShadow(LHMap2<K, V> owner) {
setOwner(owner);
Block<K, V> b = this;
for (K k : shadow.keySet()) {
if (b.keyList.size() == owner.blockSize) {
Block<K, V> overflow = new Block<K, V>(owner);
b.overflow = overflow;
b = overflow;
}
b.keyList.add(k);
b.valueList.add(shadow.get(k));
}
shadow.clear();
}
@Override
public void writeExternal(ObjectOutput arg0) throws IOException {
if (!changed)
return;
Map<K, V> map = new TreeMap<K, V>();
updateMap(map);
int sz = map.size();
arg0.writeInt(sz);
for (K k : map.keySet()) {
arg0.writeObject(k);
arg0.writeObject(map.get(k));
}
setChanged(false);
}
}
void init() {
for (int i = 0; i < N; ++i) {
addBlock();
}
}
/**
* @param hashValue
* @return a bucket number.
*/
int getDynamicHash(int hashValue) {
long unsignedHash = ((long) hashValue << 32) >>> 32;
// ^^ this long cast needed
int h = (int) (unsignedHash % (N << level));
// System.err.println("h = " + h);
if (h < split) {
h = (int) (unsignedHash % (N << (level + 1)));
// System.err.println("h < split, new h = " + h);
}
return h;
}
@Override
public V put(K k, V v) {
++totalWrites;
int h = getDynamicHash(k.hashCode());
Block<K, V> b = getBlock(h);
b.put(k, v);
return v;
}
public long getTotalWrites() {
return totalWrites;
}
private Block<K, V> getBlock(int h) {
notifyBlockRequested(h);
return blockList.get(h);
}
void blockOverflowed(Block<K, V> b, K k, V v) {
splitNextBucket();
b.addOverflowBucket();
b.put(k, v);
}
private void splitNextBucket() {
Block<K, V> b = getBlock(split);
TreeMap<K, V> map = new TreeMap<K, V>();
b.drainToMap(map);
addBlock();
System.err.printf("split N LEVEL %d %d %d \n", split, N, level);
if (++split >= (N << level)) {
++level;
split = 0;
}
for (K k : map.keySet()) {
V v = map.get(k);
int h = getDynamicHash(k.hashCode());
System.err.println(h + " ");
Block<K, V> b2 = getBlock(h);
b2.put(k, v);
}
}
private Block<K, V> addBlock() {
Block<K, V> b = new Block<K, V>(this);
blockList.add(b);
return b;
}
@Override
public void clear() {
blockList = new ArrayList<Block<K, V>>();
split = 0;
level = 0;
totalWrites = 0;// savedBlocks = 0;
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return values().contains(value);
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
TreeSet<Map.Entry<K, V>> set = new TreeSet<Map.Entry<K, V>>();
Set<K> kk = keySet();
for (K k : kk) {
final K k2 = k;
set.add(new Entry<K, V>() {
@Override
public K getKey() {
return k2;
}
@Override
public V getValue() {
return get(k2);
}
@Override
public V setValue(V value) {
return put(k2, value);
}
});
}
return set;
}
@Override
public V get(Object key) {
int h = getDynamicHash(key.hashCode());
Block<K, V> b = getBlock(h);
return b.replace((K) key, null);
}
@Override
public boolean isEmpty() {
return size() == 0;
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
kk.addAll(b.keyList);
Block<K, V> ov = b.overflow;
while (ov != null) {
kk.addAll(ov.keyList);
ov = ov.overflow;
}
}
return kk;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public V remove(Object key) {
return null;
}
@Override
public int size() {
long sz = longSize();
return (int) (sz > Integer.MAX_VALUE ? Integer.MAX_VALUE
: sz);
}
public long longSize() {
long sz = 0;
for (Block<K, V> b : blockList) {
Block<K, V> b1 = b;
while (b1 != null) {
sz += b1.size;
b1 = b.overflow;
}
}
return sz;
}
@Override
public Collection<V> values() {
ArrayList<V> list = new ArrayList<V>();
Set<K> kk = keySet();
for (K k : kk) {
list.add(get(k));
}
return list;
}
private void showStructure() {
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
Block<K, V> ov = b.overflow;
int k = 0;
while (ov != null) {
ov = ov.overflow;
++k;
}
System.out.println("Block " + i + " size " + b.keyList.size()
+ " overflow blocks = " + k);
}
}
}
Each block is a file in this implementation, because blocks are variably sized here to account for generics and variable sized key and value pairs, and overflow blocks are conceptual, not actual as on disc storage, because the block's contents and that of its overflow bucket(s), are saved as a list of alternating keys and values in this implementation. Methods for saving and loading to Object streams was used in a standard java customized object persistence way by implementing the Externalizable interface in the Block data class.
package linearhashmap;
import java.io.ByteArrayInputStream;
import java.io.ByteArrayOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.ObjectInputStream;
import java.io.ObjectOutputStream;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Random;
/**
* This class manages the LHMap2 class block disk swapping, and saves and load an instance of the LHMap2 class.
* It has been used to externally index a legacy file based database of 100,000 record master table, and 1,000,000 record
* sized child tables, and accounts for heap space available in the java virtual machine, so that OutOfMemory errors
* are avoided when the heap space is low by putting blocks back on files, and garbage collecting them.
* The main performance bottleneck appeared when loading a million record table for an index , on initial creation
* of the index.
* @author doctor
*
* @param <K>
* @param <V>
*/
public class LHMap2BlockFileManager<K, V> implements
LHMap2.BlockListener<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 2615265603397988894L;
LHMap2BlockFileManagerData data = new LHMap2BlockFileManagerData(
new byte[10000], new Random(), 0, new ArrayList<Integer>(), 0);
public LHMap2BlockFileManager(File baseDir, String name, int maxBlocks,
double unloadRatio) {
data.home = new File(baseDir, name);
if (!data.home.exists())
data.home.mkdir();
this.data.maxBlocks = maxBlocks;
this.data.unloadRatio = unloadRatio;
}
@Override
public void blockRequested(int block, LHMap2<K, V> map) {
LHMap2.Block<K, V> b = map.blockList.get(block);
if (b == null) {
int tries = 3;
File f = new File(data.home, Integer.toString(block));
do {
if (f.exists())
break;
if (!f.exists()) {
if (--tries >= 0)
fatal(block);
try {
Thread.sleep(100);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
} while (true);
try {
ByteArrayInputStream bis = new ByteArrayInputStream(data.buf);
FileInputStream fis = new FileInputStream(f);
int sz = fis.read(data.buf);
fis.close();
addByteStats(sz);
ObjectInputStream ois = new ObjectInputStream(bis);
b = new LHMap2.Block<K, V>();
b.readExternal(ois);
ois.close();
b.loadFromShadow(map);
map.blockList.set(block, b);
--data.retired;
} catch (FileNotFoundException e) {
e.printStackTrace();
fatal(block);
} catch (IOException e) {
e.printStackTrace();
fatal(block);
} catch (ClassNotFoundException e) {
e.printStackTrace();
fatal(block);
}
}
int size = map.blockList.size();
try {
long freeMemory = Runtime.getRuntime().freeMemory();
long limitMemory = (long) (data.avgBlockSize * data.unloadRatio * size);
if (block % 30 == 0)
System.err.println("free memory =" + freeMemory + " limit "
+ limitMemory);
if (map.split % 20 == 19) {
// this is just to add statistics before really needing to retire
retireRandomBlock(map, block);
++data.retired;
} else if (freeMemory < limitMemory) {
for (int i = 0; i < size / 4; ++i) {
retireRandomBlock(map, block);
++data.retired;
}
System.runFinalization();
System.gc();
}
} catch (FileNotFoundException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
}
}
private void addByteStats(int sz) {
++data.avgCount;
data.avgBlockSize = (int) ((data.avgBlockSize
* (data.avgCount - 1) + sz) / data.avgCount);
}
public void retireRandomBlock(LHMap2<K, V> map, int notThisOne)
throws FileNotFoundException, IOException {
int pick = 0;
int size = map.blockList.size();
LHMap2.Block<K, V> b = null;
for (pick = 0; pick < size
&& (pick == notThisOne || (b = map.blockList.get(pick)) == null); ++pick)
;
if (pick < size)
retireOneBlock(map, pick, b);
}
private void retireOneBlock(LHMap2<K, V> map, int pick, LHMap2.Block<K, V> b)
throws IOException, FileNotFoundException {
if (b == null)
return;
if (b.isChanged()) {
// System.err.println("Retiring " + pick);
File f = new File(data.home, Integer.toString(pick));
ByteArrayOutputStream bos = new ByteArrayOutputStream();
ObjectOutputStream oos = new ObjectOutputStream(bos);
b.writeExternal(oos);
oos.flush();
oos.close();
FileOutputStream fos = new FileOutputStream(f);
byte[] bb = bos.toByteArray();
fos.write(bb);
fos.flush();
fos.close();
if (bb.length > data.buf.length) {
data.buf = bb;
}
}
map.blockList.set(pick, null);
b = null;
}
private void fatal(int block) {
Exception e = new Exception();
try {
throw e;
} catch (Exception e2) {
e2.printStackTrace();
}
System.err.println("block " + block
+ " requested and it is not in blocklist and not a file");
for (int i : data.retirees) {
System.err.print(i + " ");
}
System.err.println(" were retired");
System.exit(-2);
}
public static boolean metaExists(File indexDir, String name) {
File home = new File(indexDir, name);
return new File(home, "LinearMap2").exists();
}
public static <K, V> LHMap2<K, V> load(File baseDir, String name)
throws FileNotFoundException, IOException, ClassNotFoundException {
File home = new File(baseDir, name);
File f2 = new File(home, "LinearMap2");
ObjectInputStream ois = new ObjectInputStream(new FileInputStream(f2));
LHMap2<K, V> map = (LHMap2<K, V>) ois.readObject();
ois.close();
loadBlocks(map);
return map;
}
private static <K, V> void loadBlocks(LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(map);
int size = map.blockList.size();
for (int i = 0; i < size; ++i) {
mgr.blockRequested(i, map);
}
}
public static <K, V> LHMap2BlockFileManager<K, V> getBlockManagerListener(
LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = (LHMap2BlockFileManager<K, V>) map.listeners
.get(0);
return mgr;
}
public static void save(File indexDir, String name,
LHMap2<?, ?> offsetMap) throws FileNotFoundException, IOException {
retireAllBlocks(offsetMap);
File home = new File(indexDir, name);
File f2 = new File(home, "LinearMap2");
ObjectOutputStream oos = new ObjectOutputStream(
new FileOutputStream(f2));
oos.writeObject(offsetMap);
oos.close();
}
private static <K, V> void retireAllBlocks(LHMap2<K, V> offsetMap)
throws FileNotFoundException, IOException {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(offsetMap);
int sz = offsetMap.blockList.size();
for (int i = 0; i < sz; ++i) {
LHMap2.Block<K, V> b = offsetMap.blockList.get(i);
// offsetMap.blockList.set(i, null); // mark for reloading as block
// destroyed after writing
if (b != null) {
mgr.retireOneBlock(offsetMap, i, b);
}
}
}
}
package linearhashmap;
import java.io.File;
import java.io.Serializable;
import java.util.List;
import java.util.Random;
public class LHMap2BlockFileManagerData implements Serializable{
/**
*
*/
private static final long serialVersionUID = 1L;
public byte[] buf;
public Random r;
public File baseDir;
public File home;
public int maxBlocks;
public int retired;
public double unloadRatio;
public List<Integer> retirees;
public int avgBlockSize;
public long avgCount;
public LHMap2BlockFileManagerData(byte[] buf, Random r, int retired,
List<Integer> retirees, long avgCount) {
this.buf = buf;
this.r = r;
this.retired = retired;
this.retirees = retirees;
this.avgCount = avgCount;
}
}
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
References
[edit | edit source]- ↑ The simplest hash table schemes -- "open addressing with linear probing", "separate chaining with linked lists", etc. -- have O(n) lookup time in the worst case where (accidentally or maliciously) most keys "collide" -- most keys are hashed to one or a few buckets. Other hash table schemes -- "cuckoo hashing", "dynamic perfect hashing", etc. -- guarantee O(1) lookup time even in the worst case. When a new key is inserted, such schemes change their hash function whenever necessary to avoid collisions.
- ↑ Wikipedia: Comparison of programming languages (mapping) shows how many programming languages provide hash table functionality.
