Circuit Idea/How the Wilson current mirror equalizes the currents
Circuit idea: "Moving" one base current from the input to the output leg of the circuit.

How do we reveal the secrets of Wilson current mirror?
[edit | edit source]The great challenge
[edit | edit source]It was a challenge to reveal the idea behind the popular BJT current mirror;[1][2][3][4] but it is a great challenge to disclosure the mystery of the legendary Wilson current mirror (Fig. 1)! Maybe, there is nothing so simple (containing only three transistors) and, at the same time, so incomprehensible and misunderstood circuit as Wilson current mirror. There are many resources that have tried to explain this sophisticated, ingenious and elegant circuit solution by using formal methods. But they do not give us what we need, first and foremost, as human beings – the basic idea(s) behind this odd, strange and exotic circuit. It is a great paradox to calculate circuit without knowing the basic idea behind it!?! So, before showing in detail how to calculate the electronic circuit we have first to show what the very basic idea is behind the circuit.
Questions to be answered
[edit | edit source]Looking at the circuit diagram (Fig. 1), we need to answer dozens of questions that are never answered.
What does the transistor Q3 do in this circuit? What is its function there? Why this current mirror contains another simpler current mirror Q1 and Q2 (why an additional simple current mirror is nested in the main current mirror)?!?! What is its function? But why this simple current mirror is reversed (why the transistors Q1 and Q2 are swapped)? Why the Q1's collector current serves as an input quantity and the Q2's collector current as an output one (we thought the Q2's collector current was the input quantity and the Q1's collector current was the output quantity)? Are there negative feedbacks in Wilson current mirror? If there are, what are they? How many negative feedbacks there are? What are their functions (why they are included)? What and how do they control – voltage or current? What are the advantages of Wilson current mirror versus current mirror with emitter degeneration? How does Wilson current mirror keep up an almost constant current (why it has an almost infinite output resistance)? Why the input and output currents are almost equal (what is the trick)? Has a MOSFET Wilson current mirror some advantage versus the simple MOSFET current mirror?
Heuristic approach
[edit | edit source]Since there are no satisfactory answers to the questions above, let's try to disclose the mystery of the famous circuit by ourselves; let's answer these questions relying mainly on our human intuition, imagination and common sense. Please, just forget all kinds "cut-and-dried" citations and begin thinking by yourself to make an exciting discussion here!
The best way of understanding and presenting electronic circuits is by reinventing them, by showing the circuit evolution.[5][6] So, let's imagine how Wilson has invented his current mirror by reinventing and building it, in order to grasp the basic ideas behind the circuit and then to present them in an attractive manner to readers. Of course, it would be wonderful if the very Wilson, if he is still alive, would expose how he has invented the famous circuit. Only, it is a well-known truth that, as a rule, due to variety of reasons, inventors do not show willingness for disclosing the process of invention.[7]
The imperfections of the simple current mirror
[edit | edit source]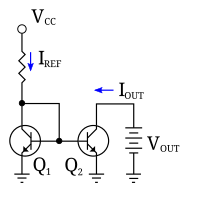
BJT. The simple BJT current mirror (Fig. 2) has two main imperfections: first, the output current differs from the input one because of the two base currents that the transistors Q1 and Q2 "suck" from the input current; second, the output current varies when the output (load) voltage changes because of the Early effect. These are completely different problems; there is no any connection between them. Wilson was clever; in the early 60's, he "killed two birds with one stone" – adding only one transistor to the humble current mirror, he managed to remove both imperfections of the simple BJT current mirror!
MOSFET. The simple MOSFET current mirror has the second imperfection only because there are no gate currents. And even in this case the Wilson idea is beneficial; it enables the MOSFET Wilson current source to keep up a constant output current (see another story about the famous circuit).
How the Wilson current mirror equalizes the input and output currents
[edit | edit source]In order to justify the name current mirror, in this circuit the output current has to follow exactly the input current. So, regarding to the current magnitudes, a current mirror is actually a current follower. The Wilson current mirror meets closely this requirement. Here we will show how the Wilson current mirror eliminates the difference between the input and output currents.
Posing the first problem of the BJT simple current mirror
[edit | edit source]
In our routine, we frequently need to equalize two quantities having different magnitudes. Let's, for example, scrutinize a popular mechanical analogy: imagine two heaps of weights are placed on the two sides of ordinary mechanical scales – for concreteness, 4 grams on the left pan and 6 grams on the right pan Fig. 3). Since there is a difference of two grams between them (4 < 6), the scales are unbalanced (inclined to the left). This mechanical analogy corresponds to the circuit of the BJT simple current mirror (Fig. 4a) consisting of transistors with ß = 4 (Fig. 4b) if we assume that one base current corresponds to one gram. The problem is how to equalize the two weights, respectively the two currents.
More generally and more precisely speaking, we want to create a copy of an original quantity but two entities are lost from the original before we make the copy. The problem is how to compensate the loss.


For this purpose, let's try to present the ideas behind this legendary circuit and its operation in a more attractive way. We know, in order to grasp the ideas behind circuits, we may visualize electrical quantities voltage and current by voltage bars and current loops. In the case of current mirrors, it is extremely interesting to show where currents flow and to visualize their magnitudes. So, we may draw two kinds of figures in this section. The first, placed on the left side of the page, will represent the respective circuit diagram with superimposed voltage and current "maps". The second, placed on the right side of the page, will visualize the magnitudes of the currents by fat lines whose thickness is proportional to the magnitude of the corresponding current.
Let's begin with presenting the simple BJT current mirror in such an attractive way (Fig. 4). You can see on the left picture (Fig. 4a) where currents flow and particularly how the transistors "suck" two base currents. The currents are represented by closed loops (every current finishes where it has started). The lines on the right picture (Fig. 4b) are actually sections of the closed current loops from Fig. 4a. The transistors are shown with extremely low ß (on this figure ß = 4) for convenience, in order to present the base currents by thick enough lines.
Equalizing the currents by "pushing" 2IB to IIN...
[edit | edit source]
How do we solve the problem of the two "sucking" IB in the simple BJT current mirror? Let's begin thinking relying on our human common sense...
We know from our daily routine the great idea of compensation: if there are some losses of "something", we might compensate them by adding the same quantity of this "thing". In our mechanical analogy, we may just take two grams from the weight box and add them to the left pan, in order to balance the scales (4 + 2 = 6) – Fig. 5.
Generally speaking, here we compensate the loss by adding two items to the original (we correct completely the original).


Well, let's put in practice this simple idea! "Electrically" speaking, since the transistors "suck" two IB, the first idea that might dawn on us is, of course, to add the same two IB (Fig. 6b). Then IOUT = IIN – 2IB + 2IB = IIN. For this purpose, we have to connect an injecting current source 2IB to the T1's collector – Fig. 6a (more precisely speaking, this is rather a current-stable resistor than a source).
Only, this has to be not an ordinary constant current source but a "following" current source that copies the current 2IB. What an idiocy! It turns out that we need another current mirror?!?
...by "sucking" 2IB from IOUT...
[edit | edit source]
With the same success, in our mechanical analogy, we may subtract two grams from the right pan and place them to the weight box, in order to balance the scales again (4 = 6 – 2) – Fig. 7. So, we may reason in similar way about the circuit...
Generally speaking, now we compensate the loss by adding two items to the copy (we correct completely the copy).


Let's now apply this "mechanical" idea to our electrical circuit... Above, we have added the two compensating base currents by injecting them into the input current (the "original" quantity). But with the same success we might add them to the output current (the "copy") by "sucking" 2IB from it (Fig. 8b). Now IIN = IOUT – 2IB + 2IB = IOUT. In this case, we have to connect a sinking current source 2IB to the T2's collector (Fig. 8a).
As before, this has to be not an ordinary constant current source but a "following" current source that copies the current 2IB.
...by both "sucking" IB from IOUT and "pushing" IB to IIN...
[edit | edit source]
We have almost reached the great Wilson's current equalizing idea... Well, let's continue thinking. It is inconvenient to create 2IB; it is easier to produce (source or sink) only IB. What do we do then?
Let's go back again to our favorite mechanical analogy; it may help us... And really, instead to add as many as two grams to the left pan or to subtract two grams from the right pan, we may balance the scales by adding only one gram from the weight box to the left pan and subtracting one gram from the right pan placing it to the weight box (4 + 1 = 6 – 1) – Fig. 9.
Generally speaking, now we compensate the loss by adding one item to the original and subtracting one item from the copy (we compensate partially both the original and the copy).


Let's now put in practice this interesting idea... For this purpose, we might connect an injecting current source IB between the positive rail and the T1's collector and a sinking current source IB between the T2's collector and the ground – Fig. 10a. In this way, we add one base current to the input current and another base current to the output current (Fig. 10b). As a result, the two currents become equal:
...by "moving" IB from IOUT to IIN...
[edit | edit source]
We have really reached the great Wilson's current equalizing idea... We may develop further the powerful idea from the mechanical analogy above just moving one gram from the right pan to the left pan! Well, let's say it again: instead to add one gram to the left pan and to subtract one gram from the right pan, we may balance the scales just by moving one gram from the left to the right pan (4 + 1 = 6 – 1) – Fig. 11. But this is not only Wilson's idea! Every vendor from the past knew and used this clever trick!
Generally speaking, now we compensate the loss by moving one item from the original (before the loss) to the copy. Thus we compensate partially both the original and the copy; we redistribute the compensating items.


Let's now put in practice this clever trick... As above, we add one base current to the input current and another base current to the output current (Fig. 12b). As a result, the two currents become again equal:
Here is the great Wilson's idea! In order to equalize the two currents, he has just "moved" one base current from the one to the other leg!
Don't you think this connection resembles a bridge circuit (the current source serves as a "bridge" between the two circuit legs)?
Realizing the Wilson's current equalizing idea
[edit | edit source]Once we revealed the brilliant Wilson's idea we have only to implement it. Let's continue thinking...


What is this mysterious element that can consume IB from one part of the circuit and can add it to the other part? Of course, there is nothing more natural for a bipolar transistor to do that "donkey work"! It "sucks" IB from the point where its base is connected and adds it to the emitter current. Then let's connect a transistor T3 in the left leg of our circuit (Fig. 13a)!
Wonderful, now it sinks the current IB from IOUT and injects the same current IB into IIN (Fig. 13b)! So, we have managed to reveal the role of the mysterious transistor T3!
In the circuit of Wilson current mirror, the transistor T3 "moves" one base current from the right to the left leg of the circuit.
Reversing the circuit to obtain the true Wilson current mirror
[edit | edit source]Only, there is something wrong in this connection because we can't change the input current in the left leg (by varying the resistor or the voltage). If we try to do that, the transistor T3 will resist to our intervention thus keeping up a constant current (see another story about the legendary circuit). Let's continue thinking.


Well, the transistor T3 has to adjust its base current so that its collector current to remain unchanged as we want. The only "thing" that can do this magic is the ubiquitous negative feedback that keeps up an almost constant voltage (this should be the same kind of negative feedback as this applied to the transistor T1).
But there isn't a feedback in this input part of the circuit; there is no connection between the T3's collector and base. Instead, there is a negative feedback implemented by T3 and T1 that are connected between the collector and the emitter of T2 in the output part of the circuit (see again Fig. 13a)! What do we do then?
Eureka! We may swap the two circuit legs: the output part can serve as an input one and the input part – as an output one. Thus we obtain finally a true Wilson current mirror (Fig. 14a)! Let's draw the final conclusion:
In the circuit of Wilson current mirror, the transistor T3 "moves" one base current from the left to the right leg of the circuit.
References
[edit | edit source]- ↑ Talk:Current mirror reveals the secrets behind the simple current mirror circuits.
- ↑ How to reverse current direction reveals the secret of the simple current mirror.
- ↑ Can a "diode" current mirror exist? begins revealing the secret of the current mirror by reinventing it.
- ↑ Building a BJT current mirror continues reinventing the simple BJT current mirror.
- ↑ The philosophy behind the Circuit idea Wikibook
- ↑ A heuristic approach to teaching analog electronics relies on human imagination, intuition and emotions.
- ↑ Why circuit ideas are hidden considers the fate of new circuit ideas.
Resources
[edit | edit source]Trying to explain the circuit by intuition
[edit | edit source]Paul Horowitz, Winfield Hill. The art of electronics, second edition, p 89. ISBN 0521370957. Well, let's look at page 89: "...with Q2 now sourcing the output current..." But why? Unfortunately, the famous authors have not also noticed the remarkable property of the Wilson current mirror to equalize the input and output currents.
Designing analog chips. The author has said about Wilson "...analog designers don't get Nobel prizes, they get a circuit named after them..." and about his creation "...by a happy coincidence the three base currents cancel..." But how? We would like to know!
Mechkov C., Equalizing the currents in Wilson current mirror, Computer science'2008 conference, 18–19 September 2008, Kavala, Greece. This is the same story as the presented above but it is written a bit more formal.
"Explaining" the circuit by formal methods
[edit | edit source]Wilson current mirror from Wikipedia is a typical example of formal approach in circuitry.
Wilson current mirror from Analogue Electronics wikibook uses the same formal approach.
Showing some historical facts
[edit | edit source]Analogue and mixed signal integrated circuit design gives interesting facts about the George Wilson invention. "The story goes that Barrie Gilbert had an informal contest with one George Wilson to see who could come up with the most useful three-transistor current source. George Wilson won and gave his name to this elegant and very effective design. 'As if by magic' the base current errors associated with the two-transistor source are almost completely cancelled out..." But we ask again, "Why?"
Are Op Amps Really Linear? in this article, Barrie Gilbert admits: "...the first reported monolithic JFET op amp was designed by my good friend George Wilson that threw in a new type of BJT current mirror, now widely known as the Wilson mirror...."