Analogue Electronics/Current Mirrors/Wilson


The Wilson Current Mirror
[edit | edit source]
The Wilson current mirror, named after engineer George Wilson, who invented the arrangement, is widely regarded as an ingenious and elegant solution to the finite-β error of the simple BJT current mirror.
In order for it to function correctly, the following conditions need to be met:
- Q1 and Q2 are be matched, so their collector currents are equal for the same base current
- All three transistors have the same common-emitter current gain, β
As Q1 and Q2 have the same emitter voltages (ground) and the same base voltages (as they are connected), the base currents are the same. We will term this current IB:
[W1]
From Condition 1 above, we can say that the collector currents in Q1 and Q2 are identical (IC):
[W2]
Now, from the basic BJT equations, we know that the base current of Q3 is given by:
[W3]
Similarly, the emitter current is also known:
[W4]
It is obvious from the diagram and KCL, that the following is true:
[W5]
Substituting from equations W1 and W2, we get
[W6]
Given that IC=βIB (Condition 2 and basic BJT equations), we have that
[W7]
Substituting for IE3 from equation W4,
[W8]
Rearranging to make IC the subject, we have
[W9]
Now, let's consider the reference current, IREF. By KCL, and then substituting from W2,
[W9]
From W3 and W9, we now have:
[W10]
Rearranging,
[W11]
Finally, simplifying by simple fractional addition and factorisation, we have:
[W12]
It is clear that if β is large, then β(β+2) is large, the denominator in the above expression approaches unity, and the output current, IO approaches the reference current IREF:
[W13]
However, due to the quadratic term, a very good approximation is achieved for much lower values of β than the simple current mirror. For example, transistors with a very modest β of 50 can theoretically expect a current deviation of about 0.75 μA. For a β of 150, this drops to 87 nA.
It should be noted that the Wilson Current Mirror is not a constant-current source. If the supply voltage, VCC changes, the output current will change. Suppose that the reference current, IREF, is supplied by a resistor to the supply voltage. Suppose the vBE of all the transistors is 0.7 V. Now, the voltage at the bases of Q1 and Q2 is therefore 0.7 V, as the emitters are at ground. The base of Q3 is therefore at (0.7+0.7)=1.4 V. This means that the reference current is given by:
[W14]
Thus, the output current will also be dependent on the supply voltage. A constant current source as the reference current will ensure a constant output current.
Output Resistance
[edit | edit source]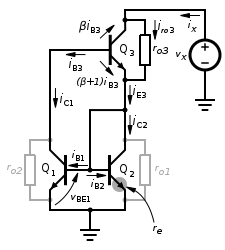
Lets consider the small-signal model on the right. The transistors have been replaced by the small-signal T-model, which has then been drawn as a large-signal BJT, with the small-signal output resistances, ro in parallel. More on this can be found here. The output resistors in Q1 and Q2 are present in this model, but they are greyed out as they do not play a part in the analysis. The reference current is deactivated in the small signal model, meaning that the base of Q3 is simply connected to the collector of Q1.
We will find the output resistance of the current mirror, Ro by applying a voltage, vx to the output and finding the relationship between this and the current that flows in the output, ix. Firstly, notice that the base current flows out of the base of Q3, and that the collector and emitter currents in Q3 are therefore reversed (these are in the large-signal BJT only and are NOT the same as iC3 and iE3, although iB3 is the same in both). This is just to remove negatives from the analysis. If they are not reversed, the analysis will still give the same result.
Firstly, recall that Q1 and Q2 are matched, so the collector currents are the same, as are the base currents. Let us call the collector currents in these simply i. Also the collector current of Q1 is equal to the (outward) base current of Q3. This leads to the following expressions:
From the common-emitter equations, we also know the base currents:
From the common-emitter equations, we can also state the current in the collector and emitter of the large signal BJT in Q3. These are shown on the diagram. From KCL, we can also show that at the collector-base connection of Q2,
The base-emitter voltage of Q1 or Q2, vbe1 is given by the (large signal) current in the emitter multiplied by the large-signal base-emitter resistor, which is usually denoted re in the T-model:
KCL at the Q3 large-signal collector/output resistor junction (paying close attention to the directions of the currents) shows that the current in the output resistor of Q3, iro3 is given by:
By Ohm's Law, we can now work out the voltage across the output resistor:
Therefore, the voltage vx, is given by the sum of this voltage and the base-emitter voltage of Q1 or Q2:
The current ix can be found using KCL at the top of the output resistor of Q3:
The output resistance, Ro is defined as follows:
Which, after cancelling the factors of i, leads to the somewhat untidy equation:
Now, re is given by the equation . See the T-model pages for more detail on this. Notice that the two fraction involving β cancel out, leaving just . Since gm is usually on the order of 20mS, this term is about 50Ω. Considering that this is going to be added to a term involving β's (in the region of 100) multiplied by ro (on the order of 50kΩ), this term is insignificant. We can now write, to a very good approximation,
Let's multiply top and bottom by β to emphasise the next point:
Now, we can say that both the "2" terms are insignificant compared to terms involving β when β is large. We can also say that the 2β term on the top of the fraction is insignificant compared to β2. We will see in moment, that although this may seem like a gross approximation, it is in fact more than accurate enough for practical purposes. Removing these terms and dividing by β top and bottom, our equation is now simply
For a β of 100, an ro of 50kΩ and an re of 50Ω, the value calculated using the full equation is 2.53MΩ, while the approximation gives 2.5MΩ. So, we can see that the approximation is well worth the massive simplification in the equation, especially as the practical value will very likely vary by more than this discrepancy anyway. This also shows the enormous output impedance of a Wilson current mirror, even for modest values of β.































