Real Analysis/Applications of Derivatives
| ←Differentiation | Real Analysis Applications of Derivatives |
Riemann integration→ |
Derivatives are also used in theorems. Even though this chapter is titled "Applications of Derivatives", the following theorems will only serve as much application as any other mathematical theorem does in relation to the whole of mathematics. The following theorems we will present are focused on illustrating features of functions which are useful in an identification sort-of-sense. Since graphical analysis is constructed using a different set of analyses, the theorems presented here will instead be applicable to only functions. However, all of what this chapter will discuss on has a graphical component, which this chapter may make reference to in order to more easily bridge a connection. In Real Analysis, graphical interpretations will generally not suffice as proof.
Higher Order Derivatives
[edit | edit source]To begin our construction of new theorems relating to functions, we must first explicitly state a feature of differentiation which we will use from time to time later on in this chapter.
Suppose be differentiable
Let be differentiable for all . Then, the derivative of is called the second derivative of and is written as .
What we have stated is that there may exist a second derivative, which is a derivative of a derivative. We will further define second derivative at a to refer to a derivation of a derivative only at the value a.
Similarly, we can define the nth-derivative of , written as
Foundation Theorems
[edit | edit source]This short section will first introduce some intriguing properties that differentiation has to offer. Concepts here will help shed insight into the latter theorems. In the previous chapter, you have been introduced to the concept that being able to take the derivative of a function implies continuity at that point. This is important to remember as each theorem will use concepts that continuity offers to justify their proof.
In this section, we will provide more groundwork.
Minimum and Maximum Points
[edit | edit source]We will now introduce two new concepts about functions, both of which you may be familiar with. We will then justify its existence by creating a theorem to go along with it.
Definitions
[edit | edit source]We will define a maximum point for a function on an interval A as such:
We will define a minimum point for a function on an interval A as such:
Both definitions complement each other, as they refer to opposing inequalities.
Existence of Minimum and Maximum Points Theorem
[edit | edit source]This proof will justify the minimum and maximum point definition by relating it to differentiation, namely through this statement
Theorem Given a function defined on which is both differentiable at and it is a maximum or minimum point, its derivative at is equal to 0
The proof is straightforward: it invokes the definition of differentiation to assert the result of the theorem.
| Application of definition. Note that the variable is any number such that the addition of it with α is still within the interval . | ||
| Algebraic Manipulations | ||
| Divide by h, which means two cases because it may be negative (and that means an inequality change!) | ||
| One sided limits are applied, which is algebraically valid if applied to both sides (which it is; limit of 0 is 0) | ||
| Merge the one-sided limits together to form a full limit, which demands an equal limit to be valid. Only one value is equal: 0. | ||
To prove the case for the minimum point, you simply reverse the initial inequality. Note that the proof will still yield the same result, namely that the derivative of the minimum point is also 0.
Convexity and Concavity
[edit | edit source]
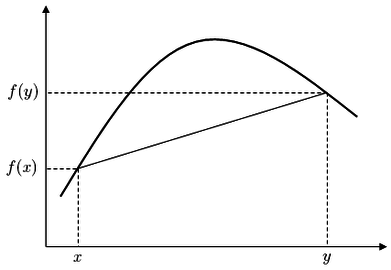
Likewise, we will now create two more complementary definitions related to functions. These are the convexity and concavity definitions, a method of describing functions based on how the function relates to some given reference point, in this case a line. Convexity and concavity mirror the visual, physical description of convex and concave, although they are described in reference to how the line protrudes out from the function instead of the other way around, so that graphically the definitions appear reversed.
Definitions
[edit | edit source]We will define convexity of a function over an interval as such:
Given , the secant line joining and for all
We will define concavity of a function over an interval as such:
Given , the secant line joining and for all
If you take the definition of convexity as is, the mathematical description will appear as such
Which can be expressed differently so that although it appears more foreign, it is more applicable to theorems.
Likewise, the definition of concavity will simply have the inequality reversed.
This definition is the one we will use in future convexity/concavity theorems in this chapter.
Corollary
[edit | edit source]The first corollary that comes from this definition is a simple, yet often not explained facet of properties coming from negating a function
Corollary Given a convex function over the interval , is concave over the interval
| Application of convexity definition. | |
| Supposing its negation and after some algebraic manipulations |
|
| The definition of concavity is reached. | |
Tangent of a Function
[edit | edit source]Conceptually, finding the derivative means finding the slope of the tangent line to the function. Thus the derivative can be thought of as a linear, or first-order, approximation of the function. This can be graphically represented by creating a tangential line using the derivative of at through this formula
Which is clearly the equation of a line translated to the point through function manipulations.
"Differentiation Produces Tangents" Theorem
[edit | edit source]This unnamed theorem is the theorem that proves our definition earlier is not wrong. Using it, our understanding of what differentiation graphically represents; a tangent line, should become rigorously clear. It is so ingrained that just in the section above, we defined what a tangent line is in reference to differentiation. There, we will prove the validity of such a statement.
How do we prove this notion? Well, we simply prove the physical concept of what being tangential is: if we have a perfectly round surface, we can imagine balancing a ruler on it and that the ruler is only balancing on one point. This physical description implies that there is a gap everywhere else, and this concept of a "gap" will be expressed mathematically by the inequality between the value of the tangent line to the curved function.
Theorem Given a function and any tangent line through some point , this tangent line will be exclusively greater than or less than the function except for , which will be equal
To begin our proof, we must first simplify the problem and assign a direction to our proof. Overall, we will [ADD OVERALL OBJECTIVE OF PROOF]
Now, we will assign cases to allow us to use our known properties properties.
Case 1: Convex
[edit | edit source]The first case we will tackle is when the function is convex over some interval .
| Suppose we animate the definition of a derivative. This means that given the definition, we analyze all values of h as it approaches 0. | |
| By definition, this is not a tangent line, but a secant line. | |
| and because | |
Case 3: Neither
[edit | edit source]Theorems about Tangents
[edit | edit source]These three theorems all relate to how a tangent relates to intersections of the function and the graph.
Rolle's Theorem
[edit | edit source]Rolle's Theorem is the introductory theorem for derivatives. This proof will open up access to many other proofs in this chapter, especially the next big differentiation theorem found in the next section, Mean Value Theorem. Rolle's Theorem is described below
Theorem Given a function which is both continuous on and differentiable on and , there exists such that
Proof
[edit | edit source]We will present two proofs for Rolle's Theorem. The first utilizes the Existence of Minimum and Maximum Points Theorem, while the second utilizes a contradiction.
Proof 1
[edit | edit source]We will first remove an obvious case. If the function is a constant function, then .
If the function is not a constant function, let such that . In other words, we know that there exists a supremum that exists in the continuous function as a consequence of the Minimum-maximum theorem. This supremum mimics the maximum point by definition.
Since it mimics the definition of a maximum, we can apply the Existence of Minimum and Maximum Points Theorem to prove the statement .
The minimum works the same way, except that we will find an infimum instead of a supremum and that the infimum definition will match up with the minimum point. The Existence of Minimum and Maximum Points Theorem still holds.
Proof 2
[edit | edit source]We will first remove an obvious case. If the function is a constant function, then .
If the function is not a constant function, let such that . In other words, we know that there exists a supremum that exists in the continuous function as a consequence of the Minimum-maximum theorem. This supremum mimics the maximum point by definition.
Without loss of generality, we can state that . In other words, because we have, though an application of a theorem, found a supremum that is greater than every value in the function and we ruled out the case that the function is constant, we can safely assert that this supremum is greater than at least the endpoints, by definition.
Assume that is valid. Thus, and hence, there exists such that contradicting the fact that is a maximum.
Similarly, we can show that the assumption leads to a contradiction. Thus, .
Mean Value Theorem
[edit | edit source]This theorem is a stronger version of Rolle's Theorem. This theorem's statement is boxed below
Theorem Given a function which is both continuous on and differentiable on , there exists such that
It is named the mean value theorem because graphically, this theorem states that if you have a function and its secant line, there will always be a tangent line somewhere on the function that is parallel to the secant line.
Note that it is a generalized version of Rolle's Theorem applied to secant lines connecting and instead of a horizontal secant line. You can see this in the theorem's equation by making . Because it is so similar, the proof is surprisingly similar in structure as well. However, it will require more algebra due to the nature of working with secant line segments instead of horizontal ones that can be easily zeroed.
Proof
[edit | edit source]The proof reduces the problem into one which can be solved using Rolle's Theorem by, in a sense, normalizing the graph based on the line i.e. the function in question is analyzed in the perspective of the line instead of the Cartesian grid.
| We create a new function based on the function and a linear function that uses the same slope as the secant line between the endpoints and .
Note that this linear function is not the secant line. This new function, based on continuity and differentiation theorems, maintains all continuity and differentiation properties given to the function . |
||
| We will now check to see if Rolle's Theorem can be applied to this new function. | ||
| The conditions of Rolle's Theorem is true - we can assert its conclusion, namely and work from there. |
| |
Cauchy Mean Value Theorem
[edit | edit source]This theorem is an even stronger version of the Mean Value Theorem, extending the secant line used in the Mean Value Theorem into other types of functions.
Theorem If are continuous on and differentiable on (without both having infinite derivatives at the same point) then there exists such that
Proof
[edit | edit source]Define the function as
Obviously, this function satisfies , and by Rolle's theorem, there is a such that .
Theorems about Change
[edit | edit source]Before we prove any more things about derivatives, we should define some facets about functions that we will use in the following proofs.
Definition of a "function increasing on an interval " Given a function and two numbers such that
Definition of a "function decreasing on an interval " Given a function and two numbers such that
If there is no interval mentioned, the interval is defaulted to the real numbers.
Armed with both of these definitions, we will now explore the simplistic concept that we learned derivatives represent: change. The following proofs will solidify these concepts on mathematically rigorous grounds and provide new tools to verify the properties of functions and lay out some tools that can be reformed to prove new concepts.
"Increasing Functions have Positive Change" Theorem
[edit | edit source]This theorem, which has no official name, is the proof that verifies the simplistic definition of derivatives as "measuring change". It states
Theorem Given a function such that for some interval , must also be increasing on the interval
Proof
[edit | edit source]This proof relies on asserting the conditions and deriving the conclusion using a theorem, namely the Mean Value Theorem.
We start by choosing any two points such that and assuming that for the entire interval.
Because the function is differentiable over , it is also continuous over . Therefore, all the conditions of the Mean Value Theorem are satisfied and we can use it.
After some algebraic manipulations,
As a reminder, .
Let this proof iterate for all possible combinations in the interval A. All implies , given the conditions.
Corollary
[edit | edit source]A similar proof works for a decreasing function. In fact,
Theorem Given a function such that for some interval , must also be decreasing on the interval
the proof is a mirror image of the previous proof.
"Second Derivative Indicates Local Min/Max" Theorem
[edit | edit source]This theorem, which has no official name, is the proof that allows you to know whether any critical points you found are local minimums or maximums. It states
Theorem Given a function such that and for some . is a local minimum
Proof
[edit | edit source]The proof involves using the conditions given to invoke the previous theorem's proof in order to infer the result.
We first invoke the definition of the second derivative
From there, we note that , which means that the equation now becomes
Given that , that means that the inequality needs to ensure its positive nature, which would mean that
| Because in order for , we can use the previous proof's result to state that because , must be increasing. | Because in order for , we can use the previous proof's result to state that because , must be decreasing. |
Since the continuous function goes from decreasing to increasing as increases, it must have stopped at the defined local minimum.
Corollary
[edit | edit source]A similar proof works when deducing whether local maximums can be done in the same manner. In fact,
Theorem Given a function ƒ such that and for some x. ƒ(x) is a local maximum
the proof is a mirror image of the previous proof.
Taylor's Theorem
[edit | edit source]Let
Let be differentiable on
Then, there exists such that
Proof
[edit | edit source]For the proof, we use the technique known as "Telescopic Sum"
Consider the function , given by,
, where the constant is chosen so as to satisfy
By Rolle's theorem, we have that there exists such that
Expanding, we have (be careful while applying the product rule!)
Which can be rearranged to give the telescopic sum:
That is, , or
Now, we can easily see that and that
but by choice, and hence we have:
QED























![{\displaystyle [x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bdff343d848c2b70c68b5c04a2479b14a9fef0)
![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)

![{\displaystyle A=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6edb111a0369489b1346e0c8d2ea1f44a0fe5c62)















![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle f'(x)=0\quad \forall x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21a85706f67ce378c3cf5f11eaa8efa46733e6b2)
![{\displaystyle \alpha \in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0039890b40418e3f7fec101e69abe60369ebebe)
![{\displaystyle f(c)=\sup f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d460a3237217291a86a19f4b4045b172835cbe4)



![{\displaystyle x_{1}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f03ee615e7879f20efa45f3c3c6296c14b53995)













![{\displaystyle {\begin{aligned}h'(x)&=f'(x)-\left[{\dfrac {f(b)-f(a)}{b-a}}(x-a)\right]'\\&=f'(x)-{\dfrac {f(b)-f(a)}{b-a}}\\0&=f'(c)-{\dfrac {f(b)-f(a)}{b-a}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/623eea4587e71ea18a7f2addd4b6d8226efc048b)


![{\displaystyle c\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/997256364b06acf0710e5d24da39e8c42991a249)

![{\displaystyle h:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1833b6178fc06e33367b794d4c27d8f9e1a9f36e)





























![{\displaystyle f:[a,x]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/67687ad801319b06b03b1b94cbf95dec40c82076)

![{\displaystyle [a,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/692f0edd0d40232c8a69ed5de7b142e1e343eff7)


![{\displaystyle \phi :[a,x]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/933998f5e39277d7d5e2785d6587481e4ab3c914)





![{\displaystyle =f'(c)+\left[{\tfrac {(x-c)f''(c)}{1!}}-f'(c)\right]+\left[{\tfrac {(x-c)^{2}f'''(c)}{2!}}-{\tfrac {(x-c)f''(c)}{1!}}\right]+\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4b80cf246b5d3a1bf8ea5bcf27918173b0d6fa2)
![{\displaystyle +\left[{\tfrac {(x-c)^{n-1}f^{(n)}(c)}{(n-1)!}}-{\tfrac {(x-c)^{n-2}f^{(n-1)}}{(n-2)!}}\right]-{\tfrac {A(x-c)^{n-1}}{(n-1)!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bfb5f589208f823ad7e863babee95cfd8a8347e)
![{\displaystyle \left[f'(c)-f'(c)\right]+\left[{\tfrac {(x-c)f''(c)}{1!}}-{\tfrac {(x-c)f''(c)}{1!}}\right]+\ldots +\left[{\tfrac {(x-c)^{n-1}f^{(n)}(c)}{(n-1)!}}-{\tfrac {A(x-c)^{n-1}}{(n-1)!}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20265370ec6728e6e4aefe73eead7d719e38501e)





