Real Analysis/Continuity
| ←Limits | Real Analysis Continuity |
Total Variation→ |
Now that we've defined the limit of a function, we're in a position to define what it means for a function to be continuous. The notion of Continuity captures the intuitive picture of a function "having no sudden jumps or oscillations". Yet, in this page, we will move away from this elementary definition into something with checklists; something with rigor. This will be important not just in Real Analysis, but in other fields of mathematics as well.
Continuity marks a new classification of functions, especially prominent when the theorems explained later on in this page will be put to use. However, if one is reading this wikibook linearly, then it will be good to note that the wikibook will describe functions with even more properties than continuity. As an example, the functions in elementary mathematics, such as polynomials, trigonometric functions, and the exponential and logarithmic functions, contain many levels more properties than that of a continuous function. We will also see several examples of discontinuous functions as well, to provide some remarks of common functions that do not fit the bill.
Definition[edit | edit source]
Given an interval and a function , continuous on I is defined as upholding the following property:
and it is notated as
Readers may note the similarity between this definition to the definition of a limit in that unlike the limit, where the function can converge to any value, continuity restricts the returning value to be only the expected value when the function is evaluated. This added restriction provides many new theorems, as some of the more important ones will be shown in the following headings.
Operations[edit | edit source]
Since limits are preserved under algebraic operations, let's check whether this is also the case with continuity.
Algebraic[edit | edit source]
We see that if and are both continuous at c, continuity still works out fine for the following situations:
| Addition | |
|---|---|
| Subtraction | |
| Product | |
| Multiple of a Function | |
| Reciprocal | |
| Division |
Note that of course, for any division, g(c) must be a valid number i.e. not 0.
This is actually a corollary when you look at the proofs for the preservation of algebraic operation for limits. Simply replace the limit values L and M with ƒ(c) and g(c) respectively.
We can use sequential limits to prove that functions are discontinuous as follows:
- is discontinuous at if and only if there are two sequences and such that .
Composition[edit | edit source]
Composition is a lot trickier though, as always, but it still works as intuition would suggest; composition of two continuous functions is still a continuous function.
If is continuous on the range of and is continuous on any interval , then the composition is continuous on A.
The proof simply works by fulfilling the definition of continuity for the composition function of and using variable substitutions based off fulfilling all requirements for those variables. As such, there is no algebra and no theorems used other than purely definitions.
| We know what is needed for continuity first. As such, we will define epsilon using the most basic definition that will fit the requirement for continuity. | Let |
| Since f must be continuous, we will also write down what we know is true—its checklist of properties fulfilling continuity. For now, we will make a slight modification to the delta variable for reasons that will be justified later. | . |
| However, has more properties than that. The key ones are what the value of and refer to. Since the function is continuous on the range of , that means that the input value of is actual the output value of . Thus, we can validly substitute the value and for the function with 's output value. | . |
| Since g must be continuous, we will also write down what we know is true, which is the definition of continuity. | . |
| The expression and is awfully similar. We can use this to our advantage by seeing if we can abuse any properties we know of. Given that the only requirement for is that it must be positive and its inequality relationship is valid for any number, and that is positive and a number, then we can put two and two together and define as . | Let |
| Thus, we abstractly strung together a definition of continuity built off what we know is true; the continuity of and . Reading the valid results of what this new implication statement suggests; that continuity for the composition of and , we are assured in our claim that the composition of and is also continuous. QED. | Thus
so is continuous on A. |
The Three Continuity Theorems[edit | edit source]
Think about what an intuitive notion of continuity is. If you can’t the image of a polynomial function always works. The smooth curve as it travels through the domain of the function is a graphical representation of continuity. However, how do we mathematically know that it’s continuous? Well, we’ll start with the Three Continuity Theorems that will verify this notion.
The Intermediate Value Theorem[edit | edit source]
This is the big theorem on continuity. Essentially it says that continuous functions have no sudden jumps or breaks.
Let f(x) be a continuous function. If and , then .
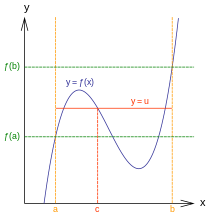
Proof[edit | edit source]
Let , and let .
Let . By continuity, .
If f(c) < m, then , so . But then , which implies that c is not an upper bound for S, a contradiction.
If f(c) > m, then since , . But since , , so = m, which implies that , a contradiction.
We will now prove the Minimum-Maximum theorem, which is another significant result that is related to continuity. Essentially, it states that any continuous image of a closed interval is bounded, and also that it attains these bounds.
Minimum-Maximum Theorem[edit | edit source]
This theorem functions as a first part in another bigger theorem. However, on its own, it helps bridge the gap between supremums and infimums in regards to functions.
Given a continuous function ƒ on [a,b] i.e. , if and , then is bounded.

Proof[edit | edit source]
Assume if possible that is unbounded.
Let . Then, is unbounded on at least one of the closed intervals and (for otherwise, would be bounded on contradicting the assumption). Call this interval .
Similarly, partition into two closed intervals and let be the one on which is unbounded.
Thus we have a sequence of nested closed intervals such that is unbounded on each of them.
We know that the intersection of a sequence of nested closed intervals is nonempty. Hence, let
As is continuous at , there exists such that But by definition, there always exists such that , contradicting the assumption that is unbounded over . Thus, is bounded over
Extreme Value Theorem[edit | edit source]
This is the second part of the theorem. It is the more assertive version of the previous theorem, stating that not only is there a supremum and a infimum, it also is reachable by the function ƒ and will be in between the interval you specified.
Given a continuous function ƒ on [a,b] i.e. , if are respectively the upper and lower bounds of , then there exist such that .

Proof[edit | edit source]
Assume if possible, but .
Consider the function . By algebraic properties of continuity, is continuous. However, being a cluster point of , is unbounded over , contradicting (i). Hence, . Similarly, we can show that .
Appendix[edit | edit source]
Continuity will come again in other branches in mathematics. You will come across not only different variations of continuity, but you will also come across different definitions of continuity too.
Uniform Continuity[edit | edit source]
Let
Let
We say that is Uniformly Continuous on if and only if for every there exists such that if and then
Lipschitz continuity[edit | edit source]
Let
Let
We say that is Lipschitz continuous on if and only if there exists a positive real constant such that, for all , .
The smallest such is called the Lipschitz constant of the function .
Topological Continuity[edit | edit source]
As mentioned, the idea of continuous functions is used in several areas of mathematics, most notably in Topology. A different characterization of continuity is useful in such scenarios.
Theorem[edit | edit source]
Let
Let
is continuous at if and only if for every open neighbourhood of , there exists an open neighbourhood of such that
It must be mentioned here that the term "Open Set" can be defined in much more general settings than the set of reals or even metric spaces, and hence the utility of this characterization.



















































![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
![{\displaystyle f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e8bf1526030f5a9f1564d4ef14c5d63350dfe9a)

![{\displaystyle [a,x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae2c07161cd155ac8fb5c82f6469286c13d767f0)
![{\displaystyle [x_{1},b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/964ceef28eee0ca6ed47d83ddd6c966ea7956b24)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle [a,b]\supseteq I_{1}\supseteq I_{2}\supseteq \ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b92c5a4800dc5943971991e4310fc0b72b29caf1)








![{\displaystyle c,d\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3242edd84bb073a138a9bbf3f4fcf83b3b5d57a5)

![{\displaystyle M=\sup(f([a,b]))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b5aaf4fcb954ca3ba533d8a4adc92d7ed45f79)
![{\displaystyle M\notin f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3187955833d418a916915b080e19758eb4ae3cac)

![{\displaystyle g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1d5103d0e36767a27715bcfc57137119294aad)


![{\displaystyle M\in f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ced025dd0e7b847c4c052fbd5065682e11b2dce)
![{\displaystyle m\in f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5faae378c13613eee594978619f5754e437720e)











