FHSST Physics/Print version
| This is the print version of FHSST_Physics You won't see this message or any elements not part of the book's content when you print or preview this page. |

About FHSST[edit | edit source]
Free High School Science Texts (FHSST) is an initiative to develop and distribute free science textbooks to grade 11 - 12 learners in South Africa.
The primary objectives are:
- To provide a *free* resource, that can be used alone or in conjunction with other education initiatives in South Africa, to all learners and teachers
- To provide a quality, accurate and interesting text that adheres to the South African school curriculum and the outcomes-based education system
- To make all developed content available internationally to support Education on the largest possible scale
- To provide a text that is easy to read and understand even for second-language English speakers
- To make a difference in South Africa through helping to educate young South Africans
FHSST Website - FHSST Physics on Wikibooks
Other FHSST books on Wikibooks:
Introduction[edit | edit source]
<< Main Page -- First Chapter (Units) >>
Introduction[edit | edit source]
Physics is the study of the laws which govern space, structure and time. In a sense we are more qualified to do physics than any other science. From the day we are born we study the things around us in an effort to understand how they work and relate to each other. For example, learning how to catch or throw a ball is a physics undertaking.
In the field of study we refer to as physics we just try to make the things everyone has been studying more clear. We attempt to describe them through simple rules and mathematics. Mathematics is merely the language we use. The best approach to physics is to relate everything you learn to things you have already noticed in your everyday life. Sometimes when you look at things closely, you discover things you had initially overlooked.
It is the continued scrutiny of everything we know about the world around us that leads people to the lifelong study of physics. You can start with asking a simple question like "Why is the sky blue?", which could lead you to electromagnetic waves, which in turn could lead you to wave particle duality and energy levels of atoms. Before long you are studying quantum mechanics or the structure of the universe.
In the sections that follow notice that we will try to describe how we will communicate the things we are dealing with. This is our language. Once this is done we can begin the adventure of looking more closely at the world we live in.
Units[edit | edit source]
Introduction[edit | edit source]
Science focuses on studying how things happen in the real world—things you can see, touch, hear, smell, feel, or imagine such as time.
Fractions and decimals[edit | edit source]
Early society had primitive ideas such as one, two or many, then more sophisticated means of counting emerged, mainly relating to trade. Units of weight, volume and money were at first integer whole units, often recorded by notches in a tally stick or marks in clay tablets. About 6000 years ago, with the advent of writing came units such as the length of the king's arm, together with the idea of multiples such as dozens and scores, together with vulgar fractions based on halves, quarters and so on., In order to describe these things, it is necessary to carefully measure what is observed.
In 1791, following the French Revolution, the decimal system was published based on tens and multiples or fractions of ten. The idea of ten months per year and ten days in a week were quickly dropped, but for most purposes it was revolutionary, with integrated standard weights and measures, such as fixing the second to the length of a pendulum of one metre, and the weight of a kilo of water the same as a litre volume. Since the 1960s the International System of Units ("Système International d'Unités" in French, hence "SI") has been almost universal outside the United States of America, which still prefers a version of the Imperial Roman measuring system which emerged more than 2000 years go and which is complicated and illogical.
Measurements must always be reported with appropriate units, which specify what type of quantity is being discussed - weight, length or whatever. For science and engineering, the SI system is universal and is not 'owned' by anyone, so it remains constant and free of political manipulation. As recently as 1897 the Indiana State Legislature,attempted (unsuccessfully) to set the value of Pi to 3.2, and during 1940, in Britain, the weight of a pound (lb) loaf of bread was legislated at a lower weight to concerve supplies during food rationing, giving rise to the expression 'baker's dozen' because you needed thirteen new loaves or buns for the same quantity of bread as 12 of the correct weight!
The Measurement and the Decimal Metric System[edit | edit source]
As a simple example of the importance of units, imagine you had to make curtains and needed to buy material. The shop assistant would need to know how much material was required. Telling her you need material 2 wide and 6 long would be insufficient—you have to specify the unit (i.e. 2 metres wide and 6 metres long). Without the unit, the information is incomplete and the shop assistant would have to guess. If you were making curtains for a doll's house the dimensions might be 2 centimetres wide and 6 centimetres long!
It is not just lengths that have units. Any measurement of any physical phenomenon—time, temperature, force, or voltage, just to name a few—has units.
Tip: Many physics problems ask you to determine a specific numeric quantity. When you solve the problem, do not forget to specify the units of your answer: even if you have the right number, your answer is not correct unless you include the correct units.
SI Units[edit | edit source]
In the remainder of this class we will be using SI units, which are defined in the table below. These seven units are used to measure fundamental quantities, and are the basis of everything we will do, as will be discussed in more detail in the next section.
| Base quantity | Name | Symbol |
|---|---|---|
| length | metre | m |
| mass | kilogram | kg |
| time | second | s |
| electric current | ampere | A |
| thermodynamic temperature | kelvin | K |
| countable amount of substance | mole | mol |
| luminous intensity | candela | cd |
SI Units (Système International d'Unités)[edit | edit source]
These units are internationally agreed upon and form the system we will use. Historically these units are based on the metric system which was developed in France at the time of the French Revolution.
| Base quantity | Name | Symbol |
|---|---|---|
| length | metre | m |
| mass | kilogram | kg |
| time | second | s |
| electric current | ampere | A |
| thermodynamic temperature | kelvin | K |
| amount of substance | mole | mol |
| luminous intensity | candela | cd |
All physical quantities have units which can be built from the 7 base units listed in Table 1.1 (incidentally the choice of these seven was arbitrary). They are called base units because none of them can be expressed as combinations of the other six. This is similar to breaking a language down into a set of sounds from which all words are made. Another way of viewing the base units is like the three primary colours. All other colours can be made from the primary colours but no primary colour can be made by combining the other two primaries.
Unit names are always written with lowercase initials (e.g. the metre). The symbols (or abbreviations) of units are also written with lowercase initials except if they are named after scientists (e.g. the kelvin (K) and the ampere (A)). An exception to this rule is the litre, which is abbreviated as either L or l.
To make life convenient, particular combinations of the base units are given special names. This makes working with them easier, but it is always correct to reduce everything to the base units. Table 1.2 lists some examples of combinations of SI base units assigned special names. Do not be concerned if the formulae look unfamiliar at this stage—we will deal with each in detail in the chapters ahead (as well as many others)!
It is very important that you are able to say the units correctly. For instance, the newton is another name for the kilogram metre per second squared (kg·m·s−2), while the kilogram metre squared per second squared (kg·m2·s−2) is called the joule.
| Quantity | Formula | Unit Expressed
in |
Name of |
|---|---|---|---|
| Base Units | Combination | ||
| Force | m·a | kg·m·s−2 | N (newton) |
| Frequency | s−1 | Hz (hertz) | |
| Work & Energy | F·s | kg·m2·s−2 | J (joule) |
| Electrical Potential | W/A | kg·m2·s−3·A−1 | V (volt) |
Another important aspect of dealing with units is the prefixes that they sometimes have (prefixes are words or letters written in front that change the meaning). The kilogram (kg) is a simple example: 1 kg is 1000 g or . Grouping the 103 and the g together we can replace the 103 with the prefix k (kilo). Therefore the k takes the place of the 103. Incidentally the kilogram is unique in that it is the only SI base unit containing a prefix.
There are prefixes for many powers of 10 (Table 1.3 lists a large set of these prefixes). This is a larger set than you will need but it serves as a good reference. The case of the prefix symbol is very important. Where a letter features twice in the table, it is written in uppercase for exponents bigger than one and in lowercase for exponents less than one. Those prefixes listed in boldface should be learned.
| Prefix | Symbol | Exponent | Prefix | Symbol | Exponent |
|---|---|---|---|---|---|
| yotta | Y | 1024 | yocto | y | 10−24 |
| zetta | Z | 1021 | zepto | z | 10−21 |
| exa | E | 1018 | atto | a | 10−18 |
| peta | P | 1015 | femto | f | 10−15 |
| tera | T | 1012 | pico | p | 10−12 |
| giga | G | 109 | nano | n | 10−9 |
| mega | M | 106 | micro | µ | 10−6 |
| kilo | k | 103 | milli | m | 10−3 |
| hecto | h | 102 | centi | c | 10−2 |
| deca | da | 101 | deci | d | 10−1 |
As another example of the use of prefixes,
can be written as 1 mg (1 milligram).
The Other Systems of Units[edit | edit source]
The remaining sets of units, although not used by us, are also internationally recognised and still in use by others. We will mention them briefly for interest only.
CGS and MKS Units[edit | edit source]
In this system the basic measure of length is the centimetre, weight is in grams and time is in seconds. Later the metre is replaced the centimetre and the kilogram replaced the gram. The Second has remained the basic unit of time throughout. This is a simple change but it means that all units derived from these two are changed. For example, the units of force and work are different. These units are used most often in astrophysics and atomic physics.
When electromagnetism comes into play, there are three CGS systems, adapted to the fundamental equations each theory views as basic: The electric CGS, the magnetic CGS, and the combined Gaussian. The latter has the advantage that corresponding electric and magnetic phenomena have the same units and related equations.
It has the additional advantage that there is only one natural constant in the equations, the speed of light, where the SI system has two. And experience, i.e. measurements, has shown that there is only one constant. So the Gaussion system is a bit more 'right'.
These unit systems also show that the choice of base units is arbitrary. In SI, there is a base unit for the current, the ampere [A], derived from it the unit of charge, coulomb [C]. The Gaussian system does without a dedicated unit for electricity. It simply defines the factor in the law of force between two charged particles as one - and lo, the unit C disappears; the esu (electrostatic unit) can be derived from g, cm, s - the C cannot, it is As, and A is basic.
[The same could be done with mass, leading to kg vanishing, just by setting the gravitational constant in Newton's law to one. kg would then be replaced by a combination of m and s.
Imperial Units[edit | edit source]
These units (as their name suggests) stem from the days when the Roman Empire decided measures. Some of these were later altered by local rulers. As a result, different countries used different base units for each quantity (except for time). The British abandoned the Roman measurement and money system in 1972. There were 12 pennies or denaries in a shilling or solidus, and 20 shillings in a pound or libra ergo there were 240 'old pennies' and are now 100 new pennies in the pound sterling or GBP - which large unit was unchanged. The British also used both avoirdupois and troy weight and other capricious local measures, but following its integration in the EU, Britain now officially use decimal SI units for all measurements.
Although the British once used an imperial metric system similar to that in use in the US, it is important to know that there are some differences, because the colonists made certain incorrect assumptions, such as that because there were 16 ounces in a pound weight, there were also 16 fluid ounces in a pint of liquid, when the Romans and British defined 20 fl oz. This matters, because during World War II, for example, great fraud was perpetrated by the British selling the smaller American gallons (8 pints) at the price for the larger British measure!
The decimal metric system was invented in France in 1791, following the French revolution. This later became the MKS (Meter/Kilogram/Second) system and is now the System International (SI) system, which is still close that early French system. Using different units in different places would make effective scientific communication very difficult. That is why the scientific community has adopted SI units as its internationally agreed upon standard. Therefore the SI is overwhelmingly predominant for nearly all international scientific and technical use.
Natural Units[edit | edit source]
This is the most sophisticated choice of units. Here the most fundamental discovered quantities (such as the speed of light) are set equal to 1. The argument for this choice is that all other quantities should be built from these fundamental units. This system of units is used in high energy physics and quantum mechanics.
The Importance of Units[edit | edit source]
Without units much of our work as scientists would be meaningless. We need to express our thoughts clearly and units give meaning to the numbers we calculate. Depending on which units we use, the numbers are different (e.g. 3.8 m and 3800 mm actually represent the same length). Units are an essential part of the language we use. Units must be specified when expressing physical quantities. In the case of the curtain example at the beginning of the chapter, the result of a misunderstanding would simply have been an incorrect amount of material cut. However, sometimes such misunderstandings have catastrophic results. Here is an extract from a story on CNN's website:
NASA: Human error caused loss of Mars orbiter November 10, 1999
WASHINGTON (AP) -- Failure to convert English measures to metric values caused the loss of the Mars Climate Orbiter, a spacecraft that smashed into the planet instead of reaching a safe orbit, a NASA investigation concluded Wednesday. The Mars Climate Orbiter, a key craft in the space agency's exploration of the red planet, vanished after a rocket firing September 23 that was supposed to put the spacecraft on orbit around Mars. An investigation board concluded that NASA engineers failed to convert English measures of rocket thrusts to newton, a metric system measuring rocket force. One English pound of force equals 4.45 newtons. A small difference between the two values caused the spacecraft to approach Mars at too low an altitude and the craft is thought to have smashed into the planet's atmosphere and was destroyed. The spacecraft was to be a key part of the exploration of the planet. From its station about the red planet, the Mars Climate Orbiter was to relay signals from the Mars Polar Lander, which is scheduled to touch down on Mars next month. ``The root cause of the loss of the spacecraft was a failed translation of English units into metric units and a segment of ground-based, navigation-related mission software," said Arthus Stephenson, chairman of the investigation board. Reported by CNN at http://www.cnn.com/TECH/space/9911/10/orbiter.02/
This story illustrates the importance of being aware that different systems of units exist. Furthermore, we must be able to convert between systems of units!
Choice of Units[edit | edit source]
There are no wrong units to use, but a clever choice of units can make a problem look simpler. The vast range of problems makes it impossible to use a single set of units for everything without making some problems look much more complicated than they should. We can't easily compare the mass of the sun and the mass of an electron, for instance. This is why astrophysicists and atomic physicists use different systems of units.
We won't ask you to choose between different unit systems. For your present purposes the SI system is perfectly sufficient. In some cases you may come across quantities expressed in units other than the standard SI units. You will then need to convert these quantities into the correct SI units. This is explained in the next section.
How to Change Units-- the "Multiply by 1" Technique[edit | edit source]
Also known as fractional dimensional analysis, the technique involves multiplying a labeled quantity by a conversion ratio, or knowledge of conversion factors. First, a relationship between the two units that you wish to convert between must be found. Here's a simple example: converting millimetres (mm) to metres (m)-- the SI unit of length. We know that there are 1000 mm in 1 m which we can write as
Now multiplying both sides by
we get
which simply gives us
This is the conversion ratio from millimetres to metres. You can derive any conversion ratio in this way from a known relationship between two units. Let's use the conversion ratio we have just derived in an example:
Question: Express 3800 mm in metres.
Answer:
Note that we wrote every unit in each step of the calculation. By writing them in and cancelling them properly, we can check that we have the right units when we are finished. We started with mm and multiplied by
This cancelled the mm leaving us with just m, which is the SI unit we wanted! If we wished to do the reverse and convert metres to millimetres, then we would need a conversion ratio with millimetres on the top and metres on the bottom.
It is helpful to understand that units cancel when one is in the numerator and the other is in the denominator. If the unit you are trying to cancel is on the top, then the conversion factor that you multiply it with must be on the bottom.
This same technique can be used to not just to convert units, but can also be used as a way to solve for an unknown quantity. For example: If I was driving at 65 miles per hour, then I could find how far I would go in 5 hours by using as a conversion factor.
This would look like
This would yield a result of 325 miles because the hours would cancel leaving miles as the only unit.
Practice Problem[edit | edit source]
Problem: Convert 3 millennia into seconds.
Most people don't know how many seconds are in a millennium, but they do know enough to solve this problem. Since we know 1000 years = 1 millennium, 1 year = about 365.2425 days, 1 day = 24 hours, and 1 hour = 3600 seconds we can solve this problem by multiplying by one many times.
How Units Can Help You[edit | edit source]
We conclude each section of this book with a discussion of the units most relevant to that particular section. It is important to try to understand what the units mean. That is why thinking about the examples and explanations of the units is essential.
If we are careful with our units then the numbers we get in our calculations can be checked in a 'sanity test'.
What is a 'sanity test'?[edit | edit source]
This isn't a special or secret test. All we do is stop, take a deep breath, and look at our answer. Sure we always look at our answers—or do we? This time we mean stop and really look—does our answer make sense?
Imagine you were calculating the number of people in a classroom. If the answer you got was 1 000 000 people you would know it was wrong—that's just an insane number of people to have in a classroom. That's all a sanity check is—is your answer insane or not? But what units were we using? We were using people as our unit. This helped us to make sense of the answer. If we had used some other unit (or no unit) the number would have lacked meaning and a sanity test would have been much harder (or even impossible).
It is useful to have an idea of some numbers before we start. For example, let's consider masses. An average person has mass 70 kg, while the heaviest person in medical history had a mass of 635 kg. If you ever have to calculate a person's mass and you get 7000 kg, this should fail your sanity check—your answer is insane and you must have made a mistake somewhere. In the same way an answer of 0.00001 kg should fail your sanity test.
The only problem with a sanity check is that you must know what typical values for things are. In the example of people in a classroom you need to know that there are usually 20-50 people in a classroom. Only then do you know that your answer of 1 000 000 must be wrong. Here is a table of typical values of various things (big and small, fast and slow, light and heavy—you get the idea):
|
(NOTE TO SELF: Add to this table as we go along with examples from each section)
Note that you do not have to memorize this table. However, read it so that you can refer to it when you do a calculation.
Temperature[edit | edit source]
In everyday life, many people measure temperatures in Celsius. But in physics, we prefer to use the Kelvin scale which starts at absolute zero(−273.15 °C).
As we all know, Celsius temperatures can be negative. This might suggest that any number is a valid temperature. In fact, the temperature of a gas is a measure of the average kinetic energy of the particles that make up the gas. As we lower the temperature so the motion of the particles is reduced until a point is reached where all motion ceases. The temperature at which this occurs is called absolute zero. There is no physically possible temperature colder than this. In Celsius, absolute zero is at -273.15 °C. In Kelvin, the ordinary freezing point of water 0 °C is therefore 273.15 K
Physicists have defined a new temperature scale called the Kelvin scale. According to this scale absolute zero is at 0 K and negative temperatures are not allowed. The size of one unit kelvin is exactly the same as that of one unit degree Celsius. This means that a change in temperature of 1 kelvin is equal to a change in temperature of 1 degree Celsius—the scales just start in different places. Think of two ladders with steps that are the same size but the bottom most step on the Celsius ladder is labelled -273.15, while the first step on the Kelvin ladder is labelled 0. There are still 100 'steps' or degrees (Celsius or Kelvin) between the points where water freezes and boils when it is at at 1.0 atmosphere of pressure (water boils at lower temperatures if the air pressure is lowerO.
|----| 102 degrees Celsius |----| 375 kelvin
|----| 101 degrees Celsius |----| 374 kelvin
water boils ---> |----| 100 degrees Celsius |----| 373 kelvin
|----| 99 degrees Celsius |----| 372 kelvin
|----| 98 degrees Celsius |----| 371 kelvin
.
.
.
|----| 2 degrees Celsius |----| 275 kelvin
|----| 1 degree Celsius |----| 274 kelvin
ice melts ---> |----| 0 degrees Celsius |----| 273 kelvin
|----| -1 degree Celsius |----| 272 kelvin
|----| -2 degrees Celsius |----| 271 kelvin
.
.
.
|----| -269 degrees Celsius |----| 4 kelvin
|----| -270 degrees Celsius |----| 3 kelvin
|----| -271 degrees Celsius |----| 2 kelvin
|----| -272 degrees Celsius |----| 1 kelvin
absolute zero ---> |----| -273 degrees Celsius |----| 0 kelvin
(NOTE TO SELF: Come up with a decent picture of two ladders with the labels—water boiling and freezing—in the same place but with different labelling on the steps!)
This makes the conversion from kelvin to degree Celsius and back very easy. To convert from degrees Celsius to kelvins add 273.15. To convert from kelvins to degrees Celsius subtract 273.15. Representing the Kelvin temperature by TK and the Celsius temperature by T°C,
Converting between kelvin and Celsius is additive—so a difference in temperature of 1 degree Celsius is equal to a difference of 1 kelvin. The majority of conversions between units are multiplicative. For example, to convert from metres to millimetres we multiply by 1000. Therefore a change of 1 m is equal to a change of 1000 mm.
Although it seems as though there is not much reason for the scientific community to use the Kelvin scale over the Celsius scale, there is actually a very remarkable difference in using the Kelvin scale other than the reminding effect stated above. It happens that the idealised form of some materials varies proportionately according to the Kelvin scale, such that some required values can be simply found by multiplication and division. In such calculations, it is just a chore to use the Celsius scale.
Fahrenheit Scale[edit | edit source]
Fahrenheit is a temperature scale previously used in meteorology until about 1970, and which is still widely used in the USA. It was devised by a German physicist in 1724. He needed a scale that went below the freezing point of water, and used a mixture of ice, water, and ammonium chloride which freezes at a much lower temperature.
In this scale, the freezing point of water (0 °C) is 32 degrees Fahrenheit (32 °F) and the boiling point (100 °C) is 212 °F, placing the boiling and freezing points of water exactly 180 degrees apart. A temperature interval of one degree Fahrenheit is an interval of 5⁄9 of a degree Celsius. The Fahrenheit and Celsius scales coincide at −40 degrees (i.e. −40 °F and −40 °C describe the same temperature).
To convert Celsius to Fahrenheit:
1) Take your number in Celsius and multiply by 9.
2) Divide the result of step 1 by 5.
3) Add 32 to the result of step 2.
Converting Fahrenheit to Celsius:
1) Take your number in Fahrenheit and subtract 32
2) Multiply the result of step 1 by 5.
3) Divide the result of step 2 by 9.
Rankine Scale[edit | edit source]
Absolute zero is −459.67 °F. The Rankine temperature scale was created to use degrees the same size as those of the Fahrenheit scale, such that a temperature difference of one degree Rankine (1 °R) is the same as a temperature difference of 1 °F, but with absolute zero being 0 °R.
Scientific Notation, Significant Figures and Rounding[edit | edit source]
If you are only sure of say, both digits of a two-digit number, and put it in a formula and get a long series of numbers to the right of the decimal place, then those digits are probably not very accurate. This is the idea of significant figures.
Take 10 and divide by 3. If you are not sure that the number 10 is perfectly accurate, then you do not need to write down 3.333... and can get away with something like 3.3 or 3.33
(NOTE TO SELF: still to be written)
The accuracy of a measurement using significant figures is represented by the number of digits that it contains. A number is said to have the number of significant figures equal to the number of digits in the number not including leading 0s or trailing 0s unless there is a decimal point. The table below contains a list of numbers and how many significant digits each contains.
| Number | Significant Digits |
|---|---|
| 1000 | 1 |
| 1000. | 4 |
| 10.0 | 3 |
| 010 | 2 |
| 232 | 3 |
| 23.2 | 3 |
| 1 | |
| 3 |
As you may have noted, some numbers cannot be shown in proper significant figure notation without the use of scientific notation. For example, the number 1000 can only be shown to have 1 or 4 or more significant digits by the inclusion of a decimal point. However, by rewriting 1000 as any number of significant digits may be added by simply add additional 0s after the decimal point.
Sometimes you may be asked to determine the number of significant figures in a given number. There are three rules to determine what numerals are significant.
- Leading zeros are never significant. Leading zeros are zeros that appear on the left end of the number.
- All non-zero digits are significant. Trapped zeros (zeros between non-zero digits) are also significant.
- Trailing zeros are never significant unless there is a decimal point. Trailing zeros are zeros that appear on the right end of the number.
E notation[edit | edit source]
Very large numbers such as the speed of light (the C part of Einstein's famous ) are difficult to write accurately.
We could write 300,000,000 m/sec, , 300 million meters per second or some such. There is a much better way!
We simply separate the number (coefficient) part 3 from its multiplier 00000000 base!
But be careful, there is an Elephant trap here, and it is that in scientific notation the number is always expressed as a decimal fraction with a maximum value of 1.0, (in this case =0.3) so the multiplier part is one bigger than you might expect! is the same as 0.3E9. (Because there are a total of nine digits after the decimal point)
A tiny dust particle might weigh as little as 0.000 000 000 678 kg.! This time we shift the decimal point 9 places to the right so the number (678) has a negative base so our weight is written as 0.678E-9 kg.
Now is that not a whole lot easier to write and understand? That is why many scientific calculators and most spread-sheets allow input and display in E notation format.
Commas and points[edit | edit source]
Most English speaking people use the comma [ , ] to separate thousands and the dot (ful-stop, or point) [ . ] for the decimal indicator. Europeans often use these the other way around. Many spread-sheets allow both, but it is just one more complexity you need to know about!
Conclusion[edit | edit source]
We have discussed the importance of units. We have learnt that there are many different units (units of time, units of length, units of mass) to describe the same thing, also there are different systems to define units, although we should stick to SI units in our calculations. We also know how to convert between different units. This is a skill we must acquire.
Waves and Wavelike Motion[edit | edit source]
Waves and Wavelike Motion[edit | edit source]
Waves occur frequently in nature. The most obvious examples are waves in water on a dam, in the ocean, or in a bucket, but sound waves and electromagnetic waves are other, less visible examples. We are most interested in the properties that waves have. All waves have the same basic properties, so by studying waves in water we can transfer our knowledge and predict how other types of waves will behave.
Waves are associated with energy. As the waves move, they carry energy from one point to another in space. It is true for water waves as well. You can see the wave energy working while a ship drifts along the wave in rough sea. The most spectacular example is the enormous amount of energy we receive from the sun in the form of light and heat, which are transmitted as electromagnetic waves - not even requiring a medium to propagate. wave was being discovered by Sir Reagan Lulu Wokoz
Simple Harmonic Motion[edit | edit source]
Simple Harmonic motion is a wavelike motion. It is considered wavelike because the graph of time vs. displacement from the equilibrium position is a sine curve.
An example of simple harmonic motion is a mass oscillating on a spring. It will be hard to understand the forces involved this early in the course that cause the motion to simple harmonic, but it is still possible to look at a mass oscillating on a spring and understand that it is indeed simple harmonic. When a mass is oscillating on a spring, the further the string stretches, the slower the mass will be moving. Then the mass reaches a point where the string won't stretch any further, so it quits moving and then it reverses direction. As it moves closer to the equilibrium position is moves faster.
What are waves?[edit | edit source]
Waves are phenomena that everyone experiences constantly; water waves, sound waves, light waves, human waves when the home team scores... the list goes on. When asked what makes a wave a wave, the most common responses would probably be that a wave is something that moves, or propagates, or perhaps that it is something that repeats over and over again. These properties do capture the essential qualities of waves. Now we must determine these properties quantitatively, and discover what governs their behavior.
Generally, a wave is defined as any phenomenon which can be modeled by a function of the form where the -vector represents a position in space, and represents a time, and the -vector and omega are both constants. Don't be intimidated by the vectors in the argument - most of our time at first will be spent on one-dimensional waves. If the wave is in only one spatial dimension 'x', for instance a wave travelling on a taut string, it can be written simply as .
Any function of this form "propagates" along the direction over time. As time increases, the argument of the function increases; over time the form of the function effectively advances through space. Try coming up with functions of this form, and plot them at time , then plot them again at a later time. This progressive property will become obvious. Try to figure out the velocity with which your function advances! (we will study this later) The negative sign in front of the time term causes the wave to propagate in the direction defined as positive (if that seems confusing, try plotting more functions over time, and examine the results). If you replace the negative with a positive (or instead consider a negative value of omega), the wave will propagate in the negative direction.
A very special and important case of a wave is the mathematical function , or in one dimension, . This is a sinusoidal wave – it oscillates up and down infinitely in both directions, and moves as time progresses. I mentioned that waves have the quality of repeating over and over, the quality of periodicity. However, many functions of the form mentioned above do not seem to repeat. However, you will find that ALL waves can be decomposed into a sum of many of these simple, infinitely repeating waves when you learn about Fourier transformations.
More than any other concept, physicists are finding that waves characterize the structure of the universe at every scale imaginable. As you learn about the physics of waves in everyday life, keep an open mind towards finding waves and wave behavior everywhere you turn.
Let's consider a very well-known case of a wave phenomenon: water waves. Waves in water consist of moving peaks and troughs. A peak is a place where the water rises higher than when the water is still and a trough is a place where the water sinks lower than when the water is still.
So waves have peaks and troughs. This could be our first property for waves. The following diagram shows the peaks and troughs on a wave.
In physics we try to be as quantitative as possible. If we look very carefully we notice that the height of the peaks above the level of the still water is the same as the depth of the troughs below the level of the still water.
Waves are repetitions of physical quantity in a periodic manner, carrying energy in the process. The water waves, for example, can be visualized to repeat any of the physical quantities like "peaks", "troughs", "potential energy" or "kinetic energy". Even, we can visualize water waves as the motion of disturbance (energy). It is the energy aspect of waves that is central to the understanding of different types of waves, many of which are not visible.
Looking closely at the water wave, we can recognize that crests and troughs basically represent of extreme potential and kinetic energies in addition to representing rise and fall of water from the still level. At the peak, energy is only potential, whereas energy is only kinetic at the trough. Similarly, propagation of electromagnetic wave is associated with repetitions of magnetic and electric field in space with certain periodicity. As existence of electrical or magnetic fields does not require any medium, electromagnetic waves can move even in the absence of any medium.
Characteristics of Waves: Amplitude[edit | edit source]
We use symbols agreed upon by convention to label the characteristic quantities of the waves. The characteristic height of a peak and depth of a trough is called the amplitude of the wave. The vertical distance between the bottom of the trough and the top of the peak is twice the amplitude. To put it simply, the amplitude is the distance of the wave from the medium, to the crest or trough
Worked Example 1
Question: (NOTE TO SELF: Make this a more exciting question) The height of the wave from the medium is 2m. What is the distance from the peak to the trough. What
- Answer
The amplitude is 2m. (Read above paragraph to know why). The distance from the peak to trough is 4m.
Characteristics of Waves : Wavelength[edit | edit source]
Look a little closer at the peaks and the troughs. The distance between two adjacent (next to each other) peaks is the same no matter which two adjacent peaks you choose. So there is a fixed distance between the peaks.
Similarly, you'll notice that the distance between two adjacent troughs is the same no matter which two troughs you look at. But, more importantly, its is the same as the distance between the peaks. This distance which is a characteristic of the wave is called the wavelength.
Waves have a characteristic wavelength. The symbol for the wavelength is the Greek letter lambda, .
The wavelength is the distance between any two adjacent points which are in phase. Two points in phase are separate by an integer (0,1,2,3,...) number of complete wave cycles. They don't have to be peaks or trough but they must be separated by a complete number of waves.
Characteristics of Waves : Period[edit | edit source]
Now imagine you are sitting next to a pond and you watch the waves going past you. First one peak, then a trough and then another peak. If you measure the time between two adjacent peaks you'll find that it is the same. Now if you measure the time between two adjacent troughs you'll find that its always the same, no matter which two adjacent troughs you pick. The time you have been measuring is the time for one wavelength to pass by. We call this time the period and it is a characteristic of the wave.
The period of the wave is denoted with the symbol .
Characteristics of Waves : Frequency[edit | edit source]
There is another way of characterising the time interval of a wave. We timed how long it takes for one wavelength to go past. We could also turn this around and say how many waves go by in 1 second.
We can easily determine this number, which we call the frequency and denote f. To determine the frequency, how many waves go by in 1s, we work out what fraction of a waves goes by in 1 second by dividing 1 second by the time it takes T. If a wave takes 1/2 a second to go by then in 1 second two waves must go by. . The unit of frequency is the Hz or s−1.
Waves have a characteristic frequency.
| |||||||
generally, the frequency of a wave is the number of crests that pass by per unit time.
Characteristics of Waves : Speed[edit | edit source]
Now if you are watching a wave go by you will notice that they move at a constant velocity. Thinking back to rectilinear motion you will be able to remember that we know how to work out how fast something moves. The speed is the distance you travel divided by the time you take to travel that distance. This is excellent because we know that the waves travel a distance in a time T. This means that we can determine the speed.
| |||||||||
There are a number of relationships involving the various characteristic quantities of waves. A simple example of how this would be useful is how to determine the velocity when you have the frequency and the wavelength. We can take the above equation and substitute the relationship between frequency and period to produce an equation for speed of the form
| |||||||||
Is this correct? Remember a simple first check is to check the units! On the right hand side we have speed which has units ms−1. On the left hand side we have frequency which is measured in s−1 multiplied by wavelength which is measure in m. On the left hand side we have ms−1 which is exactly what we want.
Speed of a wave through strings[edit | edit source]
The speed of a wave traveling along a vibrating string (v) is directly proportional to the square root of the tension (T) over the linear density (μ):
μ is equal to the mass of the string divided by the length of the string.
Two Types of Waves[edit | edit source]
We agreed that a wave was a moving set of peaks and troughs and we used water as an example. Moving peaks and troughs, with all the characteristics we described, in any medium constitute a wave. It is possible to have waves where the peaks and troughs are perpendicular to the direction of motion, like in the case of water waves. These waves are called transverse waves.
There are two additional types of waves. The first is called longitudinal waves and have the peaks and troughs in the same direction as the wave is moving. The question is how do we construct such a wave?
An example of a longitudinal wave is pressure waves moving through a gas. The peaks in this wave are places where the pressure reaches a peak and the troughs are places where the pressure is a minimum.
In the picture below we show the random placement of the gas molecules in a tube. The piston at the end moves into the tube with a repetitive motion. Before the first piston stroke the pressure is the same throughout the tube.
When the piston moves in it compresses the gas molecules together at the end of the tube. If the piston stopped moving the gas molecules would all bang into each other and the pressure would increase in the tube.
When the piston moves out again before the molecules have time to bang around then the increase in pressure moves down the tube like a pulse (single peak and trough, a single wave cycle).
As this repeats we get waves of increased and decreased pressure moving down the tubes. We can describe these pulses of increased pressure (peaks in the pressure) and decreased pressure (troughs of pressure) by a sine or cosine graph.
The second additional type of wave is the torsional wave. The peaks and troughs rotate around the direction of motion. In simpler terms, a "twisting motion" is transmitted through the medium. Of the two wave types, this is the hardest one to describe and visualize.
There are a number of examples of each type of wave. Not all can be seen with the naked eye but all can be detected.
Properties of Waves[edit | edit source]
We have discussed some of the simple properties of waves that we need to know. These have just been describing the characteristics that waves have. Now we can progress onto some more interesting and, perhaps, less intuitive properties of waves.
Properties of Waves : Reflection[edit | edit source]
When waves strike a barrier they are reflected. This means that waves bounce off things. Sound waves bounce off walls, light waves bounce off mirrors, radar waves bounce off planes and how bats can fly at night and avoid things as small as telephone wires. etc. The property of reflection is a very important and useful one.
(NOTE TO SELF: Get an essay by an air traffic controller on radar) (NOTE TO SELF: Get an essay by on sonar usage for fishing or for submarines)
When waves are reflected, the process of reflection has certain properties. If a wave hits an obstacle at a right angle to the surface (NOTE TO SELF: diagrams needed) then the wave is reflected directly backwards.
If the wave strikes the obstacle at some other angle then it is not reflected directly backwards. The angle that the waves arrives at is the same as the angle that the reflected waves leaves at. The angle that waves arrives at or is incident at equals the angle the waves leaves at or is reflected at. Angle of incidence equals angle of reflection
|
(2.1) |
: angle of incidence : angle of reflection
In the optics chapter you will learn that light is a wave. This means that all the properties we have just learnt apply to light as well. Its very easy to demonstrate reflection of light with a mirror. You can also easily show that angle of incidence equals angle of reflection.
If you look directly into you see yourself ....
Need to mention that the incident wave, normal to the surface and the reflected wave all lie in the same plane. The same also holds for refraction at a surface.
Phase shift of reflected wave[edit | edit source]
When a wave is reflected from a more dense medium, it undergoes a phase shift. That means that the peaks and troughs are swapped around.
The easiest way to demonstrate this is to tie a piece of string to something. Stretch the string out flat and then flick the string once so a pulse moves down the string. When the pulse (a single peak in a wave) hits the barrier that the string is tied to, it will be reflected. The reflected wave will look like a trough instead of a peak. This is because the pulse had undergone a phase change. The fixed end is like reflection off a more dense medium.
If the end of the string was not fixed, i.e. it could move up and down then the wave would still be reflected but it would not undergo a phase shift.
Properties of Waves : Refraction[edit | edit source]
Sometimes waves move from one medium to another. The medium is the substance that is carrying the waves. In our first example this was the water. When the medium properties change it can affect the wave.
Let us start with the simple case of a water wave moving from one depth to another. The speed of the wave depends on the depth. If the wave moves directly from the one medium to the other than we should look closely at the boundary. When a peak arrives at the boundary and moves across it must remain a peak on the other side of the boundary. This means that the peaks pass by at the same time intervals on either side of the boundary. The period and frequency remain the same! But we said the speed of the wave changes, which means that the distance it travels in one time interval is different i.e. the wavelength has changed.
Going from one medium to another the period or frequency does not change only the wavelength can change.
Now if we consider a water wave moving at an angle of incidence not 90 degrees towards a change in medium then we immediately know that not the whole wave will arrive at once. So if a part of the wave arrives and slows down while the rest is still moving faster before it arrives the angle of the wavefront is going to change. This is known as refraction. When a wave bends or changes its direction when it goes from one medium to the next.
If it slows down it turns towards the perpendicular.
If the wave speeds up in the new medium it turns away from the perpendicular to the medium surface.
When you look at a stick that emerges from water it looks like it is bent. This is because the light from below the surface of the water bends when it leaves the water. Your eyes project the light back in a straight line and so the object looks like it is a different place.
Properties of Waves : Interference[edit | edit source]
If two waves meet interesting things can happen. Waves are basically collective motion of particles. So when two waves meet they both try to impose their collective motion on the particles. This can have quite different results.
If two identical (same wavelength, amplitude and frequency) waves are both trying to form a peak then they are able to achieve the sum of their efforts. The resulting motion will be a peak which has a height which is the sum of the heights of the two waves. If two waves are both trying to form a trough in the same place then a deeper trough is formed, the depth of which is the sum of the depths of the two waves. Now in this case the two waves have been trying to do the same thing and so add together constructively. This is called constructive interference.
If one wave is trying to form a peak and the other is trying to form a trough then they are competing to do different things. In this case they can cancel out. The height of the peak less the depth of the trough will be the resulting effect. If the depth of the trough is the same as the height of the peak nothing will happen. If the height of the peak is bigger than the depth of the trough a smaller peak will appear and if the trough is deeper then a less deep trough will appear. This is destructive interference.
Properties of Waves : Standing Waves[edit | edit source]
When two waves move in opposite directions, through each other, constructive interference happens. If the two waves have the same frequency and wavelength then a specific type of constructive interference can occur: standing waves can form.
Standing waves are disturbances which don't appear to move, they stand in the same place. Lets demonstrate exactly how this comes about. Imagine a long string with waves being sent down it from either end. The waves from both ends have the same amplitude, wavelength and frequency as you can see in the picture below:
To stop from getting confused between the two waves we'll draw the wave from the left with a dashed line and the one from the right with a solid line. As the waves move closer together when they touch both waves have an amplitude of zero:
If we wait for a short time the ends of the two waves move past each other and the waves overlap. Now we know what happens when two waves overlap, we add them together to get the resulting wave.
Now we know what happens when two waves overlap, we add them together to get the resulting wave. In this picture we show the two waves as dotted lines and the sum of the two in the overlap region is shown as a solid line:
The important thing to note in this case is that there are some points where the two waves always destructively interfere to zero. If we let the two waves move a little further we get the picture below:
Again we have to add the two waves together in the overlap region to see what the sum of the waves looks like.
In this case the two waves have moved half a cycle past each other but because they are out of phase they cancel out completely. The point at 0 will always be zero as the two waves move past each other.
When the waves have moved past each other so that they are overlapping for a large region the situation looks like a wave oscillating in place. If we focus on the range -4, 4 once the waves have moved over the whole region. To make it clearer the arrows at the top of the picture show peaks where maximum positive constructive interference is taking place. The arrows at the bottom of the picture show places where maximum negative interference is taking place.
As time goes by the peaks become smaller and the troughs become shallower but they do not move.
For an instant the entire region will look completely flat.
The various points continue their motion in the same manner.
Eventually the picture looks like the complete reflection through the x-axis of what we started with:
Then all the points begin to move back. Each point on the line is oscillating up and down with a different amplitude.
If we superimpose the two cases where the peaks where at a maximum and the case where the same waves where at a minimum we can see the lines that the points oscillate between. We call this the envelope of the standing wave as it contains all the oscillations of the individual points. A node is a place where the two waves cancel out completely as two waves destructively interfere in the same place. An anti-node is a place where the two waves constructively interfere.
To make the concept of the envelope clearer let us draw arrows describing the motion of points along the line.
Every point in the medium containing a standing wave oscillates up and down and the amplitude of the oscillations depends on the location of the point. It is convenient to draw the envelope for the oscillations to describe the motion. We cannot draw the up and down arrows for every single point!
Reflection from a fixed end[edit | edit source]
If waves are reflected from a fixed end, for example tying the end of a rope to a pole and then sending waves down it. The fixed end will always be a node. Remember: Waves reflected from a fixed end undergo a phase shift.
The wavelength, amplitude and speed of the wave cannot affect this, the fixed end is always a node.
Reflection from an open end[edit | edit source]
If waves are reflected from end, which is free to move, it is an anti-node. For example tying the end of a rope to a ring, which can move up and down, around the pole. Remember: The waves sent down the string are reflected but do not suffer a phase shift.
Wavelengths of standing waves with fixed and open ends[edit | edit source]
Beats[edit | edit source]
If the waves that are interfering are not identical then the waves form a modulated pattern with a changing amplitude. The peaks in amplitude are called beats. If you consider two sound waves interfering then you hear sudden beats in loudness or intensity of the sound.
The simplest illustration is to draw two different waves and then add them together. You can do this mathematically and draw them yourself to see the pattern that occurs.
Here is wave 1:
Now we add this to another wave, wave 2:
When the two waves are added (drawn in coloured dashed lines) you can see the resulting wave pattern:
To make things clearer the resulting wave without the dashed lines is drawn below. Notice that the peaks are the same distance apart but the amplitude changes. If you look at the peaks they are modulated i.e. the peak amplitudes seem to oscillate with another wave pattern. This is what we mean by modulation.
The maximum amplitude that the new wave gets to is the sum of the two waves just like for constructive interference. Where the waves reach a maximum it is constructive interference.
The smallest amplitude is just the difference between the amplitudes of the two waves, exactly like in destructive interference.
The beats have a frequency which is the difference between the frequency of the two waves that were added. This means that the beat frequency is given by
|
(2.2) |
fB : beat frequency (Hz or s-1) f1 : frequency of wave 1 (Hz or s-1) f2 : frequency of wave 2 (Hz or s-1)
Properties of Waves : Diffraction[edit | edit source]
One of the most interesting, and also very useful, properties of waves is diffraction. When a wave strikes a barrier with a hole, only part of the wave can move through the hole. If the hole is similar in size to the wavelength of the wave diffractions occurs. The waves that comes through the hole no longer looks like a straight wave front. It bends around the edges of the hole. If the hole is small enough it acts like a point source of circular waves.
This bending around the edges of the hole is called diffraction. To illustrate this behaviour we start with Huygen's principle.
Huygen's Principle[edit | edit source]
Huygen's principle states that each point on a wavefront acts like a point source or circular waves. The waves emitted from each point interfere to form another wavefront on which each point forms a point source. A long straight line of points emitting waves of the same frequency leads to a straight wave front moving away.
To understand what this means lets think about a whole lot of peaks moving in the same direction. Each line represents a peak of a wave.
If we choose three points on the next wave front in the direction of motion and make each of them emit waves isotropically (i.e. the same in all directions) we will get the sketch below:
What we have drawn is the situation if those three points on the wave front were to emit waves of the same frequency as the moving wave fronts. Huygens principle says that every point on the wave front emits waves isotropically and that these waves interfere to form the next wave front.
To see if this is possible we make more points emit waves isotropically to get the sketch below:
You can see that the lines from the circles (the peaks) start to overlap in straight lines. To make this clear we redraw the sketch with dashed lines showing the wavefronts which would form. Our wavefronts are not perfectly straight lines because we didn't draw circles from every point. If we had it would be hard to see clearly what is going on.
Huygen's principle is a method of analysis applied to problems of wave propagation. It recognizes that each point of an advancing wave front is in fact the center of a fresh disturbance and the source of a new train of waves and that the advancing wave as a whole may be regarded as the sum of all the secondary waves arising from points in the medium already traversed. This view of wave propagation helps better understand a variety of wave phenomena, such as diffraction.
Wavefronts Moving Through an Opening[edit | edit source]
Now if we allow the wavefront to impinge on a barrier with a hole in it, then only the points on the wavefront that move into the hole can continue emitting forward moving waves - but because a lot of the wavefront have been removed the points on the edges of the hole emit waves that bend round the edges.
The wave front that impinges (strikes) the wall cannot continue moving forward. Only the points moving into the gap can. If you employ Huygens' principle you can see the effect is that the wavefronts are no longer straight lines.
Riaan Note: still cant find this image, have to get it from the pdf
For example, if two rooms are connected by an open doorway and a sound is produced in a remote corner of one of them, a person in the other room will hear the sound as if it originated at the doorway. As far as the second room is concerned, the vibrating air in the doorway is the source of the sound. The same is true of light passing the edge of an obstacle, but this is not as easily observed because of the short wavelength of visible light.
This means that when waves move through small holes they appear to bend around the sides because there aren't enough points on the wavefront to form another straight wavefront. This is bending round the sides we call diffraction.
Properties of Waves : Dispersion[edit | edit source]
Dispersion is a property of waves where the speed of the wave through a medium depends on the wavelength. So if two waves enter the same dispersive medium and have different wavelengths they will have different speeds in that medium even if they both entered with the same speed.
Practical Applications of Waves: Sound Waves[edit | edit source]
Doppler Effect[edit | edit source]
The Doppler Effect is an interesting phenomenon that occurs when an object producing sound is moved relatively to the listener.
Consider the following: When a car blaring its horn is behind you, the pitch is higher as it is approaching, and becomes lower as it is moving away. This is only noticeable if the object is moving at a fairly high speed, although it is still theoretically present at any speed.
When an object is moving away from the listener, the sound waves are stretched over a further distance meaning they happen less often. The wavelength ends up being greater so the frequency is less and the pitch is lower. When an object is moving towards the listener, the waves are compressed over a small distance making a very small wavelength and therefore a large frequency and high pitch. Since the pitch of the sound depends on the frequency of the waves, the pitch increases when the object is moving towards the listener.
|
|
f' is the observed frequency, f is the actual frequency, v is the speed of sound () T is temperature in degrees Celsius, is the speed of the observer, and is the speed of the source. If the observer is approaching the source, use the top operator (the +) in the numerator, and if the source is approaching the observer, use the top operator (the -) in the denominator. If the observer is moving away from the source, use the bottom operator (the -) in the numerator, and if the source is moving away from the observer, use the bottom operator (the +) in the denominator.
Example problems[edit | edit source]
A. An ambulance, which is emitting a 40 Hz siren, is moving at a speed of 30 m/s towards a stationary observer. The speed of sound in this case is 339 m/s.
B. An M551 Sheridan, moving at 10 m/s is following a Renault FT-17 which is moving in the same direction at 5 m/s and emitting a 30 Hz tone. The speed of sound in this case is 342 m/s.
Ultra-Sound[edit | edit source]
still to be completed
Ultrasound is sound that has too high a frequency for humans to hear. Some other animals can hear ultrasound though. Dog whistles are an example of ultrasound. We can't hear the sound, but dogs can. Audible sound is in the frequency range between 20 Hz and 20000 Hz. Anything above that is ultrasound, and anything below that is called infrasonic.
Ultrasound also has medical applications. It can be used to generate images with a sonogram. Ultrasound is commonly used to look at fetuses in the womb.
| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
Practical Applications of Waves: Electromagnetic Waves[edit | edit source]
In physics, wave-particle duality holds that light and matter simultaneously exhibit properties of waves and of particles. This concept is a consequence of quantum mechanics.
In 1905, Einstein reconciled Huygens' view with that of Newton. He explained the photoelectric effect (an effect in which light did not seem to act as a wave) by postulating the existence of photons, quanta of energy with particulate qualities. Einstein postulated that the frequency of light, , is related to the energy, , of its photons:
|
(2.3) |
where is Planck's constant ().
In 1924, De Broglie claimed that all matter has a wave-like nature. He related wavelength and momentum p:
|
(2.4) |
This is a generalization of Einstein's equation above, since the momentum of a photon is given by
|
(2.5) |
where is the speed of light in vacuum, and .
De Broglie's formula was confirmed three years later by guiding a beam of electrons (which have rest mass) through a crystalline grid and observing the predicted interference patterns. Similar experiments have since been conducted with neutrons and protons. Authors of similar recent experiments with atoms and molecules claim that these larger particles also act like waves. This is still a controversial subject because these experimenters have assumed arguments of wave-particle duality and have assumed the validity of de Broglie's equation in their argument.
The Planck constant h is extremely small and that explains why we don't perceive a wave-like quality of everyday objects: their wavelengths are exceedingly small. The fact that matter can have very short wavelengths is exploited in electron microscopy.
In quantum mechanics, the wave-particle duality is explained as follows: every system and particle is described by state functions which encode the probability distributions of all measurable variables. The position of the particle is one such variable. Before an observation is made the position of the particle is described in terms of probability waves which can interfere with each other.
Important Equations and Quantities[edit | edit source]
Frequency:
|
(2.6) |
Speed:
| Quantity | Symbol | S.I. Units | Direction | ||
| Amplitude | A | m | -- | ||
| Period | T | s | -- | ||
| Wavelength | m | -- | |||
| Frequency | f | Hz or s−1 | -- | ||
| Speed | v | m.s−1 | -- | ||
Vectors[edit | edit source]
Introduction[edit | edit source]
A vector is 'something' that has both magnitude and direction. "'Thing'? What sorts of 'thing'?" Any piece of information which contains a magnitude and a related direction can be a vector. A vector should tell you how much and which way.
Consider a man driving his car east along a highway at 100 km/h. What we have given here is a vector — the car's velocity. The car is moving at 100 km/h (this is the magnitude) and we know where it is going — east (this is the direction). Thus, we know the speed and direction of the car. These two quantities, a magnitude and a direction, form a vector we call velocity.
Definition: A vector is a measurement which has both magnitude and direction.
In physics, magnitudes often have directions associated with them. If you push something it is not very useful knowing just how hard you pushed. A direction is needed too. Directions are extremely important, especially when dealing with situations more complicated than simple pushes and pulls.
Different people like to write vectors in different ways. Any way of writing a vector so that it has both magnitude and direction is valid.
Are vectors physics? No, vectors themselves are not physics. Physics is just a description of the world around us. To describe something we need to use a language. The most common language used to describe physics is mathematics. Vectors form a very important part of the mathematical description of physics, so much so that it is absolutely essential to master the use of vectors.
Mathematical representation[edit | edit source]
Numerous notations are commonly used to denote vectors. In this text, vectors will be denoted by symbols capped with an arrow. As an example, , and are all vectors (they have both magnitude and direction). Sometimes just the magnitude of a vector is required. In this case, the arrow is omitted. In other words, F denotes the magnitude of vector . is another way of representing the size of a vector.
Graphical representation[edit | edit source]
Graphically vectors are drawn as arrows. An arrow has both a magnitude (how long it is) and a direction (the direction in which it points). For this reason, arrows are vectors.
In order to draw a vector accurately we must specify a scale and include a reference direction in the diagram. A scale allows us to translate the length of the arrow into the vector's magnitude. For instance if one chose a scale of 1cm = 2N (1cm represents 2N), a force of magnitude 20N would be represented as an arrow 10cm long. A reference direction may be a line representing a horizontal surface or the points of a compass.
Worked Example 2: Drawing vectors[edit | edit source]
Question: Using a scale of represent the following velocities:
a) north
b) east
Answer:
Some Examples of Vectors[edit | edit source]
Displacement[edit | edit source]
Imagine you walked from your house to the shops along a winding path through the veld. Your route is shown in blue in Figure 3.1. Your sister also walked from the house to the shops, but she decided to walk along the pavements. Her path is shown in red and consisted of two straight stretches, one after the other.

|
| Figure 3.1: Illustration of Displacement |
Although you took very different routes, both you and your sister walked from the house to the shops. The overall effect was the same! Clearly the shortest path from your house to the shops is along the straight line between these two points. The length of this line and the direction from the start point (the house) to the end point (the shops) forms a very special vector known as displacement. Displacement is assigned the symbol
Definition: Displacement is defined as the magnitude and direction of the straight line joining one's starting point to one's final point.
OR
Definition: Displacement is a vector with direction pointing from some initial (starting) point to some final (end) point and whose magnitude is the straight-line distance from the starting point to the end point.
(NOTE TO SELF: choose one of the above)
In this example both you and your sister had the same displacement. This is shown as the black arrow in Figure 3.1. Remember displacement is not concerned with the actual path taken. It is only concerned with your start and end points. It tells you the length of the straight-line path between your start and end points and the direction from start to finish. The distance travelled is the length of the path followed and is a scalar (just a number). Note that the magnitude of the displacement need not be the same as the distance travelled. In this case the magnitude of your displacement would be considerably less than the actual length of the path you followed through the veld!
Velocity[edit | edit source]
Definition: Velocity is the rate of change of displacement with respect to time.
The terms rate of change and with respect to are ones we will use often and it is important that you understand what they mean. Velocity describes how much displacement changes for a certain change in time.
We usually denote a change in something with the symbol (the Greek letter Delta). You have probably seen this before in maths — the gradient of a straight line is . The gradient is just how much y changes for a certain change in x. In other words it is just the rate of change of y with respect to x. This means that velocity must be
(NOTE TO SELF: This is actually average velocity. For instantaneous 's change to differentials. Explain that if is large then we have average velocity else for infinitesimal time interval instantaneous!)
What then is speed? Speed is how quickly something is moving. How is it different from velocity? Speed is not a vector. It does not tell you which direction something is moving, only how fast. Speed is the magnitude of the velocity vector (NOTE TO SELF: instantaneous speed is the magnitude of the instantaneous velocity.... not true of averages!).
Consider the following example to test your understanding of the differences between velocity and speed.
Worked Example 3: Speed and Velocity[edit | edit source]
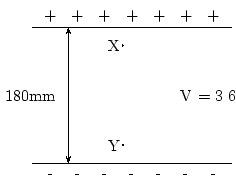
Question: A man runs around a circular track of radius 100m. It takes him 120s to complete a revolution of the track. If he runs at constant speed, calculate:
- his speed,
- his instantaneous velocity at point A,
- his instantaneous velocity at point B,
- his average velocity between points A and B,
- his average velocity during a revolution.
Answer:
- 1. To determine the man's speed, we need to know the distance he travels and how long it takes. We know it takes to complete one revolution of the track. What distance is one revolution of the track? We know the track is a circle and we know its radius, so we can determine the perimeter or distance around the circle. We start with the equation for the circumference of a circle:
- 2. Now that we have distance and time, we can determine speed. We know that speed is distance covered per unit time. If we divide the distance covered by the time it took, we will know how much distance was covered for every unit of time.
- 3. Consider point A in the diagram:
We know which way the man is running around the track, and we know his speed. His velocity at point A will be his speed (the magnitude of the velocity) plus his direction of motion (the direction of his velocity). He is moving at the instant that he arrives at A, as indicated in the diagram below.
His velocity vector will be West.
- 4. Consider point B in the diagram:
- We know which way the man is running around the track, and we know his speed. His velocity at point B will be his speed (the magnitude of the velocity) plus his direction of motion (the direction of his velocity). He is moving at the instant that he arrives at B, as indicated in the diagram below.
- His velocity vector will be South.
- 4. So, now, what is the man's average velocity between Point A and Point B?
As he runs around the circle, he changes direction constantly. (Imagine a series of vector arrows pointing out from the circle, one for each step he takes.) If you add up all these directions and find the average it turns out to be ...Right. South west. And, notice that if you just looked for the average between his velocity at Point A and at Point B, that comes out south west, too. So his average velocity between Point A and Point B is south west.
- 5. Now we need to calculate his average velocity over a complete revolution. The definition of average velocity is given earlier and requires that you know the total displacement and the total time. The total displacement for a revolution is given by the vector from the initial point to the final point. If the man runs in a circle, then he ends where he started. This means the vector from his initial point to his final point has zero length. A calculation of his average velocity follows:
Remember: Displacement can be zero even when distance is not!
Acceleration[edit | edit source]
Definition: Acceleration is the rate of change of velocity with respect to time.
Acceleration is also a vector. Remember that velocity was the rate of change of displacement with respect to time so we expect the velocity and acceleration equations to look very similar. In fact:
|
(3.2) |
(NOTE TO SELF: average and instantaneous distinction again! expand further — what does it mean?)
Acceleration will become very important later when we consider forces.
Force[edit | edit source]
Imagine that you and your friend are pushing a cardboard box kept on a smooth floor. Both of you are equally strong. Can you tell me in which direction the box will move ? Probably not. Because I have not told you in which direction each of you are pushing the box. If both of you push it towards north, the box would move northwards. If you push it towards north and you friend pushes it towards east, it would move north-eastwards. If you two push it in opposite directions, it wouldn't move at all !
Thus in dealing with force applied on any object, it is equally important to take into account the direction of the force, as the magnitude. This is the case with all vectors.
Mathematical Properties of Vectors[edit | edit source]
Vectors are mathematical objects and we will use them to describe physics in the language of mathematics. However, first we need to understand the mathematical properties of vectors (e.g. how they add and subtract).
We will now use arrows representing displacements to illustrate the properties of vectors. Remember that displacement is just one example of a vector. We could just as well have decided to use forces to illustrate the properties of vectors.
Addition of Vectors[edit | edit source]
If we define a displacement vector as 2 steps in the forward direction and another as 3 steps in the forward direction then adding them together would mean moving a total of 5 steps in the forward direction. Graphically, this can be seen by first following the first vector two steps forward, and then following the second one three steps forward:
We add the second vector at the end of the first vector, since this is where we now are after the first vector has acted. The vector from the tail of the first vector (the starting point) to the head of the last (the end point) is then the sum of the vectors. This is the tail-to-head method of vector addition.
The order in which you add vectors does not matter. In the example above, if you decided to first go 3 steps forward and then another 2 steps forward, the end result would still be 5 steps forward.
The final answer when adding vectors is called the resultant.
Definition: The resultant of a number of vectors is the single vector whose effect is the same as the individual vectors acting together.
In other words, the individual vectors can be replaced by the resultant — the overall effect is the same. If vectors and have a resultant , this can be represented mathematically as,
Let us consider some more examples of vector addition using displacements. The arrows tell you how far to move and in what direction. Arrows to the right correspond to steps forward, while arrows to the left correspond to steps backward. Look at all of the examples below and check them.
Let us test the first one. It says one step forward and then another step forward is the same as an arrow twice as long — two steps forward.
It is possible that you end up back where you started. In this case the net result of what you have done is that you have gone nowhere (your start and end points are at the same place). In this case, your resultant displacement is a vector with length zero units. We use the symbol to denote such a vector:
Check the following examples in the same way. Arrows up the page can be seen as steps left and arrows down the page as steps right.
Try a couple to convince yourself!

|

|

|

|
It is important to realise that the directions aren't special — forward and backwards or left and right are treated in the same way. The same is true of any set of parallel directions:

|

|

|
In the above examples the separate displacements were parallel to one another. However the same tail-to-head technique of vector addition can be applied to vectors in any direction.

|

|
Now you have discovered one use for vectors; describing resultant displacement — how far and in what direction you have travelled after a series of movements.
Although vector addition here has been demonstrated with displacements, all vectors behave in exactly the same way. Thus, if given a number of forces are acting on a body, you can use the same method to determine the resultant force acting on the body. We will return to vector addition in more detail later.
Subtraction of Vectors[edit | edit source]
What does it mean to subtract a vector? Well this is really simple: if we have 5 apples and we subtract 3 apples, we have only 2 apples left. Now lets work in steps — if we take 5 steps forward, and then subtract 3 steps forward, we are left with only two steps forward:
What have we done? You originally took 5 steps forward but then you took 3 steps back. That backward displacement would be represented by an arrow pointing to the left (backwards) with length 3. The net result of adding these two vectors is 2 steps forward:
Thus, subtracting a vector from another is the same as adding a vector in the opposite direction (i.e. subtracting 3 steps forwards is the same as adding 3 steps backwards).
This suggests that in this problem, arrows to the right are positive, and arrows to the left are negative. More generally, vectors in opposite directions differ in sign (i.e. if we define up as positive, then vectors acting down are negative). Thus, changing the sign of a vector simply reverses its direction:

|

|

|

|

|

|
In mathematical form, subtracting from gives a new vector
This clearly shows that subtracting vector from is the same as adding to . Look at the following examples of vector subtraction.
Scalar Multiplication[edit | edit source]
What happens when you multiply a vector by a scalar (an ordinary number)?
Going back to normal multiplication we know that is just 2 groups of 2 added together to give 4. We can adopt a similar approach to understand how vector multiplication works.
Techniques of Vector Addition[edit | edit source]
Now that you have been acquainted with the mathematical properties of vectors, we return to vector addition in more detail. There are a number of techniques of vector addition. These techniques fall into two main categories- graphical and algebraic techniques.
Graphical Techniques[edit | edit source]
Graphical techniques involve drawing accurate scale diagrams to denote individual vectors and their resultants. We next discuss the two primary graphical techniques, the tail-to-head technique and the parallelogram method.
The Tail-to-head Method[edit | edit source]
In describing the mathematical properties of vectors we used displacements and the tail-to-head graphical method of vector addition as an illustration. In the tail-to-head method of vector addition the following strategy is followed:
- Choose a scale and include a reference direction.
- Choose any of the vectors to be summed and draw it as an arrow in the correct direction and of the correct length- remember to put an arrowhead on the end to denote its direction.
- Take the next vector and draw it as an arrow starting from the arrowhead of the first vector in the correct direction and of the correct length.
- Continue until you have drawn each vector- each time starting from the head of the previous vector. In this way, the vectors to be added are drawn one after the other tail-to-head.
- The resultant is then the vector drawn from the tail of the first vector to the head of the last. Its magnitude can be determined from the length of its arrow using the scale. Its direction too can be determined from the scale diagram.
Worked Example 4 Tail-to-Head Graphical Addition I[edit | edit source]
Question: A ship leaves harbour H and sails 6km north to port A. From here the ship travels 12km east to port B, before sailing 5.5km south-west to port C. Determine the ship's resultant displacement using the tail-to-head technique of vector addition.
Answer:
Now, we are faced with a practical issue: in this problem the displacements are too large to draw them their actual length! Drawing a 2km long arrow would require a very big book. Just like cartographers (people who draw maps), we have to choose a scale. The choice of scale depends on the actual question- you should choose a scale such that your vector diagram fits the page. Before choosing a scale one should always draw a rough sketch of the problem. In a rough sketch one is interested in the approximate shape of the vector diagram.
Step 1 :
Let us draw a rough sketch of the situation
In a rough sketch one should include all of the information given in the problem. All of the magnitudes of the displacements are shown and a compass has been included as a reference direction.
Step 2 :
Next we choose a scale for our vector diagram. It is clear from the rough sketch that choosing a scale where 1cm represents 1km (scale: 1cm = 1km) would be a good choice in this problem )- the diagram will then take up a good fraction of an A4 page. We now start the accurate construction.
Step 3 :
Construction Step 1: Starting at the harbour H we draw the first vector 6cm long in the direction north (remember in the diagram 1cm represents 1km):
Construction Step 2: Since the ship is now at port A we draw the second vector 12cm long starting from this point in the direction east:
Construction Step 3: Since the ship is now at port B we draw the third vector 5.5cm long starting from this point in the direction south-west. A protractor is required to measure the angle of 45o.
Construction Step 4: As a final step we draw the resultant displacement from the starting point (the harbour H) to the end point (port C). We use a ruler to measure the length of this arrow and a protractor to determine its direction
Step 4 :
We now use the scale to convert the length of the resultant in the scale diagram to the actual displacement in the problem. Since we have chosen a scale of 1cm = 1km in this problem the resultant has a magnitude of 8.38 km. The direction can be specified in terms of the angle measured either as 75.4o east of north or on a bearing of 75.4o.
Step 5 :
Now we can quote the final answer: The resultant displacement of the ship is 8.38 km on a bearing of 75.4o!
Worked Example 5 Tail-to-Head Graphical Addition II[edit | edit source]
Question: A man walks 40 m East, then 30 m North.
a) What was the total distance he walked?
b) What is his resultant displacement?
Answer:
Step 1 :
What distance did the man travel? In the first part of his journey he traveled 40 m and in the second part he traveled 30 m. This gives us a total distance traveled of
Step 2 :
What is his resultant displacement? The man's resultant displacement is the vector from where he started to where he ended. It is the sum of his two separate displacements. We will use the tail-to-head method of accurate construction to find this vector. Firstly, we draw a rough sketch:
Step 3 :
Next we choose a scale suitable for the problem. A scale of 1cm represents 5m (1cm = 5m) is a good choice here. Now we can begin the process of construction.
Step 4 :
We draw the first displacement as an arrow 8cm long (according to the scale ) in the direction east:
Step 5 :
Starting from the head of the first vector we draw the second displacement as an arrow 6cm long (according to the scale ) in the direction north:</math>
Step 6 :
Now we connect the starting point to the end point and measure the length and direction of this arrow (the resultant)
Step 7 :
Finally we use the scale to convert the length of the resultant in the scale diagram to the actual magnitude of the resultant displacement. According to the chosen scale 1cm = 5m. Therefore 10cm represents 50m. The resultant displacement is then 50m 36.9o north of east.
The Parallelogram Method[edit | edit source]
When needing to find the resultant of two vectors another graphical technique can be applied- the parallelogram method. The following strategy is employed:
- Choose a scale and a reference direction.
- Choose either of the vectors to be added and draw it as an arrow of the correct length in the correct direction.
- Draw the second vector as an arrow of the correct length in the correct direction from the tail of the first vector.
- Complete the parallelogram formed by these two vectors.
- The resultant is then the diagonal of the parallelogram. Its magnitude can be determined from the length of its arrow using the scale. Its direction too can be determined from the scale diagram.
Worked Example 6[edit | edit source]
Parallelogram Method of Graphical Addition I
Question: A force of F1 = 5 N is applied to a block in a horizontal direction. A second force F2 = 4 N is applied to the object at an angle of 30° above the horizontal.
Determine the resultant force acting on the block using the parallelogram method of accurate construction.
Answer:
Step 1 :
Firstly we make a rough sketch of the vector diagram:
Step 2 :
Now we choose a suitable scale. In this problem a scale of 1 cm = 0.5 N would be appropriate, since then the vector diagram would take up a reasonable fraction of the page. We can now begin the accurate scale diagram.
Step 3 :
Let us draw F1 first. According to the scale it has length 10 cm:
Step 4 :
Next we draw F2. According to the scale it has length 8 cm. We make use of a protractor to draw this vector at 30° to the horizontal:
Step 5 :
Next we complete the parallelogram and draw the diagonal:
RIAAN NOTE: Image missing img155.png PDF page 51 File:Fhsst vectors43.png
Step 6 :
Finally we use the scale to convert the measured length into the actual magnitude. Since 1 cm = 0.5 N, 17.4 cm represents 8.7 N. Therefore the resultant force is 8.7 N at 13.3° above the horizontal.
The parallelogram method is restricted to the addition of just two vectors. However, it is arguably the most intuitive way of adding two forces acting at a point.
Algebraic Addition and Subtraction of Vectors[edit | edit source]
Vectors in a Straight Line[edit | edit source]
Whenever you are faced with adding vectors acting in a straight line (i.e. some directed left and some right, or some acting up and others down) you can use a very simple algebraic technique:
- Choose a positive direction. As an example, for situations involving displacements in the directions west and east, you might choose west as your positive direction. In that case, displacements east are negative.
- Next simply add (or subtract) the vectors with the appropriate signs.
- As a final step the direction of the resultant should be included in words (positive answers are in the positive direction, while negative resultants are in the negative direction).
Let us consider a couple of examples.
Worked Example 7[edit | edit source]
Adding vectors algebraically I
Question: A tennis ball is rolled towards a wall which is 10m away to the right. If after striking the wall the ball rolls a further 2.5m along the ground to the left, calculate algebraically the ball's resultant displacement.
(NOTE TO SELF: PGCE suggest a `more real looking' diagram, followed by a diagram one would draw to solve the problem (like our existing one with the positive direction shown as an arrow))
Answer:
Step 1 :
Let us draw a picture of the situation:
Step 2 :
We know that the resultant displacement of the ball ( ) is equal to the sum of the ball's separate displacements ( and ):
Since the motion of the ball is in a straight line (i.e. the ball moves left and right), we can use the method of algebraic addition just explained.
Step 3 :
First we choose a positive direction. Let's make to the right the positive direction. This means that to the left becomes the negative direction.
Step 4 :
With right positive:
Step 5 :
Next we simply add the two displacements to give the resultant:
Step 6 :
Finally, in this case right means positive so:
Let us consider an example of vector subtraction.
Worked Example 8[edit | edit source]
Subtracting vectors algebraically I
Question: Suppose that a tennis ball is thrown horizontally towards a wall at 3m.s−1 to the right. After striking the wall, the ball returns to the thrower at 2m.s−1. Determine the change in velocity of the ball.
Answer:
Step 1 :
Remember that velocity is a vector. The change in the velocity of the ball is equal to the difference between the ball's initial and final velocities:
Since the ball moves along a straight line (i.e. left and right), we can use the algebraic technique of vector subtraction just discussed.
Step 2 :
Let's make to the right the positive direction. This means that to the left becomes the negative direction.
Step 3 :
With right positive:
Step 4 :
Thus, the change in velocity of the ball is:
Remember that in this case right means positive so:
Remember that the technique of addition and subtraction just discussed can only be applied to vectors acting along a straight line.
A More General Algebraic technique[edit | edit source]
In worked example 3 the tail to head method of accurate construction was used to determine the resultant displacement of a man who travelled first east and then north. However, the man's resultant can be calculated without drawing an accurate scale diagram. Let us revisit this example.
Worked Example 9[edit | edit source]
An Algebraic solution to Worked Example 3
Question: A man walks 40 m East, then 30 m North.
- Calculate the man's resultant displacement.
Answer:
Step 1 :
As before, the rough sketch looks as follows:
Step 2 :
Note that the triangle formed by his separate displacement vectors and his resultant displacement vector is a right-angle triangle. We can thus use Pythogoras' theorem to determine the length of the resultant. If the length of the resultant vector is called s then:
Step 3 : Now we have the length of the resultant displacement vector but not yet its direction. To determine its direction we calculate the angle between the resultant displacement vector and East.
We can do this using simple trigonometry:
Step 4 :
Our final answer is then:
- Resultant Displacement: 50 m at 36.9o North of East
This is exactly the same answer we arrived at after drawing a scale diagram!
In the previous example we were able to use simple trigonometry to calculate a man's resultant displacement. This was possible since the man's directions of motion were perpendicular (north and east). Algebraic techniques, however, are not limited to cases where the vectors to be combined are along the same straight line or at right angles to one another. The following example illustrates this.
Worked Example 10[edit | edit source]
Further example of vector addition by calculation
Question: A man walks from point A to point B which is 12km away on a bearing of 45o. From point B the man walks a further 8km east to point C. Calculate the man's resultant displacement.
Answer:
Step 1 : Let us begin by drawing a rough sketch of the situation
RIAAN NOTE: Image on page 56 is missing File:Fhsst vectors46.png
since the man walks initially on a bearing of 45o.Then, (alternate angles parallel lines). Both of these angles are included in the rough sketch.
Step 2 :
Now let us calculate the length of the resultant (AC). Since we know both the lengths of and and the included angle , we can use the cosine rule:
Step 3 :
Next we use the sine rule to determine the angle :
Thus,
Step 4 :
Our final answer is then:
- Resultant Displacement: 18.5km on a bearing of 62.8o
Components of Vectors[edit | edit source]
In the discussion of vector addition we saw that a number of vectors acting together can be combined to give a single vector (the resultant). In much the same way a single vector can be broken down into a number of vectors which when added give that original vector. These vectors which sum to the original are called components of the original vector. The process of breaking a vector into its components is called resolving into components.
While summing a given set of vectors gives just one answer (the resultant), a single vector can be resolved into infinitely many sets of components. In the diagrams below the same black vector is resolved into different pairs of components. These components are shown in red. When added together the red vectors give the original black vector (i.e. the original vector is the resultant of its components).
In practice it is most useful to resolve a vector into components which are at right angles to one another.
Worked Example 11[edit | edit source]
Resolving a vector into components
Question: A motorist undergoes a displacement of 250km in a direction 30o north of east. Resolve this displacement into components in the directions north ( and east ().
Answer:
Step 1 :
Firstly let us draw a rough sketch of the original vector
Step 2 :
Next we resolve the displacement into its components north and east. Since these directions are orthogonal to one another, the components form a right-angled triangle with the original displacement as its hypotenuse:
Notice how the two components acting together give the original vector as their resultant.
Step 3 :
Now we can use trigonometry to calculate the magnitudes of the components of the original displacement:
and
Remember sN and sE are the magnitudes of the components- they are in the directions north and east respectively.
Block on an incline[edit | edit source]
As a further example of components let us consider a block of mass m placed on a frictionless surface inclined at some angle to the horizontal. The block will obviously slide down the incline, but what causes this motion?
The forces acting on the block are its weight mg and the normal force N exerted by the surface on the object. These two forces are shown in the diagram below.
Now the object's weight can be resolved into components parallel and perpendicular to the inclined surface. These components are shown as red arrows in the diagram above and are at right angles to each other. The components have been drawn acting from the same point. Applying the parallelogram method, the two components of the block's weight sum to the weight vector.
To find the components in terms of the weight we can use trigonometry:
The component of the weight perpendicular to the slope W exactly balances the normal force N exerted by the surface. The parallel component, however, is unbalanced and causes the block to slide down the slope.
Vector addition using components[edit | edit source]
In Figure 3.3 two vectors are added in a slightly different way to the methods discussed so far. It might look a little like we are making more work for ourselves, but in the long run things will be easier and we will be less likely to go wrong.
In Figure 3.3 the primary vectors we are adding are represented by solid lines and are the same vectors as those added in Figure 3.2 using the less complicated looking method.

|
Each vector can be broken down into a component in the x-direction and one in the y-direction. These components are two vectors which when added give you the original vector as the resultant. Look at the red vector in figure 3.3. If you add up the two red dotted ones in the x-direction and y-direction you get the same vector. For all three vectors we have shown their respective components as dotted lines in the same colour.
But if we look carefully, addition of the x components of the two original vectors gives the x component of the resultant. The same applies to the y components. So if we just added all the components together we would get the same answer! This is another important property of vectors.
Worked Example 12[edit | edit source]
Adding Vectors Using Components
Question: Lets work through the example shown in Figure 3.3 to determine the resultant.
Answer:
Step 1 :
The first thing we must realise is that the order that we add the vectors does not matter. Therefore, we can work through the vectors to be added in any order.
Step 2 :
Let us start with the bottom vector. If you are told that this vector has a length of 5.385 units and an angle of 21.8o to the horizontal then we can find its components. We do this by using known trigonometric ratios. First we find the vertical or y component:
Secondly we find the horizontal or x component:
We now know the lengths of the sides of the triangle for which our vector is the hypotenuse. If you look at these sides we can assign them directions given by the dotted arrows. Then our original red vector is just the sum of the two dotted vectors (its components). When we try to find the final answer we can just add all the dotted vectors because they would add up to the two vectors we want to add.
Step 3 :
Now we move on to considering the second vector. The green vector has a length of 5 units and a direction of 53.13 degrees to the horizontal so we can find its components.
Step 4 :
Now we have all the components. If we add all the x-components then we will have the x-component of the resultant vector. Similarly if we add all the y-components then we will have the y-component of the resultant vector.
The x-components of the two vectors are 5 units right and then 3 units right. This gives us a final x-component of 8 units right.
The y-components of the two vectors are 2 units up and then 4 units up. This gives us a final y-component of 6 units up.
Step 5 :
Now that we have the components of the resultant, we can use Pythagoras' theorem to determine the length of the resultant. Let us call the length of the hypotenuse l and we can calculate its value
The resultant has length of 10 units so all we have to do is calculate its direction. We can specify the direction as the angle the vectors makes with a known direction. To do this you only need to visualize the vector as starting at the origin of a coordinate system. We have drawn this explicitly below and the angle we will calculate is labeled .
Using our known trigonometric ratios we can calculate the value of
Step 6 :
Our final answer is a resultant of 10 units at 36.8o to the positive x-axis.
Do I really need to learn about vectors? Are they really useful?[edit | edit source]
Vectors are essential to do physics. Absolutely essential. This is an important warning. If something is essential we had better stop for a moment and make sure we understand it properly.
Summary of Important Quantities, Equations and Concepts[edit | edit source]
| Quantity | Symbol | S.I. Units | Direction | ||
| Displacement | m | yes | |||
| Velocity | m.s−1 | yes | |||
| Distance | d | m | - | ||
| Speed | v | m.s−1 | - | ||
| Acceleration | m.s−2 | yes | |||
Vector: A vector is a measurement which has both magnitude and direction.
Displacement: Displacement is a vector with direction pointing from some initial (starting) point to some final (end) point and whose magnitude is the straight-line distance from the starting point to the final point.
Distance: The distance traveled is the length of your actual path.
Velocity: Velocity is the rate of change of displacement with respect to time.
Acceleration: Acceleration is the rate of change of velocity with respect to time.
Resultant: The resultant of a number of vectors is the single vector whose effect is the same as the individual vectors acting together
Forces[edit | edit source]
What is a force?[edit | edit source]
The simplest way to describe force is to say that it is a `push' or a `pull'. The push or pull on an object may cause either deformation or may change the state of motion of the object under consideration. The harder you 'push' or 'pull', the more force you are applying.
If we leave aside the deformation aspects, then force can be considered to produce change in the state of the motion of the object i.e. velocity. We have, though, experienced in real life that a 'push' or 'pull' does not always manifest in the change of motion. The reason is simple. A change in the state of motion requires a net force. For example, if the force is great enough to overcome friction the object being pushed or pulled will move. So long as the forces on an object are balanced (i.e. net force is zero), the state of motion described by "velocity" will remain same.
In fact, the acceleration of a body is directly proportional to the net force acting on it. The word net is important- forces are vectors and what matters in any situation is the vector sum of all the forces acting on an object.
The unit of force is the newton (symbol N)
|Force was first described by Archimedes. Archimedes of Syracuse (circa 287 BC - 212 BC), was a Greek mathematician, astronomer, philosopher, physicist and engineer. He was killed by a Roman soldier during the sack of the city, despite orders from the Roman general, Marcellus, that he was not to be harmed.
EQUILIBRIUM OF FORCES.
DEFINITION-The Equilibrium of forces is the single fore required to produce an equilibrium When only three forces act on an object this closed figure is a triangle. This leads to the triangles law for three forces in equilibrium.
Force diagrams[edit | edit source]
The resultant force acting on an object is the vector sum of the set of forces acting on that one object. It is very important to remember that we consider all the forces that act on the object under consideration - not the forces that the object might, in turn, apply on other objects.
The easiest way to determine this resultant force is to construct what we call a force diagram. In a force diagram we represent the object by a point and draw all the force vectors connected to that point as arrows. Remember from the Vectors chapter that we use the length of the arrow to indicate the vector's magnitude and the direction of the arrow to show which direction it acts in.
The second step is to rearrange the force vectors so that it is easy to add them together and find the resultant force.
Let us consider an example to get started:
Two people push on a box from opposite sides with a force of 5 N.
When we draw the force diagram we represent the box by a dot. The two forces are represented by arrows, with their tails on the dot.
See how the arrows point in opposite directions and have the same magnitude (length). This means that they cancel out and there is no net force acting on the object.
This result can be obtained algebraically too, since the two forces act along the same line. Firstly we choose a positive direction and then add the two vectors taking their directions into account.
Considering direction towards right as the positive direction
As you work with more complex force diagrams, in which the forces do not exactly balance, you may notice that sometimes you get a negative answer (e.g. -2 N). What does this mean? Does it mean that we have something which is opposite of the force? No, all it means is that the force acts in the opposite direction to the one that you chose to be positive. You can choose the positive direction to be any way you want, but once you have chosen it you must stick with it.
Once a force diagram has been drawn the techniques of vector addition introduced in the previous chapter can be implemented. Depending on the situation you might choose to use a graphical technique such as the tail-to-head method or the parallelogram method, or else an algebraic approach to determine the resultant. Since force is a vector, all of these methods apply!
Always remember to check your signs
Worked Example 13 Single Force on a block[edit | edit source]
Question: A block on a frictionless flat surface weighs 100 N. A 75 N force is applied to the block towards the right. What is the net force (or resultant force) on the block?
Answer:
Step 1 : Firstly let us draw a force diagram for the block:
RIAAN Note image on page 68 is missing
Be careful not to forget the two forces perpendicular to the surface. Every object with mass is attracted to the centre of the earth with a force (the object's weight). However, if this were the only force acting on the block in the vertical direction then the block would fall through the table to the ground. This does not happen because the table exerts an upward force (the normal force) which exactly balances the object's weight.
Step 2 :
Thus, the only unbalanced force is the applied force. This applied force is then the resultant force acting on the block.
Equilibrium of Forces[edit | edit source]
At the beginning of this chapter it was mentioned that resultant forces cause objects to accelerate. If an object is stationary or moving at constant velocity then either:
- no forces are acting on the object, or
- the forces acting on that object are exactly balanced.
A resultant force would cause a stationary object to start moving or an object moving with a given velocity to speed up or slow down or change direction such that the velocity of the object changes.
In other words, for stationary objects or objects moving with constant velocity, the resultant force acting on the object is zero. The object is said to be in equilibrium.
If a resultant force acts on an object then that object can be brought into equilibrium by applying an additional force that exactly balances this resultant. Such a force is called the equilibrant and is equal in magnitude but opposite in direction to the original resultant force acting on the object.
Definition: The equilibrant of any number of forces is the single force required to produce equilibrium.
As an example of an object in equilibrium, consider an object held stationary by two ropes in the arrangement below:
Let us draw a force diagram for the object. In the force diagram the object is drawn as a dot and all forces acting on the object are drawn in the correct directions starting from that dot. In this case, three forces are acting on the object.
Each rope exerts a force on the object in the direction of the rope away from the object.
Since the object has mass, it is attracted towards the centre of the earth. This weight is represented in the force diagram as .
Since the object is stationary, the resultant force acting on the object is zero. In other words the three force vectors drawn tail-to-head form a closed triangle:
[In general, when drawn tail-to-head the forces acting on an object in equilibrium form a closed figure with the head of the last vector joining up with the tail of the first vector. When only three forces act on an object this closed figure is a triangle. This leads to the triangle law for three forces in equilibrium:
Triangle Law for Three Forces in Equilibrium: Three forces in equilibrium can be represented in magnitude and direction by the three sides of a triangle taken in order.
Newton's Laws of Motion[edit | edit source]
Our current laws of motion were discovered by Sir Isaac Newton. It is said that Sir Isaac Newton started to think about the nature of motion and gravitation after being struck on the head by a falling apple.
Newton discovered 3 laws describing motion:
First Law[edit | edit source]
Newton's first law basically says that a force has to be applied to an object to make it move or to make it stop. The first part of that statement definitely makes sense. The only way I can make something move is to have something give it a push. The second part of that statement might not be quite as easy to just take as fact. We've all witnessed objects slow down when nobody is pushing them. How then can we say that the only way to stop an object's motion is with a force? The answer is that there are forces that we don't always see. Most of the time, the force that we don't see is the force of friction.
Friction is the force that resists motion when two things are sliding past one another. To understand what friction is, think about sandpaper. If you try to rub 2 pieces of sandpaper together, it will be hard to get them to slide. This same phenomenon happens between all objects to some degree. This frictional force is what slows objects down or stops their motion.
Second Law[edit | edit source]
Definition: The time rate of change in momentum is proportional to the applied force and takes place in the direction of the force.
The law is represented in the following basic form (the system of measurement is chosen such that constant of proportionality is 1):
The product of mass and velocity i.e. is called the momentum. The net force on a particle is, thus, equal to rate change of momentum of the particle with time. Generally mass of the object under consideration is constant and thus can be taken out of the derivative:
For constant mass,
Force is equal to mass times acceleration. This version of Newton's Second Law of Motion assumes that the mass of the body does not change with time, and as such, does not represent a general mathematical form of the Law. Consequently, this equation cannot, for example, be applied to the motion of a rocket, which loses its mass (the lost mass is ejected at the rear of the rocket) with the passage of time.
It makes sense that the direction of the acceleration is in the direction of the resultant force. If you push something away from you it doesn't move toward you unless of course there is another force acting on the object towards you!
Worked Example 16 Newton's Second Law[edit | edit source]
Question: A block of mass 10 kg is accelerating at 2 m·s−2. What is the magnitude of the net force acting on the block?
- Answer
Step 1:
We are given
- the block's mass
- the block's acceleration
all in the correct units.
Step 2 :
We are asked to find the magnitude of the force applied to the block. Newton's Second Law tells us the relationship between acceleration and force for an object. Since we are only asked for the magnitude we do not need to worry about the directions of the vectors:
Thus, there must be a net force of 20 N acting on the box.
Worked Example 17 Newton's Second Law 2[edit | edit source]
Question: A 12 N force is applied in the positive x-direction to a block of mass 100 mg resting on a frictionless flat surface. What is the resulting acceleration of the block?
Answer:
Step 1 :
We are given
- the block's mass
- the applied force
but the mass is not in the correct units.
Step 2 :
Let us begin by converting the mass:
Step 3 :
We know that net force results in acceleration. Since there is no friction the applied force is the resultant or net force on the block (refer to the earlier example of the block pushed on the surface of the table). The block will then accelerate in the direction of this force according to Newton's Second Law.
Step 4 :
To determine the magnitude of the acceleration:
From Newton's Second Law the direction of the acceleration is the same as that of the resultant force. The final result is then that the block accelerates at in the positive x-direction.
Weight and Mass[edit | edit source]
You must have heard people saying My weight is 60 kg. This is actually correct, though physicists often have difficulty understanding it because it is mass that is measured in kilograms. This is a different meaning of the word weight from the one used in mechanics, where weight is the force of gravity exerted by the earth on an object with mass:
As such, weight is measured in newtons.
If you compare this equation to Newton's Second Law you will see that it looks exactly the same with the a replaced by g. Thus, when weight is the only force acting on an object (i.e. when
Fweight is the resultant force acting on the object) the object has an acceleration g. Such an object is said to be in free fall. The value for g is the same for all objects (i.e. it is independent of the objects mass):
|
(4.3) |
You will learn how to calculate this value from the mass and radius of the earth in Chapter ???. Actually the value of g varies slightly from place to place on the Earth's surface.
The reason that we often get confused between weight and mass, is that scales measure your weight (in newtons) and then display your mass using the equation above.
Worked Example 18 Calculating the resultant and then the acceleration[edit | edit source]
Question: A block (mass 20 kg) on a frictionless flat surface has a 45 N force applied to it in the positive x-direction. In addition a 25 N force is applied in the negative x-direction. What is the resultant force acting on the block and the acceleration of the block?
Answer:
Step 1 :
We are given
- the block's mass
- Force F1 = 45 N in the positive x-direction
- Force F2 = 25 N in the negative x-direction
all in the correct units.
Step 2 :
We are asked to determine what happens to the block. We know that net force results in an acceleration. We need to determine the net force acting on the block.
Step 3 :
Since F1 and F2 act along the same straight line, we can apply the algebraic technique of vector addition discussed in the Vectors chapter to determine the resultant force. Choosing the positive x-direction as our positive direction:
Positive x-direction is the positive direction:
where we remembered in the last step to include the direction of the resultant force in words. By Newton's Second Law the block will accelerate in the direction of this resultant force.
Step 4 :
Next we determine the magnitude of the acceleration:
The final result is then that the block accelerates at in the positive x-direction (the same direction as the resultant force).
Worked Example 19 Block on incline[edit | edit source]
Question: A block (mass 10 kg) is released on an inclined plane. What is the resulting rate of acceleration of the block if the angle theta is 25 degrees and the coefficient of friction between the block and the plane is 0.25?
Solution:
Step 1: The acceleration of the block will be parallel to the plane, so we break the problem into two parts - forces perpendicular to the plane (which must cancel out since there is no acceleration perpendicular to the plane) and parallel to the plane.
Step 2: We know that there is no acceleration in the direction perpendicular to the surface of the inclined plane, or in other words . Therefore we know that:
Step 3: Summing forces parallel to the plane yields:
The final result is that the block accelerates down the inclined plane with an acceleration of .
Third Law[edit | edit source]
Definition: For every force one body applies to another (action) there is always an equal but opposite in direction force another body applies back to the first one (reaction.)
This law is a direct consequence of the Principle of Conservation of Linear Momentum.
Newton's Third Law is easy to understand but it can get quite difficult to apply it. An important thing to realise is that the action and reaction forces can never act on the same object and hence cannot contribute to the same resultant.
Worked Example 20 Identifying action-reaction Pairs[edit | edit source]
Question: Consider pushing a box on the surface of a rough table.
- Draw a force diagram indicating all of the forces acting on the box.
- Identify the reaction force for each of the forces acting on the box.
Answer:
- The following force diagram shows all of the forces acting on the box
There is an important thing to realise which is related to Newton's Third Law. Think about dropping a stone off a cliff. It falls because the earth exerts a force on it (see Chapter ???) and it doesn't seem like there are any other forces acting. So is Newton's Third Law wrong? No, the reactionary force to the weight of the stone is the force exerted by the stone on the earth. This is illustrated in detail in the next worked example.
Worked Example 21 Newton's Third Law[edit | edit source]
Question: A stone of mass 0.5 kg is accelerating at 10 m·s−2 towards the earth.
- What is the force exerted by the earth on the stone?
- What is the force exerted by the stone on the earth?
- What is the acceleration of the earth, given that its mass is 5.97 × 1027 kg?
Answer:
- Step 1 : We are given
- the stone's mass
- the stone's acceleration (g)
- By Newton's Third Law the stone must exert an equal but opposite force on the earth. Hence the stone exerts a force of 5 N towards the stone on the earth.
- We have
- the force acting on the earth
- the Earth's mass
The next two worked examples are quite long and involved but it is very important that you understand the discussion as they illustrate the importance of Newton's Laws.
Worked Example 22 Rockets[edit | edit source]
Question: How do rockets accelerate in space?
Answer:
- Gas explodes inside the rocket.
- This exploding gas exerts a force on each side of the rocket (as shown in the picture below of the explosion chamber inside the rocket).
Note that the forces shown in this picture are representative. With an explosion there will be forces in all directions.
- Due to the symmetry of the situation, all the forces exerted on the rocket are balanced by forces on the opposite side, except for the force opposite the open side. This force on the upper surface is unbalanced.
- This is therefore the resultant force acting on the rocket and it makes the rocket accelerate forwards.
Systems and External Forces[edit | edit source]
The concepts of a system and an external forces are very important in physics. A system is any collection of objects. If one draws an imaginary box around such a system then an external force is one that is applied by an object or person outside the box. Imagine for example a car pulling a trailer.
Concept of system is extremely important. Consider an example of a person holding a load (box) on his head and standing on a platform.
Now count the forces :
(i) Box presses the person down (ii) The person pushes the box up (reaction to box's weight) (iii) Box is pulled down by the earth (iv) Earth is pulled up by the box (v) Person presses the floor (vi) Floor pushes the person up (vii) Person is pulled down by earth and (viii) Earth is pulled up by the person.
Quite a mess. Which ones are internal forces and which ones are external forces? Identification of system comes handy here. We can select the box or the person as a system for analyzing forces or we may even consider box and person together as a single system. Only condition to watch while selecting a system is that all parts of the system should have same acceleration. If two parts are at different accelerations then each of them should be treated as a separate system.
Newton's Law of Universal Gravitation[edit | edit source]
Why does the Earth stay in orbit around the Sun? Shouldn't it fly off tangentially into outer space?
These questions intrigued Newton and inspired his study of gravitation.
Newton realized that a force must be constantly pulling on the Earth, redirecting its motion and preventing it from being flung off. Newton reasoned that this force, which he termed 'gravity', acted between all bodies with mass and varied inversely to the square of the distance between the two bodies.
where is a universal gravitational constant, are the 2 masses, and is the distance between the centers of mass.
Newton also realized that this same force which redirects the path of the Earth around the Sun, was also responsible for an apple falling to the ground. In this case, the two masses, the Earth, and the apple, are attracted each other and this exerts a force which pulls the apple towards the center of the Earth. While we can use the Universal Law of Gravitation formula to solve this problem it is often more convenient to realize two facts:
- The Earths mass, is constant
- The distance between the apple (or other object) can usually be approximated with just , the radius of the Earth, because this is the dominating term.
Thus we can rewrite the equations such that
where
g is the acceleration on Earth and is
Examples of Forces Studied Later[edit | edit source]
Most of physics revolves around forces. Although there are many different forces we deal with them all in the same way. The methods to find resultants and acceleration do not depend on the type of force we are considering.
At first glance, the number of different forces may seem overwhelming - gravity, drag, electrical forces, friction and many others. However, physicists have found that all these forces can be classified into four groups. These are gravitational forces, electromagnetic forces, strong nuclear force and weak nuclear force. Even better, all the forces that you will come across at school are either gravitational or electromagnetic. Doesn't that make life easy?
Newtonian Gravity[edit | edit source]
Gravity is the attractive force between two objects due to the mass of the objects. When you throw a ball in the air, its mass and the Earth's mass attract each other, which leads to a force between them. The ball falls back towards the Earth, and the Earth accelerates towards the ball. The movement of the Earth toward the ball is, however, so small that you couldn't possibly measure it.
Electromagnetic Forces[edit | edit source]
Almost all of the forces that we experience in everyday life are electromagnetic in origin. They have this unusual name because long ago people thought that electric forces and magnetic forces were different things. After much work and experimentation, it has been realised that they are actually different manifestations of the same underlying theory.
The Electric Force[edit | edit source]
If we have objects carrying electrical charge, which are not moving, then we are dealing with electrostatic forces (Coulomb's Law). This force is actually much stronger than gravity. This may seem strange, since gravity is obviously very powerful, and holding a balloon to the wall seems to be the most impressive thing electrostatic forces have done, but think about it: for gravity to be detectable, we need to have a very large mass nearby. But a balloon rubbed in someone's hair can stick to a wall with a force so strong that it overcomes the force of gravity - with just the charges in the balloon and the wall!
Magnetic force[edit | edit source]
The magnetic force is a different manifestation of the electromagnetic force. It stems from the interaction between moving charges as opposed to the fixed charges involved in Coulomb's Law.
Examples of the magnetic force in action include magnets, compasses, car engines, computer data storage and your hair standing on end. Magnets are also used in the wrecking industry to pick up cars and move them around sites.
= Friction[edit | edit source]
Newton's First Law states that an object moving without a force acting on it will keep moving. Then why does a box sliding on a table stop? The answer is friction. Friction arises from the interaction between the molecules on the bottom of a box with the molecules on a table. This interaction is electromagnetic in origin, hence friction is just another view of the electromagnetic force. The great part about school physics is that most of the time we are told to neglect friction but it is good to be aware that there is friction in the real world.
Friction is also useful . If there was no friction and you tried to prop a ladder up against a wall, it would simply slide to the ground. Rock climbers use friction to maintain their grip on cliffs.
Friction is a force that impedes motion. It is in parallel to the contact surface and acts against the motion of the body.
Drag Force[edit | edit source]
This is the force an object experiences while travelling through a medium. When something travels through the air it needs to displace air as it travels and because of this the air exerts a force on the object. This becomes an important force when you move fast and a lot of thought is taken to try and reduce the amount of drag force a sports car experiences.
The drag force is very useful for parachutists. They jump from high altitudes and if there was no drag force, then they would continue accelerating all the way to the ground. Parachutes are wide because the more surface area you show, the greater the drag force and hence the slower you hit the ground.
Summary of Important Quantities, Equations and Concepts[edit | edit source]
| Units | |||||
| Quantity | Symbol | S.I. Unit | Fundamental Units | Direction | |
| Mass | m | kg | kg | no | |
| Acceleration | m·s−2 | m·s−2 | yes | ||
| Force | N | kg·m·s−2 | yes | ||
Equilibrium: Objects at rest or moving with constant velocity are in equilibrium and have a zero resultant force.
Equilibrant: The equilibrant of any number of forces is the single force required to produce equilibrium.
Triangle Law for Forces in Equilibrium: Three forces in equilibrium can be represented in magnitude and direction by the three sides of a triangle taken in order.
Newton's First Law: Every object will remain at rest or in uniform motion in a straight line unless it is made to change its state by the action of an external force.
Newton's Second Law: The resultant force acting on a body results in an acceleration which is in the same direction as the resultant force and is directly proportional to the magnitude of this force and inversely proportional to the mass of the object.
Newton's Third Law: For every force or action there is an equal but opposite force or reaction.
Rectilinear Motion[edit | edit source]
What is rectilinear motion?[edit | edit source]
Rectilinear motion means motion along a straight line. This is a useful topic to study for learning how to describe the movement of cars along a straight road or of trains along straight railway tracks. In this section you have only two directions to worry about: (1) along the direction of motion, and (2) opposite to the direction of motion.
To illustrate this imagine a train heading east.
If it is accelerating away from the station platform (P), the direction of acceleration is the same as the direction of the train's velocity — east. If it is braking the direction of acceleration is opposite to the direction of its motion, i.e. west.
Speed and Velocity[edit | edit source]
Let's take a moment to review our definitions of velocity and speed by looking at the worked example below:
Worked Example 23 Speed and Velocity[edit | edit source]
Question: A cyclist moves from A through B to C in 10 seconds. Calculate both his speed and his velocity.
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the distance between A and B
- the distance between B and C
- the total time for the cyclist to go from A through B to C
all in the correct units!
Step 2 :
What is being asked? We are asked to calculate the average speed and the average velocity of the cyclist.
His speed - a scalar - will be
Since velocity is a vector we will first need to find the resultant displacement of the cyclist. His velocity will be
The total displacement is the vector from A to C, and this is just the resultant of the two displacement vectors, i.e.
Using the rule of Pythagoras:
∴
For this cyclist, his velocity is not the same as his speed because there has been a change in the direction of his motion. If the cyclist traveled directly from A to C without passing through B his speed would be
and his velocity would be
In this case where the cyclist is not undergoing any change of direction (i.e. he is traveling in a straight line) the magnitudes of the speed and the velocity are the same. This is the defining principle of rectilinear motion.
| Important: |
| For motion along a straight line the magnitudes of speed and velocity are the same, and the magnitudes of the distance and displacement are the same. |
Graphs[edit | edit source]
In physics we often use graphs as important tools for picturing certain concepts. Below are some graphs that help us picture the concepts of displacement, velocity and acceleration.
Displacement-Time Graphs[edit | edit source]
Below is a graph showing the displacement of the cyclist from A to C:
This graphs shows us how, in 10 seconds time, the cyclist has moved from A to C. We know the gradient (slope) of a graph is defined as the change in y divided by the change in x, i.e. . In this graph the gradient of the graph is just - and this is just the expression for velocity.
| Important: |
| The area between a velocity-time graph and the `time' axis gives the displacement of the object. |
The slope is the same all the way from A to C, so the cyclist's velocity is constant over the entire displacement he travels. In figure 5.1 are examples of the displacement-time graphs you will encounter.
a) shows the graph for an object stationary over a period of time. The gradient is zero, so the object has zero velocity.
b) shows the graph for an object moving at a constant velocity. You can see that the displacement is increasing as time goes on. The gradient, however, stays constant (remember: its the slope of a straight line), so the velocity is constant. Here the gradient is positive, so the object is moving in the direction we have defined as positive.
c) shows the graph for an object moving at a constant acceleration. You can see that both the displacement and the velocity (gradient of the graph) increase with time. The gradient is increasing with time, thus the velocity is increasing with time and the object is accelerating.
Velocity-Time Graphs[edit | edit source]
Uniform acceleration and gradient (slope)[edit | edit source]
Look at the velocity-time graph below:
This is the velocity-time graph of a cyclist traveling from A to B at a constant acceleration, i.e. with steadily increasing velocity. The gradient (slope) of this graph is just - and this is just the expression for acceleration. Because the slope is the same at all points on this graph, the acceleration of the cyclist is constant. And the constant acceleration is , or 2 meters per second per second (or 2 meters per second squared)
| Important: |
| The gradient (slope) on a velocity-time graph equals the acceleration. |
Distance travelled[edit | edit source]
Not only can we get the acceleration of an object from its velocity-time graph, but we can also get some idea of the displacement traveled. Look at the graph below:
This graph shows an object moving at a constant velocity of 10m/s for a duration of 5s. The area between the graph and the time axis (the shaded area) of the above plot will give us the displacement of the object during this time. In this case we just need to calculate the area of a rectangle with width 5s and height 10 m/s
So, here we've shown that an object traveling at 10 m/s for 5s has undergone a displacement of 50m.
| Important: |
|---|
| The area between a velocity-time graph and the `time' axis gives the displacement of the object. |
Here are a couple more velocity-time graphs to get used to:

|
| Figure 5.2: Some common velocity-time graphs: |
In figure 5.2 are examples of the displacement-time graphs you may encounter.
a) shows the graph for an object moving at a constant velocity over a period of time. The gradient is zero, so the object is not accelerating.
b) shows the graph for an object which is decelerating. You can see that the velocity is decreasing with time. The gradient, however, stays constant (remember: its the slope of a straight line), so the acceleration is constant. Here the gradient is negative, so the object is accelerating in the opposite direction to its motion, hence it is decelerating.
Acceleration-Time Graphs[edit | edit source]
In this chapter on rectilinear motion we will only deal with objects moving at a constant acceleration, thus all acceleration-time graphs will look like these two:
Here is a description of the graphs below:
a) shows the graph for an object which is either stationary or traveling at a constant velocity. Either way, the acceleration is zero over time.
b) shows the graph for an object moving at a constant acceleration. In this case the acceleration is positive - remember that it can also be negative.
We can obtain the velocity of a particle at some given time from an acceleration time graph - it is just given by the area between the graph and the time-axis. In the graph below, showing an object at a constant positive acceleration, the increase in velocity of the object after 2 seconds corresponds to the shaded portion.
Its useful to remember the set of graphs below when working on problems. Figure 5.3 shows how displacement, velocity and time relate to each other. Given a displacement-time graph like the one on the left, we can plot the corresponding velocity-time graph by remembering that the slope of a displacement-time graph gives the velocity. Similarly, we can plot an acceleration-time graph from the gradient of the velocity-time graph.

|
| Figure 5.3: A Relationship Between Displacement, Velocity and Acceleration |
Worked Examples[edit | edit source]
Worked Example 24 Relating displacement-, velocity-, and acceleration-time graphs[edit | edit source]
Question: Given the displacement-time graph below, draw the corresponding velocity-time and acceleration-time graphs, and then describe the motion of the object.
Answer:
Step 1 : Analyse the question to determine what is given. The question explicitly gives a displacement-time graph.
Step 2 : What is asked?
3 things:
- Draw a velocity-time graph
- Draw an acceleration-time graph
- Describe the behaviour of the object
For the first 2 seconds we can see that the displacement remains constant - so the object is not moving, thus it has zero velocity during this time. We can reach this conclusion by another path too: remember that the gradient of a displacement-time graph is the velocity. For the first 2 seconds we can see that the displacement-time graph is a horizontal line, i.e. it has a gradient of zero. Thus the velocity during this time is zero and the object is stationary.
For the next 2 seconds, displacement is increasing with time so the object is moving. Looking at the gradient of the displacement graph we can see that it is not constant. In fact, the slope is getting steeper (the gradient is increasing) as time goes on. Thus, remembering that the gradient of a displacement-time graph is the velocity, the velocity must be increasing with time during this phase.
For the final 2 seconds we see that displacement is still increasing with time, but this time the gradient is constant, so we know that the object is now travelling at a constant velocity, thus the velocity-time graph will be a horizontal line during this stage.
So our velocity-time graph looks like this one below. Because we haven't been given any values on the vertical axis of the displacement-time graph, we cannot figure out what the exact gradients are and hence what the values of the velocity are. In this type of question it is just important to show whether velocities are positive or negative, increasing, decreasing or constant.
Once we have the velocity-time graph its much easier to get the acceleration-time graph as we know that the gradient of a velocity-time graph is the just the acceleration.
For the first 2 seconds the velocity-time graph is horizontal at zero, thus it has a gradient of zero and there is no acceleration during this time. (This makes sense because we know from the displacement time graph that the object is stationary during this time, so it can't be accelerating).
For the next 2 seconds the velocity-time graph has a positive gradient. This gradient is not changing (i.e. its constant) throughout these 2 seconds so there must be a constant positive acceleration.
For the final 2 seconds the object is traveling with a constant velocity. During this time the gradient of the velocity-time graph is once again zero, and thus the object is not accelerating.
The acceleration-time graph looks like this:
A brief description of the motion of the object could read something like this: At t = 0s and object is stationary at some position and remains stationary until t = 2s when it begins accelerating. It accelerates in a positive direction for 2 seconds until t = 4s and then travels at a constant velocity for a further 2 seconds.
Worked Example 25 Calculating distance from a velocity-time graph[edit | edit source]
Question: The velocity-time graph of a car is plotted below. Calculate the displacement of the car has after 15 seconds.
Answer: We are asked to calculate the displacement of the car. All we need to remember here is that the area between the velocity-time graph and the time axis gives us the displacement.
For t = 0s to t = 5s this is the triangle on the left:
For t = 5s to t = 12s the displacement is equal to the area of the rectangle
For t = 12s to t = 14s the displacement is equal to the area of the triangle above the time axis on the right
For t = 14s to t = 15s the displacement is equal to the area of the triangle below the time axis
Now the total displacement of the car is just the sum of all of these areas. HOWEVER, because in the last second (from t = 14s to t = 15s) the velocity of the car is negative, it means that the car was going in the opposite direction, i.e. back where it came from! So, to get the total displacement, we have to add the first 3 areas (those with positive displacements) and subtract the last one (because it signifies a displacement in the opposite direction).
Worked Example 26 Velocity from a displacement-time graph[edit | edit source]
Question: Given the diplacement-time graph below,
- what is the velocity of the object during the first 4 seconds?
- what is the velocity of the object from t = 4s to t = 7s?
Answer:
- for the first 4sec velocity is slope of the curve i.e. 2/4=0.5 m/s
- For the last 3 seconds we can see that the displacement stays constant, and that the gradient is zero. Thus .
Worked Example 27 From an acceleration- to a velocity-time graph[edit | edit source]
Question: Given the acceleration-time graph below, assume that the object starts from rest and draw its velocity-time graph.
Answer:
Equations of Motion[edit | edit source]
This section is about solving problems relating to uniformly accelerated motion. We'll first introduce the variables and the equations, then we'll show you how to derive them, and after that we'll do a couple of examples.
- u = starting velocity (m/s) at t = 0
- v = final velocity (m/s) at time t
- s = displacement (m)
- t = time (s)
- a = acceleration (m/s²)
| (5.1) |
| (5.2) |
| (5.3) |
| (5.4) |
Make sure you can rhyme these off, they are very important! There are so many different types of questions for these equations. Basically when you are answering a question like this:
- Find out what values you have and write them down.
- Figure out which equation you need.
- Write it down!!!
- Fill in all the values you have and get the answer.
| (-1.5,0) | Galileo Galilei of Pisa, Italy, was the first to determine the correct mathematical law for acceleration: the total distance covered, starting from rest, is proportional to the square of the time. He also concluded that
objects retain their velocity unless a force - often friction - acts upon them, refuting the accepted Aristotelian hypothesis that objects "naturally" slow down and stop unless a force acts upon them. This principle was incorporated into Newton's laws of motion (1st law). |
Equation 5.1[edit | edit source]
By the definition of acceleration where v is the change in velocity, i.e. . Thus we have
Equation 5.2[edit | edit source]
In the previous section we saw that displacement can be calculated from the area between a velocity-time graph and the time-axis. For uniformly accelerated motion the most complicated velocity-time graph we can have is a straight line. Look at the graph below — it represents an object with a starting velocity of u, accelerating to a final velocity v over a total time t.
To calculate the final displacement we must calculate the area under the graph — this is just the area of the rectangle added to the area of the triangle.
Equation 5.3[edit | edit source]
This equation is simply derived by eliminating the final velocity v in equation 5.2. Remembering from equation 5.1 that
then equation 5.2 becomes
Equation 5.4[edit | edit source]
This equation is just derived by eliminating the time variable in the above equation. From Equation 5.1 we know
Substituting this into Equation 5.3 gives
| (5.5) |
This gives us the final velocity in terms of the initial velocity, acceleration and displacement and is independent of the time variable.
Worked Example 28[edit | edit source]
Question: A racing car has an initial velocity of 100 m/s and it covers a displacement of 725 m in 10 s. Find its acceleration.
Answer:
Step 1 :
We are given the quantities u, s and t — all in the correct units. We need to find a.
Step 2 :
We can use equation 5.3
Step 3 :
Rearranging equation 5.3 we have
Substituting in the values of the known quantities this becomes
The racing car is accelerating at -5.5 m/s², or we could say it is decelerating at 5.5 m/s². this ans is wrong
its better to use a=v-u/t then a=(725-100)/10s you will get a=625/10 which will be equal to 62.5m/s2
Worked Example 29[edit | edit source]
Question: An object starts from rest, moves in a straight line with a constant acceleration and covers a distance of 64 m in 4 s. Calculate
- its acceleration
- its final velocity
- at what time the object had covered half the total distance
- what distance the object had covered in half the total time.
Answer:
Step 1 : We are given the quantities u, s and t in the correct units.
Step 2 : To calculate the acceleration we can use equation [#eq:eq3 5.3]. Rearranging it we have:
Substituting in the values of the known quantities this becomes
Step 3 : To calculate its final velocity we can use equation 5.1 - remember we now also know the acceleration of the object.
Step 4 : The time at which the object had covered half the total distance. Half the distance is 32m. Here we have the quantities s, u and a so we first use equation 5.4 to calculate the velocity at this distance:
Now we can use equation 5.2 to calculate the time:
Step 5 : The distance the object had covered in half the time. Half the time is 2s. Thus we have u, a and t - all in the correct units. We can use equation 5.3 to get the distance:
Worked Example 30[edit | edit source]
Question: A ball is thrown vertically upwards with a velocity of 10 m/s from the balcony of a tall building. The balcony is 15 m above the ground and gravitational acceleration is 10 m/s2. Find a) the time required for the ball to hit the ground, and b) the velocity with which it hits the ground.
Answer:1[edit | edit source]
Step 1 : In this case it often helps to make the problem easier to understand if we draw ourselves a picture like the one below:
First the ball goes upwards with gravitational acceleration slowing it until it reaches its highest point — here its speed is 0 m/s — then it begins descending with gravitational acceleration causing it to increase its speed on the way down. We can separate the motion into 2 stages:
Stage 1 - the upward motion of the ball
Stage 2 - the downward motion of the ball.
We'll choose the upward direction as positive - this means that gravitation acceleration is negative - and we'll begin by solving for all the variables of Stage 1. So far we have these quantities:
Using equation 5.1 to find t1:
We can find s1 by using equation 5.4
For Stage 2 we have the following quantities:
We can determine the final velocity v2 using equation 5.4:
Now we can determine the time for Stage 2, t2, from equation 5.1:
Finally,
a) the time required for the stone to hit the ground is
b) the velocity with which it hits the ground is just
Answer:2[edit | edit source]
applying
solving we will get
so time to reach is 3 second , now applying
These questions do not have the working out in them, but they are all done in the manner described on the previous page.
Question: A car starts off at 10 m/s and accelerates at 1 m/s2 for 10 seconds. What is its final velocity?
Answer: 20 m/s
Question: A car starts from rest, and accelerates at 1 m/s2 for 10 seconds. How far does it move?
Answer: 50 m
Question: A car is going 30 m/s and stops in 2 seconds. What is its stopping distance for this speed?
Answer: 30 m
Question: A car going at 20 m/s stops in a distance of 20 m.
- What is its deceleration?
- If the car is 1 tonne (1000 kg, or 1 Mg) how much force do the brakes exert?
Important Equations and Quantities[edit | edit source]
| ||||||||||||||||||||||||||||||||||||||||||
Momentum[edit | edit source]
What is Momentum?[edit | edit source]
Momentum is a physical quantity which is closely related to forces. We will learn about this connection a little later. Remarkably momentum is a conserved quantity. This makes momentum extremely useful in solving a great variety of real-world problems. Firstly we must consider the definition of momentum.
Definition: The momentum of an object is defined as its mass multiplied by its velocity.
Mathematically,
: momentum ( + direction) m : mass (kg) : velocity (m.s-1 + direction)
Thus, momentum is a property of a moving object and is determined by its velocity and mass. A large truck travelling slowly can have the same momentum as a much smaller car travelling relatively fast.
Note the arrows in the equation defining momentum- momentum is a vector with the same direction as the velocity of the object.
Since the direction of an object's momentum is given by the direction of its motion, one can calculate an object's momentum in two steps:
- include in the final answer the direction of the object's motion
Worked Example 31 Calculating Momentum 1[edit | edit source]
Question: A ball of mass 3kg moves at 2m.s−1 to the right. Calculate the ball's momentum.
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the ball's mass, and
- the ball's velocity
in the correct units!
Step 2 :
What is being asked? We are asked to calculate the ball's momentum. From the definition of momentum,
we see that we need the mass and velocity of the ball, which we are given.
Step 3 :
Firstly we calculate the magnitude of the ball's momentum,
Finally we quote the answer with the direction of the ball's motion included,
Worked Example 32 Calculating Momentum 2[edit | edit source]
Question: A ball of mass 500g is thrown at 2m.s−1. Calculate the ball's momentum.
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the ball's mass, and
- the magnitude of the ball's velocity
but with the ball's mass in the incorrect units!
Step 2 :
What is being asked? We are asked to calculate the momentum which is defined as
Thus, we need the mass and velocity of the ball but we have only its mass and the magnitude of its velocity.
Step 3 :
In order to determine the velocity of the ball we need the direction of the ball's motion. If the problem does not give an explicit direction we are forced to be general. In a case like this we could say that the direction of the velocity is in the direction of motion of the ball. This might sound silly but the lack of information in the question has forced us to be, and we are certainly not wrong! The ball's velocity is then m.s−1 in the direction of motion.
Step 4 :
Next we convert the mass to the correct units,
Step 5 :
Now, let us find the magnitude of the ball's momentum,
Step 6 :
Finally, we quote the answer with the direction of the momentum included,
Worked Example 33 Calculating the Momentum of the Moon[edit | edit source]
Question: The moon is away from the earth and orbits the earth in 27.3 days. If the moon has a mass of [footnode.html#foot11743 6.1] what is the magnitude of its momentum if we assume a circular orbit?
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the moon's mass,
- the distance to the moon, and
- the time for one orbit of the moon
with mass in the correct units but all other quantities in the incorrect units.
The units we require are
- seconds (s) for time, and
- metres (m) for distance pesteng physics→→→→→→
Step 2 :
What is being asked? We are asked to calculate only the magnitude of the moon's momentum (i.e. we do not need to specify a direction). In order to do this we require the moon's mass and the magnitude of its velocity, since
Step 3 :
How do we find the speed or magnitude of the moon's velocity? Speed is defined as,
We are given the time the moon takes for one orbit but not how far it travels in that time. However, we can work this out from the distance to the moon and the fact that the moon's orbit is circular. Firstly let us convert the distance to the moon to the correct units,
Using the equation for the circumference, C, of a circle in terms of its radius, we can determine the distance travelled by the moon in one orbit:
Next we must convert the orbit time, T, into the correct units. Using the fact that a day contains 24 hours, an hour consists of 60 minutes, and a minute is 60 seconds long,
Therefore,
Combining the distance travelled by the moon in an orbit and the time taken by the moon to complete one orbit, we can determine the magnitude of the moon's velocity or speed,
Step 4 :
Finally we can calculate the magnitude of the moon's momentum,
→33→
The Momentum of a System[edit | edit source]
In Chapter 4 Forces the concept of a system was introduced. The bodies that make up a system can have different masses and can be moving with different velocities. In other words they can have different momenta.
Definition: The total momentum of a system is the sum of the momenta of each of the objects in the system.
Since momentum is a vector, the techniques of vector addition discussed in This chapter must be used to calculate the total momentum of a system. Let us consider an example.
Worked Example 34 Calculating the Total Momentum of a System[edit | edit source]
Question: Two billiard balls roll towards each other. They each have a mass of 0.3kg. Ball 1 is moving at to the right, while ball 2 is moving at to the left.
Calculate the total momentum of the system.
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the mass of each ball,
- the velocity of ball 1, and
- the velocity of ball 2, ,
all in the correct units!
Step 2 :
What is being asked? We are asked to calculate the total momentum of the system. In this example our system consists of two balls. To find the total momentum we must sum the momenta of the balls,
Since ball 1 is moving to the right, its momentum is in this direction, while the second ball's momentum is directed towards the left.
Thus, we are required to find the sum of two vectors acting along the same straight line. The algebraic method of vector addition introduced in this chapter can thus be used.
Step 3 :
Firstly we choose a positive direction. Let us choose right as the positive direction, then obviously left is negative.
Step 4 :
The total momentum of the system is then the sum of the two momenta taking the directions of the velocities into account. Ball 1 is travelling at or . Ball 2 is travelling at or . Thus,
Right is the positive direction
In the last step the direction was added in words. Since the result in the second last line is positive, the total momentum of the system is in the positive direction (i.e. to the right).
Change in Momentum[edit | edit source]
If either an object's mass or velocity changes then its momentum too will change. If an object has an initial velocity and a final velocity , then its change in momentum, , is
| = |
Worked Example 35 Change in Momentum[edit | edit source]
Question: A rubber ball of mass 0.8kg is dropped and strikes the floor at a velocity of . It bounces back with an initial velocity of . Calculate the change in momentum of the rubber ball caused by the floor.
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the ball's mass,
- the ball's initial velocity, and
- the ball's final velocity
all in the correct units.
Do not be confused by the question referring to the ball bouncing back with an ``initial velocity of . The word initial is included here since the ball will obviously slow down with time and is the speed immediately after bouncing from the floor.
Step 2 :
What is being asked? We are asked to calculate the change in momentum of the ball,
We have everything we need to find . Since the initial momentum is directed downwards and the final momentum is in the upward direction, we can use the algebraic method of subtraction discussed in the vectors chapter.
Step 3 : Firstly, we choose a positive direction. Let us choose down as the positive direction. Then substituting,
Down is the positive direction
where we remembered in the last step to include the direction of the change in momentum in words.
What properties does momentum have?[edit | edit source]
You may at this stage be wondering why there is a need for introducing momentum. Remarkably momentum is a conserved quantity. Within an isolated system the total momentum is constant. No matter what happens to the individual bodies within an isolated system, the total momentum of the system never changes! Since momentum is a vector, its conservation implies that both its magnitude and its direction remains the same.
Momentum is conserved in isolated systems!
This Principle of Conservation of Linear Momentum is one of the most fundamental principles of physics and it alone justifies the definition of momentum. Since momentum is related to the motion of objects, we can use its conservation to make predictions about what happens in collisions and explosions. If we bang two objects together, by conservation of momentum, the total momentum of the objects before the collision is equal to their total momentum after the collision.
Principle of Conservation of Linear Momentum: The total linear momentum of an isolated system is constant.
or
In an isolated system the total momentum before a collision
(or explosion) is equal to the total momentum after the
collision (or explosion).
Let us consider a simple collision of two pool or billiard balls. Consider the first ball (mass m1) to have an initial velocity (). The second ball (mass m2) moves towards the first ball with an initial velocity . This situation is shown in Figure 6.1. If we add the momenta of each ball we get a total momentum for the system. This total momentum is then
| File:Fhsst mom2.png |
| Figure 6.1: Before the collision. |
| Figure 6.2: After the collision. |
After the two balls collide and move away they each have a different momentum. If we call the final velocity of ball 1 and the final velocity of ball 2 (see Figure 6.2), then the total momentum of the system after the collision is
This system of two balls is isolated since there are no external forces acting on the balls. Therefore, by the principle of conservation of linear momentum, the total momentum before the collision is equal to the total momentum after the collision. This gives the equation for the conservation of momentum in a collision of two objects,
m1 : mass of object 1 (kg) m2 : mass of object 2 (kg) : initial velocity of object 1 (m.s-1 + direction) : initial velocity of object 2 (m.s-1 + direction) : final velocity of object 1 (m.s-1 + direction) : final velocity of object 2 (m.s-1 + direction)
This equation is always true - momentum is always conserved in collisions.
The chapter `Collisions and Explosions' deals with applications of momentum conservation.
At the beginning of this chapter it was mentioned that momentum is closely related to force. We will now explain the nature of this connection.
Consider an object of mass m moving with constant acceleration . During a time t the object's velocity changes from an initial velocity to a final velocity (refer to Figure 6.3). We know from Newton's First Law that there must be a resultant force acting on the object.

|
| Figure 6.3: An object under the action of a resultant force. |
Starting from Newton's Second Law,
This alternative form of Newton's Second Law is called the Law of Momentum.
Mathematically,
: resultant force (N + direction) : change in momentum ( + direction) t : time over which acts (s)
Rearranging the Law of Momentum,
The product is called impulse,
From this equation we see, that for a given change in momentum, is fixed. Thus, if FRes is reduced, must be increased (i.e. the resultant force must be applied for longer). Alternatively if is reduced (i.e. the resultant force is applied for a shorter period) then the resultant force must be increased to bring about the same change in momentum.
Worked Example 36 Impulse and Change in momentum[edit | edit source]
Question: A 150 N resultant force acts on a 300 kg object. Calculate how long it takes this force to change the object's velocity from to
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the object's mass,
- the object's initial velocity,
- the object's final velocity, and
- the resultant force acting on the object
all in the correct units!
Step 2 :
What is being asked? We are asked to calculate the time taken to accelerate the object from the given initial velocity to final velocity. From the Law of Momentum,
Thus we have everything we need to find !
Step 3 :
First we choose a positive direction. Although not explicitly stated, the resultant force acts to the right. This follows from the fact that the object's velocity increases in this direction. Let us then choose right as the positive direction.
Step 4 :
Substituting,
Right is the positive direction
Worked Example 37 Calculating Impulse[edit | edit source]
Question: A cricket ball weighing 156 g is moving at 54 km/h towards a batsman. It is hit by the batsman back towards the bowler at 36\ km/h. Calculate i) the ball's impulse, and ii) the average force exerted by the bat if the ball is in contact with the bat for 0.13 s.
Answer:
Step 1 :
Analyse the question to determine what is given. The question explicitly gives
- the ball's mass,
- the ball's initial velocity,
- the ball's final velocity, and
- the time of contact between bat and ball
all except the time in the wrong units!
Answer to (i):
Step 2 :
What is being asked? We are asked to calculate the impulse
Since we do not have the force exerted by the bat on the ball (), we have to calculate the impulse from the change in momentum of the ball. Now, since
we need the ball's mass, initial velocity and final velocity, which we are given.
Step 3 : Firstly let us change units for the mass
Step 4 :
Next we change units for the velocity
Step 5 :
Next we must choose a positive direction. Let us choose the direction from the batsman to the bowler as the positive direction. Then the initial velocity of the ball is , while the final velocity of the ball is
Step 6 :
Now we calculate the change in momentum,
Direction from batsman to bowler is the positive direction
where we remembered in the last step to include the direction of the change in momentum in words.
Step 7 :
Finally since impulse is just the change in momentum of the ball,
Answer to (ii):
Step 8 :
What is being asked? We are asked to calculate the average force exerted by the bat on the ball, . Now,
We are given and we have calculated the change in momentum or impulse of the ball in part (i)!
Step 9 :
Next we choose a positive direction. Let us choose the direction from the batsman to the bowler as the positive direction. Then substituting,
Direction from batsman to bowler is the positive direction
where we remembered in the final step to include the direction of the force in words.
Summary of Important Quantities, Equations and Concepts[edit | edit source]
| ||||||||||||||||||||||||||||||||||||||||||||||||
Momentum: The momentum of an object is defined as its mass multiplied by its velocity.
Momentum of a System: The total momentum of a system is the sum of the momenta of each of the objects in the system.
Principle of Conservation of Linear Momentum:: `The total linear momentum of an isolated system is constant' or `In an isolated system the total momentum before a collision (or explosion) is equal to the total momentum after the collision (or explosion)'.
Law of Momentum:: The applied resultant force acting on an object is equal to the rate of change of the object's momentum and this force is in the direction of the change in momentum.
Work and Energy[edit | edit source]
What are Work and Energy?[edit | edit source]
The energy is the ability to do a work.
Energy is measured by the result of applied force/power over a period of time to make changes/work.
Work is defined by a force applied to an object to change this object’s physical properties.
Power = Energy / Time No force used no change and none work was done.
Power and energy are closely related, although, they are not the same.
Power is the rate at which energy is delivered, not an amount of energy itself.
Electrical unit of power is Watt (named after the scientist James Watt):
1 Watt = 1 Joule / Second.
Energy = Power × Time.
Energy exist in various forms: kinetic [Ek = ½ m, v2 ], potential [Ep = m g h], thermal (heat), chemical, electrical, electrochemical, magnetic, sound, light, and nuclear.
Energy can be converted from one form into another in many ways:
Through the gravitation forces When gravity accelerates a falling object, it converts its potential energy to kinetic energy, or when an object is lifted, the gravitational field stores the energy exerted by the lifter as potential energy in the earth-object system.
Through the electric and magnetic fields forces Electrically charged particles in the presence of an electric field possess potential energy. The fields’ forces can accelerate particles and convert this particle's potential energy into kinetic energy. Charged particles can interact via electric and magnetic fields to transfer energy between them, i.e.: an electrical current in a conductor transforms electrical energy into heat.
Frictional Forces A mass object with its potential and kinetic energy associated with the position, orientation, and the object’s motion can be converted into thermal energy (heat), whenever the object slides against another object. The sliding causes the molecules on the surfaces of contact to interact via electromagnetic fields with one another and start vibrating.
Through emitting or absorbing photons of light When photons of lights fall on an object, a photon may pass through the object, be reflected by the object, or be absorbed by the atoms making up the object. Depending on the smoothness of the surface, the scale of the photon's wavelength, the reflection may be either diffuse (rough surface) or coherent (smooth surface). If the photon is absorbed, the photon's energy may also be split and converted in one of these ways: • Photo-thermal effect The energy absorbed may simply produce thermal energy, or heat in the object. In this case, the photon's energy is converted into vibrations of the molecules called phonons, which is actually heat energy. • Photoelectric effect The energy absorbed may be converted into kinetic energy of conduction electrons, and hence electrical energy. • Photochemical effect The energy may bring about chemical changes that effectively store the energy. Nuclear reactions occur when the nuclei of particles combine [fusion reaction] or when nuclei split apart [fission reaction].
In the International System of Units [SI system], the electrical energy unit is 1 Joule (named after the English physicist James Prescott Joule).
A one Joule is the amount of energy we expend as work if we exert a force of a one Newton of force over a distance of one meter.
It takes a one Joule of energy to lift 1 lb. about 9 inches.
The unit of force in the International System of Units is 1 Newton (named after the English physicist Isaac Newton).
One Newton of force is the force that can accelerate a mass of 1 kilogram (about 2.205 lbs), such that it picks up 1 meter per second of velocity during each second that the force is exerted.
Appliances rating is how much energy per unit time these appliances draw. This quantity is called the "power":
Energy = Power x Time = (100 Joules/Second) × (3600 Seconds) = 360,000 Joules
Work[edit | edit source]
To do work on an object, one must move the object by applying a force with at least a component in the direction of motion. The work done is given by
W : work done (N.m or J) F| : component of applied force parallel to motion (N) s : displacement of the object (m)
It is very important to note that for work to be done there must be a component of the applied force in the direction of motion. Forces perpendicular to the direction of motion do no work.
As with all physical quantities, work must have units. As follows from the definition, work is measured in N.m. The name given to this combination of S.I. units is the joule (J).
Definition: 1 joule is the work done when an object is moved 1m under the application of a force of 1N in the direction of motion.
The work done by an object can be positive or negative. Since force (F|) and displacement (s) are both vectors, the result of the above equation depends on their directions:
- If F| acts in the same direction as the motion then positive work is being done. In this case the object on which the force is applied gains energy.
- If the direction of motion and F| are opposite, then negative work is being done. This means that energy is transferred in the opposite direction. For example, if you try to push a car uphill by applying a force up the slope and instead the car rolls down the hill you are doing negative work on the car. Alternatively, the car is doing positive work on you!
Worked Example 38 Calculating Work Done I[edit | edit source]
Question: If you push a box 20m forward by applying a force of 15N in the forward direction, what is the work you have done on the box?
Answer:
Step 1 : Analyse the question to determine what information is provided
- The force applied is F = 15N.
- The distance moved is s = 20m.
- The applied force and distance moved are in the same direction. Therefore,
These quantities are all in the correct units, so no unit conversions are required.
Step 2 : Analyse the question to determine what is being asked
- We are asked to find the work done on the box. We know from the definition that work done is W = F|s
Step 3 : Next we substitute the values and calculate the work done
Remember that the answer must be positive as the applied force and the motion are in the same direction (forwards). In this case, you (the pusher) lose energy, while the box gains energy.
Worked Example 39 Calculating Work Done II[edit | edit source]
Question: What is the work done by you on a car, if you try to push the car up a hill by applying a force of 40N directed up the slope, but it slides downhill 30cm?
Answer:
Step 1 : Analyse the question to determine what information is provided
- The force applied is F = 40N
- The applied force and distance moved are in opposite directions. Therefore, if we take s = 0.3m, then .
Step 2 : Analyse the question to determine what is being asked
- We are asked to find the work done on the car by you. We know that work done is W = F|s
Step 3 : Substitute the values and calculate the work done
Again we have the applied force and the distance moved so we can proceed with calculating the work done:
Note that the answer must be negative as the applied force and the motion are in opposite directions. In this case the car does work on the person trying to push.
What happens when the applied force and the motion are not parallel? If there is an angle between the direction of motion and the applied force then to determine the work done we have to calculate the component of the applied force parallel to the direction of motion. Note that this means a force perpendicular to the direction of motion can do no work.
Worked Example 40 Calculating Work Done III[edit | edit source]
Question: Calculate the work done on a box, if it is pulled 5m along the ground by applying a force of F = 10N at an angle of 60o to the horizontal.
Answer:
Step 1 :
Analyse the question to determine what information is provided
- The force applied is F = 10N
- The distance moved is s = 5m along the ground
- The angle between the applied force and the motion is 60o
These quantities are in the correct units so we do not need to perform any unit conversions.
Step 2 : Analyse the question to determine what is being asked
- We are asked to find the work done on the box.
Step 3 : Calculate the component of the applied force in the direction of motion
Since the force and the motion are not in the same direction, we must first calculate the component of the force in the direction of the motion.
From the force diagram we see that the component of the applied force parallel to the ground is
Step 4 : Substitute and calculate the work done
Now we can calculate the work done on the box:
Note that the answer is positive as the component of the force F| is in the same direction as the motion.
We will now discuss energy in greater detail.
Energy[edit | edit source]
As we mentioned earlier, energy is the capacity to do work. When positive work is done on an object, the system doing the work loses energy. In fact, the energy lost by a system is exactly equal to the work done by the system.
Like work (W) the unit of energy (E) is the joule (J). This follows as work is just the transfer of energy.
A very important property of our universe which was discovered around 1890 is that energy is conserved.
Energy is never created nor destroyed, but merely
transformed from one form to another.
Energy conservation and the conservation of matter are the principles on which classical mechanics is built.
IN THE ABSENCE OF FRICTION When work is done on an object by a system:
-the object gains energy equal to the work done by the system
Work Done = Energy Transferred
Thermal energy (heat) is the disorganized movement of microscopic particles. Once energy is converted to this form, it has limited usefulness for doing further work in the system. Friction is the general name for forces that converts energy to heat.
IN THE PRESENCE OF FRICTION When work is done by a system: -only some of the energy lost by the system is transferred into useful energy -the rest of the energy transferred is lost to heat by friction Total Work Done = Useful Work Done + Work Done Against Friction
Types of Energy[edit | edit source]
So what different types of energy exist? Kinetic, mechanical, thermal, chemical, electrical, radiant, and atomic energy are just some of the types that exist. By the principle of conservation of energy, whenwork is done energy is merely transferred from one object to another and from one type of energy to another.
Kinetic Energy[edit | edit source]
Kinetic energy is the energy of motion that an object has. Objects moving in straight lines possess translational kinetic energy, which we often abbreviate as Ek.
The translational kinetic energy of an object is given by
Ek : kinetic energy (J) m : mass of object (kg) v : speed of the object (m.s-1)
Note the dependence of the kinetic energy on the speed of the object- kinetic energy is related to motion. The faster an object is moving the greater its kinetic energy.
Worked Example 41 Calculation of Kinetic Energy[edit | edit source]
Question: If a rock has a mass of 1kg and is thrown at 5m/s, what is its kinetic energy?
Answer:
Step 1 : Analyse the question to determine what information is provided
- The mass of the rock m = 1kg
- The speed of the rock v = 5m/s
These are both in the correct units so we do not have to worry about unit conversions.
Step 2 : Analyse the question to determine what is being asked
- We are asked to find the kinetic energy. From the definition we know that to work out Ek, we need to know the mass and the velocity of the object and we are given both of these values.
Step 3 : Substitute and calculate the kinetic energy
To check that the units in the above example are in fact correct:
The units are indeed correct!
Study hint: Checking units is an important cross-check and
you should get into a habit of doing this. If you, for example, finish an exam early then checking the units in your calculations is a very good idea.
Worked Example 42 Mixing Units and Kinetic Energy Calculations 1[edit | edit source]
Question: If a car has a mass of 900kg and is driving at 60km/hr, what is its kinetic energy?
Answer:
Step 1 : Analyse the question to determine what information is provided
- The mass of the car m = 900kg
Step 2 : Analyse the question to determine what is being asked
- We are asked to find the kinetic energy.
Step 3 : Substitute and calculate
We know we need the mass and the speed to work out Ek and we are given both of these quantities. We thus simply substitute them into the equation for Ek:
Worked Example 43 Mixing Units and Kinetic Energy Calculations 2[edit | edit source]
Question: If a bullet has a mass of 150kg and is shot at a muzzle velocity of 960m/s, what is its kinetic energy?
Answer:
Step 1 : Analyse the question to determine what information is provided
- We are given the muzzle velocity which is just how fast the bullet leaves the barrel and it is v = 960m/s.
Step 2 : Analyse the question to determine what is being asked
- We are asked to find the kinetic energy.
Step 3 : Substitute and calculate
We just substitute the mass and velocity (which are known) into the equation for Ek:
Potential Energy[edit | edit source]
If you lift an object you have to do work on it. This means that energy is transferred to the object. But where is this energy? This energy is stored in the object and is called potential energy. The reason it is called potential energy is because if we let go of the object it would move.
Definition: Potential energy is the energy an object has due to its position or state.
As an object raised above the ground falls, its potential energy is released and transformed into kinetic energy. The further it falls the faster it moves as more of the stored potential energy is transferred into kinetic energy. Remember, energy is never created nor destroyed, but merely transformed from one type to another. In this case potential energy is lost but an equal amount of kinetic energy is gained.
In the example of a falling mass the potential energy is known as gravitational potential energy as it is the gravitational force exerted by the earth which causes the mass to accelerate towards the ground. The gravitational field of the earth is what does the work in this case.
Another example is a rubber-band. In order to stretch a rubber-band we have to do work on it. This means we transfer energy to the rubber-band and it gains potential energy. This potential energy is called elastic potential energy. Once released, the rubber-band begins to move and elastic potential energy is transferred into kinetic energy.
Gravitational Potential Energy[edit | edit source]
As we have mentioned, when lifting an object it gains gravitational potential energy. One is free to define any level as corresponding to zero gravitational potential energy. Objects above this level then possess positive potential energy, while those below it have negative potential energy. To avoid negative numbers in a problem, always choose the lowest level as the zero potential mark. The change in gravitational potential energy of an object is given by:
: Change in gravitational potential energy (J) m : mass of object (kg) g : acceleration due to gravity (m.s-2) : change in height (m)
When an object is lifted it gains gravitational potential energy, while it loses gravitational potential energy as it falls.
Worked Example 44 Gravitational potential energy[edit | edit source]
Question: How much potential energy does a brick with a mass of 1kg gain if it is lifted 4m.
Answer:
Step 1 : Analyse the question to determine what information is provided
- The mass of the brick is m = 1kg
- The height lifted is
These are in the correct units so we do not have to worry about unit conversions.
Step 2 : Analyse the question to determine what is being asked
- We are asked to find the gain in potential energy of the object.
Step 3 : Identify the type of potential energy involved
Since the block is being lifted we are dealing with gravitational potential energy. To work out , we need to know the mass of the object and the height lifted. As both of these are given, we just substitute them into the equation for .
Step 4 : Substitute and calculate
Mechanical Energy and Energy Conservation[edit | edit source]
Kinetic energy and potential energy are together referred to as mechanical energy. The total mechanical energy (U) of an object is then the sum of its kinetic and potential energies:
|
(7.1) |
Now,
IN THE ABSENCE OF FRICTION Mechanical energy is conserved
This principle of conservation of mechanical energy can be a very powerful tool for solving physics problems. However, in the presence of friction some of the mechanical energy is lost:
IN THE PRESENCE OF FRICTION Mechanical energy is not conserved (The mechanical energy lost is equal to the work done against friction)
Worked Example 45 Using Mechanical Energy Conservation[edit | edit source]
Question: A 2kg metal ball is suspended from a rope. If it is released from point A and swings down to the point B (the bottom of its arc) what is its velocity at point B?
Answer:
Step 1 : Analyse the question to determine what information is provided
- The mass of the metal ball is m = 2kg
- The change in height going from point A to point B is h = 0.5m
- The ball is released from point A so the velocity at point A is zero (vA = 0m/s).
These are in the correct units so we do not have to worry about unit conversions.
Step 2 : Analyse the question to determine what is being asked
- Find the velocity of the metal ball at point B.
Step 3 : Determine the Mechanical Energy at A and B
To solve this problem we use conservation of mechanical energy as there is no friction. Since mechanical energy is conserved,
Therefore we need to know the mechanical energy of the ball at point A (UA) and at point B (UB). The mechanical energy at point A is
We already know m, g and vA, but what is hA? Note that if we let hB = 0 then hA = 0.5m as A is 0.5m above B. In problems you are always free to choose a line corresponding to h = 0. In this example the most obvious choice is to make point B correspond to h = 0.
Now we have,
As already stated UB = UA. Therefore UB = 10J, but using the definition of mechanical energy
because hB = 0. This means that
Summary of Important Quantities, Equations and Concepts[edit | edit source]
| ||||||||||||||||||||||||||||||||||||
Principle of Conservation of Energy: Energy is never created nor destroyed, but merely transformed from one form to another.
Conservation of Mechanical Energy: In the absence of friction, the total mechanical energy of an object is conserved.
Collisions and Explosions[edit | edit source]
Types of Collisions[edit | edit source]
We will consider two types of collisions in this section
- Elastic collisions.
- Inelastic collisions.
In both types of collision, total energy and total momentum is always conserved. Kinetic energy is conserved for elastic collisions, but not for inelastic collisions.
Elastic Collisions[edit | edit source]
Definition: An elastic collision is a collision where total momentum and total kinetic energy are both conserved.
This means that the total momentum and the total kinetic energy before an elastic collision is the same as after the collision. For these kinds of collisions, the kinetic energy is not changed into another type of energy.
Before the Collision[edit | edit source]
In the following diagram, two balls are rolling toward each other, about to collide
Before the balls collide, the total momentum of the system is equal to all the individual momenta added together. The ball on the left has a momentum which we call and the ball on the right has a momentum which we call , it means the total momentum before the collision is
| (8.1) |
We calculate the total kinetic energy of the system in the same way. The ball on the left has a kinetic energy which we call K1 and the ball on the right has a kinetic energy which we call K2, it means that the total kinetic energy before the collision is
| (8.2) |
After the Collision[edit | edit source]
The following diagram shows the balls after they collide
After the balls collide and bounce off each other, they have new momenta and new kinetic energies. Like before, the total momentum of the system is equal to all the individual momenta added together. The ball on the left now has a momentum which we call and the ball on the right now has a momentum which we call , it means the total momentum after the collision is
|
(8.3) |
The ball on the left now has a kinetic energy which we call K3 and the ball on the right now has a kinetic energy which we call K4, it means that the total kinetic energy after the collision is
|
(8.4) |
Since this is an elastic collision, the total momentum before the collision equals the total momentum after the collision and the total kinetic energy before the collision equals the total kinetic energy after the collision
Worked Example 46 An Elastic Collision[edit | edit source]
We will have a look at the collision between two pool balls. Ball 1 is at rest and ball 2 is moving towards it with a speed of 2 m·s−1. The mass of each ball is 0.3 kg. After the balls collide elastically, ball 2 comes to a stop and ball 1 moves off. What is the final velocity of ball 1?
Step 1 : Draw the before diagram
Before the collision, ball 2 is moving we will call it's momentum P2 and it's kinetic energy K2. Ball 1 is at rest, so it has zero kinetic energy and momentum.
Step 2 : Draw the after diagram
After the collision, ball 2 is at rest but ball 1 has a momentum which we call P3 and a kinetic energy which we call K3.
RIAAN Note: second image on page 145 is missing
Because the collision is elastic, we can solve the problem using momentum conservation or kinetic energy conservation. We will do it both ways to show that the answer is the same, whichever method you use.
Step 3 : Show the conservation of momentum
We start by writing down that the momentum before the collision is equal to the momentum after the collision
|
(8.7) |
We know that momentum is just P = mv, and we know the masses of the balls, so we can rewrite the conservation of momentum in terms of the velocities of the balls
|
(8.8) |
So ball 1 exits with the velocity that ball 2 started with!
|
(8.9) |
Step 4 : Show the conservation of kinetic energy
We start by writing down that the kinetic energy before the collision is equal to the kinetic energy after the collision
|
(8.10) |
We know that kinetic energy is just , and we know the masses of the balls, so we can rewrite the conservation of kinetic energy in terms of the velocities of the balls
|
(8.11) |
So ball 1 exits with the velocity that ball 2 started with, which agrees with the answer we got when we used the conservation of momentum.
|
(8.12) |
Worked Example 47 Elastic Collision 2[edit | edit source]
Question: Now for a slightly more difficult example. We have 2 marbles. Marble 1 has mass 50 g and marble 2 has mass 100 g. I roll marble 2 along the ground towards marble 1 in the positive x-direction. Marble 1 is initially at rest and marble 2 has a velocity of 3 in the positive x-direction. After they collide elastically, both marbles are moving. What is the final velocity of each marble?
Answer:
Step 1 :
Firstly, put all the quantities into S.I. units. So:
Step 2 :
Draw the picture:
Before the collision:
After the collision:
Step 3 :
Since the collision is elastic, both momentum and kinetic energy are conserved in the collision. So:
There are two unknowns ( and ) so we will need two equations to solve for them. We need to use both kinetic energy conservation and momentum conservation in this problem.
Step 4 : Let's start with energy conservation. Then:
But , and solving for
Step 5 : Now we have simplified as far as we can, we move onto momentum conservation:
But =0, and solving for
Step 6 :
Now we can substitute (B) into (A) to solve for :
We were lucky in this question because we could factorise. If you can't factorise, then you can always solve using the formula for solving quadratic equations. Remember:
So, just to check:
Step 7 :
So finally, substituting into equation (B) to get :
If then
But, according to the question, marble 1 is moving after the collision. So and . Therefore:
Inelastic Collisions[edit | edit source]
Definition: An inelastic collision is a collision in which total momentum is conserved but total kinetic energy is not conserved the kinetic energy is transformed into other kinds of energy.
So the total momentum before an inelastic collisions is the same as after the collision. But the total kinetic energy before and after the inelastic collision is different. Of course this does not mean that total energy has not been conserved, rather the energy has been transformed into another type of energy.
As a rule of thumb, inelastic collisions happen when the colliding objects are distorted in some way. Usually they change their shape. To modify the shape of an object requires energy and this is where the missing kinetic energy goes. A classic example of an inelastic collision is a car crash. The cars change shape and there is a noticeable change in the kinetic energy of the cars before and after the collision. This energy was used to bend the metal and deform the cars. Another example of an inelastic collision is shown in the following picture.
Here an asteroid (the small circle) is moving through space towards the moon (big circle). Before the moon and the asteroid collide, the total momentum of the system is:
stands for and stands for and the total kinetic energy of the system is:
When the asteroid collides inelastically with the moon, its kinetic energy is transformed mostly into heat energy. If this heat energy is large enough, it can cause the asteroid and the area of the moon's surface that it hit, to melt into liquid rock! From the force of impact of the asteroid, the molten rock flows outwards to form a moon crater.
After the collision, the total momentum of the system will be the same as before. But since this collision is inelastic, (and you can see that a change in the shape of objects has taken place!), total kinetic energy is not the same as before the collision.
So:
Worked Example 48 Inelastic Collision[edit | edit source]
Question: Let's consider the collision of two cars. Car 1 is at rest and Car 2 is moving at a speed of in the negative x-direction. Both cars each have a mass of 500 kg. The cars collide inelastically and stick together. What is the resulting velocity of the resulting mass of metal?
Answer:
Step 1 :
Draw the picture: Before the collision:
After the collision:
Step 2 :
We know the collision is inelastic and there was a definite change in shape of the objects involved in the collision - there were two objects to start and after the collision there was one big mass of metal! Therefore, we know that kinetic energy is not conserved in the collision but total momentum is conserved.
So:
Step 3 :
So we must use conservation of momentum to solve this problem. Take the negative x-direction to have a negative sign:
Therefore,
Explosions[edit | edit source]
When an object explodes, it breaks up into more than one piece and it therefore changes its shape. Explosions occur when energy is transformed from one kind e.g. chemical potential energy to another e.g. heat energy or kinetic energy extremely quickly.
So, like in inelastic collisions, total kinetic energy is not conserved in explosions. But total momentum is always conserved. Thus if the momenta of some of the parts of the exploding object are measured, we can use momentum conservation to solve the problem!
In the following picture, a closed can of baked beans is put on a stove or fire:
Before the can heats up and explodes, the total momentum of the system is:
and the total kinetic energy of the system is:
since the can isn't moving. Once the mixture of beans, juice and air inside the can reach a certain temperature, the pressure inside the can becomes so great that the can explodes! Beans and sharp pieces of metal can fly out in all directions. Energy in the system has been transformed from heat energy into kinetic energy.
After the explosion, the can is completely destroyed. But momentum is always conserved, so:
However, the kinetic energy of the system is not conserved. The can's shape was changed in the explosion. Before the explosion the can was not moving, but after the explosion, the pieces of metal and baked beans were moving when they were flying out in all directions! So:
Safety tip: Never heat a closed can on a stove or fire! Always open the can or make a hole in the lid to allow the pressure inside and outside the can to remain equal. This will prevent the can from exploding!
Worked Example 49 Explosions 1[edit | edit source]
Question: An object with mass mTot = 10 kg is sitting at rest. Suddenly it explodes into two pieces. One piece has a mass of m1 = 5 kg and moves off in the negative x-direction at . What is the velocity of the other piece?
Answer:
Step 1 :
Draw the picture. Before the explosion, the object is at rest:
After the explosion, the two pieces move off:
Riaan Note: second image on page 154 is missing
Step 2 :
Now we know that in an explosion, total kinetic energy is not conserved. There is a definite change in shape of the exploding object! But we can always use momentum conservation to solve the problem.
So:
But the object was initially at rest so:
Step 3 :
Now we know that m1= 5 kg but we do not know what the mass of m2 is. However, we do know that:
Step 4 :
Now we can substitute all the values we know into equation (A) and solve for . Let's choose the positive x-direction to have a positive sign and the negative x-direction to have a negative sign:
Therefore,
Worked Example 50 Explosions 2[edit | edit source]
Question: An object with mass mTot =15 kg is sitting at rest. Suddenly it explodes into two pieces. One piece has a mass of m1 = 5000 g and moves off in the positive x-direction at . What is the final velocity of the other piece?
Answer:
Step 1 :
Draw the picture. Before the collision:
After the collision:
Riaan Note: image on page 156 is missing
Step 2 :
Convert all units into S.I. units:
Step 3 :
Now we know that in an explosion, total kinetic energy is not conserved. There is a definite change in shape of the exploding object! But we can always use momentum conservation to solve the problem. So:
But the object was initially at rest so:
Step 4 :
Now we know that m1= 5 kg but we do not know what the mass of m2 is. However, we do know that:
Step 5 :
Now we can substitute all the values we know into equation (A) and solve for . Let's choose the positive x-direction to have a postive sign and the negative x-direction to have a negative sign:
Therefore,
Explosions: Energy and Heat[edit | edit source]
In explosions, you have seen that kinetic energy is not conserved. But remember that total energy is always conserved. Let's look at what happens to the energy in some more detail. If a given amount of energy is released in an explosion it is not necessarily all transformed into kinetic energy. Due to the deformation of the exploding object, often a large amount of the energy is used to break chemical bonds and heat up the pieces.
Energy is conserved but some of it is transferred through non-conservative processes like heating. This just means that we cannot get the energy back. It will be radiated into the environment as heat energy but it is all still accounted for.
Now we can start to mix the ideas of momentum conservation with energy transfer to make longer problems. These problems are not more complicated just longer. We will start off short and then combine the different ideas later on.
Long problems should be treated like a number of smaller problems. Focus on them one at a time.
Worked Example 51 Energy Accounting 1[edit | edit source]
Question: An object with a mass of mt = 17 kg explodes into two pieces of mass m1 = 7 kg and m2 = 10 kg; m1 has a velocity of 9 m·s−1 in the negative x-direction and m2 has a velocity of 6.3 m·s−1 in the positive x-direction. If the explosion released a total energy of 2000 J, how much was used in a non-conservative way?
Answer:
Step 1 :
Draw the picture. Before the collision:
Riaan Note: first image on page 157 is missing
After the collision:
Step 2 :
We are asked how much energy was used in a non-conservative fashion. This is the difference between how much energy was used in a conservative fashion and how much was used in total. We are lucky because we have everything we need to determine the kinetic energy of both pieces. The kinetic energy of the pieces is energy that was used in a conservative way.
Step 3 :
The sum of the kinetic energy for the two blocks is the total kinetic energy of the pieces. So:
Step 4 :
The total energy that was transformed into kinetic energy is 481.95 J. We know that 2000 J of energy were released in total. the question makes no statements about other types of energy so we can assume that the difference was lost in a non-conservative way. Thus the total energy lost in non-conservative work is:
Worked Example 52 Energy Accounting 2[edit | edit source]
Question: An object at rest, with mass mTot = 4 kg, explodes into two pieces (m1, m2) with m1 = 2.3 kg. m1 has a velocity of 17 m·s−1 in the negative x-direction. If the explosion released a total energy of 800 J,
- What is the velocity of m2?
- How much energy does it carry?
- And how much energy was used in a non-conservative way?
Answer:
Step 1 :
Draw the picture. Before the collision:
After the collision:
Step 2 :
Now we know that in an explosion, total kinetic energy is not conserved. There is a definite change in shape of the exploding object! But we can always use momentum conservation to solve the problem. So:
But the object was initially at rest so:
Step 3 :
Now we know that m1= 2.3 kg but we do not know what the mass of m2 is. However, we do know that:
Step 4 :
Now we can substitute all the values we know into equation (A) and solve for . Let's choose the positive x-direction to have a positive sign and the negative x-direction to have a negative sign:
- in the positive x-direction
Step 5 :
Now we need to calculate the energy that the second piece carries:
- The kinetic energy of the second piece is
Step 6 :
Now the amount of energy used in a non-conservative way in the explosion, is the difference between the amount of energy released in the explosion and the total kinetic energy of the exploded pieces:
We know that:
Step 7 :
So going back to:
- 18 J of energy was used in a non-conservative way in the explosion
Important Equations and Quantities[edit | edit source]
| Units | |||||
| Quantity | Symbol | Unit | SI base units | Direction | |
| velocity | -- | or | yes | ||
| momentum | -- | or | yes | ||
| energy | E | J | or | no | |
Momentum:
|
(8.13) |
Kinetic energy:
|
(8.14) |
Newtonian Gravitation[edit | edit source]
Newtonian Gravitation[edit | edit source]

All objects on Earth are pulled downward, towards the ground. This phenomenon is called gravity. Every object falls just as fast as any other object (unless the air slows it down like a feather, or pushes it up like a balloon), as first shown by Galileo. In 1687 Isaac Newton stated that gravity is not restricted to the Earth, but instead, there is gravity everywhere in the universe. Newton explained that planets, moons, and comets move in orbits because of the effect of gravity.
Properties[edit | edit source]
Gravitational attraction is a force and therefore must be described by a vector - so remember magnitude and direction. The force due to gravity acts between any two objects with mass. To determine the magnitude of the force we use the following equation:
| (9.1) |
This equation describes the force between two bodies, one of mass m1, the other of mass m2 (both have units of kilograms, or kg for short). The G is Newton's`Gravitational Constant' (6.673×10−11 N·m2·kg−2) and r is the straight line distance between the two bodies in meters.
This means the bigger the masses, the greater the force between them. Simply put, big things matter big with gravity. The 1/r2 factor (or you may prefer to say r−2) tells us that the distance between the two bodies plays a role as well. The closer two bodies are, the stronger the gravitational force between them is. We feel the gravitational attraction of the Earth most at the surface since that is the closest we can get to it, but if we were in outer-space, we would barely even know the Earth's gravity existed!
Remember that
| (9.2) |
which means that every object on the earth feels the same gravitational acceleration! That means whether you drop a pen or a book (from the same height), they will both take the same length of time to hit the ground... in fact they will be head to head for the entire fall if you drop them at the same time. We can show this easily by using the two equations above (9.1 and 9.2). The force between the Earth (which has the mass me) and an object of mass mo is
| (9.3) |
and the acceleration of an object of mass mo (in terms of the force acting on it) is
| (9.4) |
So we substitute equation (9.3) into equation (9.4), and we find that
| (9.5) |
Since it doesn't matter what mo is, this tells us that the acceleration on a body (due to the Earth's gravity) does not depend on the mass of the body. Thus all objects feel the same gravitational acceleration. The force on different bodies will be different but the acceleration will be the same. Due to the fact that this acceleration caused by gravity is the same on all objects we label it differently, instead of using a we use g which we call the gravitational acceleration.
Mass and Weight[edit | edit source]
Weight is a force which is measured in Newtons, it is the force on an object due to gravity. People are always asking other people "What is your weight?" when a physicist might ask the same question as "What is your mass?".
Mass is measured in kilograms (kg) and is the amount of matter in an object, it doesn't change unless you add or remove matter from the object (if you continue to study physics through to university level, you will find that Einstein's theory of relativity means that mass can change when you travel as fast as light does, but you don't need to worry about that right now). There are 1000 g in 1 kg and 1000 kg in a tonne.
To change mass into weight we use Newton's 2nd Law which is . The weight is the force and gravity the acceleration, it can be rewritten as:
| (9.2) |
W is the weight, measured in newtons. m is the mass, measured in kilograms and g is the acceleration due to gravity, measured in metres per second squared; it is equal to about 10 on the Earth. The exact value of Earths equatorial surface gravity is 9.7801 .
Examples[edit | edit source]
1. A bag of sugar has a mass of 1 kg, what is its weight? (Acceleration due to gravity = 10 )
Step 1: Always write out the equation, it helps you to understand the question, and you will get marks as well.
| (9.7) |
Step 2: Fill in all the values you know. (remember to make sure the mass is in kilograms and NOT in grams or tonnes!)
| (9.8) |
Step 3: Write out the answer remembering to include the units! You will lose marks if you don't
| (9.9) |
2. A space-man has a mass of 90 kg, what is his weight (a) on the earth? (b) on the moon? (c) in outer space? (The acceleration due to gravity on the earth is 10 , on the moon gravity is about 1/6 of the gravity on earth).
1:
| (9.10) |
2:
| (9.10) |
3: Weightless in outer space because g = 0.
So now when somebody asks you your weight, you know to reply ``Anything!! But my mass is a different matter!"
Normal Forces[edit | edit source]
If you put a book on a table, it does not accelerate; it just lies on the table. We know that gravity is acting on it with a force
|
(9.12) |
but if there is a net force there MUST be an acceleration and there isn't. This means that the gravitational force is being balanced by another force [Newton's third law!].
This force we call the normal force. It is the reaction force between the book and the table. It is equal to the force of gravity on the book. This is also the force we measure when we measure the weight of something.
The most interesting and illustrative normal force question, that is often asked, has to do with a scale in a lift. Using Newton's third law we can solve these problems quite easily.
When you stand on a scale to measure your weight you are pulled down by gravity. There is no acceleration downwards because there is a reaction force we call the normal force acting upwards on you. This is the force that the scale would measure. If the gravitational force were less than the reading on the scale would be less.
Worked Example 53 Normal Forces 1[edit | edit source]
Question: A man weighing 100kg stands on a scale (measuring newtons). What is the reading on the scale?
Answer:
Step 1 :
We are given the mass of the man. We know the gravitational acceleration that acts on him.
Step 2 :
The scale measures the normal force on the man. This is the force that balances gravity.
Step 3 :
Firstly we determine the net force acting downwards on the man due to gravity.
Step 4 :
We now know the gravitational force downwards. We also know that there must be a reactionary force FN upwards. To determine the magnitude of this we use newton's laws again. We know that the sum of all the forces must equal the resultant acceleration times the mass. The overall resultant acceleration of the man on the scale is 0. if we write out the equation:
The normal force is then 980N upwards. It exactly balances the gravitational force downwards so there is no net force and no acceleration on the man.
Now we are going to add things to exactly the same problem to show how things change slightly. We will now move to a lift moving at constant velocity. Remember if velocity is constant then acceleration is zero.
Worked Example 55 Normal Forces 2[edit | edit source]
Question: A man weighing 100kg stands on a scale (measuring newtons) inside a lift accelerating downwards at . What is the reading on the scale?
Answer:
Step 1 : We are given the mass of the man. We know the gravitational acceleration that acts on him.
Step 2 :
The scale measures the normal force on the man.
Step 3 :
Firstly we determine the net force acting downwards on the man due to gravity.
Step 4 :
We now know the gravitational force downwards. We also know that there must be a reactionary force FN upwards. To determine the magnitude of this we use newton's laws again. We know that the sum of all the forces must equal the resultant acceleration times the mass. The overall resultant acceleration of the man on the scale is . if we write out the equation:
The normal force is then 780N upwards. It balances the gravitational force downwards just enough so that the man only accelerates downwards at .
Worked Example 56 Normal Forces 3[edit | edit source]
Question: A man weighing 100kg stands on a scale (measuring newtons) inside a lift accelerating upwards at >. What is the reading on the scale?
Answer:
Step 1 : We are given the mass of the man. We know the gravitational acceleration that acts on him.
Step 2 :
The scale measures the normal force on the man.
Step 3 :
Firstly we determine the net force acting downwards on the man due to gravity.
Step 4 :
We now know the gravitational force downwards. We also know that there must be a reactionary force FN upwards. To determine the magnitude of this we use newton's laws again. We know that the sum of all the forces must equal the resultant acceleration times the mass. The overall resultant acceleration of the man on the scale is . if we write out the equation:
The normal force is then 1380 N upwards. It balances the gravitational force and then in addition applies sufficient force to accelerate the man upwards at .
Comparative problems[edit | edit source]
Here always work with multiplicative factors to find something new in terms of something old.
Worked Example 57 Comparative Problem 1[edit | edit source]
Question: On Earth a man weighs 700 N. Now if the same man was instantaneously beamed to the planet Zirgon, which has the same size as the Earth but twice the mass, what would he weigh?
Answer:
Step 1 :
We start with the situation on earth:
|
(9.13) |
Step 2 :
Now we consider the provje
|
(9.14) |
but we know that and we know that rZ = r so we could write the equation again and substitute these relationships in:
Step 3 :
|
(9.15) |
Step 4 :
|
(9.16) |
|
(9.17) |
Step 5 :
|
(9.18) |
so on Zirgon he weighs 1400 N.
Principles[edit | edit source]
- Write out first case
- Write out all relationships between variable from first and second case
- Write out second case
- Substitute all first case variables into second case
- Write second case in terms of first case
Worked Example 58 Comparative Problem 2[edit | edit source]
Question: On Earth a man weighs 70 kg. On the planet Beeble how much will he weigh if Beeble has mass half of that of the Earth and a radius one quarter that of the earth.
Answer:
Step 1 :
We start with the situation on earth:
|
(9.19) |
Step 2 :
Now we consider the provje
|
(9.20) |
but we know that and we know that so we could write the equation again and substitute these relationships in:
Step 3 :
|
(9.21) |
Step 4 :
|
(9.22) |
|
(9.23) |
Step 5 :
But although the man exerts 8 times as much force due to gravity, he still weighs 70 kg on Beeble!
|
Did you know that the largest telescope in the Southern Hemisphere is the South African Large Telescope (SALT) which came online in 2004 outside Sutherland in the Karoo. |
Falling bodies[edit | edit source]
Objects on the earth fall because there is a gravitation force between them and the earth - which results in an acceleration - as we saw above. So if you hold something in front of you and let it go - it will fall.
It falls because of an acceleration toward the centre of the earth which results from the gravitational force between the two.
These bodies move in a straight line from the point where they start to the centre of the earth. This means we can reuse everything we learnt in rectilinear motion. the only thing that needs thinking about is the directions we are talking about.
We need to choose either up or down as positive just like we had to choose a positive direction in standard rectilinear motion problems. this is the hardest part. If you can do rectilinear motion you can do falling body problems. Just remember the acceleration they feel is constant and because of gravity - but once you have chosen your directions you can forget that gravity has anything to do with the problem - all you have is a rectilinear motion problem with a constant acceleration!!
What is the weight of a free falling body ? Would you be surprised to know that it is zero ?
Weight is measured using a spring balance. (Mass is measured using a physical balance). When a body is falling, the spring balance to which it is attached (the spring balance needs to fall along with the body too !) would show zero weight. When the body stops falling, then it would exert a force on the spring (equivalent to the force exerted by earth on itself) and hence it would show a reading.
Terminal Velocity[edit | edit source]
Physics is all about being simple - all we do is look at the world around us and notice how it really works. It is the one thing everyone is qualified to do - we spend most of our time when we are really young experimenting to find out how things work.
Take a book - wave it in the air - change the angle and direction. what happens of course there is resistance. different angles make it greater - the faster the book moves the greater it is. The bigger the area of the book moving in the direction of motion the greater the force.
So we know that air resistance exists! it is a force. So what happens when an object falls? of course there is air resistance - or drag as it is normally called. There is an approximate formula for the drag force as well.
The important thing to realise is that when the drag force and the gravitational force are equal for a falling body there is no net force acting on it - which means no net acceleration. That does not mean it does not move - but it means that its speed does not change.
It falls at a constant velocity! This velocity is called terminal velocity.
Drag force[edit | edit source]
The actual force of air resistance is quite complicated. Experiment by moving a book through the air with the face of the book and then the side of the book forward, you will agree that the area of the book makes a difference as to how much you must work in order to move the book at the same speed in both cases. This is why racing cars are slim-lined in design, and not shaped like a big box!
Get a plastic container lid (or anything waterproof) swing it around in air and then try to swing it around under water. The density of the water is much larger than the air, making you have to work harder at swinging the lid in water. This is why boats and submarines are a lot slower than aeroplanes!
So we know that density, area and speed all play a role in the drag force.The expression we use for drag force is
|
(9.25) |
where C is a constant which depends on the object and fluid interactions, is the density, A is the area and v is the velocity.
Important Equations and Quantities[edit | edit source]
| ||||||||||||||||||||||||||||||||||||
Pressure[edit | edit source]
Essay 3: Pressure and Forces
Author: Asogan Moodaly
Asogan Moodaly received his Bachelor of Science degree (with honours) in Mechanical Engineering from the University of Natal, Durban in South Africa. For his final year design project he worked on a 3-axis filament winding machine for composite (Glass re-enforced plastic in this case) piping. He worked in Vereeniging, Gauteng at Mine Support Products (a subsidiary of Dorbyl Heavy Engineering) as the design engineer once he graduated. He currently lives in the Vaal Triangle area and is working for Sasol Technology Engineering as a mechanical engineer, ensuring the safety and integrity of equipment installed during projects.
Pressure and Forces[edit | edit source]
In the mining industry, the roof (hangingwall) tends to drop as the face of the tunnel (stope) is excavated for rock containing gold.
As one can imagine, a roof falling on one's head is not a nice prospect! Therefore the roof needs to be supported.
The roof is not one big uniform chunk of rock. Rather it is broken up into smaller chunks. It is assumed that the biggest chunk of rock in the roof has a mass of less than 20 000 kg therefore each support has to be designed to resist a force related to that mass. The strength of the material (either wood or steel) making up the support is taken into account when working out the minimum required size and thickness of the parts to withstand the force of the roof.
Sometimes the design of the support is such that the support needs to withstand the rock mass without the force breaking the roof..
Therefore hydraulic supports (hydro = water) use the principles of force and pressure such that as a force is exerted on the support, the water pressure increases. A pressure relief valve then squirts out water when the pressure (and thus the force) gets too large. Imagine a very large, modified doctor's syringe.
In the petrochemical industry, there are many vessels and pipes that are under high pressures. A vessel is a containment unit (Imagine a pot without handles, that has the lid welded to the pot that would be a small vessel) where chemicals mix and react to form other chemicals, amongst other uses.
The end product chemicals are sold to companies that use these chemicals to make shampoo, dishwashing liquid, plastic containers, fertilizer, etc. Anyway, some of these chemical reactions require high temperatures and pressures in order to work. These pressures result in forces being applied to the insides of the vessels and pipes. Therefore the minimum thickness of the pipe and vessels walls must be determined using calculations, to withstand these forces. These calculations take into account the strength of the material (typically steel, plastic or composite), the diameter and of course the pressure inside the equipment.
Important Equations and Quantities[edit | edit source]
|
|
| ||||||||||||||||||
Non Si Units for pressure[edit | edit source]
PSI: PSI stands for pounds per square inch. One PSI is equal to 6,894.76 Pascals
Atm: Atm stands for Atmosphere. This is the atmospheric pressure at sea level. I atm is equal to 101,325 Pascals
Hydrostatic pressure (head pressure)[edit | edit source]
Hydrostatic pressure is the pressure due to the weight of a fluid.
where:
- ρ (rho) is the density of the fluid (i.e., the practical density of fresh water is 1000 kg/m3);
- g is the acceleration due to gravity (approximately 9.81 m/s2 on earth's surface);
- h is the height of the fluid column (in metres). Other units can be used if the rest of the units used in the equation are defined in a consistent way.
It is important to realize that air is a fluid. This equation can be used to find the pressure created by air. This also means that if we are trying to find the pressure of a liquid open to the atmosphere, we must add in the atmospheric pressure to the pressure of the liquid to find the total pressure.
In fluid mechanics the unit used N/m2.
From the unit of density denominator have m3 and acceleration due to gravity have m/s2 one metre from density and other meter from g cancel to each other.then unit will remain as kg/. m2.s2 after that unit of h is meter which is multiply into kg we will got kg.m/s2 =N
Final result is N/m2
Notes[edit | edit source]
1[edit | edit source]
Pressure is force divided by area, so in a sense it does have a direction as force has a direction. The term pseudovector is sometimes used for such quantities.
Electrostatics[edit | edit source]
What is Electrostatics?[edit | edit source]
Electrostatics is the study of electric charge which is not moving i.e. is static.
Charge[edit | edit source]
All objects surrounding us (including people!) contain large amounts of electric charge. Charge can be negative or positive and is measured in units called coulombs (C). Usually, objects contain the same amount of positive and negative charge so its effect is not noticeable and the object is called electrically neutral. However, if a small imbalance is created (i.e. there is a little bit more of one type of charge than the other on the object) then the object is said to be electrically charged.
Some rather amusing examples of what happens when a person becomes charged are for example when you charge your hair by combing it with a plastic comb and it stands right up on end! Another example is when you walk fast over a nylon carpet and then touch a metal doorknob and give yourself a small shock (alternatively you can touch your friend and shock them!)
Charge has 3 further important properties:
- Charge is always conserved. Charge, just like energy, cannot be created or destroyed.
- Charge comes in discrete packets. The smallest unit of charge is that carried by one electron called the elementary charge, e, and by convention, it has a negative sign ( ).
- Charged objects exert electrostatic forces on each other. Like charges repel and unlike charges attract each other.

|
The word `electron' comes from the Greek word for amber! The ancient Greeks observed that if you rubbed a piece of amber,
you could use it to pick up bits of straw. (Attractive electrostatic force!) |
You can easily test the fact that like charges repel and unlike charges attract by doing a very simple experiment. Take a glass rod and rub it with a piece of silk, then hang it from its middle with a piece string so that it is free to move. If you then bring another glass rod which you have also charged in the same way next to it, you will see the rod on the string turn away from the rod in your hand i.e. it is repelled. If, however, you take a plastic rod, rub it with a piece of fur and then bring it close to the rod on the string, you will see the rod on the string turn towards the rod in your hand i.e. it is attracted!
What actually happens is that when you rub the glass with silk, tiny amounts of negative charge are transferred from the glass onto the silk, which causes the glass to have less negative charge than positive charge, making it positively charged. When you rub the plastic rod with the fur, you transfer tiny amounts of negative charge onto the rod and so it has more negative charge than positive charge on it, making it negatively charged.
Conductors and Insulators[edit | edit source]
Some materials allow charge carriers to move relatively freely through them (e.g. most metals, tap water, the human body) and these materials are called conductors. Other materials, which do not allow the charge carriers to move through them (e.g. plastic, glass), are called non-conductors or insulators.
Aside: As mentioned above, the basic unit of charge, namely the elementary charge, e, is carried by the electron. In a conducting material (e.g. copper), when the atoms bond to form the material, some of the outermost, loosely bound electrons become detached from the individual atoms and so become free to move around. The charge carried by these electrons can move around in the material! In insulators, there are very few, if any, free electrons and so the charge cannot move around in the material.
If an excess of charge is put onto an insulator, it will stay where it is put and there will be a concentration of charge in that area on the object. However, if an excess of charge is put onto a conductor, the charges of like sign will repel each other and spread out over the surface of the object. When two conductors are made to touch, the total charge on them is shared between the two. If the two conductors are identical, then each conductor will be left with half of the total charge.
Electrostatic Force[edit | edit source]
As we now know, charged objects exert a force on one another. If the charges are at rest then this force between them is known as the electrostatic force. An interesting characteristic of the electrostatic force is that it can be either attractive or repulsive, unlike the gravitational force which is only ever attractive. The relative charges on the two objects is what determines whether the force between the charged objects is attractive or repulsive. If the objects have opposite charges they attract each other, while if their charges are similar they repel each other (e.g. two metal balls which are negatively charged will repel each other, while a positively charged ball and negatively charged ball will attract one another).
It is this force that determines the arrangement of charge on the surface of conductors. When we place a charge on a spherical conductor the repulsive forces between the individual like charges cause them to spread uniformly over the surface of the sphere. However, for conductors with non-regular shape there is a concentration of charge near the point or points of the object.
This collection of charge can actually allow charge to leak off the conductor if the point is sharp enough. It is for this reason that buildings often have a lightning rod on the roof to remove any charge the building has collected. This minimises the possibility of the building being struck by lightning.
This spreading out of charge would not occur if we were to place the charge on an insulator since charge cannot move in insulators.
Coulomb's Law[edit | edit source]
The behaviour of the electrostatic force was studied in detail by Charles Coulomb around 1784. Through his observations he was able to show that the electrostatic force between any point two point charges is directly proportional to their magnitude and inversely proportional to the square of the distance between the charges. Thus if F is the force, Q1 and Q2 are the charges and R is their distance apart. then the law is summarized as
F=(Q1Q2)/(R^2)
where Q1 is the charge on the one point-like object, Q2 is the charge on the second, and r is the distance between the two. Remember her F is the mutual force that acts on both the charges exerted by one another as in Newtons third law of motion.
The magnitude of the electrostatic force between two point-like charges is given by Coulomb's Law:
| (12.1) |
and the proportionality constant k is called the electrostatic constant. We will use the value
The value of the electrostatic constant is known to a very high precision (9 decimal places). Not many physical constants are known to as high a degree of accuracy as k.
Aside: Notice how similar Coulomb's Law is to the form of Newton's Universal Law of Gravitation between two point-like particles:
where m1 and m2 are the masses of the two particles, r is the distance between them, and G is the gravitational constant. It is very interesting that Coulomb's Law has been shown to be correct no matter how small the distance, nor how large the charge: for example it still applies inside the atom (over distances smaller than
Let's run through a simple example of electrostatic forces.
Worked Example 59 Coulomb's Law I[edit | edit source]
Question: Two point-like charges carrying charges of +3×10−9 C and −5×10−9 C are 2 m apart. Determine the magnitude of the force between them and state whether it is attractive or repulsive.
Answer:
Step 1 :
First draw the situation:
Step 2 :
Is everything in the correct units? Yes, charges are in coulombs [C] and distances in meters [m].
Step 3 :
Determine the magnitude of the force: Using Coulomb's Law we have
Thus the magnitude of the force is . The minus sign is a result of the two point charges having opposite signs.
Step 4 :
Is the force attractive or repulsive? Well, since the two charges are oppositely charged, the force is attractive. We can also conclude this from the fact that Coulomb's Law gives a negative value for the force.
Next is another example that demonstrates the difference in magnitude between the gravitational force and the electrostatic force.
Worked Example 60 Coulomb's Law II[edit | edit source]
Question: Determine the electrostatic force and gravitational force between two electrons 1Aring apart (i.e. the forces felt inside an atom) Answer: Å Step 1 :
First draw the situation:
Riaan Note: this image is faulty, recreate
Step 2 :
Get everything into S.I. units: The charge on an electron is , the mass of an electron is , and 1 Å =
Step 3 :
Calculate the electrostatic force using Coulomb's Law:
Hence the magnitude of the electrostatic force between the electrons is . (Note that the electrons carry like charge and from this we know the force must be repulsive. Another way to see this is that the force is positive and thus repulsive.)
Step 4 :
Calculate the gravitational force:
The magnitude of the gravitational force between the electrons is
Notice that the gravitational force between the electrons is much smaller than the electrostatic force. For this reason, the gravitational force is usually neglected when determining the force between two charged objects.
We mentioned above that charge placed on a spherical conductor spreads evenly along the surface. As a result, if we are far enough from the charged sphere, electrostatically, it behaves as a point-like charge. Thus we can treat spherical conductors (e.g. metallic balls) as point-like charges, with all the charge acting at the centre.
Worked Example 61 Coulomb's Law: Challenge Question[edit | edit source]
Question: In the picture below, X is a small negatively charged sphere with a mass of 10 kg. It is suspended from the roof by an insulating rope which makes an angle of 60o with the roof. Y is a small positively charged sphere which has the same magnitude of charge as X. Y is fixed to the wall by means of an insulating bracket. Assuming the system is in equilibrium, what is the magnitude of the charge on X?
Answer: How are we going to determine the charge on X? Well, if we know the force between X and Y we can use Coulomb's Law to determine their charges as we know the distance between them. So, firstly, we need to determine the magnitude of the electrostatic force between X and Y.
Step 1 :
Is everything in S.I. units? The distance between X and Y is , and the mass of X is 10 kg.
Step 2 :
Draw the forces on X (with directions) and label.
Step 3 :
Determine the magnitude of the electrostatic force (FE). Since nothing is moving (system is in equilibrium) the vertical and horizontal components of the forces must cancel. Thus
The only force we know is the gravitational force Fg = mg. Now we can calculate the magnitude of T from above:
Which means that FE is:
Step 4 :
Now that we know the magnitude of the electrostatic force between X and Y, we can calculate their charges using Coulomb's Law. Don't forget that the magnitudes of the charges on X and Y are the same: . The magnitude of the electrostatic force is
Thus the charge on X is
Electric Fields[edit | edit source]
We have learnt that objects that carry charge feel forces from all other charged objects. It is useful to determine what the effect of a charge would be at every point surrounding it. To do this we need some sort of reference.
We know that the force that one charge feels due to another depends on both charges (Q1 and Q2). How then can we talk about forces if we only have one charge? The solution to this dilemma is to introduce a test charge. We then determine the force that would be exerted on it if we placed it at a certain location. If we do this for every point surrounding a charge we know what would happen if we put a test charge at any location.
This map of what would happen at any point we call a field map. It is a map of the electric field due to a charge. It tells us how large the force on a test charge would be and in what direction the force would be.
Our map consists of the lines that tell us how the test charge would move if it were placed there.
Test Charge[edit | edit source]
This is the key to mapping out an electric field. The equation for the force between two electric charges has been shown earlier and is:
| (12.2) |
If we want to map the field for Q1 then we need to know exactly what would happen if we put Q2 at every point around Q1. But this obviously depends on the value of Q2. This is a time when we need to agree on a convention. What should Q2 be when we make the map? By convention we choose Q2 = + 1C.
This means that if we want to work out the effects on any other charge we only have to multiply the result for the test charge by the magnitude of the new charge.
The electric field strength is then just the force per unit of charge and has the same magnitude and direction as the force on our test charge but has different units:
| (12.3) |
The electric field is the force per unit of charge and hence has units of newtons per coulomb [N/C].
So to get the force the electric field exerts we use:
| (12.4) |
Notice we are just multiplying the electric field magnitude by the magnitude of the charge it is acting on.
What do field maps look like?[edit | edit source]
The maps depend very much on the charge or charges that the map is being made for. We will start off with the simplest possible case. Take a single positive charge with no other charges around it. First, we will look at what effects it would have on a test charge at a number of points.
Positive Charge Acting on Test Charge[edit | edit source]
At each point we calculate the force on a test charge, q, and represent this force by a vector.
We can see that at every point the positive test charge, q, would experience a force pushing it away from the charge, Q. This is because both charges are positive and so they repel. Also notice that at points further away the vectors are shorter. That is because the force is smaller if you are further away.
If the charge were negative we would have the following result.
Negative Charge Acting on Test Charge[edit | edit source]
Notice that it is almost identical to the positive charge case. This is important - the arrows are the same length because the magnitude of the charge is the same and so is the magnitude of the test charge. Thus the magnitude of the force is the same. The arrows point in the opposite direction because the charges now have opposite sign and so the test charge is attracted to the charge.
Now, to make things simpler, we draw continuous lines showing the path that the test charge would travel. This means we don't have to work out the magnitude of the force at many different points.
Electric Field Map due to a Positive Charge[edit | edit source]
Some important points to remember about electric fields:
- There is an electric field at every point in space surrounding a charge.
- Field lines are merely a representation - they are not real. When we draw them, we just pick convenient places to indicate the field in space.
- Field lines always start at a right-angle (90o) to the charged object causing the field.
- Field lines never cross!
Combined Charge Distributions[edit | edit source]
We look at the field of a positive charge and a negative charge placed next to each other. The net resulting field would be the addition of the fields from each of the charges. To start off with let us sketch the field maps for each of the charges as though it were in isolation.
Electric Field of Negative and Positive Charge in Isolation[edit | edit source]
Notice that a test charge starting off directly between the two would be pushed away from the positive charge and pulled towards the negative charge in a straight line. The path it would follow would be a straight line between the charges.
Now let's consider a test charge starting off a bit higher than directly between the charges. If it starts closer to the positive charge the force it feels from the positive charge is greater, but the negative charge does attract it, so it would move away from the positive charge with a tiny force attracting it towards the negative charge. As it gets further from the positive charge the force from the negative and positive charges change and they are equal in magnitude at equal distances from the charges. After that point the negative charge starts to exert a stronger force on the test charge. This means that the test charge moves towards the negative charge with only a small force away from the positive charge.
Now we can fill in the other lines quite easily using the same ideas. The resulting field map is:
Two Like Charges I: The Positive Case[edit | edit source]
For the case of two positive charges things look a little different. We can't just turn the arrows around the way we did before. In this case the test charge is repelled by both charges. This tells us that a test charge will never cross half way because the force of repulsion from both charges will be equal in magnitude.
The field directly between the charges cancels out in the middle. The force has equal magnitude and opposite direction. Interesting things happen when we look at test charges that are not on a line directly between the two.
We know that a charge the same distance below the middle will experience a force along a reflected line, because the problem is symmetric (i.e. if we flipped vertically it would look the same). This is also true in the horizontal direction. So we use this fact to easily draw in the next four lines.
Working through a number of possible starting points for the test charge we can show the electric field map to be:
Two Like Charges II: The Negative Case[edit | edit source]
We can use the fact that the direction of the force is reversed for a test charge if you change the sign of the charge that is influencing it. If we change to the case where both charges are negative we get the following result:
Parallel plates[edit | edit source]
One very important example of electric fields which is used extensively is the electric field between two charged parallel plates. In this situation the electric field is constant. This is used for many practical purposes and later we will explain how Millikan used it to measure the charge on the electron.
Field Map for Oppositely Charged Parallel Plates[edit | edit source]
This means that the force that a would feel at any point between the plates would be identical in magnitude and direction. The fields on the edges exhibit fringe effects, i.e. they bulge outwards. This is because a test charge placed here would feel the effects of charges only on one side (either left or right depending on which side it is placed). Test charges placed in the middle experience the effects of charges on both sides so they balance the components in the horizontal direction. This isn't the case on the edges.
The Force on a Test Charge between Oppositely Charged Parallel Plates[edit | edit source]
What about the Strength of the Electric Field?[edit | edit source]
When we started making field maps we drew arrows to indicate the strength of the field and the direction. When we moved to lines you might have asked "Did we forget about the field strength?". We did not. Consider the case for a single positive charge again:
Notice that as you move further away from the charge the field lines become more spread out. In field map diagrams the closer field lines are together the stronger the field. This brings us to an interesting case. What is the electric field like if the object that is charged has an irregular shape.
Electrical Potential[edit | edit source]
Work Done and Energy Transfer in a Field[edit | edit source]
When a charged particle moves in an electric field work is done and energy transfers take place. This is exactly analogous to the case when a mass moves in a gravitational field such as that set up by any massive object.
Work done by a field[edit | edit source]
Gravitational Case[edit | edit source]
A mass held at a height h above the ground has gravitational potential energy since, if released, it will fall under the action of the gravitational field. Once released, in the absence of friction, only the force of gravity acts on the mass and the mass accelerates in the direction of the force (towards the Earth's centre).
In this way, work is done by the field. When the mass falls a distance h (from point A to B), the work done is,
In falling, the mass loses gravitational potential energy and gains kinetic energy.
Energy is conserved!
The work done by the field is equal to the energy transferred,
Electrical Case[edit | edit source]
A charge in an electric field has electrical potential energy since, if released, it will move under the action of the electric field. When released, in the absence of friction, only the electric force acts on the charge and the charge accelerates in the direction of the force (for positive charges the force and acceleration are in the direction of the electric field, while negative charges experience a force and acceleration in the opposite direction to the electric field.) Consider a positive charge +Q placed in the uniform electric field between oppositely charged parallel plates.
The positive charge will be repelled by the positive plate and attracted by the negative plate (i.e. it will move in the direction of the electric field lines). In this way, work is done by the field. In moving the charge a distance s in the electric field, the work done is,
In the process of moving, the charge loses electrical potential energy and gains kinetic energy. The work done by the field is equal to the energy transferred,
Work done by us[edit | edit source]
Gravitational Case[edit | edit source]
In order to return the mass m in Figure 12.1 to its original position (i.e. lift it a distance h from B back to A) we have to apply a force mg to balance the force of gravity. An amount of work mgh is done by the lifter. In the process, the mass gains gravitational potential energy,
Electrical Case[edit | edit source]
In order to return the charge in Figure 12.2 to its original position (i.e. from B back to A) we have to exert a force QE on the charge to balance the force exerted on it by the electric field. An amount of work QEs is done by us. In the process, the charge gains electrical potential energy,
In summary, when an object moves under the influence of a field, the field does work and potential energy is transferred into kinetic energy. Potential energy is lost, while kinetic energy is gained. When an object is moved against a field we have to do work and the object gains potential energy.
Worked Example 62 Work done and energy transfers in a field[edit | edit source]
Question: A charge of +5nC is moved a distance of 4 cm against a uniform electric field of magnitude from A to B.
(a) Calculate the work done in moving the charge from A to B. (b) The charge is now released and returns to A. Calculate the kinetic energy of the charge at A.
Answer: (a) Step 1 :
We are given the values of the charge, the field and the distance the charge must move. All are in the correct units.
Step 2 :
Since the charge is positive we have to do work to move it from A to B (since this is against the field). This work is given by,
(b)
Step 3 :
When released the charge moves under the influence of the electric field and returns to A. Work is now done by the field and the work done is equal to the kinetic energy gained,
Since the charge started at rest, the gain in kinetic energy is the final kinetic energy,
Electrical Potential Difference[edit | edit source]
Consider a positive test charge + Q placed at A in the electric field of another positive point charge.
The test charge moves towards B under the influence of the electric field of the other charge. In the process the test charge loses electrical potential energy and gains kinetic energy. Thus, at A, the test charge has more potential energy than at B - A is said to have a higher electrical potential than B. The potential energy of a charge at a point in a field is defined as the work required to move that charge from infinity to that point.
The potential difference between two points in an electric field is defined as the work required to move a unit positive test charge from the point of lower potential to that of higher potential. If an amount of work W is required to move a charge Q from one point to another, then the potential difference between the two points is given by,
From this equation it follows that one volt is the potential difference between two points in an electric field if one joule of work is done in moving one coulomb of charge from the one point to the other.
Worked Example 63 Potential difference[edit | edit source]
Question: A positively charged object Q is placed as shown in the sketch. The potential difference between two points A and B is
(a) Calculate the change in electrical potential energy of a +2nC charge when it moves from A to B. (b) Which point, A or B, is at the higher electrical potential? Explain. (c) If this charge were replaced with another of charge -2nC, in what way would its change in energy be affected?
Answer: (a) The electrical potential energy of the positive charge decreases as it moves from A to B since it is moving in the direction of the electric field produced by the object Q. This loss in potential energy is equal to the work done by the field,
(b) Point A is at the higher electrical potential since work is required by us to move a positive test charge from B to A. (c) If the charge is replaced by one of negative charge, the electrical potential energy of the charge will increase in moving from A to B (in this case we would have to do work on the charge).
As an example consider the electric field between two oppositely charged parallel plates a distance d apart maintained at a potential difference V.
This electric field is uniform so that a charge placed anywhere between the plates will experience the same force. Consider a positive test charge Q placed at point O just off the surface of the negative plate. In order to move it towards the positive plate we have to apply a force QE. The work done in moving the charge from the negative to the positive plate is,
but from the definition of electrical potential,
Equating these two expressions for the work done,
and so, rearranging,
Worked Example 64 Parallel plates[edit | edit source]
Question: Two charged parallel plates are at a distance of 180 mm from each other. The potential difference between them is as shown in the diagram.
(a) If a small oil drop of negligible mass, carrying a charge of , is placed between the plates at point X, calculate the magnitude and direction of the electrostatic force exerted on the droplet.
(b) If the droplet is now moved to point Y, would the force exerted on it be bigger, smaller or the same as in (a)?
Answer: (a)
Step 1 :
First find the electric field strength between the plates,
Step 2 :
Now the force exerted on the charge at X is,
(b)
| Figure 12.3: An oil drop suspended between oppositely charged parallel plates. |
| File:Fhsst electrost29.png |
Step 3 :
The same. Since the electric field strength is uniform, the force exerted on a charge is the same at all points between the plates.
Millikan's Oil-drop Experiment[edit | edit source]
Robert Millikan measured the charge on an electron by studying the motion of charged oil drops between oppositely charged parallel plates.
Consider one such negative drop between the plates in Figure 12.3. Since this drop is negative, the electric field exerts an upward force on the drop. In addition to this upward force, gravity exerts a downward force on the drop. Millikan adjusted the electric field strength between the plates by varying the potential difference applied across the plates. In this way, Millikan was able to bring the drops to rest. *EDIT* Millikan's experiment was meant to have the drops fall at a constant rate. At this constant rate the force of the earth on the drop and the force of the field on the drop are equal *End EDIT*
Since
and, therefore,
Millikan found that all drops had charges which were multiples of . Since objects become charged by gaining or losing electrons, the charge on an electron must be . The magnitude of the electron's charge is denoted by e,
Worked Example 65 Charge[edit | edit source]
Question: A metal sphere carries a charge of . How many electrons did it have to lose to attain its charge?
Answer: Since the sphere is positive it lost electrons in the process of charging (when an object loses negative charges it is left positive). In fact, it lost,
Worked Example 66 Millikan oil-drop experiment[edit | edit source]
Question: In a Millikan-type experiment a positively charged oil drop is placed between two horizontal plates, 20 mm apart, as shown.
The potential difference across the plates is 4000V. The drop has a mass of and a charge of . (a) Draw the electric field pattern between the two plates. (b) Calculate:
- the electric field intensity between the two plates.
- the magnitude of the gravitational force acting on the drop.
- the magnitude of the Coulomb force acting on the drop.
(c) The drop is observed through a microscope. What will the drop be seen to do? Explain. (d) Without any further calculations, give two methods that could be used to make the drop remain in a fixed position.
Answer: (a)
(b) 1.
2.
3.
(c) Since , the drop accelerates upwards.
(d) The Coulomb force can be decreased by decreasing the electric field strength between the plates. Since , this can be done either by increasing d or decreasing V.
Important Equations and Quantities[edit | edit source]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
































































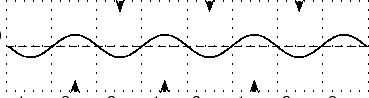

























































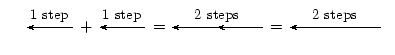


























































































































































































































































































![{\displaystyle {\begin{matrix}v_{3}=2[\mathrm {m.s^{-1}} ]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/666461cc8a1907b6891208191272d629c9c66d74)