Basic Physics of Nuclear Medicine/Print version
| This is the print version of Basic Physics of Nuclear Medicine You won't see this message or any elements not part of the book's content when you print or preview this page. |
Note: current version of this book can be found at http://en.wikibooks.org/wiki/Basic_Physics_of_Nuclear_Medicine
Atomic & Nuclear Structure[edit | edit source]

You will have encountered much of what we will cover here in your high school physics. We are going to review this material again below so as to set the context for subsequent chapters. This chapter will also provide you with an opportunity to check your understanding of this topic.
The chapter covers atomic structure, nuclear structure, the classification of nuclei, binding energy and nuclear stability.
Atomic Structure[edit | edit source]
The atom is considered to be the basic building block of all matter. Simple atomic theory tells us that it consists of two components: a nucleus surrounded by an electron cloud. The situation can be considered as being similar in some respects to planets orbiting the sun.
From an electrical point of view, the nucleus is said to be positively charged and the electrons negatively charged.
From a size point of view, the radius of an atom is about 10-10 m while the radius of a nucleus is about 10-14 m, i.e. about ten thousand times smaller. The situation could be viewed as something like a cricket ball, representing the nucleus, in the middle of a sporting arena with the electrons orbiting somewhere around where the spectators would sit. This perspective tells us that the atom should be composed mainly of empty space. However, the situation is far more complex than this simple picture portrays in that we must also take into account the physical forces which bind the atom together.
Chemical phenomena can be thought of as interactions between the electrons of individual atoms. Radioactivity on the other hand can be thought of as changes which occur within the nuclei of atoms.
The Nucleus[edit | edit source]
A simple description of the nucleus tells us that it is composed of protons and neutrons. These two particle types are collectively called nucleons, i.e. particles which inhabit the nucleus.
From a mass point of view the mass of a proton is roughly equal to the mass of a neutron and each of these is about 2,000 times the mass of an electron. So most of the mass of an atom is concentrated in the small region at its core.
From an electrical point of view the proton is positively charged and the neutron has no charge. An atom all on its own (if that were possible to achieve!) is electrically neutral. The number of protons in the nucleus of such an atom must therefore equal the number of electrons orbiting that atom.
Classification of Nuclei[edit | edit source]
The term Atomic Number is defined in nuclear physics as the number of protons in a nucleus and is given the symbol Z. From your chemistry you will remember that this number also defines the position of an element in the Periodic Table of Elements.
The term Mass Number is defined as the number of nucleons in a nucleus, that is the number of protons plus the number of neutrons, and is given the symbol A.
Note that the symbols here are a bit odd, in that it would prevent some confusion if the Atomic Number were given the symbol A, and the Mass Number were given another symbol, such as M, but its not a simple world!
It is possible for nuclei of a given element to have the same number of protons but differing numbers of neutrons, that is to have the same Atomic Number but different Mass Numbers. Such nuclei are referred to as Isotopes. All elements have isotopes and the number ranges from three for hydrogen to over 30 for elements such as caesium and barium.
Chemistry has a relatively simple way of classifying the different elements by the use of symbols such as H for hydrogen, He for helium and so on. The classification scheme used to identify different isotopes is based on this approach with the use of a superscript before the chemical symbol to denote the Mass Number along with a subscript before the chemical symbol to denote the Atomic Number. In other words an isotope is identified as:
where X is the chemical symbol of the element; A is the "Mass Number," (protons+ neutrons); Z is the "Atomic Number," (number identifying the element on the periodic chart).
Let us take the case of hydrogen as an example. It has three isotopes:
- the most common one consisting of a single proton orbited by one electron,
- a second isotope consisting of a nucleus containing a proton and a neutron orbited by one electron,
- a third whose nucleus consists of one proton and two neutrons, again orbited by a single electron.
A simple illustration of these isotopes is shown below. Remember though that this is a simplified illustration given what we noted earlier about the size of a nucleus compared with that of an atom. But the illustration is nevertheless useful for showing how isotopes are classified.
The first isotope commonly called hydrogen has a Mass Number of 1, an Atomic Number of 1 and hence is identified as:
The second isotope commonly called deuterium has a Mass Number of 2, an Atomic Number of 1 and is identified as:
The third isotope commonly called tritium is identified as:
The same classification scheme is used for all isotopes. For example, you should now be able to figure out that the uranium isotope, , contains 92 protons and 144 neutrons.
A final point on classification is that we can also refer to individual isotopes by giving the name of the element followed by the Mass Number. For example, we can refer to deuterium as hydrogen-2 and we can refer to as uranium-236.
Before we leave this classification scheme let us further consider the difference between chemistry and nuclear physics. You will remember that the water molecule is made up of two hydrogen atoms bonded with an oxygen atom. Theoretically if we were to combine atoms of hydrogen and oxygen in this manner many, many of billions of times we could make a glass of water. We could also make our glass of water using deuterium instead of hydrogen. This second glass of water would theoretically be very similar from a chemical perspective. However, from a physics perspective our second glass would be heavier than the first since each deuterium nucleus is about twice the mass of each hydrogen nucleus. Indeed water made in this fashion is called heavy water.
Atomic Mass Unit[edit | edit source]
The conventional unit of mass, the kilogram, is rather large for use in describing characteristics of nuclei. For this reason, a special unit called the Atomic Mass Unit (amu) is often used. This unit is sometimes defined as 1/12th of the mass of the stable most commonly occurring isotope of carbon, i.e. 12C. In terms of grams, 1 amu is equal to 1.66 x 10-24 g, that is, just over one million, million, million millionth of a gram.
The masses of the proton, mp and neutron, mn on this basis are:
and
while that of the electron is just 0.00055 amu.
Binding Energy[edit | edit source]
We are now in a position to consider the subject of nuclear stability. From what we have covered so far, we have seen that the nucleus is a tiny region in the centre of an atom and that it is composed of neutrally and positively charged particles. So, in a large nucleus such as that of uranium (Z=92) we have a large number of positively charged protons concentrated into a tiny region in the centre of the atom. An obvious question which arises is that with all these positive charges in close proximity, why doesn't the nucleus fly apart? How can a nucleus remain as an entity with such electrostatic repulsion between the components? Should the orbiting negatively-charged electrons not attract the protons away from the atoms centre?
Let us take the case of the helium-4 nucleus as an example. This nucleus contains two protons and two neutrons so that in terms of amu we can figure out from what we covered earlier that the
and the
Therefore we would expect the total mass of the nucleus to be 4.03298 amu.
The experimentally determined mass of a helium-4 nucleus is a bit less - just 4.00260 amu. In other words there is a difference of 0.03038 amu between what we might expect as the mass of this nucleus and what we actually measure. You might think of this difference as very small at just 0.75%. But remember that since the mass of one electron is 0.00055 amu the difference is actually equivalent to the mass of about 55 electrons. Therefore it is significant enough to wonder about.
It is possible to consider that this missing mass is converted to energy which is used to hold the nucleus together; it is converted to a form of energy called Binding Energy. You could say, as with all relationships, energy must be expended in order to maintain them!
Like the gram in terms of the mass of nuclei, the common unit of energy, the joule is rather cumbersome when we consider the energy needed to bind a nucleus together. The unit used to express energies on the atomic scale is the electron volt, symbol: eV.
One electron volt is defined as the amount of energy gained by an electron as it falls through a potential difference of one volt. This definition on its own is not of great help to us here and it is stated purely for the sake of completeness. So do not worry about it for the time being. Just appreciate that it is a unit representing a tiny amount of energy which is useful on the atomic scale. It is a bit too small in the case of binding energies however and the mega-electron volt (MeV) is often used.
Albert Einstein introduced us to the equivalence of mass, m, and energy, E, at the atomic level using the following equation:
where c is the velocity of light.
It is possible to show that 1 amu is equivalent to 931.48 MeV. Therefore, the mass difference we discussed earlier between the expected and measured mass of the helium-4 nucleus of 0.03038 amu is equivalent to about 28 MeV. This represents about 7 MeV for each of the four nucleons contained in the nucleus.
Nuclear Stability[edit | edit source]
In most stable isotopes the binding energy per nucleon lies between 7 and 9 MeV. There are two competing forces in the nuclei, electrostatic repulsion between protons and the attractive nuclear force between nucleons (protons and neutrons). The electrostatic force is a long range force that becomes more difficult to compensate for as more protons are added to the nucleus. The nuclear force, which arises as the residual strong force (the strong force binds the quarks together within a nucleon), is a short range force that only operates on a very short distance scale (~ 1.5 fm) as it arises from a Yukawa potential. (Electromagnetism is a long range force as the force carrier, the photon, is massless; the nuclear force is a short range force as the force carrier, the pion, is massive). Therefore, larger nuclei tend to be less stable, and require a larger ratio of neutrons to protons (which contribute to the attractive strong force, but not the long-range electrostatic repulsion). For the low Z nuclides the ratio of neutrons to protons is approximately 1, though it gradually increases to about 1.5 for the higher Z nuclides as shown below on the Nuclear Stability Curve.

In other words to combat the effect of the increase in electrostatic repulsion when the number of protons increases the number of neutrons must increase more rapidly to contribute sufficient energy to bind the nucleus together.
As we noted earlier there are a number of isotopes for each element of the Periodic Table. It has been found that the most stable isotope for each element has a specific number of neutrons in its nucleus. Plotting a graph of the number of protons against the number of neutrons for these stable isotopes generates what is called the Nuclear Stability Curve:
Note that the number of protons equals the number of neutrons for small nuclei. But notice also that the number of neutrons increases more rapidly than the number of protons as the size of the nucleus gets bigger so as to maintain the stability of the nucleus. In other words more neutrons need to be there to contribute to the binding energy used to counteract the electrostatic repulsion between the protons.
Radioactivity[edit | edit source]
There are about 2,450 known isotopes of the approximately one hundred elements in the Periodic Table. You can imagine the size of a table of isotopes relative to that of the Periodic Table! The unstable isotopes lie above or below the Nuclear Stability Curve. These unstable isotopes attempt to reach the stability curve by splitting into fragments, in a process called Fission, or by emitting particles and/or energy in the form of radiation. This latter process is called Radioactivity.
It is useful to dwell for a few moments on the term radioactivity. For example what has nuclear stability to do with radio? From a historical perspective remember that when these radiations were discovered about 100 years ago we did not know exactly what we were dealing with. When people like Henri Becquerel and Marie Curie were working initially on these strange emanations from certain natural materials it was thought that the radiations were somehow related to another phenomenon which also was not well understood at the time - that of radio communication. It seems reasonable on this basis to appreciate that some people considered that the two phenomena were somehow related and hence that the materials which emitted radiation were termed radio-active.
We know today that the two phenomena are not directly related but we nevertheless hold onto the term radioactivity for historical purposes. But it should be quite clear to you having reached this stage of this chapter that the term radioactive refers to the emission of particles and/or energy from unstable isotopes. Unstable isotopes for instance those that have too many protons to remain a stable entity are called radioactive isotopes - and called radioisotopes for short. The term radionuclide is also sometimes used.
Finally about 300 of the 2,450-odd isotopes mentioned above are found in nature. The rest are man-made, that is they are produced artificially. These 2,150 or so artificial isotopes have been made during the last 100 years or so with most having been made since the second world war.
We will return to the production of radioisotopes in a later chapter of this wikibook and will proceed for the time being with a description of the types of radiation emitted by radioisotopes.
Multiple Choice Questions[edit | edit source]
Click here to access multiple choice questions on atomic and nuclear structure.
External Links[edit | edit source]
- Novel Periodic Table - an interactive table providing information about each element.
- Marie and Pierre Curie and the Discovery of Polonium and Radium - an historical essay from The Nobel Foundation.
- Natural Radioactivity - an overview of radioactivity in nature - includes sections on primordial radionuclides, cosmic radiation, human produced radionuclides, as well as natural radioactivity in soil, in the ocean, in the human body and in building materials - from the University of Michigan Student Chapter of the Health Physics Society.
- The Particle Adventure - an interactive tour of the inner workings of the atom which explains the modern tools physicists use to probe nuclear and sub-nuclear matter and how physicists measure the results of their experiments using detectors - from the Particle Data Group at the Lawrence Berkeley National Lab, USA and mirrored at CERN, Geneva.
- WebElements - an excellent web-based Periodic Table of the Elements which includes a vast array of data about each element - originally from Mark Winter at the University of Sheffield, England.
Radioactive Decay[edit | edit source]

We saw in the last chapter that radioactivity is a process used by unstable nuclei to achieve a more stable situation. It is said that such nuclei decay in an attempt to achieve stability. So, an alternative title for this chapter is Nuclear Decay Processes.
We also saw in the previous chapter that we can use the Nuclear Stability Curve as a means of describing what is going on. So a second alternative title for this chapter is Methods of Getting onto the Nuclear Stability Curve.
We are going to follow a descriptive or phenomenological approach to the topic here by describing in a fairly simple fashion what is known about each of the major decay mechanisms. Once again you may have already covered this material in high school physics. But bear with us because the treatment here will help us set the scene for subsequent chapters.
Methods of Radioactive Decay[edit | edit source]
Rather than considering what happens to individual nuclei it is perhaps easier to consider a hypothetical nucleus that can undergo many of the major forms of radioactive decay. This hypothetical nucleus is shown below:

Firstly we can see two protons and two neutrons being emitted together in a process called alpha-decay. Secondly, we can see that a proton can release a positron in a process called beta-plus decay, and that a neutron can emit an electron in a process called beta-minus decay. We can also see an electron being captured by a proton. Thirdly we can see some energy (a photon) being emitted which results from a process called gamma-decay as well as an electron being attracted into the nucleus and being ejected again. Finally there is the rather catastrophic process where the nucleus cracks in half called spontaneous fission.
We will now describe each of these decay processes in turn.
Spontaneous Fission[edit | edit source]
This is a very destructive process which occurs in some heavy nuclei which split into 2 or 3 fragments plus some neutrons. These fragments form new nuclei which are usually radioactive. Nuclear reactors exploit this phenomenon for the production of radioisotopes. Its also used for nuclear power generation and in nuclear weaponry. The process is not of great interest to us here and we will say no more about it for the time being.
Alpha Decay[edit | edit source]
In this decay process two protons and two neutrons leave the nucleus together in an assembly known as an alpha particle. Note that an alpha particle is really a helium-4 nucleus.
So why not call it a helium nucleus? Why give it another name? The answer to this question lies in the history of the discovery of radioactivity. At the time when these radiations were discovered we didn't know what they really were. We found out that one type of these radiations had a double positive charge and it was not until sometime later that we learned that they were in fact nuclei of helium-4. In the initial period of their discovery this form of radiation was given the name alpha rays (and the other two were called beta and gamma rays), these terms being the first three letters of the Greek alphabet. We still call this form of radiation by the name alpha particle for historical purposes. Calling it by this name also contributes to the specific jargon of the field and leads outsiders to think that the subject is quite specialized!
But notice that the radiation really consists of a helium-4 nucleus emitted from an unstable larger nucleus. There is nothing strange about helium since it is quite an abundant element on our planet. So why is this radiation dangerous to humans? The answer to this question lies with the energy with which they are emitted and the fact that they are quite massive and have a double positive charge. So when they interact with living matter they can cause substantial destruction to molecules which they encounter in their attempt to slow down and to attract two electrons to become a neutral helium atom.
An example of this form of decay occurs in the uranium-238 nucleus. The equation which represents what occurs is:
Here the uranium-238 nucleus emits a helium-4 nucleus (the alpha particle) and the parent nucleus becomes thorium-234. Note that the Mass Number of the parent nucleus has been reduced by 4 and the Atomic Number is reduced by 2 which is a characteristic of alpha decay for any nucleus in which it occurs.
Beta Decay[edit | edit source]
There are three common forms of beta decay:
(a) Electron Emission
- Certain nuclei which have an excess of neutrons may attempt to reach stability by converting a neutron into a proton with the emission of an electron. The electron is called a beta-minus particle – the minus indicating that the particle is negatively charged.
- We can represent what occurs as follows:
- where a neutron converts into a proton and an electron. Notice that the total electrical charge is the same on both sides of this equation. We say that the electric charge is conserved.
- We can consider that the electron cannot exist inside the nucleus and therefore is ejected.
- Once again there is nothing strange or mysterious about an electron. What is important though from a radiation safety point of view is the energy with which it is emitted and the chemical damage it can cause when it interacts with living matter.
- An example of this type of decay occurs in the iodine-131 nucleus which decays into xenon-131 with the emission of an electron, that is
- The electron is what is called a beta-minus particle. Note that the Mass Number in the above equation remains the same and that the Atomic Number increases by 1 which is characteristic of this type of decay.
- You may be wondering how an electron can be produced inside a nucleus given that the simple atomic description we gave in the previous chapter indicated that the nucleus consists of protons and neutrons only. This is one of the limitations of the simple treatment presented so far and can be explained by considering that the two particles which we call protons and neutrons are themselves formed of smaller particles called quarks. We are not going to consider these in any way here other than to note that some combinations of different types of quark produce protons and another combination produces neutrons. The message here is to appreciate that a simple picture is the best way to start in an introductory text such as this and that the real situation is a lot more complex than what has been described. The same can be said about the treatment of beta-decay given above as we will see in subsequent chapters.
(b) Positron Emission
- When the number of protons in a nucleus is too large for the nucleus to be stable it may attempt to reach stability by converting a proton into a neutron with the emission of a positively-charged electron.
- That is not a typographical error! An electron with a positive charge also called a positron is emitted. The positron is the beta-plus particle.
- The history here is quite interesting. A brilliant Italian physicist, Enrico Fermi developed a theory of beta decay and his theory predicted that positively-charged as well as negatively-charged electrons could be emitted by unstable nuclei. These particles could be called pieces of anti-matter and they were subsequently discovered by experiment. They do not exist for very long as they quickly combine with a normal electron and the subsequent reaction called annihilation gives rise to the emission of two gamma rays.
- Science fiction writers had a great time following the discovery of anti-matter and speculated along with many scientists that parts of our universe may contain negatively-charged protons forming nuclei which are orbited by positively-charged electrons. But this is taking us too far away from the topic at hand!
- The reaction in our unstable nucleus which contains one too many protons can be represented as follows:
- Notice, once again, that electric charge is conserved on each side of this equation.
- An example of this type of decay occurs in sodium-22 which decays into neon-22 with the emission of a positron:
- Note that the Mass Number remains the same and that the Atomic Number decreases by 1.
(c) Electron Capture
- In this third form of beta decay an inner orbiting electron is attracted into an unstable nucleus where it combines with a proton to form a neutron. The reaction can be represented as:
- This process is also known as K-capture since the electron is often attracted from the K-shell of the atom.
- How do we know that a process like this occurs given that no radiation is emitted? In other words the event occurs within the atom itself and no information about it leaves the atom. Or does it? The signature of this type of decay can be obtained from effects in the electron cloud surrounding the nucleus when the vacant site left in the K-shell is filled by an electron from an outer shell. The filling of the vacancy is associated with the emission of an X-ray from the electron cloud and it is this X-ray which provides a signature for this type of beta decay.
- This form of decay can also be recognised by the emission of gamma-rays from the new nucleus.
- An example of this type of radioactive decay occurs in iron-55 which decays into manganese-55 following the capture of an electron. The reaction can be represented as follows:
- Note that the Mass Number once again is unchanged in this form of decay and that the Atomic Number is decreased by 1.
Gamma Decay[edit | edit source]
Gamma decay involves the emission of energy from an unstable nucleus in the form of electromagnetic radiation.
You should remember from your high school physics that electromagnetic radiation is the biggest physical phenomenon we have so far discovered. The radiation can be characterised in terms of its frequency, its wavelength and its energy. Thinking about it in terms of the energy of the radiation we have very low energy electromagnetic radiation called radio waves, infra-red radiation at a slightly higher energy, visible light at a higher energy still, then ultra-violet radiation and the higher energy forms of this radiation are called X-rays and gamma-rays. You should also remember that these radiations form what is called the Electromagnetic Spectrum.
Before proceeding it is useful to pause for a moment to consider the difference between X-rays and gamma-rays. These two forms of radiation are high energy electromagnetic rays and are therefore virtually the same. The difference between them is not what they consist of but where they come from. In general we can say that if the radiation emerges from a nucleus it is called a gamma-ray and if it emerges from outside the nucleus from the electron cloud for example, it is called an X-ray.
One final point is of relevance before we consider the different forms of gamma-decay and that is what such a high energy ray really is. It has been found in experiments that gamma-rays (and X-rays for that matter!) sometimes manifest themselves as waves and other times as particles. This wave-particle duality can be explained using the equivalence of mass and energy at the atomic level. When we describe a gamma ray as a wave it has been found useful to use terms such as frequency and wavelength just like any other wave. In addition when we describe a gamma ray as a particle we use terms such as mass and electric charge. Furthermore the term electromagnetic photon is used for these particles. The interesting feature about these photons however is that they have neither mass nor charge!
There are two common forms of gamma decay:
(a) Isomeric Transition
- A nucleus in an excited state may reach its ground or unexcited state by the emission of a gamma-ray.
- An example of this type of decay is that of technetium-99m – which by the way is the most common radioisotope used for diagnostic purposes today in medicine. The reaction can be expressed as:
- Here a nucleus of technetium-99 is in an excited state, that is, it has excess energy. The excited state in this case is called a metastable state and the nucleus is therefore called technetium-99m (m for metastable). The excited nucleus looses its excess energy by emitting a gamma-ray to become technetium-99.
(b) Internal Conversion
- Here the excess energy of an excited nucleus is given to an atomic electron, e.g. a K-shell electron.
Decay Schemes[edit | edit source]
Decay schemes are widely used to give a visual representation of radioactive decay. A scheme for a relatively straight-forward decay is shown below:

This scheme is for hydrogen-3 which decays to helium-3 with a half-life of 12.3 years through the emission of a beta-minus particle with an energy of 0.0057 MeV.
A scheme for a more complicated decay is that of caesium-137.

This isotope can decay through through two beta-minus processes. In one which occurs in 5% of disintegrations a beta-minus particle is emitted with an energy of 1.17 MeV to produce barium-137. In the second which occurs more frequently (in the remaining 95% of disintegrations) a beta-minus particle of energy 0.51 MeV is emitted to produce barium-137m – in other words a barium-137 nucleus in a metastable state. The barium-137m then decays via isomeric transition with the emission of a gamma-ray of energy 0.662 MeV.

The general method used for decay schemes is illustrated in the diagram on the right.
The energy is plotted on the vertical axis and atomic number on the horizontal axis – although these axes are rarely displayed in actual schemes. The isotope from which the scheme originates is displayed at the top – X in the case above. This isotope is referred to as the parent. The parent loses energy when it decays and hence the products of the decay referred to as daughters are plotted at a lower energy level.
The diagram illustrates the situation for common forms of radioactive decay. Alpha-decay is illustrated on the left where the mass number is reduced by 4 and the atomic number is reduced by 2 to produce daughter A. To its right the scheme for beta-plus decay is shown to produce daughter B. The situation for beta-minus decay followed by gamma-decay is shown on the right side of the diagram where daughters C and D respectively are produced.
Multiple Choice Questions[edit | edit source]
Click here to access multiple choice questions on radioactive decay.
External links[edit | edit source]
- Basics about Radiation – overview of the different types of ionising radiation from the Radiation Effects Research Foundation – a cooperative Japan-United States Research Organization which conducts research for peaceful purposes.
- Radiation and Life – from the World Nuclear Association website.
- Radiation and Radioactivity – a self-paced lesson developed by the University of Michigan's Student Chapter of the Health Physics Society, with sections on radiation, radioactivity, the atom, alpha radiation, beta radiation and gamma radiation.
The Radioactive Decay Law[edit | edit source]

We covered radioactive decay from a phenomenological perspective in the last chapter. In this chapter we consider the topic from a more general analytical perspective.
The reason for doing this is so that we can develop a form of thinking which will help us to understand what is going on in a quantitative, mathematical sense. We will be introduced to concepts such as the Decay Constant and the Half Life as well as units used for the measurement of radioactivity. You will also have a chance to develop your understanding by being brought through three questions on this subject.
Assumptions[edit | edit source]
The usual starting point in most forms of analysis in physics is to make some assumptions which simplify the situation. By simplifying the situation we can dispose of irrelevant effects which tend to complicate matters but in doing so we sometimes make the situation so simple that it becomes a bit too abstract and apparently hard to understand.
For this reason we will try here to relate the subject of radioactive decay to a more common situation which we will use as an analogy and hopefully we will be able to overcome the abstract feature of the subject matter. The analogy we will use here is that of making popcorn.
So think about putting some oil in a pot, adding the corn, heating the pot on the cooker and watching what happens. You might also like to try this out while considering the situation!
For our radioactive decay situation we first of all consider that we have a sample containing a large number of radioactive nuclei all of the same kind. This is our unpopped corn in the pot for example.
Secondly we assume that all of the radioactive nuclei decay by the same process be it alpha, beta or gamma-decay. In other words our unpopped corn goes pop at some stage during the heating process.
Thirdly take a few moments to ponder on the fact that we can only really consider what is going on from a statistical perspective. If you look at an individual piece of corn, can you figure out when it is going to pop? Not really. You can however figure out that a large number of them will have popped after a period of time. But its rather more difficult to figure out the situation for an individual piece of corn. So instead of dealing with individual entities we consider what happens on a larger scale and this is where statistics comes in. We can say that the radioactive decay is a statistical one-shot process, that is when a nucleus has decayed it cannot repeat the process again. In other words when a piece of corn has popped it cannot repeat the process. Simple!
In addition as long as a radioactive nucleus has not decayed the probability for it doing so in the next moment remains the same. In other words if a piece of corn has not popped at a certain time the chance of it popping in the next second is the same as in the previous second. The bets are even!
Let us not push this popcorn analogy too far though in that we know that we can control the rate of popping by the heat we apply to the pot for example. However as far as our radioactive nuclei are concerned there is nothing we can do to control what is going on. The rate at which nuclei go pop (or decay, in other words) cannot be influenced by heating up the sample. Nor by cooling it for that matter or by putting it under greater pressures, by changing the gravitational environment by taking it out into space for instance, or by changing any other aspect of its physical environment. The only thing that determines whether an individual nucleus will decay seems to be the nucleus itself. But on the average we can say that it will decay at some stage.
The Radioactive Decay Law[edit | edit source]
Let us now use some symbols to reduce the amount of writing we have to do to describe what is going on and to avail ourselves of some mathematical techniques to simplify the situation even further than we have been able to do so far.
Let us say that in the sample of radioactive material there are N nuclei which have not decayed at a certain time, t. So what happens in the next brief period of time? Some nuclei will decay for sure. But how many?
On the basis of our reasoning above we can say that the number which will decay will depend on overall number of nuclei, N, and also on the length of the brief period of time. In other words the more nuclei there are the more will decay and the longer the time period the more nuclei will decay. Let us denote the number which will have decayed as dN and the small time interval as dt.
So we have reasoned that the number of radioactive nuclei which will decay during the time interval from t to t+dt must be proportional to N and to dt. In symbols therefore:
the minus sign indicating that N is decreasing.
Turning the proportionality in this equation into an equality we can write:
where the constant of proportionality, λ (named lambda) is called the Decay Constant.
Dividing across by N we can rewrite this equation as:
So this equation describes the situation for any brief time interval, dt. To find out what happens for all periods of time we simply add up what happens in each brief time interval. In other words we integrate the above equation. Expressing this more formally we can say that for the period of time from t = 0 to any later time t, the number of radioactive nuclei will decrease from N0 to Nt, so that:
This final expression is known as the Radioactive Decay Law. It tells us that the number of radioactive nuclei will decrease in an exponential fashion with time with the rate of decrease being controlled by the Decay Constant.
Before looking at this expression in further detail let us review the mathematics which we used above. First of all we used integral calculus to figure out what was happening over a period of time by integrating what we knew would occur in a brief interval of time. Secondly we used a calculus relationship that the
where ln x represents the natural logarithm of x. And thirdly we used the definition of logarithms that when
then,
Now, to return to the Radioactive Decay Law. The Law tells us that the number of radioactive nuclei will decrease with time in an exponential fashion with the rate of decrease being controlled by the Decay Constant. The Law is shown in graphical form in the figure below:

The graph plots the number of radioactive nuclei at any time, Nt, against time, t. We can see that the number of radioactive nuclei decreases from N0 that is the number at t = 0 in a rapid fashion initially and then more slowly in the classic exponential manner.
The influence of the Decay Constant can be seen in the following figure:

All three curves here are exponential in nature, only the Decay Constant is different. Notice that when the Decay Constant has a low value the curve decreases relatively slowly and when the Decay Constant is large the curve decreases very quickly.
The Decay Constant is characteristic of individual radionuclides. Some like uranium-238 have a small value and the material therefore decays quite slowly over a long period of time. Other nuclei such as technetium-99m have a relatively large Decay Constant and they decay far more quickly.
It is also possible to consider the Radioactive Decay Law from another perspective by plotting the logarithm of Nt against time. In other words from our analysis above by plotting the expression:
in the form
Notice that this expression is simply an equation of the form y = mx + c where m = -l and c = ln N0. As a result it is the equation of a straight line of slope -l as shown in the following figure. Such a plot is sometimes useful when we wish to consider a situation without the complication of the direct exponential behaviour.

Half-Life[edit | edit source]
Most of us have not been taught to think instinctively in terms of logarithmic or exponential terms even though many natural phenomena display exponential behaviours. Most of the forms of thinking which we have been taught in school are based on linear changes and as a result it is rather difficult for us to grasp the Radioactive Decay Law intuitively. For this reason an indicator is usually derived from the law which helps us think more clearly about what is going on.
This indicator is called the Half Life and it expresses the length of time it takes for the radioactivity of a radioisotope to decrease by a factor of two. From a graphical point of view we can say that when:
the time taken is the Half Life:

Note that the half-life does not express how long a material will remain radioactive but simply the length of time for its radioactivity to halve. Examples of the half lives of some radioisotopes are given in the following table. Notice that some of these have a relatively short half life. These tend to be the ones used for medical diagnostic purposes because they do not remain radioactive for very long following administration to a patient and hence result in a relatively low radiation dose.
| Radioisotope | Half Life (approx.) |
|---|---|
| 81mKr | 13 seconds |
| 99mTc | 6 hours |
| 131I | 8 days |
| 51Cr | 1 month |
| 137Cs | 30 years |
| 241Am | 462 years |
| 226Ra | 1620 years |
| 238U | 4.51 x 109 years |
But they do present a logistical problem when we wish to use them when there may not be a radioisotope production facility nearby. For example suppose we wish to use 99mTc for a patient study and the nearest nuclear facility for making this isotope is 5,000 km away. The production facility could be in Sydney and the patient could be in Perth for instance. After making the isotope at the nuclear plant it would be decaying with a half life of 6 hours. So we put the material on a truck and drive it to Sydney airport. The isotope would be decaying as the truck sits in Sydney traffic then decaying still more as it waits for a plane to take it to Perth. Then decaying more as it is flown across to Perth and so on. By the time it gets to our patient it will have substantially reduced in radioactivity possibly to the point of being useless for the patient's investigation. And what about the problem if we needed to use 81mKr instead of 99mTc for our patient? You will see in another chapter of this book that logistical challenges such as this have given rise to quite innovative solutions. More about that later!
You can appreciate from the table above that other isotopes have a very long half lives. For example 226Ra has a half life of over 1,500 years. This isotope has been used in the past for therapeutic applications in medicine. Think about the logistical problems here. They obviously do not relate to transporting the material from the point of production to the point of use. But they relate to how the material is kept following its arrival at the point of use. We must have a storage facility so that the material can be kept safely for a long period of time. But for how long? A general rule of thumb for the quantities of radioactivity used in medicine is that the radioactivity will remain significant for about 10 half lives. So we would have to have a safe environment for storage of the 226Ra for about 16,000 years! This storage facility would have to be secure from many unforeseeable events such as earthquakes, bombing etc. and be kept in a manner which our children's, children's children can understand. A very serious undertaking indeed!
Relationship between the Decay Constant and the Half Life[edit | edit source]
On the basis of the above you should be able to appreciate that there is a relationship between the Decay Constant and the Half Life. For example when the Decay Constant is small the Half Life should be long and correspondingly when the Decay Constant is large the Half Life should be short. But what exactly is the nature of this relationship?
We can easily answer this question by using the definition of Half Life and applying it to the Radioactive Decay Law.
Once again the law tells us that at any time, t:
and the definition of Half Life tells us that:
when
We can therefore re-write the Radioactive Decay Law by substituting for Nt and t as follows:
Therefore
and
These last two equations express the relationship between the Decay Constant and the Half Life. They are very useful as you will see when solving numerical questions relating to radioactivity and usually form the first step in solving a numerical problem.
Units of Radioactivity[edit | edit source]
The SI or metric unit of radioactivity is named after Henri Becquerel, in honour of his discovery of radioactivity, and is called the becquerel with the symbol Bq. The becquerel is defined as the quantity of radioactive substance that gives rise to a decay rate of 1 decay per second.
In medical diagnostic work 1 Bq is a rather small amount of radioactivity. Indeed it is easy to remember its definition if you think of it as a buggerall amount of radioactivity. For this reason the kilobecquerel (kBq) and megabecquerel (MBq) are more frequently used.
The traditional unit of radioactivity is named after Marie Curie and is called the curie, with the symbol Ci. The curie is defined as the amount of radioactive substance which gives rise to a decay rate of 3.7 x 1010 decays per second. In other words 37 thousand, million decays per second which as you might appreciate is a substantial amount of radioactivity. For medical diagnostic work the millicurie (mCi) and the microcurie (µCi) are therefore more frequently used.
Why two units? It in essence like all other units of measurement depends on what part of the world you are in. For example the kilometer is widely used in Europe and Australia as a unit of distance and the mile is used in the USA. So if you are reading an American textbook you are likely to find the curie used as the unit of radioactivity, if you are reading an Australian book it will most likely refer to becquerels and both units might be used if you are reading a European book. You will therefore find it necessary to know and understand both units.
Multiple Choice Questions[edit | edit source]
Click here to access an MCQ on the Radioactive Decay Law.
Questions[edit | edit source]
Three questions are given below to help you develop your understanding of the material presented in this chapter. The first one is relatively straight-forward and will exercise your application of the Radioactive Decay Law as well as your understanding of the concept of Half Life. The second question is a lot more challenging and will help you relate the Radioactive Decay Law to the number of radioactive nuclei which are decaying in a sample of radioactive material. The third question will help you understand the approach used in the second question by asking a similar question from a slightly different perspective.
Question 1
(a) The half-life of 99mTc is 6 hours. After how much time will 1/16th of the radioisotope remain?
(b) Verify your answer by another means.
Answer:
- (a) Starting with the relationship we established earlier between the Decay Constant and the Half Life we can calculate the Decay Constant as follows:
- Now applying the Radioactive Decay Law,
- we can re-write it in the form:
- The question tells us that N0 has reduced to 1/16th of its value, that is:
- Therefore
- which we need to solve for t. One way of doing this is as follows:
- So it will take 24 hours until 1/16th of the radioactivity remains.
- (b) A way in which this answer can be verified is by using the definition of Half Life. We are told that the Half Life of 99mTc is 6 hours. Therefore after six hours half of the radioactivity remains.
- Therefore after 12 hours a quarter remains; after 18 hours an eighth remains and after 24 hours one sixteenth remains. And we arrive at the same answer as in part (a). So we must be right!
- Note that this second approach is useful if we are dealing with relatively simple situations where the radioactivity is halved, quartered and so on. But supposing the question asked how long would it take for the radioactivity to decrease to a tenth of its initial value. Deduction from the definition of half life is rather more difficult in this case and the mathematical approach used for part (a) above will yield the answer more readily.
Question 2
Find the radioactivity of a 1 g sample of 226Ra given that t1/2: 1620 years and Avogadro's Number: 6.023 x 1023.
Answer:
- We can start the answer like we did with Question 1(a) by calculating the Decay Constant from the Half Life using the following equation:
- Note that the length of a year used in converting from 'per year' to 'per second' above is 365.25 days to account for leap years. In addition the reason for converting to units of 'per second' is because the unit of radioactivity is expressed as the number of nuclei decaying per second.
- Secondly we can calculate that 1 g of 226Ra contains:
- Thirdly we need to express the Radioactive Decay Law in terms of the number of nuclei decaying per unit time. We can do this by differentiating the equation as follows:
- The reason for expressing the result above in absolute terms is to remove the minus sign in that we already know that the number is decreasing.
- We can now enter the data we derived above for λ and N:
- So the radioactivity of our 1 g sample of radium-226 is approximately 1 Ci.
- This is not a surprising answer since the definition of the curie was originally conceived as the radioactivity of 1 g of radium-226!
Question 3
What is the minimum mass of 99mTc that can have a radioactivity of 1 MBq? Assume the half-life is 6 hours and that Avogadro's Number is 6.023 x 1023.
Answer
- Starting again with the relationship between the Decay Constant and the Half Life:
- Secondly the question tells us that the radioactivity is 1 MBq. Therefore since 1 MBq = 1 x 106 decays per second,
- Finally the mass of these nuclei can be calculated as follows:
- In other words a mass of just over five picograms of 99mTc can emit one million gamma-rays per second. The result reinforces an important point that you will learn about radiation protection which is that you should treat radioactive materials just like you would handle pathogenic bacteria!
Units of Radiation Measurement[edit | edit source]

Introduction[edit | edit source]
This is the fourth chapter of a wikibook entitled Basic Physics of Nuclear Medicine.
After that rather long and detailed chapter we have just finished we will now proceed at a more leisurely pace for a short treatment of some of the more common units of measurement used in this field.
Before we do so however it is useful to consider the typical radiation environment. By doing so we will gain an appreciation of the various quantities that can be measured before considering the units which are used to express such measurements. So, we will first of all consider a typical radiation situation and then go on to consider the various units of measurement.
A Typical Radiation Situation[edit | edit source]
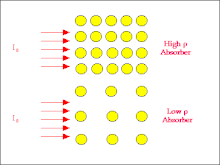
A typical radiation set-up is shown in the figure below. Firstly there is a source of radiation, secondly a radiation beam and thirdly some material which absorbs the radiation. So the quantities which can be measured are associated with the source, the radiation beam and the absorber.
This type of environment could be one where the radiation from the source is used to irradiate a patient (that is the absorber) for diagnostic purposes where we would place a device behind the patient for producing an image or for therapeutic purposes where the radiation is intended to cause damage to a specific region of a patient. It is also a situation where we as an absorber may be working with a source of radiation.
The Radiation Source[edit | edit source]
When the radiation source is a radioactive one the quantity that is typically measured is the radioactivity of the source. We saw in the previous chapter that the units used to express radioactivity are the becquerel (SI unit) and the curie (traditional unit).
The Radiation Beam[edit | edit source]
The characteristic of a radiation beam that is typically measured is called the Radiation Exposure. This quantity expresses how much ionisation the beam causes in the air through which it travels.
We will see in the following chapter that one of the major things that happens when radiation encounters matter is that ions are formed – air being the form of matter it encounters in this case. So the radiation exposure produced by a radiation beam is expressed in terms of the amount of ionisation which occurs in air.
A straight-forward way of measuring such ionisation is to determine the amount of electric charge which is produced. You will remember from your high school physics that the SI unit of electric charge is the coulomb.
The SI unit of radiation exposure is the coulomb per kilogram – and is given the symbol C kg-1. It is defined as the quantity of X- or gamma-rays such that the associated electrons emitted per kilogram of air at standard temperature and pressure (STP) produce ions carrying 1 coulomb of electric charge.
The traditional unit of radiation exposure is the roentgen, named in honour of Wilhelm Roentgen (who discovered X-rays) and is given the symbol R. The roentgen is defined as the quantity of X- or gamma-rays such that the associated electrons emitted per kilogram of air at STP produce ions carrying 2.58 x 10-4 coulombs of electric charge.
So 1 R is a small exposure relative to 1 C kg-1 – in fact it is 3,876 times smaller.
Note that this unit is confined to radiation beams consisting of X-rays or gamma-rays.
Often it is not simply the exposure that is of interest but the exposure rate, that is the exposure per unit time. The units which tend to be used in this case are the C kg-1 s-1 and the R hr-1.
The Absorber[edit | edit source]
Energy is deposited in the absorber when radiation interacts with it. It is usually quite a small amount of energy but energy nonetheless. The quantity that is measured is called the Absorbed Dose and it is of relevance to all types of radiation be they X- or gamma-rays, alpha- or beta-particles.
The SI unit of absorbed dose is called the gray, named after a famous radiobiologist, LH Gray, and is given the symbol Gy. The gray is defined as the absorption of 1 joule of radiation energy per kilogram of material. So when 1 joule of radiation energy is absorbed by a kilogram of the absorber material we say that the absorbed dose is 1 Gy.
The traditional unit of absorbed dose is called the rad, which supposedly stands for Radiation Absorbed Dose. It is defined as the absorption of 10-2 joules of radiation energy per kilogram of material.
As you can figure out 1 Gy is equal to 100 rad.
There are other quantities derived from the gray and the rad which express the biological effects of such absorbed radiation energy when the absorber is living matter – human tissue for example. These quantities include the Equivalent Dose, H, and the Effective Dose, E. The Equivalent Dose is based on estimates of the ionization capability of the different types of radiation which are called Radiation Weighting Factors, wR, such that
where D is the absorbed dose. The Effective Dose includes wR as well as estimates of the sensitivity of different tissues called Tissue Weighting Factors, wT, such that
where the summation, Σ, is over all the tissue types involved. Both the Equivalent Dose and the Effective Dose are measured in derived SI units called sieverts (Sv).
Let us pause here for a bit to ponder on the use of the term dose. It usually has a medical connotation in that we can say that someone had a dose of the 'flu, or that the doctor prescribed a certain dose of a drug. What has it to do with the deposition of energy by a beam of radiation in an absorber? It could have something to do with the initial applications of radiation in the early part of the 20th century when it was used to treat numerous diseases. As a result we can speculate that the term has stayed in the vernacular of the field. It would be much easier to use a term like absorbed radiation energy since we are talking about the deposition of energy in an absorber. But this might make the subject just a little too simple!
Specific Gamma Ray Constant[edit | edit source]
A final quantity is worth mentioning with regard to radiation units. This is the Specific Gamma-Ray Constant for a radioisotope. This quantity is an amalgam of the quantities we have already covered and expresses the exposure rate produced by the gamma-rays emitted from a radioisotope.
It is quite a useful quantity from a practical viewpoint when we are dealing with a radioactive source which emits gamma-rays. Supposing you are using a gamma-emitting radioactive source (for example 99mTc or 137Cs) and you will be standing at a certain distance from this source while you are working. You most likely will be interested in the exposure rate produced by the source from a radiation safety point of view. This is where the Specific Gamma-Ray Constant comes in.
It is defined as the exposure rate per unit activity at a certain distance from a source. The SI unit is therefore the
and the traditional unit is the
These units of measurement are quite cumbersome and a bit of a mouthful. It might have been better if they were named after some famous scientist so that we could call the SI unit 1 smith and the traditional unit 1 jones for example. But again things are not that simple!
The Inverse Square Law[edit | edit source]
Before we finish this chapter we are going to consider what happens as we move our absorber away from the radiation source. In other words we are going to think about the influence of distance on the intensity of the radiation beam. You will find that a useful result emerges from this that has a very important impact on radiation safety.
The radiation produced in a radioactive source is emitted in all directions. We can consider that spheres of equal radiation intensity exist around the source with the number of photons/particles spreading out as we move away from the source.
Consider an area on the surface of one of these spheres and assume that there are a certain number of photons/particles passing though it. If we now consider a sphere at a greater distance from the source the same number of photons/particles will now be spread out over a bigger area. Following this line of thought it is easy to appreciate that the radiation intensity, I will decrease with the square of the distance, r from the source, i.e.
This effect is known as the Inverse Square Law. As a result if we double the distance from a source, we reduce the intensity by a factor of two squared, that is 4. If we triple the distance the intensity is reduced by a factor of 9, that is three squared, and so on.
This is a very useful piece of information if you are working with a source of radiation and are interested in minimising the dose of radiation you will receive.
External links[edit | edit source]
- Radiation and Risk – covers the effect of radiation, how risks are determined, comparison of radiation with other risks and radiation doses.
- Radiation Effects Overview – results of studies of victims of nuclear bombs including early effects on survivors, effects on the in utero exposed, and late effects on the survivors – from the Radiation Effects Research Foundation, a cooperative Japan-United States Research Organization.
- The Radiation and Health Physics Home Page – all you ever wanted to know about radiation but were afraid to ask....with hundreds of WWW links – from the Student Chapter of the Health Physics Society, University of Michigan containing sections on general information, regulatory Information, professional organizations and societies, radiation specialties, health physics research and education.
- What You Need to Know about Radiation – to protect yourself to protect your family to make reasonable social and political choices – covers sources of radiation and radiation protection – by Lauriston S. Taylor.
Interaction of Radiation with Matter[edit | edit source]

We have focussed in previous chapters on the source of radiation and the types of radiation. We are now in a position to consider what happens when this radiation interacts with matter. Our main reason for doing this is to find out what happens to the radiation as it passes through matter and also to set ourselves up for considering how it interacts with living tissue and how to detect radiation. Since all radiation detectors are made from some form of matter it is useful to first of all know how radiation interacts so that we can exploit the effects in the design of such detectors in subsequent chapters of this wikibook.
Before we do this let us first remind ourselves of the physical characteristics of the major types of radiation. We have covered this information in some detail earlier and it is summarised in the table below for convenience.
We will now consider the passage of each type of radiation through matter with most attention given to gamma-rays because they are the most common type used in nuclear medicine. One of the main effects that you will notice irrespective of the type of radiation is that ions are produced when radiation interacts with matter. It is for this reason that it is called ionizing radiation.
| Radiation | Mass | Electric Charge | Velocity |
|---|---|---|---|
| Alpha Particles | relatively heavy |
double positive |
relatively slow
|
| Beta Particles | about 8,000 times lighter |
negative |
less than the velocity of light
|
| Gamma Rays | None |
None |
3 x 108 m/s in free space
|
Before we start though you might find an analogy useful to help you with your thinking. This analogy works on the basis of thinking about matter as an enormous mass of atoms (that is nuclei with orbiting electrons) and that the radiation is a particle/photon passing through this type of environment. So the analogy to think about is a spaceship passing through a meteor storm like you might see in a science-fiction movie where the spaceship represents the radiation and the meteors represent the atoms of the material through which the radiation is passing. One added feature to bring on board however is that our spaceship sometimes has an electric charge depending on the type of radiation it represents.
Alpha Particles[edit | edit source]
We can see from the table above that alpha-particles have a double positive charge and we can therefore easily appreciate that they will exert considerable electrostatic attraction on the outer orbital electrons of atoms near which they pass. The result is that some electrons will be attracted away from their parent atoms and that ions will be produced. In other words ionizations occur.
We can also appreciate from the table that alpha-particles are quite massive relative to the other types of radiation and also to the electrons of atoms of the material through which they are passing. As a result they travel in straight lines through matter except for rare direct collisions with nuclei of atoms along their path.
A third feature of relevance here is the energy with which they are emitted. This energy in the case of alpha-particles is always distinct. For example 221Ra emits an alpha-particle with an energy of 6.71 MeV. Every alpha-particle emitted from this radionuclide has this energy. Another example is 230U which emits three alpha-particles with energies of 5.66, 5.82, 5.89 MeV.
Finally it is useful to note that alpha-particles are very damaging biologically and this is one reason why they are not used for in-vivo diagnostic studies. We will therefore not be considering them in any great detail in this wikibook.
Beta Particles[edit | edit source]
We can see from the table that beta-particles have a negative electric charge. Notice that positrons are not considered here since as we noted in chapter 2 these particles do not last for very long in matter before they are annihilated. Beta-minus particles last considerably longer and are therefore the focus of our attention here.
Because of their negative charge they are attracted by nuclei and repelled by electron clouds as they pass through matter. The result once again without going into great detail is ionization.
The path of beta-particles in matter is often described as being tortuous, since they tend to ricochet from atom to atom.
A final and important point to note is that the energy of beta-particles is never found to be distinct in contrast to the alpha-particles above. The energies of the beta-particles from a radioactive source forms a spectrum up to a maximum energy – see figure below. Notice from the figure that a range of energies is present and features such as the mean energy, Emean, or the maximum energy, Emax, are quoted.
The question we will consider here is: why should a spectrum of energies be seen? Surely if a beta-particle is produced inside a nucleus when a neutron is converted into a proton, a single distinct energy should result. The answer lies in the fact that two particles are actually produced in beta-decay. We did not cover this in our treatment in chapter 2 for fear of complicating things too much at that stage of this wikibook. But we will cover it here briefly for the sake of completeness.
The second particle produced in beta-decay is called a neutrino and was named by Enrico Fermi. It is quite a mysterious particle possessing virtually no mass and carrying no charge, though we are still researching its properties today. The difficulty with them is that they are very hard to detect and this has greatly limited our knowledge about them so far.
The beta-particle energy spectrum can be explained by considering that the energy produced when a neutron is converted to a proton is shared between the beta-particle and the anti-neutrino. Sometimes all the energy is given to the beta-particle and it receives the maximum energy, Emax. But more often the energy is shared between them so that for example the beta-particle has the mean energy, Emean and the neutrino has the remainder of the energy.
Finally it is useful to note that beta-particles are quite damaging biologically and this is one reason why they are not used for in-vivo diagnostic studies. We will therefore not consider them in any great detail in this wikibook.
Gamma Rays[edit | edit source]
Since we have been talking about energies above, let us first note that the energies of gamma-rays emitted from a radioactive source are always distinct. For example 99mTc emits gamma-rays which all have an energy of 140 keV and 51Cr emits gamma-rays which have an energy of 320 keV.
Gamma-rays have many modes of interaction with matter. Those which have little or no relevance to nuclear medicine imaging are:
and will not be described here.
Those which are very important to nuclear medicine imaging, are the Photoelectric Effect and the Compton Effect. We will consider each of these in turn below. Note that the effects described here are also of relevance to the interaction of X-rays with matter since as we have noted before X-rays and gamma-rays are essentially the same entities. So the treatment below is also of relevance to radiography.
Photoelectric Effect[edit | edit source]
- When a gamma-ray collides with an orbital electron of an atom of the material through which it is passing it can transfer all its energy to the electron and cease to exist – see figure below. On the basis of the Principle of Conservation of Energy we can deduce that the electron will leave the atom with a kinetic energy equal to the energy of the gamma-ray less that of the orbital binding energy. This electron is called a photoelectron.
- Note that an ion results when the photoelectron leaves the atom. Also note that the gamma-ray energy is totally absorbed in the process.
- Two subsequent points should also be noted. Firstly the photoelectron can cause ionisations along its track in a similar manner to a beta-particle. Secondly X-ray emission can occur when the vacancy left by the photoelectron is filled by an electron from an outer shell of the atom. Remember that we came across this type of feature before when we dealt with Electron Capture in chapter 2.
Compton Effect[edit | edit source]
- This type of effect is somewhat akin to a cue ball hitting a coloured ball on a pool table. Here a gamma-ray transfers only part of its energy to a valance electron which is essentially free – see figure below. Notice that the electron leaves the atom and may act like a beta-particle and that the gamma-ray deflects off in a different direction to that with which it approached the atom. This deflected or scattered gamma-ray can undergo further Compton Effects within the material.
- Note that this effect is sometimes called Compton Scattering.
The two effects we have just described give rise to both absorption and scattering of the radiation beam. The overall effect is referred to as attenuation of gamma-rays. We will investigate this feature from an analytical perspective in the following chapter. Before we do so, we'll briefly consider the interaction of radiation with living matter.
Radiation Biology[edit | edit source]
It is well known that exposure to ionizing radiation can result in damage to living tissue. We've already described the initial atomic interactions. What's important in radiation biology is that these interactions may trigger complex chains of biomolecular events and consequent biological damage.
We've seen above that the primary means by which ionizing radiations lose their energy in matter is by ejection of orbital electrons. The loss of orbital electrons from the atom leaves it positively charged. Other interaction processes lead to excitation of the atom rather than ionization. Here, an outer valence electron receives sufficient energy to overcome the binding energy of its shell and moves further away from the nucleus to an orbit that is not normally occupied. This type of effect alters the chemical force that binds atoms into molecules and a regrouping of the affected atoms into different molecular structures can result. That is, excitation is an indirect method of inducing chemical change through the modification of individual atomic bonds.
Ionizations and excitations can give rise to unstable chemical species called free radicals. These are atoms and molecules in which there are unpaired electrons. They are chemically very reactive and seek stability by bonding with other atoms and molecules. Changes to nearby molecules can arise because of their production.
But, let's go back to the interactions themselves for the moment.....
In the case of X- and gamma-ray interactions, the energy of the photons is usually transferred by collisions with orbital electrons, e.g. via photoelectric and Compton effects. These radiations are capable of penetrating deeply into tissue since their interactions depend on chance collisions with electrons. Indeed, nuclear medicine imaging is only possible when the energy of the gamma-rays is sufficient for complete emission from the body, but low enough to be detected.
The interaction of charged particles (e.g. alpha and beta particles), on the other hand, can be by collisions with atomic electrons and also via attractive and repulsive electrostatic forces. The rate at which energy is lost along the track of a charged particle depends therefore on the square of the charge on that particle. That is, the greater the particle charge, the greater the probability of it generating ion pairs along its track. In addition, a longer period of time is available for electrostatic forces to act when a charged particle is moving slowly and the ionization probability is therefore increased as a result.
The situation is illustrated in the following figure where tracks of charged particles in water are depicted. Notice that the track of the relatively massive α-particle is a straight line, as we've discussed earlier in this chapter, with a large number of interactions (indicated by the asterisks) per unit length. Notice also that the tracks for electrons are tortuous, as we've also discussed earlier, and that the number of interactions per unit length is considerably less.

The Linear Energy Transfer (LET) is defined as the energy released per unit length of the track of an ionizing particle. A slowly moving, highly charged particle therefore has a substantially higher LET than a fast, singly charged particle. An alpha particle of 5 MeV energy and an electron of 1 MeV energy have LETs, for instance, of 95 and 0.25 keV/μm, respectively. The ionization density and hence the energy deposition pattern associated with the heavier charged particle is very much greater than that arising from electrons, as illustrated in the figure above.
The energy transferred along the track of a charged particle will vary because the velocity of the particle is likely to be continuously decreasing. Each interaction removes a small amount of energy from the particle so that the LET gradually increases along a particle track with a dramatic increase (called the Bragg Peak) occurring just before the particle comes to rest.
The International Commission on Radiation Units and Measurements (ICRU) suggest that lineal energy is a better indicator of relative biological effectiveness (RBE). Although lineal energy has the same units as LET (e.g. keV/μm), it is defined as the:
Since the microscopic deposition of energy may be quite anisotropic, lineal energy should be a more appropriate measure of potential damage than that of LET. The ICRU and the ICRP have accordingly recommended that the radiation effectiveness of a particular radiation type should be based on lineal energy in a 1 μm diameter sphere of tissue. The lineal energy can be calculated for any given radiation type and energy and a Radiation Weighting Factor, (wR) can then be determined based on the integrated values of lineal energy along the radiation track.
All living things on this planet have been exposed to ionizing radiation since the dawn of time. The current situation for humans is summarized in the following table:
| Source | Effective Dose (mSv/year) | Comment |
|---|---|---|
| Cosmic radiation | ~0.4 |
About 100,000 cosmic ray neutrons and 400,000 secondary cosmic rays penetrate our bodies every hour – and it increases with altitude!
|
| Terrestrial radiation | ~0.5 |
Over 200 million gamma-rays pass through our body every hour from sources such as soil and building materials
|
| Internal radiation | ~0.3 |
About 15 million 40K atoms and about 7,000 natural uranium atoms disintegrate inside our bodies every hour, primarily from our diet
|
| Radon and other gases | ~1.3 |
About 30,000 atoms disintegrate inside our lungs every hour as a result of breathing
|
The sum total of this Natural Background Radiation is about 2.5 mSv per year, with large variations depending on altitude and dietary intake as well as geological and geographical location.
Its generally considered that repair mechanisms exist in living matter and that these can be invoked following radiation damage at the biomolecular level. These mechanisms are likely to have an evolutionary basis arising as a response to radiation fluxes generated by natural background sources over the aeons. Its also known that quite considerable damage to tissues can arise at quite higher radiation fluxes, even at medical exposures. Cell death and transformations to malignant states can result leading to latent periods of many years before clinical signs of cancer or leukemia, for instance, become manifest. Further treatment of this vast field of radiation biology however is beyond our scope here.
Practical Radiation Safety[edit | edit source]
Radiation hazards arise since nuclear medicine involves the handling of radioactive materials. Although this risk may be small, it remains important to keep occupational exposures as low as reasonably achievable. Essential practices for achieving this aim include:
Administration
- Maintaining a comprehensive record of all radioactive source purchases, usage, movement and storage.
- Ensuring that any Codes of Safe Practice are adhered to and develop sensible written protocols and working rules for handling radioisotopes.
- Protocols for dealing with minor contamination incidents of the environment or of staff members must be established. Remember that no matter how good work practices are, minor accidents or incidents involving spillage of radioisotopes can take place.
Facility
- Storage of radioactive sources in a secure shielded environment. Specially dedicated facilities are required for the storage, safe handling, manipulation and dispensing of unsealed radioactive sources. Storage areas should be designed for both bulk radioisotope and radioactive waste. Furthermore, radioactive patients should be regarded as unsealed sources.
- Adequate ventilation of any work area. This is particularly important to minimize the inhalation of Technigas and potentially volatile radioisotopes such as I-125 and I-131. It is preferable to use fume hoods when working with volatile materials.
- Benches should be manufactured with smooth, hard impervious surfaces with appropriate splash-backs to allow ready decontamination following any spillage of radioisotopes. Laboratory work should be performed in stainless steel trays lined with absorbent paper.
- Excretion of radioactive materials by patients may be via faeces, urine, saliva, blood, exhaled breath or the skin. Provision to deal with any or all of these potential pathways for contamination must be made.
- Provision for collection and possible storage of both liquid and solid radioactive waste may be necessary in some circumstances. Most short-lived, water soluble liquid waste can be flushed into the sewers but longer lived isotopes such as I-131 may have to be stored for decay. Such waste must be adequately contained and labelled during storage.
Equipment
- Ensure that appropriate survey monitors are available to determine if any contamination has occurred and to assist in decontamination procedures. Routine monitoring of potentially contaminated areas must be performed.
- Ensure that all potentially exposed staff are issued with individual personnel monitors.
- Protective clothing such as gowns, smocks, overboots and gloves should be provided and worn to prevent contamination of the personnel handling the radioactivity. In particular, gloves must be worn when administering radioactive materials orally or intravenously to patients. It should be noted that penetration of gloves may occur when handling some iodine compounds so that wearing a second pair of gloves is recommended. In any event, gloves should be changed frequently and discarded ones treated as radioactive waste.
Behaviours
- Eating and drinking of food, smoking, and the application of cosmetics is prohibited in laboratories in which unsealed sources are utilized.
- Mouth pipetting of any radioactive substance is totally prohibited.
- Precautions should be taken to avoid punctures, cuts, abrasions and any other open skin wounds which otherwise might allow egress of radiopharmaceuticals into the blood stream.
Optimization
- Always ensure that there is a net benefit resulting from the patient procedure. Can the diagnosis or treatment be made by recourse to an alternative means using non ionizing radiation?
- Ensure that all staff, including physicians, technologists, nurses and interns and other students, who are involved in the practice of nuclear medicine receive the relevant level of training and education appropriate to their assigned tasks. The training program could be in the form of seminars, refresher courses and informal tutorials.
- A substantive Quality Assurance (QA) program should be implemented to ensure that the function of the Dose Calibrator, Gamma Camera, computer and other ancillary equipment is optimized.
The potential hazards to staff in a nuclear medicine environment include:
- Milking the 99mTc generator, drawing up and measuring the quantity of radioisotope prior to administration.
- Delivering the activity to the patient by injection or other means and positioning the now radioactive patient in the imaging device.
- Removing the patients from the imaging device and returning them to the ward where they may continue to represent a radiation hazard for some time. For Tc-99m, a short-lived radionuclide the hazard period will be only a few hours but for therapeutic isotopes the hazardous period may be several days.
- Disposal of radioactive waste including body fluids, such as blood and urine, but also swabs, syringes, needles, paper towels etc.
- Cleaning up the imaging area after the procedure.
- Contamination.
The table below lists the dose rates from patients having nuclear medicine examinations. In general, the hazards from handling or dealing with radioactive patients arise in two parts:
- External hazard: This will be the case when the radioisotope emits penetrating gamma-rays. Usually, this hazard can be minimised by employing shielding and sensible work practices.
- Radioactive contamination: This is potentially of more concern as it may lead to the inhalation or ingestion of radioactive material by staff. Possible sources of contamination are radioactive blood, urine and saliva, emanating from a patient, or airborne radioactive vapour. Sensible work practices, which involve high levels of personal hygiene, should ensure that contamination is not a major issue.

One of the most common nuclear medicine diagnostic procedures is the bone scan using the isotope Tc-99m. The exposure rate at 1 metre from a typical patient will peak at approximately 3 μSv per hour immediately after injection dropping steadily because of radioactivity decay and through excretion so that after 2 hours it will be about 1.5 μSv per hour. Neglecting any further excretion, the total exposure received by an individual, should that person stand one meter from the patient for the whole of the first 24 hours, would be ~17 μSv. For a person at 3 meters from the patient this number would reduce to 1.7 μSv and for a distance of 5 metres it would be ~0.7 μSv. These values have been estimated on the basis of the inverse square law.
Patients should be encouraged to drink substantial quantities of liquid following their scan, as this will improve excretion and aid in minimizing not only their radiation dose but also that of nursing staff.

Attenuation of Gamma-Rays[edit | edit source]

We covered the interaction of gamma-rays with matter from a descriptive viewpoint in the previous chapter and we saw that the Compton and Photoelectric Effects were the major mechanisms. We will consider the subject again here but this time from an analytical perspective. This will allow us to develop a more general understanding of the phenomenon.
Note that the treatment here also refers to the attenuation of X-rays since, as we noted before gamma-rays and X-rays are essentially the same physical entities.
Our treatment begins with a description of a simple radiation experiment which can be performed easily in the laboratory and which many of the early pioneers in this field did. We will then build on the information obtained from such an experiment to develop a simple equation and some simple concepts which will allow us generalise the situation to any attenuation situation.
Attenuation Experiment[edit | edit source]
The experiment is quite simple. It involves firing a narrow beam of gamma-rays at a material and measuring how much of the radiation gets through. We can vary the energy of the gamma-rays we use and the type of absorbing material as well as its thickness and density.
The experimental set-up is illustrated in the figure below. We refer to the intensity of the radiation which strikes the absorber as the incident intensity, I0, and the intensity of the radiation which gets through the absorber as the transmitted intensity, Ix. Notice also that the thickness of the absorber is denoted by x.
From what we covered in the previous chapter we can appreciate that some of the gamma-rays will be subjected to interactions such as the Photoelectric Effect and the Compton Effect as they pass through the absorber. The transmitted gamma-rays will in the main be those which pass through without any interactions at all.
We can therefore expect to find that the transmitted intensity will be less than the incident intensity, that is
But by how much you might ask. Before we consider this let us denote the difference between Ix and I0 as ∆I, that is
Effect of Atomic Number[edit | edit source]
- Let us start exploring the magnitude of ∆I by placing different absorbers in turn in the radiation beam. What we would find is that the magnitude of ∆I is highly dependent on the atomic number of the absorbing material. For example we would find that ∆I would be quite low in the case of an absorber made from carbon (Z=6) and very large in the case of lead (Z=82).
- We can gain an appreciation of why this is so from the following figure:

- The figure illustrates a high atomic number absorber by the large circles which represent individual atoms and a low atomic number material by smaller circles. The incident radiation beam is represented by the arrows entering each absorber from the left. Notice that the atoms of the high atomic number absorber present larger targets for the radiation to strike and hence the chances for interactions via the Photoelectric and Compton Effects is relatively high. The attenuation should therefore be relatively large.
- In the case of the low atomic number absorber however the individual atoms are smaller and hence the chances of interactions are reduced. In other words the radiation has a greater probability of being transmitted through the absorber and the attenuation is consequently lower than in the high atomic number case.
- With respect to our spaceship analogy used in the previous chapter the atomic number can be thought of as the size of individual meteors in the meteor cloud.
- If we were to precisely control our experimental set-up and carefully analyse our results we would find that:
- Therefore if we were to double the atomic number of our absorber we would increase the attenuation by a factor of two cubed, that is 8, if we were to triple the atomic number we would increase the attenuation by a factor of 27, that is three cubed, and so on.
- It is for this reason that high atomic number materials (e.g. Pb) are used for radiation protection.
Effect of Density[edit | edit source]
- A second approach to exploring the magnitude of ∆I is to see what happens when we change the density of the absorber. We can see from the following figure that a low density absorber will give rise to less attenuation than a high density absorber since the chances of an interaction between the radiation and the atoms of the absorber are relatively lower. In addition, the density determines the transmission coefficient as it relates to the sample, since the lower the density, the higher the transmission coefficient due to the porous nature of the material.
- So in our analogy of the spaceship entering a meteor cloud think of meteor clouds of different density and the chances of the spaceship colliding with a meteor.
Effect of Thickness[edit | edit source]
- A third factor which we could vary is the thickness of the absorber. As you should be able to predict at this stage the thicker the absorber the greater the attenuation.
Effect of Gamma-Ray Energy[edit | edit source]
- Finally in our experiment we could vary the energy of the gamma-ray beam. We would find without going into it in any great detail that the greater the energy of the gamma-rays the less the attenuation. You might like to think of it in terms of the energy with which the spaceship approaches the meteor cloud and the likelihood of a slow spaceship getting through as opposed to a spaceship travelling with a higher energy.
Mathematical Model[edit | edit source]
We will consider a mathematical model here which will help us to express our experimental observations in more general terms. You will find that the mathematical approach adopted and the result obtained is quite similar to what we encountered earlier with Radioactive Decay. So you will not have to plod your way through any new maths below, just a different application of the same form of mathematical analysis!
Let us start quite simply and assume that we vary only the thickness of the absorber. In other words we use an absorber of the same material (i.e. same atomic number) and the same density and use gamma-rays of the same energy for the experiment. Only the thickness of the absorber is changed.
From our reasoning above it is easy to appreciate that the magnitude of ∆I should be dependent on the radiation intensity as well as the thickness of the absorber, that is for an infinitesimally small change in absorber thickness:
the minus sign indicating that the intensity is reduced by the absorber.
Turning the proportionality in this equation into an equality, we can write:
where the constant of proportionality, μ, is called the Linear Attenuation Coefficient.
Dividing across by I we can rewrite this equation as:
So this equation describes the situation for any tiny change in absorber thickness, dx. To find out what happens for the complete thickness of an absorber we simply add up what happens in each small thickness. In other words we integrate the above equation. Expressing this more formally we can say that for thicknesses from x = 0 to any other thickness x, the radiation intensity will decrease from I0 to Ix, so that:
This final expression tells us that the radiation intensity will decrease in an exponential fashion with the thickness of the absorber with the rate of decrease being controlled by the Linear Attenuation Coefficient. The expression is shown in graphical form below. The graph plots the intensity against thickness, x. We can see that the intensity decreases from I0, that is the number at x = 0, in a rapid fashion initially and then more slowly in the classic exponential manner.
The influence of the Linear Attenuation Coefficient can be seen in the next figure. All three curves here are exponential in nature, only the Linear Attenuation Coefficient is different. Notice that when the Linear Attenuation Coefficient has a low value the curve decreases relatively slowly and when the Linear Attenuation Coefficient is large the curve decreases very quickly.

The Linear Attenuation Coefficient is characteristic of individual absorbing materials. Some like carbon have a small value and are easily penetrated by gamma-rays. Other materials such as lead have a relatively large Linear Attenuation Coefficient and are relatively good absorbers of radiation:
| Absorber | 100 keV | 200 keV | 500 keV |
|---|---|---|---|
| Air | 0.000195 | 0.000159 | 0.000112 |
| Water | 0.167 | 0.136 | 0.097 |
| Carbon | 0.335 | 0.274 | 0.196 |
| Aluminium | 0.435 | 0.324 | 0.227 |
| Iron | 2.72 | 1.09 | 0.655 |
| Copper | 3.8 | 1.309 | 0.73 |
| Lead | 59.7 | 10.15 | 1.64 |
The materials listed in the table above are air, water and a range of elements from carbon (Z=6) through to lead (Z=82) and their Linear Attenuation Coefficients are given for three gamma-ray energies. The first point to note is that the Linear Attenuation Coefficient increases as the atomic number of the absorber increases. For example it increases from a very small value of 0.000195 cm-1 for air at 100 keV to almost 60 cm-1 for lead. The second point to note is that the Linear Attenuation Coefficient for all materials decreases with the energy of the gamma-rays. For example the value for copper decreases from about 3.8 cm-1 at 100 keV to 0.73 cm-1 at 500 keV. The third point to note is that the trends in the table are consistent with the analysis presented earlier.
Finally it is important to appreciate that our analysis above is only strictly true when we are dealing with narrow radiation beams. Other factors need to be taken into account when broad radiation beams are involved.
Half Value Layer[edit | edit source]
As with using the Half Life to describe the Radioactive Decay Law an indicator is usually derived from the exponential attenuation equation above which helps us think more clearly about what is going on. This indicator is called the Half Value Layer and it expresses the thickness of absorbing material which is needed to reduce the incident radiation intensity by a factor of two. From a graphical point of view we can say that when:
the thickness of absorber is the Half Value Layer:

The Half Value Layer for a range of absorbers is listed in the following table for three gamma-ray energies:
| Absorber | 100 keV | 200 keV | 500 keV |
|---|---|---|---|
| Air | 3555 | 4359 | 6189 |
| Water | 4.15 | 5.1 | 7.15 |
| Carbon | 2.07 | 2.53 | 3.54 |
| Aluminium | 1.59 | 2.14 | 3.05 |
| Iron | 0.26 | 0.64 | 1.06 |
| Copper | 0.18 | 0.53 | 0.95 |
| Lead | 0.012 | 0.068 | 0.42 |
The first point to note is that the Half Value Layer decreases as the atomic number increases. For example the value for air at 100 keV is about 35 meters and it decreases to just 0.12 mm for lead at this energy. In other words 35 m of air is needed to reduce the intensity of a 100 keV gamma-ray beam by a factor of two whereas just 0.12 mm of lead can do the same thing. The second thing to note is that the Half Value Layer increases with increasing gamma-ray energy. For example from 0.18 cm for copper at 100 keV to about 1 cm at 500 keV. Thirdly note that relative to the data in the previous table there is a reciprocal relationship between the Half Value Layer and the Linear Attenuation Coefficient, which we will now investigate.
Relationship between μ and the HVL[edit | edit source]
As was the case with the Radioactive Decay Law, where we explored the relationship between the Half Life and the Decay Constant, a relationship can be derived between the Half Value Layer and the Linear Attenuation Coefficient. We can do this by using the definition of the Half Value Layer:
when
and inserting it in the exponential attenuation equation, that is:
to give
Therefore
and
These last two equations express the relationship between the Linear Attenuation Coefficient and the Half Value Layer. They are very useful as you will see when solving numerical questions relating to attenuation and frequently form the first step in solving a numerical problem.
Mass Attenuation Coefficient[edit | edit source]
We implied above that the Linear Attenuation Coefficient was useful when we were considering an absorbing material of the same density but of different thicknesses. A related coefficient can be of value when we wish to include the density, ρ, of the absorber in our analysis. This is the Mass Attenuation Coefficient which is defined as the:
The measurement unit used for the Linear Attenuation Coefficient in the table above is cm-1, and a common unit of density is the g cm-3. You might like to derive for yourself on this basis that the cm2 g-1 is the equivalent unit of the Mass Attenuation Coefficient.
Questions[edit | edit source]
Two questions are given below to help you develop your understanding of the material presented in this chapter. The first one is relatively straight-forward and will exercise your application of the exponential attenuation equation. The second question is a lot more challenging and will help you relate exponential attenuation to radioactivity and radiation exposure.
Question 1
How much aluminium is required to reduce the intensity of a 200 keV gamma-ray beam to 10% of its incident intensity? Assume that the Half Value Layer for 200 keV gamma-rays in Al is 2.14 cm.
Answer
- The question phrased in terms of the symbols used above is:
- We are told that the Half Value Layer is 2.14 cm. Therefore the Linear Attenuation Coefficient is
- Now combining all this with the exponential attenuation equation:
- we can write:
- Therefore
- So the thickness of aluminium required to reduce these gamma-rays by a factor of ten is about 7 cm. This relatively large thickness is the reason why aluminium is not generally used in radiation protection - its atomic number is not high enough for efficient and significant attenuation of gamma-rays.
- You might like to try this question for the case when Pb is the absorber - but you will need to find out the Half Value Layer for the 200 keV gamma-rays yourself!
- Here's a hint though: have a look at one of the tables above.
- And here's the answer for you to check when you've finished: 2.2 mm.
- In other words a relatively thin thickness of Pb is required to do the same job as 7 cm of aluminium.
Question 2
A 105 MBq source of 137Cs is to be contained in a Pb box so that the exposure rate 1 m away from the source is less than 0.5 mR/hour. If the Half Value Layer for 137Cs gamma-rays in Pb is 0.6 cm, what thickness of Pb is required? The Specific Gamma Ray Constant for 137Cs is 3.3 R hr-1 mCi-1 at 1 cm.
Answer
- This is a fairly typical question which arises when someone is using radioactive materials. We wish to use a certain quantity of the material and we wish to store it in a lead container so that the exposure rate when we are working a certain distance away is below some level for safety reasons. We know the radioactivity of the material we will be using. But its quoted in SI units. We look up a reference book to find out the exposure rate for this radioisotope and find that the Specific Gamma Ray Constant is quoted in traditional units. Just as in our question!
- So let us start by getting our units right. The Specific Gamma Ray Constant is given as:
- This is equal to:
- which is equal to:
- on the basis of the Inverse Square Law. This result expressed per becquerel is
- since 1 mCi = 3.7 x 107 Bq. And therefore for 105 MBq, the exposure rate is:
- That is the exposure rate 1 meter from our source is 891.9 mR hr-1.
- We wish to reduce this exposure rate according to the question to less than 0.5 mR hr-1 using Pb.
- You should be able at this stage to use the exponential attenuation equation along with the Half Value Layer for these gamma-rays in Pb to calculate that the thickness of Pb required is about 6.5 cm.
External Links[edit | edit source]
- Mucal on the Web - an online program which calculates x-ray absorption coefficients - by Pathikrit Bandyopadhyay, The Center for Synchrotron Radiation Research and Instrumentation at the Illinois Institute of Technology.
- Tables of X-Ray Mass Attenuation Coefficients - a vast amount of data for all elements from National Institute of Science & Technology, USA.
Gas-Filled Radiation Detectors[edit | edit source]

We have learned in the last two chapters about how radiation interacts with matter and we are now in a position to apply our understanding to the detection of radiation.
One of the major outcomes of the interaction of radiation with matter is the creation of ions as we saw in Chapter 5. This outcome is exploited in gas-filled detectors as you will see in this chapter. The detector in this case is essentially a gas, in that it is the atoms of a gas which are ionised by the radiation. We will see in the next chapter that solids can also be used as radiation detectors but for now we will deal with gases and be introduced to detectors such as the Ionization Chamber and the Geiger Counter.
Before considering these specific types of gas-filled detectors we will first of all consider the situation from a very general perspective.
Gas-Filled Detectors[edit | edit source]
As we noted above the radiation interacts with gas atoms in this form of detector and causes ions to be produced. On the basis of what we covered in Chapter 5 it is easy to appreciate that it is the Photoelectric and Compton Effects that cause the ionisations when the radiation consists of gamma-rays with energies useful for diagnostic purposes.
There are actually two particles generated when an ion is produced - the positive ion itself and an electron. These two particles are collectively called an ion pair. The detection of the production of ion pairs in the gas is the basis upon which gas detectors operate. The manner in which this is done is by using an electric field to sweep the electrons away to a positively charged electrode and the ions to a negatively charged electrode.
Let us consider a very simple arrangement as shown in the following figure:
Here we have two electrodes with the gas between them. Something like a capacitor with a gas dielectric.
The gas which is used is typically an inert gas, for example argon or xenon. The reason for using an inert gas is so that chemical reactions will not occur within the gas following the ionisations which could change the characteristics of our detector.
A dc voltage is placed between the two electrodes. As a result when the radiation interacts with a gas atom the electron will move towards the positive electrode and the ion will move towards the negative electrode. But will these charges reach their respective electrodes? The answer is obviously dependent on the magnitude of the dc voltage. For example if at one extreme we had a dc voltage of a microvolt (that is, one millionth of a volt) the resultant electric field may be insufficient to move the ion pair very far and the two particles may recombine to reform the gas atom. At the other extreme suppose we applied a million volts between the two electrodes. In this case we are likely to get sparks flying between the two electrodes - a lightning bolt if you like - and our detector might act something like a neon sign. Somewhere in between these two extremes though we should be able to provide a sufficient attractive force for the ion and electron to move to their respective electrodes without recombination or sparking occurring.
We will look at this subject in more detail below. Before we do let us see how the concept of the simple detector illustrated above is applied in practice. The gas-filled chamber is generally cylindrical in shape in real detectors. This shape has been found to be more efficient than the parallel electrode arrangement shown above.
A cross-sectional view through this cylinder is shown in the following figure:
The positive electrode consists of a thin wire running through the centre of the cylinder and the negative electrode consists of the wall of the cylinder. In principle we could make such a detector by getting a section of a metal pipe, mounting a wire through its centre, filling it with an inert gas and sealing the ends of the pipe. Actual detectors are a little bit more complex however but let us not get side-tracked at this stage.
We apply a dc voltage via a battery or via a dc voltage supply and connect it as shown in the figure using a resistor, R. Now, assume that a gamma-ray enters the detector. Ion pairs will be produced in the gas - the ions heading towards the outer wall and the electrons heading towards the centre wire. Let us think about the electrons for a moment. When they hit the centre wire we can simply think of them as entering the wire and flowing through the resistor to get to the positive terminal of the dc voltage supply. These electrons flowing through the resistor constitute an electric current and as a result of Ohm's Law a voltage is generated across the resistor. This voltage is amplified by an amplifier and some type of device is used to register the amplified voltage. A loud-speaker is a fairly simple device to use for this purpose and the generation of a voltage pulse is manifest by a click from the loud-speaker. Other display devices include a ratemeter which displays the number of voltage pulses generated per unit time - something like a speedometer in a car - and a pulse counter (or scaler) which counts the number of voltage pulses generated in a set period of time. A voltage pulse is frequently referred to in practice as a count and the number of voltage pulses generated per unit time is frequently called the count rate.
DC Voltage Dependence[edit | edit source]
If we were to build a detector and electronic circuit as shown in the figure above we could conduct an experiment that would allow us to explore the effect of the dc voltage on the magnitude of the voltage pulses produced across the resistor, R. Note that the term pulse height is frequently used in this field to refer to the magnitude of voltage pulses.
Ideally, we could generate a result similar to that illustrated in the following figure:
The graph illustrates the dependence of the pulse height on the dc voltage. Note that the vertical axis representing the pulse height is on a logarithmic scale for the sake of compressing a large linear scale onto a reasonably-sized graph.
The experimental results can be divided into five regions as shown. We will now consider each region in turn.
- Region A Here Vdc is relatively low so that recombination of positive ions and electrons occurs. As a result not all ion pairs are collected and the voltage pulse height is relatively low. It does increase as the dc voltage increases however as the amount of recombination reduces.
- Region B Vdc is sufficiently high in this region so that only a negligible amount of recombination occurs. This is the region where a type of detector called the Ionization Chamber operates.
- Region C Vdc is sufficiently high in this region so that electrons approaching the centre wire attain sufficient energy between collisions with the electrons of gas atoms to produce new ion pairs. Thus the number of electrons is increased so that the electric charge passing through the resistor, R, may be up to a thousand times greater than the charge produced initially by the radiation interaction. This is the region where a type of detector called the Proportional Counter operates.
- Region D Vdc is so high that even a minimally-ionizing particle will produce a very large voltage pulse. The initial ionization produced by the radiation triggers a complete gas breakdown as an avalanche of electrons heads towards and spreads along the centre wire. This region is called the Geiger-Müller Region, and is exploited in the Geiger Counter.
- Region E Here Vdc is high enough for the gas to completely breakdown and it cannot be used to detect radiation.
We will now consider features of the Ionisation Chamber and the Geiger Counter in more detail.
Ionisation Chamber[edit | edit source]
The ionisation chamber consists of a gas-filled detector energised by a relatively low dc voltage. We will first of all make an estimate of the voltage pulse height generated by this type of detector. We will then consider some applications of ionisation chambers.
When a beta-particle interacts with the gas the energy required to produce one ion pair is about 30 eV. Therefore when a beta-particle of energy 1 MeV is completely absorbed in the gas the number of ion pairs produced is:
The electric charge produced in the gas is therefore
If the capacitance of the ionisation chamber (remember that we compared a gas-filled detector to a capacitor above) is 100 pF then the amplitude of the voltage pulse generated is:
Because such a small voltage is generated it is necessary to use a very sensitive amplifier in the electronic circuitry connected to the chamber.
We will now learn about two applications of ionisation chambers. The first one is for the measurement of radiation exposures. You will remember from Chapter 4 that the unit of radiation exposure (be it the SI or the traditional unit) is defined in terms of the amount of electric charge produced in a unit mass of a air. An ionization chamber filled with air is the natural instrument to use for such measurements.
The second application is the measurement of radioactivity. The ionisation chamber used here is configured in what is called a re-entrant arrangement (see figure below) so that the sample of radioactive material can be placed within the detector using a holder and hence most of the emitted radiation can be detected. The instrument is widely referred to as an Isotope Calibrator and the trickle of electric current generated by such a detector is calibrated so that a reading in units of radioactivity (for example MBq or mCi) can be obtained. Most well-run Nuclear Medicine Departments will have at least one of these devices so that doses of radioactivity can be checked prior to administration to patients.

Here are some photographs of ionisation chambers designed for various applications:
Geiger Counter[edit | edit source]
We saw earlier that the Geiger Counter operates at relatively high dc voltages (for example 400-900 volts) and that an avalanche of electrons is generated following the absorption of radiation in the gas. The voltage pulses produced by this detector are relatively large since the gas effectively acts as an amplifier of the electric charge produced.
There are four features of this detector which we will discuss. The first is that a sensitive amplifier (as was the case with the Ionization Chamber) is not required for this detector because of the gas amplification noted above.
The second feature results from the fact that the generation of the electron avalanche must be stopped in order to reform the detector. In other words when a radiation particle/photon is absorbed by the gas a complete gas breakdown occurs which implies that the gas is incapable of detecting the next particle/photon which enters the detector. So in the extreme case one minute we have a radiation detector and the following moment we do not.
A means of stopping the electron avalanche is therefore required - a process called Quenching. One means of doing this is by electronically lowering the dc voltage following an avalanche. A more widely used method of quenching is to add a small amount of a quenching gas to the inert gas. For example the gas could be argon with ethyl alcohol added. The ethyl alcohol is in vapour form and since it consists of relatively large molecules energy which would in their absence give rise to sustaining the electron avalanche is absorbed by these molecules. The large molecules act like a brake in effect.
Irrespective of the type of quenching used the detector is insensitive for a small period of time following absorption of a radiation particle/photon. This period of time is called the Dead Time and this is the third feature of this detector which we will consider. Dead times are relatively short but nevertheless significant - being typically of the order of 200-400 µs. As a result the reading obtained with this detector is less than it should be. The true count rate, T, can be obtained using the following equation:
where A is the (actual) reading and τ is the dead time. Some instruments perform this calculation automatically.
The fourth feature to note about this detector is the dependence of its performance on the dc voltage. The Geiger-Müller Region of our figure above is shown in more detail below:

Notice that it contains a plateau where the count rate obtained is independent of the dc voltage. The centre of this plateau is where most detectors are operated. It is clear that the count rate from the detector is not affected if the dc voltage fluctuates about the operating voltage. This implies that a relatively straight-forward dc voltage supply can be used. This feature coupled with the fact that a sensitive amplifier is not needed translates in practice to a relatively inexpensive radiation detector.
External Links[edit | edit source]
- Inside a smoke detector - about the ion chamber used in smoke detectors - from the How Stuff Works website.
- Ionisation Chambers - a brief description from the Triumf Safety Group.
- Radiation and Radioactivity - a self-paced lesson developed by the University of Michigan's Student Chapter of the Health Physics Society with a section on gas filled detectors.
- The Geiger Counter - a brief overview from the NASA Goddard Space Flight Center, USA.
Scintillation Detectors[edit | edit source]

The second type of radiation detector we will discuss is called the scintillation detector. Scintillations are minute flashes of light which are produced by certain materials when they absorb radiation. These materials are variously called fluorescent materials, fluors, scintillators or phosphors.
If we had a radioactive source and a scintillator in the lab we could darken the room, move the scintillator close to the source and see the scintillations. These small flashes of light might be green or blue or some other colour depending on the scintillator. We could also count the number of flashes produced to gain an estimate of the radioactivity of the source, that is the more flashes of light seen the more radiation present.
The scintillation detector was possibly the first radiation detector discovered. You might have heard the story of the discovery of X-rays by Wilhelm Roentgen in 1895. He was working one evening in his laboratory in Wurzburg, Germany with a device which fired a beam of electrons at a target inside an evacuated glass tube. While working with this device he noticed that some platino-barium cyanide crystals, which he just happened to have close by, began to glow – and that they stopped glowing when he switched the device off. Roentgen had accidentally discovered a new form of radiation. He had also accidentally discovered a scintillator detector.
Although scintillations can be seen we have a more sophisticated way of counting and measuring them today by using some form of photodetector.
We will learn about the construction and mode of operation of this type of detector in this chapter. In addition, we will see how it can be used not just for detecting the presence of ionizing radiation but also for measuring the energy of that radiation.
Before we do however it is useful to note that scintillators are very widely used in the medical radiations field. For example the X-ray cassette used in radiography contains a scintillator (called an intensifying screen) in close contact with a photographic film. A second example is the X-ray Image Intensifier used in fluoroscopy which contains scintillators called phosphors. Scintillators are also used in some CT Scanners and as we will see in the next chapter, in the Gamma Camera and PET Scanner. Their application is not limited to the medical radiations field in that scintillators are also used as screens in television sets and computer monitors and for generating light in fluorescent tubes – to mention just two common applications. What other applications can you think of?
So scintillators are a lot more common than you might initially think and you will therefore find the information presented here useful to you not just for your studies of nuclear medicine.
Fluorescent Materials[edit | edit source]
Some fluorescent materials are listed in the following table. Thallium-activated sodium iodide, NaI(Tl) is a crystalline material which is widely used for the detection of gamma-rays in scintillation detectors. We will be looking at this in more detail below.
Another crystalline material sodium-activated caesium iodide, CsI(Na) is widely used for X-ray detection in devices such as the X-ray image intensifier. Another one called calcium tungstate, CaWO4 has been widely used in X-ray cassettes although this substance has been replaced by other scintillators such as lanthanum oxybromide in many modern cassettes.
| Material | Form |
|---|---|
| NaI (Tl) | crystal |
| CsI (Na) | crystal |
| CaWO4 | crystal |
| ZnS (Ag) | powder |
| p-terphenyl in toluene | liquid |
| p-terphenyl in polystyrene | plastic |
Notice that some scintillation materials are activated with certain elements. What this means is that the base material has a small amount of the activation element present. The term doped is sometimes used instead of activated. This activating element is used to influence the wavelength (colour) of the light produced by the scintillator.
Silver-activated zinc sulphide is a scintillator in powder form and p-terphenyl in toluene is a liquid scintillator. The advantage of such forms of scintillators is that the radioactive material can be placed in close contact with the scintillating material. For example if a radioactive sample happened to be in liquid form we could mix it with a liquid scintillator so as to optimise the chances of detection of the emitted radiation and hence have a very sensitive detector.
A final example is p-terphenyl in polystyrene which is a scintillator in the form of a plastic. This form can be easily made into different shapes like most plastics and is therefore useful when detectors of particular shapes are required.
Photomultiplier Tube[edit | edit source]
A scintillation crystal coupled to a photomultiplier tube (PMT) is illustrated in the following figure. The overall device is typically cylindrical in shape and the figure shows a cross-section through this cylinder:
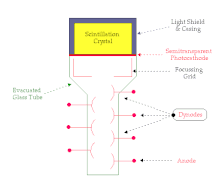
The scintillation crystal, NaI(Tl) is very delicate and this is one of the reasons it is housed in an aluminium casing. The inside wall of the casing is designed so that any light which strikes it is reflected downwards towards the PMT.
The PMT itself consists of a photocathode, a focussing grid, an array of dynodes and an anode housed in an evacuated glass tube. The function of the photocathode is to convert the light flashes produced by radiation attenuation in the scintillation crystal into electrons. The grid focuses these electrons onto the first dynode and the dynode array is used for electron multiplication. We will consider this process in more detail below. Finally the anode collects the electrons produced by the array of dynodes.
The electrical circuitry which is typically attached to a PMT is shown in the next figure:

It consists of a high voltage supply, a resistor divider chain and a load resistor, RL. The high voltage supply generates a dc voltage, Vdc which can be up to 1,000 volts. It is applied to the resistor divider chain which consists of an array of resistors, each of which has the same resistance, R. The function of this chain of resistors is to divide up Vdc into equal voltages which are supplied to the dynodes. As a result voltages which increase in equal steps are applied to the array of dynodes. The load resistor is used so that an output voltage, Vout can be generated.
Finally the operation of the device is illustrated in the figure below:

The ionizing radiation produces flashes of light in the scintillation crystal. This light strikes the photocathode and is converted into electrons. The electrons are directed by the grid onto the first dynode.
Dynodes are made from certain alloys which emit electrons when their surface is struck by electrons with the advantage that more electrons are emitted than are absorbed. A dynode used in a PMT typically emits between two and five electrons for each electron which strikes it.
So when an electron from the photocathode strikes the first dynode between two and five electrons are emitted and are directed towards the second dynode in the array (three are illustrated in the figure). This electron multiplication process is repeated at the second dynode so that we end up with nine electrons for example heading towards the third dynode. An electron avalanche therefore develops so that a sizeable number of electrons eventually hits the anode at the bottom of the dynode chain.
These electrons flow through the load resistor, RL and constitute an electric current which according to Ohm's Law generates a voltage, Vout which is measured by electronic circuitry (which we will describe later).
A number of photographs of devices based on scintillation detection are shown below:
The important feature of the scintillation detector is that this output voltage, Vout is directly proportional to the energy deposited by the radiation in the crystal. We will see what a useful feature this is below. Before we do so we will briefly analyze the operation of this device.
Mathematical Model[edit | edit source]
A simple mathematical model will be presented below which will help us get a better handle on the performance of a scintillation detector. We will do this by quantifying the performance of the scintillator, the photocathode and the dynodes.
Let's use the following symbols to characterize each stage of the detection process:
- m: number of light photons produced in crystal
- k: optical efficiency of the crystal, that is the efficiency with which the crystal transmits light
- l: quantum efficiency of the photocathode, that is the efficiency with which the photocathode converts light photons to electrons
- n: number of dynodes
- R: dynode multiplication factor, that is the number of secondary electrons emitted by a dynode per primary electron absorbed.
Therefore the charge collected at the anode is given by the following equation:
where e: the electronic charge.
For example supposing a 100 keV gamma-ray is absorbed in the crystal. The number of light photons produced, m, might be about 1,000 for a typical scintillation crystal. A typical crystal might have an optical efficiency, k, of 0.5 – in other words 50% of the light produced reaches the photocathode which might have a quantum efficiency of 0.15. A typical PMT has ten dynodes and let us assume that the dynode multiplication factor is 4.5.
Therefore
This amount of charge is very small. Even though we have used a sophisticated photodetector like a PMT we still end up with quite a small electrical signal.
A very sensitive amplifier is therefore needed to amplify this signal. This type of amplifier is generally called a pre-amplifier and we will refer to it again later.
Output Voltage[edit | edit source]
We noted above that the voltage measured across the resistor, RL, is proportional to the energy deposited in the scintillation crystal by the radiation. Let us consider how the radiation might deposit its energy in the crystal.
Let us consider a situation where gamma-rays are detected by the crystal. We learnt in Chapter 5 that there were two interaction mechanisms involved in gamma-ray attenuation – the Photoelectric Effect and the Compton Effect. You will remember that the Photoelectric Effect involves the total absorption of the energy of a gamma-ray, while the Compton Effect involves just partial absorption of this energy. Since the output voltage of a scintillation detector is proportional to the energy deposited by the gamma-rays it is reasonable to expect that Photoelectric Effects in the crystal will generate distinct and relatively large output voltages and that Compton Effects will result in lower output voltages.
The usual way of presenting this information is by plotting a graph of the count rate versus the output voltage pulse height as shown in the following figure:

This plot illustrates what is obtained for a monoenergetic gamma-emitting radioisotope, for example 99mTc – which, as we have noted before emits a single gamma-ray with an energy of 140 keV.
Before we look at it in detail remember that we noted above that the output voltage from this detector is proportional to the energy deposited by the radiation in the crystal. The horizontal axis can therefore be used to represent the output voltage or the gamma-ray energy. Both of these quantities are shown in the figure to help with this discussion. In addition note that this plot is often called a Gamma-Ray Energy Spectrum.
The figure above contains two regions. One called the Photopeak and the other called the Compton Smear. The Photopeak results because of Photoelectric absorption of the gamma-rays from the radioactive source – remember that we are dealing with a monoenergetic emitter in this example. It consists of a peak representing the gamma-ray energy (140 keV in our example). If our radioisotope emitted gamma-rays of two energies we would have two photopeaks in our spectrum and so on.
Notice that the peak has a statistical spread. This has to do with how good our detector is and we will not get into any detail about it here other than to note that the extent of this spread is a measure of the quality of our detector. A high quality (and more expensive!) detector will have a narrower statistical spread in the photopeaks which it measures.
The other component of our spectrum is the Compton Smear. It represents a range of output voltages which are lower than that for the Photopeak. It is therefore indicative of the partial absorption of the energy of gamma-rays in the crystal. In some Compton Effects a substantial scattering with a valence electron can occur which gives rise to relatively large voltage pulses. In other Compton Effects the gamma-ray just grazes off a valence electron with minimal energy transfer and hence a relatively small voltage pulse is generated. In between these two extremes are a range of scattering events involving a range of energy transfers and hence a range of voltage pulse heights. A 'smear' therefore manifests itself on the gamma-ray energy spectrum.
It is important to note that the spectrum illustrated in the figure is simplified for the sake of this introductory discussion and that actual spectra are a little more complex – see figure below for an example:

You will find though that your understanding of actual spectra can easily develop on the basis of the simple picture we have painted here.
It is also important to appreciate the additional information which this type of radiation detector provides relative to a gas-filled detector. In essence gas-filled detectors can be used to tell us if any radiation is present as well as the amount of that radiation. Scintillation detectors also give us this information but they tell us about the energy of this radiation as well. This additional information can be used for many diverse applications such as the identification of unknown radioisotopes and the production of nuclear medicine images. Let us stay a little bit longer though with the fundamental features of how scintillation detectors work.
The photopeak of the Gamma-Ray Energy Spectrum is generally of interest in nuclear medicine. This peak is the main signature of the radioisotope being used and its isolation from the Compton Smear is normally achieved using a technique called Pulse Height Analysis.
Pulse Height Analysis[edit | edit source]
This is an electronic technique which allows a spectrum to be acquired using two types of circuitry. One circuit is called a Lower Level Discriminator which only allows voltages pulses through it which are higher than its setting. The other is called an Upper Level Discriminator which only allows voltage pulses though which are lower than its setting.
The result of using both these circuits in combination is a variable-width window which can be placed anywhere along a spectrum. For example if we wished to obtain information from the photopeak only of our simplified spectrum we would place the discrimination controls as shown in the following figure:

A final point to note here is that since the scintillation detector is widely used to obtain information about the energies of the radiation emitted from a radioactive source it is frequently referred to as a Scintillation Spectrometer.
Scintillation Spectrometer[edit | edit source]
Types of scintillation spectrometer fall into two basic categories – the relatively straight-forward Single Channel Analyser and the more sophisticated Multi-Channel Analyser.
The Single Channel Analyser is the type of instrument we have been describing so far in this discussion. A block diagram of the instrument is shown below:

It consists of a scintillation crystal coupled to a photomultiplier tube which is powered by a high voltage circuit (H.V.). The output voltages are initially amplified by a sensitive pre-amplifier (Pre-Amp) as we noted above before being amplified further and conditioned by the amplifier (Amp).
The voltage pulses are then in a suitable form for the pulse height analyser (P.H.A.) – the output pulses from which can be fed to a Scaler and a Ratemeter for display of the information about the portion of the spectrum we have allowed to pass through the PHA. The Ratemeter is a display device just like the speedometer in a car and indicates the number of pulses generated per unit time. The Scaler on the other hand usually consists of a digital display which shows the number of voltage pulses produced in a specified period of time.
We can illustrate the operation of this circuitry by considering how it might be used to generate a Gamma-Ray Energy Spectrum. What we would do is set up the LLD and ULD so as to define a narrow window and place this to pass the lowest voltage pulses produced by the detector through to the Scaler and Ratemeter. In other words we would place a narrow window at the extreme left of the spectrum and acquire information about the lowest energy gamma-ray interactions in the crystal. We would then adjust the LLD and ULD settings to acquire information about the interactions of the next highest energy. We would proceed in this fashion to scan the whole spectrum.
A more sophisticated detector circuit is illustrated in the following figure:

It is quite similar to that in the previous figure with the exception that the PHA, Scaler and Ratemeter are replaced by a Multi-Channel Analyser and a computer. The Multi-Channel Analyser (MCA) is a circuit which is capable of setting up a large number of individual windows to look at a complete spectrum in one go. The MCA might consist of 1024 individual windows for example and the computer might consist of a personal computer which can acquire information simultaneously from each window and display it as an energy spectrum. The computer generally contains software which allows us to manipulate the resultant information in a variety of ways. Indeed the 137Cs spectrum shown above was generated using this approach.
External links[edit | edit source]
Nuclear Medicine Imaging Systems[edit | edit source]

Topics we have covered in this wikibook have included radioactivity, the interaction of gamma-rays with matter and radiation detection. The main reason for following this pathway was to bring us to the subject of this chapter: nuclear medicine imaging systems. These are devices which produce pictures of the distribution of radioactive material following administration to a patient.
The radioactivity is generally administered to the patient in the form of a radiopharmaceutical – the term radiotracer is also used. This follows some physiological pathway to accumulate for a short period of time in some part of the body. A good example is 99mTc-tin colloid which following intravenous injection accumulates mainly in the patient's liver. The substance emits gamma-rays while it is in the patient's liver and we can produce an image of its distribution using a nuclear medicine imaging system. This image can tell us whether the function of the liver is normal or abnormal or if sections of it are damaged from some form of disease.
Different radiopharmaceuticals are used to produce images from almost every region of the body:
| Part of the Body | Example Radiotracer |
|---|---|
| Brain | 99mTc-HMPAO |
| Thyroid | Na99mTcO4 |
| Lung (Ventilation) | 133Xe gas |
| Lung (Perfusion) | 99mTc-MAA |
| Liver | 99mTc-Tin (or Sulphur) Colloid |
| Spleen | 99mTc-Damaged Red Blood Cells |
| Pancreas | 75Se-Selenomethionine |
| Kidneys | 99mTc-DMSA |
Note that the form of information obtained using this imaging method is mainly related to the physiological functioning of an organ as opposed to the mainly anatomical information which is obtained using X-ray imaging systems. Nuclear medicine therefore provides a different perspective on a disease condition and generates additional information to that obtained from X-ray images. Our purpose here is to concentrate on the imaging systems used to produce the images.
Early forms of imaging system used in this field consisted of a radiation detector (a scintillation detector for example) which was scanned slowly over a region of the patient in order to measure the radiation intensity emitted from individual points within the region. One such device was called the Rectilinear Scanner. Such imaging systems have been replaced since the 1970s by more sophisticated devices which produce images much more rapidly. The most common of these modern devices is called the Gamma Camera and we will consider its construction and mode of operation below. A review of recent developments in this technology for cardiac applications can be found in Slomka et al (2009)[1].
Gamma Camera[edit | edit source]
The basic design of the most common type of gamma camera used today was developed by an American physicist, Hal Anger and is therefore sometimes called the Anger Camera. It consists of a large diameter NaI(Tl) scintillation crystal which is viewed by a large number of photomultiplier tubes.
A block diagram of the basic components of a gamma camera is shown below:

The crystal and PM Tubes are housed in a cylindrical shaped housing commonly called the camera head and a cross-sectional view of this is shown in the figure. The crystal can be between about 25 cm and 40 cm in diameter and about 1 cm thick. The diameter is dependent on the application of the device. For example a 25 cm diameter crystal might be used for a camera designed for cardiac applications while a larger 40 cm crystal would be used for producing images of the lungs. The thickness of the crystal is chosen so that it provides good detection for the 140 keV gamma-rays emitted from 99mTc – which is the most common radioisotope used today.
Scintillations produced in the crystal are detected by a large number of PM tubes which are arranged in a two-dimensional array. There are typically between 37 and 91 PM tubes in modern gamma cameras. The output voltages generated by these PM tubes are fed to a position circuit which produces four output signals called ±X and ±Y. These position signals contain information about where the scintillations were produced within the crystal. In the most basic gamma camera design they are fed to a cathode ray oscilloscope (CRO). We will describe the operation of the CRO in more detail below.
Before we do so we should note that the position signals also contain information about the intensity of each scintillation. This intensity information can be derived from the position signals by feeding them to a summation circuit (marked ∑ in the figure) which adds up the four position signals to generate a voltage pulse which represents the intensity of a scintillation. This voltage pulse is commonly called the Z-pulse which, following pulse height analysis, (PHA) is fed as the unblank pulse to the CRO.
So we end up with four position signals and an unblank pulse sent to the CRO. Let us briefly review the operation of a CRO before we continue. The core of a CRO consists of an evacuated tube with an electron gun at one end and a phosphor-coated screen at the other end. The electron gun generates an electron beam which is directed at the screen and the screen emits light at those points struck by the electron beam. The position of the electron beam can be controlled by vertical and horizontal deflection plates and with the appropriate voltages fed to these plates the electron beam can be positioned at any point on the screen. The normal mode of operation of an oscilloscope is for the electron beam to remain switched on. In the case of the gamma camera the electron beam of the CRO is normally switched off – it is said to be blanked.
When an unblank pulse is generated by the PHA circuit the electron beam of the CRO is switched on for a brief period of time so as to display a flash of light on the screen. In other words the voltage pulse from the PHA circuit is used to unblank the electron beam of the CRO.
So where does this flash of light occur on the screen of the CRO? The position of the flash of light is dictated by the ±X and ±Y signals generated by the position circuit. These signals as you might have guessed are fed to the deflection plates of the CRO so as to cause the unblanked electron beam to strike the screen at a point related to where the scintillation was originally produced in the NaI(Tl) crystal. Simple!
The gamma camera can therefore be considered to be a sophisticated arrangement of electronic circuits used to translate the position of a flash of light in a scintillation crystal to a flash of light at a related point on the screen of an oscilloscope. In addition the use of a pulse height analyser in the circuitry allows us to translate the scintillations related only to photoelectric events in the crystal by rejecting all voltage pulses except those occurring within the photopeak of the gamma-ray energy spectrum.
Let us summarise where we have got to before we proceed. A radiopharmaceutical is administered to the patient and it accumulates in the organ of interest. Gamma-rays are emitted in all directions from the organ and those heading in the direction of the gamma camera enter the crystal and produce scintillations (note that there is a device in front of the crystal called a collimator which we will discuss later). The scintillations are detected by an array of PM tubes whose outputs are fed to a position circuit which generates four voltage pulses related to the position of a scintillation within the crystal. These voltage pulses are fed to the deflection circuitry of the CRO. They are also fed to a summation circuit whose output (the Z-pulse) is fed to the PHA and the output of the PHA is used to switch on (that is, unblank) the electron beam of the CRO. A flash of light appears on the screen of the CRO at a point related to where the scintillation occurred within the NaI(Tl) crystal. An image of the distribution of the radiopharmaceutical within the organ is therefore formed on the screen of the CRO when the gamma-rays emitted from the organ are detected by the crystal.
What we have described above is the operation of a fairly traditional gamma camera. Modern designs are a good deal more complex but the basic design has remained much the same as has been described. One area where major design improvements have occurred is the area of image formation and display. The most basic approach to image formation is to photograph the screen of the CRO over a period of time to allow integration of the light flashes to form an image on photographic film. A stage up from this is to use a storage oscilloscope which allows each flash of light to remain on the screen for a reasonable period of time.
The most modern approach is to feed the position and energy signals into the memory circuitry of a computer for storage. The memory contents can therefore be displayed on a computer monitor and can also be manipulated (that is processed) in many ways. For example various colours can be used to represent different concentrations of a radiopharmaceutical within an organ.
The use of digital image processing is now widespread in nuclear medicine in that it can be used to rapidly and conveniently control image acquisition and display as well as to analyse an image or sequences of images, to annotate images with the patient's name and examination details, to store the images for subsequent retrieval and to communicate the image data to other computers over a network.
The essential elements of a modern gamma camera are shown in the next figure. Gamma rays emitted by the patient pass through the collimator and are detected within the camera head, which generates data related to the location of scintillations in the crystal as well as to the energy of the gamma rays. This data is then processed on-the-fly by electronic hardware which corrects for technical factors such as spatial linearity, PM tube drift and energy response so as to produce an imaging system with a spatially-uniform sensitivity and distortion-free performance.
A multichannel analyzer (MCA) is used to display the energy spectrum of gamma rays which interact inside the crystal. Since these gamma rays originate from within the patient, some of them will have an energy lower than the photopeak as a result of being scattered as they travel through the patient's tissues – and by other components such as the patient table and structures of the imaging system. Some of these scattering events may involve just glancing interactions with free electrons, so that the gamma rays lose only a small amount of energy. These gamma rays may have an energy just below that of the photopeak so that their spectrum merges with the photopeak. The photopeak for a gamma camera imaging a patient therefore contains information from spatially-correlated, unattenuated gamma rays (which is the information we want) and from spatially-uncorrelated, scattered gamma rays. The scattered gamma rays act like a variable background within the true photopeak data and the effect is that of a background haze in gamma camera images.

While scatter may not be a significant problem in planar scintigraphy, it has a strong bearing on the fidelity of quantitative information derived from gamma camera images and is a vital consideration for accurate image reconstruction in emission tomography. It is the unattenuated gamma rays (also called the primary radiation) that contain the desired information, because of their direct dependence on radioactivity.
The scatter situation is illustrated in more detail in the figure below, which shows estimates of the primary and scatter spectra for 99mTc in patient imaging conditions. Such spectral estimates can be generated using Monte Carlo methods. It is seen in the figure that the energy of the scattered radiation forms a broad band, similar to the Compton Smear described previously, which merges into and contributes substantially to the detected photopeak. The detected photopeak is therefore an overestimate of the primary radiation. The extent of this overestimate is likely to be dependent on the specific imaging situation because of the different thicknesses of tissues involved. It is clear however that the scatter contribution within the detected photopeak needs to be accounted for if an accurate measure of radioactivity is required.

One method of compensating for the scatter contribution is illustrated in the figure below and involves using data from a lower energy window as an estimate for subtraction from the photopeak, i.e.
where k is a scaling factor to account for the extent of the scatter contribution. This approach to scatter compensation is referred to as the Dual-Energy Window (DEW) method. It can be implemented in practice by acquiring two images, one for each energy window, and subtracting a fraction (k) of the scatter image from the photopeak image.
For the spectrum shown above, it can be seen that the scaling factor, k, is about 0.5, but it should be appreciated that its exact value is dependent on the scattering conditions. Gamma cameras which use the DEW method therefore generally provide the capability of adjusting k for different imaging situations. Some systems use a narrower scatter window than that illustrated, e.g. 114-126 keV, with a consequent increase in k to about 1.0, for instance.
A host of other methods of scatter compensation have also been developed. These include more complex forms of energy analysis such as the Dual-Photopeak and the Triple-Energy Window techniques, as well as approaches based on deconvolution and models of photon attenuation. An excellent review of these developments is provided in Zaidi & Koral (2004).

Some photographs of gamma cameras and related devices are shown below:
We will continue with our description of the gamma camera by considering the construction and purpose of the collimator.
Collimation[edit | edit source]
The collimator is a device which is attached to the front of the gamma camera head. It functions something like a lens used in a photographic camera but this analogy is not quite correct because it is rather difficult to focus gamma-rays. Nevertheless in its simplest form it is used to block out all gamma rays which are heading towards the crystal except those which are travelling at right angles to the plane of the crystal:

The figure illustrates a magnified view of a parallel-hole collimator attached to a crystal. The collimator simply consists of a large number of small holes drilled in a lead plate. Notice that gamma-rays entering at an angle to the crystal get absorbed by the lead and that only those entering along the direction of the holes get through to cause scintillations in the crystal. If the collimator was not in place these obliquely incident gamma-rays would blur the images produced by the gamma camera. In other words the images would not be very clear.
Most gamma cameras have a number of collimators which can be fitted depending on the examination. The basic design of these collimators is the same except that they vary in terms of the diameter of each hole, the depth of each hole and the thickness of lead between each hole (commonly called the septum thickness). The choice of a specific collimator is dependent on the amount of radiation absorption that occurs (which influences the sensitivity of the gamma camera), and the clarity of images (that is the spatial resolution) it produces. Unfortunately these two factors are inversely related in that the use of a collimator which produces images of good spatial resolution generally implies that the instrument is not very sensitive to radiation.
Other collimator designs beside the parallel hole type are also in use. For example a diverging hole collimator produces a minified image and converging hole and pin-hole collimators produce a magnified image. The pin-hole collimator is illustrated in the following figure:

It is typically a cone-shaped device with its walls made from lead. A cross-section through this cone is shown in the figure. It operates in a similar fashion to a pin-hole photographic camera and produces an inverted image of an object – an arrow is used in the figure to illustrate this inversion. This type of collimator has been found useful for imaging small objects such as the thyroid gland.
Example Images[edit | edit source]
A representative selection of nuclear medicine images is shown below:
Emission Tomography[edit | edit source]
The form of imaging which we have been describing is called Planar Imaging. It produces a two-dimensional image of a three-dimensional object. As a result images contain no depth information and some details can be superimposed on top of each other and obscured or partially obscured as a result. Note that this is also a feature of conventional X-ray imaging.
The usual way of trying to overcome this limitation is to take at least two views of the patient, one from the front and one from the side for example. So in chest radiography a posterio-anterior (PA) and a lateral view can be taken. And in a nuclear medicine liver scan an antero-posterior (AP) and lateral scan are acquired.
This limitation of planar X-ray imaging was overcome by the development of the CAT Scanner about 1970 or thereabouts. CAT stands for Computerized Axial Tomography or Computer Assisted Tomography and today the term is often shortened to Computed Tomography or CT scanning (the term tomography comes from the Greek word tomos meaning slice). Irrespective of its exact name the technique allows images of slices through the body to be produced using a computer. It does this in essence by taking X-ray images at a number of angles around the patient. These slice images show the third dimension which is missing from planar images and thus eliminate the problem of superimposed details. Furthermore images of a number of successive slices through a region of the patient can be stacked on top of each other using the computer to produce a three-dimensional image. Clearly CT scanning is a very powerful imaging technique relative to planar imaging.
The equivalent nuclear medicine imaging technique is called Emission Computed Tomography. We will consider two implementations of this technique below.
Single Photon Emission Computed Tomography (SPECT)[edit | edit source]
- This SPECT technique uses a gamma camera to record images at a series of angles around the patient. These images are then subjected to a form of digital image processing called Image Reconstruction in order to compute images of slices through the patient.
- The Back Projection reconstruction process is illustrated below. Let us assume for simplicity that the slice through the patient actually consists of a 2x2 voxel array with the radioactivity in each voxel given by A1...A4:

- The first projection, P1, is imaged from the right and the second projection, P2, from the right oblique and so on. The back projection process involves firstly adding the projections to each other as shown below:

- and then normalising the summed (or superimposed) projections to generate an estimate of the radioactivity in each voxel. Since this process can generate streaking artefacts in reconstructed images, the projections are generally filtered prior to back projection, as described in a later chapter, with the overall process referred to as Filtered Back Projection (FBP):
- An alternative image reconstruction technique is called Iterative Reconstruction, a successive approximation technique. The Maximum-Likelihood Expectation-Maximisation (ML-EM) algorithm is widely applied where a division process is used to compare the actual and estimated projections, as shown below:

- One cycle of data through this processing chain is referred to as one iteration. Sixteen or more iterations can be required in order to generate an adequate reconstruction and, as a result, computation times can be rather long. The Ordered-Subsets Expectation-Maximisation (OS-EM) algorithm can be used to substantially reduce the computation time by utilising a limited number of projections (called subsets) in a sequential fashion within the iterative process. Noise generated during the reconstruction process can be reduced, for example, using a Gaussian filter built into the reconstruction calculations or applied as a post-filter:

- Images generated using different iterations, subsets and filtration settings can be found in an online book.
- A comparison of these image reconstruction techniques is shown below for a slice through a ventilation scan of a patient's lungs:

- The gamma camera is typiclly rotated around the patient in order to acquire the images. Modern gamma cameras which are designed specifically for SPECT scanning can consist of two camera heads mounted parallel to each other with the patient in between. The time required to produce images is therefore reduced by a factor of about two. In addition some SPECT gamma cameras designed for brain scanning have three camera heads mounted in a triangular arrangement.
- A wide variety of strategies can be used for the acquisition and processing of SPECT images.
Positron Emission Tomography (PET)[edit | edit source]
- You will remember from chapter 2 that positrons can be emitted from radioactive nuclei which have too many neutrons for stability. You will also remember that positrons do not last for very long in matter since they will quickly encounter an electron and a process called annihilation results. In the process the positron and electron vanish and their energy is converted into two gamma-rays which are emitted at roughly 180o degrees to each other. The emission is often referred to as two back-to-back gamma-rays and they each have a discrete energy of 0.51 MeV.
- So if we administer a positron-emitting radiopharmaceutical to a patient an emitted positrons can annihilate with a nearby electron and two gamma-rays will be emitted in opposite directions. These gamma-rays can be detected using a ring of radiation detectors encircling the patient and tomographic images can be generated using a computer system. The detectors are typically specialised scintillation devices which are optimised for detection of the 0.51 MeV gamma-rays. This ring of detectors, associated apparatus and computer system are called a PET Scanner:

- The locations of positron decays within the patient are highlighted by the solid circles in the above diagram. In addition only a few detectors are shown in the diagram for reasons of clarity. Each detector around the ring is operated in coincidence with a bank of opposing detectors and the annihilation gamma-rays thus detected are used to build up a single profile.
- It has also been found that gamma cameras fitted with thick crystals and special collimators can be used for PET scanning.
- The radioisotopes used for PET scanning include 11C, 13N, 15O and 18F. These isotopes are usually produced using an instrument called a cyclotron. In addition these isotopes have relatively short half lives. PET scanning therefore needs a cyclotron and associated radiopharmaceutical production facilities located close by. We will consider cyclotrons in the next chapter of this wikibook.
- Standardized Uptake Value (SUV) is a semi-quantitative index used in PET to express the uptake of a radiopharmaceutical in a region of interest of a patient's scan. Its typically calculated as the ratio of the radioactivity in the region to the injected dose, corrected for body weight. It should be noted that the SUV is influenced by several major sources of variability and it therefore should not be used as a quantitative measure.
- A number of photographs of a PET scanner are shown below:
 |
 |
 |
 |
Images reconstructed using different settings of subsets and iterations for iterative reconstruction[2] are shown below:

References[edit | edit source]
- ↑ Slomka PJ, Patton JA, Berman DS & Germano G, 2009. Advances in technical aspects of myocardial perfusion SPECT imaging. Journal of Nuclear Cardiology, 16(2), 255–76.
- ↑ Maher KP, 2016. Iterations, Subsets & Gaussian Filtration, 3rd Edition (Bookemon.com]
External links[edit | edit source]
- Centre for Positron Emission Tomography at the Austin & Repatriation Medical Centre, Melbourne with sections on what PET is, current facilities, projects & research and a PET image library
Production of Radioisotopes[edit | edit source]

Most of the radioisotopes found in nature have relatively long half lives. They also belong to elements which are not handled well by the human body. As a result medical applications generally require the use of radioisotopes which are produced artificially.
We have looked at the subject of radioactivity in earlier chapters of this wikibook and have then progressed to cover the interaction of radiation with matter, radiation detectors and imaging systems. We return to sources of radioactivity in this chapter in order to learn about methods which are used to make radioisotopes.
The type of radioisotope of value to nuclear medicine imaging should have characteristics which keep the radiation dose to the patient as low as possible. For this reason they generally have a short half life and emit only gamma-rays - that is no alpha-particle or beta-particle emissions. From an energy point of view the gamma-ray energy should not be so low that the radiation gets completely absorbed before emerging from the patient's body and not too high that it is difficult to detect. For this reason most of the radioisotopes used emit gamma-rays of medium energy, that is between about 100 and 200 keV. Finally since the radioisotope needs to be incorporated into some form of radiopharmaceutical it should also be capable of being produced in a form which is amenable to chemical, pharmaceutical and sterile processing.
The production methods we will consider are nuclear fission, nuclear bombardment and the radioisotope generator.
Nuclear Fission[edit | edit source]
We were introduced to spontaneous fission in chapter 2 where we saw that a heavy nucleus can break into a number of fragments. This disintegration process can be induced to occur when certain heavy nuclei absorb neutrons. Following absorption of a neutron such nuclei break into smaller fragments with atomic numbers between about 30 and 65. Some of these new nuclei are of value to nuclear medicine and can be separated from other fission fragments using chemical processes.
The fission process is controlled inside a device called a nuclear reactor. One such reactor exists in Australia at Lucas Heights in New South Wales and many others exist throughout the world.
Nuclear Bombardment[edit | edit source]
In this method of radioisotope production charged particles are accelerated up to very high energies and caused to collide into a target material. Examples of such charged particles are protons, alpha particles and deuterons. New nuclei can be formed when these particles collide with nuclei in the target material. Some of these nuclei are of value to nuclear medicine.
An example of this method is the production of 22Na where a target of 24Mg is bombarded with deuterons, that is: 24Mg + 2H → 22Na + 4He.
A deuteron you will remember from chapter 1 is the second most common isotope of hydrogen, that is 2H. When it collides with a 24Mg nucleus a 22Na nucleus plus an alpha particle is produced. The target is exposed to the deuterons for a period of time and is subsequently processed chemically in order to separate out the 22Na nuclei.
The type of device commonly used for this method of radioisotope production is called a cyclotron. It consists of an ion gun for producing the charged particles, electrodes for accelerating them to high energies and a magnet for steering them towards the target material. All arranged in a circular structure.
Radioisotope Generator[edit | edit source]

This method is widely used to produce certain short-lived radioisotopes in a hospital or clinic. It involves obtaining a relatively long-lived radioisotope which decays into the short-lived isotope of interest.
A good example is 99mTc which as we have noted before is the most widely used radioisotope in nuclear medicine today. This isotope has a half-life of six hours which is rather short if we wish to have it delivered directly from a nuclear facility. Instead the nuclear facility supplies the isotope 99Mo which decays into 99mTc with a half life of about 2.75 days. The 99Mo is called the parent isotope and 99mTc is called the daughter isotope.
So the nuclear facility produces the parent isotope which decays relatively slowly into the daughter isotope and the daughter is separated chemically from the parent at the hospital/clinic. The chemical separation device is called, in this example, a 99mTc Generator:
It consists of a ceramic column with 99Mo adsorbed onto its top surface. A solution called an eluent is passed through the column, reacts chemically with any 99mTc and emerges in a chemical form which is suitable for combining with a pharmaceutical to produce a radiopharmaceutical. The arrangement shown in the figure on the right is called a Positive Pressure system where the eluent is forced through the ceramic column by a pressure, slightly above atmospheric pressure, in the eluent vial.
The ceramic column and collection vials need to be surrounded by lead shielding for radiation protection purposes. In addition all components are produced and need to be maintained in a sterile condition since the collected solution will be administered to patients.
Finally an Isotope Calibrator is needed when a 99mTc Generator is used to determine the radioactivity for preparation of patient doses and to check whether any 99Mo is present in the collected solution.
Operation of a 99m-Tc Generator[edit | edit source]
Suppose we have a sample of 99Mo and suppose that at time there are nuclei in our sample and nothing else. The number of 99Mo nuclei decreases with time according to radioactive decay law as discussed in Chapter 3:
where is the decay constant for 99Mo.
Thus the number of 99Mo nuclei that decay during a small time interval is given by
Since 99Mo decays into 99mTc, the same number of 99mTc nuclei are formed during the time period . At a time , only a fraction of these nuclei will still be around since the 99mTc is also decaying. The time for 99mTc to decay is given by . Plugging this into radioactive the decay law we arrive at:
Now we sum up the little contributions . In other words we integrate over in order to find the number , that is the number of all 99mTc nuclei present at the time :
Finally solving this integral we find:
The figure below illustrates the outcome of this calculation. The horizontal axis represents time (in days), while the vertical one represents the number of nuclei present (in arbitrary units). The green curve illustrates the exponential decay of a sample of pure 99mTc. The red curve shows the number of 99mTc nuclei present in a 99mTc generator that is never eluted. Finally, the blue curve shows the situation for a 99mTc generator that is eluted every 12 hours.

Photographs taken in a nuclear medicine hot lab are shown below:
 |
 |
External links[edit | edit source]
- Concerns over Molybdenum Supplies – news from 2008 compiled by the British Nuclear Medicine Society.
- Cyclotron Java Applet – a Java-based interactive demonstration of the operation of a cyclotron from GFu-Kwun Hwang, Dept. of Physics, National Taiwan Normal University, Virtual Physics Laboratory.
- Nuclear Power Plant Demonstration – a Java-based interactive demonstration of controlling a nuclear reactor. Also contains nuclear power Information links.
- ANSTO – information about Australia's nuclear organization.
- Medical Valley – contains information on what nuclear medicine is, production of nuclear pharmaceuticals, molybdenum and technetium – from The Netherlands Energy Research Foundation Petten.
Chapter Review[edit | edit source]

Chapter Review: Atomic & Nuclear Structure[edit | edit source]
- The atom consists of two components – a nucleus (positively charged) and an electron cloud (negatively charged);
- The radius of the nucleus is about 10,000 times smaller than that of the atom;
- The nucleus can have two component particles – neutrons (no charge) and protons (positively charged) – collectively called nucleons;
- The mass of a proton is about equal to that of a neutron – and is about 1,840 times that of an electron;
- The number of protons equals the number of electrons in an isolated atom;
- The Atomic Number specifies the number of protons in a nucleus;
- The Mass Number specifies the number of nucleons in a nucleus;
- Isotopes of elements have the same atomic number but different mass numbers;
- Isotopes are classified by specifying the element's chemical symbol preceded by a superscript giving the mass number and a subscript giving the atomic number;
- The atomic mass unit is defined as 1/12th the mass of the stable, most commonly occurring isotope of carbon (i.e. C-12);
- Binding energy is the energy which holds the nucleons together in a nucleus and is measured in electron volts (eV);
- To combat the effect of the increase in electrostatic repulsion as the number of protons increases, the number of neutrons increases more rapidly – giving rise to the Nuclear Stability Curve;
- There are ~2450 isotopes of ~100 elements and the unstable isotopes lie above or below the Nuclear Stability Curve;
- Unstable isotopes attempt to reach the stability curve by splitting into fragments (fission) or by emitting particles/energy (radioactivity);
- Unstable isotopes <=> radioactive isotopes <=> radioisotopes <=> radionuclides;
- ~300 of the ~2450 isotopes are found in nature – the rest are produced artificially.
Chapter Review: Radioactive Decay[edit | edit source]
- Fission: Some heavy nuclei decay by splitting into 2 or 3 fragments plus some neutrons. These fragments form new nuclei which are usually radioactive;
- Alpha Decay: Two protons and two neutrons leave the nucleus together in an assembly known as an alpha-particle;
- An alpha-particle is a He-4 nucleus;
- Beta Decay – Electron Emission: Certain nuclei with an excess of neutrons may reach stability by converting a neutron into a proton with the emission of a beta-minus particle;
- A beta-minus particle is an electron;
- Beta Decay – Positron Emission: When the number of protons in a nucleus is in excess, the nucleus may reach stability by converting a proton into a neutron with the emission of a beta-plus particle;
- A beta-plus particle is a positron;
- Positrons annihilate with electrons to produce two back-to-back gamma-rays;
- Beta Decay – Electron Capture: An inner orbital electron is attracted into the nucleus where it combines with a proton to form a neutron;
- Electron capture is also known as K-capture;
- Following electron capture, the excited nucleus may give off some gamma-rays. In addition, as the vacant electron site is filled, an X-ray is emitted;
- Gamma Decay – Isomeric Transition: A nucleus in an excited state may reach its ground state by the emission of a gamma-ray;
- A gamma-ray is an electromagnetic photon of high energy;
- Gamma Decay – Internal Conversion: the excitation energy of an excited nucleus is given to an atomic electron.
Chapter Review: The Radioactive Decay Law[edit | edit source]
- The radioactive decay law in equation form;
- Radioactivity is the number of radioactive decays per unit time;
- The decay constant is defined as the fraction of the initial number of radioactive nuclei which decay in unit time;
- Half Life: The time taken for the number of radioactive nuclei in the sample to reduce by a factor of two;
- Half Life = (0.693)/(Decay Constant);
- The SI Unit of radioactivity is the becquerel (Bq)
- 1 Bq = one radioactive decay per second;
- The traditional unit of radioactivity is the curie (Ci);
- 1 Ci = 3.7 x 1010 radioactive decays per second.
= Chapter Review: Units of Radiation Measurement =[edit | edit source]
- Exposure expresses the intensity of an X- or gamma-ray beam;
- The SI unit of exposure is the coulomb per kilogram (C/kg);
- 1 C/kg = The quantity of X- or gamma-rays such that the associated electrons emitted per kg of air at STP produce in air ions carrying 1 coulomb of electric charge;
- The traditional unit of exposure is the roentgen (R);
- 1 R = The quantity of X- or gamma-rays such that the associated electrons emitted per kg of air at STP produce in air ions carrying 2.58 x 10-4 coulombs of electric charge;
- The exposure rate is the exposure per unit time, e.g. C/kg/s;
- Absorbed dose is the radiation energy absorbed per unit mass of absorbing material;
- The SI unit of absorbed dose is the gray (Gy);
- 1 Gy = The absorption of 1 joule of radiation energy per kilogram of material;
- The traditional unit of absorbed dose is the rad;
- 1 rad = The absorption of 10-2 joules of radiation energy per kilogram of material;
- The Specific Gamma-Ray Constant expresses the exposure rate produced by the gamma-rays from a radioisotope;
- The Specific Gamma-Ray Constant is expressed in SI units in C/kg/s/Bq at 1 m;
- Exposure from an X- or gamma-ray source follows the Inverse Square Law and decreases with the square of the distance from the source.
Chapter Review: Interaction of Radiation with Matter[edit | edit source]
- Alpha-Particles:
- exert considerable electrostatic attraction on the outer orbital electrons of atoms near which they pass and cause ionisations;
- travel in straight lines – except for rare direct collisions with nuclei of atoms in their path;
- energy is always discrete.
- Beta-Minus Particles:
- attracted by nuclei and repelled by electron clouds as they pass through matter and cause ionisations;
- have a tortuous path;
- have a range of energies;
- range of energies results because two particles are emitted – a beta-particle and a neutrino.
- Gamma-Rays:
- energy is always discrete;
- have many modes of interaction with matter;
- important interactions for nuclear medicine imaging (and radiography) are the Photoelectric Effect and the Compton Effect.
- Photoelectric Effect:
- when a gamma-ray collides with an orbital electron, it may transfer all its energy to the electron and cease to exist;
- the electron can leave the atom with a kinetic energy equal to the energy of the gamma-ray less the orbital binding energy;
- a positive ion is formed when the electron leaves the atom;
- the electron is called a photoelectron;
- the photoelectron can cause further ionisations;
- subsequent X-ray emission as the orbital vacancy is filled.
- Compton Effect:
- A gamma-ray may transfer only part of its energy to a valence electron which is essentially free; ** gives rise to a scattered gamma-ray;
- is sometimes called Compton Scatter;
- a positive ion results;
- Attenuation is term used to describe both absorption and scattering of radiation.
Chapter Review: Attenuation of Gamma-Rays[edit | edit source]
- Attenuation of a narrow-beam of gamma-rays increases as the thickness, the density and the atomic number of the absorber increases;
- Attenuation of a narrow-beam of gamma-rays decreases as the energy of the gamma-rays increases;
- Attenuation of a narrow beam is described by an equation;
- the Linear Attenuation Coefficient is defined as the fraction of the incident intensity absorbed in a unit distance of the absorber;
- Linear attenuation coefficients are usually expressed in units of cm-1;
- the Half Value Layer is the thickness of absorber required to reduce the intensity of a radiation beam by a factor of 2;
- Half Value Layer = (0.693)/(Linear Attenuation Coefficient);
- the Mass Attenuation Coefficient is given by the linear attenuation coefficient divided by the density of the absorber;
- Mass attenuation coefficients are usually expressed in units of cm2 g-1.
Chapter Review: Gas-Filled Detectors[edit | edit source]
- Gas-filled detectors include the ionisation chamber, the proportional counter and the Geiger counter;
- They operate on the basis of ionisation of gas atoms by the incident radiation, where the positive ions and electrons produced are collected by electrodes;
- An ion pair is the term used to describe a positive ion and an electron;
- The operation of gas-filled detectors is critically dependent on the magnitude of the applied dc voltage;
- The output voltage of an ionisation chamber can be calculated on the basis of the capacitance of the chamber;
- A very sensitive amplifier is required to measure voltage pulses produced by an ionisation chamber;
- The gas in ionisation chambers is usually air;
- Ionisation chambers are typically used to measure radiation exposure (in a device called an Exposure Meter) and radioactivity (in a device called an Isotope Calibrator);
- The total charge collected in a proportional counter may be up to 1000 times the charge produced initially by the radiation;
- The initial ionisation triggers a complete gas breakdown in a Geiger counter;
- The gas in a Geiger counter is usually an inert gas;
- The gas breakdown must be stopped in order to prepare the Geiger counter for a new event by a process called quenching;
- Two types of quenching are possible: electronic quenching and the use of a quenching gas;
- Geiger counters suffer from dead time, a small period of time following the gas breakdown when the counter is inoperative;
- The true count rate can be determined from the actual count rate and the dead time using an equation;
- The value of the applied dc voltage in a Geiger counter is critical, but high stability is not required.
Chapter Review: Scintillation Detectors[edit | edit source]
- NaI(Tl) is a scintillation crystal widely used in nuclear medicine;
- The crystal is coupled to a photomultiplier tube to generate a voltage pulse representing the energy deposited in the crystal by the radiation;
- A very sensitive amplifier is needed to measure such voltage pulses;
- The voltages pulses range in amplitude depending on how the radiation interacts with the crystal, i.e. the pulses form a spectrum whose shape depends on the interaction mechanisms involved, e.g. for medium-energy gamma-rays used in in-vivo nuclear medicine: the Compton effect and the Photoelectric effect;
- A Gamma-Ray Energy Spectrum for a medium-energy, monoenergetic gamma-ray emitter consists (simply) of a Compton Smear and a Photopeak;
- Pulse Height Analysis is used to discriminate the amplitude of voltage pulses;
- A pulse height analyser (PHA) consists of a lower level discriminator (which passes voltage pulses which are than its setting) and an upper level discriminator (which passes voltage pulses lower than its setting);
- The result is a variable width window which can be placed anywhere along a spectrum, or used to scan a spectrum;
- A single channel analyser (SCA) consists of a single PHA with a scaler and a ratemeter;
- A multi-channel analyser (MCA) is a computer-controlled device which can acquire data from many windows simultaneously.
Chapter Review: Nuclear Medicine Imaging Systems[edit | edit source]
- A gamma camera consists of a large diameter (25-40 cm) NaI(Tl) crystal, ~1 cm thick;
- The crystal is viewed by an array of 37-91 PM tubes;
- PM tubes signals are processed by a position circuit which generates +/- X and +/- Y signals;
- These position signals are summed to form a Z signal which is fed to a pulse height analyser;
- The +/- X, +/- Y and discriminated Z signals are sent to a computer for digital image processing;
- A collimator is used to improve the spatial resolution of a gamma-camera;
- Collimators typically consist of a Pb plate containing a large number of small holes;
- The most common type is a parallel multi-hole collimator;
- The most resolvable area is directly in front of a collimator;
- Parallel-hole collimators vary in terms of the number of holes, the hole diameter, the length of each hole and the septum thickness – the combination of which affect the sensitivity and spatial resolution of the imaging system;
- Other types include the diverging-hole collimator (which generates minified images), the converging-hole collimator (which generates magnified images) and the pin-hole collimator (which generates magnified inverted images);
- Conventional imaging with a gamma camera is referred to as Planar Imaging, i.e. a 2D image portraying a 3D object giving superimposed details and no depth information;
- Single Photon Emission Computed Tomography (SPECT) produces images of slices through the body;
- SPECT uses a gamma camera to record images at a series of angles around the patient;
- The resultant data can be processed using Filtered Back Projection and Iterative Reconstruction;
- SPECT gamma-cameras can have one, two or three camera heads;
- Positron Emission Tomography (PET) also produces images of slices through the body;
- PET exploits the positron annihilation process where two 0.51 MeV back-to-back gamma-rays are produced;
- If these gamma-rays are detected, their origin will lie on a line joining two of the detectors of the ring of detectors which encircles the patient;
- A Time-of-Flight method can be used to localise their origin;
- PET systems require on-site or nearby cyclotron to produce short-lived radioisotopes, such as C-11, N-13, O-15 and F-18.
Chapter Review: Production of Radioisotopes[edit | edit source]
- Naturally-occurring radioisotopes generally have long half lives and belong to relatively heavy elements – and are therefore unsuitable for medical diagnostic applications;
- Medical diagnostic radioisotopes are generally produced artificially;
- The fission process can be exploited so that radioisotopes of interest can be separated chemically from fission products;
- A cyclotron can be used to accelerate charged particles up to high energies so that they to collide into a target of the material to be activated;
- A radioisotope generator is generally used in hospitals to produce short-lived radioisotopes;
- A technetium-99m generator consists of an alumina column containing Mo-99, which decays into Tc-99m;
- Saline is passed through the generator to elute the Tc-99m – the resulting solution is called sodium pertechnetate;
- Both positive pressure and negative pressure generators are in use;
- An isotope calibrator is needed when a Tc-99m generator is used in order to determine the activity for preparation of patient doses and to test whether any Mo-99 is present in the collected solution.
Exercise Questions[edit | edit source]
1. Discuss the process of radioactive decay from the perspective of the nuclear stability curve.
2. Describe in detail FOUR common forms of radioactive decay.
3. Give the equation which expresses the Radioactive Decay Law, and explain the meaning of each of its terms.
4. Define each of the following:
- (a) Half life;
- (b) Decay Constant;
- (c) Becquerel.
5. A sample of radioactive substance is found to have an activity of 100 kBq. Its radioactivity is measured again 82 days later and is found to be 15 kBq. Calculate:
- (a) the half-life;
- (b) the decay constant.
6. Define each of the following radiation units:
- (a) Roentgen;
- (b) Becquerel;
- (c) Gray.
7. Estimate the exposure rate at 1 metre from a 100 MBq source of radioactivity which has a Specific Gamma Ray Constant of 50 mR per hour per MBq at 1 cm.
8. Briefly describe the basic principle of operation of gas-filled radiation detectors.
9. Illustrate using a graph how the magnitude of the voltage pulses from a gas-filled radiation detector varies with applied voltage and identify on the graph the regions associated with the operation of Ionisation Chambers and the Geiger Counters.
10. Describe the construction and principles of operation of a scintillation spectrometer.
11. Discuss the components of the energy spectrum from a monoenergetic, medium energy gamma- emitting radioisotope obtained using a scintillation spectrometer on the basis of how the gamma-rays interact with the scintillation crystal.
12. Describe the construction and principles of operation of a Gamma Camera.
13. Compare features of three types of collimator which can be used with a Gamma Camera.
Further Information[edit | edit source]
Nuclear Medicine is a fascinating application of nuclear physics. The first ten chapters of this wikibook are intended to support a basic introductory course in an early semester of an undergraduate program. They assume that students have completed decent high school programs in maths and physics and are concurrently taking subjects in the medical sciences. Additional chapters cover more advanced topics in this field. Our focus in this wikibook is the diagnostic application of Nuclear Medicine. Therapeutic applications are considered in a separate wikibook, "Radiation Oncology".
Note that this WikiBooks is well past its use-by date. Some of the basic physics might still be of relevance, but the technologies and applications chapters need substantial updating.
A companion wikibook on the Basic Physics of Digital Radiography is also available.
Contents[edit | edit source]

- Atomic & Nuclear Structure
- Radioactive Decay
- The Radioactive Decay Law
- Units of Radiation Measurement
- Interaction of Radiation with Matter
- Attenuation of Gamma-Rays
- Gas-Filled Radiation Detectors
- Scintillation Detectors
- Nuclear Medicine Imaging Systems
- Computers in Nuclear Medicine
- Fourier Methods
- X-Ray CT in Nuclear Medicine
- PACS and Advanced Image Processing
- Three-Dimensional Visualization Techniques
- Patient Dosimetry
- Production of Radioisotopes
- Chapter Review
- Dynamic Studies in Nuclear Medicine
- Deconvolution Analysis
- Sonography & Nuclear Medicine
- MRI & Nuclear Medicine
- Dual-Energy Absorptiometry
The principal author of this text is grateful for the expert editorial assistance of Dirk Hünniger during his German translation of the text and his contribution to the section on the Operation of a 99m-Tc Generator.
Bibliography[edit | edit source]
- Applied Imaging Technology, 4th Ed., JCP Heggie, NA Liddell & KP Maher (St Vincent's Hospital Melbourne, 2001)
- Basic Science of Nuclear Medicine, 2nd Ed., RP Parker, PHS Smith, DM Taylor (Churchill Livingstone, 1984)
- Computed Tomography: Fundamentals, System Technology, Image Quality, Applications, 3rd Ed., WA Kalender (Wiley, 2000)
- Introduction to Nuclear Physics, H Enge (Addison-Wesley, 1966)
- Magnetic Resonance in Medicine, 4th Ed., PA Rinck (Blackwell, 2001)
- Nuclear Medicine in Urology & Nephrology, 2nd Ed., HJ Testa, PH O'Reilly & RA Shields (Butterworth-Heinemann, 1986)
- Physics in Nuclear Medicine, JA Sorenson and ME Phelps (Grune & Stratton, 1980)
- Radioisotope Techniques in Clinical Research and Diagnosis, N Veall and H Vetter (Butterworths, 1958)
- Radionuclide Techniques in Medicine, JM McAlister (Cambridge University Press, 1979).