Structural Biochemistry/Point Groups
Each molecule has a set of symmetry operations that describes the molecule's overall symmetry. This set of symmetry to classify molecules is known as point group Group theory is a powerful mathematical tool in determining the symmetry, properties, and data of complex molecules. Molecules are said to belong to the same point group if they have the same symmetry response under a set of operations. That is to say, two molecules can have totally different shapes but belong to the same point group as long as the respond the same to some symmetry operations. A molecule can only belong to one point group. It cannot belong to more than one point group.
It is important to understand that point groups is a tool for categorizing the different symmetries a molecule might have. This tries to classify molecules based on their molecular shapes and symmetries. There are various symmetry elements used to illuminate the shape of the molecule. The shape and symmetry of a molecule is highly important especially in structural biochemistry because structure determines functions of proteins and molecules. It is also important to note that many molecules are constantly going through conformational change, therefore its point group can also change. Point group is a tool for us to understand on a molecular level, symmetry. [1]
Types of Point Groups
[edit | edit source]Molecules can be separated by the symmetry elements that they contain. The different Symmetry operations can be classified into:

-Rotation operation (Cn): is rotation of 360/n degrees about a rotation axis that renders the object unchanged.. For example, ammonia (NH3) contains a threefold rotational axis, which gives it a C3 operation. Objects or molecules can have more than one rotational axis. An example of an object with more than one rotational axis is a snowflake or octahedron.

-Reflection operation (σ): is a reflection across the mirror plane where when the object remains unchanged when reflected. There are three different σ's. The first is σvwhere the mirror plane is parallel to the primary axis of rotation and an outer atom. A σd is a mirror plane that is also parallel to the primary axis of rotation but it does not pass through an outer atom, rather it is between two outer atoms. An exception to this is in Td and Dnd, in which all mirror planes are referred to as σd. The last mirror plane is such that is a horizontal reflection σh where the plane of reflection is perpendicular to the primary axis of rotation. A primary axis of rotation is the axis with the greatest number of rotational symmetry folds. Objects and molecules can also have more than one plane of reflection.
-Inversion operation (i): is a combination of a C2 rotation and a σh operation to invert the molecule across a point of inversion, which is usually taken to be the center of the molecule. It is a reflection (or inversion) through the mid-point (center) of the object or molecule.
-Improper Rotation (Sn): is the rotation of 360/n, followed by reflection through a plane perpendicular to the axis of rotation, σh. An S2 operation is identical to an inversion (both being a 180 degree rotation, followed by a reflection across the perpendicular horizontal axis).
-Identity (E): is merely a rotation by 360 degrees around an arbitrary axis that returns an equivalent configuration. Every molecule has at least an E operation.
Examples
[edit | edit source]Oh – octahedral point group – contains all symmetry elements and operation of a perfect octahedron.

C∞v : An infinite number of mirror plane parallel to an infinite number of rotation axis.

D∞v : not only has an infinite number of rotation axis and mirror planes but also has a two-fold rotation perpendicular to these infinite number of rotation axis. D∞v also has an inversion center.
C3v There is a 3-fold primary rotation axis and 3 mirror planes parallel to that axis.
D3h Designates that there are 3 two-fold rotational axes perpendicular to a three-fold primary axis and a mirror plane perpendicular to that primary axis.
How to Work a Point Group Flow Chart
[edit | edit source]All molecules have some type of symmetry or lack thereof, and can be grouped into categories (called point groups) where all molecules with the same symmetries have the same point group. To facilitate the determination of a molecule's point group, without having to exhaustively determine every one of its symmetry properties, a point group flow chart can be used. A molecule's point group can be easily determined by finding how many rotational and mirror planes it contains in a logical manner. The less symmetrical an object is, the more difficult symmetry operations are needed to determine its point group, where as the higher symmetries are more easily determined. This allows users to answer simple questions based on the shape of the molecule. If one is able to understand the point group flowchart, there requires no memorization. Therefore point group determination is quite simple, all it requires is knowledge of types of point group and some visualization. [2]
There are many other point groups such as C4v, C5v, D4h, D5h, etc. Memorizing the definition of all the point-groups is overwhelming. To simplify this, point group of a molecule can be easily found by following a flow chart. First, start with determining if the molecule is linear or not. If it is, then determine if there is an inversion center. If the molecule is not linear, check if there are two or more Cn, where n is greater than two. If yes, then determine if there is an inversion center and if there is a C5 rotation axis. If there are two or more Cn's, then check if there are Cn's at all. If so, then check if the Cn with the higher n is perpendicular to nC2. If so, then determine if the molecule has a σh or σd. If there aren't two or more Cn's, then check if there is a σh, nσv, or S2n. These are the cases where there is a Cn, but if there aren't any Cn's then check if there is a σh of inversion center. If this is done correctly, the arrival at the end of a chain will be the point group for the observed molecule.

Example of how to use the flow chart
[edit | edit source]Above is a figure of water molecule. Following the flow chart: 1. The molecule is not linear 2. The molecule does not have more than 2 axis of rotation other than the primary axis 3. The molecule has a proper C2 primary rotation 4. But the molecule does not have 2 other proper rotation axis perpendicular to the primary rotation axis 5. The molecule does not have a mirror plane perpendicular to the primary axis 6. The molecule has two mirror plane parallel to the primary axis 7. Thus, water molecule belongs to C2v point group
Above is a figure of BF5 molecule. Following the point group flow chart: 1. The molecule is not linear 2. The molecule does not have more than 2 rotation axis other than the primary rotational axis 3. The molecule has a 4-fold proper rotational axis 4. The molecule does not have 4 C2 axis that is perpendicular to the primary rotational axis 5. The molecule does not have a mirror plane that is perpendicular to the primary rotational axis 6. The molecule has 4 mirror planes that are perpendicular to the primary rotational axis 7. The molecule hence belongs to C4v point group
Above is a figure of a cyclopropane molecule. Following the point group flow chart: 1. The molecule is not linear 2. The molecule does not have more than 2 rotation axis other than the primary rotational axis 3. The molecule has a proper 3-fold rotational axis 4. The molecule has 3 perpendicular C2 axis 5. The molecule has a mirror plane perpendicular to the primary rotational axis 6. The molecule hence belongs to D3h point group
Above is a molecule octachloride osmium with an eclipse conformation. Following the flow chart 1. The molecule is not linear 2. The molecule does not have more than 2 rotation axis other than the primary rotational axis 3. The molecule has a C4 proper rotational axis 4. The molecule has 4 C2 proper rotational axis that is perpendicular to the primary rotational axis 5. The molecule does not have a mirror plane that is perpendicular to the primary rotational axis 6. The molecule has 4 mirror planes that are parallel to the primary rotational axis 7. The molecule hence belongs to D4d point group
High Symmetry Point Groups
[edit | edit source]Molecules of high symmetry are of certain geometric shapes like Linear, Octahedral (Oh), Tetrahedral (Td), and Icosahedral (Ih) shapes. Although there are some variations in these symmetries, they are often rare in nature.
-C∞v are linear molecules with an infinite number of rotations along the primary rotation axis, and an infinite number of reflection planes containing the rotation axis. They have no center of inversion, and are usually two atom molecules.
-D∞h are also linear molecules with an infinite number of rotations along the primary axis and an infinite number of reflection planes containing the rotation axis. The three main difference from a C∞v are that a C2 axes and a reflection plane exist perpendicular to the primary axis of rotation, and an inversion center.
-Td molecules have a tetrahedral geometry (but don't always have the shape of a tetrahedral). They have 4 C3 axes, 3 C2 axes, 3 S4 axes, and 6 mirror planes. However, they lack C4 axes.
-Oh molecules are most commonly those with octahedral structure. They typically have 4 C3 rotations, 3 C4 rotations, and an inversion center
-Ih molecules are identified by their C3 and C5 axes, along with its inversion center.
Low Symmetry Point Groups
[edit | edit source]C1 is a molecule with no symmetry other than the identity operation, E. Cs is a molecule with only a mirror plane and the identity operation, E. Ci contains only an inversion center and the identity operation, E.
Examples of Specific Point Groups
[edit | edit source]| Group | Intl | Orbifold | Coxeter | Order | Description |
|---|---|---|---|---|---|
| Cn | n | nn | [n]+ | n | Cyclic: n-fold rotations. Abstract group Zn, the group of integers under addition modulo n. |
| Dn | nm | *nn | [n] | 2n | Dihedral: cyclic with reflections. Abstract group Dihn, the dihedral group. |

The subset of pure reflectional point groups, defined by 1 or 2 mirrors, can also be given by their Coxeter group and related polygons. These include 5 crystallographic groups. The symmetry of the reflectional groups can be doubled by an isomorphism, mapping both mirrors onto each other by a bisecting mirror, doubling the symmetry order.
| Reflective | Rotational | Related polygons | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Group | Coxeter group | Coxeter diagram | Order | Subgroup | Coxeter | Order | |||
| D1 | A1 | [ ] | Template:CDD | Template:CDD | 2 | C1 | []+ | 1 | Digon |
| D2 | A12 | [2] | Template:CDD | Template:CDD | 4 | C2 | [2]+ | 2 | Rectangle |
| D3 | A2 | [3] | Template:CDD | Template:CDD | 6 | C3 | [3]+ | 3 | Equilateral triangle |
| D4 | BC2 | [4] | Template:CDD | Template:CDD | 8 | C4 | [4]+ | 4 | Square |
| D5 | H2 | [5] | Template:CDD | Template:CDD | 10 | C5 | [5]+ | 5 | Regular pentagon |
| D6 | G2 | [6] | Template:CDD | Template:CDD | 12 | C6 | [6]+ | 6 | Regular hexagon |
| Dn | I2(n) | [n] | Template:CDD | Template:CDD | 2n | Cn | [n]+ | n | Regular polygon |
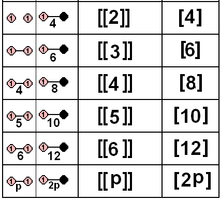
| D2×2 | A12×2 | [[2]] = [4] | Template:CDD | Template:CDD = Template:CDD | 8 | ||||
| D3×2 | A2×2 | [[3]] = [6] | Template:CDD | Template:CDD = Template:CDD | 12 | ||||
| D4×2 | BC2×2 | [[4]] = [8] | Template:CDD | Template:CDD = Template:CDD | 16 | ||||
| D5×2 | H2×2 | [[5]] = [10] | Template:CDD | Template:CDD = Template:CDD | 20 | ||||
| D6×2 | G2×2 | [[6]] = [12] | Template:CDD | Template:CDD = Template:CDD | 24 | ||||
| Dn×2 | I2(n)×2 | [[n]] = [2n] | Template:CDD | Template:CDD = Template:CDD | 4n | ||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (*) When the Intl entries are duplicated, the first is for even n, the second for odd n. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reflective subset groups
[edit | edit source]
The subset of pure reflectional point groups, defined by 1 to 3 mirror planes, can also be given by their Coxeter group and related polyhedra. The [3,3] group can be doubled, written as [[3,3]], mapping the first and last mirrors onto each other, doubling the symmetry to 48, and isomorphic to the [4,3] group.
| Schönflies | Coxeter group | Coxeter diagram | Order | Related regular and prismatic polyhedra | ||
|---|---|---|---|---|---|---|
| Td | A3 | [3,3] | Template:CDD | 24 | Tetrahedron | |
| Td×Dih1 = Oh | A3×2 = BC3 | [[3,3]] = [4,3] | Template:CDD | = Template:CDD | 48 | Stellated octahedron |
| Oh | BC3 | [4,3] | Template:CDD | 48 | Cube, octahedron | |
| Ih | H3 | [5,3] | Template:CDD | 120 | Icosahedron, dodecahedron | |
| D3h | A2×A1 | [3,2] | Template:CDD | 12 | Triangular prism | |
| D3h×Dih1 = D6h | A2×A1×2 | [[3],2] | Template:CDD | = Template:CDD | 24 | Hexagonal prism |
| D4h | BC2×A1 | [4,2] | Template:CDD | 16 | Square prism | |
| D4h×Dih1 = D8h | BC2×A1×2 | [[4],2] = [8,2] | Template:CDD | = Template:CDD | 32 | Octagonal prism |
| D5h | H2×A1 | [5,2] | Template:CDD | 20 | Pentagonal prism | |
| D6h | G2×A1 | [6,2] | Template:CDD | 24 | Hexagonal prism | |
| Dnh | I2(n)×A1 | [n,2] | Template:CDD | 4n | n-gonal prism | |
| Dnh×Dih1 = D2nh | I2(n)×A1×2 | [[n],2] | Template:CDD | = Template:CDD | 8n | |
| D2h | A13 | [2,2] | Template:CDD | 8 | Cuboid | |
| D2h×Dih1 | A13×2 | [[2],2] = [4,2] | Template:CDD | = Template:CDD | 16 | |
| D2h×Dih3 = Oh | A13×6 | [3[2,2]] = [4,3] | Template:CDD | = Template:CDD | 48 | |
| C3v | A2 | [1,3] | Template:CDD | 6 | Hosohedron | |
| C4v | BC2 | [1,4] | Template:CDD | 8 | ||
| C5v | H2 | [1,5] | Template:CDD | 10 | ||
| C6v | G2 | [1,6] | Template:CDD | 12 | ||
| Cnv | I2(n) | [1,n] | Template:CDD | 2n | ||
| Cnv×Dih1 = C2nv | I2(n)×2 | [1,[n]] = [1,2n] | Template:CDD | = Template:CDD | 4n | |
| C2v | A12 | [1,2] | Template:CDD | 4 | ||
| C2v×Dih1 | A12×2 | [1,[2]] | Template:CDD | = Template:CDD | 8 | |
| Cs | A1 | [1,1] | Template:CDD | 2 | ||
Representations
[edit | edit source]Irreducible representation is used to create a character table for that point group.
-A value of 1 means that the symmetry does not change its orbital position
-A value of 0 means the operation changes orbital's position
-A value of -1 means the orbital does not change its symmetry but inverts its sign.
Reducible representation is simply a combination of irreducible representations.
Character Table
[edit | edit source]Character tables are designated by these characters which means different operations.
-x,y,x is the transformation of the x,y,z coordinates
-Rx, Ry, Rz is the rotation about the x, y, z axes
-R is any symmetry operation like C2
-X is the character of operation
-i, j is the designation of different representations such as A1 or A2
-h is the total number of symmetry operations in the group (order)
References
[edit | edit source]- ↑ Point groups, November 14th, 2012.
- ↑ pointgroup, October 28, 2012
- ↑ The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [1]
http://en.wikipedia.org/wiki/Point_group
Miessler, Gary. Inorganic Chemistry. 4th Edition.