Sensory Systems/Computer Models/Auditory System Simulation
Computer Simulations of the Auditory System
[edit | edit source]Working with Sound
[edit | edit source]Audio signals can be stored in a variety of formats. They can be uncompressed or compressed, and the encoding can be open or proprietary. On Windows systems, the most common format is the WAV-format (w: WAV). It contains a header with information about the number of channels, sample rate, bits per sample etc. This header is followed by the data themselves. The usual bitstream encoding is the linear pulse-code modulation (LPCM, (w: Pulse-code_modulation) format.
Many programing languages provide commands for reading and writing WAV-files. When working with data in other formats, you have two options:
- You can either you convert them into WAV-format, and go on from there. A very comprehensive free cross-platform solution to record, convert and stream audio and video is ffmpeg (http://www.ffmpeg.org/).
- Or you can obtain special programs moduls for reading/writing the desired format.
Reminder of Fourier Transformations (w:Fourier_transform)
[edit | edit source]To transform a continuous function, one uses the Fourier Integral:
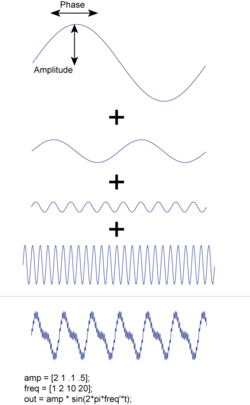
where k represents frequency. Note that F(k) is a complex value: its absolute value gives us the amplitude of the function, and its phase defines the phase-shift between cosine and sine components.
The inverse transform is given by
If the data are sampled with a constant sampling frequency and there are N data points,
The coefficients Fn can be obtained by
Since there are a discrete, limited number of data points and with a discrete, limited number of waves, this transform is referred to as Discrete Fourier Transform (DFT). The Fast Fourier Transform (FFT) is just a special case of the DFT, where the number of points is a power of 2: .
Note that each is a complex number: its magnitude defines to the amplitude of the corresponding frequency component in the signal; and the phase of defines the corresponding phase (see illustration). If the signal in the time domain "f(t)" is real valued, as is the case with most measured data, this puts a constraint on the corresponding frequency components: in that case we have
A frequent source of confusion is the question: “Which frequency corresponds to ?” If there are N data points and the sampling period is , the frequency is given by
In other words, the lowest frequency is [in Hz], while the highest independent frequency is due to the Nyquist-Shannon theorem. Note that in MATLAB, the first return value corresponds to the offset of the function, and the second value to n=1!
Spectral Analysis of Biological Signals
[edit | edit source]Power Spectrum of Stationary Signals
[edit | edit source]Most FFT functions and algorithms return the complex Fourier coefficients . If we are only interested in the magnitude of the contribution at the corresponding frequency, we can obtain this information by
This is the power spectrum of our signal, and tells us how big the contribution of the different frequencies is.
Power Spectrum of Non-stationary Signals
[edit | edit source]Often one has to deal with signals that are changing their characteristics over time. In that case, one wants to know how the power spectrum changes with time. The simplest way is to take only a short segment of data at a time, and calculate the corresponding power spectrum. This approach is called Short Time Fourier Transform (STFT). However in that case edge effects can significantly distort the signals, since we are assuming that our signal is periodic.
To eliminate edge artifacts, the signals can be filtered, or "windowed" (w: Window_function). An examples of such a window is shown in the figure above. While some windows provide better frequency resolution (e.g. the rectangular window), others exhibit fewer artifacts such as spectral leakage (e.g. Hanning window). For a selected section of the signal, the data resulting from windowing are obtained by multiplying the signal with the window (left Figure):

|

|
An example can show how cutting a signal, and applying a window to it, can affect the spectral power distribution, is shown in the right figure above. (The corresponding Python code can be found at [1] ) Note that decreasing the width of the sample window increases the width of the corresponding powerspectrum!
Stimulation strength for one time window
[edit | edit source]To obtain the power spectrum for one selected time window, the first step is to calculate the power spectrum through the Fast Fourier Transform (FFT) of the time signal. The result is the sound intensity in frequency domain, and the corresponding frequencies. The second step is to concentrate those intensities on a few distinct frequencies ("binning"). The result is a sound signal consisting of a few distinct frequencies - the location of the electrodes in the simulated cochlea. Back conversion into the time domain gives the simulated sound signal for that time window.
The following Python function does sound processing on a given signal.
import numpy as np
def pSpect(data, rate):
'''Calculation of power spectrum and corresponding frequencies, using a Hamming window'''
nData = len(data)
window = np.hamming(nData)
fftData = np.fft.fft(data*window)
PowerSpect = fftData * fftData.conj() / nData
freq = np.arange(nData) * float(rate) / nData
return (np.real(PowerSpect), freq)
def calc_stimstrength(sound, rate=1000, sample_freqs=[100, 200, 400]):
'''Calculate the stimulation strength for a given sound'''
# Calculate the powerspectrum
Pxx, freq = pSpect(sound, rate)
# Generate matrix to sum over the requested bins
num_electrodes = len(sample_freqs)
sample_freqs = np.hstack((0, sample_freqs))
average_freqs = np.zeros([len(freq), num_electrodes])
for jj in range(num_electrodes):
average_freqs[((freq>sample_freqs[jj]) * (freq<sample_freqs[jj+1])),jj] = 1
# Calculate the stimulation strength (the square root has to be taken, to get the amplitude)
StimStrength = np.sqrt(Pxx).dot(average_freqs)
return StimStrength
Sound Transduction by Pinna and Outer Ear
[edit | edit source]The outer ear is divided into two parts: the visible part on the side of the head (the pinna), and the external auditory meatus (outer ear canal) leading to the eardrum, as shown in the figure below. With such a structure, the outer ear contributes the ‘spectral cues’ for people’s sound localization abilities, making people not only have the ability to detect and identify a sound, but also have the ability to localize a sound source. [2]

Pinna Function
[edit | edit source]The Pinna’s cone shape enables it to gather sound waves and funnel them into the out ear canal. On top of that, its various folds make the pinna a resonant cavity which amplifies certain frequencies. Furthermore, the interference effects resulting from the sound reflection caused by the pinna are directionally dependent and will attenuate other frequencies. Therefore, the pinna could be simulated as a filter function applied to the incoming sound, modulating its amplitude and phase spectra.

The resonance of the pinna cavity can be approximated well by 6 normal modes [4]. Among these normal modes, the first mode, which mainly depends on the concha depth (i.e. the depth of the bowl-shaped part of the pinna nearest the ear canal), is the dominant one.
The cancellation of certain frequencies caused by the pinna reflection is called “pinna notch”. [4] As shown in the right figure [3], sound transmitted by the pinna goes through two paths, a direct path and a longer reflected path. The different paths have different length, and thereby produce phase differences. When the frequency of incoming sound signal reaches certain criterion, which is that the path difference is half of the sound wavelength, the interference of sounds via direct and reflected paths will be destructive. This phenomenon is called “pinna notch”. Normally the notch frequency could happen in the range from 6k Hz to 16k Hz depending on the pinna shape. It is also seen that the frequency response of pinna is directionally dependent. This makes the pinna contribute to the spatial cues for sound localization.
Ear Canal Function
[edit | edit source]The outer ear canal is approximately 25 mm long and 8 mm in diameter, with a tortuous path from the entrance of the canal to the eardrum. The outer ear canal can be modeled as a cylinder closed at one end which leads to a resonant frequency around 3k Hz. This way the outer ear canal amplifies sounds in a frequency range important for human speech. [5]
Simulation of Outer Ear
[edit | edit source]Based on the main functions of the outer ear, it is easy to simulate the sound transduction by the pinna and outer ear canal with a filter, or a filter bank, if we know the characteristics of the filter.
Many researchers are working on the simulation of human auditory system, which includes the simulation of the outer ear. In the next chapter, a Pinna-Related Transfer Function model is first introduced, followed by two MATLAB toolboxes developed by Finnish and British research groups, respectively.
Model of Pinna-Related Transfer Function by Spagnol
[edit | edit source]This part is entirely from the paper published by S.Spagnol, M.Geronazzo, and F.Avanzini. [6] In order to model the functions of the pinna, Spagnol developed a reconstruction model of the Pinna-Related Transfer Function (PRTF), which is a frequency response characterizing how sound is transduced by the pinna. This model is composed by two distinct filter blocks, accounting for resonance function and reflection function of the pinna respectively, as shown in the figure below.

There are two main resonances in the interesting frequency range of the pinna[6], which can be represented by two second-order peak filters with fixed bandwidth [7]:
where
and is the sampling frequency, the central frequency, and the notch depth.
For the reflection part, three second-order notch filters of the form [8] are designed with the parameters including center frequency , notch depth , and bandwidth .
where is the same as previously defined for the resonance function, and
each accounting for a different spectral notch.
By cascading the three in-series placed notch filters after the parallel two peak filters, an eighth-order filter is designed to model the PRTF.
By comparing the synthetic PRTF with the original one, as shown in the figures below, Spagnol concluded that the synthesis model for PRTF was overall effective. This model may have missing notches due to the limitation of cutoff frequency. Approximation errors may also be brought in due to the possible presence of non-modeled interfering resonances.

HUTear MATLAB Toolbox
[edit | edit source]
HUTear is a MATLAB Toolbox for auditory modeling developed by Lab of Acoustics and Audio Signal Processing at Helsinki University of Technology [9]. This open source toolbox could be downloaded from here. The structure of the toolbox is shown in the right figure.
In this model, there is a block for “Outer and Middle Ear” (OME) simulation. This OME model is developed on the basis of Glassberg and Moor [10]. The OME filter is usually a linear filter. Auditory filter is generated with taking the "Equal Loudness Curves at 60 dB"(ELC)/"Minimum Audible Field"(MAF)/"Minimum Audible Pressure at ear canal"(MAP) correction into account. This model accounts for the outer ear simulation. By specifying different parameters with the "OEMtool", you may compare the MAP IIR approximation and MAP data, as shown in the figure below.

MATLAB Model of the Auditory Periphery (MAP)
[edit | edit source]MAP is developed by researchers in the Hearing Research Lab at University of Essex, England [11]. Being a computer model of physiological basis of human hearing, MAP is an open-source code package for testing, developing the model, which could be downloaded from here. Its model structure is shown in the right figure.

Within the MAP model, there is the “Outer Middle Ear (OME)” sub-model, allowing the user to test and create an OME model. In this OME model, the function of the outer ear is modeled as a resonance function. The resonances are composed by two parallel bandpass filters, respectively, representing concha resonance and outer ear canal resonance. These two filters are specified by the pass frequency range, gain and order. By adding the output of resonance filters to the original sound pressure wave, the output of the outer ear model is obtained.
To test the OME model, run the function named “testOME.m”. A figure plotting the external ear resonances and stapes peak displacement will be displayed. (as shown in the figure below)

Summary
[edit | edit source]The outer ear, including pinna and outer ear canal, can be simulated as a linear filter, or a filter bank. This reflects its resonance and reflection effect to incoming sound. It is worth noting that since the pinna shape varies from person to person, the model parameters, like the resonant frequencies, depend on the subject.
One aspect not included in the models described above is the Head-Related Transfer Function(HRTF). The HRTF describes how an ear receives a sound from a point sound source in space. It is not introduced here because it goes beyond the effect of the outer ear (pinna and outer ear canal) as it is also influenced by the effects of head and torso. There are plenty of literature and publications for HRTF for the interested reader.(wiki, tutorial 1,2, reading list for spatial audio research including HRTF)
Simulation of the Inner Ear
[edit | edit source]The shape and organisation of the basilar membrane means that different frequencies resonate particularly strongly at different points along the membrance. This leads to a tonotopic organisation of the sensitivity to frequency ranges along the membrane, which can be modeled as being an array of overlapping band-pass filters known as "auditory filters".[12] The auditory filters are associated with points along the basilar membrane and determine the frequency selectivity of the cochlea, and therefore the listener’s discrimination between different sounds.[13] They are non-linear, level-dependent and the bandwidth decreases from the base to apex of the cochlea as the tuning on the basilar membrane changes from high to low frequency.[13][14] The bandwidth of the auditory filter is called the critical bandwidth, as first suggested by Fletcher (1940). If a signal and masker are presented simultaneously then only the masker frequencies falling within the critical bandwidth contribute to masking of the signal. The larger the critical bandwidth the lower the signal-to-noise ratio (SNR) and the more the signal is masked.

Another concept associated with the auditory filter is the "equivalent rectangular bandwidth" (ERB). The ERB shows the relationship between the auditory filter, frequency, and the critical bandwidth. An ERB passes the same amount of energy as the auditory filter it corresponds to and shows how it changes with input frequency.[13] At low sound levels, the ERB is approximated by the following equation according to Glasberg and Moore:[13]
where the ERB is in Hz and F is the centre frequency in kHz.
It is thought that each ERB is the equivalent of around 0.9mm on the basilar membrane.[13][14]
Gammatone Filters
[edit | edit source]
One filter type used to model the auditory filters is the "gammatone filter". It provides a simple linear filter for describing the movement of one location of the basilar membrane for a given sound input, which is therefore easy to implement. Linear filters are popular for modeling different aspects of the auditory system. In general, they are IIR-filters (infinite impulse response) incorporating feedforward and feedback, which are defined by
where a1=1. In other words, the coefficients ai and bj uniquely determine this type of filter. The feedback-character of these filters can be made more obvious by re-shuffling the equation
(In contrast, FIR-filters, or finite impulse response filters, only involve feedforward: for them for i>1.)

Linear filters cannot account for nonlinear aspects of the auditory system. They are nevertheless used in a variety of models of the auditory system. The gammatone impulse response is given by
where is the frequency, is the phase of the carrier, is the amplitude, is the filter's order, is the filter's bandwidth, and is time.
This is a sinusoid with an amplitude envelope which is a scaled gamma distribution function.
Variations and improvements of the gammatone model of auditory filtering include the gammachirp filter, the all-pole and one-zero gammatone filters, the two-sided gammatone filter, and filter cascade models, and various level-dependent and dynamically nonlinear versions of these.[15]
For computer simulations, efficient implementations of gammatone models are available for Matlab and for Python[16] .
When working with gammatone filters, we can elegantly exploit Parseval's Theorem to determine the energy in a given frequency band:
Perceptual Audio Coding and Filtering Properties of the Cochlea
[edit | edit source]On this page the principle mechanisms of perceptual audio coding are reviewed. The underlying psychoacoustic principles are explained and the relation to the filtering properties of the cochlea and higher cortical processing stages are pointed out.
Perceptual Audio Coding
[edit | edit source]Mp3 (MPEG-1 Layer 3, predecessor of MPEG-2 and MPEG-4 Advanced Audio Coding (AAC)) is probably still the best known audio format that exploits perceptual coding of audio signals. AAC is a more efficient extension, generally achieves better sound quality, allows for a wider range of bandwidths but relies on the same coding principles than Mp3. Both formats are standardized by ISO and IEC but only the decoder is fully specified and the encoder implementation is left open. This led to a variety of available encoders differing in reproduction quality, achievable bit-rate, performance and coding efficiency [17].
In contrast to classical signal compression algorithms, where the goal is to represent information with a minimum number of bits while maintaining signal reproduction quality, perceptual audio coding takes into account knowledge from the human auditory system and reduces bit rate by removing information that is perceptually irrelevant for most listeners. This lossy compression is achieved by exploring properties of the human auditory system and statistical redundancies. A commonly used coding bitrate for Mp3 is 128 kbit/s and efficient encoders typically achieve a factor around 10 in data reduction, when compressing CD-quality audio (16 bit PCM, 44.1 kHz, ≈ 1411 kBit/s). To state it differently, around 90 % of the data stored on a CD can not be perceived by the listener. CD-quality is what users typically expect when listening to music (There is a long debate if CD-quality is good enough to reproduce the analog original audio. Among many different expert opinions, these two references[17][18] might be of interest for further reading.). The requirement for more efficient audio coding arose from network, multimedia system and storage applications and Mp3 was originally created for the more efficient transmission of audiovisual content.
The theoretical limit of perceptual audio coding was investigated by Johnston[19], which led to the notion of perceptual entropy. Based on measurements the perceptual entropy was estimated around 2 bits per sample for CD-quality audio. State-of-the-art encoders confirm such an efficiency for transparent (near) CD-quality audio coding[20]. The quality of a perceptual coding algorithm is typically evaluated by listening tests and more recently also in combination with a standardized algorithm for the objective measurement of perceived audio quality called Perceptual Evaluation of Audio Quality (PEAQ).
Basic Architecture of a Perceptual Audio Encoder
[edit | edit source]
Most perceptual audio encoders can be described with the basic architecture shown in the figure. The analysis filter bank approximates the temporal and spectral analysis properties of the human auditory system. The input is segmented into frames, which are transformed into a set of parameters that can be quantized and encoded. The quantization and coding stage exploits statistical redundancies and relies on thresholds that are delivered by the perceptual model for bit allocation and quantization noise shaping. The perceptual model describes masking thresholds as a function of frequency for coding. Finally, the encoding stage uses standard lossless coding techniques, such as Huffman Coding. For a technical algorithm explanation and example implementation I refer to the online books of J.O. Smith.
Psychoacoustic Principles Used for Perceptual Audio Coding
[edit | edit source]The basic idea of perceptual audio coding is to shape the quantization noise such that it is masked by the audio signal itself and therefore not perceivable by the listener. This is achieved by exploiting psychoacoustic principles including the threshold of absolute hearing, critical band frequency analysis and auditory masking[20]. As the playback level is often unknown at the coding stage, typically conservative estimates regarding the absolute hearing threshold are used for signal normalization during the coding procedure. Auditory masking describes phenomena, where the perception of one sound is affected by the presence of another sound. Masking effects occur in frequency domain (simultaneous masking), as well as in time domain (non-simultaneous masking).
Simultaneous Masking
[edit | edit source]
For simultaneous masking the frequency resolution of the cochlea plays a central role. Inside the cochlea a frequency-to-place transformation takes place and distinct regions tuned to different frequency bands are created. These distinct frequency regions are called critical bands of hearing (or critical bandwidth). The critical bandwidth tends to remain constant ≈ 100 Hz up to 500 Hz and increases to approx 20 % of center frequency above 500 Hz.[20] The first 24 critical bands are described by the Bark scale. The presence of a tone leads to an excitation of the basilar membrane, which affects the detection threshold for a second tone inside its critical band (intra-band masking). In addition, also neighboring bands are affected (inter-band masking). The affection of neighboring bands is described by the spreading function. A measured spreading function for a critical-band noise masker of varying intensity is shown in the figure on the right hand side. As illustrated in the figure, a masker is more efficient in masking higher frequency bands than lower frequency bands, which is referred as the upward spread of masking. The cause of the spreading function is supposed to be a byproduct of the mechanical filter property of the cochlea, where the outer hair cells amplify the motion of the basilar membrane in order to increase frequency resolution[21]. The reason for the upward spread of masking is not clearly identified and in addition to mechanical excitation also suppression plays a role[22]. Further, as the second peak in the figure arises around 2 kHz (the second harmonic of 1 kHz) at higher sound pressure levels also the nonlinear transfer characteristic of the inner and middle ear play a role[21].
The presence of a strong noise or tone masker creates thus an excitation that is sufficient in strength on the basilar membrane to effectively block transmission of a weaker signal in its critical band and by the spread of masking also neighbouring bands are affected. Two types of simultaneous maskers have been observed: Noise-Masking-Tone and Tone-Masking-Noise. For a noise-masking-tone the presence of a tone allows to predict a threshold for the noise spectrum that is masked and for the tone-masking-noise the presence of a noise allows to predict a threshold for the tone that is masked. Different thresholds have been reported for pure tones and critical-band limited noise.[20] Regarding the perceptual coding of music, these thresholds are interpolated depending on the content of the time-frequency analysis of the perceptual encoder before the spreading function is taken into account. The objective signal-to-noise ratio (SNR) can be very low, e.g. 20 dB, but depends on the audio content, while the subjective SNR is high enough to achieve transparent coding.[21] For comparison an audio CD has a SNR of 96 dB.
Non-simultaneous masking
[edit | edit source]
Abrupt transients (or strong attacks) in audio signals can cause masking effects in time domain. The perception before (pre- or backward masking) as well as after the transient (post- or forward masking) is affected, as illustrated in the figure. The backward masking region lasts in the order of milliseconds and the forward masking region lasts longer and is in the order of tenths of milliseconds[20].
Temporal masking is still not fully understood and an active research topic. However, there is evidence that higher cortical processing is involved in this phenomena. It remains unclear if this effect is related to the integration of sounds, interruption or inhibition of neural processing and/or differences in the transmission velocities. Forward and backward masking show different characteristics and are therefore supposed to arise from different properties of the human auditory system[23].
Masking and joint stereo coding
[edit | edit source]An efficient technique common in audio coding is joint stereo coding. As the left and the right audio channels for a music signal are typically highly correlated it is sometimes more efficient to do sum/difference (L-R, L+R) coding of the audio signal. In the case of Mp3 the potential of sum/difference coding was not fully exploited, an efficient technique would compare the thresholds for left/right and sum/difference coding and dynamically chose the more efficient one. Special care has to be taken when calculating the masking thresholds, because joint channel coding can cause audible artifacts due to binaural listening.[21]
Artifacts (w: Compression_artifact)
[edit | edit source]For Mp3 and AAC the coding bit rate is chosen and not a compression factor, because the compression factor is content dependent. A lower bit rate yields to a higher compression ratio and a higher bit rate leads to a lower compression ratio with lower probability of possible artifacts. This leads to working regions (or bit rates), where a particular algorithm performs best and just improves slightly for higher bit rates.[17] In contrast to noise and distortion artifacts from playback equipment, which we are all used to when listening to CDs, audible artifacts from perceptual encoders can be annoying. If the bit rate is too low for transparent coding the resulting noise and distortions can be described as a time-varying signal, where distortions are not harmonically related, noise is band-limited and as bandwidth might change from frame to frame the signal can sound rough.[17]
Loss of Bandwidth
[edit | edit source]If the encoder runs out of bits there is a basic tradeoff between frequency bandwidth and accurate coding of lower frequency content. This can lead to a coded frequency bandwidth that changes from frame to frame that can sound very unpleasing. Generally this artifact is counteracted by limiting the frequency bandwidth for low bit rates.
Preecho
[edit | edit source]Preecho is the most difficult error to avoid and is related to the frame size of the perceptual encoder. If a strong attack of an audio signal occurs in the middle of a frame the calculated threshold for the noise might spread over the backward masking region due to the frame size and thus become audible. There are various techniques to minimize the occurrence of preechos, such as a variable frame size analysis filterbank.[17]
Relation to the Filtering Properties of the Cochlea
[edit | edit source]To sum up and conclude, perceptual coding makes extensive use of the properties of the human auditory system. The absolute hearing threshold is related to properties of the cochlea but also to acoustic and mechanic properties of the middle and outer ear. In simultaneous masking intra- and inter-critical band masking thresholds (the spreading function) arise from the filtering properties of the cochlea. However, the upward spread of masking can not only be explained by the properties of the cochlea and other phenomena such as suppression might play a role. Finally, the phenomena of temporal masking can only be explained by higher cortical processing in the auditory system and also artifacts that can arise from joint stereo coding and thus involve binaural listening for detection suggest that various stages of the human auditory system are involved.
- ↑ T. Haslwanter (2012). "Short Time Fourier Transform [Python]". private communications.
- ↑ Semple, M.N. (1998), "Auditory perception: Sounds in a virtual world", Nature, Nature Publishing Group, 396 (6713): 721–724, doi:10.1038/25447
- ↑ a b http://tav.net/audio/binaural_sound.htm
- ↑ a b Shaw, E.A.G. (1997), "Acoustical features of the human ear", Binaural and spatial hearing in real and virtual environments, Mahwah, NJ: Lawrence Erlbaum, 25: 47
- ↑
Federico Avanzini (2007–2008), Algorithms for sound and music computing, Course Material of Informatica Musicale (http://www.dei.unipd.it/~musica/IM06/Dispense06/4_soundinspace.pdf), p. 432
{{citation}}: External link in|title= - ↑ a b c d Spagnol, S. and Geronazzo, M. and Avanzini, F. (2010), "Structural modeling of pinna-related transfer functions", In Proc. Int. Conf. on Sound and Music Computing (SMC 2010), barcelona, p. 422-428
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ S. J. Orfanidis, ed., Introduction To Signal Processing. Prentice Hall, 1996.
- ↑ U. Zölzer, ed., Digital Audio Effects. New York, NY, USA: J.Wiley & Sons, 2002.
- ↑ http://www.acoustics.hut.fi/software/HUTear/
- ↑
Glasberg, B.R. and Moore, B.C.J. (1990), "Derivation of auditory filter shapes from notched-noise data", Hearing research, Elsevier, 47 (1–2): 103–138
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ http://www.essex.ac.uk/psychology/department/research/hearing_models.html
- ↑
Munkong, R. (2008), IEEE Signal Processing Magazine, vol. 25, no. 3, pp. 98--117, Bibcode:2008ISPM...25...98M, doi:10.1109/MSP.2008.918418
{{citation}}: Missing or empty|title=(help) - ↑ a b c d e f Moore, B. C. J. (1998). Cochlear hearing loss. London: Whurr Publishers Ltd. ISBN 0585122563.
- ↑ a b Moore, B. C. J. (1986), "Parallels between frequency selectivity measured psychophysically and in cochlear mechanics", Scand. Audio Suppl., no. 25, pp. 129–52
- ↑
R. F. Lyon, A. G. Katsiamis, E. M. Drakakis (2010). "History and Future of Auditory Filter Models" (PDF). Proc. ISCAS. IEEE.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ↑ T. Haslwanter (2011). "Gammatone Toolbox [Python]". private communications.
- ↑ a b c d e Karlheinz Brandenburg. Mp3 and aac explained. In Audio Engineering Society Conference: 17th International Conference: High-Quality Audio Coding. Audio Engineering Society, 1999.
- ↑ J. R. Stuart for Acoustic Renaissance for Audio. A proposal for the high-quality audio application of high-density CD carriers. 1995.
- ↑ James D Johnston. Estimation of perceptual entropy using noise masking criteria. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing of the IEEE 1988.
- ↑ a b c d e Ted Painter and Andreas Spanias. A review of algorithms for perceptual coding of digital audio signals. In Proceedings of the 13th International Conference on Digital Signal Processing of the IEEE 1997.
- ↑ a b c d e f Nikil Jayant, James Johnston, and Robert Safranek. Signal compression based on models of human perception. Proceedings of the IEEE, 81(10):1385-1422, 1993.
- ↑ Andrew J Oxenham and Christopher J Plack. Suppression and the upward spread of masking. The Journal of the Acoustical Society of America, 104(6):3500-3510, 1998.
- ↑ Renata Filippini. Unmasking auditory temporal masking, 2015. http://hearinghealthmatters.org/pathways/2015/unmasking-auditory-temporal-masking/
Human Speech
[edit | edit source]Vocal Tract
[edit | edit source]The human voice is generated by the vocal tract. While talking seems to be effortless, it requires a sophisticated motor coordination of lungs, tongue, palate, lips and teeth. On a cortical level, this motor coordination happens in Broca's Area.

Terminology
[edit | edit source]Loudness
[edit | edit source]The intensity of sound is typically expressed in deciBel (dB), defined as
where SPL = “sound pressure level” (in dB), and the reference pressure is . Note that this is much smaller than the air pressure (ca. 105 N/m2)! Also watch out, because sound is often expressed relative to "Hearing Level" instead of SPL.
- 0 - 20 dB SPL ... hearing level (0 dB for sinusoidal tones, from 1 kHz – 4 kHz)
- 60 dB SPL ... medium loud tone, conversational speech
Fundamental frequency, from the vibrations of the vocal cords in the larynx, is about 120 Hz for adult male, 250 Hz for adult female, and up to 400 Hz for children.

Formants
[edit | edit source]Formants are the dominant frequencies in human speech, and are caused by resonances of the signals from the vocal cord in our mouth etc. Formants show up as distinct peaks of energy in the sound's frequency spectrum. They are numbered in ascending order starting with the format at the lowest frequency.


Phonemes
[edit | edit source]Speech is often considered to consist of a sequence of acoustic units called phons, which correspond to linguistic units called phonemes. Phonemes are the smallest units of sound that allows different words to be distinguished. The word "dog", for example, contains three phonemes. Changes to the first, second, and third phoneme respectively produce the words "log", "dig", and "dot". English is said to contain 40 different phonemes, specified as in /d/, /o/, /g/ for the word "dog".
Speech Perception
[edit | edit source]The ability of humans to decode speech signals still easily exceeds that of any algorithm developed so far. While automatic speech recognition has become fairly successful in recognizing clearly spoken speech in environments with high Signal-to-noise ratio, once the conditions become a bit less than ideal, recognition algorithms tend to perform vary poorly compared to humans. It seems from this that our computer speech recognition algorithms have not yet come close to capturing the underlying algorithm that humans use to recognize speech.
Evidence has shown that the perception of speech takes quite a different route than the perception of other sounds in the brain. While studies on non-speech sound responses have generally found response to be graded with stimulus, speech studies have repeatedly found a discretization of response when a graded stimulus is presented. For instance, Lisker and Abramson,[1] played a pre-voiced 'b/p' sound. Whether the sound is interpreted as a /b/ or a /p/ depends on the voice onset time (VOT). They found that when smoothly varying the VOT, there was a sharp change (at ~20ms after the consonant is played) where subjects switched their identification from /b/ to /p/. Furthermore, subjects had a great deal of difficulty differentiating between two sounds in the same category (e.g. pairs of sounds with a VOTs of -10ms to 10m, which would both be /b/'s, than sounds with a 10ms to 30ms, which would be identified as a b and a p). This shows that some type of categorization scheme is going on. One of the main problems encountered when trying to build a model of speech perception is the so-called 'Lack of Invariance', which could more straightforwardly just be stated as the 'variance'. This term refers to the fact that a single phoneme (e.g. /p/ as in sPeech or Piety), has a great variety of waveforms that map to it, and that the mapping between an acoustic waveform and a phoneme is far from obvious and heavily context-dependent, yet human listeners reliably give the correct result. Even when the context is similar, a waveform will show a great deal of variance due to factors such as the pace of speech, the identity of the speaker and the tone in which he is speaking. So while there is no agreed-upon model of speech perception, the existing models can be split into two classes: Passive Perception and Active perception.
Passive Perception Models
[edit | edit source]Passive perception theories generally describe the problem of speech perception in the same way that most sensory signal-processing algorithms do: Some raw input signal goes in, and is processed though a hierarchy where each subsequent step extracts some increasingly abstract signal from the input. One of the early examples of a passive model was distinctive feature theory. The idea is to identify the presence of sets of binary values for certain features. For example, 'nasal/oral', 'vocalic/non-vocalic'. The theory is that a phoneme is interpreted as a binary vector of the presence or absence of these features. These features can be extracted from the spectrogram data. Other passive models, such as those described by Selfridge[2] and Uttley,[3] involve a kind of template-matching, where a hierarchy of processing layers extract features that are increasingly abstract and invariant to certain irrelevant features (such as identity of the speaker when classifying phonemes).
Active Perception Models
[edit | edit source]An entirely different take on speech perception are active-perception theories. These theories make the point that it would be redundant for the brain to have two parallel systems for speech perception and speech production, given that the ability produce a sound is so closely tied with the ability to identify it - proponents of these theories argue that it would be wasteful and complicated to maintain two separate databases-one containing the programs to identify phonemes, and another to produce them. They argue that speech perception is actually done by attempting to replicate the incoming signal, and thus using the same circuits for phoneme production as for identification. The Motor Theory of speech perception (Liberman et al., 1967), states that speech sounds are identified not by any sort of template matching, but by using the speech-generating mechanisms to try and regenerate a copy of the speech signal. It states that phonemes should not be seen as hidden signals within the speech, but as “cues” that the generating mechanism attempts to reproduce in a pre-speech signal. The theory states that speech-generating regions of the brain learn which speech-precursor signals will produce which sounds by the constant feedback loop of always hearing one's own speech. The babbling of babies, it is argued, is a way of learning this how to generate these “cue” sounds from pre-motor signals.[4]
A similar idea is proposed in the analysis-by-synthesis model, by Stevens and Halle.[5] This describes a generative model which attempts to regenerate a similar signal to the incoming sound. It essentially takes advantage of the fact that speech-generating mechanisms are similar between people, and that the characteristic features that one hears in speech can be reproduced by the speaker. As the speaker hears the sound, the speech centers attempt to generate the signal that's coming in. Comparators give constant feedback on the quality of the regeneration. The 'units of perception', are therefore not so much abstractions of the incoming sound, as pre-motor commands for generating the same speech.
Motor theories took a serious hit when a series of studies on what is now known as Broca's Aphasia were published. This condition impairs one's ability to produce speech sounds, without impairing the ability to comprehend them, whereas motor theory, taken in its original form, states that production and comprehension are done by the same circuits, so impaired speech production should imply impaired speech comprehension. The existence of Broca's aphasia appears to contradicts this prediction.[6]
Current Models
[edit | edit source]One of the most influential computational models of speech perception is called TRACE.[7] TRACE is a neural-network-like model, with three layers and a recurrent connection scheme. The first layer extracts features from an input spectrogram in temporal order, basically simulating the cochlea. The second layer extracts phonemes from the feature information, and the third layer extracts words from the phoneme information. The model contains feed-forward (bottom-up) excitatory connections, lateral inhibitory connections, and feedback (top-down) excitatory connections. In this model, each computational unit corresponds to some unit of perception (e.g. the phoneme /p/ or the word "preposterous"). The basic idea is that, based on their input, units within a layer will compete to have the strongest output. The lateral inhibitory connections result in a sort of winner-takes-all circuit, in which the unit with the strongest input will inhibit its neighbors and become the clear winner. The feedback connections allow us to explain the effect of context-dependent comprehension - for example, suppose the phoneme layer, based on its bottom-up inputs, could not decide whether it had heard a /g/ or a /k/, but that the phoneme was preceded by 'an', and followed by 'ry'. Both the /g/ and /k/ units would initially be equally activated, sending inputs up to the word level, which would already contain excited units corresponding to words such as 'anaconda', 'angry', and 'ankle', which had been activated by the preceding 'an'. The excitement of the /g/ or /k/
References
[edit | edit source]- ↑ Lisker, L. (1970). "The voicing dimension: Some experiments in comparative phonetics". Proceedings of the 6th International Congress of Phonetic Sciences. Prague: Academia.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help); Unknown parameter|editors=ignored (|editor=suggested) (help) - ↑ Selfridge, O.C (1959) "Pandemonium: a paradigm for learning". in Proceedings of the Symposium on Mechanisation of Thought Process. National Physics Laboratory.
- ↑ Uttley, A.M. (July 1966). "The transmission of information and the effect of local feedback in theoretical and neural networks". Brain Research. 2 (1): 21–50. doi:10.1016/0006-8993(66)90060-6.
- ↑ Liberman, M. T.; Mattingly, I. G.; Turvey (1967). "Language codes and memory codes". In Melton, A. W.; Martin, E. (eds.). Coding Processes in Human Memory. V. H. Winston & Sons. pp. 307–334.
{{cite book}}: More than one of|first1=and|first=specified (help) - ↑ Stevens, K. N.; Halle, M. (1967). "Remarks on analysis by synthesis and distinctive features". In Wathen-Dunn, W. (ed.). Models for the perception of speech and visual form: proceedings of a symposium. Cambridge, MA: MIT Press. pp. 88–102.
- ↑ Hickok, Gregory (January 2010). "The role of mirror neurons in speech and language processing". Brain and Language. 112 (1): 1–2. doi:10.1016/j.bandl.2009.10.006.
- ↑ McClelland, James L; Elman, Jeffrey L (January 1986). "The TRACE model of speech perception". Cognitive Psychology. 18 (1): 1–86. doi:10.1016/0010-0285(86)90015-0.










































