General Mechanics/Print Version

Newton's Laws: First principles

The fundamental idea of kinematics is the discussion of the movement of objects, without actually taking into account what caused the movement to occur. By using simple calculus, we can find all of the equations for kinematics. To simplify the learning process, we will only consider objects that move with constant acceleration. For the first few parts, we will also assume that there is no friction or air resistance acting on the objects.

Straight Line Motion (SLM)

The name of this section Straight Line Motion means that we begin learning about the subject of kinematics by observing motion in one dimension. This means that we will only take one axis of a 3D $(x,y,z)$ coordinate system into account. We will be using the $x$ axis as our axis of motion.

Throughout our discussion, we will look at the motion of a rigid body, one that does not deform as it moves. We idealize the rigid body by assuming that it has no dimensions and is infinitely small. This way we can talk about the entire body instead of saying, "The front of the body is at this point while the rear of the body is at some other point". Also, subscripts on the variables in our equations will indicate the initial value, $i$, and the final value, $f$, of that variable.

Displacement

To start off with we will define the term displacement. Displacement is basically the shortest route of getting from one place to another, basically it is a straight line from the starting point of motion to the ending point of motion. No matter how much movement takes place in between and what sort of things come inbetween, we only care about the first location and the second location. We will use the variable, $x$, to stand for the locations of the rigid body that we are discussing. It is a vector quantity i.e. it has both magnitude and direction, if we want to define displacement for some movement then it would be like - '50 km due North'.

In order to define motion we first must be able to say how far an object has moved. This is done by subtracting the final value of the displacement by the initial value of the displacement. Or, in other words, we subtract the initial position of the object on our coordinate system from the final position of the object on our coordinate system. It is necessary to understand that the values which you receive for this variable can be either positive or negative depending on how the object is moving and where your coordinates start:

$x=x_{f}-x_{i}\,\!$

Velocity

The term velocity, $v$, is often mistaken as being equivalent to the term speed. The basic difference between speed and velocity is that, velocity is a vector quantity, whereas speed is a scalar quantity. The term velocity refers to the displacement that an object traveled divided by the amount of time it took to move to its new coordinate. From the above discussion you can see that if the object moves backwards with respect to our coordinate system, then we will get a negative displacement. Since we cannot have a negative value for time, we will then get a negative value for velocity (Here the negative sign shows that the body has moved in the backward direction to the coordinates system adopted). The term speed, on the other hand refers to the magnitude of the velocity, so that it can only be a positive value. We will not be considering speed in this discussion, only velocity. By using our definition of velocity and the definition of displacement from above, we can express velocity mathematically like this:

${\bar {v}}={(x_{f}-x_{i}) \over (t_{f}-t_{i})}$

The line over the velocity means that you are finding the average velocity, not the velocity at a specific point. This equation can be rearranged in a variety of ways in order to solve problems in physics dealing with SLM. Also, by having acceleration as a constant value, we can find the average velocity of an object if we are given the initial and final values of an object's velocity:

${\bar {v}}={(v_{f}+v_{i}) \over 2}$

These equations can be combined with the other equations to give useful relationships in order to solve straight line motion problems. For example, to find the initial position of an object, if we are given its final position and the times that the object began moving and finished moving, we can rearrange the equation like this:

$x_{i}=x_{f}-{\bar {v}}(t_{f}-t_{i})\,\!$

Acceleration

The term acceleration means the change in velocity of an object per unit time. It is a vector quantity. We use the variable, $a$, to stand for acceleration. Basically, the sign of acceleration tells us whether the velocity is increasing or decreasing, and its magnitude tells us how much the velocity is changing. In order for an object that is initially at rest to move, it needs to accelerate to a certain speed. During this acceleration, the object moves at a certain velocity at a specific time, and travels a certain distance within that time. Thus, we can describe acceleration mathematically like this:

$a={(v_{f}-v_{i}) \over (t_{f}-t_{i})}$

Again, we can rearrange our formula, this time using our definition for displacement and velocity, to get a very useful relationship:

$x_{f}=x_{i}+v_{i}(t_{f}-t_{i})+{1 \over 2}a(t_{f}-t_{i})^{2}$

Motion with Constant Acceleration

This is the simplest kind of accelerated motion. The velocity changes at the same rate for entire duration of the motion. The displacement-time graph for motion with constant acceleration is always a parabola.

The equations of motion with constant acceleration are:

$v_{x}=v_{0x}+a_{x}t$

$v_{av}=v_{0x}t+{\frac {1}{2}}a_{x}t^{2}$

$v_{x}^{2}=v_{0x}^{2}+2a_{x}(x-x_{0})$

$x-x_{0}={\frac {1}{2}}(v_{0x}+v_{x})t$

History of Dynamics

Aristotle

Aristotle expounded a view of dynamics which agrees closely with our everyday experience of the world. Objects only move when a force is exerted upon them. As soon as the force goes away, the object stops moving. The act of pushing a box across the floor illustrates this principle -- the box certainly doesn't move by itself!

However, if we try using Aristotle's dynamics to predict motion we soon run into problems. It suggests that objects under a constant force move with a fixed velocity but while gravity definitely feels like a constant force it clearly doesn't make objects move with constant velocity. A thrown ball can even reverse direction, under the influence of gravity alone.

Eventually, people started looking for a view of dynamics that actually worked. Newton found the answer, partially inspired by the heavens.

Newton

In contrast to earthly behavior, the motions of celestial objects seem effortless. No obvious forces act to keep the planets in motion around the sun. In fact, it appears that celestial objects simply coast along at constant velocity unless something acts on them.

This Newtonian view of dynamics — objects change their velocity rather than their position when a force is exerted on them — is expressed by Newton's second law:

${\vec {F}}=m{\vec {a}}$

where ${\vec {F}}$ is the force exerted on a body, $m$ is its mass, and ${\vec {a}}$ is its acceleration. Newton's first law, which states that an object remains at rest or in uniform motion unless a force acts on it, is actually a special case of Newton's second law which applies when ${\vec {F}}={\vec {0}}$ .

It is no wonder that the first successes of Newtonian mechanics were in the celestial realm, namely in the predictions of planetary orbits. It took Newton's genius to realize that the same principles which guided the planets also applied to the earthly realm as well.

In the Newtonian view, the tendency of objects to stop when we stop pushing on them is simply a consequence of frictional forces opposing the motion. Friction, which is so important on the earth, is negligible for planetary motions, which is why Newtonian dynamics is more obviously valid for celestial bodies.

Note that the principle of relativity is closely related to Newtonian physics and is incompatible with pre-Newtonian views. After all, two reference frames moving relative to each other cannot be equivalent in the pre-Newtonian view, because objects with nothing pushing on them can only come to rest in one of the two reference frames!

Einstein's relativity is often viewed as a repudiation of Newton, but this is far from the truth — Newtonian physics makes the theory of relativity possible through its invention of the principle of relativity. Compared with the differences between pre-Newtonian and Newtonian dynamics, the changes needed to go from Newtonian to Einsteinian physics constitute minor tinkering.

Newton's first law:

"An object at rest tends to stay at rest and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an external force".

He gave this law assuming the body or the system to be isolated. If we look upon into our daily life we find that this law is applicable in reality like a bicycle stops slowly when we stop moving the pedals, this is because in our daily life there are 2 external forces which opposes the motion, these are frictional force and air resistance ( These forces aren't included in the course of an isolated system). But if these two forces are absent the above law is applicable, this can be observed in space.

Newton's second law:

"The rate change of linear momentum of an object is directly proportional to the external force on the object."

The concept behind this is - "Forces arise due to interaction between the bodies." With the help of this law we can derive this formula: $F=ma$ . In this formula, ${\vec {F}}$ means the force exerted on the object, $m$ means the mass of the object, and ${\vec {a}}$ means the acceleration of the object. Also the second law of motion is universal law in nature, i.e. it consists of both the laws. Newton assumed the body to be an isolated one, thus according to second law, if there is no interaction between bodies of two different systems( means not to be an isolated one), then there is no force that can stop or shake the object from its state of being.

Suppose two bodies are interacting with each other, then each of them would be exerting force on the other( Look from each side and apply second law of motion), it is third law.

Newton's third law:

"Every action has an equal and opposite reaction"

This means if body A exerts a force on body $B$ , then body $B$ exerts a force on body $A$ that is equal in magnitude but opposite in direction from the force from $A$ . ${\vec {F}}_{AB}=-{\vec {F}}_{BA}$

• Negative sign shows that the force is in opposite direction.

Work

When a force is exerted on an object, energy is transferred to the object. The amount of energy transferred is called the work done on the object. Mathematically work done is defined as the dot\scalar product of force and displacement, thus it is a scalar quantity. However, energy is only transferred if the object moves. Work can be thought of as the process of transforming energy from one form into another. The work W done is

$W=F\Delta x$

where the distance moved by the object is Δx and the force exerted on it is F. Notice that work can either be positive or negative. The work is positive if the object being acted upon moves in the same direction as the force, with negative work occurring if the object moves opposite to the force.

This equation assumes that the force remains constant over the full displacement or distance( depending on the situation). If it is not, then it is necessary to break up the displacement into a number of smaller displacements, over each of which the force can be assumed to be constant. The total work is then the sum of the works associated with each small displacement. In the infinitesimal limit this becomes an integral

$W=\int F(s)\,ds$

If more than one force acts on an object, the works due to the different forces each add or subtract energy, depending on whether they are positive or negative. The total work is the sum of these individual works.

There are two special cases in which the work done on an object is related to other quantities. If F is the total force acting on the object, then by Newton's second law W=FΔx=mΔx·a . However, a=dv/dt where v is the velocity of the object, and Δx≈vΔt, where Δt is the time required by the object to move through distance Δx . The approximation becomes exact when Δx and Δt become very small. Putting all of this together results in

$W_{total}=m{\frac {dv}{dt}}v\Delta t=\Delta t{\frac {d}{dt}}{\frac {mv^{2}}{2}}$

We call the quantity mv²/2 the kinetic energy, or K. It represents the amount of work stored as motion. We can then say

$W_{total}={\frac {dK}{dt}}\Delta t=\Delta K$

Thus, when F is the only force, the total work on the object equals the change in kinetic energy of the object. This transformation is known as "Work-Energy theorem."

The other special case occurs when the force depends only on position, but is not necessarily the total force acting on the object. In this case we can define a function

$U(x)=-\int ^{x}F(s)\,ds$

and the work done by the force in moving from x₁ to x₂ is U(x₁)-U(x₂), no matter how quickly or slowly the object moved.

If the force is like this it is called conservative and U is called the potential energy. Differentiating the definition gives

$F=-{\frac {dU}{dx}}$

The minus sign in these equations is purely conventional.

If a force is conservative( The force whose effect doesn't depend on the path it has taken to go through), we can write the work done by it as

$W=-{\frac {dU}{dx}}\Delta x=-\Delta U$

where is the change in the potential energy of the object associated with the force of interest.

Energy

The sum of the potential( Energy by virtue of its position) and kinetic(Energy by virtue of its motion) energies is constant. We call this constant the total energy E:

$E=K+U$

If all the forces involved are conservative we can equate this with the previous expression for work to get the following relationship between work, kinetic energy, and potential energy:

$\Delta K=W=-\Delta U$

Following this, we have a very important formula, called the 'Conservation of Energy:

$\Delta (K+U)=0$

This theorem states that the total amount of energy in a system is constant, and that energy can neither be created nor destroyed.

Power

The power associated with a force is simply the amount of work done by the force divided by the time interval over which it is done. It is therefore the energy per unit time transferred to the object by the force of interest. From above we see that the power is

$P={\frac {F\Delta x}{\Delta t}}=Fv$

where $v$ is the velocity at which the object is moving. The total power is just the sum of the powers associated with each force. It equals the time rate of change of kinetic energy of the object:

$P_{total}={\frac {W_{total}}{\Delta t}}={\frac {dK}{dt}}$

We will now take a break from physics, and discuss the topics of partial derivatives. Further information about this topic can be found at the Partial Differential Section in the Calculus book.

Partial Derivatives

In one dimension, the slope of a function, f(x), is described by a single number, df/dx.

In higher dimensions, the slope depends on the direction. For example, if f=x+2y, moving one unit x-ward increases f by 1 so the slope in the x direction is 1, but moving one unit y-ward increases f by 2 so the slope in the y direction is 2.

It turns out that we can describe the slope in n dimensions with just n numbers, the partial derivatives of f.

To calculate them, we differentiate with respect to one coordinate, while holding all the others constant. They are written using a ∂ rather than d. E.g.

$f(x+dx,y,z)=f(x,y,z)+{\frac {\partial f}{\partial x}}dx\quad (1)$

Notice this is almost the same as the definition of the ordinary derivative.

If we move a small distance in each direction, we can combine three equations like 1 to get

$df={\frac {\partial f}{\partial x}}dx+{\frac {\partial f}{\partial y}}dy+{\frac {\partial f}{\partial z}}dz$

The change in f after a small displacement is the dot product of the displacement and a special vector

$\left({\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}},{\frac {\partial f}{\partial z}}\right)\cdot \left(dx,dy,dz\right)=\operatorname {grad} f=\nabla f$

This vector is called the gradient of f. It points up the direction of steepest slope. We will be using this vector quite frequently.

Partial Derivatives #2

Another way to approach differentiation of multiple-variable functions can be found in Feynman Lectures on Physics vol. 2. It's like this:

The differentiation operator is defined like this: $df=f(x+\Delta x,y+\Delta y,z+\Delta z)-f(x,y,z)\,\!$ in the limit of $\Delta x,\Delta y,\Delta z\to 0$. Adding & subtracting some terms, we get

$df=(f(x+\Delta x,y+\Delta y,z+\Delta z)-f(x,y+\Delta y,z+\Delta z))+(f(x,y+\Delta y,z+\Delta z)-f(x,y,z+\Delta z))+(f(x,y,z+\Delta z)-f(x,y,z))\,\!$

and this can also be written as

$df={\frac {\partial f}{\partial x}}dx+{\frac {\partial f}{\partial y}}dy+{\frac {\partial f}{\partial z}}dz$

Alternate Notations

For simplicity, we will often use various standard abbreviations, so we can write most of the formulae on one line. This can make it easier to see the important details.

We can abbreviate partial differentials with a subscript, e.g.,

$D_{x}h(x,y)={\frac {\partial h}{\partial x}}\quad D_{x}D_{y}h=D_{y}D_{x}h$

or

$\partial _{x}h={\frac {\partial h}{\partial x}}$

Mostly, to make the formulae even more compact, we will put the subscript on the function itself.

$D_{x}h=h_{x}\quad h_{xy}=h_{yx}$

More Info

Refer to the Partial Differential Section in the Calculus book for more information.

Motion in 2 and 3 Directions

Previously, we discussed Newtonian dynamics in one dimension. Now that we are familiar with both vectors and partial differentiation, we can extend that discussion to two or three dimensions.

Work becomes a dot product

$W=\mathbf {F} \cdot \Delta x$

and likewise power

$P=\mathbf {F} \cdot \mathbf {v}$

If the force is at right angles to the direction of motion, no work will be done.

In one dimension, we said a force was conservative if it was a function of position alone, or equivalently, the negative slope of a potential energy.

The second definition extends to

$\mathbf {F} =-\nabla V$

In two or more dimensions, these are not equivalent statements. To see this, consider

$D_{y}\mathbf {F} _{x}-D_{x}\mathbf {F} _{y}=V_{xy}-V_{yx}$

Since it doesn't matter which order derivatives are taken in, the left hand side of this equation must be zero for any force which can be written as a gradient, but for an arbitrary force, depending only on position, such as F=(y, -x, 0), the left hand side isn't zero.

Conservative forces are useful because the total work done by them depends only on the difference in potential energy at the endpoints, not on the path taken, from which the conservation of energy immediately follows.

If this is the case, the work done by an infinitesimal displacement dx must be

$W=V(\mathbf {x} )-V(\mathbf {x} +d\mathbf {x} )=-(\nabla V)\cdot d\mathbf {x}$

Comparing this with the first equation above, we see that if we have a potential energy then we must have

$\mathbf {F} =-\nabla V$

Any such F is a conservative force.

Circular Motion

An important example of motion in two dimensions is circular motion.

Consider a mass, m, moving in a circle, radius r.

The angular velocity, ω is the rate of change of angle with time. In time Δt the mass moves through an angle Δθ= ωΔt. The distance the mass moves is then r sin Δθ, but this is approximately rΔθ for small angles.

Thus, the distance moved in a small time Δt is rωΔt, and divided by Δt gives us the speed, v.

$v=\omega r\,$

This is the speed not the velocity because it is not a vector. The velocity is a vector, with magnitude ωr which points tangentially to the circle.

The magnitude of the velocity is constant but its direction changes so the mass is being accelerated.

By a similar argument to that above it can be shown that the magnitude of the acceleration is

$a=\omega v\,$

and that it is pointed inwards, along the radius vector. This is called centripetal acceleration.

By eliminating v or ω from these two equations we can write

$\mathbf {a} =-\omega ^{2}\mathbf {r} =-{\frac {v^{2}}{r}}\mathbf {\hat {r}}$

Year 10 Force and Work 7 periods

• Possible Approach:
• Lesson Suggested Learning Outcomes Course Outline Resources
• 1 – 3  Recognise that unbalanced forces cause acceleration.
•  Investigate the relationship between the unbalanced force acting on an object, is mass *and acceleration: Newton’s Second Law. (Use Fnet = ma giving correct units for all quantities)

•**Reinforce ideas about force causing acceleration (= the rate at which speed changes)

• Experiment 1: Finding the force required to move an object (static friction)
• Discuss the factors that may affect the frictional forces acting on the block (e.g. load on *the block, surface area in contact with the bench, type of the surfaces in contact …)
• Attach a force meter to a block at rest on the bench. Pull the force meter and slowly increase *the force until the block just begins to move – record the force meter reading, tabulate data, *repeat, calculate average.
• [Or, use a bag to which washers may be added, attached to a cord and hanging over the end of *the bench to pull the block.]
• quantities and the third unknown) – a three symbol triangle may simplify the maths.
• • • • • • Homework: Coursebook – Newton’s second Law
          • force (e.g. when a force acts on a body, it moves faster and kinetic energy increases)
          • • Introduce the relationship between energy transferred and work done.
          • • Define work done in terms of the applied force and the distance through which this ********force acts (Work done = force x distance)

• • • • • • • Use the work rule to calculate work / force / distance (given two quantities and the ********third unknown) – a three symbol triangle may simplify the maths

• • • • • • Homework: Coursebook – Work Done and Energy

• • • • • • • 6 – 7  Investigate and describe the pattern of results formed from graphing ************************the effects of applied forces on a spring.

• Explore the relationships between science and technology by investigating the application of *science to technology and the impact of technology on science, e.g. Archimedes’ screw to *illustrate the principle of oits use in water irrigation or the use of springs and similar *propulsion devices in toys
• Experiment 4: Stretching Springs
• Hang a spring vertically using a clamp and stand. Add weights to the end of the spring, *measure the length of the spring after each additional weight is added. Calculate the *extension (Note: some initial weight will probably need to be added before the spring *stretches at all) Graph extension vs applied force. Interpret the graph, e.g. find the *extension for unit applied force or applied force per unit extension.

• • • • • • • • Investigate and understand the turning effect of a force.
              • Calculate the turning effect of a force = F x d where force (F) and distance (d) are *********at right angles.
              • Use the lever rule: F1d1 = F2d2 •

• Discuss and brainstorm ideas about what causes things to turn about a pivot (fulcrum).
  • • • • • • Introduce the concept of the turning effect of a force (torque).
          • • Discuss the concept levers – to increase the turning effect, use a greater distance *******(e.g. a long crowbar) and/or a greater force (e.g. a heavier weight)
          • • Use the lever rule to calculate forces and distances at right angles to the applied ********force (given three quantities and the fourth unknown).
• Experiment 5: The turning effect of a force
• Kit available from the science Office
  • • • • • • Homework: Coursebook – The Turning Effect of a Force
• Extension

Changing mass

So far we've assumed that the mass of the objects being considered is constant, which is not always true. Mass is conserved overall, but it can be useful to consider objects, such as rockets, which are losing or gaining mass.

We can work out how to extend Newton's second law to this situation by considering a rocket two ways, as a single object of variable mass, and as two objects of fixed mass which are being pushed apart.

We find that

$\mathbf {F} =m{\frac {d{\vec {v}}}{dt}}$

Force is the rate of change of a quantity, $m{\vec {v}}$ , which we call linear momentum.

Newton's third law

Newton's third law says that the force, $F_{12}$ exerted by a mass $m_{1}$ , on a second mass $m_{2}$ , is equal and opposite to the force $F_{21}$ exerted by the second mass on the first.

${\frac {d(m_{2}{\vec {v}}_{2})}{dt}}={\vec {F}}_{12}=-{\vec {F}}_{21}=-{\frac {d(m_{1}{\vec {v}}_{1})}{dt}}$

if there are no external forces on the two bodies. We can add the two momenta together to get,

${\frac {d(m_{1}{\vec {v}}_{1})}{dt}}+{\frac {d(m_{2}{\vec {v}}_{2})}{dt}}={\frac {d}{dt}}(m_{1}{\vec {v}}_{1}+m_{2}{\vec {v}}_{2})=0$

so the total linear momentum is conserved.

Ultimately, this is consequence of space being homogeneous.

Centre of mass

Suppose two constant masses are subject to external forces, ${\vec {F}}_{1},{\vec {F}}_{2}$

Then the total force on the system, ${\vec {F}}$ , is

${\vec {F}}={\vec {F}}_{1}+{\vec {F}}_{2}={\frac {d}{dt}}(m_{1}{\vec {v}}_{1}+m_{2}{\vec {v}}_{2})$

because the internal forces cancel out.

If the two masses are considered as one system, ${\vec {F}}$ should be the product of the total mass and ${\bar {a}}$ , the average acceleration, which we expect to be related to some kind of average position.

${\begin{aligned}(m_{1}+m_{2}){\bar {a}}&={\frac {d}{dt}}(m_{1}{\vec {v}}_{1}+m_{2}{\vec {v}}_{2})\\&={\frac {d^{2}}{dt^{2}}}(m_{1}{\vec {r}}_{1}+m_{2}{\vec {r}}_{2})\\{\bar {a}}&={\frac {d^{2}}{dt^{2}}}{\frac {m_{1}{\vec {r}}_{1}+m_{2}{\vec {r}}_{2}}{m_{1}+m_{2}}}\end{aligned}}$

The average acceleration is the second derivative of the average position, weighted by mass.

This average position is called the centre of mass, and accelerates at the same rate as if it had the total mass of the system, and were subject to the total force.

We can extend this to any number of masses under arbitrary external and internal forces.

• we have $n$ objects, mass $m_{1}\ldots ,m_{n}$ , total mass $M$
• each mass $m_{i}$ is at point $r_{i}$
• each mass $m_{i}$ is subject to an external force $F_{i}$
• the internal force exerted by mass $m_{j}$ on mass $m_{i}$ is $F_{ij}$

then the position of the centre of mass $R$ is

${\vec {R}}={\frac {1}{M}}\sum _{i}m_{i}{\vec {r}}_{i}$

We can now take the second derivative of $R$

${\begin{aligned}M{\vec {R}}''&=\sum _{i}m_{i}{\vec {r}}_{i}''\\&=\sum _{i}\left({\vec {F}}_{i}+\sum _{j}{\vec {F}}_{ij}\right)\end{aligned}}$

But the sum of all the internal forces is zero, because Newton's third law makes them cancel in pairs. Thus, the second term in the above equation drops out and we are left with:

$M{\vec {R}}''=\sum _{i}{\vec {F}}_{i}={\vec {F}}$

The centre of mass always moves like a body of the same total mass under the total external force, irrespective of the internal forces.

If a rigid body is initially at rest, it will remain at rest if and only if the sum of all the forces and the sum of all the torques acting on the body are zero. As an example, a mass balance with arms of differing length is shown in figure above. The balance beam is subject to three forces pointing upward or downward, the tension T in the string from which the beam is suspended and the weights M₁g and M₂g exerted on the beam by the two suspended masses. The parameter g is the local gravitational field and the balance beam itself is assumed to have negligible mass. Taking upward as positive, the force condition for static equilibrium is

$T-M_{1}g-M_{2}g=0\quad {\mbox{Zero net force}}$

Defining a counterclockwise torque to be positive, the torque balance computed about the pivot point in figure 10.7 is

$\tau =M_{1}gd_{1}-M_{2}gd_{2}=0\quad {\mbox{Zero torque}}$

where d₁ and d₂ are the lengths of the beam arms. The first of the above equations shows that the tension in the string must be

$T=\left(M_{1}+M_{2}\right)g$

while the second shows that

${\frac {M_{1}}{M_{2}}}={\frac {d_{2}}{d_{1}}}$

Thus, the tension in the string is just equal to the weight of the masses attached to the balance beam, while the ratio of the two masses equals the inverse ratio of the associated beam arm lengths.

Rotational Dynamics

There are two ways to multiply two vectors together, the dot product and the cross product. We have already studied the dot product of two vectors, which results in a scalar or single number.

The cross product of two vectors results in a third vector, and is written symbolically as follows:

${\vec {A}}\times {\vec {B}}$

The cross product of two vectors is defined to be perpendicular to the plane defined by these vectors. However, this doesn't tell us whether the resulting vector points upward out of the plane or downward. This ambiguity is resolved using the right-hand rule:

1. Point the uncurled fingers of your right hand along the direction of the first vector ${\vec {A}}$ .
2. Rotate your arm until you can curl your fingers in the direction of the second vector ${\vec {B}}$ .
3. Your stretched out thumb now points in the direction of the cross product vector ${\vec {A}}\times {\vec {B}}$ .

The magnitude of the cross product is given by

$|{\vec {A}}\times {\vec {B}}|=|{\vec {A}}||{\vec {B}}|\cdot \sin(\theta )$

where $|{\vec {A}}|$ and $|{\vec {B}}|$ are the magnitudes of ${\vec {A}},{\vec {B}}$ , and $\theta$ is the angle between these two vectors. Note that the magnitude of the cross product is zero when the vectors are parallel or anti-parallel, and maximum when they are perpendicular. This contrasts with the dot product, which is maximum for parallel vectors and zero for perpendicular vectors.

Notice that the cross product does not commute, i.e. the order of the vectors is important. In particular, it is easy to show using the right-hand rule that

${\vec {A}}\times {\vec {B}}=-{\vec {B}}\times {\vec {A}}$

An alternate way to compute the cross product is most useful when the two vectors are expressed in terms of components,

${\vec {C}}={\vec {A}}\times {\vec {B}}={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{vmatrix}}$

where the determinant is expanded as if all the components were numbers, giving

${\begin{aligned}C_{x}&=A_{y}B_{z}-A_{z}B_{y}\\C_{y}&=A_{z}B_{x}-A_{x}B_{z}\\C_{z}&=A_{x}B_{y}-A_{y}B_{x}\end{aligned}}$

Note how the positive terms possess a forward alphabetical direction, xyzxyzx... (with x following z):

With the cross product we can also multiply three vectors together, in two different ways.

We can take the dot product of a vector with a cross product, a triple scalar product,

${\vec {A}}\cdot ({\vec {B}}\times {\vec {C}})=({\vec {A}}\times {\vec {B}})\cdot {\vec {C}}$

The absolute value of this product is the volume of the parallelpiped defined by the three vectors ${\vec {A}},{\vec {B}},{\vec {C}}$

Alternately, we can take the cross product of a vector with a cross product, a triple vector product, which can be simplified to a combination of dot products.

${\vec {A}}\times ({\vec {B}}\times {\vec {C}})=({\vec {A}}\cdot {\vec {C}}){\vec {B}}-({\vec {A}}\cdot {\vec {B}}){\vec {C}}$

This form is easier to do calculations with.

The triple vector product is not associative.

${\vec {A}}\times ({\vec {B}}\times {\vec {C}})\neq ({\vec {A}}\times {\vec {B}})\times {\vec {C}}$

A nice as well as a useful way to denote the cross product is using the indicial notation

${\vec {C}}={\vec {A}}\times {\vec {B}}=\epsilon ^{ijk}\,A_{j}\,B_{k}\,{\hat {e}}_{i}$

where $\epsilon ^{ijk}$ is the Levi-Civita alternating symbol and ${\hat {e}}_{i}$ is either of the unit vectors ${\vec {\imath }},{\vec {\jmath }},{\vec {k}}$ . (A good exercise to convince yourself would be to use this expression and see if you can get ${\vec {C}}={\vec {A}}\times {\vec {B}}$ as defined before.)

Torque

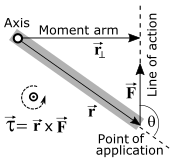
Torque is the action of a force on a mass which induces it to revolve about some point, called the origin. It is defined as

${\vec {\tau }}={\vec {r}}\times {\vec {F}}$

where $r$ is the position of the mass relative to the origin.

Notice that the torque is 0 in a number of circumstances. If the force points directly toward or away from the origin, the cross product is zero, resulting in zero torque, even though the force is non-zero. Likewise, if $r=0$ , the torque is 0. Thus, a force acting at the origin produces no torque. Both of these limits make sense intuitively, since neither induces the mass to revolve around the origin.

Angular momentum

The angular momentum of a mass relative to a point O is defined as

${\vec {L}}={\vec {r}}\times {\vec {p}}$

where p is the ordinary (also called "linear") momentum of the mass. The angular momentum is 0 if the motion of the object is directly towards or away from the origin, or if it is located at the origin.

If we take the cross product of the position vector and Newton's second law, we obtain an equation that relates torque and angular momentum:

${\vec {r}}\times {\vec {F}}={\vec {r}}\times {\frac {d{\vec {p}}}{dt}}={\frac {d}{dt}}({\vec {r}}\times {\vec {p}})-{\frac {d{\vec {r}}}{dt}}\times {\vec {p}}$

Since the cross product of parallel vectors is zero, this simplifies to

${\vec {\tau }}={\frac {d{\vec {L}}}{dt}}$

This is the rotational version of Newton's second law.

For both torque and angular momentum the location of the origin is arbitrary, and is generally chosen for maximum convenience. However, it is necessary to choose the same origin for both the torque and the angular momentum.

For the case of a central force, i.e. one which acts along the line of centers between two objects (such as gravity), there often exists a particularly convenient choice of origin. If the origin is placed at the center of the sun (which is assumed not to move under the influence of the planet's gravity), then the torque exerted on the planet by the sun's gravity is 0, which means that the angular momentum of the planet about the center of the sun is constant in time. No other choice of origin would yield this convenient result.

We already know about two fundamental conservation laws—those of energy and linear momentum. We believe that angular momentum is similarly conserved in isolated systems. In other words, particles can exchange angular momentum between themselves, but the vector sum of the angular momentum of all the particles in a system isolated from outside influences must remain constant.

In the modern view, conservation of angular momentum is a consequence of the isotropy of space—i.e. the properties of space don't depend on direction. This is in direct analogy with conservation of ordinary momentum, which we recall is a consequence of the homogeneity of space.

Angular velocity and centrifugal force

If an object is rotating about an axis, $n$ being a unit vector, at frequency $\omega$ we say it has angular velocity ${\vec {\omega }}$ . Despite the name, this is not the rate of change of an angle, nor even of a vector.

If a constant vector ${\vec {r}}$ is rotating with angular velocity ${\vec {\omega }}$ about a fixed point then

${\frac {d{\vec {r}}}{dt}}={\vec {\omega }}\times {\vec {r}}$

This says the acceleration is always at right angles to both the velocity and the axis of rotation.

When the axis is changing ${\vec {\omega }}$ can be defined as the vector which makes this true.

Note that on the left hand side of this equation ${\vec {r}}$ is a vector in a fixed coordinate system with variable components but on the right hand side its components are given in a moving coordinate system, where they are fixed.

We can distinguish them more clearly by using subscripts, $r$ for rotating and $f$ for fixed, then extend this to arbitrary vectors

${\frac {d{\vec {g}}_{f}}{dt}}={\frac {d{\vec {g}}_{r}}{dt}}+{\vec {\omega }}\times {\vec {g}}_{f}$

for any vector ${\vec {g}}$

Using this, we can write Newton's second law in the rotating frame.

${\begin{aligned}{\vec {F}}_{f}&=m{\dfrac {d{\vec {v}}_{f}}{dt}}\\&=m{\dfrac {d{\vec {v}}_{r}}{dt}}+m{\vec {\omega }}\times {\vec {v}}_{f}\\&=m{\ddot {\mathbf {r} }}_{r}+m{\boldsymbol {\omega }}\times \left(2{\dfrac {d_{2}{\vec {r}}_{r}}{dt_{2}}}+{\vec {\omega }}\times {\vec {r}}_{f}\right)\end{aligned}}$

or, rearranging

$m{\vec {a}}_{r}={\vec {F}}-2m({\vec {\omega }}\times {\vec {v}}_{r})-m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})$

The mass behaves as if there were two additional forces acting on it. The first term, ${\vec {\omega }}\times {\vec {v}}$ is called the Coriolis force. The second term is recognizable as the familiar centrifugal force.

The kinetic energy and angular momentum of the dumbbell may be split into two parts, one having to do with the motion of the center of mass of the dumbbell, the other having to do with the motion of the dumbbell relative to its center of mass.

To do this we first split the position vectors into two parts. The centre of mass is at.

$\mathbf {R} ={\frac {M_{1}\mathbf {r} _{1}+M_{2}\mathbf {r} _{2}}{M_{1}+M_{2}}}$

so we can define new position vectors, giving the position of the masses relative to the centre of mass, as shown.

$\mathbf {r} _{1}^{*}=\mathbf {r} _{1}-\mathbf {R} \quad \mathbf {r} _{2}^{*}=\mathbf {r} _{2}-\mathbf {R}$

The total kinetic energy is

${\begin{matrix}K&=&{\frac {1}{2}}M_{1}V_{1}^{2}&+&{\frac {1}{2}}M_{2}V_{2}^{2}\\&=&{\frac {1}{2}}M_{1}|\mathbf {V} -\mathbf {v} _{1}^{*}|^{2}&+&{\frac {1}{2}}M_{2}|\mathbf {V} -\mathbf {v} _{2}^{*}|^{2}\\&=&{\frac {1}{2}}(M_{1}+M_{2})V^{2}&+&{\frac {1}{2}}M_{1}{v_{1}^{*}}^{2}+{\frac {1}{2}}M_{2}{v_{2}^{*}}^{2}\\&=&K_{ext}&+&K_{int}\\\end{matrix}}$

which is the sum of the kinetic energy the dumbbell would have if both masses were concentrated at the center of mass, the translational kinetic energy and the kinetic energy it would have if it were observed from a reference frame in which the center of mass is stationary, the rotational kinetic energy.

The total angular momentum can be similarly split up

${\begin{matrix}\mathbf {L} &=&\mathbf {L} _{orb}&+&\mathbf {L} _{spin}\\&=&(M_{1}+M_{2})\mathbf {R} \times \mathbf {V} &+&(M_{1}\mathbf {r} _{1}^{*}\times \mathbf {v} _{1}^{*}+M_{2}\mathbf {r} _{2}^{*}\times \mathbf {v} _{2}^{*})\end{matrix}}$

into the sum of the angular momentum the system would have if all the mass were concentrated at the center of mass, the orbital angular momentum, and the angular momentum of motion about the center of mass, the spin angular momentum.

We can therefore assume the centre of mass to be fixed.

Since ω is enough to describe the dumbbells motion, it should be enough to determine the angular momentum and internal kinetic energy. We will try writing both of these in terms of ω

First we use two results from earlier

$\mathbf {L} =\mathbf {r} \times \mathbf {v} \quad {\mbox{and}}\quad \mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {r}$

to write the angular momentum in terms of the angular velocity

${\begin{matrix}\mathbf {L} &=&M_{1}\mathbf {r} _{1}^{*}\times \mathbf {v} _{1}^{*}&+&M_{2}\mathbf {r} _{2}^{*}\times \mathbf {v} _{2}^{*}\\&=&M_{1}\mathbf {r} _{1}^{*}\times ({\boldsymbol {\omega }}\times \mathbf {r} _{1}^{*})&+&M_{2}\mathbf {r} _{2}^{*}\times ({\boldsymbol {\omega }}\times \mathbf {r} _{2}^{*})\\&=&M_{1}\left({\boldsymbol {\omega }}\left(\mathbf {r} _{1}^{*}\cdot \mathbf {r} _{1}^{*}\right)-\mathbf {r} _{1}^{*}\left(\mathbf {r} _{1}^{*}\cdot {\boldsymbol {\omega }}\right)\right)&+&M_{2}\left({\boldsymbol {\omega }}\left(\mathbf {r} _{2}^{*}\cdot \mathbf {r} _{2}^{*}\right)-\mathbf {r} _{2}^{*}\left(\mathbf {r} _{2}^{*}\cdot {\boldsymbol {\omega }}\right)\right)\\&=&M_{1}\left({\boldsymbol {\omega }}d_{1}^{2}-\mathbf {r} _{1}^{*}\left(\mathbf {r} _{1}^{*}\cdot {\boldsymbol {\omega }}\right)\right)&+&M_{2}\left({\boldsymbol {\omega }}d_{2}^{2}-\mathbf {r} _{2}^{*}\left(\mathbf {r} _{2}^{*}\cdot {\boldsymbol {\omega }}\right)\right)\\&=&(M_{1}d_{1}^{2}+M_{2}d_{2}^{2}){\boldsymbol {\omega }}&-&\left(M_{1}\mathbf {r} _{1}^{*}\left(\mathbf {r} _{1}^{*}\cdot {\boldsymbol {\omega }}\right)+M_{2}\mathbf {r} _{2}^{*}\left(\mathbf {r} _{2}^{*}\cdot {\boldsymbol {\omega }}\right)\right)\end{matrix}}$

The first term in the angular momentum is proportional to the angular velocity, as might be expected, but the second term is not.

What this means becomes clearer if we look at the components of L For notational convenience we'll write

$\mathbf {r} _{1}^{*}=(x_{1},y_{1},z_{1})\quad \mathbf {r} _{2}^{*}=(x_{2},y_{2},z_{2})$

These six numbers are constants, reflecting the geometry of the dumbbell.

${\begin{matrix}L_{x}&=&(M_{1}d_{1}^{2}+M_{2}d_{2}^{2})\omega _{x}-(M_{1}x_{1}^{2}+M_{2}x_{2}^{2})\omega _{x}\\&&-(M_{1}x_{1}y_{1}+M_{2}x_{2}y_{2})\omega _{y}-(M_{1}x_{1}z_{1}+M_{2}x_{2}z_{2})\omega _{z}\\L_{y}&=&(M_{1}d_{1}^{2}+M_{2}d_{2}^{2})\omega _{y}-(M_{1}x_{1}^{2}+M_{2}x_{2}^{2})\omega _{y}\\&&-(M_{1}x_{1}y_{1}+M_{2}x_{2}y_{2})\omega _{x}-(M_{1}y_{1}z_{1}+M_{2}y_{2}z_{2})\omega _{z}\\L_{z}&=&(M_{1}d_{1}^{2}+M_{2}d_{2}^{2})\omega _{z}-(M_{1}x_{1}^{2}+M_{2}x_{2}^{2})\omega _{z}\\&&-(M_{1}x_{1}z_{1}+M_{2}x_{2}z_{2})\omega _{x}-(M_{1}y_{1}z_{1}+M_{2}y_{2}z_{2})\omega _{y}\\\end{matrix}}$

This, we recognise as being a matrix multiplication.

${\begin{pmatrix}L_{x}\\L_{y}\\L_{z}\end{pmatrix}}={\begin{pmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{yx}&I_{yy}&I_{yz}\\I_{zx}&I_{zy}&I_{zz}\end{pmatrix}}{\begin{pmatrix}\omega _{x}\\\omega _{y}\\\omega _{z}\end{pmatrix}}$

where

${\begin{pmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{yx}&I_{yy}&I_{yz}\\I_{zx}&I_{zy}&I_{zz}\end{pmatrix}}={\begin{pmatrix}M_{1}(d_{1}^{2}-x_{1}^{2})+M_{2}(d_{2}^{2}-x_{2}^{2})&-(M_{1}x_{1}y_{1}+M_{2}x_{2}y_{2})&-(M_{1}x_{1}z_{1}+M_{2}x_{2}z_{2})\\-(M_{1}x_{1}y_{1}+M_{2}x_{2}y_{2})&M_{1}(d_{1}^{2}-y_{1}^{2})+M_{2}(d_{2}^{2}-y_{2}^{2})&-(M_{1}y_{1}z_{1}+M_{2}y_{2}z_{2})\\-(M_{1}x_{1}z_{1}+M_{2}x_{2}z_{2})&-(M_{1}y_{1}z_{1}+M_{2}y_{2}z_{2})&M_{1}(d_{1}^{2}-z_{1}^{2})+M_{2}(d_{2}^{2}-z_{2}^{2})\end{pmatrix}}$

The nine coefficients of the matrix I are called moments of inertia.

By choosing our axis carefully we can make this matrix diagonal. E.g. if

$\mathbf {r} _{1}^{*}=(d_{1},0,0)\quad \mathbf {r} _{2}^{*}=(-d_{2},0,0)$

then

${\begin{pmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{yx}&I_{yy}&I_{yz}\\I_{zx}&I_{zy}&I_{zz}\end{pmatrix}}={\begin{pmatrix}0&0&0\\0&M_{1}d_{1}^{2}+M_{2}d_{2}^{2}&0\\0&0&M_{1}d_{1}^{2}+M_{2}d_{2}^{2}\end{pmatrix}}$

Because the dumbbell is aligned along the x-axis, rotating it around that axis has no effect.

The relationship between the kinetic energy, T, and ω quickly follows.

${\begin{matrix}2T&=&M_{1}{v_{1}^{*}}^{2}&+&M_{2}{v_{2}^{*}}^{2}\\&=&M_{1}\mathbf {v} _{1}^{*}\cdot ({\boldsymbol {\omega }}\times \mathbf {r} _{1}^{*})&+&M_{1}\mathbf {v} _{2}^{*}\cdot ({\boldsymbol {\omega }}\times \mathbf {r} _{2}^{*})\\&=&M_{1}{\boldsymbol {\omega }}\cdot (\mathbf {r} _{1}^{*}\times \mathbf {v} _{1}^{*})&+&M_{2}{\boldsymbol {\omega }}\cdot (\mathbf {r} _{2}^{*}\times \mathbf {v} _{2}^{*})\end{matrix}}$

On the right hand side we immediately recognise the definition of angular momentum.

$T={\frac {1}{2}}{\boldsymbol {\omega }}\cdot \mathbf {L}$

Substituting for L gives

$T={\frac {1}{2}}{\boldsymbol {\omega }}\mathbf {I} {\boldsymbol {\omega }}$

Using the definition

${\boldsymbol {\omega }}=\omega \mathbf {n} \quad \mathbf {n} \cdot \mathbf {n} =1$

this reduces to

$T={\frac {1}{2}}I\omega ^{2}$

where the moment of inertia around the axis n is

$I=\mathbf {n} \mathbf {I} \mathbf {n}$

a constant.

If the dumbbell is aligned along the x-axis as before we get

$T={\frac {1}{2}}(M_{1}d_{1}^{2}+M_{2}d_{2}^{2})(\omega _{y}^{2}+\omega _{z}^{2})$

These equations of rotational dynamics are similar to those for linear dynamics, except that I is a matrix rather than a scalar.

Further reading

• Modern Physics/The Uneven Dumbbell

Summation convention

If we label the axes as 1,2, and 3 we can write the dot product as a sum

$\mathbf {u} \cdot \mathbf {v} =\sum _{i=1}^{3}u_{i}v_{i}$

If we number the elements of a matrix similarly,

$\mathbf {A} ={\begin{pmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{pmatrix}}\quad \mathbf {B} ={\begin{pmatrix}B_{11}&B_{12}&B_{13}\\B_{21}&B_{22}&B_{23}\\B_{31}&B_{32}&B_{33}\end{pmatrix}}$

we can write similar expressions for matrix multiplications

$(\mathbf {A} \mathbf {u} )_{i}=\sum _{j=1}^{3}A_{ij}u_{j}\quad (\mathbf {A} \mathbf {B} )_{ik}=\sum _{j=1}^{3}A_{ij}B_{jk}$

Notice that in each case we are summing over the repeated index. Since this is so common, it is now conventional to omit the summation sign.

Instead we simply write

$\mathbf {u} \cdot \mathbf {v} =u_{i}v_{i}\quad (\mathbf {A} \mathbf {u} )_{i}=A_{ij}u_{j}\quad (\mathbf {A} \mathbf {B} )_{ik}=A_{ij}B_{jk}$

We can then also number the unit vectors, ê_i, and write

$\mathbf {u} =u_{i}{\hat {\mathbf {e} }}_{i}$

which can be convenient in a rotating coordinate system.

Kronecker delta

The Kronecker delta is

$\delta _{ij}=\left\{{\begin{matrix}1&i=j\\0&i\neq j\end{matrix}}\right.$

This is the standard way of writing the identity matrix.

Levi-Civita (Alternating) symbol

Another useful quantity can be defined by

$\epsilon _{ijk}=\left\{{\begin{matrix}1&(i,j,k)=(1,2,3){\mbox{ or }}(2,3,1){\mbox{ or }}(3,1,2)\\-1&(i,j,k)=(2,1,3){\mbox{ or }}(3,2,1){\mbox{ or }}(1,3,2)\\0&{\mbox{ otherwise }}\end{matrix}}\right.$

With this definition it turns out that

$\mathbf {u} \times \mathbf {v} =\epsilon _{ijk}{\hat {\mathbf {e} }}_{i}u_{j}v_{k}$

and

$\epsilon _{ijk}\epsilon _{ipq}=\delta _{jp}\delta _{kq}-\delta _{jq}\delta _{kp}\,$

This will let us write many formulae more compactly.

The uneven dumbbell consisted of just two particles. These results can be extended to cover systems of many particles, and continuous media.

Suppose we have N particles, masses m₁ to m_N, with total mass M. Then the centre of mass is

$\mathbf {R} ={\frac {\sum _{n}m_{n}\mathbf {r} _{n}}{M}}$

Note that the summation convention only applies to numbers indexing axes, not to n which indexes particles.

We again define

$\mathbf {r} _{n}^{*}=\mathbf {r} _{n}-\mathbf {R}$

The kinetic energy splits into

$T={\frac {1}{2}}MV^{2}+{\frac {1}{2}}\sum _{n}m_{n}{v_{n}^{*}}^{2}$

and the angular momentum into

$\mathbf {L} =M\mathbf {R} \times \mathbf {V} +\sum _{n}m_{n}\mathbf {r} _{n}^{*}\times \mathbf {v} _{n}^{*}$

It is not useful to go onto moments of inertia unless the system is approximately rigid but this is still a useful split, letting us separate the overall motion of the system from the internal motions of its part.

If the set of particles in the previous chapter form a rigid body, rotating with angular velocity ω about its centre of mass, then the results concerning the moment of inertia from the penultimate chapter can be extended.

We get

$I_{ij}=\sum _{n}m_{n}(r_{n}^{2}\delta _{ij}-{r_{n}}_{i}{r_{n}}_{j})$

where (r_n1, r_n2, r_n3) is the position of the n^th mass.

In the limit of a continuous body this becomes

$I_{ij}=\int _{V}\rho (\mathbf {r} )(r^{2}\delta _{ij}-r_{i}r_{j})\,dV$

where ρ is the density.

Either way we get, splitting L into orbital and internal angular momentum,

$L_{i}=M\epsilon _{ijk}R_{j}V_{k}+I_{ij}\omega _{j}$

and, splitting T into rotational and translational kinetic energy,

$T={\frac {1}{2}}MV_{i}V_{i}+{\frac {1}{2}}\omega _{i}I_{ij}\omega _{j}$

It is always possible to make I a diagonal matrix, by a suitable choice of axis.

Mass Moments Of Inertia Of Common Geometric Shapes

The moments of inertia of simple shapes of uniform density are well known.

Spherical shell

mass M, radius a

$I_{xx}=I_{yy}=I_{zz}={\frac {2}{3}}Ma^{2}$

Solid ball

mass M, radius a

$I_{xx}=I_{yy}=I_{zz}={\frac {2}{5}}Ma^{2}$

Thin rod

mass M, length a, orientated along z-axis

$I_{xx}=I_{yy}={\frac {1}{12}}Ma^{2}\quad I_{zz}=0$

Disc

mass M, radius a, in x-y plane

$I_{xx}=I_{yy}={\frac {1}{4}}Ma^{2}\quad I_{zz}={\frac {1}{2}}Ma^{2}$

Cylinder

mass M, radius a, length h orientated along z-axis

$I_{xx}=I_{yy}=M\left({\frac {a^{2}}{4}}+{\frac {h^{2}}{12}}\right)\quad I_{zz}={\frac {1}{2}}Ma^{2}$

Thin rectangular plate

mass M, side length a parallel to x-axis, side length b parallel to y-axis

$I_{xx}=M{\frac {b^{2}}{12}}\quad I_{yy}=M{\frac {a^{2}}{12}}\quad I_{zz}=M\left({\frac {a^{2}}{12}}+{\frac {b^{2}}{12}}\right)$

further reading

• Statics/Moment of Inertia (contents)
• Statics/Geometric Properties of Solids

Newton's Laws: A second look

So far we've tacitly assumed we can just calculate force as a function of position, set up the ODE

$m{\ddot {\mathbf {r} }}=\mathbf {F} (\mathbf {r} )$

and start solving.

It is not always so simple.

Often, we have to deal with motion under constraint; a bead sliding on a wire, a ball rolling without slipping, a weight dangling from a string.

There has to be some force keeping the bead on the wire, but we don't know what it is in advance, only what it does. This isn't enough information for us to write down the ODE.

We need a way of solving the problem without knowing the forces in advance.

How easy this is depends on the type of constraint.

• If the constraint is an inequality, as with the weight on the string, there is no straightforward analytical method.

• If the constraint can be written as a set of differential equations, and those equations can't be integrated in advance, there is an analytical method, but it is beyond the scope of this book. A ball rolling without slipping falls into this category.

• If the constraint can be written as a set of algebraic equations, and frictional forces are negligible, there is a straightforward method that solves the problem.

Generalised coordinates

Suppose we have a system of n particles satisfying k constraints of the form

$f_{k}(\mathbf {r} _{1},\cdots ,\mathbf {r} _{n},t)=0$

then we can use the constraints to eliminate k of the 3n coordinates of the particles, giving us a new set of 3n-k independent generalised coordinates; q₁, q₂, … q_3n-'k.

Unlike the components of the position vectors, these new coordinates will not all be lengths, and will not typically form vectors. They may often be angles.

We now need to work out what Newton's laws will look like in the generalised coordinates.

Derivation

The first step is to eliminate the forces of constraint.

We will need to consider a virtual displacement. This is an infinitesimal displacement made, while holding the forces and constraints constant. It is not the same as the infinitesimal displacement made during an infinitesimal time, since the forces and constraints may change during that time.

We write the total force on particle i as

$\mathbf {F} _{i}=\mathbf {F} _{i}^{a}+\mathbf {F} _{i}^{c}$

the sum of the externally applied forces and the forces of constraint.

Newton's second law states

$\mathbf {F} _{i}^{a}+\mathbf {F} _{i}^{c}=\mathbf {F} _{i}={\dot {\mathbf {p} }}_{i}$

We take the dot product of this with the virtual displacement of particle i and sum over all particles.

$\sum _{i}\left(\mathbf {F} _{i}^{a}+\mathbf {F} _{i}^{c}-{\dot {\mathbf {p} }}_{i}\right)\cdot \delta \mathbf {r} _{i}=0$

We now assume that the forces of constraint are perpendicular to the virtual displacement. This assumption is generally true in the absence of friction; e.g, the force of constraint that keeps a ball on a surface is normal to the surface.

This assumption is called D'Alembert's principle. Using it we can eliminate the forces of constraint from the problem, giving

$\sum _{i}\left(\mathbf {F} _{i}^{a}-{\dot {\mathbf {p} }}_{i}\right)\cdot \delta \mathbf {r} _{i}=0$

or

$\sum _{i}\mathbf {F} _{i}^{a}\cdot \delta \mathbf {r} _{i}=\sum _{i}{\dot {\mathbf {p} }}_{i}\cdot \delta \mathbf {r} _{i}\quad (1)$

The left hand side of this equation is called the virtual work.

Now we must change to the generalised co-ordinate system.

We write

$\mathbf {r} _{i}=\mathbf {r} _{i}(q_{1},q_{2},\cdots ,q_{3n-k},t)$

Using the chain rule gives

$\mathbf {v} _{i}=\sum _{j}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}{\dot {q}}_{j}+{\frac {\partial \mathbf {r} _{i}}{\partial t}}$

and

$\delta \mathbf {r} _{i}=\sum _{j}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}$

Note that this implies

${\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}={\frac {\partial \mathbf {v} _{i}}{\partial {\dot {q}}_{j}}}\quad (2)$

The virtual work is, dropping the superscript,

${\begin{matrix}\sum _{i}\mathbf {F} _{i}\cdot \delta \mathbf {r} _{i}&=&\sum _{i,j}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}\\&=&\sum _{j}Q_{j}\delta q_{j}\end{matrix}}$

where the Q_j are the components of the generalised force.

We now manipulate the right hand side of (1) into a form comparable with this last equation

The right hand side term is

${\begin{matrix}\sum _{i}{\dot {\mathbf {p} }}_{i}\cdot \delta \mathbf {r} _{i}&=&\sum _{i}m_{i}{\ddot {\mathbf {r} }}_{i}\cdot \delta \mathbf {r} _{i}\\&=&\sum _{i,j}m_{i}{\ddot {\mathbf {r} }}_{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}\end{matrix}}$

The terms in the coefficient of q_j can be rearranged

${\begin{matrix}\sum _{i}m_{i}{\ddot {\mathbf {r} }}_{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}&=&\sum _{i}\left[{\frac {d}{dt}}\left(m_{i}{\dot {\mathbf {r} }}_{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\right)-m_{i}{\dot {\mathbf {r} }}_{i}\cdot {\frac {d}{dt}}\left({\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\right)\right]\\&=&\sum _{i}\left[{\frac {d}{dt}}\left(m_{i}\mathbf {v} _{i}\cdot {\frac {\partial \mathbf {v} _{i}}{\partial {\dot {q}}_{j}}}\right)-m_{i}\mathbf {v} _{i}\cdot {\frac {\partial \mathbf {v} _{i}}{\partial q_{j}}}\right]\end{matrix}}$

on substituting in equation (2) from above

On taking a close look at this last equation, we see a resemblance to the total kinetic energy,

$T={\frac {1}{2}}\sum _{i}m_{i}v_{i}^{2}$

We now further rearrange to get an expression explicitly involving T.

${\begin{matrix}\sum _{i}m_{i}{\ddot {\mathbf {r} }}_{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}&=&\sum _{i}\left[{\frac {d}{dt}}\left(m_{i}\mathbf {v} _{i}\cdot {\frac {\partial \mathbf {v} _{i}}{\partial {\dot {q}}_{j}}}\right)-m_{i}\mathbf {v} _{i}\cdot {\frac {\partial \mathbf {v} _{i}}{\partial q_{j}}}\right]\\&=&{\frac {d}{dt}}\left({\frac {\partial }{\partial {\dot {q}}_{j}}}{\frac {1}{2}}\sum _{i}m_{i}v_{i}^{2}\right)-{\frac {\partial }{\partial q_{j}}}{\frac {1}{2}}\sum _{i}m_{i}v_{i}^{2}\\&=&{\frac {d}{dt}}\left({\frac {\partial }{\partial {\dot {q}}_{j}}}T\right)-{\frac {\partial }{\partial q_{j}}}T\end{matrix}}$

Putting this last expression into (1) along with the generalised force give

$\sum _{j}\left[{\frac {d}{dt}}\left({\frac {\partial T}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial T}{\partial q_{j}}}-Q_{j}\right]\delta q_{j}=0$

Since the δq_j, unlike the δr_i, are independent, this last equation can only be true if all the coefficients vanish.

That is we must have

${\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}=Q_{j}\quad (3)$

These are the equations of motion for the system, in a general set of coordinates for which all constraints are automatically satisfied.

For example, suppose we have a cylinder, mass m, radius a, rolling without slipping on a flat plane.

The kinetic energy of the cylinder is

$T={\frac {1}{2}}m{\dot {x}}^{2}+{\frac {1}{8}}ma^{2}{\dot {\theta }}^{2}$

using the results from Rigid Bodies, where x is the axis in the plane perpendicular to the axis of the cylinder, and θ is the angle of rotation.

Rolling without slipping implies

${\dot {x}}=a{\dot {\theta }}$

so we get

$T={\frac {5}{8}}m{\dot {x}}^{2}\quad {\frac {5}{4}}m{\ddot {x}}=Q_{x}$

The cylinder has the same kinetic energy as if its mass were 20% greater. If there is no torque on the cylinder then Q_x=F_x, and the cylinder behaves in every respect as though it were a 20% larger point mass.

To use (3) more generally, we need an expression for the Q_j

Suppose, as is often the case, that

$\mathbf {F} _{i}=-{\frac {\partial }{\partial \mathbf {r} _{i}}}V$

then, by definition

${\begin{matrix}\sum _{j}Q_{j}\delta q_{j}&=&\sum _{i}\mathbf {F} _{i}\cdot \delta \mathbf {r} _{i}\\&=&\sum _{i,j}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}\\&=&-\sum _{i,j}{\frac {\partial V}{\partial \mathbf {r} _{i}}}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}\\&=&-\sum _{j}{\frac {\partial V}{\partial q_{j}}}\delta q_{j}\end{matrix}}$

so, equating coefficients, the generalised force is

$Q_{j}=-{\frac {\partial V}{\partial q_{j}}}$

Putting this generalised force into (3) gives

${\frac {d}{dt}}{\frac {\partial (T-V)}{\partial {\dot {q}}_{j}}}-{\frac {\partial (T-V)}{\partial q_{j}}}=0$

since V has been assumed independent of the velocities.

In fact, this last equation will still be true for some velocity dependent forces, most notably magnetism, for a suitable definition of V, but we won't prove this here.

We call the T-V the Lagrangian, L, and write

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}-{\frac {\partial L}{\partial q_{j}}}=0$

We call these equations Lagrange's equations. They are useful whenever Cartesian co-ordinates are inconvenient, including motion under constraint.

Example

Suppose we have two identical point masses, m, connected by a string, length a. The string is threaded through an hole in a flat table so that the upper mass is moving in a horizontal plane without friction, and the lower mass is always vertically below the hole. The distance of the upper mass from the hole is r.

The position of the mass on the table is best described using polar coordinates, (r,θ). Its kinetic energy is then

${\frac {1}{2}}m\left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)$

The velocity of the lower mass is d(a-r)/dt=-dr/dt, so the total kinetic energy is

$T={\frac {1}{2}}m\left(2{\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)$

The potential energy is

$V=mg(a-r)$

where g is the gravitational acceleration.

This means

$L={\frac {1}{2}}m\left(2{\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)+mg(r-a)$

and the equations of motion are

${\begin{matrix}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\theta }}}}-{\frac {\partial L}{\partial \theta }}&=&m{\frac {d}{dt}}\left(r^{2}{\dot {\theta }}\right)&=&0\\{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {r}}}}-{\frac {\partial L}{\partial r}}&=&2m{\ddot {r}}-mr{\dot {\theta }}^{2}+mg&=&0\end{matrix}}$

The first of these equations says that the angular momentum is constant, as expected since there is no torque on the particles. If we call this constant angular momentum l then we can write

${\dot {\theta }}={\frac {l}{mr^{2}}}$

and the second equation of motion becomes

${\ddot {r}}={\frac {l^{2}}{2m^{2}r^{3}}}-{\frac {g}{2}}$

Clearly, if initially

$l^{2}>gm^{2}r^{3},\,$

then the lower ball will be pulled out of the hole, at which point these equations of motions cease to apply. They only hold when 0≤r≤a, a constraint which is not easily tamable.

Notice, we have not needed to calculate the tension in the string, which is the force of constraint in this problem.

Reformulating Newton

In the last chapter we saw how to reformulate Newton's laws as a set of second order ordinary differential equations using arbitrary coordinates:

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0$

It is often far easier to solve a problem by starting with the Lagrangian than by explicitly using Newton's laws. The Lagrangian is also more useful for theoretical analysis.

However, the Lagrangian approach is not the only useful way to reformulate Newton. There is a second, related, approach which is also highly useful for analysis; namely, writing the equations of motion as a set of first order ordinary differential equations in a particularly natural way.

To do this we will use a standard technique, familiar from your calculus studies.

Derivation

Consider the function

$H(q,p,t)={\dot {q}}_{i}p_{i}-L(q,{\dot {q}},t)$

where the $q_{i}$ are the generalised coordinates, the $p_{i}$ are a set of new variables whose meaning we will soon see, $H$ is to be a function of the $p$'s and $q$'s alone, and the summation convention is being used.

Then we have

$dH={\dot {q}}_{i}dp_{i}+p_{i}d{\dot {q}}_{i}-{\frac {\partial L}{\partial {\dot {q}}_{i}}}d{\dot {q}}_{i}-{\frac {\partial L}{\partial q_{i}}}dq_{i}-{\frac {\partial L}{\partial t}}dt\quad (1)$

but, since H is a function of the p‘s and q‘s alone we can also write

$dH={\frac {\partial H}{\partial q_{i}}}dq_{i}+{\frac {\partial H}{\partial p_{i}}}dp_{i}+{\frac {\partial H}{\partial t}}dt\quad (2)$

For these two equations to both be true the coefficients of the differentials must be equal.

Equation (2) does not contain a term in $d{\dot {q}}_{i}$, so the coefficient of that term in equation (1) must be zero. I.e,

$p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}$

which gives us a definition of the p_i. Using this in Lagrange's equations gives

${\dot {p}}_{i}={\frac {\partial L}{\partial q_{i}}}$

and equation (1) simplifies to

$dH={\dot {q}}_{i}dp_{i}-{\dot {p}}_{i}dq_{i}-{\frac {\partial L}{\partial t}}dt$

A comparison of coefficients with equation (2) now gives the desired set of first order equations for the motion,

${\dot {q}}_{i}={\frac {\partial H}{\partial p_{i}}}\quad {\dot {p}}_{i}=-{\frac {\partial H}{\partial q_{i}}}$

These are called Hamilton's equations and H is called the Hamiltonian.

Physical meaning of H and p

To see what H and the p_i's actually are, let's consider a few typical cases.

First, let's look at a free particle, one subject to no forces. This will let us see what the p_i's mean, physically.

If we use Cartesian coordinates for the free particle, we have

$L=T={\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}\right)$

The p_i's are the differential of this with respect to the velocities.

$p_{x}={\frac {\partial L}{\partial {\dot {x}}}}=m{\dot {x}}\quad p_{y}={\frac {\partial L}{\partial {\dot {y}}}}=m{\dot {y}}\quad p_{z}={\frac {\partial L}{\partial {\dot {z}}}}=m{\dot {z}}$

These are the components of the momentum vector.

If we use cylindrical coordinates, we have

$L=T={\frac {1}{2}}m\left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+{\dot {z}}^{2}\right)$

and

$p_{r}={\frac {\partial L}{\partial {\dot {r}}}}=m{\dot {r}}\quad p_{\theta }={\frac {\partial L}{\partial {\dot {\theta }}}}=mr^{2}{\dot {\theta }}\quad p_{z}={\frac {\partial L}{\partial {\dot {z}}}}=m{\dot {z}}$

This time, p_z is the component of momentum is the z direction, p_r is the radial momentum, and p_θ is the angular momentum, which we've previously seen is the equivalent of momentum for rotation.

Since, in these familiar cases, the p_i's are momenta, we generalise and call the p_i's conjugate momenta.

Note that from Hamilton's equations, we see that if H is independent of some coordinate, q, then

${\dot {p}}_{q}=-{\frac {\partial H}{\partial q}}=0$

so the momentum conjugate to q is conserved. This connection between conservation laws and coordinate independence lies at the heart of much physics.

Secondly, to see the physical meaning of H, we'll consider a particle moving in a potential V, described using Cartesian coordinates.

This time the Lagrangian is

$L=T-V={\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}\right)-V(x,y,z)$

We find that the p_i's are

$p_{x}={\frac {\partial L}{\partial {\dot {x}}}}=m{\dot {x}}\quad p_{y}={\frac {\partial L}{\partial {\dot {y}}}}=m{\dot {y}}\quad p_{z}={\frac {\partial L}{\partial {\dot {z}}}}=m{\dot {z}}$

so, again, they are the momenta

Now lets calculate H.

${\begin{matrix}H&=&{\dot {x}}p_{x}+{\dot {y}}p_{y}+{\dot {y}}p_{y}&-&L&&\\&=&m\left({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}\right)&-&{\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}\right)&+&V\\&=&{\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}\right)&&&+&V\\&=&T&&&+&V\end{matrix}}$

so H is the total energy, written as a function of the position and momentum.

This is not always true, but it will be true for all common systems which conserve energy.

In general, if we know how the energy of a systems depends on speeds and positions, we know everything about the system.

Physicists will often start work on a problem by writing down an expression for H, or L, and never bother calculating the actual forces.

Deeper meaning

If we compare Hamilton's equations,

${\dot {q}}_{i}={\frac {\partial H}{\partial p_{i}}}\quad {\dot {p}}_{i}=-{\frac {\partial H}{\partial q_{i}}}$

with the equations of geometrical optics.

${\dot {x}}_{i}={\frac {\partial \omega }{\partial k_{i}}}\quad {\dot {k}}_{i}=-{\frac {\partial \omega }{\partial x_{i}}}$

we see that both sets of equations have the same form.

If we made a substitution of the form,

$H=\alpha \omega \quad p=\alpha k$

for any α, the two sets of equations would become identical.

Now, geometrical optics is an approximation to the full solution of any wave equation, valid when the wavelength is small.

Since classical mechanics is just like geometrical optics, classical mechanics could also be small wavelength approximation to a more accurate wave theory.

This is not a proof, could be is not the same as is, but it does show that classical mechanics is compatible with wave theories, contrary to intuition.

We will see later that this is not a coincidence, classical mechanics really is a small wavelength approximation to a more accurate wave theory, namely quantum mechanics, and that, in that theory, the energy of matter waves is proportional to frequency and the momentum to wave number, just as the substitution above requires.

Hamilton's equations can also be used to construct a mathematical gadget, called a Poisson bracket, which lets us write the equations of classical mechanics in a way which makes the connections with quantum mechanics even clearer, but an explanation of how would be beyond the scope of this book.

Since classical mechanics is just like geometrical optics, there should be an analog to Fermat's principle, that light takes the quickest path, and there is.

Where light takes the quickest path from a to b, matter takes the path of least action, where the action is defined as

$\int _{a}^{b}L(x,{\dot {x}},t)\,dt$

It can be proved that this integral takes extremal values if and only if the system obeys Lagrange's equations. Saying matter takes the path of least action is equivalent to saying it obeys Lagrange's equations, or Newton's laws.

Furthermore, it turns out that in general relativity, the action is proportional to the time taken, so matter is also really taking the quickest path between two points.

We've seen that a Hamiltonian of the form

$H={\frac {\mathbf {p} \cdot \mathbf {p} }{2m}}+V(\mathbf {r} )$

describes motion under a conservative force, but this is not the most general possible Hamiltonian.

Many waves are described by another simple form, in the geometrical optics limit,

$H=f(|\mathbf {p} |)$

What happens if we consider other forms for the Hamiltonian?

Suppose we have

$H={\frac {\mathbf {p} \cdot \mathbf {p} }{2m}}+\mathbf {p} \cdot \mathbf {A} (\mathbf {r} )$

The dot product term is the simplest scalar we can add to the kinetic energy that's dependent on momentum. We'll see that it acts like a potential energy.

Using Hamilton's equations we can immediately write down equations of motion.

${\begin{matrix}{\dot {x}}_{i}&=&{\frac {\partial H}{\partial p_{i}}}&=&{\frac {p_{i}}{m}}+A_{i}\\{\dot {p}}_{i}&=&-{\frac {\partial H}{\partial x_{i}}}&=&-p_{j}{\frac {\partial A_{j}}{\partial x_{i}}}\end{matrix}}$

Note that we are using the summation convention here.

Now that we've got the equations of motion, we need to work out what they mean.

The first thing we notice is that the momentum is no longer mv. There is an additional contribution from the potential field A. We can think of this as a form of potential momentum, analogous to potential energy.

The force on the particle is

$F_{i}=m{\ddot {x}}_{i}={\dot {p}}_{i}+m{\frac {d}{dt}}A_{i}(\mathbf {r} )$

Using the chain rule, and substituting for dp/dt with the second equation of motion, we get

$F_{i}=-p_{j}{\frac {\partial A_{j}}{\partial x_{i}}}+m{\dot {x}}_{j}{\frac {\partial A_{i}}{\partial x_{j}}}$

Using the first equation, this becomes

$F_{i}=m{\dot {x}}_{j}\left({\frac {\partial A_{i}}{\partial x_{j}}}-{\frac {\partial A_{j}}{\partial x_{i}}}\right)+mA_{j}{\frac {\partial A_{j}}{\partial x_{i}}}$

The term in brackets is recognizable as being the type of thing we see in cross products. With a little manipulation, using the Kronecker delta and alternating symbol, we can write

${\begin{matrix}F_{i}&=&{\dot {x}}_{j}\left(\delta _{il}\delta _{jk}-\delta _{ik}\delta _{jl}\right){\frac {\partial A_{l}}{\partial x_{k}}}&+&mA_{j}{\frac {\partial A_{j}}{\partial x_{i}}}\\&=&{\dot {x}}_{j}\epsilon _{nij}\epsilon _{nlk}{\frac {\partial A_{l}}{\partial x_{k}}}&+&mA_{j}{\frac {\partial A_{j}}{\partial x_{i}}}\\&=&-\epsilon _{ijn}{\dot {x}}_{j}\left(\nabla \times \mathbf {A} \right)_{n}&+&mA_{j}{\frac {\partial A_{j}}{\partial x_{i}}}\\&=&-\epsilon _{ijn}{\dot {x}}_{j}\left(\nabla \times \mathbf {A} \right)_{n}&+&{\frac {1}{2}}{\frac {\partial }{\partial x_{i}}}A_{j}A_{j}\end{matrix}}$

so, writing the last line as a vector equation,

$\mathbf {F} =-m\mathbf {v} \times (\nabla \times \mathbf {A} )+{\frac {1}{2}}m\nabla A^{2}$

The force from this potential has a component perpendicular to its curl and to the velocity, and another component which is the gradient of a scalar.

If we add a carefully chosen potential energy to the Hamiltonian we can cancel out this second term.

$H={\frac {p^{2}}{2m}}+\mathbf {p} \cdot \mathbf {A} (\mathbf {r} )+{\frac {1}{2}}mA^{2}\qquad \mathbf {F} =-m\mathbf {v} \times \left(\nabla \times \mathbf {A} \right)$

This Hamiltonian can be simplified to

$H={\frac {1}{2m}}\left(\mathbf {p} +m\mathbf {A} \right)^{2}$

where the term in bracket is mv, written as a function of momentum.

This simple modification to the Hamiltonian gives us a force perpendicular to velocity, like magnetism. Because the force and velocity are perpendicular, the work done by the force is always zero.

We can use potential fields to describe velocity dependent forces, provided that they do no work.

The coefficient of A in these expression is arbitrary. Changing it amount merely to measuring A in different units so we can equally well write

$H={\frac {1}{2m}}\left(\mathbf {p} +\alpha \mathbf {A} \right)^{2}\qquad \mathbf {F} =-\alpha \mathbf {v} \times \left(\nabla \times \mathbf {A} \right)$

Having α=m means A is measured in units of velocity, which may sometimes be convenient, but we can use any other constant value of α that suits our purpose. When we come to study relativity, we'll use α=-1.

Notice that the force depends only on the curl of A, not on A itself. This means we can add any function with zero curl to A without changing anything, just as we can add a constant to the potential energy.

Furthermore, it is a standard result of vector calculus that any vector field is the sum of two components, one with zero curl, the other with zero divergence. Since the zero curl component does not affect the total force, we can require it to be zero; i.e. we can require A to have zero divergence.

$\nabla \cdot \mathbf {A} =0$

This is called a gauge condition. For the moment, it can be considered to define especially natural values for the integration constants.

Mach's principle is the name given by Einstein to a vague hypothesis first supported by the physicist and philosopher Ernst Mach.

Harmonic Oscillators

Energy Analysis

Figure 11.2: Potential, kinetic, and total energy of a one-dimensional harmonic oscillator plotted as a function of spring displacement.

For a spring, Hooke's law says the total force is proportional to the displacement, and in the opposite direction.

$F=-kx$

Since this is independent of velocity, it is a conservative force. We can integrate to find the potential energy of the mass-spring system,

$V(x)={\frac {1}{2}}kx^{2}$

Since a potential energy exists, the total energy

$E={\frac {1}{2}}kx^{2}+{\frac {1}{2}}m{\dot {x}}^{2}$

is conserved, i. e., is constant in time.

We can now use energy conservation to determine the velocity in terms of the position

${\dot {x}}=\pm {\sqrt {{\frac {2E}{m}}-{\frac {k}{m}}x^{2}}}$

We could integrate this to determine the position as a function of time, but we can deduce quite a bit from this equation as it is.

It is fairly evident how the mass moves. From Hooke's law, the mass is always accelerating toward the equilibrium position, so we know which sign of the square root to take.

The velocity is zero when

$x=\pm {\sqrt {\frac {2E}{k}}}$

If x were larger than this the velocity would have to be imaginary, clearly impossible, so the mass must be confined between these values. We can call them the turning points.

If the mass is moving to the left, it slows down as it approaches the left turning point. It stops when it reaches this point and begins to move to the right. It accelerates until it passes the equilibrium position and then begins to decelerate, stopping at the right turning point, accelerating toward the left, etc. The mass thus oscillates between the left and right turning points.

How does the period of the oscillation depend on the total energy of the system? We can get a general idea without needing to solve the differential equation.

There are only two parameters the period, T, could depend on; the mass, m, and the spring constant, k.

We know T is measured in seconds, and m in kilograms. For the units in Hooke's law to match, k must be measured in N·m^-1, or equivalently, in kg·s^-2.

We immediately see that the only way to combine m and k to get something measured in seconds is to divide, cancelling out the kg's.

Therefore T∝${\sqrt {m/k}}$

We have established the general way the period depends on the parameters of the problem, without needing to use calculus.

This technique is called dimensional analysis, and has wide application. E.g., if we couldn't calculate the proportionality constant exactly, using calculus, we'd be able to deduce by doing one experiment. Without dimensional analysis, if calculus failed us we'd have to do scores of experiments, each for different combinations of m and k.

Fortunately, the proportionality constants are typically small numbers, like $3{\sqrt {2}}$ or ${\sqrt {\pi }}/2$.

Analysis Using Newton's Laws

The acceleration of the mass at any time is given by Newton's second law

$a={\frac {d^{2}x}{dt^{2}}}={\frac {F}{m}}=-{\frac {kx}{m}}$

An equation of this type is known as a differential equation since it involves a derivative of the dependent variable . Equations of this type are generally more difficult to solve than algebraic equations, as there are no universal techniques for solving all forms of such equations. In fact, it is fair to say that the solutions of most differential equations were originally obtained by guessing!

There are systematic ways of solving simple differential equations, such as this one, but for now we will use our knowledge of the physical problem to make an intelligent guess.

We know that the mass oscillates back and forth with a period that is independent of the amplitude of the oscillation. A function which might fill the bill is the sine function. Let us try substituting,

$x=A\sin(\omega t)$

where ω is a constant, into this equation.

We get

$-\omega ^{2}A\sin(\omega t)=-A{\frac {k}{m}}\sin(\omega t)$

Notice that the sine function cancels out, leaving us with $\omega ^{2}={\frac {k}{m}}$ . The guess thus works if we set

$\omega ={\sqrt {\frac {k}{m}}}$

This constant is the angular oscillation frequency for the oscillator, from which we infer the period of oscillation to be

$T=2\pi {\sqrt {\frac {m}{k}}}$

This agrees with the result of the dimensional analysis. Because this doesn't depend on $A$ , we can see that the period is independent of amplitude.

It is easy to show that the cosine function is equally valid as a solution,

$x=B\cos(\omega t)$

for the same $\omega$ .

In fact, the most general possible solution is just a combination of these two, i.e.

$x=A\sin(\omega t)+B\cos(\omega t)$

The values of $A,B$ depend on the position and velocity of the mass at time $t=0$ .

If we wiggle the left end of the spring in the above diagram by amount d=d₀sin ω_Ft, rather than rigidly fixing it, we have a forced harmonic oscillator.

The constant d₀ is the amplitude of the imposed wiggling motion. The forcing frequency ω_F is not necessarily equal to the natural or resonant frequency of the mass-spring system. Very different behavior occurs depending on whether it is less than, equal to, or greater than ω.

Given the above wiggling, the force of the spring on the mass becomes

$F=-k(x-d)=-k(x-d_{0}\sin \omega _{F}t)\,$

since the length of the spring is the difference between the positions of the left and right ends. Proceeding as for the unforced mass-spring system, we arrive at the differential equation

${\frac {d^{2}x}{dt^{2}}}+{\frac {k}{M}}x={\frac {k}{M}}d_{0}\sin \omega _{F}t$

The solution to this equation turns out to be the sum of a forced part in which x∝ sin ω_Ft, and a free part which is the same as the solution to the unforced equation. We are primarily interested in the forced part of the solution, so let us set x=d₀sin ω_Ftand substitute this into the equation of motion, giving:

$-\omega _{F}^{2}x_{0}\sin \omega _{F}t+{\frac {k}{M}}x_{0}\sin \omega _{F}t={\frac {k}{M}}d_{0}\sin \omega _{F}t$

The sine factor cancels leaving us with an algebraic equation for , the amplitude of the oscillatory motion of the mass.

Solving for the ratio of the oscillation amplitude of the mass to the amplitude of the wiggling motion, we find

${\frac {x_{0}}{d_{0}}}={\frac {1}{1-M\omega _{F}^{2}/k}}={\frac {1}{1-\omega _{F}^{2}/\omega ^{2}}}$

where we have recognized that k/M=ω², the square of the frequency of the free oscillation.

Notice that if ω_F<ω, then the motion of the mass is in phase with the wiggling motion and the amplitude of the mass oscillation is greater than the amplitude of the wiggling. As the forcing frequency approaches the natural frequency of the oscillator, the response of the mass grows in amplitude.

When the forcing is at the resonant frequency, the response is technically infinite, though practical limits on the amplitude of the oscillation will intervene in this case -- for instance, the spring cannot stretch or shrink an infinite amount. In many cases friction will act to limit the response of the mass to forcing near the resonant frequency.

When the forcing frequency is greater than the natural frequency, the mass actually moves in the opposite direction of the wiggling motion -- i. e., the response is out of phase with the forcing. The amplitude of the response decreases as the forcing frequency increases above the resonant frequency.

Forced and free harmonic oscillators form an important part of many physical systems. For instance, any elastic material body such as a bridge or an airplane wing has harmonic oscillatory modes. A common engineering problem is to ensure that such modes are damped by friction or some other physical mechanism when there is a possibility of excitation of these modes by naturally occurring processes. A number of disasters can be traced to a failure to properly account for oscillatory forcing in engineered structures.

We often encounter systems which contain multiple harmonic oscillators, such as this:

two identical masses, m, the first attached to a wall by a spring with constant k, and the second attached to the first by another, identical spring.

If the springs weren't linked they'd both vibrate at the same frequency, ω=√(k/m). Linking the springs changes this.

To find out how the linked system behaves, we will start with the Lagrangian, using the displacements of the masses, x₁ and x₂, as our coordinates.

A moment's inspection of the system shows

$T={\frac {1}{2}}m\left({\dot {x}}_{1}^{2}+{\dot {x}}_{2}^{2}\right)\quad V={\frac {1}{2}}k\left(x_{1}^{2}+(x_{2}-x_{1})^{2}\right)$

so, using ω²=k/m,

$L={\frac {1}{2}}m\left({\dot {x}}_{1}^{2}+{\dot {x}}_{2}^{2}\right)-{\frac {1}{2}}m\omega ^{2}\left(x_{1}^{2}+(x_{2}-x_{1})^{2}\right)$

The equations of motion immediately follow.

${\begin{matrix}{\ddot {x}}_{1}&=&-\omega ^{2}(2x_{1}-x_{2})\\{\ddot {x}}_{2}&=&-\omega ^{2}(x_{2}-x_{1})\end{matrix}}\quad (1)$

To solve these equations we try a solution in trig functions

$x_{1}=A_{1}\sin \Omega t\quad x_{2}=A_{2}\sin \Omega t$

Substituting this into (1) gives

${\begin{matrix}-\Omega ^{2}A_{1}&+&\omega ^{2}(2A_{1}-A_{2})&=&0\\-\Omega ^{2}A_{2}&+&\omega ^{2}(A_{2}-A_{1})&=&0\\\end{matrix}}$

We would get the same equations from any trig function solution of the same frequency.

Gathering the coefficients of A₁ and A₂ together lets rewrite the last equation as

${\begin{pmatrix}2\omega ^{2}-\Omega ^{2}&-\omega ^{2}\\-\omega ^{2}&\omega ^{2}-\Omega ^{2}\end{pmatrix}}{\begin{pmatrix}A_{1}\\A_{2}\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}\quad (2)$

We can only solve this equation if the determinant of the matrix is zero.

$\Omega ^{4}-3\omega ^{2}\Omega ^{2}+\omega ^{4}=0$

The solutions are

$\Omega _{\pm }^{2}={\frac {3\pm {\sqrt {5}}}{2}}\omega ^{2}$

so the combined system has two natural frequencies, one lower and one higher than the natural frequency of the individual springs. This is typical.

We can also calculate the ratio of A₁ and A₂ from (2). Dividing by A₂ gives

${\frac {A_{1}}{A_{2}}}=1-{\frac {\Omega _{\pm }^{2}}{\omega ^{2}}}$

• For the lower frequency, Ω_-, which is less than ω, the ratio is positive, so the two masses move in the same direction with different amplitudes. They are said to be in phase.

• For the higher frequency, Ω₊, which is more than ω, the ratio is negative, so the two masses move in the opposite direction with different amplitudes. They are said to be in antiphase.

This behaviour is typical when pairs of harmonic oscillators are coupled.

The same approach can also be used for systems with more than two particles.

Introduction

In principle, we could use the methods described so far to predict the behavior of matter by simply keeping track of each atom.

In practice, this is not a useful approach. Instead, we treat matter as a continuum.

In this section we will see how this is done, and how it leads us back to waves.

For an example, we will consider a set of N+1 identical springs and masses, arranged as in the previous section, with spring 0 attached to the wall, and mass N free.

We are interested in what happens for large N, the continuum limit.

The system has three other parameters; the spring constant k, the particle mass Δm, and the spring rest spacing Δa, where variable names have been chosen for future convenience. These can be combined with N to give a similar set of parameters for the system.

Suppose all the masses are displaced by d from rest, with total displacement D=dN of the system end, then the total potential energy is kNd²/2 = kD²/(2N), so

• The system's spring constant is K=k/N
• The system mass is m=ΔmN
• The system rest length is a=ΔaN

If, as we increase N we change the other three parameters to keep K, m, and a constant then in the large N limit this discrete system will look like a spring with mass continuously distributed along its length.

For coordinates, we will use the displacements of each mass, x_n. For large N the displacement will vary approximately continuously with distance. We can regard it as a continuous function, x, with

$x(n\Delta a)=x_{n}\,$

The kinetic energy of the system is then simply

$T={\frac {1}{2}}\Delta m\sum _{0}^{N}{\dot {x}}_{n}^{2}$

The total potential energy is similarly

$V={\frac {1}{2}}kx_{0}^{2}+{\frac {1}{2}}k\sum _{1}^{N}(x_{n}-x_{n-1})^{2}$

From this we may deduce the equations of motion in two different ways.

Equations of motion: First approach

If we take the large N limit first, these sums become integrals.

${\begin{matrix}T&=&{\frac {m}{2a}}\sum _{0}^{N}{\dot {x}}_{n}^{2}\Delta a\\\lim _{N\rightarrow \infty }T&=&{\frac {m}{2a}}\int _{0}^{a}{\dot {x}}^{2}ds\end{matrix}}$

where s is the distance from the wall, and

${\begin{matrix}V&=&{\frac {1}{2}}kx_{0}^{2}+{\frac {1}{2}}k\sum _{0}^{N-1}(x_{n}-x_{n+1})^{2}\\&=&{\frac {1}{2}}kx_{0}^{2}+{\frac {1}{2}}K\sum \left({\frac {x(n\Delta a+\Delta a)-x(n\Delta a)}{\Delta a}}\right)^{2}a\Delta a\\\lim _{N\rightarrow \infty }V&=&{\frac {1}{2}}kx(0)^{2}+{\frac {1}{2}}Ka\int \left({\frac {dx}{ds}}\right)^{2}ds\end{matrix}}$

Since the springs always remain attached to the wall, x(0)=0.

The integrand for T is the product of the density and the square of the velocity, just as we might naively expect. Simalarly, V is the integral of the potential energy of a infinitesimal spring over the length of the system.

Using the Lagrangian will let us get equations of motion from these integrals.

It is

${\begin{matrix}L&=&{\frac {m}{2a}}\int _{0}^{a}{\dot {x}}^{2}ds-{\frac {1}{2}}Ka\int _{0}^{a}\left({\frac {dx}{ds}}\right)^{2}ds\\&=&{\frac {m}{2a}}\int _{0}^{a}({\dot {x}}^{2}-{\frac {Ka^{2}}{m}}x^{\prime 2})ds\\\end{matrix}}$

The action of the system is

$\int Ldt=\int \int {\mathcal {L}}({\dot {x}},x^{\prime })dxdt\quad {\mbox{ where }}{\mathcal {L}}={\frac {m}{2a}}({\dot {x}}^{2}-{\frac {Ka^{2}}{m}}x^{\prime 2})$

Here, we are integrating over both space and time, rather than just space, but this is still very similar in form to the action for a single particle.

We can expect that the principle of least action will lead us to the natural extension of Lagrange's equations to this action,

${\frac {d}{ds}}{\frac {\partial {\mathcal {L}}}{\partial x^{\prime }}}+{\frac {d}{dt}}{\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}={\frac {\partial {\mathcal {L}}}{\partial x}}$

This equation can be proven, using the calculus of variations. Using it for this particular Lagrangian gives

${\frac {\partial ^{2}x}{\partial t^{2}}}-{\frac {Ka^{2}}{m}}{\frac {\partial ^{2}x}{\partial s^{2}}}=0$

This is a partial differential equation. We will not be discussing its solution in detail, but we will see that it describes waves.

First, though, we will confirm that these equations are the same as we get if we find the equations of motion first, then take the large N limit.

Equations of motion: Second approach

First, we will look at the potential energy to see how it depends on the displacements.

${\begin{matrix}V&=&{\frac {1}{2}}kx_{0}^{2}+{\frac {1}{2}}k\sum _{0}^{N-1}(x_{n}-x_{n+1})^{2}\\&=&{\frac {1}{2}}k\left(x_{0}^{2}\cdots (x_{n-1}-x_{n})^{2}+(x_{n}-x_{n+1})^{2}\cdots (x_{N}-x_{N-1})^{2}\right)\\&=&{\frac {1}{2}}k\left(2x_{0}^{2}-2x_{0}x_{1}\cdots -2x_{n}x_{n+1}+2x_{n}^{2}-2x_{n}x_{n+1}\cdots x_{N}^{2}-2x_{N}x_{N-1}\right)\\&=&{\frac {1}{2}}k\left(2x_{0}^{2}-2x_{0}x_{1}\cdots 2x_{n}(x_{n}-x_{n+1}-x_{n-1})\cdots x_{N}^{2}-2x_{N}x_{N-1}\right)\\\end{matrix}}$

Notice that we need to treat the displacements of the first and last masses differently from the other coordinates, because the dependence of the Langragian on them is different.

The kinetic energy is symmetric in the coordinates,

$T={\frac {1}{2}}\Delta m\sum _{0}^{N}{\dot {x}}_{n}^{2}$

Using Lagrange's equations, we get that, for x₀

$\Delta m{\ddot {x}}_{0}+2kx_{0}=kx_{1},$

for x_N,

$\Delta m{\ddot {x}}_{N}+kx_{N}=kx_{N-1},$

and, for all the other x_n

$\Delta m{\ddot {x}}_{n}+2kx_{n}=k(x_{n+1}+x_{n-1}),$

We can replace k and Δm by the limiting values K and m using

${\frac {k}{\Delta m}}={\frac {Ka^{2}}{m\Delta a^{2}}}$

giving us

${\begin{matrix}{\ddot {x}}_{0}&=&{\frac {Ka^{2}}{m}}{\frac {x_{1}-2x_{0}}{\Delta a^{2}}}\\{\ddot {x}}_{n}&=&{\frac {Ka^{2}}{m}}{\frac {x_{n-1}+x_{n+1}-2x_{n}}{\Delta a^{2}}}\\{\ddot {x}}_{N}&=&{\frac {Ka^{2}}{m}}{\frac {x_{N-1}-x_{N}}{\Delta a^{2}}}\end{matrix}}$

Looking at the general structure of the right hand side, we see difference between the displacement at nearby points divided by the distance between those points, so we expect that in the limit we will get differentials with respect to s, the distance from the wall.

As N tends to infinity both x₀ and x₁ tend to x(0), which is always zero, so the equation of motion for x₀ is always true.

In the continuum limit, the equation for x_N becomes

${\ddot {x}}(a)=-{\frac {Ka^{2}}{m}}{\frac {1}{\Delta a}}{\frac {dx}{ds}}$

Since Δa tends to zero, for this to be true we must have x'=0 at a.

For the other displacements,

${\begin{matrix}\lim _{\Delta a\rightarrow 0}{\frac {x_{n-1}+x_{n+1}-2x_{n}}{\Delta a^{2}}}&=&\lim _{\Delta a\rightarrow 0}&{\frac {1}{\Delta a}}\left({\frac {x_{n+1}-x_{n}}{\Delta a}}-{\frac {x_{n}-x_{n-1}}{\Delta a}}\right)\\&=&\lim _{\Delta a\rightarrow 0}&{\frac {x^{\prime }((n+1)\Delta a)-x^{\prime }(n\Delta a)}{\Delta a}}\\&=&\left.{\frac {d^{2}x}{ds^{2}}}\right|_{x=a}&\\\end{matrix}}$

so we get the equation

${\frac {\partial ^{2}x}{\partial t^{2}}}-{\frac {Ka^{2}}{m}}{\frac {\partial ^{2}x}{\partial s^{2}}}=0$

just as with the other approach.

Waves

It is intuitively obvious that if we flick one of the masses in this system, vibrations will propagate down the springs, like waves, so we look for solutions of that form.

A generic travelling wave is

$x=A\sin(\omega t-\kappa x+\alpha )\,$

Substituting this informed guess into the equation gives

$-A\omega ^{2}\sin(\omega t-\kappa x+\alpha )=-{\frac {Ka^{2}}{m}}\kappa ^{2}\sin(\omega t-\kappa x+\alpha )$

so this wave is a solution provide the frequency and wavenumber are related by

$\omega ^{2}={\frac {Ka^{2}}{m}}\kappa ^{2}$

The speed of these waves, c, is

$c={\frac {d\omega }{d\kappa }}=\pm {\sqrt {\frac {Ka^{2}}{m}}}$

Thus, we've gone from Newton's laws to waves.

We can do the same starting with a three-dimensional array of particles, and deduce the equations for longitudinal and transverse waves in a solid. Everything we said about waves earlier will be true for these systems.

This particular system has two boundary conditions: the displacement is zero at the wall, and a local extrema at the free end. This is typical of all such problems.

When we take account of the boundary conditions we find that the correct solutions is a combination of standing waves, of the form

$x=A_{m}\sin \left({\frac {2b+1}{2}}{\frac {\pi s}{a}}\right)\sin \left({\sqrt {\frac {Ka^{2}}{m}}}{\frac {2b+1}{2}}{\frac {\pi }{a}}t+\alpha _{m}\right)$

where b is any integer.

If we also knew the initial displacement we could use Fourier series to obtain the exact solution for all time.

In practice, N is typically large but finite, so the continuum limit is only approximately true. Allowing for this would give us a power series in 1/N, describing small corrections to the approximation. These corrections can produce interesting effects, including solutions, but we will not calculate them here.

The continuum limit also fails for small wavelengths, comparable with the particle spacing.

Fields

In the continuum limit, the spring is described by a variable which is a function of both position and time. Variable such as this are commonly referred to as fields.

At first sight, classical fields look quite different to classical particles. In one case position is the dependent variable; in the other, it is an independent variable. However, as the above calculations suggest, fields and particles have an underlying unity, if we take a Lagrangian approach.

We can deal with both using essentially the same mathematical techniques, extracting information about both the field and the particles in that field from the same source.

E.g., once we know the Lagrangian for electromagnetism, we can deduce both the partial differential equations for the EM fields, and the forces on charged particles in those fields, from it. We will see precisely how later, when we come to study electromagnetism.

In the example above, the field Lagrangian was the continuum limit of a Lagrangian for the discrete system. It did not have to be. We can investigate the fields described by any Lagrangian we like, whether or not there is an underlying mechanical system.

So far, we've looked at waves and movement under Newton's law, and seen how the study of movement can lead us back to waves. Next, we will look at special relativity, and see how Einstein's insights affect all this.