Fractals/Iterations in the complex plane/julia

Types
[edit | edit source]Classification of Julia sets according to :
- topology
- of filled Julia set's interior
- shape[1]
- local dynamics near periodic points
- connectedness
- position of parameter c on the parameter plane [2]
Filled Julia set can have :
- an non-empty interior ( Julia set is connected )
- parabolic: filled Julia set have parabolic cycle ( c is on boundary of hyperbolic component )
- Siegel : filled Julia sets containing Siegel disc. Julia set can be locally connected or not. That depends on the rotation number. ( c is on boundary of hyperbolic component )
- attracting : filled Julia set have attracting cycle ( c is inside hyperbolic component )
- superattracting : filled Julia set have superattracting cycle( c is in the center of hyperbolic component ). Examples : Airplane Julia set, Douady's Rabbit, Basillica.
- empty interior
- disconnected ( c is outside of Mandelbrot set )[3]
- connected
- Cremer Julia sets ( c is on boundary of hyperbolic component , Julia set is connected but not locally connected)
- dendrits ( Julia set is connected and locally connected )
- Misiurewicz Julia sets (c is a Misiurewicz point )
- Feigenbaum Julia sets ( )
- others which have no [4]
topology
[edit | edit source]Julia set of root point is topologically the same as the Julia set of the child period center, but
- the center ( nucleus) Julia set is very easy to draw ( superattracting basin = very fast dynamics because critical point is also periodic point)
- while the root Julia set ( parabolic) is hard to draw ( parabolic basin and lasy dynamics)
Examples:
- t = 1/2
- Julia set of the root point = fat Basilica Julia set: c = -3/4 = - 0.75
- Julia set of period 2 center = (slim) Basicica Julia set: c = -1
- t = 1/3
- Julia set of the root point = fat Douady Rabbit: c = -0.125000000000000 +0.649519052838329i
- Julia set of period 3 center = (slim) Doudy Rabbit Julia set: c = -0.122561166876654 +0.744861766619744i period = 3
Models of Julia set
[edit | edit source]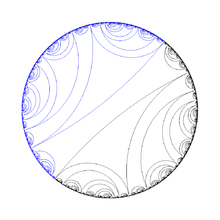
- Thurston’s invariant lamination of Julia set [5]
- graph of Julia set [6][7]
- Schreier graphs
- spine of Julia set
- disked tree model ( Hubbard trees serve as a model for Julia sets of post-critically finite polynomials[8])
- Douady’s pinched disk model[9]
- Milnor’s orbit portraits
- dendrite
- Dendritic model for Julia sets [10]
components of Julia set's interior
[edit | edit source]-
superattracting
-
parabolic
-
Inverse iteration of Siegel disc component
Douady’s pinched disk model
[edit | edit source]Dynamic rays and their landing properties are a key tool to understanding (the topology of) Julia sets of polynomials. In particular, the structure of the Julia set is determined by rays that land at a common point: at least in good cases (under the assumption of local connectivity), the knowledge of which rays land together gives a homeomorphic model for the Julia set that is known as Douady’s pinched disk model [11]
Algorithms
[edit | edit source]"... a single algorithm for computing all quadratic Julia sets does not exist."[12]
Examples:
Types
[edit | edit source]- Escape time ( attraction time to infinity ( attractor for all polynomials )
- attraction time to finite attractor inside filled Julia set )
- estimation of distance to Julia set ( DEM/J )
- Inverse Iteration Method = IIM/J
- Testing equicontinouty by Michael Becker [13]
- orbit traps [14][15]
- finding periodic repelling points using numerical methods. They are dense in the Julia set. ( Newton method [16] )
equicontinouty
[edit | edit source]"The Julia set of f then is the set of all points of G, at which this sequence of iterated functions is not equicontinous. The Fatou set is its complement. Laxly said the action of the iterated functions on near points is examined. Places, where points, which are near enough, remain near during iterations, belong to the Fatou set. Places, where points, as near they may be, are teared apart, belong to the Julia set. In the following I only consider functions, which map the Riemann sphere, i.e. the complex plane with an ideal point "infinity" added, to itself. The Julia sets are white, the Fatou sets black." Michael Becker
accuracy
[edit | edit source]- Accuracy of Computer Generated Approximations to Julia Sets by John W. Hoggard
- plane scanning
- shadowing lemma
- Numerical Precision
points
[edit | edit source]"We know the periodic points are dense in the Julia set, but in the case of weird ones (like the ones with Cremer points, or even some with Siegel disks where the disk itself is very 'deep' within the Julia set, as measured by the external rays), the periodic points tend to avoid certain parts of the Julia set as long as possible. This is what causes the 'inverse method' of rendering images of Julia sets to be so bad for those cases." ( answered Oct 26 '14 at 14:52 by Jacques Carette )[17]


compare with:
Special cases
[edit | edit source]- "The Julia set is nonempty when d ≥ 2, but the Fatou set may be empty (as demonstrated by Latt`es examples)."[18]
Names
[edit | edit source]- cauliflower = Julia set for c = 1/4 (c is the cusp of main cardioid), parabolic Julia set
- an imploded cauliflower is a Julia set for with [19], disconnected Julia set
- airplane Julia set. C is the center of period 3 component on the real axis: c = -1.75487766624669276
- helicopter z → z^3 − 0.2634 − 1.2594i
- (Douady) rabbit. C is a the center period 3 hyperbolic component of Mandelbrot set for complex quadratic map
- Cubic Rabbit z → z^3 + 0.545 + 0.539i
- dendrite. C is a tip
- the Kokopelli Julia set [20] The angle 3/15 = p0011 = 0.(0011) has preperiod = 0 and period = 4. The conjugate angle on the parameter plane is 4/15 or p0100. The kneading sequence is AAB* and the internal address is 1-3-4. The corresponding parameter rays are landing at the root of a primitive component of period 4.
- Basilica = = Julia set for c = -1 (c is the center of period 2 component)
-
airplane
-
rabbit
-
dendrite
See also
[edit | edit source]References
[edit | edit source]- ↑ blog scientific american : fractal-kitties-illustrate-the-endless-possibilities-for-julia-sets By Evelyn Lamb on September 26, 2012
- ↑ math.stackexchange question : classification-of-points-in-the-mandelbrot-set
- ↑ images of disconnected Julia sets
- ↑ Dynamics of quadratic polynomials, I: Combinatorics and geometry of the Yoccoz puzzle by Mikhail Lyubich
- ↑ Simple topological models of Julia sets by L. Oversteegen
- ↑ Combinatorial Julia Sets (1) By Jim Belk
- ↑ Jacek Skryzalin: On Quadratic Mappings With and Attracting Cycle
- ↑ Eugene1806's Blog
- ↑ Adrien Douady, Descriptions of compact sets in C. , in: Topological Methods in Modern Mathematics, Publish or Perish (1993), 429– 465.
- ↑ Hausdorff dimension of biaccessible angles of quadratic Julia sets and of the Mandelbrot set by Henk Bruin and Dierk Schleicher
- ↑ HAUSDORFF DIMENSION OF BIACCESSIBLE ANGLES FOR QUADRATIC POLYNOMIALS. VERSION OF May 8, 2017 by HENK BRUIN AND DIERK SCHLEICHER
- ↑ Computability of Julia sets by Mark Braverman, Michael Yampolsky
- ↑ Some Julia sets by Michael Becker, 6/2003. Last modification: 2/2004.
- ↑ orbit traps example video
- ↑ orbit traps making
- ↑ Newton's method in practice II: The iterated refinement Newton method and near-optimal complexity for finding all roots of some polynomials of very large degrees by Robin Stoll, Dierk Schleicher
- ↑ Clustering of periodic points for a polynomial iteration of C
- ↑ Lucjan Emil Böttcher and his mathematical legacy Stanisław Domoradzki, Małgorzata Stawiska
- ↑ [6] Douady A., Buff X., Devaney RL. and Sentenac P. Baby Mandelbrot sets are born in cauliflowers. In: Lei T. editor. The Mandelbrot set, theme and variations. Cambridge: University Press, 2000, p. 19-36.
- ↑ The Thurston Algorithm for quadratic matings by Wolf Jung









